П. АППЕЛЬ
ТЕОРЕТИЧЕСКАЯ
МЕХАНИКА
ТОМ ПЕРВЫЙ
СТАТИКА. ДИНАМИКА ТОЧКИ
ПЕРЕВОД С ПЯТОГО ФРАНЦУЗСКОГО ИЗДАНИЯ
И. Г. М А Л К И Н А
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1960

COURS DE MECANIQUE DE LA FACULTE DES SCIENCE
TRAITE
DE
MECANIQUE RATIONNELLE
PAR
Paul APPELL
MEMBRE DE L'INSTITUT
RECTEUR HONORAIRE DE L'UNIVERSITE DE PARIS
CINQUIEME EDITION, ENTIEREMENT REFONDUE
TOME PREMIER
STATIQUE. DYNAMIQUE DU POINT
PARIS
GAUTHIER-VILLARS ET Cie, EDITEURS

ОГЛАВЛЕНИЕ
От издательства		13
Введение		15
ЧАСТЬ ПЕРВАЯ
ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
Глава 1. Теория векторов		16
I. Определения		16
1.	Геометрические величины, или векторы		16
2.	Различные категории векторов		17
П. Свободные векторы. Три координаты свободного вектора		17
3.	Три координаты свободного вектора		17
4.	Геометрическая сумма произвольного числа свободных векторов	19
5.	Геометрическая разность		20
6.	Положительное направление вращения вокруг оси		20
7.	Векторное произведение двух векторов		21
III. Скользящие векторы. Пять координат скользящего вектора ....	21
8.	Общие замечания		21
9.	Теория моментов		22
10.	Аналитические выражения моментов вектора относительно осей
координат		24
11.	Пять координат скользящего вектора		25
12.	Относительный момент двух векторов /\ и Р2		25
13.	Скользящие векторы, сходящиеся в одной точке. Результи-
рующий вектор		26
14.	Произвольная система векторов. Главный вектор и главный мо-
мент 		28
15.	Изменение главного вектора и главного момента; инварианты;
центральная ось		29
16.	Сумма моментов относительно произвольной оси. Прямые нуле-
вого момента		30
17.	Упрощенные уравнения. Комплекс Шаля		31
IV. Эквивалентные системы скользящих векторов. Элементарные опера-
ции. Приведение системы скользящих векторов		32
18.	Определение эквивалентности		32
19.	Элементарные операции		33
20.	Приведение к двум векторам		34
21.	Геометрическое истолкование инварианта LX -f- MY -\- NZ ...	36
22.	Приведение двух эквивалентных систем друг к другу ....	37
23.	Пары		37
24.	Приведение к вектору и паре		39
25.	Винт		40

4	ОГЛАВЛЕНИЕ
26.	Частные случаи приведения		40
27.	Резюме		41
28.	Взаимный момент системы скользящих векторов		41
29.	Приложение общих теорем к случаю параллельных скользящих
векторов		42
V. Связанные векторы; шесть координат связанного вектора; центр па-
раллельных связанных векторов. Векторные производные ....	44
30.	Шесть координат связанного вектора. Вириал		44
31.	Центр системы параллельных связанных векторов		45'
32.	Моменты параллельных связанных векторов относительно пло-
скости 		47
33.	Векторные производные		48
VI. Полярные векторы. Аксильные векторы. Скалярные величины ...	4J
34.	Характер симметрии вектора		49
VII. Другие геометрические образы, которые могут быть использованы
в механике		51
35.	Краткий обзор		51
Упражнения		51
Глава II. Кинематика		56
1. Кинематика точки		56
36.	Определения 		56
37.	Движение точки	•		57
38.	Прямолинейное равномерное движение; скорость		57
39.	Произвольное прямолинейное движение; скорость		58
40.	Вектор скорости в криволинейном движении		5J
41.	Вектор ускорения		60
42.	Касательное и нормальное ускорения		62
II. Поступательное движение и вращение неизменяемой системы ...	63
43.	Поступательное движение		63
44.	Вращение вокруг неподвижной оси. Угловая скорость. Геоме-
трическде представление		64
III.	Скорость в относительном движении. Сложение поступательных
и вращательных движений. Скорости точек свободного тела . .	66
45.	Относительное движение; скорость		66
46.	Сложение поступательных движений		67
47.	Совокупность двух вращений		67
48.	Произвольное число вращений		68
49.	Частные случаи		6)
50.	Геометрические следствия	•		70
51.	Распределение скоростей в движущемся твердом теле		70
52.	Мгновенная винтовая ось. Касательное винтовэе движение ...	72
53.	Величина скорости точки тела		73
54.	Непрерывное движение		74
55.	Твердое тело с неподвижной точкой		75
56.	Тело перемещается параллельно неподвижной плоскости ....	75
57.	Качение и верчение подвижной поверхности по неподвижной по-
верхности 		76
IV.	Ускорения. Теорема Кориолиса 		77
58.	Распределение ускорений в движущемся твердом теле		77
59.	Ускорение в относительном движении. Теорема Кориолиса ...	77

ОГЛАВЛЕНИЕ	5
60.	Поступательное движение подвижных осей. Сложение движений	81
61.	Общие формулы для скорости и ускорения точки, отнесенной
к подвижным осям		81
Упражнения		82
Глава III. Основные законы механики. Масса и сила		86
1. Основные законы		86
62.	Неподвижные оси		86
63.	Время		86
64.	Материальная точка		86
65.	Основные законы		87
66.	Силы .'		89
67.	Закон равенства действия и противодействия		89
68.	Сложение сил. Равнодействующая		90
69.	Уравнения движения		91
70.	Равновесие		91
71.	Статика. Динамика		92
II Единицы массы и силы; однородность		92
72.	Тяжесть. Вес		92
73.	Технические единицы. Килограмм-сила		93
74.	Абсолютные единицы. Дина		94
75.	Статическое измерение сил		94
76.	Однородность		95
Упражнения .		г;6
Глава IV. Работа. Силовая функция		97
1. Материальная точка		97
77.	Элементарная работа		97
78.	Аналитическое выражение элементарной работы		98
79.	Полная работа. Единица работы		98
80.	Сила зависит от времени или скорости		99
81.	Сила зависит только от положения движущейся точки		99
82.	Частный случай, когда J1 зависит только от начального и конеч-
ного положений. Силовая функция. Потенциальная энергия . . .	100
83.	Поверхности уровня		103
84.	Примеры		105
85.	Замечание о поверхностях уровня		107
86.	Мощность		108
П. Система точек		108
87.	Работа сил, приложенных к системе точек. Силовая функция.	108
88.	Примеры		109
Упражнения		111
ЧАСТЬ ВТОРАЯ
СТАТИКА
Глава V. Равновесие точки. Равновесие системы		113
1. Материальная точка . . .		113
89.	Свободная точка		113
90.	Пример. Притяжения, пропорциональные расстояниям		115
91.	Точка, движущаяся без трения на неподвижной поверхности	116
92.	Точка, движущаяся без трения по неподвижной кривой ....	118

6	ОГЛАВЛЕНИЕ
II.	Системы материальных точек	120
93.	Система материальных точек	120
94.	Силы внутренние и силы внешние. Шесть необходимых условий
равновесия	120
95.	Разделение произвольной системы на части. Необходимые усло-
вия равновесия	123
Упражнения	123
Глава VI. Равновесие твердого тела	126
I. Приведение сил, приложенных к твердому телу. Равновесие .... 126
96.	Твердое тело ... •		126
97.	Приведение сил, приложенных к твердому телу. Равновесие . .	126
98.	Эквивалентные системы сил	 .	127
99.	Частные случаи приведения		128
100.	Другая форма условий равновесия	128
II. Приложения. Силы в плоскости. Параллельные силы. Центр тяжести 129
101.	Силы в плоскости		129
102.	Примеры		129
103.	Параллельные силы		130
104.	Центр тяжести		131
105.	Координаты центра тяжести		132
III.	Приложения. Произвольные силы в пространстве	133
106.	Примеры равновесия	133
107.	Условия, при которых силы, находящиеся в равновесии, могут
быть направлены по трем, четырем, пяти, шести прямым . . . 134
IV.	Твердое тело, подчиненное связям 	 136
108.	Метод	136
109.	Тело с неподвижной точкой	137
НО. Тело, имеющее неподвижную ось	138
111.	Тело вращается вокруг оси и скользит вдоль нее	139
112.	Тело, опирающееся на неподвижную плоскость	139
113.	Несколько твердых тел	 143
V.	Некоторые формулы для вычисления центра тяжести	143
114.	Линии		143
115.	Теорема Гюльдена		143
116.	Поверхности		144
117.	Плоские фигуры		144
118.	Теорема Гюльдена		144
119.	Объемы		145
Упражнения		145
Глава VII. Изменяемые системы	152
120.	Предварительное замечание	152
I. Веревочный многоугольник	г . 152
121.	Определение	152
122.	Натяжение	153
123.	Равновесие веревочного многоугольника. Многоугольник Ва-
риньона		153
124.	Условия на концах		155
125.	Сходящиеся силы		156
126.	Параллельные силы		157

ОГЛАВЛЕНИЕ	7
127.	Графические приложения теории веревочных многоугольников	159
128.	Кольца, скользящие на нити		162
129.	Фермы		163
II. Равновесие нитей 		164
130.	Уравнения равновесия		164
131.	Общие теоремы		166
132.	Общие интегралы		167
133.	Определение постоянных, условия на концах		167
134.	Случай, когда сила не зависит от длины дуги		168
135.	Замечание о натяжении		168
136.	Естественные уравнения равновесия нити		168
137.	Формула, определяющая натяжение, когда существует силовая
функция		169
138.	Параллельные счлы		170
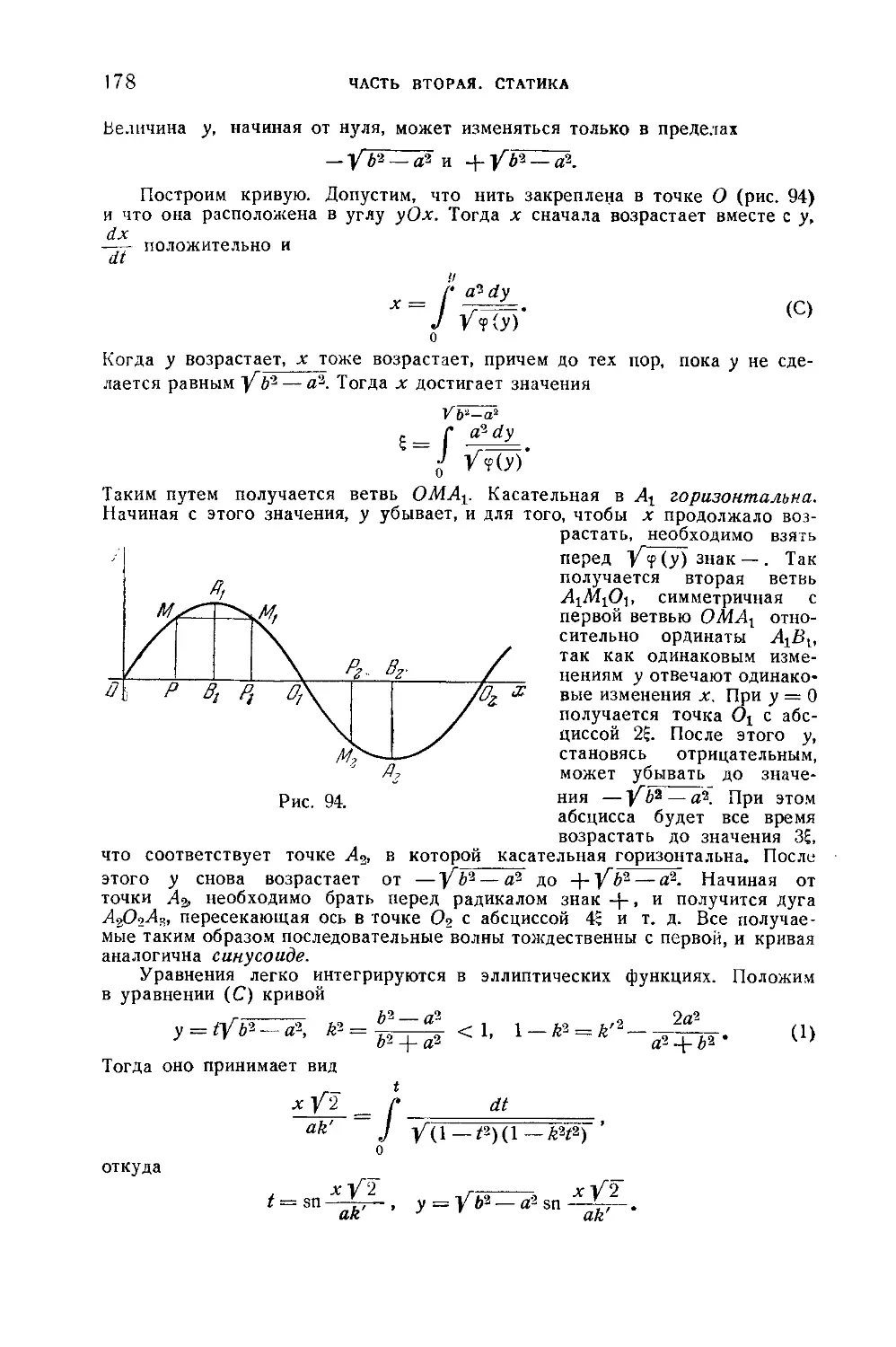
139.	Цепная линия		171
140.	Определение постоянных		173
141.	Центральные силы		175
142.	Пример существования бесчисленного множества положений
равновесия		176
143.	Равновесие нити на поверхности		180
144.	Примеры		181
145.	Естественные уравнения равновесия нити на поверхности . . .	182
III.	Исследование одного определенного интеграла		184
146.	Геометрическая задача		184
147.	Формула Тэта и Томсона . . •		188
148.	Примеры		190
149.	Та же задача на поверхности	¦		191
150.	Рефракция		193
IV.	Плоские эластики	,		195
151.	Натяжение и изгибающий момент		195
152.	Ось стержня была первоначально дугой окружности		196
153.	Случай первоначально прямолинейного стержня, сжимаемого на
концах двумя одинаковыми и прямо противоположными силами	200
154.	Стержень, изгибаемый действующим в одной плоскости по-
стоянным нормальным давлением		201
Упражнения		202
Глава VIII. Принцип возможных скоростей		208
155.	Исторический обзор	,		208
I. Формулировка и доказательство принципа в случае связей, выражаю-
щихся равенствами		209
156.	Возможное перемещение и работа		20Э
157.	Формулировка принципа		209
158.	Свободная точка		210
159.	Точка на поверхности		210
160.	Точка на кривой		212
161.	Свободное твердое тело		213
162.	Лемма		214
163.	Сочетания предыдущих связей		217
164.	Общее определение идеальных связей		218
165.	Доказательство принципа		218
166.	Замечание о работе силы		219
167.	О связях, осуществляемых при помощи тел, не имеющих массы	220

8	ОГЛАВЛЕНИЕ
II. Первые примеры. Системы с полными связями. Простые машины . .	221
168.	Системы с полными связями		221
169.	Простые машины		-^1
III Общие условия равновесия, выводимые из принципа возможных
скоростей		227
170.	Основное уравнение статики		227
171 Приведение уравнений равновесия к наименьшему числу . . .	227
172.	Голономные системы; координаты голономной системы ....	22Э
173.	Частный случай, когда выражение возможной работы есть пол-
ный дифференциал		230
174.	Приложения. Тяжелые системы		231
175.	Принцип Торричелли		232
IV.	Множители Лагранжа		233
176.	Уравнения связей ....'•		233
177.	Множители Лагранжа		234
178.	Случай неголономной системы		236
179.	Приложение принципа возможных скоростей к равновесию нитей	236
V.	Общие теоремы, выводимые из принципа возможных скоростей . .	23:)
180.	Связи допускают поступательное перемещение системы парал-
лельно оси		239
181.	Связи допускают вращение системы вокруг оси		239
182.	Связи допускают винтовое перемещение всей системы		239
183.	Приложение к условиям равновесия твердого тела		241
VI.	Неудерживающие связи	• .	241
184.	Связи, определяемые равенствами; допускаемые перемещения,
характеризуемые неравенствами		241
185.	Аналитические выражения		244
186.	Пример	-		245
187.	Связи, выражаемые неравенствами в конечной форме		248
Упражнения		250
Глава IX. Понятие о трении		255
188.	Общие сведения	¦		255
189.	Трение скольжения		257
190.	Закон трения скольжения в состоянии покоя		257
191.	Равновесие тел с трением		258
192.	Тяжелое тело, опирающееся на плоскость в нескольких точках
и находящееся под действием только одной силы F		25е*
193.	Лестница		260
194.	Веревка, навернутая на поперечное сечение цилиндра		261
195.	Трение скольжения при движении		262
196.	Трение качения в начале и во время движения		262
197.	Трение верчения		264
Упражнения		264
ЧАСТЬ ТРЕТЬЯ
ДИНАМИКА ТОЧКИ
Глава X. Общие сведения. Прямолинейное движение. Движение
снарядов		266
I. Общие теоремы		266
198.	Уравнения движения. Интегралы		266
199.	Первые интегралы		267

ОГЛАВЛЕНИЕ	9
200.	Естественные уравнения		26Э
201.	Количество движения		270
202.	Теорема о проекции количества движения		270
203.	Теорема о моменте количества движения. Закон площадей . .	271
204.	Геометрическая интерпретация двух предыдущих теорем ....	273
205.	Теорема кинетической энергии	,		273
206.	Примеры	• . .	275
207.	Замечание к интегралу кинетической энерги i		277
208.	Устойчивость равновесия свободной материальной точки. До-
казательство Лежен-Дирихле		278
II. Прямолинейное движение		280
209.	Некоторые случаи, когда движение точки прямолинейно ....	280
210.	Уравнение прямолинейного движения. Простые случаи интегри-
руемости 		281
211.	Приложение к движениям, происходящим под действием силы,
зависящей только от положения		283
212.	Движения под действием силы, зависящей только от скорости	2 il
213.	Прямолинейное таутохронное движение		297
214.	Дан закон прямолинейного движения, найти силу		2-J9
III. Криволинейное движение. Тяжелая точка в пустоте и сопротивляю-
щейся среде. Электрическая частица		301
215.	Силы постоянного направления		301
216.	Естественные уравнения		301
217.	Движение тяжелой точки в пустоте		302
218.	Определение параллельной силы по заданной траектории . . .	306
219.	Криволинейное движение тяжелого тела в- сопротивляющейся
среде 		306
220.	Движение легкого вращающегося шара в воздухе		313
221.	Движение наэлектризованной частицы в наложенных друг на
друга электрическом и магнитном полях 		315
Упражнения		319
Глава XI. Центральные силы. Эллиптическое движениэ планет	327
I. Центральные силы		327
222.	Уравнения движения		327
223.	Сила есть функция только расстояния		330
224.	Сила вида r~2 <р F)		332
225.	Обратная задача. Определение центральной силы, когда задана
траектория		333
II. Движение планет		335
226.	Следствия из законов Кеплера		335
227.	Прямая задача		336
228.	Кометы		338
229.	Спутники		ЗЗЭ
230.	Всемирное притяжение	•		340
231.	Двэйные звезды		343
232.	Задача Бертрана		343
233.	Краткие указания по поводу некоторых других задач		347
III. Элементарные сведения из небесной механики		348
234.	Задача л тел	 •		348
235.	Задача двух тел		349
236.	Масса планеты, обладающей спутником		352

jq	ОГЛАВЛЕНИЕ
237.	Определение времени в эллиптическом движении		354
238.	Геометрический метод		357
239.	Аналитические преобразования		358
240.	Элементы эллиптического движения		363
241.	Метод вариации постоянных		364
242.	Параболическое движение комет		364
243.	Параболические элементы		365
Упражнения	365
Глава XII. Движение точки по неподвижной или движущейся
кривой	372
1. Движение по неподвижной кривой	372
244.	Уравнения движения		372
245.	Устойчивость равновесия		373
246.	Движение тяжелой точки по неподвижной кривой		375
247.	Нормальная реакция. Естественные уравнения		379
248.	Математический маятник		381
249.	Движение математического маятника в сопротивляющейся среде	385
250.	Циклоидальный маятник 		387
251.	Движение тяжелой точки по кривой, расположенной в верти-
кальной плоскости, при действии трения и сопротивления среды	389
252.	Таутохроны		390
253.	Приложения		392
254.	Брахистохрона для силы тяжести		393
255.	Брахистохроны в общем случае		395
256.	Приложение теорем Томсона и Тэта к брахистохронам ....	397
257.	Брахистохроны на заданной поверхности		399
II. Движение материальной точки на изменяемой кривой	399
258.	Уравнения движения		399
259.	Уравнения Лагранжа		400
260.	Задача		402
261.	Случай неподвижной кривой		404
Упражнения	405
Глава XIII. Движение точки по неподвижной или движущейся
поверхности	410
I. Общие положения	 . 410
262.	Уравнения движения	410
263.	Уравнения Лагранжа . . .	410
264.	Приложения	414
II. Случай неподвижной поверхности	416
265.	Применение теоремы кинетической энергии		416
266.	Вывод уравнения кинетической энергии из уравнений Лагранжа	418
267.	Устойчивость равновесия в случае существования силовой функ-
ции tf	 .		419
268.	Нормальная реакция		420
269.	Естественные уравнения и нормальная реакция		421
270.	Геодезические линии		422
271.	Применение уравнений Лагранжа		424
272.	Бесконечно малые колебания тяжелой точки около наинизшей
точки поверхности		426

ОГЛАВЛЕНИЕ
11
Ш. Движение на поверхности вращения		428
273.	Геодезические линии поверхностей вращения		428
274.	Формула Клеро		430
275.	Упражнение		430
276.	Движение тяжелой точки на поверхности вращения, оСь кото-
рой Ог вертикальна	'		432
277.	Сферический маятник		433
278.	Вычисление нормальной реакции		438
279.	Интегрирование в эллиптических функциях		439
280.	Теорема Гринхилля		441
281.	Бесконечно малые колебания		441
Упражнения 		442
Глава XIV. Уравнения Лагранжа для свободной точки		447
282.	Уравнения Лагранжа		447
283.	Интеграл кинетической энергии		450
284.	Приложение		451
285.	Сферические координаты		453
286.	Эллиптические координаты в пространстве		453
287.	Эллиптичеткие координаты в плоскости ху		456
Упражнения 		457
Глава XV. Принцип Да ламбера. Принцип наименьшего действия.	458
288.	Принцип Даламбера		458
289.	Замечание о силе инерции		460
290.	Принцип наименьшего действия		460
Упражнения 		463
Глава XVI. Канонические уравнения. Теорема Якоби. Приложения	466
291.	Историческая справка		466
1. Канонические уравнения. Теорема Якоби		467
292.	Преобразование Пуассона и Гамильтона		467
293.	Частный случай, когда выражения х, у, z через q,, q%, q3 не
содержат явно времени		469
294.	Примечание		470
295.	Интеграл кинетической энергии		471
296.	Пример. Центральная сила — функция расстояния		471
II. Теорема Якоби		472
297.	Теорема Якоби		472
298.	Частный случай, когда t не входит явно в коэффициенты урав-
нения Якоби		477
299.	Геометрическое свойство траекторий		478
300.	Декартовы координаты в пространстве		479
III. Плоское движение. Движение по поверхности		481
301.	Общие положения		481
302.	Параболическое движение тяжелой точки в пустоте		483
303.	Центральная сила — функция расстояния		484
304.	Уравнения движения планеты в форме Якоби		485
305.	Геодезические линии поверхностей Лиувилля. Приложение к эл-
липсоиду 		488

12	ОГЛАВЛЕНИЕ
IV.	Движение в пространстве		490
306.	Движение планеты в сферических координатах по Якоби ....	490
307.	Движение точки, притягиваемой двумя неподвижными центрами
обратно пропорционально квадрату расстояний		493.
308.	Эллиптические координаты в пространстве		497
V.	Приложения к принципу наименьшего действия, к брахистохронам,
к равновесию нитей 		499
309.	Наименьшее действие. Свободная точка		499
310.	Точка на поверхности	,		500
311.	Параболическое движение		501
312.	Брахистохроны и фигуры равновесия нитей в случае силовой
функции. Задача рефракции		501
Упражнения		502
Именной указатель		509
Предметный указатель		511

ОТ ИЗДАТЕЛЬСТВА
Многотомный «Трактат по теоретической механике» выдающегося
французского ученого П. Аппеля A855—1930), над созданием ко-
торого автор работал на протяжении нескольких десятков лет, поль-
зуется во всех странах широкой известностью среди специалистов,
работающих в области механики. По обилию материала, полноте
и строгости изложения этот капитальный труд далеко выходит за
рамки обычного учебника и представляет собою по существу энцик-
лопедию знаний в области классической механики, отражающую уро-
вень развития этой науки к концу XVIII — началу XIX столетий.
Естественно, что при дальнейшем развитии науки и техники некото-
рые области исследований в механике значительно расширились,
а трактовка многих вопросов изменилась. Однако фундаментальный
курс Аппеля не утратил своей ценности и в наши дни.
Первые три тома трактата Аппеля были изданы в переводе на
русский язык (с 3-го французского издания) еще в 1911 г. и давно
уже стали библиографической редкостью. Настоящее издание пред-
ставляет собою новый перевод (с 5-го и 6-го французских изданий)
первых двух томов этого трактата, содержащих законченное изложение
классической механики точки, системы материальных точек и твер-
дого тела. При переводе лишь в некоторых местах (иногда без
особых оговорок) были изменены устаревшие или не поддающиеся
буквальному переводу термины и сняты рекомендации литературы.
В основном же текст перевода полностью следует оригиналу.
В связи с безвременной кончиной И. Г. Малкина научную редак-
цию текста перевода как первого, так и второго тома осуществил
С. М. Тарг.
Книга может служить хорошим пособием для студентов и аспи-
рантов механико-математических факультетов университетов и ценным
руководством для научных работников, преподавателей и инженеров,
работающих в области теоретической механики или пользующихся
этой наукой при технических исследованиях.

ВВЕДЕНИЕ
Среди математических наук первой является наука о вычисле-
ниях, которая основывается на единственном понятии о числе и
к которой стремятся свести все остальные науки. Затем следует
геометрия, которая вводит новое понятие — понятие о пространстве.
В геометрии рассматриваются точки, описывающие линии, линии,
описывающие поверхности, и т. д., но в ней никоим образом не
касаются времени, в течение которого осуществляются эти движе-
ния. Если ввести понятие времени, то получится более сложная
наука, называемая кинематикой, которая изучает геометрические
свойства движений в их соотношениях во времени, но в которой не
касаются физических причин движения. Этим последним вопросом
занимается механика. Необходимо, однако, заметить, что механика
не раскрывает действительных причин физических явлений и доволь-
ствуется заменой их некоторыми абстрактными причинами, называе-
мыми силами и способными вызвать тот же механический эффект.
Предметом механики является решение двух следующих задач:
1°. Найти движение, которое получает система тел под действием
заданных сил;
2°. Найти силы, способные сообщить системе тел заданное дви-
жение.
Прежде чем приступить к механике, мы изложим теорию геомет-
рических величин или векторов, а после этого дадим элементарные
сведения из кинематики.

ЧАСТЬ ПЕРВАЯ
ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
ГЛАВА I
ТЕОРИЯ ВЕКТОРОВ
Излагаемые в этой главе геометрические теории введены главным
образам Пуансо, Шалем и Мёбиусом. Они находят приложение во
многих важных вопросах геометрии, кинематики, механики и физики.
Так, например, векторами изображаются скорости, ускорения, вра-
щения, силы, вихри в гидродинамике и т. д.
I. Определения
1. Геометрические величины, или векторы. Геометрической
величиной, или вектором, называется отрезок прямой А1В1 (рис. 1),
имеющий начало в точке А1 и конец в точке Вх.
Если отрезок А1В1 неограниченно продолжить в обе стороны,
то получится бесконечная прямая Dlt которая называется линией
действия вектора, или его основанием.
Вектор обычно определяется следую-
щими элементами: 1) своим началом
или точкой приложения Ах; 2) своей
линией действия, совпадающей с не-
ограниченной прямой AlDl; 3) своим
направлением, обозначаемым стрелкой
У	на конце В1 и совпадающим с направ-
лением, в котором движется точка,
перемещающаяся из начала Ах к кон-
Рис. 1.	цу. Bt; 4) своим модулем Pv являю-
щимся длиной отрезка AyBv
Аналитически вектор определяется координатами (xv уи zj его
начала и (л:^, y'v г'Л его конца относительно трех осей координат,
или координатами (xv ylt zt) его начала и проекциями Xlt Ylt Zx
отрезка AJ5X на эти оси. При этом знаки проекций определяются
обычными правилами аналитической геометрии. Эти проекции, оче-
видно, равны
X1 = X[-xv Yl = y[-y1, Z^z[-Zl.	A)
Мы будем обозначать вектор одной буквой Plt представляющей его
длину или модуль и помещенной на его конце. В тех случаях, когда
можно опасаться смешения с буквами, изображающими числа, мы будем

ГЛАВА Г. ТЕОРИЯ ВЕКТОРОВ	17
обозначать вектор AiBi или Р1 также через {АгВ^, (PJ или че-
рез А^, или Р1 *).
Два вектора называются геометрически равными, если они
параллельны, имеют одинаковые модули и одинаково направлены.
Два вектора называются равными и противоположными, если они
равны, параллельны и направлены в противоположные стороны.
2.	Различные категории векторов. Все векторы, в зависимости
от того, какие физические или механические величины они предста-
вляют, могут быть разделены на три следующие категории:
1°. Прежде всего может случиться, что два геометрически равных
вектора изображают одну и ту же физическую или механическую
величину. Как мы увидим дальше, это будет, например, справедливо
для так называемых векторов моментов пары. Такого рода векторы,
не имеющие ни определенной линии действия, ни определенной точки
приложения, называются свободными.
2°. Может, однако, случиться, что два геометрически равных
вектора А1В1 и А2В2 (рис. 2) изображают одну и ту же физическую
величину лишь при условии, что они имеют	•
общую линию действия, но они изобра-	,''
жают различные физические величины,
если имеют различные линии действия.	у
Это, например, имеет место для векторов,	*'Hz
изображающих силы, действующие на твер-	,'
дое тело. Такие неотделимые от линии дей-	уЬ
ствия векторы называются скользящими.	s
3°. Может, наконец, случиться, что /'^1
изображаемая физическая величина такова,	_
что два различных вектора изображают
две различные физические величины, т. е. что вектор не может быть
отделен от своей точки приложения. Такого рода векторы назы-
ваются связанными. Связанным будет, например, вектор, изображающий
скорость движущейся точки в какой-нибудь момент времени. Дей-
ствительно, этот вектор не может быть отделен от движущейся точки.
Мы рассмотрим последовательно указанные выше три категории
векторов и будем характеризовать их некоторыми числами, которые
в известном смысле являются их координатами.
II. Свободные векторы. Три координаты свободного вектора
3.	Три координаты свободного вектора. Возьмем три оси Oxyz
(рис. 1) и обозначим через Xv Yy, Zl алгебраические значения
проекций вектора А1В1 на эти оси, причем проектирование на какую-
нибудь ось производится параллельно плоскости, проходящей через
*) Скобками обозначается еще система векторов (S) (Прим. перев.)
2 Зак, 851. П. Аппель, т. I

18	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
две другие оси. Так как два геометрически равных вектора имеют,
очевидно, одинаковые проекции и два вектора, имеющие одинаковые
проекции, геометрически равны, то свободный вектор характеризуется
тремя числами Хг, Klf Zt, которые являются его координатами.
Два вектора Рх и Р2 с проекциями Хх, Yt, Zt и Х2, К2, Z2
геометрически равны, когда
Хх = Х2, Yx = Y2, Zx = Z2;
равны и противоположны, когда
лх = — А^, ' 1 = — У2, ^i==:: — ^2»
параллельны, когда их проекции пропорциональны:
Ло	/2	^2
Случай прямоугольных осей. Направляющие косинусы вектора.
Допустим, что оси координат Ox, Oy, Oz являются прямоугольными,
и обозначим через ах, pt, 71 косинусы углов, которые образует
с этими осями вектор AtBv имеющий модуль Pt. Проектируя вектор
на эти оси, получим
Х1 = Р1а1. К1 = Р,р1. Zt = Plb	B)
и, кроме того,
Скалярное произведение двух векторов; угол между ними.
Рассмотрим два вектора Рх и Р2. Их скалярным *) произведением
(согласно мемуару Грассмана, Геометрический анализ, 1846) назы-
вается число
получаемое умножением произведения модулей этих векторов на
косинус угла между ними. В этом произведении первые два множи-
теля положительны; третий множитель cos(P1P2) положителен,
отрицателен или равен нулю в зависимости от того, будет ли
угол между обоими векторами острым, тупым или прямым.
Предполагая снова оси прямоугольными, обозначим через Xv Yx,
Zu X2, Y2, Z2 проекции обоих векторов на эти оси, а через av {Jlt
Ti- ^ Рг> Тг —их направляющие косинусы. Имеем
cos {PJ>2) = a,a2 + ргр2 + TlT2,
откуда, заменяла!, а2, ... найденными из формул B) значениями--—-,
-?-	получим формулу
"а
PxPt cos (Р,Р2) = ХхХг 4- К, К2 + ^xZ2,	C)
*) В оригинале употребляется термин «внутреннее произведение». (Прим.
перее.)

ГЛАВА I. ТЕОРИЯ ВЕКТОРОВ	19
являющуюся аналитическим выражением скалярного произведения
двух векторов и позволяющую определить косинус угла между ними.
Условие перпендикулярности двух векторов. Для того чтобы
два вектора были взаимно перпендикулярны, необходимо и доста-
точно, чтобы косинус угла между ними равнялся нулю. Таким обра-
зом, в прямоугольных осях получаем условие
ВД+^ + ад^О.	D)
Скалярное произведение двух векторов Р1 и Р2 мы будем обо-
значать символом Р1 • Р2.
Другие названия и обозначения. Дж.-В. Гиббс (Vector Analysis,
New York et Londres, 1902) употребляет для определения скалярного
произведения название прямое произведение двух векторов; О. Хэ-
висайд (Electromagnetic Theory) — название скалярное произведение
и М. Карвалло — алгебраическое произведение. Были предложены
и различные обозначения: наиболее простым обозначением скаляр-
ного произведения является запись в виде Р|Ps. Имеем Р\Р1 = Р1\Р.
Проекция вектора на ось есть скалярное произведение этого вектора
на вектор, численно равный -+-1 и имеющий данную ось своей
линией действия.
4. Геометрическая сумма произвольного числа свободных
векторов. Пусть заданы векторы (рис. 3) Pv Р2	Рп. Возьмем
произвольную точку А за исходную и построим последовательно
систему векторов, геоме-
трически равных заданным
векторам, а именно: сначала
построим вектор АСи рав-
ный P.lf в конце его — век-
тор С^С2, равный Рг, затем
вектор СгС3, равный Р3, .. .
и, наконец, вектор Сп_1Сп,
равный Рп. Вектор АСп за-	Рис-
мыкает полученный таким
образом многоугольник. Он называется геометрической суммой R
заданных векторов, а заданные векторы составляющими.
Легко убедиться, что геометрическая сумма не зависит от порядка,
в котором берутся составляющие векторы.
•Для обозначения того, что вектор R является геометрической
суммой векторов Р1% Р2, .... Рп, мы будем писать:
Я = Р1 + />2+ ... +/>„ или (Я) = (Pt)+ (/>,)+- ... +(ЯИ).
Проекции геометрической суммы векторов. Пусть Xv Yv Zv
Х2, Y2, Z2	 Xn, Yn, Zn — проекции векторов Pv P2, ..., Pn,
a X, Y, Z — проекции их геометрической суммы R. Согласно
теореме о проекциях, проекция вектора R = АСп на произвольную

20	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
ось равна сумме проекций сторон многоугольника АСЛС2 ... Сп,. т. е.
сумме проекций составляющих векторов. Таким образом, имеем
R К=У1 + К2+ ... + ГЯ,
= z1 + zs-t- ... +zn.
Равенство векторной суммы нулю. Если точка Сп совпадает-
с точкой А, то сумма R равна нулю. Для. того чтобы это имело
место, необходимо и достаточно, чтобы X, Y, Z равнялись нулю.
Примечание. Пусть Р — произвольный вектор. Если
то, взяв скалярные произведения, получим:
p.R=p.pi + p.pqJr ... +РРп.
Это равенство непосредственно вытекает также из того, что проекция век-
тора R на вектор Р равна сумме проекций векторов Ръ Р?, ..., Рп на
вектор Р.
5. Геометрическая разность. Геометрическая разность век-
торов Р1 и Р2 (рис. 4) есть вектор Q, сумма которого с векто-
ром Р2 равна вектору Рг. Проведем из некоторой точки А два
вектора АС^ и АС2, геометрически равных заданным векторам Р1
и Р2. Тогда вектор Q, г"еометри-
jfi чески равный вектору C2CV и
Т будет искомым, так как
Т
Мы будем писать
Рис. 4.	п	р 	р
V — *i — г2.
Проекции геометрической разности векторов. Пусть X, Y,
Z — проекции геометрической разности Q двух век-
торов Pj и Р2, проекции которых равны соответ-
ственно Хх, Yu Zi и Х2, Y2, Z2. Очевидно, имеем:
Х=Х)— Х2, Y=Yl—Y2, Z = Zl — Z2.
б. Положительное направление вращения во-
круг оси. Пусть Д — некоторая ось, на которой
произвольным образом выбрано положительное на-
правление, например, от г' к 2 (рис. 5). Мы будем
говорить, что точка М, движущаяся по произволь-
ной пространственной кривой С, вращается вокруг	Рис. 5.
оси в положительном направлении, если для на-
блюдателя, смотрящего по направлению от 2 к z', точка движется
справа налево. В противном случае точка вращается в отрица-
тельном направлении.
z

ГЛАВА I. ТЕОРИЯ ВЕКТОРОВ	21
Рассмотрим, например, два вектора АгР{ и ВР2 (рис. 9). Допу-
стим, что точка, перемещающаяся по направлению А1Р1, поворачи-
вается вокруг вектора ВР2, принятого в качестве оси, в каком-нибудь
направлении. Тогда из рисунка видно, что и, наоборот, точка, пере-
мещающаяся вдоль ВР2, вращается вокруг А1Р1 в том же направлении.
Ориентация координатного триэдра. Мы будем предполагать,
что координатный триэдр ориентирован таким образом, что поворот
на 90° в положительном направлении вокруг оси Ог переводит
ось Ох в ось Оу (рис. 1).
Примечание. При другом выборе положительного направления
для сохранения формул необходимо изменить ориентацию осей, при-
держиваясь указанного правила.
7.	Векторное произведение двух векторов. Проведем из какой-нибудь
точки А векторы APt и АР2, геометрически равные двум заданным сво-
бодным векторам Я, и А>, и построим на них параллелограмм APXQP2
(рис. 6V Проведем далее из точки А век-
тор AG, перпендикулярный плоскости этого
параллелограмма и содержащий столько
единиц длины, сколько единиц площади со-
держится в параллелограмме. Направле-
ние вектора АО выберем таким образом,
чтобы точка, пробегающая контур AP\QPoA,
вращалась вокруг AG в положительном
направлении. Этот вектор AG или О назы-
вается векторным, или внешним произве-
дением векторов Pi и Ро, что записывается
следующим образом:
О = Я, X Р*
Грассман называет вектор О дополнением цикла AP\QP$A, определенного
векторами Я, и Р?.
Векторное произведение Я» на Я, есть вектор АС или О', противо-
положный вектору О. Действительно, новое векторное произведение имеет
т}т же линию действия и тот же модуль, что и вектор О, но оно направлено
в противоположную сторону, так как точка, описывающая контур AP2QP\A,
должна вращаться вокруг АС в положительном направлении. Имеем:
О' = Я2 X Я,
и, следовательно,
Р2ХРх = — PiXP2-
Если Рг совпадает с Р2, то векторное произведение обращается в нуль:
Я, X Pi = 0.
III. Скользящие векторы. Пять координат
скользящего вектора
8.	Общие замечания. Рассмотрим вектор А1В1 модуля Р{, при-
ложенный в точке Ах. По предположению, если такой вектор пере-
носить вдоль его линии действия Du то он по-прежнему будет
представлять ту же самую физическую величину. При таком пере-

22
ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
Рис. 7.
носе вектор будет оставаться геометрически равным самому себе,
и, следовательно, его проекция на какую-нибудь ось не будет изме-
няться. При этом, однако, не будут изменяться и некоторые другие
геометрические величины, связанные с этим вектором.
Рассмотрим произвольную точку В пространства (рис, 7) и по-
строим треугольник ВАХВХ, имеющий вершину в точке В, а осно-
ванием — вектор Рх. Если
вектор АХВХ будет сколь-
зить вдоль прямой Dx, то
не будут изменяться следую-
щие элемента:
1°. плоскость треуголь-
ника BAxBt, являющаяся
плоскостью, образованной
прямой Dx и точкой В,
2°. площадь треуголь-
ника ВАХВХ,
3°. направление, в котором точка, движущаяся вдоль вектора от
Л, к Ви поворачивается вокруг В в плоскости BDX.
Можно заметить, что если рассматриваемую фигуру спроектиро-
вать на какую-нибудь плоскость Q в фигуру baxbx, то аналогичные
элементы в треугольнике baxbx не изменятся
при скольжении вектора Рх вдоль прямой Dx. >
Для уяснения этих обстоятельств вводятся
следующие определения.
9. Теория моментов. 1. Момент вектора
относительно точки (или векторный момент).
Момент вектора Рх относительно какой-
нибудь точки В (рис. 8) есть вектор BQV
приложенный в точке В и имеющий: 1) мо-
дуль, равный произведению Рх • 8 модуля
вектора Р, на расстояние 8 от точки В до
этого вектора, 2) линию действия, перпен-
дикулярную плоскости ВАХРХ, 3) направление такое, что точка, пере-
мещающаяся по А1Р1 от Ау к Рр поворачивается вокруг BQ^ в по-
ложительном направлении.
Модуль этого момента равен удвоенной площади треуголь-
ника ВАХР^. Он равен нулю тогда, когда либо Рх, либо 8 равно
нулю. Момент не изменяется, когда вектор Pj перемещается вдоль
своей линии действия, или когда точка В перемещается вдоль прямой,
параллельной этому вектору.
Пример. Векторное произведение О = Рх х Р%, определение которого
дано в пункте 7, равно моменту вектора Рх относительно конца вектора Я2
(рис. 6). Наоборот, векторное произведение Р2 X Р\ равно моменту век-
тора Р2 относительно конца вектора Рх.
\
Рис. 8.

ГЛАВА I. ТЕОРИЯ ВЕКТОРОВ
23
2. Момент относительно оси. Этот момент есть число положи-
тельное, отрицательное или равное нулю. Его называют иногда скаляр-
ным моментом относительно оси в противоположность векторному
моменту относительно точки. Определяется он следующим образом:
момент вектора Р, относительно
некоторой оси Д (рис. 9), на ко-
торой выбрано положительное
направление, есть алгебраическое
значение проекции на эту ось
момента вектора Pt относительно
точки, взятой на оси.
Чтобы такое определение имело
смысл, необходимо показать, что
значение момента не зависит от
выбора точки на оси. Проведем
через какую-нибудь точку В оси
плоскость П, перпендикулярную
оси, и пусть агрх— проекция
вектора А1Р1 на эту плоскость,
BGt—момент вектора Pi относи-	Рис. 9.
тельно точки В и ??gt — проекция
??G1 на ось Д. Так как угол между плоскостями А1ВР1 и ахВрх
равен углу между перпендикулярами к ним, то
2 площ.
= 2 площ. AlBP1cosGlBgl, Bgi = BGicosG1Bgl.
Но так как модуль BGt момента BGt равен удвоенной площади А1ВР1,
то его проекция Bgx равна по абсолютному значению удвоенной
площади ахВрх, а последняя величина не зависит, очевидно, от вы-
бора точки В на оси Д. Знак проекции Bgt также не зависит
от выбора точки В и будет -)- или — в зависимости от того,
будет ли точка, перемещающаяся вдоль А1Ри вращаться вокруг Д
в положительном или в отрицательном направлении.
Можно вывести несколько различных выражений для момента
вектора Pj относительно оси.
Обозначим через 8 кратчайшее расстояние между вектором и
осью, а через 6 — угол между ними. Проекция отрезка 8 на пло-
скость П равна самому отрезку, а величина рх равна Р^тб, и
поэтому момент 2Rt относительно оси Д будет
2Ht= ±Pi8= ±P18sin6,
причем знак -\- или — берется в зависимости от того, будет ли
точка, перемещающаяся вдоль АгРг, поворачиваться вокруг оси Д
в положительном или в отрицательном направлении.

ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
Отложим на оси Д в положительном направлении отрезок ВР,
длины Р2 и обозначим объем тетраэдра, имеющего Л1Р1 и ВР2 в ка-
честве противоположных ребер, через объем (Рх, Р2). При этом он
принимается положительным или отрицательным в зависимости
от того, будет ли точка, перемещающаяся от начала к концу одного
из векторов Pt или Р2, поворачиваться вокруг другого вектора
в положительном или в отрицательном направлении. Тогда момент
вектора Pt относительно Д будет
™ 	 6 объем. (/>!, Р9)
Ж1 —	р~2	~~ ¦
В самом деле, это равенство справедливо по знакам и по абсо-
лютным значениям, так как рассматриваемый объем не изменится
при перемещении вершин А1 и Pt до положений ях и рх, что при-
ведет к новому тетраэдру, объем которого V равен одной трети
произведения Р2 на площадь ахВрх; поэтому, абсолютное значение
момента, равное удвоенной площади ахВрх, равно величине 6V,
деленной на Р2.
Примечание. Из формулы Шх = ± Pfisin6 вытекает, что
момент равен нулю, когда один из трех множителей равен нулю,
т. е. когда вектор либо равен нулю, либо лежит в одной
плоскости с осью.
10. Аналитические выражения моментов вектора относительно
осей координат. Пусть дан вектор Рх с началом в точке А1 и
с концом в точке Вх (рис. 1). Обозначим через хх, yv zl коорди-
наты его точки приложения Лх и через Хх, Кх, Zx его проекции
на оси Ox, Oy, Oz. Момент Nx вектора относительно оси Ог равен
удвоенной площади проекции треугольника ОА1В1 на плоскость хОу,
причем этой величине площади приписывается знак согласно уста-
новленному ранее правилу. Но одна из вершин проекции совпадает
с точкой О, а две другие имеют в плоскости хОу координаты:
проекция точки Ау: xv, yt,
проекция точки Bt: л;1 + Л'1, yl-{-Yl.
Согласно элементарной формуле для площади треугольника,
имеющего вершину в начале координат, получим
Ni = *i CVi + Уд — Уг (*i + *д = x,Y, — yxXv
Точно так же для моментов Lx и Мх вектора относительно
осей Ох и Оу получится:
Определение векторного момента. Момент OGX вектора Pt
относительно начала О есть вектор, имеющий проекции на оси коор-

ГЛАВА I. ТЕОРИЯ ВЕКТОРОВ	25
динат, равные Lx, Мх, Nx. Это вытекает из самого определения
момента относительно оси.
Перенос начала. Если в качестве начала координат принять
любую другую точку О' с координатами х', у', z'', то .координаты
точки Ах относительно новых осей, параллельных первоначальным,
равны хх— х', ух— у', zx— z'. Проекции вектора на новые оси
остаются Хх, Yx, Zx и моменты относительно этих осей будут
Эти выражения получаются путем замены в выражениях Lv Mv Nt
величин xv ух, zx величинами xx— x', yx— y', zx— z'. Момент O'G'
того же вектора относительно точки О' есть вектор, имеющий
проекции Lx, Mi, Nx. Принимая во внимание значения Lt, Mt, Nit
можно написать
= М1 — (z'Xx — x'Zx),
11. Пять координат скользящего вектора. Шесть величин Xv
Yv Zx, Lj, Mt, Л/, удовлетворяют тождеству X1L1-\- Y1Ml-\-Z1N1 — 0,
которое выражает, что момент OGt перпендикулярен вектору AXBV
Обратно, пусть заданы шесть произвольных величин Xt, Yv Zv Lv
M,, Nv из которых первые три не равны нулю одновременно, удо-
влетворяющие тождеству
L
Уравнения
в которых х, у, z обозначают текущие координаты, определяют
прямую линию D, так как в силу предположенного тождества они
приводятся к двум независимым уравнениям. Пусть Ах — произволь-
ная точка этой прямой. Тогда вектор Рх с началом в точке Ах и
с проекциями Хх, Yx, Zx будет направлен по этой прямой D и будет
иметь моменты Lx, Mx, Nx относительно осей координат. Шесть вели-
чин Хх, Yx, Zx, Lx, Mx, N{ называются по Плюккеру координатами
скользящего вектора. Из этих шести координат пять могут быть
выбраны произвольно.
12. Относительный момент двух векторов Рх и Р2. Так называют
величину, равную 6 объемам (Рх, Ро), определенную раньше (рис. 9). Алге-
браическое выражение этой величины получается непосредственно из эле-
ментарной формулы аналитической геометрии, выражающей объем тетраэдра

26
ЧАСТЬ ПЕРВАЯ ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
в функции координат его вершин. Пусть хъ у\, zt — координаты точки А\
и пусть Хх, К], Zi — проекции вектора Рх на оси координат, наконец Lx,
Mi, Nx — его моменты относительно этих осей. Точно так же обозначим
через х2, У2, г2 координаты точки В и через X*, Y& Z& Lb М2, N2 — проек-
ции и моменты вектора Я2. Тогда, считая оси координат ортогональными
и ориентируя их таким образом, чтобы поворот в положительном напра-
влении вокруг оси Ог на 90° переводил ось Ох в ось Оу, получим с учетом
знака
6 объем. (Я,, Р2) = —
У\
х2 + Х2 у2+ Y2 г2 4- Z2 .1
Раскрывая определитель, предварительно вычтя из второй строки первую
и из четвертой третью, получим
Рис. 10.
6 объем. (Я,, Я2) = LXX2+MXY2 + NXZ2 + L2XX 4- M2YX + N2ZX,
или ввиду тождеств LxXi -\-MxYx-\- N\ZX = 0 и L2X2-\- M2Y2 4- N*Zv — 0,
имеем 6 объем. (Яг, Я2) = (Lx 4- L2) (Xx + X2) +
4- (Mi + M2) (Yx + Y2) + (Nx + N2) (Z, + Z2).
Аналитическое выражение момента отно-
сительно произвольной оси. ДаНа ось Д
(рис. 10), на которой выбрано положительное
направление от точки О' с координатами (х',
у', г') к точке О" с координатами (х", у", z").
Проекции Хь Y2, Z2 вектора О'О", предста-
вляющего собою вектор Я», и величины L2, М%,
N2 его моментов равны соответственно
х" — х', у" —у', z" — z'; y'z" — z'y",
z'x" — х V, х'у" — у*х".
Момент 5Dlt вектора Рх относительно заданной оси Д равен величине
6 объем. (Pi, Я2), деленной иа Я2, что дает:
(х"-х')^+(,У"-У')М,+(.г"-г')Nl+(y'z"-z'y")X1+(z'x"-x'z") Y,+(xfy"-y'x") Z^
"=	V(x> -x"f+(у' -y"f+ (z' - г"?
Из этой общей формулы можно для проверки получить значения мо-
ментов вектора Рх относительно осей координат. Для оси Oz, например, до-
статочно положить х' = у' = z' = х" = у" = 0 и г" = 1. Тогда момент будет
равен Nx. Точно так же для осей Ох и Оу получатся Z., и Мх.
13. Скользящие векторы, сходящиеся в одной точке. Резуль-
тирующий вектор. Пусть заданы скользящие векторы Рх, Р2, ... гРп,
линии действия которых пересекаются в некоторой точке А.
Каждый из указанных векторов можно перенести вдоль его линии
действия так, чтобы все эти векторы оказались приложенными
в самой точке А, как показано на рис. 11. Тогда результирующим
вектором рассматриваемой системы векторов называется вектор R,
равный их геометрической сумме и приложенный в точке А, либо

ГЛАВА I. ТЕОРИЯ ВЕКТОРОВ	-27
другой вектор, получающийся вследствие переноса вектора R вдоль
его линии действия. На рис. 11 результирующий вектор найден путем
последовательного построения векторов АРХ, PiQ2, •••, Qn-iQn>
геометрически равных соответствующим заданным векторам, причем
точка А принята за исходную.
Результирующий вектор R со-
впадает с AQn.
Проекции результирую-
щего вектора. Мы уже указы-
вали (п. 4), что проекции X,
Y, Z результирующего век-
тора R на оси координат равны
соответственно суммам проек-
ций составляющих векторов:
{- ... ~\-Хп,
Моменты результирую-	Рис-
щего вектора относительно
осей координат. Обозначим через х, у, г координаты точки А.
Тогда моменты вектора Pk(Xk, Yk, Zk) относительно осей коор-
динат будут:
Lk = yZk — zYk, Mk^zXk — xZk, Nk = xYk — yXk,
а моменты результирующего вектора относительно тех же осей
будут:
L = yZ— zY, M=-zX—xZ, N = xY — yX.
На основании найденных выше значений для X, Y, Z имеем
Таким образом, шесть координат X, Y, Z, L, М, N результи-
рующего вектора равны суммам соответствующих координат
составляющих векторов.
Так как произвольная ось может быть принята за координатную,
то мы видим, что проекция результирующего вектора заданной
системы векторов, линии действия которых пересекаются в одной
точке, на произвольную ось равна сумме проекций этих векто~
ров на ту же ось; момент результирующего вектора относи-
тельно оси равен сумме моментов составляющих векторов отно-
сительно этой оси. (Теорема Вариньона.)
Отсюда получаем следующее: момент результирующего вектора
системы сходящихся векторов относительно некоторой точки О
равен геометрической сумме моментов составляющих векторов.
В самом деле, если точку О принять за начало координат, то L,
М, N будут проекциями на оси координат момента OG резуль-
тирующего вектора относительно точки О, г Lk, Mk, Nk — проек-

28
ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
Р2, .
циями момента OGk вектора Рк относительно той же точки. Но
тогда предыдущие равенства как раз и показывают, что OG есть
геометрическая сумма векторов OGX, OG2	OGn.
Примечание. Иногда представляется нужным разложить задан-
ный вектор АР на другие векторы, приложенные в точке А, т. е.
найти векторы, от сложения которых получится вектор АР.
Можно, например, всегда разложить при помощи параллелограмма
вектор АР на два других, имеющих заданные направления АВ и АС,
плоскость которых содержит АР.
Точно так же при помощи параллелепипеда можно разложить АР
на три вектора, имеющих заданные направления АВ, AC, AD и
образующих триэдр.
14. Произвольная система векторов. Главный вектор и глав-
ный момент. Пусть заданы произвольные скользящие векторы Ри
., Рп, приложенные в точках Ах, А2, ..., Ап. Выберем произ-
вольную точку О пространства
и назовем:
1)	главным вектором —
геометрическую сумму OR
векторов ОР[, ОР'3, .... ОР'п,
имеющих начало в точке О и
равных заданным векторам;
2)	главным моментом
относительно точки О — гео-
метрическую сумму OG момен-
тов OGV OG2, •. •, OGn задан-
ных векторов относительно
той же точки.
Если менять положение точ-
ки О, то главный вектор не
будет меняться ни по величине,
ни по направлению, что выте-
кает из самого определения этого вектора. Напротив, главный мо-
мент OG (рис. 12) изменяется за исключением случая, когда точка О
перемещается по направлению прямой OR.
Приняв точку О за начало прямоугольных осей координат, обо-
значим через xk, ук, гк координаты точки Ак, через Хк, Yk, Zk —
проекции вектора Рк и через Lk, Mk, Nk — его моменты относительно
этих осей. С другой стороны, пусть X, Y, Z обозначают проекции
главного вектора OR и L, М, N — проекции главного момента OG
относительно точки О. Тогда, обозначая через 2 сумму, распро-
страненную на все заданные векторы, получим
Рис. 12.
(G)

ГЛАВА I. ТЕОРИЯ ВЕКТОРОВ	29
Пусть х', у', г' — координаты какой-нибудь другой точки О'.
Мы видели (п. 10), что для проекций момента O'G'k вектора Рк
относительно точки О' можно написать:
'к = Мк — (z'Xk — x'Zk),
(G'k)
Следовательно, обозначая через X', Y', Z' и L', М', N' проекции
векторов O'R' и O'G', получим:
Х' = ^Хк = Х, Y'=:Y, Z' = Z,	(/?'
L' = ^L'k = L — (y'Z — z'Y),
M' = M — (z'X—x'Z),
N' =N — (x'Y—y'X).
При помощи этих формул можно вычислить векторы R' и О'
для любой точки О' пространства, если они известны для одной
точки О. Эти формулы показывают, что главный момент O'G' от-
носительно точки О' равен геометрической сумме главного
момента относительно точки О и момента относительно
точки О' главного вектора OR в точке О.
15. Изменение главного вектора и главного момента; инва-
рианты; центральная ось. Допустим сначала, что главный вектор
отличен от нуля. Тогда главный момент G' будет отличен от G,
если только точка О' не находится на линии OR. Но проекция
главного момента на направление главного вектора есть величина
постоянная. В самом деле, имеем
R'G' cos R^G' = L'X' -f- M'Y' + N'Z',
а левая часть этого равенства на основании значений X', Y', Z'', U,
М', N' равна LX~\-MY ~\-NZ, т. е. величине постоянной. Так
как величина R' также постоянна, то
G' cos Rfb' = const == G cos RG,
что и доказывает теорему.
Вследствие этой теоремы, каковы бы ни были начало и направ-
ления прямоугольных осей координат, величины
сохраняют постоянные значения. Эти величины называются инва-
риантами системы векторов.
Согласно определению скалярного произведения двух векторов
(п. 3), можно сказать, что инвариант LX-\- MY ~\~NZ есть скалярное
произведение главного вектора и главного момента относительно

30	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
произвольной точки пространства. Ниже (п. 21) будет дано другое
замечательное геометрическое истолкование этого инварианта.
Так как главный вектор, по предположению, везде отличен от
нуля, то можно найти такую точку О'(х', у', г'), что главный
момент O'G' будет направлен по той же прямой, что и главный
вектор O'R'. Для этого необходимо и достаточно, чтобы L', М', N'
были пропорциональны X, Y, Z:
X
*• '
Эти линейные относительно х', у', z' уравнения указывают, что
геометрическое место точек О' есть прямая D'D, параллельная на-
правлению главного вектора. Эта прямая называется центральной
осью (рис. 13). Для какой-нибудь точки О' этой оси
\* главный вектор и главный момент будут лежать на этой
|	оси и будут иметь одинаковые или противоположные
1 я» направления в зависимости от того, будет ли величина
LX-\- MY-\-NZ положительной или отрицательной. При
этом главный момент g будет минимальным, так как
он совпадает со своей проекцией на главный вектор.
В частности, если R отлично от нуля, а инвариант
LX+MY + NZ
равен нулю, то проекция главного момента относительно
ЧУ произвольной точки на главный вектор равна нулю. Этот
Рис 13 момент будет перпендикулярен главному вектору, а ми-
нимальный момент O'g будет равен нулю.
Примечание. Умножая члены отношений A) соответственно
на X, Y, Z и складывая, получим для общего значения этих отно-
шений величину
LX+ MY + NZ _G cos RG
~~ R '
которая обращается в нуль, если минимальный момент равен нулю.
Случай, когда главный вектор равен нулю. В случае, когда
главный вектор равен нулю, из предыдущих формул вытекает,
что L', М', N' будут равны L, М, N. В этом случае главный момент
будет одинаковым во всех точках пространства.
Рассуждения, которые привели к понятию, центральной о.си,
в рассматриваемом случае теряют смысл. Можно условно принять
в этом случае в качестве центральной оси любую прямую, парал-
лельную главному моменту.
16. Сумма моментов относительно произвольной оси. Прямые нуле-
вого момента. Рассмотрим ось Д, соединяющую две точки О' (х', у , г')
и О" (х", у", г"). Момент Ши вектора Ph относительно этой оси определяется
одной из формул, установленных выше (п. 12).

ГЛАВА I. ТЕОРИЯ ВЕКТОРОВ	33
прямо противоположны. В самом деле, так как главный вектор ра-
вен нулю, то вектор Q равен и противоположен вектору Р. Далее,
главный момент должен равняться нулю относительно произвольной
точки. Примем в качестве нее точку А приложения вектора Р. Мо-
мент вектора Р относительно точки А равен нулю, и, следовательно,
главный момент приводится к моменту Q, и так как он должен быть
равен нулю, то линия действия вектора Q проходит через точку А,
что и доказывает предложение.
Так же, как и в алгебре, где разность двух равных величин
равна нулю и наоборот, — в теории векторов имеет место следующая
теорема:
Для того чтобы две системы скользящих векторов (S) и (So)
были эквивалентны, необходимо и достаточно, чтобы система,
образованная из векторов (S) и векторов (So), после того как
направления последних заменены на противоположные, была
эквивалентна нулю.
В самом деле, если направления всех векторов системы E0) за-
менить на противоположные, то в полученной новой системе (— 50)
главный вектор и главный момент относительно точки 0 будут от-
личаться от соответствующих элементов системы (So) только напра-
влением. Следовательно, проекции главного вектора и главного
момента всей системы, образованной путем соединения
систем (S) и (— So), будут
Х—Хо, Y — Yo, Z — Zo, L — Lo, M-Mo, N—No.
Но для того, чтобы две системы были эквивалентны,
ft
необходимо и достаточно, чтобы эти величины равнялись j
нулю, что и доказывает теорему.	!«
Мы приведем в статике (глава V) примеры наибо-
лее важных систем векторов, эквивалентных нулю.
19. Элементарные операции. Можно получить си-
стемы, эквивалентные некоторой заданной системе, при
помощи следующих элементарных действий:
1°. Присоединение или отбрасывание двух равных и
-Р'
прямо противоположных векторов. Перенос вектора Рис. 16.
вдоль линии действия.
2°. Сложение нескольких сходящихся векторов в один. Разложе-
ние вектора на сходящиеся векторы.
Перенос вектора АР в точку В, находящуюся на его линии
действия, есть следствие первого действия. В самом деле, приложим
в точке В (рис. 16) вдоль прямой АВ два равных и прямо проти-
воположных вектора Р' и —Р', из которых первый Р' равен Р.
Отбросим далее два прямо противоположных вектора Р и —Р'.
Тогда останется вектор ВР', который представляет собой не что
иное, как вектор АР, перенесенный в точку В на его линии дей-
ствия.

32	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
Наоборот, прямые комплекса, расположенные в некоторой плоскости ТС,
проходят через некоторую точку О', для которой главный момент перпен-
дикулярен к этой плоскости. Точку О' называют по Шалю фокусом плоско-
сти П. Этот фокус находится на конечном расстоянии, если только пло-
скость П не параллельна центральной оси.
Если плоскость П поворачивается вокруг некоторой прямой D, то фокус
будет перемещаться по некоторой сопряженной прямой Д. Наоборот, если
плоскость будет поворачиваться вокруг прямой Д, то ее фокус будет пере-
мещаться по прямой D.
Легко видеть, во что обратятся эти теоремы, если g или R равны
нулю.
IV. Эквивалентные системы скользящих векторов.
Элементарные операции. Приведение системы
скользящих векторов
18. Определение эквивалентности. Две системы скользящих
векторов называются эквивалентными, если их главные векторы и
главные моменты относительно некоторой точки пространства равны.
Тогда будут одинаковыми главные моменты относительно какой
угодно другой точки пространства. В частности, обе системы будут
иметь одну и ту же центральную ось и один и тот же минимальный
момент. Например, система сходящихся векторов эквивалентна глав-
ному вектору.
Пусть (S) и (So) — две системы скользящих векторов, X, Y, Z,
L, М, N — проекции на оси координат главного вектора и главного
момента относительно начала О системы (S), Хо, Yo, Zo, Lo, Mo,
No—аналогичные величины системы (So). Усло-
Р виями эквивалентности обеих систем являются ра-
венства:
X— Хо, Y = Yo, Z = Zo, L = Lo,
\д	M = M0, N = N0.
IB	I
I	Система скользящих векторов, эквивалент-
п	t-/7 ная нулю. Говорят, что система (S) эквива-
лентна нулю, если ее главный вектор и глав-
Рис. 15.	ный момент относительно какой-нибудь точки
равны нулю. Эти величины будут тогда равны
нулю и во всех других точках пространства. Эхвивалентность си-
стемы нулю выражается уравнениями
Х=0, К=0, Z = 0, /. = 0, М = 0, N— 0.
Возьмем для примера систему двух равных и прямо противо-
положных векторов, т. е. систему, образованную двумя векторами Р
и —Р, равными и направленными в противоположные стороны
вдоль прямой АВ, соединяющей их точки приложения (рис. 15).
Эта система, очевидно, эквивалентна нулю. Наоборот, если система
двух векторов Р и Q эквивалентна нулю, то эти векторы равны и

ГЛАВА I. ТЕОРИЯ ВЕКТОРОВ	33
прямо противоположны. В самом деле, так как главный вектор ра-
вен нулю, то вектор Q равен и противоположен вектору Р. Далее,
главный момент должен равняться нулю относительно произвольной
точки. Примем в качестве нее точку А приложения вектора Р. Мо-
мент вектора Р относительно точки А равен нулю, и, следовательно,
главный момент приводится к моменту Q, и так как он должен быть
равен нулю, то линия действия вектора Q проходит через точку А,
что и доказывает предложение.
Так же, как и в алгебре, где разность двух равных величин
равна нулю и наоборот,—в теории векторов имеет место следующая
теорема:
Для того чтобы две системы скользящих векторов (S) и E0)
била эквивалентны, необходимо и достаточно, чтобы система,
образованная из векторов (S) и векторов (So), после того как
направления последних заменены на противоположные, была
эквивалентна нулю.
В самом деле, если направления всех векторов системы (So) за-
менить на противоположные, то в полученной новой системе (— 50)
главный вектор и главный момент относительно точки 0 будут от-
личаться от соответствующих элементов системы (So) только напра-
влением. Следовательно, проекции главного вектора и главного
момента всей системы, образованной путем соединения
систем (S) и (— So), будут
Х—Хо, Y — Yo, Z — Zo, L — Lo, M—Mo, N—Nq.
Но для того, чтобы две системы были эквивалентны,
необходимо и достаточно, чтобы эти величины равнялись j
Р'
нулю, что и доказывает теорему	'
Мы приведем в статике (глава V) примеры наибо-
лее важных систем векторов, эквивалентных нулю.
19. Элементарные операции. Можно получить си-
стемы, эквивалентные некоторой заданной системе, при
помощи следующих элементарных действий:
Г. Присоединение или отбрасывание двух равных и
-Р*
прямо противоположных векторов. Перенос вектора Рис. 16.
вдоль линии действия.
2°. Сложение нескольких сходящихся векторов в один. Разложе-
ние вектора на сходящиеся векторы.
Перенос вектора АР в точку В, находящуюся на его линии
действия, есть следствие первого действия. В самом деле, приложим
в точке В (рис. 16) вдоль прямой АВ два равных и прямо проти-
воположных вектора Р' и —Р', из которых первый Р' равен Р.
Отбросим далее два прямо противоположных вектора Р и —Р'.
Тогда останется вектор ВР', который представляет собой не что
иное, как вектор АР, перенесенный в точку В на его линии дей-
ствия.

34	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
Покажем теперь, что оба указанных элементарных действия не
изменяют ни главного вектора, ни главного момента относи-
тельно произвольной точки.
Приняв эту точку за начало, необходимо показать, что шесть
сумм
2	2X Z
не изменяются. В самом деле, присоединение или отбрасывание
двух равных и прямо противоположных векторов означает добавле-
ние или отбрасывание в каждой сумме двух слагаемых, равных по
величине и противоположных по знаку. Замена нескольких сходя-
щихся векторов их равнодействующим вектором означает замену
сумм проекций этих векторов проекциями их равнодействующего
вектора в первых трех суммах и сумм моментов этих векторов —
моментом равнодействующего вектора в последних трех суммах. Но
это сводится к замене нескольких слагаемых в каждой из указан-
ных сумм их суммой. Точно так же
и разложение вектора на несколько
сходящихся векторов не изменяет ни
одной из шести указанных сумм.
Можно попытаться заменить при
помощи элементарных действий задан-
ную систему векторов E) более про-
стой эквивалентной ей системой.
20. Приведение к двум векторам.
/у i !	Система скользящих векторов может
/г'	\ i	быть заменена бесчисленным множест-
0	\!	вом способов двумя векторами, из ко-
у	торых один проходит через произволь-
'	ную точку.
Рис 17.	Мы покажем сначала, что система
Plt Р2	 Рп эквивалентна трем
векторам, приложенным в произвольно взятых точках О, Olt О2, не
лежащих на одной прямой (рис. 17).
Разложим вектор А^РХ на три составляющих вектора, направлен-
ных соответственно по прямым ОАХ, ОхАг, О2А1. После этого, пере-
мещая точки приложения каждого составляющего вектора вдоль
его линии действия, перенесем первый^составляющий вектор в точку О,
второй составляющий — в точку Ot и третий составляющий— в точ-
ку О2. Точно так же разложим вектор А2Р2 на три составляющих
вектора, направленных вдоль прямых ОАг, ОхАг, О2А2, перенесем
их в точки О, Ov O2 и так продолжаем далее. Векторы, приложен-
ные в точке О, имеют результирующую Rv векторы, приложенные
в точке Oj, имеют результирующую /?2, и приложенные в точке О2 —

ГЛАВА I. ТЕОРИЯ ВЕКТОРОВ
35
•прямая
результирующую R3. Таким образом, заданная система векторов за-
менилась эквивалентной системой трех векторов Rt, R2, R3, прило-
женных в трех произвольных точках О, Оь О2.
Мы разложили вектор Р1 на три вектора, направленных по
прямым OAt, Ox^!, O2AV Это разложение возможно всякий раз,
когда точка А1 не находится в плоскости трех точек О, Ои О2.
В таких случаях указанные прямые образуют триэдр. Если точка Аг
находится в плоскости ООгО2, но вектор Рг в ней не лежит, то-
точку приложения этого вектора можно переместить вдоль его ли-
нии действия так, чтобы она не лежала в указанной плоскости.
Если же сам вектор также лежит в плоскости, то его можно раз-
ложить на два вектора, направленных по ОА1 и О1А1.
Мы заменили заданные векторы тремя векторами Rv R2, R3,
приложенными в трех произвольных точках О, О1, О2. Эти три
вектора можно привести к двум. Пусть OL (рис. 18)
пересечения двух плоскостей, из ко-
торых одна проведена через точку О
и вектор R2, а другая — через точку О
и вектор R3. Выберем на этой пря-
мой произвольную точку О'. Вектор R2,
находящийся в первой плоскости, мо-
жет быть разложен на два вектора,
направленных вдоль прямых OOlt О'О^,
мы перенесем эти слагаемые — одно
в точку О, а другое в точку О'.
Точно так же вектор R3, расположен-
ный во второй плоскости, может быть
разложен на два, направленных вдоль
прямых ОО2 и О'О2\ перенесем пер-
вый из них в точку О, а второй
в точку О'. Мы получим три вектора,
приложенных в точке О, и два век-
тора, приложенных в точке О'. Первые три имеют результирую-
щую F, а два других результирующую Ф. Таким образом, система
трех векторов Rv R2, R3, а следовательно и система заданных век-
торов, заменилась эквивалентной системой двух векторов F а Ф,
из которых один приложен в произвольной точке О.
Если оба вектора, R2 и R3, и точка О расположены в одной
плоскости, то в качестве OL может быть взята любая прямая этой
плоскости, проходящая через точку О.
Существует бесчисленное множество способов приведения задан-
ной системы векторов к двум векторам. Заметим прежде всего,
что можно изменять векторы F и Ф без изменения точек О и О'
их приложения. Вообразим, в самом деле, что к двум концам от-
резка 00' приложены два равных и прямо противоположных век-
тора /и —/. Два вектора F и /, приложенные в точке О, можно

36	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
сложить и привести к одному вектору 5 и два вектора Фи —/,
приложенных в точке О', — к одному вектору ?. Система двух
векторов F и Ф заменилась, таким образом, эквивалентной системой
двух векторов 5 и 2. Вектор ? расположен в определенной плос-
кости — в плоскости, проходящей через точку О и вектор Ф. Точка
приложения О вектора 5 является произвольной. Закрепив эту точку,
можно перемещать произвольным образом точку О' по прямой О'Ъ
и, следовательно, также по всей плоскости ОО'Ф, так как модуль
вектора —/ произволен.
В общем случае два вектора F и Ф, эквивалентные всем задан-
ным векторам, не лежат в одной плоскости.
Главный вектор и главный момент первоначальной системы от-
носительно произвольной точки равны главному вектору и главному
моменту системы двух векторов отно-
сительно той же точки (рис. 19). На-
пример, если взять какую-нибудь
точку А на линии вектора F, то глав-
ный вектор AR в точке А получится
путем сложения вектора AF'', геоме-
трически равного вектору F, и век-
тора АФ', геометрически равного век-
тору Ф. Главный момент AG относи-
тельно точки А равен моменту век-
тора Ф, так как момент вектора F
равен нулю. Вектор AG будет перпен-
дикулярен плоскости АО'Ф и точка А
будет ее фокусом (п. 17).
Рис. 19.	Следовательно, фокус плоскости,
проходящей через один из векторов F
или Ф, расположен на другом векторе, и эти векторы лежат на двух
сопряженных прямых D и А.
Любая прямая, пересекающая одновременно линии действия век-
торов F и Ф, является, очевидно, прямой нулевого момента. На-
оборот, если какая-нибудь прямая нулевого момента пересекает
линию действия вектора F, то она пересекает также и линию дей-
ствия вектора Ф на конечном или бесконечном расстоянии, так как
поскольку момент вектора F относительно этой прямой равен нулю, то
и момент вектора Ф относительно нее должен также равняться нулю.
В разделе упражнений будет показано, что систему векторов
можно всегда привести к таким двум векторам, из которых Ъдин
лежит на произвольной прямой, не параллельной главному вектору.
21. Геометрическое истолкование инварианта LX-\- MY+ NZ, Обо-
значим через X', Y', Z', L', M', N', X", Y", Z", L", M", N" проекции и
моменты двух векторов F и Ф, эквивалентных заданной системе. Имеем:
Х=Х> + Х", L = L'+L", ...

ГЛАВА I. ТЕОРИЯ ВЕКТОРОВ	37
Принимая во внимание установленное ранее (п. 12) выражение для
взаимного момента двух векторов, получим:
LX + MY+NZ = (L' + L")(X' + X") + ... =6 объем. (F, Ф),
что позволяет дать замечательное геометрическое истолкование инварианта
LX + MY+NZ.
Пусть Pi, Р2	Рп — первоначальные векторы предложенной системы.
Имеем соотношения
A)
0.	B)
В силу соотношений A) и тождества B) находим также
LX + MY+ NZ = Е' {ЦХк + MiYk + NtZk + LkXt + MkYt + NkZf),
где сумма в правой части распространена на все парные сочетания индек-
сов I я к. Но выражение под знаком 2' есть взаимный момент векторов Pf
и Рк и, следовательно,
LX + MY + NZ = Б'6 объем. (Pit Pk\
п(п— 1) „
где во второй части число членов равно —i-=——. Полученные формулы
показывают, что, каким бы способом ни были приведены векторы Рк
к двум векторам F и Ф, объем тетраэдра (F, Ф) будет постоянным и
равным алгебраической сумме объемов тетраэдров, полученных путем
парных сочетаний векторов Рк (Шаль). Для того чтобы два вектора F и
Ф находились в одной плоскости, необходимо и достаточно, чтобы объем
тетраэдра Шаля равнялся нулю.
22.	Приведение двух эквивалентных систем друг к другу.
Рассмотрим сначала систему E), эквивалентную нулю. Тогда два век-
тора F и Ф, к которым мы можем привести систему, будут также
эквивалентны нулю, т. е. эти векторы, как было показано ранее (п. 18),
будут равны и прямо противоположны. Тогда можно эти векторы
отбросить и таким образом привести систему (S) к нулю.
Пусть теперь предложены две системы векторов (S) и E0), экви-
валентные между собой. Тогда эти системы могут быть приведены
одна к другой при помощи элементарных операций. В самом деле,
будем исходить из системы (S) и присоединим к ней систему
(.$о)(—*So)> образованную векторами (So) и векторами, им равными и
прямо противоположными. Это, очевидно, — одна из элементарных
операций, повторенная некоторое число раз. Совокупность систем
(S) и (— 50), будучи эквивалентна нулю, может быть приведена
к нулю при помощи элементарных операций. После этого оста-
нется система E0), что и доказывает предложение.
23.	Пары. Г. Определение. Парой, по Пуансо, называют сово-
купность двух векторов Р и —Р, равных по модулю, параллель-
ных и противоположно направленных. Расстояние АВ (рис. 20) на-
зывается плечом пары, а произведение АВ ¦ Р плеча на модуль

38	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
вектора Р называется ее моментом. Когда момент равен нулю, то й
пара эквивалентна нулю. Действительно, в этом случае равны нулю
либо оба вектора, либо плечо АВ, а тогда оба вектора прямо про-
тивоположны.
Так как пара является системой векторов, для которой главный
вектор равен нулю, то главный момент пары постоянен по вели-
чине и направлению для всех точек пространства. Этот главный
момент называется векторным моментом пары. Векторный момент
пары является, следовательно, вектором, имеющим определенный
модуль и направление, но его точка приложения может быть
выбрана в пространстве произвольно, другими словами, векторный
момент пары является вектором свободным. Чтобы уяснить, каким
является этот вектор, найдем главный момент
относительно точки О, расположенной на
плече АВ между точками А и В. Моменты
обоих векторов Р и — Р будут перпендику-
лярны к плоскости пары и одинаково напра-
влены, так как оба вектора Р и —Р имеют
Рис. 20.	одинаковое направление вращения вокруг
точки О. Следовательно, главный момент OG,
т. е. векторный момент пары, перпендикулярен к плоскости пары
и имеет модуль, равный Р • ОА-\-Р ¦ ОВ или Р ¦ АВ, т. е. равный
моменту пары.
Из предыдущего следует, что две пары с одинаковыми вектор-
ными моментами эквивалентны, так как они имеют одинаковые
главные моменты и одинаковые, равные нулю, главные векторы. Сле-
довательно, они могут быть приведены одна к другой при помощи
элементарных преобразований. Мы не входим зд/сь в подробности
этого приведения. Оно может быть произведено, согласно указа-
ниям п. 22.
Мы ограничимся формулировкой следующего заключения:
Всегда можно при помощи элементарных операций преобра-
зовать одну в другую две пары, имеющие одинаковые векторные
моменты, т. е. две пары, лежащае в параллельных плоскостях
и имеющие одинаковые моменты и одинаковые направления вра-
гцений.
2°. Сложение пар. Любое число пар всегда эквивалентно одной
паре, векторный момент которой равен сумме векторных моментов
слагаемых пар.
В самом деле, система, образованная р парами Pv —Рг;
Pt, —Р2", •••; Рр. —Рр, есть система векторов, для которой глав-
ный вектор равен нулю. Главный момент этой системы будет, сле-
довательно, одним и тем же для любой точки пространства (рис. 21).
Для нахождения этого главного момента OG относительно
точки О можно поступить следующим образом. Возьмем сначала
геометрическую сумму OGt моментов векторов Р1 и —Р\, которая

ГЛАВА I. ТЕОРИЯ ВЕКТОРОВ
-p,
равна векторному моменту первой пары, затем сумму OQ2 момен-
тов векторов Рг и —Р2, равную векторному моменту второй пары,
и так продолжаем до тех пор, пока не получим сумму OGp, равную
векторному моменту последней пары. После этого полученные
частичные суммы OGV OG2	OGp складываем вместе. Рассмо-
трим теперь пару с вектор-
ным моментом OG, равным
главному моменту. Эта одна
пара эквивалентна системе всех
заданных пар, так как эта пара
и эта система имеют одинако-
вые главные моменты, рав-
ные OG, и одинаковые глав-
ные векторы, равные нулю.
Можно при помощи эле-
ментарных операций приве-
сти заданную систему пар
к одной паре с векторным мо-	Рис. 21.
ментом OG. Если OG= О, то
эта одна окончательная пара эквивалентна нулю и тогда вся за-
данная система тоже эквивалентна нулю.
Мы не будем здесь входить в подробности относительно тех
элементарных операций, при помощи которых может быть осуще-
ствлено указанное сложение пар. Нам достаточно знать, что такое
сложение осуществимо.
24. Приведение к вектору и паре. Произвольная система век-
торов эквивалентна одному-единственному вектору, равному главному
вектору и приложенному в произвольной
точке, и одной-единственной паре с век-
торным моментом, равным главному мо-
менту относительно указанной точки.
s<p В самом деле, пусть OR — главный вектор
и OG—главный момент системы относи-
тельно произвольной точки О. Новая
система, образованная вектором R и парой
(Р,—Р) с векторным моментом OG, экви-
валентна заданной системе, так как она
имеет тот же главный вектор OR и
TOf же главный момент OG относительно точки О (рис. 22). За-
данная система может быть, следовательно, приведена к системе R,
Р, —Р при помощи элементарных операций.
Так как точка О взята произвольно, то существует бесчисленное
множество способов определения вектора и пары, эквивалентных
заданной системе. После того, как точка О уже выбрана, в качестве
пары (Р, —Р) может быть взята любая из бесчисленного множества
пар, имеющих векторный момент OG.
Рис. 22.

40	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
Если точка О взята на центральной оси DD' в точке О', то
главный вектор O'R и главный момент O'g будут лежать на этой
центральной оси. В этом случае плоскость пары (Р, —Р) будет
перпендикулярна к главному вектору R и ее момент будет мини-
мальным (рис. 23).
25. Винт. Английский ученый Болл называет предыдущую систему, об-
разованную вектором O'R (рис. 23) и парой, плоскость которой перпенди-
кулярна к этому вектору, винтом.
Точкой приложения, линией действия, направлением и модулем винта
называют точку приложения, линию действия, направление и модуль век-
тора O'R. Параметр / винта есть отношение в'еличины момента g пары
к модулю вектора R; это отношение считается положительным или отрица-
тельным в зависимости от того, будут ли век-
ХД	торы O'R и O'g иметь одинаковое или противо-
|	положное направление. Принимая эти термины,
]	мы видим, что произвольная система векторов.
ff	эквивалентна винту, линия действия которого со-
впадает с центральной осью, а модуль и напра-
,	вление совпадают с модулем" и направлением
О	j^p главного вектора. Параметр этого винта равен
величине
, g = GcosRG = LX + MY+NZ
Т ~ R	R ~ X2 + Г2 -f- Z2 -
I
у	Следовательно, / есть найденное общее значение
равных отношений, входящих в уравнения цен-
Рис. 23.	тральной оси.
Произвольное число заданных винтов всегда
складывается в один винт. Действительно, ка-
ждый заданный винт представляет собой систему трех векторов; следова-
тельно, совокупность заданных винтов представляет собою некоторую си-
стему векторов, эквивалентную согласно установленным выше правилам,
одному винту, способ определения которого известен.
Единичным винтом (vis) называется винт, у которого вектор O'R равен,
единице:
В этом случае величина / приводится к LX-\-MY-\-NZ; ее называют пара-
метром или шагом единичного винта.
Болл показал полезность понятия винта для кинематики и механики
твердого тела. Перечисление многих работ, опубликованных им по этому
вопросу, можно найти в Bulletin Bibllographlque Жино Лориа, а изло-
жение этих работ — во французском издании I Encyclopedle des Sciences
mathematlques в статье Люсьена Леви, Sur les fondements geometrlques
de la Statlque.
26. Частные случаи приведения. Может случиться, в частности,
что система векторов, не эквивалентная нулю, эквивалентна лишь
одной паре или только одному вектору.
Система эквивалентна только паре, если ее главный вектор
равен нулю.
Для того чтобы система была эквивалентна одному вектору,
необходимо и достаточно, чтобы главный вектор был отличен от

ГЛАВА Г. ТЕОРИЯ ВЕКТОРОВ	41
нуля, а минимальный момент g равнялся нулю, т. е. чтобы глав-
ный момент относительно произвольной точки пространства был
перпендикулярен направлению главного вектора. В самом деле,
для системы, состоящей из одного вектора, центральная ось совпа-
дает с этим вектором и минимальный момент равен нулю. Наоборот,
если минимальный момент обращается в нуль, то система эквивалентна
одному вектору, лежащему на центральной оси, так как пара с ми-
нимальным моментом, которую в общем случае необходимо добавить
к этому вектору, в рассматриваемом случае обращается в нуль.
Здесь /=0.
27.	Резюме. Резюмируя изложенное, получаем следующую таб-
лицу:
Система эквивалентна двум векторам, не лежа-
щим в одной плоскости. Она эквивалентна
LX~{-MY ~{-NZ^O также одному вектору, лежащему на централь-
ной оси, и одной паре, плоскость которой
перпендикулярна этой оси, т. е. винту.
j у \ %ду _|_ м7	о I Система эквивалентна двум векторам, лежащим
~*~ '	\ в одной плоскости, причем:
1 ° V2 I v2 I 72 ^ л (Система эквивалентна одному вектору,
\ лежащему на центральной оси.
2°. X=Y = Z = Q, f
/2 _i_ M2 _|_ /иг v. n {Система эквивалентна паре.
3°. Х= Y = Z=0, [
	 	 	 | Система эквивалентна нулю.
28.	Взаимный момент системы скользящих векторов. Используя
обозначения п. 18, назовем взаимным моментом двух систем векторов (S)
и (So) величину
0Z,	A)
значение которой не зависит от выбора осей координат. В самом деле, мы
можем эту величину представить в виде
-(LX+MY + NZ)- (L0X0 + M0Y0 + N0Z0),
где три члена будут инвариантами либо полной системы E)+Eо). либо одной
из систем E) или E0). Согласно истолкованию этих инвариантов, данному
в п. 21, взаимный момент систем E) и E0) равен ушестеренной сумме
объемов тетраэдров, полученных сочетанием всех векторов системы E) со
всеми векторами системы (So)-
Пусть в — кратчайшее расстояние между центральными осями обеих
систем и а — угол между ними, R и Ro — их главные векторы, лежащие
на этих центральных осях, a g и ^0 — соответствующие минимальные мо-
менты. Тогда взаимный момент обеих систем равен
± RRob sin a+ (gR0 + g0R) cos а,	B)

42	часть первая, предварительные понятия
где первый член есть взаимный момент векторов R и Ro. Эту формулу
легко вывести, если за ось Ог принять одну из центральных осей (п. 17)
и посмотреть, во что при этом обратится выражение.(I).
29. Приложение общих теорем к случаю параллельных сколь-
зящих векторов. Если все векторы некоторой системы параллельны,
то эта система эквивалентна либо одному вектору, либо одной паре;
либо нулю. В самом деле, так как моменты всех векторов относи-
тельно какой-нибудь точки направлены перпендикулярно общему
направлению этих векторов, то и главный момент, если он отличен
от нуля, будет также перпендикулярен этому направлению. Главный
вектор, если он отличен от нуля, параллелен этому направлению.
Следовательно, инвариант LX-\- MY -\-N Z обращается в нуль.
Пусть а, р, if—направляющие косинусы какой-нибудь полу-
прямой, параллельной общему направлению векторов. Обозначим
через Рх> Р2	Рп величины этих векторов, причем эти величины
будем считать положительными, если направления соответствующих
векторов совпадают с направлением выбранной полупрямой, и отри-
цательными— в противном случае. Тогда, если хк, ук, zk— коорди-
наты какой-нибудь точки приложения вектора Рк; Хк, Yk, Zk— проек-
ции этого вектора на оси координат, которые мы считаем
прямоугольными, и Lk, Mk, Nk— его моменты относительно этих
осей, то
Отсюда, полагая
где сумма распространена на все векторы системы, получим сле-
дующие выражения для проекций главного вектора и главного
момента:
Непосредственно убеждаемся в справедливости соотношения
Следовательно:
если PSgO, то система эквивалентна одному вектору;
если"Р;=0, L2-\-Mz-\-N2 > 0, то система эквивалентна одной
раре;
если Р = 0, /,=гЛ1 = ./У=0, то система эквивалентна нулю.

ГЛАВА I. ТЕОРИЯ ВЕКТОРОВ	43
Отсюда получаем необходимые и достаточные условия экви-
валентности системы нулю:
Примечание. В частном случае, когда
предыдущие условия будут выполняться, каковы бы ни были а,
§, 7- Система будет эквивалентна нулю, какое бы направление
ни задавать параллельным векторам, если только при этом не изме-
нять отношения их величин и точек приложения. Говорят, что
в этом случае система параллельных векторов находится в астати-
ческом равновесии.
Центральная ось. Результирующий вектор. Пусть Psg-0.
Тогда система эквивалентна одному вектору, алгебраическое значе-
ние которого равно Р и проекции которого суть аР, [ЗР, "[Р. Этот
вектор лежит на центральной оси. Для краткости мы будем назы-
вать его результирующим вектором системы.
Уравнения центральной оси в рассматриваемом случае прини-
мают вид
yZ — zY — L = 0, zX—xZ — M = Q, xY — yX—N=Q,
так как общее значение отношений, которые образуют уравнение
этой оси, обращается в данном случае в нуль. После подстановки
найденных ранее значений X, Y, Z, L; М, N получим:
откуда
Рх—^Ркхк Ру — ^РкУк Рг — ^Ркгк
Полагая здесь
получим
х — %	 у —
(D)
а	$	1 '
т. е. уравнение прямой D, проходящей через точку С с координа-
тами %, т), С и параллельной заданным векторам.
Когда все векторы скользят вдоль их линий действия, прямая D
не изменяется, так как не изменяются величины X, Y, Z, L, М, N.
Координаты точек приложения хк, ук, zk изменяются; поэтому
точка С(?, т), С) перемещается, но она описывает центральную ось D
заданных параллельных скользящих векторов, вдоль которой скользит
результирующий вектор.

44	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
V. Связанные векторы; шесть координат связанного вектора;
центр параллельных связанных векторов.
Векторные производные
30. Шесть координат связанного вектора. Вириал. Мы назвали
связанным всякий вектор, приложенный в определенной точКе
пространства.
Например, главный момент АО какой-нибудь системы скользящих
векторов относительно некоторой точки А есть вектор, связанный
с этой точкой А.
Для аналитического определения вектора АХВХ, связанного с точ-
кой Av необходимо задать три координаты л^, yv zx точки Ах и три
проекции Хх, Yv Zx вектора, всего шесть независимых величин,
составляющих координаты связанного вектора.
Ниже, при изложении понятия работы, а затем в третьем томе,
мы будем заниматься исследованием векторного поля,, т. е. системы
связанных векторов, приложенных в различных точках некоторой
непрерывной области пространства.
Вириал. В п. 12 мы видели, что скользящий вектор имеет пять
координат. Чтобы определить связанный вектор, достаточно добавить
к пяти координатам этого вектора, рассматриваемого как скользящий,
шестую величину, не зависящую от них. Эта величина может быть
взята, например, равной вириалу Клаузиуса относительно некоторой
заданной точки Р.
—>
Пусть AV = V—вектор, связанный с точкой А. Возьмем какую-
нибудь точку Р, которую мы будем рассматривать как конец век-
тора АР = г. Тогда вириал v вектора V относительно точки Р
есть скалярное произведение
v = Vr cos Vr
векторов V и г. Если принять точку А за начало прямоугольной
системы координат и обозначить через X, Y, Z проекции вектора V,
а через х, у, г координаты точки Р, то
Имеет место следующая теорема:
Если два геометрически равных вектора имеют одинаковые
моменты М и одинаковые вириалы v относительно одной только
точки Р, то они приложены в одной и той же точке, т. е. они
идентичны.
Допустим, что эти векторы суть AV и A'V и они приложены
в разных точках А и А'. Так как моменты равны, то эти векторы
лежат на одной прямой АА'. Кроме того, из равенства вириалов
вытекает
АР cos PAV = Ш> cos PATV',

ГЛАВА I. ТЕОРИЯ ВЕКТОРОВ	45
и, следовательно, проекции РА и PA' t(& AA' равны по величине
и знаку, т. е. точка А совпадает с точкой А'.
Следовательно, связанный вектор может быть определен своим
вириалом относительно некоторой точки Р и пятью своими коорди-
натами, если рассматривать его в качестве скользящего вектора.
31. Центр системы параллельных связанных векторов. Мы
видели (п. 29), что система параллельных скользящих векторов
с отличной от нуля геометрической суммой эквивалентна одному
результирующему скользящему вектору, лежащему на центральной
оси D системы.
Обозначим, как и раньше, через а, р, -f направляющие косинусы
прямой, параллельной векторам, через Рх, Рг, ..., Рп—-их алге-
браические величины, считаемые положительными в направлении а,
р, f, и через xv ух, гг, х2, у2, гг, .... хп, уп, гп—координаты
точек приложения этих векторов. Проекции Хк, Yk, Zk вектора Ph
суть аРк, fyPk, fPk. Мы показали (п. 29), что результирующий
вектор такой системы параллельных скользящих векторов им парал-
лелен, имеет алгебраическое значение, равное
и проекции X, Y, Z, равные величинам аР, [ЗР, fP, и, наконец,
что он лежит на центральной оси D, определяемой уравнениями
где
2^L	2Р^ г- ^PkZk	<Г\
2^ '	( }
Предположим теперь, что векторы Рк связаны со своими соот-
ветствующими точками приложения хк, ук-, zk, рассматриваемыми
как вполне определенные, и не могут скользить вдоль своих линий
действия. Тогда точка С, координаты которой выражены уравне-
ниями (С), будет вполне определенной. Эта точка называется цент-
ром заданной системы параллельных векторов, связанных со
своими точками приложения. Переместим теперь результирующий
вектор Р вдоль оси D, пока его точка приложения не совпадет с С,
и будем считать его вектором, связанным с точкой С. Полученный
таким образом результирующий вектор, связанный с точкой С,
называется результирующим вектором системы параллельных
связанных векторов.
Таким образом, если параллельные связанные векторы имеют
отличную от нуля геометрическую сумму, то результирующий
вектор будет равен этой сумме и связан с центром заданной
системы параллельных связанных векторов.

46	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
Формулы (С), определяющие координаты I, т\, С центра С парал-
лельных связанных векторов, показывают, что центр системы
параллельных связанных векторов не зависит от а, р, f, т. е.
от общего направления этих векторов; он зависит исключи-
тельно от их точек приложения (хк, ук, гк) и от отношений
их величин Рх> Р2	Рп- Зависимость точки С только от отно-
шений величин векторов вытекает из того обстоятельства, что
выражения для \, т], С однородны относительно Pv Рг	Рп,
причем порядок однородности равен нулю. Полученный результат
можно сформулировать следующим образом: Если'изменить общее
направление параллельных векторов, связанных с их точками
приложения, и одновременно пропорционально изменить их вели-
чины, то и результирующий вектор, который им параллелен,
изменится в том же, отношении, но останется приложенным
в центре этих параллельных векторов.
Замечание к случаю, когда ^Рк = 0. Если сумма векторов
JD = 2^>fc равна нулю, но три суммы ^Pkxk, 2ЛЛ> 2Л^
не обращаются в нуль одновременно, то центр С параллельных
связанных векторов уйдет в бесконечность, так как тогда по край-
ней мере одна из координат ?, т\, С становится бесконечной. В этом
случае точка С не существует.
Если одновременно
то координаты \, t\, Z, будут неопределенными и, следовательно,
центр параллельных связанных векторов будет неопределенным.
П р и м е р. Легко найти, в качестве примера, элементарные свойства
двух параллельных векторов, связанных с двумя точкаЖи ^ и i, и имею-
щих алгебраические значения Pt и Р2. Когда Р1 -\- Р2 отлично от нуля,
система имеет результирую-
/р щий вектор, т. е. эквивалент-
на одному вектору, имеющему
—	алгебраическое значение Р =
— Pi + Pi и приложенному
в точке А (центре двух парал-
лельных векторов) (рис. 24),
определяемой соотношением
АА1 Р,
Рис-24-	Ж=~р~.'
где отношение двух отрезков АА\ и АА^, как обычно принято в геометрии,
считается положительным, если отрезки имеют одинаковые направления,
и отрицательным, — в противном случае.
В частном случае, когда Рг-\- Р2 = 0, эти векторы численно равны
и противоположно направлены. Центр этих параллельных векторов не суще-
ствует. Эти векторы в общем случае образуют пару, если только они не
прямо противоположны. Если Pi -\- Р2 = 0 и оба вектора приложены в одной
точке, то центр параллельных векторов будет неопределенным.

ГЛАВА I. ТЕОРИЯ ВЕКТОРОВ
47
г'
32. Моменты параллельных связанных векторов относительно
плоскости. Формулы для координат \, т), С центра параллельных
связанных векторов, если их перевести на язык геометрии, приводят
к теореме моментов относительно плоскости.
Пусть даны произвольно направленная ось Ог и плоскость П,
которую всегда можно принять за плоскость хОу (рис. 25). Мо-
ментом какой-нибудь из парал-
лельных геометрических величин
относительно этой плоскости II
называется произведение Pkzk алге-
браического значения Рк указанной
величины на координату zk ее
точки приложения. Это понятие
введено Монжем («Курс элементар-
ной статики», Париж, 1786).
Определенный таким образом
момент есть величина положительная,
отрицательная или равная нулю,
значение которой зависит от точки
приложения геометрической вели-
чины, так что этот момент изменяется,
если указанную величину переносить вдоль ее линии действия. Основ-
ное свойство, вытекающее из этого определения, будет следующим:
Если для системы параллельных связанных векторов суще-
ствует результирующий вектор, то момент результирующего
вектора относительно плоскости равен алгебраической сумме
моментов составляющих векторов при условии, что этот ре-
зультирующий вектор приложен в центре параллельных векторов.
Для доказательства предположим сначала, что ось Ог перпенди-
кулярна к плоскости П. Тогда координата г центра параллельных
векторов определяется формулой
Рис. 25.
где P = 2^V Но эта формула как раз и выражает доказываемую
теорему.
Если ось Ог наклонена к плоскости П, то можно взять вспомо-
гательную ось Ог', нормальную к плоскости и образующую с осью Ог
угол а. Обозначим через z[, z'r .... z'n, С' координаты г точек при-
ложения, отсчитываемые параллельно этой новой оси, т. е. нор-
мально к плоскости. По предыдущему имеем:
Но координаты г' и г связаны очевидными соотношениями
^ = ^ cos a, z'2 = zzcosa	?' = Ccosa,

48	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
что после подстановки и приводит к искомому соотношению
Таким образом, теорема моментов доказана в общем виде.
Прилагая эту теорему к трем плоскостям косоугольной системы
координат, мы получим для определения координат ?, т\, С центра
параллельных векторов в косоугольной системе те же формулы,
что и в системе прямоугольной.
Примечание I. Теорема моментов относительно плоскости tnpa-
ведлива лишь в том случае, когда ^Ptz0.
Если 2^ = 0, то теорема не справедлива, так как результирующий
вектор обращается в нуль, и центр параллельных векторов уходит в беско-
нечность. Исключение будет в еще более частном случае, когда векторы
находятся в астатическом равновесии:
В этом случае координаты 6, -ц, ? неопределенны и теорема применима.
Примечание II. В частном случае, когда все векторы направлены
в одну сторону, центр параллельных векторов лежит внутри любой выпуклой
доверхности, окружающей точки приложения составляющих. В самом деле,
примем направление заданных векто-
ров Я], Р2,..., Рп за положительное,
касательную плоскость П к поверх-
ности — за плоскость лгу и в качестве
оси Ог — перпендикуляр к этой по-
верхности, направленный в ту же сто-
рону, что и поверхность (рис. 26).
Тогда координаты г всех точек
приложения векторов будут положи-
тельными, и равенство
(- __
2****
Рис. 26.
показывает, что и координата С также
положительная. Таким образом, центр
параллельных векторов расположен по отношению к произвольной каса-
тельной плоскости по ту же сторону, что и поверхность и, следовательно,
находится внутри ее.
33. Векторные производные. Пусть ОМ (рис. 27) — связанный
вектор, приложенный в фиксированной точке О. Допустим, что этот
вектор зависит от некоторой переменной и таким образом, что
если и изменяется непрерывно, то и конец М перемещается также
непрерывным образом. Можно тогда говорить, что этот вектор есть
непрерывная функция переменной и. Пусть ОМ и ОМ1— векторы,
соответствующие значениям и и a-f-Ди переменной, причем Ди
предполагается положительной. Соответствующее геометрическое
приращение вектора есть геометрическая разность (ОМ{) — (ОМ),

ГЛАВА I. ТЕОРИЯ ВЕКТОРОВ	49
т. е. вектор, равный ММ±. Отношение этого приращения к прира-
щению переменной есть вектор
Ди
имеющий ту же линию действия и то же направление, что и век-
тор MMV
Когда Дм стремится к нулю, вектор ММХ стремится к некото-
рому предельному вектору MD, касательному к кривой, описываемой
точкой М. Этот предельный вектор на-
зывается векторной производной век-	fl
тора ОМ по и.
Аналитическое определение вектор-
ной производной. Возьмем оси Oxyz
с началом в точке О. Координаты х, у, "
z точки М суть проекции вектора ОМ
на эти оси, причем проектирование на	-	|
какую-нибудь ось производится парал-
лельно плоскости двух других осей. Be-	Рис- 27.
личины х, у, z являются функциями от и.
Когда а получает приращение Дм, то точка М переходит в Мх
и х, у, г получают приращения Дх, Д.у, Дг. Так как вектор ММ
имеет проекции Дл:, Д_у, Дг, то вектор MB, равный отношению
к Дм, имеет проекции
Дх Ду Дг
¦ДгГ' 1п' "Дм*
Полагая, что Дм стремится к нулю, мы видим, что проекции произ-
водного вектора MD суть производные
dx dy dz
~Ш' ~du~' ~du~
проекций первоначального вектора.
VI. Полярные векторы. Аксиальные векторы.
Скалярные величины
34. Характер симметрии вектора. Величины, изображаемые
векторами, могут представлять собою два вида симметрии. С этой
точки зрения они подразделяются на векторы полярные и векторы,
аксиальные.
Полярные векторы. Вектор А\ВХ называется полярным, если
представляемая им физическая величина симметрична относительно
всех плоскостей, проходящих через А1В1, но не симметрична отно-
сительно плоскости, перпендикулярной к А^. Так, например, ско-
рость и ускорение представляются полярными векторами. Можно
сказать, что симметрия полярного вектора А1В1 будет такого же

50	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
вида, как и симметрия параболоида вращения вокруг оси AiBl.
Выбор направления осей и положительного направления вращения
не содержится в определении полярного вектора.
Аксиальные векторы. Вектор А1В1 является аксиальным, если
представляемая им физическая величина симметрична не только
относительно плоскостей, проходящих через AXBV но и относительно
плоскостей, перпендикулярных к А1В1, так что характер симметрии
представляемой физической величины будет таким же, как у цилиндра
вращения вокруг AtBv
Определение аксиального вектора зависит обычно от соглашения
относительно положительного направления вращения или направлений,
приписываемых некоторым циркуляциям. Например, векторный мо-
мент ВОХ некоторого полярного скользящего вектора А1В1 относи-
тельно какой-нибудь точки В есть аксиальный вектор. Действительно,
физическая величина, которую должен представлять вектор BG1,
характеризуется: 1) плоскостью, проходящей через точку В и через
ось вектора АХВ{; 2) площадью треугольника BAXBV Но оба эти
элемента симметричны относительно плоскости ВАХВХ. Направление,
приписываемое вектору BGX относительно этой плоскости, зависит
от соглашения о выборе положительного направления вращения.
Этот вектор является, следовательно, аксиальным. Представление
момента при помощи вектора обладает, таким образом, некоторым
несовершенством, так как оно вводит, вследствие произвольности
выбора положительного направления вращения, диссимметрию, кото-
рой не имеет представляемый объект. Можно избежать этой диссим-
метрии, условившись, например, изображать момент полярного век-
тора А1В1 относительно точки В при помощи некоторого круга,
описанного в плоскости ВА1В1 с центром в точке В, причем радиус
этого круга равен величине момента и на контуре круга при помощи
стрелки указано направление, в котором точка, перемещаясь вдоль
AXBV вращается вокруг центра В.
Это представление поясняет симметрию момента, но оно менее
удобно, чем обычное представление момента, с других точек зрения.
Векторный момент пары полярных векторов есть также вектор
аксиальный.
Легко показать, что векторный момент В'О' некоторого вектор-
ного момента ВО1 относительно точки В' есть вектор полярный.
Для этого достаточно установить, что вектор В'О' не зависит от
какого бы то ни было выбора положительного направления вращения.
Эти положения имеют важное значение для физики. По поводу
связанных с ними вопросов можно указать на мемуар Клейна, пере-
веденный на французский язык Г. Падэ (Annales de l'Ecole Normale
superieure, serie 3, т. VIII, 1891, стр. 87—193).
Скалярные величины первого и второго рода. Скаляром на-
зывают, обобщая уже встречавшееся заимствованное из теории
кватернионов выражение, всякую величину, определяемую одним-

ГЛАВА I. ТЕОРИЯ ВЕКТОРОВ	51
единственным Числом, как, например, плотность, температуру. Но при
этом могут представиться два случая:
а)	Рассматриваемое число не зависит от направления осей коор-
динат. Мы будем говорить, что оно является скаляром первого
рода.
б)	Число, определяющее рассматриваемую величину, меняет знак
при перемене направления осей. Такое число называется скаляром
второго рода.
VII. Другие геометрические образы, которые могут быть
использованы в механике
35. Краткий обзор. Способ представления векторных величин, кото-
рого м.ы до сих пор исключительно придерживались, очевидно, не является
единственно возможным. Можно ставить в соответствие другим механическим
вели>мнам и другие геометрические элементы. Так, например, любой системе
сил, приложенной к твердому телу, можно поставить в соответствие винты
Болла.
Скользящий вектор, рассматриваемый как совокупность двух точек,
взятых в определенном порядке, можно понимать как первое звено в ряде
величин, образованных путем присоединения в определенном порядке не
только точек, но и других простейших элементов пространства.
Э. Штуди *) занимался систематическим исследованием таких геомет-
рических величин. Он ввел следующие величины.
1°. Крест, образованный совокупностью двух прямых, из которых одна
находится на конечном расстоянии, а другая представляет собой пересечение
плоскостей, перпендикулярных к первой, и вследствие этого находится в бес-
конечности.
2°. Биплан, представляющий собой систему двух не перпендикулярных
между собой плоскостей, взятых в определенном порядке.
3°. Турникет — (moulinet), образованный точкой и плоскостью.
4°. Некоторые системы прямых, называемые моторами и импульсорами.
5°. Скользящие сферические векторы и т. д.
Мы ограничиваемся только перечислением, потому что нигде не вос-
пользуемся этими понятиями, так как до сих пор они не нашли каких-либо
важных приложений в механике. Мы отсылаем для их геометрического ис-
следования либо к сочинению Штуди, либо к статье Люсьена Леви (Lucien
Levy) во французском издании «l'Encyclopedie des Sciences mathematiques».
УПРАЖНЕНИЯ
1.	Показать, что модуль R результирующего вектора нескольких схо-
дящихся векторов Pi, Р2,	, Рп определяется формулой
R2 = 2^1 + 2'2 PiPk cos
где первая сумма распространена на все векторы, а вторая — на все их
парные комбинации.
2.	Для того чтобы система векторов была эквивалентна нулю, необхо-
димо и достаточно, чтобы обращались в нуль их главные моменты относи-
тельно трех произвольных точек, не лежащих на одной прямой.
'•;¦ Е. Study, Qeometrie der Dynamen, Leipzig, 1903 (первый выпуск
вышел в 1901).

52	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
3.	Взаимность в теории векторов. Возьмем мнимую сферу +y+}
+ 1 = 0 с центром в точке О и вектор /\ с проекциями Хи Yv Zx и момен-
тами Lx, Mh Nt. На прямой, сопряженной с Р, относительно сферы, построим
вектор Р[ с проекциями X[ = LV y[ = Ml,Z[ — Nv Это возможно, так как
направление L\, Мь Nt перпендикулярно плоскости OPV Показать, что
имеется взаимность между векторами Pt и Pv т. е. что Pt лежит на прямой,
сопряженной с Р[, и что его проекции равны моментам вектора Р[, а именно:
Xt = L'v Yt = М[, Zl — N[ (преобразование Клейна, в частном случае указан-
ное Кёнигсом).
4.	По предыдущему преобразованию системе векторов E) отвечает
некоторая система E')- Показать, что главный момент одной системы отно-
сительно точки О равен главному вектору второй системы.
5.	Если одна из предыдущих систем E) или E') приводится к паре,
то другая приводится к вектору, проходящему через точку О, и наоборот.
6.	Найти пространственные кривые, касательные к которым
являются прямыми, относительно которых момент равен нулю. Если
принять за ось г центральную ось системы, то дифференциальное уравнение
этих кривых имеет вид
fdz = xdy — у dx,
где /— параметр винта. Показать, что наиболее общая кривая, удовлетво-
ряющая этому уравнению, определяется уравнениями
z = <p (8), х = У7у (в) cos в, у = Y/VW) sin в,
где ер — произвольная функция от 6.
7.	Показать, что соприкасающаяся плоскость какой-нибудь кривой пре-
дыдущей задачи имеет фокус в точке соприкосновения.
8.	Можно бесчисленным множеством способов образовать систему из
двух векторов F и Ф, эквивалентных заданной системе векторов и таких,
что F и Ф взаимно перпендикулярны. Показать, что прямые F и Ф обра-
зуют комплекс второго порядка. К этому же комплексу придем, отыскивая
комплекс, образованный главными моментами относительно всех точек про-
странства.
9.	Если два вектора F и Ф эквивалентны заданной системе, то их общий
перпендикуляр пересекает центральную ось этой системы нормально к ней.
10.	Даны несколько пар и их результирующая пара. Показать, что пло-
щадь проекции параллелограмма, построенного на векторах результирующей
пары, на какую-нибудь плоскость равна алгебраической сумме площадей
проекций параллелограммов, построенных на векторах составляющих пар.
11.	Пусть Р', Р", ..., Р' ' — векторы, образующие систему, эквивалент-
ную нулю, и, соответственно, М', М", ...,М^—моменты какой-нибудь дру-
гой системы (S) векторов относительно осей Р', Р"	P'fc'. Доказать
соотношение
р'М'-\-Р"М"+ ... + pWAf(fc) = 0.
Следует доказать сначала теорему для одного вектора Р системы (S), вос-
пользовавшись равенством нулю главного момента векторов Р'', Р"	Р^
относительно Р.
12.	Барицентрические координаты Мёбиуса. Пусть AlAzA3Ai — неко-
торый тетраэдр. Барицентрическими координатами точки М называют алге-
браические значения Рь Р2, Рз, Р± четырех параллельных векторов, которые
необходимо приложить к вершинам А±, Ач,, А$, Ai для того, чтобы центр
этих параллельных векторов совпадал с точкой М. Показать, что:

ГЛАВА I. ТЕОРИЯ ВЕКТОРОВ
Каждой точке М отвечают значения Р,, Р2, Рв, Р±, определенные с точ-
ностью до общего множителя. Линейное однородное уравнение относительно
Pi. Ръ< Ръ< Pi определяет плоскость, расстояния которой от четырех вершин
пропорциональны коэффициентам при Рь Р%, Р3, Р±. Если эти коэффициенты
равны, то плоскость уходит в бесконечность. Поверхность порядка т пред-
ставляется однородным уравнением от-го порядка относительно Рь Р2, Р$, Р&
13. Найти результирующий винт двух взаимно перпендикулярных
сходящихся винтов.
Решение. Примем прямые, на которых лежат винты, за оси х и у к
прямую, к ним перпендикулярную, за ось г. Пусть X—вектор, а X — пара-
метр винта, лежащего на оси Ох (рис. 28). Тогда L = \Х. Обозначая через М,
Y, ц. аналогичные величины для второго винта, имеем M = \xY.
О'
м
Рис. 28.
Пусть R—сумма векторов X и Y, a G— сумма моментов L и М. Тогда
уравнение центральной оси всей системы будет
IX+zY _ pY—zX_ — xY+yX
X ~ Y ~	О
Эта ось параллельна OR и пересекает Ог в точке О', для которой
Пусть O'R' ¦—эта ось. Обозначим через R/ и G' главный вектор а
главный момент системы относительно О'. Имеем R' = R. Нужно найти G'
G'
или лучше отношение К. = —пг, т.е. параметр результирующего винта. Ноот-
R
ношение G' к R' равно отношению их проекций V и X на ось х. Таким,
путем находим:
Результирующий винт вполне определен.
14. Найти геометрическое место результирующих винтов O'R'G' преды-
дущего упражнения, когда параметры X и [л слагаемых винтов остаются
постоянными, а их векторы X и Y изменяются по модулю.
Искомая поверхность есть коноид
Кэйли назвал этот коноид цилиндроидом. Болл показал, что этот коноид,
имеет с цилиндром то общее свойство, что геометрическое место проекций
произвольной точки на образующие есть плоская кривая. Можно

54	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
дополнительно доказать, что указанная кривая является коническим сече-
нием также и для цилиндроида.
15.	Доказать в общем виде, что результирующий винт двух произволь-
ных винтов с фиксированными положениями описывает цилиндроид, когда
параметры этих винтов остаются постоянными, а их векторы изменяются.
Принять за ось Oz общий перпендикуляр к обоим винтам.
16.	Из всех нецилиндрических линейчатых поверхностей цилиндроид
является единственной поверхностью, для которой геометрическое место проек-
ций произвольной точки на образующие есть плоская кривая. (См. А р р е 11,
Bulletin de la Societe mathematique, декабрь 1900; Bricard, там же, январь
1901; Demoulin, там же).
17.	Произвольная система скользящих векторов всегда эквивалентна
шести векторам, направленным по шести ребрам тетраэдра.
18.	Пусть SABC—тетраэдр. Примем в качестве положительных напра-
влений на ребрах, выходящих из S, направления SA, SB, SC. Далее, на каж-
дом ребре основания, таком, как АВ, примем в качестве положительного
направления вращения вокруг противоположного ребра SC направление АВ.
Обозначим через ?, т), С, X, (а, ч алгебраические значения шести векторов,
направленных по SA, SB, SC, ВС, СА, АВ. Показать, что инвариант
LX -f- MY -\- NZ имеет значение
SA^ СА SB "Г" АВ
ВС SA ~ СА SB^AB SCJ'
где V—объем данного тетраэдра.
19.	Для того чтобы система скользящих векторов была эквивалентна
нулю, необходимо и достаточно, чтобы шесть составляющих ?, rj, С, X, ц, v
равнялись нулю.
20.	Для того чтобы система скользящих векторов была эквивалентна
:нулю, необходимо и достаточно, чтобы сумма моментов относительно каж-
дого из шести ребер тетраэдра равнялась нулю.
21.	Система скользящих векторов, лежащих в одной плоскости, эквива-
лентна либо одному вектору, либо одной паре, либо нулю.
22.	Система скользящих векторов, лежащих в одной плоскости, эквива-
лентна трем векторам, направленным по сторонам произвольно взятого в этой
плоскости треугольника.
23.	Для того чтобы векторнал производная какого-нибудь вектора была
всегда ему перпендикулярна,' необходимо и достаточно, чтобы этот вектор
имел постоянную длину.
24.	Для того чтобы векторная производная какого-нибудь вектора была
всегда направлена вдоль него, необходимо и достаточно, чтобы этот вектор
имел постоянное направление.
25.	Смешанное произведение трех сходящихся векторов Л/\, АР%, APS
с проекциями Хх, Yx, Z\, Хг, Y%, Z2; Х$, Y3, Z3 есть скаляр
равный по величине и по знаку объему параллелепипеда, построенного на
этих векторах.
Показать, что:
1°. Смешанное произведение меняет знак при перестановке двух мно-
жителей.
2°. Смешанное произведение трех полярных вектооов есть скаляр вто-
рого рода (п. 34).

ГЛАВА I. ТЕОРИЯ ВЕКТОРОВ	55
3°. Смешанное произведение трех аксиальных векторов есть скаляр пер-
вого рода.
4°. Смешанное произведение трех векторов есть скалярное произведение
одного из векторов на векторное произведение двух других.
26.	Центральная плоскость. Дана система связанных векторов V\,
V%	 Vn, приложенных в точках Аь А2	 Ап. Показать,' что если
точку Р перемещать параллельно главному вектору R, то существует поло-
жение Ро эт°й точки, для которого результирующий вириал относительно РОу
равный сумме вириалов всех векторов, обращается в нуль.
Геометрическое место точек Ро есть плоскость, перпендикулярная к R.
Это и есть центральная плоскость.
27.	Центр. Точка центральной плоскости, относительно которой главный
момент параллелен вектору R, есть центр.

ГЛАВА II
КИНЕМАТИКА
Кинематика оформилась как самостоятельная наука сравнительно
недавно. Уже Даламбер указал на важность изучения законов дви-
жения как такового. Но первый, кто показал необходимость пред-
послать динамике теорию геометрических свойств движения тел,
был Ампер. Эти свойства были представлены в 1838 г. Факультету
наук в Париже Понселе. В этом представлении содержались, в част-
ности, и теоремы о непрерывном перемещении твердого тела в про-
странстве, за исключением понятия мгновенной винтовой оси, кото-
рое было введено Шалем. Формулы, дающие вариации координат
точек движущегося в пространстве тела, принадлежат Эйлеру (Бер-
линская Академия, 1750). Кинематика допускает многочисленные
геометрические приложения. К ним относится, например, метод
Роберваля построения касательных, теория мгновенных центров вра-
щения, введенная Шалем, частный случай которой был дан уже
Декартом в связи с задачей о касательной к циклоиде. К ним же
относятся установленные Шалем свойства систем прямых, плоскостей
и точек, связанные с движением твердого тела и приводящие наиболее
простым образом к понятию комплекса прямых первого порядка.
В 1862 г. Резаль выпустил курс «Чистой кинематики». С появле-
нием этого курса кинематика окончательно утвердилась в качестве
самостоятельной науки.
Мы ограничиваемся здесь изложением только тех понятий, кото-
рые необходимы для дальнейшего курса механики. Так, в частности,
мы не занимаемся здесь перемещениями твердого тела, положение
которого определяется двумя или несколькими параметрами. Эти
перемещения были изучены, главным образом, Томсоном и Тэтом,
Шёнеманом, Мангеймом, Рибокуром, Кёнигсом.
I. Кинематика точки
36. Определения. Когда говорят, что тело находится в покое
или в движении, то под этим всегда понимают,что этот покой или
движение имеет место относительно некоторых других тел. Так,
объект, находящийся неподвижно на поверхности Земли, покоится
относительно Земли, сама же Земля движется относительно Солнца, и
т. д. Другими словами, наблюдают только относительные движения.

ГЛАВА II. КИНЕМАТИКА	5Т
Тем не менее представляется удобным в каждом вопросе кине-
матики выбирать систему осей, которые по определению рассматри-
ваются как абсолютно неподвижные. Тогда движение относительна
этих осей называют абсолютным движением.
Но если в кинематике выбор осей, рассматриваемых как непо-
движные, является произвольным, то в механике это будет не так.
Ниже мы увидим, что с целью возможно большего упрощения иссле-
дования явлений природы осями, которые уславливаются считать
неподвижными, являются оси, имеющие начало в центре тяжести
солнечной системы и направленные на три, так называемые, непо-1
движные звезды.
Для определения момента времени, в котором происходит какое-
нибудь явление, его относят к какому-нибудь определенному мо-
менту, называемому начальным, и задают число, которое измеряет
в как-ибс-нибудь единицах (например, в секундах среднего времени)
промежуток времени между рассматриваемым и начальным моментами.
Этому числу приписывают знак -\- или — в зависимости от того,
наступает ли рассматриваемый момент после или до начального
момента. Вследствие этого, когда
мы будем говорить о моменте вре-
мени t, буква t будет обозна-
чать положительное или отрицатель-
ное число секунд.
С целью упрощения изучения
кинематики сначала изучают движе-
ние одной точки, а после этого —
движение тел произвольной протя-
женности.
37. Движение точки. Пусть	Рис. 29.
Ox, Оу, Oz — три абсолютно не-
подвижные оси и М—движущаяся точка, координаты которой х„
у, г (рис. 29) являются заданными непрерывными функциями вре-
мени t:
Кривая, описываемая движущейся точкой, называется ее траек-
торией. Ее уравнения могут быть получены исключением t из урав-
нений, определяющих х, у, г в функции t.
Движение может быть определено еще следующим образом:
задают траекторию, далее, приняв на ней какую-нибудь точку Мо
за начало отсчета дуг и какое-нибудь направление M0S отсчета за
положительное, задают в функции времени алгебраическое значе-
ние s дуги М0М между движущейся точкой и точкой Мо.
38. Прямолинейное равномерное движение; скорость. Говорят,
что движение является прямолинейным, если траектория — прямая
линия. Если эту прямую принять за ось Ох, то оба предыдущих

58	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
способа определения движения совпадут и движение будет опреде-
ляться выражением абсциссы движущейся точки в функции времени.
Наиболее простым прямолинейным движением является то, для
которого х есть линейная функция времени:
х = at -f- b,
тде а и Ъ — постоянные. Это движение характеризуется тем, что
приращение Дл: величины х за произвольный промежуток времени Ы
пропорционально этому промежутку Ы.
Пусть М — положение движущейся точки в момент времени t,
¦& Mt — ее положение в момент t-\-kt, где Д?>0. Геометрическая
величина ММи если ее отсчитывать вдоль оси Ох, имеет алгебраи-
ческое значение, равное Дл\ Если в направлении ММХ отложить
от точки М отрезок MW, равный —гр, то геометрическая вела-
чана MW, алгебраическое значение которой равно дт, называется
скоростью равномерного движения (рис. 30). Алгебраическое
значение этой скорости равно а.
С	М	М, а	*
Рис. 30.
39. Произвольное прямолинейное движение; скорость. Рас-
смотрим произвольное прямолинейное движение, для которого х = ср (t).
Перемещение MMV которое получает точка, когда t увеличивается
на Д?, есть геометрическая величина, алгебраическое значение ко-
торой равно Длг. Если в направлении MMt отложить отрезок MW
О М М, V W	s
Рис. 31.
{рис. 31), равный . г, то вектор MW, алгебраическое значение
которого равно -rj, называется средней скоростью движущейся
точки за промежуток времени Д?. Если Д? стремится к нулю, то
вектор MW стремится к предельному вектору MV, алгебраическое
значение которого равно производной -гг или ср' (t) и который на-
зывается скоростью точки в момент t.
Например, если

ГЛАВА II. КИНЕМАТИКА	59
где а, Ь, с — постоянные, то скорость MV в момент t будет иметь,
алгебраическое значение, отсчитываемое вдоль оси Ох, равное
dx
Изменение этой скорости пропорционально изменению времени.
Говорят, что определяемое таким образом прямолинейное движение
является равнопеременным.
40. Вектор скорости в криволинейном движении. Пусть М
и Mt — положения движущейся точки в моменты t и t-\-bi. От-
ложим на хорде MMt (рис. 32) в направлении MMt отрезок MW,
равный 1 . Вектор MW называется средней, скоростью движу-
щейся точки за промежуток вре-
мени Д^. Это —скорость, которую
должна шйеть воображаемая точка,
описывающая прямолинейно и равно-
мерно отрезок прямой ММг за про-
межуток времени Ы. Когда Д^ стре-
мится к нулю, средняя скорость MW
стремится к предельному век-
тору MV, касательному к траекто-
рии, который называется скоростью
движущейся точки в момент t.
Скорость есть полярный вектор,
приложенный к движущейся точке.
Пусть л:, у, г — координаты дви-	Рис- 32.
жущейся точки. Проекции геомет-
рической величины ММ1 на оси координат будут Длг, Д.у, Дг, и,
следовательно, проекции величины MW, т. е. средней скорости, равны
Кх Ау д<г
It' ДГ' Д7"
Если Д/f стремится к нулю, то MW стремится к MV. Следовательно,
для проекций скорости в момент t имеем:
dx dy dz
Ж' dT' W
Допустим, что движение задано траекторией и выражением дуги
MJVI = s в функции t. Так как отношение дуги МMt к хорде ММХ
стремится к единице, когда Д? стремится к нулю, то для абсолют-
ного значения скорости получается
, ds
Если провести в направлении положительных дуг касательную МТ
к траектории, то скорость будет направлена по МТ или в
противоположную сторону к зависимости от того, будет ли величина

60	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
-J2 положительной или отрицательной. Следовательно, алгебраическое
значение скорости, отсчитываемой в направлении МТ, равно -^.
Если скорость v постоянна, то криволинейное движение называют
равномерным.
41. Вектор ускорения. Понятие ускорения для простейших
случаев введено Галилеем.
Пусть MV и vWjVj — скорости движущейся точки в моменты t
и t-\-bt (рис. 33, а).
М
Рис. 33.
Проведем через М отрезок MU, равный и параллельный M1Vl,
и пусть МН—геометрическая разность векторов MU и MV, т. е.
вектор, который необходимо приложить к MV, чтобы получить MU.
Если вдоль МН отложить длину Ml, равную -гг, то вектор Ml даст
среднее ускорение движущейся точки за промежуток времени Ы.
Когда Ы стремится к нулю, этот вектор стремится к пределу MJ,
который называется ускорением движущейся точки в момент t.
Ускорение есть, следовательно, полярный вектор, приложенный
к движущейся точке.
Так как плоскость VMU переходит в пределе в соприкасающуюся
плоскость, то ускорение MJ лежит в соприкасающейся плоскости.
Чтобы получить проекции ускорения на оси координат, заме-
тим, что проекция скорости MV в момент t на какую-нибудь
ось, например на ось Ох, равна -г?, а скорость MlV1 или вектор MU
имеет в момент t-\-b? проекцию на ту же ось, равную ^ + ^
Проекция вектора МН, равная разности проекций векторов MU и MV,
будет, следовательно, А -гг.	Поэтому проекции среднего ускорения
... МН
= -гг равны
dx	dy dj_
udt	*d7 dt
U '	Ы ' At '

ГЛАВА II. КИНЕМАТИКА	61
Полагая b.t стремящимся к нулю, получим для проекций ускоре-
ния MJ в момент t значения:
d2x d2y (Pz
Ж' Ш' dt2'
Годограф. Понятие ускорения можно легко свести к понятию
скорости. Проведем через произвольную фиксированную точку А
вектор Am, равный и параллельный скорости MV движущейся
точки в момент t (рис. 33, б). Когда t изменяется, вектор Am
также изменяется и его конец образует новую движущуюся точку,
описывающую траекторию h, которая называется годографом. Ско-
рость mj этой новой движущейся точки в каждый момент вре-
мени равна ускорению точки М. В самом деле, в момент t-\~M
точка т занимает положение mv причем вектор Ат^ равен и па-
раллелен вектору MlVl или MU. Поэтому вектор ттх равен
и параллелен вектору VU или МН. Средняя скорость точки т за
время Ы: есть вектор ml, направленный по ттх и равный —гт-1.
Эта средняя скорость ml равна, следовательно, и параллельна сред-
нему ускорению Ml точки М. Переходя к пределу, когда Д^ стре-
мится к нулю, мы видим, что скорость mj точки т в момент t равна
ускорению MJ точки М в тот же момент времени.
Пусть, например,
+ c', 2 = a"fi + b"t + с",	A)
где а, Ь, с, а', Ь', с', а", Ь", с" — постоянные. Тогда траекторией будет па-
рабола.
Проекции скорости будут
g	§	ft	B)
а проекции ускорения
^-2а *У-2а' —-2а"	C)
dt* ~ ' df- ~ ' df>- — ¦	К)
Последние, как видно, постоянны. Следовательно, ускорение будет посто-
янным по величине и направлению. И, наоборот, если в каком-нибудь дви-
жении ускорение постоянно по величине и направлению, то это движение
определяется уравнениями вида A). Действительно, исходя из уравнений C),
последовательным интегрированием придем сначала к уравнениям B), а за-
тем к уравнениям A). Такое движение будет подробно изучено дальше при
рассмотрении движения тяжелого тела в пустоте.
Важно заметить, что если ускорение движения постоянно по величине
и направлению, то и среднее ускорение за произвольный промежуток вре-
мени М будет иметь ту же самую постоянную величину и направление.
Действительно, если уравнения C) выполняются, то, интегрируя их, получаем
уравнения B), из которых для проекций среднего ускорения за время Д?
получаем те же значения 2а, 2а', 2а", что и для проекций ускорения в мо-
мент t.
В этом примере годографом является прямая линия, движение по ко-
торой будет равномерным.

62
ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
42. Касательное и нормальное ускорения (Гюйгенс). Рассмот-
рим какое-нибудь движение, заданное геометрически траекторией к
выражением дуги М0М или s в функции времени, причем отсчет на
этой дуге принимается положительным в каком-нибудь определенном
направлении M0S (рис. 34).
Пусть а, р, 1 — направляющие косинусы (относительно прямо-
угольных осей) касательной МТ к траектории, проведенной в сторону
положительного отсчета s, a a', J3', -у' —
направляющие косинусы главной нормали,
которая считается положительной от М
к центру С главной кривизны. Пусть, нако-
нец, МС = р есть радиус главной кривизны
траектории.
По известным формулам Серое—Френе
имеем
ds p ' ds p ' ds p *
Далее, очевидно,
dx	dx ds	 ds dy	q ds dz ds
Рис.34.	dt ~ d7 Ж= a~dt ' dt~^W' Ж~'^Ш'
Дифференцируя еще раз по времени и замечая, что
dt
da ds
'd~sdt:
(
p [at
получим для проекций ускорения
dbc ^s
a
?1 й ^?__!l^
dt*~r dt*-^~ p [dt) '
dt2 ' df- ' p [dt) •
Эти формулы легко интерпретируются. Отложим на касатель-
ной, принимая МТ за положительное направление, отрезок MJt,
алгебраическое значение которого равно Л==^«> а на нормали ММ
отрезок MJn, равный — (~Л . Тогда формулы показывают, что про-
екции ускорения на каждую из трех осей равны суммам проекций
геометрических величин MJt и MJn. Следовательно, в пространстве
ускорение MJ есть результирующая величин MJt и MJn, которые
называются касательным и нормальным ускорениями. Проекция Jt

ГЛАВА II. КИНЕМАТИКА	63
ds
ускорения MJ на касательную МТ после замены ^ через v напи-
шется так:
	d2s	dv dv ds	 1 dv*
Jt~~~d~P~~It=!idsli~~12!ls'
Проекция Jn на нормаль MC всегда положительна:
J
Ускорение MJ расположено, следовательно, в соприкасающейся
плоскости и направлено в сторону вогнутости траектории.
Примеры. 1°. Если движение прямолинейно, то р равно бесконечности
и нормальная составляющая обращается в нуль. Ускорение совпадает тогда
с касательной составляющей. Наоборот, если нормальное ускорение везде
нуль, то р обращается в бесконечность и траектория есть прямая линия.
2 . Если скорость постоянна по величине, т. е. если криволинейное дви-
жение является равномерным, то касательное ускорение равно нулю. Тогда
ускорение направлено по главной нормали и изменяется обратно пропор-
ционально радиусу кривизны. Так, если точка описывает окружность ра-
диуса R с постоянной по величине скоростью V, то касательное ускорение
равно нулю; ускорение / будет нормальным и равным V2/R, т. е. постоян-
ным по величине и направленным по радиусу. Наоборот, если в каком-нибудь
движении касательное ускорение все время нуль, то скорость будет посто-
янной по величине и движение будет равномерным.
Применение векторных производных. Можно говорить, что вектор
скорости MV движущейся точки М есть векторная производная по времени
вектора ОМ, соединяющего неподвижную точку О с точкой М. Это выте-
кает из самого определения скорости.
Вектор ускорения MJ геометрически равен производной вектора Am,
имеющего начало в неподвижной точке А и геометрически равного вектору
скорости. Это вытекает из определения ускорения при помощи годографа.
П. Поступательное движение и вращение
неизменяемой системы
43. Поступательное движение. Неизменяемой системой или
твердым телом называется совокупность точек, неизменно связан-
ных между собой.
Твердое тело движется поступательно, если оно перемещается
таким образом, что все отрезки прямых, соединяющих попарно точки
тела, остаются параллельными самим себе. Для этого, очевидно,
достаточно, чтобы триэдр, получающийся от соединения какой-ни-
будь точки А тела (рис. 35) с тремя другими его точками В, С и D,
не лежащими с Л в одной плоскости, перемещался параллельно
самому себе.
Когда тело движется поступательно, все его точки имеют оди-
наковые скорости и наоборот. В самом деле, пусть At(xu уу, zt)
и Аг{х2, уг, 22) — две произвольные точки тела. Так как отрезок.
А\Аг перемещается параллельно самому себе, то его проекции

64
ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
x 	Xi, Уг — У\> Z2 — zi на оси постоянны. Следовательно, их про-
изводные равны нулю и мы получаем:
rfyt
dt
dt
dt
dz2
A)
Это показывает, что обе точки имеют одинаковые скорости. На-
оборот, если все точки тела имеют в каждый момент времени
одинаковые скорости, то тело движется
поступательно. В самом деле, если две
точки А1 и А2 имеют одинаковые ско-
рости, то будут справедливы уравнения A),
откуда после интегрирования увидим, что
х1 — х2, Ух — У2< z\ — z% постоянны, т. е.
что отрезок АуАг перемещается парал-
лельно самому себе. Общая скорость всех
точек называется скоростью поступа-
тельного движения. Дифференцируя урав-
нения A), непосредственно убеждаемся,
что все точки тела при поступательном движении имеют в каждый
момент времени одинаковые ускорения. Общее ускорение всех точек
называется ускорением поступательного движения,
44. Вращение вокруг неподвижной оси. Угловая скорость.
Геометрическое представление. Когда тело вращается вокруг
неподвижной оси АВ (рис. 36), каждая его точка М описывает ок-
ружность, перпендикулярную к оси,
с центром Р, лежащим на оси. Скорость
точки М направлена, следовательно, нор-
мально к плоскости МАВ в сторону
вращения. Дуги, описываемые двумя раз-
личными точками за одно и то же время,
пропорциональны их расстояниям до оси.
Скорости этих точек относятся, следова-
тельно, как их расстояния до оси.
Угловой скоростью называют величину,
численно равную скорости точек, располо-
женных от оси на расстоянии единицы дли-
ны. Если эту угловую скорость обозначить
через со, то величина V скорости точки УН будет равна шМР, где МР —
расстояние от точки М до оси вращения. Когда вращение задается
углом 6, на который поворачивается тело от какого-нибудь начального
положения, и этот угол выражен в функции г, то ш равно -г.
Для определения скоростей в какой-нибудь момент t при враща-
тельном движении необходимо знать три элемента: ось вращения,
угловую скорость и направление вращения. Эти три элемента
могут быть представлены одним вектором следующим образом.
А
М
Рис. 36.

ГЛАВА И. КИНЕМАТИКА
65
Возьмем на оси вращения АВ произвольную точку А и отложим
на ней отрезок Ач> длины ш, направленный таким образом, что для
наблюдателя, стоящего в точке А и смотрящего с конца ш отложен-
ного отрезка, вращение происходит справо налево. Определяемая
таким образом геометрическая величина Лш представляет вращение*
Отождествляя вращательное движение с представляющим его векто-
ром, часто говорят, что тело совершает вращение Aw. Так как
начало вектора А может быть выбрано где угодно на оси, то, не
изменяя вращения, можно перенести
начало изображающего его вектора ш
в произвольную точку его линии.
Вращение представляется, следо-
вательно, вектором, приложенным
вдоль некоторой прямой. Этот век-
тор является аксиальным (п. 34).
Аналитические выражения про-
екций скорости точки тела.
Пусть Лш (рис. 37) — вращение
с угловой скоростью ш, а р, q,
г — проекции последней на оси Ох,
Оу, Oz, предполагаемые прямоуголь-
ными, наконец, х0, у0, z0— коорди-
наты точки А. Пусть М — точка
тела с координатами х, у, г, MV — ее скорость, Vx, Vy, Vz — про-
екции этой скорости на оси. Последние величины нам и нужно
определить.
С этой целью заметим, что скорость V точки М по величине и
направлению совпадает с моментом вектора Ак> относительно точки М.
В самом деле, эта скорость равна ыМР, перпендикулярна пло-
скости МАш и направлена таким образом, что точка, перемещаю-
щаяся от А к ш, двигается вокруг V в положительном направлении.
Нам известны (п. 9) формулы проекций иомента относительно какой-
нибудь точки (х', у', z). Прилагая эти формулы к рассматриваемому
случаю и замечая, что момент берется относительно точки х, у, z,
найдем:
Vx = q (z — z0) — г (у — у0),
Рис. 37.
Когда точка А совпадает с началом координат, эти выражения
принимают вид
Vx = qz — ry, Vy = rx —pz,
=py — qx,

66	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
III. Скорость в относительном движении.
Сложение поступательных и вращательных движений.
Скорости точек свободного тела
45. Относительное движение; скорость. Вообразим неизменяе-
мую систему E), совершающую заданное движение, и некоторую
точку М, движущуюся относительно этой системы. Система E)
может быть, например, Землей, а точка М— тяжелой точкой, предо-
ставленной самой себе на поверхности Земли и падающей по вертикали.
Для наблюдателя, увлекаемого системой E), называемой подвижной
системой отсчета, и не подозревающего об этом движении, точка М
описывает относительно си-
стемы E) некоторое движе-
ние, которое называется от-
носительным. Траектория,
скорость и ускорение в этом
движении называются отно-
сительной траекторией,
относительной скоростью
и относительным ускоре-
нием. Одновременно та же
точка совершает в простран-
стве некоторое абсолютное
движение.
На рис. 38 изображена
относительная траектория С
точки М относительно си-
стемы сравнения E). В то время, как точка М описывает эту кри-
вую С, неизменно связанную с системой E), сама система пере-
мещается в пространстве. Пусть в момент t движущаяся точка, си-
стема сравнения и относительная траектория занимают положения М,
E) и С, а в момент времени t-\-bi они за-
нимают положения Mv Et) и Cv Абсолютное
перемещение есть ММХ; точка переходит из М
в Mv следуя по некоторой траектории Са,
которая является её абсолютной траекторией.
Обозначим через М' положение, которое за-
нимает в момент ^ —(—Д/^ точка системы (S), со-
впадавшая с точкой М в момент t. Перемеще-
ние М'Мх есть относительное перемещение
точки М; перемещение ММ' называется пере-
носным перемещением. Вектор MMt есть
геометрическая сумма векторов M'Mt и ММ'. Если на каждом из
этих векторов отложить отрезки MWa, M'Wr и MWe, равные соот-
ветственно этим векторам, деленным на Ы, то полученные таким
образом векторы будут представлять собой среднюю абсолютную
скорость, среднюю относительную скорость и среднюю переносную
Рис. 38.
Рис. 39.

ГЛАВА II. КИНЕМАТИКА	67
скорость. Так как первый вектор есть сумма двух других, то
Когда Д^ стремится к нулю (рис. 39), эти векторы стремятся
к абсолютной скорости Va, относительной скорости Vr и перенос-
ной скорости Ve. Мы имеем, следовательно, геометрическое равенство
Переносная скорость, согласно предыдущему, представляет собой
скорость точки системы E), совпадающей в рассматриваемый момент
с точкой М, или скорость, которую имела бы точка М, если бы
она в занимаемом ею положении оказалась неизменно связанной
с системой E).
Мы увидим дальше, как определяется абсолютное ускорение при
помощи аналогичной формулы, но с добавочным членом. Однако
прежде мы дадим некоторые приложения предыдущей теоремы.
46. Сложение поступательных движений. Рассмотрим неизменяемую
систему (Si), движущуюся поступательно со скоростью Vb и вторую си-
стему (So), движущуюся поступательно относительно (Si) со скоростью V%
(рис. 40)."
Абсолютная скорость Va какой-нибудь точки М системы (S2) есть геоме-
трическая сумма относительной скорости этой точки, которая равна К2, и ее
переносной скорости, равной Vi- Абсолютные скорости различных точек (S2)
будут, следовательно, такими, как если бы (S2) совершала только одно посту-
пательное движение со скоростью, равной геометрической сумме двух ско-
ростей Vi и V<i- Говорят, что
два поступательных движения сло-
жились в одно. Точно так же
несколько поступательных движе-
ний складываются в одмо со ско-
Рис. 40.
Рис. 41.
ростью, равной результирующей скорости всех скоростей заданных поступа-
тельных движений.
47. Совокупность двух вращений. Пусть тело Si совершает враще-
ние А]и». Вообразим, что это тело Si содержит ось Л2о>8 и что некоторое
тело S2 совершает относительно Si вращение »2 вокруг оси Л2ш2 (рис. 41).
Найдем абсолютную скорость какой-нибудь точки М тела S2. Относи-
тельная скорость точки М относительно тела Si есть скорость, которой она
обладает во вращении «,: это момент вектора <о2 относительно точки М.
Переносная скорость — это скорость Vj, которой обладала бы точка М,

68
ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
если бы она была неизменно связана с телом Sj. Это та скорость, которая
вызвана вращением <alt или момент вектора «х относительно точки М. Абсо-
лютная скорость Va точки М равна, следовательно, результирующему мо-
менту векторов «j и <о2 относительно точки М. Эта скорость не зависит от
порядка, в котором происходят вращения ац и <о2.
Рассмотрим несколько частных случаев:
Г. Оси вращения пересекаются. Результирующий момент векторов а±
и «2 относительно произвольной точки М равен моменту их результирую-
щего вектора <о (рис. 42, а). Абсолютная скорость точки М будет, следова-
тельно, такой, как если бы тело S2 совершало только одно вращение А-^.
2°. Оба вращения «( и о>2 параллельны и не образуют пары. Система
этих двух векторов эквивалентна одному единственному вектору Аа, полу-
чаемому по известному правилу (п. 31). Следовательно, результирующий
момент относительно точки М равен моменту результирующего вектора А<*>.
Скорости различных точек тела будут, как и раньше, такими, как если бы
тело совершало только вращение « (рис. 42, б).
Я, А
Рис. 43.
3°. В случае, когда оба вращения образуют пару, результирующий мо-
мент равен вектору момента пары, какова бы ни была точка М, и все точки
тела i'3 имеют одинаковую скорость. Скорости этих точек будут, следова-
тельно, такими, как если бы тело S2 совершало поступательное движение
со скоростью, равной вектору момента пары (рис. 43).
48. Произвольное число вращений. Пусть тело 5^ совершает враще-
ние j4j«i и с ним связаны ось А^^ и тело S2, которое совершает относи-
тельно Si вращение «2. С телом S2 связаны ось А3<л3 и тело S3, совершаю-
щее относительно S2 вращение о>8, и т. д. до тела Sn, совершающего отно-
сительно Sn_i вращение <ои.
Мы будем говорить для краткости, что тело S\ одновременно совер-
шает вращения <иь <о2	<ои. Найдем абсолютную скорость какой-нибудь
точки М, неизменно связанной с последним твердым телом Sn. Эта скорость
равна главному моменту системы векторов u>lt <о2	 ап относительно
точки М. Так как это предложение установлено для случая двух вращений,
то для того, чтобы установить его в общем виде, достаточно показать, что
если оно справедливо для п — 1 вращений, то оно остается справедливым
и для п вращений.
Абсолютная скорость точки М тела Sn равна геометрической сумме его
относительной скорости Vr относительно Sn~i и переносной скорости Ve
(рис. 44). Относительная скорость точки М по отношению к Sn-\ есть ско-
рость, вызванная вращением ып, т. е. она равна моменту вектора «и отно-
сительно точки М. Переносная скорость точки М равна скорости, которую
оиа имела бы, если бы была неизменно связана с телом Sn-i, т. е. она равна
главному моменту векторов ч>1г ш2	">»-! относительно точки М. Абсо-

ГЛАВА II. КИНЕМАТИКА
69
aft
лкпная скорость есть результирующая этих двух моментов и равна, следо-
вательно, главному моменту векторов <лъ <о2	<оп относительно точки М.
Эта скорость не зависит от порядка вращений.
Задача, которая возникает при аналогичной комбинации поступательных
и вращательных движений, приводится к предыдущей путем замены ка-
ждого поступательного движения парой
вращений.
Установив это, рассмотрим вторую си-
стему векторов ш-р <i>2, ..., <о„, эквивалент-
ную первоначальной ах, ш2. ..., <ои, т. е.
такую, которая может быть получена из
первоначальной элементарными операциями.
Обе системы вращений, представляемые
этими векторами, сообщают точке М одну
и ту же скорость. Следовательно, если
рассматриваются только скорости, то одну
систему векторов <а можно заменить другой.
Вот некоторые, вытекающие отсюда
наиболее важные следствия:
1°. Система векторов эквивалентна
двум векторам, из которых один прохо-
дит через произвольно выбираемую точку.	рис_ 44.
Следовательно, скорости точек тела Sn
будут такими же, как если бы это тело совершало два вращения, ось одного
из.которых проходит через точку, выбираемую произвольно (Шаль).
2°. Система векторов эквивалентна одному вектору «, проходящему
через произвольную точку О, и паре с вектором момента OV0. Следова-
тельно, скорости точек тела Sn будут такими же, как если бы это тело
совершало одно вращение О», ось которого
проходит через произвольную точку О, ипару
вращений с вектором момента OV0, т. е.
поступательное движение со скоростью OV0
(рис. 45). Когда положение точки О меняется,
вращение О« сохраняется неизменным, а по-
ступательная скорость OVq изменяется, но
так, что произведение g = OV0 cos («, Vo)
остается постоянным.
Если DD' есть центральная ось си-
стемы векторов «i, «2, ..., «и, то эта си-
Z"*V	стема эквивалентна одному-единственному
\	„t вектору <и (вращению), направленному по
О	р DD', и паре с минимальным векторным
""о	| моментом g (поступательному движению
| pi со скоростью g), направленным также по
DD'. Скорости точек тела Sn будут та-
кими же, как если бы оно совершало вра-
щение <о и поступательное движение g
в направлении этого вращения. Это движе-
ние, эквивалентное движению болта в неподвижной гайке, называется вин-
товым движением, а ось DD' — мгновенной винтовой осью.
49. Частные случаи. Отметим некоторые частные случаи, соответст-
вующие различным исследованным случаям в теории векторов (п. 26). Если
минимальный момент g равен нулю, то система заданных вращений экви-
валентна одному-единственному вращению вокруг центральной оси. Если а
обращается в нуль, то система эквивалентна одному поступательному движе-
нию. Если (о и Vq одновременно равны нулю, то система вращений эквива-
лентна нулю: скорости всех точек тела Sn равны нулю.
/
Рис. 45.

70
ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
50. Геометрические следствия. Очевидно, что каждая теорема, уста-
новленная в главе I в теории скользящих векторов, может служить теоремой
о вращениях и поступательных движениях, сообщаемых некоторому телу Sn,
если векторы заменить вращениями, пары — поступательными движениями
со скоростями, равными их векторам-моментам, и главный момент относи-
тельно точки М — скоростью, которою обладает эта точка, двигаясь вместе
с телом. Теоремы геометрии о плоскостях и их фокусах, о сопряженных
прямых, о прямых нулевого момента имеют простое истолкование. Так, на-
пример, если плоскость П неизменно связана с телом Sn при его движении,
то фокусом плоскости II будет та ее точка, скорость которой перпендикулярна
к плоскости, и т. д.
Тот факт, что произвольное число вращений и поступательных движений,
приложенных к твердому телу, сообщают его различным точкам такие же
скорости, как и винтовое движение, находит свое настоящее объяснение
в теореме, согласно которой в наиболее общем движении твердого тела
скорости в каждое мгновение будут такими же, как в винтовом движении.
Это нам и предстоит доказать.
61. Распределение скоростей в движущемся твердом теле.
Отнесем движение к трем неподвижным в пространстве прямоуголь-
ным осям О^ХгУ^Хх. Для определения положения тела введем три
прямоугольные оси Oxyz, ориентированные так же, как и пер-
вые, и неразрывно связанные с телом (рис. 46). Достаточно знать
движение этих осей, которое определяется координатами х0, у0, z0.
подвижного начала и девятью направляющими косинусами подвиж-
ных осей относительно не-
подвижных, выраженными в
функции времени. Будем по-
лагать, что эти девять напра-
вляющих косинусов даются
следующей таблицей:
Xl
Уг
X
а
Р
т
У
ч
Pi
ь
г
h
Рис. 46.
Пусть М — точка тела, имеющая координаты х, у, z относи-
тельно подвижных осей и хи ух, zx относительно осей неподвижных.
Числа х, у, z являются постоянными, так как точка М неразрывно
связана с движущимися осями.
По формулам преобразования координат имеем:
Xi = х0 + ах + а^у -\- а2г,

ГЛАВА II. КИНЕМАТИКА	71
Дифференцируя эти выражения по t, мы получим проекции ско-
рости V точки М (рис. 46) на неподвижные оси:
у 	 ^JCi_ __ dx0 , da	dax	da2
Vx'— dt — dt ~t~x dt ~^y~dT^~z~dT'
__ dy, _ dy0	dp	dpt	dC8
V2 __ ^1 _^ ^o j ^ dy	dYi | . db ^
Для простого истолкования этих формул найдем проекции Vx,
Vy, Vz скорости V на подвижные оси. Очевидно, имеем
Вычислим правые части, заменяя в них VXl, Vyi, V2l полученными
для них выражениями и замечая, что такие величины, как
da „d$	Л
Я dt "+" Р dt ^ Т d^ ' " * -
равны нулю вследствие соотношений
a2-fP2-|-T2=l,...
Далее, примем во внимание соотношения
«i«2 + Pip2+TiT2 = 0, ав2-|-рр2+тТ2 = 0. aa1+PP1 + TTi=O.
которые продифференцируем по ^. Получим:
dp , dr
Здесь обе части мы обозначаем соответственно через р, д, г. Окон-
чательно получим:
(основные формулы)
где Vx, Vy, V% обозначают проекции скорости Vo точки О на по-
движные оси:
Vy = V°y -\- rx—pz.

72	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
Эти формулы имеют простой смысл. Они показывают, что ско-
рость V каждой точки М твердого тела есть геометрическая сумма
двух векторов: вектора V, общего для всех точек М, равного и
параллельного скорости точки О, и вектора и, изменяющегося с по-
ложением точки М и имеющего проекции qz — ry, rx—рг, ру— qx
на подвижные оси. Вектор V0 есть скорость, которую имела бы
точка М, если бы тело совершало поступательное движение со ско-
ростью V. Вектор и есть скорость, которую имела бы та же точка,
если бы тело совершало вращение Ош, имеющее проекции р, q, r
на подвижные оси. Это вращение называется мгновенным вращением.
Полученный результат выражают, говоря, что скорость произвольной
точки тела есть результирующая скорости поступательного дви-
жения, равной скорости какой-нибудь точки О тела, и скорости
вращения вокруг некоторой оси, проходящей через О.
Полученные формулы являются основными для кинематики. Когда
движение твердого тела дано, то шесть величин V°x, V°y, V°z, p, q, r
являются известными функциями времени. Наоборот, если эти вели-
чины даны в функции времени, то можно найти движение триэдра.
(См. Darboux, Lemons de Geometrie, т. I, гл. II; Кое nigs, Le-
fons de Cinematiques, стр. 119.)
Компоненты скорости по неподвижным осям легко выводятся из
полученного результата. Прежде всего, для проекций V" на непо-
движные оси имеем
dx0 dyQ dz0
dt ' dt ' dt '
Далее, обозначая через plt qlt r1 проекции мгновенного враще-
ния Ош на неподвижные оси и пользуясь формулами вращения (п. 44),
получим следующее выражение для проекции вектора и на ось Ох^
Чх (*i — г0) — rx (yt — у0).
Следовательно, проекция скорости V на Ох1 будет
,. dx-i dxQ
Два аналогичных выражения получаются для VVl и V2i.
62. Мгновенная винтовая ось. Касательное винтовое движе-
ние. Значения скоростей различных точек твердого тела таковы,
как если бы тело совершало либо одно вращательное Ош и одно
поступательное движение 0V0, либо три одновременных вращения:
вращение Ош и два вращения ш° и — ш°, образующих пару с век-
тором моментом 0V0. Согласно правилу, установленному в теории
сложения вращений, это распределение скоростей будет в то же
время таким, как если бы тело совершало одно винтовое дви-
жение вокруг центральной оси системы вектора ш, ш°, — со0. Урав-
нения этой центральной оси получатся, если искать геометри-

ГЛАВА II. КИНЕМАТИКА
73
ческое место точек, для которых скорость параллельна направлению
мгновенного вращения со (рис. 47). Таким путем для центральной
винтовой оси получатся в подвижной системе координат уравнения
—	(D)
р	q
и в неподвижной системе — уравнения
-¦го)-
L С У] — Уо)
— xo) — Pi(zi—zo)
Pi	Qi
Общее значение всех этих отношений есть
(Ох)
dxa	dy0 dz0
^4f + qy4F + ril
где g — скорость скольжения, которая принимается положительной
в направлении со.
Отдельные частные случаи, которые могут представиться, будут
следующие: если / равно нулю, то скорость скольжения обращается
со
OJ
Р'
Рис. 47.
Рис. 48.
в нуль, а если / равно бесконечности, то угловая скорость равна
нулю.
Определяемое таким образом винтовое движение называется каса-
тельным к действительному движению в момент t, так как распределение
скоростей в обоих движениях будет одинаковым. Однако это не
будет справедливым для ускорений.
53. Величина скорости точки Тела. Рассмотрим точку М (рис. 48)
тела, расположенную на расстоянии 8 от мгновенной винтовой оси DD'.
Скорость, вызванная вращением, есть вектор MU, перпендикулярный плос-
кости MDD' и равный шб; скорость, вызванная поступательным движением,

74	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
есть вектор Mg, равный и параллельный g. Результирующая скорость V
находится, следовательно, в плоскости, перпендикулярной к 8 и определяется
формулами
V2 = «ДР+gS, tg VMg = —.
&
Если точка М находится на оси DD', то ее скорость равна g и напра-
влена вдоль оси. Когда точка М описывает прямую Ь, перпендикулярную
к DD', скорость V образует гиперболический параболоид. Эти предложения
позволяют получить в простой форме распределение главных моментов во-
круг центральной оси произвольной системы векторов, причем со является
главным моментом этой системы, a g—минимальной парой (п. 17).
54. Непрерывное движение. Геометрическое место мгновенных
винтовых осей в теле есть некоторая линейчатая поверхность 2,
уравнение которой может быть получено путем исключения t иа
уравнений (D) этих осей в подвижной системе координат. Геометри-
ческое место тех же осей в абсолютном пространстве, т. е. отно-
сительно неподвижной системы координат, представляет собой дру-
гую линейчатую поверхность, уравнение которой получается из.
уравнений (Ох). В произвольный момент времени обе эти поверхности
имеют общую обрааующую, которая является мгновенной винтовой
осью для этого момента. Более того, они касаются друг друга вдоль
этой образующей. В самом деле, вообразим некоторую точку М,
описывающую на неподвижной поверхности Zt произвольную кривую
таким образом, что в каждый момент времени t она находится на
мгновенной оси, являющейся для этого момента общей образующей.
Эта же точка описывает относительно движущегося тела некоторую
кривую, расположенную на связанной с телом подвижной поверхно-
сти Е. В момент t абсолютная скорость Va этой точки М касается
в М поверхности ~LV а ее относительная скорость Vr относительно-
тела касается в М поверхности Е. Наконец, переносная скорость Ve.
возникающая вследствие движения тела, направлена вдоль общей
образующей МО, так как все точки тела, принадлежащие этой об-
разующей, являющейся мгновенной винтовой осью, только скользят
вдоль нее. Так как вектор Va есть геометрическая сумма векторов
Vr и Ve, то все эти три вектора лежат в одной плоскости. Плос-
кость Va и Ve, т. е. плоскость Va и MG, касается поверхности 2^
плоскость Vr и Ve, т. е. плоскость Vr и MG, касается поверхно-
сти Ii. Так как обе эти плоскости совпадают, то поверхности ? и,
St касаются друг друга в точке М. Но эта точка взята на образую-
щей произвольно. Следовательно, поверхности Е и ^ касаются
вдоль всей образующей.
В частном случае, когда Ve равно нулю, скорость Vr равна
скорости Va и обе касательные плоскости, определяемые — одна
образующей МО и скоростью Va, а другая — образующей МО и
скоростью Vr, по-прежнему совпадают.
Таким образом, общее движение твердого тела может быть пред-
ставлено следующим способом, указанным Понселе:

ГЛАВА II. КИНЕМАТИКА	75
Линейчатая поверхность, связанная с телом, движется по
неподвижной линейчатой поверхности, которой она касается
вдоль образующей и по которой она катится, скользя вдоль
s.nou образующей.
Рассмотрим несколько частных случаев этих теорем.
55.	Твердое тело с неподвижной точкой. Эту неподвижную
точку можно принять за начало подвижных и неподвижных осей.
Так как скорость точки О равна нулю, то скорости различных то-
чек тела будут такими, как если бы оно вращалось вокруг неко-
торой оси, проходящей через неподвижную точку (Эйлер). Эта
ось называется мгновенной осью вращения. Ось винтового движения
совпадает с ней, но скольжение в этом винтовом движении отсут-
ствует и остается только мгновенное вращение. Конечное движение
тела получится, если заставить катиться конус С с вершиной
в точке О, являющийся геометрическим местом мгновенных осей
в теле, по конусу Ct с той же вершиной О, являющемуся геомет-
рическим местом мгновенных осей в пространстве.
Точки тела, лежащие на сфере с центром в точке О, образуют сфе-
рическую фигуру неизменяемой формы, движущуюся по этой сфере.
Конусы С и Cj с вершиной в точке О пересекают эту сферу по двум
кривым с и с,, из которых первая неизменно связана с движущейся
сферической фигурой, а вторая неподвижна на сфере. Движение сфе-
рической фигуры получится, если заставить кривую с, связанную с этой
фигурой, катиться (без скольжения) по неподвижной кривой cv
56.	Тело перемещается параллельно неподвижной плоскости.
В этом случае скорости различных точек тела параллельны не-
которой неподвижной плоскости П и этот случай можно рассма-
тривать как предельный, когда неподвижная точка О удаляется
в бесконечность в направлении, перпендикулярном к плоскости П.
Сфера с центром в О, проходящая через какую-нибудь определен-
ную точку тела, переходит при этом в плоскость, параллельную
плоскости П или, если угодно, в самую плоскость П. Все точки
тела, находившиеся в некоторый момент времени на одинаковом рас-
стоянии от этой плоскости, будут и в дальнейшем находиться на
том же расстоянии от нее. Они образуют плоскую фигуру неизме-
няемой формы, движущуюся по неподвижной плоскости. Мгновенное
винтовое движение приводится теперь к вращению, ось которого
перпендикулярна плоскости П. Геометрическое место мгновенных
осей образует в теле цилиндр С, а в пространстве цилиндр С1
с образующими, перпендикулярными плоскости П. Движение тела
получится, если заставить катиться без скольжения цилиндр С по
цилиндру Cv Точки тела, лежащие на плоскости II, образуют плос-
кую неизменяемую фигуру, движение которой вполне определяет дви-
жение всего тела. Скорости различных точек этой фигуры в какой-
нибудь момент / будут такими же, как если бы фигура вращалась
вокруг некоторой точки / своей плоскости. Эта точка /, являющаяся

76
ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
точкой пересечения мгновенной оси с плоскостью П, называется
мгновенным центром вращения плоской фигуры. Конечное движе-
ние получается качением кривой с, полученной при пересечении цилин-
дра С плоскостью П, по кривой Cj, полученной при пересечении
цилиндра С1 той же плоскостью.
57. Качение и верчение подвижной поверхности по неподвижной
поверхности. Вообразим движущееся твердое тело, ограниченное некото-
рой неизменяемой поверхностью S, которая все время касается некоторой
неподвижной поверхности Sx (рис. 49). В каждый момент t некоторая точка А
Рис. 49.
движущейся поверхности 5 находится в соприкосновении с некоторой точ-
кой А| неподвижной поверхности S\. Если в момент t скорость УЛ точки А
касания поверхности S с поверхностью 5j отлична от нуля, то эта скорость
лежит в общей касательной плоскости обеих поверхностей. В самом деле,
вообразим движущуюся точку, совпадающую в каждый момент с точкой
соприкосновения обеих поверхностей. Абсолютная траектория С± этой дви-
жущейся точки лежит на поверхности S\ и ее абсолютная скорость V\ на-
правлена по касательной к Ci; относительная траектория С лежит на по-
верхности 5 и относительная скорость V касается С; переносная скорость,
вызванная движением 5, есть скорость Vo точки А поверхности S, находя-
щейся в рассматриваемый момент в соприкосновении. Так как V\ есть ре-
зультирующая векторов V и Vo, то вектор Vo, если он отличен от нуля, так
же как и векторы Vj и V, лежит в плоскости, касательной к обеим поверх-
ностям в точке А. Скорости различных точек движущегося тела будут
такими же, как если бы тело совершало поступательное движение со ско-
ростью Ко и вращение Am вокруг некоторой оси, проходящей через точку А.
Говорят, что поверхность S катится и вертится по поверхности Si,
если в каждый момент времени t скорость точки А касания этих
поверхностей равна нулю. В этом случае V% равно нулю и скорости раз-
личных точек тела будут такими, как если бы оно совершало вращение Аи>
вокруг оси, проходящей через А. Следовательно, мгновенная винтовая ось
проходит через А и скольжение не происходит. Геометрическое место
осей Аа> образует в теле S нек торую линейчатую поверхность S, а в абсо-
лютном пространстве — некоторую линейчатую поверхность Ej. Движение тела
получится, если заставить катиться поверхность Е по поверхности Е^. Гео-
метрическое место точек А на поверхности S есть кривая С пересечения
поверхностей S и 5; геометрическое место точек At на поверхности 5г
есть кривая Q пересечения поверхностей 2Х и Si. Эти две кривые С и Ci

ГЛАВА И. КИНЕМАТИКА	77
также катятся одна по другой, что вытекает из того, что скорость Vt сов-
падает со скоростью V. Мгновенное вращение Аа может быть разложено
на два: одно Аап, нормальное к обеим поверхностям и называющееся угло-
вой скоростью верчения, и другое Au>t, лежащее в касательной плоскости
и являющееся угловой скоростью качения. Когда движение таково, что
скорость верчения и>п равна постоянно нулю, то движение 5 по S, есть
качение.
IV. Ускорения. Теорема Кориолиса
58. Распределение ускорений в движущемся твердом теле.
В общем случае проекции скорости точки М тела на неподвижные
оси равны:
их-,	,
dzt
— ^
где a, b, с обозначают величины V%t — q^ -f- Г\Уо и т- Д- Диффе-
ренцируя по /, получим формулы для проекций ускорения на непо-
движные оси:
d2xx _da	dzx	dyt	dqx	drx
Заменяя первые производные ~, ... их значениями и полагая
р\-\-q\-\-г\ = ш2, найдем
^ q°
Переставляя буквы, получим выражения других проекций
d^zx
-г~ ускорения на неподвижные оси.
59. Ускорение в относительном движении. Теорема Корио-
лиса. Выше (п. 45) мы изложили очень важную теорему, устанав-
ливающую связь между абсолютной скоростью движущейся точки и
ее относительной скоростью относительно некоторой системы E).
совершающей известное движение.

78
ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
Мы ставим себе задачей доказать такого же рода теорему, свя-
зывающую между собой абсолютное.и относительное ускорения. Мы
будем пользоваться аналитическим методом, который даст также и
теорему о скоростях, доказанную ранее геометрически.
Для определения движения системы отсчета E), относительно
которой изучается относительное движение, введем три подвижные
оси Oxyz, неразрывно связанные с E), и зададим их движение так же,
как мы это делали в п. 51. Пусть М — движущаяся точка. Так как
она движется и в системе E) и в пространстве, то ее коорди-
наты х, у, z относительно подвижных осей и ее абсолютные коор-
динаты хх, уъ zx будут функциями времени. Эти координаты связаны
формулами
Х1 = Х0
-»
В22,
A)
Точка М имеет абсолютную скорость и абсолютное ускорение,
проекции которых на неподвижные оси равны
dt' dt ' dt '
(Vo)
dP ' dP '
Ее относительные скорость и ускорение имеют на подвижные оси
проекции
dx	dy	dz
~dt'	4t'	It'
d^x	d^y	d^-z
~dfi'	~d~P'	~dP'
а на неподвижные оси — проекции
dx_	dy_
dt ' i dt
r dt ~ ?l dt ~ Vi
dx . dy ,
T 77 "~i Ti 7?" "г Тг
dt
i —
]~dP
dt
<Py_
~d~P
Ж' ]
W'
d"-z
dp'
d?z
(Vr)
w
(V,)

ГЛАВА II. КИНЕМАТИКА
79
Точка М имеет также переносные скорость и ускорение, проек-
ции которых на неподвижные оси равны
dt
dt
dt
dt '
¦xdJ + y^^zW'
dt4*
dg	d*n	rf%2
<««'¦' dP "г" Л« '
3l
df* '
df-
dP
dt* *
Эти формулы получаются, если рассматривать х, у, z как постоян-
ные, так как переносными скоростью и ускорением точки М на-
зываются скорость и ускорение, которые имела бы эта точка, если бы
она была неизменно связана с подвижными осями.
Дифференцируя формулы A) по t, мы получим аналитическое
выражение теоремы, доказанной ранее (п. 45): абсолютная скорость
равна геометрической сумме относительной скорости и переносной
скорости.
После второго дифференцирования формул A) получим
d"-xx
dP
d"-x0
da dx dat dy da2dz
и две аналогичные формулы для вторых производных величин yt и zt.
Для уяснения смысла этих равенств рассмотрим вектор f, имеющий
начало в, точке М и следующие проекции на неподвижные оси:
Jx'—2\d7'dt
' __ о (d$ dx
Уг
rfctj dy , da2 dz\ ¦>
"Wdt^~dT~dt)' I
' dt dt^~ dtdl)' j
rf/ dt ' dt dt
dt2dz\
Этот вектор называется добавочным ускорением. Уравнения B)
показывают, что проекция вектора Ja на каждую из неподвижных
осей равна сумме проекций Jr, Je и f на ту же ось, т. е. что
вектор Ja есть геометрическая сумма векторов Jr, Je и /.

80
ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
Следовательно, абсолютное ускорение есть результирующая
относительного ускорения, переносного ускорения и добавочного
ускорения.
Остается найти простое истолкование вектора У. С этой целью
найдем проекции /х, f, J'z вектора / на подвижные оси. Очевидно,
имеем
Система отсчета (S), относительно которой рассматривается
относительное движение, представляет собой движущееся твердое
тело или неизменяемую систему. На основании полученных ранее
результатов мы знаем, что скорости ее различных точек в рас-
сматриваемый момент будут такими же, как если бы эта система
совершала поступательное движение и мгновенное вращение ш
с проекциями р, q, r на подвижные
оси, причем
^-^^1„ » = а-*гч-Р-л-ч-Гл
Jr-
\
со
1
г"
X
(SJ
/О,
'х,
Рис. 50.
динаты
dx
dt
dz
При помощи этих формул сразу на-
ходим:
dx	dz
Рассмотрим точку Vr (рис. 50),
имеющую в подвижных осях коор-
т. е. координаты конца вектора OV'r
dt ' dt
с началом в точке О, равного и параллельного относительной ско-
рости Vr. Тогда проекции У на оси х, у, г равны удвоенным
проекциям скорости, которую будет иметь эта точка Vr, если
угол a>OVr, предполагаемый неизменяемым, будет вращаться с угло-
вой скоростью со вокруг 0<fl, как вокруг неподвижной оси. Следо-
вательно, вектор У по величине и направлению равен удвоенной
этой скорости, т. е. удвоенному моменту вектора ш относительно
точки Vr. Этот вектор приложен в точке М. Более подробно его
можно определить так: вектор У перпендикулярен плоскости u>OVr
мгновенной оси и относительной скорости; он равен по величине

ГЛАВА II. КИНЕМАТИКА
81
удвоенному произведению ш на расстояние от точки Vr до оси Ош,
т. е. 2<oVrsin(o), Vr); наконец, он направлен по отношению к пло-
скости mOVr в ту сторону, куда мгновенное вращение ш стремится
повернуть конец V'r вектора OV'r, параллельного относительной
скорости. Итак, имеем:
(Va) = (vr)+<Уе). (Ja) =
Рис. 51.
Вектор / обращается в нуль, если один из трех множителей: о>,
или Vr, или sin(o), Vr) — обращается в нуль. Наиболее важными
являются следующие случаи.
60.	Поступательное движение подвижных осей. Сложение
движений. Если ш все время равно нулю, то и добавочное
ускорение будет все время равно нулю. Для того чтобы это
имело место, необходимо и достаточно, чтобы подвижные оси пере-
мещались поступательно. Абсолют-
ное ускорение Ja будет тогда ре-
зультирующим вектором относитель-
ного ускорения Jr и переносного уско-
рения Je.
Этот частный случай относительного
движения носит название сложения
движений. Для определения поступа-
тельного движения подвижных осей,
которые можно тогда предполагать
параллельными неподвижным осям
(рис. 51), достаточно определить дви-
жение одной точки О подвижной системы отсчета, что может быть
сделано заданием изменения вектора Ofi в функции времени.
Относительное движение точки М определяется изменением век-
тора ОМ. Абсолютное движение точки М, определяемое изменением
результирующего вектора OtM, называется результирующим двух
первых движений. Согласно предыдущему скорость и ускорение
в этом движении равны геометрическим суммам скоростей и ускоре-
ний составляющих движений.
61.	Общие формулы для скорости и ускорения точки, отне-
сенной к подвижным осям. Допустим, что подвижный триэдр Охуг
совершает известное движение. Обозначим, как и выше, через V%,
Vy, V° проекции абсолютной скорости V0 начала О на подвижные
оси, а через р, q, r—компоненты мгновенного вращения триэдра Охуг
относительно тех же осей.
Скорость. Рассмотрим точку М, имеющую относительно
осей Охуг координаты х, у, г. Относительная скорость Vr
точки М относительно триэдра имеет на подвижные оси проекции
df dt '
dt

82
ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
а переносная скорость той же точки имеет проекции (п. 51)
Vx-\-qz— ry, Vy-\-rx — pz, V°-\-py — qx.	(Ve)
Абсолютная скорость Va этой же точки, равная геометрической
сумме скоростей Vr и Ve, имеет проекции
dx
dt
-pz,
¦qx
C)
' J
Ускорение. Для получения проекций абсолютного ускорения
точки М на оси Oxyz достаточно обратиться к определению уско-
рения при помощи годографа (п. 41). Через некоторую неподвиж-
ную точку А проведем три оси Axv Ayx, Аг1г параллельные
осям Ox, Oy, Oz, и отрезок Ат, равный и параллельный абсо-
лютной скорости Va точки М. Искомое ускорение Ja равно и
параллельно абсолютной скорости точки т. Но эта точка т имеет
относительно осей Ax^Zi координаты
xl = Vax, y1 = Vay, zx^Vaz.	(m)
Скорость начала А равна нулю и мгновенное вращение триэдра Ax1y1z1
совпадает с мгновенным вращением параллельного триэдра Oxyz.
Следовательно, проекции на Ax1ylzl или Oxyz абсолютной скорости
точки т, согласно формулам, аналогичным C), равны
Поэтому для проекций абсолютного ускорения Ja имеем:
¦*ах —¦
•lay —
dt
dV,
ay
dt
+ rVax—pVaz,
^-jF+pVay—qv.
D)
Эти формулы позволяют другим путем доказать теорему
Кориолиса.
УПРАЖНЕНИЯ
1. Найти траекторию движущейся точки, зная, что она плоская и что
касательная и нормальная составляющие ускорения постоянны.
Ответ. Отсчитывая время от надлежащим образом выбранного мо-
мента и дугу s траектории от надлежащим образом выбранного начала,
найдем
%fi	4a
S = at2, 	=Ь, а = —,- s,
Р	b

ГЛАВА II. КИНЕМАТИКА	83
где р — радиус кривизны, а и Ь — постоянные. Траектория — логарифми-
ческая спираль.
2. Плоское движение определено двумя уравнениями, выражающими
полярные координаты гиб движущейся точки в функции времени. Тре-
буется найти либо непосредственно, либо при помощи теории относитель-
ного движения компоненты скорости и ускорения по радиусу-вектору и по
перпендикуляру к нему.
Ответ. Компоненты скорости —
dr
компоненты ускорения —
~df' Г~Ж
df>- \dt) ' r dt \ dt
3.	Точка описывает лемнискату
г2 = 2а2 cos 26
с постоянной по величине скоростью а. Выразить координаты точки в
функции времени и вычислить ускорение. (Эта задача предполагает зна-
комство с эллиптическими функциями.)
Ответ. Пусть s — дуга кривой, отсчитываемая от точки, для которой
6 = 0. Тогда
at = s = _ С	2а2 д>
U ~S J аУ2~УBа2 + г2)Bа2 — г2) '
откуда
г = a Y-2 cnt, cos 6 = dnt, sin 6 = ——¦ snt,
где модуль эллиптических функций равен 	. Отсюда непосредственно
найдутся х и у в функции времени.
4.	Показать, что при движении твердого тела в заданный момент
времени:
а)	геометрическое место точек тела, скорости которых пересекаются
в заданной точке, есть пространственная кубическая кривая;
б)	геометрическое место направлений этих скоростей есть конус вто-
рого порядка;
в)	геометрическое место точек, скорости которых равны по величине,
есть цилиндр вращения вокруг мгновенной винтовой оси (Шаль).
5.	Те же вопросы для ускорений.
6.	При движении твердого тела плоскости, перпендикулярные к траек-
ториям точек, лежащих в одной плоскости, проходят через одну точку.
Плоскости, перпендикулярные к траекториям точек, лежащих на одной
прямой D, проходят через одну прямую Д. Плоскости, перпендикулярные
к траекториям точек, лежащих на поверхности порядка т, огибают поверх-
ность класса т (Шаль). (Эти свойства непосредственно вытекают из свойств
плоскостей и их фокусов, указанных в п. 17.)
7.	Плоскости, перпендикулярные к траекториям двух произвольных
точек а и Ь тела, пересекают мгновенную винтовую ось D в двух точках а
и р, являющихся основаниями перпендикуляров, опущенных из а и А на
указанную ось, так что
ap = a6cos(a6, D) (Шаль),
8.	Если скорости, которыми обладают в один и тот же момент времени
различные точки тела, рассматривать как бесконечные прямые, то они

84	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
образуют комплекс второго порядка, конические сечения которого являются1
параболоидами (задача, аналогичная задаче 8 предыдущей главы).
9.	В движущемся твердом теле скорости различных точек в момент t
проектируются на плоскость, перпендикулярную к центральной оси. По-
казать, что эти проекции перпендикулярны к прямым, соединяющим проек-
ции точек на эту же плоскость с точкой ее пересечения с центральной
осью.
10.	Построение мгновенной винтовой Оса по Понселе. Через произ-
вольную точку О пространства проводят три вектора OV, OV, OV", рав-
ных скоростям трех точек тела М, М', М". Мгновенная винтовая ось
перпендикулярна плоскости ж трех точек V, V, V". Пусть т и т' —
проекции на эту плоскость двух из этих точек, М и М', a mv a m'v' —
проекции их скоростей. Перпендикуляры, восставленные в точках т и т'
к mv и m'v', пересекаются в точке встречи оси с плоскостью п. Ось таким
образом определена.
11.	Твердое тело вращается вокруг неподвижной точки. Показать, что
если мгновенная ось занимает постоянное положение в теле, то она зани-
мает также постоянное положение и в пространстве, и движение является
вращением вокруг неподвижной оси.
Обратно, если мгновенная ось неподвижна в пространстве, то она не-
подвижна также и относительно тела.
12.	Рассмотрим пространственную кривую, отнесенную к неподвижным
осям OxX^y^z^, и движущуюся по ней точку О, координаты которой являются
заданными функциями дуги s. Предположим, что движение точки О опре-
деляется уравнением s = t и рассмотрим прямоугольный триэдр Oxyz, обра-
зованный касательной Ох, направленной в сторону движения, главной
нормалью Оу, направленной в сторону радиуса кривизны р, и бинормалью Oz.
а)	Найти проекции р, q, r мгновенного вращения подвижного триэдра
на подвижные оси.
Ответ.
р =	, q = 0, г = — (т — радиус кручения)
б)	Найти уравнения мгновенной винтовой оси.
13.	Показать, воспользовавшись предыдущими результатами, что если
— = const, то кривая является винтовой линией, проведенной на произ-
вольном цилиндре (Бертран).
[Рассмотреть вспомогательный триэдр О^х'у'г' с неподвижной верши-
ной и с ребрами, параллельными подвижным осям Oxyz. Если — = const,
то мгновенная ось вращения этого нового триэдра будет неподвижна
относительно его и, следовательно, неподвижна в пространстве
(задача 11), а касательная Ох образует с направлением этой неподвижной
оси постоянный угол.]
14.	Прямая АВ пространства связана с неподвижной осью Oz, вокруг
которой она вращается с постоянной угловой скоростью со. Твердое тело С,
связанное с прямой АВ, вращается вокруг нее с той же относительной
угловой скоростью со.
Найти для этого тела мгновенную винтовую ось, неподвижную линей-
чатую поверхность ?^ и подвижную линейчатую поверхность ?.
15.	Круглый цилиндр С катится внутри круглого цилиндра С вдвое
большего радиуса и одновременно скользит параллельно образующей,
причем так, что одна из точек цилиндра С описывает неподвижную прямую,
обязательно пересекающую ось цилиндра С.
Показать, что в этом движении все другие точки тела описывают эллипсы.

ГЛАВА II. КИНЕМАТИКА	85
Это движение, если не считать движения, параллельного плоскости,
является единственным, при котором все точки движущегося тела описы-
вают плоские кривые. (См. Darboux, Comptes Rendus, XCII, или Annales
de l'Ecole Normale, 1890.)
16.	Показать, что непрерывное движение твердого тела может быть
получено следующим способом, указанным Пуансо. Конус С неизменяемой
формы, связанный с телом, катится без скольжения по конусу Ct также
неизменяемой формы, совершающему поступательное движение.
17.	Геометрическое место осей кривизны траекторий различных точек,
лежащих на прямой линии, для точек этой прямой есть гиперболоид;
геометрическое место центров соприкасающихся сфер есть пространствен-
ная кривая третьего порядка (Mannheim).
18.	К теореме Кориолиса. Если мгновенное вращение подвижной системы
отсчета есть результирующая двух вращений со' и со", то и добавочное ускоре-
ние У есть результирующая двух добавочных ускорений, соответствующих
составляющим вращениям со' и со". Если относительная скорость Vr есть
результирующая двух относительных скоростей Vr и Vr, то добавочное
ускорение У есть результирующая двух добавочных ускорений, соответ-
ствующих составляющим скоростям Vr и Vr (Resal).

ГЛАВА III
ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ. МАССА И СИЛА
Механика опирается на небольшое число основных законов, кото-
рые невозможно вывести непосредственно и к которым пришли
длинным путем индукций. Полученные из них следствия подтвер-
ждаются наблюдениями. Первая идея этих законов принадлежит
Галилею, который при исследовании законов падения тел (наклонная
плоскость, маятник, параболическое движение) ввел понятия инерции,
ускорения, сложения движений. Гюйгенс был продолжателем Галилея
в теории движения точки. Он же первый изучал движение материаль-
ной системы. Наконец, Ньютон расширил область механики откры-
тием закона всемирного тяготения.
Мы не ставим своей целью дать критический анализ основных
законов механики. Это один из наиболее тонких вопросов, требую-
щий дальнейших исследований.
I. Основные законы
62.	Неподвижные оси. Мы будем относить положение всех тел
к некоторой системе осей, которые, по определению, мы будем
считать абсолютно неподвижными осями. Эта система осей является
триэдром, с вершиной в центре тяжести солнечной системы и с реб-
рами, направленными на три звезды, называемые неподвижными
звездами.
63.	Время. Время, которым мы будем пользоваться, есть среднее
время, определяемое в космографии.
64.	Материальная точка. Для того чтобы начать с наиболее
простых задач рассматривают сперва движение настолько малой
частицы материи, что ее положение, без существенной ошибки,
может быть определено как положение геометрической точки. Такую
частицу материи называют материальной точкой. В дальнейшем
тела рассматриваются как совокупность очень большого числа мате-
риальных точек.
Одновременно с изменением положения материальная точка мо-
жет вращаться и деформироваться, но мы будем здесь заниматься

ГЛАВА III. ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ	87
только ее положением, не интересуясь тем, как она вращается и
деформируется.
Наблюдения и опыт показывают, что материальные точки воз-
действуют друг на друга. Так, например, 'материальные точки, обра-
зующие тело, называемое твердым, действуют друг на друга таким
образом, что форма тела почти сохраняется, когда его пытаются
деформировать; две наэлектризованные точки притягиваются или
отталкиваются; и т. д.
65. Основные законы. Первый основной закон. Все материаль-
ные точки, предоставленные самим себе, не имеют ускорения.
Этот закон может быть выражен еще так: материальная точка,
предоставленная самой себе, сохраняет свою скорость по величине
и направлению; она совершает относительно неподвижных осей прямо-
линейное равномерное движение; в частном случае движения может
и не быть. Этот закон известен под названием закона инерции.
Рис. 52.
Второй основной закон. Две материальные точки сообщают
друг другу ускорения, лежащие вдоль прямой, их соединяющей,
и направленные в противоположные стороны (см. оба чертежа на
рис. 52).
Изучение условий, при которых эти ускорения возникают, является
предметом экспериментальной физики. Ускорения могут возникнуть
вследствие того, что точки наэлектризованы или вследствие того,
что они друг на друга давят, или вследствие ньютоновского при-
тяжения и т. д.
Третий основной закон. Отношение численных значений уско-
рений, которые две произвольные материальные точки А к В сооб-
щают друг другу, постоянно. Другими словами, это отношение
будет одним и тем же, каковы бы ни были физические условия
возникновения ускорений, будь то наэлектризованность, взаимное
давление, ньютоновское действие и т. д.
Вследствие этого мы можем выразить отношение ускорения
точки В к ускорению точки А при помощи дроби, числителем кото-
рой является произвольно выбранная величина, которую мы обозна-
чим тд, а знаменателем другая величина тв, зависящая только от
природы точек А и В.

88	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
Таким образом, имеем
ускорение точки В тА
ускорение точки A ms
Если теперь, сохраняя точку А, возьмем вместо точки В другую
материальную точку С, то мы сможем опять выразить отношение
ускорений точек С к А дробью, числитель которой есть уже из-
бранная величина тА, а знаменатель другое число тс, характеризуе-
мое совокупностью точек А к С. Имеем, таким образом,
ускорение точки С тА
ускорение точки A nig
То же самое справедливо для всех точек D, E, F	при-
соединенных к точке А. Для каждой из них будет свой знамена-
тель mD, тЕ, тр, . ..
Образуем таблицу величин тА, тв	полученных, как мы сей-
час говорили:
тА- тв< тс	тк, ...
Эта таблица позволяет нам ответить на следующий вопрос.
К точке А присоединена какая-нибудь точка К; требуется найти
отношение ускорений, которые они сообщают друг другу. Для этого
следует только написать
ускорение точки К тА
ускорение точки А тк
Однако составленная таблица может служить для решения про-
блемы значительно более общего вида, благодаря следующему пред-
ложению, которое дополняет третий закон.
Отношение ускорений, которые две произвольные материальные
тоЧки Р и Q сообщают друг другу, равно отношению ускорений
точки Р и какой-нибудь другой точки, например А, деленному на
отношение ускорений точек Q и А, т. е.
отношение ускорений точек Р и А
отношение ускорений точек Р и Q =
отношение ускорений точек Q и А'
Следовательно, таблица величин тА, тв, ... позволяет нам ответить
на следующий вопрос: каково отношение ускорений двух произ-
вольных материальных точек? Это отношение равно обратному отно-
шению соответствующих величин т таблицы. (Можно заметить аналогию
между свойствами этой таблицы и свойствами таблицы химических
эквивалентов.)
Величины тА, тв, ... называются массами точек А, В, . . . *)
*) Раскрытие физического смысла понятия массы не является задачей
механики. (Прим. перге.)

ГЛАВА III. ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ	89*
Подведем итоги сказанному. Отношение масс двух точек равно,
по определению, обратному отношению ускорений, которые эти
точки друг другу сообщают. Если численное значение одной из масс
выбрать произвольно, то численные значения всех остальных масс
станут вполне определенными.
Четвертый основной закон. Ускорение, сообщаемое произволь-
ной материальной точке М совокупностью нескольких материальных
систем Sv S2, S3, . .. получается сложением по правилам сложения
векторов ускорений, которые сообщили бы точке М каждая из систем;
Sy, S2, S3, ..., если бы она действовала отдельно.
Все это будет строго верным лишь для абсолютных движений
относительно указанных выше неподвижных осей. Однако только
в астрономии и в некоторых исключительных опытах (например,
в маятнике Фуко) приходится действительно пользоваться указанными
осями. В огромном большинстве случаев в качестве неподвижных
осей можно принимать оси, связанные с Землей. Как показывают
наблюдения, в согласии с теорией относительных движений никаких
заметных неточностей при этом не получается.
66.	Силы. Слово сила не входит в основные законы динамики,
которые мы только что указали. В действительности, можно обойтись.
и без него. Предметом динамики является следующее: «Зная движе-
ния, которые происходят при некоторых заданных условиях, опре-
делить, какими они будут при других заданных усло-
виях». В эту задачу входят только тела и движения и ™
нет необходимости вводить сюда третьи элементы.
Тем не менее представляется удобным, с точки зре-
ния краткости, условиться о следующем. Если какая-ни-
будь точка М массы т, вследствие присутствия одной
или нескольких других материальных точек, испытывает
ускорение У, то мы будем условно говорить, что точка М
подвергается со стороны этой одной или этих нескольких
материальных точек действию силы, равной по величине
и направлению mJ. Этот вектор mJ и есть, по определе- Рис- 53"
нию, сила, действующая на точку М. Если обозначить
ее через F, то (F) — (mJ) (рис. 53). Мы видим, что сила есть поня-
тие производное, определяемое при помощи других величин. Вектор
силы есть вектор пол'ярный, так же, как и ускорение.
67.	Закон равенства действия и противодействия. Ньютон
под названием начала равенства действия и противодействия
провозгласил следующий закон. Если точка М подвергается действию
силы F, вызванной присутствием другой точки М', то эта сила
направлена по ММ', а вторая точка М' подвергается со стороны
точки М. действию силы, равной и прямо противоположной силе F.
Ньютон выразил это, говоря, что противодействие равно и противо-
положно действию. Это начало уже содержится неявно в данных выше,
законах. В самом деле, если точка М массы т подвергается действию

90	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
силы F, то это означает, что она имеет ускорение У, равное гео-
метрически (—)• Согласно второму основному закону точка М'
испытывает ускорение, направленное в противоположную сторону и
определяемое соотношением
j т 	 ^ у т 	 F
т. е. эта точка подвержена действию силы F', равной и прямо
противоположной силе F. Это и есть закон Ньютона.
Закон равенства действия и противодействия непосредственно
распространяется на взаимное действие двух произвольных систем
точек (S) и (S').
Если точки системы (S) действуют на точки системы (S')
некоторыми силами, то и наоборот, точки (S') оказывают дей-
ствие на (S), выражаемое силами, равными
и прямо противоположными первым.
Так, например, если рукой давить на стену,
то со стороны стены рука будет испытывать про-
тиводействие, выражаемое силой, равной и про-
^ . тивоположной давлению руки. Когда лошадь тянет
3 экипаж, то действие постромок на экипаж равно
и противоположно действию экипажа на постромки
и т. д.
68. Сложение сил. Равнодействующая. Чет-
вертый закон приводит непосредственно к пра-
вилу сложения сил.
Допустим, что система Sx, действуя одна
на материальную точку М, сообщает ей уско-
рение Jt. Следовательно, она действует на точку с силой Fx (рис. 54),
определяемой векторным равенством
Точно так же вторая система S2, действуя одна, сообщает точке М
при том же положении и той же скорости ускорение У, и действует
на нее с силой
и т. д. и, наконец, система Sn, действуя одна, сообщает точке М
ускорение Jn и действует на нее с силой
Если все эти силы будут приложены к точке М одновременно,
то при тех ;ке условиях они сообщат ей ускорение У, равное гео-
метрической сумме ускорений Jv У2	Уп:

ГЛАВА III. ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ	91
Сила F, которая одна сообщает точке такое же ускорение J
(рис. 54), будет
и, следовательно,
Эта единственная сила F, называемая равнодействующей данных
сил Ft, F2, ..., Fn, представляется результирующим вектором си-
стемы векторов Fv F2	Fn.
Таким образом, к сложению и разложению сил можно применить-
все, что было сказано о сложении и разложении сходящихся векторов.
69. Уравнения движения. Допустим, что на точку М массы т
действуют силы, представляемые в момент t векторами Flt F2, . . ., Fn.
Обозначим через х, у, z координаты точки М, а чере*
(Xiy Yv Zt), (Х2, Y2, Z2)	(Хп, Yn, Zn) проекции сил на оси
координат. Проекции X, Y, Z равнодействующей F будут
а проекции ускорения J—
~di*' ~W' ~W'	W
Следовательно, векторное равенство (F) = m(J) после проектиро-
вания на оси приводится к соотношениям
которые являются уравнениями движения.
В наиболее общем случае, который может представиться, равно-
действующая F зависит от положения точки, т. е. от ее коорди-
dx rfy dz
нат х, у, г, от скорости точки, т. е. от —, —, -тт и от времени.
В этом случае имеем
*-•(*.*«¦?.&?•<)
и два аналогичных выражения для Y и Z. Для того чтобы найти
движение точки под действием заданных сил, нужно проинтегрировать
уравнения движения, которые являются дифференциальными уравне-
ниями второго порядка, определяющими х, у, г в функции t.
Мы ограничиваемся здесь только указанием этой задачи. Подробно
она будет рассмотрена в начале динамики.
70. Равновесие. Несколько сил находятся в равновесии, если,
будучи приложены к точке, находящейся в покое, они не сообщат
ей никакого движения. Геометрическая сумма ускорений, вызываемых
этими силами, равна нулю. Следовательно, геометрическая сумма

92	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
этих сил, т. е. их равнодействующая, тоже равна нулю. Это условие,
необходимое для равновесия, будет, очевидно, и достаточным.
Вообще, материальная система находится в равновесии, если,
будучи в покое, она не получит никакого движения от сил, которые
на нее подействуют.
71.	Статика. Динамика. Та часть механики, где изучаются усло-
вия, которым должны удовлетворять действующие на систему точек
силы, для того чтобы система находилась в равновесии, называется
статикой. Та часть механики, где изучаются соотношения между
силами и вызываемыми ими движениями, называется динамикой.
Мы начнем с изучения статики, которая является не чем иным,
как особого вида геометрией. После этого мы будем изучать дина-
мику. Этот порядок оправдывается теми соображениями, что благо-
даря принципу Даламбера составление уравнений какой-нибудь задачи
динамики может быть приведено к решению задачи статики.
С исторической точки зрения статика является наиболее древней
частью механики. Действительно, статика восходит еще к Архимеду,
установившему в своем труде De cequiponderantibus принцип рычага.
Что же касается динамики, то ее возникновение стало возможным
лишь после открытий Галилея.
II. Единицы массы и силы; однородность
72.	Тяжесть. Вес. Тяжелая точка, падающая без начальной ско-
рости с небольшой высоты, совершает по отношению к Земле прямо-
линейное равноускоренное движение по вертикали. Ускорение g этого
движения, изменяющееся с широтой места и с высотой над уровнем
океана, имеет для Парижа значение 9,808 м/сек2. Вследствие движения
Земли этому относительному движению соответствует абсолютное дви-
жение, которое не является прямолинейным и равномерным. Отсюда
следует заключить, что на тяжелую точку со стороны Земли дей-
ствует некоторая сила; эта сила есть притяжение Земли.
Если тяжелая материальная точка удерживается каким-нибудь
препятствием, то действие Земли на нее продолжается, но эффект
этой силы изменяется. Это получается вследствие того, что препят-
ствие также оказывает на точку некоторое действие. Так, например,
если тяжелая точка, подвешенная к концу нити, неподвижна относи-
тельно Земли, то нить оказывает на нее некоторое действие, которое
является натяжением нити. Абсолютным весом точки называют
салу, равную и противоположную этому натяжению.
Если бы Земля была неподвижна, то материальная точка, под-
вешенная к нити, находилась бы в равновесии под действием натя-
жения нити и притяжения Земли. Последнее было бы, следовательно,
равно и противоположно натяжению нити, т. е. равнялось бы абсо-
лютному весу точки. Но в действительности материальная точка
яи неподвижна, ни движется прямолинейно и равномерно; натяжение

ГЛАВА III. ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ	93
и притяжение не находятся в равновесии и абсолютный вес отли-
чен от притяжения. Эта разница, однако, весьма мала и в боль-
шинстве явлений ею можно пренебрегать. Мы увидим ниже, что
тяжелая материальная точка, падающая в пустоте с небольшой высоты,
движется относительно Земли почти так же, как если бы Земля была
неподвижна и точка находилась под действием своего абсолютного
веса. Так как это движение обладает постоянным ускорением g, то
абсолютный вес р является для одного и того же места постоян-
ной силой
p = mg.
Этот вес и ускорение g изменяются с широтой места и с высо-
той над уровнем океана.
Можно представить себе абсолютный вес еще таким образом.
Допустим, что материальная точка положена на неподвижную отно-
сительно Земли руку. Рука окажет на точку действие, являющееся
вертикальной силой, направленной кверху и равной по интенсивности
абсолютному весу точки. Наоборот, по закону равенства действия и
противодействия, рука будет испытывать со стороны точки давление,
направленное вниз и равное абсолютному весу по интенсивности и
направлению. Это ощущаемое рукой давление и дает некоторое пред-
ставление об абсолютном весе. Точно так же, если точку положить
на чашу весов, то давление будет совпадать с абсолютным весом.
73. Технические единицы. Килограмм-сила. В технике обычно
принимают следующие основные единицы:
единица силы	килограмм-сила
единица длины 	 метр
единица времени	секунда среднего времени
По определению, килограмм-сила—это абсолютный вес одного
килограмма в Париже, т. е. сумма абсолютных весов в Париже
материальных точек, составляющих один литр воды при ее
наибольшей плотности. Необходимо указывать, что этот абсолют-
ный вес взят в определенном месте земного шара, например
в Париже, так как абсолютный вес материальной точки изменяется
с изменением места.
В этой системе единица массы является производной единицей.
Масса точки определяется формулой
—f
где р — абсолютный вес, выраженный в килограмм-силах, a g —
ускорение тяжести. Если сделать p = g, то ти=1. Единица массы
есть, следовательно, масса точки, абсолютный вес которой равен g
килограмм-силам. В Париже, где g = 9,808 м\секг, единица массы
есть масса 9,808 литров дистиллированной воды при 4° С.

94	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
Неудобство этой системы состоит в том, что единица силы —
килограмм является величиной, определение которой требует указа-
ния определенного места земного шара. Более того, масса тела,
являющаяся физическим свойством, присущим самому телу, выра-
жается различными числами в зависимости от того, в какой точке
земного шара определен килограмм силы. Этого неудобства можно
избежать, как это показал еще Гаусс, если в качестве основных
единиц принять единицы длины, времени и массы и уже из них
вывести единицу силы.
74. Абсолютные единицы. Дина. В этой системе в качестве
основных единиц принимаются единицы длины, времени и массы.
Единица силы будет тогда производной. Эта система основана на
том, что можно различать массы различных тел при помощи весов.
В самом деле, допустим, что в определенной точке земного шара g
есть ускорение тяжести, а р, р', р", ...—абсолютные веса мате-
риальных точек с массами т, т', т"', ... Тогда будет
p = mg, p' = m'g, p" = m"g, ...
Следовательно, если р=р', то т — т', если р = рг-\-р", то
т — т'-\-т", ... Вообще, массы материальных точек пропорцио-
нальны их абсолютным весам в одном и том же месте, т. е. их
относительным весам, полученным при помощи взвешивания на весах.
Поэтому, выбрав произвольным образом единицу массы, мы полу-
чим возможность измерять массы. Интенсивности сил будут тогда
выражаться численно по формуле
где т — масса точки, на которую действует сила, a J—вызываемое
этой силой ускорение. Если положить т и ./равными единице, то сила F
будет равна 1. Следовательно, в этой системе единица силы есть
сила, сообщающая точке единичной массы ускорение, равное еди-
нице длины при выбранной единице времени. Сообразно принципам,
выработанным Британской комиссией в 1871 г., а затем Конгрессом
электриков в 1881 г. за основные единицы приняты: для длины —
сантиметр; для массы — грамм-масса, т. е. масса одного куби-
ческого сантиметра дистиллированной воды при 4° С; для времени —
секунда среднего солнечного времени. В этой системе единиц CGS
(сантиметр, грамм, секунда) масса тела выражается тем же числом,
что и его относительный вес в граммах. Единицей силы, называемой
диной, является сила, сообщающая массе в 1 г ускорение, равное
1 см/сек2.
Абсолютный вес одного грамма в Париже равен 980,8 дин, так
как такой абсолютный вес сообщает массе в 1 грамм ускорение
9,808 м/сек2, т. е. 980,8 см[сек2.
75. Статическое измерение сил. Система мер, при которой
за единицу принят абсолютный вес, была первой, вошедшей в упо-

ГЛАВА III. ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ	95
требление. Это вызвано было тем, что первое представление о силе
человек составил по тому усилию, которое он должен был делать,
чтобы удерживать какой-нибудь груз рукой. Отсюда сравнение сил
с весом. Это сравнение может быть сделано вполне точно при помощи
динамометра. Возьмем вертикальную пружину, удлинение которой
может быть измерено при помощи делений. Подвесим к этой пру-
жине в Париже веса в 1 кг, 2 кг, ... и отметим соответствующие
удлинения. Тогда для измерения произвольной силы, действующей
на материальную точку, мы можем закрепить эту точку на конце
пружины, установить ось пружины по направлению силы и отметить
соответствующее удлинение. Мы получим тогда величину силы
в килограммах.
Это статическое измерение сил является очень важным, так как
оно показывает, что основное соотношение
выражаемое уравнениями A), не является простым тождеством-
Возьмем, например, материальную точку, на которую действует сила,
зависящая только от ее положения. Придавая точке различные поло-
жения и измеряя статически силу в каждом из этих положений, мы
сможем узнать закон изменения силы в зависимости от положения
точки. Аналитически мы узнаем проекции X, Y, Z силы в функции
координат х, у, г точки. Если потом отпустить точку и подвергнуть
ее действию указанных сил, то она придет в движение, уравнения
которого в конечной форме получатся после интегрирования урав-
нений A). В этих уравнениях проекции X, Y, Z являются изве-
стными функциями координат х, у, г.
76. Однородность. Если для приложений имеется необходимрсть
в выборе определенных единиц, то для теории в этом нет надоб-
ности. В теоретических исследованиях целесообразнее оставлять
основные единицы неопределенными, с тем чтобы получаемые фор-
мулы могли быть применены при любой системе единиц. Так как
формулы должны оставаться верными при любом выборе трех основ-
ных единиц, то они должны обладать троякой однородностью отно-
сительно длины, времени и массы. Пусть / — длина, t — время,
т — масса, v — скорость, j— ускорение, /—сила, измеренные
в какой-нибудь системе основных единиц длины, времени и массы.
Если теперь принять единицу длины в X раз меньшую, единицу вре-
мени в т раз меньшую и единицу массы в [i раз меньшую, то мерами
только что указанных величин станут
л j	X . X , Хи,
/X, U, тц, V-, j-^, f-^,
так как скорость есть отношение длины ко времени, ускорение —
отношение длины к квадрату времени, а сила — произведение
ускорения на массу. Следовательно, если основные единицы не

96	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
установлены, то формулы должны оставаться справедливыми при
любых значениях множителей X, jj., т.
Например, полупериод малых колебаний простого маятника длины I
в месте, где ускорение тяжести равно g, определяется формулой
t = :
Если изменить единицы указанным выше способом, то получится
т. е. формула не изменяется. Следовательно, она действительно
однородна.
УПРАЖНЕНИЯ
1.	Установить формулы перехода от системы единиц метр, секунда,
килограмм-сила в Париже к системе COS.
2.	Предполагая известным, что период малых колебаний простого маят-
ника зависит только от длины I и ускорения g:
t = 9(l, g),
показать, исходя из условий однородности, что t имеет вид
где ft — отвлеченное число (ft = 2я).
3.	Предполагая, что скорость v тяжелого тела, предоставленного самому
себе и падающего в пустоте без начальной скорости, зависит только от
высоты падения h и ускорения g:
v = ? (Л, g),
показать, что v имеет вид
v = ft
где ft — отвлеченное число.
4.	Зная, что скорость звука в газе есть функция только упругости е газа
и его платности d, показать, что она определяется формулой
где ft — отвлеченное число (k — отношение теплоемкостей газа при постоян-
ном давлении и постоянном объеме). Упругость — это давление газа на еди-
ницу поверхности, а плотность — масса газа в единице объема.

ГЛАВА IV
РАБОТА. СИЛОВАЯ ФУНКЦИЯ
Прежде чем излагать статику, целесообразно ввести понятие
первостепенной важности о работе силы.
I. Материальная точка
77. Элементарная работа. Пусть к материальной точке М при-
ложена сила F. Допустим, что эта точка получает какое-нибудь бес-
конечно малое перемещение ММ' (рис. 55). Тогда элементарной
работой силы F на перемещении ММ' называют ска-
->		У-
лярное произведение F на ММ':
F ¦ ММ' • cos (FMM'),	A)
т. е. произведение силы на перемещение и на косинус
угла между направлением силы и направлением пере-
мещения. Эта элементарная работа является алгебраи-
ческой величиной, положительной, отрицательной или
равной нулю, в зависимости от того, будет ли угол FMM'
острым, тупым или прямым. Когда элементарная работа положи-
тельна, силу называют движущей, а когда отрицательна — сопро-
тивлением. Если перемещение ММ' совершается за бесконечно малый
.,	ММ'
промежуток времени at, то скорость v этого перемещения равна—-гг-,
и выражение A) элементарной работы может быть представлено
в виде
Fvcos(F, v) dt,	B)
так как угол между силой и скоростью совпадает с углом между
силой и перемещением.
Элементарная работа, которая может быть написана также в виде
ММ' ¦ [Fcos(F'MM')],
равна произведению перемещения ММ' материальной точки на про-
екцию силы на направление перемещения. Если к точке М
приложено несколько сил, то работа равнодействующей этих
сил на каком-нибудь перемещении равна сумме работ соста-
вляющих сил на том же перемещении. Это вытекает из того, что

98
ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
проекция равнодействующей на направление перемещения равна
сумме проекций составляющих.
Если работу написать в виде
F ¦ [MM'cos(FMM')],
то ее можно определить как произведение силы на проекцию переме-
щения на направление силы. Следовательно, если перемещение ММ'
есть геометрическая сумма нескольких перемещений, или если скорость
точки есть геометрическая сумма нескольких скоростей, то элемен-
тарная работа силы F, соответствующая результирующему переме-
щению или результирующей скорости, равна сумме элементарных
работ силы F, соответствующих составляющим перемещениям или
составляющим скоростям.
Если элементарная работа какой-нибудь силы равна нулю, то либо
перемещение равно нулю, либо сила равна нулю, либо сила пер-
пендикулярна к перемещению.
78. Аналитическое выражение элементарной работы. Пусть х,
у, г — координаты точки М относительно трех прямоугольных осей,
x-\-dx, y-\-dy, z-\-dz — координаты бесконечно близкой точки М'
и X, Y, Z — проекции силы F на эти оси. Направляющие косинусы
силы F и перемещения ММ' равны
К. Л JL dx лу dz
F ' F ' F • ММ' ' ММ' ' ММ' '
Вычисляя cos(FMM'), мы получим следующее выражение эле-
ментарной работы в прямоугольных декартовых координатах:
F • ММ' ¦ cos (FMMf) =
Ydy-{-Zdz.
Эту формулу можно получить непосредственно, пользуясь фор-
мулой C) п. 3 для скалярного
произведения двух векторов.
и1 J^	\	7^' Полная работа. Единица
^"*	работы. Допустим, что точка М
совершает конечное перемещение
Из положения Мо в положение Mt
вдоль какой-нибудь кривой М0М1
(рис. 56) по какому-нибудь закону
движения. В положении Мо точка
находится в момент ?0, а в поло-
жении М1 — в момент tx. Пусть
к точке М приложена сила F.
Тогда полной работой силы F
на рассматриваемом конечном перемещении называется сумма эле-
ментарных работ силы F на всех бесконечно малых последова-
тельных перемещениях, из которых складывается конечное пере-
мещение. Таким образом, дуга М0М разбивается на бесконечно малые
Рис 56.

ГЛАВА IV. РАБОТА. СИЛОВАЯ ФУНКЦИЯ	99
части М0М', М'М", ... и вычисляется сумма
ff = lim [Fo • MQM' • cos(F^M')+F' ¦ M'M" ¦ cos{FrMrM")+...],
где Fo— значение силы F, приложенной к точке, когда точка на-
ходится в положении Мо, F' — значение этой силы, когда движу-
щаяся точка находится в положении М' . .. Сумма оГ и есть пол-
ная работа силы F. Ее можно вычислить с помощью интеграла
§¦ = J Xdx+Ydy^Zdz,	A)
(Жо)
выражающего сумму элементарных работ. Например, если F всюду
нормальна к траектории, то все элементы суммы равны нулю и ра-
бота обращается в нуль.
Единица работы. Если основные единицы выбраны, то полная
работа единичной силы, приложенной к точке, совершающей пере-
мещение в единицу длины вдоль направления силы, получается рав-
ной единице. Эту работу и принимают за единицу работы. Напри-
мер, если за единицу силы принята килограмм-сила, а за единицу
длины метр, то полученная единица работы будет килограммометр,
В системе CGS единица работы называется эргом.
Для вычисления оГ полезно рассмотреть несколько частных случаев.
80. Сила зависит от времени или скорости. В наиболее общем
случае, который может представиться, сила зависит от положения
точки, от ее скорости и от времени, так что X, Y, Z являются
заданными функциями переменных
dx dy dz	.
х- у- z' -Ж'-Ж'чг и '¦
В этом случае для вычисления $" надо знать движение точки из Мо
в Мх, т. е. знать выражения
ее координат в функции времени. Тогда, подставляя эти выражения х,
у, z, а также получающиеся из них дифференцированием выражения
~Ж' ~df' ~dT в 0ПРеДеленныи интеграл A), приведем его к виду
§¦ = С ф (f) dt,
и
который и позволяет вычислить оГ.
81. Сила зависит только от положения движущейся точки.
В этом случае для нахождения § достаточно знать только кри-
вую С, по которой движущаяся точка перемещается из Мо в Mt.
При этом нет необходимости знать закон, по которому точка
перемещается по кривой, так что вычисление полной работы при-
водится к задаче геометрии. Действительно, в рассматриваемом

100	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
случае можно выразить координаты точки М кривой С в функции
некоторого параметра q, изменяющегося от q0 до qt, когда точка
описывает дугу М0Ми так что
x = <?(q). y = ty(q), z = m(q).
Компоненты X, Y, Z, завися только от х, у, z, будут вдоль
кривой С некоторыми функциями от q. Поэтому, подставляя в инте-
грал A) выражения х, у, z и получающиеся из них выражения для
dx, dy, dz, получим для него формулу
4о
которая и позволяет вычислить JT.
Если ту же самую кривую точка пробегает в противополож-
ном направлении, от М^ к Мо, то полная работа станет равной —JT,
так как пределы интегрирования поменяются местами.
82. Частный случай, когда JT зависит только от начального
и конечного положений. Силовая функция. Потенциальная энергия.
Допустим, что X, Y, Z являются функциями от х, у, z, непре-
рывными и допускающими частные производные первого порядка
во всех точках области пространства, в которой расположены все
рассматриваемые кривые. Выясним, ка-
кими должны быть функции
Х{х, у, z), Y(x, у, z), Z{x, у, z)
для того, чтобы полная работа на
конечном перемещении зависела только
от начального и конечного положе-
ний Мо и Mt и не зависела от формы
кривой, по которой перемещается точка.
рис 57	Возьмем сначала две бесконечно
близкие точки Мо и Mlt лежащие
в плоскости, параллельной ху (рис. 57), причем координаты точки Мо
равны х, у, z, а координаты точки Mt равны x-\-dx, у -{-dy, z. Пере-
ведем движущуюся точку из положения Мо в положение Mv пе-
ремещая ее сначала параллельно оси Ох на отрезок длиною dx
в положение М', а затем параллельно оси Оу на отрезок dy в поло-
жение Мх. Элементарная работа на перемещении М0М' равна
Х(х, у, z)dx. В положении М' сила будет иметь значение F' и
проекцию на ось Оу, равную Y(x-\-dx, у, г). Элементарная работа
силы/7' на перемещенииM'Mj^равна, следовательно, Y(x-\-dx, y,z)dy.
Отсюда для полной работы на перемещении М0М'Мх получаем
= Х{х, у, z)dx-\-Y(x-\-dx, у, z)dy.

ГЛАВА IV. РАБОТА. СИЛОВАЯ ФУНКЦИЯ	|QJ
Если сначала переместить точку параллельно Оу на отрезок dy
в положение М", а затем параллельно Ох на отрезок dx из М"
в Ми то для работы получим
§ = Y{x, у, z)dy + X{x, y + dy, z)dx.
Мы желаем, чтобы оба эти значения § были равны. Приравни-
вая их и замечая, что
Y{x + dx, у, z)=Y(x, у, z) + ~dx,
Х(х, y + dy, z) = X(x, у, z) + ^~dy,
после очевидных преобразований получим
дУ _ дХ
дх ду '
Поступая аналогичным образом в плоскостях, параллельных другим
координатным плоскостям, получим два других необходимых условия
дг__дУ_ дХ __ 6Z
ду дг ' дг дх '
Эти условия показывают, что выражение
Xdx-\-Y dy + Zdz
есть полный дифференциал некоторой функции U независимых пе-
ременных х, у, г. Покажем, что эти условия являются также и
достаточными, по крайней мере при некоторых ограничениях,
которые мы укажем.
В самом деле, если эти условия выполнены, то будет суще-
ствовать тождество
Xdx-\-Ydy-\-Zdz = dU(x, у, г),
из которого вытекают три других:
v—du v—du 7—ди
A—~dx~' W	~д7"
Функция U, определенная с точностью только до произвольной
аддитивной постоянной, называется силовой функцией. Говорят
также, что в этом случае силы имеют потенциал; величина —U
называется потенциальной энергией.
Полная работа силы F, когда точка переходит из Мо в Mt
вдоль кривой С (рис. 58), будет тогда
(ж,)	да
$= j Xdx + Y dy-\-Zdz= J dU=Ul—UQ,

102
ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
Рис. 58.
где U1 — конечное значение, которое принимает функция U в поло-
жении Мх при непрерывном ее изменении вдоль кривой, a Uo — на-
чальное значение функции U в положении Мо.
Следовательно, если в рассматриваемой области пространства U
является однозначной функцией от х, у, г, имеющей единственное
значение в каждой точке этой области, то Uo и Ux будут вполне
определенными и полная работа JT не будет зависеть от пути, по
которому точка переходит из Мо в Mt. В част-
ности, если точка описывает замкнутый путь,
то Mj совпадает с Мо и тогда полная работа
равна нулю.
Но если функция U является многозначной, как,
например, арктангенс, то полная работа не будет
абсолютно не зависящей от пути перехода точки
из Мо в Mt. Она будет меняться в зависимости
от того, какое из значений U мы должны будем в силу непрерыв-
ности принять в точке Ми когда будем исходить из определенного
значения Uo в точке Мо. Можно также сказать, что в этом случае
полная работа по замкнутому контуру не будет обязательно равна
нулю. Эти два способа выражения будут, впрочем, идентичны, так
как, если рассмотреть два пути С и С из Мо в Мг и обозначить
через Ш и JT' полную работу на конечных перемещениях M0CMt
и MOC'MV то полная работа на замкнутом перемещении МСМ^С'М
будет равна Ш — Ш'. Следовательно, если
<^Г = |Г', то полная работа равна нулю, а
если оГ Ф Ш', то не равна нулю.
Пусть, например, U = arctg —. Проекции
силы F, равные
Y = ¦
У
'Р
Рис. 59.
являются непрерывными дифференцируемыми
функциями во всей части пространства, рас-
положенной вне кругового цилиндра сколь
угодно малого радиуса, ось которого совпа-
дает с осью Oz (рис. 59). Функция U есть
угол хОР, образованный осью Ох с проек-
цией ОР радиуса-вектора ОМ на пло-
скость ху. Поэтому, если движущаяся точка описывает замкнутую кри-
вую МСМ, не окружающую ось Oz, то полная работа равна нулю, так
как функция U при непрерывном изменении вдоль контура С принимает
в точке М свое первоначальное значение. Но если точка описывает
замкнутую кривую МСМ, окружающую один раз в положительном
направлении ось Oz, то изменение функции U будет равно 2п,
и полная работа будет также равна 2%. Если точка совершит вокруг
оси Oz в положительном направлении п оборотов, то полная работа будет
равна 2г№.
Эти соображения указаны Бертраном (Journal de I'Ecole Polytechnique,
вып. 28).

ГЛАВА IV. РАБОТА. СИЛОВАЯ ФУНКЦИЯ	ЮЗ
Вообще, для случая, когда существует силовая функция, можно
установить предложение, которое мы только выскажем, не вдаваясь
в слишком пространные аналитические подробности.
Если замкнутую кривую можно непрерывной деформацией стя-
нуть в точку, не пересекая при этом никакой точки, в которой
функции X, Y, Z перестают быть непрерывными и дифференцируе-
мыми, то полная работа силы F на этой замкнутой кривой равна
нулю.
Доказательство этого предложения может быть легко получено,
если исходить из приводимой ниже формулы.
Когда кривая С стягивается в точку Р, то ее последовательные
положения образуют некоторую поверхность S, на которой, по
предположению, функции X, Y, Z конечны, непрерывны и дифференци-
руемы. Справедлива следующая формула (формула Ампера—Стокса):
(С)	(S)
где первый интеграл берется по кривой С, а второй — по поверх-
ности 5. В силу самих условий, определяющих существование сило-
вой функции, элементы двойного интеграла по поверхности 5 всюду
равны нулю, вследствие чего § = 0.
83. Поверхности уровня. Сделаем несколько важных замечаний,
относящихся к случаю, когда существует силовая функция U.
Пусть М(х, у, г) — одно из положений материальной точки,
a My' — полупрямая, параллельная оси Оу (рис. 60). Проекция
с-	dU
силы г на эту полупрямую равна -у—, т. е. равна пределу отношения
U' —U
ММ'
когда ММ' стремится к нулю. Здесь М' — точка на полупрямой My'
и U' — значение функции U в этой точке. Так как направление
оси Оу может быть выбрано произвольно, то мы видим, что проек-
ция силы F на произвольное направление MD равна пределу от-
ношения
U" — U
ММ"
когда ММ" стремится к нулю, где М" — точка на прямой MD,
a U" — значение функции U в этой точке. Этот предел называется
производной функции U по направлению MD.

104
ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
Поверхности, определяемые уравнением
U(x, у, z) = C,
где С—постоянная, называются поверхностями уровня. Изменяя
непрерывным образом С, мы получим семейство таких поверхностей,
причем через каждую точку области пространства, в которой опреде-
лена функция U, проходит одна из этих поверхностей. Сила, действую-
щая на материальную точку в каком-нибудь ее положении М, нор-
мальна к поверхности уровня 5, проходящей через М, так как ее
Рис. 60.
проекции равны трем частным производным функции U или функ-
ции U—С. Более того, сила F направлена относительно этой по-
верхности в ту ее сторону, в которую функция U возрастает.
В самом деле, пусть MN — нормаль к поверхности уровня U, на-
правленная в сторону возрастания U. Проекция силы на эту нормаль
совпадает с самой силой. Она будет положительной или отрица-
тельной в зависимости от того, будет ли сила направлена по ММ
или в противоположную сторону. Так как эта проекция равна
lim
Ui —
где Mj — точка на MN, бесконечно близкая к М, то она положи-
тельна, ибо, по предположению, Ux > U. Таким образом, сила на-
правлена по нормали MN и ее величина F равна производной от
функции U по этой нормали, что символически может быть обо-
значено следующим образом:

ГЛАВА IV. РАБОТА. СИЛОВАЯ ФУНКЦИЯ	105
Проведем поверхность уровня SlF бесконечно близкую к S, со
стороны возрастания U. Эта поверхность пересечет какую-нибудь
нормаль MN в некоторой точке Mv Так как U принимает на по-
верхности St постоянное значение Ult то выражение
г г	т г
F = \im
в котором числитель постоянен для всех положений точки М на
поверхности 5, показывает, что сила изменяется обратно пропор-
ционально отрезку нормали к поверхности уровня 5, заключенному
между этой поверхностью уровня и поверхностью уровня, бесконечно
близкой к ней.
Поэтому распределение сил в рассматриваемом поле можно при-
ближенно представить следующим образом.
Пусть s — постоянная, выбираемая тем меньшей, чем лучшим
желательно получить приближение. Построим поверхности уровня
U=0, U = e, U=2e, ..., U = пе
U = — 8, ?/ = —2s, .... U = —ks, ...
и припишем этим поверхностям номера 0, 1, 2,..., п
— 1, —2, ..., —k, ... В точке М какой-нибудь из поверхно-
стей 5, имеющей номер р, построим нормаль в сторону поверх-
ности Sv имеющей номер р-\-\, и обозначим через М^ точку пере-
сечения этой нормали с поверхностью St. Тогда сила в точке М
направлена в сторону ММ^ и имеет приближенное значение F = е -
ММХ
84. Примеры. 1°. Сила, перпендикулярная неподвижной плоскости и
являющаяся функцией расстояния от движущейся точки до этой плоскости,
имеет силовую функцию. В самом деле, примем эту плоскость за плоскость ху
(рис. 61, а). Тогда сила будет параллельна оси Oz, проекции X и Y будут
равны нулю, a Z будет функцией только z: Z = <р (г). Элементарная работа,
равная Zdz или ydz, является полным дифференциалом функции U.
Поэтому
Поверхностями уровня будут плоскости, параллельные плоскости ху.
Так, например, если сила есть вес точки М, то, направляя ось г вертикально
вверх, получим
Z = — mg, U = — mgz -\- const.
2°. Сила, направленная по перпендикуляру, опущенному из точки М на
неподвижную ось, и являющаяся функцией расстояния от точки до этой
оси, имеет силовую функцию.
Примем эту ось за ось Oz и обозначим через р расстояние MQ от
точки М до оси и через Ф — значение силы, считая ее положительной
в направлении QM (рис. 61, б). Проекции этой силы будут
Х=Ф— , У=Ф-^-, Z=0.
р	р

106
ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
Так как р2 = л:2 + у2 и, следовательно, р dp = x dx + у rfy, то для элементар-
ной работы получаем выражение
Xdx + Ydy + Zdz = —(х dx + у dy) = Ф dp.
По предположению, Ф зависит только от р, и поэтому элементарная
работа есть полный дифференциал функции U (р), равной
?/ =
Поверхностями уровня являются цилиндры вращения вокруг оси Ог.
3е. Наконец, существует силовая функция и для силы, направление кото-
рой постоянно пересекает неподвижную точку О и которая зависит только
от расстояния движущейся точки до О (рис. 61, в).
а)
Примем точку О за начало и пусть г — расстояние ОМ, a F—величина
силы, которую мы будем считать положительной в направлении ОМ. Тогда
проекции силы равны
Fir. i-i. i-i.
и элементарная работа имеет вид
F_
г
= Fdr,
так как из соотношения х2 + У2 + ¦г2 = г2 после дифференцирования получим
xdx-\-ydy-\-zdz = rdr. По предположению F зависит только от г, по-
этому элементарная работа есть полный дифференциал функции U (г), равной
U
= С
Fdr.
Поверхностями уровня являются сферы с центром в точке О.
В частности, если точка т притягивается к неподвижному центру О
силой, обратно пропорциональной квадрату расстояния, то
F--2-
2 >

ГЛАВА IV. РАБОТА. СИЛОВАЯ ФУНКЦИЯ	107
где (л — положительный коэффициент, так как сила, направленная в сто-
рону МО, отрицательна. Тогда
В этом примере полная работа силы, когда точка переходит из бес-
конечно удаленного положения Мо в положение Mi, расположенное на рас-
стоянии r-i от притягивающего центра О, будет
Все три предыдущих закона сил являются частными случаями следую-
щего. На точку М действует сила, направленная по нормали МР к неко-
торой неподвижной поверхности S, и величина силы есть функция длины МР
этой нормали. Тогда существует силовая функция, зависящая только от МР,
и поверхности уровня параллельны поверхности S. Доказательство этого
общего случая предлагается в качестве упражнения (упражнение 7).
4°. Если на материальную точку одновременно действуют несколько сил
указанных выше типов, то силовая функция по-прежнему существует. Это
вытекает из следующей теоремы.
Если силы /"i и F& действуя на точку по отдельности, имеют
силовые функции U\ и U%, то при одновременном действии этих сил
будет также существовать силовая функция, равная U± -f- U%.
В самом деле, пусть
х _ *их у _dUx	дих
Xi~~ Yl~dy Zl~T
— проекции первой силы,
у dU,
7 _
2~
— проекции второй. Проекции равнодействующей будут, очевидно,
дЩ + Uj)	д (Ur + Ut) 7
дх '	ду
7
дх '	ду	dz
что и доказывает высказанное предложение.
85. Замечание о поверхностях уровня. Если поверхности
уровня определены только геометрически, а не их уравнением
U = const, то закон силы полностью не определяется. В самом
деле, пусть V{x, у, z)—некоторая функция, сохраняющая постоян-
ные значения на поверхностях уровня. Тогда силовая.функция будет
непременно иметь вид
где ср — произвольная функция, и для закона силы имеем:
Так как функция V произвольна, то мы приходим к выводу, что на
одной и той же поверхности уровня сила определяется лишь с точ-
ностью др произвольного постоянного множителя. Например, из

108	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
того обстоятельства, что поверхностями уровня являются сферы
с центром в точке О, следует, что сила пересекает точку О и
является функцией расстояния от движущейся точки до точки О.
86.	Мощность. Мощностью машины называют количество работы,
которое она производит за единицу времени.
Единица мощности. В системе CGS единицей мощности
является эрг/сек. Это — мощность машины, которая в секунду про-
изводит один эрг работы..
Лошадиная сила. В технической системе единицей мощности
является лошадиная сила. Это — мощность машины, производящей
в одну секунду 75 килограммометров работы.
II. Система точек
87.	Работа сил, приложенных к системе точек. Силовая
функция. Пусть на п точек Л11(а:1, ух, zj, M2(x2, У2. z2),...,
Мп(хп, уп, гп) действуют силы, причем равнодействующая сил,
действующих на первую точку, есть Ft (Хи Yl7 Zt), на вторую —
F2(X2, Y2, Z2), и т. д. Сумма элементарных работ сил Flt F2, ... ,Fn
на бесконечно малом перемещении системы равна
Х1 dxx -\- Yx dy1 -j- Zt dzx -\-
Когда силы зависят только от положения системы, т. е. когда
Ху, Yv Zj, X2, Y2, Z2, . • • являются функциями от хх> ylt zY, x2,
у2, z2, . ¦., хп, уп, zn и выражение A) есть полный дифференциал не-
которой функции U переменных xl3 ylt zu х2, у2, z2, ..., хп, уп, zn,
то говорят, что данные силы имеют силовую функцию U. В этом
случае
v dU ., dU ~ dU ,. , п
Л^ = -5—, Kft — -^—, Zft=-^—- (>fe = 1, 2	я).
Если система переходит из какого-нибудь положения Ро в какое-
нибудь положение Ри то сумма полных работ всех сил Fv F2	Fn
определяется формулой
(Р>)
= f (X1dx1-\-Y1dy1-\-Z1dzi-\-
+ X2 dx2 + Y2 dy2 -f- Z2 dzt
+
zn)= f dU.

ГЛАВА IV. РАБОТА. СИЛОВАЯ ФУНКЦИЯ	109
Работа равна, следовательно, приращению U1 — Uo, которое получает
функция U, непрерывно изменяясь при переходе системы из первого
положения во второе.
Если U есть однозначная функция координат, то значения Uo
и Ul будут единственными. Полная работа всех сил в этом случае
совершенно не будет зависеть от способа перехода системы из
одного положения в другое.
88. Примеры. Г. Даны две точки М1 и М2. Допустим, что дей-
ствие точки М1 на точку Мг выражается силой Flt направленной по
прямой МХМ2. По закону равенства действия и противодейст-
вия действие точки М2 на точку М1 выражается
силой F2, равной силе Fv но направленной противо-
положно (рис. 62). Совокупность этих двух сил назы-
вается взаимодействием двух точек. Условимся на-
зывать алгебраическим значением F взаимодействия
двух точек величину силы Fx или Fz, взятую со знаком
плюс или минус, в зависимости от того будут ли точки
отталкиваться (как на чертеже) или притягиваться. Тогда,
обозначая через г расстояние МХМ2, мы получим для
проекций сил Ft и F2 значения
Г? Х2	Х1	р У2 — У1	р г1— г\ .	fp\
Г 		t !	_	t [	__ )	уг j
г
Рис.
Вычисляя сумму элементарных работ этих двух сил, называемую
элементарной работой взаимодействия F, найдем
— [(х2 — хх) (dx2 — dxj + (у2 — ух) (dyz—dyj + {z2— zt) {dz2—dz^\.
Это выражение приводится к виду
Fdr
в силу очевидных соотношений
7-2 = (Х2 — X,f + СУ2 — y,f + (Z2 — Ztf,
rdr = (x2—Xl) {dx2—dxj + (y2— yt) (dy2—dy1) + (zz—z1) (dz2—dz1).
Если, следовательно, взаимодействие двух точек есть функция
только расстояния г между ними, а именно F = <р (г), то сумма
элементарных работ обеих сил Fv и F2 будет полным дифферен-
циалом функции
U— Г <р (г) dr.

ПО	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
Так, в частности, для двух точек, притягивающихся с силами,
пропорциональными их массам т1 и щ и обратно пропорциональ-
ными квадрату расстояния между ними
где /—постоянная, откуда
Предположим, что точки вначале были бесконечно удалены друг от
друга, а затем приблизились на расстояние г. Тогда полная работа
будет равна изменению функции U при переходе от первого поло-
, mirth
жения ко второму, т. е. /—-—-.
2°. Пусть теперь дано произвольное число точек Mlt М2, ¦ ¦ ¦, Мп.
Допустим, что любые две из этих точек Мг и Мк оказывают друг
на друга взаимное действие, алгебраическое значение которого Fik
есть функция только расстояния г^ между этими точками. Если
системе сообщить бесконечно малое перемещение, то сумма элемен-
тарных работ всех этих взаимодействий, согласно предыдущему,
будет равна
2 Fik drik,
где суммирование распространяется на все попарные комбинации
индексов i и k, причем / Ф k. Эта сумма является полным диффе-
ренциалом функции
и, следовательно, существует силовая функция. Например, для си-
стемы трех точек с массами т1, тг, щ, притягивающих друг друга
по закону пропорциональности массам и обратной пропорциональ-
ности квадратам расстояний, получается
р 	 f Щ^к
ггк
откуда с точностью до аддитивной постоянной
!3	Г31	ГП
Это значение U равно полной работе взаимодействий при пере-
ходе трех точек из положения, при котором они бесконечно уда-
лены друг от друга, в положение, которое они действительно
занимают.

ГЛАВА IV. РАБОТА. СИЛОВАЯ ФУНКЦИЯ	1 1 1
УПРАЖНЕНИЯ
1.	Какова размерность работы относительно основных единиц длины,
времени и массы? (Если взять единицу длины в X раз меньшую, единицу
времени в х раз меньшую и единицу массы в (л раз меньшую, то работа |Г
будет (А\-21Г.)
2.	Точка М притягивается или отталкивается двумя центрами О и О±
по закону обратной пропорциональности квадратам расстояний. Найти сило-
вую функцию и исследовать поверхности уровня
ом охм
3. Упругая нить, длина которой в нерастянутом состоянии равна /,
прикреплена концом к неподвижной точке О и затем растянута до длины \ > I.
Найти работу натяжения нити, когда она возвращается от длины X к пер-
воначальной длине /. Допускается, что, когда нить имеет длину г, ее натя-
жение Т пропорционально удлинению:
Ответ:
4. Пусть
U — A arctg — + В arctg У
х	° х — а
Исследовать значение полной работы вдоль замкнутой кривой С. (Эта ра-
бота имеет вид 2т%А -f- 2тВ, где т. и п — целые числа.) Если А и В несо-
измеримы, то кривую С можно провести таким образом, чтобы работа
вдоль С сколь угодно мало отличалась от любой наперед заданной ве-
личины.
5. Оболочка ограничивает объем v газа, давление которого на поверх-
ность оболочки равно р. Допуская, что р зависит только от v, показать,
что полная работа давления газа на все элементы оболочки, когда его объем
возрастает от v0 до wj, равна
I p dv.
Ответ. Разобьем поверхность на бесконечно малые элементы, рав-
ные da; на каждый из этих элементов действует нормальное давление pda;
когда объем увеличивается от v до v + dv, элемент da принимает положе-
ние da'; если, следовательно, обозначить через е проекцию перемещения
элемента da на нормаль к нему, то элементарная работа давления pda будет
равна рв da, и совокупность элементарных работ давления будет pie da.
Но е da есть объем цилиндра, противоположными основаниями которого
служат da и da'. Следовательно, I e da представляет собой приращение
полного объема. В таком случае совокупность элементарных работ
равна р dv.
6. Сила F приложена к точке неизменяемой системы, которой сообщают
элементарный поворот на угол 58 вокруг неподвижной оси Ог. Показать,
что элементарная работа этой силы равна Nbti, где N—момент силы F от-
носительно оси Ог.

112	ЧАСТЬ ПЕРВАЯ. ПРЕДВАРИТЕЛЬНЫЕ ПОНЯТИЯ
7.	На точку М действует сила F, нормальная к неподвижной поверх-
ности S. Обозначая через р расстояние от точки М до поверхности, отсчи-
тываемое по нормали F, показать, что элементарная работа силы F
равна ± F dp, где знак -\- или — берется в зависимости от того, стре-
мится ли сила увеличить или уменьшить расстояние р.
8.	Взаимодействие двух точек с массами т. и т', расположенных
на расстоянии г, равно F — —/——, где /—постоянная (закон всемирного
тяготения Ньютона). Как изменится множитель / при изменении
единиц?
г3
Ответ. Следует написать /= — F	—; во что обращаются F, г, т
mm
и т' при изменении единиц известно. Тогда / обратится в /—^-.

ЧАСТЬ ВТОРАЯ
СТАТИКА
ГЛАВА V
РАВНОВЕСИЕ ТОЧКИ. РАВНОВЕСИЕ СИСТЕМЫ
I. Материальная точка
89. Свободная точка. Для того чтобы свободная точка была
в равновесии, необходимо и достаточно, чтобы равнодействующая R
приложенных к ней сил была равна нулю, т. е. чтобы проекции
X, Y, Z вектора R были равны нулю:
^=0, К = 0, Z —0.	A)
Если в каком-нибудь положении М(х, у, г) подвергнуть точку М
действию силы R, не сообщая ей при этом никакой начальной ско-
рости, то начальное значение R может зависеть только- от х, у, z и t.
Мы будем предполагать, что от t оно не зависит. Тогда три урав-
нения A) определяют координаты положения равновесия. Если суще-
ствует силовая функция U(x, у, г), то проекции X, Y, Z являются
частными производными от О, и уравнения принимают вид
Это как раз те уравнения, которые необходимо разрешить при
нахождении макбимума и минимума функции U от трех независи-
мых переменных х, у, г. Мы покажем в динамике (гл. X) методом
Лежен-Дирихле, что если функция U действительно имеет в точке
¦Mi 0*1 > У\г- zi) максимум, то эта точка является положением
устойчивого равновесия. Это означает, что если материальную точку
каким-нибудь образом отклонить бесконечно мало от положения Mt
и сообщить ей бесконечно малую начальную скорость, то она по-
лучит движение, при котором она удаляется от положения Mt бес-
конечно мало.
Приближенное представление об этом можно получить следующим
образом. Допустим, что в точке Мг функция U имеет максимум,
значение которого равно Ut. Вблизи точки Mt функция U меньше
чем Uu и поэтому поверхность уровня будет

114
ЧАСТЬ ВТОРАЯ. СТАТИКА
где s — очень малая положительная величина, которая содержит
замкнутую поверхность, окружающую точку М1 и непрерывно стя-
гивающуюся в нее, когда е стремится к нулю (рис. 63, а). В каждой
точке М этой поверхности сила нормальна к ней и направлена
в сторону возрастания U, т. е. во внутрь. Она стремится, следова-
тельно, помешать точке М удалиться от точки Мх.
Если, наоборот, в точке Мх функция U имеет минимум и те-
перь иг есть значение этого минимума, то поверхность уровня
?/=?/j-|-e (e — положительно)
будет по-прежнему содержать замкнутую часть, окружающую точку Mv
Теперь в каждой точке М этой поверхности сила по-прежнему нор-
мальна к ней, но направлена наружу (рис. 63, б). Эта сила стремится,
следовательно, удалить точку М от точки Мх, и равновесие в точке Мх
неустойчиво.
/ 2
в)
Рис. 63.
Допустим, наконец, что в положении Mt три уравнения B) удо-
влетворяются, но что соответствующее значение Ux не является
ни максимумом, ни минимумом функции U. Тогда в окрестности
точки М1 существуют две области А и В (рис. 63, в) такие, что
в одной из них, например в А, функция U принимает значения,
меньшие чем Uy, а во второй В — значения, большие чем Uv Эти
две области разделяются поверхностью уровня S, на которой
Эта, особая поверхность уровня S, проходящая, очевидно, через
точку Mv имеет в ней коническую точку, так как, согласно B),
в ней одновременно обращаются в нуль все три частные производ-
ные первого порядка функции U — Uv Если через е обозначить
бесконечно малую положительную величину, то поверхности уровня
расположены в области Лив этой области силы стремятся вернуть
движущуюся точку в положение Mv Поверхности же

ГЛАВА V. РАВНОВЕСИЕ ТОЧКИ. РАВНОВЕСИЕ СИСТЕМЫ 115
находятся в области Вив этой области силы стремятся удалить
движущуюся точку от точки Mv так как они направлены в сто-
рону возрастания U. Следовательно, положение равновесия Mt не-
устойчиво.
Этот последний случай представляется для точки, притягивае-
мой к двум неподвижным центрам силами, обратно пропорциональ-
ными квадратам расстояний, что подробно рассматривается в теории
притяжения.
90. Пример. Притяжения, пропорциональные расстояниям. Найти
положение равновесия материальной точки, притягиваемой неподвижными
центрами пропорционально расстоя-
ниям и массам притягивающих центров.
Пусть Рь Р%, ..., Рп (рис. 64) — не-
подвижные центры и ть тг	тп —
их массы. Силы притяжения /\, F2, ...
.... Fn, действующие на материальную
точку М, направлены по МРЬ МРЬ ¦¦.	с
..., МРп; их величины равны соответ-	Ч
ственно 		_
Fl=fmtMPl, F2 =
где/— постоянная.	(afiuW	h
Пусть аь bx, сь a2, b2, c2, .... an,
*»> cn — координаты притягивающих	"ис- Ь4.
центров, а х, у, г — координаты
точки М. Проекции силы F^ на оси координат равны проекциям соответ-
ствующих отрезков MPje, умноженным на fm^. Следовательно, они равны
fmb(ak — x), fmk(bk — y), fmk(cu — z).
Отсюда для проекций равнодействующей получаем
где суммирование распространено на все силы, т. е. на все значения
k — 1, 2, ..., п. Полагая
= 2
У). г=/2«ц((Ц-г), C)
е. на
= 2
можем написать
X = /fiF —лс), Y
Рассмотрим точку G с координатами ?, т), С Она называется центром
масс системы масс Plt P%	Рп. Полученные только что уравнения
показывают, что равнодействующая сил, действующих на М, есть сила,
которую можно получить, если всю систему притягивающих центров
заменить единственной точкой G, полагая ее массу равной |х. Равно-
действующая направлена по MG и ее значение равно fix.MG. Следова-
тельно, равновесия не будет, если точка М не совпадает с центром масс
G системы.
Мы предполагали, что величины ть ть ..., тп существенно положи-
тельны. Допустим теперь, что эти числа не являются больше массами,
а лишь некоторыми коэффициентами, и предположим, что некоторые из них
отрицательны. Это равносильно предположению, что соответствующие силы
являются отталкивающими, так как проекции какой-нибудь из сил Fk

116	ЧАСТЬ ВТОРАЯ. СТАТИКА
меняют знак вместе с т^, и сила F^ меняет направление на обратное, когда />
делается отрицательным.
Если (л отлично от нуля, то приведенные вычисления сохранят силу, и
мы придем к тем же результатам. Если и- равно нулю, то три величины C)
не зависят от х, у, г, равнодействующая постоянна по величине и напра-
влению и положения равновесия нет. Если, наконец, одновременно
(а = 0, 2 тьпк = °> 2 mkbk = 0> 2 тк°к = 0>
то X, Y, Z равны нулю, каковы бы ни были х, у, z, и, следовательно,
точка М находится в равновесии в любом положении.
В рассматриваемой задаче существует силовая функция U. В общем
случае, когда (д. отлично от нуля, она будет
U = - Ц- [(? - *J + A - УУ + (С - *J1 = - Цг ^G2-
Если (л положительно, то эта функция равна нулю в точке G и отрицательна
во всех остальных точках. Она, следовательно, имеет максимум в положе-
нии равновесия, которое вследствие этого устойчиво. Когда (д. отрицательно,
имеет место обратное. Если (л равно нулю, то X; Y, Z имеют постоянные
значения /2"г&аЬ> /2wfc*fc> /2m&Cfc и силовая функция имеет вид
?/=/(-* 2 т&а& + у 2 mkbk + г 2 mkCk)-
91. Точка, движущаяся без трения по неподвижной поверх-
ности. Пусть дана неподвижная поверхность 5 (рис. 65) и на ней
точка М, находящаяся под действием заданных сил, равнодейст-
вующая которых равна F. Для того чтобы точка
находилась в равновесии, необходимо и доста-
точно, чтобы эта равнодействующая F, если она
отлична от нуля, была нормальна к поверхности.
В самом деле, если сила не нормальна к поверхности,
то ее можно разложить на две силы, из которых
одна направлена по нормали и прижимает точку
к поверхности, а другая лежит в касательной пло-
скости и заставляет точку скользить по поверхности.
Равновесия, следовательно, не будет. Если в каком-нибудь положе-
нии М сила F нормальна, то равновесие будет иметь место при
условии, что точка не может покинуть поверхность ни в ту, ни
в другую сторону. Это — случай, наиболее часто встречающийся.
Но если точка просто положена на поверхность, как какой-нибудь
предмет положен на стол, то для равновесия недостаточно, чтобы
сила была направлена по нормали; сила должна быть направлена
еще в такую сторону, чтобы она прижимала точку к поверхности.
Если точка может скользить по поверхности без трения, то дей-
ствие поверхности на точку выражается силой, которая не может
оказывать никакого сопротивления скольжению, т. е. не может иметь
никакой касательной составляющей. Эта сила, следовательно, нор-
мальна к поверхности; она называется нормальной реакцией. Когда
точка находится в равновесии, нормальная реакция равна и противо-
положна силе F. По закону равенства действия и противодействия

ГЛАВА V. РАВНОВЕСИЕ ТОЧКИ. РАВНОВЕСИЕ СИСТЕМЫ	117
точка М оказывает на поверхность действие, равное и противополож-
ное MN, которое называется давлением точка на поверхность.
Выразим все эти результаты аналитически. Пусть
f(x, у, г) = 0
—-уравнение поверхности в прямоугольных координатах и X, У,
Z — проекции силы F. Проекциями нормальной реакции MN являются
величины, пропорциональные направляющим косинусам нормали к по-
верхности, т. е. величины вида
ду	дг
Так как должно иметь место равновесие между этой реакцией и
силой F, то должны выполняться условия
дх	' ду
которые совместно с уравнением поверхности /(х, у, г) = О состав-
ляют систему четырех уравнений для определения х, у, г и X.
Пусть М — точка поверхности, координаты которой удовлетворяют
этим уравнениям. Если материальная точка не может покинуть поверх-
ность ни с одной, ни с другой стороны, то в этой точке будет
равновесие. В противном случае необходимо приписать коэффици-
енту X определенный знак. Допустим, например, что точка может
покинуть поверхность в ту сторону, где функция f(x, у, г) ста-
новится положительной. Тогда необходимо, чтобы сила была напра-
влена в сторону, где функция / (х, у, г) отрицательна. Реакция будет
направлена в противоположную сторону. Но вектор с проекциями
д1 dJL U.
дх' ду' дг
направлен относительно поверхности в ту ее сторону, где функ-
ция f(x, у, г) положительна, что вытекает из таких же соображе-
ний, какие были сделаны в п. 83 относительно поверхностей уровня,
если их применить к поверхностям f(x, у, z) = const. Так как реак-
ция N должна быть направлена в ту же сторону, то X должно быть
положительно.
В случае, когда точка не может оставить поверхность, вычисле-
ния могут быть упрощены следующим образом. Выразим прежде
всего координаты точки поверхности в функции двух параметров ql
и q2. Пусть, например,
*=<P(<7i. q2), У = ^(Як 4z)- z = <o(qv q2).
Для того чтобы имело место равновесие, необходимо и достаточно,
чтобы сила F была перпендикулярна к поверхности, т. е. к каждой
из двух кривых, которые получатся, если положить последовательно

118	ЧАСТЬ ВТОРАЯ. СТАТИКА
сначала д^— const, а затем q2 = const. Следовательно, уравнения
задачи будут
2	dq2
Величины х, у, г, которые зависят от положения точки М, будут
функциями от qx и q2, и полученные уравнения относительно qt и q2
определяют значения параметров для положений равновесия.
Интересен случай, когда выражение
Q1dq1-\-Q2dq2,
тде Qt и Q2 — левые части написанных выше уравнений, есть полный
дифференциал некоторой функции U(qlf q2). Тогда для нахождения
равновесия нужно будет приравнять нулю частные производные Qt
и Q2 функции U, т. е. искать максимум и минимум этой функции
двух независимых переменных ql и q2. Для этой функции можно
написать
U (qx, q2)~
где во второй части все величины должны быть выражены через qx
и q2. В частном случае, когда сила F имеет потенциал, будет иметь
место равенство
JXdx-\-Ydy-\-Zdz = U{x. у, г)
при любых х, у, г, и функция U (qv q2) будет существовать. Она
получится из U(x, у, г) после замены координат их выражениями
в функции qx и q2. Поверхность уровня, проходящая через поло-
жение равновесия Mv будет в общем случае касаться в этой точке
заданной поверхности 5, так как сила в точке Mt одновременно
нормальна и к поверхности уровня, и к поверхности 5.
Мы покажем в динамике, что если в каком-нибудь положении
движущейся точки функция U (qv q2) действительно имеет макси-
мум Uv то соответствующее положение равновесия устойчиво. Так
же, как и для рассмотренного выше случая свободной точки, в этом
можно отдать себе отчет, исследуя вид кривых на з.аданной поверх-
ности 5, определяемых уравнениями
U=U1 ± е.
92. Точка, движущаяся без трения по неподвижной кривой.
Пусть задана неподвижная кривая С и на ней точка М, движущаяся
без трения под действием сил, равнодействующая которых есть F.
Так же, как и в случае точки, движущейся по поверхности, убеж-
даемся, что при равновесии сила F, если она не равна нулю, должна

ГЛАВА V. РАВНОВЕСИЕ ТОЧКИ. РАВНОВЕСИЕ СИСТЕМЫ	119
быть нормальна к кривой. Если это условие выполнено, то сила F
будет уравновешиваться сопротивлением кривой, и равновесие будет
иметь место.
Действие кривой на точку выражается нормальной силой ММ,
которая называется нормальной реакцией. Точка М оказывает на
кривую давление, равное и противоположное этой реакции. Если
точка находится в равновесии, то нормальная реакция равна силе F,
но противоположна ей, а давление точки на
кривую есть сама сила (рис. 66).
Пусть
f(x,y,z) = 0, Мх. у, г) = 0
— уравнения кривой, отнесенной к трем пря-
моугольным осям, и X, Y, Z — проекции рав-
нодействующей F сил, приложенных к точке
М(х, у, z). Для того чтобы выразить, что
имеет место равновесие, достаточно написать,	Рис 66.
что сила F равна и прямо противоположна
нормальной реакции N. Эта последняя может быть всегда разложена
на две другие, направленные по нормалям MN' и ММ" к двум
поверхностям /=0 и /1 = 0, пересечение которых определяет задан-
ную кривую, так как все три направления MN, MN' и MN" лежат
в одной нормальной плоскости. Эти две составляющие MN' и MN"
реакции имеют соответственно проекции
Хдх' Хду' ldz~' lldx' ^~ду~' ll~d!'
Так как реакция и сила F находятся в равновесии, то
Эти три уравнения совместно с уравнениями кривой определяют
пять неизвестных х, у, г, X, Xt.
Можно упростить вычисления, если положить, что координаты
точки кривой выражены в функции одного параметра q при помощи
уравнений
Направляющие косинусы касательной пропорциональны произ-
водным ср'(<7)> Y (я)> ш'\Я)' и условие равновесия получится, если при-
равнять нулю величину
которую мы обозначим через Q. Каждому значению q, обращающему Q
в нуль, соответствует положение равновесия. В рассматриваемом

120	ЧАСТЬ ВТОРАЯ. СТАТИКА
случае отыскание положений равновесия всегда приводится к оты-
сканию максимума и минимума функции, зависящей только от
одной переменной. Положим
U(q)= fXdx + Ydy-\-Zdz= JQdq,
где в первом интеграле для того, чтобы он совпал со вторым, нужно
заменить величины х, у, г их выражениями через q. Условие
равновесия получится, если отыскивать те значения q, которые обра-
щают в нуль производную от U по q, т. е. если искать максимум
и минимум функции U. Если существует силовая функция U (х, у, г),
то функция U (q) получится, очевидно, заменой величин х, у, г их
выражениями через q. В этом случае поверхность уровня, прохо-
дящая через положение равновесия Mv касается в этой точке кривой.
В дальнейшем, при помощи общего метода мы покажем, что дей-
ствительным максимумам функции U (q) отвечают положения устой-
чивого равновесия. В виде упражнения (задача 7 в конце главы) мы
укажем частный метод, позволяющий убедиться в справедливости
этого предложения и основанный на том, что точка, предоставленная
самой себе на кривой, стремится перемещаться по ней в сторону
возрастания U.
II. Системы материальных точек
93.	Система материальных точек. Если система состоит из
свободных и независимых друг от друга точек, то для каждой из
них может быть повторено все, что было сказано относительно
совершенно свободной точки. Для равновесия необходимо и доста-
точно, чтобы равнодействующие сил, действующих на каждую из
точек, были равны нулю.
Та же теорема справедлива и тогда, когда на систему наложены
связи, если каждую точку рассматривать как свободную, добавляя
к приложенным к ней силам реакции связей.
Этой точки зрения мы будем придерживаться ниже в связи
с теоремой о возможной работе.
Сейчас мы разделим все силы, приложенные к системе, на две
категории: на силы внутренние и силы внешние. Мы покажем, что
для равновесия необходимо, чтобы внешние силы удовлетворяли
шести условиям, одинаковым для всех систем.
94.	Силы внутренние и силы внешние. Шесть необходимых
условий равновесия. Любую материальную систему, образованную
телами твердыми, жидкими или газообразными, можно рассматривать,
как составленную из большого числа материальных точек, подчи-
ненных некоторым связям. Так, например, твердое тело есть сово-
купность материальных точек, расстояния между которыми должны
оставаться неизменными. Общие теоремы могут быть получены, если

ГЛАВА V. РАВНОВЕСИЕ ТОЧКИ. РАВНОВЕСИЕ СИСТЕМЫ	121
написать уравнения равновесия для этих различных материальных
точек и составить из них некоторые сочетания.
Внутренними силами системы называются силы взаимодействия
между ее различными точками. По закону равенства действия и про-
тиводействия эти силы попарно равны и прямо противоположны.
Например, если точка т' системы притягивает другую ее точку т
с некоторой силой, то, наоборот, точка т притягивает точку т?
с такой же силой, но противоположно направленной.
Силы, отличные от определяемых таким образом внутренних сил,
называются внешними.
Пусть хх, yv zlt х2, у%, 22	хп, уп, zn—¦ координаты раз-
личных точек системы, массы которых mv т2, ..., тп. Если рас-
сматривать какую-нибудь одну из этих точек с массой тис коор-
динатами х, у, г, то все приложенные к ней силы можно разбить
на две категории. К первой относятся все внутренние силы, дей-
ствующие на т; проекции какой-нибудь из этих сил мы обозначим
через Хр Fj, Z^ Ко второй категории относятся все внешние силы,
действующие на ту же точку; проекции какой-нибудь из этих сил
мы обозначим через Хе, Ye, Ze. Точка т может рассматриваться как
совершенно свободная при условии, что принимаются во внимание
все действующие на нее силы как внешние, так и внутренние. Для
того чтобы она находилась в равновесии, необходимо и достаточно,
чтобы равнодействующая всех этих сил обращалась в нуль. Про-
ектируя все силы на три оси, мы получим три уравнения равновесия
A)
где знак 2 означает, что нужно взять сумму проекций всех внешних
или внутренних сил, приложенных к точке т.
Допустим, что эти уравнения написаны для всех точек системы,
и сложим почленно все уравнения, относящиеся к оси х. Получим
где знак 22 означает, что сумма распространена на все силы,
действующие на различные точки системы. Но согласно закону
равенства действия и противодействия все внутренние силы попарно
равны и противоположны. Следовательно, 22 ^1 их проекций на
ось х равна нулю, и предыдущее уравнение принимает вид
в = 0.	B)

122	ЧАСТЬ ВТОРАЯ. СТАТИКА
Аналогично получаем
о I	('
Таким образом, получены три необходимые для равновесия усло-
вия, связывающие проекции внешних сил. Три других уравнения
получатся, если ввести моменты.
Вернемся к уравнениям A). Умножим первое из них на —у,
второе на х и сложим. Имеем
2 (xYt — уХ{) + 2 (* Уе — Ухе) = 0.
Написав аналогичные уравнения для всех точек системы и почленно
сложив их, получим
Но 22№ — уХд есть сумма моментов всех внутренних сил отно-
сительно оси Ог. Это выражение будет равно нулю, так как все вну-
тренние силы попарно равны и прямо противоположны. Таким обра-
зом, мы приходим к уравнению
2C)
м аналогично к уравнениям
Полученные таким образом шесть необходимых условий B) и C)
могут быть высказаны следующим образом.
Для того чтобы произвольная система находилась в равно-
весии, необходимо, чтобы сумма проекций внешних сил на каж-
дую из трех осей и сумма их моментов относительно каждой
из этих трех осей равнялись нулю.
Эти условия можно высказать и в форме, не зависящей от каких
бы то ни было осей, следующим образом.
Для того чтобы произвольная система находилась в равно-
весии, необходимо, чтобы внешние силы составляли систему
скользящих векторов, эквивалентную нулю.
Это условие можно выразить при помощи одного из методов
первой главы. Можно, например, при помощи элементарных опера-
ций привести систему векторов к простейшему виду и окончательно
получить или два равных и прямо противоположных вектора, или рав-
ные нулю главный вектор и главный момент.
Примеры. Г. Представим себе сосуд с водой, находящейся в равно-
весии под действием силы тяжести. Рассматриваемая система образована
частицами воды. Внутренними силами являются взаимодействия между этими

ГЛАВА V. РАВНОВЕСИЕ ТОЧКИ. РАВНОВЕСИЕ СИСТЕМЫ	125
частицами. Внешними силами являются действия тел, не принадлежащих
системе, на точки системы. Этими силами будут: 1) веса частиц воды;
2) действия стенок сосуда на соприкасающиеся с ними частицы; 3) давления,
производимые воздухом на свободную поверхность. Для того чтобы имело
место равновесие, необходимо, чтобы совокупность всех этих внешних сил
образовывала систему скользящих векторов, эквивалентную нулю.
2°. Вообразим тяжелую цепь, подвешенную своими обоими концами
к двум неподвижным точкам А к В. Внешними силами, действующими на
цепь, являются: 1) веса различных звеньев; 2) действия, вызываемые непо-
движными точками А и В. Цепь тянет эти точки, и, наоборот, эти точки
действуют на цепь двумя силами FA и FB, приложенными на ее концах. Для
того чтобы было равновесие, необходимо, чтобы все внешние силы были
эквивалентны нулю. Веса образуют систему параллельных векторов, экви-
валентную одному вектору Р, равному весу цепи и приложенному в ее
центре тяжести. Три вектора Р, FA и FB и должны составлять систему*
эквивалентную нулю.
3°. Твердое тело. Если рассматриваемая система является твердым
телом, то указанные шесть необходимых условий равновесия будут также
и достаточными, что будет показано в следующей главе.
95. Разделение произвольной системы на части. Необходимые
условия равновесия. Выделим мысленно из материальной системы S
какую-нибудь ее часть Sx так, чтобы система оказалась разделенной
на две части, из которых одна состоит из точек St, а другая E — St)
из остальных точек, образующих систему. Если система находится
в равновесии, то в равновесии будет и каждая ее часть, например
часть Sv Тогда можно применить полученные результаты к части St,
рассматривая ее как систему в равновесии. Приложенные к части St
силы, внешние для нее, должны составлять систему скользящих
векторов, эквивалентную нулю. Таким путем, рассматривая последова-
тельно различные части полной системы, мы получим все необхо-
димые условия равновесия.
УПРАЖНЕНИЯ
1.	Доказать, что если п сходящихся сил находятся в равновесии, то их
общая точка приложения является центром масс п точек с равными массами,
размещенных по концам сил.
2.	Найти положение равновесия свободной точки М, притягиваемой к не-
подвижным центрам Ох, 0% •¦-, Оп силами, обратно пропорциональными рас-
стояниям. Доказать, что: существует силовая функция log МО^-МОъ ... МОп*
каждое положение равновесия О' есть центр средних расстояний между
точками, обратными к Oh относительно О'; если точки Oh лежат в одной
плоскости и если составить многочлен, корнями которого будут комплекс-
ные числа г, изображающие точки Оь то положения равновесия будут
определяться корнями производной от этого многочлена по г. (Шаль, см.
Lucas, Comptes rendus, 1879 и 1888 и Juhel-Renoy там же, 1906, и
Nouvelles Annales de Mathematiques 4 серия, т. VII, 1907.)
3.	Точка М находится в равновесии в определенном положении А под
действием определенных сил Ph Р2	Рп- На линии АР& берется точка Од,
1
причем так, что AOjc = (hPjc)'', где h и v— постоянные (чЗ: — 1). Показать,.

124	ЧАСТЬ ВТОРАЯ. СТАТИКА
что функция МО\+Х + MOl+1 + ... + МО^1 имеет максимум или мини-
мум, когда точка М совпадает с положением равновесия А. Если ч — — 1,
то эта функция должна быть заменена функцией log МО± ¦ МО2 ¦ ¦ ¦ МОп.
Если ч = 1, то А есть центр средних расстояний между точками 0%.
4.	Найти положения равновесия тяжелой точки, которая движется без
трения по винтовой линии на цилиндре вращения с вертикальной осью и
притягивается одной из точек оси пропорционально расстоянию.
Ответ. Одно положение устойчивого равновесия.
5.	Найти положения равновесия точки М, движущейся без трения по
окружности радиуса а и подверженной действию силы, направление которой
проходит через фиксированную точку А окружности и алгебраическое зна-
чение которой при положительном направлении, совпадающем с AM, равно
AM
Ответ. Три положения равновесия: два, для которых AM = а, и одно,
для которого AM = 2а. Первые два устойчивы, а третье неустойчиво.
6. Дана сила F, проекции которой X, Y, Z зависят от х, у, г. Найти
такую поверхность S, чтобы точка, движущаяся по ней без трения и подвер-
женная действию силы F, находилась в равновесии в любом положении.
Ответ. Должен существовать такой множитель ц, чтобы
l>.(Xdx + Ydy + Zdz) = df(x, у, г).
Искомые поверхности суть f(x, у, г) = const. Если существует силовая
функция, то искомые поверхности являются поверхностями уровня.
6а. Точно так же найти кривые, на которых точка находится в равно-
весии в любом положении.
(Эти кривые всегда существуют. Они должны удовлетворять уравнению
которое позволяет, выбрав произвольным образом х и у в функции пара-
метра q, определить затем г.)
7.	Точка М, находящаяся под действием силы F, может скользить без
трения по неподвижной кривой, координаты которой выражены в функциях
параметра д. К этой кривой проведена касательная МТ в сторону возраста-
ния q. Показать, что косинус угла TMF имеет знак функции, обозначенной
через Q (п. 92). Отсюда вывести, что для устойчивости равновесия при
q = qi необходимо и достаточно, чтобы функция Q обращалась в нуль, пере-
ходя от положительных значений к отрицательным, когда q достигает зна-
чение q1 и переходит через него.
8.	Найти положения равновесия точки М, помещенной на наружную
поверхность эллипсоида, если М отталкивается неподвижной точкой Р
с силой, пропорциональной расстоянию. (Так как точка М может покинуть
поверхность наружу, то необходимо принимать во внимание знак вели-
чины X. Если Р находится вне эллипсоида, то имеется одно положение
неустойчивого равновесия. Если Р находится внутри эллипсоида, положений
равновесия нет. Геометрически задача сводится к проведению из точки Р
нормалей к поверхности. Затем следует сделать надлежащий выбор осно-
ваний этих нормалей.)
9.	Точка, движущаяся по параболе у2 — 2рх = 0, притягивается непо-
движной точкой (а, Ь), лежащей в плоскости кривой, пропорционально рас-
стоянию. Найти положения равновесия. Исследовать устойчивость. Имеем
Х = р(а — х), К = (а(« — у), (х>0.

ГЛАВА V. РАВНОВЕСИЕ ТОЧКИ. РАВНОВЕСИЕ СИСТЕМЫ	125
Ординаты положений равновесия [основания нормалей, проведенных из (я, Ь)],
являются значениями у, обращающими в нуль функцию
и совпадающими со значениями, для которых функция
выраженная через у, имеет максимум или минимум. Равновесие устойчиво»
если эта функция имеет максимум. •
10. К трем вершинам А, В, С треугольника прикреплены упругие нити,
длины которых в нерастянутом состоянии равны я, р, у. Нити растягиваются
и связываются в узел. Предполагается, что сила упругости каждой нити
пропорциональна удлинению, отнесенному к единице длины (например, если
X — удлинение первой нити, то сила упругости равна к — , где k одинаково
для всех трех нитей). Какие соотношения должны существовать между
тремя длинами а, р, у, чтобы положение равновесия узла совпадало с цент-
ром тяжести треугольника?

ГЛАВА VI
РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА
I. Приведение сил, приложенных к твердому телу. Равновесие
96.	Твердое тело. Твердым телом называется совокупность
материальных точек, неизменно связанных между собой. Если
сила приложена к одной из этих точек, то говорят, что она приложена
к телу. Определяемое таким образом твердое тело является абстрак-
цией. Все естественные тела изменяют свою форму под действием при-
ложенных к ним сил. Но тела, называемые твердыми, настолько мало
деформируются, что этой деформацией в первом приближении можно
пренебречь, если только приложенные силы не слишком велики.
Согласно общим теоремам о равновесии произвольных систем для
равновесия твердого тела под действием некоторых сил необходимо,
чтобы эти силы составляли систему скользящих векторов, экви-
валентную нулю.
Но для твердого тела это необходимое условие является также
и достаточным. Это можно доказать, допуская как очевидное сле-
дующее предложение:
Две приложенные к твердому телу равные и прямо про-
тивоположные силы находятся в равновесии.
Согласно этому предложению можно, не изменяя механического
состояния твердого тела, приложить к нему или отнять от него две
равные прямо противоположные силы.
Это предложение позволяет доказать, как мы это сделали в тео-
рии векторов (п. 19), следующее свойство:
Можно, не изменяя состояния твердого тела, переносить
точку приложения любой силы вдоль ее линии действия, если
только новая точка приложения неизменно связана с телом.
Следовательно, вектор силы, приложенной к' твердому телу,
связан с прямой, т. е. является скользящим вектором.
Мы покажем, как можно привести к простейшему виду совокуп-
ность приложенных к твердому телу сил и вывести отсюда необхо-
димые и достаточные условия равновесия.
97.	Приведение сил, приложенных к твердому телу. Равно-
весие. Согласно предыдущему, состояние тела не изменится, если
выполнить следующие элементарные действия.

ГЛАВА VI. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА	127
Присоединить или отбросить две равные прямо противопо-
ложные силы; перенести силу в какую-нибудь точку на ее линии
действия.
Сложить несколько сходящихся сил в одну или разложить
одну силу на несколько сходящихся сил.
Мы видели, что все системы скользящих векторов, полученные
при помощи этих элементарных действий, эквивалентны, т. е. имеют
одни и те же главные векторы и главные моменты. Наоборот, две
эквивалентные системы скользящих векторов могут быть получены
одна из другой при помощи этих действий. Следовательно, две
системы сил, представляющие собой эквивалентные системы
скользящих векторов, могут быть заменены одна другой без
изменения механического состояния твердого тела.
Приведение к двум силам. Как было показано в теории векто-
ров, система сил (S), приложенная к твердому телу, может быть
приведена при помощи элементарных операций к двум силам F и Ф,
из которых одна приложена в произвольно выбранной точке.
Приведение к силе и паре. Как было показано в теории век-
торов, произвольная система сил (S) может быть заменена одной
силой R, равной главному вектору и приложенной в произвольной
точке О, и одной парой с вектором момента, равным главному
моменту 00 относительно точки О.
Равновесие. Для равновесия необходимо, чтобы система (S)
была эквивалентна нулю, т. е. чтобы ее главный вектор OR и глав-
ный момент OG равнялись нулю. Это условие также и достаточно.
В самом деле, если оно выполняется, то при помощи элементарных
действий все силы могут быть приведены к одной паре с момен-
том 00, равным нулю, и образованной, следовательно, двумя рав-
ными и противоположными силами, лежащими на одной прямой.
Уравнения равновесия. Обозначим через X, Y, Z суммы проек-
ций всех сил на три оси координат, а через L, М, N суммы их
моментов относительно тех же осей. Тогда необходимые и доста-
точные условия равновесия выразятся уравнениями:
Х=0, У = 0, Z=0; L = 0, M = 0, N = 0.
98. Эквивалентные системы Сил. Мы видели в предыдущем
разделе, что если две системы сил, приложенные к твердому телу,
изображаются двумя эквивалентными системами скользящих векто-
ров, то они могут быть заменены одна другой без изменения
состояния тела.
Наоборот, если две системы сил (А) и (В) могут быть заме-
нены одна другой без изменения механического состояния тела,
то они изображаются двумя эквивалентными системами скользящих
векторов.
В самом деле, рассмотрим систему (—А), получаемую из си-
стемы (А) заменой всех сил на противоположные. Эта система (— А),

128
ЧАСТЬ ВТОРАЯ. СТАТИКА
очевидно, уравновешивает систему (А). Но тогда она уравновесит
также и систему (В), которая, по предположению, производит такое же
действие, как и система (А). Следовательно, совокупность векто-
ров (—А)-\-(В) эквивалентна нулю, откуда вытекает, что система
векторов (А) эквивалентна системе векторов (В).
Когда две системы сил (Л) и (В) могут, быть заменены одна дру-
гой без нарушения механического состояния твердого тела, то их
называют эквивалентными. Мы видим, таким образом, что для
того, чтобы две системы сил были эквивалентны, необходимо и
достаточно, чтобы они представлялись двумя эквивалентными систе-
мами скользящих векторов,
99. Частные случаи приведения. Для того чтобы система (S)
имела равнодействующую, необходимо и достаточно, чтобы глав-
ный вектор OR был отличен от нуля, а главный момент 00
либо равнялся нулю, либо был перпендикулярен главному век-
тору. Тогда равнодействующая будет лежать на центральной
оси. Аналитически имеем следующие условия:
Для того чтобы система (S) приводилась к одной паре, необхо-
димо и достаточно, чтобы главный вектор равнялся нулю, а глав-
ный момент был отличен от нуля:
а
Х=0, У=0, Z = 0, OG^O.
100. Другая форма условий равновесия.
Для равновесия твердого тела необходимо и
достаточно, чтобы сумма моментов сил от-
носительно каждого из шести ребер тетра-
эдра равнялась нулю. Это условие является, оче-
видно, необходимым. Оно также и достаточно. В
самом деле, допустим, что оно выполняется для
тетраэдра ABCD. Тогда, так как суммы моментов
относительно трех ребер АВ, AC, AD, выходя-
щих из вершины А, равны нулю, то и главный
момент относительно точки А равен нулю. Сле-
довательно, все силы либо приводятся к одной равнодействующей,
проходящей через точку А, либо находятся в равновесии. Так как
эти рассуждения справедливы для каждой вершины, то силы находятся
в равновесии, ибо они не могут иметь равнодействующую, проходя-
щую одновременно через четыре вершины.
В качестве приложения докажем, что четыре силы, приложенные в четы-
рех вершинах тетраэдра (рис. 67), пропорциональные площадям противо-
положных граней и направленные нормально к ним, находятся в равновесии.
Для этого покажем, что суммы моментов относительно каждого из шести
ребер тетраэдра равны нулю.

ГЛАВА VI. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА	129
В самом деле, пусть а, [5, т, 5 — силы, приложенные к вершинам А, В, С, D
тетраэдра. Тогда
а = k ¦ пл. BCD, р = k • пл. CD А, ^ = k ¦ пл. DAB, Ь = k ¦ пл. ABC
Возьмем моменты относительно ребра CD: моменты сил у и & равны нулю,
моменты сил аир противоположны по знаку. Так как сила а напра-
влена по высоте АА', то угол между <х и CD — прямой, и кратчай-
шим расстоянием между <х и CD является перпендикуляр А'А", опущен-
ный из А' на CD; следовательно, абсолютное значение момента силы а
относительно CD равно
а. А'А" = а ¦ АА' ¦ ctg <р = k ¦ пл BCD • АА' • ctg <у = ZkVcig <p,
где V—объем тетраэдра и <р—-двугранный угол при ребре CD. Такое же
абсолютное значение имеет и момент силы р. Следовательно, сумма моментов
относительно произвольно взятого ребра CD равна нулю.
П. Приложения. Силы в плоскости.
Параллельные силы. Центр тяжести
101. Силы в плоскости. Примем плоскость, в которой лежат силы,
за плоскость ху. Очевидно, имеем:
Z = 0, 1 = 0, М = 0,
Следовательно:
если Х2-^- Y2 > D, то система приводится к одной равнодействую-
щей, лежащей в плоскости и направленной по центральной оси;
если Х=0, Y = 0, а А/^0, то система приводится к паре;
если А"=0, F = 0, А/ = 0, то система находится в равновесии.
Когда N = 0, то силы либо имеют равнодействующую, проходя-
щую через точку О, либо находятся в равновесии. Следовательно,
если сумма моментов сил относительно двух точек плоскости равна
нулю, то либо равнодействующая проходит через эти точки, либо
имеет место равновесие. Если, наконец, эта сумма равна нулю для
трех точек плоскости, не лежащих на одной прямой, то возможно
только равновесие.
102. Примеры. 1°. Возьмем в плоскости ху произвольный многоуголь-
ник и приложим к середине каждой из его сторон силу, пропорциональную
длине этой стороны, перпендикулярную к ней и направленную в сторону,
внешнюю по отношению к многоугольнику. Эти силы находятся в равно-
весии. Докажем это предложение геометрически. Сделаем это сначала для
треугольника, обозначив его через ABC (рис. 68).
Три силы A' (k ¦ ВС), В' (k • АС), С' (k ¦ АВ) пересекаются в одной
точке, как перпендикуляры в серединах сторон треугольника. Более того,
сумма их проекций на произвольную ось равна, очевидно, нулю. Следова-
тельно, эти силы находятся в равновесии.
Переходим теперь к случаю произвольного.многоугольника. При помощи
диагоналей, проведенных из одной вершины, разобьем его на треугольники.
В середине каждой стороны полученного треугольника приложим силу, про-
порциональную длине этой стороны, ей перпендикулярную и направленную

130
ЧАСТЬ ВТОРАЯ. СТАТИКА
в сторону, внешнюю по отношению к соответствующему треугольнику,
По доказанному, вся эта система сил находится в равновесии. Но в сере-
дине каждой диагонали приложены две равные и противоположно напра-
вленные силы; их можно, следовательно, отбросить, не нарушая равновесия,
и тогда останутся лишь силы, приложенные к серединам сторон многоуголь-
ника. Предложение, таким образом, доказано.
Рис. 69.
2°. Дан плоский многоугольник ABCDE (рис. 69, а), на котором избрано
какое-нибудь направление обхода. Приложим в каждой вершине этого много-
угольника силу, направленную по стороне, оканчивающейся в этой вершине,
и пропорциональную длине этой стороны. Если многоугольник выпуклый,
то эти силы приводятся к паре. В самом деле, сумма проекций этих сил на
любую ось равна нулю, так как она равна ^-кратной величине проекции
замкнутого многоугольника ABCDE, но сумма моментов относительно
произвольной точки О плоскости многоугольника отлична от нуля. Действи-
тельно, эта сумма равна
т. е.
N=±2k(na.OAB + nn.
N = ± 2k ¦ пл. ABCDE.
Таким образом, равновесия нет.
Если многоугольник вогнутый, то такого результата не получится. В
самом деле, возьмем многоугольник A'B'C'D'; сумма моментов относительно
точки О плоскости (рис, 69, б) будет равна
+ 2k (пл. D'lC — пл. В'1А').
Следовательно, равновесие получится только тогда, когда треугольники D' 1С
и В'IA' равновелики.
103. Параллельные силы. Пусть на твердое тело действуют
параллельные силы. Обозначим через а, C, f направляющие коси-
нусы полупрямой OD, параллельной направлению сил, через
Pv Р2, ..., Рп — алгебраические значения этих сил, которые мы счи-
таем положительными в сторону OD и отрицательными в противо-
положном направлении, и через хк, ук, гк— координаты точки при-
ложения Рк. Тогда могут представиться следующие различные
случаи (п. 29).

ГЛАВА VI. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА	131
1°. 2^^^. Одна равнодействующая, параллельная данному
направлению, имеющая алгебраическое значение ^Р^ и приложен-
ная в центре параллельных сил
2^ '
положение которого не зависит от направления сил.
2°. 2/>* = 0- I2 + M2 + A/2>0. Одна пара с вектором мо-
мента L, М, N.
Щ^Щ^Щ^ Равновесие.
Астатическое равновесие. Допустим, что твердое тело переме-
щается, но параллельные силы сохраняют величину, линию действия
и направление (относительно неподвижных осей) и остаются прило-
женными в одних и тех же фиксированных точках тела. Равновесие
называется астатическим, если оно осуществляется при любом
положении тела, или, что одно и то же, при любом направлении сил
относительно тела, т. е. каковы бы ни были а, р, f. Для этого
необходимо и достаточно, чтобы выполнялись уравнения
В этом случае центр сил, направленных в одну сторону, совпа-
дает с центром сил, направленных в противоположную сторону, так
что обе системы сил всегда уравновешиваются.
104. Центр тяжести. Мы уже дали определение веса матери-
альной точки: это — вертикальная сила, интенсивность которой р равна
массе точки, умноженной на ускорение тяжести g, одинаковое в
одном и том же месте для всех тел. Направление вертикали из-
меняется с изменением места; наблюдения показывают, что вели-
чина g изменяется с высотой и широтой места; но эти изменений
ничтожно малы в границах тела обычных размеров. Следовательно,
тяжелое твердое тело можно рассматривать как совокупность боль-
шого числа связанных между собой материальных точек, находя-
щихся под действием параллельных вертикальных сил, приложенных
к этим точкам и пропорциональных их массам. Равнодействующая
этих сил, равная их сумме, называется весом тела. Точка прило-
жения этой равнодействующей или центр параллельных сил, прило-
женных к материальным точкам, называется центром тяжести.
Он занимает в теле положение, не зависящее от ориентации тела, так
как если тело перемещается, то для наблюдателя, связанного с ним,
все происходит так, как если бы тело было неподвижно, а парал-
лельные силы поворачивались на один и тот же угол вокруг своих
точек приложения, что не изменяет положения центра параллельных

132	ЧАСТЬ ВТОРАЯ. СТАТИКА
сил. Таким образом, центр тяжести тела — это точка, через
которую всегда проходит его вес, каково бы ни было положение
тела. Если, следовательно, закрепить центр тяжести тела, предо-
ставив ему свободу вращаться вокруг него, то тело, находясь под
действием только тяжести, будет оставаться в равновесии в любом
положении, которое оно может принять.
106. Координаты центра тяжести. Пусть mv т2	тп — мас-
сы материальных точек, составляющих твердое тело, plt p2, ¦ • ¦,
рп— их веса, (xlt yv гх), (х2, у2, г2)	(*n, yn, zn) — координаты
этих точек, а Р и М — вес и масса всего тела. Имеем
Pk = mkg. P=Pi +P2 + • • • +Рп = Щ-
Если обозначить через ?, -ц, С координаты центра тяжести, то их
можно определить по формулам для центра параллельных сил
g
Р1 + Р2+ •¦¦ +Рп	т1 + т2+ ... +тп
или, короче,
ZP ~2т ' ^~ЪР ~2«
Отсюда видно, что положение центра тяжести в теле обычных
размеров зависит только от масс точек.
Это заключение очень важно, так как оно позволяет распростра-
нить понятие центра тяжести на системы невесомые. А именно, в не-
которых вопросах, относящихся к материальным. точкам с массами
ти т2	тп, не связанных неизменно между собой, полезно
ввести точку, координаты которой определяются предыдущими фор-
мулами. Эту точку, которую Эйлер предложил называть центром
инерции *), продолжают часто называть центром тяжести, несмотря
на то, что соображения, приводящие к понятию центра тяжести, не
применимы к рассматриваемым вопросам. Центр инерции распо-
ложен, очевидно, внутри любой выпуклой поверхности, окружающей
рассматриваемые точки (п. 32, примечание II).
Разница между центром инерции и центром тяжести для тел
больших размеров изучена Лильесштрёмом (Comptes Rendus, т. 162,
1916, стр. 155).
Если известны центры тяжести Gx и G2 двух частей тела с мас-
сами Mt и М2, то можно найти сразу центр тяжести всего тела,
так как он является центром параллельных сил Mlg и М^, при-
ложенных в точках Gt и О2. Вообще, если известны центры тя-
жести Glt G2	Op и массы Мх, М2, .... Мр нескольких частей
тела, то центр тяжести всего тела есть центр параллельных сил
Mtg, M-2g	Mpg, приложенных в точках Gu G2, .... Gp. Обо-
значая через xv ylf гъ х2, у2, г2, ..., хр, ур, гр координаты цент-
*) Ее называют также центром масс.

ГЛАВА VI. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА	133
ров тяжести этих различных частей, получим для координат S, т), С
центра тяжести тела следующие формулы:
Мрхр
г
6- м1 + м,+ ... + мр ' ^-^й* ;~^й-
Когда желают определить центр тяжести произвольного тела за-
данной формы, например какой-нибудь металлической массы, то
нужно применить полученные формулы к телу, образованному очень
большим числом материальных точек, расположенных на очень
малых взаимных расстояниях. Этой трудности можно избежать, рас-
сматривая тело как непрерывное, что не соответствует действитель-
ности, но дает вполне достаточное для приложений приближение.
Мы отсылаем читателя, желающего получить более подробное пред-
ставление о законности такой замены заданного тела сплошным,
к главе VI Механики Пуассона, относящейся к теории притяже-
ния тел. Уподобляя таким образом твердое тело некоторому сплош-
ному объему, мы предполагаем его разложенным на бесконечно
большое число бесконечно малых частей и помещаем центр тяжести
каждой из таких частей в какой-нибудь точке ее массы. Тогда фор-
мулы, определяющие координаты центра тяжести тела, разбитого на
части с массами Ми М2, . .., Мр, сохраняются при условии замены
сумм, входящих в числители и знаменатели, тройными интегралами.
Если тело имеет очень малую толщину по сравнению с другими
своими измерениями, то его уподобляют поверхности. Таким является,
например, очень тонкий лист бумаги или металла. Точно так же
имеются случаи, когда тело можно рассматривать как линию; таким
является случай длинной и тонкой нити.
Мы укажем в конце главы некоторые формулы для определения
центров инерции линий, поверхностей и объемов.
III. Приложения. Произвольные силы в пространстве
106. Примеры равновесия. 1°. Силы, приложенные в центрах тя-
жести А', В', С', D' граней тетраэдра ABCD, пропорциональные пло-
щадям этих граней, им перпендикулярные и направленные внутрь те-
траэдра, находятся в равновесии. В самом деле, эти силы по отношению
к тетраэдру A'B'C'D', имеющему вершины в центрах тяжести граней дан-
ного тетраэдра, находятся в положении, указанном в конце п. 100. Отсюда
можно заключить, что силы, приложенные в центрах тяжести граней
многогранника, пропорциональные площадям этих граней, нормальные
к ним и направленные внутрь многогранника, находятся в равновесии.
Для этого достаточно разбить многогранник на тетраэдры и применить
к совокупности этих тетраэдров те же рассуждения, что и в первом при-
мере п. 102.
В качестве предельного случая приходим к выводу, что если взять про-
извольную замкнутую поверхность и к каждому ее бесконечно малому эле-
менту приложить силу, пропорциональную площади этого элемента и на-
правленную по нормали, то полученная система сил находится в равновесии.

134	ЧАСТЬ ВТОРАЯ. СТАТИКА
2°. Пары, векторные моменты которых пропорциональны площадям
граней многогранника и направлены внутрь нормально к ним, находятся
в равновесии. В самом деле, сумма проекций моментов этих пар на про-
извольное направление равна нулю.
107. Условия, при которых силы, находящиеся в равновесии, могут
быть направлены по трем, четырем, пяти, шести прямым. Найдем, как
должны быть расположены в пространстве три, или четыре, или пять, или
шесть прямых, для того, чтобы по ним можно было направить силы, нахо-
дящиеся в равновесии. Сделаем сначала следующее замечание. Если не-
сколько сил Fx, F2, ..., Fn находятся в равновесии, то сумма их моментов
относительно произвольной оси равна нулю, поэтому, если какая-нибудь
ось А пересекает направления п — 1 сил, то момент каждой из этих сил
будет равен нулю и потому момент последней силы будет также равняться
нулю, вследствие чего ось Д пересечет линию действия этой последней силы
в точке, находящейся на конечном расстоянии или в бесконечно удаленной
точке. Это свойство сохраняется и для мнимой оси, несмотря на то, что
нельзя больше говорить о моментах относительно этой оси. В самом деле,
пусть (х', у', г') и (х", у", г") — две вещественные или мнимые точки,
Д — прямая, их соединяющая, и Хи, Уъ Zu, L^, М^, Njc— проекции и мо-
менты какой-нибудь силы />, приложенной в точке х^, у%, 2%. Условие того,
что прямая Д и сила /> находятся в одной плоскости, на основании элемен-
тарных формул аналитической геометрии, заключается в том, что величина
Шн = (х" - х') Lk + (/' - у') Мк + (г" - г') Nk +
+ (yv/ _ Z'у) Хк + (z'x" - х'г") Ук + (х'у" - у'х") Zk
равна нулю. Если силы Fh F2	Fn находятся в равновесии, то сумма
... +шп
равна, очевидно, нулю. Следовательно, если величины, ffl-i, Ш^ ..., Шп-1
равны нулю, т. е. если ось Д пересекает п — 1 первых сил, то и Шп равно
нулю и ось Д пересекает также и последнюю силу на конечном расстоянии
или в бесконечно удаленной точке. Если точка х', у', z' вещественная, то
условие Шк = 0 означает, что момент /*& относительно этой точки перпен-
дикулярен к прямой Д.
Г. Три прямых. Допустим, что по трем прямым направлены три
силы, находящиеся в равновесии. Любая ось, пересекающая две из этих
прямых, должна пересекать также и третью. Все три прямые обязательно
находятся в одной плоскости: если две из этих прямых пересекаются
в одной точке, то и третья прямая проходит через эту точку; в
противном случае, все три прямые параллельны. Эти условия необходимы.
Если они удовлетворены, то по этим трем прямым можно, очевидно, всегда
направить силы, находящиеся в равновесии.
2*. Четыре прямых. Допустим, что по четырем прямым Dx, D% D3, Dt
направлены четыре силы, находящиеся в равновесии. Любая ось Д, пересе-
кающая три из этих прямых, должна пересекать и четвертую. Следовательно,
если мы остановимся на общем случае, когда никакая пара прямых не лежит
в одной плоскости, то линейчатая поверхность второго порядка (гипербо-
лоид или параболоид), представляющая собою геометрическое место осей Д,
пересекающих одновременно три прямых, должна содержать и четвертую,
как образующую той же системы, что и три первых. Мы получаем, таким
образом, необходимое условие, указанное Мёбиусом: необходимо, чтобы
Db D2, DB, D4 были четырьмя образующими (одной и той же системы)
поверхности второго порядка. Для того чтобы показать, что это условие
является достаточным, мы воспользуемся следующим доказательством,
Данным Дарбу (статья в первом томе Механики Депейру).

ГЛАВА VI. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА
135
Возьмем на гиперболоиде четыре образующих ?>lt D2> D3, D4 одной
и той же системы. Через точку А (рис. 70) пространства проведем прямые
Аь Аъ, А3, Аь параллельные этим образующим. Направим по прямой At
силу F't и пусть Fv F'2, Fz являются составляющими по прямым Аи А2, Аа силы,
равной и противоположной силе Fit и приложенной тоже в точке А. Геометри-
ческая сумма четырех полученных таким образом сил F[, f'2, F'z, F± будет,
очевидно, равна нулю. Перенесем теперь эти силы параллельно самим себе
на прямые 0t, D2, Оя, D4, после чего получим силы Fu F9, FB, F±. Эти че-
тыре новые сильГнаходятся в равновесии. Действительно, их главный вектор
равен нулю, и их главный момент будет поэтому одинаковым относительно
всех точек пространства. Этот глав-
ный момент либо равен нулю, либо
перпендикулярен всем образующим Д
второй системы гиперболоида, так как
каждая такая образующая Д пересе-
кает четыре прямые D\, D2, D& Di
и поэтому сумма моментов относи-
тельно Д, т. е. проекция главного
момента на ось Д, равна нулю.
Отсюда следует, что главный
момент равен нулю, так как он не
может быть перпендикулярен всем
образующим одной и той же си-
стемы гиперболоида, поскольку по-
следние не параллельны одной и той
же плоскости. Таким образом, имеет
место равновесие.
Если четыре прямых Db D?, D3,
At являются образующими одной и
той же системы гиперболического па-
раболоида, то вспомогательные пря-
мые Аь А2, As, Ai лежат в одной плоскости. Тогда можно, поступая как
и в предыдущем случае, поместить на трех первых прямых Ь±, D2, Ds три
силы /j, /2, /3, главный вектор которых равен нулю, а главный момент
имеет величину а, одинаковую для всех точек пространства, и направлен
перпендикулярно ко всем образующим Д второй системы, т. е. перпенди-
кулярно второй направляющей плоскости. Точно так же можно поместить на
прямых ?>i, D2 и D4 три силы gb g%, git главный вектор которых равен
нулю и главный момент которых Ъ перпендикулярен второй направляющей
плоскости, т. е. имеет то же направление, что и а Если теперь на четырех
прямых поместить силы
Рис- 70.
полученные сложением сил первой системы, умноженных на X, и сил второй
системы, умноженных на ;а, то главный вектор будет равен нулю, а главный
момент будет перпендикулярен второй направляющей плоскости и будет
равен Xa + fJ-й. Величинами X и ц можно распорядиться таким образом,
чтобы этот момент равнялся нулю, и тогда указанные четыре силы будут
находиться в равновесии.
3°. Пять прямых. Если по пяти прямым Dx, D2, DB, Dit Db можно
направить пять сил, находящихся в равновесии, то любая прямая, пересе-
кающая четыре из них, будет обязательно пересекать и пятую. Существуют
две вещественные или мнимые секущие Д' и А", пересекающие Dy, D?, Da, D^
В самом деле, прямые Д, пересекающие Dy, ?>2, Оз. образуют поверхность
второго порядка S, которая пересекает прямую ?>4 в двух вещественных

«gg	ЧАСТЬ ВТОРАЯ. СТАТИКА
или мнимых точках р' и р". Две образующие S системы Л, проходящие
через эти две точки, образуют две секущие, пересекающие четыре прямых
?>ъ Do., D3, Di- Эти две секущие Д' и Д" должны также пересечь и пря-
мую Db. Необходимо, следовательно, чтобы существовали две прямые,
пересекающие одновременно все пять заданных прямых, или, на языке
геометрии прямых, заданные пять прямых должны принадлежать ли-
нейной конгруенции. Рассуждениями, совпадающими с предыдущими (случай
параболоида), можно показать, что это условие является достаточным.
4°. Шесть прямых. Для того чтобы по шести прямым можно было
направить шесть сил, находящихся в равновесии, необходимо и доста-
точно, чтобы эти прямые принадлежали линейному комплексу.
Применим аналитический метод, указанный Мёбиусом и Сомовым. На
одной из шести прямых Djc отложим в определенном направлении отрезок dk
единичной длины и обозначим через ак, рд., fk проекции этого отрезка на
три оси, а через lk, р.к, чк — его моменты относительно этих осей. Эти шесть
величин, связанных соотношением
= О,
пропорциональны величинам, названным Плюккером координатами прямой Dk.
Направим теперь вдоль прямой Dk силу, алгебраическое значение которой,
отсчитываемое в направлении отрезка dk, равно Fk. Проекции и моменты
этой силы равны
Если все это проделать для каждой из шести рассматриваемых прямых
(k — 1, 2	6) и написать, что шесть сил находятся в равновесии, то по-
лучится шесть уравнений
= 0, 2$	2	1
= о, I
где суммирование распространяется на все шесть сил. Из этих шести ли-
нейных и однородных уравнений можно определить для шести неизвестных
Fx, F2, ..../'e значения, неравные одновременно нулю лишь в том случае,
когда определитель, составленный из коэффициентов уравнений A), равен
нулю. Таким образом, получаем необходимое и достаточное условие
ai Pi Ь
«а Р? Тз
Рб Тб
= 0,
которое выражает, что шесть прямых принадлежат одному и тому же ли-
нейному комплексу.
Такие же вычисления показывают, что если число заданных прямых пре-
вышает шесть, то по ним всегда можно направить силы, находящиеся
в равновесии, так как шесть уравнений A) будут содержать более шести
неизвестных.
IV. Твердое тело, подчиненное связям
108. Метод. Общий метод, которым мы будем пользоваться, за-
ключается в том, что мы будем рассматривать тела как свободные,
вводя в качестве вспомогательных неизвестных реакции, вызываемые
наложенными связями, которые называются реакциями связей.

ГЛАВА VI. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА	137
109. Тело с неподвижной точкой. Рассмотрим твердое тело,
имеющее одну неподвижную точку О. вокруг которой оно может
свободно вращаться. Обозначим через Fv F2	Fn действующие
на тело силы. Такое тело может быть названо рычагом в наиболее
общем смысле этого слова. Мы занимаемся, следовательно, услови-
ями равновесия рычага.
Тело оказывает на неподвижную точку давление R (рис. 71). По
закону равенства действия и противодействия неподвижная точка
действует на тело силой Q, равной и про-
тивоположной силе R, так что тело может	,	-^	/п
рассматриваться как свободное под действием
сил Fv F2	Fn, Q. Если тело находится (L
в равновесии, то первые я сил имеют рав-
нодействующую, равную и прямо противо-
положную силе Q. Следовательно, условия
равновесия заключаются в том, что задан-
ные силы должны иметь равнодействующую,
проходящую через неподвижную точку. Это
условие является достаточным, так как если
заменить все приложенные к телу силы
указанной равнодействующей, то она уравновесится сопротивлением
неподвижной точки, со стороны которой будет действовать равная
и прямо противоположная равнодействующей сила реакции.
Мы можем прийти к этому же результату и аналитически.
В точке О выберем три прямоугольные оси координат; обозначим
через X, Y, Z, L, М, N проекции главного вектора и главного
момента относительно начала О системы сил F, приложенных
к телу, а через X', У, Z' проекции реакции Q неподвижной точки.
Условия равновесия будут:
= 0,	A)
1 = 0, М = 0, Л/ = 0.	B)
Уравнения B), не содержащие реакции, являются необходимыми
условиями равновесия. Они выражают, что приложенные к телу
силы F приводятся к одной силе, проходящей через начало О.
Уравнения A) показывают тогда, что реакция (X', Y', Z') равна и
противоположна этой равнодействующей (X, Y, Z), которая является
не чем иным, как давлением на неподвижную точку.
Рассмотрим частный случай рычага, находящегося под действием
только двух сил Fl и F2. Для того, чтобы было равновесие, необ-
ходимо и достаточно, чтобы эти силы уравновешивались реакцией Q
точки О. Для того чтобы три силы Fv F2, Q находились в равно-
весии, необходимо, чтобы силы F1 и F2 находились в одной пло-
скости с точкой О и чтобы сумма моментов сил Fx и F2 относи-
тельно точки О равнялась нулю. Это — хорошо известное элементарное
условие равновесия рычага.

138
ЧАСТЬ ВТОРАЯ. СТАТИКА
¦&"
ПО. Тело, имеющее неподвижную ось. Пусть Fv F2, ..., Fn—
силы, действующие на твердое тело. Они вызывают в различных
точках оси давления Р', Р", Р'"	а ось, в свою очередь, дей-
ствует на тело реакциями Q', Q", Of", ... Тело может рас-
сматриваться как свободное, но находящееся под действием сил
Flt F2	Fn, Q', Q", ... Для того чтобы было равновесие, не-
обходимо, в частности, чтобы сумма моментов всех этих сил отно-
сительно неподвижной оси, которую мы примем за ось г, равнялась
нулю. А так как моменты реакций Q', О", ... равны нулю, то необ-
ходимо, чтобы было
N = 0.
Это — необходимое условие равновесия. Оно и достаточно. В самом
деле, если оно выполняется, то система сил приводится к одной
силе, равной главному вектору OR и уравновешивающейся сопро-
тивлением оси, и к паре с вектором момента 00, перпендикулярным
к Ог, так как N равно нулю. Эта пара может быть повернута
в своей плоскости таким образом, чтобы ее плечо совпало с осью.
Тогда силы <p.?'i составляющие пару, будучи приложены к точкам
оси, уравновешиваются ее сопротивлением^
и тело действительно находится в равновесии.
Задача, которою мы занимаемся, пред-
ставляет собою условия равновесия ворота.
Найдем теперь реакции оси. Эти реакции
являются силами, приложенными в различных
точках тела, соприкасающихся с осью. Они
могут быть приведены к двум силам Q' и
Q", приложенным к двум точкам О и О' оси.
Такой результат может быть получен физи-
чески, если закрепить две точки О и О'
оси, сделав ее таким образом неподвижной.
Эти точки действуют на тело, развивая реакции Q и Q'. Примем
точку О за начало. Обозначим через X, Y, Z, L, М, N те же эле-
менты, что и раньше, а через X', У, Z', X", Y", Z" проекции
реакций Q' и Q". Пусть h — расстояние 00'. Мы получим условия
равновесия (рис. 72):
Х~\-Х'-\-Х"=<д, Y-\-Y'~JrY№ = 0, Z+Z'+Z" = 0,
L — ЛУ"=0, M-\-hX" = Q, N = 0.
Последнее из этих уравнений не зависит от реакций: это — необ-
ходимое и достаточное условие равновесия тела. Два предшествующих
уравнения определяют X" и Y". Подставляя эти значения в два пер-
вых уравнения, найдем X' и Y'. Но Z' и Z" связаны только одним
условием
Рис. 72.

ГЛАВА VI. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА
139
которое не позволяет определить каждую из этих реакций, если
предполагать, что тело абсолютно твердое.
С физической точки зрения реакции Q' и Q" являются, однако,
вполне определенными, так как тела в природе не обладают свойствами,
которые мы приписываем абсолютно твердым телам в теоретической
механике: они деформируются, и эта деформация вызывает действие
упругих сил. Если принять во внимание эти силы, то можно опре-
делить и каждую из последних двух реакций.
111. Тело вращается вокруг оси и скользит вдоль нее.
В этом случае реакции Q', Q", Q'" оси на тело нормальны к оси.
Приняв последнюю за ось Oz, получим
два условия равновесия
112. Тело, опирающееся на непо-
движную плоскость.
1°. Случай одной точки опоры. Рас-
смотрим сначала случай, когда тело опи-
рается на неподвижную плоскость только
одной точкой. Реакция плоскости на тело
будет нормальна к плоскости, если пред-
положить, что тело может скользить без
трения. Тело может рассматриваться как
саободное, но находящееся под действием сил Fu F2	 Fn,
непосредственно к нему приложенных, и реакции Q плоскости. Для
того чтобы было равновесие, необходимо, чтобы силы F{ имели
равнодействующую, равную и прямо противоположную реакции Q
(рис. 73), т. е. чтобы заданные силы имели равнодействующую R, про-
ходящую через точку опоры, перпендикулярную к плоскости и на-
правленную таким образом, чтобы она прижимала тело к этой пло-
скости. Это условие, очевидно, и достаточно, так как если оно вы-
полняется, то равнодействующая не вызовет скольжения тела и урав-
новесится равной и прямо противоположной реакцией плоскости Q.
Легко получить этот результат также аналитически.
2°. Случай нескольких точек опори, лежащих на одной пря-
мой. Допустим, что тело опирается на неподвижную плоскость
в точках Ах, А2	Ар прямой Ох/Во всех этих точках плоскость
развивает нормальные реакции Qt, Q2	Qp, направленные в одну
и ту же сторону (рис. 74). Эти силы имеют равнодействующую Q,
нормальную к плоскости, направленную в ту же сторону и прило-
женную в некоторой точке, лежащей между крайними точками Ах и Ар.
Для того чтобы имело место равновесие, необходимо, чтобы
заданные силы уравновешивались реакциями плоскости, т. е. чтобы
они имели одну равнодействующую, нормальную к плоскости, на-
правленную таким образом, чтобы она прижимала тело к плоскости
и чтобы ее продолжение пересекало прямую Ох в точке, располо-

140
ЧАСТЬ ВТОРАЯ. СТАТИКА
зкенной между Ах и Ар. Эти необходимые условия также и доста-
точны, так как названная равнодействующая может быть тогда
разложена на две другие силы, нормальные к плоскости и прило-
женные в двух точках опоры. Полученные силы уничтожатся сопро-
тивлением плоскости.
Чтобы выразить эти условия аналитически, примем прямую Ох
за ось х, ось г направим нормально к плоскости в ту сторону, по
которую находится тело. Тогда все реакции Qt, Q2	Qp будут
положительными. Уравнения
равновесия будут
Х=0, Y = 0,
L = 0, M — fltQj — a2Q2— ...
... — apQp = 0, N = 0,
где а1У аг	ар—абсциссы
точек опоры.
Четыре из этих уравнений,
не содержащих реакции, выра-
жают необходимые условия
равновесия. Они показывают,
что заданные силы должны
иметь равнодействующую, нормальную к плоскости ху и пересе-
кающую ось х. Третье уравнение показывает, что проекция Z
равнодействующей должна быть отрицательная, т. е. что равнодей-
ствующая должна быть направлена так, чтобы она прижимала тело
к плоскости. Пусть х — абсцисса точки пересечения равнодействую-
щей с осью Ох. Момент равнодействующей относительно оси Оу
равен М —— xZ. Следовательно, должно быть
Рис; 74.
откуда, заменяя Z его значением, получаем
Q1 + Q2+ ... +QP '
а эта величина, как известно, заключена между двумя конечными
значениями ах и ар, так как величины Qt, Q2	Qp положительны.
Таким образом, продолжение равнодействующей пересекает ось Ох
между крайними точками опоры.
Реакции плоскости должны теперь удовлетворять двум уравнениям
М — аА — a2Q2— ... — apQp=Q.

ГЛАВА VI. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА	141
Если имеются только две точки опоры, то эти уравнения определяют
обе реакции. Если точек опоры больше двух, то реакции не могут
быть определены из этих соотношений. Они могут быть определены,
если считать тело упругим.
3°. Общий случай. Предположим, что твердое тело опирается на
плоскость в нескольких точках Аи Аг, .... Ар% не лежащих на одной
прямой. Со стороны плоскости возникают нормальные реакции
Qv Q2	Qp, имеющие одну равнодействующую Q, так как они все
направлены в одну сторону.. Как мы видели в теории сложения па-
раллельных сил, точка пересечения этой равнодействующей с пло-
скостью лежит внутри любого выпуклого многоугольника, охваты-
вающего все точки опоры. В частности, она находится внутри опор-
ного многоугольника, который является выпуклым и вершинами
которого служат точки опоры. Этот многоугольник охватывает все
остальные точки опоры. Для равновесия необходимо, чтобы заданные
силы уравновешивали равнодействующую реакцию Q. Следовательно,
заданные силы должны иметь равнодействующую, нормальную к пло-
скости и направленную так, чтобы она прижимала тело к плоскости
и пересекала эту плоскость внутри опорного многоугольника. Этих
условий достаточно, так как при сделанных предположениях можно
всегда разложить равнодействующую на три силы, нормальные к
плоскости и приложенные к точкам опоры, и эти силы уничтожатся
сопротивлением плоскости.
Возьмем ту же систему осей. Твердое тело можно рассматривать
как свободное, но находящееся под действием сил Fu F2	Fn,
Qv Q2	Qp. Условия равновесия будут
X=Q, Y=0, N = Q,	A)
+ ... -|-Qp=0.
M — «A — a2Q2 — ... —apQp =
где av bx, a2, b2, ...—координаты точек опоры.
Уравнения A), не содержащие реакций, выражают необходимое
условие равновесия, заключающееся в том, что заданные силы имеют
равнодействующую, нормальную к плоскости. В самом деле, вели-
чина LX-\-MY -\-NZ равна нулю и равенство Z —0 возможно
только при условии, что все реакции равны нулю, так как последние
либо равны нулю, либо положительны. В этом частном случае, когда
все реакции равны нулю, Z, L и М будут равны нулю, и тогда будут
находиться в равновесии непосредственно приложенные силы. Отбра-
сывая этот очевидный случай равновесия, мы видим, что силы
F{, F2, .... Fn должны иметь равнодействующую, нормальную к пло-
скости. Необходимо, кроме того, чтобы проекция Z была отрица-
тельная, как это видно из первого уравнения B), и чтобы равно-

142
ЧАСТЬ ВТОРАЯ. СТАТИКА
действующая пересекала плоскость внутри опорного многоугольника,
что вытекает из двух последних уравнений B). Если имеются только
три точки опоры, то уравнения B) позволяют определить три реак^
ции. Если их больше, то необходимо принять в расчет упругость тела.
4°. Приложения. Чтобы показать, как можно составить вспомогательные
условия равновесия, рассмотрим прямоугольный стол, опирающийся четырьмя
ножками на горизонтальную плоскость.
Пусть AtA2AsAi— стол, на который мы положим произвольные
тела. Пусть Р — равнодействующая весов тел и стола и А — ее точка
пересечения со столом. Обозначим через Вь В2, В3, В4 (рис. 75) точки
опоры. Примем неподвижную горизонтальную плоскость за плоскость ху,
центр опорного прямоугольника за
Дг	начало координат и прямые, парал-
дельные его сторонам, за оси х и у.
Координаты точек опоры Вь Вь Вя,
В± будут соответственно (а, Ь),
( — a,b), (—a, —b), (a, —b). Пусть
х, у — координаты точки А. Обозна-
чим через Qi, Q?, Q%, Q± реакции
плоскости. Напишем сначала общие
уравнения равновесия, которые здесь
имеют вид:
—«0,+лОз + «<?8 — aQi +
Рис.
: = 0.J
A)
Чтобы получить еще одно уравне-
ние, мы допустим, что грунт не явля-
ется абсолютно твердым и что он оседает в каждой точке на очень малую
величину, пропорциональную давлению на грунт в этой точке. Обозначим
через еъ е2, е8, е4 величины, на которые ножки углубляются в грунт. Тогда,
по предположению,
Точка О, рассматриваемая последовательно как середина отрезков
B2Bit опустится на величину
00' =
Следовательно, должно быть
-, ОО' =
+ Ч = ?2 + Ч
откуда
B)
Если имеются р точек опоры, то, напнсав, что после деформации
грунта они остаются в одной плоскости, мы получим р — 3 условий, которые
совместно с тремя общими уравнениями позволят определить все реакции.
В нашем частном случае из уравнений A) и B) после их разрешения
относительно Qlt Q2> Фз> Qi получаются для этих величин значения
a b

ГЛАВА VI. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА
143
где величине Qi соответствуют знаки (++), <Эз—знаки (	1- ), Q3—знаки (	)
и Q^ — знаки (+•—). Необходимо, чтобы все эти значения были положитель-
ными, а для этого точка А должна находиться внутри ромба с вершинами
в серединах ребер стола. Если точка А находится вне этого ромба, напри-
мер со стороны Ах (рис. 75), то реакция Qs будет отрицательной, а осталь-
ные три будут положительными. Так как это невозможно, то следует предпо-
ложить, что ножка Вв не оказывает больше давления на грунт и надо вычи-
слять реакции Qb Q2, Qi так, как если бы стол был поставлен только
на три ножки, для чего нужно в уравнениях A) положить Q3 = 0.
113. Несколько твердых тел. Для нахождения условий равно-
весия системы, состоящей из нескольких твердых тел, соединенных
взаимными связями, можно применить следующий метод: нужно вы-
разить, что каждое из тел системы находится в равновесии под дей-
ствием сил, непосредственно к нему приложенных, и под действием
на него реакций остальных тел. Эти последние силы подчинены
закону равенства действия и противодействия. Мы не будем зани-
маться здесь приложением этого метода. Мы увидим дальше, что
принцип возможных скоростей дает значительно более быстрый метод
для решения подобных вопросов.
V. Некоторые формулы для вычисления центра тяжести
114. Линии. На линии АВ возьмем две точки Р и Р' (рис. 76) и обо-
значим через т массу дуги РР'. Отношение ^р- есть средняя плотность
РР'
дуги РР'. Если это отношение не зависит от положения точек Р и Р', то
говорят, что линия АВ однородна. Если оно изменяется, то плотностью линии
в точке Р называют предел р средней
плотности дуги РР', когда точка Р' стре-
мится к Р. Плотность р, изменяясь с по-
ложением точки Р, является функцией па-
раметра, определяющего положение точки Р
на кривой. Пусть ds— бесконечно малый
элемент кривой, содержащий точку Р с ко-
ординатами х, у, г. Масса dm этого эле-
мента равна р ds и, обозначая через М всю
массу кривой, а через ?, rlt С координаты
ее центра тяжести, имеем
М = С ?ds, Mt= С х? ds,
М'Ч = I УР ds< -М* = I z? ds.
Рис. 76.
Если линия однородна, то средняя плотность р будет постоянной и масса М
будет тогда р/, где I — длина кривой. Для €, ij, С получим:
; = ixds, /tj = [yds, fc= izds.
115. Теорема Гюльдена. Площадь поверхности, образованной вра-
щением плоской кривой вокруг оси, расположенной в ее плоскости, и

144	ЧАСТЬ ВТОРАЯ. СТАТИКА
ее не пересекающей, равна длине этой кривой, умноженной на длину
окружности, описываемой ее центром тяжести, в предположении, что
кривая однородна.
В самом деле, отнесем плоскую кривую к оси вращения, принятой за
ось Ох, и перпендикулярно к последней направим ось Оу. Элемент ds с ор-
динатой у образует при вращении элемент поверхности dA, который можно
отождествить с боковой поверхностью усеченного конуса, так что
dA =
Следовательно,
— 2п Су ds =
что и доказывает теорему.
Если ось пересекает кривую, то найденное выражение для А предста-
вляет не полную поверхность, а разность между поверхностями, образован-
ными вращением частей кривой, расположенных по одну и по другую сто-
рону оси, так как в интеграле А элемент у ds будет положительным или
отрицательным, в зависимости от того, находится ли элемент ds выше или
ниже оси.
116.	Поверхности. Пусть /и — масса элемента поверхности с площадью а.
Отношение /и/а есть средняя плотность элемента а. Плотность р поверхно-
сти в точке Р есть предел отношения /и/а, когда а есть бесконечно малый
элемент, окружающий точку Р. В общем случае р будет функцией двух
параметров, определяющих положение точки Р на поверхности. Когда плот-
ность р постоянна, поверхность называется однородной.
Пусть da — бесконечно малый элемент поверхности, окружающий точку Р
с координатами х, у, г. Масса этого элемента равна dm = p da и, обозначив
через М всю массу, а через Z, щ, К. координаты центра тяжести, получим
М = | I р da. Mi = I I XO da, Mi\ = I I yp da, MZ = I I 20 da.
J J	J J	J J JV	J J
У однородной поверхности плотность р — постоянна, масса М равна р5,
где 5 — площадь поверхности, и мы получаем
SZ= С С xda, Stj= f f yda, SC= Г Г 2 da.
117.	Плоские фигуры. Примем плоскость фигуры за плоскость ху.
Координата С будет тогда равна нулю. Элемент da будет иметь разные
выражения в зависимости от принятой системы координат. Например, в поляр-
ных координатах /-ив элемент da будет равен г dr d%, в декартовых косо-
угольных координатах с углом а между осями он равен sin a dx dy, ...
В частности, для однородной фигуры, отнесенной к прямоугольным
декартовым координатам, формулы принимают вид
S = С С dx dy, SC = Г Г х dx dy, Sr\= f j у dx dy, S? = Г Г г dx dy,
где одно интегрирование всегда может быть выполнено.
118.	Теорема Гюльдена. Объем, образованный плоской фигурой,
вращающейся вокруг оси, лежащей в ее плоскости и не пересекающей ее,
равен площади фигуры, умноженной на длину окружности, описываемой
центром тяжести этой фигуры, принимаемой за однородную.
Какой-нибудь элемент dx dy фигуры S при вращении вокруг оси Ох
описывает элемент объема, равный разности объемов цилиндров, описанных
прямоугольниками ABCD и A'B'CD (рис. 77), т. е. с точностью до величин
третьего порядка равный
2*у dx dy.

ГЛАВА VI. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА
145
Обозначая объем через V, получим
У
= 2п С Г у dx dy =
что и доказывает теорему.
Заметим, что если ось пересекает фигуру, то полученная формула будет
представлять разность объемов, описанных частями фигуры, расположенными
по одну и по другую сторону оси.
Как на обобщение этой теоремы, укажем
на исследования Кёнигса об объемах, описывае-
мых кривыми (Journal de Jordan, t. V, 1889). См.
также заметку Адамара в Bulletin de la Societe
mathematique de France, seance du 7 dec. 1898.
119. Объемы. Возьмем в твердом теле
объем V, заключающий массу т. Отношение mjv
называется средней плотностью выделенной
части тела. Когда объем v стремится к нулю,
стягиваясь в точку Р, то отношение mjv стремится
к пределу р, который называется плотностью в
точке Р. Эта величина р является функцией
координат точки Р, и, когда она постоянна, тело
называется однородным.
Масса dm элемента объема dv, окружающего точку Р с координа-
тами х, у, z, равна р dv. Следовательно, обозначая через М всю массу,
получим формулы
Рис. 77.
Mi = Г Г Г хр dv, Mt\ = j j С yp dv, Ж= Г Г Г гр dv.
Если тело однородно и имеет объем V, то М = pV и
У? = С С С х dv, Vt) = jjf у dv, VI = С С С z dv.
Выражение dv зависит от избранной системы координат. В косоугольной
декарт©вой системе необходимо принять dv равным k dx dy dz, где через k
обозначен объем параллелепипеда с ребрами, равными единице и парал-
лельными осям координат. В сферических координатах г, 6, <р для dv полу-
чается выражение г- sin в dr db df и т. д.
В случае однородного тела можно всегда начинать с выполнения одного
интегрирования и привести тройные интегралы к двойным.
УПРАЖНЕНИЯ
1. Система сил, приложенных к твердому телу, отнесена к косоугольным
осям. Показать, что уравнения равновесия имеют тот же вид, что и в прямо-
угольных осях:
2. Рассматривается плоский замкнутый многоугольник; ко всем его сто-
ронам, кроме одной, прилагаются силы, пропорциональные этим сторонам,
им перпендикулярные, лежащие в плоскости этого многоугольника и напра-
вленные^ по отношению к нему наружу. Показать, что эти силы имеют
равнодействующую, перпендикулярную к последней стороне и пропорцио-
нальную ей.

146	ЧАСТЬ ВТОРАЯ. СТАТИКА
3.	Доказать, что если несколько сил, приложенных к твердому телу,
находятся в равновесии или приводятся к паре, то центр тяжести равных
масс, помещенных в концах этих сил, совпадает с центром тяжести равных
масс, помещенных в точках их приложения (Крофтон).
4.	Вдоль сторон замкнутого пространственного многоугольника Р напра-
вляют в одну и ту же сторону обхода силы, равные сторонам. Показать:
1) что эти силы приводятся к паре; 2) что если построить в плоскости этой
пары многоугольник II с площадью, равной половине момента пары, то
проекция многоугольника Р на произвольную плоскость имеет такую же
площадь, как и проекция многоугольника П на ту же плоскость (Гишар).
5.	Дан выпуклый плоский четырехугольник ABCD. Направить по сто-
ронам этого четырехугольника четыре силы, находящиеся в ра.вновесии.
(См. Мёбиус, Статика, § 29.)
6.	Центр системы сил, лежащих в плоскости и имеющих равно-
действующую. Дана плоская фигура А\А%...Ап неизменяемой формы,
к различным точкам которой приложены силы F\, F2, ..., Fn, расположен-
ные в плоскости фигуры и имеющие равнодействующую R. Будем пере-
мещать фигуру в ее плоскости, предполагая, что силы Fb F%, ..., Fn
остаются приложенными в тех же точках А\, Л2, ..., Ап движущейся
фигуры и сохраняют неизменными свои величины' и направления. Тогда
равнодействующая R будет также сохранять неизменными свою величину
и направление и будет проходить через некоторую точку С, неизменно
связанную с движущейся фигурой и называемую по Мёбиусу центром
сил Fb F2, ..., Fn.
7.	Случай пары. Главные направления. Допустим теперь, что силы
F\, F%, ..., Fn образуют пару. Тогда перемещая фигуру в своей плоскости
и сохраняя постоянными величины и направления сил, можно всегда при-
вести фигуру в положение равновесия.
Существуют два взаимно перпендикулярных направления ОР и OQ,
неизменно связанных с движущейся фигурой и обладающих следующим
свойством: когда фигура приведена в то ее положение, где имеет место
равновесие, и каждая из сил Fji разложена на две составляющие Р^ и Q&,
параллельные соответственно ОР и OQ, то каждая из систем параллельных
сил P]i и Qfc находится в равновесии. Эти направления называются глав-
ными (Мёбиус).
8.	На дощечке укреплены две магнитные стрелки, линии полюсов кото-
рых имеют длину а и b и пересекаются под прямым углом в своих сере-
динах. Дощечка плавает в неподвижной жидкости. Найти: 1) положение
равновесия; 2) главные направления (упр. 7). Известно, что действие Земли
на правильно намагниченную стрелку, т. е. такую, которая имеет только
два полюса и только одно нейтральное направление, приводится к паре,
силы которой постоянны по величине и направлению и приложены в полюсах.
Обозначим в рассматриваемой задаче через Р общее значение горизонталь-
ных проекций сил пары, действующих на стрелку а, а через Q ту же вели-
чину для стрелки Ь. Силы Р и Q направлены по магнитному меридиану
места.
9.	Центральная плоскость в твердом теле, находящемся п'од дей-
ствием сил, главный вектор которых не равен нулю. Пусть на твердое
тело действуют силы, главный вектор которых не равен нулю. Допустим,
что когда тело перемещается, каждая из сил сохраняет постоянными свою
величину и направление и остается приложенной в одной и той же точке
тела. Это, например, имеет место для тяжелого тела, образованного соеди-
нением нескольких намагниченных тел. В этом случае действие Земли на
каждый магнит создает пару, силы которой постоянны по величине и напра-
влению и приложены в полюсах магнита, а полный вес системы также
является силой, постоянной по величине и направлению, приложенной в опре-
деленной точке тела. Эта система сил имеет главный вектор, равный весу.

ГЛАВА VI. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА	147
Очевидно, что поступательное перемещение тела ничего не изменяет
в его состоянии и поэтому достаточно исследовать эффект вращений.
Рассмотрим прямую Ор и разложим каждую силу Fk на составляю-
щую рк, параллельную Ор, и на силу, к ней перпендикулярную. Если про-
извольным образом менять направление Ор, то геометрическое место цен-
тров » параллельных сил рк будет, в общем случае, плоскостью, называемой,
.по Мёбиусу, центральной плоскостью. Она не меняет свое положение
в теле, какова бы ни была его ориентация. В некоторых частных случаях
геометрическое место может быть прямой линией (центральная линия),
а также и точкой (центр сил).
10. Теорема Миндинга. Будем перемещать произвольным образом
тело, предполагая все время, что силы постоянны по величине и направле-
нию. Существует бесчисленное множество положений, при которых силы F^
приводятся к одной равнодействующей. Совокупность этих равнодействующих
образует в теле множество лучей, которые пересекают два фиксированных
конических сечения (фокальные конические сечения), находящихся в двух
взаимно перпендикулярных плоскостях. (См. Crelle, т. 14, 15.)
• 11. Оси равновесия. Рассмотрим свободное твердое тело, удовлетворяю-
щее указанным выше условиям: когда тело меняет свое положение, дейст-
вующие на него силы сохраняют величину и направление и остаются
приложенными к одним и тем же точкам тела. Как мы уже говорили,
поступательное перемещение ничего не меняет в состоянии тела и
поэтому достаточно исследовать влияние вращений. Допустим, что
тело в рассматриваемом положении находится в равновесии, и положим, как
и Мёбиус (Статика, гл. VIII), что
где суммы распространены на все силы. Мёбиус назвал осью равновесия
прямую, при повороте вокруг которой на произвольный угол тело остается
в равновесии. Для того чтобы ось Oz была осью равновесия, необходимо и
достаточно, чтобы, кроме шести уравнений рав ;овесия, выполнялись сле-
дующие условия:
F = 0, G = 0, / + т = 0.
12.	Астатическое равновесие. Говорят, что равновесие является аста-
тическим, когда при тех же условиях в отношении сил, что и в предыдущем
упражнении, это равновесие существует, каково бы ни было заданное поло-
жение тела. Для этого необходимо, чтобы каждая из трех осей координат
Ox, Oy, Oz была осью равновесия, т. е. чтобы, кроме шести условий равно-
весия, выполнялись еще следующие шесть условий:
F=0, G = 0, tt=0, 1 = 0, от = 0, л = 0.
Эти условия, необходимые для астатического равновесия, являются и
достаточными.
13.	Если на тело действуют две постоянные по величине и направлению
силы, приложенные в двух фиксированных точках, то всегда существует ось,
параллельная заданному направлению, причем такая, что если ее закрепить,
то тело будет оставаться в безразличном равновесии во всех положениях,
которое оно может принимать (Мёбиус).
14.	Если тело находится в астатическом равновесии и действующие
силы параллельны данному направлению, то система параллельных сил
находится в равновесии. Центр тех из этих параллельных сил, которые
направлены в одну сторону, совпадает с центром параллельных сил, напра-
вленных в противоположную сторону.

148	ЧАСТЬ ВТОРАЯ. СТАТИКА
15. Рассмотрим твердое тело, находящееся под действием сил, прило-
женных в фиксированных точках этого тела и постоянных по величине и
направлению. Каковы необходимые и достаточные условия для того, чтобы
можно было привести тело в состояние астатического равновесия присоеди-
нением только одной силы, приложенной в фиксированной точке Р и
постоянной по величине и направлению?
Ответ:
и две аналогичные пропорции, в которых х должен быть заменен через у
или z. Тогда точка Р существует и называется центром сил си-
стемы. В этом случае координаты точки и>, подлежащей определению
в упражнении 9, не зависят от положения тела. Эта точка как раз и будет
точкой Р.
16.	Найти также условия, чтобы существовала центральная линия,
т. е. чтобы точка « описывала прямую. В этом случае всегда можно при-
соединить к системе две силы, чтобы осуществить астатическое равновесие.
17.	Если точка и> описывает плоскость (центральную плоскость), то
можно соответствующим образом присоединить к системе три силы, чтобы
осуществить астатическое равновесие.
18.	Твердое тело, вращающееся вокруг неподвижной точки, находится
под действием сил, приложенных в неизменно связанных с телом точках
и постоянных по величине и направлению. Каким условиям должны удовле-
творять эти силы, чтобы тело оставалось в равновесии во всех положениях,
которые оно может принимать вокруг неподвижной точки (астатическое
равновесие рычага)?
19.	Тот же вопрос в предположении, что тело может вращаться
вокруг оси.
23. Тот же вопрос в предположении, что тело может не только вра-
щаться вокруг оси, но и скользить вдоль нее.
21.	Твердое тело, которое может вращаться вокруг неподвижной точки
или оси, находится под действием сил, приложенных в неизменно связанных
с телом точках и постоянных по величине и направлению. Найти положения
равновесия тела. (См. упражнение 23; см. также My аньо, Lecons de Мёса-
nique analytique d'apres Cauchy, стр. 234.)
22.	Дана система сил, приложенных к твердому телу, и произвольный
триэдр OP, OQ, OS. Каждая из сил F^ разложена на три составляющие /»ftt
qk, sk, параллельные ребрам триэдра. Обозначим через А центр параллель-
ных сил рк и через Р=~^Рк их равнодействующую, а через В и q, С и s
—то же для сил qk и sft. Показать, что произведение площади треугольника ABC
на объем параллелепипеда, имеющего ребра р, q, s, постоянно, какова бы
ни была ориентация триэдра OPQS (Миндинг).
23.	Упражнения к теореме Миндинга. 1°. Взята произвольная пря-
мая Д, опирающаяся на два фокальных конических сечения, найденных
в упражнении 10. Показать, что существует положение тела (т. е. система
значений девяти направляющих косинусов), при котором силы приводятся
к одной равнодействующей, направленной по Д. (Нужно заметить, что так
как подвижные оси могут совпадать с неподвижными, то определитель
девяти косинусов равен + 1; целесообразно выразить косинусы через углы
Эйлера.)
2°. Через произвольную точку Р тела можно провести четыре прямых,
опирающихся на два фокальных конических сечения. Существуют, следова-
тельно, четыре положения тела, для которых силы имеют равнодействующую,
проходящую через точку тела.

ГЛАВА VI. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА	149
3°. Если силы, действующие на тело, остаются постоянными по величине
и направлению и приложены в фиксированных точках тела и если, кроме
того, эти силы приводятся к паре, то существует четыре положения равно-
весия тела.
(В самом деле, пусть Fv F2, ..., Fn— силы и А\, Ля, ..., Ап—-точки
их приложения. Главный вектор R сил F2, F^, ..., Fn равен и противопо-
ложно направлен силе F\. Согласно предыдущему существует четыре поло-
жения тела, при которых силы F%, F%, ..., Fn имеют одну равнодействую-
щую R, проходящую через точку Аг тела. Эти четыре положения будут,
очевидно, положениями равновесия, поскольку для них R и F± равны и
прямо противоположны.)
Предыдущие теоремы имеют место в наиболее общих случаях. Для
частных положений сил число 4 может быть увеличено и стать даже бес-
конечным.
24. Твердое тело находится в рассматриваемом положении в равно-
весии. Спрашивается, будет ли при предположениях упражнения 11 суще-
ствовать для него ось равновесия.
Решение. Достаточно исследовать, существует ли ось равновесия Oz'.
проходящая через О. Для этого отнесем систему к новым осям Ох',
Оу', Oz', образующим со старыми углы, косинусы которых равны а, я', а",
P. P', P"i Т> т'> t"i и найдем соответствующие этим новым осям величины
F'', G', Н', V, т', п'. Если для сокращения положить
tn-\-n = f, n-\-l = g, l-\-m = h
и обозначить через /', g', h' аналогичные величины относительно новых
осей, то придем к следующему результату. Рассматривая квадратичную
форму
ф (и, и', и") = /и5 + gu'2 + hu — 2Fu'u" — 1Оа"и — 2Нии',
можно написать:
/' = ф (a, a', a"), g' = ф (р, р', $"), А' = ф (Т, Т', f").
G =
¦¦¦)¦
Для того чтобы ось Oz', направление которой определяется косинусами у,
у', ¦("' была осью равновесия, необходимо и достаточно, чтобы y, Y> Л" удо-
влетворяли уравнениям
которые выражают, что дискриминант формы ф равен нулю.
25.	Найти положения равновесия однородного тяжелого стержня АВ,
один из концов которого прикреплен при помощи нерастяжимой и не имею-
щей массы нити АО к неподвижной точке О, а другой конец скользит
без трения по горизонтальной плоскости.
26.	Даны материальные точки с массами ть /и2, ..., тп. Пусть
М-—сумма их масс, G — их центр тяжести и А — произвольная точка.
Доказать два соотношения:
2	¦ АО"-,
где /ге;/И? обозначает расстояние между точками т.{ и /и& (Лагранж).

ЧАСТЬ ВТОРАЯ. СТАТИКА
27. Центры тяжести однородных линий. Дуга круга. Доказать, что
расстояние от центра круга до центра тяжести дуги круга есть четвертая
пропорциональная между дугой, радиусом и хордой.
28.	Дуга цепной линии у = —[еа -\- е "). Доказать, что центр тяже-
сти дуги цепной линии имеет ту же абсциссу, что и точка пересечения
касательных к ней в концах А к В. Если точка А есть вершина кривой,
то ордината центра тяжести равна половине ординаты точки пересечения
нормали, проведенной в точке В, с осью Оу.
29.	Однородные плоские фигуры. Доказать, что если однородная плоская
фигура имеет прямолинейный диаметр, сопряженный с некоторым, напра-
влением хорд, то центр тяжести лежит на этом диаметре..
30.	Центр тяжести площади треугольника совпадает с центром
тяжести трех равных масс, помещенных в трех вершинах; центр тяжести
площади трапеции лежит на прямой, соединяющей середины оснований Ъ
и В и делит эту прямую в отношении 2В -\- b к 2Ь + В.
31.	Центр тяжести части плоскости, ограниченной дугой цепной
линии АВ, осью х (основанием цепной линии) и двумя ординатами то-
чек Аи В. (Абсцисса центра тяжести равна абсциссе центра тяжести дуги АВ;
его ордината равна половине ординаты центра тяжести дуги АВ.)
32.	Неоднородные фигуры. Центр удара. Дана плоская фигура 5. Рас-
смотрим прямую АА' в ее плоскости и допустим, что плотность р в какой-
нибудь точке пропорциональна расстоянию 5 от этой точки до прямой АА'.
Центр тяжести G полученной таким образом материальной поверхности на-
зывается центром удара относительно оси АА' фигуры S, если считать ее
однородной. Эта точка встречается в теории удара, а также в гидростатике.
Доказать, что центр удара G и ось АА' образуют систему полюсов и поляр
относительно неподвижного мнимого конического сечения, центр которого
совпадает с центром тяжести площади S, если считать ее однородной.
Ответ. Примем за начало центр тяжести площади S, предполагаемой
однородной, и обозначим через da элемент этой площади. Интегралы I I x da
и I I у da, распространенные на площадь, равны нулю. Можно выбрать
такое направление прямоугольных осей х Оу, чтобы J I xy da также рав-
нялся нулю. Тогда I Г da = S. Положим, кроме того, что
J J х"- da = a*S, j f y"-da = b"-S.
Пусть их -\-vy -(-I =0 — уравнение прямой АА'. Предполагаемая плотность
площади S в точке (х, у) будет
k
р=	 (илг-f vy-\-1) (k — постоянная).
Координаты точки G будут тогда 5 = а2и, ij = b2v, и эта точка является
х2 у2
полюсом прямой А А' относительно мнимого конического сечения — -j- т? ~Ь
-J- 1 = 0. Можно также сказать, что точка G симметрична с точкой О от-
носительно полюса прямой АА' для вещественного конического сечения
х°- v2
_ 4- -	1=0
Й2 + 2,2	- U-

ГЛАВА VI. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА	151
33.	Криволинейные однородные поверхности. Пусть S — часть сфери-
ческой поверхности радиуса R, а — ее проекция на диаметральную плоскость
и 5 — расстояние от ее центра тяжести до этой плоскости. Доказать фор-
мулу
34.	Однородные объемы. Если однородный объем имеет диаметральную
плоскость, сопряженную некоторому направлению хорд, то центр тяжести
лежит в этой плоскости. Например, тетраэдр (центр тяжести совпадает
с центром тяжести четырех равных масс, помещенных в четырех вершинах),
усеченный цилиндр (центр тяжести есть середина прямой, параллельной
образующим и соединяющей центры удара обоих оснований относительно
прямой их пересечения).
35.	Даны три косоугольные оси Ox, Oy, Oz. Обозначим через S3 пло-
щадь сечения однородного тела плоскостью, параллельной плоскости хОу,
а через $', •/]', г — координаты центра тяжести площади этого сечения, пред-
полагаемой однородной. Доказать, что центр тяжести тела имеет координаты
z,	г,	г,
VS = к Г S2S' dz, V-ц = k J SeV dz, FC = к j Sez dz,
где z0 и z-l — координаты z плоскостей, ограничивающих тело, V— его объем
/ Г' \
I V" = k I Sz dz I и k — объем параллелепипеда, основание которого парал-
\	?„	/
лельно плоскости ху и имеет площадь, равную единице, и образующие ко-
торого параллельны оси Oz и равны по длине единице.
(Разбить тело на бесконечно тонкие слои плоскостями, параллельными
плоскости ху.)
36.	Из предыдущего упражнения следует, что если центры тяжести парал-
лельных плоских сечений лежат в одной плоскости, то центр тяжести тела также
лежит в этой плоскости. Если центры тяжести сечений расположены на пря-
мой, то центр тяжести объема также лежит на этой прямой. Это последнее
обстоятельство имеет место для части тела вращения, заключенной между
двумя плоскостями, перпендикулярными оси, и для объема, ограниченного
поверхностью второго порядка и двумя параллельными плоскостями.
37.	Если Se есть функция второй степени относительно г, то обозначая
через So, Si, а площади обоих оснований и равноотстоящего от них сечения,
а через h — высоту тела, получим
Расстояния от центра тяжести объема до обоих оснований So и Sj относятся
как St + 2с к So + 2s- Формулы эти применимы к усеченным пирамидам и
конусам, а также к частям поверхностей второго порядка и линейчатых по-
верхностей, заключенных между двумя параллельными плоскостями.
38. Для тел, указанных в предыдущем упражнении, справедлива следую-
щая теорема: центр тяжести тела совпадает с центром тяжести трех
масс, помещенных в центрах тяжести обоих оснований и среднего се-
чения и равных соответственно площадям оснований а учетверенной
площади среднего сечения. (Дарбу, Статья в «Механике» Депейру,
стр. 383—388.)

ГЛАВА VII
ИЗМЕНЯЕМЫЕ СИСТЕМЫ
120.	Предварительное замечание. В главе V мы указали необ-
ходимые условия равновесия произвольной материальной системы
в следующей форме.
Если произвольная система находится в равновесии, то при-
ложенные к ней внешние силы (т. е. все силы, отличные от
взаимных реакций различных частей) образуют систему сколь-
зящих векторов, эквивалентную нулю, in. e. удовлетворяют усло-
виям равновесия сил, приложенных к твердому телу.
То же условие должно выполняться для внешних сил, приложен-
ных к любой части материальной системы, если рассматривать ее
как отделенную от остальной части.
Об этом можно составить себе представление на основании
следующих рассуждений, основанных на идее затвердевания: если
система находится в равновесии, то последнее, очевидно, сохранится,
если все точки станут неизменно связанными между собой, т. е.
если система затвердеет. Внешние силы должны уравновешиваться
для полученного таким образом твердого тела и, следовательно, они
удовлетворяют общим условиям равновесия твердого тела. Эти необ-
ходимые условия не будут, вообще говоря, достаточными. Мы при-
меним эти рассуждения к некоторым изменяемым системам.
I. Веревочный многоугольник
121.	Определение. Так называют систему материальных точек Ми
М2	Мп, каждая из которых связана с последующей при помощи
гибкой нерастяжимой нити. К каждой из этих точек приложена соот-
ветственно одна из сил Fv F2	Fn, под действием которых
фигура может иметь некоторое положение равновесия в виде пло-
ского или пространственного многоугольника. Исследуем условия
равновесия такого многоугольника.
Рассмотрим сначала случай, когда имеются только две точки Mt
и М2 и две силы Fx и Ft. Равновесие может иметь место лишь
тогда, когда внешние силы Fl и F2, действующие на точки Mt и М2,
равны и прямо противоположны. Это необходимое условие не будет
достаточным. Кроме того, силы должны иметь такое направление,

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ
155
М, Д
в м2
Рис. 78.
при котором нить растягивается. Если силы будут направлены так,
чтобы точки сближались, то равновесия не будет. Чтобы в этом слу-
чае оно все таки было, нужно заменить нить твердым стержнем
(рис. 78).
122.	Натяжение. Допуская, что равновесие имеет место, возь-
мем на нити MtM2 (рис. 78) произвольную точку А и выделим
часть МХА. Полученная нить МгА рань-
ше находилась в равновесии. На нее
действовали только сила Ft и часть '
нити АМ2. Необходимо, следовательно,
заменить это действие .силой, рав-
ной и противоположно направленной
силе Fv Эта сила называется натяжением в точке А. Она равна
по абсолютному значению силе Fx и одинакова во всех точках
нити. Точно так же часть АМ2 находится в равновесии под дей-
ствием силы F2 и натяжения, приложенного в точке А в сто-
рону АМУ. Наконец, произвольная часть АВ нити находится в равно-
весии под действием натяжений,
приложенных на обоих концах в
направлениях АМХ и ВМ2.
Вообще, если рассматривается
произвольная часть веревочного
многоугольника, находящегося
в равновесии, например часть
PM3M4M6M6Q, полученная рас-
сечением нитей М2М3 и М6М7
в точках Р и Q, то можно счи-
тать, что она находится в равно-
весии под действием сил, непо-
средственно приложенных к его
вершинам М3, М4, Мл, Ме(рис. 79)
и под действием натяжений сто-
рон РМ3 и M6Q, приложенных
в точках Р и Q в направлениях М3Р и MeQ. Эти силы и два
натяжения удовлетворяют условиям равновесия сил, приложенных
к твердому телу.
Например, если силы F3, Fit F6, Fe имеют одну равнодействую-
щую R, то должно быть равновесие между натяжениями М3Р и MeQ
крайних сторон и этой равнодействующей. Следовательно (п. 107),
эти крайние стороны должны пересекаться в некоторой точке на
линии действия равнодействующей R.
123.	Равновесие веревочного многоугольника. Многоугольник
Вариньона. Рассмотрим веревочный многоугольник, находящийся
в равновесии под действием сил, приложенных к его различным вер-
шинам. Чтобы исключить всякие недоразумения с направлением натя-
жений, будем обозначать через Tiii+i натяжение стороны Mj/Wj+1,

154	ЧАСТЬ ВТОРАЯ. СТАТИКА
которое она испытывает в направлении MiMi+l, а через Ti+1, { то
же самое натяжение, но в противоположном направлении, так что 7\, $+1
и Ti+1, i являются равными и прямо противоположными силами.
Допустим, что рассекаются стороны М2М3 и М6М7 в точках Р
и Q и рассматривается часть РMiMiMbMiQ веревочного многоуголь-
ника. Эта часть находится в равновесии под действием натяжений Т32
и Гв7, приложенных в точках Р и Q, и заданных сил F3, F4, Fb, Fs,
приложенных к промежуточным вершинам. Точка М3, рассматривае-
мая как свободная, находится под действием силы F3 и двух натя-
жений Т32 и Ти, примыкающих к этой точке нитей; эти три силы
находятся, следовательно, в равновесии. Точно так же точка М4
находится в равновесии под действием непосредственно приложен-
ной силы F4 и двух натяжений Т43 и 745, примыкающих к этой точке
нитей, и т. д. Выражая таким же образом, что каждая вершина на-
ходится в равновесии под действием приложенной к ней силы и двух
натяжений примыкающих к ней нитей, мы и получим условия равно-
весия.
Эти условия очень просто выражаются при помощи следующего
построения, приводящего к многоугольнику Вариньона. Через произ-
вольную точку А (рис. 79) проведем вектор АА2, равный и1 парал-
лельный натяжению Т32 первой рассматриваемой стороны и через
точку А2 вектор А2АЯ, равный F3. Так как три силы Т32, F3, Tu
находятся в равновесии, то вектор А,А, замыкающий треуголь-
ник АА2А3, равен и параллелен силе Т34, и поэтому вектор АА3
равен силе Ti3. Теперь, так как силы Т43, F4 и Т45 находятся в рав-
новесии, то, проведя через конец А3 вектора АА3, равного и парал-
лельного силе Г43, вектор А3А4, равный силе F4, получим вектор А4А,
равный силе Т45, а противоположно направленный вектор АА4 равен
силе Ты. Продолжая так шаг за шагом, придем в конце концов
к вектору АЪА6, равному и параллельному силе Fs, и к вектору ААв,
равному натяжению Т76. Полученный таким образом многоуголь-
ник АА\А3 ... называется многоугольником Вариньона.
Резюмируя сказанное, мы видим, что для того, чтобы рассматри-
ваемая часть РМ3М4М6М6B (рис. 79) веревочного многоугольника
была в равновесии, необходимо и достаточно, чтобы после построе-
ния векторов А2А3, А3А4, А4АЪ, АЬА6, равных и параллельных си-
лам F3, Ft, Fb, Fe, приложенным в вершинах, можно было найти
такую точку А, чтобы векторы АА2, АА3, АА4, АА6, АА6 были
параллельны векторам РМ3, Ж3М4, Ж4М6, M6MS, M^Q и направлены
в стороны, им противоположные. Это последнее условие вытекает
из того, что такой вектор, как АА3, должен быть равен натяжению Т43,
которое направлено в сторону М4М3.
Эти условия также и достаточны. Если они выполняются, то каж-
дая вершина Mi будет находиться в равновесии под действием силы Fi
и двух натяжений T\ti-\ и Tii+1, равных соответственно векторам
Л,4^_! и АгА.

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ
155
Главный момент крайних натяжений Т32, Г67 и сил F3, F4, Fb, F6
будет равен нулю, так же как и главный момент каждой из сил Ft
а двух натяжений Titi_lt Tiii+1, приложенных в точке Мц. Следо-
вательно, рассматривая моменты сил и натяжений относительно одной
и той же точки, мы получим векторы, для которых можно построить
многоугольник, аналогичный многоугольнику Вариньона.
Может случиться, что будут выполнены все условия равновесия,
кроме тех, которые касаются направления натяжений сторон. Тогда
некоторые из сторон будут сжиматься вместо того, чтобы быть рас-
тянутыми, и равновесия не будет. Для того чтобы оно было, надо
заменить эти стороны твердыми стержнями, которые способны со-
противляться сжатию.
124. Условия на концах. Указанные нами условия равновесия
должны выполняться для любой части многоугольника. Крайние вер-
шины веревочного многоугольника могут быть подчинены разного
вида условиям, которые называются условиями на концах.
1°. Свободные конца. Может случиться, что веревочный много-
угольник
Мп является свободным в пространстве и его
п
концы Мх и Мп свободны
и находятся под действием
заданных сил Ft и Fn. До-
пустим, для упрощения, что
п = 5и, следовательно, рас-
сматривается многоуголь-
ник М1М2М3М4МЪ. Тогда
натяжения крайних звеньев
МгМ2 и М4МЪ известны.
В самом деле, так как Мх
находится в равновесии под
действием Fx и натяже-
ния Т12, то это натяжение
равно и противоположно Fx.
Точно так же Ти равно и
противоположно Fb. Если построить многоугольник Вариньона, соот-
ветствующий полному веревочному м ногоугольнику, то первое звено А Ах
будет равно и параллельно Fv второе АХА2 равно и параллельно
F2, и т. д., последнее А4АЬ равно и параллельно Fb (рис. 80). Построен-
ный таким образом многоугольник является многоугольником сил Fx,
F2, F3, F4, Fb. Этот многоугольник должен быть замкнутым, т. е.
точка Аъ должна совпадать с точкой А, так как силы Fk должны
удовлетворять условиям равновесия сил, приложенных к твердому
телу, и их главный вектор должен равняться нулю. Натяжения
Tk+u k равны и параллельны диагонали ААк многоугольника Ва-
риньона.
2°. Концы Мг и Мп закреплены в неподвижных точках. Не-
обходимо тогда принять в качестве вспомогательных неизвестных.
Рис. 80.

156
ЧАСТЬ ВТОРАЯ. СТАТИКА
силы Ft и Fn, представляющие действия неподвижных точек на
концы Мх и Мп или, что то же, натяжения Т2 и Тп_1п.
3°. Веревочный многоугольник замкнут. Многоугольник замкнут,
когда последняя точка Мъ непосредственно ¦ связана с первой Мг
при помощи нити. В этом случае можно применить общие условия
равновесия и построение Вариньона ко всему многоугольнику, раз-
резав мысленно нить МХМЬ в двух точках Р и Q и приложив
вдоль МХР натяжение Т1Ь и вдоль MbQ натяжение 751. Тогда надо
будет провести через точку А век-
тор АА0, равный и параллельный на-
тяжению Т1Ь и далее векторы А0Аг,
АХА2	А±АЪ, равные и параллель-
ные силам Fv F2	Fb (рис. 81).
Натяжения нитей будут равны и па-
раллельны векторам AAV АА2, .. .
..., АА6, причем натяжение Т15 будет
/С равно и параллельно вектору АА0, на-
тяжение Т21 равно и параллельно век-
тору ААХ и т. д, натяжение Тк+1>к —
вектору ААк и т. д. Последнее натяже-
ние Т16 будет равно и параллельно
г* вектору ААЪ; точки Аъ и Ав совпа-
дают, так как АА0 также равно Tib.
Следовательно, для равновесия зам-
кнутого веревочного многоугольника
необходимо и достаточно: 1) чтобы
многоугольник сил, непосредственно приложенных, был замкнут;
2) чтобы существовала такая точка А, для которой каждая из
сторон МГМГ+Х веревочного многоугольника была параллельна и
противоположно направлена диагонали ААГ.
Примечание. Если число сторон веревочного многоугольника не-
ограниченно возрастает, причем каждая из этих сторон стремится к нулю,
то как этот многоугольник, так и многоугольник Вариньона обращаются
в кривые. Этот предельный случай будет изучен в параграфе II.
В общем случае фигура равновесия будет пространственным много-
угольником. Этот многоугольник будет плоским в случаях, когда силы
/¦"a,..., Fn-i сходятся или параллельны.
125. Сходящиеся силы. Если все силы F, кроме крайних Fx и Fn,
пересекаются в одной точке, то независимо от того, будет ли много-
угольник замкнутым или нет, его фигура равновесия будет плоской и
моменты всех натяжений относительно точки пересечения сил будут
равны.
Пусть О — точка пересечения сил. Как мы видели, можно считать, что
материальная точка М2 находится в равновесии под действием силы F% и
натяжений Т^ и 7з- Так как эти силы уравновешиваются, то они лежат
в одной плоскости, и, следовательно, точки Mi, jW2. jW3, О находятся
в одной и той же плоскости Р. Таким же путем убеждаемся, что точки М%,
М3, jW4, О тоже лежат в одной плоскости, которая совпадает с Р, так как
имеет с ней три общие тоЧМй О, 7И2; М3, и так далее. Следовательно,
Рис. 81.

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ
157
фигура равновесия является плоской, и ее плоскость проходит через
точку О.
Так как точка М% находится в равновесии под действием сил F2,, Тц,
Тгг, то алгебраическая сумма моментов этих сил относительно точки О
равна нулю. Но так как момент силы F2 равен нулю, то сумма моментов
сил 7*21 и ^23 Равна нулю, откуда вытекает, что момент силы Тп равен
моменту силы 7"гз. Продолжая таким
же образом дальше, убеждаемся, что
все натяжения Tr, r+i имеют одинако-
вые моменты относительно точки О
(рис. 82).
126. Параллельные силы. Фигура
равновесия будет также плоской,
когда все силы, кроме двух крайних,
параллельны. В этом случае проек-
ции натяжений на перпендикуляр
к общему направлению сил равны.
Первая часть этого предположения
докажется так же, как и для сходя-
щихся сил. Для доказательства второй
части-замечаем, что так как силы F2, 7"a,
7^ находятся в равновесии, то сумма
их проекций на направление хх', перпендикулярное силам, равна нулю.
Но так как проекция силы F2 равна нулю, то отсюда следует, что проек-
ция 7"х2 равна проекции 7з и точно так же равна проекции Т<ц и т. д.
Допустим, например, что оба конца многоугольника подвешены к двум
неподвижным точкам и что силами, действующими на промежуточные
вершины, являются веса. Тогда мно-
гоугольник будет находиться в вер-
тикальной плоскости, проходящей
через две неподвижные точки. Допу-
стим, кроме того, что имеется гори-
зонтальное звено ММ±, натяжение
которого мы обозначим через То.
Натяжения следующих звеньев ММо,
ММ*
будут Т12, Т.
23» • - ¦>
X
Рис. 83.
ные и параллельные силам рь рч,
одной вертикали, а диагонали АВЬ
М2МВ, ... и равны натяжениям 71,
*„. _ Л ,„„ _ Pi+Pi
tg al — ~Y~ > 'g a2 —	j-
7 = 7l COS (Xj = 72 COS a2 =
Если предположить, что число вершин i
растает, причем каждая сторона стремится
углы наклона к горизонту обозначим
через alt 0.9, ... На точки Мь
М% ... действуют веса рь р?, ...
Для построения в рассматриваемом
случае многоугольника сил для ча-
сти Мо, Мь М% •¦¦. веревочного
многоугольника (рис. 83) необходимо
провести через некоторую точку А
в направлении М^М^ вектор АВ,
равный и параллельный натяжению Та,
далее — векторы ВВХ, ВХВЬ ..., рав-
,.. Точки В, Вь Во, ... находятся на
АВо, ... параллельны сторонам М^М<>,
ТВо. Имеем, следовательно:
Р1+Р2+ ••• +Рк
= Тк+1, к cos ак.
М^Мъ ... неограниченно воз-
нулю, то многоугольник

158
ЧАСТЬ ВТОРАЯ. СТАТИКА
превратится в такую кривую, что, обозначая через а угол наклона касатель-
ной в точке М к горизонту, через Т—натяжение в этой точ"ке, через Р —
вес дуги MQM, отсчитываемой от наинизшей точки Мо, где натяжение
равно То, мы сможем написать
tg<x = -?, T0=Tcosa.
1 о
Например, если вообразить однородную тяжелую нить, находящуюся
в равновесии, то вес нити от наинизшей точки Мо до точки М пропор-
ционален дуге М0М, длину которой обозначим через s. Следовательно, для
кривой равновесия (цепной линии)
(а — постоянная). Ниже мы дадим уравнение этой кривой в конечной
форме (п. 139).
Если тяжелая нить не однородна, но ее линейная плотность р (как она
определена в п. 114) есть известная функция дуги s, отсчитываемой от Мо, то
Р =
tg a = — I р ds.
о
где а, как и раньше, — постоянная.
Висячие мости. Будем предполагать, что подвесные стержни верти-
кальны, находятся на одинаковых расстояниях друг от друга и одинаково
нагружены. Мы будем пренебрегать весом этих стержней и каната. Будем,
наконец, предполагать, что канат симметричен относительно вертикальной
плоскости, перпендикулярной к его собственной плоскости, и что он абсо-
лютно гибок и нерастяжим. Примем вертикальную плоскость, содержащую
канат, за плоскость чертежа, прямую ее пересечения с плоскостью сим-
метрии за ось у и прямую хх' ее пересечения с плоскостью моста,
которая предполагается горизонтальной, за ось х. Будем предполагать
число стержней четным, т. е. что в середине многоугольника имеется
горизонтальное звено М0М1 (рис. 83). Обозначим через а расстояние между
стержнями и через хj, у& координаты вершины Ми- Координаты вершины Mi
будут я/2, Ь. Координаты остальных вершин могут быть подсчитаны после-
довательно по формулам
**-!
в которых tg<*fc_j равен
* о
так как веса рь р2,
равны вдному
о
и тому же весу р. Таким путем найдем:
JtL\
То	z у 0
Это последнее уравнение может быть непосредственно получено, если
заметить, что внешние силы, приложенные к части М^М^ ... М^, образуют
систему векторов, эквивалентных нулю, вследствие чего сумма их моментов
относительно точки ,Мк равна нулю.

ГЛАВА VII. ИЗМЕНЯЕМЫЕ. СИСТЕМЫ	159
В этих выражениях имеется еще неизвестное натяжение То.	Оно
может быть определено, если известна точка подвеса последней	вер-
шины М„. Пусть h — высота этой точки; тогда
что и определяет TQ. Вершины многоугольника находятся на параболе
с вертикальной осью. В самом деле, если в равенствах
изменять k непрерывным образом, то точка х, у опишет параболу с верти-
кальной осью и вершины многоугольника будут точками этой параболы,
соответствующими целым, значениям к. Легко, кроме того, показать, что
звенья многоугольника касаются в своих серединах другой параболы
с вертикальной осью.
Если число стержней будет очень большим, а звенья очень малыми, то
многоугольник можно будет отождествить с кривой, которая, согласно
вышеизложенному, будет обязательно параболой. В этом можно также
убедиться, если заметить, что тангенс угла наклона звена М^М^+х про-
порционален абсциссе его середины. Если многоугольник отождествляется
с кривой, то угловой коэффициент касательной в какой-нибудь точке этой
кривой пропорционален абсциссе этой точки, что является характерным
свойством параболы с вертикальной осью.
127. Графические приложения теории веревочных много-
угольников. Геометрические и механические свойства веревочных
многоугольников послужили поводом к возникновению новых теорий,
начало которым было положено в заметке Понселе и которые были
впоследствии подробно разработаны в руководствах графической
статики Кульмана, Кремоны, Мориса Леви, Руше. Можно указать
также на элементарную книгу Зейрига в серии- Aide-Memoire Леоте
и на книгу П. Монтеля «Статика и сопротивление материалов»
(Gauthier-Villars, 125). Мы ограничимся здесь рассмотрением неко-
торых примеров.
1°. Графическое определение равнодействующей нескольких сил,
лежащих в одной плоскости. Пусть в плоскости задано произвольное
число сил, например, заданы четыре силы Fb Fa, F9, Fit имеющие равно-
действующую, не равную нулю. Построим многоугольник этих сил, проведя
через некоторую точку Аъ вектор АЬАХ, равный и параллельный силе Flt
через точку Ах — вектор АхА?, равный и параллельный силе F%	на-
конец, через точку А%—вектор A3Ait равный и параллельный силе Fit и
перенумеруем стороны этого многоугольника, обозначая буквой г сторону,
равную и параллельную силе Fr. Равнодействующая сил Fx, Ft ..., F±
равна и параллельна стороне AsAt, имеющей номер 5. Возьмем в плоскости
точку А и соединим ее с вершинами Аъ, Аь А%, А9, А± многоугольника
сил. Обозначим через (г, s) диагональ, соединяющую точку А с точкой
пересечения сторон г и s. Мы получим таким образом многоугольник
Вариньона. Построим соответствующий веревочный многоугольник. Для
этого проведем произвольную прямую L$Mx, параллельную диагонали E, /),
и обозначим через М^ точку, в которой она пересекает направление
силы Fj. Через Мг проведем прямую М^М?, (рис. 84), параллельную диаго-
нали (/, 2), и обозначим через М-,: точку ее пересечения с направлением силы /^
и т. д. ... , через точку ЛЦ проведем М^ъ параллельно D, 5). Эта последняя

160
ЧАСТЬ ВТОРАЯ. СТАТИКА
прямая пересечет первую ?5VHi в точке Мъ, через которую проходит
равнодействующая. В самом деле, если мы заменим прямые LbMy МХМЪ ...
	, М±МЪ нитями или жесткими стержнями, перенесем силы Fj, F2, FH, Ft
в точки Mlt M2	М{ на их
линиях действие и приложим к
крайним нитям Ь5М%, MiN--, натя-
жения, равные диагоналям (Л 5)
и D, 5) многоугольника Варинь-
она, то получим веревочный мно-
гоугольник, находящийся в рав-
новесии. Согласно принципу за-
твердевания (п. 120) существует
равновесие между крайними натя-
жениями, направленными по сто-
ронам MiL&, jM47V5, и силами Fu
F% F3, Fit приложенными в вер-
шинах. Равнодействующая этих
последних сил будет, следова-
тельно, равна и прямо противопо-
ложна равнодействующей двух
крайних натяжений и будет про-
ходить через точку Мц пересече-
ния сторон Lr,Mi и М±Ы§. Таким
образом, равнодействующая будет
найдена, так как она по вели-
чине и направлению определяется
вектором АЪА^.
Если изменять положение пер-
вой стороны L5Mb перемещая ее
параллельно самой себе, то веревочный многоугольник будет менять
свою форму, а точка М5 будет перемещаться по линии действия равнодей-
ствующей сил Flt F2, F3, F±.
Сумма моментов сил относительно
произвольной точки О плоскости. Сумма
моментов сил относительно точки О равна
моменту равнодействующей R, т. е. равна
Rb, где 8—расстояние от точки О до
силы R. Проведем через точку О (рис. 85)
линию PQ, параллельную линии действия
равнодействующей, и пусть Р и Q — точки
пересечения этой прямой с крайними
звеньями MtMr, и 7И47И5. Треугольники
PQM5 и А±АЬА, имея параллельные сто-
роны, подобны. Построим высоты Л15// —8
и АК. этих треугольников. Так как
А±А$ = R, то получим
R
Рис. 84.
Рис. 85.
~,
Точка А выбрана произвольно и по-
этому можно принять АК= 1. Тогда мо-
мент Rb будет измеряться отрезком PQ.
Теорема. Точка А выбрана произвольно. Выбирая для этой точки
другое положение А', мы придем при помощи указанных выше построений
к другому веревочному многоугольнику L'b, М[, М'2, М'3, М'^ ы'ъ, крайние

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ	161
звенья которого также пересекаются на линии, действия равнодействую-
щей (рис. 84).
Более того, справедлива следующая теорема:
Точки пересечения соответствующих сторон MjcMjc+l и MkMrt.+l
первого и второго веревочных многоугольников лежат на прямой Д,
параллельной АА' (рис. 84)..
В самом деле, допустим, что первый веревочный многоугольник
разрезан в точке В какой-нибудь стороны, например, стороны М3М±.
Часть LbMiMiM$B этого многоугольника находится в равновесии
под действием * сил Fu F2, Fs, и натяжений Tlr>, Т?А крайних
сторон M\Lft и МЯВ. Следовательно, натяжения 75 и 74 имеют равно-
действующую, равную и противоположную равнодействующей сил Fb F^, Fx.
Применяя те же рассуждения к части Ь5М±М2М3В второго многоугольника,
который мы предполагаем разрезанным в точке В' стороны М'3м[, мы най-
дем, что натяжения крайних сторон M^L5 и М%В', которые мы обозначим
через 75 и TSi, имеют равнодействующую, равную и противоположную
равнодействующей сил Fv F2, F3. Таким образом, натяжения Г13 и Ти
имеют равнодействующую, равную равнодействующей натяжений т'хь и Тш_
Мож»ю также сказать, меняя направления двух последних натяжений, что
совокупность четырех векторов 75, Tsi, 71, Ti3 эквивалентна нулю. Равно-
действующая двух натяжений 71 и 73, проходящая через точку пересече-
ния сторон MsMi и M3Mit равна и прямо противоположна равнодействую-
щей Д двух натяжений 75 и ТЬ1, проходящей через точку пересечения
сторон L;>Mi и LbMv Следовательно, точка пересечения сторон M-iMi и
М3М± находится на фиксированной прямой Д. То же самое будет справед-
ливо для точки пересечения двух любых соответствующих сторон обоих
многоугольников. Эта фиксированная прямая Д параллельна АА', так как
натяжение Г15 равно и параллельно AAh и направлено в сторону АА^,
а натяжение ТЬ1 равно и параллельно А:,А' и направлено в сторону А:,А';
следовательно, равнодействующая Д этих двух натяжений равна и парал-
лельна равнодействующей сил АА;> и А,А', т. е. силе АА'.
2°. Построение замкнутого веревочного многоугольника, соответ-
ствующего системе лежащих в плоскости уравновешивающихся сил.
В плоскости дана система сил Fit Fit ..., Fb (рис. 84), находящихся в равно-
весии, т. е. таких, главный вектор и главный момент которых равны
нулю. Построим многоугольник сил Ai А2... Аъ. Это будет замкнутый
многоугольник со сторонами /, 2, 3, 4, 5, соответственно параллельными
силам Fit F%	Fr,. Возьмем далее в плоскости произвольную точку А.
Этой точке можно поставить в соответствие замкнутый веревочный много-
угольник следующим образом.
Соединим эту точку с различными вершинами многоугольника сил и
пусть (г, s) — прямая, соединяющая точку А с точкой пересечения сторон г
и s. Таким путем получится шесть прямых (/, 2), B, 3) ..., E, 1). Построим
затем замкнутый многоугольник М^М.^М^М^М^, вершины которого лежат,
соответственно на осях векторов Fb Fo	F5, а стороны M5Mt, MtM% ...
..., М±МЛ параллельны сторонам E,"/), (/, 2), ..., D, 5). На основании
случая, рассмотренного раньше, можно произвольно выбрать положение
стороны Мг^Мх или LbM\, последующие стороны М\М^ М%М$, ..., Л^М-, бу-
дут тогда определенными и точка М:, пересечения сторон LbMi и AI.tiVj
будет находиться на линии равнодействующей сил fi, F.^ ..., Fit т. е. на

162
ЧАСТЬ ВТОРАЯ. СТАТИКА
линии силы F5, которая равна и прямо противоположна этой равнодействую-
щей. Построенный многоугольник будет, следовательно, замкнутым.
Построенный таким образом многоугольник Mi М% ... М6 называется
веревочным многоугольником, соответствующим точке А. Если предполо-
жить, что точки Mi, М&..., Мь заменены материальными точками, а сто-
роны М^Мъ MiM9, ..., М5Мг — нерастяжимыми нитями, и перенести все
силы в точки Mi, M^,..., Me,, то получится находящийся в равновесии
замкнутый веревочный многоугольник, в котором натяжение стороны MrMs
равно и параллельно отрезку (г, s). Может случиться, что некоторые из
сторон подвержены сжатию; тогда необходимо заменить их твердыми стер-
жнями. Это имеет место на рис. 84 для сторон МгМь и MrtM4.
Если взять другую точку А', то ей будет соответствовать другой вере-
вочный многоугольник AfjAfgAfg ... Соответствующие стороны этих мно-
гоугольников, как было показано, пересекаются на прямой Д, параллель-
нон АА'.
Если бы силы Ft,..., Fb вместо того, чтобы находиться в равновесии,
приводились к паре, то это обнаружилось бы при построении, так как L-aMx
и M±Ns не пересекались бы на линии силы F$ и равнодействующая R
сил Fb F?, F8, FA лежала бы на прямой, параллельной силе F& но не сов-
падающей с ней.
3°. Частный случай. Пример взаимных фигур. Допустим, что силы
Fi, F%	F& находящиеся в равновесии, пересекаются в одной точке О
(рис. 86). Веревочный многоугольник (О)
Мг М? ... М5, построенный указанными
выше приемами, и многоугольник Ва-
риньона (A) Ах A2 ... Аь будут тогда
взаимными. Под этим надо понимать
следующее. В веревочном многоуголь-
нике M-iMv ... М$ натяжения 7i>
Ту,,..., Тгъ сторон МоМь ММо,...,
М^Мг, соответственно равны и парал-
лельны диагоналям AAi, ААо, ..., АА$
многоугольника Вариньоиа. Приложим
в вершинах Ai, Аь ..., Ас, много-
угольника Вариньона вдоль каждой из
этих диагоналей силы Рь Я2. •••> Рь
равные и параллельные соответствую-
щим сторонам МчМ\, М^Мч,,	, М^М^
веревочного многоугольника, и заменим
стороны AiAo, A2AS,..., А5А^ нитями.
Построенный таким образом новый
веревочный многоугольник AiA2 .., Ас,
будет в равновесии, и натяжения сторон
1,2,3,... будут равны и параллельны
диагоналям ОМЬ ОМо, ... первоначаль-
ного веревочного многоугольника, ко-
торый, таким образом, является многоугольником Вариньона для нового
геревочного многоугольника. Короче говоря, каждый из двух веревочных
многоугольников (.Л) и (О) является многоугольником Вариньона для другого.
128. Кольца, скользящие на нити. Допустим, что гибкая нерастяжи-
мзя нить закреплена своими концами в двух неподвижных точках А и В и
что по ней могут скользить без трения бесконечно малые кольца. К этим
кольцам приложены известные силы. Нужно найти положение равновесия
системы.
Если имеется только одно кольцо С (рис. 87), то сила F должна быть
Сассектрисой угла АСВ. Это вытекает из того, что кольцо С может рас-
сматриваться как точка, скользящая без треиия по эллипсу с фокусами

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ
163
в точках А и В, причем сила должна быть нормальна к эллипсу и направ-
лена наружу, т. е. так, чтобы нить натягивалась. Давление кольца на нить
будет тогда равно силе F. Элемент нити, находящийся в точке С, будет
находиться под действием двух натяжений 7" и 7" и силы F. Так как
последняя является биссектрисой угла между силами 7" и 7" и должна их
уравновесить, то эти натяжения равны между собой
F=2T cos?.
Теперь можно без труда исследовать случай нескольких колец. Если
имеет место равновесие, то каждая из сил направлена по биссектрисе двух
частей нити, примыкающих к соответствую-
щему кольцу, натяжение 7" нити везде оди-
наково и если Fb F%, ... — действующие \	у в
силы, аъ а2, ... — последовательные углы
между частями нити, то (Пуансо) ..
7=._ Fx ^ F2
2 cos ~ 2 cos ~
Так как система находится в равно-
весии, то последнее, очевидно, сохранится,
если каждое кольцо закрепить в занимае-
мом им положении. Следовательно, к этой
фигуре равновесия можно применить все,
что сказано относительно веревочных мно-
гоугольников. Для рассматриваемого случая все натяжения одинаковы и все
вершины Аъ А,, А3,... веревочного многоугольника (рис. 79), кроме
вершины А, лежат на сфере с центром в вершине А. Если многоугольник
плоский, то все вершины находятся на окружности с центром в точке А.
129. Фермы. Рассуждения, аналогичные тем, которыми мы поль-
зовались для веревочных многоугольников, приводят к условиям
равновесия ферм, т. е. систем прямолинейных стержней, весом кото-
рых пренебрегаем, соединенных своими концами при помощи шар-
ниров. Предполагается, что вся система находится под действием
сил, приложенных только в шарнирах (иначе, в узлах). Так как
каждый из стержней, например АВ, должен находиться самостоятельно
в равновесии под действием двух сил, приложенных к его концам,
то эти силы, являющиеся действиями узлов А и В на стержень,
должны приводиться к двум равным и противоположно направлен-
ным сжатиям или растяжениям. Каждый узел будет находиться в
равновесии под действием непосредственно приложенных к нему сил
и реакций примыкающих к нему стержней. Последние направлены
вдоль соответствующих стержней, так как по закону равенства
действия и противодействия действия стержней на узлы равны и про-
тивоположны действию узлов на стержни.
Пример. Система шести невесомых стержней, образующих правиль-
ный шарнирный тетраэдр SABC (рис. 88), подвешена с помощью трех вер-
тикальных ннтей АА', ВВ', СС так, что основание ABC горизонтально.

164
ЧАСТЬ ВТОРАЯ. СТАТИКА
К вершине S подвешен груз Р. Найти натяжения нитей и силы растяжения
и сжатия стержней. Обозначим через 6 общее значение трех сил, растяги-
вающих стержни SA, SB, SC. Проектируя на вертикаль и приравнивая нулю'
сумму проекций трех сил в и силы Р, при-
ложенных в узле S, получим
Р— бУ6~=О, 6 =
так как косинус угла между ребром SA и
вертикалью равен . Стержни основа-
о
ния испытывают сжатия; обозначим че*
рез р общее значение этих сжимающих
сил, а через Г— общее значение натяже-
ний нитей АА', ВВ', СС. Точка А нахо-
дится в равновесии под действием силы 6,
натяжения Т и двух сил р. Проектируя эти
силы на вертикаль АА', получим:
Т =
Рис.
что ясно непосредственно, так как три
силы Т уравновешивают груз Р. .Проекти-
руя далее четыре силы, приложенные в точке А, на высоту AD тре-
угольника ABC, получим
б Уз о уз
о
так как cos DAB =
УЗ
и cos SAD =
уз:
II. Равновесие нитей
130. Уравнения равновесия. Найдем условия равновесия не-
растяжимой, гибкой нити, находящейся под действием непрерывных
сил. Эта задача может рассматриваться, как предельный случай ве-
ревочного многоугольника, но мы рассмотрим ее непосредственно.
Обозначим через s длину дуги, отсчитываемую от какого-нибудь
начала А в каком-нибудь определенном направлении АВ (рис. 89).
Мы будем предполагать, что внешние силы, действующие на эле-
мент ds, могут быть представлены в виде одной силы Fds, по-
рядка ds, приложенной в какой-нибудь точке этого элемента,
Проекции этой силы будут
Xds, Yds, Zds,
где X, Y, Z—-проекции вектора F, называемого силой, отнесен-
ной к единице длины.
Если отбросить часть нити MB и рассматривать оставшуюся
часть AM, то для сохранения ее равновесия необходимо будет

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ
165
приложить в точке М одну-единственную силу Т, так как нить
предполагается идеально гибкой. Сила Т называется натяжением
нити. Обозначим через а, р, -у направляющие косинусы этого натя-
жения; его проекции суть
Та,
Ту
Если же, разрезав нить в точке М, отбросить часть МА, то
согласно закону равенства действия и противодействия, для сохра-
нения равновесия части MB необхо-
димо приложить в точке М силу — Т.
Проекции этого нового натяжения равны
— 7а, — Ц, — Ту
Разрежем нить в двух бесконечно
близких точках М и Mt и сохраним
только элемент MMV Этот элемент бу-
дет в равновесии под действием прило-
женной к нему силы F ds и двух натя-
жений —Т и 7*5, котврые заменяют дей-
ствие отброшенных частей нити. Если
через аг, $,, fi обозначить направляющие косинусы натяжения 7\,
то его проекции будут
Напишем, что суммы проекций трех сил равны пулю. Тогда,
замечая, что
получим
d(Ta.)-\-Xds = 0,
A)
Моменты трех сил —Т, 7\ и F ds относительно оси х равны,
соответственно,
— Су7-7— гЩ. УхТ^г — zJ.^, (yZ-zY)ds,
где через х, у, z и Xj, yv zx обозначены координаты концов дуги ds.
Следовательно, сумма моментов сил —Т и 7\ равна d(yTf — z TP)
и по теореме моментов имеем:
B)
d (У 7"т — z Щ + (yZ — zY) ds = О,
d B Та — х Ту + (zX— xZ) ds — О,
d {x T$ — у Та) + (xY — уХ) ds = 0.

jg6	ЧАСТЬ ВТОРАЯ. СТАТИКА
Развертывая первое из уравнений B), можем написать
— T$dz — zd GB) -+- (yZ — zY) ds = 0.
В силу уравнений A) члены с у и z уничтожаются, и тогда
остается
Второе из уравнений B) показывает, что
dx	dy	dz ф
~—т=т;
это означает, что натяжение направлено по касательной к кривой.
К этому же результату можно прийти, рассматривая нить как предел
веревочного многоугольника. Общее значение трех отношений равно,
очевидно, + ds; но натяжения должны быть направлены так, чтобы
нить растягивалась. Для этого натяжение Т должно быть направлено
в сторону возрастающих дуг. Поэтому надо взять знак -j-. Следо-
вательно,
a — ds' V — ds' 1 — dJ'
Внеся эти выражения в уравнения A), получим:
C)
и ¦, равнения B) являются следствиями уравнений C).
131. Общие теоремы. Из уравнений A) и B) непосредственно
получаем две следующие теоремы.
Если сила F перпендикулярна какой-нибудь оси, например
оси Ох, то проекция натяжения на эту ось постоянна. Дей-
ствительно, из условия Х=0 получается Та— const.
Если сила F постоянно находится в одной плоскости с ка-
кой-нибудь осью, например с осью Ох, то момент натяжения
относительно этой оси постоянен. Действительно, из условия
yZ — zY = Q получается у Т-^ — гТф == const.
Эти две теоремы являются частными случаями следующей.
Если сила F всюду вдоль кривой принадлежит линейному
комплексу, то момент натяжения относительно комплекса по-
стоянен. В самом деле, если сила принадлежит линейному ком-
плексу, то должно выполняться уравнение вида
рХ-\- qY + rZ + a (yZ — zY) -+- b (zX— xZ) + с (xY — yX) = 0,

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ	167
где р; q, г, а, Ь, с — постоянные. Заменяя в этом уравнении X че-
рез —т^-,..., (yZ — zY) — через -т- (у\— z$)T, мы приведем его
к уравнению, проинтегрировав которое, получим
Это уравнение выражает, что относительный момент (п. 28) натяже-
ния и системы векторов, имеющих координаты р, q, r, а, Ь, с,
постоянен. (Пеннакьетти, Rendiconti del Circolo math, di Pa-
lermo, т. VI.)
132. Общие интегралы. Наиболее общим случаем является тот,
когда сила F, отнесенная к единице длины, зависит от положения
и направления в пространстве элемента ds и от его положения на
нити. Тогда X, Y, Z будут функциями от х, у, z, s, -?-, -~, -?-.
CIS CIS CIS
При этих условиях написанные выше три уравнения равновесия C)
совместно с уравнением
Is} ~"г>~' -т-« —I — 1
образуют систему четырех дифференциальных уравнений, определяю-
щих х, у, г и Г в функции s. Это — уравнения первого порядка от-
носительно Т, но второго относительно х, у, г. Следовательно, их
общий интеграл содержит шесть произвольных постоянных, в каче-
стве которых могут быть, например, приняты значения шести вели-
~ dx dy	„	л
чин х, у, z, I, -=—, —- при начальном значении s = s0. Таким об-
uS CIS
разом, в общем случае
1	m (v С С	С Л
..	,it /Р /~> Г1	О \
у ~-~. ш^о, L*j, ^-*2» ••*, ^fi/>
г— соE, С1( С2	С6),
Г = /(в. С,. С2	С,).
133. Определение постоянных, условия на концах. Шесть
произвольных постоянных можно определить по условиям на кон-
цах. Эта задача будет наиболее простой для случая нити задан-
ной длины /, закрепленной своими концами Мо (х0, у0, z0) и Мх (х1; ух, Zj).
Приняв точку Мо за начало отсчета дуг и написав, что при s —О
и при s = l величины х, у, z обращаются в координаты точек Мо
и Mv мы получим шесть уравнений для определения шести по-
стоянных. Далее необходимо будет исследовать эту систему, которая
может допускать одно, два и даже бесчисленное множество решений.
Можно также предположить, что нить закреплена на одном
конце М0(х0, у0, г0), а на другом имеет бесконечно малое колечко,

168	ЧАСТЬ ВТОРАЯ. СТАТИКА
которое может скользить без трения по неизменяемой кривой С, за-
данной уравнениями
ЧГ(*. у. г) = 0. }
Тогда три уравнения для определения постоянных получатся из
условия, что при s = 0 величины х, у, z равны xo,yo,zo. Остальные
уравнения определятся из условий, что при S —/ значения хг, уг, zt
величин х, у, г удовлетворяют уравнениям (С) кривой и что на-
правление натяжения, т. е. касательной в точке Ми нормально
к этой кривой, так как кольцо может скользить без трения. Таким
путем получится шесть уравнений для определения постоянных.
Точно так же, если конец М1 нити может двигаться без трения
по заданной поверхности, то надо выразить, что при s — l значения
xi> У1' zi удовлетворяют уравнению поверхности и что касательная
в точке Мг к ней нормальна.
134. Случай, когда сила не зависит от длины дуги. Часто слу-
чается, что X, Y, Z не содержат явно s. Заменяя тогда всюду в равен-
ствах C) ds через \f<tx2 -f- dy2 -f- йгг, можно будет принять х в ка-
честве независимой переменной и тогда получатся три уравнения для
определения у, г и Г в функции х. Общий интеграл будет тогда со-
держать только пять постоянных, например значения, которые при-
нимают у, г, Т, —-, — при начальном значении х — х0. Пусть
C1. С2	С6),
* = <!»(*, с„ с2	с6),
T = f(x, Cu С2	С5)
— общие интегралы. Если мы захотим выразить, что нить имеет
заданную длину и закреплена своими двумя концами в точках
(х0, _у0, 20) и (Xj, yx, zj, то нужно выразить, что величины у, z
принимают значения у0, z0 при х = х0 и значения ух, zx> при х = лгх
и что длина нити равна /. Мы получим пять уравнений, необходимых
для определения постоянных.
135.	Замечание о натяжении. Найденное решение будет непри-
емлемо, если Т не будет положительным во всех точках кривой,
так как если для какого-нибудь элемента натяжение Т будет отри-
цательным, то этот элемент будет испытывать сжатие, а не натяже-
ние. Можно истолковать решение, в котором Т отрицательно, если
предположить, что на нить нанизаны бесконечно малые твердые бу-
синки. Каждая такая бусинка будет испытывать давление со стороны
предыдущей и последующей и равновесие будет осуществлено (Пуансо).
136.	Естественные уравнения равновесия нити. Так называют
уравнения равновесия, не зависящие от выбора осей координат. Мы
уже обозначили через а, р, -у направляющие косинусы касательной Mt

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ
169
в направлении возрастающих дуг; обозначим через а', р', f' на-
правляющие косинусы главной нормали Мп, направленной в сторону
вогнутости (рис. 90), и через р—радиус кривизны. Известны фор-
мулы Френе и Серре:
da 	a' d$ 	Р' di _ 1'
ds p ' ds р ' ds р
и, следовательно, первое уравнение равновесия
может быть написано в следующем виде
ds ' p
Таким образом, получаем три уравнения
dT ,1
Р'
' = —т ——г'- I
' ds ' о ' I
D)
Эти уравнения показывают, что F есть результирующая двух
отрезков, отложенных соответственно на касательной и на главной нор-
мали и имеющих алгебраические значения,
отсчитываемые в направлениях Mt и Мп, "\f
равные —-j- и	. Сила F
F	ds	p
находится,
следовательно, в соприкасающейся плоско-
сти кривой и направлена в сторону выпук-
лости и в сторону убывания натяжения. Ее
проекции на касательную, главную нормаль
и бинормаль определяются формулами
F	F	F ° ^
Рис. 90.
которые и являются естественными урав-
нениями равновесия.
Если сила всюду нормальна к нити, то Ft = 0. Тогда произ-
водная -г- тоже равна нулю. Следовательно, натяжение Т постоянно.
137. Формула, определяющая натяжение, когда существует
силовая функция. Умножим уравнения равновесия D) соответственно
на а, р, f и сложим. Тогда, заменяя а, В,
получим	dT=
rfy
через —, —, —,
ds ds ds
dz),

170	часть вторая, статика
что является не чем иным, как первым из естественных уравнений E).
Это последнее уравнение очень важно. Оно позволяет сразу опре-
делить натяжение, когда X, Y, Z зависят только от х, у, z и
имеют силовую функцию U(x, у, г). Тогда, обозначив через k
постоянную, получим
что позволяет определить натяжение в конечной форме, не зная фи-
гуры равновесия. Это значение натяжения следует внести в.уравне-
ния равновесия, после чего они приведутся к двум уравнениям.
Когда U принимает свое первоначальное значение, то то же самое
будет и с натяжением. Следовательно, если U — однозначная функ-
ция, то натяжение будет одним и тем же во всех точках нити, ле-
жащих на одной и той же поверхности уровня. Но если функция U
не однозначна, если, например, U = arctg—, так что поверхности
уровня суть плоскости у = xtgC, и если нить пересекает какую-
нибудь из этих плоскостей несколько раз, то натяжение может иметь
одно из значений С + lm. Здесь можно повторить для натяжения все,
что было сказано в главе IV относительно полной работы.
138. Параллельные силы. Наиболее простым случаем будет тот,
когда внешние силы параллельны одному и тому же направлению.
Фигура равновесия будет тогда плоской кривой, плоскость которой
параллельна направлению сил, и проекция натяжения на перпенди-
куляр к этому направлению будет постоянна. Эти два свойства могут
рассматриваться как следствия аналогичных свойств, полученных для
веревочного многоугольника. Мы докажем, однако, эти свойства не-
посредственно.
Допустим, что ось Оу параллельна общему направлению сил.
Тогда X и Z будут все время равны нулю и после интегрирования
первого и последнего из уравнений равновесия C) получим
ds	ds
Исключим из этих уравнений Т. Получим
Adz — Bdx=0,
откуда
Az — Bx = C.
Это — уравнение плоскости, параллельной оси Оу. Следовательно,
первая часть нашего предложения доказана. Примем эту плоскость
за плоскость ху. Тогда можно составить два уравнения равновесия

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ	171
Внося во второе уравнение значение Т из первого и обозначая
,	dy
через у производную ~, получим соотношение
A dy' + У ds = 0,	F)
которое является дифференциальным уравнением фигуры равновесия.
В наиболее общем случае равновесия нити сила может быть функ-
dx dy ^ „
цией шести величин х, у, z, s, -j—, -?-. Сейчас, поскольку кривая
плоская, имеем 2 = 0 и \jA ~\-утА = 1- Следовательно, Y должно
быть функцией переменных х, у, s, у'. В случае, когда Y зависит
только от одной из величин х, у, s, у', задача приводится к квад-
ратурам.
Пусть, например, Y = f (x). Заменяя ds его значением У\ -\-у'гйх,
мы видим, что переменные у' и х разделяются, и после интегриро-
вания получается
A In (у + УгТ72) + //(*) *х = С.
Из этого уравнения можно определить у' в функции х, после
чего у находится новой квадратурой.
Пусть теперь Y = f(y). Тогда можно принять ds=	-7	dy
и в уравнении F) переменные сразу разделяются. В случае, когда
существует силовая функция, натяжение, как мы видели, может быть
вычислено сразу.
Наконец, если Y есть функция только s или только у', то
уравнение F) интегрируется сразу.
Естественное уравнение. Пусть а — угол между касательной к кривой
равновесия и осью х и пусть р — радиус кривизны в точке касания. Если
написать, что абсолютная величина нормальной составляющей силы есть —,
то получим
Y cos a = —
Р
и так как проекция Т cos а силы натяжения на ось Ох равна постоянной
величине А, то дифференциальное уравнение кривой будет
Кр cos2 а — А.
Это уравнение идентично уравнению F). Если, например,
у= К
COS2 a '
то из предыдущего уравнения получим для р постоянное значение, и сле-
дозательно, фигура равновесия есть окружность.
139. Цепная линия. Приложим эти вычисления к нахождению фигуры
равновесия однородной тяжелой цепочки. Галилей считал, что этой фигурой
является парабола. Ошибку Галилея исправил Гюйгенс.

172
ЧАСТЬ ВТОРАЯ. СТАТИКА
Пусть р — вес единицы длины цепочки. На элемент ds действует
сила pds, направленная по вертикали. Следовательно, фигурой равновесия
является плоская кривая, расположенная в вертикальной плоскости, прохо-
дящей через точки подвеса. Примем эту плоскость за плоскость ху и на-
правим ось у вертикально вверх. Тогда
Yds = —pds, Y^—p,
и уравнения равновесия будут:
Ady' — pds=0.
A)
B)
Можно всегда предполагать, что А — число положительное. Действи-
тельно, Т — существенно положительно; следовательно, если на кривой
выбрать такое направление обхода, чтобы х и s возрастали одновременно,
то производная -j- будет положительной и постоянная А будет, вследствие
этого, тоже положительной. Мы можем обозначить ее через ра, где а —
положительная величина. Заменим ds его зна-
0
ya.fi)
/ *
ds = + 1Л + у'г dx.
Тогда уравнение примет вид
d/ 	dx
Интегрируя, найдем
о, д
Рис. 91.
х,
У' + V\ + у'г = е1Г
C)
Отсюда следует, что
= -е а	D)
Складывая эти два уравнения, получим у' и, снова интегрируя, найдем
уравнение кривой
/ х—х„	х—з.
с-хл
Перенесем начало в точку Ot (лг0, у0) (рис. 91); тогда новое уравнение
кривой будет
=il»-
Это — уравнение цепной линии, которая симметрична относительно
оси O-iy-t', ось OiXt называется ее основанием.
Вычитая уравнение D) из уравнения C), получим
.У\
а

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ	173
а из формулы A) получим для натяжения
Г= А * = A /lT?2 = А Ь. = рУ1.
ах	а
Отсюда мы видим, что натяжение нити в точке М равно весу части
нити, длина которой равна ординате MQ этой точки над базой. Следова-
тельно, если в точке М поместить бесконечно малый блок и дать возможность
части нити, расположенной выше точки М, свободно свешиваться, то равно-
весие не нарушится, если свешивающаяся часть будет равна MQ.
140. Определение постоянных. 1°. Концы закреплены. Уравнениз
цепной линии содержит три постоянных х0, у0, а, которые определяются из
условий на концах. Согласно принятому ранее условию постоянная а должна
быть положительная. Примем за начало О точку закрепления, расположенную
более низко, и направим ось х таким образом, чтобы вторая точка закрепле-
ния Р находилась в квадранте между положительными координатными осями.
Пусть а и р — координаты этой точки, I — длина нити (рис. 91). Напишем
условия, выражающие, что кривая проходит через обе точки О @, 0) и Р(а, р):
a—а
Я t	п .	п \	in\
Чтобы получить третье уравнение, напишем, что нить должна иметь
длину /. Имеем
rfs = y Ц-/2^ = ЛЬ о- +е о- Jdx,
и, интегрируя в пределах от 0 до а, получим длину нити:
f a—Х„	a— xtl	Xn Xi,\
I- U
T
Вычитая равенство A) из равенства B), мы исключим у0 и получим
t=j[e а +е а -е а-еа).	D)
Уравнения C) и D) определяют а и х0. Из них легко находим:
(а-Х„	_Ж,\	_Хь1 а_	\
е~^ —е ") = ае " U5" — lj'
/ Х„	У--ХЛ	Ж../	_Л\
1-$=а\еа -е а ) = аеа \\~е а ) .
Для исключения х0 достаточно почленно перемножить эти равенства. Тогда
-~ \
+ е а —2/.
(	г)
Скобка равна квадрату величины \е2а — е ia); следовательно,
/ JL
= ±а\е2а-

174
ЧАСТЬ ВТОРАЯ. СТАТИКА
Может показаться, что следует рассматривать два знака. Но согласно
/ — -—\
а\е2а-е 2а),
выбору осей величины а и а, и поэтому также а\ет— е 2а/. должны быть
положительными, вследствие чего надо брать только знак +. Положим
?- = и. Неизвестная и положительна и для нее уравнение имеет вид
a	1u
Нам нужно найти положительные решения этого уравнения. Заменяя его
правую часть разложением в ряд, получим
Vp — ю	и2	и4	П
и'-
1-2-3-4-5
Здесь правая часть монотонно возрастает от 1 до бесконечности, когда и
возрастает от 0 до бесконечности. Вследствие этого для того, чтобы суще-
ствовал положительный корень, необходимо и достаточно, чтобы левая часть
была больше 1. В этом случае уравнение будет иметь один и только один
положительный корень. Следовательно, единственным условием возможности
задачи будет
^>i
т. е. длина нити должна быть больше расстояния между точками подвеса.
Если это условие выполнено, то можно будет определить и и, проследив
за всем ходом вычислений, можно легко убедиться, что для трех по-
стоянных а, х0, у0 будет получаться одна-
единственная система значений. Следова-
тельно, в этом случае существует одно
и только одно положение равновесия.
Пусть и' — положительный корень ура-
внения для и. Это уравнение имеет
также отрицательный корень —и'. Пуансо
интерпретирует это решение следующим
образом: перевернутая цепная линия, для
которой и = — и', является фигурой равно-
весия особого свода, образованного рав-
ными бесконечно малыми, идеально отпо-
лированными твердыми шариками.
2°. Концы скользят по двум прямым.
Допустим, что однородная тяжелая це-
почка имеет длину I и что ее концы А
и В скользят без трения по двум данным
прямым PQ и PR, расположенным в одной вертикальной плоскости (рис. 92).
Требуется определить постоянные х0, у0, а таким образом, чтобы цепная
линия пересекала обе прямые линии под прямым углом и чтобы ее
?уга АВ между этими линиями имела заданную длину I.
Предлагая аналитическое решение в качестве упражнения, мы дадим
здесь геометрическое решение задачи. Мы будем основываться на том, что
; ве цепные линии, имеющие параллельные основания, подобны, и что,
наоборот, фигура, подобная цепной линии с горизонтальным основанием,
является другой цепной линией, расположенной таким же образом. Вообра-
зим вспомогательную цепную линию С с горизонтальным основанием и
проведем к ней две нормали А'Р' и В'Р', параллельные заданным пря-
мым QP и RP, что всегда возможно и притом единственным образом, так

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ
175
как при изменении х от — со до + оо угловой коэффициент касательной
к цепной линии принимает один и только один раз любое заданное
значение. Дуга А'В' будет иметь некоторую длину /'. Перенося угол А'Р'В'
вместе с дугой А'В' в угол Р, получим дугу цепной линии А"В" длины/',
нормальную к обеим заданным прямым и имеющую горизонтальное осноза-
нис. Искомая дуга АВ будет тогда подобна дуге А"В" относительно точки Р,
так как касательные к обеим дугам в точках А и А", а также в точках В
и В" параллельны. Отношение подобия равно ///'. Следовательно, доста-
точно поставить в соответствие каждой точке М' дуги А"В" точку М
, РМ I	..
таким образом, чтобы -рттг = -jr • и точка М опишет искомую дугу. Реше-
ние будет, следовательно, единственным. Более того, мы видим, что если при
таких же условиях на двух прямых расположить несколько цепных линий
различной длины, находящихся в равновесии, то они все будут подобны
относительно точки Р.
141. Центральные силы. Фигура равновесия является плоской кривой
и ее плоскость проходит через точку пересечения сил; момент сил
натяжения относительно этой точки постоянен.
Эти предложения могут быть рассматриваемы как следствия аналогич-
ных предложений, установленных для веревочных многоугольников, но мы
установим их непосредственно.
Мы видели (п. 131), что если момент силы F относительно оси
равен все время нулю, то момент силы натяжения относительно
этой оси постоянен.
Так как внешние силы пересекаются в одной точке, то мы можем
принять эту точку за начало координат. По юлько что высказанной теоремо,
примененной к трем осям координат, имеем:
ds
ds
dy
ds
ds
dx\
/ dy	dx
\ ds	ds
Умножая эти уравнения соответственно на х,
у, z и почленно складывая, получим
Ах -Y- By -\- Cz = 0.
О
Следовательно, кривая равновесия является	рис 93
плоской и ее плоскость проходит через начало
координат.
Если эту плоскость принять за плоскость ху и обозначить через F силу,
отнесенную к единице длины, считая ее положительной, если она отталки-
вающая, и отрицательной, если она притягивающая, то проекции этой силы
будут
Уравнения равновесия могут быть преобразованы следующим образом
(рис. 93).
Уравнение моментов относительно оси Ог, как мы установили, дает
ds

176	ЧАСТЬ ВТОРАЯ. СТАТИКА
С другой стороны, имеем
Вводя полярные координаты г и 0, мы приведем эти уравнения к виду
Наиболее простым будет случай, когда F есть функция от г вида <?(/")•
Тогда будет существовать первый интеграл, который легко найти. В самом
деле, так так сила F потенциальная, то Т получается при помощи квадратуры
у
Имея силу натяжения, легко найти дифференциальное уравнение кривой
равновесия. Для этого нужно подставить значение Т в первое уравнение,
которое после этого примет вид
то уравнение интегрируется в квадратурах. Действительно,
Подставляя это выражение в предыдущее уравнение, предварительно возве-
денное в квадрат, и разрешая относительно dO, получим уравнение кривой
[*
1	а 	 1
°~~ J
±
Если, например, положить F—k (k — постоянная), то
и уравнение кривой будет содержать эллиптический интеграл. Но если
приписать силе Т значение Т = — kr (k < 0), то искомая кривая будет
равносторонней гиперболой с центром в точке 0.
Естественное уравнение. Пусть V—угол между касательной к нити
и продолжением радиуса-вектора ОМ. Расстояние от полюса О до касатель-
ной равно г sin V (рис. 93). Условие того; что момент силы натяжения
постоянен, будет иметь вид
7Vsin V=C.
Далее, написав, что проекция силы F на нормаль равна Г/р, получим
FsinV=—.
Р
Исключая Т из этих двух уравнений, получим дифференциальное уравнение
кривой в виде
Fp r sin3 V = С.
142. Пример существования бесчисленного множества положений
равновесия. Нить закреплена в двух точках оси Ох и каждый элемент
нити отталкивается от оси силой, пропорциональной его длине и

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ	177
расстоянию от этого элемента до оси. Эта задача возникает при
нахождении положения равновесия невесомой нити, вращающейся с постоян-
ной угловой скоростью вокруг оси Ох («прыгалки»).
Так как все силы, действующие на нить, пересекают ось Ох, то момент
сил натяжения относительно этой оси постоянен вдоль всей нити. Но так
как нить прикреплена к двум точкам оси, то момент сил натяжения на
концах равен нулю. Следовательно, этот момент будет равен нулю всюду,
и мы имеем
„/ dz	dy\ .
Т у -т	z —f- — О,
\^ ds	ds )
откуда
dy dz л
—	= 0, у = mz,
у г	у
где m — постоянная. Отсюда видно, что фигура равновесия находится
в плоскости, проходящей через ось Ох. Примем ее за плоскость ху. Тогда
сила, действующая на элемент ds, будет перпендикулярна к оси Ох, про-
порциональна ординате у и будет отталкивающей
Y ds = fi у ds.
Уравнения равновесия будут
Из первого уравнения имеем Т —— = А, где постоянную А можно всегда
считать положительной, отсчитывая дугу s в направлении, в котором х
возрастает вместе с s. Подставляя это значение Т во второе уравнение и
полагая
dx у ' А а"- '
приведем его к виду
У' dy' _ 2y rfy
Интегрируя это уравнение, получим
где постоянная й2 должна быть обязательно положительной, так как левая
часть уравнения положительна. Уединяя радикал, возводя уравнение в квадрат
и заменяя у' его значением—^-, получаем
dx= ±
a"- dy
Так как нить прикреплена к оси Ох, то уравнение должно иметь
вещественное значение для у', когда у = 0; следовательно, Ь- > а\ Обозна-
чая через <р (у) стоящий под радикалом многочлен четвертой степени,
получим
ср (у) = (fi -j- a' — у2) (b'i — а'- - у-5).

178
ЧАСТЬ ВТОРАЯ. СТАТИКА
Величина у, начиная от нуля, может изменяться только в пределах
—аз и
— а\
Построим кривую. Допустим, что нить закреплена в точке О (рис. 94)
и что она расположена в углу уОх. Тогда х сначала возрастает вместе с у,
dx
	 положительно и
dt
7
c&dy
(С)
Когда у возрастает, х тоже возрастает, причем до тех пор, пока у не сде-
лается равным Yb'1 — а1. Тогда х достигает значения
<f-dy
Таким путем получается ветвь ОМА\. Касательная в А\ горизонтальна.
Начиная с этого значения, у убывает, и для того, чтобы х продолжало воз-
растать, необходимо взять
перед У<р (у) знак — . Так
получается вторая ветвь
AiMiOi, симметричная с
первой ветвью ОМАХ отно-
сительно ординаты А\В\,
так как одинаковым изме-
нениям у отвечают одинако-
вые изменения х. При у = О
получается точка Ох с абс-
циссой 2?. После этого у,
становясь отрицательным,
может убывать до значе-
рис 94.	ния — У~62 — а\ При этом
абсцисса будет все время
возрастать до значения 3?,
что соответствует точке А2, в которой касательная горизонтальна. После
^	^ — я2.
этого у снова возрастает от — У^Ь2 — я3 до -f- }^Ь2 — я2. Начиная от
точки А% необходимо брать перед радикалом знак -f-, и получится дуга
А2ОоАя, пересекающая ось в точке О2 с абсциссой 4S и т. д. Все получае-
мые таким образом последовательные волны тождественны с первой, и кривая
аналогична синусоиде.
Уравнения легко интегрируются в эллиптических функциях. Положим
в уравнении (С) кривой
fe?	^	CD
Тогда оно принимает вид
'2_ = /•	dt_
J УA— &)(\
откуда
ak'
ak'

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ
Дифференциал ds дуги кривой будет
179
Сделав в этой формуле подстановку A), мы получим для абсциссы ? точки
и для длины X дуги OAi следующие два выражения:
ак' Г	dt_	= ак'
~ У2" J У(Т — *2)A — б2*2) ~ У2
a /* (l-\-k2 — 2k*P)dt
~ k'Y2 J У(Т— fi)(\ — k4*
Щ'
B)
так как для точки Д величина г! равна 1.
Когда X и ? даны, причем X должно быть больше, чем ?, так как
дуга ОАХ больше своей проекции OBV то постоянные величины а и №
имеют единственную систему значений при условии, что А2 < 1. В самом
деле, вычисляя X — % и X-f-?,
имеем	У
X-? ,.o
IV
a
l
/V
1
1
J 	^2
— k4*
dt
dt
C)
При ?2 = 0 отношение в	р qj-
правой части равно нулю; при
увеличении &2 числитель будет,
очевидно, возрастать, а знаменатель убывать и, следовательно, отношение
будет возрастать. При й2 = 1, оно обратится в единицу. Таким образом, это
отношение проходит один и только один раз через заданное значение
¦. , >¦¦ Следовательно, постоянная k2 будет иметь одно и только одно зна-
чение. Тогда из выражения B), написанного для ?, получим для а единствен-
?У
ное значение
1\к
Определение постоянных. Так как нить имеет заданную длину I и
закреплена в точке О и в точке О' оси Ох с абсциссой а, то может предста-
виться бесчисленное множество случаев.
1°. Нить имеет только одну полуволну между О и О' (рис. 95).
Тогда ? равно половине а, а X — половине /. Величины ? и X известны
и постоянная k2 имеет значение, определяемое формулой C); после
этого a = —

.gQ	ЧАСТЬ ВТОРАЯ. СТАТИКА
2°. Нить имеет две полуволны между О и О'. Тогда ? = — ' X = —,
a k- имеет то же значение, что и в предыдущем случае, так как -?	=-
К — а
имеет то же значение т——. После этого
X-f- а
3°. Вообще, если нить имеет п полуволн между О и О', то ; = -^- ,
i. = —, k- имеет всегда одно и то же значение, но а — ' , .
Следовательно, существует бесчисленное множество положений равно-
весия, которые все подобны первому относительно точки О с отношением
подобия i/з, 113, ..., х/п. (См. А п п е л ь и Л я к у р, Theorie des ionctions
elliptiques.)
143. Равновесие нити на поверхности. Пусть f(x, у, z) = 0 —
уравнение поверхности, отнесенное к трем прямоугольным осям. Нить
находится под действием непрерывных внешних сил. Обозначим
через F {X, Y, Z) силу, отнесенную к единице длины, в рассматрива-
емой точке.
Нить может скользить без трения, и реакция поверхности на эле-
менте ds направлена по нормали. Пусть N — реакция, отнесенная
к единице длины; ее проекции равны
, df xdf , df
дхг ду' dz '
Можно считать, что нить находится в равновесии под действием сил
F ds и Nds, имеющих равнодействующую Ф ds. Применяя общие
формулы равновесия нитей, имеем три уравнения
S-ds = O, \
дх	|
A)
которые совместно с уравнениями
определяют х, у, z, T и X в функции 5. Когда X. известно, то
известной будет также и нормальная реакция, которая направлена
относительно поверхности /=0 в сторону, где / положительно
или отрицательно, в зависимости от того, будет ли X положительно
или отрицательно. Так же, как и для свободной нити, если X, Y, Z

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ	181
не содержат явно s, можно привести число неизвестных к четырем,
заменяя везде ds через
и вычисляя, например, г, у, Т, X в функции х.
Для нахождения натяжения в общем случае мы имели
dT = — (Xdx-\-Ydy-\-Zdz).	B)
Здесь эта формула переходит в следующую:
Так как нить лежит целиком на поверхности, то коэффициент при X
обращается в нуль и остается та же формула B), что и для сво-
бодной нити. Если имеется силовая функция U(x, у, z), то
Например, если положить тяжелую однородную нить на поверхность,
.то, направляя ось Ог вертикально вверх, найдем, что сила F параллельна
этой оси, направлена в противоположную сторону
и равна по абсолютному значению весу р единицы Л у	/В
длины нити. Тогда
dT = pdz, T = p(z — h).
Рассмотрим плоскость z — h. Только что полу-
ченная формула показывает, что натяжение в точке М
(рис. 96) равно весу части нити, равной расстоя-
нию MQ от точки М до этой плоскости. Если, сле-
довательно, удалить часть MB нити и оставить све-
шиваться через блок в точке М часть нити, рав-
ную MQ, то равновесие не нарушится.
144. Примеры. 1°. Геодезические линии. Наи-	рис gg
более простым будет тот случай, когда на нить,
растянутую на поверхности, не действуют никакие
другие силы, кроме нормальной реакции N. Тогда предыдущее уравнение
переходит в dT — 0 и натяжение нити получается постоянным. Нить рас-
положится по геодезической линии поверхности. Действительно, так как
соприкасающаяся плоскость в какой-нибудь точке должна содержать силу Лг,
то она будет нормальной к поверхности, что характеризует геодезическую
линию.
Применим это к сфере. Так как реакции проходят через центр, то нить
находится под действием центральных сил. Следовательно, ее фигура равно-
весия лежит в плоскости, проходящей через центр, и будет поэтому дугой
большого круга.
Известно, что линия наименьшей длины, соединяющая две точки на
поверхности, является одной из геодезических линий, проходящих через эти
точки. Однако было бы неточным сказать, что каждая из геодезических
линий будет минимальной по сравнению с бесконечно близкими линиями.
Например, дуга большого круга, большая 180°, соединяющая две точки на
сфере, является геодезической линией. Между тем возможно найти между
этими двумя точками путь бесконечно близкий и в то же время более
короткий. Наоборот, на замкнутом цилиндре все геодезические линии,

182	ЧАСТЬ ВТОРАЯ. СТАТИКА
являющиеся винтовыми линиями, будут минимальными. Существует бес-
численное множество этих линий, соединяющих две точки на поверхности.
Их можно получить, натянув по поверхности между этими точками нить и
обернув ее один, два, ... раза вокруг цилиндра.
2°. Сферическая цепная линия. Фигура равновесия однородной тяжелой
нити на сфере была исследована Бобилье (Жергоннь, 1829), Миндингом
(Crelle, т. 12) и затем Гудерманом (там же, т. 33), который дал выраже-
ния интегралов при помощи эллиптических функций. Решение было допол-
нено Клебшем (Crelle, т. 57, § 6), Бирманом (Dissertation inaugurate, Бер-
лин, 1865) и Шлегелем (Programm des K6niglichen Wilhelms Gymnasium,
Берлин, 1884).
Приняв центр сферы за начало координат, направив ось z вертикально
вверх и, обозначив через р вес единицы длины нити, получим сначала для
натяжения Т значение p(z— h) (п. 143). Так как равнодействующая сил
(веса и реакции), приложенных к ds, находится все время в одной плоскости
с осью Oz, то момент натяжения относительно этой оси постоянен. Следова-
тельно, взяв в плоскости хОу полярные координаты гиб, получим
где С — произвольная постоянная. Заменив в этом уравнении Т его значе-
нием и написав А вместо С, получим дифференциальное уравнение фигуры
равновесия
(z — h)r*dQ = A ds.
Для интегрирования этого уравнения возведем его в квадрат и заметим,
что вследствие соотношения
г = Л[а> — z2,
где а — радиус сферы,
ds2 = rfr* +	д8Дг3
Разрешая относительно df), получим
Аа dz
откуда определяем выражение 8 через z при помощи квадратуры. Пере-
менная z может принимать лишь такие значения, для которых многочлен
9 (z) = (Л — zf (а2 — г5) — Л2
положителен. Следовательно, обозначая через гй координату z какой-нибудь
точки нити, например одной из точек закрепления, имеем q> (z0) > 0. Но <р (а)
и <р(—а) отрицательны, и поэтому многочлен y(z) имеет один корень а
между z0 и а и один корень р между z0 и —а. Переменная z может изме-
няться только между пределами аир. Кривая на сфере расположена между
двумя параллелями аир, которых она попеременно касается. Коорди-
наты х, у, z точки кривой можно выразить через однозначные функции
параметра и, определяемого уравнением
. adz
du = -
Y(h — zy (a9- — z2) — A*
(См. статью Аппеля в Bulletin de la Societe mathematique, 1885 и статью
Гомеца Тейксейра в Annales scientificos da Academia Polytechnica do Porto,
т. IV, 1909.)
145. Естественные уравнения равновесия нити на поверхности.
Пусть АА'—кривая равновесия, At — касательная к ней в точке А в напра-
влении положительных дуг, An — нормаль в точке А к поверхности, считав-

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ
185
мая положительной в направлении от точки А к центру кривизны О нор-
мального сечения, проведенного через At, и R— радиус кривизны АО этого
сечения (рис. 97). Если С — центр кривизны нити в той же точке А и-
АС = р — радиус кривизны нити, то по теореме М*нье р = R cos 8, где 8
угол САО. Обозначим, наконец, через Ар проек-
цию направления АС на касательную плоскость
к поверхности в точке А. Элемент ds нити нахо-
дится под действием заданной силы Fds и
нормальной реакции N ds, считаемой положи-
тельной в направлении АО. Равнодействующая
(F) -f- (N) двух сил F и ЛГ, на основании естест-
венных уравнений равновесия свободной нити,
dt	T
равна равнодействующей сил-—-т- и	, на-
правленных соответственно по At и АС. Следо-
вательно, сумма проекций сил F и N на какую-
, „ dT
нибудь ось равна сумме проекции сил	— и
Т
ds
Рис. 97.
	на ту же ось. Спроектируем силы (F) и
(Л7) последовательно на оси At, Ар, An. Тогда, обозначая через Ft, Fp, Fn
проекции на эти оси силы ¦F, получим
— — =Ft, — — sinb = Fp, — — cos 8 = Fn + N.
Из последнего уравнения получим реакцию N:
TV =	cos » — /•„ =	- — tn.
9	К
Первые два уравнения являются естественными уравнениями равно-
Р
является.
весия нити на поверхности. В этих уравнениях величина
радиусом геодезической кривизны нити.
Например, для сферической цепной линии (п. 144) Fn обозначает проек-
цию веса р на радиус сферы; следовательно, Fn равно р—. Так как R
равно радиусу а сферы и Т равно p(z—h), то нормальная реакция для
сферической цепной линии равна — — {2z — Л). Если нить находится между
двумя бесконечно близкими сферическими поверхностями, то она давит на
внутреннюю сферу в точках, где это значение N положительно, и на внеш-
нюю сферу — в точках, где оно отрицательно. Точки, где Л'' = 0, являются
в горизонтальной проекции точками перегиба.
Вернемся к общему случаю. Допустим, что нить находится в равно-
весии и будем деформировать поверхность таким образом, чтобы длины
начерченных на ней линий не изменялись. Тогда геодезическая кривизна этих
линий остается неизменной. В то же время сохраним для натяжения нити
те же значения и изменим F таким образом, чтобы Ft и Fp не изменились.
Тогда два естественных уравнения равновесия будут по-прежнему удовле-
творяться, и нить останется в равновесии. Изменится только реакция N.
ц Вследствие *гого нахождение фигуры равновесия нити на развертываю-
щейся поверхности может быть сведено к случаю, когда эта поверхность —
плоскость. Например, фигура равновесия тяжелой однородной цепочки на

184	ЧАСТЬ ВТОРАЯ. СТАТИКА
поверхности вертикального цилиндра является кривой, которая при развер-
тывании цилиндра на вертикальную плоскость обращается в цепную линию.
Фигурой равновесия тяжелой однородной цепочки на круговом конусе
с вертикальной осью является кривая, которая при развертывании конуса
обращается в фигуру равновесия нити, каждый элемент которой притяги-
вается или отталкивается неподвижной точкой (вершиной конуса) с постоян-
ной по величине силой. Дифференциальное уравнение этой кривой было
нами найдено (п. 141).
III. Исследование одного определенного интеграла
146. Геометрическая задача. Нахождение фигуры равновесия
нити в случае существования силовой функции может быть сведено
при помощи интересного приема к отысканию максимума или мини-
мума некоторого определенного интеграла, который встречается
также при определении брахистохрон, при доказательстве принципа
наименьшего действия и в общей задаче рефракции.
Пусть ср(х, у, г) — непрерывная функция декартовых координат
точки, определенная в некоторой области пространства, включающей
все кривые, которые мы будем рассма-
тривать. Разрешим сначала следующую
задачу геометрии.
Среди всех кривых, соединяющих две
неподвижные точки А а В (рис. 98),
найти такие, которые обращают ин-
теграл	{В)
I = Г ср(я, у, z)ds
(h
в максимум или минимум. В этом
интеграле ds обозначает элемент длины
кривой, и интеграл распространен на всю кривую между точками ,4
и В. Нетрудно представить себе, что для некоторых кривых С
интеграл / имеет максимум или минимум. Например, если функ-
ция v{x, у, z) положительна при всех значениях х, у, г, то инте-
грал / будет положительным и не сможет обратиться в нуль; он будет
тогда, очевидно, иметь минимум. В частности, если ср (л:, у, г)= 1,
то значение интеграла / равно длине кривой, соединяющей точки А
и В, и кривая С, вдоль которой интеграл имеет минимум, есть
прямая АВ.
Пусть, в общем случае, С — кривая, обращающая интеграл в макси-
мум или минимум. Выразим координаты х, у, z точки М этой кри-
вой в функции какого-нибудь параметра q, который изменяется
в пределах от а до Ь, когда точка М описывает дугу АМВ. Обо-
значим через х', у', ?.' производные от х, у, z по q л
положим

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ	185
Имеем
ds = R dq,
и интеграл / вдоль С будет иметь значение
ь
1= fy(x, у, z)Rdq.
а
Для того чтобы выразить, что интеграл / имеет минимум, доста-
точно выразить, что значение /t того же интеграла, взятого вдоль
произвольной кривой С,, бесконечно близкой к С и соединяющей
точки А и В, больше чем '/.
Пусть ;, ij, С — произвольные функции от q, обращающиеся
в нуль на пределах а и b и имеющие производные ?', г{, С.
Положим
x1 = x-\-eJ-, _y1 = _y-feT]> г1 = г-\-ег„	(Mx)
где s — бесконечно малая постоянная. Когда q изменяется от а до Ь,
точка Мх с координатами xl3 yt, zy описывает кривую Cv беско-
нечно близкую к С и проходящую через точки А к В. Имеем вдоль
кривой Cj
Для оценки значения разности /х — /, т. е. вариации 8/ интеграла
при переходе от кривой Сх к кривой С, разложим /t по возрастаю-
щим степеням а, останавливаясь на членах второго порядка. Имеем
A'f + (У
где написано ср вместо <р (лг, у, г). Перемножая почленно, получим
Умножая обе части на Л/, интегрируя от а до b и замечая, что

186	ЧАСТЬ ВТОРАЯ. СТАТИКА
получим
Освободимся от X', тг)', С' интегрированием по частям. Имеем
ь
/их г, ,
ь	ь	ь
dx t
и две аналогичные формулы для членов с т\' и С. Следовательно,
окончательно,
где положено
Проинтегрированная часть равна нулю, так как Е, i\, Z, обра-
щаются в нуль на пределах а и Ь. Для того чтобы интеграл / вдоль
кривой С был максимумом или минимумом, надо, чтобы знак
разности /j — / сохранялся при любых бесконечно малых поло-
жительных или отрицательных значениях е. Надо, следовательно,
чтобы коэффициент J при s равнялся нулю, так как, в противном
случае, для достатоточно малых значений s разность 1Х — / будет
иметь знак величины sJ. Следовательно, для того чтобы был макси-
мум или минимум, необходимо, чтобы интеграл, который мы обозна-
чили через У, равнялся нулю, и это должно быть каковы бы ни
были произвольно выбранные функции ?, -ц, С. Но это условие тре-
бует, чтобы в интеграле J коэффициенты при ?, -ц, С были тож-
дественно равны нулю; в противном случае, выбирая для ?, -ц, С
такие функции, которые при всяком значении q имеют такие же
знаки, как и соответствующие коэффициенты, мы сделаем положи-
тельными все элементы интеграла J, который, очевидно, будет тогда
отличным от нуля. Таким образом, искомая кривая С, осуществляю-

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ	187
щая максимум или минимум, должна удовлетворять уравнениям
~дх
C)
,/ dx\
Эти три уравнения приводятся к двум, что может быть непосредственно
проверено, если их сложить, умножив предварительно на —г-, -~
dz
и -у—; тогда, принимая во внимание хорошо известные соотношения
dz \2 , dx.dx.dy.dy.dz.dz
Ы=1' -did-dJ + -dJd-dJ+-dTddi = °>
мы придем к очевидному тождеству
Уравнения C) после замены ds выражением Ydx* -j- dy2 -\- dzz
приводятся к двум уравнениям второго порядка, общий интеграл
которых определяет у и z в функции х и четырех произвольных
постоянных:
с2, с3. с4). j
Постоянные определяются из того условия, что кривая проходит
через две заданные точки А и В, откуда получаются четыре урав-
нения для определения четырех постоянных. Таким образом опре-
деляются искомые кривые, соединяющие две точки. Не все эти кри-
вые дают для интеграла максимум или минимум, но среди них нахо-
дятся именно те, которые осуществляют максимум или минимум.
Так как общие уравнения кривых С содержат четыре произвольных
постоянных, то одна из этих кривых определяется четырьмя усло-
виями. Кроме исключительных случаев можно, например, предполо-
жить, что кривая проходит через заданную точку и имеет в ней
заданную касательную. Легко проверить, что если ср — постоянная,
то кривые С, получаемые интегрированием уравнений C), как мы
это знали уже заранее, являются прямыми
Уравнения C) показывают, что искомые кривые С являются
фигурами равновесия нити, находящейся под действием силы F,
имеющей силовую функцию — <р (х, у, г), причем натяжение
нити должно иметь значение <р(х, у, г). Наоборот, пусть нить

1*8
ЧАСТЬ ВТОРАЯ. СТАТИКА
находится в равновесии и уравнения равновесия суть d\T'—— )-+-
+ -J— ds—0	причем Т — — (U-{-h). Если на нити взягь две
фиксированные точки А и В, то фигура равновесия в общем случае
придает максимальное или минимальное значение интегралу
в
и во всех случаях обращает в нуль вариацию этого интеграла,
(Мёбиус, Статика, ч. 2, гл. VII).
147. Формула Тэта и Томсона. Проделанные нами вычисления, при
несколько иной интерпретации, приводят к важной теореме Тэта и Том-
сона. Пусть С—-дуга одной из кривых, удовлетворяющих уравнениям C),
имеющая концы Л и В, и пусть
Ci — другая кривая, бесконечно
близкая к первой и имеющая
концы A-i и В1, бесконечно близ-
В ( 9Э К
Р
i 1
кие к А и В (рис. 9Э). Как и
выше, можно перейти от кривой С
к кривой С;, полагая
с той только разницей, что ej, ет],
Л не обращаются больше а нуль
на пределах, а и Ь, но при q — а
имеют значения (е?),, (ет,),, (tC)b
равные проекциям на оси координат отрезка AAV а при q = b — значения (e?)g,
(?Y|).>, (е')о, равные проекциям отрезка ВВ\. Разность /t — / значений инте-
грала \ <? ds вдоль кривых С| и С по-прежнему определяется из формулы B),
в которой проинтегрированная часть, образующая первый член, не равна
больше нулю, в то время как интеграл У, стоящий во втором члене, равен
нулю, так как кривая С удовлетворяет, по предположению, уравнениям C) и
все элементы интеграла / равны нулю. Следовательно, пренебрегая а фор-
муле B) членом второго порядка малости е2К. имеем
о
,, |л dx , dy . _ dz \
1	\\ ds ' ds	ds )
Значения е?, щ, еС на пределах а и b указаны выше; обозначим
через <р (А) и у (В) значения функции ? в точках А и В; заметим,
наконец, что так как —г-, —~, —— суть направляющие косинусы а, <$, •(
ds ds ds
касательной МТ к кривой С, направленной в сторону возрастания дуги, т. е.
от А к В, то значения указанных величин на обоих пределах равны напра-
вляющим косинусам alt Pj, fi и а2, [Ц, -[з ДВУХ касательных Л^ и ВТ-> на
обоих концах. Следовательно, для 6/ получается выражение
6/ =
еу2 Ь] ? {В) - [(
h + (^)i Tl) f

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ	189
которое имеет простую геометрическую интерпретацию. Величина
(в$Jа2 + (^),р2 + (еСJТ?
представляет собою проекцию отрезка BBt на касательную ВТ2; она равна
ВВ\ cos T^BBi, точно так же вторая величина, содержащаяся в о/, равна
ЛА] cos ТгААх. Окончательно,
§/ = BBjcf (В) cos T\BBl — AAtf (A) cos 7\AAL,
или в более симметричной форме
Ы = — ААгу (A) cos BAAi.— 55^ (В) cos АВВЪ	D)
так как угол АВВг является дополнительным к углу Т2ВВ1, а угол BAAt
равен углу ТуАА^.
Формула D) Тэта и Томсона совершенно аналогична хорошо известной
элементарной формуле, выражающей изменение длины отрезка прямой, и
получающейся из этой при ср = 1 (см. Бертран, Кдос дифференциального
исчисления, стр. 22).
Следствия, которые получаются из формулы D), тождественны с теми,
которые выводятся из аналогичной формулы для прямых в теории разверток
и в теории параллельных кривых и
поверхностей. Мы укажем здесь те
следствия, которые приводят к интерес-
ным результатам в теории брахистохрон,
в. теории принципа наименьшего дей-
ствия и в задаче рефракции. Мы пред-
полагаем в последующем, что функция <р
не обращается в нуль в рассматривае-
мой области пространства.
1°. Приложение. Даны две поверх-
ности S и I. Какую кривую нужно
провести от одной поверхности к
другой, для того, чтобы интеграл I,
взятый вдоль этой кривой, имел мак-
самум или минимум} Пусть А и В	р ,л«
(рис. 100) — две неизвестные точки,	и '
в которых искомая кривая пересекает
обе поверхности. В частности, эта кривая будет одной из тех, соединяющих
точки А и В, которые обращают интеграл / в максимум или минимум.
Следовательно, это — одна из кривых С, определяемых уравнениями (о). Для
определения точек А и В заметим, что при переходе от кривой АСВ. кото-
рая обращает интеграл / между двумя поверхностями в максимум или
минимум, к произвольной бесконечно близкой кривой, и, в частности,
к другой бесконечно близкой кривой С, вариация о/ должна быть равна
нулю. Вычислим эту вариацию при переходе от кривой АСВ к другой
бесконечно близкой кривой С; пусть это будет кривая АЕВ^, которая
выходит из той же самой точки А и оканчивается в точке Вг поверх-
ности 2. Тогда на основании полученной выше формулы
Ы = — Mltf (В) cos ABBV
Так как вариация S/ должна быть равна нулю, то нулю должен быть
равен косинус. Следовательно, угол АВВХ должен быть.прямым для всех
положений точки В± на поверхности S и искомая кривая С нормальна
к. этой поверхности. Точно так же она нормальна и к поверхности S.
В частности, если ^=1, то получается известный элементарный результат,

190
ЧАСТЬ ВТОРАЯ. СТАТИКА
заключающийся в том, что для нахождения кратчайшего расстояния между S
и 2 нужно провести общую нормаль к обеим поверхностям. Отсюда видно,
что искомая кривая является фигурой равновесия нити, концы которой
скользят без трения по двум поверхностям, причем натяжение равно q> и
силовая функция равна —у. Очевидно, что та же теорема будет справедлива,
если одну из поверхностей заменить неподвижной кривой или точкой.
2°. Теорема Тэта и Томсона. Если рассматриваются кривые С,
выражаемые уравнениями C) и нормальные к заданной поверхности S
и если на каждой из этих кривых откладывается от точки А, в кото-
рой она пересекает поверхность S, дуга АВ такая, что интеграл
(-В)
г= С yds,
взятый вдоль этой кривой, имеет постоянное значение, одинаковое для
всех кривых, то геометрическое место точек В есть поверхность 2,
нормальная ко всем кривым.
В самом деле (рис. 100), если перейти от кривой С к бесконечно
близкой кривой С1? то вариация S/, заданная формулой D), равна, по пред-
положению, нулю, но так как cos BAAt = 0 в силу того, что кривая С нор-
мальна к 5, то и cos АВВх = 0, и кривая С нормальна к 2.
Эта теорема, которая содержит как частный случай (у = 1 > теорию
параллельных поверхностей, справедлива, очевидно, и в предельном случае,
когда поверхность S сводится к сфере
бесконечно малого радиуса, т. е. когда
кривые С проходят через неподвижную
точку.
148. Примеры. 1°. Пусть функция
у (лг, у, г) имеет вид pz. Будем рассматри-
вать кривые, проведенные только в части
пространства, расположенной над плоско-
стью ху. Кривые С являются фигурами
равновесия нити, на каждый элемент кото-
рой действует вертикальная сила. Проек-
ция последней на ось Ог равна —pds,
причем натяжение Т равно pz. Следова-
тельно, кривые являются цепными ли-
ниями, лежащими в вертикальных плоско-
стях и имеющими основания в горизон-
тальной плоскости х Оу. Действительно,
мы видели, что если z0 есть ордината основания находящейся в равновесии
цепочки, то натяжение Т равно p(z— z0); следовательно, z0 должно быть
равно нулю.
Этот результат имеет интересное геометрическое толкование. Возьмем
в вертикальной плоскости zOx две точки А и В, лежащие над осью Ох, и
кривую AM В, соединяющую эти точки (рис. 101). Площадь поверхности,
образованной вращением этой кривой вокруг оси Ох, равна
(.В)
О
д
\
\
\
\
т
\
\
\
N Ч
——/
/ /
г/
//
в
/I
/I
/ /
'Ум
с
Рис. 101.
f
zds.
Следовательно, кривая АМВ, описывающая наименьшую площадь, есть
цепная линия, соединяющая обе точки А я В к имеющая основанием ось Ох.
Если искать цепную линию, удовлетворяющую этим условиям, то окажется,
что она не всегда существует. Например, если обе точки А и В имеют

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ	191
одинаковые ординаты, то она существует только в том случае, когда
половина угла при вершине С равнобедренного треугольника АСВ, имею-
щего основание АВ и вершину в точке С на оси, меньше угла DCT =
=33° 32', который образован осью симметрии CD (рис. 101) и касательной СТ
к цепной линии, проведенной из точки пересечения оси симметрии с осно-
ванием. Мы не будем здесь указывать условий существования цепной линии
при произвольном положении точек А и В. Эти условия установлены
впервые Гольдшмидтом (Determinatio superficiei mimoe, etc., Гёттинген, 1831).
Когда цепная линия не существует, то кривая АМВ, при вращении
которой описывается минимальная площадь, состоит из двух ординат АА'
и ВВ' заданных точек и отрезка оси Ох, заключенного между А' и В'.
В самом деле, дифференциальные уравнения кривой суть
dx
Из первого имеем рг —— = k. Если k не равно нулю, то получается цепная
линия. Если цепной линии нет, то это решение должно быть отброшено.
В этом случае следует положить k — 0, и, следоват&гьно,
dx
pz —— = 0.
r ds
Это показывает, что либо г равно нулю, либо х постоянен. Таким образом,
часть кривой, не совпадающая с осью Ох, состоит из прямых, к ней пер-
пендикулярных.
2°. Пусть 9 = — и по-прежнему рассматриваются точки и кривые, рас-
положенные над плоскостью хОу. Все кривые С лежат в вертикальных
плоскостях, причем в одной из них, а именно в плоскости zOx, они имеют
дифференциальные уравнения
z ds } • \z ds
которые приводятся к одному уравнению. В первом уравнении заменим ds
через ydx2 -\- dz^ и затем разделим в нем переменные. Получим
1 dx 1	_,	zdz
	= —, или dx = +	—.
z ds с	у с2 — z2
Это уравнение интегрируется сразу. Обозначая через а новую постоянную,
найдем
(,х — af -
т. е. уравнение окружности с центром на оси Ох. Следовательно, в про-
странстве кривые С суть окружности, перпендикулярные к плоскости ху.
Через две точки А и В проходит, очевидно, одна и только одна из этих
окружностей.
Геометрия, в которой эти окружности С играют ту же роль, что и
прямые в обычной геометрии, и в которой сохранено элементарное понятие
угла, а за длину дуги какой-нибудь кривой принимается интеграл / —,
распространенный на эту дугу, является неэвклидовой геометрией Лоба-
чевского.
149. Та же задача на поверхности. Нахождение фигуры равновесия
нити на поверхности в случае, когда существует силовая функция, также
приводится к определению максимума или минимума некоторого определен-
ного интеграла.

J92	ЧАСТЬ ВТОРАЯ. СТАТИКА
Среди всех кривых, проведенных на неподвижной поверхности S а
соединяющих две ее заданные точки А и В, нужно найти те, которые
обращают интеграл
(В)
г=/
<?(х, у, z)ds
U)
в максимум или минимум.
Пусть С — искомая кривая, a Q — проведенная на поверхности между
теми же двумя точками А и В бесконечно близкая кривая. Обозначим
через х, у, г координаты точки М кривой С. Тогда координаты бесконечно
близкой к ней точки Мг кривой С) будут
-*Ч = х + Ьх, У1 = у + 8у, z\ = г-\- Ьг,
где для краткости несколько изменены обозначения, принятые в п. 146, и
пишется 8дг, Ьу, Ьг вместо в?, ет), еС
Если отбросить величины, содержащие е3, то согласно выкладкам, при-
веденным в п. 146 для вариации 8/ интеграла /, соответствующей переходу
от кривой С к кривой Q, имеющей те же концы, получается выражение
(А)
В рассматриваемом случае эта вариация должна быть равна нулю при
переходе не к произвольной бесконечно близкой кривой, но к бесконечно
близкой кривой, лежащей на поверхности. Вследствие этого не все три
вариации Ьх, Ьу, Ьг произвольны; если
f(x, у, z) = О
есть уравнение поверхности 5, то должно выполняться условие
bx+b +Ъг=Ог	B)
дх п ду J п дг
которое выражает, что вариация функции f(x, у, z) равна нулю при пере-
ходе от С к Cj, и которое показывает, что одна из вариаций, например Ьх,
есть функция двух других вариаций Ьу и Ьг, которые остаются произвол^
ными. При этом условии, обозначая через X произвольную функцию, по-
лучим
(В)
\ дх ~ ду у ~ дг
W
Вычтем этот равный нулю интеграл из 8/. Получим
(В)

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ
193
где член с bz аналогичен двум первым членам. Эта вариация в/ должна
быть равна нулю, каковы бы ни были X, Ьу и bz. Мы можем распорядиться
величиной X таким образом, чтобы коэффициент при Ьх обратился в нуль.
Тогда величина, стоящая под знаком интеграла, будет содержать только
члены с 5 у и bz, и так как 8/ должно равняться нулю при любых Ьу и bz,
то коэффициенты при этих двух вариациях должны тоже равняться нулю.
Таким образом, при подходящем выборе X получаются три следующих урав-
нения, которые мы выписываем с обратными знаками:
дх
'(»#)+(-?+'?)*-»
Эти уравнения, вместе с уравнением поверхности, определяют искомые кри-
вые С.
Но эти уравнения в точности совпадают с уравнениями равновесия
нити, лежащей на поверхности S, когда силовая функция равна —<р и
натяжение равно <р. Мы получаем, таким образом, результат, тождественный
с тем, который мы получили для кривых в пространстве.
Пример. Если 9 = 1, то интеграл / определяет длину кривой АВ. Сле-
довательно, если искать на поверхности линии наименьшей длины, соеди-
няющие две точки Л и В, то получится фигура равновесия нити, которая лежит
на поверхности и на которую не действуют никакие непосредственно прило-
женные силы (п. 144).
150. Рефракция. Покажем вкратце, что этот же интеграл I ? (х, у, г) ds
встречается в общей задаче рефракции. Этот факт, по крайней мере
в наиболее простых случаях, был отме-
чен уже Мопертюи, Иваном Бернулли
и Эйлером. Лаплас даже рассматривал
с этой точки зрения двойную рефракцию
(Memoires de l'lnstitut, 1809).
Когда световой луч переходит из
пустоты в однородную среду, (рис. 102),
ограниченную произвольной поверхно-
стью S, то он подчиняется двум следую-
щим законам:
1°. Падающий луч АР, преломлен-
ный луч РА^ и нормаль PN к поверх-
ности S находятся в одной плоскости.
2°. Справедливо соотношение
sin г
sin r
= п,
где I — угол APN, r — угол AtPNx ил — постоянная, называемая показа-
телем преломления среды относительно пустоты или абсолютным по-
казателем преломления.
Пусть (М) и (Мх) — Две однородные среды с абсолютными покааателями
преломления л и nlt разделенные поверхностью 5. Если световой луч пере-
ходит из первой среды во вторую, то первый закон сохраняется и
sin / _ rii
sin г ~~ п

194	ЧАСТЬ ВТОРАЯ. СТАТИКА
Напомнив эти законы, переходим к следующей задаче.
Пусть А и Аг — две заданные точки по одну и другую стороны от S,
а Р— произвольная точка на этой поверхности. Каково должно быть поло-
жение точки Р, чтобы сумма
а = ПАР + ПХ А^Р
была минимумом? Покажем, что минимум получится тогда, когда две пря-
мые АР и РА1 удовлетворяют закону преломления при переходе из среды (М)
в среду (Мх). В самом деле, если обозначить через а, Ь, с координаты
точки А, через alt bt, с,—координат» точки Ах и через х, у, z—коорди-
наты точки Р, то расстояния АР и АХР будут соответственно иметь значения
Y(x - а? + (у - bf + (г - с)» и /(* - о^» + (у - Ьх? + (г - с^.
Сумма а будет функцией двух независимых переменных х и у, так как z есть
функция от дг и у, определяемая уравнением f(x, у, г) = 0 поверхности 5.
Для того чтобы найти значения х и у, обращающие с в минимум, необхо-
димо приравнять нулю частные производные от а по х и у, что приводит
к двум уравнениям
)
^	cx)~.
=	1- Пх	=	= 0,
РА	РАх
-cx)^
	— = 0,
п=Пх
РА
которые вместе с уравнением поверхности определяют координаты точки Р.
Определив таким образом эту точку, сделаем замену осей координат: примем
точку Р за начало (рис. 102), за ось Oz примем нормаль в сторону точки А
и за плоскость гх плоскость, содержащую А, так что координата b точки А
будет равна нулю, а координаты а и с будут положительны. Величины х,
у, z, -J—, -;— будут тогда для точки Р равны нулю и полученные уравнения
примут вид
^3^
РА РАХ
Второе уравнение показывает, что точка Ах также лежит в плоскости zPx,
что выражает первый закон преломления. Первое уравнение показывает,
что «1 отрицательно и, если через (иг обозначить углы, образуемые от-
резками АР и РАх с нормалью Pz, то из этого уравнения получим
п sin I — tix sin г = 0,
так как ajPA и — ах\РАх равны sin / и sin г. Это — второй закон преломления.
Таким образом, искомый минимум получается вдоль пути, по которому луч
идет от i к Л].
Вообразим теперь несколько поверхностей Si, S^ ..., Sp, разделяющих
однородные среды. Пусть над St находится среда с абсолютным показателем
преломления п, между Si и S2 — среда с показателем nv между S2 и
Sj — среда с показателем «g, и, наконец под Sp — среда с показателем пр.
Возьмем в первой среде точку А, в последней среде точку В и рассмотрим
мивгвугольник АР^Ръ ... РрВ с вершинами на каждой из поверхностей,

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ
195
идущий от точки А к точке В (рис. 103). Если искать, каким должен быть
этот многоугольник для того, чтобы сумма
была минимумом, то согласно предыдущему получится, что он должен быть
тем путем, по которому идет световой луч от А к В, следуя законам
преломления.
Допустим, наконец, что число поверхностей неограниченно увеличивается
и притом так, что стороны многоугольника, так же как и разности п — л1(
щ—п2, ..., стремятся к нулю. Тогда сово-
купность рассмотренных сред превратится
в непрерывную среду, в которой абсолют-
ный показатель преломления п будет не-
прерывной функцией у(х, у, г) координат.
Многоугольник, по которому следует свето-
вой луч, превратится в кривую, а сумма а
станет интегралом
/=
nds.
Рис. 103.
Таким образом, путь светового луча
из точки А в точку В совпадает с кривой,
которая обращает интеграл / в минимум и для которой мы составили диф-
ференциальные уравнения. По этому вопросу можно указать на статью
О. Бонне (Nouvelles Annales de Mathematiques, 1887). Эти же кривые были
исследованы Викером (Comptes Rendus, т. CVII1, стр. 330). Наиболее суще-
ственные их свойства были даны еще Эйлером в его «Теории брахистохрон».
IV. Плоские эластики
151. Натяжение и изгибающий момент. Пусть дан однородный
упругий стержень, длина которого велика по сравнению с его тол-
щиной и который имеет по всей своей длине одинаковые попереч-
ные сечения. Осью стержня называют геометрическое место центров
тяжести его поперечных сечений. Естественным состоянием равно-
весия стержня является та его форма, которую он принимает, когда
на него не действуют никакие силы, которые стремились бы его
деформировать, например, когда он положен на стол. Если к стержню
приложить силы, стремящиеся его изогнуть, то он изменит свою форму
и придет в новое состояние равновесия, которое называется вы-
нужденным состоянием равновесия, соответствующим данным силам.
Мы исследуем здесь наиболее простые случаи равновесия, когда
изогнутая ось стержня (эластика) является плоской кривой. Но сна-
чала укажем некоторые общие предложения, касающиеся такого рода
задач.
Рассмотрим упругий стержень, ось которого в естественном со-
стоянии имеет вид плоской кривой Со, и пусть р0 — радиус кривизны
в какой-нибудь точке М этой кривой. Допустим теперь, что стержень
деформируют, приложив к нему некоторые силы, но деформируют

196
ЧАСТЬ ВТОРАЯ. СТАТИКА
так, чтобы не изменилась длина стержня и чтобы его ось осталась
плоской и приняла новую форму С. Радиус кривизны в точке М
будет теперь р. В этом положении вынужденного равновесия силы
упругости определяются следующими законами.
Если разрезать стержень в точке М, то для сохранения равно-
весия нужно будет к сечению в точке М приложить силу Т, лежа-
щую в плоскости кривой С и пару с вектором момента, перпендику-
лярным к этой плоскости, численное значение которого N {изгибаю-
щий момент) пропорционально изменению кривизны, так что
n = b(-—-
\ Р Ро
где В — постоянный коэффициент, зависящий от природы стержня.
152. Ось стержня была первоначально дугой окружности.
Рассмотрим наиболее простой случай, когда ось стержня была первона-
чально дугой окружности М1АМ2 или прямой, так что — = const.
Пусть к концам Мх и Мг стержня приложены две силы 7\ и Т2,
лежащие в плоскости его изогнутой оси при равновесии, и две пары Л/,
и Wj с моментами, перпендикулярными к этой плоскости.
Обе силы Т1 и Т2 равны и противоположно направлены, так
как единственными действующими на стержень внешними силами,
сумма проекций которых на произвольное направление должна рав-
няться нулю, являются силы 7\ и Т2 и пары Nt и N2.
В' О В
О
aj
Рис. 104.
С другой стороны, так как сумма моментов внешних сил отно-
сительно любой точки плоскости равняется нулю, то силы Тг и Тг
составляют пару, которая уравновешивает пары Nt и Л/2.
Примем за ось Ох (рис. 104) прямую, параллельную силам 7\ и Тг.
Пусть М — произвольная точка оси стержня. Если стержень разре-
зать в точке М, то часть МХМ будет находиться в равновесии под

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ	197
действием следующих внешних сил: 1) силы Tt и пары TV,, дей-
ствующих на конце Мх\ 2) силы Т и пары N, действующих в точке М.
Пара N имеет момент
V Р Ро /	К
Эти внешние силы, приложенные к дуге МХМ, уравновешиваются.
Следовательно, сила Т равна по величине силе 7\, но направлена
противоположно ей. С другой стороны, сумма моментов всех внеш-
них сил относительно любой точки плоскости должна равняться
нулю. Возьмем сумму моментов относительно точки О; тогда, обо-
значая через у и уг ординаты точек М и Ми имеем
или, заменяя Т через 7\ и N его значением A), получим уравне-
ние
Если сила Т1 равна нулю, т. е. если к концам стержня при-
кладываются только пары, то из этого уравнения получаем для 1/р
постоянное значение, и фигура вынужденного равновесия будет другой
дугой окружности.
Оставляя этот случай в стороне, разрешим уравнение относи-
тельно 1/р и в получившейся правой части вынесем Т^/В в качестве
множителя за скобки. Получим уравнение вида
где через с2 обозначена положительная постоянная В/Т1 и через
b — другая постоянная. Ось х всегда можно переместить параллельно
самой себе так, чтобы последняя постоянная исчезла и чтобы урав-
нение равновесия приняло вид
Таким образом, получено дифференциальное уравнение кривой, форму
которой примет ось стержня. Для интегрирования этого уравнения
обозначим чере^ 6 угол, образованный нормалью в точке М с осью Оу
(рис. 104); если точка М переместится на ds, то нормаль повер-
нется на угол rf6 и мы получим
rfe	i_ _ у
ds p с" '

198
ЧАСТЬ ВТОРАЯ. СТАТИКА
откуда, дифференцируя, получим
i 1 dy	1 . ,
; == —=¦ -5==- =	S-Sinl
! c2 ds	c"
dx
C)
так как -р-= — sin 9 и -т- —cos6.
Умножим обе части уравнения C) на j- и проинтегрируем. По-
лучим
где
откуда
2 , й , . .
=-s(cos6+a), ds=
¦произвольная постоянная. Теперь находим
с cos 6 rf6
D)
dx = cos б ds =
± /2 (cos
cos 6 rf8
+/2^08
E)
Здесь нет необходимости добавлять постоянную, так как всегда
можно в качестве оси Оу выбрать нормаль к кривой, перпендику-
лярную к оси Ох. С другой стороны, имеем
F)
Формулы E) и F) определяют х и у в функции б. Здесь нужно
различать три случая в зависимости от того, будет ли |л лежать
внутри промежутка (—1, +1), или будет больше 1, или рав-
няться 1.
Укажем вкратце форму кривой в этих трех случаях. Анализ будет
основываться на следующих замечаниях.
Условимся отсчитывать дугу s кривой от точки А, лежащей на оси Оу
(рнс. 104), и примем в качестве положительного направления для s направ-
ление движения точки, абсцисса которой, будучи в начале равна нулю, ста-
новится положительной. Когда кривая описывается в этом направлении, s
всегда возрастает; следовательно, ds всегда положительно и в формуле D}
радикал всегда имеет тот же знак, что и db. Этот знак радикала должен
быть сохранен во всех последующих формулах. Из формул
dy	dx
-г- — — sin 6, -j- = cos 9	GV
ds	ds
видно, что при возрастании s координаты у и х возрастают или убывают
в зависимости от того, положительны или отрицательны величины — sin ft
и cos 8. Наконец, точками перегиба являются те точки кривой, в которых
она пересекает ось х, так как уравнение B) показывает, что р обращается
в бесконечность при у = 0, и наоборот.
Ось Оу является осью симметрии кривой.

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ
199
— COS a.
Первый случай. — 1 < ft < 1. В этом случае можно положить ft =
и радикал, содержащийся в формулах, принимает вид
/2 (cos 6 + ц) = Л[2 (cos в — cos а).
Для того чтобы он был вещественным, необходимо, чтобы в, начиная от
нуля, изменялось между —а и -\- а. Когда в изменяется от 0 до а, полу-
чается дуга АВ (рис. 104, а; рис. 105, а, б, в); когда 6 изменяется от 0
до —о, получается симметричная дуга АВ'.
г)
В точках В и В' кривая пересекает ось Ох под углом о, так как нор-
маль в точке, например, В образует с осью Оу угол а. Абсцисса точки В
на основании формулы E) будет
COS 6 fif6
s 6— cos a)'
(8)
где радикал берется положительный.
Когда угол о — острый или прямой, величина х0 получается положитель-
ной, так как все элементы интеграла положительны (кривая на рис. 105, а);
когда а возрастает, начиная от л/2, величина х0 будет сначала положитель-
ной (форма на рис. 104, а), затем обратится в нуль при некотором значе-
нии а0 величины а (форма на рис. 105, б) и после этого становится отри-
цательной (форма на рис. 105, в); когда а близко к я, тогда х0 отрицателен
и очень велик; это вытекает из того, что при а = я получается Xq = —со;
действительно, тогда
п
COS
2cos
а этот интеграл равен —оо. В предельном случае, когда ft = 1, кривая будет
иметь форму, указанную на рис. 105, г с асимптотой Ох.
Если s продолжает возрастать, начиная от точки В, то угол в будет
обязательно убывать, так как он не может быть больше а. Начиная с зтого

200
ЧАСТЬ ВТОРАЯ. СТАТИКА
момента, нужно будет перед радикалом брать знак минус. Когда в изме-
няется от а до —а, получается новая ветвь кривой, симметричная первой
относительно В, и т. д. Получается бесконечное число одинаковых волно-
образных линий, как в синусоиде.
Второй случай. Если р. > 1, то в может изменяться от 0 до 2щ у и 1/е>
никогда не обращаются в нуль; кривая имеет вид, указанный на рис. 104, б.
Интегрирование в этих двух случаях может быть выполнено в эллипти-
ческих функциях (см. Аппелль и Лякур, Principes de la theorie des fonctions
elliptiques, приложения).
Третий случай. В промежуточном случае, когда ц. = 1, кривая, как мы
уже говорили, будет иметь асимптотой ось Ох, так как х0 = —ею (рис. 105, г).
В этом случае все интегрирования могут быть выполнены в элементарных
функциях.
153. Случай первоначально прямолинейного стержня, сжимаемого
на концах двумя одинаковыми и прямо противоположными силами.
Наблюдения показывают, что первоначально, прямолинейный упругий стер-
жень, к концам которого приложены две одинаковые и противоположно на-
правленные силы Т, не изгибается до тех пор, пока значение Т не пре-
высит некоторого предела; говорят, что тогда имеет место продольный изгиб.
Когда Т меньше этого предела, единственно возможной фигурой равновесия
является прямолинейная форма. Лишь при значениях Т превосходящих ука-
занный предел, возможны изученные выше криволинейные фигуры равно-
весия. Найдем этот предел.
В рассматриваемом случае, так как ось стержня в естественном состо-
янии прямолинейна, то — = 0 и из формулы A) для пары получаем
Ро
N=B —.
Р
Эта пара обращается, следовательно, в нуль одновременно с кривизной.
Но мы предположили, что к обоим концам В' и В" стержня приложены
две силы Т, равные, противоположно направленные и не образующие пары;
отсюда вытекает, что для обоих концов N = 0 и — = 0, следовательно, эти
Р
концы являются точками перегиба, как указано на рис. 105, а. Когда
стержень очень мало отклоняется от первоначальной прямолинейной формы,
величина а очень мала. Она равна нулю для прямолинейной формы. До-
пустим, что стержень может принять волнообразную фигуру равновесия,
показанную на рис. 105, а, с п волнами, и определим постоянную а, зная
длину / стержня и сила Т на обоих концах В' и В". Постоянная с
будет тогда известна и равна УВ/Т. Согласно выражению D) для ds, дуга АВ
имеет длину
Y2 (cos 6 — cos о)
Сделаем подстановку
cos 6 = 1 — 2 sin3 - , cos a = 1 — 2 sins — ,
тогда
а
dd
= с f	,
t 2|/ sin»-J-sin» 1

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ
201
Обозначим, для краткости, sin-K- = ? и сделаем замену переменной
sin -^- = ku.
Когда 6 изменяется от 0 до а, тогда и изменяется от 0 до 1 и мы имеем
где
К=
Для всей длины I стержня, равной 2пАВ, получаем
= 2псК, К=~
2пс
2пс
(Ю)
Это уравнение, в котором fc = sin-^- неизвестно, определяет угол а. Для
того чтобы фигура равновесия с п волнами существовала, необходимо и
достаточно, чтобы из этого уравнения получалось для k значение, заклю-
ченное между 0 и 1. Но при k=0 имеем, согласно равенству (9), К = -к-;
при возрастании k интеграл К, постоянно возрастает, так как возрастает
подынтегральное выражение, и при k = 1 интеграл К становится бесконеч-
ным. Таким образом, когда k изменяется от 0 до 1, интеграл К проходит
один и только один раз через любое значение, больше чем тс/2. Для того
чтобы уравнение A0) имело для k решение, необходимо и достаточно,
чтобы
2пс ^ 2 '
Заменяя с его значением
находим
Т>
Таким является условие существования фигуры равновесия с п волнами.
Наименьшее значение нижнего предела для Т соответствует значению п=\.
Следовательно, для того чтобы существовала возможная фигура равновесия
с одной волной, необходимо, чтобы
/2 "
Если давление Т меньше этого предела, то единственно возможной
фигурой равновесия будет прямая линия.
154. Стержень, изгибаемый действующим в одной плоскости по-
стоянным нормальным давлением. Эта задача исследована Морисом Леви
(Comptes Rendus, т. XCVII, стр. 694); интегрирование по-прежнему выпол-
няется в эллиптических • функциях, как это показано в Traite Альфена
и в Principes de la theorie des fonctions elliptiques Аппеля и Лякура.

202	ЧАСТЬ ВТОРАЯ. СТАТИКА
УПРАЖНЕНИЯ
1.	Натянутая невесомая нить проходит через находящиеся на одинако-
вых расстояниях неподвижные кольца Аь А2, ..., Ап. Показать, что если
имеет место равновесие, то натяжение постоянно и давление на каждое
кольцо Aji обратно пропорционально радиусу окружности, проведенной через
это кольцо Ак и через два других соседних с ним кольца vl^-i и ylfc+1.
Вывести отсюда предельным переходом закон давления на кривую для неве-
сомой нити, протянутой по этой кривой, по которой она может скользить
без трения (Пуансо, Statique).
2.	Невесомая нить заданной длины закреплена своими концами в двух
неподвижных точках А а В. По этой нити могут скользить без трения два
кольца Mi и М.% находящихся соответственно под действием сил F\ и F2,
заданных по величине и направлению. Найти положение равновесия системы.
(Надо воспользоваться сказанным в конце п. 128.)
3.	Для веревочного многоугольника, находящегося в равновесии, нужна
взять моменты <р* сил и моменты т4д. натяжений относительно некоторой
точки. Показать, что для этих векторов можно построить многоугольник,
аналогичный многоугольнику Вариньона, заменив векторы Ft и Т^ век-
торами <р^ И Xfft.
4.	Показать, что если веревочный многоугольник находится в равно-
весии, то, построив векторы, сопряженные относительно некоторой сферы
(мнимой) силам и натяжениям, и прямые, сопряженные сторонам так, как
об этом указывалось в упражнении 3 в конце главы I, мы получим новый
многоугольник, находящийся в равновесии. Стороны одного многоугольника
являются прямыми, сопряженными сторонам второго; вершины одного суть
точки, сопряженные плоскостям, образованным двумя последовательными
сторонами другого.
5.	Фермы. Теорема Ренкина (см. Philos. Magazine, т. XXVII, 1864,
стр. 92; Максвелл, там же, стр. 250). Силы, приложенные к узлам про-
странственной фермы, находятся в равновесии, когда они перпендикулярны
и пропорциональны граням многогранника, ребра которого лежат в пло-
скостях, проведенных через неподвижную точку О нормально стержням:
фермы.
Решение. Предполагая, что многогранник из стержней находится
в равновесии, построить многогранник, образованный векторами, сопряжен-
ными силам и натяжениям относительно мнимой сферы с центром О в соот-
ветствии с методом, указанным раньше (упражнение 3 в конце главы I).
(См. статью Гидо Гука, Crelle, т. 100, стр. 365.)
6.	Шарнирный четырехугольник, образованный четырьмя стержнями не-
изменной длины а, Ь, с, d, находится под действием четырех сил, приложен-
ных в его четырех вершинах. Каковы должны быть эти силы, чтобы было-
равновесие? (Эта задача решена Мёбиусом, Статика.)
7.	Шарнирная система Фусса. Рассматривается плоский многоугольник,
образованный твердыми материальными стержнями, сочлененными своими
концами шарнирно. В плоскости многоугольника в середине каждой сто-
роны, перпендикулярно к ней, приложены силы, пропорциональные длинам
соответствующих сторон. Доказать, что фигурой равновесия является впи-
санный в окружность многоугольник.
8.	Радиус кривизны, находящейся в равновесии тяжелой однородной
нити, изменяется пропорционально квадрату натяжения (Мёбиус).
9.	Рассмотрим несколько одинаковых однородных нитей, вытянутых сна-
чала по прямым линиям от точки Р до точек N, Nu ЛГ3	ЛГ4, лежащих на
одной вертикали. После этого точка Р несколько смещается по горизонтали
таким образом, что она приближается к вертикали и переходит в точку М.
Тогда эти нити, которые предполагаются тяжелыми, расположатся по цепным
линиям. Доказать:

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ	203
1)	что все цепные линии имеют одинаковый параметр а;
2)	что их вершины лежат на цепной линии того же параметра а, об-
ращенной вогнутостью к основанию и имеющей вершину в точке М (Мёбиус).
10.	Найти положения равновесия однородной тяжелой нити, подчинен-
ной указываемым ниже условиям на концах, причем длина нити предпо-
лагается заданной:
1°. Один из концов закреплен в точке А, другой проходит через бес-
конечно малый блок, находящийся на такой же высоте как и точка А,
и затем свободно свешивается.
2°. Нить проходит через два бесконечно малых блока, расположенных
на одной высоте, и оба конца свободно свешиваются. (Ответ: обе свеши-
вающиеся части имеют одинаковую длину и оканчиваются у основания
цепной линии; имеются два положения равновесия: одно устойчивое, другое
неустойчивое.)
3°. Оба конца скользят без трения по Двум одинаковым соприкасаю-
щимся внешним образом окружностям, центры которых лежат на одной
высоте.
4°. Нить замкнута и проходит через два бесконечно малых блока А
и В. [Ответ: две цепные линии ASB и AS'В с общим основанием; если
через более низкий блок А провести горизонталь AU'U, пересекающую
обе кривые в точках U' и U, то длины обеих цепных линий обратно пропор-
циональны дугам BU и B'U (Мёбиус).]
5°. Оба конца закреплены в неподвижных точках, находящихся на одной
высоте; вдоль нити мож'ет скользить без трения бесконечно малое кольцо М,
к которому подвешен груз Р. (Ответ: кольцо расположится на середине
нити; обе части МА и MB суть две цепные линии с общим основанием;
в точке М получается угловая точка; натяжения дуг МА и MB уравно-
вешиваются грузом Р.)
11.	Найти фигуру равновесия, которую принимает под действием ветра
прямоугольный парус ABCD, закрепленный двумя противоположными краями
на двух вертикальных реях АВ и CD. (Действием веса пренебрегаем; пред-
полагается, что ветер дует горизонтально и его давление на элемент паруса
нормально к этому элементу и пропорционально его площади и квадрату
нормальной составляющей скорости ветра. Можно считать очевидным, что
парус примет форму цилиндра с вертикальными образующими и что вид
прямого сечения не зависит от высоты. Следовательно, достаточно выразить,
что полоса между двумя плоскостями двух бесконечно близких прямых
сечений находится в равновесии. Эту полосу можно отождествить с гибкой
нерастяжимой нитью. Прилагая к ней естественные уравнения, найдем, что
она примет форму цепной линии и что натяжение постоянно.)
12.	Найти фигуру равновесия нити, на каждый элемент которой дей-
ствует вертикальная сила, пропорциональная горизонтальной проекции этого
элемента. (Парабола — предельный случай веревочного многоугольника вися-
чих мостов.)
Определить постоянные, зная, что нить имеет заданную длину и за-
креплена в двух заданных точках.
13.	Найти фигуру равновесия тяжелой нити, плотность которой из-
меняется пропорционально длине дуги s, отсчитываемой от наиболее низкой
точки.
k
14.	Тот же вопрос, полагая, что плотность равна 	(окружность).
C0S2-
а
15.	Определить закон изменения плотности тяжелой нити в функции s
Для того, чтобы под действием веса она приняла форму наперед заданной
кривой (параболы с вертикальной осью, окружности и т. д.). Ответ на этот
вопрос получится, если исходить из естественного уравнения (п. 138).

204	ЧАСТЬ ВТОРАЯ. СТАТИКА
16. Цепная линия одинакового сопротивления. Так называют цепь
переменной толщины такую, что в фигуре равновесия толщина в каждой
точке пропорциональна натяжению в этой точке. В этом случае вероятность
разрыва во всех точках одинакова (Кориолис). Требуется определить урак-
нение этой кривой и закон изменения толщины.
Ответ. Пусть а— прямое сечение цепи, изменяющееся с s, p— вес
единицы объема; вес элемента ds равен pa ds. Если за начало координат
принять наиболее низкую точку, то уравнение кривой будет
у_
е а cos — = 1,
а
а для закона изменения толщины о получим
х
a cos —
а
17. Найти фигуру равновесия нити, на каждый элемент ds которой дей-
ствует сила F ds, пересекающая неподвижную ось и нормальная к ней,
причем F есть функция только расстояния г от элемента до оси.
Ответ. Принимая заданную ось за ось Oz и обозначая через лив
полярные координаты в плоскости х Оу, получим три уравнения:
= - f Fdr, т?- =
,1	ds
Каков бы ни был закон силы получается дифференциальное уравнение
вида
которое показывает, что касательные к кривой принадлежат линейному
комплексу.
18.	Частный случай предыдущей задачи, когда F = \ir (ц — постоянная),
при произвольных условиях на концах. Эта задача исследована Клебшем
при помощи особого метода, который будет изложен в аналитической меха-
нике (Crelle, т. 157, стр. 93).
Мы рассмотрели (п. 142) случай, когда оба конца нити закреплены
в точках оси.
19.	Найти фигуру равновесия нити в плоскости, зная, что на каждый ее
элемент действует сила, пропорциональная этому элементу и образующая
с ним постоянный угол. [Применить естественные уравнения; кривая является
логарифмической спиралью (О. Бонне).]
29. Найти закон вертикальной силы, под действием которой нить рас-
полагается по заданной плоской кривой.
[Задача не будет вполне определенной, если в формулировке ничего
не добавить относительно природы силы. Чтобы задача стала определенной,
необходимо задать переменную, в функции которой должна быть выражена
сила. Если нить лежит в плоскости хОу и сила Yds параллельна оси Оу,
то Y может быть выражен в функции одной из величин х, у, s, а, где
а — угол касательной с осью Ох, или в функции нескольких из этих вели-
чин сразу. Например, если заданная кривая есть окружность х2 + у2 — а2=0,
то естественное уравнение (п. 138) будет

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ	205
X
далее, так как tg а =	— и s = aa, то
*—*?*•	<3>
r=—^~г-	<4>
a cos2 —
Это — различные законы, отвечающие заданной окружности.]
Наоборот, найти фигуру равновесия нити, находящейся под действием
вертикальной силы, закон которой выражается одной из предыдущих фор-
мул A), B), C), D). Получатся совершенно разные кривые в зависимости
от взятого закона. Все они при надлежащем подборе постоянных могут
оказаться окружностью х2-\- у2 — а3 = 0.
21. Найти закон центральной силы, под действием которой нить рас-
положится по заданной плоской кривой.
[Здесь можно повторить те же замечания, что и в предыдущем упраж-
нении. Принимая центр сил за начало координат и обозначая через г и в
полярные координаты, .получим
^ dr \Wdb )'
где F рассматривается как положительная или отрицательная величина
в зависимости от того, будет ли сила отталкивающей, или притягивающей.]
Пример:
АаС
окружность, г = 2а cos 6, ds = 2а db, F = —ц- .
22.	Найти фигуру равновесия нити, каждый элемент которой Притяги-
вается или отталкивается неподвижным центром обратно пропорционально
квадрату расстояния. (Получится уравнение вида — = а + 6 cos/ив, или
1	1	\
— = а + b ch /ив, или, как промежуточный случай, — == а + *в2. J
23.	Если одна и та же кривая является фигурой равновесия нити под
действием силы F\ при натяжении 7\, и силы F% при натяжении Т<>, то она
является также фигурой равновесия нити под действием силы (F) = (ktF{) -\r
-+- (k2F2) при натяжении (T) = (k-jT{)-\-(k2T2), где &t и k2 — постоянные.
Использовать естественные уравнения.
24.	Свободная нить под действием заданной силы F располагается по
некоторой кривой С. Эту кривую осуществляют материально и протягивают
по ней нить, подвергнув ее действию той же силы F. Показать, что в этом
втором случае нормальная реакция кривой С на элемент ds лежит в со-
прикасающейся плоскости и имеет значение kdsjf, где k — постоянная,
ар — радиус кривизны.
25.	Пусть М — произвольная точка нити, находящейся в равновесии.
Показать, что главный момент относительно точки М всех внешних сил,
действующих на нить от конца Мо до точки М, равен нулю (Мёбиус). (Этот
результат выводится из принципа затвердевания в применении к дуге М0М-
Можно вновь установить результаты, указанные в тексте, применив это
условие к части находящейся в равновесии цепной линии, заключенной

206	ЧАСТЬ ВТОРАЯ. СТАТИКА
между вершиной Мо и точкой М, и приняв в качестве вспомогательной
переменной натяжение То в точке Мо.)
26.	Для тяжелой цепочки переменной плотности, находящейся в равно-
весии на сфере, гиперболоид, у которого образующими одного семейства яв-
ляются натяжения в точках Л и В, и вертикаль, проведенная через центр
тяжести дуги АВ, проходит через центр сферы. (Для доказательства следует
предположить, что дуга АВ затвердела и заметить, что приложенные к этой
дуге внешние силы: натяжения в точках А и В, вес и равнодействующая
реакции сферы должны уравновешиваться.)
27.	Найти фигуру равновесия гибкой и нерастяжимой невесомой нити,
по которой проходит электрический ток и которая находится под действием
магнитного полюса О.
[Геодезическая линия кругового конуса с вершиной в точке О (Дарбу).]
Напомним, что действие полюса О на элемент ds, находящийся на рас-
стоянии г от точки О, нормально к плоскости О ds и равно по величине
•—g- sin (r, ds).
28.	Среди кривых, проведенных на заданной поверхности S между
двумя точками, рассматриваются те кривые С, которые обращают в минимум
интеграл ^=1 f ds, т. е. кривые, которые были определены в п. 149.
Показать, что при переходе от какой-нибудь такой кривой АВ к бесконечно
близкой кривой AtBv лежащей на поверхности, вариация интеграла по-
прежнему определяется формулой Тэта и Томсона. Вывести отсюда такие
же следствия, как и для кривых С в пространстве (п. 147).
29.	В плоскости zOx рассматриваются цепные линии, имеющие осно-
ванием ось Ох и пересекающие нормально заданную кривую С. На каждой
нз этих цепных линий от точки А, в которой она пересекает кривую С,
откладывается дуга АВ такая, что она описывает при вращении вокруг
оси Ох определенную площадь S. Доказать, что геометрическое место
точек В есть кривая С, нормальная к каждой цепной линии. (Приложение
теоремы Томсона и Тэта.)
30.	Даны две неподвижные точки А и В и неподвижные поверхности
Si, S2, •-., Sp (рис. 103, п. 150). Рассмотрим точки Ру, Р%, ..., Рр, которые
могут скользить без трения по этим поверхностям. Допустим, что первая
точка Р\ притягивается к точке А постоянной по величине силой л и
к точке Р2 постоянной по величине силой щ; вторая точка Р2 притягивается
к точке Ру постоянной силой % и к точке Я3 постоянной силой п2 и т. д.
Доказать, что положением равновесия системы является путь светового луча,
идущего от А к В и подчиняющегося законам преломления, указанным
в тексте.
31.	Доказать, что путь АР1Р2...РрВ светового луча от А к В по
законам преломления (п. 150) совпадает с фигурой равновесия веревочного
многоугольника, вершины которого А и В закреплены, а вершины Pv P2	Рр
могут скользить без трения по поверхностям Sb S2, ..., Sp и для которого
натяжение стороны PJJDk+1 равно пк (Другая форма условий предыдущей
задачи.)
32.	Если вдоль кривой (п. 146), соединяющей точки А и В, функция
<f (x, у, г) принимает положительные и отрицательные значения, то
интеграл	^щ
9 (х, у, z) ds,
взятый по этой кривой, не может быть ни максимумом, ни минимумом.
(Вейерштрасс. См. заметку Кобба Annales de la Faculte des Sciences de
Toulouse, 1891).

ГЛАВА VII. ИЗМЕНЯЕМЫЕ СИСТЕМЫ	207
33. Пусть А и В— две точки, из которых одна расположена выше,
а другая ниже плоскости хОу. Если среди кривых, соединяющих эти две
точки, искать ту, которая обращает в максимум или минимум интеграл
(В)
/ *•*.
где п — целое положительное четное число, то получится, что эта кривая
состоит из двух перпендикуляров АА' и ВВ', опущенных из точек А и В
на плоскость хОу и из прямой А'В'.
34.	Рассмотрим функцию <р (х, у, г), конечную и непрерывную в области
пространства, расположенной по одну сторону от некоторой поверхности S,
на которой эта функция принимает постоянное значение k. Пусть tpt (х, у, z) —
— другая функция, конечная и непрерывная по другую сторону этой поверх-
ности 5 и принимающая на ней постоянное значение kx. Пусть, наконец,
А — точка в первой области, а В — во второй. Найти, какой кривой нужно
соединить эти две точки, чтобы получить максимум или минимум для
интеграла
(Р)	(-В)
/= Г 9 (¦*. У- *) ds + J <fi(x, у, z)ds,
(Л)	(Р)
где Р — точка пересечения искомой кривой с поверхностью 5.
(Дуги АР и ВР являются кривыми, образующими, соответственно, первый
и второй интегралы в максимум или минимум; касательные t и tx к этим
кривым в точке Р лежат в одной плоскости с нормалью к поверхности 6
в той же точке и образуют с этой нормалью углы / и ilt для которых
sini _ kx \
sin^ k ')
35.	Если дугу АР перемещать нормально к некоторой поверхности 2,
которую она пересекает в точке А, и если на кривых АР и ВР предыду-
щего упражнения отложить такие дуги, что интеграл / будет иметь по-
стоянное значение, то геометрическим местом точек В будет поверх-
ность Et, нормальная к дугам Ра. (Это свойство доказывается при помощи
соотношения Тэта и Томсона (п. 147), которое надо последовательно при-
менить к вариации каждого из обоих интегралов, составляющих /.)
36.	Упругий прямолинейный вертикальный стержень, находящийся
в естественном состоянии, имеет заделанный конец А. Другой его конец В
подвергается действию вертикальной силы Т. Каков предел силы Т, начиная
с которого стержень изгибается?

ГЛАВА VIII
ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ
155. Исторический обзор. Принцип возможных скоростей при-
менялся Галилеем в теории некоторых простых машин и затем
Валлисом в его «Механике». Декарт пользовался правилом, похожим
на правило Галилея, для того, чтобы свести всю статику к одному
единственному принципу. Но (цитируем дословно Лагранжа) «Иван
Бернулли был первым, понявшим общность принципа возможных
скоростей и его полезность для решения задач статики. Это видно
из одного из его писем к Вариньону, датированного 1717 годом,
которое последний поместил в начале девятого раздела своей «Новой
Механики», раздела, целиком посвященного доказательству справед-
ливости для различных приложений принципа, о котором идет речь,
и посвященного его использованию. Этот же принцип привел впо-
следствии к появлению другого принципа, предложенного Мопертюи
в 1740 г. в Memoires de l'Academie des Sciences de Paris под названием
«Закона покоя», и развитого затем в более общей форме Эйлером
в 1751 г. в Memoires de l'Academie de Berlin. Наконец, этот же
самый принцип лежит в основе принципа, данного Куртивроном
в Memoires de l'Academie des Sciences de Paris за 1748 и 1749 гг.
И вообще я считаю возможным утверждать, что любой общий прин-
цип, который, быть может, будет еще открыт в науке о равновесии,
будет не чем иным, как тем же принципом возможных скоростей,
рассматриваемым с иной точки зрения и иначе выраженным. Но этот
принцип не только сам по себе является очень простым и очень
общим: он обладает, кроме того, особо ценной и уникальной выго-
дой, позволяющей выразить в одной общей формуле все задачи,
которые можно предложить на равновесие тел». (Лагранж, Аналити-
ческая механика, часть первая, § 17.)
После Лагранжа было предложено несколько доказательств прин-
ципа возможных скоростей. Одно из наиболее известных принадлежит
Амперу; изложение его можно найти, например, в Механике Депейру.
Позднее К. Нейман предложил другое доказательство (Berichte der
SSchsischen Gesellschaft der Wissenschaften, март, 1886). Мы изложим
здесь классическое доказательство, основанное на анализе различных
видов простых связей.

ГЛАВА VIII. ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ	209
I. Формулировка и доказательство принципа
в случае связей, выражающихся равенствами
156. Возможное перемещение и работа. Пусть М — материальная
точка, к которой, среди других сил, приложена также сила/7. Допу-
стим, что этой точке сообщено произвольное бесконечно малое пере-
мещение ММ'; это сообщенное точке перемещение называют воз-
можным перемещением для того, чтобы отличить его от действи-
тельного перемещения, которое эта точка совершает под действием
приложенных к ней сил. Элементарная работа
FMM' cos FMM'	A)
называется возможной работой силы F, соответствующей переме-
щению ММ'. К этой возможной работе можно тогда применить все,
что говорилось об элементарной работе (глава IV). Ограничимся
напоминанием двух следующих предложений.
Для одного и того же возможного перемещения ММ' возможная
работа равнодействующей нескольких сил, приложенных к точке М,
равна сумме работ составляющих сил.
Если возможное перемещение ММ' есть геометрическая сумма
^нескольких перемещений, то работа одной и той же силы на пере-
мещении ММ' равна сумме работ этой силы на составляющих пере-
мещениях.
Если обозначить через 8^ бесконечно малый промежуток времени,
в течение которого осуществляется возможное перемещение ММ',
ММ'
то вектор V, равный —^— и направленный по ММ', называется воз-
можной скоростью, сообщенной точке М. Заменяя ММ' через V ot,
можно написать возможную работу в виде
FVcos(F, V)bt,	B)
так как угол между силой F и вектором V равен углу между этой
силой и перемещением ММ'.
Аналитически, в прямоугольной системе, если проекции силы
обозначить через X, Y, Z, а проекции перемещения через ох, Ьу, Ьг,
то возможную работу можно выразить следующим образом:
Мы будем брать возможную работу в форме A); первоначально
ее чаще брали в форме B). Если будет употребляться форма B)
и если будут рассматриваться возможные перемещения нескольких
различных точек, то условимся считать, что для всех этих точек
промежуток 8^ имеет одно и то же значение.
157. Формулировка принципа. Установив это, рассмотрим систему
точек, подчиненных связям без трения, которые могут быть выражены
при помощи равенств. Разделим все силы, приложенные к различным

210	ЧАСТЬ ВТОРАЯ. СТАТИКА
точкам, на две группы: реакции связей, происходящие от связей,
наложенных на систему, и силы непосредственно приложенные,
или заданные силы, которые действуют на систему. Тогда принцип
возможных перемещений формулируется следующим образом.
Необходимые и достаточные условия равновесия системы
заключаются в том, что для любого возможного ее перемеще-
ния, допускаемого связями, сумма возможных работ непосред-
ственно приложенных сил равна нулю.
Мы сначала установим справедливость этого принципа для неко-
торого числа простых случаев.
158. Свободная точка. Пусть дана совершенно свободная мате-
риальная точка и пусть X, Y, Z — равнодействующая непосредственно
приложенных к ней сил. В этом случае любое перемещение будет
возможным, так как отсутствуют связи. Возможная работа, соответ-
ствующая какому-нибудь из этих перемещений, есть
Если точка находится в равновесии, то X, Y, Z равны нулю и,
следовательно, действительно сГ = О, каково бы ни было перемеще-
ние Ьх, Ьу, 8г. Наоборот, если оГ = 0, каковы бы ни были 8х, Ьу, Ьг,
то
Х=0, К = 0. Z = 0,
и точка находится в равновесии.
159. Точка на поверхности. Рассмотрим точку, которая может
перемещаться без трения по неподвижной поверхности
/(х, у, 2)= О
и находится под действием силы F. В этом случае имеется одна
связь, выражаемая предыдущим уравнением, и единственными пере-
мещениями, допускаемыми этой связью, являются те, которые про-
исходят по поверхности. Если точка находится в равновесии, то сила
будет нормальна к поверхности и, следовательно, ко всем возможным
перемещениям. Тогда возможная работа будет равна нулю на всех
этих перемещениях. Наоборот, если работа § равна нулю на любом
перемещении ММ!, лежащем на поверхности, то из выражения
$=FMM'cos(F, MM')
следует, что либо F = 0, либо cos(F, MM') —0, т. е. либо сила
равна нулю, либо сила нормальна к поверхности. В обоих случаях
имеет место равновесие.
Выведем снова в качестве упражнения уравнения равновесия точки
на поверхности, исходя из принципа возможных скоростей. Мы
должны иметь

ГЛАВА VIII. ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ	211
при единственном условии, что приращение Ьх должно быть связано
с произвольными приращениями Ьу и Ьг соотношением
дх ' ду ¦* ' аг
которое выражает, что перемещение ММ' происходит по заданной
поверхности. Умножим это уравнение на X и сложим с предыдущим.
Получим
каковы бы ни были X, Ьу, bz. Выберем X так, чтобы обратить в нуль
первый коэффициент. Тогда, так как Ьу и bz произвольны, их коэф-
фициенты должны тождественно равняться нулю. Таким образом,
получим одновременно:
Это — действительно уравнения равновесия, полученные нами ранее
другим путем (п. 91). Сила, вызванная связью, является нормальной
реакцией N поверхности, и написанные уравнения равновесия пока-
зывают, что точка М, предполагаемая совершенно свободной, нахо-
дится в равновесии под одновременным действием заданной силы и
силы, имеющей проекции Х-jp-, Х'-^-» ^ТГ~' Отсюда следует, что
эта последняя сила представляет собой не что иное, как нормальную
реакцию. Эта реакция называется реакцией связи; она происходит
от связи, наложенной на точку.
Если поверхность задана в форме
то для всех вариаций 8^ и 8^2 величин qt и q2 перемещение 8х,
by, bz, определяемое этими уравнениями, будет происходить по поверх-
ности. Возможная работа
Xbx-\-Yby~\-Zbz
для такого рода перемещения примет вид
и условия равновесия будут те же, что и полученные ранее:
Примечание. Во всех случаях, независимо от того, будет ли
точка находиться в равновесии или нет, для любого возможного
перемещения, допускаемого связью, работа реакции связи, т. е. нор-
мальной реакции, равна нулю.

212	ЧАСТЬ ВТОРАЯ. СТАТИКА
160. Точка на кривой. Если материальная точка вынуждена оста-
ваться на неподвижной кривой
f(x, у, г) = 0, Л(х, у, z) = 0,
то единственным перемещением, допускаемым этой связью, будет
перемещение по кривой. Непосредственно видно, что если имеет
место равновесие, то работа заданной силы на возможном переме-
щении равна нулю, так как сила нормальна к кривой, и, наоборот,
если работа на возможном перемещении равна нулю, то сила либо
равна нулю, либо нормальна к перемещению, причем в обоих слу-
чаях имеет место равновесие. Выведем отсюда уравнения равновесия,
которые уже были получены нами ранее (п. 92).
Мы должны иметь
ff == ХЬх + Y Ьу -|- Z bz = 0
для всех перемещений, допускаемых связями, т. е. для всех ох,
Ьу, bz, удовлетворяющих уравнениям
¦* ^ dz
дх '^ ду ^ дг	дх ' ду ¦* ^ dz
которые выражают, что перемещение происходит ио кривой. Следо-
вательно, только одна из величин Ьх, by, bz, например bz, остается
произвольной. Умножим теперь два последних уравнения на X и Xj
и сложим их с первым. Получим:
каковы бы ни были X, Хи bz. Если X и Xt определить так, чтобы
два первых коэффициента равнялись нулю, то и третий тоже должен
будет обратиться в нуль, так как выражение должно равняться нулю
при любом 8г. Следовательно, имеем одновременно
Эти уравнения выражают, что существует равновесие между непосред-
ственно приложенной силой и силой, имеющей проекции
Klx"^Kldx' A7^~Ai-gy-. Ла7+Л11Г-
Эта сила является нормальной реакцией связи.

ГЛАВА VIII. ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ	213
Если уравнения кривой представлены в виде
то возможная работа будет
§¦ = (Хер' -|- Kf
и условие равновесия будет
В рассматриваемом случае, так же как и в предыдущем, незави-
симо от того, будет ли точка находиться в равновесии, или нет,
для любого перемещения, допускаемого связями, работа нормальной
реакции связи равна нулю.
161. Свободное твердое тело. Пусть свободное твердое тело
находится под действием заданных сил Fv F2, • • -. Fn. Это тело
образовано большим числом материальных точек, вынужденных оста-
ваться на неизменных расстояниях друг от друга. Это и будут связи,
наложенные на систему. В этом новом случае единственными возмож-
ными перемещениями, допускаемыми связями, являются те, при кото-
рых форма тела остается неизменной. Пусть для одного из этих
перемещений а, Ъ, с обозначают проекции скорости поступательного
движения, а р, q, r — проекции мгновенной угловой скорости. Эти
шесть величин могут быть выбраны совершенно произвольно, так
как твердому телу можно сообщить какое угодно перемещение. Ско-
рость точки (х, у, z) имеет проекции
Vx=a-\-qz— ry, Vy = b-\-rx—pz. Vs =
так что возможная работа
силы /\, приложенной к точке (xv, _yv> zv), равна
JTV = Xv (a + <7*v — ryj M + Kv (b + rxv — pzj bt +
Мы можем это выражение написать так:
Щ	& — z% Kv
Н- Я BЛ — x^ZJ + г (*, Fv —
Следовательно, сумма работ на возможных перемещениях всех непо-
средственно приложенных сил будет

214	ЧАСТЬ ВТОРАЯ. СТАТИКА
Если тело находится в равновесии, то коэффициенты при шести
произвольных величинах равны нулю и мы действительно имеем
для любого перемещения, допускаемого связями, и, наоборот, если
оГ равно нулю, каковы бы ни были эти произвольные величины, то
необходимо, чтобы коэффициенты равнялись нулю, т. е. чтобы
выполнялись условия равновесия.
Вне зависимости от того, находится ли тело в равновесии или
нет, сумма работ реакций связей, которые являются здесь силами
взаимодействия между точками системы, равна нулю для любого
перемещения, допускаемого связями. В самом деле, пусть М1 и
М2 — две точки тела, находящиеся на расстоянии г друг от друга.
Точка Мх оказывает на точку М2 какое-то действие Fv направлен-
ное по М1М2, а точка М2 согласно закону равенства действия и
противодействия оказывает на точку Мх равное и прямо проти-
воположное действие F2 (п. 88, рис. 62). Эти две силы являются
реакциями связи, вызванными взаимодействием обеих точек М1 и
М2, связанных между собой так, что они остаются на неизменном
расстоянии друг от друга. Для того чтобы осуществить эту связь,
можно вообразить, что обе точки связаны между собой твердым
стержнем, лишенным массы. Условимся, как и раньше, называть
алгебраическим значением силы F взаимодействия обеих точек
абсолютное значение этого действия, взятое со знаком -\- или —
в зависимости от того, отталкиваются точки или притягиваются.
Для произвольного возможного перемещения, сообщенного обеим
точкам, сумма работ обеих сил равна (п. 88)
Fir.
Если возможные перемещения, сообщенные обеим точкам, до-
пускаются наложенной на них связью, согласно которой расстоя-
ние г между ними должно оставаться постоянным, то 8г = 0
и сумма работ реакций связи равна нулю. То же самое имеет
место для всех взаимных действий попарно взятых точек тела, что
и доказывает высказанное предложение.
162. Лемма. Замечания, сделанные в трех рассмотренных при-
мерах, мы возведем сейчас в общее правило и докажем следую-
щую лемму.
Независимо от того, будет ли система материальных
точек находиться в равновесии или нет, сумма возможных
работ реакций связей на любом возможном перемещении, до-
пускаемом связями, равна нулю. При этом является сущест-
венным предположение, что трения нет.
Достаточно, очевидно, доказать эту лемму для каждой связи
системы и поэтому мы переходим к обзору различных видов
связей. Мы разобьем их на две категории:

ГЛАВА VIII. ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ	215
1)	связи тел системы с другими неподвижными телами;
2)	связи тел системы между собой.
Первая категория, а) Наиболее простым является случай, когда
твердое тело имеет неподвижную точку; единственно возможным
перемещением будет вращение вокруг этой точки; работа реакции
связи или реакции неподвижной точки будет равна нулю, так как
ее точка приложения при таком движении тела не перемещается.
То же самое будет иметь место и в случае, когда тело имеет две
неподвижные точки, т. е. вращается вокруг неподвижной оси.
б)	Допустим, что какая-нибудь поверхность S, связанная
с каким-нибудь телом системы, скользит без трения по какой-
нибудь неподвижной поверхности 5'. Реакцией связи будет нормальная
реакция MN этой поверхности S' на S
(рис. 106); ее точкой приложения яв-
ляется точка М поверхности S, нахо-
дящаяся в соприкосновении с S'. Так
как перемещение этой точки должно
находиться в общей касательной плос-
кости поверхностей S и S', то работа
нормальной реакции равна нулю. Одна
из обеих поверхностей S или S' может	Рис-
вырождаться в линию или в точку.
в)	Допустим, наконец, что поверхность S, связанная с каким-
нибудь твердым телом системы, катится и вертится без скольжения
по неподвижной поверхности S' (п. 57). Реакция МР поверх-
ности S' на S (рис. 106) по-прёжнему приложена в точке М по-
верхности S, находящейся в соприкосновении, но эта реакция не
будет больше нормальной, так как связь между 5 и Sr противо-
действует скольжению. Сообщим системе перемещение, допускаемое
рассматриваемой связью, т. е. сообщим поверхности S качение и
верчение по поверхности S', и пусть Vr—возможная скорость
точки М. Возможная работа силы Р будет при этом PVrcos(P, Vr)bt.
Эта работа равна нулю, так как при скольжении и верчении ско-
рость Vr точки соприкосновения М равна нулю.
Наиболее простым примером такого рода связи будет следующий.
Колесо S, оставаясь в неподвижной плоскости, катится без
скольжения по неподвижной кривой S' (рис. 106). Эту связь можно
осуществить, снабдив колесо и кривую бесконечно малыми зубцами,
находящимися в зацеплении друг с другом, или закрепив лишен-
ную массы нерастяжимую нить в какой-нибудь точке А окружности
колеса и протянув ее по окружности до точки касания М и далее
по кривой S' до некоторой неподвижной точки В, где она должна
быть закреплена.
Вторая категория, а) Пусть сначала два движущихся твердых
тела сочленены в точке О. Реакциями связи будут равные и прямо
противоположные реакции Р и Р' обоих тел. Так как их точки

216
ЧАСТЬ ВТОРАЯ. СТАТИКА
приложения совпадают при всех допускаемых перемещениях, то
сумма возможных работ этих двух сил равна нулю. То же самое
будет, справедливо, если оба тела должны все время иметь больше
двух общих точек, например если они связаны шарниром.
б) Рассмотрим теперь две поверхности, связанные с телами системы,
обе находящиеся в движении и вынужденные скользить без трения одна
по другой (рис. 107). Реакции связей, являющиеся реакциями N и N'
этих поверхностей, равны, противопо-
ложно направлены и нормальны к об-
щей касательной плоскости в точке
касания. Пусть V и V — возможные
скорости точек М и М' поверхно-
стей S и S'', находящихся в рассматри-
ваемый момент в соприкосновении. Эти
скорости не будут одинаковыми, так
как можно, например, получить пере-
мещение, допускаемое связями, если одну
поверхность закрепить неподвижно, а
Рис. 107.	другую заставить скользить по ней.
Обозначая через Vn и V'n, проекции
соответствующих возможных скоростей V и V на N и N', получим
следующее выражение для полной возможной работы
§' = 8; (NVn + N'V'n,) = Nbt (Vn + V'n).
Так как движением поверхности S относительно поверхности S'
является скольжение, то относительная скорость Vr точки М по
отношению к поверхности S лежит в общей касательной плоскости,
и для абсолютной скорости точки М получаем
где Ve — переносная скорость точки М. Эта переносная скорость Ve
является, по определению, скоростью точки системы отсчета S',
совпадающей с точкой М, т. е. скоростью V точки М'. Следова-
тельно, имеем
и, проектируя на направление N'N, получим
так как Vr лежит в касательной плоскости и ее проекция равна
нулю. Но V^ = —V'n,, так как обе эти величины обозначают

ГЛАВА VIII. ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ	21?
проекции одного вектбра V на два прямо противоположных на-
правления N и N'; следовательно,
К + К- = <>-
и работа JT равна нулю.
в) Допустим, наконец, что какое-то твердое тело системы огра-
ничено поверхностью S (рис. 108), которая катится и вертится по
некоторой поверхности S', являющейся частью тела, также при-
надлежащего системе. Взаимное действие двух поверхностей S и 5'
в их точке касания не будет больше нор-
мальным к общей касательной плоскости,
так как оно препятствует скольжению.
Пусть МР — действие поверхности S' на
поверхность S, приложенное в точке каса-
ния М, принадлежащей поверхности 5,
а М'Р' — реакция поверхности S на по-
верхность S'', приложенная в точке касания,
принадлежащей поверхности 5'. Эти две
силы равны и противоположны. Сообщим
системе перемещение, допускаемое связями,	Рис. 108.
т. е. такое, при котором S и S' переме-
щаются и S катится по S'. Пусть, как и раньше, V и V— возмож-
ные скорости точек М и М', Vp и Vp> —их проекции соответ-
ственно на МР и М'Р'. Сумма возможных работ обеих реакций
связи Р и Р' равна
Г = Ы (PVp+P'V'p) = РЫ (Vp + V'pl).
Так как движение S относительно S' является качением и вер-
чением, то относительная скорость Vr точки М относительно S'
равна нулю; переносная скорость точки М так же, как и раньше,,
равна скорости V точки М' и общая формула
принимает вид
iV) = {V).
Так как обе скорости V и V равны, то их проекции V и V',
на два противоположных направления равны по величине и обратны
по знаку. Поэтому работа § равна нулю.
163. Сочетания предыдущих связей. Связи, осуществляемые
в машинах, являются сочетаниями предыдущих. Так, легко включить
в число связей, рассмотренных выше, связи, осуществляемые при
помощи нитей или цепей. Вообразим, например, что две точки М
и М\ системы связаны между собой нерастяжимой цепью, про-
тянутой частью своей длины по некоторой поверхности 5, по кото-
рой она может скользить без трения, причем эта поверхность 5
либо неподвижна, либо движется. Эта связь является сочетанием.

218	ЧАСТЬ ВТОРАЯ. СТАТИКА
предыдущих; звенья цепи являются твердыми телами; каждое из них
сочленено со следующим в точке или вдоль оси; те из них, кото-
рые находятся в соприкосновении с поверхностью, скользят без трения
по поверхности S. Одна из точек, например Mlt могла бы, сверх
того, быть неизменно связанной с поверхностью 5: это было бы
еще одной связью, рассмотренной выше. К такого рода связям отно-
сятся, в частности, связи, осуществляемые при помощи блоков.
164.	Общее определение идеальных связей*). Мы видели, что
в случаях наиболее простых связей и их сочетаний сумма возмож-
ных работ реакций связей равна нулю на любом возможном пере-
мещении, допускаемом связями, если только отсутствует трение.
Для связей более сложной природы, например, для связей, выра-
жаемых уравнениями, это свойство принимается как определение
самого понятия отсутствия трения; связи будут без трения, или
идеальными, если на любом допускаемом ими перемещении сумма
работ реакций связей равна нулю.
165.	Доказательство принципа. Рассмотрим систему материаль-
ных точек М1г М2, .... Мп, подчиненных заданным связям и на-
ходящихся под действием непосредственно приложенных сил. Обо-
значим через х„, у„ 2V координаты какой-нибудь из этих точек Ж,
и через Хч, Kv, Zv — проекции равнодействующей /\ непосредственно
приложенных к ней сил.
Мы хотим доказать следующее предложение: для того, чтобы
система в каком-нибудь положении была в раановесии, необ-
ходимо и-достаточно, чтобы при сообщении системе произволь-
ного возможного перемещения, допускаемого связями, сумма
возможных работ непосредственно приложенных сил равнялась
нулю.
Это условие необходимо. Действительно, если равновесие имеет
место, то каждая точка Mv находится в равновесии под действием
всех приложенных к ней сил как заданных, так и реакций связей.
Более точно можно рассматривать эту точку как свободную при
условии приложения к ней некоторых сил F'4, F"	вызванных
связями. Точка будет тогда находиться в равновесии под действием
заданных сил, имеющих равнодействующую /\, и реакций связей Fr,
F" ... Для произвольного возможного перемещения, сообщенного
этой точке, сумма работ всех этих сил равна нулю. То же самое
справедливо для любой точки системы, и поэтому если всем точкам
системы сообщить произвольные перемещения, допускаемые или не-
допускаемые связями, то сумма работ всех сил как заданных, так и
реакций связей будет равна нулю:
*) В оригинале «связи без трения». Термин «идеальные связи» в ори-
гинале не применяется. (Прим. перев.)

ГЛАВА VIH. ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ	219
Здесь §d — сумма работ заданных сил, a §l — сумма работ реакций
связей. Но если перемещения допускаются связями, то на основании
предыдущей леммы оГь равна нулю и, следовательно, также
Условие является и достаточным. Если для всех перемещений,
допускаемых связями, сумма Шо работ заданных сил равна нулю,
то система находится в равновесии. Для доказательства нам доста-
точно показать, что если система не находится в равновесии, то
существует, по крайней мере, одно перемещение, допускаемое
связями, для которого qJId отлично от нуля. Действительно, если
система не находится в равновесии и предоставлена самой себе, то
она начнет двигаться. Перемещения, которые при этом получат
точки, будут допускаемые связями и каждая точка М„, рассматри-
ваемая как свободная, переместится в направлении равнодействующей
всех действующих на нее сил Fv, F[, F", ... как заданных, так w
реакций связей. В этом действительном перемещении все начальные
скорости равны нулю; но мы можем сообщить системе возможное
перемещение, при котором каждая точка перемещается в том же
направлении, что и при действительном перемещении, но при кото-
ром не все возможные скорости точек Mv равны нулю. Тогда сумма
работ сил Fv, F'v, F", равная работе их равнодействующей, будет
положительной, так как перемещение происходит в направлении
этой равнодействующей. Так как то же самое имеет место дл*
каждой точки системы, то сумма §'z>'-\-$'l работ заданных сил и
реакций связей для рассматриваемого перемещения будет положи-
тельной, отличной от нуля. Но это перемещение допускается связями.
Следовательно, §ь равно нулю и мы получаем
Отсюда следует, что если для всех перемещений, допускаемых
связями, Шг> равно нулю, то равновесие будет иметь место.
166. Замечание о работе силы. Произведенный нами анализ
различных возможных связей выдвигает со всей очевидностью один
вопрос, на котором не бесполезно остановиться. Речь идет о том,
что при вычислении элементарной работы силы, как возможной так
и действительной, не следует смешивать материальную точку,
к которой приложена сила, с геометрической точкой ее приложения.
В выражениях элементарной работы
FMM'cos(F, MM'), FVcos(F, V)bt
ММ' и V обозначают бесконечно малое перемещение и скорость
материальной точка, к которой приложена сила, а не пере-
мещение и скорость геометрической точки приложения силы. На-
пример, если колесо катится по неподвижной кривой С (рис. 109),

220
ЧАСТЬ ВТОРАЯ. СТАТИКА
и
то реакция Р кривой приложена к материальной точке М колеса,
находящейся в соприкосновении с кривой; после промежутка вре-
мени 8^ колесо примет бесконечно близкое положение, в соприкосно-
вении будет новая точка М1 колеса и реакция Рх будет приложена
в точке Мх; что касается материальной точки М, находившейся
в соприкосновении первоначально, то она займет положение М'.
В выражение работы силы входит именно перемещение ММ' и ско-
ММ' .
рость —г-,— (эта скорость равна нулю вследствие качения) мате-
риальной точки М, а не переме-
щение ММг и скорость
геометрической точки приложе-
ния этой силы.
167. О связях, осуществляе-
мых при помощи тел, не имею-
щих массы. Иногда бывает, что
в системе, движущейся или на-
ходящейся в равновесии, имеются
тела, массами которых, по сравне-
нию с массами других тел системы,
пренебрегают и считают эти тела
лишенными массы. Это предположение можно осуществить, выразив,
что силы, приложенные к телу без массы, находятся в равновесии.
В самом деле, уравнения движения точки имеют вид
т
¦ = Х. m^=Y, »^ = .
где X, Y, Z — проекции равнодействующей всех сил, приложенных
к точке. Если точка т принадлежит движущейся системе, то ее
ускорение конечно и, следовательно, если она имеет очень малую
массу, то величины X, К, Z будут также малыми. Если предположить,
что /к= 0, то и X, К, Z должны быть равны нулю и силы, прило-
женные к точке, уравновешиваются. Если теперь вообразить систему
без массы, то масса каждой точки системы будет равна нулю, все
приложенные к этой точке силы будут находиться в равновесии
и, следовательно, совокупность всех приложенных к системе сил
будет тоже находиться в равновесии.
Если, например, две точки М и М' связаны между собой при
помощи твердого стержня, не имеющего массы, то действия
стержня на обе точки выражаются двумя равными и прямо противо-
положными силами F и F". В самом деле, если действие стержня на
точку М есть F, то действие точки М на стержень есть —F; точно
так же действие точки М' на стержень есть —F'. Следовательно,
силы, действующие на стержень суть F и —F' и так как они уравно-
вешиваются, то они равны и прямо противоположны. Мы снова
приходим таким образом к связи, разобранной ранее (п. 161).

ГЛАВА VIII. ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ	221
Рассмотрим еще две материальные точки М и М'', связанные нерас-
тяжимой нитью, не имеющей массы и лежащей на неподвижной
или движущейся поверхности 5, по которой она может скользить
без трения. Пусть Т и Т'—действия, оказываемые нитью наточки М
и М' и, следовательно, —Т и —Т' действия, оказываемые на нить
этими точками. На нить действуют: на концах силы —Т и —Т', а на
часть, соприкасающуюся с поверхностью 5,—нормальные силы, выз-
ванные реакцией поверхности. Так как нить должна быть в равно-
весии, то ее натяжение везде одинаково и она должна расположиться
по геодезической линии поверхности (п. 144); в частности и Т = Т'.
Этот род связи встречается среди разобранных выше (п. 163); он
приводит к некоторым геометрическим следствиям, которые мы
укажем в качестве упражнений в конце главы (упражнения 1 и 2).
II. Первые примеры. Системы с полными связями.
Простые машины
168.	Системы с полными связями. Говорят, что система мате-
риальных точек является системой с полными связями (с одной сте-
пенью свободы), если ее положение зависит только от одного пара-
метра. В такой системе каждая точка описывает определенную
неподвижную кривую и положение одной точки на траектории опре-
деляет положение всех остальных точек. Например, твердое тело,
вращающееся вокруг оси, является системой с полными связями: поло-
жение тела зависит только от угла, на который оно повернулось от
начального положения. Каждая точка ^ела описывает окружность,
перпендикулярную к оси вращения, с центром на этой оси; положе-
ние одной из этих точек определяет положение всех остальных. Винт,
движущийся в неподвижной гайке, цепь, скользящая по неподвижной
кривой, являются системами с полными связями.
Эти системы являются наиболее простыми из всех, так как им
можно сообщить только одно возможное перемещение, допускаемое
связями, а именно то, которое получится, если бесконечно мало
изменить единственный параметр, определяющий положение системы.
Следовательно, существует только одно условие равновесия такой
системы.
169.	Простые машины. Простые машины являются системами
с полными связями. На машины действуют две силы: одна Р, называ-
емая движущей силой, и другая R, называемая сопротивлением.
Для нахождения условия равновесия машине сообщают единственное
бесконечно малое возможное перемещение, допускаемое связями.
Пусть в этом перемещении SP — проекция на направление Р пере-
мещения АА' точки А приложения движущей силы, а oR— проекция
на R перемещения ВВ' точки В приложения сопротивления (рис. ПО).
Тогда условие равновесия будет
Р IP -4- R oR = 0.

222	ЧАСТЬ ВТОРАЯ. СТАТИКА
Вводя вместо перемещений возможные скорости, получим условие
и
где Up — проекция на Р возможной скорости U точки Л и Уд —
проекция на R возможной скорости V точки В. Следовательно, при
равновесии движущая сила и со-
противление находятся в отноше-
нии, обратном отношению проек-
ций возможных скоростей точек
приложения этих сил на направле-
--д- ния сил. Это — то, что Галилей
высказал в следующей форме:
«То, что выигрывается в силе,
теряется в скорости».
1°. Клановый пресс. Клин есть
равнобедренная треугольная призма,
зажатая между двумя толстыми досками, из которых одна неподвижна,
а другая перемещается горизонтально. Движущей силой является верти-
кальное давление, действующее на основание клина, которое предполагается
горизонтальным. Сопротивлением является горизонтальная сила R, противо-
Рис. ПО.
действующая перемещению горизонтальной подвижной доски. Рассмотрим
возможное перемещение, при котором клин переходит из ABC в А'В'С,
(рис. 111) опускаясь при этом на
ВН=ЪР.
Перемещение bR равно IB' со знаком минус, т. е. если угол С равен 2а, то
bR = — 257? tg о = — 25Я tg о.
Следовательно, условие равновесия будет
РЬР—
или
Применение клина тем выгоднее, чем меньше угол.
2°. Винтовой пресс. Допустим, что движущей силой является сила Р,
перпендикулярная оси Вг винта (рис. 112) и приложенная в точке А на расстоя-

ГЛАВА VIII. ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ
223
нии а от этой оси нормально к плоскости АгВ, а сопротивление R действует
вдоль самой оси. При бесконечно малом повороте 59 — единственном пере-
мещении, допускаемом связями, проекция на Р дуги винтовой линии, описы-
ваемой точкой А, есть дуга круга радиуса а с центральным углом 56:
8Р = а 56.
Что касается hR, то оно имеет значение
5/? =	|-56,
где h — шаг винта, так как перемещение винта вдоль
оси пропорционально его повороту, а шаг h есть зна-
чение этого перемещения при полном повороте винта.
Условие равновесия имеет вид
Ра 88 — R А- 88 = О, Р = A- R.
Отсюда следует, что выгодно увеличивать расстоя-	Рис- 112.
ние а и уменьшать шаг винта.
3°. Коромысловые весы Квинтенса. Весы состоят из коромысла ABC
(рис. 113), вращающегося вокруг точки О и несущего при помощи шарнирно
связанных с ним стержней ВВ' и СС две горизонтальные платформы, из
которых одна опирается
в / на неподвижное лезвие,
а другая в F на лезвие FF',
неразрывно связанное с
платформой 1С. Взвешивае-
мое тело помещают на верх-
нюю платформу и уравнове-
шивают гирей Р, подвешен-
ной в точке А таким обра-
зом, что коромысло ABC
занимает горизонтальное по-
ложение. При бесконечно
малом повороте 56 коро-
мысла вокруг оси, очевидно,
В О
г
I
В'
Рис. 113.
имеем
ЬР = ОА
Что касается перемещения hR, то оно будет зависеть от положения груза на
площадке FB', если только эта площадка не перемещается параллельно
самой себе, т. е. если точки F и В' не повышаются на одинаковые величины.
Чтобы выразить это условие, заметим, что точка В' поднимается на ту же
величину, что и В, т. е. на ОВ 58; точка С поднимается на величину ОС 88,
на ту же величину поднимается точка С. Точка F', увлекающая за собой
и точку F, поднимается на ._ ОС 58. Следовательно, искомое условие бу-
1С
дет следующее:
IF' OB
ОС
1С'
Оно выражает, что прямые 01 и BF' пересекаются на СС. При таком
предположении имеем
bR

224
часть Вторая, статика
и весы будут в равновесии, если будет выполнено условие
ОВ
P OB
РОЛ 58 — /?OB 88 = 0, -5- = -
ОА
и все происходит так, как если бы взвешиваемое тело было непосредственно
подвешено в точке В.	id/ti / ^ ni\
4° Весы Роберваля. Шарнирный параллелограмм ADLU (рис. lit;
может поворачиваться вокруг середин О и О' двух противоположных сторон,
причем эти точки лежат на одной вертикали. Стороны AD и ВС будут, оче-
видно, оставаться вертикальными. Если к ним прикрепить две площадки,
Рис. 114.
то их возможные перемещения будут равны, но противоположных знаков, так
что для равновесия положенных на них двух грузов Р и R необходимо, чтобы
эти грузы были одинаковы. Так же, как и в случае коромысловых весов,
условие равновесия не зависит от положения тел на площадках. Более того,
равновесие будет иметь место во всех положениях: оно
будет безразличным.
До сих пор мы пренебрегали весом стержней. Так
как веса вертикальных стежней AD и ВС одинаковы,
то сумма их возможных работ равна нулю и так как
веса стержней АВ и CD приложены в неподвижных точ-
ках О и О', то сумма их работ также равна нулю.
В действительности стержни АВ и CD заменяются твер-
дыми телами с весами р и /, центры тяжести которых
находятся в точках g и g', когда линии АВ и CD
горизонтальны. Допустим, что равновесие установлено
в этом положении. При возможном перемещении си-
стемы точки g и g' перемещаются нормально к р и р ,
описывая дуги окружностей с центрами соответственно
в точках О и О'. Следовательно, сумма возможных
работ весов будет по-прежнему равна нулю и усло-
вием равновесия будет всегда Р = R. Только равнове-
сие не будет безразличным, так как в другом положе-
нии в расчет войдут работы весов р и р'.
5°. Кривошипный механизм. Стержень ЛО
(рис 115) шарнирно связан концом А с неподвижной
осью, а концом О-со стержнем ОВ длины Ь, конец которого В скользит
без тоения по вертикали, проходящей через точку А. На палец F. неиз-
менно*^ связанный Рс АО, действует движущая сила FP, ™™РУЮ *""
считать перенесеной в точку Е ее направления, являющуюся основанием пер-
пендикуляра опущенного из точки А на Р. Сопротивлением является вер-
тикальная сила ?/?i, препятствующая движению точки В.
Рис. 115.

ГЛАВА VIII. ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ
225
Единственным перемещением, допускаемым связями, будет то, которое
получится, если повернуть стержень АО на угол 8а. При этом перемещении
работа силы Р будет
/>5Р=— РАЕЪа.
Работа сопротивления равна — R Ьх, где х — расстояние АВ. Из треуголь-
ника АОВ имеем
?2 = хъ _{_ а2 __ 2ах cos a,
и, дифференцируя, получаем
О — хЪх — a cos а Ьх + ах sin а 5а,
откуда
.	ах sin о
Ьх =	:	Во,
х — a cos a
так что условие равновесия будет
R
Р =
ах sin о
АЕ х— acos a
Я"
Проведем OD и АС перпендикулярно к АВ и обозначим через С точку
пересечения последнего перпендикуляра с продолже-
нием линии ВО. Имеем
х АС
OD = a sin a, BD = х — а cos а, -=^ =
BD ОО
и условие равновесия напишется в такой простой форме:
_Р_ _ хОР _ АС
R ~ АЁВЪ~~ЖЁ '
6°. Полиспасты и тали. Полиспаст состоит из
двух систем блоков, каждая из которых смонтирована
в общей обойме, причем блоки насажены на общую ось
или на отдельные оси. Первая система неподвижна, а вто-
рая движется (рис. 116). Допустим, что каждая система
состоит из трех блоков: первая — из блоков А, А', А" и
вторая — из блоков Av A'v A"l. В неподвижной точке В
обоймы первой системы закреплена веревка, которая по-
следовательно перекидывается через AiA, АХА', ... Дви-
жущая сила Р является натяжением, действующим на
свободный конец веревки. Сопротивлением R является
груз, подвешенный внизу подвижной системы. Шесть частей веревки, заклю-
ченных между обеими системами блоков, можно рассматривать как па-
раллельные. Так как общая длина нити остается неизменной, то при
перемещении свободного конца нити на ЬР, каждая из ее частей, заклю-
ченных между двумя системами блоков, укоротится на -тгЬР. Это выра-
жение, взятое с обратным знаком, является значением bR и при равно-
весии получаем
1
я,
я;
я;
7°. Нерастяжимая цепь, скользящая без трения по неподвижной
кривой. Пусть А и В — концы цепи, толщина которой принимается беско-
нечно малой, F—сила, непосредственно приложенная к элементу ds.

226
ЧАСТЬ ВТОРАЯ. СТАТИКА
Рис. 117.
находящемуся в точке С, Ft — проекция этой силы на касательную к кривой
в точке С в направлении АВ. Сообщим системе единственно возможное пере-
мещение, допускаемое связями, при котором вся цепь целиком, а вследствие
этого и каждый ее элемент, скользит вдоль кривой на общую величину СС,
равную Ъа (рис. 117). Возможная работа силы F равна Ffba; приравнивая
сумму этих работ нулю и замечая, что 8а может быть выведено из суммы
в качестве общего множителя,
получим условие равновесия
Это условие достаточно, если
предположить, что цепь во всех
точках растянута, а не сжата. На-
пример, если на цепь не действуют
никакие силы, кроме двух сил Р
и R, приложенных к концам, то
условие равновесия будет
Pt + Rt=0.
8°. Равновесие несжимаемой
жидкости в очень узкой трубке.
Уже Галилей пользовался принципом возможных скоростей для доказатель-
ства основных теорем гидростатики. Декарт и Паскаль также пользовались
этим принципом для изучения движения жидкостей. Для того чтобы можно
было приложить принцип возможных скоростей к жидкости, пренебрегая
работой внутренних сил, необходимо, чтобы работа внутренних сил жидкости
или реакций связей равнялась нулю при любом возможном перемещении,
допускаемом связями, т. е. чтобы соседние молекулы оставались на постоян-
ных расстояниях (несжимаемая жидкость) и чтобы не было внутренних
трений (идеальная жидкость). Мы
позаимствуем пример у Лагранжа
(Статика, раздел 7).
Рассмотрим несжимаемую
жидкость, заключенную в беско-
нечно тонкой трубке заданной
формы, поперечное .сечение ко-
торой о) изменяется по заданному
закону. Для большей точности
можно себе представить, что
трубка образована перемещаю-
щимся бесконечно малым пло-
ским элементом, остающимся все
время нормальным к заданной кривой S (рис. 118). Пусть А и В — концы
жидкой колонки, удерживаемой двумя бесконечно малыми поршнями,
dm — элемент этой колонки в положении С, где поперечное сечение
равно (о. Обозначим через F силу, приложенную к элементу dm, и через Ft —
ее проекцию на касательную к кривой S в направлении АВ, т. е. на нормаль
к «. Сообщим жидкости единственно возможное для нее перемещение,
допускаемое связями, перемещение, при котором вся колонка совершает
скольжение как целое на бесконечно малую величину. При этом скольжении
элемент dm, находящийся в С, описывает по кривой S дугу Is, так что <¦> bs
равно количеству жидкости, проходящей через сечение о> трубки. Вследствие
несжимаемости жидкости необходимо, чтобы это количество было всюду
одинаковым. Можно положить ш 6s = а, гце <х — одинаково на всем протяжении
трубки. Работа F равна тогда F os или — Ft, и сумма возможных работ
Рис. 118.

ГЛАВА VIII. ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ	227
непосредственно приложенных сил равна о \^—-. Следовательно, необходи-
мое и достаточное условие равновесия будет
предполагая, что колонка сжата во всех своих точках.
Например, если единственными силами, приложенными к жидкости,
являются нормальные давления Ро и Рь приложенные к поршням А и В
с сечениями ш0 и u>t, то условие равновесия будет
Примечание. К этому же самому уравнению равновесия жидкости
можно прийти при следующих условиях. Представим себе замкнутый сосуд
произвольной формы, из которого выведены две цилиндрические трубки А
и В с сечениями ш0 и cot. Допустим, что сосуд заполнен жидкостью, на
которую не действуют никакие непосредственно приложенные силы, и что
трубки закрыты двумя поршнями А и В, на которые действуют нормальные
давления Ро и Рх. Если поршень А вдвинуть на бесконечно малую величину е0,
то внутренний объем уменьшится на еошо; необходимо, следовательно, чтобы
поршень В поднялся на такую величину tb что еошо = t{al. Так как сумма
возможных работ Ро и Рь очевидно, равна Ро?о — Р^ь то имеем уравнение
равновесия
Р Р = 0, />t — Pt o0 = 0.
На этой зависимости основано устройство гидравлического.пресса.
III. Общие условия равновесия, выводимые из принципа
возможных скоростей
170. Основное уравнение статики. Мы будем следовать методу,
указанному Лагранжем. Пусть задана система, образованная л точками
МЛхх, уи zj, ,442.(*2. У*, г2)	, Мп(хп, yh, гп)
и подчиненная связям, выражаемым такими равенствами, какие раг-
сматривались в предыдущем..
Обозначим через F^(X^, Vv, 2V) равнодействующую заданных сил,
действующих на точку М.,. На основании принципа возможных ско-
ростей составляем уравнение
2 (X, Ьх, + У., Ъу„ + Zv 32v) = 0,	A)
v = l
которое должно удовлетворяться для всех перемещений bxw, o_yv, 8.г„,
допускаемых связями. Можно сказать, что это уравнение является
общим уравнением статики.
171. Приведение уравнений равновесия к наименьшему числу.
В каждой частной системе для получения наиболее общего возмож-
ного перемещения, допускаемого связями, необходимо и достаточно

228	ЧАСТЬ ВТОРАЯ. СТАТИКА
сообщить k параметрам qv q2, . . ., qk произвольные вариации о^,
8<72, • • • , %qk. Тогда говорят, что рассматриваемая система имеет k
степеней свободы.
Например, для получения наиболее общего перемещения точки
по поверхности (п. 159) необходимо и достаточно сообщить двум
параметрам произвольные вариации bqt и bq2; следовательно, точка на
поверхности является системой с двумя степенями свободы.
Для получения наиболее общего перемещения свободного твердого
тела достаточно сообщить ему три произвольных бесконечно малых
поступательных перемещения, параллельных трем осям координат,
и повернуть его на три произвольных бесконечно малых угла вокруг
этих трех осей. Следовательно, свободное твердое тело является
системой с шестью степенями свободы.
Возьмем еще систему, образованную твердой материальной окру-
жностью, которая катится без скольжения по неподвижной
плоскости Р (обруч). Для выражения связи нужно написать, что
скорость материальной точки, находящейся в соприкосновении, равна
нулю. Следовательно, для того чтобы сообщить обручу перемещение,
допускаемое связью, необходимо и достаточно сообщить ему враще-
ние на бесконечно малый угол вокруг произвольной оси, проходящей
через точку касания. Но это элементарное вращение может быть
всегда разложено на три: одно bq1 вокруг нормали к неподвижной
плоскости в точке касания А, другое bq2 вокруг касательной к обручу
в точке А, и третье bq3 вокруг нормали к обручу, проведенной
в точке А в неподвижной плоскости. Следовательно, обруч образует
систему с тремя степенями свободы.
Вернемся к общему случаю системы с k степенями свободы.
Так как, по предположению, перемещение системы определяется беско-
нечно малыми вариациями bqv bq2, .... bqk, то вариации bxv bylt
bzv Ьх2, Ьу2, Ьг2, ¦ ¦ ¦ координат различных точек системы будут
определенными, если известны bqv bq2, .. ., bqk. Для этих вариаций
должны иметь место выражения вида
= cn bql -\- c12 bq2 -f- . . . —|- clk bqk,
8^v = cvl S^j —|- cv2 8<72 -\- ... -\- cvft bqk,
Если внести эти выражения в основное уравнение статики
B)

ГЛАВА VIII. ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ
229
то оно примет вид
Qi
в котором
C)
= 2 (^A
Так как уравнение C) должно выполняться при любых Ьди
Ьд2, ..., oqk, то должно быть одновременно
Qi = 0, Q2 = 0	 Qk = 0.	D)
Таким образом, получились k необходимых и достаточных урав-
нений равновесия. Число этих уравнений в точности равно числу
степеней свободы системы.
172. Голономные системы; координаты голономной системы.
Говорят, согласно Герцу (Oeuvres completes, т. Ill), что система
с k степенями свободы является голономной, когда существует такая
система параметров qt, q2,..., qu, что координаты xv, jyv, 2V раз-
личных точек системы выражаются в функции этих параметров
е конечной форме
х* — Ь (Яи Яг	Як)>
У-, = 1\ @1. ?2	Як)'
А, = ш, (Як Яг	Як)>
(^=1.2	л).
E)
Параметры glt q2	Як будут тогда координатами голономной
системы; их численные значения определяют положение системы.
Для получения возможного перемещения, допускаемого связями, до-
статочно дать этим параметрам произвольные бесконечномалые
приращения 8<7i, §<72	8<7л- Таким путем на основании равенств E)
получится
ъУ*=т&Ъг + -
dq,
... +-
F)
Эти формулы являются частными случаями выражений B), поскольку
правые части выражений, написанных для 8xv, 8jv, 8zv, являются пол-
ными дифференциалами функций от qlf q2, .... qk, что не имеет
места в общем случае B).
Подставляя выражения F) в основное уравнение статики A), мы
получим уравнения равновесия в форме
Q1 = 0. Q2 = 0	 Qk = 0,	G)

230	ЧАСТЬ ВТОРАЯ. СТАТИКА
в которых
Большинство систем, встречающихся в приложениях, являются
голономными. Например, твердое тело, которое вращается вокруг оси
и скользит вдоль нее, является голономной системой, так как его
положение зависит от двух координат: угла; на который оно повер-
нулось от некоторого начального положения, и длины, на которую
оно совершило скольжение от этого положения.
Твердое тело, вращающееся вокруг неподвижной точки, является
голономной системой, так как положение тела определяется тремя
координатами, которыми могут быть, например, углы Эйлера, между
осями, связанными с телом, и осями неподвижными.
Напротив, окружность, катящаяся без скольжения по неподвижной
плоскости (обруч), не представляет собою голономной системы. Это
вытекает из того, что обруч обладает тремя степенями свободы (п. 171)
и в то же время его положение на плоскости, по которой оно
катится, не может быть определено тремя координатами. Уже Лагранж
рассматривал неголономные системы в своей Аналитической меха-
нике (раздел IV, п. 2, т. I, изд. Бертрана).
173. Частный случай, когда выражение возможной работы
есть полный дифференциал. Полученные выше общие результаты
принимают интересную форму, когда выражение возможной работы
где Qv Q2, • • • , Qie суть функции параметров q, является полным
дифференциалом некоторой функции U от параметров qx, q2	qk,
т. е. когда
О dU п ди	П ди
В этом случае дифференциальные уравнения равновесия совпадают
с уравнениями, определяющими максимум и минимум функции U. Мы
покажем в динамике, что если для определенной системы значений
величин q эта функция U действительно имеет максимум, то соответ-
ствующее положение равновесия является положением устойчивого
равновесия (Лежен-Дирихле).
Случай существования силовой функции, т. е. случай, когда выра-
жение
является полным дифференциалом некоторой функции от величин хг,
yv zv х2, У2- z2	хп, уп, г„, относится к только что рассмот-
ренному, так как если заменить координаты и дифференциалы коор-

ГЛАВА VIII. ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ
231
динат их выражениями через q и Ьд, то рассматриваемая сумма
останется полным дифференциалом. Но обратное, вообще говоря,
неверно: может случиться, что Qibql~\-Q2bq2-\- ... ~\~Q]ebqk будет
полным дифференциалом и в случае отсутствия силовой функции.
174. Приложения. Тяжелые системы. Когда система, для которой
ищутся положения равновесия, находится под действием только сил
тяжести, являющихся непосредственно приложенными силами, то, оче-
видно, существует силовая функция непосредственно приложенных
сил. В самом деле, полагая, что ось Ог направлена вертикально
вниз, получим для точки т{, имеющей вес т$, возможную работу,
равную triigbzi. Следовательно, для суммы возможных работ получится
Л
/Г G' В'
где С—ордината центра тяжести. Тогда положениями равновесия
будут те, для которых 8? равно нулю. Они совпадают с теми поло-
жениями, которые получаются при нахождении максимума или мини-
мума координаты С, рассматриваемой как функция от k геометрически
независимых параметров qu q2, • • •, <fa, определяющих положение
системы.
Приме р ы. 1°. Найдем положение равновесия однородного тяжелого
стержня АВ (рис. 119), скользящего без трения своими концами по кониче-
скому сечению, фокальная ось которого вертикальна (система с одной степеиью
свободы). Прежде всего очевидными положениями равновесия, если только
они возможны, будут горизонтальные по-
ложения. Для нахождения остальных поло-
жений равновесия рассмотрим директрису
DD' и пусть АА' и ВВ' — расстояния от
точек А и В до этой директрисы. Расстоя-
ние прямой DD' от центра тяжести G, на-
ходящегося на середине стержня АВ, равно
-,АА' + ВВ' .
Но если е — эксцентриситет и F—
фокус, соответствующий директрисе DD',
то, как известно, АА' и ВВ' равны соот-
ветственно — AF и —BF, откуда полу-
чаем
2е
Рис. 119.
Следовательно, расстояние GG' будет максимумом или минимумом одно-
временно с AF-\-BF, а последняя сумма будет, очевидно, минимумом, когда
прямая АВ проходит через фокус F. Таким образом, если прямая может
проходить через фокус, то каждое ее положение является положением равно-
весия. В случае, показанном на фигуре, когда прямая проходит через F, она
будет находиться в неустойчивом положении равновесия, так как в этом
положении ее центр тяжести будет выше, чем в соседних положениях. Она

232	ЧАСТЬ ВТОРАЯ. СТАТИКА
будет в устойчивом положении равновесия, когда будет проходить через
другой фокус Flt как это видно, если взять вторую директрису DXDV
1°. Тяжелая, однородная или неоднородная цепочка, концы которой
закреплены или могут скользить по неподвижным кривым или поверхностям,
занимает положение равновесия, являющееся тем из возможных положений,
этой цепочки, при котором высота ее центра тяжести имеет максимум или
минимум. Например, из всех однородных кривых заданной длины /, прохо-
дящих через две неподвижные точки, та из них, центр тяжести которой
занимает самое низкое положение, является найденной ранее (п. 140) цеп-
ной линией. Отсюда следует, что если на плоскости взять неподвижную
ось Ох и две неподвижные точки А и В, то из всех кривых заданной
длины /, лежащих в этой плоскости и проходящих через эти точки, цепная
линия опишет при вращении вокруг оси Ох поверхность наименьшей пло-
щади. В этом убеждаемся на основании теоремы Гюльдена, так как опи-
санная площадь, равная / • 2nGG', обращается в минимум одновременно
С GO'. Можно оставить в стороне условие относительно длины и вновь
установить, по Крайней мере частично, один полученный ранее результат.
Из всех кривых, лежащих в плоскости и проходящих через А и В, та, ко-
торая описывает наименьшую площадь, является некоторой цепной линией.
В самом деле, пусть С — эта кривая. Она является, в частности, одной из
всех кривых такой же длины, что и сама кривая С, описывающих наимень-
шую площадь. Следовательно, она действительно является цепной линией,
имеющей основание, параллельное оси Ох. Остается среди всего этого бес-
численного множества цепных линий найти ту, которая описывает наимень-
шую площадь. Последняя, как мы видели (п. 148, пример 1), является той,
которая имеет основанием ось Ох.
175. Принцип^Торричелли. Мы видели как следствие принципа воз-
можных скоростей, что для нахождения положений равновесия тяжелой
системы достаточно „приравнять нулю
вариацию высоты центра тяжести.
Лагранжу принадлежит важное замеча-
ние, что если принять, как и Торри-
ffc ! челли, в качестве очевидного прин-
ципа это условие равновесия тяжелой
системы, то отсюда можно будет вы-
вести принцип возможных скоростей
во всей его общности (Аналитическая
; ,	механика, том I, Статика, отдел I и
Xj7li	отдел III, § V). Пусть, в самом деле,
имеется система материальных то-
р 12л	чек Мх, Мъ ..., Мп, на которые на-
ложены заданные связи и действуют
заданные силы Flt F2, ..... Fn (рис. 120).
Рассмотрим определенное положение системы, в котором точки занимают
положения шх, щ, ..., тп, а силы имеют значения /j, /2, ..., fn. На напра-
влении силы /, вообразим неподвижную точку Оч на некотором расстоя-
нии т^О^ — г,. Если сместить бесконечно мало систему из рассматриваемого
определенного положения, то точка т„ перейдет в mv и возможная работа
силы /v будет равна —/, Ьг.„ так как имеем (п. 84, пример III):
\т,
8rv = — mvm^ cos {/,, m^m[).
Следовательно, сумма возможных работ сил /, будет

ГЛАВА VIII. ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ
233
Требуется доказать, что необходимым и достаточным условием того,
что рассматриваемое частное положение представляет положение равновг-
сия, является равенство нулю величины §".
Для этого заметим, что мы можем заменить действие силы /, натяже-
нием нерастяжимой нити, закрепленной в точке mv проходящей через беско-
нечно малый блок Ov и несущей натягивающий груз р„ равный /„. Если мы
проделаем эту операцию с каждой из сил /v, то мы заменим предложенную
систему тяжелой системой и первоначальная система будет служить лишь
для нахождения соотношений между грузами /?.,. Тяжелая система может нахо-
диться или не находиться в равновесии в том же самом положении. Но для
того, чтобы тяжелая система находилась в равновесии, необходимо и доста-
точно, чтобы вариация Ь? ординаты центра тяжести грузов рч равнялась
нулю; эта вариация определяется формулой
РК = р1Ьг1+ргЬгъ+ ... +pnbzn
где ось z направлена вертикально вниз, Р — общий вес и zb z2, ..., zn^
координаты центров тяжести грузов рь р2, ..., рп. Очевидно, что Ъгч = —Ьг,г
так как нить т.фчРч имеет постоянную длину. Следовательно, имеем
так как рч = /„. Для того чтобы первоначальная система была в равновесии,
необходимо и достаточно, чтобы 8? = 0, т. е. чтобы для любого перемеще-
ния, допускаемого связями, обращалась в нуль величина JT. что и представ-
ляет принцип возможных скоростей во всей его общности.
Примечание. Если материальной системе с нитями и с грузами pt,
ро, ..., рп придать какое-нибудь положение, отличное от рассматриваемого
частного, то заданными силами будут Fb F2	Fn, а натяжения нитей M±Oi,
М2О2, • ••> равные р%, р2	рп, будут отличаться и по величине и по на-
правлению от сил Fi, F2, ..., Fn. Однако в рассматриваемом частном положе-
нии ni\, m2> •••> тп заданные силы равны натяжениям, так что если это
положение является положением равновесия системы под действием задан-
ных сил, то оно будет положением равновесия и под действием натяжений.
Но так как для положения, даже бесконечно близкого к щ, т2, ..., тп,
силы F., отличаются от натяжений, то может случиться, что это положение
равновесия системы будет устойчивым под действием заданных сил /\ и
неустойчивым под действием грузов р^.
В упражнениях F) будут указаны некоторые свойства положений
равновесия системы, аналогичные только что подробно изложенным, в част-
ности свойство, указанное Гауссом и Мёбиусом, относительно минимума
суммы квадратов.
IV. Множители Лагранжа
176. Уравнения связей. Пусть дана система, образованная а
точками
v г,), М2(х2, у2, г2)
Мп(хп> уп, гп)
и подчиненная связям, выражаемым соотношениями между их коор-
динатами вида
i. Уи
i. Уи
2, у2, z2
2, у2, г2
хп, уп, гп) =
*„, уп, гп) =
/л(-«I. Уи гх, хг, уг, г2, ¦¦-. хп, уп, zn) = 0.
A)

234	ЧАСТЬ ВТОРАЯ. СТАТИКА
Число h этих уравнений должно быть меньше числа Зл коорди-
нат, ибо если бы оно равнялось Зи, то все Зл координат определя-
лись бы этими уравнениями. Положим поэтому,
й = 3л — k.
Такая система будет голономной, так как при помощи равенств A)
можно выразить все координаты в функциях подходящим образом
выбранных из них k координат. Система" имеет, следовательно, k
степеней свободы. В случае, когда k=\, система будет с пол-
ными связями, так как ее положение зависит только от одного
параметра, например, от одной подходящим образом выбранной
координаты.
Обозначим через FV(X,, Kv, Zv) равнодействующую заданных сил,
действующих на точку /И„. Тогда на основании принципа возможных
скоростей имеем уравнение
2 ix% ьхч + к, ьу,+z, a*v) = о,	B)
v = l
которое должно выполняться для всех перемещений 8xv, 8_yv, §2V,
допускаемых связями.
177. Множители Лагранжа. Перемещения точек М связаны h
соотношениями, которые получаются дифференцированием уравне-
ний A), а именно:
дух
дхх 1 ' dyt ^l ' dz{ l '	' дгп "
C)
Эти h соотношений между Зл вариациями координат показывают,
что k из этих вариаций могут быть выбраны произвольно. Назовем
эти вариации независимыми вариациями, а остальные, определяе-
мые уравнениями C),—зависимыми вариациями.
Для нахождения условий равновесия применим метод множителей
Лагранжа. Умножим уравнения C) соответственно на неопределенные
множители \, Х2	Хл и сложим их с уравнением B); после этого
определим множители таким образом, чтобы в полученной сумме
обратить в нуль коэффициенты при h зависимых вариациях; тогда
коэффициенты при независимых вариациях должны также обратиться
в нуль; в результате требуется" определить X таким образом, чтобы
обращались в нуль все коэффициенты, и мы получаем Зл совместных

ГЛАВА VIII. ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ	235
уравнений:
2	я).
ду'	D)
Эти уравнения совместно с h уравнениями связей A) составляют пол-
ную систему Зи-)-А уравнений, определяющих Зл координат и h
вспомогательных неизвестных X.
Таковы общие уравнения равновесия.
Как только коэффициенты X будут известны, так сейчас же можно
будет определить и реакции связей. В самом деле, мы видим, что
уравнения равновесия не изменятся, если отбросить связь /, = 0 и
присоединить к заданным силам, действующим на точку Л1„, силу
с проекциями \. -J^-, \, -—¦, X, -J^-; эта сила является действием
связи на точку М„, т. е. тем, что мы называем реакцией связи. Мы
непосредственно имеем величину этой силы; ее направление -у-^,
-3-1-, -^-t- нормально к поверхности, которая получится, если пред-
положить, что в уравнении /, = 0 всем координатам, кроме хч, уч,
2„ приданы численные значения, соответствующие положению рав-
новесия, а координаты xv, _yv, 2V являются текущими.
Пример. Применим предыдущие рассуждения к равновесию веревоч-
ного многоугольника с п сторонами, концы которого закреплены в двух
заданных точках. Здесь будет п уравнений связи, а именно:
У, — г,+,J-^ = 0 (v = 0, 1,2	л-1),
причем координаты х0, у0, z0 и хп, уп, zn даны. Общие уравнения равно-
весия будут
v —1 1
Г
V J-\	Уу —У.,-1 1 ) У, — У-, + \ л
Z, + V,_t	+^,	=0.
Они действительно совпадают с теми, которые получатся при помощи эле-
ментарных методов, если выразить, что сила /\ уравновешивается натяже-
ниями двух нитей, оканчивающихся в точке Afv. Так как коэффициенты при X
в этих уравнениях равны направляющим косинусам сторон веревочного мно-
гоугольника, то эти X являются абсолютными значениями натяжений.

236	ЧАСТЬ ВТОРАЯ. СТАТИКА
причем последние направлены вдоль сторон. Мы действительно видим, что они
нормальны к поверхностям
(*,-г1±& = 1-' или А.-*
где только xv у„, гч являются переменными, так как эти поверхности яв-
ляются сферами с центрами в точках Afv+t и -M,_i.
178. Случай неголономной системы. Тот же метод применим
к такой системе точек, для которой возможные перемещения, допу-
скаемые связями, определяются h соотношениями вида
Ап Ъхх+Вп Ьу, + Сп 82,+.. . +Л1П Ъхп+В1п Ьуп+С1п Ьгп = 0, )
ЪхпАГВ2пЪупАГСгпЬгп = О, \ E)
I
Ahnbxn-!rBhnbyn-{-Chnbzn=O, J
где коэффициенты А. В, С суть функции координат и где левые
части не являются точными полными дифференциалами, как в пре-
дыдущем пункте. Мы видим, что по-прежнему & = 3я—-h вариаций
Sxv, S_yv» ^2V произвольны. Далее, поступая с этими соотношениями E)
так же, как и с соотношениями C), мы получим уравнения равно-
весия в виде
F)
+ х„вЛч = о,
(v=l, 2	л).
179. Приложение принципа возможных скоростей к равновесию
нитей. Пусть ds — элемент нити nXds, Yds, Z ds — проекции равнодей-
ствующей приложенных к нему внешних сил. Для возможного перемещения,
сообщенного элементу ds, работа этой силы равна
где Ь*, Ьу, Ъг должны рассматриваться как функции дуги s, так как каждый
элемент нити получает перемещение, изменяющееся с его положением на
нити. Для равновесия необходимо и достаточно, чтобы сумма элементарных
работ
была равна нулю для всех перемещений, допускаемых связями. Допустим
для определенности, что нить закреплена обоими концами; тогда 5*, Ъу, bz
обращаются в нуль на обоих пределах интеграла. Так как, кроме того, нить
нерастяжима, то

ГЛАВА VIII. ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ	237
откуда выражая, что вариация левой части равна нулю и замечая, что ва-
. dx d Ьх
риация производной равна производной от вариации, например, о —— = —-—,
получим
dx db± dy_ dby_ dz_ dlz_ _
ds ds ~f ds ds """ ds ds	K >
Это условие показывает, что в качестве Ъх и Ьу можно принять произ-
вольные функции от s, обращающиеся в нуль на пределах 0 и /; Ьг опре-
деляется из соотношения B):
dbz _ Idx dbx . dy dby\
ds ~~ \ dz ds dz ds j '
Отсюда, интегрируя и замечая, что Ьг обращается в нуль вместе с s, получим
z ds ' dz ds
Но необходимо, чтобы Ьг обращалось в нуль и на втором конце, где
s = /; следовательно, Ьх и Ьу должны удовлетворять условию
z ds ' dz ds
о
Необходимо теперь выразить, что $ обращается в нуль. для любых
функций Ьх, by, bz, обращающихся в нуль на пределах и удовлетворяющих
соотношениям B) и C). Обозначим через X пока произвольную функцию
дуги s и через k — постоянную. Имеем
Интегрируя последние члены по частям и полагая Т = — IX -\- k —r-1,
мы можем иаписать
так как проинтегрированная часть обращается в нуль на пределах.
Для того чтобы было равновесие, необходимо и достаточно, чтобы это
выражение Ш было равно нулю, каковы бы ни были функции Ьх, Ьу и X от s.
Распорядимся функцией I так, чтобы обратить в нуль коэффициент при bz.
Тогда оставшееся выражение должно обращаться в нуль, каковы бы ни были
функции Ьх и Ьу в промежутке @, /); для этого необходимо, чтобы

238	ЧАСТЬ ВТОРАЯ. СТАТИКА
коэффициенты при Ьх и Ьу были также равны нулю. (Это рассуждение анало-
гично рассуждениям в п. 177). Таким образом получаем уравнения равновгсия
совпадающие с теми, которые были установлены непосредственно.
Частный случай. Допустим, что X, Y, Z являются частными производ-
ными функции U (х, у, z, s) по х, у, г:
у dU v dU	dU
ox	ay	dz
Тогда
г	/
g = J (Xbx + Yby + Z Ъг) ds = 5 J U(x, y, z, s) ds,
о	о
и, следовательно, для получения положения равновесия нужно искать коор-
динаты х, у, z в функции величины s, обращающие в максимум или мини-
мум интеграл
Г U (л:, у, z, s) ds
о
при условии A). Например, для неоднородной тяжелой нити вес элемента ds
лмеет вид g<f(s)ds; направив ось z вертикально вверх, имеем
U = — gzy (s),
и положение равновесия обращает в максимум или минимум интеграл
I
— gjz<f(s)ds,
о
т. е. высоту центра тяжести.
В общем случае, для определения натяжения имеем уравнение
dT + Xdx + Ydy + Z dz = 0,
которое при рассматриваемом предположении обращается в
..,№, . ди . . dU j n
dT + з— dx Л- -з— dy + -3— dz = 0.
дх ' ду * dz
Но при увеличении s на ds имеем
dU J , d
-^— dx -f ^— dy + s~ dz+ -5-
dx ' dy * ^ dz	ds
.„ dU J , dU J , dU J , dU .
du = -^— dx -f ^— dy + s~ dz+ -5- ds,
dx ' dy * ^ dz	ds
откуда
dT + dU — ~ds = 0.
ds
Следовательно, если U не зависит от s, то получаем
как мы это видели и ранее (п. 137). В этом частном случае, когда U не
зависит от s, только что изложенная теория позволяет непосредственно
установить результаты, уже полученные в параграфе III, главы VII; таким
образом, эти результаты оказываются связанными с принципом возможных
скоростей.

ГЛАВА VIII. ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ	239
V. Общие теоремы, выводимые из принципа
возможных скоростей
180. Связи допускают поступательное перемещение системы
параллельно оси. Допустим, что связи допускают поступательное
перемещение всей системы параллельно оси, которую мы примем за
ось Ох. В основном уравнении статики
приложенном к этой системе, для рассматриваемого частного пере-
мещения нужно положить
Ъу, — О, Ьг, = 0, 8^=8*2 = ... =Ьхп.
Вынося в нем за скобку общий множитель 8;tv, получим
Для равновесия системы необходимо, следовательно, чтобы сумма
проекций на рассматриваемую ось Ох непосредственно приложенных
сил равнялась нулю.
181.	Связи допускают вращение системы вокруг оси. Допустим,
что связи допускают вращение всей системы как целого вокруг оси,
которую мы примем за ось Ог. Обозначая через rv и 6V полярные
координаты проекции точки (xw, у„ zv) на плоскость хОу, имеем
хч = /¦„ cos 6V, _yv = rv sin 8V.
Для того чтобы выразить, что система получает рассматриваемое
перемещение, нужно, оставляя rv и гч постоянными, изменить все
полярные углы 8„ на одну и ту же величину 56. Таким путем для Ьх^,
§_У„, 82V получаются значения
§.*:„ = — rv sin 9,88 = — ^,86, S_yv = jcv 39, 8^ = 0.
Сумма возможных работ непосредственно приложенных сил для
этого частного перемещения равна
2 (*, Ьху + Kv by, + 2, ozw) = 88 2 (*Х — УМ
т. е. она равна произведению 88 на сумму N моментов непосредст-
венно приложенных сил относительно рассматриваемой оси. Для
равновесия необходимо, чтобы эта сумма N равнялась нулю.
Мы видим, что понятие момента относительно оси вводится, таким
образом, наиболее естественно.
182.	Связи допускают винтовое перемещение всей системы.
Примем за ось Ог ось винтового движения. Пусть 86 — бесконечно
малый угол, на который система поворачивается вокруг оси Oz,
а Ьг—величина скольжения вдоль этой оси. Положим 82 = /89,
/ будет тем, что мы назвали параметром винтового движения. Так

Связи
Никаких связей
Неподвижная точка О
Неподвижная ось Ог
Тело вращается вокруг оси Ог и скользит
вдоль нее
Тело покоится на плоскости хОу:
1) одной точкой О
2) несколькими точками на оси Ох . .
3) несколькими точками, не лежащими
на прямой
Степени
свободы
6
3
1
2
5
4
3
Возможные перемещения
параллельно
Ох, Оу, Ог
—
—
Ог
Ох, Оу
Ох, Оу
Ох, Оу
вокруг
Ох, Оу, Ог
Ох, Оу, Ог
Ог
Ог
Ох, Оу, Ог
Ох, Ог
Ог
Условия равновесия (число которых
равно числу степеней свободы)
X=Y=Z=L=M=N=O
L=M=N=O
N = O
Z = N = O
X=Y=Lr=M = N = O
X=Y=L=N=O
X=Y=N=O
•fi
>
О
tr
га
ч
О
¦в
>
>
я

ГЛАВА VIII. ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ	241
как бесконечно малое перемещение каждой точки системы есть гео-
метрическая сумма перемещения вращения и перемещения скольжения,
то сумма возможных работ непосредственно приложенных сил равна
сумме работ на каждом из указанных перемещений в отдельности.
Для этой суммы имеем
§ = Ьг 2 Zv + 89 2 (*VKV — yJC%) = 89 {N +/Z),
где N — сумма моментов относительно оси Oz, a Z — сумма проек-
ций на эту ось. Для равновесия необходимо, следовательно, чтобы
N-\-fZ=0.
Примечание. Выражение Ш представляет собой относительный
момент двух систем векторов, из которых одна образована непосред-
ственно приложенными силами, а другая имеет центральной осью
ось Oz винтового движения, главным вектором 89 и минимальным
моментом 8г = /86 (п. 28).
183.	Приложение к условиям равновесия твердого тела.
В таблице на стр. 240 мы обозначаем через A!", Y, Z, L, М, N проек-
ции на оси координат главного вектора и главного момента относи-
тельно начала О сил, непосредственно приложенных к твердому телу.
Мы указываем, кроме того, число степеней свободы твердого
тела, подчиненного различным рассматриваемым связям. Для свобод-
ного тела это число равно шести, так как положение свободного
твердого тела зависит от трех координат х0, у0, г0 какой-нибудь
точки О тела и трех независимых углов (например, углов Эйлера),
которые определяют положение прямоугольного триэдра Oxyz, свя-
занного с телом, относительно неподвижного триэдра О^^у^.
VI Неудерживающие связи
184.	Связи, определяемые равенствами; допускаемые перемещения,
характеризуемые неравенствами. Может случиться, что система подчинена
связям, определяемым равенствами, но что возможные перемещения, допу-
скаемые этими связями, определяются неравенствами. В этом случае говорят,
что система подчинена неудерживающим связям.
Представим себе, например, материальную точку, положенную на гори-
зонтальный стол, который она может покинуть, переместившись вверх. При-
мем за ось Oz направленную вверх вертикаль. Предположив, что связь
осуществлена, имеем z = 0, но возможные перемещения, допускаемые этой
связью, будут таковы, что
Представим себе теперь две точки М{х, у, г) и М1(х1, уъ z{), связанные
невесомой нерастяжимой нитью длины /; наибольшее расстояние между этими
точками равно /, но это расстояние может быть и меньше, так как нить
не препятствует точкам приближаться друг к другу. В предположении,
что связь осуществлена, т. е. что нить натянута, имеем
/¦2 =

242	ЧАСТЬ ВТОРАЯ. СТАТИКА
а возможные перемещения, допускаемые этой связью, либо оставляют рас-
стояние г равным /, либо уменьшают его:
6г<0.
Так как
ri = {х _
то эти перемещения определены неравенством
(х - хО (Ьх - bxi) + (у - у,) (By - By,) + (г - гг) (8г - 8*0 < 0.
Вообще можно представить себе систему из п точек xv yv, г„ подчи-
ненную таким связям, что когда они все осуществлены, возможные переме-
щения, допускаемые этими связями, определяются некоторыми равенствами
и некоторыми неравенствами:
Ап В*, + Вп By, + Сп 8г, + ... + Аы Ьхп + Вы Ьуп + С,„ Ьгп = 0,
Ап Ъхх + Вп ЬУ1 + Cnbzx+ ... + А2п Ьхп + В2п Ьуп + С2П Ьгп = 0,
Ад1 бдг, + Bgl By, + Cfll 8^ + ... + Л^ Sjfn + Bfln Ву„ + Сдп bzn = 0;
... + Ад+2, „ Ьхп + Вд+2, п Ьуп + Сд+2, п	j
+ Sfti ВУ1 + См Bart + ... + ^ft« 5xn+Bhn Ьуп + Сй„ 6гп < 0. J
Мы имеем таким образом Л соотношений: ? равенств и Л — ? неравенств.
Мы будем предполагать, что левые части всех неравенств либо отрица-
тельны, либо равны нулю, чего можно всегда достичь, изменив, в случае
необходимости, знаки обеих частей.
Мы ставим себе задачей найти для такого рода систем положения равно-
весия, при которых все связи осуществлены.
Полезно разбить перемещения, допускаемые связями, на две категории:
1) неосвобождающие перемещения и 2) освобождающие перемещения. Мы
будем называть освобождающими перемещениями такие перемещения, для
которых левые части соотношений B) равны нулю, как и для соотноше-
ний A):
Aj+u I bxi + ¦ ¦ ¦ + Cff+i, n8*» = о,
Очевидно, что каждому неосвобождающему перемещению соответствует
такое же перемещение, ему равное, но противоположное по направлению, так
как если левые части равенств A) и B) равны нулю для какой-нибудь системы
значений Bxv, byv 5гч, го они будут также равны нулю, если у всех Вхч,
5у„ Ьг., переменить знаки на обратные.
Наоборот, мы назовем освобождающим перемещением такое перемеще-
ние, для которого хотя бы одна из левых частей соотношений B) не равна
нулю, например:
Л+1. \Ьх\+ ¦¦¦ + Сд+и п *гп < 0.
В этом случае перемещение, равное и противоположное, не допускается
связями, так как если переменить знаки у Ьхч, Ьуч, bz,, на обратные, то не-
равенство не будет выполняться.
Теорема о возможной работе для такого рода связей формулируется так:
Для того чтобы в положении, при котором все связи осуществлены,
имело место равновесие, необходимо и достаточно, чтобы для всех

ГЛАВА VIII. ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ	243
возможных перемещений, допускаемых связями, сумма работ заданных
сил была равна нулю ила была отрицательной, причем нулю она должна
быть равна для неосвобождающих перемещений, равна нулю или отри-
цательной для освобождающих перемещений:
Необходимость условия. Для доказательства, что условие необходимо,
достаточно показать, что в случае неудерживающих связей для любого
перемещения, допускаемого связями, сумма возможных работ реакций
связей либо равна нулю, либо положительна: равна нулю для неосвобож-
дающих перемещений, равна нулю или положительна для других перемещений.
В самом деле, возьмем, например, точку, положенную на некоторую по-
верхность, которую она может покинуть в какую-нибудь сторону. Нормаль-
ная реакция поверхности будет, очевидно, направлена в ту сторону, в кото-
рую точка может покинуть поверхность. Следовательно, если точке сообщить
перемещение, при котором она покидает поверхность (освобождающее пере-
мещение), то работа реакции будет положительна; она будет равна нулю
только в том случае, когда реакция также равна нулю. Если точке сообщить
перемещение по поверхности (неосвобождающее перемещение), то работа
реакции будет равна нулю.
Возьмем теперь две точки, связанные не имеющей массы нерастяжимой
нитью. Если нить натянута, то реакциями связи будут натяжения Т на обоих
концах, стремящиеся сблизить точки. Если обе точки переместить таким
образом, чтобы расстояние не изменилось (неосвобождающее перемещение),
то сумма работ натяжений будет равна нулю (п. 88); но если при перемеще-
нии точки сближаются (освобождающее перемещение), то сумма работ натя-
жений будет, очевидно, положительной; она будет равна нулю лишь
в частном случае, когда натяжение также равно нулю.
Резюмируя сказанное для всех перемещений, допускаемых связями
получаем
где §L, как и прежде, обозначает сумму работ реакций связей и знак
равенства следует брать для неосвобождающих перемещений.
Установив это, допустим, что система находится в равновесии. Каждая
точка, как мы это подробно разобрали в п. 165, будет находиться в равно-
весии под действием всех приложенных к ней сил как непосредственно
заданных, так и реакций связей, и если системе сообщить какое-нибудь
возможное перемещение, то получится
где §D — сумма работ заданных сил. Но если перемещение допускается
связями, то, как мы видели, $L > 0 и, следовательно,
Таким образом, высказанное условие является необходимым, причем знак
равенства соответствует неосвобождающим перемещениям.
Достаточность условия. Для доказательства, так же как и в п. 165,
покажем, что если равновесия нет, то существует по крайней мере одно
перемещение, допускаемое связями, для которого сумма работ ffD заданных
сил отлична от нуля и положительна. В самом деле, если равновесия нет,
то система приходит в движение и совершает перемещение, допускаемое
связями. В этом действительном перемещении каждая точка перемещается
вдоль равнодействующей всех приложенных к ней сил как непосредственно

244	ЧАСТЬ ВТОРАЯ. СТАТИКА
заданных, так и реакций связей. Работа этой равнодействующей, равная сумме
работ составляющих сил, будет, следовательно, положительная, и мы имеем
fz>+IT?>0.	C)
Но в действительном перемещении сумма J~? работ реакций связей
равна нулю. Это очевидно, если действительное перемещение является неос-
вобождающим перемещением, так как к нему может быть приложено все,
что было сказано о работе реакций связей, в случае, когда последние выра-
жаются равенствами. Но то же самое будет по-прежнему справедливо и
в случае, когда действительное перемещение является освобождающим
перемещением; это вытекает из того, что если действительное перемещение
является освобождающим перемещением для какой-нибудь связи, то соответ-
ствующая реакция связи равна нулю и, следовательно, ее работа также
равна нулю.
Например, возьмем какую-нибудь точку, лежащую на поверхности, кото-
рую она может покинуть в какую-либо сторону. Соответствующая реакция
связи будет нормальной реакцией. Если точка приходит в движение под
действием приложенных к ней сил, то могут представиться два случая: либо
точка переместится по поверхности (неосвобождающее перемещение) и тогда
работа реакции будет равна нулю, либо она покинет поверхность (освобождаю-
щее перемещение), но тогда реакция будет равна нулю, так как, по предположе-
нию, поверхность не удерживает точку и работа реакции будет по-прежнему
равна нулю. Теперь возьмем две точки, связанные нитью. Если обе точки
под действием приложенных к ним сил приходят в движение, то могут
представиться два случая: или нить остается натянутой (равенство) и сумма
работ натяжений равна нулю (п. 88), или точки сближаются (неравенство),
но тогда нить не будет более натянутой, натяжения будут равны нулю и их
работа по-прежнему будет равна нулю.
Резюмируя изложенное, можно сказать, что для действительного пере-
мещения сумма работ реакций связей равна нулю,
и, следовательно, согласно неравенству C) для действительного переме-
щения
что и требовалось доказать.
Примечание. Таким образом, доказанное условие является и необ-
ходимым и достаточным. Его можно высказать более кратко: для равновесия
необходимо и достаточно, чтобы на всех перемещениях, допускаемых
связями, было
D)
Отсюда само собой будет вытекать, что для неосвобождающих пере-
мещений
Действительно, если для неосвобождающего перемещения получится §D < О,
то, так как противоположное перемещение будет также допускаться связями,
для этого нового перемещения получится |Го > 0, и, следовательно, усло-
вие D) не будет более выполняться для всех допускаемых связями пере-
мещений.
185. Аналитические выражения. Пусть на точки наложены связи, вы-
ражаемые равенствами и неравенствами такого вида, как A) и B). Если обо-
значить через Хч, К,, Z, проекции равнодействующей заданных сил, прило-
женных к точке (xv, у„ ,г„), то для того, чтобы выразить, что имеет место

ГЛАВА VIII. ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ
245
равновесие, надо написать, что для всех перемещений, удовлетворяющих
соотношениям A) и B), выполняется неравенство
2
+ Y, Ьуч + Zv 5г.,) < 0.
E)
Начнем с того, что приравняем нулю сумму в левой части соотношения
для всех неосвобождающих перемещений, т. е. для всех перемещений,
которые получатся, если приравнять нулю левые части равенств A) и B).
Таким путем, при помощи методов п. 171 и 177, будут найдены положения
равновесия.
После этого останется выбрать среди найденных положений те, при кото-
рых для каждого освобождающего перемещения сумма работ заданных сил
равна нулю или отрицательна. Таким путем получатся все возможные поло-
жения равновесия, при которых все связи осуществлены.
Допустим, например, что использованы множители Лагранжа. Написав,
что при всех неосвобождающих перемещениях сумма работ приложенных
сил равна нулю, получим, как в п. 178, следующие необходимые условия
равновесия:
F)
= О,
где n = 1, 2, ..., п.
Возьмем теперь какое-нибудь положение равновесия, определяемое
этими уравнения'ми. Чтобы они были применимы, необходимо и достаточно,
чтобы множители Xff+l, lg+2, ¦¦-, Хл, соответствующие соотношениям B),
были отрицательны. Действительно, сообщим системе освобождающее пере-
мещение 8лг„, 5у„, 52\,, удовлетворяющее соотношениям A) и B). Вычисляя
сумму 2 (Xv 5xv -f- Y-fiy-t + Z$z-i) ПРИ помощи уравнений F), мы видим, что
коэффициенты при X], Х2, ..., Xff равны нулю в силу соотношений A) и остается
—	\+i (Ад+1,1 Ьх1 + Вд+\, 1 Ь
—	^д + Ъ (Ад+2,15-*! + ¦••) —
Cg+U
i+ ¦¦¦)¦	G)
Эта сумма должна быть отрицательная при любых перемещениях, удовле-
творяющих соотношениям B), при которых коэффициенты перед множителями
\+v ^0+з. ••-. Xh либо отрицательны, либо
равны нулю.	О	X
186. Пример. Найдем положение равнове-
сия тяжелой точки т, прикрепленной к не-
подвижной точке О при помощи невесомой и
нерастяжимой нити длины / и лежащей на на-
ружной поверхности неподвижного горизонталь-
ного цилиндра вращения.
Примем точку О за начало; вертикаль, на-
правленную вниз, —за ось Oz; прямое сечение
цилиндра — за плоскость гОх; ось Оу будет
тогда горизонтальна.
Сечение цилиндра плоскостью zx будет	р ,91
окружностью радиуса R, которую мы предпо-
ложим целиком расположенной внутри угла хОг
(рис. 121). Обозначим через а я с координаты центра С этой окружности.
Обозначим далее через В наивысшую точку окружности и предположим, чтс
длина I нити больше длины ОВ, но меньше длины касательной к окружности,

246	ЧАСТЬ ВТОРАЯ. СТАТИКА
проведенной из точки О, так что когда нить натянута, точка т будет лежать
на цилиндре.
Предполагая, что обе связи осуществлены, получим
! = 0, \
'	(8)
Возможные перемещения, допускаемые первой связью, таковы, что они
либо оставляют неизменным, либо уменьшают расстояние От, перемеще-
ния же, допускаемые второй связью, либо оставляют неизменным, либо
уменьшают расстояние от точки т до оси цилиндра, так что
Ь\(х — «)« + (гг—с)«]>6,
или, производя дифференцирование и меняя знаки во втором неравенстве
xbx + yby+zbz^Q, \
— (х — а)Ьх — (г — с)Вг<0. )
Так как единственной заданной силой является вес, то для равновесия
необходимо и достаточно, чтобы при условии осуществления соотношений (8)
выполнялось неравенство
mgbz^O	A0)
для всех перемещений (9).
Для упрощения вычислений мы применим метод, который, очевидно,
может быть распространен на общий случай. Примем в качестве независи-
мых переменных левые части соотношений (9), положив
= ЬХ, \
— (х — а)Ьх — (г — сM 8 I
где ЬХ и 8(а — две произвольные бесконечно малые величины. Разрешая эти
уравнения относительно Ьх и bz, имеем
_ (с — z) ЬХ — z ?(а — (с — z) у Ьу j
Х~(а_х)ьх^х~™{а__х) ь' I	A2)
~~	az — сх	' j
Для того чтобы получить наиболее общее перемещение, допускаемое
связями, можно принять, что Ьу, ЬХ и 5[л произвольны при условиях
8A < 0,	A3)
являющихся условиями (9), написанными в новых переменных. Для равно-
весия, согласно соотношению A0), необходимо, чтобы величина mg bz, или,
что то же, величина bz, была отрицательна или равна нулю для всех этих
перемещений.
Возьмем сначала неоевобождающае перемещения ЬХ =0, Ър = 0. Для
того чтобы было равновесие, необходимо, чтобы для всех этих перемеще-
ний величина mgbz или bz равнялась нулю. Но если ЬХ = 0, В[л = 0, то
для Ьг из равенства A2) получаем
— (а — х) у Ьу
az — сх
и чтобы эта величина была равна нулю при любом Ьу, необходимо и доста-
точно, чтобы

ГЛАВА VIII. ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ	247
Это необходимое условие равновесия распадается на два: у = 0 и
а — х = 0. Рассмотрим последовательно каждый из этих случаев.
Первый случай, у = 0. Полагая в уравнениях связи (8) у = 0, получим
два соотношения
= Р,
определяющих два положения равновесия в точках А и А' пересечения
окружности основания цилиндра с окружностью, лежащей в плоскости xz
и описанной из точки О как из центра радиусом, равным /. Обозначим
через х, у, z координаты одного из этих положений. Чтобы узнать, при-
годно ли оно, дадим точке т в этом положении какое-нибудь освобождаю-
щее перемещение, т. е. такое, для которого
8Х < 0, 8A < 0.
Необходимо, чтобы при таком перемещении работа mgbz заданной силы
была или отрицательна, или равна нулю. Но при у = 0 из выражения A2}
для Ъг получим
(а — х) ЬХ — х S(a
Ьг=-
аг — сх
и это выражение должно быть или отрицательным, или равным нулю,
когда 8а, и 8(а или отрицательны, или равны нулю.
Для положения А величины az ~-сх и а —¦ х отрицательны, а х поло-
жительна; следовательно, bz имеет отрицательные значения при всех осво-
бождающих перемещениях, и положение А пригодно.
Для положения А' величины .а — х, х и az — сх положительны; bz не
будет отрицательным при всех отрицательных или равных нулю значениях 5Х.
и ?(а. Например, при 5Х = 0 и 5(а < 0 величина bz получается положитель-
ной. Положение А' не пригодно. Это видно сразу, так как если точку т
положить на поверхности цилиндра в А', то она упадет.
Второй случай. Положим теперь х = а. Тогда из второго из уравне-
ний (8) связей имеем
~ г	up
Это показывает, что искомые положения лежат либо на наивысшей обра-
зующей z = с — R, либо на наинизшей образующей z = с -j- R цилиндра.
Согласно первому соотношению (8) они лежат на пересечении этих обра-
зующих со сферою радиуса I, описанной из точки О как из центра. Эта
сфера пересекает верхнюю образующую B(z = с — R) в двух симметричных
относительно плоскости zx точках Е и Е и не пересекает нижней обра-
зующей (г — с -\- R). Проверим, будет ли одно из этих положений Е и Ег
пригодно. Координаты этих положений будут
х — а, у==^0, z = c — R.	A4)
Для того чтобы положение было пригодно, нужно, чтобы для всех
освобождающих перемещений получалось
mg bz < 0.
Но значение A2) Для Ьг при условиях A4) для координат рассматри-
ваемых положений будет
, _ je?|i 	6(х
~~ az — сх к
При всех освобождающих перемещениях Ьу. < 0 значение bz отрица-
тельно или равно нулю; следовательно, оба положения Е и Е пригодны.

248	ЧАСТЬ ВТОРАЯ. СТАТИКА
Можно к этой задаче применить, в качестве упражнения, метод мно-
жителей Лагранжа. Тогда положения равновесия определятся соотношениями
: — Х2 (х — а) = О,
= 0,
mg -\- \±z — Х2 (z — с) = 0,
где Xj и Х2 должны быть отрицательными или равными нулю.
Примечание. В соответствии с общим методом мы нашли положе-
ния равновесия в предположении, что связи осуществлены, т. е. что урав-
нения связей (8) удовлетворяются.
187. Связи, выражаемые неравенствами в конечной форме. В пре-
дыдущих параграфах мы предполагали, что связи выражаются равенствами.
Но мы предполагали, что связи осуществляются таким образом, что пере-
мещения, допускаемые связями, выражаются неравенствами. Мы показали,
как можно найти все положения равновесия, при которых все связи осу-
ществлены.
Можно поставить более общую задачу следующим образом.
Представим себе систему точек, подчиненных связям, из которых одни
выражаются g равенствами в конечной форме:
/i (хъ Уъ *ь х2, Уъ z2	хп, уп, zn) = 0,
Уь *i. . ••-. хп, yn,zn) = 0,	(]5)
fg (*i> Уъ гъ	••¦< хп, У п. г„) = 0,
а другие выражаются h — g соотношениями неравенств тоже в конечной
форме:
/ (ъ Уь *1	хп, уп, гп) <0,
2(-«1. Уъ гь ¦¦¦< хп, Уп< гп) <0.
A6)
/ft (-«i. Уь гь .... хп, уп, zn) < 0. J
Тогда задача нахождения всех положений равновесия системы под дей-
ствием заданных сил распадается на несколько других задач, исследованных
выше.
Мы будем говорить для краткости, что связь fg+\ осуществлена, если
система находится в положении, при котором функция fg+i\X\,yi, z^, ...,xn,
уп, zn) равна нулю и что указанная связь не осуществлена, если функция
fg+i удовлетворяет неравенству связи A6)
/ff+i < 0.
То же самое будет для остальных связей fg+%, •¦-, /j,.
Тогда различные положения равновесия распадаются на следующие:
1°. Могут существовать положения равновесия, при которых все
связи fg+i, fg+2> •••tfh осуществлены, а перемещения, допускаемые свя-
зями, сохраняют функции f\,f%, ...,fg равными нулю, а функции/fl+],
/л+ь ••¦./п или сохраняют равными нулю, или делают отрицательными.
При этих условиях перемещения, допускаемые связями, удовлетворяют g
равенствам
В/1 = 0, 5/3 = 0	 5/^ = 0
и h — g неравенствам
..., S/ft<0.
Положения равновесия этого рода будут как раз те, которые выведены
методами п. 184.

ГЛАВА VIII. ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ	249
2°. Могут существовать положения равновесия, при которых одна
из связей A6) не осуществлена, а остальные осуществлены. Например,
можно искать положения равновесия, при которых
fg+l < О
0, /а+3 = 0	 Д = 0.	A7)
Тогда снова получится такая же задача, как в п. 184, при которой
осуществлены связи A5) и A7), а допускаемые перемещения удовлетворяю^
равенствам
8/i = 0. 5/2=0	 5/3 = 0
и неравенствам
«Д<0 S/<0»Д<0.
Но из этих положений равновесия системы нужно взять только,
для которых выполняется условие
fg+i < 0-
3°. Точно так же могут существовать положения равновесия, при
рых не осуществлены два, три или вообще р связей A6), например,
/я+1<0, /а+2<0	/в+,<0,	A8),
а осуществлены остальные:
= 0	 Д = 0.	A9)
Возможные перемещения, допускаемые связями, удовлетворяют
ствам A5) и неравенствам
Ve+,+i<0. «/,+,+*< 0	 5Д<0.	B0)
Эти положения равновесия находятся методом п. 184 без условий A8)t
Однако из найденных таким образом положений равновесия нужно coxpa-t
нить только те, для которых выполняются неравенства A8).
4°. Могут, наконец, существовать положения равновесия, при которых^
ни одна из связей /fl+i, /#+2> •••, Д не осуществлена. Они найдутся, если,
определять положения равновесия системы, подчиненной только связям A5),
Но из полученных положений равновесия следует сохранить, дищь те, для
которых выполняются неравенства
0, /ff+2<0, .... Д<0.
Пример. В примере предыдущего пункта мы определили положения
равновесия точки, предполагая, что нить натянута и что эта точка лежит
на поверхности цилиндра, т. е. предполагая, что осуществлены обе связи
- — /2 = 0,
(х — af + (г — cf — #2 = 0.
В более общей постановке можно искать положения равновесия, при
которых
х°- + У2 + г"- — Р < 0,
(х — йJ + (г — с)"- — /
Тогда сначала нужно взять в обоих соотношениях знаки равенства, 4TQ
даст уже найденные положения равновесия.

250	ЧАСТЬ ВТОРАЯ. СТАТИКА
Затем нужно будет искать положения равновесия, при которых
Х2 + у2 + г2 — /2 < О,
(х — яJ + (z — сJ — #з = О,
т. е. при которых нить не натянута, но точка находится на цилиндре. Тогда
в качестве возможных положений равновесия получатся все точки образую-
щей В, расположенные между найденными выше положениями Е и Е'.
Точно так же нужно будет искать положения, для которых
*2 + У2 + ¦** — Р = О,
(х* — af + (z — с)* — /?* ^ О,
т. е. нить натянута, но точка находится вне цилиндра. Очевидно, получится
вертикальное положение равновесия нити.
Наконец, остается найти положения, для которых
*2 + У2 + ^ — Р < 0.
(х — af + (г — еJ — № > 0,
т. е. нить не натянута и точка лежит вне цилиндра. Таких положений равно-
весия не существует.
УПРАЖНЕНИЯ
1. Проверить, что если две точки М (х, у, z) и М' (х', у', z") системы
связаны нерастяжимой и невесомой нитью, проходящей через некоторую
кривую С, то сумма работ реакций связей (натяжений нити в точках М и
М') равна нулю для перемещения, допускаемого связью.
Ответ. Обозначая через А (а, Ь, с) точку, в которой нить опирается
яа кривую, и через Т натяжение, одинаковое вдоль всей нити, получим,
после приведений, для суммы работ натяжений, приложенных в точках М
и М', значение
равное нулю, так как не имеющий массы элемент ds нити, расположенный
в точке А, находится в равновесии под действием двух натяжений на его
концах и нормальной реакции кривой, вследствие чего эта реакция является
¦биссектрисой угла МАМ'.
2. Проверить тот же вопрос для случая, когда обе точки М и ЛГ свя-
заны невесомой нитью, скользящей без трения по неподвижной поверх-
ности S.
Нить располагается по прямолинейной части МА, затем по поверхности S
вдоль геодезической линии АА' и, наконец, снова по прямолинейной части А'М';
натяжение нити вдоль всей ее длины имеет одно и то же значение Т. Эти
свойства вытекают из того, что, поскольку нить не имеет массы, то при-
ложенные к ней силы находятся в равновесии. Обозначая через {а, Ь, с) и
(а', о', с') координаты точек А и А', имеем
МА + АА' + А'М' = const.
Если сообщить системе возможное перемещение, допускаемое связями, то
дуга АА' перейдет в A^Ay и при попытке проверить, что сумма работ натя-
жений в точках М и М' равна нулю, придем к геометрическому соотно-
шению
8 (АА') + AAV cos A^AA' + А?~А[ cos XjJA = 0,

ГЛАВА VIII. ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ	251
выражающему свойство геодезических линий поверхности. (Упражнение
в конце предыдущей главы для случая ср = 1.)
3.	Диск, ограниченный кривой С, движется в плоскости. Невесомая нить
закреплена в точке М контура С диска, обернута вокруг него и затем про-
тянута до точки М' системы, где она закреплена. Проверить, будет ли сумма
работ реакций связи равна нулю для перемещения, допускаемого этой
связью.
(Достаточно заметить, что связь входит в число связей, рассмотренных
в тексте, так как точка М' вынуждена скользить без трения по одной
из разверток кривой С. Можно также повторить рассуждения п. 162.)
4.	Равновесие простого домкрата- Машина состоит из шестерни радиу-
са а, которую при помощи рукоятки длины b заставляют вращаться вокруг
своей оси. Эта шестерня находится в зацеплении с зубчатой рейкой, так
что при вращении шестерни вокруг оси рейка перемещается вдоль самой себя.
Движущая сила Р приложена в конце рукоятки перпендикулярно к ней,
а сопротивление /? противодействует перемещению рейки. (Условие равно-
весия: РЬ — Ra = 0.)
5.	Дифференциальный ворот. Эта машина состоит из двух неизменна
связанных между собой цилиндров с общей осью, но разных радиусов г и г'.
Веревка, несущая блок, навернута вокруг обоих цилиндров в противопо-
ложных направлениях. Движущая сила Р приложена перпендикулярно к ру-
коятке радиуса а, а сопротивление R вызывается грузом, подвешенным к
блоку. [Условие равновесия 2aP = (r — r')R.]
6.	Принцип минимума суммы квадратов расстояний. (Мёбиус и
Гаусс, Crelle, т. 4.) Дана система точек Мь М2	Мп, находящаяся под дей-
ствием сил Р1г Р2	Рп- Система находится в равновесии в положении тх,
т2	тп, где силы имеют значения ph p2	рп. Отложим от точки т±
в направлении силы рх отрезок тх0х, равный рх/к, от точки т2 в направ-
лении р2 — отрезок т^Оч, равный p2/k	где k — отличная от нуля посто-
янная. Возьмем после этого произвольное положение М\, М2	Мп си-
стемы и приложим к точкам Мх, Л1?, •.., Мп силы Я,, Р2, ..., Рп, направ-
ленные соответственно по прямым MxOi, М2О2	МпОп и равные kM^Qi,
kM%02, ..., kMnOn. Под действием этих новых сил система будет по-преж-
нему находиться в равновесии в том же положении тх, т2, ..., тп, так как
в этом специальном положении силы Pv Р2,	, Рп совпадают с Р\,р2	рп.
Так как новая система сил Р[, Р'2< ..., Р'п имеет силовую функцию
то, как мы видим, рассматриваемое положение равновесия обращает, вообще
говоря, эту функцию в максимум или минимум и во всяком случае в этом
положении равновесия вариация функции U обращается в нуль.
Прилагая теорему к простейшему случаю, мы видим, что если точка т
находится в равновесии под действием трех сил тОх, тО2, тО%, то это
положение равновесия будет тем положением точки М, для которого сумма
МО\ + МО\ + Ш1
имеет минимум, что является хорошо известным свойством центра тяжести
треугольника OiO2O3.
7. Вообще рассмотрим систему точек Мх (хь уь zt), M% (x2, y2, z2), ...
.... Мп (х„, уп, zn), подчиненных заданным, не зависящим от времени
связям, и находящихся под действием непосредственно приложенных сил,
причем для простоты мы будем считать, что силы, действующие на точку М\,
приведены к одной силе Ру (XL, Yx, Zx), силы, действующие на точку М2, — к

252	ЧАСТЬ ВТОРАЯ. СТАТИКА
одной силе Ро, (X2, Y%, Z%), ... Допустим, что эта система имеет определенное
положение равновесия, для которого точки Mi, Л42	Мп занимают опреде-
ленные положения mv т2	тп с координатами (аь Ьь с{), (а2, Ь2, с2), ...,
(ап, Ьп, сп), а соответствующие силы имеют определенные значения рь
р2, .... рп с соответствующими проекциями (Аь В1г Сх), (А%, В2, С2), ...
..., (Лп, Вп, Сп).
Составим функцию U от хъ уь гх, х2, у2, г-,	хп, уп, zn, частные
„ dU dU dU
производные которой g—, -т—, j— принимают значения Ait Bt, Q (/ = 1,
2, .... п), когда система находится в рассматриваемом положении равнове-
сия, т. е. когда координаты хь уь zlt x2, y2, z% ..., хп, уп, гп принимают
значения щ, bb Cj, a^, bit cit ..., ап, Ьп, сп. Та же система, находясь под дей-
ствием сил Pv Я2> ..., Рп, имеющих силовую функцию U, будет по-прежнему
находиться в равновесии в том же самом положении т^, т2, ..., тп, так как
в этом положении силы Р[, Р'2	Р'п совпадают с силами рь рь ..., рп.
Следовательно, в общем случае, функция U имеет в этом положении равно-
весия максимум или минимум и во всчком случае ее вариация в этом поло-
жении равна нулю.
8.	Двойной тяжелый конус, образованный двумя одинаковыми конусами,
соединенными основаниями, положен на две пересекающиеся прямые, оди-
наково наклоненные к горизонту^ причем так, что центр тяжести конуса
находится в вертикальной плоскости, делящей пополам угол между обеими
прямыми. Найти условия равновесия (система тяжелая, 8? = 0).
Геометрически необходимо и достаточно, чтобы плоскость, проходя-
щая через центр тяжести и две точки касания конуса с прямыми, была
вертикальной, или чтобы линия пересечения касательных плоскостей к кону-
сам в точках касания была горизонтальна.
Аналитически, если т обозначает половину угла раствора конусов,
а — угол наклона плоскости обеих прямых к горизонту, р — половину угла
между вертикальными плоскостями, проведенными через эти прямые, то
условие равновесия будет tg a = tg m tg р. (А. Ф л ё р и, Annales de Mathe-
matiques, 1854.)
9.	Применив положение о том, что равновесие тяжелой системы полу-
чается, если приравнять нулю вариацию высоты G центра тяжести, доказать,
что свободной поверхностью находящейся в равновесии тяжелой жидкости
является горизонтальная плоскость.
10.	Если три точки ть ть ms связаны таким образом, что площадь
треугольника ть /п2, /п8 постоянна, и если на точки действуют три силы Ръ
Ръ Р8, то для равновесия необходимо и достаточно, чтобы эти силы лежали
в плоскости треугольника и чтобы они были перпендикулярны противопо-
ложным сторонам треугольника и им пропорциональны.
Если четыре точки связаны таким образом, что объем тетраэдра с вер-
шинами в этих точках постоянен, и если на них действуют четыре силы,
то для равновесия необходимо и достаточно, чтобы эти силы были перпен-
дикулярны противоположным граням тетраэдра и им пропорциональны
(К. Нейман).
11.	Однородный тяжелый стержень О А вращается в вертикальной пло-
скости вокруг своего закрепленного конца О. Нить, прикрепленная к концу А,
перекинута через находящийся на одной вертикали с О бесконечно малый
блок В и несет на своем конце противовес Q, скользящий без трения по
находящейся в той же вертикальной плоскости кривой С.
Какова должна быть эта кривая, чтобы равновесие системы было без-
различным? (Подъемный мост Белидора.)
[Необходимо, чтобы центр тяжести системы перемещался горизонтально.
-Приняв точку В за начало, найдем, что в полярных координатах уравнение

ГЛАВА VIII. ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ	253
кривой имеет вид г2 — г (а -\- b cos 8) -)- с = 0. Это — овал Декарта; в частном
случае, когда с — О, будет улитка Паскаля.]
12.	Тот же вопрос в предположении, что кривая С проходит через В
и что вместо того, чтобы быть натянутой, нить протянута по кривой
(циклоида).
13.	Найти положение равновесия однородного тяжелого стержня длины 2а,
расположенного в вертикальной плоскости и опирающегося на непо-
движную точку О, по которой он может скользить, а концом А — на вер-
тикальную стену.
E? = 0. Если Ъ — расстояние от точки О до стены, то для равновесия
получается О А = Уab"*; эта величина должна быть меньше а.)
14.	Однородный тяжелый стержень АВ длины 2а опирается на край
полуокружности, диаметр которой 2/? горизонтален, а конец его лежит на
этой же полуокружности. Найти положение равновесия. (Наклон / стержня
дается уравнением 4/? cos2/ — a cos I—2R = 0; для возможности равновесия
a Y&	а
необходимо, чтобы было -~— > R > -^.
15.	В вертикальной плоскости даны две неподвижные кривые С и С.
Две тяжелые точки с массами т и т' скользят без трения по этим кривым
и связаны друг с другом невесомой и нерастяжимой нитью, проходящей
через бесконечно малый блок О. Одна из этих кривых дана. Какой должна
быть другая кривая, чтобы равновесие было безразличным? Если взять гори-
зонтальную полярную ось, то необходимо и достаточно, чтобы
тОт sin 8 + т'От' sin 8' = const.
16.	Рассматриваются два одинаковых однородных стержня АВ и АС,
связанных шарнирно в точке. А и касающихся вертикальной окружности
таким образом, что точка А находится на одной вертикали с центром.
Найти положение равновесия. (Если 2/ — длина стержня, а — угол их на-
клона с горизонтом, R — радиус круга, то tg3a-)-tga	 = 0. Имеется
/\
одно положение равновесия. Устойчиво ли оно?)
17.	Равнобедренный тяжелый однородный треугольник, высота кото-
рого h и равные стороны имеют длину а, лежит своими тремя вершинами на
поверхности сферы. Найти положение равновесия (Вриглей).
18.	Равносторонний однородный тяжелый треугольник ABC находится
в вертикальной плоскости. Его вершина А скользит без трения по верти-
кальной прямой Ох, а середина М стороны АВ прикреплена к неподвижной
точке О этой прямой при помощи невесомой и нерастяжимой нити.
Найти положения равновесия. Исследовать их устойчивость. Если обо-
значить через а угол ОМ с осью Ох, то задача приведется к нахождению
максимума и минимума функции sin (а + ^Ь
19.	Однородный тяжелый эллиптический диск лежит в вертикальной
плоскости и касается горизонтальной оси, по которой он может скользить
без трения. По контуру диска обернута нить, несущая на конце заданный
груз. Найти положения равновесия системы. (Можно привести эту задачу
к следующей: провести к эллипсу параллельные касательную и нормаль
таким образом, чтобы отношение их расстояний до центра было заданным.)
20.	Однородная тяжелая пластинка ABCDE, лежащая в вертикальной
плоскости, имеет следующую форму; АВ — горизонтальная прямая длины х,
ВС—вертикаль длины b, CD — горизонталь длины с, меньшей чем х,
DE—дуга неизвестной кривой Г, выходящей из точки D и поднимающейся
над CD со стороны точки А; и, наконец, ЕА — вертикальная прямая.
Пластинка может свободно вращаться вокруг точки И, предполагаемой

254	ЧАСТЬ ВТОРАЯ. СТАТИКА
закрепленной, и находится под действием веса и горизонтальной силы F, при-
ложенной в точке Е. Какой должна быть форма кривой Г, чтобы равновесие
имело место при любом положении ограничивающей ординаты ЕА, т. е.
каково бы ни было х (Ь и с рассматриваем как постоянные)? (Фурман).
Если взять горизонтальную и вертикальную оси с началом в точке D,
— +СХ
то уравнение этой кривой получится такое: у-\-Ъ = be"
21.	Найти такие кривые, чтобы однородная тяжелая цепь длины /, сколь-
зящая по ним без трения, была в равновесии в любом положении.
Ответ. Если взять вертикальную ось Oz и обозначить через /(s) пери-
одическую функцию периода /, то необходимо и достаточно, чтобы коорди-
ната z какой-нибудь точки кривой была связана с дугой s соотно-
шением z = f(s). Гак, можно принять z = a sin—— , где k — целое число.
22.	Дана направленная вверх вертикальная прямая ОВ и два невесомых
стержня BD и ОС, связанных шарнирно в точке С, расположенной мвжду В
и D. Стержень ОС вращается вокруг точки О, а конец В стержня BD
скользит без трения по неподвижной прямой ОВ. К точке D подвешен груз.
Найти положения равновесия. В каких случаях равновесие будет безраз-
личным?
23.	Шесть одинаковых однородных стержней веса р связаны шарнирно
своими концами и образуют шестиугольник, лежащий в вертикальной пло-
скости. Сторона АВ этого шестиугольника закреплена неподвижно в гори-
зонтальном положении; остальные стороны расположены симметрично
относительно вертикали, проходящей через середину АВ.
Какую направленную вертикально вверх силу F нужно приложить к
середине горизонтальной стороны, противоположной АВ, чтобы система была
в равновесии? (F=3p).
24.	Твердое тело с пятью степенями свободы. Положение свободного
твердого тела в пространстве зависит от шести параметров (п. 183). Если
между этими параметрами установить какое-нибудь соотношение, то тело
будет иметь только пять степеней свободы и его положение будет зависеть
от пяти параметров q±, q% ¦.., qr,- Доказать, что если тело поместить теперь
в какое-либо определенное положение, то все возможные перемещения,
допускаемые наложенными на него связями, должны удовлетворять следую-
щему геометрическому условию. Существует такая неподвижная прямая D,
что проекция на нее скорости поступательного движения, сообщенной опре-
деленной точке тела, находится в постоянном соотношении с проекцией на
ту же ось сообщенной телу мгновенной угловой скорости вращения. Нужно
заметить, что координаты хй, у0, zq определенной точки тела и девять на-
правляющих косинусов осей Ox, Оу, Oz прямоугольного координатного три-
эдра, связанного с телом, относительно неподвижных осей О\Х±, уг, z± (п. 51)
будут функциями пяти параметров qi. Тогда, если сообщить этим параметрам
произвольные вариации hq±, bqSt ..., о^5 в течение промежутка времени W, то
проекции У°х, V°y, V°z возможной скорости точки О на оси Охуг и ком-
поненты р, q, r возможной мгновенной угловой скорости вращения по тем
же осям будут линейными однородными функциями от -Щ-, ~, ¦¦¦> -Щ-•
Исключение этих пяти произвольных величин приведет к линейному одно-
родному уравнению, связывающему величины Vx, V%, Vi, p, q, r, коэффи-
циенты которого будут функциями от qb q2, ¦ ¦., q~D- Интерпретация этого урав-
нения даст высказанную теорему. (В п. 201 Treatise of natural Phylosophy
Тэта и Томсона можно найти описание механизма, позволяющего осуще-
ствить такого рода связи.)

ГЛАВА IX
ПОНЯТИЕ О ТРЕНИИ
188. Общие сведения. До сих пор мы рассматривали твердые
тела как идеально твердые и идеально отполированные и допускали,
что если два тела, находящиеся в покое или в движении, соприка-
саются друг с другом в какой-нибудь точке и могут скользить друг
по другу, то их взаимодействие нормально к общей касательной
плоскости в этой точке.
Это предположение противоречит опыту. Естественные тела не
являются ни идеально твердыми, ни идеально гладкими. Когда два
естественных тела 'находятся в соприкосновении, то никогда касание
не происходит в одной точке; оба тела испытывают деформации,
вообще говоря, очень малые, вследствие которых касание проис-
ходит по малой части поверхности. Эти деформации постоянны, когда
тела находятся в равновесии, и становятся переменными, когда одно
тело скользит по другому. Тогда они вызывают колебания моле-
кул и поэтому развивается тепло или электричество, на возникно-
вение которых затрачивается часть работы
движущих сил.
Эти сложные явления становятся до-
ступными для расчета, если предположить,
что к нормальной реакции добавляются ка-
сательная сила и пары.
Вообразим два движущихся твердых
тела А и В (рис. 122), находящихся в сопри-
косновении. Пусть т — точка тела Л, находя-
щаяся в соприкосновении с телом В. Как
мы видели в п. 57, относительные скорости
различных точек тела А по отношению
к телу В, рассматриваемому как неподвиж-
ное, будут такими, как если бы тело А обла-
дало: 1) поступательной скоростью, называемой скоростью сколь-
жения и совпадающей с относительной скоростью Vr точки т,
лежащей в общей касательной плоскости к поверхностям тел в т;
2) мгновенным вращением с угловой скоростью ш вокруг оси, про-
ходящей через точку т.; слагающая юп этой угловой скорости по
общей нормали в т к обеим поверхностям называется скоростью
Рис. 122.

256	ЧАСТЬ ВТОРАЯ. СТАТИКА
верчения, а слагающая <x>t, лежащая в касательной плоскости, назы-
вается скоростью качения. Когда мгновенная угловая скорость ш
равна нулю, то говорят, что относительное движение тела А по
отношению к телу В является скольжением в собственном смысле
слова; когда относительная скорость точки т равна нулю, то сколь-
жение отсутствует и относительное движение тела А по отношению
к телу В является качением и верчением. Следовательно, в общем
случае имеют место одновременно скольжение, качение и верчение.
С точки зрения динамической, когда два движущихся твердых
тела А а В находятся в соприкосновении и давят друг на друга,
то оба тела деформируются и касание не происходит в одной точке
(рис. 122). Оба тела соприкасаются по некоторой весьма малой пло-
щадке и в каждой точке они воздействуют друг на друга. Согласно
теоремам о приведении системы сил, приложенных к твердому телу,
совокупность таких действий на какое-нибудь из тел может быть
приведена к одной силе, приложенной в произвольно выбранной точке,
и к паре. Так как тела соприкасаются по очень малой площадке,
то с точки зрения геометрической можно считать, что касание
происходит в одной единственной точке т, которую мы будем на-
зывать геометрической точкой касания. Тогда действие тела В на
тело А можно свести к следующим элементам:
1)	к силе N, приложенной к телу А в геометрической точке каса-
ния т и направленной по нормали к соприкасающимся поверхностям;
эта сила является нормальной реакцией, препятствующей взаимному
проникновению тел;
2)	к силе F, приложенной в той же точке т и лежащей в общей
касательной плоскости к соприкасающимся поверхностям, проведен-
ной в точке т; эта сила является трением скольжения, препят-
ствующим скольжению;
3)	к паре G, вектор момента которой нормален к соприкасающимся
поверхностям; эта пара является парой трения верчения, противо-
действующей верчению;
4)	к паре Н, вектор момента которой лежит в общей касательной
плоскости соприкасающихся поверхностей и направлен по касатель-
ной составляющей u>t мгновенной угловой скорости вращения; эта
пара является парой трения качения, препятствующей качению.
Действие тела А на тело В выражается силами и парами, противо-
положными предыдущим. В общем случае влияние пар О и Н очень
мало по сравнению с влиянием сил N и F. Мы начнем с изучения
вопросов, в которых этими парами можно пренебречь, и вернемся в
последующих пунктах к специальному изучению трения скольжения
и верчения.
Мы предполагали, что оба тела А а В касаются по очень
малой площадке, которую можно рассматривать как точку. В неко-
торых вопросах оба тела могут иметь бесчисленное множество
геометрических точек касания; так, например, будет для куба,

ГЛАВА IX. ПОНЯТИЕ О ТРЕНИИ	257
лежащего на плоскости. Тогда предыдущие соображения должны быть
применены к каждой геометрической точке касания.
189.	Трение скольжения. Первые опыты по изучению трения
скольжения были проделаны Кулоном и были повторены генералом
Мореном. Но этот вопрос требует нового исследования. Необходимо
различать два случая трения скольжения: 1) трение в состоянии покоя
и, в частности, трение в начале движения; 2) трение в состоянии
движения.
190.	Законы трения скольжения в состоянии покоя. Возьмем тяже-
лый брусок, лежащий на горизонтальном столе. Система находится
в равновесии, и поэтому сила давления стола на брусок имеет в дан-
ном случае равнодействующую N, нор-
мальную к столу, равную и противо- /^	\/V
положную весу Р тела (рис. 123).
Приложим теперь к телу в вертикаль-
-Q
p
ной плоскости, проходящей через его
центр тяжести, и как можно ближе —
к столу горизонтальную силу Q, ин-
тенсивность которой постепенно уве-
личивается, начиная от нуля. Пока эта
сила Q очень мала, тело не будет сколь-	Рис, 123.
зить и будет оставаться в равновесии.
Следовательно, необходимо, чтобы реакция R стола на тело была
равна и противоположна равнодействующей веса Р и силы Q. Эта
реакция может быть разложена на две: нормальную N, равную и
прямопротивоположную силе Р, и. касательную F, равную и противо-
положную силе Q. Эта касательная составляющая и является силой
трения. Для угла р между R и нормалью N имеем
1ч	i
Если постепенно увеличивать Q, то наступит момент, когда эта
сила достигнет, значения Ф, при котором тело приходит в движение.
Соответствующее значение Ф силы F называется трением в начале
движения; соответствующее значение ср угла р, для которого
	 Ф
называется углом трения.
Можно говорить также, что скольжение начинается лишь с того
момента, когда равнодействующая сил Р и Q, приложенных к телу,
образует с нормалью угол, превосходящий ср.
Кулон измерял значения Ф и ср на опыте, позволявшем осуще-
ствить предыдущие условия (на повозке, которую тянули возрастаю-
щими силами). Он пришел к следующим трем законам.
1°. Трение в начале движения не зависит от площадей поверхно-»
стей, находящихся в соприкосновении.

258
ЧАСТЬ ВТОРАЯ. СТАТИКА
2°. Оно зависит от природы этих поверхностей.
3°. Оно пропорционально нормальной составляющей реакции, или,
что приводится к тому же, нормальной составляющей давления.
Постоянное отношение / силы трения Ф в начале движения к нор-
мальной реакции N, или к нормальному давлению Р, называется
коэффициентом трения:
Угол трения ср определяется тогда формулой
tg<f>=/.
Угол р, при котором существует равновесие, меньше ср.
Например, если тело и стол сделаны из металла, то при отсут-
ствии смазки
/ = 0,19, ср=10°46'.
Примечание. Выше мы говорили, что силу Q нужно прила-
гать возможно ближе к плоскости. Вот из каких соображений де-
лается это ограничение. Если сила Q приложена слишком высоко,
то до того, как она достигнет предельного значения Ф, при котором
начнется скольжение, равнодействующая Q и Р может выйти за осно-
вание тела; тогда она не будет уравновешиваться, и тело опрокинется.
191. Равновесие тел с трением. 1°. Одна точка каса-
ния. Рассмотрим тело 5, положенное на другое тело S', с ко-
„	 „ торым оно соприкасается по очень малой ча-
г	"* сти поверхности. Мы будем предполагать
последнюю приведенной к одной точке А.
Реакция R тела S' на тело 5 складывается
из нормальной реакции N и касательной реак-
ции F (рис. 124), направление которой не-
известно и максимум которой равен /ЛЛ
Угол р между R и N будет, следовательно,
меньше угла трения ср. Для того чтобы тело 5
было в равновесии, необходимо, чтобы суще-
ствовало равновесие между непосредственно
приложенными к телу 5 силами и реакцией R,
или чтобы силы, приложенные к телу, имели
одну равнодействующую, равную и прямо
противоположную силе R, т. е. а) проходя-
щую через точку А, б) направленную так,
чтобы прижимать тело 5 к телу S' и в) образующую с нормалью AN
угол, меньший, чем угол трения.
Эти необходимые условия достаточны, так как если они выпол-
нены, то можно предположить, что равнодействующая непосредственно
приложенных сил перенесена в точку А и разложена на две силы:
на нормальную силу Р и на касательную силу Q; под действием
Рис. 124.

ГЛАВА IX. ПОНЯТИЕ О ТРЕНИИ	259
этих сил скольжения не будет, так как угол равнодействующей с нор-
малью меньше ср, вследствие чего (рис. 123)
?</. Q<Pf.
и касательная составляющая меньше, чем трение в начале движения.
Если рассматривать конус вращения С с осью AN, описанный
прямой AD, образующей с AN угол ср, то для равновесия необхО-*
димо и достаточно, чтобы силы имели равнодействующую, проходя-
щую через А и лежащую внутри конуса С.
Из предыдущих рассуждений можно заключить также, что любая
приложенная к телу сила, проходящая через точку А и образующая
с нормалью угол, меньший чем ср, т-. е. сила, лежащая внутри конуса С,
уравновешивается реакцией тела S', так как эту силу можно разложить
так, как мы только что указали.
2°. Несколько точек касания. Вообразим тело 5, покоящееся
в точках Av А2, .... Ар на нескольких телах Su S2, .... Sp
с коэффициентами трения, равными соответственно /t, /2	/р
и с углами трения срх, ср2, .... срр. На тело 5 действуют заданные
силы Fif F2, . ¦ ¦, Fn; требуется определить условия равновесия.
Реакция тела <SV на тело 5 есть сила #v, приложенная в точке А,
и образующая с нормалью Л/, угол, меньший угла трения ср„, т. е.
эта сила лежит внутри конуса С„ с вершиной Л,, осью Л/„ и углом <р„.
Для того чтобы было равновесие, необходимо и достаточно, чтобы
заданные силы Fv /%_, .... Fn уравновешивались системой сил реак-
ций Rv R2, ¦.., Rp, удовлетворяющих предыдущим условиям, т. е.
чтобы система заданных сил была эквивалентна системе сил —Ru
—R2, ...,—Rp, проходящих соответственно через точки Ли А2	Ар
и лежащих внутри конусов С1з С2, .. ., Ср. Эти последние силы все
уравновешиваются реакциями поверхностей Sv S2, .... Sp.
3°. Бесконечное число точек касания. Если тело 5 соприка-
сается с некоторыми телами по площадкам конечной протяженности,
то необходимо и достаточно, чтобы система сил Fv F2, ..., Fn была
эквивалентна системе какого угодно числа сил, пересекающих пло-
щадки соприкосновения и образующих с нормалями в точках пере-
сечения углы, меньшие соответствующих углов трения.
Примечание. Эти условия аналитически выражаются при по-
мощи неравенств; поэтому в общем случае существует бесчисленное
множество положений равновесия, образующих непрерывные множества.
192. Тяжелое тело, опирающееся на плоскость в нескольких точках
и находящееся под действием только одной силы F. Для того чтобы
тело било в равновесии, необходимо и достаточно:
1)	чтобы сила F была направлена так, чтобы она прижимала тело к пло-
скости;
2)	чтобы она составляла с нормалью угол, меньший угла трения <р;
3)	чтобы она пересекала плоскость внутри ©порного многоугольника,
определяемого, как в п. 112.

260
ЧАСТЬ ВТОРАЯ. СТАТИКА
Эти условия необходимы. В самом деле, пусть, как и в п. 112, А^,
Аъ ..., Ар — точки касания тела с плоскостью и Ru R2, ..., Rp — ре-
акции плоскости в этих различных точках. Если представить себе ось Oz,
направленную нормально к плоскости в сторону, где находится тело, то все
эти реакции будут направлены в ту же сторону от плоскости и будут со-
ставлять с осью Oz углы меньше ср. Так как совокупность сил Rlt R%, .. .,RP, F
находится в равновесии, то реакции Rb R2, ..., Rp имеют равнодействую-
щую, которая, очевидно, равна и прямо противоположна силе F. Но главный
вектор реакций направлен, очевидно, в ту же сторону от плоскости, что и
ось Oz, и образует с ней угол, меньший ср; следовательно, сила F напра-
влена в противоположную сторону и тоже образует с осью Oz угол, мень-
ший ср. Чтобы показать необходимость третьего условия, возьмем какую-
нибудь сторону А(Ак опорного многоугольника; сумма моментов сил Rlt
R2, ..., Rp и F относительно этой стороны должна равняться нулю; моменты
всех сил Rb R2, ..., Rp относительно этой стороны имеют одинаковые
знаки; сила F должна иметь момент противоположного знака и должна
поэтому пересекать плоскость в точке А, лежащей по отношению к AiAy,
по ту же сторону, что и остальные точки опоры. Так как это имеет место
для каждой из сторон опорного многоугольника, то точка А находится
внутри этого многоугольника.
Эти необходимые условия и достаточны. В самом деле, если они выпол-
нены, то можно всегда разложить силу F на одинаково с ней направленные
параллельные силы, приложенные в точках опоры А±, А%	Ар. Все эти
составляющие уравновешиваются сопроти-
влением плоскости.
193. Лестница. Лестница АВ опи-
рается на горизонтальный пол и вертикаль-
ную стену; допустим, что средняя линия
лестницы лежит в плоскости, перпендику-
лярной полу и стене (рис. 125); эту пло-
скость мы примем за плоскость чертежа.
Обозначим через G центр тяжести
лестницы и стоящего на ней в произволь-
ном положении человека и найдем усло-
вия равновесия, предполагая, что коэффи-
циенты трения в точках А и В равны одной
и той же величине f и, следовательно, углы
трения имеют одно и то же значение ср.
Если лестница образует со стеной
угол р, меньший угла трения ср, то будет
иметь место равновесие при любом поло-
жении точки G. В самом деле, всегда
можно перенести вес Р, приложенный в точке G, вдоль его направления
и разложить на две силы, из которых одна направлена по DB нормально
к стене, а другая по линии DA, образующей с нормалью AN к полу
угол DAN, меньший р и, следовательно, меньший угла трения; обе эти
составляющие уравновешиваются.
Допустим теперь, что угол лестницы со стеной превышает угол тре-
ния ср. Так как вес и реакции стены и пола должны уравновешиваться,
то эти три силы пересекаются в одной точке и лежат в плоскости чертежа.
Проведем в точках А и В нормали AN и BN к стене и к полу и затем
две прямые АК.М и ALQ, образующие с AN угол ср, и две прямые BQ
и BL, образующие с BN тоже угол ср. Эти четыре прямые, являющиеся
прямыми пересечения плоскости чертежа с рассмотренными в общем слу-
чае конусами, образуют четырехугольник MQLK- Так как реакции стены и
пола образуют с нормалями углы, меньшие ср, то их точка пересечения
находится внутри четырехугольника MQLK- Так как линия действия силы Pf
Нис. lib.

ГЛАВА IX. ПОНЯТИЕ О ТРЕНИИ
261
т. е. вертикаль, проведенная через точку G, должна проходить через упо-
мянутую точку пересечения реакций стены и пола, то для того, чтобы было
равновесие, необходимо, чтобы эта вертикаль пересекала площадь четы-
рехугольника. Это условие будет тогда и достаточным, так как если вер-
тикаль G пересекает этот четырехугольник, то, взяв точку D на этой вер-
тикали внутри четырехугольника, мы можем перенести в нее вес Р и здесь
разложить его на две силы, направленные по DA и DB, которые уравно-
весятся реакциями стены и пола.
Примем О А и ОВ за оси Ох и Оу и обозначим через а и Ь расстоя-
ния ОА и ОВ. Ближайшая к стене точка М, будучи пересечением двух
прямых
ВМ (y — b = xf) и AM
имеет абсциссу
f
r_a-bf
1
являющуюся положительной величиной, так как, по предположению, ajb
больше чем /, ибо угол р больше у. Для равновесия .необходимо и доста-
точно, чтобы абсцисса S центра тяжести G была больше х. Пусть т —
масса лестницы и mt — масса человека, стоящего на лестнице на расстоянии
хг от стены. Тогда, чтобы выразить, что S больше х, напишем:
a — bf
m -Tf -f- m^Xi
т-\-тг
откуда можно определить нижнюю границу для хх. Чтобы при любом поло-
жении человека равновесие было устойчиво, необходимо и достаточно,
чтобы
а	¦
т
a — bf
SA/ds
Эта формула определяет верхнюю гра-
ницу угла р, тангенс которого равен а\Ь.
194. Веревка, навернутая на по-
перечное сечение цилиндра. Пусть
веревка положена на поперечное се-
чение выпуклого цилиндра, по которому
она может скользить с трением. Коэф-
фициент трения равен /. Касание
происходит по дуге АВ (рис. 126);
веревка натягивается на концах Мй
и Mi натяжениями 7 и 7"i, при-
чем Т1\^Т0. Найдем условия равно-
весия, предполагая, что веревка на-
ходится в состоянии, когда она готова
начать скользить в сторону АВ. Этим самым мы найдем верхний пре-
дел, больше которого не должно быть натяжение Ть чтобы осуществля-
лось равновесие. Пусть s — дуга AM, ds — элемент, находящийся в точке М,
Nds — абсолютное значение нормальной реакции цилиндра, которая напра-
влена наружу, /N ds — абсолютное значение касательной реакции, которая
направлена в сторону МА. На основании естественных уравнений равнове-
сия нити имеем
dT.-fN = 0, — — N=0,
Р
Рис. 126.
ds

262	ЧАСТЬ ВТОРАЯ. СТАТИКА
так как значение реакции, отсчитываемой по главной нормали, равно — Nds,'
а отсчитываемой по касательной Mt в сторону возрастания дуг равно —
fN ds. Исключая N, получим
dT fds ..
ds
так как р=——, где а — угол между касательной Mt и фиксированной
касательной Т0М0. Следовательно, интегрируя от точки Мо до точки М\ и
обозначая через в угол между конечными касательными, или равный ему
угол АОВ между конечными нормалями, получим
1пГ1-1пГ0=/в, 7\=Г0/е.
Таково верхнее значение, больше которого не должна быть величина Ти
чтобы осуществлялось равновесие. Если веревка обвивается несколько раз
вокруг цилиндра, то угол в может быть больше чем 2п. Эта формула по-
казывает, что малым натяжением 7 можно уравновесить значительное
натяжение Ть полагая 6 достаточно большим. (Пуассон, Traite de
Mecanique, § 303.)
Интересные упражнения можно найти в сочинении английского ученого
Джеллета.
195.	Трение скольжения при движении. В случае движения
трение будет вполне определенным. Допустим, что движущееся твер-
дое тело, ограниченное поверхностью S, соприкасается с телом Sr
в точке А. Если имеется трение, то реакция тела S' на тело 5 рас-
падается на две силы: нормальную N, которая называется нормаль-
ной реакцией, и касательную F, которая является силой трения и
подчиняется трем следующим законам:
1°. Сила трения направлена в сторону, противоположную отно-
сительной скорости материальной точки А по отношению к 5.
2°. Она не зависит от величины этой скорости.
3°. Она пропорциональна нормальной реакции: F = fN; коэффи-
циент / является коэффициентом трения в начале движения.
Согласно опытам Гирна эти законы применимы главным образом
в случае непосредственного трения (т. е. когда трущиеся поверх-
ности сухие). Они должны быть изменены, если поверхности разде-
лены смазывающим веществом; в этом случае отношение F/N зави-
сит от скорости и от N. (См. Comptes Rendus, т. XCIX, стр. 953.)
196.	Трение качения в начале и во время движения. Выше
(п. 188) мы определили в общем виде пары, представляющие сопро-
тивление качению и верчению. Возьмем простой случай цилиндра.
Если цилиндр может катиться и скользить по плоскости, то при
вычислениях можно следующим образом учесть деформацию тела и
колебания молекул. Пренебрежем протяженностью деформации и
допустим, что цилиндр касается плоскости по образующей А. Допу-
стим, кроме того, что на цилиндр действуют силы, лежащие в пло-
скости поперечного сечения, которую мы примем за плоскость чер-

ГЛАВА IX. ПОНЯТИЕ О ТРЕНИИ
263
тежа. Приведем эти силы к точке А. Тогда мы получим Одну
силу AR, приложенную в точке цилиндра, совпадающей с точкой А,
я одну пару О, вектор момента которой перпендикулярен плоскости
чертежа. Разложим AR (рис. 127) на две силы: одну АР, нормаль-
ную к плоскости, и другую AQ, параллельную плоскости. Сила Q
вызывает скольжение цилиндра; пара G вращает его вокруг обра-
зующей, по которой происходит касание, т. е. вызывает качение ци-
линдра по плоскости,так как при
¦качении эта образующая является
мгновенной осью вращения.
Допустим сначала, что пара О
равна нулю. Тогда может возник-
нуть только скольжение; для того
чтобы его не было, необходимо
и достаточно, чтобы
Q<Pf.
A)
где /—коэффициент трения сколь-
жения. Допустим, что это усло-
вие выполнено, и восстановим
пару AG, вектор момента которой
нормален к плоскости фигуры.
Если нет никакого сопротивления
качению, то эта пара, как бы мала она ни была, заставит тело ка-
титься. Опыт, однако, показывает, что это не будет так и что ка-
чения не будет, пока момент G пары меньше некоторого предела:
G<Pb,
B)
где Р, как и выше, обозначает нормальную составляющую силы R,
а 8— линейный коэффициент, называемый коэффициентом тре-
ния при качении. Согласно Кулону и Морену этот коэффициент 8 не
зависит от силы R и радиуса кривизны поперечного сечения катя-
щегося цилиндра, по крайней мере в некоторых пределах.
Если этот коэффициент 8 известен, то условиями равновесия
цилиндра на плоскости будут уравнения A) и B), из которых одно
выражает, что нет скольжения, а другое, что нет качения. В этом
случае плоскость разовьет реакцию, состоящую из одной силы R',
равной и противоположной силе R, и пары О', равной и противо-
положной паре G. Пара G' возникает вследствие того, что касание
имеет в действительности конечную протяженность возле точки А
и при приведении сил реакций плоскости к точке А получится сила
и пара. Эта пара Q' есть пара трения качения.
Полученный результат можно представить еще следующим обра-
зом: для того чтобы выразить, что имеется равновесие, нужно вы-
разить, что непосредственно приложенные к цилиндру силы (котот

264	ЧАСТЬ ВТОРАЯ. СТАТИКА
рые предполагаются лежащими в плоскости поперечного сечения)
уравновешиваются нормальной силой N (равной и противоположной
силе Р) и касательной силой F (равной и противоположной силе Q),
приложенными в точке А, и парой с вектором момента О', парал-
лельным образующим. Эти силы и пара удовлетворяют неравенствам
F < Nf, G' < №.
Может случиться, что одно из условий A) и B) выполняется,
а другое нет. Тогда в первое мгновение цилиндр катится без сколь-
жения или скользит без качения. Если не выполняется ни одно из
этих условий, то одновременно будет и скольжение и качение в том
смысле, что элементарное перемещение цилиндра будет склады-
ваться из скольжения и вращения вокруг образующей, по которой
происходит касание.
Если цилиндр уже находится в движении, то допускают, что при
качении реакция плоскости, противодействующая качению, все время
имеет максимальное значение, так что во время качения пара, пред-
ставляющая трение качения, все время равна Nb, где N—нормальная
составляющая реакции плоскости. Точно так же, если происходит
скольжение, то касательная составляющая F реакции равна все время
Nf (п. 195). Если одновременно происходят и качение и скольже-
ние, то необходимо ввести совместно оба трения. В этом случае,
обычно, пренебрегают трением качения.
197. Трение верчения. Можно допустить в наиболее простых
случаях, что при равновесии момент пары трения верчения меньше
чем sN, где е—линейный коэффициент, аналогичный 8. При движе-
нии этот момент равен sN. Для более подробного изучения трения
верчения мы отсылаем к докторской диссертации Леоте (Париж, 1876).
УПРАЖНЕНИЯ
1.	Тяжелое твердое тело положено на наклонную плоскость, наклон
которой можно изменять. Показать, что скольжение будет происходить в том
случае, если наклон плоскости равен углу трения или больше его.
2.	Найти условие равновесия клинового пресса, принимая во внимание
трение между обеими щеками клина и брусьями (п. 169, рис. 111); Обозначая
через / коэффициент трения между обеими щеками и брусьями, получим
в предельном случае, когда клин начинает скользить,
p=2R	#
COS a — /sin a
3. Найти положение равновесия тяжелого однородного стержня АВ,
концы которого скользят с трением по двум плоскостям, из которых одна
горизонтальна, а другая вертикальна. (Необходимо, чтобы вертикаль центра
тяжести проходила через общую часть обоих конусов вращения с верши-
нами в точках А и В, оси которых нормальны к обеим плоскостям, а по-
ловины углов при вершинах равны углам трения.)

ГЛАВА IX. ПОНЯТИЕ О ТРЕНИИ	265
4.	В предыдущей задаче предполагается, что точка В, в которой стер-
жень опирается на вертикальную плоскость, перемещается по вертикали
в этой плоскости. Определить: 1) крайние точки, между которыми должна
перемещаться точка В по этой вертикали и 2) кривую, внутри которой
должна находиться точка А, чтобы было равновесие.
5.	Однородный тяжелый цилиндр вращения положен на наклонную пло-
скость таким образом, что его образующие горизонтальны. Известен коэф-
фициент В трения качения. Какое наименьшее значение нужно придать
наклону плоскости, чтобы началось качение? (В этом упражнении допу-
скается, что качение начинается при меньшем наклоне плоскости, чем
при скольжении.)
6.	Однородная тяжелая цепь положена на поперечное сечение круглого
цилиндра, ось которого горизонтальна, таким образом, что концы свеши-
ваются с обеих сторон цилиндра. Каковы возможные положения равновесия
если предположить, что имеется трение?

ЧАСТЬ ТРЕТЬЯ
ДИНАМИКА ТОЧКИ
ГЛАВА X
ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ.
ДВИЖЕНИЕ СНАРЯДОВ
I. Общие теоремы
198. Уравнения движения. Интегралы. В главе Ш мы видели,
что если точка М находится в движении под действием некоторых
сил, имеющих равнодействующую F, то ускорение j этой точки и
сила F имеют одинаковые направления и их величины связаны соот-
ношением
F = mj,
где т — масса точки. Говоря на языке алгебры, мы получили диф-
ференциальные уравнения движения.
Пусть х, у, я — координаты движущейся точки относительно
трех произвольных осей, X, Y, Z—составляющие силы F по этим
осям. Проекции силы F равны проекциям ускорения у, умноженным
на массу т, и мы получаем таким образом три уравнения движения
Если предположить, что точка М совершенно свободна, то дей-
ствующие на нее силы зависят, в общем случае, от положения, ско-
рости и времени. Следовательно, проекции X, Y, Z равнодействую-
ще dv dz ,
щей являются заданными функциями от х, у, г, -%-т, —п-> -гг, t,
т. е. от х, у, z, х', у', z', t, если употреблять обозначения
Лагранжа для производных: —тт = х', ... Тогда уравнения A) обра-
зуют систему трех совместных дифференциальных уравнений второго
порядка, определяющих х, у, z в функции t. Эту систему можно
заменить системой шести совместных уравнений первого порядка
dx 	 , dy 	 , dz 	 ,
dt	dt -^	dt
dx^__X_ <W_—L. dz'
dt m ' dt m ' dt
d')

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ	267
определяющих переменные х, у, г, х', у', г' в функции t. Общие
интегралы этих уравнений содержат шесть произвольных постоянных;
они имеют вид:
х = ср (t, Ct, С2, С3, С4, С5, С6), |
.У = Y (*• ^1> ^2> ^3" ^4> ^5> ^б)> (¦	V >
^	 .. г t. (^ Г С Г1 Г* /°1 I
6 — ш^, Oj, о2, ^з» о4, ^5' ^6/» J
откуда получаем:
х — ср {t, ьи ..., с6;,
,/	,.//•* /^	/^ л !
2 — Ш (,Г, Cj, . . . , Св/), J
где ср', ф'. ш' обозначают производные от ср, ф, ш по времени /.
В каждой частной задаче произвольные постоянные должны быть
определены при помощи начальных условий. Задаются положение
и скорость движущейся точки в момент t = t0, нужно определить
Ct, C2	С6 так, чтобы при t — t0 величины х, у, z приняли
наперед заданные значения лг0, у0, г0, а величины х', у', г' — на-
перед заданные значения x'Q, y'o, г^. Чтобы такое определение было
возможным, каковы бы ни были заданные начальные значения для
X, у, z, х', у', г', необходимо, чтобы можно было разрешить, по
.крайней мере теоретически, шесть уравнений B) и C) относительно
Сх, С2, .... С6, т. е. чтобы эти уравнения B) и C), в которых
Ct, С2, ..., С6 рассматриваются как неизвестные, не были ни несов-
местными, ни неопределенными. Тогда для этих шести постоянных
получатся значения вида
ck = fa(t, х, у, z, х', у', z') (fc= 1, 2	6),	D)
которые непосредственно определят численные значения постоянных,
когда заданы начальные значения переменных х, у, г, х', у', г'.
Допускается, что заданным начальным условиям отвечает
сколько одно движение. Это обстоятельство, в котором мы будем
убеждаться во всех примерах, изучаемых дальше, вытекает из тео-
ремы Коши при условии, что X, Y, Z являются регулярными функ-
циями от лг, у, г, х', у', г', t. Но это предполагается во всех слу-
чаях, встречающихся в явлениях природы. Вследствие этого, если
каким-нибудь образом удастся найти какое-нибудь возможное движе-
ние, т. е. удовлетворяющее уравнениям движения и начальным,усло-
виям, то это движение будет тем, которое действительно совершает
точка.
199. Первые интегралы. Первым интегралом уравнений дви-
жения называется соотношение вида
Ф(Л х, у, г, х', у, г', С) = 0,
связывающее t, x, у, г, х', у', г' и одну произвольную постоян-

268	часть третья, динамика точки
ную С и имеющее место вследствие уравнений движения, каковы
бы ни были начальные условия. Можно всегда представить это соот-
ношение, разрешенным относительно С и написать его в виде
C = f(t, х, у, г, х', у, г').	E)
Нетрудно непосредственно проверить, что соотношение такого
вида является первым интегралом. Дифференцируя по t, получим
д* л. д/ г' -Х- д/ «' -4- df ?' л- д/ d<ix л_ df а*У л- д/ d'2 — о
JfT'dx ~^"ду~у "•" dz ^~~d?~1v^"W4&^"W df* —"'
или, заменяя вторые производные от х, у, z их значениями, взятыми
из уравнений движения, получим
dt ' дх ' ду •* ' дг ' т \дх ' ду ' дг
Это последнее уравнение содержит только величины t, x, у, г, х',
у', г' и так как оно должно иметь место, каковы бы ни были на-
чальные условия, т. е. каковы бы ни были значения, приписываемые
этим величинам, то оно должно удовлетворяться тождественно.
Практическая полезность какого-либо первого интеграла с точки
зрения интегрирования уравнений A) заключается в том, что он поз-
воляет понизить на одну единицу число неизвестных. В самом деле,
соотношение E) позволяет выразить одну из неизвестных х, у, г*
х', у', z' как функцию остальных неизвестных и t.
Несколько первых интегралов
r=/1(^> x, у, z, x', у', z'), '
l = f2(t. x, y, z, x', y, z'),
1 =/»(*¦ x< У> z> x'> У> z')
F)
являются независимыми, когда из них нельзя исключить все вели-
чины х, у, z, х'', у', г'. Если такое исключение возможно, то оно
приведет к соотношению между постоянными С, С"	C(v\ кото-
рое, очевидно, не может содержать независимую переменную tr
являющуюся произвольной. Отсюда следует, что число независимых
первых интегралов, которые можно найти, равно шести, так как
если v больше 6, то всегда можно исключить шесть величин х, у,
г, х', у, z'.
Если известны v первых интегралов F), то в уравнениях A'}
можно уменьшить на v единиц число неизвестных. Действительно,
из уравнений F) можно выразить v этих неизвестных в функции
6 — v остальных неизвестных и времени t.
Например, шесть уравнений D), полученных после разрешения
общих интегралов уравнений движения относительно произвольных
постоянных, образуют шесть независимых первых интегралов.

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
269
Наоборот, если известны шесть независимых первых интегралов
вида F), где целое число v равно шести, то из этих уравнений
после разрешения относительно х, у, г, х', у', г' получится общий
интеграл уравнений движения.
Аналогичные рассуждения применимы, как мы увидим дальше,
и к движению точки по кривой или по поверхности.
По вопросам анализа, с которыми шы здесь столкнулись, мы от-
сылаем к нашему Cours d'Analyse a l'Ecole Centrale, гл. XXII.
200. Естественные уравнения (Эйлер). Возьмем на траектории
начало О дуг. Движение по этой кривой определено, если дуга
ОМ — s является известной функ-
цией времени. Проведем касатель-
ную МТ ъ сторону положитель-
ных дуг (рис. 128). Условимся
считать скорость положительной,
если движение происходит в сто-
рону МТ, и отрицательной, если
ОНО ПРОИСХОДИТ В Обратную СТО-
рону. Тогда скорость по вели-
чине и знаку будет
ds
В
5 г
v =
dt
Рис. 128.
Пусть J—ускорение движущейся точки. Как известно, его
проекции на касательную и главную нормаль выражаются соответ-
ственно формулами (п. 41):
.	dv_	d*s_ ,
Ф
а проекция на бинормаль равна нулю. Так как вектор силы равен
вектору ускорения, умноженному на массу, то обозначая через Ft,
Fn, Fb проекции силы F на касательную, главную нормаль и бинор-
маль, получим:
dv
dt
d-s
mv
Эти три уравнения образуют систему, эквивалентную трем уравнениям
движения. Так как Fn всегда положительно, a Fb всегда равно нулю,
то сила всегда лежит в соприкасающейся плоскости траектории и
направлена в сторону вогнутости последней.
Если сила все время нормальна к траектории, то Ft = 0, ско-
рость постоянна и сила обратно пропорциональна радиусу кривизны.
Если сила все время касательна к траектории, то Fn = m — = 0
и так как v не равно нулю, то р равно бесконечности, т. е. траек-
тория есть прямая линия.

270	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Можно установить отмеченные уже Маклореном интересные ана-
логии между этими уравнениями и уравнениями равновесия нити.
Мёбиус указал большое число таких аналогий в своей Статике, так же
как и Оссиан Бонне в томе IX Journal de Mathematiques и П. Серре
в своей Theorie nouvelle des lignes a double courbure (Mallet-Ba-
chelier, 1860). (См. упражнения.)
Мы переходим теперь к выводу теорем, позволяющих во многих
случаях найти первые интегралы.
201. Количество движения. Количеством движения точки М
называют вектор MQ, который направлен по линии скорости в ту же
сторону, что скорость, и длина которого равна произведению ско-
dx
рости на массу: mV. Так как проекции скорости на оси равны -гг,
dy dz	,
-тг, -yi, то проекции количества движения будут
dx	dy	dz
m4 m- m
Моменты количества движения относительно осей координат равны
dx	dz\	I dy	d
так что момент количества движения относительно точки О есть
вектор 00', проекции которого равны только что написанным вели-
чинам.
202. Теорема о проекции количества движения. Первое урав-
нение движения может быть написано так;
d I dx
{
Так как ось х произвольна, то это уравнение выражает следующее:
Производная по времени от проекции количества движения
на какую-нибудь ось равна проекции на ту оке ось равнодей-
ствующей всех сил, приложенных к движущейся точке.
В частности, если сумма проекций сил на ось все время равна
нулю, то по этой теореме получается первый интеграл. В самом
деле, приняв эту ось за ось Ох, имеем
d I dx \ „	dx .
где значение постоянной А равно проекции на ось Ох начального
количества движения. Интегрируя вторично, получим
т. е. движение проекции точки на ось Ох является равномерным.
Пример. Параллельные силы. Если сила F параллельна опре-
деленному направлению, то траектория будет лежать в плоскости,
параллельной этому направлению. В самом, деле, приняв за ось Ох

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
271
прямую, параллельную равнодействующей силе F, имеем Л"=(
Y = 0. Следовательно,
dx ,	dy „
что является уравнением плоскости, параллельной оси Oz. Эта пло-
скость, в которой происходит движение, определяется начальными
условиями; она является плоскостью, проведенной через начальную
скорость параллельно постоянному направлению силы.
203. Теорема о моменте количества движения. Закон пло-
щадей. Из уравнений движения можно вывести теорему, аналогичную
предыдущей, для момента количества движения. Два уравнения
путем преобразований приводятся к одному
хт ¦
которое можно написать так:
dfi
т. е. производная по времени от момента количества движения
относительно какой-нибудь оси
(оси Oz) равна моменту равно-
действующей всех сил, приложен-
ных к точке, относительно той
же оси.
Из этой теоремы получается пер-
вый интеграл уравнений движения
в случае, когда xY — уХ=0, т. е.
когда равнодействующая сил, прило-
женных к материальной точке, нахо-
дится все время в одной плоскости
с осью Oz. Этот интеграл будет
dy	dx 	„
Он имеет очень простую геометриче-	Рис. 129.
скую интерпретацию, а именно:
пусть (рис. 129) Р — проекция движущейся точки М на плоскость ху
и Ро — начальное положение этой проекции. Рассмотрим сектор,
ограниченный проекцией траектории и двумя радиусами ОР0 и ОР.
Обозначая через 5 площадь этого сектора, отсчитываемую в напра-
влении положительного вращения вокруг оси Oz, имеем
-ydx).

272	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Следовательно, предыдущее уравнение принимает вид
2 dS _c
откуда, интегрируя, находим
Другими словами, площадь S пропорциональна времени, в течение
которого она была описана. В этом случае говорят, что для
проекции движения на плоскость ху справедлива теорема площадей.
Постоянная площадей С, входящая в предыдущую формулу, равна
отношению удвоенной площади, описанной радиусом-вектором ОР,
к затраченному на это времени. Она определяется начальными усло-
виями, а именно: она равна значению, принимаемому в начале дви-
жения величиной х-^2	У~йГ< Т- е- моменту начальной скорости
относительно оси Oz.
Наоборот, если теорема площадей применима к проекции движе-
ния на плоскость хОу относительно точки О, то сила находится
в одной плоскости с осью Oz, так как уравнение х~ — у-?- = С
после дифференцирования принимает вид
а2У	dT-x .
Х dfl У dP ~~ U>
откуда
хУ — уХ=0.
Пример. Центральные силы. Допустим, что равнодействую-
щая F сил, приложенных к точке, является центральной, т. е. ее
направление все время проходит через неподвижную точку О. Если
эту точку принять за начало, то момент F относительно каждой из
трех координатных осей будет равен нулю и теорема площадей
будет применима к проекциям движения на каждую из трех коор-
динатных плоскостей. В этом случае траектория будет лежать в пло-
скости, проходящей через центр сил. В самом деле, имеем три урав-
нения:
dy	dx 	„
x~dT~~y~df — Ll
dz	dy .
y-dt-z-d7 = A'
dx	dz n
zx B
Умножая их на х, у, z и складывая, найдем
Ax-{-By-\-Cz = 0,
т. е. уравнение плоскости, проходящей через точку О. Эта пло-
скость определяется начальной скоростью и точкой О.

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
273
204. Геометрическая интерпретация двух предыдущих теорем. Про-
ведем через точку О вектор OR, равный и параллельный равнодействующей
всех сил, приложенных к точке, и вектор OR', равный и параллельный ко-
личесэву движения точки (рис. 130). Точка R'
имеет координаты:
dx
~~dt
dy
~-
dt
Tdz
Уравнения движения, выражающие тео-
рему проекций количества движения на каж-
дую из координатных осей, имеют вид
da — X _"
It ~ ' dt
v dt —
Рис. 130.
и обозначают, что скорость V геометриче-
ской точки R' в каждый момент времени
равна и параллельна силе R.
Точно так же, пусть 00 — момент равнодействующей сил, приложенных
к точке М, относительно точки О и пусть OG' — момент количества дви-
жения относительно той же точки. Координаты X, (л, ч точки G' выражаются
равенствами
dz	dy
dx
dy
dx
(C)
проекции вектора OG суть
L = yZ — zY,
^zX — xZ, N=xY—yX.
(G)
И мы приходим к уравнению — = N; точно так же получаются урав-
нения
dt
	/
dt
= М,
выражающие, что точка G' обладает в каждый момент времени ско-
ростью V", равной и параллельной вектору OG. В, этом заключается
аналогия между обеими предыдущими теоремами.
Например, если равнодействующая сил, действующих на движущуюся
точку, проходит через неподвижную точку О, то величины X, (л, ч будут по-
стоянными и отрезок OG во время движения будет оставаться неподвиж-
ным. Мы видели, что в этом случае траектория будет плоской; она будет
находиться в плоскости, перпендикулярной к OG.
205. Теорема кинетической энергии. Возьмем уравнения дви-
жения
d^-x v	d"-y ,,	d?-z 7
m	X	Y mZ
и сложим их почленно, умножив предварительно первое уравнение

274	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
на dx, второе на dy и третье на dz. Получим
т ("Ж dx + llk аУ+% dz) = Xdx + ydy + z dz.
Замечая, что квадрат скорости равен
можно это уравнение написать следующим образом:
. mv2 ,, . , ,, , , ., .	,,ч
d —к— = X dx-\- Y dy-\-Zdz.	A)
Произведение -к mv2 половины массы на квадрат скорости
называется кинетической энергией *). Предыдущее уравнение
может быть поэтому выражено следующим образом:
Дифференциал кинетической энергии за промежуток вре-
мени dt равен элементарной работе равнодействующей сил, дей-
ствующих на точку, за тот же промежуток времени. Действи-
тельно, правая часть
X dx-\-Ydy-\-Zdz
уравнения является элементарной работой силы X, Y, Z на дейст-
вительном перемещении dx, dy, dz, которое совершает точка за
промежуток времени dt. Работу равнодействующей X, Y, Z можно,
как мы видели (п. 77), заменить суммой работ отдельных сил, при-
ложенных к движущейся точке.
Уравнение A) вытекает также сразу из первого из естественных
уравнений движения	,
Умножая на ds и заменяя —г? через v, получим уравнение
d ~- = Ft ds,
в котором правая часть равна элементарной работе силы F на пере-
мещении ds.
Если уравнение A) проинтегрировать от момента t0 до момента t,
то, обозначая через v0 скорость в момент t0, получим
mv'1 mvl Г
—.	^-= / Xdx-\-Y dy-\-Z dz,	B)
•^	*¦ J
t,
что выражает следующую теорему:
*) В оригинале вместо названия «кинетическая энергия» автор поль-
зуется устаревшим и вышедшим теперь из употребления названием гживая
сила», причем живой силой автор называет величину mv2. {Прим. перев.^

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ	275
Изменение кинетической энергии точки за произвольный про-
межуток времени равно полной работе сил, приложенных
к точке, за тот же промежуток времени.
С точки зрения оценки полной работы следует, как мы показали
в главе IV, различать три случая:
1°. В наиболее общем случае, когда X, Y, Z зависят от х, у,
г, х', у', г', t, для вычисления полной работы надо знать выра-
жения координат х, у, z в функции t, т. е. надо знать движение.
2°. В случае, когда X, Y, Z зависят только от х, у, г, для
вычисления полной работы достаточно знать траекторию движущейся
точки между положением Мо, которое она занимает в момент t0, и
положением М, занимаемым в момент t.
3°. Наконец, если равнодействующая X, Y, Z зависит только от по-
ложения движущейся точки и имеет силовую функцию U (х, у, z), т. е
Xdx-\-Ydy + Zdz = dU{x, у, z),
то можно вычислить полную работу, зная только положения Мо
и Ж. В этом случае теорема кинетической энергии приводит
к первому интегралу. Действительно, выполняя интегрирование
в правой части уравнения B), получим
~2	2~ = t/(x, у, z) — U(x0, у0, г0),
или
-y = t/(*. у, z) + h,
2
mv0
где h обозначает произвольную постоянную —.	U (х0, у0, z0); эта
постоянная называется постоянной кинетической энергии. Согласно
этому уравнению скорость движущейся точки становится тою же
самою, что и раньше, каждый раз, когда функция U принимает
прежнее значение. Если U является однозначной функцией от х,
у, г, то можно говорить, что скорость движущейся точки прини-
мает одинаковые значения, когда она возвращается на одну и ту же
поверхность уровня U(x, у, г) = const. Когда функция U много-
значна, как, например, U{x, у, г) —arctg—, то скорость не обя-
зательно принимает одинаковые значения, когда точка возвращается
на одну и ту же поверхность уровня, так как на определенной по-
верхности уровня функция U (х, у, z), а вследствие этого и полная
работа принимают различные значения вдоль пути (см. п. 82).
20.6. Примеры. Г. Рассмотрим движущуюся в пустоте совершенно сво-
бодную тяжелую точку. Если ось Ог направить вертикально вверх, то так
как единственной силой, приложенной к точке, является вес, проекции кото-
Р°ГОСУТЬ	*=0, Y = 0, Z = -mg,

276	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
то по теореме кинетической энергии получаем уравнение
. mv"-
d -у- = — mg dz,
правая часть которого является полным дифференциалом, что показывает,
как это уже отмечалось много раз, что вес имеет силовую функцию.
Интегрируя, получим
V2 V*
Это уравнение показывает, что скорость принимает одно и то же числен-
ное значение всякий раз, когда точка находится на одной и той же высоте,
т. е. возвращается на ту же поверхность уровня.
Вообще, если точка находится под действием вертикальной силы, являю-
щейся функцией от г, то
Х = 0, к=0, Z = <f(z),
откуда
mv2 mvl Г
<((z)dz, ~2	r^J
Поверхностями уровня по-прежнему являются горизонтальные плоскости.
Во всех этих движениях траектории являются плоскими кривыми (п. 202,
пример).
2°. Рассмотрим точку М, притягиваемую неподвижным центром О по
закону обратной пропорциональности квадрату расстояния. Притягивающая
сила имеет вид тц/г2, где (л — постоянная, а г—расстояние ОМ. Алгебраи-
ческое значение этой силы, отсчитываемой в направлении ОМ, равно — m\x.jr%
и, как мы видели в п. 84, элементарная работа этой силы равна — —?- dr.
Следовательно, по теореме кинетической энергии имеем
mv9-	тр.	v2 — vl ( 1 1
*-2-=-75-^ —2— ^Л
или
Поверхностями уровня являются сферы (л//- = const; скорость принимает
одинаковые численные значения на одинаковых расстояниях от притягиваю-
щего центра О.
Вообще, если точка М находится под действием центральной силы,
являющейся функцией от г, и алгебраическое значение этой силы, отсчиты-
ваемое в направлении ОМ, есть ср (/¦), то
d	()d	^
3°. Рассмотрим тяжелую точку М, притягиваемую неподвижным цен-
тром А по закону обратной пропорциональности квадрату расстояния и
отталкиваемую неподвижным центром А' пропорционально расстоянию
(рис. 131). Направим ось Oz вертикально вверх, так что элементарная ра-
бота веса равна — mg dz. Если мы обозначим через г расстояние AM, то
алгебраическое значение притягивающей силы F, отсчитываемой в направ-

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
277"
m\>.jr2, а элементарная работа равна ——^-dr. Наконец,.
лении AM, есть
если мы обозначим через /¦' расстояние МА', то алгебраическое значение-
отталкивающей силы F', пропорциональной расстоянию, есть пць'г', а ее
элементарная работа равна mp'r'dr'. По теореме кинетической энергии
дифференциал d-7-mv'i равен элементарной ра-	,-.
боте равнодействующей приложенных к точке	z
сил, т. е. сумме работ составляющих сил, и мы
имеем
Правая часть этого равенства является полным
дифференциалом, так что существует силовая
функция; в этом можно было убедиться и за-
ранее, на основании теорем, установленных в гла-
ве IV. Следовательно, интегрируя и деля на т,
получим
Рис.131.
Силовая функция здесь по-прежнему однозначна и скорость принимает оди-
лаковые значения каждый раз, когда движущаяся точка проходит через-
одну и ту же поверхность уровня
= c°nst.
Это — поверхности шестого порядка. Они приводятся к сферам, если (i равно
нулю, т. е. если отбрасывается притягивающий центр А.
207. Замечание к интегралу кинетической энергии. Интеграл
кинетической энергии
— = t/(x, у, z) + h
показывает, что движущаяся точка не может выйти из области про-
странства, в которой величина U(x, у, г)-\- h положительна, так
как левая часть равенства существенно положительна. Когда эта
область не содержит всего пространства, она, вообще говоря, огра-
ничена поверхностью уровня, имеющей уравнение
U(x, у, z) + h = 0.
Вид этой поверхности зависит от постоянной кинетической энергии,
т. е. от начального положения и от величины начальной скорости,
но не от ее направления. В упражнениях будет показано, какими
будут эти поверхности в рассмотренных выше примерах.
Это очевидное замечание, важные приложения которого можно
найти в трудах Хилла (Acta mathematica, т. VIII), Болена, (там же,,
т. X), Дарвина (там же, т. XXI, и Mathem. Annalen, т. LI), приво-
дит непосредственно к теореме Лежен-Дирихле об устойчивоста
равновесия.

278	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
208. Устойчивость равновесия свободной материальной точки.
Доказательство Лежен-Дирихле. Рассмотрим свободную точку
М(х, у, г), находящуюся под действием сил, равнодействующая
которых (X, Y, Z) имеет силовую функцию U (х, у, г):
у dU v dU 7 dU
дх ' ' — ду '	дг '
Положения равновесия точки найдутся, если приравнять нулю X, Y, Z,
т. е. если искать максимумы и минимумы функции U. Если в задан-
ном положении О точки функция U имеет максимум, то соот-
ветствующее равновесие устойчиво. Примем это положение О за
начало и предположим, что функция U обращается в нуль в точке О,
что всегда возможно, так как эта функция определяется с точно-
стью до аддитивной постоянной, которою всегда можно распоря-
диться так, чтобы функция U обращалась в нуль в заданной точке.
Чтобы точнее уяснить понятие максимума, опишем вокруг точки О
выпуклую поверхность S, например, сферу или куб с центром О,
размеры которых достаточно малы для того, чтобы внутри поверх-
ности 5 и на ней самой функция U была отрицательна и, за исклю-
чением начала О, отлична от нуля.
Выбрав поверхность 5 сколь угодно малой, покажем, что суще-
ствуют два положительных числа е и ч), обладающих следующими
свойствами: поместив движущуюся точку в начальном положении на
расстоянии от О, меньшем чем е, и сообщив ей начальную скорость,
.меньшую чем т), мы получим такое движение точки, при котором
эта движущаяся точка останется внутри поверхности S. В самом
деле, функция U на поверхности 5 отрицательна и отлична от нуля;
•следовательно, можно указать достаточно малое положительное
число р такое, что на поверхности 5 постоянно будет
— U>p, U+p<0.
Поместим теперь точку М в начальное положение М0(х0, у0, г0)
внутри поверхности 5 и сообщим ей начальную скорость v0. Для
движения, которое точка начнет совершать, на основании теоремы
¦кинетической энергии будет
т,л	(mv\	\
ш	I Г I [	°	I Г \	/4
где Uo есть значение функции U в точке Мо, причем отрицатель-
ное. Определим начальное положение и скорость условием
для чего достаточно, например, принять
mv\ p

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ	279
Первое из этих неравенств определяет для v0 верхний предел и,
равный Yplm' далее, так как функция U непрерывна и обращается
в нуль в начале, то существует такое достаточно малое положитель-
ное число е, что если расстояние ОМ0 меньше чем е, то —-Uo будет
меньше чем р/2. Тогда, придавая движущейся точке начальное поло-
жение, находящееся от точки О на расстоянии, меньшем чем е, и
сообщая ей начальную скорость, меньшую чем \р\т, мы удовле-
творим неравенству B) и вследствие этого, на основании теоремы
кинетической энергии A), удовлетворим также неравенству
?	C)
которое показывает, что движущаяся точка не может выйти за-
поверхность 5. В самом деле, если точка достигнет поверхности S,
то U-\-р станет отрицательным и кинетическая энергия, являю-
щаяся существенно положительной величиной, станет меньше
отрицательной величины, что является абсурдом. Теорема таким
образом доказана. Например, если точка притягивается центром О
пропорционально расстоянию, то О является положением устойчи-
вого равновесия (п. 90).
В полученном движении можно указать верхний предел для ско-
рости, так как поскольку U отрицательно, то по формуле C) mv2/2
меньше чем р п v меньше чем "|/2р//я.
Обратное предложение. Вероятно, что обратное предложение
также справедливо. Если в точке, представляющей изолированное
dU dU dU
положение равновесия, производные -з—, -з—, -^— обращаются
в нуль, но функция U не имеет максимума, то соответствующее
равновесие будет неустойчивым. Это предложение для широкого
класса случаев доказано Ляпуновым (Journal de Mathematiques, т. Ill,
1897, стр. 81)*) и Адамаром (там же, стр. 364). Но если рассмат-
риваемое положение равновесия не является изолированным, то
может случиться, что равновесие будет устойчивым, но функция U
не будет максимумом. Это показал Пенлеве (Comptes Rendus, т. 12j,
1904), который привел пример:
В этом примере начало координат является положением устойчивого
равновесия, но функция U не имеет максимума.
*) Русский перевод этой статьи А. М. Ляпунова приложен ко второму
и третьему изданиям (Гостехиздат, 1935 г. и 1950 г.) его докторской дис-
сертации «Общая задача об устойчивости движения». См. также
А. М. Ляпунов, Сочинения, т. II, Изд-во АН СССР, 1956. {Прим. перев.у

280	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Примечание. Когда для точки, находящейся под действием
силы, не имеющей силовой функции, имеется некоторое положение
равновесия, то для того, чтобы узнать, устойчиво оно или нет, надо
исследовать движение, которое получит эта точка, если ее удалить
на бесконечно малое расстояние от положения равновесия и сообщить
ей бесконечно малую скорость.
II. Прямолинейное движение
209. Некоторые случаи, когда движение точки прямолинейно.
1°. Силы постоянного направления. Если движущаяся точка, выхо-
дящая из некоторого положения Мо, находится под действием силы
постоянного направления и если ее начальная скорость Vo равна
нулю или параллельна этому направлению, то траекторией будет
прямая D, проведенная из Мо параллельно заданному направлению.
Это свойство можно рассматривать как очевидное из соображений
симметрии, так как нет никакой причины, которая заставила бы
точку сойти с этой прямой D в ту или другую сторону. Можно это
свойство установить также аналитически. Оси координат можно всегда
выбрать так, чтобы сила, была параллельна оси Ох. Тогда проекции К
и Z силы на оси Оу и Ог будут равны нулю и поэтому
dt4- ~U1 dt>-
откуда
аУ _ „ ^ _
где а и b — проекции начальной скорости на оси О у и О г; но так
как эта скорость равна нулю или параллельна оси Ох, то а и b
равны нулю. А если производные величин у и г равны нулю, то
эти величины постоянны,
У = У<* * = г0
я точка перемещается по линии, параллельной оси Ох.
2°. Центральная сила. Если точка, выходящая из Мо, находится
под действием силы, направление которой все время проходит через
неподвижный центр- О, и если начальная скорость Vo равна нулю
или направлена по прямой ОМ0, то точка останется на прямой ОМ.
Этот результат также очевиден из соображений симметрии. Его
можно получить аналитически, приняв О за начало и заметив, что на
основании теоремы, изложенной в п. 203 для проекций движения на
все три координатные плоскости, имеет место закон площадей.
Имеем, например,
х dt у dt ~ь>

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ	281
где с—момент скорости относительно оси Ог. Но в начальны*
момент скорость либо равна нулю, либо проходит через точку О.
Ее момент относительно оси Ог равен нулю и С — 0. Следовательно*
dx 	 dy
~х~ ~
и, интегрируя от начального момента времени до момента t, получим
ln-i-=InJL, JL=JL.
х0	Уо	х0 Уо
Точно так же, проектируя на плоскость уОг, найдем
JL = JL
Уо. г0 '
Следовательно, точка остается на прямой ОМ0.
3°. Учет сопротивления среды. Предыдущие теоремы останутся
справедливыми и в том случае, если присоединить к рассмотренным
силам силу сопротивления среды, направленную в сторону, противо-
положную скорости. Это по-прежнему вытекает из симметрии и.
может быть установлено аналитически в качестве упражнения.
4°. Точка, вынужденная двигаться по прямой. Можно, наконец,
представить себе точку, находящуюся под действием заданных сил
и описывающую прямую,, например, точку, находящуюся в прямоли-
нейной трубке бесконечно малого поперечного сечения. Тогда со
стороны трубки возникает сила реакции, но равнодействующая всех
приложенных к точке сил будет направлена по прямой, так как она
равна произведению массы на ускорение.
210. Уравнение прямолинейного движения. Простые случаи
интегрируемости. Возьмем частный случай, когда движение прямо-
линейно, и примем прямую, описываемую точкой, за ось Ох. Урав-
нение движения будет
d2x v	/1Ч
т~ж==х-	A)
Наиболее общим случаем будет тот, когда X одновременно
зависит от х, v и t. В этом случае
так как алгебраическое значение скорости v есть -?-. Это—диффе-
ренциальное уравнение второго порядка, позволяющее определить х
в функции t. Общий интеграл содержит две произвольные постоянные:
x — f(t, с, с').
Эти постоянные определяются из начальных условий:
*о = /('о. с. С), vQ = ft(t0, с, с').

282	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Может случиться, что аналитическое выражение силы изменяется
з зависимости от положения точки или направления скорости. При-
лер такого рода встретится в упражнениии 4 п. 211.
Интегрирование дифференциального уравнения A) приводится
к квадратурам, когда X содержит только одну из величин х, v и t.
1°. Сила зависит только от положения. Пусть сначала
d2x
Умножая обе части на ^—тг, получим
и, интегрируя, найдем
Это уравнение представляет собой не что иное, как уравнение кине-
тической энергии, примененное к рассматриваемому частному случаю.
Для определения постоянной положим х — х0, что даст для h зна-
чение mv\. Если выполнить вышеуказанную квадратуру, то получатся
уравнения вида
Здесь нет никакой неопределенности в выборе знака, так как при
jc — xQ должно быть I , j —t^. Следовательно, перед радикалом
нужно ставить тот знак, какой имеет v0. Если v0 равно нулю, то
движение будет происходить в сторону силы, что опять определяет
знак радикала. Тогда можно написать
dx	t_t = f dx
'	° J
dt =
Это уравнение, разрешенное относительно х, выражает закон рас-
стояния; непосредственно оно выражает время, необходимое для пере-
мещения на данное расстояние. Мы исследуем его более подробно
дальше (п. 211, пример 6), после того, как рассмотрим несколько
Простых частных случаев.
2°. Сила зависит только от скорости. Допустим теперь,
что X есть функция только скорости V. Написав
dv	.	,, mdv
т —г?- = ф iv), ut =¦
at i ч •

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ	283!
и проинтегрировав, получим
= J
V
mdv
«о
Так как их = v dt, то
V
ш^	С mvdv ,
ил ¦'-- 	т—г— t	л 	 I 	;—г— —— -
Здесь х к t получились выраженными в функции вспомогательной:
переменной v. Последнее уравнение mv dv = cp (v) dx вытекает также
из теоремы кинетической энергии, так как cp (v) dx есть элементар-
ная работа силы и mv dv = d-к- mv2.
3°. Сила зависит только от времени. Если, наконец, X есть-
функция только времени t, то имеем
Интегрируя первый раз, получим
t
т —тг =
to
После второго интегрирования найдем
t t
4>(f)dt\dt
211, Приложение к движениям, происходящим под действием силы,,
зависящей только от положения.
1°. Вертикальное движение тяжелого тела в пустоте.
В качестве оси примем направленную вверх вертикаль, проходящую
через начальное положение точки. Обозначим через v0 алгебраическое зна-
чение начальной скорости, которое предполагается вертикальным. Сила,
действующая на точку, равна в каждый момент времени —mg, и поэтому
уравнение движения будет
d"-x	d°-x	...
m m	8	A)
Интегрируя первый раз,, находим
dx _
dt ~v-
B)
причем время отсчитывается от того момента, когда точка начинает дви-
гаться. Интегрируя второй раз, получим
g	C)

284	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
если абсциссы отсчитываются от начального положения точки. Если v0 поло-
жительно, то скорость, будучи вначале положительной, затем убывает и
обращается в нуль по истечении промежутка времени vo/g. Начиная с этого
момента, скорость становится отрицательной и неограниченно увеличи-
вается по абсолютному значению. Исключая t из равенств B) и C), найдем
v-* = vl — 2gx.
К этому же соотношению можно прийти, применяя теорему кинетической
,	... _ dx
энергии, т. е. умножая обе части равенства A) на 2 —т— и интегрируя.
Таким образом,
При сделанном нами предположении, что v0 > О, точка начинает двигаться
вверх и в начале движения ее скорость положительна. Следовательно, перед
радикалом надо взять знак-}-. Пока х будет увеличиваться до v^/2g, скорость
будет уменьшаться до нуля, после чего точка начнет падать и тогда перед
радикалом надо будет взять знак —. Полученное нами выражение для скорости
показывает, что на одной и той же высоте, как при движении вверх, так и
лри движении вниз, точка имеет скорость, одинаковую по абсолютному
значению. Точка проходит на
т.-а	.	9т°й высоте каждый раз через
. - *" *	" * * -,	одну и ту же поверхность
У-'-хо-.,_	"-.	 уровня.
	^Г ~у	~^Ъ ~2	З7	2°. Движение материаль-
~~~--Я-Ь---~~	ной точки, притягиваемой
неподвижным центром О про-
Рис. 132.	порционально расстоянию.
Примем точку О (рис. 132)
за начало, а за ось — пря-
мую ОМа, которая будет траекторией. В качестве положительного напра-
вления примем ОМ0, где Мо — начальное положение точки, и обозначим
через «о начальную скорость.
Рассмотрим случай притяжения. В этом случае сила в какой-нибудь
момент времени будет равна •— (хх, где у- положительно, каково бы ни было
положение точки, справа или слева от 0. Полагая — = k\ получим уравнение
движения
S"+ ** = <>•	О)
Это уравнение является линейным уравнением с постоянными коэффи-
циентами без правой части. Его общий интеграл имеет вид
х = A cos kt -j- В sin kt,
где А и В — две постоянные. Скорость v есть производная от х по t:
v = — Ak sin kt -f Bk cos kt.
Для определения постоянных дадим величинам х и v начальные значе-
ния х0 и Vq, которые они имеют при t = 0. Получим
х0 = A, vо = Bk.
Значение х будет тогда
х = х0 cos kt -j- —- sin kt.	B)
rv

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ	285
Следовательно, движение является простым колебанием периода Т = -=—
(вперед и обратно). Для нахождения амплитуды колебания положим:
х0 = a cos а, —д~ = — a sin a,
Тогда
х = a cos (kt + a).	C)
Следовательно, х изменяется от — а до + а, т. е. амплитуда равна а.
Если начальная скорость равна нулю, то
X = Хо COS ftf.
В этом случае время, необходимое точке для достижения положения О,
равно четверти периода Т, т. е. тс/2*. Оно не зависит от х0. Этот резуль-
тат выражают, говоря, что движение является таутохронным.
Применение теоремы кинетической энергии. Умножая обе части урав-
нения движения на 2dx и интегрируя, получим
- — -««¦+*.
При х = х0 должно быть v = v0; следовательно,
и h является существенно положительной величиной, большей, чем №х% или
равной ей; следовательно, мы можем предположить, что h = №а2, причем
а^г-х0. Тогда уравнение движения принимает вид
и время ? определяется элементарной квадратурой
ее
/• rf-r
приводящейся к арксинусу. Мы приходим, таким образом, с иной точки
зрения к уравнению движения B). Формула D) показывает, что х может
изменяться только между — а и -f- а для того, чтобы радикал был веществен-
ным. Когда х изменяется от — а до -fa перед радикалом D) следует брать
знак +, а когда х уменьшается от -{-а ло — а, нужно брать знак — .
3°. Точка отталкивается неподвижным центром пропорционально
расстоянию. Уравнение движения
dZx ,„ d"-x .,
dfi	* dfi KX~v
является линейным с постоянными коэффициентами и его общий интеграл
имеет вид
х-х0
где х0 и v0 — начальные абсцисса и скорость. Если
»в = — kx0'

286	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
то уравнение для х принимает вид
X = Х(Р~Ы.
В этом случае точка неограниченно приближается к отталкивающему центру,
никогда его не достигая, так как при неограниченном возрастании времени
абсцисса х стремится к нулю.
Применение теоремы кинетической энергии. Можно применить другой
метод исследования и интегрирования.
Умножим обе части уравнения движения на 2 —-гг и проинтегрируем.
Получим
где h = i/ц — k2x\. Следовательно,
~=± fk
Допустим сначала, что v0 > 0. Тогда точка будет все время удаляться от
отталкивающего центра и ее скорость будет неограниченно возрастать
вместе с х.
Допустим теперь, что v0 < 0. Так как в начале движения скорость
отрицательна, то перед корнем нужно взять знак —. Пусть h > 0. Пока
точка приближается к началу 0, ее скорость уменьшается до значения у^/г;
с этой скоростью движущаяся точка проходит через начало О и удаляется
с неограниченно возрастающей скоростью. Если h отрицательно, то его
можно положить равным —k?a2
В	и тогда получим
Рис. 133.
где а обязательно меньше х0,
так как при х = х0 скорость t/0
вещественна. Следовательно, движущаяся точка приближается к точке А
(рис. 133) с абсциссой а и приходит в эту точку за конечный промежуток
времени, так как время, необходимое для прохождения отрезка пути х0 — х,
равное
1 Г —&х
стремится к некоторому пределу Т, когда х стремится к а. По истечении
промежутка времени Т скорость меняет знак и точка неограниченно
удаляется от Л с постоянно возрастающей скоростью.
Интересно исследовать промежуточный случай, когда h = 0, или
vo= ±kx0.
Положим
vo= — kx0;
тогда
Скорость неограниченно уменьшается по мере того, как точка неогра"
ниченно приближается к началу О. Но она не может достигнуть его за

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ	287
конечный промежуток времени, так как время, необходимое ей для того,
чтобы подойти к началу на расстояние х, равно
X
— dx 1 . Хп
а это выражение неограниченно возрастает, когда х стремится к- нулю.
Точка О отличается той особенностью, что она является положением
неустойчивого равновесия; движущаяся точка, помещенная в начало О без
начальной скорости, останется в покое; но если ее немного удалить, то
отталкивание удалит ее еще больше. Чаще всего, когда движущаяся точка
приближается к положению неустойчивого равновесия со скоростью, стре-
мящейся к нулю, она к этому положению неограниченно приближается,
никогда его не достигая.
4°. Движение точки, притягиваемой неподвижным центром, обратно
пропорционально квадрату расстояния.
Когда х положителен, тогда Х = —f*/-*a> если •* отрицателен, то
надо принять X—^jx^. Мы рассмотрим первый случай. Тогда уравнение
движения, если положить ц = mk2, будет
<Г-х	№
df*
	 ЛХ
dt
Умножим его на- 2 —гг и проинтегрируем. Получим выражение теоремы
кинетической энергии
/ dx \я Ж-
Ы) ==—+h'
где h = v\	. Предположим, что точка выходит из Л^ с начальной
х0
скоростью щ, которая или отрицательна, т. е. направлена к точке О, или
равна нулю. Тогда вначале нужно принять
и движущаяся точка будет приближаться к точке О с неограниченно возра-
стающей скоростью, что физически невозможно, так как тогда удар дол-
жен был бы произойти раньше, чем расстояние между обеими точками обра-
тится в нуль.
Если точке сообщается движение в положительную сторону, то сначала
надо принять
dx
Если h ]> 0, то по мере того, как х возрастает, скорость v убывает, но
остается все время больше чем У^Л; следовательно, точка будет неограни-
ченно удаляться и так как при этом ее скорость стремится' к }fh> T0 через
некоторое время движение можно рассматривать как равномерное.
Если h = 0, то движущаяся точка обязательно достигнет любого поло-
жения на прямой, как бы удалено оно ни было, так как между точкой Мо
и произвольной точкой Р с абсциссой р скорость больше чем Y^^/p; из
этого следует, что движущаяся точка неограниченно удаляется со скоростью,
стремящейся к нулю.

288	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Если h отрицательно, то, полагая Л =	, приведем уравнение дви-
жения к виду
dx	/~2й2 2k°-
причем а > х0 (рис. 134), так как радикал должен быть вещественным при
х = х0. Скорость будет сначала направлена в положительную сторону
и будет уменьшаться, пока х воз-
„,	i	—	1	1	 растает. Движущаяся точка будет
О Мо	В	Л	приближаться сколь угодно близко
к точке А с абсциссой а и до-
Рис. 134.	стигнет ее за конечный проме-
жуток времени. После этого
движение переменит направление, так как сила — притягивающая и она
стремится, как и в случае, когда vo-^O, привести точку в начало О.
Задачу можно рассмотреть еще иначе, выполнив квадратуру, которая
определит t в функции х. В самом деле, имеем
t =
2й3
Если положить	1- h = и2, то задача сведется к интегрированию рацио-
нальной дроби.
5°. Точка притягивается неподвижным центром пропорционально я-й
степени расстояния:
Х = — \>.хп.
В этом случае, если точка помещена без начальной скорости на рас-
стоянии х0 от начала, то она его достигнет за промежуток времени
о
В этом выражении определенный интеграл является эйлеровым интегра-
лом в/ ¦ , -у). Отсюда ясно, что единственным значением л, при ко-
тором Т не зависит от х0, является п = 1 (пример 2).
6°. Исследование общего случая. Сила имеет вид X = т<р (х) и урав-
нение движения будет
После первого интегрирования получим (теорема кинетической энергии)
или
Допустим для определенности, что f{x) является рациональной дробью.
Знак перед корнем в начале движения определяется направлением, в кото-
ром точка начинает двигаться.

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ	289
Допустим, например, что следует взять знак +; тогда движущаяся точка
будет удаляться в положительном направлении. Единственными особенностями
являются нули и бесконечности функции f(x). Допустим, что при воз-
растании х мы придем сначала к точке, в которой функция / бесконечна.
В этом случае движущаяся точка будет перемещаться с неограниченно воз-
растающей скоростью в положение А, соответствующее этой бесконечности;
данный результат и дает решение задачи. (Физически такой случай невоз-
можен). Допустим теперь, что первой особенностью является простой нуль.
Тогда можно написать
/(де) = (а —дс)ф(л-),
где ф не обращается в нуль между х0 и а, и мы получим
При этом функция ф (х) в промежутке от х0 до а должна быть положитель-
ной для того, чтобы -77 было вещественным. Движущаяся точка подходит
сколь угодно близко к точке А с абсциссой а, так как на отрезке М0В
(рис. 134) скорость не обращается в нуль и, следовательно, превосходит
некоторую положительную величину v±. Поэтому движущаяся, точка обя-
зательно достигает' положения В. Но она достигает также за конечный про-
межуток времени и положения А, так как время, необходимое ей. для про-
хождения расстояния от х0 до х, равное
/у
dx
остается конечным, когда х стремится к а. В точке А скорость обращается
в нуль и дальнейшее движение будет происходить в направлении силы.
При этом точка обязательно пойдет обратно, так как если х перейдет
через а, то -гг станет мнимым. Если особенность х — а будет двойным или
кратным корнем, то движущаяся точка будет сколь угодно близко под-
ходить к точке А, но не достигнет ее за конечный промежуток времени,
так как, предполагая корень двойным, имеем
и вследствие этого
где функция ii (x) будет по-прежнему положительной между х0 и а. Время
X
С dx
J (a —дОУТС*)"
необходимое движущейся точке для прохождения расстояния от х0 до х,
неограниченно возрастает, когда х стремится к а. Можно заметить, что если
х = а является двойным корнем, то соответствующее положение является
положением неустойчивого равновесия. Действительно,

290	Часть третья, динамика точки
и, кроме того,
/« = 2 Jf(x)dx + h.
Отсюда, дифференцируя, получим для силы выражение
которое действительно обращается в нуль при х = а. Но если сила при х = а
обращается в нуль,' то соответствующее положение А есть положение рав-
новесия. Оно неустойчиво, так как если точку бесконечно мало удалить от
этого положения, сообщив абсциссе х значение, меньшее чем а, но беско-
нечно к нему близкое, то вышенаписанное выражение, в котором ф (х) по-
ложительно вблизи х — а, показывает, что X станет отрицательным; следо-
вательно, точка стремится двигаться в отрицательном направлении и еще
более удаляться от положения равновесия.
Часто встречающимся частным случаем является следующий: точка выхо-
дит из положения х0 со скоростью Vq и первыми особенностями, которые
встречаются при увеличении х или при его уменьшении, являются два простых
нуля а и с функции f{x), где а > х0 > с. Тогда можно написать
где <\> {х) — положительно между а и с. В этом случае имеем
X
dx
где попеременно нужно брать знаки -f и —»так как, согласно предыдущему
движущаяся точка будет колебаться между двумя точками А и С с абсцис-
сами а и с (см. рис. 134). Продолжительность колебания (вперед и назад)
равна
~=2/ /(д_х(==
Если, следовательно, х рассматривать как функцию от t (обращение
интеграла), то х будет периодической функцией с периодом Т. Согласно тео-
реме Фурье х можно разложить в тригонометрический ряд вида
х = a0 + at cos — + bt sin -=- + a2 cos -=- + b2 sin -=- + ...,
сходящийся при всех значениях ?. Определение коэффициентов ап и 6„ пред-
ставляет большие трудности, кроме случая, когда <li {x) является относительно х
многочленом степени, меньшей или равной двум. Тогда х является круговой
или эллиптической функцией аргумента t. По вопросу вычисления этих
коэффициентов в общем случае отсылаем к работе Вейерштрасса «Ueber
eine Oattung reel periodischer Funktionen» (Monatsbericht der Akad. der Wissen,
zu Berlin). Можно получить приближенную формулу для закона движения,
применяя метод, указанный Аппеллем (Comptes Rendus, т. 160, 1915, стр. 419).

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ	291
212. Движения под действием силы, зависящей только от
скорости. Вертикальное движение снаряда в сопротивляющейся
среде. До сих пор мы рассматривали примеры, в которых сила за-
висела только от положения точки. Перейдем теперь к кругу во-
просов, в которых приходится рассматривать материальную точку,
находящуюся под действием силы, зависящей только от скорости.
Вообразим тяжелое тело, движущееся в такой сопротивляющейся
среде, как воздух. Среда оказывает на каждый элемент поверхности
тела некоторое действие и все эти действия складываются в одну
силу и одну пару, приложенные к телу. В частном случае, когда
снаряд является телом вращения и совершает поступательное дви-
жение, параллельное оси вращения, из соображений симметрии оче-
видно, что пара равна нулю и что равнодействующая всех действий
среды на элементы поверхности тела является силой, направленной
вдоль оси в сторону, противоположную движению. Такое явление
можно наблюдать, например, когда шар или снаряд цилиндрическо-
конической формы падает в неподвижном воздухе по вертикали.
Займемся этим частным случаем. Согласно теореме движения
центра тяжести, которую мы докажем позднее, движение центра
тяжести будет таким, как если бы в нем была сосредоточена вся
масса тела и если бы в него были перенесены параллельно себе все
приложенные к телу внешние силы. Следовательно, центр тяжести дви-
жется, как тяжелая точка, находящаяся под действием вертикальной
силы R, направленной в сторону, противоположную скорости. Мы
приходим таким образом к необходимости исследовать движение
материальной точки под действием ее веса и силы сопротивления R.
Опыт показывает, что при очень малых скоростях сопротивление почти
пропорционально скорости v. Если скорость заметна, но все же меньше
чем 200 м/сек, то сопротивление изменяется пропорционально V2. При
больших скоростях необходимо ввести члены с V3 или с v%. Нельзя,
по-видимому, выразить закон сопротивления простой формулой. Сиаччи
предложил формулу, совпадение которой с экспериментом заслуживает
внимания. Эта формула была исследована Шапелем в Revue d'Artil-
lerie (т. XLVIII, апрель — сентябрь 1896). Мы будем исходить из
общего предположения, что сопротивление выражается в функции
скорости формулой
R = mg<? (v),
где <?(v)— положительная и возрастающая функций от V. Так как тело,
если его предоставить самому себе без начальной скорости, будет
падать, то сопротивление при -у = 0 должно быть меньше веса,
и, следовательно, ср(О)< 1. Допустим, кроме того, что для каждого
положительного значения переменной функция ср (t») имеет конечную,
положительную и не равную нулю производную. Через X обозначим
то значение v, при котором сопротивление равно весу, т. е. ср(Х)= 1.

292	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
1°. Нисходящее движение. Предположим, что движение является
нисходящим (рис. 135). Примем за начало исходное положение тела,
а за ось — вертикаль, направленную вниз. Уравнение движения будет
m~di* = mg — R = mg—mg<? (v)
или
Так как ср (X) = 1, то можно написать
откуда при помощи квадратуры найдем время в функции скорости:
I	dv
R	«•
Кроме того, заменяя в равенстве A) dt через dx/v, по-
лучим
М	,	v dv
gdx
Таким образом, координата также определяется как функ-
ция скорости при помощи квадратуры
v
gx= /*__ч*>
J <р (X) —
Рис. 135.
Формула A) показывает, что -тт имеет тот же знак, что и разность
ср (X) — ср (v). Предположим, что начальная скорость, которая по усло-
вию положительна, меньше величины X. Тогда вначале производная —г
будет положительна и скорость с течением времени будет возрастать
от своего начального значения v0. Скорость будет увеличиваться
до тех пор, пока разность срМ— f(v) будет оставаться положи-
тельной, т. е. пока v не достигнет значения X. Покажем, что v не
может достигнуть значения X за конечный промежуток времени.
В самом деле, в уравнении B) подынтегральное выражение
' . —р-у обращается в бесконечность при v = X и притом таким
образом, что п\_—гт" стремится к пределу 1/ср'(Х). Вследствие
этого интеграл становится бесконечным при •у = Х. Уравнение C)
показывает, что х также становится бесконечным для этого значе-
ния скорости v. Отсюда вытекает, что скорость все время воз-
растает, но стремится к конечному пределу X.

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ	293
_	,	,	dv
Если начальная скорость v0 больше X, то производная -г?
будет вначале отрицательной и скорость будет уменьшаться, при-
ближаясь к X. Так же, как и выше, можно убедиться, что tux
неограниченно возрастают, когда v стремится к X.
Итак, какова бы ни была окорость в начальный момент, она
будет стремиться к одному и тому же пределу X и по истечении
достаточно большого промежутка времени движение станет почти
равномерным со скоростью X. Отсюда следует, что если начальная
скорость будет в точности равна X, то движение будет точно рав-
номерным. Заметим, что дифференциальное уравнение A) действи-
тельно допускает решение v = X.
Допустим, что в воздухе падают два одинаковых однородных
шара, массы которых различны. При одинаковых скоростях сопро-
тивление будет одинаковым; следовательно,
mg<?(v) = m1g<f1(v).	D)
Обозначим через X и Xt предельные скорости для обоих шаров,
определяемые уравнениями ср(Х)=1, q>1(X1)=l. Легко видеть, что
если тх > т, то Xt > X. В самом деле, полагая в равенстве D)
¦v = X, получим:
Следовательно, cpt (X) меньше единицы и так как функция ср4 — воз-
растающая, то X, > X. Это показывает, что большей массе соот-
ветствует большая предельная скорость, что находится в соот-
ветствии с опытом, показывающим, что более тяжелые тела падают
в воздухе быстрее.
В качестве упражнения можно положить
gf (V) = kvn.
При п целом, квадратуры, которые нужно выполнить, касаются ра-
циональных дробей. Если п — число рациональное, л = — , то, полагая v = и3,
по-прежнему приведем задачу к рациональным дифференциалам.
Если, например, п = 1, то уравнение B) можно проинтегрировать, и мы
получим
k
откуда находим первый интеграл
X — v = (l — vo)e-kt.
Здесь мы действительно приходим к общим результатам: X — v имеет знак
X — «0 и когда t неограниченно возрастает, показательная функция стре-
мится к нулю и v стремится к X. Заменяя v через — и интегрируя, найдем
It - х = — j (X — v0) е-м + С.

294	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Так как при / = О должно быть х = О, то
Таким образом, для х как функции времени получаем
— e~kt
где скорость \ заменена ее значением g/k.
Покажем теперь, что если k стремится к нулю, то уравнение, опреде-
ляющее х, становится уравнением вида х = v^t -\- — gfl, которое определяет
свободное падение в пустоте. В самом деле, если в предыдущем равенстве
мы заменим е~ы его разложением в ряд, то получим
„,g-,(?+...)]+,[,_.(?_...)].
и если k = 0, то останется
х = vot + ^ ?&¦
2°. Восходящее движение. Направим теперь ось Ох вертикально
вверх (рис. 136). По-прежнему R — mgy(v) и уравнение движе-
ния будет
т. е.
dv
р Откуда, как и раньше, выведем:
V
V
7	_ С vdv
~~ ~ J 1
_ С
gX ~~ ~ J 1 + ф (w) '
Рис. 136.	„о
В этом случае -^ всегда отрицательно и скорость все время
уменьшается. Она обращается в нуль по истечении конечного про-
межутка времени
~~ g J I
О
dv
g
«0
и наибольшая высота, которой достигнет движущаяся точка, будет
о
„	 1 Г vdv
7 У ьГГы •

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ	295
Если ср (v) равно нулю, то получаются формулы движения в пустоте
о	о
1 g J "'¦ "' g
Когда функция ср (t>) не равна нулю, то она положительна. Вследствие
этого подынтегральное выражение в Н всегда меньше подынтеграль-
ного выражения в #,; поэтому Н меньше чем Нх и точка в воздухе
поднимается на меньшую высоту, чем в пустоте. Точно так же Т
меньше чем Гп и точка затрачивает меньше времени для поднятия
на наибольшую высоту, чем при движении в пустоте.
По истечении времени Т точка останавливается и затем начинает
падать по закону, установленному выше для нисходящего движения
при отсутствии начальной скорости. Когда точка проходит через свое
начальное положение, она имеет скорость, меньшую чем щ. В самом
деле, она поднимается на меньшую высоту, чем если бы она была
брошена вверх в пустоте с той же начальной скоростью; кроме того,
она падает тоже медленнее, так как ее падение замедляется сопро-
тивлением воздуха. По этим двум причинам скорость при возвра-
щении будет меньше, чем та же скорость при движении в пустоте,
т. е. меньше чем v0.
Полагая снова gy (v) = kvn, мы сумеем легко выполнить интегрирования
в случае л = 1. Имеем
V
= - f
J
»0
откуда, потенцируя, получим
g + kv=(g + kvo)e-kt.	(с)
Точка поднимется на максимальную высоту по истечении временя
Заменим в уравнении (с) скорость v через -гг и проинтегрируем. По-
лучим
gt + kx = (g + kv0) -^	.
Полагая k стремящимся к нулю, мы придем к формуле движения в пустоте
—	1
Положим теперь л = 2. Тогда, заменяя через У? величину g/k, получим
dv	1

296
ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
откуда, полагая р = С\ имеем
— tY~kg).
Постоянная р определится из начального условия v0 = X tg p. Время, не-
обходимое для поднятия на максимальную высоту, на которой v = 0, равно
R	dx
Т = . - Исходя из выражения для скорости, в котором v = —, после
У kg	at
квадратуры найдем
1 , cos(p— tY~kg)
k	cosp
3°. Прямолинейное движение тяжелой материальной, точки по на-
клонной плоскости с учетом трения и сопротивления среды.
Точка, пущенная из положения О (рис. 137) по линии Ох наибольшего
наклона плоскости, опишет прямую, наклон которой к горизонту мы
обозначим через /. Силами, приложенными
к точке, являются вес mg, сопротивле-
ние среды, которое мы будем считать про-
порциональным vn, R = mkvn, направленное
в сторону, противоположную скорости, нор-
мальная реакция N плоскости и, наконец,,
сила трения F, также направленная в сто-
рону, противоположную скорости. Эта
сила, согласно экспериментальным законам
трения (п. 195), не зависит от скорости
точки и пропорциональна нормальной
реакции: F — /N, где / есть коэффициент
трения.
Исследуем подробно нисходящее дви-
жение. Возьмем ось Ох, направленную
вниз, как на чертеже, И перпендикулярную к ней ось Оу. Выписав оба
уравнения движения, имеем
О
Рис. 137.
d?x
m-772=mgsinl — >
m-j?=N—mgcost.
Так как у все время равно нулю, то
N = mg cos /, F = fN = fmg cos /.
Заменив R его значением mkvn, получим уравнение
—гр = (g sin l — fg cos 0 — kvn.
^ Необходимо различать три случая в зависимости от того, будет ли пер-
вый член положительным, отрицательным или равным нулю.
Первый случай: tg/ >/. В этом случае первый член gsini — fgcos / по-
ложителен. Обозначая его через g', получим
Это уравнение идентично уравнению нисходящего движения по вертикали
в сопротивляющейся среде и отличается от него лишь заменой g через §•'.
Скорость, следовательно, стремится к (g'jk)n>

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ	297
Второй случай: tg / < /. Первый член отрицателен, и, обозначая его
через g±, мы получим уравнение
<Г'Х	. _
идентичное уравнению восходящего движения по вертикали с заменой g
на gi- Скорость будет уменьшаться и обратится в нуль по истечении ко-
нечного промежутка времени Т. Следовательно, к этому времени точка до-
стигнет некоторого положения А, в котором сопротивление воздуха и тре-
ние скольжения при движении уничтожаются, так как скорость обращается
в нуль. Точка будет оставаться все время в этом положении, так как если бы
-она начала двигаться, то сразу возникли бы силы трения и сопротивления
среды, которые вновь обратили бы скорость в нуль. Следовательно, в этом
положении А имеет место изученное в главе I равновесие между весом и
наклонной реакцией плоскости, вызванной трением покоя.
Третий случай: tg / = /. В этом случае получится уравнение:
dfi ~ RV ' dt~ V •
Следовательно, скорость будет убывать, так как ее производная отри-
цательна. Будет ли она обращаться в нуль? Интегрируя, получим
если л отлично от 1, и
если л = 1. Следовательно, если л больше или равно 1, то t неограниченно
возрастает, когда v стремится к нулю: движение продолжается неопреде-
ленное время со скоростью, стремящейся к нулю.
Если л меньше 1, то t стремится к определенному пределу Т, когда v
¦стремится к нулю:
1 —л
По истечении этого времени скорость обратится в нуль и точка остано-
вится, так как при скорости, равной нулю, пропадет, как ив предыдущем
случае, сопротивление.
Пройденное расстояние х будет конечным или бесконечным в зависи-
мости от того, будет ли л меньше или больше чем 2.
213. Прямолинейное таутохронное движение. Говорят, что
прямолинейное движение является таутохронным, если точка, начи-
нающая движение без начальной скорости и находящаяся под действием
заданных сил, затратит одно и то же время для достижения опреде-
ленного конечного положения, каково бы ни было ее положение в
начальный момент.
1°. Равнодействующая сил зависит только от положения
точки (метод Пюизб). Примем точку прибытия или точку тауто-
.хроназма за начало О. Пусть X—равнодействующая приложенных

298	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
к точке сил, х0— абсцисса начального положения, которую мы пред-
полагаем положительной. По теореме кинетической энергии имеем
По предположению, X является функцией от х и, очевидно, от-
рицательной, так как точка должна двигаться к началу О, каково бы
ни было ее начальное положение, для чего сила должна быть везде
направленной к О. Положим для краткости
где ср(лг) — положительная функция, возрастающая вместе с х и обра-
щающаяся в нуль при х — 0. Уравнение примет вид
Отсюда для определения времени Т, необходимого точке для дости-
жения положения О, можно вывести формулу
у = 1/ ¦?- '	dX
0 V *(*„)-
Положим
ср (л:) = г, ср (*0) = z0, х — ф (г),
где (|)—функция, обратная ср. Получим
2 J у1^г
Для того чтобы движение было таутохронным, необходимо и до-
статочно, чтобы Т не зависело от *0, т. е. от г0. Чтобы выразить
это, напишем, что производная от Т по параметру г0 равна нулю.
Чтобы избавиться от бесконечных членов в выражении этой произ-
водной, сделаем пределы не зависящими от г0, положив г — гои*
Тогда
г-— с
о
dT ¦w/"m' f

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ	299
или, возвращаясь к переменной г = гои,
Т._,/^Г ?
dzo-V 2 J
Это выражение должно быть равно нулю, каково бы ни было z0,
для чего подынтегральная функция должна тождественно обращаться
в нуль. В противном случае можно будет выбрать г0 настолько ма-
лым, чтобы в пределах от 0 до z0 эта функция имела постоянный
знак и тогда интеграл не будет равен нулю. Следовательно, функ-
ция ф должна удовлетворять дифференциальному уравнению
из которого получим
Так как ф(г) обращается в нуль вместе с г, ибо переменные г
и х обращаются в нуль одновременно, то С' = 0 и ф (г) = 2С]Лг.
Из уравнения х = <]> (г) получим, наконец,
дг2
откуда видно, что ср (л:) = -j-^- и
Следовательно, единственной зависящей только от х силой, вы-
зывающей прямолинейное таутохронное движение, является притяже-
ние, пропорциональное расстоянию. Это движение было рассмотрено
выше (п. 211).
2°. Равнодействующая сил зависит от положения а скорости точки.
Мы ограничимся для этого случая лишь некоторыми библиографическими
•ссылками. Лагранж указал (Memoires de Berlin, 1765 и 1770) общий закон
силы, при которой таутохронизм будет обязательно иметь место и который
как частный случай содержит предыдущий закон. Но, как заметил Бертран,
формула Лагранжа не дает всех законов для силы, при которых движение
<5удет таутохронным.
Отметим также статью Бриоши, содержащую формулу, более общую,
чем формула Лагранжа (Annali ... da Tortolini, Rome, 1853 и Mecanique de
Jullien, т. I), и статью Гатона де ла Гупийёра (Journal de Lioville, 2 сер.,
т. XIII). (См. упражнение 5 и 6.)
214. Дан закон прямолинейного движения, найти силу. Эта задача
будет определенной в зависимости от того, будет ли дан общий закон пря-
молинейного движения с двумя произвольными постоянными илн только
частный закон движения.
А. Допустим, что дано
х = <р (t, хе, v0),	A)

300	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
где х0 — начальное положение точки при t = 0 и i>o — начальная скорость»
Нужно найти закон силы, способной сообщить заданное движение точке,
пущенной из произвольного положения х0 с произвольной скоростью v0. Эта
задача является определенной. Имеем
dx	/0.
—тт- = ф' {t, Xq, «о),	(/)
ut
Х=т -^р- = ту"(t, х0, v0).
Разрешая уравнения A) и B) относительно х0 и v0 и подставляя в вы-
ражение для X, получим искомый закон
Пример. Если заданное движение определяется формулой
х0
то
Б. Если, наоборот, дан только частный закон движения, не содержащий
произвольных постоянных, или содержащий только одну произвольную по-
стоянную, то задача будет неопределенной. Допустим, например, что постоян-
ной нет вовсе и что дано
х = ч (О-	C)
Тогда имеем
v = <f' (О, X = ту" (t).
Из этих уравнений можно бесчисленным множеством способов получить
выражение для X в функции х, v и t. Следовательно, существует бесчислен-
ное множество законов для силы, способной произвести заданное частное
движение.
Вопрос может стать точнее, если заранее подчинить X некоторым усло-
виям. Так, например, если подчинить выражение X условию, что оно дол-
жно зависеть только от положения х, то задача становится определенной,
так как надо будет найти t из уравнения движения C) и внести его в выра-
жение для X. Задача получается тоже определенной, если наложить условие,
согласно которому X зависит только от v или только от t.
Пример. Пусть х = sin t. При t = 0 получаем х0 = 0, Vq = 1. Из этого-
уравнения имеем
v = cos t, X = — т sin t.
Отсюда получаем следующие законы для силы:
— т sin t,	(a>
G)
(Ь)
и далее, комбинируя первое равенство бесчисленным множеством способов.
Если мы будем искать наиболее общие движения, производимые этими силами,
то\ получатся весьма различные движения, но все они при частных начальных

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ	301
условиях хй = 0, v0 = 1 обратятся в заданное движение х = sin t. Так, на-
пример, для первых четырех законов силы получатся следующие движения:
X = Sin t + Ct + С,	(а)
.* = slntf + C) + C',	(p)
л: = С cos < 4" С' sin f,	G)
* = С cos -?= + С" sin -yp + sin t.	(8)
Все эти движения при подходящем выборе постоянных С и С обращаются
в j: = sin t.
III. Криволинейное движение. Тяжелая точка в пустоте
и в сопротивляющейся среде. Электрическая частица
215. Силы постоянного направления. Допустим, что сила, дей-
ствующая на материальную точку, все время параллельна некоторому
фиксированному направлению. В этом случае траектория будет ле-
жать в плоскости, содержащей начальную скорость и направление
силы. Этот результат можно считать очевидным из соображений сим-
метрии (п. 202). Примем плоскость траектории за плоскость ху и
направим ось Оу параллельно силе. Тогда уравнения движения будут
<Рх n	cPy v
Первое из этих уравнений приводится к следующему
dx	-it
-~тг = а, x = at-\-b,
т. е. проекция точки на ось Ох движется по этой оси равномерно.
Постоянные а и Ь определяются из условия, что при t = t0 должно
быть х = х0, (-37-) =*о- ^ наиболее общем случае второе уравне-
ние имеет вид
rf2y л /	dx dy ,\
После замены х выражением at-\-b оно преобразуется в уравне-
ние вида
"" dt* ~~ V d '
идентичное с уравнением прямолинейного движения. Если его можно
проинтегрировать, то задача будет решена.
216. Естественные уравнения. В рассматриваемом случае естествен-
ные уравнения упрощаются. Возьмем прямоугольные оси. Пусть а—-угол,
образованный скоростью с осью Ох (рис. 138). Проектируя на нормаль.

302
ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
имеем
Kcos =
ту*
Второе уравнение получится при проектировании на касательную. Однако
dx
проще исходить из наиденного выше свойства, что проекция —г— скорости
У
равна некоторой постоянной а, откуда
v cos a = а.
Исключая скорость из обоих уравений, по-
лучим естественное уравнение траектории
Кр cos2 a = const.
Если, например, положить Y = const., то
получится уравнение
р cos2 а = к,
являющееся естественным уравнением па-
раболы.
217. Движение тяжелой точки в пу-
стоте. За начало координат примем на-
чальное положение точки, ось у направим
вертикально вверх, а ось х— по горизонтали в плоскости траектории.
Уравнения движения будут
О
Рис. 138.
т
_
dt*
! — mg.
Обозначая через а угол, образованный начальной скоростью «о с осью Ох,
получим из первого уравнення
A)
B)
dx
— = t»0 cos a,
X = V(,t COS о.
Второе уравнение также интегрируется сразу и мы получаем
dy
dt
¦ = — gt + v0 sin a,
gfi
'	-7Z
Уравнення A) и A') определяют скорость:
У2 = v\ COS2 а + (у0 Sin а — gtJ = vl — 2gy.
d')
B')
C)
Численное значение скорости в каждый момент времени получается таким,
как если бы точка падала без начальной скорости из положения с ордина-
той VQpg. Формула C) непосредственно вытекает из теоремы кинетической
энергии.
Исключая t из равенств B) н B'), получаем уравнение траектории
Это — парабола с вертикальной осью, обращенная вогнутостью вниз (рис. 139).

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
303
Если угол а отрицательный, то, как видно из равенства A'), -^ будет
все время отрицательным. Следовательно, у будет монотонно убывать, и дви-
жущаяся точка никогда не пройдет через вершину параболы.
dy
Допустим теперь, что а > 0. Тогда -^-, или, что то же, у', будет вна-
чале положительным, и точка будет подниматься. Она будет подниматься
У
D
В
Д
Рис. 139.
до тех пор, пока у' не обратится в нуль, что произойдет по истечении про-
межутка времени t0, определяемого уравнением
. _ «о sin a
Так как при этом высота точки достигнет своего максимума, то ее скорость
на основании равенства C) будет иметь минимум. Координаты наивысшей
точки 5 параболы — ее вершины — будут
х0 = voto cos a =
«о sin 2o
Уо =
= ^- sin3 а.
По истечении промежутка времени t$ проекция у' скорости станет отри -
дательной и движущаяся точка начнет опускаться. На одной и той же вы-
соте, как при движении вверх, так и при движении вниз, точка будет иметь
одинаковую по абсолютному значению скорость. В частности, она пройдет
через точку А, находящуюся на одной высоте с точкой О, со скоростью t»0.
Горизонтальное расстояние ОА равно удвоенной абсциссе х0 вершины:
vl sin 2а
Чтобы при заданной начальной скорости расстояние ОА имело возможно
большее значение, необходимо, чтобы sin 2я имел максимум, т. е. чтобы

304	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
угол о был равен 45°. Допустим, что требуется попасть в точку В оси Ох,
абсцисса которой меньше, чем —. Наклон стрельбы определится формулой
о
sin 2а = А- ОВ.
Отсюда видно, что имеются два решения, оба отличные от 45е. Следовательно,
в точку В можно попасть по двум параболам. Легко убедиться, что по
нижней параболе точка попадает в цель В за более короткий промежуток
времени.
Можно определить геометрически положение параболы, соответствующей
заданному углу а. Для этого заметим, что все параболы, которые получаются
при изменении угла а, имеют общей директрисой прямую D с ординатой
v^j2g. В самом деле, параметр параболы, описываемой движущейся точкой,
vl cos2 a vl sina a
равен р =	 и так как ордината вершины равна у0 = ——^	, то
уравнение директрисы будет
Следовательно, это — прямая D, находящаяся на высоте, которую достигнет
движущаяся точка, если ее бросить вертикально вверх со скоростью w0.
Этот результат становится наглядным, если исходить из уравнения C)
(с1х\Ъ /rfy\2
-ту-) + (-77} , то это уравнение показы-
at ) \atI
«о
вает, что в мнимых точках пересечения траектории с прямой у = у-
получается —+-= ±1. Следовательно, эта прямая является директрисой
параболы.
Установив это, допустим, что дана касательная к траектории в начале
координат. Тогда фокус F будет находиться на такой прямой OF, что пря-
мая Ov0 будет биссектрисой угла FOD. Кроме того, он будет находиться на
окружности радиуса OD, описанной из точки О, как из центра. Следова-
тельно, он находится на пересечении этой окружности с прямой OF. Построе-
ние показывает, что геометрическим местом фокусов парабол является окруж-
ность с центром в точке О радиуса OD.
Поставим себе задачей найти угол, под которым нужно выпустить сна-
ряд, чтобы попасть в заданную точку Mi {хь у{) плоскости. Введя обозна-
чение tg a = и и подставив в уравнение траектории координаты хь у! задан-
ной точки Mi, так как траектория должна пройти через эту точку, получим
для определения и уравнение второй степени
У1=—
Условием вещественности корней является выражение
i4

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
305
Для его геометрического
уравнение
истолкования рассмотрим параболу, имеющую
	у —
C)
Эта парабола имеет параметр v^jg и вершину в точке х — 0, у = к- ,
т. е. в точке D; следовательно, ее фокус находится в начале координат.
Условие вещественности B) выражает, что точка М± должна быть внутри
этой параболы («параболы безопасности») или на ней. Если точка My на-
ходится внутри параболы безопасности, то уравнение для и имеет два раз-
личных вещественных корня и тогда в точку My можно попасть двумя раз-
личными способами, выпуская снаряд под двумя различными углами (рис. 139).
Если точка My находится на параболе безопасности, то уравнение для и
имеет двойной корень и тогда в точку My можно попасть только одним
способом. В случае, когда уравнение для и имеет два различных корня,
имеются две траектории, проходящие через Мь соответствующие двум зна-
чениям а.у и ах угла а. Время, затрачиваемое на достижение точки My по
обеим траекториям, равно соответственно
U=-
COS
*;=¦
v0 cos c^
Более короткое время соответствует меньшему из углов ах и а%.
Парабола безопасности является огибающей траекторий, получаю-
щихся при изменении угла а, т. е. величины и. В самом деле, для нахо-
ждения огибающей кривых, представляемых ура-
внением A), в котором и — переменный параметр,
достаточно выразить, что это уравнение, рассматри-
ваемое как уравнение относительно и, допускает
двойной корень. Но это как раз то, что мы делали
для нахождения параболы безопасности.
Эти результаты могут быть также легко полу-
чены и геометрически (рис. 140). Пусть нужно по-
строить параболу, проходящую через две точки и
имеющую заданное направление. Ее фокус, как мы
видели, находится на окружности радиуса OD с цен-
тром в точке О. Он должен также находиться на
окружности с центром в точке Му, через которую
должна проходить парабола, и радиусом, равным
перпендикуляру МуР, опущенному из точки My на
директрису D. Эти две окружности могут пересечься
в двух точках: F и F'. Следовательно, могут быть две
параболы. Чтобы эти окружности пересекались, не-
обходимо, чтобы расстояние ОМг между центрами было меньше суммы и
больше разности радиусов. Последнее условие, очевидно, выполняется, так
как ОМу > OQ, a OQ есть разность радиусов. Следовательно, достаточно
написать
Рис. 140.
Проведем прямую Д на расстоянии 2 OD от оси х и продолжим M-JP до
точки пересечения П с этой прямой. Тогда условие, которое должно выпол-
няться, примет вид
МуО < МХП.

306	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Но геометрическое место точек, для которых М^О — Л^Д является пара-
болой с фокусом в начале координат и директрисой Д; это и будет пара-
бола безопасности. Если точка М± находится внутри этой параболы, то в нее
можно попасть двумя способами; если она находится на параболе, то имеется
только одна траектория, проходящая через эту точку. Для такой точки М±
фокус траектории и фокус параболы безопасности лежат на одной прямой
с точкой М^. Элементарное построение, определяющее касательную
в точке М±, показывает, что эта касательная является одной и той же для
обеих парабол. Отсюда вытекает, что парабола безопасности является оги-
бающей всех траекторий.
218. Определение параллельной силы по заданной траектории. Мы
исследовали задачу, заключавшуюся в том, что по заданной силе, параллель-
ной оси Оу, нужно было найти движение, которое эта сила сообщала мате-
риальной точке. Можно задаться обратной задачей: зная плоское движение,
при котором проекция точки на ось х движется по этой оси равномерно,
найти закон сил, параллельных оси у, которые могут вызвать это движение.
Зададимся траекторией y=f(x), по которой движется точка под дей-
ствием силы, параллельной оси Оу. По предположению, x=at-{-b и уравнение
траектории определит у в функции t, если заменить в нем х его значением.
Тогда получим
Следовательно, закон силы будет такой:
Г==т~ж = та2/"(ЛГ)-
Полученное выражение силы можно преобразовать при помощи уравне-
ния траектории. Иа этого уравнения можно, например, определить х в функ-
ции у и выразить силу через эту одну переменную, но можно также заме-
нить часть значений х через у, а другую часть — через t или —тг', в общем
виде закон изменения силы можно выразить так:
где ЧГ — произвольная функция. Эта сила действительно обращается
в ma?fa(x) на заданной траектории. Если, исходя из одного из этих
законов для силы, определить вызванное ею движение, то при подходящем
частном выборе начальных условий получится заданная траектория у = f(x).
Возьмем, например, окружность
Применяя вышесказанное, получим законы
У=4-. У=
y	_
(ф — л:2J
Для этих двух законов получатся два совершенно различных семейства кони-
ческих сечений, но каждое из них содержит окружность у = Y № — -*2-
219. Криволинейное движение тяжелого тела в сопротивляю-
щейся среде. Когда снаряд находится в движении, его центр тяжести
движется так, как если бы в нем была сосредоточена вся масса

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ	307
тела и к нему были приложены все действующие на снаряд внешние
силы.
В случае, которым мы занимаемся, на центр тяжести действуют
две силы: вес снаряда и сопротивление R среды, которое является
равнодействующей поверхностных сил (давлений и трений),' перене-
сенных параллельно им самим в центр тяжести. Эти поверхностные
силы, взятые в совокупности, могут, вообще говоря, приводиться
к результирующей силе R, приложенной в центре тяжести, и к паре.
Если форма снаряда произвольна, то о направлении этой равно-
действующей ничего не известно, и эта сила может вывести центр
тяжести из вертикальной плоскости, в которой он выпущен в момент
t — О. Но если снаряд является сферическим и он не вращается, то
равнодействующая лежит в вертикальной плоскости, содержащей
скорость центра тяжести G и вследствие симметрии траектория этой
точки является плоской. Для возможно большего упрощения мы
допустим, кроме того, что эта равнодействующая является силой R,
направленной в сторону, противоположную скорости v центра тя-
жести. Сила R будет возрастающей функцией скорости v. Мы на-
зовем эту силу R сопротивлением воздуха.
Если допустить, что сопротивление R лежит в вертикальной
плоскости, проходящей через центр тяжести, то можно доказать
аналитически, что траектория плоская. В самом деле, отнесем дви-
жение к трем прямоугольным осям Ох, Оу, Ог, причем ось Oz на-
правлена вертикально вверх. Если через Rx, Ry, Rs обозначить
проекции силы R, то уравнения движения будут:
=Rs — mg.
Из первых двух выводим
d">-x
df-	dfi
Но так как предположено, что вектор R прямо противоположен
—?- и —
Вследствие этого предыдущее соотношение принимает вид
v, то проекции Rx и Ry пропорциональны производным —?- и — .
dx	dy
It	Hi
откуда, интегрируя, найдем
dy , ,, dx
i -L. = In С —;т •
dt	at

308
ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Потенцируя и снова интегрируя, получим
у = Сх-\-С
Отсюда следует, что кривая является плоской и ее плоскость вер-
тикальна. Это — плоскость горизонтальной проекции начальной ско-
рости.
Примем эту плоскость за плоскость ху, начальное положение
движущейся точки за начало координат, ось Оу направим верти-
кально вверх, а ось Ох по отношению к Оу направим в ту же сто-
рону, в какую направлена начальная скорость.
Будем исходить из естественных уравнений движения. Обозначим
через s дугу ОМ траектории, через а — угол скорости v с осью Ох
и через р — радиус кривизны МС
(рис. 141). Действующие на точку
силы суть вес mg и сопротивление R.
Их равнодействующая всегда располо-
жена относительно касательной R со
стороны отрицательных у. Но так как
эта сила всегда направлена в сторону
вогнутости, то траектория направлена
вогнутостью в сторону отрицатель-
ных у. Следовательно, угол а будет
все время уменьшаться. Его начальное
значение равно известной величину о^.
В наивысшей точке траектории он обращается в нуль и далее про-
должает уменьшаться. Мы увидим в дальнейшем, что его предельное
значение равно —-к/2.
Проектируя силы на касательную Mv, получим (п. 200)
Рис. 141.
т
dt
= Ft = — mg sin a — /?.
В этом уравнении R есть функция скорости, которую мы напи-
шем так:
R = mgtf (v).
Поэтому
|	(t»)].	A)
Проектируя теперь на нормаль, получим
= mg cos a.
Но
ds
ds dt
dt

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ	309
Здесь нужно взять знак минус, так как с возрастанием s угол а убы-
вает, а р есть абсолютное значение радиуса кривизны. Внося это-
значение в предыдущее уравнение, получим
Уравнения A) и B) позволяют найти t и v в функции а. Исключим,
из них dt, деля их почленно друг на друга; получим уравнение
4-=tga + ^>.	CV
v d a & ' cos a	K ¦
Это — уравнение первого порядка. Отсюда находим v в функции а:
После этого из уравнения B) получим
Можно выразить также х и у в функции а при помощи новых
квадратур. В самом деле, имеем:
а
dx = v cos а dt, x==	 /[<|i (а)]2 da,
а,
а
dy = v sin a, dt, у —	/ [<]) (a)]2 tg a da.
а.
Таким образом, если удастся найти функцию ф(а)- т0 задача приве-
дется к простым квадратурам.
Выражение
dt __ \ у
da	g cos a '
определяющее dt, показывает, что когда а больше, чем — тс/2, про-
dt
изводная -^- отрицательна и с уменьшением а время действительно
увеличивается. То же самое справедливо и для х, так как dx=v cos adt.
Что касается у, то он сначала увеличивается, пока а не достигает зна-
чения a = 0, после чего —^- меняет знак, у уменьшается и движу-
щаяся точка опускается. Для нахождения значений х, у, t, соот-
ветствующих наивысшей точке, нужно в интегралах положить a = 0.
Годограф. Уравнение v = ф (а) является уравнением в полярных,
координатах годографа скорости точки, так как v есть радиус-век-
тор точки годографа, а a — угол, который он образует с осью Ох~

310	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Естественное уравнение. Если функция <]i известна, то легко
найти естественное уравнение кривой. Действительно, мы нашли, что
следовательно,
cos a g cos а
Случай интегрируемости Лежандра. Мы исследуем со всеми подроб-
ностями случай, когда, по предположению, сопротивление определяется фор-
мулой
где все три постоянные а, Ь, п. положительны. Мы будем предполагать,
что а меньше единицы, так как в противном случае, если тело отпустить
без начальной скорости, его вес будет меньше силы сопротивления mga, и
тело не будет падать.
Для рассматриваемого движения уравнение C) примет вид
dv 	 . а -\- bvn
v da °	cos о
Разделив обе части на —vn/n и приняв за новую переменную l/i/n, получим
Для интегрирования этого линейного уравнения положим
—- = ра,
после чего получим
da , dp .	Л . а \ . nb Л
Р -г- + Q -г- + n PQ tg а -А	) -4	= 0.
* da ч da ' гч \ s ' COS a) ' cos a
Выберем q таким образом, чтобы обратить в нуль коэффициент при р; по-
лучим уравнение
da	na da
— = — П tg a da	,
q	s	cos a
допускающее частный интеграл
In q = n In cos a — na In tg I ¦=- + -j- j,
•При этом значении q нам останется	для определения р проинтегрировать
уравнение
dp _	nb
da ~	q cos a

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ	311
Интегрируя это уравнение в пределах от а0 до а и обозначая через «fa зна-
чение q при а = а0 и через v0 начальную скорость, получим
= —Кг = С— nb
qvn	J
da
q cos a
где постоянная С имеет значение 	, в чем убеждаемся, положив a = о0.
Подставив сюда найденное выше значение для функции q, получим v в функ-
ции а. После этого найдем х, у, t по формулам D) и E).
Покажем, что если а убывает до —я/2, то время неограниченно увели-
чивается, и у становится бесконечным, но отрицательным, тогда как v и х
оба имеют определенные пределы, так что кривая имеет вертикальную
асимптоту на конечном расстоянии и движение стремится стать прямолиней-
ным и равномерным.
В самом деле, выражение, определяющее величину —— после умноже-
ния на q, может быть написано следующим образом:
-—¦ =• —У-	nbq I
v	<7n<	«/
da
qcosa
Когда а стремится к —~-, q стремится к нулю, так как а меньше 1; с дру-
гой стороны, интеграл в правой части обращается при этом в бесконечность.
Так как член —*-^ стремится к нулю, то достаточно найти предел второго-
члена правой части, который может быть написан в виде отношения
-nb
q cos
	_
Я
со _
принимающего вид —. Отношение производных по а равно
nbqda
cos a dq '
q da
или, заменяя ~-— его вычисленным выше значением, получим
— sin a — а '
Полагая, наконец, а —	—, найдем, что 1/и" стремится к пределу -=	 ,
at» — к пределу
Л —

312	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Интеграл, определяющий х [формула E) ],
(А
-- ! Г
•—1J
V2da,
остается конечным, когда а стремится к —я/2. Действительно, так как v
стремится к конечному пределу X, то подынтегральное выражение остается
конечным и поэтому конечным будет х, который стремится к значению
«о
2
v"-da.
С другой стороны, t становится бесконечным при а = —- . Действительно,
g J
V da
cos a
«0
и подынтегральное выражение обращается в бесконечность при а = —7-
и притом таким образом, что 	la -)- -^-} стремится к определенному пре-
делу X. Следовательно, этот интеграл ведет себя вблизи а =	^-, как
Ida
т. е. обращается в бесконечность. По той же причине выражение
а
неограниченно возрастает, когда а стремится к — я/2. Таким образом, вы-
сказанные выше предложения установлены.
Найденной предел \ для скорости, так же как и в случае прямолинейного
нисходящего движения, является корнем уравнения
Примечание. Если в каком-нибудь определенном частном случае
желательно выполнить квадратуры или по крайней мере приближенно вы-
числить значения v, х, у, t вблизи а = —^ > то проще всего положить
da	2и
(а , я\ du da
-п + Т I. -— =	 . COS а =
2 ' 4 / и cos а
1+и2'
Переменная и, вначале положительная, равна 1 при а = 0 и стремится к нулю,
когда а стремится к — я/2.

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
Значение q принимает вид
»-«а 2п и"'
q =
A + иТ A + "Т
где показатель п' положителен, так как а меньше 1. Подставляя это значе-
1
ние q в выражение для ——, найдем
2™ и"'
Когда л целое, квадратура может быть выполнена. Это выражение легко-
поддается разложению в ряд.
Замечание по поводу интегрирования уравнения C). Мы видели, что
задача приводится к квадратурам, если из уравнения C) удается определить v
в функции а. Поэтому представляет интерес исследовать это уравнение и
указать случаи интегрируемости. Это сделал Сиаччи в двух статьях в Com-
ptes Rendus, т. СХХХП и СХХХШ, 1901. С другой стороны, для выполнения
интегрирования можно привести уравнение C) при помощи подстановки*).
v [sin а + 9 (v)] = —
к уравнению
-|J = v [срз (v) - 1] гз - Щ (V) + t/9' («)] г\
т. е. к виду
^ = сог3 + с^ + с2г + с3,
исследованному многими авторами (Рожер Лиувилль, Comptes Rendus,.
6 сентября, 1886; Ann ель, Sur les invariants de quelques equations differen-
tielles, Journal de Jordan, т. 5, 1891; П е н л ё в е, Annales de l'Ecole Normale
superieure, т. VIII, 1891; Эллиот, там же, т. VII, 1890). Следует отметить
также работы Драха, определившего все виды функции у (v), при которых
уравнение C) интегрируется в квадратурах (Comptes Rendus, 1914).
220. Движение легкого вращающегося шара в воздухе. Карьер
исследовал экспериментально траектории в воздухе легких однородных сфе-
рических ядер, вращающихся вокруг оси, перпендикулярной плоскости траек-
тории центра. Он установил вид различных траекторий в зависимости
от величины и направления вращения. Результаты даны в статье в Jour-
nal de Physique theorique et appliquee, т. V, 1916. Существенным является
то, что при постоянном вращении получаются траектории, которые вместо
вертикальных асимптот, как это было выше, имеют асимптоты, наклоненные
в ту или иную сторону, в зависимости от направления вращения. Причину
этих отклонений следует искать главным образом в трении о воздух поверх-
ности ядра. Это трение вызывает элементарные действия, которые, будучи
перенесены параллельно самим себе в центр тяжести, имеют равнодействую-
щую, зависящую от направления и скорости вращения. Вид траекторий,
*) См. А п п е л ь, Archiv der Mathematik und Physik, т. 5, 1903.

314	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
найденный Карьером, можно объяснить, если принять следующую гипотезу
о полном эффекте сопротивления и трения воздуха *):
Движение центра тяжести будет таким, как если бы точка с мас-
сой т, равной всей массе ядра, находилась под действием своего веса mg
и сопротивления R = mgy (*>), возрастающего вместе со скоростью v
точки, но не направленного в сторону, противоположную скорости, а обра-
зующего с вектором, противоположным скорости v, острый угол ф,
положительный или отрицательный, в зависимости от направления
угловой скорости вращения в>. Угол ф возрастает вместе с а и обращается
в нуль при и> = О **).
Эта гипотеза указывает на то, что сопротивление R, которое при о> = О
прямо противогГоложно скорости v, отклоняется вследствие вращения в сто-
рону, противоположную направлению вращения, на острый угол <\>, являющийся
возрастающей функцией угловой скорости » я обращающийся в нуль при
*> = 0. На малом участке траектории скорость ш и угол ф остаются приблизи-
тельно постоянными.
Обозначая, как и раньше, через а угол между i/ и Ох и приняв те же
оси, что и на рис. 141, получим при R = mg<f(v) уравнения движения:
d (v cos а)	/|,ч rf (t» sin a)	/ ч , / i i ч
dt	'- ^—g<t (f) cos (а + ф),	dt—'- — — g<( (v) sin (a + ф) — g,
откуда, исключая dt, получим дифференциальное уравнение годографа
[<f (v) sin ф — cos a] dv = v [<f (w) cos ф — sin a] da,
определяющее i/ в функции a, если i/ рассматривать как постоянную. Это
уравнение при ф = 0 переходит в классическое уравнение.
В частном случае, когда сила R пропорциональна скорости v,
R = mg~,
уравнения движения приводятся к линейным уравнениям, определяющим
координаты х и у в функции t.
Случай, когда мгновенное вращение шара имеет произвольное на-
правление. В предыдущих экспериментах ядро вращалось вокруг оси, пер-
пендикулярной плоскости траектории. Производились также эксперименты,
в которых мгновенная ось вращения имела произвольное, но известное
направление. В этом случае траектория была, вообще говоря, простран-
ственной кривой. Предполагается, что та же самая гипотеза относительно
полного эффекта сопротивления среды может быть сделана и для такого
рода движений. Сопротивление R = mgy (v) вместо того, чтобы быть
противоположным, вектору скорости v центра тяжести G, имеет на~
правление, которое находится поворотом вектора — v на острый угол ф
вокруг оси Ga> мгновенного вращения шара в сторону, противоположную
этому вращению; этот угол ф является возрастающей функцией от
мгновенной угловой скорости и> и обращает в нуль при <л = 0. Таким об-
разом, если ось мгновенного вращения касательна к траектории или угловая
скорость равна нулю, то сопротивление будет противоположно скорости.
По затронутым здесь вопросам можно указать на статью лорда Рэлея
«On the irregular flight ef a tennis-balb (Messenger of mathematics, n°. 73,
1877) и на статью Гринхилла (Messenger of mathematics, т. IX, 1880).
*) Ann ель, Journal de Physique theorique et appliquee, т. VII, 1917
стр. 5 и 49.
**) Этот и следующий результаты являются прямым следствием теоре-
мы Н. Е. Жуковского о подъемной силе. (Прим. перев.)

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
315
221. Движение наэлектризованной частицы в наложенных друг на
друга электрическом и магнитном полях. Рассмотрим материальную-
частицу М массы т, имеющую заряд г и движущуюся в пространстве со ско-
ростью V.
Представим себе сначала неподвижные электрические заряды .на непо-
движных телах, создающие электрическое поле, в котором электрическая сила,
действующая на электрический заряд +1, помещенный в точке (х, у, г),
имеет проекции Р, Q, R, определяемые формулами
Я = —— О-—— R= дУ
~ дх '	ду ' ~ дг '
где V — потенциал электрического поля. Тогда сила, действующая на массу т,.
несущую заряд е, будет иметь проекции еЯ, eQ, e.R.
Допустим, что, кроме того, имеется магнитное поле, в котором состав-
ляющие вектора напряженности поля Н равны Нх, Ну,
Нг (направление Н считается совпадающим с направ- '
лением силы, действующей на положительный по-
люс магнита). Тогда сила F, с которой это поле дей-
ствует на движущуюся частицу, определяется следующим
., dx dy
законом: пусть х, у, z — координаты частицы М; —т—, —f- ,
dt ' dt
dz
—r,	проекции ее скорости v;с — скорость света; сила/7
перпендикулярна к плоскости векторов Я и v и рав-
на 	sin (H, v). Если заряд е положительный, то
М
Рис. 142.
сила F направлена в сторону, откуда кратчайшее совме-
щение вектора Н с v видно против хода часовой стрелки (рис. 142)р
следовательно,
Если оси координат расположены обычным образом, то проекции силы F
будут
и две аналогичные формулы получатся круговой перестановкой букв. Сле-
довательно, уравнения движения частицы будут
d?x
dy*
т .._ =
dz
dx
dz
A)
Если электрическое и магнитное поля произвольны, то об интегрирова-
нии этих уравнений сказать ничего нельзя, за исключением того, что непо-
средственно следует из теоремы кинетической энергии. Эта теорема дает
так как работа силы F равна, очевидно, нулю. Следовательно, имеете»

316	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
первый интеграл
где V—потенциал электрического поля. В частном случае, если электричес-
кое поле равно нулю, то скорость постоянна:
Тогда можно исключить время, вводя дугу траектории s соотношением
ds = «о dt.
Первый частный случай. Электрическое поле равно нулю, магнит-
ное поле создается единственным магнитным полюсом, помещенным
л начале О.
При этих условиях сила магнитного поля X, Y, Z имеет силовую функцию
вида U = —, где г — расстояние У-*2 + У2 + z". Тогда уравнения движения,
если в них положить
Щ
будут
' ' dz
Ж
dx dz
ds	ds
dy\
ds )'
B)
ds У ds
Прежде всего очевидно, что траектория С является геодезической линией
конуса с вершиной в точке О и направляющей С. Действительно, так -как
скорость постоянна, то сила F направлена по главной нормали к С и, с дру-
гой стороны, сила F в точке М перпендикулярна образующей ОМ и ско-
рости v, т. е. нормальна к рассматриваемому конусу. Но при помощи анализа,
принадлежащего Дарбу (примечание VII к т. I «Механики» Депейру), можно
показать, что этот конус будет круговым. Из уравнений B), если сделать над
ними преобразования, приводящие к теореме моментов относительно оси Ог,
получим
d*y d'lx\ z I dx dy . dz\
	V	I = — I X —!	\- V —-—h Z	I —
ds* ds2 / r3 \ ds ' J ds ds)
_ z dr 1 dz _ d I z\
~7* ds T ds ~~~ds\r )'
¦Следовательно, интегрируя, получим
JxJ!y-y**) = -± + c.
r\ds J ds j	r
и точно так же
dz dy \	x
dz
ds
ds ds /	r
I dx dz\	у . „

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
317
где А, В, С — постоянные. Если эти уравнения умножить соответственно
на г, х, у и сложить, то получится
О = — г + Ах + By + Сг,
C)
т. е. уравнение конуса, на котором лежит траектория. Это — конус враще-
ния вокруг оси, перпендикулярной к плоскости Р, имеющей уравнение
Ах + By + Сг = О,
так как уравнение C) показывает, что конус является геометрическим
местом точек, для которых отношение расстояний до точки О к расстояниям
до плоскости Р, проходящей через точку О, постоянно.
Итак, траектория является геодезической линией кругового конуса с вер-
шиной в точке О. Этот результат, отмеченный Пуанкаре, объясняет инте-
ресное явление затягивания катодных лучей магнитным полюсом, открытое
в 1895 г. Биркеляндом (Archives des Sciences physiques et naturelles, т. VI,
1898, стр. 205).
Второй частный случай. Постоянные электрическое и магнитное
поля. Интегрирование выполняется легко, когда оба поля постоянны. Возь-
мем оси так, чтобы ось Ог была параллельна силе X, У, Z магнитного поля
и чтобы плоскость гОх содержала постоянную силу Р, Q, R электрического
поля.
Тогда X, Y, Q будут равны нулю и общие уравнения движения A)
принимают вид:
т —гпг = вн— i
т-
-= +eZ
dx
dt
D)
где коэффициенты постоянны. Возьмем за начало координат начальное поло-
жение движущейся точки в момент t = 0. Обозначая через р, г и о> постоян-
tP tR tZ
ные 	, 	,	, получим после первого интегрирования:
dx
dt
~dt
a,)
= — <ox + b,
E)
где a, b, с — постоянные интегрирования, равные проекциям начальной ско-
рости на оси. Далее исключение у приводит к линейному уравнению
dPx
в котором за неизвестную можно принять величину х	^- и из кото-
О)	00"
рого получается
h	n
+ «).	F)

318
ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
где А и а — новые постоянные. После этого из первого уравнения E) имеем
a pt
у =	— + A cos (ш/ 4- а).	F'>
О)	О) '	\ i /	\ г
Постоянные А и а таковы, что л: и у обращаются в нуль при * = 0. Инте-
грируя третье из уравнений E), получим
Таким образом мы получили уравнения движения в конечной форме.
Движение можно рассматривать как составленное из равномерного кру-
гового движения и параболического движения с постоянным ускорением,
параллельным оси Ог. В самом деле, если положить
х2 — A sin (a>t -f о), уа = A cos {at -]- a), z2 = 0,
(8)
то можно написать
у =
Рис. 143.
Точка Mi с координатами х±, уь г^ совершает параболическое движение
в плоскости, параллельной плоскости zOy, с постоянным ускорением, рав-
ным г и параллельным оси Oz. Точка М2 с координатами Хо, у2 z% описывает
в плоскости хОу окружностей
z	^-	^ радиуса А с центром в точке О,
с угловой скоростью о). Поло-
жение точки к моменту вре-
мени t может быть получено
путем построения результи-
рующей векторов ОМХ и ОМ^,
т. е. путем проведения через
точку М\ вектора М^М,' рав-
ного и параллельного век-
тору ОМ2 (рис. 143).
Движение точки М можно
тогда представить следующим
образом: круг С постоянного
радиуса А с центром в точке Ми
параллельный плоскости ху, совершает поступательное параболическое дви-
жение с постоянным ускорением, а точка М равномерно описывает окруж-
ность этого круга по тому же закону, по которому точка М2 описывает
окружность Со-
Изменяя постоянные р, г, ш или Р, R, Z, мы иолучим частные случаи,
приводящие к изящным результатам. Если R = 0, т. е. если электрическое
поле перпендикулярно магнитному, то г = 0 и точка Mt совершает прямо-
линейное равномерное движение. Получающаяся в общем случае парабола
заменяется сейчас прямой и в зависимости от начальных условий можно
в частных случаях получить в качестве траектории винтовую линию, цик-
лоиду и т. д.
Третий частный случай. Исследования Штё'рмера о полярных
сияниях. На основании идей, высказанных в 1896 г. Биркеляндом и в 1900 г.
Аррениусом, некоторые физики пришли к мысли, что полярные сияния а
соответствующие магнитные возмущения вызываются электрическими части-
цами (катодными или сходными с ними лучами), приходящими из пространства
и движущимися по траекториям, определяемым действием земного магнетизма.

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ	319
Задача вычисления этих траекторий упрощается, если предположить, что
частицы очень далеки от Земли, примерно на расстоянии более миллиона
километров. Тогда можно рассматривать магнитное поле Земли как образо-
ванное одним элементарным магнитом, помещенным в центре Земли, ось
которого совпадает с земной осью. Именно при таких упрощающих
предположениях задача рассматривалась Карлом штёрмером в статье, по-
мещенной в Archives des Sciences physiques et naturelles de Geneve, т. XXIV,
1907. Штёрмеру удалось получить важные результаты без интегрирования
уравнений задачи. Ему, в частности, удалось объяснить некоторые сущест-
венные моменты опытов Биркелянда и более новых опытов Вилляра. Недо-
статок места не позволяет нам изложить здесь эту теорию, требующую
длинных вычислений.
УПРАЖНЕНИЯ
1.	Найти прямолинейное движение точки, притягиваемой неподвижным
центром с силой, обратно пропорциональной кубу расстояния: X =	^-.
Ответ.
А
2.	Найти прямолинейное движение точки между двумя притягивающими
центрами, например центрами Земли и Луны, предполагаемыми неподвиж-
ными и притягивающими с силами, обратно пропорциональными квадрату
расстояния.
Ответ. Обозначая расстояние между обоими неподвижными центрами
через а и принимая один из них за начало координат, имеем
mk'2
В рассматриваемом случае между обоими центрами имеется положение
неустойчивого равновесия Е. Если точка не находится в этом положении и
ей сообщается начальная скорость в направлении этого положения, доста-
точно большая для того, чтобы она прошла через это положение, то она упадет
во второй притягивающий центр. Если скорость точки обратится в нуль до
того, как она достигнет положения Е, то она упадет в первый притягивающий
центр. Если, наконец, алгебраическое значение скорости обращается в нуль
в точке Е, то движущаяся точка неограниченно приближается к ? со ско-
ростью, стремящейся к нулю, но никогда этого положения не достигнет.
3. Пусть x=f(t, jc0, w0) — уравнение движения, вызванного силой
X = ср (д:), зависящей только от положения точки, причем д:0 и «о — началь-
ные абсцисса и скорость. Доказать, что другая точка с той же массой,
абсцисса которой равна
где а — постоянная, движется под действием силы Xi = oflX, если начальная
абсцисса и скорость равны х0 н v0.
В частности, если а = У—1, то точка, движение которой задается фор-
мулой
движется под действием "силы Х1 = — X (Comptes Rendus, 30 декабря 1878).
Применить к случаям

320	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
4.	Показать, что если закон таутохронного движения входит в формулу
Лагранжа, то при присоединении к действующей силе сопротивления, про-
порционального скорости, по-прежнему получится таутохронное движение.
5.	В прямолинейном движении выразить скорость v в функции х и х0
так, чтобы соответствующее движение было таутохронным.
Ответ. Приняв точку таутохронности за начало, предположим, что ско-
рость написана в следующей форме:
1	1
v
X
где ? обозначает отношение —. Это выражение v должно, по предположе-
но
нию, обращаться в нуль при х = х0, т. е. при 5 = 1. Время, затрачиваемое
точкой для достижения начала, равно
1
f = - f xo9(xo,
я
Т= —
о	о
где х заменен через лго?. Так как интеграл Т не зависит от х0, то его произ-
водная
1
дТ
__ Г д [хо9 Uo, б)] d,
J	дх0
дхр J	дх0
о
должна равняться нулю. Обозначим через в (дг0, 6) интеграл
д [хо<( (х0, 6)] ^
дх0 ai'
о
так что
д [хо<( (х0, 6)] _ дд (х0, S)	„
дхй	dS
Функция в обращается в нуль при 6 = 0, и условие таутохронности заклю-
чается в том, что в должна обращаться в нуль также и при 6=1. Наоборот,
если в есть произвольная функция от jf0 и 5, обращающаяся в нуль при
6 = 6 и 5 = 1, то интеграл -^— равен нулю. Интегрируя уравнение A) по хй
и рассматривая ? как переменную, не зависящую от Xq, получим
dx0 + X E),
где Х(?) — произвольная функция от 6, а а — произвольная постоянная. Сле-
довательно, для I/ получается выражение
v= ¦

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ, ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ	321
где g — произвольная функция от х0 и 6, подчиненная единственному :усло-
вию, что она обращается в нуль при 5 = 0 и 6 = 1. После квадратуры надо
заменить 5 через xjx0. Так как скорость должна обращаться в нуль при
? = 1 и должна оставаться конечной, то требуется, кроме того, чтобы знат
менатель* обращался в бесконечность при ? = 1 и был отличен от нуля при
изменении 5 от 1 до 0.
После того как v будет найдено в функции х и х0, для нахождения
dv
закона силы достаточно будет исключить х0 из v и из —j—., что можно будет
сделать лишь при определенном выборе функции 6 (х0, ?). Таким путем полу-
dv ,, .
чим —z—=/(jc, v), и для силы получим
r = mv —z— = mv f(x, v).
Например, если 8 тождественно равно нулю, то мы опять придем к слу-
чаю, когда дифференциальное уравнение движения однородно относительно х
и v. Бертран уже давно заметил, что общая формула прямолинейного тауто-
хронного движения должна содержать произвольную функцию от двух пере-
менных.
6. Таутохронные движения (метод Гишара). Рассмотрим произвольные
таутохронные движения. Движущаяся точка выходит из положения х0 и
приходит в начало координат за промежуток времени, который мы можем
принять равным единице. Скорость щ точки в начале координат изменяется
с изменением х0. Возьмем обратное движение; точка выходит из начала
в момент t = 0 с переменной начальной скоростью v0; она достигает поло-
жения х0, изменяющегося вместе со,к моменту времени t = 1. Для этого
движения имеем
v=*(\ — t)f{t. v0),	A)
где / обращается в v0 при t = 0; более того, / положительно при вся-
ком v0 и при t, заключенном между 0 и 1. Отсюда, обозначая через \ уско-
рение, получим:
x = J(l-t)f(t,vo)dt,	B)
Из формул A) и B) находим t и v0 и подставляем в формулу C); тогда
получим у = П (х, v). Полагая, наконец, F = — mU. {x, v), получим тауто-
хронное движение.
7. Найти силы, под действием которых происходят следующие движения:
х — х0 cos t -f- fо s'n t>
X = Xo COS t -\- V0 Sin t + gt2.
8. Точка, совершающая прямолинейное движение, находится под дей-
ствием только силы сопротивления R — ту (v), являющейся непрерывной
функцией скорости v, существенно положительной и возрастающей вместе
с v. Доказать: 1) если <р @) отлично от нуля, то точка в течение конечного
промежутка времени, описав конечный путь, остановится; 2) если <р @) равно
нулю и притом так, что произведение v~nf(v) стремится к отличному от

322	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
нуля пределу, когда v стремится к нулю, то точка останавливается, если п
меньше единицы, и продолжает неограниченно двигаться со стремящейся
к нулю скоростью, когда п равно или больше 1; в этом втором случае путь,
пройденный точкой, будет конечным, если п меньше 2, и бесконечным
при л, равном или большем 2.
9. Найти движение точки, притягиваемой плоскостью пропорционально
расстоянию.
10. Определить движение точки, находящейся под действием силы,
параллельной оси Ог и имеющей выражение
Z
(Ax + By-t Сг + Df
г ли
•7_	P
(Ax* + 2Bxy + Cy2 + 2Dx + 2Ey + F)'1
где ft, A, B, C, D, E, F—постоянные.
Ответ. Траектории — конические сечения, каковы бы ни были началь-
ные условия.
11.	Найти движение тяжелой точки в сопротивляющейся среде при
законе сопротивления R, определяемом формулой
R = mg (А + В In v),
где А и В — постоянные.
Этот закон можно рассматривать как предельный случай принятого
в тексте закона
R = mg (a + bvn).
, В , В
Для этого достаточно положить а = Л	, о = — и заставить п стре-
п	п
миться к нулю.
12.	Завершить вычисления в тексте п. 219, полагая п — 1 и а «= -j.
Можно выполнить все квадратуры.
13.	Тяжелая точка движется в сопротивляющейся среде. Доказать, что
если R обозначает сопротивление, то между ординатой у и абсциссой х
точки траектории существует соотношение
d%y	2gR
dxs	v4 cos3 a '
где v — скорость и а — угол между касательной и горизонталью Ох.
В частности, если сопротивление пропорционально V*, то дифференциаль-
ное уравнение траектории будет
|Де Спарр, Comptes Rendus, 23 и 30 мая 1892 и Memorial de I'Artilierie
de la Marine, 1892.)
14. Найти движение тяжелой точки в сопротивляющейся среде пря
сопротивлении, пропорциональном кубу скорости.
Эта задача может быть разрешена в эллиптических функциях. (См.
Аппель и Лякур, Principes de la theorie des fonctions elliptique,
стр. 225; см. также две статьи де Спарр a, Bulletin de la Societe mathema-
tique, 1900 и 1901.)

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ	323
15. Точка движется в плоскости	хОу под действием силы с соста-
вляющими
x_dU_	у_Ш_
ду'	dx'
где U — функция от х и у. Доказать, что уравнения движения имеют пер-
вый интеграл
dx dy
16. Точка движется в плоскости хОу под действием силы, составляющие
которой X я Y являются функциями от х и у, удовлетворяющими условиям
дХ_ = _дУ_ dX^_dY
ду ~ дх ' дх ~~ ду '
Доказать, что интегрирование уравнений движения может быть выполнено
в квадратурах.
Ответ. В этом случае величина X-\-lY является функцией <р(г) ком-
плексной переменной г = х + 1у. Оба уравнения движения можно свести
в одно
и интегрирование приводится к двум последовательным квадратурам, нз
которых первая
а вторая определяет t ,в функции г. (Лекорню, Comptes Rendus, т. CI,
стр. 1244; Journal de I'Ecole polytechnique, вып. LV.)
17. В более общей постановке, если
ад*- = Ь— —= —
ду ~~ дх ' дх ду '
где а и Ь — постоянные, интегрирование уравнений движения приводится
к квадратурам.
Ответ. Этот случай приводится к предыдущему при помощи под-
становки
Х=±\ ЬХ', Y=Y —aY'. x=Y bx', у = У— ay'.
18. Точка движется в пространстве под действием силы, составляющие
которой X, Y, Z являются функциями от х, у, г, удовлетворяющими соотно-
шениям
д~х ~ ду ~~ дг ' йу" ~~ ~дг ~~ Ш' ~дг~д~х Ну'
Доказать, что интегрирование уравнений движения приводится к квадратурам.
Ответ. Обозначая через а и о2 комплексные кубические корни из еди-
ницы и полагая
X + у + z = р, x + ay + a^z = q, х
=P, X + аУ + **Z = Q, X+a*Y+aZ=R,

324	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
найдем> что Р есть, функция только от р, Q — только от q и /?--~-'только
от г. Тогда уравнения движения эквиваленты трем следующим:
каждое Из которых интегрируется в квадратурах. Пример:
X = х* + Чуг, Y=z* + 2ху, Z = y4--\- 2гх.
(Comptes Rendus, 19 марта 1877.)
19.	Если дана материальная точка, находящаяся под действием силы,
зависящей только от положения, то интегралы дифференциальных уравнений
движения остаются вещественными при замене t значением t У—1 и проек-
ций х'а, у'о, z'o начальной скорости значениями —х'о Y~ 1 - —Уц 'У—1 ,
— г0 У"—1. Полученные таким образом новые выражения являются уравне-
ниями нового движения, которое будет совершать та же самая материальная
точка, если при тех же начальных условиях на нее будет действовать сила,
равная и противоположная той, которая вызвала первое движение. (Comptes
Rendus, 30 декабря 1878.)
20.	Тяжелая материальная точка движется в сопротивляющейся среде,
сопротивление R которой является функцией скорости v и предполагается
направленным в сторону, противоположную скорости v: R = mg<f (о). Допустим,
кроме того, что функция <р (и) непрерывна, положительна и возрастает вместе
с v. Доказать следующие общие предложения:
1°. Если tp(O)'> 1, то точка за конечный промежуток времени описывает
конечную дугу траектории, заканчивающуюся в точке, где касательная верти-
кальна и куда движущаяся точка приходит со скоростью, равной нулю. После
этого движущаяся точка остается в покое, так как если она будет стремиться
начать движение, то возникающее сопротивление будет больше веса. (Этот
случай может, например, представиться при движении с трением тяжелой
точки по наклонной плоскости.)
2°. Если iy @) < 1 (случай артиллерийских. снарядов)^ то движущаяся
точка будет описывать кривую с бесконечной ветвью, обладающей верти-
кальной асимптотой; скорость точки стремится к пределу X, равному корню
уравнения 1 — <р (г/) = 0, которое, очевидно, на основании предположений,
сделанных относительно функции <$(v), обладает только одним корнем.
3°. Если <р @)= 1, то v стремится к нулю и х стремится к конечному
пределу; но1 для t и у могут представиться различные случаи в зависимости
от закона, по которому tp (v) стремится к нулю, когда к нулю стремится v.
Если*>-"[1 — <р(»)] остается конечным, то получаются результаты упраж-
нения 8.
Указа ни е. Применяя уравнение C), стр. 528, получим уравнение
COS a
v cos a = v0 cos aoe a°	,
которое показывает, что v cos a стремится к нулю, когда а стремится
к —' -я-; разрешая его относительно », получим выражение, принимающее
вид -тг- при a = —-^-. При помощи обычных методов, обозначая через vx
предел скорости it, выводим условие

ГЛАВА X. ОБЩИЕ СВЕДЕНИЯ. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ	325
которое показывает, что v^ равно нулю или корню уравнения 1—<р(») = 0-
Исследование завершается при помощи формул стр. 528 (Морен).
21. Аналогия между равновесием нити и движением точки. Эта ана-
логия получается непосредственно из сравнения естественных уравнений
равновесия нити (п. 136) с уравнениями движения точки. Таким путем полу-
чаются следующие теоремы.
а)	Если каждый элемент нити находится в равновесии под действием
силы Fds и если натяжение равно Т, то материальная точка массы т, опи-
сывающая кривую, образованную нитью, со скоростью v, равной kT в каждой
точке (k — постоянная), находится под действием силы Ф, направленной про-
тивоположно силе F и равной по величине mk% FT или mk Fv. Можно, на-
оборот, перейти от движения точки к равновесию нити. Для этого достаточно
_ v	_	Ф
положить Т = -г и силу г равной численно —-г— и направленной противо-
положно силе Ф.
б)	Материальная точка, находящаяся под действием вертикальной силы,
направленной вверх и пропорциональной скорости, описывает цепную линию.
в)	Нить, у которой каждый элемент ds находится под действием силы,
„ , k ds
обратно пропорциональной ее натяжению Fds = —=—, принимает форму
параболы. (Можно также говорить, что эта сила Fds изменяется пропор-
ционально горизонтальной проекции ds, так как Т — — С А
г)	Если уравнения равновесия нити преобразовать так, как при получении
законов площадей (п. 203) и кинетической энергии (п. 205), то получатся
теоремы, выражаемые уравнениями
dy dx
ds ds
из которых первое имеет место, когда вдоль всей нити момент силы относи-
тельно оси Ог равен нулю (п. 131).
д) Аналогичные теоремы можно вывести и для равновесия нити на
поверхности, если сравнивать с движением точки по поверхности. (См.
Мёбиус, Statique, часть вторая, глава VII и Поль Серре, Theorie des
lignes a double courbure, Mallet-Bachelier, 1860.)
22.	Если несколько масс m, m', m", ..., находящихся соответственно
под действием сил F, F', F", ..., зависящих только от координат, выходят
из одной и той же точки А с одинаковыми по направлению, но разными по
величине скоростями v0, v'o, v0, ... и описывают одну и ту же кривую ABC,
то произвольная масса М, находящаяся под действием равнодействующей
сил aF, a'F', a"F", ..., где а, а', а", ... —положительные или отрицатель-
ные постоянные, и выходящая из точки А со скоростью Ко, имеющей то же
направление, что и v0, v'o, ..., опишет ту же самую кривую, если только
начальная кинетическая энергия массы М определяется формулой
,.,,3	2	/ / /2	// // //2
MV0 = amv0 -j- a m v0 -\- a m v0 +...
(Бонне, Примечание ко второму тому «Аналитической механики» Лагранжа.)
Эта теорема доказывается при помощи естественных уравнений движения.
23.	Если равнодействующая F сил, приложенных к свободной точке,
принадлежит неподвижному линейному комплексу, то момент количества
движения относительно этого комплекса постоянен.

326	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Ответ. По предположению, существуют постоянные а, Ь, с, р, q, r
такие, что
рХ + q Y + гЪ + a (yZ — zY) + Ь (гХ — xZ) + с (лгК — уХ) = 0.
Заменяя X, У, Z через тх", ту", тгГ и интегрируя, получим
рх' + qy' -+- гг' -\- а (уг' — гу') + Ь (гх' — хг') + с (ху' — ух') = const.,
что и выражает подлежащее доказательству свойство.
24. Найти движение наэлектризованной частицы, находящейся под дей-
ствием неподвижной электрической массы, помещенной в точке О, и един-
ственного неподвижного магнитного полюса, также находящегося в точке О.
Ответ. Точка описывает на круговом конусе с вершиной в точке О
траекторию, которая при развертывании конуса переходит в коническое
ссчеиие с фокусом в точке О; движение подчинено закону площадей. (См.
Ann ель, Annaes scientificos da Academia Polytechnica do Porto, т. IV,
1909.)

ГЛАВА XI
ЦЕНТРАЛЬНЫЕ СИЛЫ. ЭЛЛИПТИЧЕСКОЕ ДВИЖЕНИЕ ПЛАНЕТ
1. Центральные силы
222. Уравнения движения. Сила называется центральной, если
ее направление все время проходит через неподвижную точку. Эта
точка называется центром силы. Примем центр силы за начало
координат и условимся обозначать через F абсолютное значение силы,
взятое со знаком + или — в зависимости от того, будет ли сила
отталкивающей или притягивающей. Мы видели ранее (п. 203),
что в случае действия центральной силы траектория точки является
плоской кривой, плоскость которой проходит через центр силы. Эта
плоскость определяется начальным положением и начальной скоростью
дчижущейся точки. Если начальная скорость направлена по радиусу-
вектору, то плоскость эта становится неопределенной, но тогда дви-
жение будет прямолинейным и будет происходить по радиусу-вектору.
Возьмем плоскость траектории за плоскость ху. Тогда проекции
силы, согласно принятому условию относительно знака F, будут F —
и F —. Мы можем воспользоваться общими уравнениями плоского
движения; однако проще исходить из уравнений, получаемых по
закону площадей и по теореме кинетической энергии.
Интеграл площадей
х dt y dt~u'
если пользоваться полярными координатами, может быть написан
следующим образом:
"?-*	<¦>
Мы видим, что С есть момент начальной скорости относительно
оси Ог. Пусть v0 — начальная скорость и р0 — расстояние до нее от
начала. Тогда абсолютное значение постоянной С равно pQvQ; при
этом нужно взять знак -\- или — в зависимости от того, будет ли
происходить движение в сторону положительного или отрицатель-
ного вращения вокруг оси Oz. Пусть г0, Во — координаты точки Мо,

328
ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
т0 — угол между начальной скоростью Movo и продолжением ОМО
(рис. 144). Имеем
р0 = r0 sin кH,
и поэтому абсолютное значение постоянной площадей будет
С = rov0 sin т]0.
Если условиться считать угол тH положительным от продолжения MQOr
радиуса-вектора в сторону положительных вращений, то это равен-
ство будет справедливо и по знаку, так как г0 и v0 считаются положи-
тельными, и знак постоянной С совпадает со знаком sin тH. Эта
постоянная С может обратиться
в нуль только тогда, когда нулю
равен один из множителей r0, vty
или sinifH. В последнем случае дви-
жение будет происходить по ра-
диусу-вектору.
Применим теперь теорему кине-
~х тической энергии. Получим
Рис. 144.
¦=Fdr.
B)
Уравнения A) и B) вполне определяют движение. Они служат для
нахождения г и 6 в функции времени.
Скорость имеет выражение
При помощи равенства A) из этого выражения можно исключить
или dt, после чего получаем:
или
C)
D)
1 (dr\*
если заменить -7I;™) чеРез \~Jt
Наиболее простой случай будет тогда, когда сила зависит только
от расстояния г. Тогда задача приведется к квадратурам, так как F dr
будет полным дифференциалом и из уравнения B) получим v2 в функ-
ции г; подставляя это значение г>2 в уравнения C) и D), найдем t
и 9 при помощи квадратур.
Вернемся к общему случаю. Мы можем получить еще два важных
уравнения, заменяя v2 его значениями C) и D) в уравнении кинети-

ГЛАВА XI. ЦЕНТРАЛЬНЫЕ СИЛЫ. ДВИЖЕНИЕ ПЛАНЕТ	329
чгской энергии. Взяв сначала равенство C) и написав уравнение
кинетической энергии в виде
\_dmtfi_	 dr_
2 dt ~ dt'
мы получим
di\~2 [\dl/ ' 7J (	df'
выполнив дифференцирование и разделив на ~, найдем
что мы представим в виде
Это уравнение определяет относительное движение точки по
радиусу-вектору. Оно показывает, что движение происходит так,
как если бы радиус-вектор бил неподвижен, а сила, действую-
щая на точку, была увеличена на тС2/г3. Это же уравнение опре-
деляет г в функции t, когда F зависит только от г или от г и /.
Используем теперь для подстановки в уравнение кинетической
энергии выражение D). Написав уравнение кинетической энергии в
1 drmfl cdr
виде -j rf9 ¦ = F щ , мы получим
тС2
2 L\ М .
d~
Выполним дифференцирование и заменим производную .» - ее зна-
чением 	а Ж' РазДелив затем на -т? , мы получим следующую фор-
мулу, установленную Бине:
Это уравнение может служить для определения г в функции 9, т. е.
для нахождения уравнения траектории, если F зависит только от г
или же и от л и от 9. Знаки обеих частей уравнения F) показывают,
что сила всегда направлена в сторону вогнутости траектории; в самом
/	1\
деле, как известно, величина I	1—~шг~\ отрицательна или поло-
жительна в зависимости от того, будет или не будет траектория
обращена к полюсу своей выпуклостью. Если в каком-нибудь
положении движущейся точки сила равна нулю, то в этом положении
траектория имеет точку перегиба.

330	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
223. Сила есть функция только расстояния. Исследуем пол-
нее важный случай, когда
/=" = ?(/¦).
Уравнение B) интегрируется сразу, и мы получаем
Чтобы найти зависимость между г и t, заменим v2 его значением C)
и мы получим уравнение вида
dt
Следовательно, t определяется простой квадратурой. После этого
легко найдется уравнение траектории; в самом деле, из уравнения A)
имеем
М=?м= Cdr
/-а	+ г у ф (О
и для нахождения 8 надо выполнить квадратуру.
Теперь нужно определить знак, который следует брать перед
корнем. Он определяется следующими условиями. Известно, что
dr
проекция скорости на радиус-вектор равна —г-; знание начальной
I dr\
скорости позволяет знать знак величины \—тг) ', вначале надо 6paib
\"' /о
перед корнем этот знак и сохранять его до тех пор, пока -с (г)
не обратится в нуль, а затем определится и знак, который нужно
будет взять впоследствии. Никакой трудности не возникает, когда
(Jj(r0) равно нулю, т. е. когда начальная скорость перпендикулярна
радиусу-вектору. Тогда рассмотрим уравнение движения по радиусу-
(dr\
вектору; начальная скорость \-тг) этого движения равна нулю, и это
\ «г /о
движение будет происходить так, как если бы радиус-вектор был непо-
шС1
движен, а сила была равна F -|	ц~; если эта вoqб*paжaeмaя сила
вначале положительна, то г будет вначале возрастать и нужно брать
знак плюс; если она отрицательна, то г будет сначала уменьшаться
и нужно брать знак минус. Допустим, наконец, что Fo-\	— = 0.
г»
В этом случае для наблюдателя, связанного с радиусом-вектором,
точка остается неподвижной, так как она движется по радиусу-век-
тору так, как если бы он был неподвижен, а точка предоставлена
самой себе в положении, в котором воображаемая сила равна нулю.
Траектория будет окружностью радиуса г0, и в силу закона площа-
дей движение будет равномерным.

ГЛАВА XI. ЦЕНТРАЛЬНЫЕ СИЛЫ. ДВИЖЕНИЕ ПЛАНЕТ
331
Посмотрим теперь, какие начальные условия нужно сообщить
точке, чтобы осуществить это круговое движение. Необходимо,
чтобы начальная скорость была перпендикулярна радиусу-вектору,
т. е. чтобы цо= ± -д-, откуда С=± rovo, и чтобы fo-f-—^-=0,
откуда, заменяя С его значением, найдем
У
т
Это значение будет вещественным только тогда, когда Fo отри-
цательно, т. е. когда сила — притягивающая.
Пример. Наиболее важными приложениями предыдущей теории
являются случаи, когда сила пропорциональна расстоянию и когда сила
обратно пропорциональна квадрату расстояния.
Второй случай будет подробно рассмотрен в тео-
рии движения планет; займемся здесь первым слу-
чаем и рассмотрим сначала точку, притягиваемую
точкой О (рис. 145) с силой, пропорциональной
расстоянию;
F = — mklr, v" = — k2r^ 4- h.
Рис. 145.
Вышеизложенные общие методы позволяют найти
уравнение траектории и время. Но проще исходить
из уравнений движения
d^x	(Ру	,,
Л9. — п. л,	- — к. у,
которые будут такими же и в косоугольных координатах. Общие интегралы
этих линейных уравнений с постоянными коэффициентами будут
/	i
х0	у0
х = х0 cos kt + -г— sin kt, у = у0 с0? bt -)- -j- sin kt,
где x0, y0 — проекции на оси координат скорости движущейся точки в мо-
мент t = 0 (п. 211). Если, в частности, принять за ось Ох начальный радиус
вектор, а за ось Оу прямую, параллельную начальной скорости, то получим
X = Г0 COS kt, у = ~- Sin kt,
tz
откуда для траектории находим уравнение
являющееся уравнением эллипса, отнесенного к двум сопряженным диа-
метрам 1а' и 2Ь', где длины а' — Го и Ь' = -?-, Продолжительность обра-
щения по эллипсу равна -г-. Так как за начальный момент времени может
быть принят произвольный момент, то мы видим, что скорость точки в про-
извольном положении равна kb', где Ь' — длина полудиаметра, параллельного
скорости, т. е. сопряженного радиусу-вектору.

332	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Если движущаяся точка отталкивается центром О пропорционально
расстоянию, F = mk2r, то получатся уравнения движения, которые могут
быть выведены из предыдущих заменой k коэффициентом k >A— 1. Следова-
тельно, выбрав оси, как и выше, получим
g-kt	щ gkt — g-kt
'и 2 ' ' k 2
Траектория будет гиперболой
х*-
с центром в точке О. Скорость в какой-нибудь точке будет По-прежнему
равна произведению k на длину полудиаметра, параллельного скорости.
224. Сила вида /—2фF). Якоби показал, что можно привести
задачу к квадратурам в случае, когда центральная сила выражается
формулой вида F = г~2 ср F), т. е. когда сила является однородной
функцией декартовых координат х, у с показателем однородно-
сти —2, В этом случае из формулы
1
получаем для определения траектории уравнение
г , 1 _ у (В)
Р "г" г ~~ тС-'
которое является линейным с постоянными коэффициентами и. со
второй частью. Общий интеграл этого уравнения имеет вид
— = A cos б -f В sin 9 -f- <]> (б).
где А и В — произвольные постоянные, а <|>F) — частный интеграл
уравнения, который всегда может быть найден при помощи квадратур.
_з
Пусть, например, F = — т;хг~2 (cos 28) 2, где [л — вещественная поло-
жительная или отрицательная постоянная. В этом случае дифференциальное
уравнение будет
его общий интеграл имеет вид
— = A cos в + В sin в — -^ У cos 26 ,
или, в декартовых координатах,
A - Ac-By)» = i? (*•->«).

ГЛАВА XI. ЦЕНТРАЛЬНЫЕ СИЛЫ. ДВИЖЕНИЕ ПЛАНЕТ
393
Это — уравнение конического сечения, касающегося двух прямых ОР и OQ
(рис. 146). Уравнение прямых имеет вид х2— у2 = 0. Эти жрямые каса-
ются сечения в точках, где они пересекаются с прямой 1 — Ах— By = 0,
которая изменяется вместе с начальными условиями. Начальное положение
движущейся точки лежит обязательно или в углу POQ, или в углу, противо-
положном ему относительно вершины, так
как вне этих углов выражение F ком-
плексно. Допустим для определенности,
что кривая является эллипсом. Если [л по-
ложительно, то траектория состоит из ча-
сти дуги QMP, так как она должна быть
обращена вогнутостью к точке О; когда
движущаяся точка приходит в одно из по-
ложений Р или Q, то сила обращается
в бесконечность, и задача теряет смысл.
Если (а отрицательно, то движущаяся
точка описывает часть дуги QNP.
Время может быть определено из урав-
нения площадей
¦
в котором г следует заменить его значе-
нием в функции 8. Если постоянные А и В
специальным образом не подобраны, то по-
лучающийся интеграл будет эллипти-
ческим.
Примечание. Точно так же приводится к квадратурам и более общая
задача, когда выражение силы имеет вид
Рис. 146.
где k — постоянная. При этом по-прежнему придется интегрировать линей-
ное относительно \\г уравнение с постоянными коэффициентами и со второй
частью.
225. Обратная задача. Определение центральной силы, когда
задана траектория. Поставим себе следующую задачу.
Точка описывает плоскую траекторию по закону площадей
относительно некоторого неподвижного центра. Найти силу,
вызывающую это движение.
Прежде всего, эта сила — центральная. В самом деле, примем
неподвижную точку за начало; тогда по закону площадей имеем
уравнение
откуда, дифференцируя, получим
Это уравнение показывает, что ускорение, а следовательно, и
сила все время проходят через начало. Пусть F — алгебраическое

334	часть третья. Динамика точки
значение силы. Тогда на основании равенства F)
По условию известно уравнение траектории /(г, 6) = 0, которое
определяет — в функции 9: — = ср @). Следовательно, получаем
? (в)+ <р" (он.
Если на характер силы F заранее не налагается никаких ограниче-
ний, то задача представляет неопределенность, так как г и 9 связаны
заданным уравнением, вследствие чего можно преобразовать бесчислен-
ным множеством способов выражение для F. Можно, и это обычно
требуется, выразить F в функции одного только г, для чего нужно
исключить 9 из предыдущего уравнения и из уравнения траектории.
Примеры. 1°. Рассмотрим случай конического сечения, описываемого
по закону площадей относительно фокуса и обращенного к этому фокусу
вогнутостью. Приняв фокус за полюс, имеем уравнение конического сечения
у ==	_
Р
где р — параметр и е — эксцентриситет. Отсюда находим
_ тС-
рг* •
Следовательно, сила является притягивающей, изменяющейся обратно
пропорцивнально квадрату расстояния.
2*. Если ту же задачу рассматривать для ветви гиперболы, обращенной
выпуклостью к фокусу, так что ее уравнение имеет вид
1 е cos в — 1
г	Р
то
тС°-
F =
Таким образом, для силы получается тот же закон, но она будет отталки-
вающей.
3°. Большинство встречающихся в подобных задачах кривых заключено
в уравнении
Г* = a cos kb + b,
где a, b, k — постоянные. Если предположить, что эти кривые описываются
по закону площадей относительно начала, то для силы, выраженной

ГЛАВА XI. ЦЕНТРАЛЬНЫЕ СИЛЫ. ДВИЖЕНИЕ ПЛАНЕТ	335
в функции г, получится
F- Г,Г(^+1)(Д2-^) ,
°" L г2*+3 "•
J'
(Частные случаи: при .k = —1 имеем конические сечения с фокусом в
полюсе; при k = —2 имеем конические сечения с фокусом в центре; при
k = 1 имеем улитку Паскаля; при ? = 2, ft = 0 имеем лемнискату, ...)
II. Движение планет
226. Следствия из законов Кеплера. Во всем последующем
изложении речь будет идти только о движении центра тяжести пла-
нет. Согласно теореме, которую мы докажем впоследствии, центр
тяжести движется, как точка, в которой сосредоточена вся масса
планеты и в которую перенесены параллельно самим себе все при-
ложенные к планете силы.
Законы движения планет выведены Кеплером из наблюдений
Тихо Браге. Эти законы следующие:
1°. Планеты описывают вокруг Солнца плоские кривые по
закону площадей;
2°. Эти кривые являются эллипсами с фокусом в Солнце;
3°. Квадраты звездных времен обращения планет пропорцио-
нальны кубам больших осей их орбит.
Из этих законов Ньютон вывел закон для силы, вызывающей
эти движения.
Так как траектория плоская и имеет место закон площадей отно-
сительно центра Солнца, то сила является центральной, проходящей
через эту точку. Так как траектория является эллипсом с фокусом
в Солнце, то сила, действующая на планету, обратно пропорцио-
нальна квадрату расстояния от планеты до Солнца. Для этой силы
мы получили выражение («ервый пример предыдущего пункта)
t	рг* •
где С — постоянная площадей, а р — параметр конического сечения.
С1
Полагая а = —, можно написать
г ——-рг-
Последний закон Кеплера показывает, что jj. не зависит от рас-
сматриваемой планеты. В самом деле, постоянная площадей С равна
удвоенному отношению площади, описанной радиусом-вектором, к за-
траченному на это времени; если Т—продолжительность обращения,
то радиус-вектор описывает за время Т площадь nab; следовательно,
Так как р равно —¦, то для р. получаем выражение
С- 4тгЗдз

336	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
По закону, о котором мы говорили, отношение -™- будет одина-
ковым для всех планет; поэтому сила для любой планеты будет
Итак, каждая планета притягивается к центру Солнца силой, про-
порциональной массе планеты и обратно пропорциональной квадрату
расстояния от планеты до Солнца.
227. Прямая задача. После установления этого результата
Ньютон обратился к следующей задаче.
Найти движение материальной точки, притягиваемой не*
подвижным центром с силой, обратно пропорциональной квадрату
расстояния.
Центральная сила выражается формулой
F— 2Vl
r —— г2 .
По закону кинетической энергии имеем
d+. = -?dr. «¦ = ¦
Но по теории центральных сил [формула D)]
-•[(#¦4
Подставляя это значение -у2 в предыдущее равенство, получим
\M I ^ г* ~~ СП г
Это — дифференциальное уравнение траектории; его можно предста-
вить так:
Положим
г — С2 — v у & ^ С2 •
Тогда уравнение для р будет
\d6j	v'	УЬ^
откуда, интегрируя, найдем
8 — а = ± arc cos р, р = cos F — а).

ГЛАВА XI. ЦЕНТРАЛЬНЫЕ СИЛЫ. ДВИЖЕНИЕ ПЛАНЕТ	337
Уравнение траектории принимает вид
где корень можно всегда предполагать положительным, так как,
если бы он был отрицательным, то, прибавляя я к произвольной
постоянной а, мы сделаем его положительным. Получилось уравне-
ние конического сечения, имеющего фокус в полюсе. Действительно,
известно, что общее уравнение конических сечений с полюсом
в фокусе есть
-= — + -cos(8 — a),
где р— параметр, а е — эксцентриситет. Сравнивая два последних
уравнения, найдем
а-
р
что уже было установлено ранее, и
и, наконец, подставляя сюда значение р, получим
Это выражение определяет вид конического сечения, который
зависит только от знака постоянной h кинетической энергии.
Если h отрицательно, то траектория есть эллипс, так как е < 1.
Если h равно нулю или положительно, то траектория — парабола или
гипербола. Значение постоянной h кинетической энергии равно
Оно зависит только от численного значения начальной скорости,
но не от ее направления. Следовательно, если при определенных
начальных условиях траектория есть эллипс, то она останется эллип-
сом, если движущуюся точку бросить из того же положения и с той
же скоростью, но в любом другом направлении.
Вычисления, которые мы произвели, содержат неявно и случай
отталкивания. Для исследования этого случая достаточно во всех
формулах считать р. отрицательным. При этом условии постоянная h
будет обязательно положительной и всегда будет получаться ветвь
гиперболы. Эта ветвь гиперболы обращена своей выпуклостью к на-
чалу, так как сила направлена в сторону вогнутости траектории.

338	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Займемся случаем эллипса, полагая h < О, и выразим элементы
траектории через начальные значения переменных. Мы нашли
откуда
или, вводя полуоси эллипса,
Это последнее соотношение определяет большую ось эллипса, кото-
рая зависит только от постоянной уравнения кинетической энергии.
После этого малая ось определится формулой
^ V- ^ О
"a	f/.
Вычислив таким образом большую полуось а, можно легко по-
строить эллипс, зная начальное положение Мо и начальную ско-
рость v0. Для этого нужно взять точку Р, симметричную фокусу
относительно касательной v0, соединить точку Р с точкой Мо и
отложить на прямой РЛ10 длину РМ0О' — 2а; точка О' будет вторым
фокусом эллипса.
228. Кометы. Кеплер не изучал движения комет, считая их ми-
молетными метеорами. Ньютон, заметив, что материальная точка,
притягиваемая Солнцем обратно пропорционально квадрату расстоя-
ния, может описывать не только эллипс, но и параболу, и ветвь
гиперболы с фокусом в Солнце, пришел к мысли, что кометы,
так же как и планеты, описывают эллипсы, в фокусе которых на-
ходится Солнце. Он только предположил, что в то время как пла-
неты описывают лежащие почти в одной плоскости эллипсы с малыми
эксцентриситетами кометы описывают очень вытянутые эллипсы,
лежащие в произвольных плоскостях. Они появляются у нас редко
потому, что мы их видим только на части траектории, наиболее
близкой к Солнцу. Так как большая ось орбиты кометы очень велика,
то эта близкая к Солнцу часть орбиты почти такая же, как
если бы большая ось была бесконечной, т. е. эллипс был бы пара-
болой с теми же фокусом и вершиной. Ньютон пришел таким обра-
зом к мысли, что вблизи Солнца комета должна описывать по за-
кону площадей дугу параболы с фокусом в Солнце. Ему предста-
вился случай проверить эти догадки на комете, появившейся в 1680 г.
Галлей, современник Ньютона, произвел такую же проверку на двад-
цати четырех кометах. Все последующие наблюдения также подтвер-
дили взгляды Ньютона.

ГЛАВА XI. ЦЕНТРАЛЬНЫЕ СИЛЫ. ДВИЖЕНИЕ ПЛАНЕТ	339
Вообразим комету массы т, описывающую по закону площадей
дугу параболы с фокусом в центре Солнца. Эта комета будет нахо-
диться под действием силы, направленной к Солнцу, выражение ко-
торой, как мы показали выше, имеет вид
t- р г*'
где р — параметр дуги параболы. Для другой кометы, с массой т',
мы точно так же получим силу
т'Сг 1
/=" = — ¦
Наблюдения показывают, что отношения С2//? и С /р' равны между
4-к-а3
собой и имеют общее значение, равное величине —™— для какой-
нибудь планеты. Следовательно, выражение центральной силь*, дей-
ствующей на комету, так же, как и для планет, будет
F = _ т(х
Г2 '
где коэффициент у. имеет одно и то же значение для всех комет и
для всех планет.
Мы приходим таким образом к результату, что Солнце притяги-
вает произвольную точку массы т, находящуюся на расстоянии г
от центра, с силой, равной по абсолютной величине —?-. где ^. — коэф-
фициент притяжения, присущий Солнцу и представляющий притяже-
ние Солнцем материальной точки с массой, равной единице, находя-
щейся на единичном расстоянии от центра.
229. Спутники. Наблюдения показывают, что спутники в своих
движениях вокруг планет следуют очень близко законам Кеплера.
Отсюда вытекает, что каждая планета притягивает своих спутников
с силой, пропорциональной их массе и обратно пропорциональной
квадрату их расстояний до центра планеты. Притяжение планет дей-
ствует также и на тела, лежащие на их поверхности. Оно, как мы
видели в главе III, приводит к понятию о силе тяжести. С каждой
планетой связан некоторый коэффициент притяжения X таким обра-
зом, что притяжение этой планетой точки массы т1, помещенной
на расстоянии гх от центра, равно —-. Этот коэффициент X из-
меняется при переходе от одной планеты к другой.
Таким образом, именно притяжение Земли, которому подвергаются
тела, находящиеся на ее поверхности, заставляет их падать верти-
кально, когда они отпущены без начальной скорости, или описывать
дугу параболы, когда они брошены под углом. Эта парабола
является не чем иным, как частью очень вытянутого эллипса, фокус
которого находится в центре Земли. Это вытекает из того, что

340	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
притяжение Землей внешней материальной точки является почти таким
же, как если бы'вся масса Земли была сосредоточена в ее центре. Сле-
довательно, сила, удерживающая Луну на ее орбите, будет той же
природы, что и сила тяжести.
Ньютон проверил это следующим образом. Пусть at — большая
полуось лунной орбиты, 7\—продолжительность обращения и т1 —
масса Луны. Притяжение Луны Землею выражается так:
f2 г2 '
Так как эксцентриситет лунной орбиты весьма мал, то будем эту
орбиту рассматривать как окружность с центром в центре Земли.
Тогда rl = a1 и
F =	й— /и,.
Т\
С другой стороны, тяжелая точка массы mv находящаяся на поверх-
ности Земли, т. е. на расстоянии от центра, равном радиусу р
Земли, находится под действием притягивающей силы, которая, как
мы увидим дальше, мало отличается от веса и которую мы отожде-
ствим с весом
Так как эти две силы находятся в отношении, обратном квадратам
расстояний ах и р, то, принимая во внимание, что а1 = 60р,
получим
F' а\
^ 60*
откуда
Но
2-пгр = 4 ^ 107 м,
Т= 27 суш. 7 час. 43 мин. = 39643 • 60 сек..
Подставляя и выполняя вычисления, найдем значение ^ = 97
сек0- '
мало отличающееся от среднего ускорения силы тяжести на поверхности
Земли g-=9,8 —j. Небольшое различие вызвано сделанными при-
ближениями и полностью исчезает при более точных вычислениях.
230. Всемирное притяжение. Таким образом. Солнце притягивает
планеты, кометы и вообще все тела; планеты в свою очередь при-
тягивают своих спутников, тела, находящиеся на их поверхности и
вообще все тела; они должны, следовательно, притягивать также и

ГЛАВА XI. ЦЕНТРАЛЬНЫЕ СИЛЫ. ДВИЖЕНИЕ ПЛАНЕТ	341
Солнце. С Солнцем и с каждой из планет связан определенный коэф-
фициент притяжения.
Пусть М — масса Солнца; т, т', т", ...—массы ^различных
планет; (J- — коэффициент притяжения Солнца и X, X', X", .. . —коэф-
фициенты притяжения планет. Если Солнце и планета т находятся
на расстоянии г, то притяжение Солнцем планеты равно по абсо-
лютной величине -^-, а притяжение планетой Солнца равно —g- .
В силу закона равенства действия и противодействия эти два притя-
жения должны быть равны и, следовательно,
та = Мк, -?г = —.
М т
Сопоставляя Солнце с планетами, мы получим ряд равных от-
ношений
где через / обозначено общее значение этих отношений. Тогда вели-
чина притяжения Солнцем произвольной планеты может быть напи-
сана так:
fMm
где М — масса Солнца, т — масса планеты и/—коэффициент, оди-
наковый для всех планет.
Этот результат, обобщенный Ньютоном, выражает закон всемир-
ного тяготения.
Две материальные точки с массами т и т', помещенные на
расстоянии г друг от друга, притягиваются с силой ™ . По-
стоянный коэффициент / есть притяжение единицы массы единицей
массы на единице расстояния.
Первое экспериментальное определение постоянной всемирного
тяготения было получено из опытов Кавендиша (Phylosophical Tran-
sactions, 1798). Эта постоянная была очень точно измерена в опытах
Корню и Байля (Comptes Rendus, m. LXXVI и LXXXVI).
Мемуар Кавендиша переведен на французский язык и опубликован
в XVII выпуске Journal de l'Ecole polytechnique A815). Бюржесс
в Comptes Rendus за 21 и 28 августа 1899 г. указал способ опре-
деления постоянной /.
В системе CGS имеем:
-1
/=0,68-10"'=
38622
Подробности относительно измерения / можно найти в Cours
de Physique Виоля (т. 1, стр. 294).

342	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Средняя плотность Земли. Определение постоянной / весьма
важно, так как, зная ее, можно определить массу и, следовательно,
среднюю плотность Земли. В теории притяжения доказывается,
что шар, образованный концентрическими однородными слоями,
притягивает внешнюю точку так, как если бы вся масса шара
бнла сосредоточена в его центре. Допуская, что Земля приближенно
удовлетворяет этому условию, и обозначая через /мир массу и
радиус З^мли, найдем, что притяжение Землей единицы массы, на-
ходящейся на ее поверхности, равно /—. С другой стороны, это
притяжение, как мы это увидим в теории относительного равновесия
(глава XXII), мало отличается от веса g единицы массы. Следова-
тельно, имеем приближенно
откуда находим т.
Зная массу Земли, можно определить ее среднюю плотность,
вычислив плотность, которую должен иметь однородный шар, радиус
и масса которого равны радиусу и массе Земли. Эта средняя плот-
ность, отнесенная к воде, равна 5,5. Она значительно Дольше плот-
ности поверхностных слоев. Отсюда следует, что слои Земли, лежа-
щие на большой глубине, имеют значительно большую плотность,
чем поверхностные слои.
Размерность /; естественный час. Значение коэффициента / зависит
от выбора основных единиц длины, времени и массы. Так как для притяже-
ния двух масс
с *тт'
то отсюда получаем
f- Fri
J~~ mm' ¦
Следовательно, если взять единицу длины в X раз меньшую, единицу
времени в z раз меньшую и единицу массы в ;л раз меньшую, то новое зна-
чение /, как мы видели в п. 76, будет
Допустим, что мы условились раз навсегда принимать за единицу массы
массу куба со стороной, равной единице длины, заполненного каким-нибудь
определенным веществом, например водой при 4°; тогда
и / не будет изменяться с изменением единицы длины, а будет изменяться
лишь с изменением единицы времени. Если единицу времени взять в х раз
меньшую, то / перейдет в ~. Взяв в качестве единицы времени секунду
среднего времени, получим:

ГЛАВА XI. ЦЕНТРАЛЬНЫЕ СИЛЫ. ДВИЖЕНИЕ ПЛАНЕТ
и, выбрав в х раз меньшую единицу времени, получим для / значение
Примем х—	. Тогда / будет иметь значение 1. Новая единица вре-
ooO'Z
мена Судет равна 3862 секундам среднего времени; она мало отличае:ся
от часа. Липпман предложил называть ее естественным часом (Comptes
rendus, 8 мая 1899).
На основании сказанного естественным часом является единица времени,
которую нужно принять для того, чтоэы при произвольной единице длины и
при единице массы, равной массе единичного куба воды, для постоянной
всемирного тяготения получилось значение /= 1.
231.	Двойные звезды. Закон тяготения, открытый Ньютоном, распро-
страняется за пределы солнечной системы. В самом деле, весьма вероятно*
что этот закон управляет движением двойных звезд. Вот что показывают
наблюдения этих движений. Заметим, прежде всего, что наблюдения не-
посредственно дают нам не действительную орбиту звезды-спутника вокруг
главной звезды, а проекцию этой орбиты на касательную плоскость к не-
беснои сфере, т. е. на плоскость, проведенную через главную звезду Е
перпендикулярно радиусу ТЕ, соединяющему Землю Т с этой звездой. Эта
проекция и является видимой орбитой звезды-спутника. Наблюдения показы-
вают, что
1) видимая орбита описывается по закону площадей вокруг главной
звезды Е;
-) эта орбита является зллипсом, в котором главная звезда Е занимает
произвольное положение, отличное от фокуса.
То обстоятельство, что имеет место закон площадей для проекции дви-
жения на плоскость, проведенную через звезду Е перпендикулярно к ра-
диусу ТЕ, соединяющему Землю со звездой, показывает (п. 2Ш), что сила,
действующая на звезду-спутник, постоянно пересекает прямую ТЕ. Так как
это справедливо для всех двойных звезд и так как положение, занимаемое
в пространстве Землей, никак не связано с двойными звездами, то естественно
допустить, что сила, действующая на звезду-спутник, постоянно пересекает
главную звезду Е. Так как сила центральная, то траектория будет плоской и
так как ее проекция — эллипс, то она сама является эллипсом. В таком слу-
чае можно попытаться дать себе отчет и в природе силы, вызывающей
это движение. Так как на каждую звезду-спутник действует сила, направлен-
ная к главной звезде и заставляющая звезду-спутник описывать эллипс,
то закон этой силы, очевидно, таков, что движение спутника по кониче-
скому сечению, не зависит от того, каковы были начальные условия движе-
ния спутника. Для нахождения' этой силы необходимо решить следующу.о
задачу.
232.	Задача Бертрана. Найти закон центральных сил, зависящих
только от положения движущейся точки, и заставляющих ее описывать
коническое сечение, каковы бы ни были начальные условия.
Эта задача была поставлена Бертраном в т. LXXXIV Comptes Rendus н
разрешена одновременно Дарбу и Альфеном. Дарбу изложил свое реше-
ние в примечании в конце «Механики» Депейру. Мы изложим решение
Альфена с некоторыми изменениями, позволяющими упростить вычисления.
Этот метод Альфена основан на составлении дифференциального уравнения
конических сечений.
Общее уравнение конического сечения, разрешенное относительно у,
у = ах + Р + Уя^з + 2bx + С

344	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
содержит пять произвольных коэффициентов о, р, а, Ь, с. Дифференцируя
дважды и обозначая через у', у", ... производные от у по х, найдем
у" = (ас — 62) (дл-2 -f- 26л: + с) 2.
Следовательно, величина у" 3 является многочленом второй степени отно-
сительно л: и ее третья производная равна нулю. Таким путем получается
данное Альфеном дифференциальное уравнение конического сечения:
_~г) = 0.
Это — уравнение пятого порядка.
Установив это, рассмотрим точку массы 1, находящуюся под действием
центральной силы Flt зависящей только от координат (хь у{) точки прило-
жения относительно двух прямоугольных осей ОуХх, Orfi, имеющих начало
в точке Оу, через которую проходит сила. Если время обозначить через ty,
то уравнения движения будут
-F	2L-p
dtl ~ Ч' < ~
где
Интеграл площадей имеет вид
dyi	dxi _
Сделаем преобразование *)
х = ^ у — _L	B)
Л	У1	'
и положим
dt = — "иг •
Тогда получим
dx	dty	d^i dti	dy 	 1 dyi dti 	 dyi
~dt ~	yj	dt ~a> dt ~ yl d^ dt ~ dti '
Отсюда
У	о	»2	j,	3
—J- = 0, -4=-^—=-F —.	C)
dt2	dt1 dtl dt	rx
Эти уравнения показывают, что зависимость движения точки (л:, у) от
времени t такова же, как материальной точки, находящаяся под действием
силы
Vs
*) См. А р р е 11, De l'homographie en Mecanique (Comptes rendus,
4 февраля 1899 и American Journal of Mathematies, т. XII и XIII).

ГЛАВА XI. ЦЕНТРАЛЬНЫЕ СИЛЫ. ДВИЖЕНИЕ ПЛАНЕТ	345
постоянно параллельной оси Оу. Эта сила Y является функцией от х^ и ух и,
следовательно, на основании соотношений B) — также функцией от х и у.
Если точка (xv yi) описывает коническое сечение, то точка (л:, у) также
описывает коническое сечение, являющееся томографическим преобразова-
нием первого, и наоборот. Таким образом, мы привели задачу к отысканию
закона параллельных сил Y, заставляющих их точку приложения ' описывать
коническое сечение при любых начальных условиях. Эта задача может быть
разрешена следующим образом.
Так как уравнения движения имеют вид
-о
dt°- ' df>- ~ '
то —=г = а и дифференциальное уравнение траектории будет
где Y — функция от х и у. Обозначим через у', у", ... производные от у
по х. Выражение E) для у" должно удовлетворять дифференциальному
( Г
р	()
( —Г
\у" 3 / =
б
( Г
уравнению \у" 3 / =0 конических сечений, каковы бы ни были начальные
условия. Обозначив через jj. постоянную, положим
Y 3=,х \(х, у), К =(![*(*, у)]Т.	F)
Тогда [<р (лг, у)]'" = 0. Произведя действия, получим:
ду '
4* = ^!l + Зу' дЦ + Зу'2 dS(f + у'3 ^L +
9 длг* + У дх** ду + у дл: ду* + У ду* +
+ Зу" ( ^2у + у' **L\ + у'" *L
+ йу \дхду ^у ду*)+У ду'
Так как на основании равенств E) и F)
У a* f ' у	2 яа ?
то уравнение <р'" = 0 напишется так:
iH	Л$ v'2 ^5L 4- v'3 ^ 4-
* ду + dy дх ду9-
Это условие должно выполняться при любых начальных условиях, поэтому
оно должно тождественно удовлетворяться, каковы бы ни были х, у, у'

346	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
и. -г, так как в начале движения эти четыре величины произвольны. Имеем,
следовательно,
-о
дх* "' ду	?	^
^!||l|l	%1(р)* ,	(8)
т дх ду дх ду	т ду* \ ду)
Условия G) показывают, что <в является многочленом второй степени
' Т Х И У' <р (х, у) = Лл:2 + 2Вд:у + Су"- + 2?>л: + 2?у + F.
Этот многочлен должен удовлетворять условиям (8); здесь необходимо разли-
чать два случая в зависимости от того, равен ли коэффициент С нулю
или нет.
&-¦¦?
Г. CsO. Тогда -~^ = 2С и второе из тождеств (8) дает выражение
f=±(Bx + Cy + ET-,
которое удовлетворяет, как это можно непосредственно проверить, также
и первому из тождеств (8).
2°. С = 0. Тогда из второго тождества (8) имеем -—- = 0, т. е. <р не
зависит от у. Следовательно,
В = С = Е = 0,
и пеивое из тождеств (8), очевидно, удовлетворяется.
Таким образом, имеется два закона параллельных сил, отвечающих
требованиям задачи. Эти законы на основании равенства F) выражаются
формулами:
я
{Вх + Су
).
(Ах°- + IDx + F)k
Следовательно, имеется также два закона для центральных сил, удовлет-
воряющих требованиям задачи. На основании формул преобразования B) и D),
Уг	Уу	П
эти силы определяются формулами:
з
(Вхх + Еух + С? '
(Axi+2
Это и будут два закона сил, открытых Дарбу и Альфеном.

ГЛАВА XJ. ЦЕНТРАЛЬНЫЕ СИЛЫ. ДВИЖЕНИЕ ПЛАНЕТ	347
Если перейти к полярным координатам лгц = rx cos 9, yt — rt sin 8, то полу-
чатся два следующих закона сил:
A'Г,
фгх cos в + Erx sin в + Cf' r\ (A cos2 в + 2D sin в cos в + Fsin* в) "
где вместо (лС2 написано у.'..
Если допустить, что действие звезды на какую-нибудь материальную
точку зависит только от расстояния г между точкой и звездой, а не от напра-
вления в радиуса-вектора, то обе силы не должны зависеть от 6, и тогда
для первой силы требуется, чтобы В = Е — О, а для второй, — чтобы D = О,
A— F. Вместе с тем эти случаи являются единственными, когда для обоих
законов сил существует силовая функция. Законы сил при этом будут
С3 "
tLr	^	L
При первом законе, когда сила пропорциональна расстоянию, точка при-
ложения будет описывать коническое сечение с центром в центре сил. Это
не будет справедливым для двойных звезд, так как если центр действитель-
ной траектории звезды-спутника совпадает с главной звездой, то то же будет
и для видимой траектории.
Таким образом, остается только второй закон, согласно которому сила
изменяется обратно пропорционально квадрату расстояния. Это—закон Нью-
тона. Согласно этому закону звезда-спутник будет описывать вокруг главной
звезды эллипс, в фокусе которого находится главная звезда. Для' нахожде-
ния действительной траектории спутника необходимо разрешить следующую
задачу геометрии.
Зная проекцию эллипса на плоскость и зная, что один из его фоку-
сов находится в определенной точке Е плоскости, определить этот
эллипс в пространстве.
Задача имеет два решения, симметричных относительно плоскости
проекции.
233. Краткие указания по поводу некоторых других задач. Руко-
водствуясь аналогичными идеями, Бертран решил следующую задачу:
Зная, что сила, вызывающая движение планеты вокруг Солнца,
зяниеит только от расстояния и такова, что она заставляет свою
точку приложения описывать замкнутую кривую, каковы бы ни были
начальные условия, если только скорость не превосходит некоторого
предела, найти закон этой силы.
Бертран доказал (Comptes rendus, т. LXXVII), что единственными зако-
нами, удовлетворяющими этим условиям, являются
-*• -*•
из которых первый не подходит по причинам, указанным выше.
В т. LXXX1V Comptes rendus Бертран решил еще следующую задачу.
Зная, что сила, действующая на точку, зависит только от положе-
ния точки и заставляет ее описывать коническое сечение с фокусом
в определенной точке S, каковы бы ни были начальные условия, найти
закон этой силы.
Он доказал, что сила должна обязательно проходить через точку 5 и
быть обратно пропорциональной квадрату расстояния. Следовательно, если
принять первый закон Кеплера как общий' закон и допустить, кроме того.

348	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
что сила, действующая на планету, зависит только от ее положения,
то только из этих предположений вытекает закон Ньютона.
В связи с этой работой Бертран поставил следующую задачу:
Зная, что сила, зависящая только от положения точки, заставляет,
точку при любых начальных условиях описывать коническое сечение,
найти закон этой силы.
Эта задача была сведена Альфеном и Дарбу (Comptes Rendus, т. LXXXIV)
к частной задаче, решение которой было изложено выше (п. 232). Альфен
доказал аналитически, что если сила, зависящая только от положения точки,
заставляет точку при всех обстоятельствах описывать плоскую траекторию,
то сила является либо центральной, либо параллельной постоянному напра-
влению. Дарбу дал элементарное доказательство этого предложения (приме-
чание, помещенное в «Механике» Депейру).
Наконец Кёнигс (Bulletin de la Societe mathematique, т. XVII) исследовал
вопрос о том, какой должна быть центральная сила, зависящая от расстояния,
чтобы ее точка приложения описывала при любых начальных условиях алге-
браическую кривую. Он пришел к законам — fir и — С-!1-
III. Элементарные сведения из небесной механики
234. Задача п тел. Мы только что видели, каким путем Ньютон
пришел к закону всемирного тяготения. Теперь речь идет о том,
чтобы, исходя из этого закона, объяснить движение небесных тел
и, в частности, тел, образующих солнечную систему: Солнца, планет,
их спутников и комет. При изучении относительных движений этих тел
можно совершенно пренебречь действием звезд вследствие огромных
расстояний до звезд по сравнению с размерами солнечной системы *).
Двумя основными задачами небесной механики являются сле-
дующие: 1) найти движение центров тяжести небесных тел; 2) найти
движения небесных тел вокруг, их
*2	™ центров тяжести.
Мы ограничимся здесь некото-
рыми указаниями о первой задаче.
Рассмотрим группу, образованную
Рис 147	планетой Р и ее спутниками Е,
?',... (рис. 147). Движение центра
тяжести G этой группы будет та-
ким, как если бы в нем были сосредоточены массы планеты и всех
ее спутников и в него были бы перенесены параллельно самим себе
все действующие на группу внешние силы. Пусть М — любая другая
точка солнечной системы. Так как ее расстояние от различных точек
группы Р, S, ?', • .. очень велико по сравнению с размерами группы,
то равнодействующая F сил притяжений, действию которых под-
вергается точка М со стороны группы, будет почти такой, как
если бы группа была заменена одной точкой той же массы, поме-
щенной в G; доказывается в теории притяжения. Наоборот, при-
тяжения, которые оказывает точка М на различные точки группы
*) Автор всюду употребляет выражение «центр тяжести» вместо «центр
Инерции» или «центр масс». (Примеч. перев.)

ГЛАВА Xh ЦЕНТРАЛЬНЫЕ СИЛЫ. ДВИЖЕНИЕ ПЛАНЕТ	349
Р, Б, ?'ъ ..., будут силами, равными и противоположные пре-
дыдущим; ,если их перенести параллельно им самим в точку G,
то они будут иметь равнодействующую F', равную и прямо проти-
воположную силе F. Следовательно, действие группы Р, ,Ъ, 2', ...
на точку М и движение центра тяжести G группы будут почти такими,
как если бы вся масса группы была сосредоточена в ее центре
тяжести.
Поэтому можно вначале рассматривать солнечную систему, как
образованную ограниченным числом материальных точек, притяги-
вающихся по закону Ньютона и помещенных: одна—в центре
тяжести Солнца, другая — в центре тяжести Меркурия, третья —
в центре тяжести Венеры, четвертая—в центре тяжести Земли и
Луны, пятая—в центре тяжести Марса и его двух спутников
и т. д.
Полагая число групп равным п, мы получим, написав уравнения
движения п центров тяжести, Ъп дифференциальных уравнений вто-
рого порядка, — по три для каждого центра тяжести. Эти уравне-
ния, интегрирование которых составляет задачу п тел, допускают
семь известных первых интегралов> которые мы укажем как прило-
жения общих теорем о движении системы. Современные средства
анализа не допускают выполнения интегрирования этих уравнений.
Тем не менее в небесной механике оказалось возможным при по-
мощи этих уравнений вычислить с достаточной степенью точности
движение, центров тяжести небесных тел благодаря тому, что массы
всех тел солнечной системы очень малы по сравнению с массой
Солнца. Так, масса Юпитера, наибольшая во всей системе, не со-
ставляет тысячной доли массы Солнца. Приведя число тел к трем,
получим знаменитую задачу трех тел.
235. Задача двух тел. Рассмотрим Солнце и определенную пла-
нету, как две материальные точки, совпадающие с их центрами тяжести.
Так как массы остальных тел солнечной системы очень малы по сравне-
нию с массой Солнца, то в первом приближении мы положим их
равными нулю. Другими словами, допустим, что солнечная система
состоит из Солнца и одной единственной планеты. Мы приходим
таким образом к простой задаче двух тел, для которой можно
найти все интегралы. В небесной механике исследуется, каким
образом, после того как эти интегралы будут вычислены, надо их
изменить, чтобы рассчитать действия остальных тел солнечной
системы.
Пусть М и т — массы Солнца S и планеты Я, а а, р и ?, •*•
у, z-—их координаты. Так как абсолютное значение силы притяже-
fMm
ния обеих точек равно -—^ , то проекции силы, действующей на
Солнце S, будут
/Mm х — a	fMm у — fJ /Mm z — 7
-72 —» ~72 ~r ' -72 ~r -

350
ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
а проекции силы, действующей на планету Р, будут иметь те же
выражения, но с обратными знаками. Тогда будем иметь уравнения
движения:
., d-a /Mm x — ч
(S)
m
%
dta-
dfi
d"-x
d"-y
dfi
/Mm
/*2
/Mm
/Mm
/Mm
r
y —
r
r
r
p-
r
T
X
У
z
(P)
Легко проинтегрировать эту систему, определяющую а, {3, f. •*> З'» г
в функции ^, присоединяя к ней соотношение
Сложим почленно соответствующие уравнения систем (S) и (Р).
Тогда получим три уравнения вида
О
Рис. 148.
которые, если обозначить через \, •»), С
координаты центра тяжести системы, т. е.
.	 Ма-\-тх
К~ М+т
преобразуются к виду:
^5.-0 -^—0
dt°- ~~ • d(* ~
Эти три уравнения показывают, что центр тяжести системы
совершает прямолинейное равномерное движение, т. е. выражают
лишь частный случай общей теоремы о движении центра тяжести.
Найдем теперь относительное движение точки Р по отношению
к S. Для этого перенесем оси в точку S (рис. 148) и пусть xl% yv гх —
новые координаты планеты Р:

ГЛАВА XI. ЦЕНТРАЛЬНЫЕ СИЛЫ. ДВИЖЕНИЕ ПЛАНЕТ	351
Если из уравнений (S) вычесть уравнения (Р), сократив их пред-
варительно на М и т, то они примут вид:
d"-xx __ f(M + m) xy
ffiyx _ f(M + m) y,
dp ~~	/-2 r
d?zx _ f(M + m) г,
dP ~~	r"-	r '
Это — уравнения относительного движения. Их вид показывает,
что точка хх, ух, гх движется относительно точки S так, как если бы
последняя была неподвижна, имела бы массу М-\-т вместо М и
продолжала бы притягивать точку Р по закону Ньютона. Действи-
тельно, вышенаписанные уравнения являются уравнениями движения
точки массы т, притягиваемой к неподвижному началу силой
f(M-\-m)m	„	и.т	г, ял i ч
—	з— — • имеющей вид -i-j-, где p = f(M-\-m).
Отсюда следует, что к этому движению применим первый закон
Кеплера: относительная траектория является коническим сечением,
имеющим фокус в точке S и описываемым по закону площадей.
Так как речь идет о планете, то это коническое сечение является
эллипсом, и если вычислить элементы этого эллипса, то, обозначив
через а большую полуось и через Т — период обращения,'мы полу-
чим соотношение, связывающее эти два элемента:
Мы замечаем, что отношение a3IT2 не зависит от т.
Если коэффициент / известен (п. 230), то из этого соотношения
можно получить приближенное значение для М-\-т.
Для другой планеты с той же степенью приближения имеем
откуда выводим
т
а* а\ 1 + -м
т\
г- п 1 , т
1 1 +
М
Так как отношения т/М и m-jNl будут порядка тысячных долей,
то мы видим, что член в правой части очень близок к единице.
Вследствие этого третий закон Кеплера является только приближен-
ным законом.

3.52
ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
236. Масса планеты, обладающей спутником. Полученная
нами формула
об.та-
- -р.
позволяет, как показал Ньютон, вычислить массу планеты
дающей спутником.
Пусть т и т-х — массы пла-
неты Р и ее спутника ? (рис. 149).
Силы Ф и Ф' — действия Солнца и
других планет на рассматриваемую
планету и ее спутник — почти па-
раллельны и пропорциональны мас-
сам, так как расстояние гх от планеты
до ее спутника очень мало по сравне-
нию с расстояниями от этой же пла-
неты до других тел солнечной си-
стемы. Поэтому если мы обозначим
через X, Y, Z проекции сил при-
тяжения этими другими телами единицы массы планеты, то уравне-
ния движения планеты и ее спутника будут:
¦у
Рис. 149.
— X
** = «,*-
d'-Zx
л
fmmx
fmmx
Л
fmm\
2
Гх
fmmx
Л
fmm-x
r\
У\ —
Г\
*\ —
Уг-
Z\~
1
У
i
г
- X
¦у
-Z
(P)
(S)
Перенесем оси параллельно самим себе в точку Р и пусть Хи Ул>
Z\—новые координаты спутника 1:
х[ = Хх — х, у[ = Ух — У,
= г1 — г.
После сокращения на множители /кит, мы получим, вычитая
уравнения (Р) из уравнений (Е), три уравнения относительного

ГЛАВА XI. ЦЕНТРАЛЬНЫЕ СИЛЫ. ДВИЖЕНИЕ ПЛАНЕТ
353
движения
<Гх\
df-
dt-
п
f(m +
Щ)
щ)
щ)
х\ \
i
/
Г\ '
(
в которых силы Ф и Ф' исчезли.
Из уравнений BХ) видно, что спутник описывает вокруг планеты
эллипс так, как если бы эта планета была неподвижной и притяги-
вала свой спутник с силой —-— ? ——. Если обозначить через их
большую полуось орбиты спутника, а через 7\— его период обра-
щения, то получим
/(m + /Bl)
Так как, с другой стороны, для самой планеты
то, деля эти равенства почленно друг на друга, получим
1+ -^Ъ-
т.	т.
а?
Если масса спутника очень мала по сравнению с массой планеты,
1 + Ш\ 1пг	,
то отношенае -гЧ	—г почти равно единице и мы приближенно
1 -f- mIM	r
имеем
что позволяет вычислить отношение массы планеты к массе Солнца.
При выводе последней формулы мы предположили, что масса тх
очень мала по сравнению с массой т. Этого нельзя сделать, если
мы пожелаем применить наши вычисления к системе, образованной
Землей и Луной. В этом случае прибегают к другому приему.
Формула
/B) = i^	A)
справедлива всегда. С другой стороны, если на поверхности Земли

354	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
взять материальную точку с массой, равной 1, то можно будет опре-
делить, как мы это покажем впоследствии, силу притяжения А этой
точки Землею. Известно, что если считать Землю сферической и
состоящей из однородных концентрических слоев, то ее притяжение
будет равно притяжению материальной точки массы т., находящейся
в центре Земли. Другими словами, для силы притяжения имеем
* = ?.	B)
где р— радиус Земли. Исключая / из равенств A) и B), находим
искомое соотношение
М _ 4д2а»	.
т ~ Т*Ар
По вопросу об определении масс небесных тел мы отсылаем к заметке
Тиссерана, опубликованной в l'Annuaire du Bureau des Longitudes
за 1894.
237. Определение времени в эллиптическом движении.
Вернемся опять к задаче двух тел и вспомним, что планета Р массы m
движется относительно осей, имеющих неизменные направления и
проведенных через центр S Солнца так, как если бы Солнце было
неподвижным, но имело массу, равную своей истинной массе М,
увеличенной на т. Планета движется тогда вокруг Солнца как
материальная точка массы т, находящаяся
под действием центральной силы
р	 , {М -+- т) т 	 (л/ге
г ¦— —/	^	" —¦	~рг>
где
Орбитой является эллипс с фокусом
в точке S, плоскость которого мы примем
Рис. 150.	за плоскость ху. Обозначая через р пара-
метр этого эллипса, через а — его большую
полуось и через е — его эксцентриситет, мы получим, как это было
показано в п. 227, следующие выражения для постоянной площадей С
и постоянной h кинетической энергии
Вершина А (рис. 150), ближайшая к Солнцу, называется периге-
лием, а вершина А' — афелием. Обозначим через ш угол, образо-
ванный радиусом-вектором перигелия и осью Sx, а через w — угол ASP
между радиусом-вектором г — SP планеты и прямой SA; этот угол
называется истинной аномалией. Полярный угол xSP связан
с аномалией очевидным соотношением 6 = w -\- о, где со — постоянная.

ГЛАВА XI. ЦЕНТРАЛЬНЫЕ СИЛЫ. ДВИЖЕНИЕ ПЛАНЕТ	355
Вычислим теперь время, затрачиваемое планетой для достижения
какой-нибудь точки траектории. Мы нашли
а, с другой стороны, для скорости после исключения db при помощи
теоремы площадей г2 dQ = C dt получается выражение
Следовательно,
\dt ) ~*~ г* ~ г	а'
Разрешая уравнение относительно \—гг) и заменяя С2 его значе-
нием |аиA — е2), получаем:
(drY— j*a(l — g2) ¦ 2р.	j^
\dt ) ~	r°- "+" г а '
что может быть написано так:
Отсюда
Обозначим через т момент прохождения планеты через перигелий.
Тогда г после момента т будет сначала увеличиваться, ~^- будет
положительным и в вышенаписанном равенстве нужно будет взять
знак -\-. Этот знак нужно сохранять, пока г возрастает от своего
минимального значения г = а — с = а{\—е) до своего максималь-
ного значения /¦—a(l-j-e). Положим
а — г = aecos a,
что возможно, так как а — г все время меньше, чем ае\ перемен-
ная и за полный период обращения изменяется от 0 до 2тс. Тогда
получим уравнение
1/ —dt = a{\—e cos и) da,
V ' а
которое непосредственно интегрируется, и так как при t = i вели-
чина и обращается в нуль, то
— у ^-(t — t) = H — esina.
а У а

356	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Таким образом, / выражено в функции к, а к связано с г соотно-
шением
r = a{\ — ecosu).	A)
Если надо вычислить положение движущейся точки в момент t,
то первое из этих уравнений определит к, а второе позволит вычи-
слить г.
Введенный нами угол и называется эксцентрической аномалией.
Обычно пишут левую часть уравнения, связывающего г и и, в виде
n(t — 1), полагая
Тогда n(t — 1) есть то, что называют средней аномалией. Так как
для (а было найдено значение

V1
то п —-^, где Т — период обращения, и уравнение для и прини-
мает вид
n{t — т) = и — esinu;	B)
оно показывает, что действительно должно быть л = —, так
как правая часть увеличивается на 2т: одновременно с и, т. е. после
каждого оборота. Коэффициент п = -1=- называется средним движе-
нием. Полученное нами уравнение носит название уравнения Кеп-
лера.
Мы выразили г в функции к; остается теперь выразить в функ-
ции а истинную аномалию w. Для этого будем исходить из уравне-
ния эллипса в полярных координатах:
	а A-е»)
1 -f- e cos w'
В этом уравнении числитель равен параметру р. Приравнивая это
значение г найденному выше значению а{\—ezosu), получим урав-
нение
1 — е cos и = .—:	,
1 + е cos w
откуда находим:
*	„ . „ w A + е) A — cos и)
1 — cos да = 2 stn2 -^ = ,
2	1 — е cos a
-*)<1+со8И) 2fl(l-g)cos»|


ГЛАВА XI. ЦЕНТРАЛЬНЫЕ СИЛЫ. ДВИЖЕНИЕ ПЛАНЕТ
357
и, извлекая квадратные корни, получаем
У г sin •?-= Vа (
~
^. C)
Эти формулы, удобные для вычислений при помощи логарифмов,
позволяют определить г и w в функции и. Делением получаем из
них соотношение
w 	1 Г \ -\-е а
связывающее истинную и эксцентрическую аномалии.
238. Геометрический метод. Для определения положения пла-
неты на ее орбите в момент времени / можно применить геометрический
метод, который указывает смысл введенных выше переменных. Из-
вестно, что эллипс можно рас-
сматривать как проекцию описан-
ного круга, который нужно по-
вернуть вокруг большой оси А А'
на угол, косинус которого ра-
вен Ь\а. Пусть М — точка эллипса
и М' — соответствующая точка
описанного круга (рис. 151). Тогда
пл(Л!/М)=4„л<А1'/М).
Д'
Угол MFA есть угол w, названный ранее истинной аномалией,
а угол М'ОА равен эксцентрической аномалии и. В самом деле,
площадь сектора M'FA равна
M'FA = M'OA-
M'OF = -^ а2и	;г а2е sin к,
т. е.
и, следовательно,
M'FA = -—¦ (и — е sin и),
Ж/^Л = —н- (« — е sin к).
Площадь этого сектора пропорциональна времени, затрачиваемому на
то, чтобы описать ее. Следовательно, если обозначить через (t — t)
это время, а через Т период обращения, то должно быть
пл (MFA)	 шЬ
Заменяя MFA его значением, получим
аЬ
(и — е sin и)
nab

358	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
откуда
-=г- (t — г) = м — е sin и.
Полагая п = 2тг/7\ мы придем к уравнению Кеплера
а — е sin и = п {t — 1).
Для нахождения геометрического смысла средней аномалии п (t—т)
вообразим движущуюся точку, выходящую из А одновременно с пла-
нетой и пробегающую описанную окружность равномерно, причем
так, чтобы прийти в А' одновременно с планетой. К моменту t эта
точка будет в М"\ угол \ = М"ОА будет средней аномалией. В са-
мом деле,
Этот угол С меньше угла и, если sin и положителен (рис. 151).
Что касается выражения г в функции «, то оно получается из
того, что отношение расстояний от точки эллипса до фокуса и до
соответствуюшей директрисы DD' равно е. Следовательно, имеем
г = еМК = е (OD — ОН) = е (^ — a cos и) = а A — е cos a),
так как расстояние OD от центра до директрисы равно а/е.
239. Аналитические преобразования. Для вычисления положения пла-
неты в момент t необходимо сначала найти эксцентрическую аномалию и
при помощи уравнения Кеплера
¦\ri = n(t — z)\.	A)
После этого найдутся.все остальные координаты, которые все выражаются
в функции и. Какова бы ни была дуга С, уравнение A) Кеплера имеет один
корень, который мы обозначим через и. В самом деле, С заключается между
двумя целыми числами, кратными я:
Ы < ? < (k + 1) it.
В функции ср (и) = и — е sin и — С положим и = kit; тогда получим
с (kn) = ks. — С < О,
в то время как
Т [(* 4-1)«] = (* + 1)« — С > 0.
Следовательно, между kit и (й-|- 1)я всегда имеется вещественный ко-
рень. Более того, этот корень будет единственным, так как производная
<р' (и) = 1 — е cos и всегда положительна, поскольку е заключается между
О и 1.
Iе. Последовательные приближения. Единственный вещественный ко-
рень уравнения A) можно вычислить последовательными приближениями
"ледующим образом.
Пусть «о —• произвольная вещественная дуга. Положим
«1 = е sin и0 4- С,
м2 = е sin «t -f- С,
= е sin

ГЛАВА XI. ЦЕНТРАЛЬНЫЕ СИЛЫ. ДВИЖЕНИЕ ПЛАНЕТ
359
Кёнигс указал следующий метод, позволяющий доказать, что величины
ыг, Uo, ..., ип действительно стремятся к искомому корню и и оценить пре-
дел ошибки при замене ип через и. Этот метод является приложением
к уравнению Кеплера общих результатов, заключающихся в работах Кёнигса
по функциональным уравнениям (Annales de PEcole Normale, 1884. и 1885).
Обозначая через и единственный вещественный корень, имеем
и
е sin
Но так как
то можно также написать
Щ — и
С —я = -
щ — и
- е sin и,
sin и,- — sin a
щ — и
s n -=-=—
1C Щ 4- и	2
щ — и	щ — \
Так как модули величин
cos -Ц|— и
sin
и{ — и
щ — и
меньше единицы, то
Ui + x — U
щ — и
Отсюда умножением выводим
Но е заключается между 0 и 1, а е" стремится к нулю, когда п неогра-
ниченно возрастает; следовательно, предел ип равен искомому корню и.
Таким образом, последовательность величин и0, at, ..., ип имеет предел «.
Более того, предыдущее неравенство показывает, что эти величины не-
прерывно приближаются к своему пределу и. Этот факт замечателен, так
как «о выбрано совершенно произвольно. Если каким-нибудь образом уда-
лось найти приближенное значение для и, то его можно принять за «0 и
тогда «j, и-,, ... будут еще более приближаться к и. Допустим, что в каче-
стве и0 принято, как это часто делают, само значение С. Мы нашли
и„ — и
< ё"
Но из соотношения
получается
и, следовательно.
и — е sin и = С
< е
I ип — а |
Мы нашли, таким образом, оценку совершаемой ошибки. Например, для
Земли приблизительно е = fk и достаточно трех действий (п = 3), чтобы
получить и с семью точными десятичными знаками.
2°. Номограмма. Д'Окань, прилагая к уравнению Кеплера общие методы
номографии, дал в Bulletin de la Societe mathematique de France (т. XXII, 1894)

360	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
номограмму для решения этого уравнения. Эта номограмма позволяет быстро
получить первое приближенное значение для неизвестной, исходя из кото-
рого можно, применяя строгие методы, найти более точные приближения.
3°. Ряд Лагранжа. При помощи ряда Лагранжа можно получить разло-
жения и, sin и, cos и, и — С, г, ... по возрастающим степеням е. Рассмотрим
уравнение вида
« = С + е/(й),
определяющее и в функции переменных С и е; обозначим через и тот из
корней этого уравнения, который стремится к С, когда е стремится к нулю
Лагранж поставил себе задачей разложить заданную функцию F(u) этого
корня в ряд, расположенный по возрастающим положительным степеням е.
Он дал для этого формулу
'(I)] +
"¦ "+" га!	d^-'	Г"'
Мы отсылаем за доказательством этой формулы к курсу анализа Эрмита
и к мемуару Рушё (Journal de l'Ecole Polytechnique, вып. XXXIX).
В уравнении Кеплера имеем
/(С) = sin С
и за функцию F(u) можао последовательно принимать эксцентрическую
аномалию и, или радиус-вектор а(\—е cos и), или любую другую функцию и,
разлагающуюся по степеням е. Так, например,
и = I + е sin С + ^ 2 sin 21 + -^ BГ- sin 3C — 3 sin С) +
cos и = cos С + -| (cos 2t — 1) + тртр- C cos ЗС — 3 cos Q + ... .
Лаплас первый нашел, что эти разложения сходятся до тех пор, пока е
остается меньше 0, 662743 ... Коши подтвердил этот результат более пря-
мым методом.
4°. Функции Фурье — Бесселя. Предыдущие разложения сходятся для
планет, но перестают сходиться для некоторых периодических комет, опи-
сывающих вокруг Солнца очень вытянутые эллипсы. Тогда можно применить
для cos и, sin и	cos ju, sin ju, где j —- целое положительное число, метод
разложения в ряды по функциям Фурье — Бесселя, пригодные для всех зна-
чений эксцентриситета, заключенных между 0 и 1. Чтобы показать идею этих
разложений, заметим сначала, что уравнение Кеплера
и — е sin и = t
определяет и как нечетную функцию переменного С, так как это уравнение
не перестает удовлетворяться при одновременной перемене знаков у С и и.
Более того, если средняя аномалия С увеличивается на 2я, то на столько же
увеличивается и эксцентрическая аномалия и. Вследствие этого cos/'u и
и sin ju, где j — целое положительное число, будут функциями переменного 'С,
не изменяющими своих значений, когда С увеличивается на 2я, причем пер-
вая будет четной, а вторая — нечетной. Известно, что любая конечная и
непрерывная вещественная функция переменной С, не изменяющаяся, когда С
увеличивается на 2к, разлагается по формуле Фурье в ряд по синусам и
косинусам /С, где / = 1,2, ... В случае, когда разлагаемая функция от
? — четная, разложение содержит только косинусы и свободный член;

ГЛАВА XI. ЦЕНТРАЛЬНЫЕ СИЛЫ. ДВИЖЕНИЕ ПЛАНЕТ	361
в случае, когда эта функция нечетная, разложение содержит только синусы
и не имеет свободного члена.
Следовательно, для cos/и и sin ju мы получаем, используя обозначения
из первого тома Небесной механики Тиссерана, разложения следующего
вида:
cos ju = -j pf + p\j) cos С + p(j] cos % 4- ... + />У> cos Й + ..., (a)
sin ун =	q[j) sin С -f q$ sin 2C + ... 4- q{/> sin it 4- ...	F)
Здесь коэффициенты определяются известными формулами
?- р[>1 = / cos ju cos /С dQ, ~ q{->] = / sin ju sin /C rfC,
о	о
из которых первая может быть получена сразу умножением обеих частей
разложения (а) на cos V, (К, и интегрированием от 0 до я, после чего все
члены правой части, кроме члена, соответствующего pfj\ обратятся в нули.
Мы займемся сейчас вычисленизм коэффициентов р^\ коэффициенты q^
вычислятся аналогичным образом. Прежде всего, полагая I = 0, имеем
J
\№ = J cos ju
о
или, заменяя С переменной и — е sin и и замечая, что если и изменяется от
О до л, то С будет изменяться тоже от 0 до я, имеем
Т.
— рУ> = / cos ju (I — е cos и) du.
о
Этот интеграл равен нулю при j > 1; при у = 1 он равен —яе/2. Следо-
вательно,
Далее, интегрируя по частям, находим (г > 0)
X	TI	ТС
/1 I	'	/*
cos уи cos lZd? = —-. tus ум sin it	т	/ sin ju sin г' rf^.
о
Проинтегрированная часть равна нулю; после замены в другой части
произведения синусов разностью косинусов и величины С ее значением
и — е sin и найдем
ТС	TZ
У~> = j- / cos [(z — y')« — /e sin «] rf« — ~- I cos
0	О

362	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Сюда и входят функции Фурье—Бесселя, которые можно определить
следующим образом. Пусть k — целое число и х — параметр. Выражение
1 Г
Jk (х) = — / cos (й<р •— х sin cf) df
о
определяет функцию Фурье — Бесселя. Существует, следовательно, бесчи-
сленное множество функций Фурье — Бесселя, соответствующих всем поло-
жительным, или отрицательным, или нулевым значениям целого числа k.
Легко видеть, что всегда можно считать k положительным. В самом деле,
меняя <f на тс — <р', получим dtp = — dy' и из написанного выше интеграла
находим:
It
Jk(x) — -	— I cos (—k<f' — х sin tp') df' = (—1) J-ji(x).
0
Эта формула позволяет переходить от отрицательных индексов к положи-
тельным. Функция J^ (x) является целой трансцендентной функцией от х, со-
держащей х* множителем; раскладывая эту функцию по степеням х, найдем
4
k\
1-2.3(*+1)(*+2)(*+3)
Согласно этим обозначениям мы получаем следующие значения для
коэффициентов />У':
pf^ — lJi-jil^-Ji
Точно так же находим
Подставляя эти значения в выражения для cosy« и sin/м, мы получим
искомые разложения, сходящиеся при всех значениях е между 0 и 1. Так,
например,
COS U = — -j-Г 7j I1'*-! №>	"'<+!
4=7
Если в этом разложении найти коэффициенты при е, е2, ..., то мы снова
получим те же значения, что и в написанной ранее формуле Лагранжа. Тем
не менее оба эти разложения совершенно различны. Разложение Лагранжа
расположено по степеням е и сходится только при значениях е, меньших
некоторого предела; только что полученное разложение расположено по
косинусам и синусам целых кратностей С и сходится при всех значениях е
от 0 до 1.
Более подробные сведения о функциях Фурье — Бесселя можно найти
в сочинении Тодгунтера, On Laplace's, Lame's and Bessel's Functions

ГЛАВА XI. ЦЕНТРАЛЬНЫЕ СИЛЫ. ДВИЖЕНИЕ ПЛАНЕТ 363
и в Traite de Mecanique celeste Тиссерана, из которой мы многое заимство-
вали. До Бесселя эти функции встречаются у Фурье. По этому вопросу
можно указать на статью Аппеля и на несколько статей Пере? Акимова
и Жуковского (Comptes rendus годы 1915, 1916, 1917).
240. Элементы эллиптического движения. Эллиптическое дви-
жение планеты определяется в пространстве шестью постоянными. Про-
ведем через центр S Солнца (рис. 152) три оси Sx, Sy, Sz с неизменными
направлениями. В настоящее время обычно принимают за плоскость ху
плоскость эклиптики на 1 января 1850 г.,
за положительные оси Sx и Sy — прямые,
направленные в точку весеннего равно-
денствия и в точку летнего солнцестояния
той же эпохи, и за положительную ось Sz
направление на северный полюс эклиптики.
Плоскость орбиты планеты пересекает
плоскость ху по линии NN', кото-
рая называется линией узлов. Точка
N пересечения орбиты с плоскостью
эклиптики является восходящим узлом.	' р „
Это —точка, которую пересекает пла-
нета, когда ее координата г переходит от отрицательных значе-
ний к положительным. Другой узел N' является нисходящим. Для
определения плоскости орбиты задают угол 6 = xSN, который
считается положительным от Sx к Sy и называется долготой восхо-
дящего узла, и угол наклонения <р между плоскостью орбиты и пло-
скостью эклиптики; этот угол <р измеряется углом между перпенди-
кулярами в точке N к прямой SN, из которых один лежит
в плоскости эклиптики и направлен в сторону движения Земли, т. е.
от Sx к Sy, а другой лежит в плоскости орбиты и направлен
в сторону движения планеты (или кометы). После того как плоскость
орбиты установлена, надо определить положение и размеры эллипса.
Пусть А — перигелий; обозначим через ш сумму углов xSN и NSA,
причем последний угол отсчитывается от SN в сторону движения;
угол ш называется долготой перигелия. Угол NSA равен ш — 6.
Этот угол определяет положение эллипса; для определения размеров
этого эллипса задают его большую полуось а и его эксцентриситет е.
Наконец, для указания закона, по которому планета описывает свою
орбиту, задают период обращения Т или среднее движение га = -^-
и момент х прохождения через перигелий. Заметим, что а и Т
не независимые величины, так как они связаны установленным ранее
соотношением (п.236):
где М — масса Солнца, a m — масса планеты. Итак, для определения
движения планеты или периодической кометы необходимо знать шесть

1564
ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
постоянных 9, ср, ш, а, е, х, которые называются шестью
элементами эллиптического движения. Вместо -х часто вводят
элемент е, определяемый формулой
• лт — i
и называемый средней долготой в нулевую эпоху. Тогда прямо-
угольные координаты х, у, г планеты определяются в функции t
и шести эллиптических элементов формулами вида
: = fl(t, 9, ср,
t, 9, ср, со, а, е, г), |
t, 9, ср, и, а, е, е), >
: = /з(Л 9, ср, (в, а, е, г),
(А)
которые нам нет надобности здесь приводить.
241. Метод вариации постоянных. Если бы солнечная система
состояла из Солнца и только одной планеты, то шесть элементов
эллиптического движения сохраняли бы в течение неопределенного
времени свои значения. Но, как мы видели, эллиптическое движе-
ние является лишь первым приближением для движения планеты.
Действие других планет на рассматриваемую планету сказывается
в возмущении этого эллиптического движения. Для представления
возмущенного движения, которое является действительным движе-
нием планеты и которое несколько отличается от эллиптического
движения, сохраняют формулы (А), рассматривая
в них шесть элементов 9, ср, u>, a, e, s не как по-
стоянные, но как-функции от t. С течением времени
под действием других планет эти элементы будут
получать приращения 89, 8ср, 8ш, 8й, Ье, 8е, которые
называются возмущениями элементов и которые
вызовут соответствующие возмущения координат х,
у, г. Раздел небесной механики, посвященный вы-
числению этих приращений, называется теорией
возмущений.
242. Параболическое движение комет. Пред-
ставим себе комету М, описывающую параболу, фо-
кус которой находится в центре Солнца, что имеет
место для огромного большинства комет. Обозначая через w угол,
образованный радиусом-вектором SM = г с радиусом-вектором SA
перигелия (рис. 153), напишем:
Ряс. 153.
г =
¦ COS W
W
2 cos" -g-
На основании интеграла площадей имеем
г2 clw = С dt =
dt.

ГЛАВА XI. ЦЕНТРАЛЬНЫЕ СИЛЫ. ДВИЖЕНИЕ ПЛАНЕТ	365
где т — масса кометы, а М — масса Солнца. Действительно, из рас-
смотренной нами задачи двух тел вытекает, что комета движется вокруг
Солнца так, как если бы Солнце было неподвижно, а сила, с кото-
рой оно притягивает комету, равнялась
f(M-\-m)m 	 (лот
f
Постоянная площадей будет тогда C = Yv-P — 1/Л/(М + т)/?. Сле-
довательно,
-dt=. dm
p'k	w
r	2 cos4 -^-
откуда, интегрируя	и обозначая через т момент прохождения через
перигелий, найдем
p3U	¦ ' ё 2 ' 3 ё 2 '
Таково уравнение третьей степени относительно ig -=-, которое необ-
ходимо решить, чтобы найти поло'жение планеты в момент t. Урав-
нение имеет только один вещественный корень. Полагая в этом
уравнении р = 1q и замечая, что У~М-\-т можно заменить через у М,
так как массой т кометы можно вполне пренебречь по сравнению
с массой Солнца, мы можем представить уравнение в виде
t—х ,/ 2
/'
q'k
Существуют численные таблицы корней этого уравнения для ряда
значений левой части, причем масса М Солнца принята равной 1.
243. Параболические элементы. Для определения параболической
орбиты кометы задают пять независимых элементов б, <р, ш, х и q,
из которых первые четыре имеют те же значения, что и для планет,
г q = ~ обозначает расстояние перигелия (см. «Небесную меха-
нику» Тиссерана).
УПРАЖНЕНИЯ
1. Для движения точки, притягиваемой к неподвижному центру О
силой F = — mknr, пропорциональной расстоянию, было показано, что трае-
ктория является эллипсом с центром в точке О и что скорость точки в произ-
вольном положении М пропорциональна полудиаметру Ь'', сопряженному
с ОМ: v = kb'. Показать, что, пользуясь этими результатами, можно с по-
мощью теорем площадей и кинетической энергии доказать теоремы Апол-
лония.
Ответ. Пусть. ОМ — г = а'. Теорема площадей выражается равенством
pv = С. Но это произведение pv равно взятой k раз площади парал-
лелограмма, построенного на а' и Ь'. По теореме кинетической энергии
2г2 = Л, откуда к9- (а'% + б'2) = А.

366	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
2. Найти движение точки под действием центральной с.1лы, выраженной
формулой
где а и Ь — постоянные.
Ответ. Для нахождения траектории нужно проинтегрировать уравнение
которое является линейным с постоянными коэффициентами относительно 1/г.
Форма общего интеграла меняется в зависимости от знака 1 -j- -=%. Когда эта
величина равна нулю, 1/а будет многочленом второй степени относительно 9;
когда она положительна и квадратный корень из нее рационален, траекто-
рия есть алгебраическая кривая.
3.	Найти движение точки, когда
т (д + Ь cos 26)
/•-	рь	•
Ответ. Надо проинтегрировать уравнение
7,1 а + b cos 26
—щ.—I	—	?i	 '^ — постоянная площадей).
Его интеграл имеет вид
- = A cos 6 + В sin 6 — -JL _)-.—¦ cos 26.
Траектория является алгебраической кривой четвертой степени при любых
значениях А, В, С, если только b не равно нулю. В последнем случае траек-
тория будет коническим 'сечением, так как закон притяжения станет законом
Ньютона.
После этого при помощи квадратуры можно определить t из интеграла
площадей.
4.	Найти движение точки, когда
г2 (a cos2 6 + 26 sin 6 cos 6 4- с sin2 8K/a r2 (a cos 26 4- Р sin 26 4- i)k '
где a, b, с—постоянные, a а, р, f имеют значения: я = —^— , р = Ь, -\ = й ~j~c .
(Это один из законов центральной силы, найденных Дарбу и Альфеном.)
Ответ. Если положить ф (в) = о cos 26 4- Р sin 26 4- ?> то придется про-
интегрировать уравнение
Если a2 -J- р2 — y2 или б2 — ас отличны от нуля, то, как легко убедиться,
это уравнение допускает частный интеграл вида
- = Хугф(в), Х= Сцаг + р_^у

ГЛАВА XI. ЦЕНТРАЛЬНЫЕ СИЛЫ. ДВИЖЕНИЕ ПЛАНЕТ 367
Следовательно, уравнение траектории будет
у = Л cos в + В sin 8 -f
с произвольными постоянными А, В, С или А, В, X. Это — коническое сечение,
касающееся двух неподвижных прямых, определяемых уравнением
,F)
<j/ (8) = 0 или а (х9- — у2) + 2рх;у + ? (х* + у2) = й
-|-Р2— ?2 = 0 или
вид k cos 6 -j- / sin
и траектория будет
Если а2-|-Р2— ?2 = 0 или Ь2 — ас = 0, то фF) = »2F), где функция
о>F) имеет вид k cos 6 -j- / sin 6. Уравнение имеет частное решение вида
1	х
— = A cos 8 -j- В sin 8 + -
Это — уравнение конического сечения, касающегося в начале координат
неподвижной прямой о> (8) = 0 или kx -\- 1у = 0.
5. Доказать, что если удастся найти траекторию точки, движущейся под
действием центральной силы /г= гпФ A/г, в), то удастся найти траекторию и
в том случае, когда сила
/=i = тФ ( — — a cos 6 — b sin 8, 6 \ A — ar cos 8 — br sin 8) ~2,
где а и 6 — постоянные.
Ответ. Предполагается, что можно проинтегрировать уравнение
и нужно доказать, что тогда можно проинтегрировать уравнение
^2-i
C-
r \ \	r2	/ 1
-Ш- + -1 =—Ti	-a	¦ , n.9 Ф1— — a cose — 6 sine, i
d№ ^ r I	A — ar cos 8 — 6r sin вJ \ г
Но второе уравнение приводится к первому подстановкой
— =	(- a cos 8 -j- Ь sin в.
6. Зная, что под действием силы F = tmxr точка описывает коническое
сечение с центром в начале координат, найти траекторию точки, движущейся
под действием силы
1/1	\8
г"Л— — a cos6 — Ъ sin в)
(второй из законов силы, найденных Дарбу и Альфеном).
Ответ. Этот вопрос является приложением задачи 5. Общее уравнение
траектории, описываемой под действием силы Fv имеет вид
— = a cos 8 -f b sin 8 + \ra cos2 8 -j- 2p cos 8 sin 6 + f sin2 6,
где a, p, -f — три произвольные постоянные. Эта траектория является таким

368	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
коническим сечением, что поляра начала координат относительно него
является фиксированной прямой ах -j- by—1 = 0.
/ 7. Годограф. При движении планеты вокруг Солнца откладывают от
центра Солнца отрезки, равные и параллельные скоростям планеты в ее
различных положениях. Найти геометрическое место концов этих отрезков,
называемое годографом скорости.
Ответ. Годографом является окружность, центр которой находится на
ординате фокуса и которая содержит фокус внутри себя. Это можно доказать,
опираясь на соотношение pv — С, или на то, что геометрическое место проек-
ций фокуса на касательные есть круг, или на то, что фигура, обратная кругу,
есть круг.
8.	Для нахождения годографа скорости точки, описывающей плоскую кри-
вую по закону площадей вокруг центра О, надо: а) построить подеру г (у)
этой кривой относительно центра О (геометрическое место оснований, опу-
щенных из центра О на касательные к кривой); б) найти инверсию подеры
[кривую р (9), где р = k'r, k = const. — радиус инверсии]; в) повернуть инвер-
сию подеры на 90° вокруг О.
Для того чтобы годограф был окружностью, необходимо и достаточно,
чтобы подера траектории была окружностью. В этом случае сама траекто-
рия будет коническим сечением с фокусом в точке О и сила будет обратно
пропорциональна квадрату расстояния.
9.	Точка описывает по закону площадей окружность, проходящую через
центр площадей О. Найти закон силы: 1) в функции расстояния г, 2) в виде
(в)/гя.
Ответ.
> г* ' '
10. Найти движение точки под действием центральной силы F= — 2m\>. 'гъ,
|1>0.
Ответ. По теореме кинетической энергии имеем г/2 — _!_ _j_ h Нужно
различать случаи, когда величина h = vZ	— положительна, отрицательна
У
'0
или равна нулю. Пусть h < 0. Тогда дифференциальное уравнение траекто-
рии будет
Cdr	Cdr
db=-
Vhr± — СЧ"- + (л у h {г"- — а9-) (г2 + *2)
где явно указано, что один из корней многочлена относительно г2 положи-
телен, а другой отрицателен.
У — h (да 4- Ь*А
Полагая г = a cos tp и 	-^	 = g, найдем в нормалинои форме
У— № sin2 p
Следовательно, <p = am[g(d — й0)] и уравнение траектории получается
в виде
(в —60)].
Время можно определить по формулам
Cdt = r*de, Ct =а°- JCn2[?F — 60) I rfe ,
где интеграл может быть выражен через функции 6 и Н Якоби.

ГЛАВА XI. ЦЕНТРАЛЬНЫЕ СИЛЫ. ДВИЖЕНИЕ ПЛАНЕТ	369
Если положить b — со, h = 0, hb1 = — ц в'2 = — С-, k"- = 0, то, как вы-
текает из соотношений между коэффициентами и корнями, получится окруж-
ность г = a cos F — tH).
11. Функции Бесселя. Доказать следующие соотношения:
^	A)
\ xi } ч	w
Эти соотношения можно легко проверить, если заменить функции J их
выражениями в "виде определенных интегралов. Возьмем, например, первое.
Действие сведется к доказательству соотношения
I k cos (fop — х sin tp) flf<p — " / {cos [(? 4-1) tf — x sin tf] -\-
0	0
+ cos [(k — 1) у — x sin tp]} dy = 0
или, заменяя сумму двух косинусов произведением косинусов, к доказатель-
ству соотношения
¦к.
I cos (ky — х sin tf) (k dy — x cos tf dy) = 0.
0
Это соотношение очевидно, так как после интегрирования получается выра-
жение sin (?tf — х sin tf), обращающееся в нуль на пределах.
12. Развернуть Ju(x) B ряд по целым возрастающим положительным
степеням х.
Ответ. Можно воспользоваться выражением Jk (x) в виде определен-
ного интеграла; коэффициенты разложения будут содержать интегралы вида
I cos &tf sin"' tp rftp, I sin Atp sin Wi
которые легко вычисляются заменой sin»" tp синусами и косинусами углов,
кратных tp.
Можно также воспользоваться дифференциальным уравнением C), под-
гтпзляя в него Jk{x) в виде ряда
¦4 М = хк\ай + щ у + й, |у + ... + а.,^- + .
и вычисляя коэффициенты при помощи рекуррентных формул.
13. Теорема Эйлера. Время У, затрачиваемое кометой для про-
хождения по параболической траектории от точки Р до точки Р', можно
найти из формулы
где гиг' — радиусы-векторы обоих положений Я и Я', а <з — хорда РР'.

370	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
(Мы докажем эту теорему ниже, в п. 304. См. также Тисе еран
Mecanique celeste, стр. 112.)
14.	Точка, притягиваемая неподвижным центром по закону Ньютона,
описывает гиперболическую траекторию. Вычислить также положение в каж-
дый момент времени.
Применить тот же метод, что и для эллипса (п. 237); это введет лога-
рифмы и показательные функции вместо функций тригонометрических и им
обратных.
15.	Метод последовательных приближений для решения уравнения Кеп-
лера (п. 239). Пусть и — корень уравнения. Доказать следующие предложения.
1)	На тригонометрической окружности отложим от начала А дуг две
равные и противоположные по знаку дуги AM и AM', равные по абсолют-
ному значению -=- — е. Если конец дуги ? лежит на дуге МАМ', то cos и
положителен; если нет, то отрицателен.
2)	Если cos и положителен, что зависит от расположения С, то все зна-
чения последовательности ult и2, ..., и», . - - начиная с некоторого момента?
будут приближаться к и, причем или все с избытком или все с недостатком.
3)	Если, наоборот, cos и отрицателен, то приближенные значения корня и,
начиная с некоторого момента, будут попеременно приближаться к и то
с избытком, то с недостатком, наподобие непрерывных дробей.
16.	Притягивающий центр с абсциссой ? колеблется на оси Ох по за-
кону S = a cos nt. Этот центр притягивает свободную материальную точку М
пропорционально расстоянию. Найти движение точки М.
(Проекция траектории на плоскость уг будет эллипсом с центром
в точке О.)
17.	Найти движение точки, вызванное центральной силой, пропорцио-
нальной v2r/f, где v — скорость точки, г — расстояние от нее до центра сил
и р — радиус кривизны траектории. (Р е з а л ь, Comptes rendus, т. ХС,
стр. 769.)
18.	Найти движение точки, находящейся под действием центральной
силы постоянной величины. Исследовать траекторию. (8 определяется как
функция г эллиптическим интегралом. Ниже, при изложении естественных
уравнений движения трчки на поверхности, мы увидим, что к этой задаче
можно привести исследование движения тяжелой точки по конусу вращения
с вертикальной осью.)
19.	Найти движение материальной точки, находящейся под действием
центральной силы
Г
гд^ а — начальное расстояние точки от притягивающего центра. Начальная
скорость перпендикулярна начальному радиусу-вектору и равна Ща.
(Траектория является инверсией эллипса относительно его центра.)
20. Найти движение точки, находящейся под действием центральной
силы
f- cos3 0 *
(Траектория — коническое сечение; частный случай законов, найденных
Альфеном и Дарбу.)
21. Центральные силы с сопротивлением среды. Точка массы 1 дви-
жется под действием центральной силы F и сопротивления R, касательного
к траектории. Доказать, что траектория плоская. Далее, приняв плоскость
о	dy dx
траектории за плоскость ху и обозначив через о величину х -f- — у -г- , че-

ГЛАВА XI. ЦЕНТРАЛЬНЫЕ СИЛЫ. ДВИЖЕНИЕ ПЛАНЕТ	371
рез р—рассюяние от центра сил О до касательной и через р— радиус кри-
r S9- „	S dS
визны, доказать формулы г =	^ ¦— , /< = — -дг -^.
dx	S dx
(Можно исходить из тождества — = — 	—-г- , которое нужно про-
дифференцировать, вспомнив, что х dy — у dx = p ds, dy d-x — dx d'2y = —,
f = -rr = —.) В частности, если R = kv2, то получается интеграл S = Ае~кз,
заменяющий интеграл площадей, причем s — описанная дуга кривой. (С и-
а ч ч и, Comptes rendus, т. LXXXVIII.)
22.	Доказать, что если в предыдущем упражнении предположить, что
сопротивление пропорционально скорости, R = kv, то будет существовать
интеграл
5 = Се~ы.	(Эллиот.)
23.	Найти движение точки массы 1 под действием централ ьной силы
U.4 Зц.3 „
равной —~	~-. Этот закон сил, с достаточной для астрономии точностью,
является приближенным выражением притяжения удаленной точки сферои-
дом. (Г ю л ь д е н, Comptes rendus, т. XCL, стр. 957.)
24.	Определить движение материальной точки, притягиваемой неподвиж-
ным центром, пропорционально расстоянию, при воздействии сопротивления
среды, пропорционального скорости.
(Траектория плоская; для определения х и у в функции от t получаются
линейные дифференциальные уравнения с постоянными коэффициентами.
25.	Материальная точка, притягиваемая массой М, описывает круговую
орбиту радиуса а. Обозначим через 8 период обращения, приняв за
единицу времени естественный час (/=1). Имеем 6 = 2гс Уа^/М. Если
М — масса куба воды со стороной а, то М = а3, 6 = 2я. Тогда материаль-
ная точка будет стрелкой абсолютных часов; за каждую единицу времени
она будет описывать дугу, равную радиусу. (Липпман, Comptes rendus,
8 мая 1899.)
26.	Исследовать изменение элементов траектории планеты или кометы
,п
под действием сопротивления среды, определяемого равенством R — k —-t.
п'
Г"
Показать, что большая ось постоянно убывает; что эксцентриситет не изме-
няется, если п-\- п' = 1, и уменьшается, если п-\-п' > 1; что круговое дви-
жение устойчиво в обоих этих случаях.
(Нужно продифференцировать по а и и2 формулы п. 237, вводя cos и.)
(А. Веронне, Comptes rendus, т. CLXXII, CLXXVII.)

ГЛАВА XII
ДВИЖЕНИЕ ТОЧКИ ПО НЕПОДВИЖНОЙ
ИЛИ ДВИЖУЩЕЙСЯ КРИВОЙ
I. Движение по неподвижной кривой
244. Уравнения движения. Пусть дана кривая, по которой дви-
жется точка, и MF — результирующая действующих на эту точку
внешних сил. Точка оказывает на кривую некоторое давление и кри-
вая действует на точку равной и прямо противоположной реакцией,
которая будет нормальна к кривой, если предположить, что отсут-
ствует трение. Вследствие этого точка может рассматриваться как
свободная в пространстве при условии, что к ней прилагаются
сила F и реакция MN (рис. 154). Так как
положение точки на кривой зависит только
от одного параметра, то для определения
движения достаточно только одногр уравнения,
не содержащего реакции. Это уравнение мы
.получим по теореме кинетической энергии
в виде
¦"¦«^i
Рис. 154.
Ydy-j-Zdz.
Уравнение не содержит реакции N, так как последняя, оставаясь
нормальной к перемещению, не производит никакой работы.
Для завершения вычислений нужно выразить координаты точки
кривой в функции некоторого параметра q:
Тогда имеем
= ш (q).
Xdx -f Y dy + Z dz = (Х-/ H- YY -f Za>') dq = Q dq,
B)
где Q обозначает выражение Л"<р'-|-Кф'-f-Za/. В наиболее общем
случае, который может представиться, сила зависит от положения
движущейся точки, ее скорости и времени. Тогда компоненты X,

ГЛАВА XII. ДВИЖЕНИЕ ТОЧКИ ПО КРИВОЙ	373
У. /., а следовательно, и Q будут функциями от q, ~ н /, и уравнение
кинетической энергии, написанное в виде
будет дифференциальным уравнением второго порядка, определяю-
щим q в функции t.
В частном случае, когда сила зависит только от положения точки,
Q будет функцией только от q, и интегрирование уравнения приводится
к квадратурам. Действительно, уравнение кинетической энергии будет
о
mv~ mvn
Из этого уравнения можно найти (-тт\ в функции q, для чего
нужно заменить vz его значением A). Получим
Таким образом, задача решается двумя последовательными
квадратурами. Выражение -^ содержит два знака. В начале движения
известно, какой знак нужно взять, так как знак начальной скорости
определяет знак начального значения -~. Этот знак нужно сохранять
do
до тех пор, пока ~ не обратится в нуль; если по истечении ко-
нечного промежутка времени функция f (q) обратится в нуль, то
скорость тоже обратится в нуль; тогда направление касательной со-
ставляющей силы определит направление движения, а следовательно,
da
и знак -j-.
Если существует силовая функция U(x, у, z), то первое инте-
грирование производится сразу. Имеем
tnv"' ,,,	„ , ,
-y- = C/(x, у, z) + h,
где значение h равно —„	U (х0, у0, 20). После замены х, у, z их
выражениями через q, вычисления завершаются так, как указано выше.
245. Устойчивость равновесия. Допустим, что сила X, Y, Z
зависит только от положения движущейся точки. Тогда величина О
будет функцией только от q и для нахождения положений равновесия
нужно найти значения q, обращающие Q в нуль (п. 92). Эта задача

374	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
сводится к тем же вычислениям, что и при нахождении максимума
и минимума функции
определенной с точностью до аддитивной постоянной. Мы хотим дока-
зать, следуя Лежен-Дирихле, что если для какого-нибудь значе-
ния q = a эта функция U действительно имеет максимум, то соответ-
ствующее положение равновесия устойчиво.
Мы можем для упрощения положить а = О, так как это равно-
сильно замене параметра q новым параметром q — а. Мы можем
также предположить, что функция U(q) обращается в нуль в рас-
сматриваемом положении равновесия при q = 0, так как это сводится
к подходящему выбору произвольной постоянной, которую можно
добавить к U, т. е. нужно принять
U{q)= fQdt.
Тогда при q — О функция U (q) будет иметь максимум, равный
нулю; это значит, что если е — произвольная положительная по-
стоянная, меньшая некоторой, наперед заданной величины, то при
всех значениях q, отличных от нуля и удовлетворяющих единствен-
ному условию
— е<?<е,	A)
функция U(q) будет отрицательной.
Считая, что число е выбрано сколь угодно малым, сместим точку
из положения равновесия в некоторое начальное положение, соот-
ветствующее значению q0 параметра q, заключенному между —ей -\-г,
и сообщим ей начальную скорость г»0. Докажем, что можно найти
два, таких положительных числа аир, что при выполнении только
двух условий
точка в своем последующем движении не выйдет за крайние положе-
ния, соответствующие значениям + г параметра q, и даже не достигнет
этих положений. В самом деле, так как величины U (в) и U{—е)
отрицательны и не равны нулю, то можно найти положительное
число р, которое будет одновременно меньше, чем—U (е) и меньше,
чем — U (—в), так что сумма U {q)-\-p, будучи положительной
при q=0, станет отрицательной при q— + г. При движении точки,
согласно теореме кинетической энергии, будет

ГЛАВА XII. ДВИЖЕНИЕ ТОЧКИ ПО КРИВОЙ
375
Определим v0 и д0 из условий
"Щ
Из первого неравенства получаем для г»0 верхний предел а, равный
Yplm ; второе неравенство в силу непрерывности функции U (q),
обращающейся в нуль при q = О, требует, чтобы q0 было по абсо-
лютному значению меньше некоторого положительного предела |3.
Тогда, если эти начальные условия выполнены, получим
~<U(q)+p.
Отсюда видно, что q не может достигнуть пределов + е, так как,
если q достигнет какого-нибудь из этих пределов, то кинетическая
энергия mv2/2, являющаяся существенно положительной величиной,
должна оставаться меньше правой части, которая при <?= ±е ста-
новится отрицательной, что является абсурдом. Следовательно,
равновесие действительно устойчиво.
Примечание. Когда сила зависит от скорости, величина Q
do
зависит по-прежнему от q и еще от —-. Для нахождения положений
равновесия нужно найти значения q, обращающие в нуль Q при усло-
вии, что — — 0. Если какое-нибудь положение равновесия будет най-
дено, то для того, чтобы узнать, устойчиво оно или неустойчиво,
нужно будет исследовать движение точки, предположив, что она
бесконечно мало смещена из этого
положения равновесия и что ей
сообщена бесконечно малая ско-
рость. Примером того, как это
нужно делать, служит теория ма-
тематического маятника, подвер-
женного действию сопротивления
среды, пропорционального ско-
рости. В дальнейшем мы дадим
систематическое изложение иссле- о
дования малых движений около по-
ложения устойчивого равновесия.
246. Движение тяжелой точ-
ки по неподвижной кривой.
Возьмем три прямоугольные оси, причем ось Oz направим вертикально
верх. Проекции силы равны (рис. 155)
Х=0, К = 0, Z = — mg,
элементарная работа силы тяжести есть —mgdz, и уравнение
П

376	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
кинетической энергии будет
что можно написать в виде
где обозначено
h
	trrz Q,
g
Рассмотрим плоскость II, уравнение которой г —а. Расстояние МР
от движущейся точки до этой плоскости равно а — г, так что ско-
рость определяется формулой
г/2 = 2gPM.
Отсюда видно, что численное значение скорости будет такое, как
при падении точки по вертикали из Р в М без начальной скорости.
Допустим, что рассматриваемая кривая замкнута. Могут предста-
виться два случая в зависимости от того, будет ли плоскость П пе-
ресекать эту кривую или нет. Каково бы ни было начальное поло-
жение Мо точки, ей всегда можно сообщить такую достаточно боль-
шую начальную скорость v0, чтобы плоскость П была расположена
сколь угодно высоко, так как
Допустим, что г»0 настолько велико, что плоскость П находится
над кривой. Тогда скорость никогда не обратится в нуль и движу-
щаяся точка будет бесконечное число раз оборачиваться по своей
траектории. Движение будет периодическим, наибольшая скорость
будет в наинизшей точке, а наименьшая — в наивысшей.
Допустим теперь, что плоскость П пересекает кривую. Пусть А
и А' — две последовательные точки пересечения. Допустим, что точка
начинает движение из наинизшего положения Мо дуги АМА' в сто-
рону А. Легко видеть, что движущаяся точка подойдет к положению А
сколь угодно близко; в самом деле, скорость между Л10 и В будет все
время больше, чем V 2gBBv где ВВХ — расстояние от точки В до
плоскости П, и точка обязательно придет в положение В за конечный
промежуток времени. Если касательная в Л не горизонтальна, то дви-
жущаяся точка достигнет этого положения. Действительно,
v* = 2g(a — z) или
откуда
ds
± Ya — .

ГЛАВА XII. ДВИЖЕНИЕ ТОЧКИ ПО КРИВОЙ	377
Будем отсчитывать дуги от положения Мо, а время от начального
момента. Так как s должно возрастать вместе с t, то в написанном
уравнении нужно взять знак плюс, и мы получим
M=dz.
Ya—z
ds
Если касательная в точке А не горизонтальна, то — будет оставаться
конечным при г == а и подынтегральное выражение будет обращаться
в бесконечность порядка 1/2. Следовательно, этот интеграл остается
конечным, когда г стремится к а. Время Т, нужное для достижения
точки А, будет тогда определяться формулой
V2gT= С *
J у а —
После достижения положения А движущаяся точка будет возвращаться
к Мо, куда она придет со скоростью v0 и дальше будет двигаться
по дуге Л10А' аналогичным образом в течение времени 7\, если ка-
сательная в точке А' не горизонтальна. Движение будет, следова-
тельно, колебанием между точками А и А', и продолжительность
каждого простого колебания будет Т-\-Т'.
'Можно указать два предела, между которыми должно заклю-
чаться Т; эти два предела будут тем ближе друг к другу, чем меньше
дуга М0А. Если положить
то, как известно, будет
~ds
где р — радиус кривизны и у' — косинус угла, который образует этот
радиус кривизны с осью Oz; этот косинус положителен, так как угол
острый. Пусть k и К—пределы для у'/р на рассматриваемой дуге;
тогда между точками Мо и А будет
ds"- ^ *•
откуда, интегрируя, заключаем, что
так как эта функция, обращающаяся в нуль при s = 0, согласно пре-
дыдущему неравенству, монотонно убывает. Вследствие этого моно-
тонно убывающей будет и первообразная функция z	ту-s2. Написав,

378	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
что она больше своего конечного значения, получим-
I— Z
где / — длина дуги М0А. Заменяя в выражении для Т величину
1/уа — z правой частью этого неравенства, получим
2
о '
Точно так же, исходя из неравенства -3-5	k^>0, найдем
Если уменьшать начальную скорость таким образом, чтобы пло-
скость П приближалась к точке Мо, то обе величины К и k будут
одновременно стремиться к одному и тому же пределу, а именно,
к значению f'/р в наинизшей точке, которое мы отметим индексом
нуль. Поэтому, когда колебание будет иметь бесконечно малую ампли-
туду, продолжительность одного простого полуразмаха будет равна
-^7", а продолжительность простого размаха будет равна
i—
'—, если для части МОАГ траектории величина ¦-]¦'/? имеет
o
тот же предел, что и- для части М0А. В частности, если.траектория
является окружностью радиуса R в вертикальной плоскости, то по-
лучится известное выражение для продолжительности бесконечно
малого размаха ^^fRjg.
Вернемся теперь к колебаниям конечной амплитуды и рассмотрим
случай, когда касательная в точке А горизонтальна. Вспомним фор-
мулу, определяющую время:
z ds
Когда г стремится к а, тогда 5 стремится к длине / дуги М0А,
а стоящие под знаком интеграла выражения 1/уа — г и -г- неогра-
ниченно возрастают. Приняв s за независимую переменную, получим

ГЛАВА Х1Г. ДВИЖЕНИЕ ТОЧКИ ПО КРИВОЙ	379
Пусть X — порядок малости величины а — z относительно 5 — I вблизи
s = /. Тогда подынтегральное выражение будет обращаться в беско-
нечность порядка Х/2 относительно	. Если Х/2>-1, то интеграл,
определяющий /, будет неограниченно возрастать; если, напротив,
Х/2 < 1, то интеграл останется конечным. Первый случай представится
для обыкновенной точки, для которой Х = 2; в этом можно убедиться,
рассматривая z как функцию от s и разлагая ее по формуле Тэйлора
вблизи s = l и замечая, что -г- обращается, по предположению,
в нуль при s = Z. Второй случай может представиться для точки воз-
врата, для которой в общем случае Х = 3/2. Если, следовательно, А
является обыкновенной точкой с горизонтальной касательной, то дви-
жущаяся точка будет неограниченно приближаться к этому положению,
никогда его не достигая. Если А является точкой возврата, то дви-
жущаяся точка может достигнуть точки возврата А со скоростью,
равной нулю, после чего она остановится в этом положении равно-
весия. Такой пример мы найдем в
упражнении 5.
247. Нормальная реакция. Есте-
ственные уравнения. Если применить -
естественные уравнения движения (п.
209), то получатся: во-первых, одно
уравнение, определяющее движение, и,
во-вторых, два уравнения, определяю-
щие нормальную реакцию.	i^
Проведем в точке М касатель-
ную МТ в сторону возрастания дуг.	Рис. 156.
Пусть МС = р —радиус главной кри-
визны (рис. 156); проведем бинормаль MB. Так как единственными
силами, действующими на точку М, будут сила F и нормальная реак-
ция N, то естественные уравнения движения для рассматриваемого
случая будут:
„	dv
Fn + Nn = m^-,	B)
Fb + Nb = 0.	C)
Первое из этих уравнений, являющееся не чем иным, как уравне-
нием кинетической энергии в другой форме, определяет движение
по кривой, так как оно не содержит реакции; два других опреде-
ляют составляющие Nn и Nb реакции. Вычисление упрощается, если
имеется силовая1 функция U. В этом случае уравнение кинетической
энергии имеет вид
?

380	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
и, внося это значение v2 в уравнение B), можно будет определить
реакцию, не зная движения.
Уравнение A), написанное в виде
„	dv ds	dv 1 d(mv")
*	ds dt	ds 2 ds
действительно идентично с уравнением кинетической энергии. Оно
показывает, что движение не изменится, если деформировать кривую,
не изменяя ее длины, и изменять при этом силу таким образом, чтобы
не изменялась ее касательная составляющая. Эта операция отразится
только на нормальной реакции. В частности, таким путем можно, не
изменяя движения, преобразовать кривую линию в прямую и свести
задачу к вопросу прямолинейного движения.
Дополнение. В качестве дополнения к сказанному выше, докажем сле-
дующую теорему:
Пусть свободная точка, начинающая двигаться из положения Мо, с после-
довательными начальными скоростями v0, v0, ..., под действием сил, соответ-
ственно равных F', F", ..., описывает одну и ту же траекторию С. Допустим
теперь, что эта точка начинает движение по неподвижной кривой, имеющей
форму траектории С, и что при этом на точку одновременно действуют
силы a'/1', aF", ..., где а', а", ... — постоянные; тогда в этом движении
нормальная реакция кривой будет направлена по главной нормали и
будет обратно пропорциональна радиусу кривизны.
Пусть v', v",...—¦ скорости, которыми последовательно обладает точка
в серии свободных движений. Естественные уравнения какого-нибудь из этих
движений, например первого, будут
в'	dv'	, dv' о'	V2	. Л ]
При несвободном движении в уравнения войдут нормальные реакции
неподвижной кривой, и уравнения движения примут вид
dv i _/ , w _// ,
~dl!='1 Ft + a Ft+
n rr
a Fn+ ¦¦¦'
Отсюда, на основании уравнений A) получим сначала N^ = 0, а затем
dv , , dv' . „ ,. dv" .
V —г- — а V	\- a"v" —z	\- ¦ ¦ ¦
ds	ds ~	ds '
и, интегрируя, найдем
1»2 = е _|_ а'у'2 _|_ a"v"'2 + ....
где постоянная с имеет значение
2	/ '2	// г/2
v0 — а то — а v0 — ...

ГЛАВА XII. ДВИЖЕНИЕ ТОЧКИ ПО КРИВОЙ
381
Наконец,
, mv
m
9
P	P
>. — a'v'- — *"v-
P
= 0 и доказывает теорему, кото-
Это равенство совместно с равенством
рую мы имели в виду.
Начальными скоростями можно распорядиться таким образом,чтобы по-
стоянная с была равна нулю. В этом случае реакция будет все время рав-
няться нулю и точка свободно опишет заданную кривую. Этот последний
результат установил Бонне.
Например, материальная точка может свободно описывать один и тот же
эллипс под действием пяти следующих сил: притяжения, обратно пропорцио-
нального квадрату расстояния со стороны каждого из фокусов, притяжения,
пропорционального расстоянию со стороны центра и, наконец, притяжений
со стороны осей, обратно пропорциональных кубу расстояний. Если, следова-
тельно, заставить точку описывать эллипс под
одновременным действием всех этих пяти сил при
произвольных начальных условиях, то давление
на эллипс будет обратно пропорционально ра-
диусу кривизны.
248. Математический маятник. Математи-
ческий маятник состоит из тяжелой материаль-
ной точки, движущейся без трения по" окружно-
сти, расположенной в вертикальной плоскости
(рис. 157).
Возьмем оси, указанные на чертеже, и до-
пустим, что точка приведена в движение из са-
мого низкого положения Мо (г0 = — I) с началь-
ной скоростью v0. По теореме кинетической энер-
гии имеем
F
= 2g(a-z), a=-l+ ¦?.
Рис. 157.
1°. Допустим сначала, что прямая И (г = а) пересекает окружность в двух
точках А и А', т. е. что а < I, или v0 < 2Ylg- Тогда, как мы видели, движе-
ние будет изохронным колебанием между точками А и А'. Для исследования
движения примем в качестве переменной угол М0ОМ = 8. Имеем:
г = —/ cos в, а = — I cos a,
где а. — угол наибольшего отклонения М0ОА.
В этой переменной выражение скорости будет
_ ds _ М
V~~dl~~ ей
и уравнение кинетической энергии примет вид
Уравнение можно переписать так:

382	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
откуда
'	db
Мы взяли знак плюс, предположив, что точка поднимается. Отсчитывая
время от момента, когда точка выходит из Мо, получим
/f.-/
rfT
4 — sin- ^r
Полагая
. е	а
Sin -fj- = USin-y
получим далее
?¦/ = Г-	rfa	(^ = sln^).
/ ./ }АA — u")(l — *%')	V	2/
Следовательно, задача свелась к эллиптическому интегралу, и только что
написанное уравнение может быть заменено следующим *):
« = snUl/ -&-).
т. е.
О	а
sin -^- = sin — sn \t
/*)•
COS тг =
Таким образом, координаты / sin 6 и / cos 6 движущейся точки выражены как
однозначные функции времени.
Для нахождения времени Т, затрачиваемого точкой для перехода из Мо
в А, надо изменять 0 от 0 до а, и, следовательно, и от 0 до 1. Полагая,
как обычно,
1
,/ V A — м2) A — &?и2)
о
получим для Т значение KYljg и продолжительность простого колебания
будет 2KYl!g- Если эту величину добавить к t, то точка займет положе-
ние М', симметричное с М, и sin 6 изменит свой знак, что является провер-
кой известной формулы
sn (х + 2Я) = — sn x.
*) См. Аппе ль и Лякур, Principes de la theorie des fonctions ellip-
tiques.

ГЛАВА XII. ДВИЖЕНИЕ ТОЧКИ ПО КРИВОЙ	383
Полезно знать разложение величины Т по степеням sin у, т.е. вели-
чины К по возрастающим степеням k. Для получения этого разложения напи-
шем по формуле бинома
У1 — k.4"-	2	2-4	2-4-6...2л
и, опираясь на легко устанавливаемую формулу
1
u*Mdu тс 1 -3-5 ... Bл— 1)
'Л —и1- 2 2 • 4 ¦ 6 ... 2л
о
получим
и, следовательно,
Для бесконечно малых колебаний (а = 0) получаем, таким образом,
Для колебаний с незначительной амплитудой можно заменить sin -у углом -=¦
и ограничиться только двумя первыми членами разложения. Получим
2°. Нам нужно теперь рассмотреть случай, когда прямая П не пересекает
окружности, т. е. когда а > I. Уравнение кинетической энергии и2 = 2g(a — г)
может быть написано в виде
2/
или, положив k'1 — —:—-, в виде
а + I
Величина № меньше 1, так как а больше /. Разрешая это уравнение отно-
сительно dt и полагая к = -^ ——	, получим
6	«	О
, kt
r . 	 2	у
=lvri

384	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Примем, наконец, м = sin -=- в качестве новой переменной. Тогда
о
т. е. sin -у = sn (Xt). Отсюда найдем
О
cos _ = у 1 — sn- (\t) = en (It).
Время Т, необходимое точке для достижения наиболее высокого положения,
получится при изменении 6 от 0 до л или при изменении и от !) до 1; сле-
довательно
3°. Остается, наконец, рассмотреть промежуточный случай, когда пря-
мая II касается заданной окружности, т. е. когда а = I. Тогда интегрирование
можно выполнить при помощи показательных функций, так как модуль /г2
предыдущих эллиптических функций делается равным 1. В самом деле, вер-
немся к уравнению кинетической энергии v = 1g(a — z). Напишем
Р E Г=2g {i+Uo& e)=igi cos'2 4 •
Интегрируя, получим
4
cos —
Постоянная интегрирования равна нулю, так как t должно обращаться в нуль
одновременно с 6. Когда t неограниченно возрастает, в, возрастая, стремится
к пределу тс; движущаяся точка неограниченно приближается к наивысшему
положению, никогда его не достигая. Оно является положением неустойчи-
вого равновесия.
Вычисление реакции. Реакция в каждой точке направлена по радиусу
окружности; она считается положительной в сторону центра и отрицательной
в противоположном направлении. Пусть тогда N—ее алгебраическое значе-
ние; второе естественное уравнение принимает вид
Р
так как N совпадает со своей проекцией на главную нормаль. С другой сто-
роны (рис. 157),
_	„ mgz
Fn — — mg cos в = -f- ,
v* = 2g(a-z\
и радиус кривизны р равен длине / маятника; поэтому

ГЛАВА XII. ДВИЖЕНИЕ ТОЧКИ ПО КРИВОЙ	385
Следовательно, когда точка поднимается по окружности, реакция уменьшается,
и ее максимум, существенно положительный, имеет место в наиболее низ-
кой точке. Эта реакция обращается в нуль и меняет знак в точках, в ко-
торых окружность пересекается с прямой z = -~-.
о
Если сообщить точке движение в трубке, изогнутой по окружности, то,
как вытекает из изложенного выше, точка будет давить на внешнюю стенку
трубки, когда реакция Лг положительна, и на внутреннюю, когда реакция
отрицательна. Чаще всего движущаяся точка связывается с неподвижной точ-
кой при помощи гибкой нити. Когда реакция положительна, нить остается
натянутой; если же после обращения в нуль реакция должна стать отрицатель-
ной, то точка будет стремиться приблизиться к центру, и нить не сможет
удержать ее на окружности. Если пренебречь массой нити, то точка покинет
окружность в положении /(, где N=0 и начнет свободно перемещаться под
действием веса; следовательно, она опишет параболу, касающуюся окруж-
ности в точке, где обе кривые имеют общий радиус кривизны. В самом
деле, скорость точки, так же как и действующие на нее силы, с момента,
когда она покидает окружность, будут изменяться непрерывно; естественное
уравнение, определяющее mv2jf, показывает, что радиус кривизны также
изменяется непрерывно, и вследствие этого обе кривые будут действительно
соприкасающимися в точке К- Парабола, имеющая вертикальную ось, опре-
деляется из условия касания в рассматриваемой точке *).
Найдем теперь, какие условия должны дополнительно выполняться, чтобы
точка или покинула окружность, или осталась на ней. Рассмотрим прямые
Д (г = -q-) и П (г = а) (рис. 157). Если а отрицательно, то реакция никогда
не обратится в нуль, так как прямая Д будет расположена над прямой П.
Точка, колеблясь между А и А', никогда этой прямой не достигнет и реак-
ция будет везде положительная. Точно так же, если 2а/3 больше чем /, то
прямая Д будет вне окружности и реакция не обратится в нуль; точка будет
периодически непрерывным образом описывать окружность. Следовательно
реакция может обратиться в нуль, только если
О а —
или, заменяя а его значением, если
' <vo<
где Vq, как и выше, обозначает скорость в самой низкой точке.
249. Движение математического маятника в сопротивляющейся
среде. Если не пренебрегать сопротивлением среды, в которой происходит
движение, то достаточно к силам jV и —mg, действующим на точку, доба-
вить третью силу R, направленную по касательной к траектории в сторону,
противоположную движению, и возрастающую вместе со скоростью.
Уравнение кинетической энергии или первое естественное уравнение
d2s
представится тогда в виде
ml —р? = — mg sin в — R,
*) Речь идет о касании второго порядка. (Прим. перев.)

386
ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
в котором силы спроектированы на касательную, направленную в сторону
положительных дуг.
1°. Рассмотрим случай малых колебаний в среде, в которой сопротивле-
ние пропорционально скорости. При этих предположениях имеем
ml ~lR dt'
и уравнение движения после замены sin 6 на в примет вид
Это уравнение одинаково пригодно как для восходящего движения, так и для
нисходящего, так как знак силы R изменяется с направлением движения.
Уравнение движения является линейным уравнением с постоянными коэффи-
циентами. Для его интегрирования положим
в =ert,
и тогда для нахождения г получим уравнение
r2 + 2kr + ¦?- = О,
r = — k ±y k"- — J-.
Если предположить сопротивление небольшим, то оба эти корня будут
комплексными и мы можем написать
так что общий интеграл уравнения движения будет
в = е~ы (A cos (it + В sin ц/).
Угловую скорость найдем из равенства
™ = е-м [(?ц _ Ak) cos fi* — (Ац + Bk) sin fit],
at
Допустим, что движущаяся точка опускается без
начальной скорости из положения Мо; пусть
60 — угол начального отклонения. Полагая в пре-
дыдущих формулах t = 0, мы видим, что
Рис. 158.
При этих значениях постоянных для угловой скорости получим
dt	V-
Движущаяся точка, выходя из Мо, опишет дугу окружности и дойдет
до точки Mi (рис. 158), в которой скорость обращается в нуль. Продолжи-
тельность ti этого полуразмаха есть первое значение переменной t, обра-
т. е. tx = —. После этого точка будет двигаться обратно
до положения М2, в которое она придет к моменту t2 = — и т. д. Колеба-
щающее в нуль —гг,

ГЛАВА XII. ДВИЖЕНИЕ ТОЧКИ ПО КРИВОЙ	387
ния будут изохронными, как и в пустоте, но продолжительность каждого из
этих колебаний несколько увеличится, так как (i < ~\Гgjl и, следовательно,
Для изучения изменения амплитуды возьмем снова выражение, для в:
6 = е~ы (в0 cos & -|	? sin |
Полагая tx — — , найдем
/tie
Следовательно, Sj < fl0. К моменту to = — будет 63 = Ьое~ * и т. д. Сле-
довательно, амплитуды изменяются по закону геометрической прогрессии
со знаменателем —e~kizlv".
2°. Уравнение движения легко интегрируется в случае колебаний с конеч-
ной амплитудой и в случае сопротивления, пропорционального квадрату скоро-
сти. Для восходящего движения имеем
а уравнение нисходящего движения получится, если заменить й2 величи-
*	//ft
ной —&2. Примем за новую переменную 8'=-т-. Имеем
М' __ db' М _ db' _ 1 tf F'2)
dt ~ d§ dt ~~ dd ~ d%
и уравнение движения станет линейным относительно б'2:
— -г- sin 6.
2 dO ' ~ " - I
Уравнение без правой части имеет общий интеграл 8'2 = Ае~2к'ь. Бу-
дем искать частный интеграл полного уравнения в виде б'2 = X cos 6 -}- р sin в.
Легко видеть, что для того, чтобы удовлетворялось предложенное урав-
нение, достаточно взять
и общий интеграл будет
Отсюда можно найти в при помощи квадратуры, которая для случая
очень малых амплитуд может быть выполнена в конечной форме.
250. Циклоидальный маятник. Под этим термином мы понимаем мате-
риальную точку, перемещающуюся без трения по циклоиде с горизонтальной
осью, расположенной в вертикальной плоскости и обращенной вогнутостью
вверх.
Примем за начало самую низкую точку кривой и за ось z — направлен-
ную вверх вертикаль; пусть R—радиус образующего круга.
Напомним прежде всего некоторые элементарные свойства циклоиды. Рас-
смотрим какое-нибудь положение образующего круга и соответствующее

388
ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
положение точки М, описывающей циклоиду. Нормалью к кривой будет пря-
мая MB (рис. 1о9), центр кривизны находится в точке ?, симметричной к М
относительно В, и геометрическое место центров кривизны ? является циклои-
дой, одинаковой с заданной и с вершинами в точках А и А'. Наконец, каса-
тельная МС равна половине дуги ОМ, которую мы обозначим через s.
В прямоугольном треугольнике ВМС имеем
т. е.
М С2 = ВС ¦ СР,
ds
Проекция веса на касательную, равная — mg—, будет —mg — . Сле-
довательно, уравнение кинетической энергии, или естественное уравнение,
будет	jv	•
df-
X
4R
Мы вновь получили такое же уравнение, как и в случае прямолинейного
движения материальной точки, притягиваемой неподвижным центром про-
порционально расстоянию. Общий
2	интеграл этого уравнения будет
О'
s = A cos t~
JL
он приводится к виду
У
если в начальный момент дуга
s = So, а начальная скорость равна
нулю. При этих условиях время,
	необходимое для достижения наи-
более низкой точки, равно T = vYRjg- Период колебания не зависит,
следовательно, от начального положения точки, т. е. от амплитуды: движе-
ние будет таутохронным.
Гюйгенс осуществил циклоидальный маятник следующим образом: в точке
возврата О' развертки он закрепил нить длины 4R, равной дуге О'А раз-
вертки. По указанным выше свойствам, если нить заставить последовательно
огибать обе дуги О'А и О'А', то конец М нити опишет рассматриваемую
циклоиду.
Нормальная реакция. Одно из естественных уравнений движения будет
Но
v*- = 2g(a — z), p = 2MB, Fn = — mg cos a = — mg
2R —
где через а обозначен угол между нормалью и вертикальной линией и 2R —

ГЛАВА XII. ДВИЖЕНИЕ ТОЧКИ ПО КРИВОЙ	389
равно проекции MB на вертикаль. Тогда
_ mg (а — г) mg BR — г)
MB "•" MB
В частном случае, когда точка отпускается без начальной скорости из
точки возврата, имеем а = 2R, первое отношение станет равным второму
и реакция будет
— z) _
'	мв - "w
t. e. она будет по модулю равна, а по направлению противоположна удво-
енной нормальной составляющей веса (Эйлер).
251. Движение тяжелой точки по кривой, расположенной
в вертикальной плоскости, при действии трения и сопротивления
среды. Допустим, для определенности, что кривая обращена вогну-
тостью вверх и что точка движется в
направлении, противоположном напра-
влению O'S, принятому за положитель-
ное направление отсчета дуг (рис. 160).
Обозначим через а угол между го-
ризонталью и касательной МТ, прове-
денной в сторону положительных дуг.
Силами, действующими на точку, будут
вес mg, нормальная реакция N, сила
трения /Л/ (п. 195) и сопротивление
среды R = ту (v). Последние две силы направлены в сторону, противо-
положную скорости, т. е. по касательной МТ. Естественными урав-
нениями будут:
т -г^ = — mg sin a -|- fN -\- my (v),
	= N — mg cos a.
Исключая N из этих двух уравнений и заменяя -t-j производной
dv I d(v°)
—гг ==^>-'—\—-, получим уравнение
ul	Z US
A)
Вдоль кривой переменные аир являются известными функциями
дуги s. Мы имеем, следовательно, дифференциальное уравнение пер-
вого порядка, определяющее v в функции s. После того, как эта
функция будет найдена, величина t выразится через s при помощи
квадратуры. Если сопротивление равно нулю или пропорционально
квадрату скорости \y(v) = kv2], то уравнение будет линейным отно-
сительно v2 и можно будет закончить вычисления.

390	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Точка кривой, в которой sin a—/cos а обращается в нуль, яв-
ляется предельным положением равновесия для движущейся точки,
если принимать во внимание трение и считать при этом / коэф-
фициентом трения в момент начала движения (п. 190).
252. Таутохроны. Выше мы нашли, что движение тяжелой точки
по циклоиде является таутохронным. Рассмотрим общий случай движе-
ния точки по любой заданной материальной кривой, под действием сил,
тоже заданных. Говорят, что кривая является таутохроной, если
на ней существует точка О' такая, что движущаяся точка, предо-
ставленная самой себе без начальной скорости, приходит в положе-
ние О' за одно и то же время, каково бы ни было ее начальное
положение. Точка О' называется точкой таутохроназма.
Необходимо различать два случая, а именно: будет ли точка на-
ходиться под действием сил, зависящих только от ее положения,
или зависящих также и от скорости.
Первый случай. Силы зависят только от положения. Тогда возни-
кает следующая задача
Пусть F (X, Y, Z), где X, Y, Z — функции только х, у, z —
суть заданные силы. По какой кривой нужно заставить двигаться
без трения точку, чтобы движение было таутохронным?
Допустим, что одна из этих таутохронных кривых найдена, и
будем отсчитывать дуги от точки таутохронизма О'. Имеем уравне-
ние движения
dfi	*	ds ' ds ' ds
Вдоль кривой координаты х, у, z являются функциями дуги s.
Следовательно, X, Y, Z будут также определенными функциями от s
и в уравнении правая часть Ft является функцией от s. Это уравнение
будет тогда совпадать с уравнением прямолинейного движения, проис-
ходящим по оси O's под действием силы Ft, зависящей только от
положения точки. Требуется, чтобы это движение было таутохронным.
Но мы видели, на основании метода Пюизё (п. 213), что необходи-
мое и достаточное условие таутохронизма заключается в том, что
сила Ft должна быть вида —k2s, где k2 — положительная постоян-
ная. Следовательно, для того, чтобы предложенная кривая была
таутохроной, необходимо и достаточно, чтобы
ds ' ds ' ds	'
Всякая кривая, удовлетворяющая этому единственному условию, будет
таутохроной. Точка таутохронизма s = 0 будет, очевидно, положе-
нием устойчивого равновесия для точки, движущейся по этой кривой.
Чтобы закончить решение, можно произвольно задаться вторым
условием. Вот, например, два различных способа выбора этого до-
полнительного условия.

ГЛАВА XII. ДВИЖЕНИЕ ТОЧКИ ПО КРИВОЙ	391
1°. Можно заставить кривую находиться на заданной поверхности
/(*. у, г) = 0.	B)
Это уравнение и уравнение A) совместно с очевидным уравнением
\~dsf ~T~\ds) ^\ds) —l
определяют х, у, z в функции t. Интегрирование этих уравнений
введет еще две произвольные постоянные, кроме k2, которая уже
выбрана произвольно. Если сила имеет силовую функцию, то урав-
нение A) сразу проинтегрируется, так как тогда
Xdx-\- Ydy + Zdz = dU(x, у, z) = — k2sds,
откуда
U(x, у, г) = -Ц--\-С.
2°. Вместо того, чтобы заставлять кривую находиться на задан
ной поверхности, можно потребовать, чтобы она была также тауто-
хроной с той же самой точкой таутохронизма для другого закона
силы Xlt Yx, Zx, зависящей только от положения движущейся точки.
Для этого необходимо и достаточно, чтобы, кроме уравнения A),
удовлетворялось еще уравнение
1 ds ' * ds	1 ds
Оба уравнения A) и A') совместно с уравнением C) определяют х,
у, z в функции s. Полученная кривая будет таутохроной и для
силы ~КХ-\-\>.Х1	где X и ja—положительные постоянные.
Если вторая сила имеет силовую функцию Ux так же, как и пер-
вая, то будет еще
k'2s2
?/,(*, у, z) =	\	1-С,.
и тогда искомая кривая будет находиться на поверхности
ki\U(x, у, z) — C) = k*[U1{x, у, z) — Cx\.
Второй случай. Силы зависят от скорости. Допустим, что
сила X, Y, Z может зависеть, но может и не зависеть от скорости.
Кроме того, имеется сила сопротивления среды, которая является
функцией скорости: /? = ср(г)), где v равно -?. Уравнение движе-
ния по искомой кривой будет
dt2	ds ' ds	ds ' T \ dt
где x, у, z — функции от s. Правая часть, в которой первые члены
dx dv dz	*	j.
зависят от х, у, z, —?-, —?-, -тг, может быть выражена в функ-

392	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
ции s и —ff- Тогда уравнение будет совпадать с уравнением прямо-
линейного движения точки по оси O's под действием силы, завися-
шей от положения и скорости. Для этого случая не известны необ-
ходимые и достаточные условия таутохронизма; известно лишь, что
таутохронизм будет иметь место, если сила следует некоторым опреде-
ленным законам, например законам, установленным Лагранжем (п. 213).
Следовательно, для нахождения таутохронных кривых нужно при-
равнять, если это возможно, выражение
v d x	dy	dz . ,(ds^
одному из этих законов сил, например, закону Лагранжа.
Мы не рассматриваем здесь подробно этот случай, так же как
и случай, когда к сопротивлению среды добавляется трение. Мы
отсылаем читателя к статье Дарбу (Mecanique de Despeyrous, т. 1,
добавление XIII), к статье Гатона де ля Гупийера (Journal de Liou-
ville, т. XIII, серия 2) и к статье Адамара (Proces-verbaux des
seances de la Societe des Sciences physiques et naturelles de Bor-
deaux, 7 февраля 1895).
253. Приложения. 1°. Тяжелая точка, движущаяся при отсутствии
сопротивления среды и трения. Прежде всего можно свести нахождение
пространственных таутохронных кривых под действием веса к нахождению
плоских кривых. В самом деле, вообразим пространственную таутохронную
кривую С и рассмотрим цилиндр, проектирующий эту кривую на горизон-
тальную плоскость. Если развернуть этот цилиндр на вертикальную пло-
скость, удерживая его образующие вертикально, то кривая С перейдет
в плоскую кривую С той же длины, а касательная, составляющая Ff веса
точки, не изменится. Вследствие этого движение не изменится, и новая кри-
вая будет 'таутохроной. Обратная операция позволяет переходить от пло-
ской кривой С' к пространственной С.
Докажем, что единственной таутохроннои кривой для веса в вертикаль-
ной плоскости является циклоида.
Примем за начало точку таутохронизма на таутохроннои кривой, а ось z
направим вертикально вверх. Так как заданная сила является весом, то для
рассматриваемого случая Х=0, К = 0, Z = —mg и касательная составляю-
щая Ft силы равна —mg—. Эта составляющая должна иметь вид —k2s.
Следовательно, обозначая через Л2 положительную постоянную, имеем
dz .,	№si
без добавления постоянной, так как z обращается в нуль одновременно с s.
Это уравнение характеризует циклоиду с горизонтальным основанием и
с вершиной в начале.
2°. Два закона сил. Мы видели, что таутохронная кривая определяется
с точностью до постоянных, когда требуют, чтобы таутохронизм имел место
отдельно для двух различных законов сил при одной и той же точке тауто-
хронизма для обоих законов.
Найдем, например, кривую, которая является таутохроной: 1) для
силы тяжести и 2) для силы притяжения, имеющей постоянную интенсив-
ность /и исходящей от вертикальной оси. Примем эту ось за ось Oz, счи--

ГЛАВА XII. ДВИЖЕНИЕ ТОЧКИ ПО КРИВОЙ	393
тая ее направленной вверх. Мы можем всегда выбрать начало и ось Ох
таким образом, чтобы точка таутохронизма лежала на оси Ох на расстоя-
нии а от начала.
Так как в рассматриваемом случае первая сила имеет силовую функ-
цию — gz, а вторая — силовую функцию — /г, где г — расстояние от дви-
жущейся точки до оси Ог, то имеем два условия таутохронизма:
— gz =	g—, —/r =	r2	fa,
так как при s == 0 должно быть г = 0 и г = а.
Эти уравнения можно представить в более простом виде:
где ft и с — положительные постоянные.
Исключение s2 показывает, что кривая должна лежать на поверхности
r = a+yz,	B)
являющейся круговым конусом с осью Oz. Чтобы закончить определение
кривой, введем цилиндрические координаты г, Ь л г.
Элемент ds^ дается равенством
ds2 = dh + r9- d№ + dz\.	C)
Выразим s и z в функции г при помощи предыдущих формул. Из урав-
нения B) и из второго уравнения A) имеем
г = у(г — a), s=/2c(r — a).
Подставляя в равенство C) и сокращая, получим уравнение горизонтальной
проекции
где а — положительная постоянная, большая чем а. Так как кривая выходит
из точки таутохронизма г = а, 6=0, то нижний предел интегрирования
принят равным а.
Горизонтальная проекция кривой заключена между двумя окружностями
г = а и г = а. Она касается первой из них и нормальна ко второй, на кото-
рой она имеет точки возврата. Интегрирование при помощи очевидной под-
становки
ц
г — а
приводится к интегралу от рациональной функции.
254. Брахистохрона для силы тяжести. Найдем сначала бра-
хистохрону для силы тяжести. Даны две точки А и В, из кото-
рых более высокой является точка А. Найдем, при помощи
какой кривой С нужно соединить эти две точки для того, чтобы
тяжелая материальная точка, пущенная из точки А без начальной

394
ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
скорости, скользя по этой кривой, достигла точки В за наи-
более короткий промежуток времени.
Эта кривая является брахистохроной для силы тяжести или кри-
вой наиболее быстрого ската (рис. 161).
Примем за начало точку А, за ось г— вертикаль Az, направлен-
ную вниз, за плоскость xz — вертикальную плоскость, содержащую
обе точки А и В. Если тяжелая точка массы т скользит без тре-
ния по кривой С при начальной скорости в точке А, равной нулю,
то ее скорость в положении т опреде-
ляется по закону кинетической энергии:
v2 = 2gz.
ds
Заменяя V через
мент дуги, имеем
dt
где ds — эле-
(-В)
= f ¦
ds
Y*
где t— время, необходимое точке для
прихода в В.
Для того чтобы это время было наименьшим, необходимо опре-
делить кривую С таким образом, чтобы обратить в минимум напи-
санный выше интеграл, который можно представить в виде
(В)
Г <?(х, у, z)ds,
где ср=-у=. Мы нашли ранее (глава VII, § III), что кривая, обра-
щающая в минимум интеграл такого вида, является фигурой равно-
весия нити под действием силы с силовой функцией —ср (л:, у, г),
при этом натяжение нити равно ср (х, у, z). Три дифференциальных
уравнения, которые мы установили для этой кривой, приводятся,
как мы видели, к двум.
Для задачи, которую мы сейчас рассматриваем, ср(х, у, z) = —^=.
и сила, действующая на нить, вертикальна, так как -^- = 0, -^ = 0;
поэтому фигура равновесия будет лежать в вертикальной плоскости,
проходящей через обе заданные точки. Если эту плоскость принять
за плоскость xz, то для нахождения кривой достаточно будет одного
уравнения. Мы возьмем первое из общих уравнений
d ф —
дх'
которое приводится к виду
d
_ dx\ = Q
г ds)
dx_
ds

ГЛАВА XII. ДВИЖЕНИЕ ТОЧКИ ПО КРИВОЙ	395
откуда
dx2 = c2z ds2 = сгг {dx2 + dz2).
Переменные разделяются и, полагая —5- = 2R, получим
Это—дифференциальное уравнение циклоиды, основанием которой
является ось Ох. Легко найти уравнения кривой в обычной форме,
полагая
Z = R(\— cos 6);
тогда
dx = 2R sin2 -^-db, x =
Так как циклоида должна проходить через точку А, то х0 = О
и А является точкой возврата (рис. 161). Для окончательного опре-
деления циклоиды С, проходящей через обе точки А и В, нужно
построить какую-нибудь циклоиду С с основанием Ах и точкой
возврата А, соединить А и В прямой, пересекающей циклоиду С
в точке В' и произвести затем над циклоидой С преобразование
подобия, приняв за центр точку О и за отношение подобия отноше-
ние АВ' к АВ.
Мы предположили для упрощения, что начальная скорость, с ко-
торой точка выходит из положения А, равна нулю. Если мы хотим
найти кривую наибыстрейшего ската из А в В, предполагая, что
точка начинает двигаться из А по этой кривой с начальной скоро-
стью v0, то достаточно будет заменить интеграл
/" ds
J Y*
интегралом
/
dz
V	2g
Кривая будет по-прежнему циклоидой с горизонтальным основа-
ло
нием, но это основание будет находиться на высоте г = —^—"
Оссиан Бонне непосредственно доказал, что циклоида действи-
тельно осуществляет наименьшее время ската.
255. Брахистохроны В общем случае. Рассмотрим точку, находящуюся
под действием силы F, имеющей силовую функцию U{x, у, г). Найдем
кривую С, которою нужно соединить две точки А и В для того, чтобы точка,
двигающаяся по этой кривой и вышедшая из А с заданной начальной ско-
ростью v0, пришла в В за наиболее короткий промежуток времени (рис. 161).
Эта кривая С является брахистохроной для заданного закона силы. Обозначая

396	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
через х0, у0, z0 координаты точки А, имеем по теореме кинетической
энергии
~2	^-=U(x, У' z) —
или. полагая
Л==—2	^(*о. Уо. *о), v = ~dt'
имеем
(В)
ds
Y2U(x, у, z) + 2h' " m	J Y^U (x, у, z) 4- 2A
Таков будет интеграл, который требуется обратить в минимум. Он при-
надлежит к общему типу, изученному в главе VII, § III, если в последнем
положить
<f (х, у, г) =		.
У 2U(х, у, z) + 2h
Согласно тому, что мы получили в главе VII для кривых, обращающих
в минимум интеграл
(Л)
| ?(•*. У, z)ds,
(А)
искомая кривая является фигурой равновесия гибкой нити под действием
силы Ft с проекциями
д	1	д	1	д	1
дх Y2(U+h)'	ду У2(?/+Д) '	dz
1
причем натяжение нити равно
Получаемые таким путем уравнения даны Рожером (Journal de Liou-
ville, 1848).
Известно, что задачу можно свести к квадратурам, если фиктивная
сила Fv а следовательно, и сила F являются зависящими от расстояния
силами притяжения неподвижной точкой, или прямой, или плоскостью.
Теорема Эйлера. При движении по брахистохроне нормальная
реакция направлена по главной нормали; она равна по модулю и проти-
воположна по направлению удвоенной нормальной составляющей дей-
ствующей силы.
В самом деле, будем рассматривать кривую как фигуру равновесия нити.
Составляющие фиктивной силы F±, действующей на нить, которою мы, по
предположению, заменяем кривую, будут:
з
~~Т" dU
Yx ={2(U + h)] 2 ^f-,
ду

ГЛАВА XII. ДВИЖЕНИЕ ТОЧКИ ПО КРИВОЙ	397
а натяжение нити будет
1
т =
С другой стороны, сила, фактически действующая на движущуюся точку,
имеет проекции
dU дЦ дЦ
дх ' ду ' дг '
Естественные уравнения равновесия нити здесь имеют вид
Так как проекции силы Fj, на декортовы оси равны проекциям силы Р
умноженным на [2({/ +Л)]~5'3, то так же будут преобразовываться и проек-
ции на нормаль и бинормаль. Следовательно,
откуда
или, на основании теоремы кинетической энергии,
Fn = -m — .	B)
Возьмем теперь естественные уравнения движения. Имеем
или, принимая во внимание равенства A) и B),
Nb = 0, N=-2Fn.
Эти два равенства и доказывают высказанное предложение, которое мы
уже проверили для циклоиды (п. 250). По поводу этой теоремы можно ука-
зать на статью Андуайе (Comptes rendus, т. С).
Гатон де ля Гупийер дополнил исследование брахистохрон, разобрав
случай одновременного действия сил, зависящих от скорости, и сил трения
и разрешив обратную брахистохронам задачу (Memoires de l'Academie,
т. XXVII и XXVIII).'
256. Приложение теорем Томсона и Тэта к брахистохронам.
В главе VII мы указали несколько интересных свойств кривых, обращаю-
щих в минимум интеграл вида
(В)
1= j ?(лг, у, z) ds.	A)
W
Эти свойства, если их, в частности, приложить к брахистохронам, полу-
чают простое выражение. Брахистохроны в случае сил, имеющих силовую
функцию U(x, у, г), получаются как кривые, обращающие в минимум инте-
грал
(В)
t= f r 1 - ds,	B)
U)

398	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
где h имеет определенное значение. Если эта постоянная выбрана, то во всех
рассматриваемых движениях начальное положение и величина начальной
скорости связаны соотношением
-2	U (х0, у0, z0) = h.
Следовательно, интеграл A) совпадает тождественно с интегралом B), если
принять
9 (х, у, г) = ¦ ,		,
и значение интеграла / вдоль участка АВ какой-нибудь кривой будет
в точности равно времени t, которое понадобится точке массы единицы,
чтобы переместиться по этой кривой под действием рассматриваемой силы
и при указанных начальных условиях из А в В.
Брахистохроны будут тогда кривыми, которые раньше были названы
кривыми С (п. 146), зависящими от четырех произвольных постоянных. На-
пример, если принять U — — gz, h = О, то брахистохроны будут циклоидами,
лежащими в вертикальных плоскостях ниже плоскости ху и имеющими точки
возврата на плоскости ху.
Возвращаясь к общему случаю, мы можем основную формулу Тэта и
Томсона выразить так:
Пусть АСВ и А-^С^Вг— две бесконечно близкие брахистохроны, опи-
сываемые точкой массы 1, — первая за время t, а вторая за время t-\-bt;
тогда имеем (п. 147)
BAA,
	 cos BAA,	Ш1 _ cos ь
где UA и UB являются значениями функции U на концах А и В.
Тогда из формулы Тэта и Томсона, полученной в п. 147, вытекают
следующие результаты:
1°. Если заданы две неподвижные поверхности S и 2, то кривая, кото-
рую нужно провести между ними таким образом, чтобы движущаяся по ней
при указанных начальных условиях точка описала ее за минимальное время,
является брахистохроной, которая одновременно нормальна к обеим поверх-
ностям. Теорема остается справедливой, если одна или обе эти поверхности
заменяются кривой или точкой.
Например, если даны точка А и плоскость Р, то кривая, которую нужно
провести от А до плоскости таким образом, чтобы пущенная по этой кри-
вой из А без начальной скорости тяжелая точка достигла плоскости за
кратчайший промежуток времени, является циклоидой с горизонтальным
основанием, лежащей в вертикальной плоскости, имеющей в А точку воз-
врата и пересекающей нормально плоскость Р.
2°. Если взять брахистохроны, нормальные к поверхности S и по каж-
дой из них в момент t = 0 пустить при указанных начальных условиях оди-
наковые материальные точки, то в любой момент времени t все эти точки
будут находиться на поверхности S', также нормальной к брахистохронам.
(Эта теорема была указана уже Эйлером.)
Например, если взять все циклоиды, имеющие в точке А точку возврата
и вертикальную касательную Аг, и по каждой из них в момент t = 0 пустить
из А без начальной скорости тяжелую точку, то в момент t все эти точки
будут находиться на поверхности S', нормальной ко всем циклоидам. В данном
примере поверхность S сводится к точке А; поверхность S' будет, очевидно,
поверхностью вращения вокруг Az.
Мы предлагаем в качестве упражнения проверить это утверждение.

ГЛАВА XII. ДВИЖЕНИЕ ТОЧКИ ПО КРИВОЙ	399
3". Наконец, формула Тэта и Томсона позволяет высказать для бра-
хистохрон теоремы, аналогичные свойствам разверток, если заменить в клас-
сических формулировках длины дуг промежутками времени, которые за-
трачивает для их описания точка, скользящая по ним без трения. Мы не
будем здесь останавливаться на этом вопросе, который мы предлагаем в ка-
честве упражнения.
257. Брахистохроны на заданной поверхности. Требуется среди
кривых, лежащих на заданной поверхности f(x, у, z) = О и соеди-
няющих две точки А и В, найти такую, которая обращает интеграл
(-В)
ds
I
в минимум. Эта задача получится такая же, как и рассмотренная
в п. 149, если подставить <р (х, у, г) вместо ..	—. Она при-
YV ^	y<2.{U+h)	F
водится к нахождению равновесия нити на заданной поверхности.
II. Движение материальной точки на изменяемой кривой
258. Уравнения движения. Рассмотрим точку, скользящую без
трения по кривой, положение и форма которой изменяются с тече-
нием времени. В неподвижных осях уравнения этой кривой будут
f{x, у, z, 0 = 0. Л(х, у, г, t) = 0.
Нормальная реакция N кривой имеет проекции
Х^+Х^, Х-^ + Х^, Х^
дх ' 1 дх	ду ^ * ду ' дг
и точку можно рассматривать как свободную, но находящуюся под
действием равнодействующей F заданных сил и реакции N. Тогда
уравнения движения будут:
т~Ш=-
tn —~- =
W~' " Jy"lr''dy~t
d^z „ , , df . . d/t
/ra —775- = Z -4- л -5—\- л, -^-i-.
dfi	' дг ' x dz
A)
Эти три уравнения совместно с уравнениями кривой определяют
х, у, г, т. е. движение точки, и X, \, т. е. реакцию, в функции
времени. Следует заметить, что реакция не исчезает в уравнении
кинетической энергии. В этом можно убедиться аналитически, умно-
жая уравнения A) соответственно на dx, dy, dz и складывая. В по-
лученном равенстве коэффициенты при X и Xt не будут равны нулю.
В самом деле, когда t увеличивается на dt, тогда х, у, z увеличи-

400
ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
ваются на dx, dy, dz и так как
оставаться равной нулю, то
функция f(x, у, г, t) должна
Следовательно, коэффициент при X
так же коэффициент при X, обращается в
обращается в
~лТ^- Точно
Этот результат ясен и геометрически, так как действительное
перемещение точки происходит не по касательной к движущейся
кривой и работа реакции не равна нулю. Для исключения реакции
пользуются методом, рассматриваемым ниже.
259. Уравнения Лагранжа. Пусть q — параметр, определяющий
положение точки на кривой С. К моменту t координаты какой-нибудь
точки кривой и, в частности, движущейся точки будут
если будет известно, как изме-
Движение точки будет известно,
няется q с течением времени.
Умножим уравнения движения A) соответственно на -j—, ¦—-, -3-
и сложим. Коэффициенты при X и \ обратятся в нуль, так как они
будут отличаться множителем от косинусов углов, образуемых каса-
тельной к кривой С с нормалями к каждой из поверхностей /=0,
f1 = 0. Тогда останется
ду
где положено
дх
дг
Это и есть уравнение движения, определяющее значение пара-
метра q, служащего для фиксирования положения точки на кривой
в функции времени. Чтобы придать этому уравнению более удобную
форму, мы применим к нему важное преобразование, введенное Лаг-
ранжем, с которым мы снова встретимся в самой общей задаче дина-
мики голономных систем.
Обозначим через q' производную параметра q по времени и через
х', у', z' проекции скорости точки на оси координат. Согласно
формуле х — ср (q, t), абсцисса движущейся точки зависит от вре-
мени и непосредственно, и через параметр q, потому что последний
в свою очередь является функцией от t. Имеем
дх
дх

ГЛАВА XII. ДВИЖЕНИЕ ТОЧКИ ПО КРИВОЙ	401
Рассматривая х' как функцию трех переменных q, q', t, имеем
очевидные равенства
дх' 	 дх дх' __ д*х , &'-х
dq' dq ' dq dq2 ^ ~"~ dq dt'
Последняя формула показывает, что
дх' _ d I dx \
dq dt \~dq~)'
В самом деле, -g— зависит от t и непосредственно и через q; по-
этому
Ж\~dq ) = ~5ф q ~^"dqdi'
Для у и г получаются аналогичные формулы:
ду' 	 ду ду' 	 d I ду\
д^~"Щ' ~0q~~~dJ\dq)'
dz' 	 dz_	dz^_	d I дг\
dq' ~ dq '	~5q~ ~ ~dt \~dq )'
Установив это, мы можем	уравнение B) написать следующим
образом:
d2x	dx'	o	дх
так как —^- равно —п-, -•• оаменяя в последнем	уравнении	-г—,
ду дг	дх' ду' dz'
-J-, -j- полученными выше значениями —тт, -jV,	-=-r, а произ-
d I dx\ d i dy \ d I dz \	dx' dy'	dz'
водные -тг|-з—)> -ут\-г-], тг[— их значениями	—,—, —4—	—,
dt \ dq ]' dt \ dq )' dt \oq )	dq ' tiq '	oq
будем иметь:
, dx' , dy , , d
d r I
или, обозначая через Т кинетическую энергию точки,
окончательно получим
dt \dq' I dq —У'	D)
Это и есть уравнение движения по Лагранжу. После замены х',
У, z' их значениями по формуле C) и ей аналогичными, величина Т
станет функцией от q, q' и t, причем второй степени относительно q'.
26 Зак. 851. П. Аппель, г. 1

402	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Как только эта функция будет вычислена, можно будет сразу соста-
вить уравнение D).
Написанное выше значение Q можно определить следующим обра-
зом. Представим себе, что движущейся точке сообщено возможное
перемещение, которое получится, если кривую С сделать неподвиж-
ной в занимаемом ею в момент t положении и переместить точку по
этой кривой. Или аналитически представим себе, что точке сообщено
перемещение, которое получится, если t считать постоянным, а пара-
метр q увеличить на bq. Тогда будет
5, dx -, 5	ду 5 5, dz »
Для этого возможного перемещения работа заданной силы X,
У, Z равна
Следовательно, величина Q является коэффициентом при Sg в вы-
ражении возможной работы.
Если существует силовая функция U(x, у, z), или же, вообще,
если X, Y, Z будут частными производными по х, у, z какой-то
функции U{x, у, z, t), содержащей время, то будет также
Q-
Ч~ dq •
где последняя производная вычислена в предположении, что в функ-
ции U{x, у, z, t) координаты заменены их вы-
ражениями через q и t. Действительно, так как
U зависит от q через х, у, г, то, очевидно,
имеем
dU __ dU dx . dU dy . dU dz _
dq dx dq "' dy dq "' dz dq
= xdX	dy +Z^. = Qm
dq ' dq ' dq ^
26Э. Задача. Материальная точка скользит
без трения по окружности, лежащей в горизон-
Рис. 162.	тальной плоскости хОу и вращающейся с по-
стоянной угловой скоростью « вокруг odnou из
своих точек О, которая закреплена неподвижно. HcCAedoeamb deujwenue
точки, пpedпoлaгaя, что на нее не действует никакая Henocpedcmeenno
приложенная сила.
Пусть А — точка окружности, диаметрально противоположная неподвиж-
ной точке; угол хОА изменяется пропорционально времени. Отсчитывая t
от того момента, когда это г угол равен нулю, найдем (рис. 162):

ГЛАВА XII. ДВИЖЕНИЕ ТОЧКИ ПО КРИВОЙ	403
Пусть С — центр окружности, а М — движущаяся точка. Мы будем опре-
делять положение точки М на окружности углом АСМ = 8, который будет
играть роль параметра д. Проектируя контур ОСМ на оси, получим z = 0
и
х = R cos at + R cos @ -)- at),
у = R sin at + R sin (8 + at).
Обозначая через х', у', 8' производные от х, у, 8 по t, имеем:
х' = — R<» sin at — R (Ъ' + a) sin (8 + at),
у' = Ru, COS at + R (8' + a>) COS (8 + at).
T = -—¦ К + F' + a)"- 4- 2o) (8' 4- a) cos 8],
mR°- (8' 4- со 4- ш cos 8), -gg- = — «/? « (8' + со) sin в.
Так как заданных сил нет, то
<?=0.
Следовательно, уравнение D) после всех приведений будет иметь вид
- = — о>2 sin 8.
df-
Сравнивая это уравнение с уравнением движения математического маят-
ника
мы видим, что относительное движение точки М для наблюдателя, который
движется вместе с окружностью, будет движением математического маят-
ника, причем точка А будет играть для него роль наиболее низкой точки.
Продолжительность двойного бесконечно малого размаха, равная 2л'уг//^,
будет здесь 2тс/со; она в точности равна продолжительности одного оборота
окружности. Продолжительность конечных колебаний будет больше.
Для вычисления нормальной реакции Л^ будем исходить из общих урав-
нений движения, которые в данном случае имеют вид
т~ = — N cos (в + at), m-^- = — Nsin(e + at),
так как точка находится под действием только силы N. Из этих уравнений
находим
N = ~ т ["Ж cos (й + at) + "Жsin (t) + at)]'
что можно написать так
N= -m JL [-g- cos (в 4- W) 4- -§- sin (8 4- »
(в' 4- «) [ -~sinF + «0 + % cos (в 4- *>0].
Заменяя в этой формуле —— и —jj- их значениями, получим
N—mR [a'i cos 0 + С' 4" ШИ-
26*

404	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Это выражение зависит от 8'. Реакция, следовательно, не будет одина-
ковой при прохождении движущейся точки через одну и ту же точку окруж-
ности в одну или другую сторону, так как знак 6' не будет одинаковым
в обоих случаях.
Если движущаяся точка отталкивается от центра О силой, пропорцио-
нальной расстоянию ОМ = г, то эта сила, равная fmr, будет иметь силовую
функцию U = —у— , которая, будучи выражена через 8, примет вид
Тогда
и уравнение движения сохранит вид уравнения движения математического
маятника, для которого g/l будет равно (ш2+/).
261. Случай неподвижной кривой. Само собой понятно, что изло-
женный метод, будучи общим, применим и к движению точки по непо-
движной кривой. При этом обычно можно выбрать параметр q таким
образом, чтобы х, у, г, выраженные в функции q, не содержали
явно t:
X = f (q), У = ^ (q), 2 = ш (q);
тогда
т. е. Т будет однородной функцией второго порядка относительно q'•
Уравнение Лагранжа
dt \ dq' ) dq ч
должно совпадать с уравнением кинетической энергии, так как при
неподвижной кривой применение теоремы кинетической энергии при-
водит к единственному уравнению движения. Это легко проверить.
В самом деле, умножая уравнение Лагранжа на q', получим
, d i дТ \ , дТ . ,
*)	Q
или
дТ\ dq' дТ__ дТ
~W)~~dT dq' q dq ~ W'
дТ
Но вследствие однородности функции Т произведение q' -5—Г равно 2Т
и более того, так как Т зависит от t только через q и q', то
dt ~ dq' dt ~" dt

ГЛАВА XII. ДВИЖЕНИЕ ТОЧКИ ПО КРИВОЙ	405
Поэтому уравнение принимает вид
dt	dt vv
или
dT = Qdq,
что действительно является уравнением кинетической энергии.
УПРАЖНЕНИЯ
1.	Материальная точка, вынужденная двигаться по окружности, при-
тягивается или отталкивается одной из точек этой окружности. Найти, каким
должен быть закон силы, чтобы реакция была постоянной.
2.	Две материальные точки А я В с одинаковыми массами, вынужденные
скользить без трения одна по оси Ох, а другая по оси Оу, притягиваются
друг к другу с произвольной силой, являющейся функцией /(/") их взаимного
расстояния г. Они начинают движение без начальной скорости. Доказать,
что они одновременно достигнут начала координат [лиценциатская *), Бордо].
3.	Определить такую кривую, чтобы тяжелая точка, скользящая по этой
кривой без трения, приобретала в каждый момент скорость, вертикальная
составляющая которой имеет постоянное значение (лиценциатская, Париж).
4.	Материальная точка массы т прикреплена к концу невесомой нити,
навернутой на плоскую кривую С; точка отталкивается центром кривизны
кривой С, соответствующим той ее точке, в которой нить отделяется от этой
кривой. Сила отталкивания есть функция расстояния от движущейся точки
до центра кривизны.
1°. Составить общие уравнения, определяющие закон движения и натя-
жение нити.
2°. В случае, когда отталкивающая сила пропорциональна расстоянию,
а точка вначале лежит на кривой С и не имеет начальной скорости,
обратить внимание на вид закона движения и выражения натяжения нити.
3°. Допустив, наконец, что отталкивание обратно пропорционально ква-
драту расстояния, определить кривую, для которой предыдущий закон B°)
сохраняет силу (лиценциатская, Пуатье).
5.	В вертикальной плоскости рассматривается кривая, являющаяся оги-
бающей отрезка прямой постоянной длины, один конец которого скользит
по горизонтальной прямой Ох, а другой — по вертикальной прямой Oz.
Исследовать движение тяжелой точки, скользящей без трения по этой кривой.
В частности, найти время, затрачиваемое движущейся точкой для достижения
точки возврата на оси Ох, если она начала двигаться из наиболее низкой
точки с такой начальной скоростью, что постоянная кинетической энергии
равна нулю (v2 — Igz).
6.	Найти такую кривую, лежащую в вертикальной плоскости, что если
по ней заставить двигаться материальную точку, то реакция этой кривой
должна находиться в постоянном отношении k к нормальной составляющей
силы тяжести (k = 1 — прямая, k = 2.— циклоида, ...).
7.	Тяжелая точка начинает двигаться без начальной скорости по внешней
части параболы, лежащей в вертикальной плоскости и имеющей горизон-
тальную ось. Найти точку, в которой движущаяся точка покидает параболу
(точку срыва).
*) То есть задача, предложенная на экзаменах на степень лиценциата.
{Прим. перев.)

40б	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Если через h обозначить высоту начального положения над осью, то
ордината у искомой точки будет положительным корнем уравнения
уЗ + 3/?2у — 2p-h = О (р — параметр).
8.	Если два маятника с грузами Mt и уИ2, находящимися на одной и
той же окружности С, выходят в разные моменты из одного и того же
начального положения с одинаковыми скоростями, то прямая МгМ^, соеди-
няющая грузы, огибает окружность С. Допустим, что маятники совершают
круговое движение, и обозначим через Т продолжительность обращения
каждого из маятников, а через т — промежуток времени, отделяющий начала
их движений. Если х соизмеримо с Т, то прямые, соединяющие положения
маятников в моменты t, t-\-i, t-\-2z, t-\-iz,	, образуют многоугольник,
вписанный в С и описанный около С. (Это упражнение является не чем
иным, как применением метода Якоби для вывода теоремы Понселе; см.
А л ь ф е н, Traite des fonctions elliptiques.)
9.	Рассмотрим неподвижные прямые, проходящие через точку А, и допу-
стим, что в момент tu из А по всем этим прямым начинают двигаться без
начальной скорости одинаковые точки, притягиваемые неподвижным цен-
тром О пропорционально расстоянию. Доказать, что все эти точки одновре-
менно приходят в положения, совпадающие с проекциями точки О на про-
бегаемые ими прямые.
• 10. Материальная точка остается на кривой, определяемой уравне-
нием вида
S2 = ср (г),
где z — ордината, s — дуга, отсчитываемая от некоторой точки кривой,
а ср — произвольная функция.
Требуется исследовать движение этой точки, предполагая:
1)	что она находится под действием силы, параллельной оси z и опре-
деляемой равенством
Z = —g-*V <*)¦
где k — заданная постоянная;
2)	что она испытывает, кроме того, сопротивление, пропорциональное
скорости. Результат применить к случаю, когда
ср (z) = а*-пгп — ai=a?-n(zn — an\
где а — заданная длина.
Исследовать частный случай, когда отсутствует начальная скорость,
и определить время, необходимое точке для достижения положения s = 0,
соответствующего z — а. Рассмотреть случай, когда п = 2. (Лиценциатская.)
11. Найти плоскую таутохрону для точки, притягиваемой неподвижным
центром, лежащим в плоскости таутохроны, с силой, пропорциональной рас-
стоянию г (п. 252).
Требуется найти кривую, для которой г dr — ks ds. Рассматривая кривую
как огибающую движущейся прямой
X COS a — у Sin a = ср' (а),
получим для определения функции ср (а) линейное уравнение с постоянными
коэффициентами
A —?2) </'(«) —*?(«) = 0.
Это уравнение интегрируется в тригонометрических или показательных
функциях В первом случае имеем эпициклоиду. (П ю и з ё, Journal de
Liouville, т. IX.)

ГЛАВА XII. ДВИЖЕНИЕ ТОЧКИ ПО КРИВОЙ	407
12. Задача Абеля. Определить кривую, лежащую в вертикальной пло-
скости и обладающую следующим свойством: на этой кривой существует
такая неподвижная точка О, что тяжелая точка, пущенная без начальной
скорости по кривой из начального положения, находящегося на высоте h
над О, приходит в точку О за время Т, являющееся наперед заданной функ-
цией Т = <р (h).
[Пусть s = <\> (z)—-соотношение между дугой ОМ кривой, отсчитываемой
от точки О, и ординатой точки М. Имеем
Пусть а — вещественная переменная, большая чем h. Абель умножает обе
dh
части равенства на -==. и интегрирует по Л от 0 до и:
у и—¦ h
г— Г <e(h)dh = f dh Г у (z) dz
J yir=~h J fir^hJ Yh—z '
О '	0 '	0 '
Переменив порядок интегрирования в правой части, найдем для интеграла
этой части значение п<\/ (и). Искомая функция будет выражаться определенным
интегралом, содержащим заданную функцию tp. Например, если ср (/г) == const.,
то опять получится циклоида.]
13.	Определить таутохрону для тяжелой точки в вертикальной плоскости,
принимая во внимание трение и сопротивление среды, пропорциональное v3.
(Задача приводится к линейному уравнению относительно tA)
14.	Задача Эйлера и Саладини. Какую кривую нужно провести в вер-
тикальной плоскости из точки О, чтобы тяжелая точка, пущенная по этой
кривой из О без начальной скорости, пришла в произвольное положение М
на этой кривой за то же время, какое ей потребовалось бы, если бы она
скользила вдоль хорды ОМ} (Получается лемниската; Эйлер, т. II его
Механики, 1736; Саладини, Memoires de l'Istituto nazionale italiano, 1804;
см. статью Фуре «Bulletin de la Societe mathematique», т. XX.)
15.	Задача Бонне. Доказать, что найденная в предыдущем упражнении
лемниската будет обладать тем же свойством, если вес заменить силой при-
тяжения к точке О, пропорциональной расстоянию (Journal de Mathematique
pures et appliquees, т. IX, стр. 116).
16.	Задачи Фуре. 1°. Материальная точка, находящаяся в плоскости
под действием силы, имеющей определенную силовую функцию, выходит
из начала О с заданной начальной скоростью. Найти систему подобных
кривых (С), проходящих через начало О, причем таких, чтобы точка, дви-
гающаяся по какой-нибудь из этих кривых, описывала, начиная от точки О,
любую дугу в такое же время, какое ей понадобилось бы для пробега соот-
ветствующей хорды.
2°. Дана на плоскости система кривых (С), проходящих через точку О
и гомотетичных относительно этой точки. Найти силу, имеющую силовую
функцию, под действием которой движущаяся точка, получив заданную на-
чальную скорость, описывает, начиная от точки О, произвольную цугу любой
из кривых (С) за то же время, какое ей потребовалось бы для описания
соответствующей хорды.

408	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Первая из этих задач имеет решение лишь при условии, что начальная
скорость равна нулю и что силовая функция в полярных координатах имеет
вид ф —щ Ч2 С)! Уравнение искомых кривых будет тогда
Г 9(")
_ Г 9(
J Ч>' i
где k — произвольная постоянная.
Вторая задача также невозможна, если начальная скорость не равна
нулю. Если уравнение кривой имеет вид r = k<o(b), то силовая функция
получится, если в написанном выше выражении, в котором ф — произвольная
функция, положить
(Фуре, Comptes rendus, т. СШ, стр. 1114 и 1174; Journal de 1'Ecole Poly-
technique, вып. 56.)
17.	Синхронные кривые и поверхности. В плоскости дано семейство
проходящих через точку О кривых С, уравнения которых зависят от
одного параметра. В момент t = 6 по каждой из этих кривых из точки О
начинают двигаться одинаковые материальные точки с одинаковой для всех
заданной начальной скоростью v0, находящиеся под действием силы, имеющей
заданную силовую функцию. Найти кривую S, представляющую собою геоме-
трическое место этих точек в один и тот же момент t.
Эти кривые S образуют семейство, зависящее от параметра V, их назы-
вают кривыми, синхронными первым.
Если кривые С, проходящие через точку О, расположены в пространстве
и зависят от двух параметров и если пустить по этим кривым в момент t — О
со скоростью v0 материальные точки, находящиеся под действием сил, имею-
щих данный потенциал, то геометрическим местом таких точек к моменту t
будет поверхность S, называемая синхронной поверхностью.
18.	Примеры синхронных кривых. Скорость v0 предполагается равной
нулю; силой является вес; кривые С являются прямыми, проходящими через
начало и лежащими в вертикальной плоскости (кривые S — окружности),
(Эйлер).
Сила является весом, а кривые С суть циклоиды в вертикальной пло-
скости с горизонтальными основаниями и точками возврата в точке О.
[Синхронные кривые S ортогональны к циклоидам; это вытекает (п. 256)
из того, что циклоиды С являются брахистохронами для рассматриваемого
закона сил.] (Эйлер).
Сила является притяжением к точке О, пропорциональным расстоянию,
а кривые С суть окружности х^-\-у2 — 'lay = 0, где а — переменный пара-
метр. (Синхронные кривые S суть прямые, проходящие через начало.)
(Лег у, Annales de la Faculte des Sciences de Toulouse, т. VI.)
19.	Даны в плоскости два семейства кривых (А) и (С), проходящих
через точку О. Можно ли найти такую потенциальную силу F, чтобы
под ее действием материальная точка, выходящая с определенной ско-
ростью из начала О и движущаяся по какой-нибудь из кривых (С), при-
ходила в любую точку М этой кривой за такое же время, за какое она
пришла бы в М, двигаясь вдоль проходящей через М кривой семейства (А).
Кривые (А) можно назвать траекториями, а кривые (С) синодальными
линиями; при этом очевидно, что их роли можно поменять. Задача может
быть всегда решена бесчисленным множеством способов. Задача Фуре отно-
сится к случаю, когда траектории прямолинейны и синодальные кривые по-
добны относительно точки О. (Де Сен-Жермен, Bulletin des Sciences Mathe-
matiques, 1889.)

ГЛАВА XII. ДВИЖЕНИЕ ТОЧКИ ПО КРИВОЙ	409
20.	Доказать, что между траекториями, синхронными и синодальными
кривыми существует следующее соотношение: пусть MA, MB, MC—соот-
ветственные касательные, проведенные в сторону движения к тем из этих
линий, которые пересекаются в точке М. Тогда
2АМВ = it + АМС
и
2СШ = п + СМ А
(Фуре, Comptes rendus, т. СШ и де Сен-Жермен, Bulletin des Sciences ma-
thematiques, 1889.)
21.	Доказать, что если синхронные кривые ортогональны к траекториям,
то последние совпадают с синодальными кривыми и обращаются в брахи-
стохроны для рассматриваемых сил. (Там же.)
22.	Найти движение тяжелой материальной точки по прямой, неизменно
связанной с вертикальной осью, вокруг которой она вращается с постоянной
угловой скоростью.
23.	Найти движение тяжелой материальной точки по вертикальной
окружности, неизменно связанной с вертикальной осью, вокруг которой она
вращается с постоянной угловой скоростью. Предполагается, что проекция
оси на плоскость окружности проходит через ее центр.
24.	Показать, что задача о таутохроне для случая, когда существует
силовая функция, приводится к интегрированию одного дифференциального
уравнения с частными производными второй степени и первого порядка.
(Кёнигс, Comptes rendus, 1 мая 1893.)

ГЛАВА XIII
ДВИЖЕНИЕ ТОЧКИ ПО НЕПОДВИЖНОЙ
ИЛИ ДВИЖУЩЕЙСЯ ПОВЕРХНОСТИ
I. Общие положения
262. Уравнения движения. Дана поверхность S, которая может
изменять как свое положение, так и свою форму, и пусть
f(X,y,2,t) = 0	A)
—уравнение этой поверхности в прямоугольных координатах. В ча-
стном случае, когда поверхность неподвижна, это уравнение не будет
содержать времени t. Материальная точка М с координатами х, у, z
скользит без трения по этой поверхности и находится под действием
заданных сил, равнодействующая которых F имеет проекции X, Y, Z.
Требуется найти движение точки. Со стороны поверхности на точку
будет действовать нормальная реакция TV, проекции которой будут
величинами вида
Хд-1 Х^ XdJ	(N1
кдх' ду' kdz-	т
Точку можно рассматривать как свободную, находящуюся под
действием сил F и N. Уравнения движения будут
m=K + X	m=Z^k	B)
Эти уравнения совместно с уравнением A) поверхности образуют
систему четырех уравнений, определяющих х, у, z и X в функции t.
Для нахождения уравнений, определяющих х, у, z в функции /,
необходимо из уравнений B) исключить X, что приведет к двум
уравнениям. После того, как движение будет найдено, значение X,
а следовательно, и величина реакции, найдется из любого урав-
нения системы B) или из комбинации этих уравнений.
263. Уравнения Лагранжа. Метод Лагранжа, который мы сейчас
изложим, сходен с тем, которым мы пользовались для изучения дви-
жения точки по кривой (п. 259). Всегда возможно выразить коор-
динаты точки поверхности S и, в частности, движущейся точки М,
в функции двух параметров qx и q2:
х = <Р (<7i> <72' О. У = *]>(.Я1. Яг> t), г — ш (qv q2, t).	C)

ГЛАВА XIII. ДВИЖЕНИЕ ТОЧКИ ПО ПОВЕРХНОСТИ	411
Эти выражения таковы, что если из них исключить ql и q2, то вновь
получится уравнение A) поверхности. Они содержат явно время t,
которое входит в уравнение A). В частном случае, когда поверх-
ность S неподвижна, уравнение A) не будет содержать времени и можно
будет распорядиться так, чтобы выражения C) для х, у, z также
не содержали времени явно.
Чтобы знать движение, достаточно знать, как выражаются через t
параметры qu q2, определяющие положения движущейся точки. Для
нахождения qx и q2 требуются два уравнения, которые могут быть
составлены следующим образом. Умножив уравнения B) соответственно
дх ду dz
на г—, -^-, -к- и сложив их, получим:
dq dq oq
/ d^x дх , d2y ду . d2z дг \
V df- dqx ~ df- dqx ^ df- dqj
где
В этом равенстве коэффициент kt исчез вследствие соотношения
д/ дх . д/ ду . df dz	_
дх dqt ду dqy dz dqx '
которое выражает, что нормаль к поверхности нормальна и к кри-
вой, которую опишет точка C), если, сохраняя постоянными q2
и t, изменять только параметр qt; эта кривая лежит на поверхно-
сти 5. Точно так же, умножая уравнения движения B) соответственно
дх ду dz
на з~> -JT- > з~ и складывая, получим уравнение
dq<> dq2 dq2	J
(d^x дх . d?y ду . d2z dz\	 _	,.,.
m \~Ш dq~2 'df-~dq~o~{~ ~df-Iq~>) ~~ ^2'	(
где
Уравнения D) и D') и будут определять ^, и дг в функции t.
Их можно написать в значительно более простой форме. Обозначим
через q\ и q'% производные от q1 и q2 по t и через х', у', z' проекции
~dl' ~di' ~Ш СК0Р0СТИ точки. Уравнение D) можно представить в виде

412	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
так как, очевидно,
dt\ dqx)	dt\oqx)	dt* dqL
Но, на основании равенств C), x зависит от t и непосредственно
и через q1 и q2, которые являются функциями от /; следовательно,
х'= — ff'4-— '-+-—	(1
™	дх
1очно так же -г— зависит от ; и непосредственно и через ql
и <72; следовательно,
В выражении F) будем рассматривать х' как функцию перемен-
ных qy, q2, q[, g'2, t. Тогда найдем, что
т. е.
дх' дх дх' &*х / д^х
дх'	дх дх'	 d /дх
Аналогичные вычисления приводят к следующим результатам:
ду'	ду ду'	 d / ду\
dq[ dqt' dqx dtXdqJ'
dz'	 dz dz'	 d i dz\
do dqi' Oqi dt \dq\)'
Заменяя в уравнении движения E) величины
дх ду dz d idx\ d I ду\ d Idz\
dqi' dqt' dqt' dt\dqj' dtydqj' dt\dqj
найденными для них сейчас значениями, получим уравнение
d Г / , дх' , , ду' . , dz' \ 1	I , dx' . . dy' . , dz'\
-r,\m | x —, 4- v -^y + z' —; I — mix' ^	H'j-4-2 ;.— )¦
at \ \ dq.	dq,	oq,	\ дЯ\	oqx	dqj
dt
или
dT\ dT
где положено

ГЛАВА XIII. ДВИЖЕНИЕ ТОЧКИ ПО ПОВЕРХНОСТИ	413'
Точно так же, преобразуя уравнение D'), найдем
-J- = Q2-	G')
Уравнения G) и G') являются уравнениями движения по Лагранжу.
Чтобы получить их, достаточно вычислить величину Т, равную кине-
тической энергии точки; в этой величине нужно заменить х', у', 2''
их значениями, такими, как F), чтобы выразить Т через qv q.z,
q'v q'2 и t; после этого можно составить уравнения G) и G').
В этих уравнениях правые части Q1 и Q2 вычислены выше.
Их можно определить еще следующим образом: сообщим точке воз-
можное перемещение по поверхности 5, т. е. такое, которое по-
лучится, если, оставляя t постоянным, дать величинам <?, и q2 при-
ращения §<7Х и bq2. Проекции этого возможного перемещения на оси
координат будут
8х =
Ьу =
02 =
дх
ду_
дг
да,
bqx
ЬЧ1
1 да» чг
+ — 8
, дг .
+ ^— 0G,.
Отсюда, учитывая найденные выше значения Qx и Q2, получим для
возможной силы F выражение
ХЬх + Y оу + Z 8г = Ql bqt -f- Q2 bq2.
Таким образом, для нахождения величин Qx и Q2 достаточно опре-
делить коэффициенты при S<7j и о<72 в выражении возможной ра-
боты силы F на произвольном перемещении, осуществляемом на
поверхности S в положении, которое эта поверхность занимает в мо-
мент t.
Чтобы получить, в частности, Qx, нужно сообщить точке воз-
можное перемещение, которое получится, если, оставляя постоян-
ными q2 и t, изменить только qx на величину ее вариации 5^; тогда
соответствующая возможная работа силы F будет Qfiqv Точно так же,
чтобы получить Q2, нужно взять возможное перемещение, при кото-
ром постоянны О] и t2; работа силы F будет тогда равна Q2 bq2.
Если существует силовая функция О (х, у, г) или выполняется
более общее условие, согласно которому X, Y, Z являются частными
производными функции U(x, у, г, t), содержащей время, то
п ди п ди

414
ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Действительно, U(x, у, г, t) зависит от qx и q2 через х, у, г
и, следовательно,
dU__dUdx_.dU_dy_,dV^dz^__ удх , v ду_ 7д?_п
dqx — дх dqt "•" ду dqt "+" dz dqx ~ Л dqx^~ Y dqx^~ dqt ~ Wl>
Аналогичное выражение получим и для Q2.
264. Приложения. Г. Движение точки на неподвижной плоскости
в полярных координатах. Найдем движение точки на плоскости хОу, при-
няв за параметры 9i и <7г Две полярные координаты гиб. Формулы, опре-
деляющие х, у, г в функции двух параметров, для рассматриваемого случая
будут следующие:
х = г cos 9, у — г sin 6, z = 0.
Допустим, что на точку действует сила F, лежащая в плоскости и имеющая
проекции (X, Y, О). Функция Т будет
а уравнения движения —
dt\dr'
Так как <7i = Л Я?= ", то
Л |Xi_\	^L — Г)
л-1 Ля' I лв — V»
Qt=A^+ K|l = ^cose+ysin8,
Q? = X |^ -f- Y p- = — Xr sin 8 + Kr cos 8.
Функции Qt и Q2 можно найти и непосредственно. Обозначим через R
и /> составляющие силы по радиусу-вектору
в направлении возрастания г и по прямой,
к нему перпендикулярной в направлении воз-
растания 8. На перемещении or вдоль ра-
диуса-вектора E2=const.) работа силы F, равная
сумме работ сил Р и R, приводится к
виду R Ьг, так как работа силы Р равна нулю
(рис. 163). Следовательно,
О
\
\
р^
\
у
у/
s
Y
У'
Рис. 163.
Точно так же для возможного переме-
' х щения, которое получается, если предполо-
жить, что 9i> T- е- г, остается постоянным,
а 8 изменяется, н которое происходит по
окружности радиуса ОМ и равно г В6, ра-
ру	ру
бота силы F сводится к работе силы Р и равна Рг
вательно	г> п
р	р
Имеем, следо-
Учитывая найденные значения
d . ,.	»„,•)
и Q2, получим уравнение движения:
-л 4
Когда сила является центральной, Р все время равно нулю, и мы
получаем	rf.
(закон площадей).
dt

ГЛАВА XIII. ДВИЖЕНИЕ ТОЧКИ ПО ПОВЕРХНОСТИ
415
2°. Найти движение без трения тяжелой точки на плоскости, рав-
номерно вращающейся вокруг горизонтальной оси, лежащей в этой пло-
скости.
Будем отсчитывать время от того момента, когда вращающаяся пло-
скость совпадает с плоскостью хОу, которую мы предполагаем горизонталь-
ной, принималось вращения за ось х. Если 6 — угол у OR между движущейся
плоскостью и плоскостью ху (рис. 164),
то в = at, где (о — угловая скорость вра-	z
щения. Уравнение вращающейся пло-
скости ROx будет тогда
у sin at — г cos at = 0.
Применяя общие формулы B62), полу-
чим уравнения движения:
а*у
т—? = X sin at,
dt2
сРг
т —g = — mg — I cos coif,
Рис. 164.
причем нормальная реакция будет в точ-
ности равна величине X. Для фиксирования
положения точки М на движущейся плоскости воспользуемся координатами х
и г в системе осей Ox, OR, причем х будет играть роль параметра qv a. r —
роль параметра q2. Формулы преобразования будут
X = X, у = Г COS at, Z = Г Sin at,
и для функции Т получим
Для действующей силы mg существует силовая функция
U = — mgz — — mgr sin n>t.
Следовательно:
дТ _
дТ -от
ои -о
дТ
"' дх
дТ
Ь7
dU
дг
= 0,
= «-v.
= — mg sin at.
Уравнения движения будут
или
rfV
— a4 = —g sin at.

416	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Первое из этих уравнений показывает, что проекция Q точки М на ось х
движется равномерно. Второе уравнение, будучи линейным с постоянными
коэффициентами, интегрируется и имеет общий интеграл
г = Aemt + Ве~ш* + J^ sin at.
2а-
Для нахождения уравнения проекции траектории на плоскость yz до-
статочно заменить в этом соотношении Ы углом в. Тогда
Представляет интерес частный случай, когда начальные условия таковы,
что А и В равны нулю; для этого достаточно, чтобы точка была брошена
от оси вращения таким образом, чтобы ее проекция на прямую R имела на-
чальную скорость, равную g/2a. Тогда уравнение проекции траектории на
плоскость yz будет
Г = ^ 81Пв.
Это — окружность, касающаяся в точке О оси Оу. Траектория будет вин-
товой линией.
Для вычисления нормальной реакции возьмем снова одно из уравнений
движения:
т —! = X sin wt.
dti
Заменяя в нем у его значением г cos wt, имеем
fd2r	dr	\
т [ ГП* COS at — 2м —- Sin u>t — mV COS at] = I Sin at.
\dP	dt	I
Отсюда, вспоминая уравнение, определяющее г,
-l^^r — g sin at,
получим
\ = — mg cos at — 2ma ——.
Эта формула, в которой г следует заменить его значением через t, опре-
деляет в функции t нормальную реакцию, которая в рассматриваемом слу-
чае совпадает с L
II. Случай неподвижной поверхности
265. Применение теоремы кинетической энергии. Указанный
нами общий метод применим всегда. Но если поверхность непо-
движна, то возможны упрощения, которые следует указать. В этом
случае уравнение поверхности имеет вид
f(x,y, z) = Q,
и действительное перемещение, которое совершает точка, будет пер-
пендикулярно к нормальной реакции -N: Если применить теорему ки-

ГЛАВА XIII. ДВИЖЕНИЕ ТОЧКИ ПО ПОВЕРХНОСТИ	417
нетической энергии, то работа этой нормальной реакции будет равна
нулю, и мы получим уравнение
не зависящее от реакции. Этим уравнением можно всегда заменить
одно из уравнений Лагранжа. Мы убедимся сейчас, что оно действи-
тельно представляет следствие уравнений Лагранжа.
Если поверхность движется, то нормальная реакция не исклю-
чится при применении теоремы кинетической энергии, так как действи-
тельное перемещение dx, dy, dz точки не будет перпендикулярным
к нормальной реакции. В самом деле, в момент t поверхность
будет в положении S и точка в положении М на поверхности S;
к моменту t-\~dt поверхность будет в S' и точка в М' на поверх-
ности S'; перемещение ММ' не будет перпендикулярно к реакции N.
Вернемся к случаю неподвижной поверхности. Из уравнения кине-
тической энергии сразу получаем первый интеграл, если существует
силовая функция U(x,y, z) :
Может еще случиться, что Xdx-\-Y dy~\-Z dz не является пол-
ным дифференциалом, но становится таковым в силу соотношения
/(х, у, z) = 0. Если, например, точка поверхности определяется двумя
параметрами ql и q2, то
и выражение Xdx-\~ Ydy -\-Zdz, если заменить в нем X, Y, Z, xt у, z
их значениями в функции qx и q2, обращается в Q\dql-^rQidq2. Если
выражение Qidqi-\-Q2dq2 является полным дифференциалом функ-
ции U (q1, q2). то интеграл кинетической энергии будет иметь вид
или
T=U-\-h,
ибо Т как раз и есть кинетическая энергия.
Этим последним уравнением можно заменить наиболее сложное
из уравнений Лагранжа, и таким путем получатся два уравнения для
определения qv и q2 в функции /.
Пример. Рассмотреть движение точка на поверхности геликоида
с направляющей плоскостью, когда точка притягивается или отталки-
вается осью геликоида,, с силой, пропорциональной расстоянию (рис. 165).
Пусть г и в — полярные координаты точки М геликоида, лежащей на
образующей CD. Декартовы координаты этой точки будут:
х = г cos в, у = г sin в, z = ?9.
27 Зак. 851. П. Аппель, т. I

418
ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Сила, действующая на точку, равна F=my.r и направлена по CD. Изве-
стно, что в этом случае имеется силовая функция
п	г%
и = та. -j^.
Определяя точку поверхности параметрами гиб, которые заменяют д1
и q2, имеем
Уравнения движения Лагранжа будут
у поэтому следующие:
dr' „,9	d
—3	Г в'1* = (*/•, .	 [(^2 1 Г2) 6'] =0.
dt	dt
Второе из этих уравнений показывает,
что
Рис. 165.	(г2 + ft2) 6' = С.
Вместо первого уравнения воспользуемся интегралом кинетической энергии
I) в'2 _ „г2 = ft.
Исключив в' из двух последних уравнений, получим уравнение движения
по радиусу-вектору:
г'2 _|	.	_— рг2 = Л,
или
Таким образом, t выражается через г при помощи квадратуры. Точно
так же найдем, что 9 выражается через г при помощи второй квадратуры.
Для этого достаточно в последнем уравнении заменить dt его значением
С(>
При исследовании формы кривой необходимо различать два случая
в зависимости от того, положительно или отрицательно (л (отталкивание
или притяжение). Если (J- положительно, то кривая может иметь бесконечные
ветви, что видно из того, что при неограниченном возрастании г вели-
чина (—jj-1 не перестает быть положительной. Наоборот, если ;х отрица-
тельно, то г может возрастать только в некоторых пределах. В частном
случае, когда (л. = 0, точка перемещается по поверхности без непосред-
ственно приложенной силы (по инерции). Тогда t выразится через г эллип-
тическим интегралом. В этом частном случае точка, как мы увидим дальше
(п. 270), будет описывать геодезическую линию геликоида:
266. Вывод уравнения кинетической энергии из уравнений
Лагранжа. Если поверхность неподвижна, то выражения х, у, z
в функции qt и; q2 могут быть выбраны таким образом, чтобы они
не содержали t явно. Тогда Г.будет однородной квадратичной функцией

ГЛАВА XIII. ДВИЖЕНИЕ ТОЧКИ ПО ПОВЕРХНОСТИ	419
величин q'y и q'2 и на основании теоремы об однородных функциях
получим тождество
,_дТ__, г дТ __2Т
Установив это, возьмем оба уравнения Лагранжа
d I дТ \ _^Т_	о
dqt !'
dq2 V2
и сложим их, умножив предварительно первое на q'y, а второе
на q'r Мы получим одно уравнение, которое может быть написано
следующим образом:
dt + dq't dt + dQl Я^
/IT
Первая скобка равна 27, а вторая равна —тг, так как Т зависит
от t через q'v q'v qv qr Следовательно, предыдущее уравнение
можно написать в виде
dT „
или, умножая его на dt, получим
что и является уравнением кинетической энергии, так как Qldq1-{~
-^rQidq2 есть элементарная работа силы {X, Y, Z). Если Qirf^-j-
-\-Q2dq2 является полным дифференциалом функции U (qt, q2), то
интеграл кинетической энергии будет
Он заменит одно из уравнений Лагранжа.
267. Устойчивость равновесия в случае существования
силовой функции U. Как мы видели в статике, для нахождения
значений qt и q2, соответствующих положению равновесия точки,
необходимо составить два уравнения: Q1 = 0, Q2 = 0. В частном
случае, когда Q1dq1-{-Q2dq2 является дифференциалом функ-
ции U (qv q2), уравнения равновесия совпадают с уравнениями,
которые нужно написать при нахождении максимума или минимума
функции U {qv q2).
27*

420	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Мы хотим доказать, следуя Лежен-Дирихле, что если для
какой-нибудь системы значений ql^=al, <72 = я2 функция U имеет
максимум, то соответствующее равновесие устойчиво. Доказательство
совпадает с данным ранее (п. 208) для свободной точки. Укажем
его в немногих словах. Можно всегда предполагать, что максимум
имеет место при qx = 0, q2 = 0, так как это приведет к выбору
новых параметров q1 — ах и q2 — а2, и что этот максимум U @, 0)
равен нулю, так как это равносильно вычитанию из U(qv q2) не-
которой постоянной, что допустимо, поскольку эта функция опре-
деляется с точностью до постоянной. Согласно определению мак-
симума, функция U будет тогда отрицательной и отличной от нуля
вблизи рассматриваемого положения равновесия Р. Проведем на
поверхности малую замкнутую кривую С, окружающую Р. На этой
кривой функция U отрицательна и не равна нулю. Следовательно,
существует такое малое положительное число р, что функция U-\-p
будет на кривой С тоже отрицательна. Сместим теперь точку из
положения равновесия Р в близкое положение Мо, лежащее внутри С,
где U принимает значение Uo, и сообщим ей скорость v0. Получим
Выберем начальное положение и начальную скорость так, чтобы
выполнялись условия
™1 р	р
2	~2~'	° ~2~'
что вследствие непрерывности потребует, чтобы v0 и расстояние РМ0
были меньше некоторых пределов. При этих условиях точка не
выйдет за кривую С и даже ее не достигнет, так как из уравнения
кинетической энергии получаем неравенство
—
a U А-р делается отрицательным на граничной кривой С.
268. Нормальная реакция. После того как движение станет
известным, для нахождения реакции достаточно будет найти X из
какого-нибудь одного уравнения движения B) (п. 262). Допустим,
что точка свободно положена на поверхность, т. е. что она может
сойти с нее в какую-нибудь сторону. Для того чтобы точка остава-
лась на поверхности, необходимо, чтобы реакция была направлена
в ту сторону, куда точка может от поверхности удалиться. По
одну сторону поверхности функция f(x, у, z) положительна, а по
другую сторону отрицательна. Для того чтобы реакция была,
например, направлена в область положительных /, необходимо, как
мы это видели в статике в связи с равновесием точки на поверх-
ности, чтобы коэффициент X был положителен. Если \ в какой-

ГЛАВА ХШ. ДВИЖЕНИЕ ТОЧКИ ПО ПОВЕРХНОСТИ	421
нибудь момент обращается в нуль и меняет знак, то точка покидает
поверхность и задача сводится к случаю свободной точки.
269. Естественные уравнения и нормальная реакция. Отметим
на траектории, лежащей на поверхности, начало дуг А (рис. 166). Пусть
М — произвольное положение движущейся точки. Проведем через эту
точку касательную МТ в направлении возрастающих дуг, и пусть С —
центр кривизны нормального сечения по-
верхности, касающегося МТ, R — MC—его
радиус кривизны. За положительное напра-
вление нормали к поверхности мы примем
направление МС. Пусть также МС—глав-
ная нормаль траектории и р = МС— ее
радиус кривизны. Обозначим через 6 угол
между соприкасающейся плоскостью ТМС
траектории и нормалью к поверхности.
На основании теоремы Менье имеем
Рис. 166.
Проектируя направление МС на касательную плоскость, мы
получим полупрямую МР, на которой мы будем рассматривать на-
правление проекции отрезка МС' как положительное. Пусть
теперь Ft, Fn, /^ — проекции силы F на прямые МТ, МС, МР,
а N — алгебраическое значение нормальной реакции. Мы знаем, что
равнодействующая сил F и N разлагается на две силы, из которых одна
равна m —гг и направлена по МТ, а другая равна m — и напра-
влена по МС; эта система двух сил эквивалентна системе, образо-
ванной силами F и N. Приравнивая суммы проекций сил каждой из
этих систем на оси МТ, МР, МС, имеем:
dv „ mv2 . о „ тф „о с , \Т
m4f = Ft, — sin 6 = /^, _-cosb = Fn-)-N.
Этим уравнениям можно придать более простую форму. Обозначим
через рд радиус геодезической кривизны - р е и воспользуемся най-
денным выше соотношением —?-g- = /?. Тогда предыдущие урав-
COS О
нения примут вид
«1 ^	f	F+W
Если имеется силовая функция, то ——= U -\- h, и последняя из
предыдущих формул позволит вычислить нормальную реакцию без
предварительного определения движения при условии, что известен
радиус кривизны R.
Из этих уравнений можно вывести интересное следствие. Под-
вергнем поверхность такой деформации, чтобы длины начерченных

422	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
на ней линий не изменились. При таком преобразовании радиусы
геодезической кривизны не изменяются. Если, следовательно, из-
менить силу F таким образом, чтобы не изменилась ее проекция
на касательную плоскость, то первые два из написанных выше уравне-
ний, определяющие движение, не изменятся и движение будет
таким же, как и в первом случае. Изменится только нормальная
реакция. Мы видим, таким образом, что траектория тяжелой точки,
двигающейся на вертикальном цилиндре, получится навертыванием
на этот цилиндр параболы с вертикальной осью. Точно так же траек-
тория тяжелой точки на круговом конусе с вертикальной осью
получится навертыванием на этот конус плоской траектории точки,
движущейся под действием постоянной центральной силы.
270. Геодезические линии. Наиболее простым будет тот случай,
когда на точку, положенную на неподвижную поверхность, не дей-
ствуют никакие силы. Тогда уравнение кинетической энергии
будет al—о~
==0; оно показывает, что скорость остается постоян-
ной. Траектория точки будет геодезической линией поверхности,
так как ее соприкасающаяся плоскость должна содержать единствен-
ную действующую на точку силу — нормальную реакцию. Это сле-
дует также и из второго естественного уравнения, которое обра-
ти .	1 п
щается в 	= 0, откуда вытекает — = 0, так как v постоянно,
?д	Рд
а условие — = 0 характеризует геодезические линии. Последнее
естественное уравнение позволяет вычислить нормальную реак-
.» яги2 ,,	on
цию Л/ = _ . Можно заметить, что в рассматриваемом случае о = 0,
„ тФ
вследствие чего к = р и нормальная реакция имеет значение 	.
Она изменяется обратно пропорционально радиусу кривизны траек-
тории.
Общие уравнения движения приводятся теперь к виду
dP>	dx '	dfi	dy '	df-	dz
При помощи уравнения ds = vodt здесь можно исключить время, для
чего достаточно в предыдущих формулах заменить dt% через (——) .
Примечание. Если поверхность имеет прямолинейные образую-
щие, то они будут одними из возможных траекторий, так как
если точку пустить по какой-нибудь образующей, то она будет
продолжать двигаться по ней в силу закона инерции, а реакция
поверхности будет равна нулю.

глава хщ. движение точки по поверхности	423
Пример. Геодезические линии эллипсоида. Приложим предыдущие
результаты к эллипсоиду
Мы пишем здесь в знаменателях а, Ь, с, чтобы те же вычисления в за-
висимости от знаков а, Ь, с давали геодезические линии эллипсоида или
гиперболоида.
Уравнения движения могут быть написаны так:
d9-x _ х_ <Ру _ у_ &z _ ?
dp ~* a ' dP ~* Ь ' dt9- ~^ с "	()
Как всегда, имеем первый интеграл v = v0. Для нахождения второго
используем метод Дарбу. Продифференцировав два раза подряд уравне-
ние A), получим
х d9-x у d*y , г (Рг . 1 / dx \« 1 / dy \а 1 / <te \a _
или в силу уравнений B)
,,.v 1 оГж 1 dy 1 й
Умножим теперь уравнения B) соответственно на	-т-, "С ~ir >	jT
и сложим. Получим
/ х dx у dy г dz\_
^ \ a2 dt ~т~ b* dt "*" с2 rf^ j
~ИЧГ dt9- + * ~dT dt4- + с Л оГ^ '
Если мы разделим почленно уравнение D) на уравнение C), то получим
х dx у dy_ . z dz I dx_ d^x . \_ dy_ dty , l_ dz_ d*z
~a?~dT~T~Fi~~dF~T~~c*~d7 ~a~dT dP +T~dT dt9- ^ с dt dt*
^ '
Cfl + *2 ¦+ C2
Каждый из числителей с точностью до постоянного множителя равен про-
изводной от знаменателя; следовательно, найденное уравнение можно про-
интегрировать и получить
Исключая время при помощи уравнения кинетической энергии -^г =
получим
и^)ЬЫ Ш ЫJconst- (
dx \« ,1 / dy \2 ,1 / d2 \21
Таково дифференциальное уравнение геодезических линий эллипсоида.
Простая геометрическая интерпретация этого уравнения приведет к теореме,
установленной Иоахимсталем: если р — расстояние от центра эллипсоида
до касательной плоскости в точке М геодезической линии, D — длина

424	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
полудиаметра, параллельного касательной, проведенной в точке М к геодези-
ческой линии, то вдоль всей этой линии произведение pD постоянно. Дей-
ствительно, так как направляющие косинусы касательной в точке М
dx dy dz
равны -г— , -~, ——, то координаты конца параллельного полудиаметра
US CIS CIS
будут
D dx D аУ D dz
ds ' ds ' ds
Написав, что эта точка принадлежит эллипсоиду, имеем
D2 а\ ds ) "г" b\ds ) """ с \ds
Уравнение касательной плоскости в точке М будет
J^L + JL + I^ !_o-
а + * + с — 1-°-
расстояние от начала координат до этой плоскости определяется формулой
pi аг "Г Ь2 -Г С2 •
откуда на основании равенства E) действительно получаем
pD = const.
Эта теорема применима также и к линиям кривизны эллипсоида. Действи-
тельно, мы увидим дальше, что эти линии соответствуют особым решениям
уравнения E). (Дарбу, Mecanique de Despeyroux, т. 1.)
Для завершения интеграции нужно выразить координаты х, у, г точки
эллипсоида через ее эллиптические координаты qv q%. Тогда перемен-
ные 9i> Ч2 разделятся и интегрирование приведется к квадратурам. К этому
вопросу мы вернемся вновь при рассмотрении приложения метода интегри-
рования Якоби (глава XVI).
271. Применение уравнений Лагранжа. Обычно для нахожде-
ния геодезических линий предпочтительнее поступать следующим
образом, используя уравнения Лагранжа. Пусть
* = <P(?i. Яг)- ^ = Ф(?1. Яг). z = <o(qu q2)
— выражения координат точки поверхности в функции двух пара-
метров.
Тогда квадрат линейного элемента произвольной кривой, прове-
денной на поверхности, выразится так
ds2 = dx2 4- dy* + dz* = an dq\ + 2an dqx dq2 + a22 dq\.
Если для упрощения мы положим массу точки равной 1, то
получим

ГЛАВА ХШ. ДВИЖЕНИЕ ТОЧКИ ПО ПОВЕРХНОСТИ	425
и уравнения движения будут
Одно из этих уравнений, более сложное, будет в дальнейшем
заменяться интегралом кинетической энергии Г = А, или
Мы имеем таким образом два уравнения (из которых одно
второго порядка, а другое первого), определяющие qx, qt в функции t.
Пример. Поверхность такова, что при подходящем выборе криво-
линейных координат, определяющих ее различные точки, можно выра-
жение линейного элемента ds привести к виду
ds3 = и (du2 + dv1).
Требуется найти конечное уравнение геодезических линий. Во что пре-
образуются эти линии, если сделать карту, на которой каждой точке поверх-
ности с координатами и, v будет соответствовать точка плоскости
с прямоугольными координатами, имеющими те же самые значения'}
(лиценциатская, Париж, 1887).
„,	, ,	du dv
Обозначая через и и v производные —т- и -тт и полагая массу точки
равной 1, получим
T=±u{u'2 + v'2)
и так как нет непосредственно приложенных сил, то уравнения Лагранжа
будут
^-(tttt')-I^_^'2 = o. A(BD') = a	(l)
Мы знаем заранее первый интеграл этих уравнений, а именно инте-
грал кинетической энергии Т = h, или
du \2 Л. i dv VI h	(9\
dF)+(w)\-h-	B>
Второе из уравнений A) дает другой первый интеграл
и^=С.	C)
С2
Исключая dt из этих двух уравнений и полагая —г- — 2а, получим диф-
ференциальное уравнение геодезических линий
dv^'a du
Отсюда, интегрируя и обозначая через Ь другую постоянную интегрирова-
ния, получим
(и —6J = 4a(a — a).

426	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Это и есть уравнение искомых геодезических линий в конечной форме.
Если и и v рассматривать как прямоугольные координаты точки плоскости,
то кривые будут параболами, имеющими директрису на оси v. Поверхность,
для которой мы нашли геодезические линии, развертывается на поверхность
вращения. (См. Дарбу, Theorie generate des surfaces, часть 3, гл. II.)
272. Бесконечно малые колебания тяжелой точки около наинизшей
точки поверхности. Рассмотрим на поверхности точку О, в которой каса-
тельная плоскость горизонтальна и поверхность в окрестности этой точки
расположена над этой касательной плоскостью. Это положение О является
положением устойчивого равновесия для тяжелой материальной точки, движу-
щейся без трения по поверхности. Мы исследуем бесконечно малые колеба-
ния около этого положения равновесия. Примем точку О за начало коор-
динат, ось Ог направим вертикально вверх, а осн Ох и Оу — по касательным
к линиям кривизны, проходящим через точку О. Если координату z поверх-
ности разложить для малых значений х и у по формуле Маклорена, то
уравнение поверхности будет иметь вид
где добавочный член у {х, у), пе крайней мере, третьего порядка относи-
тельно х п у, а р и q — оба главных радиуса кривизны поверхности в точке О.
Так как материальная точка является тяжелой, то имеется силовая функция
U=-gz,
которую мы написали в предположении, что т = 1. Функция Лагранжа Т
имеет вид
т ^ С v'2 _j_ ,i'2 i -,'24
1 = yU +У +г ),
где
дх	ду
При малых колебаниях около рассматриваемого положения равновесия х
и у остаются очень малыми; составляющие х' и у' скорости также очень
малы, так как сама скорость, как мы видели (п. 267), очень мала. Мы будем
рассматривать х, у, х', у' как величины одного и того же порядка. В выра-
жении Т будут тогда содержаться два члена второго порядка и третий
член г'2 четвертого порядка. Мы пренебрежем им по сравнению с двумя
первыми и получим
Если в выражении U заменить г его значением, то разложение U
начнется двумя членами второго порядка, которые мы только и сохраним,
пренебрегая членами более высокого порядка. Получим
Уравнения Лагранжа в применении к переменным хну, играющим роль
параметров q± и q%, будут
d I дТ \ дТ _ дЦ
Т \
'Ш\дхт)~~д7~~~дх~
d 1дТ \ дТ _ дЦ
dt \ ду' ) ду ~ ду '

ГЛАВА XIII. ДВИЖЕНИЕ ТОЧКИ ПО ПОВЕРХНОСТИ
427
Но поскольку Т не содержит ни х, ни у, они примут вид
df- ~~~p X' ~dW~ д~У'
Эти уравнения сразу интегрируются:
х = A cos (t у ~ + а) , у = В sin
A)
где А, В, а, р — произвольные постоянные, которые должны быть определены
по начальным условиям. Таким образом, мы получили бесконечно малые
колебания. Координата х принимает свое первоначальное значение через
промежуток времени 2я
— , а координата у — через промежу-
ток 2л
Т/
Если эти два периода соизмеримы, то горизонтальная проек-
ция траектории будет алгебраической кривой, которая получается исключе-
нием t из уравнений A). Траектория будет трансцендентной, если оба
периода несоизмеримы. В этом случае движе-
ние обладает некоторыми своеобразными осо-
бенностями. Рассмотрим в плоскости ху прямо-
угольник, образованный прямыми х = + А,
у = + В. Кривая, определяемая уравне-
ниями A), касается бесчисленное множество
раз сторон этого прямоугольника. Так, эта
кривая касается стороны х — А (рис. 167)
при всех значениях t вида
{k — целое).
Рис. 167.
Более того, траектория некоторым образом как бы покрывает всю пло-
щадь этого прямоугольника. Мы это докажем, установив, что для произволь-
ной точки Р с координатами ? и т) внутри прямоугольника существует
бесчисленное множество значений t, при которых движущаяся точка под-
ходит к Р на расстояние, меньшее любого заданного числа. Пусть в самом
деле, X и р. — дуги, определяемые формулами
? = A COS (X + а), 1) = В COS (ft ¦+" Р)-
Если переменному t придать значение вида
t—y ?- (X + 2Ы) (k — целое число),
то абсцисса х движущейся точки будет равна ?, а ее ордината у будет
иметь вид
у = В cos у I- (X + 2йя) + 2?'я + р ,
где ft' — произвольное целое число. По предположению, числа ряд не-
соизмеримы; следовательно, можно определить два целых .числа, k и к'
таким образом, что
п
q	n -r

428	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
будет отличаться сколь угодно мало от любого заданного числа и, в част-
ности, от fi. При соответствующих значениях t координата у будет отли-
чаться сколь угодно мало от В cos (ц -f- р), т. е. от ¦»), и так как при этом
х будет равняться ?, то движущаяся точка пройдет сколь угодно близко от Р.
III. Движение на поверхности вращения
273. Геодезические линии поверхностей вращения. Мы ставили
целью составить два уравнения, не содержащих нормальной реак-
ции, и получили в качестве таковых уравнение кинетической энер-
гии и одно из уравнений Лагранжа. В случае движения точки на поверх-
ности вращения мы всегда будем иметь два не зависящих от реакции
уравнения, применив теорему кинетической энергии и теорему момента
количества движения относительно оси вращения, так как нормальная
реакция лежит в одной плоскости с осью вращения и ее момент
относительно этой оси равен нулю. Приложим, в частности, этот
метод к определению геодезических линий поверхностей вра-
щения.
Примем ось вращения за ось г. Если уравнение меридиа-
на в плоскости xz есть z = ср (х), то уравнение поверхности
будет, очевидно, 2 = ср(г), где г = У^хг-\-у2 есть расстояние от
точки до оси. Обозначим через гиб полярные координаты проек-
ции Р движущейся точки на плоскость хОу. Для координат точки
поверхности получим следующие выражения в функции двух пара-
метров <7i и <72:
х = г cos 6, y = rsinQ, 2 = cp(r).
Выражение квадрата линейного элемента будет
ds2 = dx2 + dу2 + dz2 = A + =р'2) dr2 + г2 db2,
где ср' = ср'(г). Так как мы ищем геодезические линии, то займемся
исследованием движения точки, скользящей по поверхности без воз-
действия какой бы то ни было заданной силы. На эту точку будет
действовать только реакция. Тогда по теореме кинетической энергии
имеем
/ ds \2 „
Далее теорема момента количества движения показывает, что для
проекции движения на плоскость ху справедлив закон площадей
(п. 203), т. е.
r2dB = C dt.
Из этих двух уравнений получаются два первых интеграла.

ГЛАВА XIII. ДВИЖЕНИЕ ТОЧКИ ПО ПОВЕРХНОСТИ	429
Покажем, что интегрирование приводится к квадратурам. В самом
деле, интеграл кинетической энергии после замены ds2 его значе-
нием принимает вид
dr2 (l + <Р'2) + гг d№ = v\ dt2.
Чтобы получить проекцию траектории на плоскость ху, исключим
отсюда dt при помощи уравнения площадей. Тогда найдем
2
dr2 A + <Р/2) + гг d№ = -J- г4 d№;
или, полагая -^г= ~рг и разрешая относительно dv, получим
Знак, который нужно взять, определится из рассмотрения направле-
ния начальной скорости. Уравнение геодезической линии в конечной
форме будет
Это уравнение содержит две постоянные k и C, которые можно,
например, определить из условия, что геодезическая линия проходит
через две заданные точки. Из этих двух постоянных лишь первая
влияет на форму кривой; изменение второй постоянной дает поворот
геодезической линии вокруг оси поверхности.
Обозначив через da элемент дуги меридиана, получим
do2 = dr* + dz2 = (l + cp/2) dr2,
и дифференциальное уравнение геодезических линий можно будет
написать в другом виде:
db±kda
г Yr°- — К>-
Примечание. В рассматриваемом случае имеем
где <р' — функция от г. Одно из уравнений Лагранжа будет
dt \ d6' / дЬ ~ и#
Так как Т не содержит 8, то -^- равно нулю и мы получим
Таким образом, мы снова приходим к уравнению площадей.

430	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
274.	Формула Клеро. Если обозначить через t угол, под ко-
торым геодезическая линия поверхности вращения пересекает мери-
диан, проходящий через точку М этой линии, а через г — расстоя-
ние от точки М до оси, то для всех точек линии выполняется
соотношение
rsini = k.	A)
В самом деле, если рассматривать точку, описывающую геодези-
ческую линию при предыдущих условиях, то момент количества
движения, или, что приводится к тому же, момент скорости точки
относительно оси будет постоянным. Постоянное значение этого
момента как раз равно' постоянной С площадей на плоскости, пер^
пендикулярной оси, так как момент скорости относительно оси Oz
равен г2-тт ¦ Разложим скорость v движущейся точки М на две
составляющие, из которых одна f sin г касается параллели, проходя-
щей через точку М, а другая vcosI касается меридиана. Момент
скорости относительно оси вращения равен сумме моментов этих
двух составляющих, но так как момент второй равен нулю, то,
следовательно, момент скорости равен моменту rvsini только первой
составляющей. Следовательно,
rv sin i = C.
Но так как v = v0, то отсюда получается уравнение A), причем
С
постоянная к имеет значение ¦— и поэтому совпадает с той, которая
входит в уравнение геодезической линии (п. 273).
Примечание. Соотношение^ A) не характеризует геодези-
ческих линий. Если линия удовлетворяет этому уравнению, то она
является либо геодезической линией, либо параллелью. Действи-
тельно, уравнение A), очевидно, удовлетворяется для параллели, так
как для нее г = k, i — -^. Это решение является особым инте-
гралом r — k, dr — 0 уравнения (G).
275.	Упражнение. Геодезические линии поверхности, образованной
вращением равносторонней гиперболы вокруг своей асимптоты. Урав-
нение поверхности будет
	 а2
г
Поэтому в приведённых выше формулах нужно заменить у (г) через —
и для проекций геодезических- линий "получится уравнение
Для того чтобы 6 было вещественным, необходимо, чтобы г было
больше k\ следовательно* .асривая-! находахсй :вне; круга- радиуса Ь. Можно,

ГЛАВА XIII. ДВИЖЕНИЕ ТОЧКИ ПО ПОВЕРХНОСТИ
431
однако, полагать г = k, так как при этом значении подынтегральное выра-
жение обращается в бесконечность вместе с	- и интеграл остается
yr — k
конечным. Повернув оси на подходящий угол вокруг оси Ог (рис. 168),
можно добиться того, чтобы 6 равнялось нулю при г = k, и мы получим
6 =
- — k°- r
Начиная от значения k, r может неограниченно
рушения вещественности 8; при этом 6,
возрастая вместе с г, будет иметь некото-
рый предел, так как при неограничен-
ном возрастании г подынтегральное выраже-
ние стремится к нулю, как и —. Этот пре-
дел Ф будет
возрастать без на-
v J ? г*- — № г "
Чтобы узнать, существует ли асимп-
тота, параллельная этому направлению ф, до-
статочно, как известно, выяснить, будет ли
полярная подкасательная г2-т- иметь предел	Рис. 168.
при бесконечном г. Этот предел, если он
существует, равен расстоянию от полюса до асимптоты. В данном случае
выражение
г~+4
имеет предел k. Следовательно, кривая имеет асимптоту D, касающуюся
окружности радиуса к. Можно доказать, что угол
лагая для этого — = и, имеем
Y =
больше, чем —. По-
-4V
du.
Если k = оо, то i[/ = —; когда k уменьшается, этот угол увеличивается,
и если предположить, что k становится очень малым, то подынтегральное
выражение будет становиться все большим и большим и ф будет неогра-
ниченно возрастать. Следовательно, ф имеет какое-то значение, заключенное
между -=- и оо. Взяв перед интегралом знак —, мы получим вторую ветвь
кривой, симметричную первой относительно оси х.

432	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Таким же путем можно исследовать геодезические линии поверхностей
вращения второго порядка, детальный анализ которых можно найти в Traite
des fonctions elliptiques, т. II, глава VI, Альфена. Для произвольных поверх-
ностей вращения получается, что если меридиан имеет бесконечные ветви,
то и геодезические линии имеют бесконечные элементы. Если на поверх-
ности имеется самая короткая параллель, то эта параллель будет геодези-
ческой линией, и в общем случае будут существовать геодезические линии,
асимптотически к ней приближающиеся. Для подробного изучения этих кри-
вых отсылаем к Legons sur la theorie des surfaces Дарбу (часть З).
276. Движение тяжелой точки на поверхности врадцения,
ось которой Oz вертикальна. Интегрирование уравнений движения
приводится к квадратурам. Прежде всего по теореме кинетической
энергии имеем
"
где v2 = 2gz-\- h, причем ось г направлена вниз. Теорема площадей
справедлива, и мы имеем
/-2 dB = С dt.
Если уравнение поверхности есть z=w(r), то
Исключая из этих трех уравнений время и скорость, получим
dr2 (l + ср'2) + г2 dV = [2g ср (г) + h]
Переменные сразу разделяются и 6 выражается через г при помощи
квадратуры:
f	72 саг
е
J y [2gf(r
ri — С-
Точно так же интегрирование приводится к квадратурам всякий
раз, когда движущаяся точка находится под действием силы, имею-
щем силовую функцию, зависящую только от г.
Для алгебраической поверхности Кобб указал случаи, при которых
задача приводится к эллиптическим функциям (Acta mathematica, т. X).
Интересное аналитическое исследование движения тяжелой точки
на поверхности вращения можно найти в статье Отто Штауде (Acta
mathematica, т. XI).
Примечание. Тяжелая точка, движущаяся по поверхности
вращения, может описывать параллель поверхности лишь в том слу-
чае, когда вершина конуса нормалей вдоль этой параллели находится
над ней.
В самом деле, уравнение поверхности имеет вид
или

ГЛАВА XIII. ДВИЖЕНИЕ ТОЧКИ ПО ПОВЕРХНОСТИ	433
Обращаясь к общим уравнениям движения на поверхности, имеем:
Для того чтобы траектория была параллелью г = z0, необходимо,
чтобы эти уравнения удовлетворялись при условии 2 —20, x = r0cos6,
у = rosin 6. С другой стороны, по теореме площадей г2—- = С = rovo,
где начальная скорость v0 обязательно касается параллели; отсюда
6 = —2- . Поэтому обязательно должно быть
и0 х v~	у
\ = — mg.	tx = S — f'i.r0),	^y = g— <?'(rQ).
Эти два последних уравнения приводятся к следующему:
Следовательно, ср' (г0) должно быть отрицательным. Если это условие
выполнено, то вершина конуса нормалей находится над параллелью.
Если точке, находящейся на параллели, сообщить скорость
^о = V— g/VP'(/о).
то она будет двигаться по этой параллели.
Этот результат легко проверяется геометрически. Для этого
достаточно выразить, что равнодействующая веса и нормальной
l
реакции направлена к центру параллели и равна 	.
го
277. Сферический маятник. Сферический маятник состоит из тяжелой
точки, движущейся без трения по неподвижной сфере. Примем за начало
координат центр сферы и направим ось г вертикально вверх. В цилиндри-
ческих координатах уравнение сферы будет
г9- + г* = /з,
где / — длина маятника.
Течка находится под действием двух сил: силы тяжести и нормальной
реакции сферы; следовательно, по теореме кинетической энергии имеем
так как работа реакции равна нулю. Более того, так как обе силы лежат
в одной плоскости с осью Ог, то можно применить закон площадей к проек-
ции движения на плоскость хОу:
r2dd = C dt.
Эти три уравнения определяют z, r и в в функции t.
Найдем сначала г. Для этого нужно исключить г и 9. Уравнение кине-
тической энергии можно переписать так:
28 Зак. 851. П. Аппель, т. I

434	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Из уравнения сферы г—\Р— z2 получим
— zdz
С другой стороны, из уравнения площадей имеем
.„ С dt	С dt
Подставляя в уравнение кинетической энергии, получим
Г- (-^j-J ¦ Bgz + h) (P — z°-) — С2.
Полагая
найдем окончательно:
Idz
Таким образом, время выражается через z эллиптическим интегралом. Знак
перед радикалом определяется начальными условиями. Сомнение может воз-
/ Лг \ п
никнуть лишь в том случае, когда (—т—) = 0; тогда нужно будет выяснить,
\ «' /о
должно ли z увеличиваться или, наоборот, уменьшаться для того, чтобы <f (z)
оставалось положительным.
Формула dd = —— показывает, что проекция движущейся точки на
плоскость хОу все время поворачивается в одну и ту же сторону вокруг
оси z, если только С не равно нулю; в последнем случае 6 будет оставаться
постоянным, и мы получим математический маятник. Если в этой формуле
заменить г2 и dt их выражениями через z, то получим
.„	±Cldz
dv =
Таким образом, ( и в определены в функции z; после этого г найдется из
уравнения сферы. Чтобы уравнения были вещественными, необходимо, чтобы
многочлен <р (г) был положителен. Этот многочлен имеет три вещественных
корня. Чтобы в этом убедиться, достаточно подставить вместо z последовательно
значения — оо, — /, Zq, + I, для которых у (¦?) примет соответственно значе-
ния -\- со, — С2, ср (z0), — С2, и заметить, что так как Z(, является начальным
. ч ,	dz
значением z, то у (г0) будет положительным, так как начальное значение —т-
вещественно. Следовательно, имеются два вещественных корня а и [В в про-
межутках ( -\-1, z0) и (z0, — I) и один корень f в промежутке ( — /, —со).
Сумма попарных произведений этих корней равна — /2; следовательно,
Так как а и р заключены между — /и -(- /, то Р -\- оф положительно, но f
отрицательно и поэтому а -\- р положительно; следовательно, параллель,
равноотстоящая от параллелей z = а и z = (В, лежат всегда ниже центра, и
корень а всегда положителен. Переменная z, начальное значение которой г0
лежит между а и р, остается, всегда заключенной в этом промежутке, гак
как, если бы она из него вышла, то <р (z) стало бы отрицательным.

ГЛАВА XIII. ДВИЖЕНИЕ ТОЧКИ ПО ПОВЕРХНОСТИ
435
Допустим для определенности, что z, начиная с г = г0, сначала убывает.
Тогда перед радикалом нужно будет взять знак минус и z будет умень-
шаться до значения р, так что когда точка достигнет параллели ВВ' {г = Р)
в Вл, ее траектория будет иметь горизонтальную касательную, так как в этом
dz	dd
положении —— обращается в нуль, а производная —т- отлична от нуля.
Ctt	(Ль
Начиная с этого момента, движущаяся точка будет продолжать поворачи-
ваться вокруг оси z в том же направлении, но она будет при этом опу-
скаться до параллели г=а, описывая дугу,
касающуюся в А± этой параллели (рис. 169).
После этого она будет подниматься до па-
раллели г = р и т. д. Время, затрачиваемое
точкой для перехода из А\ в В% будет
Idz
и оно будет таким же, как и время, не-
обходимое для описания дуг В1А1, В2А2
и т. д.
Если начальная скорость точки напра-
влена вдоль одной из крайних параллелей,
*го в начале движения будет —— = 0.
Это — сомнительный случай, о котором мы
говорили выше. Если точка начинает дви-
жение по параллели г = % то z должно возрастать и перед радикалом
нужно взять знак плюс; во втором случае, когда движение начинается вдоль
параллели z = а, нужно взять знак минус.
Меридианные сечения, проходящие через точки касания траектории с
крайними параллелями являются для траектории плоскостями симметрии.
В самом деле, рассмотрим две точки М и М' ветвей А±В^ и А^В^, лежащие
на одной параллели. Если 9, 6', Oj — значения 8, соответствующие точкам
М, М' и Аи то имеем
С Idz
(/2-
с/"
Следовательно, обе точки М и М' действительно симметричны относительно
меридиана точки Av Кроме того, промежутки времени, затрачиваемые дви-
жущейся точкой для пробега дуг МАг и А\М', одинаковы, так как они оба
имеют одно и то же значение
а
Idz
Построим теперь проекцию траектории на-плоскость ху. Мы будем раз-
личать два случая в зависимости от .того,, лежат ли крайние параллели на
одной полусфере, или нет.
28*

436
ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Первый случай. Обе крайние параллели лежат на нижней полусфере.
Расположенная ниже окружность г = а проектируется внутрь окружности
z = р; кривая, касающаяся поочередно этих окружностей, имеет вид, изобра-
женный на рис. 170; кроме того, мы увидим, что эта кривая не может иметь
точек, перегиба. Наблюдателю, расположенному на оси г, кажется, что дви-
жущаяся точка описывает овал, который перемещается в направлении дви-
жения. Ниже мы покажем, что угол BjOAx больше прямого.
Рис. 170.
Рис. 171.
Второй случай. Допустим теперь, что обе крайние окружности распо-
ложены по разные стороны экватора. Проекция окружности z = а будет
по-прежнему лежать внутри окружности г = р, так как я -f- p > 0. С другой
стороны, проекция траектории должна касаться экватора в точке Е. Она
имеет указанную на рис. 171 форму; при этом она может иметь точки
перегиба.
Доказательством высказанного выше свойства, что угол W = В1ОА1 всегда
больше прямого, мы обязаны Пьюизё (Journal de Liouville, 1842). Этот угол
имеет значение
J W- — &
Cldz
Мы обозначили через а, р, f корни функции <р (г) и, следовательно, имеем
тождество
? {г) = Bgz + h) (P- - 0) - С = 2^ (а - z)(z - р) (г - 7).
Раньше, приравнивая друг другу члены с г, мы получили
Теперь мы можем написать, заменяя ? этим значением,
Полагая в этом тождестве z = I, получим

ГЛАВА XIII. ДВИЖЕНИЕ ТОЧКИ ПО ПОВЕРХНОСТИ	437
Обозначая
имеем
;_v.
и поэтому
ар]
к
Для оценки пределов этого интеграла определим пределы, между которыми
заключен последний множитель г (а -|- Р) + /2 -f" аР- Допустим, что найдены
два положительных числа Р и Q таких, что для значений г, заключенных
между а и р, выполняется неравенство
Тогда интеграл W будет заключен между двумя пределами, которые полу-
чатся, если в нем величину г (а -j- р) -)- /а -|_ ар последовательно заменить
величинами Р и Q:
JJL С	ldz	<w<AB_ f
YP ¦' (I2 — z°AY(a — z)(z — №	YO J (I2 —
YP j	J
Определенный интеграл, входящий в это неравенство, содержит квадрат-
ный корень из квадратного трехчлена и может быть поэтому легко вычи-
71 I 1 , 1 \
слен. Для него получается значение — j —г -\- -щ-1, и предыдущее неравенство
принимает вид
(А + В) < W < —%г {А + В).
2YQ
—^==- (А + В) < W < —%
2YP	2YQ
Первый выбор пределов Р и Q, который сразу приводит к теореме
Пьюизё, будет следующий: множитель z(a 4- Р)+ Р1 + «р убывает или воз-
растает одновременно с z, потому что коэффициент а -\- р положителен; так
как z заключен между -\-1 и — /, то этот множитель заключен между
/ (а + Р) + Р + «Р и — / (а + Р) 4- Р- + ар, т. е. между В2 и А2. Следовательно,
можно принять Р = В2, Q = А%, и мы видим, что Ч*1 заключено в пределах
"( I + ~х) и "o'I^+'r')' кажДый из которых больше чем я/2. Если на-
чальная скорость очень велика, то оба эти предела будут очень близки к я.
Действительно, при неограниченном возрастании v0 величины А и С2 также
неограниченно возрастают, и уравнение <р (z) = 0 после деления всех его чле-
нов на А принимает вид
Р — г?- — р2 = 0,
где р2 — некоторая постоянная. При этих условиях корень у многочлена <р (г}
обращается в бесконечность, а корни аир стремятся к корням только что
написанного трехчлена, которые равны и противоположны по знаку. Следо-
вательно, в предельном случае имеем C = — аи оба найденных нами предела
для ЧГ равны я. Таким образом, мы видим, что когда v0 неограниченно воз-
растает, то Ч*1 стремится к я; траектория стремится тогда обратиться в боль-
шой круг. Альфен доказал (Traite des fonctions elliptiques, т. II), что угол ЧГ

438	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
не может стать больше предела т.. Сен-Жермен установил это же свойство
более элементарным путем (Bulletin des Sciences mathematiques, 1896, 1898,
1901 и Memoires de l'Academie de Caen, 1901).
Вернемся на время к общему случаю. Мы можем найти более узкие
пределы для значения 4'. В самом деле, так как множитель z (а + $) + I- + =Ф
возрастает или убывает вместе с z, то в интеграле, определяющем Х1", этот
множитель будет заключен между крайними значениями, которые он прини-
мает при z = а и z = р. Мы можем, следовательно, принять
/2, 0 =
и тогда получим
2 Уа2 + 2ар + Р	2 У> + 2=Ф -г Г- '
Когда 3 стремится к а, оба эти предела становятся равными и мы имеем
Р>а	2 /За2 + /2
Эта формула позволяет определить значение W, когда траектория заключена
между двумя бесконечно близкими параллелями. Если, кроме того, обе эти
бесконечно близкие параллели находятся вблизи самой низкой точки сферы,
то а будет очень мало отличаться от /, a W — от -к/2. В этом последнем
случае траектория близка к маленькому эллипсу. Такой же результат мы
получим дальше при рассмотрении бесконечно малых колебаний.
278. Вычисление нормальной реакции. Будем считать нормальную
реакцию положительной, если она направлена к центру сферы. Общая
формула
установленная раньше (п. 269), сразу позволяет найти N. В самом деле,
радиус R равен радиусу / сферы, v'1 = 2gz -f- h и Fn есть проекция веса mg
mgz
на радиус, равная	~—; следовательно, имеем
Эта реакция будет такой же линейной функцией от z, как и в случае мате-
матического маятника. Если точка прикреплена невесомой гибкой нитью
к центру сферы, то она покинет эту сферу в тот момент, когда реакция
обратится в нуль. После этого реакция становится отрицательной, и точка
падает, описывая параболу, соприкасающуюся с прежней ее траекторией
на сфере.
Если точка не может покинуть сферу, если она, например, находится
между двумя бесконечно близкими жесткими сферическими оболочками, то
она будет давить на внешнюю оболочку, когда реакция положительна, и на
внутреннюю, когда реакция отрицательна. В этом случае горизонтальная
проекция траектории будет иметь точку перегиба в том месте, где N обра-
щается в нуль. Действительно, в произвольном положении движущейся
точки соприкасающаяся плоскость траектории содержит равнодействующую
?ил N и mg; в точке же, где 7V = 0, соприкасающаяся плоскость содержит
только вес mg; следовательно, она будет вертикальна, и горизонтальная
проекция рассматриваемой точки-будет точкой перегиба. Этот случай не

ГЛАВА XIII. ДВИЖЕНИЕ ТОЧКИ ПО ПОВЕРХНОСТИ	439
может иметь места, когда аир оба положительны, так как тогда г будет
оставаться положительным и реакция —~ -)- ЧЩЕ. будет существенно поло-
жительной (см. упражнение 24).
279. Интегрирование в эллиптических функциях. Полученные нами
формулы могут быть преобразованы таким образом, чтобы переменные
выражались однозначными функциями t. Этим мы сейчас и займемся. Мы
нашли
dt=
Будем отсчитывать время от того момента, когда точка проходит через
самое низкое положение у1}. Мы должны будем взять перед радикалом знак
минус, вследствие чего получим:
Idz
J
I	J Y{a-Z){z-$)(z-i) '
Для приведения этого интеграла к канонической форме, положим
а _ z = (а — Р) и\
Так как z изменяется между предельными значениями а и р, то и колеблется
между 0 и 1. Из последнего равенства выводим
Z = a — (а — р)н2, dz= — 2 (а — $)udu
и, подставляя в значение для t, получим
I	J У(а — 1)A — и2)A —kill*) '
где положено
Р
Величина k2 существенно положительна и меньше 1, так как а — наиболь-
ший из трех корней: а > р > f. Полагая, наконец,
К~	21
имеем
U
J 1/-A_Ц2)A_
т. е.
и = sn \t,
откуда
Z = а — (а — р) Stl2 It.

440	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Таким образом, г является двоякопериодической функцией переменного t.
Один из периодов вещественный и равен
If
du
Заметим, что Ya — г, Уг — р, Уг—1 являются однозначными функ-
циями времени. В самом деле,
У* — z = У о —
sn
M z — p = y a — р У 1 — Ф--=-уа~ pen It,
Y* — 1 = Y<*~—1 Y^-^tfi = Уа — Y dn U
Чтобы выразить х и у как функции времени, вспомним, что мы получили
d%= Cdt
Если теперь заменить здесь z полученным для него ранее значением, то
-тт станет рациональной функцией от sn \t; разложив ее на простые дроби
по методу Эрмита, можно будет выполнить интегрирование так, как это
указывается в теории эллиптических функций. Получающаяся таким путем
функция 6 не будет однозначной, но можно показать, что х и у получатся
однозначными функциями времени t. Действительно, имеем
e J p -г
Можно доказать, что показательная функция не имеет критических точек,
кроме как при значениях t, соответствующих значениям z = ± /, и что
произведение
не имеет этих критических точек и будет однозначной функцией от t.
Отсюда получится, что и вещественная часть х и мнимая часть у будут обе
однозначными функциями от t. Этот метод принадлежит Тиссо (Journal de
Liouville, 1852).
Эрмит дал прямое доказательство этого же самого свойства (Crelle, m. 85).
Непосредственное отыскание функций хну сводится к интегрирова-
нию дифференциального уравнения второго порядка, являющегося частным
случаем уравнения Ляме, исследованного Эрмитом (Sur quelques applications
des fonctions eiliptiques). Действительно, мы установили ранее, что если
N обозначает реакцию, то
d2jc	Nx „7 т
mw=~-r- N=T
и поэтому
&х _
d?>-	/a
Заменив в этой формуле z найденным выше значением, мы получим
йР?	3g[a — (a — P)sn2X*]-f h
dfl ~ X	l°-

ГЛАВА XIII. ДВИЖЕНИЕ ТОЧКИ ПО ПОВЕРХНОСТИ	441
Это — линейное уравнение, частные интегралы которого определяют не
только x(t), но и у (t), так как уравнение для у
tPy _ Ny
dt'i ~ I
будет таким же, как и уравнение для х. Если теперь положить It = t', то
предыдущее уравнение примет вид
dt'1	¦
где А' обозначает постоянную. Это — уравнение Ляме
^- = х \п (п + 1) К>- sns f + A'],
в котором п = 2.
280. Теорема Гринхилла. Мы обязаны Гринхиллю следующим интерес-
ным замечанием. Если сферическому маятнику сообщить на уровне центра
горизонтальное движение, то существует линейная комбинация интегралов,
определяющих 8 и t, являющаяся псевдоэллиптическим интегралом, т. е.
таким, который может быть выражен в элементарных функциях. В самом
деле, так как начальные значения г и у в момент ?=0 приняты равными
нулю, то, обозначая через vg начальную скорость, которая предполагается
горизонтальной, имеем
С = lv0, h = v%
		Pv0 dz
¦-/-¦
t:	¦	ldZ
Из этих уравнений, как легко проверить, имеем
~Yi ==arcsin~" =
или, обозначая через <р угол маятника с вертикалью, т. е. вводя z = / cos tp,
получим
Это соотношение совместно с тем, которое определяет z или / cos tp
через эллиптические функции от ,t, позволяет выразить х, у, г как одно-
значные функции от t.
281. Бесконечно малые колебания. Вводя нормальную реакцию N,
имеем следующие уравнения движения маятника:
&х	Nx	d?y	Ny d*z	Nz	...
т1т=- — ' тШ = -~Г' ma? = mg--r-	A>
Если колебания достаточно малы, то л: и у будут оставаться очень
малыми. Мы будем рассматривать их как бесконечно малые первого порядка

442	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
и будем пренебрегать членами второго порядка. Ограничиваясь такой сте-
пенью приближения, получим 2=1, так как по формуле Тэйлора имеем
и второй член разложения есть член второго порядка. Таким образом, при-
ближение, о котором мы говорим, сводится к допущению, что движущаяся
точка не покидает касательной плоскости. Последнее из уравнений A) упро-
щается:
N — mg.
Подставляя это значение в два первых, получим уравнения
dp ~ I ' dt>-~ I y>
совпадающие с уравнениями движения точки под действием центральной
силы, пропорциональной расстоянию. Траектория будет эллипсом с центром
на оси г. Это видно из того, что полученные линейные уравнения имеют
общие интегралы
х = A cos t у | + В sin t y-j-. y = A' cost y-f- + В' sin 11/ -f- •
Допустим, что при t = О
dx . dy
x = x0, y = yo. -ar = b -af=v°'
что равносильно проведению плоскости zOx через одну из вершин малого
эллипса. Тогда получатся следующие значения постоянных:
А = х0, тГ=0, В=0, B'=vo^/—,
¦откуда
j-, у = v0 у j- sin t у -j-.
Исключая t, получим непосредственно уравнение эллипса J). Период обра-
щения равен 2я у —.
Можно улучшить приближение, сохранив члены второго порядка. Для
этого достаточно во вторых частях уравнений A) заменить N его значением,
полученным из первого приближения. Это вычисление выполнено Тиссераном
(Bulletin des sciences mathematiques, 1881).
Другие методы приближения даны Резалем (Mecanique generale, т. 1,
стр. 180) и де-Спарром (Annales de la Societe scientifique de Bruxetles, 1892).
УПРАЖНЕНИЯ
1. Точка М с массой, равной 1, двигается по поверхности, заданной
в прямоугольных координатах уравнением
х2 + У2 = \ (es + е-2J-
!) О степени точности этого результата см. Крылов А. Н., ЖРФХО,
т. 609, 128 и Лекции о приближенных вычислениях, изд. 5, Москва 1950,
§ 82 (Прим. перев.).

ГЛАВА XIII. ДВИЖЕНИЕ ТОЧКИ ПО ПОВЕРХНОСТИ	443-
Она притягивается каждым элементом оси z с силой, равной отношению длины
элемента к четвертой степени расстояния до точки М. Исследовать движе-
ние, которое может получить точка, и найти проекцию траектории на
плоскость ху. Исследовать случай, когда в начальный момент точка нахо-
дится на оси х и имеет скорость, равную 1/ -=¦ и образующую с пло-
скостью ху угол, равный 45° (лиценциатская, Кан).
4. 2. Невесомая точка движется по сфере х^ -\- у2 -f- г2 — /?а = 0 под дей-
„ mk2
ствием силы, направленной нормально к плоскости ху и равной ——,
где k- — постоянная. Найти движение и нормальную реакцию.
(Траектория — сферическое коническое сечение.)
3.	Рассмотрим материальную точку М с массой, равной 1, находящуюся
под действием силы F, проекции которой на три прямоугольные оси коор-
динат равны частным производным силовой функции U (х, у, г). Уравнение
?/ = const представляет поверхность уровня, пересечение которой с произ-
вольной поверхностью S можно назвать линией уровня на поверхности S.
Определить эту последнюю поверхность таким образом, чтобы точка М,
вынужденная на ней оставаться и предоставленная без начальной скорости
действию силы F, описывала траекторию С, ортогональную всем линиям
уровня. Если, например, на точку М действует только вес, то она должна
падать на искомой поверхности вдоль линии наибольшего ската.
Доказать, что синус угла, под которым поверхность уровня пересекает
поверхность S, изменяется в различных точках линии пересечения в отно-
шении, обратном силе F. (А. де Сен-Жермен, Journal de Math., ок-
тябрь, 1876.)
4.	Свободная точка, находящаяся под действием только сопротивления
среды, описывает прямую. Доказать, что точка, движущаяся по поверхности
и находящаяся под действием только сопротивления среды и трения, описы-
вает геодезическую линию.
5.	Тяжелая материальная точка, оставаясь на поверхности сферы
радиуса а, притягивается пропорционально расстоянию неподвижной точкой В,
находящейся на вертикали Ог и проходящей через центр О сферы;
расстояние ОВ — Ь. Даны значение (л. притяжения на единицу расстояния,
ускорение g силы тяжести, начальная скорость k движущейся точки,
предполагаемая горизонтальной, и, наконец, начальное расстояние h от точки
до горизонтальной плоскости Оху, проходящей через центр сферы. Тре-
буется: 1) найти границы, между которыми изменяется во время движения
координата z точки; 2) определить движение в частном случае, когда при-
тяжение неподвижной точки В в центре сферы равно и противоположно
весу.
6.	Найти движение точки, движущейся на сфере и притягивающейся
диаметральной плоскостью пропорционально расстоянию. Задача сводится
к интегрированию уравнения Ляме. [К о б б, Comptes rendus, т. CVIII-]
7.	Геодезические линии эллипсоида. Как следствие доказанного в тексте
(п. 279) соотношения pD = const., доказать следующие предложения.
Если О и О' — две шаровые точки эллипсоида, не лежащие на одном
диаметре, то МО и МО'— геодезические линии, соединяющие точку М с
этими точками, а эти две линии одинаково наклонены к каждой из линий
кривизны, проходящей через точку М.
Если точка М описывает линию кривизны, то сумма или разность дуг
геодезических линий МО ± МО' — постоянна. (См. Journal de Liouville, 1846.)
8.	Найти геодезические линии тора. (Ре за ль, Comptes rendus, т. ХС,
стр. 937.)
9.	Найти геодезические линии поверхности, образованной вращением
цепной линии вокруг основания F определяется через г эллиптическим
интегралом первого рода, который сразу приводится к нормальной форме).

444	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
9 bis. Найти геодезические линии однополостного гиперболоида, обра-
X*	22
зеванного вращением гиперболы —ъ	— =1, Обозначая через е эксцен-
триситет гиперболы, получим для проекций геодезических линий такое
уравнение:
= kdr Г еЧ* — а9-
~ г V (г2 — я2) (г2 — k1)'
Следовательно, 6 выражается интегралом, который приводится к эллипти-
ческим. Кривая имеет форму, аналогичную указанной в п. 275. При k = a
она асимптотически приближается к горловому кругу г — а; при k = — кри-
вая обращается в образующую.
10. Кривизна геодезических линий поверхностей вращения. Пусть R
и R' — главные радиусы кривизны в точке поверхности вращения, г—радиус
соответствующей параллели, I — наклон рассматриваемой геодезической
линии к меридиану, р — ее радиус кривизны. Вывести формулу
~R+\R' ~R) ~
где k, как и в тексте, представляет собою постоянное значение произведе-
ния г sin ? вдоль рассматриваемой геодезической линии. (Р е з а л ь, Nouvel-
les Annales, фев., 1887.)
11.	По поверхности двигается тяжелая точка. Доказать, что можно взять
начальную скорость настолько большой, что траектория на некотором рас-
стоянии от начального положения точки будет сколь угодно мало отли-
чаться от геодезической линии.
12.	Найти геодезические линии поверхности вращения
16а2 (х"- + у?) = z"- {2а"- — z"-).
Можно положить
а	( , и	и\
г = — cos н, z = a I sin у — cos -=-1.
Эти геодезические линии имеют вид пространственной восьмерки; все
они замкнуты и имеют одинаковую длину. (Т а н н е р и, Bulletin des Sciences
mathematiques, 1892, стр. 190.)
13.	Даны две тяжелые точки, притягивающиеся друг к другу пропор-
ционально расстоянию. Первая из них двигается по вертикали, а другая
на плоскости, образующей с горизонтом угол а. Найти движение этой систе-
мы двух точек.
Рассмотреть частный случай, когда: а) т' = т\ б) начальное положение
совпадает с положением равновесия; в) проекции начальной скорости второй
точки на горизонталь и на линию наибольшего наклона плоскости равны,
каждая, начальной скорости первой точки; г) sin а = — .
Рассмотреть также случай, когда плоскость горизонтальна, т. е. а = 0.
14.	Движение точки на сфере под действием силы, постоянно лежа-
щей в плоскости меридиана, проходящего через движущуюся точку.
Предполагается, что радиус сферы равен единице и что положение точки
определяется долготой 8 и углом у, дополнительным к широте; на точку
действует сила, постоянно находящаяся в плоскости меридиана; обозначим
через F проекцию силы на касательную плоскость к сфере, причем F считается
положительной или отрицательной в зависимости от того, будет ли эта соста-
вляющая направлена в сторону возрастающих или убывающих значений у.

ГЛАВА XIII. ДВИЖЕНИЕ ТОЧКИ ПО ПОВЕРХНОСТИ	445
Доказать справедливость следующих формул, аналогичных соответствующим
формулам в теории центральных сил и, в частности, формуле Бине:
F = -
(П. С е р р е, Theorie geometrique et mecanique, etc., стр. 195.)
Пример. Если F имеет значение . , , то траектория будет сфери-
ческим коническим сечением с фокусом в полюсе (аналогия с движением
планет).
15.	Установить формулы такого же, как в примере 14, характера для
движения точки на поверхности вращения под действием силы, постоянно
находящейся в плоскости меридиана движущейся точки.
16.	Преобразование движений. В неподвижной плоскости дана мате-
риальная точка массы 1, находящаяся под действием силы F, проекции
которой X и Y суть функции только координат х и у движущейся точки.
Уравнения движения будут
d"-x _ d"-y _
Заменив независимую переменную t переменной tx, связанной с t соотноше-
нием
...	(U
х (а"х + Ь"у + с"J '
сделаем гомографическое преобразование
	ax + by-\-c	a'x-i-b'y + c'
1 а"х + b"y + c"' J1 а"х + Ь"у + с" '
Доказать, что точка (хх, ух) двигается во времени tx, как точка массы 1, на-
ходящаяся под действием силы Ft, проекции которой Хь Yx зависят только
от хх и ух. Траектория точки (хх, ух) является томографическим преобразо-
ванием траектории точки (х, у) и направление силы Fx есть гомографическое
преобразование направления силы F.
Если сила F—центральная, то сила F± тоже центральная или параллель-
ная постоянному направлению. (Ann ель, Comptes rendus, т. CVIII,
стр. 224.)
17.	Доказать обратное: если надо найти наиболее общее преобразование
вида
хх = <р (х, у), ух = <\> (х, у), ^dtt=l (x, у) dt
такое, что новая сила Fx зависит только от координат xt и уь и это
имеет место, какова бы ни была сила F, зависящая от х и у, то получается
только вышеуказанное гомографическое преобразование. (American Journal,
т. XII.)
18.	Преобразование сферического движения в плоское. Даны сфера (S)
радиуса 1 и касающаяся ее плоскость (Я); каждой точке Мх на сфере ста-
вится в соответствие проекция М этой точки на плоскость (Я) при помощи
радиуса, идущего от центра к М^, это хорошо известная в теории географиче-
ских карт так называемая центральная проекция; она ставит в соответствие
любой прямой плоскости (Я) большие круги на сфере (S) и наоборот. С точки
зрения аналитической, если точку касания плоскости (Я) и сферы (S) при-
нять за полюс полярных координат на плоскости и на сфере, то, обозначая

446	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
через (и« полярные координаты точки М на плоскости, а через ер и в —
полярные координаты точки М± на сфере (ср— дополнение широты ив —
долгота), получим следующие формулы преобразования:
р = tg <р, ш = в.	(а)
Уравнения Лагранжа плоского движения будут
df>- ?\dt
где R и Q — функции от р и ю. Точно так же, если рассматривается на сфере
точка массы 1, перемещающаяся в течение времени ^, то уравнения движе-
ния будут
где Фи 8 — функции от ср и 6. Доказать, что если над уравнениями плоского
движения (Ь) сделать преобразование центральных проекций, определяемое
формулами (а), и если между ( и (t установить соотношение
dt-i = cos3 ср dt,
то уравнения (Ь) примут вид уравнений (с), где
COS2 cp '	COS3 ср
Следовательно, любому движению на плоскости соответствует движение на
сфере и обратно. Траекторией одной из точек будет преобразование при по-
мощи центральных проекций траектории второй точки (Ann ель, American
Journal, т. XIII). Приложить это преобразование к примеру 14.
19.	Доказать более общее предложение, что таким же путем можно
преобразовать движение точки на поверхности постоянной кривизны в дви-
жение на плоскости. (Дотевилль, Annales de l'Ecole Normale superieure,
1890.)
20.	Точка, на которую не действует никакая заданная сила, движется на
плоскости, вращающейся с постоянной угловой скоростью ш вокруг непо-
движной оси, с которой она неизменно связана. Найти движение и вычислить
реакцию (де Сен-Жермен).
21.	Найти длину кривой, описываемую сферическим маятником в гори-
зонтальной проекции и в стереографической проекции в случае Гринхилла
(п. 280) (Гринхилл).
22.	Установить уравнения движения точки на поверхности с трением.
(Апсель, Comptes rendus, 15 фев., 1892; см. также М а й е р, Sachsische
Qesellschaft, 5 июня, 1893.)
23.	Найти движение с трением тяжелой точки на круговом цилиндре
с вертикальной осью. (Де Сен-Жермен, Bulletin des Sciences mathema-
tiques, август, 1892.)
24.	Доказать, что если точка, движущаяся по поверхности без трения,
находится под действием силы постоянного направления, то проекция траек-
тории на плоскость, перпендикулярную силе, имеет точку перегиба: 1) когда
реакция обращается в нуль; 2) когда соприкасающаяся плоскость траектории
нормальна к поверхности (де Спарр, т. CXIX). Это будут два случая,
когда соприкасающаяся плоскость траектории вертикальна.

ГЛАВА XIV
УРАВНЕНИЯ ЛАГРАНЖА ДЛЯ СВОБОДНОЙ ТОЧКИ
282. Уравнения Лагранжа. В предыдущих главах мы вывели
для точки, движущейся по неподвижной или движущейся поверхности
или по кривой, уравнения движения, указанные Лагранжем. Тот же
метод позволяет написать уравнения движения свободной точки,
причем в любой системе координат. Этот метод тем более важен,
что он применим к движению произвольной голономной системы.
Допустим, что декартовы координаты х, у, г движущейся точки
относительно трех прямоугольных осей координат выражены через
новые координаты qx, q2, q3 формулами
x==t? (<7i> Чг< li)' y = ty(<lv <Ь <7з). 2 = 0)(qlt q2, q3).
Требуется написать уравнения движения в новой системе координат,
т. е. написать дифференциальные уравнения, определяющие qx, q2, q3
в функции времени. Для этого можно было бы взять те же уравне-
ния движения, которые определяют х, у, г в функции t и преобра-
зовать их к новым переменным, определяемым вышенаписанными
формулами. Но такое вычисление было бы слишком длинным, а метод
Лагранжа имеет целью именно избежать длинные вычисления. Этот
метод применим также и в том случае, когда декартовы координаты
являются заданными функциями не только трех новых координат qv
q2, q3, но и времени. С точки зрения геометрической это означает,
что указанный метод применим также и в случае, когда новая си-
стема координат подвижна, причем движение ее известно.
Поэтому, чтобы исследовать наиболее общий случай, мы предпо-
ложим, что х, у, г являются заданными функциями параметров qx, q2,
q% и времени t:
•* = <Р (?i. <72' <7з. *), y = <\>(ql, q2, q3, t), z = m(qv q2, q3, t).
Чтобы найти уравнения движения в новой системе координат,
т. е. дифференциальные уравнения, определяющие qt; q2, <7з в функ-
ции времени, напишем уравнения движения в декартовых координатах

448	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
..	дх	ду dz
Умножим, соответственно, эти уравнения на -=—¦,	-з^-i -з—• и
3V	dqi	dqx dq,
почленно сложим их. Получим
-x дх , rf2y ду . A fe\ ,,	...
где положено
q^X^+Y^L + Z^-.
"<7i	"<7i	dqx
Так как X, Y, Z являются заданными функциями координат х, у, г
и их производных по t, то легко вычислить Qt в функции qv q.2. q3
и их производных по t. Далее для вычисления левой части заметим,
что предыдущее уравнение может быть написано в виде
_с/_ Г ldx_ дх . dy ду . dz_ J)z
dt I \ dt dqt ' dt dqx ' dt dt
~MVdt d
Для упрощения записи Лагранж обозначает:
y ' dt	'
dt	' dt y ' dt
d<h_ t
dt yi' dt 42' dt ~"^3'
Тогда, взяв производные по t от обеих частей уравнения
*=?(?!. 42. 4i. t),
получим
. дх , , дх , . дх , . дх
Отсюда, так же как и в п. 263, выводим формулы
дх __ дх/_ J_ (^\ __ дх^_
^х ~~ dq[ ' dt \dqt)~ dqi '
Точно так же получаются тождества
ду 	 д/_ jL(_^y\	jW_
dqi ~~ dq[ ' di \dqi)~ dqx '
dz dz' JL(J^L\dz'
~d<h~~l)q[' 'd7\~dq7)~'~d<h'
Поэтому, уравнение B) можно написать так
' дх> j_ ' дУ' _j_ ' dz>

ГЛАВА XIV. УРАВНЕНИЯ ЛАГРАНЖА ДЛЯ СВОБОДНОЙ ТОЧКИ	44&
Положим теперь
Следовательно, Т обозначает кинетическую энергию точки. Если за-
менить х\ у', г' их значениями C), то Т станет функцией пере-
менных <7i> Яг< <?з> t< я[> я'->< Яу При таком обозначении непосред-
ственно видно, что уравнение B') можно переписать в виде
dq[
Путем таких же вычислений получим:
dq2
d I дТ \ дТ =
dqs
Выражение Т содержит qx, q2, q3 и их первые производные; от-
сюда следует, что полученные нами уравнения Лагранжа будут вто-
рого порядка. Следовательно, их общие интегралы содержат шесть
произвольных постоянных, которые определяются из начальных условий.
Если известно выражение dsz в системе координат qx, q2, q$, то
m I dsX2
можно сразу найти Т, так как Г—-^-1 -тЛ .
Вычисление правых частей. В равенствах, выражающих Q4, Q3, Q3,
можно заменить X, Y, Z их значениями, но часто можно вычисление
упростить. Допустим сначала, что имеется силовая функция U. В этом
случае
	 dU у	 dU 7 __ 0U
дх '	ду '	dz '
и поэтому
— — jLl j_ — ду -4- — дг
^] Ox dqx ' ду dqx ' dz Oqx '
Если теперь предположить, что в выражении силовой функции U
координаты х, у, г заменены их значениями в функции qx, q2, q3,
то предыдущее уравнение запишется следующим образом:
dU
Точно так же будет
dU О - dU
Эти формулы пригодны и тогда, когда X, Y, Z являются част-
ными производными по х, у, г функции U{x,y,z,t), содержащей
явно время, хотя в этом случае нельзя больше говорить, что сила
имеет силовую функцию.
29 Зак. 851. П. Аппель, г. I

450	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
В наиболее общем случае можно также упростить вычисление
величин Qt, Q2, Q3. Дадим в уравнениях преобразования координат
х = <?(Я1, q2,q3.t), y = ty(qit q2, q3, t), z = w(qv q2, q3, t)
времени t определенное значение и допустим, что qlt q2, q3 полу-
чают произвольные возможные приращения oqlt bq2, bq3. Тогда при-
ращения координат х, у, z будут:
s	дх j , дх s , ^ ,
Ь +р_
dq1 Ч1~ dq2
ь
s	& , .	dz ь , дг 5
t)qt V1 '	dq2 V2 ' dq% чз
Элементарная работа силы на	соответствующем возможном переме-
щении равна
или в силу предыдущих равенств
И если предположить, что возможное перемещение совершается
по кривой q2 = const., ^з = const., то элементарная работа будет
равна Qx bqlt что и позволяет определить Qv Точно так же полу-
чаются Q2 и Q3.
Мы видим, таким образом, что имеется полная аналогия с урав-
нениями, найденными для движения по кривой и по поверхности.
Единственное различие заключается в числе параметров qv q2, . ..,
которое для точки на кривой равно 1, для точки на поверхности
равно 2 и для свободной точки равно 3.
283. Интеграл кинетической энергии. В случае, когда суще-
ствует силовая функция U (х, у, z), по теореме кинетической энергии
получим первый интеграл
T = U-\-h,
где Т обозначает кинетическую энергию. Этот интеграл, являясь
следствием уравнений движения, является также следствием уравне-
ний Лагранжа и может заменить одно из них.
Проверим непосредственно, что интеграл кинетической энергии
действительно является следствием уравнений Лагранжа. Остано-
вимся лишь на более простом случае, когда х, у, z, выраженные
через qx, q2, q3, не содержат явно t. В этом случае для хг, у', zr
получатся выражения вида
, дх , . дх , . дх ,
Х	+ ?+

ГЛАВА XIV. УРАВНЕНИЯ ЛАГРАНЖА ДЛЯ СВОБОДНОЙ ТОЧКИ 451
и Т будет однородной функцией второй степени относительно q'v q'v q'^
По теореме об однородных функциях имеем
После этого возьмем уравнения Лагранжа, в которых Qv Q2, Q3
dU dU dU
заменены через -s—, -ч—, -^—, и, умножив их предварительно на
Яу ч'.>> Чу сложим. Получим
d ( дТ \ _i_ ' Л I дт \ i ' d I дТ
дТ , дТ , дТ ' dU , , dU . , dU
п	dU	,,
Правая часть этого уравнения равна, очевидно, ~тг, так как Ь
зависит от t только через qx, q2, q3. Что касается левой часги, то
ее можно написать так:
дТ . , дТ . , дТ
++q
„ дТ . „ дТ . „ дТ . , дГ . , дТ . , дТ
где q", q"^, q"z—вторые производные от qlt q2, q3 по времени.
На основании уравнения A), полученного из теоремы об одно-
родных функциях, первая скобка равна 27. Что касается второй
скобки, то она является развернутым выражением производной ~гт-,
так как Т зависит от t через параметры qv qz, q3, q'v q'2, q'y и урав-
нение B) приводится к следующему виду:
d	dT _ dU
dt (Z1)	dt " dt '
т. e.
dT=dU,	T==U-\~ft.
что и является интегралом кинетической энергии. В приложениях
наиболее сложное из трех уравнений Лагранжа заменяют этим пер-
вым интегралом.
284. Приложение. Задача. Найти движение материальной точки,
которая притягивается или отталкивается неподвижной осью с силой,
являющейся заданной функцией расстояния (рис. 172).
Мы уже видели (п. 84), что в этом случае имеется силовая функция
I Ф dr, которую мы обозначим через /я/(г).
29*

452
ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Мы будем определять положение точки ее цилиндрическими координа-
тами г, Ь, z. Тогда получим
т (ds\"j т , ,о	о ,о.
Вследствие этого, уравнения Лагранжа после сокращения на т будут
1Г 2' = °-
Интегрируя два последних уравнения, получим
г'д' = С,	A)
z' = а.	B)
Заменим теперь первое уравнение Лагранжа интегралом кинетической энер-
гии. Имеем
z	1
Если заменить здесь z' и 6' их значе-
ниями из равенств A) и B), то получим
C)
—у Это — уравнение вида
из которого можно определить время простой
Рис. 172.	квадратурой.
Можно было сразу написать уравне-
ния A), B) и C), не пользуясь уравнениями
Лагранжа. В самом деле, так как сила все время пересекает ось Oz,
то к проекции движения на плоскость ху применим закон площадей,
что приводит к уравнению A). Так как составляющая силы по оси Oz
равна нулю, то -тщ = 0, z' = а и мы получаем уравнение B). Наконец, урав-
нение C) есть не что иное, как уравнение кинетической энергии.
Исключив из уравнений A) и B) время, мы получим дифференциальное
уравнение
г"- db = — dz,
а
которому удовлетворяют траектории каков бы ни был закон сил. Если это
уравнение написать в декартовых координатах, то получится
х dy — у dz = k dz.
Такое уравнение уже встречалось в упражнении 6 в конце главы I как диф-
ференциальное уравнение кривых, касательные к которым являются прямыми
нулевого момента.

ГЛАВА XIV. УРАВНЕНИЯ ЛАГРАНЖА ДЛЯ СВОБОДНОЙ ТОЧКИ
453
285. Сферические координаты. Пусть р, 6, и — координаты точки М
(рис. 173). Положим
Тогда имеем
= ?Lvi = \ (р'2
f-
и, следовательно, уравнения Лагранжа будут
^ (тр') - /яр (б'2 + «>'2 sins 6) = <2ь
— (mps6') — mp2co'2 sin в cos В = Q2,
Для вычисления Qu Q%, Q3 применим указанный ранее метод. Обозна-
чим через R, Q, Р составляющие силы F соответственно по радиусу-векто-
ру г, по перпендикуляру к плоскости zOM и по перпендикуляру к плоскости
составляющих R, Q; величины Р, Q, /? считаются положительными, когда
они направлены в сторону возрастания соответствующих координат д, и> или 6.
Для возможного перемещения вдоль ра-
диуса-вектора (#2 = const., ^з = const.) эле-
ментарная работа равна Rbr и, следова-
тельно,
На перемещении р ЬЬ, для которого р
1} и> остаются постоянными, элементарная
работа равна Яр 86. Имеем поэтому
Qi = -Pp.
Если,
ными р и
вершаться
в точке О'
наконец, оставлять неизмен-
в, то перемещение будет со-
по окружности с центром
и радиусом р sin в; элементар-
р
ная работа будет, следовательно,
Qa sin 6 5<и, и мы получим
равна
Рис. 173.
Если сила F пересекает ось г, то Q будет равно нулю, и из тргтьего
уравнения Лагранжа найдем
/яр?
)' = const.
Это уравнение выражает, что проекция точки на плоскость ху движется по
закону площадей.
286. Эллиптические координаты в пространстве. В эллиптической
системе координат точка М в пространстве определяется параметрами трея
пересекающихся в этой точке поверхностей второго порядка, софокусны:.
заданной. Пусть
r2	и 2	,2
A)
— —1 =0
а — \ ' b — \~ с — /.
уравнение поверхностей второго порядка, софокусных поверхности
? + 7 + Т = 1-

454	часть третья, динамика точки
Если для определенности мы положим а > b > с, то при X < с уравнение A)
представит вещественный эллипсоид, при Ь > X > с оно представит одно-
полостный гиперболоид, при а>\>Ь— двуполостныи гиперболоид и, на-
конец, при \>а—-мнимый эллипсоид. Через каждую точку пространства
проходят три таких софокусных поверхности. В самом деле, если х,
у, z рассматривать как заданные величины, то уравнение A), третьей
степени относительно X, будет иметь три вещественных корня, из
которых один меньше с, другой заключен между с и Ь, и третий —
между b и а. Это можно проверить, подставляя в левую часть урав-
нения указанные ниже значения X и замечая, что знаки левой части
будут определяться следующей таблицей, в которой г — очень малое поло-
жительное число:
Значения параметра X	— со с — г с-\-г Ь — е Ь + г а — в й + ; -4-со
Соответствующие знаки левой
части уравнения A) 	—	+ — + — -f-	— —
Положение корней		q^	q2	qi
Обозначим эти три корня в порядке убывания их величин через qb q2,
qs. В случае X = q1 получается двуполостныи гиперболоид, в случае
X = <72—¦ однополостный гиперболоид и в случае X = qB — эллипсоид.
Как хорошо известно, эти три поверхности пересекают друг друга орто-
гонально. Например, две поверхности
v-2	ф	?1
U —	+	4-	—1=0
a— q2 b — q2 c — q^-
пересекаются ортогонально, так как условие
J,=0
дх дх ~*~ ду ду ' дг дг
как это можно непосредственно проверить, идентично уравнению
Три величины q^, q->, q% называются эллиптическими координатами точки
М (х, у, г).
Чтобы выразить декартовы координаты х, у, г через qv q%, q$, заметим,
что <?1> 9г. Чг являются тремя корнями уравнения A) относительно X. По-
этому имеем тождественно
~*~й — X ' с — X	(я—Х)F— Х)(с — X)
(Х-
Умножая обе части этого тождества на а — X и полагая затем X = а,
получим
,_ (а — gi)(a — 92) (а— 9з)
(й)(с)

ГЛАВА XIV. УРАВНЕНИЯ ЛАГРАНЖА ДЛЯ СВОБОДНОЙ ТОЧКИ
Точно так же найдем
455
J'~	{c-b)(a-b) _" *
о = (с — д1)(с — д2)(с — д3)
{a — c)(b-c)
Вычислим теперь в этой системе координат выражение для as-. Взяв
логарифмические производные обеих частей написанных выше равенств, имеем:
2rfx _ dqx	dq^	dq3
х <7r — a q2 — a qA — a'
dqx
У
Яг
dq?
!•> — b
; +
Отсюда для 4ds2 получится выражение вида
dy2
= Ml dq\
dq3
dq\
я dq\.
В нем нет членов с dq1dq,, ..., так как поверхности пересекаются ортого-
нально. Легко проверить соотношение
I	У2	I 	г1	= 0
(а — qt) (а — q2) ^ (Ь — q{) (b — q?) л (с — qt) (с — q2)
которое выражает, что коэффициент при dq1 dq2 равен нулю. Величины Мь
Мч, М% имеют следующие значения:
Х2	у°.	z-
Если взять производные от обеих частей тождества B) по X и затем по-
ложить X = qb то, заметив, что в результате этой подстановки все члены
второй части, содержащие множителем
X — <7i> обратятся в нуль и поэтому не
будет надобности их вычислять, найдем	'
где /(X) обозначает произведение
(а — А)(#—X) (с — X). Точно так же по-
лучим
7Ш
Рис. 174.
Заметим, что если, в частности,
рассмотреть дугу кривой С\ пересе-
чения двух поверхностей q^ — const, и q3 = const, (рис. 174), то дифферен-
циал dsx этой дуги получится, если положить
dq2 = dqs = 0.
Отсюда
l^dqt.

456
ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Точно так же, обозначая через ds2 и rfs3 дуги кривых С2 и С3, по ко-
торым пересекаются поверхности д1 — const, <?з= const, и поверхности
qx = const., q2 — const., получим
ds2 = -у У"Л13 d^2' ^5з = -к YM% dg3.
Тогда дугу ds любой кривой можно рассматривать как диагональ прямо-
угольного параллелепипеда со сторонами dsx, ds2, ds3.
Величина Т выражается в виде
/2
и уравнения Лагранжа теперь легко составить. Так как вид левых частей
этих уравнений очевиден, то ограничимся определением правых частей.
Разложим силу F на три составляющие Fb F2, FB, касающиеся соответ-
ственно кривых Сь Сг, Cs, считая эти составляющие положительными в на-
правлении перемещения точки М вдоль каждой из этих кривых при увеличе-
нии только одной эллиптической координаты и при сохранении постоянными
двух других. Сообщим точке М возможное пе-
ремещение §slt при котором q2 и q& остаются
постоянными, a <7l увеличивается на bq±. Тогда
возможная работа силы F будет с одной стороны
равна Q| bqL. С другой стороны, так как работы
сил F2 и Fs будут на рассматриваемом переме-
щении равны нулю, то работа силы F будет равна
Следовательно, имеем
Рис. 175.
и точно так же
Q2 = -
f3Ym3
¦2
287. Эллиптические координаты в плоскости ху. Эти координаты
можно вывести из предыдущих формул. Чтобы получить точку М на пло-
скости хОу, достаточно в этих формулах положить z = 0, q3 = с. Тогда
точка М будет определяться двумя эллиптическими координатами q1 и q2h
которые являются корнями уравнения второй степени относительно К
представляющего софокусные конические сечения. Через каждую точку М
плоскости проходят два таких конических сечения: гипербола, соответ-
ствующая значению <?i параметра X, и эллипс, соответствующий значению q2.
Тождество B) в рассматриваемом случае принимает вид
^1 . ^_.
(l — gi)(k — q2)

ГЛАВА XIV. УРАВНЕНИЯ ЛАГРАНЖА ДЛЯ СВОБОДНОЙ ТОЧКИ 457
Можно также получить либо непосредственно, либо как предельный случай
предыдущих формул, формулы преобразования координат:
хо = (a — 9i)(« — q*)	2 = (Ь — Чд (Ь — д.-,)
Выражение ds3 квадрата элемента дуги на плоскости хОу будет
4 V 1	2 -/'
где
\$\ — ^) \Я{ — ^) J \q° — &) iq2 — b)
Отсюда
Наконец, если силу Z7, действующую на точку М в плоскости хОу, раз-
ложить на две составляющие, направленные по касательным к проходящим
через точку М гиперэоле и эллипсу (рис. 175), то получим
п ^Ж п F
Wl = 	о	. V2 =
УПРАЖНЕНИЯ
1.	Пусть гОг' — вертикальная однородная ось, продолженная неограни-
ченно в обе стороны. Все элементы этой оси притягивают материальную
точку М пропорционально их массам и обратно пропорционально четвертой
степени расстояния. Кроме того, на точку М действует,ее вес. Исследовать
движение, предполагая, что проекция начальной скорости точки М на пло-
скость MOz вертикальна. Траектория определится, если рассматривать ее
как пересечение цилиндра, параллельного Ог, и поверхности вращения,
имеющей Ог осью. Рассмотреть частный случай, когда начальная скорость
горизонтальна (лиценциатская, Монпелье).
2.	В уравнениях равновесия свободной нити под действием силы, имею-
щей силовую функцию U(х, у, г), сделана замена переменной
dt T
Эти уравнения обратятся в дифференциальные уравнения движения точки
с массой 1 под действием силы, имеющей силовую функцию -k(U-\- tif.
Используя сказанное, распространить уравнения Лагранжа на равнове-
сие нити, находящейся под действием силы, имеющей силовую функцию
(Comptes rendus, т. XCVI, стр. 688).

ГЛАВА XV
ПРИНЦИП ДАЛАМБЕРА. ПРИНЦИП НАИМЕНЬШЕГО
ДЕЙСТВИЯ
288. Принцип Даламбера. Принцип Даламбера позволяет свести
процесс составления уравнений динамики к составлению уравнений
статики.
Этот принцип, который мы здесь изложим для свободной мате-
риальной точки и для точки, движущейся по поверхности или по
кривой, применим к любой задаче динамики. Он позволит нам под-
вести итог всей теории движения точки.
Рассмотрим материальную точку М массы т, находящуюся под
действием сил, равнодействующая которых R имеет проекции Rx,
Ry, Rz. Уравнения движения этой точки могут быть написаны так:
Будем рассматривать наряду с векторами, представляющими при-
ложенные к точке М силы, вектор Ml с проекциями —т-г^,
d°-y	cPz „
—т Ttfi' —т Hf> ' с*тот вектор, численно равный произведению
массы на ускорение и направленный противоположно ускорению,
называется силой инерции, хотя это никоим образом не будет силой,
приложенной к точке. Тогда уравнения выражают, что геометрическая
сумма векторов MR и Ml равна нулю, или, что в каждый момент
времени существует равновесие между силой инерции и силами,
действительно приложенными к точке.
Вывод уравнений движения из принципа Даламбера. На осно-
вании только что сказанного, для нахождения уравнений движения
точки при любых условиях достаточно выразить, что имеет место
равновесие между всеми силами, приложенными к точке, и силой инер-
ции. Но это можно сделать методами статики. Можно, например,
применить теорему о возможной работе. Для этого нужно различать
среди сил, приложенных к точке, силы заданные и реакции связей.
Через X, Y; Z мы обозначим проекции заданных сил.
Чтобы написать, что существует равновесие между силами, дей-
ствующими на точку, и силой инерции, достаточно написать, что на

ГЛАВА XV. ПРИНЦИП ДАЛАМБЕРА НАИМЕНЬШЕГО ДЕЙСТВИЯ	459
всех возможных перемещениях 8jc, by, bz, допускаемых связями,
существующими в момент t, сумма работ заданных сил {X, Y, Z)
и силы инерции!— т ~7п < —т 7М' —т Ш) Равна НУЛЮ:
= Ь.	B)
Следует различать три случая:
1°. Свободная точка. Ьх, by, Ьг произвольны. Если, как в п. 282,
применяется произвольная система координат qv q2, q%, то, заменяя
qv q2, q3 вариациями 8^, 8^2, bq3, получим:
j дх j . dx j . dx s
где 8^^ 8^2' ^q3 произвольны.
Подставляя Ьх, by, Ьг в равенство B) и приравнивая результат
нулю при произвольных 8<71( bq2, Zq3, получим уравнения движения
в форме, указанной в п. 282, из которых мы вывели уравнения
Лагранжа для свободной точки.
2е. Точка на поверхности. Пусть
f(x, у, г, t) = 0
есть уравнение поверхности, которая для общности предполагается
движущейся. Давая переменному t определенное значение, мы видим,
что Ьх, by, bz должны удовлетворять условию
~ 8х -4- ~ о у + -г-02 = О,
дх ' ду ¦* ' dz
выражающему, что возможное перемещение допускается связью, су-
ществующей в момент t. Если, как в п. 263, выразить координаты
точки поверхности в функциях двух параметров, то получим
j дх j. , дх j
ох = з— °<7i + з— So?, . ..
dqx V1 ' dq-2 ^
и соотношение B) должно иметь место, каковы бы ни были S^t
и 8<72- Таким путем получатся уравнения движения в форме D) п. 263.
3°. Точка на кривой. Пусть
f{x. у, z, 0 = 0, Л(*, у. z, 0 = 0
— уравнения кривой. Величины Ьх, Ьу, Ьг должны удовлетворять
двум условиям

460	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Допустим, что координаты точки кривой выражены в функции
одного параметра:
х = ? (д, t), y = ty (q, t), 2=co (q, t).
Тогда наиболее общее перемещение на кривой в положении, которое
она занимает в момент t, получится, если дать величине q прираще-
ние oq. Поэтому имеем
5 дх Л * ду * Л дг *
ъх = -5- оа, о у = -/- оо, uz = -г- оо,
и уравнение B), после сокращения на множитель Zq, примет вид
/d"-x дх еру ду tPz dz\_ дх	ду	дг_
m\4F~dq'^rW dq^"aWdq~)~A ~dq~ ~^ Y ~dq~ ~^ ^ dq '
из которого мы вывели уравнение Лагранжа (п. 259).
289.	Замечание о силе инерции. Допустим, что материальная точка,
находящаяся под действием сил /*\, F^, ..., Fn и поставленная в некоторые
начальные условия, начинает двигаться. Отбросим теперь силы FbF% ...,Fn,
возьмем материальную точку в руку и сообщим ей рукой то же самое дви-
жение. Тогда действие руки на точку будет в каждый момент t равно равно-
действующей R сил Fb Fv,,..,,Fn, действовавших при первом экспери-
менте, или равному, где j—ускорение. Следовательно, по закону равенства
действия и противодействия, давление точки на руку в каждый момент вре-
мени равно и противоположно силе R или ту, таким образом, это давление
равно силе инерции. Необходимо, однако, заметить, что это давление будет
силой, действующей на руку, но не на точку.
290,	Принцип наименьшего действия. Этот принцип может быть при-
ложен к движению точки под действием силы, имеющей силовую функцию,
причем точка либо может быть свободной, либо должна скользить по непо-
движной поверхности. Принцип позволяет объединить уравнения движения
в одно, написав, что вариация некоторого интеграла равна нулю. Во втором
томе мы укажем другие принципы, как, например, принцип Гамильтона, прин-
цип Гаусса, которые применимы в более общих случаях. Принцип наимень-
шего действия был указан Мопертюи. Пример его можно найти в работе
Эйлера De motu projectorum. Лаплас, Лагранж, Пуассон излагали этот прин-
цип в форме, способной вызвать возражения. Якоби первый изложил его
в строгом виде. В Sitzungsberichte Берлинской Академии A887) можно найти
интересную статью Гельмгольца по истории принципа наименьшего действия.
Свободная точка. Если свободная точка находится под действием силы,,
имеющей силовую функцию U (х, у, z), то интеграл кинетической энергии
имеет вид
*	o, *„) + *].	A)
В принципе наименьшего действия сравниваются лишь такие движения,
для которых постоянная h имеет одинаковые значения. Таким образом, везде
в дальнейшем h является определенной постоянной. Следовательно, можн^
по произволу задать начальное положение лг0, у0, zQ движущейся точки, и
тогда ее начальная скорость определится по величине (но не по направле-
нию) из второго соотношения A). Положения движущейся точки и кривые,
которые мы рассматриваем, расположены, разумеется, в области простран-
ства, где функция
U(x,y,z) + h
положительна.

ГЛАВА XV. ПРИНЦИП ДАЛАМБЕРА НАИМЕНЬШЕГО ДЕЙСТВИЯ	461
Пусть А и В — две неподвижные точки. Тэт и Томсон называют дей-
ствием вдоль кривой С, соединяющей эти две точки, интеграл
(В)
<Л= f f2(U + h)ds,	B)
где вместо U (х, у, г) мы пишем U. Предполагается, что этот интеграл бе-
рется вдоль кривой С, элемент дуги которой обозначен через ds. Принцип
наименьшего действия может быть сформулирован следующим образом.
Кривые, соединяющие две неподвижные точки А и В и обладающие
тем свойством, что вариация действия равна нулю при переходе от одной
из этих кривых к любой другой, бесконечно близкой и проходящей через
те же точки, являются траекториями, которые фактически опишет
материальная точка, начавшая движение из одной из этих неподвиж-
ных точек в таком направлении, что она приходит во вторую.
Можно также сказать, что если среди всех кривых, идущих от точки А
к точке В, отыскивать кривые, для которых действие имеет минимум, то
эти кривые среди траекторий, соединяющих точки А и В. Это следует из
того, что для нахождения таких кривых нужно прежде всего приравнять
нулю вариацию действия.
Чтобы доказать это предложение, заметим, что интеграл Л будет вида
(В)
у (х, у, г) ds,
)
где
4{x,y,z)=Y2(U+h).	C)
Следовательно, чтобы получить дифференциальные уравнения кривых,
которые могут обратить интеграл Л в минимум, нужно применить уравне-
ния C) п. 146, заменив в них <р его значением C). Таким путем мы получим
для искомых кривых дифференциальное уравнение
ds\ дх f2(U+h)
о,
и два аналогичных. Примем за независимую переменную величину t, опре-
деленную соотношением
V™ds	E)
)
Тогда дифференциальные уравнения D) кривых, которые могут обратить
интеграл Л в минимум, станут следующими:
dPx _ dU	d"-y _ dU	d?z _ dU
m dP ~ Ш ' m~aW~~Jy" m~dT*~ dz'
Это — уравнения движения свободной точки, причем уравнение E) является
уравнением кинетической энергии с частным значением h. Таким образом,
теорема доказана.
Итак, кривые, дающие для действия Л относительный минимум, т. е.
значение, меньшее, чем вдоль всякой кривой, бесконечно близкой, нужно
искать среди траекторий, идущих от А к В. Вопрос о том, дает ли найден-
ная траектория, соединяющая две точки А и В, относительный минимум для Л,
в действительности не является существенным с точки зрения самого прин-
ципа. Он аналогичен вопросу, дает ли в действительности геодезическая линия,

462	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
соединяющая две фиксированные точки на заданной повзрхности, относитель-
ный минимум для расстояния двух точек на поверхности (см. Дарбу, Тпёо-
rie des surfaces, ч. 3, глава V). Так как коэффициент при ds в интеграле Л
положителен, то действие всегда положительно и всегда существуют кривые,
идущие от Л к В, вдоль которых имеет место минимум интеграла Л. Эти кривые
образуются траекториями. Существует также между А и В кривая, которая
дает абсолютный минимум. Эта последняя кривая, обязательно составленная из
дуг, дающих каждая в отдельности относительный минимум, состоит, следова-
тельно, из дуг траекторий.
Не существует кривых, дающих для интегралов Ж относительный мак-
симум, так как если С есть произвольная дуга, проведенная между А к В,
то всегда можно построить бесконечно близкую кривую С", вдоль которой
действие будет больше, чем вдоль С. Для этого достаточно взять в каче-
стве С синусоидальную кривую с бесконечно малыми амплитудами, прохо-
дящую С.
Точка на поверхности. Пусть на неподвижной поверхности 5 дана точка,
находящаяся под действием силы, имеющей силовую функцию U (х, у, г).
Для нее по-прежнему имеем интеграл кинетической энергии A). Будем сра-
внивать между собой движения, которые совершаются на поверхности S при
одном и том же значении постоянной h. Тогда имеем следующую теорему.
Кривые, проведенные на поверхности между двумя неподвижными
точками А и В и обладающие тем свойством, что вариация действия
равна нулю при переходе от одной из этих кривых ко всякой другой
бесконечно близкой кривой, проведенной на поверхности между теми же
точками, являются траекториями движущейся точки, соединяющими
эти две неподвижные точки.
Следовательно, если мы ищем кривые, идущие на поверхности от Л к В,
вдоль которых действие имеет минимум, то их надо выбирать среди траекторий.
Чтобы доказать это, достаточно приложить к случаю у = Y'?(U-\- h)
уравнения, которые мы дали (п. 149) для кривых, лежащих на поверхности,
и обращающих I у ds в минимум. Эти уравнения, так же как и выше, непо-
средственно преобразуются в уравнения движения точки на поверхности
с заданной постоянной h кинетической энергии.
Например, если на точку не действует никакая сила (?/=0), то траекто-
риями будут кривые, которые получатся, если искать кривые, обращающие
(В)
в минимум интеграл I У~2/г ds, т. е. если искать наиболее короткие линии
(А)
на поверхности. Получатся, следовательно, геодезические линии (п. 270).
Справедливо более общее предложение, что задача отыскания траекторий
на поверхности S при заданной силовой функции U эквивалентна задаче
отыскания геодезических линий на другой поверхности S'. В самом деле,
представим себе вспомогательную поверхность S', на которой линейный эле-
мент определяется равенством
где ds—линейный элемент поверхности 5. Тогда нахождение траекторий на
поверхности S приведется к нахождению кривых, обращающих I ds' в ми-
нимум, т. е. к нахождению геодезических линий на поверхности 5'.
Если мы на минуту вернемся к случаю свободной точки, находящейся
под действием силы, имеющей силовую функцию, то мы увидим, что на
основании принципа наименьшего действия задача определения траекторий
точки является распространением на случай трех переменных задачи о геоде-
зических линиях.

ГЛАВА XV. ПРИНЦИП ДАЛАМБЕРА НАИМЕНЬШЕГО ДЕЙСТВИЯ	463
Мы не станем входить в подробности этой теории, относящейся больше
к геометрии, чем к механике, отсылая читателя к главам VI и VII второго
тома сочинения Дарбу «Lecons sur la Theorie des surfaces».
Мы вернемся, однако, к этому принципу в аналитической механике.
УПРАЖНЕНИЯ
1.	Формулы Тэта и Томсона. Если взять две бесконечно близкие
траектории АВ и А\ВЬ то вариация действия при переходе от первой ко
второй будет
Ь<А = — V2(UA+h)- AAt cos A^AB — Y~2(LJB -f h) ¦ BB^ cos B^BA,
где UA и UB являются значениями функции U в точках А и В [эта фор-
мула совпадает с установленной в п. 147, если только заменить <р выраже-
нием /2G7+Tj].
2.	Теорема Тэта и Томсона (п. 147. 2°). Если из различных точек Мо
поверхности 5 по нормалям к ней начинают двигаться одинаковые мате-
риальные точки, для каждой из которых силовая функция есть U, а настоя-
щая кинетической энергии есть h, и если на каждой траектории взять дугу M0Mt
такую, что действие на участке от Мо до Mt этой траектории имеет определен-
ное значение, одинаковое для ссех траекторий, то геометрическим местом
точек Mi будет поверхность Sb нормальная к траекториям. Важный частный
случай этой теоремы получится, если предположить, что поверхность S
вырождается в сферу с нулевым радиусом. Тогда все траектории будут выхо-
дить из одной определенной точки Mq со скоростью, определенной по вели-
чине, но переменного направления.
Если потребовать, чтобы движение было плоским или происходило на
поверхности, то формулировка, очевидно, останется той же, если заменить
поверхности 5 и Si кривыми.
Если (J = §, то эти теоремы переходят в классические теоремы о парал-
лельных поверхностях или параллельных кривых на поверхности.
3.	Свойство, аналогичное свойству разверток. Если рассматривать
траектории АВ, нормальные в точке А к неподвижной кривой и касающиеся
в точке В другой кривой D, и если обозначить через А'В' и А"В'( два по-
ложения траектории, то можно высказать следующую теорему: действие вдоль
дуги А"В" равно действию вдоль дуги А'В', сложенному с действием вдоль
дуги В'В" огибаемой кривой D.
Та же теорема имеет место и при движении точки на поверхности для
траекторий, нормальных к неподвижной кривой.
Если U = О, то эти теоремы переходят в классические теоремы о раз-
вертках.
4.	Приложить принцип наименьшего действия к движению тяжелой точки
в пустоте в вертикальной плоскости (п. 217, рис. 139). Действие будет тогда
иметь вид
Г У~2Л — 2gy ds.
Возьмем в плоскости две точки, из которых одна — начало О, а дру-
гая — точка М1. Кривая, для которой действие от О до М\ имеет минимум,
есть одна из траекторий, по которой движется тяжелая точка, брошенная
из О со скоростью v0 = y'2h, причем так, что она достигает точки Мг. Если М1
находится внутри параболы безопасности — огибающей траекторий, выходя-
щих из точки О, то существуют две траектории, ведущие из точки О
в точку Mi- Доказать, что относительный минимум имеет, место для той
параболы, для которой точка приходит в М\ до касания с параболой

464	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
безопасности (на рис. 139 это — внутренняя парабола) (правило Якоби). Если
точка Мг достаточно близка к точке О, то дуга ОМг внутренней параболы
также дает абсолютный минимум для действия, но этого не будет, если
точка Mi близка к параболе безопасности. Так, если точка Mi находится на
параболе безопасности, например в точке А, то траектория ОА по-прежнему
дает для действия относительный минимум, но не абсолютный. Это можно
доказать, опираясь на результаты предыдущего упражнения, если приложить
их к параболе безопасности, которая рассматривается как обобщенная раз-
вертка точки О. (Рассуждения совпадают с теми, которые дал Дарбу, Lecons
sur la Theorie des surfaces, ч. З, гл. V.)
5.	Если в предыдущем примере точка Mt находится вне параболы безо-
пасности, то не существует траектории, идущей от О к Мх, но в то же время
должна существовать кривая, обращающая действие между О и Afj в ми-
нимум. Доказать, что эта кривая образована двумя перпендикулярами, опу-
щенными из точек О и Afj на прямую 2Л — 2gy — О и частью этой прямой,
заключенной между этими перпендикулярами (результат, аналогичный резуль-
тату п. 148).
6.	Исследование траекторий тяжелой точки на вертикальной плоско-
сти хОу производится так же, как исследование геодезических линий на
поверхности S', линейный элемент которой определяется формулой
ds'2 = Bft — 2gy) (dx*- + df-).
Доказать, что эта поверхность развертывается на поверхность вращения,
и составить уравнение меридиана. Если положить 2Л — 2gy = и, 2gx = v,
то вновь получится упражнение п. 271.
7.	Приложить принцип наименьшего действия к движению планет и раз-
решить для этого движения вопросы, аналогичные предыдущим D, 5 и 6).
(См. Якоби, Vorlesungen tiber Dynamik *), лекция 6.)
8.	Пусть <f(x, у, z) — положительная функция от х, у, г, а А и В — две
неподвижные точки. Кривые С, соединяющие эти точки, вдоль которых ин-
теграл I <f(x, у, г) ds имеет минимум, суть: 1) фигуры равновесия нити, для
которой натяжение есть <р, а силовая функция — <р; 2) брахистохроны
для точки массы 1, когда силовая функция равна -%-.	—- , а началь-
<?2(х, у, г)
\Г2
ная скорость в точке *0, у0, z0 равна —	-; 3) траектории свободной
<Р (¦% Уо> го)
точки массы 1 для силовой функции у2 (х, у, г) при начальной скорости,
равной Y2-f(x0' Уо- го)- ((-'м- Андуайе, Comptes rendus, т. С, стр. 1577;
Викер, т. CVI, стр. 458.)
9. Те же теоремы имеют место и для кривых, проведенных на непо-
движной поверхности и обращающих I <f ds в минимум.
10. Кривая, описываемая точкой под действием заданной силовой функ-
ции, обращающая в минимум интеграл I vn ds, где v = V (U + h), имеет
в каждой точке К, радиуса кривизны р, направленный по той же прямой, что
и радиус кривизны р1 траектории, которую движущаяся точка описала бы,
если бы она оказалась в положении К, свободной; при этом р = pj/Л и
когда п < 0 откладывается в сторону, противоположную той, куда отло-
жен радиус кривизны pj.
Наиболее интересным случаем будет тот, для которого п = — 1; тогда
кривая будет брахистохроной. Таким образом вновь устанавливается связь
*) Имеется русский перевод (ОНТИ, 1936). (Прим. перев.)

ГЛАВЛ XV. ПРИНЦИП ДАЛАМБЕРА НАИМЕНЬШЕГО ДЕЙСТВИЯ	465
между траекториями и брахистохронами, указанная в упражнении 8. (В и к е р,
Savants etrangers и статья Жор дана, Comptes rendus, т. CVIII, стр.330.)
11. Вывести из принципа наименьшего действия уравнения Лагранжа.
Возьмем, например, случай свободной точки, отнесенной к системе коор-
динат qh q2, qz. Функция U будет функцией этих координат, а
ds = яи dq^ -\- ...-(- 2ai0 dq^ dq2 -\- .. ¦
Теперь нужно определить qlt q% q?, в функции вспомогательного пере-
менного q таким образом, чтобы интеграл
Ь
был минимумом. Делая в полученных уравнениях замену переменной по фор-
муле E) на странице 811, получим уравнения Лагранжа. Согласно упражне-
нию 8 мы приходим, таким образом, к возможности приложения уравнений
Лагранжа к фигуре равновесия нити. (Comptes rendus. т. XCVI, стр. 668.)

ГЛАВА XVI
КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМА ЯКОБИ.
ПРИЛОЖЕНИЯ
291. Историческая справка. Уравнения движения свободной
точки или точки, движущейся по поверхности или по кривой как
подвижным, так и неподвижным, были составлены Лагранжем в одина-
ковой для всех этих случаев форме с той лишь разницей, что число
параметров, подлежащих определению в функции времени, равно
трем для свободной точки, двум для точки на поверхности, и одному
для точки на кривой (пп. 259, 263, 282). Мы увидим дальше,
что уравнения самой общей задачи динамики системы могут быть со-
ставлены в этой же форме, но число параметров будет каким
угодно, при условии, что связи могут быть выражены в конечной
форме и что эти параметры действительно являются коорди-
натами.
Излагаемые ниже преобразования и теоремы применимы только
в том случае, когда проекции X, Y, Z равнодействующей заданных
сил, приложенных к точке, суть частные производные функции
U(t, х, у, z), которая может содержать явно время /. Уравнения
Лагранжа будут тогда иметь вид:
где v— 1, 2, 3 для свободной точки, v= 1, 2 для точки на поверх-
ности и v = 1 для точки на кривой. Мы будем вести изложение,
предположив для определенности, что точка свободна, v=l, 2, 3;
тогда будут три уравнения и три параметра qlt q2, q3. Но, как мы
увидим, выкладки не будут зависеть от числа уравнений A).
Преобразование, начатое Пуассоном и законченное Гамильтоном,
позволяет написать уравнение в форме, которая содержит частные
производные только от одной функции и которая очень удобна для
теоретических исследований.
Эта форма привела Якоби к замечательной теореме об интегри-
ровании уравнений движения.

ГЛАВА XVI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМА ЯКОБИ	467
I. Канонические уравнения. Теорема Якоби
292. Преобразование Пуассона и Гамильтона. Пуассону при-
надлежит идея принять за переменные величины
дТ	дТ	дТ
Pi = ~гт • Рг = ~гт • Ръ = -—г ¦	B)
dq1	dq2	dq3
Эти уравнения, будучи линейными относительно q'v q'r q'3, так
как Т есть квадратичная функция этих величин, могут быть раз-
решены относительно q', q'2, q'3 в виде:
^=/i(<7i> Яг. Яз. Р\. Рг> Рз- 0> ]
я'2 = А(Я1. Яг. <7з. A. Pi' P> t), 1	C)
<7з = /зО71> Яг< Яг. Pi. Рг. Pi. t). j
Посмотрим, во что обратятся уравнения Лагранжа, если в них
заменить q'v q'9, q'3 этими выражениями.
Прежде всего, первые члены уравнений A) -г (—Г\ обратятся
at \ dq, J
просто в -р.
Для преобразования второго члена — ^— дадим в выражении Т
переменным qlt q2, q3, pv p2, ръ произвольные бесконечно малые
приращения S^i- ^Яг< ^Яъ> %Pv ^Pz> %Рз> оставляя переменную t постоян-
ной. При этом величины q'v q'2, q'^ получат приращения 8^, 8^, S^,
определяемые соотношениями C), в которых t остается постоянным.
Тогда функция Г, зависящая от qv q2, q3, pt, p2, p3 и /, получит
приращение ЪТ, определяемое формулой
dq-i.	dq2	dq^	dqx	dq2	dq3
или в силу уравнений B)
87 = Щх ^ + 5^	^
что можно написать так
^ 8<7i + ^3 8?2 + ^ 89з - 9l 8Pl — q2
Полагая для краткости
20* Зак. 851. П. Аппель, т. I

468	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
представим это равенство в виде
дТ	дТ «	дТ
что является первым выражением для дифференциала ЪК. С другой
стороны, допустим, что К выражено при помощи системы новых
переменных qx, q2, q3, pu p2, p3, t. Когда qu q2, q3, pu p2, p3 полу-
чают рассматриваемые произвольные приращения, тогда оК опре-
деляется формулой
оК=~Ь 4-—о -4-~ 3 -t- — S 4- —3 -4- —S
Это выражение должно совпадать с первым, каковы бы ни были
3<7i> 3^2. 3?з> 3/?i, §р2, ^Рз- Следовательно,
_дТ_ = дК_ i _дК_ Cv — 1 2 34	D)
В этих уравнениях частные производные берутся в предположении,
что Т выражено через qv q2, q3, q'v q'r q'y а К выражено через
Qv Чг< Яз< Р\< Рг> Рз- В силу уравнений D) уравнения Лагранжа A)
принимают вид
Рассмотрим разность
Я=/<— U.
Функция U, зависящая только от х, у, 2, t, выражается через t и
через переменные qlt q2, q2, в то время как К зависит от времени,
от переменных qt, q2, q3 и еще от переменных рх, рг, р3. Таким
образом, имеем
др.,~~ д~р~~,' ^ dq~, ~~ W,
и уравнения E), если полагать последовательно v=l, 2, 3, обра-
тятся в следующие:
dt ' дрг'	dt dp?'	dt дря' I	.„.
dpi	 дН dp?	 дН dp?,	 дН i
dt	dqt' dt	dq^' dt	dqn' J
Это и будут канонические уравнения движения, данные Гамиль-
тоном. Они будут первого порядка и число их равно шести. Они
определяют шесть переменных qv q2, q3, pv p2, ръ в функции вре-
мени и шести произвольных постоянных. Для определения движения
системы достаточно найти значения параметров <?,, q2, q3 в функции
времени, так как только они участвуют в определении положения
точки.

ГЛАВА XVI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМА ЯКОБИ	469
293. Частный случай, когда выражения х, у, г через qu q2, q3
не содержат явно времени. Вычисления упрощаются, если опре-
деление новых координат qx, q2, q3 не зависит от времени, т. с.
если выражения х, у, г через qv q2, qa не содержат t. Тогда будет
к=т.
В самом деле, в этом случае Т будет однородной функцией второго-
порядка относительно q'v q'2> q's и мы получим (пп. 261, 265, 283)
,дТ. ,дТ . ,дТ О7,
dqx	dq2	dq3
Но на основании уравнений B) левая часть представляет собой не
что иное, как р^[~\-p2q'2-{-p3q'r Следовательно,
и функция Гамильтона Н принимает вид
T — U.
В этом случае преобразования, которые надо выполнить, чтобы
перейти от квадратичной формы Т, выраженной через q'v q'2, q'3,
к форме Т, выраженной через ри р2, р3, совпадают с теми, которые
надо выполнить для перехода от квадратичной формы к форме
сопряженной, как, например, для перехода от уравнения конического-
сечения в точечных однородных координатах к его уравнению в одно-
родных тангенциальных координатах.
Если положить
27 - anqf + a^fi + a^ + 2a12q[q2 + 2a^'2q'3 + 2а31 q'3q[,
или в более сжатой форме
2Т = 2 аач'$'к (aik = flfti).
то получим
1
Р2 = ~гт = a2iq[ + a22q2 + a2Sq's,
Рз = -/-= asiq[ -f «32^ + «339з-

470	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Отсюда, обозначая через D дискриминант квадратичной формы, т. е.
определитель девяти величин aik, а через Aik — -3	минор, со-
tic
ответствующий элементу а^, получим
Я', = -^ (AnPi + Алр2 + Av3ps) (v = 1, 2,3),
и поэтому
294. Примечание. Для того чтобы выполнить преобразование Гамиль-
тона, нужно было предположить, что уравнения B) разрешимы относи-
тельно qv q2, q3. Такое разрешение всегда возможно. Возьмем, например,
случай, когда равенства, определяющие значения новых переменных, не содер-
жат явно времени. Тогда Т будет однородной функцией второго порядка, т. е,
квадратичной формой относительно qv q2, q's, и определитель из коэффициен-
тов при неизвестных в уравнениях B) будет дискриминантом этой квадра-
тичной формы. Если он равен нулю, то можно найти систему значений (^Л ,
\Ч-2) • (9з) для Qv Q2' Q® не равных одновременно нулю, для которых все
частные производные от Т относительно этих переменных обращаются в нуль.
Но это невозможно, так как на основании соотношения
о_ / дТ , / дТ . , дТ
2Т 11^г + 41гт+<1зТг
aq1	aq2	dq3
эти значения переменных обратят в нуль и функцию Т, а так как Т является
кинетической энергией, то оно не может обратиться в нуль при веществен-
ных значениях qv q2, qs, т. е. при действительном движении точки. Мы
видим, таким образом, что рассматриваемый определитель действительно
всегда отличен от нуля и разрешение уравнений B) всегда возможно.
Если выражения х, у, г через qlt q%, q3 содержат явно время, т. е.
х = ? (ft, qo, <73. 0. У = Ф (?1, Чъ> Чъ> 0. г = а> (qv qb qz, t),
то кинетическая энергия
Бе будет больше однородной относительно q[, qt, q'z. Но определитель коэф-
фициентов при qv q2, q3 в уравнениях B) будет тогда дискриминантом
квадратичной формы
получаемой, если взять в Т члены второго порядка. Этот дискриминант не
может быть равен нулю, ибо в противном случае функция 7^ обращалась
бы в нуль при вещественных значениях qv q2, qz, не равных нулю одно-
временно. Но тогда существовало бы возможное перемещение точки, полу-
чающееся, если, оставляя t постоянным, изменить #i> Q">, Is- и Для этого
1 Ъ* Ь S2 + ?
#i Q Is
1 Ъх* -Ь Sy2 + ?г- ri ,
перемещения возможная кинетическая энергия -^-пг	 ' ¦	 была бы
равна нулю, что невозможно.

ГЛАВА XVI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМА ЯКОБИ	471
295. Интеграл кинетической энергии. Мы видели раньше, что
в случае, когда существует силовая функция U(x, у, г), имеется
интеграл кинетической энергии вида
Мы убедились в этом (пп. 261, 265, 283), предполагая, что вы-
ражения х, у, z через qt, q2, q3 не зависят от времени. Таким
образом, получается первый интеграл канонических уравнений, ко-
торый может быть выведен из них непосредственным вычислением.
Чтобы убедиться в этом, предположим по-прежнему, что выра-
жения х, у, z через qv q2, q3 не содержат t. В этом случае ни Т,
ни U, ни Н, которое равно Т—U, не содержат t. Если теперь
предположить, что в функции Н параметры qv q2, q3 и величины рх,
р2, р3 заменены выражениями, которые они должны принять в функ-
ции времени в силу уравнений F), то на основании теоремы о слож-
ных функциях получим
dH 	 дН dqt , дН dq-> . дН dq^ .
' | "Л/Г Tt г"
dt dqt dt > dq-г dt ' dq3 dt
дН dpi дН_ dp^
' др± dt ~т~ др2 dt '
dp± dt ' dp2 dt ' dp3 dt
Но' на основании канонических уравнений имеем
дН dq, . дН dp, _ дН дН дН дН _
dq, dt ' др., dt dq., dp, др., dq,
и остается
—r- = 0 или Л = й, или Т—U = h.
dt
Если выражения х, у, z через qv q2, q3 зависят от времени,
то Н не будет больше равно Т — U и не будет существовать инте-
грал H=h. В этом случае Н будет содержать явно время и полная
dH
производная —тг, взятая в предположении, что <7i> q2, ,q3, pv p2, p3
рассматриваются как функции t, будет содержать' еще один член,
а именно: частную производную —^т- от функции Н по содержащейся
в ней явно переменной t, и после предыдущих сокращений получится
dH _ dH
dt ~ dt '
296. Пример. Центральная сила — функция расстояния. Приведем
для примера к каноническому виду уравнения движения точки на плоскости
под действием центральной силы, являющейся функцией расстояния. Примем
центр сил за начало координат и введем полярные координаты гиб, ко-
торые будут играть роль параметров ql и q?i. Полагая массу равной единице,
получим для кинетической энергии выражение

472	часть третья, динамика точки
Силовая функция U является функцией переменного г, т. е. U = f (r).
Так как Т однородно относительно г' и в', то
Я = Г - ?/= I (г'2 + г26'2) - Y (г).
Переменные р± и р2 определяются уравнениями
откуда получаем
Следовательно, выражение Н в этих новых переменных будет иметь вид
и канонические уравнения будут
dr 		dd р9
dp, pi
Эти уравнения определяют г, 0, рх и рг в функции ^. Из последнего
уравнения имеем ръ = С, и, подставляя во второе, получим г2 -^- = С, что
является уравнением площадей. Исключая рг из первого и третьего и за-
меняя ръ величиной С, получим уравнение
которое было выведено непосредственно в главе XI, как уравнение, опре-
деляющее движение по радиусу-вектору.
Теорема кинетической энергии выражается уравнением Т—U — h
или H = h.
II. Теорема Якоб и
297. Теорема Якоби. В канонических уравнениях F) Н является
функцией второй степени относительно pv p2, р3. Теорема Якоби
справедлива для любых уравнений вида F), в которых Н является
произвольной заданной функцией от рх, pv p3, qv q2, q3, t. Мы
будем писать ее в виде H(pl, p2, p3, qit q.2, q3, t), чтобы сделать
явными входящие переменные. Основа теоремы Якоби заключается
в том, что канонические уравнения являются уравнениями характе-
ристик дифференциального уравнения с частными производными
первого порядка
+н	"qд

ГЛАВА XVI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМА ЯКОБИ 473
определяющего V в функции qx, q2, q3, t, рассматриваемых как не-
зависимые переменные. Леиая часть этого уравнения получается, если
к члену —yjt добавляется функция, в которую обращается Н, когда
dV dV dV
в нем заменяют рх, р2, рг производными -=—, -^—, -^—.
Гамильтон показал, что если известен общий интеграл уравнений
движения, представленных в канонической форме, то из него можно
вывести полный интеграл этого уравнения с частными производными.
Якоби дополнил эту теорему, доказав, что, обратно, если известен
какой-нибудь полный интеграл этого уравнения с частными произ-
водными, то из него можно получить общий интеграл уравнений
движения. Как мы только что говорили, это уравнение с частными
производными, которое мы будем называть уравнением Якоби,
подобрано таким образом, что уравнения движения F) являются для
него дифференциальными уравнениями характеристик согласно извест-
ному методу интегрирования уравнений с частными производными
первого порядка. Мы не будем, однако, пользоваться этим методом.
Выясним сначала, какую форму должен иметь общий интеграл
канонических уравнений. Уравнения F) образуют систему шести
уравнений первого порядка, определяющих qx, q2, q3, рх, p2, р%
в функции t. Их общий интеграл представляется уравнениями вида
<7v = ^\(?. ai' аг> аъ> *i> *2> *з)>
pv = Ow(t, ах, а2, a3, bv b2, b3)
(v=l, 2, 3) с шестью произвольными постоянными ах, а2, с;>
Ьх, Ьг, Аз-
Уравнение с частными производными первого порядка (J) опре-
деляет некоторую функцию V переменных qx, q2, q3, t, рассматри-
ваемых как независимые. Известно, что по Лагранжу полным инте-
гралом уравнения с частными производными первого порядка
называется решение этого уравнения, содержащее столько произволь-
ных постоянных, сколько в нем содержится независимых переменных.
В рассматриваемом случае полный интеграл должен содержать четыре
произвольных постоянных. Но уравнение (J) содержит только произ-
водные от V. Поэтому, если оно обладает каким-нибудь решением V,
то оно будет иметь и другое решение V-\— const. Следовательно,
для того, чтобы иметь полный интеграл, достаточно найти решение
У(<?1> <72. <7з- t, ax, а2, а3)	(С)
с тремя произвольными постоянными ах, а2, аъ, из которых ни
одна не является аддитивной; тогда функция V +const, будет
полным интегралом. Эта последняя постоянная, которую можно
всегда добавить, не играет никакой роли в теореме Якоби. Последняя
формулируется следующим образом: если для уравнения (J) найден
полный интеграл вида (С), то конечные уравнения движения*

474	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
дающие общий интеграл системы канонических уравнений, будут
дУ_ __ _^К._Л dV __
__ дУ	_ дУ	__ dV
dq± ' 2 dq2 '	dq3 '	*• 2
где bit b2, b3—произвольные постоянные.
Три уравнения (JJ, разрешенные относительно qv q2, q3, опре-
деляют эти величины как функции времени и шести постоянных av
а2, а3, bv b2, b3. Если эти значения подставить в уравнения (J2), то
последние определяют ри р2, р3 в функции времени и тех же по-
стоянных. Необходимо показать, что полученные таким образом вы-
ражения являются общим интегралом канонических уравнений
dt~dp,' dt — dq, ly—L.-.V-	W
Уравнения (Jx) образуют систему трех совместных уравнений
относительно qv q2, q3, t, определяющих qlt q2, q3 в функции t.
Будем искать производные от qv q2, q3 no t по теореме о неявных
функциях, для чего продифференцируем уравнения (J,), рассматривая
в них qv q2, q3 как функции t. Таким путем получим:
. dW dqt , dW dq,	dW dqb _
' da^ dqt dt ' dat dq2 dt ' da^ dq3 dt	'
аг dt ' da^ dqt dt ' dat dq2 dt ' da^ dq3 dt
dW dqt	dW dq2	&V dg3
"г" da^dqx dt ~1r da,dq2 dt ' da2dq& dt	'
da2dt ^ da2dql dt '^ да*дд2 dt ' da2dq3 dt
d°-V , d?V dqt . dW dq2 . d"±V иЧЧ п
да3 dt ~ das dq± dt ~r das dq2 dt ' das dq3 dt	J
dqY
Из этих трех уравнений первой степени можно найти
dq9 dq3	,
~1Г' ~Ж~ и НУЖНО убедиться в том, что значения этих производных
удовлетворяют уравнениям F), т. е., что они равны соответственно
дН дН дН „	,
производным -д—, -5—, ——. Но так как в общем случае система
OPl	°Pi dP3
уравнений первого порядка имеет только одно решение, то доста-
точно убедиться, что уравнения G) удовлетворяются, если в них
dq± dq, dq*	дН дН дН „
вместо -~, —^г, -±г подставить -з—, ——, -^—. Достаточно,
dt dt at	дрх др2 дря
например, проверить, выполняется ли тождество
д"-У	д"-У дН , д"-У дН , д"У дН __
da^dt ' da1dq1 dpt ' da1dq2 др2 ' da1dq3 др3	^ '
после того как в нем величины qlt q2, q3, plt p2, p3 будут заменены
их значениями в функции t и шести произвольных постоянных, полу-
ченными из уравнений (Jx) и (J2). Но мы сейчас докажем, что это
уравнение является тождеством относительно qx, q2, q3, t, av a2, a3,
если в нем заменить pv p2, p3 их значениями (J2). В самом деле,

ГЛАВА XVI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМА ЯКОБИ	475
если в уравнение (J) подставить вместо v полный интеграл (С),
то полученное от этой подстановки равенство будет тождественно
равно нулю, каковы бы ни были qv q2, q.u t, av а2, й3. Частные
производные этого равенства относительно каждой из величин
Qv Яг< Яз< t, #i, а2, as будут также тождественно равны нулю. Напи-
шем, что частная производная по аг уравнения (J) равна тожде-
ственно нулю:
' I	/ ДТ/ \ Я/у. Ал	I	/ Л1/ \ Л/, An	"• '" /
)	d
так как левая часть равенства (J) зависит от ах через член —,— и вели-
чины -5— , -д—, -5—., входящие в Н. Зто тождество (8 ) в точности
<% dq2 dq3	ч '-
выражает то, что мы хотим доказать, а именно, что выражение (8)
является тождеством, когда в нем plt p2, р3 заменены значениями (J2).
Точно так же убеждаемся, что подстановка значений -^—, -^—, -^—¦
дрх др2 дрЛ
вместо -—, —~-, ~- в два других уравнения G) обращают их
в тождества.
Мы доказали, что значения qv q2, q3, определяемые уравнениями (J^,
dq., дН	,
удовлетворяют уравнениям —-~- = -т—; остается убедиться в том,
что значения pv p2, р3, определяемые уравнениями (J2), удовлетво-
ряют уравнениям
dp., __ дН
dt	dq^ '
Проверим это для pv Так как -^— зависит от t непосредственно
и через qu q2, q3, то из уравнений (J2) получим
dPl 	 д^У	. V- У и.Щ .	U- V	и.Ч:>
dt dq± dt dq\ dt dq1 dq9 dt dq1 dq3 dt
Требуется показать, что полученное выражение для —~- совпадает
-\ ТТ
с выражением	^—^в силу равенств (JJ и (J2). Но мы только что
dqx dq<y dq4	дН дН дН
доказали, что —¦, -~ , -~ совпадают тождественно с ^—, ^—, ^—;
dp,
подставляя эти значения в вышенаписанное выражение для —^~ и
дН
приравнивая результат величине	-,—, мы получим уравнение
д?У dW дН	д*У дН	д^У дН _ дН
~А Л	*	А~% Д	'	!л	А	1 ~л	^	 	' 		"* I	(У)

476
ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
которое должно быть тождеством в силу равенств (Jt) и (J2). Пока-
жем, как мы это делали выше, что оно тождественно удовлетво-
ряется при замене pv рг, р3 значениями (J2). Действительно, если
подставить в левую часть уравнения Якоби (J) полный интеграл V,
то результат такой подстановки будет тождественно равен нулю при
любых значениях qx, q2, q3, t, av a2, a3. Следовательно, производ-
ная этой левой части по qx будет также тождественно равна нулю.
Написав это, получим уравнение
dt
дН
&*У
^ 2 Г
дН
дН dW
(dV\ dqx dq2 " /dV\
\dq2)	\dqj
= 0, (90
выражающее, что равенство (9) обращается в тождество, если в нем
dV dV dV
вместо pv p2, Рз подставить _,_,_.
Таким образом, теорема Якоби доказана. Интегрирование урав-
нений движения сведено, следовательно, к нахождению полного инте-
грала уравнения (J). Наоборот, если бы мы пожелали классическими
методами проинтегрировать уравнение Якоби, то нам пришлось бы
сначала проинтегрировать канонические уравнения. Можно, сказать,
что две задачи анализа: интегрирование канонических уравнений и
нахождение полного интеграла уравнения (J) — эквивалентны в том
¦смысле, что решение одной задачи влечет за собой и решение другой.
Примечание. Мы допустили, что система уравнений первой сте-
dql dq<± dq%
пени G) относительно
¦определитель
—~
—тр, ~гг
имеет только одно решение, т. е. что
Д =
д'-V	д°-У
дах
д"-У	д"-У	д"-У
дао dqx да2 dq2 дао dqs
d"-V	д-У	d^V
не равен нулю. Но этот определитель является функциональным определи-
dV dV dV	.
телем производных -=—, -г—, -^—, рассматриваемых	как функции от aL, a2,
до-\ dqo 0q^\
дУ dV	dV ?
а*. Если этот определитель равен нулю, то -^—, -,—, -^— будут связаны
oqx oqo	с^з
соотношением вида
Ф(^,^ iiiUo	do)
\ dqx dq-> dq^)
с коэффициентами, не зависящими от ах, аъ д3, т. е. являющимися функ-
циями от qx, q?, q3, t. Но тогда функция V не будет больше полным инте-
гралом уравнения Якоби, так как она удовлетворяет не только уравнению
Якоби, но еще и уравнению A0), которое не содержит t и поэтому отли-
чается от уравнения Якоби. Но, как известно, существенным свойством пол-
ного интеграла является то, что по исключении содержащихся в нем постоян-

ГЛАВА XVI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМА ЯКОБИ	477
ных мы придем к заданному уравнению с частными производными, но не
к какому-либо другому. Поэтому определитель Д не может равняться нулю
(см. Гурса, Equations aux derivees partielles, стр. 97).
Из того, что Д не равно нулю, можно заключить также, что шесть
постоянных, входящих в интегралы (Jj) и (J2) канонических уравнений,
действительно различны, т. е. что можно определить а^, а?, а3 таким обра-
зом, чтобы при t = t0 величины qlt q?, q^ приняли произвольные значения,
после чего можно определить bb bo, Ьъ так, чтобы при t — t0 вели-
чины pi, р2, рз тоже приняли любые наперед заданные значения.
298. Частный случай, когда t не входит явно в коэффи-
циенты уравнения Якоби. Такой случай имеет место в механике,
когда выражения х, у, z через qv q2, qs не содержат явно времени
и когда имеется силовая функция U (х, у, г). Тогда, как мы видели
в п. 293,
H(Pv Рг> Ps' <7i> <?2> qs) = T — U,	A1)
где Т — квадратичная форма от рг, р2, р3. В этом случае можно
удовлетворить уравнению Якоби функцией V вида
V-^ — ht-\-W,	A2)
где h — постоянная, a W — функция от qb q2, q3, но не от t.
Подставляя эту функцию V в уравнение (J) Якоби и замечая, что
dV ___	dV dW
dt — "• dq,, — dq4 '
мы получим для определения W уравнение
dW diV dW
g
Достаточно будет определить полный интеграл W (qt, q2, д3> а. Р. Щ
этого уравнения (J'), содержащий, кроме h, две постоянные аир,
из которых ни одна не является аддитивной. Тогда, приняв
q2, qs, a, p, /г),
получим полный интеграл уравнения Якоби с тремя постоян-
ными а, р, h, играющими роль постоянных av a2, а3.
Интегралы (J{) и (J2) уравнений движения, если через а', C' и —10
обозначить другие постоянные, играющие роль Ь1з Ьг, Ь3, будут
тогда иметь вид:
dW	dW	dW
P
Первые два уравнения (З'Л, не содержащие t, определяют траек-
торию движущейся точки в системе координат qlt q2, q3. Третье
уравнение определяет время, затрачиваемое для прихода в какое-
нибудь место на этой траектории.

478	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Постоянная h будет тогда постоянной интеграла кинетической
энергии. Действительно, уравнение (J') в силу значений вели-
dW dW dW	/r,N ,
чин -д—, -д—, -5— в уравнении (J9) обращается в следующее:
i Ocli °Чъ	ч i>
H(pv p2, р3, 4l, q2, g3) — h = 0,
т. е. в интеграл кинетической энергии (п. 295).
299. Геометрическое свойство траекторий. Докажем следую-
щее геометрическое свойство: Если постоянным а, C, h придать
произвольные фиксированные значения, а постоянные а.', C' изме-
нять, то траектории, определяемые двумя первыми уравне-
ниями (З'Л, будут нормальны к поверхностям, имеющим урав-
нение W = const.
Эту теорему легко доказать, если воспользоваться декартовыми
координатами, как мы это покажем в следующем пункте в качестве
упражнения. Здесь мы докажем эту теорему в любой системе координат,
чтобы иметь способ доказательства, который мог бы быть пригоден
в дальнейшем при рассмотрении движения системы.
Заметим, что необходимое и достаточное условие перпендикуляр-
ности двух бесконечно малых перемещений dx, dy, dz и Ьх, by, bz
имеет вид
Если мы, в частности, допустим, что dx, dy, dz являются дей-
ствительным перемещением движущейся точки по траектории за про-
межуток времени dt, а Ьх, Ьу, Ьг— произвольное перпендикулярное
к нему перемещение, то, разделив условие ортогональности на dt и
обозначив через х', у', z' производные от х, у, z no t, мы можем
написать его в виде
bz = Q.	A3)
При переходе от декартовых координат к новым координа-
там qv q2, <73 мы полагали
х = ? (<7i, q2, <7з). y = *?{qi, <72. <7з)> г = со (qv q2, q3).
Отсюда
„/	 ду ,. а?
х —й^1 + -5гГ
Далее
dqt 41 ' dq-2 чг ' dq3 46' ' '
где bqv bq2, bq3 — бесконечно малые вариации координат qu q2, q3,
соответствующие перемещению Ьх, Ьу, Ьг. Если вспомнить, что кине-
тическая энергия выражается в виде

ГЛАВА XVI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМА ЯКОБИ 479
то условие ортогональности A3), как это легко проверить, можно
представить в виде
-гт 8<7i + -гт 8<?2 + —т §9з = О,
<ty	dq	dq
или, на основании принятых ранее обозначений, в виде
=O.	A4)
Вернемся теперь к интересующей нас теореме. Мы хотим доказать,
что траектория точки, определенная как указано в формулировке,
нормальна к той из поверхностей
W(qv <72, q3, а, $, А) = const.,	A5)
которая проходит через рассматриваемое положение движущейся
точки. Для этого достаточно показать, что скорость х', у', z' дви-
щущейся точки перпендукулярна к любому перемещению bqv bq%, bq3,
происходящему по поверхности A5), т. е. удовлетворяющему условию
dW * , dW ъ , dW s .
Другими словами, достаточно показать, что это условие A6) необ-
ходимо влечет за собой условие, ортогональности A4). Но это оче-
видно на основании теоремы Якоби, так как значения pv p2, р3.
вытекающие из этой теоремы [уравнения C'2\ предыдущего пункта],
будут
dW	dW	dW
P	P	P
Следовательно, условие A6) влечет за собой равенство A4) и
скорость точки, будучи нормальной к любому перемещению, совер-
шаемому по поверхности W — const., нормальна к этой поверхности.
300. Декартовы координаты в пространстве. Предположим, для про-
стого примера, что д1г q%, qs обозначают декартовы координаты:
x = qb y = q* z= q3,
/	Г	Г	/.	I
х =qv У =q2, ? = <Is
и примем для простоты массу материальной точки, равной единице. Тогда
Г = 1 (*'* + /*+г'2),
и если допустить, что существует силовая функция U{x, у, z), то функция
Гамильтона будет
HTU

480	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Необходимо выразить эту функцию через переменные х, у, г и вспомо-
гательные переменные pit р%, р3, определяемые формулами
дТ	дТ	дТ ,
x	y	Z
так чтобы функция Гамильтона приняла вид
— U (х, у, z).
Вследствие этого канонические уравнения будут
dx _	dy _	dz _
rfpj 	 dU dp->t 	 dU dps dU
~W = l)x'' ~dT=~d~y~' ~dT = 'dz''
Исключение переменных р из этих уравнений приведет, очевидно, к обыч-
ным уравнениям движения.
Посмотрим, что дает в этом случае метод Якоби. Этот метод состоит
в том, что нужно найти для дифференциального уравнения
dV 1 17 dV\2 I dV\2 / dV\S]
-W + l[\d7) +['dy') +\ЧГ) \~U{x'y'z) = 0
полный интеграл, т. е. интеграл, содержащий три не аддитивные постоян-
ные. Так как время не входит явно в это уравнение, то можно положить
V= — ht+ W(x, у, z),
где h — постоянная, и достаточно, чтобы функция W удовлетворяла соотно-
шению
¦-U + k.	(У)
Если для этого уравнения с тремя переменными будет найден полный
интеграл
W(x, у, z, а, р, К),
содержащий две новые постоянные а и {3, из которых ни одна не является
аддитивной, то теорема Якоби показывает, что конечные уравнения движе-
ния будут
i^	IE	dW
да -а' д? ~Р'	t + ~W f°-
Два первых уравнения представляют траекторию, а последнее опреде-
ляет время, затрачиваемое движущейся точкой для прихода в какое-нибудь
положение на ее траектории. Кроме того, для рь р?, р3 получаем значения
dV	dV	dV
р	Р
и так как рь ръ ръ равны здесь х', у', z',	а V равно —ht -\- W(x, у, z),
то имеем
, _ dW , __ dW	, _ dW
~~ ~спГ' у ~ ду '	~ dz '

ГЛАВА XVI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМА ЯКОБИ	481
Эти формулы определяют проекции скорости точки, выраженные	в функ-
ции ее координат через частные производные одной функции W.	Так как
эта функция удовлетворяет уравнению (J")> то
что представляет собой не что иное, как интеграл кинетической энергии.
Следовательно, Л, как мы уже видели, является постоянной интеграла кине-
тической энергии.
Мы можем, между прочим, легко проверить геометрическое свойство
траекторий. Дадим постоянным а, р, ft какие-нибудь определенные значения.
Написанные выше выражения для х', у', г' через частные производные
функции W показывают, что в каждой точке (х, у, г) скорость нормальна
к той из поверхностей W— const., которая проходит через эту точку. Но
скорость касается той из траекторий
dW , dW „,
да	 dp """
которая получается, если а' и р' подобраны так, чтобы эта траектория про-
ходила через рассматриваемое положение движущейся точки. Следовательно,
все траектории, получающиеся при изменении я' и р', нормальны к поверх-
ностям W = const. Это и является геометрическим свойством траекторий,
установленным выше в общей системе координат qlt q2, ?з-
III. Плоское движение. Движение по поверхности
301. Общие положения. Очевидно, что все вышеизложенное
прилагается к движению на плоскости или к более общему слу-
чаю,— движению на поверхности, при условии использования двух
координат ql и q2 вместо трех. Функция
зависит тогда от ри р2, qlt q2 и t, и уравнение Якоби имеет вид
Если известен полный интеграл V(ql, q2, t, av a2) с двумя про-
извольными постоянными аи а2, из которых ни одна не является
аддитивной, то конечные уравнения движения будут
dV _,	dV _,
__ dV	_ dV
Pi-Sq^- p*-jj;-
Если система координат qv q2 определена независимо от времени
и если функция U не зависит явно от времени, то время t не будет
входить в коэффициенты уравнения (J). Тогда можно положить
qlt qt, a, h),
31 Зак, 851. П. Аппель, т. I

482	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
где W(qv q2, a, h) — полный интеграл уравнения
W dW
- *¦ *)-°	<*>
с неаддитивной постоянной а. Уравнения движения будут тогда
dW _ , 	 dW _
да	*	' dh
причем первое из них является уравнением траектории. Кроме того,
_dW_	_ dW
Pl dqx ' ^2 dq2 '
Траектории, получающиеся при изменении а', нормальны
к кривым W = const.
Рассуждения, совпадающие с изложенными ранее для движения
свободной точки, позволяют установить и эту теорему.
Условие ортогональности скорости х', у', г' и перемеще-
ния Ъх, Ьу, Ьг будет
lz = Q.	(a)
На поверхности в рассматриваемом случае будем иметь
* = <P(<7i. <72)> У =
Кроме того,
dqo, 4
%-
dq2
Условие (а) можно тогда написать так:
dq1	dq2
или
Л8?1+А8?2 = О-	(«О
Чтобы установить, что траектории —^— = а' ортогональны
к кривым
W(qlt q2, a, h) = const.,	(b)
достаточно показать, что скорость точки ортогональна к пере-
мещению 8ft, 8<72, лежащему на этой кривой, т. е. к перемещению,
удовлетворяющему соотношению

ГЛАВА XVI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМА ЯКОБИ	483
_ - dW dW
Но по теореме Якоои ¦ , ¦ и -д— равны р1 и р2 и, следова-
тельно, условие (с) влечет за собой условие ортогональности (а').
302. Параболическое движение тяжелой точки в пустоте.
Примем, как и в п. 217, горизонтальную ось в плоскости траектории за
ось Ох, направленную вверх вертикаль — за ось Оу и введем декартовы
координаты х и у. Полагая т = \, найдем U — — gy, и уравнение, опре-
деляющее функцию W, напишется так:
Так как х не входит в коэффициенты, то существует решение вида
W = ах + <р (у).
Действительно, подставляя это выражение для W в уравнение, получим
откуда, разрешая относительно у' (у) и интегрируя по у для нахождения ер (у),
получаем решение
W = ax+ С Y2h — <& — 2gy dy.
Уравнение траектории будет тогда
dW ,	Г	dy
-д-=я', Х — а	у -	=gf	A)
**	J /2/г — аз — 2^у
и время i можно определить из формулы
Выполняя квадратуру, получим уравнение
+ у2Л
о
Возводя это уравнение в квадрат, представим его в виде трехчлена вто-
рой степени относительно х, из которого можно определить у. Таким обра-
зом, мы непосредственно убеждаемся, что траектория A) является действи-
тельно параболой с вертикальной осью. Что касается уравнения, определяю-
щего t, то, исключив интеграл из равенств A) и B), мы можем написать
его в виде
t-t0-——.
Это уравнение выражает, что горизонтальная проекция точки совершает
dW	dW
равномерное движение. Кроме того, уравнения р± = -^— , /?2 = ^— в данном
случае будут х' = а', у' = Y^h — & — 2^у
Траектории, соответствующие изменению а', получаются одна из другой
поступательным перемещением, параллельным оси Ох. Все эти параболы
31*

484
ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
касаются прямой с ординатой
=—
, являющейся геометрическим местом
их вершин. Кривые W= const, суть полукубические параболы (рис. 176)
,	1
aX — j- BA — а3 — 2gyJ = const.,
получаемые все из одной поступательным перемещением, параллельным
оси Ох. Все эти полукубические параболы нормальны к прямой АВ с ор-
Рис. 176.
динатой —=	, и эти прямые являются геометрическим местом их точек
возврата. Они ортогональны к предыдущим параболам на основании тео-
ремы п. 301.
303. Центральная сила — функция расстояния. Мы видели (п. 296),
что если начало координат взять в центре сил и если силовая функция
равна ЧГ (г), то в полярных координатах гиб функция Н будет иметь вид
Применим метод Якоби. Уравнение, определяющее W, для которого
требуется найти полный интеграл, будет следующего вида:
Так как в это уравнение не входит явно в, то будем искать интеграл
в виде
W = at) + R,
где R зависит только от г. Тогда нужно, чтобы эта функция R удовлетво-
ряла обыкновенному дифференциальному уравнению
откуда находим

ГЛАВА XVI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМА ЯКОБИ	485
Следовательно, полный интеграл уравнения Якоби для W имеет вид
и конечные уравнения движения будут
~ш~ J
dr
dr
/^
= t-t0.
Первое уравнение определяет траекторию, а второе — время, необходимое
точке для достижения заданного положения на этой кривой.
Значения pt и рь если это понадобится, найдутся из равенств:
= ? = /"
дг V
dW
Последнее уравнение показывает, что а есть не что иное, как постоянная
площадей, так как р2 равно /-28'.
Из теоремы кинетической энергии мы знаем, что Н должно оставаться
постоянным в течение всего времени движения. Мы можем проверить это
предложение, воспользовавшись полученными
сейчас формулами. Действительно, если мы в вы- У
ражении
заменим переменные pi и /?2
получим
их значениями, то
что и подтверждает, что h действительно	р ._^
является постоянной интеграла кинетической
энергии, как мы это доказали ранее.
Траектории, получающиеся при изменении а, что равносильно враще-
нию одной из них вокруг полюса, ортогональны к кривым W = const.; эти
кривые также получаются вращением какой-нибудь одной вокруг полюса.
304. Уравнения движения планеты в форме Якоби. Возьмем начало
координат в Солнце, плоскость траектории примем за плоскость ху и обо-
значим через г расстояние МО от планеты до Солнца (рнс. 177). Весь во-
прос сводится к нахождению полного интеграла уравнения
A)
так как сила притяжения равна — -^ и поэтому силовая функция равна — .
Следуя методу предыдущего примера, мы найдем полный интеграл, который
будет уравнением движения планеты в классической форме.
32 Зак. 851. П. Аппель, т. I

486	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Якоби нашел другой полный интеграл следующим образом. Пусть А —
произвольная точка на оси х и О А = г0. Обозначим через р расстояние МА,
так что
Р = У(* — /"оJ + У2- г = V*2 + У2,
и положим
з = г+р, з'= г — р.
Покажем, что функция
представляет собою полный интеграл уравнения A) с произвольной постоян-
ной г0> отличной от аддитивной. В самом деле, так как а и а' зависят от х
и у через г и р, то имеем:
B)
откуда, возводя в квадрат, складывая и замечая, что члены, содержащие
произведение двух квадратных корней, уничтожаются, получаем
В этом выражении коэффициент при h равен двум; чтобы вычислить
коэффициент при ja, заметим, что имеем тождественно
г?	гр
Гр	Гр	Гр
2(г
откуда найдем, что члены с ja приводятся к —.
Таким образом, мы убеждаемся, что функция W является интегралом
уравнения Якоби A) с постоянной Гц. Уравнения движения в конечной форме
теперь будут
№ь t t dW	(to

ГЛАВА XVI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМА ЯКОБИ	487
Первое уравнение представляет собою траекторию. Написав его в раз-
вернутом виде, найдем:
— Г0
V a'
-/
¦ <»+'•>'/ 7^ + 7
: =k,
так как а и а' зависят от г0 и
да _ dp _ л: — /-Q	да' _ «Зр 	л: —- Го
й/"о ~ дг0 ~~	р ' дг0 ~~ ~~ дг0 ~ р '
Выражение под знаком интеграла представляет собою производную от
и уравнение траектории после приведений принимает вид
+	( +
го ' 2 V	Р
D)
Приведем это уравнение к такому виду, чтобы оно содержало только
расстояния от движущейся точки до двух неподвижных точек О и А. Исходя
из тождеств
гг — Л — р2
2 2 п 2 0 <
Г — р = /ХГп — Тс\, X — Гп — 	ft-	¦—- ,
/-о)(
Р
напишем уравнение
р	2рг0
x-r0 2r0p+/-2-
р	V а + г0 ^ 2
1
^ 2
где й' — новая постоянная. Это является, следовательно, уравнением траек-
тории в биполярной системе координат с полюсами в точках О и А.
Такой вид уравнения непосредственно показывает, что траектория прог
ходит через точку А, так как, освободившись от знаменателя р и положив
р = 0, г = / и, следовательно, а = а' = г0, мы, очевидно, удовлетворим этому
уравнению.
На основании того, что мы знаем о движении планет, это уравнение
представляет собою коническое сечение, род которого зависит только от
знака постоянной Л кинетической энергии (п. 227).
Чтобы вычислить время, затрачиваемое планетой для достижения ка-
кой-нибудь точки ее орбиты, достаточно написать второе из уравнений C),
32*

488	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
которое на основании значения W представится в виде легко вычисляемой
квадратуры
1/
2
Эта формула выражает через радиусы-векторы г и р время, отсчитываемое
от момента, когда планета проходит через точку А, так как в этой точке
р = 0, а = а' и ^ —10 обращается в нуль.
В случае параболической орбиты h равно нулю (п. 227). Тогда получается
формула, установленная Эйлером, но часто несправедливо приписываемая
Ламберту. В этом случае
(s+'o)
1 Г
j (s+'J
7=
*>-	^
Эта формула определяет время, затрачиваемое точкой для перехода из по-
ложения А в положение М, выраженное в функции радиусов-векторов г0
и г точек А и М и хорды /Ш = р.
Следует заметить, что в этой формуле перед вторым корнем надо со-
хранять знак минус до тех пор, пока корень не обратится в нуль, т. е. до
тех пор, пока угол АОМ остается меньше 180°, так как в треугольнике АОМ
сторона р может стать равной сумме двух других сторон только тогда, когда
угол АОМ становится равным 180°. После этого нужно изменить знак вто-
рого корня. Эта формула играет важную роль в методе Ольберса определе-
ния орбит комет (см. Тиссеран, Mecanique celeste т. 1, стр. 114). В случае,
когда h отлично от нуля, формула E) после квадратуры представит собою
обобщение формулы Эйлера на случай эллиптических и гиперболических
орбит, данное впервые Гауссом. (Си. Я к о б и, Vorlesungen iiber Dynamik,
лекция 25.)
305. Геодезические линии поверхностей Лиувилля. Приложение
к эллипсоиду. Лиувилль заметил, что можно при помощи квадратур найти
геодезические линии поверхностей, для которых квадрат линейного элемента,
при подходящем выборе параметров q-i и q2, может быть представлен
в форме
«й« = (Л - А2) (Bt dq\ - B2 dq%
где Ах и Вх зависят только от qt, а А% и ?2—только от q%. Чтобы полу-
чить геодезические линии, достаточно найти траектории материальной точки
массы 1, движущейся по поверхности и не подверженной действию никакой
силы. Тогда
= ~ (Л -

ГЛАВА XVI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМА ЯКОБИ	489
Уравнение Якоби, если в нем положить V = — ht -\- W, будет, следовательно,
B1\dq1J B2\dq?J	ч 1 г"
или
B1\dqi)	1~~Bo\(??2/	*
Приравняв каждую из этих двух величин одной и той же постоянной 2а,
легко получим полный интеграл W, образованный суммой двух функций, из
которых одна зависит только от ?i, а другая только от q2. Этот интеграл
есть
W =
Г У72В2 (kA2 + a) dq2.
Уравнение геодезических линии будет тогда -^— = я , а время опре-
делится из формулы t — to = -jT- :
/	dqt -f- / —-—	dq2 = a ,	A)
Так как по теореме кинетической энергии скорость точки постоянна, то
ds = У2А dt, s — s0 = 1^2/1 (* — ^0).
Второе соотношение определяет дугу геодезической линии.
Приложим этот метод к эллипсоиду. Пусть
—+ 4г-4--	1=0	B)
— уравнение эллипсоида с тремя неравными осями. Рассмотрим софокусные
поверхности
Через каждую точку пространства проходят три такие поверхности,
соответствующие трем значениям qb <7->, <73 величины \ (п. 286). В частности,
через точку М, взятую на эллипсоиде B), проходит сам рассматриваемый
эллипсоид, соответствующий значению X = 0 (<73 = 0), и две другие софо-
кусные поверхности, соответствующие значениям q± и q2 величины I. Мы
примем эти два параметра qt и q2 за координаты точки М на поверхности.
Согласно теореме Дюпена, кривые q-i = const, и q2 = const, являются линиями
кривизны эллипсоида. Для величины ds% в эллиптических координатах мы
нашли ранее (п. 286) выражение вида
rf52 = _L (Af l dql + M2 dq\ + Ms dql).
Так как сейчас <?3 = 0, то dq3 = 0. Тогда, заменяя jVft и Mz их значе-
ниями при q3 = 0, получим

490
ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Эта величина rfs3 действительно имеет форму, данную Лиувиллем, причем
Ч\	Ч*
(<*-<
(а — д2) (b — q2) (с — q2)
Подставляя эти значения в общие уравнения A), получим уравнение
геодезических линий и дуги этих кривых в форме, данной Якоби. Эти урав-
нения содержат ультраэллиптические интегралы. Вейерштрасс дал обраще-
ние этих интегралов, выразив д± и Чг в виде однозначных функций неко-
торого параметра.
Более подробные сведения о поверхностях Лиувилля можно найти
в «Lecons sur la Theorie generale des surfases» Дарбу (часть З, глава I) и
в премированной работе Кёнигса (Savants etrangers, 1894).
IV. Движение в пространстве
306. Движение планеты в сферических координатах по Якоби («Vor-
lcsungen», лекция 24). Примем за плоскость ху плоскость эклиптики, за
ось х — прямую, соединяющую Солнце с точкой весеннего равноденствия,
и определим положение планеты ее сферическими координатами г, <р, <j/, где
4< — долгота планеты, а ^ — ее широта (рис. 177а). Оси ориентированы, как
в астрономии. Переменные г, у, <\> играют роль
параметров дь д2, дл.
Для силовой функции имеем U = — , при-
чем масса планеты принята равной единице.
Из выражения ds в сферических координатах
непосредственно имеем
Т = ~ (г'2
Далее
г* f2 cos* т).
дТ
= ~ЩГ = г~ V cos
Рис. 177а.
Подставляя найденные отсюда значения г', у', у в Т, получим
Следовательно, уравнение с частными производными для W будет
<¦>
Для данного частного вида уравнения A) можно найти полный интеграл
в виде
W = R + Ф + W,
где R, Ф, W являются соответственно функциями переменных г, у, ф.

ГЛАВА XVI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМА ЯКОБИ	491
Для того чтобы W удовлетворяло уравнению A), необходимо, чтобы было
Это уравнение после выделения членов с г можно написать таким образом:
Левая часть" зависит только от <р и ф, а правая только от г, следовательно,
это равенство возможно лишь в том случае, когда каждая часть в отдель-
ности равна одной и той же постоянной величине G3, так как в уравнении A)
переменные г, у, ф независимы. Следовательно, имеем
Ф'2-1
COS5* <p
или
V2 = (G°- — Ф'2) COS2 (p.
Повторяя те же рассуждения, что и выше, мы увидим, что обе части послед-
него равенства должны в отдельности равняться одной постоянной L2, вслед-
ствие чего
W = L, W = Ы/
и
COS2
Таким образом, полный интеграл уравнения A) есть
и конечные уравнения движения имеют вид
dW _ dW	dW
да ~L> ~Ж~Ь> -gF
т. е.
(I)
(II)
/
¦ = < — ta.	(Ill)
Два первых уравнения, не содержащих t, определяют траекторию. Чтобы
дополнить решеяие, укажем на смысл входящих в эти формулы постоянных.

492	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Мы знаем, что для планеты орбита является эллиптической; наибольший и
наименьший радиусы-векторы, соответствующие афелию и перигелию, равны
аA_|-е) и а A—е)\ с другой стороны, уравнение (Ш) показывает, что
Следовательно, корни подкоренного выражения должны соответствовать
максимуму и минимуму радиуса-вектора; поэтому эти корни равны а(\-\-е)
и а(\—е) и на основании зависимости между корнями и коэффициентами
получаем
Найдем теперь смысл величины L. Для того чтобы из уравнения (II)
можно было получить вещественное значение для <\/, когда задана функция ср,
необходимо и достаточно, чтобы выполнялось неравенство
G^>0
COS2cp
и для каждого значения <?, удовлетворяющего этому условию, соответствую-
щее значение <р, определяемое из уравнения (I), должно быть обязательно
вещественным, так как орбита является вещественным эллипсом. Поэтому ср
имеет верхний предел arccos -=г и может этого предела достигать. Но, оче-
видно, что наибольшим значением угла <? является угол / между плоскостью
орбиты и плоскостью эклиптики, и мы должны иметь
-=г = cos i, L =У р-р cos /.
Нам нужно теперь установить нижние пределы интегралов. Мы примем
для этих пределов г = аA—е), что соответствует перигелию, и у = 0, что
соответствует узлу /V. Тогда уравнение (III) показывает, что t0 есть время
прохождения через перигелий, а уравнение (И),— что фо есть долгота узла.
Для вычисления С допустим, что планета находится в перигелии. Тогда
уравнение (I) обратится в следующее:
. у а-- —
COS г tp
где 9i — широта перигелия. Принимая во внимание соотношение L — G cost,
мы можем написать
/
cos у
Os2 ср — COS2/
или, интегрируя,
	—
sin i
I = С, sin a, = sin / sin C.
)	T
Пусть N и Р (рис. 1776) являются точками пересечения радиусов-векторов
восходящего узла и перигелия со сферой радиуса 1, имеющей центр в точке О,
a PQ — <fx — широта перигелия. В треугольнике NPQ имеем
sin »1 = sin NP sin /,

ГЛАВА XVI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМА ЯКОБИ
493
что показывает, что С равно NP, т. е. углу между радиусами-векторами
перигелия и восходящего узла.
307. Движение точки, притягиваемой двумя неподвижными цент-
рами, обратно пропорционально квадрату расстояния. Задача движения
точки, притягиваемой двумя неподвижными
центрами с силой обратно пропорциональной
квадрату расстояния, была впервые приве-
дена к квадратурам Эйлером для случая
плоского движения. Лагранж дал общее
решение, которое Якоби связал с методами
интегрирования, излагаемыми в этой главе.
Эллиптические квадратуры, встречающиеся
в интегралах, далч Лежандру важный при-
мер для приложения его теории эллиптиче-
ских интегралов.
Этому же вопросу посвящены диссер-
тации Серре, Дебова и Андраде *) (во Фран-
ции) и работа Кёнигсбергера (в Германии),
озаглавленная <:De motu puncti versus duo
centra attractb (Берлин, 1860) и содержа-
щая приведение эллиптических интегралов
к функциям в.
Примем за ось Ох (рис. 178) прямую, соединяющую оба притягивающих
центра Ох и О2, за начало координат — точку, лежащую посредине между
ними, и обозначим через 2е расстояние OiO3.
Пусть Оу\ и OzL — две другие неподвиж-
ные оси, образующие с осью Ох прямо-
угольный триедр. Для определения поло-
жения в пространстве движущейся точки М
введем сначала угол 9, который образует
плоскость MOlOv, проведенная через дси-
жущуюся точку и ось Ох, с плоско-
стью хОу\, этот угол измеряется углом
у. между осью Oyt и следом Оу плоско-
сти MOiOo, на плоскости y\Ozx.
Определив таким образом плоскость
уОх, мы обозначим для фиксирования по-
ложения движущейся точки на этой пло-
скости через х и у ее декартовы коорди-
наты ОР и OQ относительно осей хОу
и через Qi и q2 ее эллиптические коор-
динаты в той же плоскости, определенные
системой софокусных конических сечений с фокусами Ох и Од (п. 287). Коор-
динаты точки М относительно неподвижных осей суть х, ух, zlt и мы имеем
Ух= У cos 6, zx — У sin 9.
Отсюда для квадрата линейного элемента получаем
ds2 = dx2 + dy\ + dz\ = dx2 + dy2 + / d%\
Если мы теперь воспользуемся для определения положения точки (х, у)
в плоскости хОу эллиптическими координатами qx и до, являющимися кор-
нями уравнения
Рис. 178.
*) Andrade, Journal de l'Ecole Polytechnique, вып. 60, 1890.

494	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
то по установленным ранее формулам (п. 287)
Ь—а	' у	а—Ь
y =
имеем:
N==	щ=У
(а— Ч\)(а — Я")	, _ (b — qx) (b — д2)
у	а
dq\ + N2 Oft},
Следовательно, в рассматриваемой системе координат квадрат линейного эле-
мента равен
ds' = т (A'i d(f\ + N2 dil) + у2 rfe2,
где N±, iV2 и у2 должны быть заменены их выражениями через qx и q%, на-
писанными выше.
Примем массу точки за единицу. Тогда кинетическая энергия будет
1 ,	,2	/2ч	1	/3
где бив' играют роль параметров qs и qs. Если через гх и г2 обозначить
расстояние от движущейся точки до обоих фокусов, то алгебраические зна-
чения сил притяжения со стороны этих фокусов равны —^ и ——, а сумма
2
их элементарных работ —^ brt	1- Ьг2 есть полный дифференциал силовой
функции
y_Hi i Из
Но так как квадрат большой полуоси эллипса, проходящего через точку М,
равен а — qt, то сумма Г\ + г2 расстояний от точки М до обоих фокусов
будет
Точно так же квадрат поперечной полуоси гиперболы, проходящей через
точку М, равен а — q2, и мы имеем
r-i. — гг = 2 У'а — q2,
откуда
Г1 = Ya— Ч\ + Уа — ?2. ^2 — У а — ?1 — У й — ^2-
После приведения к общему знаменателю, получим
где для краткости положено
так что f/i зависит только от дл, а б'о — только от q2, что весьма суще-

ГЛАВА XVI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМА ЯКОБИ	495
ственно для дальнейшего. Вспомогательные переменные рь р2, р9 равны
здесь частным производным от Т по q'v q'2 и б':
Разрешая эти уравнения относительно qv q2 и б' и подставляя затем в функ-
цию Гамильтона #= Т—U, получим
Заменяя N\, N2 и у2 их значениями в функции qx и q2 и замечая, что можно
написать
1	а—Ь
f-	(.b — Ях) (Ь — q2)
мы представим окончательно функцию Н в виде
_ а — Ь / 1	1 \
Чъ—Я\ \ b — qi b — q2)'
Теперь легко написать уравнение Якоби; мы напишем сразу уравнение для W,
получающееся, как и раньше (стр. 481), путем подстановки V = — ht-\-W-
Можно найти полный интеграл вида
W = аЬ + /?i + R*
где /?! зависит только от qb а /?2 — только от ^2- Действительно, подставляя
в предыдущее равенство это выражение W и освобождаясь от знаменателей,
мы получим для определения /?j и R2 уравнение, которое можно написать
в виде
где правая часть зависит только от qlt а левая часть — только от q2. Так
как в уравнении с частными производными параметры q1 и q2 являются не-
зависимыми переменными, то единственный способ, которым можно удов-
летворить этому последнему соотношению, не устанавливая зависимости
между q1 и q2, заключается в приравнивании каждой части в отдельности
одной и той же постоянной 2р. Разрешим после этого полученные таким
образом уравнения относительно -^—^ и -=—-. Тогда, полагая
dqx dq2

496	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
мы получим
Эти выражения определяют й] и й в квадратурах и для искомого полного
интеграла получается выражение
с тремя произвольными постоянными а, C и /г, из которых ни одна не
является аддитивной. Для получения траекторий нужно теперь приравнять
постоянным а.' и р' частные производные от W по а и [3:
¦(а
-Ь)а Г	dq"	-
J 4(&-<?t)V SJiqO
— (а — Ь) а
J 4F — .
(T)
Второе из этих уравнений, устанавливающее соотношение между qt и q*,
представляет относительную траекторию в движущейся плоскости хОу; пер-
вое уравнение определяет угол вращения этой плоскости. Чтобы получить
время, приравняем частную производную от W по h разности t — ^0:
_J_ Г qt dqx	1 Г
4 J YsJIqJ 4 J
Таким образом, задача приведена к квадратурам. Эти квадратуры яв-
ляются эллиптическими, как в этом можно убедиться, полагая qx — а = sf
и q2 — a —st,, так чтобы S^ и So, стали рациональными относительно Si и s^.
Что касается выражений для вспомогательных переменных р(, р.„ р%, то
для их нахождения нужно взять частные производные от W по qv, qn, 6:
Последняя формула выясняет смысл постоянной о. В самом деле, из
уравнения, определяющего /?3, мы имели Яз = )'28' (стр. 874). Следовательно,
интеграл ps = а дает
у2й' — а,
что выражает возможность применения закона площадей к проекции движения
на плоскость У\Ог^, так как у и в являются полярными координатами проек-
ции движущейся точки на эту плоскость. Это обстоятельство можно было
предвидеть заранее, так как силы, действующие на точку, пересекают ось Ох.
В частном случае, когда начальная скорость точки пересекает ось Ох,
траектория будет, очевидно, находиться в плоскости M-fiiOo, определяемой
начальным положением точки и обоими притягивающими центрами. В этом
можно убедиться и из уравнений. В самом деле, постоянная а будет в этом
случае равна нулю и первое из уравнений G") траектории обратится в сле-
дующее:
6 = я'.

ГЛАВА XVI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМА ЯКОБИ	497
Это показывает, что плоскость уОх останется неподвижной. Второе из
уравнений (Т) определит траекторию в эклиптических координатах.
Интегрирование уравнения Эйлера. Допустим, что не только а = О,
но и р., = (л2 = 0. Тогда плоскость уОх будет неподвижной, траектория будет
плоской и так как сил нет, то эта траектория будет прямой линией на
плоскости уОх. При этих предположениях второе из уравнений (Т) после
замены f(q\) и /(?2) их выражениями примет вид
Г	^	+ Л,-	^	¦	=Р'- (Е)
Следовательно, это уравнение представляет прямую, и оно может быть ото-
ждествлено с уравнением прямой линии в эллиптических координатах, ко-
торое будет, очевидно, алгебраическим относительно q± и q2. Таким путем
мы воспроизвели, следуя Лагранжу, очень важный результат, данный Эйле-
ром и выражающий, что уравнение (Е) допускает алгебраический интеграл.
На этом результате основывается сложение эллиптических функций.
Примечание. Таким же путем можно привести к квадратурам за-
дачу о движении точки, находящейся под действием сил, которые в приме-
ненных нами координатах имеют силовую функцию вида
где U-l — произвольная функция только переменного qlt а ?/2 — функция
только переменного q%. Например, эта форма силовой функции сохранится,
если к предыдущим силам (притяжениям к неподвижным центрам О± и О3
по закону обратной пропорциональности квадрату расстояния) присоединить
силу притяжения к точке О, пропорциональную расстоянию, силу притяже-
ния, перпендикулярную к плоскости y\Qzl и обратно пропорциональную кубу
расстояния х, и силу притяжения, перпендикулярную оси Ох и обратно
пропорциональную кубу расстояния у.
Отметим, в заключение, работу Вельде «Ueber einen Specialfall der Be-
wegung eines Punktes welcher von zwei festen Centren angezogen wird» (Бер-
лин, изд-во Р. Партнера, 1889) (Bulletin des Sciences mathematiques, 1890
стр. 125). Вельде рассматривает задачу плоского движения в предположении
что силы притяжения к фокусам О^ и О2 равны соответственно	1 — [*Гь
•—-2 — (х/-2 и что движущаяся точка притягивается центром О пропорцио-
нально расстоянию.
308. Эллиптические координаты в пространстве. Мы нашли (п. 286}
НТО
Тогда
Pi = -4 Mi4v Р-г = -
Допустим, что силовая функция имеет вид

(-71 — Я2) (<7i - Яз) ^ (<?2 - <?з) (?2 - ft) ^ (?з - Чк) (?з - 4°)

498	часть третья, динамика точки
где Ui — функция одной только переменной qlt i/2— функция одной только
переменной q^. и U$ — только переменной qa. Имеем
Если мы подставим вместо М\, М-->, Мъ их значения (п. 286), то уравне-
ние для W будет следующее:
к . о Г	/(ft)	(dW\*	f(q2)	tdWV ,
L (?. — ?г) (?i — <7з) W?i / (?з — <7з) (9s — ?i) \ ^2 /
Для нахождения полного интеграла этого уравнения при сделанных
относительно U предположениях заметим, следуя Якоби, что при любых
Значениях постоянных аир выполняется тождество
¦+Jq
в чем можно убедиться, написав, что сумма вычетов рациональной относи-
тельно q функции
2а. + 2Во -4- hq-i
равна Л. Тогда уравнение для IF при замене Л этим выражением может
быть написано следующим образом:
(qi—q*)(qi—q{)
Это уравнение имеет, очевидно, интеграл
где положено
2S4- = 2а + 2P?i + Н\ ~ Ut (/=1,2, 3).
Действительно, это выражение для W обращает в нуль каждый из трех
членов уравнения с частными производными. Для нахождения траекторий
приравняем теперь постоянным а' и fj' частные производные от W по а и р:
/,	/а
,.	— + /
YSif(qt) J
YS,f(q2)
В частном случае, когда нет сил, т. е.
Uу = Uг = f/3 = О,

ГЛАВА XVI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМА ЯКОБИ	499
эти уравнения должны представлять прямую линию в пространственных
эллиптических координатах. Они эквивалентны двум алгебраическим соот-
ношениям между qlt q2, q3: что составляет первое обобщение результата
Эйлера, указанное в конце предыдущего упражнения, и частный случай
теоремы Абеля, приложенной к ультраэллиптическим интегралам первого
рода. Что касается времени, то мы получим его, приравнивая t — tv частной
„ dW
производной ¦ , .
В виде упражнения будет показано, что силовая функция принимает
вышеуказанную форму, когда на движущуюся точку одновременно действуют
притяжение к центру, пропорциональное расстоянию, и притяжения, нормаль-
ные к трем главным плоскостям софокусных поверхностей и изменяющиеся
в отношении, обратном кубу расстояний.
V. Приложения к принципу наименьшего действия,
к брахистохронам, к равновесию нитей
309. Наименьшее действие. Свободная точка. Допустим, что на
свободную точку массы 1 действует сила, имеющая силовую функцию
U(x, у, г). Мы видели, что если постоянная живых сил h имеет определен-
ное значение, то траектории, проходящие через две заданные точки А и В,
являются кривыми, обращающими в нуль вариацию действия
= С
A)
Эти траектории легко найти, если известен полный интеграл уравнения
Якоби относительно W в произвольной системе координат:
W dW dW
Для дальнейшего полезно написать это уравнение в явной форме. Мы
видели (п. 293), что Т является квадратичной формой от рь р2, р8:
2Г =
кроме того, //= Т—U. Уравнение Якоби, получающееся заменой р«, р<>,
dW dW dW
производными -^—, -j—, -з—, имеет вид
<% dq^ dqz
Пусть теперь W (qb q%, qs, a, p, h) — полный интеграл этого уравнения,
a Wo и W\ — значения, которые он принимает в точках А и В. Мы знаем,
что уравнения траекторий в конечной форме суть
с четырьмя постоянными а, р, a', p'.
Чтобы найти траектории, проходящие через точки А к В, надо опре-
делить эти постоянные, подставив в уравнения D) координаты точек А и В.
Тогда будет
dW	dW	dWi	dW

500	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Вычитая, получим
да	"'	dp	'	v"'
Эти два последних уравнения определяют а и р, а предыдущие уравне-
ния E) определяют а' и р'. Каждой системе значений аир, заданной урав-
нениями F), соответствует траектория, проходящая через, точки А и В, для
которой справедлива следующая замечательная теорема: значение действия
вдоль траектории АВ определяется формулой
Л=Щ— Wo.
В самом деле, найдем, каково будет элементарное приращение dW
функции W, соответствующее бесконечно малому перемещению dqb dq2, dq%,
совершаемому по этой траектории. Мы можем предположить, что qlt q2, q^
являются координатами материальной точки, брошенной таким образом,
чтобы она описала рассматриваемую траекторию. Тогда
(б')
или, подставляя q-jit, q2dt, qzdt вместо dqb dq^, dq9 и рь />,, ръ вместо
dW dW dW
-з— . -з— > -з— . получим
dqx dq2 dq3
dW = ( Plq[ + p2q'2 + Psq'B) dt.
Так как рь рь ps суть частные производные от Т по qv q%, q's и так как
кинетическая энергия Т равна -=-1— j , то на основании теоремы об одно-
родных функциях имеем
-^-ds.
dt
Но по теореме кинетической энергии скорость — равна У? (U -f- h); отсюда
dW = f2(U+h) ds.
Следовательно, значение действия, вычисленного вдоль траектории от А
до В, окончательно будет
(¦В)	{?)
Л = Г У (U + h) ds= f dW^Wi— Wo,
(A)	(A)
что и надо было доказать.
310. Точка на поверхности. Те же заключения справедливы и для
движения точки по плоскости или по произвольной неподвижной поверх-
ности, когда существует силовая функция.
Кинетическая энергия будет тогда квадратичной формой относи-
тельно q[, q!a или относительно pv p2:
-^ {Апр\ + 2AliPlp2 + A22pf), G)
где

ГЛАВА XVI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМА ЯКОБИ	501
Н равно Т—U и уравнение Якоби для W будет
Если W (qb q9, a, h) есть полный интеграл, то уравнение траекторий будет
3W
¦ - = а' и действие вдоль траектории, идущей от А до В, равно W± — Wo,
причем а определяется уравнением —-—^	— = 0. (Более подробное
исследование этих свойств см. в «Legons sur la Theorie des surfaces» Дарбу,
т. II, главы VI и VII).
311. Параболическое движение. Для параболического движения тяже-
лой точки в вертикальной плоскости мы нашли (п. 302)
W = ax--± <2A-as-2gy).
Значение действия вдоль одной из двух параболических траекторий,
идущих от точки (дг0, Уо) к точке (хъ y{), равно
1	1
Л = а (X! - х0) - -L [BЛ - а? - 2gyx) * - BА - at - 2g70J ] ,
где а — один из двух корней уравнения
x-l - Ч + | [BА - «2 _ 2gyif - BА - «г- 2^уо)Т] = 0.	(9)
Это уравнение после приведения к рациональному виду будет биквад-
ратным относительно а. После того как одно из значений аа будет выбрано,
знак величины а определится из уравнения (9), в котором член xt — хй и
коэффициент при — имеют известные знаки.
312. Брахистохроны и фигуры равновесия нитей в случае силовой
функции. Задача рефракции.. Если мы для краткости заменим в предыду-
щих равенствах 2(?/ + Л) величиной <р2, где <f — функция координат, то
увидим, что результаты, полученные для свободной точки, могут быть
выражены следующим образом. Кривые, соединяющие две точки А и В
и обращающие в минимум интеграл
(-В)
/= Г yds,	A0)
будут известны, если известен полный интеграл W{q^, q% q%, a, E) уравнения
Якоби C) относительно W, в котором 2{U-\-h) заменено величиной ср2;
Их уравнения будут
и значение интеграла / вдоль одной из этих кривых равно W\ — Wo, причем
постоянные аир вычисляются, как и раньше, при помощи уравнений F).
33 Зак. 851. П. Аппель, т. 1

502	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Например, в прямоугольных декартовых координатах достаточно знать пол-
ный интеграл уравнения
(dW\2 (dWy (dwy
Точно так же, чтобы найти на неподвижной поверхности кривые, соеди-
няющие две точки А и В и обращающие в минимум интеграл /, достаточно
иметь полный интеграл W (qv g2, а) уравнения Якоби (8) относительно W,
в котором нужно заменить 2{U-\-h) величиной <р2. Получится уравнение
1 Г, (dWy 9. dW dW	(dWyi
Искомые кривые будут тогда иметь уравнение —^— = о.', и интеграл A0)
вдоль одной из этих кривых равен W± — Wo.
Но мы видели, что к нахождению кривых, обращающих в минимум
интеграл вида A0), можно свести три следующие задачи:
1)	определение фигуры равновесия нити, свободной или лежащей
на поверхности, когда действуют силы, имеющие силовую функцию
(п. 146);
2)	общую задачу рефракции (п. 150);
3)	определение брахистохрон для точки, свободной или движущейся
по поверхности, когда существует силовая функция (пп. 255 и 257).
Эти задачи могут быть, следовательно, приведены к нахождению полного
интеграла уравнения с частными производными вида A1) или A2). Значение
интеграла A0) вдоль одной из этих кривых, идущих от А к В, есть Wx— Wo.
В частном случае брахистохрон значение этого интеграла определяет время,
затрачиваемое точкой для пробега дуги АВ брахистохроны. (См. К л е б ш,
Journal de Crelle, т. 57, стр. 93; Аппель, Comptes rendus, 12 марта 1883 и
Annales de la Faculte de Toulouse, 1887; Андуайе, Comptes rendus, m. C,
стр. 1577; Марколонго, Rendiconti della R. Accademia delle Scienze di
Napoli, июль, 1888.)
УПРАЖНЕНИЯ
1. Если в канонических уравнениях положить t = —t'', то уравнения
сохранят ту же форму, но р будут играть роль параметра q и наоборот.
Сделать отсюда вывод, что для получения интегралов уравнений движения
достаточно знать полный интеграл уравнения с частными производными
dV „(	dV dV dV
и написать интегралы уравнений движения.
2.	Тот же вопрос для движения точки по поверхности или по кривой.
3.	Применить метод Якоби к следующим примерам.
а)	Движение точки, находящейся под действием силы, постоянной по
величине и направлению, и силы притяжения к неподвижному центру по
закону обратной пропорциональности квадрату расстояния. Этот случай
является предельным для задачи, разобранной в п. 307; достаточно предпо-
ложить один из притягивающих центров в бесконечности; софокусные кони-
ческие сечения обратятся тогда в софокусные параболы. (Селлерье, Bul-
letin des Sciences mathematiques, 1891; Сен-Жермен, Nouvelles Annales,
1892.)
б)	Движение сферического маятника.
4.	Привести к канонической форме уравнения движения точки по непо-
движной или движущейся кривой. Применить затем теорему Якоби. (Доста-

ГЛАВА XVI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМА ЯКОБИ	503
точно применить общие теоремы, допустив, что параметры сводятся
к одному qi.)
5.	Рассмотреть приложение метода Якоби к математическому маятнику.
6.	Рассмотреть приложение метода Якоби к задаче п. 260.
В этой задаче, полагая т = \, имеем
Имеется только один параметр 8, играющий роль параметра q^; кроме
того, G = 0. Нужно положить
Н = Л6' —Т—и = ^ (б'2 —
или, в функции pi,
Уравнение Якоби будет
Оно имеет полный интеграл
у= W — ht+ С аМ+ С /2аш + 2А db\
с постоянной h. Тогда уравнение движения будет
^= const. = — R?t0, t — to=
Из вида а следует, что это уравнение идентично уравнению движения мате-
матического маятника.
7.	Дана поверхность, линейный элемент которой может быть приведен
к форме Лиувилля (п. 305). Обозначим через i угол, который образует
в каждой точке определенная геодезическая линия с кривой q% = const., про-
ходящей через эту точку. Доказать, что вдоль всей этой линии
Ai sin2 i + Аг cos21 = const.
(Л и у вил ль, Journal de Mathematiques, 1844.)
8.	Приложить метод п. 305 к нахождению геодезических линий на пло-
скости, пользуясь эллиптическими координатами на плоскости.
Дифференциальное уравнение геодезических линий (прямых линий) будет
в этом случае уравнением Эйлера. Тогда уравнение прямой в эллиптических
координатах будет интегралом уравнения Эйлера (Лагранж, см. п. 307).
Уравнение, определяющее дугу геодезической линии C05), будет выражать
теорему сложения для эллиптических интегралов второго рода. (Дарбу,
Lecons sur la Theorie generale des surfaces, т. Ill, стр. 13.)
9.	Приложить метод п. 305 к нахождению геодезических линий сферы,
пользуясь эллиптическими координатами на сфере. (См. Дарбу, там же,
т. II, стр. 422.) Имеем
= (cos 2fi — cos 2v) (	fJ^	х- Н
\ cos 2jx cos 2c
, cos 2ц — cos 2с cos 2с — cos 2м
33*

504	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Формула относительно дуги геодезической линии (большого круга) даст
тогда формулу сложения для эллиптических интегралов третьего рода.
(Дарбу, там же, т. III, стр. 13.)
10. Приложить метод Якоби к нахождению по п. 312 фигуры равновесия
однородной тяжелой цепочки.
П. Пользуясь обозначениями п. 305, доказать, что можно привести
к квадратурам задачу движения точки по поверхности Лиувилля, когда
силовая функция имеет вид —-	, где C/t зависит только от qb a b\ —
ТОЛЬКО ОТ Qo.
Рассмотреть, в частности, движение на эллипсоиде точки, притягиваемой
центром пропорционально расстоянию (Якоби). Доказать, что в этом движении
давление точки на эллипсоид изменяется пропорционально кубу расстояния
от центра до касательной плоскости, проведенной к эллипсоиду в движущейся
точке. (А с т о р, Bulletin des Sciences mathematiques, 1889, стр. 294.)
12. Метод Эллиота для случая сопротивления, пропорционального
скорости. Мы допустили в предыдущей главе, что составляющие X, Y, Z
равнодействующей заданных сил, приложенных к движущейся точке, суть
частные производные некоторой функции U (х, у, z, t). Мы обязаны Эллиоту
остроумным замечанием, что уравнения движения можно привести к кано-
ническому виду и вследствие этого применить метод Якоби также и в том
случае, когда к силе X, Y, Z присоединена сила сопротивления, пропорцио-
нальная скорости. Возьмем, например, движение точки массы 1 по непо-
движной или движущейся поверхности f(x, у, z, t) = 0 под действием силы
dU dU dU
с проекциями -т—, -з— . -г- и сопротивления, пропорционального скорости,
, dx , dy	, dz ч,г
с проекциями —k~J7> —^ 7Г '	— ~нТ ^ —постоянная). Уравнения дви-
жения будут
?	ddUdf
следо-
Чё==-кШ+-дх + 1Гл'---
Сделаем замену независимой переменной, положив ? = е~м и,
вательно, приняв f за новую переменную. Имеем
dt	dt' dfi	dt'	dt'2
и первое уравнение примет вид
d"-x __ \ дЦ X df
dt'2 k4'2 дх ^ k'4'2 dx'
Два других уравнения преобразуются аналогичным образом. Следовательно,
если положить
гЩХ,у,г,Ъ Х
t=—~\nt',
к
то уравнения примут вид
d»-x _dU' , df
dt'2 дх	дх

ГЛАВА XVI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМА ЯКОБИ	505
т. е. обратятся в уравнения движения точки -без сопротивления среды на
поверхности fix, у, г,	— In t'\ — 0. К этому последнему движению можно
применить методы Пуассона, Гамильтона и Якоби. После того, как будут
найдены в конечной форме общие интегралы уравнений движения B), доста-
точно будет заменить в них ? через <?~Ц чтобы получить общие интегралы
предложенных уравнений движения A).
Этот же метод преобразования можно применить, очевидно, к движению
свободной точки, или точки, скользящей по неподвижной или движущейся
кривой, когда на нее действует сила сопротивления среды, пропорциональная
скорости. (Эллиот, Comptes rendus, 1893; Annales de l'Ecole Normale,
август, 1893.)
13. Приложить предыдущий метод Эллиота к следующим примерам.
1°. Точка движется по неподвижной поверхности, для которой
ds1*- = E dun- + IF dudv+G dv\
причем силовая функция равна U и на точку действует пропорциональная
скорости V сила сопротивления среды, равная kV.
Ответ. Если W (и, v, а, C) — полный интеграл уравнения
то уравнения движения суть
2°. Точка движется по неподвижной кривой, для которой ds% = ЕйФ,
при сопротивлении среды, равном kV.
Ответ. Если W(и, а.) есть интеграл уравнения
то конечное уравнение движения есть
<?и ^— = а',
до.
3°. Завершить вычисления для случая свободной материальной точки,
притягиваемой неподвижным центром с силой, обратно пропорциональной
расстоянию, и подверженной сопротивлению среды, пропорциональному ско-
рости. (Эллиот, Annales de l'Ecole Normale, август, 1893.)
14. Приведение уравнений равновесия свободной нити к канонической
форме. Пусть дана свободная нить, элемент ds которой находится под дей-
ствием силы, имеющей проекции ^—«fs, ^—<&• ~Т~ ds' где ^ — заданная
функция от х, у, z, s. Если через qly q-2, Чг обозначить координаты х, у, zr

506
ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
Tdx	dy
ds' ds'
„dz
ds~'
то получим
а через р±, р%, ръ — величины
Т —у р\-\- р\-\- р\. Если, наконец, положить
то уравнения равновесия могут быть приведены к канонической форме
dq,_dH_ Ф1__^Я
ds dp., ' ds	dq.,	' '
Применить к этим уравнениям теорему Якоби. Таким путем получится
другое доказательство теоремы Клебша (Journal de Crelle, т. 57). (См. Comp-
tes rendus, т. XCVI, 1883, стр. 688 и статью Марколонго «Rendiconti della
R. Academia delle Scienze de Napolb, 1888.)
15.	Привести точно так же к канонической форме уравнения равновесия
нити, скользящей по поверхности. (Comptes rendus, т. XCVI, 1883, стр. 688.)
16.	Доказать, что определитель коэффициентов при qv q2, qa в уравне-
ниях B) п. 292 равен квадрату функционального определителя величин
х, у, г, рассматриваемых как функции параметров qb g2, q3.
17.	Материальная точка скользит без трения по поверхности однород-
ного эллипсоида вращения и притягивается элементами этого эллипсоида
по закону Ньютона. Найти движение. (Якоби, Crelle, т. 24.)
(По теории притяжения, сила притяжения точки эллипсоидом имеет
проекции X — — fx, Y = —fy, Z = — gz, где fug — постоянные, а ось Ог
является осью вращения.
18.	Найти движение точки, находящейся под действием ньютоновского
притяжения к двум подвижным центрам, описывающим неподвижную окруж-
ность таким образом, что они постоянно находятся на двух концах одного
и того же диаметра, а движущаяся точка всегда находится в плоскости,
определенной этим диаметром и осью окружности. (Д е б о в, Journal de Liou-
ville, т. XIIIj.)
19.	В случае эллиптических координат на плоскости задача интегриро-
вания уравнений движения точки приводится к квадратурам, когда силовая
функция имеет вид
U =
В пространстве задача приводится к квадратурам, когда силовая функ-
ция имеет вид
1
1
1
1
щ
и?
Яг
/ =
1 q2
1 дв
1 Яг Я\
1 Яъ 4%
где функции UI, U% GS являются каждая функцией соответственно пара-
метров qlt q% и q3. (Лиувилль, Journal de Liouville, т. XII^)

ГЛАВА XVI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ. ТЕОРЕМА ЯКОБИ	507
Убедиться, что к этой форме можно привести силовую функцию, обратно
пропорциональную степени движущейся точки относительно одной из софо-
кусных поверхностей, например,
ц-	k
(получится, что U-i, (Jo, иъ равны —, —, — где С — постоянная ). (Bul-
\	Ч\ <7г <7з	)
letin de la Societe mathematique de France, т. XIX, стр. 102.)
К этой форме можно привести силовую функцию для точки, скользящей
по эллипсоиду и притягиваемой центром пропорционально расстоянию (см.
Лиувилль, Journal de Liouville, т. XII); тот же вопрос исследован Шель-
бахом (Crelle, т. 44, стр. 380).
20. При системе плоских эллиптических координат предполагается,
что движущаяся точка находится под действием силы, имеющей силовую
функцию —	-, где U\ и ?/» зависят соответственно от q± и q->. Во что
Яг — Чч
обратится задача, когда оба фокуса будут неограниченно сближаться до-
слияния в точке 07
Ответ. Полагая в формуле п. 287 а = Ъ + Е> где е — бесконечно мало,
получим qt =a — jxs, q2^a — r\ х»- = рг*. у = A — ц)г2, U = iMz_ll?!>r
где г — радиус-вектор, исходящий из центра. Следовательно, U есть сумма
двух членов, из которых один зависит только от г, а второй однороден
относительно координат с показателем однородности — 2. (Лиувилль,
Journal de Liouville, т. XIj.)
f 21. Система эллиптических координат и ее предельные случаи являются
единственными вещественными системами, допускающими приведение квад-
рата линейного элемента плоскости к форме Лиувилля
(предельными случаями являются: прямоугольные координаты, когда оба
фокуса находятся в бесконечности, параболические координаты, когда только
один из фокусов находится в бесконечности, и, наконец, полярные коорди-
наты, когда оба фокуса сливаются). (Лиувилль, Journal de Liouville,
т. XI и XII. См. премированные работы, Comptes rendus, seance publique,
декабрь 1892, стр. 1122.)
22.	Зная полный интеграл W (х, у, z, a, p, h) уравнения с частными про-
изводными п. 300, можно всегда вывести из него другой интеграл W того же
уравнения, который обращается в нуль на заданной поверхности ср (х, у, г) = 0.
(Метод Лагранжа получения общего интеграла из полного.) Если этот инте-
грал определен, то траектории, нормальные к заданной поверхности, будут
нормальны к поверхностям W = const., и действие на отрезке одной из этих
траекторий между двумя из этих поверхностей будет одинаковым для всех
траекторий. (См. Дарбу, Lecons sur la Theorie generale des surfaces, т. II,
гл. VI и VII.)
23.	В плоском движении силовая функция предполагается вида
U= Ахт + Вуп,
где А и В — произвольные постоянные, а т и п — целые числа. Доказать,
что уравнение Якоби для W имеет полный • интеграл, алгебраический
относительно х и у.
Вывести отсюда, что можно получить бесконечное число ортогональных
алгебраических систем, включающих в себя и заданную алгебраическую

508	ЧАСТЬ ТРЕТЬЯ. ДИНАМИКА ТОЧКИ
кривую (Дарбу, Lecons sur la Theorie generate des surfaces, т. И, гл. VI,
п. 549).
24. Теорема о произвольном решении W уравнения с частными про-
изводными Якоби.
Пусть W (х, у, г) — произвольное решение уравнения с частными про-
изводными, содержащее или не содержащее постоянных. Кривые, нордмаль-
ные к поверхностям
W (х, у, z) = const.,
являются траекториями, которые получатся, если точку поместить в произ-
вольном месте одной из поверхностей, например W = 0, и пустить ее нор-
мально к поверхности с такой скоростью, чтобы постоянная кинетической
энергии имела определенное значение А.

ИМЕННОЙ УКАЗАТЕЛЬ
Абель 407, 499
Адамар 145, 279, 392
Акимов 363
Альфен 201, 343, 348, 366, 367, 370,
406, 432, 437
Ампер 103, 208
Андраде 493
Андуайе 397, 464, 502
Аполлоний 365
Аппель 54, 180, 182, 201, 290, 313,
314, 322, 326, 344, 363, 382 445,
446, 502
Аррениус 318
Архимед 92
Астор 504
Байль 341
Белидор 252
Бернулли И. 193, 208
Бертран 84, 102, 189, 230, 299, 321,
343, 347
Бессель 360, 363, 369
Бине 329, 445
Биркелянд 317, 318
Бирман 182
Бобилье 182
Болен 277
Болл 40, 51, 53
Бонне 195, 204, 270, 325, 381, 395,
407
Бриоши 299
Бюржесс 341
Валлис 208
Вариньон 27, 153, 159, 202, 208
Ваши 86
Вейерштрасс 206, 290
Вельде 497
Веронне А. 371
Викер 195, 464, 465
Вийар 319
Виоль 341
Вриглей 253
Галилей 60, 86, 92, 171, 208, 222
226
Галлей 338
Гамильтон 460, 466, 473
Гаусс 94, 233, 251, 460, 488
Герман 316
Герц 229
Гиббс Дж.-В. 19
Гирн 262
Гишар 146, 321
Гольдшмидт 191
Грассман 18, 21
Гринхилл 315, 441, 446
Гудерман 182
Гук Г. 202
Гупийер де ла 299, 392, 397
Гурса Э. 477
Гюйгенс 62, 86, 171
Гюльден 143, 371
Даламбер 56, 92, 458
Дарбу 72, 85, 134, 151, 206, 316, 343,
348, 366, 367, 370, 392, 423, 426, 432,
462, 463, 464, 490, 501, 503, 504, 507,
508
Дарвин 277
Дебов 493, 506
Декарт 56, 208, 226
Депейру 134, 151, 208, 343, 348
Де Спарр 322, 442, 446
Джеллет 262
Д'Окань 359
Дотевилль 446
Драх 313
Дюпен 489
Жордан 465
Жуковский 363
Зейриг 159
Иоахимсталь 423

510
ИМЕННОЙ УКАЗАТЕЛЬ
Кавендиш 341
Карвалло 19
Карьер 313
Квинтенс 223
Кёнигс 52, 56, 145, 348, 359, 409,
490
Кёнигсбергер 493
Кеплер 335, 338, 347, 351, 356
Клаузиус 44
Клебш 182, 204, 502, 506
Клейн 50, 52
Клеро 430
Кобб 206, 432, 443
Кориолис 77, 85, 204
Корню 341
Коши 267, 360
Кремона 159
Крофтон 146
Кулон 257, 263
Кульман 159
Куртиврон 208
Кэйли 53
Лагранж 149, 208, 226, 230, 232, 266
299, 325, 360, 392, 400, 410, 447, 460*
493
Ламберт 488
Лаплас 193, 360, 460
Леви Л. 40, 51
Леви М. 159, 201
Легу 408
Лежандр 310, 493
Лежен-Дирихле 13, 230, 277, 374, 420
Лекорню 323
Леоте 159, 264
Лильесштрём 132
Липпман 343, 371
Лиувилль 313, 488, 503, 506, 507
Лобачевский 191
Лориа 40
Лякур 180, 201, 322, 382
Ляме 440
Ляпунов 279
Майер 446
Маклорен 270
Максвелл 202
Мангейм 56, 85
Марколонго 502, 506
Мёбиус 16, 52, 134, 136, 146, 188, 202,
232, 251, 270, 325
Менье 183, 421
Миндинг 147, 182
Монж 47
Монтель 159
Мопертюи 193, 208, 460
Морен 257, 263, 325
Муаньо 148
Нейман 208, 252
Ньютон 86, 89, 112, 335, 336, 338, 348,
366
Ольберс 488
Падэ 50
Паскаль 226, 253
Пеннакьетти 167
Пере 363
Плюккер 25, 136
Понселе 56, 74, 84, 159, 406
Пуанкаре 317
Пуансо 16, 37, 85, 163, 168, 174, 202
Пуассон 133, 262, 460, 466
Пэнлеве 279, 313
Пюизё 297, 390, 406, 436
Резаль 56, 85, 370, 442, 443, 444
Ренкин 202
Рибокур 56
Роберваль 56, 224
Рож ер 396
Руше 159, 360
Рэлей 315
Саладини 407
Селлерье 502
Сен-Жермен 408, 437, 443, 446, 502
Серре 62, 169, 270, 325, 445, 493
Сиаччи 291, 313, 371
Сомов 136
Стоке 103
Таннери 444
Тейксейра 182
Тиссеран 354, 361, 362, 365, 370, 442,
488
Тиссо 440
Тодгунтер 362
Томсон 56, 188, 254, 397, 461
Торричелли 232
Тэйлор 379
Тэт 56, 188, 254, 397, 461
Флери А. 252
Френе 62, 169
Фуко 89
Фуре 407
Фурье 290, 360, 363
Фусс 202
Хэвисайд 19
Хилл 277

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
511
Шаль 16, 31, 37, 56, 69, 83
Шапель 291
Шельбах 507
Шёнеман 56
Шлегель 182
Штауде 432
Штермер 318
Штуди 51
Эйлер 56, 75, 132, 148, 193, 195, 208,
230, 269, 369, 389, 396, 398, 407, 408,
460, 488, 493
Эллиот 313, 371, 504, 505
Эрмит 360, 440
Якоби 332, 368, 406, 424, 460, 464, 488
490, 493, 504, 506
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абака 359
Абеля задача 407
Ампера — Стокса формула 103
Аномалия истинная 354
—	средняя 356
—	эксцентрическая 356
Аполлония теоремы 365
Афелий 354
Белидора мост подъемный 252
Бертрана задача 343
Бесселя функции 369
Бине формула 329, 445
Биплан 51
Бонне задача 407
Брахистохрона 184, 189, 393, 408, 464,
499, 501
Вариация 234
Вариньона многоугольник 153,159, 202
—	теорема 27
Вектор 16
—	аксиальный 49
—	главный 28
—	полярный 49
—	результирующий 26, 43, 45, 51
—	свободный 17
—	связанный 17, 44
—	скользящий 17, 21
—	— сферический 51
—	скорости 59
—	ускорения 60
Верчение 76, 255
Вес 92, 131
—	абсолютный 92
Весы коромысловые Квинтенса 223
—	Роберваля 224
Взаимодействие 109
Винт 40, 51, 53
Вириал Клаузиуса 44, 55
Возмущения элементов эллиптиче-
ского движения 364
Ворот 138
—	дифференциальный 251
Вращение мгновенное 72
Вращение системы 239
—	— неизменяемой 63
Время 86
Гамильтона принцип 460
— функция 469
Гаусса принцип 460
Геометрия 15
¦— Лобачевского 191
Гидростатика 226
Годограф 61, 309, 368
Грамм-масса 94
Гринхилла теорема 441
Гюльдена теорема 143, 232
Давление точки на поверхность 117
Даламбера принцип 92, 458
Движение абсолютное 57
—	винтовое 69
	 касательное 72
—	комет параболическое 364
—	криволинейное 59, 301
—	непрерывное 74
-— относительное 56, 66
—	параболическое 86
—	планет 335, 485, 490
—	плоское 481, 497
—	по наклонной плоскости 296
—	по поверхности 481
¦— поступательное 63
—	прямолинейное 57, 280
—	равномерное 60
—	равнопеременное 59
—	результирующее 81
—	снаряда 266, 291
—	среднее 356
—	таутохронное 285, 297, 320, 321,388
—	тяжелого тела в пустоте 61, 283
Действие 461, 499
Дина 94
Динамика 92
—	точки 266
Динамометр 95
Дисимметрия 50
Диск 251

512
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Диск эллиптический 253
Долгота восходящего узла 363
—	перигелия 363
—	средняя в нулевую эпоху 364
Домкрат 251
Дополнение цикла, определенного
векторами 21
Дуализм в теории векторов 52
Дюпена теорема 489
Единица абсолютная 94
—	массы 92
—	мощности 108
—	основная 93
—	производная 93
—	работы 98
—	силы 92
—	техническая 93
Жидкость несжимаемая 226
Задача Абеля 407
—	Бертрана 343
—	Бонне 407
—	п тел 349
—	рефракции 501
—	Фуре 407
—	Эйлера и Саладини 407
Закон всемирного тяготения 86, 112,
340
—	инерции 87
—	площадей 271, 327, 414
—	«покоя> 208
—	равенства действия и противодей-
ствия 8Э
Законы Кеплера 335, 351
—	механики основные 86
—	преломления 194
Звезда двойная 343
Звезды неподвижные 87
Значение взаимодействия алгебраи-
ческое 109
Изгиб продольный 200
Измерение сил статическое 94
Импульс 51
Инвариант системы векторов 29, 36,
54
Инерция 86
Интеграл кинетической энергии 277,
417, 425, 450, 460, 471
•— общий 167
—	первый уравнения движения 267
—	полный уравнения с частными
производными 473
Качение 76, 256
Квннтекса весы коромысловые 223
Кеплера законы .335, 351
—	уравнение 356, 370
Килограмм-сила 93
Килограммометр 99
Кинематика 15, 56
Клаузиуса вириал 44
Клеро формула 430
Клин 222
Колебание бесконечно малое 426, 441
—	простое 285
Количество движения 270
Комета 338
Комплекс линейный (Шаля) 31, 136,
166, 204, 325
Конгруенция линейная 136
Коноид 53
Координаты барицентрические Мё-
биуса 52
—	голономной системы 229
—	Плюкера 25
—	прямой 136
—	эллиптические 453
Кориолиса теорема 77
Косинус направляющий вектора 18
Коэффициент трения 258, 296
	 качения 263
Кривая синодальная 408
—	синхронная 408
Кривизна главная 62
Лагранжа множитель 233, 245
—	ряд 360
—	уравнение движения 400, 410, 424,
466
—	формула 320
Лебедка 225
Лежен-Дирихле метод 113
Линия винтовая 84
—	геодезическая 181, 422
—	действия вектора 16
—	узлов 363
—	центральная 147
—	цепная 150, 158, 171
	одинакового сопротивления 204
	сферическая 182
Лобачевского геометрия 191
Лучи катодные 317
Ляме уравнение 440
Масса 86, 89
—	планеты, обладающей спутником
352
Машина простая 221
Маятник 86, 96, 406
—	математический 375, 381, 403, 503
—	сферический 433, 502
—	Фуко 89

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
513
Маятник циклоидальный 387
Мёбиуса координаты барицентриче-
ские 52
Менье теорема 183, 421
Метод Лежен-Дирихле 113
—	Ольберса определения орбит ко-
мет 488
Механизм кривошипный 224
Механика небесная 348
Миндинга теорема 147
Многоугольник Вариньона 153, 159,
202
—	веревочный 152, 235
¦— опорный 141
Множитель Лагранжа 233, 245
Модуль вектора 16
Момент векторный (вектора относи-
тельно точки) 22
—	векторов относительный 25
•— взаимный 41
—	главный 28
—	изгибающий 195
¦— количества движения 270
—	относительно плоскости 47
—	пары 38
—	— векторный 38
—	скалярный (вектора относительно
оси) 23
Мопертюи принцип 208
Мост висячий 158
—	подъемный Белидора 252
Мотор 51
Мощность 108
Направление вращения положитель-
ное 20
—	главное 146
Натяжение 195
—	нити 92, 111, 153, 165
Начало равенства действия и проти-
водействия 89
Нить нерастяжимая 164
—	тяжелая 158
—	упругая Ш, 125
Нормаль главная 62
Однородность линии (поверхности,
тела) 143
—	формул 95
Ольберса метод определения орбит
комет 488
Операции элементарные 32
Ориентация координатного триедра
Оси абсолютно неподвижные 86
Основание вектора 16
—	цепной линии 172
Ось винтовая мгновенная 69, 72, 84
—	вращения мгновенная 75
—	равновесия 147
—	стержня 195
—	центральная 29, 43
Падение свободное в пустоте 294
Пара 37
«Парабола безопасности» 305, 463
Параметр винта 40
—	винтового движения 239
Парус 203
Перемещение возможное 209, 402
—	действительное 209
—	относительное 66
—	переносное 66
—	поступательное 239
—	равенства (неравенства) 242
—	системы винтовое 239
Перигелий 354, 365, 492
Пластинка тяжелая 253
Плечо пары 37
Плоскость наклонная 86
—	центральная 55, 146, 148
—	эклиптики 363
Плотность газа 96
—	средняя 145
	 Земли 342
Плюккера координаты 25
Поверхность синхронная 408
—	уровня 103
Показатель преломления абсолютный
193
Полиспаст 225
Постоянная всемирного тяготения 341
—	кинетической энергии 275
Потенциал 100, 108
Правило Якоби 464
Преобразование томографическое 445
—	движений 445
—	Пуассона и Гамильтона 466
Пресс винтовой 222
—	гидравлический 227
—	клиновидный 222, 264
Приведение системы скользящих век-
торов 32, 37
Принцип возможных скоростей 143,
208
—	Гамильтона 460
—	Гаусса 460
—	Даламбера 92, 458
¦— затвердевания 152, 160
¦— минимума суммы квадратов рас-
стояний 251
—	Мопертюи 208
—	наименьшего действия 184, 189,
458, 499

514
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Принцип рычага 92
—Торричелли 232
Притяжение всемирное 86, 112, 340
—	Земли 92
—, пропорциональное расстоянию 115
Проекция центральная 445
Произведение векторов векторное
(внешнее) 21, 54
	скалярное (внутреннее, прямое,
алгебраическое) 18, 19
Производная векторная 44, 48, 54, 63
—	по направлению 103
«Прыгалки» 177
Прямая нулевого момента 30
Пуассона и Гамильтона преобразо-
вание 466
Работа 97
—	возможная 209, 242, 456
—	движущая 97
—	полная 98, 275
—	элементарная 97, 274, 450
	 взаимодействия 109
Равновесие 91, 113
—	астатическое 43, 131, 147
—	веревочного многоугольника 153
—	ворота 138
—	естественное (вынужденное) 195
—	естественных тел с трением 258
—	нити 164, 180, 236, 270, 325, 457,
499, 505
—	рычага 137
—	системы 120
—	твердого тела 126
—	точки 113
—	устойчивое 113
Равнодействующая 90
Радиус геодезической кривизны 183
Реакция нормальная 116, 119,256,262,
379, 388, 420, 438
—	связей 136, 210, 235
Ренкина теорема 202
Рефракция 184, 189, 193
Роберваля весы 224
Рычаг 92, 137
Ряд Лагранжа 360
Связь без трения 218
—	идеальная 218
—	неудерживающая 241
—	полная 221
Сила 15, 86, 89
•— внешняя 120
—	внутренняя 120
¦— движущая 221
—	«живая» 274
—	заданная 210
—	инерция 453
Сила «лошадиная» 108
—, отнесенная к единице длины 164
—	постоянного направления 280
—	центральная 272, 280, 327, 471, 484
Система голономная 229, 447
—	изменяемая 152
—	материальных точек 120
—	неголономная 236
—	неизменяемая 63
—	с полными связями 221
—	сравнения 66
—	тяжелая 231
—	шарнирная Фусса 202
Скаляр, род его 50
Скольжение 255
Скорость 57
¦—• абсолютная 67
•— верчения угловая 77
—	возможная 206
—	звука в газе 96
—	качения угловая 77
—	относительная 66
—	переносная 67, 79
—	поступательного движения 64
—	средняя 58
—	угловая 64
Сложение движений 66, 81
—	сил 90
Спутник планеты 339
Статика 92, 113
Степень свободы 228
Стержень твердый 153
—	тяжелый 231, 253
Таутохрона 390, 406, 407
' Тело, опирающееся на неподвижную
плоскость 139
—, перемещающееся параллельно не-
подвижной плоскости 75
—	с неподвижной осью 138
—	твердое 63, 126
—• —, подчиненное связям 136
—	— с неподвижной точкой 75
	 свободное 213
Теорема Вариньона 27
—	Гринхилла 441
—	Гюльдена 143, 232
—	движения центра тяжести 291, 350
—	Дюпена 489
—	кинетической энергии 273, 285,
302, 315, 327, 372, 416
—	Кориолиса 77
—	Менье 183, 421
—	Миндинга 147
—	моментов относительно плоскости
47
Теорема о возможной работе 120

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
515
Теорема Ренкина 202
—	Эйлера 369, 396
—	Якоби 466, 472
Теоремы Аполлония 365
Теория возмущений 364
—	моментов 22
—	притяжения 348
Теплоемкость газа 96
Тетраэдр Шаля 37
Торричелли принцип 232
Точка материальная 86, 97, 113, 210,
212
—	свободная 113, 123, 447, 499
—	срыва 405
—	таутохронизма 297, 390
—	тяжелая 301, 324
Траектория 57, 408, 464, 478
-— относительная 66
Трение 256, 262
Турникет 51
Тэйлора формула 379
Тэта и Томсона формула 188, 206,
207, 463
Тяжесть 92
Угол наклонения 363
—	трения 257
—	Эйлера 230
Упругость газа 96
Уравнение движения Лагранжа 400
410, 424, 447, 466
—	Кеплера 356, 370
—	Ляме 440
—	статики основное (главное) 227
—	Якоби 473
Уравнения движения 91, 266
—	естественные 168
—	канонические 466
—	равновесия 120, 127
—	— нити 164, 168
—	упрощенные 31
Ускорение 60
—	добавочное 79
—	касательное 62
—	нормальное 62
—	относительное 66
—	переносное 79
—	поступательного движения 64
—	среднее 60
Условия на концах веревочного мно-
гоугольника 155
—	равновесия 120, 127
Устойчивость равновесия 113, 278,
373, 384, 419
Ферма 163, 202
Фигура 'равновесия 174, 464, 501, 504
Фокус Шаля 32
Формула см. название
Формулы для вычисления центра тя-
жести 143
—	Френе —Серре 62, 169
Фуко маятник 89
Функции Бесселя 369
—	Якоби 368
Функция Гамильтона 469
—	силовая 97, 100, 108, 169, 275, 501
—	Фурье—Бесселя 360
Фуре задача 407
Фусса система шарнирная 202
Центр 55
•— вращения мгновенный 56, 76
—	инерции 132
—	параллельных связанных векторов
44
	¦ сил 131
—	сил 146, 148
—	тяжести 115, 131, 143
—	удара 150
Цепь 123, 183, 206, 225, 232, 254, 265.
504
Цилиндроид 53
Час естественный 343
Частица электрическая 315
Число степеней свободы 228
Шаг единичного винта 40
Шаля комплекс линейный 31
—	тетраэдр 37
—	фокус 32
Эйлера и Саладини задача 407
—	теорема 369, 396
—	угол 230
Эквивалент химический 88
Эквивалентность пар 38
—	систем сил 127
—	системы скользящих векторов 32
Эклиптика, плоскость 363
Эластика 195
Элементы эллиптического движения
363
Энергия кинетическая 274
Эрг 99
Якоби правило 464
—	теорема 466, 472
—	уравнение 473
—	функции 368