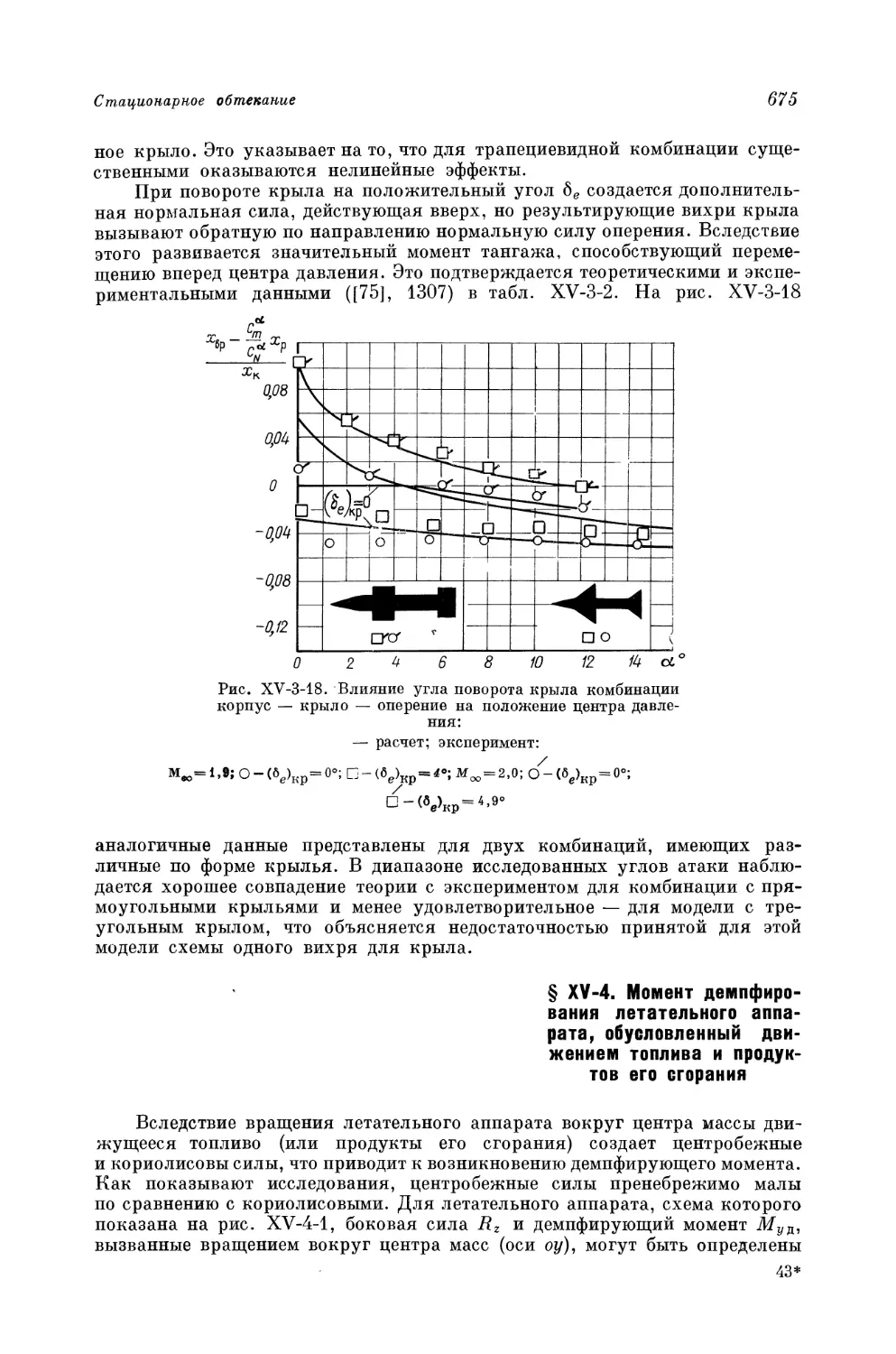
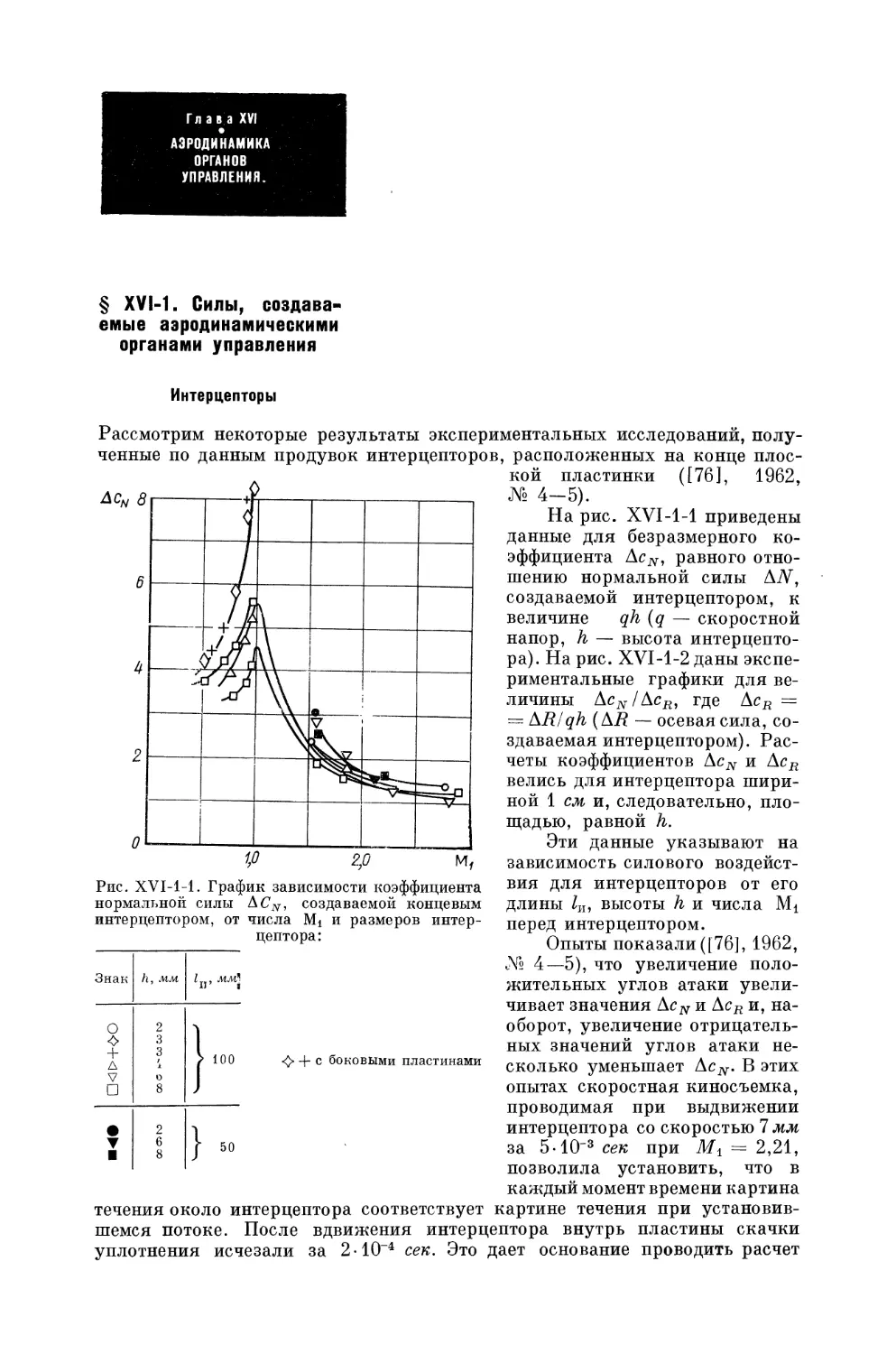
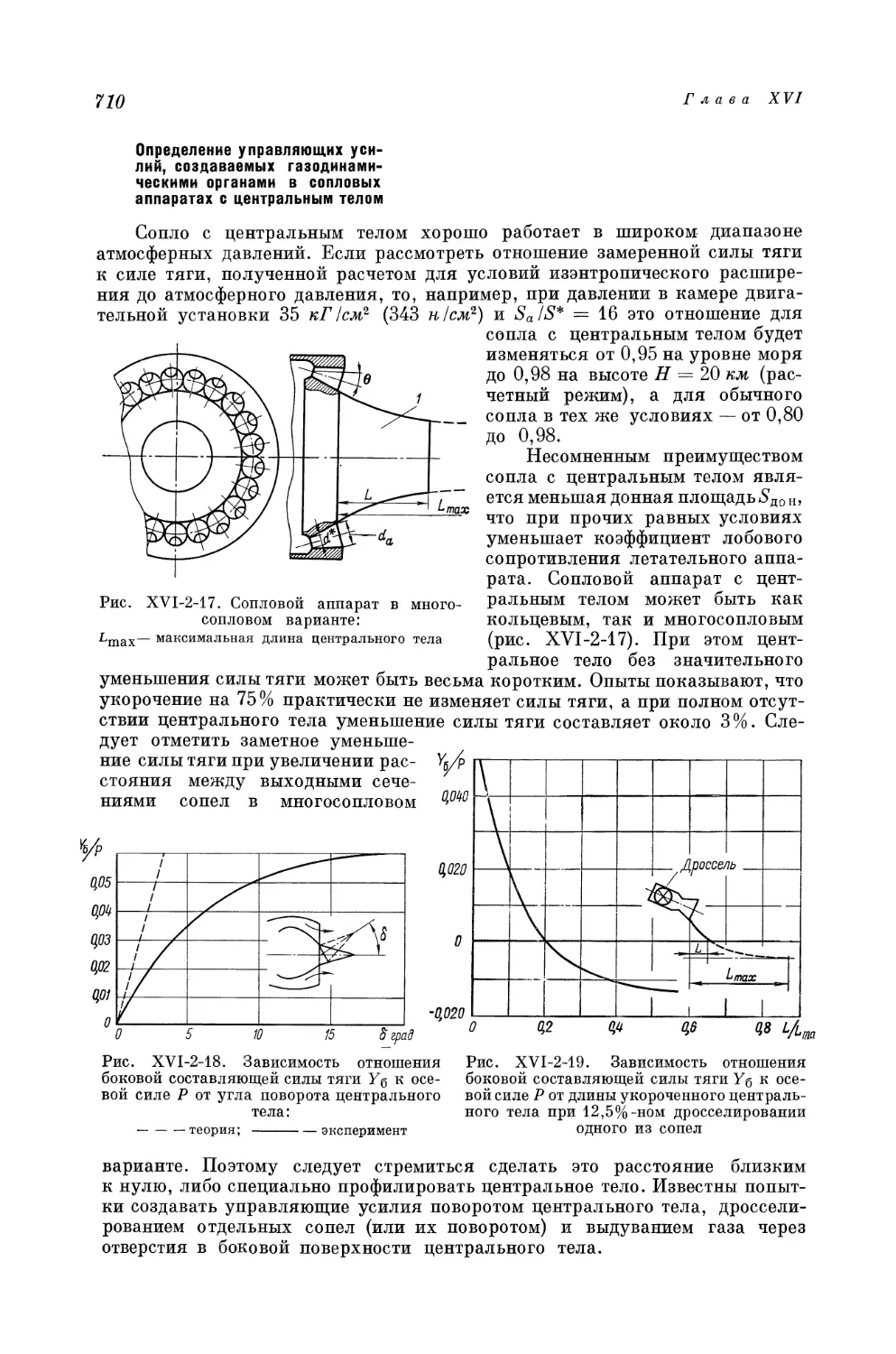
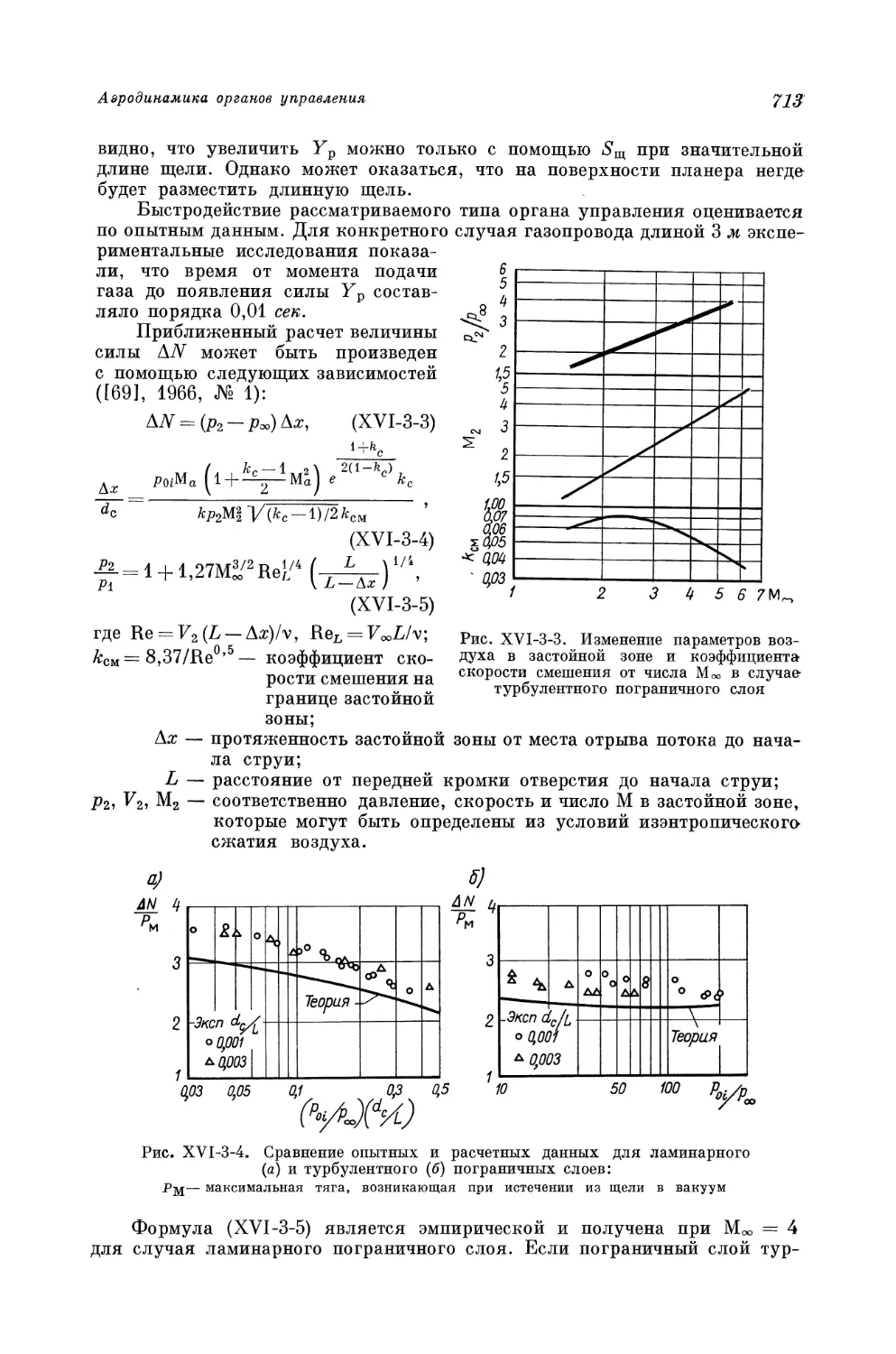
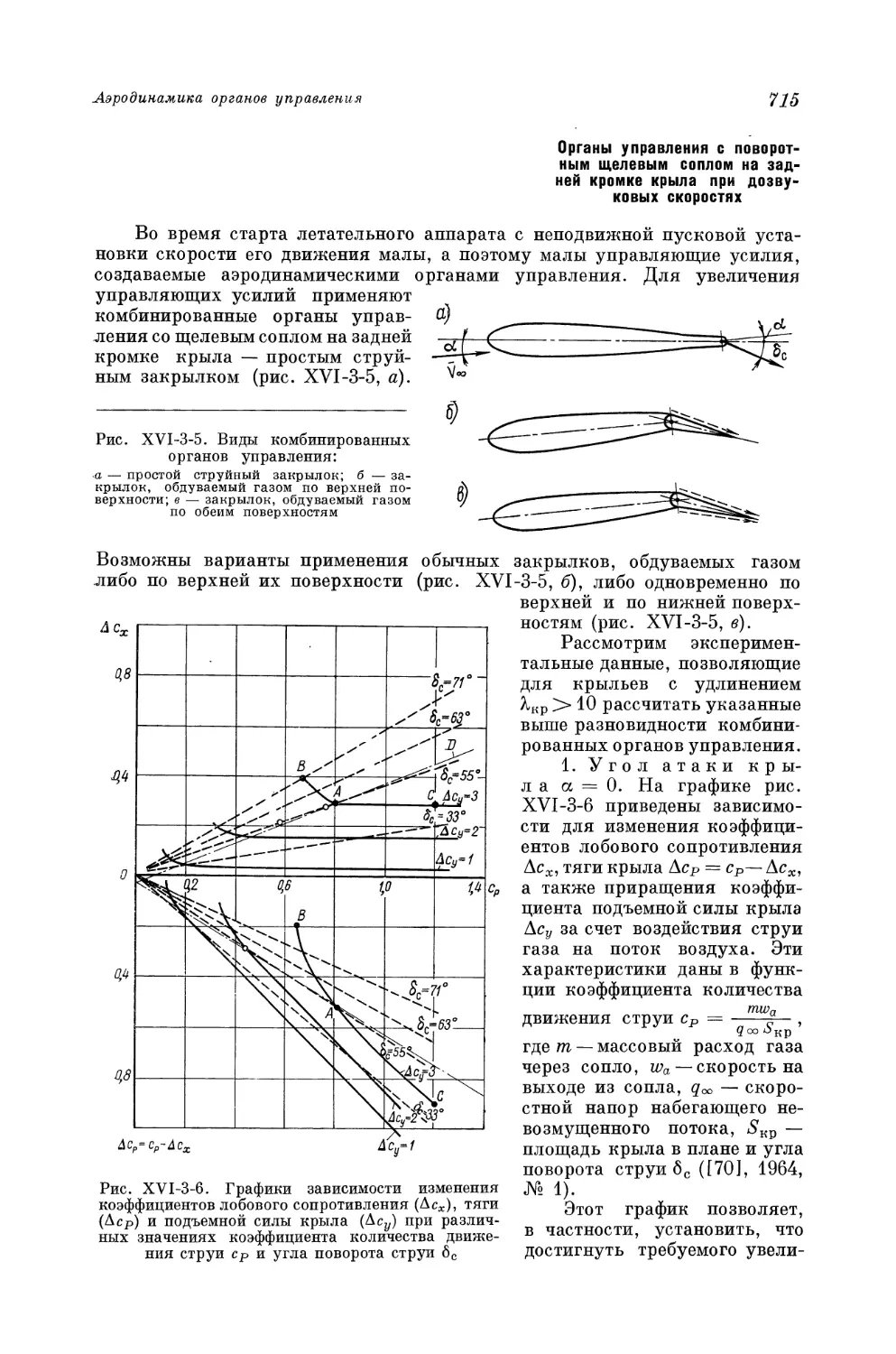
Author: Краснов Н.Ф. Кошевой В.Н. Данилов А.Н. Захарченко В.Ф.
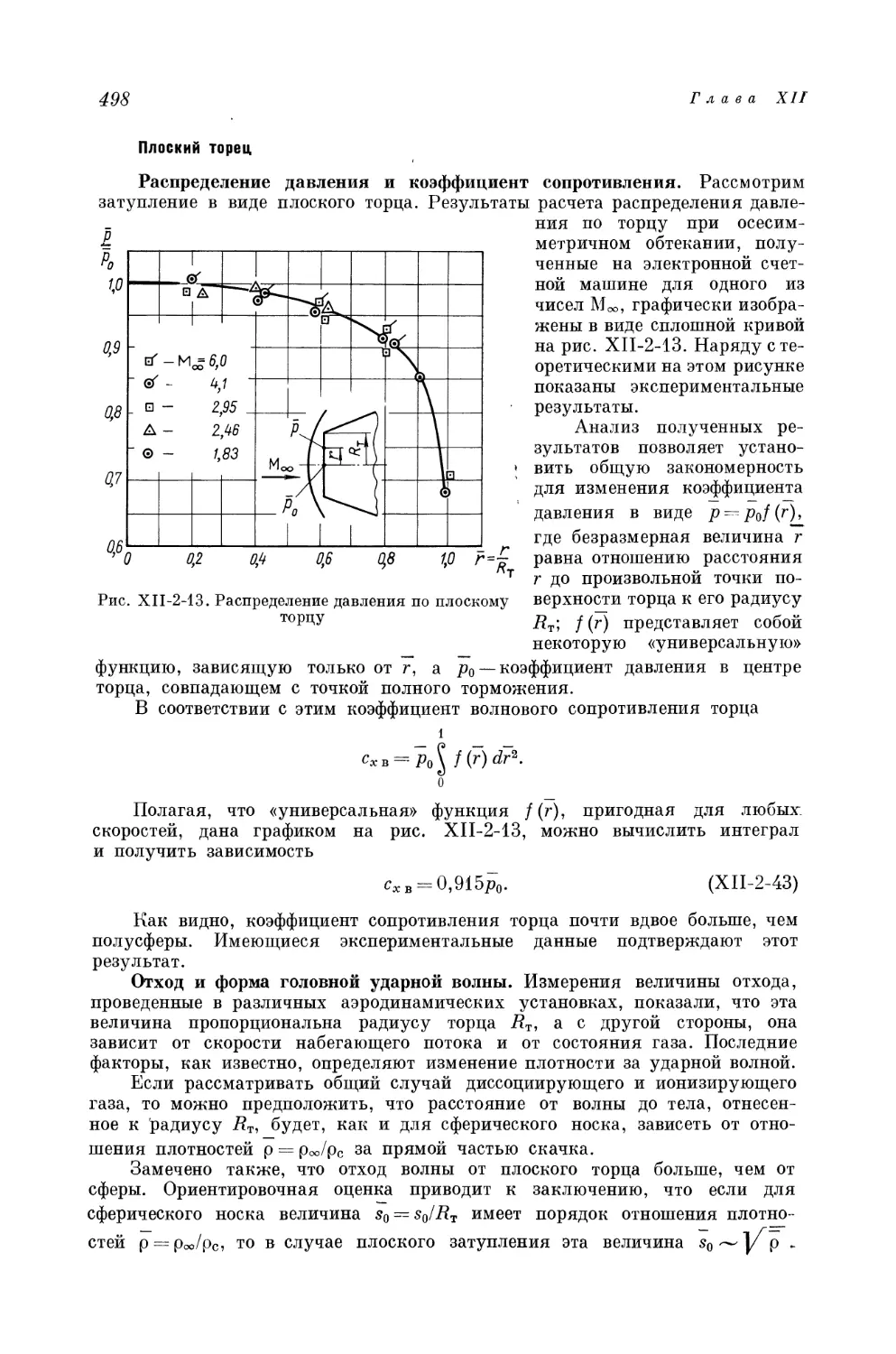
Tags: техника средств транспорта летательные аппараты ракетная техника аэромеханика
Year: 1968
Text
Н-Ф-КРАСНОВ
ВН-КОШЕВОЙ
АН-ДАНИЛОВ
В-Ф-ЗАХАРЧЕНКО
аэродинамика
ракет
ПОД ОБЩЕЙ РЕДАКЦИЕЙ ПРОФ.НФ-КРАСНОВА
Допущено
Министерством
высшего
и среднего
специального
образования
СССР
в качестве
учебного
пособия
для студентов
технических
ИЗДАТЕЛЬСТВО
ВЫСШАЯ
ШКОЛА
МОСКВА 1968
УДК 629.136
К-78
Краснов
Николай Федорович
Кошевой
Всеволод Николаевич
Данилов
Анатолий Николаевич
Захарченко
Вадим Федорович
АЭРОДИНАМИКА
РАКЕТ
НАУЧНЫЙ РЕДАКТОР
Я. М. К О Т Л Я Р
РЕДАКТОР
Г. И. ФУФАЕВА
ХУДОЖНИК А. Т. ЯКОВЛЕВ
ХУДОЖЕСТВЕННЫЙ РЕДАКТОР
Н. К. ГУТОРОВ
ТЕХНИЧЕСКИЙ РЕДАКТОР
Э. М. ЧИЖЕВСКИЙ
КОРРЕКТОР
С. Р. ЛАНОВЕНКО
Т-14448 Сдано в набор 4/1—68 г. Подп.
к печати 16/Х—68 г. Формат 70xl08/ie
Объем 48,25 печ. л. усл. п. л. 67,55 Уч.-изд. л.
57,01 Изд. № стд-41 Тираж 10.000 экз. Цена
2 р. 23 к. Зак. 114
БЗ-39/31 от 30/V-68 г.
Москва, К-51, Неглинная ул., д 29/14,
Издательство «Высшая школа»
Московская типография № 16
Главполиграфпрома Комитета по печати при
Совете Министров СССР
Москва, Трехпрудный пер., 9
Рецензенты:
1. Н. С. АРЖАНИКОВ, проф.
2. И. П. Гинзбург, проф.
2-4-2
БЗ—30 31—68
ПРЕДИСЛОВИЕ
Современная аэродинамика развивается по двум основным направлениямт
одно из которых связано с дальнейшим развитием и совершенствованием
методов определения силового воздействия среды на движущиеся в ней тела,
другое — с исследованием и расчетом тепловых процессов на стенке
летательного аппарата, сопровождающихся различными физико-химическими
превращениями. Второе направление превратилось в самостоятельный раздел
аэродинамической науки — аэротермодинамику. Аэротермодинамические
исследования ведутся в основном самостоятельно, с использованием данных обычной
(«силовой») аэродинамики. В последние годы по мере совершенствования
математического аппарата все большее число аэродинамических задач, связанных
с определением силового воздействия и теплопередачи, решается во
взаимосвязи. Однако во многих случаях практически оправдано предположение
независимости силовых и тепловых процессов и проведение их расчета отдельно.
В соответствии с этим распределение параметров газа при обтекании поверх -
ности (давление, напряжение трения, температура и т. д.) находится без учета
теплопередачи на стенке. Вычисление же тепловых потоков может
осуществляться отдельно с использованием этих параметров.
Исследование распределения давления, температуры, плотности (так
называемых «невязких» параметров) ведется путем решения соответствующих
уравнений газодинамики для невязкого (идеального) газа. Полученные «не-
вязкие» параметры используются для решения уравнений пограничного слоя
и вычисления распределения касательных напряжений по поверхности
летательных аппаратов.
При движении летательных аппаратов с очень большими скоростями
воздух вблизи поверхности тела разогревается до очзнь высоких температур,
при которых происходят химические реакции. Учет влияния реакций на
величину и распределение давления, температуры и других параметров составляет
важнейшую особенность современной аэродинамики, которая нашла отражение
в настоящей книге.
Значительное место в книге отводится исследованиям нестационарного
обтекания тел различной формы, которые в настоящее время приобрели
большое значение.
Изложению прикладных вопросов аэродинамического расчета различного
вида крыльев и корпусов и их комбинаций предшествует в настоящей книге,
рассмотрение общих положений аэродинамики. Соответствующие материалы;
помещены в первом разделе, который содержит понятия о силах, моментах
и аэродинамических коэффициентах (гл. I), описание формы летательных;
аппаратов и их элементов (гл. II), основные соотношения теории газовых
течений (гл. III), общие методы решения аэродинамических задач (гл. IV).
При рассмотрении аэродинамических характеристик весьма важно с
практической точки зрения обоснованно расчленить суммарные значения этих
характеристик на отдельные составляющие, обладающие свойством аддитив-
4: Предисловие
Принцип расчленения аэродинамических характеристик на отдельные компоненты
применен для изолированных корпусов и крыльев, а также для их комбинаций. В
последнем случае аэродинамические силы и моменты определяются в виде суммы
соответствующих характеристик (для изолированных корпуса, крыльев и оперения) и
интерференционных поправок. Этот принцип положен также в основу изложения вопросов
нестационарной аэродинамики, когда аэродинамические характеристики вычисляются
отдельно с учетом соответствующих дополнительных нестационарных течений,
накладываемых на стационарное обтекание.
Современная аэродинамика накопила значительный опыт по определению
аэродинамических характеристик изолированных корпусов и крыльев, а также различных
конфигураций летательных аппаратов. В гл. II рассматриваются наиболее
распространенные формы отдельных элементов летательных аппаратов, дается классификация ракет
различного назначения по их аэродинамическим схемам и летным свойствам, анализ
общих аэродинамических свойств современных летательных аппаратов, различные типы
рулевых устройств, их аэродинамические характеристики.
Система дифференциальных уравнений аэрогазодинамики, лежащая в основе
решения задач обтекания, рассматривается отдельно для двух основных видов движения:
-свободного потока и течения в пограничном слое. Система уравнений для свободного
потока позволяет рассчитать в общем случае сильно возмущенное вихревое течение с
учетом влияния высоких температур, при которых может происходить диссоциация и
ионизация. Решение уравнений для пограничного слоя дает возможность найти параметры
трения и теплопередачи при наличии химических реакций и диффузии, обусловленной
шаличием в слое молекулярных, ионных и электронных компонент.
Решение задач о сверхзвуковом обтекании связано с исследованием течения за скач-
шами уплотнения. С этой целью рассматриваются основные зависимости, определяющие
параметры потока за скачками для наиболее общего случая, учитывающего химические
процессы, которые протекают в газе за ударными волнами при гиперзвуковых
скоростях. При этом учитываются явления релаксации, так как процессы возбуждения могут
характеризоваться значительным временем запаздывания.
Эффективным методом решения аэродинамических задач является метод конечных
разностей (метод сток). В частности конечные разности используются при расчетах по
методу характеристик, основные зависимости которых даются в книге для общих случаев
двухмерных диссоциирующих вихревых течений (плоского и пространственного осе-
симметричного). Большой вклад в разработку метода сеток применительно к расчету
пространственного обтекания заостренных тел в общем случае, когда учитываются
химические реакции, внесен группой научных сотрудников Математического, института
АН СССР (К. И. Бабенко, Г. П. Воскресенский и др. [4]).
При рассмотрении аэродинамического расчета изолированных крыльев и корпусов
большое место отведено методам определения параметров обтекания тонких тел при
небольших сверхзвуковых скоростях (методы источников и малых возмущений).
Применение метода характеристик позволяет перейти при расчете обтекания к телам
любой формы и произвольным числам Маха набегающего потока.
Значительное место при рассмотрении аэродинамики крыльев и корпусов отведено
методам расчета силового воздействия и теплопередачи при гиперзвуковых скоростях
обтекания.
Аэродинамические характеристики изолированных корпусов и крыльев
рассмотрены также при дозвуковых и околозвуковых (трансзвуковых) скоростях.
Наряду с аэродинамикой заостренных крыльев и корпусов в настоящее время
получили развитие исследования обтекания затупленных поверхностей.
Рассматриваемые в книге результаты этих исследований относятся, в частности, к определению
отхода и формы ударной волны, вычислению давления и скорости на затупленной
передней части поверхности, а также к расчету обтекания периферийных участков
затупленного тела. Практический интерес представляют решения задач об обтекании под большим
углом атаки (до 90°) крыла в виде плоской пластинки, а также задачи о круговом
обдуве корпуса.
Предисловие g
В результате исследования возмущенного течения под влиянием затупления
установлено существование «невязкого» высокоэнтропийного слоя малых скоростей,
определены его свойства. Правильное использование этих свойств позволяет путем наиболее
целесообразного подбора формы и размеров затупленного носка снизить тепловые
потоки. Таким образом, затупление надо в известном смысле рассматривать как средства
тепловой защиты летательного аппарата.
В книге нашли отражение теоретические и экспериментальные результаты
исследований теплопередачи на поверхностях, имеющих в общем случае произвольную
переднюю часть. Рассматривается расчет тепловых потоков на затупленных телах с учетом
предыстории пограничного слоя, а также происходящих в нем химических реакций.
С ростом скоростей полета наряду с передачей тепла в пограничном слое за счет
теплопроводности существенной становится диффузионная теплопередача,
представление о которой дается для случаев конечной скорости химической реакции и бесконечно
быстрой рекомбинации. При изложении этих вопросов указываются пути управления
диффузионной теплопередачей, заключающиеся в применении контактирующих
материалов с различной каталитической способностью.
Аэродинамический расчет изолированных крыльев носит вспомогательный
характер и входит составной частью в определение суммарных аэродинамических
характеристик летательных аппаратов, представляющих собой комбинацию корпуса с различными
несущими, стабилизирующими и управляющими поверхностями. Самостоятельное зна
чение аэродинамика крыла будет приобретать по мере появления аппаратов типа
«летающее крыло». Аэродинамические исследования корпусов произвольной формы и особенно
тел вращения могут иметь самостоятельное значение, так как многие летательные
аппараты ракетного типа по своей аэродинамической схеме являются телами вращения или
изготовлены в виде корпуса, близкого по форме к телу вращения. По этой причине
аэродинамика корпуса (тела вращения) изложена в книге наиболее полно. Наряду
с отмеченными выше проблемами, общими для крыльев и корпусов, освещается ряд
специфических вопросов аэродинамики корпуса.
Современный высокоскоростной летательный аппарат по своей аэродинамической
схеме представляет собой комбинацию корпуса (обычно тела вращения), крыльев,
оперения и управляющих устройств. Вследствие аэродинамической интерференции между
указанными элементами полные силы и моменты для комбинации не равны сумме
соответствующих характеристик для изолированных корпуса, крыльев, оперения и рулей.
Поэтому при расчете суммарных аэродинамических характеристик должны быть учтены
эффекты взаимодействия. В последнем разделе книги проблемы интерференции
излагаются на основе аэродинамической теории тонкого тела как для стационарного, так
и для неустановившегося обтекания тонких составных конфигураций. Разработанные
в этой теории методы расчета интерференции распространяются на случай
линеаризованного обтекания, когда учитывается влияние чисел Маха. Интерференция при
больших скоростях движения комбинированных тел произвольной толщины является
наименее разработанной проблемой современной аэродинамики. Экспериментально
установлено, что по мере увеличения сверхзвуковых скоростей полета эффекты взаимодействия
становятся менее t существенными. Это [объясняется сужением зон взаимного влияния.
Поэтому аэродинамические характеристики комбинации корпусов с несущими,
стабилизирующими и управляющими устройствами при больших скоростях приближенно можна
определять путем суммирования соответствующих аэродинамических характеристик для
изолированных элементов этой комбинации.
Современные управляемые летательные аппараты обеспечиваются
аэродинамическими, газодинамическими или комбинированными органами управления. Выбор
типа органа управления обусловлен конструктивными особенностями, назначением
и условиями полета летательного аппарата. Нахождение управляющего усилия
является важной частью аэродинамического расчета, так как во многом определяет летные
свойства летательного аппарата в целом. Поэтому вопросу расчета эффективности рулей
указанных трех типов в книге уделено большое внимание. Силовые и моментные
характеристики аэродинамических органов управления излагаются в рамках аэродинамиче-
g Предисловие
ской теории тонкого тела с использованием поправок, получаемых по линеаризованной
теории. Расчет эффективности других типов органов управления излагается на основе
имеющихся экспериментальных данных с учетом применения элементарных
соотношений газодинамики. Аэродинамические проблемы, связанные с органами управления,
разработаны недостаточно. Необходимы дальнейшие теоретические и
экспериментальные исследования.
В целом книга знакомит читателя с основными теоретическими положениями
современной аэродинамики больших скоростей, методами расчета силового и теплового
воздействия среды на летательный аппарат и его отдельные элементы, а также с
важнейшими характеристиками течений газа при различных его состояниях.
С целью облегчения перевода использованных единиц измерения физических
величин в новые, соответствующие принятой Международной системе (СИ), в конце
книги приведена специальная переводная таблица. В численных примерах для
сопоставления даются величины, полученные с учетом Международной системы единиц
измерения.
Заслуженный деятель науки и техники, проф. Н. С. Аржаников и проф. И. П.
Гинзбург, выполнили большую работу по рецензированию рукописи, дали весьма ценные
советы и указания, которые были учтены при окончательном редактировании книги.
Авторы сознают, что их труд не свободен от недостатков и с благодарностью
примут все замечания читателей.
РАЗДЕЛ
ПЕРВЫЙ
овщие
определения
аэродина
мики
ПОНЯТИЕ
О СИЛАХ,МОМЕНТАХ
И АЭРОДИНАМИЧЕСКИХ
КОЭФФИЦИЕНТАХ.
§ 1-1. Систем ы осей координат
Силовое воздействие среды. Воздействие среды на движущееся в ней тело
сводится к появлению на его поверхности непрерывно распределенных сил
нормального давления, а также касательных напряжений, обусловленных
вязкостью среды. Все эти силы (рис. 1-1-1) приводятся к одному главному
вектору F аэродинамических сил и главному вектору М момента этих сил
относительно какой-либо точки приведения. Причем, такой точкой может
быть произвольная точка тела, в частности, центр тяжести, острие носка
и т. д. В инженерной практике имеют дело не с векторами F и М, а с их
проекциями на оси какой-либо
системы координат. Наиболее [У
распространенными из них
являются система поточных
(скоростных) осей координат и
система связанных осей
координат.
Система поточных
(скоростных) осей координат. В этой
системе координат (рис. 1-1-1)
продольная ось х совпадает с
направлением скорости полета,
ось у лежит в вертикальной
плоскости симметрии
обтекаемого тела, а ось z
перпендикулярна плоскости х, у и
направлена так, что оси х, у, z
образуют правую систему координат.
Иногда поточная система
применяется в другом виде. Ее
продольная ось х совпадает с
направлением скорости потока,
а ось у лежит в плоскости, в
которой расположены вектор
скорости Foo и связанная ось х±.
Система связанных осей координат. В этой системе, жестко связанной
с. летательным аппаратом (см. рис. 1-1-1), ось х± направлена к носку
параллельно хорде крыла, а у летательного аппарата, обладающего осесимметрич-
ным корпусом, ось Xi совпадает с продольной осью симметрии корпуса.
Ось ух связанной системы лежит в вертикальной плоскости симметрии, а ось
Zi направлена вдоль размаха правого крыла (правая система координат).
Иногда применяется связанная система координат, оси которой
изображены на рис. 1-1-2. Ось х± направлена от носка к хвосту тела по потоку. При
наличии горизонтальной и вертикальной симметрии оси z± и г/i лежат
соответственно в горизонтальной и вертикальной плоскостях симметрии,
образуя правую систему координат.
Рис. 1-1-1. Схема действующих на летательный
аппарат аэродинамических сил и моментов в
поточной (х, у, z) и связанной (х±, у±, г±) системах
координат
10
Глава I
Наряду с поточной и связанной системами координат в
аэродинамических исследованиях применяется в отдельных случаях система так
называемых полусвязанных осей координат. В этой системе продольная ось х2
совпадает с проекцией вектора скорости Foo на вертикальную плоскость
симметрии летательного аппарата.
Вертикальная ось у2
расположена также в этой плоскости,
называемой плоскостью угла
атаки. Ось z2 совпадает с осью z±
связанной системы координат.
Взаимное расположение
осей координат различных
систем. Величина и направление
действия сил и моментов
зависят при данной скорости
движения от ориентировки тела
относительно вектора скорости
Рис. 1-1-2. Связанная (хи yt1 zt) и поточная полета или, ^сли
рассматриваем у, z) системы координат етсд обращенНое движение,
относительно направления
скорости набегающего потока Foo. Следовательно, величина и направление
действия сил и моментов зависят от взаимного расположения систем
координат, связанных с потоком и телом.
Взаимное расположение поточной и связанной систем координат
определяется (см. рис. 1-1-1) углом атаки а — углом между осью Oxt и
проекцией вектора Foo на плоскость х^Оу^ и углом
скольжения рск— углом между вектором Foo
и плоскостью XiOyi.
Зная углы а и рск, можно по данным
координатам точки, например в поточных
осях, найти ее координаты в связанной
системе, и наоборот. Для этой цели следует
воспользоваться соответствующими
формулами аналитической геометрии, дающими
зависимость для пересчитываемых координат от
косинусов углов между осями
рассматриваемых систем, а также выразить эти углы
через а и рск.
Следует иметь в виду, что углы,
определяющие положение летательного аппарата
относительно направления полета, зависят от
выбора систем координат, связанных с
потоком и аппаратом, что в известной мере
является произвольным. В частности, для систем, изображенных на рис. 1-1-2,
такими углами, которыми наиболее удобно характеризовать положение тела,
являются углы асиф. Первый из них можно назвать условно углом тангажа,
второй — крена.
Зная эти углы, также можно найти связь между координатами точки
в связанной и поточной системах.
По значениям ас и ф могут быть определены углы атаки и скольжения
®<si &и Рг, Ps (рис. 1-1-3). Соответствующие расчетные формулы приведены
в табл. 1-1-1.
Углы скольжения принимаются положительными, если поток набегает
с правой стороны, f"^ ^ t,,,,1
Рис. 1-1-3. Углы атаки и
скольжения (составляющие скорости Foo
даны в связанной системе
координат)
Понятие о силах, моментах и аэродинамических коэффициентах 11
Таблица 1-1-1
Углы атаки и скольжения
Расчетные зависимости
для углов атаки
V оо
= sinaccos ф;
= tgaccos9.
для углов скольжения
sin рв— *-
V оо
= sin ac sin ф;
tgps=-^i-=
— tgac sinф.
Составляющие скорости потока
(рис. 1-1-3) в связанной системе
координат
Fxl = VooCOsac;
Vyi = Foo sin ac cos ф;
VZl= —Уоо sin ac sin ф.
При малых углах атаки и скольжения
= accos ф.
§ 1-2. Силы, моменты
и их аэродинамические
коэффициенты
Составляющие аэродинамических сил и моментов. Аэродинамические
коэффициенты. Вектор полной аэродинамической силы F, а также главный
вектор-момент М можно представить в виде суммы трех составляющих
по осям выбранной системы координат. В поточной системе координат
где i, /, А —единичные векторы соответственно по осям х, у, z.
Аналогично будут написаны выражения для векторов F я М в связанной системе
координат с той разницей, что составляющими вектора силы будут Хи У1?
Zb а вектора-момента — Mxv Myv MZv
Проекции вектора F на оси х, у, z поточной системы координат
называются соответственно силой лобового сопротивления X, подъемной Y и
боковой Z силами. Соответствующие проекции того же вектора на оси xt, yt, zi
связанной системы координат называются продольной (осевой) (Xi или /?),
нормальной (Yi или N) и поперечной (Zi) силами.
Проекции вектора М в той или другой системе координат называются
одинаково, а именно: составляющие Мх и МХ1 относительно продольной
оси—моментом крена, составляющие Му и МУ1 относительно осей у и у^ —
моментом рысканья, составляющие Mz и MZl относительно поперечной
оси—моментом тангажа.
Как следует из теории подобия, величину любой аэродинамической силы
можно представить как произведение скоростного напора ^=0,5pooFL =
12 Г л а в а I
= 0,5&ML/?oo на некоторую характерную площадь и коэффициент с, т. е.
cqS (например, сила лобового сопротивления X = cxqS и т. д.).
Составляющая момента представляется аналогичным произведением
с добавлением в него в качестве сомножителя параметра I с линейной
размерностью (например, Mx = mxqSl).
По значению аэродинамических сил и моментов можно определить
безразмерные коэффициенты пропорциональности сит, так называемые
аэродинамические коэффициенты этих сил и моментов. В частности, для
коэффициентов аэродинамических сил и моментов справедливы формулы
C c C (Ltl)
m-5b m=
Коэффициенты cx, су, cz называются соответственно аэродинамическими
коэффициентами силы лобового сопротивления, подъемной и боковой сил,
а коэффициенты тх, m,v, mz — соответственно аэродинамическими
коэффициентами моментов крена, рысканья и тангажа.
В связанной системе координат для характеристики соответствующей
составляющей силы или момента вводятся аналогичные коэффициенты.
Коэффициенты сил обозначаются через cXl(cR), cyi(cN), cZl и называются
соответственно аэродинамическими коэффициентами продольной (осевой),
нормальной и поперечной сил. Коэффициенты момента обозначаются тХ1Г
mw тч и называются так же, как в поточных координатах.
Пересчет аэродинамических характеристик с одной системы
координат на другую. Необходимость такого пересчета возникает, в частности,
в том случае, когда аэродинамические исследования осуществляются в одной
какой-либо системе координат, а траекторные расчеты — в другой. Обычно
в этом случае ведется пересчет аэродинамических характеристик со
связанной системы, в которой они получены, на поточную, в которой ведутся
исследования полета. Обратный пересчет необходим, например, когда
аэродинамические характеристики, полученные по результатам летных испытаний,
сравниваются с расчетными данными, найденными в связанных
координатах.
В качестве иллюстрации приведем формулы для пересчета коэффициентов
силы и моментов со связанной на поточную систему координат. Используя
таблицу направляющих косинусов [30], можно найти выражение для
аэродинамического коэффициента силы лобового сопротивления
Сх = Cr c°s ос cos рск — ex sin a cos |3CK -f- cZl sin рСк- (1-2-3)
Соответствующая зависимость для коэффициента момента
тх — тХ1 cos a cos рск — тУ1 sin a cos (3Ск + ^z± sin (3Ск- (1-2-4)
Пересчет других коэффициентов осуществляется аналогично.
Расположение осей координат в случае аэродинамических
исследований тел вращения. При исследовании обтекания без скольжения тел
вращения оси хи jji связанной и х, у поточной систем координат выбираются
таким образом, чтобы они располагались в одной вертикальной плоскости,
являющейся плоскостью симметрии обтекаемого тела (рис. 1-2-1).
Вертикальная плоскость симметрии часто называется нулевой
меридиональной плоскостью. Так как в ней производится отсчет угла атаки, то ее
называют также плоскостью угла атаки.
Понятие о силах, моментах и аэродинамических коэффициентах
13
Рис. 1-2-1. Схема расположения осей
координат при аэродинамических
исследованиях тел вращения
Любая другая плоскость, проходящая через продольную ось и
называемая меридиональной, образует с вертикальной плоскостью угол у, который
также называется меридиональным
(см. рис. 1-3-3).
При указанном выборе осей
координат вектор F располагается в
вертикальной плоскости симметрии, а
вектор М ориентирован по нормали к ней.
Следовательно, движение тела в
поточной системе координат будет
определяться лобовым сопротивлением X,
подъемной силой У и моментом
тангажа Mz, или соответственно
аэродинамическими коэффициентами сх,
■Су, mz; в связанной системе
координат—осевой силой R, нормальной
силой N и продольным моментом Mz,
или соответственно аэродинамическими
коэффициентами cR, cN и mz.
Коэффициенты лобового сопротивления сх и подъемной силы су в
поточной системе координат выражаются через коэффициенты продольной cR
и нормальной cN сил в
связанной системе (см. рис. 1-2-1)
следующим образом:
сх = cR cos a — cn sin a;
су = cN cos a -f cR sin a. (1-2-5)
Знак угла а на рис. 1-2-1
отрицательный.
Пересчет момента с
одной точки приведения на
другую. Момент обладает тем
свойством, что его величина
и направление зависят от
точки приведения,
относительно которой рассматривается
момент. Поэтому при
переходе от одной точки приведения к другой необходимо производить
соответствующий пересчет момента. Наиболее часто это применяют по
отношению к моменту тангажа и соответствующему аэродинамическому
коэффициенту в предположении, что угол скольжения рск = 0. Пересчет
коэффициента момента mz с одной точки приведения О, на другую О2 (рис 1-2-2)
ведется по формуле у 2 КУ * ;
Рис. 1-2-2. Схема для пересчета момента с одной
точки приведения на другую
(1-2-6)
например длина тела вращения, или хорда
где I — характерная длина,
крыла Ъ (рис. 1-2-2).
Поляра. Качество летательного аппарата. Важнейшими
аэродинамическими характеристиками летательного аппарата являются поляра и
аэродинамическое качество. Поляра устанавливает зависимость между подъемной
силой и лобовым сопротивлением или между нормальной и осевой силами
зависимость cx = fi{cy) называется полярой первого рода, зависимость
сх\ — /г(сУ1) [или cR~f2(cN))— полярой второго рода.
и
Г л ав а 1
Аэродинамическое качество летательного объекта
Центр давления и фокус. Центром давления летательного аппарата
называется точка приложения равнодействующей аэродинамических сил.
Коэффициент центра давления (рис. 1-2-3) является безразмерной величиной
и определяется как отношение расстояния до центра давления от какой-либо
фиксированной характерной точки
9f
к характерной длине (I или Ъ)
сц- д "
(1-2-8)
Коэффициент сц# д можно
рассчитать по известным значениям момента
тангажа и нормальной силы и
выразить через аэродинамические
коэффициенты:
сц. д — jsfb — CN \ )
Для летательных аппаратов, не
имеющих горизонтальной симметрии,
их летные свойства удобнее оценивать
не по центру давления, а по
фокусному расстоянию. Чтобы установить смысл понятия «фокус летательного
аппарата», воспользуемся известной зависимостью для коэффициента момента,
вычисляемого относительно произвольной точки с координатой хп, лежащей
на хорде несимметричного профиля,
(1-2-9)
Рис. 1-2-3. Схема к определению центра
давления
rnz — m
хп
z0
S^"*'
CV>
где mz0 — коэффициент момента относительно передней кромки при нулевой
подъемной силе.
Второе слагаемое в правой части определяет приращение момента,
связанное с изменением угла атаки. В качестве характерного линейного
размера принята хорда профиля Ь. Здесь рассматриваются малые углы атаки,
при которых су « cN.
Из (1-2-9) следует, что на хорде можно выбрать такую точку xn = xF
(фокус), относительно которой момент не будет зависеть от су.
Координата фокуса
X 771 I
дтг
дс7.
XF — —г— —
xf _ _
дтг
(1-2-10)
Очевидно, фокус —это такая точка, относительно которой
аэродинамический момент сохраняет постоянное, независящее от угла атаки значение,
т. е. точка приложения равнодействующей всех добавочных сил, вызванных
углом атаки. Зависимость между центром давления и фокусом определяется
соотношением
mz0-]-(dmz/dCy) су ^^ ^ — (1-2-11)
СЦ- Д г.."
' — сц. д. О
где
= rnzOlcy, a x~F взято по абсолютной величине.
Понятие о силах, моментах и аэродинамических коэффициентах
15
Для тел симметричной конфигурации mz0 и, следовательно, сЦш д 0 равны
нулю, и центр давления совпадает с фокусом. Если у симметричного тела
су —>0, то и mz—>0;
коэффициент центра давления
стремится к конечной величине,
равной
dmz
дсу у
У несимметричного тела,
например у профиля, при су —■> О
коэффициент момента стремится
к конечной величине mz0 и,
следовательно, сц> д —> оо.
Шарнирный момент. Этот
момент, действующий на органы
управления,
Mm = mmqbpS^ (I-2-12)
где тпш — коэффициент
шарнирного момента;
6Р и 5Р — средняя геометрическая хорда и площадь в плане органа
управления (руля).
Коэффициент момента тпш является при заданных условиях полета
(скорость, высота) функцией угла атаки летательного аппарата а и угла 6Р
отклонения руля (рис. 1-2-4).
Рис. 1-2-4. Шарнирный момент органа
управления
§ 1-3. Лобовое
сопротивление
Крылатый летательный аппарат
Коэффициент сх лобового сопротивления летательного аппарата можно
представить в виде суммы коэффициента сх0, происхождение которого
обусловлено влиянием вязкости и сжимаемости и не связано с подъемной
силой, и дополнительного коэффициента схи обусловленного подъемной
силой (коэффициент индуктивного сопротивления). В соответствии с этим
суммарный коэффициент сопротивления
сх — сх0~Т~сх1* {L-O-L)
Коэффициент сопротивления с^о можно представить как сумму
соответствующих коэффициентов сопротивлений для изолированных корпуса, крыльев,
оперения, органов управления и других элементов летательного аппарата,
а также дополнительной величины, обусловленной интерференцией между
различными элементами летательного аппарата.
Рассмотрим, например, комбинацию, состоящую из корпуса, поворотных
крыльев и неподвижных хвостовых стабилизаторов (рис. 1-3-1). Значение cxi
зависит от коэффициента подъемной силы рассматриваемой комбинации,
вычисляемого по (1-4-1').
При малых углах атаки корпуса а и небольших углах установки
крыла 6 (небольших отклонениях хорды крыла от продольной оси ракеты)
коэффициент индуктивного сопротивления
cxi — 1CNт(кр, on) + CN оп(т, кр)] а + CN кр(т) (& + б),
(1-3-2)
16
Глава 1
где cNT(Kp,on), cNOn(T, кр), слгкр(т) —коэффициенты нормальной силы,
соответственно: корпуса в присутствии крыла и оперения; оперения в присутствии
корпуса и крыла; крыла в присутствии корпуса.
Здесь учтено, что при отклонении крыла относительно оси корпуса
на угол б появляется дополнительная составляющая коэффициента
сопротивления бсдгКр(т, оп)« Заменяя в (1-3-2) аэродинамические коэффициенты в
соответствии с их значениями (1-4-3) и отбрасывая член, содержащий
произведение малых величин аг (е — угол скоса потока, см. рис. 1-3-1), получим
сх1 = К,а? + Z262 + Kzab, (I-3-3)
где Кг, К2, Z3 — соответствующие комбинации угловых производных.
Рис. 1-3-1. Скос потока за крылом
Далее преобразуем полученное выражение, поделив его на величину с2м,
Где Cn — коэффициент нормальной силы комбинации, определяемый
равенством (1-4-5). В результате выражение (1-3-3) примет вид
Имея в виду, что углы атаки и установки малы, можно в (1-3-4)
заменить cN на су. Обозначая, далее, правую часть равенства (1-3-4) через К,
получаем формулу для сопротивления (1-3-1) в следующем виде:
Кривая, определяемая этим уравнением, называется параболической
полярой сопротивления.
Из уравнения видно, что сопротивление при К«const изменяется
в зависимости от подъемной силы по квадратичному закону. Причем,
минимум сх, равный cxi), достигается при нулевой подъемной силе.
Исследования показывают, что аналогичная параболическая зависимость
сх - с% = К {су - суу или Асх = К(Асу)*
(1-3-6)
может иметь место и в более общем случае обтекания, когда углы атаки
не обязательно остаются малыми. Этот более общий случай характерен тем,
что минимум сопротивления с°х достигается не при нулевой подъемной силе,
а при некотором конечном ее значении Су.
Кривая, отображающая эту зависимость, показана на рис. 1-3-2.
Параметр К характеризует увеличение сопротивления при возрастании подъемной
силы и является постоянной величиной. Касательная к параболе, выходящая
из начала координат, определяет максимальное качество
Понятие о силах, моментах и аэродинамических коэффициентах
где наивыгоднейший коэффициент подъемной силы
17
Для летательного аппарата с горизонтальной симметрией коэффициент с°у
равен нулю.
Анализ аэродинамических свойств с помощью кривой сопротивления
может быть проведен как для комбинации корпусов с несущими
управляющими и стабилизирующими поверхностями, так и для изолированных
составных частей. Во всех случаях эти
свойства будут полностью
определяться соответствующими
значениями Сх, С у Я К [СМ. (1-3-6)].
Обобщенная поляра. В более
общем случае коэффициент
лобового сопротивления сх изменяется
по закону
сх = Сх0 + Кс». (1-3-5')
Кривая, представляемая этим
уравнением, называется
обобщенной полярой. Коэффициент К и
показатель степени п являются
функциями числа Моо и Re.
Рис. 1-3-2. Поляра сопротивления
В соответствии с (1-3-5') максимальное аэродинамическое качество
сх ) max n \ cxq
п-1
(1-3-7')
Значение (су1сх)тах
подъемной силы
и величине
соответствует наивыгоднейшему коэффициенту
£*9
(1-3-8')
Кспу
сх0
1
тг — 1
Для летательных аппаратов с крыльями, обладающими тонким
профилем, при дозвуковых, околозвуковых и средних сверхзвуковых скоростях
можно принять п&2. При гиперзвуковых скоростях для указанных
аппаратов лучшим приближением является п л? 3/2.
Корпус
Существует различный подход к разделению сопротивления,
действующего на тело со стороны воздуха, на составные части. В наиболее общем
случае сопротивление можно разделить на составляющую, обусловленную
силами давления, действующими по нормали к поверхности, и составляющую,
связанную с касательными силами трения, возникающими на поверхности
из-за вязкости воздуха.
Первая составляющая сопротивления называется сопротивлением
давления, вторая — сопротивлением трения.
Обычно сопротивление давления разделяют в свою очередь на две
составляющие, а именно сопротивление от давления на боковую поверхность
(головное сопротивление) и сопротивление от давления на донный срез
(донное сопротивление).
2-114
28 Г л а в а I
Таким образом, суммарное сопротивление
Х^Хр + Хдон + Ху, (1-3-9)
где члены справа представляют соответственно головное сопротивление г
донное и сопротивление трения.
Переходя к аэродинамическим коэффициентам, запишем выражение
для суммарного коэффициента сопротивления, отнесенного к площади 5
наибольшего (миделевого) сечения тела вращения
°х = я^мид = Схр "*" °х дон
где справа представлены соответственно коэффициенты головного и донного-
сопротивлений и сопротивления трения.
Если известно распределение нормального давления по поверхности, то
°хР = -* \ Р cos (тг, Foo) dS60K; (I-3-10)
(#г, F«,) Л5ДОН, (1-3-11)
=^(р — poo)lq — коэффициент давления;
cos (тг, Foo) — косинус угла между вектором FTO и нормалью п к
поверхности корпуса в рассматриваемой точке;
S6oK и £дон — соответственно боковая и донная поверхности корпуса.
Для плоского донного среза, где cos (n, Foo) = const, обычно давление
принимают постоянным во всех точках. Если принять, что нормаль п на
плоскости среза совпадает с направлением продольной оси, то cos (тг, Foo) —cos a.
При этом
сх дон = Рдон СО8а5дон, (1-3-1 Г)
ГДе *-> дон = *Ь дон/*^ мид •
Для малых углов атаки
сх дон ~ Рдон^дон* (I-O-11 )
Коэффициент сопротивления трения определяется по распределению
касательных напряжений
cxf = -о \ cfx cos (t, Foo) dS6oK, (1-3-12)
^МИД е)
где CfX~%lq — местный коэффициент трения;
cos (t, Foo) — косинус угла между вектором Foo и касательной t к
поверхности корпуса.
При аэродинамических исследованиях удобнее иметь дело с осевой
силой, совпадающей по направлению с осью корпуса. Суммарная
осевая сила
т. е. равна сумме трех составляющих, а именно осевой силы Rp от
давления на переднюю часть (или просто осевой силы от давления), осевой силы Ддок
от донного давления (донной осевой силы) и осевой силы трения Rf.
Понятие о силах, моментах и аэродинамических коэффициентах
19
Переходя к коэффициентам сил, получим:
R
Змид
— cRp + CR дон + cRfi
(1-3-13')
где cR — коэффициент суммарной осевой силы;
Сддон» cRf — соответственно коэффициенты осевой силы от давления,
донной осевой силы и осевой силы трения.
Составляющие осевой силы и их коэффициенты можно определить,
если известно распределение нормального давления и касательного
напряжения по поверхности корпуса.
Рассматривая корпус в виде
тела вращения и пользуясь схемой,
изображенной на рис. 1-3-3, можно
получить следующие выражения
для коэффициентов составляющих
полной осевой силы:
НР
R
1 Р dr2 ,~ р - j
— — \ —— ах \ р ау;
я е) dx <0
О О
(1-3-14)
= Рдон^дон» (1-3-15)
1 я
1ДОН
о
(1-3-16)
Здесь г = г/г
j — отношение
радиуса корпуса в
некотором сечении
к радиусу миде-
левого сечения;
х = х/хк — расстояние до
этого сечения по оси,
отнесенное к
длине корпуса;
{= хк/2гШ1Щ — удлинение тела
вращения.
Рис. 1-3-3. К выводу зависимостей,
определяющих аэродинамические характеристики
тела вращения по известному распределению
нормального и касательного напряжений
ращения.
Выражения (1-3-14) и (1-3-16) написаны для общего случая
несимметричного обтекания тела вращения, когда угол атаки не равен нулю. При
нулевом угле атаки (осесимметричное обтекание)
t = 4ЯК \ cfxr dx.
О
(1-3-16')
Крылья (несущая поверхность)
Составляющие сопротивления. Сопротивление несущей поверхности
где Х-р — сопротивление от давления;
Xf — сопротивление трения.
2*
20 Глава I
От сил можно перейти к аэродинамическим коэффициентам
где сх— полный коэффициент сопротивления;
схр — коэффициент сопротивления от давления;
cXf — коэффициент сопротивления трения. *
Коэффициенты сопротивления обычно относят к площади крыла
в плане 5кр. Если известно распределение давления по поверхности крыла, то
Коэффициент сопротивления трения вычисляется по распределению
касательных напряжений:
Формула (1-3-18) справедлива для крыльев любой формы и в частности
для крыльев с острой или затупленной задней кромкой. Для крыла с
затупленной задней кромкой сопротивление от давления включает также
сопротивление за счет разрежения, возникающего за кромкой. Эту составляющую,
аналогичную донному сопротивлению тела вращения, называют
сопротивлением задней кромки.
Коэффициент сопротивления задней кромки можно найти по известному
распределению давления /?3. к на затупленной поверхности площадью S3, K
сх з. к = -J— *\ Рз. к cos (/г, Foo) dSa, K, (1-3-19')
где рз. к — коэффициент давления на задней кромке в рассматриваемой точке;
cos (rc, Foo) — косинус угла между вектором Foo и нормалью п к
затупленной поверхности кромки в той же точке.
Сохраняя обозначение схр для коэффициента сопротивления давления
передней части крыла, запишем выражение для полного коэффициента
сопротивления
сх = схр + сх з. к + cxf. (1-3-17")
Профиль. Применим теперь полученные соотношения для вычисления
аэродинамических характеристик профиля крыла, считая, что
распределение давления и напряжения трения по профилю известно.
Коэффициент сопротивления от нормального давления, отнесенный
к хорде профиля Ъ (рис. 1-3-4),
Схр = у g> P cos (тг, Foo) ds, (1-3-20)
где <ё — криволинейный интеграл по контуру профиля;
ds — элемент дуги контура.
Коэффициент сопротивления трения также находится в результате
вычисления криволинейного интеграла
Cfxcos (t, Foo) ds. (1-3-21)
Понятие о силах, моментах и аэродинамических коэффициентах
21
Полный коэффициент сопротивления профиля будет равен сумме
коэффициентов схр и cXf. Причем, полный коэффициент, как и его составляющие,
рассчитывается по площади крыла единичной ширины, равной ЪЛ.
Рассмотрим, как вычисляются соответствующие аэродинамические
коэфй
фициенты в связанной системе координат
совпадает с хордой (рис. 1-3-4).
Коэффициент осевой силы
от давления
cRp =-г-hp cos (n, Xj) ds, (I-3-22)
а коэффициент осевой силы
трения
Л г*
cRf = у Ф Cfx cos (t, Xi) ds,
(1-3-23)
горизонтальная ось
которой
Рис. 1-3-4. Силы, действующие на крыло
где cos(ft, хх) и cos (t, х^) — косинусы углов соответственно между внешней
нормалью п и касательной t к контуру в данной точке и осью xt.
Если cos (t, Xt) = cos P, то cos (n, x^) = sin (3. Для ds имеем соотношение
ds = dxjcos$. Поэтому, переходя от криволинейных к обычным интегралам,
получим следующие выражения для составляющих аэродинамических
коэффициентов:
(1-3-24)
(1-3-25)
cRf=
где xi = xl/b;
dyjdxi — производная от функции */i = /(#i), определяемая уравнением
контура.
Индексы «н», «в» указывают, что соответствующие параметры берутся
на нижнем и верхнем участках контура профиля.
Суммарная величина коэффициента осевой силы
CR — CRJ> + CRf* (1-O-ZO)
В значение cRp можно включить и сопротивление тупой задней кромки,
если она имеется. Однако удобней выделить эту часть сопротивления и,
приняв, что кромка расположена по нормали к оси хи представить ее
в следующем виде:
СЕз.к = Рз.кСз.к, (1-3-27)
где с3, к = с3.к/Ь — безразмерная высота задней кромки.
В соответствии с этим коэффициент осевой силы
Cr = CRp + Сдз.к + CRf. (1-3-26')
Для крыла бесконечного размаха прямоугольной формы в плане
коэффициент сопротивления равен его значению, найденному для профиля.
На участке такого крыла с площадью £кр сила сопротивления X — cxqSKV.
Чтобы определить коэффициент сопротивления крыла конечного
размаха произвольной формы в плане с площадью SK$, необходимо знать
значения коэффициентов сх для ряда сечений (профилей), выбранных вдоль
22
Глава I
размаха I (рис. 1-3-5). Соответствующая величина коэффициента
сопротивления крыла определяется интегрированием по размаху
иг
с* =
cxb(z)dz.
(1-3-28)
Другие формы представления сопротивления. При разделении
сопротивления крыла на составляющие можно выделить ту из них, которая
связана с образованием подъемной силы. Эта составляющая Хг называется
индуктивным сопротивлением. При добавлении ее к той части
сопротивления, которая не связана с образованием подъемной силы и называется
профильным сопротивлением крыла Хпр, получаем полное сопротивление
Рис. 1-3-5. К определению аэродинамических
характеристик крыла
Если схпр и cxi соответственно коэффициенты профильного и
индуктивного сопротивлений, то выражение для коэффициента полного
сопротивления представится в виде суммы
cxl. (I-3-29)
Профильное сопротивление состоит из сопротивлений давления и
трения и определяет полное сопротивление, когда cxi равно нулю.
Коэффициент сопротивления профиля можно написать по аналогии
с выражением (1-3-6) также в следующем виде (см. рис. 1-3-2):
сх = сх пр + Ксу {су - 2с°у). (1-3-30)
В этой формуле выделена составляющая сяпр| не зависящая от угла
атаки, и составляющая cxi, обусловленная подъемной силой. Первая
составляющая
Схщ> = с$ + К(с1)*; (1-3-31)
вторая
cxi = Kcy(cy-2cl). (I-3-32)
При наличии горизонтальной симметрии с°у = 0 и сх пр = с°х, a cxi = Кс2.
Особенности сопротивления крыльев при сверхзвуковых скоростях!
при расчете сопротивления крыльев, движущихся со сверхзвуковыми
скоростями, должны быть учтены некоторые особенности их обтекания. Эти
особенности относятся к крыльям с дозвуковой передней кромкой.
Подробнее о дозвуковой и сверхзвуковой кромках крыла рассказано на стр 55
Понятие о силах, моментах и аэродинамических коэффициентах 23
Передняя кромка крыла будет дозвуковой, если перпендикулярная к ней
составляющая скорости набегающего невозмущенного потока Vnoo меньше
чзкорости звука аоо. При этом профиль крыла обтекается дозвуковым
потоком (см. рис. 1-3-5). У критической точки 0' (точки полного торможения),
располагающейся при наличии угла атаки недалеко от передней кромки
на нижней стороне крыла, поток разветвляется и часть его движется
вперед, обтекая переднюю кромку. При безотрывном обтекании на передней
кромке возникает зона разрежения, которая создает подсасывающую силу,
снижающую сопротивление. Эта сила, как показывают исследования,
пропорциональна коэффициенту, величина которого равна асу. Если
коэффициент пропорциональности обозначить через [х, то подсасывающая сила
будет \iacy.
Обозначим далее через cRp коэффициент осевой силы от давления
для крыла с симметричным профилем, не зависящей от подсасывающей
силы. Тогда суммарный коэффициент осевой силы при некотором угле атаки
cR = cRp + \iacy + cRf.
Полагая, что углы атаки небольшие, и поэтому Cn ~ су1 получим
в соответствии с (1-2-3)
сх = — асу (1 - \i) + cRp + cRf. (1-3-33)
При а = 0
Сх = сх0 = (сЛр)о + (cRf)0. (1-3-33')
Аэродинамические свойства крыла можно характеризовать
коэффициентом увеличения сопротивления
тг Асх сх — сх0 (1 — р) cRp — (cRp)0 cRf — (cRf)0 /т о on
А = — = — = £— Н 2 1 (L-6-64)
С
2
у Су
где Су=дСу/да = су/а.
Исследования показывают, что главным членом, от которого зависит iT,
является первый член — (1 — fi)/cy, определяемый в основном сопротивлением
давления, распределение которого обусловлено волновыми явлениями и
взаимодействием внешнего потока с вихревым следом за крылом. Коэффициент |х
отличен от нуля для дозвуковых и равен нулю для сверхзвуковых
передних кромок.
Второй член в формуле (1-3-34) обусловлен разностью осевых сил,
зависящих от давления, при афО и а = 0. Эта разность, как показывают
исследования, пропорциональна произведению относительной толщины
профиля Д/й и угла атаки. Величина cRp—(cRp)o может увеличиться за счет
отрыва пограничного слоя.
Наконец, третий член связан с изменением сопротивления трения
в зависимости от угла атаки. Это изменение настолько мало, что
практически его можно не учитывать.
§ 1-4. Подъемная сила
Крылатый летательный аппарат
Рассмотрим общее выражение для подъемной силы летательного
аппарата, представляющего собой ту же комбинацию корпуса, крыла и
оперения, для которой выше было получено соотношение для сопротивления.
Подъемная сила
т, кр)» (1-4-1)
24 Глава!
где ^(кр, оп) — подъемная сила корпуса (тела) в присутствии крыла и оперения;
^кр(т) — подъемная сила крыла в присутствии корпуса;
^оп(т, кр) — подъемная сила оперения в присутствии корпуса и крыла.
! Соответствующая величина коэффициента подъемной силы
Су ~ С1ут(кр, оп) ~Ь сукр(т) ~\~ суоп(т, кр)» (1-4-1 )
Написанные выражения учитывают влияние на суммарную подъемную
силу интерференции между отдельными элементами летательного аппарата.
Если из полной величины подъемной силы удается выделить отдельные
составляющие, зависящие от интерференции, то коэффициент подъемной
силы
СУ ~ СУ т Т" су кр т* су оп т" &Су т(кр, оп) ~\~ kCy кр(т) Ч" ^су оп(т, кр)>
где первые три составляющие относятся к изолированным корпусу, крыльям
и оперению, а остальные члены определяют дополнительные,
интерференционные составляющие подъемной силы.
Вместо подъемной силы и ее составляющих можно рассматривать
нормальную силу и соответствующие составляющие, характеризующие
несущую способность летательного аппарата.
Суммарный коэффициент нормальной силы
Cjv— Cjvt(kp, оп) + С]укр(т) + С;Уоп(т,кр)' (1-4-2)
По коэффициенту нормальной силы можно найти коэффициент
подъемной силы, воспользовавшись формулой перехода от связанной к поточной
системе координат. Предположим, что наряду с малыми углами атаки а
малыми являются и углы б установки крыла относительно оси корпуса.
Тогда составляющие нормальной силы
== Cn т(кр,
c
кр(т) = с% Кр(т)а + cN Kp(T)S; ? (1-4-3)
CN оп(т, кр) = Cn оп(т,[кр) (<Я — 8),
где индексы сверху «ос» и «б» — частные производные от коэффициента
нормальной силы соответственно по а и б;
е — угол скоса потока за крылом.
Таким образом, суммарный коэффициент нормальной силы
с% 0П(т, кр)£> (1-4-4)
где
a a i а , а 6^ Лв
Cn = Cn кр(т) "Г CN т(кр, оп) "Г Cn оп(т, кр)» CN = C]v кр(т)«
Последний член в правой части (1-4-4) характеризует влияние
интерференции крыла с оперением на нормальную силу. Это влияние невелико,
если учесть, что площадь оперения относительно мала. Однако влияние
интерференции на момент может оказаться существенным ввиду болыпога
плеча хвостового оперения.
Пренебрегая интерференционным членом в правой части (1-4-4), найдем
зависимость
-ft-=CN-jr- + CN, (1-4-0}
характеризующую чувствительность летательного аппарата к управляющим
усилиям, создаваемым крылом. Параметр управляемости cN/8 зависит
для заданной конструкции аппарата и определенной скорости полета только
от отношения а/б.
Понятие о силах, моментах и аэродинамических коэффициентах 25
Корпус
Подъемную силу корпуса Y можно представить в виде суммы двух
составляющих Yp и У/, первая из которых зависит от распределения
нормального давления, вторая — от распределения касательных напряжений.
Суммарный коэффициент подъемной силы
где Сур — коэффициент подъемной силы от нормального давления;
Cyf—коэффициент подъемной силы от трения.
Составляющие коэффициента подъемной силы можно рассчитать, если
известно распределение давления и касательного напряжения по корпусу:
сур = т \ Р sin К v°°) dS> (I-4-7)
Cyf = -j \ cfx sin (t, Foo) dS. (1-4-8)
(S)
Здесь S — полная поверхность корпуса, включающая боковую поверхность
и площадь донного среза. Обычно влияние составляющей подъемной силы
за счет трения за дном не учитывают из-за малости этой составляющей,
поэтому в (1-4-8) принимают 5 = 5б0к.
Составляющая подъемной силы, возникающая за счет донного давления,
хотя и остается малой, но может оказывать более существенное влияние
на подъемную силу корпуса, чем составляющая от трения. Коэффициент
составляющей подъемной силы за счет донного давления
1 Р ~~ —
с — ——^— \ т) si п (yi V^ I cl■ j ^Т II Q^
Если расчет сУДОЯ производится отдельно, то в (1-4-7) следует принять
S = S6oi{, определяя, таким образом, составляющую подъемной силы,
зависящую от распределения нормального давления по боковой поверхности.
Если донный срез плоский, то sin (n, Foo) = sin а. Принимая также,
что за дном /?дон = const, найдем
су дон = Рдон sin а£дон. (I-4-9')
Для малых а коэффициент сУдОн = Рдона^дон«
Коэффициент нормальной силы
cN = cNp + cNf, (1-4-10)
где cNp — составляющая, обусловленная действием нормального давления
на боковую поверхность;
Cnj — составляющая, возникшая от сил трения.
Для корпуса в виде тела вращения (см. рис. 1-3-3) составляющую
коэффициента cNp нормальной силы можно найти по известному
распределению давления при помощи формулы
N 1 я
Р ^\rdx \pzosd (1-4-11)
Вторая составляющая cNf вычисляется по известному распределению
касательного напряжения
1"
°Nf = <т^£~ = я1" I Г tg ^ dx \ Cfx C0S y
где tgp = dr/dx.
26 Глава I
Крылья (несущая поверхность)
Подъемную силу крыла или вообще какой-либо несущей поверхности
можно выразить, как и подъемную силу корпуса, в виде суммы двух
составляющих, одна из которых обусловлена действием сил нормального
давления, другая — сил трения. В соответствии с этим суммарный
коэффициент подъемной силы изображается формулой (1-4-6).
Составляющие вычисляются по формулам
z, Vсо) dSw (I-4-13)
cfx sin (t, Foo) dSKV>. (1-4-14)
Если крыло имеет затупленную заднюю кромку, то целесообразно
из составляющей cyv выделить часть подъемной силы, происхождение
которой связано с подсасывающим эффектом на задней кромке. Коэффициент
этой подъемной силы
су 8. к =-г- \ psin(n,Voo)dS3mK. (I-4-15)
Коэффициент подъемной силы от трения обычно рассчитывается без
учета влияния сил трения за задней кромкой.
Формулы (1-4-13), (1-4-14) используют для определения составляющих
подъемной силы профиля. Полагая хорду профиля равной Ъ и относя
аэродинамические коэффициенты к площади 6-1, запишем
Сур = у | р sin (и, Foo) ds; (I-4-16)
у
cyf=-jj cfx sin (*, Foo) ds. (1-4-17)
Здесь вместо интегрирования по площади *SKp производится вычисление
криволинейного интеграла по дуге контура профиля s.
Рассмотрим общие выражения для коэффициента нормальной силы
профиля и его составляющих. Для суммарного коэффициента нормальной
силы действительна формула (1-4-10), в которой cNp — коэффициент
нормальной силы крыла, рассчитанный по распределению нормального давления;
cjvy — коэффициент нормальной силы, вычисленный по распределению
касательного напряжения. Расчетные формулы для этих коэффициентов следующие:
= T§p sin (n' Xi^ ds; (I-4-18)
1 с*
cNf = у у cfx sin (*, х±) ds. (I-4-19)
От криволинейных интегралов можно перейти к обычным:
1 о
cNp = I Рв dx± + J рн dx±; (I-4-20)
о 1
Понятие о силах, моментах и аэродинамических коэффициентах 27
Зная коэффициент нормальной силы и его составляющие и пользуясь
соответствующими формулами перехода от связанной к поточной системе
координат, можно определить коэффициент подъемной силы профиля.
По коэффициенту су = сур + cyf определяется подъемная сила участка
€ площадью £кр прямоугольного крыла бесконечного размаха Y = cyqSKV.
Для крыла конечного размаха произвольной формы в плане суммарный
коэффициент подъемной силы находится путем интегрирования по размаху
элементарных величин подъемной силы
1/2
суЪ (z) dz, (I-4-22)
где су — коэффициент подъемной силы профиля.
§ 1-5. Момент
Крылатый летательный аппарат
Аэродинамический момент, действующий на летательное устройство
произвольной формы, может быть рассчитан относительно любой точки.
В аэродинамических исследованиях удобнее в качестве такой точки
приведения выбрать фиксированную точку, связанную с телом и не меняющую
своего положения в полете. В дальнейшем будем вести этот расчет
относительно носка корпуса летательного устройства или центра тяжести,
рассматривая его положение фиксированным.
В общем виде, когда летательное устройство состоит из отдельных
элементов (корпус, крыло, оперение и т. д.), момент определяется как
сумма составляющих от корпуса, крыла, оперения и других элементов
с учетом влияния интерференции.
Рассмотрим общее выражение для коэффициента момента тангажа.
Коэффициенты моментов крена и рысканья могут быть представлены
аналогично. Для комбинации корпус — поворотное крыло — стабилизатор имеем
mz = m2T(Kp} on) + ^ZKp(T) + ^2On(T, КР)- (1-5-1)
Здесь индексы имеют тот же смысл, что и выше.
В свою очередь каждую составляющую коэффициента момента можно
определить, если известны нормальная и осевая составляющие силы и
соответствующие плечи, т. е. расстояния по осям х и у до центра давления.
Например, для корпуса составляющая mz Т(Кр, оп) = (<?л^ц. д + Сцуц. д)Т(кр, оп>»
где хц, д = хц. д/жт, г/ц. д = уц. R/xT (#ц. д» Уц. д — координаты центра давления,
хТ — характерный линейный размер). Для всего летательного устройства
коэффициент момента
3
mz = 2 (слгЯц. д + сцуц. д)ь (1-5-2)
г=1
где суммирование ведется по всем элементам (корпус, крыло, оперение).
При вычислении момента положительное направление соответствует
вращению в кратчайшем направлении от оси х к оси г/.
Для комбинации корпус — поворотное крыло — стабилизатор коэффициент
момента при заданной скорости полета можно представить как функцию
mz = /(а, б). При малых углах а и б имеет место линейная зависимость
28 Г лав а I
момента от углов атаки и отклонения крыла, в соответствии с которой
™<z = т?а + тп?хЬ + mz0, (1-5-3)
где mz0 — коэффициент момента при а = б = 0. Для конструкции с
горизонтальной симметрией mz0 = 0.
Корпус
Аэродинамический момент, действующий на корпус, как и силу, можно*
представить в виде суммы двух составляющих — моментов сил давления
и сил трения. В соответствии с этим суммарный коэффициент продольного
момента (момента тангажа)
™<z = m>zp + и&*/» (1-5-4)
где mzp — коэффициент момента сил от нормального давления;
mZf — коэффициент момента сил трения.
Каждую составляющую можно определить интегрированием по
поверхности корпуса элементарных величин моментов, создаваемых соответственно
силами от нормального давления и касательных напряжений. Составляющая
или
mzv =
С5 ~~
\ р [х sin (п, хЛ — у cos (/г, хЛ] dS. (I-5-6)
При определении знаков составляющих можно пользоваться рис. 1-3-3.
Рассматриваемый элемент поверхности dS выбран таким, что для нега
dr/dx>0 и, следовательно, моменты от элементарных величин нормальной
и осевой сил будут отрицательными. Так как в соответствии с рис. 1-3-3
знак dcNp отрицательный, то перед первыми членами в выражениях для mzp
поставлен знак «плюс».
Составляющая коэффициента момента от трения
или
mzf = —^— \ cfx [x sin (t, x±) — у cos (t, xt)] dS. (1-5-7')
При исследовании моментных характеристик корпуса можно исключить
влияние донного среза, так как практически оно оказывается весьма малым.
Тогда во всех приведенных формулах интегрирование будет вестись по
боковой поверхности.
Рассмотрим моментные характеристики для корпуса в виде тела
вращения (см. рис. 1-3-3) при условии, что момент и его составляющие
вычисляются относительно носка. Коэффициент момента сил от нормального
давления
М 1 ~ я
— = \ rxdx \ р cos у dy —
Д*к я } .} * * *
о о
1 я
\r2tg$dx \ pcosydy. (I-5-8)
о о
Понятие о силах, моментах и аэродинамических коэффициентах 29
Если тело тонкое, то второй член в этой формуле будет малым.
Составляющая момента от сил трения также найдется в результате
интегрирования по поверхности
1 л
mzf = s zjх = ■— \ xr tg (5 dx \ cfx cos у dy —
МИД K Q q
1 л
\ r2 dx \ CfXcosy dy. (1-5-9)
0 0
Составляющая момента, как и составляющие аэродинамических сил,
зависящие от трения, не всегда по порядку величин такие, как
составляющие от нормального давления. Исследования показывают, что влияние
трения оказывается более существенным в случае тонких и длинных тел,
обтекаемых под большими углами атаки.
Крыло и профиль
Момент и соответствующий коэффициент для крыла обычно вычисляются
относительно оси 2, проходящей через вершину крыла (см. рис. 1-3-5).
Полный коэффициент момента расчленяется на составляющую mzp,
зависящую от распределения нормального давления, и составляющую mZf,
зависящую от распределения касательного напряжения.
По аналогии с соответствующими выражениями для корпуса
10— —
т \ [xpsin(n1xi) — ypcos (п, х^] doKp; (1-5-10)
^GAX _ «у
sin (t, x^ — yCfX cos (t, Xi)] dSKp. (1-5-11)
Из формул следует, что коэффициенты момента отнесены к площади
крыла в плане £Кр и средней аэродинамической хорде bGAX.
Соответствующие расчетные зависимости для профиля имеют вид
криволинейных интегралов:
1 £ ~
mzp =: — (^-p[x sin (п, х^ — у cos (n, xt)] ds; (I-5-12)
1 i?
mzf=z — <!b CfX [x sin (t, Xi) — ycos(t, x^] ds, (1-5-13)
x которые вычисляются по дуге контура s.
Определяя момент, который в данном случае рассчитывается
относительно передней кромки, как сумму моментов для верхней и нижней частей
контура, получим
1 0
mzp =
о
о
о
— У1в (^/х)в] dxi +
и (1-5-15)
l
= xjb\ y\~yjb.
30 Глава I
Коэффициент момента профиля равен сумме составляющих, т. е. mz =
= mZJ>-r-mZf. Если известно распределение величины mz вдоль размаха
крыла заданной формы в плане (см. рис. 1-3-5), то можно найти
суммарный коэффициент момента крыла относительно оси z*:
1/2 1/2
где хп — расстояние от оси zt до передней кромки крыла.
При наличии у крыла поперечной V-образности коэффициент момента
1/2 1/2 1/2
яг^ кр = —— V хп (z) Ъ (z) cN dz + \ b2 (z) mzdz^p \ cRb (z) у dz . (1-5-16')
oKpC?CAX Le) e) e) J
0 0 0
При положительной V-образности (крылья приподняты) перед третьим
членом в правой части должен стоять знак «минус», при отрицательной
(крылья опущены) — «плюс».
§ 1-6. Применение
аэродинамических
характеристик для
исследования
устойчивости тел
в полете
Статическая устойчивость
Продольная и поперечная устойчивость. При движении тела
случайное возмущение (начальный толчок при сходе со стартового устройства г
порывы ветра, отклонения от заданного режима работы двигателя и т. д.)
может привести к изменению углов атаки и скольжения. Возникающий
вследствие этого момент приводит после прекращения действия возмущения
к дальнейшему изменению этих углов.
Если при этом изменении углы а и (Зск Ьтремятся к первоначальным
значениям, то полет называется статически устойчивым. Если отклонение
продолжает возрастать, то полет называется статически неустойчивым.
Статическая устойчивость подразделяется на продольную статическую
устойчивость, статическую устойчивость пути и поперечную статическую
устойчивость.
При наличии продольной статической устойчивости возникающий
продольный момент будет стабилизирующим, т. е. будет стремиться вернуть
угол атаки к прежнему значению. В этом случае направление изменения
момента Мг (и соответственно коэффициента mz) будет противоположно
направлению изменения угла а. Следовательно, условие продольной
статической устойчивости можно выразить неравенствами dMJda < 0 или dmjda =
В случае продольной статической неустойчивости возникает
опрокидывающий дестабилизирующий момент, который стремится еще больше
изменить угол атаки. Следовательно, условием продольной статической
неустойчивости будет неравенство дМ2/да>0 или dmz/da = m?>0.
Статическая устойчивость пути, очевидно, характеризуется
неравенством дМу/д$Ск<® или дту/д$ск = ту<0; статическая неустойчивость пути —
Понятие о силах, моментах и аэродинамических коэффициентах 31
неравенством 9Му/дрск > 0 или дту/д$ск = т% >0. В первом случае
направления изменений момента рысканья и угла скольжения различны, во
втором — одинаковы. Соответственно моменты будут стабилизирующими
и дестабилизирующими моментами пути.
Мерой поперечной статической устойчивости (или статической
устойчивости крена) является производная дМх/д$ск или дтх/д$ск = тх. Если
производная тх << 0, то летательный аппарат обладает поперечной статической
устойчивостью. Если ?Пх>0, то имеет место поперечная статическая
неустойчивость.
Летательный аппарат нейтрален в отношении продольной статической
устойчивости, устойчивости пути или поперечной статической устойчивости,
если справедливы равенства т% — О, т1 = 0, тх = 0.
Коэффициент центра давления. Фокус. Одним из параметров
статической устойчивости является коэффициент центра давления. В частности,
параметром продольной статической устойчивости является коэффициент
центра давления, определяемый из условия хц, д = хц. д II = mz/cN, где
#ц. д — расстояние до центра давления от точки, относительно которой
определяется продольный момент.
Пусть такой точкой является носок тела. Тогда в качестве
характеристики (критерия) статической устойчивости можно принять расстояние
между центром тяжести хц, т и центром давления #ц.гд. Если разность
#ц. д — #ц. т положительна (#ц. т = Хц. T/Z), т. е. центр давления расположен
за центром тяжести, то полет будет статически устойчивым. При переднем
расположении центра давления (разность хц, д — хЦш т отрицательна) . имеет
место статическая неустойчивость.
Критерий #ц.д — хц, т иногда называют запасом статической
устойчивости. Он может быть положительным (статическая устойчивость),
отрицательным (статическая неустойчивость) и нулевым (нейтральность в
отношении продольной устойчивости).
Если момент тангажа определяется относительно центра тяжести,
то параметр хц. д можно непосредственно рассматривать как критерий
устойчивости. В линейном диапазоне углов атаки величину хц, д можно
представить в виде хц, K — dmz/dcN. Если dmzldcN<^0, то полет будет статически
устойчивым; при dmz/dcN^>0— неустойчивым.
Параметру.n=dmz/dcNназывается коэффициентом продольной устойчивости.
Для несимметричных конструкций или для симметричных конструкций
с отклоненными рулями удобнее применять в качестве критерия
статической устойчивости вместо коэффициента центра давления безразмерное
фокусное расстояние. Принимая во внимание (1-2-9), напишем равенство
определяющее коэффициент mzi момента относительно поперечной оси,
проходящей через некоторую точку с координатой хТ, через коэффициент mz
момента относительно передней точки аппарата и коэффициент нормальной
силы cN. Знаки в (1-6-1) выбраны таким образом, что момент положителен,
когда он действует в сторону увеличения угла атаки, и отрицателен — когда
действует в обратном направлении.
Точка с координатой xT = xF, при которой dmzldcN-\-xF — §, является
фокусом. Безразмерная координата фокуса xF определяется по следующей
формуле:
32 Г л а в а I
Таким образом,
mzi = mz0 — (xF — хт) cN, (1-6-3)
где ~хт может быть безразмерной координатой центра тяжести. Тогда из (1-6-3)
следует, что при заднем относительно центра тяжести расположении фокуса
полет будет статически устойчивым, при переднем — неустойчивым, т. е.
степень статической устойчивости летательного аппарата зависит от
взаимного положения его фокуса и центра тяжести.
Условие балансировки. Это условие, необходимое для осуществления
статически устойчивого прямолинейного полета в продольной плоскости,
имеет вид mz = 0. Выполнение этого условия обеспечивается путем
отклонения на соответствующий угол руля высоты полета. Приняв в (1-5-3) mz — 0,
получим уравнение полета в условиях балансировки
m6z8 + mz0 = 0. (1-6-4)
Из этого уравнения находят балансировочную характеристику,
представляющую собой отношение угла атаки к углу отклонения рулевого органа.
Для заданной конструкции и скорости эта характеристика является
функцией угла б. Для симметричной конструкции балансировочное отношение а/б
не зависит от угла отклонения руля и определяется формулой
4-=-^-. d-6-5)
Динамическая устойчивость
Понятие динамической устойчивости. Анализ производных
аэродинамических моментов по а или рск позволяет установить, обладает ли тело тем
или иным видом статической устойчивости. Однако для оценки летных
качеств движущегося тела недостаточно такого анализа, так как он не дает
ответа на вопрос о характере движения тела после прекращения действия
возмущения, о величинах параметров, определяющих это движение. В самом
деле, если известно, например, что производная dmjda отрицательна и что,
следовательно, центр давления расположен за центром тяжести, то можно
сделать вывод лишь о продольной статической устойчивости. Но нельзя
сказать, например, какова будет амплитуда колебаний угла атаки при том
или ином значении параметра начального возмущения, и каким образом
по времени будет происходить ее изменение. На все эти и другие вопросы
отвечает теория динамической устойчивости.
Теория динамической устойчивости опирается на результаты
аэродинамических исследований, полученных на режимах неустановившегося
обтекания. Таким образом, на тело, ориентировка которого меняется со
временем, будут действовать, в отличие от статических условий, дополнительные
аэродинамические нагрузки, эффект которых зависит от времени.
Демпфирующий момент. К числу этих нагрузок относится
демпфирующий момент, возникающий в том случае, когда на траектории полета тело
совершает вращательное движение относительно центра масс. По своей
природе этот момент является тормозящим и направленным, следовательно,
в сторону, обратную вращению.
Понятие о силах, моментах и аэродинамических коэффициентах
33
Рассмотрим выражение для демпфирующего момента, создаваемого
оперением, в частном случае, когда аппарат движется без скольжения с
постоянной скоростью и одновременно вращается относительно оси z, проходящей
через центр масс, с некоторой угловой скоростью Qz (t) (рис. 1-6-1).
В результате такого движения возникает продольный аэродинамический момент
от оперения MZ1 зависящий от составляющих скорости поступательного
движения Vx, Vy, а также от угловой скорости Qz, т. е. Mz = f(Vx, Vy, Qz).
Вводя обозначения Vy/V^^a; QzLr. 0/Foo = Aar. 0, где Lr. 0— расстояние
от центра масс аппарата до фокуса оперения; Ааг. 0 — приращение угла
Рис. 1-6-1. Схема возникновения демпфирующего момента
оперения
атаки оперения, вызванное вращением, и, полагая VJVoo « 1, можно
написать выражение для коэффициента момента в виде mz = MJqSl =
— ф (а, А аг. о). Здесь ф — функция угла атаки и приращения Ааг. 0.
Полагая а и Ааг. о малыми, функцию ф для симметричных конструкций можно
представить в виде суммы ф = фаос ~j-фА0Сг- ° Даг. 0, где производные фа
и фЛаг- и постоянные.
Если фа = пи и с
5=Даг. о = —ZyV^ ° ) >
то
М z =
mz zqSlcoz.
(1-6-6)
Вторая составляющая момента, зависящая от угловой скорости,
называется демпфирующим моментом и обозначается М2Д = m®zqSl(dz или
Мед - ^pooFooQ^2^, (1-6-7)
которая определяет демпфирующий момент в зависимости от коэффициента
демпфирующего момента mZA и угловой скорости вращения.
Исследования показывают, что (1-6-7) может быть отнесена к
летательному аппарату в целом. Демпфирующий коэффициент будет зависеть
в линейном диапазоне его изменения от угловых скоростей только от
конструктивных особенностей летательного аппарата.
Критерии динамической устойчивости. Подобно критериям статической
устойчивости имеются критерии динамической устойчивости. Чтобы
рассмотреть эти критерии, воспользуемся уравнением вращательно-колебатель-
ного движения тела около центра тяжести
где А — экваториальный момент инерции;
Мъ — момент тангажа относительно центра тяжести, определяемый (1-6-6).
3-114
34 Г л а в а Г
Будем рассматривать такое движение, при котором наклон траектории
тт ^z °°г
меняется незначительно. Производную тг* можно представить в виде mzz —
=zrn^Voo/li так как Qz = a = da/dt. Следовательно, (1-6-8) приводится к виду
а + ata + а2а = 0, (1-6-9)
где
Для дальнейшего анализа примем, что скорость вдоль траектории
не меняется и, следовательно, аэродинамические коэффициенты остаются
постоянными. Если также принять, что А = const, то коэффициенты аи а%
в (1-6-9) будут постоянными. Общее решение такого уравнения следующее:
где ки к2— корни характеристического уравнения k2jraik + a2 = 0,
определяемые выражением
Постоянные С1? С2 находятся из начальных условий. Как показывают
исследования, наибольшее влияние на устойчивость полета оказывает
начальный толчок, характеризуемый в момент времени t — 0 начальной угловой
скоростью a = a0 и углом а = 0. Для этих условий постоянные
и решение (1-6-10) принимает вид
a = ±-aob-1e-bit(ebt-e-bt), (1-6-10')
где
Рассмотрим случай статической устойчивости, когда производная
т% <0 и, следовательно, а2>>0. Если при этом иметь в виду, что в
реальных условиях демпфирующий момент значительно меньше
стабилизирующего и что поэтому | а2 \ > Я^, то для а можно получить зависимость
a = аф-Ч-^ sin (bt), (1-6-10")
в которой Ъ = У\ а21 — к\.
Из (1-6-10") видно, что изменение угла атаки носит характер
периодических колебаний. Так как величина Xt всегда положительна, то эти
колебания будут затухающими и, следовательно, движущееся тело обладает
продольной колебательной устойчивостью.
Анализируя зависимость (1-6-10") для угла атаки, можно установить
некоторые критерии колебательной устойчивости (или динамической
устойчивости). К числу таких критериев относятся период колебаний
T = 2n(\m2\qSlA — Kl) 2 (I-6-11)
и частота колебаний
со = Ц- = (| mz | qSlA'1 - Х1)~г. (1-6-12)
Понятие о силах, моментах и аэродинамических коэффициентах 35
Важным критерием колебательной устойчивости является
логарифмический декремент затухания, равный натуральному логарифму отношения
амплитуд колебаний соответственно в моменты времени ti и t±-}-T, т. е.
Величина этого критерия зависит от периода колебаний и параметра
Чем больше аэродинамический коффициент демпфирования | т%|, тем
больше логарифмический декремент и тем быстрее по времени затухают
колебания.
Наряду с логарифмическим декрементом критерием динамической
устойчивости является время уменьшения амплитуды вдвое
Параметр А,ь определяющий оба названные критерия, рассматривается
также в качестве самостоятельной характеристики динамической
устойчивости, называемой коэффициентом затухания.
Наконец, приведем еще один критерий устойчивости —длину волны
колебания, определяемую из выражения
Практически целесообразно обеспечивать такие аэродинамические
свойства движущегося тела, при которых коэффициент затухания достаточно
велик, так как при этом время t2 будет мало, хотя несколько возрастает
длина волны колебания, что нежелательно. Обычно стремятся длину волны
уменьшить. Для этого нужно увеличить стабилизирующий момент, что
в свою очередь приведет к такому положительному явлению, как
уменьшение амплитуды колебания.
Ранее рассмотрен случай, когда тело обладает статической
устойчивостью, обеспечивающей ему также продольную колебательную
устойчивость. Аналогичный анализ может быть проведен для тела, у которого нет
статической устойчивости, т. е. производная т?>>0.
Решая (1-6-9), получим зависимость для а, указывающую на
незатухающий апериодический характер движения, которое уже не будет
колебательным. С течением времени угол атаки будет неограниченно возрастать.
В этом случае тело обладает продольной динамической неустойчивостью.
Обобщенный метод анализа устойчивости движения летательного
аппарата. Более общее выражение по сравнению с (1-6-10) для угла атаки
баллистического снаряда приведено в [55] и имеет вид
а - el^y [d/o (v) + C2Y0 (v)], (1-6-17)
где /0 (v) и Yo (v) — функции Бесселя нулевого порядка соответственно
первого и второго рода от аргумента
v = VT2e~^\ (I-6-18)
Параметр lt представляет собой фактор «динамической устойчивости»:
36 Г л а в а I
а параметр Z2 — фактор «статической устойчивости»:
U— — ^Рз^мид a (J^A 2 . /т а от
В приведенных соотношениях G — вес аппарата;
0О — начальный угол наклона траектории к горизонту;
хк — длина аппарата;
#вр — радиус вращения аппарата;
с* и га" — производные по а: Су{ = дсу/да, т% = дтх1да.
Две другие производные от коэффициента момента даются выражениями
dmz . a dmz , fi
~~l7
причем
Wz = lfer; ^ = ft (" = tw)- (1-6-22)
Решение (1-6-17) получено для условий неравномерного полета
баллистической ракеты в атмосфере, изменение плотности в которой определяется
экспоненциальным законом:
где р3 —плотность на уровне моря;
Р — высотный градиент плотности, принимаемый постоянной величиной;
у — высота над уровнем моря.
Постоянные интегрирования Сг и С2 в (1-6-17) определяются начальными
условиями при входе в плотные слои атмосферы. Если начальная угловая
скорость вращения Qz0=:0, а угол атаки а = ао=т^О, то постоянная С2 = 0,
и решение принимает вид
а = aoe~he-VyJo ^ (I-6-23)
Фактор статической устойчивости Z2 в наиболее распространенных
случаях имеет порядок ~105.
Фактор динамической устойчивости lt может существенно отличаться от
указанного значения. В частности, когда влияние демпфирования на
колебательное движение велико, то Zt может принимать отрицательные значения
(например, 1± = —10). В этом случае по мере уменьшения высоты угол
атаки колеблется около нуля с резко уменьшающейся амплитудой, близкой
по величине к нулю. Если фактор динамической устойчивости Zt = 0, то
затухание колебаний будет более медленным и у земли амплитуда может
быть отличной от нуля.
Для Zi > 0 (например, 1^ « 10) имеем случай практически
недемпфированного движения, когда затухание колебаний на некоторой высоте
прекращается и по мере приближения к земле наблюдается значительное
увеличение амплитуды.
Влияние колебаний аппарата можно учитывать при расчете теплопере- '
дачи, интенсивность которой несколько изменяется по сравнению с
интенсивностью, когда колебаний нет. Это изменение теплопередачи может,
естественно, приниматься во внимание при создании соответствующей
системы охлаждения.
Понятие о силах, моментах и аэродинамических коэффициентах
37
Х1
§ 1-7. Аэродинамические
характеристики
летательных аппаратов
при неустановившемся
движении
Общая зависимость для силы или момента. Ранее были рассмотрены
зависимости, определяющие силы, моменты и их коэффициенты. Эти
зависимости отвечали только на вопрос о том, как найти ту или иную
аэродинамическую характеристику, если закон распределения нормального давления
и касательных напряжений известен, а не о том, при каких условиях это
распределение возникло. Между тем для исследования аэродинамических
свойств реального объекта, в частности для исследования распределения
давления и касательных
напряжений, имеет значение
предыстория движения, т. е.
каким путем достигнуто
данное положение тела на
траектории, фиксируемое
определенными значениями угла
атаки и скольжения.
Например, достигнуто ли оно в
условиях, когда вращение
отсутствует и тело движется
вместе с центром масс вдоль
траектории поступательно Рис- 1"7"1- Схема Действия вращающих моментов
с постоянной скоростью, или
же оно достигнуто в условиях, когда движение тела характеризуется^™
только скоростью центра масс, но также угловой скоростью вращения тела
относительно центра масс.
Первый случай, если говорить строго, не реализуется в полете, но
может быть воспроизведен в экспериментальных аэродинамических
установках, и, очевидно, он соответствует установившемуся обтеканию при
фиксированных углах атаки и скольжения. Полученные в результате
эксперимента аэродинамические коэффициенты называются статическими
коэффициентами.
Второму случаю движения тела, которое характеризуется вращением,
будет соответствовать неустановившееся обтекание. Такой характер
обтекания обусловливает изменение в распределении местных сил по сравнению
с установившимся обтеканием. Вследствие этого возникают дополнительные
динамические составляющие аэродинамических сил и моментов. Такой
составляющей является демпфирующий момент, выражение для которого
было получено в частном случае плоского движения (без скольжения),
характеризующегося постоянными поступательной—Foo и угловой Qz
скоростями.
В наиболее общем случае неустановившееся движение летательного
аппарата будет определяться тремя составляющими скорости — Foo (i) центра
масс в связанной системе Vxl(t), Vyi(t), Vzi (t) (рис. 1-7-1), а также
составляющими угловой скорости Q(t) в той же системе QXi(t), Qyi(t), Qzi(t),
причем все эти составляющие зависят от времени.
Любую силу или момент можно представить в виде функциональной
зависимости
F = f(Vxi, Vvl, Vzi, Qxl, Qwl> Qzl> VxU Vyi, Vzi, Qxi, Qyl, Qzl), (1-7-1)
38
Г лав а I
показывающей, что нестационарные аэродинамические характеристики
определяются не только мгновенным динамическим состоянием тела, т. е.
параметрами Vxi1 Vyi, Vzl, Qxi, Qyi, Qzl в данный момент времени на
траектории, но и первыми производными от этих параметров по времени Vxl, VyiJ
Vzu ЙХ1, Qyl, Qzi.
В частном случае при плавном изменении параметров можно
ограничиться функциональной зависимостью
F = f(Vxi, Vyi, Vzi, Qxi, Qyi, Qzi). (1-7-2)
На практике задачи о неустановившемся обтекании бывают связаны с
изменением геометрической формы летательных аппаратов в полете за счет,
в частности, упругих деформаций. Влияние этого изменения формы на
аэродинамические характеристики можно учесть введением параметра б (хи уи
zi4 t), равного по величине приращению местного угла атаки, а также
производной от этого параметра по времени dbldt.
Безразмерные кинематические параметры. При исследовании
аэродинамических коэффициентов сил и моментов эти коэффициенты
рассматривают как функции, зависящие от безразмерных кинематических параметров,
имеющих вид
_
и —
vx
- dV.
xi
dt
a = ■
da I
dt 2Fo
dQ
xi
I*
_ dQyl
&
dt 2VI
dQzi I*
~~dT 2VI
(1-7-3)
Здесь a, pcK — соответственно углы атаки и скольжения;
Z — характерная длина.
В частности, для коэффициентов нормальной силы и продольного
момента
и, а, а,
Li _i л .
= f2(u,u, а, а, рск, рск, сох, сох,
у, coz, coz, б, б); (1-7-4)
у, coz, coz, б, б). (1-7-5)
Производные устойчивости. Предположим, что функциональные
зависимости (1-7-4) и (1-7-5) можно разложить в ряд Тейлора относительно
точки, определяемой некоторыми значениями начальной скорости Fooo,
Vxw, Fyio, Fzio и нулевой угловой скоростью Й0 = 0-
При малых нестационарных возмущениях действителен линейный закон
изменения аэродинамических коэффициентов от кинематических параметров.
Тогда, исключая из рассмотрения параметры б и б, т. е. не учитывая
влияния деформации, получим для аэродинамических коэффициентов
выражения:
cN = ст
: = ^20 + niPu + mu и 4- mai
Z Z 7.
(1-7-6)
(1-7-7)
Производные с^ = dcNldu, с1^ = dcN/du и т. д. называются производными
устойчивости.
Понятие о силах, моментах и аэродинамических коэффициентах 39
Рассмотрим принятую классификацию производных устойчивости.
Производные устойчивости вида с", с<*, с^ и т. д., которые определяются
в результате дифференцирования коэффициентов соответственно по и, а и рск,
называются статическими производными устойчивости и относятся к первой
группе производных.
Частные производные от коэффициентов по одной из переменных со*,
щ, (oz и т. д. составляют вторую группу и называются вращательными
производными (с^х, cpi, c^z и т. д.).
В третью группу производных устойчивости входят производные по
ускорению, определяемые как частные производные от коэффициентов по одной
из производных и, сох, (ду или (oz.
Имея в виду, что производные с^, с^ и т. д. вычисляются путем
дифференцирования аэродинамических коэффициентов также по производным
(в данном случае по а, рск и т. д.), отнесем условно эти производные
устойчивости к производным по ускорениям. Таким образом, к этой группе
относятся производные с^, с®Л, с^у, с** и т. д.
Так как число аэродинамических коэффициентов сил и моментов равно
шести, то в первую группу войдут 18 статических производных
устойчивости, во вторую—18 вращательных производных. Третья группа будет
включать 36 производных по ускорению.
Если нестационарные возмущения перестают быть малыми, то
существенной особенностью становится нелинейность зависимостей,
характеризующих обтекание. В этом случае в разложениях (1-7-6) и (1-7-7) надо оставлять
члены выше первого порядка. В частности, сохраняя квадратичные члены,
получим производные второго порядка, такие как т^&х = д2ту/да дсох и другие.
Исследования показывают, что практическое значение имеет лишь часть
производных первого и небольшое число производных второго порядка. Эти
производные приводятся в табл. 1-7-1.
Некоторые производные устойчивости, приведенные в табл. 1-7-1,
представляют особый интерес для исследования динамических свойств
летательного аппарата и имеют специфические названия. Среди этих производных
можно назвать уже упоминавшиеся статические производные устойчивости
т^, т$, т$, характеризующие такое важное свойство, как «жесткость»
соответственно продольного, бокового и поперечного колебательных движений
аппарата, и определяющие частоты этих колебаний.
Производная т™ часто называется статической производной продольной
устойчивости, т$~ статической производной устойчивости пути, или
коэффициентом флюгерной устойчивости, т$ — статической производной
поперечной устойчивости.
Вращательные производные и производные по ускорениям воздействуют
на движение как параметры демпфирования. В соответствии с этим
производные m®z, m™ называются коэффициентами продольного демпфирования,
т®у, т$ —коэффициентами демпфирования рысканья, т®х —коэффициентом
демпфирования крена.
Важное значение при вращательном движении имеет эффект Магнуса.
Он заключается в том, что при продольном вращении тела с угловой
скоростью Qx и при наличии угла атаки или угла скольжения возникают сила
и момент, пропорциональные произведению апх или рск&2х? причем силы
эти направлены перпендикулярно плоскостям, в которых лежат углы а и рск.
40
Глава I
Таблица 1-7-1
Производные устойчивости
Статические производные
4
4
Вращательные производные
°R
А
CN
со
czx
*
со
coz
°z
со
CO
mz
тхУ
CO
mxZ
CO
ml/
Производные по ускорениям
4
-
CR
1
CN
A
CO
4
4
•
•
-
CO^. /
•
cox
z
Производные устойчивости второго порядка
Аэродинамические коэффициенты этих сил и моментов пропорциональны
соответственно асох и Рсксо^. Поэтому производные от коэффициентов по асох
и река)*, например с*®*, с^ск®х, т%®х, т?гск(*х, называются производными
устойчивости Магнуса.
Происхождение другой группы сил и моментов связано с
одновременным вращением аппарата около двух осей и имеет, следовательно,
гироскопический характер. Гироскопические силы и моменты пропорциональны
произведению двух угловых скоростей. Например, при одновременном
вращении около осей хну эти дополнительные силы и моменты
пропорциональны произведению йхйу, а соответствующие аэродинамические
коэффициенты— произведению co^coj/. Поэтому производные от коэффициентов
по сохо)у (с®Л, т®х<ду и т. д.) называются гироскопическими производными
устойчивости.
Понятие о силах, моментах и аэродинамических коэффициентах 41
Частные случаи движения. С целью упрощения исследования
характеристик устойчивости можно пользоваться методом разделения сложного
движения летательного аппарата на отдельные его составляющие. В каждом
таком частном случае движения устойчивость изучается независимо от других
видов движения. Этот метод предполагает выделение отдельных характерных
видов движения или их комбинаций, которые являются определяющими
при оценке устойчивости всего летательного аппарата.
В табл. 1-7-2 приведены несколько характерных видов движения,
исследование которых имеет важное практическое [значение.
[Таблица I-7-24
Различные виды движения и соответствующие им скорости
^\^^ Составляющие
^"■""--^^^ скорости
Вид движения ^^^--^^^
Движение тангажа и крена
Движение тангажа без крена
Движение крена без тангажа
Движение без тангажа и крена
Vx
X
Va)
±
i м i
°х
±
мм
Примечание. Знак «+» обозначает составляющую скорости, не равную нулю, знак «—»—
составляющую скорости, равную нулю.
Упрощение исследования частного вида движения может быть
достигнуто, если исключить влияние ускорений. Практически это оправдано,
когда движение аппарата развивается достаточно медленно. При
необходимости учесть ускорение можно ввести поправку к аэродинамическому
коэффициенту в виде члена, равного произведению первой производной
устойчивости по ускорению и соответствующего безразмерного параметра ускорения.
Таким образом, можно, в частности, изучать устойчивость движения
тангажа, которое иногда называют главным видом движения. Устойчивость
движения тангажа (или продольная устойчивость) определяется продольным
демпфированием, зависящим в свою очередь от производных mf и m®z.
Иногда смешивают между собой производные т% и m®z, полагая, что
между ними нет различия. Это различие можно установить, если
рассмотреть два вида движения, один из которых характеризуется условием а = 0у
&2ф0, другой—условием а=#=0, Qz = 0.
Первый вид движения (рис. 1-7-2) характеризуется тем, что угол атаки,
равный углу между мгновенным направлением вектора Foo и связанной
с телом осью, не меняется и, следовательно, производная а = 0. Однако
при этом движении образуется переменный угол Ф между некоторым
фиксированным направлением и осью, связанной с телом. Поэтому Qz = d'&/dt^Q.
В частном случае, когда Qz = const, траектория на рис. 1-7-2, а
характеризует движение аппарата, выполняющего «мертвую петлю».
На рис. 1-7-2, б показан второй вид движения, соответствующий уело-
•
вию а =7^=0, £lz = 0. Это движение может возникнуть в случае свободного
падения с постоянным ускорением. При падении угол # между
фиксированным направлением и осью тела остается постоянным, а меняется угол а
между мгновенным направлением полета и осью тела.
Глава I
V
Рис. 1-7-2. Виды неустановившихся движений:
а — а = 0, Ф = &z = const; б — а = const, ф = Qz = 0; а = ао + Аа =
Voo', oL = g/Voo\ I — ось тела, 2 — фиксированное направление:
з — мгновенное направление полета
-* const
Рис. 1-7-3. Виды неустановившихся движений:
а — а = 0, O = Q;z = .Bsin(pf; б— а = Asincof, o = Qz = 0; e — a = 0=
Понятие о силах, моментах и аэродинамических коэффициентах 43
Таким образом, производная # = Qz = О, а производная по времени
от угла атаки афО. В данном случае эта производная а = const.
Каждый из рассмотренных видов движения встречается редко. Обычно
возникают продольные колебания, являющиеся комбинацией этих двух
движений. Такие колебания хорошо описываются синусоидальными
зависимостями для производных а или # = Qz
z
где А, В— амплитуды,
со, ф — частоты колебаний.
Уравнения (1-7-8) определяют гармонический закон изменения
производных а, Ф. Можно рассмотреть три вида движения, каждый из которых
описывается таким законом. Первый вид движения (рис. 1-7-3, а)
соответствует условию а = О, О = Qz ~В sin ф£. В этом виде движения ось тела,
совпадая с направлением полета (а = 0), совершает вдоль траектории колебания
в соответствии с гармоническим законом # — Bsinqt.
Второй вид движения (рис. 1-7-3, б) характеризуется тем, что ось тела
не меняет своей ориентировки вдоль траектории, так что ^ = # = 0. При
этом вследствие наличия вертикальной скорости меняется угол атаки в
соответствии с гармоническим законом для производной а.
Наконец, третий вид движения, показанный на рис. 1-7-3, в, возникает
в случае прямолинейной траектории движения центра масс тела, ось
которого меняет свой наклон к направлению полета по гармоническому закону.
В этом случае углы а и # совпадают, следовательно, а = #, а суммарная
производная продольного демпфирования равна т% + т®*.
Если одновременно с движением тангажа совершается движение крена,
то при исследовании устойчивости по крену должно быть учтено влияние
производной демпфирования крена, равной т^ + m®z.
Соответствующие значения коэффициентов демпфирования находятся
• • • • .
в виде производной (т% + mfz) а и (mj -f m®z) а, где производная а
определяется по гармоническому закону (1-7-8). Вводя обозначения ao = A/Q,z,
Sh = Qzl/Voo-, получим
Безразмерный параметр Sh = Qzl/Vco называется числом Струхаля
и является важнейшим критерием подобия при неустановившемся обтекании.
Пересчет производных устойчивости при изменении положения точки
приведения. При определении суммарных нестационарных характеристик
по известным их значениям для отдельных элементов летательного аппарата
необходимо привести каждое из этих значений к одной точке приведения,
выбранной для аппарата в целом. Таким образом, должен быть произведен
пересчет производной устойчивости с одной точки приведения на другую.
Предположим, что для некоторой несущей поверхности известны
аэродинамические характеристики и производные устойчивости, рассчитанные
для некоторой точки приведения 0 (см. рис. 1-2-2). Требуется определить
соответствующие характеристики относительно другой точки 01?
расположенной от точки 0 на расстоянии х = х[.
44
Глава Г
Для упрощения задачи примем, что с^0 — mz0 = 0, а также равны нулю
составляющие аэродинамических коэффициентов, обусловленные изменением
• • • •
скорости поступательного движения, т. е. с^и = с^и = т^и = 0. При этих
допущениях
cN = с* а + с%а + с%чог + cj*az; (I-7-10)
mz =
(1-7-11)
где производные для точки отсчета 0 известны.
Для новой точки приведения 0i соответствующие коэффициенты
записываются в виде
ст = с*\а±
Как следует из рис. 1-2-2,
(I-7-107
(1-7-1Г)
Vqo
где a)z =
o, x = x'Jb, и далее
а1 = ос —2coz#; cozl = coz; cozl = coz. (1-7-12)
Теперь воспользуемся тождествами ст = cN и zn^! — mz — cNx. Внося
в левые части тождеств выражения (Т-7-12) и приравнивая соответствующие
коэффициенты при a, a, coz, coz, получим следующие зависимости для
производных устойчивости:
i
= та_са; тах = та_
cx
Гл а в а II
ФОРМЫ
ЛЕТАТЕЛЬНЫХ
АППАРАТОВ
И ИХ ЭЛЕМЕНТОВ.
Основными элементами, из которых состоит современный летательный
аппарат, являются планер, двигательная установка, оборудование и
полезный груз.
Основным объектом аэродинамических исследований, в результате
которых определяется силовое воздействие воздушной среды, является
планер. Планер летательного аппарата (или просто летательный аппарат)
включает в себя корпус, крылья, оперение, органы управления и некоторые
другие устройства, объединяемые в понятие надстроечных элементов.
Так как аэродинамические характеристики летательного аппарата
ов значительной степени определяются аэродинамическими
характеристиками изолированных частей — корпуса, крыльев и др., то представляет
интерес рассмотреть форму, а также некоторые наиболее общие
аэродинамические свойства этих частей.
§ 11-1. Формы корпусов
летательных аппаратов
Корпус летательного аппарата в большинстве случаев является телом
шращения и состоит из трех элементов: передней головной части, средней
ш задней (или хвостовой)
части, называемой иногда
кормой.
Головная часть. На рис.
П-1-1 показаны возможные
«схемы головных частей,
представляющих собой
заостренные тела вращения,
сплошные или с протоком. Такие
«формы головных частей
снижают аэродинамическое
сопротивление корпуса, но
уменьшают его полезный
объем. Головные части обычно
имеют коническую, оживаль-
ную или параболическую
форму, а иногда
представляют собой комбинацию этих
форм.
Оживальная головка
■—1
1
I
Рис. П-1-1. Форма заостренных головных частей
(сплошных и с протоком):
а — конус; б — оживальная (параболическая) касательная
головная часть: в — оживальная (параболическая)
секущая головная часть; г — комбинированная головная часть
(конус с оживалом)
имеет образующую в виде
дуги окружности некоторого
радиуса (рис. Н-1-2).
Сопряжение головки с цилиндрическим участком может быть осуществлено либо
по касательной, либо под некоторым углом р Ф 0. В первом случае ожи-
вальную кривую называют касательной, во втором — секущей. Уравнение
оживальной кривой в безразмерной форме
>2 ^-^ /Ч—1)2]1/2 — 1} Ч-1, (П-1-1)
46
Глава IГ
где -й = /?/(2гмид), А,МИд = хМИд/(2гМИд)~удлинение головной части {хшт~ее-
__ абсолютная длина);
X =
Непосредственно из рис. П-1-2 можно найти зависимость между
удлинением Ямид и безразмерным радиусом R оживальной образующей
Кшц, - VR-0,25. (П-1-2)
При исследовании обтекания оживальных поверхностей необходимо знать,,
как изменяется наклон касательной вдоль образующей. Чтобы найти закон
этого изменения, продифференцируем (И-1-1):
о dr I dr
* P ~ dx ~ 2ХМИД ^х ~
— ■ ■ — IX ~~ х J I л. п^ (X —• А
х Из полученного выражения можно найти >
в частности, наклон касательной у острия тела
Рассмотрим параболическую головную часть.,
характерные геометрические параметры которой
Рис. п-1-2. Форма и геометри- такие же' как * на Рис-О11Л'2- Координаты точек
ческие параметры оживальной параболической кривой удовлетворяют в общем
головной части тела вращения: случае уравнению
1 — касательная оживальная кри- , 9 ч .
вая О = 0 в точке А), 2 — секу- Г = X (п + ОХ + CXZ +•••)• (11-1-4)
щая оживальная кривая (|5 Ф О
в точке А) Из класса параболических образующих
рассмотрим частный ее вид, получаемый щ
уравнения (Н-1-1), в котором безразмерный радиус R принят достаточно большим.
В этом случае в (Н-1-2) величиной 0,25 можно пренебречь. Если, например,
допустимая погрешность не превышает 3%, то это можно сделать при Л>4.
В результате найдем приближенную зависимость Д = ЯмИД. Подставляя ее
в (Н-1-1) и производя упрощение, получим уравнение параболической
образующей, которое в безразмерной форме имеет вид
Дифференцируя по х, найдем тангенс угла между осью тела и
касательной к образующей
(П-1-6)
1
Отсюда для угла наклона касательной у острия имеем tg §Q^{drldx)x=o ■=
1/^мид- Имея в виду это выражение, уравнение (П-1-6) преобразуем к виду
-X).
(II-1-6-)
Подобно оживальной кривой, параболическая образующая может быть
касательной и секущей. Тела с параболической образующей обладают
важным свойством, которое вытекает из (П-1-5) и состоит в том, что вся
их бесконечная совокупность характеризуется одинаковой зависимостью
относительной толщины г/гшия от безразмерной координаты х/хмид>.
Формы летательных аппаратов и их элементов
47
Среди этой совокупности могут быть геометрические подобные тела,
отличающиеся своими линейными размерами в одно и то же число раз.
Такие тела, очевидно, имеют одинаковое удлинение и их можно совместить
друг с другом путем равномерной, т. е. одинаковой для всех направлений
деформации.
Однако совокупность параболических тел включает в себя и такие
формы, которые можно совместить только путем неравномерной
деформации. Представим себе тела с различными удлинениями. Введя новый
масштаб для радиальной координаты, можно сдеформировать тело в
вертикальном направлении, но это не даст полного совмещения, для осуществления
которого надо принять другой масштаб и для осевой координаты. Такое
преобразование одного тела в другое
называется аффинным. В соответствии с этим
тела с параболической образующей
называются аффинно-преобразованными или
аффинно-подобными. Очевидно, конические
тела, образующие которых даются
уравнением в безразмерной форме г = х, харак-
Рис. 11-1-3. Формы затупленных головных частей:
а — конус с плоским затуплением; б — ступенчатый
конус с плоским затуплением; в — конус с
касательным сферическим носком; г — цилиндр с касательным
сферическим носком; д — конус с секущим
сферическим носком; е — цилиндр с секущим сферическим
носком; ж — оживальная (параболическая) головная
часть с плоским затуплением; з — комбинированная
головная часть (конус с оживалом) с плоским
затуплением; и — оживальная (параболическая) головная
часть с касательным сферическим носком; к —
оживальная (параболическая) головная часть с секущим
сферическим носком
теризуются также одинаковым распределением относительных толщин иу
следовательно, будут являться аффинно-подобными.
В отличие от параболических и конических тел у оживальных головок
с изменением удлинения меняется распределение по длине относительных
толщин, что непосредственно вытекает из (П-1-1). Вследствие этого нельзя
аффинно преобразовать одну оживальную головку в другую. Таким
образом, тела оживальной формы не являются аффинно-подобными, за
исключением тех случаев, когда головки имеют одинаковое удлинение, т. е. подобны
геометрически. Однако в тех случаях, когда удлинения велики (Ямид > 2),
оживальная форма, как указывалось, незначительно отличается от
параболической. Поэтому изменением распределения относительных толщин по
длине при переходе от одного тела к другому можно пренебречь и считать
оживальные головки аффинно-подобными.
Во многих конструкциях летательных аппаратов головные части могут
иметь затупленные формы. Их применяют прежде всего при очень высоких
скоростях полета, когда основным требованием, предъявляемым к
головным частям, является способность противостоять действию очень высоких
температур. Однако весьма часто затупленной формой обладают
летательные аппараты, имеющие небольшие скорости, что может быть обусловлено
конструктивными особенностями, назначением аппарата и т. д.
Практически всегда приходится иметь дело с затупленным телом, так
как технологически невозможно добиться абсолютно острой головки.
На рис. П-1-3 показаны различные формы затупленных носков
конических головок, а также головок криволинейной формы. Затупленный носок
48 Г л а в а II
может быть выполнен в виде степенной головки, образующая которой задана
уравнением
где показатель степени 0 < п < 1.
Разновидностью степенной головки является сферическое тело,
уравнение образующей которого получается из (П-1-7) при условии, что п = 0.
Рис. П-1-4. Головные части со сферическим носком:
1 — криволинейная образующая; 2— сферический носок; з —
касательная прямолинейная образующая; 4 — секущая прямолинейная
образующая
Летательные аппараты, выполненные в виде сферы или имеющие в
качестве головной части сферический носок, распространены весьма широко.
При этом образующая основного участка, идущего за сферическим носком,
может быть как криволинейной, так и
прямолинейной (рис. 11-1-4). Наиболее
распространены тела с прямолинейной
образующей в виде конуса. Уравнение
этой образующей
X
Рис. П-1-5. Цилиндрическое тело со
сферическим носком:
1 — касательная образующая; 2 — секущая
образующая
где rT = /?TcospK, xT = RTctg$Kcos$K\
RT и рк— соответственно радиус
сферы и угол наклона образующей
конуса. В случае, если за сферическим
носком следует цилиндрический участок
(рис. П-1-5), то (Зк = 0 и г=гт = /?т,
т. е. поверхность сферического носка
касается цилиндра.
Носок конуса или цилиндра может
быть выполнен и таким образом, что
их поверхности не будут касательными к сфере. В этом случае сферический
носок оказывается секущим (рис. П-1-5).
При исследовании обтекания сферических носков используется
уравнение образующей сферического носка, которое можно получить из уравнения
(11-1-1) оживальной кривой, приняв в нем гмид = хшщ = R = RT. Тогда
>2 = 1 —(ж —I)2, (II-1-9)
где r = r/RT;'~x = x/RT.
Тангенс угла наклона касательной в данной точке образующей к оси
(П-1-10)
Формы летательных аппаратов и их элементов
49
Сферическая форма затупления включает в себя два семейства носков,
выполненных в виде секущих и касательных сфер. Касательный
сферический носок характеризуется радиусом сферы RT. Если его величина равна
нулю, то затупление будет «нулевым» и, следовательно, носок заострен
(рис. И-1-6). С увеличением радиуса возрастают размеры носка. Причем
максимальная величина этого радиуса при заданных гмид и рк равна RT =
/|З
ид/С03|Зк.
Если рассмотреть плоский торец конуса или цилиндра, то затупленный
носок, построенный около этого плоского торца с радиусом RT, имеет
в общем случае форму
секущей сферы с различными
радиусами (рис. П-1-7). Его наименьшая
величина равна RT = rT/cos (Зк
и RT = гт, причем первое
значение соответствует сферическому
носку, касательному к
поверхности конуса, второе — сферическому
носку, касательному к поверхности
цилиндра.
В том случае, когда
затупленная поверхность плоская, т. е.
выполнена в виде плоского торца(рис.
П-1-7), ее можно рассматривать как сферу с бесконечно большим радиусом.
Сферический касательный носок и плоский торец являются двумя
характерными формами затуплений, которые можно представить как границы
интервала, содержащего другие возможные формы.
Обе эти характерные формы представляют интерес и при исследовании
аэродинамики затупленных тел с какой-либо промежуточной формой носка,
Рис. П-1-6. Конус с различной степенью
затупления по сфере
Рис. П-1-7. Конус (а) и цилиндр (б) со сферическим и
плоским затуплением:
X — секущий сферический носок, 2 — сферический касательный
носок, 3 — плоский торец
так как дают возможность оценить крайние значения тех или иных
аэродинамических параметров, которыми они обладают.
Сферический носок и плоский торец можно рассматривать как частные
случаи эллиптической поверхности. На рис. И-1-8 изображены конус
и цилиндр с такой формой затупления. Геометрическими характеристиками
эллиптического носка являются его большая и малая оси, причем их
ориентировка может быть различной. На рис. П-1-8 изображен частный случай,
когда большая ось перпендикулярна к оси тела. Если обе оси равны, то
эллиптическое затупление переходит в сферическое. Когда малая ось равна
нулю, эллиптическая поверхность вырождается в плоскость.
Так же как и сферическое затупление, эллиптический носок может быть
секущим и касательным. В последнем случае радиус RT меньшего основа-
4-114
о
Глава If
Ф
Рис. И-1-8. Конус (а) и цилиндр (б) с
эллиптическим затуплением
ния конуса, вообще говоря, не равен примыкающей к нему полуоси. Строго
это равенство соблюдается, когда носок сопрягается с цилиндром.
Приближенно его можно принять и для конуса, обладающего малым углом |3К.
Наряду с указанными формами затуплений можно привести еще один
вид поверхности, который изображен на рис. Н-1-9. Показанное здесь
затупление представляет собой плоский,
торец с круглой фаской радиуса г.
Когда г = гт, затупление
приобретает сферическую форму; в случае-
г = О поверхность превращается в.
плоский торец.
Аэродинамические
характеристики затупленных тел существенно*
зависят при заданном типе носка от
степени затупления, под которой
условимся в дальнейшем понимать
отношение радиуса основания носка гт-
к радиусу наибольшего сечения тела
гмид. Наряду с этим важное значение*
имеет величина геометрического
параметра самого затупления. Таким
параметром для сферического носка
является отношение (Дт)кас/^т> в
котором (Дт)кас~РаДиУс касательного
сферического носка. Этот параметр
изменяется в интервале от 1 до 0. Для
эллиптического носка таким
параметром может быть отношение
полуосей Ъ = Ъ/а, которое для цилиндрического тела меняется в интервале-
0 <!& •< 1, а для конического — в интервале 0 ■< Ъ < 1.
При небольших углах рк у конических тел за один из характерных
размеров носка удобно выбрать его высоту А (см. рис. П-1-7), а за другой —
радиус гт. Тогда параметр затупления можно определить как отношение1
А = А/гт, которое будет меняться в интервале 0 <; А <; 1.
На рис. II-1-9 видно, что в качестве параметра затупления,
выполненного в виде торца с круглой фаской, можно выбрать величину г = г/гт,
которая для цилиндрического и конического тел с малым углом |3К будет
меняться в интервале 1 <; г <! 0.
Средняя часть. Средняя часть корпуса обычно выполняется в виде
цилиндра. Вместе с тем она может быть выполнена в отдельных случаях
Рис. 11-1-9. Конус (а) и цилиндр (б) с
затуплением в виде торца с круглой фаской
Рис. 11-1-10. Виды корпусов летательных аппаратов с
воздухозаборниками:
а — круглыми; б — полукруглыми; в — кольцевыми
и в виде усеченного конуса, причем наклон образующей делается
небольшим. У летательных аппаратов с воздушно-реактивным двигателем (ВРД)
Формы летательных аппаратов и их элементов
51
средняя часть корпуса может иметь либо кольцевой уступ, либо один или
несколько секторных уступов, обеспечивающих расположение
воздухозаборников (рис. П-1-10).
Средняя часть корпуса может иметь несимметричную форму. В
частности, корпус не круглого, а овального сечения (рис. И-1-11) используется
для размещения воздухозаборников 1 ВРД.
Рис. И-1-11.
Овальная форма корпуса
с двумя
воздухозаборниками
Рис. 11-1-12. Формы
суживающейся хвостовой части:
а — конус; б — касательная ожи-
вальная (параболическая)
хвостовая часть; в — секущая ошиваль-
ная (параболическая) хвостовая
часть; г — комбинация оживала
и конуса
а)
5)
—И- -
1 1-~
J
^
Рис. П-1-13. Форма раширяю-
щейся хвостовой части:
а — коническая; б — оживальная
Хвостовая часть (корма). Эта часть выделяется из корпуса как его
элемент, имеющий постепенно уменьшающийся (или увеличивающийся) по»
направлению к донному срезу диаметр.
Основное назначение хвостовой части с уменьшающимся диаметром —
уменьшить полное сопротивление. Формы хвостовой сужающейся части
показаны на рис. П-1-12.
Рис. П-1-14. Формы донного среза для сплошных тел и тел
с протоком:
а — цилиндрической части; б — конической суживающейся части
В некоторых случаях форма хвостового участка выбирается из
конструктивных соображений. Причем она может быть и расширяющейся.
В последнем случае (рис. П-1-13) хвостовая часть способствует улучшению
устойчивости летательного аппарата, но увеличивает его сопротивление.
Донный срез ограничивает корпус или его хвостовую часть. Он может
представлять либо сплошную торцевую поверхность, либо плоское кольцо
(рис. И-1-14). Конструктивно корпус выполняется иногда в такой форме,
когда четко выраженный донный срез отсутствует. В этом случае донная часть.
4*
52
Глава 11
может представлять собой поверхность произвольной формы. На форму
донной части, например, оказывает влияние сопловой блок двигательной
установки. На рис. Н-1-15 представлены некоторые возможные формы
донных частей корпуса с соплами.
Рис. 11-1-15. Формы хвостовых частей
корпуса с соплами:
в — односопловой блок; б — четырехсопловой блок
Рассмотренными формами затупленных и заостренных носков, как
и в целом корпусов, не исчерпывается, конечно, все их многообразие. Здесь
приведены лишь наиболее простые формы, которые в известной степени
отражают это многообразие и являются типичными.
11-2. Формы несущих,
управляющих,
стабилизирующих
и вспомогательных
поверхностей
Профиль. Аэродинамические свойства крыла в значительной степени
определяются его профилем, представляющим собой контур крыла,
лежащий в сечении, перпендикулярном его плоскости. Ориентировка плоскости
сечений в известной мере произвольная: она может быть перпендикулярна
передней кромке, совпадать по направлению с корневой хордой и т. д.
Средняя линия
Рис. 11-2-1. Произвольный профиль крыла в равномерном
невозмущенном потоке под углом атаки а
В общем случае профиль может иметь криволинейную форму и не
обладать симметрией (рис. П-2-1). Форма профиля задается уравнениями yiB =
= /в (xi) и У in — /н (#i) соответственно верхней и нижней частей его
контура.
Основные геометрические параметры профиля показаны на рис. П-2-1.
Обычно имеют дело с безразмерными параметрами: относительной
наибольшей толщиной Л = Alb; безразмерным расстоянием до места наибольшей
Формы летательных аппаратов и их элементов
53
толщины хс = хс/Ь; относительной стрелой прогиба Ai = AJb и
безразмерным расстоянием до нее xci = xci/b.
При наличии горизонтальной симметрии уравнения верхнего и
нижнего контуров имеют вид (z/i)B,H — ± / (#i), где знак «плюс» относится
к верхнему, а «минус» — к нижнему контуру. Средняя линия совпадает
с хордой, а стрела прогиба равна нулю.
В современных конструкциях летательных аппаратов,
предназначенных для полетов с большими скоростями, несущие и стабилизирующие
поверхности могут иметь один из следующих профилей: ромбовидный,
модифицированный ромбовидный и чечевицеобразный профиль (рис. П-2-2) [23].
Первые два профиля отличаются простотой изготовления. Преимущество
ромбовидной формы заключается в обеспечении крылу большей жесткости
а)
Ф
Рис. П-2-2. Профили сверхзвуковых несущих и
стабилизирующих поверхностей:
а — ромбовидный; б — модифицированный ромбовидный; в —
чечевицеобразный
по сравнению с модифицированной формой. С точки зрения аэродинамики
некоторым преимуществом обладает модифицированный профиль, так как
при одинаковой с ромбовидным профилем ширине он может обеспечить
меньшее сопротивление и большее аэродинамическое качество.
У чечевицеобразного профиля сопротивление еще меньше, чем у
модифицированного (при одинаковой относительной толщине). Выбором
соответствующих углов заострения передней и задней кромок можно добиться
хорошей жесткости крыла.
Увеличивая углы заострения передней кромки, следует учитывать
возможность возрастания волнового сопротивления, а также повышенную
чувствительность режима обтекания к изменению углов атаки. Так, с
увеличением углов заострения уменьшаются углы атаки, при которых наступает
режим обтекания с отошедшей
волной, когда резко возрастает
сопротивление, нарушается безотрывный
характер течения, ухудшается
устойчивость полета.
Основное отличие
сверхзвукового профиля от дозвукового
заключается в его симметричности
относительно хорды и в заострении
передней кромки. Характер обтекания
и распределения давления при
сверхзвуковой скорости таков, что
искривление средней линии профиля,
выгодное при дозвуковой скорости, не
дает здесь особых преимуществ.
Форма в плане. Современные
летательные аппараты обладают
крыльями самой различной формы
в плане. Выбор этой формы зависит
от назначения летательного аппарата и диапазона его скоростей. При выборе
формы крыла в плане определяется не только его контур, но и все
геометрические параметры как размерные, так и безразмерные. Представление об
Рис. II-2-3. Основные геометрические
параметры обобщенной схемы крыла в плане
£4 . Г лав а II
основных геометрических параметрах можно получить из рис. П-2-3, на
котором изображена схема крыла современного летательного аппарата.
Аэродинамические коэффициенты крыла заданной формы в плане и при
данной скорости полета зависят от углов стреловидности хп и к3
соответственно передней и задней кромок; удлинения крыла X = l/bcv или X=l2/SKl>
(5кр = Z6cp —площадь крыла в плане); относительных размеров корневой
и концевой хорд (соответственно foKp — &кр/ЬСр, ^кц = ^кц/^ср)-
Важнейшей геометрической характеристикой, широко используемой
в аэродинамических исследованиях, является средняя аэродинамическая
хорда (САХ). Под САХ понимают хорду эквивалентного крыла
прямоугольной формы в плане, обладающего при той же площади в плане, что
и у заданного, одинаковыми с ним аэродинамическими характеристиками.
Коэффициент момента эквивалентного крыла
|в5 = с"Е + 1Л-Св8Ё£
где хА, уА — координаты передней кромки эквивалентного крыла,
отсчитываемые от оси z, проходящей через переднюю кромку заданного крыла
(рис. П-2-3).
Приравнивая 77г|кр значению тп2Кр (1-5-16'), можно получить
1/2
L/CAX Li \lI'l>■■rA-JKID/ \ iivvU \*> / U//> ,
0
1/2
xA = 2 (cjsrS^y1 \ Cjsfb (z) xn dz\
о
1/2
yA = 2 (crS^Y1 \ cRb (z) yn dz.
0
Таким образом, САХ, а также координаты хА и уА, являясь
интегральными величинами, будут, строго говоря, зависеть от распределения местных
аэродинамических параметров по размаху крыла. Практически полагают,
что САХ и координаты хА и уА зависят только от геометрических
характеристик крыла. В соответствии с этим средняя аэродинамическая хорда
1/2
Ьсах = -§— \ Ъ2 (z) dz,
о
а координаты
1/2 1/2
2 С5 2 {*
хА = -^— \ Ъ (z) xu dz; уА = -о— \ Ъ (z) yu dz.
о о
Для стреловидного крыла с концевыми кромками, параллельными
корневой хорде,
где г] = Ькр/6кц —обратное сужение крыла.
Относительная координата
где X — удлинение крыла.
•Формы летательных аппаратов и их элементов
55
Угол стреловидности по передней кромке %и связан с углом
стреловидности хп по линии, проходящей через п-е доли хорд (см. рис. И-2-3),
соотношением
. 4я Ti —1
Центр давления или фокус крыла в практических случаях отсчитывают
от начала средней аэродинамической хорды, располагающейся вдоль
корневой хорды крыла (см. рис. П-2-3).
Применение средней аэродинамической хорды в качестве характерного
^геометрического параметра удобно в том отношении, что длина этой хорды
Рис. 11-2-4. Типичные формы крыльев в плане современных
высокоскоростных летательных аппаратов
ш положение фокуса (центра давления) относительно ее передней кромки
остаются почти неизменными с изменением формы крыла в плане при
сохранении площади крыла.
Типичные формы крыльев в плане современных высокоскоростных
летательных аппаратов приведены на рис. II-2-4. Характерной
особенностью всех крыльев является наличие передней стреловидности, главным
назначением которой является снижение сопротивления благодаря
уменьшению нормальной составляющей скорости невозмущенного набегающего
потока (Voon = Foo cos %).
У аппаратов, предназначенных для полетов с дозвуковыми скоростями,
при общем снижении сопротивления, сдвигается в сторону большей
скорости волновой кризис («звуковой барьер»).
У сверхзвуковых летательных аппаратов с крыльями, обладающими
большой стреловидностью, обеспечивается более плавный переход через
звуковой барьер, без значительного увеличения сопротивления, что имеет
очень важное значение для сохранения устойчивости полета.
Аэродинамические характеристики крыла при сверхзвуковой скорости
существенно зависят от того, является ли передняя кромка дозвуковой или
сверхзвуковой.
Передняя кромка крыла называется дозвуковой, если она лежит внутри
конуса Маха с вершиной в передней точке крыла (рис. И-2-5), так как
при этом нормальная к кромке составляющая скорости набегающего потока
будет меньше скорости звука (Vnoo < апоо, МпОо < 1).
Таким образом, крыло находится в условиях дозвукового обтекания,
лри котором заостренная передняя кромка оказывается невыгодной. Можно
улучшить условия обтекания и добиться более благоприятных
аэродинамических характеристик, в частности, получить большее аэродинамическое
качество, слегка закруглив переднюю кромку.
56
Глава 11
Улучшение аэродинамических характеристик будет обусловлено
возникновением разрежения в окрестности передней кромки, что приводит
к образованию подсасывающей силы и, как следствие, к уменьшению
сопротивления.
Следует иметь в виду, что снижения сопротивления можно достигнуть
только при правильном выборе радиуса закругления, величина которого
зависит от угла атаки. При отклонении от некоторых оптимальных значений
этих параметров эффект снижения сопротивления не достигается. Это
связано с тем, что, например, при уменьшенных радиусах закругления и
повышенных углах атаки возникает срыв потока и сопротивление возрастает.
Передняя кромка крыла называется сверхзвуковой, если она лежит вне
конуса Маха (см. рис. И-2-5, б), так как число Маха потока в направлении
нормали к кромке будет при
этом больше единицы. Учитывая
особенности сверхзвукового
обтекания, желательно, чтобы
передняя кромка была
заострена.
Подобно передней кромке,
задняя и боковая кромки также
могут быть дозвуковыми и
сверхзвуковыми, что существенно-
отражается на обтекании крыла.
Дозвуковая задняя кромка
образует с горизонтальной осью
симметрии крыла угол, меньший
угла Маха (см. рис. П-2-5, а).
Распределение скорости и
давления на крыле внутри угла
Маха зависит от концевых
потерь, обусловленных
перетеканием воздуха через боковую
кромку, когда она является дозвуковой (см. рис. П-2-5, а, боковая
дозвуковая кромка лежит внутри конуса Маха). Эффект перетекания приводит
к уменьшению подъемной силы в этой области крыла.
Чтобы исключить неблагоприятное воздействие боковой кромки, ее
делают сверхзвуковой, размещая вне конуса Маха (см. рис. П-2-5, б).
Особенность, связанная с наличием дозвуковой кромки, состоит также
в том, что на всем участке крыла внутри угла Маха будет сказываться ее
влияние, которое в ряде случаев может оказаться неблагоприятным. Чтобы
исключить это влияние, заднюю кромку выполняют сверхзвуковой,
придавая ей больший угол наклона, чем угол Маха (см. рис. П-2-5, б).
Из сказанного можно сделать вывод, что при соответствующем выборе
формы крыла в плане можно получить необходимые аэродинамические
характеристики. Как видно из рис. П-2-4, разные формы крыла с
прямолинейной передней кромкой могут быть получены путем соответствующего
преобразования крыла треугольной формы (см. рис. И-2-4, а). Треугольное
крыло обладает всеми положительными свойствами крыльев со стреловидной
передней кромкой и, кроме того, имеет ряд благоприятных особенностей,
приобретающих существенное значение в некоторых условиях полета.
Так, установлено, что в трансзвуковой области полета центр давления
крыла перемещается незначительно, что облегчает стабилизацию и
управление летательным аппаратом. Аэродинамическое качество треугольного
крыла при сверхзвуковых скоростях выше, чем у некоторых других крыльев,
в частности, у обычного стреловидного (см. рис. П-2-4, д), так как отсут-
Рис. И-2-5. Характер кромок крыла при
сверхзвуковом полете:
а — передняя, задняя и боковые кромки дозвуковые;
б — эти же кромки сверхзвуковые
Формы летательных аппаратов и их элементов 57
стьует отрицательное воздействие концевого эффекта. Наконец, у
треугольного крыла имеются некоторые конструктивные преимущества, позволяющие
сделать его прочным и жестким и использовать достаточно большую
внутреннюю полость для размещения оборудования и топлива. Благодаря
размещению органов управления вдоль задней кромки, перпендикулярной
продольной оси летательного аппарата, повышается их эффективность.
Все отмеченные и некоторые другие положительные качества
треугольных крыльев проявляются, естественно, в определенных условиях полета.
Треугольные крылья обычно используются для высокоскоростных
сверхзвуковых летательных аппаратов. При изменении условий полета и
назначения летательного аппарата треугольные крылья могут оказаться
неэффективными и должны быть заменены другими.
На рис. П-2-4 приведены возможные схемы крыльев, которые
используются помимо треугольных. Каждую такую схему можно рассматривать
как улучшенный вариант треугольного крыла.
На рис. II-2-4, б ж в изображены четырехугольные крылья. У первого
крыла более передний, у второго — несколько сдвинутый назад центр
давления. Первое крыло обладает меньшей, второе — несколько большей
подъемной силой.
Пятиугольное крыло, схема которого изображена на рис. Н-2-4, а,
по своим свойствам достаточно близко к треугольному, если скос концевой
кромки невелик. Такой скос, хотя и несколько уменьшает площадь несущей
поверхности, избавляет крыло от непрочной заостренной кромки, к тому же
испытывающей сильное воздействие нагрева.
Две другие модификации (см. рис. И-2-4, д и е) относятся к типу
шестиугольных крыльев, близких по своим характеристикам к четырехугольным
при условии, что скос боковых кромок невелик.
Важная особенность пятиугольных и шестиугольных крыльев с
достаточно развитыми концевыми хордами состоит в том, что обтекание участков
крыла, примыкающих к задним кромкам, будет в большой степени зависеть
от обтекания боковых кромок, что должно быть учтено при проектировании
этих крыльев.
На рис. Н-2-4, ж изображена схема восьмиугольного крыла с
передней кромкой, выполненной в виде ломаной линии. Такое крыло можно
рассматривать как комбинацию стреловидного и треугольного крыльев. Оно
обладает тем свойством, что положение центра давления в трансзвуковой
области полета практически не меняется в отличие от обычного
стреловидного крыла, у которого центр давления сдвигается к передней кромке с ростом
скорости полета.
Прямоугольные крылья с обычным удлинением не имеют широкого
применения. Основными причинами этого являются значительное
сопротивление, которое резко возрастает при достижении волнового кризиса,
наблюдаемого уже при сравнительно небольших числах Моо < 1, а также
значительное перемещение центра давления в трансзвуковой области
полета.
В последнее время в конструкции высокоскоростных летательных
аппаратов вводятся в качестве несущих и управляющих элементов
прямоугольные крылья малого удлинения. Вследствие благоприятной интерференции
с корпусом такие крылья обладают достаточно хорошими
аэродинамическими характеристиками.
Выбор формы крыла в плане является одним из самых ответственных
моментов в разработке конструкции летательного аппарата и должен быть
основан на глубоких теоретических и экспериментальных исследованиях,
учитывающих назначение летательного аппарата и конкретные условия его
полета.
58
Глава II
Кольцевое крыло. В качестве оперения и несущих
поверхностей применяют кольцевые крылья (рис. И-2-6). Такое крыло
характеризуется углом установки профиля а0 относительно продольной оси симметрии,
радиусом г0 окружности, проходящей через задние кромки сечений
(«донный» радиус), удлинением 2ro/b (Ъ — хорда профиля). Применяя кольцевое
крыло, можно при той же подъемной силе обеспечить меньшие поперечные
габариты летательного аппарата. Крыло обладает достаточно большой
жесткостью, что практически исключает флаттер.
Благодаря продольной симметрии, крыло позволяет легко создавать
управляющую силу в любом направлении без крена, обеспечивая тем самым
высокую маневренность при полете. Большие критические углы атаки
обеспечивают надежную работу крыла в достаточно широком диапазоне углов
«х-
Рис. 11-2-6. Кольцевое крыло
атаки. Повышению несущих возможностей кольцевого крыла способствуют
пластины (пилоны), крепящие крыло на корпусе. Кроме того, пилоны играют
роль стабилизаторов, обеспечивающих статическую путевую и продольную
устойчивость.
Особенно ощутимо проявляются преимущества кольцевого крыла при
его установке на аппарате с воздушно-реактивным двигателем, когда оно
используется одновременно как устройство для забора воздуха из
атмосферы. Удобно оно также для летательных аппаратов, стартующих
вертикально или из ограниченного пространства.
К недостаткам кольцевого крыла относятся более слабая, чем у
плоского, зависимость подъемной силы от угла атаки и повышенное
сопротивление за счет пилонов. Кольцевое крыло не обеспечивает поперечной
устойчивости летательного аппарата. Его подъемная сила уменьшается
вследствие неблагоприятной интерференции с корпусом. Причем это
неблагоприятное влияние тем значительнее, чем ближе к корпусу расположено
крыло.
Крутка крыла. Улучшения аэродинамических характеристик крыла
можно достигнуть при помощи крутки крыла, которая бывает двух видов —
аэродинамическая и геометрическая.
Метод аэродинамической крутки состоит в смещении по размаху крыла
(относительно передней кромки) места расположения наибольшей толщины
профиля, т. е. в изменении относительного расстояния хс — хс1Ъ (см.
рис. И-2-1). Крыло в этом случае остается плоским.
При геометрической крутке относительные размеры профиля
сохраняются постоянными, но изменяется вдоль размаха крыла угол, который
составляет хорда профиля с направлением корневой хорды. Таким
образом, крыло оказывается как бы закрученным и приобретает форму
искривленной поверхности.
Формы летательных аппаратов и их элементов
59
Основное назначение крутки состоит в том, чтобы создать лучшие
условия обтекания концевых участков крыла, при которых обеспечивается более
выгодное распределение давления, и как следствие, повышение
аэродинамического качества крыла и улучшение характеристик Уст™Гяагаюшие?я
пели служат некоторые вспомогательные поверхности, располагающиеся
Sa крыле в частности аэродинамические гребни и выступы на передней
гребни представляют собой небольшие выступы
Рис. Н-2-7. Консоль крыла (1)
с аэродинамическими гребнями (2)
Рис. Н-2-8. Форма крыла с
выступом:
I _ аэродинамический выступ;
2 — «наплыв»
2-Я таких гребня. Их назначение состоит в том, чтобы воспрепятствовать
перетеканию пограничного слоя вдоль размаха крыла и уменьшить срыв
ПОТОВ^стоКОаНзЦрОоВДИнамических гребней используется и ^™%^™™>
представляющее собой выступ на передней части крыла (рис. И-2-8), которое
Se препятствует перетеканию пограничного слоя. Передняя часть про-
Гиля выступающей части крыла делается в виде загнутого носка («наплыва»),
!тсОбеспечивает более плавное обтекание без отрыва пограничного слоя на
SSt^hS поверхности, аэродинамическая и геометрическая
крутка могут использоваться как самостоятельно, так и в комбинации
npvr с другом В частности, крутка может быть комбинированной - аэро-
Хами4ской и геоМеТричёской одновременно. Эти средства повышения
эффективности крыла используются в основном для аппаратов с
дозвуковыми скоростями полета и оказываются недостаточно эффективными при
СвТх-уковыек^лья обычно являются плоскими и в некоторых слу-
чаях могут иметь небольшую аэродинамическую крутку.
Расположение крыльев и оперения на корпусе. На летательнш:
аппаратах не предназначенных для широкого маневра по курсу и выполненных
по обычной5 так называемой, самолетной схеме, применяется, как правило
монопланное расположение крыльев на корпусе (рис. П-2-9, в). Крылья
могут быть поворотными или снабжены элеронами для создания
управляющих усилий, обеспечивающих маневр по курсу при одновременном выполне-
Изч1тырехвидов монопланной компоновки - низкоплапной, средне-
планной, высокопланной и парасольнои (см. рис. Н-2-9, б, в, г, О) - в схе-
I' г а в а И
мах высокоскоростных конструкций чаще встречается среднепланная
компоновка. Она обеспечивает лучшие условия обтекания места соединения крыла
с корпусом, при которых пограничный слой имеет меньшую тенденцию
к срыву.
Монопланная компоновка может быть усовершенствована введением
так называемой V-образности — прямой и обратной (см. рис. П-2-9, е, ж).
Прямая V-образность способствует повышению статической поперечной
устойчивости, обратная — ее уменьшению. Обратная V-образность
применяется для стреловидных крыльев, с тем чтобы понизить высокую степень
поперечной устойчивости, создаваемую крылом, и тем самым облегчить
управление полетом.
Для выполнения широкого маневра в пространстве на летательных
аппаратах устанавливаются крылья по так называемой нормальной или плюс-
образной (+), а также крестообразной или иксобразной (X) схемам (см.
Рис. П-2-9. Различные варианты расположения крыльев на корпусе
летательного аппарата:
а — бипланное; б — низкопланное; в —среднепланное; г —высокоплаыное; д—па-
расольное; е — с прямым V; ж —с обратным V; з — Х-образное; и
(--образное; к — тандемное
рис. П-2-9, з, и). Такие крылья являются одновременно органами
управления или используются для размещения на них рулей. При нормальной
и крестообразной схемах обеспечивается маневр по курсу без
предварительного накренения.
Следует иметь в виду, что ни та, ни другая схема не дает выигрыша
в подъемной силе. Однако как средства управления крестообразные крылья
имеют некоторые преимущества. В практических случаях часто
выбор схемы определяется главным образом конструктивными
соображениями.
Расположение крыльев в этих схемах обычно симметричное, их размах
и площадь небольшие. Небольшая площадь предопределяет применение
таких крыльев для аппаратов с большими скоростями, при которых
обеспечивается значительная подъемная и управляющая силы.
В тех случаях, когда необходимо обеспечить повышенную подъемную
силу при заданных площади и размахе крыльев, применяют тандемное
расположение поверхностей (см. рис. П-2-9, к). При этом задние крылья
могут одновременно выполнять роль хвостового оперения.
Схемы расположения оперения на корпусе отличаются большим
разнообразием по сравнению с крыльями. Это связано с особой ролью оперения
Формы летательных аппаратов и их элементов
61
как стабилизирующих и управляющих органов, форма и расположение
которого могут существенно меняться даже при небольших изменениях
в компоновке корпуса, крыльев, двигателя и других элементов летательного
аппарата.
При всем многообразии можно выделить две основные схемы —
нормальную (+) и крестообразную (X), которые применяются самостоятельно
ж, кроме того, служат известной основой для построения других схем
(рис. И-2-10, а, и). Естественно, что по своим общим аэродинамическим
свойствам изолированное оперение идентично крыльям. Однако в
компоновке с другими элементами на корпусе эти свойства оперения могут
существенно меняться, что влияет на выбор конкретной схемы, обусловливая
отклонение от обычной нормальной или крестообразной схем.
На рис. Н-2-10, б-т- з показаны различные видоизменения нормальной
схемы, в которых нашло отражение стремление вынести горизонтальные
или вертикальные консоли
оперения вверх или в
стороны, с тем чтобы уменьшить
отрицательное влияние на
1.
Рис. 11-2-10. Различные схемы расположения
оперения на корпусе летательного аппарата
Рис. П-2-11. Взаимное
расположение крыла (7) и оперения (2) на
корпусе летательного аппарата
них возмущенного потока от крыльев или струи реактивного двигателя.
В этих целях может быть использована также крестообразная схема и ее
модификации (см. рис. П-2-10, и-^г-м)
Оперение, обладая вертикальной симметрией, во многих случаях не
имеет горизонтальной симметрии, как это видно на рис. И-2-10, б-^-ж.
В оперении без горизонтальной симметрии удалены некоторые
недостаточно эффективные элементы нормальной или крестообразной схемы.
Например, на схемах «г-^-ж» рис. И-2-10 отсутствует нижний киль; на схеме «к»
отсутствует один киль, а оставшийся ориентирован вертикально вниз; на
схеме «л» отсутствуют два нижних киля.
Правильная ориентировка оперения по отношению к крыльям, а также
к корпусу и двигателю имеет существенное значение для обеспечения
необходимых аэродинамических характеристик летательного аппарата.
Располагая оперение и его отдельные элементы на корпусе, следует
следить за тем, чтобы неблагоприятное влияние самого корпуса, а также
крыльев и двигателя было минимальным. Например, с целью уменьшения
интерференции крыла, выполненного по нормальной схеме, схема оперения
может быть выбрана крестообразной (рис. Н-2-11).
62 Г л а в а II
§ 11-3. Органы управления
Основные типы органов управления. Траекторию неуправляемого
летательного аппарата, испытывающего лишь действие силы сопротивления
и веса, обычно называют естественной или баллистической. Для такой
траектории характерно отсутствие какой-либо искусственно созданной
управляющей аэродинамической или другой силы, нормальной к
траектории. Траектория управляемого летательного аппарата, необходимая
для выполнения определенного маневра, будет отличаться от естественной
траектории благодаря дополнительному управляющему усилию,
совпадающему по направлению с нормалью к вектору скорости полета. Устройства,,
обеспечивающие необходимую управляющую силу, называются органами
управления. Органы управления входят в систему управления движением
летательного аппарата, под которой понимают комплекс аппаратуры
и устройств, обеспечивающих измерение отклонений фактического
движения летательного аппарата от необходимого направления полета,
формирование соответствующего сигнала и создание управляющей силы.
В зависимости от физического характера управляющей силы органы
управления можно разделить на три основных типа: аэродинамические,,
газодинамические и комбинированные.
Аэродинамические органы управления создают управляющую силу
путем изменения условий внешнего обтекания и, следовательно,
управляющая сила по своему происхождению является аэродинамической. Орган
управления является средством, изменяющим величину и направление
вектора аэродинамических сил.
Действие газодинамических органов управления основано на
использовании эффекта, вызванного изменением направления газовой струи,
истекающей из сопла реактивного двигателя. Управляющая сила возникает
в результате отклонения вектора силы тяги от направления касательной
к траектории.
В некоторых конструкциях газодинамических органов управления
используются специальные управляющие реактивные двигатели.
Комбинированные органы управления при создании управляющей силы
используют одновременно эффекты аэродинамических и газодинамических
органов управления.
Аэродинамические органы управления. Органы управления этого типа
применяются для летательных аппаратов, движущихся в достаточно
плотных слоях атмосферы. Их можно разделить на следующие группы: рулевые-
поверхности, роллероны, интерцепторы, поворотные крылья и средства
механизации летательного аппарата.
Рулевые поверхности, или просто рули, размещаемые
в различных местах летательного аппарата, можно классифицировать
следующим образом (рис. II-3-1): а) органы управления типа поворотного
оперения; б) концевые органы управления; в) органы управления,
расположенные вдоль задней кромки несущей поверхности.
В свою очередь, концевые органы управления могут быть разделены
на обычные концевые рули и органы управления с рулевой компенсацией
(рис. II-3-2).
Органы управления, расположенные вдоль задней кромки, могут быть
внутренними и внешними рулями, занимающими часть кромки или
размещенными по всему размаху (рис. П-3-3).
Рулевые поверхности летательных аппаратов служат в качестве рулей
поворота, рулей высоты, элеронов и элевонов.
Формы летательных аппаратов и их элементов
63*
Рули поворота в среднем положении располагаются вдоль продольной
оси аппарата. Отклонение их от среднего положения вызовет поворот
летательного аппарата вправо или влево.
Рули высоты располагаются перпендикулярно плоскости рулей
поворота. Их отклонение обеспечивает изменение направления полета в
вертикальной плоскости и, следовательно, изменение высоты. Комбинация рулей
поворота и высоты дает возможность управлять летательным аппаратом:
а)
\|7
VJ
Рис. П-3-1. Основные типы рулевых
поверхностей:
а — полностью подвижные; б — концевые; в
—расположенные вдоль задней кромки
а)
Рис. 11-3-2. Типы концевых рулей:
а — обычный концевой руль; б — с
компенсацией
одновременно в двух взаимно перпендикулярных плоскостях, т. е.
осуществлять практически любой маневр в пространстве.
Известна другая схема управления летательным аппаратом в
пространстве, в которой используются рули высоты и элероны (рули крена).
Элероны — это две рулевые поверхности, расположенные на задних
кромках консолей крыла и отклоняющиеся в разные стороны, что приводит
к накренению летательного
аппарата. При одновременном
повороте руля высоты
появляется горизонтальная
составляющая управляющей силы,
поворачивающая летательный
аппарат в нужную сторону.
Элевоны, в отличие от
элеронов, отклоняются в любую
сторону независимо друг от
друга, поэтому они использу-
а)
Л\ Л\
7
ф
■Е
/
/7\
Рис. 11-3-3. Типы рулей, расположенных вдоль,
задней кромки:
а — с постоянной хордой; б — с обратным сушением:,
1 —внутренний руль; 2 — внешний, 3 — по всему
размаху
ются одновременно и как рули
крена и как рули высоты.
Роллероны.
Разновидностью элерона является
рулевое устройство,
называемое роллероном. В отличие от
обычного элерона, управляющая
плоскость роллерона поворачивается благодаря гироскопическому эффекту,
возникающему при вращении диска, помещенного внутри руля (рис. П-3-4).
Ось вращения диска z/i перпендикулярна к плоскости роллерона, который;
свободно вращается вокруг оси zu жестко связанной с крылом или
оперением. Перед полетом диск раскручивается до требуемой угловой скорости,,
а во время полета эта скорость поддерживается воздействием набегающего^
потока воздуха на зубцы диска, выступающие из элерона. При вращении
роллерона вместе с крылом вокруг продольной оси х^ летательного аппарата,
(под действием возмущающего момента крена) возникает гироскопический
момент Мг (рис. П-3-4), который стремится повернуть роллерон вокруг
64
Глава II
Х1
Рис. 11-3-4. Схема работы роллерона
1 — корпус; $2 — крыло; з — роллер он
4 — диск; 5 — ось вращения роллерона
6 — ось вращения диска
оси Zx на некоторый угол бр. Отклонение плоскости роллерона от
плоскости крыла создает момент, который будет парировать действие
возмущающего момента крена. Поэтому роллероны могут использоваться в качестве
средства стабилизации летательного
аппарата по крену [811.
Интерцептор представляет собой
тонкую пластинку, которая
располагается в крыле и может выдвигаться
над его поверхностью (рис. Н-3-5).
Управляющий эффект обусловлен
торможением потока, когда интерцептор
находится в выдвинутом положении [23].
При торможении потока
происходит увеличение давления на части
поверхности крыла перед интерцептором;
кроме того, интерцептор способствует
повышению скорости обтекания
противоположной стороны крыла и,
следовательно, некоторому снижению
давления, что приводит к увеличению
результирующего управляющего
усилия. Управляющий эффект
интерцептора несколько снижается из-за
уменьшения давления за ним, происходящего
вследствие турбулизации пограничного
слоя, роста его толщины и, как
следствие, отрыва, зона которого при
значительном выдвижении интерцептора простирается до задней кромки. Этот
отрицательный эффект невелик, когда поверхность за интерцептором
сравнительно небольшая.
Если полет осуществляется при сверхзвуковых скоростях, то картина
обтекания выдвинутого интерцептора изменяется (рис. И-3-6, а) ([76], 1962,
дго 4—5). Перед интерцептором и за ним происходит срыв потока,
образуются застойные зоны. Внешний поток движется около этих зон, подобно
потоку около непроницаемых
клиньев, образуя систему ударных
волн и волн разрежения. График
распределения давления,
изображенный на рис. Н-3-6, б,
показывает, что несмотря на разрежение
за интерцептором возникает
управляющее усилие, направленное вниз.
Для повышения
эффективности управления интерцепторы
приводятся в колебательное движение, амплитуда и частота которого обычно
не регулируются. Величина управляющей силы изменяется путем
перемещения центра колебания. Чем ближе центр к поверхности крыла, тем больше
время, в течение которого интерцептор будет выдвинут и, следовательно,
больше будет управляющая сила.
Преимуществом интерцепторов перед рулями является их меньший вес
(включая привод). Поэтому интерцепторы применяются обычно в
летательных аппаратах с малым весом.
Недостаток интерцепторного управления заключается в том, что оно
не обеспечивает летательному аппарату резкого маневра и увеличивает
лобовое сопротивление.
Рис. 11-3-5. Схема работы интерцепторного
управления:
1 — интерцептор; 2 — центр колебания
интерцептора; 3 —крыло
Формы летательных аппаратов и их элементов
65
Поворотное крыло представляет собой обычное крыло,
имеющее возможность поворачиваться относительно корпуса вокруг поперечной
оси летательного аппарата. Преимущество такого органа управления состоит
в обеспечении большого управляющего усилия при малых углах отклонения.
Летательный аппарат с
поворотным крылом обладает способностью
совершать на траектории быстрый
маневр, который начинается сразу
после отклонения крыльев, так как
при этом не нужно поворачивать
корпус с большим моментом инерции.
Поворотное крыло может
совмещать функции управления
продольным движением аппарата и
управления креном.
К недостаткам поворотного кры- ч
ла следует отнести большие шарнир- 0)
ные моменты, требуемые для его
поворота, хотя мощность привода не
очень велика, так как углы, а также
скорости поворота небольшие.
Недостатком является также некоторое
увеличение лобового сопротивления
летательного аппарата из-за зазоров
между поворотным крылом и
корпусом.
При повороте на большие углы,
когда совершается резкий маневр,
нагрузка на крылья значительно
возрастает, что приводит к
возникновению большого изгибающего момента, приложенного к корпусу.
Следовательно, летательный аппарат с поворотным крылом должен обладать
повышенной прочностью.
Средства механизации летательного аппарата.
Особое место среди аэродинамических органов управления занимают
различные средства механизации
летательного аппарата,
позволяющие изменять его
аэродинамические характеристики [23].
Средства механизации
размещаются в различных местах
конструкции и обычно
предназначены для управления какой-
либо определенной
аэродинамической характеристикой.
Рассмотрим группу средств
механизации, расположенных на
крыле и предназначенных для управления подъемной силой. К ним относятся
предкрылки, закрылки, щитки и другие устройства. Общий эффект от
применения этих средств заключается в том, что они обеспечивают на больших
углах атаки увеличение подъемной силы при сравнительно малом
возрастании лобового сопротивления.
Предкрылок (рис. П-3-7, а) — это небольшая по размерам часть крыла,
расположенная в передней части основной несущей поверхности и
отодвигающаяся вперед на больших углах атаки. В образовавшуюся щель устрем-
5-114
-4 СМ
Рис. 11-3-6. Картина обтекания интерцеп-
тора сверхзвуковым потоком:
а — картина обтекания выдвинутого интерцеп-
тора (области срыва потока 1 и 2, система
скачков уплотнения 3,4, 5 и волна разрежения б);
б — распределение избыточного дав ления по
поверхности крыла около интерцептора
Рис. П-3-7. Схемы, улучшающие
аэродинамические характеристики крыла:
а — предкрылок; б — закрылок; в — щиток; г —
носовой щиток
66
Глава И
ляется по направлению снизу вверх струя воздуха, которая обеспечивает
более плавное обтекание верхней стороны профиля, так как увеличивает
кинетическую энергию воздуха в пограничном слое и задерживает его срыв.
Таким образом, срыв потока отодвигается на углы атаки большие, чем без
предкрылка. Иногда предкрылки делаются не по всей длине консоли крыла,
а только перед отклоняющимися рулевыми поверхностями, чтобы
предотвратить срыв потока с этих рулей и сделать их
работу эффективной при больших углах
отклонения.
Закрылок (рис. И-3-7, б) представляет
собой, как и предкрылок, небольшую по
размерам часть крыла, но в отличие от него
располагается на задней кромке основной
несущей поверхности, являясь как бы ее
продолжением. Закрылок отклоняется вниз,
создавая дополнительный подпор под крылом
и тем самым увеличивая подъемную силу
крыла. Между закрылком и крылом может быть
предусмотрена щель, позволяющая улучшить
обтекание верхней стороны крыла и
обеспечить дополнительное увеличение подъемной
силы.
Щиток (рис. Н-3-7, в) является частью
крыла, размещаемой на нижней его стороне
и имеющей возможность отклоняться вниз.
Отклоненный щиток создает подпор под
крылом и увеличивает подъемную силу. Между
отклоненным щитком и крылом образуется
застойная вихревая зона с пониженным
давлением. Благодаря этому происходит
отсасывание пограничного слоя, что предотвращает
его отрыв и улучшает характеристики крыла
при больших углах атаки.
Носовой щиток (рис. П-3-7, г) в отличие
от щитка помещается на передней кромке
крыла. Отклонение носового щитка при
больших углах атаки позволяет в условиях
полета с дозвуковыми скоростями цредотвратить срыв потока с острых
передних кромок крыла, используемых в сверхзвуковых летательных аппаратах.
Отсос и сдувание пограничного слоя. К средствам механизации крыла
можно отнести специальные устройства, предназначенные для отсоса и сду-
вания пограничного слоя, в результате которого предотвращается его срыв,
обеспечивается более плавное обтекание поверхности и, как следствие,
повышение подъемной силы крыла.
Отсос производится при помощи вакуум-насосов через щель или систему
отверстий (рис. И-3-8, а), расположенных вблизи предполагаемого места
отрыва пограничного слоя.
Сдувание пограничного слоя (рис. И-3-8, б) производится при помощи
нагнетательных насосов также через щели и отверстия. Причем они
располагаются несколько выше по потоку перед местом предполагаемого отрыва
пограничного слоя. Оси щелей и отверстий должны составлять с
направлением касательной к контуру профиля острый угол.
Физический эффект от отсоса и сдувания одинаков и состоит в
увеличении кинетической энергии частиц воздуха в пограничном слое, благодаря
чему уменьшается их торможение. При этом в первом случае этот эффект
Ы
Рис. 11-3-8. Управление
пограничным слоем крыла:
а — отсос; б — сдувание; в —
увеличение коэффициента подъемной силы
с и критического значения угла
атаки а с ростом интенсивности
отсоса пограничного слоя (I — без отсоса
р (
2 — слабый отсос, з — сильный отсос
Формы летательных аппаратов и их элементов
67
достигается в основном за счет повышения скорости, а во втором — также за
счет увеличения массы воздуха, протекаемой через пограничный слой.
Эффективность отсоса или сдувания пограничного слоя видна из
рис. Н-3-8, 6.
Крыло с переменной стреловидностью. Одним из средств механизации
летательного аппарата является устройство, позволяющее изменять в полете
стреловидность крыльев или оперения (рис. П-3-9). Такое устройство может
оказаться полезным для крылатых
летательных аппаратов, движущихся в
большом диапазоне скоростей (от
дозвуковых до больших сверхзвуковых),
так как создает наивыгоднейшие
условия для движения. Например, чтобы
преодолеть зону трансзвуковых
скоростей с минимальным сопротивлением и
предотвратить флаттер, крылу придают
наибольший угол стреловидности. В
области больших до- и сверхзвуковых
скоростей крыло выводят в положение,
соответствующее меньшему углу
стреловидности. При малых скоростях,
например при взлете, полет совершается
с прямым крылом. Изменение
стреловидности увеличивает подъемную силу
и повышает эффективность
аэродинамических органов управления.
Управление становится более эффективным
благодаря некоторому смещению центра
давления ближе к головной части.
Тормозные щитки. Для уменьшения скорости полета применяют
специальные устройства — тормозные щитки, повышающие сопротивление
движению. На летательных аппаратах они размещаются у задней кромки крыла
Рис. П-3-9. Летательный аппарат с
крылом с изменяющейся стреловидностью
Ф
Рис. 11-3-10. Средства уменьшения скорости полета:
а — тормозные щитки у задней кромки крыла; б — тормозные щитки в
хвостовой части корпуса; в — гирлянды металлических дисков на тросе
(рис. П-3-10, а) или в хвостовой части корпуса (рис. Н-3-10, б). Большая
сила сопротивления, тормозящая движение, возникает вследствие отклонения
щитков на значительные углы, близкие к 90°.
К числу аэродинамических средств торможения относятся также
металлические диски, соединенные тросом (рис. И-3-10, в), и
парашюты.
Обычно парашют применяется на заключительной стадии процесса
торможения, которой предшествует торможение щитками или дисками (или
совместно щитками и дисками).
Газодинамические органы управления применяются в тех условиях,
когда аэродинамические органы управления делаются малоэффективными,
;5*
68
Глава II
например, в разреженных слоях атмосферы или при малых скоростях
движения летательного аппарата (в частности, при старте с Земли).
На рис. П-3-11 показаны устройства, которые обеспечивают создание
управляющего усилия путем поворота двигателя в целом (рис. П-3-11, а)
и поворота только одного сопла (рис. И-3-11, г).
Поворот основного двигателя даже на малые углы обеспечивает большие
управляющие силы. Однако для осуществления поворота требуется
приложение значительных усилий.
Рис. П-3-11. Схема газодинамических органов
управления:
а — поворот основного двигателя; б — поворот верньерного
двигателя; в — включение неподвижных управляющих двигателей;
г — поворот сопла; д — поворот насадка; е — газовые рули;
ж — дефлекторы; з — впрыск жидкости в сверхзвуковую часть
сопла; и — перераспределение силы тяги путем перекрытия сопла
в многосопловом блоке (сопло 1 открыто, сопла 2 закрыты)
Использование поворотного сопла позволяет уменьшить усилия,
необходимые для поворота, однако при этом возникает ряд затруднений,
связанных, в частности, с загрязнением и выгоранием подвижного сочленения
сопла с камерой двигателя, что приводит к ненадежной работе всего рулевого
устройства.
Конструктивно более простыми являются рулевые устройства,
использующие поворотные насадки и так называемые дефлекторы (рис. И-3-11, д, ж).
Поворотный насадок охватывает струю основного реактивного двигателя,
находясь, таким образом, все время под воздействием продуктов сгорания.
Работа такого насадка достаточно эффективна, однако он быстро выходит
из строя вследствие загрязнения и выгорания. Дефлекторы вводятся в струю
газа лишь тогда, когда необходимо создать управляющую силу. Поэтому
они обладают большей надежностью и долговечностью.
В качестве органов управления можно использовать газовые рули,
размещаемые в конце сопла основного двигателя (рис. П-3-11, е). Откло-
Формы летательных аппаратов и их элементов
69
нение струи газа, вызываемое рулями, приводит к созданию достаточно
больших управляющих усилий. Однако газовые рули, являясь
эффективным средством управления, обладают существенными недостатками.
Оказывая значительное сопротивление газовому потоку, они уменьшают
эффективное значение тяги. Кроме того, под воздействием высоких температур
и больших скоростей газа рули выгорают, быстро выходя из строя.
Одна из современных конструкций газодинамического органа
управления основана на принципе изменения направления вектора силы тяги
основного двигателя путем впрыска жидкости или газа в сопло
(рис. И-3-11, з).
Механизм возникновения управляющего усилия состоит в следующем»
Поток жидкости или газа, подводимый в сверхзвуковую часть сопла через
отверстие 1, взаимодействует со сверхзвуковым потоком газообразных
продуктов сгорания топлива и, отклоняясь от первоначального направления,
течет в области 2.
При обтекании основным потоком этой области образуется скачок
уплотнения 3, за которым происходит поворот потока и, как следствие,
повышение давления. В результате возникает боковая управляющая сила Y§.
Изменяя расход жидкости, впрыскиваемой в сопло, можно
регулировать величину управляющей силы. Направление силы можно изменять,
вводя жидкость через различные отверстия, расположенные по
окружности поперечного сечения сопла.
Особенность этого рулевого устройства состоит в том, что возникновение
управляющей силы практически происходит без уменьшения силы тяги
основного двигателя. Объясняется это тем, что уменьшение тяги вследствие
потери механической энергии потока газа при переходе через скачок
уплотнения компенсируется ростом тяги благодаря увеличению массы истекающих
газов. Более того, силу тяги можно несколько увеличить, если в качестве
впрыскиваемой жидкости применить окислитель, который, вступая в
химическую реакцию с недогоревшим топливом, увеличит полноту сгорания.
Управление полетом возможно путем перераспределения силы тяги
за счет перекрытия одного или нескольких сопел маршевого двигателя,
расположенных по окружности (рис. И-3-11, и). В результате образуется
эксцентриситет реактивной силы и
управляющий момент.
Газодинамические органы управления,
схемы которых были рассмотрены, могут быть
объединены в один класс рулевых устройств,
выполненных с использованием основного
двигателя. Второй класс объединяет рулевые
устройства, выполненные в виде специальных
управляющих двигателей. Одно из таких устройств
(рис. II-3-11, б) представляет собой поворотный
(так называемый верньерный) реактивный
двигатель с боковым соплом.
Управляющую силу можно создавать также
специальными неподвижными двигателями с
соплами, расположенными перпендикулярно оси
летательного аппарата (рис. И-3-11, в).
Комбинированные органы управления.
Схема комбинированного органа управления
приведена на рис. Н-3-12. Основным элементом управляющего устройства
является поворотное сопло, обычно устанавливаемое на задней кромке крыла
или оперения и выполняемое в виде узкой щели некоторой длины.
Управляющее усилие возникает в результате истечения воздуха из сопла, накло-
Рис. 11-3-12. Схема
комбинированного органа управления:
а — щелевое сопло; б — струя;
Р — реакция струи; Рв —
вертикальная составляющая реакция
струи; Д У — дополнительная
подъемная сила крыла,
появляющаяся за счет перераспределения
давлений по контуру крыла; Рр —
горизонтальная составляющая
реакции струи
уд Г л а в а II
ненного под определенным углом к хорде крыла. Это усилие складывается
из двух компонент. Одна из них равна нормальной составляющей Рв силы
тяги, создаваемой поворотной щелью. Вторая равна нормальной
составляющей аэродинамической силы AY, которая возникает вследствие
перераспределения давления на несущей поверхности, обусловленного взаимодействием
набегающего потока и струи воздуха, истекающей через щель [80].
Принципиально по этой схеме работает так называемый реактивный
интерцептор. Струя газов в нем направляется через щель в крыле вверх или
вниз. Изменение подъемной силы происходит как благодаря реактивной
силе интерцептора, так и за счет перераспределения давления.
Недостатком комбинированных органов управления является их
небольшая эффективность в разреженных слоях атмосферы и при небольшой
скорости полета. Несмотря на кажущуюся простоту, они оказываются
достаточно сложными в конструктивном отношении и неудобны в эксплуатации
из-за необходимости иметь источники сжатого газа или жидкости.
§ 11-4. Аэродинамические
схемы летательных
аппаратов
Для обеспечения необходимой дальности полета, устойчивости и
управляемости, а также для выполнения ряда других тактико-технических
требований должна быть осуществлена соответствующая аэродинамическая
компоновка летательного аппарата.
Под аэродинамической компоновкой понимают рациональный выбор
размеров, внешних форм, взаимного расположения корпуса, крыла,
оперения, органов управления и других элементов летательного аппарата.
При окончательной отработке конструкции эти задачи должны решаться
совместно, с тем чтобы обеспечить согласование размеров, формы и
взаимного расположения. Однако на начальном этапе проектирования выбор
схемы и расчеты можно вести раздельно. Более того, принципиальная
аэродинамическая схема может быть намечена исходя из тактико-технических
требований, без конкретизации формы отдельных элементов.
Правильный выбор аэродинамической схемы летательного аппарата
может быть осуществлен с учетом накопленного практического опыта в
авиационной и ракетной технике, использования имеющихся теоретических
и экспериментальных данных.
Аэродинамические схемы летательных аппаратов делят на два класса.
К первому классу относятся аэродинамические схемы неоперенных
летательных аппаратов. Корпус таких аппаратов не имеет каких-либо резко
выступающих поверхностей. Аэродинамические схемы неоперенных
летательных аппаратов различаются в зависимости от того, является ли
летательный аппарат управляемым или неуправляемым.
Неоперенным управляемым летательным аппаратом является ракет&
дальнего действия с отделяющейся головной частью (рис. II-4-1, а).
Стабилизация ракеты на активном участке траектории осуществляется при помощи
газодинамических органов управления (например, поворотных сопел 1).
К неоперенным неуправляемым летательным аппаратам принадлежат
так называемые турбореактивные снаряды (рис. И-4-1, б), стабилизация
которых обеспечивается быстрым их вращением вокруг продольной оси.
Ко второму классу относятся схемы оперенных летательных аппаратов,
на корпусе которых могут быть установлены несущие и стабилизирующие
поверхности.
Формы летательных аппаратов и их элементов
71
Аэродинамические схемы оперенных летательных аппаратов могут быть
разделены на бескрылые и крылатые, а также на схемы с совмещенным крылом
и оперением.
Схемы бескрылых оперенных летательных аппаратов включают схемы
неуправляемых и управляемых летательных аппаратов.
Ракета, выполненная по схеме неуправляемого бескрылого оперенного
летательного аппарата, изображена на рис. II-4-1, в. Оперение на корпусе
Рис. 11-4-1. Аэродинамические схемы летательных аппаратов:
а — неоперенная управляемая ракета; б — турбореактивный снаряд; в —
бескрылый неуправляемый летательный аппарат; г — бескрылый управляемый
летательный аппарат; д — схема «утка»; е — схема «нормальная», ж — схема
«бесхвостка»; з — схема «бесхвостка» с дестабилизатором; и —«бесхвостка» со
стабилизатором к — схема «летающее крыло»
является неподвижным и выполняет роль стабилизаторов. Управляемый
аппарат (рис. П-4-1, г) может быть снабжен поворотными консолями
оперения (1) или иметь газодинамические рули.
Летательные аппараты, выполненные по схеме крылатого оперенного
летательного аппарата (рис. П-4-1, е) и по схеме с совмещенным крылом и
оперением 1 (рис. 11-4-1, ж),
являются управляемыми и
могут быть объединены в одну
группу крылатых
управляемых летательных
аппаратов.
Схемы крылатых
управляемых аппаратов
можно разделить в зависимости
от принятого способа
управления на нормальную
схему, схему «утка» и
схему «бесхвостка».
В нормальной схеме
(рис. П-4-1, е)
управляющее оперение 1
расположено за крылом 2 в хвосто-
Рис. 11-4-2. Управление летательным аппаратом по
нормальной схеме:
а — положение до поворота; б — положение после поворота
летательного аппарата
вой части летательного аппарата, что обеспечивает ему ряд преимуществ
аэродинамического и конструктивного характера [80].
При таком расположении рулей возмущения от них не влияют на крыло,
следовательно, условия его обтекания более благоприятны. Рули могут
обеспечить резкий маневр летательному аппарату при сохранении их плав-
72 Г л а в а II
ного обтекания. Это достигается поворотом руля на достаточно большой
первоначальный угол атаки б (рис. И-4-2), который затем в полете
уменьшается на величину угла атаки акр аппарата, что способствует
предотвращению срыва потока.
Конструктивно рули в хвостовой части можно выполнить таким образом,
чтобы было обеспечено дифференциальное отклонение горизонтальных
консолей, необходимое для создания крена.
Можно рассмотреть схему, в которой задние поверхности работают
попарно, как рули высоты и направления, обеспечивая тем самым
управление по тангажу и курсу, а пара рулей, расположенных на крыльях,— как
элероны. Применяется также схема с фиксированными задними
поверхностями, в которой управление по тангажу, курсу и крену осуществляется
соответствующими отклонениями крыльев. Достаточно надежная
стабилизация по крену обеспечивается в этой схеме отклонением пары передних
рулевых поверхностей в разные стороны.
В рассмотренных схемах облегчается условие балансировки
относительно центра тяжести, обеспечивается большая свобода в расположении
и выборе относительных размеров аэродинамических поверхностей, а также
в выборе схемы управления. При заднем расположении рулей достигается
некоторая выгода, связанная с обеспечением прочности, так как изгибающие
моменты, приложенные к корпусу, оказываются сравнительно небольшими.
При использовании нормальной схемы следует учитывать и ее
недостатки.
1. Хвостовое оперение, находясь в зоне возмущенного потока, за
крылом, подвергается неблагоприятному силовому воздействию, носящему
обычно ударный периодический характер. Вследствие этого оперение
испытывает сильную тряску — так называемый бафтинг. Желая избежать баф-
тинга, стремятся перенести оперение выше плоскости крыла за пределы
возмущенного потока, хотя при этом снижается жесткость, что может явиться
причиной флаттера оперения.
2. Вследствие того, что углы атаки крыла и рулей имеют разный знак
и, следовательно, создаваемые ими подъемные силы направлены в
противоположные стороны, суммарная подъемная сила летательного аппарата
несколько снижается.
3. По этой же причине возникает дестабилизирующий эффект при
отклонении рулей, вследствие чего расстояние между центром тяжести
и центром давления летательного аппарата уменьшается. Это несколько
ухудшает статическую устойчивость. Кроме того, если рули расположены
на небольшом расстоянии от центра тяжести, это может уменьшить
демпфирующий момент от оперения и, как следствие, ухудшить динамическую
устойчивость; периодические колебания, возникающие на траектории,
будут затухать медленнее.
В схеме «утка» (см. рис. II-4-1, д) управляющее оперение 1 находится
перед крылом 2 в носовой части летательного аппарата и располагается
впереди центра тяжести. Положительные качества этой схемы проявляются
в том, что рули не испытывают влияния возмущений от крыла и поэтому
оказываются более эффективными. Вследствие того, что знаки углов атаки
рулей и крыла одинаковы и подъемные силы, создаваемые ими, направлены
в одну сторону, суммарная подъемная сила летательного аппарата
возрастает [80].
Так как при отклоненном руле дестабилизирующий момент
уменьшается, то достигается некоторое улучшение статической устойчивости по
сравнению с нормальной схемой. Улучшаются также характеристики
демпфирования вследствие того, что рулевое устройство находится обычно на
большем удалении от центра тяжести.
Формы летательных аппаратов и их элементов
73
р
Некоторые выгоды схемы «утка» в конструктивном отношении связаны
с тем, что рули имеют сравнительно небольшие размеры и поэтому малые
шарнирные моменты. Кроме того, при переднем расположении рулей и
соответствующего оборудования удобнее размещать в средней и хвостовой
частях баки с топливом и двигательную установку.
Недостатки рассматриваемой схемы, ограничивающие ее практическое
применение, состоят в следующем.
1. На крыло воздействует скошенный рулями поток, что приводит
к уменьшению истинного угла атаки и снижению подъемной силы. Этот
эффект усиливается в случае небольших удлинений крыла, когда почти
вся поверхность его подвергается воздействию скошенного потока.
2. Рули нецелесообразно применять в качестве элеронов для
управления по крену, так как вследствие скоса потока за ними крылья создают
противоположный по
знаку момент крена, и эффект
от элеронов практически
исчезает. Более того, из-за
малости плеча момент от
элеронов может быть даже
меньше момента крена,
возникающего вследствие
скоса потока. Этот
недостаток можно устранить,
применяя на неподвижных
крыльях элероны,
управляемые независимо от
передних рулей, что однако
приводит к
конструктивным трудностям и
утяжелению аппарата.
3. Рулевые
поверхности находятся в
неблагоприятных условиях обтекания вследствие больших углов атаки, равных
сумме угла атаки крыла акр и угла отклонения руля б (рис. П-4-3).
При больших углах атаки происходит срыв потока с рулей, который, как
показывают наблюдения, сопровождается возникновением продольных
колебаний летательного аппарата.
4. Расположение управляющего оперения впереди центра тяжести
обусловливает некоторый дестабилизирующий эффект. При этом
положение центра давления меняется в зависимости от отклонения рулей, что
затрудняет сохранение заданного диапазона изменения координаты центра
давления.
5. Нагрузки на рули и изгибающие моменты, приложенные к корпусу,
оказываются большими, чем в нормальной схеме, так как углы атаки рулей
велики.
6. В схеме «утка», предполагающей использование длинной носовой
части корпуса для размещения рулей, возникает трудность в обеспечении
путевой устойчивости. Эта трудность обусловлена большими
дестабилизирующими моментами носовой части и необходимостью иметь развитое
вертикальное хвостовое оперение с большим плечом относительно центра
тяжести.
В схеме «бесхвостка» изолированное управляющее оперение отсутствует,
а рулевые устройства 1 расположены на задней кромке несущей
поверхности 2, которая представляет собой совмещенные крылья и хвостовой
стабилизатор (см. рис. II-4-1, з), или же их функции выполняет крыло (см.
Рис. П-4-3.
Управление летательным аппаратом по
схеме «утка»:
а — положение до поворота; б — положение после поворота
летательного аппарата
У 4 Г л а в а II
рис. II-4-1, и). Возможно также в схеме «бесхвостка» применение
газодинамических органов управления, расположенных в кормовой части. Это
увеличивает маневренность летательного аппарата, так как плечо действия
управляющих усилий, приложенных к органу управления, получается
большим.
Если площадь аэродинамических поверхностей велика, то снаряд
называют крылатым; при небольшой площади эти поверхности играют роль
стабилизаторов, и летательный аппарат представляет собой обычную
баллистическую ракету. В соответствии со схемой на рис. II-4-1, ж летательный
аппарат может иметь фиксированное горизонтальное крыло треугольной или
трапециевидной формы, а управление по курсу осуществляется отклонением
вертикальных поверхностей. Управление по тангажу и крену производится
при помощи расположенных на задних кромках крыла рулей, которые могут
отклоняться в двух противоположных направлениях.
Преимуществом такой аэродинамической схемы является отсутствие
скосов потока, снижающих эффективность рулей и крыльев. Использование
рулей на горизонтальных крыльях делает более надежным управление
по крену, так как в такой схеме исключается возможность обратного влияния
крена. Статическая устойчивость достаточно независима от движения по
тангажу, курсу и крену.
Летательные аппараты, выполненные по схеме «бесхвостка», могут иметь
неуправляемое оперение, расположенное как впереди, так и позади центра
массы.
Необходимость в таком оперении возникает при стремлении улучшить
характеристики устойчивости и демпфирования. На рис. II-4-1, з показано,
что летательный аппарат имеет в носовой части неподвижные поверхности,
выполняющие функции дестабилизаторов 3, которые уменьшают
чрезмерную статическую устойчивость, придаваемую сильно развитой в хвостовой
части несущей поверхностью. Дестабилизатор одновременно играет роль
демпфирующего устройства.
Из рис. II-4-1, и видно, что неподвижное оперение 1 может быть
расположено позади поворотного крыла 2. Оно обеспечивает статическую
устойчивость, улучшает демпфирующие свойства летательного аппарата.
Разновидностью «бесхвостки» является схема «летающее крыло» (см.
рис. II-4-1, к), в которой корпус летательного аппарата почти полностью
вписывается в очертание крыла.
Летательный аппарат, выполненный по схеме «бесхвостка», выгодно
отличается в конструктивном отношении, что обусловлено компактностью,
сравнительной простотой внешней формы. Отсутствие изолированного
управляющего оперения уменьшает лобовое сопротивление, снижает вес
конструкции. По этой же причине крыло не испытывает неблагоприятное
воздействие скоса потока.
Схеме «бесхвостка» присущ также ряд недостатков.
1. Летательный аппарат, выполненный по этой схеме, не приспособлен
для'резких маневров, так как рули расположены обычно на небольшом
расстоянии от центра тяжести и не могут обеспечить значительного
управляющего момента. Большой управляющий момент можно создать путем
увеличения управляющей подъемной силы, что достигается увеличением
поверхности рулей или их отклонением. Однако при этом повышается
потребная мощность для поворота органов управления, возрастает вес
летательного аппарата.
2. Вследствие того, что центр тяжести площади крыльев и центр тяжести
конструкции расположены близко друг от друга, демпфирующий момент мал
и поэтому летательный аппарат не обладает хорошими характеристиками
.демпфирования.
Формы летательных аппаратов и их элементов
75
а)
3. Устойчивость и управляемость ухудшаются вследствие сильной
зависимости координаты центра давления от скорости. Например, для
одной из конструкций, выполненной по схеме «бесхвостка», при Моо = 1,5
запас устойчивости по сравнению с дозвуковой скоростью больше
в 2,5 -=- 3 раза, что резко ухудшает управляемость, тогда как у
летательных аппаратов, выполненных по схеме
«утка», это увеличение составляет лишь
1,3-т-1,5.
Схемы многоступенчатых
летательных аппаратов. Принципиально эти
схемы не отличаются от уже
описанных схем летательных аппаратов. До
разделения схема многоступенчатого
летательного аппарата может быть
принята управляемой неоперенной (см.
рис. II-4-1, а) или управляемой
оперенной (рис. II-4-4). Последняя схема
может применяться в различных
модификациях, о которых говорилось выше.
Эти схемы могут быть отнесены и к
ступеням летательного аппарата,
оставшимся после разделения.
Однако для многоступенчатых
летательных аппаратов характерны
определенные особенности в их
аэродинамической компоновке, обусловленные
тактико-техническими требованиями,
предъявляемыми к аппарату в
целом (до разделения) и к отдельным
ступеням.
Аппарат в целом должен быть
устойчив и управляем. В этих целях в схеме
управляемого неоперенного летательного аппарата (рис. II-4-5)
предусматриваются газодинамические органы управления. При этом в
аэродинамическом смысле неоперенный корпус может и не обладать статической
устойчивостью. На рис. II-4-4 показана схема с оперением,
которое служит для обеспечения устойчивости и
управляемости. В некоторых конструкциях предусматриваются
дополнительные газодинамические органы управления,
функционирующие на активном участке полета.
Аэродинамическая схема оставшейся после разделения
ступени летательного аппарата может сохраняться, как это
видно на рис. II-4-4, или видоизменяться в зависимости от
назначения ступени и условий ее полета. На рис. II-4-4
показано, что после разделения первой ступени оставшиеся части
могут быть выполнены по схемам неоперенных (см. рис. II-4-4, а),
оперенных бескрылых (см. рис. 11-4-4, б) и крылатых (см.
рис. II-4-4, в) летательных аппаратов.
В первом случае оставшаяся ступень может быть
последней ступенью и выполнять функции отделяющейся головной
Рис. II-4-5. Схема многоступенчатой ракеты:
1, 2ц г^ соответственно первая, вторая и третья ступени
Рис. 11-4-4. Аэродинамические схемы
многоступенчатых летательных
аппаратов:
а — вторая ступень неоперенная; б —
вторая ступень оперенная; в — вторая ступень
крылатая; 1 — первая ступень; 2 —
вторая ступень
76 Г лав а II
части. Во втором случае оставшаяся ступень может выполнять
аналогичные функции (с той разницей, что головная часть будет оперенной) или
играть роль второй ступени для неоперенной отделяющейся головной части.
Наконец, в третьем случае оставшаяся ступень является последней и играет
роль самостоятельного летательного аппарата (зенитные ракеты,
планирующие аппараты).
Неоперенные отделяющиеся головные части (последние ступени)
выполняются по схемам управляемых и неуправляемых летательных
аппаратов, которые могут быть снабжены средствами стабилизации или
оставаться статически неустойчивыми при движении в плотных слоях
атмосферы.
Степень симметрии летательного аппарата относительно его продольной
оси. Общая аэродинамическая компоновка летательного аппарата
характеризуется степенью симметрии относительно его продольной оси, т. е. углом
поворота, необходимым для полного совмещения очертаний аппарата.
Самолеты или ракеты, выполненные по так называемой самолетной
схеме, имеют очертания, которые совмещаются только при повороте на
360°. Такая форма соответствует предельному случаю отсутствия симметрии
относительно продольной оси. Существуют летательные аппараты, у
которых совмещение их формы происходит при повороте на 180° (конфигурации
с симметрией относительно продольной оси в 180°).
Ракетная аэродинамическая схема характеризуется более высокой
степенью симметрии. Выполненные по этой схеме летательные аппараты
обладают симметрией, меньшей 180°. Типичными являются аппараты с
конфигурацией, обладающей симметрией в 120 или 90° относительно продольной
оси. Особенно широко распространены схемы с симметрией в 90° (так
называемые крестообразные или иксобразные конфигурации). Их
аэродинамическое преимущество по сравнению с самолетной схемой заключается в
получении больших боковых управляющих усилий без создания
предварительного крена. Это позволяет обеспечить высокую скорость маневра в любой
плоскости, хотя и приводит к увеличению сопротивления и веса
конструкции. Вследствие симметрии результирующая аэродинамическая сила
аппарата, наклоненного к направлению вектора скорости полета, всегда
лежит в плоскости продольной оси и вектора скорости, так что
соответствующие производные продольной и боковой устойчивости равны между
собой.
Одна из существенных особенностей ракетных схем состоит в
применении конфигураций с малым удлинением аэродинамических поверхностей.
Это обусловливает нелинейность аэродинамических характеристик, которая
усиливается интерференцией между различными элементами летательного
аппарата (между крылом и оперением, крылом и корпусом и т. д.), а также
наличием больших угловых скоростей вращения.
§ 11-5. Влияние назначения
и тактико-технических
требований на выбор
аэродинамических схем
летательных аппаратов
Выбор той или иной аэродинамической схемы тесно увязан с
назначением летательного аппарата и тактико-техническими требованиями, в
соответствии с которыми устанавливаются взаимное расположение точек старта
и цели, вид траектории движения, тип двигательной установки, системы
Формы летательных аппаратов и их элементов 77
управления, характерные особенности конструкции. Таким образом,
определенному летательному аппарату соответствует конкретная
аэродинамическая схема, обеспечивающая выполнение тактико-технических
требований.
Тип летательного аппарата
и особенности
аэродинамической схемы
Рассмотрим типы современных летательных аппаратов и
соответствующие аэродинамические схемы. В качестве фактора, определяющего тип
аппарата, примем взаимное расположение точек старта и цели полета.
При этом используем общепринятое наименование типа летательного
аппарата, например «космос-космос» (место старта и цели полета в космосе),
«космос-земля» (место старта в космосе, цели — на земле) и т. д.
«Космос-космос». Поскольку движение происходит в безвоздушном
пространстве, форма летательного аппарата практически не влияет на
аэродинамические характеристики и, следовательно, на параметры траектории.
Поэтому выбор
целесообразной аэродинамической схемы ~\ *\
в обычном понимании, как ' - h '
это имеет место для условий
полета в плотных слоях
атмосферы, в данном случае не
имеет смысла. Форма
летательного аппарата
определяется конструктивными со- Рис п_ЪЛ Вид летательных аппаратов типа
ображениями. Он может «космос — земля»:
быть неуправляемым ИЛИ а — неоперенный; б — крылатый летательный аппарат
управляемым. В качестве
органов управления применяются газодинамические устройства,
обеспечивающие ориентировку в пространстве и корректирование траектории.
«Космос-земля». Отличительная особенность этих летательных
аппаратов состоит в том, что они входят в земную атмосферу с очень большой
скоростью, поэтому испытывают сильное влияние аэродинамического нагрева.
Основное требование заключается в уменьшении этого нагрева и в
предохранении летательного аппарата от разрушения. С этой целью в
аэродинамической схеме предусматривают применение головных частей и кромок крыльев,
покрытых слоем огнеупорных защитных обмазок, использование тормозных
ракетных двигателей для уменьшения скорости полета и, следовательно,
снижения теплопередачи. Некоторые участки поверхности летательного
аппарата защищаются от перегрева путем создания условий,
обеспечивающих преждевременный срыв пограничного слоя с этих участков.
Аппарат «космос-земля» может выполняться по схемам управляемого
или неуправляемого неоперенного (рис. II-5-1, а) и крылатого (рис. II-5-1, б)
летательных аппаратов.
В качестве средства стабилизации неуправляемых летательных аппаратов
используется стабилизирующая юбка, представляющая собой пустотелую
хвостовую часть конструкции. Для управления применяются
газодинамические и аэродинамические управляющие устройства.
«Воздух-земля» и «воздух-воздух». Аэродинамические схемы
летательных аппаратов этого типа должны удовлетворять условиям движения в
плотных слоях атмосферы со скоростями, при которых все аэродинамические
эффекты проявляются достаточно сильно, за исключением
аэродинамического нагрева, не имеющего в данном случае существенного значения.
Наиболее широко применяются аэродинамические схемы одноступенчатых one-
78
Глава II
ренных бескрылых или крылатых управляемых и неуправляемых
летательных аппаратов.
Органы управления обычно комбинированного или аэродинамического
типа. К управляемым летательным аппаратам иногда предъявляют
повышенные требования в отношении маневренности. Поэтому аэродинамическая
схема должна предусматривать мощные органы управления.
Осуществляя аэродинамическую компоновку, необходимо учитывать
особенности старта с летательного аппарата-носителя, обладающего
определенной скоростью полета. Если старт производится по направлению полета
носителя, то следует предусмотреть меры для предотвращения разворота
стартуемого летательного аппарата в сторону носителя.
При старте под углом к направлению полета носителя возникает эффект
поперечного обтекания вследствие наличия у летательного аппарата
дополнительной составляющей ско-
; 2 3 * рости движения, что может
привести к ухудшению
устойчивости и кучности. Поэтому органы
стабилизации и управления
должны обеспечивать
ликвидацию неблагоприятных
последствий поперечного обтекания.
Одна из особенностей
аэродинамической схемы может
состоять в том, что вследствие
ограниченного пространства,
занимаемого стартовым
устройством, хвостовой стабилизатор
выполняется в виде
раскрывающегося оперения.
«Земля-земля». В связи с большим разнообразием аэродинамических
схем летательных аппаратов типа «земля-земля» целесообразно
рассматривать эти схемы, классифицируя их по дальности и виду траектории.
Межконтинентальные дальности. Баллистические
траектории (рис. П-5-2, траектория 1). Как правило, летательные
аппараты с такой траекторией являются многоступенчатыми с отделяющейся
головной частью и выполняются по аэродинамической схеме без оперения.
На активном участке траектории управление и стабилизация обеспечиваются
газодинамическими органами, на пассивном участке — управляющими
ракетными двигателями, которые придают необходимую устойчивость последней
ступени (отделяющейся головной части) и позволяют осуществить
корректировку траектории ([69], 1968, № 1); [80].
Аэродинамические схемы головных частей рассматриваемых
летательных аппаратов должны удовлетворять тем же требованиям, что и схемы
летательных аппаратов типа «космос-земля». В дополнение к этим схемам
в целях уменьшения сопротивления затупленных головных частей на
восходящей ветви траектории в плотных слоях атмосферы может устанавливаться
острый баллистический наконечник, который сбрасывается на большой
высоте.
В тех случаях, когда летательный аппарат «земля-земля» является
одноступенчатым без отделяющейся головной части, в аэродинамической
схеме предусмотрено оперение, обеспечивающее надежную стабилизацию
на пассивном участке траектории. На активном участке устойчивость
и управление могут обеспечиваться газодинамическими органами.
В некоторых случаях аэродинамическая схема управляемой
баллистической ракеты с отделяющейся головной частью может также иметь опере-
Рис. П-5-2. Виды траекторий
межконтинентальной дальности:
1 — баллистическая; 2 — планирующая; 3 —
рикошетирующая;
4 — настильная
Формы летательных аппаратов и их элементов
79'
с*
2,0
1,0
0,5
г
к
о-
—
— —
5 10 15 20 AL
Рис. 11-5-3. Аэродинамическое
сопротивление баллистической.
ракеты и ее головной части
ние. Оно предусматривается в том случае, если для стабилизации на
траектории статически неустойчивой ракеты потребуются такие мощные
газодинамические органы управления, которые практически невыполнимы.
Оперение в хвостовой части ракеты обеспечит перемещение центра давления
ближе к центру тяжести и уменьшение статической неустойчивости ракеты.
Это позволит выполнить приемлемые по размерам и весу газодинамические
органы управления.
Баллистическая ракета испытывает влияние сильного
аэродинамического нагрева. Конвективный тепловой поток к аппарату весьма велик и лишь
сравнительно небольшая его часть может быть рассеяна в атмосферу в виде
лучистой энергии. Для сохранения аппарата
необходимо, чтобы ему было передано в виде
тепла минимальное количество кинетической
энергии. С этой целью головные части
выполняются в виде плохо обтекаемых (затупленных)
тел с большим сопротивлением от давления и
малым общим сопротивлением трения,
обеспечивающим снижение конвективной
теплопередачи.
На рис. И-5-3 показаны кривые
изменения в зависимости от числа Маха
коэффициента лобового сопротивления типичной
баллистической ракеты (нижняя кривая), а также
головной части, используемой для
пилотируемого тормозного спуска [78].
Плакирующие траектории (см. рис. II-5-2,
траектория 2). Летательные аппараты с такой
траекторией движутся в плотных слоях
атмосферы без приложения силы тяги. Скорость
аппарата в конце работы двигателя должна быть
достаточна для создания подъемной силы,
равной разности веса и центробежной силы. В
аэродинамической схеме должны бдоь
предусмотрены крылья, позволяющие обеспечить
необходимую подъемную силу и максимальное
аэродинамическое качество с целью достижения
наибольшей дальности полета.
Компоновка летательных аппаратов
многоступенчатая или одноступенчатая с органами
управления и стабилизации. При многоступенчатой компоновке крылья
располагаются на последней ступени, совершающей планирующий полет на
нисходящей ветви траектории.
Планирующий полет в плотных слоях атмосферы происходит с большой
скоростью, поэтому летательный аппарат подвергается длительному
воздействию больших тепловых потоков. Это предъявляет дополнительные
требования к аэродинамической схеме, связанные с уменьшением теплопередачи
и нагрева поверхности.
Однако отвод тепла для планирующих ракет является менее сложной
задачей, так как при планировании кинетическая энергия переходит в
тепловую постепенно и, в противоположность баллистическим ракетам,
интенсивность конвективной теплопередачи невелика. Следовательно, значительная
часть тепла может быть излучена в окружающее пространство при
температурах стенки, допустимых в отношении прочности материала.
Рикошетирующие траектории (см. рис. П-5-2, траектория 3).
Летательные аппараты с такими траекториями занимают промежуточное положение
О
Рис. Н-5-4. Поляра
крылатого летательного аппарата
80 Г лав а II
между двумя предыдущими. Головная часть выполняется по схеме
крылатого управляемого летательного аппарата, благодаря чему- обеспечивается
рикошетирующий характер полета на пассивном участке траектории, при
котором пребывание в плотных слоях атмосферы чередуется с движением
в разреженной среде. Это позволяет получать достаточно большие дальности
полета.
Для достижения максимальной дальности полета необходимо чтобы
в тот период времени, когда рикошетирующая ракета находится в плотных
слоях атмосферы, коэффициент подъемной силы соответствовал
наибольшему отношению су1сх.
При движении в разреженных слоях атмосферы снижается
теплопередача к поверхности. Интенсивность подвода тепла сильно возрастает при
рикошетировании, так как время пребывания в плотной среде мало. Условия
теплопередачи при этом практически оказываются такими, как для
баллистической ракеты. В целях снижения максимальной скорости
теплопередачи, а также полного количества тепла, передаваемого во время входа
в плотные слои атмосферы, передние кромки крыла и корпус должны быть
затуплены. Чтобы не допустить увеличения сопротивления, передние кромки
должны быть сильно скошены. Поэтому в планирующих и рикошетирующих
гиперзвуковых летательных аппаратах целесообразно применять треугольное
крыло. Типичная поляра такого крыла летательного аппарата показана
на рис. П-5-4 [78]. Для малых углов атаки и очень больших чисел Маха
коэффициент индуктивного сопротивления cxi = Кс™ стремится к
предельному значению cxi = csy/2}/~2.
Настильные траектории (см. рис. П-5-2, траектория 4). К летательным
аппаратам, обладающим такой траекторией, относятся обычные самолеты
и самолеты-снаряды, скорости полета которых могут быть как до-, так
и сверхзвуковыми. Их аэродинамическая схема включает в качестве
необходимого элемента крыло для компенсации действия силы тяжести. Так
как полет происходит в плотных слоях атмосферы, то используют
комбинированные или аэродинамические органы управления.
В аэродинамической схеме должны быть предусмотрены средства,
обеспечивающие стабилизацию и управление в условиях, когда старт
осуществляется при помощи ракетных ускорительных двигателей. Необходимая
устойчивость должна быть обеспечена в полете в условиях заправки
летательных аппаратов со специальных самолетов-заправщиков.
Средние дальности. Полет на средние дальности совершается
летательными аппаратами обычно по баллистической траектории
(баллистические ракеты) или настильной (самолеты и самолеты-снаряды). Их
компоновка может быть многоступенчатой и в наиболее общем виде выполняться
по аэродинамической схеме управляемых оперенных крылатых летательных
аппаратов. Отдельные конструкции могут выполняться с некоторыми
отклонениями от этой схемы, например, баллистические ракеты, которые
обладают более простыми схемами, описанными выше.
При средних дальностях дополнительное упрощение обусловлено
меньшими скоростями на нисходящей ветви траектории и, как следствие,
меньшими тепловыми потоками. Поэтому защита от аэродинамического
нагрева облегчается, головная часть может быть сохранена заостренной.
Такая форма головной части обусловливает снижение сопротивления,
что приводит к повышению скорости и сокращению времени полета.
Уменьшение длительности нахождения на траектории повышает точность стрельбы,
так как летательный аппарат в течение более короткого промежутка
времени испытывает неблагоприятное воздействие ветра, изменения температуры
и плотности воздуха и, следовательно, меньше отклоняется от расчетной
траектории.
Формы летательных аппаратов и их элементов
81
Рис. 11-5-5. Оперенные снаряды:
а — мина; б — подкалиберный снаряд
(П — разъемный поддон)
Малые дальности. Баллистические траектории.
Летательные аппараты с такой траекторией являются неуправляемыми оперенными
бескрылыми или неоперенными. В аэродинамической схеме должны быть
предусмотрены средства, обеспечивающие повышение точности стрельбы.
Такими средствами являются косорасположенные лопасти хвостового
оперения, с помощью которых в полете достигается проворачивание оперенного
летательного аппарата вокруг продольной оси, улучшающее кучность.
Такой же эффект создают тангенциальные сопла реактивных двигателей.
Аэродинамические силы и моменты летательного аппарата с такой
аэродинамической схемой должны определяться с учетом проворачивания и
конструктивных особенностей, связанных с косым расположением оперения
и наличием тангенциальных сопел, с учетом влияния струи на внешнее
обтекание.
Настильные траектории. К летательным аппаратам с такой
траекторией относятся противотанковые ракеты и артиллерийские снаряды,
предназначенные для борьбы с наземными
подвижными и неподвижными целями.
Противотанковые ракеты
выполняются по аэродинамической схеме
управляемых крылатых, а
артиллерийские снаряды — по схеме
неуправляемых оперенных и неоперенных
летательных аппаратов.
Схемы неуправляемых оперенных
снарядов (мин) могут иметь некоторые
разновидности, определяемые размахом
оперения по отношению к поперечным
размерам корпуса. Если размах
оперения равен или меньше диаметра
наибольшего поперечного сечения корпуса, схема летательного аппарата носит
название подкалиберной (мины с малыми скоростями, рис. П-5-5, а); если
больше, то схема называется надкалиберной (рис. П-5-5, б) ([69], I960, № 2).
«Земля-воздух» и «земля-космос». Летательные аппараты этих типов
применяют для противовоздушной и противоракетной обороны, а также
для атмосферных и космических исследований.
Если они предназначены для полетов на больших высотах, то
выполняются многоступенчатыми. Для полетов на небольшие дальности возможен
одноступенчатый вариант с двухрежимной работой двигателя, при которой
тяга в момент разгона обеспечивается большой, а после набора заданной
высоты (или достижения определенной скорости) — резко уменьшается.
Летательные аппараты для космических целей выполняются обычно
управляемыми неоперенными.
Аэродинамическая схема ракет типа «земля-воздух» должна обеспечить
большую маневренность. Поэтому в ней предусматриваются крылья,
оперение, мощные управляющие органы, которые могут быть выполнены по
одной из схем — нормальной, схеме «утка» или «бесхвостка». В последней
схеме часто используются поворотные крылья.
Для атмосферных и космических исследований используются
специальные исследовательские ракеты (метеорологические, геофизические, медико-
биологические).
Компоновка таких ракет может быть самой разнообразной в
зависимости от конкретных задач, для выполнения которых они предназначены.
На рис. П-5-6 показаны одно- и двухступенчатые летательные аппараты.
У одноступенчатых ракет может оказаться достаточным стабилизатор 1
из трех лопастей (рис. П-5-6, а). У ракеты, выполненной по двухступенча-
6-114
82
Глава II
той схеме, стабилизатор 1 стартового двигателя может состоять из трех
лопастей, а основной ступени 2 — из четырех (рис. И-5-6, б).
Ракеты для исследовательских целей могут быть управляемыми и
неуправляемыми. Управление может осуществляться с помощью газоструйных
рулей или поворотом камеры сгорания. Угловая ориентация ракеты
относительно продольной оси производится с помощью специальных реактивных
сопел.
Специфические особенности ракет могут быть обусловлены наличием
системы спасения головной части с комплексом измерительных устройств.
Поэтому в аэродинамическую схему включается отделяющаяся головная
Рис. П-5-6. Аэродинамические схемы метеорологических ракет:
а — одноступенчатая; б — двухступенчатая ракета
часть (см. рис. И-3-10, б). Ее торможение при входе в плотные слои
атмосферы осуществляется с помощью специальных тормозных средств, в
качестве которых используются гирлянды тормозных дисков, тормозные щитки,
раскрывающиеся после отделения, и парашюты.
«Глубина-глубина». Летательные аппараты этого типа предназначены
для движения в воде. Обычно они выполняются по аэродинамической схеме
управляемых оперенных бескрылых летательных аппаратов. Управление
обеспечивается аэродинамическими (или точнее гидродинамическими)
органами, которые могут быть связаны с системой самонаведения.
В схеме должно учитываться влияние на аэродинамические
(гидродинамические) характеристики аппарата возможного забора воды в качестве
топлива для реактивного двигателя.
«Воздух (земля)-глубина». Летательные аппараты такого типа должны
входить в воду со сравнительно небольшой скоростью. Иначе из-за
больших перегрузок, возникающих при погружении, потребуется обеспечить
повышенную прочность корпуса и других частей летательного аппарата, что
приведет к увеличению его веса.
Для уменьшения скорости предусматривают меры, обеспечивающие
повышение сопротивления. С этой целью головную часть выполняют
затупленной, летательный аппарат снабжают тормозными парашютами, щитками,
раскрывающимися при подходе к воде.
Принципиальная схема аппаратов этого типа такая же, как летательных
аппаратов типа «глубина-глубина».
Тип двигательной установки
и особенности
аэродинамической схемы
Ракетная двигательная установка. Так как ракетный двигатель
работает без поступления кислорода воздуха, то воздухозаборные устройства как
один из элементов аэродинамической схемы отсутствуют.
Формы летательных аппаратов и их элементов
83
а)
Двигательная установка чаще всего размещается в кормовой части
корпуса летательного аппарата, что оказывает влияние на центровку
аппарата, взаимное расположение центра тяжести и центра давления и,
следовательно, на устойчивость и управляемость. Кроме того, на форму
хвостовой части и условия ее обтекания
влияет размещение сопел.
Существенные особенности в
аэродинамической схеме связаны с
применением нескольких
двигательных установок, размещаемых в
«пакете» вокруг корпуса летательного
аппарата (рис. П-5-7), а также с
использованием ракетных двигателей
в качестве стартовых ускорителей.
Такое расположение двигателей
требует дополнительных средств
стабилизации.
В обоих случаях двигатели
отделяются после окончания работы.
В связи с этим к аэродинамической
схеме предъявляются требования,
чтобы в момент отделения были
обеспечены необходимые устойчивость
и управляемость. Лобовое
сопротивление, испытываемое двигательной
установкой, должно быть достаточно,
чтобы быстро произвести ее
отделение от корпуса.
Реактивная двигательная
установка. Двигатели этого типа
(прямоточные, турбореактивные) используют для своей работы кислород
воздуха, который поступает из воздухозаборников, установленных на
летательном аппарате.
Размеры воздухозаборных устройств, их число, характер
расположения, режим работы существенно изменяют условия обтекания и
аэродинамические свойства летательного
аппарата, что в свою очередь
влияет на тяговые и
экономические характеристики двигателей.
Для обеспечения наименьших
потерь полного давления и
создания тем самым лучших условий
работы двигателей воздухозабор-
ные устройства должны
размещаться на летательном аппарате
Рис. П-5-7. Размещение двигательных
установок на летательных аппаратах:
а —«пакет» ракетных двигателей вокруг
корпуса летательного аппарата; б — реактивные
двигатели вместе с воздухозаборными устройствами
расположены в гондолах на пилонах
Рис. 11-5-8. Схема расположения
воздухозаборников в месте соединения крыла с
корпусом
так, чтобы они не затенялись
крыльями, оперением и другими
выступающими частями, т. е. чтобы
в зоне входа в воздухозаборное устройство поток испытывал как можно,
меньшие во змущения.
С этой целью нежелательно размещать воздухозаборное устройство»
вблизи поверхности корпуса на большом удалении от носовой части, если*
входной канал оказывается в зоне пограничного слоя с достаточно
большой толщиной и поступающий воздух будет иметь большие потери полного*
давления.
84
Глава II
Вид аэродинамической схемы летательного аппарата с реактивным
двигателем зависит от расположения воздухозаборных устройств. На
рис. П-1-10, а, б показаны схемы с боковыми
воздухозаборниками, на рис. П-1-10, в — с
кольцевым; на рис. П-5-8 и П-1-11 показаны
схемы с воздухозаборниками 1, размещенными
соответственно в месте соединения крыла с
корпусом и в корпусе некруглого поперечного
сечения.
Расположение воздухозаборников по
длине летательного аппарата показано на
рис. П-5-9, а, б. При большом удалении
воздухозаборника от носовой части летательного
аппарата перед входом в него должны быть
предусмотрены устройства для отсоса
пограничного слоя. Возможно вынесение входного
сечения воздухозаборника за пределы
пограничного слоя (рис. П-5-9, б). Все это
предотвращает срыв потока воздуха и улучшает
характеристики работы воздухозаборников.
С целью снижения потерь давления
воздуха, поступающего в двигатель, и повышения
эффективности его работы воздухозаборные
устройства вместе с двигателями могут
располагаться в виде гондол на крыльях или
специальных пилонах (см. рис. И-5-7). В этой
схеме для повышения устойчивости и
улучшения управляемости предусмотрено хвостовое
оперение.
Особенность аэродинамической схемы
сверхзвуковых летательных аппаратов с
прямоточными воздухореактивными двигателями
(ПВРД) обусловлена наличием специальных
ускорительных двигателей, обеспечивающих
скорость движения, необходимую для начала
устойчивой работы ПВРД. Это утяжеляет
хвостовую часть конструкции и для обеспечения необходимой устойчивости
требует установки стабилизаторов.
Рис. П-5-9. Возможные схемы
расположения
воздухозаборников по длине летательных
аппаратов:
а — кольцевой воздухозаборник 1,
в — четыре боковых полукруглых
воздухозаборника 2, входное
сечение которых вынесено за
пределы пограничного слоя
Г л а в a III
ОСНОВНЫЕ
СООТНОШЕНИЯ
В ТЕОРИИ
ГАЗОВЫХ ТЕЧЕНИЙ.
§ 111-1. Особенности
течения газа с очень
большими скоростями
Изменение физико-химических
свойств и термодинамических
характеристик воздуха с
температурой
Удельные теплоемкости. Значительное увеличение скоростей летательных
аппаратов привело к необходимости учитывать в аэродинамических
исследованиях специфические особенности газовых течений, обусловленные
изменением физико-химических свойств воздуха. Если в «обычной» сверхзвуковой
аэродинамике учитывалось свойство сжимаемости как важнейшее
проявление особенности течения с большими скоростями, а влиянием температуры
на термодинамические параметры, в частности, удельные теплоемкости, пре-
небрегалось, то при гиперзвуковых скоростях на первое место выдвигаются
особенности, связанные с влиянием высоких температур, возникающих за
ударными волнами и в пограничном слое. Благодаря этому влиянию
теплоемкости газа возрастают вследствие возбуждения колебательных уровней
внутренней энергии.
Исследования ударных волн и пограничного слоя показали, что все
соотношения обычной аэродинамики достаточно надежны, пока условия
течения газа существенно не отличаются от условий, для которых приемлема
предпосылка о неизменности удельных теплоемкостей и возможности
применения уравнения состояния совершенного газа р = RpT, где R —
абсолютная газовая постоянная, р и Т — соответственно плотность и
температура газа. Необходимость учитывать изменение теплоемкости с
температурой наступает раньше, чем необходимость применять уравнение состояния,
отличное от уравнения для совершенного газа. Например, как показывают
исследования, становится целесообразным учитывать изменение удельных
теплоемкостей с температурой при переходе через прямую ударную волну,
начиная с чисел Моо набегающего потока порядка 3-f 4. При этом до
значений чисел Моо = 64-7 можно сохранить уравнение состояния
совершенного газа, а также уравнение для скорости звука а2 = kRT (к = cpfcv —
показатель адиабаты, равный отношению удельной теплоемкости ср при
постоянном давлении к удельной теплоемкости cv при постоянном объеме).
Для расчета истинных удельных теплоемкостей в зависимости от
температуры можно воспользоваться термодинамическими таблицами или
интерполяционными формулами. Такие формулы, полученные для условий
термодинамического равновесия и в предположении линейной зависимости
удельных теплоемкостей от температуры, имеют вид
ср = 0,2317 + 0,000221Г; cv = 0,1647 + 0,000221Г, (Ш-1-1)
где ср и с0 в ккал/кГ-град.
В соответствии с приближенной оценкой влияния температуры на
удельную теплоемкость при р = const
86
Глава III
где ф — зависит от температуры (рис. Ш-1-1); индекс «оо» соответствует
параметрам невозмущенного потока или вообще каким-либо начальным значениям.
Для Т > 1000° К можно принять
Ф = 0,1. При Гоо = 288° К теплоемкость
Ср оо = 0,24 ккал/кГ -град (103 дж /кг-град).
Формула (Ш-1-2) применяется до
значений Т = 2000—2500° К, при которых
колебательные степени свободы оказываются
полностью возбужденными.
Кинетические коэффициенты. Трение
и теплопередача в пограничном слое
зависят от таких кинетических коэффициентов
газа, как коэффициенты динамической
вязкости |х и теплопроводности Я.
Установлено, что при отсутствии диссоциации
вязкость воздуха зависит лишь от
температуры и практически не зависит от
давления. При этом имеется несколько
зависимостей, связывающих между собой вязкость и температуру. В
частности, степенная зависимость
т°к
Рис. 111-1-1. Изменение показателей
степени ср, п, х в формулах для
определения теплоемкости, вязкости
и теплопроводности
Цоо
(Ш-1-3)
Показатель степени п в свою очередь зависит от температуры
(рис. Ш-1-1). При сравнительно небольших ее значениях можно принимать
п = 0,76 (или 3/4). В соответствии с графиком на рис. Ш-1-1 для
достаточно большого интервала температур средняя величина п « 0,7. Причем
начальное значение |х можно принимать равным |Лоо = 1,82-10~6 кГ-сек/м2
(1,79-10~5 н-сек/м2), что соответствует Гоо = 288° К.
В приближенных расчетах формулу (Ш-1-3) можно применять до
температур порядка 2000—2300° К, т. е. пока не наступит диссоциация. При
температурах, меньших 1500° К, несколько лучшие результаты дает
формула Сэзерленда
\х ( Т \ 2 1-1-
1 + 111/Г
(Ш-1-4)
Так же как вязкость, теплопроводность при температурах до 2000° К
практически не зависит от давления и может быть определена как функция
вязкости и удельной теплоемкости:
ср—0,0374
сп —0,0374
(Ш-1-5)
где ср и cv имеют размерность ккал/кГ *град, a \i и X — соответственно
кГ-сек/м2 и ккал/м-град-сек (или нсек/м2 и впг/м-град).
Более простой является степенная формула
(Ш-1-6)
в которой показатель х в свою очередь зависит (рис. Ш-1-1) от температуры. Для
приближенных расчетов можно принять х = 0,85 и ^оо = 5,53-10~3 ккал/мх
Хсек-град (23,2 em/м-град) для Гоо = 261°К
Основные соотношения в теории газовых течений
87
Диссоциация и ионизация
Термодинамические функции воздуха при высоких температурах. С
увеличением скорости полета воздух за ударной волной или в пограничном слое
разогревается настолько, что колебательные степени свободы оказываются
полностью возбужденными. При дальнейшем повышении температуры атомы
преодолевают внутримолекулярные силы, в результате чего двухатомная
молекула диссоциирует на две отдельные одноатомные молекулы. Этот
процесс диссоциации характеризуется весовой долей одноатомного газа а = Gi IG
{Gi— вес части газа, находящейся в атомарном состоянии, G — общий вес
газа). Параметр а называется степенью диссоциации.
Т°К
Рис. II1-1-2. Молярные и атомарные концентрации компонент
воздуха (кислорода и азота) в зависимости от температуры
и давления (в скобках указано давление в атмосферах)
При еще более высокой температуре воздуха наряду с диссоциацией,
которая завершается при температуре порядка 6000° К, происходит
ионизация воздуха. Основной причиной ионизации является соударение молекул
в их тепловом движении. Поэтому такой процесс называют
термоионизацией. Его интенсивность характеризуют степенью ионизации, равной
отношению количества ионизированных атомов к их общему числу.
Как показывают исследования, водород и азот, например, полностью
термически ионизированы (степень ионизации равна единице) при
температурах соответственно 10 000 и 17 000° и давлении 1 атм.
При диссоциации и ионизации воздух заметно перестает следовать
уравнению состояния для совершенного газа. Становится недействительным
предположение о постоянстве температуры торможения, на котором
основываются, в частности, обычные уравнения ударной волны. Поэтому они
должны получаться с учетом физико-химических превращений воздуха при
высоких температурах.
Важным элементом расчетов этих течений является определение
термодинамических параметров и кинетических коэффициентов
диссоциированного и ионизированного воздуха, а также его состава. В настоящее время
имеются достаточно подробные данные об этих параметрах и коэффициентах,
а также о составе воздуха в условиях термодинамического равновесия при
температурах от 1000 до 20 000° К и давлениях от 0,001 до 1000 атм,
полученные с помощью электронных счетных машин группой советских
ученых под руководством члена-корреспондента Академии наук СССР проф.
ьпГкал/кГ
12500
Т °К =12000 11SO0114001100010600 10200 9800 9400 9000
10000
7500
2,0
2,5 3,0 3,5 4J
Рис. Ш-1-3. Диаграмма энтальпия — энтропия
5,0 S"
Основные соотношения в теории газовых течений
89
А. С. Предводителева [28]. Соответствующие расчеты проводились для
температур от 1000 до 6000° К без учета ионизации, так как ее влияние в этом
интервале температур пренебрежимо мало. В интервале температур от 6000
до 20 000° К учитывалось влияние ионизации. Для упрощения вычислений
использовалась гипотетическая схема так называемой однократной
ионизации, которая полностью завершалась при Т = 12 000° К и р — 0,001 атм.
1,0
Рис. Ш-1-4. Параметры воздуха при высоких температурах в
условиях термодинамического равновесия:
Veo= 1,293 пГ/м*\ 7^ = 273,2° К; R= 29,27 кГ - м/кГ • град; RT^^
= 8-103 кГ-м/кГ
По полученным результатам были построены графики атомарных и
молекулярных концентраций (рис. Ш-1-2), а также i- ^-диаграмма (диаграмма
энтальпия-энтропия), приведенная на рис. Ш-1-3, где также изображены
кривые р = const и Т = const [28].
На рис. Ш-1-4 эти графики перестроены таким образом, что вместо
давления они содержат плотность и вместо абсолютных значений приведены
безразмерные энтальпия i/RToo и энтропия SIR.
/* г/г -моль
29
10
О 1000 2000 3000 Ш0 5000 6000 7000 8000 9000 10000 11000 12000 т°К
Рис. III-1-5. Средний молекулярный вес воздуха при высоких температурах
Основные соотношения в теории газовых течений
91
и
ft
н
ft
Н
I
и
I
\Юккал/м-сек -град
trim
Dm
I \ / V/
'/ /\/\ Y/A
w
ж
10000
Рис. Ш-1-7. Коэффициент теплопроводности воздуха-при высоких температурах
»
•^
Основные соотношения в теории газовых течений QS
Важным для практических расчетов являются графики (рис. III-1-5),
позволяющие определить молекулярный вес |хср диссоциированного и
ионизированного воздуха в зависимости от температуры и давления. Как видно из
графиков, средний молекулярный вес с температурой уменьшается.
Рассматривая модель воздуха в виде однородного двухатомного газа,
можно для определения степени диссоциации применить формулу
Дальтона
а ,
М-ср
где |хср о, Н'ср — соответственно средние молекулярные веса недиссоциирован-
ного воздуха (двухатомный газ) и диссоциированной среды. Величина
jxcpo = 29, а [Лср определяется как функция р и Т по графикам на рис.
Ш-1-5.
При помощи еще одного семейства кривых, приведенных на рис. Ш-1-6,
можно найти значение скорости звука как функции у ир.
Кинетические коэффициенты. Приближенный анализ показал, что при
высоких температурах вязкость воздуха, находящегося в равновесном
состоянии, может быть определена с точностью до 10% вплоть до
температуры 9000° К по формуле Сэзерленда (Ш-1-4). Однако более точные
исследования указывают на то, что для диссоциированного воздуха \i зависит не
только от температуры, но и от давления. Это учитывается уточненной
формулой Сэзерленда
/ Т \21 + 111/Гсо/ 1 1,42 \
\TooJ 1 + 111/2* и+О.вЭсА/см"1 1 + 1,26см/сА/ '
где см, сА — концентрации соответственно молекул и атомов, причем для
бинарной смеси см + с а — 1.
Концентрации можно заменить через степень диссоциации ос, а именно
€а = ее, см = 1 — ос. При отсутствии диссоциации (а = 0) зависимость
(III-1-8) переходит в обычную формулу Сэзерленда. При полной диссоциации
{а = 1) член в скобках в (III-1-8) равен 1,42, следовательно, увеличение
вязкости по сравнению с недиссоциированной средой составляет 42%.
При высоких температурах коэффициент теплопроводности, как и
коэффициент |1, зависит от температуры и давления. На рис. Ш-1-7 приведены
результаты теоретического исследования коэффициента теплопроводности
в предположении, что воздух представляет собой реагирующую бинарную
смесь газов. При исследовании высокоскоростных потоков могут оказаться
весьма полезными данные о кинетических коэффициентах и параметрах
состояния воздуха, приведенные в работе [13].
Основные зависимости для
двухатомного
диссоциирующего газа
Степень диссоциации. С целью упростить исследование диссоциации
воздух можно представить как некоторый условный двухатомный газ,
состоящий из симметричных молекул одного вида, которые в результате
двойных соударений диссоциируют на два атома. В свою очередь атомы
могут рекомбинировать в молекулы путем тройных соударений. Эта схема
позволяет изучить механизм диссоциации чистого диссоциирующего
двухатомного газа [73, 1957, № 1].
Предполагается, что диссоциация является равновесной. Это означает,
что в химической реакции, определяемой, например, простейшим уравне-
94
Глава III
нием бинарного процесса
А + А,
(Ш-1-9)
скорости протекания реакций слева направо rD и справа налево rR
(соответственно скорости диссоциации и рекомбинации) одинаковы.
Исследования течений диссоциирующей среды связаны с определением
степени равновесной диссоциации а. Для упрощения расчета воздух можно*
рассматривать как механическую смесь, состоящую из чистых
диссоциирующих компонентов, а именно азота N2 и кислорода О2.
Степень равновесной диссоциации а определяется в химической
термодинамике соотношением
1 — а
т
в котором
пА
(Ш-1-10)
(Ш-1-11)
Здесь па — число атомов элемента А в некотором объеме;
^А2— число молекул газа А2 в том же объеме.
В (Ш-1-10) входят величины р<?, Та, представляющие собой
соответственно характеристические плотность и температуру. Вычисления
показывают, что характеристическая температура диссоциации для кислорода
Та = 59 000° К, для азота Та = 113 000° К. Характеристическая
плотность несколько меняется в зависимости от температуры (табл. III-1-1).
Так как это изменение невелико, то для приближенных исследований можно
принять среднюю величину р^, равную для кислорода 150 г/см3, для азота —
130 г /см*.
Таблица II1-1-1
Характеристические параметры диссоциации
Элемент
Кислород
Азот
Воздух
атм
2,3-107
4,МО7
3,7-107
ккая/кГ
3,7-103
8,0-103
7,1-103
м2/сек2
1,5-107
3,4-107
3,0-107
м/сек
3,9-103
5,8-103
5,4-103
pd, г/смЗ
1000<Т<5000°К
150
130
135
5000<Т<7000°К
130
125
126
Вместо температуры в (Ш-1-10) можно включить энтальпию i [см.
(ГП-1-14') и (Ш-1-16')]. Тогда степень диссоциации будет определена в
функции i и р. На рис. Ш-1-8 показана соответствующая зависимость для ос
от безразмерных величин p/pd и ilua- Параметр иа называется
характеристической энергией диссоциации, равной удельной теплоте диссоциации
на 1 г молекул А2,
где тА — масса атома;
D — энергия диссоциации молекулы А2.
По степени диссоциации а можно определить, используя формулу-
Дальтона (Ш-1-7), средний молекулярный вес смеси |хер.
Основные соотношения в теории газовых течений
95
В табл. Ш-1-1 представлены наряду с рассмотренными параметрами
pd и ud также характеристические давление/^ и скорость Vd, понятия о
которых будут даны ниже.
1,0
0,8
0,6
ОА
Рис. Ш-1-8. Диаграмма для определения степени диссоциации
двухатомного газа в зависимости от отношения ijud и параметра lg (р^/р)
Уравнение состояния. Рассмотрим уравнение состояния газовой смеси,
возникшей в результате диссоциации двухатомных молекул. Это уравнение
можно получить, если воспользоваться зависимостями для определения
давления смеси р, а также парциального давления компоненты pt
А, (Ш-1-13)
где к — газовая постоянная, отнесенная к одной молекуле (постоянная
Больцмана);
индекс <ш> обозначает газовую компоненту.
В дальнейшем атомарную составляющую (i = 1) будем фиксировать
индексом «А», молекулярную (i =^2) — индексом «М».
Так как концентрация компоненты ct = р*/р, т. е. для атомарной и
молекулярной составляющих соответственно с± = сА = а = рА/р, с2 = сш = 1 — а =
= рм/р» т0 из (Ш-1-13) найдем при условии, что тш = 2тА, уравнение
состояния
р = ЛгрТ(1 + а), (Ш-1-14)
где к/(2?пА) — газовая постоянная для 1 г компоненты А2 в смеси.
Отнеся (Ш-1-14) к состоянию, определяемому характеристическими
параметрами, получим зависимость для характеристического давления pd =
= 0,5kpdTd/mA. Так как энергия диссоциации молекулы А2 равна D=-kTd,
то, очевидно, pd = 0,5Dpd/mA.
Характеристическая скорость, о которой упоминалось, определяется
формулой Vd = 1г*/2. Соответствующие значения pd и Vd для кислорода
и азота приведены в табл. Ш-1-1.
Уравнения термодинамики. Представляют интерес некоторые
уравнения термодинамики двухатомного диссоциирующего газа. В частности,
уравнение для внутренней энергии единицы массы газа имеет вид
иЗ^+Л" (Ш-1-15)
дв Г л а в а III
Разделив и и Т на соответствующие характеристические параметры udi
Td, это уравнение можно привести к безразмерному виду
п=ЪТ + а, (Ш-1-15')
где u = u/ud, T=TlTd.
Наряду с (Ш-1-15') можно написать уравнение для энтальпии, причем
также в безразмерной форме
Р
где i = i/ud, p = p/pd, p = p/pd.
Используя понятия характеристических параметров, можно привести
к безразмерному виду также уравнение состояния (Ш-1-14)
р = рТ(1 + а). (Ш-1-14')
Внося выражение (Ш-1-15') для и в соотношение (Ш-1-16) и используя
(Ш-1-14'), получим для энтальпии
Смесь двухатомных газов. Так как молекулярные веса азота и кислорода
близки, то в известной мере можно считать оправданной модель воздуха как
аддитивную смесь двухатомных газов. При этом можно учесть различие
в характеристических температурах азота и кислорода.
Кислород начинает диссоциировать при значительно более низких
температурах, чем азот, и оказывается полностью продиссоциировавшим
тогда, когда азот вступает в стадию развившейся диссоциации.
Если за начало диссоциации N2 принять температуру 3500° К, то при
этой температуре степень диссоциации двухатомной модели воздуха будет
определяться относительной массой кислорода в смеси, т. е. значением 0,235.
При Т > 3500° К степень диссоциации модели воздуха
где а02 — степень диссоциации чистого кислорода.
После завершения диссоциации О2 при температурах Т > 3500° К
величина аОз = 1 и степень диссоциации воздуха
а = 0,235 + 0,765aN2, (HI-1-18)
где cxn2 — степень диссоциации чистого азота, а величина 0,765 определяет
объемную долю N2 в воздухе.
Для полностью диссоциированного воздуха ао2 = ащ = 1 и,
следовательно, а — 1.
Таким образом, при приближенном расчете степени диссоциации, а также
других параметров принимается упрощенный массовый состав недиссоции-
рованного воздуха, включающий 76,5% N2 и 23,5% О2 (в состав
атмосферного азота условно включен 1% инертных газов).
Наряду с формулами (Ш-1-17) и (Ш-1-18) можно применять
приближенный метод, основанный на определении эффективных значений
характеристических параметров диссоциации воздуха в соответствии с массовыми
долями азота и кислорода. Например, эффективное характеристическое
давление диссоциации
pd = 0,765a* N2 + 0,235pd 02,
/?dN2> Pd o2 — соответственно характеристические давления диссоциации
азота и кислорода.
Основные соотношения в теории газовых течений д?
Аналогично можно вычислять эффективные значения других
характеристических параметров.
Подсчитанные таким образом для воздуха эффективные значения pd, ud,
Vd приведены в табл. Ш-1-1.
Энтальпия равновесной диссоциации. Если воздух рассматривается
в виде смеси азота и кислорода, то энтальпия смеси
^0
in - с6 ^0 = {iRc)o2 + {1rC)^ (IIH-20)
>J ch
A=N, О
где энтальпия диссоциации к-й компоненты равна в соответствии с (Ш-1-12)
iRk = Dk/(2mh) = udk.
Значения iRk приведены в табл. Ш-1-1, а концентраций — на графике
(рис. Ш-1-2). Для двухатомной модели газа
где а — степень диссоциации модели газа;
ud = iR — характеристическая энергия диссоциации 1 г молекулы воздуха.
Если принять, что весь кислород диссоциирует до начала диссоциации
азота, то атомарная концентрация обусловлена только распадом кислорода
и, следовательно, с = а = 0,235.
В соответствии с этим
1л = 0,235(i л) оа-
Если условия таковы, что диссоциация кислорода происходит
неполностью, то iD <C 0,235 {ir)o2 и концентрация (степень диссоциации смеси)
с = а < 0,235.
При высоких температурах и малых давлениях вслед за кислородом
диссоциирует азот. Энтальпия диссоциации смеси
iRc = iRa = iD = 0,235 (iB)Oa + (с - 0,235) (*B)Na. (III-1-21)
Для грубой оценки величины iD можно использовать таблицы или
графики термодинамических функций. В этом случае по температуре Т
и давлению р находится энтальпия ia с учетом диссоциации, a iD
определяется в виде разности
где ia=o — энтальпия при этой же температуре, но без учета диссоциации.
Для приближенных вычислений ее величины можно применить формулу
(Т \ Ф
в которой для Т > 1000° К показатель степени ф = 0,1, а удельная
теплоемкость ср0 принимается при температуре То = 273° К равной
0,24 кшл/кГ-град.
Определение характеристических параметров воздуха как модели
двухатомного чистого диссоциирующего газа, представляющего собой смесь N2
и О2, обусловливает ту особенность, что рассматриваемая газовая среда
в начальном (недиссоциированном) состоянии оказывается как бы
предварительно нагретой. Этому состоянию с возбужденными колебательными
уровнями энергии соответствует показатель адиабаты к = 1,33.
Строго говоря, по отношению к обычным условиям полета такая среда
не является реальной. Тем не менее приведенные выше соотношения имеют
практическое значение. Дело в том, что переход через ударную волну,
возникающую перед телом, представляет собой неравновесный процесс.
7-114
98 Г л а в a III
Практически можно считать, что даже при очень высоких скоростях
и, следовательно, больших температурах за волной диссоциация
непосредственно за ее фронтом равна нулю, но колебательные уровни возбуждены.
Таким образом, свойства реального и гипотетического газа за ударной
волной совпадают.
При этом точность расчетов возрастает по мере увеличения скоростей
полета, когда газ за ударной волной разогревается до весьма высоких
температур.
Релаксационные явления
Неравновесные течения. Рассмотренные выше методы расчета
термодинамических параметров с учетом физико-химических превращений отражают
предположение о равновесности протекающих процессов. Это
предположение заключается в соответствии уровней внутренних степеней свободы
параметрам, характеризующим состояние газа. Например, при
сравнительно невысоких температурах (небольших скоростях) устанавливается
равновесие между температурой и колебательной степенью свободы, что
соответствует равновесию между температурой и удельной теплоемкостью.
При высоких температурах (больших скоростях), когда газ диссоциирует,
равновесный процесс характеризуется соответствием, с одной стороны,
между степенью диссоциации, с другой — температурой и давлением.
Наконец, при еще более высоких температурах (очень больших
скоростях) можно говорить о равновесных процессах возбуждения электронных
уровней и ионизации.
В равновесном течении при внезапном изменении температуры также
мгновенно устанавливаются соответствующие внутренние степени свободы,
причем диссоциацию и ионизацию можно рассматривать как проявление
новых степеней свободы. Таким образом, в этих случаях отсутствует
запаздывание в установлении степеней свободы, т. е. время достижения равновесия
равно нулю.
Практически равновесное течение наблюдается при сверхзвуковом
обтекании тел потоками с числами Моо > 4—5 в условиях, соответствующих
высотам 10—15 км и меньше. Это объясняется тем, что при возникающих
в этих условиях максимальных температурах порядка 1000—1500° К
главная часть внутренней энергии приходится на поступательные и
вращательные степени свободы, которые при внезапных изменениях температуры
практически устанавливаются мгновенно, так как для достижения
равновесия достаточно всего несколько молекулярных столкновений. По этой
причине поступательные и вращательные степени свободы обычно называют
«активными».
С увеличением скоростей и, следовательно, температур значительная
часть внутренней энергии приходится на колебания, затем диссоциацию,
возбуждение электронных уровней и ионизацию. Реально протекающие
процессы таковы, что эти уровни энергии устанавливаются медленнее, чем
поступательные и вращательные, так как для этого нужно значительно
большее число столкновений. Поэтому колебательные и диссоциационные
степени иногда называют «инертными». Таким образом, инертным степеням
свойственно запаздывание в достижении равновесия, называемое релаксацией.
То время, в течение которого достигается равновесие, т. е. устанавливается
соответствие между температурой и энергетическим уровнем, называется
временем релаксации.
Релаксационные процессы определяются тем, какая степень свободы
приходит в возбуждение. Если при внезапном изменении температуры
возникают колебания, то соответствующий неравновесный процесс называется
Основные соотношения в теории газовых течений QQ
колебательной релаксацией. Он характеризуется запаздыванием
теплоемкости при изменении температуры. Если температура повышается, то
теплоемкость увеличивается вследствие изменения молекулярного движения от
перемещения и вращения к перемещению, вращению и вибрации. Время,
в течение которого колебательное движение приходит в равновесие,
называется колебательным временем релаксации. В неравновесном
диссоциирующем газе при внезапном изменении температуры происходит запаздывание
в изменении степени диссоциации. Это объясняется тем, что, в частности, при
быстром увеличении температуры скорость образования атомов превышает
скорость их исчезновения, т. е. скорость диссоциации больше, чем
рекомбинации. С энергетической точки зрения требуется относительно небольшое
число столкновений, чтобы вызвать диссоциацию. А чтобы осуществлялись
рекомбинации, необходимы сравнительно редко встречающиеся
столкновения трех частиц.
С течением времени скорости прямой и обратной реакций
выравниваются. Время, которое требуется для получения равновесной
концентрации (или степени диссоциации), называется диссоциационным временем
релаксации.
При температурах приблизительно до 10 000° К основными являются
колебательные и диссоциационные релаксационные процессы.
Релаксационными явлениями, связанными с возбуждением электронных уровней
молекул и атомов, а также ионизацией, можно пренебречь, так как на долю
этих степеней при указанных температурах приходится малая часть
внутренней энергии.
Неравновесность оказывает существенное влияние на различные
процессы, сопровождающие течения газа с очень большими скоростями. В
частности, колебательная и диссоциационная релаксация изменяет параметры
газа при переходе через ударные волны и при обтекании тел, что в свою
очередь влияет на процессы трения, теплообмена, а также на
перераспределение давления.
Уравнение для скорости химических реакций. Изучение неравновесных
течений заключается в совместном исследовании движения среды и
химических процессов, происходящих с конечными скоростями. Формально это
выражается в том, что к обычной системе уравнений газовой динамики
добавляется уравнение для скорости химических реакций.
В целях упрощения исследований можно использовать уравнение,
отнесенное к простой бинарной реакции диссоциации и рекомбинации чистого
диссоциирующего двухатомного газа (Ш-1-9), причем в этой зависимости
скорости диссоциации и рекомбинации не равны и, следовательно,
химическая реакция протекает с некоторой скоростью. Равновесие достигается,
когда скорость образования новых молекул в результате рекомбинации
атомов будет равна скорости исчезновения молекул, диссоциирующих на
атомы. Таким образом, истинная скорость реакции диссоциации
где а — текущее значение степени диссоциации.
С целью получения общих выражений для скоростей диссоциации и
рекомбинации необходимо воспользоваться соотношениями из химической кинетики.
Рекомбинация двух атомов А в молекулу А2 при соударении с третьей
частицей В изображается формулой А + А + В —> А2 + В, где В —частица,
kR
уносящая энергию рекомбинации; fcR — константа скорости рекомбинации.
Эта константа определяется из уравнения для скорости рекомбинации
^}В = 2*Я[А]*[В]. (Ш-1-23)
7*
100
Глава III
Квадратные скобки обозначают концентрацию в единицах моль/см3,
kR имеет размерность см61моль2-сек.
Для бинарной смеси атомов и молекул сумма концентраций
следовательно,
= ^; [А2] = Ш. =
[В] = [А] + [А2] =
(ПИ-24)
причем сА = а, см = 1 — а. Внося соотношения (Ш-1-24) в (Ш-1-23),
получим зависимость для скорости рекомбинации
6/ 2 rR=№) =kR(-£-Y аЦ1 + а). (Ш-1-25)
кнсм6/моль2-сек R x Jj '" R{~ l v ;
W20
п19
\
\
\
\
Рассмотрим простую схему реакции
диссоциации А2 + В->А + А+В, отобра-
hD
ю1
W1
2 3 4 5 6 7 8-1O~3T°K
Рис. III-1-9. Изменение
коэффициента скорости рекомбинации
в воздухе в зависимости от
температуры
2 + В>А + А+В
№ hD
жающую процесс распада молекулы в
результате парных соударений. Здесь kD— константа
скорости диссоциации, В — вторая частица,
участвующая в парном столкновении с
молекулой и передающая ей энергию диссоциации,
В соответствии с принятой схемой
скорость диссоциации
Подставляя соотношения (Ш-1-25) и
(Ш-1-26) в (Ш-1-22), получим
где Kv =
(Ш-1-22')
Для равновесных процессов эта величина
определяется как константа
термодинамического равновесия. При некоторых
предпосылках константа справедлива и для
неравновесных реакций.
Имея это в виду и полагая в (111-1-22')
daldt = 0, найдем в равновесном случае
значение Кр = 2а!/(1 ~ а*), где ае —
равновесная степень диссоциации. Используя (Ш-1-10),
получим
2а2 9пл
10
Рис. III-1-10. Кривые времени
релаксации при атмосферном
давлении:
?. 2 — экспериментальные времена
колебательной релаксации
соответственно О2 и N2; 3—4 — расчетные
времена релаксации для
диссоциации соответственно О2 и N2
Подставляя это выражение в (Ш-1-22'),
найдем
где
(Ш-1-28)
Как видно из (III-1-27), для исследования
неравновесных течений важно знать
коэффициент скорости рекомбинации. Этого достаточно для определения скорости
диссоциации, так как можно воспользоваться константой термодинамического
равновесия.
На рис. Ш-1-9 представлены осредненные экспериментальные
значения коэффициента скорости рекомбинации, полученные для давления при-
Основные соотношения в теории газовых течений 101
близительно в одну атмосферу. Предполагается, что эти значения
соответствуют нижнему пределу скорости рекомбинации.
Время релаксации. Уравнение (Ш-1-27) можно несколько
преобразовать. С этой целью используем понятие о константе равновесия, пригодное
для условий неравновесного и равновесного течений. Тогда отношение
e-i/f/p можно заменить величиной а?/(1 —ае), что после подстановки
в (Ш-1-27) даст
~ = ае-а, (111-1-27')
dx
где
Параметр tD представляет собой время релаксации. В его определении
заключается важнейшая задача физики релаксационных процессов.
Некоторые данные о диссоциационном времени релаксации для кислорода и азота
экспериментально получены в ударных трубах (рис. Ш-1-10).
Анализ показывает, что вычисленные времена релаксации для
диссоциации приблизительно на порядок меньше, чем для рекомбинации. Поэтому
для оценки эффектов релаксации надежнее пользоваться временем для
рекомбинации, хотя грубую оценку можно сделать и по времени для прямой
реакции.
То же можно сказать о колебательной релаксации, имея в виду, что
в реальных процессах время возбуждения до заданной температуры меньше
времени затухания колебаний при обратном процессе, начинающимся от той
же температуры.
Для оценки времени релаксации для рекомбинации кислорода или
азота можно воспользоваться приближенным выражением
+ ? 2 <ш-1-30)
где «О» обозначает конечные значения параметров.
Из (Ш-1-30) видно, что чем больше начальные плотность и температура,
тем быстрее протекает реакция и, следовательно, меньше время релаксации.
Эта же формула указывает на уменьшение tD с увеличением давления, что
подтверждается графиками на рис. Ш-1-11. Видно, что увеличение
давления на три порядка обусловливает уменьшение времени релаксации
приблизительно в десять раз (давление р на графике отнесено к атмосферному р<х>з
на уровне моря). Исследования показали, что времена релаксации для
диссоциации в воздухе меньше, чем в чистом азоте или кислороде.
Равновесные процессы. Как с качественной, так и с количественной
стороны, равновесные течения изучены лучше, чем неравновесные.
Вследствие неодинаковости времени релаксации для разных уровней
возбуждения, в одной и той же области потока по одним степеням свободы
может установиться равновесие, в то время как по другим будут наблюдаться
релаксационные явления.
Приближенная модель процесса может быть построена на основе
предположения, что равновесие достигается последовательно по степеням
свободы, т. е. если какая-либо степень свободы находится в стадии
установления равновесия, то все «низшие» степени свободы полностью возбуждены,
а «высшие» не возбуждены вовсе.
Последовательность наступления равновесия с ростом температуры
может быть представлена по степеням свободы в следующем порядке:
поступательные, вращательные и колебательные степени, диссоциация,
возбуждение электронных уровней, ионизация. При рассмотрении, например,
102
Глава III
, сек
области установления равновесия колебаний первые две степени свободы
можно считать полностью возбужденными, а все последующие — не
возбужденными.
Такая схема неприемлема для некоторых газов, в частности для азота
при высоких температурах, так как ионизация начинается до того, как
полностью произойдет диссоциация. Это объясняется
тем, что энергии диссоциации и ионизации азота
различаются между собой только в полтора раза.
Аналогичное явление наблюдается в воздухе при
Ю~*[\—I 1 1 1 сравнительно небольших температурах. На рис.
Ш-1-11 видно, что при температурах, больших
3200° К, время релаксации для диссоциации
кислорода меньше, чем время установления колебаний
азота. Следовательно, равновесие при диссоциации
кислорода будет достигнуто до того, как
установятся колебания в азоте.
Диффузионные явления
в пограничном слое
\
\
Та-1-
\
if
ч
-2
Т°К
Рис. Ш-1-11. Время
релаксации для
диссоциации кислорода
Диффузионный поток вещества и перенос тепла.
При изучении явлений, связанных с обтеканием тел
высокоскоростным потоком, приходится иметь дело
с неравномерным нагревом, приводящим к
пространственному распределению как температур, так и
состава газа. Возникающие градиенты температур вызывают поток тепла путем
молекулярной теплопроводности. А наличие переменной концентрации
атомов продиссоциированных молекул приводит к передаче энергии за счет
диффузии атомов, выделяющих тепло при рекомбинации в молекулы. Из
этих основных составляющих формируется тепловой поток к поверхности.
Диффундирующие компоненты газа, перенося энтальпию, являются
своеобразными источниками потока энергии, который может даже
превысить при определенных условиях поток за счет теплопроводности.
Тепловой поток, возникающий при рекомбинации диффундирующих
атомов какой-либо компоненты воздуха,
?д«(»Д| (Ш-1-31)
где Q — диффузионный поток вещества; iR— теплота рекомбинации атомов
в молекулы, величина которой, очевидно, равна теплоте диссоциации молекул
компоненты воздуха.
Будем рассматривать в дальнейшем простую бинарную смесь атомов
и молекул, характеризующуюся коэффициентом бинарной диффузии D
[м2/сек].
Приняв, что с [кГ/кГ] обозначает массовую концентрацию атомарной
компоненты, можно определить ее диффузионный поток поперек
пограничного слоя
ду
(Ш-1-32)
Влияние скорости реакции в газовой среде. Диффузионная
теплопередача зависит от скорости реакций в пограничном слое. В общем
случае, характеризующемся конечными значениями скорости, рекомбинация
частично протекает в самой газовой среде, а оставшиеся атомы
диффундируют к стенке. Таким образом, тепло выделяется не только в толще
пограничного слоя, но и на поверхности тела.
Основные соотношения в теории газовых течений 203
Для анализа этого процесса имеет большое значение исследование двух
предельных случаев. Первый из них характеризуется бесконечно большой
скоростью рекомбинации, так что в каждой точке потока устанавливается
термодинамическое равновесие и диффузия вещества к стенке отсутствует.
Химическая реакция и, следовательно, тепловыделение происходят в самом
пограничном слое. При этом диффузионная теплопередача обусловлена
наличием профиля равновесных концентраций.
В практических случаях условия течения, близкие к такому
гипотетическому «равновесному» пограничному слою, будут иметь место, когда
скорость диффузии пренебрежимо мала по сравнению со скоростью
диссоциации и рекомбинации (а в случае ионизации — также и электронных
реакций).
Во втором предельном случае рекомбинация протекает бесконечно
медленно, т. е. химические реакции не происходят. Следовательно, несмотря
на то, что диффузия атомов возникает, однако рекомбинация отсутствует
и энергия в пограничном слое не выделяется. Практически это может иметь
место в потоке, если время химической реакции велико по сравнению с
характерным временем движения частиц. Такие потоки называются
«замороженными».
В замороженном течении атомы, образующиеся при диссоциации,
диффундируют по направлению к холодной стенке, где затем рекомбинируют.
Освобождающаяся при этом энергия зависит от каталитических свойств
стенки, проявляющихся в различных значениях скорости каталитической
рекомбинации.
Рекомбинация на стенке. Каталитический эффект стенки в общем
случае характеризуется конечной скоростью каталитической реакции
рекомбинации. В наибольшей мере свойства стенки как катализатора проявляются
в предельном теоретическом случае бесконечно быстрой рекомбинации.
В другом предельном случае, когда скорость бесконечно мала, стенка
является некаталитической. В общем случае конечной скорости тепло,
выделяющееся на стенке, определяется потоком вещества в установившемся
режиме
где кСТ — константа скорости каталитической реакции на стенке;
m — показатель степени, учитывающий характер каталитической
реакции (1</тг<2). В частном и наиболее простом случае
реакции первого порядка можно принять m — 1.
В соответствии с законом сохранения массы (пренебрегая термической
диффузией)
Из (Ш-1-33) следует, что в предельном случае диффузии,
соответствующем бесконечно большой скорости рекомбинации (кст ~ оо), атомы
достигают стенки даже при условии нулевой концентрации на стенке (сст = 0).
В случае некаталитической стенки (кст = 0) поток атомов равен нулю, так
как концентрация всегда конечна. Следовательно, поток тепла за счет
диффузии равен нулю. В первом предельном случае катализ происходит
бесконечно быстро, во втором, наоборот, с бесконечно малой скоростью.
Условия существования равновесного и «замороженного» потока. Эти
условия определяются, с одной стороны, средним временем £ДИф диффузии
атомов к стенке и с другой — средним временем £хим жизни этого атома.
Если £диф значительно больше £Хим> т0 химическая реакция произойдет
раньше, чем атом достигнет стенки, и в пограничном слое возникнет местное
204 Глава III
термодинамическое равновесие. Таким образом, условие существования
равновесия будет £ДИф = £ДИф/£хим > 1. Относительное время £ДИф
называется параметром скорости рекомбинации.
При малом времени диффузии (£ДИф <С 1) реакция протекает настолько
медленно, что практически рекомбинация начинается лишь на стенке и,
следовательно, газ течет как замороженный.
Время диффузии £ДИф можно вычислить как время перемещения частиц
к стенке через пограничный слой. Что касается времени жизни атома, то
при его оценке возникают трудности, обусловленные недостаточной
изученностью химических процессов рекомбинации. Приближенно £хим можно
определить по формуле (Ш-1-30), в которой параметры То, р0 определяются
для недиссоциирующей среды, а Г, р — для равновесно диссоциирующего
газа на внешней границе пограничного слоя. Наряду с этим для вычисления
относительного времени диффузии можно пользоваться выражением
где i?0— универсальная газовая постоянная;
pfQ, Т'о — параметры газа в точке полного торможения обтекаемого тела;
X — градиент скорости в этой точке (он определяется ниже);
kt — константа скорости рекомбинации.
О константе скорости рекомбинации имеется весьма мало данных.
Известно, в частности, что для рекомбинации кислорода при Т = 300° К
произведение /^Г"1»5 = 5-Ю4 см6/молъ2-сек.
Безразмерный параметр £ДИф является критерием подобия процессов,
которые характеризуются скоростью рекомбинации, а также временем
диффузии атомов через пограничный слой.
Формула (Ш-1-34) показывает, что замороженный поток существует
на больших высотах и при низких скоростях полета. При этом
замораживание может, по-видимому, сдерживаться возрастающими с подъемом на
высоту скоростями рекомбинации.
До сих пор рассматривались случаи, когда газ находится на внешней
границе пограничного слоя в термодинамическом равновесии. Однако в
разреженной среде вследствие больших времен диссоциационной релаксации
частицы при подходе к границе слоя могут не находиться в состоянии
равновесия. Это усложняет анализ. Можно упростить исследование, если
предположить, что при низкой плотности и небольших скоростях диссоциация будет
задерживаться и, следовательно, возникнут условия «замороженного» течения.
Применяя в этом случае стенку из некаталитических материалов, мошна
задержать увеличение теплового потока. Некоторый рост его произойдет
за счет передачи энергии молекулами, не успевшими продиссоциировать.
Критерий каталитического процесса. В качестве этого критерия
используется так называемая рекомбинационная (или каталитическая) способность
у = Nr/N, где N — полное число атомов, падающих на единичную
площадку в единицу времени; Nr — часть рекомбинирующих атомов.
В соответствии с (III-1-33) при т = 1 число атомов Nr = QcJniA =
= kCTcCTpCT/mA. Общее число атомов N = рА (2птАкТС1:)~1/2. Поскольку рА =
= пАкТст и сстрст = ^А^А5 то рекомбинационная. способность
v-^-к (2тспгА\1/2
У~ N -^{ кТст ) •
На рис. III-1-12 приведены экспериментальные значения каталитической
способности ряда материалов. На этом же графике нанесены линии
постоянных кст. Изучение рекомбинации кислорода показало, что каталитическая
способность исследованных материалов настолько низка, что их использо-
Основные соотношения в теории газовых течений
105
вание в качестве покрытий может уменьшить теплопередачу. При этом
больший эффект достигается от применения стекла, меньший — от хлоридов,
обладающих большей зависимостью каталитической способности от
температуры.
Рекомбинация атомарного азота изучалась на различных
металлических и неметаллических поверхностях. Выяснилось, что большинство
металлов оказывает сильное
каталитическое воздействие на
атомарный азот. Неметаллические
материалы обладают обратным
свойством, что обусловливает
низкую рекомбинационную
способность азота. В частности,
на стекле измеренная при
парциальном давлении азота
10"3 атм величина у = 3-10~5.
Исследования
рекомбинации чистых азота и кислорода
имеют важное практическое
значение, так как позволяют
оценить ожидаемые
каталитические эффекты при изучении
теплопередачи воздуха. При
этом можно предположить, что
рекомбинация воздушной смеси ускоряется вследствие промежуточных
реакций между кислородом и азотом, поэтому увеличивается суммарная
каталитическая способность и, как следствие, возрастает теплопередача.
300
Рис.
Каталитическая способность
некоторых материалов
§ III-2- Система основных
уравнений
Задача об обтекании гела содержит ряд неизвестных. Если
рассматривать в качестве основных четыре неизвестных, а именно скорость, давление,
плотность и температуру, то для их отыскания необходимо иметь систему
из четырех независимых уравнений (одного векторного и трех скалярных).
При этом часто оказывается целесообразным перейти от этого числа
неизвестных к большему и тогда соответственно возрастает число
уравнений системы. Так, например, вместо полной скорости обычно отыскивают
ее составляющие по осям системы координат, наиболее удобной для решения
данной задачи. В общем случае таких составляющих будет три и,
следовательно, число уравнений системы возрастет до шести. Увеличение числа
уравнений достигается тем, что вместо одного уравнения движения в
векторной форме записывают три уравнения в проекциях на соответствующие оси
координат.
Наряду с основными неизвестными в уравнения обычно входят и
другие параметры, такие, как напряжение трения, энтальпия, энтропия,
удельные теплоемкости, скорость звука, тепловой поток и др. Тогда система
уравнений дополняется соответствующими уравнениями, связывающими
между собой новые неизвестные.
Получаемая система уравнений отражает в наиболее общей форме
важнейшие закономерности газовых течений. При этом их вывод
базируется на совокупности предпосылок, составляющих определенную
физическую схему рассматриваемого течения.
106
Глава III
Схематизация потока и процессов, происходящих в нем, лежит в основе
любой аэродинамической задачи, так как позволяет максимально упростить
уравнения, причем схема может быть более или менее сложной, в
соответствии с тем, какой характер имеет само течение.
Одна из таких физических схем основывается на теории Прандтля,
согласно которой поток около обтекаемого тела рассматривается невязким
(свободный поток) вне тонкого пограничного слоя и вязким внутри него.
Эта схема позволяет упростить уравнения, при помощи которых изучаются
явления как в той, так и в другой частях потока.
Таким образом, рассматривая частные случаи движения, можно добиться
упрощения уравнений, описывающих эти течения.
Ниже рассматривается система уравнений в наиболее общем виде,
а также приводятся ее частные случаи, соответствующие свободному потоку
и течению в пограничном слое. При этом в каждом из частных случаев даются
уравнения, отображающие различные специфические особенности
(физические схемы) реальных потоков.
Уравнение движения
Общий вид уравнения движения. Рассмотрим первое уравнение системы,
а именно уравнение движения жидкой частицы. Вывод его основан на
принципе Даламбера. Применив этот принцип к частице жидкости в виде эле-
р dudz
Рис. 111-2-1. К выводу уравнения движения газа:
т — объем газа; S — поверхность. Масса газа в объеме т равна С p dx
ментарного параллелепипеда (рис. Ш-2-1) при условии, что массовые силы
не учитываются, можно получить уравнение движения в векторной форме [14]
dt p V
(Ш-2-1)
p \ dz l dy l д.
Векторы поверхностных сил рХ1 ру, pz можно представить в виде
Рк = Pkxh + Pkyh + Pkzh, (III-2-2)
где Pkx, Pkyi Pkz — проекции этих векторов на оси х, у, z; к принимает
последовательные значения х, z/, z;
Ч» hi h—единичные векторы по соответствующим осям.
Основные соотношения в теории газовых течений 107
Вектор скорости
где VX1 Vy, Vz — проекции этого вектора на оси координат.
От (Ш-2-1) в векторной форме можно перейти к уравнениям Навье —
Стокса:
dvx _ 1 dp , v d ,д. rT7,
dt p dx 3 dx
dVy 1 dp v d
dt p dz/ 3 dz/
dVz 1 dp . v d
(Ш-2-1')
где
dx ' dy ' dz
dVx __ dVx v dVx v dVx у dVx
Эти уравнения для физической схемы пограничного слоя,
предложенной Прандтлем, преобразуются в так называемые уравнения Прандтля для
пограничного слоя, а вне его — в уравнения Эйлера для невязкого
(идеального) газа.
Уравнения движения идеальной среды. Широкий класс задач связан
с расчетом распределения параметров потока около различных тел в
условиях обтекания невязким (идеальным) газом. Уравнение движения
идеального газа можно получить из (Ш-2-1'), отбросив в нем члены в правой
части, учитывающие влияние вязкости. В результате найдем
*L= -Igradp, (III-2-3)
где градиент давления
-, dp т . dp т , dp т /ттт о /\
grad р = ——i\ -\——12 H—^^з* (111-2-4)
Это уравнение называется уравнением Эйлера. Учитывая (Ш-2-4) для
градиента давления в декартовых координатах, уравнение Эйлера можно
написать в развернутой форме
(III-2-5)
Эти уравнения применяются для исследования пространственного
(трехмерного) неустановившегося обтекания тел. В результате их решения
получают распределение так называемых невязких газодинамических параметров.
При изучении двухмерного неустановившегося потока (например, при
обтекании профилей) следует применить два уравнения системы (Ш-2-5).
Если движение установившееся, то частные производные по времени равны
нулю.
При исследовании обтекания тел вращения удобно применять
уравнение Эйлера в цилиндрических и сферических координатах.
wx
dt
dVy
dt
dt
+vx-
+ vx
dVx
dx
dVz
dx
dvy
1 V dVz I
1 l* dy '
т/ dVx
z dz
T z dz
* z dz
1
P
1
P
1
P
dp
dx
dp
dp
dz
108
Глава III
Если х, г, у — цилиндрические координаты (рис. Ш-2-2), то градиент
давления
др т dp т . 1 dp -~.
~dx~li "• ~dr~ *2 ' 7" ~^у" *3'
Тогда, обозначив составляющие скорости в цилиндрических
координатах через Fx, Fr, Fv, уравнение движения (Ш-2-3) в проекциях на
координатные оси получим в виде:
ОТГ
■V,-
dt
дх
dt
дг
ду
dt
дх
дг
ду
ду
v у
-^•=—-^■5 (I"-2"6)'
Эти уравнения применяются для исследования неустановившегося
обтекания тел вращения произвольной формы под углом атаки
(несимметричное обтекание).
Система упростится при осесимметричном обтекании, когда угол атаки
равен нулю (пространственный двухмерный поток), так как выпадут
производные по у и состав-
ляющая Vy.
Из (Ш-2-6) следует
частный вид уравнения
движения,
соответствующего чисто радиальному
потоку,
dVr v dVr __ 1 dp
(III-2-7)
**x
Рис. Ш-2-2. Составляющие местной скорости потока
в цилиндрических координатах
который применяется для
исследования
нестационарного движения газа за
цилиндрической ударной
волной 1. Эта волна
возникает при расширении
поршня 2, который можно
рассматривать как
некоторую непроницаемую
подвижную поверхность
(рис. Ш-2-3). Ниже будет
показано, что между
высокоскоростным потоком
около тела вращения и
течением газа при его
вытеснении поршнем
существует аналогия, которая
используется при решении
задач сверхзвуковой
аэродинамики.
Рассмотрим теперь уравнение движения в сферических координатах
г, О, я|) (рис. Ш-2-4), которое применяется, в частности, для исследования
сверхзвукового обтекания конусов. Чтобы получить это уравнение, напишем
prdQ
Рис. II1-2-3. К выводу уравнений движения и
неразрывности для течений газа за цилиндрической ударной
волной
^Основные соотношения в теории газовых течений
109
^выражение для градиента давления в сферических координатах
\ др т
Обозначив, далее, через Fr, Fe, F^, составляющие скорости по
соответствующим осям выбранной системы координат^ получим (Ш-2-3) в
развернутой форме:
OVr+y^dVr
dVr
dt
dt
dt
dr
+
dVr
r 56 ' rsin0 д'ф
+ Уг^- + -^~
dr
r dr
г дв
r sin 6
p dr '
i^ctge = l dp .
r pr ^e '
r ae ' rsini
• + ■
dp
» sin @
(III-2-8)
При симметричном обтекании параметры течения не зависят от
переменной гр, поэтому из (Ш-2-8) выпадут производные по if), а также
^составляющая F^.
Наряду с рассмотренными
системами распространена
нормальная (или естественная) система
координат (рис. Ш-2-5). В случае
плоского течения или при осевой
симметрии потока одна из осей
этой системы совпадает с
касательной к дуге s линии тока,
другая — направлена по нормали п
к линии тока в данной точке.
Уравнения движения относительно
осей нормальной системы
координат можно получить, если
воспользоваться (Ш-2-3) и заменить градиент давления величиной
Рис. II1-2-4. Составляющие местной скорости
потока в сферических координатах
дп
вектор полного ускорения—значением
где касательная составляющая ускорения при установившемся движении
W8 = V8(dVs/ds), а нормальная составляющая Wn = Vl (d$/ds), причем |5 —
угол наклона линии тока. Следовательно, уравнения движения будут иметь
вид
J
ds
L
ds
p ds '
p dn
В теории пограничного слоя обычно применяется криволинейная система
координат. Такую же систему оказалось удобным применить и для
изучения течения в тонком слое невязкого газа между ударной волной и криво-
110
Глава III
линейной поверхностью при очень больших скоростях полета. Положение
произвольной точки М в этой системе (рис. Ш-2-6) определяется
расстояниями у по нормали к поверхности и х вдоль образующей.
я?,
Рис. Ш-2-5. Нормальная • Рис. Ш-2-6. Криволинейная система
(естественная) система ко- координат
ординат:
1 » линия тока
При установившемся течении около плоского контура или
симметричном обтекании тела вращения уравнения движения
(Ш-2-10)
где R — радиус кривизны контура.
Уравнение движения в пограничном слое. Схема вывода обобщенного
уравнения движения для двухмерного пространственного осесимметричного
vx
i + y/R
vx
l + y/R
дх '
дх '
T/ dVx
У ду
dVv
vxvy
R + y
R + y
l
i + y/R
1 dp
P ay •
1 dp
p d.z '
& • (2Strf)dydx
Рис. II1-2-7. К выводу уравнения движения газа в
пограничном слое
и плоского пограничного слоя воспроизведена на рис. Ш-2-7. Важное
условие, положенное в основу вывода, заключено в малости толщины
пограничного слоя б по сравнению с линейными размерами тела (если характерный
линейный размер L, то условие малости б будет ЫЬ < 1). При этом др/ду = О,
т. е. давление внутри пограничного слоя в различных точках,
расположенных на нормали к контуру тела, не меняется и равно значению давления
Основные соотношения в теории газовых течений 111
на границе слоя. Вследствие малости толщины пограничного слоя можно
также пренебречь кориолисовым ускорением. Тогда уравнение движения
в слое будет
т/ дух л-v dVx 1 др \ — d(r*x)
где 8 = 0 для плоского и 8=1 для осесимметричного пограничного слоя.
Это уравнение пригодно для исследования как ламинарного, так
и турбулентного пограничного слоя, в котором параметры,
характеризующие течение в слое, принимаются осредненными, и пульсационные
значения параметров исключаются. В соответствии с этим в (Ш-2-11) значения
Vx, Vy, p, p надо принимать осредненными, а напряжение трения
определять из выражения т= (|ы + М<т) (dVJdy). В этом выражении |ыт
—коэффициент турбулентной вязкости (в отличие от \х — коэффициента обычной
молекулярной вязкости в ламинарном пограничном слое).
В ламинарном пограничном слое jiT = 0, напряжение трения т = |1Х
X (dVJdy) и уравнение движения перепишется так:
х дх ' у ду р дх г£р ду у ду
В общем случае, когда газ испытывает физико-химические
превращения, коэффициент {х меняется поперек пограничного слоя. Когда эти
превращения отсутствуют или они малы, можно принять \х = const. При
исследовании пограничного слоя около плоского контура применяются
уравнения (Ш-2-11) и (Ш-2-12), из которых следует исключить радиус г.
Уравнение неразрывности
Формы уравнения неразрывности. Это уравнение относится к числу
основных уравнений аэродинамики и используется совместно с уравнением
движения для исследования обтекания тел.
В математической форме оно отражает условие, что если газ протекает
через некоторый фиксированный объем т без образования пустот и
разрывов, то полная масса газа \ p(Vn)dS, протекающая за единицу времени
(S)
через поверхность S, ограничивающую этот объем, равна изменению
секундной массы в рассматриваемом объеме— \ др/dtdx (п — внешняя нормаль
к поверхности). В соответствии с этим получаем уравнение
которое называется уравнением неразрывности. Полностью его вывод дан
в работе [2]. Внося в (Ш-2-13) выражения для div (pF) = д (pVx)/dx +
+ d(pVy)/dy + d(pVz)/dz, получим:
или, учитывая, что dp/dt = dp/dt + Vx(dp/dx) + Vy(dp/dy) + Vz(dp/dz), будем
иметь
Глава III
Чтобы получить уравнение неразрывности в цилиндрических
координатах, воспользуемся выражением
дх ' дг ' г ду
Тогда уравнение неразрывности
Из него следует частный вид
^ + ^ = 0. (Ш-2-16)
Это уравнение применяется для исследования нестационарного течения
газа за цилиндрической волной (см. рис. Ш-2-3).
Приведем уравнение неразрывности в сферических координатах. С этой
целью воспользуемся выражением для дивергенции
г* дг "^ г sine дв ^ г sine дЦ "
После подстановки этого выражения в (Ш-2-13) получим
др 1 д (Pr2Fr) I ^(pFesine) ! a (pFj)
Г^Г + Т ^ +sln~e ae Hsln^ дф =и-
Уравнение неразрывности для плоского или осесимметричного течения
получается соответственно из уравнения (Ш-2-14) или (Ш-2-15):
= °. (Ш-2-18)
в котором 8 = 0 для плоского потока и 8 = 1 для пространственного
двухмерного течения (y = r, Vy = Vr).
Уравнение неразрывности пространственного двухмерного потока в
сферических координатах получается из (Ш-2-17), если в нем опустить
четвертый член в левой части.
Уравнение неразрывности для установившегося течения в нормальной
системе координат (см. рис. Ш-2-5) получается как условие сохранения
расхода при протекании газа между двумя близкими поверхностями тока
(пространственный двухмерный поток) или линиями тока (плоский
двухмерный поток).
Уравнение неразрывности
|Р + !££ + dl*v° + llEl 8 = о, (Ш-2-19)
дп l ds l ds l у ч '
где 8 = 0 для плоского потока и 8 = 1 для пространственного течения.
Если рассмотреть криволинейную систему координат (см. рис. Ш-2-6),
то
д (рг*Ух) д[рг*Уу{1+у/В)] = а (Ш-2-20)
дх ду ' ^ '
При исследовании пограничного слоя это уравнение можно упростить,
имея в виду, что толщина слоя мала. Пренебрегая величиной y/R по
сравнению с единицей, найдем
Чх) НРг°Уу)
' ду v '
дх ' ду
Преобразование уравнения неразрывности. На практике часто
применяют уравнение, которое получают из уравнения неразрывности при исклю-
Основные соотношения в теории газовых течений
213
чении из него плотности с помощью уравнения движения. При этом может
быть использована любая система координат.
Если рассматривать потенциальное неустановившееся течение в
декартовых координатах, то преобразованное уравнение неразрывности будет
представлять собой уравнение в декартовых координатах для потенциала
скоростей ф [14]:
(Ш-2-22)
где производные ц>х — ду/дх, Ц)хх = д2Ц)/дх21 (pxt = d2y/dxdt, qtt — d2q)/dt2 и т. д.
Аналогичное уравнение для потенциала ср в цилиндрических
координатах имеет вид
г2
4>у
2 Фгуфгфу 2 фхуфкфу
,
Фг
, ф7 \ ZVxVxt 2фгФг^ 2фуФу^ уи ^Q /ттт 2„23}
' а2г2 / а2 а2 а2г2 а2 • \ " " /
а2 г
Из (Ш-2-22) получается уравнение, которое используется для
исследования двухмерного неустановившегося потенциального течения (плоского
или пространственного):
I 2П 2 2
Ффф Фф
(Ш-2-24)
При исследовании установившегося обтекания из уравнений
исключаются все члены, содержащие частные производные по времени.
Установившееся пространственное потенциальное обтекание можно
изучать при помощи уравнения для потенциала скоростей в сферических
координатах
1а *ГЛ m i (\ ^ \ Фее » 1а У% \
\1~~ а* ) ф7Г"^ I1 а*г*) г2 "^ V Л-2 sin2 9 J
г2 sin2 9
a2r2 sin2 9
/ Ф2е^п29 + Ф|ч Фг /
V a2r2sin29 / г "^ V
а2г2 sin2 9
9ectg9 A
r2 ~U*
(Ш-2-25)
Для пространственного двухмерного течения (Ш-2-25) принимает более
простой вид вследствие того, что производные по of) равны нулю.
Приведенные уравнения для потенциала скоростей являются основными
в аэродинамике изэнтропических (безвихревых) течений, отличительным
свойством которых является постоянство энтропии во всей области потока.
Если не учитывать влияния вязкости, то таким свойством обладает
дозвуковое возмущенное течение около обтекаемого тела. Изэнтропическим
будет и сверхзвуковое возмущенное течение, если оно находится за
прямолинейным скачком уплотнения, так как энтропия за ним всюду одинакова.
В случае небольших чисел Моо поток за криволинейным скачком
практически мало отличается от изэнтропического, поэтому для его
изучения можно применять уравнение для потенциала скоростей. Решение этого
уравнения дает лучшие результаты по мере того, как обтекаемое тело
становится все более тонким.
8-114
114 Глава III
При больших числах Моо сверхзвуковое обтекание существенно зависит
от вихревого характера движения газа за криволинейным скачком
уплотнения, поэтому при его исследовании следует исходить из уравнения
неразрывности, преобразованного с помощью уравнения движения
в общем виде.
Укажем вид этого уравнения для различных систем координат, имея
в виду случай установившегося двухмерного течения.
Декартовы и цилиндрические координаты:
Сферические координаты:
(Ш-2-27)
~~ a* ) H7 W \д^^ гЙвГг I1 a4 00 ■+*~Т~
Нормальные (естественные) координаты:
Линеаризация уравнений. Приведенные выше дифференциальные
уравнения являются нелинейными и относятся к общему случаю
возмущенного течения газа, параметры которого могут значительно отличаться
от соответствующих параметров невозмущенного потока. В задачах
обтекания эти уравнения используются для изучения возмущенного потока в тех
случаях, когда форма обтекаемых тел произвольная и обтекание происходит
под любым углом атаки.
Во многих случаях, представляющих практический интерес,
обтекаемые тела являются тонкими, а углы атаки — небольшими, поэтому
возмущенное течение около таких тел мало отличается от невозмущенного. Для
слабовозмущенного течения можно линеаризовать дифференциальные
уравнения.
В соответствии с определением слабовозмущенного, или
линеаризованного, потока его параметры можно выразить в следующем виде:
F = Foo + F, а^аоо + а'; р = роо + р/; р = Роо + р'; 5г = 5Оо + 5/, (Ш-2-29)
где индексом «оо» обозначены параметры невозмущенного течения, а
штрихом— малые добавочные величины параметров, возникающие за счет
возмущения.
Из выражения S = SooJrS/ следует, что линеаризованный поток
характеризуется новой энтропией. Однако, как показывают исследования,
добавочная величина *S" настолько мала, что ею можно пренебречь, и
поэтому линеаризованный поток можно рассматривать изэнтропическим. В
соответствии с этим следует считать, что перед тонким заостренным телом
криволинейный скачок уплотнения вырождается в волну возмущения
бесконечно малой интенсивности.
Линеаризованный поток можно охарактеризовать потенциальной
функцией cp^cpoo-fq/, складывающейся из потенциала ср<х> невозмущенного
течения и добавочного потенциала q/ возмущенного потока (потенциала
возмущения), являющегося малой величиной.
Линеаризованные уравнения, получающиеся в результате
преобразования (Ш-2-22) и (Ш-2-23) с учетом (Ш-2-29) и выражения для q> = ф«> + q/,
имеют следующий вид [51]:
(1 - ML) Ф;* + ц'уу + q'zz-~4xt--^L= 0;
(1-му ф;х+ф;,+^+^--^<ы -$-=о. (ш-2-31)
Основные соотношения в теории газовых течений 215
В результате упрощения (Ш-2-24) при условии, что из него
исключены производные по времени, получают линеаризованное уравнение для
установившегося двухмерного (плоского L или пространственного) течения
(1-МУч4с + ф;у + 8-^ = 0. (Ш-2-32)
Уравнение для функции тока. }Для исследования неизэнтропических
течений вместо (Ш-2-26) или (Ш-2-27) более удобно применять уравнения,
преобразованные к переменной i|), называемой функцией шока.
Для преобразования (Ш-2-26) используют соотношения
для преобразования (Ш-2-27) — зависимости
U = - rWr sin 9 -£- ; -^ = rWe sin 9 -£-, (Ш-2-34)
dv po or р0 '
где ро — плотность при полном изэнтропическом* торможении.
В дальнейшем для исследования обтекания тел сверхзвуковым
потоком будем использовать (Ш-2-26), преобразованное к функции тока я|х
Вид этого уравнения [58]
fe-1
(Ш-2-35)
где производные ^хх = д2^/дх2, ^ху = д2^/дхду, ^уУ = д2^/ду21 V=V/V
(F а орос) фя
где производные ^хх = д2^/дх2, ^ху = д
(Fmax — максимальная скорость); функци
m3iX
Здесь Ро — давление при полном изэнтропическом торможении.
Если вдоль скачка давление торможения не меняется, то dpo/dty = O
и, следовательно, /(я|)) = 0. В этом случае (Ш-2-35) определяет функцию
тока для потенциального (изэнтропического) течения.
В области за криволинейным скачком уплотнения давление
торможения меняется при переходе от одной линии тока к другой, и, понятно,
что / (\|)) =^0. Следовательно, (Ш-2-35) описывает неизэнтропический
(вихревой) поток.
Так как изменение давления торможения поперек линий тока
обусловлено изменением энтропии S, то (Ш-2-35) можно преобразовать к виду,
содержащему энтропию, если воспользоваться уравнением
J_ dRL - k dS
р0 Ар - (fc-l)Cp*l>-
Уравнение диффузии
Диффузионные процессы, протекающие в пограничном слое, зависят
от распределения концентрации компонентов смеси. Одним из соотношений
для его определения является уравнение диффузии.
Как и уравнение неразрывности, оно также является уравнением
сохранения массы с той особенностью, что выражает условие сохранения
диффундирующей компоненты смеси.
8*
116 Глава III
Предположим, что химических реакций не происходит и,
следовательно, скорость Wt образования атомов или молекул в результате
диссоциации или рекомбинации равна нулю. Тогда, пренебрегая диффузионным
потоком в направлении оси х, а также тепловой диффузией, можно
получить уравнение неразрывности для i-й компоненты смеси (или, как его
называют, уравнение диффузии) из уравнения (Ш-2-21), если в нем
заменить величину preVx на preVxCi, а выражение preVy~ на рггУусь — Qu
где Qi — диффузионный поток поперек пограничного слоя. Если же в газе
происходят химические реакции, сопровождающиеся появлением новых или
исчезновением старых частиц, то в правой части полученного уравнения
появится член rzWu учитывающий дополнительный расход компоненты.
Таким образом, уравнение диффузии i-ж компоненты будет
где величина коэффициента диффузии D считается одинаковой для каждой
пары диффундирующих компонент бинарной смеси.
Уравнение (III-2-38) упрощается, если состав газа «заморожен» и в нем,
следовательно, химические реакции не происходят. В этом случае надо
принять Wt=0.
В уравнении диффузии можно перейти от концентрации к степени
диссоциации а бинарной смеси. Для этого воспользуемся соотношениями
сА —ее, см = 1 —ее. В частности, для атомарной компоненты уравнение
неразрывности
д(Рг>ух*) »(pr%«)= a / 5,te> S]V 2_ж
дх ' ду ду V ду ) ' v '
Приведенные уравнения можно отнести и к ламинарному и к
турбулентному пограничному слою, В первом случае величина D является
коэффициентом ламинарной диффузии D = Вл и определяется как параметр
молекулярного переноса. Во втором случае коэффициент диффузии
складывается из коэффициентов ламинарной /?л и турбулентной DT диффузии,
т. е. вместо D в уравнение войдет величина Дт + £>т- Другие
газодинамические параметры, а также концентрацию следует рассматривать как
осредненные величины.
Уравнение количества
движения
Общий вид уравнения. При исследовании газовых течений иногда
удобно использовать уравнения движения в иной форме, которую можно
получить, рассматривая протекание газа через какую-либо фиксированную
поверхность или сечение.
Если в качестве такой поверхности взять поверхность
параллелепипеда, изображенного на рис. Ш-2-1, и применить теорему о количестве
движения, согласно которой изменение количества движения равно
импульсу внешних сил, то получим уравнение количества движения (уравнение
импульсов)
дрх. , ?Рх , дРг _ д (рУ) . д (рУхУ) , ПрУуУ) , д (pVzV)
дх "*■ ду Чг~дГ~~д1 г- дх 1 Yy ' Tz "
Установившееся движение идеального газа. Так как в этом случав
равна нулю частная производная по времени и отсутствуют силы, завися-
Основные соотношения в теории газовых течений 217
щие от вязкости, то (Ш-2-39) принимает вид
- grad Р = Ш& + д^Л + Щ11. (Ш-2-40)
Практический интерес представляет уравнение количества движения
газа в канале с постоянным сечением, т. е. для одномерного случая.
Из (Ш-2-40) следует, что в этих случаях dp/dx = — d (pV2x)/dx.
Проинтегрировав по х между двумя произвольными сечениями <<1» и «2», получим
Этот закон, а также другие два закона сохранения массы и энергии
лежат в основе теории газовых течений.
Уравнение количества движения для пограничного слоя. Рассмотрим
установившееся движение в двухмерном пограничном слое, в котором
выполняется условие малости его толщины.
В результате совместного преобразования уравнений движения
(Ш-2-11) и неразрывности (Ш-2-21), в которых радиус г принимают для
данного сечения слоя постоянной величиной, равной его значению г0
на стенке, получим следующее уравнение [57]:
(Ш-2-42)
где т0 — напряжение трения на стенке;
V&, Рб — скорость и плотность на границе слоя.
По своему физическому смыслу левая часть определяет изменение
количества движения некоторой массы газа, протекающей через сечение
пограничного слоя. Поэтому (Ш-2-42) называется уравнением количества
движения для пограничного слоя. Это уравнение называется также
интегральным соотношением Кармана.
Интегралы в левой части (Ш-2-42) представляют собой важнейшие
характеристики пограничного слоя
6*= \ (*~ш) *»* б**= \ w-, t1-^)dy- <ш-2-43)
о о
Параметры б* и б** называются соответственно толщиной вытеснения
и толщиной потери импульса. Первый из них характеризует уменьшение
секундного расхода, а второй — уменьшение количества движения (импульса)
при протекании газа через сечение пограничного слоя вследствие
торможения потока.
Уравнение энергии
Общий вид уравнения энергии. К числу основных уравнений
аэродинамики относится уравнение энергии. В математической форме оно
отражает закон сохранения энергии, согласно которому изменение кинетической
и внутренней энергии движущейся частицы равно работе внешних сил
плюс приток энергии за счет переноса тепла извне.
Будем считать, что работа совершается поверхностными силами,
возникающими от нормального давления и касательного напряжения. Что
касается переноса тепла, то он происходит, если не считать диффузионной
теплопроводности, путем молекулярной теплопроводности, излучения и
диффузии газов.
118 Глава III
В соответствии с этим уравнение энергии для массы газа,
заключенной в произвольном объеме т (см. рис. Ш-2-1), будет иметь вид
4г I p (lT + M) dx= I P-VdS+ I qTdS+ J edx + jj
CO (S) (S) (т) (S)
где grT, дд — соответственно потоки тепла путем теплопроводности и
диффузии в единицу времени и через единицу поверхности;
8 — поток от излучения единицы массы в единицу времени;
и — внутренняя энергия единицы массы газа;
рп—вектор поверхностной силы.
Уравнение энергии для пограничного слоя. Рассмотрим сначала
уравнение энергии для ламинарного пограничного слоя при наличии в нем
химических реакций и диффузии. Для этой цели воспользуемся общим
уравнением (Ш-2-44). Входящий в него тепловой поток от молекулярной
теплопроводности определяется по формуле qT == — X (дТ/дп).
Количество тепла, переносимое диффундирующими газами,
причем энтальпия i-ж компоненты
т
т . С" г . rjT ! /т \ Т. _!_ (j \.
о
где Cpi — удельная теплоемкость компоненты;
т
it= \ Cp^d^ — его энтальпия как совершенного газа;
о
(^хим)г—химическая энергия образования компоненты; ее величину
можно принять равной нулю для молекул.
Для атомов эту величину следует считать отрицательной и равной
(^хим)г=—Ir, где дл энергия диссоциации на единицу массы атомарных
компонент. Очевидно, энтальпия смеси газов £ = 2С^*.
г
Если отнести (Ш-2-44) к условиям течения в двухмерном пограничном
слое и использовать криволинейные координаты, то уравнение энергии
ду \ ду ) ^-^ 1 ду '
г
где для бинарной смеси атомов и молекул
di = (
причем средняя теплоемкость смеси
(Ср)ср = S (cp) i ci
г
Первый член справа представляет собой молекулярную составляющую
средней теплоемкости, второй — атомарную.
Уравнение (Ш-2-45) можно преобразовать, если использовать
выражение для энтальпии торможения fo = i + F2/2. В результате получим
Основные соотношения в теории газовых течений 219
Преобразуем (Ш-2-46) применительно к бинарной смеси двух
компонент, для которой сумма концентраций см + са — 1 и, следовательно, дсм/ду =
— —dcpjdy. Учтем, что так как энтальпия смеси £=2^с* и средняя
теплоемкость смеси (ср)ср = ]>] с% (ср)и то для бинарного состава
di = (cp)Cp dT + (ia—Ы) dc
(p)p A.
Отсюда можно найти частную производную дТ/ду. Подставляя ее
в (Ш-2-46) и используя уравнение неразрывности (Ш-2-21) для
преобразования правой части, получим
д (prBvxi0) , д (prsvyio) _ д (А^д1±\ ,
дх ' ду ду \ Рг ду ) ^
#)^] (Ш-2-47,
где Рг = [г (Ср)ср/А, — число Прандтля;
Sc = |ix/(pZ>) — число Шмидта.
Отношение этих чисел Pr/Sc = Le называется числом Льюиса — Семенова.
Эти параметры являются критериями переноса энергии. Число Рг
определяет ту часть кинетической энергии, которая преобразуется в тепловую,
следовательно, для газов Рг<1. Физический смысл параметра Шмидта
заключается в том, что он характеризует соотношение между кинетической
энергией частиц и энергией, переносимой путем диффузии. Так же, как
и число Прандтля, параметр Sc<l, причем число Sc<Pr.
Параметр Льюиса — Семенова представляет собой отношение
интенсивности теплопередачи путём массообмена в результате диффузии к
интенсивности теплообмена путем теплопроводности. В общем случае Le>l.
Можно предположить, что числа Прандтля и Шмидта равны. Тогда
параметр Le = 1 и интенсивность обоих процессов одинакова. Формально
в этом случае последний член в правой части (Ш-2-47) выпадает. Это
указывает на отсутствие влияния диффузии в пограничном слое. Так как
процессы теплопроводности и диффузии протекают с одинаковой
интенсивностью, то избыточная химическая энергия на границе слоя полностью
преобразуется в тепловую на стенке.
Наиболее общий случай характеризуется тем, что в пограничном слое
Pr>Sc и, следовательно, число Le>l. Это указывает на то, что
превращение химической энергии в тепловую происходит неполностью.
Наряду со случаем Le = 1 можно рассмотреть теоретический случай,
-когда Рг = 1. При этом (Ш-2-47) еще больше упрощается, так как
выпадает средний член справа. Из физических соображений следует, что в этом
случае вся кинетическая энергия внешнего потока преобразуется на стенке
в тепло.
Важное значение для практики имеют исследования численных
значений указанных выше параметров. Теоретически установлено, что для двух-
компонентной атомно-молекулярной смеси число Шмидта меняется весьма
мало в широком интервале температур. Например, если при Т = 252° К
значение Sc = 0,495, то при Т = 3360° К параметр Sc = 0,482. Тоже можно
сказать и о характере изменения числа Прандтля, значение которого
приблизительно равно 0,71. Если принять число Шмидта равным его среднему
значению Sc = 0,49, то параметр Льюиса
Р1_^рИ1 pZ>___ pDcp _0I71_, ,,
Sc ~~ X ii X ~0A$~~ '
120 Глава III
По имеющимся данным этот параметр слабо зависит от температуры
вплоть до значений Т = 9000°К.
Анализируя (Ш-2-47), следует иметь в виду его частный вид,
соответствующий отсутствию диффузии. В этом случае уравнение не будет
иметь третьего члена справа и его можно рассматривать как уравнение
энергии для «замороженного» течения. Причем, входящая в него энтальпия
торможения i0 не учитывает химическую энергию, освобождаемую при
рекомбинации атомов.
От энтальпии i0 можно перейти к температуре торможения, при этом
принимаем, что энтальпия io = cpTo. Таким образом, уравнение
энергии диссоциирующего газа без учета диффузии будет отличаться от
уравнения энергии совершенного газа лишь тем, что в нем вместо
температуры торможения фигурирует полная энтальпия.
Можно рассмотреть случай малых скоростей, который характеризуется
незначительным влиянием сжимаемости, а также пренебрежимо малым
количеством выделяемого тепла вследствие трения и преобразования
кинетической энергии. Тогда уравнение энергии
r*Vx °L + r%Щ- = -±-4- (rS 1Г-) ■ (Ш-2-48)
дх и ду рср ду \ ду I v '
Уравнение энергии для турбулентного пограничного слоя можно
получить, осуществив некоторые формальные преобразования в (Ш-2-47) и введя
в него параметры, характеризующие процессы переноса в турбулентном
пограничном слое. В результате получим
I M* /T Л \ I М"Т /Т Л\ II /ТТТ О / О\
X -£- (Le -1) + -gr- (LeT ~ 1) И- , (Ш-2-49)
где Ргт = [лт (ср)Ср/А,т и LeT = pZ) (cp)cp/XT — соответственно турбулентные числа
Прандтля и Льюиса — Семенова;
Ят — коэффициент турбулентной
теплопроводности.
Все газодинамические и термодинамические параметры в (Ш-2-49)
надо рассматривать осредненными.
Учет влияния диффузии связан с решением (Ш-2-49). При этом важно
определить величину турбулентного числа Льюиса—Семенова. Некоторые
исследования указывают на то, что число LeT приблизительно такое же,j как
для ламинарного течения, и лишь немного отличается от него в меньшую-
сторону.
Уравнение состояния
К числу основных уравнений аэродинамики относится уравнение-
состояния, которое для реальной среды можно записать в виде
= Ф(Р, Л'. (Ш-2-50)
где Л —абсолютная газовая постоянная совершенного газа;
ср — функция, определяющая отклонение свойств реального газа от
совершенного.
Если этого отклонения нет и ср = 1, то
p = RpT.
Основные соотношения в теории газовых течений 221
Неравенство ср Ф 1 обусловлено изменением физико-химических свойств
воздуха при очень высоких давлениях или значительном повышении
температуры. В первом случае большую роль играют межмолекулярные силы,
учитываемые известным уравнением Ван-дер-Ваальса.
Характерными в аэродинамике являются такие процессы, когда
в результате значительного повышения температуры возникает диссоциация
и ионизация. Функция ср в этом случае определяет значение газовой
постоянной несовершенного газа Ru = q>R. Записывая величину i?H как отношение
универсальной газовой постоянной Ro к молекулярному весу, найдем
выражение ср (р, Т) = (^cpVl^cp» где в числителе молекулярный вес недиссоцииро-
ванного, а в знаменателе — диссоциированного воздуха. Функция ср>1,
так как при диссоциации молекулярный вес воздуха уменьшается.
Учитывая, что абсолютная газовая постоянная R = R0/(\iCV))q, уравнение
состояния диссоциирующего газа можно написать в виде
р = срДрГ - ^^ RpT = -^ рТ. (Ш-2-52)
^ср М-ср
В частном случае диссоциирующего двухатомного газа функцию ср
можно выразить через концентрацию атомарной компоненты или, что то же
самое, через степень диссоциации а. Пусть массовая концентрация
произвольной компоненты сг, а ее молекулярный вес [Л^. Тогда, очевидно,
средний молекулярный вес смеси [хср найдется из соотношения |^ср S (^^М'О = 1^
г
в котором знак суммирования определяет число молей смеси. Для
двухатомного диссоциирующего газа 2 ct == ci + сг — !• Очевидно, что сА = с а = ее,
г
с2 = см=1 — ос, 2(iA=fxM=(fxCp)o- Следовательно, ср= ([хср)0/fxcP = 1 +а.
Уравнение состояния после подстановки ср в (III-2-50) принимает вид
где в соответствии с (Ш-1-14) газовая постоянная R~kl(2rriA).
Условие сохранения энтропии
При исследовании изэнтропических течений исходят из условия,
согласно которому энтропия вдоль линии тока остается постоянной. Это
условие можно написать как равенство нулю скалярного произведения двух
векторов, а именно:
FgradS-0, (III-2-54)
где градиент энтропии (вектор grad£) нормален к направлению касательной
к линии тока в данной точке. Условие (Ш-2-54) можно раскрыть, если
воспользоваться конкретной системой координат. Так, например, в
декартовой системе
Если применяются другие системы, то в соответствующем виде
представляются вектора V и grad*$\ а затем определяются скалярные произведения.
Начальные и граничные
условия
Решение дифференциальных уравнений, описывающих обтекание тел,
должно удовлетворять определенным начальным и граничным условиям
этого обтекания. Начальные условия определяются параметрами в начальный
момент времени движения и, очевидно, имеют смысл для неустановившегося
обтекания.
122 Глава III
Граничные условия накладываются на решение любой задачи о движении
таза и должны выполняться в каждый момент времени этого движения,
причем эти условия могут быть самыми разнообразными. Граничное условие
для давления, например, определяется известным его значением на какой-либо
граничной поверхности. Ею может быть граница между возмущенным и
невозмущенным потоками, на которой известно невозмущенное давление. Другой
границей является поверхность скачка уплотнения, за которой также известно
давление. В области между скачком и обтекаемым телом это давление
определяет граничное условие точно так же, как в задаче о скачке граничное
условие для давления определяется его величиной в невозмущенном потоке.
Решения уравнения сверхзвукового обтекания должны удовлетворять
условиям течения газа на поверхности тела и условиям в невозмущенном
лотоке перед скачком уплотнения (или условиям непосредственно за скачком
уплотнения).
Рассмотрим граничные условия, используемые при решении задач
обтекания. Если должно выполняться условие безотрывности обтекания,
то вектор скорости V в любой точке поверхности с уравнением F {х, у, z) = 0
будет направлен по касательной к поверхности, следовательно, будет равно
нулю скалярное произведение векторов V и grad.F, т. е.
Раскрывая вектора V и gradF, получим граничное условие,
соответствующее безотрывному обтеканию в декартовых координатах
Аналогичные выражения могут быть получены в других системах координат.
Для двухмерного обтекания условие (III-2-57) принимает вид
или
ZL=_iggl или ^ = |.
Ух dF/ду Vx dx
При безотрывном потенциальном обтекании граничное условие,
накладываемое на потенциал ф в соответствии с равенством (Ш-2-57), принимает вид
9F , dF , OF n
я* it+ч* ж+фг "*"=°-
В случае двухмерного течения
!*IL=*!LU (111-2-58')
<рх dx ч
Заменяя обозначения, получаем условие безотрывного обтекания тела
вращения
£=■£• <ш-2-59>
или для потенциального обтекания
^2L=^L. (111-2-59')
Приведенные граничные условия относятся к случаю обтекания тел
идеальным потоком.
При исследовании пограничного слоя решения соответствующих
уравнений должны удовлетворять условиям на стенке и на внешней границе слоя.
Условия на стенке заключаются в том, что скорость потока на ней равна
нулю, т. е. при у —О скорость F = 0. На внешней границе, т. е. при у — 8,
скорость V равна ее значению в свободном потоке, а т = 0.
Юсповные соотношения в теории газовых течений 223
При изучении тепловых процессов задают условия на стенке и на
границе слоя для параметров, определяющих теплопередачу. В частности
температура должна удовлетворять условию, чтобы на границе обтекаемого
тела она равнялась температуре стенки, а на границе слоя — температуре
невязкого потока. Распределение теплового потока по толщине слоя должно
быть таково, чтобы на границе слоя его значение равнялось нулю.
При изучении диффузионных явлений накладываются граничные условия
на величину концентрации ct. Обычно требуют, чтобы на границе слоя
ж на границе обтекаемого тела концентрация принимала заданные значения.
§ 111—3- Изэнтропическое
течение
Случай постоянных теплоемкостей. Рассмотрим установившееся течение
сжимаемой среды. Для этого случая дифференциальные уравнения (Ш-2-5),
в которых частные производные по времени следует принять равными нулю,
могут быть проинтегрированы. Этот интеграл, впервые полученный Д. Бер-
нулли, имеет вид [2]
где с имеет постоянное значение вдоль данной линии тока.
Интеграл (Ш-3-1) относится к общему случаю непотенциального
течения. Этот интеграл упрощается в случае изэнтропического течения, для
которого можно воспользоваться уравнением адиабаты dp = (kplp) dp,
преобразованным с учетом выражения для энтальпии i = Тср = cpp/(pR) к виду
dp — pdi. После подстановки в (Ш-3-1), интегрирования и определения
константы из условия полного торможения, для которых эта константа равна
энтальпии торможения i0, получим уравнение Бернулли в следующем виде:
•^ + * = *о. (Ш-3-2)
Отнеся это уравнение к условиям набегающего потока, получим
]L + i^^L + ioo. (Ш-3-2')
Таким образом, энтальпия торможения i0 определяется энтальпией
зи скоростью набегающего потока. Произведя замену i — cvpl(pR), получим
уравнение Бернулли в виде
V2 , к р ^оо , к рсо
Энтальпии торможения соответствуют определенные значения других
параметров торможения, а именно давления р0, плотности р0, температуры Го.
Текущее значение того или иного параметра пропорционально его
величине в условиях полного торможения и зависит от местной скорости.
Соответствующие формулы для расчета давления, плотности,
температуры следующие:
k 1
к *1; T = iyt, (Ш-3-4)
где величина А определяется по выражению А = 1 — F2. Причем, в этом
выражении от безразмерной скорости F = F/Fmax можно перейти к местному
числу M = F/a или относительной скорости K = V/a*, где а* — критическая
224 Глава III
скорость, a Fmax = а* у -j^—^. В первом случае А= [l + ^- М2)
1 — ——Д2). Из сравнения этих значений видно, что
между X и М имеется связь:
+1(^)""1. (Ш-3-5)
По значению X можно определить критическую скорость как а* = V/X.
Сравнивая другую пару выражений для А, можно найти зависимость
между V и М, а именно:
V = j/l- (l + ^M2)"1 . (Ш-3-6)
Из приведенных формул можно получить приближенные соотношения
для гиперзвуковых скоростей (М > 1):
2k 2
_P_ = Bk-i^ _9_ = въ-^ -£- = В\ (Ш-3-7)
Poo poo -* сю
где £ = Моо/М.
Что касается формулы (Ш-3-6), то она также несколько упрощается:
^ 1 1 \
Ф
где Foo = Foo
Интеграл Лагранжа. Для потенциального неустановившегося движения
сжимаемого газа дифференциальные уравнения Эйлера могут быть
преобразованы к выражению, называемому интегралом Лагранжа [51]
Произведя замену р = (рр^/рсх>)1/&, найдем формулу для давления
. (Ш-3-10)
Рассмотрим случай, когда возмущения потока таковы, что второй член
в квадратных скобках мал по сравнению с единицей. Разлагая в ряд
по биному и сохраняя только первые два члена, получим
Представим F2 в этой формуле в виде F2 ~V2oo-{-2vxVoo + vl-\-v2zl где vx,
Vy, vz — составляющие скорости возмущения, и заменим ф^ — q^. Переходя
к коэффициенту давления, получим
Для установившегося течения ср^ = 0.
Коэффициент давления можно выразить через составляющие скорости
vx\-> vyi, vzi в связанной системе координат, что позволит оценить влияние
углов атаки и скольжения [51]. С этой целью воспользуемся следующими
зависимостями:
vx = vxi + vyiac cos ф — vzlac sin cp;
vy = — vxiac + vyi cos ф — vziac sin cp;
vz = vyi sin ф + vzi cos ф.
Основные соотношения в теории газовых течений 125
Внеся эти зависимости в (111-3-11') и сохраняя только квадратичные
члены vl± и v\v получим
р = — 2 (vxi + vylac cos ф — vziac sin ф) — (u2yl + v\x) — 2% . (IH-3-12)
Здесь постоянные Foo и Vlo включены соответственно в значения
составляющих скорости и производной ф*. Вводя углы атаки а и скольжения рск,
найдем
р = - 2 (vxi + vyi$CK - vzia) - (v*yl + v2zl) - 2Ф;. (Ш-3-12')
При обтекании тонких крыльев можно принять, что
р= -2vxi- 2% • (Ш-3-13)
Для установившегося течения % — 0 и
P=-2vxi. (Ш-3-13')
При исследовании обтекания тонких тел вращения целесообразно перейти
к цилиндрическим координатам, приняв в (III-3-10) V2 — FL + 2Foo^х + ^r + Vy.
В соответствии с этим
р=—2их— (v2r + v2y) — 2Ф;. (Ш-3-14)
Изэнтропическое течение диссоциирующего и ионизирующего газа.
При исследовании течения диссоциирующего и ионизирующего газа
необходимо учитывать зависимость термодинамических параметров как от
температуры, так и от давления. С этой целью используются таблицы и диаграммы
термодинамических функций воздуха при высоких температурах. Наиболее
важной из них является диаграмма, две разновидности которой приведены
на рис. Ш-1-3 и Ш-1-4. Дополнением к таблицам или диаграммам является
уравнение (Ш-3-2), позволяющее по известной энтальпии определить
местную скорость изэнтропического течения или, наоборот, по скорости вычислить
энтальпию. В частном случае течения недиссоциирующего газа с переменными
теплоемкостями термодинамические параметры зависят только от местной
температуры.
§ 111-4. Основные
зависимости для определения
параметров за скачком
уплотнения
Уравнения косого скачка
уплотнения
Рассмотрим основные зависимости, позволяющие рассчитать равновесные
параметры диссоциирующего и ионизирующего газа за криволинейной
ударной волной. В качестве параметров, подлежащих определению, примем
давление р2, плотность р2, температуру Г2, скорость F2, энтальпию £2,
энтропию «$2, скорость звука а2, средний молекулярный вес (j^cpb? угол
наклона скачка вс (или угол отклонения потока рс). В соответствии с числом
отыскиваемых параметров необходимо составить систему из девяти
уравнений. Причем известными в этих уравнениях являются параметры до скачка.
Рассмотрим на рис. Ш-4-1 схему криволинейной ударной волны,
которую можно представить как бесконечную последовательность косых скачков.
Для одного из таких скачков, поверхность которого совпадает с касательной
к поверхности криволинейной волны, построены треугольники скоростей
126
Глава III
до скачка (параметры с индексом «1») и после него (параметры с индексом
«2»). Из этих треугольников нетрудно определить вспомогательные
соотношения для вычисления нормальных (индекс «п») и касательных (индекс т)
составляющих скорости
Ftl = F4 cos 9С; Fwl = F1sinec; I
c-pc); F»2 = F2sin(ec-pc). J
В тех случаях, когда для анализа криволинейной ударной волны
применяется угол со, равный углу наклона радиуса кривизны Rc ударной
волны к направлению скорости
набегающего потока (рис. Ш-4-1),
в соотношениях (Ш-4-1) надо
осуществить замену 9с = я/2 —со. И&
этих соотношений можно
получить зависимость
V,
tgec
tg(ec-pc)
*П\ _ b&VC /TTT / 9V
тока
Рис. Ш-4-1. Схема криволинейной ударной
волны
гими уравнениями системы
массы (расхода) —
импульса —
энергии —
А
основанную на том, что
касательные составляющие скорости до и
после скачка равны, т. е. VXl = VX2.
Эта зависимость — первое
уравнение системы —■ позволяет найти
угол наклона скачка. Тремя дру-
являются уравнения сохранения:
(Ш-4-3
(Ш-4-4)
V2
уп2
(Ш-4-5)
и скорость звука
зависимостей этих
в диссоциирующем газег
параметров от давления
Еще четыре уравнения, позволяющие определить энтальпию, энтропию,
средний молекулярный вес
представим в виде общих
и температуры:
*2 = /i(ft, T2); (III-4-6)
£2 = /2(Р2, Т2); (Ш-4-7)
(М'Ср)2 == /з {Р2ч Т2)\ (III-4-8)
«2 = Д(Р2, Т2). (Ш-4-9)
Эти параметры находят с помощью таблиц или графиков
термодинамических функций воздуха по известным давлению и температуре.
Девятое уравнение получается из уравнений состояния, отнесенных
к условиям до и после скачка,
р2 — Pi = i?0 |\P2^ PiTj 1 ^ (Ш-4-10)
Представим основные параметры за ударной волной через относительное
изменение нормальных составляющих скоростей, т. е. через величину
AVn - AVn/Vni = (Vni - Vn2)/Vni.
Основные соотношения в теории газовых течений 227
Находим
-HL^l-AfV, (III-4-11)
Р2
где для недиссоциирующего набегающего потока
Отношения температур и энтальпий
AF.) -g^ , (111-4-13)
Другие параметры также могут быть выражены через величину AF^
и известные параметры набегающего потока. Так как эта величина в
соответствии с (Ш-4-11) определяется отношением плотностей p2/pi, то, следо-
вательно, другие неизвестные относительные параметры, а именно ~^-
т 1 Pi
в (Ш-4-12), ^ в (Ш-4-13), -^ в (Ш-4-14) и т. д. могут быть представ-
■* 1 li
лены как функции p2/pi. Кроме того, вместо величин Vni или Мл1
в формулы можно ввести соответственно значения Vnl = V± sin 0С и Mni =
^MiSinGc. Таким образом, решение задачи о косом скачке при известном
угле наклона сводится к отысканию отношения плотностей p2/pi или, что
то же самое, к определению величины AVn с помощью уравнений (Ш-4-13),
(Ш-4-14):
AF» = А + У А* —В; (Ш-4-13')
(Ш-4-14')
где
(Ш-4-15)
Уравнения (Ш-4-13/) и (Ш-4-14') решают методом последовательных
приближений.
Расчет косого скачка
уплотнения с помощью таблиц или
графиков термодинамических
функций воздуха при очень
высоких температурах
При решении задачи об ударной волне в диссоциированном и
ионизированном газе в качестве начальных данных выбираются параметры воздуха
на какой-либо высоте Н (давление р^ температура Ти плотность р1 и др.)»
а также величина нормальной составляющей скорости Ущ.
Задаваясь в первом приближении значением AF7l = l, соответствующим
предположению о полном торможении потока за ударной волной (Vn2 — 0),
находят из (Ш-4-12) давление/^, а из (Ш-4-14)—энтальпию i2i равную,
очевидно, энтальпии торможения i0. Пользуясь затем i — S-диаграммой,
определяют температуру Т2, а по рис. Ш-1-5 — средний молекулярный вес
128
Глава III
((icp)2. При этом вместо диаграммы и графиков можно использовать
соответствующие таблицы термодинамических функций воздуха, что повысит
точность расчетов.
По найденным значениям р2, Т2, (M<cpb ПРИ помощи уравнения
состояния можно определить плотность р2 и уточнить по (Ш-4-11) значение AVn.
Затем по этому значению во втором приближении по (Ш-4-12) и (Ш-4-14)
найдем соответственно давление и энтальпию, а по ним при помощи таблиц
или графиков уточним температуру и средний молекулярный вес. Зная
А
40
30
20
10
н=о
20 j
w
hzSL
-—-^
■
//=
?
80
-80 км
10
15
20
Рис. II1-4-2. Значение отношения температур воздуха после и
до скачка с учетом диссоциации и ионизации:
сплошная линия — Тг = 220° К; пунктирная — Tt = 350° К
уточненные значения р2, Т2, (^срЬ» можно во втором приближении по
уравнению состояния найти плотность. Приближения заканчивают по
достижении заданной точности.
Расчеты косого скачка можно осуществлять также при задании
параметров набегающего потока (включая число М4) и угла рс-
В качестве первого приближения определяют угол скачка 0С для
недиссоциирующего газа (см. об этом ниже), затем по (Ш-4-11), (Ш-4-12),
(Ш-4-14) находят соответствующие значения AFn, p2 и р2. Используя эти
значения, вычисляют по таблицам [29] или графику [13] температуру Т2
и средний молекулярный вес ([ЛсрЬ* _
Далее по (111-4-13') и (Ш-4-15) уточняют AFn, а по (Ш-4-2) —tg9.
и угол 0С. По указанным выше формулам уточняются остальные параметры
При диссоциации и ионизации относительные величины
параметров газа за ударной волной зависят не только от температуры, что
было характерно для случая переменных теплоемкостей, но и от давления.
Зависимость параметров газа за скачком от числа Mni изображена
графически на рис. Ш-4-2-Ш-4-4. Расчеты отношений температур и плотностей
проводились для усредненных значений температуры Т1 = 220 и 350° К,
равных вероятному минимуму и максимуму, которые выбраны в
зависимости от изменения температуры воздуха по высоте в случае
пониженных и повышенных среднегодовых значений.
Полученные данные показывают, что диссоциация и ионизация
обусловливают значительное изменение равновесной температуры и плотности по
сравнению со случаем постоянных теплоемкостей (к = 1,4 = const).
Что касается давления, то оно значительно слабее зависит от физико-
химически^: превращений воздуха. Отношение p2/pi мало отличается от мак-
Основные соотношения в теории газовых течений
129
симальной величины p2/pi = 1 +&iMni, определяемой только условиями
набегающего потока, но не изменением структуры и физико-химических
свойств воздуха за ударной волной.
Рассмотренный метод расчета может быть отнесен в равной мере
к косому и к прямому скачкам уплотнения. В применении к прямому
скачку этот метод упрощается, так как заранее известно, что 6c = jt/2
и рс = 0. Следовательно, скорость Vni надо положить равной Vu а Мд1 = М1.
Таким образом, в приведенных выше
соотношениях при переходе к прямому скач- р2/р1 н=80 км
ку формально отбрасываем индексы «га». 20
Расчеты параметров газа за косым
скачком следует дополнить
вычислением угла рс (или 8С), а также числа Mi /5
(или скорости Vi). Для этой цели
необходимо воспользоваться соотношениями
71
_ мд1
sin9c
(Ш-4-16)
—%о
80
У*
/Н=20км
зации:
сплошная линия — Tt = 220° К, пунктир-
tldn. — 1 1 — «5OU 1л.
800
600
400
200
Н=80км
Н=0км
/
fQ
15
20
15 20
Первое отношение позволяет
определить по найденному значению /SVn
c (или tfc) при условии, что один ела Mni с учетом диссоциации и иони-
из углов задан. По другим двум
формулам подсчитываются скорость Vi или
число М1в
Для удобства расчетов можно
вычислить заранее углы рс по заданным
величинам 6С, составить
соответствующую таблицу или прстроить график.
Тогда с их помощью для какого-либо
значения A Vn, которому соответствуют
ранее вычисленные величины
отношений p2lpu p2/pi и т. д., можно по
одному из известных углов Эс или рс
найти другой.
Расчеты показывают, что в реаль- Рис. III-4-4. Зависимость отношения
ном газе отклонение потока больше, давлений после и до скачка от чи-
чем в совершенном газе при А = 1,4. ела Мд1 с учетом диссоциации и иони-
Это приводит к тому, что в разогре- зации: Г, ^=220 К
том газе отошедший скачок возникает
позднее, чем в холодном. Число М за большей частью косого скачка
превышает его значения в случае постоянных теплоемкостей, однако при
приближении к прямому участку наблюдается некоторое снижение этого
числа.
Расчет параметров потока в точке полного торможения. Важным
практическим применением теории прямой ударной волны является расчет
параметров в точке полного торможения затупленного тела. Этот расчет
осуществляется следующим образом. По найденным значениям i2, p2
с учетом диссоциации и ионизации по i — S-диаграмме или таблице
термодинамических функций воздуха определяют энтропию S2. Рассматривая
нулевую линию тока и считая, что течение вдоль нее изэнтропическое,
принимают на этом основании энтропию S'Q в точке полного торможения,
равной ее значению S2 за ударной волной. Кроме того, в этой точке можно
9—114
130
Глава III
р'0=Ю~5кГ/см2
найти энтальпию i'0 = ii + 0,5Vl. Зная теперь S'o и i'o, можно найти по той же
диаграмме i — S или термодинамическим таблицам остальные параметры,
а именно р'о, Т'о, р'о и т. д. Результаты
расчета будут соответствовать заданной высоте
полета.
С изменением высоты будут меняться
условия обтекания и, следовательно,
параметры в точке полного торможения. Эта
зависимость графически изображена на рис. Ш-4-5.
Кривые позволяют определить температуру Т^
и давление р'о в функции скорости F4 и
высоты полета Н.
Пример. Рассчитать параметры воздуха за
косым скачком уплотнения для следующих
условий: число Mt=-ll, угол рс = 45°, высота полета
м2 Н~^> км- По таблице стандартной атмосферы
9Л F
о'=1(ЮкГ/см ~ км' таолице стандартной атмос
ч ' (приложение № 2) для высоты 5 км находят:
2000 ШО 6000 V, м/сек
Рис. II1-4-5. Давление и
температура в критической точке
затупленного носка
Pi= (J*) р3 = 5,334.Ю-1-1,033 = 0,551 кГ/см2;
\ Рз *
р1= (Р±\рз=6,012- Ю-1- 0,1249 -0,0751 \кГсек*/м*;
\ р /
^ = 255,6° К; ^ = 320,5 м/сек; ^ср1 ,
Определяют скорость полета: F1 = M1a1 =
= 11-320,5 = 3526 м/сек. По данным [29] находят
А?! = 1,405, ср1 = 1002 м2/сек2-град и вычисляют энтальпию i1 = cplr1 = 1002-255,6 =
= 0,2562- 10е м2/сек2 (61,19 ккал/кГ). Из графика на рис. 37 работы [17] находят
угол вс = 60^ при отсутствии диссоциации. Имея в виду, что при наличии
диссоциации угол скачка будет меньше, задаются в первом приближении значением 0с = 55°,
для которого подсчитывают:
P2-=(P2/Pi) Pi=- HO-0,551 -=55,65 кГ/см2]
h = Н + 0,5F| sin2 0сА7д (2 — AVn) = 0,2562 -106 +
+ 0,5-35262 sin2 55°.0,877 (2 — 0,877) =4,36-106 м2/сек* (1042 ккал/кГ).
По таблицам [29] или графику [13] находят, зная i2 и р2» значения 72 = 3357° К
и jiCp2= 28,7, затем определяют
_
f sia28r —1 _ 1,405-II2-sin2 55° — 1
" 2-l,405.112sin255
= 0 495.
\ 1 / 3357 28^97_ \
I "" 1,405-И2-sin2 55^ I 255,6 28,7 ) '
~ /ciMf sin2 6С
По этим данным производят расчеты во втором приближении
— 5 = 0,495+ ~|/0,4952 — 0,1074 = 0,8659;
0,8659- Т/0,86592-4 (1-0.
Значению 9С=56°25Г соответствуют во втором приближении
' = 103,2;
р2 = 0,551 -103,2 = 56,74 кГ/см2;
i2 = 0,2562-106 + -^35262-sin2 56°25'.0,8659 (2 — 0,8659) = 4,49-106 м2/сек2 (1072 ккал/кГ).
Из таблиц [29] или из графика [13] по уточненным значениям i2 и р2 определяют
7'2 = 3424°К и (хср2 = 28,64.
Вычисления в третьем приближении дают 0С = 56°.
Основные соотношения в теории газовых течений 231
Вновь полученное значение угла достаточно близко к найденному в предыдущем
приближении, поэтому дальнейшее уточнение можно не производить.
Итак, принимают 0с = 56°; р2 = 56,7 кГ/см2;
г2 = 4,49.106 м2/сек2; Г2 =
По таблицам [29] или графику [13] находят
^2 = 2,18 ккал/кГ-град (9,15-103 м2 / сек2 - град);
Si = l,77 ккал/кГ-град (7,4-103 м2/сек2»град); а2 = 1094 м/сек.
Далее подсчитывают
V2n = Vi (1 —Д7П) sin 6С = 3526 (1 — 0,8659) sin 56° = 383 м/сек;
P2 = Pi/(1-AFti) = 0,0751/(1-0,8659) = 0,575 кГ-сек*/м*;
V2 = V2n/sm (ec-pc) = 383/sin (56 — 45) =2007 м/сек;
М2 = V2/a2 = 2007/1094 = 1,835.
Параметры воздуха в точке полного торможения за косым скачком уплотнения
^ = дУ2 = 9Д5-10» м2/сек2-град;
= 6,47.10» м2/сек2.
По диаграмме г — jS* [13] находят
/?о = ЗЗО кГ/см2; 7^ = 4490° К; Ро = 2,4 кГ-сек2/м*.
Ударная волна в чистом диссоциирующем двухатомном газе.
Используя систему уравнений (Ш-4-2)— (Ш-4-10), а также зависимости
для определения термодинамических функций и степени диссоциации
чистого диссоциирующего двухатомного газа, можно сравнительно просто
рассчитать параметры за ударной волной.
Комбинируя уравнения импульса (Ш-4-4) и уравнение энергии
р2 Z
в котором давление и плотность отнесены соответственно к
характеристическим параметрам pd и pd, а скорость—к характеристической величине Vd>
можно получить
7Ts;( /?jf) (Ш-4-18)
где
D = | (7 + а2) (1 + а2) а2. (Ш-4-19)
Выражение (Ш-4-18) получено при условии, что до скачка газ недис-
социирован (а1 = 0), скорости Vni очень велики и можно пренебречь
энтальпией i{ невозмущенного потока, а также отбросить некоторые величины
с более высоким порядком малости.
Уравнение (Ш-4-18) решается совместно с уравнениями (Ш-1-10),
(Ш-1-14/), (Ш-1-16') и уравнением для энтальпии
l2 =^- AVn (2^AVn). (III-4-20)
Вычисления ведутся методом последовательных приближений. Считая
скорость Vni известной, задаются в первом приближении отношением
плотностей p2/pi (или величиной AFn). По величине ЬУп, которую в случае
задания p2/pi находят по (Ш-4-11), определяют из выражения (Ш-4-20)
энтальпию 72. Затем по этому значению и относительной плотности р2/р<*
9*
132 Г лава III
из графиков на рис. Ш-1-8 определяется в первом приближении степень
диссоциации. После этого проводится повторный расчет, в результате
которого при помощи (Ш-4-18) и (Ш-4-19) уточняется величина АУп и
остальные параметры.
При приближенных оценках величины AVn (a2) и других параметров
воздуха за ударной волной может быть использован изложенный метод,
хотя он разработан для чисто диссоциирующих двухатомных газов. При
этом характеристические параметры диссоциации должны быть найдены для
воздуха как для модели газа, состоящей из смеси азота и кислорода
в соответствии с их массовым составом.
Как показывают расчеты, для реального воздуха параметры несколько
отличаются от тех, которые получаются по изложенному методу для
двухатомной воздушной модели. Так, для скорости Vni = l,5Fd = 8,l км/сек
плотность реального воздуха за скачком р2 = 14,7р1, что приблизительно
на 5% больше, чем для двухатомной модели воздуха.
Скачок уплотнения в потоке
газа с постоянными теплоемко-
стями
Система уравнений. В случае скачка уплотнения в потоке газа с
постоянными теплоемкостями система упрощается, так как средний молекулярный
вес воздуха не меняется, кроме того, остаются постоянными удельные
теплоемкости. Такие параметры, как скорость звука и энтальпия, зависят
только от температуры. Энтропия определяется из термодинамики идеального
газа. На основании сказанного уравнения (Ш-4-6) — (Ш-4-9) запишутся
так:
i2 = cvT2\ S2 = cvlnM:; )
р2 > (Ш-4-21)
(И'ср)2 = (М'вр)1 = И'вр = const; a\ = kRT2. J
Уравнение (Ш-4-10) также упростится
P2~Pi = R (P2T2-PtTi). (Ш-4-22)
Уравнения (Ш-4-2) — (Ш-4-5) сохраняются.
Формулы для расчета ^ параметров. Решая упрощенные уравнения
(Ш-4-13'), (Ш-4-14'), получают выражение для относительного изменения
нормальной составляющей скорости
AVn = (1 —б) [1 — (М4 sin 9С)-2], (Ш-4-23)
где 6 = (£-)( + )
Подставляя (Ш-4-23) в (Ш-4-11) и (Ш-4-12), получим следующие
расчетные зависимости:
р2 Mjsin29c
Pi"" (l-6) +
lI*- = (l + 8)Ml sin2 0c— б, (III-4-25)
при помощи которых можно найти формулы для расчета других
параметров. В частности, формула для отношения температур получается, если
воспользоваться уравнением состояния
Tl Pi 92
Этому отношению температур равно отношение энтальпий, а также
квадратов скоростей звука после и до скачка.
Основные соотношения в теории газовых течений 133
Расчет параметров за прямым скачком осуществляется с помощью
приведенных соотношений, если принять 0с = я/2.
Углы наклона скачка и вектора скорости потока. Из соотношений
(Ш-4-24) и (Ш-4-25) следует, что параметры за скачком уплотнения
определяются не только числом М4, но и углом 6С наклона скачка.
Расчетная зависимость для этого угла получается из формул (Ш-4-2)
и (Ш-4-23) и имеет вид
Угол рс наклона вектора скорости может быть определен по формуле
~sin
е0) м;]"1. (ш-4-28)
Характер изменения угла рс вдоль волны зависит от того, является
она отошедшей или присоединенной. В первом случае изменение угла рс
начинается от значения (5с = 0 Для «прямого» участка, затем он достигает
максимального (критического) значения, соответствующего определенной
величине 6С, после чего уменьшается, принимая на бесконечности, где
скачок вырождается в волну возмущения, нулевое значение. Во втором
случае присоединенной волны угол рс уменьшается в интервале от рс = Рсо
до рс = 0, где начальное значение угла рсо определяется условием обтекания
острия тела.
Число М и скорость за ударной волной. Число М2 определяется из
выражения
(i-fl)Mjcos«ec mi-4-29)
Для определения скорости за ударной волной применяется формула
-р. = cos2 6С + (^-)2sin2 Gc, (Ш-4-30)
в которой отношение плотностей может быть заменено по выражению
(Ш-4-24).
Энтропия и давление торможения. Важным практическим следствием
теории скачков является расчет энтропии и зависящего от нее давления
торможения.
Неизэнтропический характер перехода через скачок проявляется в
возрастании энтропии, которое определяется из выражения
Между изменением энтропии и уменьшением давления торможения
за скачком имеется однозначная зависимость
Заменив разность энтропии по (Ш-4-31), получим
ро L б (1-
р'° = fi Г 1 1 2б
UL 1-6) J
26 (л , О we . ОЛ \ 26
(Ш-4-33)
Анализ приведенных зависимостей показывает, что за скачком
уплотнения отношение давлений р'0/р0 всегда меньше единицы. Причем, чем
134 Глава III
больше угол 9С при том же числе Ши т. е. чем сильнее скачок, тем больше
потери давления торможения и, следовательно, меньше отношение р'0/р0.
Годограф скорости. Решение задачи об определении параметров потока
за косым скачком уплотнения может быть получено из уравнения
годографа скорости, представляющего собой геометрическое место концов
векторов скорости за скачком уплотнения. Уравнение годографа получается
из общих соотношений для косого скачка и имеет вид:
где Xw = W2la*, Xu = U2la*1 A1 = F1/a*, a W2 и U2 обозначают соответственно
вертикальную и горизонтальную составляющие скорости.
Уравнение (Ш-4-34) позволяет определить все параметры ударной
волны для заданных условий набегающего потока и значений угла
отклонения потока рс. Так как А,^ = Xv tg|3С, то, решая его совместно с (Ш-4-34),
можно найти непосредственно за скачком составляющие скорости Xw, V/
и, следовательно, полную скорость X = V^Xw + ЬЬ* Из (Ш-4-34) следует, что
одно решение дает большую скорость, другое — меньшую. При этом можно
указать наибольшее критическое значение угла |3С = (3Kp, которому
соответствует однозначное решение для скорости.
Большая скорость реализуется в присоединенном скачке, возникающем
перед заостренным телом, причем такая скорость достигается до момента,
пока ни в одной точке волны угол поворота не превосходит критической
величины, т. е. |3С << ркр, и сохраняется, следовательно, докритическое
течение.
Такая же скорость имеет место за той частью отсоединенной волны,
где угол поворота меньше критического.
Меньшая скорость реализуется только за отсоединенным скачком на той
его ветви, которая примыкает к «прямой» части и где имеет место
сверхкритическое течение.
С помощью годографа скорости можно определить угол наклона скачка,
используя формулу tgQc = (ki — kjjj/Xw Значению угла 6 = arcsin (1/M4)
соответствует волна бесконечно малой интенсивности (волна Маха), а
величине 6 = я/2 —прямой скачок.
Как видно из (Ш-4-27), имеется два различных решения для угла 6С.
Первое из них (знак «плюс» перед корнем) соответствует ударной волне,
близкой по форме к прямому скачку. Второе решение (знак «минус» перед
корнем) определяет наклон ударной волны той же интенсивности под
меньшим углом. Большее значение угла 0С реализуется для отсоединенного,
а меньшее —для присоединенного скачка уплотнения.
Скачок уплотнения при очень больших скоростях (постоянные
теплоемкости). При очень больших скоростях параметр MiSin0c может
значительно превышать единицу, что позволяет упростить зависимости для
расчета течения за скачками уплотнения.
Формула (Ш-4-24) будет
*±* И (Ш-4-24')
,. = ±
pi к — 1 б
Выражение (Ш-4-25) упрощается:
g S, (Ш-4-25')
где Kc — MiSinBc или при малых углах наклона скачка КС = М19С.
Основные соотношения в теории газовых течений 135
Коэффициент давления за скачком найдется из (Ш-4-25'):
После упрощения (Ш-4-23) получим
AF» = 1 — S. (Ш-4-23')
Аналогичным путем могут быть получены приближенные формулы для
других параметров.
Полученные таким образом зависимости соответствуют случаю, когда
значение Кс весьма велико. Представляет интерес рассмотреть расчетные
зависимости для тех реальных случаев, когда число М4 оказывает влияние
на параметры обтекания. Предположим, что возникающие скачки
наклонены под малыми углами; тогда возможно упростить расчет углов 6С.
С этой целью, воспользовавшись выражениями (III-4-2), (Ш-4-3), (Ш-4-24),
после преобразования с учетом того, что 0С и (Зс малы, найдем
err л г -,
С Лс 1 . \л | I/ Л 1 / /Л £\2 Х^-2 /ТТТ / QCL4
При K^MjP—^ oo отношение Эс/рс стремится к пределу, равному
Комбинируя (Ш-4-25) и (Ш-4-35) при условии, что в первом из них
принимается sin 9С « Эс, можно найти приближенную формулу для
коэффициента давления
4- = 2 -g- = ^- [1 + V1 + 4 (1 - б)2 K"2J. (Ш-4-36)
В пределе при К —■» оо
-£г = "13у- (Ш-4-36')
Выражение для AFn можно получить из (Ш-4-23) в следующем виде
Отсюда видно, что в пределе при К—>оо эта величина стремится
к значению (111-4-23').
Из (Ш-4-29) можно получить упрощенную формулу для определения
числа М2:
[i±|A^A)]-^Lr, (Ш-4-38)
где Кс определяется как функция параметра К по (Ш-4-35).
Некоторые соотношения для криволинейной ударной волны.
Отсоединенная криволинейная волна всегда имеет хотя бы одну точку, в которой
касательная плоскость перпендикулярна к направлению скорости
набегающего потока. Эта точка принадлежит «прямой» части ударной волны.
Линию тока, проходящую через эту точку, называют нулевой линией
тока. Вдоль нее течение происходит без изменения направления и,
следовательно, угол наклона радиуса кривизны элемента ударной волны,
расположенного на этой линии, равен нулю.
По мере перемещения вдоль волны этот угол возрастает и, кроме того,
значительней становится поворот потока.
236 Глава III
Характер изменения угла поворота потока вдоль криволинейной
ударной волны определяется производной
cffic __ (1 — d)2 Mf cos* со—(1 —6)Mfcos2co + 2(l — 6)2Mf cos2 о) — (1 — 6)Mf— (1— 6)2
~5gT"~ (1 —6 + 6Mfcos2co)2+(M?coscosinco)2 '
(HI-4-39)
найденной в результате дифференцирования (Ш-4-28).
Аналогично могут быть найдены соотношения, позволяющие найти
изменение других параметров. В частности, производные
d In p __ 2Mf cos со sin со (1 + 6) # ,j yj , ,q^
d<* ~~ (1 + 6) M| cos2 со —б '
—6)tgco (Ш-4-41)
+ 6Mfcos2co
dco 2 l_6 + 6Mfcos2co
служат для расчета изменения давления и плотности. Они показывают, что
по мере приближения к нулевой линии тока давление и плотность
монотонно возрастают, достигая максимальной величины в вершине волны при
(0 = 0.
Составной частью аэродинамических исследований является изучение
геометрических свойств криволинейной ударной волны, связанное, в
частности, с определением радиуса Вс кривизны поверхности, а также
характера его изменения вдоль волны.
Если уравнение у = f (х) представляет в общем виде уравнение
образующей волны в некоторой плоскости хоу, то радиус кривизны образующей
в некоторой точке
з
R° = "£■= - <* + У'*)* W1' (Ш-4-42)
где dl — элемент дуги образующей; y' = dyldx7 у" = d2y/dx2, причем г
Изменение радиуса кривизны вдоль волны
^ = До (у'Г2 [(1 + У'2) У'"-3*/' {у")?- (Ш-4-43)
Предположим, что образующая волны имеет форму параболы х = ау2»
Тогда
Rc = (2а)-1 (Аа2у2 + 1)3/2. (Ш-4-44)
Причем в точке у = 0, через которую проходит нулевая линия тока,
величина Rc = Rco = l/(2a).
Выражение (Ш-4-43) для параболической волны будет
^ = 3,-^. (Ш-4-43')
где Rc определяется по (Ш-4-44).
Экспериментальные данные указывают на то, что образующую
отошедшей криволинейной волны вблизи нулевой линии тока можно
аппроксимировать также гиперболой
г2 ^i_i
а2 б2 "
с полуосями а и &• В этом случае
А-Д. [! + (!+£)£]•". (Ш-4-45)
где Rco = b2/a — радиус кривизны на оси (х = у =
В соответствии с (Ш-4-45) производная
(l +4]. (Ш-4-46)
i?c0 V аЛсо/
Основные соотношения в теории газовых течений 237
Эффекты релаксации в ударных
волнах
Физическая картина неравновесного процесса. В результате перехода
газа через ударную волну происходит преобразование части кинетической
энергии в энергию активных и инертных степеней свободы. Так как для
активных степеней — поступательных и вращательных — равновесие
устанавливается в течение очень малого промежутка времени, соизмеримого
со временем перехода газа через толщину скачка, то практически можно
считать, что установление равновесия происходит мгновенно. Таким
образом, за ударной волной температура будет такой, как в газе с постоянными
удельными теплоемкостями.
В соответствии с этой схемой инертные степени свободы непосредственно
за скачком не возбуждены. Так как эти степени имеют конечное время
релаксации, причем значительно большее, чем время перехода через толщину
реального скачка, то достигнутая начальная температура будет
уменьшаться до тех пор, пока инертные степени (сначала колебания, затем
диссоциация, возбуждение электронных уровней и, наконец, ионизация) не
достигнут равновесия. Этот процесс сопровождается увеличением плотности и
некоторым ростом давления. Возрастет также от нуля до равновесного значения
степень диссоциации (а при очень высоких температурах — степень
ионизации).
Расчет неравновесного течения за прямым скачком уплотнения. Задача
заключается в том, чтобы оценить протяженность зоны неравновесности или,
как говорят, длину пути релаксации, а также определить неравновесные
параметры за ударной волной. Для этой цели необходимо решить систему,
состоящую из уравнения одномерного установившегося движения
■ dx p ~dx '
а также уравнений энергии (III-4-17), состояния (Ш-1-14') и уравнения
(Ш-1-27) для скорости химической реакции.
Эта система уравнений с учетом обозначений, введенных в § Ш-1,
напишется следующим образом:
1 dV2 I dj _n>
2 ~^Г Р dx ~ '
(Ш-4-47)
dx pi
где г — xlL (L — некоторый характерный линейный размер), а параметр
(Ш-4-48)
причем вместо последнего уравнения системы (Ш-4-47) можно применить
одно из уравнений (111-1-27').
Написанная система уравнений отображает случай неравновесного
течения вдоль произвольной линии тока. Если рассмотреть «нулевую» линию
тока, проходящую через прямую часть скачка уплотнения, то система
несколько упростится. В частности, вместо уравнения движения можно
138
Глава III
0,40
0,30
0,20
0,10
f
/ 2 3
/ . Ударная
1 болна
i
-—-
-2
-1
О
1 Цх
применить уравнение импульса для сильной ударной волны
p + pV2 = piV21. (III-4-49)"
Тогда в системе (Ш-4-47) останется одно дифференциальное уравнение
для скорости химической реакции.
Начальные условия при интегрировании этого уравнения определяются
параметрами непосредственно за ударной волной, которые находятся из
теории обычного ударного перехода, т. е.
в предположении, что диссоциация
отсутствует и, следовательно, при х — О
величина а = 0. Давление вдоль «нулевой»
линии тока рассматривается постоянным и не
зависящим от неравновесности.
На рис. Ш-4-6 приведены результаты
численного интегрирования при условии
равновесия по колебательным степеням свободы
(кривая t0 = 0). В качестве среды выбран
кислород, для которого коэффициент скорости
рекомбинации по экспериментальным данным
принят равным kR = 8,4-1014 см6/моль2-сек.
Кривая на рис. Ш-4-6 позволяет оценить
неравновесную степень диссоциации в зоне
релаксаций, возрастающую от нуля
непосредственно за ударной волной до
равновесного значения а = ае в конце пути
релаксации.
График на рис. Ш-4-7 иллюстрирует
изменение плотности в неравновесной
области. В соответствии с характером изменения
степени диссоциации плотность возрастает
от ее значения для недиссоциирующего газа
до величины плотности при равновесной
диссоциации.
На тех же рис. Ш-4-6 и Ш-4-7 показаны
кривые (tv Ф 0), учитывающие время tv
релаксации по колебательным степеням.
Можно заметить, что колебания атомов приводят
к возрастанию степени диссоциации и
отношения плотностей по сравнению с их
равновесными значениями (при tv = 0). Это
обусловлено тем, что колебания не достигли
равновесия и непоглощенная часть энергии
дополнительно расходуется на диссоциацию.
Такое возрастание степени диссоциации
и плотности в зоне релаксации имеет место
не только в двухатомном газе, но и в воздухе
при 4000° К. Объясняется это тем, что при
достижении за скачком такой температуры
в азоте могут быть почти не возбуждены колебания и непоглощенная
колебательная энергия способствует дополнительной диссоциации кислорода
и, как следствие, увеличению плотности воздуха.
Данные о степени диссоциации позволяют оценить неравновесную
температуру, например, по приближенной формуле
Т—а
Рис. Ш-4-6. Изменение
неравновесной степени диссоциации
кислорода за ударной волной:
1 —tv = 20tD; 2 — tv~btD; 3—
колебания в равновесии (tv = 0)] M\= 13;
р1==5,65 мм ргп, ст.; Ti = 295°K;
tv — время колебательной релаксации;
tD — время релаксации диссоциации
1Z
10
-Л
(■■
/3
/
/
/
/
/
\ \
\ \
/ 3
-2
-1
Рис. Ш-4-7. Изменение
отношения плотностей кислорода после
и до скачка уплотнения при
неравновесном течении в сжатом слое:
1,2, 3 — СМ. рис. Ш-4-6
Т =
4 + а
(Ш-4-50)
Основные соотношения в теории газовых течений
139
в которой для больших скоростей принимается i — 0,5 V\. Можно также
применять и уравнение состояния (Ш-1-14'). По расчетным данным,
приведенным на рис. Ш-4-6 и Ш-4-7, температура меняется от 9700° К
непосредственно за ударной волной (х = 0) до равновесного значения 3700° К.
Приведенные результаты, как указывалось, относятся к кислороду,
поскольку параметр скорости рекомбинации kR более достоверно известен
именно для этого газа. Для приближенной оценки влияния
неравновесности на течение воздуха можно вое-
А
А
12
\
X
4v
~~~
1J2
иая
л
Ъпно
1
S
пользоваться той же системой
уравнений, отнеся ее к двухатомной
модели воздуха, состоящей из
аддитивной смеси кислорода и азота. В
этом случае коэффициент с в (II1-4-48)
определяется для кислорода, а все
остальные параметры, в частности,
степень равновесной диссоциации ае,
характеристические плотность и
давление и т. д. находятся для
двухатомной модели воздуха.
На рис. Ш-4-8 показано
распределение плотности и температуры
воздушной смеси кислорода и азота
в зоне релаксации за ударной волной
при Mt = 14,2; 2\ = 300° К; р± = 1 ммртп. ст. Сплошные кривые построены
в предположении мгновенного колебательного возбуждения, пунктирные —
без учета колебательного возбуждения. Из этих результатов следует, что
колебания играют существенную роль. Без учета их температура за скачком
равна 12 000° К, а для полностью возбужденного состояния 9770° К, т. е.
значительно ниже.
Из рис. Ш-4-8 также видно, что протяженность неравновесной
зоны сравнительно невелика и составляет, примерно, 8—10 мм, причем
в конце зоны вибрационное возбуждение практически не имеет значения.
Поэтому в расчетах равновесной диссоциации можно принимать скорости
колебательного возбуждения бесконечно большими, рассматривая, таким
образом, газ перед началом диссоциации полностью возбужденным.
0 Z 4 6 8 s,mm
Рис. Ш-4-8. Влияние неравновесной
диссоциации на плотность и температуру за
ударной волной
ОБЩИЕ МЕТОДЫ
РЕШЕНИЯ
АЭРОДИНАМИЧЕСКИХ
ЗАДАЧ.
§ IV-1. Метод
характеристик
Nfx и)
М(*о,Уо)
Общие уравнения для
характеристик
Условие совместности. В числе методов, применяющихся в сверхзвуковой
аэродинамике, важное место занимает метод характеристик, который
позволяет графически или численно решить уравнения движения газа и, в
частности, рассчитать течение за стационарной ударной волной при условии, что
это течение сверхзвуковое.
Рассмотрим метод характеристик применительно к установившимся
двухмерным сверхзвуковым вихревым и безвихревым газовым потокам.
Решаемые при помощи этого метода уравнения (Ш-2-24) для потенциала скоростей
ф и (Ш-2-35) для функции тока г|)
являются квазилинейными дифференциальными
уравнениями в частных производных
второго порядка гиперболического типа.
Решения этих уравнений ф = ф (#, у)у
а|) = о|) (х, у) геометрически изображаются
в пространстве, определяемом
координатными системами х, z/, ф или х, г/, г|),
интегральными поверхностями. В этих
системах плоскость х, у рассматривается как
основная и называется физической или
плоскостью независимых переменных.
Решения (Ш-2-24) и (Ш-2-35) будут
однозначно определены, если их подчинить
определенным дополнительным условиям. Такими дополнительными
условиями является задание на некоторой начальной кривой АВ (рис. IV-1-1)
значений искомой функции ф (х, у) или г|) (#, у) и одной из ее первых
производных фх (tyx) или <ру (i|)y). Отыскание по этим начальным данным в
окрестности кривой АВ функции ф или if), удовлетворяющей заданному
уравнению и начальным условиям, составляет содержание задачи Коши,
С геометрической точки зрения решение задачи Коши заключается
в отыскании интегральной поверхности в пространстве х, у, ф (или х, у, г|)),
которая проходит через заданную пространственную кривую ф = ф (хАВу
уАв) или г|) = г|) (хАВ, уАВ) и имеет в точках этой кривой заданные
касательные плоскости. Решение задачи Коши применительно к сверхзвуковым
течениям и разработка в связи с этим соответствующего метода
характеристик принадлежат проф. Ф. Франклю.
Чтобы рассмотреть задачу Коши, представим уравнения (Ш-2-24)
и (Ш-2-35), написанные для установившегося течения, в следующем виде:
0
Рис. IV-1-1. К методу характеристик:
АВ — начальная кривая, 1 —
характеристика первого семейства; 2 — характе-
ристика второго семейства
Аи + 2Bs + Ct + Н = О,
(IV-1-1)
где и = ц)
изводные;
= q>xy ( =
t = ууу ( = уруу) — вторые частные
проОбщие методы решения аэродинамических задач 241
А, В, С — коэффициенты при соответствующих вторых частных производных
в уравнениях (Ш-2-24) и (III-2-35), а слагаемое Н объединяет
все остальные члены этих уравнений.
Решение (IV-1-1) в окрестности начальной кривой АВ находится в виде
ряда Тейлора
п=1
где Ах = х0 — х, Ау = у0 — У (рис. IV-1-1); значения производных берутся
в точках кривой АВ; вместо ф может фигурировать функция тока г|). Очевидно,
это разложение определяет искомое решение, если на начальной кривой
известны значения функции ф (или г|)), а также ее производных любого
порядка. Но на этой кривой заданы только искомая функция и ее первые
производные р = фх (=г|)ж), q = фу (=i|)y). Следовательно, необходимо
указать способ отыскания на кривой АВ значений производных порядка выше
первого.
Найдем сначала уравнения, с помощью которых могут быть определены
вторые производные. Так как производных три (и, s, t), то нужно составить
столько же независимых уравнений для их определения. Первым из них
является (IV-1-1), которое будем рассматривать на начальной кривой АВ.
Два других получаются из следующих соотношений, также рассматриваемых
вдоль начальной кривой:
Таким образом, система уравнений для определения вторых
производных будет:
Аи + 2Bs + Ct= — Я; ^
dxu + dys + o-t = dp; \ (IV-1-3)
o-u-\-dxs-\-dyt = dq. J
Если для главного и частных определителей системы ввести
обозначения соответственно А, Аи, Д5, Д$, то вторые производные на кривой
определятся из соотношений
"=x;s=x-;<=x- (IV-*-4)
Из этих равенств следует, что если главный определитель не равен
нулю на АВ, то производные и, s, t вычисляются однозначно. Если же
кривая АВ такова, что вдоль нее этот определитель равен нулю, т. е.
А 2В С
dx dy 0
0 dx dy
и, следовательно,
= 0,
то вторые производные либо вовсе не определяются через ф, р и gv либо
определяются неоднозначно.
142 Глава IV
Нетрудно видеть, что (IV-1-5), которое можно переписать как
представляет собой дифференциальное уравнение двух однопараметрических
семейств вещественных кривых, если только В2 — АС > О (F2 — а2 > 0)г
т. е. если поток сверхзвуковой. Такие кривые, в каждой точке которых
главный определитель системы (IV-1-3) равен нулю, называются
характеристиками, а уравнение (IV-1-5) — характеристическим. Угловые
коэффициенты, вычисляемые по (IV-1-5'), определяют характеристические
направления.
Из сказанного ясно, что для однозначного определения вторых
производных должно быть выполнено условие: направление начальной кривой
в любой ее точке не должно совпадать с характеристическим.
В отношении однозначного определения высших производных,
входящих в ряд (IV-1-2), действует то же условие А Ф 0. Таким образом, если на
начальной кривой А Ф 0, то, составляя системы, подобные (IV-1-3), можно
последовательно определить любые производные, входящие в ряд (IV-l-2)r
и тем самым найти искомое решение ф или г|з в окрестности начальной кривой.
В теории сверхзвуковых течений особое место занимает случай, когда
начальная кривая АВ совпадает с одной из характеристик, и вдоль нее равен
нулю не только главный определитель системы (IV-1-3), но и частные
определители Аи = As = At = 0. При этом можно показать, что если, например,
определители А и А* равны нулю, то равенство нулю остальных двух
определителей удовлетворяется автоматически. В этом случае система (IV-1-3)
имеет решения, хотя и неоднозначные.
Уравнения
А 2В —Н
Д = 0, Д,=
0 dx dq
в развернутой форме имеют вид
dx dy dp
= 0
А (у' dq - dp) -2Bdq + Hdx = 0. (IV-1-7)
Эта система уравнений составляет математическую основу метода
характеристик. Уравнения (IV-1-6) и (IV-1-7) называются условиями
совместности. Первое из них определяет два семейства кривых (характеристик) в
физической плоскости, второе — два семейства кривых, называемых
характеристиками в плоскости р, q.
Из уравнений (IV-1-6) и (IV-1-7) видно, что каждой точке на
характеристике в плоскости х, у соответствует определенная точка на соответствующей
характеристике в плоскости р, q. Это и позволяет использовать
характеристики для расчета газовых течений.
Уравнение (IV-1-7) представляет собой условие, которому должны
удовлетворять значения первых производных р и q функции ф или г|э на
начальной кривой АВ в том случае, когда эта кривая — характеристика,
для того чтобы система (IV-1-3) имела решение. Таким образом,
отличительное свойство характеристик состоит в том, что если вдоль кривой, не
являющейся характеристикой, начальные условия можно задавать
произвольно, то вдоль характеристики этого сделать уже нельзя.
Характеристики в физической плоскости. Два семейства характеристик
в физической плоскости определяются различными вещественными корнями
Я1|2 =dy/dx характеристического уравнения (IV-1-5), рассматриваемого как
квадратное уравнение относительно dy /dx. После замены в этом уравнении
Общие методы решения аэродинамических задач
143
коэффициентов А, В, С их значениями в соответствии с уравнениями (Ш-2-24)
или (Ш-2-35) получим дифференциальное уравнение для характеристик
где «1» соответствует первому семейству характеристик, «2» — второму.
Найдем угол jx между характеристическим направлением для какой-
либо точки А потока и направлением вектора скорости V в той же точке.
Этот угол можно найти при помощи
(IV-1-8), если отнести его к местной У
системе координат хи у± с началом
в точке Лис осью хи совпадающей
с направлением вектора V. При этом
условии Vx = F, Vy = О и,
следовательно, на основании (IV-1-8)
х
\
Рис. IV-1-2. К определению физического
смысла характеристик:
1 — направление характеристики первого
семейства в точке А; 2 — характеристика первого
семейства с угловым коэффициентом Xi; з —
направление характеристики второго семейства
в точке А\ 4 — характеристика второго
семейства с угловым коэффициентом К2
Отсюда видно (рис. IV-1-2), во-
первых, что вектор скорости делит
пополам угол между
характеристиками, выходящими из одной точки,
и, во-вторых, что угол между этим
вектором скорости и
характеристикой есть угол Маха. Следовательно,
физический смысл характеристики
состоит в том, что она представляет
собой такую линию, в каждой точке которой направление касательной
совпадает с направлением одной из линий возмущения, исходящей из той же
точки.
Заметим теперь (рис. IV-1-2), что угол наклона характеристик к
горизонтальной оси равен |3 + |х. Следовательно, уравнение (IV-1-8) для
характеристик можно написать также в виде
= tg(p±(x)» (IV-1-9)
где р —угол между вектором скорости V и осью х.
Существенно, что уравнения для характеристик (IV-1-8), а
следовательно, и вид характеристических кривых одинаковы как для вихревых,
так и потенциальных двухмерных течений.
Характеристики в плоскости годографа скоростей. Если в (IV-1-7)
величину у' заменить первым корнем характеристического уравнения у'= К±,
то оно будет представлять первое семейство характеристик в плоскости р,
q. Аналогичная замена у' вторым корнем у'= Х2 дает уравнение для второго
семейства характеристик в той же плоскости. Полученные таким образом
уравнения для характеристик можно несколько преобразовать,
воспользовавшись известным свойством корней квадратного уравнения (IV-1-5),
согласно которому 2В = А (А,1?2 + ^2,i)» Внося это соотношение в (IV-1-7),
получим его в таком виде:
A(dp + k2.idq) + Hdx = 0, (IV-1-7')
причем, в этом уравнении индекс «2» соответствует первому семейству
характеристик, а «1» — второму.
В отличие от (IV-1-5') для характеристик в физической плоскости
конкретная форма уравнения (IV-1-7') зависит от того, какое исследуется
течение: плоское или пространственное, вихревое или потенциальное.
244 Глава IV
Каждому из указанных видов течения соответствует свое уравнение
для ф или г|) и, следовательно, выражение для коэффициента Н.
Для получения в наиболее общем виде уравнения для характеристик
в плоскости р, q рассмотрим вихревое двухмерное сверхзвуковое течение
и (Ш-2-35) для функции тока. Введем в (IV-1-7') коэффициенты уравнения
(Ш-2-35):
Здесь функция /(г|)) дана выражением (Ш-2-36), из которого видно,
что она определяется значением вихря dVyldx — dVxldy. В свою очередь для
вихря в газодинамике известно соотношение
dvx
которое указывает на зависимость вихря от градиента энтропии по
нормали к линии тока. Следовательно, функцию / (г|э) можно представить в виде
Функции р и q (IV-1-7') заменим в соответствии с (III-2-33)
выражениями
1 1
а угловые коэффициенты — их значениями Х2,4 = tg (p =F \i).
Вводя далее полярные координаты (3 и F, определяемые выражениями
Vx — V cos [3, Vy — V sin |3, после ряда преобразований получим уравнение [58]
которое представляет собой уравнение для характеристик в плоскости
годографа скорости. Верхний знак соответствует характеристикам первого
семейства, нижний — второго.
Вместо градиента энтропии в уравнения для характеристик в плоскости
годографа можно ввести градиент давления торможения dp'Jdn, используя
зависимость
dS _ R dPo _ Р d *n fto /TV \ \*\\
^гг />0 dn dn v 7
Характеристики плоского
потенциального потока
Уравнения для характеристик в физической плоскости в этом случае
имеют вид (IV-1-9). В плоскости годографа соответствующие уравнения
получаются из (IV-1-12), если принять 8 = 0 O
Интегрируя от V = a*(X = l) до некоторого произвольного значения
скорости, найдем уравнение для характеристик
Общие методы решения аэродинамических задач 245
где Р* — начальный угол отклонения потока;
со = ^ ctg \i Щ- = \ ctg \х -^ . (IV-1-16)
а* 1
В этом выражении dXIX находится с помощью (Ш-3-5):
dk dM
М
После подстановки, вычисления соответствующего интеграла в
пределах от М = 1 до некоторого значения М > 1 и [преобразования с учетом
того, что ctg \х = ]/М2 — 1, найдем
со = |/|^| arctg ]/щ (М2- 1) -arctg ]/"М2 - 1. [(IV-1-17)
Из этого выражения видно, что угол со является функцией только
числа М. Если ввести относительную скорость X = V/a*, то этот угол можно
представить в виде зависимости со = со (А,). Кривая, построенная по (IV-1-17),
является эпициклоидой.
Таким образом, уравнения (IV-1-15) для характеристик плоского потока
геометрически соответствуют двум семействам эпициклоид, причем они
располагаются в кольце, внутренний радиус которого равен %—1, а
наружный— Л = [(/с + 1)/(&—1)]1/2. Знак «плюс» перед функцией со (X)
соответствует эпициклоиде (характеристике) первого семейства, а знак «минус» —
второго.
Физический смысл угла со состоит в том, что он представляет собой
угол (5 отклонения потока при его изэнтропическом расширении от
направления, соответствующего числу М = 1, до направления, характеризуемого
некоторым произвольным числом М>1, равного верхнему пределу в
интеграле (IV-1-16).
Угол отклонения потока в произвольной точке можно определить
следующим образом. Предположим, что известно начальное число Mi>l.
В результате расширения потока число М увеличивается и достигает
величины М2>М!. Этим числам МА и М2 соответствуют углы щ и со2
отклонения течения от направления потока с числом М = 1, которые могут быть
определены из выражений ^ = со (M4) и р2 = со (М2). Следовательно, угол
отклонения от первоначального направления равен Ар = р2 ~ Pi = «(М2) —
-©(МО.
Расчет параметров потока можно вести в ином порядке, а именно по
известному значению числа Mi и величине угла Ар отклонения потока от
первоначального направления определять соответствующее этому
направлению число М2. Для облегчения таких расчетов в табл. IV-1-1 приведены
значения функции со = со(М), вычисленные по (IV-1-17) для различных
чисел М при к = 1,4. В той же таблице приведены углы наклона линии
возмущения (углы Маха), рассчитанные по формуле (j, = arcsin (1/M).
При гиперзвуковых скоростях уравнение для функции со, а
следовательно, расчеты по методу характеристик упрощаются. Действительно,
(IV-1-16) при очень больших М можно написать
м
2 Р <Ж
что после интегрирования дает
10-114
146
Глава IV
Таблица IV-1-1
Значение угла ю отклонения плоского сверхзвукового потока
и угла IX наклона линии возмущения в зависимости от местного числа М
при fe = l,4
м
1,00
1,10
1,20
1,30
1,40
1,50
1,60
1,70
1,80
1,90
2,00
2,10
2,20
2,30
2,40
2,50
2,60
2,70
2,80
2,90
3,00
3,10
3,20
3,30
3,40
3,50
3,60
3,70
3,80
3,90
(0°
0,000
1,336
3,558
6,170
8,987
11,905
14,861
17,810
20,725
23,586
26,380
29,097
31,732
34,283
36,746
39,124
41,415
43,621
45,746
47,790
49,757
51,650
53,470
55,222
56,907
58,530
60,091
• 61,595
63,044
64,440
90,000
65,380
56,443
50,285
45,585
41,810
38,682
36,032
33,749
31,757
30,000
28,437
27,036
25,771
24,624
23,578
22,620
21,738
20,925
20,171
19,471
18,819
18,210
17,640
17,105
16,602
16,128
15,680
15,258
14,857
м
4,00
4,10
4,20
4,30
4,40
4,50
4,60
4,70
4,80
4,90
5,00
5,10
5,20
5,30
5,40
5,50
5,60
5,70
5,80
5,90
6,00
6,10
6,20
6,30
6,40
6,50
6,60
6,70
6,80
6,90
(0°
65,785
67,082
68,333
69,541
70,706
71,832
72,919
73,970
74,986
75,969
76,920
77,841
78,732
79,596
80,433
81,245
82,032
82,796
83,537
84,256
84,955
85,635
86,296
86,937
87,561
88,168
88,759
89,335
89,895
90,441
14,478
14,117
13,774
13,448
13,137
12,814
12,556
12,284
12,025
11,776
11,537
11,308
11,087
10,876
10,672
10,476
10,287
10,104
9,928
9,758
9,594
9,435
9,282
9,133
8,989
8,850
8,715
8,584
8,457
8,333
м
7,00
7,10
7,20
7,30
7,40
7,50
7,60
7,70
7,80
7,90
8,00
8,20
8,40
8,60
8,80
9,00
9,20
9,40
9,60
9,80
10,00
10,20
10,40
10,60
10,80
11,00
11,20
11,40
11,60
11,80
12,00
(0°
90,973
91,491
91,997
92,490
92,970
93,440
93,898
94,345
94,781
95,208
95,625
96,430
97,200
97,936
98,642
99,318
99,967
100,589
101,188
101,763
102,316
102,849
103,362
103,857
104,335
104,796
105,241
105,671
106,087
106,489
106,879
8,213
8,097
7,984
7,873
7,776
7,662
7,561
7,462
7,366
7,272
7,181
7,005
6,837
6,677
6,525
6,379
6,240
6,107
5,979
5,857
5,739
5,626
5,518
5,413
5,313
5,216
5,123
5,032
4,945
4,861
4,780
Уравнения (IV-1-17) и (IV-1-18) могут быть использованы для расчета-
обтекания сверхзвуковым потоком выпуклого угла (рис. IV-1-3, угол
ABC > 180°). Возмущенное течение около
такого угла называется течением Прандтля —
Майера.
При обтекании угла В поток
претерпевает расширение, которое начинается вдоль
линии Маха БЕ (^ = arcsin 1/Моо) и
заканчивается на линии Маха BD (\х0 = arcsin 1/MO).
Эти линии Маха, как и промежуточные линии
Маха вида BF, являющиеся прямыми
линиями, соответствуют характеристикам первого
семейства и вдоль них скорости не меняются.
Изменение скорости будет происходить при
переходе от одной линии Маха первого
семейства к другой. Это изменение скорости можно
проанализировать при помощи (IV-1-17) или
(IV-1-18).
Чтобы найти число М на промежуточной характеристике BF, которой
соответствует заданный угол отклонения потока (3, найдем вначале полный
угол со = (Ооо + Р» где сооо находится из (IV-1-17) или (IV-1-18) по задан-
Рис. IV-1-3. Обтекание выпуклого
угла сверхзвуковым потоком
(течение Прандтля — Майера)
Общие методы решения аэродинамических задач 247
ному Моо. Зная со, можно вычислить при помощи тех же уравнений (IV-1-17)
и (IV-1-18) соответствующее местное число М. Местное число Мо на
стенке ВС определяется по значению угла о)0 = (Ооо + Ро- Угол е между линией
Маха BF и вертикалью определяется из условия 8 = я/2 — (fi — Р), где
x arcsinl/M
Свойства течения Прандтля — Майера можно использовать для решения
задачи о непрерывном сверхзвуковом обтекании выпуклой криволинейной
поверхности (эта задача будет рассмотрена ниже).
Схема решения задач по
методу характеристик
Система уравнений для характеристик. При помощи (IV-1-16) можно
преобразовать уравнение (IV-1-12) для характеристик в плоскости
годографа и таким образом использовать свойства эпициклоид для расчета
двухмерных неизэнтропических течений.
В результате система уравнений для характеристик будет следующая:
а) для первого семейства
б) для второго семейства
где
y_ sin ft sin M* . л _ sin2 P cos \i .
l~ C
_ sin p sin fx . _ sin2 p cos \i
~ cos(P + |^) ' l~ cos(P-(i) '
Как указывалось, вместо градиента энтропии [можно ввести градиент
давления торможения dp'Jdn, используя зависимость между ними (IV-1-13).
Для двухмерного изэнтропического (потенциального) течения
уравнения для характеристик принимают вид:
а) для первого семейства
d (со - р) - 8 — I = 0; (IV-1-26)
у
б) для второго семейства
d (со + р) - е — ттг-О. (IV-1-28)
Для плоского потока в уравнениях надо принять е==0, для
пространственного осесимметричного 8 = 1.
Методика численного расчета. Определение поля скоростей
возмущенного течения по методу характеристик складывается большей частью из
решения двух самостоятельных задач. Первая из них связана с
определением скорости в точке пересечения характеристик разных семейств,
выходящих из двух близко расположенных точек, в которых скорости известно^
вторая задача заключается в расчете скорости в месте пересечения твердый
стенки с характеристикой, если она проведена из точки% лежащей вблизи!
10*
148
Глава IV
Плоскость х,у
Плоскость р,с{
о
О
В
х
в
стенки, и если в этой точке известна скорость. Эти задачи являются чисто
кинематическими, так как метод характеристик дает возможность
непосредственно найти скорость.
При этом следует иметь в
виду, что в общем случае
неизэнтропического течения
в качестве начальных
данных одной скорости
недостаточно, и должны быть
заданы другие параметры
(энтропия, давление торможения).
Рассмотрим первую
задачу. По ее условию в двух
соседних точках А и В
физической плоскости (рис.
IV-1-4, а) известны числа
МА, МБ и другие параметры,
в том числе значения
энтропии SA, SB и нужно найти
параметры потока в точке С,
Рис. IV-1-4. К расчету скорости сверхзвукового
потока по методу характеристик:
1 — элемент характеристики первого семейства; 2 —
элемент характеристики второго семейства; а —первая задача;
б — вторая задача
в которой пересекаются
элементы характеристик
первого и второго семейств (число Мс, ьугол наклона вектора скорости рс,
энтропия Sc и др.). Кроме того, необходимо найти координаты хс, у с точки С.
Все численные расчеты основаны на использовании уравнений для
характеристик (IV-1-19) — (IV-1-22), которые записываются в конечных
разностях:
а) для первого семейства
Аув = tg (РБ + \iB) AxB; (IV-1-29)
= 0; (IV-1-30)
(IV-1-31)
,0, (IV-1-32)
у А ил z_wc/
где
б) для второго семейства
А У а = tg
— Ра)
Уа
An
sinpa sin [iB
тА =
COS(pA-fXA)
sin2
\ib m
;1
^_ sin2 |3А cos \iA
1 "cos(pA — [iA)
(IV-1-33)
Таким образом, уравнения (IV1l-29) — (IV-1-32) записаны в
предположении, что коэффициенты I, т, с, t сохраняются при перемещении вдоль
элементов характеристик постоянными и равными их значениям в
начальных точках А ж В.
Для определения координат хс, Ус необходимо решить систему
уравнения (IV-1-29) и (IV-1-31) для элементов сопряженных характеристик
ъ физической плоскости
Ус —
—Уа = (*с —au)tg (Ра —
Общие методы решения аэродинамических задач
249
Расчет скорости в точке С и угла Рс связан с решением системы
уравнений (IV-1-30) и (IV-1-32) для сопряженных характеристик в
плоскости годографа. Величина этих параметров зависит, очевидно, от
значения ASIAn, определяющего изменение энтропии при переходе вдоль
нормалей к линиям тока, проходящим через точки
В ж А.
Из рис. IV-1-5 видно, что
AS = SA-SB
An
где
AC sin \iA-{-BC sin \iB '
*С — хв
cos (pB
О
cos (рА —М-а) '
Введя обозначения
е = (хс — хА) sin (iA cos (PB + ц,в);
f=(xc — xB) sin |1Б cos (pA — |^a)» л ос
получим Рис. IV-1-5. К расчету
скорости по методу характеристик
&S _ (о а — Sb) cos (Рь + М'б) cqs (на — №а) (IV-1-34^ с Учетом вихревого характера
An
потока
Абсолютная величина энтропии в точке С определяется из соотношения
Sc = ASB + SB = ^- ВС sin Ив + SB = ^"^ /
Градиент давления торможения по нормали к линии тока определяется
с помощью формулы, аналогичной (IV-1-34): .
Ар'о _ (РОА~РОВ) C0S
cos Фа-Va)
где рол, Ров — давления торможения соответственно в точках А ж В.
Знак отношения Ap'JAn зависит от характера изменения давления
торможения при перемещении по нормали к линии тока от точки А к точке В.
В случае обтекания тел с криволинейной ударной волной давление
торможения уменьшается при переходе к линиям тока, расположенным ближе
к поверхности тела. Это и понятно, так как при этом переходе волна
становится более интенсивной и протекание через нее сопровождается большим
возрастанием энтропии. Если точка В находится ближе к поверхности, то
величина Ар'0/Ап = (р'оА—р'ов)/Ап положительна, так как давление
торможения ров в этой точке меньше, чем в точке А. Давление торможения
в точке С, лежащей на пересечении характеристик разных семейств,
проведенных через точки А и В, вычисляется по аналогии с (IV-1-35) из
выражения
РОС = РОВ Н
/TV л о
(lV-1-ч
Неизвестными в системе уравнений (IV-1-30) и (IV-1-32) являются
приращения АсоБ, Лсоа* ДРя и ДРл- Число этих неизвестных можно
сократить до двух, если иметь в виду, что
Асов = АсоА + соА — озв; Арв = АрА + рА —Рб-
В соответствии с этим (IV-1-32) преобразуется к виду
250 Глава IV
Решая это уравнение совместно с (IV-1-30) относительно переменной ДрБ,
получим
По найденному значению Дрв из (IV-1-30) или (IV-1-38) находим
вторую неизвестную величину АсоБ. Теперь можно вычислить для точки С
углы Рс = Рв+Дрв и сос = сов + Дсов. Затем с помощью табл. IV-1-1
определяют в этой точке по величине о)с число Мс и угол возмущения fxc.
При необходимости могут быть найдены другие параметры, а именно
давление, плотность, температура и т. д. Вычисляемые таким образом
параметры представляют собой первое приближение, так как вдоль элементов
характеристик коэффициенты I и т, а также координаты рассматриваемых
точек принимались постоянными и равными их соответствующим значениям
в точках А и В. Эти параметры можно уточнить, если в уравнения
(IV-1-30) и (IV-1-32) подставить вместо 1В, тА, ув, уА величины,
вычисленные как средние между заданными в точках А, В и полученными
в точке С в первом приближении. Осуществляя расчеты, нужно иметь
в виду, что начальные точки А и В не должны находиться на одной и той
же характеристике.
Рассмотрим вторую задачу, сформулированную выше и заключающуюся
в определении скорости в точке В, которая расположена на пересечении
элемента DB характеристики второго семейства с контуром тела (см. рис.
IV-1-4, б). Причем скорость в точке D по величине и направлению, а также
координаты точки известны.
Определение скорости в точке В ведется непосредственно с помощью
уравнения (IV-1-32), если отнести его к условиям вдоль элемента
характеристики второго семейства DB и записать в конечных разностях
В этом уравнении приращение A$D = $B—$D представляет разность
углов наклона векторов скорости в точках В и D. Причем в точке В
угол fig определяется (в соответствии с условием безотрывного обтекания
поверхности) наклоном касательной к ней в этой точке, т. е. tgpB = (dy/dx)B.
В свою очередь величина tg(5B вычисляется по уравнению образующей
y = f(x) и координатам хВ1 ув, которые находятся в результате совместного
решения уравнений
У в — yD=(xB — xD)tg(^D — \iD) и yB = f(xB). (IV-1-41)
Подсчитав градиент давления торможения
Арр _ (Ров — Род) cos (рв—\iB)
An ~~ (xD — xB)sm\xB
и подставив его в (IV-1-40), можно определить приращение Асо^, найти
но нему угол оав = A(x)D -f (oD и вычислить число Мв, а также
соответствующий угол Маха \хв.
Рассмотренная методика численного расчета относится к общему случаю
вихревого двухмерного течения. Эти расчеты упрощаются для изэнтропи-
ческого течения. Соответствующая система уравнений для характеристик,
написанная в конечных разностях, имеет следующий вид:
/Общие методы решения аэродинамических задач
а) для первого семейства
Л*/в = tg фв + |хв) Ахв;
Ашв - Ар
б) для второго семейства
s -^в- lB = 0; (I V-1-43)
У В
= tg (pA - \iA) AxA;
В (IV-1-43) и (IV-1-45) для плоского потенциального течения надо
принять 8 = 0, для пространственного осесимметричного 8 = 1. Можно
рассмотреть также случай плоского неизэнтропического течения.
Соответствующие уравнения для характеристик имеют вид (IV-1-30) и (IV-1-32), в
которых следует принять 8 = 0.
Характеристики в
диссоциирующем газе
Уравнения для характеристик в физической плоскости, выбранной
в потоке диссоциирующего газа, имеют вид (IV-1-19) и (IV-1-21) с той
особенностью, что местные числа М и соответствующие углы Маха
jli = arcsin (a/V) нужно вычислять с учетом зависимости скорости звука как
от температуры, так и от давления.
Чтобы учесть влияние диссоциации при определении параметров потока,
их следует рассматривать как функции местного числа М или, что то же
самое, угла Маха, вычисленных указанным методом. Имея это в виду,
можно применить в расчетах уравнения для характеристик в плоскости
годографа (IV-1-12), осуществив в нем некоторые преобразования.
Эти преобразования вытекают из условия, что для однородного набе-
тающего потока di= —VdV. Кроме того, показатель адиабаты к и газовую
постоянную следует заменить их значениями для несовершенного газа,
т. е. к = кК, i? = i?H, причем Rn = R0/\icv. Произведя эти преобразования
и присоединив уравнения (IV-1-19) и (IV-1-21), получим следующую систему
уравнений для характеристик диссоциирующего неизэнтропического течения:
а) для первого семейства
6 sin Li . dx sin2 jx cos u dS
б) для второго семейства
r / \ 7 dx sin В sin ix dx sin2ucosix dS Л
— f(a) du — 8 t^ ^—т-5 7^ ^-—— = 0,
/ \r/ г у cos($ — \i) kHRH cos(p —jx) dn '
где
При проведении численных расчетов уравнения для характеристик
представляются в конечно-разностной форме и полученная система решается
методом итераций. Эта система отличается от соответствующей системы
для совершенного газа функцией f(\x) и произведением kHRH. Для
совершенного газа
^+с;;^ kHRH = kR.
252 Глава IV
Причем для реального газа функция /([л), как видно, не может быть
представлена в явной форме. В расчетах течений реального газа удобнее
применять вместо /([г) отношение z(\i) = f (\i)/f°(\х), а вместо кяВи —
отношение kR = kHRJkR = kK(\xcv)Q/kixcv, которые для совершенного газа равны
единице.
Существенным элементом расчетов является определение местного
значения функции z(\i). Зная условия набегающего потока, вычисляют
энтропию за ударной волной и для заданного ряда возможных значений
скоростей Vo, Vij ..., Vt находят соответствующий ряд значений энтальпии
ii = i0Jr015Vl — O,5Ff. По энтропии и энтальпии при помощи таблиц или:
графиков термодинамических функций определяют давление, температуру,
скорость звука, а затем число М* и угол \it наклона линии возмущения
в данной точке. Полученные данные позволяют построить кривую i (fx),
найти производную di/d\i = f (\i) и вычислить функцию z(\i).
Уравнения для характеристик (IV-1-47) и (IV-1-49) упрощаются в
случае диссоциирующего безвихревого потока, так как производная dS/dn = 0.
Еще проще уравнения для плоского диссоциирующего безвихревого потока,,
так как дополнительно выпадает из уравнений третий член в связи с тем,.
что 8 = 0.
§ IV-2. Конические
течения
Сверхзвуковой поток около некоторых заостренных тел (конус, крылья
треугольной формы в плане) обладает тем свойством, что вдоль каждой
прямой, проходящей через вершину тела, параметры течения сохраняются
одинаковыми и меняются при переходе от одной прямой к другой. Такой
поток называется коническим.
Уравнения конического потока могут быть получены из общих
уравнений газодинамики. В сферических координатах с началом в вершине тела
условие коничности потока состоит в том, что производные от параметров
по координате г должны быть равны нулю. В частности, равны нулю
производные dVr/dr, dV^ldr, dV^ldr, др/дг. Приняв также, что коническое
течение установившееся, получим для него уравнения движения и
неразрывности в следующем виде:
Т/ дУт i 7ф dVr Т/2 172 О-
2pFr sin ф + * <py *> + Щ± = 0. (IV-2-2)
Эта система уравнений описывает нетаэнтропический конический поток.
Если течение является безвихревым (или с известным приближением
принимается таковым), то можно применять уравнение для потенциала
скоростей конического потока.
В соответствии с основным свойством конического потока решение
для потенциальной функции отыскивается в виде
(IV-2-3)
Общие методы решения аэродинамических задач 253'
Вычисляя производные, найдем составляющие скорости
(IV-2-4)
где введены обозначения ц = у/х, е = z/x; F^ = dF/дц, Fs = dF/de.
Определяя из (IV-2-4) вторые производные срхх, фуу, ф22 и внося их в
уравнение (II1-2-30), описывающее слабовозмущенный поток, получаем уравнение
для линеаризованного конического течения
(1 - a'V) F^ + (1 -<*'2е2) Fee-2er|a'»Л,е - 0, (IV-2-5)
где
Рассмотрим коническое безвихревое течение в сферических координатах.
Общее решение для потенциальной функции такого потока
Ф = г^(9, if). (IV-2-6).
Составляющие скорости
7Г ФГ ^; 7в ^^
Отсюда следует важное соотношение теории конических течений
позволяющее дополнительно упростить систему (IV-2-1) и (IV-2-2)
для несимметричного конического потенциального течения. Еще более
простой вид система уравнений будет иметь для симметричного конического
потока вследствие того, что составляющая скорости F^ = 0h равны также
нулю все производные по if>. Комбинируя полученные в результате
упрощения уравнения движения и неразрывности, придем к следующему
уравнению для конического симметричного течения
Это уравнение можно получить из (III-2-27), приняв dVrldr = dV$ldr — 0,
№ V
§ IV-3. Метод источников
Метод источников позволяет получить в общем виде решение
уравнения (Ш-2-30) для потенциала скоростей слабовозмущенного потока.
Физически этот метод основан на возможности замены течения, представляемого
уравнением (Ш-2-30), потоком от единичного источника или от системы
источников, распределенных по какому-либо закону.
Потенциальную функцию источника можно получить следующим обра^-
зом. Пусть QH — мощность точечного источника несжимаемой жидкости.
Тогда в системе координат хн, г/н, zE потенциал источника cpH= —
где
Обычно имеют дело с системой непрерывно распределенных
источников, элементарную мощность которых можно представить в виде dQH — fHdo,
гДе /н—плотность или интенсивность распределенных источников, do = d&dt) —
элементарная площадка на плоскости у = 0.
154
Глава IV
Как следует из (Ш-2-30), при условии срг = О между координатами
^н> Упч %н Для несжимаемого потока и х, у, z для дозвукового течения
имеется следующая аффинная связь: хя = х (1 — М2)""1/2; ун = у; zH = z. Поэтому
для дозвукового источника элементарный потенциал
dcp = — / do/4nR, где R = Vx2 + (I — M2) (y2 + z2).
Непосредственной подстановкой можно убедиться,
что выражение для dcp удовлетворяет уравнению
(Ш-2-30) как для дозвуковых, так и для
сверхзвуковых установившихся течений.
Для сверхзвуковых скоростей выражение для dcp
действительно не для всей области течения, а только
для той ее части, где #2>(М2 — i)(y2jrz2). Таким
образом, источники оказывают влияние на течение
внутри пространства, ограниченного поверхностью,
Рис. IV-3-1. Область ин- описываемой уравнением х2 = (М2 — 1) (у2 + z2). Эта
тегрирования при опреде- т\/г
лении потенциала скоро- поверхность является конусом Маха с углом нак-
стей по методу источников лона образующей \i = arcsin (1/M). В соответствии
с этим находится область интегрирования при
определении потенциала скоростей в исследуемой точке (рис. IV-3-1,
точка А) от источников, распределенных на некоторой плоскости
поверхности. Потенциал скоростей
Ф (X, У^)
где а —область интегрирования;
1/2jt — постоянный коэффициент, включенный в значение функции /(е,
Для двухмерного случая
Ф ^» У) -
/ (е) de
У(Я —8)2 — (М2 — 1)у2'
(IV-3-2)
где верхний предел соответствует границе влияния сверхзвукового источника.
Найденное выражение для потенциала скоростей составляет основу
метода источников, согласно которому обтекаемое тело заменяется системой
непрерывно распределенных источников и стоков. Закон распределения
источников, т. е. вид функции / (е, £) должен быть таким, чтобы в
результате наложения невозмущенного потока на течение от этих источников
были бы удовлетворены граничные условия обтекания.
При обтекании поверхностей с образованием подъемной силы
возмущенное течение должно быть заменено не только источниками и стоками,
но и диполями. Это следует из того, что дифференциальное уравнение
обтекания удовлетворяется, если потенциальная функция слагается из источ-
ноков (стоков) и некоторой дополнительной функции, называемой диполем.
Физически диполь представляет собой течение, образуемое в результате
такого неограниченного сближения источника и стока одинаковой
интенсивности Q, при котором сохраняется постоянным произведение Qh, где h
расстояние между источником и стоком. Эта константа называется
интенсивностью или моментом диполя.
Потенциал диполей можно определить из следующих соображений.
Пусть источники и стоки, расположенные по обе стороны от плоскости у = О
на расстоянии соответственно y = h/2 и г/ = —/г/2, сближаются, так что
Л —>0. Результирующий потенциал фДИп = ^ (дфист/дг/), т. е.
д ? ? hf (8, £) dz dt /ТЛТ о оч
фдип = — \ \ , 2 2~ ' (IV-.3-3)
о
где hf = m(e, Q —функция распределения интенсивности (момента) диполя.
Общие методы решения аэродинамических задач 255
§ IV-4. Теория
сверхзвукового обтекания тонких
тел с произвольным
поперечным сечением
Решение уравнения
потенциала
Потенциал скоростей. В основе теории установившегося сверхзвукового
обтекания тонких тел лежит линеаризованное уравнение потенциала,
которое в системе цилиндрических координат х, г, у имеет вид (Ш-2-31).
Решение этого уравнения, в котором принимается ф* = 0, можно
получить в общем виде при помощи преобразования Лапласа [51]. В
соответствии с этим потенциал ф (#, г, у) преобразуется к виду Ф (р, г, у) при помощи
оператора
L [Ф (х, г,у]^1 <грхф (х, г, у) dz, (IV-4-1)
о
где р — параметр преобразования. При этом Ь[у(х, г, у)] = Ф(р, г, у).
Применяя преобразование Лапласа к отдельным членам уравнения
(Ш-2-31), получаем
1г[ф„.]=Фгг; £,[фг] = Фг; Ыц)уу] = Фуу, Ь[цхх] = Фххр\
(Здесь учтено,- что ф (0, г, у) = 0, фя (0, г, y)=0.)
В результате изображение уравнения (Ш-2-31) будет
Ф + ^Ф а'2р2Ф где а'2= M2-l. (IV-4-2)
Общее решение (IV-4-2) может быть получено по методу Фурье в виде ряда
оо оо
Ф= 2 (Cnsinny-]-Dncosny)In(a'pr)+ 2 (Еп sinпу+ Fn cosпу) Кп (а'рг).
П=0 71=0
(IV-4-3)
Коэффициенты Сп, Dn, En, Fn в общем случае зависят от р и
выбираются таким образом, чтобы удовлетворялись граничные условия.
Функции 1п и Кп представляют собой функции Бесселя мнимого
аргумента. Как показывают исследования, в случае сверхзвукового
обтекания заостренных тел физический смысл имеет только функция Кп (функция
Макдональда). Поэтому в уравнении (IV-4-3) следует положить Сп = 0;
Dn = 0. Вводя вместо коэффициентов Еп и Fn величины Ап и 8п, получаем
решение для Ф в следующем виде:
Ф = Л#о (а» + S АпКп (а» cos (пу + 8п). (IV-4-4)
п=1
Величина 6^ представляет собой некоторый фазовый угол.
В том случае, когда поперечные размеры тела весьма малы,
выражение (IV-4-4) может быть представлено в более простом виде. Именно этот
случай рассматривается в аэродинамической теории тонкого тела. Для малых
значений г имеем [51]:
К, (а» = ^г [1 + 0 (г» In г)];
156 Глава IV
где О — обозначает порядок величины;
С — постоянная Эйлера.
Тогда (IV-4-4) принимает вид
оо
71=1
Чтобы перейти к потенциалу ф, надо применить обратное
преобразование Лапласа к членам в правой части (IV-4-5). Введем обозначения
bo
(x) =L"i [ -
^ (x) = An (x) - iBn (x) = L-i [fc^- (4j)nAn(p) eibn
Тогда
(IV-4-6)
i i i. i V Мл cos rav + 2?n sin иу /т^7 7 7Ч
Ф - a0 In r + &o + 2j -^ T^ * (IV-4-7)
n=l
Из этого выражения можно выделить составляющую потенциальной
функции срг, обусловленную толщиной тела, и составляющую фа, которая
характеризует положение тела в потоке:
Фг = ао1пг+Ьо; (IV-4-8)
у Лд cos тгу + ^п sin ^гу ^ (IV-4-9)
п=1
Таким образом, полный потенциал
Потенциал скоростей при несимметричном обтекании тонкого тела
вращения. Для тонкого тела вращения потенциальную функцию можно
получить в более простом и конкретном виде. С этой целью исходят
из уравнения движения, отнесенного к связанным с телом осям хъ yt1 zt
(рис. IV-4-1). В цилиндрических координатах уравнение будет аналогично
(Ш-2-31) с заменой в нем х, г, у соответственно на хи г, у.
Поток около тонкого тела вращения можно рассматривать состоящим
из двух, наложенных друг на друга течений (см. рис. IV-4-1): продольного
(симметричного) со скоростью Foo cos a ~ Foo и поперечного со скоростью
Foo sin a c*± FooOc. Продольное обтекание обусловливает составляющую
потенциала фг, зависящую от толщины тела, поперечное обтекание —
составляющую фа, связанную с углом атаки.
Непосредственной подстановкой можно убедиться в том, что выражение
J У(Ж8)2а'2г2 Ч '
У(Ж1_8)2_а'2г2 Xi дх1 J У(Ж1_8)2_а'
действительно удовлетворяет уравнению (Ш-2-31).
Функция / (е) определяет интенсивность распределения источников
(стоков), а т (г) — интенсивность распределения диполей.
Выражение (IV-4-11) представляет собой потенциальную функцию,
соответствующую линейной теории обтекания тел вращения. Дальнейшее
упрощение может быть осуществлено в рамках теории обтекания весьма
тонкого тела, у которого радиус г0 мал по сравнению с расстоянием хи
Общие методы решения аэродинамических задач
157
а величина fa— е)/а'г является большой (за исключением малой окрестности
вблизи носка, что не имеет существенного значения).
При этом условии составляющая
±—а'г
(IV-4-12)
Для тонкого тела обратный гиперболический косинус можно
приближенно представить в виде arch [fa — e)/a'r] ~ In [2 fa — е)/а'г]. В
результате получим уравнение dytldr——f(xi — a'r)/r.
а)
st
Vcc^V-
В х
У*
дх
Рис. IV-4-1. Несимметричное обтекание тела вращения:
а — связанная система; б — поточная система координат
Так как на поверхности тела
дг
Ут
Foo
dr __S'
dx*
2nr
(IV-4-13)
где S (Xi) — закон изменения площади поперечного сечения тела по его
длине, то
/fa-aV) - - Vo°S27l{Xi)~ • (IV-4-14)
Следовательно,
ф* = -
д
XI
В этом выражении в значение <pt включена скорость F<x>.
Чтобы получить функцию фа для тонкого тела, необходимо во втором
члене в правой части (IV-4-11) перейти к пределу при г —> 0. В результате
найдем фа = (cos у/г) га fa), где функция т(х1) определяется из условия
безотрывного обтекания
(IV-4-16)
" dx± щ
Но условие (1/Foo) dytldr — drldxi выполняется при симметричном
обтекании. Следовательно, m fa) = aFoor2. В соответствии с этим
cosy
2
(IV-4-17)
где фа — функция, включающая постоянную
158
Глава IV
Комплексный потенциал. Исследования показывают, что при обтекании
сжимаемым потоком тонкого тела плотность меняется весьма мало, так что
отношение р/роо = 1 + 0 (t2), где t — относительная толщина тела. С
точностью до величины О (t2) можно считать, что p/p^c^l, следовательно,
j-r 1 д\р j-r dip
т г dv ' ^ дг
(IV-4-18)
или
dtp
*Р . J__^_= *L aV-4-184
dy ' г ду дг v '
В теории функций комплексного переменного эти уравнения, как
известно, называются уравнениями Коши — Римана и выражают условие, что
функция
является аналитической функцией комплексного переменного £ =
— z-\-iy. Функция (IV-4-19) называется комплексным потенциалом.
а)
Плоскость
У
1 0
i
—-».
С
)
V
1
ф
Плоскость б
-ш
Рис. IV-4-2. Физическая плоскость Z = z -t~ iy (а) и
преобразованная плоскость а = г\ 4- £§ (б)
Таким образом, обтекание сжимаемым потоком тонкого тела может быть
охарактеризовано комплексным потенциалом. Плоскость, в которой
определяется течение, называется физической плоскостью комплексного
переменного t> = z-\-iy (рис. IV-4-2, а).
Потенциал ф можно рассматривать как действительную часть
функции W (t). Имея (IV-4-7) для ф, выражение для комплексного потенциала
W (Q можно получить следующим образом. В (IV-4-7) заменим In r на 1п£,
а выражение под знаком суммирования — величиной ап/^п, в результате
получим
(IV-4-20)
71=1
В соответствии с формулой ф = ф? + фа можно написать аналогичное
выражение для комплекрного потенциала
Граничное условие. Коэффициенты, входящие в (IV-4-20), определяются
из граничного условия, в соответствии с которым направление скорости
в некоторой точке обтекаемой поверхности должно совпадать с касатель-
Общие методы решения аэродинамических задач 159s
ной к поверхности в той же точке. Пусть рассматриваемая точка А
(см. рис. IV-4-1) расположена в поперечной плоскости обтекания ВС,
перпендикулярной поточной оси х, и одновременно лежит в поточной
плоскости (продольной плоскости, содержащей нормаль v к контуру тела
в поперечной плоскости в точке А и параллельной поточной оси х).
Кривая AD на рис. IV-4-1, проходящая через точку А, является пересечением
поверхности тела с поточной плоскостью. Наклон этой кривой к оси х
в точке А определяется производной dvldx. По условию безотрывного
обтекания отношение составляющих скорости VvIVx = dvldx или (d(p/dv)/(F<x>+
+ д<р/дх) — dvldx. Так как осевая возмущенная составляющая скорости
ду/дх < Foo, то граничное условие
-^- = -£-. (IV-4-22)
- &v дх v '
в котором скорость Foo включена в значение потенциальной функции ср.
Определение коэффициентов ао(х), Ъ0(х). Для определения ао(х)
рассмотрим произвольную окружность некоторого радиуса г, расположенную
в плоскости поперечного обтекания тела, и вычислим интеграл по этому
контуру
2я 2л; оо
I l№~ 2 £k - ny) rdy = 2na0.
0 0 n=l
Интеграл по этому же контуру можно вычислить, используя граничное
условие (IV-4-22),
2 л 2я
dw , £ dv , £ dr j 1 d P 9 . d^ (ж) о, / ч
dv д дх Ъ dx * 2 dx j r ^ v n
0 0
где S (x) — площадь поперечного сечения тела. Таким образом,
ао(х)=^-. (IV-4-23)
Для определения коэффициента Ь0(х) воспользуемся (IV-4-6). Применяя
теорему о свертке оригиналов [51], получаем
X
Ъо (х) =JL [S' (x) ln-^-— I In (ж- e) ^ (e) de] . (IV-4-24)
0
Аэродинамические силы
и моменты
Подъемная и боковая силы. Подъемную силу Y можно определить,
вычислив изменение количества движения жидкости при протекании через
контрольную цилиндрическую поверхность S2 некоторого радиуса г
в направлении оси у и через донную торцевую поверхность S3 в том же
направлении (рис. IV-4-3, а)
) I (+^)^dS3. (IV-4-25)
I (%% ) I
( 82) (S3)
Вычисляя изменение количества движения при протекании в
направлении оси я, найдем боковую силу
?= - I (H I
(S2) (S3)
160
Глава I
Протекание жидкости через поверхность S± не дает составляющих
подъемной и боковой сил, так как эта поверхность расположена в
невозмущенной области, где
ду/ду = d^jdz = 0 и изменение
количества движения в
поперечном направлении равно
нулю.
При обтекании тонкого
тела изменение плотности
мало, поэтбму в (IV-4-25) и
(IV-4-26) можно принять
Рис. IV-4-3. Контрольная цилиндрическая поверх-
ность (а) с двумя контурами (б)
Р Р
Вместо сил Z и У удобно
рассматривать комплексную
величину F = ZAr iY.
После подстановки Y и Z получим для этой величины выражение
(IV-4-27)
(s2)
-* S (•+■£)(#+'£) *»
(Ss)
где q^PcJl/2, p = (p — poo)/q.
Формулу (IV-4-27) можно преобразовать, воспользовавшись
соотношениями
dW _ dcp __ . дер dW _ дф . дЦ)
а также выражением для коэффициента давления
i 2 . / да> \ 2П 5ф
dW dW
В результате получим
2
(82)
(82)
ду
(IV-4-27')
Первые два интеграла могут быть вычислены по формуле Стокса для
некоторого произвольного кругового контура К радиуса г1? охватывающего
контрольную поверхность S2 (см. рис. IV-4-3, б). Так как dS2 = r1dydx1
2 1
2 я 1
то в соответствии с формулой Стокса интеграл вида \ /^2=\ \
(S2) О О
Рассмотрим также контур С, совпадающий с контуром донного сечения.
По формуле Стокса
(S3)
Так как dz-\-i dy =■-dt, и
ностью радиуса г1? то
К С
delv = riieiv dy, а контур совпадает с
окруж2я 1
о о
Общие методы решения аэродинамических задач 261
С учетом указанных преобразований
2я 1 — _
F о-£ J* Р Р /О 5Ф dW dW dW
С 0 0
По мере увеличения радиуса контура г4, который может быть выбран
произвольным, возмущения уменьшаются. В пределе при г —> оо
составляющие возмущенной скорости ду/дг, dW/dy и dW/d£ и, следовательно, двойной
интеграл обращается в нуль. С учетом этого получим для комплексной
силы выражение F=—2д£(Ьфй£. Произведя дополнительные преобразова-
(IV-4-28)
с
ния [51], можно найти более удобную для расчета формулу
где £д = 2Д + и/д; зд, уА — координаты центра тяжести площади основания
тела S (1); производная t)'fft = dt)jSy/dx.
Выделяя из (IV-4-28) действительную и мнимую части, получим
соответственно боковую и подъемную силу.
Момент. В комплексной форме
о
Интегрируя по частям и полагая х = 1, получим после некоторых
преобразований
Щ^ = 4mat (1) + 2i[S' (1) £д + S (1) И -
1
- 4л1 J ai йж — 2я5 (1) 2Д. (IV-4-29)
о
Действительная часть этой комплексной функции дает момент
относительно оси z (продольный момент Mz), мнимая — момент относительно оси у
(путевой момент Му).
Сопротивление. Его величина, определяемая изменением количества
движения при протекании жидкости в направлении оси х через
контрольную поверхность, изображенную на рис. IV-4-3, а, равна
(Si) (S3)
(S2)
В этом выражении можно осуществить некоторые упрощения,
используя уравнение сохранения расхода
(Si) (Sa) (S3)
и формулу для коэффициента давления
^ q дх L\dr)~*~r2\dy)j*
Полагая р = р^ и пренебрегая величиной дц>1дх по сравнению с
единицей, получим после подстановки ер из (IV-4-7) и некоторых преобразований
11-114
162 Глава IV
формулу для сопротивления
о о
2я
In -rj^-гS" (e) de- f cp -Ц- dS. (IV-4-30)
Эта формула определяет волновое сопротивление тонких продолговатых
тел, включающих тела вращения и корпуса с произвольным поперечным
сечением. Первые два члена дают сопротивление, обусловленное
распределением толщины по длине тела независимо от формы и наклона поперечного
сечения. Это сопротивление не зависит от угла атаки и, следовательно,
от подъемной силы.
Третий член определяет сопротивление, зависящее от наклона
поперечного сечения. Так как q> = cpt-\-<pa, где сра — потенциал, обусловленный
поперечным обтеканием, то часть сопротивления будет зависеть от
подъемной силы. Исследования показывают, что эта часть сопротивления равна
0,5aY\ Таким образом, полное сопротивление
где Хо — сопротивление при нулевой подъемной силе.
Метод конформного
преобразования
Выше было показано (IV-4-18), что при обтекании тонкого корпуса
потоком с большой скоростью течение в поперечной плоскости (нормальной
к продольной оси тела) может рассматриваться потенциальным и
независящим от числа Маха. Такое течение может быть изучено при помощи
комплексного потенциала (IV-4-19), зависящего от формы контура тела в
поперечном сечении.
Комплексный потенциал определяют во многих задачах со сложной
формой контура косвенным путем при помощи метода конформного
преобразования. Чтобы воспользоваться этим методом, необходимо знать
комплексный потенциал обтекания круглого цилиндра. Метод конформного
преобразования позволяет перейти от этого частного случая к построению
комплексных потенциалов потоков, обтекающих контуры произвольной формы.
Сущность метода конформного преобразования достаточно полно
изложена в работе [1]. Напомним кратко некоторые основные положения этого
метода. Допустим, что в некоторой области S плоскости комплексного
переменного Z> = z + iy задана аналитическая функция <т = /(£) = г) + i£> т. е.
такая функция, которая в каждой точке рассматриваемой области
однозначна и дифференцируема. Совокупность точек a = /(£), соответствующих
точкам области S, образует в плоскости а (преобразованной плоскости)
новую область *51в Следовательно, однозначная аналитическая функция
a = / (£) осуществляет отображение области S плоскости £ = z + iy
на область S1 преобразованной плоскости сг = г| + ££.
Таким образом, указанное отображение может быть осуществлено, если
известна формула преобразования o = f(Q (отображающая функция),
устанавливающая связь между комплексными переменными а и £. В качестве
примера рассмотрим преобразование Н. Е. Жуковского
Общие методы решения аэродинамических задач
163
Примем, что £> = ziJriyi (zi и ух — связанные координаты для обтекаемой
поверхности) и G = r[-\-i£). Следовательно,
Величина г20/(ц + 11) равна г£(*] —^)/(12 + т)2). Предположим, что в
плоскости комплексного переменного а = т] + i| задан круг радиуса г0 с центром
Рис. IV-4-4. Конформные преобразования круга на области
с иной границей
в начале координат, уравнение которого г\ —
этого формула преобразования будет:
(рис. IV-4-4). С учетом
Отсюда находим, что zt = 2%; г/± = 0. Этот результат показывает, что
для точек окружности координата z± является действительной величиной,
изменяющейся в пределах от +2г0 до —2г0 (при изменении -ц от +г0
до —г0) и от —2г0 до +2г0 (при изменении т] от —г0 до +г0).
Следовательно, при помощи формулы Жуковского осуществлено преобразование
круга радиуса г0 в отрезок действительной оси длиной 4г0 (см. рис. IV-4-4,
где введено обозначение s=--2r0). Такой отрезок можно рассматривать как
плоское крыло с размахом 25.
Подбирая специальным образом формулу конформного преобразования,
можно преобразовать круг в другую фигуру, совпадающую по форме с
поперечным сечением обтекаемого тела. В подборе такой формулы состоит
одна из задач теории обтекания тонких тел с заданной конфигурацией
поперечного сечения.
Для конфигураций поперечных сечений летательного аппарата типа
корпус — плоское крыло, изолированного плоского крыла или
продолговатого эллипсоида (см. рис. IV-4-4) получены формулы конформного
преобразования [51[, которые можно представить в общем виде
ИЛИ L = (
(IV-4-32)
п=0
где коэффициенты сп, кп — комплексные числа.
Формулы (IV-4-32), частный вид которых для указанных конфигураций
приведен в табл. IV-4-1, осуществляют преобразования, сохраняющие
направление и величину скорости потока на бесконечности.
По данным табл. IV-4-1 можно определить потенциалы при поперечном
обтекании эллипсоида, комбинации корпуса и крыла, а также плоского крыла,
если известна потенциальная функция для кругового цилиндра.
Рассмотрим два случая обтекания цилиндра, исследованные в теории
плоских несжимаемых течений. В первом случае цилиндр с фиксированным
контуром радиуса г0 обтекается однородным поперечным потоком со
скоростью Vo (рис. IV-4-5, а) под углом ср к вертикальной оси £. Комплексный^
164
Глава IV
Таблица IV-4-1
формулы конформного преобразования
Вид конформного
преобразования
Преобразование круга
в эллипс
Преобразование круга
в комбинацию корпуса
и плоского крыла
Формулы преобразования
~'
а*_
s
Преобразование круга
в плоское крыло
Примечание. «+» — для верхней полуплоскости; «-» — для нижней
полуплоскости.
потенциал такого возмущенного течения
W (а) = — iVoe-i(P (o—^
(IV-4-33)
Во втором случае однородный поперечный поток отсутствует, и
возмущенное течение в поперечном направлении вызывается расширением контура
л цилиндра радиуса г0 с
равномерен Ц Е, \ ной радиальной скоростью Vr (рис.
IV-4-5, б). Такое течение
аналогично потоку от точечного
источника, комплексный потенциал
которого
W (a) = r0Vr In а. (IV-4-34)
Если рассмотреть
продолговатое тело с переменной по длине
площадью поперечного сечения,
обтекаемое в осевом направлении,
то в каждом поперечном сечении
потенциал скоростей можно
определить при помощи формулы
(IV-4-34). При наличии
одновременно поперечного течения, имеющего место в случае обтекания
продолговатого тела под углом атаки, необходимо добавить комплексный потенциал
(IV-4-33).
Построение комплексного потенциала для заданной конфигурации
в плоскости £, = z-\-iy осуществляется путем замены в (IV-4-33) и (IV-4-34)
функции о на £ по формулам конформного преобразования.
Рис. IV-4-5. Обтекание круглого цилиндра:
а — цилиндр в однородном потоке; б — течение
около равномерно расширяющегося цилиндра
Общие методы решения аэродинамических задач
165
§ IV-5. Метод обратимости
потока
Этот метод применим к расчету аэродинамических характеристик
тонких изолированных крыльев, а также их комбинаций с тонким корпусом
в условиях, когда возмущения в потоке малы и, следовательно, углы
атаки являются малыми. При этом набегающий поток может быть как
сверхзвуковым, так и дозвуковым.
Рассмотрим основное соотношение метода обратимости применительно
к условиям обтекания двух тонких крыльев с одинаковой формой в плане,
Рис. IV-5-1. Обтекание крыдьев 1 и 2 прямым и обратным
потоками
но с различной изогнутостью несущей поверхности [6], [41]. Предположим,
что обтекание крыла 1 набегающим потоком с некоторой скоростью Foo
в указанном на рис. IV-5-1 направлении характеризуется распределением
коэффициента давления р1 и соответствующего ему местного угла атаки oq.
Рис. IV-5-2. Обтекание комбинации корпус — крыло —
руль прямым и обратным потоками
Обтекание с той же скоростью второго крыла в противоположном
направлении характеризуется величинами р2, ос2. Метод обратимости устанавливает
следующее интегральное соотношение:
J J J-J Др2сч dS, (IV-5-1)
(S) (S)
в котором величины Ар1? а4, Др2, а2 измерены в одной и той же точке,
причем Api, Ap2 представляют собой перепады коэффициентов давления
на нижней и верхней сторонах крыла в прямом и обращенном потоках.
При использовании соотношения (IV-5-1) следует иметь в виду, что
оно применимо при любом распределении местных углов атаки по
поверхности крыльев при прямом и обратном обтекании. В частности, если
аг = а2 = const, то из (IV-5-1) получаем, что подъемные силы обоих крыльев
одинаковы.
Глава IV
Соотношение (IV-5-1) может быть использовано в более общем случае,
когда имеется некоторая комбинация, состоящая из корпуса и крыла.
Причем крыло может быть оснащено рулевыми элементами (рис. IV-5-2).
В этом случае (IV-5-1) принимает вид
S. (IV-5-2)
<Sp+SKP+Sr)
Для иллюстрации применения метода обратимости потока и
соотношения (IV-5-2) рассмотрим частный случай, когда корпус отсутствует (£т = 0).
Пусть требуется найти подъемную силу неотклоненного крыла при условии,
что угол поворота руля равен некоторому малому значению ах — б. Таким
образом, на крыле местный угол атаки ^ = 0, а на руле а± = Ь. Примем,
что при обращенном обтекании крыла и руля угол атаки на всей
поверхности один и тот же и равен а2 = б.
Внося значение углов атаки в (IV-5-2), получим
= \\ Ар2 dS.
Здесь левая часть определяет отыскиваемую подъемную силу крыла
при отклоненном на угол б руле. Из полученного выражения следует, что
ее можно определить как подъемную силу, создаваемую неотклоненным
рулем в условиях обтекания крыла обращенным потоком под общим углом
атаки б.
Таким образом, метод обратимости потока позволяет привести более
сложную задачу об обтекании крыла с отклоненным рулем к достаточно
простой задаче об аэродинамических характеристиках поверхности с
неотклоненным рулем.
§ IV-6. Общие
выражения для производных
устойчивости оперенного
тела вращения. Метод
присоединенных масс
Применительно к тонким оперенным телам разработан эффективный
метод определения производных устойчивости, названный методом
присоединенных масс или инерционных коэффициентов [14], [51].
Этот метод применим в тех случаях, когда имеется взаимодействие
только между корпусом и крылом (оперением), а влияние вихрей от крыла
на оперение отсутствует. Влияние интерференции между крылом и
оперением учитывается специальными методами.
Рассмотрим оперенное тело (рис. IV-6-1), которое движется с некоторой
скоростью Foo и одновременно вращается с угловой скоростью Q. Начало
координат связанных осей ж, у, z совпадает с центром тяжести, оси £, т), £
выбраны параллельными осям х, у, z и начало координат О' системы £т]£
находится в произвольной точке оси х.
В плоскости поперечного обтекания, совпадающей с плоскостью т]0'£,
потенциал скоростей
101 ср = иц>! + иц)2 + Йхфз> (IV-6-1)
где и и и — составляющие поступательной скорости движения тела в
рассматриваемой плоскости;
Qx — угловая скорость вращения вокруг продольной оси.
Юбщие методы решения аэродинамических задач
167
Потенциалы ф1? ф2 определяют течения, возникающие при движении
плоского контура с единичными скоростями, параллельными осям О'ц и (?'£,
•а ф3 характеризует поток от
вращения контура вокруг
продольной оси с единичной
угловой скоростью.
В силу того, что выбрана
подвижная система координат,
жестко связанная с телом,
потенциалы фь ф2, ф3 не зависят
от времени. Зависимость от
времени суммарного
потенциала ф обусловлена изменением
во времени скоростей и, v, Qx.
Потенциал ф определяет течение
в поперечной плоскости,
влияющее на производные
устойчивости. Составляющая
потенциала для продольного обтекания
не имеет значения, так как оно не оказывает влияния на эти производные.
Если функция ф и ее составляющие определены, то можно найти
распределение скорости при поперечном обтекании и кинетическую энергию
газа, заключенную в некотором объеме т (рис. VI-6-1) и равную
т. (IV-6-2)
(т)
Применяя к этому уравнению преобразование Грина, получим
выражение для кинетической энергии газа на единицу длины в направлении оси х:
Рис. IV-6-1. К определению производных
устойчивости оперенного тела вращения
(IV-6-3)
где С —контур, состоящий из очертания поперечного сечения тела и
внешней границы рассматриваемого объема т;
п — внешняя нормаль;
Z —дуга контура С.
Из (IV-6-3) видно, что кинетическая энергия определяется девятью
•слагаемыми, каждое из которых включает в себя коэффициент вида
Vl дП
dl,
(IV-6-4)
называемый коэффициентом присоединенных масс или инерционным
коэффициентом поперечного сечения.
Формулу (IV-6-4) можно видоизменить, если воспользоваться условиями
Коши—Римана dqldn = dtyldl, dq>/dl= —dty/dn. После простых
преобразований получаем
(IV-6-4')
где по аналогии с потенциалом скоростей функция тока представляется
в виде суммы трех составляющих
h. (IV-6-5)
168 Глава IV
Применим к (IV-6-4) частную формулу Грина, справедливую для
потенциальных функций ф1, фг и ф3:
с с
Таким образом, Л^ = Я^, следовательно, вместо девяти членов в (IV-6-3)
останется шесть. Тогда для кинетической энергии
2Г == Хпи2 + Xzzv2 + X33Q% + 2X12uv + 2Xi3uQx + 2X23vQx. (IV-6-3')
где и и v — скорости, которые можно заменить значениями
и== 6 F ■ | О х' v — ctF — О >х ^IV-6-6\
Подъемная и боковая силы, а также момент крена, действующие
на тело, определяются по известной кинетической энергии:
dZ d_ /дТ\ ^ дТ_ # (IV 6 7^
4г-= —т- (—) —Six—; (IV-6-8)
ах dt \ dv ) ди v
^=— 4-(-S-)+»-?--»-?-• (IV-6-9)
Полная производная d/dt определяется с учетом изменения параметров
для фиксированного поперечного сечения. Для некоторого произвольного
параметра /, являющегося функцией времени t и расстояния х до начала
координат (рис. IV-6-1),
где dx/dt = — Foo,
d д т-г д
~dt^~dt~ool)xm
Моменты тангажа Mz и рысканья Му находятся из уравнений
dx dx ' dx dx
Интегрирование ведется от основания тела с координатой х=—хА
до носка с координатой х = хн. Таким образом, все [моменты вычисляются
относительно осей, проходящих через центр тяжести.
Удобнее перейти к аэродинамическим коэффициентам. С этой целью
полученные выражения для сил следует разделить на 0,5pooF?o5r, а
моментов— на 0,5pooFL57. Для определения производных устойчивости необходимо
соответствующим образом продифференцировать выражения для
коэффициентов су ~ cN, cZy mx, my, mz. Дифференцируя последовательно по а, р,
сох = Qxl/2Voo, (dy = Qyl/2Voo, coz = QzZ/2Foo, получим статические и враща-
тельные производные; дифференцируя по а = allZVoo, P=|3//2Foo, cox = coxZ2/2FL,
coy = coyZ2/2FL, coz = (ozZ2/2FL, Foo = FooZ/2FL, найдем производные
устойчивости по ускорениям.
Статические производные устойчивости имеют следующий вид:
с%=- 4^522 - 2l22 - 4сож512;
с% = - 4fco512 - 2 J12- 4аяД11;
с» = - 4foo512 - 2i^2 + 4соя522;
Общие методы решения аэродинамических задач 269
- 2А
и
- 4Fco523 - 2 J23 + 4аБ12 + 2p (Bu - BZ2)
- 8согС12 + 4<йу (Cit - С22);
ml = - AfooBi3 - 2 Аи + 2а (5И - £22)
- 4coz (Си - С22) - 8(oyCiZ; (IV-6-16)
ml
- 4FroC12 - 2 [S12 + A12 (f) дон] + 4сожС22;
l = -4F.CH-2 [5U + In (y) 1 + 4©*C12; (IV-6-18)
L \ ^ / ДОНJ
m? = + 4^22 + 2 [i522 +122 (у) дон] + 4сожС12; (IV-6-19)
m\ = 4FooC12 + 2 [B12 + Ai2 (у)дон] + 4сояСи. (IV-6-20)
Вращательные производные определяются выражениями:
с%х = — 4/23 —
c7=-4i"12(-f) -8сожС„; (IV-6-22)
\ I / ДОН
C12; (IV-6-23)
дон
- 8(о2С22 + 8ювС12; (IV-6-24)
^ = _ 4/и (-1) дон + 8о)жС12; (IV-6-25)
Г = 4i;2 (у) дон -8сожС22; (IV-6-26)
tx = - 4l33 + 4а£13 - 4р523 - 8cozC13 - 8coyC23; (IV-6-27)
ДОН
- 8со2 (Du - D22) - l6«>yDiZ; (IV-6-28)
V = 4l23 (у) - 8аС12 - 4p (Cu - C22) - 8u)x
V * / дон
+ 16(ozZ)12-8co!/(Z>11-Z)22); (IV-6-29)
^ = - 4 Гя13 + Лз fу) 1 + 4аС22 + 4рС12 + 16сожС23 -
|_ \ " / ДОН J
Z?12; (IV-6-30)
4 [J12 (^) дон + С12] -8(oKZ)22; (IV-6-32)
4 [£23 +123 (у) дон] + 4аС12 + 4рСи +
16о)жС13 - 8cozZ)12 + 8(oyZ?u; (IV-6-33)
170 Глава IV
т?> = 4 [112 (у)2дон + С12] + 8v>xDu; (IV-6-34)
,n?z = - 4 Г i"22 (-f)2 + С221 - 8юж£»12. (IV-6-35)
L \ W дон J
Производные по ускорениям
; (IV-6-36)
(Ox / d ®i/ //"* . л^2 //"* . /ТЛ7" d. Q7\
Сдг = —4Ш2з) C^v — —4^12» ciV — ^^22» (1Y-O-O/)
c? = -*4£12; cf = - 45U; cj" = - 4a512 - 4pJ?14; (IV-6-38)
<£= = _4fi13; cf»= -4CU; cf = 4C12; (IV-6-39)
m*=- 4Z?23; mg = - 4£13; ml" = - 4a£23 - 4p£13; (IV-6-40)
77ZX = —4Ш33, Шх = —^^13? ^x ==^^23» (IV-D-'Hj
/nj, = —4612; 772j, = —46-11; ^ =—4a612 — 4(э6ц; (IV-d-42)
772^ = — 4613; myJ = — 4/>и; ттгу 12' (lV-b-4d)
77iz — 4622; щ=4612; 7722 =4a622 + 4p612; (lv-b-44)
mfx = 4C • mfv = 4:D * mfz= 4Z) . (IV-6-45)
В выражениях для производных устойчивости введены безразмерные
параметры Bjft, C^, Z?^, которые определяются для значений i, к
соответственно 1; 2; 3 соотношением
Eik= \ Aikxndx. (IV-6-46)
хдон
Здесь
Параметры Aik представляют собой безразмерные коэффициенты
присоединенных масс, связанные с размерными коэффициентами присоединенных
масс Xik соотношениями:
л 11 л л 12 л ^22
•^•11 == "7—с" » ^12 = -^21 == "7—с" ' -^22 == "Г—о~ '
Роо^ Роо1^ Роо^
/4 = Л = 13 Л ___ Л ___ 23 /| __ 33
В отличие от Aik параметры Aik, входящие в выражения для
производных устойчивости, определяют безразмерные коэффициенты присоединенных
масс, найденные для поперечного сечения тела у основания с контуром С,
по которому ведется интегрирование в формуле (IV-6-4).
Определение производных устойчивости связано с вычислением
коэффициентов присоединенных масс по формулам (IV-6-4) или (IV-6-4'). Из (IV-6-4)
видно, что коэффициенты Х^ для заданной формы тела могут быть найдены,
если известны потенциалы скоростей при поперечном обтекании ср17 ср2, ф3,
а также производные по нормали к контуру поперечного сечения.
Общие методы решения аэродинамических задач 171
Эти производные можно определить непосредственно, рассматривая
условия на границе контура. Так как производная ду/дп представляет
собой скорость точки контура в направлении нормали, то
дф! ду дф2 dz_ дф3 1 с?/-2 1 d(y2 + z2) пхта л
дп dl ' "5л dl ' дп 2 dl 2 dZ • V1V °-^°;
От потенциалов q^ можно перейти к комплексным потенциалам
Wi = q>i-\-i'tyi. С учетом (IV-6-48) выражения для коэффициентов
присоединенных масс
f (Wft - ii|)fe) d£, (IV-6-49)
где £ = z + £z/, а коэффициент А последовательно принимает значения 1, 2, 3.
Коэффициент присоединенной массы
^jW3-i^)d (Ш, (IV-6-50)
где Z = z — iy.
Интегралы, содержащие функцию тока, определяются из граничных
условий на контуре. С этой целью по (IV-6-48) и условиям Коши — Римана
следует найти значения функций тока на контуре я]^, г|з2, if>3. После их
подстановки под интегралы Ф % й£ найдем для /с = 1 и 2 соответственно
с
значения 5С, —iSc, определяемые площадью поперечного сечения, а для
k = 3 получим, при условии, что форма сечения симметричная, нулевое
значение интеграла.
Комплексный потенциал Wk находится при помощи конформного
преобразования заданного поперечного сечения в плоскости £ = z + iy в круг
некоторого радиуса г0 в плоскости а = т] + ^> осуществляемого по общей
формуле (IV-4-32). Если потенциал Wk (о) для круга известен, то,
производя подстановку g = o(Z), можно получить комплексный потенциал Wk(Z)
в физической плоскости £.
Наиболее просто получаются потенциалы W±, W2, характеризующие
обтекание тела при его движении соответственно вдоль осей z и г/. С этой
целью можно воспользоваться выражением (IV-4-33). Положив в нем F«> = 1,
<р = 0, получим формулу W = о — Гд/ст, которая определяет комплексный
потенциал для неподвижного цилиндра, обтекаемого в направлении оси у
набегающим потоком с единичной скоростью.
По сравнению с формулой (IV-4-33) знак «минус» перед i изменен
на знак «плюс», так как в нашем случае положительные значения
координаты у отсчитываются вниз.
Полученный потенциал равен величине W2 (£) + ££, характеризующей
поперечное обтекание неподвижного тела в плоскости £, причем W2 [£ (о)]
представляет собой комплексный потенциал для подвижного цилиндра
в плоскости а. Заменив £ по (IV-4-32), получим
n=0
Аналогично получаем комплексный потенциал обтекания в плоскости а
при направлении потока по оси z
оо
Wi [I (а)] = — -^-+ ^ ^ • (IV-6-52)
п=0
272 Глава IV
При определении комплексного потенциала W3 можно исходить из
выражения ImVF3 = Im(iif)3), указывающего что W3 — мнимая часть потенциала я|)3.
Причем потенциал я|)3 должен удовлетворять условию для функции тока
на границе подвижного тела dq>3/dn = dty/dl, в соответствии с которым
гЬ= -±(z* + y*)=~(z + iy) {z-iy)=-\&. (IV-6-53)
Таким образом, отыскание потенциала W3 связано с решением задачи
Дирихле об определении в некоторой области функции г|)3 по граничному
условию (IV-6-53).
Общее выражение для определения W3 может иметь вид
Im W3 = Im ( —i Щ . (IV-6-54)
В это выражение следует внести £ из (IV-4-32), а также ряд
оо
^+2-=Ь (IV-6-55)
п=0
в котором о»=с2/сг. В результате этих подстановок комплексный потенциал
оо
^з=-*2^. (IV-6-56)
П=1"
Вычисления коэффициента присоединенных масс можно производить
непосредственно по (IV-6-4). При этом потенциал ц>г и функция тока г|)&
находятся из выражения для комплексного потенциала W — ф + ity.
Пример. Определим коэффициенты присоединенных масс для эллипса
с полуосями а и Ъ. С этой целью найдем комплексные потенциалы Wu W2,
воспользовавшись конформной формулой (см. табл. IV-4-1)
^ri' (IV-6-57)
отображающей внешность эллипса в плоскости £ на внешность круга радиуса
го = О,5 (а + Ь).
Потенциал W± определяется по (IV-6-52). Чтобы определить
коэффициенты ряда кп, надо воспользоваться выражениями (IV-6-57) и (IV-4-32).
Сравнивая их, найдем, что ki = (a2 — Ь2)/4, а остальные коэффициенты ряда
равны нулю.
Внося значение для ки получим
W±=-^. (IV-6-58)
Аналогично найдем уравнение
W2=-i^. (IV-6-59)
Комплексные потенциалы можно определять также из граничных
условий для функций тока. Проиллюстрируем это на примере комплексного
потенциала Wle
Из условия на границе контура г|^± = г/ получим зависимость Im W4 =
= Im£. Внося в эту зависимость под знак Im вместо £ выражение (IV-6-57),
получим после простых преобразований - формулу Im Wi = Im (— r0b/o),
действительную на круге. Обобщая эту формулу, получим (IV-6-58).
Аналогично найдем выражение для W2. С этой целью исходим из
граничного условия г|з2= — х или Im^F2 = Im ( — it,). После подстановки сюда t,
из (IV-6-57) придем к уравнению (IV-6-59).
Общие методы решения аэродинамических задач 173
Для определения потенциала W3 воспользуемся выражением (IV-6-56).
Внося в него £ из (IV-6-57), а также
после преобразований получим комплексный потенциал
W3=-i{a2-pr» . (IV-6-60)
Коэффициенты присоединенных масс вычисляются по формуле (IV-6-4').
При вычислении удобно перейти к полярным координатам г0, 6. Например,
комплексный потенциал W± записывается в виде W±=—(r0b)lo——be~iQ.
Тогда потенциал скоростей ф! = — b cos 0, а функция тока г^ = b sin 8.
Аналогично представляются W2, W3 и находятся соответствующие
выражения для потенциалов и функций тока.
Внося выражения для ср*, tyk в (IV-6-4') и интегрируя от 0 до 2л,
получим следующие значения коэффициентов присоединенных масс:
К\ = лрооЬ2; А,22 = ярооа2; Х33 = -^ яроо (а2 — Ь2)2; Х12 = Л13 = А,23 = 0. (IV-6-61)
Из приведенного примера видно, что для эллипса коэффициенты
присоединенных масс Xik равны нулю, если 1фк. Эта особенность сохраняется
для всех тел, поперечное сечение которых обладает свойством симметрии.
§ IV-7. Приближенные
методы расчета обтекания
поверхностей
Метод Ньютона. Этот метод применяется для приближенного расчета
давления при очень больших скоростях обтекания. Он основан на
корпускулярной теории Ньютона (или теории «ньютонова торможения»), согласно
которой частицы газа испытывают возмущения только при ударе о твердую
стенку и полностью теряют нормальную к стенке составляющую количества
движения. Избыточное давление определяется этой потерей количества
движения в соответствии с формулой р — Роо = РосУ1, где Vn — нормальная
к стенке составляющая невозмущенной скорости. Разделив на скоростной
напор q = 0,5pooVlo, получим формулу Ньютона для коэффициента давления
p2,
Эту формулу можно представить также в виде
p = 2cos2T], (V-7-Г)
где г\ — угол между вектором скорости Foo и нормалью к поверхности.
Отнесем формулу (IV-7-Г) к какой-нибудь фиксированной точке
поверхности, наклон которой^ определяется углом т|*. Для этой точки местный
коэффициент давления p0 = 2cos2r]*. Присоединяя (IV-7-Г), получим
усовершенствованную формулу Ньютона для коэффициента давления в
произвольной точке поверхности
174
Глава IV
Эта формула дает лучшее приближение, чем (IV-7-Г), так как
величина ро вычисляется достаточно точно для начальной точки поверхности,
которой может быть, в частности, коническое острие заостренного тела или
точка полного торможения на затупленной поверхности. В последнем случае
cosrj* = l и
\. (IV-7-3)
Приведенные формулы определяют давление, возникающее при
поступательном движении тела. Между тем поступательное движение может
сопровождаться вращением относительно центра тяжести, что может оказать
существенное влияние на перераспределение давления.
Чтобы учесть это влияние, следует воспользоваться формулой (IV-7-1),
в которой Vn должна быть определена в ^иде суммы двух составляющих,
Рис. IV-7-1. К опеределению составляющей скорости,
нормальной к обтекаемой поверхности у = / (z, х)
а именно нормальной компоненты невозмущенной скорости и нормальной
составляющей скорости, индуцируемой в рассматриваемой точке при
наличии вращения.
Таким образом, определение давления по методу Ньютона связано
с вычислением суммарной величины составляющей скорости, нормальной
к поверхности тела.
Рассмотрим произвольную поверхность (рис. IV-7-1) с уравнением
y = f(z, х), обтекаемую потоком с большой скоростью Foo. Угол атаки,
измеряемый в плоскости уОх, образован вектором Foo и положительным
направлением оси х. Чтобы найти составляющую скорости Vnoo
поступательного потока, нормальную к элементу dS в точке А, следует вычислить
скалярное произведение вектора Foo и единичного вектора п внутренней
нормали к рассматриваемому элементу поверхности. Из рис. IV-7-1 видно,
что вектор Foo = Foo cos ai + Foo sin а/. Единичный вектор п можно
представить в виде п = cosaxi -\-cosayj'-\- cosazk, где i, /*, к — единичные векторы^.
ах, ау, az — углы, образуемые вектором п с направлениями осей координат.
у
Косинусы этих углов
ду/дх
cos ах =
—1
cosaz =
dy/dz
В соответствии со значениями векторов
щая скорости поступательного потока
Vnoo = Foo cos a cos ax -f F^ sin a cos ay
(IV-7-3')
и п нормальная
составляю(IV-7-4)
Общие методы решения аэродинамических задач 275
Предположим, что обтекаемое тело совершает вращательное движение
с некоторой угловой скоростью Q = Qxi + £iyj' + Qzk.
Добавочная скорость, индуцируемая в рассматриваемой точке А, равна
векторному произведению v — QxR, где R — радиус-вектор для точки А.
Если их, vy, vz являются составляющими вектора v, то нормальная к
площадке dS составляющая VnQ скорости
VnQ = vx cos ах + vy cos ay + vz cos ocz. (IV-7-5)
Радиус-вектор R может быть представлен в виде R = xAi -j- yAj -f- zAk,
где xA, yA, zA — расстояния до точки А от центра вращения. Таким
образом, вектор индуцированной скорости
v=vxi + vyj + vzk = (QyzA — QzyA) i — (QxzA — QzxA) j +
+ (QxyA-QyXA)~k. (IV-7-6)
Из этого выражения непосредственно определяются составляющие их,
vy, vz, входящие в (IV-7-5) для Vuq. Определив значения Fnoo, VnQ, можно
найти суммарную величину нормальной составляющей скорости Vn=VnOo-\-
-\-Vn& и, следовательно, коэффициент давления (IV-7-1). Его величину
можно представить в виде суммы двух составляющих
P = Pv + Pa, (IV-7-7)
где первый член
Pv = 2^- (IV-7-8)
характеризует приращение давления от поступательного движения, второй
член
Ра = 4- (2Vn~VnQ + V^) (IV-7-9)
К оо
дает составляющую, обусловленную вращательным движением.
По известной внешней форме обтекаемой поверхности и распределению
давления могут быть определены аэродинамические характеристики (силы,
моменты и их коэффициенты).
Применение метода Ньютона ограничено, очевидно, теми участками
поверхности тела, которые обращены в сторону набегающего потока и
испытывают столкновение с частицами газа. Границей этого участка является
некоторая кривая, вдоль которой нормальная компонента скорости Vnoo
и, следовательно, коэффициент давления pv равны нулю. Из (IV-7-4)
следует, что уравнение этой кривой
cos a cos ах + sin a cos ау = 0. (IV-7-10)
За пределами этой кривой, в так называемой «затененной» зоне,
давление в которой обозначим через ре, при оценке коэффициента ре — (2 /kMlo) X
X (ре/роо — 1) можно исходить из разных соображений. Полагая,
например, что М -> оо, получим ре = 0. Можно также принять условие, что
скорости остаются конечными, хотя и очень большими по величине, так что
Моо > 1, а в «затененной» зоне образуется полный вакуум (ре = 0).
Соответствующая величина коэффициента давления будет ре = — 2/kM%y.
Метод Ньютона в принципе применим для произвольных потоковт—
плоских или пространственных. Однако, как показывают
экспериментальные данные, для плоских течений он дает менее удовлетворительные
результаты, чем для пространственных. Это значит, например, что распределение
давления по профилю крыла, полученное при помощи этого метода, будет
менее точным, чем по телу вращения.
176 Глава IV
Метод, сочетающий теорию скачков уплотнения и течений разрежения.
Этот метод, позволяющий определять параметры сверхзвукового обтекания
на заостренной поверхности, состоит в следующем. Вычисление параметров
на заостренном носке, с которого начинается расчет, осуществляется с
помощью теории скачков уплотнения, а на последующих участках,
расположенных вниз по потоку, претерпевающему расширение, параметры находятся
по теории Прандтля — Майера.
В этом методе предполагается, что сверхзвуковое обтекание
заостренного носка («острия») может быть плоским (поток около клина) или
пространственным (течение около конуса). Что касается сверхзвукового обтекания
остальной части поверхности, то оно рассматривается как плоское.
Для расчета такого плоского сверхзвукового обтекания можно
воспользоваться аналитическими зависимостями для эпициклоид-характеристик
двухмерного течения. Каждой точке эпициклоиды соответствуют
определенные значения местного числа М и угла отклонения потока при его изэн-
тропическом расширении от начального состояния с числом М = 1 и
давлением, равным критическому р*. Отсюда следует, что каждой точке
эпициклоиды соответствует в то же время определенное значение отношения
давлений
Эта формула позволяет вычислять давление в тех точках потока, в
которых состояние газа изменилось в результате изэнтропического расширения
или сжатия. При этом начальные параметры изэнтропического течения
определяются сразу за скачком уплотнения, где поток отклонился от
первоначального на некоторый угол |30 и где местное число М равно какому-либо
значению М2 > 1.
Предположим, что требуется найти давление в некоторой точке
поверхности, касательная к которой образует с направлением вектора Foo угол р.
С этой целью по величине М2 находим при помощи (IV-1-17) или из
табл. IV-1-1 угол со2, равный углу поворота потока, расширяющегося от
М = 1 до М = М2>1. Затем находим полный угол поворота со = со2 +
+ Ро — Р> по которому из табл. IV-1-1 определяем местное число М. Внося
это число в (IV-7-11), вычисляем отношение р/р*, а затем коэффициент
давления
При использовании этого метода для расчета гиперзвукового
обтекания тонких заостренных тел можно воспользоваться упрощенным
уравнением (IV-1-18) для эпициклоид. Если отнести это уравнение к условиям
потока непосредственно за скачком уплотнения, то получим
Для произвольной точки на контуре со = со2 + р0 — р.
В результате связь между углом со и числом М примет весьма
простой вид
Остальные параметры, такие, как давление, плотность, температура,
скорость потока, рассчитываются по найденному числу М при помощи
(Ш-3-7) или (Ш-3-8).
Общие методы решения аэродинамических задач 277
В частности, из (Ш-3-7) можно получить зависимость для расчета
коэффициента давления
_ 2k _
2
_ _
Р __ ( М2 \ ft-l / Pk 2 \
Число М2, входящее в эту формулу и в (IV-7-14), также определяется
по упрощенным соотношениям для клина или конуса.
Выражение для коэффициента давления в произвольной точке
криволинейной поверхности можно представить в общем виде
§£}/Р(М2,ро-р),
гДе /р — некоторая функция, зависящая от числа М2 за ударной волной на
заостренном носке и угла поворота потока (30 — Р-
Эта функция для заданного М2 не зависит от формы поверхности.
Параметры с индексом «2» определяются в зависимости от того, каким является
Рис. IV-7-2. Взаимодействие волн при сверхзвуковом
обтекании плоского контура
поток перед заостренным носком — плоским (крыло) или
пространственным (корпус).
Применение изложенного метода более оправдано для расчета плоских
сверхзвуковых потоков, в частности, около крыльев. Неточность метода
обусловлена неучитываемым взаимодействием обтекаемой поверхности со
скачком уплотнения (рис. IV-7-2) в области правее отраженной волны АС.
В случае, когда исследуется обтекание заостренных корпусов,
погрешность обусловлена заменой пространственного течения за ударной волной
плоским.
По мере увеличения скоростей расчет по изложенному методу дает
более удовлетворительные результаты. Для крыльев его можно
рассматривать точным, когда отраженная от ударной волны в точке А' простая
волна разрежения не пересекает поверхность (рис. IV-7-2).
Для тонких тел точность возрастает по мере увеличения параметра
К = Мооро- Экспериментальные исследования показывают, что хорошие
результаты получаются, когда К > 1, а углы атаки невелики.
При больших углах атаки существенное отклонение от
экспериментальных результатов наблюдается на наветренной стороне поверхности, что
связано с большим влиянием вязкости, которое не учитывается
рассматриваемым методом.
Этим методом можно рассчитывать, в отличие от метода Ньютона,
обтекание тех ^участков поверхности, которые имеют отрицательный наклон
к направлению скорости Foo, т. е. принадлежащих «затененной» зоне. Из
12-114
178
Глава IV
содержания самого метода следует, что он может дать в некоторой области
отрицательную величину коэффициента давления, которая обнаруживается
экспериментально. При этом удовлетворительное соответствие с
экспериментальными данными имеет место в том случае, когда за «ударной» областью
непосредственно следует «затененная» зона. Метод следует применять с
известной осторожностью для оценки параметров сверхзвукового обтекания
достаточно удаленных от носка хвостовых сужающихся участков тела, так как
он не учитывает всех сложных процессов течения около предшествующих
участков.
Одна из особенностей этих процессов состоит в том, что они связаны
со взаимодействием потока и ударной волны, существенно влияющим на
изменение параметров газа.
К недостаткам метода надо также отнести и то, что в нем не учитывается
предыстория движения частиц газа..Для этого метода неважно, как двигалась
Рис. IV-7-3. Схема, иллюстрирующая метод
«касательных» конусов
частица к данному месту, а существенным является ее местоположение.
Таким образом, параметры в какой-либо точке будут одними и теми же,
независимо от того, какой по форме является поверхность на
предшествующем участке, если только сохраняются постоянными углы заострения р<>
и наклона |3 поверхности в рассматриваемой точке.
Сказанное относится и к головным, и к концевым участкам тела. Однако,
если эти недостатки, как показывают экспериментальные данные, почти
не проявляются в передней части, то у кормы отклонение от
действительной картины может быть более существенным.
Метод «касательных поверхностей». Для иллюстрации этого метода
рассмотрим решение задачи о симметричном сверхзвуковом обтекании
заостренного тела вращения. Коэффициент давления в некоторой точке А
поверхности тела, расположенного в потоке с числом Моо > 1, принимается
по величине таким, как на касательной к этой точке конической
поверхности, обтекаемой потоком с тем же числом Моо (рис. IV-7-3). Таково
содержание метода «касательных конусов», который, как видно, позволяет
исследовать обтекание поверхности с криволинейной образующей, используя
данные о сверхзвуковом потоке около более простой по форме конической
поверхности.
Этот метод можно распространить на заостренные поверхности
произвольной формы, полагая коэффициент давления в любой точке поверхности
равным его значению в той же точке на соответствующей касательной
поверхности (метод «касательных поверхностей»).
При выборе формы касательной поверхности, что является
существенным моментом расчета, должна учитываться форма исследуемой обтекаемой
поверхности (рис. IV-7-4). Например, для крыла касательная поверхность
является плоскостью с передней кромкой, обладающей той же стреловид-
Общие методы решения аэродинамических задач
179
ностыо, что и линия АВ, в точках которой определяется давление. Для
заостренного тела вращения касательной поверхностью является круглый
конус.
Угол заострения касательной поверхности равен углу, образованному
касательной к данной точке поверхности с вектором FTO. При наличии угла
атаки касательная поверхность должна строиться так, чтобы она обтекалась
при нулевом угле атаки (рис. IV-7-5). Таким образом, давление в какой-
Рис. IV-7-4. Построение касательной поверхности около
крыла и корпуса:
1 — плоская касательная поверхность к крылу; 2 — коническая
касательная поверхность к корпусу
либо точке заостренной поверхности, обтекаемой под углом атаки,
принимается таким, как на соответствующей касательной поверхности при
условии, что для нее а = 0.
Можно рассмотреть другую разновидность метода касательных
поверхностей, основанную на гипотезе равенства скоростей в точке касания
реальной и касательной поверхности. В соответствии с этой гипотезой коэффициент
давления определяется по формуле рс = [2/(Ш^)] (рс/роо — 1), в которой
величина абсолютного давления
вычисляется по скорости Vc и
давлению торможения р'о. Это
давление определяется для
заданного Мое по углу скачка у острия
тела (индекс «с» относится к
величинам, рассчитываемым по
гипотезе равенства скоростей).
Расчет на основе гипотезы одинаковых скоростей можно упростить,
воспользовавшись результатами, полученными по гипотезе одинаковых
давлений. Так как скорости, вычисленные на основе обеих гипотез, равны,
то можно найти зависимость
Рис. IV-7-5. Касательная поверхность при
наличии угла атаки
. 2(v —
Г
(IV-7-18)
где рц — коэффициент давления, соответствующий гипотезе одинаковых
давлений; величина v равна отношению vo/v, в котором коэффициент v =
— Ро/Ро рассчитан по давлению торможения р"0 для местной касательной
поверхности с углом наклона |3 к вектору Foo, а величина v0 = р'0/р0
определена по давлению торможения р'о для касательной поверхности с углом
наклона 0О.
12*
180 Глава IV
Таким образом, чтобы рассчитать коэффициент давления рс, надо
вначале найти на местной касательной поверхности значение рд и определить
отношение v = vo/v. Это отношение у острия равно единице, а для тех
точек, где |3 < р0, величина v < 1. Поэтому коэффициент рс примет, как
следует из (IV-7-18), в некотором сечении нулевое значение, а далее вниз по
потоку окажется отрицательным.
Возможность получения отрицательных величин коэффициента
давления принципиально отличает метод «касательных поверхностей», основанный
на гипотезе одинаковых скоростей, от метода, основанного на гипотезе
одинаковых давлений, по которому коэффициент давления может быть либо
больше, либо равен нулю.
Экспериментальные данные и некоторые теоретические исследования
показывают, что при умеренных числах Моо в удаленных от носка участках
возникают четко выраженные области разрежения. Это подтверждает, что
при таких скоростях гипотеза одинаковых скоростей более реальна, чем
гипотеза одинаковых давлений.
При очень больших числах Моо почти вся поверхность с положительным
наклоном находится под положительным избыточным давлением, что не
согласуется с гипотезой одинаковых скоростей, дающей неправдоподобно
малые значения давления.
По смыслу рассматриваемый метод применим для расчета потока в тех
точках, где наклон касательной поверхности к направлению вектора F<x>
составляет угол р >0. При этом в точке, где (3 = 0, давление рд принимается
равным давлению р<х> невозмущенного потока и, следовательно, коэффициент
давления в этой точке рц = 0. Таким образом, для площадок с
отрицательным наклоном (Р < 0) этот метод, строго говоря, неприменим.
Однако для грубой оценки коэффициента давления в «затененной» зоне
можно воспользоваться методом «касательных поверхностей». При этом
предполагается, что коэффициент давления на площадку с углом Р < 0
будет по знаку отрицательным, но равным по абсолютной величине
коэффициенту давления на площадку с положительным углом наклона (Р > 0).
Формула Буземана. В соответствии с ньютоновской корпускулярной
теорией аэродинамическая сила возникает в результате соударения частиц
газа с поверхностью. Основная концепция этой теории заключена, таким
образом, именно в эффекте удара.
Выводы ньютоновской теории можно получить из теории ударной волны,
произведя в соответствующих выражениях предельный переход при условии
fc—>-1, Моо -»■ оо, что соответствует полному прилеганию ударной волны
к поверхности и, следовательно, бесконечно малой толщине сжатого слоя.
В реальных условиях обтекания ударная волна не может подойти
вплотную к поверхности. Поэтому частицы, испытав удар при переходе через
скачок уплотнения, продолжают движение по искривленным траекториям.
Это приводит к тому, что давление на поверхности тела отличается от
давления непосредственно за скачком.
Принципиально такое же явление будет в гипотетическом потоке при
Моо->-оо, &->1. Частицы газа, перейдя ударную волну, совпадающую
с поверхностью, продолжают свое движение в бесконечно тонком слое по
геодезическим линиям поверхности.
Скорость этого движения F2, вычисляемая из теории скачка
уплотнения при к ->■ 1, Моо -> оо, равна V2 = У\ cos P (индексы 1 и 2 относятся
соответственно к параметрам потока до и за скачком).
Движение по искривленной траектории приведет к возникновению
центробежной силы, которая изменит давление на поверхности тела по
сравнению с его значением, получаемым по теории Ньютона.
Общие методы решения аэродинамических задач 181
Величина этой силы, определяемая массой перешедших через скачок
частиц в единице объема (плотность р2) и центробежным ускорением V\IR,
где R — радиус кривизны обтекаемого контура, равна р2УУК- Следовательно,
элементарная величина давления, создаваемого этой силой в тонком слое
толщиной dn, будет йрць = (p2Vl/R) dn.
Произведение $2V2dn можно заменить выражением, получаемым из
уравнения расхода p2F2/ (x) dn = р^ dS, в котором / (х) = 1 для плоских
и f(x) = 2nr(x) для пространственных симметричных течений; S — площадь
поперечного сечения. Тогда элементарное центробежное давление
Rf(x)
Интегрируя это соотношение по S и учитывая, что за ударной волной
давление равно piFJ sin213, найдем [38]
8
p=PiFjrsinap—r7i-g ^ cosflds] . (IV-7-19)
О
Эта формула, полученная Буземаном, определяет давление не только
в зависимости от местного наклона площадки относительно вектора Foo, но
и от формы поверхности на всем участке между площадкой и передней точкой.
Для тонких тел, у которых углы |3 всюду малы (cosji^l, sinp^ji),
влияние формы поверхности предшествующего участка оказывается
пренебрежимо малым. Формула (IV-7-19) принимает вид
(IV-7-20)
Заменив радиус кривизны его значением для тонкого тела R= — (d2yldx2)~1
и перейдя к коэффициенту давления, получим
где у — координата точки поверхности крыла (плоский поток) или корпуса
(пространственное течение).
В последнем случае у равен радиусу г образующей тела вращения.
Подобно усовершенствованной формуле Ньютона можно написать формулу
Буземана для коэффициента давления
Для тонкого тела
ИЛИ
Р~ PS
где v = 1 для плоских течений; v = 2 — для симметричных пространственных
потоков.
Приведенные зависимости отличаются от соответствующих формул
Ньютона наличием второго члена в скобках, характеризующего влияние
кривизны контура и учитывающего, следовательно, влияние на давление
цетробежных сил.
Как показывают исследования, при условии к = 1,4 это влияние будет
реальным в случае обтекания вогнутых поверхностей.
182 Глава IV
Для тел с выпуклой поверхностью поправка на влияние центробежных
сил физического смысла не имеет, поэтому для расчетов лучше применять
формулу Ньютона. Однако для тонких поверхностей она дает завышенные
значения давления при условии Моо—>оо, к —>1 и, следовательно, в этом
случае предпочтительней оказывается формула Буземана.
§ IV-8. Аэродинамический
нагрев
Полет в атмосфере сопровождается передачей тепла от окружающей среды
к летательному аппарату, когда на близком расстоянии от его поверхности
температура газа становится выше температуры тела. Области высоких
температур возникают вследствие торможения потока в ударных волнах
и в пограничном слое, что вызывает увеличение статической энтальпии
воздуха.
Расчет теплопередачи заключается в определении: а) скорости передачи
тепла в точке полного торможения; б) скорости теплопередачи в любой
другой точке стенки; в) полного теплового потока к поверхности. Решение
первой задачи позволяет правильно рассчитать систему охлаждения или
выбрать другие средства, обеспечивающие предохранение поверхности
от перегрева. Решение двух других задач даст возможность определить
участки, где достигаются чрезмерные тепловые напряжения и возможно
разрушение поверхности с тем, чтобы предпринять практические меры
предосторожности.
Рассмотрим некоторые общие понятия теории аэродинамического нагрева.
Параметры теплопередачи
Температура и энтальпия в пограничном слое. Рассмотрим выражения,
определяющие температуру и энтальпию для условий полного торможения
в пограничном слое.
Если никакого переноса энергии не происходит, т. е. не совершается
работа сил вязкости, отсутствует теплопроводность, диффузионный или
радиационный потоки тепла, то температура торможения
где Vx — скорость в некоторой точке по сечению пограничного слоя;
Т — статическая температура в этой точке;
(Ср)Ср — средняя удельная теплоемкость для интервала температур То — Г.
Температура Го, являющаяся мерой полной энергии, не меняется
по толщине слоя и определяется параметрами Т§, V& на внешней границе
пограничного слоя в соответствии с выражением
Произведя в этом выражении подстановки
и (ср)ср
где Мб — число Маха на свободной границе;
к — средняя величина показателя адиабаты для интервала температур
Общие методы решения аэродинамических задач 183
получим приближенное соотношение
при постоянных теплоемкостях следует принять к = к = const. В тех случаях,
когда теплоемкость сильно меняется с температурой вследствие диссоциации
и ионизации и ее нельзя заменить средним значением, целесообразно вместо То
использовать энтальпию торможения, определяемую выражениями
; | * __ . , б /Ту О_О\
&о = ^ о~ ^ '—2~ ' llv ° ^
где i и £б — соответственно энтальпия в произвольной точке пограничного
слоя и на его внешней границе.
При постоянных теплоемкостях по аналогии с (IV-8-1") для расчета i0
можно применить формулу
Рассмотрим теперь случай, когда стенка является теплоизолированной
{адиабатической) и процессы, происходящие в пограничном слое,
характеризуются переносом энергии. При этом из-за работы сил трения происходит
нагрев стенки, сопровождающийся теплопередачей путем теплопроводности
во внешние слои. Нагрев будет возрастать, пока не установится равновесие
между теплопередачей от внутренних слоев к внешним и притоком тепла
из-за работы сил вязкости. Соответствующая температура стенки Тг
называется температурой равновесия или температурой восстановления и,
очевидно, она меньше температуры торможения То. Это снижение температуры
стенки можно охарактеризовать коэффициентом восстановления
г = £е£, (IV-8-3)
указывающим на то, как близка температура восстановления к температуре
торможения.
При диссоциации и ионизации лучше перейти к энтальпии
восстановления iT и соответствующей величине коэффициента восстановления
В соответствии с (IV-8-3) и (IV-8-4) выражения для температуры
ш энтальпии восстановления имеют следующий вид:
Тг = Тб + Г~Щ^; 7V^a(l+rbliMi), (IV-8-5)
ir = 4 + r^', *r=;6(l+r-^-Ml) , (IV-8-6)
где (ср)ср и к— средние значения для интервала температур Тг — Т&.
Коэффициент восстановления определяется по общей формуле r = Prm,
в которой 7/1 = 1/2 для ламинарного и т=ЦЗ для турбулентного
пограничного слоя. Число Прандтля Рг, а значит, и коэффициент г зависят от физико-
химических превращений в газе. Однако эта зависимость невелика, и в
приближенных расчетах можно принять коэффициент восстановления постоянным
и равным гл = 0,85 для ламинарного и гт = 0,88 — 0,9 для турбулентного
пограничного слоя.
Определяющие параметры. Течение в сжимаемом пограничном слое
при больших скоростях характеризуется определенным законом изменения
184 Глава IV
по толщине слоя температуры, энтальпии и других термодинамических
и кинетических параметров газа. На практике течение в слое характеризуют
определяющими параметрами, представляющими собой некоторые осреднен-
ные и постоянные для рассматриваемого сечения величины температуры,
энтальпии, плотности и т. д.
Пограничный слой с такими параметрами рассчитывается по
соотношениям для несжимаемого газа. Получаемые данные о трении и теплопередаче
весьма хорошо согласуются с экспериментальными результатами, найденными
при отсутствии диффузии для течения вдоль поверхности с постоянным
давлением (например, около пластинки или конуса), в широком диапазоне
скоростей (7б = ЗОО-г-7000 м/сек), температур (-Г6-450-Т-65000 К; Гст = 300-ч-3000°К)
и давлений (ра = 0,1 ч- 10 атм).
Параметры, от которых зависят свойства такого условного несжимаемого
пограничного слоя, вычисляются в зависимости от температуры при
некоторой энтальпии г*, лежащей между крайними значениями г, имеющимися
в пограничном слое. По данным Эккерта [50]
i* = 0,5 (*ст + i6) + 0,22 (ir - i6), (IV-8-7)
где гст и iq — энтальпии газа соответственно на стенке и на внешней
границе слоя;
ir — энтальпия восстановления.
Зависимость (IV-8-7) может быть представлена также в другом виде:
где
Определяющая энтальпия зависит от структуры пограничного слоя,
а также от числа Моо. Имеется ряд соотношений, позволяющих рассчитывать
величину i* отдельно для ламинарного и турбулентного пограничных слоев,
а также для различных интервалов чисел Моо. Формула (IV-8-7) выгодна
отличается от этих соотношений своей универсальностью и может быть
применена с известным приближением как для ламинарного, так и для
турбулентного течений в довольно широком диапазоне чисел Моо.
Как видно из (IV-8-7), для вычисления i* необходимо знать энтальпию
на стенке гст. В наиболее важном для практики случае, когда температура
поверхности поддерживается на нужном уровне, энтальпия стенки будет
известна. Если же разогрев протекает самопроизвольно, то определение iCT
связано с решением задач о теплопередаче между стенкой и газом.
Из двух параметров, входящих в (IV-8-7), известной обычно является
энтальпия ig на внешней границе слоя. Что касается энтальпии
восстановления, то она определяется из выражения
ir = ib + r*^~, (IV-8-8)
в котором коэффициент восстановления г* в общем случае может
рассчитываться как определяющий параметр при помощи выражения r* = (Pr*)m,
где число Прандтля Pr* = c$\i*lk* (значок «*» означает определяющие
значения всех величин).
Соотношение (IV-8-7) используется в общем случае диссоциирующего
газа, а также в том случае, когда газ в пограничном слое разогревается
до температуры, при которой диссоциация не наступает, но теплоемкости
меняются.
Общие методы решения аэродинамических задач
185
В первом случае определяющую температуру находят, как функцию
р и i**. Для вычислений можно использовать таблицы или диаграммы
состояния воздуха при очень высоких температурах.
Во втором случае для нахождения определяющей температуры можно
применить соотношение (IV-8-7), в котором энтальпия заменяется
температурой в соответствии с выражением
/ \ //тг т \ /ТЛ7 $к Q\
где энтальпия ik может принимать значения ir, iCT или £*, а температура
Tk — соответственно ТГ1 Тст или Т7*. Средняя теплоемкость (ср)Ср вычисляется
для интервала температур Tk — T&. В результате
замены вместо (IV-8-7) получим зависимость для £*
определяющей температуры Г*, причем темпера- i$
туру восстановления найдем по (IV-8-5), в
которых г заменяется величиной г*.
Когда удельные теплоемкости не зависят от 8
температуры (при температуре, примерно, 700 —
— 800° К и ниже)
Г* = ±(Гб + ГСт) + 0,22(Гг-Гб).
Внося [в это соотношение значение для Тт
и Т01 получим
т _ т it
-/от — -/ ст/i о
- IV-8-1. Определяющая
энтальпия (пунктирные ли-
б
сплошные — с учетом
диссоциации при давлении
р = 100 кГ/см2, штрих-
пунктирные — при р =
= 0,001 кГ/см2)
^ энтальпия (пунктирные ли
Для теплоизолированной стенки в приведен- Нии без учета диссоциации,
ных зависимостях для определяющих значений
энтальпии и температуры следует принять Гст — Тт.
На рис. (IV-8-1) показаны значения
определяющей энтальпии, вычисленной по (IV-8-7) для
не диссоциированного и диссоциированного газа.
Термодинамические функции и кинетические коэффициенты вычисляются
в зависимости от определяющей температуры по формулам
£=(Я*; ■£■=(■£■)*•> f=(f)"
Уравнение теплового баланса. Это уравнение в^общем виде определяет
суммарный тепловой поток дст, идущий на нагревание стенки. Его величина
равна разности подводимого qu к поверхности и отводимого от нее q0
тепловых потоков, т. е. qCT = qu~-Qo-
Подводимый тепловой поток возникает вследствие: разогрева
пограничного слоя, вызванного трением (конвективный qK и радиационный драд потоки
тепла); солнечной qG и земной радиации q3; передачи тепла от
оборудования q0Q. Таким образом,
Отводимый поток складывается из тепловой энергии, излучаемой
нагретой поверхностью (#Из), поглощаемой материалом стенки и рассеиваемой
в окружающую среду при уносе массы (qao) и тепла, отводимого различными
охлаждающими устройствами (дОх)-
Следовательно,
Яо = 2из + 2аб + дох- (IV-8-12)
186 Глава IV
В балансе тепла поток от оборудования, а также тепло, отводимое путем
охлаждения, могут иметь большой удельный вес. Проблемы, связанные
с допустимыми значениями qo6 и потребными величинами дох, носят прежде
всего конструктивно-технологический характер.
Конвективный тепловой поток. При скоростях обтекания, когда
химические реакции в пограничном слое отсутствуют, величина удельного
конвективного теплового потока определяется при помощи видоизмененного
закона Ньютона
Як = ссст (Тт - Тст). (IV-8-13)
В условиях очень больших скоростей химические процессы играют
существенную роль, и при расчете теплопередачи следует учитывать
изменение энтальпии в соответствии с формулой
*>—*ст),
\ср)ст
где аст — коэффициент теплоотдачи;
(ср)ст — удельная теплоемкость для условий газа на стенке.
Для характеристики теплового потока вместо размерного коэффициента
теплоотдачи удобно применять безразмерные критерии теплопередачи, а именно
число Стантона
и число Нуссельта
St = -- ?« . ч = т/а;т ч (IV-8-15)
где I — произвольный линейный размер;
Хст — коэффициент теплопроводности газа у стенки.
Связь между этими двумя числами устанавливается соотношением
Nu-StRePr, (IV-8-17)
где число Рейнольдса Re = Vbp6l/\iQ; число Прандтля Рг = (ср)ст|1бАст«
В определении величины аст или безразмерных коэффициентов
теплопередачи заключается основная задача теории аэродинамического теплообмена.
Радиационный тепловой поток. В результате сильного
повышения температуры за ударной волной или в пограничном слое значительно
увеличивается концентрация окиси азота в воздухе, вследствие чего он
перестает быть оптически прозрачным и становится источником
радиационного теплового потока.
Оптические свойства воздуха характеризуются некоторым параметром 8,
представляющим собой излучательную способность единицы длины
излучающего слоя и имеющим размерность 1/1. Для излучающего слоя толщиной s0
безразмерной характеристикой излучательной способности будет величина es0,
называемая эффективной излучателъиой способностью ваза.
По закону Стефана — Больцмана излучаемое абсолютно черным телом
тепло драд = аГ4. Для учета прозрачности в эту формулу должна быть введена
некоторая функция f(&s0), зависящая от эффективной излучательной
способности и характеризующая степень черноты газа. Таким образом,
радиационный тепловой поток к стенке
где G = 5,85-10~9 кГм/м2 сек град"1—коэффициент излучения абсолютно
черного тела; >■
Т — температура излучающего газа.
Формула (IV-8-18) относится к тому случаю, когда стенка не излучает
и ее температура 77ст<;3000оК.
Общие методы решения аэродинамических задач
187
На рис. IV-8-2 приведена кривая, характеризующая изменение
функции / (es0) в зависимости от эффективной излучательной способности. Эту
кривую можно аппроксимировать
уравнением /
/ = l_exp(-es0),
которое дает ошибку не более 20%.
Из рис. IV-8-3 [11], на котором
приведены результаты экспериментальных
исследований, видно, что параметр 8
зависит от температуры и плотности воздуха.
В интервале температур 8000°К<Г< ° 2 k ts°
< 16 000° К семейство кривых, изображен- ~ ттг о о тт х
тлт о о Рис. IV-8-2. Изменение функции
ное на рис. IV-8-3, хорошо аппроксими- f {eSo)> характерИзующей радиаци-
руется формулой онный поток в критической точке
р \ 1.28 /Г°К\6354
8 = 0,138 (JL-y" (^5?)— «-1, (IV-8-20)
где рооз — плотность атмосферного воздуха у поверхности Земли.
Солнечная и земная радиация. Радиационный поток тепла
от Солнца
где г|) — угол между направлением солнечных лучей к нормалью к
поверхности тела;
q— излучательная способность Солнца, зависящая в основном от высоты
полета, а также от метеорологических условий и зенитного
расстояния Солнца.
Для средних географических условий значения q для Солнца в зените
и без учета поглощения лучей атмосферой приведены на рис. IV-8-4. Данные
о коэффициенте рс, учитывающем
поглощательную способность
материала, приведены в табл. IV-8-1 [6].
Удельный тепловой поток от
земного излучения весьма мал. Для удоб-
0,3
-6
-10
Рис. IV-8-3. Экспериментальные данные об
излучательной способности газа
/
(
1
п
— -
50 Нкм
о
Рис. IV-8-4. Зависимость
излучательной способности Солнца от высоты
полета
ства его можно рассматривать в виде суммы двух составляющих: величины
^с. 31 представляющей собственно радиационный поток Земли, и теплового
потока д0. з> отраженных от земной поверхности и облаков солнечных лучей.
Исследования показывают [11], что для условий полета на высоте 500 км
величина qCs приближенно может быть найдена по формуле
qCm з = 0,007 (1 + 2 cos Ф) р8, (IV-8-22)
где ф — угол между нормалью к поверхности и линией тело — Земля.
188
Глава IV
Таблица IV-8-1
Поглощательная способность материала (значения коэффициента рс, р3)
^^^---^^^ Вид радиации
Материалы ^"~"~"--—^^^
А1
Fe
Ni
Сплавы:
типа дуралюмин;
легированные стали
Изоляционные материалы:
плексиглаз
стекло
Крашеные поверхности:
темные
светлые
От Земли (Э3)
0,04-
0,06-
0,04-
0,04-
0,12-
-0,10
-0,74
-0,39
-0,55
-0,62
0,89
0,85
0,80-^0,99
0,80^-0,90
От Солнца (р_)
1 с
0,10-^0,49
0,45
0,40
0,53
0,60
—
0,97
0,14^-0,18
Примечание. Данные о коэффициентах 03, рс приведены для интервала температур
стенки 200-600° С.
Имеющиеся экспериментальные данные указывают на возможность вести
расчет максимальной величины радиационного потока Земли по формуле
Ышах-двРз. (IV-8-23)
Значения q3 и (33 приведены соответственно на рис. IV-8-5 и в табл. IV-8-1.
Данные об удельном тепловом потоке q0.3 являются также
экспериментальными и получены для условий, что тело расположено на высоте 500 км
на линии Земля — Солнце [11].
Согласно этим данным
200
ч
>
12
20
q0. з = 0,016 (1 + 2 cos ф) р8. (IV-8-24)
Лучистый тепловой
поток от поверхности стенки.
Тепловой поток, излучаемый с
единицы поверхности стенки,
определяется по закону Стефана — Боль-
Нки цмана
яИо = еаТ74, (IV-8-25)
Рис. IV-8-5. График зависимости q3 от вы- ^ х '
соты Н где 8 — степень черноты поверхности
или коэффициент излученияг
зависящий от материала, способа обработки поверхности и ее температуры.
Данные о коэффициенте излучения приведены в работе [11].
Коэффициент излучения повышается при увеличении шероховатости
поверхности. Если высота бугорков шероховатости превышает в несколько
раз длину волны излучения, то зависимость коэффициента излучения 8Ш
шероховатой поверхности от коэффициента излучения 8 гладкой поверхности
можно выразить формулой
еш=е[1 + 2,8(1-8)2]. (IV-8-26)
При этом длина волны излучения максимальной интенсивности зависит
от температуры и равна
(IV-8-27)
Общие методы решения аэродинамических задач 189
Уравнение для расчета температуры тонкой обшивки. Предположим,
что обшивка летательного аппарата представляет собой тонкую стенку
и прогревается мгновенно по всей толщине. В этом случае удельный
тепловой поток, поглощаемый стенкой,
gCT = CT8-^f, (IV-8-28)
где с, у, S — соответственно теплоемкость, весовая плотность материала
обшивки и ее толщина.
После подстановки величины дст в уравнение теплового баланса qCT =
z=qn — q0 получим уравнение для расчета температуры тонкой обшивки
= аСТ (Тт- Тст) + драд + qc + ?з + ?об - еаПт ~ gOx- (IV-8-29)
Это уравнение решается численными методами, если известны траектория
полета, начальная температура обшивки, ее материал и толщина. В результате
получаем зависимость Гст от времени t. Из (IV-8-29) вытекают следующие
принципиально возможные пути снижения температуры стенки: 1)
уменьшение конвективного теплового потока путем снижения осст. Снижение
коэффициента теплоотдачи достигается в условиях полета в разреженной атмосфере.
Коэффициент аст существенно уменьшается при ламинарном пограничном
слое; 2) применение искусственного охлаждения. Весьма эффективно, в
частности, охлаждение путем испарения жидкости через поры в обшивке; 3)
увеличение черноты поверхности; 4) применение теплоизолирующих обмазок
с большой теплоемкостью.
Равновесная радиационная температура. Предположим, что тепловой
режим, характеризующийся только подводом конвективного теплового потока
от пограничного слоя к стенке и отводом от нее тепловой энергии путем
радиации, является установившимся, т. е. температура стенки не меняется
со временем и dTCT/dt = O. При этом (IV-8-29) принимает вид
аст (Тг - Тст) = еаГ*т. (IV-8-30)
Температура стенки, определяемая этим уравнением, называется равно-
«весной радиационной температурой и обозначается Те.
Это понятие отличается от температуры восстановления, которая по своему
определению является температурой поверхности в отсутствие излучения,
а. также внутреннего отвода и подвода тепла. Поэтому температуру Тг
иногда называют температурой адиабатической стенки.
Температура Те представляет собой некоторый верхний предел для
излучающей поверхности, достигаемый в том случае, когда разогретая стенка
полностью излучает всю получаемую энергию. Эта температура при очень
больших тепловых потоках нереальна, так как она настолько велика, что
не может быть достигнута до того, как разрушится материал (оплавление,
сублимация, сгорание). Однако в некоторых случаях равновесная
радиационная температура может оказаться реальной, например на поверхности
планирующих летательных аппаратов. При планировании кинетическая энергия
переходит в тепловую постепенно, и интенсивность конвективного теплового
потока может оказаться сравнительно небольшой, так что вполне реальна
возможность излучения всей поглощаемой энергии при той равновесной
температуре, которая допустима для конструкции.
Уравнение (IV-8-30) включает в себя неизвестные аст, ТСт, Тг. Поэтому
оно должно быть дополнено двумя независимыми соотношениями для этих
параметров, получаемыми в теории пограничного слоя. Решение системы
уравнений позволит найти температуру Тст = Те.
Равновесную радиационную температуру можно определить
непосредственно из (IV-8-30), задавшись значениями Тг и аст/е. При этом темпера-
190
Глава IV
туру восстановления можно рассчитать по энтальпии, ir равной при
больших скоростях значению iP = 0,5FJo. Решение (IV-8-30) приведено
на рис. IV-8-6 и позволяет сделать вывод, что основным способом снижения
равновесной радиационной температуры является уменьшение отношения аст/е.
Понятие равновесной радиационной температуры можно обобщить на тот
случай, когда учитываются другие виды подводимой энергии, а также отвод
8200
5500
4400
3300
Т=220О°К
150 200 250 300 350
Рис. IV-8-6. Зависимость равновесной радиационной
температуры Те от параметров a/s и Тг
тепла охлаждением, в частности qc, q3 и qox. В этом случае уравнение
определения Тст будет
^ст \* г — ■* сту ~т~ (/с ~т~ (/з =:r Sui ст "т~ Чох* \А * "^
Связь между трением и теплопередачей. Коэффициент теплопередачи aCTr
входящий в уравнение теплового баланса, может быть при некоторых
упрощающих предпосылках связан сравнительно простыми соотношениями с
параметрами, характеризующими трение газа о стенку. Эти соотношения войдут
в систему уравнений для определения аэродинамического нагрева.
Чтобы получить эти соотношения, рассмотрим уравнения движения
(Ш-2-12) и энергии (Ш-2-46) применительно к условиям течения в
ламинарном пограничном слое. Если в этих уравнениях принять р = const,
то они будут описывать сверхзвуковой пограничный слой около конуса
или пластинки, или с известным приближением, около поверхности с малой
кривизной. Если дополнительно принять, что числа Прандтля и Шмидта
равны единице, то
у ду ду \ У
т/ diQ д
рт У у
дх
г);
ду
(IV-8-32)
(IV-8-33)
ду V г" ду
Перейдя в уравнениях к переменным Vx-=VJVb\ 6 = (&о—1ст)1{Чь — Ч?),
можно заметить, что Vx и 9 удовлетворяют одному и тому же уравнению-
и одним и тем же граничным условиям: на стенке значения Vx и 9 равны
нулю, на границе слоя —единице. Следовательно, согласно теореме о
единственности решения, функции Vх и 9 должны совпадать, т. е.
in — ir.T Vx
Общие методы решения аэродинамических задач 191
Рассматривая условия на стенке, где (dio/dy)CT = (di/dy)crB = [cp (дТ/ду)]СТ,
и имея в виду, что удельный тепловой поток на поверхности q — — (X дТ/ду)ст,
а напряжение трения %QT=[\i>{dVxldy))w, получим выражение для теплового
потока
&об— *ст Г (Х% \ 1 "I
(ср)ст L \ М- / ст ^б J
Здесь величина в квадратных скобках представляет собой местный
коэффициент теплоотдачи ах. С другой стороны, известно, что местный
коэффициент трения CfX — 2TCT/p6F|. Следовательно, между двумя этими
коэффициентами имеется связь
(IV-8-34)
Нуссельта
(IV-8-35)
Из этого выражения следуют зависимости для местного числа Нуссельта
где Rex = p&Vdx/\iCT, и местного числа Стантона
St« = ^.. (IV-8-36)
Установленная связь между параметрами трения и теплопередачи
является приближенной, так как в действительности числа Рг и Sc
отличаются от единицы. Влияние этих чисел можно учесть, если выражения
для критериев Нуссельта и Стантона записать в виде
Nux = у cfx Re* A (Pr, Sc); Stx = у cfxf2 (Pr, Sc), (IV-8-37)
где fi и /2 — некоторые функции чисел Pr и Sc.
Физически учет влияния этих чисел, отличных по величине от единицы,
означает, что избыточная химическая и кинетическая энергия преобразуется
в тепло на поверхности неполностью. Конкретный вид зависимостей /l7 /2
определяется в результате решения уравнений пограничного слоя при условии,
что Рг=т^1, Sc=t^1 (Le^l). Исследования показывают, что если не
учитывать влияния диффузии (Le=l), то Д^Рг1/3, а /2 = Рг-2/3. Таким образом,
для местного критерия Стантона
St*==^-/2 --^-Pr-2/3. (IV-8-38)
От местного критерия Стантона можно перейти к его средней величине,
опустив индекс <ш>. При этом можно принять, что местное и среднее числа
Прандтля одинаковы.
Формула (IV-8-38) имеет большое практическое значение и отображает
аналогию Рейнольдса, согласно которой критерий теплопередачи зависит
в основном от того же параметра, что и коэффициет трения — от числа Rex.
В соответствии с этим величина /2 = Рг~2/3 называется фактором аналогии
Рейнольдса.
Как показывают исследования, формула (IV-8-38) пригодна и для
турбулентного пограничного слоя с той разницей, что коэффициент трения
и параметр /2 должны вычисляться по соответствующим зависимостям для
турбулентного пограничного слоя. В частности, величину /2 можно
определять по формуле
/2 = [1 + 2,135 Re"0'1 (Pr-l)]"i. (IV-8-38')
При вычислении средней величины числа Стантона параметр /2
оказывается равным
/2 = [1 + 2,2ReJM (Pr-1)]"1. (IV-8-38")
192 Глава IV
Расчеты показывают, что, как и для ламинарного течения, величина /2
при отсутствии диффузии в турбулентном пограничном слое может быть
принята с известным приближением равной /2=Рг-2/3. Чтобы учесть
влияние числа Рг, целесообразно перейти от энтальпии гоб = i& + 0,5Fe к энтальпии
восстановления ir. Тогда для местного теплового потока можно получить
qx = -£f-(ir-in), (IV-8-39)
где
ax = Stxp6V6(cp)CT. (IV-8-40)
Расчет теплопередачи по определяющим параметрам. Влияние физико-
химических процессов на теплопередачу в пограничном слое при высоких
температурах может быть учтено путем использования определяющих
параметров. В частности, применяя аналогию Рейнольдса, получим для
определяющей величины числа Стантона
St* = ^-fix, ' (IV-8-40')
где местный коэффициент трения с*х, как и число Прандтля, вычисляется
по определяющим параметрам.
В соответствии с этим тепловой поток к стенке
откуда коэффициент теплопередачи
Определим число Нуссельта в виде
Nu* . q*c^x
^6 vr гсту
Следовательно, у
Nu* = St*Re*Pr, (IV-8-35')
где
Re* = V6pbxl\i6; Pr = срб|ябД6.
Обобщенные критериальные зависимости можно использовать для
ламинарного и турбулентного пограничных слоев.
Теплопередача в ламинарном
пограничном слое на
криволинейной поверхности
Суммарный тепловой поток. В общем случае обтекания какой-либо
поверхности с очень большой скоростью при наличии градиента температуры
и концентрации тепловой поток от диссоциирующего газа к стенке можно
рассматривать, если пренебречь конвекцией, как сумму двух составляющих,
а именно теплового потока путем теплопроводности qT и диффузионной
теплопередачи дд, т. е. q — q^ + qju.
Зависимости для составляющих теплопередачи в наиболее простой форме
могут быть получены в том случае, если рассматривать модель воздуха,
представляющую собой бинарную смесь атомов и молекул,
характеризующуюся коэффициентом диффузии атомов D. Если пренебречь влиянием
Общие методы решения аэродинамических задач 293
на теплопередачу ионизации, то суммарный тепловой поток
где Le = pDcp/K — число Льюиса — Семенова;
1а, с а — энтальпия (энергия диссоциации на единицу массы) и
концентрация атомарной компоненты;
ср — средняя удельная теплоемкость смеси.
В (IV-8-41) ср и X принимаются для «замороженного» течения в
пограничном слое.
Если диссоциация в пограничном слое отсутствует, что имеет место
при небольших скоростях обтекания, то поток тепла определяется
теплопроводностью в соответствии с формулой qT=—(k/cp) (di/dy). Такой будет
теплопередача и в «замороженном» пограничном слое при наличии
некаталитической стенки, на поверхности которой не происходят реакции
рекомбинации, так что концентрация в слое са = ы не меняется.
Представляет интерес теоретический случай гиперзвукового обтекания,
когда Le —1 и в соответствии с (IV-8-41) тепловой поток q= —(Я/ср) (di/dy),
т. е. определяется градиентом энтальпии и не зависит от механизма
теплопередачи. Атомы, ударившиеся о холодную каталитическую поверхность,
рекомбинируют на ней мгновенно, выделяя ту же энергию, что при
мгновенной рекомбинации в пограничном слое. Удельный тепловой поток
соответствует термодинамическому равновесию в пограничном слое.
Для определения более точной величины теплового потока необходимо
знать реальное значение Le^l, что дает возможность учесть диффузионные
эффекты и перенос тепла путем теплопроводности.
Предельный случай, характеризующийся диффузионной теплопередачей,
может иметь место при очень больших скоростях, когда, как показывают
исследования, величина г а (dcAldy)/(di/dy) близка к единице. Как видно
из выражения (IV-8-41), в нем остается только вторая, диффузионная
составляющая теплопередачи.
Теплопередача при термодинамическом равновесии. Для определения
равновесной теплопередачи необходимо решить систему уравнений для
ламинарного пограничного слоя, включающую уравнения неразрывности (Ш-2-21),
движения (Ш-2-12) и энергии (Ш-2-47) при условии, что в последнем
уравнении принимается Sc = Pr(Le —1). Если, кроме того, положить
в (Ш-2-12) и (Ш-2-47) r = r0 = co:nst (r0 — координата точки контура тела),
то система уравнений примет следующий вид:
|
Ох ду
p Ух~~~д^~ + ¥У~д^~) = ~~dT + 'oY [P
ду
д
ду Ur WJ+^LTl1 Рг
Следуя Лизу [50], введем переменные Дородницина
ц = ™r° \rBj^dy; x=\ p6F6Li6r2e dx, (I V-8-42)
(2x) /2 с) Рб с) N '
v 7 о о
откуда
•—-= P~6i/2 » -^^Рб^б^28- (IV-8-42')
13-114
194 Глава IV
Для дальнейших преобразований используем функцию тока, которая
определяется соотношениями (Ш-2-33). В новых переменных т], £ выражение
для функции тока можно представить в виде я|? (х, г)) = (2х)1/2 f (ц). В
соответствии с этим отношение скоростей запишется в врще VJV6 = df (ц)1дг\ =
= /'(ц). Введя далее функцию g (rj) = io/io6 (fo6 = *б + 0,5F|), определяющую
отношение энтальпий, можно получить уравнения движения и энергии,
преобразованные к новым переменным:
")' + //" + Р [f- (/')2] = 0; (IV-8-43)
где частные производные, обозначенные штрихом, вычисляются по т|;
параметр р]х = р|л/рб[хб.
Функции /(ri) и g(T)), являющиеся решениями этой системы уравнений,
должны удовлетворять следующим условиям:
/(0) = /'(0)=0; /'ft)->l прит|-*оо;
g (0) = #ст (х); g' (0) = 0; g ft) -> 1 при n -> оо
Система может быть решена численными методами. При этом для
условий гиперзвукового обтекания в уравнениях можно осуществить
дополнительные упрощения. В частности, можно принять р|л = 1. Кроме того,
так как число Прандтля является слабой функцией температуры, то его
можно считать постоянным и равным некоторому среднему значению для
данного сечения пограничного слоя. При больших сверхзвуковых скоростях
принимается, что приближенно отношение энтальпий io/^o6 = рб/р = g" (т|).
Полученные решения дают значения функций g и / в зависимости от
координаты пограничного слоя г). Так как в общем случае параметры
свободного потока, включая градиент скорости р, меняются вдоль поверхности,
то значения g и / будут также зависеть от координаты х. Таким образом,
решения не являются подобными (автомодельными).
Исследования, однако, показывают, что при некоторых условиях
обтекания можно получить автомодельные решения, пригодные для любого
сечения пограничного слоя. Это будет иметь место, когда V%l2ir — р(я — 1,
градиент скорости (3 = const, а число Прандтля равно некоторой постоянной
для данных условий величине. При этих условиях уравнения становятся
автомодельными:
/'" + /f + P [g- (/' )2] = 0; (IV-8-43')
Рг"1 g" + /£' + 2(1- Рг"1) (/'/")' = 0. (IV-8-44')
В результате численного интегрирования этих уравнений можно найти
значения функций /' и g' в зависимости от числа Прандтля Рг, отношения
плотностей рб/рст ^ £ст и градиента скорости р = (2io/i6) d In VJd In x.
Особый интерес представляет случай сильно охлажденной стенки, когда
отношение плотностей Рб/рСт С 1- Расчеты показывают, что в то время как
производная /', а следовательно напряжение трения, существенно зависит
от градиента скорости, величина g\ определяющая теплопередачу, является
слабой функцией параметра р.
Поэтому производную g' можно вычислять при нулевом градиенте
давления. Такие расчеты показывают, что на стенке производную g' (0) =
= (dg/df])ci можно принять равной для всей затупленной поверхности
0,47 Р*/з
Общие методы решения аэродинамических задач
По значению производной g' (0) ^ОДТРг1/3 определяется удельный
тепловой поток при термодинамическом равновесии
=*^^Pr*/3(AV (IV-8-46)
2 (ср)ст \ду)ст v '
Внося значение производной (йт)/йг/)ст, найденное при помощи (IV-8-42),
полагая, далее, что Рст^ст = рбЩ и заменяя i0& на ir~ ц§ [1 -f (]^Pr — 1) х
"Р8/2Ь найдем
(IV-8-47)
где функция
^^\\У^Г\^\ (IV-8-48)
2 /?0 (О0 Р оо L е) Ро ^оо О)0
о
Здесь о)б = |^б/Лб^б [^б = /?о/(М'ср)б]? ^ индекс «О» обозначает параметры
в точке полного торможения.
Для теплового потока в точке полного торможения расчетная
зависимость получается из условия, что р/р'о = 1, соб/оо^ = 1; г с^х; Vq = Xx
(X— dVd/dx = const). Эта зависимость имеет вид
qT. о = 0,47Рг-2/зу^4iT V^+i ■ (IV-8-49)
Тепловой поток, обусловленный диффузией. Для количественной
оценки теплопередачи, обусловленной диффузией, можно рассмотреть
«замороженный» пограничный слой при условии, что на его границе достигается
термодинамическое равновесие. В этом случае эффект диффузии проявляется
в тонком слое, примыкающем непосредственно к каталитической стенке, так
как скорости рекомбинации настолько малы, что атомы доходят до
поверхности без рекомбинации в пограничном слое.
В соответствии с этой схемой тепловой поток от молекулярной
теплопередачи определяется отдельно в результате решения уравнений для
равновесного пограничного слоя.
Вторая составляющая суммарного теплового потока, возникающая
за счет диффузии, должна определяться на основе уравнения диффузии
(Ш-2-38). В результате его решения находится градиент концентрации
атомарной компоненты на стенке, от которой в соответствии с (Ш-1-32)
зависит диффузионный поток вещества.
Для отыскания решения преобразуем это уравнение к новым
переменным т] и х, в результате чего получим
)' = 0, (IV-8-50)
где z—переменная, определяющая безразмерную концентрацию в
соответствии с выражением z = c/c&\ штрихом обозначены производные по т).
Уравнение (IV-8-50) можно упростить, положив число Sc равным
некоторой постоянной для данных условий величине, параметр pjx = 1
и, приняв, что профиль концентраций остается одинаковым вдоль
пограничного слоя, т. е. dz/dx — O.
С учетом сказанного уравнение для функции z примет вид
Scfz' + zT = Q. (IV-8-50')
Из этого уравнения следует, что получаемое решение является
автомодельным.
13*
196 Глава IV
Уравнение (IV-8-50') решается совместно с уравнениями (IV-8-43')
и (IV-8-44') при соответствующих граничных условиях. Для функций g и /
эти условия были указаны ранее. Решение для функций z должно
удовлетворять на внешней границе (г]~ оо) условию z(oo)~l; на стенке
граничное условие имеет вид (Ш-1-33). В новых переменных х, г\ это условие
записывается в предположении, что т — 1,
Так как решение (IV-8-50') не зависит от координаты х, то можно
рассмотреть сечение пограничного слоя у точки полного торможения.
Вблизи критической точки значение переменной # может быть
вычислено по (IV-8-42) при условии, что г~х, F6=Xr, а величина p6F6 = const.
Приняв, далее, что рб^б^РоМчр найдем граничное условие
z' (0) = у 9М„ -Ь^г z (0). (IV-8-51')
Интегрируя (IV-8-50') дважды, получаем
z(t|) —s(0) = z'(0) J в о dr\.
Численные расчеты показали, что для т] — оо величина интеграла равна
приблизительно (0,47 Sc1/3)""1. Поэтому
z' (0) = 0,47 Sc1/3 [1 - z (0)1. (IV-8-52)
Внося значение zf (0) из (IV-8-51'), найдем безразмерную концентрацию
на стенке
z (0) = i£2L = Г ( Ро^о Л */2 ^ст + 1Т1 . (IV-8-53)
w ^б L V (е + 1)Х / 0,47Sc1/3pCT£> J V ;
Из (IV-8-53) и (IV-8-52) следует, что при бесконечно быстром катализе
(/сст~оо) безразмерная концентрация на стенке z(0) = 0, а производная
z' (0) = 0,47Sc1/3. В другом предельном случае бесконечно медленной
каталитической реакции (кСТ = 0) концентрация на стенке остается такой, как
на внешней границе слоя, т. е. z(0) = l, а производная 2'(0) = 0.
Величину теплового потока, выделившегося при рекомбинации на стенке
в точке полного торможения, можно получить после подстановки градиента
концентрации (IV-8-52) в формулу (III-1-32) с заменой величины z (0)
по выражению (IV-8-53). Эта зависимость имеет вид
<?д = 0,47 V7+1 (р#;Х)1/2 Sc-2/з 1дСвф, (IV-8-54)
где iR — средняя энергия диссоциации на атом;
каталитический коэффициент
»!1 _ (IV_8.55)
Рст^ст J
Смысл этого коэффициента заключается в том, что он учитывает
влияние конечной скорости рекомбинации, так как в выражение для него входит
параметр кст.
В одном из предельных случаев, когда кст ~ оо, коэффициент ф = 1,
что соответствует выделению максимального количества тепла при
рекомбинации. В другом предельном случае бесконечно медленной реакции
Общие методы решения аэродинамических задач
197
(kCT = 0) коэффициент ф = 0. При этом физический процесс протекает таким
образом, что дополнительное тепло не освобождается.
Полный тепловой поток к стенке будет определен, если тепло от
диффузии сложить с теплом от теплопроводности.
При наличии градиента концентрации теплопередача от молекулярной
теплопроводности
Ub) (IV-8-56)
где iD = iRc6 — средняя энергия диссоциации на атом, умноженная на
массовую концентрацию атомов (сб = осб) на внешней границе
слоя;
q% —теплопередача при отсутствии градиента концентрации.
В результате сложения qT и дд получим
q = q)j, [1 -|- (JLe ф — 1) Id\, \\ v-o-o/)
где ij) = ij^lir»
Вводя числа Нуссельта и Рейнольдса
<7(*р)ст* . __ F6pCTx
iMUcT — 1 /- —г ? ^"ст — ?
Аст ^7* ^СТ/ М*СТ
получим для безразмерного критерия теплопередачи
~Р^- 0,47 1/вТТРгс~т2/3 [1 + (Ье2/Зф-1)7^]. (IV-8-58)
Формулы (IV-8-57) и (IV-8-58) могут быть использованы для расчета
теплопередачи как в точке полного торможения, так и в произвольной
точке на стенке. При этом число Le и коэффициент ф определяются для
условий в точке полного торможения и принимаются постоянными для всей
поверхности.
Значения gj и iD подсчитываются в зависимости от положения
рассматриваемой точки на стенке.
Для более детального изучения влияния рекомбинации целесообразно
рассмотреть- отношение количества тепла д, выделяющегося при конечной
скорости рекомбинации, к теп- _
ловому потоку д^ст^оо в случае
бесконечно быстрого катализа
**СТ-оо
7Й^(1-ф)*
(IV-8-59)
Из формулы (IV-8-55)
видно, что каталитический
коэффициент ф зависит не только от
скорости рекомбинации, но и от
скорости полета. Эта
зависимость показана на рис. IV-8-7.
Приведенные данные указывают
на важность учета конечной
скорости рекомбинации, а
также на возможность уменьшить
теплопередачу путем применения обшивки из некаталитического материала.
Так как вблизи поверхности такой обшивки рекомбинация не происходит,
Рис. IV-8-7. Изменение теплопередачи в
зависимости от скорости полета (Foo км /сек) и
скорости рекомбинации (// = 60 км, RT =i 0,3 ж,
Тсг = 700° К):
а — некаталитическая стенка (стекло), б —
промежуточная поверхность (окислы), в — катализаторы
(металлы)
198
Глава IV
то весь тепловой поток будет обусловлен неравновесной диссоциацией,
поглощающей значительную тепловую энергию. В результате этого и
произойдет уменьшение теплового потока. В предельном случае при ф = О
тепловой поток определяется по (IV-8-56).
Теплопередачу, обусловленную диффузией, можно охарактеризовать
каталитическим параметром
1 = РстАст [0,47 /F
связанным с коэффициентом ф зависимостью
л,- Ф
(IV-8-60)
(IV-8-60')
Ч
На рис. IV-8-8 ^приведены результаты расчета по формулам (IV-8-57,
IV-8-60') значений q = q/qT в зависимости от параметра % для случая,
когда отношение iD/ir = 0,5, а
поверхность носка сильно охлаждается,
так что концентрация на ней сст = 0.
Если стенка остается достаточно
горячей, то химическая реакция будет
протекать до установления
термодинамического равновесия с конечной
концентрацией сст = 0, что приведет
к уменьшению теплового потока.
Соответствующее значение
каталитического коэффициента в (IV-8-59)
будет определяться выражением
0,8
\
>
/А
/Ж
ж/
А
///л
у/
/
0,6
. 0,01 0J 1,0 10 X
Рис. IV-8-8. Теплопередача в зависимости
от параметра рекомбинации на стенке и
числа Льюиса — Семенова
ф =
(л gCT \
Входящая в (IV-8-59) величина
причем для бинарной смеси можно принять с& ■=<%$; сст = аст. Для большей
точности расчетов по (IV-8-59) в выражение iD = iD/ir вместо ir надо подставить
значение ir — iCT.
Факторы, уменьшающие диффузионную теплопередачу. Наряду с
константой скорости каталитической рекомбинации рассмотрим ряд других
факторов, разумное использование которых может привести к снижению
диффузионного потока вещества и теплопередачи.
1. Из (IV-8-54) и (IV-8-55) следует, что диффузионную теплопередачу
можно снизить, увеличив градиент скорости \ = Vq /x. В частности, если
рассмотреть сферический носок, то так как для него величина % изменяется обратно
пропорционально радиусу сферы, снизить тепловой поток можно, уменьшив
радиус носка»
2. Как видно из рис. IV-8-7, с увеличением скорости полета тепловой
поток от диффузии в реальном случае конечной скорости рекомбинации
уменьшается. Это объясняется тем, что наряду с увеличением полной
теплопередачи увеличивается доля тепла, затрачиваемого на диссоциацию. При
этом, следовательно, уменьшается доля энергии, выделяемая в результате
химической реакции на стенке.
3. Для эффекта теплопередачи имеет значение и температура стенки.
Из (IV-8-55) видно, что коэффициент ф в основном зависит от произведения
Рст&ст» которое, в свою очередь, определяется величиной Гст. При этом, если
скорость рекомбинации является сильной функцией температуры стенки
Общие методы решения аэродинамических задач JQ9
(например, для одной из марок стекла рст&ст ^ У3/2), то плотность меняется
несколько слабее.
Таким образом, величина рСТкСТ примерно пропорциональна
температуре стенки. Отсюда следует, в частности, что с уменьшением ТСт будет
уменьшаться и коэффициент ф. Значит, низкие температуры поверхности
препятствуют выделению большого количества химической энергии. Правда,
при этом имеет место и другой эффект, а именно большой подвод тепла
к стенке путем конвекции.
Квазиравновесный пограничный слой. В дополнение к схеме
«замороженного» течения можно рассмотреть квазиравновесный пограничный слой,
который характеризуется локальным равновесным распределением
концентрации. Локальная равновесная концентрация может быть найдена по
распределению энтальпии поперек пограничного слоя при помощи таблиц
или графиков термодинамических функций воздуха, находящегося в
термодинамическом равновесии.
В свою очередь распределение энтальпии находится в результате
решения уравнения движения и уравнения энергии, в котором сохраняется
диффузионный член. Это уравнение с переменными х, г\ будет
где параметр
число Льюиса — Семенова принято постоянным, а индекс «р» означает
дифференцирование при постоянном давлении.
Система уравнений решается с учетом следующих граничных условий:
Параметры Рг, р|х и d определяются для заданного сечения в первом
приближении с помощью термодинамических таблиц или графиков для
воздуха, находящегося в термодинамическом равновесии, по известным
условиям на стенке и на границе слоя. После решения уравнений и
определения функций g, / указанные параметры могут быть учтены. Определив
градиенты энтальпии и концентрации, можно вычислить теплопередачу с
учетом диффузии. Расчеты показывают, что в квазиравновесном пограничном
слое величина теплового потока определяется аппроксимирующей
зависимостью
q = q% [l + (Le0.52 - 1) ■£] . (IV-8-63)
Несколько большая величина показателя степени при числе Льюиса —
Семенова в выражении (IV-8-57) по сравнению со значением этого
показателя в случае равновесного пограничного слоя физически объясняется тем,
что диффузия сквозь толщу «замороженного» слоя оказывает более
существенное влияние на теплопередачу. При этом несмотря на указанную
разницу в значениях показателя степени суммарные тепловые потоки все же
чотличаются мало.
Чтобы определить, будет ли течение в пограничном слое в окрестности
200
Глава IV
в точке торможения;
точки торможения равновесным или «замороженным», можно воспользоваться
эмпирической зависимостью для параметра скорости рекомбинации [471
■ 2,5 /5000°КЧО,2 Дт_ (IV-8-64)
где 7?т —радиус сферы [м];
Foo —скорость полета [м/сек];
р"— отношение плотности РооН к плотности
Т'о — температура в точке торможения.
Значение С > 0,1 соответствует равновесному пограничному слою*
в то время как С< 10~5 — «замороженному». Из (IV-8-64) видно, что
отклонение от равновесия увеличивается с высотой. Эта формула может быть
применена для приближенной оценки параметра скорости рекомбинации
также около затупленного двухмерного тела (клина).
«Замороженное» течение в пограничном слое, возникающее около точки
торможения, сохраняется и на удаленных участках обтекаемой
поверхности. Если в окрестности точки торможения холодной стенки течение
равновесное, то отклонение от равновесия наблюдается ниже по потоку в
невязком газе вследствие увеличения разрежения. Зная плотность рб невязкого
течения на поверхности, можно оценить отклонение от равновесия для этого
течения при помощи формулы
|в = (Ж)2, (IV-8-65)
^о V Ро /
где С0 — параметр скорости рекомбинации (IV-8-64), вычисляемый для точки
торможения.
«Замораживание» постепенно распространяется по толщине пограничного
слоя, и если выполняется неравенство
<0,01, (IV-8-66)
то пограничный слой оказывается полностью «замороженным».
Влияние скорости рекомбинации в газе. Случай конечной скорости
рекомбинации в пограничном слое является наиболее реальным, так как
в действительности не будет ни
«замороженного», ни равновесного течений.
На рис. IV-8-9 показаны
результаты расчета фактора теплообмена
1
С
Nu
[ст
0,71д
ir — iCT) V
(IV-8-67)
п-2
1
ю
для различных значений параметра
скорости рекомбинации С, данного
соотношением (Ш-1-28). Причем в.
одном случае стенка была
каталитической, в другом — некаталитической.
Кривая 1 на рис. IV-8-9
характеризует полный тепловой поток к
каталитической поверхности. Как
видно, его величина практически не
зависит от параметра скорости
рекомбинации.
Такое выравнивание потоков
тепла при малых скоростях
рекомбинации («замороженное» течение) объясняется каталитическим действием стенки^
а при больших скоростях — обратным эффектом, связанным с малым ката-
Рис. IV-8-9. Параметр теплопередачи в
зависимости от скорости рекомбинации (Тст—
=300° К; Le = 1,4; Рг = 0,7; iCT/ir =
= 0,0123; а =0,5310):
1 — каталитическая поверхность; 2 — неката-
литическад поверхность; 3 — каталитическая
поверхность (тепловой поток путем
теплопроводности)
Общие методы решения аэродинамических задач 201
литическим влиянием поверхности (равновесный пограничный слой).
В последнем случае процесс заключается в том. что атомы не успевают
достигнуть стенки путем диффузии и рекомбинируют в самом пограничном
слое. Таким образом, практически расчет теплового потока при наличии
каталитической стенки можно вести без учета диссоциации.
Сравнивая на рис. IV-8-9 кривую 1 с кривой 3, характеризующей
поток тепла к каталитической стенке путем теплопроводности, можно
определить ту часть теплового потока, которая подходит к каталитической
поверхности вследствие диффузии. При больших значениях параметра С,
соответствующих высоким скоростям рекомбинации, процесс в
пограничном слое близок к равновесному, и влияние диффузии в направлении
к стенке уменьшается. В этом случае основная часть тепла подводится путем
теплопроводности.
Кривая 2 изображает тепловой поток к некаталитической стенке. Видног
что для «замораживания» пограничного слоя требуются гораздо меньшие
значения параметра С, чем при каталитической стенке. Это объясняется
тем, что вблизи некаталитической поверхности скапливается большое
количество атомов, что приводит к увеличению скоростей рекомбинации в
пограничном слое. Поэтому, чтобы «заморозить» течение, необходимо не допустить
такой повышенной концентрации, что возможно при меньших значениях
параметра С.
Параметр С при заданной температуре изменяется пропорционально
квадрату плотности. Это значит, что если для атмосферных условий
вблизи земли, где параметр С достаточно велик, течение в пограничном слое
будет равновесным, то на большой высоте оно может оказаться
«замороженным».
Если принять, что эти два крайних состояния разделяет диапазон
значений С, равный примерно 104, то для перехода в «замороженное» состояние
плотность должна уменьшаться в 100 раз. Это соответствует изменению
высоты в 30 км. Из (IV-8-64) также следует, что чем меньше радиус
сферического носка, тем меньше высоты, необходимые для достижения
«замороженного» состояния.
Таким образом, тепловой поток к поверхности, обтекаемой
диссоциированным газом с образованием ламинарного пограничного слоя, может быть
рассчитан по (IV-8-63) для равновесного и по (IV-8-57) — для
«замороженного» слоя. При этом тепловой поток зависит главным образом от
произведения рб(Хб на внешней границе пограничного слоя. Если стенка
каталитическая, то диссоциация не влияет на тепловой поток, который
практически остается таким, как в недиссоциированном пограничном слое.
Если стенка не является катализатором, то расчет теплопередачи надо
вести с учетом диссоциации. При этом суммарный тепловой поток будет
меньше, чем к каталитической стенке, когда скорость диффузии
значительно превышает скорость рекомбинации в пограничном слое.
§ IV-9. Влияние вязкого,
взаимодействия на
параметры обтекания
Пока толщина пограничного слоя около обтекаемого тела мала по
сравнению с поперечными размерами тела и толщиной ударного слоя,
исследование процессов диссоциации, обусловленных вязкостью и
теплопроводностью, можно ограничить областью потока внутри пограничного слоя, и
считать, что пограничный слой не оказывает влияния на свободное невязкое
202 Глава IV
течение. В соответствии с этой гипотезой об отсутствии обратного влияния
пограничного слоя на свободный поток на поверхности тела устанавливается
такое же давление, как в свободном невязком потоке. Из этого
следует, что расчет давления можно вести, отвлекаясь от свойства вязкости
газа.
Чем длиннее тело, тем больше толщина пограничного слоя и тем менее
достоверной становится гипотеза об отсутствии обратного влияния слоя
на свободный поток, тем сильнее будет вязкое взаимодействие между
пограничным слоем и свободным потоком. Толщина слоя возрастает при
больших скоростях обтекания вследствие влияния высокой температуры, что
также будет усиливать эффект вязкого взаимодействия. В таких случаях
расчет давления на поверхности, так же как и других параметров обтекания,
надо вести с учетом влияния вязкости. Вязкое взаимодействие будет
оказывать дополнительное влияние на процессы диссоциации.
Чтобы учесть эффекты вязкого взаимодействия, можно воспользоваться
вместо уравнений Эйлера уравнениями движения в общем виде, выведенными
с учетом реальных свойств газа. Однако практически такой расчет
осуществить трудно. Экспериментальные исследования показали, что хорошие
результаты по учету вязкого взаимодействия могут быть получены, если
исходить из предположения, что существует фиксированная граница между
свободным невязким потоком и взаимодействующим с ним пограничным
слоем. Обратное влияние утолщенного пограничного слоя заключается
в некотором поджатии газа в области невязкого течения, обусловленном
отклонением Линий тока. Давление и другие параметры на стенке будут
такими, как при невязком обтекании эквивалентного тела с сечением,
увеличенным за счет условной толщины вытеснения. «Невязкие» параметры,
индуцированные пограничным слоем, в свою очередь влияют на рост его
толщины [59].
В случае гиперзвукового обтекания тонких заостренных тел при расчете
вязкого взаимодействия можно исходить из того, что местные «невязкие»
параметры зависят от угла наклона касательной плоскости к поверхности
эквивалентного тела
При исследовании вязкого гиперзвукового взаимодействия для тонких
тел [59] условно выделены две области: слабого и сильного взаимодействия,
для которых получены достаточно простые аналитические расчетные
зависимости. В области слабого взаимодействия отклонение линий тока, а
следовательно, индуцированное давление мало. Эффект сильного взаимодействия
проявляется в большем отклонении линий тока и соответственно в более
значительном увеличении давления. Для плоской пластинки область
сильного взаимодействия близка к передней кромке, а область слабого
взаимодействия расположена вдали от нее.
Для обеих указанных областей взаимодействия индуцированное
давление на тонком заостренном теле можно рассчитать по методу касательных
поверхностей, используя гиперзвуковой параметр подобия
(^) -^-, (IV-9-2)
где К = МооР.
Областям слабого и сильного взаимодействия соответствуют предельные
значения параметров К* < 1 и К* > 1.
Наряду с рассмотренным основным видом взаимодействия,
обусловленным отклонением линий тока невязкого течения, существует еще один вид —
вихревое взаимодействие. Оно состоит в том, что на процессы, происходя-
Общие методы решения аэродинамических задач
203
щие в пограничном слое, влияет не только распределение скорости, но также
ж распределение вихрей во внешнем потоке. Вихревое взаимодействие
возникает при наличии пограничного слоя, толщина которого соизмерима с
толщиной ударного слоя, и когда имеется сильный искривленный скачок
уплотнения. За таким скачком вихрь в слое невязкого газа имеет тот же порядок,
что и средний вихрь в пограничном слое, обусловленный действием
касательных напряжений.
В качестве параметра для оценки вихревого взаимодействия можно
выбрать величину
£> = М, (IV-9-3)
представляющую собой отношение вихря £н в невязком течении к среднему
вихрю V&/8 в пограничном слое при малой скорости. Если Q < 1, то
вихревым взаимодействием можно пренебречь, а при Q ~ 1 это взаимодействие
следует учитывать, так как оно приводит к увеличению трения и
теплопередачи.
Расчеты показывают, что в области слабого и сильного взаимодействия
вихревое взаимодействие проявляется незначительно, и может иметь
существенное значение в окрестности точки полного торможения на
затупленном теле.
§ IV-10. Особенности
обтекания тел с затупленной
передней частью
Важное для практики аэродинамическое свойство затупленных тел
заключается в том, что при движении в атмосфере с очень большими
скоростями они по сравнению с заостренными телами нагреваются и разрушаются
меньше.
Рассмотрим, какими газодинамическими явлениями обусловлено
свойство затупленных тел. На рис. IV-10-1 изображена схема потока около
затупленного тела произвольной формы.
Перед телом образуется отошедшая
криволинейная ударная волна с переменной
интенсивностью в различных точках ее
ловерхности. Вдали от носка ударная
волна вырождается в обычную волну
возмущения с бесконечно малой интенсивностью
л углом наклона 0С = jjtoo = arcsin 1/M«>.
Максимальная интенсивность будет в
вершине волны, где Эс = я/2.
Так как в окрестности носка угол вс
мало отличается от я /2, то, следовательно,
соответствующий участок волны будет
обладать достаточно большой
интенсивностью, близкой к интенсивности прямого
скачка.
Переход частиц газа через такой
сильный скачок уплотнения будет
сопровождаться значительными потерями полного
напора и повышением энтропии. В
результате этого поверхность тела будет покрыта
слоем некоторой толщины, в котором газ
обладает высокой энтропией.
Рис. IV-10-1. Схема обтекания
затупленного тела:
1 —«звуковые» точки; 2 — ударная
волна; 3 — звуковая линия тока; 4 —
высокоэнтропийный слой
204 Глава IV
В таком слое, строго говоря, вследствие неодинаковой степени
торможения в различных точках ударной волны течение будет характеризоваться
некоторым градиентом скорости в направлении нормали, как показано на
рис. IV-10-1. Однако, если пограничный слой имеет значительно меньшую
толщину и если угол наклона ударной волны близок к прямому на участке,
через который проходит слой уменьшенных скоростей, то в этом слое
градиент скорости можно не учитывать, что упрощает расчеты. Скорость в таком
слое меньше, чем на заостренном корпусе или клине. Вблизи поверхности
область течения, характеризующаяся малыми скоростями (и следовательно,
малыми числами Маха и Рейнольдса), оказывает решающее влияние на
формирование процессов в пограничном слое.
Существенная обобенность обтекания состоит в том, что под влиянием
затупления изменяется режим течения в пограничном слое. Вследствие
уменьшения местных чисел Рейнольдса, подсчитываемых по скорости на
границе слоя, ламинарный пограничный слой переходит в турбулентный
гораздо ниже по течению и, таким образом, протяженность ламинарного
пограничного слоя возрастает. Это способствует снижению трения и
уменьшению тепловых потоков к стенке.
Снижение тепловых потоков, обусловленное повышением энтропии газа
при переходе через скачок уплотнения, называется энтропийным эффектом.
При этом следует иметь в виду, что энтропийный эффект сводится не только
к уменьшению скорости на внешней границе пограничного слоя, но и к
уменьшению плотности газа, т. е. к снижению чисел Рейнольдса. Вместе с тем
увеличение энтропии приводит и к увеличению по сравнению с заостренным
телом температуры на внешней границе пограничного слоя. В этом
проявляется противоположный эффект высокоэнтропийного слоя, приводящий
к некоторому повышению теплового потока от пограничного слоя к стенке.
Однако суммарный энтропийный эффект при соответствующем подборе
степени и формы затупления, как показывают расчеты и экспериментальные
исследования, приводит к уменьшению тепловых потоков.
Волновое сопротивление затупленного тела по сравнению с
заостренным, как правило, возрастает. Однако для некоторых тонких тел с малым
затуплением (например, конусов) имеет место снижение сопротивления,
которое объясняется тем, что несмотря на повышение давления в
окрестности затупленного носка, на значительной части тела возникает
пониженное давление. Сопротивление конуса или клина с полууглом |3 и длиной як
становится соизмеримым с сопротивлением носка с малым диаметром
(толщиной) D? только в том случае, если xK/DT ~ [|3 (г + 3)/(е + I)]2 (е = О
для клина и 8 = 1 для конуса). Таким образом, малое затупление оказывает
гораздо большее влияние на величину полного сопротивления крыла, чем
удлиненного корпуса. Ниже по течению от носка ударная волна
сравнительно далеко отходит от поверхности тела. В этой области распределение
давления зависит от затухания волны, испытывая малое влияние
предыстории обтекания. На удлиненных участках затупленной поверхности
устанавливается такое же давление, как на заостренной.
Главный эффект от применения затупления заключается не в изменении
сопротивления, которое при малой степени затупления оказывается
сравнительно небольшим, а в существенном уменьшении теплопередачи.
Из сказанного ясно большое практическое значение аэродинамических
исследований тел с затуплением. Однако важность таких исследований
обусловлена не только применением преднамеренно затупленных тел. Дела
в том, что в действительности все тела вращения в какой-то мере являются
затупленными, так как технологически невозможно выполнить идеально
острый носок. Затупление увеличивается от случайных механических
воздействий, кроме того, носок может затупиться при оплавлении в случае
Общие методы решения аэродинамических задач
205
движения тела с очень большой скоростью в плотной газовой среде. Многие
летательные аппараты и их отдельные элементы могут иметь затупленную
форму, обусловленную конструктивными соображениями. Таким образом,
вместо тел с абсолютно острыми носками на практике приходится иметь
дело с телами, обладающими затуплением.
Оценим относительную величину сдвига точки перехода ламинарного
пограничного слоя в турбулентный вследствие наличия затупления,
предположив, что критические числа Рейнольдса будут одинаковыми для острого
и затупленного тел. Для этих тел (соответственно индексы «ос» и «з») имеет
место равенство
fVpxY =
V М- /ос
/з
Из этого равенства вытекает следующая формула для относительного
сдвига точки перехода
В этой формуле все параметры относятся к точке перехода.
Если рассмотреть конические или клиновидные тела, то так как вдоль
образующей каждого из них
параметры потока постоянны, можно
написать
Re3
хъ_^ (VpxX
хк \ \i ) к
__
Vpx
ReK
0,6
0,2
1
I
\
Конус
20°
—
1/1°
1
\
Клин
-
Re3 *
(IV-10-1)
Здесь индексы «к» и «з» относятся
теперь соответственно к острому и
затупленному конусам или
клиньям, а все величины, входящие
в среднюю и правую части формулы
(IV-10-1), относятся к
произвольным сечениям обоих конусов с одинаковой координатой х. Из (IV-10-1) получим
16
Рис. IV-10-2. Влияние затупления на число
Рейнольдса для конуса и клина
Рк
Рз
Примем, что ix3/^k = {TJTv)n, и условимся считать давления на
заостренном и затупленном телах одинаковыми. Тогда рк/рз = TJTK. Имея в виду,
что
лолучим для отношения чисел Рейнольдса
. к — 1 ,,о \ „ , 1
Re»
Мя
(IV-10-2)
206 Глава IV
Числа Мк и М3 вычисляются соответственно из формул
где Рк — давление на заостренном теле;
Рок —Давление торможения за косым скачком перед острым клином
или конусом;
(р^)0с=я/2 — давление торможения за прямым скачком уплотнения.
Отношение Re3/ReK приведено на рис. IV-10-2 для конуса и клина.
Видно, что существенное уменьшение чисел Рейнольдса и, как следствие,,
значительный сдвиг точки перехода характерны для тонких конусов
и клиньев, причем влияние затупления более заметно с увеличением Моо-
РАЗДЕЛ
ВТОРОЙ
•
аэродина -
мика
несущих,
ставилизи-
рующих
управляющих
поверхностей
Глава V
РАСЧЕТ
АЭРОДИНАМИЧЕСКИХ
КОЭФФИЦИЕНТОВ.
§ V-1. Дозвуковые и
околозвуковые скорости
Влияние сжимаемости на
давление
Метод Христиановича. Задача об обтекании заданного профиля
потенциальным потоком с некоторым числом Моо < Ма>Кр (Моокр < 1 —
критическое число Маха) связана с решением уравнения (Ш-2-24), в котором
принимается 8 = 0, а скорости выражаются через потенциал скоростей.
В результате решения распределение скоростей и давлений находится
с учетом влияния сжимаемости.
В такой постановке задача оказывается весьма сложной. Упрощение
достигается расчленением задачи на две более простые. Первая из них
связана с определением распределения давления рнс при обтекании профиля
несжимаемым потоком, вторая — с вычислением поправки к значению рнс,
учитывающей влияние сжимаемости.
Рассмотрим вторую задачу, т. е. будем считать, что распределение
давления в несжимаемом потоке известно, и требуется найти распределение
давления с учетом сжимаемости.
В 1902 г. С. А. Чаплыгин, путем введения новых независимых
переменных V, $ (V — модуль скорости, (3 — угол наклона вектора скорости
к оси я), точно преобразовал нелинейные уравнения газовой динамики для
потенциала ф и функции тока я|) в линейные уравнения. Академик С. А. Хри-
стианович [37] , используя эти уравнения, создал строгую теорию расчета
давления с учетом влияния сжимаемости при докритических скоростях
обтекания профилей.
По этой теории задача об обтекании профиля потоком газа с
дозвуковыми скоростями сводится к задаче об обтекании профиля видоизмененной
формы потоком несжимаемой жидкости. Следовательно, для применения
метода Христиановича необходимо знать относительную скорость
набегающего сжимаемого потока Хоо — Foo/a*, форму данного профиля, правило
перехода от данного профиля к фиктивному и от истинного сжимаемого
потока к фиктивному несжимаемому, а также распределение коэффициента
давления рис около фиктивного профиля при обтекании его несжимаемым
потоком.
В том случае, если заданный профиль достаточно вытянут, форма
видоизмененного профиля почти не меняется. Поэтому можно считать
действительный и фиктивный профили одинаковыми. Тогда метод Христиановича
позволяет достаточно просто пересчитывать давление рнс на любое значение р,
соответствующее заданному Моо.
Для этой цели служит зависимость между относительной скоростью X
сжимаемого потока и скоростью Л фиктивного несжимаемого течения
(табл. V-1-1). Величина А определяется из формулы
14-114
210
Глава V
в которой скорость фиктивного набегающего потока Л с» считается величиной
известной и определяется из табл. V-1-1 по заданному значению Хоо.
Определив Л, можно найти из той же табл. V-1-1 значение Я, по (Ш-3-4) вычислить
истинное давление/?, а затем коэффициент давления р == (р —poo)/q.
Таблица V-1-1
X
А
1
А
X
А
0
0
0
0
0
0
,50
,4734
,800
,6857
0,05
0,0500
0,55
0,5144
0,825
0,6988
Зависимост!
0,10
0,0998
0,60
0,5535
0,850
0,7110
0,
0,
0,
0,
0,
0,
15
1493
625
5722
875
7223
0,
0,
о,
о,
о,
о,
20
1983
650
5904
900
7324
МЛ)
0,25
0,2467
0,675
0,6080
0,925
0,7413
0,30
0,2943
0,700
0,6251
0,950
0,7483
0,
0,
0,
0,
0
о,
35
3410
725
6413
975
7546
0
0
0
0
1
0
,40
,3862
,750
,6568
,000
,7577
0
0
0
0
,45
,4307
,775
,6717
Пересчет давления с одного числа Моо на другое. Предположим, что
известно распределение коэффициента давления р± сжимаемой жидкости
при некотором числе Mooi- Теория Христиановича позволяет пересчитать
этот коэффициент на другое число Моог и получить соответствующие
значения р2-
Вычисления ведутся следующим образом. Вначале определяем
отношение давлений pi/p<x> в рассматриваемой точке, где известно р±:
Затем из формулы
находят Я4. По значению Я1? а также величине Яоо! определяют из
табл. V-1-1 соответственно Ai и Л«>1. По этим данным и формуле (V-1-1)
.А-
л?
Рис —
(V-1-1')
\х>1
подсчитывают рпс- Далее определение коэффициента давления в сжимаемом
потоке ведется в последовательности, указанной ранее. Определяют по Я<х>2
из табл. V-1-1 значение Лоо2> затем из формулы рнс = 1 — (Л2/Лоо2)2 находят
Л2. Возвращаясь снова к табл. V-1-1, определяют по Л2 значение Я2,
подсчитывают р2 и, наконец, величину коэффициента р2.
Критическое число Маха. Определение критического числа Маха при
помощи рассматриваемого метода ведется следующим образом.
Предполагается, что местная звуковая скорость, которой соответствует
критическое число Маха набегающего потока МосКр> возникает в том месте
профиля, где в случае обтекания профиля несжимаемым потоком возникает
наибольшее разрежение, т. е. там, где коэффициент давления pHC =
Расчет аэродинамических коэффициентов 211
Зная pHcmin7 можно подсчитать Лоо по (V-1-1), где в соответствии
с данными табл. V-1-1 следует положить Л = 0,7577. Таким образом,
скорость фиктивного набегающего потока
Лоо = -4==-- (V-1-2)
Vl— РнспНп
Далее, по табл. V-1-1 определяется критическая скорость Лоокр» & по
формуле
ivlooKp = Аоокр I—2 2~~^оокр! (V-l-oj
критическое число Маха.
Приближенные зависимости. Между коэффициентами давления р и ряс
можно установить приближенную зависимость, соответствующую некоторой
упрощенной модели действительной связи между давлениями, даваемой
методом Христиановича. Эта зависимость, известная в литературе как
формула Кармана —Тзяна, следующая:
Проф. Г. Ф. Бураго предложил приближенный метод пересчета
давления с учетом влияния сжимаемости [6], дающий практически такие же
результаты, как и метод Христиановича.
Важным следствием метода Бураго является установление весьма
эффективной и простой зависимости между Pucmin и Моокр-
Рнстш = 1 - -4— [Y1 + 0.2MLKP + (1 + 0,2MLKp)3T . (V-l-5)
оМооКр L -J
Линеаризованное обтекание. Рассмотренный метод расчета давления
с учетом сжимаемости учитывает влияние больших возмущений,
возникающих при обтекании профилей.
В том случае, когда эти возмущения оказываются слабыми (профиль
тонкий), зависимость между давлениями в сжимаемом и несжимаемом
потоках может быть получена в весьма простой форме.
С этой целью воспользуемся линеаризованным уравнением (Ш-2-30)
для потенциала скоростей. Для установившегося течения оно упрощается:
(1-МУф« + Фге = 0. (V-1-6)
Если ввести новые переменные
где Vioo; Foo — скорости соответственно фиктивного несжимаемого и
действительного сжимаемого потоков, у — произвольная постоянная, то (V-1-6)
преобразуется в уравнение (<p'1)xixi + (<f'1)yjyi = 0, описывающее течение
несжимаемой жидкости. Таким образом, задача об обтекании заданного
профиля сжимаемым потоком сводится к задаче об обтекании некоторого
другого профиля несжимаемым потоком.
Из (V-1-7) следует, что между коэффициентами давления в
соответствующих точках существует зависимость Рнс — уР- Связь между формой
профилей устанавливается при помощи условий их безотрывного обтекания:
VyJVioo^dyJdxi и VyIVoo = dyldx, из которых находим: yt = yy (1 — М^)~1/2*
Полагая у = (1 — ML)1/2, приходим к выводу, что оба профиля —в
сжимаемом и несжимаемом потоках — одинаковы по форме и имеют одинаковые
углы атаки. Следовательно, между коэффициентами давления в соответ-
14*
212 t Г лав а V
ствующих точках существует следующая связь:
Это соотношение называется формулой Прандтля — Глауэрта. Нетрудно
заметить, что оно может быть получено из (V-1-4), если принять ~рнс
достаточно малыми.
Пример. Пусть в некоторой точке профиля при обтекании его потоком
несжимаемой жидкости коэффициент давления рНс — 0,5. Определим значение jiT в той же
точке профиля при обтекании его потоком сжимаемой жидкости со скоростью
Яоо = 0,5 (Моо = 0,4663).
По значению Хоо = 0,5 из табл. V-1-1 определяем величину Лоо = 0,4734 и из
соотношения (V-1-1) находим соответствующее значение Л = 0,3348 для выбранной точки.
Из той же табл. V-1-1 по найденному значению Л определяем Я = 0,3434.
Давление в рассматриваемой точке профиля
Зная р/роо, можно подсчитать коэффициент давления
- 2(р/рос-1) 2-0,082 псо
ml ~i,4-0,4663'-u>Mtf-
Расчет по приближенной зависимости (V-1-4) дает значение р = 0,547, а по (V-1-8)
линеаризованной теории — менее точный результат р = 0,565.
Произведем пересчет коэффициента давления р4 = 0,539, полученного для
скорости Xooi = 0,5, на другую скорость набегающего потока Яоо2 = 0,7.
Определяем отношение давлений Pi/p<x> в точке, где известно р± = 0,539:
^ + t ; +1 = 1,08.
Poo £ *
Из соотношения
k
в котором
находим
Я1 = 0,3434.
По значениям ^t и Xooi из табл. V-1-1 определяем соответственно Л4 = 0,3348
и Aooi = 0,4734, а по (V-1-1') подсчитываем рнс — 0,5 — величину коэффициента давления
в рассматриваемой точке заданного профиля, обтекаемого несжимаемой жидкостью.
Дальнейший расчет полностью повторяет начальную часть данного примера.
По значению Яоо2 = 0,7 находим из табл. V-1-1 Лоо2 = 0,6251, по (V-I-I) — величину
Л2 = 0,442, а по табл. V-1-1 — значение Я2 —0,4632. Давление в рассматриваемой точке
/?2 = l,187poo, а коэффициент давления р2 = 2 (р2АРоо —1)/&mL2 = 0,6. Для определения
критического числа МооКр зададимся минимальным значением рнс при обтекании
профиля потоком несжимаемой жидкости рнс mln= —1,17 и по (V-1-2) подсчитаем
величину
1/21/2
Из табл. V-1-1 по найденной величине Лоо определяем Яожр^О^, а затем
по (V-1-3)—число Моокр = 0,515.
Подъемная сила [6]
Нестреловидные крылья. В несжимаемом потоке коэффициент
подъемной силы крыла с несимметричным профилем может быть определен
по формуле
Г
Расчет аэродинамических коэффициентов
213
где
а — угол атаки;
а0 — угол атаки при нулевой подъемной силе;
^кр — удлинение крыла;
ao = dcyiiC/da — коэффициент, вычисляемый для профиля. Теоретическое
значение коэффициента а0 для тонкой пластинки равно 2я.
Для относительных толщин симметричного профиля с ^0,2 этот
коэффициент мало зависит от формы и линейно изменяется по с в соответствии
с формулой [61]
Экспериментальная проверка показывает, что действительные значения
аоэ несколько меньше теоретических а0 и зависят от угла заострения (33
задней кромки, числа Re = bFoo/Voo и положения точки перехода на профиле.
Если точка перехода расположена на расстоянии 0,56, то для Re = 108
действительное значение аоэ ПРИ Рз = О (пластинка) равно 0,97а0, а при
tg рз = 0,2 величина аоэ = 0,85а0; для Re = 106 этот коэффициент
соответственно равен аоэ = 0,9а0 и аоэ —0>74а0. Если точка перехода расположена
на передней кромке (пограничный слой полностью турбулентный) и Re = 108,
то аОэ = О,97ао фз = 0) и аОэ = О,82ао (tg|33 = 0,2). Если Re = 106, то аСэ =
= 0,9а0 (рз = 0) и аоэ = 0,68а0. При оценке значений аоэ для
интервалов 106<:Re<;108, 0<tgP3<!0,2 можно пользоваться линейной
интерполяцией.
Параметр т в (V-1-9) учитывает форму крыла в плане и может быть
представлен в виде зависимости % = %(т, т)), где m = XKV,/aOi ц — сужение.
Приближенная зависимость для т имеет вид
т = 5,88т1(/тг)т2(т1),
где функции т4 (т) и т2 (х\) приведены в табл. V-1-2.
Коэффициенты 6 и % [6]
Прямоугольные крылья (т] =
(V-1-11)
Таблица V-1-2
6
т
1/2
0,019
0,10
3/4
0,034
0,14
1
0,049
0,17
1,25
0,063
0,20
1,5
0,076
0,22
1,75
0,088
0,24
Ч
6
т
0,
о,
1
049
17
Трапецие
4/3
0,026
0,10
В И Д
ные
0
0
крылья
2
,011
,03
0
0
4
,016
,01
0
0
с»
,141
,17
Примечание. Данные для трапециевидных крыльев получены при условии, что А,
214 Глава V
Учет влияния сжимаемости на коэффициент подъемной силы может быть
осуществлен в достаточно простой форме для крыльев с тонким профилем,
обтекаемым под малым углом атаки, поток около которых будет
слабовозмущенным. Чтобы получить расчетные зависимости, рассмотрим
линеаризованное уравнение (Ш-2-30) для потенциала скоростей при условии, что
в нем производные по времени равны нулю. Введем переменные
1 —Mo
и преобразуем к ним уравнение (Ш-2-30).
В результате получим уравнение Лапласа
дх\ П~ ду\ т" dz\
которое можно рассматривать как уравнение для потенциала скоростей
возмущенного течения несжимаемой жидкости в координатах ж1? у±, zt.
При переходе к новым переменным хорда крыла станет больше в ]/l — ML
раз, а размах не изменится, так как zi = z.
Рассмотрим толщину профиля. Из условий безотрывного обтекания
(dq)'/dy1)/Voo = dy1/dx1 (несжимаемый поток) и (dy'/dy)/Voo = ду/дх (сжимаемое
течение) следует, что
dyj __ dy
dz± dx
Таким образом, в несжимаемом потоке форма сечений по потоку
не меняется, следовательно, не меняются и углы атаки сечений.
Коэффициент давления на крыле рх = — 2 (d(p7d#i) = — 2 (дер'1дх) ]/~1 — ML, т. е. будет
в У~1—ML раз меньше, чем на профиле в сжимаемом потоке. Поэтому
коэффициенты подъемной силы для обоих крыльев будут связаны
соотношением Су нс = Су Vl — ML •
Для крыла в несжимаемом потоке коэффициент подъемной силы
Суис=
Из условий х± = х/У1 — М1о и Zi = z получим зависимость между
удлинениями крыльев в несжимаемом и сжимаемом потоках
Поскольку коэффициенты подъемной силы фиктивного крыла в
несжимаемом потоке и заданного крыла в сжимаемом течении связаны
соотношением Су не = CyVl — ML и а' = а, то на основании (V-l-13), (V-1-14) для
крыла в сжимаемом потоке:
где %' вычисляется по формуле (V-1-11), в которой параметр т следует
принять равным т = ЯкрУ1 — MUa0.
Расчет аэродинамических коэффициентов
215
В частности, для крыла эллиптической формы в плане с тонким
симметричным профилем (ао = 2я, ао = О)
°"^=. (V-1-16)
Стреловидные крылья и крылья малого удлинения. Для стреловидных
крыльев при расчете коэффициента подъемной силы в несжимаемой жидкости
следует пользоваться более общей по сравнению с (V-1-9) формулой
где m = Xp()
т — параметр, вычисляемый по формуле (V-1-11) с учетом нового
значения т.
Для крыла с заданными параметрами Якр, а0, т), % расчет ведется
следующим образом. Вычисляется параметр т = Якр/(а0 cos %), затем из табл. V-1-2
/
к
^>
г
V
^-—
^——
*-—
— —
N
■—
.——^
— —
— -
——
45°
60°
О
Рис. V-1-1. Производная с^нс для стреловидного крыла
с сужением т] = 1 j
находится т1в Далее, определив по заданному т] из табл. V-1-2 величину т2,
находим т и, наконец, подсчитываем сунС' На рис. V-1-1 приведены
результаты расчета по (V-1-17).
Для крыльев малого удлинения порядок членов, входящих в
знаменатель формулы (V-1-17), оказывается таким, что возможно упростить эту
«формулу, в результате чего
> = —— (а — а0).
(V-1-18)
Если крыло тонкое, то влияние сжимаемости следует учитывать по
соотношению (V-1-14), а также выражению
дающему связь между углами стреловидности % 'и % соответственно для
крыльве в несжимаемом и сжимаемом потоках. Сужение крыла т] для обоих
крыльев остается одинаковым.
Чтобы определить коэффициент подъемной силы с учетом сжимаемости,
вычисляем по заданным значениям Мое, Якр и % параметры \g%', ЯкР, т'
ж т' и применяем формулу (V-1-17)
лА,кр (а — а0)
Су ~~ УГ я)2 • (V-1-20)
216
Глава V
Величина т' обычно невелика по сравнению с единицей, и
необходимость ее учета возрастает по мере увеличения удлинений и углов
стреловидности, а также с уменьшением чисел Моо. В приближенных расчетах
подъемной силы можно принять величину т такой, как в несжимаемом
потоке. Тогда расчетная формула для коэффициента подъемной силы с
учетом сжимаемости принимает следующий вид:
зхЯКГ) (а — ал)
"•= , (V-1-21)
■у
гъкр
Для крыльев малого удлинения коэффициент подъемной силы, как
указывалось, можно рассчитывать по (V-1-18).
Производную с^ = дсу/да можно представить в виде [61]
где / — некоторая функция сужения г] = &кр/Ькц и параметра
определяемого по углу стреловидности %1/4 крыла на линии 1/4 хорд.
Исследования показывают, что функцию / (т), %1/4) можно принять прибли-
орг
1
1
i
/
/
/
/
/
*•—
-—
, —
-.—'
^—
^—-
——-
^ —
— -
оо
"8
-/
N
—.
——
1
^ к ~'57,3
—
\
\
\
OS*
\
\
\
-60 -W -20 0 20 НО 60 80
Рис. V-1-2. Наклон кривой коэффициента подъемной силы
стреловидных крыльев [(Р =j/"l — М^,; к = аОд х
xyi-Ml/2n; Xi/4= arctg [tg Xi/4 (1 - M^)"1/,])
женно равной /(х1/4)- На графике рис. V-1-2 показаны теоретические
кривые са, построенные для r\ = 2. Эти кривые позволяют найти с известным
приближением величину са для произвольных значений т), если известны
экспериментальные значения аод — (дсу/да)э для профиля при Моо<;Моокр-
Данные рис. V-1-2 применимы для больших углов атаки, если отсутствует
срыв потока. При этом значение аоэ можно определять по правилу
Прандтля—Глауэрта аОэ = «оэ (1— М^)~1/2, где аоэ — экспериментальное
значение са для профиля в несжимаемом потоке.
Эффективность органов управления. Орган управления, занимающий
полностью или часть размаха крыла у задней кромки, изменяет подъемную
Расчет аэродинамических коэффициентов
217
силу крыла в зависимости от угла бр отклонения руля. Эффективность
органа управления на профиле определяется производной аор = дсу/д6р
коэффициента подъемной силы профиля по углу бр руля. Теоретическое
значение величины аор, полученное для линейной области зависимости
коэффициента подъемной силы профиля (при Моо = 0) от угла атаки а и угла
2,0
б)
06
Ofi
-
—
——
Eg
^^
^^
^^
^—'
—.
— —
. ■
-—
.—
■
:- -*■
■
.
--—
.
. "
. ■
'
-i
'
———
—
——-
^~.—
^-
•—
-
■
— —
-*
^- '
■
,
—
. '
-
__——
. -*
—
.—•
.—■-—
,
—
. —
, —
——
. ■
, ■
„— '
— -
———
. —
—
.
/
«« \/ъ
1,00
0,98
0,94
0,90
0,86
0,82
0,78
0,7U
0,2
ЦЗ
ьр/ь
Рис. V-l-3. Эффективность органа управления на
профиле при обтекании несжимаемым потоком:
а — теоретические значения аор = дсу/ддр; б — отношение
аорэ/аор = (дсу/д6рэ)/(дс Vd6p) по экспериментальным данным
отклонения бр, приведено на рис. V-l-3, a [61]. При малых углахматаки
эти кривые следует применять для значений бр«<15°. Поправка к
величине аор, найденная по экспериментальным данным для аор = аорэ,
приведена на рис. V-1-3, б. Значение а^1а0 для заданного профиля можно
определить при помощи (V-1-10) и линейной интерполяции по данным на стр. 213.
218
Глава V
При Моо<Мкр эффективность рулей управления aov,u= Сут,
расположенных вдоль всего размаха на крыльях с сужением, прямыми кромками,
концевыми хордами, параллельными корневой хорде, и постоянным
отношением fop/б, может быть оценена параметром
арр. м/врр. э _ , / Ьр л ул_Шъ \ fV-1-22)
аом/аоэ V- b i
где аом = СуМ — наклон кривой подъемной силы крыла определяется
по рис. V-1-2. Определение указанного параметра эффективности можно
вести по данным рис. V-1-4, которые применимы для линейного изменения
коэффициента су от а и бр.
Эффективность органа управления аор. м> занимающего часть размаха
крыла и простирающегося до корневой хорды крыла, можно определить
при помощи полуэмпирического со-
/1 I I I I отношения
#0р. м = #0р. m^j (\-L-6O)
где
+ к3 sin [arctg (tg %i/2 У 1 — ML)]}.
(V-l-24)
Коэффициенты кп являются
функциями сужения крыла х\ и отношения
Zp/Z =1Р, в котором Zp — расстояние
между концевыми кромками рулей;
I — размах крыльев. Коэффициент kt
является слабой функцией сужения
и приближенно равен
A:1=7p(l-KZp). (V-1-25)
^Шо - 6)
Рис. V-1-4. Эффективность органов
управления на стреловидных крыльях; значение
(д)/(д/дд)
Для расчета
можно применять
мость
коэффициента кг
линейную зависи*
(дсу/да)м/(дсу/да)э &2 = а (1 — Zp), (V-1-26)
в которой для т] = 1; 2; оо соответственно а——0,017; —0,007; 0,015.
Коэффициент к3 приближенно равен
k3 = b(l-lm), (V-1-27)
где для т) = 1; 2; оо соответственно Ъ = 0,088; 0,112; 0,129. При определении
коэффициентов к2, к3 для промежуточных значений ц можно применить
линейную интерполяцию. Для случаев, когда корневая хорда органа
управления (руля) не совпадает с корневой хордой крыла, величина аоР.м равна
разности между эффективностями двух рулей, размахи которых Zp. кц и Zp. кр
равны соответственно расстояниям между внешними (концевыми) и
внутренними (корневыми) хордами органов управления.
Максимальный коэффициент подъемной силы. Для приближенного
расчета коэффициента подъемной силы можно использовать зависимость
с -с К 1 + cosx (V-1-28)
cymax — kymaxnp1*-1!! 2 ' \т /
cv max пр — максимальный коэффициент подъемной силы профиля;
X —угол стреловидности;
Кц — коэффициент, зависящий от сужения крыла. Значения этого
коэффициента приведены в табл. V-1-3.
где су
Расчет аэродинамических коэффициентов
219
Таблица V-1-3
Значения коэффициента Кц
кц
1
0,90
2
0,94
3
0,93
4
0,93
Величину су max крыла с отклоненным рулем можно определять по
приближенной формуле
Су max 6 = Су тах + 0,0755рб COS2 Xcp, (V-1-29)
где £р = SV/SKV — отношение части площади крыла, обслуживаемой рулем,
ко всей площади;
Хер —средний угол стре- £
ловидности,
определяемый по формуле 12
2 г| — 1
(V-1-30)
Параметр б, зависящий от угла
отклонения и относительной хорды
руля, может быть определен с
помощью рис. V-1-5, причем
относительная хорда выбирается средней по
длине руля.
Пример. Рассчитаем коэффициент
подъемной силы крыла с рулем при ско- ~
рости полета Моо = 0,6 под углом атаки и IV uu ии ш v
а = 5°. Геометрические характеристики Р
Р Рис. V-1-5. График для определения пара-
^кр — 8/3; т) — 2; %п = 45°; с = 0,1. метра 6
Угол атаки, соответствующий нулевой подъемной силе, ао=—2°.
Эффективные значения параметров
/
//
/
/
/
/
/
/
>-
.——
0,2
0,1
10
30
50
70
-MIo = у Т/1 — 0,62 = 2,136;
m' \ I/ л ivf5 //Лпрпч v'V 9
т — ЛКР У •"■ — -lVIoo/ V"0 ^Ufc) X / — ^'
где параметр а0 принимается равным 2я.
По (V-1-11) определяем т' с учетом тп' и rj:
т' = 5,88-0,107.0,03 = 0,0189.
Применяя (V-1-20), находим
3,14-2,67(0,0873 + 0,0349)
,28-0,6246) =-0,545,
■ = 0,341.
Максимальный коэффициент подъемной силы подсчитываем по зависимости
{V-1-28), приняв для профиля су тах пр = 0,9.
Имея также в виду, что согласно табл. V-l-З величина ТГ^ —0,94, находим
еу max = 0,9-0,94
= 0,722.
Значение су тах крыла с рулем определяем по (V-1-29). Пусть в этой формуле
р = 0,4. Положив значение средней по размаху относительной хорды руля Ьрср=0,2,
220 Глава V
а угол отклонения 6р = 60°, найдем по рис. V-1-5 параметр 6 = 12. Определив затем
по значению
2 т| — 1 ^ 2 2 —1_ 3
1 873~2ТТ~4"
величину cos %ср = 0,80, подсчитываем
6 = 0,722 + 0,075-0,4.12-0,82 = 0,95.
Правила подобия для околозвуковых течений. Эти правила позволяют
унифицировать расчеты аэродинамических характеристик крыльев,
обтекаемых потоками с числами Мто, близкими к единице. При помощи правил
подобия можно по известному значению аэродинамического коэффициента
для крыла при данном Моо получить для другого числа М^ и
видоизмененного (деформируемого) крыла соответствующую величину
аэродинамического коэффициента.
Для установления правила подобия следует воспользоваться
приближенным уравнением для потенциала скоростей в трансзвуковой области
(1 - ML) фхх + Ъу + Vzz = (к + 1) М^ф*ф*х, (V-1-31)
где ф = ф/7оо. Уравнение (V-1-31), вывод которого дан в работе [6],
отличается от соответствующего уравнения линейной теории наличием
нелинейной правой части. Введем новые переменные (обозначены штрихами)
x(l-Ml)-i/2 = x' (1-W*ri/2; у = у'\ z = z'; фс"1^'(7')"1, (V-1-32)
где с — относительная толщина профиля.
Если подставить эти переменные в (V-1-31) и ввести дополнительное
условие
то получим уравнение в новых переменных, внешний вид которого точно
совпадает с (V-1-31). Это уравнение описывает подобный поток около крыла
видоизмененной формы. Зависимости, описывающие деформацию крыла,
нетрудно получить из (V-1-32):
(V-l-34)
Формулы (V-l-33) и (V-l-34) называются критериальными
зависимостями.
Пользуясь (Ш-3-13') и критериальными зависимостями, можно
установить связь между аэродинамическими характеристиками подобных крыльев,
расположенных в подобных потоках.
В частности, связь между коэффициентами давления, а также
коэффициентами подъемной силы будет следующей:
. - ML - су (с')-1 У 1 - М^2; [ (V-1-35)
ас~* = а (с у1. j
Таким образом, расчет аэродинамических характеристик крыльев
в трансзвуковом потоке при любом числе Моо может быть сведен к расчету
для одного какого-либо числа Моо и последующему пересчету на любое
число Моо по вышеприведенным формулам.
Расчет аэродинамических коэффициентов
221
Рассмотренные зависимости теории подобия могут быть распространены
на малые сверхзвуковые скорости. Для этого необходимо во всех
выражениях произвести замену ]/*1 — ML на УМ2^ — 1.
Правила подобия дают возможность установить некоторые зависимости,
позволяющие систематизировать экспериментальные данные. Рассмотрим,
в частности, однопрофильные прямоугольные крылья с относительной
толщиной с. В соответствии с теорией подобия
общая зависимость для производной са
cic
ЮОЗ
0,01
—4
с
1
1
1
/
'
— -
/
1
имеет вид
(V-1-36)
Рис. V-1-6. Подъемная сила прямо- Рис. V-1-7. Подъемная сила прямоугольных
угольного крыла при Моо = 1. крыльев при околозвуковых скоростях
В частном случае при Моо = 1 первый [критерий подобия в скобках
равен нулю и
- -1/3). (V-1-37)
Таким образом, величина с^с1^3 является функцией одной переменной
^крС1/3 и может быть, следовательно, изображена графически в виде одной
кривой.
Для расчета производных с^ прямоугольных крыльев при различных
околозвуковых числах М^ нужна уже сетка кривых, определяемая уравне-
■нием (V-1-36).
На рис. V-1-6 представлены экспериментальные данные при Моо = 1
для прямоугольных крыльев с ромбовидным профилем. Эти данные
показывают, что при А,крс1/3 < 1 зависимость для са можно представить в виде
.с« = яЛкр/2.
На рис. V-1-7 приведены более полные экспериментальные данные для
прямоугольных крыльев с различными профилями. Этими данными можно
пользоваться для приближенной оценки аэродинамических характеристик
также и для трапециевидных крыльев при небольшом сужении.
Для стреловидных крыльев малого удлинения (Якр<!3) производную са
можно определять методами, установленными для дозвуковых потоков.
Пример. В ычислим коэффициент подъемной силы изолированного крыла
(см. пример на стр. 219) с симметричным профилем, относительная толщина которого
с = с/Ь = 0,04 при Моо = 9.,95, если известен коэффициент подъемной силы крыла
^0 = 0,295 при Моо = 0,9.
222 Г л а в а V
Определим относительную толщину профиля видоизмененного крыла, используя
зависимость (V-1-33):
(1-0,92)3/2 _(1-0,952)
0,92-0,04 ""
3/2
отсюда с' = 0,013.
По формулам (V-1-34) для видоизмененного крыла находим
' = 35°36').
По зависимости (V-1-35) подсчитываем
I УТ=*Е От VEEg; 0,295 = 0,134.
с Vi-MZ °'04 Vi-0,95*
Соответствующий угол атаки
Лобовое сопротивление
Докритические скорости (Моо < МооКр) • В соответствии с (1-3-1)
коэффициент лобового сопротивления определяется как сумма коэффициентов
профильного и индуктивного сопротивлений. Коэффициент профильного
сопротивления можно вычислять по формуле [26]:
cXIip = 2cxf (0,93 + 2,8с) (1 + 5сМу, (V-1-38)
где 2сXf — коэффициент трения плоской пластинки с длиной, равной
средней хорде крыла, и с таким же, как у крыла, положением точки перехода
ламинарного пограничного слоя в турбулентный. Его величина вычисляется
в общем случае с учетом сжимаемости (см. гл. VI).
Для прямых (нестреловидных) крыльев точку перехода в первом
приближении можно считать совпадающей с абсциссой максимальной толщины
профиля. При малых скоростях для стреловидных крыльев с достаточна
большим углом стреловидности можно принимать пограничный слой
полностью турбулентным.
Индуктивное сопротивление крыла в несжимаемом потоке
сх*=^(1+6), (V-1-39)
где
6 = 20,4161(ти)62(т|). (V-1-40)
В этой формуле б4 находится из табл. V-1-2 как функция параметра
т = Хкр/а0, а 62 —из той же таблицы в зависимости от сужения т). В частном
случае крыла эллиптической формы в плане 6 = 0.
Для стреловидного крыла расчет коэффициента 6 ведется по формуле
(V-1-40) и табл. V-1-2 при условии, что т = Якр/(а0 cos %).
Влияние сжимаемости на коэффициент индуктивного сопротивления
учитывается формулой
где cxi0 находится по (V-1-39).
Расчет аэродинамических коэффициентов 223
На режимах, предшествующих срыву потока, сопротивление равно
примерно теоретическому минимальному значению [41]
-^-, (V-1-42)
а на больших углах атаки оно приближается к величине
сх = сх пр + су tg a. (V-1-42')
Сверхкритические скорости (Моо>МооКр). В приближенных расчетах
можно считать, что сопротивление крыла при сверхкритических скоростях
обусловлено в основном местными ударными волнами. Коэффициент
волнового сопротивления нестреловидного крыла можно рассчитывать по
формуле [26]:
схв = (0,25*+ 1,2*2-0,45х5) cXBmax, (V-1-43)
где сХВтах — максимальное значение коэффициента волнового
сопротивления, достигаемое при Моо = 1;
х—~ параметр, равный
Моо Моокр ,,т ,, , /ч
Ж = -П -• (V-1-44)
1 — Моо кр
Критическое число М^ кр определяется по приближенной формуле
Мое кР = 1 - 0,7^/2 - 3,2сСз/2. (V-1-45)
Величина схвтах может с известным приближением рассматриваться
как функция относительной толщины профиля с:
СХ в max = - 0,017 + 0,0081с, (V-1-46)
где с берется в процешах.
Рассчитываемое по (V-1-43) сопротивление соответствует диапазону
ММ1
Р
Чтобы найти участок кривой волнового сопротивления между Моо = 1
и числом Моо, несколько большим единицы, следует воспользоваться (V-2-9).
Третье слагаемое в (V-2-9), не зависящее от угла атаки, при звуковой
скорости должно быть заменено коэффициентом (V-1-46). Вычислив
значение схво по (V-2-11), можно построить промежуточный участок кривой,
который позволит приближенно найти значения схво в околозвуковом
диапазоне между Moo^l и числом Моо, несколько большим единицы.
Теперь надо найти ту часть волнового сопротивления в этом диапазоне,
которая зависит от угла атаки. При Моо^Моокр волновое сопротивление
отсутствует, а при Моо>1, когда поток около крыла полностью
сверхзвуковой, эта часть сопротивления определяется двумя первыми слагаемыми
в выражении (V-2-9). Интерполируя, найдем промежуточные значения
добавочной величины коэффициента волнового сопротивления.
Таким образом, полный коэффициент сопротивления
схв = схв0 + Ас2у, (V-1-47)
где А—-параметр, определяемый при помощи интерполяции между
значениями
А^ОСМоо-Моонр) и A
Пример расчета А приведен на рис. V-1-8.
Суммарную величину коэффициента лобового сопротивления крыла при
числах Маха, расположенных в диапазоне Моокр <Моо<^1, можно получить
224
Глава V
0,1
У
сложением коэффициентов волнового, профильного и индуктивного
сопротивлений. Теоретические и экспериментальные исследования показывают,
что волновое сопротивление зна-
Л чительно превышает профильное
0,3\ 1 1 и индуктивное.
В околозвуковом диапазоне
при Моо > 1 профильное
сопротивление можно определять как
сопротивление трения.
Индуктивное сопротивление для
прямого крыла в этом случае
невелико и с известным
приближением его можно не учитывать.
Стреловидные крылья.
Составляющая коэффициента
волнового сопротивления сх в о,
не зависящая от а, равна
1 —
CKcos3x]. (V-1-48)
0,5
0J5
,кр
Рис. V-1-8. График для определения параметра А
Входящая в эту формулу величина SCK представляет собой отношение
площади части крыла, работающей как скользящее крыло, ко всей площади
и определяется по выражению
(V-1-49)
Величина c^BOnp равна коэффициенту волнового сопротивления части крыла,
которая условно принимается работающей как прямое крыло и
определяется по фактическому числу Моо,
действительному значению су и по
относительной толщине профиля^с в сечении,
параллельном плоскости симметрии.
Коэффициент сх в о ск относится к
части крыла, работающей как скользящее
крыло, и определяется изложенными
выше способами по эффективным
значениям числа Моо Эф = Моо cos %,
коэффициента подъемной силы су эф = cy/cos %
и относительной толщины профиля
Су
0,k
0.2
ОМ
0,2
О
I
(
/
1
S
/
/
•Ж
=0,8-
0°
0,04 0,06 с
Приближенное выражение для
второй составляющей коэффициента
сопротивления, зависящей от а, имеет вид
С*вг = ЛстР4> (V-1-50)
где
Астр — •
в
cos2 %
+ SCK) COS х
этой формуле А
г
Л
у
/
%=60°
/
/
i
/
/
7
45°
/г
/
30°
0'
0,02
0,04
0,06 0,08 Сх
(V-1-51)
пр ОТНОСИТСЯ К
работающей как прямое
части крыла,
крыло, и определяется для
су\ параметр
Рис. V-1-9. Поляры крыльев различной
стреловидности (^кр =4; т] = 2; с =0]06'
При Моо = МоокрСхпр = 0005)
М
нои величины с7.
фактических значений М», с и действитель-
Аск относится к части крыла, работаю-
Расчет аэродинамических коэффициентов 225
щей как скользящее крыло, и определяется для МооЭф, с9ф' суэф
(см. рис. V-1-8).
На рис. V-1-9 приведены результаты расчета по изложенной методике
для конкретных условий.
Пример. Подсчитаем коэффициент волнового сопротивления стреловидного крыла,
геометрические характеристики которого определяются следующими параметрами:
Якр = 8/3; г] = 2; хп = 45°; ё~=0,1. Крыло движется под углом атаки а = 5° со
скоростью, которой соответствует число Моо = 0,8. Угол атаки, при котором cv—0, равен
оо=-2°.
Предположим, что для Моо = 0,8 и а = 5° коэффициент подъемной силы крыла
равен 0,382. Этому значению соответствует следующее значение критического числа
Маха [см. (V-1-45)]:
Моокр = 1—0,7 У ОД — 3,2-0,1.0,3821,6 = 0,703.
Так как заданное число Маха Моо = 0,8]>МооКр> то, следовательно, полет будет
соответствовать сверхкритическому режиму обтекания.
Коэффициент волнового сопротивления
где сх в0 вычисляется при помощи (V-1-48). Вычислим некоторые параметры, входящие
в это выражение. Безразмерная величина
Параметр сх в0 Пр находится при помощи зависимости (V-1-43) по значению (V-1-44)
_0,8—0,703
*— 1—0,703 ~~ '
и величине (V-1-46)
сх в тах= -0,017 + 0,0081.10 = 0,064.
Применяя (V-1-43), получим
сх во пр = (0,25.0,327 + 1,2.0,3272-0,45-0,3275) 0,064 = 0,013.
Подсчитаем далее коэффициент ехвОск [см. (V-1-43)].
Для этого определяем
МооЭф = Моо cos Хп = 0,8-0,7071 = 0,57;
су Эф = су /cos Хп = 0,382/0,7071 = 0,54;
сх в max эф = —0,017 + 0,0081.14,1 = 0,097;
Моокр эф = 1—0,7 1/0441—3,2-0,14Ь0,541»5 = 0,558;
«эф = (мооаф —Моокр эф)/(1 — Моокр эф) = (0,57—0,558)/(1 —0,558) =0,027;
затем подсчитываем
сх во ск== (0,25.0,027 + 1,2.0,0272—0,45.0,0275) 0,097 = 0,0074.
Используя (V-1-48), находим
**во = у [(1 — 0,544) 0,013+ (1 + 0,544) 0,0074-0,70713] =0,005.
Подсчитаем индуктивную составляющую сопротивления cXBf. С этой целью
найдем коэффициент Астр, входящий в (V-1-50). Неизвестными параметрами в этой
формуле являются Апр и Аск. Значение Апр можно найти, зная Моо, с и су> по рис. V-1-8
или по интерполяционной формуле
1,5 — 1
Вычисления дают величину Апр = 0,034.
15-114
226
Глава V
Аналогично определяем по значениям М«>эф» сэф и суэф величину Аск = 0,003.
С учетом полученных данных
А = [ Т^4
,544) 0,7071 >0,00з] =0,0017;
Следовательно,
Правила подобия. Наряду с соотношениями, приведенными выше, при
расчете сопротивления для условий полета с околозвуковыми скоростями
можно использовать зависимости, вытекающие
из теории подобия:
7
7
ч-5/З.
Для прямоугольного крыла правило
подобия по сопротивлению имеет следующую
функциональную зависимость:
(V-1-53)
с2-1/3
у 1'3 Для & = 0 имеем
Рис. V-1-10. Сопротивление Сх
прямоугольного крыла при "^5/3~~ <!
Моо =1 С
При Моо = 1 зависимости (V-1-53) и (V-1-54) упрощаются:
Сх
сГо1/3
сх
^5/3
(V-1-54)
(V-1-53')
(V-1-547)
Кривая, представляющая функцию (V-1-54'), изображена на рис. V-1-10.
Она построена на основе экспериментальных данных для прямоугольного
крыла с ромбовидным профилем.
Рис. V-1-11. Сопротивление прямоугольных крыльев при
околозвуковых скоростях
Расчет аэродинамических коэффициентов
227
Экспериментальные данные о сопротивлении прямоугольных крыльев
при околозвуковых скоростях приведены также на рис. V-l-11, V-1-12.
Л
0
с =3^
~\
vis
У/
,——*
———
Л
——
У175
у
^-—
^——
1,0
0,6
«- ■"
0,25
i
==
^^
==:
' "
О
-2,0 ~1,6 -1,2 -0,8 -0,4 0 0,4 0,8 1,2 1,6
С2/з
Рис. V-1-12. Сопротивление прямоугольных крыльев при
околозвуковых скоростях
Эти данные можно использовать для приближенных расчетов сопротивления
крыльев с профилями различных типов. Причем крылья могут быть не
только прямоугольные, но и слегка трапециевидные.
Момент и фокус (центр
давления)
Как показывают исследования, точка фокуса (центр давления) у
современных симметричных профилей с относительной толщиной порядка с = 0,04,
обтекаемых несжимаемым потоком, расположена от носка на расстоянии
22 — 25% длины хорды; у крыла эта точка лежит на средней
аэродинамической хорде и удалена от ее передней кромки на такое же относительное
расстояние.
Для расчета положения центра давления (фокуса) при дозвуковых
скоростях можно пользоваться приближенной формулой
(V-1-55)
где Сц.дпр — расстояние до центра давления профиля в долях средней
аэродинамической хорды;
F (т]) — функция, характеризующая влияние сужения на положение
центра давления. Значения этой функции приведены в табл.
V-1-4.
Таблица V-1-4
Значения функции F (ц),
характеризующей влияние сужения на положение центра давления
Л
1,0
1,5
1,7
2,0
2,5
3,0
4,0
5,0
6,0
-0,022
-0,005
0,006
0,012
0,016
0,022
0,024
0,025
Как указывалось, для профилей с толщиной с порядка 0,04
величину Сц.дпр в (V-1-55) можно принимать равной 0,22 — 0,25.
Относительное расстояние центра давления (фокуса) хЦт д/&сах от начала
средней аэродинамической хорды для стреловидных крыльев при малых
15*
228
Глава V
о}з
■
= 00
—-
— —
-
\
——-
^
—-^"
-y-
20
40
скоростях и малых углах атаки можно определить из графиков на
рис. V-1-13 [61]. Пунктирные линии показывают значение хц.д/ЬСАХ для
крыльев с нестреловидной зад-
ней кромкой.
Влияние
сжимаемости на
полоя^ение центра давления
крыльев стреловидной формы,
обтекаемых линеаризованным
дозвуковым потоком, показано
на рис. V-1-14. Пунктирные
кривые получены
экстраполяцией данных теоретического
расчета.
Исследования показывают,
что в околозвуковом диапазоне
скоростей (МооКр<Моо< 1) по
мере увеличения числа Моо центр
давления несколько смещается
назад. По найденному значению
коэффициента подъемной силы и
указанной выше величине центра
давления можно определить
коэффициент момента профиля или
крыла при докритической
скорости обтекания.
Из теории подобия следует,
что между коэффициентами
момента тонких крыльев,
расположенных в сжимаемом и
несжимаемом потоках под
одинаковыми углами ата ки,
существует зависимость
Ofi
0,3
0,2
1-
" ■
-.2
=====
■
А,
=====
— —
-
-
4,
^
, '
^
20
Рис. V-1-13. Положение центр а]' давления
(фокуса) крыла при малых скоростях обтекания и
углах атаки. Пунктирные линии характеризуют
положение центра давления для крыла с
нестреловидной задней кромкой
Vi-mI
(V-l-56)
Коэффициент mZHC
определяется для крыла, обтекаемого
несжимаемым потоком и сдефор-
мированного в соответствии с формулами подобия (V-1-14) и (V-1-19).
Рассмотрим, как определяется момент крыла с отклоненными
закрылками. Если расчет ведется относительно оси, проходящей через центр
тяжести, то коэффициент продольного момента
(V-1-57)
= Шг 0 + A"lz 0 зак — (xF — XT) (cy + Асу 8ак),
где Хг и xF — соответственно координаты центра тяжести и фокуса,
отсчитываемые от передней кромки;
mz о — коэффициент момента при су = 0;
&mz о зак = — 0,25Асу зак; (V-1-58)
величина _
ДСу зак = 0,07558а„б cos2 ХсР. (V-1-59)
Пример. Подсчитаем коэффициенты центра давления и момента для крыла
со следующими геометрическими характеристиками:
Х,кр = 8/3; г) = 2; с -0,04; tg/n=l; tgx3 = 0,5.
Расчет аэродинамических коэффициентов
229
Предположим, что крыло, имеющее симметричный ромбовидный профиль (для
такого крыла ао = О), движется под углом а = 5° со скоростью полета, которой
соответствует число Моо = 0,6. Для этих условий коэффициент подъемной силы су — 0,255.
0.5
<J4
0,3
77=OO
KptqXi/=4
m "
—. —
— —
_
— "
— —
, ■
q
/
1 —
n
и
0,2
т -
щ
в——'
и. —
— —
— —
□
- —
0
у
j
У
1»
\
Акр//-М
=
•£2
•—-
——-
V
\
44
it
0,3
0,2
6 5 4 3 2 10 7 6 5 4 3 2 10
z
ч
— ,
\
>
Рис. V-1-14. Влияние сжимаемости на положение центра
давления (фокуса) стреловидных крыльев
Примем что величина сц.дпр для заданного профиля равна 0,25.
Расчет сц. д ведем по (V-1-55), в которой F(y\)— 0,006 (см. табл. V-1-4),
264
Вычисляем коэффициент центра давления
(-*.|-+щ) 0,006 = 0,
и коэффициент момента
г = еисц. д = 0,255-0,264 = 0,0673.
§ V-2. Сверхзвуковые
скорости
Обтекание тонкой пластинки
Применяя метод характеристик для плоских двухмерных течений и
теорию скачка уплотнения, можно рассчитать сверхзвуковое обтекание тонкой
пластинки (рис. V-2-1, V-2-2).
Расчет осуществляется отдельно для верхней и нижней сторон. Для
исследования обтекания верхней стороны, где течение характеризуется
дополнительным расширением потока, используется общее соотношение метода
230
Глава V
характеристик (IV-1-17), дающее возможность рассчитать поток, когда
числа Моо и углы атаки произвольные. В двух частных случаях это
соотношение упрощается.
Первый из них относится к линеаризованному обтеканию (числа Моо
и углы а невелики). Из (Ш-2-30) находим формулы для расчета
соответственно добавочной возмущенной скорости и коэффициента давления на
верхней стороне:
,—1
Второй случай характеризуется гиперзвуковым обтеканием (числа
Моо > 1, углы а произвольные). Для определения местных чисел М следует
применять (IV-1-18), а для вычисления
давления— (IV-7-12).
При исследовании течения на нижней
стороне пластинки, где поток испытывает
сжатие, можно рассматривать общий
случай, характеризующийся произвольными
Рис. V-2-1. Тонкая пластинка в сверхзвуковом Рис. V-2-2. Схема обтекания
потоке сверхзвуковым потоком
пластинки под углом атаки
значениями числа Моо и угла атаки. Расчет параметров в этом случае
следует вести по общим соотношениям теории скачка уплотнения. В
частности, давление на нижней стороне определяется по (Ш-4-25).
Как и для верхней стороны, можно рассмотреть два частных случая
течения: линеаризованное (Моо и а невелики) и гиперзвуковое (Моо > 1,
углы атаки произвольные).
В случае линеаризованного обтекания расчет течения со слабым
сжатием на нижней стороне можно производить по методу характеристик,
применяя формулы, аналогичные (V-2-2),
* хк — 1
(V-2-2)
Расчет гиперзвукового потока осуществляется по теории сильной
ударной волны. В частности, давление определяется по (Ш-4-19).
Результаты расчета параметров обтекания тонкой пластинки под углом
атаки, а также коэффициентов волнового сопротивления и подъемной силы
приведены в табл. V-2-1.
При гиперзвуковых скоростях обтекания на той стороне пластинки, где
возникает скачок уплотнения, газ претерпевает химические превращения.
В общем случае течение вдоль линии тока от скачка до пластинки будет
происходить с переменной плотностью. Однако, если ударный слой тонкий,
Расчет аэродинамических коэффициентов
231
Таблица V-2-1
Параметры обтекания тонкой пластинки под углом атаки
Условия обтекания
Параметр
обтекания
Формула
Примечание
Линеаризованное обтекание
ПрИ Моо > 1
(угол атаки а
мал)
Очень большие
скорости
Моо>1
(угол атаки а
произвольный)
Произвольные
числа Моо > 1
(угол атаки
также
произвольный)
Коэффициент
давления
Коэффициент
волнового
сопротивления
Коэффициент
подъемной
силы
Угол между
волной
возмущения и
направлением Fq
Число М
Давление
Коэффициент
давления
Плотность
Температура
Скорость
Горизонтальная
составляющая
скорости
Вертикальная
составляющая
скорости
Коэффициент
давления
— 2а
2а
4а2
4а
М
Моо л & —1
-5j- = l ^-Мооа
2k
Poo \ 2 °° )
2k
Р / Mop \
Роо V М j
У = / Моо \
Гоо V М )
Moo \k~l
2
x(sins»ec-M-«)
4
P =
fc+1
Верхняя
сторона
(разрежение)
Нижняя
сторона
(уплотнение)
Углы а
принимаются
положительными
Верхняя
сторона
М>МО
При а >
> (Л-1)Моо
поток
отрывается от
передней кромки
и формула
недействительна
Нижняя сторона
232
Глава V
Продолжение табл. V-2-1
Условия обтекания
Параметр
обтекания
Формула
Примечание
Числа Мое > 1
(угол атаки
произвольный)
Числа Моо > 1
(углы атаки
малы)
Плотность
Угол наклона
скачка
уплотнения
Соответственно
те же
параметры, что и при
Моо>1
Добавочная
величина
горизонтальной
составляющей
скорости
Вертикальная
составляющая
скорости
Давление
Плотность
Величина Кс
Коэффициент
давления
Число М
Poo k — 1
| 2 1
-1
— 1
= Foo(l-
sin2 6r
°° sin 0C cos 6C
tg a =
poo
2
X
A + l
(1-
A — I
sin 6C cos 0C x
2 Sin2 0c^ 1
FFT
2 Kc 1
"A+l K*
■ = 1
-i)
-1
c
~k + i
M
/A-l , 2 z.
,11" 2
a L A(A —1)
1/2
Нижняя сторона
oo
Расчет аэродинамических коэффициентов
233
Продолжение табл. V-2-1
Условия обтекания
Параметр
обтекания
Формула
Примечание
Суммарные
аэродинамические
коэффициенты
Коэффициент
волнового
сопротивления
Для К < 1
2k
Коэффициент
подъемной
силы
, = (А4 1)сб2
су = 2яа
Мо
ОО
то изменением плотности можно пренебречь и считать, что на стенке
относительная величина р^роо/рс^р^рз. Для этого случая коэффициент
давления на пластинке
— 2 sin2 а
р
=
(l-p)cos2(0c-a)
/Л7 о о\
При фиксированном значении а можно, задавшись, например, р,
определить угол G с присоединенного скачка, применив соотношения
гиперзвуковой теории:
tg е^р-'/г/Ог,); /(г)) = 2г](1±КГ^4^)-\ (V-2-4)
где
(V-2-5)
Интервалу 0<г]<0,5 соответствует интервал изменения функции /(т]):0<
</(т])<1. По разности 6С—а определяется значение cos2 (9С — а).
Воспользовавшись соотношением (Ш-4-14), в котором /SVn=i — р, можно
определить, задавшись F^i/2, энтальпию г2, а по термодинамическим таблицам,
зная г2 и р^р^/р, вычислить давление р2. По значению р2 при помощи
(Ш-4-12) можно уточнить Fnl, а затем найти скорость набегающего потока
Foo = Fnl/sin9c. Для больших скоростей, при которых волна примыкает
к стенке, cos(0c — а) « 1 и коэффициент давления
(V-2-5')
Профиль в сверхзвуковом
потоке
Распределение давления. Рассмотрим заостренный профиль,
расположенный в сверхзвуковом потоке под углом атаки (рис. V-2-3). Задачу об
обтекании профиля можно решить, применяя метод характеристик. В
приближенном виде эта задача может быть решена, применяя метод, сочетающий
теорию плоских течений (теорию Прандтля — Майера) и теорию скачков
234
Глава V
уплотнения. Причем течение Прандтля — Майера может исследоваться при
помощи соотношений метода характеристик для плоских потоков.
Для тонких профилей и небольших углов атаки приближенное решение
может быть получено в явной форме. С этой целью функция р = /(в), где
в — угол между
касательной к профилю в данной
точке и вектором Foe,
представляется в виде ряда
по степеням малого
параметра в. Коэффициенты
при 0П представляют
собой соответствующие
производные дрп/д@п и
определяются по уравнению
эпициклоиды в = со (М) +
+ const и выражению для
давления в изэнтропиче-
I
Рис. V-2-3. Тонкий профиль, обтекаемый под углом
атаки: / — область течения с расширением; // —
область течения со сжатием
кий, то, ограничившись в разложении
где
ском потоке.
Так как профиль тон-
членом с 02, получим
(V-2-6)
(V-2-7)
У
1 °
1
6
При в<0 формула (V-2-6) относится к течению расширения, при
6;>0 — к течению сжатия. Причем течение сжатия может происходить
изэнтропически или быть связано
с переходом через скачок.
Формула (V-2-6) соответствует теории
второго приближения,
разработанной проф. Буземаном, а в СССР —
проф. А. А. Лебедевым. В теории
первого приближения принимается ~
Аэродинамические
коэффициенты в линеаризованном потоке.
Толщину профиля можно подо- Рис. V-2-4. Геометрические характеристики
брать настолько малой, что в фор- профиля с криволинейным контуром (i — сред-
муле (V-2-6) можно принять с2 = О няя линия профиля)
и, следовательно, воспользоваться
теорией первого приближения. Полагая, что в = г/' + а, получим
линеаризованные зависимости для расчета давления на верхней и нижней
сторонах профиля:
2(у'в-а) - 2(-у'н-
где производные
Ув
dx
dx
вычисляются по известным уравнениям ув = ув (х) для верхнего и ун = ун (х)
нижнего контуров (рис. V-2-4). Если профиль симметричный, то |г/в| =
||
Расчет аэродинамических коэффициентов 235
Используя формулы для коэффициентов давления рв и рн, можно
получить следующую зависимость для подъемной силы заостренного
тонкого профиля с произвольным сечением:
с„ = -=#==. (V-2-8)
Для тонкого профиля, принадлежащего крылу стреловидной формы
бесконечного размаха, коэффициент подъемной силы
4а cos % ,v 9 я,,
С7, = (V Z )
Имеется в виду, что передняя кромка сверхзвуковая, так что
os%>l.
Коэффициент волнового сопротивления
где x = x/b.
При нулевом угле атаки
С* в = С* во = -wj , ^ (Ув2 + Ун2) CS. (V-2-10)
В этой формуле
следовательно,
где ^! — коэффициент, зависящий от формы и размеров профиля, точнее,
от параметра хс, равного отношению расстояния от носка до места
наибольшей толщины к хорде (рис. V-2-5).
Значения этого коэффициента приведены в табл. V-2-2 [6]. В таблице
принято, что для нижней и верхней сторон значения хс одинаковы.
Коэффициент cxbq определяет сопротивление, обусловленное толщиной
и формой профиля, и не зависит от угла атаки.
Две первые составляющие в (V-2-9) определяют ту часть полного
сопротивления профиля, которая зависит от угла атаки.
Составляющая, обусловленная подъемной силой
ae (V212>
не зависит от размеров и формы профиля.
Вторую составляющую, зависящую от угла атаки и формы профиля,
1
сх в2 = - -7== \ (Ув + Ун) dl (V-2-13)
V OO п
236
Глава V
Таблица V-2-2
Значения коэффициента к^ и относительного расстояния xG
до места максимальной толщины
Вид профиля
Ромбовидный
Клиновидный
»
Параболический симметричный
Клиновидный с одной плоской
стороной
То же
»
Параболический с одной плоской
стороной
Образованный двумя дугами
окружности
можно написать также в виде
0,5
0,4
0,3
0,5
0,5
0,4
0,3
0,5
0,5
2fti
4
4,16
4,76
5,33
8,32
9,52
10,67
16/3
(V-2-14)
х
где dyldx представляет собой производную, которая вычисляется по урав-
нению у = -^ (у в + У и) средней линии профиля. Вторая составляющая
связана с одновременным влиянием угла атаки и формы профиля. Эта
составляющая равна нулю, когда задняя кромка
заострена, или, при отсутствии
заострения, когда профиль симметричный.
Для наиболее широко
распространенных симметричных профилей или
профилей, заостренных с обоих концов,
(V-2-15)
Приведенные формулы могут быть
применены к слабоизогнутым крыльям,
установленным под малым углом атаки.
Обтекание профиля с учетом
нелинейного эффекта. Расчет такого
обтекания осуществляется при помощи зависимости (V-2-6) для коэффициентов
давления. Для верхней стороны профиля
Рис. V-2-5. Геометрические
характеристики профиля с
прямолинейными стенками
Рв = с± (г/в — а) + с2 (Ув1 — а)2;
для нижней стороны
(V-2-16)
(V-2-17)
Интегрируя по поверхности профиля заданной формы, можно получить
соотношения для коэффициентов подъемной силы и волнового сопротивления:
—а0),
2с2А3,
(V-2-18)
(V-2-19)
Расчет аэродинамических коэффициентов
237
где а0 —угол атаки, при котором су = 0 (угол нулевой подъемной силы),
вычисляется по формуле
ао=—~А2. (V-2-20)
Величины А2, В2 и Аъ, зависящие от формы профиля, определяются
следующим образом:
В2 =
(V-2-21)
(y*)(yBy]dx. \
о 1
Комбинируя (V-2-18) и (V-2-19) и пренебрегая в полученном
выражении членами высших порядков, найдем уравнение поляры профиля
с2
сх = 17— щсу + сх в0, (V-2-22)
где cxbq — коэффициент волнового сопротивления при нулевой подъемной
силе, равный
сх в0 = 2с±В2 - 2с2А3. (V-2-23)
Значения коэффициентов А2, В2, А3 для некоторых типов профилей
приведены в табл. V-2-3.
Таблица V-2-3
Значения коэффициентов А2, В2, А3 для расчета аэродинамических коэффициентов
Форма профиля
Примечание
Профиль,
образованный дугами
•окружности;
профиль имеет
вертикальную симметрию
{рис. V-2-6, а)
При наличии
горизонтальной
симметрии
Профиль,
образованный двумя
трапециями (рис. V-2-6, б)
Те же формулы
•относятся к
ромбовидному профилю
Величина сн<0
Величина св>0
Для
симметричного профиля
Профиль,
образованный дугами
окружностей
различного радиуса
{рис. V-2-6, в)
Для профиля
с горизонтальной
симметрией
238
Глава V
Профиль с минимальным сопротивлением. Определив минимум
функции сопротивления, выражаемой (V-2-23), можно найти форму профиля
с заданной относительной толщиной, соответствующую величине
а)
Рис. V-2-6. Геометрические характеристики профилей:
а — профиль, образованный дугами окружности (профиль имеет вертикальную
симметрию); б — профиль, образованный двумя трапециями; в — профиль, образованный
дугами окружности различного радиуса
Исследования показывают, что таким профилем является клиновидный
профиль с относительным расстоянием до места максимальной толщины
Ъл 1 t л , со
Коэффициент минимального волнового сопротивления
сх во min =
1 —■■§- с2
(V-2-24)
(V-2-25)
Определяя зависимость сопротивления от размеров профиля заданной
формы, можно установить, что наименьшая величина схво достигается (при
условии, что максимальная относительная толщина задана), когда толщины
верхней и нижней частей профиля одинаковы, т. е. когда профиль
обладает горизонтальной симметрией. В частности, для профиля, образованного
дугами окружности,
(4^) (V-2-26)
Место максимальной толщины профиля, соответствующее значению
коэффициента схво (V-2-26), определяется относительным расстоянием
(V-2-27)
Для симметричного профиля, образованного двумя трапециями с
заданными значениями Ь1? &3> с» наименьшее сопротивление
1 с* с
(b + Ь)» C
(V-2-28)-
достигается при условии, что
_\ = i (j I
h+b 2 I
_ \
b3 J
(V-2-29).
При размещении крыла на конкретной конструкции летательного
аппарата важное значение преобретают его прочностные характеристики,.
Расчет аэродинамических коэффициентов 239
во многом зависящие от формы профиля и его момента инерции
относительно хорды. Поэтому важно определить минимальное сопротивление
профиля при заданном моменте инерции. Как показывают вычисления, это
сопротивление для профиля, образованного двумя трапециями, равно
(V-2-30)
Соответствующий этому сопротивлению момент инерции
/ = 1с3Ь4; (V-2-31)
другие размеры профиля
Ь1 + Ь3 = »-, &2 = у. (V-2-32)
Профиль с максимальным аэродинамическим качеством. Анализируя
выражения (V-2-22) и (V-2-23), можно установить, что максимальное
качество, равное
^]1/2, (V-2-33)
имеет место при условии, что
cy = 2[cicXB0]l/2. (V-2-34)
При фиксированной относительной толщине профиль с максимальным
качеством будет ромбовидным с относительным расстоянием до места
наибольшей толщины, определяемым (V-2-24). Толщины верхней и нижней
частей профиля
( !) ±() (V-2-35)
В соответствии с этим формула для максимального качества
27^2 7s
^Л =27—^2 7s. (V-2-36)
Подъемная сила и сопротивление стреловидного крыла бесконечного
размаха. Для стреловидного крыла бесконечного размаха со сверхзвуковой
передней кромкой (M«>cos%:>1) аэродинамические коэффициенты, а также
соответствующие силы можно определить по значениям с°у и схв для
профиля прямого крыла при условии, что в качестве числа Маха набегающего
потока принимается величина Mooc = MooCos %. Таким образом, во всех
приведенных формулах для су и схв при переходе к профилю, принадлежащему
стреловидному крылу бесконечного размаха, следует произвести замену
Моо на Moo cos %'
Подъемная сила и сопротивление профиля в направлении скорости Foo
вычисляются по формулам
Y = \ фооУ^Лф cos2 x; (V-2-37)
Хв = 4" с% вРооУ^кр cos3 х, (V-2-38)
откуда следует, что для стреловидного крыла
су = с°у cos* х\ (V-2-37')
cXB = cXBcos3X' (V-2-38')
240
Глава V
Для симметричных профилей
4а cos
с°хв=>
2В2
(V-2-39)
(V-2-40)
Для крыла с дозвуковой передней кромкой (Moo cos % <С 1) при
вычислении аэродинамических коэффициентов профиля, расположенного в
направлении составляющей скорости MooCos%, следует использовать методы
аэродинамики дозвуковых или околозвуковых течений.
Центр давления. В случае линеаризованного обтекания тонкого
профиля центр давления расположен в середине хорды, и, следовательно,
коэффициент центра давления сЦш д =
= #ц.д/Ь = 1/2. Отклонение от этой вели- ^у_
чины связано с нелинейным эффектом, да
Сй dn
0,25
А1
J
/
/
\
1
\
\
\
'—
сх
__
о
1
_
сц.а i
Су Г
— ^
ри с
—-«
1=2°
——
0 0 0
Рис. V-2-7. Аэродинамические коэффициенты
прямоугольного крыла бесконечного размаха
Юсх
ОМ 2,0
О?-
0,2
ш -
дс
То
У
с
СхЬ
у
/
\
О
10 20 30 40 Х°
Рис. V-2-8. Влияние стреловидности
на аэродинамические характеристики
крыла бесконечного размаха (М«> =
== 2, с =0,08)
обусловленным влиянием толщины профиля и его формы. Этот эффект
проявляется в перераспределении давления, которое вычисляется по (V-2-3).
Если рассмотреть обычно применяющийся симметричный профиль,
то выражение для коэффициента центра давления будет [26]
где
Г \Шоо) —
4(M5o—l) '
(V-2-41)
(V-2-42)
Коэффициент к2 зависит от формы профиля. Для ромбовидного
профиля &2 = 1; Для профиля, образованного двумя окружностями, &2 = 4/3.
Коэффициент центра давления профиля, принадлежащего
стреловидному крылу,
_ 1 Г , кгс (ML cos2 % — 2)2 + 0,7Mt>cos4x'
^ц.д — ~2 \_ cos~x
(V-2-43)
На рис. V-2-7, V-2-8 показаны графики изменения аэродинамических
коэффициентов крыльев бесконечного размаха в диапазоне от звуковых
до сверхзвуковых скоростей.
Расчет аэродинамических коэффициентов 241
§ V-3. Подъемная сила и
момент тонких крыльев
конечного размаха.
Сопротивление, зависящее от
подъемной силы
Рассмотрим аэродинамические характеристики крыльев конечного
размаха с малой, но конечной толщиной при условии, что углы атаки
невелики. Иными словами, будем искать линеаризованное решение
уравнения (V-1-6) для потенциала скоростей.
Отыскиваемый потенциал скоростей ф' можно представить в виде
суммы ф^ + ф2, где ф^ — потенциал обтекания крыла заданной толщины при
нулевом угле атаки; фз — потенциальная функция, полученная из условия
обтекания бесконечно тонкой пластинки той же формы в плане, что
и у крыла при заданном угле атаки.
В соответствии с этим подъемная сила крыла равна подъемной силе
пластинки, а сопротивление будет складываться из двух компонент:
сопротивления крыла заданной толщины при а = 0 (су = 0; профиль принимается
симметричным) и сопротивления пластинки при афО.
Треугольное крыло. Рассмотрим крыло треугольной формы в плане
со сверхзвуковыми передними кромками. Для вычисления
распределения давления и аэродинамических коэффициентов можно воспользоваться
методом источников, на основе которого проф. Н. А. Красилыцикова в 1947 г.
решила задачу о сверхзвуковом обтекании крыла конечного размаха.
В общем случае потенциал скоростей от системы источников и стоков,
которой заменяется заданная поверхность, дается выражением (IV-3-1).
Для плоской пластинки функцию /(е, |) следует принять равной некоторой
константе /0. Тогда потенциал скоростей в некоторой точке А от системы
источников
ф = — /о \ de\ -—s-
<У <у I/ /«. о\2 Ш* *<
Область интегрирования определяется площадью, получаемой в
результате пересечения плоскости у ~0 с поверхностью конуса Маха (конуса
возмущения) и ограниченной, следовательно, уравнением параболы
{x-zy = af*[y* + {z-l)% (V-3-2)
где х, у, z— координаты точки А. Интеграл (V-3-1) можно вычислить
непосредственно. Имея в виду зависимость (V-3-2), найдем, что первый
определенный интеграл равен я. Так как, кроме того, &i = xAl и г2 = хА—
— а'г/А, где xAl — точка пересечения конуса Маха с плоскостью г/ = 0,
соответствующая значению z~zA, то отыскиваемый потенциал в точке А
У=-^т(хА-а'у-хА1). (V-3-3)
Вертикальная составляющая скорости
^=!г=я/о- (v-3-4)
Такое же значение скорости будет в том случае, когда точка расположена
на плоскости г/ = 0.
Если поверхность обтекается под углом атаки а, то из условия безотрыв-
ности обтекания f0 = aVoo/?i.
16-114
242
Глава V
Предположим, что крыло в виде тонкой пластинки треугольной формы
имеет бесконечный размах (рис. V-3-1). В зоне /, расположенной между
передней сверхзвуковой кромкой и образующей конуса Маха с вершиной
в точке О, составляющие осевой возмущенной скорости и коэффициент
давления определяются по
ф \ 5) обычной теории линеаризо-
~~ " ванного обтекания
КоМо^/
cos %
lo cos2 x—1
л/о cos %
- 2а cos х
* 1 / О
(V-3-5)
Рис. V-3-1. Обтекание треугольного крыла: У Moo cos2 % 1
а — со сверхзвуковыми передними кромками; б — с дозву- (V-3-6)
ковыми передними кромками ^ тг
Рассмотрим область 11,
расположенную внутри
конуса Маха. Добавочная составляющая скорости в точке А является
результатом действия источников, распределенных в областях ADE, ВСО ж В DO.
Причем в области В DO интенсивность источников равна, но противоположна
по знаку интенсивности в области ADE.
Источники в области ADE индуцируют скорость, определяемую
соотношением (V-3-5). Области В DO соответствует величина скорости
(V-3-7)
где
Интегрируя, найдем
/о
а1 Vl-д2
arccos
п(1-<х) '
(V-3-8)
где n = tg%/a\ o = tg%zA/xA, причем
Скорость, индуцируемая источниками, расположенными в области ВСО,
находится из выражения, аналогичного (V-3-7), и может быть представлена
в виде
/о
= arccos
(V-3-9)
где |тг|<1, |тг|><7>0.
Суммируя (V-3-5), (V-3-8) и (V-3-9), получаем осевую составляющую
скорости в точке А для области //:
/о
(V-3-10)
Следовательно, в этой области коэффициент давления [58]
где знак « —» относится к верхней стороне, знак « + »— к нижней стороне
крыла.
Расчет аэродинамических коэффициентов 243
Коэффициент подъемной силы
C
p
где
dS = у х2 ctg % da; £кр = -1 х2 ctg x«
Внося рн и рв из (V-3-11), получим для су формулу, из которой следует,
что для треугольного крыла со сверхзвуковой передней кромкой
коэффициент подъемной силы не зависит от угла стреловидности и определяется
так же, как для плоской нестреловидной пластинки.
Коэффициент сопротивления, обусловленный волновыми потерями,
(V-3-12)
Это сопротивление, зависящее от подъемной силы, можно определить
так же, как индуктивное сопротивление треугольного крыла со
сверхзвуковыми передними кромками. Так как выполняются условия конического
течения, то центр давления расположен на расстоянии 2/3 корневой хорды
от вершины.
Распределение давления, а следовательно, аэродинамические
коэффициенты для треугольного крыла с дозвуковыми передними кромками
(см. рис. V-3-1) будут иными, что обусловлено дозвуковым характером
обтекания поверхности.
Течение около крыла, установленного под углом атаки а, эквивалентно
потоку от непрерывно распределенных диполей, потенциальная функция
для которых дается формулой (IV-4-4).
Так как течение около крыла носит конический характер, то все
параметры зависят от переменной t==^/s и функцию распределения диполей
можно представить в виде т(&, £) = е/ (t). Имея это в виду, выражение
для потенциала диполей будет
/О 81
4
= ^ / (t) dt ^ ^ ,_ „ ,_ ' (V-3-13)
—to 0
где £0>—^o — представляют собой значения 2=:tgYn, соответствующие
передним кромкам;
е± — определяется из условия, что сверхзвуковые возмущения
распространяются внутри конуса Маха.
В соответствии с этим при е —ej подкоренное выражение в (V-3-13)
становится равным нулю.
В результате интегрирования получим
Фдип= I Ff(t)dt, (V-3-14)
-'о
где
F = yn-s/2a'2 (—L-. + arcthg) . (V-3-15)
n = l-(a't)2; 1= * (V-3-16)
В соответствии с (V-3-16) функция F зависит от переменных z//#, z/x, e/g.
16*
244 Глава V
Функция f(t), представляющая интенсивность распределенных
источников, находится из условия безотрывности обтекания крыла, в соответствии
с которым (Vy)y=o = Vooa = (дудии/ду)у==о- Следовательно,
Как показывают исследования, функцию / (t) можно представить в виде
f (г) —fo~\/tl — t2, где /0 — некоторая постоянная величина. Значение этой
постоянной можно найти из (V-3-17) в результате подстановки в него
заданной функции f(t). Интегрируя, найдем
где EQfl — a'2120) — полный эллиптический интеграл второго рода с
параметром к = ]/"1 — а' Ч20;
я/2
Е= ^ (1 — A2sin2i|5)1/2di|>. (V-3-18r)
с)
О
Переходя к у—>0, получим
Фдип = лт (е, I) = ^^ , (V-d-19)
откуда осевая составляющая
В соответствии с vx определяется коэффициент давления на верхней (—)
и нижней ( + ) поверхностях крыла:
где угол a берется по абсолютной величине.
По давлению можно найти коэффициенты подъемной силы и момента.
Для крыльев произвольной формы в плане
^ = ^+1 И (Рн-Ра)ейсй; (V-3-22)
(V-3-23)
где коэффициент момента рассчитан по корневой хорде 6кр;
Учитывая, что для треугольного крыла г) = оо, и производя
несложные преобразования, получаем
l J (Рн-А)Л; (V-3-24)
о о
(Pn-~P*)dt. (V-3-25)
tgTn J
Расчет аэродинамических коэффициентов
245
Внося значения рИ и рв из (V-3-21), находим
(V-3-26)
(V-3-27)
Из этих выражений следует, что коэффициент центра давления
треугольного крыла равен 2/3.
Приведенные формулы для су, mz можно упростить для частного
случая крыла с очень малым удлинением. Принимая а'£0—>0, найдем, что
Е (к) —> 1 и, следовательно,
су = 2п tg упа» mz = -g- л tg упа.
(V-3-28)
Вводя удлинение ^кр =
= 4 tg уп, получим
1 1
(V-3-29)
Ее ли a't0 —> 1, то Е (к) —> л/2
и формула для су принимает вид,
аналогичный случаю крыла со
сверхзвуковыми кромками.
1,4
0,5
1
/
/
/
/
/
/
/
/
if
/
1 \Г\ 'п\
у
у
П~
о-с=8%
п-с=3%
П D 1
1
"i О С
I
1
i
!
)
/
1
1 №
О
\
Значения производной с\
0,5
1,0
у>
рассчитанные для треугольных
крыльев с до- и сверхзвуковыми
передними кромками,
представлены на рис. V-3-2 в функции
Рис. V-3-2. Теоретическая кривая для
коэффициента подъемной силы треугольного крыла.
Экспериментальные данные:
О — 1 = 8%, D — с«= 3%
На том же рисунке нанесены экспериментальные данные для крыльев
с симметричным профилем, образованным дугами окружностей. Наибольшая
разница между экспериментальными и теоретическими результатами имеет
место для значений a't0, близких к единице, т. е. когда передняя кромка
становится почти звуковой.
Сопротивление крыльев с дозвуковой передней
кромкой. Наличие у крыльев острой дозвуковой передней кромки
обусловливает отрыв с нее вихрей и, как следствие, увеличение сопротивления. Чтобы
предотвратить отрыв вихрей, переднюю кромку несколько скругляют. Так
как скорости на кромке остаются достаточно большими, то давление будет
очень малым и появится подсасывающая сила, уменьшающая
сопротивление. Если обозначить коэффициент подсасывающей силы схи, то суммарный
коэффициент сопротивления крыла с дозвуковой передней кромкой
сх = суа~схи. (V-3-30)
Исследования показывают, что
В соответствии с этим
'яХ
'Кр
(V-3-31)
2
су
яХ
кр
-(а%)а]. (V-3-30')
Если а70=1 (передняя кромка звуковая), то cx = c2yl%KV. Для крыльев
с очень малым удлинением (а70—>0) сж = 4/лЯкр> что совпадает с выраже-
246
Глава V
нием для коэффициента индуктивного сопротивления в случае несжимаемой
жидкости.
Крылья в виде четырех-, пяти- и шестиугольных пластин [58]. Методы
теории обтекания треугольных крыльев могут быть использованы для
расчета аэродинамических характеристик крыльев в виде четырех-, пяти-
и шестиугольных пластин со сверхзвуковыми задними и боковыми
кромками (рис. V-3-3). Обтекание таких крыльев характеризуется
отсутствием зон взаимного влияния хвостовых и боковых участков,
ограниченных пересечением конусов Маха с крылом, т. е. течение у боковых и
задних кромок будет чисто сверхзвуковым.
Формулы для расчета давления на поверхности крыльев указанной
формы будут такими же, как и для треугольной пластины, и выбираются
Рис. V-3-3. Крылья со сверхзвуковыми задними и боковыми кромками:
а — четырехугольное крыло с вырезом; б — четырехугольное крыло с приставкой;
в — пятиугольное крыло; г — шестиугольное крыло
с учетом вида передней кромки — до- или сверхзвуковой. По картине
давлений интегрированием можно определить коэффициенты подъемной силы,
момента и сопротивления.
Приведем результаты, полученные для четырехугольного крыла. В
случае дозвуковой передней кромки
(V-3-32)
(V-3-33)
,= ftgTn [J+b2 rccQs8_
' 3(1 —е)Я(Л) L(l+s)3/2
е(4-е»П
1 —s2 J *
Для крыльев со сверхзвуковыми передними кромками
1
(1__8)
arccos n
arccnanA
8a
2 —n?(l+82)
тгтр arccos щ —
8(3 —82)
(1-82)
- arccos n — -
(V-3-34)
(V-3-35)
где n = g%g\ x\
Расчеты по приведенным формулам можно упростить, если
четырехугольные крылья мало отличаются по форме от треугольных. В этом
случае при условии, что |е| < 1,
1—8
1-е '
(V-3-36)
Расчет аэродинамических коэффициентов
247
где Суд, mz&— коэффициенты подъемной силы и момента треугольного крыла;
величина
=1_ 4 f з-37)
где %ш Хз — углы стреловидности соответственно передней и задней кромок;
xOi xK — размеры крыла, показанные на рис. V-3-3.
У крыльев типа «ласточкин хвост» (рис. V-3-3, а) величина е
положительна, а для ромбовидных пластин (рис. V-3-3, б)— отрицательна.
0yU 0,6 0,8 ' £0
/77
Рис. V-3-4. Графики для расчета подъемной силы
четырехугольных пластин (т = tg yn/tg \i)
CCJ
/
/
Qfi
6=0
\
i
•
-0Л
[^
4
/
w
— —
—
— —
— -
- 1
'1
—• —
-
0
OA
06
0,8
/77
Рис. V-3-5. Графики для расчета коэффициента центра
давления четырехугольных крыльев (т — tg Vn/tg Iх)
В частном случае, когда у крыла со сверхзвуковой передней кромкой
значение tg%Jtg\i > 1, параметр г практически не влияет на коэффициент су,
и вырез или приставка будут изменять подъемную силу почти]
пропорционально изменению площади пластины.
На рис. V-3-4 показаны кривые
для четырехугольных пластин, полученные по линейной теории при условии,
что задние кромки являются сверхзвуковыми. На рис. V-3-5 приведены
результаты расчета, характеризующие положение центра давления у этих пластин.
Аналогичные кривые, построенные для пятиугольной пластины,
показаны на рис. V-3-6-HV-3-8.
Лобовое сопротивление крыльев рассчитывается следующим образом.
Если кромка сверхзвуковая, то независимо от формы пластины
Сх = Суа = ^ (т>1). (V-3-38)
248
Глава V
Если передняя кромка дозвуковая, этот коэффициент надо уменьшить
на величину коэффициента подсасывающей силы, т. е. расчет следует вести
по (V-3-30). Величина
подсасывающей силы
0,75
0,5
0,25
/
/
/
п
//
/л
W
У
У/,
/
'//
V,
г*-
/у
У/
у
/у
у
А
L2
f
А
<?
у
/
6
,5-
/
/?
'/+
у,
/
4
3,5
у
/
т
-?
F=ii
(V-3-39)
(см. рис.
Рис. V-3-6. Графики для расчета
коэффициента подъемной силы пятиугольных крыльев
малого удлинения
Зоны влияния,
для шестиугольного
где I — размах крыла
V-3-3).
Разделив величину F на
произведение qSKp, где £кр — площадь
пластины заданной формы,
получим схи.
Для четырехугольного крыла,
мало отличающегося от
треугольного, расчет можно вести по формуле
«*п = 1^. (V-3-40>
где (схп)д вычисляется по (V-3-31)
для треугольной пластины.
Рассмотрим крылья с
дозвуковыми боковыми кромками,
полагая, как это имеет место на
практике, что задние кромки являются
сверхзвуковыми. Расчет обтекания
таких крыльев оказывается более
сложным, что обусловлено
образованием зон влияния у боковых
кромок и необходимостью учета
перетекания газа в этих зонах с одной
стороны пластинки на другую.
расположенные внутри конусов iMaxa, показаны
крыла на рис. V-3-9. В зоне / течение определяется
4
10
0,9
3.5 А
У
1
1
**~
**■
=
— ■
^<-
^^
^»
р —
:^
■ess
— —
2
—■
rsss
— —
)
——
аа
——
=
■as
=
10
15
Рис. V-3-7. Графики для расчета коэффициента подъемной
силы пятиугольных крыльев большого удлинения
дозвуковыми передними кромками и при расчете потока надо учитывать
их влияние на перетекание с нижней стороны на верхнюю (или наоборот).
Расчет аэродинамических коэффициентов
249
В зоне // на обтекание сказывается влияние правой боковой кромки,.
а в зоне /// добавляется еще влияние левой кромки.
Обтекание носит симметричный характер относительно оси х, поэтому
можно рассматривать зоны /, //, ///, расположенные по одну сторону от оси х.
0,5
0,3
3/
J_
Ц
/
/
"I
//
1/
/
1*
/
с
r;
/
\
I I
7?n
с
I
ю
Рис. V-3-8 Коэффициент центра давления
пятиугольного крыла (сцд = .Гцд/6Кр)
При заданной скорости набегающего потока параметры в
рассматриваемой точке поверхности шестиугольного крыла (рис. V-3-10) или era
суммарные аэродинамические ког^фшшенты в наиболее общем случае зави-
Рис. V-3-9. Схема обтекания шестиу- Рис. V-3-10. Геометрические
гольного крыла с дозвуковыми перед- размеры шестиугольного крыла
ними и боковыми кромками и задними
сверхзвуковыми кромками
сят от комплекса безразмерных геометрических характеристик пластины^
а именно удлинения Хкр, сужения ц = ЬКТ)/ЬКЦ и углов %и и %3 (или
соответствующих им величин уи и ^з)-
В зоне /, расположенной за дозвуковой передней кромкой,
коэффициент давления определяется по (V-3-21). Для этой зоны
характерным параметром является угол наклона передней кромки Yn (или угол
стреловидности %п)-
Применяя метод источников и стоков, можно определить давление
в зонах // и ///. Как показывают исследования, в зоне II коэффициент
давления
- + 2a tg уп
"" E(k)
tg6
z 1-tgG/tgYn
(V-3-41)
250
Глава V
где }z = 2zll, tgQ = z/x. В зоне /// избыточное давление равно нулю, что
обусловлено противоположным по знаку влиянием на течение в этой зоне
передних и боковых кромок, в результате чего добавочная осевая
составляющая скорости оказывается равной нулю.
Внося значения рн и рв из (V-3-41) в (V-3-22) и (V-3-23), можно
вычислить коэффициенты подъемной силы и момента. Чаще всего встречается
случай, когда зона /// отсутствует и
остаются только зоны /, // (волны
возмущения АС и BD, выходящие из передних
точек боковых кромок, как показано на
рис. V-3-11, пересекаются вне крыла).
При определении аэродинамических
коэффициентов для пятиугольного крыла
следует принять tg%3 = Q. Для
четырехугольных крыльев г] = оо.
Рассмотрим аэродинамические
характеристики шестиугольных крыльев со
сверхзвуковыми передними и
задним и и дозвуковыми боковыми кромками
(рис. V-3-11).
Обтекание такого крыла носит
сложный характер и характеризуется влиянием
боковых кромок на параметры в зонах ///,
/F, V. В [зонах /, // течение будет таким,
как на треугольном крыле со
сверхзвуковыми передними кромками.
В зоне / добавочная осевая
составляющая скорости и коэффициент давления
определяются соответственно по формулам (V-3-5) и (V-3-6), а в зоне// — по
формулам (V-3-10) и (V-3-11).
Используя метод источников, можно определить аналогичные величины
в остальных зонах. Приведем значения коэффициентов в зонах ///, /F, V.
В зоне /// коэффициент давления
Рис. V-3-11. Схема обтекания
шестиугольного крыла со сверхзвуковыми
передними и задними кромками и
дозвуковыми боковыми кромками
р=±
-А;
в зоне IV
в зоне V
где
(V-3-42)
(V-3-43)
ppns
Л-arccos
Az = arccos "2j
n(x—0,5aXKpz
В приведенных формулах параметр а =
(V-3-44)
(V-3-45)
Расчет аэродинамических коэффициентов
251
м„
Применяя (V-3-22) и (V-3-23), можно определить для шестиугольного
крыла коэффициенты подъемной силы и момента. Чтобы перейти к
пятиугольному крылу, надо принять tg%3 = Q-
Практический интерес представляет случай обтекания, когда линии
возмущения ОБ и АС пересекаются на крыле (рис. V-3-12, а) или когда
эти линии пересекаются вне крыла (рис. ч ^
V-3-12, б). Расчет распределения
давления должен производиться с учетом
числа и принятой нумерации зон
влияния. На рис. V-3-12, а видно, что таких :
зон четыре {I — IV), а на рис. V-3-12, б —
три (I — III).
Применяя (V-3-22) и (V-3-23),
можно убедиться, что хотя распределение
давления носит различный характер,
аэродинамические коэффициенты,
соответствующие обеим схемам обтекания,
одинаковы.
Прямоугольное крыло. На рис.
V-3-13 показано прямоугольное крыло, „ лтолп m
* J ^ ' Рис. V-3-12. Шестиугольные крылья
у которого передняя и задняя кромки со сверхзвуковыми передними и зад-
сверхзвуковые, боковые —дозвуковые. В ними кромками и дозвуковыми боко-
зоне / имеет место обычное сверхзву- выми кромками
ковое течение, и давление определяется
по (V-3-6) для тонкой пластинки при условии, что cos% = l.
В зоне //, где на течении сказывается влияние боковой кромки,
- arcsin
in j/
tgB
(V-3-46)
Если зоны // для правой и левой боковых кромок пересекаются, то
в образовавшейся зоне пересечения /// (см. рис V-3-13, б) коэффициент
Давления рш == (рц)лев + (Ри)прав — Pi-
Рис. V-3-13. Схема обтекания прямоугольного крыла:
а — зоны II не пересекаются; б — обтекание с образованием зоны III\ в —
многократное пересечение волновых зон
Для случаев обтекания, схематически изображенных на рис. V-3-13
и соответствующих условию Якр ]/~М^ — 1 > 1, при выполнении которого
линии Маха BD и АС пересекаются соответственно в точках Е и F на
задней кромке крыла (рис. V-3-13, б),
(V-3-47)
(V-3-48)
%-4atg|1(l—
Глава V
а)
Хкп-ot 6 4 Z 0 2 4 6 8 10
Рис. V-3-16. Изменение величины Су/Якр изолированного крыла в за
личных зна
Расчет аэродинамических коэффициентов
яп.\
4,0
|\\
\
ч ч
N
^-—■
У
у
*.—
—■
-■^
——9
J-4
-Мое*'
Л/1
г-
4 2 О Z
6 8 10 AKp-od
8 10 ЛКрс/
tT 4 2 0 2
m
I
Л
j
VJ -
'А
Л*
i
ч
\\
\\
у
■ул
J-
—
\
\
1
/
50
/fi'fi
$
6 8 fO
висимости от параметров
чениях г\
— 1; ?ч = А,Кр tg Xi/, при раз-
Глава V
Лкр-л 6
Ф
2,0
-
«^
-^
-^и
^-*
**~
—-—
^-^^
^=^"
. 1 —
——
—
■- —
-——
» —
—»-
» ■
3
2
1 .
О
в Акрс*
Рис. V-3-17. Изменение величины сц. д. изолированного
= ^кР tg %1/2 при различ
Расчет аэродинамических коэффициентов
ф
сц.Э
■MM
№.-1
а5
——
— —
i=
Э»
——
Af5
/
о
О 2 4 6 Акр-с*
AKp-ct' 6
^5
О 2 U 6
Ф
^? 2
6 Акр-et'
крыла в зависимости от параметров Д,кра', Я4 =
ных значениях х\
256
Глава V
Обтекание носит более сложный характер, если ХКРУМ.1, —1<1. В этом
случае (рис. V-3-13, в) возникают новые волновые области, образованные
op
Ofi
4
у
/
/
у
^—
Рис. V-3-14. Кривая для расчета подъемной силы
прямоугольного крыла конечного размаха
в результате пересечения падающих и отраженных от боковых кромок волн
возмущения. Для определения коэффициента су крыла можно пользоваться
данными, приведенными на рис. V-3-14.
Приведенные результаты для су и mz
позволяют найти коэффициент центра
давления сц. д = хц. д/6кр = mjcy (рис. V-3-15).
Коэффициент сопротивления
прямоугольного крыла
сх = асу = 4а2 tg fx (l —^-) . (V-3-49)
При расчетах аэродинамических
коэффициентов в практических случаях
удобнее пользоваться графиками, показанными
на рис. V-3-16, a — e, V-3-17, а —ей
характеризующими изменение величины Су/Хкр
на
US
03
/
/
!
I
+—
——-
——
.;
о
5
10
и коэффициента
параметров
сц# д в зависимости от
Рис. V-3-15. Коэффициент центра
давления прямоугольного крыла
конечного размаха
По величине сц. д, равной отношению расстояния до центра давления
к корневой хорде &кр, можно определить расстояние до центра давления
в долях средней аэродинамической хорды
^ ^Ц. Д ( 3 ™ "£э Хп Л ~Т" "1 Л \Л "Т" *■) /тт о trrv\
Сп/тт = = ^усц. д g — J <Ху1^п . (V-d-bU)
§ V-4. Сопротивление
крыльев конечной
толщины
Треугольное крыло в плане. Для определения сопротивления,
обусловленного толщиной, необходимо исследовать обтекание крыла при
нулевом угле атаки (нулевой подъемной силе). Исследование можно осуществить
при помощи метода источников.
Рассмотрим крыло треугольной формы в плане с малой толщиной [58].
С газодинамической точки зрения такое крыло эквивалентно системе рас-
Расчет аэродинамических коэффициентов
257
пределенных источников (стоков), потенциал скоростей которых определяется
по (IV-3-1).
Функция /(е, |), определяющая интенсивность источников, находится
из условия безотрывности обтекания. Имея в виду (V-3-4), получим
f = U=^~, (V-4-1)
где уг — угловой коэффициент касательной к профилю в рассматриваемой
точке.
Для определения добавочной осевой составляющей скорости на крыле
со сверхзвуковой передней кромкой можно использовать формулы (V-3-5)
и (V-3-9) .с заменой в них /0 выражением (V-4-1). В соответствии с этим
получим следующие зависимости
для коэффициента давления. В зоне
между волной Маха и передней
кромкой
Р=,,%-тг-. (V-4"2)
м,
в области, расположенной внутри
угла Маха,
Р =
X
X
Рис.У-4-1. Треугольное крыло конечной
толщины с дозвуковой передней кромкой в
сверхзвуковом потоке
(V-4-3)
Для расчета [течения около
крыла с дозвуковой передней
кромкой следует использовать (IV-3-1) при условии, что пределы интегрирования
определяются с учетом распределения источников в области между линиями
Маха АС и АЕ и соответствующими участками передних кромок (рис. V-4-1).
Потенциал скоростей для точки А можно представить в виде трех
составляющих, определяемых действием источников в зонах ОС В, OBAF
и FAE. В соответствии с этим формула (V-3-1) будет
(V-4-4)
При условии, что источники распределены в плоскости г/ = 0, функция
Непосредственно из рис. V-4-1 можно найти значение координат zc и zE.
определяемых положением точки А. Осуществляя дифференцирование
в (V-4-4) по х, находят дополнительную осевую составляющую скорости,
а затем определяют выражение для коэффициента давления
(V-4-5)
Если точка Ах расположена между передней кромкой крыла и волной
Маха, то, осуществляя расчеты, аналогичные проведенным для точки А,
17 — 114
258
Глава V
с учетом того, что на гточку А действуют источники, расположенные
в заштрихованной области рис. V-4-1, получим для коэффициента давления
:arch
(V-4-6)
О
Треугольное крыло с ромбовидным профилем. Схема
такого крыла показана на рис. V-4-2. Расчет сопротивления,
обусловленного толщиной крыла, можно осуществить, используя приведенные выше
результаты для треугольного
крыла с постоянным наклоном
у контура профиля.
При определении
аэродинамических характеристик следует
иметь в виду три расчетных
случая (рис. V-4-3):
а) передние кромки, а
также линии АВ и АС
максимальных толщин профиля являются
сверхзвуковыми (1 > п > пс,
где п = tg Хп tg (х, пс = tg %с tg [x);
0
f
►о
/ А
С
В i
X
Рис. V-4-2.
Треугольное крыло
профилем
с ромбовидным б) передние кромки
являются дозвуковыми, а линии АВ и
АС—сверхзвуковыми (п > 1 >пс) \
в) линии АВ и АС являются дозвуковыми (тг>ггс>1).
Рассмотрим случай: 1 >п'>пс. Распределение давления на участке ОБА
рассчитывается по (V-4-2) в области, расположенной между граничной
волной Маха и передней кромкой, а при помощи выражения (V-4-3) — в зоне,
находящейся внутри угла Маха.
Интегрируя по площади ОБА, получим
величину составляющей полного
коэффициента сопротивления
а'п
•F(n,
(V-4-7)
где b1 =
KP—(см. рис. V-4-2);
F — функция, равная
F(n, 61)=
Гт + arcsin (Ml}. (V-4-8)
L2 JJ v /
X
Рис. V-4-3. Расчетные случаи
обтекания треугольного крыла: «i—i»—
кромки OB (ОС) и АВ [АС) сверхзвуковые
(1 > п > пс); «2—2»— кромка ОВ —
дозвуковая, кромка А В — сверхзвуковая
(п > 1 > Гсс); «3—3»— кромки ОБ и
А В дозвуковые (п > пс > 1)
Вторая составляющая
сопротивления обусловлена действием источников,
вызывающих вертикальную
составляющую скорости vy = г/^Foo и влияющих на
течение в области ABD с наклоном у'2.
Давление во внешней и внутренней по отношению к углу Маха зонах
участка крыла ABD вычисляется соответственно по формулам (V-4-2) и
(V-4-3). Интегрируя по площади ABD, получим
(V-4-9)
Чтобы вычислить третью составляющую сопротивления, необходимо
учесть влияние источников, расположенных на участке ABD и имеющих
Расчет аэродинамических коэффициентов
259
интенсивность fo = VOQ(y2 — y[)/n. С учетом этой интенсивности давление
в соответствующих зонах определяется по (V-4-2) и (V-4-3) при условии,
что в этих формулах величина у[ заменяется на у'2—у'г
Производя интегрирование по площади ABD, получим
У2 — Ух)
авс
Зкр
(V-4-10)
Суммируя составляющие, найдем полный коэффициент сопротивления
крыла cx = cxi + cx2 + cx3.
Во втором случае п > 1 > пс сопротивление вычисляется аналогично
при условии, что на передней части крыла давление находится из (V-4-6),
В соответствии с этим находится
схы/4с"2
9.1
о,з
0,5
0J
первая составляющая
сопротивления для участка ОАВ, а также
вторая составляющая от
источников fo = y'1Vao/n, распределенных
по области ABD. Величина сх3,
соответствующая сверхзвуковой
кромке АВ и зависящая от
источников, расположенных в области
ABD с интенсивностью /0 = (у2 —
—Уд Voo/n, определяется по
формуле (V-4-10).
Для третьего случая,
характеризующегося тем, что кромки ОВ
и АВ дозвуковые и, следовательно,
п>пс> 1> три составляющие
сопротивления вычисляются так же,
как в предыдущем случае, с той
особенностью, что кромка АВ
дозвуковая и поэтому Ь1^>1.
К этим трем составляющим надо добавить сопротивление,
обусловленное влиянием на область АЕВ источников с интенсивностью /0 = (у2 —
— y'dVoo/л, распределенных на участке 4BD. Так как в области АЕВ
давление находится по (V-4-6), то третья часть сопротивления выражается
зависимостью
Cxi = MM=idI 2^.^. J° 1_ arch /g dQ_ (y_4rll)
V с 4 v v
Суммируя составляющие, найдем коэффициент полного сопротивления
Рис. V-4-4. Изменение коэффициента
сопротивления треугольного крыла с ромбовидным
профилем и сверхзвуковой передней кромкой
в зависимости от положения максимальной
толщины при различных углах стреловидности
х 2j xk
На рис. V-4-4 и V-4-5 приведены результаты расчета параметра
сопротивления сха'/4с2 для треугольного крыла со сверхзвуковой (рис. V-4-4) и
дозвуковой (рис. V-4-5) передними кромками в зависимости от \—Ъх для
различных значений n = tg%ntg\i.
Четырехугольное крыло с ромбовидным профилем. Изложенная схема
расчета обтекания треугольного крыла по методу источников может быть
использована для вычисления сопротивления крыла произвольной формы
в плане.
Рассмотрим четырехугольное крыло с ромбовидным профилем (рис. V-4-6).
Поток около крыла можно представить как суммарное течение от трех
систем источников, имеющих треугольное распределение. Первая система
17*
260
Глава V
источников распределена в треугольнике OBL (рассматриваем половину
крыла) и имеет интенсивность U = y'VJn\ источники второй системы
с интенсивностью /0 = (у'2 — у[) VoJn распределены в треугольнике ABD и,
наконец, источники третьей
системы, имеющие отрицательную
интенсивность fo= — y'2Vaoln>,
распределены в области DBL.
В наиболее общем случае
в некоторой точке на
поверхности крыла дополнительная
осевая составляющая скорости,
а следовательно, давление будут
определяться в результате
сложения составляющих,
полученных от каждого
распределения источников. В зависимости
от угла стреловидности или
положения каждого из трех
распределений источников
относительно рассматриваемой точки
поверхности коэффициент
давления будет определяться урав-
2,0
1,0
0,5
\
S; —
\
\
_x
\
1
1,3
\
\
\
\
\
J
f'5t-
i
1
\
\
\
f
i
\
\
\
Д
\;
\
/
<s
**•
--"
\
/\
^\
\
f
1,1
4
VI x
«^
***
у
f
1
7
/
/
/
/
/
Ofi
0,3
0,8 1-
Рис. V-4-5. Изменение коэффициента
сопротивления треугольного крыла с дозвуковой
передней кромкой в зависимости от положения
максимальной толщины
нениями (V-4-2), (V-4-3), (V-4-5),
(V-4-6).
Пусть кромки крыла OB, AB
и DB дозвуковые. Тогда можно
рассмотреть четыре области ozDv zDlzAl, zAiZd2 и Zd2z, каждая из которых
характеризуется одним и тем же положением зон распределения
источников. Следовательно, внутри зоны около каждого сечения будет одинаковое
х
X
Рис. V-4-6. Четырехугольное крыло с ромбовидным профилем
распределение давления, и профили будут иметь одинаковые местные
коэффициенты сопротивления.
Обтекание профиля EGJ с координатой z± (0 < zi < zDl) рассчитывается
следующим образом. На участке EF с наклоном у[ коэффициент давления,
зависящий от распределения источников в треугольнике OBL, вычисляется
Расчет аэродинамических коэффициентов 261
по (V-4-5). На участке FG с таким же наклоном следует, кроме того,
учесть влияние источников в зоне ABL. Следовательно, к величине (V-4-5)
надо добавить значение коэффициента, вычисленного по (V-4-6) при
условии, что у[ заменяется на у'2 — у[, а о вычисляется относительно точки В,
располагающейся в начале координат.
На участке профиля GH с наклоном у2 вторую составляющую давления
необходимо вычислять по (V-4-5) при условии замены в ней у[ на у2 — у[>
Наконец, на четвертом участке профиля HJ к рассмотренным двум
составляющим надо добавить третью составляющую, обусловленную
действием источников в треугольнике DBL и определяемую по (V-4-6) с заменой
в ней у[ на — у2.
Аналогично исследуется обтекание крыла в сечениях с координатами
z2, z3, zi. В сечении с координатой z2 следует рассмотреть также четыре
участка. На первом участке, расположенном между передней кромкой
и линией Маха ААи будем иметь одну составляющую коэффициента
давления, определяемую по (V-4-5). На втором участке, ограниченном линиями
Маха ААХ и DD2, следует добавить составляющую, вычисляемую по (V-4-6)
с заменой у[ на у'2 — у[. Третий участок профиля располагается между
линией DD2 и кромкой АВ. К двум предыдущим составляющим
коэффициента давления добавляется третья, которая находится по (V-4-6) при
условии, что у'х заменяется на — у2, а вершина D считается расположенной
в начале координат. На четвертом участке, примыкающем к задней кромке,
составляющие давления определяются по аналогии с третьим участком.
В сечении z3 следует рассмотреть три участка профиля, а в сечении
z4 — два. Так как сечение z4 располагается за волной DD2, то на поток
в каждой точке этого сечения будут влиять одновременно три
распределения источников.
Если кромки крыла сверхзвуковые, то для определения коэффициента
давления вместо (V-4-5) надо использовать (V-4-3).
Расчет обтекания симметричного крыла с ромбовидным профилем
по изложенному методу показывает, что коэффициент сопротивления,
обусловленный влиянием толщины, может быть представлен в виде
сх = ^г f (п. Ъа , bo), (V-4-12)
f — функция, зависящая от параметров тг, 61? Ь2, имеет различный вид,
определяемый соотношениями между величинами указанных параметров.
В результате исследований получен вид функции / в следующих трех
случаях: п < b2, b2<in<db1 и п\>Ь±.
Расчеты a'cjc2 по (V-4-12) приведены на рис. V-4-7, а, б в
зависимости от п — — для различных значений Ьх и Ь2.
Стреловидное крыло с криволинейным профилем.
Методом источников можно рассчитать обтекание тонкого стреловидного
крыла с криволинейным профилем.
Предположим, что тонкий профиль является симметричным и образован
дугами окружности (рис. V-4-8). Для определения коэффициента давления
в некоторой точке поверхности А следует воспользоваться приведенными
выше формулами метода источников и произвести суммирование
составляющих давления, индуцированных различными распределениями источников.
Сначала следует рассмотреть распределение источников с
интенсивностью fo^y'oVoJtt, определяемой начальным наклоном касательной к
профилю. Полагая, что передняя кромка дозвуковая и применяя (V-4-5), полу-
262
Глава V
чим для оэффициента давления
- —м^
яа' У^2 —1
где
tg [i; a4 = ^
а)
с
)z
WIR
ля.
*f-крыло Вес конечного размаха
~ЪГО,5-
0,5
1,0
2ft n
e)
-
— ■—
^■*-
f
/
<^
*/=
Й
7
7/
/
~?
0,5
/
I)
Ml
//I/
/I
/
/
\
Л
\\
\
fp-крыло бесконечного
/JU3M
axa
Qfi
W
15
(V-4-13)
Рис. V-4-7. Коэффициент волнового сопротивления крыла в
зависимости от п = 1/п для различных значений Ь± и Ь2
В точке А индуцируется давление от источников с интенсивностью dy\
распределенных в треугольнике с вершиной в точке С (рис. V-4-8):
■т —Ady' , , /" rfi—о%
яа V п2 — 1 r -1 — "2
(V-4-14)
Расчет аэродинамических коэффициентов
263
где
(72
__ za tg Хп
= •
Если а>1, то приращение коэффициента давления вычисляется в
соответствии с (V-4-6):
^^ (V-4-15)
От дифференциала dz/' можно перейти к величине dy' = (dy'/dx) dx =
= [(dy'/dx)tg ХпУл/вЦ da2, где для дуги окружности dy'ldx = — 2y'Jb.
Рис. V-4-8. Стреловидное крыло с криволинейным
профилем
Чтобы получить полную составляющую давления, следует
проинтегрировать (V-4-14) от G2 = Gi до а2 = 1, a (V-4-15) — от сг2 = 1 до о2 = п. Если
точка А расположена так, что испытывает влияние источников с
интенсивностью /0= —y'0VoJn>, расположенных в треугольнике с вершиной В, то при
интегрировании (V-4-15) следует
вместо предела сг2 = п взять предел
о2 = аВ1 где о в = [tg %uza/(xa —
—хв)]<.п.
Третья составляющая
давления в точке А будет определяться
указанным распределением
источников /о = — y'0VJii
- _ — 4г/р 1 /"л2 — 1
~~~ па' 1/^==ТаГ У G% —1#
(V-4-16)
Суммируя полученные состав-"
ляющие, можно найти для данной
точки полный коэффициент
давления.
Распределение давления около
профиля с контуром в виде дуги
окружности, подсчитанное по изложенному методу для Моо = 1,4 и %п=г60°
в зависимости от отношения zlb, показано на рис. V-4-9. Изменение местного
коэффициента сопротивления по размаху крыла приведено на рис. V-4-10.
Крылья произвольной формы в плане. По методу источников задача
об обтекании крыла произвольной формы в плане может быть сведена
к задаче об обтекании треугольных поверхностей. В соответствии с этим
с
+2,0
О
-2,0
со
Рис. V-4-9. Распределение давления вдоль
ХОРДЫ кРыла с Углом стреловидности 60°
264
Глава V
методом заданная поверхность в плане дополняется до поверхности
треугольной формы. Тогда можно считать, что поток около заданной
поверхности индуцируется источниками с по-
~* ^ ложительной интенсивностью,
распределенными на треугольной поверхности,
и источниками противоположного знака,
распределенными на достроенной части
поверхности, которая также
расчленяется на отдельные участки треугольной
формы.
В качестве примера рассмотрим
шестиугольное крыло как крыло
треугольной формы с законцовкой в виде среза
с хордой MN (см. рис. V-4-6).
Рис. V-4-10. Распределение профиль- Расчет обтекания такого крыла ве-
ного сопротивления по размаху крыла дется следующим образом. Достроив
с углом стреловидности 60° и сим- крыл0 до треугольной формы О DC, pac-
метричным профилем, образованным r r * г *
006
0,04
0,02
0
-0,01
N
S
\
1
Моо=>,4; 0-0,1
о
дугами окружности (1 —прямое крыло;
2 — стреловидное); по оси абсцисс —
считывают течение от распределенных
по площади О DC источников. При этом
расстояние от корневого сечения поток на участке OMD (MD — линия
в долях корневой хорды Маха) останется таким, как и для
заданного крыла. Полученные параметры
для конца MDN надо уточнить, так как он будет испытывать влияние
источников противоположного знака в треугольнике MNC.
Общее соотношение для расчета сопротивления стреловидного крыла
конечного размаха. Полное сопротивление аэродинамически плоского крыла
Сх = cxf + сх вО +
(V-4-17)
где А — некоторый коэффициент.
Величина этого коэффициента определяется характером передней кромки.
При сверхзвуковой передней кромке 4= (с*)""1, при дозвуковой Л<(с^)"1.
Величина схво представляет собой
коэффициент волнового сопротив- сх
ления крыла при ос = 0. Эту
величину удобно выражать через
коэффициент волнового сопротивления
профиля схв с помощью зависимости
(V-4-18) 0
>
/
— —
з
где
Рис. V-4-11. Изменение коэффициента
пропорциональности сх в формуле (V-4-20) по ли-
(V-4-19) нейной теории (г\ =2; хс = 0,5; ^кр tg % =
V ' 36
; хс
= 3,67)
Коэффициент пропорциональности сх в рамках линейной теории можно
представить в виде функции [6]
(V-4-20)
В качестве примера на рис. V-4-11 представлена кривая сх для
стреловидного крыла с сужением т] = 2, абсциссой хс = 0,5 и величиной ^
Расчет аэродинамических коэффициентов
265
= 3,67. Причем угол % (рис. V-4-12) измеряется относительно передней
кромки.
В тех случаях, когда крыло имеет несимметричный профиль (см. рис.
V-2-5) с различным положением максимальной толщины хСня хс в на
нижней и верхней сторонах, коэффициент схв0 следует определять в виде суммы
сх в0 в, (V-4-21)
сх во =
где первое слагаемое относится к нижней стороне, второе — к верхней.
На рис. V-4-13 для иллюстра- с
ции приведены кривые волнового х °
сопротивления схво крыльев раз-
0,02
от
1_
,—■—
-
к
(\
A
/ J
L
г"
t/7 ^ i4 /^ ^ 2,0 Moo
Рис. V-4-12. Геометрические ха- Рис. V-4-13. Волновое сопротивление
рактеристики стреловидного крыльев
крыла
личной формы в плане. Профиль всех крыльев — чечевицеобразный с
относительной толщиной с = 0,05.
Подобие. Обозначим индексом «*» параметры (геометрические и
аэродинамические) стреловидного крыла при Моо =у 2.
Можно показать, что геометрические параметры крыльев при любом
числе Моо > 1 и при Moo = V2 будут связаны между собой соотношениями
(V-4-22)
Соответствующая связь между аэродинамическими коэффициентами этих
крыльев и их сечений будет следующей:
иц. д *•
(V-4-23)
(V-4-24)
266
Глава V
3,0
zp
1,0
Таким образом, чтобы рассчитать параметры при некотором числе
>1, надо, чтобы они были известны для крыла с несколько
другими значениями сужения г]* и
удлинения ^, но с теми же, что у
заданного, формой сечения и углами атаки.
На рис. V-4-14 приведены в качестве
примера теоретические кривые Су* = /(^#)
для стреловидных;крыльев при различных
значениях tg%* и при сужении т]* = 1.
Для того чтобы воспользоваться
этими кривыми для других чисел
-д ^ Моо>1, достаточно в соответствии с
57 А* приведенными формулами преобразо-
Рис. V-4-14. Зависимость с* = f (Я*) вания произвести на рис. V-4-14 замену
для стреловидных крыльев при различ- величине^, Я*, tg %# произведениями
ных значениях tg %% и сужении г\* = 1
§ V-5. Нелинейная задача
о сверхзвуковом обтекании
крыльев
/
/
/77=
/
/
0,2
—-—
m=tg\*
и—
—1/» 1
Применение метода
ристик
характеу i
Расчет обтекания заостренного профиля. В общем случае, когда
заостренный криволинейный профиль произвольной толщины обтекается
сверхзвуковым потоком, число Мое которого также может быть произвольным,
расчет местных аэродинамических параметров газа может быть осуществлен
при помощи метода характеристик.
Расчет производится следующим образом. В окрестности заостренной
передней кромки выбирается достаточно малая клиновидная поверхность О А
(рис. V-5-1), на которой параметры обтекания вычисляются по теории косого
скачка уплотнения. В результате строится прямолинейный участок скачка ОС
и определяется точка его пересечения С
с простой прямолинейной волной,
проведенной из точки А. Эта волна АС
совпадает с характеристикой, которую
можно условно назвать
характеристикой первого семейства.
Обтекание криволинейного контура,
расположенного вниз по течению от
точки А, зависит от формы этого
контура, значения параметров газа в
точках на характеристике АС, а также
от взаимодействия с ударной волной,
в результате которого сама ударная
волна приобретает криволинейную
форму. При этом можно выделить
участок контура AL, где влияние
криволинейной ударной волны отсутствует. Этот участок можно определить, если
из близко расположенных точек F, G и т. д. провести прямолинейные
характеристики первого семейства до пересечения в точках D, Е и т. д.
с соответствующими элементами характеристик второго семейства. Элемент
характеристики второго семейства NL, проведенный из точки N, пересечет
контур профиля в точке L, которая будет являться границей отыскивае-
Рис. V-5-1. Схема расчета
сверхзвукового обтекания профиля по методу
характеристик
Расчет аэродинамических коэффициентов 267
мого участка потенциального (безвихревого) обтекания, не зависящего от
течения за криволинейной волной.
На этом участке местное число М определяется по теории простой
волны, известной как теория потенциальных течений разрешения Прандтля —
Майера (см. стр. 146). По этой теории, например, для точки F угол
расширения потока с начальным условием М = 1 будет равен (dF — рА —
— $F + a)A. Соответствующее число MF в точке F находится по табл.
IV-1-1. Аналогично ведется расчет для других точек контура, включая
точку L.
Чтобы найти давление, надо воспользоваться формулой
где М —местное число Маха;
р'о — давление торможения потока за скачком ОС. Величина этого
давления принимается одинаковой как для точек 4, F, . .., L, так и для всех
других точек, лежащих вниз по потоку от точки L.
Коэффициент давления вычисляется по (IV-7-12). В области,
расположенной между характеристикой второго семейства CL и криволинейной
стенкой, поток будет вихревым и зависит от условий течения
непосредственно за криволинейной ударной волной, форма которой имеет вид ломаной
линии, выстраиваемой постепенно в ходе решения задачи. Для расчета
потока должен быть использован соответствующий метод характеристик
в сочетании с теорией ударной волны.
Рассмотрим, как рассчитывается течение в треугольнике CDH. Оно
будет определено, если найдены параметры потока в точках С, D и Н.
В точке С параметры газа находятся как параметры непосредственно
за ударной волной. В точке D параметры будут такими, как в точке F,
в частности \xD = \iF, $d = Pf- Поэтому можно найти наклон характеристики
DH к оси х, который будет определяться углом $D + [iD.
Чтобы определить течение в точке Н, лежащей на скачке уплотнения
и характеристике DH, надо совместно рассмотреть уравнения для скачка
и характеристики. Причем уравнение для характеристики должно быть
написано с учетом завихренности течения. В результате решения
соответствующей системы уравнений определяется разность углов
где
По значению Д{Уо можно найти
Acdd = соя оъ = ApD £5 ^2. Cdi (у52)
np0D Атг
затем определить сон и соответствующее число Мя. По значениям Мн и угла
pjf = APd -f Pd определяется угол наклона скачка Qqh в точке Н. Параметры
газа в этой точке можно уточнить, если повторить вычисления, имея новое
значение роя» соответствующее параметрам Мн и 0с н»
Теперь можно найти параметры в точке /, лежащей на пересечении
двух характеристик HJ и EJ соответственно второго и первого семейств.
С этой целью используем уравнения для характеристик, учитывающие эффект
завихренности течения. В результате их совместного решения получаем
(V-5-3)
268 Глава V
где
_ sin2 \xH cos \iH _ sin2 цЕ cos \лЕ
H~ со8фя-М ' Е~ cos(PE + |iE) '
Ро = Рон — Рое\
Аи, = Я/ sin [iH -f- ВС sin \iE.
Этому значению Др# соответствует разность
Да,л = Ш/-Шв = Аря + ^МСл. (V-5-4)
Таким образом, для точки / могут быть вычислены углы р/? coj, |ij
и число Mj.
Аналогично определяются параметры газа в других точках
рассматриваемой области, лежащих на криволинейном скачке или в узлах
сопряженных характеристик.
Последним элементом расчета является определение параметров
вихревого потока в точках, расположенных на контуре. Рассмотрим для примера
точку S. Так как она лежит на контуре и одновременно на характеристике
второго семейства PS, то можно применить уравнение для этой характеристики
Ло)Р = cos - соР = - ДРр + Ц£ ^-, (V-5-5)
где
An = PS sin [ip.
Входящая в это уравнение величина Лрр равна разности ps — Pp> в
которой угол ps известен по условию. Вычислив АсоР, находим в точке S
значения cos, fis, Ms.
Составной частью расчетов является определение координат точек,
расположенных в узлах сетки характеристик, на скачке уплотнения или
на контуре.
Рассмотрим для примера точку пересечения / двух сопряженных
характеристик HJ и EJ. Ее координаты г/j, Xj определяются в результате решения
уравнений
*//-^=(^-^)tg(Ps + M; |
В качестве иллюстрации рассчитаем координаты точек Н и S. Первая
из них расположена на скачке и характеристике первого семейства. Поэтому
ее координаты уН1 хн определяются решением уравнений
ун—Ус = {хн—*с) tg еся;
Ун — Уо=(хн — xD)tg(fiD+iiD).
Вторая точка S расположена одновременно на контуре и характеристике
второго семейства PS. Поэтому для определения ее координат ys, xs
применяем уравнения
1
). J ( " " )
У8 = ПХв); \
-Ур = {xs ~хр) tg (РР -11Р). I
Аналогично определяются координаты других точек.
Рассмотренный метод расчета обтекания может быть использован и в том
случае, когда профиль расположен под углом атаки. Если величина угла
атаки такова, что угол между касательными к контуру у острия и векто-
Расчет аэродинамических коэффициентов 269
ром Foo меньше 180°, то расчет надо вести с учетом образования ударной
волны снизу и сверху профиля, как это предполагалось при изложении
схемы расчета.
Если угол наклона одной из касательных к вектору F<x> равен или
больше 180°, то на соответствующей стороне скачок не образуется, и поток
надо рассчитывать по теории Прандтля—-Майера, т. е. по формулам простой
волны.
Указанный метод расчета позволяет непосредственно найти
распределение чисел М по профилю. По значению М можно найти давление, а затем
подсчитать, пользуясь формулами (1-3-20), (1-4-16) и (1-5-12),
аэродинамические коэффициенты.
Стреловидное крыло. Для приближенного определения
аэродинамических характеристик крыла со стреловидной передней кромкой можно
воспользоваться «методом полос», согласно которому поверхность стреловидного
крыла представляется в виде
совокупности полос малой
ширины, ориентированных по
направлению вектора
скорости набегающего потока
(рис. V-5-2). Основное
предположение состоит в том, что
для каждой такой полосы
сверхзвуковое течение
рассматривается двухмерным и взаи- Рис. V-5-2. Схема расчета сверхзвукового обтека-
модействие между полосами ния профиля по методу полос:
отсутствует. Поэтому течение i — полосы; 2 — местные профили
может рассчитываться, в
частности, по методу характеристик для двухмерных потоков. Хорошие
результаты по методу полос получаются для больших скоростей, однако, для
приближенной оценки этот метод можно использовать и при небольших
сверхзвуковых скоростях.
Если профиль тонкий, а числа ML невелики, то местный поток может
быть рассчитан по линеаризованной теории.
Суммированием по размаху аэродинамических характеристик для каждой
полосы можно оценить величину аэродинамической силы, момента или
соответствующего коэффициента. С этой целью следует применить формулы
{1-3-28), (1-4-22) и (1-5-16).
Аэродинамические
характеристики при очень больших
(гиперзвуковых) скоростях
Применение метода Ньютона. В основе метода Ньютона,
использующегося для приближенного определения аэродинамических характеристик
профилей при гиперзвуковых скоростях, лежит расчетная зависимость (JV-7-2).
Входящая в нее величина р*, представляющая собой коэффициент давления
на соответствующей стороне в передней заостренной точке профиля,
вычисляется по точной теории обтекания пластины. Угол между направлением
нормали к профилю и вектором Foo равен г]*. В произвольной точке профиля,
где коэффициент давления р, этот угол равен г].
Косинусы углов г]*, т] определяются из уравнения (IV-7-4) в результате
вычисления отношения VnOolVoo — cost], в котором значения cosax и cosa^
находятся по формулам (IV-7-3). Так как dyldx = tg$, где Р —угол между
.касательной к профилю и хордой, а dyldz = 0, то cosax = sin |3, cosау = — cos (i.
270
Глава V
Следовательно,
■у
cos т] = ™°° = cos a sin р — sin a cos р = sin (р — а).
' оо
В носовой точке, где Р = р0,
cos т)* = cos a sin р0 — sin а cos р0 = sin (Po — а) •
Таким образом, (IV-7-2) можно написать в виде
— —* (cos a sin р— sin a cos Р)2 —^ sin2(P —а)
"^ sin2(P0 —а)
^
(V-5-9)
(V-5-9')
(V-5-10)
^ ^ (cos a sin Po — sin а cos p0)2
Эта формула применима для положительного наклона местной площадки,
т. е. для тех случаев, когда сами значения р имеют положительный знак,
причем предельное значение р = 0. В точках контура, где реализуется это
значение, должно выполняться условие сс = р, из которого можно найти
координаты точек, являющихся границами «затененной зоны» (рис. V-5-3).
Соответственно для верхней и нижней
частей профиля уравнения для
определения этих координат имеют вид
Рис. V-5-3. Границы «затененной»
зоны на профиле (1 — затененная
зона)
уравнение контура ув = ув(х),
В точках, которые лежат в «затенен-
ной зоне», следует принимать в
соответствии с теорией Ньютона коэффициент р — 0.
Распределение давления находится
отдельно на верхней стороне профиля, где
и на нижней стороне, где ун = Ун(х)~
Соответствующие формулы для коэффициента давления имеют вид
- _-„ sin2(PB-a) . " -» sin2(PH-g)
Рв ~ Рв sin2 (Ров - а) ' Ри ~ Рн sin2 (рОн - а) '
(V-5-12)
Коэффициент р* определяется из теории косого скачка уплотнения
в общем случае для произвольных значений углов рОв> Рон- В соответствии
с этим формулы пригодны как для тонких, так и для толстых профилей,
обтекаемых потоками с очень большими Моо при произвольных а. В том
случае, если профили тонкие и углы атаки малы, формулы (V-5-12)
упрощаются:
Применяя формулу для рн> следует иметь в виду, что угол рн
вычисляется по уравнению контура г/н = Уя (#) в предположении, что координаты г/н,
как и г/в, являются по знаку положительными. Следовательно, углы
рн = (dy/dx)H в начале профиля по знаку положительные, а у задней кромки
могут принимать отрицательные значения.
Из теории косого скачка уплотнения для коэффициента давления р*
имеем
где для верхней стороны вов = рОв — а? Для нижней-
дельном случае при Моо©о —-> °°
' (V-5"13)
©он = Рон —«. В пре-
(V-5-14)
Расчет аэродинамических коэффициентов
271
Так называемой чистой ньютоновской теории соответствует значение
к = 1, при котором
(V-5-15)
-а)2. J
По распределению давления можно вычислить аэродинамические
коэффициенты. Коэффициент
подъемной силы
r, (V-5-16) SL
где # = у, или, учитывая, что в
«затененной зоне» р = 0, можно
написать
Cy=\P*dx—\^ pBdx, (V-5-16') Рис. V-5-4. Профиль с параболическим
о о туром
кон-
где хн, хв — безразмерные координаты точек на границе «затененной зоны»
_ __ соответственно на нижней и верхней сторонах профиля;
Рн, Рв — коэффициенты давления, вычисляемые по формулам (V-5-12)
и (V-5-12'). V '
Коэффициент волнового сопротивления
1
сх = I (- Рн@н + Рв©в) dx. (V-5-17)
о
После подстановки значений 0н = рн — а и 6В = |3В — а найдем
^н __ ^в
сх = асу — ^ рнрн dx + ^ рврв йж*. (V-5-17')
о о
Коэффициент момента относительно передней кромки
1
mz= — \ (рн~-р
(V-5-18)
или
о о
В качестве примера рассмотрим расчет аэродинамических характеристик
симметричного профиля, контур которого образован параболической кривой
второго порядка у = 4ж(1 —ж), где ~y = ylym, ~х=х12хт (рис. V-5-4).
Уравнения контуров соответственно на нижней и верхней сторонах
= 2сх(1~х),
где
с = 2ут1Ь = 2ут/2хт.
Определяем углы рн и рв:
272
Глава V
Координаты точек на границе «затененных зон» находим из условий
(У OJ(\ оГ" \. п О7 (\ 9^Г \
\Jj LuKs I J. ZJ.X-jj ) , LA/ Ci\s II /LiUs-ft I ,
из которых видно, что
хк = ^- = ^(а + 2с); хв = -± = -=-(2с — а).
Осуществляя интегрирование в (V-5-16') и (V-5-17') при условии, что
сс<<2с, а р%, ръ определяются по (V-5-14), получаем выражения для
коэффициентов подъемной силы и
сопротивления:
±t-); (V-5-19)
где
(V-5-20)
(V-5-21)
ю
Рис. V-5-5. Поляры для пластинки и двух
тонких профилей
вии с этим для коэффициентов
Аналогично по (V-5-18)
определяется коэффициент момента.
Формулы (V-5-19) и (V-5-20)
недействительны для случая
а>2с, т. е. когда углы атаки
оказываются равными или
большими угла наклона профиля у
передней кромки. В этом случае
вся верхняя сторона будет
расположена в «затененной зоне» и,
следовательно, пределы
интегрирования #н = 1, ,гв = 0. В соответст-
подъемной силы и сопротивления получим
4 ~оЛ (V-5-22)
схв = р* (4ас2 + а3). (V-5-23)
Таким же путем можно подсчитать аэродинамические коэффициенты
для различных профилей,
если задана их форма.
Как указывалось,
«чистой» теории Ньютона
соответствует к—Л и,
следовательно, значение р* = 2. Для
этого значения на рис. V-5-5
и V-5-6 показаны поляры
профилей, соответствующие
формулам (V-5-19) и (V-5-20).
Анализ кривых показывает, в
частности, что треугольный
профиль по своему
аэродинамическому качеству имеет
10
20
60
Рис. V-5-6. Поляры для профилей крыла, натк-
денные при помощи формулы Ньютона
преимущество перед ромбовидным при достаточно больших углах атаки.
Метод, использующий теорию скачков уплотнения и течений
разрежения. Для расчета давления по этому методу следует применить формулу
Расчет аэродинамических коэффициентов 273
(IV-7-16), в которой параметры с индексом «2» и функция ср имеют (при
условии, что крыло тонкое, а числа М<х> очень велики) следующий вид:
Р2 _ /fc-l
2k К* fc~M ( fc-1 I11Г-»Л"1/2-
Aj 1+ Л JJ
1Г-»Л"1/2-
Л° JJ '
2ft
JcMlo
где Zi^MooQo-
После преобразований формулу (IV-7-16) можно привести к виду
2k
'-■иг М1-'('-£)]"-•}• (V-5-24»
где
fif <v-5-25>
я- <v-5-2e>
Если угол атаки достаточно велик, то скачок у верхней поверхности
профиля не образуется и распределение давления можно найти по формуле
простой волны
2fe
где угол в отсчитывается от направления вектора Foo.
2
При |Моо6|<-7—г коэффициент давления принимается равным нулю.
/с —• 1
При расчете по (V-5-24) следует иметь в виду, что она применима,
когда возмущения, отраженные от точки С ударной волны, не достигают
контура. Если же поверхность обтекаемого профиля искривлена, то
возмущения, отраженные от ударной волны, вообще говоря, следует учитывать
при определении давления. Однако, как показывают исследования,
интенсивность этих возмущений, даже при больших сверхзвуковых скоростях,
невелика.
Формулой (V-5-24) можно пользоваться с погрешностью менее 10%
при Моо>3 и 0< 25°. Ее точность повышается при к, близких к единице
(см. рис. V-5-12).
Влияние физико-химических превращений. Ранее рассмотрен метод
расчета обтекания применительно к идеальному газу. При гиперзвуковых
скоростях, когда свойства газа отличаются от свойств идеального газа,
возмущенное течение можно определить по методу характеристик,
учитывающему влияние равновесных химических реакций [уравнения (IV-1-46) —
(IV-1-50)].
Для упрощения задачи вместо течения, находящегося в
термодинамическом равновесии, можно рассмотреть «замороженное» течение, в котором
газ имеет тот же равновесный состав, что и в некоторой определенной точке
18-114
274 Глава V
или на некотором участке за ударной волной. Такое течение будет
соответствовать большим временам химических реакций по сравнению с
характерным временем перемещения частиц.
Для «замороженного» состояния диссоциированного газа, который
первоначально состоял из двухатомных молекул, действительно уравнение
p = p(l + a)RT=:pRfT, где Rf = R (1 + а) — газовая постоянная для
«замороженного» состояния. Степень диссоциации а определяется для
равновесных условий непосредственно за ударной волной и принимается постоянной
для всего течения. «Замороженный» газ будет характеризовать наряду
с модифицированной газовой постоянной Rf также эффективный показатель
изэнтропы kf = (cp/cv)f.
Для «замороженного» состояния, при котором скорости любых
химических реакций очень малы и колебательные уровни энергии не успевают
возбуждаться из-за большого времени релаксации, показатель изэнтропы
kf = (7 + 3a)/(5 + a). Второе «замороженное» состояние характеризуется
временем релаксации для химической рекомбинации, значительно большим,
чем время релаксации для колебательных степеней свободы, которые за
ударной волной полностью возбуждены. Для этого состояния kf =
= (9 + а)/(7 — а). Отличие указанных двух видов «замороженных» состояний
можно обнаружить, если рассмотреть случай сс = О. Тогда для первого
состояния «замороженный» газ имеет /^ = 7/5, для второго — с полностью
возбужденными колебательными уровнями — kf = 9/7.
Расчет «замороженного» возмущенного течения около профиля можно
вести по j методу характеристик при помощи соотношения (IV-1-17) или
(IV-1-18), если использовать эффективное значение kf. Для нахождения
этого значения следует в том случае, когда вид «замороженного» состояния
известен, определить за ударной волной равновесную степень диссоциации а.
Для установления вида «замороженного» течения необходимо знать
соответствующие времена релаксации для газа.
Решение для условий термодинамического равновесия. В работе [18]
рассмотрен метод решения задачи о течении равновесно диссоциирующего
газа около выпуклой поверхности (см. рис. IV-1-3), основанный на
использовании диаграмм термодинамических функций воздуха при высоких
температурах [13]. Это течение описывается дифференциальным уравнением
сф =dVr
Где уг — радиальная составляющая скорости, совпадающая по направлению
с лучом, проведенным из вершины выпуклого угла;
параметры F = cjVl + 2с2; А = 2 (i0 — с0).
Коэффициенты сп определяются из условия изэнтропичности течения,
имеющего вид ^ = с0 + с4а + с2а2, при помощи таблиц или диаграмм i — a
(энтальпия — скорость звука) для некоторого интервала изменения
энтальпии. В результате интегрирования дифференциального уравнения получим
зависимость между углом поворота и параметрами газа с учетом
диссоциации.
Для заданных начальных условий течения эти параметры, как и в
случае постоянных теплоемкостей, зависят от полного угла поворота со = сОоо +
+ 6, где сооо — начальный угол поворота, отсчитываемый от направления
вектора скорости, соответствующего М = 1.
В работе [18] приведены таблицы углов (Ооо, рассчитанных для
различных значений энтропии S и энтальпии торможения i0 = ioo + 0,5Vlo.
Прибавив к значению сооо заданный угол поворота потока Р и определив а> =
=т(Ооо + Р> можно по тем же таблицам найти местные параметры газа
Расчет аэродинамических коэффициентов
275
У ^
х
(i, F, a, M). Соответствующие давление и температура определяются при
помощи таблиц или графиков термодинамических функций воздуха по
известным значениям i и S.
В качестве примера [18] вычислим параметры г воздушного потока
(с начальными условиями Foo = 2500 м/сек; £=1,4'104 м2/сек2-ерад; ioo =
= 28,87 -106 м21сек2) при повороте его на угол р = 20°. Энтальпия
торможения i0 = 28,87 • 106 + 0,5 - 25002 = 31,995 • 106 мЧсек2. По табл. [18] находим
для этого значения i0 и заданной энтропии 5=1,4-104 ж21сек2-град угол
0)00 = 4,19° и подсчитываем со = 4,19°+ 20° = 24,19°. По этому углу из той
же таблицы находим возмущенные параметры: F = 3472 м/сек; а = 1955 м/сек;
М = 1,776; t = 25,973 • 106 м21сек2. Для нахождения распределения
параметров диссоциирующего газа по выпуклой поверхности заостренного
профиля следует поступить
следующим образом. Вначале
определяются параметры диссоциирующего
газа непосредственно за скачком
на носке профиля. Эти параметры
рассматриваются в качестве
начальных при решении задачи о
повороте потока. Зная, в частности,
начальные энтальпию ic и
скорость звука ас, можно по
диаграмме i — а [13] найти энтропию S Рис. V-5-7. Профиль произвольной формы
и с учетом полной энтальпии с «затененной» зоной 1
iQ — ioo + O.bVlo определить по
таблице [18] начальный угол поворота сооо. Задавшись местным углом р>
наклона касательной к контуру профиля, можно найти угол со — сооо + Р*
а затем, пользуясь таблицей [18], определить в этой точке параметры газа.
Метод «касательных поверхностей». Для заостренного профиля
произвольной формы (рис. V-5-7) коэффициент давления может быть вычислен
при помощи метода «касательных поверхностей». Этот метод состоит в томг
что давление в некоторой точке профиля принимается таким, как на
плоской пластинке, наклоненной к направлению скорости набегающего потока
под углом, равным углу между касательной к контуру в данной точке
и вектором Foo.
Исходными выражениями для расчета являются формулы для плоской
пластинки. Если угол атаки равен а, то на нижней стороне пластинки
коэффициент давления в соответствии с (V-5-13), в которой принято 0о = а^
будет
(V-5-28)
Для верхней стороны можно использовать (V-5-27) с заменой в ней 9 на ос.
Практически такие же результаты получаются по выражению [6]
Эти формулы дают хорошие результаты, когда параметр Мооос>0,5.
Обозначим местный угол атаки для касательной плоскости через ©. Тогда
при положительном угле 0 коэффициент давления в соответствующей точка
(V-5-30y
276 Глава V
при отрицательном угле
Местный угол атаки
в = г/н — ос (на нижней стороне);
в = г/в — а (на верхней стороне),
причем
y'H = Jl!L (на нижней стороне),
y'B = -j^- (на верхней стороне),
a yH = fR (х) и г/в = /в (ж) — уравнения соответственно нижнего и верхнего
контуров.
В предельном случае при Моо —■> оо
[ (V-5-32)
р = и (6 < 0). j
По известному коэффициенту давления можно найти другие
аэродинамические коэффициенты.
При малых углах атаки коэффициент подъемной силы вычисляется
по (V-5-16).
Эту формулу можно представить в виде
су = Су оо + Асу, (V-5-33)
где
1
су оо — V (рн оо — рв оо) dx — (V-5-34)
о
коэффициент подъемной силы профиля при Моо—>оо, а добавочный член
1
Асу — К (Дрн — Арв) dx (V-5-35)
о
учитывает влияние числа Моо. Коэффициенты давления соответственно
равны
роо = (к + 1)в2 (0>О); ]
_ V ; V ' (V-5-36)
Роо = 0 (6<0), J
а величина Ар определяется выражениями
(V-5-37)
Формулу (V-5-18) для коэффициента момента относительно передней
кромки можно представить в виде
z, (V-5-38)
Расчет аэродинамических коэффициентов
277
где
т,= —
— Рвоо) хdx;
(V-5-39)
(V-5-40)
Коэффициент лобового сопротивления профиля с местными углами
атаки вн и вв на нижней и верхней сторонах определяется по (V-5-17').
Так как
i
Amz — — \ (Арн — А/?в)
то
где
сх в — \сх в)оо
в)оо = су ооа — \ (рн ооу'н —
нг/н — Арвг/;) dx + Acya.
(V-5-43)
Рис. V-5-8. Клиновидный профиль
Рассмотрим в качестве примера клиновидный профиль (рис. V-5-8).
Местные углы атаки соответственно на нижней и верхней сторонах следующие:
где с = с/Ь.
Если углы атаки а < с/2, то
где
причем значению Ki соответствует величина 84 = вн и значению К2 — в2 = 9В.
В соответствии с полученными величинами
К2); (V-5-44)
i—if2); (V-5-45)
МооС2
2МооС2
Если а>с/2, то
Moo
M
f-,
(V-5-46)
(V-5-47)
278
Глава V
где
(V-5-48)
к k+i J" i/l I Г 4
В частном случае тонкой пластинки надо принять с = 0. В
соответствии с этим
(V-5-49)
=]'•
В предельном случае при
оо
(V-5-50)
(V-5-49')
(V-5-50')
Профиль произвольной формы. Пользуясь изложенным методом,
можно рассчитать аэродинамические коэффициенты для профиля
произвольной формы. При этом должны быть известны уравнения для нижнего
и верхнего контуров, т. е. функции
2SL
280
200
120
40
V
у
У
^~
1
Г <^
У
оо
1200
2000
Рис. V-5-9. Поляры для клиновидного
профиля
т. е.
!/нМ иув(а;).
Расчеты показывают, что, подобно
клиновидному профилю,
коэффициенты подъемной силы (момента) и
волнового сопротивления профиля
произвольной формы, отнесенные
соответственно к значениям с2 и с3, являются
функциями отношения а/с.
Соответствующие формулы для
трех типов профилей приведены в
табл. V-5-1 [6]. Анализ этих формул
показывает, что поляра профиля,
выражаемая зависимостью су/с2 = f (cx в/с3),
является слабой функцией отношения
а/с. Поэтому для приближенного
определения величины су/с2 как функции
сх в/с3, в случае какого-либо
произвольного профиля, можно
пользоваться кривыми, в частности для
клиновидного профиля (рис. V-5-9).
По данным табл. V-5-1 можно
определить коэффициент центра давления
(V-5-51)
хц. д
тг
На рис. V-5-10 приведены кривые, характеризующие изменение
коэффициента центра давления для трех профилей. Центр давления для плоской
пластинки находится на половине хорды пластинки, следовательно, сц. д. = 1/2.
Для расчета качества следует воспользоваться равенством
Су оо
сх в
СХ оо
(V-5-52)
Аэродинамические коэффициенты нрофиля при очень больших числах Мо
Таблица V-6-1
g
№
п/п
Тип профиля
Коэффициент подъемной силы
Vе2 ^ сг?«>/с2 +' Лсу/с2
а/1 У' I
а/11/' | > 1
ДС
а/|у'|
Параметр М001в|,
определяющий
коэффициент Кп
1
ML с2
(а —
-=- X
X
X (2КХ+К2-К3)
X
Ki
Моо а
(а—2с)
(а + 2с)
1 \2
! 4)
Кг
Mc
(-i)
Продолжение табл. V-5-1
№
п/п
1
2
3
Тип профиля
См. тип профиля из п. 1, стр. 279
См. тип профиля из п. 2, стр. 279
См. тип профиля из п. 3, стр. 279
Коэффициент сопротивления
(СХВ>оо/«3
а/| у' |«: 1
(fc+l)X
-12^ + 8)
С '
(*+1)х
се/1 У1 > i
(А+1)уХ
с3
к(к-\-1)Х
АсЛв/с3
a/|i/'|^l
М^С2 1 С
-T*.(f-»)]
1 х
■«['•(f+т)-
-"(т-4)]
а/1 У | > 1
1 х
x[^(f+i) +
+'•(7-0]
4- Г'» -■+
М^,С2 L с
+T^(f+2)+
м^2
+*.(Т-Т)]
Параметр М^ |в|,
определяющий
коэффициент Кп
Ki
Кг
Kt
Кг
Кг
Ki
Кг
Моо(а + е)
Моо(а —с)
МооОС
Моо(а —2с)
Мое, (а + 2с)
Моо(а + у)
Моо (а ^-1
Продолжение табл. V-5-1
п/п
1
2
3
Тип профиля
См. тип профиля из п. 1, стр. 279
См. тип профиля из п. 2, стр. 279
См. тип профиля из п. 3, стр. 279
Коэффициент момента
т /с2 = m _./c2-|-Am /с2
а/|у'|г£ 1
* с
* С 1
с
1
х (-^—-^-+1)
\ С2 С 9
1
а/|,'К.1
1
х(^! + |-^2-
-т*.)
«/|„'|>1
X (•*»■ 4 ^"^ -Ло)
1
схэ
1
- X
Параметр Моо|в|,
определяющий
коэффициент Кп
к,
к2
Кк
Моо (а + с)
Моо (а —с)
Моо (а —2с)
Мое (а + у)
Мое (а~у)
Оо
N
282
Глава V
При очень больших числах Моо эту величину можно оценить по
формуле K = cyJcXoo.
Если ввести обозначения Суоо/с2 = сУоо; (схв)оо/с3 = (сЛВ)оо, то
ЬУоо
e в) о
(V-5-53)
На рис. V-5-11 приведены значения Кс для трех профилей с
прямолинейным контуром.
02
Рис. V-5-10. Коэффициент центра давления профилей
при очень больших числах Моо
Переменные теплоемкости. Рассмотрим обтекание профиля потоком
совершенного газа с очень большими скоростями, когда показатель
изэнтропы за ^'скачком меняется и сохраняет некоторое фиксированное
значение к2<.коо. Коэффициент
давления в некоторой точке тонкого
профиля с углом в >> 0 в
соответствии с методом касательных клинье в
где
Метод касательных к линьев
можно уточнить, если учест ь
влияние кривизны, обусловлив ающей
действие центробежных сил.
Соответствующая формула, получ енная
для очень малых значений 1/р,
Рис. V-5-11. Кривые для расчета аэродинами- имеет вид
ческого качества профилей с прямолинейным _ __ 2w
контуром р — 2®2(1—р)"1 Л-, (V-5-54')
где у— координата точки профиля, отсчитываемая по нормали к
направлению вектора F«>;
R — радиус кривизны профиля.
Расчет аэродинамических коэффициентов
283
Расчет по формуле Буземана. Для вогнутых профилей при к = 1,4
и для выпуклых — при к—>оо более удовлетворительные результаты, чем
метод Ньютона, дает при расчете давления формула Буземана (IV-7-22).
Полагая в этой формуле /(я) = 1, получим для профиля расчетную
зависимость о
Р =
sin*
— -i- \ cos
(V-5-55)
Для тонкого профиля можно применять (IV-7-21), приняв в ней v=l,
'-■к
р
0,08
0,04
ft J
l\
V
2 \
VCO
^—
1 .
\
<=%05
ОЛ
0,8
о
Qfl X
(¥-5-55')
где у — у(х) — уравнение
контура профиля.
На рис. V-5-12 приведены
для сравнения результаты
расчета распределения
давления при помощи формул
Ньютона и Буземана, а также
по методу характеристик.
Видно, что при к = 1,05
формула Буземана дает
результаты, близкие к результатам
по методу характеристик.
Закон подобия при
обтекании профилей.
Исследованиями установлено, что параметрами подобия при обтекании тонких
профилей являются величины К = МооС и а/с. Это, в частности, вытекает из
метода «касательных поверхностей». Общий вид формул подобия для сопро-
тивления и подъемной силы
следующий:
Рис. V-5-12. Распределение давления по профилю
(Моо = оо; 7= 0,1):
1 — по формуле Ньютона; 2 — по формуле Буземана;
3 — по методу, использующему соотношения на скачке
и в простой волне; О — по методу характеристик
■£ = *■, (К, Я . (V-5-56)
с2 V с /
Рис. V-5-13. Зоны влияния при очень
больших числах Моо
При К—>оо отношения схв/с3,
Су/с2 становятся функциями только
одного параметра а/с, что
подтверждается расчетами по методу
Ньютона и формуле Буземана.
Крылья конечного размаха.
Расчет обтекания крыльев
конечного размаха можно вести по
«методу» полос. При очень больших скоростях этот метод дает более
удовлетворительные результаты, чем при умеренных числах Моо.
Это объясняется тем, что при больших скоростях значительно
сужаются зоны влияния боковых кромок, а также зона влияния на крыло
вблизи корневого сечения возмущений, идущих из вершины (рис. V-5-13),
которые оказываются весьма малыми по сравнению с общей площадью крыла.
Для расчета гиперзвукового обтекания профиля (полосы) можно
применить один из изложенных выше методов, а для вычисления суммарных
284
Глава V
аэродинамических коэффициентов крыла заданной формы в плане —
интегрирование вдоль размаха полученных для полосы аэродинамических
характеристик.
При вычислении суммарных характеристик можно воспользоваться
формулами подобия (V-5-56), которые должны рассматриваться как выражения
для местных аэродинамических коэффициентов. В том случае, когда вдоль
размаха относительная толщина профиля не меняется, формулы (V-5-56)
будут давать значения аэродинамических коэффициентов для всего крыла.
§ V-6. Донное
сопротивление. Вязкое
взаимодействие
\
\
\
\
Донное сопротивление. У крыльев с затупленной задней кромкой
к составляющим сопротивления, вызванным трением и давлением на переднюю
часть, добавляется донное сопротивление. Исследования показывают, что
донное давление, определяющее донное
сопротивление, существенно зависит от структуры
пограничного слоя на участке между задней
кромкой (точкой отрыва) и точкой прилипания
на осевой линии, в которой сходится
пограничный слой, оторвавшийся от задней кромки.
Чисто турбулентное и ламинарное
течения. Если точка перехода ламинарного
пограничного слоя в турбулентный расположена
выше по течению, чем точка отрыва (донный
срез), то на участке между этой точкой и
точкой прилипания течение будет чисто
турбулентным. Изменение донного давления для
этого случая показано на рис. V-6-1.
Кривая, характеризующая отношение донного
давления за тупым основанием профиля к давлению невозмущенного потока,
определяет донное давление для профилей с относительно тонкими
турбулентными слоями в соответствии с формулой рдоп(роо=и (Moo). В более общем случае
формула должна отражать зависимость донного давления также от толщины
пограничного слоя. Имеющиеся
экспериментальные данные
указывают на более общую
зависимость
Рдон ,
0,5
0,4
0,3
ffl 1,5 2,0 2,5 3,0 Мс
Рис. V-6-1. Изменение донного
давления за профилем с
относительно тонким пограничным слоем
Сдон
задней
где сдон — толщина
кромки.
Вводя число Рейнольдса,
получим
Рдон , /м Ъ
Роо
.Re1'5
)■
О
(V-6-2)
Рис. V-6-2. Влияние числа Рейнольдса на донное
давление при турбулентном пограничном слое
где Ъ — хорда профиля.
Аналогичную зависимость можно получить и для чисто ламинарного
пограничного слоя, когда точка перехода расположена ниже по потоку, чем
Расчет аэродинамических коэффициентов
285
точка прилипания:
Рдоя
Роо
"ДОН
Re1/2
(V-6-3)
Экспериментальные кривые, соответствующие формуле (V-6-1),
приведены на рис. V-6-2.
Смешанное течение. Смешанный пограничный слой имеет место в том
случае, когда точка перехода лежит между точкой отрыва и точкой
прилипания. При таком режиме течения изучение донного давления представляет
особые трудности, что связано прежде всего с неясностью в определении
W
0,8
0,6
0,2
/
— /
/
■
о
от
0,08
0J6
Рис. V-6-3. Изменение донного давления за профилем
при смешанном пограничном слое
точки перехода. Экспериментальное исследование донного давления при
наличии смешанного пограничного слоя велось путем продувок моделей
крыльев в аэродинамических трубах. Результаты измерений позволяют
сделать вывод, что относительную величину донного давления можно
представить при помощи (V-6-1), и изобразить графически в виде семейства
кривых, как это показано на рис. V-6-3. Донное давление за профилем при
увеличении параметра b/(cAOnRei/2) возрастает. При малых числах Рейнольдса
(больших значениях этого параметра) между точками отрыва и прилипания
практически имеет место ламинарный пограничный слой, и донное давление
оказывается большим, что характерно для чисто ламинарного течения.
На величину донного давления оказывают влияние и другие параметры,
в частности, угол атаки, нагрев или охлаждение пограничного слоя.
Вязкое взаимодействие. Рассмотрим изменение давления на
поверхности заостренного профиля, обусловленное взаимодействием гиперзвукового
пограничного слоя с невязким потоком.
Слабое взаимодействие. При слабом взаимодействии давление
изменяется по сравнению с первоначальными условиями на небольшую величину.
Слабому взаимодействию соответствуют [см. формулу (IV-10-2)] значения
К*<1 или d8*/<£z<P при произвольном К = Моо р. На тонких клиньях
такие взаимодействия появляются при малых углах атаки и больших числах
Re и М или при умеренных сверхзвуковых скоростях и малых числах Re.
286 Глава V
На толстых клиньях слабое взаимодействие имеет место при больших углах
атаки на той стороне клина, где происходит сжатие.
Используя теорию косого скачка уплотнения и метод касательных клиньев,
можно определить для клина с ламинарным пограничным слоем и углом
наклона стенки р* —13 -f- db*ldx следующее соотношение для индуцированного
давления [59]:
^ *i*+i>+...., (V-6-4)
где
g (^)2j2di. (v-6-5)
Величина %н представляет собой гиперзвуковой параметр взаимодействия,
определяемый соотношением
Хн = М*<£/2Ве^/2. (V-6-6)
Индекс «н» относится к начальным условиям в однородном течении
невязкого газа около клина. Остальные параметры следующие:
(V-6-7)
(V-0-У)
Коэффициенты А ж В зависят от числа Прандтля. Для Рг = 1 значения
4 = 0,865; 5-0,166; для Рг = 0,725 коэффициенты А = 0,968; Б = 0,145.
Для теплоизолированной стенки можно принять
l ^ dn=(k-l)D, (V-6-10)
где для Рг=1 величина D== 0,599, а для Рг = 0,725 значение D = 0,556.
Для очень холодной стенки Тст/Тн < 1 и приближенно
dH=(k-l)B. (V-6-11)
В обоих частных случаях индуцированное давление определяется только
параметрами К и %н. Если ввести параметр взаимодействия
~ MV/2Re~1/2
поределяемый по условиям в невозмущенном течении, то отношение %н/% будет
зависеть только от /£ = Моо-|3. Для К > 1 имеем
к(к — 1) '
Так как fiH~ Mip2 для [л — Г, то (Моо/Мн) (х~н/#) — х/#2.
Следовательно, по порядку величины изменение давления
£-1~*н-£г. (V-6-12)
Расчет аэродинамических коэффициентов
287
Для плоской пластинки с нулевым углом атаки К = 0, Ji = J2 = l.
Экспериментальные данные, полученные для теплоизолированной пластинки,
подтверждают результаты, получаемые по (V-6-4) для к =1,4, Рг = 0,725
для отношения давлений
-£- = 1 + 0,31х + 0,05?. (V-6-13)
Роо
Хорошее соответствие между экспериментом и формулой слабого
взаимодействия наблюдается до значений гиперзвукового параметра % = 3 -=- 4.
Исследования показывают, что местный тепловой поток и равновесная
температура стенки очень мало зависят от индуцированного давления.
Местный коэффициент трения меняется более существенно в соответствии
с зависимостью
(V-6-14)
« ("-■£)*■
где cfxi Cfx— местные коэффициенты трения соответственно при наличии
индуцированного давления и без него; производная
" "* — . (V-6-15)
dx н Мн
Сильное взаимодействие. Область сильного взаимодействия
характеризуется тем, что <J8*/dx>$ и К* > 1. Эта область образуется при обтекании
пластинки под небольшим углом атаки при условии, что числа Маха достаточно
велики, а местные числа Рейнольдса небольшие.
Для анализа сильного взаимодействия можно использовать метод
касательных клиньев, который приводит к следующей зависимости для
индуцированного давления:
8* К*~\ (V-6-16)
где K* =
(f )
Выражение для р/р^ можно представить в виде
(V-6-17)
рд р
го слоя. Для пластинки К =
Здесь р0 зависит от степени охлаждения стенки gCT = iCT/i08- Для А = 1,4
и Рг=1 значения р0 приведены в табл. V-6-1. Коэффициенты ри р2, Рз
определяются экспериментально или из теории гиперзвукового погранично-
"1ооВ = 0и
Таблица V-6-1
(V-6-18)
J/OO
Для теплоизолированной стенки
расчеты при Рг = 1, А: = 1,4 дают
р2 = 0,759. Следовательно,
-2- = 0,514х + 0,759. (V-6-18')
Роо
Эта формула согласуется с
экспериментальными данными для значе-
*» ~~~ лугЗ 1/2 т~% —*1/2 о с^ • 7
нии % = М.ооСоо Иехоо =о,э—/.
Для оценки изменения коэффициентов трения и теплопередачи при
сильном взаимодействии можно воспользоваться соотношениями
-1/2. а* — оТ,1/2_ Q
Параметры
0
0
0
1
г
СТ
,2
,6
,0
для
расчета вязкого
взаимодействия
0
0
0
0
с
,208
,279
,412
,549
S
0,0788
0,105
0,155
0,187
0
0
0
0
Vo
,149
,232
,377
,514
TCT) '
(V-6-19)
Коэффициенты ens для к = 1,4; Рг = 1 приводятся в табл. V-6-1.
Глава V
§ V-7. Аэродинамика
затупленных крыльев при
больших сверхзвуковых
скоростях
Обтекание затупленной
передней кромки профиля
Отход и форма ударной волны. Рассмотрим обтекание передней части
профиля, контур которой имеет произвольную криволинейную форму
(рис. V-7-1).
Обтекание затупленной кромки характеризуется образованием отошедшей
криволинейной ударной волны. Как доказывают исследования, расстояние s0
от ударной волны до критической точки зависит от радиуса кривизны волны
на оси Rc0 и числа Моо. Отношение so/Rco определяется выражением
к — 1
1 + 2.
— 1
(V-7-1)
В пределе при Моо—-> сю и к = 1,4 отношение so/Rco = 0,1586. При очень
больших скоростях необходимо учитывать влияние диссоциации и ионизации
газа в ударном слое. В этом случае вместо
(V-7-1) следует пользоваться
выражением [59]:
М
*со
2р2
х
Рис. V-7-1. Затупленная передняя
кромка профиля в сверхзвуковом потоке
2р2 J
(V-7-2)
которое получено из условия, что
ударная волна концентрична поверхности
криволинейного носка. Отношение р2 =
^Рг/Роо следует рассчитывать по
плотности р2 непосредственно за вершиной
ударной волны (за «прямой» ее частью)
с учетом физико-химических
превращений. Формулу (V-7-2) можно
применять только в тех случаях, когда числа
Моо (и, следовательно, отношение р2) достаточно велики. Из формулы видно?
что в пределе при р2—>оо отход становится равным нулю, т. е. ударная
волна вплотную прилегает к
поверхности носка.
Теоретические и
экспериментальные исследования позволяют сделать
вывод о том, что диапазон чисел Моо,
в котором наблюдается зависимость
относительного отхода so/RcO только
от плотности, можно расширить, если
в качестве функции рассмотреть
величину sop'Q/Rc0, а за аргумент
принять отношение плотностей р'о = р^/роо,
FLJo
К
— 1
— !■
0/2
0,20
Рис. V-7-2. Параметр, характеризующий
расстояние до ударной волны от точки
полного торможения цилиндра
где pQ —плотность в критической точке, которая при больших скоростях
мало отличается от плотности р2 непосредственно за ударной волной.
Расчет аэродинамических коэффициентов
289
На рис. V-7-2 показано изменение величины s0p'0/Rco в зависимости
от отношения 1/р^. Кривая, как и формулы (V-7-1) и (V-7-2), позволяет
определить радиус кривизны волны /?со, если предварительно найден отход s0.
Из физических соображений следует, что отход s0 при заданных
условиях набегающего потока зависит от радиуса кривизны RT носка на оси.
На основании теоретических
исследований построена кривая (рис. -^
V-7-3), позволяющая найти отно- т
шение sQ/(2RT) в зависимости от
числа Моо.
Приведенные результаты соот- 2
ветствуют условиям, которые
характеризуются достаточно
большими числами Рейнольдса и, следо- /
вательно, пренебрежимо малым
влиянием вязкости газа на течение
между волной и стенкой. Это имеет
место в том случае, когда газ в
ударном слое не очень разрежен
и остается достаточно плотным.
Распределение давления и
скорости. С известным
приближением расчет распределения давления по криволинейному затупленному носку
можно вести по усовершенствованной формуле Ньютона (IV-7-3).
Для плоского контура формула Ньютона дает менее
удовлетворительные результаты, чем для пространственного тела; в частности,
распределение давления на цилиндре, обтекаемом в поперечном направлении, хуже
согласуется с экспериментальными данными, чем для сферического носка.
В случае очень больших скоростей набегающего потока при расчете
возмущенного течения можно исходить из предположения постоянной
плотности в ударном слое. В соответ-
ствии с этим [59] коэффициент дав-
ления вблизи критической точки ци-
линдра можно выразить соотношением
1
I
\
\
i
Мех:
*
Рис. V-7-3. Относительное расстояние от
скачка до цилиндра
'0,8
\
ч
\
\
\
г
80
120
шо 9
Рис. V-7-4. Распределение давления около
цилиндра
где р2 = р2/роо определяется по
плотности р2 непосредственно за прямой
частью ударной волны.
Приведенная формула,
отображающая плоский двухмерный характер
обтекания цилиндра, пригодна для
значений угла р, мало отличающихся
от ох/2, т. е. для окрестности вблизи точки полного торможения. Что касается
периферийных участков с небольшими углами (3, то некоторое
представление о распределении давления на этих участках дает рис. V-7-4, где
приведены экспериментальные данные для Моо = 2 (на рисунке ф = я/2 —Р).
Пользуясь данными о распределении давления, можно подсчитать
по (VI-3-16) распределение скорости. Если для расчета давления применяется
формула Ньютона (IV-7-3) и имеется в виду линейный закон изменения
скорости, то скорость F4 на цилиндре находится по формуле V4 = VooRTyH,
19-114
290 Глава V
в которой коэффициент К (градиент скорости) подсчитывается по формулам
(VI-3-12) или (VI-3-13).
В данном случае при определении скорости и при расчете давления
не учитывается отличие плоского обтекания от пространственного. Можно
показать, что при очень больших скоростях это отличие невелико, но оно
становится существенным с уменьшением скоростей обтекания.
Аэродинамические коэффициенты. Для заданной формы носка
аэродинамические коэффициенты или соответствующие им силы определяются
в результате интегрирования по контуру.
Практический интерес представляет расчет коэффициента волнового
сопротивления затупленного носка. Пусть длина участка этого носка (вдоль
хорды) равна хК9 и носок является симметричным относительно хорды.
Коэффициент сопротивления, отнесенный к длине всего носка (его хорде),
£ ££*•• <v-7-4>
О
В частном случае, когда контур носка является дугой окружности,
выражение для схв будет
ft cos2JU /V 7
Для контура в виде полуокружности (Р = 0)
cXB = jPo- (V-7-5')
Расчет обтекания профиля с криволинейным затупленным контуром
по ньютоновской теории. Расчет распределения давления для профиля
с затупленным носком с применением формулы Ньютона ведется так же,
как и для профиля с заостренной передней кромкой.
В общем случае у таких профилей могут возникать «затененные зоны»
с нулевым избыточным давлением как на верхней, так и на нижней
сторонах, когда местные участки контура имеют отрицательный наклон к
направлению скорости набегающего потока.
Расчеты несколько упрощаются, когда такие участки отсутствуют
и когда, следовательно, весь контур взаимодействует с частицами газа.
В этом случае всюду на контуре избыточное давление будет положительным.
Для удобства расчетов можно из всего контура условно выделить его
носовую затупленную и периферийную части. Аэродинамический коэффициент
вычисляется как сумма двух составляющих для каждой из этих частей.
Рассмотрим, в частности, выражение для лобового сопротивления
профиля в виде симметричного клина с круглым носком, обтекаемого под
нулевым углом атаки. Если длина носка хк, а всего профиля хп и угол наклона
плоскости клина |3, то коэффициент сопротивления, рассчитанный по длине хи,
cos2 p\ xK sin» ft ( хк\~] /v 7 ftt
Это значение сх в можно принять равным коэффициенту осевой силы,
когда рассматривается обтекание профиля под углом атаки и скоростной
напор вычисляется по выражению 0,5pooFL cos2 p. Осевая сила
_ РооТ^ СЭ32 ft
Яр — схр 2 Хп"
Следовательно, коэффициент осевой силы, отнесенный к скоростному
напору pooFL/2,
сЖр = сявсо8ар. (V-7-7)
Расчет аэродинамических коэффициентов
291
Затупление в виде плоской
пластинки
Схема обтекания и система уравнений [47]. Рассмотрим схему потока
в координатах X, У около передней кромки профиля, представляющего
собой плоскую пластинку шириной 26 (рис. V-7-5). Перед пластинкой
возникает криволинейная волна, расстояние до которой от критической точки
определяется величиной sQ. Составляющие
скорости, отнесенные к Foo, в произвольной точке
линии тока обозначим через VY = Fy/Foo', Vx =
Для расчета невязкого двухмерного течения
около пластинки, характеризующегося
возникновением криволинейной ударной волны,
необходимо воспользоваться системой
газодинамических уравнений, включающей уравнение
неразрывности, уравнения движения в проекциях
на оси У и X и уравнение энтропии.
Решение такой системы в общем случае
представляет весьма сложную задачу.
Упрощение системы может быть достигнуто на основе
модели ньютоновского двухмерного течения,
когда величина 1/р2 = р<х>/р2 равна нулю, а волна
прилегает непосредственно к поверхности
пластинки. Считая скорость обтекания достаточно
большой и течение близким к предельному
случаю ньютоновского, можно рассматривать
величину р = б0 как малый параметр (р = б0
представляет собой отношение плотностей для
прямого скачка уплотнения) и представить.
величины, характеризующие течение, в виде ряда по этому малому
параметру. Разложение основано на определении порядка газодинамических
величин за ударной волной, которое осуществляется при помощи следующих
соотношений:
Рис. V-7-5. Двумерный
плоский сверхзвуковой поток
около затупленного носка:
1 — область внешнего разложения;
2 — область внутреннего разло-
Р2
— Poo = l — 80 — tg26c;
где P2 =
Poo — Poo/poo »^oo J ^2 — &
I- I Л I
(V-7-8)
(V-7-9)
^g2Oc); (V-7-10)
tg6c; (V-7-11)
(V-7-12)
), ioo = ioJ(0,Wlo), а величина
°o =
(V-7-13)
Когда 80-^0 и скачок прилегает к носку, тангенс угла наклона скачка
к вертикальной оси имеет порядок 8(/2, т. е. tgec = (9(8o/2). В соответствии
с этим определяется порядок величин других параметров, а именно:
92
Введем новую координату х = Z6"1/2, сохранив при этом прежнее значение
переменной У, которую для удобства обозначим y = Y. Учитывая порядок
19*
292 Г лава V
величин параметров за скачком, можно для возмущенной области потока,
примыкающей к скачку, выразить величины, характеризующие обтекание
в виде разложений по степеням малого параметра б0:
у)+...; (V-7-14)
Vy = 8l/2v(x, у)+...; (V-7-15)
р - рх = 1 + 80р (х, у) + ...; (V-7-16)
р = б-1 + р(^, »)+..., (V-7-17)
где и, v, р, р — некоторые безразмерные функции переменных х = Хбо"1/2, y — Y.
С учетом вида разложений (V-7-14) — (V-7-17) и новой координаты
x = X8'oi/2 можно получить упрощенную (предельную) форму уравнений
для возмущенного потока. Рассмотрим, в частности, уравнение
неразрывности d(pVx)/dX -\-д (pVY)/dY = 0. После соответствующих подстановок
получим
Сравнивая члены в левой части уравнения, можно заметить, что
первый и третий из них имеют более высокий порядок малости и ими можно
пренебречь. Тогда уравнение примет вид
Заменяя производные их значениями ди/дХ = (ди/дх)8^1/2, dv/dY =
= dv/dy, получим ди/дх + ди/ду = 0. Следовательно, в координатах х, у
уравнение неразрывности преобразовано к виду для несжимаемой жидкости.
Аналогично можно получить упрощенную форму для остальных уравнений
системы. В результате система уравнений будет
*L + V*L = _^L; (V-7-20)
дх ду дх v '
(V-7-21)
дх 1 ду
Уравнение (V-7-19) получено при условии, что в уравнении
vx (dVY/dX) + vY (dVY/dY) = - (i/p) др/dY,
преобразованном к переменным y — Y, x = X8^i/2 с учетом разложений
(V-7-14)— (V-7-17), член др/dY пренебрежимо мал и можно принять
др/ду = О.
Из этого следует, что давление в направлении оси Y = y не меняется.
Первые два уравнения системы позволяют определить поле скоростей. Третье
и четвертое уравнения служат для вычисления давления и поправки
к плотности.
Граничные условия определяются условиями течения непосредственно
за скачком уплотнения и на поверхности носка. Из выражений (V-7-9) —
(V-7-11), (V-7-14) — (V-7-16), а также соотношения (dX/dY)2 = tgSc следует,
Расчет аэродинамических коэффициентов 293
что функции и, v, p должны удовлетворять на ударной волне условиям
; (V"7-22)
p2. (V-7-23)
Как показывают исследования, условие и/и —> 0 на поверхности не может
быть удовлетворено, так как двухмерное течение, описываемое системой
уравнений (V-7-18) — (V-7-21), вблизи этой поверхности не имеет места.
Если говорить точнее, то здесь величины скоростей имеют другие порядки,
чем вблизи ударной волны, хотя порядки величин давления и плотности
остаются одинаковыми во всей области потока между скачком и носком.
Поэтому область течения между криволинейной волной и пластинкой
приходится разбивать на две части — внешнюю и внутреннюю области
разложения (см. рис. V-7-5). Течение во внешней области описывается системой
(V-7-18) — (V-7-21) и условиями (V-7-22) —(V-7-23). Что касается
внутренней области, где должно выполняться условие безотрывности обтекания
м/у—>0, то применительно к ней параметры потока можно представить
в виде следующих разложений:
;,*/)+...; (V-7-24)
2/)+...; (V-7-25)
p-Pco = l + 6oP(J,y) + ...; (V-7-26)
p = p-i + p (x, y) + ..., (V-7-27)
где
# —переменная, соответствующая внутренней области, определяется
равенством # = 6^1/ (X— s0);
и, v, р, р — переменные, аналогичные переменным и, v, p, p во внешней
области разложения.
После подстановки разложений (V-7-24) — (V-7-27) в уравнения
неразрывности, движения и энтропии можно получить
"IT + Ж = °; (V"7"28)
-^- = 0; (V-7-29)
дх v ;
Z-^ + v -^-^-—; (V-7-зо)
дх ОУ ду
~ д(Р-Ъ + ~ д(р-р) = 0> (V-7-31)
дх ду
Из второго уравнения видно, что давление не зависит от переменной
х и зависит только от г/.
Решение этой системы уравнений должно удовлетворять граничным
условиям на стенке
u(o,y)=0; v(o,y) = V6(y), (V-7-32)
где Vq — скорость на стенке, определяемая интегрированием (V-7-30) при
условии, что и = 0, связана с давлением формулой
р6 (у) + -*М = Const. (V-7-33)
294 Глава V
Для заданного у эта величина будет определять давление во всей
внутренней области. Следовательно, др/ду = —2V6 (dV6/dy) и (V-7-30)
превращается в чисто кинематическое соотношение. Решая уравнения (V-7-28)
и (V-7-30), можно найти значения скоростей и(х,у) и v(x,y),
удовлетворяющие граничным условиям на стенке (V-7-32).
Решения уравнений для внешней и внутренней областей,
удовлетворяющие соответственно граничным условиям на скачке и стенке, подчиняют
дополнительно условиям сопряжения на границе между обеими областями,
что позволяет однозначно определить течение в исследуемой области.
Результаты решения уравнений. Не останавливаясь на методе решения
уравнений и на сопряжении полученных решений, приведем лишь основные
результаты, имеющие практическое значение для аэродинамических
расчетов.
Отход и форма ударной волны. Расстояние до ударной волны
в безразмерном виде
50 = ^ = - 1,23б£/2 In 8j/2. (V-7-34)
Уравнение кривой ударной волны можно представить в виде следующей
аппроксимирующей зависимости:
y = l,32*M66JT0i23, (V-7-35)
где y = y/b, х = х/Ь.
Давление и скорость. Расчетная формула для коэффициента
давления
- = .Ре-Poo = 2[i + борб -)h (V7_36)
Функцию рб (у) можно аппроксимировать выражением
у + у)2] • (V-7-37)
Следовательно, коэффициент давления
|j2] (V-7-38)
Расчет скорости на стенке ведется по формуле VyJVoo = b0VQ, в
которой V6 вычисляется по уравнению (V-7-33). Внося в (V-7-33) значение
р6 (у) из (V-7-37), найдем аппроксимирующую зависимость для расчета
скорости
Отсюда определяется градиент скорости в критической точке
1=^-№) =|SO. (V-7-40)
Сопротивление. Интегрированием по поверхности пластинки
определяется ее сопротивление. Используя при этом (V-7-38), можно получить
соотношение для коэффициента сопротивления, отнесенного к размаху
пластинки 26,
1
c*B=i§T= I Pedy = 2(l-0,9560). (V-7-41)
О
Аэродинамический расчет крыла. Методы расчета гиперзвукового
обтекания пластинки при ее поперечном расположении в потоке могут быть
Расчет аэродинамических коэффициентов 295
применены для определения аэродинамических характеристик крыла в
следующих случаях.
С помощью этих методов рассчитывается обтекание передней плоской
затупленной кромки профиля крыла, имеющего близкий к нулю угол атаки.
Обтекание периферийной части профиля может быть определено,
например, по корпускулярной теории Ньютона, а суммарные аэродинамические
характеристики крыла —по «методу полос».
Можно рассмотреть другой случай движения крыла, характеризующийся
углами атаки, близкими к 90°. Этот вид движения может иметь место при
входе летательного аппарата в плотные слои атмосферы с гиперзвуковыми
скоростями, когда крылья используются как тормозные средства,
обеспечивающие максимальное лобовое сопротивление.
Для расчета обтекания крыла используется «метод полос», в
соответствии с которым течение вдоль пластинки (полосы) предполагается плоским.
Поток около крыла аппроксимируется с помощью ряда пластин, каждая
из которых считается установленной перпендикулярно к направлению
скорости набегающего потока. При этом суммарный аэродинамический
коэффициент крыла будет таким, как для изолированной пластинки. В
частности, суммарный коэффициент сопротивления будет равен величине (V-7-41).
При применении «метода полос» следует иметь в виду, что он дает
более удовлетворительные результаты для тех участков крыла, которые
достаточно удалены как от концевой, так и от корневой хорды, и где
течение по своему характеру близко к плоскому.
Суммарные аэродинамические характеристики крыла конечного размаха,
рассчитанные по «методу полос», надо рассматривать как ориентировочные,
требующие проверки и уточнения либо более строгими теоретическими
методами, либо экспериментальным путем.
Профиль с малым затуплением
Как показывают исследования, сопротивление профиля с малым
затуплением при умеренной сверхзвуковой скорости можно получить в
результате суммирования сопротивления затупления и сопротивления остальной
части профиля, вычисленного в соответствии с теорией обтекания
заостренных тел без учета малого влияния на это
сопротивление возмущений, идущих из дозву-
ковой области.
При очень большой сверхзвуковой
скорости это влияние может оказаться значитель-
ным. Для оценки длины L участка профиля, —— .
на котором сказывается влияние малого затуп- V I L
х
р
ления толщиной d, можно воспользоваться
выражением L/d!~p~3, в котором |3 —
характерный угол наклона поверхности. Например,
если (5 = 0,1, то малое затупление
значительно изменяет картину течения и распределе- Рис. V-7-6. Пластинка конечной
ние давления на длине L ~ 1000J. толщины в свеРхзвУК0В0М потоке
Пластинка конечной толщины.
Рассмотрим пластинку малой толщины d, обтекаемую потоком с очень большой
сверхзвуковой скоростью (рис. V-7-6). Исследования проф. Г. Г. Черного [38]
показали, что распределение давления по поверхности пластинки
характеризуется общей зависимостью
d) '
(V-7-4
296
Глава V
где Pi — некоторая функция параметров к, (cxML) 1xld;
Сх __ коэффициент сопротивления затупления.
Уравнение кривой головного скачка уплотнения
.Х = д1 (к, тжт) ' (V-7-43)
где Ri — некоторая функция тех же параметров, которые следует
рассматривать как параметры подобия при гиперзвуковом обтекании
затупленной пластинки.
Формулы (V-7-42) и (V-7-43) хорошо подтверждаются расчетами
по методу характеристик для пластинки с плоским закругленным затупле-
ю
ю"
• + х — клинобидная кромка
о —закругленная кромка
• 5,00
+ 6,86
х 9,50
о 14,0
сх' Расчет п •+
1,326 п9 методу
1,374
ЩО
по методу
характеристик
10'
-4
10
-з
10
-2
10
ri
If
У'
.—■—■
1.0
0.5
1,0
1,8
Рис. V-7-7. Распределение давления на пластинке
с клиновидной (# + X) и закругленной (О)
кромкой. Сопротивление закругленной кромки
2 _
вычислялось по формуле сх = ~~-р0. Сплошная
линия — по формуле (V-7-44)
Рис. V-7-8. Функции %, %и
используемые при расчете обтекания
пластинки конечной толщины и
затупленного клина
нием, а также с клиновидным носком, выбранным таким образом, что
на нем возникает звуковая скорость (рис. V-7-7).
При очень большой скорости полета давление роо мало по сравнению
с давлением за скачком. В этом случае влияние параметра роо и вместе
с ним числа Моо несущественно, и зависимости (V-7-42) и (V-7-43)
принимают более простой вид:
где % и %i — функции, зависящие только от показателя адиабаты.
Значения этих функций изображены сплошными линиями на рис. V-7-8.
Аппроксимирующие зависимости для функций % (к) и %х (к) (пунктирные
кривые на рис. V-7-8) имеют вид
Расчет аэродинамических коэффициентов
297
Величины, определяемые формулами (V-7-44) и (V-7-45), следует
рассматривать как главные члены рядов, получаемых в результате разложения
функций Pi и Rt при условии, что параметр x/(cxMl,d) имеет малые значения.
При расчетах необходимо иметь в виду, что удовлетворительные
результаты по приведенным формулам получаются в тех случаях, когда числа
Рейнольдса, рассчитанные по
толщине пластины, превосходят 2000. 2Р
Тонкий клин с малым затуп- ДК^Х
лением. Для расчета распределения
давления по поверхности
затупленного клина с половиной угла при
вершине рк теория гиперзвуковых
течений дает общую формулу
0,1
0,2 0,3
* мл
Рк х \ ^ /у_7-49) ^ис* V-7-9. Распределение давления на клине
р
с малым затуплением. Пунктирная линия —
клин с острой кромкой
(V-7-48)
Форма ударной волны
характеризуется зависимостью
d-AtgZ^"
В этих выражениях Р2 и R2
представляют собой некоторые
функции параметра 4 tg3^^/^^); cx — коэффициент сопротивления
затупленного носка. Зависимости (V-7-48) и (V-7-49), полученные при условии, что
начальное давление не учитывается, графически показаны на рис. V-7-9
и V-7-10.
Величина 4 tg3 $Kz/(cxd) является параметром подобия при
гиперзвуковом обтекании затупленного клина. При меньших скоростях, когда учиты-
Поберхнот
2
ь мина
1^"
0,2
Рис. V-7-10. Форма головной волны перед клином:
1 — с затуплением; 2 — заостренный клин; з — скачок на
большом удалении от носка, совпадающий по направлению
со скачком перед заостренным клином
вается влияние противодавления, необходимо ввести еще один параметр
МооС (с — относительная толщина клина, равная 2tg|3K), а в общем случае —
и показатель адиабаты к, учитывающий свойства газа.
298
Глава V
Полное сопротивление Хкл клина длиной хк с затупленной передней
кромкой
(V-7-50)
где X — половина сопротивления затупления.
Коэффициент сопротивления клина
сх кл = 2 [1 + Р2 (*)] tg2 pK, (V-7-51)
где t = 4 tg3 pK#K/(cx<i).
График зависимости (V-7-51) при небольших значениях t приведен на
рис. V-7-11. Большим значениям £ соответствует приближенная зависимость
g2 Рк. (V-7-52)
25
20
15
\
\
ч
Клан
щ
с остр
1MKOU
ой
0,1
U2 0? 0,4 А}
Рис. V-7-11. Коэффициент сопротив-
ления затупленного клина
Закон подобия. Изменение
клина характеризуется законом
а при очень большой скорости
Если сопротивление затупленной
поверхности вычисляется как сумма
сопротивлений затупления и заостренного клина,
можно применить зависимость (V-7-52),
заменив в ней 2klt на 211.
Центр давления профиля с
затуплением. Центр давления профиля с
затуплением смещается вперед по сравнению с
положением центра давления для того же
профиля с заостренной кромкой.
Это смещение может быть
значительным. Так, например, для профиля в виде
затупленной пластинки центр давления при
очень большой скорости расположен на рас-
стоянии ^ Длины пластинки от передней
кромки, а не в середине, как у бесконечно
тонкой пластинки.
коэффициента сопротивления затупленного
подобия, общее выражение для которого
Ь, К, К*),
где параметры подобия
/г — м г- К
С3
(V-7-53)
(V-7-54)
(V-7-55)
В (V-7-53), (V-7-54) функции F и .Foo определяются соответственно
параметрами к, К, К* и к, К**. Размер d дается в долях длины клина.
Распределение давления по поверхности клина и координаты точек
головной ударной волны определяются общими соотношениями теории подобия
-±Z— = Ps(K*-1z, к, К); (V-7-56)
(V-7-57)
Расчет аэродинамических коэффициентов 299
которые при очень большой сверхзвуковой скорости имеют вид
^ )-ix,k]; (V-7-58)
)-11
С
Ч, к]. (V-7-59)
Функции Р3, R3 определяются параметрами К*х, к, К, а Лх>,
^(подпараметрами К**х, к; х я у измерены в долях длины клина.
Влияние стреловидности на сопротивление. Возрастание сопротивления,
обусловленное затуплением передней кромки, ослабляется для стреловидных
крыльев. Исследования показывают [55], что сопротивление цилиндрического
стреловидного крыла приближенно можно найти при помощи формулы
Cxx = cxX=0(l-sinx). (V-7-60)
§ V-8. Кольцевые крылья
Несжимаемый поток. Подъемная сила кольцевого крыла при нулевом
угле атаки может быть определена при помощи формулы [6]:
в которой Хкр = 2rlb — удлинение;
ао = сао — dcyjda — параметр, относящийся к профилю крыла.
Подъемная сила вычисляется по выражению У = 2cyqrb, где 2гЬ —
площадь горизонтальной проекции крыла.
Коэффициент индуктивного сопротивления кольцевого крыла
Пусть cxQ — коэффициент сопротивления крыла при су~ О, отнесенный
к площади 2гЪ. Следовательно, лобовое сопротивление
Хо = 2cx0qrb. (V-8-3)
Эту же силу можно определить по выражению
Хо = cxpqS = 2cxpqzirb, (V-8-3')
где S = 2nrb — поверхность цилиндра радиуса г и длиной Ь, равной хорде
профиля;
схр — коэффициент сопротивления профиля при су = 0.
Сравнивая оба выражения для Хо, найдем
сх0 = лсхр. (V-8-4)
В соответствии с этим полный коэффициент лобового сопротивления,
рассчитанный как и коэффициент подъемной силы, по площади
горизонтальной проекции крыла
г —г -L-r —rrr I °У (Y-R-*\\
сх — СхО\~сХ1 — %рт 9тг^ ' \\ о О)
Продольный момент, обычно определяемый относительно координатной
оси z, создается только подъемной силой. Чтобы определить его величину,
можно исходить из того, что центр давления крыла (а для несимметричного
профиля — фокус) будет занимать на оси такое же положение относительно
передней кромки, как и центр давления профиля, т. е. считать, что
Сц. д. кр — Сц, д.пр* (V-O-b)
300 Г лав а V
Таким образом,
Мг = УСц.д.прЬ,
а его коэффициент
Шг ~ 2qrb2 ~^УСЦ-Д-ПР* (V-o-7)
Влияние сжимаемости. Это влияние при дозвуковой скорости полета
можно учесть при помощи следующих формул:
rxi= с*'сн -. (V-8-9)
Т/1ML v }
Здесь коэффициенты сусн и с^^сн для крыла в несжимаемом потоке
вычисляются по удлинению ЯОкр = Якр ]/"1 — Mlo.
Исследования показывают, что положение центра давления (фокуса)
в линеаризованном сжимаемом потоке не меняется.
Сверхзвуковые скорости. В сверхзвуковом потоке взаимное влияние
сечений слабее, чем в дозвуковом. Причем, это влияние снижается по мере
того, как возрастают числа Моо.
Если конус возмущения, идущий от передней кромки какого-либо
сечения, не пересекает хорду диаметрально противоположного сечения, то
взаимодействие сечений в первом приближении можно не учитывать.
В таком случае можно считать, что каждое сечение в плоскости у = const
будет находиться под углом атаки, равным av = acos у. Следовательно,
коэффициент подъемной силы сечения в той же плоскости
с'у = с°уаау = с°уаа cos у = с°у cos у, (V-8-10)
где с0 — коэффициент подъемной силы профиля при угле атаки а.
Принимая, что для элемента крыла с площадью dS — Ъг dy подъемная
сила dYr в плоскости у = const определяется равенством
Найдем действительную подъемную силу элемента
dY = dYf cos у = c
Подъемная сила крыла
QooV2 OooV2
dY = dYf cos у = c'y °° °° Ъг cos у dy = с0 °°2 °° Ъг cos2 у dy.
2л
Y = c°qbr \ cos2yc?y =
о
Следовательно, коэффициент подъемной силы
У jt
Cy = ~2qbF:=Ycv'
(V-8-
Подсасывающая сила на передней кромке кольцевого крыла в
сверхзвуковом потоке отсутствует, поэтому коэффициент лобового сопротивления,
обусловленный подъемной силой,
cxi = cya. (V-8-12)
Коэффициент лобового сопротивления при су = 0 находят по (V-8-5),
приняв в ней схр равным коэффициенту сопротивления профиля при су = О
и заданном числе Моо.
Фокус крыла будет занимать такое же положение относительно
передней кромки, как и фокус профиля сечения при одинаковом числе Моо.
Расчет аэродинамических коэффициентов
301
Лобовое сопротивление, обусловленное подъемной силой, не вызывает
продольного момента вследствие симметричного распределения подъемной
силы относительно оси z. В силу осевой симметрии крыла коэффициент mz
также будет равен нулю.
§ V-9. Крестообразные
крылья
Схема потока около крестообразных крыльев показана на рис. V-9-1.
При расчете аэродинамических характеристик таких крыльев можно исходить
из того, что при 2-ф = 90° (г|) — угол наклона консоли к оси z^ и малом угле
атаки влиянием скольжения
каждого плана на
коэффициенты Су, сх, mz можно пренебречь.
При сверхзвуковых
скоростях в силу того, что каждый
план расположен в плоскости
симметрии другого плана, с
известным приближением будет
оправдано предположение, что
взаимное влияние между ними
практически отсутствует.
Учитывая сказанное,
каждый план крестообразного крыла Рис. V-9-1. Схема потока около крестообразного
с углом г|) = 45° будет иметь такие крыла
же аэродинамические
характеристики, какие он имеет в изолированном виде при той же скорости обтекания.
При угле атаки а крестообразного крыла эффективный угол атаки
каждого плана (рис. V-9-1) будет равен:
= ■==£ cos 1
= a cos г|) =
а~\/2
(V-9-1)
Полагая производную по углу атаки коэффициента подъемной силы
изолированного плана равной cjja, найдем коэффициенты подъемной силы
су1 и су2 обоих планов в крестообразном крыле:
— су2 — су
,0 Т/2
-My 2 — ~у 2
где с°у — коэффициент подъемной силы изолированного плана при угле атаки а.
Коэффициент подъемной силы всего крестообразного крыла, отнесенный
к площади одного плана,
су = {сп + су2) cos -ф = с°у cos -ф У2 = с°у, (V-9-2)
т. е. оказывается равным коэффициенту подъемной силы изолированного
плана при том же угле атаки а.
Коэффициент сопротивления, обусловленный подъемной силой и
отнесенный к площади одного плана, как и для обычного крыла, найдется в виде
cxi = Ac2y. (V-9-3)
При дозвуковых скоростях Ас^ 1/(лА,кр), где Якр — удлинение отдельного
крыла; при сверхзвуковых скоростях А = 1/сОа (если отсутствует
подсасывающая сила на передних кромках крыльев).
Лобовое сопротивление крестообразного крыла при су = 0 будет в два
раза больше лобового сопротивления обычного крыла, поэтому сх = 2с°х, где
коэффициенты сх и сх отнесены к площади одного плана.
30Z
При установке крестообразного крыла на корпусе (см. рис. XV-1-3)
необходимо учитывать взаимное влияние планов и корпуса. В первом
приближении это влияние для каждого плана можно учитывать отдельно.
Найденные таким образом коэффициенты с0, с£, с®а для отдельного плана
подставляют затем в вышеприведенные формулы для получения характеристик
крестообразного крыла с учетом влияния корпуса.
§ V-10. Нестационарная
аэродинамика крыла
Пластина в сверхзвуковом
потоке
В случае, если крыло обтекается нестационарным потоком, что
соответствует условиям, при которых оно совершает колебательное движение, та
1,6
12
— -,
.
О)
/у
Л
Л.
г
St
0,8 1,6 2,4
аэродинамические характеристики дополнительна
зависят от параметров, определяющих это движение.
Для наиболее распространенного вида
гармонических колебаний на рис. V-10-1, V-10-2 [6]
представлены в качестве примера теоретические
зависимости нестационарных характеристик
плоской пластинки бесконечного размаха для Моо = О
и Моо = 3. Коэффициенты моментов, приведенные
на рис. V-10-1, V-10-2, соответствуют точке
приведения, расположенной от передней кромки на
расстоянии ;гвр = 0,25 Ь.
Зависимость производных устойчивости от
удлинения для прямоугольных и треугольных крыльев,
расположенных в дозвуковом потоке, показана на
рис. V-10-З-ч-V-10-8. Приведенные данные
указывают на то, что при малых Хкр влияние чисел Стру-
халя St на нестационарные характеристики
уменьшается. Такое же явление наблюдается при
сверхзвуковых скоростях. Причем с ростом Моо эффект
числа St также уменьшается (рис. V-10-9, V-10-10).
При решении практических задач приходится
иметь дело с числами St порядка 0,05-4-0,07.
Поэтому с определенной степенью точности можна
пользоваться нестационарными характеристиками
при числах St—> 0, т. е. считать, что производные
устойчивости не зависят от частоты колебаний. В
соответствии с этим предположением и для xBV =
= 0,25 Ъ получены следующие значения
производных устойчивости для пластины бесконечного размаха, обтекаемой
сверхзвуковым потоком в условиях гармонических колебаний:
Рис. V-10-1.
Нестационарные аэродинамические
характеристики
прямоугольной пластины бесконечного
размаха (ось вращения
расположена на расстоянии 1/4
хорды; #вр = xBV/b =0,25)
cf,=
(ML-I)3'2
C°z--±.
1
Умасо-1 '
__7 1_
12
6 (М^о-1)3/2
5 1
1 1
(V-10-1)
(V-10-2)
(V-10-3)
(V-10-4)
А
7
С*
<^—
1,
i
с?
2,
\
2St
0,8
1,6
2fi 3,2 St
/
1
к
>
**•—'
У*
. ■
.
*- •
^——
—
-0
/
-0,8
-1,2
4,6
Рис. V-10-2. Нестационарные
аэродинамические характеристики
прямоугольной пластины бесконечного
размаха (#вр = 0,25)
т?
Рис. V-10-4. Коэффициент т^
(сплошные линии — для
прямоугольных, пунктирные — для
треугольных крыльев); Якр — удли-
нениё; #вр = 0,25
0£
0,8
Qfi
0,2
/
/
/
/
/
/
/
/
\.
/
'' St=2
2
xSt=2
1 0,25
3
'1 0^25
~0,2
Рис. V-10-3. Коэффициент т% (сплошные
линии —- для прямоугольных, пунктирные —
для треугольных крыльев) Хкр — удлинение.
Ось вращения крыльев расположена на
расстоянии 1/4 корневой хорды, т. е. #вр = 0,2Ь
Л'
м ~о
St=0,25
\
St=2
0,5
\
=^=
2
\
=^=
/
Q25
>'?
-0,6
-Ц4
-0,2
0
-0,12
-ори
А
Г
1
/И
St=0,25^
^ St-2
St=H2;
0,25-0,5
? Лкр
5 Ак
Рис. V-10-5. Коэффициенты mfz и m®z
(сплошные линии — для
прямоугольных, пунктирные — для треугольных
крыльев)[ А,кр — удлинение; xBV =0,25
0,8
/
I
St=0,25
\
St=2
M^O
7 ^ J Лкр
Рис. V-10-6. Коэффициент c®z (сплошные
линии — для прямоугольных,
пунктирные —для треугольных крыльев); ^кр —
удлинение; #вр = 0,25
304
Глава V
Рис. V-10-8. Коэффициенты с® и Су (сплошные
линии — для прямоугольных, пунктирные >
для треугольных крыльев); А,кр — удлинение;
^вр = 0,25
Рис. V-10-7. Коэффициент c®z (сплошные
линии — для прямоугольных, пунктирные — для
треугольных крыльев); £кр — удлинение,
^вр = 0,25
0,2
-0,2
~0£
'0,6
St=2
/1 А
SU0,25\
1 0,5
у/
\
\
л
/
//
А
st=
0,25
St=2
,о
0,8
Ofi
/
/.
0t2l
—I—
к
^ч
0,25
3 Л
кр
0,6
ол
' 0
\
\
ч
\
ч
7"
\
"^—,
3
0,8
0,5
1,5 St
4 3
- т
\
\
\
М^12
>^
1,5
1,0
1,5 St
-0,2
-0,4
0,2
1 2
Рис. V-10-9. Зависимость
нестационарных аэродинамических
характеристик прямоугольного крыла от
числа Моо (Хкр=1, а;Вр=0,25)
Рис. V-10-10. Коэффициенты с^
и с^ в зависимости от
удлинения прямоугольного крыла
Расчет аэродинамических коэффициентов
Приведенные зависимости можно использовать с известным
приближением в практических расчетах для любого другого закона изменения
кинематических параметров от времени, если выполняется условие St—>0. В этом
состоит гипотеза «гармоничности».
Крылья в дозвуковом потоке
В практических случаях можно пренебречь влиянием изменения
скорости на аэродинамические характеристики (за исключением движений
с весьма большими ускорениями). Принимая также, что угол скольжения
Рск^О» Для аэродинамических коэффициентов получим
су = Суо + <V* + с*а + cvx®z + Cyz(x>z; (V-10-5)
mz = mz0 + т%а -f- maa + тг°*(йг + m^(az. (V-10-6)
Для расчета производных устойчивости можно использовать графики
на рис. V-10-З-н V-10-8, соответствующие несжимаемой среде (Моо = 0).
Сжимаемость (для чисел Моо<Моокр) можно учесть, применив теорию
подобия дозвуковых течений. Причем соответствующие зависимости будут
относиться только к статическим производным устойчивости и к
вращательным производным по coz.
Методика расчета заключается в следующем. По заданной форме крыла,
его удлинению и числу Моо определяются геометрические параметры
фиктивного крыла, расположенного в несжимаемом потоке,
(V-10-7)
где параметры с индексом «не» относятся к несжимаемому потоку. Затем
с помощью соответствующих графиков или зависимостей находят
производные устойчивости для фиктивного крыла. По найденным величинам
вычисляются соответствующие коэффициенты для крыла в сжимаемом потоке
(V-10-8)
(V-10-9)
1-ЛЙо 1Л-М2оо '
Производные момента крена [61]. Теоретические значения
производной демпфирования крена тхх = дтх/д(ох ((ux = QI/2V<x>, где I — размах
крыльев) для крыльев с сужением и прямыми кромками при дозвуковом
обтекании (Моо<МооКр) приведены на рис. V-10-11. Из данных на этом
рисунке следует, что производная тхх зависит от параметра &,
представляющего собой отношение действительного (экспериментального) наклона кривой
подъемной силы профиля к теоретическому значению, а также от сужения
т] = Ькр/Ькци угла xi/4 = arctg [(1 — М2)1/2 tg X1/4] в градусах. Производная т®*,
как и все последующие производные, определяется для связанных с крылом
осей координат (рис. V-10-11).
При скольжении летательного аппарата возникает дополнительный
поперечный момент, величина которого при малых углах скольжения равна
(dmjdfi) Рек — т^хРск- Статическая производная поперечной устойчивости тх
зависит в общем случае от формы крыла в плане и числа Моо. Для малых
скоростей обтекания (Моо = 0) экспериментальные значения тх даны на рис.
20-114
306
Глава V
l
-
кр
Ли,
10
8
6
5
3
2
»-—
*~
m ■
N
4,
4
s
—
0,5
4
Ofi*
-20 0 20
0,2 х
0,1
15
^—■
■1 ■
■ 1
■ —
\J
\
x
s
\
\
s
^4
s
0,5
02
60 Х^град. -20 0 20 40 60 Х/град.
Рис. V-10-11. Производные демпфирования крена для стреловидного
крыла при дозвуковых скоростях
Рис. V-10-12. Статическая производная
поперечной устойчивости для
стреловидных крыльев при малых скоростях
(сплошные линии для т] = 1, пунктир-
^— ные — т) = 2)
Рис. V-10-13. Изменение перекрестной
вращательной производной т®у
стреловидного крыла в несжимаемом потоке:
сплошные линии — т] = 1;
пунктирные — г\ = 2:
± 60°; 2-xi/4«±50°; 3~
7.1/4 ==±40°; 4-Х1/4=г0о
—I /77.
0,3
0,2
, ■
7
A
ди
—/— *■
A
in
4
—
ин
-:
—i
1 2 д
5 6 7 Д
кр
Расчет аэродинамических коэффициентов
307
V-10-12 в зависимости от удлинения Якр для г] = 1 и г| —2. Производные Шх
слабо зависят от сужения г), поэтому приближенно можно считать т£
функцией только удлинения Якр и угла стреловидности.
Момент крена меняется при вращении аппарата около вертикальной
оси с угловой скоростью Qy. Это изменение равно т®у1щч где (oy = Qyl/2Vo,>.
0,1
0,1
-0,2
.
—
—!
j
—
Ш т.
II "
Х=60'
¥
-40
-50
-60
8 А,
кр
Рис. V-10-14. Изменение отношения статической
производной путевой устойчивости
к значению с2у в
зависимости от угла стреловидности и удлинения крыла
Теоретические значения перекрестной вращательной производной
устойчивости ШхУ для стреловидных крыльев с сужением и прямыми кромками
в несжимаемом потоке показаны на рис. V-10-13. Чтобы учесть влияние
сжимаемости на производные ®
У
Am,
'1 О
-0,4
- 60
20
и /ПхУ, следует воспользоваться
преобразованиями (V-10-7) — (V-10-9).
Производные путевого
момента [61]. Изменение коэффициента
путевого момента обусловлено
скольжением и вращением вокруг
продольной и вертикальной осей
с угловыми скоростями
соответственно (ох и соу. Возникающие при
этом дополнительные величины
коэффициента путевого момента
равны глубок (при скольжении), т®/ых
(при вращении вокруг оси х), тщу(оу
(при вращении вокруг оси у).
Теоретические значения статической
производной путевого момента для
стреловидных крыльев без сужения,
которое не имеет существенного
значения, можно при дозвуковом обтекании (Моо = 0) определить по рис.
V-10-14. Производную от путевого момента т®* (перекрестную производную
от угловой скорости поперечного движения) можно определить при помощи
вспомогательных коэффициентов Am* и Ат2 по формуле
+ Ат2 (<£)пр, (V-10-10)
Г
У//
W
/п
1
/
у
\
<
-
■■
J{? -
Am?
8 Я
О
кр
Рис. V-10-15. Изменение коэффициентов Amt
и Ат2, определяющих статическую
производную путевого момента (центр вращения
совпадает с фокусом крыла)
ntf* =
где Су — коэффициент подъемной силы крыла
а производная
20*
SOS
Глава V
т^ е> равна производной от профильного сопротивления. Коэффициенты
и Дга2 изображены на рис. V-10-15 для стреловидных крыльев без сужения,
которое практически не ока-
Ц1\~~\ (ч^ | | | | | | | | | | | | |v icn] зывает влияния на значения
этих коэффициентов. В
соответствии с данными рис.
V-10-15 в несжимаемом потоке
коэффициент Атг зависит от
-qj\ 1 1 I I I I I—I—LJ I I—I—LJ—I—L_J угла стреловидности % и удли-
=
х=
щ
О 1
8 А
кр
нения
-Ofi
-0,8
-2,0
/
/
i
/
У
у'
——
—
■ ■
—
—
--
—
—
50
о'-
1
7 -
,кр, а коэффициент
— только от удлинения.
Производная
демпфирования пути
(V-10-11)
где коэффициент профильного
сопротивления
(^х)пр — Сх
п%
кр
. (V-10-12)
8 А
кр
Рис. V-10-16. Изменение коэффициентов А7тг3 и Ат4,
определяющих производную демпфирования пути
(центр вращения совпадает с фокусом крыла)
Коэффициенты Ат3 и
даны для стреловидных
крыльев, обтекаемых несжимаемым
потоком, на рис. V-10-16. С
известным приближением
можно считать эти коэффициенты независящими от сужения. Влияние сжимаемости
на производные путевого момента можно учесть при помощи
преобразований (V-10-7) — (V-10-9).
Крылья в сверхзвуковом
потоке (теория тонкого тела)
Общие соотношения для производных устойчивости крыльев
произвольной формы. Если выполняется условие, при котором величина а'Хкр
близка к нулю, то производные устойчивости могут быть вычислены по
теории тонкого тела. Исследования показывают, что их значения не зависят
от числа Моо, а определяются геометрическими параметрами крыла.
Рассмотрим крылья произвольной конфигурации, но с одинаковым
расположением консолей (рис. V-10-17). Определение производных будем
вести относительно связанных осей координат #, г/, z, начало которых может
не совпадать с центром тяжести площади.
Движение крыла характеризуется углами атаки а и скольжения рСк,
а также составляющими угловой скорости йх, Qy, Qz. Поступательное
перемещение со скоростью Foo может быть неравномерным.
Производные устойчивости для крыльев по теории тонкого тела
определяются выражениями (IV-7-11) — (IV-7-45). Входящие в них величины Bik,
Ctk, Dik, Atk зависят от коэффициентов присоединенных масс, определяемых,
в свою очередь, в зависимости от формы поперечного сечения крыльев. Эти
коэффициенты найдены для нескольких конфигураций крыльев, из которых
рассмотрим двух-, трех- и четырехконсольные конфигурации. Причем двух-
консольное крыло в поперечном сечении выглядит в виде отрезка прямой
на горизонтальной оси в плоскости £. Пусть размах крыла (т. е. длина
отрезка) равен 2Z. Преобразование этого отрезка в крз^г радиуса г0 в плос-
Расчет аэродинамических коэффициентов
309
кости о осуществляется при помощи конформной формулы (см. табл. IV-4-1)
£ = а + -7Г' (V-10-13)
где г0 = 1/2.
Используя соотношения (IV-6-51) и (IV-6-52), можно найти
комплексные потенциалы W2, Wi4 а применяя зависимости (IV-6-53) и (IV-6-54) —
определить потенциал W3. Коэффициенты присоединенных масс находят
по формулам (IV-6-4) или (IV-6-4').
Осуществляя расчеты, следует иметь в виду, что в направлении оси z
составляющая скорости Vz не вызывает возмущений, поэтому сразу можно
указать, что коэффициенты присоединенных масс Я11 = Я12 = Я13 = 0.
of
Ьт
/7=4
Рис. V-10-17. Система обозначений для крыла при
определении производных устойчивости (п — число консолей)
При вычислении коэффициентов присоединенных масс для других форм
поперечных сечений крыльев следует использовать формулу (IV-6-4),
преобразовав ее соответствующим образом с учетом формы трех- или четырех-
консольного крыла.
При рассмотрении консоли, наклоненной к оси у или z, следует
применить разложение скоростей Vy, Vz на составляющие в направлении
консоли и по нормали к ней.
Расчеты показывают, что для всех трех конфигураций коэффициенты
присоединенных масс Я12, ?4з> ^23 равны нулю. Что касается других
коэффициентов, то они имеют следующие значения [51]: двухконсольное крыло
(плоская конфигурация) —
Х 0; Я яР/2; X 3tpZ4; (V1014)
трехконсольное крыло —
Хи = Х22 = 0,793jtpoJ2; ^зз = 0,533pooZ4; (V-10-14')
четырехконсольное крыло (крестообразная конфигурация) —
Яи = Х22 = jtpoo/2; Х33 = ~ pooZ4. (V-10-14w)
Зная коэффициенты присоединенных масс, можно найти при помощи
выражений (IV-6-47) коэффициенты Aik. Ввиду того что коэффициенты
присоединенных масс Я12 = Я13 —Я2з = 0, то также равны нулю
соответствующие коэффициенты Aik, т. е. Ai2 = Ai3 = A23 = 0.
Г лава V
Приняв в формулах (IV-6-47) в качестве характерных параметров
площадь крыла (S = SKV) и величину 2lm=bm, получим следующие выражения
для коэффициентов Aiiy А22, А33 на задней кромке:
двухконсольное крыло —
^кр ' 8 fr^
трехконсольное крыло —
Ап = А22 = 0,793л; -£- ; Л3з - 0,533 ■
^кр
четырехконсольное крыло —
Приняв в этих формулах l = lm=-bml2, получим значения
коэффициентов Ац, Л22> ^зз Для условий на задней кромке. При этом следует иметь
в виду, что коэффициенты Ai2i Ai3, А2Ъ равны нулю.
По коэффициентам Aik можно вычислить при помощи (IV-6-46)
коэффициенты Bik, Cik, Dik. Девять этих коэффициентов, соответствующих
индексам ik—12, 13, 23, равны нулю вследствие того, что Ai2 = Ai3 = ^23 = 0.
Это значительно упрощает формулы (IV-6-11) — (IV-6-45).
Определение других значений коэффициентов Bik, Cik, Dik no (IV-6-46)
требует знания формы консолей в плане. Причем консоли могут отличаться
по форме от обычных треугольников, в частности, иметь криволинейные кромки.
В качестве примера рассмотрим расчет производных устойчивости для
тонкого плоского треугольного крыла и четырехконсольной (крестообразной)
конфигурации.
Треугольное крыло. Основные обозначения для этого крыла показаны
на рис. V-10-17. В качестве характерной площади примем площадь крыла
£кр=:0,56тс, а в качестве характерного линейного размера — размах 2lm=bm.
После подстановки значений Ац (V-10-14) в (IV-6-46) и интегрирования
в предположении, что начало координат совпадает с центром тяжести
(.Гц т = с/3), получим
где удлинение крыла
Якр = ЬУ5кр = 2bjc. (V-10-19)
Внося Ац, В и, С а и Dn в общие выражения для производных
устойчивости (IV-6-11) — (IV-6-45), получим их значения для треугольного крыла.
Статические производные устойчивости имеют следующий вид:
с&=—t^-^iF; 4 = °; (V-10-20)
с« = -|ясоя; СР = 0; (V-10-21)
---1Р+ттк7; "S—t-S5 (V"10-22)
~; m3 = 0. (V-10-24)
^кр z
Расчет аэродинамических коэффициентов
311
Вращательные производные
Производные по ускорениям
cN~ 3 л; cN
\У Z
N
^кр
(V-10-25)
(V-10-26)
(V-10-27)
* ; (V-10-28)
(V-10-29)
(V-10-30)
(V-10-31)
(V-10-32)
^кр *" УЛКР " ±Ос»Лкр
Остальные производные по ускорениям равны нулю. Используя
выражения для производных, следует иметь в виду, что все параметры
вычислялись по характерной длине
Ьт. Например, юЛ = Qxbm/2Foo, -^ г
V=Voobm/2Vlo1 где
производная V = dV/dt.
Ряд производных
устойчивости зависит от ускорения
поступательного движения.
Если влияние этого
ускорения отсутствует или
пренебрежимо мало, то надо
принять V=0.
Приведенные зависимости
позволяют проанализировать
отдельные виды движения, например, движение крена, движение при наличии
только продольного демпфирования и т. д. Осуществляя анализ, следует
помнить, что эти зависимости пригодны только для крыльев малого удлинения
при условии, что произведение а'А,кр невелико.
При выполнении такого условия крыло располагается вблизи оси
конуса возмущения. При больших числах М«о или с ростом удлинения
приведенные зависимости дают все менее удовлетворительные результаты.
Влияние удлинения и числа Моо будет рассмотрено ниже.
Четырехконсольное (крестообразное) крыло. Основные размеры крыла,
у которого все четыре консоли одинаковы, обозначены на рис. V-10-18.
Внося соотношения (V -10-15) для Ап в (IV-6-46), получим следующие
зависимости для Вц, Сц, Da'.
г> п П п п ТС Г 1 (л t ХЦ. Т
Рис. V-10-18. Система обозначений для
крестообразного крыла при определении производных
устойчивости
(V-10-33)
(V-10-34)
312 Глава V
Формулы для Сц, Dit пригодны для любого положения начала
координат выбранной связанной системы. Если начало координат поместить
в центр тяжести площади крыла, то надо принять хц т/с=—1/3. В этом
случае С±1 = С22= -л/(36Якр), /)11==/)22 = 4л/(135А»р).
Производные устойчивости (IV-6-11) — (IV-6-45) записывают
следующим образом.
Статические производные устойчивости:
<$=-|-Якр-|-яГ; 4=-|-я©1с; (V-10-35)
С« = |ясож; сЭ=-^р-|яГ; (V-10-36)
^ ^f (V-10-37)
вращательные производные:
2я n , 2я # со 2я # со 2я /Л7 4П qqv
—о~ Р ^1—qT ®у» N 0% ^а' ^N Ч~ ' ^V-IU-ОУ/
^1а+ 2^Юг; Л = -^; сиг== 2^Юж; (V-10-40)
32jc со сх со 32зт /тт лл /nw
СО; ^; ^00^ (V-10-42)
32j! (о • то%= 32я9 (о • (V-10-43)
v'vkp 13оАкр 13оЛкр
TO«Z==__i^; (V-10-44)
производные по ускорениям:
4= -| я; с^-АяР; с«» = ^-; (V-10-46)
<*=-5l-; (V-10-47)
4 ^ (V-10-48)
лкр
Г7—a; mr2:= =—. (V-10-49)
При вычислении производных за характерную площадь принята
величина ^кр = fomc/2, а за характерную длину — размах крыла у основания
2lm = bm. Параметры сох, соу, coz, V, а также их производные определяются*
как и для плоского крыла, по характерной длине Ът,
Влияние удлинения крыла
и числа Моо на производные
устойчивости
Треугольное крыло. Теория тонкого тела дает производные
устойчивости, не зависящие от числа Моо. Эта теория не позволяет установить
влияние на производные и удлинения, хотя, как будто оно и входит в соот-
Расчет аэродинамических коэффициентов
313
ветствующие выражения. Дело в том', что появление величины А,кр в этих
выражениях обусловлено не физическим процессом, а формальным выбором
характерных геометрических параметров.
Чтобы установить зависимость производных устойчивости от М«> и Хкр,
следует воспользоваться результатами сверхзвуковой линеаризованной теории.
Рассмотрим треугольное крыло. Независимой переменной для производных
устойчивости является величина а'А,Кр = 4а' tgyUi где уп — полуугол при
вершине крыла. Характерной площадью при вычислении производных
является площадь крыла £кр, а характерной длиной —размах Ът.
0,8
Ofi
-0,015
-0,010
0,005
0,015
0
>
Z
'3
5 Акр
\
\
ч
\
ч
к*
Ч
\
<
■——.
■—^
Рис. V-10-19. Зависимость для произ- Рис. V-10-20. Отношение производных устой-
водной поперечной устойчивости^тре- чивости треугольного крыла, вычисленных по
угольного крыла при Моо =~\/2'; линеаризованной теории и теории тонкого
1 — по теории тонкого тела; 2 — по
линеаризованной теории; О — угол р = 5° для
крыла с передней дозвуковой кромкой
тела:
х; 5 -
Для выяснения влияния удлинения и числа Моо сопоставим наиболее
важные производные устойчивости, полученные в теории тонкого тела
и линеаризованной теории. Это сравнение позволит также установить
возможность применения и степень точности теории тонкого тела. Будем
рассматривать случай, когда продольное ускорение отсутствует и F = 0.
Статические производные устойчивости. Анализ
производных устойчивости для моментов будем вести с учетом того, что моменты
вычисляются относительно центра тяжести крыла, вокруг которого
происходит вращение. Иное расположение центров момента и вращения будет
указано особо. Расчеты по аэродинамической теории тонкого тела дают:
значение т™ = 0, т. е. такое, как по линеаризованной теории. Это
указывает на достаточно хорошее приближение, полученное по теории тонкого
тела. В то же время результат т% = 0 показывает, что в рамках линейной
теории нельзя определить влияние числа Моо на статическую производную
устойчивости.
Если центр моментов не расположен в центре тяжести, то та=^0.
Кривая продольного момента, вычисленная по линеаризованной теории
в том случае, когда ось вращения проходит через начало хорды, а передняя
кромка является сверхзвуковой, показана на рис. V-10-25. Исследованиями
установлено, что производная т% не зависит от удлинения треугольного крыла^
В результатах для производной поперечной устойчивости тР, имеются
различия. На рис. V-10-19, где приведены расчетные данные для случая
Моо = ]/2, видно, что у треугольного крыла значения т% близки по обеим
теориям до тех пор, пока передняя кромка не становится звуковой (а'Якр^^.
Причем для дозвуковой кромки производная т% по линеаризованной теории
остается отрицательной (стабилизирующей), для сверхзвуковой — положи-
314:
Г лава V
тельной (дестабилизирующей). В зоне перехода от до- к сверхзвуковой
кромке различие между теориями особенно заметно.
На изменение стреловидности, а следовательно, и на значения момента
крена влияет угол скольжения. С ростом угла рск передняя кромка становится
-звуковой и раньше появляется дестабилизирующий эффект. Когда кромка
переходит из до- в сверхзвуковую, зависимость тх от рск отклоняется от линейной.
Рассмотрим производные от коэффициентов нормальной силы и введем
обозначение
(V-10-50)
Здесь в числителе —производная,
и равная
лЛкР/(2Я)
4/а'
cNt
полученная
при
при
по линеаризованной теории
4
в знаменателе —производная, найденная по теории тонкого тела и равная
€<*т~ лЛ,кр/2. Функция Е в (V-10-51) является полным эллиптическим
интегралом второго рода с параметром к = [1— (аЯкр/2)2]1/2.
Кривая cn, построенная в зависимости от параметра а'Якр, приведена
на рис. V-10-20. Излом кривой происходит при значении а'Хкр = 4, когда
кромка становится звуковой. По мере роста удлинения или числа Моо
теория тонкого тела дает все более заниженные значения. На рис. V-10-20
показана кривая с% для треугольного крыла со сверхзвуковой передней кромкой.
Вращательные производные и производные по
ускорениям. Одна из вращательных производных, а именно производная
демпфирования крена в линеаризованной теории определяется выражениями
j
при
тде К — полный эллиптический интеграл первого рода
я/2
К=
(V.10_52)
(V-10-52r)
с параметром к= [1 — (а'Якр/2)2]1/2.
Эта же производная в теории тонкого тела т®%= — яХкр/32. Отношение
производных ШхХ = тп^!Шх^ показано на рис. V-10-20. По теории тонкого
тела значения производных ниже, чем по линеаризованной теории, хотя
разница меньше, чем для производной с<*.
Продольное демпфирование зависит от производных mz по а и coz,
которые различным образом определяются по обеим теориям. По
линеаризованной теории
— лк2 _./Л ^ , \
\ (V-10-53)
16
при
при
(V-10-54)
Расчет аэродинамических коэффициентов
315
Производные по теории тонкого тела mfz = — я/(ЗЯкр), т^ = —я/9А,кр.
По известным значениям производных можно вычислить отношения m®z
и яг?, для которых кривые показаны соответственно на рис. V-10-20 и V-10-21.
Производные от коэффициентов нормальной силы определяются по
линеаризованной теории:
2я
ЗА;2
2 |
—-^J при а'Я
кр
4;
= 0 при а'Якр>4;
2л Г ЗА;2 (
= За'2 (2№ — \\ /
2а/2+3
За'2 L(
— 16
J при а'Акр < 4;
при а'Лкр>4.
(V-10-55)
(V-10-56)
Производные по теории тонкого тела определяются выражениями с%% =
— 2л/3, с?ут = 2л;/3. Соответствующие производные по wz и а по обеим тео-
0,8
¥
кр
риям определяют отношения cN и cN.
Кривая erf приведена на рис. V-10-20,
а для с% — на рис. V-10-21.
Для сверхзвуковой кромки крыла
кривые cN, с^, построенные по
данным линеаризованной теории,
показаны на рис. V-10-24 и V-10-27 (ось
вращения проходит через начало
корневой хорды).
Анализ имеющихся данных
позволяет установить, что при очень
малых удлинениях теория тонкого
тела может быть достаточно надежно
использована для расчета
производных. Однако при больших удлинениях
эта теория пригодна лишь для
качественных оценок, например, положения
центров давления и стабилизирующих э ффектов при демпфировании
При малых удлинениях координата центра давления в случае вращения
вокруг центра тяжести определяется по теории тонкого тела:
\
\
\
\
' \
2
X
3
4
5ос'Л
-Ц8
Рис. V-10-21. Отношение производных
устойчивости треугольного крыла,
вычисленных по линеаризованной теории и теории
тонкого тела
^кр
3
2л
(V-10-57)
Таким образом, центр давления расположен за центром тяжести и,
следовательно, демпфирующий момент является стабилизирующим. При а/Хкр>4
в соответствии с линеаризованной теорией с^г = 0, а значения тщх не равны
нулю и являются отрицательными. Это означает, что центр давления
перемещается за крыло на бесконечное расстояние. Следовательно, качественная
картина стабилизации при демпфировании, предсказанная теорией тонкого
тела, сохраняется.
Однако качественным анализом по теории т онкого тела надо пользоваться
с осторожностью. Например, при движении, связанном с изменением по вре-
316
Глава V
мени угла атаки (а^О), коэффициент центра давления по теории тонкого
тела определяется величиной
z
г«кр
1 с
"12 Ът
(V-10-58)
/
M'
d
2z4v
к
h
a
(u.6)
*■ 1
(a
Рис. V-10-22. К пересчету производных
устойчивости с одного центра вращения
(центра моментов) на другой
Следовательно, нормальная сила с%а всегда является стабилизирующей.
Из линеаризованной теории следует, что координата центра давления будет
такой же, как по теории тонкого тела.
Однако, как видно из рис. V-10-21,
при некоторых значениях а'Якр
нормальная сила с^а становится
отрицательной. Это означает, что возникает
дестабилизирующий эффект, не
предсказываемый теорией тонкого тела.
В общем случае центр вращения
может не совпадать с центром
моментов, т. е. с точкой, относительно
которой определяются моменты. При
этом иногда приходится пересчитывать производные с одного центра вращения
(или центра моментов) на другой. Формулы пересчета имеют вид
(V-10-59)
(V-10-60)
(V-10-61)
тп?* = (т?у-2(т?)'±+(с%<у±-2±±с%. (V-10-62)
В этих формулах коэффициенты со штрихами являются значениями
производных для заданных центра вращения или центра момента (эти центры
в общем случае не совпадают); остальные коэффициенты соответствуют новым
положениям этих центров. Причем новые центры моментов и вращения
находятся позади старых на расстояниях соответственно 1± и Z2 (рис. V-10-22).
Характерным размером является некоторая длина Z, которая для крыла
выбирается равной размаху Ът.
Моменты крена, обусловленные вращением вокруг оси г/, по
линеаризованной теории определяются формулой
т* ъ =
(V-10-63)
в то время как в теории тонкого тела тх% = л;а/(9Якр). Различие
существенное. Отношение соответствующих производных
...I"- (V-10-64)
При Якр—>0 это отношение mxv-^>\.
Силы и моменты от эффекта Магнуса. Силы и моменты
от эффекта Магнуса возникают при косом обтекании крыла, совершающего
вращение вокруг продольной оси. Эти силы пропорциональны произведениям
асох или рскО)х- В частности, боковая сила Z ~ acox, момент рысканья Му ~ а(ох.
1,5
0,5
\
i.
Рис. V-10-23. Зависимость с^ от
удлинения и числа Моо при сверхзвуковых
скоростях (St = 0)
5МО
Рис. V-10-26. Зависимость т^ от
удлинения и числа Моо при сверхзвуковых
скоростях (St = 0)
1,5
1,0
0,5
\
\
\
\
\
\
*«ч
Рис. V-10-24. Зависимость с% от
удлинения и числа Моо при
сверхзвуковых скоростях (St = 0)
Рис. V-10-27. Зависимость cNz от
удлинения и числа Моо при
сверхзвуковых скоростях (St =0)
-0,5
\
\
ч
ч
\
-0,05
-0,025
\\\
X
V
\ \
\
\
\
\
ч
Й
Рис. V-10-25. Зависимость т™ от удлинения „,.,„„„„ '<*>,
ш числа М.О при сверхзвуковых скоростях Рис- V"10"28' Зависимость Cjv* от удли-
/§t __ q\ нения и числа Моо при сверхзвуковых
скоростях (St =0)
318
Глава V
В поточных осях производные устойчивости для боковой силы и момента
рысканья определяются по линеаризованной теории в таком виде:
(V-10-65)
—(1 — №) К] '
(V-10-66)
При а/Якр>4 обе производные равны нулю.
Коэффициентам (V-10-65) и (V-10-66) в теории тонкого тела
соответствуют выражения с™* = -^- , т* ®* = -_ _5_ . Кривая для отношения с?Шх
приведена на рис. V-10-20. Как
видно, при а'Якр — 4 обе теории
отличаются качественно.
-w
-0,5
\
\
\
\
\
\
ч
Рис. V-10-29. Зависимость
от уд Рис. V-10-30. Зависимость m z от удлинения
линения и числам» при сверхзвуковых и числа Мсо при сверхзвуковых скоростях
(St = 0)
скоростях (St =0
Прямоугольное крыло. Некоторые данные о производных устойчивости
для прямоугольного крыла, полученные в линеаризованной теории, приведены
на рис. V-10-23-^ V-10-30. В отличие от треугольных крыльев производные
устойчивости зависят от удлинения (на рисунках сплошной линией
обозначены характеристики для прямоугольного крыла, пунктирной — для
треугольного) .
Исследования показывают, что при сверхзвуковых скоростях зависимость
вращательных производных от числа Струхаля тем меньше, чем меньше числа
Струхаля и чем меньше удлинение крыла. При этом в диапазоне чисел St,
встречающихся на практике, можно с достаточной степенью точности
пользоваться значениями аэродинамических характеристик, полученных при
St—>0.
Соответствующие данные для коэффициентов вращательных производных,
рассчитанных при условии, что оси вращения и моментов проходят через
начало корневой хорды крыла, представлены на рис. V-lO-23-f- V-10-30.
Характеристики демпфирования движения крена. Исследуем отдельно
вращение крыла относительно оси х с угловой скоростью Qx (рис. V-10-31),
в результате которого возникает демпфирующий момент крена Мх,
направленный в противоположную сторону вращения и равный Мх = mxSKplq.
Расчет аэродинамических коэффициентов
В общем случае коэффициент демпфирующего момента крена
319
тх = т%шх + тхх«ух. (V-10-67)
В практических случаях ускорения сох малы, поэтому можно написать, что
™* = /ю£здх. (V-10-67')
Рис. V-10-31. К определению момента демпфирования
при крене
Применяя «метод полос», найдем для крыла в целом
, , 1
2S-
кр
(V-10-68)
где z = 2zll;
cfya — производная для данного сечения, определяемая из условия
,а Qxz л.а_ - (V-10-69)
в котором
Другие обозначения видны из рис. V-10-31.
По известной зависимости для данного крыла bz2lhcv, а также величине
с'уа (z, Moo) как функции координаты z и числа Моо можно вычислить по
(V-10-68) производную коэффициента демпфирования.
Глав а VI
ТРЕНИЕ
И ТЕПЛОПЕРЕДАЧА
НА
КРЫЛЬЯХ.
§ VI-1. Параметры трения
при| обтекании плоской
пластинки
Однородный пограничный слой
Несжимаемый пограничный слой. Рассмотрим расчет параметров трения для
пластинки, обтекаемой несжимаемым потоком. В результате этого расчета
определяются такие параметры пограничного слоя, как толщина слоя,
условные толщины вытеснения и потери импульса. Эти параметры, как будет
показано, могут быть использованы для расчетов более сложных случаев
течения газа в пограничном слое, характеризующихся влиянием сжимаемости
и высоких температур, а также криволинейной формой обтекаемой
поверхности.
Рассмотрим основные зависимости для несжимаемого пограничного слоя
около пластинки, предполагая, что пограничный слой имеет некоторую
конечную малую толщину бнс, а распределение скорости по сечению
ламинарного и турбулентного пограничных слоев характеризуется соответственно
параболическим законом, предложенным Польгаузеном,
и законом «корня седьмой степени» (по Карману)
Ух I У
являющимся частным случаем более общего закона «корня степени к»
Внося выражения (VI-1-1) и (VI-1-2) в интегральное соотношение
(Ш-2-42), найдем толщину пограничного слоя:
хк
где хк — длина пластинки;
х = х/хк — безразмерная координата; Re =
Напряжение трения на стенке тст. нс определяется в результате
подстановки выражения (VI-1-4) для толщины слоя в формулы
первая из которых относится к ламинарному, вторая —к турбулентному
пограничному слою. В результате получим
Тст. не = ЯрбП Re",
где Rex = F6^/v —местное число Рейнольдса.
Трение и теплопередача на крыльях
321
По напряжению тст. Нс можно найти местный коэффициент трения
cfx не =Х-^ = С Re-, (VI-1-7)
где q^^
Используя (VI-1-7), определяют среднюю величину этого коэффициента
1
cf нс = I cfxnc <£ = D Ren. (VI-1-8)
о
Значения коэффициентов А, В, С, D и показателей степени т, п
приведены в табл. VI-1-1.
Т а б лица VI—1—1
Значения коэффициентов и показателей степени в
для параметров пограничного слоя
Пограничный слой
Ламинарный
Турбулентный
А
5,8
0,37
в
0,332
0,0289
С
0,664
0,0578
формулах
D
1,33
0,074
m
1
2
1
5
п
1
2
1
5
Другие результаты для турбулентного пограничного
слоя. Формулу (VI-1-8) для коэффициента турбулентного трения с/т нс
надежнее применять, если число Re не превышает 106. Для больших
значений лучшие результаты дают другие зависимости. Например, для значений
чисел Re в диапазоне 106 <г_ Re <C 109
cf т. не - 0,427 (lg Re - 0,407)"2'46. (VI-1-9)
Для диапазона 5 • 106 << Re < Ю10 может быть применена также формула
U67# (VI-1-10)
Числам Рейнольдса в диапазоне 2-106<Re«< 1010 соответствует
зависимость
cf т. не = 0,032 Re-0»145. (VI-1-11)
При больших числах Рейнольдса можно рассматривать универсальной
формулу Прандтля — Шлихтинга для расчета среднего коэффициента
турбулентного трения
Такой же универсальной можно рассматривать формулу Шульца —
Грюнова для вычисления местного коэффициента турбулентного трения
0 37
Cfx т. НС = (lgRex)2,584 ' (VM-13)
в которой числа Rex могут меняться вплоть до 109.
Толщину пограничного слоя с профилем скоростей, характеризующимся
степенным законом (VI-1-3), можно определять по выражению
(VI-1-14)
2 1—114
322
Глава VI
где
(Л+ 2) J
а коэффициент С по данным Висхарда
С = 0,917*"+ 2,343.
Значения В и С приведены в табл. VI-1-2.
Значения параметров В и С
Таблица VI—1—2
к
С
В
6
0
5
,93
,544
6
7,84
0,445
8
0
7
,74
,370
8
9,71
0,311
10
0
9
,6
,274
И
0
10
,5
,261
При определении показателя * можно пользоваться формулой
* = 2,35 (lg Re** -1), (VI-1-15)
в которой число Re** = F66**/v6-
Между условными толщинами вытеснения б* и потери импульса б**
и толщиной бнс пограничного слоя в несжимаемой жидкости имеется
следующая зависимость:
6т. но (VI-1-16)
1
Пример. Определим параметры пограничного слоя на пластинке для следующих
условий:
Foo = 200 м/сек; Н = 2000 м; v6 = 0,1715-10"4 м2/сек*; х = 1 м.
Решение производится методом последовательных приближений. В качестве
первого приближения принимаем показатель степени в законе распределения скоростей
к = 7,46 и подсчитываем соответствующие значения коэффициентов В и С:
В =
L (1 + 3)
fe+l 2k
ft+3- ft+3
7,46+1
7,46
L(7,46 + 3) (7,46 + 2)
По (IV-1-14) определяем толщину слоя:
2
2-7,46
"Т 9,18 ~7>46+3 = 0,343.
По (VI-1-16) находим
*** к
От. НС = ~Г=:
7,46
(Л+1) (Л+2)
(7,46 + 1) (7,46 + 2)
0,0153 = 0,0014 м.
Далее определяем
Re** =
0,1715-10-4
Трение и теплопередача на крыльях 323
и подсчитываем значение к во втором приближении:
к = 2,35 (lg Re** —1) = 2,35 (lg 16 300-1) = 7,55.
По этому к уточняем параметры пограничного слоя:
С = 0,917-7,55 + 2,343 = 9,266; £ = 0,338;
6Т нс = 0,01545 щ б**нс = 0,00143 м\
Этим данным соответствует значение
1=2,35 (lg 16 680-1)= 7,57.
Поскольку полученная величина к незначительно отличается (~ 0,2%) от
значения в предыдущем приближении, можно считать величину к — 7,57 и
соответствующие ей параметры пограничного слоя окончательными.
Влияние высоты. Это влияние выражается в изменении с высотой
числа Рейнольдса. Если вблизи земли это число Re3 = Mooa3xK/v3 (^з и v3—
соответственно скорость звука и коэффициент кинематической вязкости
вблизи земли), а на некоторой высоте число Re = MooaxK/v, то для него
можно написать
Re = Re8/i (Я) /2 (Я) /3 (Я), (VI-1-17)
где
представляют собой функции, определяющие изменение плотности, скорости
звука и коэффициента динамической вязкости с высотой. Значения этих
функций находят с помощью соответствующей таблицы (см.
приложение № 2).
Влияние сжимаемости (при отсутствии теплообмена). Значения
параметров пограничного слоя, в частности напряжения и коэффициента
трения, будут существенно отличаться от их значений для несжимаемого
потока при больших скоростях обтекания вследствие действия таких
факторов, как сжимаемость, нагревание и теплообмен.
Расчет этих параметров с учетом указанных факторов может вестись
различными методами в зависимости от характера происходящих тепловых
процессов. Рассмотрим расчет, основанный на предположении, что
теплообмен отсутствует (хотя имеет место аэродинамический нагрев пограничного
слоя) и любые возможные физико-химические процессы не учитываются.
Если предположить, что нагревание происходит без какого бы то
ни было изменения внутренней энергии (работой сил вязкости,
теплопроводностью или радиацией пренебрегаем), то влияние нагревания на
параметры пограничного слоя проявится в зависимости этих параметров
от числа Mr».
Для ламинарного пограничного слоя соответствующая зависимость
имеет вид
с/л = (1 + 0,03М1)~1/3. (VI-1-18)
Cf Л. НС
Для турбулентного пограничного слоя вид зависимости для отношения
Cf Jcf T. не от числа Мб будет определяться в общем случае величиной
показателя степени в законе изменения скорости, т. е. значением к или, что
тоже самое, значением числа Рейнольдса. Однако, как видно из рис. VI-1-1,
изменение 4 от 5 до 9, что соответствует изменению числа Рейнольдса
от 106 до 108, практически не сказывается на величине отношения cfT/cfTHC.
21*
324
Глава VI
Поэтому практически можно считать, что это отношение не зависит
от величины к (числа Рейнольдса). В соответствии с данными на рис. VI-1-1
зависимость отношения коэффициентов трения от числа Мб для
турбулентного слоя представляется в виде
с/т
.= (1+!^!м!)\
(VI-1-19)
с/ т. не V ' 2
где t= —0,43 для 6<Мб<15 и t= —0,39 для 0<Мб<6.
Экспериментальное исследование влияния температуры стенки на
отношение с/т/с/т. нс показало, что в турбулентном потоке это влияние невелико
и в практических расчетах его можно не учитывать, если при этом расчет
коэффициентов трения производится по параметрам на внешней границе слоя.
При этом формула будет более точной
для теплоизолированной
(адиабатической) стенки.
Наряду с (VI-1-19) может быть
использована зависимость, найденная акад.
А. А. Дородницыным,
с/т = 0,472 §Ol
X
\
к=5
Рис. VI-1-1. Отношение с/т/с^т#нс для
турбулентного пограничного слоя в
зависимости от числа М§ при различных
значениях к
0,5
или формула Лютера
ю Mfc c/T = 0,0631exp(-0,172M62)Re-0'182,
(VI-1-21)
которые дают лучшие результаты для
чисел Рейнольдса, лежащих в диапазоне
106<Re<1010.
Толщины пограничного слоя с
учетом сжимаемости и температуры стенки
могут быть вычислены при помощи (VI-1-4), если перейти в ней к
определяющим параметрам. По найденной таким образом толщине слоя могут
быть определены по (VI-1-16) толщины вытеснения и потери импульса.
При расчетах по (VI-1-14) следует внести в значение к поправку,
вызванную влиянием числа Маха. Это можно сделать, применив выражение
(VI-1-15), в котором
Re** = 0,036 ReM (l + AzIm?)' . (VI-1-22)
Величины б** и б* можно вычислить непосредственно при помощи
выражений
1 1
v6)d U J' б - К1 ~
о
d vt
(VI-1-23)
о о
в которых принимается VJV6 = (y/8)i/h; VxIV^ = (T0~TCT)l{T06-~TCT), где
Tq, Tqc — температуры торможения соответственно в пограничном слое
и свободном потоке. При этом плотность определяется из уравнения p = pRT
при условии, что в пограничном слое др/ду = О.
Толщины потери импульса и вытеснения, отнесенные к толщине
пограничного слоя и рассчитанные для закона «корня седьмой степени»,
выражаются следующим образом:
бГ 85,2 [1-0,098 (9-Ъ)] (1-0,78С)
(VI-1-24)
Трение и теплопередача на крыльях
325
где
G=
-Ml
0,197 {1_
—0,15
== {^-[1 + 0,465 (A-
Результаты расчета значений 6J* /бт и 6*/6т приведены на рис. VI-1-2
и VI-1-3 в зависимости от Мб и относительной температуры стенки
1 СТ = 1 ст/-* О*
5т
0,9
0,7
0,5
0,3
0,1
0,04
0,02
о
Рис. VI-1-2. Отношение б**/бт в
зависимости от числа М5 и
относительной температуры стенки Тст
/71,
'/ ///
У/
к=7
Л?
7/Х
/77/7
7/
1/
\ 0,5
W 1>°
\ X 9 П .
10
м5
Рис. VI-1-3. Отношение 6*/бт в
зависимости от числа Мб и
относительной температуры стенки ТСт
По значениям б?*/бт можно подсчитать, используя формулу 6** =
= (1/2) CfXTx, толщину пограничного слоя:
CfT
нс о"**/6т.нс
(VI-1-26)
Отношения б?*/бт и 8*/8т получены для условий, при которых не
учитывается влияние ламинарного подслоя. Исследования показывают, что это
влияние на величину б?/бт невелико и его можно не учитывать.
Что касается толщины потери импульса, то влияние ламинарного
подслоя может оказаться существенным, причем оно возрастает по мере умень-
326 Глава VI
шения Re6 и роста Мб- Величина б**/бт может быть представлена общей
зависимостью
1 т ^ п-'т- ««5, M6)iV2(M6, Ree),
где (6**/6T)Re6=oo — отношение толщины потери импульса к толщине слоя,
когда ламинарный подслой отсутствует (см. рис. VI-1-2); Re6^F66/V6. Для
частного случая теплоизолированной стенки (Тст = 1) функция
N± = l + 0,004 (Мб -10) (1 - 0,125 Re6).
Функция N2 рассчитывается по формуле
где h = 3,9 — 0,6 VM6—3 при Мб>3 и й = 3,9 при 1<М6<3. ПриМб<1
значение N2 = 1.
Влияние высоких температур на течение в пограничном слое.
Вследствие торможения потока в пограничном слое и повышения температуры
изменяется плотность газа, что оказывает влияние на параметры
пограничного слоя. В этом проявляется свойство сжимаемости и зависимость
параметров пограничного слоя от числа Маха.
С ростом скоростей температура увеличивается и пограничный слой
разогревается настолько, что в нем могут происходить химические реакции.
В результате наряду с изменением плотности изменяются также другие
физические параметры газа. Эти явления имеют решающее значение при
формировании процессов трения и теплообмена в пограничном слое. Однако их
учет связан с достаточно большими трудностями. Поэтому были предприняты
попытки отыскать сравнительно простые приближенные методы расчета
пограничного слоя при очень высоких скоростях обтекания. Один из методов,
рассматриваемый ниже, основан на использовании зависимостей, полученных
в результате исследований пограничного слоя в несжимаемой среде. Вблизи
поверхности всегда имеются области, где поток сильно заторможен и,
следовательно, газ близок по свойствам к несжимаемой среде. Если считать,
что течение в этой области оказывает основное влияние на процессы трения
и теплопередачи, то, следовательно, можно использовать для исследования
пограничного слоя те зависимости, которые по внешней форме сходны с
соотношениями для несжимаемой среды. Разница будет заключаться в том, что
в эти зависимости войдут параметры, определяемые в соответствии с местными
значениями температуры в пограничном слое. Причем, как показали
исследования, удовлетворительные результаты получаются в том случае, если
расчет вести по определяющей температуре Г* и соответствующим ей
определяющим значениям энтальпии £*, плотности р*, коэффициентов |х*, v* и т. д.
Рассмотрим некоторые зависимости для расчета пограничного слоя
по определяющим параметрам.
Ламинарный пограничный слой. Вводя определяющие
параметры, можно получить соотношения, учитывающие влияние высоких
температур. В частности, в соответствии с (VI-1-4), толщина
высокотемпературного пограничного слоя
«.-«„,(£$)"■. (VI-1-4-)
Аналогично можно определить толщину вытеснения и толщину потери
импульса в общем случае с учетом диссоциации и температуры стенки. Наряду
Трение и теплопередача па крыльях 327
с расчетом по методу определяющей температуры вычисления толщин можно
вести, используя обычные уравнения пограничного слоя. При условии, что
ср — const и Рг = 1 в результате решения этих уравнений получены
зависимости, позволяющие определять параметры пограничного слоя, близкие к
действительным, в функции температуры стенки и числа Mg. Эти зависимости
имеют следующий вид:
6J =-^ = 1,6* (fOT +0,18 Д) (l—I*)"1; (VI-1-29)
_ *##
6£* = —=
xk
где ТСТ = ТСТ/Т0; коэффициент
K=\ -ШТГ'
Здесь x = x/xk, число Re = F6^fe/v6; коэффициент Яст находят по одной из
формул (VI-3-2).
При замене в этих формулах ТСТ на Т& можно вычислить
коэффициент Xq.
Беря за исходную формулу (VI-1-5), найдем зависимость для
напряжения трения
т т °Л Р /Т7Т Л С/\
1ст. л — 1ст. л. не "т ~— • V v А"1"^ /
°л.нс Рб
Отношение напряжений трения равно отношению местных и средних
коэффициентов трения
тст. л __ cfx л _
тст. л.нс с/хл.нс с/л.нс
Из (VI-l-4/) видно, что при повышении температуры увеличивается
толщина ламинарного пограничного слоя. Напряжение трения, несмотря
на повышение вязкости, уменьшается, что обусловлено снижением плотности,
которая оказывает доминирующее влияние на трение. Соотношения для
расчета параметров пограничного слоя упрощаются при отсутствии диссоциации,
когда можно принять Рб/р* = Т*/Т&, [х*/^хб = (Т*/Т&)п.
Расчет напряжения трения по методу определяющей температуры
(энтальпии) при заданных параметрах потока на внешней и внутренней
границах ламинарного пограничного слоя проводится в следующей
последовательности.
Сначала находится определяющая энтальпия. Для этой цели можно
применить (IV-8-7) или зависимость, полученную для ламинарного
пограничного слоя
.„ _ 0,563 Рг* . 0,1264-0,437 Рг* . , 0,211 Рг* т/2
1 — 0,1264-Рг* ЧЛ 0,126 + Рг* *ст+ 1,53+Рг* Уб'
При этом в качестве первого приближения определяется величина i*,
рассчитываемая по числу Рг* = Ргст на стенке. Затем по этой величине V*
находится число Рг* во втором приближении и т. д.
Практически можно ограничиться расчетом определяющей энтальпии
в первом приближении, т. е. вычислять i* no (VI-1-32), полагая в ней
Рг* = Ргст.
328
Глава VI
При этом максимально возможное отклонение коэффициента трения,
а также теплопередачи от их истинных значений не превышает 10%.
По определяющей энтальпии при помощи таблиц или графиков
термодинамических функций воздуха находят определяющую температуру, затем
1,25
Q75
16-216°К
/0
/5
20 Мо
~'~0 5
Рис. VI-1-4. Зависимость сул~|/Ке°° (Reoo=Re=V6^/v5) в
функции числа Моо и относительной энтальпии гст = —т^-
(ламинарный пограничный слой)
0,075
0,05
0,025
Jcr0,2
15
Рис. VI-1-5. Зависимость с/ -j/Reoo в функции числа Моо и
относительной энтальпии гст = гСтЛ'о (турбулентный пограничный слой)
подсчитывают величину с = р*(ы*/рб^1б и вычисляют местный и средний
коэффициенты трения:
где
где
(VI-1-33)
Если коэффициент трения определяется для обеих сторон пластинки,
то полученный результат следует удвоить.
Трение и теплопередача на крыльях 329
Турбулентный пограничный слой. Если исходить из степенного
закона (VI-1-2) распределения скорости и соответствующего ему выражения
(VI-1-4) для несжимаемого пограничного слоя, то, вводя определяющие
параметры, можно найти формулу для толщины пограничного слоя:
R __ Я / М-* Рб \ 1/5 Л/Т 1 А"\
От - от. нс у— — J . (V1-1-4 )
Внешний вид формул для напряжения и коэффициентов трения тот же,
что и у выражений (VI-1-5') и (VI-1-31). Разница состоит в том, что толщину
слоя надо принимать в соответствии с соотношением (VI-1-4"). Применяя
(VI-1-8) для расчета коэффициента трения плоской пластинки в несжимаемом
потоке, можно получить обобщенное выражение для коэффициента трения:
B (£)-(£)'~. (VI-,-34)
в котором для ламинарного пограничного слоя п = —1/2, а для
турбулентного п=—1/5. Зависимость произведения c/Re~n от ряда параметров,
вычисленная с учетом диссоциации, показана на рис. VI-1-4 и VI-1-5.
Для расчета коэффициента трения в диссоциированном пограничном слое
можно также применять формулу
полученную из общих уравнений турбулентного пограничного слоя. В этой
формуле С/от — коэффициент трения, рассчитанный для соответствующих
местных величин Мб, Гст/Гб и Йеб = ^6Д?б, но при отсутствии диссоциации;
с*б> сбст—степени диссоциации соответственно на внешней границе слоя и на
стенке, которые для воздуха могут определяться в предположении, что он
является двухатомной моделью газа.
Местный коэффициент трения
с,От = 0,058Re, (^)~°'27 (l + tzl гщ)~^ =
= с, от. нс (^)Г-°'27 (1 +■*=! гЩ) -°'55, (VI-1-36)
где ~Rex = V6x/v6.
Расчеты ведутся при условии, что температура стенки задана. Некоторые
данные о коэффициенте cfoT приведены на рис. VI-1-б-т-VI-1-8.
Изменение величины cfXT/cfoT, рассчитанной по VI-1-35, графически
изображено на рис. VI-1-9. Из данных на рис. VI-1-9 следует, что влияние
диссоциации сказывается либо в увеличении коэффициента трения на 22%,
еслиаб = 1, аст = 0, поверхность каталитична и атомы полностью рекомбини-
руют на стенке, либо в уменьшении на столько же в другом случае, когда
а6 = 0, аст = 1 и поверхность не является катализатором.
Приведенные выше формулы для расчета пограничного слоя через
определяющие параметры могут быть отнесены к любому случаю течения. В
частности, им может быть течение около адиабатической стенки, т. е. ненагре-
ваемой и неохлаждаемой. Если теплообмен в газе отсутствует, то изменение
термодинамических параметров поперек слоя будет адиабатическим. Тогда
приведенные выше формулы будут отражать влияние сжимаемости (числа Моо)
на параметры пограничного слоя.
«г*
-——
— —
— —
— и.
—■ —
—■ —
1
=5
в.
ст
8
а- - -
а- - х
— — ..
0,5 ' /
1,0 '/
1,5 7 /
з,о/
%
*—у
/
7=
м
0
а—
7
1
— -
—
—-
—-
—
:—-—
:=
— —
— —
-——
———.
1——-.
——
— -
= :-
~-«-
— -..
—-•
ю7
Рис. VI-1-6. Местный коэффициент трения на
пластинке в несжимаемом турбулентном потоке
10
——.
g
т
—V /
Г0'2 5
щ
1ft
1Я'
*
-^
-—.
<
ч-
Г"
-9
ш.
—
——.
— —
— —
-——«
—•
-—.
—в
—«.
—».
—--
—--,
— «..
— -.
в -
- в
« в
« В
Ю7
10*
Рис. VI-1-7. Местный коэффициент трения на
пластинке в сжимаемом потоке при отсутствии диссоциации
(аб=аст =0)
10'
L
__ I
"■-^^^^-~
_/ / /
— —
г,
15 ///
1,5 V /
з,о/ /
*—-
—
г-
—>
——
■—. -»
"-1ВВ
—--.
—-«
—«
-*—.
"—в
"в,
==;
ю7
ю8
Re-
Рис. VI-1-8. Местный коэффициент трения на пластинке
в сжимаемом потоке при отсутствии диссоциации
(аб = аст = 0), Мб^=4
331
При этом формулы позволяют достаточно наглядно рассмотреть
качественную картину такого влияния. Сжимаемость будет доминировать при умеренных
скоростях полета, когда разогрев невелик. Благодаря этому газ будет менее
«жестким» и, следовательно, более
податливым к изменению плотности. Из сказанного
вытекает, что предпосылка о несжимаемости газа
в пограничном слое при умеренных скоростях
менее достоверна, чем при больших, когда
вследствие значительного повышения
температуры жесткость газа возрастает, и он ведет себя
как несжимаемая среда. Поэтому приведенные
формулы, содержащие определяющие
параметры, более достоверны в применении к расчету
пограничного слоя при очень больших
скоростях. При этом весьма важен тот факт, что
определяющие параметры вычисляются с учетом
температуры (энтальпии) газа на стенке,
которая участвует в формировании процессов трения
и теплообмена.
Схема расчета параметров турбулентного
пограничного слоя по методу определяющей
энтальпии при заданных условиях на свободной
границе слоя и стенке будет та же, что и для
ламинарного.
В том случае, когда параметры на стенке
не даны, а должны быть определены расчетом,
вычисление параметров трения как для
ламинарного, так и для турбулентного пограничных
слоев ведется совместно с расчетом тепловых потоков и температуры
поверхности с применением соответствующих уравнений теплопередачи.
Приближенный расчет турбулентного трения на пластинке (по
В. М. Иевлеву). Местное напряжение трения
1, (VT-1-37)
1,1
1,0
°>9
П Q
/
/
/
1
/
/
/
1ft
Рис. VI-1-9. Отношение
коэффициента трения на пластинке
с учетом диссоциации к его
значению при отсутствии
диссоциации
(105<Re6<108; 0<Мб<4;
0,04 < 77ст/Гб<1,0)
где
Ai = 0,
'224 + 3,966 • Ю-4;
= 1,175 Re*;
H-i
(VI-1-38)
(VI-1-39)
(VI-1-40)
Параметр рх представляет собой некоторую плотность, определяемую
соотношением
(VI-1-41)
Pi,р2—плотности соответственно при теплосодержаниях iu i2:
Й VI
(VI-1-42)
Величина \xt в (VI-1-40) определяется как вязкость при
теплосодержании i±.
332
Глава VI
—-с '
Ax
j
X
Смешанный пограничный слой
Точка перехода. Критическое число Рейнольдса. Приступая к расчету
пограничного слоя, следует проанализировать характер пограничного слоя
на пластинке и установить, является ли он чисто ламинарным, смешанным
или чисто турбулентным. Если пограничный слой является смешанным,
необходимо определить положение точки
перехода хт (рис. VI-1-10).
Строго говоря, переход ламинарного в
турбулентный пограничный слой происходит
постепенно, и тем не менее можно четко
зафиксировать начало и конец области
перехода. В связи с этим можно говорить о
критических числах Рейнольдса, одно из
которых соответствует началу, а другое —концу
перехода.
Началу области перехода соответствует
минимальное критическое число Рейнольдса,
Рис. VI-1-10. Смешанный погра- ниже которого все колебания в ламинарном
ничный слой на пластинке пограничном слое затухают. Из рис. VI-1-11,
где показано изменение коэффициента
сопротивления трения в несжимаемом потоке в зависимости от числа Rex ~ V&x/vq,
видно, что минимальное критическое число приблизительно равно 106.
За точкой минимума cfx следует резкое, почти скачкообразное
возрастание местного коэффициента трения, который достигает максимального
значения, соответствующего границе области перехода и максимальному
критическому числу Рейнольдса, равному примерно 5-Ю6. Правее этой границы
устойчивым будет турбулентный
пограничный слой.
Опытные данные показывают, что
наличие ламинарного участка и
области перехода не влияет на закон
развития турбулентного пограничного слоя
после точки перехода. Следовательно,
за точкой перехода можно
использовать зависимости, полученные в
предположении, что течение в пограничном
слое полностью турбулентное.
Положение точки перехода на
поверхности тела зависит от многих
факторов, основными из которых являются
степень турбулентности потока,
состояние поверхности, температурный фак- Рис. VI-1-11. Изменение коэффициента
тор и число Мб.
В дальнейшем будем
рассматривать точку перехода, соответствующую
критическому числу Рейнольдса, которое определяется как среднее между
его значениями для начала и конца перехода.
Таким образом, принятая схема соответствует бесконечно малому
размеру области перехода.
Влияние степени турбулентности в несжимаемой жидкости на число ReKp
в точке перехода приведено на рис. VI-1-12 [степень турбулентности,
откладываемая по оси абсцисс, измеряется в процентах и равна (1/F) х
0,007
0,006
0,005
0,00k
0,003
\
\
\
\
\
V
)
сопротивления трения в несжимаемом
потоке в зависимости от числа Rex
X Y(l/S) (и'2 + v'2 + w'2) • 100, где и', v', wr — пульсационные составляющие
скорости; V — средняя скорость потока].
Трение и теплопередача на крыльях
333
С увеличением числа М§ влияние степени турбулентности на ReKp
уменьшается и при Мб>4н- 5 это влияние можно не учитывать (рис. VI-1-13).
Влияние состояния поверхности на ReKp, характеризующегося
параметром А/б* (А —высота бугорков шероховатости, б* — толщина вытеснения),
ReKp 10-6
к
\
'
■—-.
—-—.
— —
— —
Рис. VI-1-12. Влияние степени турбулентности в несжимаемой жидкости
на число Рейнольдса в точке перехода
при различных Мб показано на рис. VI-1-14. Можно заметить, что с
увеличением числа Мб шероховатость оказывает на критическое число Рейнольдса
все меньшее влияние, которым можно пренебречь при Мб > 4-4-5.
Охлаждение обтекаемой поверхности способствует стабилизации
пограничного слоя и повышению критических чисел ReKp. Критерием
устойчивости течения в пограничном слое
является температурный фактор
Tci = TCT/Tr, в зависимости от
которого на рис. VI-1-15
показано изменение величины
При охлаждении
поверхности уменьшается толщина
вытеснения пограничного слоя,
следовательно, при достижении
некоторого значения б* < А эффект
от охлаждения будет снижен за
счет влияния на критическое
число Рейнольдса шероховатости. Рис. VI-1-13. Влияние степени турбулентности
По данным рис. VI-1-15 по- на критическое число Рейнольдса при различ-
строена универсальная кривая ных числах м* (по Ван-Драйсту)
(рис. VI-1-16), характеризующая _
изменение величины ReKp/(ReKp^ _.ч от параметра (Гст — 1)/М1, включающего
в себя, как видно, температурный фактор и число М6.
Анализ приведенных данных показывает, что с ростом числа Мб
уменьшается влияние на переход ламинарного пограничного слоя в турбулентный
таких факторов, как степень турбулентности, шероховатость, охлаждение
стенки.
По теоретическим и экспериментальным данным о критических числах
Рейнольдса можно построить графики, определяющие области устойчивого
Глава VI
Рис. VI-1-14. Влияние состояния поверхности на
критическое число Рейнольдса
%
ФЧ
2,0
X
\
3
\
\
\
\|
\
0,5 0,6
0,7 0.8
-0,02
Рис. VI-1-15. Влияние температурного
фактора ~ГСТ = Тст/Тг на отношение
ReKp/(ReKp)-T :
; - Ван-Драйст Мб = 3,65
3 - » Щ=2»7
2 - Джен Мб= 3,0
4 — БрауЕШнг Mg = 1,85
5 — Занесений Mg = 1,67
Рис. VI-1-16. Экспериментальная
кривая, характеризующая изменение
величины ReKP/(ReKP)- от параметра
_ ■/ст~1
(Тст -
Трение и теплопередача па крыльях
335
ламинарного пограничного слоя. Один из таких графиков показан
на рис. VI-1-17, где области внутри кривых i, 2 соответствуют устойчивому
ламинарному пограничному слою, обнаруженному в экспериментах на
пластинке.
Определив точку перехода, можно осуществлять расчет параметров
пограничного слоя отдельно для области чисто ламинарного и чисто
турбулентного течений. Однако за точкой Т (см. рис. VI-1-10) зависимости
для расчета турбулентного пограничного слоя не могут быть
непосредственно применены, так как слой начинается не с нулевой толщины,
а с какого-то конечного значения. Чтобы избежать этой несогласованности,
надо найти условное начало турбулентного пограничного слоя, определяемое
на рис. VI-1-10 точкой О'. С этой целью
можно воспользоваться одной из следующих
двух схем.
В соответствии с первой схемой
принимается, что расстояние Ах до точки (У,
являющейся началом условной пластинки с
полностью турбулентным слоем, должно быть таким,
чтобы обеспечить толщину турбулентного
пограничного слоя бвт в месте перехода,
равную толщине ламинарного слоя на длине хт.
При малых скоростях это приводит к условию
где Ai =
числа Рейнольдса
Неякр =
Рис. VI-1-17. К определению
области устойчивого ламинарного
пограничного слоя:
1 — пластина (труба); 2 — пластина
(полет); з — конус (полет)
Здесь критическое число Re* Kp может
быть найдено по данным, приведенным выше. Вместе с тем для
приближенного учета влияния больших скоростей можно также воспользоваться
определяющими параметрами. В этих целях выражения для чисел Рейнольдса
можно представить в следующем виде:
где Re^p для несжимаемого пограничного слоя может быть принято
равным (2-7-5) 106. Так как координата хт известна, то можно найти
величину Ах.
Согласно второй схеме предполагается, что в точке перехода одинаковы
не толщины пограничного слоя, а толщины потери импульса б** для
ламинарного и турбулентного слоев и из этого условия вычисляется
величина Ах. Расчетная формула будет аналогична (VI-1-43) с той разницей,
что коэффициенты Аи А2 надо принять соответственно равными 0,808
и 0,036. По второй схеме значения для Ах будут несколько больше, чем
по первой. Можно предположить, что среднее между значениями Ах,
которые дают обе эти схемы, лучше будет соответствовать действительности.
После того как найдена точка О', можно приступить к вычислению
толщин пограничного слоя, распределения касательных напряжений и
местных коэффициентов трения, используя при необходимости зависимости,
включающие определяющие параметры.
Средний коэффициент трения для пластинки длиной хк, обтекаемой
смешанным пограничным слоем, в соответствии с рис. VI-1-10 определяется
336
Глава VI
формулой
_
cf не —
f л. нс — г" с/ т. нс — С/ т. нс —Г~ 1
х'
хк
(VI-1-44)
ГТТР X — СС — '
Число Рейнольдса для первого коэффициента С/Л.нс вычислено по длине хТ1
для второго коэффициента с}тяс—по длине х\ для третьего коэффициента
с/т. нс—по длине Ах.
Трение на пластинке,
расположенной под углом атаки
Рассмотрим пластинку, обтекаемую сверхзвуковым потоком с
присоединенным скачком уплотнения. Расчет трения ведется для каждой стороны
отдельно при условии, что течения сверху и снизу
независимы. Одно из них возникает как течение
с постоянной скоростью за косым скачком
уплотнения, другое —также с постоянной скоростью как
течение расширения за простой волной.
Поэтому для определения местных и средних
коэффициентов трения используются приведенные
выше зависимости. Причем заданными являются
параметры на нижней и верхней сторонах пластинки,
вычисляемые по теории скачка уплотнения и теории
течений разрежения Прандтля — Майера.
Расчет можно вести в общем случае с
применением метода определяющей энтальпии. Силы трения,
действующие на нижнюю и верхнюю поверхности
пластинки, соответственно равны
о
/
is
/|
/
М^20
4^
4
8
12
Рис. VI-1-18. Отношение
/ н
q скоростных напоров
на нижней (сплошные
линии)и верхней
(пунктирные линии) стороне
пластинки к скоростному
напору qoc = PooF^/2
где g =
причем
где qR = pHFH/2, qB = pBFB/2 — скоростные напоры, cf H,
ct в — средние коэффициенты трения соответственно на
нижней и верхней сторонах.
Суммарная сила трения пластинки, наклоненной
под углом а,
"~/* Ra = RfR + RfB = 2cfaqxKi (VI-1-45)
а коэффициент
1 '" ' " 7в), (VI-l-46)
у у
Следовательно,
где
угла
Ufa
Rf*=o
h
an
~q — Ян ' a
^н g ' yB
атаки Rfa^o
Ча к
cfa=0 a
Cfa=Q Ш
Яв
Я
= 2cfa=oqxll
2
Cf в —
'" Cfa=0 q"
(VI-1-47)
(VI-1-48)
На рис. VI-1-18 приведены отношения скоростных напоров qK и qB1
а на рис. VI-1-19 — значения коэффициентов кап и кав для ламинарного
и турбулентного пограничных слоев.
Ф
/
1
1 \
/
7 Л
'А
сС=16°
\
/
/у
/
У
/
к/
^—.——
>
J
/1
/12у
'А
/
/
/
—
t±±
О 5 10 15 М^ 0 5 W 15 М^
Рис. VI-1-19. Коэффициенты кан на нижней поверхности (сплошные линии) и кав на
верхней поверхности (пунктирные линии):
а — турбулентный слой; б — ламинарный слой. Относительная энтальпия на стенке; Т„т = 0,2
СТ
Рис. VI-1-20. Суммарные
значения коэффициента
ка для пластинки.
Сплошные линии —
высота Н =0 км, пунктир- 3
ные — Н = 60 км:
а — турбулентный слой; б —
ламинарный слой.
Относительная энтальпия на стен- I
ке; 1'ст= 0,2
/
/
//
/
//
/
/
/
I /
/
8/
//
У:
ф
/.
/j
is.
oC=16°j
/
/
0 5
/5 Мо
0 5 10 15 Мо
тсмещ
о ю м^
Рис. VI-1-21. Влияние точки перехода на коэффициенты трения при очень
больших скоростях
4
0,6\ \s
Яе=Ю7
7ст=0'2
22-114
338 Глава VI
На рис. VI-1-20 показаны графики для суммарных значений ка,
полученные для условий, что на стенке iCT = £CT/ir = 0,2.
На рис. VI-1-21 показана зависимость коэффициента трения от
координаты точки перехода при различных числах М<х> и значениях Re = 106
и 107. Эта зависимость, как следует из данных на рис. VI-1-21,
уменьшается с ростом Моо и снижением чисел Re.
§ VI-2. Теплопередача на
плоской пластинке
Несжимаемый поток
Теплопередача от несжимаемого пограничного слоя к плоской стенке
в какой-либо точке может быть охарактеризована местным числом Стантонаг
определяемым в соответствии с формулами (IV-8-38), (VI-1-7) в виде
Среднее по длине пластинки число Стантона
i (VI-2-2)
Значения коэффициентов С и D и показателя степени п приведены
в табл. VI-1-1.
Для ламинарного пограничного слоя местное и среднее значения
параметра /2 (соответственно f2x и /2Ср) одинаковы и вычисляются по формуле
f2x = /2ср = Рг~2/3. Для турбулентного пограничного слоя значения f2x и /2Ср>
можно принимать такими же, как для ламинарного слоя, однако для
большей точности f2x следует вычислять по (IV-8-38'), а /2ср — из (IV-8-38").
Влияние больших скоростей
Формулы (VI-2-1) и (VI-2-2) применимы для расчета тепловых потоков
не только при малых, но и при больших скоростях, когда существенно
влияние сжимаемости, и параметры, от которых зависит теплопередача,
претерпевают изменение вследствие кинетического нагрева.
В этом случае расчет теплопередачи можно вести по определяющей
энтальпии, применяя (IV-8-7). При этом расчет можно вести в общем случае
диссоциирующего ламинарного или турбулентного пограничных слоев.
Удельный тепловой поток лучше определять из выражения
gCT = St?p6F6 (ir — iCT). (VI-2-3)
Ламинарное течение. Как показывают исследования, для
ламинарных потоков значение /2х лучше принимать равным 0,437 (1,3 + Рг*)/Рг*.
В соответствии с этим число Стантона в (VI-2-3)
^T)=°'145 ^ Y
где С = р**/
Число Нуссельта, вычисляемое по определяющим параметрам,
- gcfPT = 0,145 (1,3 + Рг*) УШГХ. (VI-2-4')
Трение и теплопередача на крыльях 339
Из приведенных соотношений следует, что изменение величины р\х
по толщине пограничного слоя является важным фактором, влияющим
на трение и теплопередачу.
При приближенной оценке местного числа Нуссельта можно исходить
из экспериментальных данных [46], согласно которым
NuJ = 0,33 (Re*)0'5 (Pr*)0'33. (VI-2-4")
где ReJ = F6^/v*.
Если принять Pr* постоянной величиной, равной 0,74, то Nu* =
= 0,3(Re*)0'5.
При температуре стенки ниже предела диссоциации удельный тепловой
поток дСт = ах{Тг — ТСт), где
Среднее число Стантона
StSp = 0,29 Щ^ ]/JL , (VI-2-5)
где R F/
Для расчетов ламинарных тепловых потоков без учета диссоциации
и при сръ = const можно пользоваться формулой
=ах (ТТ-ТСТ) = 0,332 (-Ш!«_)Г<"/15 X
V МстРст/
X -——I Act I/ -—-11-icTJrr 1 CT, lvl ^ °/
где ТСТ = ТСТ/ТГ.
Значения р,* и р* рассчитываются по температуре Г*, которая в свою
очередь должна выбираться с учетом состояния стенки.
Если TCT<iTr (стенка нагреваемая), то Г* находится из формулы
где Го — температура торможения набегающего потока.
Если ТСТ>ТГ (стенка охлаждаемая), то следует принять Г* = ГСТ. При
малых скоростях обтекания пластинки определяющая температура Т* = Т&.
Приближенный расчет турбулентной теплопередачи на пластинке
(по В. М. Иевлеву). Удельный тепловой поток может вычисляться по формуле
qcT = A2pxV^ (VI-2-8)
где
А2 - 0,9Л [1,1 + 2,58 (1 - Рг)3 2о,о75]; (VI-2-9)
= 0,9 ^4- (Pr-0,9); (VI-2-11)
Z
Входящие в приведенные зависимости величины рх, ц, z определяются
по формулам на стр. 331.
При приближенных оценках теплопередачи можно пользоваться
эмпирическим соотношением [46] для числа Нуссельта:
Nu* = q™ep6X = 0,029 (Re*)0'8 (Pr*)0'4. (VI-2-13))
A5 (ir — 1Ст)
22*
340 Глава VI
Если принять Рг* = 0,74, то
Nu* = 0,026 (ReJ)0'8. (VI-2-14)
Для холодной стенки при отсутствии на ней диссоциации
теплопередача qCT = ах (Тг — Гст), где
ах = 0,026 2± (Re*)0'8. (VI-2-15)
Для пластинки, расположенной под углом атаки, теплопередача
определяется для каждой стороны отдельно, а затем суммируется. Этот расчет
связан с определением параметров невязкого возмущенного потока. При
•сверхзвуковом обтекании с присоединенным скачком определение невязких
параметров ведется по теории скачка уплотнения, а на стороне, где скачок
не возникает, — по теории Прандтля —Майера.
Теплопередача на пластинке,
расположенной перпендикулярно
к направлению набегающего потока
(ламинарный пограничный слой)
Рассмотрим тепловой поток к пластинке, обтекаемой под углом атаки
а, = 90° (см. рис. V-7-5). В этом случае перед пластинкой возникает
отсоединенная криволинейная ударная волна. Вследствие сильного торможения
потока за ударной волной пограничный слой около пластинки может
рассматриваться на всей поверхности ламинарным.
Удельный тепловой поток при термодинамическом равновесии и условии,
что стенка сильно охлаждена, а отношение р^х = р^л/рстМ^ст = 1 рассчитывается
при помощи формул (IV-8-42) и (IV-8-46). Положив в них cog^co^ k = 0,
х = у, получим следующие расчетные зависимости [47]:
qT = 0,47 Pr-2/з (p6fx6)1/2 V'JhrF (у), (VI-2-16)
где
Значение функции F (у) может быть найдено при помощи экстраполя-
ционных формул (V-7-38) и (V-7-39), по которым вычисляются отношения
давлений Рб/Ро и скорости Fa/Foo. В соответствии с (V-7-39) отношение
давлений
Р6 *-У.
Ро 2 —б0
Внося значение Рб/р'о, а также величину F^/Foo, определяемую из (V-7-39),
получим
где
и
" ГТпТТ^- • (VI-2-20)
Трение и теплопередача на крыльях
В точке полного торможения
h (0) = у (2 - б0); h (0) = [| (2 - б0)]1/2. (VI-2-21)
Учитывая (VI-2-20), получим для F(0) выражение
или F (0) = |/Т , (VI-2-20')
F(0)=2M-
так как в соответствии с (V-7-40) значение (4/3) б0 =Д. У кромки пластинки
(у = 1) значения Д (у) и /2 (у) будут следующими:
h (1) - 3,46 (1 -2б0); /2 (1) = 1,79 (1 - 1,2бо)1/2. (VI-2-21')
Отбрасывая малые величины порядка 8JJ, получим
F (1) - 1,2 (1 —1,1560) F (0), (VI-2-20")
где F (0) определяется при помощи (VI-2-20').
В (VI-2-16) входят плотность ps и коэффициент динамической вязкости \i6,
в общем случае являющиеся переменными величинами вдоль размаха
пластинки.
Их значения можно было бы определить следующим образом. Вначале
для точки полного торможения по i0 и р0 определяется энтропия S'o, что
можно сделать по таблицам или графикам термодинамических функций,
учитывающим в общем случае диссоциацию и ионизацию. Затем, полагая
течение вдоль стенки изэнтропическим, находят по местному давлению р&
и энтропии S'o местную плотность рб, а также температуру 7V Вязкость
можно определить, в частности, по формуле Оэзерленда по значению 2V
Расчеты показывают, что изменение плотности и коэффициента вязкости
по сравнению с их значениями в точке полного торможения мало и имеет
порядок бр.
Поэтому с точностью до бц параметры рб и \iq можно принять
постоянными и равными соответствующим значениям р^ и \i'o в точке полного
торможения. Число Рг можно также принять постоянным и равным значению
этого числа в той же точке полного торможения.
Таким образом, изменение теплопередачи будет определяться
функцией F (у). Для произвольной точки
^Jl (VI-2-22)
?то F(0)
где <7то — теплопередача в критической точке, равная
. (VI-2-23)
При гиперзвуковых скоростях энтальпию торможения можно определять
по формуле i0 = 0,5Vlo.
Из (VI-2-20") следует, что у кромки пластинки (у = 1) тепловой поток
?T = l,2gT0(l-l,1560). (VI-2-24)
В зависимости от б0 величина qT может быть больше или меньше, чем
в точке полного торможения.
Вместо размерной величины можно использовать безразмерный критерий
теплопередачи
Re^/2Stx=0,47Pr-2/3 (£S-M.)i/2F ft), (VI-2-25)
\Poo f-loo /
Глава VI
где Reb = FooPoob/[Aoo;
Stx = ax/(pooVooCp) = qT/(pooVooir)-
Для определения безразмерного критерия теплопередачи в критической
точке функцию F (у) в (VI-2-25) надо принять равной F (0) (VI-2-20'). Таким
образом, отношение коэффициентов Стантона для произвольной точки и точки
полного торможения будет аналогичным отношению (VI-2-22), т. е. равно
F(y)/F(0).
Теплопередача на отклоненной пластинке. Изложенная
методика расчета теплопередачи относится к случаю, когда поток набегает
на пластинку под углом атаки а = 90°. При отклонении потока от этого
направления, т. е. при а < 90°, можно предположить, что распределение
тепловых потоков по размаху будет определяться теми же соотношениями,
что и при а = 90°, в которых скорость Foo заменена составляющей FooSina0
В соответствии с этим теплопередача в критической точке при а<90.
?то = (gT0)a=90 sin5/2a. (VI-2-26)
Для безразмерного критерия теплопередачи в критической точке
получим зависимость
Rel/2 (St)0 = [Rel/2 (St)0]a=90 sin5/2a. (VI-2-27)
Для расчета распределения теплопередачи по размаху отклоненной
пластинки используется формула (VI-2-22).
Средняя теплопередача. Интегрируя по поверхности, определяют
средний удельный тепловой поток:
1
Подставляя под интеграл значение для qT (VI-2-16) и функцию F (у)
в виде (VI-2-20), получаем
дср = 1,13 (1 -0,7560) gT0. (VI-2-28)
В зависимости от отношения плотностей средний тепловой поток на
пластинке может быть больше или меньше его значения в точке полного
торможения. Например, для б0 = 0,2 значение #Ср —0»96дт0, а для 60 = 0,05
получаем gCp = l,09gT0.
Влияние диффузии. Экспериментальными исследованиями получен
следующий результат для параметра полного удельного теплового потока
в точке торможения при наличии диффузии [59]:
^ (]-°'4Г1 + (Ье0,52_1)^1 (VI-2-29)
Это соотношение учитывает изменение величины р\х по толщине
пограничного слоя и пригодно при температуре стенки, не превышающей
температуру торможения.
Удельный тепловой поток определяется следующими соотношениями:
g.faW Re = ^(5)0. .(VI-2-30)
Чтобы найти распределение теплового потока по пластинке с учетом
диффузии, можно исходить из предположения, что влияние числа Льюиса-
Семенова в различных точках будет таким, как в точке полного
торможения. Следовательно, можно использовать формулу (VI-2-22), которая
пригодна для сильно охлажденной поверхности и не учитывает влияния гради-
Трение и теплопередача на крыльях 343
*ента скорости. Чтобы учесть это влияние, можно воспользоваться зависимостью
44,
Яо F(0) £Ст0
в которой отношение g'c?/gcT0 определяется эмпирической формулой
Д^ = 0,82 (1 + 0,096р1/2) l~gcT . (VI-2-32)
Коэффициент
l6 ^ In £ гбРб с) ^*У
О
§ VI-3. Трение и
теплопередача на крыльях
конечной толщины
Крыло с заостренной передней
кромкой
При рассмотрении пограничного слоя около плоской пластинки скорость
вне пограничного слоя вдоль оси х принималась постоянной. Следовательно,
давление будет также постоянным, и градиент давления dp/dx = 0. В
отличие от прямолинейной стенки на криволинейных поверхностях скорость
на внешней границе пограничного слоя является переменной функцией
координаты х. На этой границе давление будет меняться вдоль оси х,
а значит, градиент давления dp/dx^O, что следует учитывать при расчете
лограничного слоя.
Рассмотрим влияние градиента давления на ламинарное трение.
Приводимые ниже результаты основаны на предположении, что число Рг = 1,
а коэффициент динамической вязкости пропорционален температуре. Как
показывают исследования, эти допущения при условии постоянных тепло-
емкостей вносят малую погрешность в результаты расчета параметров
пограничного слоя.
Для определения течения в пограничном слое можно использовать
уравнения движения (Ш-2-11), неразрывности (Ш-2-21) и энергии (Ш-2-47),
при условии, что рассматривается двухмерное плоское течение. Кроме того,
в уравнении (Ш-2-47) принимается равным нулю последний член в правой
части, а энтальпия торможения i0 заменяется температурой торможения
0 (p)
Система уравнений преобразуется к переменным Дородницына,
имеющим вид
где
_ Ро ' <0 Po ° Ро
0 0 0
Ро \ 2г'о/ Ро Т Ро
Коэффициент динамической вязкости, входящий в уравнение движения,
определяется из выражения
■£-=*^, (vi-3-i)
344
Глава VI
где А, в соответствии с (Ш-1-5) или (Ш-1-6) определяется соотношениями
К= t^?)71'1 или Х== Vj^tI^IIi ' (VI-3-2)
при
ный
условии, что температура стенки задана.
В результате преобразования система уравнений принимает вид,
сходс системой для несжимаемой жидкости. Ее решение ведется с учетом
граничных условий на стенке (Т = ТСТг
Ух = Vy = 0) и на границе слоя
[(dVJdif])1]==6 = 0]1 где б —значение
переменной т] на границе слоя.
В качестве закона изменения
скорости по сечению пограничного слоя
выбирается параболическая
зависимость Vx = а^ц -f а2т[2 -f ^зЛ3 + • • • ^е"
личина местного напряжения трения
Ро
ldV
0,25
Рис. V1-3-1. Значения Cfxsl]/Re для
различных профилей, вычисленные по формуле
(VI-3-3)
Не излагая подробно решения^
приведем основные результаты.
Местный коэффициент трения
X
Г1 + 4
<* г Ъек(х)
2 7^(^(5^4-1)
(У1-з-
4 tr
где Хб вычисляется по одной из
формул (VI-3-2), в которых Тст заменяется?
Коэффициент
где
7+8Г_
с, (VI-3-4)
Положив в (VI-3-3) значения
V'& = 0 и А: (#) = лг, получим формулу
для коэффициента трения на плоской
пластинке, на которой градиент
давления равен нулю.
В качестве примера по (VI-3-3)
вычислены значения cfx ]/Re для
параболического профиля с уравнением
г//Ь = 0,12 (х/Ъ) (l—x/b),
параболической стенки с уравнением у/Ь = 0,05 (х/b)2, а также для пластинки,
расположенной в потоке с числом Моо = 3 и имеющей температуру Тст = 1
(теплоизолированная стенка). Из представленных на рис. VI-3-1 результатов расчета
следует, что наличие отрицательного градиента давления приводит к увели-
Рис. VI-3-2. Значения cfxn\' Re для
параболической стенки с уравнением у = 0,05 х2
при различных величинах Тст (Моо = 3,0)
Трение и теплопередача на крыльях
345
чению трения, а положительного, наоборот, к уменьшению его величины
по сравнению с пластинкой (V& = 0).
На рис. VI-3-2 и VI-3-3 показаны кривые, построенные по (VI-3-3),
характеризующие одновременное влияние температуры стенки и градиента
давления. Охлаждение стенки увеличивает трение при положительном
градиенте давления (рис. VI-3-2), как и при его отсутствии (пластинка). Что
касается влияния отрицательного
градиента давления (рис. VI-3-3),
то оно неодинаково по своему
характеру для различных участков
профиля. В начале профиля при
охлаждении стенки трение становится
больше, а на периферийных
участках, наоборот, меньше.
\V
N
-. /
Ik
'II!/}.
JJJJ .
—-—i
0
0,25
0,50
0,75
0,10
0,05
\
0
10 Ma
Phc.VI-3-3. Значения Cfxл Y Re для
параболического профиля с уравнением у = 0,12а: (1 —
— х) при различных величинах Гст (Моо =
= 3,0)
Рис. VI-3-4. Координата точки отрыва
при условии, что скорость на профиле
меняется по линейному закону (у^ =
= 1 — х), а стенка теплоизолирована
Полагая местный коэффициент трения (VI-3-3) равным нулю, можно
определить координату точки отрыва ламинарного пограничного слоя. Более
точные исследования показывают, что эту координату лучше определять
из уравнения
_ 7ik& = ___JA_. (vi-3-5)
V6(l-Vl/2i0) 5Гст + 1 V }
На рис. VI-3-4 показаны результаты расчета по уравнению (VI-3-5)
координаты точки отрыва х — хотр при условии, что скорость вдоль профиля
меняется по линейному закону (Vq = 1—x), а стенка теплоизолирована
(Гст=1).
Приближенный расчет трения и теплопередачи на профиле. Этот расчет
основан на использовании решений для безградиентного сжимаемого
пограничного слоя, т. е. на применении соответствующих зависимостей,
полученных для плоской пластинки.
Излагаемый ниже метод дает удовлетворительные результаты для
контуров с малой кривизной, обтекание которых характеризуется малыми
продольными градиентами давления, не оказывающими почти никакого влияния
на профиль скорости. Влияние градиента давления может быть учтено
соответствующим подбором эффективной длины при определении числа Рейнольдса.
Метод состоит в том, что контур заостренного профиля, обтекаемого-
с присоединенной ударной волной, разбивается на ряд небольших
прямолинейных участков. Таким образом, в схеме расчета рассматривается про--
346
Глава VI
филь, принадлежащий крылу единичного размаха, которое состоит из
совокупности пластинок малой длины (рис. VI-3-5).
В начале расчета определяются параметры невязкого потока. С этой
делью может быть использована теория скачков уплотнения и теория
Прандтля — Майера. При этом
возмущения предполагается, что на
каждой пластинке (грани)
«невязкие» параметры являются
величинами постоянными.
Рассмотрим две
разновидности метода, одна из
которых основана на
предположении равенства толщин слоя
при переходе от одной
пластинки к другой, а другая —
равенства толщин потери
импульса.
Гипотеза равенства
толщин пограничного
слоя. Расчет трения может быть осуществлен по универсальным формулам
как для ламинарного, так и для турбулентного пограничного слоя. Причем
для турбулентного слоя используется закон «корня седьмой степени».
Рассматривая грань 1 на верхней стороне, где параметры свободного
(невязкого) потока известны, можно найти по длине грани х± и значениям рь
Fi, jXi число Re1 = p1F1.r1/[x1.
Коэффициент трения, который можно считать средним по величине
для грани, находят по формулам для пластинки по определяющим
параметрам с учетом структуры пограничного
слоя или при помощи графиков на рис.
VI-l-4-г- VI-1-5 в зависимостиот числа Mt
и относительной энтальпии iCTi. Из рис.
VI-1-4, VI-1-5 находят величину (CfRe'^^
а затем подсчитывают коэффициент
Скачок
Рис. VI-3-5. Схема потока при сверхзвуковом обте-
-кании профиля с прямолинейными стенками и
присоединенной ударной волной
Рис. VI-3-6. К расчету трения и
теплопередачи на профиле
Переходя к грани 2 (рис. VI-3-6),
принимают, что толщина пограничного слоя
в начале этой грани такая же, как и в конце
грани 7. Но слой такой толщины в начале
грани 2 можно рассматривать как результат обтекания фиктивной пластинки
длиной #ф2 —#2 = Яд2 потоком с числом М2. Длина хд2 фиктивного
дополнительного участка может быть найдена из указанного выше условия
равенства толщин пограничного слоя, т. е. из выражения
j
где числа Рейнольдса Re{ и Refl2 вычисляются по местным значениям
скорости V± и Fa2 = F2, длинам х±, £д2 и, в общем случае, по определяющим
значениям коэффициентов кинематической вязкости v* и vjj^ — vf.
Средний коэффициент трения на длине Хф2, соответствующей силе тре-
лия Хф2, будет
Так как на фиктивном участке длиной Хт&, где действует сила трения Хд2,
коэффициент трения с, д2 = (c/Re-^ReJk, T0 сила трения на грани 2
Трение и теплопередача на крыльях 347
Имея в виду, что (cf Re~n)A2 = (cf Re~n)<fr2 = (cf Re"n)2, получим для
коэффициента трения на грани 2
В соответствии с этим для любого £-го участка
сfl = (cf Re-"), [Re5 i (-^- +1) - Re£, x-ff] . (VI-3-6)
При этом полная длина фиктивного элемента x$\=xRi-\-Xi, где длина х%
определяется рекуррентной системой уравнений
ХЛ гИвд i = Хф, г-1 Щ, i-1, (VI-3-7)
в которых числа Рейнольдса в общем случае вычисляются по определяющим
параметрам.
Рассчитав, таким образом, коэффициенты трения и соответствующие
силы на нижней стороне, проводят аналогичный расчет для верхней стороны.
Суммируя, можно найти силу трения профиля
N
Xf= ^XfiCosQt,
%=i
где Xft — силы трения на нижней и верхней гранях;
0j — углы наклона граней к направлению вектора Foo;
i~ номер грани;
TV —общее число граней на нижней и верхней сторонах.
Общее выражение для силы трения на какой-либо грани имеет вид
где скоростной напор qt = ptV\l2 определяется по соответствующим невязким
параметрам на рассматриваемой грани.
По известным значениям коэффициента трения на местных пластинках
при помощи аналогии Рейнольдса может быть вычислено число Стантона
и определен удельный тепловой поток.
Гипотеза одинаковых толщин потери импульса. Расчет
по этой гипотезе, как и в предыдущем случае, может быть осуществлен как
для ламинарного, так и для турбулентного пограничного слоя. Примем
при этом, что пограничный слой недиссоциирован, удельные теплоемкости
постоянны, а влияние сжимаемости на коэффициент трения проявляется
в его зависимости только от числа Маха.
Для грани 1 коэффициент трения определяется как для обычной
пластинки по значению 'Rei = VixJv^ и числу М^ При переходе ко второму
участку для определения числа Рейнольдса по параметрам этого участка
следует знать фиктивную дополнительную длину #Д2, учитывающую
предысторию развития пограничного слоя. Эта длина вычисляется исходя из
гипотезы о том, что толщина потери импульса остается неизменной на границе
перехода от первого участка ко второму. В соответствии с этим
где левая часть равна (1/2) (cfx)1, а правая (1/2) (с/#)Д2. Поэтому можно
написать, учитывая зависимость Cfi и СуД2 от сжимаемости, выражение
для определения длины жд2:
Г
L
1~ n
J
д _/]. Г
где п определяется в зависимости от вида пограничного слоя по табл. VI-1-1.
348 Глава VI
Отношения Cflcf Нс Ддя первого и второго участков определяются в
зависимости от соответствующих значений чисел М4 и М2 на этих участках
с использованием формул (VI-1-18) для ламинарного пограничного слоя
и зависимостей (VI-1-19) — (VI-1-21) для турбулентного слоя.
Для произвольного i-то участка фиктивная длина определяется из условия
1 п
*г-1 + *д*-1 L (cf/cfHc)i J "L (Цб/Рб^б)*
Если предположить, что профиль скорости в турбулентном слое меняется
по более общему закону «корни степени к», то в этом случае (VI-3-8)
примет вид
fe+3 2
(cf/cfHC)i J L
(VI-3-9>
Определив фиктивные длины пластинки хж *, можно перейти к вычислению
коэффициентов и сил трения на гранях.
Коэффициент трения на первой грани
/нс
Для второго участка
СП - {-$-) , Г(С,»)Ф2 (-^-+1) - (С/нс)д2-^
где (с/нс)ф2 и (с/нс)д2 определяются по формулам для несжимаемой жидкости
и для значений чисел Рейнольдса, вычисленных соответственно по длинам
и xR2 и по параметрам на втором участке.
Для произвольного i-то участка
Зная числа Рейнольдса Re^ = Т7ф^фг/^ь значения(^д i + Xi)/xt, можно
определить толщины пограничного слоя в конце каждой грани.
Определив коэффициенты трения, можно вычислить удельную
теплопередачу с учетом влияния градиента давления на криволинейной поверхности.
Для этой цели можно воспользоваться формулами (VI-2-1) и (VI-2-2),.
вытекающими из аналогии Рейнольдса.
Теплопередача на затупленной
поверхности крыла
Точка полного торможения. Передняя кромка может иметь плоское
затупление. В этом случае тепловой поток в точке полного торможения
рассчитывается по (VI-2-23) для плоской пластинки, обтекаемой
гиперзвуковым потоком.
Для точки полного торможения, принадлежащей криволинейной
затупленной поверхности носка, расчет термодинамически равновесной
теплопередачи следует вести по формулам (IV-8-47) и (IV-8-48). Принимая в них
е=^0, получим
q = qT0 = 0,47 Рг-2/з V$
Здесь градиент скорости X определяется при очень больших числах
Маха из выражения
Трение и теплопередача на крыльях
349
При умеренных сверхзвуковых скоростях величину к можно получить
из формулы Ньютона для распределения скорости
{__
2 2 ~~ fe—1
Foo (&[(k — l)Moo + 2]\-/l к — 1 (к — 1) Moo -4- 2~| 11/2
i — о И-Н о г г • (Vl-o-lo)
I (Л + DMSo L 2 2Ш«(А: — 1) J J
дх)х=о
2RT
Расчет теплопередачи с учетом диффузии и изменения величины р[х
поперек пограничного слоя, а также для произвольных значений ТСТ можно
осуществлять при помощи формул (VI-2-29) и (VI-2-30).
Если крыло обладает стреловидностью,
теплопередача в критической точке передней кромки
будет меньше, чем у прямого. Уменьшение
теплопередачи можно оценить с помощью графика на
рис. VI-3-7.
Распределение теплового потока по
поверхности носка. При гиперзвуковых скоростях
обтекания носка с сильно охлаждаемой поверхностью
и при условии, что произведение р\х поперек
слоя не меняется, распределение равновесного
теплового потока рассчитывается по формуле
(IV-8-47), в которой функция F (х) определяется
^IV-8-48). При условии, что е=^0; соб = <°о> она
принимает вид
0,6
0,2
02-
\
\
\
\
О
20
60
p
Po
LJ Po v°o
Рис. VI-3-7. Влияние
стреловидности крыла на
теплопередачу в точке полного
торможения передней кромки
Согласно усовершенствованной ньютоновской формуле давление на
криволинейной поверхности носка
Р о . , 1
Ро
= COS2 К] +
(VI-3-15)
где г] — угол между касательной к контуру и направлением радиуса кривизны.
Распределение местной скорости
(¥]Г- (VM-16)
Для криволинейного контура произвольной формы значение функции
F (х) находится в результате численного интегрирования.
В частном случае, когда контур представляет собой дугу окружности
некоторого радиуса i?T, определение теплопередачи может быть упрощено,
что достигается использованием линейного закона изменения скорости вместо
(VI-3-16):
(VI-3-16')
Voo~~ \ дх ) х=(Г
Вместо dx в (VI-3-14) следует подставить RTd(p. В результате
несложных преобразований для отношения тепловых потоков в произвольной точке
и точке полного торможения получим
где функция
D (Ф) = ф2 (1 + —i-г) + sin Ф (2Ф cos ф-sin Ф) (1 - —^) . (VI-3-18)
В пределе при ф-^0 отношение gT/gTo—->1; в конце носка, где ф = я/2,
это отношение qT/qTQ = 1,8/AM^
350 Г л а* а VI
При небольших сверхзвуковых скоростях для приближенного расчета
распределения теплопередачи по плоскому контуру можно пользоваться
выражением
q = А Pr-2/з Rex-i/n P6F6 (iT- iCT), (VI-3-19)
где соответственно для ламинарного и турбулентного течений ^4 = 0,57
и 0,042, лг = 2 и 5. Разность энтальпий можно рассчитывать, учитывая
небольшой нагрев
ir-icT = cp \ (Tr-TCT), (VI-3-20)
т
ст
где ср I —теплоемкость, вычисляемая как среднее для интервала темпе-
т
ст
ратур Тг-Тст.
Число Рейнольдса определяется из выражения Re = p6F6x/[x6.
Кроме случаев обтекания со сверхзвуковыми скоростями, формула
(VI-3-19) может быть применена и для дозвуковых потоков, когда
теплопередача оказывается относительно небольшой. С возрастанием скоростей
температура в пограничном слое увеличивается, что необходимо учитывать
при расчете теплопередачи. С этой целью в (VI-3-19) следует перейти к
определяющим параметрам.
Осуществляя расчеты, следует иметь в виду, что вблизи критической
точки течение всегда будет ламинарным. Граница ламинарной области
определяется критическим числом Рейнольдса, устанавливаемым обычно
из эксперимента.
Влияние диффузии и нагрева стенки. Если предположить,
что влияние диффузии в произвольной точке поверхности будет таким, как
в точке полного торможения, а также принять температуру стенки
произвольной (стенка необязательно сильно охлаждена), то отношение тепловых
потоков
j_ = ^ _
*° V2z9'oli'o (dV6/dx)0
где х определяется из (IV-8-42), а отношение £ст/£сто~ по (VI-2-32).
Удельный тепловой поток q0 в точке полного торможения вычисляется по (VI-2-30).
Влияние стреловидности. Для крыла с закругленной по
некоторому радиусу передней кромкой и с углом стреловидности %
теплопередача в точке торможения или ее среднее значение для затупленной
поверхности кромки могут быть определены согласно данным работы [55] при
помощи формулы
?% = 9x=o-cos4/3x. (VI-3-22)
§ VI-4. Температура стенки
Стационарный нагрев
Равновесная радиационная температура стенки при отсутствии
внутреннего охлаждения. При отсутствии внутреннего охлаждения и лучистого
потока к стенке, а также различных утечек тепла равновесная температура
определяется из уравнения (IV-8-30). График изменения этой температуры
в зависимости от Тт и а/г показан на рис. IV-8-6. Однако пользоваться
этим графиком для определения Гст = Те нельзя, так как значения Тг и а
неизвестны, и сами они определяются в ходе решения уравнения (IV-8-30)/
одновременно с температурой Те.
Трение и теплопередача на крыльях
351
700
600
Решение осуществляется методом последовательных приближений с
привлечением соответствующих соотношений для трения и теплопередачи. При
этом заданными являются число Моо, высота полета и угол атаки, по
которым находят распределение параметров «невязкого» обтекания на
поверхности крыла.
Чтобы найти равновесную температуру в какой-либо точке поверхности,
определяют для нее в качестве первого приближения температуру Тт = Т& +
+ r(Vl/2), где г = ]^Рт (ламинарный пограничный слой) или г = У~Рг
(турбулентный пограничный
слой). Затем задаются
несколькими значениями температуры
Гст, которые должны быть
несколько меньше Тт.
Для каждого значения ТС1:
находят разность qCT = ах (Тг —
—Тст) — гоТ1т и строят кривую
зависимости qCT от Гст- Полагая
gCTr=0, определяют на графике
значение равновесной
температуры Гст = Те.Жз условия
равенства конвективного и
радиационного теплового потоков по
значению ГСт = Те МОЖНО УТОЧНИТЬ
коэффициент теплопередачи ах,
а также коэффициент трения.
По найденной равновесной
температуре можно уточнить температуру восстановления, определив во
втором приближении коэффициент восстановления г, затем повторить расчет
температуры Те.
Можно получить значение ТС1: непосредственно численными расчетами.
В этом случае должны быть известны, по крайней мере, два значения дСт1
и qCT2, первое из которых положительное, а второе — отрицательное по знаку.
Зная соответствующие им температуры ГСТ1 и ТСТ2 и используя линейную
интерполяцию, найдем значение Тст~Те, соответствующее дст = 0:
m m
ст2 ■* ст1
Точка перехода
W
Рис. VI-4-1. Характер распределения
равновесной радиационной температуры по поверхности
профиля:
I — ламинарный слой; II — турбулентный слой; III —
переходная область
> = 1 ст1
(VI-4-1)
Расчет равновесной температуры необходимо вести с учетом наличия
на обтекаемой поверхности смешанного пограничного слоя, используя для
определения параметров трения и теплопередачи соответствующие зависимости.
В связи с этим должны быть найдены критические числа Рейнольдса и
определены точки перехода.
При больших скоростях равновесная температура и связанные с ее
определением другие параметры вычисляются методом определяющей
энтальпии (температуры).
В качестве иллюстрации на графике рис. VI-4-1 приведены результаты
расчета равновесной температуры для параболического профиля при
сверхзвуковой скорости обтекания. Расчет проведен без учета влияния
продольного градиента давления для фиксированных значений г = у 0,71 —0,84
и г = 1^0,71 =0,89 по числу Рг = 0,71.
При построении графика, подобного изображенному на рис. VI-4-1,
следует учесть переходную область, в окрестности которой тепловые потоки
меняются по некоторой кривой. Изломы на кривой не должны иметь места,
так как в реальных условиях возникают продольные потоки тепла,
приводящие к выравниванию температуры.
352 Глава VI
Равновесная температура стенки, охлаждаемой изнутри. Рассмотрим
случай, когда при отсутствии подвода внешнего радиационного потока
от стенки с помощью какого-либо охладителя отводится некоторое
количество тепла дОх- При стационарной теплопередаче уравнение теплового
баланса будет qK — #из — Яох — 0 или
аГгт = ^(Г;-Гст), (VI-4-2)
С/
где Т'г — приведенная температура восстановления, определяемая из условия
Гг = Тг[1-д0Х/(ахТг)].
Так как величиной удельного теплового потока qox обычно задаются,
то, следовательно, задача об определении равновесной радиационной
температуры стенки ТСт решается в принципе так же, как и без охлаждения.
Отличие состоит лишь в том, что вместо температуры восстановления
определяется ее приведенное значение Т'г.
Из V1-4-2 видно, что равновесная температура стенки ТСт = Те при
наличии охлаждения снижается.
По найденному значению ТСт можно определить внешнюю То& и
внутреннюю Твн температуры стенки, предполагая, что изоляция (если она есть)
и обшивка нагреваются до температуры, соответствующей установившемуся
теплообмену, и, следовательно, через них проходит одно и то же количество
тепла, равное
(f) (f) = ,ox (VI-4-3)
и зависящее от коэффициентов теплопроводности материала изоляции
и обшивки. Если принять, что их значения постоянны, то в результате
интегрирования по толщине изоляции бИЗОл (в данном случае внешней)
и обшивки боб получим
*А ^б (VI-4-4)
Нестационарный нагрев
При нестационарном нагреве температура стенки меняется со временем.
Если рассмотреть тонкостенные металлические обшивки с большой
теплопроводностью, то можно пренебречь влиянием на нагрев температурного
градиента по толщине и считать, что стенка прогревается мгновенно. Для
расчета температуры стенки следует воспользоваться уравнением (VI-8-29),
в котором для простоты можно принять, что имеет место только излучение
внешней поверхности.
При интегрировании дифференциального уравнения (VI-8-29) задаются
некоторой начальной температурой, которой может быть, в частности,
равновесная радиационная температура, возникающая при движении тела с
постоянной скоростью и на одной высоте. Это движение предшествует моменту
времени, с которого начинается нестационарный процесс (разгон или
торможение летательного аппарата).
Задавшись произвольным интервалом времени At и зная из расчета
траектории значение числа М<х>, соответствующее моменту t + Atf можно
определить параметры невязкого обтекания, а также значения aix и Тг1 в
некоторой точке поверхности при стационарной теплопередаче. По этим данным
определяется в первом приближении производная
1} (сТб)об) (VI-4-5)
а затем уточняется температура стенки
Гст2 = AT + Гст1 = (-^f-) i At + TCTl.
Трение и теплопередача на крыльях
353
По этой температуре определяются во втором приближении значения а2,
ТГ2, ГСт2> затем производная (VI-4-5) и, наконец, температура ТСтз- При
этом, если интервал времени выбран достаточно малым, то при расчете
производной (VI-4-5) можно ограничиться первым приближением.
На рис. VI-4-2 показано примерное изменение по времени температуры
тонкой стенки в некоторой точке поверхности обтекаемого тела,
движущегося сначала ускоренно (до момента времени т = 20 сек, как видно на графике),
а затем замедленно. Как показывают расчеты, температура обшивки отстает
от роста температуры адиабатической
стенки, и имеет место тепловая
инерция, обусловленная теплоемкостью
обшивки.
В случае полета на больших
высотах, где аэродинамическим
нагревом можно пренебречь, уравнение для
расчета нестационарной температуры
тонкой обшивки будет
dTc
t°c
500
300
- ст
dt
го
с?) об
200
100
/
А-
V
/
/
/
--
\
у
1
К
К
2
><
——
10 20 30 <*0 50
<2Г сек
Рис. VI-4-2. Температура обшивки при
переменной скорости полета:
1 — температура адиабатической стенки Тг', 2 —
действительная температура обшивки
где дл — подводимый к поверхности
лучистый поток.
В общем случае при переменной
величине дл приведенное уравнение
решается путем численного
интегрирования.
При умеренных скоростях полета
в плотных слоях атмосферы
радиационный поток тепла в окружающую среду можно не учитывать.
Пренебрегая также лучистой энергией, подводимой к стенке, и полагая, что
количество тепла, поглощаемое тонкой обшивкой, равно количеству тепла,
передаваемому ей пограничным слоем, можно написать
(суб)об dTCT = а (Тт - Тст) dt.
Имея в виду, что (суд)Об> а и Тг являются слабыми функциями времени
и принимая эти параметры постоянными, найдем после интегрирования при
начальном условии £ = 0, ТСТ = ТО
Тст = Тт-(Тг-То)е-~*, (VI-4-6)
где t= — atI(суд)об-
Изложенная схема расчета нестационарной теплопередачи неприменима
к низкотеплопроводным материалам (защитные покрытия), а также к толстым
металлическим обшивкам, для которых характерен неравномерный нагрев
по толщине, в результате чего наружная поверхность может иметь
значительно более высокую температуру, чем внутренняя. Расчет распределения
температуры по толщине такой обшивки изложен в работе [11], где также
приведен метод определения потребной толщины термоизоляционного
покрытия.
Температура стенки при
солнечном нагреве
На больших высотах (порядка 100 —150 км и выше) аэродинамический
тепловой поток незначителен по сравнению с лучистой энергией.
Пренебрегая рассеиванием тепла вдоль поверхности, можно считать, что уравнение
баланса тепла при стационарном процессе имеет вид
23—114
354 Глава VI
Практически на больших высотах тепловым излучением Земли и
отраженной от нее солнечной энергией дот можно пренебречь. В соответствии
с этим qc = диз и, следовательно,
|-^созг|))1/4, (VI-4-7)
откуда видно, что максимальная температура будет при чр = 0. Практически
можно воспользоваться постоянным значением qG = 0,332 ккал/м2-сек,
которому соответствует температура стенки
Для вращающегося сферического аппарата усредненная температура
поверхности
(А)1/4. (VI-4-8)
§ VI-5. Степень
затупления передней кромки
крыла, обеспечивающая
наибольшее снижение
тепловых потоков
Эффект затупления проявляется в уменьшении местных чисел Re, что
сдвигает точку перехода ламинарного пограничного слоя в турбулентный
и, как следствие, снижает трение и тепловые потоки. Это снижение будет
наибольшим, когда затупление сдвигает точку перехода к задней кромке.
Следовательно, степень затупления должна быть настолько большой, чтобы
число Рейнольдса на внешней границе пограничного слоя было близко
к значению этого числа, подсчитанного по уменьшенной скорости V^
высокоэнтропийного невязкого потока для всего участка ламинарного течения.
Положение точки перехода определяется критическим числом Рейнольдса ReKp,
подсчитываемым по скорости V&. Поэтому затупление должно быть
достаточным для того, чтобы поток, замедленный в высокоэнтропийном «невязком» слое,
покрывающем пограничный слой, обладал в конце тела нужной величиной F6.
Как показывают исследования [50], в качестве верхней границы этого
слоя можно принять линию тока, проходящую через «звуковую» точку
с координатой ys на отошедшей ударной волне (см. рис. IV-10-1). Расход
газа через сечение площадью z/s-1 будет равен pooVooi/s- Это же количество
протекает через слой уменьшенных чисел Re некоторой толщины А,
соответствующей произвольному сечению тела с координатой х. Следовательно,
Vi откуда толщина «невязкого» слоя
где рб, V6 — соответственно плотность и скорость в рассматриваемом сечении,
рассчитанные для невязкого обтекания поверхности с учетом влияния
затупления. При определении этих параметров можно исходить из условия,
что на некотором удалении от затупленного носка давление устанавливается
таким, как на остром теле. При расчетах «невязких» параметров с учетом
диссоциации используются графики или таблицы термодинамических
функций воздуха. Зная давление и вычисленную среднюю величину энтропии Sq
(между вершиной волны,и «звуковой» точкой или, при более упрощенных
расчетах, по значению So за прямой частью скачка), находят при помощи
Трение и теплопередача на крыльях
355
этих таблиц в заданном сечении плотность ра и энтальпию £$. Затем
по уравнению г0 = jr6 -[- 0,5^1 вычисляют скорость V&. Скорость и плотность
газа в удаленных от носка сечениях
потока при постоянных теплоемко-
стях могут быть вычислены
соответМ 5
ственно по формулам
fe-i
poo poo РО
где местное число Маха
(VI-5-2)
(VI-5-3)
I /
ft
/
5°
20°
M-
^
8
12
16
20
0 4 ^
Рис. VI-5-1. Местное число Маха на
поверхности затупленного клина
УЗТ
Рассчитанные по этой формуле числа М на затупленном клине
приведены на рис. VI-5-1. Давление торможения р'о определяется с целью
уточнения расчетов как среднее между соответствующими значениями в точках В
и S (см. рис. IV-10-1), первая из которых
4 расположена непосредственно за прямой
частью ударной волны, а вторая — на
криволинейном участке и является
«звуковой» .
Зная параметры рб и F6, а также
координату «звуковой» точки ys на
ударной волне, можно определить
толщину «невязкого» слоя.
На рис. VI-5-2 приведены
результаты расчета указанным способом
величины А, отнесенной к координате yST
«звуковой» точки на затупленном по
сфере клине,
А
ys
ysr ysT
Для расчета потребного затупления
(величины yST) поставим условие, чтобы
толщина ламинарного слоя в точке
перехода равнялась толщине слоя малых
q 20 скоростей. Следовательно, условия, из
которых может быть определена вели-
Рис. VI-5-2. Отношение толщины «не- чина z/ST, будут
вязкого» слоя А на затупленном клине
к координате «звуковой» точки на
сферическом- носке (сплошная кривая
вычислена для точного значения у sly
пунктирная — для yslysn = 0,5)
V
1
/,0-
/
/ .
у
/
/
' /
/ ^
—J /
/
/
/
у-о-
5°
/
(VI-5-6)
Из второй формулы (VI-5-6)
следует, что если A/?/st — 1> то координата
«звуковой» точки у$т — 6л- Для определения толщины ламинарного слоя
в точке перехода на поверхности затупленного клина можно воспользоваться
23*
356 Глав а VI
соответствующей зависимостью для плоской пластинки при условии, что
входящие в нее параметры принимаются такими, как на затупленном клине.
Толщина ламинарного слоя в точке перехода
-^ = 5,8(Ве£р)йл1/2, (VI-5-7)
где хи — расстояние до точки перехода.
Критическое число Рейнольдса может быть вычислено по определяющим
параметрам для затупленного клина, т. е. (Кекр)кл = (^б#пР*/(А*)кл« Так как
критическое число Рейнольдса считается величиной известной, то можно
определить длину ламинарного участка
Хп~\
затем толщину пограничного слоя в точке перехода
• <VI-5-8>
Требуемое затупление уменьшается, если учесть влияние условной
толщины вытеснения, увеличивающей эффективную толщину клина и,
следовательно, толщину невязкого слоя уменьшенных чисел Рейнольдса. В
соответствии с этим координата «звуковой» точки
)\ (VI-5-9)
Если принять, что б* = 0,125бл (условная толщина, как и толщина
слоя, вычисляется в общем случае по определяющим параметрам на
затупленном клине), то
РАЗДЕЛ
ТРЕТИЙ
аэродинамика
корпусов
АЭРОДИНАМИЧЕСКИЕ
КОЭФФИЦИЕНТЫ
ПРИ ДОЗВУКОВЫХ
И ОКОЛОЗВУКОВЫХ СКОРОСТЯХ.
§ VIM. Дозвуковые
скорости
Сопротивление трения. При упрощенных расчетах сопротивления
трения корпусов могут быть использованы зависимости для плоской пластинки.
Полученные результаты следует считать весьма приближенными, так как
не учитывается пространственный характер течения и форма обтекаемой
поверхности.
Если cXf представляет собой коэффициент сопротивления трения пластинки
с длиной, равной длине корпуса, то сила сопротивления трения Xf = cqS
где $бок — боковая поверхность корпуса.
Пограничный слой около корпуса
в реальных условиях оказывается
смешанным: на передней части он
ламинарный, на остальной турбулентный. В
соответствии с этим средний коэффициент
сопротивления корпуса, рассчитанный
по миделевому сечению,
с
~~~о
^мид
xf л ~с
мид
Г Cxf Л
7 Re-1(f
Рис. VII-1-1. Влияние сжимаемости на
критическое число ReKP тела вращения
(VII-1-1)
где cxfK и cxf л — коэффициенты
турбулентного трения пластинки; первый из
них находится по числу Рейнольдса,
подсчитанному по длине корпуса,
второй—по числу Рейнольдса,
вычисленному подлине ламинарного участка; величина cxfn представляет собой средний
коэффициент ламинарного трения пластинки, длина которой равна
протяженности ламинарного слоя на корпусе. Величины 5б0к и £л представляют собой
соответственно полную боковую поверхность корпуса и часть этой
поверхности, соответствующую длине ламинарного слоя.
Длина ламинарного участка в общем случае зависит от формы корпуса,
числа Моо, температуры стенки и шероховатости ее поверхности. В наиболее
простом случае абсолютно гладкой поверхности, обтекаемой несжимаемым
потоком, при наличии отрицательного градиента давления критическое число
Рейнольдса для продолговатого корпуса можно принимать равным ReKp = 10 .
О влиянии сжимаемости на критическое число Рейнольдса для тела вращения
можно судить по графику на рис. VII-1-1.
Для оценки величины ReKp можно пользоваться данными, относящимися
к плоским двухмерным течениям, имея при этом в виду, что для корпусов
действительные значения ReKp оказываются несколько больше. Ниже будут
изложены более подробные данные о критических числах Рейнольдса
для корпусов.
Сопротивление от давления. При дозвуковых скоростях
распределение давления, которое необходимо знать для вычисления соответствующей
составляющей сопротивления, может быть найдено достаточно надежно
360
Глава VII
лишь экспериментальным путем. При этом, как показали исследования,
для удлиненных корпусов различие между давлениями в несжимаемом
и дозвуковом сжимаемом потоках [невелико.
Рис. VII-1-2. Критическое число МооКр тела
вращения
\
\
\
0
\v"
II
зо\
\
+о;г
60 0
-о,2
К -о,б
У 1
90
.4-
у
120//
f.
~3
/
(
150 18
Рис. VII-1-3. Распределение
давления по сфере:
1 __ потенциальное течение; 2 — Re >
Для нахождения коэффициента давления р при докритическом числе Маха
можно воспользоваться значениями коэффициента давления рнс для
несжимаемого потока и формулой пересчета
— М2 ^-о»5
(VII-1-2)
Для приближенной оценки критического числа Маха может служить
график на рис. VII-1-2. Для поверхностей с большой кривизной
распределение давления зависит от того, при каких значениях числа Рейнольдса —
докритических или сверхкритических — происходит обтекание. Это видно на
рис. VII-1-3, где показано распределение давления по сфере.
Коэффициент головного сопротивления, обусловленного давлением
и трением на передней части корпуса (профильное сопротивление),
определяется по эмпирической формуле [26]
(VII-1-3)
в которой коэффициент формы
*ф = 1,86 —0,175Хф +0,014-
(VII-1-4)
Параметр Яф называется
приведенным удлинением и определяется
из выражения
Рис. VI1-1-4. Сопротивление некоторых
тел вращения
Коэффициент сопротивления тре~
ния cXf, отнесенный к миделевому
сечению, вычисляется с учетом
сжимаемости и в зависимости от характера
течения в пограничном слое.
Полное сопротивление. Его следует рассматривать как сумму головного
(профильного) и донного сопротивлений (см. § XIV-2). Экспериментальна
полученные данные о коэффициентах полного сопротивления для неко-
Аэродинамические коэффициенты при до- и околозвуковых скоростях
361
торых тел вращения, обтекаемых несжимаемым потоком, показаны в виде
кривых на рис. VII-1-4 [16]. Согласно этим данным коэффициент
сопротивления трения
сх,= 0,014
МИД
(VII-1-6) ф~
При обтекании тел потоками с
большими скоростями на
сопротивление оказывает влияние сжимаемость.
Однако при докритических числах
Маха это влияние, как видно из
экспериментальных данных,
представленных на рис. VII-1-5, невелико и
выражается обычно в некотором
увеличении коэффициента сопротивления.
Сопротивление корпуса
существенно зависит от формы носовой
части (рис. VII-1-6).
Экспериментальным данным, приведенным на
рис. VII-1-6 [16] (модель 1),
соответствует эмпирическая зависимость для
коэффициента сопротивления
продолговатого тела вращения с плоским
передним носком:
х
0,003
10-10°
8
6
4
2
0~
<^
0,4 0,8 Ма
у
0£ 0,8 Моо
НеХк(х^0,6м)
^—
0,8
Рис. VI1-1-5. Точка перехода (а),
сопротивление (б) и число Рейнольдса (в) для
тела вращения (г) при различных числах
Моо; 1 — точка перехода
Летные испытания сферических снарядов показали, что до значений
числа Моо •< 0,5 полный коэффициент сопротивления может быть принят
постоянным и равным сж = 0,4923 ([72], № 4, 1945).
сх
V
1
/
/
у
//
1
'А
4
I6
ш
7
0,2
0,6 0,8
Рис. VI1-1-6. Влияние формы носовой части тела
вращения на коэффициент лобового сопротивления:
I — окружность; II — эллипс
Нормальная сила, момент. Исследования показывают, что при
дозвуковых скоростях нормальная сила и момент тонких корпусов могут быть
362 Глава VII
определены по тем же соотношениям, что и при сверхзвуковом обтекании.
Коэффициенты нормальной силы и момента можно вычислить соответственно
по формулам (XI-3-31) и (XI-3-40), учитывающим влияние отрыва потока
на аэродинамические характеристики.
§ VII-2. Околозвуковые
скорости
Подобие околозвуковых потоков
Уравнение околозвукового симметричного течения. Линеаризованные
уравнения движения газа неприменимы в случае околозвуковой
(трансзвуковой) скорости потока, обтекающего тело вращения, даже если оно
является тонким. Это становится понятным, если вспомнить, что при
линеаризации уравнений разность квадратов скоростей а2 — Vx заменялась ее
приближенным значением а% — FL. Но эту замену нельзя делать в
условиях трансзвуковых скоростей. Действительно, разность а2 — V% в
линеаризованном потоке, равная alo— Vlo— V'xVoc (k-\- 1), может быть заменена
приближенным ее выражением alo— F^ потому, что член VxV00(kJr\) мал
по сравнению с alo — Vlo.
Между тем в условиях трансзвуковых течений, когда скорость потока
близка к звуковой, величина FiFoo(A; + l), определяемая добавочной
составляющей возмущенной скорости V'x, будет соизмерима с величиной разности
alo — Vlo и, следовательно, линеаризация уравнений невозможна. Однако
при некоторых предпосылках основные уравнения хотя и не линеаризуются,
но могут быть упрощены. Полученные упрощенные уравнения [43]
существенно облегчают исследование трансзвуковых симметричных течений.
Рассмотрим уравнение для потенциала скоростей установившегося,
симметричного трансзвукового потока, которое получается в результате
упрощения (Ш-2-22).
Определим потенциал возмущения ср' соотношениями
*L =& = Vx--a-, ^=<p; = F,
Потенциал возмущения соответствует такому характеру течения около
тонкого тела вращения, когда местная скорость мало отличается от
критической скорости а* и, следовательно, производная ду'/дх невелика.
Потенциал ср' должен, очевидно, удовлетворять условиям «на
бесконечности»:
Вводя в (Ш-2-22) потенциал ср' и принимая во внимание, что при
скорости Foo, близкой к звуковой, можно пренебречь квадратом величины
ср*/а, получим дифференциальное уравнение для потенциала установившегося
трансзвукового потока:
9 ф'
*Ф** + £* Фгфг* = Фгг + — . (VII-2-3)
Это уравнение нелинейное относительно ср'; оно сложнее, чем
линеаризованное, и в то же время проще общего уравнения (Ш-2-22) для
потенциала скоростей.
Закон подобия потоков. Закон подобия для трансзвуковых потоков,
обтекающих тела вращения с различными удлинениями, но с подобным
Аэродинамические коэффициенты при до- и околозвуковых скоростях 363
распределением толщин (например, конические и параболические),
получается присоединением к упрощенному уравнению (VII-2-3) граничных
условий (VII-2-2) и условий безотрывного обтекания
^ = £ = 5- (VH-2-4)
Заменяя в (VII-2-4) производную drldx величиной drldx = s (х/хк)/Хк,
где s (х/хк) — некоторая функция, характеризующая наклон образующей,
^к~ %Jdmm — удлинение тела, получаем
Соотношение (VII-2-5) указывает на то, что по порядку величины
потенциал на поверхности тела q/ ~ га*Ак. Исходя из этой оценки, можно
ввести аффинные переменные g, т), связанные соотношениями
а потенциал ср' представить в виде
где Г =- (А: -f1)/2 — параметр, учитывающий влияние на подобие потоков
свойства газа, определяемого показателем адиабаты;
^oo = Voo/a* — относительная скорость набегающего потока.
Введение множителя 1— Х^ определяется условием на бесконечности,
а функция F (|, т|) подлежит определению.
В результате преобразования к новым переменным и упрощения
(некоторыми членами можно пренебречь вследствие их малости) уравнение
VII-2-3 будет таким:
где
При одинаковых значениях параметра К уравнение (VII-2-8) описывает
целый класс потоков, обтекающих тела вращения с большим удлинением
и одинаковым законом распределения толщины. Параметр К, таким образом,
выражает закон подобия потоков с околозвуковой скоростью. Причем,
подобие здесь надо понимать в том смысле, что потоки описываются одним
и тем же по форме уравнением (VII-2-8).
Коэффициенты давления и сопротивления. Сначала найдем общую
формулу для коэффициента давления. С этой целью воспользуемся зависимостью
у2 4- V2 \ ъ^Т
1')
и заменим в ней V% приближенным выражением
При этом (а*)2 определим через скорость набегающего потока в
соответствии с условием «на бесконечности» cpioo — Foo — а* следующим образом;
где ф^оо вычисляется из соотношения (VII-2-2).
364 Глава VII
Разлагая полученное выражение в ряд и сохраняя в нем лишь два
члена, получим
р — Роо= — Poo (cpi — cpioo)Foo — у роофг2,
откуда коэффициент давления
Далее, найдем осевую составляющую скорости
Принимая во внимание приближенное соотношение 1 — Veda* =
= (1 —А,оо)/Г, а также зависимости (VII-2-5) и (VII-2-12), можно формулу
(VII-2-11) привести к следующему виду:
р * Р(К, £), (VII-2-13)
где функция
Р(К, g)=_2K(l+-^)-*2(£)
и для данной точки с безразмерной координатой £ зависит только от
параметра подобия К.
Найдем теперь общее выражение для коэффициента сопротивления
от давления. Для этого в (1-3-14) подставим коэффициент р, определяемый
соотношением (VII-2-13). В результате получим
схр * £>(К), (VII-2-15)
где -О (К) — функция, зависящая от параметра подобия К, определяется
из выражения
1
Z? = 4 ^ Л„Р (К, -) Ftgpd£. (VII-2-16)
Найденные для коэффициентов р и схр зависимости показывают, что
при одном и том же значении параметра К трансзвуковые течения около
тел вращения являются подобными в том смысле, что величины Др
и ^исхр остаются одинаковыми.
Таким образом, при изучении обтекания тел потоками с
околозвуковыми скоростями основным параметром, характеризующим такое обтекание,
является величина К. Поэтому закон подобия потоков по параметру К
можно положить в основу экспериментальных и теоретических исследований
околозвуковых аэродинамических характеристик тел. При этом для
параметра К может быть использовано соотношение, несколько отличное от
формулы (VII-2-9):
которое точнее отображает подобие.
Более строгий подход приводит к выводу, что законы подобия
оказываются по сравнению с выражениями (VII-2-13), (VII-2-15) несколько
Аэродинамические коэффициенты при до- и околозвуковых скоростях
365
сложнее, а именно:
к
С
JE(M0O) К, к, I);
[-Сг (Moo» Ак, /с),
(VII-2-18)
(VII-2-19)
где В, С, Е, G — некоторые функции.
Переменные, от которых они зависят, указаны в формулах (VII-2-18)
и (VII-2-19).
Подобие в соответствии с этими формулами будет относиться не к
функциям рЯк и сх-р%\, а соответственно к произведениям
Тонкое заостренное тело с криволинейной образующей. Исследования
показывают, что для семейства аффинно-подобных тонких заостренных тел
вращения второе слагаемое в формуле
(VII-2-18) имеет вид р
///
/
1
Х=85
^^
X
-
— 1
хк
Ofi у-—
О
0,2 0,4 0,6 Ofi $*j^
(VII-2-20)
Формула (VII-2-20) вместе с
соотношением (VII-2-18) позволяет
обобщать единичные экспериментальные
данные для данного числа М<х> и
конкретной модели с каким-либо
удлинением на различные значения Хк.
На рис. VII-2-1 показано, в
частности, экспериментальное
распределение давления при М<х> = 1 около
параболического тела вращения с
удлинением Як=6. По этому распределению
и значению лк = 6 в каждой точке
с заданной координатой | = xlxK
были подсчитаны с помощью правила
подобия (VII-2-18) функции В(1). Затем, пользуясь той же формулой
(VII-2-18) и имея значения функции В (£) для Хк = 6, были вычислены
коэффициенты давления в соответственных точках более тонкого тела
вращения с удлинением А,к = 8,5. Полученные результаты хорошо согласуются
с экспериментальными данными [16].
Внося выражение (VII-2-18) для р в (1-3-14), можно получить
следующий закон подобия для коэффициента сопротивления:
Рис. VI1-2-1. К пересчету коэффициента
давления для параболического тела
вращения:
эксперимент; —■ по формуле
(VII-2-18)
4 С (К)
1 [^(^к)]2
из которого может быть найдена функция G, входящая в выражение
(VII-2-19).
Закон подобия (VII-2-21) упрощается, если тело имеет донный срез,
совпадающий с миделевым сечением, или заканчивается заостренной
хвостовой частью, так как в обоих случаях производная площади поперечного
сечения S' (#к) = 0.
Приведенные зависимости, отображающие закон подобия, пригодны для
чисел Моо в окрестности единицы, причем результаты расчета хорошо согла-
366
Глава VII
суются с экспериментальными данными при звуковом или слегка
сверхзвуковом обтекании.
Тонкий заостренный конус с цилиндрической хвостовой частью.
Особенность обтекания такого тела околозвуковым или звуковым потоком
состоит в том, что в угловой точке устанавливается всегда звуковая скорость.
Поэтому давление в этой точке может быть рассчитано заранее. В
остальных точках конуса параметры потока находятся теоретически путем решения
уравнения (VII-2-8) или экспериментально.
Это решение приводит к следующей зависимости, позволяющей
рассчитывать коэффициент давления при Моо = 1:
где
2 1-| ДЛЯ
= l для
(VII-2-22)
(VII-2-23)
На рис. VII-2-2 показана кривая, рассчитанная по формуле (VII-2-22)
для конуса с углом рк = 7°. Она хорошо согласуется с экспериментом.
Используя имеющиеся данные —
теоретические или экспериментальные,
полученные для условий, характеризующихся
какими-либо конкретными значениями М^
и рк, и зная правило подобия (VII-2-22),
можно рассчитывать распределение давления
около семейства тонких конусов. Это
распределение будет соответствовать обтеканию
конических тел с различными числами Моо,
но такими, при которых параметр К
сохранялся бы постоянным.
Правило подобия, аналогичное (VII-2-22),
можно получить и для Моо ф 1. С этой
целью воспользуемся формулами (VII-2-18) —
(VII-2-20). Так как для конуса S (х) =
р
0,15
0,10
0,05
\
X
^ ....
Hi
\~
Г7
Li
\
\
I
О
0,2 Ofi
Рис. VI1-2-2. Коэффициент
давления на остром конусе (Моо =1)
следующий:
Як = 0,5/рк, то коэффициент давления (VII-2-18) будет
р = 4Рк5 (К, I) — 2рк In [4РкМоо (к +1)1/2]. (VII-2-24)
Выражение для коэффициента сопротивления, соответствующее (VII-2-21),
СхР = ^-С (К) - 2fK In
(VII-2-25)
При Моо = 1 соотношения (VII-2-24) и (VII-2-25) упрощаются, так как
в этом случае параметр К = 0. В частности, выражение, позволяющее
определить коэффициент сопротивления, будет
(cxp)Moo=i = — Рн(1,09 + 41прк). (VII-2-26)
В том случае, когда числа М^ отличны от единицы, для тонкого тела,
вместо общей формулы (VII-2-25) можно использовать более конкретную
зависимость
к). (VII-2-27)
Аэродинамические коэффициенты при до- и околозвуковых скоростях
367
Применение этой формулы ограничивается значениями параметра К,
удовлетворяющими неравенству
К =
М2 — 1
€ 1.
(VII-2-28)
Суммарное сопротивление
различных тел вращения при
трансзвуковых скоростях
Экспериментальные данные [16] о лобовом сопротивлении заостренного тела
вращения с оперением приведены на рис. VI1-2-3. Эти данные показывают,
что коэффициент сопротивления быстро растет, начиная со значения Моо =
— 0,8 и достигает максимума приблизительно при Моо = 1,1.
1,0
0,6
0,2
*s
Moo
Voo
r
/
/
0,2
4
/
/
'Л
0А 08
2.0 Мо
0
30
60
Рие. VII-2-3. Коэффициент
сопротивления бомбы
Рис. VII-2-4. Сопротивление
конических головных частей
при Моо = 1 (эксперимент)
Экспериментальные данные [16] о сопротивлении заостренных конических
и оживальных головок при звуковой скорости полета (Моо = 1) приведены
соответственно на рис. VII-2-4 и VII-2-5.
Затупление носовой части приводит к возрастанию сопротивления как
в до-, так и в сверхзвуковой зонах, однако увеличение сопротивления при
переходе трансзвуковой области оказывается менее интенсивным, чем для
заостренных корпусов.
Это видно на рис. VI1-2-6 и VI1-2-7, где приведены результаты
экспериментов соответственно для сферы и затупленного по торцу цилиндра.
Для сферы сопротивление возрастает в два раза, для цилиндра примерно
в 2, 3 раза, в то время как для заостренного корпуса (рис. VII-2-3)
сопротивление увеличивается более чем в 7 раз.
В итоге анализа как приведенных, так и других экспериментальных
данных, могут быть сделаны следующие выводы:
1) коэффициент лобового сопротивления достигает своей максимальной
величины сх тах при числах Моо, несколько больших единицы и
расположенных в интервале, границы которого приблизительно определяются
значениями Моо = 1,1 и Моо = 1,5;
2) доминирующее влияние на величину сх тах оказывает форма головной
части тела.
Этими выводами можно практически руководствоваться при
приближенной оценке максимальной величины коэффициента лобового сопротивления.
Для этой же цели можно пользоваться экспериментальной кривой, пока-
368
Глава VII
занной на рис. VI1-2-8 и представляющей зависимость коэффициента сх тах
от удлинения Ямид головной части. Эту зависимость можно представить
интерполяционной формулой
ft
0,30
0,25
о?о
0,15
0,10
0,05
= -£-'- + 0,014Я
мид.
(VII-2-29)
Второй член справа в этой формуле
оценивает величину коэффициента
сопротивления трения.
30
60
А
Рис. VI1-2-5.
Сопротивление оживальных головных
частей при Моо = 1
(эксперимент)
0,5
О
г—
Моо
•о
мо
Рис. VII-2-6. Коэффициент
лобового сопротивления сферы
(экспериментальные данные)
Наивыгоднейшее удлинение головной части, которое в соответствии
с формулой (VII-2-29) определяет наименьшее значение коэффициента схтах,
равно девяти. Таким удлинением обладает весьма тонкое тело, у которого
Рис. VII-2-7. Сопротивление цилиндри- Рис. VI1-2-8. Максимальная величина коэф-
ческого тела вращения с плоским тор- фициента сопротивления тел вращения (1,1 <
цом: < Моо < 1,5):
А —сопротивление головной части; Б— дон- В — сопротивление трения
ное сопротивление; В—сопротивление трения
сопротивление трения в общем балансе сил, из которых складывается
суммарное сопротивление, оказывается по удельному весу самым большим.
Анализ теоретических и экспериментальных данных об обтекании
полусферы потоками с различными скоростями, в том числе и околозвуковыми,
позволил установить, что расчет коэффициента сопротивления от давления
можно вести по формуле [16]
(VII-2-30)
Аэродинамические коэффициенты при до- и околозвуковых скоростях
369
Этот закон «арктангенса» можно применить также к расчету
коэффициента давления в критической точке сферы
р0 = 1,35 ^-
[1,96 (1 - Moo)].
(VII-2-31)
Формулы (VH-2-30) и (VII-2-31) дают удовлетворительные результаты
как для околозвуковых скоростей, включая значение числа Моо = 1, так
и для более широкого диапазона этих чисел от Моо = 0 до М^ порядка 7 — 8.
Расчет сопротивления заостренных тел, основанный на принципе
«стационарности» местного числа Маха. В соответствии с этим принципом
считается, что производная (5М/^Моо)моо=1 = 0> т- е. местное число М не
изменяется и остается «замороженным», когда число М^ набегающего потока
проходит через единицу.
Диапазон чисел Моо, в котором распределение местных чисем М
«заморожено», сравнительно узок. Так, например, для конуса с углом (Зк = 25°
этот диапазон определяется значениями 0,9-f-1,1, а для угла рк = 7° —
числами Моо, равными 0,99-^-1,01.
Используя принцип «стационарности» местного числа М, можно
получить зависимость, которая позволяет вести расчет сопротивления
заостренной головки при околозвуковых скоростях. Предположим, что распределение
местных чисел М известно. Тогда соответствующее значение скорости
V2
v оо
1)М2
<VII"2-32>
а коэффициент давления
Используя эту зависимость для коэффициента давления, а также
выражение (VI1-2-32), найдем после соответствующих подстановок в формулу
(1-3-14) соотношение, позволяющее рассчитать коэффициент сопротивления
конической головки:
1 о h
схр - ^|г { I [2X(~_i)b; Y* &* -1} . (VII-2-34)
Разлагая выражение в квадратных скобках в ряд и отбрасывая члены,
содержащие разности М^ — 1 во второй и более высокой степенях, получим
«** = -Ш1- {[^ТТГ^-1)] I [пРтЙ^+г-]5^^'-1}' (VH-2-35)
оо I Q
Полагая Моо = 1, из этого выражения находим формулу, определяющую
сопротивление при звуковой скорости полета
1 к
_2_
к
о
Если теперь принять в соответствии с принципом стационарности, что
местное число М инвариантно по отношению к числу Моо, близкому к
единице, то интеграл в (VII-2-35) можно заменить по выражению (VII-2-36).
В результате получим формулу, позволяющую рассчитать коэффициент
сопротивления при околозвуковых скоростях:
(VII-2-37)
24-114
370
Глава VIГ
где значения (cxp)moo=i могут быть определены для конических и оживаль-
ных головок по экспериментальным кривым на рис. VII-2-4 и VII-2-5 [16].
Зависимости для схр позволяют найти наклон кривой сопротивления
в точке, которой соответствует значение Моо = 1. Дифференцируя схр по Мое
и полагая Моо = 1, получим
1,0
//
у
у
/
р
о
35°
25°
20°
^—
■/л °
-10
-— -
111111•
— -
дс
хр
Г, (схр)м»=1 1
L 2 J '
oo=i k + 1 L 2
(VII-2-38)
В экспериментах с конусами
установлено, что грубая оценка величины (схр)м^=1 при
помощи экстраполяции кривой
сопротивления, построенной для Moo^l, дает хорошие
результаты при определении наклона кривой
схр для Моо.
На рис. VII-2-9 и VII-2-10 приведены
экспериментальные данные о сопротивлении:
конуса и оживальной головки при
околозвуковых скоростях. Эти данные
удовлетворительно согласуются с результатами расчета
коэффициента сопротивления в околозвуковой,
области и наклона кривой схр в точке М^ — 1.
Согласно измерениям в аэродинамических
установках на моделях тел вращения с
криволинейными головной и хвостовой частями коэффициент волнового сопротивления
1
с = - D (К)
эф
где ХЭф = аг + Хкр -f АЯЦ — представляет собой эффективное удлинение, равное
сумме удлинений головной Яг и хвостовой Якр частей тела и некоторой
величины АЯц, учитывающей влияние
промежуточного цилиндра на
обтекание переднего и заднего участков.
0,6
о,г
Рис. VI1-2-9. Зависимость cxv
конических головных частей от М<х>:
эксперимент;
экстраполяция
(VII-2-39)
12
8
4
0
/
/
/
:^=
-4 О
12
20
28 К
Рис. VII-2-10 Сопротивление оживаль
ных головок при транс- и
сверхзвуковых скоростях
Рис. VII-2-11. Функция,
определяющая волновое сопротивление тела
вращения при околозвуковых
скоростях
поверхности. Величина АХЦ выбирается обычно равной трем. Функцию D (К)
находят по графику на рис. VII-2-11 в зависимости от параметра
— 1). (VII-2-40)
Аэродинамические коэффициенты при до- и околозвуковых скоростях
371
0,05
0,04
0,03
0,5
¥
03
^ '
Q J
оамц
д
—U
Г-
0}4 0,5
0,7 0,8 0,9 1,0 1,1
Нормальная сила и центр давления. Наблюдениями установлено, что
для тонких тел вращения коэффициент нормальной силы в окрестности
звуковой скорости может достигать максимального значения, превышающего
значения коэффициента cN при дозвуковых скоростях на 25 — 35%.
Этот вывод можно проиллюстрировать данными на рис. VII-2-12,
показывающими зависимость величины cN/a от числа М^ для малых углов атаки
порядка ос = 0ч-3°. В соответствии с этими данными отношение cN/a
достигает максимального значения при Моо = 1,0, причем, оно примерно на 35%
больше той величины cN/a,
которая соответствует числу Моо = 0,4;
С увеличением нормальной
силы возрастает и момент. В
результате положение центра
давления может практически не
изменяться. Это видно на рис.
VI1-2-12, где представлены
результаты измерения
коэффициента центра давления
цилиндрического тела с параболической
головной частью.
Зафиксированное изменение этого коэффици- Рис- VII-2-12. Изменение cN/a и сц д тела вра-
ента при переходе через скорость щения с паРаб™ической образующей
звука составляет всего около 2%.
Подобная картина наблюдается также при экспериментальных
исследованиях обтекания конусов. Известно, что коэффициент центра давления
конуса при сверхзвуковых скоростях равен примерно 0,667. При дозвуковой
скорости, как показывает опыт, например для конуса с половиной угла
при вершине (Зк = 15, он меньше на 4%, т. е. центр давления расположен
ближе к острию. При переходе через скорость звука коэффициент центра
давления конуса незначительно увеличивается, достигая при Моо = 1,0
значения 0,65.
У тел, представляющих собой комбинацию из головного конуса и
цилиндрического хвостового участка, как показывают экспериментальные данные,
цилиндрический участок, непосредственно примыкающий к конусу, сдвигает
центр давления к дну конуса. Это явление имеет место как при дозвуковых
скоростях, так и при переходе через скорость звука. Величина сдвига
зависит от длины примыкающего к конусу цилиндрического участка. Однако
этот эффект проявляется практически лишь до определенных значений
относительной длины цилиндрического участка.
Для тонких конусов увеличение коэффициента центра давления в
интервале чисел Моо = 0,7 ч- 1,2 за счет влияния цилиндрического участка длиной
примерно 0,5ймид составляет 5-т-7%.
При длине цилиндрического участка 0,75ймид это увеличение достигает
7 —13%, и величина сц. д оказывается близкой к максимальному значению.
При дальнейшем увеличении длины цилиндра положение центра давления
практически не меняется.
Чтобы иметь представление об изменении коэффициента центра
давления всего тела, составленного из конуса и цилиндра, необходимо учесть
несущую способность не только головной части, но и цилиндрического
участка. Наличие этого участка приводит к дополнительному сдвигу центра
давления назад.
У тела с параболической головной частью центр давления в условиях:
перехода через скорость звука практически не перемещается.
2.4»
Глава VIII
КОНУС
В СВЕРХЗВУКОВОМ
ПОТОКЕ.
§VIII-1. Осесимметричное
сверхзвуковое обтекание
конуса
м
Система уравнений
Рассмотрим круглый заостренный конус с половинным углом рк при
вершине, обтекаемый осевым сверхзвуковым потоком. Задача заключается в том,
чтобы рассчитать течение газа между этим конусом и возникающим перед
ним скачком уплотнения, имеющим вид конической поверхности. При этом
необходимо также определить угол наклона 6С образующей конического
скачка (рис. VIII-1-1). С этой целью
рассмотрим систему уравнений
применительно к такому случаю обтекания,
когда газ за скачком под влиянием
высоких температур претерпевает
физико-химические превращения.
Будем считать, что в
возмущенной области устанавливается
термодинамическое равновесие. Примем, далее,
что отыскиваемое решение для конуса
должно обладать свойством, согласно
которому параметры газа сохраняются
постоянными на поверхности любого
промежуточного конуса (в том числе
и конусов с углами 0 = 6С и 0 = |3К)
и меняются при переходе с одной
поверхности на другую. Поток, который соответствует такому решению,
называется коническим. С учетом его свойства частная производная от любого
параметра по координате г (рис. VIII-1-1) равна нулю, и тогда из
уравнений (II1-2-8) можно получить первые два уравнения системы
dVr т/_.
Рис. VII1-1-1. Схема обтекания острого
конуса сверхзвуковым потоком газа (1 —
скачок уплотнения)
dVQ
dQ
(VIII-1-1)
(VIII-1-2)
В соответствии с числом определяемых неизвестных параметров к этим
двум уравнениям надо добавить уравнение неразрывности (Ш-2-17),
записываемое в виде
" Fe % + 9 ^ж + pVQ ctg 0 = О, (VIII-1-3)
(VIII-1-4)
[И
• = ic + -^. (VIII-1-5)
а также уравнение
Р = (1*ср)с Р Т
Рс И'ср Рс *(
получаемое из уравнения состояния (Ш-2-52), и уравнение энергии
F2
2
Конус в сверхзвуковом потопе
373
В этих уравнениях индексом «с» обозначены параметры непосредственно
за скачком уплотнения. В рассматриваемую систему должны войти также
общие зависимости (Ш-4-6) н- (Ш-4-9) для расчета энтальпии, энтропии,
среднего молекулярного веса и скорости звука.
Постоянные теплоемкости
Рассмотрим решение для частного случая, когда диссоциация отсутствует
и удельные теплоемкости при переходе через ударную волну не меняются.
Для этого случая система состоит из уравнения (VIII-1-1), а также
уравнения
(VIII-1-6)
получаемого в
с учетом того,
результате комбинации уравнений (VIII-1-2) и
что dp!dQ = a2 (dp/dQ), где квадрат скорости
(VIII-1-3)
2 =
[(
В результате совместного
решения этих двух дифференциальных
уравнений может быть найдено
распределение скоростей VT и Vq. Этого
достаточно для полного решения
задачи, так как по скоростям при
помощи уравнения Бернулли могут быть
найдены остальные газодинамические
параметры (давление, температура
и т. д.).
Численное интегрирование
дифференциальных уравнений для
нахождения VT и Vq ведется при
следующих граничных условиях на конусе
и скачке. Условие на конусе заключается в том, что на его поверхности
нормальная составляющая скорости VQ = 0, т. е. dVr/dQ = Vq = О при е = рк
(см. рис. VIII-1-1).
Используя уравнение (III-4-34) ударной поляры, можно получить
условие на скачке уплотнения
Рис. VIII-1-2. К определению граничных
условий на скачке уплотнения около
острого конуса
где
Л+1
= vcr/v
с г' * max?
Fcr, Vcq — соответственно радиальная и нормальная составляющие скорости
на скачке уплотнения.
Уравнение получено с учетом того, что (рис. VIII-1-2)
Fc г = Vc roo = Foo cos ec. (VIII-1-8)
Расчеты начинают с того, что по известной скорости набегающего
потока вычисляют для заданного значения угла 6С параметры за скачком
FCr, Fce, а также скорость звука ас. Затем, зная эти граничные условия,
в результате численного интегрирования последовательно находят параметры
на ряде промежуточных конических поверхностей. Вычисления заканчивают,
когда будут удовлетворены граничные условия на конусе: соответствующий
угол 6 равен углу конуса рк, значение Vr = FK — полной относительной
скорости на его поверхности.
374 Глава VIII
Расчеты можно производить также в обратном порядке, задавшись
условиями на конусе (углом (Зк, скоростью FK). В результате находят
параметры газа, а также угол наклона скачка, возникающего перед заданным
конусом.
Решение в виде ряда Тейлора. Для численного расчета потока около
конуса можно воспользоваться разложением в ряд Тейлора. Представим
в виде такого ряда выражение для радиальной составляющей скорости,
отнесенной к ее максимальному значению:
'Kr (8-р„) + ..(9f)№
где V^l — значения производных dnVr!dQn на поверхности конуса.
Эти производные определяются по известной скорости на конусе,
причем первая производная V'Kr равна нулю, так как нормальная составляющая
скорости на нем VKe = V'Kr = 0. Для второй производной из (VIII-1-6)
получим
[(l^)] (l—S
] (
где a = a/Vmax.
Если рассмотреть поверхность конуса, то Э = рк> Fr = FK, V'r = VKr = Q
и, следовательно, V'^r= —2FK.
Применяя последовательное дифференцирование уравнения (VIII-1-6),
определяют третью и более высокие производные. С учетом этого ряд
(VIII-1-9) можно записать
где h = Q — рк, а коэффициенты а3, а4 даются при к = 1,4 соотношениями
Дифференцируя (VIII-1-11) по Э, найдем ряд, представляющий
нормальную составляющую скорости:
ZL = _ 2/г + За3/г2 - 4а4&3 + . .. . (VIII-1-13)
Формулы (VIII-1-11) и (VIII-1-13) позволяют вычислить составляющие
скорости вблизи конуса и далее последовательно (шагами) определить
составляющие скорости на промежуточных конических поверхностях. Для
этой цели используется ряд
Vrh = Vrh
где Vrh — радиальная составляющая скорости на конической поверхности
с углом наклона образующей 6 + h\
Vrh-i— та же составляющая на соседнем промежуточном конусе с углом 0;
Fr/i-i —значение первой производной на том же конусе.
В практических расчетах лучше брать среднее
V'V
По аналогии с (VIII-1-14) можно написать выражение для производной
Конус в сверхзвуковом потоке
375
При этом первую и вторую производные в правой части находят при
помощи уравнения (VIII-1-6). Формула (VIII-1-15) дает возможность
вычислить нормальную составляющую скорости на промежуточной конической
поверхности
vQh = veh-i+hv;h-i +... . (viii-i-16)
Основной операцией при осуществлении этих вычислений является
определение по формуле (VIII-1-10) второй производной на предыдущей
конической поверхности.
Перемещаясь в ходе вычислений с одной поверхности на другую,
расчеты заканчивают, когда угол 9, полученный от сложения угла |3К и всех
Рис. VIII-1-3. К определению параметров газа около конуса
заданных интервалов h = AQ, окажется равным величине 6 = 6С,
подсчитанной по (VIII-1-7). Эта величина определит угол наклона скачка, а
значения Vr = Vcr, Vq = Vcq будут являться соответственно радиальной и
нормальной составляющими скорости за ним. Определив составляющую Vcr
и угол 0С по (VIII-1-8), можно найти скорость набегающего потока.
Таблицы, графики, приближенные формулы. В работе [4] показано,
что в случае сверхзвукового обтекания конуса газодинамические величины
являются функциями Моо, рк и координаты g = (r — B)/(W — В), где В и W —
расстояния соответственно от оси до поверхности конуса и до ударной
волны (рис. VIII-1-3).
Результаты численных расчетов осесимметричного обтекания конусов
представлены в приложении № 1 (табл. VIII-1-1 и VIH-2-2).
В табл. VIII-1-1 даны значения газодинамических функций VX1 Vr, p
и р, которые являются безразмерными и отнесены к следующим величинам:
осевая и радиальная составляющая скорость (в цилиндрических
координатах) отнесены к критической скорости звука а*, плотность —к величине роо
и давление— к рооа*2. В этой же таблице дано значение Wx, равное тангенсу
угла наклона ударной волны к оси конуса.
В табл. VIII-2-2 приведены значения коэффициента волнового
сопротивления конуса cXB = cRp, вычисленные по данным табл. VIII-1-1. Величина
схв равна коэффициенту давления на конусе.
Для расчета параметров потока по табличным данным (с индексом «т»)
следует воспользоваться формулами Vx = VXTa*, Vr = VrTa*, p = ртрооа*2,
р = ртроо, где a:¥2 = [2/(k + l)]a2oo + [(k — l)/(k + l)] FL. Тангенс угла наклона
образующей промежуточного конуса находится по заданному значению
координаты I при помощи tg6 =--rlx =-- tgf5K + g (Wx — tg (3K).
Для определения температуры, давления и плотности по известной
скорости могут быть применены формулы (III-3-4), которые удобнее предста-
376
Глава VIII
вить в следующем виде:
Poo
т
Л.
т \k-i
\l/(ft-l
1
(VIH-1-17)
где V2 = (F? + F|)/Fmax; параметр vo = p'o/po представляет собой отношение
давлений торможения после и до скачка и определяется в зависимости
от числа Моо и угла 0С по формуле (Ш-4-33).
В результате обработки вычислений могут быть рекомендованы
следующие приближенные формулы для расчета коэффициента давления и угла
наклона скачка уплотнения:
(VIII-1-18)
(VIII-1-19)
Mo
рк = схв = (0,0016 + 0,002M~2) (рк)1 '7;
sin ес = 1 - cos рк + (l + -h=L Ml sin2 рк)
/2
где |3К — угол конуса в градусах.
Практически расчет по этим формулам ведется в широком диапазона
значений рк и Моо с точностью до 5%. Нижние допустимые пределы для рк
и Моо определяются теми их значениями, при которых поток между конусом
и скачком остается сверхзвуковым. Погрешность выражения (VIII-1-19)
возрастает с увеличением Моо и рк, когда значительным становится влияние
диссоциации (Моо > 10-г-15, рк > 30 ~ 40°).
Исследования показывают, что скорость звука в возмущенной области
меняется настолько слабо, что ее можно принять постоянной и равной
соответствующему значению непосредственно за скачком. Расчеты, проведенные
при этом предположении, показали хорошие результаты. Например, при
Моо = 3 и 9С = 28°11/ погрешность в определении угла конуса по сравнению
с точной теорией составила 0,08%, а скорости на его поверхности —
около 0,2%.
Таблица VIII—1—2
Минимальные значения числа М^, для которого возможен конический
режим обтекания
(теоретические данные)
к
Моо min
5
1,0129
7,5
1,0294
10
1,0528
12,5
1,0828
15
1,1193
17,5
1,1622
20
1,2115
22,5
1,2673
25
1,3301
30
1,4820
35
1,6814
40
1,9582
Расчеты обтекания конусов дают удовлетворительные результаты пока
сохраняется конический режим течения между конусом и скачком
уплотнения. Минимальные значения числа Моо, для которых по теоретическим
данным возможен конический поток, даны в табл. VIII-1-2.
Гиперзвуковые скорости. По выражениям для составляющих скорости
в виде рядов Тейлора можно найти сравнительно простое приближенное?
решение задачи об обтекании конуса при очень больших числах Моо.
Конус в сверхзвуковом потоке
При таких скоростях скачок достаточно близко приближается к
поверхности конуса и разность углов 9С —рк становится настолько малой, что при
помощи рядов (VIII-1-11) и (VIII-1-13) можно написать следующие
соотношения для составляющих скорости потока на скачке уплотнения:
(VIII-1-20)
Fee = FH [- 2 (9c-pK) + (9c-pK)2ctgpK -...]. (VIII-1-21)
Эти соотношения могут быть использованы для расчета угла наклона
скачка уплотнения. С этой целью напишем уравнение расхода (Ш-4-3)
в виде
Так как составляющая скорости набегающего потока, нормальная
к скачку уплотнения, равна Fooe = Foo sin 9C, то с учетом соотношения
(VIII-1-8) зависимость (VIII-1-22) преобразуется в выражение
. (VIII-1-22')
Если рассматривается обтекание с очень большими скоростями при
условии, что углы наклона скачка 0с и разность 9С — |3К малы, то из (VIII-1-20),
(VIII-1-21) и (VIII-l-22/) можно получить следующую формулу для угла
наклона скачка уплотнения:
где
К0 = Моовс; Ki^MoopK.
Из (VIII-1-23) видно, что при разных соотношениях углов рк и чисел
Моо, но при соблюдении постоянства параметра Кь величина Ко у всех
конусов будет одинаковой.
Найдем выражения для определения параметров на конусе, а также его
волнового сопротивления. С этой целью воспользуемся соотношением pjpoo =
= (Рк/Рс) (Рс/Роо), в котором величина pjpoo найдется по (Ш-4-25), а
значение pjpe — o помощью уравнения адиабаты pKlpc = {aJaG)2k^k-i\
Для скоростей звука на конусе и скачке имеем формулы
на основании которых
где Fcr и Fce определяются при помощи выражений (VIII-1-20) и (VIII-1-21).
Вычисляя скорость звука ас с учетом (Ш-1-26), имея в виду, что
числа Моо перед скачком очень велики и можно допустить некоторые
упрощения, а также определяя из (Ш-4-25) давление рс, получаем формулу для
давления на конусе
С помощью этой формулы Нетрудно вычислить коэффициент давления
на конусе рк= (2/A:ML) (Рк/Роо — 1), равный его коэффициенту волнового
сопротивления.
378 Глава VIII
По величине коэффициента давления определяют функцию
сопротивления
А 2(+1)K|i . (VIII-1-26)
Этой формулой функция сопротивления фактически определяется лишь
в зависимости от одного параметра К4, потому что Ко в свою очередь, как
видно из (VIII-1-23), зависит от этого параметра.
Таким образом, течения с очень большими числами Моо около конусов
оказываются подобными в том смысле, что при одинаковых параметрах
подобия К4 будут одинаковыми и функции сопротивления.
Формулой (VIII-1-26) неудобно пользоваться, так как приходится
определять промежуточный параметр Ко. Практически удобнее аппроксимирующая
зависимость
2 (к+1) (fe+7) и2 (л , 1 тг-3/2
которая для & = 1,4 имеет вид
РкМ^ = сявМ^ =
Как следует из самого вывода формул (VIII-1-23) и (VIII-1-26), они
будут тем точнее, чем больше число Моо и чем, следовательно, ближе к
поверхности тонкого конуса расположен скачок уплотнения. Те значения схв = рК,
которые соответствуют значениям параметра К^ > 1, лучше согласуются
с точной теорией и экспериментом.
Предельный случай. В предельном случае, когда Моо—^оо,
формула (VIII-1-23) для угла наклона скачка уплотнения принимает вид
Соответствующее значение для коэффициента давления получается
из (VIII-1-26) в таком виде:
или, с учетом (VIII-1-28),
Сравнивая это выражение с (IV-7-3), в котором в случае тонкого конуса
величина cos2r] заменена квадратом угла конуса рк> можно видеть, что
разница между ними заключена в значениях коэффициента при рк- Очевидно,
формула (VIII-1-30), учитывающая особенности обтекания конуса, является
более точной, чем (IV-7-3). Формула (VIII-1-30) совпадает с (IV-7-3), если
принять k = l.
Формулу (VIII-1-30) можно распространить на конуса произвольной
толщины, для которых коэффициент давления
ш2Рк. (VIII-1-30')
Эту формулу называют усовершенствованной формулой Ньютона для
конуса.
Оценка величины возмущений при обтекании тонкого
конуса. Полученные выше соотношения позволяют оценить величины
возмущений, возникающих в потоке около конуса в условиях обтекания его
с очень большими скоростями. Определим вначале из уравнения (VIII-1-20)
скорость на конусе. Полагая Fce = Foo (I — 0,5(3^), найдем
Конус в сверхзвуковом потоке 379
Из этого выражения следует, что вертикальная составляющая скорости
У г == ^к sin Рк ~ Т^кРю а горизонтальная Vx = FK cos j3K ~ FK.
Таким образом, осевая составляющая скорости возмущения, равная
Уоо [(Эс — |3К)2 — 0,5РкЬ будет на порядок меньше, чем вертикальная.
Следовательно, процесс сжатия газа при обтекании конуса в основном
обусловлен смещением частиц воздуха поперек потока, в то время как характер
течения в продольном направлении претерпевает весьма малые изменения.
Пренебрегая этим изменением скорости, т. е. принимая продольную
составляющую равной скорости набегающего потока, полагают, что процесс
смещения частиц происходит только в плоскости, нормальной к оси конуса. Этот
процесс является одним из частных примеров действия закона плоских сечений.
Если рассмотреть предельный случай, которому при к — 1,4
соответствуют значения углов скачка 6С = 1,093рк, то предельная величина
возмущенной скорости на конусе будет FK = Foo (I — О,5|3к)- Следовательно,
лродольное возмущение можно оценить величиной — 0,5FooPk-
Как видно, эта величина определяется квадратичной зависимостью от
малого параметра Р^. Причем, вместо угла в качестве малого параметра
может быть выбрана величина, обратная удлинению конуса, т. е. 1 М,к,
представляющая собой его относительную толщину.
Если ввести для малого параметра в общем случае обозначение т, то
на основании оценки возмущений, полученной для условий на конусе,
лродольное возмущение в произвольной точке потока оценивается
величиной Foot2, а поперечное — значением FooT.
Для оценки возмущений давления можно воспользоваться
выражением (VIH-1-27), из которого найдем, что на конусе коэффициент давления
имеет порядок р# ~ (3^, а следовательно, абсолютное давление оценивается
величиной рК ~ £>ooMLPk- На основании этой оценки в любой точке потока
около конуса давление можно оценить величиной р ~ /?ооМ^т2, которая, как
.видно, будет значительно превосходить давление невозмущенного потока.
Что касается плотности, то для оценки возмущений можно исходить
из (III-4-24). Так как рассматриваются очень большие скорости, когда
Моо0с = Ко > 1, то можно сделать вывод, что плотность в возмущенном
потоке приблизительно на порядок выше, чем в невозмущенном. Таким
образом, и в отношении плотности возмущения оказываются большими.
Несмотря на большие возмущения давления и плотности, тем не менее
удалось, как было показано, достигнуть упрощения задачи об обтекании
конуса потоками с очень большими скоростями и получить достаточно
простые расчетные эависимости. Это оказалось возможным вследствие
малости возмущений скорости.
При этом следует отметить, что рассмотренная выше оценка возмущений
распространяется на случай обтекания любого тонкого тела с произвольной
образующей. Поэтому, как и для конуса, математически может быть
достигнуто упрощение решения задачи об обтекании такого тонкого тела с
большой сверхзвуковой скоростью.
Влияние диссоциации и
ионизации
При расчете обтекания с учетом изменения состава воздуха
используется в прежнем виде часть уравнений системы, а именно уравнения
(VIII-1-1), (VIII-1-4) — (VIII-1-6). Разница заключается в применении
более общих зависимостей для определения скорости звука, энтальпии,
энтропии и среднего молекулярного веса. Расчет начинается с определения
за косым скачком параметров газа по заданному углу 6С и известным
значениям poo, Too, Foo. Затем по уравнениям (VIII-1-1) и (VIII-1-6) вычисляют
первые производные для условий на скачке, подсчитывают составляющие
380
Глава VII}
скорости Vr и Vq и разность энтальпий i — ic на соседней конической
поверхности с углом 9С — А0. Полагая, что поток за скачком во всей
области изэнтропический и его энтропия S = Sc = const, можно определить по-
энтропийной диаграмме или таблицам,
зная i и S, давление и температуру на
этой поверхности. По найденным
значениям Тир определяют скорость звука,
средний молекулярный вес и плотность.
Ведя аналогичные расчеты, перемеща-
Н-50км
ун^Окм
400
200
у
/
/
■н=ь
1
V
Жоез учета
f диссоциации
20
60
500
О
20
Рис. VII1-1-4. Давление на конусе
с учетом диссоциации: Too =
222° К; Мое = 23,5
Рис. VIII-1-5. Температура на
конусе с учетом диссоциации:
Too = 222° К; Мое = 10
ются к соседней промежуточной конической поверхности и т. д. Вычисления
заканчивают, когда на одной из таких поверхностей нормальная
составляющая скорости окажется равной нулю. Полученные параметры будут
принадлежать поверхностям
обтекаемого конуса.
Эти параметры, как
видно, зависят от температуры,
и давления набегающего
потока, в то время как при
отсутствии диссоциации в
случае обтекания разогретым
газом с переменной
теплоемкостью параметры обтекания
зависят от Too и не зависят от
Роо. Некоторые результаты
расчета параметров обтекания
конуса потоками с большими
скоростями приведены на рис.
VIII-1-4 4- VIH-1-6.
Характер изменения этих
параметров при наличии диссоциации
и ионизации тот же, что и
непосредственно за скачком. В частности, изменение давления оказывается
таким же малым. Что касается температуры и плотности, то они меняются
существенно. Причем, это изменение тем больше, чем толще конус.
Если углы конуса невелики, то даже при значительных скоростях эти
параметры на конусе испытывают небольшое влияние физико-химических
10
20
30
Рис. VII1-1-6. Плотность на конусе с учетом
диссоциации, Гоо = 222° К; Мое =10
Конус в сверхзвуковом потоке
381
с
46
45
43
42
\
<
н=
30 км
\
4
\
\
\
10
15
20 Мс
Рис. VIII-1-7. Изменение угла
наклона скачка уплотнения перед
конусом:
реальный газ;
совершенный газ
превращений. Например, расчеты показывают, что при Моо = 24 плотность
почти не меняется с высотой вплоть до углов |3К = 15°, а при Моо = 10
{рис. VIII-1-6) — до углов рк = 35°. Таким образом, интервал углов, внутри
которого влияние высоких температур не сказывается, расширяется с
уменьшением скорости. Такое же явление наблюдается с уменьшением высоты.
Утолщение конуса вызывает более
интенсивный разогрев и, как следствие,
диссоциацию и ионизацию, которые могут
существенно влиять на параметры обтекания. Для
иллюстрации на рис. VIII-1-7 показано это
влияние на изменение угла наклона скачка
перед 40-градусным конусом. Величина угла
наклона скачка уменьшается по сравнению
со значением этого угла при постоянных
теплоемкостях (к = 1,4). На том же рис.
VIII-1-7 показано изменение угла 6С,
рассчитанное для гипотетического совершенного
газа с показателем адиабаты Тс = 1,2. Видно,
что при очень больших скоростях схема
гипотетического газа дает удовлетворительные
результаты. Из этого следует, что параметры
возмущенного течения около конуса при
таких скоростях в основном определяются
физико-химическими свойствами разогретого
за ударной волной газа, и прежде всего
отношением удельных теплоемкостей.
Сказанное относится к таким
параметрам, как плотность, температура, угол
скачка. Что касается давления, то оно, как
отмечалось, практически не меняется по
сравнению с совершенным газом. Его величина
зависит почти целиком от условий
набегающего потока. Причем максимальное
избыточное давление не может превысить значения
PooF^o. Расчеты же по фиктивному отношению
удельных теплоемкостей к = 1,2, как видно
на рис. VIII-1-8, дают заниженные значения
давления.
Исследования обтекания конуса
потоком реального газа можно упростить, если
скорость звука за ударной волной принять
постоянной. Выше было показано, что это
предположение при постоянных
теплоемкостях незначительно отклоняет получаемые
результаты от точных.
Численное интегрирование (VIII-1-6) при а = ас = const выявило,
что при наличии диссоциации точность расчета оказывается большей.
Например, для нормальных условий (Too = 288° К, рос = 1кГ /см2 =
= 9,807-104 н/м2) перед скачком с углом 8С = 14° при Моо = 14
погрешность в определении угла рк составляет 0,06%, а скорости — 0,002%.
При условии постоянства скорости звука задача в основном
заключается в определении скоростей на промежуточных конических
поверхностях. Что касается таких параметров, как энтальпия, давление, плотность
и температура, то их расчет может осуществляться независимо и после того,
как найдено поле скоростей.
400
300
200
100
0
к
к=1,2
V
//
/
10
15
20 Мс
Рис. VIII-1-8. Давление на
конусе в диссоциированном газе:
О— Я = 0 км; □ — Я = 30 км;
А — Я = 60 км; сплошная и
пунктирная линии — совершенные газы
с постоянными теплоемкостями
382 Глава VIII
При очень большой скорости расчет обтекания упрощается вследствие
того, что благодаря близости ударной волны к конусу и, следовательно,
малой толщине возмущенной области потока производную dVQ/dQ можно
принять в этой области постоянной и равной ее значению непосредственно
за скачком, а производную dVr/dQ — равной 0,5 Fc0, т. е. средней
величине между значениями на скачке и конусе.
При этих предпосылках можно непосредственно определить угол
обтекания конуса и скорость на нем:
рк = вс —|Ав|; FK = 7Kr = Fcr-O,5Fce|Ae|>
где lAGI^F^^
Решение с постоянной плотностью. При очень
больших скоростях обтекания конуса ударный слой оказывается
достаточно тонким, и вследствие того, что давление в нем мало меняется,
плотность вдоль линии тока можно практически принять постоянной. Таким
образом, значение р = роо/рс = Pi/p2 непосредственно за скачком будет
определять плотность на конусе.
Решение уравнений движения газа около конуса дает приближенное
соотношение для коэффициента давления [59]:
рк = 2 sin2 р„ [(1 - 0,25р) cos2 (9С - pK)]-i. (VIII-1-33)
Расчеты показывают, что эта формула дает хорошие результаты для
значений р, равных, примерно, ОД и меньше.
Чтобы вычислить по формуле (VIII-1-33) коэффициент давления, надо
знать углы скачка 6С, относительную плотность р при заданных параметрах
набегающего потока и угле конуса рк. В ходе расчетов можно поступить
следующим образом. Задавшись величиной р, определяют угол
присоединенного скачка по формуле гиперзвукового обтекания конуса:
(|) 5/(т0, (VIII-1-34).
где
/ (т,) = 2т, (1 + /Г^Г2)-1; г] = (|)1/2 (1 -1) -1 tg pK. (VIII-1-35)
Значения г] меняются от 0 до 0,5, а соответствующие величины
функции /(г))— от 0 до 1. По разности углов 0С —Рк подсчитывают cos2(Gc —рк).
Причем, для малых значений 8С — рк можно принять cos (9С — рк)^1.
По формулам (III-4-14) и (III-4-12) подсчитывают соответственно
энтальпию i2 и давление р2, затем по термодинамическим таблицам, зная i2 и р2,
находят р2,уточняют угол Эс и коэффициент давления.
Расчеты упрощаются, если воспользоваться эмпирической зависимостью
для определения угла наклона скачка перед конусом ([70], № 12, 1964)
102Моо sin 9С = 39 - lg poo + 0,5 (206 + lg Poo) Moo sin pK, (VIIi-1-36)
где poo — атмосферное давление в кПсм2.
Точность этой формулы при MooSin6c>6 составляет, примерно, 1%.
Расчет по формулам (VIII-1-34) — (VIII-1-36) не требует применения таблиц
термодинамических функций. По известным значениям Моо, Рк и роо при
помощи (VIII-1-36) определяют 0С, а затем, используя (VIII-1-34) и (VIII-1-35),
путем одного-двух приближений находят р, после чего подсчитывают рк
по (VIII-1-33).
Пример. Произведем расчет обтекания острого конуса с углом рк = 45° при
условии, что Me» = 20, а параметры набегающего потока соответствуют высоте
Конус в сверхзвуковом потоке
383
Н = 5 км. Для этих параметров по таблицам стандартной атмосферы находим
/>oo=Pi=0,56-^5 ; Г0О=7т1 = 255,7о; aoo=a1 = 320,5 —; p^p^ 0,0733 / .
cjh сек м^
Для удобства дальнейших вычислений приведем уравнение (VII1-1-34) при помощи
(VIII-1-35) к виду
(VIII-1-37)
з tg2 рк
'4)г
Энтальпию и давление за скачком уплотнения определяем при помощи равенств
^ [ ^
В качестве первого приближения примем р —0,108, и для этого значения найдем
tg9c = 1,1298 (0С==48°29').
Следовательно, учитывая, что Fnl = Foo sin 0C и i1 = c-pTi, энтальпия
., = 1002.255,7+ **»^°'->"»' ((„o,,O8.)a.i,367.1O.
и давление
2
202320,52
,u
(4_0>108)
]-,
По диаграмме i — р [13] определяют р2 = 0,6
6475.10. к
затем подсчитывают
соответствующий параметр р = 0,1095.
Расчет во втором приближении дает угол 0с = 48°32\
По этим значениям р и 8С при помощи формулы (VII1-1-33) находят коэффициент
давления на конусе
Рк-2-0,70722 Г Г 1 — 0,25-0,1095 \ cos2 (48°32/-45°)l~1 = 1,032.
Воспользовавшись формулой (VII1-1-36), для заданных условий обтекания находят
sin 9С = ^^^20 [39-lg 0,56 +0,5 (206+lg 0,56) 20 sin 45°]-
= 0,7456 и Gc = 48°13'.
Для нахождения плотности применяют зависимость (VIII-1-34), которую
преобразуют к виду
2 tg Рк 1 (VIII-1-38)
1 —
tgec
У "(-4Г
После ряда приближений находят р = 0,1. Соответствующий этой величине
коэффициент давления практически не отличается от значения, полученного выше.
Автомодельное решение. В работе [4] показано, что решение задачи
об обтекании круглого конуса при наличии химических реакций является
автомодельным относительно параметра £ = (г — B)I(W — В) (см. рис. VIII-1-3).
Газодинамические величины в точке с координатой £ зависят при заданной
скорости полета от угла конуса |3К, давления, плотности и температуры
набегающего потока.
В табл. VIII-1-3 сравниваются результаты расчета обтекания конуса
с рк = 20° при Моо —15 и 20 соответственно для случаев, когда химические
реакции учитываются и когда воздух не претерпевает физико-химических
превращений (к = 1,4). В этих таблицах приведены безразмерные параметры
Vxla*, Vr/a*, p/pood*2, р/роо, рассчитанные для условий в невозмущенном
потоке при Моо = 15 для а* = 1962 м/сек, росД*2 = 0,1567 am (ОД 537- 10ьн/м2),
384
Глава VIII
Таблица VIII—1—3
Газодинамические параметры на круглом конусе с углом полураствора (JK = 20°,
рассчитанные с учетом химических реакций и при Jc = 1,4 — const
I
и
0,2
0,4
п a
и, о
0,8
Л (Л
1,1)
\"-
Параметры ^ч.
Vx
р
9
Vx
Р
9
Vx
Vr
Р
9
Vx
Vr
р
9
Vx
Vr
p
9
Vx
Vr
P
9
0с == OW/dx
к..
с учетом
химических реакций
2,113
0,769
0,738
6,022
2,118
0,754
0,737
6,012
2,124
0,740
0,732
5,985
2,129
0,726
0,725
5,940
2,135
0,711
0,715
5,877
2,140
0,697
0,703
5,797
0,405
= 15
k = 1,4
2,109
0,768
0,742
5,410
2,116
0,751
0,741
5,401
2,122
0,735
0,736
5,375
2,128
0,719
0,727
5,332
2,134
0,703
0,716
5,274
2,141
0,687
0,702
5,199
0,410
с учетом
химических реакций
2,127
0,774
0,732
7,031
2,132
0,762
0,730
7,021
2,136
0,749
0,727
6,992
2,141
0,737
0,721
6,945
2,146
0,725
0,712
6,879
2,150
0,713
0,702
6,794
0,398
= 20
k = 1,4
2,121
0,772
0,739
5,727
2,127
0,756
0,737
5,718
2,133
0,741
0,733
5,692
2,139
0,726
0,725
5,649
2,145
0,711
0,714
5,591
2,151
0,696
0,701
5,516
0,407
а при Мое = 20 для а* = 2604 м/сек, ртса*2 = 0,2759атп(0,2706-105 н1м2).
Значения 71оо=250о, р™=0,292• 10"2 ат(0,2864-103 н1м2), р*,=0,412-10"2 кг/м3
соответствуют примерно атмосферным условиям на высоте 40 км.
Решение при помощи рядов [18]. Представим решения для
составляющих Vr и Fe [см. рис. (VIII-1-1)] в виде рядов
Vr = Л + А,Н +1А2Н* + i A3HS +...;
(VIIM-39)
_ _ J_
где #=ес-е.
Для определения коэффициента A-t воспользуемся системой уравнений
(VIII-1-1) — (VIII-1-5) и граничными условиями. На поверхности скачка
■ = Fce;
-1
на поверхности обтекаемого тела
(VIII-1-41)
(VIII-1-42)
Конус в сверхзвуковом потоке 385
В соответствии с граничными условиями
А) = Vc r = Foo cos 6C;
At=-Vee;
А2 = -Fcr-(Fcectg9C + Fcr) (1 —
(VIII-1-43)
= -Л- (Л + 42ЯК), (VIII-1-44)
лк
где #К = 0С — рк.
Значение Як находят из решения уравнения
Коэффициент Ля определяют по заданному углу скачка Эс и
вычисленным с учетом диссоциации значениям для этого скачка Vcq и ас. По
найденным Ап определяют поле течения вокруг конуса с соответствующим
заданному значению 0С углом |3К — 6С — Нк.
Влияние неравновесности
Мы рассмотрели два случая невязкого обтекания конуса. Один из них
связан с постоянными теплоемкостями, другой — с равновесной
диссоциацией и ионизацией в области между волной и телом. Оба случая можно
считать предельными и расположенными на границах интервала, внутри
которого размещаются неравновесные течения газа в возмущенной области.
Первый случай характеризуется тем, что химические и физические
свойства газа в возмущенной области остаются такими же, как
непосредственно за ударной волной, причем переход через нее совершается при
постоянных теплоемкостях. Таким образом, газ рассматривается
«замороженным» во всей возмущенной области. Для этого предельного состояния
характерно отсутствие возбуждения энергетических уровней. При этом
в качестве дальнейшего приближения можно принять, что непосредственно
за фронтом волны колебательные степени свободы приходят в равновесие,
а затем остаются «замороженными». Если рассмотреть газ, состоящий
полностью из двухатомных молекул, то для «замороженного» состояния
показатель А: = 9/7.
Другой случай имеет ту особенность, что во всей возмущенной области,
в том числе непосредственно за фронтом ударной волны, диссоциирующий
газ находится в равновесии. Исследования показывают, что имеется отличие
в значениях параметров обтекания в двух предельных случаях. Например,
в «замороженном» потоке угол скачка и температура на поверхности больше,
а плотность и давление, наоборот, меньше, чем соответствующие значения
этих параметров в равновесном диссоциирующем потоке. Причем
«замороженное» течение можно рассматривать с невозбужденными или
возбужденными колебательными уровнями.
Если температуры недостаточно высоки, чтобы развилась
диссоциация, то предельные случаи будут характеризоваться, с одной стороны,
«замороженным» потоком с постоянными теплоемкостями, а с другой,—
течением с возбужденными во всей области вибрационными уровнями.
Таким образом, второй предельный случай будет характеризоваться в
зависимости от температуры равновесным возбуждением колебаний или
равновесной диссоциацией.
Если при очень высоких температурах первый предельный случай
рассматривается как «замороженное» течение, то эта предпосылка оказывается
более оправданной, когда времена релаксации колебаний меньше, чем дис-
социационной релаксации. Оба предельных случая рассчитываются как
25-114
386
Глава VIII
конические течения. Что касается промежуточного неравновесного
обтекания, то оно не является коническим. Понятно, что исследование параметров
обтекания представляется задачей
более сложной.
Для ориентировочной оценки
можно предположить, что они
меняются от значений на носке для
«замороженного» течения до равновесных
величин в конце длины пути
релаксации, т. е. там, где достигается
равновесная степень диссоциации (или
колебательное равновесие). Схема
этого явления изображена на рис.
VIII-1-9. Сплошные кривые
соответствуют случаю, близкому к
равновесному 1 почти во всей области,,
а пунктирные — к «замороженному» 2.
При этом первый случай более
вероятен на малых высотах, второй — на
больших.
Из этой качественной оценки
следует, что неравновесные течения
изменяют аэродинамические
характеристики. В частности, сопротивление
оказывается больше по сравнению
с «замороженным» и меньше — по сравнению с равновесным случаем. Однако
эта разница невелика. Если же рассмотреть влияние неравновесности на
подъемную силу, то оно может оказаться более значительным.
Рис. VIII-1-9. Неравновесные параметры
на конусе
§ VMI-2. Конус под углом
атаки
Некоторые результаты расчета
сверхзвуковых конических
течений
Рассмотрим результаты расчета сверхзвуковых конических течений
по методу конечных разностей, полученные группой научных сотрудников
под руководством проф. К. И. Бабенко [4]. Решение задачи о течении около
бесконечного конуса, обтекаемого под углом атаки, является
автомодельным. Соответствующие газодинамические функции зависят только от двух
переменных, являющихся известными комбинациями исходных. В качестве
таких переменных можно взять угол 7 и переменную I = (г — В) /(w — В).
В табл. VIII-2-1 и VIH-2-2 приведены реультаты расчета
сверхзвукового обтекания конусов идеальным газом с постоянным показателем адиабаты
k = 1,4 (см. приложение № 1). Поля течений, приведенные в табл. VIH-2-1,
рассчитаны в цилиндрической системе координат х, г, ф (д = я/2 — у),
причем полуплоскость Ф = 0 (у = л) расположена с наветренной стороны
(см. рис. VIII-1-3).
В качестве параметров выбраны число Моо, углы конуса рк и атаки а,
а в качестве независимых переменных Ф и £ = (г — В) I(W — В). Значения
составляющих скорости Fx, Vr, V# отнесены к критической скорости звука
а*, плотность — к значению роо, давление — к рооа*2. Для каждого
значения д в табл. VIII-2-1 приведено значение Wx = dW/dx, равное тангенсу
Конус в сверхзвуковом потоке
387
угла между осью х и образующей ударной волны в соответствующей
меридиональной плоскости.
Значения аэродинамических коэффициентов в связанной системе
координат, рассчитанные по формулам
приведены в табл. VIII-2-2. В этой же таблице даны значения
коэффициента момента mzv.
Коэффициенты волнового сопротив-
ления сх в и подъемной силы сур в
поточной системе определяются по формулам
перехода
Схв = Crv cos a + Cnp sin a;
сур = сдгр cos а — cRp sin а.
Для расчета параметров потока по
табличным данным(с индексом «т ») следует
воспользоваться формулами Vx —• VxTa*
(аналогично находят другие составляющие
Vr и Fe), р = ртроо; р-Ртрооа*2.
При заданных х, £, Ф» расстояние г
от оси конуса определяется формулой
0,2
У
Анализ результатов расчета
обтекания конусов
Данные, содержащиеся в табл. VII1-2-1,
позволяют сделать некоторые общие
выводы о неосесимметричном обтекании
круглых конусов, а также обнаружить
отдельные характерные особенности конического
течения.
Форма ударных волн. Ударные волны,
следы которых в поперечной плоскости
могут заметно отличаться от окружности,
по форме разделяются на два вида. Первый
вид характеризуется тем, что расстояние
от волны до конуса в наветренной стороне
(Ф = 0) меньше, чем в подветренной {& =
180°). Второй вид, наблюдаемый при
больших углах конуса и числах М»,
характерен меньшим расстоянием в
подветренной стороне. Таким образом, можно найти
отдельные значения рк и М<х> и
соответствующие им углы Ф, отличные от 0 и я,
при которых волна наиболее удалена от
поверхности конуса. Обычно максимальное
расстояние до ударной волны
соответствует углу д = 180°.
Зависимость параметров газа от значения координаты |. При малых:
углах атаки эта зависимость близка к линейной и отклоняется от нее при
возрастании а.
■■ ■
А
1—
— —
— —.
1—-*«
■——
"*—-
,
1—-^
—
3,0
0 0,2 0,и Q6 0,8 / <f
Рис. VIII-2-1. Зависимость
давления и плотности около конуса от
координаты |:
а-1 —Моо = 5; рк=30°; а = 5°; 2 - М^^
«=5; рк=15°; а =10°; б-1-Моо = 7;
Эк=30°; а=5°; (#=0,90°; 180°); 2-
Моо = 7; Зк = 30°; а=15° (#=0,90°; 180°);
388
Глава VIII
Плотность газа, как и давление вблизи поверхности конуса, обычно
больше, чем вдали от нее (рис. VHI-2-1). Однако при больших а в некоторых
меридиональных плоскостях плотность возрастает вплоть до ударной волны.
На поверхности конуса (1 = 0) величины параметров газа (кроме
давления) могут резко отличаться от значений в соседней по 5 точке (§ = 0,05),
что объясняется отличием величины
энтропийной функции р /рк на конусе
и в соседней точке.
Зависимость газодинамических
функций от угла #. Эта зависимость
оказывается существенно
нелинейной, причем изменение параметров
газа с уменьшением угла Ф будет тем
больше, чем больше угол атаки.
Составляющая скорости V® имеет резко
выраженный максимум, достигаемый
для малых а при значении й,
близком к 90°. С увеличением Моо и
уменьшением разности (Зк — а
максимум смещается в сторону больших
углов д. Зависимость давления и
плотности от угла Ф графически
изоN
•ч
ч
NS
\
\
ч
ч.
0,5
1,0
135
W
бражена на рис. VIII-2-2.
Р
1,0
0
■р
+~-—-
"— .-
i
3s= 180s
Рис. VII1-2-2. Зависимость давления
и плотности около конуса от угла О:
^к=30°; а=15°; 2-Ш^^
а= 5°
Рис VIII-2-3. Зависимость давления от
Мех, при (Зк = 25°, а = 10°:
сплошная линия — на поверхности конуса,
пунктирная —на поверхности ударной волны
Изменение параметров газа в зависимости от числа Моо. Все
газодинамические функции изменяются монотонно по числу Маха и производные
их убывают по абсолютной величине.
Окружная составляющая скорости независимо от значения угла Ф
на конусе уменьшается, а непосредственно за ударной волной увеличивается
с ростом Моо.
Характер изменения давления, существенно меняется при изменении
угла 'О1 и слабо зависит от £ (рис. VIII-2-3).
Конус в сверхзвуковом потоке
389
Влияние угла конуса рк и угла атаки а. Зависимость газодинамических
функций от угла |3К существенно нелинейная. При этом характер поведения
каждой газодинамической функции по |3К (кроме V&) мало зависит от | и Ф.
Величина V® на конусе с увеличением |3К уменьшается, а за ударной волной
возрастает.
ю
20
30
Рис. VIII-2-4. Зависимость давления
и плотности от угла конуса:
сплошная линия —на поверхности конуса,
пунктирная — на поверхности
ударной волны (Моо = 5, а = 5)
1,5
1,0
0,5
у
90°
■^ 180'
10
4,0
3,0
2,0
Ч
90е
180°
Рис. VII1-2-5. Зависимость
давления и плотности от угла атаки а
конуса при Моо =7, |3К = 20°:
£=0; £=0,5; £-=1
При малых углах атаки (а < 5°) можно приближенно считать, что
газодинамические функции зависят линейно от а. При больших а
зависимость становится нелинейной. Характер поведения газодинамических
функций с изменением угла а мало меняется от координаты £, а от координаты
д зависит существенно.
Кривые, характеризующие зависимость давления и плотности от рк и а>
показаны соответственно на рис. VIII-2-4 и VIII-2-5.
390
Глава VIII
Таблицы Копала
Некоторые данные о сверхзвуковом обтекании круглых конусов
получены 3. Копалом и опубликованы в виде специальных таблиц ([62] н- [64]).
Табличные данные получены с использованием решения Стоуна для
уравнений конического потока. Позднее А. Ферри указал на ошибку, допущенную
в решении Стоуна и предложил простой способ улучшения этого решения.
Рассмотрим некоторые расчетные зависимости для определения
аэродинамических коэффициентов круглого конуса при помощи таблиц Копала.
Коэффициент осевой силы
K+
(VIII-2-2)
Таблица VIII—2—3
Значения коэффициентов, необходимых для расчета параметров потока
при сверхзвуковом обтекании конуса под углом атаки (fc = l,4)
к
N
кт
0,40
0,45
0,50
0,55
0,60
0,65
0,70
0,75
0,80
0,85
0,95
0,97
68,653
55,162
46,309
39,708
34,452
30,091
26,363
23,101
20,184
17,518
12,566
11,568
,0901
,2330
,4028
,5956
,8165
,0750
,3869
2,7794
3,3041
4,0748
9,0999
15,146
0,07243
0,05784
0,05113
0,04666
0,04318
0,04028
0,03772
0,03539
0,03319
0,03101
0,7151
0,7195
0,7188
0,7171
0,7152
0,7138
0,7132
0,7139
0,7168
0,7224
0,7518
0,7650
0,0884
0,0753
0,0886
0,1140
0,1508
0,2001
0,2630
0,3408
0,4354
0,5495
0,8791
0,9815
0,28
0,53
0,91
1,43
2,11
3,04
4,30
6,10
8,68
12,34
0,25
0,14
0,15
0,23
0,33
0,43
0,53
0,61
0,66
0,71
0,03
0,06
0,10
0,16
0,24
0,34
0,44
0,55
0,66
0,77
0
0
0
0,0001
0,0002
0,0008
0,0027
0,0089
0,0295
0,1011
0,40
0,45
0,50
0,55
0,60
0,65
0,70
0,75
0,80
0,85
0,95
61,679
51,757
44,559
39,043
34,620
30,959
27,854
25,163
22,784
20,639
16,805
1,1916
1,3382
1,5144
1,7178
1,9541
2,2345
2,5787
3,0217
3,6345
4,5010
16,855
0,12292
0,10428
0,09362
0,08614
0,08034
0,07557
0,07148
0,06785
0,06455
0,6682
0,6731
0,6752
0,6769
0,6793
0,6827
0,6874
0,6933
0,7009
0,7107
0,7416
0,2337
0,2408
0,2772
0,3287
0,3899
0,4585
0,5331
0,6130
0,6992
0,7939
1,0309
0,37
0,64
1,04
1,57
2,26
3,13
4,16
5,33
6,31
0,48
0,39
0,41
0,45
0,48
0,50
0,48
0,42
0,32
0,09
0,15
0,21
0,28
0,34
0,40
0,45
0,51
0,57
0,0004
0,0007
0,0016
0,0038
0,0091
0,0214
0,0492
0,1113
0,2521
0,35
0,40
0,45
0,50
0,55
0,60
0,65
0,70
0,75
0,85
0,90
68,507
58,043
50,281
44,424
39,835
36,124
33,045
30,435
28,180
24,433
22,834
1,2175
1,3144
1,4672
1,6531
1,8714
2,1297
2,4431
2,8387
3,3694
5,5457
9,5928
0,21723
0,17594
0,15498
0,14162
0,13199
0,12650
0,11841
0,11325
Р
0,6152
0,6238
0,6297
0,6348
0,6401
0,6459
0,6524
0,6596
0,6675
0,6862
0,6978
оп о
0,4748
0,4251
0,4444
0,4880
0,5422
0,6017
0,6642
0,7288
0,7952
0,9375
1,0161
1,34
0,75
0,69
1,05
1,50
2,01
2,50
2,82
2,66
0,72
0,55
0,50
0,47
0,43
0,37
0,29
0,04
0,11
0,17
0,22
0,27
0,31
0,35
0,40
0,0042
0,0046
0,0079
0,0152
0,0301
0,0587
0,1120
0,2099
-0,1406
-0,1523
-0,1635
-0,1737
-0,1825
-0,1898
-0,1951
-0,1983
-0,1990
-0,1971
-0,2101
-0,2217
-0,2327
-0,2423
-0,2503
-0,2566
-0,2614
-0,2651
-0,2684
-0,2761
-0,2786
-0,2873
-0,2967
-0,3057
-0,3141
-0,3222
-0,3305
Конус в сверхзвуковом потоке 391
коэффициент нормальной силы
Коэффициенты KD, KD2, #к» d, KN приведены в табл. VIII-2-3. Функции
У к = 1^к/^тах^ (ак)2 = (^к)2/1^тах вычислены соответственно по скорости
течения Fk и скорости звука а£ на конусе, обтекаемом под нулевым углом
атаки. При симметричном обтекании конуса KD = np°J8.
Угол наклона образующей скачка
9 = eg — as cos у + а2 [ [i0 + fx2 cos 2у + у ctg рк (1 — cos 2 у) ] , (VII1-2-4)
где [х0, [х2, 8 —находят из табл. VIII-2-3;
0? — угол образующей скачка уплотнения перед конусом при
а = 0.
Особый интерес представляют образующие поверхности скачка,
лежащие в вертикальной плоскости симметрии (у = 0 и я). Углы наклона этих
образующих
(VIII-2-5)
где а —угол атаки в радианах принимается по абсолютной величине.
Первая зависимость в (VIII-2-5) относится к образующей, лежащей
в теневой (7 = 0), а вторая —к образующей, лежащей в наветренной
стороне (у = я).
Приближенный расчет
обтекания при больших скоростях
Для указанного расчета давления на круглом конусе при наличии угла
атаки может быть применен метод «касательных поверхностей». В качестве
касательной поверхности выбирается местный касательный конус,
построенный около образующей, на которой отыскивается давление. Угол местного
конуса
Рк = Рк - a cos у + ~ ctg pK sin2 7. (VIII-2-6)
По значению этого угла при помощи соответствующих формул, таблиц
ж графиков находят давление и другие параметры симметричного обтекания
конуса, которые принимаются равными их значениям на образующей,
принадлежащей реальной конической поверхности. Таким образом определяется,
в частности, коэффициент давления как функция угла у при заданных М<х>,
а и рк.
Для предельного случая Моо ->• оо расчет коэффициента давления можно
осуществить при помощи комбинации метода «касательных конусов» и метода
Ньютона. При этом используется формула (VIII-1-30), в которой вместо
угла рк принимается угол р^.
ПРИМЕНЕНИЕ
РАЗНОСТНЫХ МЕТОДОВ
ДЛЯ РАСЧЕТА ОБТЕКАНИЯ ТЕЛ
С КРИВОЛИНЕЙНОЙ ОБРАЗУЮЩЕЙ.
§ IX-1. Расчет осесимме-
тричного сверхзвукового
обтекания заостренного
тела вращения по методу
характеристик (17)
Потенциальное обтекание. Для расчета потенциального потока около
заостренного тела вращения при нулевом угле атаки (рис. IX-1-1)
применяется система разностных уравнений для характеристик (IV-1-25) —
(IV-1-28) при условии, что 8 = 1.
Расчет обычно начинают с определения конического потока около
острия, которое в малой окрестности носка можно заменить конусом (на
рис. IX-1-1 его границей является точка К). В результате на образующих
OD, О А и других промежуточных конических поверхностях (включая
образующие конуса О К и скачка OS) определяются скорости, а также углы со,
(л и р. При этом углы 0 промежуточных конусов выбирают произвольно,
но так, чтобы интервалы А8 были достаточно малы и обеспечивали
достижение заданной точности.
Проводя расчеты, целесообразно сопровождать их построением сетки
характеристик, изображенной на рис. IX-1-1. Вначале строят элемент KD
характеристики первого семейства, причем данными для этого являются,
известные в точке К углы |хк и $к. Концевая точка D элемента является
точкой его пересечения с соседней образующей OD. Ее координаты xDr
rD находятся в результате совместного решения уравнений
г к — rD={xK — ^D)tg(|3K + fxK); rD = xDtgQD. (IX-1-1)
Аналогично находят координаты остальных точек характеристики
первого семейства, являющейся границей конического потока, причем с целью
получения более точных данных можно вести расчет координат по средним
значениям углов (3 и \х между соседними точками К ж D, D в. А ж т. д.
Наряду с координатами в каждой точке на этой характеристике,
включая точку S ее пересечения со скачком, будут известны скорости по величине
и направлению, а также число М, углы со, jx, |3. Теперь задача сводится
к отысканию поля скоростей в области между характеристикой и
образующей обтекаемого тела.
Вначале вычисляют параметры в точке В, лежащей на пересечении
образующей тела и элемента DB характеристики второго семейства. Затем по
найденной скорости в точке В и известным из решения задачи о конусе
параметрам в точке А подсчитывают параметры в точке С, лежащей на
пересечении элемента АС характеристики второго семейства и элемента ВС
характеристики первого семейства. В процессе вычислений определяют
углы Р и со, а по со находят число М и угол \х, причем, эти расчеты можно
вести с помощью табл. IV-1-1. Аналогичные вычисления позволяют
определить параметры во всех точках второго ряда, включая точку N.
Дальнейший расчет заключается в том, чтобы найти параметры газа в точке
пересечения элемента характеристики, проведенной через точку N, со скачком
При этом должен быть вычислен также наклон скачка в точке пересечения
Применен, разности, методов для расчета обтекания тел с криволин. образующей 393
Практически в целях получения лучшего приближения характеристику
проводят не из точки N, а из точки F, расположенной между точками N
и S. При таком построении характеристики ее элемент, примыкающий
к скачку, оказывается достаточно малым.
Координаты точки F, а также другие параметры к ней (М, со, |jl: |3)
вычисляют по известным их значениям в точках S и N линейной
интерполяцией. После этого можно составить уравнения для элемента FH
характеристики первого семейства физической плоскости, а также для элемента
соответствующей характеристики того же
семейства в плоскости годографа.
Решая уравнение для характеристики
в плоскости х, г совместно с уравнением
прямолинейной образующей скачка, найдем в
первом приближении координаты точки Н.
Чтобы определить скорость в этой точке,
надо рассмотреть наряду с условиями на
характеристике также условия на скачке, так
как точка Н одновременно лежит и на его
поверхности. Характеристика FH,
подходящая к скачку, является по своей природе
волной разрежения, возникшей на поверхности
тела. Встречая скачок уплотнения, эта волна
уменьшает его интенсивность и,
следовательно, наклон, угол которого следует определить.
Одним из неизвестных параметров в точке Н является угол наклона
вектора скорости |3Н, определяемый приращением A$F угла р вдоль элемента
FH : |3Н = AfiF + |3F. Предположим, что вдоль элемента скачка SH угол (5
меняется на величину A$F. Этому изменению будет соответствовать
приращение числа М, равное AMg = (dM/d$)$F A$F.
Если принять, что в точке S отклонение потока за скачком такое, как
в точке F, т. е. определяется углом |3F, то по этому отклонению можно
вычислить соответствующее число Ms, а затем найти в первом
приближении число М в точке Н:
О
Рис. IX-1-1. Схема для расчета
обтекания тела вращения методом
характеристик
Входящую в (IX-1-2) производную (dMld$)$F можно вычислить по теории
скачка уплотнения, используя формулу
(IX-1-3)
Расположенные в правой части этого выражения две производные в свою
очередь определяются по формулам
^ (1Х-4-4>
Далее определяют изменение числа М при переходе вдоль характеристики
от точки F к точке Н, т. е. величину ДМр = Мн — M.F. С этой целью
подставляют сюда вместо Мн выражение (IX-1-2), в результате чего находят
ДМ„ = ]
(IX-1-6)
•394
Глава IX
Переходя от числа М к углу со, получают
др о^, (IX-1-7)
-Ж" • (1Х"!-8)
(IX-1-9)
Относя к элементу FH уравнение (IV-1-26) для характеристики первого
семейства и решая его совместно с уравнением (IX-1-6), находят
где
а функция g (M) в свою очередь определяется выражением
rF
AcoF = A$F + Xh~Xf i¥% (IX-1-11)
По величине Д<% можно подсчитать в точке Н угол соя и найти затем
число Мн и угол возмущения \х>н. В этой же точке подсчитывают угол
§н = Дрр + pF, по которому уточняется угол наклона скачка. Его величина будет
меньше, чем у конического скачка,
причем уменьшение, как отмечалось,
обусловлено ослаблением интенсивности скачка.
Р
0,16
0,12
-0,04-
К
г*
—
X
о
2,0 3,0
0,18
0,14
0,10
0,06
0,02
Л
\
-—.
^-—
■-.
4'1
I Амиа-^миэ|
^—
■— —
.
■ .
—
-
- 2,28
— 2J8
— $®
— £76
1
ма
Рис. IX-1-2. Распределение коэффи- Рис. IX-1-3. Коэффициенты волнового со-
циента давления на поверхности па- противления параболической головной
раболической головной части, вы- части, рассчитанные с применением метода
численное методом характеристик характеристик
Закончив расчет для точки Н, приступают к вычислениям для
следующего ряда точек и т. д. Таким образом определяют поле скоростей (чисел М)
при обтекании заостренного тела вращения с любой образующей, заданной
в виде плавной кривой.
По значениям чисел М в точках пересечения характеристик с образующей
тела можно найти другие параметры, а именно температуру, плотность
и давление. В частности, в точке В
где To,
p0 — параметры изэнтропически заторможенного потока,
определяемые по формулам
Применен, разности, методов для расчета обтекания тел с криволин. образующей 395
Коэффициент Vo = p'0lpo, представляющий собой отношение давлений
торможения после и до скачка, может быть найден по формуле (Ш-4-33)
в зависимости от числа М<х> и угла конического скачка 9С у острия. По
найденной абсолютной величине Давления подсчитывается его коэффициент
pB = (llkMlo) I(PbIPo) (PolPoo) — 1]. Распределение коэффициента давления,
вычисленное по методу характеристик для параболического тела вращения
с удлинением А,мид = 3,8 при Моо = 2;3 и 3,92, показано на рис. IX-1-2.
На рис. IX-1-3 приведены данные о коэффициенте волнового сопротивления,
полученные по известному распределению давления около тел той же
параболической формы (по Франклю).
Вихревое обтекание. С увеличением числа Моо сверхзвукового потока
интенсивность криволинейного скачка перед телом вращения возрастает
настолько, что становится необходимым учитывать выхревой характер
течения. В этом случае следует применить систему уравнений для характеристик
(IV-l-19)^-(IV-l-22), которая позволяет численно решить дифференциальное
уравнение (Ш-2-35) для функции тока и тем самым рассчитать вихревое
течение в области между скачком и телом вращения.
В примере обтекания тела вращения с коническим элементом (см.
рис. IX-1-1) вихревое течение будет наблюдаться за скачком, начиная
от точки S, лежащей в конце его конического участка. Нижняя граница
вихревой области совпадает с характеристикой SG второго семейства,
выходящей из той же точки. Течение на участке потока, ограниченном этой
характеристикой и коническим скачком, будет потенциальным. Следовательно,
здесь расчет поля скоростей ведется по методу характеристик для
потенциального течения.
В зоне, расположенной выше кривой SG, необходимо исходить из теории
характеристик применительно к вихревому движению. В качестве примера
вычислим скорость в точке Н (см. рис. IX-1-1), которая расположена на
криволинейном участке скачка уплотнения.
Вначале следует найти величину (i/p'o) &р'01&п, которая учитывает
изменение давления торможения при переходе от точки F к точке Я, приняв, что
это изменение будет таким, как вдоль искривленного участка скачка SH.
При этом в точке S давление торможения pos будет определено при помощи
{Ш-4-33) по значениям числа Моо и угла конического скачка.
Полагая, далее, что отклонение потока за скачком уплотнения в точке Н
равно углу наклона вектора скорости в точке F, находят угол наклона
скачка 0ся и подсчитывают давление торможения роя-
Определим теперь расстояние вдоль нормали к характеристике между
точками F и Н:
An = (FH) sin ц, = C0S7p;;^ sin ц, (IX-1-14)
и найдем изменение давления торможения на этом участке:
= -J_ P'm~/os . (IX-l-15)
Так как точка Н лежит на скачке уплотнения, то для отыскания в ней
параметров потока наряду с уравнением для характеристик первого семейства
следует учесть условие (IX-1-6) на скачке. Таким образом, для отыскания
приращения угла Д|3^ придем к выражению, аналогичному зависимости
(IX-1-10), с той разницей, что в нем будет член, обусловленный вихревым
влиянием:
396
Глава IX
Moo
о 6
и 12
d-шЪ
3
6
K.-Z
-И
Используя далее (IX-1-11), можно вычислить приращение AcoF,
подсчитать угол соя и число Мя. Определив затем угол $н = ApF + pF, по
значениям этого угла, а также числа Мн находят угол 6СН наклона скачка в точке Н.
В результате в этой точке можно уточнить отношение давлений торможения.
Далее переходят к расчету параметров в соседней точке / (см. рис. IX-1-1),
который осуществляется так же, как в точке С рассмотренного выше примера
(см. рис. IV-1-5). Приведенные в этом
примере зависимости будут
действительны, если в них перейти от
обозначений для точек А, В и С к
соответствующим обозначениям для точек
Я, N и /.
Так шаг за шагом определяют
координаты точек Я, /, ..., L
характеристики второго семейства, а также
газодинамические параметры в них.
По найденным параметрам в точке L
можно определить скорость и другие
параметры в точке R, расположенной
на контуре тела. При этом ее
геометрические координаты вычисляют в
результате совместного решения
уравнений образующей тела и прямой,
проведенной через точку L под углом
Рь~M'L- Наряду с этим к числу
известных параметров можно отнести
угол наклона вектора скорости в точ-
-2
О
ол
0,8 1,2 1,6 2,0
Рис. IX-1-4. Распределение давления около
тел вращения с параболической головной
частью (а =0):
ке R, равный углу наклона
касательной в ней к контуру. Также известно
давление торможения p'or, которое
будет тем же, что и в точках К,
В, ... G, принадлежащих одной и той же линии тока. Поэтому можно
найти изменение давления торможения вдоль характеристики LR:
1 — с учетом вихревого движения за скачком;
2 — для потенциального движения за скачком
(IX-1-17)
Применяя затем уравнение характеристики второго семейства, находим
Так как в этом выражении приращение Арь считается известной
величиной и равной ЛРь = Рй~Рь> то можно подсчитать разность Асоь, вычислить
в точке R угол (oR = Дсоь + <*>ь> найти в ней число Мв, а также давление
и другие параметры с учетом влияния вихревого характера течения.
Как отмечалось, это влияние оказывается значительным при больших
скоростях. Расчеты показали, что, например, для параболической головки
с удлинением Ямид = 5 при значении параметра К1 = МОоДмид = 1, которому
соответствует число Моо^б, волновое сопротивление возрастало из-за
вихревого влияния всего на 5% по сравнению с его величиной в потенциальном
потоке. В то же время при К4 = 4 (Моо — 20) оно увеличивается более чем
на 25%. Эффект возрастания сопротивления с физической точки зрения
объясняется тем, что на образование вихрей необратимо затрачивается
дополнительная часть кинетической энергии потоку.
На рис. IX-1-4 показано распределение давления, найденное по методу
характеристик для двух тел с параболической головной частью при условии,
Применен, разности, методов для расчета обтекания тел с криволин. образующей 397
что параметр K1 = MOotgp0 = MooAMHA = 2. На графике видно повышение
давления по сравнению с потенциальным обтеканием. Это следует учитывать
о 3
09
к
хмас
9
)
) . У
Йр
^миЗ
Аи*
—/—i
/
V
0,8
-вв I 1 1 1 1 1 *- -0,2
I/ Ц¥ цо у: 4^ ХМ1Ю ^ Ч^ ЦО '^^
Рис. IX-1-5. Распределение давления по поверхности параболических тел вращения
в практических случаях, начиная, примерно, со значений параметра К± =
= 1,2 ч-1,5. При меньших его значениях вихревым влиянием можно пренебречь.
График на рис. IX-1-4
подтверждает действие закона
подобия .по параметру К4 не только
в отношении конусов, но также
и в отношении аффинно-подобных
тел вращения с криволинейной
образующей, какими являются
тела параболической формы. Вид
но, что обтекание двух
различных тел с одним и тем же пара*
метром К4 характеризуется одной
кривой для функции давления.
О
Рис. IX-1-6. Область
применения закона
подобия для тел оживаль-
нойгформы
(заштрихована область
сомнительного подобия)
О
-Of
-0,2
-о,з
£--16
W
ч ^ !2
0,8
1,2
13
Рис. IX-1-7. Графики для определения
давления на поверхности тел с оживальной
головной частью:
а — для головной части; б — для цилиндрической
Область применения закона подобия можно расширить, используя
экспериментальные или теоретические данные для различных величин К1в В каче-
398 Глава IX
стве иллюстрации такие данные, полученные по методу характеристик для
тонких цилиндрических тел с параболической головной частью при условии г
что Ki^l и 0,5, приведены на рис. IX-1-5.
Существует предельное значение параметра Кь ниже которого закон
подобия для криволинейной головки недействителен. Это значение
устанавливается из анализа возможности использования закона подобия для
конического острия (рис. IX-1-6).
В соответствии с.пределами применимости закона подобия,
устанавливаемыми графиком на рис. IX-1-6, проведены расчеты по методу
характеристик распределения давления около тонких цилиндрических тел вращения
с параболической (или оживальной) головкой. Результаты этих расчетов
в обобщенном виде представлены на рис. IX-1-7.
Интегрированием давления по поверхности можно получить коэффициент
волнового сопротивления. В результате обработки данных, полученных
по методу характеристик и уточненных экспериментально, найдена
следующая зависимость для расчета коэффициента волнового сопротивления ожи-
вальных головок с половиной угла при вершине 10°<р<45° при числах Моог
расположенных в интервале 1,5<Моо<3,5:
где рк — коэффициент давления в конической вершине;
^мид — удлинение тела вращения, определяемое по (И-1-2) либо из
выражения XMIW = l/[2tg(0,5p0)].
Давление на цилиндрической части при очень больших скоростях
обтекания. Методом характеристик было рассчитано обтекание
цилиндрической поверхности корпуса с головными частями, имеющими форму
оживала и конуса, при скорости, соответствующей числу Моо = 20. Результаты
расчета показывают, что коническая головка вызывает большие изменения
давления на цилиндре, чем оживальная.
С данными расчета давления по методу характеристик хорошо
согласуются результаты, получаемые по эмпирической формуле
-L- = 0,55 + 0,061A»Ml, VbTa — , (IX-1-20)
Poo %
где сх в — коэффициент сопротивления головной части;
х — расстояние, измеренное от места сопряжения головки с цилиндром.
Образующая скачка уплотнения удовлетворительно аппроксимируется
уравнением
гмид
Зависимости (IX-1-20) и (IX-1-21) справедливы для 0,4<Ямид<4
>4i
Метод «местных конусов». Результаты расчета обтекания по методу
характеристик являются в известной мере эталонными и служат в качестве
критерия при оценке данных, получаемых при помощи различных
приближенных способов. Сравнение показывает, что особенно близкие к методу
характеристик результаты дает метод «местных (или касательных) конусов»
(см. § IV-7) при расчете обтекания заостренного тела вращения с
образующей без излома.
Достаточно удовлетворительное совпадение результатов свидетельствует
о том, что метод «местных конусов» позволяет в какой-то степени учесть
вихревой эффект, имеющий место за криволинейной ударной волной.
Если в методе «местных конусов» используется гипотеза «одинаковых
давлений», то давление в данной точке образующей определяется как давле-
Применен, разности, методов для расчета обтекания тел с криволин. образующей 399"
ние на конусе с полууглом при вершине, равным углу наклона
касательной. Применяя гипотезу «одинаковых скоростей», расчет давления следует
вести по формуле (IV-7-17), а коэффициент давления— по выражению
(IV-7-18).
Кривые, характеризующие изменение коэффициента рс в зависимости
от величин tgp0 и tg|3, показаны для двух значений Моо = 2 и 5
на рис. IX-1-8 и IX-1-9. Зная распределение давления рс, можно
определить соответствующий
коэффициент волнового
сопротивления схв.с. Вместе с тем его
величину можно рассчитать
приближенно, если использовать
зависимость (IV-7-18),
связывающую между собой
коэффициенты рс и рд. Соответствующее
расчетное соотношение
получается в результате применения
выражений (1-3-14) и (IV-7-18):
1
(IX-1-22)
где г = -
'ДОН
Эта формула определяет
коэффициент сопротивления,
отнесенный к площади донного среза
секущего тела с радиусом Гдон»
который может отличаться от
радиуса миделевого сечения
касательной головки. Формулу (IX-1-22)
можно упростить, если
рассмотреть случаи обтекания, когда функция v мало изменяется вдоль тела вращения.
При этом условии оказывается возможным' величины v и v — 1 вынести
из-под знака интеграла соответствующими средними значениями, и формула
(IX-1-22) примет вид
Рис. IX-1-8. График распределения давления
около тела вращения, построенный на основе
гипотез «одинаковых давлений» и «одинаковых
скоростей» (Моо =2)
-схв. д^ср Н
2(уср —
(1Х-1-23)
где с'хв. д — коэффициент сопротивления, отнесенный к площади донного среза
ягдон и вычисленный на основе гипотезы одинаковых давлений. Этот
коэффициент определяется по (1-3-14), в которой следует принять р=^рц.
По (IX-1-23) расчет ведется, примерно, до значений v, укладывающихся
в интервале 0,8<v<l. Если это условие не выполняется, надо применять
общую формулу (IX-1-22). Однако и в этом случае расчет может быть
упрощен. Как показывают исследования, распределение функции v вдоль
параболической или оживальной головки может быть приближенно
представлено уравнением _
где х-^х/хмт. _
Кроме того, установлено, что коэффициент давления рд можно оценить
по выражению рд = рк(1 — #) ' » в котором рк — коэффициент паттения
400
Глава IX
у острия тела вращения. С учетом этих приближенных зависимостей
формула (1Х-1-22) после вычисления [интеграла будет
Vb. с = с'хв.д-0,667гДон (1 - v0) Г (1 -0,552?ДОН + 0,0687ДОН-
-0,189гд
Р +
оо J
(IX-1-25)
ГДе Гдон — Гдон'гмид-
Для головки, у которой гДон = ''мид5 эта формула принимает вид
В ней коэффициенты схв. с и сжв.д отнесены к площади яг
МИД-
О
0,75
0J 0,2 0,3 ОЛ 0,5 0,6 0,1 0,8
Рис. IX-1-9. График распределения давления около тела
вращения, построенный на основе гипотез «одинаковых
давлений» и «одинаковых скоростей» (Моо = 5)
Для параболической головки коэффициент
Если его величина относится к площади nrl'0'H некоторого произвольного
сечения, то
с'х,. д = Fk (1 -0,49?ДОН + 0,0567ДОН - 0,1517ДОН). (IX-1-28)
Сравнение с методом характеристик и опытными данными показывает,
что формулой (IX-1-26) можно пользоваться в тех случаях, когда числа М '
расположены в интервале 2<М«<(6-7), а значения удлинений
удовлетворяют неравенству Яннд< (2- 2,2). Такими удлинениями обладают
достаточно толстые тела вращения Формула (IX-1-27) для указанных условий
дает завышенные результаты. Например, для параболической головки с
удлинением Ямид = 2 подсчитанная при 1^ = 2 по этой формуле величина с
почти вдвое больше, чем по методу характеристик. Более удовлетворител!-
Применен, разности, методов для расчета обтекания тел с криволин. образующей 401
ные результаты (IX-1-27) дает при замене численного коэффициента 0,415
параметром, зависящим от Моо. Соответствующее выражение для
коэффициента волнового сопротивления
с»а 3+мГ ' (IX-1-29)
причем оно пригодно для удлинений Ямид>2,5 и интервала 1,5 < Моо < 6.
§ IX-2. Метод сеток
Опыт и теория показывают, что при больших числах М^ возникает
необходимость учитывать не только влияние вихревого характера течения,
но и таких факторов, как пограничный слой и различные эффекты,
наблюдаемые в нем (сжимаемость, диссоциация, теплопередача между стенкой
и газом). Значительное влияние оказывают также колебательные
возбуждения и диссоциация воздуха, которые могут возникнуть при очень высоких
скоростях обтекания вследствие значительного повышения температуры
в невязкой области потока между ударной волной и поверхностью тела.
Расчет этой области при условии, что газ претерпевает
физико-химические превращения, может быть осуществлен методом характеристик. С этой
целью следует воспользоваться системой уравнений для характеристик
(IV-1-29) — (IV-1-32), написав их в конечных разностях. Принципиальная
схема расчета та же, что и для потока с постоянными теплоемкостями.
Разница будет состоять в расчете конического течения около острия, а также
в определении параметров газа в остальной части потока, которые должны
вестись с учетом диссоциации и ионизации газа. С этой целью могут быть
использованы таблицы или графики термодинамически равновесных функций
воздуха при высоких температурах.
В работе [4] для расчета обтекания тел с учетом равновесных
химических реакций между компонентами воздуха, а также реакций ионизации
применен разностный метод, называемый методом сеток, при помощи которого
совместно решены обычные уравнения газовой динамики и уравнения
химической кинетики. Определение параметров потока, а также
термодинамических функций осуществлялось для диссоциирующего и ионизирующего
воздуха, первоначальный объемный состав которого выбирался следующим:
азот —78,08%, кислород —20,95%, аргон — 0,97%. Рассмотрим некоторые
результаты указанных расчетов.
Осесимметричное обтекание. Тела вращения, для которых проводились
расчеты, имели головной конус, сопряженный при помощи кривой
четвертого порядка с основным конусом или цилиндром. В приводимых таблицах
(см. приложение № 1) и графиках результаты расчета обтекания получены
для чисел Моо -=15 и 20, температуры 77Оо = 250°К и давления /Эоо = 0,292х
X Ю"2 am (0,2864-103 н/м2). При этом для Моо = 15 значение а* = 1962 м/сек,
Рооа*2 —0,1567 am (0,1537-105 н/м2), а для М^ = 20 — а* = 2604 м/сек,
р^а*2^0,2759 am (0,2706-105 н/м2). Плотность набегающего потока
принималась равной роо = 0,412 -10"5 г/см3.
Газодинамические функции, приведенные для некоторых значений х и £,
представляют собой осевую и радиальную составляющие скорости Vx и Vr,
отнесенные к а*, давление р, отнесенное к рсх>а*2, и параметр р,
представляющий собой отношение плотности к величине роо. Значение х=1
соответствует длине головного конуса до точки сопряжения с переходной
кривой. Табл. IX-2-1 (см. приложение № 1) содержит газодинамические
функции обтекания тела с головным конусом (рк = 40°) и основным конусом
2 6-114
402
Глава IX
(Рк = 20° и 10°) при Моо = 20 и 15. В табл. IX-2-2 (см. приложение № 1)
приведены результаты расчета обтекания тела, состоящего из головного-
конуса с полууглом при вершине рк = 40°, сопряженного с цилиндром, при
Моо = 20 с учетом равновесных химических реакций и для к = 1,4.
Исследования показывают, что вниз по потоку слой больших градиентов функций
становится тоньше и он «прижат» непосредственно к стенке, а области
течения, имеющие конический характер, увеличиваются. На удалении от носка
порядка # = 20-т-30 газодинамические функции при £ = 0,05 близки к их
значениям в коническом потоке.
В области интенсивного расширения потока влияние равновесных
химических реакций сильнее всего сказывается на плотности и давлении.
Несимметричное обтекание. В табл. IX-2-3 (см. приложение № 1)
приведены результаты расчета параметров Vx, Vr, F&, р, р при
*2
а =
3,0
2fi
W
1
L
7 Ч
:
X
Г г
/#=90°
15
20
Рис. IX-2-1. Изменение давления на поверхности тела (сплошные
линии) и на поверхности ударной волны (пунктирные линии)
и Моо = 20 для тела, состоящего из головного конуса с половиной угла при
вершине 46,9° и хвостового цилиндра. Значения Vx, Vr, V® отнесены к а*,,
величина р — к роо^*2, а р —к плотности набегающего потока роо.
Газодинамические функции даны для ряда значений # = -5—v, x и %.
Координата х является безразмерной и отнесена к длине головного конуса,
а переменная \ определяется из выражения
где Ф = Ф (х, #) —некоторая функция, значения которой
в табл. IX-2-4 (см. приложение № 1).
По данным этой таблицы можно перейти от координаты
1,4<#<2,4 по формуле
£ = 21{[Ф2 + 4(1-Ф)!]1/2 + Ф}-1.
(IX-2-1)
приведены
£ к £ при
(IX-2-2)
Для х < 1,4 и х > 2,4 значение £ =1.
На рис. IX-2-1, IX-2-2 приведены графики, построенные по результатам
расчета давления и температуры воздуха с учетом равновесных химических
Применен, разности, методов для расчета обтекания тел с криволин. образующей 403
реакций при Моо = 20 для тела, состоящего из двух конусов (передний конус
заостренный). Очень сильное изменение давления и плотности происходит
на участке от х = 1 до х = 2, особенно на поверхности тела (g = 0). Непо-
Т°К
f ■
V\\
\\^
******
й=0°
-&=90°
}}=180°
°° 90°
180°
5000
4000 -
3000
2000
О 5 10 15 20 &к
Рис. IX-2-2. Изменение температуры на поверхности
тела (сплошные линии) и на поверхности ударной волны
(пунктирные линии)
средственно за ударной волной (6 = 1) изменения также довольно
значительные, но более плавные. На поверхности тела при #>3 газодинамические
функции, как и значения термодинамических параметров, уже почти не
зависят от х. За ударной волной такое явление наблюдается при х >> 15.
§ IX-3. Влияние угла
атаки на лобовое
сопротивление
Как показывают экспериментальные исследования, коэффициент лобового
сопротивления заостренных тел вращения изменяется в соответствии с
формулой
(l + )
в которой сх0 — коэффициент лобового сопротивления при нулевом угле атаки;
z = sin2 (a/2);
е — некоторый коэффициент, зависящий в основном от формы
тела вращения.
В частности, для заостренной пули калибра 12,7 мм в диапазоне 1,5 <
<Моо<2,2 значение 8^87, а для снаряда калибра 20 мм в том же
диапазоне чисел Маха е с^ 80.
Зависимость (IX-3-1) была подтверждена после обработки результатов
опытных отстрелов снарядов при скоростях более 450 м/сек и значениях
0<z<0,l (0<a<37°). При меньших скоростях оказалось, что линейная
зависимость не имеет места и следует пользоваться более общим
соотношением
сх = сх0 (1 + atz
(IX-3-2)
26*
£04: Глава IX
в котором в зависимости от условий обтекания необходимо учитывать члены
со второй и даже с более высокими степенями z.
Приведенные формулы для коэффициентов лобового сопротивления
относятся к случаю достаточно больших углов атаки. Если же они невелики
(порядка 0 ч-5°), то при приближенных расчетах можно исходить из
выражения (1-2-5), которое дает для малых углов атаки: cx — cR + cN\a,\. В этой
формуле, как показывают экспериментальные и теоретические исследования,
коэффициент осевой силы изменяется в зависимости от угла атаки
незначительно. Например, в результате продувок в аэродинамической трубе
установлено, что при изменении угла атаки от 0 до 5° величина cR модели
в виде цилиндра с коническим носком возрастала приблизительно на 2 —
2,5%. Поэтому в первом приближении коэффициент осевой силы может быть
принят постоянным и равным соответствующему значению cR0 при нулевом
угле атаки. Тогда расчетная формула для коэффициента сопротивления
упростится:
сх = с по + cN | а |. (IX-3-3)
В соответствии с этой формулой расчет сх при несимметричном
обтекании связан с предварительным вычислением коэффициента осевой силы для
а = 0 и коэффициента нормальной силы при заданном угле атаки.
ГИПЕРЗВУКОВЫЕ
СКОРОСТИ.
§Х-1. Обтекание тонких
тел с очень большими
скоростями
Рис. Х-1-1. Положение скачка
уплотнения при умеренных (1) и очень
боЛЬШИХ (2) ЧИСЛаХ Моо
Система уравнений
Упрощение уравнений. Решение задачи о гиперзвуковом обтекании
тонких тел вращения основано на использовании упрощенных уравнений
аэродинамики, полученных из условий малости возмущений скорости.
Упрощение уравнений существенно отличается от линеаризации
уравнений при небольших Моо, хотя линеаризация также достигается на основе
предположения о малости возмущений. Так как числа Моо невелики,
то упрощение уравнений (линеаризация),
достигается путем отбрасывания членов,
содержащих возмущения в первой и более
высокой степенях, т. е. имеющих
соответственно порядок т, т2 и т. д. (например,
МооТ< 1, М^т2 < 1).
Соответствующая этому случаю
картина потока изображена на рис. Х-1-1.
Особенность такого линеаризованного
потока состоит в том, что толщина тела
мала по сравнению с расстоянием между
телом и скачком.
Напротив, при очень высоких
скоростях скачок находится вблизи тела (рис. Х-1-1), влияние которого
на возмущенное течение больше, чем в линеаризованном потоке.
Хотя возмущения малы, но произведение Moot может быть порядка
единицы. В этом случае членами с первой степенью возмущения, если они
содержат параметр Moot, пренебрегать нельзя, так как их порядок тот же,
что и остающихся в уравнении. Упрощение достигается тем, что
отбрасываются члены порядка т2 и выше, если малый параметр т входит самостоя-
тельно, а не вместе с Моо.
Несмотря на упрощения, система уравнений обтекания остается
нелинейной и, таким образом, нелинейность оказывается существенным свойством
уравнений для течений газа с большими числами Моо.
Преобразуем уравнения симметричного установившегося обтекания
([71], № 3, 1954). Введем для этой цели безразмерные координаты £, г),
определяемые из условий
х = х-^. г = хх^ш (Х-1-1)
Так как т < 1 (по условию малости толщины тела), то, следовательно,
г < х, что соответствует полученному выше выводу о существовании около
тела при очень больших скоростях обтекания тонкого сверхзвукового слоя,
в котором происходит изменение всех параметров потока. Соотношения (Х-1-1)
представляют собой формулы аффинного преобразования.
406
Глава X
Аналогично в соответствии с оценками изменения скорости, давления
и плотности в коническом потоке, которые были сделаны ранее, можно
написать
V — V М ~~ ~
Ух — " оо [ I ~
% Ц)]\ Vr = FootF^ (£, т|); (Х-1-2)
р = РсокМ2оо%2р(1, г]); p = poop(g, г)), (Х-1-3)
где Fg, УЦ1 р, р — новые безразмерные переменные, от которых зависят
действительные значения скорости, давления и плотности.
Подставив выражения (Х-1-1) — (Х-1-3) в уравнения движения (Ш-2-5)
и неразрывности (Ш-2-15) для случая установившегося симметричного
обтекания, а также условие сохранения энтропии (Ш-2-54) и, отбросив члены,
имеющце по сравнению с единицей порядок г2, получим
(Х-1-4)
(Х-1-5)
dl r^ дц
д~Р
дц
= 0. (Х-1-6)
Эти уравнения, составляющие основу теории малых возмущений,
используются при исследовании неизэнтропического (непотенциального) обтекания
тонких тел вращения гиперзвуковым
потоком.
Закон плоских сечений.
Сущность этого закона состоит в том, что
движущееся с очень высокой
скоростью тело вызывает лишь
поперечное смещение частиц воздуха. Такое
движение газа возникает при
вытеснении его плоским цилиндрическим
поршнем. Следовательно, можно
провести аналогию между плоским
неустановившимся движением газа за
расширяющимся поршнем и
стационарным потоком около конуса.
Представим, что в момент
времени t = 0 поршень (рис. Х-1-2)
мгновенно начинает движение с на-
Рис. Х-1-2. К закону «плоских сечений»:
1 — невозмущенные частицы газа; 2 —
возмущенные частицы; з — ударная волна; 4 — путь
поршня; 5 — путь ударной волны; 6 — поршень
чальной скоростью F, создавая
впереди себя плоскую цилиндрическую
ударную волну, фронт которой
перемещается со скоростью D. Расстояния R = Vt и R = Dt, проходимые
соответственно поршнем и ударной волной, изобразятся в плоскости (i?, t)
прямыми, которым в физической плоскости (г, х) соответствуют образующие
конуса и скачка уплотнения. Таким образом, неустановившееся плоское
течение за равномерно расширяющимся поршнем соответствует
стационарному обтеканию конуса.
При использовании этой аналогии физическая координата оказывается
подобной времени t. Если поршень расширяется неравномерно по какому-
либо произвольному закону R (t), то следы движения поршня и фронта
ударной волны изобразятся в плоскости (i?, t) кривыми, которым в плоскости
(г, х) будут соответствовать криволинейные образующие тела вращения
и скачка (рис. Х-1-2).
Гиперзвуковые скорости 407
Следовательно, нестационарный плоский поток газа за неравномерно
расширяющимся поршнем аналогичен установившемуся течению около тела
о криволинейной образующей. В этом состоит обобщенный закон плоских
сечений, который, как видно, вытекает непосредственно из аналогии с
движением поршня. При расчете обтекания по этому закону параметры потока
получаются с точностью до величины т2 по сравнению с единицей.
Закон плоских сечений, схематично изображенный на рис. Х-1-2,
станет более наглядным, если рассмотреть необращенную систему,
включающую в себя неподвижную среду и движущееся тело. Выделим из этой среды
-слой частиц, расположенный в некотором сечении, перпендикулярном
к направлению движения. Тогда наблюдатель, находящийся в этом сечении,
увидит, что при движении тело, проникая сквозь слой частиц, раздвигает
их и заставляет смещаться только в данном плоском сечении. Теперь понятно,
что роль поршня играет поверхность тела, представляющая собой
непроницаемую для частиц газа подвижную границу.
Если образующая этого тела задана уравнением г = / (#), то,
интерпретируя время как t = xlVoo, найдем соответствующую этому уравнению
-зависимость для измерения радиуса поршня в виде R = / (tV<x>)>
Дифференцируя по t1 найдем скорость расширения поршня Vr = dR Idt.
Если рассматривается обтекание конуса, то г = афк, следовательно,
R = Vooftxt и Vr = dR Idt = FoopK- Последнее выражение позволяет
сделать вывод, что закон подобия для течений с очень большими скоростями
непосредственно вытекает из закона плоских сечений.
Действительно, возмущенная скорость частиц на поверхности конуса,
совпадающая в эквивалентной задаче о поршне со скоростью его
расширения, будет одной и той же, если сохранится произведение FooPK- Тогда для
разных значений F<x> и |3К установившиеся потоки около конуса (или
эквивалентные нестационарные движения газа под плоским цилиндрическим
поршнем) будут отличаться лишь линейным масштабом. Так как
конические тела являются аффинно-подобными, то, очевидно, аналогичные выводы
могут быть распространены и на другие аффинно-подобные тела, в частности
тела с параболической образующей.
Граничные условия. Решения уравнений (Х-1-4) — (Х-1-6) должны
удовлетворять граничным условиям на поверхности тела и в
невозмущенном потоке.
Если известно уравнение г — %Ъ{х) образующей тела вращения, то
условие на границе тела напишется так:
условия невозмущенного потока
fs_»0, 7л->0; р -» (AMJoT*)"1; р-> 1 при £-> оо. (Х-1-8)
Кроме этого, должны быть соблюдены также условия на скачке
уплотнения, поверхность которого можно описать уравнением r~is(x). В
частности, условие, которому должна удовлетворять функция F^, может быть
определено из соотношения (Ш-4-2) для косого скачка.
С этой целью из указанного соотношения находят формулу для
изменения нормальной составляющей скорости при переходе через скачок. Затем,
имея в виду, что Vni = Vnoo = F<x> sin Gc; Vn2 = Vx tg (9C — (Зс), а числа Mt = Moo
настолько велики, что можно принять Vx = Foo cos 6C c^l Foo и заменить синус
ж тангенс углами, получим
1\
408 Глава X
Нетрудно заметить, что в этом выражении величина Foo0c представляет
собой радиальную составляющую скорости Vr непосредственно за скачком.
Заменим эту составляющую ее значением
где в соответствии с уравнением образующей скачка r = xs (х) малый
параметр
dr rds(x)-\-l 0С
dx L dx J s' (x) '
Вводя затем Ко = Moo9c и заменяя х новой переменной £, получим
Условия на скачке уплотнения для функций р и р получаются из
соотношений (Ш-4-24) и (Ш-4-25), если в первом из них заменить p%/pi
выражением
Pl
получающимся из условий
dr
dx
ds{x)
dx
Ko =
P2 _
Pl
Moo
P
poo
s'(x) '
9c,
= p.
а во втором сделать замену
Перейдя затем от х к переменной £, в результате несложных
преобразований найдем
- 2Ж;- (к — 1)
Р
(X-l-10)
В результате решения уравнений (Х-1-4) — (Х-1-6) для заданной формы
обтекаемой поверхности заостренного тела вращения и числа Моо
определяются параметры газа в возмущенной области потока, расположенной между
этой поверхностью и скачком уплотнения. Одновременно с этим, как
результат решения указанных уравнений, находится форма поверхности скачка
уплотнения.
Уравнение для функции тока. Решение задач об обтекании тел
вращения, имеющих криволинейную образующую, связано с учетом изменения
за скачком уплотнения энтропии при переходе от одной линии тока к другой.
Чтобы облегчить это решение, полученные выше уравнения
преобразуются к функции тока г|), определяемой соотношениями (Ш-2-33).
Гиперзвуковые скорости 409
Если в этих соотношениях перейти к переменным £, т), включив в
значение функции тока i|) = 1F постоянные для данных условий величины Foo, т
и хк, то в рассматриваемом случае малых возмущений получим
откуда следует, что
Для преобразования уравнений (Х-1-4) — (Х-1-6) к переменной W
представим производную др/дц в виде
ь л до
где (x)=zp/pk представляет собой функцию, зависящую от изменения
энтропии при переходе от одной линии тока к другой и определяемую,
следовательно, функцией W.
Обозначив производную d(d/dW через со' и заменив р соотношением (Х-1-10),
получим уравнение для функции тока
Давление при принятых обозначениях
Расчет обтекания3
Рассмотрим решение уравнения (Х-1-14) для функции тока, которое
позволяет рассчитать параметры газа в окрестности острия.
Решение отыскивается по следующей схеме. Вначале находят решение
уравнения применительно к обтеканию конического острия с углом ро.
Причем, в этом случае уравнение решается точно. Затем, рассматривая
малую окрестность криволинейной
поверхности и вводя поправку в функцию
тока для течения около конуса, находят
новое решение того же уравнения
(Х-1-14), которое будет учитывать в пер-
вом приближении влияние на функцию
тока кривизны поверхности вблизи носка.
После этого можно получить решение
задачи во втором приближении. Рис- Х"1"3' Расчетная схема течения
т» /лг л л /\ около конуса:
Решение уравнения (Х-1-14) для 1 _ скачок уплотнения; 2 _ конус; стрел.
КОНуСа (рИС. Х-1-о). Обтекание КОНуса ками указаны направления отсчета углов
характеризуется постоянством энтропии
во всей области за скачком уплотнения. Поэтому производная со' в (Х-1-14)
равна нулю. В виду конического характера течения функция тока
где Э — относительный угол промежуточной конической поверхности,
определяемый из условия 0 = r/(Qcx) = т)/£.
Угол наклона скачка Эс следует рассматривать как малый параметр,,
который ранее был обозначен через т.
420 Глава X
Внося выражение (Х-1-16) в (Х-1-14), получим обыкновенное нелинейное
дифференциальное уравнение
где /' и /" — соответственно первая и вторая производные по 9;
со0 — постоянное для данных условий значение отношения p/pk за
скачком уплотнения. Причем, это отношение определяется из
выражений (Ш-4-24) и (Ш-4-25) в следующем виде:
0)0 =
L
J •
Решение уравнения (Х-1-17) должно удовлетворять граничным условиям
на скачке уплотнения, которые получаются из соотношений (Х-1-10), (Х-1-11),
(Х-1-16) и (Х-1-18). В частности, условия для функции /(0) и ее
производной /' (6) находят следующим образом. Вначале определяют общие
выражения для /' (9) и / (9). С этой целью вычисляют с помощью соотношений
(Х-1-10) и (Х-1-11) производную Ч^ = £/'(0) = т)р, из которой находят
/' (в) = (л/5) р.
Функцию /(0) определяют из соотношений (Х-1-10), (Х-1-12), (Х-1-16)
в виде
Если теперь в полученных выражениях для /' (0) и / (0) принять 0 = 1
и воспользоваться зависимостями (Х-1-12) для Уц и р, то можно придти
к следующим условиям на скачке уплотнения:
Условие безотрывного обтекания требует, чтобы функция тока на
поверхности тела была равна нулю. Если уравнение образующей конуса задано
в виде r = 0cfoc, то это условие будет /(Ь) = 0.
Уравнение (Х-1-17) интегрируется при заданных граничных условиях
численным методом. Причем, интегрирование удобно вести от условий
на скачке уплотнения до условий на поверхности конуса. Полученное при
этом значение $К = Ьвс и будет углом того конуса, при обтекании которого
образуется скачок уплотнения с углом 0С, соответствующим заданному
параметру Ко.
Кроме угла [Зк, находят значение производной /' на поверхности конуса,
что позволяет подсчитать коэффициент давления:
Рк _ 2(рк — Роо) оГ®0 ( f'\k 1
Pi" AKJpoo -гЫ\Т) —
где Ki-MoopK.
Результаты, найденные по теории малых возмущений, близки к данным
точной теории.
Учет влияния кривизны в первом приближении. Предположим, что
образующие тела вращения и скачка уплотнения представлены соответственно
уравнениями
( ) (\) (Х-1-22)
где 0О —угол наклона скачка уплотнения у острия (рис. Х-1-4).
При решении (Х-1-17) в случае криволинейной поверхности условия
непосредственно за скачком уплотнения для функций W и со определяются
Гиперзвуковые скорости 411
соотношениями, которые находят с помощью зависимостей (Х-1-10), (Х-1-11)
и (Х-1-18). Причем, эти условия будут зависеть от местного наклона скачка.
Учитывая, что рассматривается малая окрестность носка, можно
упростить определение условий на скачке для W и со, воспользовавшись
разложением в этой окрестности рассматриваемых функций в ряды по параметру
К = МооЭс, рассчитанному по местному углу
скачка. Постоянный для данных условий пара- r l
метр Ко, рассчитанный по углу скачка 60
у острия (# = г = 0), будет К0 = Моов0.
Условия для функции тока
непосредственно за скачком уплотнения будем
определять через условия для ее производных
*Р6 и\ о
Рассмотрим, как находят условие для Рис. Х-1-4. Обозначения для уг-
производной Ч^, имея в виду, что для другой лов наклона касательной к обра-
лроизводной Yn нахождение условия на скач- зующей тела вращения (1) и
скачке будет аналогичным. Прежде всего, заметим, ка Уплотнения (2)
что, как следует из выражений (Х-1-9) -=-
-4-(Х-1-11), функция Т| зависит от значения параметра К. Разлагая эту
функцию в ряд по параметру К в окрестности острия и ограничиваясь
двумя членами разложения, найдем
Ys = Y5(K0)+-5M (К-Ко). * (Х-1-23)
Здесь значение функции "ЧР^ (Ко) определяется с помощью соотношений
«(Х-1-9) — (Х-1-11). С учетом того, что
s w - 6о dx - Ко.
функция Y| имеет вид
Полагая здесь К = К0, находят значение ^()
Чтобы найти производную dW^/dK |к=к0^ наД° продифференцировать
(Х-1-24) по К и принять в полученном выражении К = К0.
Далее из (Х-1-22) для образующей скачка определяют разность
С учетом найденных при К = К0 выражений для функции ¥^ и ее
производной по К, а также разности К —Ко условие для производной W%
на скачке уплотнения будет
£-1) [
:-l)K§\
Аналогично находят условие для производной
4
l)K§ г.
-1) К02 L +2 + (*-1) Kg
Условие для функции © будет
ft U 4(fc
J
(X-l-27)
412 Глава X
Как и в задаче о конусе, необходимо задаваться видом искомого
решения (функции тока). Примем, что это решение в основном определяется
значением функции тока для конуса у острия тела с образующей,
наклоненной под углом Ро = 9(А а влияние кривизны в первом приближении
учтем линейной поправкой. В соответствии с этим решение будем искать
в виде
¥ (£, г,) = £*/ (9) - lci*g (6), (Х-1-28>
где g (9) — некоторая функция, учитывающая влияние кривизны образующей.
Очевидно, это решение должно удовлетворять также условию на
конической поверхности скачка у острия, которое можно определить, полагая:
g(Q) = O и /(9)-0,5, в виде ¥ = 0,5ri2 = 0,5g2. .
Значением функции тока определяется энтропийная функция со(¥)г
которую можно представить в виде ряда с сохранением в нем только
второго члена:
со (¥) = ©о (1 + Щ1с VZ¥), (X-1-29)
где со0 дается соотношением (Х-1-18), а
Внося выражения (Х-1-28) и (Х-1-29) в уравнение (Х-1-14) и
группируя члены прэ одинаковых степенях £, придем к двум уравнениям. Одно
из них является нелинейным уравнением для функции /(9), совпадающим
с уравнением (Х-1-17) для конуса, другое — линейным уравнением для
функции g(Q), имеющим вид
где gf и g" —первая и вторая полные производные от функции g(9) по 9.
Коэффициенты в последнем уравнении
\
\ (х-1-32>
Дифференциальное уравнение (Х-1-31) может быть проинтегрировано
численно. При этом условия на скачке, которым должны удовлетворять
отыскиваемые по этому уравнению функции g (Q) и #'(9), получаются
с помощью выражений (Х-1-25), (Х-1-26), (Х-1-28) при 8 = 1:
g (1) = _Ко -————-— . (А
При проведении численных расчетов заданными параметрами могут
быть те значения Ко, которые были выбраны при расчете обтекания
конуса. Интегрирование ведется шаг за шагом от известных условий на скачке
уплотнения с использованием тех же интервалов, что и в задаче о конусе.
В результате находится функция g и ее производная g' для каждого значения
угла 9, включая его величину 8 = 6, соответствующую условиям на
коническом носке.
Гиперзвуковые скорости
413
После того как определены функции / и g и их производные, можно
найти форму скачка уплотнения, а также рассчитать в первом приближении
давление.
Форма скачка уплотнения, как видно из уравнения (Х-1-22),
определяется коэффициентом Z, который равен отношению кривизны скачка к
кривизне образующей тела. Этот коэффициент находят из уравнения (Х-1-28)
при условии, что функция тока на
ловерхности равна нулю
/'
-27W • <хл**>
Давление будет равно его
значению на конусе плюс некоторая по-
лравка, линейная относительно х и
зависящая от начального градиента
давления, величина которого
W
0,6
ОА
0,2
др_
дх
[f'(b)]k -
/
1
«-
.
■4
(Х-1-35)
Рис. Х-1-5. Зависимость коэффициента I
от Kii
асимптотическое значение при Ki—>°о;
I — скачок уплотнения, 2 — тело вращения
где параметр R"o практически мо-
ткет рассматриваться для достаточно
тонкого тела как кривизна
образующей у острия.
Результаты интегрирования уравнения (Х-1-31) приведены на графиках
рис. Х-1-5 и Х-1-6 и в табл. Х-1-1. Результаты, относящиеся к коэффи-
д- циенту Z, можно аппроксимировать следую-
d(p0R'lx) Щбй зависимостью:
- 4кг1-1,51 (Х-1-36)
5,0
\
V
-4
^^
'_ ~
Аппроксимация начального градиента
давления может быть осуществлена по
формуле
др , = 4,929 - 0,429КГ3/2 -
3
Рис. Х-1-6. Величина начального
градиента давления в зависимости
от критерия подобия К4:
2 — по теории малых возмущений; 2 —
по методу конических течений и течений
разрежения: 3 — по методу «местных»
конусов (гипотеза «одинаковых давлений»)
- 0,645 (Ki -1) К
Г2
(Х-1-37)
Обе формулы дают
удовлетворительное приближение в интервале
,
При расчете распределения
давления исходят из формулы, полученной
в результате разложения в ряд по степеням малого параметра х, причем,
в этом ряду ограничиваются линейным членом:
"=p*+ix или pz
др
-X,
(Х-1-38)
где рк _ коэффициент давления на коническом носке.
Кривизну До находят из уравнения образующей, написанного в виде
(Х-1-39)
414
Глава X
Форма образующей поверхности скачка уплотнения определяется по
уравнению (Х-1-22), которое может быть представлено несколько иначе, а именно:
0 1 ' TV' О /V Л ОО'\
ох + -у Rox2. (Х-1-22 )
В качестве примера найдем вид кривой скачка уплотнения, а также
распределение давления в окрестности острия тела вращения с
параболической образующей.
Таблица Х-1-1
Результаты расчета функций g(b), g' (&), I и начального градиента давления
Ki
0,3765
0,6599
1,150
2,469
3,988
оо
ё(Ъ)
5,170
1,800
1,573
2,101
2,487
2,931
ё' Ф).
—8,502
—3,640
—4,073
—6,820
—8,638
—10,76
г.
0,0426
0,2346
0,5106
0,8039
0,8921
0,9586
1 др
ЭоД'о дх
ь
5,532
4,662
4,514
4,684
4,802
4,929
Из уравнения параболы можно найти в точке
^мид и кривизну образующей
= г — 0 угол конуса
0 — 5^2 — —
\-i
Тогда уравнение образующей скачка напишется в виде
Для определения вида кривой распределения давления воспользуемся
(Х-1-38). Подставляя в него полученное значение кривизны R'o^= — Р0/#мид».
найдем
Р Рк др —
Нетрудно заметить, что конкретная форма скачка уплотнения и
величина коэффициента давления в рассматриваемой точке данного тела
определяются только параметром К^^МооРо*
так как от него в свою очередь зависят
параметр Ко и коэффициент I.
Второе приближение. Решение
задачи о расчете потока во втором
приближении связано с отысканием более
точного, чем (Х-1-28), выражения для
функции тока. Анализ результатов этого
решения показывает, что для тонких
заостренных головных частей расчет
коэффициента давления во втором прибли-
"7 го"°° жении можно вести по формуле
Рис. Х-1-7. Характер изменения про-
изводнои а/-<Г,
1Ь
10
5
-
в зависимости от
асимптотическое значение при Кх—>оо * ' 2
в которой величины pJ(Ro)2 = Рк/Ро и др/д (Rq
_ д (RoRox)
—^|—х2, (Х-1-40)
д (Rox)2
определены соотноше-
Гипераву новые скорости
ниями (Х-1-21) и (Х-1-35), а также аппроксимирующими выражениями
(VIII-1-27') и (Х-1-37). Зависимость для второй производной д2р/д (i?o#)2,
приведенная на рис. Х-1-7, может быть определена при помощи формулы
Г2
-Ь) КГ, ()
которая дает удовлетворительные результаты для значений Кь
расположенных в интервале 1<К1<оо, когда коэффициент 6 = 22,5 и в интервале
0,5<К!<1, когда 6 = 19,2.
При этом определение второй производной при помощи (Х-1-41)
позволяет несколько расширить область, в которой вычисляется распределение
давления. Однако такой расчет не дает полного представления о характере
распределения давления по всей поверхности тела.
Чтобы дополнить результаты, полученные по теории малых возмущений,
рассмотрим некоторые приближенные методы для расчета обтекания тел.
§ Х-2. Применение
приближенных методов
расчета обтекания тел
вращения потоками с очень
большими скоростями
Метод «местных конусов»
Симметричное обтекание. Рассмотрим разновидность этого метода,
основанную на гипотезе одинаковых давлений. Следовательно, для расчета
распределения давления около тела вращения с произвольной образующей можно
воспользоваться формулой (¥111-1-27'), если в ней параметр К4 определять
по углу местного конуса f5.
Для тонкого тела вращения с параболической образующей и местным
углом наклона касательной |3 = |3О(1—х) получаем уравнение кривой
распределения
р
2
О
Р
= 2,091 [(1-х)
где К-i = МооРо определяется по углу местного конуса у острия.
Представляет интерес сравнить значения первых производных от
коэффициента давления у острия, найденные с помощью формулы (Х-2-1) и по
теории малых возмущений, в частности, из выражения (Х-1-37). Вычисляя
производную, имея в виду формулу (Х-2-1), найдем
4— = -4,182 (1 + 0,036КГ3/2). (Х-2-2)
)
На графике рис. Х-1-6 показаны изменение начального градиента давления,
вычисленного по этой формуле, и соответствующие результаты теории малых
возмущений. Видно, что точность расчета по методу местных конусов
уменьшается с ростом параметра КА.
Сравнивая давления в окрестности острия, подсчитанные по теории
малых возмущений и по методу «местных конусов», можно сделать вывод,
что последнему методу свойственно некоторое завышение давления, хотя
разница в результатах и невелика.
Такое заключение, естественно, можно сделать и в отношении
коэффициента волнового сопротивления. Приближенную зависимость для него можно
получить, если ввести выражение (Х-2-1) в формулу (1-3-14) и затем про-
416
Глава X
интегрировать. В результате получим
^ = 0,697 + 0,213КГ3/2.
Ро
(Х-2-3)
Если применить другую разновидность метода «местных конусов»,
основанную на гипотезе одинаковых скоростей, то сравнение показывает, что для
больших чисел Моо получаемые давления оказываются заметно заниженными.
Учет влияния переменности теплоемкости. Рассмотрим частный случай
гиперзвукового обтекания тонкого тела вращения, при котором за ударной
волной совершенный газ имеет фиксированное значение показателя изэнтропы
к2<коо. Для расчета давления на местном конусе можно применить
формулу [59]
(Х-2-4)
,2
/Loo Г
где К1=МооР>1;
г —радиальная координата точки корпуса;
R — радиус кривизны образующей в этой точке. Таким образом, эта
формула учитывает влияние кривизны поверхности.
Обтекание под углом атаки. Применительно к расчету
несимметричного обтекания тела вращения с произвольной образующей метод «местных
конусов» состоит в следующем.
Принимается, что линия, касательная к
контуру тела в некоторой точке поверхности
(рис. Х-2-1), одновременно является
образующей конуса, симметрично
обтекаемого невозмущенным потоком. Угол
этого «местного конуса» можно
определить из выражения
г ctg p sin2 у, (Х-2-5)
Рис. Х-2-1. Построение «местного
конуса»
где Р — угол между касательной к
образующей и осью тела.
Если определить параметры на таком
конусе при а = 0, то в соответствии с
идеей метода «местных конусов» эти
параметры будут именно теми, которые характеризуют действительный поток
в рассматриваемой точке поверхности при заданном угле атаки.
Расчеты и сравнение с экспериментальными данными показывают, что
при числах Моо порядка Зч-4 и ниже, а также малых углах атаки
необходимо исходить, применяя метод «местных конусов» для вычисления
параметров на поверхности заостренных тел вращения с небольшим удлинением
головной части, из гипотезы одинаковых скоростей. По найденной на основе
этой гипотезы скорости расчет давления и плотности ведется с учетом
энтропии струйки, протекающей в рассматриваемой меридиональной плоскости
через скачок уплотнения непосредственно у острия.
При больших скоростях лучшие результаты дает гипотеза одинаковых
давлений. По найденному на основе этой гипотезы давлению расчет скорости
и плотности осуществляется с учетом той же энтропии.
Метод «местных конусов» ограничен в применении точками, в которых
касательные к поверхности параллельны направлению набегающего потока.
Очевидно, в этом случае углы «местных конусов» равны нулю. Причем, из
условия Рк = 0 можно получить значения соответствующих углов наклона
этих касательных к оси тела. Действительно, полагая рк = 0, найдем
Гиперзвуковые скорости £27
из (Х-2-5), что
Р = a cos у - ^ ctg P sin2 у. (Х-2-6)
В точках поверхности, положение которых определяется этими углами,
давление будет равно в соответствии с гипотезой одинаковых давлений
статическому давлению невозмущенного потока. Если же расчет ведется
на основе другой, гипотезы одинаковых скоростей, то в той же точке без
изменения по сравнению с невозмущенным течением останется скорость.
Однако метод «местных конусов» можно применить для оценки
параметров потока и за пределами указанной границы в так называемой
«теневой» зоне. С этой целью следует рассмотреть условный «местный конус»
с «отрицательным» углом рк, рассчитанным по той же формуле (Х-2-5).
Тогда коэффициент давления, найденный по абсолютному значению (5К,
надо рассматривать для данной точки «теневой» зоны отрицательным по знаку.
Метод сочетания конических
течений и течений разрежения
Осесимметричное обтекание. Содержание метода конических течений и
течений разрежений было изложено в § IV-7. Расчетная формула для
коэффициента давления
ir
где К1 = МОсР0;
Мс и рс — число М и давление непосредственно за скачком уплотнения
у острия;
рк — коэффициент давления на коническом носке.
Число МС = М2 находится из (Ш-4-29) или (Ш-4-38), а давление
рс = р2 определяется при помощи формулы (Ш-4-36). Коэффициент
давления рк и абсолютная величина давления рк на коническом носке вычисляются
из (VIII-1-27).
Применение этой формулы проиллюстрируем на конкретном примере
расчета симметричного обтекания заостренного тела вращения с углом
конического носка р0 = 0,2 при условии, что число Моо = 10 (К4 = 2).
Прежде всего, найдем число Мс = М2 на коническом носке. Для этой цели,
полагая к = 1,4, определим вначале по формуле (VIII-1-23) Ко = Моо6с =
= 2,38. Применяя затем (Ш-4-29), вычислим М2 = 6,73. При очень
больших числах Моо давления рс и рк отличаются мало, поэтому в (Х-2-7)
можно принять (pc//?K)(k-i)/2^ 1 считая, таким образом, что Мс
приближенно равно числу Мк, на коническом носке. Для заданного значения Kj. = 2
из (Х-1-21) определяем на коническом носке рк/Ро = 2,2. Вычислим
давление в той точке, где угол наклона касательной (3 = 0,1. В этом случае поток
отклоняется, начиная от вершины, на угол Др = (30 — Р = 0,1. Внося
полученные данные в выражение (Х-2-7), найдем для выбранной точки
р 1$1 = 0,543. Если рассмотреть более удаленную точку, для которой р = 0,
то здесь р/Ро = —0,085. Соответствующие значения чисел М, вычисленные
по (IV-7-14), будут равны 7,83 и 9,27.
Сравнение показывает (см. рис. Х-1-6), что начальный наклон кривой
распределения давления, рассчитанный по методу сочетания конических
течений и течений разрежения, ближе к результатам теории малых
возмущений, чем к методу «местных конусов». На это же указывают результаты
расчета по методу характеристик.
2 7—114
£28 Глава X
По распределению давления при помощи (1-3-14') вычисляют
коэффициент осевой силы.
Для заданной формы тела вращения коэффициент сопротивления
представляется в общем виде, как функция
где Kt = Мооро-
Рассмотрим в качестве примера тело вращения с параболической
образующей, уравнение которой в безразмерной форме г = х (2 — х). Внося г
и значение р по (Х-2-7) под интеграл (1-3-14'), производя интегрирование в
пределах от 0 до 1 (численно или графически), можно определить cRp в функции К^
и ML. Подсчеты показывают, что величина сдрМ» является возрастающей
функцией от параметра К* = Моо|30. Для выбранного в рассмотренном
выше примере значения К4 = 2 величина cRpMlo = 2,86, а для значения
КА = 3 эта величина cRpMlo = 6,09. Конкретные значения cRp для корпуса
с заданным удлинением Ямид = 1 /Ро соответствует определенному числу
Моо, вычисляемому из условия Моо = К^мид. Например, для Ямид = 3
число Моо = 6, а соответствующее значение cRp = 2,86/36 = 0,079.
Рассмотренный метод можно применить для расчета обтекания корпуса с учетом
изменения свойств газа за ударной волной при очень высоких температурах.
С этой целью, как было указано при исследовании потока около профиля,
можно исходить из того, что течение за скачком «замороженное» и газ имеет
постоянное значение показателя &2, определяемое для условий
непосредственно за скачком.
В соответствующих формулах метода характеристик вместо к надо
принять к2.
Оценка параметров обтекания хвостовой сужающейся части тела. Число
М на этом участке можно оценить таким же образом, как на головной части.
Предположим, что хвостовая часть тела вращения выполнена
сужающейся и имеет произвольную форму с плавным контуром. Так как в
каждой точке угол |3С наклона образующей этого участка известен, то можно
определить угол поворота потока, начиная от условий на носке. Его
величина равна Ар = Ро — Рс- Причем угол Рс здесь отрицателен по знаку.
Пусть, в частности, угол Рс = —0,1. В этом случае А(3 = 0,2 — (—0,1) =
= 0,3, а следовательно, в соответствии с формулой (IV-7-14) число М в
рассматриваемой точке равно 11,4. Применяя формулу (IV-7-15), найдем
WPo = —0,293. Как видно, влияние сужения привело к увеличению
разрежения.
Рассчитав подобным образом распределение давления, можно, исполь-
-2
гдон
зуя формулу с^= \ \р | dr2, вычислить дополнительную часть волно-
1
вого сопротивления от влияния кормы. Если в рассмотренном примере она
выполнена в виде усеченного конуса с углом Рс = — 0,1, на поверхности
которого коэффициент давления постоянен и равен р = — 0,293^, то
cfB = 0,293р; (1 -5Дон). (Х-2-8)
Недостатки метода, о которых указывалось в § IV-7, обусловливают
неточность расчета обтекания головной и особенно хвостовой частей тела
вращения, где отклонение от действительной картины может быть более
существенным. Если рассматривать среднюю цилиндрическую часть, то
по своему содержанию метод лишен возможности отобразить хотя бы
приближенно возможную картину ее обтекания. Поэтому его можно
использовать лишь для ориентировочного расчета параметров обтекания тела.
Гиперзвуковые скорости
419
Неосесимметричное обтекание. В приложении к неосесимметричному
потоку около заостренного тела вращения метод состоит в том, что число М
и другие параметры на носке в каждой меридиональной плоскости берутся
из решения задачи об обтекании конуса под углом атаки, а поток за носком
в соответствующей меридиональной плоскости рассчитывается как
двухмерное сверхзвуковое течение разрежения, известное под названием течения
Прандтля — Майера.
Решая задачу о неосесимметричном обтекании конуса, находим число
М2 на конусе для выбранного угла у, а из формулы (IV-1-17) или
табл. IV-1-1 — соответствующий угол со2. Затем расчет ведется так же, как
для симметричного случая, а именно находитвя полный угол поворота со,
а)
Р
0,1
0,1
\
\
S
К,=1,68
п
«Г 1,01
2
/
3
,
- —1
0,8
3
V
о—
-» —
Кг 1,01
=^
—
х
Рис. Х-2-2. Распределение коэффициента давления по
поверхности оживального тела вращения:
а — а = 5°; б — а = 15°; 1 — подветренная; 2 — боковая;
3 — наветренная образующие
под которым надо понимать сумму угла поворота о2 и местного (или
абсолютного) угла отклонения ро — р, а по значению со = со2 + ф0 ~ Р) из
табл. IV-1-1 определяется местное число М. Зная это число, можно
подсчитать абсолютное давление и коэффициент давления. При очень больших
числах Моо для расчета распределения давления около тонких заостренных
тел вращения можно воспользоваться формулой, аналогичной (Х-2-7):
2fe
где параметр К^, равный Мооро, определяется по углу «местного конуса»
у острия Ро = Ро — ее cos у для заданного угла 7 меридиональной
плоскости. Число Мк и коэффициент давления ря определяются по параметру К^
для «местного конуса». Для вычисления рн применяется формула (VIII-1-27).
Значение Мк можно принимать равным числу Мс непосредственно за
скачком, вычисляемому при помощи (II1-4-38) по параметру Ко = Мообс,
который в свою очередь находится из (VIII-1-23) по величине К^ = Мооро*
27*
420
Глава X
В результате применения (Х-2-9) для заданных формы корпуса,
значений Моо и а находится распределение коэффициента давления по
поверхности тела, т. е. функция р = р (х, у). Получаемые данные тем точнее, чем
больше Моо и значения параметра подобия К4 = Моо/Хмид. Это видно из
рис. Х-2-2, где приведены результаты исследований распределения
давления около оживальных головок с удлинениями Ямид = 3 и 5 при Моо = 5,05
и углах атаки а = 5 и 15°. Лучшее приближение теории к эксперименту
наблюдается для большего значения параметра Kt = 1,68, т. е. для тела
с удлинением Ямид = 3. Для
А
А
0,8
0,6
Ofi
0,2
А
/
/
1,01
1
/
/
15 U
10 15 ct°
Рис. Х-2-3. Зависимость коэффициента
нормальной силы оживальной головки от угла
атаки, Моо = 5,05:
О — эксперимент; расчет
головки с удлинением Ямид = 5 (Kt = 1,01)
приближенный расчет дает по
сравнению с экспериментальными
результатами несколько заниженные
значения на верхней стороне тела.
Такое явление имеет место
практически при всех значениях Kt > 1,
хотя точность расчета падает при
снижении величины параметра
подобия. Если этот параметр меньше
единицы, то, как правило,
приближенные вычисления
оказываются неприемлемыми.
Из сопоставления данных
можно также сделать вывод, что
приближенный метод дает лучшие
результаты по мере снижения угла
атаки. При этом отклонение в
распределении давления по теоретическому расчету от эксперимента при
больших а объясняется влиянием вязкости поперечного потока, особенно на
верхней стороне тела, что не учитывается приближенной теорией. Причем
это влияние возрастает с увеличением числа Моо.
Аэродинамические коэффициенты при неосесимметричном обтекании
корпуса определяются по найденному распределению давления при помощи
формул (1-3-14), (1-4-11), (1-5-8) путем численного или графического
интегрирования. Причем в (1-5-8) для коэффициента момента вторым членом
вследствие малой толщины корпуса можно пренебречь. Вычисления
коэффициента осевой силы по (1-3-14) показывают, что вследствие малости углов
атаки величина cRp при а Ф 0 практически не отличается от
соответствующего значения при а = 0, следовательно, cRp c±l cxb.
Вычисления коэффициентов нормальной силы и момента показывают,
что выражения для них могут быть для заданной формы тела в общем
случае представлены соответственно в виде
1
, / а
4.
тгр = /
м
Для параболической образующей г = х (2 — х) значения cNvbl[oo
оказываются следующими:
0
0,
0,
1,
2
6
0
0,6
0
0,393
1,22
2,46
0
0
1
3
1,0
,600
,79
,32
0
0
2
4
,793
,42
,33
2
0
1,
3,
5,
,5
00
30
79
4
0
1,
4,
8,
,0
36
74
20
Гиперзвуковые скорости 421
На рис. Х-2-3 вычисленные коэффициенты нормальной силы
сравниваются с экспериментальными величинами. Совпадение результатов, как
видно, удовлетворительное. Однако лучшее соответствие теории и
эксперимента наблюдается при большем значении параметра подобия.
Исследования показывают, что при гиперзвуковом обтекании тонких
заостренных корпусов с параболической оживальной образующей расчет
коэффициента центра давления можно вести по приближенной формуле
Сц.д= Хц-я =S-[l^K1 (l-i^-)l , (X-2-10)
где К4 = Моо(30-
Удовлетворительные результаты получаются по этой формуле для
значений Ki<0,5 -г- 0,6. Зная коэффициент центра давления, можно найти
по формуле mzp = xn^cNp коэффициент момента относительно носка корпуса.
§ Х-3. Метод Ньютона
Давление
В соответствии с этим методом расчет давления ведется по
формуле (IV-7-2), в которой значения cos2 r\ и cos2 т|* определяются при помощи
(IV-7-4).
Так как рассматривается тело вращения, то (IV-7-2) будет
~ _~* ( sin p cos a —sin a cos p cosy \2
V ~~ V у sin Po cos а — sin а cos p0 cos у / '
sin Po cos а — sin а cos p0 cos у
где р* — коэффициент давления на коническом носке, который
рассчитывается по обычной теории сверхзвукового неосесимметричного обтекания
конуса и для заданных значений угла |30 и числа Моо является функцией
углов а и у.
В случае нулевого угла атаки (Х-3-1) упрощается:
где р* уже не зависит от а и у и является для заданных условий осесимме-
тричного обтекания величиной постоянной.
В тех случаях, когда скорости настолько велики, что давление
практически перестает зависеть от числа Моо, в (Х-3-1) можно произвести замену
параметра p*/cos2ri* на величину р (k) = pK/sin2»'|3K, определяемую из
(VXII-1-30') в виде
Следовательно, можно написать, что
p = p(k) (sin P cos a — sin a cos P cos у)2. (Х-3-4)
Коэффициент осевой силы
Внося выражение (Х-3-1) в (1-3-14), находим зависимость для расчета
коэффициента осевой силы
Crp = 4 \ Ямид —-^- г tg P dx, (X-3-5)
«1 ЗХ
Глава X
Jt ,
p* (sin p cos a — sin a cos |3 cos y)2
422
где
В случае использования (Х-3-4)
я
А (ук) = p{k) \ (sin P cos a — sin a cos |3 cos у)2 dy
и после интегрирования
А Ы = Р (А) [ (я — 7к) (cos2 a sin213 + \ sin2 a cos2 p) +
sin2p — sin2acos2PcosyK)l . (X-3-7)
Пределы интегрирования ук и х'к (или в размерной форме х'к) зависят
от геометрической формы тела и угла атаки. Чтобы установить их, надо
>M
Рис. Х-3-1. Образование «затененной» области при обтекании
тела вращения под углом атаки
исходить из особенности обтекания тела «ньютоновым потоком», которая,
как уже было отмечено, состоит в том, что на его поверхности создается
некоторая «затененная» область, в которой не происходит удара частиц.
~~" Граница этой области (рис. Х-3-1) определяется кривой, на которой,
как и всюду за ней, давление равно нулю. Поэтому значения пределов ук
и Хц (или соответствующей координаты гк) определяются в зависимости
от положения границы «затененной» области. В соответствии с IV-7-10
значение угла 7к найдется из условия tg p/tg a = cos ук или для малых а и Р —
из условия p/a = cosYK.
При расчете величины х'к, представляющей собой расстояние от острия
до наиболее удаленной точки, в которой давление равно нулю, исходят
из условия Р = — а. В соответствии с этим условием уравнение для
определения х'к (или гк) принимает вид
(X-3-8)
При вычислении пределов следует иметь в виду два возможных случая
обтекания. Первый случай характеризуется тем, что угол атаки а меньше
угла ро конуса у острия тела (см. рис. Х-3-1). В этом случае, пока
текущее значение угла р наклона образующей больше или равно углу а,
значение предела ук = 0. Когда угол р становится меньше угла атаки, то
значение ук будет больше нуля. В частности, при р=0 угол ук = я/2, а в случае
Р = — а величина ук = я.
Гиперзвуковые скорости
423
Очевидно, для цилиндра всегда ук = л;/2, так как у него р = 0. Для этих
двух значений р существенно упрощается вид функции Л(ук),
представленной формулой (Х-3-7). В частности, формула (Х-3-7) при р = 0, ук = л/2
принимает вид А (ук) = -i- p (A) sin2 а, а в случае Р = — а, ук = я величина А (ук) = 0.
Предел хк определяется положением точки на нижней образующей, где
начинается «затененная» зона. Причем, как видно на рис. Х-3-1, в общем
случае значение х'к отличается от полной длины тела.
При а < р0 на криволинейной головке образуется небольшая по размеру
«затененная» зона и приближенно можно принять Як^^мид и х'к = 1. Так
как в этом случае 7к = 0, то
А (ук) = лр (k) (cos2 a sin2 р + у sin2 a cos2 Р) . (Х-3-9)
Следовательно,
1
cRp = КгщР{к) J (cos2 a sin2 р + i- sin2 a cos2 р) г tg P dx. (X-3-10)
Предположим, что задана параболическая головка с
г = х(2 — х). Для нее tg Р = tgP0<l — х), где
= tg2 p/(l + tg2 P). После
соответствующих подстановок в (Х-3-10)
и вычисления интеграла можно
подсчитать cRp.
Второй случай имеет ту
особенность, что угол атаки больше или сС
равен углу конуса у острия (рис.
Х-3-2). В этом случае, если а = ро,
то, очевидно, значение уК = 0
соответствует месту у острия.
Непосредственно за ним начинается «за-
уравнением
и sin2 p =
х
Рис. Х-3-2. Образование «затененной» области
(заштриховано) на теле вращения при а > (30
тененная» область, в которой всюду ук>0. Эта область, как показано на
рис. Х-3-2, простирается до дна, следовательно, координата х'к~хк.
Коэффициент давления р* на носовом конусе как в первом, так и во
втором случаях может определяться по методу «местных конусов».
Для нулевого угла атаки входящая в выражение (Х-3-5) функция А (ук) =
— (jtp*/sin2 ро) sin2 p и, следовательно, формула для коэффициента осевой
силы, равного коэффициенту вол-
„Затененная"зона нового сопротивления, принимает
вид
sin* frd?.
(Х-3-11)
В этой формуле верхний
предел г = 1 интеграла определяется
тем, что «затененная» зона (рис.
Х-3-3) начинается с места
наибольшего поперечного сечения
тела. Рассматривая параболическое тело, для которого tgp = tgp0K 1 — г,
2 P
Рис Х-3-3. Схема обтекания тела вращения при
а = 0
р р р
и производя соответствующую замену величины sin2 P, получим после
интегрирования
cRp =
1
J
(Х-3-12)
424
Глава X
Когда Хшщ > 2, эта формула может быть представлена в более
простом виде:
1
^мид
(Х-3-13)
Если тело вращения тонкое, то Ямид~1/ро и cRp^ р*/3.
Таким образом, коэффициент сопротивления параболической головки
оказывается втрое меньше его величины для конического носка. Полагая
р* = р (к) Ро> найдем, что, в
частности, при к = 1,4
величина cRp = О,697Р*.
Характер изменения cRp в
зависимости от а для
параболической головки при р (к) = 2
показан на рис. Х-3-4.
Коэффициент осевой
силы конуса. Так как для
конуса Р = РК = const, то,
следовательно, функция
А (уК), определяемая (Х-3-6),
будет величиной постоян-
0}5
0,3
У i
20
60
80
ной. Поэтому
Рис. Х-3-4. Зависимость коэффициента осевой силы
для параболической головки от угла атаки
(Х-3-14)
Если угол конуса
больше угла атаки, что
соответствует первому случаю, то «затененная» зона отсутствует, угол ук = 0и,
следовательно А(уК)=А (0) (см. Х-3-9), где Р = РК. Для тонкого конуса
(Тк) = А (0) = жр{к)
+ ^
(Х-3-15)
Если угол конуса меньше угла атаки (второй случай, рассмотренный
выше), то сверху возникает «затененная» зона (рис. Х-3-5)и функция А (уК)
должна определяться по (Х-3-7).
При нулевом угле атаки коэффициент осевой силы cRp = cXB=- p(k) sin2 PK,
что при к = 1,4 дает величину 2,091 sin2 PK.
Чтобы учесть влияние числа Маха, можно использовать приближенную
зависимость
( ApL) sinPK. (X-3-16)
Влияние расширения потока в «затененной» зоне. До сих пор мы
рассматривали чистый «ньютонов поток», в котором коэффициент давления
для «затененной» зоны
принимался равным нулю.
Коэффициент осевой силы в этом
предельном случае определяется по
(Х-3-5).
В действительности, при
отклонении от предельного
случая, когда числа Моо остаются
конечными, хотя и очень боль-
Рис' Х"3-5' «Затененная» зона на конусе
шими, величина cRp будет
отличаться от того значения, которое получается по (Х-3-5). Одна из причин состоит
в том, что эта формула не учитывает влияния разрежения в «затененной» зоне.
Гиперзвуковые скорости 425
Результаты можно уточнить, если для оценки коэффициента осевой силы
применить более общее выражение
лк л
ЯГмид
\\prig$dx d7, (Х-3-17)
которое учитывает влияние «затененной» области.
Для удобства представим этот коэффициент в виде суммы двух
составляющих:
cRp = cRvt + AcRpi (X-3-18)
где crpt — коэффициент осевой силы, возникающей вследствие торможения;
&crp — добавочная величина коэффициента, вызванная влиянием
разрежения в «затененной» зоне.
Значение crpt вычисляется по формуле (Х-3-17), а величина ДсДр — из
выражения
\ \ er tg p dx dY, (X-3-19)
Гмид
которое получается из условия, что интегрирование при определении
коэффициента осевой силы продолжено в «затененную» зону. В этом выражении
нижний предел х'к равен расстоянию от острия до начала «затененной» зоны
на верхней стороне тела.
Коэффициент давления ре в этой зоне определяется по формуле ре =
= (2/kMlo) (ре/роо — 1) и в общем случае, очевидно, будет величиной переменной.
Для приближенной оценки влияния «затененной» зоны принимают
коэффициент давления во всех точках постоянным и равным ре= — 2/(кМ2ос).
При этом исходят из того предположения, что при очень больших скоростях
в «затененной» зоне образуется вакуум (ре = 0). Тогда
В частности, для конуса интегрирование при возникновении «затененной»
зоны ведется от 0 до ^к, следовательно,
т. е. суммарная осевая сила несколько снижается. Если затенение
отсутствует (ук=:0), то добавочная, отрицательная по знаку, осевая сила исчезает.
У тела вращения с криволинейной образующей при нулевом угле атаки
«затененная» область полностью захватывает хвостовую часть. Так как в этом
случае xK = xK=$Mim, уК = л, то
^(1-^Он) (Х-3-22)
и, следовательно, осевая сила несколько возрастает.
Форма головной части с
минимальным сопротивлением
Применение формулы Ньютона. Формулу Ньютона р = pooF^o sin213
можно использовать для определения вида образующей тела вращения с
минимальным сопротивлением при очень больших скоростях. С этой целью, имея в виду
формулу (1-3-14), а также зависимость p = pooV2oo (dr/ds)2, напишем выражение
426 Глава X
для силы сопротивления при симметричном обтекании
r (-^)2 dr. (X-3-23)
г
о
Задача заключается в том, чтобы определить уравнение образующей
r = f(x), которому соответствует минимум функции Rp. Решая эту задачу,
можно принять ([72], 1962, № 1), что минимум сопротивления определяется
при условии постоянства боковой поверхности S и объема тела W, т. е.
S X
S = 2л \ г ds = const; W = л [ г2 dx = const. (X-3-24)
Решение этой изопериметрической вариационной задачи сводится к
исследованию на безусловный экстремум функционала:
ИЛИ
где Я4, Я2 —некоторые постоянные, называемые множителями Лагранжа.
Составляя для последнего функционала уравнение Эйлера
в котором rr = dr/ds и
получим уравнение, которому должна удовлетворять минимизирующая
функция. Это уравнение после подстановки выражения (Х-3-26) в (Х-3-25) с
учетом, что dF/ds = 0, принимает вид
(dWi/2 1 Л О
Постоянные Я1? Я2 можно определить из условий, что при г —0
производная (dr/ds)0 = sm$o, а при т* = гмид эта производная равна нулю. В
результате уравнение минимизирующей функции
£2"2} (X-3-27,
Примем в этом уравнении местный наклон и = dr/ds за параметр. Тогда
само уравнение дает выражение для определения координаты г точек
образующей:
= YY~tf (l *\ . (Х-3-27')
V sin3p0/
Уравнение для расчета координаты х
Гиперзвуковые спорости
427
Проинтегрируем это уравнение с учетом выражения (Х-3-27') в
пределах от г = гмид, х = хк до текущих значений г, х. Получим
гмид,
откуда
'МИД
(Х-3-29)
Отсюда накодим, полагая х =
и = sin p0, длину головки
г
Гмиа
^ми9
Уравнения (Х-3-27) и (Х-3-29)
представляют в параметрической
форме образующие тела вращения с
минимальным сопротивлением. Семейство
таких образующих, построенных для
различных значений угла |30,
приведено на рис. Х-3-6. Образующая тела
минимального сопротивления
удовлетворительно аппроксимируется кривой
€ уравнением
^_)3/4. (х-3-31)
#Мид /
Используя параметрические
уравнения минимизирующей кривой, можно получить выражения для
сопротивления, а также для боковой поверхности и объема тела вращения. Внося
зависимость (Х-3-27') в (Х-3-23), найдем
0,
J-
5 \
о)
\
-■—
\
/
о 4
м
гмид
«5
-",5
-W
Рис. Х-3-6. Семейство образующих тел
минимального сопротивления
у - у sin2 р0) , (Х-3-32)
откуда коэффициент сопротивления
ГМИЯ
^sin'po (l -|sin2po) . (Х-3-33)
Формулы для вычисления боковой поверхности и объема
S = -
1
V
\
х~
X
■■ "
JJC.
<
/
^=
/
иа
— _
S
—
(Я
-
25-
20-
15 -
10 -
5 -
На рис. Х-3-7 видно, как
изменяются значения минимального
сопротивления в зависимости от
угла заострения носка |30. На том
же рисунке нанесены кривые,
характеризующие изменение безмерных
величин хк/гмид, б'/гмид, И7гмид.
Эти кривые, а также графики на
рис. Х-3-6 показывают, что форма
образующих весьма близка к
оживал ьной кривой. Вместе с тем
обнаруживается тенденция к большей длине по сравнению с оживальной
головкой при том же самом значении |30, а такжеJ к ^более четко выраженной
конусности в передней части.
0,1
О 10
30
50
70
Рис. Х-3-7. Параметры головных частей
минимального сопротивления
428
• Глава X
Таблица Х~3-1,&
Волновое сопротивление головных частей наивыгоднейшей формы
1
Параметры
•^мид» ^*мид
^бОК' ^МИД
W rl
УУ т, «МИД
2
d
d
d
i,6ojA2jl
f ^мид
W
5,33 T
3
X
МИД
•^мид
0,598 ^бок
/ С ^Т
^' ° 2
"МИД
2
0,098 ^ок
4
лмид
<i
*^мид
л б? ^МИД
0 ооо ЙМИД
1,60 |/4^
5,44 —з—
5
ООК
1,0У1жМИд, «мид
W
6-05^
о оо "l/тд/ -.
о, ^о 1/ ки т^мид
^бок
6
схв
0,288Лмид
0,564Ямид
0,321А/мид
0,307Хмид
Примечания. Графа 1 —заданные геометрические параметры головки; графы 2
—5—расчетные геометрические параметры оптимального тела вращения; графа 6—вычисленная величина
минимального коэффициента волнового сопротивления.
Таблица Х-3-1,6
Форма образующей оптимальной головки
Заданные
параметры
Координаты точки
1/
рд
перехода 1о=*о/х
мид,
Уравнение первого участка образующей
•^мид» ^мид
^бок» ^мид
ГУ т, «МИД
УУ гр * *Ст\/ГГ¥ТТ
g0 = 0,704, Г]о = О,76
g0 = 0,802, г)0 = 0,778
go = 0,385, т]0 = 0,617
Ло V go
Ло go
g0
где h (ц) =
go Л(т)0)-Л(0) '
2tj2 —1
2,73 —
p, к)
Ф = arccos [0,73 +|Г4т]2 (1 — ^2)] х
X [2,73-1
= 0,463, т]о = 0,637
Примечание: функции F и Е представляют собой соответственно неполные
эллиптические интегралы первого и второго рода.
Гиперзвуковые скорости 429
Использование формулы Буземана. Оптимальные формы головок
оказываются несколько иными, если для их определения использовать формулу
Буземана (VI-7-19). Решение вариационной задачи ([68], 1960, в. 6; 1963,
в. 3; [70], 1963, № 1) приводит к выводу, что образующая головки с
минимальным сопротивлением состоит из двух последовательно расположенных
участков кривых. На первом из них всегда будет положительное по знаку
избыточное давление, на втором — величина избыточного давления равна нулю.
В табл. X-3-la и б приведены результаты решения шести задач по
определению минимального коэффициента волнового сопротивления и уравнения
образующей соответствующей головки. Исходными условиями являлись
задание в различных комбинациях попарно длины хШИД головки, диаметра миде-
левого сечения ^мид, объема WT, боковой поверхности Sqok. ^ зависимости
от заданной комбинации параметров определялись относительные координаты
точек перехода £о = ^о/^мид, Ло^^о/^мид первого участка кривой ко второму.
При этом уравнение образующей на втором участке оказывается одним
и тем же и имеет вид
r1 = T^=[l-^f-(l-i)]1/3, (X-3-35)
где 1 < g = ^/^мид < 5о-
Коэффициент нормальной силы
Тело вращения с произвольной образующей. Расчетная зависимость
для коэффициента нормальной силы получается после подстановки
выражения (Х-3-1) для коэффициента давления в (1-4-11):
2 v" "' ч ' (X-3-36)
где функция
я _
р* (sin р cos a — sin а cos р cosy)2 cos у ,
(sin Po cos a- sin а cos po cos 7)2 аУ>
а верхний предел хк представляет собой расстояние от острия до наиболее
удаленной точки на поверхности тела, за которой начинается «затененная» зона.
Если для коэффициента давления принимается формула (Х-3-4), то можно
вычислить интеграл Х-3-37, и функция В (у) находится в явном виде:
+ sinyK ["cos2 a sin2 P— — sin2asin2fJcos yK + y sin2 а cos213 (cos2 ук + 2)1 } .
(Х-3-38)
Величина предела х'к вычисляется в соответствии с приведенными выше
возможными расчетными случаями.
Для первого из этих случаев значительно упрощается выражение (Х-3-38)
для функции В (ук). Выше указывалось, что пока выполняется условие а <(3,
значение -ук = 0, следовательно,
Когда же текущее значение угла Р становится меньше угла а, величина
7к>0. В частности, если Р = 0, то ук = п/2 и
В (ук) = В (я/2) = -1- sin2 a cos2 Pp (А).
Если Р = — а, то ук = я и В (ук) = В(п) = 0.
430
Глава X
В рассматриваемом случае а < (50 можно пренебречь влиянием «затененной»
зоны, тогда
1
cNp = р (к) Хмид sin 2а ^ sin 2£r ds. (Х-3-39)
о
Подынтегральная функция зависит от формы образующей. В частном
случае параболической головки
= s(2-s) и sin2p=
где
ук:
Во втором случае «затененная» область, которой соответствуют значения
• 0, начинается непосредственно за передней точкой и, следовательно,
значение функции В (ук) надо
вычислять по (Х-3-38).
Если углы атаки малы, то
влияние «затененной» зоны пренебрежимо
мало. В этом случае, внося в (Х-3-36)
выражение для В(ук)= — p(&)a(3jt,
получим
cNp = p(k)a. (Х-3-40)
Результаты расчета коэффициен-
3
2
п
30
50
70
та нормальной силы по (Х-3-36) для
параболической головки приведены
на рис. Х-3-8.
Нетрудно заметить, что цилинд-
Рис. Х-3-8. Зависимость коэффициента
нормальной силы для параболической головки
от угла атаки
рическому участку (ж>1),
следующему за криволинейной головкой, соответствует постоянное значение
подынтегральной функции в (Х-3-36). Из (Х-3-38) следует, что, так как В(ук) =
= — у р (k) sin2 a, то коэффициент нормальной силы цилиндрического участка
cnp = 1JT ?(*) Яч sin2 a- (X-3-41)
Коэффициент нормальной силы тонкого конуса. Учитывая, что для
конуса функция В (ук) = const, из (Х-3-36) можно получить
П- (Х"3-42>
Используя (Х-3-38) для функции #(ук), можно представить (Х-3-42)
в более конкретном виде, если рассмотреть частные случаи обтекания.
Так как в первом случае a < Рк, то ук = О, В (ук) = В (0) =
= — яр (к) sin 2a sin 2(3/4, и, следовательно,
л
sin 2a.
При малых углах^а и |3К
(Х-3-43)
(Х-3-44)
зс), определяе-
(Х-3-45)
Для тонкого конуса при малых углах атаки и Ы1 последняя формула
дает значение (dcNp/da)a==o = 2, которое, как будет показано ниже, точно
соответствует линеаризованному обтеканию.
Из (Х-3-43) можно найти начальный наклон кривой
мый производной
да ) а=0
Гиперзвуковые скорости
431
2,0
Следовательно, можно сделать вывод, что наклон кривой и величина
cNp слабо зависят от числа Моо во всем диапазоне от малых до очень
больших его значений. Этот
вывод подтверждается резуль- fdcNp) 1
татами точного расчета за- \ du/^Jg cos2L
висимости от Моо величины 2,5
(dcNp/da)a==o cos"2 |3K для
конусов с различными
значениями угла рк.
На рис. Х-3-9, где
приведены эти результаты,
также видно, что влияние числа
Моо оказывается тем
меньше, чем толще конус и чем
больше число Моо. Вместе
с тем сравнение
показывает, что теория Ньютона
при оценке коэффициента
нормальной силы лучше
согласуется с точными данными, если при расчете величины В (ук) принять k = l.
Во втором случае при а > рк величина ук > 0 и значение В (ук) надо
вычислять по формулам (Х-3-37) и (Х-3-38).
Влияние расширения потока в «затененной» зоне. Для оценки
коэффициента нормальной силы с учетом влияния разрежения в «затененной»
зоне вместо (Х-3-36) надо применять более общее выражение
|
Я =.9/7°
/ 20
Ш^
Г\1—
15° 1
4
^=
__——
Mm ^^*~~
1/оо
—
^
^^
„I —
SSSSBMI
ь
12
Рис. Х-3-9. Изменение начального наклона кривой
коэффициента нормальной силы конуса в зависимости
от Моо и угла рк
'МИД
\ \ Р cos yr dx dy.
(Х-3-46)
о о
При этом величину коэффициента нормальной силы можно представить
в виде суммы двух составляющих:
cNp = cNpT + AcNp, (X-3-47)
где с^р т рассчитывается по формуле (Х-3-36) из условия торможения,
a AeNp определяется для «затененной» области с помощью (Х-3-46).
Рассмотрим подробней, как находится AcNp. Примем, как и прежде,
что в «затененной» зоне коэффициент давления ре = (2/Miy (ре1р<х> — 1) везде
одинаков. С учетом этого, после подстановки значения ре в (Х-3-46), найдем
яг
МИД
(X-3-48)
Зная форму тела в «затененной» области, а также границы этой области,
можно определить AcNp. В частности, для тонкого конуса абсолютная
величина
а для цилиндра,
(Х-3-49)
(Х-3-50)
Наибольший эффект от разрежения в «затененной» зоне будет
соответствовать полному вакууму, т. е. когда всюду в этой зоне ре = рек = рец
и, следовательно, ре = рек = Рец = ~2/(Ш2оо).
432
Глава X
На рис. Х-3-10 показаны результаты расчета при а = 5 и 10°
коэффициента нормальной силы тела вращения, составленного из конуса и
цилиндра, с учетом поправок, вычисленных по формулам (Х-3-49) и (Х-3-50),
и при условии, что коэффициент давления ре в «затененной» зоне принят
равным нулю. Видно, что экспериментальные данные располагаются в
промежутке между результатами, полученными соответственно с учетом и без
учета поправок. Можно заметить также, что с уменьшением угла атаки
ослабевает и влияние «затенения».
Из того же рис. Х-3-10 следует, что при угле атаки а = 5°, т. е. таком
же, как угол конуса, экспериментальная кривая оказывается достаточно
0,5
—^
Jo
<
с
, <
— -<
>-—<
и
—1
;
*• — ,
S
*^^._ оС
OL
-10°
= 5°
5 6 7 89]
20 30
Рис. Х-3-10. Расчет влияния расширения
потока в «затененной» зоне на коэффициент
нормальной силы по теории Ньютона:
1 —ре = 0; 2 — Ре = — 2/feM2; о —эксперимент
Рис. Х-3-11. Изменение dcNp/dx вдоль
продольной оси:
1 — для конуса; 2 — для цилиндра по
теории Ньютона; 3 — при больших; 4 — при
малых сверхзвуковых скоростях
близкой к кривой, найденной по теории «ньютонова торможения» без
поправки. Это объясняется отсутствием «затененной» зоны на конусе, а также
небольшим влиянием «затенения» на цилиндре.
Влияние цилиндрического участка тела на коэффициент нормальной
силы. Как показывают расчеты и экспериментальные исследования, это
влияние зависит от формы головной части и числа Моо.
На рис. Х-3-11 приведен график распределения коэффициента
нормальной силы на цилиндрической части тела, следующей за конической
головкой. Этот график позволяет оценить роль цилиндрического участка
в создании нормальной силы при различных скоростях.
При относительно небольших сверхзвуковых скоростях (Моо = 2 -=- 3)
коэффициент местной нормальной силы уменьшается в направлении вниз
по потоку и примерно на расстоянии (2 -f- 2,5) ймид от места сопряжения
цилиндрической и конусной частей тела становится равным нулю. При более
высоких числах Моо, лежащих в диапазоне 3 < Моо < 6, распределение
коэффициента местной нормальной силы оказывается таким, что его
среднее значение становится наибольшим.
Дальнейшее возрастание числа Моо сопровождается все меньшим
изменением коэффициента нормальной силы, и его величина совершенно
отчетливо стремится к некоторому постоянному значению, определяемому
приближением по теории Ньютона.
Чтобы установить количественные характеристики для оценки влияния
при больших числах Моо цилиндрического участка, рассмотрим вначале
некоторые общие соображения об изменении начального наклона кривой cNp.
Гиперзвуковые скорости
433
Для тела, форма которого изображена на рис. Х-3-12, коэффициент
нормальной силы можно представить в виде общей зависимости
(Х-3-51)
Для того случая, когда вся хвостовая часть является цилиндрической,
т. е. ха — хц и dROn = dmia, эта зависимость
civp = /(p0, j^-, М*,, а) . (Х-3-51')
Если углы атаки малы, то cNp можно рассматривать линейной
функцией а и, следовательно, выражение для коэффициента нормальной силы
напишется в виде cNp = (dcNp/da)a==Q a,
где производная я
JQL,
амип /
амид
(Х-3-52)
представляет собой некоторую
функцию ф от переменных ро,
Рассматривая формулу (Х-345) Рис. х.3.12. Расчетная схема для тела вра-
и рис. A-tD-У, можно сделать вывод, щения:
ЧТО Коэффициент НОрмалЬНОЙ СИЛЫ 1 — головная часть с произвольной образующей;
ичмрттдртгя тгптт^тгттчтгтоттт.т1п ттпп 2—цилиндрическая часть; з — коническая кор-
Ивменяется приОЛИЗИТеЛЬНО Про- мовая, 4 — коническая головная части
порционально cos2130. Однако, если
рассматривать тонкие тела с углами р0, не превышающими 10—15°, то
влияние угла заострения будет малым и тогда можно принять, что
да М=0
0,02
/
ч
^мид
, м.
(Х-3-52')
Эта зависимость была
положена в основу эксперимента с
двумя моделями тел, имеющими
цилиндрические хвостовые
элементы. У одной из них
головная часть была конической, у
другой — оживальной.
Результаты эксперимента,
приведенные на рис. Х-3-13 [16],
показывают, что когда длина
цилиндрического участка
достигает порядка 3<2МИД, наклон
кривой коэффициента нормальной
силы у обеих моделей
практически одинаков.
При большой относительной
длине цилиндра порядка Хц =
— 8 -ь 9 и выше начальный
наклон кривой cNp практически не
зависит от величины Хц.
Как показывают экспериментальные данные, с увеличением числа Моо
наклон кривой уменьшается, причем при Моо > 8 -^ 9 наклон кривой равен
углу, который получается для конуса по теории «ньютонова течения». Это
28-114
8
12
А,
Рис. Х-3-13. Зависимость (dcNp/da)a=a0oT Хц для
цилиндрического, корпуса с тонкими носовыми
частями:
коническая головка; оживальная
головка; коническая и оживальная головки
434
Глава X
согласуется с выводом, который следует из (Х-3-41) и состоит в том, что при
Моо->оо цилиндрический участок не дает составляющей начального наклона.
Нелинейная зависимость нормальной силы от угла атаки. Если наклон
кривой коэффициента нормальной силы не зависит от угла атаки, то
величина cNp может быть вычислена, например, с
помощью графика на рис. Х-3-13, откуда снимаются
данные о начальной производной, и линейной
зависимости cNp = (dcNp /да)а=оа.
Однако с увеличением угла атаки зависимость
коэффициента нормальной силы от а отклоняется от
линейного закона
1Аг~
1ft
0,6
Jo
Ч
О
а + AcNp,
(X-3-53)
12 ссс
Рис. Х-3-14. Изменение
коэффициента
нормальной силы и его
составляющих для
цилиндрического тела с тонким
заостренным носком
(Мое = 4)
нение параметра Ac
Np
где добавочный член AcNp отображает нелинейную
зависимость коэффициента нормальной силы от угла
атаки.
Графическая интерпретация формулы (Х-3-53)
на основе экспериментальных данных приведена на
рис. Х-3-14. Как и следовало ожидать, для углов
а < 15°, при которых проводились эксперименты,
величина AcNp пропорциональна а2, т. е.
добавочный член характеризует квадратичную зависимость.
Следовательно, параметр AcNp/a2 не зависит от угла
атаки и определяется, очевидно, в общем случае
геометрическими размерами цилиндра и скоростью
потока, что конкретно может быть установлено при
помощи экспериментальных исследований. По
результатам исследований при углах атаки а <! 15°
построены кривые (рис. Х-3-15), характеризующие изме-
/а2 в зависимости от Моо и относительной длины
цилиндрической части тела. На том же рисунке показана предельная
прямая, построенная на основе фор- л
мулы (Х-3-41). ^
Имея кривые (dcNp/da)a==o и
AcNp /а2 (см. рис. Х-3-13 и Х-3-15),
можно приближенно оценить
значение коэффициента нормальной
силы при очень больших числах
Моо. Для этого необходимо,
задавшись углом -атаки, найти для
нескольких чисел Моо на рис. Х-3-13
значения начального наклона
кривой коэффициента нормальной
силы, а на рис. Х-3-15 — величины
AcNpi а затем по (Х-3-53)
подсчитать cNp. По этим значениям можно
построить кривую, а затем
экстраполировать ее таким образом,
чтобы при Мое порядка 15—20 она
достигла значения, определяемого
по теории «ньютонова торможения»
(прямая 1 на рис. Х-3-10). Экстраполяционная кривая позволит приближенно
оценить коэффициент нормальной силы для промежуточных значений
числа Моо.
16
/
5°
z
С
Рис. Х-3-15. Изменение АсЖр/а2в зависимости
от относительной длины цилиндра и числа Мое
Гиперзвуковые скорости
435
Влияние сужающейся хвостовой части тела вращения. Это влияние
можно оценить при больших числах Моо с помощью экспериментальной
кривой (рис. Х-3-16), характеризующей изменение начальной производной
коэффициента нормальной силы в зависимости от донного сужения, а также
числа Моо.
Экспериментальная кривая графически изображает функцию
<х=0
-1
(Х-3-54)
V
s
\
0,H-
■С А
причем A (dcNplda)a=Q представляет собой изменение начальной производной.
Физически кривая отражает то наблюдаемое при опытах явление, что в
пределах 0,4<<2Дон/^мид<ОД величина / (Моо) уменьшается, примерно,
линейным образом с уменьшением отношения
Опытами также установлено, что
форма образующей хвостовой части тела
играет меньшую роль в изменении
величины коэффициента cNp по сравнению
с донным сужением.
Из анализа данных на рис. Х-3-16
следует, что эффект хвостового сужения
оказывается значительным при малых
скоростях. Это согласуется с
известным выводом линеаризованной теории,
по которому при нулевом сужении
(йдон/^мид = 0) коэффициент нормальной
силы равен нулю.
Что касается больших чисел Моо,
то,как видно из рис. Х-3-16, уже при
Моо = 8ч-9 влияние кормы исчезает. Такое же явление имеет место в
случае приближения по теории Ньютона, когда хвостовая часть расположена
в «затененной» зоне, следовательно, угол атаки равен или меньше угла
наклона образующей этой части тела. В ином случае появляется
стабилизирующий эффект, так как хвостовая часть выходит из «затененной» зоны,
образуя зону торможения.
Коэффициенты момента и центра
давления
Приближенная оценка коэффициента момента. Подставляя в (1-5-8)
выражение для коэффициента давления, находим
-0,03
-0,01
Рис. Х-3-16. Зависимость начального
наклона кривой cNV от числа Моо для
корпуса, имеющего хвостовое сужение
xrB (Тк) dx
г2 tg p£ (7к) dx, (X-3-55)
где функцию В (ук) находят по (Х-3-37) или (Х-3-38). Если тело тонкое,,
то вторым членом в (Х-3-55) можно пренебречь.
При определении интеграла в (Х-3-55) можно использовать значения
В (ук), которые были получены в ходе предшествующих вычислений
коэффициента нормальной силы. Вычисляемый по этой формуле коэффициент
момента отнесен к длине тела хк.
Расчет по (Х-3-55) с применением численного или графического
интегрирования целесообразно вести только для головной части. Что касается
цилиндрического участка, то формулу для определения коэффициента
28*
Глава X
момента цилиндра т% можно получить непосредственно, подставив
найденное выше выражение В (^к) = — (2/3)/? (к) sin2 а в рС-3-55^. Принимая во
внимание, что в рассматриваемом случае Ямид = Яц, г = 1, #к = 1, находим
(тх'р)ц = ■ р„ Яц sin2 a. (X-3-56)
Здесь характерным размером является длина цилиндрической части.
Полученное по этой формуле значение коэффициента (т'2р)ч соответствует
величине момента, рассчитанного относительно точки на переднем торце
цилиндра. Если момент сил, действующих на цилиндрический участок,
рассчитать относительно другой точки, расположенной от торца на
расстоянии х, то соответствующая величина коэффициента, отнесенного к длине хц,
будет
т% = о ^ц sin2 a. (X-3-57)
оя Хц
Относя коэффициент момента к какой-либо другой характерной длине,
в знаменателе формулы (Х-3-57) надо сделать соответствующую замену.
В частности, если за характерный размер взять длину головки или полную
длину тела, то вместо хц следует подставить соответственно хмид и хК =
мид Ь ц
Приняв для тела с криволинейной образующей головной частью и
хвостовым цилиндром характерный размер, определяемый полной длиной хк,
и вычислив момент относительно острия, получим для коэффициента момента
„%>=*Е£>-ЬЦ sin2 а (1 + 0,5-5^3-)-%«_. (Х-3-58)
Складывая эту величину с коэффициентом момента для головной части,
отнесенным к длине всего тела, найдем суммарный коэффициент
mzp = т% + mTzv -~ . (Х-3-59)
Расчет коэффициента момента головки mvzv можно упростить, если
принять предположение, что влияние «затененной» зоны^не учитывается. В этом
случае для тонкой головки
J (^)> (X-3-60)
где WT — объем, занимаемый телом.
Коэффициент момента сил для конуса. Принимая во внимание, что
для конуса функция В (ук) является величиной постоянной, коэффициент
момента
Функция 5(ук), вычисляемая по (Х-3-38), в первом случае обтекания
(а<рк, ук^О) упрощается и коэффициент момента
mzp = £Ж sin 2a cos2 рк (1 + tg2 р„). (Х-3-62)
Во втором случае (а>рк, ук>0) значение в В(ук), вычисляемое
по той же формуле (Х-3-38), сохраняет более сложный вид, а коэффициент
момента находится из (Х-3-55).
Тело вращения, состоящее из конуса и цилиндра. Выражение для
оценки коэффициента момента сил, действующих на такое тело, получается
достаточно просто, так как известны коэффициенты момента отдельно для
конуса и цилиндра. Если выбрать в качестве характерного размера длину
Гипердвуковые скорости
437
тела хк и исходить из (Х-3-38) для функции В (ук), то
я/? {к) tg Po Зя ц
В том случае, когда а<р0, в этой формуле надо принять В(уК) =
= —р(к)к sin 2a sin 2(3ОМ.
Приближенная оценка коэффициента центра давления. Имея в виду,
что коэффициент центра давления равен отношению коэффициента момента
к коэффициенту нормальной силы и используя формулы (Х-3-36) и (Х-3-55),
получим для тонкого тела выражение без учета влияния «затененной» зоны:
ч. д — ^ xrB (yK) dx
о
гВ (уЕ)
(Х-3-64)
где хк = — .
хк
Коэффициент центра давления можно подсчитать в каждом конкретном
случае путем вычисления интегралов в выражении (Х-3-64). Если же
предварительно были подсчитаны
коэффициенты mZp и cNp, то значение q) r
Сц. д, отнесенное к длине тела хк, 0_
вычисляется по формуле сц. д = ~1
= mZp/cNp.
Формулы для приближенной
оценки коэффициента центра
давления. Наряду с рассмотренными
выше соотношениями для оценки
предельной величины сц. д можно
рекомендовать другие приближенные
зависимости. Одну из них можно
получить при помощи формул
(Х-3-40) и (Х-3-60):
^ц.д
Ц- Д
= !-■
(Х-3-65)
Рис. Х-3-17. Схемы для расчета положения
центра давления различных тел
Эту формулу следует
использовать для условий обтекания
тонкой криволинейной головки,
которым соответствуют зависимости
(Х-3-40) и (Х-3-60), причем длина
головки #к—#мид.
Для тела вращения с
образующей, близкой по форме к оживаль-
ной или параболической (рис. Х-3-17, б), как показывают исследования,
величину коэффициента центра давления можно приближенно определять по формуле
хп д 0,67 —0,75гк + 0,2й,
Сц. д = -~^ = YZI 0 25-2 ' (Х-3-66)
которую можно применять в том случае, если а<ро,га безразмерная длина
0<жк<С(1Д-т-1,2). Таким образом, рассматриваемое тело может иметь
хвостовую сужающуюся часть небольшой длины.
Если заменить эту часть цилиндром (рис. Х-3-17, а), то коэффициент
центра давления полученного тела следует рассчитывать по другой формуле
0,73+ 0,67аХмид (4-1) /v Q А7Ч
сц. д = - = . (Х-о-о/)
як[1,57+1,33оймид0гк — 1)]
438 Глава X
Используя эту формулу, необходимо соблюдать условия а <С Ро и^к>1.
Анализируя зависимость (Х-3-67), можно придти к выводу, что с ростом
длины тела центр давления смещается ко дну, стремясь при хк —> оо к
предельному положению, определяемому величиной сц. д = 0,5.
Для определения коэффициента центра давления конуса воспользуемся
(Х-3-64). Так как для конуса величина В (ук) постоянная, то в этой
формуле ее можно сократить. После интегрирования найдем значение
коэффициента сц. д = 2/3. Такое же значение получается, если рассмотреть предельное
положение центра давления для криволинейной головки с бесконечно малой
длиной, когда ее форма совпадает с конусом. Из (Х-3-67) находим, что
lim сЦт д = 2/3 ~ 0,667. Если к конической головке присоединить цилиндр,
то для такого тела
Сц. д —
,81 Цех) ^к ' ^ " ™'
Из этой формулы получаем при Хц = 0, т. е. в случае отсутствия
цилиндрического участка, величину сц.д = 0,667 для чистого конуса. Когда же
цилиндр очень длинный, то коэффициент центра давления стремится к
предельному значению сц. д = 0,5.
Сравнивая два тела одинакового удлинения с конической и
параболической (или оживальной) головными частями, можно на основе результатов,
получаемых по формулам (Х-3-67) и (Х-3-68), заключить, что для
конического тела характерно более заднее расположение центра давления.
Зависимость коэффициента центра давления от числа Моо. Расчеты
по приведенным формулам дают предельные значения коэффициентов центра
давления, практически совпадающие с теми, которые соответствуют
реальным, но достаточно большим числам Моо порядка 15—20. При меньших
значениях Моо расчет коэффициента центра давления можно осуществлять
следующим образом.
Полагая, что заданное тело состоит из нескольких элементов,
используем для расчета величины ст формулу (XI-3-45). Входящий в нее
коэффициент с* головной части определяют с помощью графика на
рис. Х-3-13 по формуле с^р — (dcNp/da)a=o a, a коэффициент с^ находят
из рис. Х-3-15 при условии, что с?* равен поправке AcNp, учитывающей
влияние цилиндрической части.
Наконец составляющая с*® для хвостовой части может быть найдена
с помощью рис. Х-3-.16. По нему определяют величину A (dcNp/da)a=o
в зависимости от Моо и отношения dR0H/dM1/lJl, а затем вычисляют
составляющую с«р — A (dcNp/da)a=:o a.
В соответствии с формулой (XI-3-45) необходимо определить координаты
центров давления каждого элемента. Для головной части с криволинейной
образующей при приближенных расчетах центр давления можно принять
расположенным на расстоянии #ц. д ~ 0,5#мид, а для конической головки —
на расстоянии хЦш д с^. 0,667ямид. Что касается центров давления
цилиндрического и хвостового участков, то их можно считать расположенными на
середине этих участков тела.
По найденным коэффициентам нормальной силы и координатам
центров давления подсчитывают сумму их произведений 2 (cNp)i (хЦш д)г,
находят величину 2 (cNp)iy а затем в соответствии с (XI-3-46) определяют
коэффициент сц. д.
По вычисленным для ряда чисел Моо значениям этого коэффициента
можно построить кривую. Если кривую экстраполировать таким образом,
Гиперзвуковые скорости
чтобы при Моо порядка 15—20 она указала тот результат, который следует
из теории Ньютона, то полученная кривая позволит найти сц. д для
промежуточных чисел Моо, включая их большие значения. Анализ влияния числа
Моо показывает, что переход к меньшему его значению сопровождается
уменьшением коэффициента центра давления, так как положение центра
давления оказывается ближе к острию в сравнении с предельным случаем
при Моо ->■ оо.
Увеличение коэффициента центра давления с ростом скорости
обусловлено тем, что при этом, как видно из рис. Х-3-11, возрастает
стабилизирующий момент цилиндра в результате того, что положительную силу создает
все большая его часть. В предельном случае при М<х> ->■ оо «работает» весь
цилиндрический участок. Причем центр давления расположен достаточно
далеко от острия. При меньших же числах Моо значительная часть цилиндра
практически не является несущей.
До чисел Моо порядка 2—3 нормальная сила создается лишь на длине
примерно (2 -г- 2,5) ^мид. В этом случае наблюдается меньшее
стабилизирующее влияние цилиндрического участка, обусловленное, с одной стороны,
меньшей нормальной силой и, с другой,— более сдвинутым вперед центром
давления. Поэтому может оказаться, что при одном и том же положении
центра тяжести тело вращения с достаточно развитой цилиндрической
частью будет статически устойчивым при очень больших скоростях и
неустойчивым — при меньших их величинах.
Рассмотренные вопросы были связаны с определением при очень
больших числах Моо аэродинамических коэффициентов, зависящих от
распределения нормального давления по боковой поверхности. Суммарные значения
этих коэффициентов будут зависеть также от донного давления.
Если строго следовать теории «ньютонова торможения», то при числах
Моо ->■ оо коэффициент донного давления нужно принять, как указывалось,
равным нулю.
В соответствии с этим донный срез находится в «затененной» зоне и,
следовательно, не оказывает влияния на аэродинамические коэффициенты.
Однако в тех случаях, когда коэффициенты определяются при реальных
больших числах Моо, можно приближенно оценить влияние донного
давления, как это было рекомендовано при учете расширения потока в
«затененной» зоне на боковой поверхности тела, т. е. считать, что при больших
числах давление за дном равно нулю и, следовательно, рдои = —2/(кМ2оо).
В соответствии с этим коэффициент осевой силы сйдон = (2/&ML) ^дон-
Применение формулы Буземана. С целью учета влияния на давление
центробежных сил, возникающих при движении частиц газа по
искривленной траектории, следует воспользоваться формулой Буземана (IV-7-22).
Полагая в этой формуле / (х) = 2яг, получим следующее выражение для
определения коэффициента давления на поверхности тела вращения:
s
п* / А (* \
р = . о о sin2 р —«—5- \ cos р аЬ . (Х-оо-оУ)
^ sin2 ро V 2nrR «3 /
о
Для тонкого тела можно воспользоваться формулой (IV-7-24). Приняв
в ней v = 2, найдем _
f-5-Йт) • (Х-3-70)
В частном случае тонкого тела с параболической образующей
R= —(^мид^мид)?"1 7* ^ ^мид^ (2 — х), р = Ро (1—%), р0 = ^
Следовательно, полагая р* = рк, получим
р=рк[(1—ж)2 — -J(2—5)1 . (Х-3-71)
Из этого выражения видно, что центробежные силы способствуют
уменьшению давления.
В результате этого кривая, рассчитанная по (Х-3-71), показывает
значительное разрежение в конце тела. Однако экспериментальные данные
и теоретические исследования по методу характеристик не подтверждают
этих результатов. В действительности при больших числах Моо разрежение
практически исчезает, а возникающее давление оказывается очень близким
к тому, которое получается по уточненной теории Ньютона.
Таким образом, для тел вращения с выпуклой поверхностью поправка
на влияние центробежных сил снижает точность расчета. Поэтому для
таких тел при к = 1,4 следует применять теорию Ньютона без учета
центробежных сил. Наоборот, для тел с вогнутой поверхностью эта теория
дает худшие результаты и, как уже отмечалось, расчет обтекания
необходимо вести по формуле Буземана. Давления, получаемые по формуле
Ньютона, оказываются завышенными. К такому завышению эта формула
может привести в том случае, когда давление за ударной волной и давление,
рассчитанное по теории Ньютона, будут одинаковыми и, следовательно,
сохранится лишь эффект уменьшения давления за счет центробежных сил.
Такое явление будет иметь место при Моо —>■ оо и к-+• 1, когда в пределе
волна и поверхность тела совпадут. Следовательно, при обтекании
выпуклых тел горячим воздухом (к «< 1,4) с очень большими Моо точность формулы
Буземана будет возрастать. В пределе при Моо —>- оо и fc—>- 1, когда
плотность в слое становится бесконечной, формула Буземана дает точные
значения давления.
Закон подобия при неосесиммет-
ричном обтекании
Выше было установлено, что при очень больших скоростях и нулевом
угле атаки закон подобия для тонких тел вращения определяется
параметром Ki = Moo(30> причем малый параметр |30 может быть углом конуса,
углом наклона образующей у острия или относительной толщиной тела.
Например, коэффициент давления в произвольной точке на
поверхности тела p~$lf (К 1, х), где /(Кь #) —некоторая функция, зависящая от
параметра К4 и безразмерной координаты точки. Коэффициент
сопротивления того же тела схв — ^%F(K1)^ где F (Кй) — некоторая функция,
определяемая параметром К1в
При неосесимметричном обтекании аэродинамические коэффициенты
зависят от угла атаки. Покажем, что обтекание тел будет подобным, а
следовательно, их аэродинамические коэффициенты сохранятся одинаковыми,
если наряду с постоянством параметра К4 будет соблюдено равенство величин
К2 = а/ро. С этой целью воспользуемся выражением (Х-3-1), в котором
коэффициент давления р* на тонком коническом острие выразим в
соответствии с методом «местных конусов» в виде р* = 6|фр (К^), где фр (К4) —
некоторая функция, зависящая от параметра К1# Если угол «местного конуса»
представить при малых углах атаки как 6К = (30 — a cos 7, то, очевидно,
р(Ро ^Фр^О
Следовательно,
4 (£)2. (Х-3-72)
Гиперзвуковые скорости
441
Таким образом, если у двух аффинно-подобных тел соблюдено равенство
параметров К2 и Кь то в соответственных точках поверхности с одинаковыми
значениями у и |3/ро величины р/$% будут одинаковыми.
Подставляя найденную зависимость (Х-3-72) в формулу (1-3-14),
получим общее выражение для коэффициента осевой силы:
^ = q>*(KlfK2). (X-3-73)
Ро
Чтобы получить соответствующую зависимость для коэффициента
нормальной силы, произведем аналогичную подстановку в (1-4-11). При
этом имеем в виду, что входящая в
эту формулу координата г будет на
порядок меньше х, т. е. г ~ $ох, так
же как гмид ~ Ро^мид или гмид ~ Ро^к-
После интегрирования придем к
общей зависимости для коэффициента
нормальной силы:
h
cNp
= <pw(K1>K2). (X-3-74) 0,6
Таким образом, семейство
аффинно-подобных тел, обтекаемых
потоками, у которых, кроме параметра
К4, одинаковы и величины К2,
характеризуется постоянными значениями
0,2
ОД,
к"
0 с
135°
90°
-8 0 8 16 2k Ka
Рис. Х-3-18. Распределение давления по-
поверхности конуса при нессимметричном
обтекании
В предельном случае при Moo ->
—>оо (КА ->■ оо) параметром подобия
для аэродинамических
коэффициентов остается только величина К2. Это,
в частности, видно на примере конуса, для которого коэффициент давления
(Х-3-75)
в в соответствии с формулами (Х-3-14) и (Х-3-42)
CRp п
(Х-3-76)
1
Закон подобия по параметрам Kt и К2 достаточно хорошо
подтверждается расчетами и экспериментальными данными. Эти данные обнаруживают
важную особенность, заключающуюся в том, что закон подобия сохраняет
свою силу даже при небольших значениях параметра Кь хотя этот закон был
получен в предположении таких больших чисел Мте, что при малых
значениях р0 должно выполняться условие Ki > 1.
Это хорошо видно на рис. Х-3-18, где приведены экспериментальные
данные о распределении давления в зависимости от угла атаки на
поверхности двух конусов с углами (Зк = 0,166 и 0,102 при Мое = 2,75 и 4,46.
Произведение Моорк дает для обоих тел одинаковое значение К4 = 0,455.
При эксперименте давление измерялось в точках, соответствующих углам
Y = 0; 45°; 90°; 135° и 180°. Найденная в результате измерений функция
рк/роо'— 1 нанесена на график для каждого из конусов и фиксированного
угла 7 в зависимости от параметра К2-
Как видно из графика, значения функции давления для соответственных
точек обоих конусов определяются практически одной и той же кривой.
Некоторое отклонение наблюдается при больших значениях параметров К2
442
Глава X
на верхней стороне конуса. Это объясняется появляющимся при увеличении
угла атаки отрывом потока, что не учитывается законом подобия по К2.
Таким образом, используя для практических целей закон подобия
по параметру К2, следует иметь в виду, что он ограничен малыми
значениями углов атаки. Что касается чисел Моо, то закон подобия по параметру
К.! пригоден практически для достаточно большого диапазона их значений.
Оценка точности приближенных
методов
На рис. Х-3-19 [51] графически представлены данные, позволяющие
установить в зависимости от параметра подобия Kt = Моо/Ямид величины
тех ошибок, которые дает тот или иной приближенный метод расчета
обтекания оживальных головок по сравнению с методом характеристик. Можно
О Ц4 0,8 1}2 1,6 К1 2,0
Рис. Х-3-19. Точность приближенных методов расчета
волнового сопротивления при нулевом угле атаки по
сравнению с методом характеристик:
1 — метод «местных» конусов (гипотеза одинаковых
давлений;) 2 — метод «местных» конусов (гипотеза одинаковых
скоростей); з — линеаризованная теория; 4 — метод
сочетания конических течений и течений разрежения; 5 —
ньютоновская теория
заметить, что линеаризованная теория (см. § XI-2) дает небольшие
погрешности при значениях параметра подобия меньше единицы.
В отличие от этого метода точность ньютоновской теории, первого
метода «касательных конусов» (гипотеза одинаковых давлений) и метода,
сочетающего коническую теорию и теорию разрежения, повышается с
увеличением параметра подобия Ki. Ошибки второго метода «местных конусов»,
основанного на гипотезе одинаковых скоростей, меньше, чем первого метода,
для параметров подобия, не превышающих значения Kt = 1,2. Таким
образом, лучшие результаты расчета обтекания при умеренных сверхзвуковых
скоростях, когда Ki<l,2, получаются по методу «местных конусов»,
основанному на гипотезе одинаковых скоростей. При значениях параметра
Ki > 1,2 предпочтение следует отдать первому методу «касательных конусов»,
который, однако, по точности уступает методу, сочетающему конические
течения и течения разрежения. На рис. Х-3-19 видно, что наибольший
разброс по точности, снижающийся по мере увеличения параметра Кь дает
ньютоновская теория.
Глава XI
•
АЭРОДИНАМИКА
ТОНКИХ КОРПУСОВ
В ЛИНЕАРИЗОВАННОМ ПОТОКЕ.
§ ХМ. Применение метода
источников
Уравнения линеаризованного обтекания. Для исследования
аэродинамических характеристик тонких корпусов, обтекаемых линеаризованным
потоком, используют уравнение (Ш-2-31), которое для условий
установившегося обтекания будет
(1 - му у'**+ф;г+-4т щу+у ф; = о. (xi-i-i)
При симметричном обтекании это уравнение упрощается:
(1 - Ml) Ф;х+Ф;г+1Ф; - о. (xi-i-2)
Граничные условия. Уравнения (XI-1-1) и (XI-1-2) составляют
теоретическую основу аэродинамики линеаризованных течений. В результате
решения этих уравнений находят потенциал возмущения ф', который должен
удовлетворять условию на границе тела (Ш-2-58/). Это условие,
относящееся к общему случаю течения с большими возмущениями, можно несколько
преобразовать. С этой целью напишем выражения для составляющих скорости
набегающего потока в цилиндрических координатах:
Vxoo = Foo cos a; Vroo = Foo sin a cos у; Vyoo = — Foo sin a sin y. (XI-1-3)
В соответствии с этим потенциальная функция для набегающего потока
ф^ =z(foo = .rFoo cos a + rVoo sin a cos y. (XI-1-4)
Это выражение представляет собой условие, которому должен
удовлетворять наряду с условием на границе тела потенциал скоростей
возмущенного течения. Это требование соответствует тому, чтобы решения для
составляющих скорости удовлетворяли в невозмущенном потоке условиям (XI-1-3).
Если искомая потенциальная функция
ф = #Foo cos a + rVoo sin a cos 7 + ф' (#» г, 7), (XI-1-5)
то в соответствии с условием (XI-1-4) добавочный потенциал ф' (х, г, у)
в невозмущенном потоке должен быть равен нулю. На самой же
поверхности тела его величина должна удовлетворять условию безотрывное™
течения
Фг _ FooSinacosy + (p;Or, r, у) _ dr
Фх ~~~ V°o cos a + ф^. (х, г, у) ~ dx ^ '
Для линеаризованного обтекания это условие упрощается, так как
искомую потенциальную функцию Ф (XI-1-5), полагая cosa^l, sin a«a,
можно представить в виде
Ф = xVoo + rVoo a cos у + ф' (х, г, у). (XI-1-7)
Вычисляя производные от суммарной потенциальной функции Ф, найдем
составляющие скорости возмущенного течения:
Vx = Foe + q>i; Fr = aFoc cos у + Ф;; Fv = - aFoo sin у + ^- . (XI-1-8)
444 Г лава XI
Имея в виду эти соотношения, получим условие (XI-1-6) безотрывного
обтекания при наличии угла атаки:
[^ + q>i (х, г, у)] ~£^ = aFoo cos у + q>'r(x, r, у). (XI-1-9)
Если обтекание осесимметричное, то XI-1-9 упрощается:
[Foo + ф; (*, г)] -g-=Ф; (х, г).
Потенциал скоростей линеаризованного потока, обтекающего тело
вращения под углом атаки, можно представить в виде суммы трех составляющих:
потенциала невозмущенного потока фоо, потенциала возмущенного осесиммет-
ричного течения ф^ (х, г) и потенциала от нарушения симметрии у'2(х, г, у).
В теории линеаризованных течений ф^ и Ц)2 рассматриваются как
функции, которые определяют независимые друг от друга потоки. Поэтому
каждая из этих функций, как решение уравнения движения, должна
удовлетворять определенным граничным условиям. В частности, ф^ должна
удовлетворять условию (XI-1-10) осесимметричного обтекания. Что касается
потенциала ц>'2, то для него соответствующее условие на границе тела можно
получить из (XI-1-9). С этой целью (XI-1-9) перепишем следующим
образом:
(Foo + (pi* + ф2х) -^" = OcVoo COS у + Щт + ф2Г, (XI-1-11)
где ч\х = дч'г1дх, Ч2Х = дуудх и т. д.
Имея в виду равенство (XI-1-10), в котором ф^, Фг заменяются
соответственно на щх, ф^г и отбрасывая член (dr/dx) ф2Л с меньшим порядком,
получим из (XI-1-11) условие безотрывного обтекания
V2r= -aFoo cos у. (XI-1-11')
Общие выражения для потенциальной функции и давления. Расчет
распределения газодинамических параметров около тонкого тела вращения
в линеаризованном потоке в случае установившегося обтекания под углом
атаки основывается на использовании дифференциального уравнения (XI-1-1)
для потенциала возмущения ф'. Ранее указывалось, что решение этого
уравнения отыскивается как сумма потенциалов Ф^фоо + Фх + Фз соответственно
для невозмущенного потока, осесимметричного обтекания ф^ (х, г) и течения
при нарушении симметрии <р'2(х, г, у).
На основании (XI-1-2) и (XI-1-1) для определения ср^ и у'2 получим
уравнения
(1 - Ml) Ф'1яя + щтт + ^ = 0; (XI-1-12)
(1 - ML) Ф2хх + Ф2гг + Аг Ф277 + у Ф2г = 0. (XI-1-13)
Таким образом, параметры неосесимметричного обтекания тела
вращения будут найдены, если решить две самостоятельные задачи: задачу об
обтекании тела под нулевым углом "атаки и задачу о добавочном течении,
возникающем от нарушения симметрии. При этом решение второй задачи
получается при помощи решения первой и можно показать, что между
Ф^ и фз существует определенная связь.
С этой целью продифференцируем по г уравнение осесимметричного
возмущенного течения:
Аэродинамика тонких корпусов в линеаризованном потоке 445
Сравнение этого уравнения с уравнением (XI-1-13) и учет граничного
условия (XI-1-11') показывает, что
Следовательно, полный потенциал возмущения при неосесимметричном
обтекании:
ф' = ф; _ М cos у. (XI-1-15)
Мы рассмотрели случай установившегося обтекания. Однако
выражение (XI-1-14) для фз распространяется также на нестационарный поток,
в чем можно убедиться, если в качестве исходного использовать более общее
уравнение (Ш-2-31).
Определив с учетом граничных условий полную величину добавочного
потенциала ср\ вычисляют скорости, а затем давления, используя
уравнение (Ш-3-14). Заменив радиальную составляющую скорости в соответствии
с условием безотрывного обтекания приближенной величиной Vr = Voo(dr/dx),
a V'x и Vy — их выражениями через добавочный потенциал ф', являющийся
в данном случае функцией координат х, г, у и времени t, найдем
- (XI4-16)
Величину коэффициента давления можно представить в виде суммы двух
составляющих, а именно p = Pi + Pz- Одна из составляющих р4 определяется
по условиям продольного осесимметричного обтекания при помощи формулы
^ (■£■)
а другая p2 — no условиям поперечного обтекания в зависимости от угла
атаки:
Если режим обтекания установившийся, то частные производные по
времени (pi* и ф2* в этих выражениях равны нулю. Можно представить и такой
случай, когда осесимметричная составляющая потока является
установившейся и коэффициент давления
где производная ф^ представляет собой безразмерную величину, отнесенную
к Foo.
При условии, что поперечное обтекание оказывается нестационарным,
расчет коэффициента давления надо вести по формуле (XI-1-18). Если же
и поперечное обтекание установившееся, то
где постоянная Foo включена в значение потенциала ф^.
Формулу (XI-1-18) для р2 можно упростить, если учесть зависимость
(XI-1-14) для фа, а также условие (XI-1-17), которым воспользуемся для
оценки отношения ф2Г/г.
Представим зависимость (XI-1-14) в виде ф2= — (1/г) [г (dq'Jdr)] cos у.
Как будет показано (см. стр. 448), величина dy'1/dr = Vir при г—^0 имеет
структуру / (х)/г и, следовательно, произведение rVir при г—>0 стремится
446 Глава XI
к предельному значению f{x). Из этого будем исходить при оценке
отношения ф2<у/г« Дифференцируя (XI-1-14) по у, найдем, что при достаточно
малых г
а вычисляя производную по г, определим добавочную радиальную
составляющую скорости (то же при г —> 0):
V2r = ф2г = 72" / (Я) COS у.
Эта составляющая на поверхности тела по условию (XI-1-11') равна
— aFoo cos у. Следовательно, функция f(x)= — aV^r2, поэтому (р2у/г =
= —aFoo sin у. После подстановки этого выражения в (XI-1-18) получим
= - 2 [q>2* + 4 (4 sin2 Т ~ 1) + Ф2«] ,
где производная ф2« является безразмерной величиной, отнесенной к квадрату
скорости Vlo.
Полная величина коэффициента давления при неустановившемся
обтекании под углом атаки
причем вторая производная щгх является здесь безразмерной величиной,
отнесенной к квадрату скорости Via.
В случае стационарного режима
р2= -2 [-yirx cos у + -у-(4 sin2 7-1)] . (XI-1-23)
Следовательно, полная величина коэффициента давления
причем производные ф1Х, щгх, входящие в выражение (XI-1-24), зависят
только от переменных х, г.
Подставив это выражение в (1-3-14), замечаем, что основная
составляющая коэффициента осевой силы не зависит от угла атаки и определяется
условиями осесимметричного обтекания. Добавочная величина обусловлена
нарушением симметрии и зависит от квадрата угла атаки.
С точностью до величин второго порядка малости можно пренебречь
влиянием а, считая, что для вычисления коэффициента осевой силы
достаточно определить распределение давления около тела вращения при его осе-
симметричном обтекании. Найденный в результате расчета коэффициент
волнового сопротивления и будет равен коэффициенту осевой силы.
Метод источников. Из полученных зависимостей следует, что задача
о линеаризованном обтекании тонкого тела будет решена, если найден
добавочный потенциал скоростей ф^ осесимметричного потока. При этом его
величина непосредственно используется для вычисления распределения
скоростей и давлений, а также волнового сопротивления при нулевом угле атаки.
Для определения ф^ применим метод источников. По этому методу
добавочный потенциал скоростей отыскивается по (IV-3-3). Принимая в этом
выражении у = г и включая знак «минус» в значение функции /(е), получим
где а' = УШ^1
Аэродинамика тонких корпусов в линеаризованном потоке
447
Закон распределения источников, т. е. вид функции /(б), должен быть
таким, чтобы в результате наложения невозмущенного потока на течение
от этих источников одна из линий тока суммарного потока совпала с образующей
тела вращения. Иначе говоря, потенциальная функция q^ должна
удовлетворять условию безотрывного обтекания.
Используя метод источников, следует иметь в виду, что при
сверхзвуковом течении возмущения от источников распространяются только внутри
конусов возмущения с вершинами в источниках.
Таким образом, если представить систему непрерывно распределенных
по оси тела источников (рис. XI-1-1), то скорость и другие параметры
г
/2
I
^«—
X
A(x,r)
arc sin
X
Рис. XI-1-1. Схема распределения сверхзвуковых
источников по оси тела вращения:
1 — образующая тела; 2 — кривая распределения интенсив-
ностей источников; з — линии тока от источников; 4 — линия
возмущения
в любой точке А (х, г) будут определяться теми возмущениями, которые
исходят из источников, расположенных вверх по течению, начиная от точки
6 = х — a'r и кончая точкой 8 — х = 0. В точке 8 — х = 0 интенсивность
источника равна нулю, так как предполагается, что при 8<0 возмущения
отсутствуют. Это означает, что вершина обтекаемого тела находится
в точке х—0.
Из сказанного станут понятны значения пределов интегрирования
в выражении (XI-I-25). Вид кривой /(е) [или /(#)], представляющей закон
распределения источников для тонкого тела с произвольной образующей,
приведен на рис. XI-1-1. Эта кривая определяет непрерывный характер
малых возмущений при линеаризованном обтекании.
Чтобы найти общие зависимости для скорости и давления,
преобразуем (XI-1-25) с помощью новой переменной:
z = arch -
Учитывая, что
ch z = -
a'r
(XI-1-26)
i; e =-- j, — a'r ch z\ ds = — a'r sh z dz,
найдем, подставив эти выражения под интеграл (XI-1-25):
arch(x/a'r)
Ф^= \ f (x — a'rchz) dz.
(XI-1-25')
Для потенциала возмущения при обтекании под углом атаки имеем
выражение (XI-1-14). Учитывая это и дифференцируя по г (XI-l-25r)t
448 Глава XI
найдем
arch (я/a'r)
cp^a'cosy \ т(х — a' rchz) ch zdz, (XI-1-27)
о
где т — производная по аргументу х — a'rchz от функции /, т. е.
т = f (x —a'rchz).
Переходя в выражении (XI-1-27) от переменной z к переменной
в = х~a'rchz и имея в виду, что m(s) = f(s), получим
х-а'г
, _ cosy е т(в) (x — z)dE
fXI-1 2Т)
y(a:_8)2__(a')2r2- v - - ;
Интеграл ц>'2 представляет потенциал диполей, а функция m (г)
описывает закон их распределения. Следовательно, добавочное возмущение от
диполей эквивалентно возмущению, вносимому в поток телом при неосесиммет-
ричном обтекании.
Заменяя тело распределенными вдоль его оси диполями, следует
учитывать, что в сверхзвуковом потоке возмущения от диполей, как и
возмущения от источников, распространяются только вниз по потоку и в
пределах конуса возмущения.
§ XI-2. Осесимметричное
обтекание
Расчет скорости и давления
Дифференцируя функцию ср^, определяемую выражением (XI-1-25'),
по а: и г и полагая интенсивность источника у острия / (е) = / (0) = 0,
получим для составляющих скорости
f (x —a'rchz) dz; (XI-2-1)
о
arch(x/a'r)
9ir = Fr=— a' [ f (x —a'rchz) chzdz. (XI-2-2)
о
Чтобы рассчитать по этим формулам составляющие скорости,
необходимо знать функцию /(е). С целью определения вида этой функции
преобразуем выражение (XI-2-2) к переменной 8 в соответствии с условием (XI-1-26)
у ± \
г J, i/(x_e)2_(aV)2
X— ОС Т
Примем допущение, что значение интеграла для точек поверхности
мало отличается от его предельного значения на оси, т. е. при г—>0.
В соответствии с этим
Fr=-}/(*). (XI-2-3)
Это выражение уже было использовано выше при определении порядка
величины rVr вблизи оси (стр. 445).
Принимая, что на поверхности весьма тонкого тела составляющая Vr
определяется выражением (XI-2-3), и используя приближенное условие
Аэродинамика тонких корпусов в линеаризованном потоке 449
безотрывного обтекания Vr«drldx (получаемое из точного соотношения
Vr/(l + V'x) при условии, что 1 + Fi«l), найдем уравнение кривой
распределения источников для такого тела:
Дифференцируя эту функцию по х, находим производную
Предположим, что образующая задана в виде кривой параболического
типа:
г- 2 епхп^. (XI-2-6)
71=0
Если это выражение для г внести в (XI-2-5) и расположить в
полученном соотношении члены по степеням х, то придем к следующему общему
виду производной:
k
f(x)=- 2 dmx™. (XI-2-7)
m=0
Выражение (XI-2-7) является приближенным для производной от
функции распределения источников в случае произвольного тела вращения, так
как при его получении было использовано приближенное условие
безотрывного обтекания. Чтобы уточнить эту зависимость, можно ввести в
уравнение (XI-2-7) поправочные коэффициенты а0 и а4, которые будут
определены в ходе решения самой задачи. Тогда, вводя вместо х переменную е,
•
напишем функцию /(е) в таком виде:
и
/ (е) = - (о0 + at 2 dmem). (XI-2-8)
m=l
Теперь заменим в уравнении (XI-2-2) производную /(е) выражением
(XI-2-8), приняв в нем г = х — a'rchz. В результате несложных
преобразований получим для радиальной составляющей скорости
Fr = a'(aoi? + aiTi), (XI-2-9)
где
archu archu k
I chzdz; r\= J 2 dm(x-a'rchz)mchzdz; u = -^.
0 0 m=i
Аналогичную зависимость можно найти для осевой составляющей
возмущенной скорости. С этой целью внесем выражение (XI-2-8) для
производной / в (XI-2-1), в результате чего найдем
где
archu archu k
Й= j <fe; ф= J 2 dm(x — a'rchz)mdz.
0 0 m=i
Нетрудно видеть, что в выражениях (XI-2-10) и (XI-2-12) приходится
иметь дело с вычислением интегралов вида
archu
In= I (ch z)ndz, (XI-2-13)
о
29—114
450 Глава XI
причем, если ограничиться значением & = 3, то нетрудно убедиться в том,
что в каждое из уравнений (XI-2-9) и (XI-2-11) входят функции £?, &£,
значения которых определяются из выражений
7-о_ г . i' — ill T •
i\ = u2li — 2ul2 + /3; i? = uzL — ЪиЧ2 + 3ul3 — /4;
f-I - i =ul -I - \ (XI-2-14)
Из соотношений (XI-2-13) и (XI-2-14) вытекает, что функции С и i™
зависят только от параметра и. Эти функции, вычисленные для значений
параметра и от 1 до 12,2, приведены в табл. XI-2-1.
Чтобы определить коэффициенты а0, а4, лучше воспользоваться условием
безотрывного обтекания
dr Vr a'(a
Отнесем это условие к переднему коническому элементу тела вращения.
Тогда, имея в виду, что k = m = l и, следовательно, т] == 'ф = 0, получим
0 (4)о + аО?
где величины (i?)0, (^)0 определяются из выражений (XI-2-10) и (XI-2-12) при
условии, что на коническом острие (х = г = 0) параметр ^ = и0 = 1/(а'р0)•
Следовательно,
(*!)о = /^Г17!", (4)о = arch Mo. (XI-2-17)
Коэффициент а0 предполагается постоянным для всего тела.
Коэффициент at каждый раз вычисляется, исходя из условия (XI-2-15)
безотрывного обтекания в рассматриваемой точке поверхности:
Значения функций i°x, ir, а также т) и i|) находят по величине и
в той же точке.
Подставляя в формулы (XI-2-9) и (XI-2-11) найденные коэффициенты
а0, аи можно определить добавочные составляющие скорости. Используя
затем (XI-1-19), вычисляют коэффициент давления.
В качестве иллюстрации рассмотрим применение изложенного метода
к расчету обтекания тела вращения с параболической образующей вида
г = х (2 — х). В этом случае
/(в)=-[
k
Сравнивая выражения (XI-2-19) и (XI-2-8), видим, что 2 dmem =
m=l
= 8 —82/2. Полагая, далее, что в уравнении (XI-2-19) переменная & = х —
— a'rchz, получим в результате подстановки / под интегралы функций ц
(XI-2-10) и i|) (XI-2-12) выражения для этих функций:
mix ^ (XI-2-20)
где w = r. , г=— .
^ЛМИД ГМИД
Функции i%, ir находят по параметру и либо с помощью формул (XI-2-10)
и (XI-2-12), либо из табл. XI-2-1.
) тН 4f OS О
> 00 CM vf к-О 00 CD СО СО
) OQ ^H OS OS ч^ CM D"^ *"^
)OrHlN CD CO CO l>-OS
О CNl *tfCO
OS CO 00 CO
Nt1 OS П 00 vj
OOlOCOOSD-
гн О OS OS СО Ч* СО 00 00 vt< vft>-00vfC5
О Ю xj< CO 00 l>- CO ^ CM
oo ooo
■< CO ч-н CO
и чН CM CM
CO<©00-rHt> GO (>• О !>- 00 CM О CM OS -«н OOOCOCOvjH CM l>» О -
CO vf Ю !>• 00 О CM Ю t^ О vF 00 CM CO CM t>- vf О 00 CD Ю "<^ Ю С
rHr^HrHlM CM CM CO CO *<F Vf Ю CD CO I>- 00 OS О '
О5 F О
о as csi
vt СО О
нч СМ
_ _ t^ 00 4F t^
00 <O !>• O> OS vf
CO 00 CM 00 COO
см см —
CO OS CO vf
CM О 00 OS
t*- со
CO OilMOCOCD
rHCOIxM-H CMCOOiCSlNt'
О О О CM vf OOCOO^OOOO
h 4t< чн Ю OOCMO'Ht* CO CD О 00 О I> «sh
5 CM CM ЧР OS 00 О Ю CO CD CM CO !>• !>• О OS
CO 00 00 чРСО
о os"oo"oogso"
CO CO CO CO CO C
О Ю Ю CM Ю C
CO 00 (МЮ1>
CO CO !>• CD CD
О ЧР 00 CO 00
ООООО
ч-t CO 00 l> Ю n}< OS 00 CO
CO OS Ю CM OS I>- Ю CO CM тн
со"со"ч1н"ю"ю" со" i>" со" оэ* о"
■« CO 4f CO
~s смю
co"l>^co"c "
CO^OOtO CDtCMO^
О5 СО С- СМ 00 C005CDCOO
> 1>О5 CD О 00 O5 С
DsJ< CM CM vf CO ^ С
1 CM CM CM CM CM CM COCOCOCOCO
OOCMCDO^ 00 СО 1> СМ
со^гюю ю со со t
см со см ^
00 СО "чн О CD О СМ О СМ О Ю 00 О О 00 СО СО OS СО О vj< О5 СО СО О СО CD O5 СМ -ф СО 00 О CM Sf CD 1> 00
И0 СО СО 00 *^ Ю СО СО 00 О "^ CM v^ Ю Ю СО 1>» 1>» 00 О5 G5 OJOOHri ^r-i гн СМ СМ СМ СМ СО СО СО СО СО СО
О Nf CO 00 Oi CM ^ t* O5 h vf CD 00 О CM 4f CO 00 О CM vF CD 00НСОЮ1> O)H0QlOt> С5НСОЮ1> О^НС
СО ^ 00
СО СО 00 О ^ CM v^ Ю
t*- O5 "^h vf CD 00 О CM
1> 1> 00 О5 G5 OJOOHri ri гн СМ СМ СМ СМ СО СО СО СО СО СО
00 О CM vF CD 00тНСОЮ1> O)rH0QlOt> С5"НСОЮ1> О^гНС
00 гг
< vt1 Ю Ю СО
5 О Ю
Ю CD CD CD
OS CO t>» rH
СМСОСОСОСО
ЮСОСОСОСО
t^OOOOOOOO 00 05QOO
I
I
§>
и
О)
И
со
THlOSfMrH CM
OOCMvfCO COCOC
О О О CM ЧР CD CMC
CO О OS 00OS 00
Ю t^ О CM CM "
CD sf CD OS
fiO5l OS
СМСМтг<ОСМ
о о о о о
1>-ОЭСО!>-СМ ООС^СОСМСО
coco см о n
THrHCSHNCM
P O> OS rrH CD vt^ CO r-l CD CO
эчрг-смсо псосмоочл
DCOCO^nJI ЮЮСОСО^
OS OS CM CO 00 Ю
I> НСОЮСОГ>
00 CO^IXMO
CM CD 00 vf 00
CM t>* t** CO ^sf rH LO iO *чР OS CM ч
ООСМСОчН 00 CD CD 00 гн С—-
5I>CDN COl>.OSCOOO t^ t^ 00
5 l>- 00 чн CD CO CM ЧР C^ CO-H-HSfCT»
О П П CM CO
OCM4t<COOS ^rns^t-C
Hr(r(r(<H CMCMCMC
> CO l> С
) CO CO *
ч CO CO l>- CM t> CM t>- COQlOrHN хИ 00 CO OS CD
• ■ - iococot>N oo oo os о о гч см ---^
МЫМЮСО НОСОООЮ МО1>ЮгН
OI>t>00rH CD CM OS t^-t>- 00 О CM CO -чн
OS-rH vf t>--<H njh CO "чн Ю OS CO 00 CM CD тн
Ю 00 00 CD CM CO CM 00
CD CM OS О. СО Ю Ю Ю
OO^Oit1 OS
ЮПОЗФО C0t>*COC
ОСМСОЮОО ОСМЮС
нем cMcMcococo
CDt^t^t-00 OOOSOSOO чНСМСМСОСО
l>00 05O"H
«a
Й
Ю CO !>• CO
со ^tp^
CD t>- 00 С
о" о"о"о"-
-r^COvf OOrH
СО^ЮсЬсО I>-66o6osO ОчНчНСМСМ CMCOCOn^n^ v^lOlOLOCO COCOCDI>I>
"cm" cm cm"cm"cm"cm" cm cm"cm"cm"cm" cm cm"cm cm"cm" cm"cm"cm"cm"cm" cm cm cm cm"cm" cm"cm cm"со"со" со"со"со"со"
JCM^^cM OSCD
) CO t-mo со см с
)OSOSOO Or(
CMCOV^CDOO OCMNtCOOO ОСМ^ФСООО OCMv^cOOO ОСМЧРСООО ОСМЧ^СООО OCM*<}<CD00 OCMvfcOOO О ^ 00 CM CO
п'гн'тн'-.Н^^Н4 См'сМ CM См"см" CO* CO* CO* CO* CO s^s^s^s^ vjT l/flO* lO\niO CD* CD со" СО* Co" t^ D-Г tr-T t-^Ttr-Г Oo"oo"oo"o040o" Os"oToTo"o" ^тгГ^
452
Глава XI
Найденные значения г) и г|) позволяют определить для данной точки
коэффициент аи а по нему —составляющую скорости возмущения Fi = cpix.
Подставляя ее в формулу (XI-1-19), можно подсчитать коэффициент давления.
При этом следует иметь в виду, что составляющая коэффициента давления
Api = — (drldxf может быть найдена заранее, если известна форма тела.
В частности, для параболической головки Api=—§\ (1—х)2.
Этот метод может быть использован для приближенного расчета
обтекания тел вращения, представляющих собой сочетание различных элементов.
Например, можно рассмотреть тело, состоящее из головки и цилиндрического
участка. При этом к концу его может быть
присоединен хвостовой сужающийся элемент
поверхности или участок какой-либо другой
формы.
На рис. XI-2-1 приведено распределение
давления, подсчитанное для цилиндрического
и хвостового участков тела вращения при
Моо = 1,5. Как видно, вниз по потоку
давление вдоль цилиндрической части, начиная
с конца головки, возрастает, в то время как
обтекание сужающейся хвостовой части
сопровождается на большем участке увеличением
разрежения.
Для сравнения на рис. XI-2-1 нанесены
кривые, рассчитанные по методу
характеристик и по методу «местных конусов».
Для обтекания цилиндрического участка
характерно восстановление давления до атмо-
6 х/*над сФеРного, которое происходит почти полностью
на длине, отсчитываемой от конца головки,
несколько большей двух диаметров.
Понижение давления на сужающейся хвостовой части
\
К2
\
\
"V
о,з
0J
-0,1
-0,3
Рис. X1-2-1. Давление на
поверхности корпуса, имеющего пара-
болические головную и кормовую наблюдаетСя не на всей длине. Видно, что
1 — по методу характеристик; 2 —
линеаризованная теория; з — метод
«местных конусов»
вблизи донного среза или хвостового
заострения давление несколько возрастает.
Точность изложенного метода расчета
линеаризованного обтекания растет по мере
увеличения заострения. Для очень тонких тел может отпасть необходимость
вводить поправочные коэффициенты а0, ал в выражение (XI-2-7). В этом
случае следует исходить из условия (XI-2-4), которое можно переписать
в виде / (х) = -~ ^^ = — S' (х)/2л, где S (х) = кг2 — текущее значение
площади поперечного сечения тонкого тела. Тогда
(XI-2-21)
Переходя в этом выражении к переменной 8 с последующей заменой
ф —#_a'rchz, затем подставляя найденную производную /(в) под
интеграл (XI-2-11), получим
arch и
V'x=--ir I S"(x-a'rchz)dz. (XI-2-22)
о
Если форма тела задана, то можно найти функцию S, определить ее
вторую производную S" и затем вычислить интеграл (XI-2-22), что даст
возможность подсчитать добавочную составляющую скорости.
Аэродинамика тонких корпусов в линеаризованном потоке 453
Пусть, например, задана параболическая головка, уравнение образующей
которой
г = (х/2ХШИД) (2 — х/хмт).
Следовательно, площадь поперечного сечения и вторая производная
функции S соответственно (с заменой х на е)
Лмид
(XI-2-23)
Производя замену е на х — a'rchz в выражении для второй
производной и подставляя ее под интеграл (XI-2-22), после интегрирования получим
V*=—§t> (XI-2-24)
где
в,- I
Отличие в результатах двух изложенных методов можно обнаружить,
если сравнить, например, осевые составляющие скорости на коническом
острие. По первому методу [формула (XI-2-11)] и по второму [формула
(XI-2-24)] эти составляющие соответственно определяются зависимостями
^i = — Ро («S&o 1Ро (Й)о + «' (^)оГ1; ^=-4г^=-Р;(Й)о. (XI-2-24')
Лмид
Нетрудно заметить, что второе выражение можно получить из первого,
если конус очень тонкий. Действительно, в этом случае член (30 (^х)о
в квадратной скобке имеет более высокий порядок малости и им можно
пренебречь. Что касается оставшегося члена, то при малых значениях (50 он
приводится к виду а' (£?)0 « Рё1-
Формулы (XI-2-24') позволяют оценить порядок величины возмущения
в потоке около тонкого конуса. Добавочная возмущенная составляющая
скорости, как видно, имеет порядок квадрата малого угла конуса. В общем
случае произвольной образующей эта составляющая имеет порядок г2.
Радиальная составляющая возмущенной скорости в соответствии с условием
безотрывного обтекания Vr = dr/dx, следовательно, имеет порядок т. Таким
образом, возмущения в продольном направлении на порядок меньше, чем
в поперечном. Поэтому в (XI-1-19) для давления были сохранены члены,
содержащие квадраты возмущений в поперечном направлении.
Закон подобия для функции давления и коэффициента сопротивления.
Рассмотрим зависимость для коэффициента давления
Р = 4г—(^)2- (XI-2-25)
Из формулы (XI-2-24) видно, что функция fii для данной точки
с координатой х зависит от параметра u — xl(a'r) и удлинения Ямид, которое
в свою очередь определяет угол р0 У острия (Ро = 1/^мид)- Параметр и можно
представить в общем виде, как u = uQh(x), где, в частности, для
параболической образующей функция h(x) = 2 (2 — x)"1.
На основании сказанного в общем виде коэффициент давления
p = №N(uo;x), (XI-2-26)
где N — некоторая функция параметра и и безразмерной координаты х>
454
Глава XI
Используя (1-3-14), найдем общую зависимость для коэффициента
волнового сопротивления:
с*в = Р;ЯЫ, (XI-2-27)
где D — некоторая функция параметра щ.
Формулы (XI-2-26) и (XI-2-27) позволяют сделать следующий вывод
о подобии потоков около тел вращения. Если эти потоки характеризуются
одинаковыми по значению
параметрами щ, то в соответственных точках
будут одинаковыми отношения р/$20,
что непосредственно следует из
формулы (XI-2-26). Из другой формулы
(XI-2-27) вытекает, что в
газодинамически подобных потоках тела
вращения испытывают такие осевые
усилия, что отношения схв/$1, для этих
тел будут одинаковы. Таким образом,
критерием подобия потоков в данном
случае является параметр
щ = (а'РоГ1 = (Ро VW^i)'1.
(XI-2-28)
Соотношение (XI-2-26) можно
представить в несколько ином виде для
О
Рис. XI-2-2. Область возможного
применения закона подобия для конических
головных частей (заштрихована область
сомнительного подобия)
тех случаев, когда числа Моо
достаточно велики и можно принять
I^Mto — 1 с^. Моо. С этой целью введем
параметр подобия К1 = МОоАМИд =
= Моо(Зо- Умножая (XI-2-26) на ML и учитывая выражение для параметра
подобия, получаем соотношение для функции давления:
-^ 1 =Nt (Кц ж). (XI-2-29)
Рос IV 1» / V /
Таким образом, в данной точке ж функция давления зависит только
от параметра подобия K^MoojV
Закон подобия по этому параметру подтверждается расчетом
распределения давления по методу характеристик. Причем удовлетворительные
результаты получаются лишь для значений К1? меньших единицы.
Закон подобия по параметру К4 (или щ) оказывается сомнительным при
некоторых сочетаниях чисел Моо и удлинений Ямид.
Физически это имеет место при отклонении действительного течения от
линеаризованного для тел с малым удлинением, с большой толщиной или при
очень больших числах Моо. Чтобы сохранить линеаризованный характер
течения, необходимо по мере увеличения чисел Моо больше заострять тело. При
этом, как следует из (XI-2-24), должно сохраняться неравенство щ>1.
Из выражения щ = (а'Ро)"1 следует, что если тело вращения достаточно
тонкое, т. е. удлинение велико, то для сохранения неравенства щ > 1
должно быть выполнено условие Моо>1. Если же число Моо—> 1, то, как
следует из (XI-2-28), возмущенная скорость по абсолютной величине
достигает бесконечно большого значения, что физически невозможно. Таким
образом, теория линеаризованных течений и законы их подобия пригодны при
одновременном соблюдении двух неравенств Хмид > KML — 1 и Моо>1.
Области возможного применения теории линеаризованных течений
и законов их подобия приведены на рис. IX-1-6 (для оживальной головки)
и на рис. XI-2-2 (для конуса), где заштрихованный участок соответствует
Аэродинамика тонких корпусов в линеаризованном потоке
455
сомнительному подобию. В соответствии с этими данными расчеты не
рекомендуется вести для малых удлинений А,мид<;2 и небольших чисел Моо.
При этом в практических случаях следует выбирать числа Моо не менее
1,3-1,5.
Если на рис. IX-1-6 и XI-2-2 провести прямые Ki~const,
соответствующие значениям параметра, меньшим единицы, для которых подобие
дает удовлетворительные результаты, то с помощью этих прямых для
данного числа Моо можно найти соответствующее удлинение головной части.
Подобие по параметру Кг определяет также подобие для функции
волнового сопротивления М1оСхв.
Умножив обе части формулы (XI-2-27) на М^о, получим общее
выражение для этой функции MloCXB = H (Ki).
Коэффициент волнового
сопротивления
Волновое сопротивление тонкого конуса. Найденное соотношение
(X1-2-24) для осевой добавочной составляющей возмущенной скорости
на конусе позволяет определить коэффициент давления на нем и,
следовательно, его коэффициент волнового
сопротивления.
В соответствии с (XI-1-19) находим
рк = схв = 2 (i°x)KA - p2K, (XI-2-30)
где 0,3
0,2
0J
ч
[со ^
0'
о
1
Рис. X1-2-3. Коэффициент волнового
сопротивления для острого конуса:
точная теория;
линеаризованная теория
{^х)к? (^?)к — функции, вычисляемые
соответственно из выражений (XI-2-17)
в результате подстановки
параметра щ = (а'рк)"1.
Приведенная формула может быть
несколько упрощена для значений wo>3:
JK = Сх в = № (4,606 lg 2щ -1). (XI-2-31)
Сравнение результатов расчета
коэффициента волнового сопротивления по
формуле (XI-2-30) и по точной теории проведено на рис. XI-2-3. Вплоть до
больших чисел Моо для тонких конусов наблюдается хорошее
согласование результатов. Значительное расхождение между ними возникает при
небольших числах Моо для более толстых конусов, что видно из рис. XI-2-3
на примере конуса с углом (Зк — 20°. Очевидно, поток около такого конуса
существенно отклонился от линеаризованного. Поэтому, применяя
изложенные методы расчета обтекания, надо строго придерживаться указанных выше
правил определения допустимых чисел Моо и углов (Зк, при которых
не нарушается линеаризованный поток.
Волновое сопротивление тел вращения, составленных из конических
элементов. На рис. XI-2-4 приведены несколько возможных схем тел
вращения, включающих отдельные конические элементы. В общем случае для
расчета коэффициента волнового сопротивления тел необходимо знать
распределение давления по их поверхности. На рис. XI-2-5 приведены
экспериментальные данные об этом распределении при Моо = 2, полученные
в результате продувки модели тела вращения, состоящего из конической
головки, цилиндрической части и хвостового усеченного конуса. При расчете
по линеаризованной теории получаем, примерно, такие же данные.
Расчет обтекания хвостового участка вызывает определенные трудности,
обусловленные тем, что, строго говоря, это обтекание может быть рассчи-
456
Глава XI
тано, если найдены параметры потока на участке поверхности,
предшествующей хвостовой части, в том числе на цилиндрическом участке.
Такой полный расчет может вестись и по линеаризованной теории
и по методу характеристик. Однако расчет связан с большой затратой
времени. Между тем практически имеется необходимость в простых способах
приближенной оценки параметров обтекания на корме, в частности
давления, что дает возможность найти составляющую полного сопротивления,
учитывая влияние хвостового участка.
С этой целью можно использовать формулу (VIII-1-18), которая для
головного конуса, как отмечалось, дает почти точное значение коэффициента
Рис. X1-2-4. Формы тел
вращения
Рис. X1-2-5. Кривые распределения
давления около корпуса, составленного из
конических элементов:
эксперимент; — по формуле
для конуса
волнового сопротивления. При этом, как видно из рис. XI-2-5,
действительная величина коэффициента давления на кормовом коническом элементе
оказывается меньше, чем получающаяся по формуле (VIII-1-18). Поэтому
распределение давления, найденное по этой формуле, надо рассматривать
как приближенную оценку действительной картины. Использование формулы
(VIII-1-18) позволяет найти сравнительно простую, хотя и весьма
приближенную, зависимость для оценки коэффициента волнового сопротивления тел
вращения, состоящих из конических элементов.
Предположим, что pi и р2 представляют собой коэффициенты давления
соответственно на переднем и заднем конусах, а безразмерная величина
£дон определяет хвостовое сужение, равное отношению £дон = ^дон/^мид ==
= (^дон/^мид)2. Тогда, применяя (1-3-14), получим
I у» /4 С" \ /VT О QO\
С% в — р^ —}— р2 \ •*• ~"~ *^ДОН/ • ^Л-1-^l-O^^
Здесь первое слагаемое дает сопротивление головного конуса с£в = .р1» а
второе—сопротивление ХВОСТОВОЙ (КОРМОВОЙ) ЧаСТИ С^в = р2(1—£дон)-
Внося в формулу (XI-2-32) вместо ри рг их выражения в соответствии
с (VIII-1-18), найдем
" 7](1_5дон), (XI-2-33)
где Poi» Рог — углы головного и хвостового конусов в градусах.
Аэродинамика тонких корпусов в линеаризованном потоке
457
Из выражения в правой части этой формулы можно выделить часть
сопротивления
<£рв = 0,002 (0,8 + М-2) (рО2)1>7 (1-Лон), (XI-2-34)
приходящуюся на хвостовой элемент. Эту часть можно определить, если
воспользоваться результатами, которые приведены на рис. XI-2-6. Одни
из этих результатов получены по линеаризованной теории, другие —по более
точной теории с учетом второго приближения, причем все результаты
найдены для конических хвостовых частей тела в предположении, что они
0,05
V
0,3 0,4 0,5 0,6 0,7 0,8 03 1,0
•MS,-/'
0 0,1 0,2 0,3 0Ц 0,5 0,6 0,7 0,8 0,9 1,0 5Япн
Рис. XI-2-6. Кривые для определения коэффициента волнового сопротивления
конических кормовых частей
достаточно удалены от носка. В этом случае давление перед хвостовой
частью полностью восстанавливается, а следовательно, скорость равна ее
значению для набегающего потока.
При расчетах с помощью кривых на рис. XI-2-6 вначале по известным
данным определяют удлинение хвостовой части по формуле Якр = ^кр
или из выражения Якр = (1 — £ДоН) (2Ро2) 1» затем подсчитывают параметр
(М1о~ 1)1/2 ^Акр)"1. По этому параметру из графика находят произведение
, из которого и определяют значение с^в.
Расчеты, проведенные с помощью данных на рис. XI-2-6, показывают,
что лучше, чем по формуле (XI-2-34), результаты получаются, если
воспользоваться аппроксимирующей зависимостью
Скр= 0,002 (0,8 + M~J) (ft,)1'7 Vi-Snm. (XI-2-35)
Тогда, добавляя к этой составляющей сопротивление головного конуса
стхв = 0,002 (0,8 + М-2) (Р^)1'7, (XI-2-36)
получим формулу для расчета коэффициента полного сопротивления:
СХъ = (
Если у головного и хвостового конусов углы
(XI-2-37) принимает вид
(XI-2-37)
одинаковы, то
(XI-2-38)
458
Глава XI
Хвостовая часть может быть выполнена не только сужающейся,
но и расширяющейся. В последнем случае донный срез оказывается больше
миделевого сечения. Вследствие этого коэффициент сопротивления тела
вращения становится еще больше. Причем сопротивление будет тем больше,
чем больше угол конусности и удлинение хвостового конуса.
Исследование составляющей сопротивления, возникающей из-за
расширяющегося хвостового конуса, представляет сложную проблему. Она
упрощается, если угол конусности невелик. В этом случае можно было бы
ф
зу
—;
v—
■—.
5
/
0,3 0,5 0,7
*~х
Рис. X1-2-7. Графики (а и б)
для определения давления и
волнового сопротивления
расширяющейся части корпуса
(в) (1,5<Моо<3,5; 5°<Ро2<
<^ 20°). Номерам кривых 2, 2,
3,4, 5 соответствуют
отношения г/г0, равные 1,25; 1,5; 1,75;
2; 3; схъ отнесено к
максимальной площади уширения
воспользоваться методом характеристик. Если же углы велики, то обтекание
можно исследовать достаточно надежно только с помощью эксперимента.
Однако для грубой прикидки значений параметров обтекания можно
воспользоваться методом «местных конусов», полагая при этом, что перед
расширяющейся конической кормой газ движется со скоростью набегающего
потока.
В соответствии с этим методом сопротивление определяется как часть
сопротивления полного конуса с тем же углом наклона образующей.
Коэффициент волнового сопротивления конической кормы будет, следовательно,
зависеть от удлинения хвостового конуса Якр = ^кр/^МИд (или от угла
конусности Рог)? величины Snon и числа Моо.
Графики, позволяющие определить давление и коэффициент с^в,
приведены на рис. Х1-2-7,а, б ([70] 1963, № 41).
Волновое сопротивление тонкого тела вращения с произвольной
образующей. Общий случай расчета коэффициента волнового сопротивления
связан с вычислением распределения давления и последующим применением
формулы (1-3-14).
Такой общий способ расчета дает возможность достаточно точно
получить необходимые результаты для любого тела вращения, возможные формы
которого приведены на рис. XI-2-8.
Наряду с этим, так же как и в случае расчета обтекания тел
вращения, составленных из конических элементов, можно рассмотреть приближен-
Аэродинамика тонких корпусов в линеаризованном потоке
459
ные зависимости, позволяющие сравнительно просто оценивать коэффициент
волнового сопротивления тел вращения произвольной формы.
Головки различных фЪрм. На рис. XI-2-8 видно, что головки
играют двоякую роль. Они могут представлять собой самостоятельный
летательный объект (рис. XI-2-8, модели,№ 1, 2) или являться составным
передним элементом тела вращения (рис. XI-2-8) модели № 3 — 6. В
последнем случае сопротивление
головки является частью
полного сопротивления всего тела.
Обтекание головки можно
рассчитать по методу «местных
конусов», применяя формулу
(XI-2-31).
Для тонкой головки с
параболической образующей и
местным углом наклона
касательной в произвольной точке
Р = (30 (1 — х) приближенная
зависимость для расчета
давления имеет вид
(XI-2-39) N6
где K^MoofV
По этой зависимости
можно рассчитать, применяя
(1-3-14'), коэффициент
волнового сопротивления головки:
N1
N2
N3
Л/4
in
Ш
А М
Kj 18 j *
Рис. X1-2-8. Некоторые формы корпусов с
произвольной образующей
(XI-2-40)
Используя эту формулу,
следует иметь в виду, что она получена для полной головки (рис. XI-2-8,
модель № 2). Не представляет труда получить аналогичную зависимость для
укороченной головки (рис. XI-2-8, модель № 1).
Наряду с формулой (XI-2-40) для расчета волнового сопротивления
тонких параболических или оживальных головок можно воспользоваться
несколько более общими выражениями (IX-1-26) и (IX-1-27). Однако
последняя формула для полной головки дает завышенные значения коэффициента
волнового сопротивления. Лучшие результаты получаются, если вместо
коэффициента 0,415 принять значение 0,332:
Сл.в=:0,332рк. (XI-2-41)
Хвостовая сужающая часть. Расчет распределения около
хвостовой части с сужением может быть осуществлен по методу характеристик.
При этом, если цилиндрическая часть достаточно длинная, то расчет
начинается от места сопряжения цилиндра с кормой, где местную скорость
можно принять равной скорости невозмущенного потока.
Полученные при этом предположении результаты показали, что
коэффициент давления в некоторой точке поверхности хвостового элемента зависит
от значений tg|3 и отношения координат r/х. Угол р определяет наклон
к оси тела касательной к образующей в рассматриваемой точке, а коорди-
460
Глава XI
ната х равна расстоянию от этой точки до точки пересечения линии
возмущения, проведенной через начало кормы, с осью тела. Кривые,
характеризующие изменение коэффициента давления на хвостовом участке в зависимости
от параметров t~p и r/х для различных чисел Моо, приведены на рис. Х1-2-У.
-0,10
-0,05
о
Г£др=-о,зо
-0,25
-0,20
'~ -0,15
-0,10
-0,075
-0,050
- tqp=-0,025
0,25
0.5 г/х
Рис. XI-2-9. Кривые, характеризующие изменение коэффициента
давления на кормовой поверхности тела при различных числах Моо
По распределению давления можно вычислить величину
дополнительного коэффициента сопротивления с£Р, являющегося результатом влияния
кормы. Такие данные, полученные для хвостового элемента, выполненного
в виде параболического тела вращения, приведены на рис. XI-2-10.
Из этих графиков видно, что величина с*р зависит от удлинения кормы
^кр = #Кр/йМИд (якр — длина хвостового участка), донного сужения £дон
и числа Моо. Причем сами графики отражают закон изменения функции
4?1кРс£в в зависимости от параметров (2KKV)"1 l/ML — 1 и £дон. Последний пара-
Аэродинамика тонких кропусов в линеаризованном потоке
461
метр зависит, как в этом нетрудно убедиться, от удлинения реальной кормы Якр
и удлинения А,мид = tg~1p02 = #Мид/^мид некоторого фиктивного параболического
тела, полученного в результате наращивания хвостового участка до полной
головки, как это показано на рис. XI-2-9. Соответствующая зависимость
для Злон имеет вид 5A0H= (1 — А!РАмид)2-
3,0
2,0
V
0,5
ОА
%3
0,2
0,10
0,06
0,05
I
Sdw=0,336
/
0,502
-J,652 -
0,801
"^—
■*-—-
——.
■
-—--
—«=
"--—■
^
=^—
.
- —
— —
— —
-1
02
0,3
0,5
0,5 0,6 %7 0,8 0,9 SanH
Рис. X1-2-10. Сопротивление хвостовой сужающейся
части с параболической образующей:
ЯКр _ якр/<гмид (графики получены методом характеристик)
На рис. XI-2-11 приведены кривые, рассчитанные по методу
характеристик и позволяющие определить волновое сопротивление расширяющейся
кормы параболической формы.
Помимо метода характеристик для приближенной оценки влияния
кормы на волновое сопротивление, можно пользоваться методом «местных
конусов».
462
Глава XI
Рассмотрим применение этого метода для хвостовой части, выполненной
в виде параболического тела с сужением £дон. Примем, что у фиктивной
головки, построенной на
основе заданного хвостового
элемента, удлинение будет Хмт,
а соответствующий ему угол
конуса у острия —Р02 (Рис-
XI-2-8, модели № 3, 4, 6).
Тогда, если рк2 представляет
собой коэффициент давления
на хвостовом конусе
(отрицательный по знаку), то с
помощью (1-3-14) найдем, что
1
скрв== ? pK2dr2. (XI-2-42)
Рис. X1-2-11. К расчету волнового сопротивления -^
расширяющейся кормы параболической формы дон
^кр = W^ Подставляя в эту формулу
рк2 из (VIII-1-18) с заменой
рк на р = 57,3ро (1 — ^)? уточняя затем полученную зависимость при помощи
данных£метода характеристик, получим приближенную формулу
где рК2 — коэффициент давления на конусе с углом рО2-
С учетом (XI-2-43), а также выражения (XI-2-41) полный коэффициент
волнового сопротивления тела с головной и хвостовой частями
параболической формы будет
схв = 0,332рк1 + 0,4рк2 [1 - 2,415*& (1 - 0,49ВД + 0,05б£дон - 0,151^)],
(XI-2-44)
где Рк1 — коэффициент давления, вычисляемый для конуса с углом р01.
В том случае, когда корма тела представляет собой конус с донным
сужением 5д0ш полный коэффициент волнового сопротивления вычисляется
по более простой формуле
схв = 0,332рк1 + рк2 Kl-^дон, (XI-2-45)
где /?К2 — находится по известному углу (302 конического элемента.
Весьма тонкий корпус
Приведенные выше соотношения для определения волнового
сопротивления относились к тонким телам, у которых параметры обтекания более
или менее существенно зависят от числа Моо, причем, как показывают
исследования, эта зависимость уменьшается по мере того, как тело становится
более тонким. В теоретически предельном случае при г —> 0 сверхзвуковое
возмущенное течение уже не будет зависеть от сжимаемости. Практически
это соответствует весьма тонкому корпусу с большим удлинением.
Отмеченный предельный случай рассматривается в аэродинамике в специальном ее
разделе под названием «аэродинамика тонких тел».
В соответствии с этой теорией зависимость для коэффициента волнового
сопротивления находится из общего выражения (IV-5-30). Конкретный вид
этого выражения зависит от формы тонкого корпуса.
Аэродинамика тонких корпусов в линеаризованном потоке 463
Тело, заостренное с обоих концов. Для такого тела S'(l) = 0. Кроме
того, равен нулю последний член в формуле (IV-4-30), так как контур С,
по которому вычисляется интеграл, стянут в точку. Поэтому коэффициент
волнового сопротивления
1 1
Xr -1 J J S"(x)S"(l)ln\x-l\dxdg. (XI-2-46)
0 о
Такое же соотношение будет и в том случае, когда угол а = 0 и тело
имеет цилиндрическое основание. Действительно, в этом случае производная
S' (1) — 0. Кроме того, по условию безотрывного обтекания равна нулю
в конце тела и радиальная составляющая скорости <9cpo/dv. Поэтому второй
и третий члены в правой части (IV-4-30) равны нулю, и формула для
коэффициента сопротивления принимает вид (XI-2-46).
Тело без осевой симметрии с круговым основанием. Угол атаки а = 0.
Для тела, у которого в общем случае отсутствует осевая симметрия, но
имеется круглое основание, формула (IV-4-30) для сопротивления может
быть представлена в более конкретном виде. С этой целью напишем выражение
функции dr/dx, определяемой для точек донного сечения, в виде ряда [51]:
оо
(■£■)«-! = 2 /2mcos2m (-J—?) , (XI-2-47)
171=0
где /2m — некоторые безразмерные величины.
Вычисляя производную (дуо/дг)х=={ по уравнений) (IV-4-7) и имея в виду,
что (д($о/дг)ХЯЛ1 = (dr/dx)x=={, найдем коэффициенты Ап и Вп, затем определим
интеграл (Ь ф0 (<5cpo/dv) dx = \ ф0 (9<po/dr) r0 d0. Внося полученное значение
с о
интеграла в формулу (IV-4-30), найдем для коэффициента волнового
сопротивления
1 1
1
2-%|25-- (XI-2-48)
Для тела вращения, обладающего осевой симметрией, формула (XI-2-48)
упрощается, так как последний член в ней оказывается равным нулю.
В упрощенном виде формула определяет сопротивление тела, которое в более
общем случае имеет хвостовое сужение. В конце такого тела производная
5/(1) = 0.
Форма тела вращения с
минимальным волновым
сопротивлением
Соответствующим подбором формы можно добиться того, чтобы при
заданных условиях (скорость полета, угол атаки, объем, длина тела и т. д.) полное
сопротивление было наименьшим. Рассмотрим тела минимального волнового
сопротивления — оптимальные головки, полученные в аэродинамической теории
тонкого тела при условии, что угол атаки равен нулю. Форма этих головок
найдена в результате вычисления функции (XI-2-46), определяющей
волновое сопротивление.
464 Глава XI
Корпус, симметричный относительно средней точки оси, с нулевой
площадью поперечного сечения на концах. Такой корпус, носящий
название тела Сирса —Хаака [51], имеет минимальное волновое сопротивление
с„ = -^ (XI-2-49)
при условии, что объем тела задан. Распределение площади вдоль оси дается
формулами
s (Q)=-aSrsin3e;s (it) - *-„=is£' (XI-2-50)
где угол 0 связан с координатой х зависимостью
х = -|- хк (1 + cos 6). (XI-2-51)
Из этой зависимости видно, что передней точке (х = 0) соответствует
угол 9 = я, концевой (х = хк) — значение 6 = 0. Для средней точки с
координатой х = хк/2 (место максимального поперечного сечения) величина 9 = я/2.
Оптимальная головка с площадью донного сечения #мид. Форма
оптимальной головки получена Карманом. Она обеспечивает минимальное
волновое сопротивление при заданных длине тела хк и площади донного среза
^(^к) = ^дон при условии, что в концевой точке S'(xK) = 0. Следовательно,
у этого тела S (хк) — £д(Ш = £мид- Коэффициент сопротивления такой головки
f (XI-2-52)
Распределение площадей вдоль оси дается уравнением
S (х) = -£и« ( я - 0 + -у sin 20) , (XI-2-53)
2W
где £Мид = , угол 9 связан с х зависимостью (XI-2-51). В отличие от тела
хк
Сирса —Хаака, у которого месту максимального сечения (х = хк/2)
соответствует угол 9 = я/2, у головки Кармана этому сечению (х = хк)
соответствует 9 = 0.
Уравнение (XI-2-53) описывает образующую, принадлежащую слегка
затупленному тонкому телу вращения. Несмотря на затупление,
сопротивление все же остается весьма малым, так как благодаря влиянию носка хвостовые
участки тела оказываются расположенными в области пониженного давления.
Сопротивление тел оптимальной формы мало зависит от условий
обтекания. Это означает, что если, например, головка Кармана будет помещена
в поток с очень большой скоростью, то ее форма и для этих условий будет
близка к оптимальной. Таким образом, оптимальная форма головной части
с точки зрения минимального сопротивления при заданных условиях мало
зависит от закона, используемого для вычисления распределения давления.
§ Xl-З. Обтекание тел
вращения под углом атаки
Распределение давления при
неосесимметричном обтекании
Основные зависимости. Задача о неосесимметричном обтекании сводится
к определению коэффициента р2 добавочного давления, возникающего в
результате нарушения симметрии обтекания. Это давление зависит от потенциала
возмущения ц>'2 при поперечном обтекании, который является интегралом
Аэродинамика тонких корпусов в линеаризованном потоке
дифференциального уравнения (XJ-1-13), и в общем виде может быть выражен
формулой (XI-1-14). Полная величина коэффициента давления при неосесим-
метричном обтекании р = Pi + P2, где pt зависит только от переменных х, г,
а р2 еще и от переменной у.
Поэтому в линеаризованном потоке коэффициент нормальной силы
определяется в соответствии с формулой (1-4-11) как:
1 я
^ \ rdx
о о
Таким образом, коэффициент нормальной силы зависит только от
условий неосесимметричного обтекания. Чтобы вычислить этот коэффициент,
необходимо найти распределение коэффициента р2, расчет которого связан
с вычислением добавочного потенциала ф^, определяемого выражением (XI-1-27)
или (XI-1-27').
К уравнению для ц'2 необходимо присоединить условие (XI-1-11')
безотрывного обтекания. Включив для упрощения постоянную величину Foo
в значения добавочной осевой V'x и радиальной V'r составляющих
возмущений скорости и дифференцируя (XI-1-27) сначала по х, а затем по г, найдем
archu
ф2я = Vx — a' cos у \ т (х—a'rchz) ch z dz; (XI-3-2)
с
archu
ф2Г = V'r= — (ar)2cosу \ m(x — aVch z)ch2zdz, (XI-3-3)
0
где производная
m = m' (e) |8=x-a'rchz
Приравнивая правые части соотношений (XI-3-3) и (XI-1-11'), получим
уравнение
archu
сс--=(а')2 § т(х — a'rchz)ch*zdz (XI-3-4)
о
для определения функции т(е).
На основании полученного выражения (XI-3-2) для добавочной осевой
составляющей скорости находим коэффициент давления
archu
рг= —2а' cosy \ т(х — a'rchz)chzdz — а2 (4sin2у —1). (XI-3-5)
о
Как видно, в этом выражении появился квадратичный член,
позволяющий уточнить величину коэффициента давления. Если углы атаки очень
малы, то этим членом можно пренебречь, и тогда
archu
р2=—2arcos7 \ т(х —a'rchz) chzdz. (XI-3-6)
о
Расчет параметров потока. Рассмотрим один из способов расчета,
основанный на использовании в качестве первого приближения закона
распределения диполей по оси весьма тонкого тела. Соответствующий этому закону
вид функции т(х) можно найти из уравнения (XI-3-4), приняв в нем
е = х — а'г chz:
= ar\
ar\ (XI-3-7)
30—114
466 Глава XI
Для весьма тонкого тела (у такого тела г очень малы) величина осг2
может быть принята в первом приближении равной его значению при г—>0.
х
Тогда аг2 = \ т (г) (х —-г)йг. Полагая и = х — е, dv = mds и интегрируя
о
х
по частям, имея в виду, что у острия 77i(O)=O, получаем \ т (е) de, = аг2.
о
Отсюда находим закон распределения диполей вдоль оси весьма тонкого тела
m = 2ar(dr/dx). Интересно отметить, что этот закон имеет такой же характер,
как и закон распределения источников.
Приведенная зависимость для функции т может быть использована
для расчета обтекания тела, отличающегося от весьма тонкого, по аналогии
с тем, как это было сделано в § XI-2 в связи с применением первого
[приближения для функции / распределения источников в симметричном случае.
В качестве иллюстрации рассмотрим конкретный случай обтекания тела
с параболической образующей.
Имея в виду полученное выражение для функции т, найдем производную
•
т/г (е). Корректируя найденный таким образом закон распределения этой
производной введением постоянных коэффициентов а0, аи получим
(XI-3-8)
Переходя в этом уравнении от 8 к переменной z и включая в
коэффициенты а0, аА постоянную а', найдем
т(х — aVchz) = а{а0 + at (и — chz)m[l~-0,5т (и — chz)]}. (XI-3-9)
Внося это выражение для функции т в уравнение (XI-3-4), получим
после интегрирования условие безотрывного обтекания
aoJr + «1 (jr - 0,5m;J!) = (a')"1. (XI-3-10)
Отсюда можно найти оба коэффициента а0 и at. Чтобы определить первый
коэффициент, надо отнести условие (XI-3-10) к коническому острию (я = е = 0);
второй коэффициент найдется из того же условия, написанного для
произвольной точки поверхности. В результате получим
В выражениях (XI-3-10) и (XI-3-11) /T представляет собой некоторую
функцию, которая зависит только от параметра и = х/(а'г). В частном
случае функция (jг)о зависит от параметра и = щ = (а'Ро)"1 на коническом острие.
Чтобы получить зависимость для добавочной осевой составляющей
возмущенной скорости при поперечном обтекании, внесем выражение (XI-3-9)
в уравнение (XI-3-2) и проинтегрируем:
Vx = a cos
\ а' (/•)
где f% — некоторая функция того же параметра и.
Введенные функции /J? и /S аналогичны функциям С и i2»
рассмотренным при исследовании осесимметричного обтекания.
Если иметь в виду несколько более общий случай задания производной
тгг(е), в частности, в виде параболы третьей степени [в уравнение (XI-3-8)
войдет член с е3], то после подстановки ее в выражения (X1-3-2) и (X1-3-3)
Аэродинамика тонких корпусов в линеаризованном потоке 467
придем к соотношениям, включающим функции:
jx = /j; jx = uli — /2; /I == и<2>1\ — 2и12 + /з!
_ (XI-3-13)
где /д —функции, представляющие собой интегралы вида (XI-2-13). Можнсг
обратить внимание на то, что функции у£ совпадают с соответствующими
функциями С, введенными в осесимметричном случае. Значения других
функций у?, определяемых формулами (XI-3-13), подсчитаны для различных
параметров и и приведены в табл. XI-3-1. Пользуясь этой таблицей, как
и табл. XI-2-1 для расчета осесимметричного обтекания, надо иметь в виду,
что они вычислены для значений параметра и от 1 до 12,2. При
необходимости, если по ходу расчета окажется, что значения и не укладываются
в табличные, следует вычислить соответствующие величины функций in, jn
по формулам (XI-2-14) и (XI-3-13), и тем самым дополнить таблицы.
Такая необходимость может возникнуть при исследовании обтекания тонких
и длинных тел потоками с малыми числами Моо.
Определение добавочной составляющей скорости Vx при заданных а
и cosy по формуле (XI-3-12) связано, как видно, с вычислением значений
функций /я, /'? и параметра т в рассматриваемой точке, а также величины
(jr)o для конуса у острия.
Найдя эту составляющую, можно подсчитать по (XI-1-23) добавочную
величину коэффициента давления:
p2^-2acosY(^-)~-^(4sin2Y-l), (XI-3-14)
где отношение V'xl(ao,osy) не зависит от a cos у и определяется из
выражения (XI-3-12).
Рассмотренный способ расчета неосесимметричного обтекания можно
упростить. С этой целью воспользуемся результатами теории обтекания
очень тонких тел. При этой теории при определении закона распределения
диполей, например, в виде (XI-3-8) нет необходимости осуществлять
корректировку с помощью коэффициентов а0 и а±.
Для очень тонкого тела вращения функция т может быть
представлена в виде т = (aln)Sf (x), а ее производная т— (а/я) S"(x). В
соответствии с этим добавочная осевая составляющая скорости
arch u
^=-^-cosy jj S"(x-a'rchz)chzdz. (XI-3-15)
о
В качестве примера рассмотрим применение этой зависимости для
расчета обтекания тела вращения с параболической образующей. Для такого
тела вторая производная S" дается выражением (XI-2-23). Подставляя его
под интеграл (XI-3-15), получим
Vx=^- cos 7Q2, (XI-3-16)
где
arch и -, ~
S"(x-a'rchz)chzdz=~ (2i°r ^r
^мид ч и
J мид
О
Изложенные методы могут быть использованы для оценки скорости и,
следовательно, давления на цилиндрической и хвостовой частях тела.
30*
468
Глава XI
Таблица XI-3-1
Значения функций j™ (и)
и
1
1,1
1,2
1,3
1,4
1,6
1,8
2,0
2,2
2,4
2,6
2,8
3,0
3,2
3,4
3,6
3,8
4,0
4,2
4,4
4,6
4,8
5,0
5,2
5,4
5,6
5,8
6,0
6,2
6,4
6,6
6,8
7,0
7,2
7,4
7,6
7,8
•8,0
.8,2
8,4
8,6
8,8
9,0
9,4
9,8
10,2
10,6
11,0
11,4
11,8
12,2
0
0,4736
7090
8824
0,1120-10
1523
1894
0,239Ы0
2869
3380
3925
4506
0,5124-10
5780
6472
7202
7966
0,8778-10
9623
0,1051.Юа
1143
1239
0,1339-Ю2
1443
1551
1663
/1779
0Д899.102
2022
2150
2282
2417
0,2556-102
2700
2847
2999
3154
0,3313-102
3476
3644
3814
3990
0,4169-102
4540
4927
5327
5747
0,6177-Ю2
6631
7096
7578
0
0,3090-10-1
8394
0,1719-10°
2688
5378
8758
0,1317-10
1843
2467
3197
4039
0,5001-10
6092
7316
8682
0,1020-Ю2
0,1187-Ю2
1371
1573
1792
2030
0,2288-Ю2
2566
2865
3187
3531
0,3899-Ю2
4291
4708
5151
5621
0,6118-Ю2
6644
7198
7783
8399
0,9045-Ю2
9723
0,1044-Ю3
1118
1196
0,1278-103
1452
1642
1846
2067
0,2305-103
2563
2837
3130
0
0,2300-Ю-2
0,1450-10-1
4021
8462
0,2446-10°
5519
0,9632-10°
0,1599-10
2450
3579
5024
0,6827-10
9040
0,1172-Ю2
1491
1868
0,2309-Ю2
2821
3409
4081
4844
0,5703-102
6678
7763
8974
0,1032-Ю3
0,1180-Ю3
1344
1524
1721
1936
0,2171-Ю3
2426
2703
3002
3326
0,3674-103
4049
4453
4884
5348
0,5842-103
6935
8171
9563
0,1112-104
0,1287-Ю4
1483
1698
1937
0
0,1173-Ю-3
0,3326-10-2
0,1031-10-1
2862
0,1191-100
4409
0,7850-100
0,1490-10
2740
4536
7103
0,1086-102
1538
2158
2954
3959
0,5209-Ю2
6745
8609
0Л085-103
1330
0,1669-Ю3
2040
2472
2974
3552
0,4214-103
4971
5831
6803
7899
0,9130-Ю3
0,1051-104
1204
1376
1565
0,1779-104
1997
2262
2541
2849
0,3189-104
3950
4855
5916
7154
0,8592-104
0,1026-105
1216
1437
Аэродинамика тонких корпусов в линеаризованном потоке 469
Причем хвостовая часть должна быть слегка сужающейся или слегка
расширяющейся, чтобы сохранить линеаризованный характер обтекания.
Закон подобия потоков. В соответствии с (XI-3-16) функция Fi/(acosY)
зависит в данной точке от параметра и. В § XI-2 было показано, что этот
параметр в свою очередь определяется его значением и0 на конусе у острия,
а также некоторой функцией h от переменной х, т. е. u = uQh(x),
Следовательно, если учесть, что функция (/?)0 зависит от того же параметра и0,
то для добавочного коэффициента давления можно написать в соответствии
с (XI-3-16) общее выражение
р2= — 2а$0С(и01 i)cos7 — а2 (4 sin2 у — 1), (XI-3-18)
где G — некоторая функция, зависящая для данной точки поверхности
от величины щ.
Рассмотрим случаи, когда число М«> велико, а тело вращения имеет
параболическую образующую, так что его удлинение Ямид = 1/р0. Тогда,
умножив выражение (XI-3-18) на ML, найдем
-gj— 1 = оЛмидК^! (Klf x) cos 7 - (аХмт)2 KJ (4 sin2 у -1), (XI-3-19)
где В1-—некоторая функция, определяемая в данной точке
параметром Ki^MooP.
Обозначив параметр аЯмид через К2, напишем (XI-3-19) в общем виде
■^—l=£(Ki, K2, J, у). (XI-3-20)
Из этого выражения видно, что функция давления в данной точке
зависит от К1? К2, которые являются параметрами подобия потоков,
обтекающих тонкие тела вращения под углом атаки.
В соответствии с (1-4-11) и (1-5-8) от этих же параметров будут зависеть
коэффициенты нормальной силы и момента:
Е(Ки К2); Mlmzp = F(Ku K2),
где Е и /" — некоторые функции параметров К4 и К2.
Коэффициент нормальной силы
Тело вращения с произвольной образующей. Если известно
распределение величины добавочного коэффициента р2 при неосесимметричном
обтекании, то можно вычислить коэффициент нормальной силы. Для этого
применим формулу (1-4-11). Имея в виду, что
я
\ (4 sin2 у — 1) cos у dy = О,
о
получим
\ -Ь- 7dx;x = ^. (XI-3-22)
а cos у ^мид
Эту формулу для частного случая тела вращения с параболической
образующей можно преобразовать к виду
CNP = 4Kma\^-ydt, (XI-3-23)
_ '°
где t = x2[l — (/3)]
470
Глава XI
Практический интерес представляет исследование изменения вдоль тела
функции V'x/(ос cos у). Эта функция определяет элементарную величину
коэффициента нормальной силы, отнесенную к единице длины тела, в
соответствии с формулой
Zk * ff^4. (XI-3-24)
a cos у 4аА,мид dx r
Из рис. XI-3-1 видно, что на длине приблизительно в 2 ^мид, начиная
от конца головки, элементарная величина коэффициента нормальной силы
v'
cccosy ,
0,1
0,1
О
Рис. XI-3-1. Изменение функции Fi/(acos7) вдоль
комбинированного тела вращения
становится равной нулю и затем принимает в хвостовой части возрастающие
к донному срезу отрицательные значения. Практически влияние
цилиндрического среднего участка тела на нормальную силу мало. Что же касается
кормы, то ее влияние может оказаться существенным в тех случаях, когда
длина и сужение достаточно велики.
Исследования показывают, что коэффициент нормальной силы тонких
тел при малых углах атаки почти не зависит от числа Моо и удлинения.
В частности, на рис. XI-3-2 видно, что
у двух тел вращения с удлинениями
^мид = 3 и 5 до значений углов атаки
порядка 4—5° коэффициенты cNp при
Моо = 5,05 практически одинаковы, хотя
с увеличением удлинения наблюдается
тенденция к возрастанию
коэффициентов нормальной силы.
Данные,, приведенные на рис.
XI-3-2, указывают на почти линейную
зависимость коэффициента cNp от угла
атаки, близкую к виду
cNp=:2a. (XI-3-25)
о,ч
0,3
0,2
n
1»
h
j
I
о
2.5
10
Рис. X1-3-2. Изменение коэффициента
нормальной силы в зависимости от угла
атаки двух тел вращения:
Mqo = 5,05; сплошная линия по формуле
(XI-3-25); О О — экспериментальные данные
при
г = 5, Q □ — то же, при X
мид-
Примечателен факт, что такое
значение коэффициента нормальной силы
дает линеаризованная теория для очень
тонких тел вращения. Чтобы показать
это, следует найти распределение коэффициента давления в предельном
случае бесконечно тонкого тела, т. е. при г -> 0. Этот предельный случай
рассматривается, как уже указывалось, в аэродинамике тонкого тела.
Согласно этой теории коэффициент давления можно найти, если перейти
в выражении (XI-3-5) к переменной & = х —a'rchz и найти предел вели-
Аэродинамика тонких корпусов в линеаризованном потоке 471
чины р2 при г -»- 0. Вычисление предела дает
Рг= ~2crosy m-a2(4sin2Y-l). (XI-3-26)
Так как функция m = 2ar (dr/dx), то в рассматриваемом случае
добавочный коэффициент давления
р2 = - 4а cos у -Jt - а2 (4 sin2 Y -1). (XI-3-27)
Если внести это выражение в (XI-3-1), то после вычисления интеграла
получим зависимость
н, (XI-3-28)
которая при отсутствии хвостового сужения (SA(m — 1) совпадает с
формулой (XI-3-25).
Таким образом, аэродинамика тонкого тела устанавливает тот же
линейный характер зависимости коэффициента нормальной силы от угла атаки,
который ранее был обнаружен экспериментально. Физически эта теория
правильно отражает и влияние формы хвостовой части, заключающееся
в уменьшении cNp при наличии сужения кормы (SR(m < 1).
При этом следует заметить, что те же экспериментальные исследования
показывают, что у реальных тел, отличающихся от весьма тонких, величина
cNp скорее пропорциональна относительному донному диаметру с?дон, чем
сужению £Дон« Имея это в виду, будем, однако, в дальнейшем изложении
использовать теоретический результат (XI-3-28). Формулу (XI-3-25), как
показывают исследования, можно применять для приближенной оценки
величины коэффициента нормальной силы сравнительно недлинных тонких
тел вращения с удлинением порядка 3—5.
Наиболее интересной для практики задачей является определение
коэффициента нормальной силы тела вращения, представляющего собой
в общем случае комбинацию головной части некоторой формы,
промежуточного цилиндра и хвостовой части. Если тело имеет цилиндрическую
корму, то основным его несущим элементом является головка, поэтому
при изменении ее геометрических характеристик будет меняться и
коэффициент нормальной силы.
Эксперименты показывают, что, например, с увеличением удлинения
головной части возрастает и коэффициент нормальной силы. Следует, однако,
заметить, что при небольшом изменении геометрических характеристик
достаточно заостренных головок изменение коэффициента нормальной силы
невелико.
Экспериментально проверялась также зависимость этого коэффициента
от формы заостренной головки тел с одинаковыми относительными длинами
цилиндрических участков. Оказалось, что, например, у тела с
параболической головной частью коэффициент нормальной силы несколько больше,
чем у тела с конической головкой того же удлинения.
Установлено, что эта зависимость обусловлена также влиянием головной
части на обтекание примыкающего к ней цилиндрического участка. В
частности, в случае параболической или оживальной головки на длине цилиндра
в 2-f-З ймид при небольших числах Моо вследствие такого влияния может
создаваться дополнительная отрицательная нормальная сила.
В случае конической головки на той же длине возникает, наоборот,
дополнительная положительная нормальная сила, что хорошо видно на
рис. XI-3-3. Эта сила на цилиндре возникает вследствие того, что на нижней
его части создается положительное, а на верхней отрицательное избыточное
давление.
472
Глава XI
Ф
$
0,1
о
-0,1
р
0,3
0,2
0,1
О
Нетрудно заметить, что перепад давлений в сечении, расположенном
на расстоянии примерно в 3 ^мид, практически исчезает. При этом несущая
часть цилиндра создает дополнительную нормальную силу, большую, чем
в том случае, когда перед цилиндром имеется параболическая головка.
Более того, в последнем случае эта дополнительная сила оказывается
настолько малой, что практически ее можно не учитывать. В то же время
для тела с конической головкой такой учет может быть целесообразным.
Исходя из сказанного и учитывая имеющиеся экспериментальные данные,
коэффициент нормальной силы, зависящий от давления, для цилиндрических
тел с параболической или оживальной
головкой можно рассчитывать по формуле
(XI-3-25). Оказывается, что таким же
образом можно вести расчет для тел с
головным конусом. Вероятно, совпадение
коэффициентов обусловлено тем, что
уменьшение по сравнению с параболической
головкой нормальной силы конуса
перекрывается ее возрастанием за счет
цилиндрического участка, примыкающего к
головной части.
Если цилиндрическое тело
заканчивается хвостовым участком какой-либо
формы, отличной от цилиндра, то в
результате перераспределения на нем давления
возникает дополнительная составляющая
нормальной силы. Эта составляющая
уменьшает величину суммарной
нормальной силы, если хвостовая часть будет
сужающейся (£дОН < 1), и наоборот,
увеличивает, если она расширяющаяся. В обоих
случаях, как показывают
экспериментальные исследования, нормальная сила тела
вместе с хвостовой частью может быть
приближенно оценена по формуле (XI-3-28), причем эта формула не
учитывает зависимости коэффициента cNp от числа Моо, хотя исследования
обнаруживают существование этой зависимости, правда, небольшой. При этом
с увеличением числа Моо наблюдается тенденция к некоторому возрастанию
коэффициента cNp.
Влияние отрыва потока. Приведенная оценка нормальной силы не
учитывает влияния отрыва потока. Если это оправдано для коротких тел,
обтекание которых практически носит безотрывный характер, то для длинных
тел при оценке нормальной силы следует учесть влияние отрыва,
наблюдающегося при поперечном обтекании тела вязкой средой со скоростью FooSina
(рис. XI-3-4).
Для элемента поверхности длиной dx (рис. XI-3-4) дополнительная
нормальная сила, обусловленная отрывом,
10\
Рис. X1-3-3. Распределение
давления по конусу и примыкающему
к нему цилиндрическому участку
(эксперимент):
а — верхняя, б — боковая, в — нижняя
образующие
dNf = с
2r dx =-. dcNf
f МИД»
где с — некоторый коэффициент, определяемый условиями течения в
пограничном слое.
В соответствии с этим
dcNf = с 2— Slrl a dx-
к Гмид
Аэродинамика тонких корпусов в линеаризованном потоке
473
Интегрируя в пределах от х0Т до хк, получим
к
2 sin2 а Г-
\
rdx\
(XI-3-29)
координата хот равна расстоянию до сечения на цилиндре, где начинается
отрыв потока.
Исследования показывают, что это расстояние непостоянно и зависит
от угла атаки, числа Моо, числа Рейнольдса и формы корпуса. На рис. XI-3-5
приведена приближенная зависимость величины хот от угла атаки при
Моо = 2 для цилиндра с оживальной головкой. Нетрудно заметить, что
в общем случае хот > #мид и с
увеличением углов атаки появляется
тенденция к начальному образованию вихрей
и отрыву в области перехода оживаль- ^
ной части к цилиндру. При
ориентировочных расчетах можно исходить из
Рис. X1-3-4. Влияние нормальной
составляющей скорости Foo sin а на обтекание
тела вращения
Рис. X1-3-5. Расстояние до области отрыва
пограничного слоя на подветренной стороне
тела вращения
того, что начало отрыва совпадает с началом цилиндрического участка,
т. е. нижний предел интеграла в (XI-3-29) хот = хшщ. Для корректировки
расчетных результатов следует пользоваться данными, аналогичными
графику на рис. XI-3-5.
При наличии хвостовой части нет особой необходимости вычислять
интеграл в (XI-3-29). Вполне допустимо заменить корму в этом случае
цилиндром с удлинением Якр = xKV /ймид. В соответствии с этим
_4_
я
sin2
(XI-3-30)
где Хц=(^к — xMm~xKV)/dmm — удлинение цилиндрического участка тела.
При небольших углах атаки
/
^Nf ~ С — (Ац -J- Акр/ & • (Al-O-oU )
Коэффициент с, как показывают экспериментальные исследования,
зависит от того, будет пограничный слой турбулентным или ламинарным.
Для ламинарного течения в диапазоне чисел Re = Voodumlv от 2-Ю4 до
2-105 величина с приблизительно равна 1,2. Пока отсутствуют другие данные,
можно для приближенных вычислений пользоваться этим значением для
других чисел Re. Для турбулентного обтекания можно принять с с^. 0,3—0,4.
С учетом дополнительной нормальной силы суммарная величина
коэффициента нормальной силы
cN =
а2
(XI-3-31)
474
Глава XI
/о
/
/о
с
1
/
/
/
•
*--
8
16 24 Ыа
0,2
Ofi
0,6
0,8
V
\°
о
р°
о
8
16 а°
Рис. X1-3-6. Коэффициенты нормальной силы и центра
давления заостренного тела вращения. Полное удлинение
тела равно 21, удлинение головки А,мид — 4,75:
теория тонкого тела; — с учетом отрыва
пограничного слоя при поперечном обтекании; С — эксперимент при
М = 2
>
i
h
V
к
4
T
i
1
1
8 16 24
--»
^*-
M^2
A
-—
2
//
7
:r
-2
-1
■»/.
чц.9
[ '1
.0
ц.8
f
2
3
0
4
8 6
12 4
16 2
Рис. X1-3-7. Изменение c^v и сц#д цилиндрических тел с
конической и оживальной головками:
.цифры 1, 2, 3, 4 на кривых соответствуют цифрам на схеме тела и
представляют условную длину
-Аэродинамика тонких корпусов в линеаризованном потоке 475
На рис. XI-3-6 приведены экспериментальные данные, которые
сравниваются с результатами расчета по теории тонкого тела [формула (XI-3-28)],
«а также по формуле (XI-3-31), учитывающей влияние отрыва. Нормальная
сила, определяемая по теории тонкого тела, действует лишь на
расширяющейся части корпуса перед областью отрыва, а вязкие поперечные силы
действуют за этой областью. При увеличении угла атаки эти силы
возрастают пропорционально а2, в то время как нормальная сила, вычисленная
по теории тонкого тела, растет пропорционально а. Формула (XI-3-31)
дает результаты, удовлетворительно согласующиеся с экспериментом.
Некоторые экспериментальные результаты по определению
коэффициента cN для цилиндрических тел с коническими и оживальными головками
приведены на рис. XI-3-7.
Коэффициент нормальной силы тонкого конуса. Для расчета этого
коэффициента необходимо знать распределение добавочного коэффициента
давления. Чтобы найти его, воспользуемся выражениями (Х1-3-14)и(Х1-3-16),
комбинируя которые получим
^||a«(4sin»Y-l), (XI-3-32)
(xi-3-зз)
где индекс «О» заменен индексом «к».
Подставив значение р2 в (XI-3-1), найдем
Для очень тонкого конуса (|3К—»0) из этой формулы можно найти
cNp = 2a.
Коэффициент момента сил
Тело вращения произвольной формы. Не рассматривая пока влияние
отрыва, будем считать, что коэффициент момента зависит от распределения
добавочного давления и от положения точки приведения, относительно
которой вычисляется момент. Примем, что такой точкой является носок тела.
Коэффициент момента определяется выражением (1-5-8), которое дает
величину mzp, отнесенную к полной длине тела хк. Наряду с этим можно
получить зависимость для коэффициента момента mzv, отнесенного к любой
другой характерной длине, например, к длине головной части хМШ№. С этой
целью следует применить соотношение
m'zv = ™<zp -r^~ = rrizp т-^~ • (XI-3-34)
%ид лмид
Выражение для коэффициента момента, отнесенного к полной длине
тела, можно получить из (1-5-8), имея в виду зависимость (XI-1-24) для р2:
о
В частном случае параболической образующей эта формула может быть
написана несколько иначе:
т*Р = К ) ^^j dl' (XI-3-35 )
О
где 1=1с3 (2/3— ж/4).
Чтобы вычислить коэффициент момента, используя формулу (ХТ-З-Зб'),
сначала следует найти значения функции Fi/(acosy) в зависимости
476
Глава XI
от величины Z, а затем применить численное или графическое
интегрирование (рис. XI-3-8).
Коэффициент момента конуса. Используя (X1-3-32) для добавочного
коэффициента давления на конусе, можно получить из соотношения (XI-3-35)
формулу для расчета коэффициента момента:
2 а
Wlzp— о 77Г
о С6 Ui
(XI-3-36)
Коэффициент момента очень тонких тел вращения. Если внести
(XI-3-27) в формулу (1-5-8), то получим
= -2а
(XI-3-37)
где WT — объем тела вращения;
Wn = xKSmm— объем цилиндра, основание которого равно площади
наибольшего поперечного сечения, а высота —длине тела.
Если момент определяется относительно точки, расположенной от носка
на расстоянии хц. т, то
[(^ ) ^] (XI-3-37')
Формула (XI-3-37) для реальных тонких тел вращения верна лишь
в отношении порядка величины коэффициента момента. Более удовлетвори-
ос cosi
0,2
0,1
О
-0,1
0,2
т.,
1,0
—^
Т
1
\
Z'
ь
\
Рис. X1-3-8. Графическое
определение коэффициента момента
1
Рис. X1-3-9. Угловая
производная от коэффициента момента
тонкого конуса:
1 — точная теория; 2 — расчет по
методу источников; 3 — по теории
тонкого тела
тельные результаты по этой формуле получаются для тонких тел
произвольной формы без хвостового сужения. Для тонких конических головок она
дает также неплохое приближение. Например, для конуса, у которого
5Д0Н = 1 и ИУУГц = 1/3, значение mzp = — 1,33 а оказывается близким
к достаточно хорошему результату для mzp, равному —1,27 а и получаемому
по (XI-3-36) при Моо = 1,87 для конуса с углом (Зк = 0,1.
Данные, приведенные на рис. XI-3-9, также показывают, что результаты
расчета с помощью формулы (XI-3-37) производной т% = dmzp/da для того же
конуса хорошо согласуются с точной теорией. Из результатов расчета
по точной теории видно, что у тонких конусов производная т% почти
не зависит от числа Моо.
Влияние отрыва. Отрыв потока на верхней части обтекаемой
поверхности приводит к появлению дополнительного момента тангажа.
Элементарная величина этого момента (рис. XI-3-10)
dMzf = — х dNf = — (
Ci
= -dm.
•zf
PooF2oc
2 ■
'МИД *
Аэродинамика тонких корпусов в линеаризованном потоке
477
откуда
2 с sin2 a
к «3
rxdx.
(XI-3-38)
"МИД
Если хвостовая часть тела невелика по длине, то при вычислении
коэффициента момента от сил, вызванных отрывом потока, эту часть тела
можно заменить цилиндром, после чего приведенная формула упростится
и при условии малых углов атаки
Полный коэффициент момента является суммой составляющей от
давления, определяемой по формуле (XI-3-37), и составляющей, возникающей
при отрыве потока и вычисляемой из т ^
выражения (XI-3-39), т. е.
X
1
dx
—<
Рис. XI-3-10. К определению момента
от сил трения
Для цилиндрического тела с
конической головкой эта формула дает более
удовлетворительные результаты, чем для
такого же тела, имеющего сужающуюся
или расширяющуюся хвостовую часть.
Более надежные данные по
сравнению с формулой (XI-3-40) могут быть получены экспериментальным путем.
Если предварительно определены коэффициенты нормальной силы и центра
давления, то коэффициент момента
тг = С]усц.п. (XI-3-41)
Коэффициент центра давления
Конус и тело вращения произвольной формы. Из формул (1-4-11)
следует, что при небольших углах атаки центр давления тонкого конуса при
отсутствии влияния вязкости расположен от острия на расстоянии 2/3 его
длины, следовательно, сц д = 2/3. Практически влияние вязкости на
величину этого коэффициента пренебрежимо мало.
Для тела вращения произвольной формы, если учитывать только
распределение давления, его коэффициент центра давления определяется при
помощи формул (1-4-11) или (1-5-8). В линеаризованном потоке этот коэффициент
X
МИД
. Д — "
Т/' 1 Т/'
\[—Z—rdxT [—^—^cdx. (XI-3-42)
L«) a cos у J J a cos у v '
о о
Эта формула не учитывает влияния отрыва и поэтому пригодна для тел
со сравнительно короткой цилиндрической частью.
Функция VJ (аъоъу) и, следовательно, коэффициент центра давления
не зависят от угла атаки. Для тонких тел вращения с параболической
образующей и удлинениями приблизительно до 5 расчет сц. д можно вести по
приближенной формуле
сц д = —— Ю~2(11 -г^о) х, (XI-3-43)
где щ = (а'Ро)"1-
478
Глава XI
r [ r=x(2-x)
Ц.В
Коэффициент центра давления, вычисленный по этой формуле, отнесен
к длине головной части, т. е. сц,д = хц, дАг и соответствует условиям
линеаризованного обтекания. Безразмерная величина х, входящая в формулу
(XI-3-43), определяется отношением х — х/хМ1/щ и должна удовлетворять
условию (1,1-М,15)>я>0 (рис. XI-3-11).
Из формулы (XI-3-43) видно, что коэффициент центра давления слабо
зависит от числа Моо. С увеличением Моо центр давления несколько
сдвигается ко дну тела. Это объясняется тем, что
с возрастанием скорости разрежение в конце
головки уменьшается и, следовательно,
ослабляется дестабилизирующий эффект хвостового
х участка. При Моо = 2,5 — 3 разрежение
практически исчезает, а при больших числах Маха
возникает уже положительное избыточное
давление, поэтому концевая часть головки
начинает играть роль своеобразного
стабилизатора.
При небольших скоростях (Моо < 1,5)
центр давления может смещаться к острию
тела, так как нормальная сила на передней
части головки будет возрастать значительней,
чем на ее конце.
Стабилизация головных частей.
Коническая головка или головка с произвольной
образующей будут обладать статической устойчивостью в том случае, если центр
давления расположен за центром тяжести, т. е. ближе ко дну тела. При
этом запас устойчивости определяется в процентах из соотношения
у^*ц.д-*ц,т 10QO/^
Рис. X1-3-11. Геометрические
параметры корпуса, необходимые
для расчета коэффициента центра
давления
Для обеспечения положительного запаса устойчивости можно, очевидно,,
при заданной форме головки, а значит, при заданном значении
коэффициента сц. д утяжелить носовую часть и сдвинуть тем самым центр тяжести
к острию.
Можно также добиться положительного запаса устойчивости, сдвигая
ко дну тела его центр давления. Для этой цели используются различные
способы стабилизации. К их числу, в частности, относится стабилизация
с помощью оперения. Применяются также другие аэродинамические
устройства.
Стабилизация оперением применяется наиболее широко. Она основана
на том, что оперение, расположенное в конце тела, создает дополнительную
силу, благодаря которой центр давления перемещается ко дну.
Этот же эффект достигается использованием так называемых
стабилизирующих юбок. Поясним этот способ стабилизации на примере тела
вращения в виде конической головки. Предположим, что мы имеем сплошной
конус. Так как его центр тяжести расположен от носка на расстоянии 3/4
высоты (рис. XI-3-12, a), a центр давления —на расстоянии 2/3, то ясно,
что такое тело в полете будет статически неустойчиво, так как в данном
случае запас устойчивости отрицателен и равен
У=(сц.д-хц.т) 100= (|—-|) Ю0= -8,34%.
Теперь присоединим ко дну конического тела стабилизирующую юбку.
Она мож'ет являться либо усеченным пустотелым конусом, представляющим
собой продолжение основного тела (рис. XI-3-12, б), либо тем же конусом,.
Аэродинамика тонких корпусов в линеаризованном потоке
479
но с меньшим углом наклона образующей (рис. XI-3-12, в), либо
пустотелым цилиндром (рис. XI-3-12, г). Все эти варианты стабилизирующих
устройств определяются в основном конструктивными соображениями.
Наиболее простым для расчета запаса устойчивости является вариант,
когда коническая юбка является продолжением основного конуса. В этом
случае при незначительном весе юбки можно считать, что положение центра
давления всего стабилизированного тела
не меняется и его безразмерная
координата
_ *ц. т _ 3 h
Хц-д"~ ht ~ 4 ^ '
а)
•*—у— *А
i
1
3/4 h
1
1!
где h — высота основной головки;
hi — высота всего тела со
стабилизирующей юбкой.
Центр давления такого тела будет
расположен от острия на расстоянии
2/3/г1а Следовательно, коэффициент
центра давления равен 2/3, а запас
устойчивости у = -| [1 — (9/8) (Л/АО! 10°0/°-
Подбором величины h можно добить- Рис. X1-3-12. Схема взаимного
располося того, что центр давления
расположится между дном и центром тяжести
и запас устойчивости окажется
положительным. Обычно на практике запас устойчивости берется в пределах
8 — 10%. Исходя из выбранной его величины, определяют потребное
отношение h/hi.
Аналогичный способ стабилизации с помощью конической юбки может
быть применен и в том случае, когда основная головка имеет криволинейную
жения центра давления и центра
тяжести у конического тела
а)
5)
Рис. X1-3-13. Схема взаимного расположения центра
давления и центра тяжести у головок произвольной
формы
образующую (рис. XI-3-13). Как показывают эксперименты, коэффициент
центра давления тела, изображенного на рис. XI-3-13, аш представляющего
собой неполную головку с конической юбкой при значении hi порядка
(1,5 — 2) /г, равен примерно 0,5 — 0,55. При этом он слабо зависит от числа
Моо, угла атаки и длины стабилизирующей юбки, хотя и обнаруживается
тенденция к некоторому увеличению коэффициента сц.д при возрастании
угла атаки или же при переходе к большей длине юбки.
Представляет интерес анализ характера изменения у такого тела
коэффициента нормальной силы. Его величина практически не зависит от числа
Моо. Влияние угла атаки выражается линейной зависимостью
Cn = (2,5 ~-3) а.
480 Глава XI
На рис. XI-3-13, б представлена другая форма полной (или
касательной) головки со стабилизирующей юбкой.
Как показывают исследования, для таких головок с удлинением Хг =
= 3,5 — 5 и стабилизирующими юбками, имеющими удлинение А,кр — 1,5 — 2,5
и относительный диаметр донного среза ^ДОн = ^донМиид = 1,5 — 1,8,
коэффициент центра давления сц. д = агд. д//^! примерно равен 0,55 — 0,60, причем
меньшее из этих значений соответствует более короткой и узкой
стабилизирующей юбке.
Длину hi тела со стабилизирующей юбкой при известном значении
длины h, а также заданном положении центра тяжести выбирают так же,
как и в примере с коническим телом.
Коэффициент центра давления длинных тел. В том случае, когда
к головной части присоединяется дополнительный достаточно длинный
участок, на положение центра давления такого тела определенное влияние будет
оказывать отрыв потока. Это влияние, возрастающее по мере увеличения
угла атаки, приводит к смещению центра давления ко дну и, следовательно,
к повышению статической устойчивости.
Рассмотрим случай, когда коническая головка с удлинением кг
заканчивается цилиндром некоторой длины Хц^мид, который, в свою очередь, снабжен
сужающейся или расширяющейся хвостовой частью с относительной длиной
^кр = #кр/^мид. При условии Яц> 1,5 — 2 для приближенной оценки
коэффициента центра давления тонких тел вращения с небольшим сужением
(£дон ~ 0,9 —1,1) можно пользоваться формулой
(XI-3-44)
Эту формулу можно применять для ориентировочной оценки величины
сц. д, имея в виду при этом, что в действительности центр давления будет
расположен ближе к острию, чем это получается по расчету. Это видно,
например, из рис. XI-3-6, где приведены экспериментальные данные для
длинного заостренного тела вращения. Аналогичные результаты, полученные
для цилиндрических тел с коническими и оживальными заостренными
головками, показаны на рис. XI-3-7.
С увеличением числа Моо у тела с расширяющейся кормой наблюдается
тенденция к уменьшению величины сц.д. Так, для одного из тел вращения
с конической расширяющейся кормой коэффициент центра давления при
Моо = 4 оказался меньше примерно на 7%, чем при Моо = 2. Следовательно,
увеличение числа Моо привело к некоторой дестабилизации.
Более удовлетворительные результаты по формуле (XI-3-44) получаются
в том случае, когда сужение или расширение в конце тела отсутствует и,
следовательно, в этой формуле надо принять <5ДОН = 1 и Хкр = 0.
Помимо приведенных формул, приближенный, расчет коэффициента
центра давления тела произвольной формы может быть произведен при помощи
аэродинамических коэффициентов, известных для отдельных элементов этого
тела. Поясним это на примере с телом вращения, схема которого
изображена на рис. XI-3-14.
Расчленим это тело на такие элементы, для каждого из которых
известны создаваемая им нормальная сила, а также точка ее приложения.
Вычислим относительно точки О сумму моментов сил, которая равна произведению
суммарной нормальной силы на ее плечо хц. д, представляющее собой
расстояние от носка до отыскиваемого центра давления всего тела:
2. д ±
д,
Аэродинамика тонких корпусов в линеаризованном потоке
481
где индексы «г», «ц», «кр» обозначают нормальную силу и координату точки
еэ приложения соответственно для головной части, цилиндра и кормы,
причем, под Л^ц будем понимать нормальную силу, возникающую
вследствие отрыва потока и действующую на цилиндрический участок тела, т. е.
Учитывая, что N = NT -f Nn ± 7VKP и вводя затем вместо сил их
коэффициенты как для всего тела, так и для каждого из его элементов,
получим уравнение для
коэффициента центра давления всего
тела
— JL /г ~~г _1_
х
г
0
*ц.Э.
х'и..З.
! л?цра
Г '
р
■ КР Кр \ /"VT О / С\
j,. д zn <^iY #ц. д/5 (Al-o-40)
в котором суммарный
коэффициент нормальной силы
Cjv—Сдг+Сдг rh Сдг. Знак «плюс»
соответствует расширяющейся
корме, обусловливающей
эффект стабилизации, а знак Рис. X1-3-14. Схема для расчета коэффициента
«минус» — сужающемуся хво- центра давления корпуса
стовому элементу,
создающему отрицательную по знаку нормальную силу. В выражении (XI-3-45)
содержатся также безразмерные координаты хЦт д = хц. дАгк, хц = хц/хктл. хк? =
В общем случае, если тело вращения состоит из нескольких элементов,
формула для расчета коэффициента центра давления имеет вид
Рассмотрим, как определяются отдельные величины, входящие в
формулу для расчета коэффициента центра давления. Коэффициент нормальной
силы cN всего тела подсчитывается по (XI-3-31). Значение cTN для головной
части должно быть вычислено с учетом влияния примыкающего к ней
цилиндра. В этом случае рекомендуется вычисление вести по формуле
cN = За. Координата Хцш д центра давления этой части тела также будет
испытывать влияние цилиндра, причем, так как обычно примыкающая
к головке часть цилиндра является несущей, то она несколько сдвигает
центр давления головной части назад по сравнению с его положением для
изолированной головки. Для конической головки с цилиндром этот сдвиг,
например, составляет около 5 —10%. Следовательно, при вычислении
координаты Хц, д для такой головки с примыкающим цилиндрическим участком
можно принимать ее значение равным хтц, д = (2/3) (1,05-4-1,10) #мид, т. е. в этом
случае безразмерная координата
2 К
Хц. д —
ц- д
-(1,05-^-1,10).
(XI-3-47)
Для параболической головки расчет ведется по обычной формуле
#ц. д = сц.д (ЯмидАк), причем, если головка подходит по касательной к
цилиндрической части, то коэффициент сЦш д берется по формуле (XI-3-43). Если же
головка укороченная, то значение этого коэффициента, полученное по (XI-3-43),
следует увеличить примерно на 5 — 10%. Это вызывается тем, что в
рассматриваемом случае примыкающий к головке цилиндрический участок ста-
31-114
482
Глава XI
новится несущим, как и цилиндрический участок, примыкающий к
конической головной части.
Рассмотрим теперь ту часть коэффициента нормальной силы и
соответствующее ей значение безразмерной координаты центра давления, которые
обусловлены поперечным обтеканием. Коэффициент нормальной силы
цилиндрической части можно опреде-
сц.Э.
лять по формуле
— CNf = COL* (Лк — t
(XI-3-48)
считая, что корма дает такую
же составляющую,
обусловленную отрывом, как
цилиндрический участок равной длины.
Безразмерную координату
Хц, д центра давления найдем,
исходя из предположения, что
нормальная сила при
поперечном обтекании тела распределяется по его участку длиной Як — А,мид
равномерно и, следовательно, центр давления здесь расположен в середине, т. е.
Рис. XI-3-15. Схема для расчета коэффициента
центра давления оперенного тела вращения
Абсолютную величину коэффициента нормальной силы, создающейся
на хвостовой сужающейся или расширяющейся части тела в результате
перераспределения давления при невязком обтекании, в соответствии с (XI-3-28)
можно подсчитывать по формуле
4Р = 2а (5Дон -1) • (XI-3-50)
Точку приложения нормальной силы в первом приближении можно
считать расположенной в середине кормы. В соответствии с этим
безразмерная координата
г л \
-~КР *Ф л 1 ЛКр /VT Q 1Г/1 \
*Л = -=- = 1~о-Х" • (XI-3-51)
Стабилизация длинных тел вращения. Стабилизация длинных тел
вращения, как и коротких, может осуществляться с помощью оперения, а также
специальных аэродинамических устройств. Наиболее распространенной
является стабилизация оперением.
При этом, если известен коэффициент с™ нормальной силы оперения,
отнесенный к миделевому сечению тела, а также безразмерная координата
х™х = ХцПд/хк центра давления оперения, то в соответствии со схемой,
приведенной на рис. XI-3-15, найдем следующее выражение для коэффициента
центра давления оперенного тела:
WT. Я — - "
(XI-3-52)
cn ~
Здесь с1^ и с%и — соответственно коэффициенты нормальной силы
корпуса и оперения;
—коэффициент центра давления корпуса и безразмерная
координата центра давления оперения.
Коэффициент нормальной силы корпуса определяется по формуле
n — CiVP как сУмма тРех составляющих соответственно для головки,
ск и
Аэродинамика тонких корпусов в линеаризованном потоке 483
цилиндра и кормы. Рекомендации для их расчета были изложены ранее.
Коэффициент центра давления корпуса Сц. д находят из выражения (XI-3-45).
При вычислении аэродинамических характеристик корпуса следует
учитывать влияние оперения, которым снабжено тело вращения. Это же
относится и к расчету характеристик оперения, которое будет испытывать
влияние корпуса. Таким образом, необходимо, чтобы расчеты осуществлялись
с учетом интерференции между корпусом и оперением. При оценке запаса
статической устойчивости оперенного тела вращения можно вести вычисление
коэффициентов нормальной силы корпуса и оперения, как и координат
центров давления, изолированно для каждого из этих элементов, т. е. беа
учета интерференции. Точность этих расчетов возрастает с увеличением
скоростей обтекания. Координата центра давления оперения может быть
принята расположенной в середине средней аэродинамической хорды.
Надлежащим подбором площади оперения можно добиться того, что
центр давления оперенного тела окажется позади центра тяжести и тем
самым будет обеспечен положительный запас устойчивости. Если задаться
его величиной, то можно при выбранной форме стабилизатора определить
его площадь в плане. __
Действительно, так как запас устойчивости У = (сц. д— хЦт т) 100%, где
с ц. д и хц, т соответственно коэффициент центра давления и безразмерная
координата центра тяжести оперенного тела, то, очевидно, сц а = хц т +
+ У/100%.
Далее, общее выражение для коэффициента с°р можно написать в виде
с^ = (с™)' (£опА$мид), где (с^У — коэффициент нормальной силы оперения,
отнесенный к площади в плане стабилизаторов. При приближенных расчетах
с учетом интерференции в площадь Sou включается и часть площади корпуса
(подфюзеляжная часть), расположенная под оперением.
С помощью выражения (XI-3-52) можно найти отношение площади
оперения с учетом подфюзеляжной части к площади наибольшего сечения
тела вращения:
Задаваясь запасом устойчивости в 8 —10%, можно по этой формуле найти
необходимую величину относительной площади оперения 50ш при которой
этот запас устойчивости обеспечивается.
Другим весьма эффективным способом стабилизации является
использование хвостового расширяющегося конуса. Так же, как и оперение, он
создает положительную по знаку подъемную силу и тем самым сдвигает
центр давления ко дну тела.
Для определения коэффициента центра давления при таком способе
стабилизации можно пользоваться формулой (XI-3-45). Заменив в ней
коэффициенты с*у и с"Р их значениями, например, по формулам с^ = 2а и с^ =
= 2а(5дОН—1)» получим __ _ _
IX • Л /V И • II \ jUjUxi 'II- II /А7"тог"/\
=^-J=L- . (Xl-o-54)
При помощи этого выражения для заданного запаса устойчивости
и выбранной длины кормы можно найти необходимое уширение хвостовой
части, т. е. величину безразмерной площади:
31*
Глава XI
Анализируя это выражение, можно установить, что при^весьма малых
углах атаки (а—>0) и заданных других условиях величина £дон принимает
наибольшее значение. Этой величине соответствует, очевидно, при выбранной
длине кормы наибольший угол наклона образующей конуса.
Сопротивление, обусловленное
подъемной силой
При обтекании корпуса под углом атаки появляется дополнительное
сопротивление, обусловленное возникновением подъемной силы. Это
сопротивление можно рассматривать как результат влияния вихрей, сбегающих
с корпуса и изменяющих распределение давления на его поверхности.
Сопротивление, обусловленное подъемной силой, эквивалентно индуктивному
сопротивлению крыльев конечного размаха. Его величину можно
определить [51], рассмотрев контурный интеграл в формуле (IV-4-30). Внесем
под интеграл значение Фо = ф* + фа> гДе ф* и Фа определяются
соответственно выражениями (IV-4-15) и (IV-4-17). Тогда те члены, которые
содержат фа, дадут отыскиваемую составляющую сопротивления Хг. Полагая
в соответствии с условием безотрывного обтекания дц)а/дг= —asin0, найдем
Соответствующее значение коэффициента сопротивления
^Szo*oc\ (XI-3-56)
где 5Дон^£донА$мид- Приведенные формулы можно выразить через подъемную
силу Y = 2ягд0НДО или коэффициент этой силы
Действительно, Xt=-^Ya или
cxi=\cya. (XI-3-58)
Сопротивление, обусловленное отрывом потока. Это сопротивление
но своей природе является сопротивлением давления. Оно не связано с силами
поверхностного трения и возникает из-за отрыва потока с верхней стороны
корпуса, обтекаемого под углом атаки, и, как следствие, образования
вихрей. Таким образом, сопротивление при наличии поперечного обтекания
обусловлено силами, нормальными к оси тела. Если суммарная нормальная
сила, возникающая при таком обтекании, найдена, то, умножив ее на угол а,
можно определить дополнительную силу сопротивления. В соответствии
с (XI-3-30') коэффициент этой силы
cxf = c±(Xn + Kv)a3. ' (XI-3-59)
При расчете величины cxf надо иметь в виду, что сопротивление при
поперечном обтекании, как и дополнительная подъемная сила, возникает,
начиная с некоторых углов атаки, когда происходит отрыв потока и, как
следствие, перераспределение давления на верхней стороне.
При более точном анализе отрыва следует учитывать, что на
протяженность области отрыва влияет положение точки перехода ламинарного
пограничного слоя в турбулентный. С ростом угла атаки точка перехода смещается
к головной части и это вызывает более ранний отрыв и образование вихрей.
Для упрощения расчетов можно считать, что дополнительная сила
сопротивления появляется при любых малых углах атаки и протяженность
области отрыва, начинающаяся в конце головки, равна Хц + Я1ф.
АЗРОДИНАМИКА
ЗАТУПЛЕННЫХ
ТЕЛ ВРАЩЕНИЯ.
§Х1М. Невязкое обтекание
затупленного носка
Общее решение для носка
произвольной формы
Изучение аэродинамики всего затупленного тела связано с исследованием
обтекания его передней части, выполненной в виде затупленного носка
какой-либо формы. Результаты этих исследований являются основой для
расчета параметров потока на остальном участке тела. С другой стороны,
эти же результаты имеют самостоятельное значение, так как позволяют
определить аэродинамические характеристики затупленного носка.
Суммарные аэродинамические характеристики тела могут быть определены
сложением составляющих для носка и остального участка.
При этом необходимо указать, что если обтекание периферийной части
тела зависит от затупления, то условия течения около самого носка
определяются лишь его формой, точнее говоря, формой части носка до
«звуковой» точки на его поверхности. Из этого следует, что задача об обтекании
затупленного носка является автономной, т. е. решается независимо.
Ниже рассматривается невязкое обтекание. Тем не менее отыскиваемое
решение имеет большое практическое значение, так как оно позволит
определить основные условия течения вне пограничного слоя, которые
необходимо знать при исследовании процессов трения и теплопередачи,
формируемых в самом пограничном слое.
К настоящему времени создан ряд методов решения задачи об
обтекании затупленного носка. Некоторые авторы основывали свои методы на
задании формы и положения ударной волны, найденных, например, из
эксперимента. После этого решали обратную задачу: система нелинейных
дифференциальных уравнений в частных произвольных интегрировалась
приближенно при известных граничных условиях на криволинейной
ударной волне и таким образом рассчитывался поток около затупления. При
этом определялась сама форма носка.
Академик А. А. Дородницын предложил метод интегрирования, который
сводится к численному решению в некоторой области аппроксимирующей
системы обыкновенных дифференциальных уравнений [10]. В частности,
этот метод может быть использован, когда граница области, например
криволинейная ударная волна перед затуплением, является заранее
неизвестной. Следовательно, ее форма и положение могут определяться в процессе
решения задачи об обтекании носка. Используя этот метод, О. М. Бело-
церковский осуществил расчет обтекания затупленных симметричных тел
с отошедшей криволинейной ударной волной ([68], 1960, XXIV, вып. 3).
Рассмотрим систему уравнений для решения этой задачи. При расчете
смешанного (дозвукового, звукового и сверхзвукового) вихревого течения
газа, возникающего между криволинейной ударной волной и затупленным
носком произвольной формы, удобнее использовать систему уравнений
в сферических координатах (рис. ХН-1-1). Так как рассматривается осе-
симметричное обтекание, то в эту систему войдут уравнения движения
486
Глава XII
(Ш-2-8) и неразрывности (III-2-17) в упрощенной форме, а также условие
(Ш-2-54) изэнтропического течения газа.
Для осуществления расчетов удобнее уравнение движения
преобразовать с помощью уравнения Бернулли и ввести функцию тока Т. Тогда
полная система уравнений будет
дг
~дв~
д (rpVQVr sin 6) ■■ /o- f -
дв ~
»(r%Vr sin 0) . d(rrF@sine)
дг
дв
(Х1Ы-1)
где
Здесь введены безразмерные параметры V = V/Vmax, р = р/роо, p =
r = r/l, где Z является некоторым характерным
Ударная
болна
линейным размером тела.
Энтропийная функция /, изменяющаяся
при переходе от одной линии тока к другой,
т. е. зависящая от функции тока i|),
определяется соотношением S — cv In /.
Система из четырех уравнений (ХП-1-1)
х позволяет рассчитать неизвестные Vr, Fe, /
и \р. Ее решение должно удовлетворять
граничным условиям на поверхности носка и
ударной волны. На поверхности затупленного
носка, уравнение образующей которого r = ro(Q),
должны выполняться равенства
Рис. ХП-1-1. Расчетная схема
потока около затупления
причем энтропийную функцию находят для условий перехода через вершину
ударной волны, записываемых в форме
-— (!L=±\kv-2k[vz (/g~1)2(l F2 Л Ш1-1-4)
Граничные условия на ударной волне с образующей г = г0 (0) -f- s (в),
где s~ расстояние вдоль луча, 0 = const от контура тела до волны, находятся
по теории криволинейного скачка уплотнения и имеют вид
Vr = Vy sin 9С + Vx cos 6C; V@ = Vx sin 9C + Vy cos 9C;
vv = (Fc - Vx) ctg 9C;
— 1-ПТ (sin2 Gc — ;
(XII-1-5)
Из выражений для
функции.
и р находят граничное условие для энтропийной
Аэродинамика затупленных тел вращения
С решением системы уравнений (ХП-1-1) по методу А. А. Дородницына
можно познакомиться по специальной литературе ([68], 1960, вып. 3).
Численное интегрирование может вестись на электронной счетной машине. В
результате рассчитываются потоки около тел с отошедшей ударной волной, причем
тела могут иметь различную форму затупления, в том числе в виде сферы,
торца, криволинейной поверхности с изломом и т. д. Эффективность
указанного метода определяется именно возможностью применения
быстродействующих электронных счетных машин, на которых окончательные
результаты получаются с требуемой точностью.
Результаты расчетов позволяют судить о форме и положении ударной
волны, о величине и характере распределения параметров потока между
волной и затупленным носком.
§ XII-2. Приближенные
методы расчета обтекания
носков различной формы
У
Сферический носок
Система уравнений и решение для окрестности точки полного
торможения (критической точки). Одной из наиболее характерных точек
сферического носка является точка полного торможения. Изучение течения в ее
окрестности представляет интерес
прежде всего потому, что оно свя- шш"
зано с такой практической
задачей, как определение тепловых
потоков, которые могут достигать
здесь наибольшей величины. Ниже
показано, что эта величина зависит
от начального градиента скорости
вдоль сферической поверхности.
Начальный градиент скорости
может быть найден в результате
исследования невязкого обтекания
затупленного носка. Наряду с
этим решение задачи о течении
вблизи критической точки
позволяет определить расстояние от
волны до тела, а также распределение газодинамических параметров в этой
небольшой области, причем решение может быть получено в общем случае
с учетом физико-химических превращений газа.
Рассмотрим решение сформулированной задачи ([72], 1957, № 1).
С этой целью воспользуемся уравнениями движения (Ш-2-10) и
неразрывности (III-2-20) в криволинейной ортогональной системе. Начало
координат этой системы совпадает с критической точкой, координата х отсчитывается
вдоль поверхности, а у — по нормали к ней (рис. ХН-2-1).
Если принять, что исследуется область в окрестности критической
точки и набегающий поток имеет очень большую сверхзвуковую скорость,
то исходные сложные уравнения могут быть упрощены. В самом деле, при
этих условиях поток за ударной волной по своим свойствам практически
несжимаем, так как число М2 мало отличается от его значения [(к — 1) /2/с]1/2,
соответствующего случаю предельного течения (при Моо —>■ оо, к = const)
за прямым скачком. Следовательно, в рассматриваемой окрестности
плотность можно принять постоянной и равной р— роо/р, где р = роо/рс> а рс—
Рис. ХП-2-1. Составляющие скорости потока
около затупленного носка в криволинейных
координатах
488
Глава XII
плотность за ударной волной в критической точке. Таким образом, в
уравнениях движения и неразрывности переменную плотность р можно заменить
постоянной величиной роо/р.
Так как рассматриваются большие скорости, то в этом случае ударная
волна будет близко подходить к поверхности тела. При этом область
возмущенного течения располагается в тонком слое некоторой толщины s, весьма
малой по сравнению с радиусом кривизны R поверхности вблизи
критической точки.
Таким образом, если принять, что s/R < 1, то, очевидно, и y/R < 1,
так как 0 <?/<$. Следовательно, в уравнениях для газодинамического потока
величиной y/R по сравнению с единицей можно пренебречь. Кроме того,
в уравнениях (Ш-2-10) можно пренебречь третьими членами в левой части,
так как они имеют меньший порядок опять же вследствие того, что у < R,
а также х < R. Наконец, уравнение неразрывности для условий вблизи
критической точки можно упростить, если принять г я^ х.
С учетом указанных упрощений система уравнений (Ш-2-10) и (Ш-2-20)
принимает вид
(ХП-2-3)
Решение этой системы должно удовлетворять условиям на поверхности
тела в произвольной точке, где при у = 0 нормальная составляющая скорости
Fy=0, затем в критической точке, в которой при у = х = 0 составляющие
Vx = Vy = 0- Кроме того, решение должно удовлетворять условиям течения
непосредственно за ударной волной. Эти условия, написанные для
составляющих скорости в точке А, расположенной на расстоянии s от поверхности
носка, имеют вид (рис. ХИ-2-1)
Vy= -Fsin(P-pc). (XII-2-5)
Для полной скорости V и давления р в текущей точке А в соответствии
с выражениями (Ш-4-24) и (Ш-4-12) и с учетом того, что непосредственно
за скачком р = роо/р будем иметь условия
^- = (р2 sin2 9С + cos2 Эс)1/2; (ХП-2-6)
у оо
Из уравнений (ХН-2-1) и (XII-2-2) можно исключить давление и
плотность. С этой целью эти уравнения продифференцируем соответственно по у
и х. Приравнивая затем результаты дифференцирования и используя
уравнение (ХН-2-3), получим
где функция (выражение для вихря)
со, = dVJdy - dVyldx. (XII-2-9)
Таким образом, задача заключается в отыскании решений уравнений
(ХН-2-3) и (ХП-2-8), удовлетворяющих указанным граничным условиям.
Аэродинамика затупленных тел вращения 489
Предположим, что решение для Vx в окрестности оси х = О можно найти
в виде ряда
Vx = а0 (у) + а, (у) х + а2 (у) х2 + аъ{у)х* + . . . , (ХП-2-10)
в котором х является малым параметром. Структуру этого ряда можно
несколько упростить. Действительно, из условия нечетности, в соответствии
с которым одинаковым по величине, но различным по знаку значениям х
соответствуют равные по абсолютному значению, но противоположные по знаку
составляющие скорости Vx, в разложении сохранятся члены только с
нечетными степенями, т. е.
Vx = а4 (у) х + а3 (у) х* + . .. . (ХИ-2-11)
Учитывая, что рассматривается малая окрестность вблизи критической
точки, членами, содержащими х в третьей и более высокой степени, будем
пренебрегать. Таким образом, приходим к выражению Vx = a± (у) х.
Введем функцию
чтобы
Г(у) = ах(у) и F(0) = 0. (XII-2-13)
Тогда
Vx = xF'(y). (XH-2-14)
Подставляя это выражение для Vx в уравнение неразрывности (ХИ-2-3),
найдем зависимость для другой составляющей скорости
Vv=-2F(y) + f(x). (XII-2-15)
Но по условию безотрывности обтекания Vy(x, 0) = 0, т. 6.-2^(0) +
+ /(д:) = 0, и так как ^(0) = 0, то f(x)=O.
Следовательно,
Vy=-2F(y). (XII-2-16)
Внося соотношения для Vx и Vy в (ХН-2-8), получим уравнение
F"'(y) = 0, (XII-2-17)
которое имеет общее решение
-^- = F(y)=C0 + Ciy + C2y\ (XII-2-18)
Так как F(0) = 0, то С0 = 0. Два других коэффициента можно
определить, если воспользоваться условиями на ударной волне вблизи
критической точки при х—>0. В частности, так как в точке С скорость Vy = Vc =
= —2(Cis0JrC2sl) и угол 9С = л/2, то на основании (ХП-2-6), с учетом
направления оси г/, получаем, что Fc= —pFoo и, следовательно,
См + Сгй-^-. (ХИ-2-19)
С другой стороны,
Vx = xFf (у) = х(С± + 2С2у). (ХН-2-20)
Приравнивая эту скорость ее значению на ударной волне в соответствии
с (ХП-2-4) и переходя к пределу при х—>0, получим
1. cos(P-Pc)
Х
490 Глава XII
Предел в левой части можно вычислить следующим образом. Из
рис. ХП-2-1 видно, что в произвольной точке угол Р — Рс = -^—Сп + Рс)-
Следовательно, cos (|3 — рс) — sin (т] + рс), а для малых величин г| и рс можно
принять sin (т) + Рс) — Л + Рс- Тогда
= I /fex I
Лт V СО )х^0 #сО
х_+0 х х->0
где со —угол наклона радиуса кривизны скачка к оси потока; i?c0 —радиус
кривизны скачка на этой оси.
Отношение
(К) =Л*РсЛ
V со )х-+о V dco /рс->о
равно величине 1/р —1. Это значение можно получить с помощью формулы
(Ш-4-23), в которой надо ввести замену AVn/Vni = 1 — р, Эс = я/2 — со и перейти
к пределу при со—>0. Приняв отношение R^IR^ равным приблизительно
единице, найдем
^ + 2^0 = ^-. (ХИ-2-21)
К уравнениям (ХП-2-19) и (ХИ-2-21) добавим еще одно соотношение
(так как они содержат три неизвестных константы Си Сг, sQ). Это
соотношение вытекает из выражения для вихря за ударной волной. В соответствии
с (ХН-2-20) получаем для условий на поверхности тела зависимость сог =
= dVxldy = 2С2х. С другой стороны, из теории криволинейной ударной волны
известно, что вихрь
^ —or -г V°° (1 — р)2 sin 9C cos 9C dQc
СОг — ZO2^ — f_ =- —т— •
sin (9С — рс) У р2 sin2 9С + cos2 6С ах
Переходя в этом выражении к пределу при х—>0, получим
С2 = (1~р)2 i%-. (ХП-2-22)
1 pR
Подставляя С2 в уравнения (ХП-2-19) и (ХН-2-21) и решая их совместно,
найдем коэффициент 6\ и величину отхода So:
(ХН-2-23)
(ХН-2-24)
где А = 1 —р.
Можно получить и другое выражение для величин s0. Так, в работе [59]
показано, что при больших скоростях обтекания и постоянной плотности
за ударной волной, расположенной концентрично относительно сферической
поверхности, отход
(/| ) (XII-2-24')
Это решение справедливо для малых р (порядка 0,1 и меньше).
Начальный градиент и распределение скорости. Из (ХП-2-20) следует,
что на контуре обтекаемого тела, где у = 0, скорость Vx = Cix, т. е. с учетом
(ХП-2-23)
Vx = + ТЛГ^А2 ~^~ х. (ХН-2-25)
Так как при х > 0 или х <с 0 должно быть соответственно Vx > 0 или
Vx<i0, то ясно, что в этой формуле, а значит, и в равенствах (ХП-2-23)
и (XI1-2-24) должен быть выбран нижний знак. Учитывая сказанное, можно
по найденным коэффициентам С\ и С2 определить составляющие скорости
Аэродинамика затупленных тел вращения
491
в возмущенном потоке
V
УУ о~ / Т/14-А2
А2
/1 —А2 А2
рЛс0 p2i?2 У
со
(ХП-2-26)
где рЯс0 выражается через s0 по формуле (ХН-2-24).
Как уже отмечалось, для определения теплопередачи необходимо знать
величину градиента скорости в критической точке. Согласно (ХП-2-25)
(ХП-2-27)
Экспериментальные исследования показали, что эта зависимость,
полученная для случаев обтекания с очень высокими скоростями, может быть
использована в приближенных ^
расчетах и при сравнительно не- А27Т
больших скоростях. Это следует,
например, из рис. ХН-2-2, где
приведены экспериментальные
значения безразмерного
градиента скорости %D\IVоо (Дг = 2J?T).
В формулу (ХН-2-25),
которую перепишем в виде Vx = кх,
можно ввести вместо х
центральный угол г), определяемый из
выражения х = k\Rt. Тогда Vx =
= Ai?Tr], что указывает на
линей0,8
г
— —
— т.
— —
Ifi
3.0
5,0 Мо
Рис. ХП-2-2. Градиент скорости в критической
точке тела:
1 — теория; 2 — эксперимент
ную зависимость Vx от tj.
Напомним, что эта зависимость
получается из анализа обтекания
малой окрестности носка потоком с очень большой скоростью. Однако
экспериментальные исследования показали, что линейный закон изменения
скорости действителен на значительно
большем участке криволинейной
поверхности, а также при
сравнительно небольших числах М«>.
Это подтверждается данными
на рис. ХП-2-3, где показаны
значения безразмерной скорости
Vx/(kD?) на полусферическом носке,
вычисленные по измерениям в
аэродинамической трубе для четырех
различных чисел Моо. Можно
заметить, что линейный закон хорошо
выдерживается до значений угла
г] = 45 — 50° и практически
сохраняется с небольшим отклонением
от него при более высоких
значениях Т).
Соответствующая этому закону
формула Vx = XRTv) может быть
х, где х = x/DT, а безразмерный градиент скорости
Рис. ХП-2-3. Распределение скорости
сферической головной части
представлена в виде Vх = \
по
Я = /)Д/7оо. Экспериментальные и теоретические данные для этого градиента
492
Глава XII
приведены на рис. ХИ-2-4, причем градиент скорости определен по
приближенной зависимости
WxA _ 1 i/2(A)-/>oo) (ХН-2-27')
дх ) х=0 RT * Ро
которая получена на основе усовершенствованной формулы Ньютона р =
= p0cos2r\. При помощи этой формулы можно оценить распределение
скорости по сферическому носку. Для этого следует применить выражение*
получаемое из условия изэнтропического течения за ударной волной,
где коо — отношение теплоемкостей в невозмущенном потоке;
к — среднее отношение теплоемкостей за головным скачком уплотнения,
которое при очень высоких температурах может достигать
значения к= 1,1 — 1,2.
Отношение давлений, входящее в (ХП-2-28), в соответствии с формулой
Ньютона равно
Ч (ХИ-2-29)
-Е- — cos21
Ро
Ро
причем при достаточно больших числах Моо величина р<х>/р'о может быть
принята приблизительно равной (&ML)"1.
Из (XI1-2-28) нетрудно получить упрощенные зависимости для
скорости и градиента ее в окрестности критической точки:
(ХИ-2-30)
в которых
К=\ ^=
Это выражение для К, а значит, и сами формулы (ХП-2-30) можно
упростить, если рассматривать очень большие скорости. Тогда в (ХН-2-31)
_ можно принять равными нулю величины,
обратно пропорциональные ML- С другой
стороны, упрощение достигается тем, что
поток в окрестности острия принимается
несжимаемым. В соответствии с этим можно
написать: р'о = р + — p'0V%. Давление здесь
можно заменить по формуле (ХП-2-29),
в которой ввиду малости т] принимаем
cosrj^l, sin т] с^. т] = xRT.
Дифференцируя затем Vx по х, придем к формуле
(ХП-2-27/) для градиента скорости. В этой
формуле при больших скоростях можно под
корнем пренебречь величиной р<х>1р'о.
Для некоторого диапазона скоростей, охватывающего дозвуковые и
средние сверхзвуковые скорости, в окрестности критической точки
Vx = %Voo^- . (ХИ-2-32)
OcboN
о
7ГЪ—-
— —
т
3 —
1
О 2 4 6 8 Мс
Рис. ХП-2-4. Градиент скорости в
критической точке сферы:
О — эксперимент
В этой формуле для несжимаемого потока
градиент скорости
их
; = 1,5 и, следовательног
(ХН-2-33)
Аэродинамика затупленных тел вращения
493
С увеличением числа Моо значение % уменьшается.
может быть найдено из эмпирического выражения
При М^ > 1 оно
Х = 0,8М-°'232. (ХП-2-34)
Представляет интерес оценить размеры области несжимаемого потока,
а также расстояние до звуковой точки на сфере. С этой целью можно
воспользоваться соотношением (ХП-2-28) для изэнтропического течения, считая,
что оно начинается от критической точки. С
известным приближением условия в этой точке
можно считать такими, как непосредственно за
прямой частью ударной волны.
В частности, таким путем определена
область недиссоциированного несжимаемого
течения при к = 1,4 в предположении, что за ее
пределами местные числа М>0,3. Схематично эта
область изображена на рис. ХИ-2-5. На рис.
ХП-2-6 показано найденное тем же способом
и при тех же условиях угловое расстояние до
точек на сфере, где местные числа М = 0,3
и М = 1.
Эти результаты хорошо согласуются с теми
данными о положении «звуковых» точек на сфере
рис. ХН-2-7, которые были получены на
электронной счетной машине по методу А. А. Дородницына. Рис. ХП-2-7 дает также
представление о форме «звуковых» линий при различных числах Моо и
положении «звуковых» точек на ударной волне. Соответствующие этим точкам
углы наклона ударной волны показаны на рис. ХИ-2-6. В реальных
условиях области несжимаемых и дозвуковых сжимаемых течений будут меньше,
\
Рис. XI1-2-5. Расположение
области несжимаемого потока
(М <! 0,3) в окрестности
критической точки сферы, Моо =
= 5,1; роо/р2 -0,2; к =1,4;
1 — ударная волна, 2 —
поверхность тела
2 1
80
60
W
20
\
-5—
—
ц, —
/ '
А1)
ЧУ
м.
Рис. ХП-2-6. Положение «звуковых» точек на
сфере (1) и на ударной волне (2). Угловое
расстояние (3) до границы несжимаемой
области на сфере (до точки, в которой число
М = 0,3)
/////% м
//// / * линии4
*—
оо=
— —
3
6
оо
1,0
0,5
0,5
Рис. ХП-2-7. Расположение
ударных волн и «звуковых»
линий около сферической
поверхности при различных
числах Моо
чем по приведенному расчету. Это обусловлено тем, что колебательные
возбуждения молекул или диссоциация за ударной волной при больших
скоростях приводят к снижению температуры. Это способствует
уменьшению скорости звука. Следовательно, при той же скорости на сфере местные
числа М возрастут и точки М = 0,3 и М = 1 сдвинутся.
Распределение давления и коэффициент сопротивления. Полученные
результаты для скорости позволяют найти распределение давления в тонком
ударном слое в окрестности оси, а также на поверхности тела вблизи кри-
494 Глава XII
тической точки. С этой целью можно воспользоваться уравнением Бернулли
для несжимаемой среды, из которого нетрудно получить выражение для
коэффициента давления в произвольной точке ударного слоя:
p= P~vi =PA+il\Tt) (rt) -(it) J- (m-2-35>
Так как слой тонкий, то коэффициент давления рА и скорость
непосредственно за ударной волной в точке ее криволинейной поверхности можно
приближенно заменить соответственно значениями рс и Vc за прямой частью
в точке С. Эти значения, как следует из формул (ХП-2-7) и (ХИ-2-6),
равны соответственно
Понятно, что для условий на осевой (нулевой) линии тока Ра = Рс,
a VA = VC. Тогда коэффициент давления в произвольной точке на этой линии
(ХП-2-35')
где Fj,/(pFoo) вычисляется по формуле (ХП-2-26).
Задаваясь различными значениями y/s0, можно подсчитать в каждой
точке на осевой линии тока коэффициент давления. В частности, в
критической точке поверхности, где Vy = 0, этот коэффициент
ро = 2-р- (ХИ-2-36)
Распределение давления на поверхности тела в окрестности критической
точки можно подсчитать по формуле (ХИ-2-35), в которой следует принять
Vy = 0, a Fx=Xr. Тогда _
[(^)2] (ХП-2-37)
Подставляя сюда значение градиента К в соответствии с формулой
(ХП-2-27) и полагая Rc0 = RT, получим
^Ь-Ш2]- <хп-2-38>
Эта формула выведена для малых значений х. Однако исследования
показывают, что формула (ХП-2-38) после простого преобразования может
быть распространена на значительно больший участок поверхности тела.
Действительно, так как x/RT с^. г) ~ sinr], то, очевидно, р=(2 — p)cos2r] и,
следовательно, р — /?0cos2r). Таким образом, получили усовершенствованную
формулу Ньютона. Экспериментальные исследования указывают на то, что эта
формула позволяет с достаточно высокой точностью рассчитать
распределение давления практически на всей поверхности полусферы, хотя точность
несколько снижается в конце затупленного носка, где ньютоновская теория
дает несколько заниженные результаты по сравнению с экспериментальными.
В соответствии с (1-3-14) расчетная формула для коэффициента волно-
sin2 n
вого сопротивления сферического носка имеет вид схв~ \ pdsm2r\.
_ _ о
Внося в эту формулу р = р0 cos2 г] и интегрируя, найдем
(ХН-2-39)
В частности, для полусферы (т| — я/2) коэффициент схв —
Аэродинамика затупленных тел вращения
495
Эксперименты по измерению сопротивления полусферы без учета
донного давления (рис. ХП-2-8) подтверждают формулу (ХИ-2-39), показывая,
что ее точность возрастает с увеличением скорости. Для углов, близких
к т) = я/2, формула Ньютона не дает
правильных результатов. СЬ
Исследования показали, что в ус-
ловиях равновесно диссоциирующего
газа при скоростях полета Foo>
> 3000 м/сек распределение давления
на всей передней поверхности сферы
хорошо аппроксимируется уравнением
W
0,9
0,8
р
_. 1 '/>-п.
f
1
([77], 1966, № 1)
10 /4 18 22 26 Мс
Р°
= 1-1,17 sin2 ц + 0,225 sin6 ц.
Рис. ХП-2-8. Коэффициент волнового со-
«_ j _ „q противления полусферы
В диапазоне 10<[Моо<40 распределение давления практически не
зависит от числа Маха. Для ^чисел Моо>3 и значений А; =1,4 (диссоциация
не учитывается)
- (1,525 — 1,85р) sin2 т| + (0,487 — 1,32р) sin4 т), (ХИ-2-39")
-£-=1-
Ро
где
/с 4-1
Коэффициенты волнового сопротивления сферического сегмента с углом
полураствора ц > х\* (т]* — центральный угол, соответствующий «звуковой»
точке на сфере), вычисленные по распределению давления (ХП-2-39')
и (XI1-2-39"), соответственно равны
J f_ZL (2 — 1,17 sin2 -л + ОД 13 sin6 т]) — 21 ; (ХН-2-40)
Шо
.POO
V |[(,
Шоо I Р°°
(ХИ-2-40')
Для определения коэффициента сопротивления полусферы или ее части
надо найти давление р'о в точке полного торможения. С этой целью можно
п определить (с учетом физико-
химических превращений)
отношение плотностей р = роо/р2 за
прямой частью волны, а затем
по формуле (ХП-2-36) вычислить
коэффициент давления и
соответствующее значение р'о. Для
приближенной оценки давления
торможения при очень больших
числах Мое можно применить
1,0
0,8
0,6
0,2
7
п т
п
| П
гг1
Рис. ХП-2-9. Коэффициент лобового
сопротивления сферы (эксперимент)
формулу р'0/роо = Ш1э.
При определении
сопротивления сферы следует учитывать
влияние давления на задней
части поверхности. Как видно из экспериментальных данных на рис. XI1-2-9,
это влияние будет существенным при небольших сверхзвуковых скоростях.
При Моо > 5 практически этим влиянием можно пренебречь, полагая, что
сх в ^0,5р7- При к = 1,4 значение схв = 0,92, что хорошо совпадает сданными
496
Глава XII
рис. ХП-2-9, полученными для «холодного» потока. Можно заметить, что
наибольшее значение сопротивления сферы достигается приблизительно при
Моо^1.До Моо с^ 4 оно падает и при дальнейшем увеличении скорости
почти не изменяется. При наличии диссоциации и ионизации сопротивление
с ростом числа Моо несколько увеличивается (см. рис. ХИ-2-8).
Исследования показывают, что полное сопротивление сферы зависит
не только от числа Моо, но и от числа Рейнольдса. Это видно на рис. ХИ-2-10,
10ь
Рис. XI1-2-10. Сопротивление сферы в зависимости от
числа Моо и Re =2i?TFoo/Voo
где приведены результаты экспериментального определения суммарного
коэффициента сопротивления сферы в зависимости от Моо и Re = 2Fooi?T/voo [55].
Зависимость сопротивления от Моо и Re уменьшается по мере роста
скоростей обтекания.
Отход и форма ударной волны. Величина отхода s0 может быть
определена по (ХП-2-24), которая была выведена для случая очень больших
скоростей, когда можно принять RCO = RT1 чему соответствуют, как
показывают эксперименты, р<0,1. Однако эту же формулу можно использовать
и при меньших скоростях (больших р), когда Rc0^> RT. Только в этом
случае при помощи (ХП-2-24) находят относительную величину отхода
s0 = s/Rc0. Для того чтобы определить абсолютную величину s0, надо
найти Дс0. При заданных условиях набегающего потока величина Rc0
определяется радиусом сферы i?T, причем, как показывают исследования, радиус
кривизны волны линейно зависит от RT.
Если учесть это и исходить из предположения, что на оси волна кон-
центрична сфере, то тогда Rc0 = Rc0/RT= (I — s^)'1. Эксперименты
показывают, что концентричность нарушается тем больше, чем меньше числа Моо.
Лучший результат получается, если пользоваться зависимостью
Тогда отход, отнесенный к радиусу сферического носка,
(ХИ-2-41)
(ХП-2-42)
Результаты расчета по формулам (ХП-2-42) и (ХП-2-24) приведены
на рис. ХИ-2-11.
Аэродинамика затупленных тел вращения
497
Для значений р<0,5 близкие к этим результатам величины
относительного отхода получаются по эмпирической зависимости
2
S0 ="T-
(ХИ-2-42')
Для построения ударной волны перед затупленным носком необходимо
знать, кроме расстояния s0, также вид образующей волны. С достаточным
приближением можно
принять, что волна имеет форму
параболы
сSo
iCO
или гиперболы
(X
а)2 У2 _ л
Полуоси гиперболы а л b
определяются из условий
0,8
0,6
0,2
ч
V
s
ч
3'
?
——.
=====
■
■■■■■
——.
1
3456789 ±=
Рис. ХН-2-11. Величина относительного отхода
ударной волны перед сферой (1) и плоским
притуплением (2). Расчет по формуле (ХИ-2-42) (3)
Построенная таким
образом образующая ударной
волны близко совпадает с экспериментальной практически для любых чисел М«>,
причем приближение улучшается по мере увеличения этих чисел. Кривая,
характеризующая изменение радиуса Rc0 в
соответствии с формулами (ХН-2-41) и (ХП-2-24),
приведена на рис. ХП-2-12.
По данным работы ([77] 1966, № 1) радиус
кривизны волны на оси при очень больших
скоростях обтекания
Rc0 = (0,935 - 1,05р) ДТ| (ХП-2-41')
0,8-
\
Г
J
\
N
/к
"со
т
1=Ь
Г
Рис. ХП-2-12. Радиус
кривизны ударной волны перед
сферой
где 0,06<р<0,2.
Зная форму ударной волны, можно
определить параметры непосредственно за нею в
любой точке ее поверхности. В частности, можно
найти распределение чисел М2 и то место, где
число М2 — 1. Для этого в случае
диссоциирующего газа следует поступить следующим
образом. Задавшись рядом значений со = я/2 — 0С,
решают для каждого из них задачу о косом
скачке уплотнения с учетом диссоциации. При
этом определяются местные значения F2 и а2,
а следовательно, и числа М2. Одному из заданных углов о) = со(1) будет
соответствовать число М2 = 1. Расстояние от оси до точки на ударной волне,
в которой М2 = 1, равно приближенно
г = Rc0 sin co(1).
Для оценки величины г можно воспользоваться обычной теорией косого
скачка, в частности формулой (Ш-4-29).
Задавшись рядом углов 6С, можно найти то его значение, которому при
известном Mi — Моо соответствует число М2 = 1. График изменения углов 6С,
рассчитанных указанным способом для к = 1,4, показан на рис. ХН-2-6.
32-114
498
Глава XII
Плоский торец
Распределение давления и коэффициент сопротивления. Рассмотрим
затупление в виде плоского торца. Результаты расчета распределения
давления по торцу при осесим-
метричном обтекании,
полученные на электронной
счетной машине для одного из
чисел Моо, графически
изображены в виде сплошной кривой
на рис. ХП-2-13. Наряду с
теоретическими на этом рисунке
показаны экспериментальные
результаты.
Анализ полученных
результатов позволяет
установить общую закономерность
для изменения коэффициента
давления в виде p~Pof(r)i
где безразмерная величина г
равна отношению расстояния
г до произвольной точки
поРис. ХП-2-13. Распределение давления по плоскому
Т0РЦУ
верхности торца к его радиусу
i?T; / (г) представляет собой
некоторую «универсальную»
функцию, зависящую только от г, а р0 — коэффициент давления в центре
торца, совпадающем с точкой полного торможения.
В соответствии с этим коэффициент волнового сопротивления торца
1
f(7)d7\
Полагая, что «универсальная» функция /(г), пригодная для любых
скоростей, дана графиком на рис. ХП-2-13, можно вычислить интеграл
и получить зависимость
(ХИ-2-43)
Как видно, коэффициент сопротивления торца почти вдвое больше, чем
полусферы. Имеющиеся экспериментальные данные подтверждают этот
результат.
Отход и форма головной ударной волны. Измерения величины отхода,
проведенные в различных аэродинамических установках, показали, что эта
величина пропорциональна радиусу торца RT, а с другой стороны, она
зависит от скорости набегающего потока и от состояния газа. Последние
факторы, как известно, определяют изменение плотности за ударной волной.
Если рассматривать общий случай диссоциирующего и ионизирующего
газа, то можно предположить, что расстояние от волны до тела,
отнесенное к радиусу Лт, будет, как и для сферического носка, зависеть от
отношения плотностей р = роо/рс за прямой частью скачка.
Замечено также, что отход волны от плоского торца больше, чем от
сферы. Ориентировочная оценка приводит к заключению, что если для
сферического носка величина s0 — so/RT имеет порядок отношения
плотностей р = ро0/рс, то в случае плоского затупления эта величина s0—]/р -
Аэродинамика затупленных тел вращения
499
Выражение для относительного отхода, найденное по
экспериментальным данным, может быть представлено следующим образом:
-р
(ХИ-2-44)
с
Радиус кривизны волны на оси, определяющий ее форму вблизи торца,
оказывается, как и отход, пропорциональным радиусу плоского затупления.
Причем, для относительной величины радиуса
кривизны Rc0 =-- RCO/RT можно написать
очевидное выражение (i?co)n=: (V5o)n, в котором^
как и прежде, s0 = sQ/Rc0, а индекс «п»
обозначает параметры для плоского торца.
Аналогичная зависимость (Лсо)сф = ($о/5)сф
может быть отнесена и к сфере. При этом, как
показывают экспериментальные исследования,
величины относительных отходов s0 для сферы
и торца оказываются приблизительно
одинаковыми. В соответствии с этим одинаковыми
будут и отношения so/Rco. Поэтому для
относительного радиуса кривизны волны перед
торцом можно написать
(Дсо)п - ~!Ф- (^со)сф. (ХН-2-45)
5
3
У
У
\
1 0
г
X
■
8 _/__
Рис. XI1-2-14. Радиус кривизны
ударной волны перед критической
Относительный отход (£0)п для торца, а точкой плоского Т0РДа
также величины (£0)Сф и (Дсо)сф для сФеРы
определяются соответственно по формулам (ХН-2-42') и (ХИ-2-41).
Зависимость (ХИ-2-45) можно представить в более простом виде, если
принять, что волна концентрична сфере. В этом случае
(^со)сф = 1 + (5о)сф'
(ХН-2-46)
Используя далее формулы (ХН-2-42/) и (ХН-2-44), найдем для
плоского торца
Лс0^0,52 (3-р) [р(1-р)Г1/2. (ХИ-2-47)
График этой зависимости для Rc0 приведен на рис. XI1-2-14.
Нетрудно видеть, что в соответствии с (ХП-2-47) при р -> 0 величина
Rc0 ->■ оо, так как волна в пределе соприкасается с плоской поверхностью
торца.
Положение «звуковой» точки на ударной волне определяется методамиг
которые были указаны при изучении обтекания сферы.
Что касается обтекаемой поверхности, то «звуковая» точка на ней
совпадает с острой кромкой торца, что подтверждается экспериментальными
данными.
Вследствие того, что в угловой точке торца скорость звуковая, а
следовательно, известно местное число М = 1, в этой точке можно определить
давление.
Рассматривая течение изэнтропическим вдоль линии тока между
точкой полного торможения и «звуковой» точкой, можно написать для
давления
^зв^ ( 2 \
Ро U2+l/
fe2
k2-l
32*
500
Глава XII
где к2— отношение теплоемкостей, рассчитанное для условий за прямой
частью скачка. При небольших скоростях к2 = к{ и, следовательно,
давление рзв в «звуковой» точке определяется по обычной формуле.
При больших скоростях надо учесть изменение теплоемкостей. Если
принять, что р~ (к2—1)/(&2 + 1)» то приближенно
■^- = 0,5 (1-р).
Ро
(ХП-2-48)
Согласно этой формуле давление в точке излома торца примерно вдвое
меньше, чем в точке полного торможения.
Градиент скорости в критической точке. Было показано, что для сферы
градиент скорости обратно пропорционален радиусу поверхности i?T.
Следовательно, с возрастанием этого радиуса градиент скорости уменьшается
и в пределе при RT ->■ оо, т. е. для плоского затупления, равен нулю.
Этот вывод следует из выражения (ХИ-2-27'). Исследования
показывают, что градиент скорости в критической точке плоского торца отличен от
нуля. На основании этого можно предположить, что плоский торец влияет
на поток аналогично сферической поверхности некоторого радиуса i??.
Такой вывод подтверждается наблюдениями за формой ударной волны.
Можно подобрать такой эквивалентный радиус сферы Л?' при котором
кривизна волны на оси будет приблизительно одинаковой с кривизной волны
перед торцом. Тогда
Отсюда эквивалентный радиус
/гт =.
(ХН-2-49)
(йсо)сф
где RT = DTf2 — радиус торца.
Используя формулу (ХП-2-27'),
можно определить градиент скорости
в критической точке сферы
эквивалентного радиуса:
V~iM«> где
-■ СО
Рис. ХИ-2-15. К определению
эквивалентного радиуса (А = А/Лт)
-1/2
Градиент скорости, определяемый
по (ХП-2-50), предполагается таким,
как в точке полного торможения на торце. Это предположение, конечно,
не является строгим и должно быть дополнительно проверено
экспериментальными исследованиями. Имеющиеся данные рис. ХП-2-15 показывают,
что при больших скоростях формула (ХП-2-50) дает приблизительно
правильное решение.
Другие формы затупленных
носков
Распределение давления и сопротивление. Рассмотрим плоское
затупление с круглой фаской (закруглением) (рис. ХП-2-16, кривая 2), а также
затупление по сферическому сегменту с радиусом большим, чем у
полусферы (рис. XI1-2-16, кривая 5).
Аэродинамика затупленных тел вращения
501
Исследования показывают ([72] 1961, № 11), что в дозвуковой области
на распределение давления несколько выше по потоку, начиная от точки
полного торможения, оказывают влияние форма и радиус кривизны контура
вблизи места его резкого изгиба.
У плоских носков с закругленными кромками определяющим
параметром является относительный радиус закругления г— r/RT, у носков со
сферическим сегментом — безразмерный радиус сферы г — r/RT (или
безразмерная высота сегмента А = A/i?T), причем для второй формы носка
влияние места изгиба будет
сказываться в том случае,
если в нем устанавливается
звуковое течение.
Экспериментальные
исследования при Мею = 5,8
показали, что режим звуковой
скорости в точке излома
сохраняется до значений угла
наклона сферической
поверхности в этой точке риз > 45°.
Для значений 67° < риз <
<90° форма ударной волны
вблизи носка практически не
зависит от величины радиуса
кривизны носка. «Звуковая»
точка на ударной волне лежит
на пересечении волны с
нормалью, проведенной из точки
излома. При риз ->■ 67°
поверхности носка и ударной
волны почти концентричны.
Для значений угла наклона 0 0£ 0,4 0,6 0,8 1,0
образующей в точке излома
45° < Риз < 67° имеет место
режим обтекания,
характеризующийся тем, что «звуковая»
точка на ударной волне по
мере уменьшения! радиуса
сегмента смещается к оси тела, в то время как «звуковая» точка на теле
остается в месте излома. Форма волны все больше отличается от формы
носка, а распределение давления приближается к тому, которое имеет место
на полусфере.
Давления выравниваются, когда контур в точке излома наклонен под
тем же углом, что и в «звуковой» точке на полусфере. В частности, для
Моо = 5,8 это имеет место в том случае, когда в месте излома 0 < риз< 45°.
При этом режиме обтекания уменьшение радиуса закругления носка
вызывает смещение «звуковой» точки на поверхности тела от места излома к оси.
Распределение давления не меняется, так как от места излома, где скорость
сверхзвуковая, возмущения в дозвуковую область не проникают.
Характер изменения величины р/ро, приведенной на рис. ХП-2-16,
относительно слабо зависит от числа Моо, что подтверждается данными на
рис. ХП-2-17, где показано экспериментально найденное распределение
величиныр/ро около поверхности сферического сегмента с углом г\ = 20°, 21
для двух чисел Моо = 2,01 и 4,76. У такого носка место излома и «звуковая»
точка совпадают.
s
Рис. ХП-2-16. Распределение давления по
затупленным поверхностям различной формы:
g* — координата «звуковой» точки на поверхности
затупления; I — возможное положение «звуковой» точки;
•Э£ — место сопряжения круглой фаски с плоским торцом
502
Глава XII
Экспериментальные исследования, проведенные при средних числах Моо,
обнаружили линейную зависимость коэффициента волнового сопротивления
носка с закруглением от безразмерного параметра г, которая представляется
в виде
Схв= (СХ в)п — 1(Сх в)п — (СХ в)сф] Г. (ХН-2-51)
Можно предположить, что эта зависимость сохранится и при больших
скоростях.
С известным приближением формулу (ХП-2-51) можно распространить
на тела с затупленными носками, выполненными в виде сферического сег-
д
\
• ч*-
' 0
а
\
Г.
-2JM
, i
\
V
0,9
0J
О 0,2 Oft ?i рад
Рис. ХП-2-17. Давление на
затупленной поверхности при
различных числах М:
а —«звуковая» точка
0,2
4
So
fen
¥
^
= /^
Рис. ХП-2-18. Относительный
отход ударной волны у плоского
затупления с круглой фаской
(эксперимент)
мента с увеличенным радиусом Лсф > i?T, а также в виде эллипса, хотя,
если говорить строго, эксперименты указывают на некоторое отклонение
от линейной зависимости. _
При использовании формулы (ХП-2-51) в этих двух случаях параметр г
надо заменить соответственно на Ъ и А.
Отход и радиус кривизны волны. Аналогичная линейная зависимость
обнаруживается и для относительного отхода ударной волны перед носком
с закруглением.
На рис. ХП-2-18 изображен экспериментально полученный график
изменения величины s0 — so/RT от параметра затупления г = r/RT при
Моо = 5,8. Как видно, форма поверхности тела в «звуковой» области
оказывает сильное влияние на отход и кривизну волны.
Предполагая, что этот закон сохранится для произвольных значений
числа Моо, напишем по аналогии с формулой (ХП-2-51) общее выражение,
позволяющее оценить величину относительного отхода:
= Ып — [Ып — Ысф] Г'
(ХП-2-52)
Экспериментальные данные, полученные на моделях носков со
сферическим сегментом, указывают на близкий к линейному характер изменения
sQ в зависимости от относительной высоты сегмента для интервала ее
значений — 0,1<"А<0,45.
Соответствующая приближенная зависимость для относительного отхода
20г/-ч Лл-г
(ХН-2-53)
Аэродинамика затупленных тел вращения 503
где А — значение относительного отхода при А = 0,45. В соответствии
с некоторыми экспериментальными данными это значение можно
принять равным приблизительно 2 ($0)сф-
Экспериментальные исследования позволили также приближенно
установить характер зависимости для относительного радиуса кривизны ударной
волны на оси. Для тела с закруглением эта зависимость носит
гиперболический характер на всем участке 0<г<1, причем, по мере уменьшения
радиуса закругления уменьшается и радиус кривизны. Соответствующая
эмпирическая зависимость
Rc0 = ^1 = -= (^01п(^с0Ч _ . (ХИ-2-54)
Что касается затупления в виде сферического сегмента, то для случая
почти плоского носка ( — 0,1 < Д<0,45) относительный радиус, как и отход,
почти линейно зависит от параметра А. В указанном интервале значений А
относительный радиус кривизны
r = № = , (ХН-2-55)
9В + 2О[(Д)Я]Л
где В — значение i?c0, соответствующее величине А = 0,45. По
экспериментальным данным приблизительно В = (1,8 ч- 2) (Ёсо)сф-
Эквивалентный радиус сферы и градиент скорости в критической точке.
При вычислении этих параметров исходят из тех же предпосылок, которые
были сделаны при изучении обтекания торца. Эквивалентный радиус сферы,
соответствующий какому-либо носку, определяется по выражению (XI1-2-49),
в котором числитель должен быть рассчитан по (ХП-2-54) или (ХП-2-55).
Градиент скорости в критической точке будет определен по формуле
(ХП-2-50) после того, как найден эквивалентный радиус. Согласно
сделанным предположениям, получаемые значения являются ориентировочными,
поэтому всякий раз их рекомендуется проверять и уточнять экспериментально.
Результаты таких исследований при уменьшенных числах Моо приведены
на рис. ХП-2-15. Здесь видно, что формула (ХП-2-50) хорошо согласуется
€ экспериментальными данными для сферического сегмента с параметром
д — 0,4, хотя в этом случае угловая точка все еще является «звуковой»
(наибольшее значение А, соответствующее звуковой скорости, равно А —
= 0,45).
Имеющиеся данные показывают, что формулу (ХП-2-50) можно
использовать для расчета градиента скорости в критической точке сегментных носков
даже для значений А, несколько меньших 0,4, начиная с величин примерно
0,3—0,35. Для тела с почти плоским носком (радиус закругления достаточно
велик, так что А ->- 0) приближенное значение градиента скорости в точке
полного торможения [55]
Ю-.-ъЪУЯ^ <хп-2-50'>
Сферическая поверхность
с «затупленной» передней
частью
Расчет давления при круговом обдуве с очень большой скоростью
«затупленной» сферы, представляющей собой комбинацию части сферы
с поверхностью произвольной формы (рис. ХП-2-19), можно вести по
усовершенствованной формуле Ньютона
~р = р0 (cos a sin p — sin a cos р cos у)2. (ХН-2-56)
504
Глава XII
Приняв коэффициент давления в «затенной» зоне ре=^0, определим
коэффициент осевой силы cRp в соответствии с (Х-3-5) по формуле
A(yK)rtg$dx,
(XII-2-57)
где хк—координата точки, соответствующей началу «затененной» зоны
в нижней части поверхности;
А (Тк) — функция, определяемая выражением (Х-3-6).
Рис. ХП-2-19. Расчетная схема для «затупленной» сферы
Коэффициент нормальной силы определяется по формуле (Х-3-36)
х'
к
(ХП-2-58)
где В (ук) — функция, вычисляемая по выражению (Х-3-37).
Рис. ХП-2-20. Коэффициент осевой (а) и
нормальной (б) сил для «затупленной» сферы
20 40 60 80 100 120 140 160 сСс
Рис. ХН-2-21. Коэффициенты момента (а) и
центра давления (б) для «затупленной» сферы
При помощи (Х-3-55) определяется коэффициент момента
(ХН-2-59)
Аэродинамика затупленных тел вращения 505
Зная коэффициенты mzP и cNp, можно определить коэффициент центра
давления сц,д. = mzp/cNp. Расчеты по приведенным формулам могут быть
осуществлены для углов атаки, изменяющихся от 0 до я, т. е. для случая
кругового обдува. На рис. ХП-2-20 и ХП-2-21 показаны результаты расчета
обтекания сферы, соединенной с половиной эллипсоида, для различных
значений отношения полуосей т = alb = a/RT. Значение m — 1 соответствует
сферической поверхности, m — 0 — плоскому торцу. С качественной
стороны эти результаты хорошо согласуются с экспериментальными данными.
Менее удовлетворительное совпадение количественных характеристик
объясняется неточностью метода расчета, не учитывающего, в частности, влияние
давления в «затененной» зоне.
§ XII-3. Обтекание
потоками больших скоростей
цилиндрических и
конических тел с малым
затуплением
Аналогия с неустановившимся
движением поршня
Влияние малого затупления. Исследования показывают, что влияние
малого затупления на обтекание всего тела неодинаково в различных
условиях и зависит, в частности, от скорости набегающего потока. Так,
эксперименты позволили установить, что при умеренных числах М<х> это влияние
незначительно и распространяется лишь на небольшую окрестность тела
вблизи носка.
При очень больших скоростях влияние затупления существенно
возрастает. Затупленный носок изменяет характер течения в возмущенной
области длиной в десятки и сотни диаметров затупления, причем, чем тоньше
тело, тем протяженней эта область и, следовательно, эффективней действие
затупления. К сказанному следует добавить, что эффект затупления зависит
также от вида затупленного тела, например, он значительно больше для
профиля, чем для тела вращения.
В частности, сопротивление затупленного профиля всегда возрастает
но сравнению с заостренным, причем, этот рост может оказаться весьма
большим. Однако у тела вращения оно может не только не увеличиться,
а наоборот, даже уменьшиться.
Характер обтекания тела будет зависеть от степени затупления,
которую можно определить отношением 2RT/L. Степень затупления и
соответствующий ей эффект обтекания определенным образом согласуются с
методами исследования аэродинамики затупленных тел. В частности, если
размер затупления мал (2RT/L < 1), то это исследование можно провести
в предположении, что тело остается заостренным, а эффект от затупления
заменяется действием на обтекающий поток сосредоточенных сил со стороны
затупления.
В такой постановке задача была решена проф. Г. Г. Черным [38]. Чтобы
яснее представить себе предложенный метод, напомним об аналогии между
установившимся обтеканием конуса и нестационарным движением газа
за цилиндрической ударной волной, возникающей перед поршнем. Согласно
этой аналогии возмущенный поток около конуса эквивалентен в неподвижной
относительно тела поперечной плоскости течению газа, возникающему
перед цилиндрическим поршнем. Для наблюдателя, расположенного в этой
плоскости, такое течение аналогично потоку, возникающему при
распространении взрывной волны.
506 Глава XII
Таким образом, возмущенный поток около конуса аналогичен течению,
образующемуся при взрыве в момент времени t = 0 длинного
концентрированного цилиндрического заряда. Начальная энергия газа принимается
равной ее значению в невозмущенном течении, что обусловлено отсутствием
силового воздействия на газ перед взрывом (или перед поршнем) со стороны
острого носка.
Однако при наличии затупления действующая на газ сила не равна
нулю. Эта сила, равная лобовому сопротивлению X затупленного носка,
действуя на газ, произведет работу, сообщив ему некоторую энергию Е.
Таким образом, начальная энергия, приходящаяся на единицу длины
концентрированного заряда, отождествляется с сопротивлением носка.
Ограничившись симметричным обтеканием, можно теперь
сформулировать задачу о движении цилиндрического поршня, эквивалентную
обтеканию затупленного тела. В покоящемся газе, расположенном вдоль
некоторой прямой, в начальный момент времени происходит взрыв, в результате
которого газу сообщается удельная энергия Е. В этот же момент времени
в газе в месте взрыва возникает течение, анологичное потоку перед
цилиндрическим поршнем, движущимся со скоростью V.
Решение задачи заключается в том, чтобы определить возникающее
перед поршнем движение. Это решение позволит в эквивалентной задаче
о стационарном обтекании найти форму ударной волны перед затупленным
конусом, а также распределение давления по его поверхности. При
переходе к этой задаче надо принять
где сх — коэффициент сопротивления затупления.
Таким образом, в общем случае задача об обтекании затупленного
конуса сводится к задаче о взрыве с последующим расширением поршня.
Следует заметить, что эта аналогия относится к области течения, не
слишком близкой к носку тела, где возмущение скорости в продольном
направлении мало, и, следовательно, действителен закон плоских сечений.
Система уравнений. Подобного рода задачи, связанные с
исследованием движения под поршнем, удобнее решать, используя уравнения не в
форме Эйлера (см. гл. III), а в виде, предложенном Лагранжем. Написанные
в таком виде уравнения отображают движение отдельной частицы. Если
рассматривать, как в нашем случае, одномерное радиальное движение под
цилиндрическим поршнем, то решение этих уравнений определит
координаты г и параметры состояния частицы для любого момента времени t.
Если в] начальный момент времени t = О координата частицы гь то ее
текущая координата г будет являться функцией времени t и начальной
координаты ги т. е. г = f (ru t). Параметры состояния при известных их
начальных значениях (например, плотности |3оо, давлении роо, энтропии Soo
и т. д.), также являются функциями начальной координаты г4 и времени t.
Кратко изложим вывод основных уравнений в форме Лагранжа,
используя рис. Ш-2-3. Приравнивая нулю сумму сил инерции (dVr/dt) p X
X(2nrdr-l) и сил давления (др/дг) (2nr-l) dr, действующих на частицу
объемом 2nrdr-l, получим уравнение движения
Уравнение неразрывности получается из условия сохранения массы
частицы при ее движении. В соответствии с этим условием, если в
начальный момент времени масса была pOo(2nridri-l), то такой же она останется
и в момент времени t. Следовательно,
2яг drp =
Аэродинамика затупленных тел вращения
Так как это условие действительно в любой момент времени, то полную
производную drldri можно заменить частной производной drldr^ Тогда
уравнение неразрывности примет вид
дг, - рг • (All-d-d)
Если ввести новую лагранжеву переменную /тг^рооГ^/2, то уравнения
движения и неразрывности в этой переменной будут
Эти уравнения решаются при условии изэнтропичности течения под
лоршнем. В математической форме условие постоянства по времени
энтропии частицы
° "*"£(£) ° (ХИ-З-4)
Первое выражение относится к более общему случаю, когда в газе
могут происходить физико-химические превращения, второе — соответствует
изэнтропическому течению с постоянными теплоемкостями.
Полученную систему уравнений дополним уравнением энергии,
отнесенным к тем же условиям за цилиндрической ударной волной. Если
рассматривать движение газа под поршнем, начавшееся после взрыва, то
согласно этому закону полная (кинетическая и внутренняя) энергия движущегося
газа в каждый момент времени равна выделившейся на единице длины
энергии Е при взрыве, начальной энергии Е± и работе расширения поршня.
Следовательно,
2я \ 1-^ + и) prdr = E + 2n \ Uooprdr + 2n \ prdr,
r0 0 0
где и и Uoo — удельные внутренние энергии с размерностью квадрата
скорости;
р~ давление газа на поршень;
г0 и г —расстояния соответственно до поршня и ударной волны.
Рассматривая случай постоянных теплоемкостей, когда и = cvT =
= [l/(k — l)]p/p, а также имея в виду, что Vr = dr/dt и r^oodri = rp dr,
найдем
S G (4
го 0
Наконец, получим уравнение импульсов, которое вместе с уравнением
энергии оказывается наиболее удобным для решения задач о движении газа
под цилиндрическим поршнем. Уравнение импульсов можно получить
из уравнения движения, написанного в виде
dVr -, dp ,
рг —-- dr= —^r-r dr.
f dt dr
После интегрирования по толщине возмущенного слоя найдем
г V
J ^l. рГ dr = - J r dp. (XII-3-6)
508
Глава XII
Обтекание затупленного
цилиндра
Решение эквивалентной задачи о неустановившемся движении
цилиндрического поршня позволяет рассчитать обтекание затупленного цилиндра.
При этом предполагается, что распределенный вдоль некоторой прямой
линии заряд при взрыве сообщает газу начальную энергию Е.
Возникающее в результате этого взрыва движение газа соответствует
условию, когда у поршня скорость V = 0. В общем случае параметрами,
определяющими это движение за ударной волной, являются начальное
а) р
р
V
0,06
Ofik
0,02
Ofi1
I
~C0ST p'o
//4
p x~^~~
-Точка сопряжения
1—-
\
i_
г
— ■■
p
Poo
3
2
1
\
\
I ^
*PocS
I.
4
\
\
^.
0
Рис. XI1-3-1. Распределение давления на образующей цилиндрического корпуса со
сферическим носком:
О эксперимент; по (XII-3-12); по (ХИ-3-10')
давление р<х> и плотность роо, энергия взрыва Е (работа, отнесенная к
единице длины), отношение теплоемкостей к, расстояние г от линии взрыва
и время t. Если вычисляются безразмерные характеристики
возмущенного течения, например относительное давление, то они будут являться
функциями также безразмерных комбинаций, составленных из указанных
выше определяющих параметров.
Так как один из этих параметров, а именно отношение теплоемкостей кг
является безразмерной величиной, то в соответствии с теорией
размерностей [31 ] дополнительные безразмерные комбинации должны быть
составлены из остальных пяти параметров. Вследствие того, что три из них имеют
независимые размерности, очевидно, можно составить еще две независимые
безразмерные комбинации, а именно pLJ? rlE1-1*, poot/ipooE)1/*.
Таким образом, отыскиваемые величины за ударной волной после
приведения их к безразмерному виду будут зависеть от этих трех безразмерных
параметров. Два последние из них можно преобразовать, произведя замены
при помощи (ХП-3-1). Тогда система безразмерных параметров примет вид
Отсюда следует, что форма головной ударной волны перед
затупленным цилиндром определяется общей функциональной зависимостью
(ХИ-3-8)
Мо
Аэродинамика затупленных тел вращения
509
Общая зависимость для распределения давления по поверхности цилиндра
находится из условия г = 0 и имеет вид
(ХП-3-9)
30
25
20
15
10
В формулах (ХП-3-8), (ХИ-3-9) функцииЯжР зависят от величин
и к, представляющих параметры подобия. Существование этих параметров
позволяет обобщать получаемые единичные экспериментальные результаты
на группу подобных потоков около цилиндрических затупленных тел. Для
иллюстрации сказанного рассмотрим экспериментальные данные о
распределении давления, полученные для Мею = 7,7
и к = 1,4 при продувке модели цилиндра
с полусферической головкой (рис. ХИ-3-1, а).
Для обобщения этих данных подсчитаны
значения параметра (x/DT) /(Mlo\fcx), в котором
в соответствии с условием эксперимента
коэффициент сх найден для числа Моо = 7,7.
Отношения x/DT приняты такими, как в
эксперименте. Построенный по этому
параметру график на рис, ХП-3-1, б
(экспериментальные данные [16]) может служить для
вычисления давления при произвольных
значениях числа Моо. Аналогичный график,
обобщающий экспериментальные результаты по
исследованию формы ударной волны,
которые были получены при тех же условиях (к =
= 1,4, Моо = 7,7), приведен на рис. ХП-3-2.
В некоторых случаях общие зависимости
(ХП-3-8) и (ХП-3-9) могут быть
преобразованы к более конкретному виду. Это
возможно, например, при очень большой
скорости обтекания, когда начальное давление газа роо пренебрежимо мало по
сравнению с давлением за очень сильной ударной волной. В этом случае
из перечисленных определяющих параметров выпадает давление р^.
Следовательно, давление на цилиндре можно представить в виде зависимости
Ар~р = Р(к, рос, E,t).
Последние три параметра под знаком функции Р имеют независимые
размерности и из них нельзя образовать безразмерной комбинации.
Следовательно, по основной теореме теории размерностей величина Ар должна
-определяться выражением
А
V
/
/
/
8J_ 2х_ -2
Рис. XI1-3-2. Кривая для
определения формы головной волны
перед цилиндрическим корпусом
со сферическим носком
где fi(k) — некоторая функция, зависящая от отношения теплоемкостей.
После замены Е и t их выражениями (ХП-3-1) можно написать
Показатели степени определяются с помощью основной формулы
размерности, имеющей вид степенного одночлена, а именно:
ML"1!7"2 = [ML-3]x[MLT-*]y[T]z,
/где М, L, Т — соответственно независимые размерности массы, длины и вре-
510
Глав а XII
мени. Отсюда найдем, что x = y = l/2, z = l. Следовательно,
(ХП-3-10)
Аналогичную зависимость можно получить для координат точек ударной
волны. Напишем вначале общее выражение для радиуса волны в виде
rc = R(k, poo, E, t), где R—некоторая функция параметров, указанных в
скобках, используя затем теорию размерностей,
/ которая была применена при выводе общей
зависимости для функции давления, т. е.
представляя величину гс в виде
0,15
0,05
/А
(
>
———
0,5
где gi(k)—некоторая функция, зависящая
от показателя адиабаты к, получим
формулу для безразмерной координаты
1,0 1,2 1,4 1,6 1,8 к и^
Рис. ХП-3-3. Графики для опреде- В формулах (ХП-3-10) и (ХИ-3-11)
ления расчетных коэффициентов, функции /(А) и g(k), зависящие от без-
входящих в формулы (ХП-3-10) и размерного отношения k = cplcv, определя-
(ХП-3-11) ются в результате точного решения задачи
о сильном взрыве линейного заряда.
Полученные численные значения этих функций представлены графически на рис.
ХИ-3-3. В соответствии с этими значениями, а также принятой величиной
сх^0,94 из (ХП-3-10), можно получить выражение
-^L. (ХИ-3-10')
Следует иметь в виду, что эта формула, как и более общая зависимость
(ХИ-3-11), является первым приближением, так как не учитывает влияния:
начального давления.
Были предприняты попытки учесть влияние начального давления.
В результате проведенных исследований получена более точная формула
£- - 0,066ml -^ + 0,405 + ^Ц^
Роо
Мо
(ХП-3-12)
Как видно из рис. ХП-3-1, расчет по этой формуле лучше согласуется
с экспериментом. Формула (ХП-3-12), относящаяся к цилиндру со
сферическим носком, может быть распространена на цилиндрические тела с
произвольной формой затупления. Для случая к = 1,4 обобщенная формула
будет иметь следующий вид:
Роо
х^ + 0,405 + 0,15-
(ХП-3-13)
Если цилиндр снабжен сферическим носком, для которого принимается
сх^0,94, то эта формула переходит в зависимость (ХП-3-12) при прежнем
условии к = 1,4.
Аналогичные зависимости получены для определения формы ударной
волны. Находя из графика на рис. ХП-3-3 значения g(k) для к = 1,4 и
принимая, как прежде, сх=-0,94, получим в соответствии с (ХН-3-11)
следующую формулу для расчета в первом приближении радиуса точки на ударной
Аэродинамика затупленных тел вращения 511
волне около цилиндра со сферой:
(ХИ-3-1Г)
Более точная зависимость, учитывающая влияние противодавления,
(ХН-З-14)
Эта зависимость, распространенная на общий случай, когда перед
цилиндром имеется затупление произвольной формы,
-%- = 0,795 (сх)1/4 (-£-) U2\l+ Jf -£. - 4f5- {£.) 21 . (ХП-3-15)
^Т V VT I L Moo I/ Cx ^T MooCx V ^Т / J
Используя соотношения (ХН-3-10) — (ХП-3-15), следует иметь в виду,
что они дают удовлетворительные результаты для участков тела, удаленных
от основания носка приблизительно на величину его радиуса.
Соответствующие значения х, отсчитываемые от критической точки носка (см. рис. ХИ-3-1),
в практических расчетах следует выбирать из условия #> (2 -г-2,5) RT.
Обтекание тонкого конуса
с малым затуплением
Основные уравнения и метод решения. Случай Ki = oo. Для расчета
обтекания тонкого конуса с очень большой сверхзвуковой скоростью
воспользуемся аналогией с задачей о неустановившемся движении газа с
цилиндрическими волнами.
Полагая, что при больших скоростях слой газа между поршнем и
ударной волной весьма тонок, уравнение энергии (ХН-3-5') несколько упростим:
4р. ( * )2 + ^F4p = #- + #^+ \ ргоЛ-о. (ХН-3-5")
4 i \ dt ) 2 (к — 1) ^ 2л 2 (к — 1) J v '
о
Можно упростить и уравнение импульсов (ХИ-3-6). Так как слой
возмущенного газа рассматривается тонким, то это уравнение будет
p~Poo)rdt. (XII-3-6')
Примем в этих уравнениях величину drldt = г постоянной во всей
возмущенной области и равной скорости частиц непосредственно за ударной
волной, имея в виду, что скорость можно определить из теории скачка
уплотнения. В теории стационарного скачка относительное изменение
скорости определяется выражением
2
Foo — Vo 2 / л Яоо
Обращая движение, при котором со скоростью Voo=~ D = гс в
неподвижном потоке перемещается ударная волна, найдем скорость частиц за нею:
Как известно, эта формула учитывает начальное давление газа.
Далее, имея в виду, что возмущенный слой является тонким, примем
координату г равной расстоянию до ударной волны, а радиус поршня г0
равным Ut, где [7 — скорость расширения поршня. Внесем теперь в уравне-
512 Глава XII
ния (ХП-3-5") и (ХИ-3-6') выражение (ХП-3-16) для г, а также значения
r = rc, ro = Ut и перейдем в полученных уравнениях к безразмерным
величинам с помощью масштабов длины L = El{npooU*) и времени L/U. В
результате найдем
tdt;
о
где Ар = (р — Poo)/(pocU2), a K1 = C7(^oo/poo)-1/2==MOotgpK —параметр подобия.
В общем случае решение этих уравнений для произвольных значений t
может быть получено численным интегрированием.
Рассмотрим предельный случай, когда К.!—>оо. Кроме того, примем,
что время t мало, так что начальная энергия газа в возмущенной области
и работа расширения поршня будут также малы по сравнению с
выделившейся при взрыве энергии. В этом случае уравнения (ХП-3-17) и (XII--3-18)
существенно упрощаются:
3j-Ap = l; (ХИ-3-17')
r\rc -—- = 2 J Aprc dt. (XII-3-18')
о
Исключая из этих уравнений Ар, получим
2 ^(')
Это уравнение имеет единственное решение для гс (£), удовлетворяющее
условию гс (0) = 0 и существующее при всех £>0. При] малых t решение
имеет вид
44(НГ?1)'|1/4 (хп-з-20)
По этой формуле можно вычислить координаты точек ударной волны.
Подстановка значения (ХП-З-20) для гс в (ХН-З-!?') дает возможность
найти давление
Переходя к размерным параметрам и имея в виду зависимости (ХН-3-1),
найдем соотношения для определения формы ударной волны и
распределения давления на поверхности конуса:
()"s; (ХП-3-20Ч
Р—
1/2 D
T
Р^оо Х
в которых коэффициенты
1 Г8(/с + 1)2 (А; —1)-|1/4 а _Г fe —1 "[1/2
1)2 (А; —1)-|1/4 а _Г fe —1 "[1/2
Аэродинамика затупленных тел вращения
513
Нетрудно заметить, что соотношения (ХП-3-20') и (ХП-3-21')
отличаются от соответствующих зависимостей для цилиндрического тела лишь
значениями коэффициентов у и v. Эти значения графически изображены
на рис. ХП-3-3.
В соответствии с формулой (ХП-3-21') коэффициент давления,
принимающий бесконечно большое значение в передней критической точке, быстро
уменьшается по мере удаления от носка. При этом на некотором участке
его значения оказываются
существенно меньше, чем на заостренном
конусе.
Такое явление наблюдается, в
частности, на конусе со сферическим
носком. Для сравнения примем, что
0,1
о i9e 0,16-0,20
а 3,2 0,33-0fi8
Л 4,0 0,41-0,53
2,5
2fl
3,01
Рис. XI1-3-4. Коэффициент давления на
поверхности конуса с плоским
затуплением Мое = 6,85:
• коническая теория
\
\
f.
с
1,5
Рис. XI1-3-5. Коэффициент
сопротивления тонкого конуса с плоским
затуплением
коэффициент давления на заостренном конусе в соответствии с теорией
Ньютона /Гк = 2(3К, а коэффициент сопротивления сферического носка сх = 1.
При /с = 1,4 коэффициент v = 0,125. В этом случае
р _ 0,0625 DT
х
Рк
Р'к
Если, предположим, угол конуса (Зк = 0,1, то =- = 6,25(DT/x). Теперь
Рк
ясно, что на расстоянии х > 6,25/)т от носка давление на затупленном
конусе становится меньше, чем на заостренном.
Эта качественная особенность, установленная для предельного случая
Ki = оо, сохраняется, как показывают исследования, и при конечных
значениях параметра Кь в частности, при его значениях порядка единицы.
Формула (ХП-3-21') не позволяет выяснить характер изменения
давления по всей поверхности конуса, а годится лишь для сравнительно
небольших значений х.
Исследования, подтвержденные экспериментально, показывают, что
на значительном удалении от носка коэффициент давления, как и углы
наклона скачка, стремится к величинам, определяемым условиями
обтекания заостренного конуса.
Отмеченные особенности в распределении давления наглядно видны
на рис. ХИ-3-4, где представлены результаты продувки при Моо = 6,85
затупленного по торцу конуса с углом (Зк = 10°. Можно заметить, что
минимум давления достигается на расстоянии около 10 диаметров затупления,
а восстановление давления до значения на заостренном конусе происходит
на длине, в 10 раз большей. Пониженное давление на значительной части
затупленного конуса может привести к тому, что его сопротивление окажется
меньше, чем заостренного.
33-114
514 Глава XII
На рис. XII-3-5 приведен график, позволяющий рассчитать
сопротивление затупленного конуса. Из этого графика видно, что при некоторой
длине конуса его сопротивление становится минимальным.
Минимум коэффициента сопротивления достигается в соответствии
с графиком на рис. XII-3-5 при относительной длине конуса
х _0,96 т
DT ~~ р^ V
В частности, для конуса со сферическим носком (сх = 1) и углом
(5К = 0,1 величина x/DT = 68.
Минимальное сопротивление затупленного конуса меньше, чем
заостренного, приблизительно на 10%. В тех случаях, когда оптимальная длина
не выдерживается, сопротивление слабо затупленных конусов при очень
больших скоростях практически оказывается таким, как у заостренных.
Исследования показывают, что у слабо затупленных тонких тел
давление на конической части оказывается существенно меньше его величины
на остром конусе, причем по мере удаления от носка оно сравнительно
медленно восстанавливается до давления на остром конусе. Однако при
обтекании толстого конуса разница в давлениях резко уменьшается, а
процесс восстановления практически завершается вблизи затупления. Как
показывают эксперименты, для затупленного по сфере 40-градусного конуса
при Моо = 6 на расстоянии, несколько большем диаметра затупления,
от точки полного торможения давление на конической части практически
равно его значению на остром конусе. Это указывает на практическую
возможность оценивать давление на конической части тела по теории
обтекания острого конуса.
Что касается сферического носка и небольшой окрестности вблизи него,
включая коническую часть, то, как видно на рис. ХИ-3-1, хорошее
приближение к экспериментальным данным дает усовершенствованная формула
Ньютона р = р0 cos2ri.
Закон подобия. Произвольные числа Моо. Приведенные выше
соображения о характере обтекания затупленных тел позволяют вывести закон
подобия, которому подчинено обтекание затупленного конуса.
При выводе общих зависимостей, характеризующих обтекание
затупленного цилиндра, было установлено, что это обтекание определяется
безразмерными параметрами (ХП-3-7). Если рассматривается тонкий
затупленный конус, то к совокупности параметров, определяющих давление, надо
добавить угол |3К. Тогда, аналогично случаю обтекания заостренного конуса,
в число безразмерных параметров, от которых зависит обтекание,
дополнительно войдет параметр подобия КА = Моо|Зк-
Эти безразмерные параметры должны определять безразмерные
характеристики потока. Если рассматривается давление, то, как следует из теории
Ньютона, его избыточная величина на конусе р — poo ~ pooFL^K. Исходя
из этой оценки, избыточное давление можно определить как р — роо =
= pooFLPIp, где р — некоторая безразмерная характеристика для давления.
Следовательно, коэффициент давления на поверхности конуса
Р
TW1 = Р<*•'' К" *>' (ХИ-3-22)
где функция Р, равная 2р, определяется наряду с параметром Kj также
безразмерной величиной
Ц #-, (ХИ-3-23)
кз
Аэродинамика затупленных тел вращения $25
которую можно рассматривать как некоторую условную относительную
координату. При этом, как уже отмечалось, исследуемое сечение должно
отстоять от основания затупления не менее чем на величину его радиуса i?T.
В дальнейшем для конических тел с затуплением координату х будем
отсчитывать вдоль оси тела от основания носка, так что в расчетах следует
принимать х > i?T.
По аналогии с (ХП-3-8) закон подобия для координат точек ударной
волны:
"5- = *^*1' К" *>' (ХП-3-24)
где Ф—некоторая функция параметров х-1, КА; к.
Границы действия закона подобия можно расширить, заменив угол |3К
величиной tH. |3К. В соответствии с этим законом при обтекании конусов
с малым затуплением, отличающихся углами |3К и диаметром носка /)т,
безразмерные величины, определяемые соотношениями (ХП-3-22) и (ХП-3-24),
будут одинаковыми при равных относительных координатах x/DT, если
сохраняются величины к и значения параметров подобия
Параметр К3 отражает специфические особенности обтекания
затупленного конуса.
Изложенный закон подобия может быть распространен на затупленные
тела произвольной формы, но с аффинно-измененными образующими. В этом
случае вместо угла |3К необходимо ввести другой параметр т,
характеризующий относительную толщину тела.
§ ХН-4. Применение метода
характеристик к расчету
обтекания затупленных
тел вращения
Система уравнений для характеристик. Изложенные выше
теоретические методы применимы к исследованию обтекания затупленных тел
потоками с очень большими скоростями. В практических случаях может
оказаться необходимым расчет потока в области за затупленным носком также
при относительно небольших сверхзвуковых скоростях. Такой расчет
в области чисто сверхзвукового течения между ударной волной и
поверхностью тела может быть осуществлен методом характеристик. При этом,
так как ударная волна перед затупленным телом имеет криволинейную
форму, то должен быть применен метод, учитывающий влияние
завихренности.
Следовательно, в качестве расчетных зависимостей могут быть
использованы уравнения (IV-1-20) и (IV-1-22) для сопряженных характеристик
вихревого сверхзвукового потока. По этим уравнениям можно при
заданных условиях численно рассчитать параметры течения в некоторой области,
включающей поверхность тела и ударную волну.
Однако метод характеристик отличается чрезвычайной громоздкостью
вычислений. Поэтому расчеты были связаны с очень большой затратой
времени, что не способствовало широкому распространению на практике
этого метода.
С появлением быстродействующих электронных счетных машин
указанный недостаток метода характеристик перестал иметь существенное
значение. Вместе с тем оказалось, что использование машин с целью решения
33*
516 Глава XII
на них общепринятых уравнений для характеристик (IV-1-20) и (IV-1-22)
является неэффективным. Эти уравнения не приспособлены для машинного
счета, так как в них входит целый ряд функций (в частности,
показательных и тригонометрических), которые требуют дополнительной затраты
машинного времени на их вычисление.
В связи со сказанным возникла необходимость усовершенствовать
метод характеристик, приспособив его для расчетов на электронной машине.
Эту работу проделал П. И. Чушкин ([68], I960, вып. 5), который также
осуществил на электронной машине расчеты сверхзвукового обтекания ряда
конических тел со сферическим носком.
Чтобы усовершенствовать уравнения для характеристик (IV-1-20)
и (IV-1-22), целесообразно перейти в них к искомым функциям a' = ctg\i =
Тогда система уравнений (IV-1-20) и (IV-1-22) для сопряженных
характеристик в физической плоскости и в плоскости годографа,
преобразованная к этим новым переменным, напишется так:
первое семейство —
—-= *\ ~ т; (ХП-4-1)
d% + К da' + L dr -P dS = 0; (XII-4-2)
второе семейство —
dx cc' + g
dl~К da' -Ndx + P dS = 0, (XII-4-4)
где
2(a/)g(62 + l) t =
[б(а')2 + 1] '
p_ a'
Для расчетов энтропии Гудобнее выразить ее через функцию тока \|),
если совместно преобразовать зависимости (Ш-2-23) и соотношение для
энтропии с учетом новых переменных а', |, причем, вместо функции г|?
целесообразнее перейти к ее модификации W в соответствии с выражением
Записывая дифференциал dyp в виде
r dr
и заменяя частные производные я|)х, чрг по формуле (II1-2-33), найдем после
введения переменных а', £ уравнение для модифицированной функции тока:
По найденной функции W можно определить энтропию S. Так как
рассматривается изэнтропическое течение и, следовательно, на данной линии
тока W = const энтропия постоянна, то для этой цели можно применить
зависимость между W и 5, полученную из условий на ударной волне.
Система, состоящая из уравнений (ХП-4-1)—(ХИ-4-5), а также
уравнения, связывающего между собой S и W, решается численно. С этой целью
каждое из уравнений представляется в конечно-разностной форме.
Схема решения двух задач, графически изображенных на рис. IV-1-4,
та же, что и в обычном методе характеристик, изложенном в гл. IV. Третья
Аэродинамика затупленных тел вращения
517
задача, связанная с расчетом точки Н на ударной волне (см. рис. IX-1-1),
может решаться в данном случае следующим образом.
В точкеН, положение которой пока неизвестно, задаются произвольным
значением угла наклона волны 0сй, несколько меньшим, чем в соседней
точке F. Затем из соотношений на ударной волне определяют величины
-2 _
ан-
н
2 + (/с-1)М2оо '
1/2
9с Я А —
— °Ро) PO '
Координаты xHj rH точки Н находят в результате решения методом
итераций системы, состоящей из уравнения для характеристики первого
семейства вида Ах = тАг и уравнения параболы, которой представляется
участок волны FH.
Приближения заканчивают, когда удовлетворяется уравнение для
характеристики второго семейства:
1н — £я- + KN (a'H — aN) + LN (rH — rN) — PN (SH — SN) = 0.
По найденным параметрам в точке Н определяется модифицированная
функция тока
4'
42
40
М
Граничные условия. Для того чтобы применить рассмотренный метод
характеристик для расчета сверхзвуковой части течения около
затупленного тела вращения, необходимо знать параметры на какой-либо граничной
кривой. Если они известны, то
можно определить поле
параметров в области между этой кривой,
поверхностью тела и скачком
уплотнения, причем образующая
скачка уплотнения строится
постепенно в ходе решения. Если
рассматривается тело со
сферическим носком, то начальные данные
могут быть известны на участке
нормали АВ, проведенной к
сферической поверхности и
расположенной в полностью сверхзвуковом
слое вблизи «звуковой» линии CD
(рис. XI1-4-1). Эти данные
определяются различными методами.
Одним из наиболее точных
является, в частности, метод
интегральных соотношений, изложенный
1
0,5
0
1,5
У 8,0
/о
/
/
0,5
1
0,5
0
Рис.
ХП-4-1. Распределение параметров по
толщине ударного слоя:
точное решение; ооо — формула (ХП-4-7);
й й
р; фру ();
S/R — отношение энтропии к газовой постоянной
ранее.
Может быть использован
также и приближенный способ,
который заключается в следующем.
Около сферического носка строится вначале образующая ударной волны по
уравнению г2 — 2Rc0(x + s0). Затем вблизи «звуковой» точки на сфере
выбирается произвольная точка А, через которую проводится нормаль А В
518 Глава XII
к поверхности носка (рис. ХП-4-1). Теперь распределение некоторого
параметра вдоль нормали может быть задано полиномом
П= S адп, (ХИ-4-6)
в котором у = y/s, a s — толщина ударного слоя в рассматриваемом
сечении. Независимая переменная у меняется от нуля на стенке до единицы
на ударной волне.
При достаточно больших скоростях и, следовательно, малых толщинах
ударного слоя в полиноме можно ограничиться тремя членами и принять
Неизвестный коэффициент а0 определяется из условия на стенке при
у = 0. Причем параметры на ней рассчитываются приближенно по
усовершенствованной теории Ньютона или находятся экспериментально.
Для определения двух других коэффициентов используются условия
на ударной волне при у = 1, где параметры находятся по углу 6С ее наклона
в точке В и числу М<х>, а также известное значение производной дЛ/ду в
точках В (у = 1) или А (у = 0). Знание этой производной дает возможность
найти коэффициент а± в виде а± = (дИ/ду)^0.
На рис. ХП-4-1 показаны результаты точного расчета распределения
некоторых параметров, в частности, чисел М, углов (3 и безразмерной
энтропии S /R, к которым, как видно, близки данные, полученные с помощью
параболической зависимости (XI1-4-7).
Для определения начальных данных вдоль выбранной нормали может
быть использован непосредственно метод характеристик. С этой целью
вдоль произвольной дуги EF заданной ударной волны (рис. ХП-4-1)
выбирают густой ряд точек. Так как в каждой из этих точек параметры известны,
то можно применить уравнения для характеристик. В результате их
решения находится сетка характеристик, в узлах которой становятся известными
параметры потока в области между дугой EF и сопряженными
характеристиками ЕА и FA. По этим данным можно найти параметры вдоль нормали.
Именно так были получены результаты, приведенные на рис. ХП-4-1.
Ход вычислений и некоторые результаты. Теперь, когда вдоль
выбранной нормали зафиксирован ряд точек, в каждой из которых параметры
известны, можно применить уравнения
для характеристик в
конечно-разностной форме. В результате
последовательного применения этих уравнений мето-
£ у^/Й^"^" Дом итераций вычисляются параметры
в точках первого ряда вблизи нормали.
п,„ х Причем одна из точек ряда, а именно
**-—-^ I—•- верхняя, находится на пересечении
характеристики первого семейства и по-
Рис. ХП-4-2. Сетка характеристик для верхности ударной волны, а другая —
затупленного конуса нижняя — на пересечении
характеристики второго семейства и образующей
тела. Все остальные точки лежат на пересечении сопряженных
характеристик, выходящих из соседних точек на нормали.
Затем по аналогии находятся координаты точек следующего ряда,
вычисляются в них параметры и т. д. Описанным методом на электронной
машине были проведены расчеты обтекания серии конусов со сферическим
носком при различных скоростях. Причем углы конусов равнялись f5K = 0;
20; 30 и 40°, а числа Моо = 3; 4; 6; 10 и оо. Отрезок нормали АВ разбивался
Аэродинамика затупленных тел вращения
519
на 48 интервалов. На рис. ХП-4-2 построена схема потока около
затупленного конуса с углом (Зк = 20° при Моо — 6, дающая представление о форме
образующей поверхности ударной волны 1 и сетке характеристик 2. Здесь же
показана характеристика первого семейства FE, выходящая из точки
сопряжения сферы и конуса и ограничивающая ту часть потока, которая
сформирована при обтекании сферического носка и за которой начинается течение,
обусловленное влиянием не только сферы, но и
основной части тела. £
Таким образом, характеристика FE аналогич- Ро[
на KS (см. рис. IX-1-1), разделяющей конический
поток от течения, возникшего при обтекании
криволинейной поверхности.
Распределение давления на затупленном по
сфере конусе с углом (Зк = 20°, подсчитанное по
методу характеристик на электронной машине для
трех чисел Моо, представлено на рис. ХП-4-3. Там
же для сравнения пунктирными прямыми показаны
давления на заостренных конусах. Как видно,
затупление на некотором участке уменьшает
давление, причем его относительное изменение
возрастает с увеличением числа Моо.
Таким образом, при небольших скоростях
поток около периферийной части затупленного тела
почти не отличается от течения возле острого
конуса. Это указывает на возможность
приближенно рассчитывать сопротивление затупленного конуса путем
суммирования сопротивлений носка и периферийного участка конуса, на котором
давление принимается таким, как на заостренной поверхности.
Такой же вывод можно сделать и в отношении утолщенного
затупленного тела, распределение давления на котором при любых скоростях мало
отличается на основном участке от соответствующего распределения на
заостренном теле. Разумеется, из этого анализа необходимо исключить
небольшую окрестность периферийной поверхности, непосредственно
примыкающую к носку, где давление может меняться существенно.
0J
О
Рис. ХП-4-3.
Распределение давления по
образующей затупленного конуса:
давление на остром
конусе
§ ХМ-5.
Влияние
атаки
угла
Исследование неосесимметричного обтекания затупленных конусов
показывает, что принципиальные особенности, связанные с изменением давления
вдоль образующих, лежащих в различных меридиональных плоскостях,
являются такими же, как при нулевом угле атаки. Это, например, видно
из экспериментальных результатов, полученных для конуса со
сферическим носком при Моо = 5,8 и углах атаки а = 4 и 8° (рис. ХП-5-1). На
нижней и верхней образующих давление после критической точки постепенно
снижается, достигая минимума на некотором удалении от носка. После
этого оно возрастает, принимая значения, близкие к тем, которые имеются
при обтекании острого конуса. Экспериментальные исследования показали,
что для значений а<4-^ 5° распределение давления можно с известным
приближением представить уравнением
р = pa=z0 — aB cosy + а2 (С cos2y + D) (XII-5-1)
В этом уравнении коэффициенты В, С и D не зависят от угла атаки,
поэтому для их определения могут быть использованы результаты измере-
520
Глава XII
ния или расчета распределения давления вдоль трех произвольных
образующих тела при данном угле атаки.
Уравнение (ХП-5-1) упрощается, если углы атаки настолько малы,
что можно пренебречь членом аЮ. Тогда в уравнении (XI1-5-1) должны
Рис. ХП-5-1. Давление на затупленном по сфере конусе,
обтекаемом под углом атаки:
острый конус (теория); А—для верхней образующей;
В — для нижней образующей
быть определены два коэффициента В ж С, что можно сделать,
воспользовавшись данными для давления на образующих, расположенных в
плоскостях у = 0 ж у = п. Для очень малых значений а в уравнении (ХП-5-1)
можно ограничиться вторым членом, приняв
р = ра=0 — аВ cos у. (ХП-5-2)
§ XI1-6. Метод Ньютона
Расчет аэродинамических коэффициентов тел вращения с затупленным
криволинейным носком при гиперзвуковом обтекании можно вести на основе
усовершенствованной формулы Ньютона (Х-3-1) для давления.
Рис. ХИ-6-1. Схема расчета обтекания затупленного конуса по
методу Ньютона
Существенным элементом расчета является определение для заданной
формы корпуса границ «затененной» зоны. Рассмотрим корпус в виде
конического тела со сферическим носком (рис. ХП-6-1). Образующая на участке
Аэродинамика затупленных тел вращения 521
О <о;<а;к имеет вид дуги окружности, а на участке #к<ж</к —
прямой с уравнениями
где хК1 rK — координаты точки сопряжения сферы и цилиндра.
Из рис. XII-6-1 видно, что rK = i?TcospK; xK = Дт(1 — sinpK). В качестве
характеристики затупления можно ввести отношение 7*— 1К1ГК, где 1^ =
= ^мид/tg Рк — длина незатупленного конуса. В качестве другого параметра
затупления целесообразно рассмотреть отношение радиусов RT = Дт/гмид,
которое, как видно из рис. XII-6-1, равно
RT = -^ - . ™S.P* (1 - Т). (ХИ-6-2)
гмид ■*■ sin Рк
Предположим, что имеется в виду наиболее общий случай обтекания,
когда «затененная» зона захватывает часть конической поверхности и сферы.
Граница «затененной» зоны определяется из условия ре — 0, что дает cos yK=--
= tgp/tga. На сфере граничная кривая является окружностью радиуса i?T,
плоскость которой наклонена к оси г под углом а (см. рис. ХН-6-1). На
конусе граница «затененной» зоны определяется уравнением cosyk =
— tgPK/tga — const. Часть сферы до точки с координатой xa = RT(i — sin a)
полностью обтекается потоком и, следовательно, ук = 0.
Коэффициент осевой силы определяется при помощи формулы (Х-3-5)
следующим образом:
А1 (ук) г tg Р dx + \ А2 (ук) г tg P dx +
0 la хк
(XII-6-3)
Функция А± соответствует участку полного обтекания сферического носка
и определяется из (Х-3-6) при условии, что ук=:0. Значение tg$ = dr/dx =
— (RT — x)/r. Для вычисления второго интеграла в (XII-6-3) следует
заменить А2(Ук) выражением (Х-3-6), в котором принимается yK = arccos (tgp/tg a)
и tg Р = (i?T — x)lr и тем самым учитывается влияние «затененной» зоны
на сферическом носке. Наиболее просто вычисляется третий интеграл,
соответствующий коническому участку, для которого следует принять ук =
= arccos tgPK/tga; А3 (ук) = const; tg p — tg PK = const и произвести замену г
в соответствии со вторым соотношением (ХН-6-1). Вычислив интегралы
в (XII-6-3), получим для коэффициента осевой силы
^i + flJAci, (XII-6-4)
где ct — коэффициент осевой силы, действующей на незатупленный конус.
(ХП-6-5)
Параметр Aci определяет добавочную составляющую коэффициента
осевой силы вследствие влияния затупления:
_ iJ£Jk sin 2a Sin 2pK (2 + 3 cos2 pK).
Угол 7К определяется по углу конусности при помощи формулы cos yK =
= tgPK/tga. Если рк>а, то «затененная» зона на корпусе отсутствует, еле-
522
Глава XII
довательно, угол ук = 0 и коэффициент осевой силы
cRp = 2 sin2 рк + sin2 a (1 - 3 sin2 рк) + R% -^^ (2-3 sin2 a). (ХИ-6-7)
При осесимметричном обтекании в приведенных выражениях следует
принять а = 0 и ук — 0. Результаты расчета коэффициента cRp для этого случая
приведены на рис. ХП-6-2. Для незатупленного конуса параметр Дт = 0.
Формула (ХИ-6-4) позволяет определить коэффициент осевой силы для
условий кругового обдува. Соответствующие результаты расчета для значений
0,2
м —
■
/
j
'
у
>
f
/
с
к}
S
/
/
у
Л
/
ЕЙ
/
//
/
1
0,2
0,6 0,8
20
I
%0,y
hO
MfOP
60
80
\
\'
\\
20
\
\\
V
\
no
\
\
Рис. XI1-6-2. Коэффициент осевой
силы затупленного конуса,
вычисленный по ньютоновской теории
(нулевой угол атаки)
Рис. ХН-6-3. Коэффициент осевой силы
затупленного конуса, вычисленный по
ньютоновской теории (круговой обдув)
J3K = 15°, i?T = 0,9 и 0,6 показаны на рис. ХН-6-3. Величина cRp при а = 180°,
т. е. на плоском торце (в точке полного торможения) принята равной 2.
Коэффициент нормальной силы определяется по аналогии с (ХП-6-3)
также в виде суммы трех составляющих. Имея в виду (Х-3-36), напишем
-2
'МИД
В (Тк) rdx+\B (Vk) rdx+\B (Тк) г dx] . (XII-6-8)
Функция В (ук) для каждого из трех участков интегрирования
определяется из (Х-3-37) соответственно по значениям ук = 0, ук = arccos (tg p/tg a)
и ук = arccos (tgPK/tgа). В результате вычисления интегралов и
преобразований получим
где с2 — коэффициент нормальной силы острого конуса;
Величина Дс2 определяет уменьшение коэффициента нормальной силы
вследствие влияния сферического носка:
Ас2 = с2 cos2 рк + с3,
где
sin 2pK [5 sin2
arctgf
п 6Vcosa
sin2 pK (1 — 3 sin2 a]. (XII-6-12)
Аэродинамика затупленных тел вращения
523
При отсутствии «затененной» зоны (сс<|Зк) угол ук = 0 и
cNp = cos2 рк sin 2сс (1 - -^ cos2 рк) .
(ХИ-6-13)
Влияние цилиндрического участка на коэффициент cNp учитывается
добавлением величины AcNp = (16/3n)^sin2a. Результаты расчета
коэффициента нормальной силы по (ХП-6-9) приведены на рис. ХН-6-4. Можно
заметить, что цилиндрический участок увеличивает максимальное значение cNp.
Используя формулу (Х-3-55), можно вычислить коэффициент момента,
представив каждый интеграл в
этой формуле как сумму трех %
интегралов: первый из них
соответствует участку поверхности
от 0 до ха; второй — от ха до хк
и третий — от хк до ZK. Величину iQ
nR%(a-\-RT) в знаменателе еле- '
дует заменить значением лг^т1к.
Произведя вычисления,
получим
2 sin 2а 1—7
TTlzv— о = =~~
I
Здесь
(ХИ-6-14)
i
W/
f
I
I
У
1
//
* /
/
/
f J
/
/
s
)
)
6y
s
N.
Кт=0,9
■ч
\
\
>
\
\
\
^ \
4
\
\
\
\
\
\
\
ч
ч
\
\
х
(ХИ-6-15)
0,5
О 20 40 60 80 100 /20 ПО 160 ос°
Рис. ХН-6-4. Коэффициент нормальной силы
затупленного конуса фк = 15°):
без цилиндрической части; с
цилиндрической частью длиной 0,334й1,/г„тг
МИД
Параметр I = 1К11'К1 а коэффициенты с2 и с3 даются соответственно
выражениями (ХП-6-10) и (ХН-6-12). При отсутствии «затененной» зоны ук = 0 и
/T^jcos^s^af-^^^
(ХН-6-16)
По значениям mzp и cNp находим коэффициент центра давления сц.д =
= ^ц д/^к = WzplcNp. В частном случае, когда «затененная» зона соответствует
<у„ = 0), из (ХИ-6-16) и (ХИ-6-13) находим
сц.ц —
3 cos2 pK
^-(2-3 sin pK)
(ХП-6-17)
Для заостренного конуса (Лт^=0) получаем выражение сц. д = 2/(3 cos2 PK).
Цилиндр с полусферическим носком. В случае обтекания цилиндра
с носком какой-либо формы, в частности полусферическим, «затененная» зона
яри любом значении угла атаки всегда будет захватывать половину
цилиндрической поверхности и, следовательно, ук = я/2. На носке «затененная» зона
начинается от точки (в плоскости у = 0)> гДе угол $ = а, и захватывает вниз
по потоку часть полусферы, расположенной между плоскостью, наклоненной
к оси г под углом а, и передним основанием цилиндра. Вычисления показы-
524 Глава XII
вают, что для цилиндра с полусферическим носком
cRv = cos4 -J-; (XH-6-18)
cNp = sin a cos2 -^- + 4~ (2К — !) sin2 а; (ХН-б-19)
m^ = _J_rsinacOs2-^ + -4-(44 — l)sin2a] , (XII-6-20)
где Як^/к/(2гмид) —удлинение корпуса.
Применение усовершенствованной формулы Ньютона. Приведенные
выше результаты найдены, исходя из обычной формулы Ньютона, в
соответствии с которой избыточное давление на площадку, образующую с нормалью
к вектору Foo угол а, равно р — p0o = p0oVl0cos2a1 а коэффициент давления
р = 2 cos2 а. При обтекании конуса или какого-либо другого тела со сферическим
носком под небольшим углом атаки точка полного торможения располагается
на сфере, и для расчета обтекания затупленного корпуса можно применить
усовершенствованную формулу Ньютона (Х-3-1). Соответствующие выражения
для аэродинамических коэффициентов можно получить из формул (ХП-6-7)г
(ХП-6-13) и (ХН-6-16), введя в них коэффициент р0 и приняв углы а малыми:
Crp = Ро [sin2 рк + ^ (1 - 3 sin2 рк) + Щ ^^ (2 - За2)] ; (ХН-6-21)
cNp = Poa cos2 рк (1 _ -JL cos2 рк ) ; (X И-6-22)
-(l-T) + ^-ggyL(2--3smpK)] . (ХП-6-23)
При переходе к заостренному конусу в этих формулах следует принять
i?T = 0, а величину р0 заменить на р(к) согласно (Х-3-3).
Для цилиндра с полусферическим носком использование
усовершенствованной теории Ньютона приводит вместо формул (ХП-6-18) -н (ХИ-6-20)
к выражениям
^; (XII-6-24)
cNp = ^ [1 + -^ (2ЯК -1) a] a; (XII-6-25)
mzp = ^[l +-3^- (4Я2к-1) а] £-. (ХП-6-26)
§ ХП-7. Обтекание
затупленных тел криволинейной
формы
Общее решение. Задача об обтекании затупленных тел с криволинейной
образующей может быть решена на основе закона плоских сечений,
выражением которого является аналогия с неустановившимся движением газа под
цилиндрическим поршнем.
Как известно, в общем виде это одномерное движение описывает система
уравнений (ХН-3-2') и (ХН-3-3'). Следуя Г. Г. Черному [38], находят
решение уравнений с помощью разложения искомой функции в ряды по
степеням 6 = (к— 1)/(к+ 1). Для параметров газа за ударной волной эти
соотношения, в частности формула (Ш-4-12) для давления, выражаются через
Аэродинамика затупленных тел вращения $25
относительную плотность роо/рг- С увеличением скорости эта величина
уменьшается, достигая в предельном случае при М<х> —> оо и k = const значения роо/р2 = б.
Если учитывать физико-химические превращения за ударной волной,
то величина роо/р2 будет меньшей. Таким образом, вблизи поверхности
ударной волны образуется слой сжатого газа, в котором возмущенные параметры
по порядку величины будут такими, как непосредственно за волной, т. е. и для
них определяющим параметром является отношение плотностей в набегающем
потоке и в невозмущенном слое. Чем больше скорость, тем интенсивнее волна
и тоньше слой, в котором происходит уплотнение.
Эту возмущенную область газа за волной можно рассматривать как
своеобразный пограничный слой вблизи нее, в котором происходит основное
изменение давления газа. В предельном случае, когда уплотнение в этом
слое бесконечно велико, т. е. роо/рз^гО, избыточное давление газа за волной
равно р2 — Poo = pooVlo sin2 P и совпадает со значением, полученным по теории
Ньютона. Толщина слоя становится бесконечно малой.
В реальных случаях течения давление отличается от предельного, причем
критерием этого отличия является параметр роо/рг- Из сказанного вытекает
возможность искать решение задачи о течении газа в тонком слое вблизи
волны в виде рядов по степеням параметра б = роо/р2. Из формул,
приведенных в § Ш-4, можно видеть, что параметры газа за ударной волной
определяются именно этим малым параметром.
Имея в виду систему уравнений (ХИ-3-2'), (ХИ-3-3') и (ХН-3-4),
представим ее решение в виде рядов
+...; P = Po + bpi+...; р = -^- + р1+... . (ХН-7-1)
• • •
Внося ряды в эти уравнения и обозначая dro/dt — rQ; d2r0/dt2 = r0,
получим систему уравнений
д :'' д a Ро
dm -v' >v~ '° dm > иь vpj .
служащую для определения вида функций г0, р0, Ро- Интегрируя уравнения,
найдем
Po, (XII-7-3)
где ro(t)« P(t), # (т) — некоторые произвольные функции.
В результате той же подстановки получим систему уравнений
dm ~Po>V ° dm ~ r0 fi dt* ' { .^.jj ^ ,,
Po "" Po
которым удовлетворяют функции ги ри р1# Интегрирование уравнений дает
выражения для этих функций
.. m m } (XII-7-5)
l ^l |
где r*(t), p*(t), 'O1! (m)—некоторые произвольные функции;
m* —нижний предел интегралов, который выбирается
также произвольно.
526
Глава Х1Г
Для определения произвольных функций следует воспользоваться уело-
виями на ударной волне и на поверхности поршня. Условия на ударной волнеv
движущейся со скоростью D относительно невозмущенного течения, имеют вид.
т =
; рс = (1 — б)
(XII-7-6).
Пользуясь правом выбора произвольной функции ro(t), примем ее такой,
чтобы она соответствовала закону распространения ударной волны, т. е.
положим ее равной ro = rc(t). Тогда скорость этого распространения будет
D = drjdt = rc. При таком выборе, очевидно, на ударной волне функция гЛ — 0.
Условия, которым должны удовлетворять на ударной волне другие члены
в разложениях, будут получены, если выражения (ХИ-7-6) для рс и рс
приравнять соответственно их значениям, представленным в виде рядо&
(ХП-7-1). В результате найдем
Ро = РооГс; Pi = — po
6+ (1-6)-^-
^
-1
(ХН-7-7)
При помощи условий (ХП-7-6) и (ХП-7-7) на ударной волне можно*
определить произвольные функции в выражениях (XII-7-3), (XII-7-5). В
частности, внося Ро — рооГ2с и т = 0,5рооГс во второе выражение (XII-7-3), найдем
Аналогично можно найти другие функции, после подстановки которых
в соотношения (XII-7-3) и простых преобразований определяются величины
Ро и р0:
А) = рооГ^ + Т роогсгс —\г~
-
I/ft
(ХН-7-8)
где г = дг/дх — производная от переменной г, определяющей лагранжеву
координату т. Причем, если t представляет собой момент времени,
который соответствует координате т*(гс), то некоторое время т
определяет произвольную лагранжеву координату ударной?
волны т (г).
Таким же путем получаются формулы для ?\, ^ и р^
m*PooK+0,5rcrc —
rc m
rc poo
k I/ft ■
771*
771*
p0
(ХН-7-9)
Так как обычно задана форма тела вращения, что соответствует заданию-
закона движения поршня rT(t), то необходимо связать дополнительным уело»
Аэродинамика затупленных тел вращения 527
вием с этим законом функцию гс. Условие, в котором члены второго и более
высокого порядка малости отброшены, имеет вид
г = гс + Ьг± = гт.
Из него найдем, что
г^Лг-6'I^IU (ХП-7-10)
где функция [rjlm* определяется первым выражением (ХП-7-9) при условии,
что верхний предел интеграла т = 0 (условие на поршне). Заметим, что
в этом выражении величину гс в правой части можно заменить на гт. Это
следует из того, что после замены гс на гс — гТ — бгА в нем появится третий
член порядка б2, которым можно пренебречь.
Обтекание тела вращения с образующей степенной формы. Рассмотрим
приложение изложенного метода к расчету обтекания тела вращения
степенной формы [38].
При очень больших скоростях обтекания, когда поо/D < 1, давлением
перед ударной волной можно пренебречь. Тогда ее скорость будет
определяться выражением
где /(*, роо) — некоторая функция от t и роо.
Так как эти две величины имеют независимые размерности, то
где величина В является некоторой константой. Обозначив Bp™ — Ci, напишем
для скорости распространения волны
и определим закон ее движения
Входящая сюда постоянная С4 имеет кинематическую размерность LT~in+1).
По аналогии с выражением для гс можно написать зависимость для
закона расширения поршня:
г* = -4т*п+1. (ХИ-7-12)
Заменяя в последнем выражении t на t = xlVoo, получим уравнение
образующей обтекаемого тела
S\ (ХИ-7-12')
которое имеет вид степенного одночлена. В частном случае п = 0 приходим
к уравнению для конуса.
Имея (ХН-7-11) для гс, а также соответствующую ему зависимость
можно определить произвольные функции, представленные в общем виде
уравнениями (ХИ-7-8) и (ХП-7-9). После подстановки и соответствующих
преобразований с учетом того, что величина поо/D считается пренебрежимо
малой, получим
+" (1^)] |
(1] |
\ (ХП-7-13)
528
Глава XII
Аналогично получаем зависимости для функций (ХН-7-9):
Pl = 9ooD* [тЧ' (т)-1 (^ +1)
4) т/ И
(ХП-7-14)
где
а величина /' (т) = d/ (m)/dm.
Из зависимостей (ХИ-7-9) и (ХИ-7-14) видно, что рассматриваемое
движение носит автомодельный характер, так как все безразмерные параметры
определяются одной безразмерной
величиной т = т/т*. _Pj_
Зависимость между законами Рс
движения поршня и ударной волны,
0,1,
г
>—о—<
Г
п
>• !
i
= В
\
\
X
\
п„-
X
-0,к
0,2
0,2
0,6
0,2
/
0
^—
X
гс
—
п
А
-ом
-0,2
О
09
Рис. ХП-7-1. Величина гт/>с для
тела степенной формы:
ооо — точное решение;
по (ХП-7-22)
— решение
Рис. XI1-7-2. Отношение давления на
поверхности тела вращения с образующей
степенной формы к давлению за ударной
волной
определяемая соотношениями между коэффициентами С и Си получается из
формул (ХП-7-11) и (XII-7-12) с использованием выражения (ХИ-7-14) для гА:
— --= -J- = 1 ~^-J (0), (ХИ-7-16)
где / (0) — значение функции J (ш) при лг = О.
В задаче об обтекании тела зависимость (XI1-7-16) дает отношение
координат точек соответственно поверхности тела и ударной волны. Графически
эта зависимость представлена на рис. ХН-7-1.
При помощи функций (ХИ-7-13) и (ХН-7-14), а также уравнений (ХП-7-1)
можно найти соотношения, позволяющие определять параметры газа в
возмущенном слое между ударной волной и обтекаемым телом. В частности,
на поверхности тела (ш = 0) давление
1
Аэродинамика затупленных тел вращения $29
причем давление непосредственно за ударной волной
а функция Р (0) = рТ/рс [Р (0) определяется из (ХП-7-17)]. По этой функции,
графически изображенной на рис. XI1-7-2, можно рассчитывать
сопротивление тела степенной формы. При этом будем исходить из формулы
X = 2л \ pTrT drT
о
и выражения для давления
Рт = РсР (0) = -^ PooDW (0) = ^ pJ^P (0).
Выразим входящее сюда произведение C\t2n через гс и гт с учетом
соотношений (ХП-7-11) и (ХИ-7-12). Затем внесем полученное выражение для р
под интеграл и после его вычисления будем иметь
—
X—^-о С*р{0) )
+ () С ) 2 (
где i? (0) = rT/rc — рассчитывается по формуле (ХИ-7-16).
Чтобы рассчитать сопротивление, необходимо наряду с параметрами
набегающего потока знать также уравнение образующей тела. В формуле
(ХП-7-18) в качестве параметра, характеризующего форму тела, входят
радиус наибольшего сечения гт = гмид, показатель п и постоянная С.
В практических случаях можно задаться величинами п, гмид и
удлинением X = #мид/(2гмид) и построить образующую по уравнению
гт = Ахп+1 = 1 Г'я+1> (2rMm)~n Xn+1.
Определив по этому уравнению значение коэффициента А, можно
вычислить коэффициент С, который в соответствии с зависимостью (ХИ-7-12')
равен A(n + l)Vl+i.
Из (ХП-7-18) следует, что не при всяких значениях показателя п в законе
расширения поршня (ХП-7-12), т. е. не для всякой степенной формы
существует решение. В частности, видно, что значение интеграла
расходится при [nl(n-\-1)] <С — 1. При значениях п, соответствующих этому
неравенству, сопротивление оказывается равным бесконечности, что нереально.
Сопротивление, вычисляемое по (ХП-7-18), по величине конечным будет
у тел, уравнение образующей которых характеризуется показателем лг >> —1/2.
Если же п<С~ 1/2, то автомодельного решения не существует. Это значит,
что распределение параметров в поперечных плоскостях между телом и ударной
волной не обладает свойством подобия и, следовательно, давление, плотность,
скорость нельзя выразить в форме
В этом случае поток в некотором сечении должен зависеть от своей
предыстории, определяемой особенностями геометрической формы тела. Из
анализа уравнения образующей (ХИ-7-12) следует, что при п~^> —1/2 наряду
с заостренными телами (тг>0) это уравнение представляет также
затупленные формы ( — -n-<
34—114
530
Глава XII
Приближенный характер формулы (ХН-7-18), обусловленный
представлением решений в виде рядов (ХН-7-1) с учетом членов порядка 6=(&—1)/(й?+1),
ограничивает использование этой формулы значениями п, несколько
большими — 1/2. Это видно на рис. ХИ-7-3, где нанесена кривая изменения
коэффициента сопротивления, соответствующая формуле
IX I \п-\-\у г (U) 1 /YTT 7 4Q\
сх — Ш 2 == ь\\ o~F)—ХТ\ Р2 (0\ Т* ' (ЛИ-/-1а/
в которой удлинение тела А,мид = х/(2гт) = 1/т. Заметим, что формула (ХН-7-19)
получается из (ХН-7-18) при условии, что значение интеграла при нижнем
пределе равно нулю, а постоянная
0,3
-ол
Рис. XI1-7-3. Коэффициент сопротивления
тел вращения с образующей степенной
формы:
О О О — точное решение;
по (ХП-7-25)
- решение
Сравнение с результатами точного
решения (рис. ХИ-7-3) показывает, что
точность формулы (ХП-7-19)
уменьшается вблизи значений п == —1/2. То
же можно отметить и в отношении
формы ударной волны.
Соответствующая расчетная зависимость (ХП-7-16)
дает менее удовлетворительные
результаты по сравнению с точной теорией
вблизи того же значения п = —1/2
(см. рис. ХН-7-1).
Анализ результатов, приведенных
на рис. ХП-7-3, позволяет сделать
вывод, что существует такое тело
вращения со степенной формой, которое по сравнению с другими, имеющими то
же удлинение, обладает наименьшим сопротивлением. Из этих результатов
следует, что минимум функции сДмид достигается приблизительно при п = —0,29
и равен 0,38, в то время как для конуса СаЛмид==0>52, что больше, примерно,
на 37%. Таким образом, при очень больших скоростях затупленное тело
вращения с криволинейной образующей, обладающее по сравнению с заостренным
конусом преимуществами в отношении лучших условий для отвода тепла,
может выгодно отличаться от конуса также меньшим сопротивлением.
Полученные выше зависимости относились к тому случаю, когда в
разложениях (ХИ-7-1) учитывались члены порядка б = (к — 1)/(к + 1). Естественно,
что эти зависимости упрощаются, если учесть только главные члены. В
частности, формулы (ХН-7-16) и (ХИ-7-17) принимают вид
Д(0) = ^=-^ = 1; (ХН-7-16')
= РсР(0), (ХН-7-17')
а формула (ХИ-7-19) для коэффициента сопротивления
(ХИ-7-19)
Определяя минимум сх при фиксированном удлинении Ямид, можно найти,
что этот минимум достигается при п = —1/3. Этому значению соответствует
минимальная величина
1 (ХИ-7-20)
\ 2 »
^МИД
Аэродинамика затупленных тел вращения
531
меньшая, чем для конуса в рассматриваемом приближении, для которого
ПО НЬЮТОНОВСКОЙ теории Сх = 1/(2ЯмИд)«
Применение формулы Ньютона. Расчет давления по (ХП-7-17) может
осуществляться для точек поверхности тела вращения степенной формы,
г
-ж
Рис. XI1-7-4. Сравнение теоретического и экспериментального
распределения давления около симметрично обтекаемого
эллипсоида
расположенных на некотором удалении от затупленного носка. Что касается
поверхности носка, то здесь усовершенствованная теория Ньютона дает
удовлетворительные результаты
при расчете распределения
давления около сферических тел.
Исследования показывают, ,что
такие же результаты
получаются для тел с иной
криволинейной формой.
Это, в частности, видно на
рис. XI1-7-4, где наряду с
результатами расчета по формуле
р = р0 sin2^ приведены
экспериментальные данные о
распределении давления около
симметрично обтекаемых эллипсоидов.
Удовлетворительные
результаты получаются и при использовании усовершенствованной формулы
Ньютона ([66], 1964, № 4) для расчета обтекания эллипсоида под углом атаки
(рис. ХН-7-5):
-_ ро (cosal/ 1 — г2 — rfsinacosy) /v O/|
P~sin2p0 1 +г2 (72-1) ' (A11-/-Z1)
где Ро — угол между касательной к контуру тела в передней точке и
направлением вектора V^ г = r/Ъ; t = alb (Ьжа — полуоси эллипса, рис. ХП-7-5);
р0 — коэффициент давления в критической точке эллипсоида. Вычисления
могут быть упрощены, если вместо (ХП-7-21) применить эмпирическую
зависимость
Р (г, у) = Pi (г) + р2 (г) cos у, (ХИ-7-22)
где
— - 1 —
(ХИ-7-23)
34*
Рис. XI1-7-5. Схема к расчету обтекания
эллипсоида
532
Глава XII
В соответствии с формулой (ХП-7-22) давление в какой-либо точке
поверхности определяется его значениями в точках, лежащих на
образующих эллипсоида, соответствующих углам у = О и я.
Интегрируя давление по поверхности, можно определить коэффициент
осевой силы. Величина этого коэффициента, как показывают расчеты и
сравнение с экспериментом, меняется незначительно в довольно большом
диапазоне углов атаки — 15°<а<15°. Сравнение показывает, что лучшее
согласование экспериментальных и теоретических результатов наблюдается
при больших сверхзвуковых скоростях. Однако теория Ньютона дает
достаточно удовлетворительное для практических целей приближение и при
сравнительно небольших скоростях, когда давление определяется вблизи
критической точки. По мере удаления от носка теоретически найденное
давление становится меньше, чем измеренное в эксперименте.
Расчетные результаты можно несколько улучшить путем «склеивания»
распределения давления, найденного на передней части по формуле
Ньютона, с распределением давления, которое на нижележащем участке находят
по теории течения разрежения Прандтля — Майера. В свою очередь,
решение по теории Прандтля — Майера «склеивается» с решением, получаемым
по формуле (ХИ-7-17).
§ ХП-8. Влияние
неравновесности на параметры
невязкого обтекания
затупленных тел
ДозБукобая
область "
Неравновесное течение в
областях с большим
перерасширением и малыми градиентами
давления
Области течения газа около затупленного тела. Если рассмотреть
характер обтекания затупленного тела, то можно установить три области течения
газа (рис. ХП-8-1). Первая из них
непосредственно примыкает к затупленному
носку, располагаясь между осью потока
и «звуковой» линией. Она характеризуется
почти постоянным давлением, близким к
давлению полного торможения.
Перемещаясь вдоль линии тока в этой области
почти постоянного и очень большого
давления, газ, будучи после перехода через
ударную волну в состоянии неравновесной
диссоциации, получает возможность
быстро возвратиться в равновесное состояние.
Причем, равновесие соотвествует
некоторому среднему значению давления и
энтальпии в этой области.
Вторая область потока начинается от
звуковой «линии» и характеризуется на
некотором участке резким уменьшением
давления. Она может заканчиваться (в
зависимости от формы тела за носком)
течением с положительным, нулевым или
отрицательным градиентами давления. На участке значительного
перерасширения состояние диссоциирующего газа не успевает следовать за. равновес-
Рис. ХП-8-1. Схема течения газа
около затупленных тел:
а — затупление по сфере; б — плоское
затупление с круглой фаской;1 —
ударная волна; 2 — «звуковая» линия; з —
ударный слой низких скоростей; 4 —
линия тока
Аэродинамика затупленных тел вращения
533
0,2
ным, поэтому термодинамическая неравновесность является существенным
свойством движущегося газа.
В третьей области течения, расположенной в периферийной части тела
и характеризующейся небольшим изменением давления, газ будет
стремиться к равновесному состоянию.
Таким образом, при расчете невязкого обтекания возникает
необходимость учета неравновесности. При этом, как показывают исследования,
давление практически мало меняется при переходе от неравновесного
состояния к равновесному. Основываясь на этом факте, оказалось возможным
оценить влияние неравновесной молекулярной диссоциации на такие
параметры невязкого течения, как степень
диссоциации, плотность и температура при заданном
распределении давления, близком к реальному. При
этом принимается, что распределение давления
подчиняется одному и тому же закону независимо
от условий движения тела.
Расчет неравновесного течения. Этот расчет
связан с интегрированием системы уравнений
(Ш-4-47) при некоторых заданных константах и
граничных условиях. Результаты, приведенные
ниже, получены с использованием значений С =
= 6-1014 см31г-сек и pd = 125 г /см3. Граничными
условиями при интегрировании уравнений
являлись условия на «звуковой» линии, причем
соответствующие параметры на этой линии
определялись при заданной скорости полета Foo и
некоторой высоте Н как параметры равновесного
течения в области полного торможения.
Линия тока, вдоль которой вычислялись
неравновесные параметры течения, располагалась
вниз по течению от «звуковой» области.
Принималось, что давление на этой линии тока
устанавливается таким, как при расширении одномерного
потока в соответствии с законом Прандтля — Май-
ера. Предполагалось также, что протяженность выбранной линии тока с
таким распределением давления будет порядка радиуса сферического носка
или четверти радиуса плоского торца (или торца со слабой круглой фаской).
Принятая протяженность первоначального сверхзвукового расширения
определяет характерный линейный размер L.
На рис. ХП-8-2 показано распределение давления, подсчитанное
на основе теории Прандтля — Майера при условии перехода линией тока
веера расширения, начиная от «звуковой» точки ([72], 1960, № 11). Для линии
тока с постоянным радиусом кривизны г угол расширения принимался
равным v = х = х/г. Некоторые результаты численного интегрирования
системы (Ш-4-47), приведенные на рис. XI1-8-3 -г- ХП-8-7, получены для
различных высот и скоростей полета. Кроме того, в каждом случае расчеты
проводились для нескольких значений характерной длины L (или, что то же
самое, параметра ф).
Из рис. XI1-8-3 можно сделать вывод о характере изменения
неравновесной диссоциации. Здесь же в порядке сравнения показа ы кривые
изменения степени равновесной диссоциации, полученные для реального воздуха
(В) и модели двухатомного газа (А). Можно заметить, что при скоростях
Foo > 5 км /сек разница между величинами степени равновесной
диссоциации в двух последних случаях невелика. Из анализа приведенных
результатов видно, что изменение степени диссоциации а вдоль линии тока по
О,"
Рис. ХП-8-2. Падение
давления вдоль линии тока при
расширении газа по закону
Прандтля Mt
534
Глава XII
сравнению с начальным равновесным значением аОе весьма мало даже на
значительном удалении. О таком состоянии газа говорят, что оно близко к
«замороженному», характеризующемуся тем, что в газе реакции не происходят
и, следовательно, его химический состав не меняется.
0,45
6) а
UJ 0,7
0,65
0,60
0,55
0,50
\
L-3
\\
30 м
А
— —
В
О 0,4 0,8 х
0,70
0,65
0,60
0,55
0,50
\
1
/
А
•С
О 0,4 0,8 х
0,25
0,20
0,15
0,10
$
к
Зм
30 м,
300м
о
=x/L
об
0,25
0,20
0,15
0,10
L=30m/
300м
А'
—-—
В'
Фа
0,25
О 0,4 0,8 х
0,15
0,10
А
В
О 0,4
х
Рис. ХП-8-3. Влияние неравновесности на степень диссоциации вдоль
линии тока:
А — двухатомный газ; В — реальный воздух; а — Я = 47 км, V^ = 7,G км/сек\
б — Я = 61 ?ш; Vqo = 7,6 км/сек; в — Н = 75 клс, Vqq = 7,6 куи/сск; г — Я = 47 клс;
¥^ = 4,6 км/сек; а —Я =61 клс, Уоо = 4,6 км/сек; е — Я = 75 клс, Voo = 4,6 км/сек
Можно условиться в практических случаях считать течение
«замороженным», если состав газа отличается от исходного примерно на 5%. Тогда,
если at — степень неравновесной диссоциации в конце рассматриваемого
участка расширения, то для «замороженного» состояния должно быть
выполнено условие, согласно которому параметр
Г | j 1 . 1 . неравновесной диссоциации
причем этот параметр включает величину а1е,
представляющую собой степень равновесной
диссоциации в конце того же участка. Если
параметр а4 равен нулю, то это означает
полный переход в состояние равновесия.
Практически можно считать, что такое состояние
наступило, если о^ < 0,05. Возвращаясь к гра-
1 _J / фикам на рис. ХП-8-3, можно отметить, что
Op oc-x/L на высотах СВЬ1Ше 47 км при скоростях
полета 5—8 км/сек течение в области
сверхзвукового расширения вблизи затупленных тел
будет практически «замороженным».
При какой-либо фиксированной скорости
полета и длине L течение оказывается ближе
к «замороженному» при возрастании высоты.
С уменьшением скорости при прочих равных условиях параметр at
возрастает, что объясняется уменьшением местной плотности. Увеличение «заморо-
\
N
ч
N
4
Л
"3
0 0,2 0,4 0,6
Рис. ХП-8-4. Изменение
плотности при неравновесном течении
двухатомной модели газа:
Н= М км, Vqo = 4,6 км/сек, 1 - L =
= 0,3 м; 2 — L— 6 м\ 3 — L = 30 м;
4 — L= оо (равновесное течение)
Аэродинамика затупленных тел вращения
535
женности» наблюдается при уменьшении характерной длины L, что связано
с уменьшением времени пребывания частиц газа в рассматриваемой точке,
в течение которого в
рекомбинации успевают принять
лишь немногие атомы.
2RJ
V2
—-,
^7
<£
5 4
i i
3
/■
~4-—
"-—.
2
=bz
—' —.
-—
/
i
———
О 0J 0,2 0,3 Ofi 0,5 0,6 0,7 0,8 x=x/L
Рис. ХП-8-5. Распределение температуры при
неравновесном течении двухатомной модели газа Н =
= 47 км, Voo = 4,6 км/сек:
1 — l= оо (равновесное течение); 2 - L = 300 м; 3 — Ь —
= 30 м\ 4-L=3 м\ 5-L=0,S м
ТТ 0,14
Из приведенных на рис.
ХП-8-4 и ХП-8-5 результа- о,12
тов следует, что отклонение
от равновесия обусловливает qjq
снижение плотности и
повышение температуры. В свою 0,08
очередь это приводит к
существенному изменению мест- 0,06
ных чисел Re. При этом, как
показывают расчеты,
отклонение от равновесного течения
оказывает слабое влияние на
перераспределение давления.
По результатам
численного интегрирования
уравнений (III-4-47) на рис. XII-8-6 построены графики, дающие возможность
оценить по известной величине ф параметр неравновесной диссоциации а4.
За областью сверхзвукового расширения течение попадает в зону слабо
изменяющегося давления, которую практически можно принимать за область
постоянного давления, что упрощает
анализ. Этот случай близок к
действительному, если к затупленному носку
примыкает конический участок.
Перемещаясь в области с
постоянным давлением, частицы газа получают
возможность возвратиться в
равновесное состояние, соответствующее
постоянным значениям энтальпии и давления.
Неравновесные параметры в процессе
такого перехода определяются в
результате интегрирования только последнего
уравнения системы (Ш-4-47).
Начальные условия определяются
«замороженными» параметрами в конце
рассмотренного выше участка сверхзвукового
расширения (длина х отсчитывается от этого
конуса). Полученные результаты
показывают, что при скорости 4,6—7,6 км /сек
течение на участке, примыкающем к
носовой части, практически продолжает
оставаться «замороженным» на
расстоянии не менее 6—9 м, причем это
расстояние, относящееся к высоте порядка
45—47 км, возрастает для больших
значений Н. Например, для высоты Н =
= 61 км длина L увеличивается до 30 м.
Некоторые результаты расчета для
высоты ZT = 47 км приведены на рис.
ХП-8-7. Отклонение от «замороженного» состояния и приближение к
равновесным условиям происходит наиболее быстро при больших скоростях.
Рис. XI1-8-6. Изменение параметра
неравновесной диссоциации в различных
условиях:
1-Н=47 ш, УОО = 4,6 км/сек; 2-Н =
= 61 км, Vqo = 4,6 км/сек; 3-Я =47 км,
1^ = 6,1 км/сек; 4 - Я = 61 км, V^ =
= 6,1 км/сек; 5—Н= 47 км, У^ = 7,С км/сек;
6 — Н = 61 км, Vоо =7,0 км/сек
536
Глава XII
х=о
Явление «замораживания» потока свойственно не только области с
нулевым градиентом давления, но в еще большей степени — течению с
отрицательным его значением, которое возникает,
rtx-p-^f например, при обтекании цилиндра. Такая
повышенная чувствительность к
«замораживанию» объясняется тем, что снижение
давления обусловливает уменьшение
плотности. В последнем уравнении системы
(Ш-4-47) член в правой части,
характеризующий рекомбинацию, существенно
зависит от плотности, изменяясь
приблизительно пропорционально квадрату ее величины.
Из приведенного анализа
неравновесного течения около затупленного тела
можно сделать следующий практический
вывод. Так как вся зона течения,
связанная с областью сильной ударной волны,
продолжает оставаться «замороженной»
почти на всей длине затупленного тела, то
в этом ударном слое расчет параметров
невязкого обтекания вдоль линии тока
можно вести из условия изэнтропического течения при к2 = 1,1—1,2 (точное
значение кг рассчитывается для условий полного торможения). В
соответствии с этим температуру и плотность в данной точке находят из выражений
0,16
Щ
Q08
0,04
О
^^
■—
--
—-
^^
^^—
———
Зм
~—±—
15
17,5
20
22,5
Рис. XI1-8-7. Изменение степени
диссоциации вдоль конической
поверхности в условиях постоянного
давления (Н = 47 км)
р'о
р'о
(ХП-8-1)
Влияние неравновесности на
положение и форму ударной
волны
Рассмотрим следующие два предельных случая, характеризующие
качественно это влияние. Первый из них обусловлен полностью «замороженным»
течением за ударной волной, когда газ ведет себя как среда с постоянными
теплоемкостями, которые можно определить, если принять, что
вибрационные степени свободы устанавливаются за ударной волной мгновенно. Однако
для выяснения наибольшего эффекта можно исходить из того, что
равновесие для этих степеней не устанавливается.
Во втором предельном случае газ в сжатом слое находится в условиях
равновесной диссоциации.
Ранее были изложены методы расчета относительного отхода ударной
волны в обоих предельных случаях обтекания. В соответствии с
результатами расчета в первом случае волна оказывается наиболее удаленной от
критической точки, во втором, наоборот, она расположена на самом близком
расстоянии от этой точки.
Между этими предельными случаями находятся реальные
неравновесные течения, характеризующиеся промежуточным расположением ударных
волн. Для того чтобы охарактеризовать такие течения, целесообразно ввести
параметр неравновесности, определяемый следующим образом. Из
последнего уравнения системы (Ш-4-47) следует, что для течения за прямым
скачком уплотнения величину (Сроо)"1 можно рассматривать как временный
масштаб диссоциации, а параметр Foo(Cpoo)"1 — как линейный масштаб тече-
Аэродинамика затупленных тел вращения
537
ния. Тогда в качестве безразмерного параметра неравновесного течения
можно принять отношение какого-либо линейного размера тела к линейному
масштабу течения.
Для сферы линейным размером может
быть ее диаметр DT. Следовательно,
параметр неравновесности в этом случае
0,2
У
f,
/
—
1
У
/1
/
1
0,2 0,й Q6
Рис. XI1-8-8. Изменение степени
диссоциации вдоль нулевой линии
тока (от ударной волны до
критической точки тела):
171 л V\o Poo
-~— = 1; = 10-6; 1 - Л= 100;
2-А=50; 3-Л=10; 4-A=i
об
ор
Если этот параметр Л равен нулю, то
имеем недиссоциированный («замороженный»)
поток, что обусловлено бесконечно медленной
химической реакцией.
Большие значения Л соответствуют
быстро протекающим реакциям и, следовательно,
диссоциация начинается вблизи волны и
захватывает почти всю область между волной
и поверхностью тела. При Л -> оо равновесие
достигается сразу после волны.
Для анализа течения между волной и
телом можно воспользоваться локальным
значением параметра Л = Я, вычисленным по
местной скорости V на нулевой линии тока,
т. е. величиной
A, = Z)TCpOoF-1. (XII-8-2')
В критической точке, где V = О, этот параметр X = оо и,
следовательно, вблизи нее достигается равновесная диссоциация. Физически такое
явление объясняется чрезвычайно замедленным течением в окрестности точки
торможения, способствующим
установлению термодинамического равновесия.
Если исходить из равновесного
течения на поверхности тела, то
качественно распределение концентраций
атомарной компоненты вдоль нормали к
стенке будет характеризоваться ее
постепенным уменьшением в направлении
к ударной волне, где степень
диссоциации равна нулю. Теоретический
профиль концентраций можно рассчитать,
решив систему уравнений для
обтекания области критической точки
совместно с последним уравнением системы
(Ш-4-47) неравновесного течения. Для
одного из частных случаев рассчитан-
Q15
0,10
0,05
О
20
60
Л
Рис. ХП-8-9. Относительный отход
ударной волны перед сферой как функция
параметра неравновесности:
- = 1;
-=10-6
ный таким образом профиль концентраций приведен на рис. ХП-8-8.
Наряду с этим одним из результатов решения является возможность
расчета расстояния от ударной волны до тела. На рис. ХП-8-9 графически
представлено изменение относительного отхода в зависимости от параметра
неравновесности Л. Сравнивая результаты, можно заметить, что отход
в двух предельных случаях, т. е. в «замороженном» и равновесном течениях,
может отличаться вдвое. Приблизительно такой же характер носит
изменение радиуса кривизны волны на оси.
Случай неравновесности на поверхности. Отношение
характеристических времен TD = tD/tS0 (tso — время пребывания частиц в зоне
неравновесной реакции) может быть использовано для ориентировочной оценки
условий, при которых возникает неравновесная химическая реакция настен-
538 Глава XII
ке. Очевидно, такая реакция произойдет в том случае, если £^>1, т. е.
когда атомы достигают поверхности тела прежде, чем прореагируют.
Для оценки протяженности L участка поверхности с химической
реакцией надо сравнить характеристическое время реакции с характеристическим
временем пребывания частиц в зоне неравновесности на рассматриваемом
участке. При этом время пребывания рассчитывают с использованием
величины da/dt, которая определяет скорость изменения степени диссоциации,
обусловленного исчезновением атомов вследствие рекомбинации. Время этого
исчезновения, очевидно, равное характеристическому времени пребывания
в зоне реакции, определяется из уравнения
dt __ dx I
1a~~da V *
Для приближенной оценки можно принять dx/da ~ Ыа0, где а0 —•
степень неравновесной диссоциации в точке торможения. Следовательно,
время пребывания можно представить в виде L/(a0V), где V — скорость
частицы вдоль поверхности вблизи точки торможения. Примем, что эта
скорость по величине того же порядка, что и средняя скорость между
скачком и телом, равная 0,5F0. Таким образом, отношение характеристических
времен можно представить в виде
tV /YTT Я Ч\
(Xll-8-d)
*L = _-=__.
От этого выражения нетрудно перейти к зависимости
_ LtL =lDaoSo, (ХП-8-3')
где L = L/RT.
Так как мы рассматриваем зону реакции, то в ней, очевидно, должно
выполняться условие £l>1- Следовательно, длина этой зоны, начиная
от точки торможения, будет
На участке поверхности с такой длиной в пограничный слой поступают
атомы, не участвовавшие в химической реакции.
Процесс рекомбинации завершается в пограничном слое и оказывает
известное влияние на процессы трения и теплопередачи. При этом следует
подчеркнуть, что распределение давления практически не зависит от
эффектов неравновесности.
Уточнение режима течения в зоне торможения (в критической точке
и в некоторой области вниз по течению) позволяет оценить изменение
плотности и температуры, если этот режим оказывается неравновесным.
Увеличение температуры и уменьшение плотности на внешней границе слоя
приводит к изменению теплового потока на этом участке поверхности по
сравнению с состоянием равновесия. Можно предположить, что, несмотря
на увеличение температуры, тепловой поток несколько снизится вследствие
уменьшения плотности.
До сих пор все расчеты велись в предположении, что параметр скорости
рекомбинации kR не зависит от температуры. Однако в действительности
температура оказывает существенное влияние на этот параметр. В частности,
согласно некоторым экспериментальным данным для кислорода
[^УсмУмоль2-сек. (ХИ-8-5)
В соответствии с этой формулой вычисленное выше время релаксации
можно уточнить, если ввести поправочный коэффициент (Г/3500)2.
Следовательно, уточненное время релаксации
Ч)2- (хп-8-6>
Гла в а XIII
НЕСТАЦИОНАРНАЯ
АЭРОДИНАМИКА
КОРПУСОВ.
§ XIII-1. Линеаризованное
обтекание тел вращения
Основные зависимости
Общие определения. Рассмотрим задачу об обтекании тела
линеаризованным неустановившимся потоком. Как и в случае установившегося
обтекания, для ее решения применим метод источников с той разницей, что
обтекаемое тело заменяется системой неустановившихся источников (стоков)
и диполей ([72], 1951, № 8).
Предположим, что в линеари- г
зованном сверхзвуковом потоке г=г(х)
с некоторым числом Моо
происходит дополнительная поперечная
продувка со скоростью W (#, £),
зависящей от времени t и
координаты х произвольного сечения тела
вращения (рис. ХШ-1-1). Таким
1
\w(x,t)
Рис. XIII-1-1. Схема неустановившегося обте-
образом, этот дополнительный по- кания тела вращения в поперечном направ-
ток является неустановившимся. лении
Следуя методу источников, можно
рассматривать потенциал скоростей такого потока как потенциал от
неустановившихся источников и диполей, у которых соответственно мощность
и момент меняются по времени.
При этом потенциал скоростей от неустановившихся источников и
диполей, размещенных на оси тонкого тела, определяется из линеаризованного
уравнения (III-2-31). Интеграл этого уравнения ф' отыскивается в виде
суммы двух потенциалов: ф^ — потенциала осесимметричного обтекания,
который не дает возмущений, приводящих к возникновению нормальной
силы, и ф^ — потенциала от нарушения симметрии, обусловливающего
появление нормальной силы. Как и в случае установившегося обтекания,
решение для добавочного потенциала ф^ может отыскиваться в виде (XI-1-14).
Что касается решения для ф{, то оно представляет собой интеграл
линеаризованного уравнения неустановившегося обтекания
-фгг —7~фг
2МО
(XIII-1-1)
где индексы х, г обозначают соответствующие частные производные.
Потенциал неустановившегося источника (стока). Представим решение
уравнения (XIII-1-1) в виде
;= -т)(ж, г)ехр [т (*_
(ХШ-1-2)
где со —угловая частота колебания тела в необращенном движении;
г](£, г) —некоторая функция, зависящая от переменных х, г.
При этом т] (0, г) = ч)х(О, г) = 0, что физически соответствует отсутствию
возмущений на линии х = 0.
540 Глава XIII
После подстановки выражения (ХШ-1-2) для q^ в уравнение (ХШ-1-1)г
оно преобразуется к виду
Ът + уУ]г- (а')2 Т1« - ^yt г, = О, (XIII-1-3)
Дифференциальное уравнение (XIII-1-3) может быть решено
операционным методом, который основан на интегральном преобразовании
Лапласа. Этот метод в применении к данному случаю состоит в том, что изучается
не сама функция т] (х, г), называемая оригиналом, а ее так называемое
изображение. Такое преобразование функции rj (x, г) по отношению к
переменной х осуществляется следующим образом. Функция т] (х, г) умножается
на экспоненциальную функцию exp (—sx), а затем производится
интегрирование в пределах от 0 до оо. В результате получаем
оо
т] (s, г) = \ ехр (— sx) ц (х, г) dx, (XIH-1-4)
о
где г] (^, г) —функция, называемая изображением (по Лапласу) функции
у](х, г);
s — некоторая комплексная величина, являющаяся оператором:
преобразования.
В результате преобразования Лапласа (ХШ-1-4) получаем
обыкновенное дифференциальное уравнение для изображения
dr
(ХШ-1-5)
Из вида уравнения (ХШ-1-5) становится понятным смысл
осуществленного преобразования — оно уменьшило число переменных на единицу и тем
самым позволило перейти от уравнения в частных производных (XIII-1-3)
к обыкновенному дифференциальному уравнению (ХШ-1-5). Полученное
уравнение относится к одной из разновидностей уравнения Бесселя,
имеющему ограниченное на бесконечности решение
где Ко — функция Макдональда.
Отыскав изображение г), следует найти оригинал г|. Для этого
необходимо воспользоваться обращением преобразования Лапласа.
Окончательное выражение для искомой функции имеет вид
т) (*, г) = [*«- (а'г)*Г1/2 cos {^-^ [х'~ {a'rff2 } , (ХШ-1-7)
которое действительно при условии (х — aV)>0.
На основании выражений (ХШ-1-2) и (ХШ-1-7) получим соотношение
для потенциала неустановившегося точечного источника. Если источники
с переменной интенсивностью / (е) непрерывно расположены вдоль оси х,
то потенциальная функция
q)j = exp (mt) X
*-*''/(в) ехр Г-^^^
х ^ L аоо(а) =! Uoo(a /9 >—. ши-1-8)
Потенциал неустановившегося диполя. Дифференцируя потенциальную
функцию ср^ по г, найдем в соответствии с (XI-1-14) добавочный потенциал ср^
неустановившегося диполя. Прежде чем осуществлять операцию
дифференцирования, преобразуем выражение (ХШ-1-8) к переменной z = arch [{x — e)/(a>)].
Нестационарная аэродинамика корпусов $41
Продифференцировав затем по г и вновь переходя к переменной г = х — aVchz,
найдем выражение для потенциала неустановившегося диполя
г
х—а'г
' — е) х
sin
I
аоо{а')*г
X
X
(XIII-1-9)
Граничное условие. Граничное условие для определения функции /(е),
входящей в (XIII-1-9), получается из условия безотрывности обтекания. Это
означает, что потенциал возмущенного движения от неустановившегося диполя
Рис. XII1-1-2. Случаи движения тела вращения:
а _ гармоническое колебательное движение относительно центра
тяжести тела; б — гармоническое колебание тела, нормальное
к продольной оси; в — установившееся вращение тела
относительно поперечной оси, проходящей через центр тяжести
должен быть таким, чтобы на поверхности тела или, учитывая малость его
толщины, на оси х исчезла нормальная составляющая скорости, т. е.
выполнялось условие, аналогичное (XI-1-11'),
(ХШ-1-10)
Это условие принимает различные формы в соответствии с конкретным
случаем обтекания, сопровождающимся тем или иным видом движения тела.
Рассмотрим возможные случаи движения тела, имеющие практический
интерес в связи с исследованием колебательной устойчивости.
Гармоническое колебательное движение тела
относительно поперечной оси, проходящей через центр
тяжести (рис. ХШ-1-2, а). В этом случае движение определяется
уравнением
a = a0 exp (tot), (XIII-1-11)
где а0 —начальная амплитуда, равная значению угла атаки в момент
времени t = 0.
Глава XIII
Колебания тела обусловливают в обращенном движении возникновение
неустановившегося возмущенного течения, поперечная составляющая скорости
которого
W(x, t) = Vooa0ex1p(m) + ^(x-x4mT). (ХШ-1-12)
Так как
-^- = а,ш ехр (Ш), (ХШ-1-13)
то граничное условие примет вид
Л$к == _ а0 ехр (icot) cos у [(7*, + ^ (х — хц, т)]. (ХШ-1-14)
Гармоническое колебание, нормальное к продольной
оси тела (рис. XIII-1-2, б). В этом случае движение характеризуется
поперечной составляющей скорости
W (t) = Wo ехр (Ш), (ХШ-1-15)
где Wo — нормальная скорость колебательного движения в момент
времени £ = 0.
Следовательно, условие (ХШ-1-10) напишется в виде
J*El = _ Wo ехр (Ш) cos у. (ХШ-1-16)
Установившееся вращение тела относительно центра
тяжести (рис. XIII-1-2, в). Составляющая скорости в некоторой точке
поверхности тела, имеющего в рассматриваемом случае постоянный угол
атаки а0, определяется выражением
W (х) = a0Foo + Qz(x — хц, т), (ХШ-1-17)
где Qz — угловая скорость вращения. Граничное условие будет
Ц + Qz (х - хц, т)] cos у. (ХШ-1-18)
Граничные условия служат для определения закона распределения
источников, т. е. вида функции /(е). В случае очень тонкого тела вид этой
функции можно найти следующим образом. Сначала преобразовывают
выражение (ХШ-1-9) к переменной z = arch [(# —е)/а'г)] и вычисляют частную
производную ср2Г. Затем, снова преобразовав полученное выражение для этой
производной к переменной & = х — a'rchz, переходят к пределу при г—>0.
К найденной предельной зависимости присоединяют написанные выше
граничные условия. Тогда предельное значение частной производной ср2Г,
которое рассматривается в теории тонкого тела для случая неустановившегося
обтекания, будет
■?Г= -^ехр (Ш) cosy, (XIII-1-19)
где S (х) = лг2 — площадь поперечного сечения, отстоящего от острия тела
на расстоянии х.
Определение аэродинамических коэффициентов. Выражение для
потенциальной функции и граничное условие необходимо дополнить
соотношениями, определяющими в общем виде аэродинамические коэффициенты.
Одним из этих соотношений является формула (XI-1-21) для добавочного
коэффициента давления, возникающего в результате неустановившегося
поперечного обтекания. Внося вместо р2 выражение для этого коэффициента
в соответствии с формулой (XI-1-21) под интеграл (XI-3-1), получим для
Не стационарная аэродинамика корпусов 543
коэффициента нормальной силы
cNp = - ■/- \£- г dx, (XIII-1-20)
°мид J tot5 У
где
Рассмотрим теперь зависимость, определяющую коэффициент момента
относительно оси, проходящей через центр тяжести. С этой целью
воспользуемся формулой (1-5-8), которую преобразуем к виду
Выражение для коэффициента осевой силы, как следует из формул
(1-3-14) и (XI-1-21), не изменяется по сравнению со случаем
установившегося обтекания.
Аэродинамические коэффициенты
в условиях колебаний
низкой частоты
Общее выражение для потенциальной функции. Решение задачи
об определении аэродинамических характеристик при неустановившемся
сверхзвуковом обтекании тела вращения упрощается, если этому обтеканию
соответствуют в необращенном движении колебания низкой частоты. Если
представить выражение (ХШ-1-9) в виде ряда по степеням параметра
k = Moo(ur/(a'Voo), который называют приведенной гармонической частотой,
то можно убедиться в том, что для частот порядка аооа//хк потенциал
неустановившегося обтекания может быть с достаточной степенью точности
представлен в виде линейной зависимости от параметра к. Переходя в этой
зависимости к переменной z = arch [(x — е)/(а'г)], найдем в первом
приближении
arch и
Фз = cos у ехр (icot) \a' \ f (x — a'r ch z) chzdz —
-a'rchs)efe]. (XIII-1-23)
Вычислим теперь производные от cpg по х и t, необходимые для
определения коэффициента давления. Полагая f — m, получим
archu
ф2х = a' cos у ехр (icot) Г \ га (х —air ch z) chzdz —
о
archu
archu
— ШосЛ \ m(x — a'rchz)dzl; (XIH-1-24)
о
archu
2^ = a'ico cos у ехр (Ш) Г ^ m{x — a'r ch z) chzdz —
о
m (x — air ch z) dz] . (XIII-1-25)
о
archu
544 Глава XIII
Вид функций т и т определяется из условия (ХШ-1-19), а также
граничных условий для каждого конкретного случая движения тела.
Гармоническое колебательное движение тела
относительно центра тяжести. В этом случае вид функций т и т можно
определить следующим образом. Вначале из выражений (ХШ-1-14),
(ХШ-1-19) найдем функцию
/ (е) = ^р~ а0 [Foo + ш (е - хЦи т)]. (ХШ-1-26)
Затем, вычисляя первую и вторую производные, находим соответственно
т (8) = -^- ao iVn + ш (е- а?ц. т)] + -^ коа0; (ХШ-1-27)
т(е) = ^1^- а0 [Foe + т (г — хц, т)] + ^-^ шсс0. (ХШ-1-28)
Внесем в уравнения (ХШ-1-24) и (ХШ-1-25) эти выражения,
предварительно перейдя в них к переменной z = arch [(x — e)/(aV)]. Вычисляя затем
интегралы и используя формулу (XI-1-21), получим
(ХШ-1-29)
где
о
Q±= \ S'(x — a'rchz)chzdz; (XIII-1-30)
archu
О
Q2= ^ S'(x — a/rchz)(x — a'rchz)chzdz; (XHI-1-31)
archu
0
archu
Внося р"; из (ХШ-1-29) в (ХШ-1-19), (ХШ-1-22) и вычисляя затем
производные
получим
(ХШ-1-35)
Производные устойчивости очень тонких тел можно получить из
приведенных выражений, если функции Qn заменить соответствующими
значениями из аэродинамики тонкого тела. Чтобы найти эти значения,
необходимо в выражениях (XIII-1-30) — (XIII-1-32) перейти к переменной г=-х —
— aVchz и после этого осуществить предельный переход при г—>0.
Подставив найденные таким образом значения функции Qn в выражения
Нестационарная аэродинамика корпусов
(ХШ-1-34) и (ХШ-1-35), получим
. (ХШ-1-37)
Гармоническое колебание в направлении,
нормальном к продольной оси тела. Функция /(е) для этого вида
движения определяется в соответствии с выражениями (ХШ-1-16) и (ХШ-1-19)
следующим образом:
а функция т и ее производная т имеют вид
Перейдя к переменной z и подставляя найденные из выражений
(XIII-1-39) функции т ж т в формулы (ХШ-1-24) и (ХШ-1-25), получим
соответствующие значения ф2х и ср2*, а затем по (ХШ-1-21) —коэффициент
давления. Внося значения этого коэффициента в (ХШ-1-20) и (ХШ-1-22)
и дифференцируя, получим производные устойчивости
2а'
где
—к
а 2 \ yQi Ц---^\гхйх,
(ХШ-1-42)
Зависимости для производных устойчивости, вытекающие из
аэродинамической теории тонкого тела, имеют вид
с»р= s2Wtx ; (ХШ-1-43)
= 25ДОН [^ ^ - (й ^дон)"1 J 5 (ж) ж efe] . (ХШ-1-44)
о
Установившееся вращение вокруг центра тяжести.
В этом случае функция / (е) задается уравнением
/ (е) = £|> [a0FM + Йг (8- хц.,)]. (ХШ-1-45)
Дважды продифференцировав это выражение по е, найдем
7(8) = т = ^ [aoFoo + Q2 (е - ягц. т)] + ^^ Й*. (ХШ-1-46)
Перейдя в этой формуле к переменной z и подставив полученное
выражение для т в (XI-3-2), найдем ф2Х> а затем коэффициент давления
35-114
546
Глава XIII
При помощи р'2 можно вычислить коэффициенты нормальной силы
и момента, обусловленные вращением, а затем и их производные
*J
J («■+£-^-*)rte <XIIM-47>
где
о
dcNp
'^zp
(ХШ-1-49)
Производные устойчивости, соответствующие аэродинамической теории
тонкого тела, имеют вид
& (^) (ХШ-1-50)
Результаты расчета производных устойчивости по приведенным формулам
для тела вращения параболической формы приведены на рис. XIII-l-3-r-
0,6
0,5
Ofi
0,3
--
о
С z
^&
—-^
/77.
i
■Р
'"zp
-1,0
-0,8
■r-Ofi
1,4
1,8 2,0 2,2 Мо
О
Рис. ХШ-1-3. Изменение
производных устойчивости тела
вращения в зависимости от числа Моо
при вращении с постоянной
угловой скоростью
1,4 1,6
Рис. XI11-1-5. Изменение
производных устойчивости тела вращения
в зависимости от Моо при
гармонических колебаниях, нормальных
к продольной оси
JZLl 0,15
1,6 ~8 W 2,2 M^
Рис. XIII-1-4. Изменение
производных устойчивости тела
вращения в зависимости от числа Мое
при гармонических колебаниях
около центра тяжести
n
1,2
1,0
,2т
———
-
Tot
V
m
mzp
' /,4 1,6 0 2,0 2,2 Моо
Рис. XII1-1-6. Изменение
производных устойчивости тела вращения
в зависимости от Моо при
движении с постоянным углом атаки
-f-XIII-1-5. Образующая этого тела имеет вид г ^=0,02 (10а; — х2), а коор
дината центра тяжести, отсчитываемая от начала координат хЦщ т = 5. Штри-
Кестационарная аэродинамика корпусов
ховыми линиями на этих рисунках показаны результаты, полученные
по теории тонких тел. Для сравнения на рис. XIII-1-6 приведены
статические производные устойчивости, вычисленные для того же тела, по
формулам линеаризованной теории
да
dmzp хц. - -
да хк
" —" О
^-гх dx, (XIII-1-53)
а также по формулам аэродинамической теории тонкого тела (штриховые
линии)
с« =24^; (ХШ-1-54)
°мид
а о ^Д^Н / ^Ц. Т WT л\ /vttt л гг\
mzv = 2^ +^ 1 . ХШ-1-55
§ X111-2. Применение
метода Ньютона
Заостренное тело вращения
Рассмотрим аэродинамические характеристики корпуса, совершающего
наряду с поступательным движением с гиперзвуковой скоростью также
вращение с некоторой угловой скоростью Qz относительно центра тяжести.
Коэффициент давления определяется общей формулой (IV-7-7) в виде
суммы двух составляющих, одна из которых обусловлена поступательным
движением, другая —демпфированием, возникающим вследствие вращения.
Первая составляющая pv дается формулой (Х-3-1), вторая равна
в соответствии с выражением (IV-7-9) величине
Ра= —-гг^ {гЩ$ + х — #ц.т) (cosasin(3 —
— sin a cos р cos у) cos |3 cos у -j- -^- cos2 у cos2 Р (г tg |3 + z — ^ц. т)2»
(ХШ-2-1)
Коэффициент осевой силы корпуса, испытывающего вращение около
центра тяжести, в соответствии с формулой (1-3-14)
де х =
cRp = —p. J г tg p dx J (ру + рп) dy, (XIII-2-2)
О 7К
х
мид
Эту формулу можно представить в виде
cRp = (сЛр)0=о + ^ {crp)q dx, (XIII-2-3)
где ,
= ^ = ± Кт г tg p I pQdy. (ХШ-24)
35*
$48 Глава XIII
Коэффициент осевой силы (снр)а--=о при отсутствии вращения определяется
формулой (Х-3-5). Вторая составляющая в (ХШ-2-3) зависит от угловой
скорости вращения Qz и, как видно, выражена в виде интеграла от местного
коэффициента осевой силы c'Rv. Если рассмотреть обычно встречающийся
на практике случай малых угловых скоростей, то вторым членом в (ХШ-2-1)
можно пренебречь, тогда
(crpYq = —J^P sin 2р sin a (r tg Р + х - хц, т) X
X [(я — 7к) — sin ук (cos 7к — 2 tg p ctg a)]. (XIII-2-4')
Вычисление пределов х'к и ук, определяемых протяженностью и формой
«затененной» зоны, изложено в § Х-3. Вращательная производная
Для коэффициента нормальной силы можно написать аналогично
(XII1-2-3) выражение
х'к
cNp = (cnp)q=o + \ (cnp)'q dx, (XIII-2-6)
о
X
где х =
В этой^формуле (cNp)q=o определяется по (Х-3-36) с сохранением в ней
знака «минус», а величина
я
(cnpYq = —^~ = ^- г \ р& cos у dy. (XIII-2-7)
дх Я <j)
В результате подстановки под интеграл выражения (ХШ-2-1) для ра, в
котором оставлен первый член с QJVoo, получим
4Q ~г%
(cNv)'Q= — ' z MHAsin2pcosa(rtgP + 3; — хЦлТ) X
X
Вращательная производная
О
Рассмотрим выражения для суммарного коэффициента продольного
момента корпуса относительно центра тяжести и соответствующей
вращательной производной. Коэффициент момента
хк п
Р r (r *S Р + 2яА,мид — 2^ц. Дмид) cos у dx dy,
о
(XIII-2-10)
где
— х m - г m - хц- т
Нестационарная аэродинамика корпусов 549
Или, учитывая выражение (ХШ-2-7),
mzp = -щ- ^ (г tg р + 2х Хшт — 2хц. т Ямид) [(cNp)Q==0 + (c'Np)Q] dx,
где в соответствии с (Х-3-36)
^р ^РЫ г, (ХШ-2-12)
а производная (cNp)q равна (ХШ-2-7).
Вращательная производная
о
Для цилиндрического участка тела в приведенных формулах следует
принять р = 0, ук = я/2. В соответствии с этим (crp)q — (cNp)'q = 0.
При некоторых углах атаки, меньших р0 у острия, «затененная» зона
на криволинейной головке может иметь небольшую протяженность, так что
можно принять #к=1, а величину ук = 0. В этом случае
-~ = *мид sin а { sin 2р (г tg р + 2яЯмид — 2хц. ТА,МИД) г dx; (XIII-2-14)
°° о
1
dcNp 2#мид Л # —
■^г- = —7т cos а \ sin 26 (г
dmzp
О
1
cos a \ si
о
Если углы а>ро, то влияние «затененной» зоны будет значительным
и следует пользоваться более общими зависимостями, в которых угол
7K = arccos(tgp/tga). В «затененной» зоне можно принять коэффициент
давления ре = 0.
Для расчета суммарных аэродинамических коэффициентов следует
воспользоваться формулами
= Ыа=0 + ^й, (ХШ-2-17)
В последней формуле
I . (ХШ-2-18)
о
По найденным значениям га2р и cNp определяется коэффициент центра
давления c^K = inzplcNp.
Затупленный конус
Аэродинамические коэффициенты затупленного по сфере конуса,
совершающего вращение с угловой скоростью Qlz, следует вычислять по формулам
(ХШ-2-3), (ХШ-2-6), (XIII-2-11), в которых интегралы представляются
в виде суммы трех интегралов, каждый из которых соответствует области
550
Глава XIII
обтекания, установленной в § ХП-6. С учетом протяженности областей
обтекания первый интеграл вычисляется в пределах от 0 до х&, второй —
от ха до хк и третий —от хк до /к (см. рис. ХП-6-1).
В соответствии с (XII1-2-3) суммарный коэффициент осевой силы
(ХШ-2-19)
= (cRp) Q=0 + А (Сдр)й,
где (сяр)й=о вычисляется по формуле (ХИ-6-4), а добавочная величина
коэффициента A (cRp)q, вызванная вращением,
A (cRp)Q = Я, - хц. ТВ2,
где #ц. т = #ц. т/£к — относительная координата центра тяжести.
Коэффициенты
(ХШ-2-20)
(l— -^l
cos a sin 2pK (b3 + R* sin2 рк).
(XIII-2-21)
Здесь (oz = QzlK/Voo; -йт^^т/^м
RT — радиус сферического носка);
— длина незатупленного конуса,
3sinpK); 1
[
(ХШ-2-22)
Коэффициент нормальной силы
cNp = (cNph=o + A (cNp)Q, (XIII-2-23)
где (cNp)q=0 находится по (XII-6-9) при отсутствии вращения.
Добавочная составляющая, обусловленная угловой скоростью,
A (cNp)q = Ai — хц, ТА2,
где
к —ctgatgPK)x
А2 = 2coz (l — 3£- ] b3 cos a cos2 рк + coz&2 (I + sin2 a) +
+ -д- ©г cos2 рк ^^ cos а (4 tg a ctg рк — ctg a tg рк) (Ь3 — Ь4);
, _ Лт sin2 а (4 + 3 sin2 ftK)--sin2 gK
Л~~^" -•-•"/4—3sm*pK) — si
(ХШ-2-24)
(XIII-2-25)
(XIII-2-26)
Нестационарная аэродинамика корпусов 551
Суммарная величина коэффициента продольного момента относительно
центра тяжести с координатой #ц>т определяется по выражению
mzp = Kp)Q=o + A (mzp)Qi (XIII-2-27)
где (mzp)Q=Q вычисляется без учета демпфирования при помощи формулы
{ХН-6-14). При вычислении следует учесть, что момент определяется
относительно точки #ц# т. В соответствии с этим (m^Q^o = mzp — cNpx4.Ti где mzp
находится из (XII-6-16), a cNp — из (Х-3-36). Составляющая демпфирования
A (mzp)Q = F~ 2Агхц. т + А< т, (ХШ-2-28)
где Ai и А2 определяются выражениями (ХШ-2-25). Параметр
к [2 cos а (1 - Jk) {Ъ\ + Ъь) + b2bsRl sin2 рк (1 + sin2 а) +
+ f
где
f Щ (4 *8а ct^ P«-Ctg а tg P«) (&i + bs - bsb^ sin2 Рк cos2 P«>]' (XI11-2-29)
рк_^ дв cos6 рк> (ХШ-2-30)
При отсутствии «затененной» зоны, когда а<рк, угол ук = 0, и,
следовательно, параметры, определяющие демпфирование, будут проще:
Bi = -^Д sin а; В2 = 2cozfo3 sin а cos2 рк; (ХШ-2-31)
i44 = ^Ь- cos а; Л - 2со2&3 cos а cos2 рк; (ХШ-2-32)
р^ 2coz cosa щ + ъъ (ХШ-2-33)
72 COS2pK Ъ3 •
Для^ [заостренного конуса характеристики демпфирования могут быть
получены при условии, что i?T =0, Z = l:
_ ^ (XIII-2-34)
Б2 = 2сог sin a cos2 pK [ (l —^-) + ^ tg pK ctg a] ;
, = 2co2 cos a cos2 6К Г f 1 -^ + [ (ХШ-2-35)
+ ^^ (^ tg a ct^ Рк — tg Рк ctg a) J ;
Если а<рк, то «затененная» зона отсутствует, угол ук^О и,
следовательно,
4
sin a; Вг = 2coz sin a cos2 рк; (ХШ-2-37)
о
± = -s- coz cos a; ^42 = 2coz cos a cos рк; (ХШ-2-38)
о
(XUI-2-39)
552
Глава XIII
Для цилиндра со сферическим носком коэффициенты Bii2 и Аи2
принимают вид
Bi = -^- sin а (1 + eos а); В2 = ^- сог sin а (1 + cos а); (ХШ-2-40)
(ХШ-2-42)
По этим коэффициентам можно, используя формулы (ХШ-2-20)
и (ХШ-2-24), определить составляющие демпфирования для коэффициентов
2,0
W ^
У'
/
/
/
s
у'
— '
■*"-•
_
к
Т\
Л
ч
\
ч
\
ч
ч
\
\
\
2,0
80
120
160 сс°
<
J
/
/
/
/
/
-**
^=0,0
\
>Я=039
^1
\
Ч
\
s
\
\
\
Ч
V
\
ч
\
\
\
\\
\
\
\
N
V
Л
\
\\1 N
!
ч,
80
120
160
Рис. XII1-2-1. Параметры демпфирования дА±/д(йг и дА2/д(о2, вычисленные по
ньютоновской теории, для конуса со сферическим затуплением (Рк = 15°):
конус с цилиндрической хвостовой частью длиной 0,334 <^мид; без
цилиндрической части
осевой и нормальной сил. Коэффициент момента демпфирования
Л () |^(l + i2) ^А)
(ХШ-2-43)
При круговом обдуве, когда углы атаки достигают значений а > 90°,
следует учесть влияние на демпфировать донной плоскости, введя в
значение A (mzp)Q поправку
№ = сог ДЁк. Cos a. (XIII-2-44)
Результаты расчетов по этим
формулам приведены на рис.
XIII-2-1 и ХШ-2-2. На рис. ХШ-2-1
показаны значения производных
у
s
—
s
u..
**^
4r0R
\
ч
ч
s
S;
\
•-
—
0 U0 80 120 160 cL°
Рис. ХШ-2-2. Параметр демпфирования dF/d(dz,
вычисленный по ньютоновской теории, для
затупленного по сфере конуса (|3К = 16°):
с цилиндрической хвостовой частью
; без цилиндрической части
= Аг г\
= А2 г в за-
висимости от а, найденные при
круговом обдуве затупленного ко-
нуса с рк = 15° и i?T = 0,6 и 0,9.
причем в ОДНОМ Случае КОНуС
имел цилиндрический хвостовой
участок длиной хц = 0,334 ймид. На рис. ХШ-2-2 для этих же условий
приведены расчетные данные для производной dF/d(uz=F z.
■ — конус
длиной 0,334 L
Нестационарная аэродинамика корпусов
553
§ XI11-3. Дополнительное
силовое воздействие,
обусловленное вращением
корпуса вокруг продольной оси
При вращении корпуса вокруг продольной оси симметрии возникает
дополнительная боковая сила AZ (так называемая сила Магнуса),
вычисляемая по формуле
AZ = сД2д£мидсох, (ХШ-3-1)
где
q = 0,5pooF?o; (ox = ^xdUVL-Ptl2VOo\ cAz = (dcAz/da) a;
dcAz SX2
да
(7,834-16,53со^2);
(ХШ-3-2)
Формула (XIII-3-1) получена для цилиндрического тела с плоским дном
и пригодна для небольших углов атаки а<5ч-7° и условий обтеканияг
при которых пограничный слой
сохраняется ламинарным.
Координата (#ц. д)д2 точки
приложения магнусовой силы,
отсчитываемая от носка корпуса,
вычисляется из формулы
со8
ч
V
к
1,6 Z,0
Ofi 0,8
Рис. XII1-3-1. Сила Магнуса при больших углах.
атаки корпуса
(ХШ-3-3)
Момент этой силы относительно
носка AM = AZ (хц. Д)Д2. Для
турбулентного пограничного слоя
эффект Магнуса возрастает
примерно на 30 — 40%. Этот эффект
слабо зависит от формы носка,
степени его затупления, наличия каких-либо кольцевых выступов или
желобков на корпусе. В то же время форма хвостовой части летательного аппарата
оказывает существенное влияние на величину AZ. В частности, округление
задних кромок у дна может сильно изменить силу Магнуса и обусловить
нелинейность изменения AZ в зависимости от угла атаки а даже при малых
значениях этого угла.
Отмеченная нелинейность усиливается с увеличением углов атаки. Чтобы
учесть этот эффект, можно воспользоваться графиком на рис. XIII-3-1, где
даны экспериментальные значения величины
в зависимости от
хоо ПОП к оо ПОП/
= Foo sin a/a*,,
полученные для корпусов с удлинениями от 3 до 9. Величина Snp равна
площади продольного сечения корпуса. Данные рис. XIII-3-1 позволяют
определить силу Магнуса с точностью до 10 ч-20%.
Пример. Определим силу Магнуса и момент этой силы для неоперенного корпуса,
вращающегося вокруг продольной оси и совершающего полет с угловой скоростью
Qa; = 600 1/сек, на высоте Ъ км с Моо = 2 под углом атаки а = 5°. Геометрические
£54 Глава XIII
размеры корпуса следующие: жц = 970 мм; хт = Ь60 мм; ^мид = 250 лш. Расстояние от
носка до центра массы хц, т = 830 мм.
В соответствии с этими размерами условная длина £ = #ц + 0,5.гг = 970 + 0,5-560 =
= 1250лл; удлинение К = 1/с1мид = 1250/250 = 5.
По таблицам стандартной атмосферы находим для высоты 5 км: роо=0,07506 кГсек2/м*;
л?оо = 22,09 • Ю-6 м2/сек2; а^ = 320,4 м/сек.
Скорость полета на этой высоте
= 2-320,4 = 640,8 м/сек,
число Рейнольдса
Vool 640,8-1,25
' Voo 22,09-10-6 —"" ^ *
По формуле (XI11-3-2)
-^L = 8'52 |/9 , [7,834- 16,53 ( 690Q;/°r:2ft5 )2 5*1=0,0721.
da (0,36.108)1/2 {I V 2-640,8 / j
Так как скоростной напор
q = pJf^/2 = 0,07506 • 640,82/2 = 1,54-104 кГ/м2:
площадь миделевого сечения ^мид = л^ид/4 = jt-0,252/4 = 0,0491 м2, то в соответствии
с (XII1-3-1) сила Магнуса
AZ = 0,0721 (-^3-) 1,54-104.0,0491 ^§^- = 0,477 «Г.
По формуле (XII1-3-3) находим
Расстояние между точкой приложения силы Магнуса и центром массы
летательного аппарата
&х= ( Хц'Д ) I — яц.т = 0,695.1250-830 = 870—830 = 40 мм.
Момент от силы Магнуса
AM = AZ-A^ = 0,477-0,04 = 1,9-Ю-2 крм.
Предположим, что угол атаки увеличен на 10° и необходимо учесть нелинейный
эффект. Из рис. (XIII-3-1) по МооПоп = Моо sin a = 2-sin 10 = 0,347 находим
- Роо^по -SWO =0,18.
Для летательного аппарата с конической головной частью площадь продоль-
еого сечения
(-g-0,56 + 0,97) 0,25 = 0,3
По этой величине продольного сечения и поперечной скорости обтекания Foonon =
ооПопаоо = 0,347-320,4 = 111 м/сек подсчитываем силу Магнуса
AZ = 0,18 Г-i- 0,07506.1112.0,312 ( ^'ш5 ) 1 =17'5 кГ*
Глава XIV
ТРЕНИЕ
И ТЕПЛОПЕРЕДАЧА
ПРИ БОЛЬШИХ СКОРОСТЯХ.
§ XIV-1. Трение и
теплопередача на корпусе
Пограничный слой около тела вращения. Уравнения для пограничного слоя
около тела вращения можно преобразовать к уравнениям для пограничного
слоя плоского двухмерного газового потока [57]. Уравнения движения и
неразрывности для осесимметричного ламинарного пограничного слоя (рис. XIV-1-1)
будем рассматривать соответственно в виде (Ш-2-12) и (Ш-2-21) при условии,
что величина 8=1, а радиус г принят равным его значению г0 для корпуса.
Полагая 8 = 1, г = г0, для совершенного газа с постоянными теплоемкостями
уравнение энергии получается из (III-2-45) в следующем виде:
Используем формулы преобразования, предложенные Манглером [57]:
\йх\ y = -^roy; (XIV-1-2)
(XIV-1-3)
) = р(х); T{xLy) = T(x, у); р(х, у) = р(х, у);
И* \хч У) ~ И1 \х>> У/f
где d — некоторая характерная длина;
с — произвольный масштабный множитель.
Составляющие скорости связаны с функцией тока соотношениями
2
ду
дх
При помощи приведенных
формул преобразования уравнения
движения (Ш-2-12), неразрывности
(Ш-2-21) и энергии (XIV-1-1)
преобразуются к соответствующим
уравнениям для плоского
двухмерного пограничного слоя,
распределение давления вдоль которой
подчиняется условию р(х)=р (х).
Параметр х связан с длиной дуги х образующей тела вращения формулой
(XIV-1-2). Очевидно, что в соответствующих точках плоскопараллельного
и осесимметричного течений параметры газа на внешних границах
пограничных слоев имеют одинаковые значения.
Рис. XIV-1-1. Система координат для
преобразования Манглера:
1 — образующая корпуса; 2 — граница
пограничного слоя
556 Глава XIV
Рассмотрим соотношение между напряжениями трения. Для
плоскопараллельного течения тст = Мчзт (dVJdy)CT, а для осесимметричного тст = И-ет X
X (dVx/dy)CT. Учитывая зависимость (XIV-1-2) для г/, найдем отношение
irCT/TcT=(c/d)r0, в котором eld определяется из первого выражения (XIV-1-2).
В результате замены получим
т / гт-2
тст / xr0
Координату а; можно выбрать равной длине дуги х образующей. Если
перейти к осевой координате х, уравнение образующей написать в виде
X
г0 = /(#), то длина дуги будет равна \ yrlJr(dr/dx)2dx.
о
Следовательно,
ст о
Из второго соотношения (XIV-1-2) получим зависимость между толщи-
нами пограничного слоя
б тст
Для использования указанных зависимостей необходимо знать уравнение
образующей тела вращения. Если это уравнение задано в виде г = ахт,
то отношение тст/тст будет являться функцией показателя т. На удаленных
от носка участках криволинейной поверхности, где изменение давления вдоль
образующей пренебрежимо мало, течение в пограничном слое тела вращения
может быть приближенно определено из течения в пограничном слое
на плоской пластинке, обтекаемой равномерным потоком под нулевым углом
атаки при таких же значениях параметров газа, что и в невязком потоке
около корпуса, и при той же температуре стенки.
Для полностью турбулентного пограничного слоя расчет можно вести
по формулам
^31 = (1 + 2т)1/5; 4- = (1 + 2m)-i/b. (XIV-1-4")
тст б
На основании равенства (XIV-1-4) можно получить зависимость [41] для
сопротивления трения тела вращения произвольной формы
где х — длина дуги, отсчитываемая вдоль меридионального контура;
хк — длина тела вращения.
Сопротивление трения
где cXf — средняя величина коэффициента трения для плоской пластинки
длиной хк;
— боковая (смачиваемая) поверхность тела.
Трение и теплопередача при больших скоростях S57
Для турбулентного течения преобразование Манглера дает выражение
для сопротивления трения [41]
Конус. Для конуса показатель m = l; dro/dx = tg$K; r0 — #tg|3K,
следовательно, в случае ламинарного пограничного слоя
Таким образом, в соответствующих точках поверхностное трение на конусе
в ]/3 больше, а толщина пограничного слоя в ]/3 меньше, чем на плоской
пластинке.
По формуле, аналогичной зависимости (XIV-1-6), определяются
местные с* и средние с* значения коэффициентов трения
которые отнесены к скоростному напору возмущенного потока дк =
Если перейти к скоростному напору невозмущенного течения д«> = PooVL/2,
то в формулах (XIV-1-7) появится сомножитель рк^к/роо"^.
В случае полностью турбулентного пограничного слоя на конусе
}
Для определения среднего коэффициента сопротивления трения,
рассчитанного по площади миделевого сечения конуса, необходимо воспользоваться
формулой
-w S ^* (Х№1-10)
где х = х/хку а координата х отсчитывается по оси, совпадающей с осью
конуса. Коэффициент cfx зависит от числа Рейнольдса, которое определяется
по длине, отсчитываемой вдоль образующей. Подставляя под интеграл
значение cfx, получим
где I—длина образующей конуса; значения Сип определяются из табл. VI-1-1.
Коэффициент А для ламинарного пограничного слоя равен ]/г31 а для
турбулентного А = У^З.
Цилиндр. Для цилиндрического тела т = 0, следовательно,
Таким образом, если принять, что «невязкие» параметры на цилиндре
сохраняют постоянные значения, то напряжение трения и толщины
пограничного слоя будут такими, как на плоской пластинке, имеющей
такую же температуру стенки и «невязкие» параметры, что и на цилиндре.
558 Глава XIV
Полученный результат относится и к ламинарному и к турбулентному
пограничному слою.
Теплопередача. Для расчета теплопередачи на конусе используем
формулу (IV-8-41'), в которой заменим коэффициент трения его значениями
для конуса. Местное и среднее значения числа Стантона будут определяться
соответственно соотношениями
st,^4c™(РгГ2/3; st=4С-/Л(Ргг2/3- (xiv-i-i2)
Коэффициенты теплоотдачи ажиа вычисляются на основе формул (IV-8-40').
Метод определяющей энтальпии. Для того чтобы учесть
влияние высоких температур, в приведенных формулах необходимо перейти
к определяющим параметрам.
Местный коэффициент ламинарного трения, вычисленный по этим
параметрам для конуса,
где величины с = р*(х*/рк|хк, Re^ = VKpKx/\iK вычисляются по параметрам
свободного потока на конусе (индекс «к» соответствует индексу «б»).
Число Стантона
St* - 9KvJirT-iCT) = d V lfc' (XIV-1-14)
где d можно рассчитывать по одной из формул
d = 0,575 (Рг*)-2/3 или d = 0,251 (1,3 + Pr*)/Pr*.
Число Нуссельта, вычисляемое по определяющим параметрам,
VRe^ kK(ir — iCT)
Расчеты турбулентного трения и теплопередачи могут быть
осуществлены аналогично. При этом используется закон «корня седьмой степени».
Исследования показали (В. М. Иевлев), что удовлетворительные
результаты для местного коэффициента трения и удельного теплового потока
получаются соответственно по формулам (VI-1-37) и (VI-2-8), в которых параметр
z = 0,54 Re*. (XIV-1-16)
В тех случаях, когда предположительно устанавливается равновесная
радиационная температура, расчеты трения и теплопередачи на конусе
ведутся по методу последовательных приближений. Для иллюстрации
изложим порядок расчета параметров трения и теплопередачи, имея в виду,
что в пограничном слое газ диссоциирован. Этот расчет начинается с
определения параметров идеального обтекания конуса, а именно давления рк,
плотности рк, энтальпии iK, скорости FK. Затем задаются приближенным
значением числа Прандтля Рг* = 0,71, а также энтальпией
теплоизолированной стенки iCT = iK + 0,5]/Рг*7к и вычисляют по формуле (IV-8-7)
определяющую энтальпию i*. По ее величине, а также давлению рк находят
с помощью таблиц или графиков термодинамических функций
определяющую температуру Г*. Используя, далее, уравнение состояния, находят
плотность р*=рк[Хср/(/?07т*)> причем средний молекулярный вес |ХсР
вычисляют по значениям f и рк.
В дополнение к этим параметрам рассчитывают вязкость, затем
вычисляют в первом приближении по выражению (XIV-1-12) число Стантона,
а по нему удельный тепловой поток
qCT = StlpKVK(ir— iCT),
Трение и теплопередача при больших скоростях 559
где
е / rp \ #
Решая после этого уравнение qCT = есгГст, определяют во втором
приближении равновесную радиационную температуру Тст = Те. По
найденной температуре можно вновь провести расчеты, уточнив значения чисел
Pr*, St* и величину Тст = Те. Для турбулентного пограничного слоя расчеты
производятся аналогично.
Когда диссоциация отсутствует, равновесная радиационная
температура может определяться в результате решения уравнения
■Э^хРк" к \Ср)ст \+ г — •* сту == ^оУ ст.
Осуществляя расчеты, следует оценить протяженность ламинарного
пограничного слоя, определив критическое число Рейнольдса. Как
показывают исследования (подробней об этом см. § XJV-3), критическое число Re
определяется наряду с местным числом Мб=Мк также относительной
температурой стенки Тст/Тг (рис. XIV-3-4), причем имеет место приблизительно
пропорциональная зависимость между ReKP и Тст/Тг (см. рис. XIV-3-4).
Охлаждение стенки ведет к увеличению протяженности ламинарного слоя.
Критическое число Рейнольдса для случая равновесной радиационной
температуры рассчитывается путем последовательных приближений. Анализ
показывает, что величина равновесной радиационной температуры зависит
от режима течения в пограничном слое и координаты точки обтекаемой
поверхности, причем эта температура возрастает по мере приближения
к острию.
Переход к турбулентному пограничному слою также способствует
увеличению температуры стенки, причем температура может оказаться
настолько высокой, что материал обшивки будет разрушаться. Чтобы охладить
стенку, можно повысить излучательную способность поверхности. Однако
практически не удается обеспечить степень черноты более 0,8. Поэтому
приходится охлаждать внутреннюю поверхность стенки или защищать
обшивку изоляцией. При необходимости делается и то и другое.
Предположим, что при охлаждении изнутри стенки с температурой
ТСт = Те = 1500° К отводимый тепловой поток qox = 30 ккал/м2-сек,
коэффициент теплоотдачи в рассматриваемой точке поверхности аох = 2,56 X
X 10~2 ккал/м2-сек-град, температура восстановления в ней Тт = 4400° К.
По этим данным находим q%xl{uoxTT) = 0,27 и приведенную температуру
Т'г = 3200° К. В соответствии с формулой (VI-4-2) равновесная температура
стенки Тст = Те = 1380° К, т. е. охлаждением удалось снизить
температуру на 120°.
По найденному значению Тст определим внешнюю и внутреннюю
температуру обшивки, используя формулу (VI-4-4).
§ XIV-2. Влияние вязкости
на сопротивление. Донное
сопротивление
Влияние вязкого взаимодействия
на параметры обтекания
Для расчета «невязких» параметров с учетом влияния пограничного
слоя необходимо найти закон изменения толщины вытеснения по длине тела
и ввести поправку в уравнение образующей. С этой целью можно
воспользоваться результатами теории сверхзвукового пограничного слоя для пло-
660
Глава XIV
ской пластинки и конуса, основанной на применении определяющих
параметров.
Приняв в (Ш-2-43) р = рб и произведя замену Vx/Vq по уравнениям
(VI-1-1), получим для толщины вытеснения ламинарного слоя выражение
^нс. л = 36/8, а для турбулентного — 6НС. т = 6/8. Внося в эти выражения
соответствующие формулы для толщин, получим
Ь*=В (^-Y xm, (XIV-2-1)
WsPdJ
где для ламинарного слоя В = 1,74, п = т~ 1/2; для турбулентного
# = 0,046; лг = 1/5; гтг = 4/5. Переходя к определяющим параметрам, найдем
(XIV-2-2)
Если рассмотреть конус| в сверхзвуковом вязком потоке, то толщины
вытеснения можно вычислить по формуле
6* Л—1 £* /Vf\7" О Q\
* = А Юпл, (XIV-2-d)
в которой для ламинарного пограничного слоя А = ]/3, для
турбулентного А = у^З.
В соответствии с этим текущая радиальная координата образующей
фиктивного тела rK = r-{- 6kCosPk. Входящая сюда условная толщина
л*__ АРптт (XW-9 А\
°к — а~ х ? vA1 v £-4)
где
Р = Si £* Ж.. (XIV-2-5)
И-б Р Рб^б
Для ламинарного слоя А = 1,02, для турбулентного А = 0,037.
В этой формуле координата х представляет собой расстояние от острия
вдоль образующей конуса
произвольного сечения пограничного
слоя и равна х = г /sin рк.
Фиктивное тело отличается от конуса
и имеет криволинейную
образующую. Однако для упрощения
расчетов можно сохранить
поверхность конической. При этом
исРис. XIV-2-1. Схема к расчету условной
толщины вытеснения
ходят из некоторой средней
величины приращения угла Др
кажущегося конуса, которая
вычисляется по формуле Ар = бд/L. Причем в этой формуле условная толщина 6д
определяется из выражения (XVI-2-4) для хк = L, т. е. для сечения
пограничного слоя у донного среза. Таким образом, угол кажущегося конуса
Рк = Рк + ЛР- Для этого угла и производятся все расчеты невязких
параметров на конусе.
Рассмотрим теперь тело вращения произвольной формы.
Принимая, что носок тела представляет собой конический элемент малой длины
(рис. XIV-2-1), найдем в конце его толщину вытеснения
6J - IP?*?1, (XIV-2-47)
где Pi рассчитывается из выражения (XIV-2-5) по параметрам на
коническом носке.
Следующий малый участок криволинейной поверхности заменим
усеченным конусом с длиной образующей х2 и предположим, что он является
продолжением фиктивного конического тела с длиной образующей х2ф.
Трение и теплопередача при больших скоростях
В конце этого фиктивного конуса условная толщина равна б* и вычисляется
по формуле _(XIV-2-4'). Следовательно, для фиктивного конуса имеем
выражение б* = АР%х™ф, из которого можно найти длину х2ф его образующей.
Причем функция Р2 подсчитывается по параметрам на втором участке.
Зная теперь длину образующей х2ф + х2 фиктивного конуса с учетом длины
второго участка, можно приближенно подсчитать толщину вытеснения
в точке В поверхности тела (рис. XIV-2-1):
Аналогично можно вычислить толщину вытеснения в точке С:
где функция Р3 находится по параметрам на третьем участке, а длина х3ф
фиктивного конуса подсчитывается с помощью выражения
61 = API (х2ф + х2)т = АРп3х7ф.
Обобщая приведенные соотношения, можно написать зависимость для
условной толщины на произвольном i-ou участке:
б? - АРпг (xt ф + Xi)m, (XIV-2-6)
где длина хгф образующей фиктивного конуса находится из условия
6?_i =ЛР?_1 (х^1ф + х^)п = АР^хТф. (XIV-2-7)
Для получения координаты точки образующей кажущегося тела надо
воспользоваться тем же выражением.
В случае теплоизолированной поверхности изложенный метод расчета
предполагает совместное решение двух задач. Первая из них связана с
определением невязких параметров, вторая — с расчетом параметров трения
и теплопередачи.
Для упрощения расчетов можно не учитывать влияния теплопередачи
и высоких температур на термодинамические характеристики и
кинетические коэффициенты газа. Тогда эффект больших скоростей сведется к
влиянию сжимаемости (числа Моо) на толщину пограничного слоя и, как
следствие, на невязкие параметры. Приближенную оценку невязких параметров
на криволинейной поверхности можно осуществлять, применяя зависимости
для условной толщины несжимаемого пограничного слоя. В случае сильно
охлажденных потоков (например, в аэродинамических трубах), хорошее
совпадение полученных данных с экспериментальными наблюдается даже
при том условии, что расчет произведен по формулам для плоской пластинки.
Вязкое взаимодействие на тонком конусе при гиперзвуковой скорости
обтекания. Для определения «невязких» параметров на тонком конусе при
гиперзвуковых скоростях можно воспользоваться методом «местных
конусов» и формулой (VIII-1-27), в которой К1 = МОоРк заменяется значением
К* = Ki + Moo (d8*ldx) = Моо (Рк + d§*ldx). Производная d&*/dx для
ламинарного пограничного слоя вычисляется по выражению [59]
*»Ь^** (XIV-2-8,
dx уз V "|/Rex н УЗ Мн
в котором dH, с„, ReXII даны соотношениями (V-6-9), a % — формулой (V-6-6).
Число Мн находится из теории обтекания тонкого конуса без учета вязкого
взаимодействия. Приведенное соотношение для d8*/dx относится к
произвольной температуре стенки Тст. Для частных случаев
теплоизолированной и холодной стенки значения du определяются соответственно по
формулам (V-6-10) и (V-6-11).
36-114
562 ' Глава XIV
При слабом взаимодействии, когда индуцированное давление мало
отличается от первоначального, йб*/Лг<|Зк (значения К1 = МооРк
произвольные). В этом случае параметр гиперзвукового взаимодействия % изменяется
до значений примерно 3—3,5. Сильному взаимодействию, при котором
£* » 1 и dd* Idx > |3К соответствуют величины %н > З-т-3,5.
Трение
Приближенная оценка коэффициента сопротивления трения для
корпуса может быть осуществлена по формулам
Cxf л = Cxf л-« » cxf т = Cxf т -^ , (А1 V -Z-У)
Г 4,96.10-4 дуд 0,0396 / 1 О.ЬУдЧП S6oK /YTV 9
L ^1 + О.ОЗМ^ ^бок "*" У1 + 0,12М^ Ueo,i45 ^бок ) J ^1ИД • У^1 ^'
первая из которых применяется в случае полностью ламинарного, вторая —
полностью турбулентного пограничного слоя. Величины с^/л и cXfT
являются коэффициентами сопротивления трения плоской пластинки
соответственно для ламинарного и турбулентного пограничных слоев.
Соответствующая расчетная формула для коэффициента сопротивления
трения при смешанном пограничном слое имеет вид (VII-1-1). Если
коэффициенты турбулентного и ламинарного трения в (VI1-1-1) определять
соответственно по формулам (VI-1-8) и (VI-1-10), а влияние сжимаемости учитывать
при помощи зависимостей (VI-1-18) и (VI-1-19), то, принимая критическое
число Рейнольдса равным 6,5 • 106, получим
f
Эксперименты в аэродинамических трубах при небольших
сверхзвуковых скоростях (Моо с^. 1,5-7-2) показали, что можно использовать для
расчета сопротивления трения формулы, полученные для плоской пластинки
в предположении несжимаемого пограничного слоя.
Улучшение результатов вычисления сопротивления трения связано
с учетом влияния формы поверхности тела вращения. При этом упрощенный
способ расчета трения для тонкого и длинного тела заключается в замене
головной части эквивалентным конусом, а остальной части — цилиндром.
Как и на эквивалентном конусе, параметры газа на цилиндре можно
рассматривать постоянными. Их значения обычно принимаются такими, как
параметры набегающего потока.
Угол эквивалентного конуса можно определить по формуле рк. э =
= \ |3<2#. В частном случае параболической головки |3К. э = 0,5р0-
о
Суммарная величина коэффициента сопротивления трения
комбинированного тела (эквивалентный конус + цилиндр)
где А — постоянная для ламинарного и турбулентного пограничных слоев
соответственно равна ]/"3 и УЗ;
$бок — боковая поверхность действительной головной части;
б'бок — поверхность остальной части тела (цилиндра).
Коэффициент с}к в этой формуле рассчитывается из выражений для
плоской пластинки, но по параметрам на эквивалентном конусе. Для расчета
коэффициента с°" надо поступить следующим образом. Вначале определяют
Трение и теплопередача при больших скоростях
фиктивную длину цилиндра Хф, на которой при заданных на цилиндре
параметрах образовался бы пограничный слой с толщиной, равной ее
значению в конце конуса.
Приравнивая соответствующие выражения для толщин, найдем
' <XIV-2-12>
где #к.э — длина образующей эквивалентного конуса; п=Л и 1/4
соответственно для ламинарного и турбулентного слоев.
Теперь можно определить коэффициент трения
±fS-c,.^. (XIV-2-13)
Здесь коэффициент Cft ф+ц рассчитан по длине Хф + хц, a cf — по
фиктивной длине Хф.
Смысл этой формулы заключается в том, что она определяет
сопротивление трения цилиндрической части как разность сопротивлений цилиндра
с фиктивным участком и фиктивного участка.
Вместо расчета по методу эквивалентного конуса можно производить
вычисления, используя метод «местных конусов» и понятие о фиктивной
длине конуса. При этом длина фиктивного конуса определяется по формуле
(XIV-2-7). Найденное распределение местных касательных напряжений
позволяет рассчитать суммарную силу трения, вычислить распределение
тепловых потоков и полную теплопередачу.
В основу расчета коэффициентов трения могут быть положены
соотношения, учитывающие влияние сжимаемости (в них непосредственно входит
число Моо), а при очень больших скоростях — зависимости с
определяющими параметрами.
При вычислении параметров теплопередачи необходимо перейти к
местным коэффициентам трения. Выражения для этих коэффициентов на
эквивалентном конусе и на цилиндре соответственно будут
cfx = Ac?i; cfx = A'cf*. (XIV-2-14)
Причем коэффициент с/ц рассчитывается по длине Хф + х, где х —
расстояние от начала цилиндрической части.
В первой формуле (XIV-2-14) значение коэффициента А выбирается
как для обычного конуса, в зависимости от того, каким будет пограничный
слой — ламинарным или турбулентным. Во втором выражении (XIV-2-14)
величина А' может быть принята равной единице, если толщина
пограничного слоя во много раз меньше радиуса цилиндра. При этом условии для
турбулентного пограничного слоя на цилиндре расчет трения и
теплопередачи может быть осуществлен по формулам тонкой пластинки.
Донное сопротивление
Сверхзвуковые скорости. Одной из составляющих полного
сопротивления является донное сопротивление, обусловленное возникновением за тупым
основанием тела разрежения. Возникновение разрежения связано со
взаимодействием между пограничным слоем, отрывающимся у дна тела, внешним
потоком и газом в задонном пространстве (застойной зоне) (рис. XIV-2-2).
Внешний поток играет роль эжектирующей среды, а пограничный слой —
своеобразной перегородки, препятствующей эжекции; газ в застойной зоне
ведет себя как эжектируемая среда. Эжектирующий эффект и,
следовательно, величина донного давления рдон зависят от того, каким является
пограничный слой в области между точкой отрыва А и точкой прилипания 5,
36*
564
Глава XIV
расположенной на оси: полностью ламинарным, смешанным или полностью
турбулентным. Кроме того, донное давление зависит от ряда других
факторов, таких, как угол атаки, форма тела в целом и, в частности, конфигурация
у основания, числа Маха и Рейнольдса, температура стенки.
Характер течения в пограничном слое, как известно, определяет
толщину слоя, которая при ламинарном течении будет меньше, при
турбулентном — больше. Эффект эжектирования носит противоположный характер:
при ламинарном слое этот
эффект больше, при
турбулентном — меньше.
Следовательно, в первом случае,
донное давление оказывается
меньше, во втором — больше.
Наиболее сложным для
анализа является случай
смешанного течения,
характеризующийся тем, что точка
перехода расположена между
точками отрыва и
прилипания. Можно предположить,
что влияние такого
смешанного пограничного слоя на
донное давление будет носить промежуточный характер между тем влиянием,
которое оказывают чисто ламинарный и чисто турбулентный пограничные
слои.
Зависимость донного давления от формы тела обусловлена влиянием
конфигурации поверхности на толщину пограничного слоя в точке отрыва,
Рие. XIV-2-2. Схема течения газа за дном тела
вращения:
1 — область внешнего потока; 2 — пограничнай слой;
3 — застойная зона; 4 — область расширения; 5 — область
сжатия; 6 — нижняя граница пограничного слоя; 7 —
верхняя граница пограничного слоя
200 tC
0
15 &
'02
Рис. XIV-2-3. Зависимость донного давления от
температуры стенки (1) и полуугла |302 кормовой части (2)
(турбулентный пограничный слой)
а также на среднее давление (обозначим его р') и число М' внешнего
невязкого потока в окрестности дна. На рис. XIV-2-3, где показаны
экспериментальные данные, видно, что увеличение угла конусности кормы приводит
к увеличению донного давления и, следовательно, к уменьшению
коэффициента донного сопротивления.
Изменение числа Маха сказывается на изменении величины среднего
давления, а также профиля скорости в пограничном слое в точке отрыва
и, как следствие, на эжектирующем эффекте. При этом с ростом числа Маха
донное давление всегда снижается.
Донный эффект, как указывалось, зависит от вида пограничного слоя
в окрестности хвостовой части. При этом для одного и того же вида
пограничного слоя зависимость донного давления от числа Рейнольдса оказывает-
Трение и теплопередача при больших скоростях
565
ся небольшой. Это, в частности, видно из рис. XIV-2-4, где приведены
данные измерений донного давления в случае турбулентного течения.7
Наблюдается лишь небольшое, теоретически предсказываемое увеличение донного
давления при уменьшении числа Рейнольдса.
Влияние малого угла атаки на донное давление оказывается небольшим.
Из экспериментальных данных на рис. XIV-2-5 можно видеть, что с
увеличением угла атаки при турбулентном обтекании донное давление
постепенно уменьшается. С ростом скорости обтекания величина донного
давления будет также уменьшается, так как оно приближается к своему
предельному значению, равному нулю.
Донное давление зависит от расположения задней кромки консолей
хвостового оперения. Когда кромки прямоугольного оперения расположены
Р'
0,8
0,7
0,6
-
/
2
0,2
0,3
-0,23
-0,22
-0,21
-020
2
1
=====
Г*
О
Рис. XIV-2-4. Влияние числа Рейнольдса на Рис. XIV-2-5. Влияние угла атаки
донное давление (эксперимент): на "7 :
7 М' = 1,5; 2 JVT = 2 1,2, 3 — для отношений *7гдон, равных
соответственно 0,876, 0,756, 0,992
у основания донное сопротивление возрастает по сравнению с
изолированным корпусом, Сдвиг вперед оперения на величину, приблизительно в одну
хорду, приводит к тому, что донное сопротивление остается таким, как для
изолированного корпуса. Наряду^.с изменением места расположения на
данное сопротивление влияет также толщина профиля и форма консолей
оперения в плане.
При нагреве пограничного слоя его толщина возрастает, а донное
давление вследствие этого увеличивается (см. рис. XIV-2-3). При охлаждении
пограничного слоя путем отвода тепла через поверхность наблюдается
обратный эффект — толщина слоя уменьшается, а донное давление
снижается. Этот эффект наблюдается при полете с большой сверхзвуковой скоростью,
когда стенка принудительно охлаждается, и температура пограничного
слоя оказывается ниже той температуры, которая устанавливается для
адиабатической стенки.
На рис. XIV-2-6 показаны экспериментальные результаты
исследования донного давления, полученные для серии тел вращения различной
формы, на поверхности которых образуется турбулентный слой. Различие
в форме связано с неодинаковой конфигурацией хвостовой части тел.
Универсальность кривой на рис. XIV-2-6 достигнута введением таких параметров,
как среднее давление внешнего обтекания р' и число М', представляющее
собой среднее число Маха внешнего потока вдоль длины смешивания и
соответствующее давлению р'. Число М' можно рассматривать как параметр
подобия: независимо от конфигурации хвостовой части отношение p^0Jpf
остается постоянным для одного и того же значения М'.
Чтобы определить при помощи кривой на рис. XIV-2-6 донное давление
для заданной формы тела вращения, надо предварительно найти
соответствующее этой форме среднее давление р' вдоль длины застойной области.
С этой целью можно воспользоваться гипотезой о том, что р' равно
давлению в конце условного цилиндра, являющегося продолжением тела за дон-
666
Глава XIV
ным срезом и имеющего диаметр и длину, равные диаметру донного сечения.
Величина р' может быть найдена либо теоретически!(например, по методу
характеристик), либо экспериментально. Результаты расчета давления р1
Ры
Р'
0J
0,5
0,3
0,1
Рис. XIV-2-6. Изменение рдон
в зависимости от числа М'
(турбулентный пограничный слой)
7
\
\
\
\
<
\
ч
I
!
i
ч
м'
Рис. XIV-2-7. Среднее давление
в застойной области
по методу характеристик для цилиндрического тела с носовым конусом
приведены на рис. XIV-2-7.
Для цилиндрических тел с длиной цилиндра, равной трем-четырем
Ймид, МОЖНО ПРИНЯТЬ р' CzL Poo-
Донное давление можно найти по формуле
Рдон
Рдон
(XIV-2-15)
Роо Роо Р' ' V '
в которой отношение pR0H/pf определяется из рис. XIV-2-6 по числу М'.
Связь между р' и М' определяется также выражением
(XIV-2-16)
где р'о — давление торможения, соответствующее участку скачка,
примыкающему к острию головной части. Данные на рис. XIV-2-6 можно
представить в виде зависимости донного давления от некоторой
функции fi (M') как
I™L = 2Lfi(M'), (XIV-2-17)
Роо Роо
соответствующей пренебрежимо малой толщине пограничного слоя. В более
общем случае толщина оказывает влияние на донное давление, что можно
учесть введением функции /(М', бд/ймид):
Рдон р'
в - v - - а , ■ (XIV-2-18)
Роо Роо \ "МИД /
где бд — толщина пограничного слоя у дна. Относительная толщина турбу-
лентного слоя длиной I имеет порядок -^~Re~1/5, а ламинарного —
-^^Re-1/2. Поэтому для турбулентного слоя
Роо
^е1'5
)■
(XIV -2-19)
Трение и теплопередача при больших скоростях
567
а для ламинарного
Рдон
(XIV-2-20)
где fi, /2 — некоторые функции параметров, указанных в скобках.
Донное давление можно определять с известным приближением без учета
влияния числа Рейнольдса. Коэффициент донного давления при
турбулентном течении
=-К2 (0,29 + 0,
где
(XIV-2-21)
(XIV-2-22)
тивления с
х дон
+
кр.
V2
Экспериментальные
Формула (XIV-2-21) применима для интервала 1<;Моо<5 и для
сравнительно коротких тел. В соответствии с (XIV-2-21) коэффициент
донного сопротивления
сх дон = Кг (0,22 + 0,13 sin^/s рО2)*з £донв
(XIV-2-23)
При фиксированной длине кормовой
части тела увеличение угла |3О2 приводит к
уменьшению *УДОН и, как следствие, к снижению
сх дон» Однако при этом будет увеличиваться
составляющая сопротивления сх кр
вследствие снижения давления на боковой
поверхности кормы. Можно определить такое
значение угла конусности (302, которому будет
соответствовать минимум суммарного сопро-
Ц10
0,14
0,10
0,06
Р
с"
\
60°
-"— —
/
,2
о
ю
Рис. XIV-2-8. Влияние кормового
сужения на сопротивление
кормовой части:
ламинарный (I) и турбулентный (2)
пограничные слои
кривые на рис. XIV-2-8 показывают, что
минимум сопротивления будет
приблизительно при рО2 = 7°.
В случае, если корпус имеет большое
удлинение х к/^мид, целесообразно учитывать
влияние этого удлинения на донное
давление. При выводе эмпирической зависимости можно исходить из того, что
величина Re1^, фигурирующая в общей формуле (XIV-2-19) оказывает
незначительное влияние на донное давление в сравнительно большом
диапазоне изменения чисел Re. С учетом этого, как показывают
экспериментальные исследования, коэффициент
рдон= -1,144 К* (2 -К^М"2. (XIV-2-24)
Здесь Ki = MooДЭф, где эффективное удлинение
>,эф = ^_. (XIV-2-25)
В соответствии с выражением для рДОн коэффициент донного
сопротивления ,
Е = 1,144 к^г-к^м;
-2 ■
^дон-
(XIV-2-26)
Приведенные формулы, учитывающие влияние хвостового сужения, дают
удовлетворительные результаты для £дон> 0,4—0,5 и сравнительно
небольшого среднего угла наклона образующей хвостовой части (8—10°).
568 Глава XIV
Параметр К± является параметром подобия. При одинаковых его
значениях для различных по форме тел и чисел Моо сохраняются одинаковыми
величины рДонМ2о и схяокМ1оISдон- Применяя формулы (XIV-2-24) и (XIV-2-26),
следует иметь в виду, что они пригодны для значений Ki<l. Если же
К4 > 1, то расчет надо вести по формулам
Рдон - - 1,43 М"2; сх дон = 1,43 М^2 £дон, (XIV-2-27)
соответствующим возникновению за дном абсолютного вакуума.
Донное давление при смешанном пограничном
слое за точкой отрыва. Смешанное течение за точкой отрыва
может возникнуть, например, в случае, когда благодаря охлаждению стенки
ниже равновесной температуры ламинарный пограничный слой становится
более протяженным и может перейти точку отрыва.
Положение точки перехода, а следовательно, донное давление, как
показывают эксперименты в аэродинамических трубах, зависят от тех же
параметров М', бд/с?мид. При оценке донного давления для смешанного
пограничного слоя следует учитывать, что его величина изменяется между
значениями, соответствующими чисто ламинарному и чисто турбулентному
течению. Для чисто ламинарного течения точка перехода близка к точке
прилипания, а для чисто турбулентного пограничного слоя эта точка близка
к точке отрыва.
Дозвуковые скорости. Измерения показывают, что, как и при
сверхзвуковых скоростях, донное разрежение, а следовательно, донное
сопротивление при Моо < 1 зависят от состояния поверхности тела, его длины и
донного сужения, т. е. от тех же факторов, которыми определяются свойства
пограничного слоя. Следовательно, должна быть связь между донным
давлением, донным сопротивлением и трением.
В качестве параметра, характеризующего донное давление, можно
ввести коэффициент cxf дон = cfX (S6oK ЛУдон^где cXf дон — коэффициент
трения, отнесенный к площади донного среза, cXf — тот же коэффициент,
рассчитанный по боковой поверхности тела.
Экспериментальные данные позволили установить следующую связь
между коэффициентом сх/ДОн и коэффициентом донного давления:
рдон= °^L. (XIV-2-28)
V cxf дон
Вводя коэффициент трения cxf=-cXf (^бок/^мид), отнесенный к миделе-
вому сечению, можно найти выражение для коэффициента донного
сопротивления, рассчитанного по площади SMm
с*дон = ^(-^) . (XIV-2-29)
Имеющиеся экспериментальные данные указывают на возможность
использования формул (XIV-2-28) и (XIV-2-29) для приближенных расчетов
донного давления и сопротивления также и в трансзвуковой области
обтекания, т. е. для чисел Моо порядка единицы.
Донное давление при наличии струи газа. Экспериментальные
исследования донного давления у тела вращения с действующим соплом, т. е.
при условиях, соответствующих работающему реактивному двигателю,
показали, что при заданном числе Моо давление на донном кольце тела
существенно зависит от давления на срезе сопла. При этом, чем больше давление
на срезе, тем больше давление на кольце.
Донное давление зависит также от параметров набегающего потока —
его скорости и статического давления. В ходе исследования этой зависимости
Трение и теплопередача при больших скоростях 369
наблюдались следующие характерные явления: 1) при давлении на срезе
сопла 1 кГ/см2 (9,807-104 н/м2), статическом давлении потока в трубе
0,4 кГ/см2 (3,921-104 н!м2) и числе Моо = 1,87 на кольце возникало
разрежение; 2) при сохранении давления на срезе сопла 1 кГ /см2 и уменьшении
статического давления в трубе до 0,16 кГ /см2 (при этом число Моо потока
возрастало до 2,5) избыточное давление на кольце равнялось нулю; 3) когда
статическое давление в трубе уменьшалось еще больше, достигая 0,1 кГ /см2
(поток в трубе разгонялся до Моо = 3), на кольце появлялось уже не
разрежение, а давление. При этом скорость потока в трубе оказывалась равной
или большей скорости в струе вытекающего из сопла газа. Возникающая
при этом разница между величинами статического давления на срезе сопла
и в трубе приводит к интенсивному перемешиванию газа за дном и к
заполнению вакуума. В результате может появиться сила, подталкивающая тело
в направлении движения.
Первое из описанных явлений возникает при работе сопла в условиях,
близких к расчетному режиму (давление на срезе приблизительно равно
статическому давлению в потоке). Если статическое давление на срезе сопла
существенно меньше давления в потоке, то образующееся разрежение может
оказаться даже больше того, которое возникает при неработающем
двигателе. В том случае, когда сопло двигателя работает в условиях, близких
к расчетным, для приближенной оценки коэффициента донного
сопротивления можно пользоваться формулой (XIV-2-26), заменив в ней сужение
£дОН величиной SK = а?к/«?МИд, где SK — площадь кольца донного среза
или, в общем случае, той части дна, которая не занята сопловыми
устройствами.
Снижение донного давления, наблюдающееся при отклонении корпуса,
оказывается незначительным при малых углах атаки и мало влияет на
донное сопротивление.
§ XIV-3. Определение
степени затупления,
обеспечивающей
максимальное снижение тепловых
потоков
Толщина «невязкого» слоя низких скоростей. Методика расчета
толщины «невязкого» слоя низких скоростей для затупленного конуса в принципе
такая, как для затупленного клина (см. § VI-5).
Полагая, что в качестве верхней границы высокоэнтропийного
«невязкого» слоя можно принять линию тока, проходящую через «звуковую»
точку с координатой rs, расположенную на отошедшей ударной волне перед
затупленным конусом (см. рис. IV-10-1), расход газа через поперечное
сечение площадью nrl будет равен pooFooJtrs.
Это же количество протекает через так называемый слой «уменьшенных
чисел Re» некоторой толщины Д, соответствующей произвольному сечению
тела с радиусом г и, следовательно,
f
откуда толщина «невязкого» слоя
д = ^ _Р^ !± J^l , (XIV-3-2)
где р, V — соответственно плотность и скорость в рассматриваемом сечении,
рассчитанные для невязкого обтекания поверхности с учетом
влияния затупления.
670
Глава XIV
Определение этих параметров можно в практических случаях
упростить, приняв с известным приближением, что на некотором удалении от
затупления давление устанавливается таким, как на остром теле. В частности,
это было видно на примере обтекания затупленного
конуса.
Расчет плотности р и скорости V при этом
условии с учетом диссоциации на затупленной
поверхности изложен в § VI-5. Определение указанных
параметров для к = const ведется при помощи
формул (VI-5-2) — (VI-5-4). Местные числа М3,
рассчитанные по формуле (VI-5-4) для затупленного конуса
при условии, что давление на нем такое, как на
заостренной конической поверхности, приведены на
рис. XIV-3-1.
Внося в формулу (XIV-3-2) значения скорости
и плотности, можно определить по известной
координате «звуковой» точки на ударной волне толщину
слоя «уменьшенных чисел Re» и площадь поперечного
сечения этого слоя 2ягА = Fs.
На графике рис. XIV-3-2 приведены кривые для отношения площадей
Рис. XIV-3-1. Числа М
на поверхности
затупленного конуса,
обтекаемого невязким потоком
2ягА
лг2
Р
(XIV-3-3)
Здесь rST — координата «звуковой» точки на сферическом носке.
Приближенные расчеты величины FS/FST могут быть приведены при
условии, что координата точки rST вдвое больше координаты «звуковой»
точки на ударной волне, т. е. отношение r2s/rlT= 0,25.
Из рис. XIV-3-2 видно, что при сделанных
предположениях отношение площадей FS/FST для
затупленных по сфере конусов с малыми углами |3К
имеет порядок единицы. Для конусов,
затупленных по торцу, слой малых скоростей будет
несколько толще. Если принять, что координаты
«звуковых» точек на торце и ударной волне
приблизительно одинаковы, т. е. rs = rST — i?T, то
в соответствии с формулой (XIV-3-3) отношение
площадей Fs /FST будет вчетверо больше, чем для
конуса со сферой. Для расчета толщины слоя
низких скоростей можно воспользоваться
формулой (XIV-3-2) или, если дана зависимость для
отношения площадей FS/FST, выражением
Л==1^7!^- (XIV-3-4)
Приближенные расчеты толщины слоя
уменьшенных скоростей для конуса со сферическим носком
можно производить при условии FS/FST = 0,25,
ас плоским торцом Fs/FSt = 1- Соответствующие
расчетные зависимости имеют вид
Д=4--
(XIV-3-5)
Рис. XIV-3-2. Отношение
площади сечения /> = 2л;гД
слоя малых скоростей на
конусе к площади FST =
=яг|т; сплошные кривые—
точные расчеты по формуле
(XIV-3-3); пунктирные
кривые — приближенные
значения для отношения
г?/^т = 0,25
Расчет потребного затупления. При определении потребного затупления
(величины rST) можно поставить условие, чтобы толщина ламинарного слоя
Трение и теплопередача при больших скоростях 571
бл равнялась толщине слоя малых скоростей. Следовательно, условия,
из которых может быть определена величина rST, будут следующими:
бл = * -^ ^ ^- или 6„ = -/^ 41- * (XIV-3-6)
Z р Гц V г s T 2гп
где гп — радиус сечения затупленного конуса в ожидаемой точке перехода.
В частности, из второй формулы (XIV-3-6) следует, что если FS/FST c^ 1,
то координата rST должна быть порядка величины ]/^2rn6n, равной, как видно,
среднему геометрическому между диаметром тела и толщиной пограничного
слоя в точке перехода.
Для определения толщины ламинарного слоя в точке перехода на
поверхности затупленного конуса можно воспользоваться зависимостью
(XIV-1-6), причем величину 6£л следует вычислять по критическому
значению Re*p, применяя формулу для тонкой пластинки
°Л _К Q/C* 4-1/2
в которой хП — расстояние до точки перехода.
Критическое число Re^p = F6#np*/u* может быть рассчитано в общем
случае по определяющим параметрам для затупленного конуса.
В целях упрощения расчетов вместо определяющих параметров (х* и р*
можно использовать параметры невязкого обтекания затупленного конуса,
полученные без учета влияния определяющей температуры.
Так как критическое число Рейнольдса обычно считается величиной
известной, то можно определить длину ламинарного участка хп =
= |a,*ReKp/(F6p*), а затем толщину пограничного слоя в точке перехода
Если рассмотреть случай постоянных теплоемкостей, то формула для
расчета потребного затупления примет вид
-fe+i
В этой формуле величиной ReSp, как указывалось, обычно задаются;
отношения р'о/ро, Ат/Л* и число М на затупленном конусе определяют по
известному значению М<х>. В случае прикидочных расчетов величину rST/rs
для сферического носка и торца можно принять соответственно
равными 2 и 1.
Произведя необходимые вычисления в правой части формулы (XIV-3-8),
можно найти значение функции П. Зная радиус
tg рк
и координату хп, можно по формуле
(XIV-3-9)
подсчитать требуемое затупление rST, точнее, координату «звуковой» точки
на носке. Для «затупления в виде торца эта координата даст величину радиуса
торца, так как RT = rST1 а для сферического носка его радиус найдется по
формуле RT = rST/sin т), причем в этой формуле угол т), под которым
расположена «звуковая» точка на сфере, находят из рис. XII-2-6.
572
Глава XIV
/
о
1
Moo— 7
1
62
7
/if
i
1 П
V
>
4
Рб
<°7
\
}}
8 12
Рис. XIV-3-3. Область
устойчивости ламинарного
пограничного слоя на
затупленном конусе
(внутренняя область относительно
сплошной кривой):
q — острый и П —
затупленный конуса
Некоторые данные о критическом числе Рейнольдса. Определение
критического числа Рейнольдса связано с исследованием устойчивости
пограничного слоя. Установлено, что по мере охлаждения стенки устойчивость
ламинарного пограничного слоя повышается. Физически это объясняется
тем, что с понижением температуры газа вблизи поверхности растет
плотность и вследствие этого возрастает кинетическая
энергия газа в том же объеме. Понятно, что
частицы с большой энергией менее подвержены
влиянию возмущающих пульсаций. При этом замечено,
что при очень больших скоростях число
Рейнольдса, как критерий устойчивости, играет менее
существенную роль по сравнению с такими
параметрами, как относительная температура стенки
ТСТ1Т6 (Тст1Тоо или Тст1Тг) и число Мб на внешней
границе пограничного слоя (или для заданных
условий обтекания — число Моо).
Теоретическими исследованиями определена
потребная для полной стабилизации ламинарного
пограничного слоя величина относительной
температуры стенки в зависимости от местного числа М&
(рис. XIV-3-3). Из этого рисунка видно, что при
Мб > 8 пограничный слой не может быть
устойчивым независимо от интенсивности охлаждения.
Также можно заметить, что границы устойчивости
расширяются с уменьшением отношения Тст/Ть*
Отсюда следует, что торможение внешнего потока,
сопровождающееся уменьшением числа Мб и
повышением температуры Tq, будет оказывать
стабилизирующее влияние (если при этом поддерживается постоянная
температура стенки соответствующим охлаждением).
Выше было отмечено, что такое торможение можно осуществить,
применяя вместо острого тела затупленное. Таким образом, затупление является
важным средством стабилизации
ламинарного пограничного слоя. Действительно,
температура на внешней границе слоя больше
у затупленного, чем у заостренного тела, и,
следовательно, при сохранении постоянной
температуры стенки отношение TctJTq будет
меньше. Кроме того, уменьшаются местные
числа Мб- Из сказанного ясно, почему
затупление, как это видно на рис. XIV-3-3,
сдвигает условия на внешней границе
пограничного слоя из области неустойчивости в зону
стабильности.
Область неустойчивости, расположенная
вне кривой на графике рис. XIV-3-3,
необязательно является областью полной турбу-
лизации. В этой области слою свойственны
турбулентные включения, возникновение
которых связано с моментом перехода
ламинарного течения в турбулентное.
Завершение этого перехода происходит при критическом числе Рейнольдса.
На рис. XIV-3-4 приведены экспериментальные результаты по
определению этого числа, полученные Ван-Драйстом в аэродинамической трубе.
Экспериментальная модель острого конуса охлаждалась изнутри, чем обес-
Рис. XIV-3-4. Изменение
критических чисел Рейнольдса на
конусе:
" " 2—0,8;
значения
Тст/Тг: 1 — 0,7;
5—0,9; 4—1,0
'Трение и теплопередача при больших скоростях
печивалось изменение отношения Tct/Tq. Продувки велись при различных
числах Моо.
Анализ кривых показывает, что с уменьшением температуры стенки
критические числа Рейнольдса возрастают, причем характер изменения
этих чисел во многом зависит и от чисел Мб. При Мб > (3,8 ч- 4) критические
числа Рейнольдса практически остаются постоянными.
Если поверхность охлаждается (ТСТ/ТГ < 1), значения ReKP
увеличиваются, причем при оценке изменения ReKP можно исходить из того, что
их значения приблизительно обратно пропорциональны относительным
температурам стенки Гст/Гг, определяемым выражением
. (XIV-3-10)
На величину ReKP известное влияние оказывает градиент давления
на стенке. Причем отрицательный градиент благоприятен для
повышения устойчивости и, следовательно, увеличения критического числа
Рейнольдса. Наоборот, при увеличении давления вдоль потока, т. е.
положительном градиенте, создаются условия для преждевременной турбулиза-
ции, и величина ReKp уменьшается.
Если рассмотреть обтекание затупленного тела, в частности конуса,
то на его поверхности имеются области с различным характером изменения
давления. Непосредственно за точкой полного торможения на некотором
участке тела давление снижается и, следовательно, устанавливается
отрицательный градиент статического давления, благоприятный для
стабилизации ламинарного пограничного слоя. Далее по потоку на некотором
удалении от носка начинается торможение, вследствие чего возникает
положительный градиент. Это приводит к уменьшению устойчивости. Однако такое
неблагоприятное влияние положительного градиента практически
оказывается незначительным. Все же при окончательном выборе размера
затупления влияние отрицательного градиента целесообразно учесть, несколько
увеличив против расчетного этот размер.
В качестве примера рассчитаем сдвиг точки перехода при Моо = 10
на гладкой поверхности затупленного конуса с углом |3К = 10°. Рассмотрим
сферический носок и вычислим, прежде всего, координату «звуковой» точки
rs. Из уравнения образующей волны х = ar2 = r2 /(2Rc0) найдем отношение
гя = #со ( dr \-i
RT RT V dx
в котором безразмерный радиус кривизны волны Rc0/RT определяется как
функция отношения плотностей рс/роо за прямой частью волны и перед нею.
Для условий полета вблизи земли при Моо = 10 вычисляем с учетом
диссоциации отношение рс/роэ = 7,4, а затем из графика на рис. XII-2-12
находим величину Rc0/RT = 1,2. При помощи другого графика на
рис. ХП-2-6 определяем угловую координату «звуковой» точки на волне
со = 22°30\ затем находим угол наклона скачка 9CS = 67°30' и tg 0CS =
= (dr'ldx)s = 2,41. Следовательно, rsIRT = 1,2/2,41 с^ 0,5. Из того же
рис. ХП-2-6 находим угловую координату «звуковой» точки на сфере
^9Т = 42°30', которая определяет относительную линейную координату
rSTIRT = 0,676. Таким образом, отношение координат «звуковых» точек
rsT/rs = 0,676/0,5 = 1,35.
Найдем, далее, отношение давлений торможения р'о/ро как среднее
между их значениями в вершине и «звуковой» точке ударной волны.
Используя формулу (И 1-4-33), по значениям Моо = 10 и M«>sin9ce = 10sin67°30' =
— 9,24 вычисляем отношения давлений торможения после и до скачка,
574 Глава XIV
а затем определяем среднее отношение давлений
_р^ = 3,14 + 4,52 10_3 = з 83.10-8в
Ро *
После этого на рис. XIV-3-1 определяем число М на затупленном конусе
М3 = 2,8, а по рис. XIV-3-4 — критическое число ReKP = 8,7-106, причем
при определении этого числа задаемся относительной температурой стенки
Тст/Тг = 0,7, что соответствует отношению
-0,7 (1+0,169- 2,8а) = 1,58.
В результате подстановки всех найденных величин в формулу (XIV-3-8)
находим значение функции
Координата точки перехода на остром конусе
Для выбранного конуса местное число Мк = 7,6. Принимая, далее, что
полет происходит на высоте примерно 22 км и, следовательно, коэффициент
кинематической вязкости VooH = 20voo0, получим из формулы (XIV-3-11)
значение хп = 0,438 м.
Чтобы определить соответствующую координату для затупленного
конуса, оценим по рис. IV-10-2 уменьшение для этого конуса числа
Рейнольдса, т. е. найдем отношение Re3/ReK = 0,071. В соответствии
с этими данными координата точки перехода с учетом влияния затупления
_ 0,438 _ 6
и~ 0,071 ~ '
По этой величине можно подсчитать координату «звуковой» точки
на сфере:
rsт = 0,5Шп cos рк sin"1 r]s T + [0,25 (Шп cos рк sin"1 k\s t)2 + Шд sin рк]"*1/2?
а затем радиус сферического затупления RT = ■. ST и отношение площади
Sill T)ST
затупленного носка к площади поперечного сечения конуса в точке
перехода $Сф. Если эта точка расположена у донного среза, то вся поверхность
конуса покрыта ламинарным пограничным слоем.
Решение можно упростить, если участок образующей ударной волны
представить в виде дуги окружности радиуса Rc0. В этом случае
гв = i?co cos 8C 8; rST = i?Tsinr]ST.
Следовательно,
Sin Т)5 т м /„
cos0cs ~ '
В соответствии с этими данными подсчитывают параметры затупления *
Влияние пограничного слоя. Вычисленное указанным способом
потребное затупление может быть уточнено, если учесть влияние условной толщины
вытеснения пограничного слоя. Действительно, из физических соображений
следует, что эффект влияния вязкости на обтекание можно, как отмечалось,
Трение и теплопередача при больших скоростях 575
учесть, если рассмотреть невязкий поток около условного тела с поперечными
размерами, увеличенными на толщину вытеснения 6£. Следовательно, слой
низких скоростей оказывается сдвинутым на величину 6£. Из сказанного
ясно, что при расчете потребного затупления надо исходить из равенства
А = бл — SJ. Определить 8J можно по формуле для конуса
В свою очередь, условная толщина блпл, рассчитанная по определяющим
параметрам, может быть найдена по формуле для несжимаемой среды
6*ПЛ /О /О\ &ПЛ
л =(3/8)б
Таким образом, для затупленного конуса с учетом влияния толщины
вытеснения
/ бпл \
A = 6n-6S = 0,36*n (-f- . (XIV-3-12)
Сопоставляя эту формулу с выражением (XIV-3-7), можно сделать
вывод, что требуемое затупление в рассматриваемом случае уменьшается.
Изложенный метод расчета потребной степени затупления основан
на предположении о неизменности формы профиля слоя низких чисел М.
Однако в действительности вниз по потоку происходит деформация этого
профиля, обусловленная диссипацией (рассеянием) «невязкого» слоя низких
скоростей за счет поступления в него все большего количества воздуха
с низкой энтропией. Такое явление разрушения высокоэнтропийного потока
эквивалентно воздействию уменьшенного затупления.
Некоторые исследования показывают, что при полетах на небольших
высотах диссипацией профиля слоя уменьшенных скоростей можно
пренебречь на участке ламинарного пограничного слоя длиной до х с^. 1000А.
При большей протяженности обтекаемой поверхности целесообразно
учитывать эффект диссипации, что можно сделать, несколько увеличив
первоначально вычисленное затупление.
§ XIV-4. Теплопередача
на корпусе
Поверхность криволинейной
формы
Для расчета удельного теплового потока от ламинарного пограничного
слоя к криволинейной сильно охлаждаемой стенке в случае равновесной
диссоциации газа и при условии, что поперек слоя величина pjx = const,
следует воспользоваться соотношениями (IV-8-47) и (IV-8-48). Приняв 8=1,
получим
q = 0,5 Pr-2/з VV^y0 irF, (XIV-4-1)
где функция
F 1/2" (р/р'о) (F6/Fqq) г ,YT , 9.
b = Г5 Ш2- ' (XIV-4-2)
2 J (P/P'o) (V6/Vco)^dx\
В формуле (XIV-4-1) в энтальпию iT включено ускорение силы тяжести
g = 9,81 м/сек2, так что размерность ir будет ккал-м/кГ-сек2.
576 Глава XIV
Заостренный корпус
Конус. Для конической поверхности в (XIV-4-1) и (XIV-4-2) следует
принять р = р'о, V6 = VU, РоК = Рк|^к. Следовательно,
qK = 0,808 Рт~2/Нг ]/ pKlifK , (XIV-4-3)
где индексом «к» обозначены параметры на конусе; координата х отсчиты-
вается от носка вдоль образующей поверхности.
Суммарный тепловой поток на конусе
J qKrdx. . (XIV-4-4)
о
После подстановки сюда qK из (XIV-4-3) получим
<?к = 0,812 Pr-2/з tg $KSKir у Рк^к^/2 , (XIV-4-5)
где SK = я#к sin рк — боковая поверхность конуса с длиной образующей хк
и углом полураствора рк.
Заостренная головка произвольной формы. При вычислении тепловых
потоков по формуле (XIV-4-1) можно принять при больших скоростях
р = р* sin2 p/sin2 р0, где р* — коэффициент давления на заостренном
коническом носке. Следовательно,
[ ] (XIV-4-6)
Используя связь между давлением и скоростью для изэнтропического
течения, можно найти скорость F6 на поверхности слоя. Внося р и F6
в (XIV-4-2), можно вычислить функцию F и подсчитать по формуле
(XIV-4-1) удельный тепловой поток.
При приближенных вычислениях в случае больших чисел Моо местную
скорость на головке можно определить по формуле Ньютона V& =■-- Vm cos рк,
что позволит получить более простое соотношение для F и, следовательно,
для q.
Наряду с этим для приближенной оценки распределения местных
потоков можно применить метод «местных конусов» и формулу (XIV-4-3).
Удельный тепловой поток в точке А (см. рис. IV-7-3), определяемый этой формулой,
соответствует местной конической поверхности с половиной угла при
вершине Р и расстоянию О'А=хк вдоль ее образующей. Если начало
выбранной системы координат расположить в носке и продольную ось направить
по оси корпуса, то радиальная координата точки А, в которой определяется
удельный тепловой поток, r = xKsinp. В соответствии с этим удельный
тепловой поток в точке А:
q - 0,608 Рг-2/3*г j/p^sinp ^ (XIV-4-7)
:где рб, ?}1б» 1^6 — параметры невязкого потока на местной конической
поверхности. Суммарный тепловой поток на участке корпуса
длиной х (г)
= 1,216л Pr-2/3ir [ l/^^fdr. (XIV-4-8)
) V Sill р
Трение и теплопередача при больших скоростях 577
Если удельный тепловой поток на местной конической поверхности
вычисляется по критерию Стантона St* = |/~3 StJJn, найденному по определяющим
параметрам [q — StJp6F6 (ir — *ст)]» то
St* p6V6 (ir - iCT) r cos"1 p dx, (XIV-4-9)
о
где x — длина корпуса, измеряемая по оси.
§ XIV-5. Точка полного
торможения на
затупленном носке
Равновесная диссоциация. Приняв в выражении (IV-8-49) 8 = 1,
получим для теплового потока в критической точке, принадлежащей
затупленному телу вращения,
q0 = 0,664 Pr-2/з (kp'oli'oy/4r. (XIV-5-1)
Это выражение получено для переохлажденной поверхности, на которой
температура ТСТ1 а следовательно, энтальпия iCT пренебрежимо малы по
сравнению с соответствующими значениями Тг и ir. В тех случаях, когда
охлаждение не обеспечивает достаточно низкой температуры стенки,
например, при рассеивании тепла только излучением, т. е. когда
устанавливается сравнительно высокая равновесная радиационная температура,
необходимо учитывать значения iCT.
Экспериментальные исследования показали, что для случаев
разогретой стенки формула для дов основном сохраняет тот же вид, что и (XIV-5-1).
Различие состоит в том, что вместо iT в новую формулу войдет величина
ir — iCT, а также дополнительный множитель, учитывающий изменение
произведения pfx поперек пограничного слоя в окрестности критической
точки. Расчетная зависимость имеет следующий вид:
п O7fi4Pr-0,6/ln'ii'W^/ 7 \lc\ ii W1U /YTV ^ 9\
где
В соответствии с формулой (XIV-5-2) и выражениями
Nu = ^Ст°0г —' ст)'У Re = "e^~^2 (XIV-5-3)
безразмерный критерий теплопередачи
^= = 0,763 Рг^4 (^J^)-0'4. (XIV-5-2')
Исследования показывают, что РстМ'ст/роМ'о ^ 1» следовательно,
тепловой поток увеличивается по сравнению с его значением для сильно
охлажденной поверхности. Формула (XIV-5-2) пригодна для температур
поверхности, не превышающих температуру торможения. Из этой формулы следует,
что при больших скоростях, когда диссоциация оказывается значительной,
теплопередача определяется скорее градиентом энтальпии, чем
температуры. При таких скоростях энтальпию восстановления ir можно вычислять
как энтальпию торможения по формуле ir = 0,5FL.
При отсутствии диссоциации в формуле (XIV-5-2) можно перейти от
разности энтальпий к разности температур, если воспользоваться заменой
т — ^ст — £р. ст V-* г *~"~ •*• ст/>
37-114
578 Глава XIV
где удельная теплоемкость ср. ст рассчитывается как среднее между
значениями на охлаждаемой и изолированной стенке с температурами
соответственно Тст и Тт. Из приведенных формул следует, что подводимое к стенке
тепло зависит от величины параметров на внешней границе пограничного
слоя. В свою очередь, эти параметры определяются из условия обтекания
затупленного носка в точке полного торможения.
Обработка численных результатов расчета при очень больших
сверхзвуковых скоростях позволила получить приближенную формулу для
расчета удельного теплового потока в точке полного торможения
_ 31500 -,/рооя / Fqq \ 3,25 / *ст \ ккал (Y1V Ъ А\
д°~уТтУ "^TlTri I1 гГ]"^Г' (XIV-5-4)
где Vc — первая космическая скорость, равна 7,93 км/сек;
рооя? роо з — плотность атмосферы соответственно на некоторой высоте И
и у земли;
i?T— радиус сферы, м.
Энтальпия восстановления может быть принята равной энтальпии:
торможения.
Формула (XIV-5-4) дает значение теплового потока, определяемого
не только теплопроводностью, но и диффузионным переносом тепла
вследствие рекомбинации атомов на каталитической стенке. Если же поверхность
сферы не является каталитической (например, поверхность неметаллической
обшивки), то формула (XIV-5-4) будет давать заниженный тепловой поток.
Неточность формулы будет возрастать с увеличением высоты, когда все
большим становится отклонение состояния газа от равновесного. С
практической точки зрения применение некаталитической поверхности может
оказаться выгодным, так как малые скорости рекомбинации незначительно
изменяются на некаталитической поверхности, что обусловливает поглощение
тепла за счет диссоциации и как следствие уменьшение теплового потока
к стенке. При проведении расчетов можно задаться энтальпией стенки,
исходя из максимально допустимой температуры обшивки.
Наряду с этим тепловые потоки могут быть рассчитаны из условия их
равенства тепловым потоком при излучении. В условиях полета это равенство
может быть обеспечено соответствующим подбором скорости и высоты
(плотности воздуха). С этой целью задаются степенью черноты поверхности г
и ее температурой, которая в данном случае будет равновесной.
Найдя радиационный тепловой поток аеГст и внося его в уравнение
(XIV-5-4), определяют требуемую связь между скоростью и плотностью
воздуха, а следовательно, и высотой. В этих условиях полета охлаждение
происходит путем излучения тепла нагретой поверхностью.
При умеренных сверхзвуковых скоростях удельный тепловой поток
к точке полного торможения носка можно вычислять по формуле
q0 = 0,763PrF0'6 Ур^ДсР[(Тг^Тст), (XIV-5-2")
где k = (dV&/dx)xsss$ может быть принята равной (3/2) Foo/i?T (как для
несжимаемой жидкости) или подсчитана по формуле (VI-3-16).
Согласно экспериментальным данным удельный тепловой поток в точке
торможения торца
q0T = (0,55 ± 0,05) досф. (XIV-5-5)
Влияние завихренности во внешнем потоке. Приведенные зависимости
для теплового потока получены из условия, что поток в «невязком» слое,
примыкающем к стенке, является равномерным и, следовательно, градиенты
скорости поперек слоя, обусловленные завихренностью, равны нулю.
В действительности же скорость не остается постоянной, а возрастает от зна-
Трение и теплопередача при больших скоростях
579
чения на стенке, соответствующего параметрам торможения за прямым
скачком, до некоторой величины на условной границе слоя, и,
следовательно, в потоке возникает завихренность.
Эффект завихренности проявляется в каждой точке поверхности,
включая точку полного торможения, причем отношение теплового потока д03,
вычисленного с учетом влияния этого эффекта, к его величине qOi
найденной в случае пренебрежения завихренностью, зависит от ряда факторов,
в том числе от числа Моо и высоты полета.
Расчеты, например, показали, что при Моо = 20 в критической точке
полусферы на высотах 90 и 60 км это отношение дОз/#о соответственно равно
1,3 и 1,04. Таким образом, в плотных слоях атмосферы эффект
завихренности практически можно не
учитывать, в то время как в
разреженной среде расчетную
теплопередачу целесообразно
скорректировать в сторону
некоторого увеличения.
Важнейшим параметром,
определяющим влияние
завихренности на теплопередачу,
является число Рейнольдса,
рассчитанное по# радиусу сферы
и газодинамическим
характеристикам в критической точке
1М
ч
ч
/
\
■и
А
1
1
6 8 10 2 U 8
1 Ю1
4 68 10
RQW'2
И-о
Рис. XIV-5-1. Влияние завихренности"на
теплопередачу в критической^ точке:
гг=—~; Тг = 2000°К
При определении этого чис- *r=—~
ла следует иметь в виду, что
при больших скоростях можно принять iT = 0,5 У*,. На рис. XIV-5-1
представлена экспериментально найденная зависимость отношения qOQ/qo от Re
для двух значений числа Моо = 8 и 20, которая может быть использована при
уточнении теплового потока. Видно, что для числа Моо = 8 эффект
завихренности существенно меньше, чем для Моо = 20. Данные на рис. XIV-5-1
получены для условий, когда температура в критической точке Т'о = 2000° К.
При повышении температуры влияние завихренности возрастает. Однако
даже при значительном повышении температуры это возрастание невелико.
Например, при увеличении температуры на 1000° К теплопередача от влияния
завихренности возрастает всего на 3—4%.
Радиационный поток от перегретого ударного слоя. Радиационный
поток тепла в окрестности критической точки можно вычислять по формуле
#рад = / (es0) ст (Т'о)* при условии, что отход волны s0 определяется с
учетом пространственной формы носка. Наряду с этим можно пользоваться
экспериментальной зависимостью для удельного теплового потока от
излучения газа в окрестности] критической точки сферы
ft.-2.12.M4.,
ИЛИ
(XIV-5-6,
где RT —- в м; Voo — в м/сек.
Определяя эквивалентный радиус, можно вычислить радиационный
поток в критической точке носка, отличного по форме от сферы, в частности
для торца.
37*
580
Глава XIV
На рис. XIV-5-2 показано типичное распределение радиационного
и аэродинамического даэр тепловых потоков на траектории при
некоторых условиях полета. Можно заметить, что радиационный поток
принимает большие значения на малых высотах. При
этом наибольшая его величина соответствует
максимуму аэродинамического теплового потока
и составляет, приблизительно, одну треть этого
максимального значения.
Влияние диффузии. Влияние диффузии на
теплопередачу рассмотрено в § IV-8.
Изменение удельного теплового потока при наличии
диффузии определяется формулой (IV-8-57),
в которой каталитический коэффициент ф
учитывает влияние конечной скорости
рекомбинации. Наибольшее количество дополнительного
тепла, выделяемого вследствие диффузии, соот-
ветствует бесконечно большой скорости
рекомбинации, при которой коэффициент ф = 1 и,
следовательно,
0,5
У
/
40
/а
3
эру
/
/
/
{
\
\
24
Рис. XIV-5-2. Сравнение
величин аэродинамического и
радиационного потоков тепла в
критической точке сферы:
t — время полета в сек; q —
тепловой поток (кшл/сек см2)
_ 1) -£.] . (XIV-5-7)
В качестве примера оценим максимальную
величину теплового потока при бесконечно
быстром катализе и при условии, что Моо = 15, роо =
= 0,1 кГ/см2 (0?981-104 н/м2) (этому давлению соответствует высота
атмосферы //^16 км). По исходным данным подсчитываем давление в
критической точке р'о = fokMloPoo/2 = 30 кГ/см2 (29,4-104 н/м2). Величина энтальпии
в ней
а2 М2 А
°%°° =2430 ккал/кГ (1018-104 дж/кг).
По этому значению ir и давлению pQ из рис. Ш-1-3 находим темпера-
ТУРУ 2гтг = 5500°К. Соответствующая ей энтальпия недиссоциированного газа
ккалЫГ (7460-103 дж/кг).
Следовательно, энтальпия диссоциации
iD = ir — ia==0 = 2430 —1780 = 650 ккалЫГ (2720.103 дж/кг),
а отношение iD/ir = 0,267. Если принять число Le = 1,45, то эффект
диффузии в соответствии с формулой (XIV-5-7) определяется величиной дтах/#т ~
= 1,075.
При очень больших скоростях отношение iDliT близко к единице. Если
принять iD/ir = 1, то при ф = 1 отношение дтах/#т = Ье2/з. Для Le = 1,45
величина дтах/^т = 1,28, т. е. наибольшее увеличение теплового потока
составляет 28%. По экспериментальным данным параметр теплопередачи,
учитывающий влияние диффузии,
I/Re
= 0,763
Для вычисления удельного теплового потока по этому параметру
необходимо воспользоваться формулами (XIV-5-3).
Трение и теплопередача при больших скоростях
581
§ XIV~6. Криволинейная
затупленная поверхность
Ламинарная теплопередача
Случай термодинамического равновесия. Рассмотрим некоторые
зависимости, позволяющие рассчитать в условиях термодинамического
равновесия тепловой поток в произвольной точке заданной криволинейной
поверхности. С этой целью воспользуемся формулой, определяющей отношение
теплового потока q в произвольной
точке, к его значению q0 в точке
полного торможения [50]:
д _ F _ 1 {р1р'ъ)Уьг i/X
90
1
Но
0,8
1/2
0,6
0,4
0,2
- ■> J
ч(
ъ
\
- ^
^—
20
60
80
Г
(XIV-6-1)
Полусфера. Как показывают
исследования, распределение теплового
потока по сферической поверхности,
рассчитанное на основе формулы (XIV-6-1)
и ньютоновского закона изменения
давления р=ро cos2 т], удовлетворительно
согласуется с экспериментальными
данными для чисел Моо порядка двух и выше. Чтобы рассчитать тепловой поток,
будем иметь в виду, что на этой поверхности закон изменения скорости
в зависимости от центрального угла очень близок к линейному вплоть до
значений г) = 75 -f- 80°. Поэтому примем в дальнейшем, что скорость на
внешней границе пограничного слоя Vq — XRTt\. Учитывая, что
Рис. XIV-6-1. Распределение теплового
потока по поверхности сферы
(ламинарный пограничный слой):
Тст = const, Тст/Тб«1
и имея в виду, что при больших скоростях в соответствии с формулой
Ньютона отношение давлений
(XIV-6-2)
-±г = cosa л + -^f- sin* ri = cos12 ri 4- -y^- sina ti,
Ро ' Ро ' ' ' ЛМ^ "
напишем зависимость (XIV-6-1) в более конкретной форме:
_i- = 2т| sin 2т] (1 —■ 2 j cos2
где функция
D V1 лм» ) Ь2 :
1 —COS4T]\
8 J
В том случае, когда (&«> ML)""1 < 1> Для оценки распределения тепловых
потоков можно воспользоваться более простым выражением
— = 2r)sin г] cos2 г] [т]2 к-
т| sin 4ti , 1 —
/
/VT,r с /ч
(XIV-6-4)
Нетрудно видеть, что это выражение точно определяет величину
теплового потока в предельном случае при Моо = оо. В реальных случаях формулу
(XIV-6-4) можно применять для Моо > 10, что подтверждается рис. XIV-6-1,
582
Глава XIV
где построено семейство кривых, рассчитанных по формулам (XIV-6-2)
и (XIV-6-4) при условии, что в каждой точке поверхности температура
стенки постоянна и достаточно низка (Гст/^б С 1)- Приведенные кривые
показывают, что теплопередача достигает максимума в критической
точке и уменьшается на удаленных участках полусферы вследствие снижения
плотности.
Уточнение по экспериментальным данным [16]. Формула (XIV-6-2)
достаточно удовлетворительно отражает реальное распределение тепловых потоков
для тех больших чисел Моо, для которых действительно соотношение
Poolp'o = (kooMlo)'1. Однако при не очень больших скоростях формула
оказывается недостаточно точной, особенно для участка поверхности вблизи
0,9
0,8
0,7
0,6
1
%
0,60
0,50
0,40
F
\
dS S
% ЦзА
—
8 12 16 MQ
2,5
7У5
Рис. XIV-6-2. Величина
параметра давления р в
зависимости от числа Моо
Рис. XIV-6-3. Средняя
величина теплового потока
к полусферической
поверхности (ламинарный
пограничный слой)
точки с координатой ф = 90°, где действительные значения тепловых потоков
больше, чем определяемые теоретически по формуле (XIV-6-2). Это
обусловлено тем, что статическое давление здесь несколько выше, чем атмосферное,
которое получается по приближенной формуле Ньютона.
Для уточнения формулы (XIV-6-2) примем распределение давления по
сфере
i(^)in2r1' (XIV-6-5)
где р' — давление в точке г] = 90°.
С учетом этого выражения формула (XIV-6-4) принимает вид
q (1 — р sin2r|) г] sin г\
В этой формуле введены обозначения
(XIV-6-6)
(XIV-6-7)
Экспериментально найденная зависимость функции р от числа Моо
(рис. XIV-6-2) показывает, что для чисел М > 6 величина |3 практически
постоянна. Наиболее сильное изменение функции р наблюдается при
Моо < 3. Следовательно, при соответствующих скоростях существенно
меняется в зависимости от давления и отношение тепловых потоков q/q0.
Трение и теплопередача при больших скоростях
583
Исследования тепловых потоков, проведенные для М<х> > 10; iCT <C i0 и
условий равновесной диссоциации ([66], 1966, № 2), показали, что распределение
величины qlq0 можно аппроксимировать формулой
■ = 0,55+ 0,45 cos tj.
(XIV-6-8)
Po,Po>
— я
Moo jf
л
si
V
/l
Эта формула носит универсальный характер и пригодна также для
малых скоростей движения и произвольных значений iCT, если эти значе-
яия соответствуют сильно охлаждаемой стенке.
По распределению давления около сферы можно вычислить среднюю
величину дСр/#о Для затупления. Изменения этой величины в зависимости
от числа Моо показаны на рис. XIV-6-3.
Плоский торец. Расчеты показывают, что тепловые потоки к
плоской поверхности значительно меньше, чем к сферической. Это
объясняется не только меньшей поверх- л ф
ностью торца, но и более
интенсивным торможением потока на
нем, что, в частности, приводит 2,0
и существенному уменьшению
скорости и продольного
градиента К на внешней границе
пограничного слоя.
Если картина распределе- о 0/t 0,8, x=x/r^
ния параметров обтекания
известна, то приближенный ха- Рис. XIV-6-4. Распределение теплового потока
рактер изменения отношения на торце (ламинарный пограничный слой):
qlq0 МОЖНО Определить С ПО- значени* Роо/р;: 1 -0,05; 2- 0,15; з -0.25#- 0,35
мощью формулы (XIV-6-1), в
которой надо принять г = х. На рис. XIV-6-4 показаны результаты расчета
этого изменения для нескольких значений величины роо/р^ которым
соответствуют различные скорости набегающего потока. При очень больших
числах Моо (кривая 1, отношение плотностей для точки полного
торможения роо/ро = 0,05) удельные тепловые потоки возрастают при приближении
к острой кромке торца. Это объясняется доминирующим влиянием роста
давления (плотности) на увеличение тепловых потоков, претерпевающих некоторое
снижение за счет возрастания скорости вблизи острой кромки.
При снижении скорости обтекания характер распределения удельных
тепловых потоков изменяется (кривые 2, 3, 4, соответствующие значениям
отношений плотностей роо/ро = 0,15; 0,25; 0,35).
До некоторой величины x = xlRT<ii отношение q/q0 увеличивается,
достигая при определенном значении я, зависящем от числа М^,
максимальной величины, а затем снижается.
Снижение удельного теплового потока объясняется тем, что вблизи острой
кромки при сравнительно небольших скоростях обтекания уменьшение
давления может оказать решающее влияние и, несмотря на рост скорости,
тепловой поток после достижения некоторой наибольшей величины начинает
снижаться.
Формула (XIV-6-1) позволяет приближенно оценить распределение
тепловых потоков около произвольной затупленной поверхности с заданной
формой образующей r = f(x).
Для этой цели необходимо предварительно произвести для заданных
условий полета (число Моо, высота Я) расчет распределения давления р,
скорости F6 при невязком обтекании затупленной поверхности, принимая
бо внимание, что давление торможения р'о находится для условий за «прямой»
584
Глава XIV
частью ударной волны. По найденному распределению скорости и давления
вычисляется интеграл ^JLv6r*dx. Определив далее по распределению
^ о °
скорости градиент Я скорости в точке полного торможения, находим
отношение удельных тепловых потоков q/q0 в рассматриваемой точке обтекаемой
поверхности затупленного носка и в точке полного торможения. На
рис. XIV-6-5 приведены результаты такого расчета для плоского торца
с круглой фаской радиусом г = 0,25Дт. Там же нанесены экспериментальные
Рис. XIV-6-6. Теплопередача на
эллипсоиде вращения:
-sin2 3
Рис. XIV-6-5. Распределение
теплового потока на торце со
скругленными кромками (ламинарный
пограничный слой):
О — эксперимент; по (XIV-6-1)
данные, показывающие, что скругление несколько изменило распределение
тепловых потоков по сравнению с торцом, но вместе с тем сохранило
тенденцию к росту теплопередачи при подходе к скруглению, характерную
для торца, обтекаемого потоком с очень большим числом Моо.
Значительное снижение плотности газа в зоне сопряжения
затупленного носка с цилиндрической поверхностью (x = xlRT>\) обусловливает
резкое уменьшение тепловых потоков. На цилиндрической поверхности
удельный поток составляет менее 10% от его значения в точке полного
торможения и с известным приближением может быть рассчитан для
условий обтекания плоской пластинки.
Эллипсоид вращения. Формула (XIV-6-1) может быть
использована для расчета ламинарной теплопередачи при обтекании различных
по форме тел вращения. Результаты этого расчета, показывающие
изменение относительной величины q/q0 в зависимости от безразмерного давления
на эллипсоидах с различным соотношением полуосей а/b, приведены на
рис. XIV-6-6. Малые значения отношения alb соответствуют затупленным
носкам с повышенным сопротивлением, в то время как большие величины
alb представляют тела с уменьшенным сопротивлением.
Тепловой поток в критической точке эллипсоида может быть вычислен,
например, по формуле (XIV-5-4), в которой значение ]/"./?? надо заменить
величиной }/Ь2/а. Затем по графику на рис. XIV-6-6 можно найти
теплопередачу в произвольной точке поверхности. Безразмерное давление в этой
точке определяется по ньютоновской теории или по экспериментальным
данным.
Трение и теплопередача при больших скоростях
Коническая поверхность. Рассмотрим расчет теплового
потока на поверхности усеченного конуса со сферическим носком. Примем,
что на конической поверхности «невязкие» параметры газа постоянны
и равны соответствующим их значениям в конце сферы. В частности, скорость
а отношение давлений
JL = cos2 TjK +
РО
Радиальная координата произвольной точки поверхности конуса г =
= хк sin т]к, где хк представляет собой расстояние вдоль поверхности,
отсчитываемое от воображаемой вершины острого конуса и определяемое
зависимостью
Теперь можно подставить приведенные выше соотношения для V§r
р/р'о и г в формулу (XIV-4-2). Интеграл в знаменателе, определяемый в
пределах от 0 до хк, вычисляется как сумма двух интегралов: одного — с
пределами от 0 до х = i?TT]K (или для углов — от 0 до т]к) и другого — с пределами
от i?T ctg |3K до хк. Первый интеграл соответствует значению теплового
потока в конце сферического участка (или, что то же самое, в начале
конической поверхности). Понятно, что распределение теплового потока на
передней криволинейной поверхности такое же, как и полученное ранее для
сферы. Второй интеграл
G
где функция
а угол t]k = jt/2 — |3К. После необходимых преобразований получим для
расчета тепловых потоков
где
Входящая в последнее выражение функция D определяется по (XIV-6-3)
для значения т] = т]к. Безразмерная величина хк в (XIV-6-9) равна xK/RT.
Следует иметь в виду, что зависимость действительна только на конусе,
т. е. для значений #K>ctgPK.
На основе приведенных формул можно рассчитать распределение
тепловых потоков в предельном случае при Моо -> оо. Соответствующие
зависимости для функций А (|3К) и В (Рк) принимают вид
А (Рк) = -^ sin P« (|~ рк)V2 : (XIV-6-10').
586
Глав а XIV
О
0,8
Рис. XIV-6-7. Распределение теплового
потока вдоль поверхности затупленного конуса
(ламинарный пограничный слой):
ст
ст
—— < 1; Гст = const;
1; 1 — по формуле
(XIV-4-3); 2 - по формуле (XIV-6-9)
В практических случаях этими формулами можно воспользоваться,
если Moo sin рк > 1. На рис. XIV-6-7 нанесены кривые, рассчитанные по
формулам (XIV-6-9) — (XIV-6-11) для сильно охлаждаемой поверхности
^^ (^ст < Т&). Там же представлены
^>^\ результаты расчета по формуле
(XIV-4-3), относящиеся к
поверхности эквивалентного острого
конуса, скорость на котором
вычисляется по выражению FK = Xi?Tr]K.
На рис. XIV-6-7 видно, что
при углах рк = 30 и 40°
распределение теплового потока на
затупленном и эквивалентном
заостренном конусах практически
одинаково, в то время как на
поверхности тонких затупленных тел
тепловые потоки меньше, чем на
поверхности соответствующих
эквивалентных конусов.
Анализ формулы (XIV-6-9)
показывает, что тепловой поток на
участках поверхности,
расположенных по потоку ниже
критической точки, приблизительно пропорционален х~1/2. Поэтому представилось
возможным ввести в качестве параметра теплопередачи величину {q/qo) Vх /^т»
зависящую от местного угла наклона поверхности |3 и от числа Моо. При
помощи соответствующей расчетной кривой,
приведенной на рис. XIV-6-8, можно достаточно
просто определить тепловой поток как на
поверхности затупленного носка, так и на
периферийных участках. Получаемые по рис. XIV-6-8
результаты оказываются лучшими для близких
к носку участков поверхности.
Влияние диссипации профиля низких
скоростей. Приведенные выше зависимости, а также
сделанные выводы относятся к случаю, когда
диссипация профиля низких скоростей не
учитывается. Наличие диссипации снижает эффект
затупления, что проявляется в увеличении
теплового потока. Однако это явление имеет
значение для удаленных участков поверхности, где
тепловой поток возрастает до величины,
соответствующей заостренному конусу. Вблизи
носка тепловой поток будет близок к расчетному.
Эффект диссипации приближенно можно
оценить, если на чертеже нанести тепловые
потоки, рассчитанные для затупленного тела
вблизи носка и для заостренного — вдали от него, а затем, задавшись некоторой
длиной, провести интерполяционную кривую. Для плотных слоев атмосферы
эта длина должна выбираться большей, чем для разреженных.
Тепловые потоки на цилиндрической поверхности. В том случае, когда
сферический носок заканчивается цилиндрическим участком, распределение
тепловых потоков можно рассчитать с помощью формул (XIV-4-1) и (XIV-4-2)
лри условии, что на этом участке р/р'о = (коо ML)"1, F6 = 0,5AJ?Tjt, т. е. когда
80 60 40 20
Рис. XIV-6-8. Параметр
ламинарной теплопередачи
Трение и теплопередача при больших скоростях 587
параметры принимаются такими, как в конце сферы, где r] = jt/2. Так как
на цилиндре r = i?T = const, то выражение (XIV-4-1) для тепловых потоков
принимает вид
^ К ^"1/2' (XIV-6-12)
где дгц = Жц/7?т, а #ц отсчитывается от начала цилиндрического участка.
Функция 2)Т1==я/2 определяется по формуле (XIV-6-3), в которой угол ц
принимается равным л/2:
к(^) (XIV-6-13)
Если в формуле (XIV-4-2) использовать замену р/р'о = Pl^H)
тепловой поток в критической точке q0 определить по выражению (XIV-5-1)
и рассмотреть при этом достаточно удаленные точки на цилиндре, для
которых хц > 1, то придем к зависимости
q = 0,27 Pr-2/3ir |/РвИ*цв , (XIV-6-14)
которая при эквивалентной скорости щ = 0,ЪХЕТп совпадает с формулой для
теплового потока на плоской пластинке. При малых числах М<х> скорость щ
близка к значению 7б, и в этом случае формула (XIV-6-14) точно
совпадает с формулой для пластинки.
Экспериментальные исследования показывают, что на цилиндре
достижение тепловых потоков, близких по значению к потокам на пластинке,
происходит даже несколько раньше, чем это следует из теории, практически
уже вблизи места сопряжения. Если принять число Рг = 0,71, то в
соответствии с формулой (XIV-6-14) в рассматриваемом случае щ ~ V& параметр
теплопередачи
St/Re = 0,34, (XIV-6-15)
что совпадает со значением для несжимаемой среды.
Расчет теплового потока к стенке с произвольной температурой.
Соотношение (XIV-4-1), как указывалось, получено при условии, что
произведение pjx поперек пограничного слоя остается величиной постоянной и не
учитывается влияние градиента давления. Это предположение правильно, если
стенка сильно охлаждается. В ином случае необходимо исходить из того,
что параметр pjx является переменным и теплопередача, кроме того, зависит
ют параметра |3, определяемого градиентом давления
X
р = ~ 21Г ^ (I PsV6r2 dx) ^ fo7^)"1* (Xiv-6-16)
0
Как показывают исследования, в рассматриваемом случае отношение
удельного теплового потока в произвольной точке поверхности к его
значению в точке полного торможения определяется выражением
-fk- j(XIV-6-17)
где
X
х= \
о
о
Отношение
0,937 (l-gCT) (1+o,O96/р). (XIV-6-18)
588
Глава XIV
Удельный тепловой поток q0 в точке полного торможения определяется
по формуле (XIV-5-2).
Влияние завихренности. При рассмотрении теплообмена в критической
точке было отмечено, что эффект завихренности проявляется в повышении
теплопередачи. Такое же явление наблюдается и в произвольной точке
поверхности.
На рис. XIV-6-9 показаны результаты исследований эффекта
завихренности в различных условиях. Имея эти кривые, а также значения
теплопередачи в критической точке, можно для
заданных конкретных условий
построить ориентировочную кривую и
оценить величину теплового потока q%
с учетом влияния эффекта
завихренности в произвольной точке поверхности.
Влияние диффузии. Для уточнения
расчетов в связи с влиянием диффузии
могут быть использованы зависимости,
подобные тем, которые применялись при
анализе тепловых потоков в
критической точке. Исследования показывают,
что одной из таких зависимостей может
служить выражение
О
1,0 s/rt
Рис. XIV-6-9. Влияние завихренности
потока на теплопередачу в
произвольной точке сферической поверхности:
1 — Н:== ои км; Ъ/L = Z0; Кб == p»ibm v It'/М'л ===
= 1470; ft =1,4; Кт=0,6 At; 2-Tq =
= 2900°К; Re=1000, Моо = 8; 3 - То =
= 2000°К; Re=3570; M^ = 8
-1) f-] , (XIV-6-19)
в котором qT— тепловой поток без
учета диффузии в произвольной точке
поверхности — вычисляется в общем случае при помощи формулы (XIV-6-17).
Показатель р зависит от условий течения в пограничном слое.
Ранее было показано, что в критической точке при «замороженной»
диссоциации этот показатель (3 = 2/3, а при равновесном процессе |3 ==^0,52.
Для периферийных областей поверхности точных данных о величине (3 нет.
Приближенные расчеты показывают, что в случае «замороженного»^течения
для интенсивно охлаждаемой плоской пластины можно принять |3 = 2/3.
Сопоставляя данные для критической точки и пластины, можно попытаться
использовать значение "р = 2/3 для оценки влияния диффузии на
теплопередачу к удаленным участкам поверхности тела вращения. При этом
выражение в квадратных скобках формулы (XIV-6-19) можно истолковать как
поправку на влияние диффузии к коэффициенту трения. Следовательно,
(XIV-6-20).
где Cf0— коэффициент трения без учета диффузии.
Теплопередача через
турбулентный пограничный слой
Метод расчета. Практически некоторая часть периферийной
поверхности затупленного тела омывается турбулентным пограничным слоем.
Следовательно, на этой части теплопередача от газа к телу значительно
возрастает. На рис. XIV-6-10 приведены в качестве иллюстрации
экспериментальные результаты, полученные на цилиндре со сферическим носком
([72], 1958, № 12). Видно, что в интервале значений чисел Re от 4-Ю5 да
6-Ю5 ламинарное течение (область /) переходит в турбулентное (область П)>
при этом теплопередача увеличивается почти в пять раз.
Трение и теплопередача при больших скоростях
589
6
4
2
103
8
6
4
2
к
6
Ч
Измерения показали, что для расчета турбулентной теплопередачи
можно применять формулу (IV-8-38), в которой число Прандтля принимается
как для ламинарного пограничного
•слоя, хотя в турбулентном потоке это -р^
число будет иным. Коэффициент
поверхностного трения, необходимый
для вычислений по формуле (IV-8-38),
принимают в случае сильно
охлаждаемой поверхности таким, как для
несжимаемой жидкости, причем
находят его по параметрам на внешней
границе слоя, предполагая, что
распределение скорости по сечению
пограничного слоя подчиняется закону
корня седьмой степени.
Если стенка охлаждается слабо, и \ , , , , | Y/л Л , i i i I rPj.
то при расчете теплопередачи, а
следовательно, трения, лучше
пользоваться определяющими параметрами.
При этом внешний вид применяемых
соотношений остается таким, как для
несжимаемой среды. Rex =
На криволинейной поверхности,
обтекаемой турбулентным
пограничным слоем, вблизи критической точки сферы*, где распределение скорости
подчиняется закону F6 = кх, расчет теплопередачи при умеренных
сверхзвуковых скоростях можно вести по формуле
'- Vcc
—;
: I
1 III
- .х VS
I.
у
л
i in
Ю4 2
4 6 810° 2 U
68106 2
4 6810'
Рис. XIV-6-10. Теплопередача на цилиндре
со сферическим носком в зависимости от
числа Рейнольдса:
Nu
Рг
qx
Рг=0,72
q = 0,042 Р г-2/з Г
(ТТ ~ Тст).
(XIV-6-21)
При сравнительно низких числах Рейнольдса пограничный слой является
полностью ламинарным и распределение удельной теплопередачи
характеризуется наличием максимума q в точке торможения. При высоких числах
Рейнольдса, когда пограничный слой на некотором расстоянии от точки
торможения турбулизируется, вблизи точки перехода через скорость звука
наблюдается второй максимум скорости передачи тепла. Исследования
показывают [78], что при относительно холодной полусферической носовой
части в гиперзвуковом потоке с числами Рг = Le = 1 отношение
наибольшей удельной теплопередачи gmax T в точке перехода через скорость звука
для турбулентного пограничного слоя к максимальному удельному
тепловому потоку gmax л в точке торможения
(XIV-6-22)
где Лг-вд, плотность роо имеет размерность кГ • сек21м* и берется для
соответствующей высоты атмосферы. Значение #тахл = #о вычисляется по
формуле (XIV-5-4).
Влияние диффузии. Можно ожидать, что механизм теплопередачи,
обусловленный влиянием диффузии, будет аналогичен тому, который имеет
место в полностью ламинарном пограничном слое. На этом основании можно
воспользоваться соотношением (XIV-6-19), вытекающим из теории
ламинарной теплопередачи. Согласно экспериментальным данным в этом
соотношении величина Le^ — 1 принимается равной приблизительно 0,4. В
соответствии с этим зависимость для расчета теплопередачи на затупленной
590
Глава XIV
поверхности принимает вид
(XIV-6-23)
Полезные сведения о теплопередаче на затупленной поверхности
с малым продольным градиентом давления могут быть получены из теории,
обтекания плоской пластинки. Одна из зависимостей для пластинки,
распространенная на поверхность вращения, имеет вид
(XIV-6-24)
(для конуса А = у^З, для цилиндра Л^1).
Если исходить из формулы (XIV-6-19), то в ней следует величину
—1 принять равной 0,4, а значение qT вычислять по выражению
igL [2
(XIV-6-25)
Энтальпия диссоциации, входящая в формулу (XIV-6-24), рассчитывается
для атомарно-молекулярной смеси азота и кислорода при условии, что на
стенке степень диссоциации аст Ф О, по следующей формуле:
—скст) i
— скст)
(XIV-6-26)
Для сильно охлажденной поверхности расчеты упрощаются, так как
аст = скст == 0. Кроме того, iCT < ir, следовательно, влиянием энтальпиж
газа на стенке можно пренебречь.
Теплопередача на затупленном носке. При определенных условиях
турбулентный пограничный слой образуется на поверхности затупленного
носка. Точку перехода ламинарного течения в турбулентное можно
определить, зная критическое число Рейнольд-
са. В рассматриваемых условиях
целесообразней вычислять это число по
толщине потери импульса б**, т. е.
принимать, что
Для критического числа Рейнольд-
са в результате экспериментальных
исследований на серии затупленных
поверхностей в виде эллипсоидов
вращения (включая полусферу) найдено
Рис. XIV-6-11. Параметр, учитывающий
влияние местного градиента давления (XIV-6-27)'
и геометрической формы тела на
критическое число Рейнольдса где размерность Ъ — длины полуоси
эллипса — в м, а скорости — в м/сек.
Параметр ф зависит от положения рассматриваемой точки на поверхности
тела и формы этой поверхности. В частности, для эллипсоида величина г|>
может быть определена по рис. XIV-6-11.
Трение и теплопередача при больших скоростях
591
Толщина потери импульса, по которой определено критическое число
Рейнольдса, вычисляется при помощи формулы
6** =
Го,491 (1 —0,09р0'4)
РстИ/с
°'39
] , (XIV-6-28)
X
где функция 8 дается формулой 8 = \ p&V6\i6r2 dx, а коэффициент (5 опреде-
0
ляется по выражению
ft _ о d In V6
p~z dine "
Из (XIV-6-28) видно, что толщина потери импульса зависит от степени
охлаждения стенки. Это подтверждается экспериментальными
результатами, полученными на
цилиндрическом теле с полусферическим носком
(рис. XIV-6-12).
300
о
2fi x/Rj
Рис. XIV-6-12. Толщина потери
импульса на затупленной
поверхности с различной степенью
охлаждения:
17,5; Мм=2,2; 3 - го/гп
: 9,5;
О 0,5 1,0 1,5 х
Рис. XIV-6-13. Изменение
критического числа Рейнольдса вдоль
поверхности конуса (характерная
длина — толщина потери
импульса)
'1,8; 4 — эллипсоид вращения:
= 17,5;
= 2,2
600
200
— -
' 30 50 70 90s
/3
/z
A—
4
—-
Определив значения ReKp и б**, можно вычислить координату точки
перехода, за пределами которой процессы теплопередачи будут определяться
турбулентным режимом течения в
пограничном слое. При этом расчет '
критического числа Рейнольдса
можно вести с помощью
экспериментального графика на рис. XIV-6-13,
полученного для сферического носка
с присоединенным к нему
30-градусным конусом. Данные этого графика
соответствуют очень сильно
охлажденной стенке. Критическое число
Рейнольдса существенно зависит от
того, насколько снижена температура
стенки. Влияние степени
охлаждения на число ReKP можно оценить по
рис. XIV-6-14, где приведены
экспериментальные данные для цилиндра
с полусферическим носком. Кривые
на этом рисунке можно использовать
не только для криволинейной поверхности носка, но и для периферийной.
На рис. XIV-6-15 соответствующая связь между числом ReKp и параметром
охлаждения £0/^ст в графическом виде представлена более наглядно.
0
0,8
1,6
2,4 x=cc/Rr
Рис. XIV-6-14. Критическое число
Рейнольдса на охлаждаемой поверхности:
-Z -го/гст=9,5; 1^=1,8; 2-io/i = 17,5;
Мю=2,2; «3-го/гст = 29,5; МОО=2,5; 4-
эллипсоид вращения: го/*ст = 17,5; 1^=2,2;
Кекр =
S92
Глава XIV
Расчет турбулентной теплопередачи, которая возникает за переходным
участком, должен вестись с учетом предыстории пограничного слоя, т. е.
с учетом тех процессов, которые протекают в нем выше по течению.
Соответствующая расчетная зависимость сходна с формулой для ламинарной
теплопередачи и имеет вид
Nu __ 0,029 Рг1/3(рб[гб)5/4*У1/4 h-2/5
J&Jb - х Пг >
где число Нуссельта
Nu = -
ir — iCT)
Величина Re дается формулой
Re = Re h? ; Re =
(XIV-6-29)
(XIV-6-30)
(XIV-6-31)
Отношения плотностей, коэффициентов динамической вязкости и
скоростей определяются так:
* Рг ' б Нт ' 6 УГГ
Входящий в формулу (XIV-6-29) параметр
(XIV-6-32)
Prh
(XIV-6-33)
Все величины с индексом «г» соответствуют энтальпии (температуре)
восстановления и с известным приближением могут быть рассчитаны для
Рис. XIV-6-15. Изменение критического Рис. XIV-6-16. Распределение параметра
Рй бй
р
числа Рейнольдса в зависимости от степени
охлаждения:
1 — цилиндр со сферой, x/RT~ 2,4-^3,2; 2 —
цилиндр с эллипсоидом x/RT— 2,0 ч- 3,0
р
турбулентной теплопередачи:
О - эксперимент
условий торможения. Линейные безразмерные параметры в этой формуле
отнесены к радиусу сферы i?T.
Как видно из (XIV-6-29), интегрирование начинается от условий в
критической точке, где х = 0. При этом отыскиваемое значение параметра
теплопередачи будет соответствовать тем участкам поверхности (или
значениям х), которые расположены за точкой перехода ламинарного течения
в турбулентное. На рис. XIV-6-16 приведены экспериментальные данные,
а также (пунктирная кривая) результаты расчета параметра турбулентной
теплопередачи по формуле (XIV-6-29). За исключением переходного участка
Трение и теплопередача при больших скоростях
593
теоретические результаты удовлетворительно согласуются с
экспериментальными.
Рассчитав тепловой поток, можно определить местный коэффициент
турбулентного трения, если воспользоваться уравнением, выражающим
аналогию Рейнольдса,
п _ рг-2/з o*F* (i 7 ^ с*т fXTV-fi-44^
Исследования показывают, что расчеты теплопередачи можно вести
на основе соотношений, полученных для тонкой пластинки, которые, как
известно, не учитывают влияния
продольного градиента давления. Если к тому же
не учитывается эффект диффузии в
пограничном слое, то формулы для параметра
теплообмена можно применять в следующем
виде:
Nu _ 0,029 Рг1/3 ( p6V6x ^4/5 jie
Re4/5 "
V Ji6 / х
(XIV-6-35)
или
Nu° = NuLe=3i, g=i = 0,
(XIV-6-36)
Рис. XIV-6-17. Параметр,
учитывающий влияние градиента
давления и формы тела на теплопередачу
Результаты расчета по (XIV-6-35)
представлены на рис. XIV-6-16 сплошной линией.
Несколько большая точность достигается
при условии, если расчет ведется по определяющей энтальпии
чину можно уточнить, применив вместо (IV-8-7) выражение
Ее вели-
= 0,5^т + 0,22
ir + *б (0,5 — 0,22 Pr1/3), (XIV-6-37)
в которое входит число Прандтля в явном виде. Определяющие параметры,
соответствующие этому значению энтальпии, входят, в частности, в числа
Рейнольдса и Нуссельта
Nu =
qc*x
X*(ir-iCT) '
(XIV-6-38)
Дальнейшее уточнение приведенных формул связано с учетом
продольного градиента давления и диффузии. Чтобы осуществить это, следует
воспользоваться полуэмпирической зависимостью
Nu
, вф!
= 1,0376 (a?) fl + (LeP-l) . *D. 1 . (XIV-6-39)
Nu° q°
Коэффициент G (x) учитывает влияние местного градиента давления.
Как видно из графика на рис. XIV-6-17, величина G (х) зависит от
относительного давления в данной точке поверхности, а также от формы этой
поверхности. Выражение в квадратных скобках дает поправку на эффект
диффузии. Величина Le^ — 1 в этом выражении, как показывают
экспериментальные данные, может быть принята равной 0,58.
38-114
594
Глава XIV
§ XIV-7. Сравнение трения
и тепловых потоков на
заостренном и
затупленном конусах
Конус и сферический носок. Для оценки влияния затупления на
суммарную величину теплового потока представляет интерес определить
вначале, насколько отличаются тепловые потоки на заостренном конусе и
соответствующем сферическом носке (рис. XIV-7-1). Рассмотрим ламинарную
теплопередачу [50 ].
Ее суммарная величина на заостренном конусе определяется по
формуле (XIV-4-5). Для расчета теплового потока на поверхности
соответствующего вписанного сферического шаро-
«сф
0,7
0,6
0,5
\
1
к
V
n
frf-A
вого сегмента можно
формулу
*1к
использовать
-^-) sin tj
0
12
16
20
в которой отношение q/qo берется по
формулам (XIV-6-1) или (XIV-6-6),
а поверхность сферического сегмента
Рис. XIV-7-1. Сравнение тепловых потоков
для сферических и конических носков
(ламинарный пограничный слой):
Верхний предел интеграла цк =
= п/2 — |3К. Задаваясь различными
условиями обтекания или, что то же,
системой параметров Мс»; Тст/Т&;
рк; жк, можно определить отношение тепловых потоков на сфере и конусе,
т. е. величину <?сф/<?к- Часть результатов таких расчетов, проведенных
для конусов с половинными углами раствора |3К = 10, 20° и при условии, что
поверхность охлаждается до температуры набегающего потока, показана
на рис. X1V-7-1. Из этих результатов следует, что тепловые потоки для
сферического носка меньше, чем для конического.
Коническое тело с заостренным и затупленным носками. Если на
затупленной и заостренной конических поверхностях пограничные слои будут
однотипными, то трение и теплопередача на обеих поверхностях не будут
существенно отличаться. Расчеты показывают, например, что снижение
теплопередачи на затупленном конусе составляет не более 5%.
Существенное преимущество затупленной поверхности проявляется
тогда, когда большая ее часть покрыта ламинарным слоем, в отличие от
заостренного тела, на котором пограничный слой турбулентный.
Чтобы убедиться в этом, рассмотрим соотношения между
коэффициентами трения и теплопередачи для заостренного и затупленного конусов.
В соответствии с формулами для местных коэффициентов трения их отношение
„пл
(XIV-7-1)
где Aa =
пл
Тогда
Ак =
£/_з_ ^
ReK \l/2
«(г-)
Re-3/io.
(XIV-7-2)
Для оценки влияния затупления на средний коэффициент трения
необходимо в (XIV-7-2) заменить коэффициент 16 на величину 25,6. Как
Трение и теплопередача при больших скоростях 595
видно, для того чтобы воспользоваться этой формулой, следует вначале
найти числа Рейнольдса для заданных точек на затупленной и заостренной
конических поверхностях.
Чтобы иметь представление о порядке величины, характеризующей
снижение трения, можно задаться какими-либо ожидаемыми значениями
этих чисел. Если принять для примера, что на остром конусе ReK = 1010,
а на затупленном Re3 = ReK/25, то ламинарный местный и средний
коэффициенты трения на затупленной поверхности уменьшатся по сравнению с их
значениями для турбулентного пограничного слоя соответственно в 12
и 7,5 раз.
Формулу (XIV-7-2) можно использовать, присоединив к ней зависимость,
отражающую аналогию Рейнольдса, также для оценки уменьшения
теплопередачи к затупленной поверхности. При этом с целью упрощения можно
принять, что с известным приближением числа Прандтля для обоих тел
одинаковы. Тогда при условии, что iCT < £г, отношение тепловых потоков
16 ( )Re z^. . (XIV-7-3)
Як \ ReK / fXK cp к TT K v '
Полагая, что два последних отношения в правой части меняются мало,
вычисляя коэффициент динамической вязкости по формуле (Ш-1-3), а
величину Re3/ReK— по выражению (IV-10-2) и принимая п = 3/4, можно
получить более простую зависимость для оценки отношения местных тепловых
потоков на затупленном и заостренном конусах:
(XIV-7-3')
При оценке отношения средних значений тепловых потоков
коэффициент 16 надо заменить на 25,6. В соответствии с формулой (XIV-7-3')
тепловые потоки на затупленном теле могут уменьшаться существенно.
Например, у 10-градусного конуса при Моо = 20, М3 = 3 и Re3 = 106
местный тепловой поток снизится в 17 раз, а средний — в 11.
Экспериментальные исследования показывают, что в действительности снижение
оказывается меньше. Это объясняется в основном тем, что турбулизация
наступает раньше, чем достигается расчетное критическое число Рейнольдса,
и турбулентный пограничный слой покрывает значительную часть
поверхности, на которой практически тепловой поток остается таким, как на остром
конусе.
Экспериментальные исследования показывают, что коэффициент
турбулентной теплопередачи при небольших скоростях обтекания конуса [46]
а = тг~Ттст = °'022 ^Г Ке2'8Рк'33> (XIV-7-4)
где рк — угол конуса, измеряемый в радианах;
х — расстояние от носка вдоль образующей до точки, в которой
определяется теплопередача; число Rex = Foo^/voo.
Используя соотношение (XIV-7-4), можно определить, применяя
формулу (VI-4-6), температуру тонкой обшивки в некоторый момент времени
полета.
§ XIV-8. Влияние вязкости
на внешний поток около
затупленного тела
Оценка влияния вязкого взаимодействия. При изучении влияния
вязкости на параметры внешнего (невязкого) потока, в частности на
распределение статического давления, необходимо учитывать роль затупления в фор-
38*
596 Глава XIV
мировании пограничного слоя. Установлено, что если число Рейнольдса,
вычисленное по диаметру носка DT и определяемое соотношением ReD =
= FooPoo^t/M'oo, достаточно велико, то влияние давления в невязком потоке
у затупленного носка является доминирующим и именно величина и
характер его распределения определяют развитие пограничного слоя.
Обратное влияние пограничного слоя на внешний поток невелико.
Однако по мере удаления от носка, вследствие роста толщины пограничного
слоя, это влияние усиливается. В частности, из-за роста толщины слоя может
существенно увеличиться давление, что в свою очередь влияет на параметры
пограничного слоя. Исследования показали, что для тел вращения
расстояние L от затупленного носка, на котором дополнительное сопротивление
вследствие увеличения давления при вязком взаимодействии становится
соизмеримым с сопротивлением затупления, определяется формулой
где Ъ — некоторый коэффициент, зависящий от условий обтекания.
В результате экспериментальных исследований в аэродинамической
трубе для теплоизолированной цилиндрической поверхности (Тст = Тт) при
Моо = 15 было найдено, что величина Ъ равна приблизительно двум.
Влияние вязкости существенно ослабляется в условиях свободного
потока, при которых температура поверхности значительно ниже
температуры восстановления, и поэтому пограничный слой более тонок, чем на
теплоизолированной стенке. В частности, при Тст = ЪТоо и Моо = 15 для
воздуха коэффициент Ъ ~ 20.
Таким образом, влияние вязкого взаимодействия зависит от теплового
режима стенки, чисел Моо и Re^. В качестве примера оценим это
взаимодействие на поверхности сферы DT = 1 м для условий ее полета на высоте
порядка 82—83 км со скоростью, определяемой числом Моо = 15.
Вычисленное по этим данным число Re^ = 2640. Следовательно, для
теплоизолированной стенки (Ь = 2) в соответствии с формулой (XIV-8-1) величина L/DT =
— 23, а в свободном потоке (Ъ = 20) при температуре стенки Тст = ЪТоо эта
величина будет в десять раз больше, т. е. L/DT = 230.
Как видно, при выбранном значении числа ReDT для более коротких
реальных тел, т. е. с меньшей относительной длиной L/DT, чем найденные
в примере, влиянием вязкости можно пренебречь. Однако с уменьшением
чисел Rej)T или увеличением Моо расчетные значения L/DT могут оказаться
меньше, чем относительная длина реального тела, и влияние вязкого
взаимодействия будет существенным. Например, при Re#T = 225, Моо = 15
и Тт — Тст значение L/DT = 2. В этом случае дополнительное
сопротивление носка из-за увеличения давления, связанного с нарастанием толщины
пограничного слоя, становится соизмеримым с сопротивлением носка вблизи
затупления на длине L = 2DT. Указанные рекомендации по расчету вязкого
взаимодействия пригодны лишь для больших чисел ReDT и оказываются
сомнительными для малых их значений. В настоящее время трудно сказать
точно, где находится граница применимости теории этого взаимодействия,
характеризующаяся некоторым предельным значением ReDT. Отдельные
данные показывают, что ориентировочной оценкой нижнего предела может
являться число Re/)T ~ 102.
«Эффективная» форма тела. Учет влияния вязкого взаимодействия
на параметры внешнего обтекания заключается в расчете невязкого течения
около тела «эффективной» формы, которая получается в результате смеще-
Трение и теплопередача при больших скоростях 597
ния контура заданного тела на величину, равную толщине вытеснения
пограничного слоя. Рассматривая удаленные участки тела, где продольный
градиент давления мал, расчет толщины вытеснения с известным
приближением можно вести на основе теории пограничного слоя около пластинки
с использованием преобразования Манглера.
Обобщенная формула для толщины вытеснения ламинарного
пограничного слоя имеет вид
Здесь А и п приведены в табл. VI-1-1. Коэффициент Nt = 8/3 для
ламинарного и N± — 8 для турбулентного пограничного слоя. Коэффициент
N2 = 1 для цилиндра, обтекаемого как ламинарным, так и турбулентным
пограничным слоем. Для конической поверхности он имеет различные
значения: в случае ламинарного пограничного слоя N2 = ]/3, турбулентного
N2 = ул3. Расчет числа Rex в формуле (XIV-8-2) следует вести по
эквивалентной скорости, вычисленной с учетом влияния затупления. Для тела
со сферическим затуплением эта скорость равна скорости в конце носка
Fa = XRTr\K, где для конуса т)к = я/2 — рк, для цилиндра т]к = я/2.
Плотность и вязкость, по которым вычисляется число Re^, находятся для
горячей стенки, в частности, теплоизолированной по определяющей
температуре, а для сильно охлажденной поверхности (Гст < ТТ) они принимаются
такими, как на внешней границе пограничного слоя, т. е. рассчитываются
как параметры невязкого обтекания с учетом влияния затупления. Длина
х может отсчитываться вдоль криволинейной образующей носка от точки
торможения.
В практических расчетах число Re^ может вычисляться по формуле
(IV-10-2) или находиться по графикам на рис. IV-10-2.
В качестве иллюстрации применения формулы (XIV-8-2) рассмотрим
вычисление толщины вытеснения для затупленного по сфере (i?T = 0,25 м)
конуса с углом |3К — 10° и цилиндра длиной 10 м с сильно охлажденной
стенкой. Примем те же условия полета, что и в приведенном выше примере
(Моо = 15, Н = 30 м). Для заостренного конуса длиной 10 м число Re =
= 9-Ю7, для цилиндра соответствующее число Рейнольдса, подсчитанное
по невозмущенным параметрам, Re = 5,28-107. Такой цилиндр можно
рассматривать как острый конус с нулевым углом наклона образующей.
Полученные числа Рейнольдса оказываются больше критического, и,
следовательно, на заостренных поверхностях пограничный слой будет
турбулентным. Так как затупление снижает числа Рейнольдса на конусе в 30,
а на цилиндре в 48 раз, то пограничный слой ламинаризуется практически
на всей длине и, следовательно, можно применять формулу (XIV-8-2).
Подставляя в нее уменьшенные числа Рейнольдса, получим в конце конуса
б* = 7,2 мм, а в конце цилиндра б* = 20,7 мм. Более существенным будет
влияние вязкости при турбулентном течении. Вычисления дают для конуса
-6* = 18,7 мм, для цилиндра б* = 29,3 мм.
Изменение б* для теплоизолированной стенки оказывается более
значительным, чем для охлажденной. Как показывают расчеты, определяющая
температура для нее будет приблизительно в 10 раз больше, чем на внешней
границе. Следовательно, учитывая изменение р и \х от температуры, число
Рейнольдса, найденное по определяющим параметрам, уменьшится в 50 раз.
В соответствии с этим толщина вытеснения для ламинарного пограничного
слоя увеличится примерно в 7 раз, а для турбулентного — в 2,2 раза.
Существенное увеличение толщины вытеснения связано с уменьшением местных
чисел Рейнольдса. Таким образом, затупление тела, увеличение высоты
598
Глава XIV
полета, рост средней температуры пограничного слоя — все эти факторы
способствуют изменению «эффективной» формы.
После того как определена «эффективная» форма тела путем смещения
контура в направлении нормали на величину б*, распределение давления
и других «невязких» параметров вычисляется для этой новой формы. Одной
из характеристик новой формы, в частности для конуса, является его
«эффективный» угол, который может быть приближенно найден по формуле Рк =
— Рк + S*/L, где б* — условная толщина на заданной длине образующей L.
Если же дан цилиндр, то его «эффективной» формой можно считать конус
с углом, равным б*/£.
Более точным является определение «эффективной» формы конуса или
цилиндра как видоизмененной поверхности вращения с
криволинейной образующей. «Эффективный» криволинейный контур сохранится также
и в том случае, когда обтекаемое тело имеет заданный криволинейный
контур.
Для полученных «эффективных» криволинейных поверхностей расчет
давления можно вести по формуле Ньютона р = р0 sin2P9, в которой для
конуса угол Рэ = рк + arctg (d6* Idx)
Р
0,6
0,2
\
1
V
2
/
1 1 1
/ миЭ
i
О 0,1 0,2 0,3 Qfi 0,5 0,6
0,7 £
L
Рис. XIV-8-1. Влияние пограничного слоя
на распределение давления:
1 — невязкое обтекание; 2 — с учетом
влияния пограничного слоя; M^sie^; Re =
определяется наклоном
«эффективной» образующей к направлению
скорости набегающего потока.
Для достаточно удаленных от
затупления участков тела при
вычислении приращения угла Ар =
= arctg (<2б* Idx) наклона контура от
влияния толщины вытеснения можно
воспользоваться формулой (XIV-8-2).
Дифференцируя по х, получим
^-=^шг^- <XIV-8-3)
_ y°°L =з ЗЮ5 Для тонкого тела «эффективный»
v°° угол наклона контура рэ = рк +
+ йб* Idx. На рис. XIV-8-1 показано
влияние пограничного слоя на распределение давления на примере
обтекания потоком гелия поверхности тела вращения степенной формы.
Существенное увеличение давления вследствие вязкого взаимодействия объясняется
очень большим числом Моо, сравнительно малым значением Re и наличием
теплоизолированной поверхности.
Увеличение сопротивления произойдет не только из-за возрастания
давления в свободном потоке, но и вследствие увеличения трения,
обусловленного влиянием на пограничный слой индуцированного давления. В
результате суммарный коэффициент сопротивления будет определяться
соотношением
— /» | , /» , _] р _] \р | А /» , | А л
х — ихр i bxf \ ьх дон \ LAUxpp г LALxfp i ^^х/к?
схр, cxf, схдон — соответственно коэффициенты сопротивления
давления, трения и коэффициент данного сопротивления,
вычисленные без учета вязкого взаимодействия;
&cxppi &cXfp — коэффициенты добавочных сопротивлений, вызванных
соответственно изменением давления и трения
вследствие вязкого взаимодействия.
Коэффициент Лсх/К характеризует изменение сопротивления трения,
обусловленное поперечной кривизной тела. В табл. XIV-8-1 приведены
результаты расчета составляющих коэффициента сопротивления затуплен-
Трение и теплопередача при больших скоростях
599
Таблица XIV-8-1
Сопротивление затупленного конуса
Коэффициент
сопротивления
и его составляющие
сХ
Схр
cXf
сздон
Абсолютная
величина
0,1300
0,0427
0,0643
0,0061
Проценты
100
32,9
49,5
4,7
Коэффициент
сопротивления
и его составляющие
&схрр
Лсх/К
Абсолютная
величина
0,0069
0,0037
0,0063
Проценты
5,3
2,8
4,8
ного по сфере конуса с углом (Зк = 8° и степенью затупления Rr Ir дон = 0,035
для условий Мое - 15,3 и Re = Fooi?T/voo = 8,4.10* ([70], 1964, № 11).
Суммарная величина сх, приведенная в табл. XIV-8-1, хорошо
согласуется с экспериментальным значением сх = 0,1290. Анализ компонент
полного сопротивления показывает, что его главную часть (87,1%) составляют
сопротивления схр + cxf + сх дон, вычисленные без учета вязкого
взаимодействия. Ориентируясь на данные табл. XIV-8-1, в практических случаях
0,5
0,3
0,2
0,1
О
i
о,"
о
Обозн.
о
о
Л
X
Иоо
15,21-16,30
14,89-15,19
12,3943,24
10-13,07
100
200
300 а.%град'
х v a
Dv x av ov
*-*
Л
А
I
100 200 300 а2, град
i
/у п ^
Iй
Г
„Л П
у А о
100
200 300 *\град^ °
200
300 сс2,ерад2
Рис. XIV-8-2. Аэродинамические характеристики слегка затупленного по сфере конуса
(Р„ = 8°, Ят/гДон = 0,035)
можно оценить дополнительные компоненты сопротивления,
обусловленные вязким взаимодействием и влиянием поперечной кривизны
поверхности.
На рис. XIV-8-2 приведены экспериментальные данные об
аэродинамических коэффициентах для слегка затупленного по сфере конуса (рк = 8°,
600 Глава XIV
^т/^дон = 0,035) при различных значениях гиперзвуковых чисел М<х>.
Эти данные получены с учетом вязкого взаимодействия. Коэффициент
лобового сопротивления меняется по квадратичной зависимости от угла атаки
и увеличивается с ростом числа Моо. Статические производные с", т%, как
и коэффициент центра давления сц. д = £ц. д/як> могут рассматриваться как
функции, не зависящие от угла атаки и числа Маха.
РАЗДЕЛ
ЧЕТВЕРТЫЙ
•
аэродина
мические
характеристики
летательного
аппарата
Глава XV
СТАЦИОНАРНОЕ
ОБТЕКАНИЕ.
§ XV-1. Расчет
аэродинамических коэффициентов
с учетом интерференции
для комбинации,
состоящей из тонкого корпуса
и крыла
D D +
Общие определения
Тело вращения или корпус какой-либо другой геометрической формы,
используемые в качестве элемента конструкции летательных аппаратов,
могут быть снабжены крыльями, оперением и рулевыми элементами.
При рассмотрении аэродинамики корпусов в комбинации с несущими,
стабилизирующими и управляющими поверхностями возникает сложная
и пока недостаточно разрабо- >
тайная проблема учета интер- Щ к v
ференции между различными
элементами летательного
аппарата.
В результате
интерференции сумма
аэродинамических сил и моментов, взятых
отдельно (изолированных)
крыла и корпуса, оперения
и корпуса, корпуса, крыла
и оперения и т. д., не равна
полной силе или моменту
комбинации, состоящей из
соответствующих элементов
и представляющей собой единое целое (рис. XV-1-1). Таким образом,
отдельно взятые элементы — корпус, крыло, оперение, рули, будучи соединены
в единую конструкцию летательного аппарата, как бы теряют свои
индивидуальные аэродинамические характеристики и приобретают вследствие
интерференции новые.
Суммарные аэродинамические характеристики летательного аппарата
можно определить как сумму этих характеристик для изолированных
составных элементов, а также дополнительных величин, называемых
интерференционными поправками. В частном случае, который рассматривается ниже,
поправки обусловлены интерференцией корпуса с крылом. В соответствии
с этим в аэродинамической теории тонкого тела [51] нормальная сила
комбинации корпус — крыло (рис. XV-1-2) представляется в виде
NT. KV^-NT + NKV + АЛГТ + ДЛГкр,
где первые два члена представляют собой соответственно нормальные силы
для изолированного корпуса и крыла; Д2УТ — дополнительная нормальная сила
корпуса, обусловленная влиянием крыла; AiVKp — дополнительная нормальная
Рис. XV-1-1. Схема интерференции между
корпусом и установленными на нем крылом и оперением:
а — изолированные элементы; б — элементы, соединенные
в одной конфигурации
604 Глава XV
сила крыла, вызванная интерференцией с корпусом. Введем обозначения
ДД/"Т = iVT(KP) и NKJ? + AiVKp = Л^кр(т) (нормальная сила крыла в присутствии
корпуса). С учетом этих обозначений
NT. кр = iVT + Л^кр) + ^kp(t) . (XV-1-1)
Для удобства расчетов две последние составляющие в формуле (XV-1-1)
можно написать следующим образом:
ZKp7VKp; (XV-1-2)
#T^KP, (XV-1-3)
где
iVKp — нормальная сила изолированного крыла;
КТ1 Ккр — коэффициенты интерференции. Под изолированным крылом
понимается крыло, состоящее из соединенных вместе двух консолей.
Рис. XV-1-2. Основные части комбинации крыло —
корпус (ф =0, ас ф 0):
1 — хвостовая часть; 2 — крыльевая часть; з — носовая
часть
В соответствии с формулами (XV-1-2) и (XV-1-3) нормальная сила
комбинации корпус — крыло
NT. «р = NT + (Кт + #кР) iVKP. (XV-1-4)
При появлении крена возникает дополнительное интерференционное
взаимодействие, изменяющее нормальную силу крыла. Приращение нормальной
силы
А^кр = Жф7Укр, (XV-1-5)
где Ку — коэффициент интерференции, обусловленный креном.
Суммарная нормальная сила при крене
+ KKJ> + KJ Лгкр. (X V-1-6)
Аналогично можно представить выражение для момента. Таким
образом, расчет взаимного влияния между корпусом и крылом связан с
определением коэффициентов интерференции. Нормальная сила корпуса
лгт=#т.и;УкР, (xv-i-7)
где КТг и — некоторый коэффициент, связывающий нормальные силы
изолированных корпуса и крыла. Таким образом,
NT, кр - (Кт. И + Кт + Кк» + Ку) NKJ?. (XV-1-8)
Переходя к аэродинамическим коэффициентам, получим
Мт. кр = (£т,и + Кт + #кр + Яф) CN кр.
Стационарное обтекание
605
Если рассматривается линейная зависимость нормальной силы от угла
атаки, то cN = c^a и, следовательно,
(с%)*. кр = (КТ. и + Кт + #кр + К*) с% Кр, (XV-1-9)
где коэффициенты К следует рассматривать как отношения производных
соответствующих коэффициентов нормальной силы по углу к
производят CW
Зависимости для
аэродинамического расчета с учетом
интерференции
Аэродинамическая теория тонкого тела позволяет получить
зависимости для расчета аэродинамических характеристик комбинации крыло —
корпус с учетом интерференции. Комбинация может быть не только плоской,
состоящей из корпуса с парой
несущих консолей, но и
крестообразной, включающей две пары
несущих консолей. При определении
сил и моментов будем пользоваться
системой координат х\ у', z' (рис.
XV-1-2), оси которой совпадают
с осями симметрии тела при ф — О,
ас Ф О, а также системой хи уи
z1? оси которой связаны с телом
при любых значениях ас и ф. При
этом силы, действующие на
консоли при крене (ф Ф 0), удобнее
определять в системе хи уи zi (рис.
XV-1-3).
Шарнирный момент консоли
Мш вычисляется относительно оси,
направленной по нормали к
продольной оси тела, как
произведение нормальной силы и координаты центра давления, отсчитываемой от
носка бортового сечения консоли. Пересчет момента на любую другую
точку отсчета может быть произведен обычными методами.
Интерференция крестообразного крыла с корпусом. Рассмотрим
наиболее общий случай, когда комбинация, состоящая из крестообразного
крыла и корпуса, находится в потоке под углом атаки ас и накренена на
угол ф (рис. XV-1-3). Исследование аэродинамических характеристик
такой комбинации и выяснение интерференционного взаимодействия между
крыльями и корпусом основано на представлении потенциальной функции
возмущенного течения в виде суммы ф = фа=0 + фа + Фз- Значения фа
и фз представляют собой потенциалы возмущений при независимых
обтеканиях со скоростями VooOL и Foof3cK> т- е- в направлениях нормали
соответственно к плоскости горизонтальных консолей с полуразмахом s (x) и
плоскости вертикальных консолей с полуразмахом t (x).
Потенциалы фа и фз определяются из комплексных потенциалов Wa,
W$, которые в свою очередь находятся при помощи конформного
преобразования круга на плоскости о = £ + щ в круг с парой плоских консолей на
плоскости £ = Zi + ijji. Это преобразование осуществляется по формуле,
приведенной в табл. IV-4-1. Потенциал Wa получается из (IV-4-33) при
условии ф = 0 в результате замены величины а — г\ /а по указанной формуле
из табл. IV-4-1, а также подстановки Fo = FooCc = Fooccc cos ф. Чтобы
найти полную величину потенциала TFa, надо включить в нее потенциаль-
Рис. XV-1-3. Коэффициенты сил и моментов,
действующих на консоли крыла и на всю
комбинацию крыло — корпус
606 Глава XV
ную функцию потока, параллельного оси г/ь равную iVoodt,. Осуществив
указанные операции, найдем
Составляющие скорости при поперечном обтекании вычисляются по
формуле wa — iva = dWJd^.
Комплексный потенциал W& при поперечном обтекании в направлении
(Зск со скоростью FooPck = VooO^c sin ф получается в результате замены
в (XV-1-10) значений а на (Зск и s на t. Что касается составляющих скорости,
то они вычисляются по формуле w$ — iv$ = dW&/d£. Выделяя
действительные части из комплексных величин Wa, Wq, можно найти потенциалы
фа и ф3. Добавляя к сумме этих функций потенциал фа==0 (IV-4-8), определим
суммарную потенциальную функцию ф = фа=о + фа + Фз-
Полные составляющие скорости определяются суммированием трех
компонентов:
(XV4-11)
w = (pz==Wa=QJi J
Внося величины и, v, w в (Ш-3-12'), находим коэффициенты давления
в возмущенном потоке, обтекающем рассматриваемую комбинацию корпуса
и крыла. Коэффициент давления в общем случае равен
p-=f(aCi4>, 5, t, r, xu г/i,^), (XV-1-12)
причем xi отсчитывается от начала корневой хорды консоли. Относя
выражение для р к условиям на корпусе (yl = r2 — zl), найдем коэффициент
давления рТ(кр) на корпусе в присутствии крыла. Обозначив индексом «н»
коэффициент давления в нижней части корпуса, а индексом «в»
—величину этого коэффициента в симметричной точке на верхней части корпуса,
найдем избыточный коэффициент давления Арт. (Кр) — р" (кр) + Рт. (кр)'.
4ас cos Ф [(1-т-з4) s' + 2r8 (l + r;-2z») г']
АРт- (КР) ~ [(i+r;)»
где rs = r/s; rt=-rlt, zr-=zjr\ yt
zs = zjs; zt = zjt\ rf = dr/dx^ s' = ds/dx±.
Чтобы определить коэффициент давления на консоли ркр (т) в
присутствии корпуса, следует в общем выражении (XV-1-12) принять z± = 0 (для
вертикальных консолей) и */i = 0 (для горизонтальных консолей). Для
вертикальных консолей у± меняется от +г до ± t. Координата zi для
горизонтальных консолей меняется от ± т до ± s. Как показывают вычисления,
для правой консоли избыточный коэффициент давления в присутствии
корпуса
4
i
где введены новые величины rz = r/z1; ysz=
Стационарное обтекание
Для левой консоли следует принять в приведенном выражении угол ср,
большим на я. Выражение избыточного коэффициента давления на
вертикальных консолях будет аналогичным (XV-1-14), с той разницей, что
величину z± надо заменить на у±. Угол ср для нижней консоли заменяется
величиной ф + я/2, а для верхней —ф + Зтс/2. Это определение углов ср следует
отнести и к формуле (XV-1-13) при вычислении по ней давления в точках
сопряжения с консолями.
Анализируя выражения (XV-1-13) и (XV-1-14), можно сделать вывод,
что первые члены в правых частях (обозначим их соответственно Ар? (КР)
и А/?кр (Т)) определяют нагрузку, симметрично распределенную на правой
и левой консолях и зависящую от параметров только горизонтальных
консолей. При фиксированном угле a = accoscp значения Др?(Кр), А/Лф(т) будут
одними и теми же при любых ср, в том числе при отсутствии крена, когда
Ф = 0 и, следовательно, ос = ас.
Вторые члены в формулах (XV-1-13) и (XV-1-14) (соответственно
Д/?т(кр)> Аркр (т)) дают одинаковые по величине, но разные по знаку нагрузки
на правую и левую консоли. Эти нагрузки, имеющие асимметричный
характер, зависят от угла крена и формы вертикальных консолей. Таким образом,
коэффициенты давления можно рассматривать в виде суммы двух величин:
А'Рт1Ш = Др°(кр) + Аи? (кр); (XV-1-13')
В формулы (XV-1-13) и (XV-1-14) входит производная г' = drldxu
характеризующая влияние переменности радиуса в месте сопряжения с крылом.
Исследования показывают, что это влияние незначительно. Поэтому в
дальнейшем примем г' = 0.
Аэродинамические силы. Интегрируя давление по поверхности
корпуса и крыла, можно найти нормальную силу Nu расположенную в
плоскости угла атаки a — accoscp, и боковую силу Z1? нормальную к этой
плоскости:
Nt = 2jtas2m (l-rt + ri) qoo; (XV-1-15)
Zt = - 2ярск4 (1 - r? + rf) goo; (XV-1-16)
где rs = r/sm; rt = r/tm; sm и tm — размах соответственно горизонтальной и
вертикальной консолей.
Нормальная сила N, лежащая в плоскости угла атаки ас,
N = Ni cos ф — Zi sin ф. (XV-1-17)
Боковая сила, совпадающая с направлением оси z',
Z; = Ni sin Ф + Zd cos ф. (XV-1-18)
Для симметричной крестообразной комбинации tm — sm, следовательно,
N - 2яас5^ (1 - rl + ri) qoo. (XV-1-19)
Что касается боковой силы, то, как следует из (XV-1-18), она равна
нулю. Таким образом, нормальная сила, расположенная в плоскости угла
атаки ас, остается неизменной при любом угле крена.
Коэффициенты интерференции. Как указывалось выше, можно
принять производную г'=0. Это означает, что будет рассматриваться случай,
когда корпус в месте сопряжения с крылом представляет собой круговой
цилиндр. Нормальная сила части корпуса до крыла равна, как видно
из (XV-1-19), Nr = 2nacr2qoo и создается носовой частью на участке до места
сопряжения с цилиндром, который не является несущим. Так как для крыла
£кр?оо, то коэффициент #т. И7 входящий в (XV-1-7), будет
608
Глава XV
равен
(XV-1-20)
Если цилиндрический участок корпуса, расположенный между крылом
и носовой частью, длинный, то при определении нормальной силы следует
учесть составляющую, создаваемую этим участком и обусловленную
отрывом потока.
В соответствии с (XV-1-2) коэффициент интерференции для крыла Ккр =
= Л7'кр(т)М^кр- Нормальную силу крыла iVKP(T) с учетом влияния корпуса
можно вычислить, интегрируя
давление по поверхности крыла и
полагая в (XV-1-14) производную
г'=0. В табл. XV-1-1 приведены
результаты расчета интерференции
комбинации корпус — крыло
треугольной формы (рис. XV-1-4) с
учетом, что для изолированного крыла
NK$ = 2л;ас cos q)(sm — г)2.
Коэффициент интерференции
является функцией отношения rs —
= r/sm. Радиус корпуса вдоль хорды
крыла или оперения может
меняться. В этом случае для упрощения расчетов выбирают среднее значение радиуса
на длине хорды или оперения. В предельном случае при г = О комбинация
переходит в крыло, и величина .йГКр = О. По мере того как r/sm приближается
к единице, консоли крыла становятся очень малыми и, как следует из формулы
(XV-1-21)
где ас — угол атаки корпуса; а z — расстояние от оси тела до
рассматриваемого сечения консоли, местный угол атаки такой весьма малой консоли
будет равен 2ас. Коэффициент интерференции Ккр = 2, следовательно,
эффективность консоли возрастает вдвое. Значения KKV>, полученные для
треугольного крыла, практически могут быть годны для всех тонких комбинаций
независимо от их размаха.
Т а б лиц а XV-1-1
Коэффициенты интерференции и координаты центра давления
при наличии угла атаки
Рис. XV-1-4. Комбинация треугольного крыла
и корпуса
г
0
од
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,000
1,077
1,162
1,253
1,349
1,450
1,555
1,663
1,774
1,887
2,000
0
0,133
0,278
0,437
0,611
0,800
1,005
1,227
1,467
1,725
2,000
/ Ц. Д(Х \
V ькр /кр(т)
0,667
0,657
0,650
0,647
0,646
0,647
0,650
0,654
0,658
0,662
0,667
/Лц.доЛ
V ьКр /т(кр)
0,500
0,521
0,542
0,563
0,581
0,598
0,613
0,628
0,641
0,654
0,667
Z — Г
Ц. ДОС
sm~r
0,424
0,421
0,419
0,418
0,417
0,417
0,416
0,418
0,420
0,422
0,424
Стационарное обтекание
609
Коэффициент интерференции для корпуса определяется из (XV-1-3)
в виде отношения KT = NT(Kp)/NKI>, в котором
-Л/т. (кр) = ■
. кр"
^кр.'(т)
— NT.
(XV-1-22)
Суммарная нормальная сила JVT. кр вычисляется для угла атаки а
по формуле (XV-1-15). Имея в виду, что iVKp(T) =NKpKlw, a NT--= 2тсаг2доо,
получим для коэффициента интерференции зависимость
Кт = (1 + rs)2 — ZKP. (XV-1-23)
Значения Кт, вычисленные по формуле (XV-1-23), приведены в табл.
XV-1-1. Эти значения не зависят от формы крыла в плане, а определяются
только параметром rs = r/sm.
Рассмотрим, как вычисляется коэффициент интерференции для крыла,
обусловленный креном. Величина этого коэффициента определяется из
формулы (XV-1-5) в виде Ку = ANKV/NKV>. Добавочную нормальную силу крыла
A7VKp при крене находят путем интегрирования по поверхности
коэффициента давления АркР(т), равного второму члену в (XV-1-14). Так как суммарная
сила AiVKp для двух консолей равна нулю, то для определения величины
Ку следует рассмотреть одну консоль, например правую, для которой Лгкр =
= Jta (sm — r)2 goo. Интегрируя по поверхности консоли, найдем, что
величина Кф пропорциональна отношению f5CH/tg e (tg e = dsldx1 — const) и
некоторой функции Кц, зависящей от параметра rs = r/sm. Эта функция,
используемая также в качестве коэффициента интерференции
Значения коэффициента
О
*кр Рек
в зависимости
~К tg8
■^^ф ft
Рек
ОТ
отношения rs = r/sm
приб
ведены в табл. XV-1-2. Они вычислены для комбинации корпуса с
треугольным крылом и будут меняться при переходе к другой форме крыла.
В этом случае данные табл. XV-1-2 можно использовать как
ориентировочные.
Т а б лица XV-1-2
Коэффициенты интерференции и координаты центра давления
при наличии крена (корпус—треугольное крыло)
г
sm
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
h
0,
0,
о,
о,
о,
о,
о,
о,
о,
0,
0
Плоские
637
687
681
649
597
529
447
382
246
128
комбинации
V Ькр /кр(т)
0,667
0,667
0,677
0,688
0,699
0,709
0,719
0,729
0,736
0,744
0,750
2ц.дф г
sm-r
0,524
0,518
0,531
0,546
0,560
0,575
0,588
0,601
0,614
0,616
0,647
к
0,
0,
о,
о,
о,
о,
0,
о,
о,
о,
0
Крестообразные комбинации
352
447
490
508
502
471
417
342
244
127
Рц.дчЛ
V ькр /кр(т)
0,667
0,654
0,660
0,673
0,687
0,700
0,714
0,725
0,734
0,743
0,750
2ц.дф г
sm~r
0,556
0,532
0,530
0,540
0,554
0,569
0,585
0,598
0,612
0,625
0,637
Коэффициент Кц, определяющий асимметричную нагрузку, необходим
для расчета момента крена от сил, действующих на крылья. Вычисление
аналогичного коэффициента интерференции для корпуса не имеет смысла,
39-114
610 Глава XV
так как асимметричная нагрузка практически не оказывает влияния на силы
и момент, действующие на корпус.
Центр давления. Вычислим координаты центра давления для
правой горизонтальной консоли (zn, да)Кр (Т)» (хц. да)кр(т)» имея в виду случай,
когда влияние угла крена отсутствует. Координата
(*ц. да)кр (т) = I А^кр wZ±ds [ J АЙр (т)^]"1, (XV-1-25)
(S) (S)
где dS = dxidzi, a избыточный коэффициент давления на консоли ДрКр(т)
равен первому члену в (XV-1-14).
Координата
(*ц. да)кр (т) = J А^р {T)XidS [ J АЙР (т) dS]"1. (XV-1-26)
(S) (S)
Здесь ^ и, следовательно, координата (хц, да)кр (т) отсчитываются от начала
консоли. Безразмерные значения (хц. да/^кр)кр (т) и (гц, да — г)кр (Т)/(*т — г)?
вычисленные при помощи формул (XV-1-26) и (XV-1-25), приведены в табл.
XV-1-1. Величины (хц, да/6Кр)кр (т) мало отличаются от значения 2/3 для
изолированного крыла, составленного из консолей, что указывает на слабое
влияние интерференции.
Аналогично вычисляются координаты центра давления (2Ц. ДФ)Кр(Т)>
(#ц. дф)кр(т)» являющегося точкой приложения добавочной подъемной силы,
вызванной поворотом на угол крена. Расчетные формулы будут теми же,
с той разницей, что вместо значения Аркр (Т) надо взять величину Дркр (т) >
равную второму члену в (XV-1-14). Вместо размерных координат удобнее
пользоваться безразмерными параметрами (гц, Дф—г)кр (т)/ (sm—r); (хц. ДФ)Кр(т)/^кр-
Значения этих параметров, рассчитанные указанным методом, приведены
в табл. XV-1-2. Центр давления корпуса (хц, да)Т(кр) с учетом влияния
крыла можно определять при условии, что ср = 0, так как влияние крена
незначительно. Расчетная формула имеет вид
(хц. да)т (кр) - j[ АЙ(кр)* sin в dS [ J А^(кр) sm в dS]"i, (XV-1-27)
(h (S)
где dS = r d@ dxu а угол 0 отсчитывается по оси oz±. Значения (хц. да/Ькр)т (Кр),
подсчитанные по формуле (XV-1-27) и отнесенные к корневой хорде консоли
&кр, приведены в табл. XV-1-1. Расстояние от носка до центра давления
(*ц. яа)т (кр) = хг + (^2) т ш Ькр, (XV-1-28)
где ^ — расстояние от носка корпуса до начала корневой хорды консоли.
Значения (яц. да — г)/ (sm~г), приведенные в табл. XV-1-1, близки к
величине 4/Зтс, имеющей место при эллиптическом распределении нагрузки,
и не зависят от формы крыла в плане. Этот результат показывает, что
интерференция крыла с корпусом не оказывает существенного влияния
на положение центра давления крыла по размаху.
Продольное положение центра давления крыла зависит от его формы
в плане, и значения (^ц. да/6кр)кр(Т), приведенные в табл. XV-1-1, подсчитаны
по формуле (XV-1-26) для треугольного угла.
Применяя теорию тонкого тела к прямоугольным крыльям, можно
установить, что центр давления расположен на передней кромке, что физически
невозможно. При определении реальной координаты центра давления можно
предположить, как и для треугольного крыла, что интерференция оказывает
слабое влияние на ее величину и, следовательно, эту координату можно
принять равной ее значению для изолированного крыла. Если применить
Стационарное обтекание
611
линеаризованную теорию, то
• д<%\ _
кр /кр(т)
— 2
р —3
(XV-1-29)
где а'Якр>1. (XV-1-30)
Исследования показывают, что координата центра давления
трапециевидного крыла в присутствии корпуса с хорошей точностью может быть принята
Рис. XV-1-5. Координаты центра давления для
изолированных крыльев, вычисленные по линеаризованной теории для
сверхзвуковых скоростей (а' > 1)
такой же, как для изолированного крыла. На рис. XV-1-5 показаны
значения (хЦш д/ЬКр)кр для изолированного треугольного (Я = &Кц./^кр = 0)?
трапециевидного (X = 1/2) и прямоугольного (X = 1) крыльев. Кривые, вычисленные по
сверхзвуковой линеаризованной теории, экстраполируются до предельных величин,
kn L
< кр/*р
46
"''
0,2-
1—
in
1
ZJ Щ
\
г[ 1
.-X
1
1
1 1 1
1
1
1\
\
\
1
\
1
\\
\
\
\
/
О 12 3 4 5 6 7 ot'AKp
Рис. XV-1-6. Коэффициенты центра давления для
изолированных крыльев, вычисленные по
линеаризованной, теории для дозвуковых скоростей (а' < 1)
получаемых по теории тонкого тела при а'Хкр^О. Значения (хц, д/6)Кр
для дозвуковых скоростей приведены на рис. XV-1-6.
По данным графиков (хц. да/^крЬр^ (#ц. да/ЬКр)кр(т), a расстояние относка
корпуса до центра давления
#ц. да — хт ~\~ \хц. да/^кр)кр (т)^кр* (X V-1-ol)
Плоская комбинация корпус — крыло. Чтобы получить соответствующие
выражения для аэродинамических параметров плоской комбинации корпус —
крыло, необходимо принять t = r. В частности, формулы (XV-1-13) и (XV-1-14)
39*
612
Глава XV
для избыточного коэффициента давления принимают следующий вид (при
условии, что кроме t = r, производная г' =dr/dx1 = 0):
4ccccos(p (I — rj) s' 32zszr (1 — z*
-
АЛф(т)
Т (КР) ~~ \(\— 2\2
4ссс cos ф (1 — r|) s'
^ —1) (^ —1) а| sin ф cos ф
; (XV-1-32)
. (XV-1-33)
По этим значениям давления для плоской комбинации подсчитаны
коэффициенты интерференции К^, а также центров давления (хц, ДФ)Кр (т), (zn. ДФ)кр (т)>
которые приведены в табл. XV-1-2.
Для случая, когда крен отсутствует (ср = О), формулы для
коэффициентов давления еще более упрощаются:
Л~ "-**'' (XV-1-34)
(XV-1-35)
[(1+,2)2_422]1/2 '
Эти зависимости можно отнести и к крестообразной комбинации,
движущейся без крена. Соответствующие аэродинамические характеристики,
подсчитанные по формулам (XV-1-34) и (XV-1-35), приведены в табл. XV-1-1.
Формулы для расчета аэродинамических коэффициентов. Знание
коэффициентов интерференции, координат центров давления, а также
аэродинамических характеристик для изолированного крыла и корпуса позволяет
вычислить с учетом влияния интерференции аэродинамические характеристики
отдельных элементов летательного аппарата, а также комбинации в целом.
В табл. XV-1-3 приведены все формулы, необходимые для подобных
расчетов аэродинамических коэффициентов тонких плоских и крестообразных
комбинаций. Эти формулы получены для крыльев нулевой толщины,
которые поэтому не возмущают поток при продольном обтекании и нулевом угле
атаки.
Таблица XV-1-3
Формулы для аэродинамического расчета тонких плоских и крестообразных
комбинаций с учетом интерференции
Название
коэффициента
Расчетные формулы
Корпус — крыло (плоская комбинация)
/. Силы и моменты, действующие на правую консоль
Коэффициент
силы
{см. рис. XV-1-3)
Коэффициент
шарнирного
момента консоли
Коэффициент
момента крена
1 а \ ^ф/1 ^
— с%\ ассозф + —— I — cjj I а2з1пфсозф
^ / кр ig 8 V Z /кр
X
кр
\хц. д. ф)кр (т)
'кр
\хц. д. а)кр. (т)
a£sin(pcos(p; xK — длина корпуса
1 а \ (2ц. да)кр (т)
у cn J
(2ц. д. ф)кр (т) .
х а2.sin Ф cos '
Стационарное обтекание
613
Продолжение табл. XV-1-3
Название
коэффициента
Расчетные формулы
//. Силы и моменты, индуцируемые на корпусе крылом
Коэффициент
нормальной силы
(см. рис. XV-1-3)
Коэффициент
боковой силы
Коэффициент
продольного
момента
Коэффициент
момента крена
(с2')т (кр) =
'N )кр ас sin ф cos ф
(хц. д. а)т. кр
)кр ; ас С
///. Суммарные силы и моменты плоской комбинации
Коэффициент
нормальной силы
Коэффициент
боковой силы
Коэффициент
продольного
момента
Коэффициент
момента крена
= cN
z')t (кр) +^кр (с^)кр <*с sin ф cos ф
гх / ач ^Ц* Д- а^кР(т) о
(кр) -#кр (CN )кр 1 ac COS2 ф
а\ ^* д* °^КР (т)
с% )кр ас cos ф
Корпус — крестообразное крыло (крестообразная комбинация)
/. Силы и моменты, действующие на правую консоль
Коэффициент
нормальной силы
Коэффициент
шарнирного
момента консоли
Коэффициент
момента крена
(cni)k
Wk
Формулы те же, что и для плоской комбинации. В этих
формулах коэффициент Ку и величина Сгц. д. ф)Кр<т>
должны определяться по табл. XV-1-2 для крестообразной
комбинации
II. Силы и моменты, индуцируемые на корпусе крылом
Коэффициент
нормальной силы
Коэффициент
боковой силы
Коэффициент
продольного
момента
Коэффициент
момента крена
(cn)t (кр) = Кт (^у)кр ас
\т2')т (кр) = —Лт Vcat
Ч- Д- а)т(кр)
614
Глава XV
Продолжение табл. XV-1-3
Название
коэффициента
Расчетные формулы
III. Суммарные силы и моменты крестообразной комбинации
CN = CN т + С^т + ^кр) (с%)кр аС
mz, =
[КТ
. д. а
хц. д. а)кр (т)] (cn)kp ас
= Ni cos ф — Zi sin ф
Коэффициент
нормальной силы
Коэффициент
боковой силы
Коэффициент
продольного
момента
Коэффициент
момента крена
Нормальная
сила
Боковая сила
Нормальная
сила к
направлению оси х
Расчет интерференции
«нетонких» комбинаций
Коэффициенты интерференции. Результаты расчета коэффициентов
интерференции тонких комбинаций могут быть положены в основу
определения подъемной силы «нетонких» конфигураций. Этот метод состоит в том,
что аэродинамический коэффициент для такой конфигурации вычисляют
по коэффициенту интерференции, найденному из теории тонкого тела,
и аэродинамическому коэффициенту изолированного крыла, взятому по
линеаризованной теории или из эксперимента. Например, коэффициент (с^)кр(т) =
= ^Гкр(с^)кр, где .йГкр находится по табл. XV-1-1, a (cN)Kp определяется
с учетом влияния числа М*» устанавливаемого в линеаризованной теории.
Аналогично пишутся и другие интерференционные характеристики.
Таким образом, предполагается, что коэффициенты интерференции не
изменяются при переходе к нетонким комбинациям. Исследования показывают,
что для коэффициента Ккр это предположение оправдывается полностью.
Что касается коэффициента КТ, то его значения, соответствующие теории
тонкого тела, действительны для условия
Если выполняется условие
>4, (XV-1-37)
то аэродинамическая теория тонкого тела не дает таких хороших
результатов, как в предыдущем случае.
Более удовлетворительные данные об интерференции можно получить,
если рассчитать для заштрихованной площади корпуса (рис. XV-1-7)
фактическую нормальную силу, возникающую в присутствии крыла. В
соответствии с этой схемой корпус предполагается плоским, установленным под
нулевым углом атаки.
Стационарное обтекание
615
Для крыла со сверхзвуковой передней кромкой величина этой
нормальной силы, развивающейся на корпусе с хвостовой частью (рис. XV-1-7, б),
N
( р)
nV(a'tge)2-l .}
arccos
-П+ltge
(XV-1-38)
где a' tge> 1.
Аналогично для дозвуковых передних кромок
2г
na'(a'
где a' tge< 1.
Интегралы (XV-1-38) и (XV-1-39) выражаются в элементарных
функциях. Разделив каждое из найденных значений на нормальную силу
изолированного крыла q<x>SKV (cN)Kp = •
= ?оо5кр (^)крос с удлинением а) 7
4 {sm — г)
(XV-1-40)
получим соответствующие
зависимости для коэффициентов
интерференции Кт. Анализ полученных
зависимостей показывает, что
величина KT=KT(l-]-X) (sm/r—l) а' (^)кр
является функцией только af tg 8
и 2а/г/6кр. Значения Кт
представлены на рис. XV-1-8, б. Данные этого
рисунка соответствуют случаю,
когда концевой эффект не оказывает влияния на часть корпуса,
заштрихованную на рис. XV-1-7. При этом условии волна Маха АВ, исходящая
из передней кромки концевой хорды крыла, проходит за точкой С задней
кромки корневой хорды. График на рис. XV-1-8, б применяется в том
случае, если расстояния от задней кромки крыла до донного среза
удовлетворяют неравенству
Рис. XV-1-7. Схема расчета подъемной силы
с учетом интерференции между крылом и
корпусом:
а — плоская модель для расчета влияния крыла на
корпус без хвостовой части; б — плоская модель
для расчета влияния крыла на корпус с хвостовой
частью
(XV-1-41)
Если это неравенство не выполняется, то коэффициенты интерференции
и относительные координаты центра давления можно находить линейной
интерполяцией между значениями, определяемыми графиком на рис. XV-1-8, б.
При отсутствии у корпуса хвостового участка позади крыла расчет
коэффициента интерференции следует вести при помощи тех же формул
(XV-1-38) и (XV-1-39), в которых верхний предел интеграла 6Кр + с&'г|
заменяется на &кр. Соответствующие значения параметра Кт приведены на рис.
XV-1-8, а. Сравнение с данными рис. XV-1-8, б показывает, что при
больших значениях 2a'r/6Kp хвостовая часть корпуса, расположенная за крылом,
оказывает существенное влияние на величину нормальной силы,
обусловленной интерференцией с крылом.
616
Глава XV
При дозвуковых скоростях эффект хвостовой части приблизительно
одинаков, так как участки корпуса, расположенные вниз по потоку,
обладают значительно меньшей
несущей способностью, чем при
сверхзвуковых скоростях.
Влияние крыла на
положение центра давления корпуса.
Координата центра давления
корпуса может оказаться
чувствительной к изменению числа
Моо, даже если комбинация
корпус — крыло является тонкой.
Ее величина определяется
различными методами для
сверхзвуковых и дозвуковых
скоростей.
Сверхзвуковые
скорости. Для сверхзвуковых
скоростей можно использовать
плоскую модель корпуса, которая
применялась для определения
нормальной силы на корпусе в
присутствии крыла. Момент от
нормальной силы корпуса с
хвостовой частью, обусловленный
влиянием крыла со
сверхзвуковой передней кромкой,
1,6 20 2,k 2,8 3,2 3,6 2а.'г
0,8 1,2 1,8 2,0 2Л 2,8 3,2 3,6 J
Мц (кр) = -
oOCtgE
jxy(a/tg8)2 —1
IX
Рис. XV-1-8. Графики для расчета влияния
крыла на нормальную силу корпуса:
а — без хвостовой части; б — с хвостовой частью;
|SL) (JHL- i);
X
arccos
' + a'T] tge
' \ 6—
корпуса от влияния двух консолей
с дозвуковой передней кромкой
(XVI-1-42)
Этот результат надо
удвоить, чтобы получить момент
крыла. Аналогично для крыла
2г
;УЕ/«'-т|
(XV-1-43)
Координата центра давления получается в результате деления величин
Мт(кр), определяемых по (XV-1-42) и (XV-1-43), соответственно на значения
^)? определяемых формулами (XV-1-38) и (XV-1-39):
( *Ц-ДОЧ
'* ^кр / т (кр)
м.
т (кр)
М,
т (кр)
(XV-1-44)
Результаты расчета величины (хц. д.а/&кр)т(кр) для комбинации корпуса
с крылом, обладающим сверхзвуковой и дозвуковой передними кромками,
Стационарное обтекание
617
представлены на рис. XV-1-9, б. Можно заметить, что влияние параметра af tg t
на координату центра давления мало.
При отсутствии хвостового участка корпуса за крылом интегрирование
(XV-1-42) и (XV-1-43) ведется при условии, что верхний предел равен 6кр.
Результаты расчета относительной координаты центра давления представлены
на рис. XV-1-9, а. Кривые на рис. XV-1-9 действительны для условий
> 4. Диапазону малых Л
удлинений, для которого - '*
)/т(кр)
Ofi 0,8 1,2 1,6 2,0
Ф
) 2,0
16
Ok
yS
y^
y^
<y*
y>
6
cP
А, соответствуют диа- V
граммы на рис. XV-1-10,
построенные при условии,
что часть корпуса выступает
за крыло, а независимыми
переменными являются
эффективное удлинение а'А,кр
и обратное сужение Х =
= Ькц/ЬкР; в качестве
параметра выбрано отношение
радиуса к полуразмаху
rs = rlsm. Значения
(^ц. д. а/Ькр)т (кр) ДЛЯ Ос'^кр =
= 0 получены по теории
тонкого тела, а для rs =
= rlsm = 0 — по
линеаризованной теории для
изолированного крыла;
пунктирные кривые построены
методом экстраполяции до
Значения \%ц. д. а/С'кр/т (кр)
при а'Хкр^О. Сравнение
показывает, что значения
(хц. д. а/^кр)т (кр)?
вычисленные по линеаризованной
теории при наличии
хвостового участка корпуса для ос'Хкр;>0, сильно отличаются от величин,
найденных по теории тонкого тела. Когда хвостовой участок отсутствует,
различие значительно снижается, что особенно заметно для крыла с
дозвуковыми передними кромками. В этом случае практически при оценке влияния
интерференции на координату центра давления корпуса можно пользоваться
аэродинамической теорией тонкого тела.
Дозвуковые скорости. Для определения центра давления корпуса
в присутствии крыла используется модель П-образного вихря, верхняя часть
которого проходит вдоль линии четвертей хорд крыла (присоединенный вихрь),
а две боковых вихревых линии располагаются по потоку (свободные вихри),
причем одна из них может лежать внутри хвостовой части корпуса (см.
рис. XV-2-7). Рассмотрим линию четвертей хорд с эллиптическим
распределением циркуляции:
0,4 Ofi
1,6 2,0
2,4 2J3
2arr
Рис. XV-1-9. Графики для расчета влияния крыла на
положение центра давления корпуса:
a — без хвостовой части; б — с хвостовой частью
(XV-1-45)
Предположим, что zt представляет собой координату свободного вихря,
проходящего внутри корпуса. Следовательно, подъемная сила элементарного
618
Глава XV
участка несущей линии, обусловленная влиянием присоединенного вихря,
Элементарная величина момента относительно оси z, проходящей через
вершину линии четвертей хорд,
2fi
)
*
—•*
/
=^*
ф
'—
у
/
'
0,2
~T
rs=o
bsssa
■-- -
_..
I
I —
——
V"
\]
■7
/
0,1
0 12 3 4 5
1,6
12
Oft
^кр
is
f>
V
* /
0,6,
if
/
у
^—■
0,1
0,2
»——
—
.—■
r—
1
08
1
f/
ft-,
1
N
/
[A
V
/
/
/
/
/
у
у
3
—'
I
V
i
ому
0,2
5
^—-
кр
^--
X-/
i—h
Ф
i
О
^кр
Рис. XV-1-10. Диаграммы для определения относительной
координаты центра давления корпуса с хвостовой частью
за крылом при сверхзвуковой скорости (пунктирные линии
получены экстраполяцией). Условие применения:
Следовательно, расстояние до центра давления от начала несущей линии
г г
где (хц. д. а)т(кр) измеряется от передней кромки корневой (бортовой) хорды.
Стационарное обтекание
619
Внося Г из (XV-1-45), заменяя х по выражению х = (tge)1/4 (z — r)
и интегрируя, получим расстояние до центра давления и относительную
величину (хц, д. а/^кр)т(кр)- Результаты вычислений приведены на рис. XV-1-11
0,2
0,1
О
0,4
if
%
—
/
<*'
\Joo
7
\f
—
^>
^^
<
■
—
rs=
0
\
-Л
-\
liiii
V
V
-V
\
4—
/
V
X=o
7
—
0,2
0J
/
/
^-—
\-
1
г-
Рис. XV-1-11. Диаграммы для определения относительной
координаты центра давления корпуса с учетом влияния
крыла при дозвуковой скорости (пунктирные линии
получены экстраполяцией)
и соответствуют условию а'Якр = 0 для тонкого тела. Как видно, эти
результаты зависят от вида передней кромки и отношения r/sm и не зависят
от числа Мое.
Более точные исследования, проведенные на основе линеаризованной
теории, показывают, что коэффициент центра давления зависит от
параметров а'^кр и r/sm, a также от формы крыла. Это видно из рис. XV-1-11, где
приведены результаты вычислений для трех видов крыльев — треугольного,
трапециевидного (X =1/2) и прямоугольного. Кривые для а'Якр<4
экстраполированы до значения (#ц. д. а/^кр)т (кр)? соответствующего теории
тонкого тела.
Пример. Вычислим с учетом интерференции силы и моменты, действующие на
правую консоль в виде треугольного крыла на корпусе, а также на всю крестообразную
комбинацию крыло — корпус (размеры указаны на рис. XV—12). Примем углы ас =
= 0,3 (17,2°), ф = 22,5°, число Моо = 2 и используем приведенные выше соотношения,
620
Глава XV
таблицы и графики. Все полученные результаты внесем в табл. XV-1-4, из которой
видна последовательность вычислительных операций.
В расчете принято, что ось продольного момента проходит через точку передней
кромки в месте соединения крыла с
корпусом. В качестве характерной длины I
выбрана корневая хорда 6кр, а в качестве
характерной площади — площадь
изолированного крыла.
Данный пример рассчитывается с
учетом, что производная (с^)кр определялась
не по аэродинамической теории тонкого
тела, а по линеаризованной теории.
Линеаризованная теория использовалась также
и при уточнении величины (яц. да/ЬКр)т(кр>
с учетом влияния хвостовой части (см.
рис. XV-1-9). Эта величина оказалась
Рис. XV-1-12. Форма и размеры модели,
использованные в примерах расчета
интерференции для крестообразной комбинации:
4,50
4,00
хх.в
2,67
г
0,75
sm
2,75
ной силы iVKp. (T) расположена от носка на расстоянии
(#ц. д. а)кр (т) = %г+ [ Ь^~}'кр(т) ^КР*
После подстановки данных находим
равной 0,85, т. е. значительно больше
значения 0,556, полученного в теории
тонкого тела.
По данным табл. XV-1-1 можно
найти координаты центров давления
крыла и корпуса с учетом
интерференции. Точка приложения нормаль-
(XV-1-47)
Точка приложения нормальной силы корпуса iVT(KP), обусловленной
влиянием на корпус крыла, определяется координатой
р' (XV-1-48)
равной в данном примере величине
(*ц. д. а)т(кр) - 4,5 + 0,85 • 4 = 7,9.
Расстояние до центра давления корпуса определяется по теории тонкого
тела при помощи формулы
\%Ц. Д/Т —
I 1 2 I 1
4 ЗТГмИТТ#л/гт;гтг '
(XV-1-49)
полученной из условия, что несущей частью корпуса является только
криволинейная головка длиной #Мид- В формуле (XV-1-49) WT — объем этой головки.
С учетом значения (хц. д)т для изолированного корпуса, создающего
нормальную силу iVT, координата центра давления комбинации корпус —крыло
(хц. д. а)кр(т)^кр(т) + (хц. д. а)т(кр)-^т (кр)+(хц. д)т^т ^ . ^
ХЦ' Д = ^кр(т) + ^т(кр)+^т • ( }
Используя эту формулу, можно учесть, что при высоких числах Маха
и длинных корпусах некоторая часть подъемной силы создается
цилиндрическим участком позади криволинейной головки, следовательно, хц, д будет
больше, чем по формуле (XV-1-49). Поэтому для получения более точных
данных лучше пользоваться результатами линейной теории или
экспериментальными данными. В том случае, когда крылья создают наибольшую часть
общей подъемной силы и доля корпуса невелика, можно применять
линейную теорию и формулу (XV-1-49).
Таблица XV-1-4
Пример расчета сил и моментов для крестообразной комбинации корпус — крыло с учетом интерференции
3
1
г
Sm
0,75
2775
0,27
2
Из табл.
XV-1-1
по (1)
1,23
3
XV iji
Из табл.
XV-1-1
по (1)
0,39
4
/#ц. да\
V ^кр /кр(т)
Из табл.
XV-1-1
по (1)
0,648
5
/•£ц. да\
V ^кр /т(кр)
Из табл.
XV-1-1
по (1)
0,556
6
£ц. да~ г
Из табл.
XV-1-1
по (1)
0,418
7
2ц. да
По (6)
1,586
8
Из табл.
XV-1-2
по (1)
0,500
9
£ц. дф — г
Из табл.
XV-1-2
по (1)
0,537
10
2Ц. Дф
По (9)
1,91
11
/£Ц. Дф\
V ^кр /кр(т)
Из табл.
XV-1-2
по (1)
0,669
12
а'
1,730
13
2а'г
^кр
Из рис.
XV-1-12
и по (12)
0,650
14
tge
Из рис.
XV-1-15
0,500
Продолжение табл. XV-1-4
15
a4ge
По
(12)
и
(14)
0,866
16
(*ц. доЛ
^ ^кр /т(кр)
Из рис.
XV-1-9, б
по (13)
и (15)
0,850
17
к
У 1 - (a' tg 8)2
0,500
18
Е(к)
По
форм.
(V-3-18')
1,47
19
(4)кр
По форм.
(V-10-51)
(Yn=e),
(14) и
(18)
2,14
20
Табл.
XV-1-3
по (19),
(14),
(2), (8)
0,399
21
тш
Табл.
XV-1-3
по (14),
(19)
(2), (8),
(4),
(И)
—0,526
22
(тхх)к
Табл.
XV-1-3
по (10),
(7), (2)
(8), (4),
(19)
-0,160
23
(сДг)т(кр)
Табл.
XV-1-3
по (3),
(19)
0,25
24
(с2')т (кр)
Табл.
XV-1-3
по (3)
0
25
(т<2')т(кр>
Табл.
XV-1-3
по (3),
(16), (19)
-0,212
26
(civ)Kp. т
Табл.
XV-1-3
по (2),
(3),
(19)
(cn)t+
+ 1,04
27
OV^Kp. т
Табл.
XV-1-3
0
28
OvW.t
Табл.
XV-1-3
по (2),
(3), (16)
(4), (19)
(mz,)T-
-0,725
29
("VWt
Табл.
XV-1-3
0
622 Глава XV
§ XV-2. Изменение
аэродинамических свойств
оперения под влиянием
крыла
Общее выражение для
нормальной силы
Если перед оперением, расположенным на корпусе, отсутствуют другие
несущие или управляющие поверхности, то расчет интерференции для
оперения и корпуса ведется точно так же, как для крыла и корпуса. В том же
случае, когда на корпусе перед оперением имеется крыло, при определении
аэродинамических характеристик оперения следует учитывать дополнительное
влияние крыла.
Рассмотрим случай, когда крыло и оперение летательного аппарата
жестко закреплены на корпусе и углы их установки относительно
продольной оси аппарата равны нулю. Предположим, что скольжение отсутствует
и нормальная сила линейно зависит от угла атаки. Тогда коэффициент
нормальной силы с учетом интерференции
cN = (c%)KVa (Ккр + #т)кр -^p- + (#кр + Кт)т. о X
X (c%)T. 0(a-e)% + (cJS)T<z-^ . (XV-2-1)
Здесь (cn)t. о = (дсм/да)г. о~производная по углу атаки а от коэффициента cn
нормальной силы изолированного
горизонтального оперения;
(ККр + ЛГт)кр — суммарный коэффициент интерференции для
комбинации корпус — крыло;
(Кт + Ккр)т. о — тот же коэффициент для комбинации корпус —
оперение;
£кр и £г. о—площади изолированных крыла и горизонтального
оперения без учета части, занятой корпусом;
S — площадь крыла в плане с учетом части, занятой
корпусом;
8 —угол скоса потока за крылом при угле атаки а;
а — 8 = аэ. г. о — эффективный угол атаки оперения, возникший
вследствие скоса потока за крылом.
Формула (XV-2-1) может быть использована для определения
нормальной силы и в том случае, когда имеется скольжение (крен). С этой целью
к сумме коэффициентов К^ + Кт необходимо добавить коэффициент ЛГФ,
учитывающий интерференцию при появлении угла крена ср, а угол а
заменить значением a = accoscp. Вычисленная при помощи формулы (XV-2-1)
сила по абсолютной величине будет равна модулю вектора, расположенного
в плоскости угла атаки а.
В линейном диапазоне изменения cN по углу атаки
(XV-2-2)
Стационарное обтекание
623
Входящая в формулу (XV-2-2) величина с% определяется
дифференцированием выражения (XV-2-1) по а:
Змид
(XV-2-3)
Во многих применяемых схемах летательных аппаратов Sr, 0 «S
и *Sr. 0/S С 1. Кроме того, часто значительно меньше единицы оказывается
и величина 1 — del da. Поэтому формулу (XV-2-3) можно заменить
приближенным выражением
S& (р^1 \ (ТС | tz \ *^кр I (рР^\ мид .^-~- е\ /\
Приведенные зависимости непригодны для больших возмущений, когда
закон изменения аэродинамической силы отличается от линейного и необхо-
ди мо учитывать нелинейные эффекты. Учет нелинейных эффектов представляет
значительно более сложную задачу. Во многих случаях, имеющих
практический интерес, влияние больших углов атаки может быть определено только
экспериментально. Таким же путем устанавливается, как правило, тот
«предельный» угол атаки, при котором еще сохраняются линейные соотношения.
Исследования показывают, что с ростом числа Моо величина
«предельного» угла атаки уменьшается.
Угол скоса потока за крылом
Дозвуковой поток. Угол скоса потока в точке за крылом, удаленной
от центра давления (фокуса) на расстояние Lr. 0, может быть определен
по формуле [6]:
CN
2кХ
кр
где I — размах;
Хкр = Z/&Cp — удлинение крыла.
Параметр
к = Т%КР > (XV-2-6)
где Cjvo — коэффициент нормальной силы корневого сечения.
Угол скоса потока можно полагать постоянным по размаху оперения,
равным его значению в точке, совпадающей с центром давления (фокусом)
оперения, расстояние до которого LT.O. Формулу (XV-2-5) можно применять
с известным приближением для
крыльев и оперения любой формы в плане
при условии, что они располагаются
в одной плоскости.
Если по высоте крыло и оперение
располагаются в разных плоскостях
и расстояние между ними г/г. 0 (рис.
XV-2-1), то расчет будет сложнее.
Можно указать приближенную зависи-
У
мость, пригодную и для таких случаев:
8 = 46,2 ^L. kxk2ks град. (XV-2-7)
Phc.|XV-2-1. Смещение оперения по высоте
относительно плоскости крыла:
1 — фокус
Входящие в эту формулу коэффициенты ки учитывают влияние на угол
скоса расстояния LT0 (/c^, характера расположения оперения по высоте
624
Глава XV
относительно плоскости хорд крыла (к2) и сужения крыла (к3). Значения
этих коэффициентов даны на рис. XV-2-2 — XV-2-4.
Сверхзвуковой поток. Характеристики оперения, расположенного за
крылом, можно приближенно определить по углу скоса потока за
изолированным крылом. Таким образом, в этом случае влияние на угол скоса
интерференции между крылом и корпусом не учитывается.
h
0,8
0,6
0,4
О
0,2
0,6 у
Рис. XV-2-2. Кривая для расчета
коэффициента к± в формуле (XV-2-7)
Рис. XV-2-3. Кривая для расчета
коэффициента к2 в формуле (XV-2-7)
На рис. XV-2-5 [6] приведены значения углов скоса потока за
изолированными крыльями прямоугольной формы в плане двух различных
удлинений в зависимости от расстояния L от передней кромки, отнесенного к хорде
1,2.
0,8
f
———
^-—|"
*
1,8
2,6
L/ъ
Рис. XV-2-4. Кривая для расчета коэффициен- Рис. XV-2-5. Скос потока за пря-
та &з в формуле (XV-2-7) моугольным крылом
Ь. Кривые, показанные на рис. XV-2-6, дают возможность определить углы
скоса в любой точке за треугольными крыльями в зависимости от
относительной продольной координаты точки L = LlbKV и ее безразмерного
расстояния от плоскости у = ут. 0/ЬКр, а также параметра 60 =
(gxT
Расчет оперения должен вестись по эффективному углу атаки с учетом
интерференции оперения с корпусом. При ориентировочной оценке
аэродинамических характеристик оперения можно ограничиться учетом
влияния только эффективного угла атаки.
Несущая способность
летательного аппарата с неподвижными
крыльями и оперением при
сверхзвуковых скоростях
Коэффициенты интерференции оперения с крылом. Реальные
характеристики оперения можно считать зависящими от угла аэ.г.о. только в
грубом приближении. Уточнение можно сделать, приняв, что средний угол
Стационарное обтекание
625
скоса, а значит, и величина аэ.г.о. будут определяться также
интерференцией между крылом и корпусом.
Наряду с этим можно воспользоваться выводами теории вихрей из
аэродинамики тонкого тела, дающими возможность вычислять непосредственно
ту часть аэродинамического
коэффициента, которая создается
оперением под влиянием
интерференции с крылом. По этой
теории, одинаково пригодной
для дозвуковых и
сверхзвуковых скоростей, вихревая
схема для крыла, соединенного
с корпусом, принимается такой,
как показано на рис. XV-2-7.
0,8
0,4
0,8
0,8
^**
1 —-
1———
—■—■
. ■
%:°
02
■
-—•
—
/Во
«——-
т.
Ш=
.. ■—
^——
1,8
Рис. XV-2-6. Скос потока за
треугольным крылом
Рис. XV-2-7. Вихревая схема, применяемая при
расчете интерференции крыла и оперения:
2 — внешний вихрь; 2 — внутренний вихрь
При положительном угле атаки вихри лежат выше плоскости
хвостового оперения, и их направление совпадает с направлением скорости
набегающего потока.
Таким образом, задача об интерференции оперения с крылом сводится
к задаче об интерференции оперения с вихрем. Эффект от интерференции
определяется интенсивностью и расположением внешнего вихря
относительно оперения. В качестве одной из характеристик интерференции
оперения, зависящих не от интенсивности, а только от расположения вихря
введем безразмерный параметр ton, определяемый из выражения [51]:
* (т. оп)в — '
Nr
— r)o
(XV-2-8)
Параметр £оп называют так же, как и величину ZKp, коэффициентом
интерференции. Однако, в отличие от коэффициента ZKp, коэффициент iou
40-114
626 Глава XV
учитывает изменение подъемной силы комбинации оперение — корпус
под влиянием крыла (вихря).
В формуле (XV-2-8) iV(T. 0П) в — нормальная сила оперения в
присутствии корпуса, обусловленная влиянием крыла (вихря); Го— интенсивность
вихря; Nonla — нормальная сила изолированного оперения на градус
угла атаки; (sm—г)оп — разность размаха оперения и радиуса корпуса
в месте его соединения с задней кромкой оперения.
Величина iV(T. 0П) в должна быть добавлена к значению, определяемому
при помощи формулы (XV-2-1), если расчет ведется не по эффективному углу
атаки, а по углу атаки корпуса (углу а). Обычно величина Л^т.0П)в
отрицательная, так как нормальная сила из-за наличия вихрей, сбегающих с крылау
уменьшается.
Если интерференция крыла с оперением не уменьшает несущей
способности хвостового оперения, то iV(T. Оп) в — 0 и ion = 0. Можно рассмотреть
другой крайний случай, когда в результате интерференции с крылом
подъемная сила хвостового оперения полностью исчезает. В этом случае ion < О
и принимает наименьшее из всех возможных значений.
Расчет нормальной силы оперения, обусловленной интерференцией
с крылом (^У(Т.оп)в)« Этот расчет можно вести по формуле (XV-2-8),
которая действительна для плоской схемы комбинации корпус — крыло —
оперение (или для крестообразной комбинации при нулевом угле крена).
В этой формуле циркуляцию скорости Го можно определить следующим
образом. Пусть Г представляет собой интенсивность распределения
циркуляции за консолью крыла (см. рис. XV-2-7) на участке (sm — г)кр, т. е.
между боковой кромкой крыла и корпуса. Тогда нормальная сила крыла
-^кр(т) =2pooFoo \ Tdz. Если принять, что вихревая пелена заменена вих-
рем с интенсивностью 10, равной циркуляции в корневом сечении кон-
<sm>Kp
соли, то \ Tdz = Го (zv — г)кр, где zv — боковая координата вихря.
Имея в виду, что дополнительная нормальная сила неподвижного крыла
(бкр = 0)
(^) (XV-2-9)
кр ,
можно найти циркуляцию Го. Внося ее в формулу (XV-2-8), получим
р я, I яГ 1 р
7- V оа> /кр V да /оп /YV 0 п,ч
. оп)в = ^оп о^т; Tv 71 ~\ » (л-V -^-о )
°я \sm — г;оп \zv — г)кр
где
' \1Г~) ~~пР0ИЗВ0Дные соответственно для изолированного крыла
и оперения;
£кр> Son — площади двух консолей соответственно изолированного
крыла и оперения;
($т)оп — размах оперения с учетом корпуса;
т*кр> ^оп — соответственно радиусы корпуса в месте расположения:
крыла и оперения.
Приняв некоторую величину S за характерную площадь, получим
коэффициент нормальной силы
dcN £
. оп)в =
= io
Стационарное обтекание
627
где удлинение изолированного оперения
(XV-2-11)
Для того чтобы применить формулу (XV-2-10), следует знать
координаты вихря zv, yv в хвостовой части летательного аппарата. Для
упрощения расчетов можно принять, что вихри, сбегающие с задней кромки крыла,
совпадают с направлением потока и не смещаются в поперечном
направлении. Если также принять, что координата расположена над центром тяжести
площади оперения, рассчитанной с учетом части площади, занятой
корпусом, то координата
yv = х^а - Ьш6кр, (XV-2-12)
где #кр — расстояние от задней кромки крыла до центра тяжести указанной
площади;
Ьт — расстояние от задней кромки до шарнирной линии крыла (рис. XV-2-7).
Значения координаты zv, которые могут быть определены по табл.
XV-2-1, не зависят от формы крыла в плане или корпуса
впереди линии наибольшего размаха крыла, так как в теории тонкого
тела потенциал и, следовательно, циркуляция определяются
только поперечным течением в рассматриваемой плоскости.
Таблица XV-2-1
Горизонтальная координата сбегающего вихря
(поперечное положение центра тяжести вихревой пелены)
г = г
sm
(*v-r\
1 1
V sm ' /кр
0,
0
786
0
0,
,i
769
0
о,
,2
760
0
0,
,3
757
0
0,
,4
757
0
0,
,5
759
0
0,
,6
763
0
0,
,7
768
0
о,
,8
774
0
0/
9
?80'
1
0,
,о
786
Максимальное отклонение между значениями отношения [ ———) из
\sm — г /кр
табл. XV-2-1 и соответствующими значениями для изолированного крыла
(я/4 = 0,786) составляет приблизительно 3%. Такое малое различие
позволяет определять значение zv комбинации корпус — крыло по данным для
изолированного крыла, рассматривая также и нетонкие комбинации.
Для изолированного крыла линеаризованная теория дает
"2
(XV-2-13)
где
frcp — произведение коэффициента нормальной силы профиля в
среднем сечении на среднюю хорду.
Формула (XV-2-13) получена в предположении, что максимальная
циркуляция соответствует месту среднего сечения. Результаты расчета
отношения (zv — г) /(sm — г) при помощи формулы (XV-2-13) приведены на
рис. XV-2-8 для прямоугольного (X = ЬКц/ЬКр = 1)» трапециевидного
(X = 1/2) и треугольного крыла (К = 0). Пунктирные кривые находились
экстраполяцией данных линеаризованной теории до значения я/4,
получаемого по теории тонкого тела при нулевом удлинении.
Найденные выражения для zv определяют боковое положение вихря
на крыле. Исследования показывают, что это значение zv отличается от
боковой координаты вихря на оперении. Так как более точные данные отсут-
40*
628
Глава XV
ствуют, то в принятых расчетах значение zv на оперении берется таким,
как на крыле.
В соответствии с выражением (XV-2-8) коэффициент интерференции
можно рассматривать как отношение двух безразмерных величин:
нормальной силы и безразмерной интенсивности вихря. Если нормальные силы
вычислять не по теории тонкого тела, а по линеаризованной теории, то
коэффициент интерференции практически остается величиной постоянной.
Таким образом, вычислив коэффициент ion по теории тонкого тела, его
величину можно использовать для расчета интерференции нетонких
конфигураций, укладывающихся в рамки линеаризованной теории. В этом
z,,-r
Рис. XV-2-8. Относительная координата, определяющая поперечное
положение вихревого жгута
состоит смысл введения коэффициента интерференции оперения. В общем
случае его величина зависит от параметров X = (Ькц/Ькр)ои; (r/sm)on;
(bKV/afsm)on; (zv/sm)on и (yv/sm)ou- Для вычисления коэффициента iou
эффективным является метод полос в предположении, что рассматривается плоская
модель. Расчеты по этому методу показывают, что величина iou практически
не зависит от отношения (Ькр/а'sm)on. Результаты этих расчетов показаны
на рис XV-2-9, XV-2-10, XV-2-11 для комбинации корпуса с треугольным
(X = 0), трапециевидным (X = 1/2) и прямоугольным (X = 1) оперениями.
На этих рисунках нанесены кривые iou = const, построенные по параметрам
X и (r/sm)on в зависимости от (zo/sm)on и {yjsm)oil. Для треугольного крыла
максимальное значение соответствует расположению вихря в плоскости
оперения вблизи конца с внутренней стороны. Для других крыльев
появляется бесконечный максимум, когда вихрь расположен на конце.
Таким образом, за исключением треугольных крыльев со сверхзвуковыми
передними кромками, теория полос непригодна для положений вихря
вблизи конца.
Метод полос дает более удовлетворительные данные, когда вихрь
расположен снаружи оперения, и менее точные — при внутреннем расположении.
На рис. XV-2-12 показаны в зависимости от отношения (zv/sm)on величины
[(*оп. л — ^опУ^оп.л! 100%, рассчитанные по значению £оп. л» найденному
по линеаризованной теории при (r/sm)ou = 0,2, (bKp/a'sm)on = 0,5 для
комбинации с прямоугольным оперением (X = 1). Кривые на этом рисунке
позволяют уточнить значения ion, определяемые по методу полос при помощи
графиков на рис. XV-2-9, XV-2-10 и XV-2-11. Уточнение целесообразно
производить, когда коэффициент интерференции определяется при внутреннем
расположении вихря.
Как видно из рис. XV-2-9, XV-2-10 и XV-2-11, коэффициент
интерференции при фиксированных значениях X, (r/sm)0Ii является функцией только
безразмерных координат вихря (zv/sm)ou, (yv/sm)on и не зависит от интен-
Стационарное обтекание
629
2,0 2U 2,8
(4
Рис. XV-2-9. Изменение коэффициента интерференции для комбинации
корпус — треугольное оперение
630
Глава XV
У
/
/
/
/
/
1
/
7/
1
1-0£
IJ
/
л
/ \
/,
/у
/
/
/
у
'к
//■
^/
f /
А
/^
/У
/
-у —— ~
У 1,5
.—-
Ч
Ъ&о \ \
№°i \ i
— —
^.
^
\
\
\
\
N
\
\
(r/sm)on='^;o,6;
\
\
Г
I
\
\
\
\
\
\
\
\
\
\ \
ч
\
\
\
1,6
0,8
0,4—
OM
0,8
1,2
2,0
Рис. XV-2-10. Изменение коэффициента интерференции для комбинации
корпус — трапециевидные крылья
Стационарное обтекание
631
О ОЛ 0,8 1,2 1,6 2,0 fz17L ) 2,8
Рис. XV-2-11. Изменение коэффициента интерференции для комбинации
корпус — прямоугольное крыло
632
Глава XV
сивности вихря. Представляет практический интерес ввести параметр
интерференции, зависящий от интенсивности вихря. Таким параметром,
характеризующим степень интерференции является коэффициент эффективности
оперения
NT. кр. оп—7VT. кр
ЛОП = дг дт 7 (Л V-2-14)
равный отношению приращения нормальной силы при установке хвостового
оперения на комбинацию корпус — крыло к приращению нормальной
силы при установке хвостового
оперения на изолированный корпус.
Коэффициент эффективности оперения
показывает, на сколько уменьшается
несущая способность оперения в
результате интерференции с крыльями.
Величину т]оп можно написать также в виде
Лоп = 1+/(т;^ ■ (XV-2-15)
О 0,2
Рис. XV-2-12. Погрешность при
вычислении коэффициента интерференции
по методу полос для комбинации
корпус — прямоугольное крыло [r/sm =0,2;
(Ькр/а'я™) оп = 0,5, Хоп=1]
Разность сил
= NT. on -
можно представить в виде АЛ" = а£, где
коэффициент i определяется при помощи
соотношения, учитывающего
интерференцию между корпусом и оперением.
По аналогии с соотношением для AN
можно написать зависимость iV(T. 0П)в = — е&, которая учитывает изменение
нормальной силы оперения вследствие скоса потока на угол 8, вызванного
интерференцией от крыла. Таким образом, можно установить связь между
коэффициентом эффективности и углом вертикального скоса потока за
крылом
, 8
ОС
(XV-2-16)
Учитывая, что а и 8 малы, величину г/а можно заменить производной
(de /^а^о-
Выражение (XV-2-16) используется для приближенной оценки угла сг
бокового скоса при наличии скольжения. В этом случае коэффициент
эффективности следует отнести к вертикальному оперению, а отношение 8/а
заменить величиной а/(3Ск — do/d$CK.
Центр давления оперения. Координата центра давления оперения, как
и нормальная сила, изменяется под влиянием вихрей крыла. С достаточным
приближением можно считать, что точка приложения нормальной силы,
обусловленной вихрями крыла, совпадает с центром давления оперения для
комбинации корпус — оперение, т. е.
(#ц. д.[а)оп(в) = (*ц. д. а)оп(т)- (XV-2-17)
Приближенная оценка интерференции оперения. Рассмотрим два метода
приближенной оценки интерференции. Один из них основан на
упрощенной модели течения, в соответствии с которой за крылом образуется
плоская вихревая пелена, располагающаяся в плоскости хвостового оперения.
Предполагается, что оперение расположено в плоскости крыла. Таким
образом, те участки оперения, которые «покрываются» вихревой пеленой,
не будут давать нормальной силы. Если размах оперения (sm)ou меньше
или равен размаху крыла (sm)Kp, то эффективность оперения равна нулю.
Это непосредственно следует из формулы (XV-2-14), в которой надо принять
■*» т. кр. оп = ■*» т. кр'
Стационарное обтекание QS3
В том случае, когда (sm)on > («т)кр> суммарная нормальная сила
NT. Кр. оп комбинации корпус — крыло — оперение (с учетом носовой части)
вычисляется по формуле (XV-1-15), в которой (sm)Kp надо заменить
величиной (sw)on> а Радиус корпуса г за крылом полагать постоянным. Очевидно^
это значение NT, кр. оп будет точно равно нормальной силе NTm оп
комбинации корпус — оперение при отсутствии крыла. Внося выражения для
NT. Kp. оп и NTm on в формулу (XV-2-14), а также имея в виду зависимость
(XV-1-15) для NTt кр и соотношение NT = 2nr2qooa, найдем коэффициент
эффективности хвостового оперения
({—Г2 )2 Г2
п \ кр^ оп /YV9 \Я\
^ оп' Лкр
где rKp = r/(sm)Kp, гоп = г/(5т)0П-
Формула (XV-2-18) может применяться для условий (sm)on> (sm)KV.
Рассмотрим второй метод оценки интерференции. В отличие от первого
он основан на использовании схемы течения, согласно которой вихревая
пелена заменяется двумя П-образными вихрями, расположенными в
плоскости крыла оперения. В действительности, направление вихрей ближе
к направлению невозмущенного течения, чем к направлению консолей
оперения. Для этой модели коэффициенты эффективности оперения можно
вычислять по формуле (XV-2-18) или по выражению
«п -1 16 (1-r»)2 ron
где rv = r(zv;
zv — поперечная координата сбегающего вихря.
Формулы (XV-2-18) и (XV-2-19) применяются для случаев, когда
zv < (sm)on- При расчете значения гоп радиус корпуса может приниматься
равным величине гоп, отличной от значения гкр у крыла.
Крестообразная комбинация. Изложенные методы расчета
интерференции плоской комбинации корпус — крыло — оперение могут быть
применены к расчету интерференции крестообразной комбинации для любых
углов крена, произвольных значений размаха вертикального и
горизонтального оперения.
В основе метода лежит предположение, что крестообразная
комбинация представляется в виде аддитивной совокупности двух плоских
комбинаций, одна из которых образована корпусом и горизонтальными консолями
крыла и оперения, другая — корпусом и вертикальными консолями крыла и
оперения. Принимается, что горизонтальные консоли обтекаются
составляющей поперечной скорости aFoo = VooOLc cos ф, а вертикальные — составляющей
Рск^оо = Fooocc sin ф.
Интерференция рассчитывается независимо для горизонтального и
вертикального оперения в связанных осях г/ь z^. Затем аэродинамические
характеристики комбинации пересчитываются на связанные оси у'', z .
Если рассматривается плоская комбинация при наличии крена, то в
полученных выражениях надо принять размах вертикального оперения равным
радиусу корпуса.
Для примера рассчитаем для конфигурации оперение — корпус
коэффициент нормальной силы, обусловленной влиянием вихрей, возникающих
за крылом (рис. XV-2-13), при условии,, что Моо = 2, а = 5°, (Зск = О
(скольжение отсутствует). Результаты и последовательность расчета
представлены в табл. XV-2-2.
С целью определения координаты yv сначала находим координату
центра тяжести оперения (треугольник ОВС на рис. XV-2-13), затем опре-
634
Глава XV
Пример расчета интерференции
1
V sm / кр
Из рис.
XV-2-13
0,2
2
\sm— rl кр
Из табл.
XV-2-1
по (1)
0,760
3
Из рис.
XV-2-13
по (2)
2,27
4
(*„)кр
(5т)оп
Из рис.
XV-2-7
и по (3)
1,25
5
Из рис.
XV-2-13
3,99
6
(Уо)кр
Из форм.
(XV-2-12)
и по (5)
0,348
деляем расстояние #кр = 3,99. Величину yv вычисляют по формуле (XV-2-12).
Производные {dcNlda)KV и (dcN/da)0U определяются по формуле (V-10-51)
линеаризованной теории. При этом учтено, что передние кромки консоли
крыла и оперения при Моо = 2 являются сверхзвуковыми.
tfl-f.
Ди -(Ь\
Рис. XV-2-13. К примеру расчета интерференции
оперения с крылом:
3,75
(Wkp
2,25
хц
3,16
(Won
1,25
хк
10,5
(вт)кр
2,81
(sm)on
1,81
2г
1,125
а0
5
8°
45
При расчете (с^)(Т. 0П)в п<> формуле (XV-2-10) за характерную площадь
принята площадь изолированного крыла (пары консолей) Suv. По данным
табл. XV-2-2 можно подсчитать коэффициент эффективности оперения.
С этой целью воспользуемся формулой (XV-2-15), которую можно
представить через коэффициенты нормальной силы в виде
|0П ^ (
Стационарное обтекание
оперения с корпусом
635
Таблица XV-2-2
7
Ыкр
(sm)on
Из рис.
XV-2-13
и по (6)
0,19
8
гоп
Из рис.
XV-2-9
по(1),(4),(7)
—1,80
9
■^кр
Из табл.
XV-1-1
по (1)
1,16
10
(dcN\
\ да ) кр
Из форм.
(V-10-51)
иМоо = 2
2,31
11
(dcN\
V да ) оп
Из форм.
(V-10-51)
и 1^ = 2
2,31
12
(cn)(t. on) в
Из форм.
(XV-2-10)
При£=:£кр
—0,029
В этой формуле в качестве характерной можно принять любую площадь
S, в частности площадь крыла S = 5кр. При этом условии коэффициент
нормальной силы комбинации крыло — корпус, вычисленный с учетом
интерференции, равен (cN)T, on = (KKV + Кт) (с^)кр = 1,62а, а коэффициент
нормальной силы изолированного кор- с
пуса (cN)T = 2а£МИд/#Кр = 0,396а.
В соответствии с полученными
данными коэффициент эффективности
оперения
_, -0,029 _
Лоп—1-t- (1,62 —0,396) (5/57,3)""
= 1-0,27-0,73.
Таким образом, эффективность
оперения уменьшилась и составляет
73%. Такое снижение несущей
способности оперения не приведет к
существенному уменьшению суммарной
подъемной силы комбинации, так как
площадь крыла значительно больше,
чем оперения. Однако влияние
интерференции на моментные
характеристики и, следовательно, на
статическую устойчивость может оказаться
более существенным из-за большого
плеча хвостового оперения. В
рассмотренном примере при а ->• 0 запас
статической устойчивости
уменьшается приблизительно на 3%.
С возрастанием угла атаки
неблагоприятное воздействие
интерференции снижается. Это объясняется тем, что вихрь продолжает двигаться по
направлению потока, а оперение с ростом а опускается вниз, что приводит
к увеличению координат zvi yv и, как следствие, к уменьшению | iou |. Если
бы положение вихря по отношению к оперению не менялось, то
неблагоприятное влияние интерференции носило бы линейный характер, так как
интенсивность вихря пропорциональна углу атаки. Из этого следует, что в
реальном случае моментная характеристика будет нелинейной (рис. XV-2-14),
и статическая устойчивость с возрастанием угла атаки будет увеличиваться.
У/
4 8 12 ос
k 8 12. с£
Рис. XV-2-14. Коэффициенты момента и
нормальной силы для комбинации
корпус — крыло — оперение:
без интерференции; с учетом
интер ференции
636
Глава XV
Неблагоприятное влияние интерференции на устойчивость можно
уменьшить, разместив оперение выше крыла (рис. XV-2-15). В этом случае
характеристики оперения, которое по
форме будет крестообразным, улуч-
6 шаются при малых углах атаки, когда
"" вихри достаточно удалены от
оперения. По мере увеличения углов атаки
верхние консоли оперения
оказываются все ближе к вихрям, и
неблагоприятное влияние интерференции
возрастает. После того как оперение
перейдет через вихрь и будет
удаляться от него, неблагоприятное
влияние снижается.
Интерференция оперения с
крылом, обусловленная наличием скачков
уплотнения. Кроме интерференции,
связанной с образованием вихрей,
-т..
Рис. XV-2-15. Влияние горизонтального
оперения на моментные характеристики
комбинации корпус — крыло — оперение:
1 — без интерференции; 2 — с учетом
интерференции для обычного оперения; з — с учетом
интерференции нетандемного крестообразного
оперения; 4 — крыло; 5 — вихрь; 6 —
вертикальное оперение; 7 — горизонтальное оперение
при больших сверхзвуковых
скоростях имеет место дополнительное
интерференционное взаимодействие. При таких скоростях над крылом
появляются скачки уплотнения (рис. XV-2-16), которые, взаимодействуя с оперением,
дополнительно изменяют его характеристики. На рис. XV-2-16 видно, что
при малом угле атаки (а = 5°) горизонтальное оперение расположено в зоне
между хвостовым скачком и веером расширения. Вследствие этого оно
оказывается для потока, прошедшего через веер расширения, под нулевым
Рис. XV-2-16. Влияние интерференции оперения с крылом при возникновении
скачков уплотнения:
1 — коэффициент эффективности г]оп = 0; 2 — Г)оп = 1; з — реальная кривая; 4 — крыло;
5 — веер расширения; 6 — хвостовой скачок уплотнения
углом атаки и не будет создавать подъемной силы. Практически
эффективность оперения близка к нулю (т]оп = 0). С увеличением угла атаки (на
рис. XV-2-16 для примера показан угол атаки а = 20°) угол скачка
относительно плоскости крыла возрастает и его плоскость может оказаться
впереди оперения. Так как линия тока за скачком близко совпадает с
направлением набегающего потока, то оперение в значительной мере восстанавливает
свою эффективность. Некоторое снижение подъемной силы обусловлено
уменьшением числа М и скоростного напора за скачком. Кривая,
показывающая характер изменения момента оперения вследствие влияния скачков
\ уплотнения и расширения, изображена на рис. XV-2-16. Она проходит между
линиями, соответствующими, с одной стороны, полной потере эффективности
= 0), с другой — его полному восстановлению (г)оп = 1).
Стационарное обтекание
637
§ XV-3. Влияние
интерференции на
аэродинамические характеристики
органов управления
Полностью подвижные плоские
органы управления
Углы отклонения. Аэродинамические характеристики подвижных
органов управления зависят для данных условий полета от углов их отклонения.
Пусть значения этих углов для горизонтальных консолей будут 8i для
левой консоли и б2— для правой. Примем,
что положительным по знаку угол будет
в том случае, если крыло отклоняется вниз
(рис. XV-3-1). По значениям 8t и б2 можно
вычислить продольный 8е и поперечный ба
углы отклонения:
(XV-3-1)
^е — 2 » va — 9
Если 84 и б2 равны и одинаковы по знаку,
т. е. 81 = б2, то 8е = б4 = б2. Это значение
угла отклонения 8е соответствует
продольному управлению. Если же углы отклонения
равны по величине, но противоположны по
знаку, то Sa = 8± — — б2. Углу ба будет
соответствовать поперечное управление при
помощи горизонтальных крыльев.
Пусть углы б3 и б4 характеризуют
отклонение соответственно верхней и нижней
консолей и примем, что угол отклонения вправо будет по знаку
положительным (рис. XV-3-1). По значениям этих углов можно определить путевой бг
и поперечный 8а' углы отклонения:
г= о » 6о' = —S • (AV-d-2)
Рис. XV-3-1. Крестообразная
конфигурация полностью
подвижных рулей
Если б3 = б4 (углы б3 и б4 равны по величине и одинаковы по знаку),
то угол бг, равный 63 = 64, характеризует путевое управление; в том случае,
когда 63 = — б4 (углы б3 и б4 равны по величине и противоположны по
знаку), угол 6а/ = б3 = — б4, и определяет отклонение, создаваемое при
поперечном управлении.
Изменение нормальной силы. Рассмотрим, как определяется
нормальная сила полностью подвижных органов управления, расположенных на
корпусе в плоской конфигурации. Когда угол отклонения горизонтальных
консолей 8е не равен нулю и корпус наклонен под некоторым углом атаки а,
нормальная сила комбинации крыло — корпус может быть представлена
суммой
Л^т. кр = Л^(т. кр)а + N(t. кр)6е> (XV-3-3)
где iV(T. Кр)а — нормальная сила при нулевом отклонении органов управления
и некотором угле атаки (бе = 0, а^О);
^(т. кр)б — нормальная сила комбинации при отклонении рулей и
нулевом угле атаки корпуса (бе^0, а = 0).
638
Глава XV
уже
Схема действия сил показана на рис. XV-3-2. Величина N(Tm кр)а была
определена выше. С целью определения второй составляющей Л^
Рис. XV-3-2. Схема действия нормальных сил
при подвижном органе управления
можно воспользоваться резуль-
татами аэродинамической
теории тонкого тела,
распространив их с помощью
линеаризованных решений на нетонкие
тела и тем самым найдя
зависимость подъемной силы от числа
Моо. В соответствии с теорией
тонкого тела значение iV(T.KP)e
можно представить в виде суммы
-ЛГ(т. Кр)бе = ^Kp(T)6e + -#т(кр)6е»
(XV-3-4)
где первый член представляет
собой нормальную силу крыла,
отклоненного на угол де при
наличии влияния корпуса,
второй — нормальную силу
корпуса, обусловленную его
интерференцией с крылом. Каждую из
этих составляющих можно
выразить в виде
= kN кр,
(XV-3-5)
где &кр, кт — коэффициенты интерференции, обусловленные отклонением рулей
на угол де при а = 0;
iVKp — нормальная сила изолированного крыла. Таким образом,
./V (f. кр)б х^КР ~1 *^Т/ * КР• V"^^ —О—О)
Можно также написать, что
г) бе, (XV-3-7)
откуда коэффициент нормальной силы комбинации, отнесенный к некоторой
произвольной площади 5, равен
(СЛ')(Т. кр) 6е =
Зкр
(XV-3-8)
При наличии угла атаки корпуса и одновременном отклонении крыльев
и оперения соответственно на углы (бе)кр и (бв)оп компоненты коэффициента
нормальной силы, действующей на комбинацию корпус —крыло—оперение,
будут следующими:
1. Коэффициент нормальной силы носовой части корпуса
а. (XV-3-9)
2. Коэффициент нормальной силы крыла в присутствии корпуса
Мкр (т) - [KKVa + &кр (6в)кр] (с&)кР. (XV-3-10)
3. Коэффициент нормальной силы корпуса в присутствии крыла
= [Кта + кт ( ^
Стационарное обтекание
639
4. Коэффициент нормальной силы оперения в присутствии корпуса
(без учета влияния вихрей крыла)
(^iV/on(T) == 1-**-оп^ ~т" "'on \^e/onj \Cn)oti "~о— » (2\.\-о-±А/
*^кр
где Кои и коп определяются для оперения так же, как и для крыла.
5. Коэффициент нормальной силы корпуса в присутствии корпуса
(без учета влияния вихрей крыла)
Ыт (оп) = 1(Кт)опа + (&т)оп (Se)onl (<&)оп 4^ , (XV-3-13)
Лкр
где (Кт)ои, (Ат)оп находятся по параметрам для оперения аналогично
коэффициентам Кт, кт, определяемым по параметрам крыла.
6. Коэффициент нормальной силы оперенного участка, вызванной
влиянием вихрей крыла,
/ \ . (С1у)кр (civ)on t KPa i *Ф (Ое)кр] (5^ — won /лт-тт о
(Cn)(t. on) в = ^оп о^ /- Z\ . (X V-d-14)
Эта формула получена из выражения (XV-2-10), в котором величина ZKpcc
заменена значением ^кра + &кр(бе)Кр, а за характерную площадь принято £кр.
Наряду с этой составляющей
возникает также сила, обусловленная
действием вихрей от крыла на участок
корпуса, расположенный между оперением
и крылом. Эта сила
X
X
(XV-3-15)
и зависит от расположения линейных
вихрей интенсивностью Го на крыле и
оперении. Так как это расположение на
крыле принято таким, как на оперении,
N
В аэродинамической теории тонкого
тела коэффициент &кр определяется как Рис. XV-3-3. Значения &кр для комби-
функция параметра rs = r/sm. Соответ- нации корпус — прямоугольное крыло
ствующие значения этого коэффициента
приведены в табл. XV-3-1. Из данных таблиц, пригодных для тонкой
комбинации корпус —крыло, видно, что коэффициент &кр незначительно
отличается от единицы. Это показывает, что несущая способность полностью
подвижных тонких крыльев или оперения в присутствии корпуса почти
не изменяется по сравнению с изолированными крыльями.
Применительно к нетонким комбинациям значения &кр при
определенных условиях отличаются от данных линеаризованной теории, что следует
из рис. XV-3-3, где эти данные показаны применительно к комбинации
корпус — прямоугольное крыло. Если а/Якр<2, то можно использовать
для прямоугольных крыльев в комбинации с корпусом значения &кр из
теории тонкого тела. Когда эффективное удлинение а/Якр>2 и Моо>1, то
лучшие результаты получаются, если использовать имеющиеся данные для ккр
из линеаризованной теории.
Метод расчета Лкр по теории тонкого тела может быть применен
и при дозвуковых скоростях, что в известной мере объясняется
независимостью коэффициента интерференции от числа Моо.
Для определения коэффициента кт имеются данные только теории
тонкого тела, которые указывают на то, что
kT = KKV-kKp. (XV-3-16)
640
Глава XV
Величины кт, зависящие от отношения r/sm, даны в табл. XV-3-1.
Таблица XV-3-1
Коэффициенты интерференции и координата центра давления
поворотной консоли при 6е Ф 0, а = 0
г
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
-кр
1,000
1,077
1,162
1,253
1,349
1,450
1,555
1,663
1,774
1,887
2,000
*кР
1,000
0,963
0,944
0,93>
0,935
0,940
0,948
0,958
0,971
0,985
1,000
0
0,114
0,218
0,317
0,414
0,510
0,607
0,705
0,803
0,902
1,000
ь
кр
0
0,118
0,231
0,338
0,442
0,542
0,641
0,736
• 0,827
0,916
1,000
Ккр
0
0,123
0,239
0,349
0,454
0,551
0,646
0,737
0,827
0,915
1,000
Рц.дбА*
V Ькр /кр(т)
0,667
0,669
0,668
0,666
0,665
0,664
0,663
0,664
0,666
0,667
0,667
* Треугольное крыло.
Коэффициент кт может сильно отличаться от единицы, что
свидетельствует о существенном влиянии крыла на несущие свойства корпуса.
Из табл. XV-3-1 следует приближенная зависимость для коэффициента
интерференции
£t = t-s = -^. (XV-3-17)
sm
Если предположить, что крыло «передает» корпусу часть своей подъемной
силы независимо от того, создается ли эта сила под влиянием угла атаки а или
угла установки бе, то можно написать равенство kT/kKV = KT/KKpi из
которого следует еще одна приближенная зависимость
кр
(XV-3-18)
Как и коэффициенты &кр, значения кт применимы для тонких
конфигураций. Однако в приближенных расчетах они используются и для нетонких
конфигураций. Применяя формулу (XV-3-18) и используя имеющиеся
данные для А;кр, Кт из линеаризованной теории, можно уточнить значения кт.
Приведенный метод расчета пригоден, когда впереди органа управления
нет несущих поверхностей. В ином случае необходимо учитывать
уменьшение подъемной силы, обусловленное влиянием крыла, применяя
изложенные выше способы расчета интерференции.
Центр давления. Вследствие поворота органов управления будет
изменяться положение центра давления. Координату центра давления при сс = О,
8еф0 можно определить из выражения
(*,. д б)кр =
кр (т)
(XV-3-19)
Эта координата отсчитывается от носка корпуса. Величина хкр
представляет собой расстояние от носка до передней точки корневой хорды, а второй
член в формуле (XV-3-19) определяет относительное расстояние от этой
точки до центра давления органа управления при условии, что его угол
поворота деф0. Значения ( ?' ' ) для треугольного крыла приведены
V °кх> I КР (т)
Стационарное обтекание
641
в табл. XV-3-1. Влияние интерференции на координату центра давления
треугольных консолей мало. Это дает основание считать, что с хорошим
приближением центр давления
для крыла любой формы в плане
i / кр(т)
может быть принят таким, как \
для изолированного крыла, т. е.
(^ц. д. б)кр(т) = (^ц. д. б)кр-
Расчет (#ц. д. б)кр Для
изолированного крыла может быть
осуществлен не по теории
тонкого тела, а по линеаризованной
теории. Для сравнительно
простой комбинации корпус
—поворотное крыло прямоугольной
формы в плане эта теория
позволяет более точно вычислить
также смещение центра давления
вследствие влияния корпуса при*
условии а = 0, 8еф0 (рис.
XV-3-4).
Если корпус отклонен на
угол атаки а, а крыло
дополнительно отклонено относительно оси корпуса на угол бе, то центр давления крыла
QJ3L
0,48
ОМ
Ш
[
^—
Л-
3
2^
- —
-——
— —
———
S
. J
1
———
- ■
0,2 OJt 0,6 0,8
s *m
Рис. XV-3-4. Кривые для расчета смещения
центра давления крыла под влиянием корпуса при
условии а = 0 бе Ф О
р.(т)
■'кр»
где
кр(т)
кр(т)
кр. (т)
(XV-3-20)
(XV-3-21)
Аналогичное выражение будет и для комбинации корпус — оперение.
При повороте органа управления наряду с изменением положения центра
давления крыла вследствие интерференции с корпусом меняется координата
точки приложения дополнительной нормальной силы корпуса, обусловленной
влиянием крыла. Приближенно можно принять, что изменение будет таким,
как в случае образования нормальной силы под влиянием угла атаки
корпуса, т. е.
(^) кр- (XV-3-22)
Координату центра давления можно отсчитывать также от центра
тяжести. Если расстояние до него от передней точки корневой хорды (хц. т)кр,
то координата центра давления
(#ц. д. а)т(кр) = (#ц. т)кр + у—g )т(кр) ^КР* (XV-3-23)
При расчете положения центра давления на корпусе с учетом влияния
крыла принимается, что центр давления нечувствителен к тому, развивается
ли подъемная сила от угла атаки или от угла поворота крыла (оперения).
В СООТВеТСТВИИ С ЭТИМ (хц. д. а)т(кр) = (Жц. д.в)т(кр).
Центр давления для полной комбинации корпус—крыло — оперение
определяется формулой
)кр (т) (сЛг)кр(т) + (жц. д)т(кр) (с^)т(кр) + (жц.
{хц. д)т(оп) (сЛ')т (оп) + (хц. д)оп(в) (civ)on(B)
. д — '
41-114
{cN)
kp (т) + (cn)t (кр) + (cn)t (on) + (C2v)on (т) + (civ)on (в)
(XV-3-24)
642 Глава XV
где (Civ)on(B) и (хц. д)оп(в) — соответственно коэффициент нормальной силы
и центр давления, обусловленные влиянием вихрей крыла.
Величина (хц. д)Оп(в) принимается равной (хц. д)оп(т)« Значения хц. д и cN,
входящие в (XV-3-24), определяются в общем случае с учетом влияния угла
атаки а и углов поворота крыла и оперения. В частности, (#ц. д)кР(т)
находится по формуле (XV-3-20), в которой (хц. д/6Кр)кр. (т) определяется из (XV-3-21).
Соответствующая координата для корпуса, расположенного под крылом,
(*ц. д)т (кр) = #кр + [j^) т (кр) Ькр, (XV-3-25)
где
/ хц. Д. а \ ( «ц. д. б
(г ч А та I —г I + ктбе —т I
*\ V & т g V & т(кр) (XV-3-26)
/ хц. Д. а \ ( «ц. д. б \
(г ч А та I —г I + ктбе —т I
*Ц-Д\ = V &кр /т(кр) т g V &кр /
&кр /т(кр) Кт<х + ктЬе
т(кр)
В знаменателе этого выражения написана величина, определяющая
коэффициент нормальной силы корпуса в соответствии с формулой
Ыт(кр) = {К*а + ЛЛ) (с^)кр. (XV-3-27)
Аналогично можно представить соотношения для отсека оперения.
Продольная эффективность. Продольная эффективность органов
управления определяется степенью изменения коэффициента продольного
момента mz в зависимости от изменения угла 8е при симметричном отклонении
горизонтальных консолей и равна производной dmzldbe. Эта производная
обычно отрицательна для хвостового оперения и положительна для органа
управления, выполненного по схеме «утка». Если определять продольный
момент относительно центра тяжести, то продольная эффективность
(XV-3-28)
т(кр) V ^кр /Kp
где I — некоторая характерная длина.
Если перед органом управления располагается какой-либо несущий
элемент, необходимо учесть влияние интерференции с этим элементом на
величину продольного момента.
Поперечная эффективность. Поперечная эффективность определяется
производной момента крена тх по углу ба при дифференциальном
отклонении горизонтальных органов управления. Производная дтх/д8а, обычно
отрицательная по знаку, равна
Ш- (XV-3-29)
Здесь А,кр = 4 (sm — r)2/SKV — удлинение крыла;
/ — некоторая функция отношения rs = r/sm, которая
в соответствии с линейной зависимостью
определяется равенством
/ = 0,167 (1 + 3,71re). (XV-3-30)
Значения функции / соответствуют весьма тонкому телу. Пользуясь
теорией линеаризованного обтекания, можно уточнить эти значения для
реального тонкого тела и тем самым учесть влияние числа Моо
/=/т.н|4т£1£5' (xv-3-31)
где величина /тн вычисляется по формуле (XV-3-30), полученной по теории
тонкого тела.
Стационарное обтекание 643
Дробь в формуле (XV-3-31) представляет собой отношение угловых
коэффициентов кривых cN(a) для изолированного крыла, подсчитанных
по линеаризованной теории и по теории тонкого тела. Это отношение для
треугольных крыльев имеет вид
ПРИ а
(XV-3-32)
где Е (к) — полный эллиптический интеграл второго рода с модулем
1/2
[(М
Якр — удлинение крыла.
При выборе места расположения органов управления, обеспечивающих
создание поперечного момента, необходимо учитывать следующее. Если
за органами управления располагаются какие-либо несущие поверхности,
то при дифференциальном отклонении органов управления в результате
интерференции с ними несущие поверхности создают момент крена, обратный
по направлению моменту от самих органов управления. По этой причине
органы управления, располагающиеся впереди несущих поверхностей,
например рули типа «утка», не являются достаточно эффективными для
поперечного управления.
Пример. Определим продольную и поперечную эффективность полностью
подвижных консолей хвостового оперения при Моо = 2 для комбинации корпус — крыло—
оперение, размеры и форма которой показаны на рис. XV-2-13. Пусть центр тяжести
комбинации расположен на расстоянии (яц. т)Оп = 3,95 от передней точки корневой
хорды оперения (индекс «кр» заменим на индекс «оп»).
Для вычисления дтх/дде воспользуемся формулой (XV-3-28). Входящие в нее
коэффициенты кои, кТ найдем из табл. XV-3-1 по значению (r/sm)ou — 0,562/1,81 =
-0,310: кои = 0,936, кт = 0,327.
Относительная координата центра давления (£ц. д-б/^оп)оп(т) принимается равной
(^ц. д а/&оп)оп<т) и определяется по табл. XV-1-1. Для треугольной консоли находим
(•^ц. д б/^оп)оп(т> = 2/3. Центр давления на корпусе определяем в соответствии с
формулой (XV-3-25) при помощи табл. XV-1-1, имея в виду, что хвостовая часть за
оперением отсутствует. Относительная координата центра давления (яц# д б/^оп)т(оп) = 0,556.
Приняв за характерную длину I среднюю аэродинамическую хорду крыла,
проходящую через центр тяжести консоли и равную &сах~^'5> и учитывая, что для
изолированного оперения (с^)Оп — 2,31, после подстановки всех величин в формулу
(XV-3-28) получим
дтг 1,25 Г / 3,95 \ / 3,95 \ П
"557=—U" L0'936l0j667+T2^j+°'327 ^556 + X25-)J2'3l=-9,24.
Вычислим далее поперечную эффективность. По формуле (XV-3-30) и значению
rs~r/sm = 0,310 находим величину /тн = 0,359.
Так как удлинение изолированного оперения
■ 4(*m-r)2 4(1,812-0,562)2
Аоп = £ = 1"252 = 4'00»
а величина а'= ]/ЛМ^о —1 = 1,73, то а'А,оп = 6,92. Поэтому в соответствии со второй
формулой (XV-3-32)
По формуле (XV-3-29)
-^~-= —0,359.0,368-4= —0,53.
Используя выражение (XV-3-8) и принимая за характерную площадь S = i
определяем для оперения наклон кривой cN (6e):
dCN ^ = 2,31 (0,936 + 0,327) = 2,9.
(т оп) б
41*
644 Глава XV
Полностью подвижные
крестообразные органы управления
Продольная эффективность. Для крестообразной конфигурации
полностью подвижных рулей при наличии крена продольную эффективность
в плоскости угла а = ас cos ф можно найти по формуле (XV-3-28), не
учитывая влияния скорости скольжения, т. е. полагая, что взаимодействие
между консолями отсутствует. Из формулы (XV-1-17) следует, что при
наличии угла крена продольная эффективность возрастает. Если при ф = О
нормальная сила N всей комбинации создается только горизонтальными
консолями, отклоненными на угол б, то при повороте системы на некоторый
угол ф в создании нормальной силы участвуют все четыре консоли.
Суммарная нормальная сила в вертикальной плоскости будет N (cos ф + sin ф),
что, например, при ф = 45° дает N]/~2.
Путевая эффективность. Эта характеристика, определяемая
производной дту/д8г, зависит от изменения путевого момента при симметричном
отклонении вертикальных рулей. Величину dmz/d8r в плоскости угла
Рек = &с sin ф можно вычислить по формуле (XV-3-28) без учета влияния
угла а.
Поперечная эффективность. Анализ продольной и путевой
эффективности крестообразных рулей осуществляется так же, как для плоских
органов управления, и без учета интерференции между консолями. Однако для
поперечной эффективности подобные методы расчета не дают
удовлетворительных результатов, так как под влиянием горизонтальных рулей при
их дифференциальном отклонении происходит перераспределение давления
на вертикальных консолях, причем на одной из сторон создается
положительное давление, на другой — отрицательное. В результате этого возникает
обратный поперечный момент, противоположный по направлению моменту
от отклонения рулей. Результирующий поперечный момент и
соответствующая величина поперечной эффективности будут, следовательно, меньше.
Изменение поперечной эффективности можно вычислить по приближенной
зависимости
Л (-|^) =0,16cos (^-rs) -0,12rs(l-rs). (XV-3-33)
Несмотря на снижение поперечной эффективности горизонтальных
органов, все же результирующая поперечная эффективность крестообразной
конфигурации будет больше, чем плоской, вследствие влияния
вертикальных рулей.
При осуществлении расчетов применительно к нетонким телам
значения, полученные по теории тонкого тела, нужно уточнить при помощи
(XV-3-31).
Взаимодействие между
органами управления
Для полного представления об аэродинамических свойствах
летательного аппарата необходимо знать наряду с характеристиками, связанными
с непосредственным влиянием углов атаки, скольжения и отклонения
органов управления, также о тех эффектах, которые появляются вследствие
Бзаимодействия органов управления. Одним из них является эффект
поперечного момента от вертикальных крыльев, имеющий место при
дифференциальном отклонении горизонтальных рулей. Рассмотрим с качественной
стороны возможные виды взаимного влияния между органами управления.
Взаимодействие, не связанное с отклонением органов управления.
Предположим, что комбинация корпус — крыло совершает полет под неко-
Стационарное обтекание 645
торым углом атаки с одновременным накренением и проанализируем эффекты
взаимодействия в случае, когда крылья, являющиеся органами
управления, не отклонены.
1. Благодаря взаимному влиянию полей давления от корпуса
конечной толщины и крыльев при наличии углов атаки и скольжения (крена)
возникают дополнительные подъемные силы от горизонтальных и верти-
кальных консолей. Взаимодействие, обусловленное толщиной корпуса,
можно при наличии только угла атаки условно определить как
взаимодействие вида «угол атаки — толщина», приводящее к созданию на
горизонтальных консолях подъемной силы одного направления. При появлении угла
скольжения возникает дополнительное взаимодействие вида «угол
скольжения — толщина», вызывающее подъемную силу также одного
направления на вертикальных консолях. Возникающие силы в результате
указанного взаимодействия обоих видов действуют в плоскостях соответственно
углов а и (Зск.
2. Второй вид взаимодействия обусловлен взаимным влиянием полей
давления от корпуса и крыльев при наличии углов атаки и скольжения
(взаимодействие вида «угол атаки — угол скольжения»). Для плоской
комбинации это приводит к возникновению на правой и левой консолях
дополнительных подъемных сил разного направления и, как следствие, к
образованию поперечного момента, стремящегося уменьшить накренение.
В случае крестообразной комбинации взаимодействие вида «угол атаки —
угол скольжения» дополнительно приводит к тому, что на вертикальных
консолях образуется момент, равный по величине, но противоположный
по знаку моменту на горизонтальных консолях. В результате суммарный
момент крена равен нулю.
Взаимодействие, обусловленное отклонением горизонтальных рулей*
Такого рода взаимодействие возникает при отклонении горизонтальных
рулей с целью создания продольного момента или получения необходимого
поперечного момента. Наиболее общий случай взаимодействия
характеризуется наличием углов атаки и скольжения.
1. Рассмотрим эффекты взаимодействия, когда рули отклоняются
симметрично на угол бе для обеспечения продольного управления.
а. Предположим вначале, что скольжение отсутствует ((Зск = 0). В
случае плоской комбинации при симметричном отклонении консолей на угол бе
появляется дополнительная подъемная сила, одинаковая по величине и знаку
на правой и левой консолях. Это наблюдается и в случае крестообразной
формы, так как взаимодействие с вертикальными консолями отсутствует.
Рассмотренное взаимодействие относится к виду «угол бе — толщина»
и качественно оказывается таким же, как взаимодействие вида «угол атаки —
толщина».
б. Если отклонение рулей на угол 8е сопровождается скольжением,
то появляется взаимодействие вида «угол бе— угол |3СК». Для плоской
комбинации оно качественно такое же, как взаимодействие вида «угол (3Ск —
угол атаки» в результате которого образуется поперечный момент,
стремящийся уменьшить угол крена. Для крестообразной комбинации эффект
взаимодействия оказывается аналогичным: на вертикальных консолях
возникают добавочные подъемные силы, создающие поперечный момент того же
знака, что и на горизонтальных консолях.
2. Рассмотрим эффекты взаимодействия, возникающие в том случае,
когда горизонтальные органы используются для создания поперечных
моментов, т. е. когда они играют роль элеронов.
а. Пусть скольжение и угол атаки отсутствуют. В результате
взаимодействия корпуса с горизонтальными рулями при их дифференциальном
отклонении на угол ба возникают дополнительные поперечные моменты
646 Глава XV
(взаимодействие вида «угол ба— толщина»). При этом на горизонтальных
и вертикальных консолях образуется поперечный момент, уменьшающий
угол крена.
Если угол атаки не равен нулю, то в случае крестообразной
комбинации возникает взаимодействие вида «угол а — угол ба», приводящее к
созданию боковой силы одного знака (отрицательного) на вертикальных
консолях. Дополнительных сил на горизонтальных консолях не возникает.
Таким образом, у плоской комбинации отмеченное взаимодействие
отсутствует. Рассмотренное явление аналогично указанному выше
взаимодействию вида «угол рск— толщина» и, как видно, обусловливает образование
у крестообразной комбинации путевого момента.
б. При наличии скольжения дифференциальное отклонение
горизонтальных консолей на угол ба приводит к появлению у плоской комбинации
дополнительной, положительной по знаку, подъемной силы. В случае
крестообразной конфигурации на вертикальных консолях взаимодействие не
проявляется. Таким образом, когда горизонтальные консоли используются
в качестве элеронов, создается продольный момент как для плоской, так
и для крестообразной конфигураций.
3. Наконец, можно рассмотреть взаимодействие, обусловленное
использованием горизонтальных органов управления одновременно для
продольного и поперечного управления. Отклонение рулей, характеризующееся
углами 8е и ба, приводит к созданию дополнительной подъемной силы на
вертикальных консолях, в то время как на горизонтальных органах
управления никакой дополнительной силы не возникает. Общий вывод из анализа
взаимодействия в рассмотренных случаях заключается в том, что у плоской
конфигурации при отклонении органов поперечного управления изменяется
поперечная эффективность и появляется продольный момент. У
крестообразной конфигурации, кроме того, возникает путевой момент.
Указанные эффекты взаимодействия обусловлены отклонением
горизонтальных консолей. Новые интерференционные эффекты возникнут при
отклонении вертикальных органов управления. Их анализ может быть
осуществлен аналогично тому, как это было сделано в случае
горизонтальных консолей. Следует также учесть, что изложенные выводы относятся
к тонким телам и крыльям малого удлинения.
Органы управления,
расположенные вдоль задней
кромки несущих поверхностей
Органы управления, расположенные вдоль задней кромки несущих
поверхностей, могут занимать всю или часть задней кромки консоли. Если
они занимают всю заднюю кромку, то их можно рассматривать как
полностью подвижные органы управления и применять методы аэродинамического
расчета, изложенные выше. Часто встречаются случаи, когда органы
управления занимают часть кромки и притом небольшую. Если интерференция
корпуса с несущей поверхностью оказывает незначительное влияние на
аэродинамические характеристики рулевого органа, как, например, на
координату центра давления, то для расчета этих характеристик можно
применять результаты обычной сверхзвуковой теории, относящиеся к
изолированным поверхностям.
Более сложными являются исследования аэродинамики органов
управления в том случае, когда интерференция между корпусом и крылом
оказывает существенное влияние на рули. Если орган управления,
расположенный на задней кромке, имеет большое удлинение, то его аэродинамика
может быть исследована при помощи элементарной теории стреловидности.
Стационарное обтекание
647
Применение обычной сверхзвуковой теории. При применении этой
теории следует обращать внимание на следующие факторы:
1) являются ли передняя и задняя кромки органов управления
сверхзвуковыми или дозвуковыми;
2) совпадают ли концевые хорды руля с направлением потока;
3) как расположен орган управления: распространяется ли он до
концевой хорды крыла или находится на некотором удалении от этой хорды;
в последнем случае важно знать, пересекает ли внешний конус Маха
от органа управления концевую хорду
крыла или нет;
4) наконец, следует учитывать,
пересекает ли внутренний конус Маха от
органа управления корневую хорду крыла.
Исследование органов управления с
дозвуковыми передними и задними кром-
2,0 V
А/р
—-^
—
Ч
\
..г
У
\
Л
/
0,8 Г
Рис. XV-3-5. Схема отражения для органов
управления с дозвуковой передней кромкой:
а — задняя кромка сверхзвуковая; б — задняя
кромка дозвуковая; линии Маха; ось
вращения руля
Рис.
XV-3-6. Эффективность
органов управления:
1 — внешние органы управления;
2 — внутренние органы управления;
sj==smp» sm=lm кр
ками представляет известную трудность, обусловленную наличием
многократного отражения волн возмущения на рулевой поверхности (рис. XV-3-5).
Учет влияния интерференции между крылом и корпусом. Этот учет
необходим, когда органы управления расположены на крыльях малого
размаха. Метод обратимости в сочетании с теорией тонкого тела дает
возможность вычислить эффективность концевых органов по подъемной силе.
Рассмотрим комбинацию корпус — крыло — руль (рис. XV-3-6) с
неподвижным крылом и поворотным концевым рулем, поперечный размер
которого определяется величиной smKp — <?mp. Эффективность рулей найдем при
условии, что корпус и, следовательно, крыло расположены под нулевым
углом атаки (ат = оскр = 0), а руль отклонен на угол б (сср = б).
Чтобы найти нормальную силу Nv комбинации от отклонения рулей,
будем рассматривать обращенное движение и примем, что в таком движении
(см. рис. IV-5-2) комбинация располагается под общим углом атаки а9 = б
Тогда из (IV-5-2) найдем
i dS = J J Ap2 dS.
(XV-3-34)
P p
Здесь левая часть определяет отыскиваемую нормальную силу одной
консоли ЛГР, отнесенную к скоростному напору g^. Для вычисления правой
части внесем под интеграл величину Ар2 = А^кР(т), выраженную
формулой (XV-1-14), в которой примем ср = О; ас = б; r' = Q; s = ztge; s' = tge =
= const. Полагая, что dS = dxdz и интегрируя по х, в пределах от z/tge
648
Глава XV
до sm/tge, а по у от st до sm (рис. XV-3-6), получим выражение
для iVp. Отнеся его к силе iVKp = 2#оо6л; [($ткр — $тР)] изолированного крыла,
образованного соединением двух концевых органов управления вместе,
получим отношение
N-
кр
■ — (1 — rf) arcsin
'pi's
arcsin
(XV-3-35)
Ts — 7/Sm, 5p — Sm р/(£пг)кр*
Хотя это отношение получено при помощи формулы (XV-1-14),
отнесенной к условиям на треугольном крыле, тем не менее, как показывают
исследования, оно применимо для крыла произвольной формы. Величина Nv /iVKp
зависит только от геометрических параметров на задней кромке. Кривая,
характеризующая изменение величины NV/NKV, показана на рис. XV-3-6.
Вычисляя значение iVKp для изолированного крыла с учетом его формы
и полагая отношение NV/NKV таким, как в теории тонкого тела, можно учесть
влияние числа Моо на эффективность концевых органов управления. В
частности, изолированное крыло (руль) может иметь треугольную форму с
корневыми хордами, расположенными по потоку, как это показано на рис. XV-3-6.
Данные рис. XV-3-6 можно использовать также для расчета эффективности
внутренних органов управления. При помощи этого рисунка находят
эффективность (iVp/iVKP)r органов управления, простирающихся от корпуса до
конца крыла (swp = г); затем определяют значение (Nv/NKV)Bni для
внешнего управления (smp > г). По этим
величинам находят силы (Np)r и (Nv)Bm.
Рассматривая теперь внутренний руль как
разность двух внешних органов
управления, простирающихся до конца крыла,
находят для внутреннего органа Nv =
= (Nv)r — (iVp)Bin. Если для
соединенных вместе внутренних рулей
нормальная сила -/VKP, то эффективность будет
равна iVp/7VKP.
Элементарная теория стреловидности.
Если орган управления, расположенный
на задней кромке, имеет достаточно
большое удлинение, то его эффективность
можно рассчитать, пользуясь
элементарной теорией стреловидности.
Предположим, что ось вращения руля (рис. XV-3-7), совпадающая с его передней
стреловидной кромкой, является сверхзвуковой. Тогда нормальная сила,
развиваемая органом управления при отклонении на угол бп, измеренный
в направлении нормали к оси вращения, в соответствии с двухмерной
теорией стреловидности будет определяться выражением
Рис. XV-3-7. Стреловидный орган
управления большого удлинения:
1 — крыло; 2 — ось вращения; з — орган
управления
Nn = No
,М'ЯО~1
ML-cos-»x
= iV0
loo cos2x—1
(XV-3-36)
Здесь No — нормальная сила при нулевой стреловидности, рассчитываемая
по площади руля 5Р из выражения
?р, (XV-3-37)
Стационарное обтекание
649
где goo — скоростной напор, вычисленный по числу Мое,;
60 —угол отклонения руля] в направлении набегающего потока (60 =
8 )
x)
(c<n)o — производная от коэффициента нормальной силы по углу атаки,
равная (^)о = 4(М2оо-1)"1/2.
Как видно из формулы (XV-3-36), применимой для Moo cos % > 1,
стреловидность приводит к увеличению эффективности руля по нормальной силе.
Когда Moo cos %->- 1, формула теряет силу. При этом условии происходит
отделение скачка от органов управления, что можно избежать, обеспечив,
чтобы положение оси вращения было сверхзвуковым.
Нелинейные эффекты
Влияние щелей. Одна из причин нарушения линейной зависимости
аэродинамических характеристик рулей от угла отклонения связана с
образованием щелей между органами управления и корпусом или вблизи оси
вращения. Щели способствуют снижению перепада давления у корневой хорды
(рис. XV-3-8) и, следовательно,
уменьшению нормальной силы. В реальных
условиях вязкого обтекания пограничный слой
как бы перекрывает малые щели, поэтому
практически они не оказывают своего от-
линейность не
0,8
0,6
•
r
_£_
\
r
J
\
рицательного
нарушается.
влияния, и
v- Г
■^ i
^3
Рис. XV-3-8. Влияние щелей
на распределение нормальной
силы (без учета вязкости):
1 — щелей нет (g/sm = 0); 2 —
размер щели g/sm — 0,0025
Рис. XV-3-9. Влияние щелей при
большом отклонении рулей
Снижение эффективности и нелинейность возникают при достаточно
больших щелях, вид которых меняется при значительном отклонении
подвижных органов управления (рис. XV-3-9). Изменение аэродинамических
характеристик и нарушение линейности в этом случае объясняется
перераспределением давления на корпусе вследствие влияния крыла. Поджатие потока
на нижней поверхности консоли приводит к повышению давления на корпусе
и, как результат, к возникновению пары сил.
Влияние больших углов отклонения руля и толщины профиля. Это
влияние может привести к изменению аэродинамических характеристик по
сравнению с линейной теорией. К сожалению, для крыльев малых и средних
удлинений нелинейная теория не разработана.
Если органы управления имеют достаточно большие удлинения, то
для оценки влияния высоких порядков углов атаки на аэродинамические
характеристики можно применить теорию скачков и течений разрежения.
Нелинейный эффект можно учесть сравнительно простым путем, используя
650
Г лава XV
также теорию приближения второго порядка, предложенную Буземаном,
которая, в частности, применима для оценки влияния толщины органа
управления, расположенного на задней кромке крыла (рис. XV-3-10).
В соответствии с этой теорией коэффициенты давления на поверхности
профиля выражаются формулами (V-2-16) и (V-2-17). При помощи этих
формул можно путем интегрирования подсчитать коэффициент нормальной
Рис. XV-3-10. Орган управления с симметричным профилем
(яВр — расстояние до оси вращения; smax, А г — максимальные
толщины соответственно крыла и руля)
силы органа управления. Для симметричной формы профиля руля
коэффициент нормальной силы, отнесенный к хорде
ъ
CN=T——
2c262(smax — 5ДОН)
^вр
(XV-3-38)
вр
где xBV — расстояние от передней точки корневой хорды до оси вращения
руля.
Обозначения других геометрических параметров даны на рис.ХУ-3-10.
Коэффициенты сь с2 находятся по формуле (V-2-7). Первый член в (XV-3-38)
Рис. XV-3-11. Отрыв пограничного слоя на руле,
расположенном на задней кромке:
I — орган управления; II — пограничный слой; 2 — точка
перехода; 2 — точка отрыва; з — точка прилипания; а —давление
без учета вязкости, б — давление с учетом отрыва
определяет нормальную силу (cN)s=0 несущей поверхности нулевой толщины,
второй дает поправку на влияние толщины. Таким образом, хотя линейный
эффект по углу поворота руля сохраняется, все же имеет место отклонение
от линейной теории из-за влияния толщины. Уменьшение нормальной силы
органа управления определяется выражением
__4 С2
*дон
s=0
Ъ — х
вр
(XV-3-39)
Стационарное обтекание
651
0,8
о
"4 /
/
/
у)
/
20
40 ос°
Рис. XV-3-12. Подъемная
сила и сопротивление
треугольного крыла
Если задняя кромка не затуплена, то в этой формуле следует принять
Влияние отрыва потока. Отрыв пограничного слоя, обычно
начинающийся вблизи оси вращения руля, приводит к перераспределению давления
(рис. XV-3-11) и, как следствие, к некоторому изменению аэродинамических
характеристик.
Максимальная величина подъемной силы. Вблизи угла атаки, при
котором достигается сушах, наблюдается существенное отклонение от
линейного закона изменения подъемной силы по углу
атаки. В большинстве практических случаев
нелинейная зависимость для подъемной силы
получается экспериментально. На рис. XV-3-12
приведены типичные кривые изменения
аэродинамических коэффициентов для изолированного
треугольного крыла при больших углах атаки, в том
числе коэффициента подъемной силы.
При установке на корпусе такого крыла в
качестве подвижного руля его максимальная
подъемная сила определялась бы суммой угла
отклонения руля и угла атаки корпуса, которая будет
меньше, чем критический угол атаки на рис.
XV-3-12. Это объясняется дополнительным
влиянием корпуса на крыло. Кроме того, на
критический угол атаки могут оказать влияние щели.
Исследования, проведенные для изолированных
крыльев в диапазоне чисел Моо от 1,6 до 2,3,
выявили одну особенность, состоящую в том, что для крыльев с
удлинением более 1,4 и различной формы в плане — треугольных, прямоугольных,
стреловидных, трапециевидных—максимальные значения коэффициента
подъемной силы приблизительно одинаковы и равны 1,05 ± 0,05. Причем,
критические углы атаки во всех случаях были близки к 40°. Этот результат
может оказаться полезным при исследовании аэродинамических
характеристик при больших углах атаки различных комбинаций, включающих
несущие элементы указанной ранее формы.
Шарнирный момент полностью
подвижных крыльев
Вычисление шарнирного момента органа управления относительно
оси вращения ведется в следующей последовательности.
1. Определяют коэффициенты нормальной силы руля {cN)a (для угла
атаки) и (cN)6 (для угла отклонения) с учетом интерференции с корпусом.
2. Находят координату центра давления хц.т крыла при а Ф 0 и неот-
клоненном руле. С этой целью вначале определяют координату центра
давления изолированного крыла, затем вводят поправку на влияние
интерференции и толщины. Влияние интерференции на положение центра
давления невелико. Расчеты показывают, что у треугольных крыльев
максимальное смещение центра давления составляет 2% длины корневой хорды.
Изменение координаты центра давления вследствие влияния толщины также
невелико и его можно учесть при помощи теории второго приближения
Буземана. Для профиля, симметричного относительно вертикальной оси,
смещение центра давления определяется из формулы
Д*ц.д = -^, (XV-3-40)
где
662 Глава XV
Коэффициенты mz и cN для профиля определяются по формулам
™z = у ci (*н — sB) + у с2а (sn + FB); (XV-3-41)
с^ = 2qa + -c2(s2H-sl), (X V-3-42)
где 5Н, 5В — соответственно максимальные толщины нижней и верхней частей
профиля, отнесенные к хорде Ьсах-
Расстояние до центра давления относительно передней точки корневой
хорды, вычисленное с учетом толщины и отнесенное к Ькр, будет
Ч) ~ I"^ L~Д^'д ^Г ' (XV-3-43)
где (#ц.д/Ькр)Кр — относительная координата центра давления
изолированного тонкого крыла.
Для крыла треугольной формы эта величина может быть принята
равной 2/3. Поправка на толщину, как показывают исследования, составляет
не более 3—4% длины корневой хорды.
3. Вычисляют поправку к координате центра давления тонкого
изолированного крыла учитывающую влияние толщины руля и интерференции
при его отклонении, и находят расстояние до центра давления #ц.дб ПРИ
а = 0. Поправка, обусловленная интерференцией, мала и, в частности
для треугольных рулей составляет не более 1% длины корневой хорды.
4. Находят шарнирный момент как сумму моментов, вызванных углом
атаки и углом отклонения руля
JK(^J} <xv-3-44)
где #вр — расстояние от передней точки корневой хорды до оси вращения
руля. В формуле (XV-3-44) коэффициент шарнирного момента
отнесен к средней аэродинамической хорде.
Изложенная методика расчета пригодна для органов управления любой
формы в плане, однако используемые в ней данные аэродинамической теории
тонкого тела о влиянии интерференции дают -более удовлетворительные
результаты для треугольной формы и менее точные для прямоугольных
крыльев. При определении взаимного влияния корпуса и отклоненного
руля прямоугольной формы на подъемную силу и положение центра
давления лучше использовать данные линеаризованной теории, согласно
которым поправка на смещение центра давления при отклонении органа
управления больше, чем по теории тонкого тела, примерно в два раза.
Пример. Вычислить коэффициент шарнирного момента при Мею = 2, ос = 0,1; 6 = 0,2
для полностью подвижного органа управления треугольной формы с размерами,
показанными на рис. XV-3-13. Профиль руля симметричный, двояковыпуклый с
относительной толщиной 5тах = 5тах/6Кр = 0,05.
Сначала найдем коэффициенты нормальной силы по значениям углов а и б:
(cN)a = KKVot (с^)кр; (cN)6 = &кр6 (с^)кр.
Так как крыло имеет сверхзвуковую переднюю кромку, то
По значению rs = r/sm — 0,25 находим в табл. XV-3-1 коэффициенты
интерференции .ЙГкр = 1,21, &кр = 0,94. Теперь определим по формуле (XV-3-43) координату центра
давления с учетом толщины, имея в виду, что в этой формуле величина
2 1,47 0Q50Q/l2
Стационарное обтекание
653
Полагая, что
мулу (XV-3-43) находим
= 2/3 и принимая хЦт д/&кр = 2/3, после подстановки в
фор, =-g—0,042 4- = 0,667 — 0,028 = 0,639.
OKp 6 О
Эту величину необходимо уточнить, имея в виду влияние угла атаки, при помощи
формулы
- { Х\Д> а ) » (XV-3-45)
1 кр V 0Кр / кр(т)
в которой первый член определяет координату центра давления изолированного крыла,
второй — в комбинации с корпусом.
Из табл. XV-1-1 для rs = 0 и /-s = 0,25 соответственно находим (хц, д.а/^кр)кр =
= 0,667, (.Гц. д> а/^кр)кр(т) = 0,648. Следовательно, Аа:ц^д/а = 0,019 и относительная коор.
дината центра давления с учетом влияния
толщины (хц. д, а/&кр)кр= 0,639 — 0,019 = 0,620.
Сдвиг центра давления при отклонении руля
/ зц.д.б \ / хц. д. б \
А^ц. д. 6 = I —z ~ —г
V ^кр /кр V с?кр /кр(т)
(XV-3-46)
где первый член определяет координату
центра давления изолированного крыла, второй —
в комбинации с корпусом.
Из табл. XV-3-1 для rs = 0 и rs = 0,25
соответственно находим (хц, д. б/&Кр)кр = 0^667,
(хц. д. б/&кр)крст) = 0,667. Следовательно,
&х ц. д. б = 0 и в соответствии с полученными
данными относительная координата центра
давления при отклонении руля (хЦг д/ЬКр)б =
= 0,639 — 0 = 0,639. После подстановки в
(XV-3-44) находим коэффициент шарнирного
момента
Рис. XV-3-13. Подвижный орган управ
ления в примере расчета:
г
1
sm
4
*вр
2
ЬКР
3
smax
0,05
0,025
+ 0,94-0,2 (у—0,639)1=0,038.
Пример расчета аэродинамических
характеристик комбинации корпус — крыло—
оперение. Экспериментальные данные.
В качестве примера в табл. XV-3-2
приведены результаты расчета суммарных
аэродинамических характеристик плоской
комбинации корпус — крыло — оперение, схема
которой изображена на рис. XV-2-13, для
Моо = 2. В качестве характерных геометрических размеров выбраны длина комбинации
хк и площадь двух консолей крыла без учета площади, занятой корпусом. Все линейные
геометрические параметры являются безразмерными и отнесены к радиусу
цилиндрической части корпуса, принятому за единицу (г = гмид=1). Расстояние от носка до
центра, вращения в соответствии с рис. XV-2-13 равно £вр = 9,35.
При определении коэффициентов (с^)кр, (с^)ош (cjv)t использовались, по
возможности, экспериментальные данные либо результаты сверхзвуковой линеаризованной
теории, приведенные во II и III главах, и, таким образом, достигалась большая
точность вычислений по сравнению с теорией тонкого тела.
В табл. XV-3-2 графы 1 — 36 содержат исходные геометрические величины
комбинации и вспомогательные параметры, вычисленные с учетом заданного числа Моо.
В графах 37 — 51 и 52 — 65 приведены результаты расчета интерференционных
характеристик для комбинаций соответственно корпус —крыло и корпус —оперение. При этом
в графах 38, 38' даются коэффициенты А;т, вычисленные соответственно по
аэродинамической теории тонкого тела и линеаризованной теории. В дальнейших расчетах
используется значение &т = 0,23, полученное по линеаризованной теории.
В графах 66 — 71 помещены данные об обтекании изолированной криволинейной
головки, графы 72 — 102 содержат суммарные аэродинамические характеристики
комбинации корпус —крыло —оперение. Причем часть этих характеристик дается без учета
654
Глава XV
Пример расчета аэродинамических характеристик
Корпус —
1
По
условию
2
2
а'
Л/ м2 7
1,73
3
г
4
sm
5
Ьк. ц
6
Ькр
7
tg 8
8
*кр
По условию
1
5
0
4
1
6,66
9
Я
(5)
(6)
0
10
rs
(3)
(4)
0,2
11
а' tg 8
(2)(3)
1,73
12
Зкр
[(4)-(3)].(6)
16
13
*из
Г(4)-(3)]3
(12)
4
Корпус — опере
24
К
(20)
(21)
0
25
rs
(18)
(19)
0,31
26
a' tge
(2)(22)
1,73
27
Son
X(21)
4,94
28
*из
[(19)-(18)]« ,
(27) l
4
29
а'*из
(2)(28)
6,92
30
2а'г
Ькр
2 (2) (18)
(21)
1,56
31
Л i 1 \ /л
аЛи3и 1 a'tge/(1 ' Я)
(29) [i+ " 1[1 + (24)]'
1 ^ 1
10,9
Интерференция комбинации
42
\ Ькр /кр(т)
Табл. XV-3-1
по (10)
0,67
43
(хц. да>кр
(8)+ (41) (6)
9,26
44
(*ц. дб^р
(8)+ (42) (6)
9,34
45
хвр (хц. да^кр
(17) —(43)
0,09
46
*вр " (хц. дб^кр
(17) —(44)
0,01
47
Рц.дсЛ
V Ькр /т(кр)
Рис. XV-1-9, б
по (15)
0,94
Интерференция комбинации
56
Рц. доЛ
V Ькр /оп(т)
Табл. XV-1-1
по (25)
0,647
57
Гц.дб^
V Ькр >/оп(т)
Табл. XV-3-1
по (25)
0,666
58
(хц.д а^оп
(23)+ (56) (21)
17,7
59
(хц. дб^оп
(23)+ (57) (21)
17,8
60
*вр ^хц.д а^оп
(17)-(58)
—8,40
Стационарное обтекание
комбинации корпус—крыло—оперение (рис. XV-2-13)
655
Табл. XV-3-2
крыло
14
а'Яиз
<«(..,
6,92
ние
32
Scn
SKP
(27)
(12)
0,308
15
2а'г
ЬКр
О(2)(3)
" (6)
0,86
16
(14) [i
1 . М 1 (
1 (11) J [1 ' (
9)]
10,9
Корпус
33
гмид
34
хмид
35
*мид
36
wT
По условию
1
5,67
3,14
8,82
17
*вр
17'
-к
По условию
9,35
18,7
Корпус — оперение
18
г
19
sm
20
Ькц
21
Ькр
22
tge
По условию
1
3,22
0
2,22
1
23
*оп
По
условию
16,3
Интерференция комбинации корпус — крыло
37
*кР
Табл.
XV-3-1
по (10)
1,16
38
Кт
Табл.
XV-1-1
по (10
0,28
38'
Рис. XV-1-86
по (15),(И)
и а'с£ = *
0,23
корпус — крыло
48
<*ц.Д«>т
(8)+ (47) (6)
10,4
49
*вр-(*Ц.да>т
(17) —(48)
— 1,05
50
/zv-ry
\sm-r)
'кр
Рис. XV-2-8
по (14)
и А,= 0
0,678
51
<Фкр
Глава II
(теория)
(4/57,3)/(2)
0,0404
39
*кР
Табл.
XV-3-1
по (10)
0,94
40
К
Табл.
XV-3-1
по (10)
0,22
41
(-
:ц. да'
Ькр ^
кр(т)
Табл.
XV-1-1
по (10)
0,65
Интерференция комбинации
корпус — оперение
52
Табл.
XV-3-1
по (25)
1,26
53
Рис.
XV-1-8, a
по (30),
(26) и
а'с£ = 4
0,130
54
feon
Табл.
XV-3-1
по (25)
0,940
55
*т
Табл.
XV-3-1
по (25)
0,330
корпус -
*зр-<
(17)
-
— оперение
61
хц. дб^оп
-(59)
8,40
62
(*ц.д«Л
Ькр >/т(оп)
Рис. XV-1-9, а
по (30)'
0,670
63
<*ц.да>т
(23) + (62)(21)
17,8
хвр
(17)
64
-(63)
8,40
«кр
0,
65
(са)
on
4
57,3 (2)
0124
656
Глава XV
66
*кр
(35)
(12)
0,196
Аэродинамические
67
а
2
57,3
0,035
характеристики изолированного корпуса
68
^ТН «#>кр *«*
(67) 6б
(51) (66)
0,171
(криволинейной
69
wT
хмидьмид
(36)
(34)(35)
0,495
Полной комбинации (корпус—крыло—оперение) без учета влияния вихрей
!
79
а0
0
5
10
15
(
'(54)
74
А)
J\ on. т
+ (55)] (65)
0,0158
Нормальная
80
(V
4,
4,
4,
4,
о
кр
9
9
9
9
81
(Von
0
0
0
0
(с
сила полной
82
iV^T. кр. опа
(72) (79)
0
0,402
0,804
1,20
{[(37) (45) +(38')
+ [(52) (60)
-
комбинации без учета
83
б
(73) (80)
0,229
0,229
0,229
0,229
75
ССч
z't. кр. оп
(49) + (68) (71)]
+ (53) (64)] (65)}
0,00573
влияния вихрей
84
(Скг) (6 )
v N ои.т v е'оп
(74)(81)
0
0
0
0
(51) +
1
(17)'
крыла
85
(82) + (83) + (81)
0
0
1
1
229
631
03
43
Нормальная сила полной комбинации с учетом влияния
91
Ьш
92
хкр
93
<VsmW
94
95
*ср«
96
feKP (бс>кр
Стационарное обтекание
657
Продолжение табл, XV-3-2
головки)
70
ПО
(69) и (34)
2,87
71
авр-(хц.д)т
(17)-(70)
6,48
крыла
76
[(39) (46)+ (40)
(5)
(4")] ■.. -й,ч'
(1 / )
-0,00048
Аэродинамические характеристики
72
(сЛ^т кр. оп
[(37) + (38') + (68)] (51) + [(52) + (53)] (65)
0,0804
73
' iV^Kp. т
[(39)+ (40)] (51)
0,0468
Расстояние вихря крыла от оперения
77
<mz>on. т
[(54) (61)+ (55) (64)]
(«5)
(17')
-0,0071
78
/ z \
V LSm /on
{(50) [1 (Ю)]
1 (10)} (19)
1,152
Момент и центр давления полной комбинации без учета влияния вихрей крыла
86
<mz%.KP.ona
(75) (79)
0
—0,0287
—0,0573
—0,0862
87
Ар. т <блР
(76) (80)
0,00235
—0,00235
-0,00235
-0,00235
88
^mz'on. т ^ е^оп
(77)(81)
0
0
0
0
вихрей крыла
97
~^~ ^кр (бРкр
98
Форм.
(XV-3-14)
(cn\t. оп)в
99
CN
89
mz
(86) +(87) + (88)
—0,00235
-0,0310
-0,0596
—0,0886
90
<*.р-*ц.д>/*к
(89)/(85)
—0,0105
—0,0492
—0,0577
—0,0621
Момент и центр давления лолной
комбинации с учетом вихрей крыла
100
on) в
101
т
2
102
42-114
658
Глава XV
Нормальная сила полной комбинации с учетом влияния
91
1,560
а= 0°
а=.- 5°
а= 10°
а= 15°
92
7,12
6 = 4,9°
6 = 4,9°
6 = 4,9°
6 = 4,9°
93
L(y^M/JJ {•>*■) \°v)l ^rj 3(i9)
-0,0413
0,151
0,344
0,536
94
Рис. XV-2-9
no (93), (78)
и (25)
-2,16
-2,02
-1,71
— 1,44
95
(37)(79)
0
5,80
11,6
17,4
96
(39)(80)
•$, 60
4,60
4,60
4,60
Суммарные значения статических производных
103
корпус
(68) (51) = 0,0069
корпус — крыло
[(37) + (38') + (68)] (51) = 0, 0631
корпус — оперение без носка корпуса
[(52) + (53)] (65) = 0,0172
корпус — крыло — оперение
примечание
Из рис. XV-2-9 для yv= 0,zu/sm= 1,152 и rs = 0, 31
находим гоп= — 2,2
Примечание. В скобках приведены номера граф, из которых берутся расчетные данные.
влияния вихрей крыла, а окончательные результаты (графы 78 — 102) включают
интерференционную поправку, обусловленную взаимодействием крыла и оперения. В
заключение вычислены суммарные величины статических производных (с^)а_,б ч _0,
(т?)сс=(6е)кр=0' (4)а=(6е)кр=о и (wz)a=(6e)Kp=o и их компоненты для изолированного
корпуса (криволинейной головки), а также для комбинаций корпус —крыло и корпус —
оперение (без головной части корпуса). Из полученных данных видно, что
доминирующую роль в создании нормальной силы комбинации играет отсек крыла, а в
создании момента — отсек оперения.
Расчеты, аналогичные табл. XV-3-2, были выполнены для других
комбинаций. В табл. XV-3-3 приведены результаты этих расчетов для
комбинаций корпус — крыло, в табл. XV-3-4 — для комбинаций корпус —
Стационарное обтекание
659
Продолжение табл, XV-3-2
вихрей крыла
97
(95)+ (96)
4, 60
10,4
16,2
22,0
98
(94) (97) (51) (65) [(19)-(18)] 57,3
2л (28) (50)[(4)-(3)](32)
—0,0303
-0,0636
-0,0840
-0,0965
99
(85)+ (98)
0,1987
0,5674
0,9460
1,3340
Момент и центр давления полной
комбинации с учетом вихрей крыла
100
(98)(61)
(17')
0,0136
0,0286
0,0378
0,0434
101
(89)+ (100)
+0,0112
-0,0024
-0,0218
-0,0452
102
(101)
(99)
0,0565
-0,0042
—0,0230
—0,0338
устойчивости и их компоненты
104
(т?)а=(*ЛР=0
<10(J>7<)71> -0,0024
[(37) (45)+ (38') (49) +
+ <68)<7i)]-i5*L=;<>,0021
[(52)+(53)] (65)=0,0172
(75) + [(103) - W1-щгу- ~ 0,00223
105
(с^)а = <6ЛР=°
(73) = 0,0464
[(52)(61) + (53)(64)]-fp^-=
= - 0,00775
(73) + [(103) -(72)] Щ^ =
= 0,0405
106
(76)= - 0,00048
(76)+ [(104)-(75)]-^ =
= 0,00236
крыло — оперение. Для сравнения в этих таблицах указываются
экспериментальные характеристики, полученные для различных значений чисел
Моо и Re = FoobcAx/v (Ьсах — средняя аэродинамическая хорда
изолированного крыла) ([75], 1307). Для некоторых комбинаций радиус корпуса
на участке сопряжения с крылом или оперением был переменным. В этих
таблицах smax/b—максимальная толщина профиля, отнесенная к хорде.
Сопоставления теоретических и экспериментальных величин делаются
для производных по а от коэффициентов нормальной силы (при а = 0)
и для коэффициентов центра давления (£ц.д/#к)т.кр целой комбинации, так
как такие сопоставления для отдельных компонентов комбинации
невозможны из-за отсутствия в необходимом количестве соответствующих
экспериментальных данных. Удовлетворительное совпадение суммарных теорети-
42*
Т аблица XV-3-3
Теоретические и экспериментальные значения аэродинамических характеристик плоских комбинаций крыло— корпус.
Геометрические параметры комбинации, значение чисел Мто, Re = FTO (&CAX) /v^
о*
и/п
Схема комбинации
Мо
Re-10-6
к
гмид
а'Х.
из. кр
Ькр
'МИД
1 —а
la
б
в
2а
б
За
б
Якр
ХЬ
\
о,6
0,20
0,70
0,90
1,50
2,00
1,20
1,70
1,86
1,86
1,86
1,0
1,0
0,59
0,59
22,5
22,5
22,5
14,7
14,7
31,8
31,8
0,483
0,483
0,483
—
0,440
0,440
0,440
0,450
0,450
0,912
0,912
3,43
2,49
1,52
4,47
6,93
2,66
5,50
9,45
9,45
9,45
45,0
45,0
45,0
45,0
0,546
0,546
0,546
0,000
0,000
0,000
0,000
0,992
0,992
0,992
1,000
1,000
1,000
1,000
0,179
0,179
0,179
0,201
0,201
0,254
0,254
Продолжение табл. XV-3-3
и/и
Схема комбинации
Re-10-6
'МИД
~кр
а'к,
из. кр
'МИД
4а
0,50
0,90
1,45
1,99
4,25
6,58
2,76
2,34
19,6
19,6
19,6
19,6
1,000
1,000
1,000
1,000
0,380
0,380
0,380
0,380
1,73
0,87
2,10
3,45
26,5
26,5
26,5
26,5
0,000
0,000
0,000
0,000
1,000
1,000
1,000
1,000
0,243
0,243
0,243
0,243
ас
0,60
3,67
16,7
0,521
0,386
2,19
35,0
0,352
1,000
0,160
Г
0,10
0,57
11,7
0,322
0,260
5,62
0,0
0,88
1,000
0,115
<■
0,10
0,62
11,7
0,322
0,185
5,52
18,3
0,38
1,000
0,115
Т7
0,10
0,10
0,62
0,62
11,7
.41,7
0,322
. 0,322
0,223
0,261
5,52
5,52
9,3
0,0
0,38
0,38
1,000
1,000
0,115
0,115
Продолжение табл. XV-3-3
№
п/п
9а
б
10а
б
Схема комбинации
\^
0,75
1,07
0,75
1,07
Re • 10-6
1,27
1,25
1,31
1,29
гмид
24,0
24,0
24,0
24,0
*к
0,606
0,606
0,637
0,637
0,388
0,388
0,499
0,499
a'\i3. кр
1,49
0,83
1,60
0,90
*п
60,0
60,0
0,0
0,0
0,0
0,0
0,0
0,0
г
гмид
0,981
0,981
0,861
0,861
г
0,158
0,158
0,139
0,139
2—а
11а
б
в
12
13
и
г
L
и
1,62
1,93
2,40
,00
1,50
0,40
0,40
0,40
0,26
19,5
19,5
19,5
27 9
22,9
—
—
—
0,501
0,501
0,501
0,860
0,148
1,66
2,14
2,84
1,73
2,98
0,0
0,0
0,0
0,0
26,6
1,000
1,000
1,000
1,000
0,500
1,000
1,000
1,000
1,000
0,986
0,350
0,350
0,350
0,333
0,486
X
Продолжение табл. XV-3-3
№
п/гг
14а
б
15а
б
16а
б
Схема комбинации
А
+
«„
1,50
2,00
1,62
1,93
1,50
2,00
Re • 10-6
0,70
0,70
0,31
0,28
1,00
1,00
гмид
22,9
22,9
21,8
21,8
14,7
14,7
—
—
0,632
0,632
0,870
0,870
0,450
0,450
а из. up
3,30
5,11
1,57
2,03
0,75
1,16
п
14,0
14,0
60,0
60,0
80,4
80,4
0,461
0,461
0,305
0,305
0,000
0,000
г
гмид
1,000
1,000
1,000
1,000
1,000
1,000
г
0,250
0,250
0,465
0,465
0,600
0,600
3-а
17
18
п
и
к
1,92
1,40
0,20
1,25
25,0
31,8
0,920
0,412
5,13
2,27
0,0
0,0
1,0
0,0
1,0
1,0
0,228
0,216
с*.
Продолжение табл. XV-3-3
JSft
п/п
19a
б
Схема комбинации
1 1
^— t
*^ 1
1,40
1,90
Re • 10-6
1,51
1,51
гмид
31,8
31,8
хк
—
0,389
0,389
а из. кр
1,13
1,87
о
0,0
0,0
1,0
1,0
г
гмид
1,0
1,0
г
0,216
0,216
п/п
la
б
в
2а
б
За
б
4а
б
в
г
Кт. и
0,08
0,07
0,06
0,11
0,17
0,15
0,25
0,14
0,12
0,13
0,15
к
0,
0,
о,
о,
о,
о
0
0
0
0
0
т
24
24
24
23
23
20
14
35
,35
,35
,35
к
1,
1,
1,
1,
1
1
1
1
1
1
1
14
14
14
16
16
21
21
,20
,20
,20
,20
з,
2,
2,
4,
4
3
4
1
1
2
3
нормальная сила
47
83
02
00
00
10
00
,97
,13
,69
,71
0,27
0,19
0,12
0,44
0,68
0,48
1,00
0,28
0,16
0,34
0,55
5,
4,
2,
6,
6
4
6
3
1
4
6
Аэродинамические
1-6 (а ф
т. кр
05
10
90
01
24
86
40
,34
,89
,50
,31
Теория
/*ц. д\
хк т
0,229
0,229
0,229
0,190
0,190
0,207
0,207
0,102
0,102
0,102
0,102
v
характеристики
0, 6 = 0)
центр давления
. дач
хк /т.(кр)
0,480
0,478
0,474
0,675
0,710
0,966
0,969
0,452
0,441
0,606
0,632
(^
0,
0,
о,
0,
о,
о
0
(0
(0
(0
(0
/кр.(т)
485
485
485
636
636
969
969
,428)
,428)
,477)
,477)
/*ц.д
хк
0,
0
о
0
0
0
0
0
0
0
0
/т.кр
47
47
47
60
59
,89
,84
,40
,40
,47
,47
Эксперимент
нормальная
сила
—
—
—
0,43
0,90
—
—
—
—
—
—
(a'ciy)T< кр
4,70
3,94
3,08
5,69
7,09
4,91
7,26
3,36
2,18
4,40
5,95
(
центр
давления
хк )т' КР
0,47
0,47
0,47
0,60
0,60
0,90
0,85
0,40
0,40
0,43
0,43
5 | 0,05 10,221 1,13 | 2,51
0,13
3,51
0,505
0,541
3,64
0,52
Продолжение табл. XV-3-3
и/и
Теория
нормальная сила
(а'с
кр
центр давления
V *„ /т
• т(кр)
/*ц. дач
V х /к
а? /кр(т)
. кр
Эксперимент
нормальная
сила
кр
центр
давления
/т. кр
|
1
6
7
8а
б
9а
б
10а
б
0,14
0,14
0,14
0,14
0,05
0,04
0,05
0,04
0,15
0,15
0,15
0,15
0,23
0,21
0,19
0,19
1,09
1,09
1,09
1,09
1,13
1,13
1,11
1,11
4,13
4,12
4,12
4,12
1,76
1,22
1,84
1,31
0,60
0,58
0,58
0,58
0,09
0,05
0,09
0,05
5,30
5,27
5,27
5,27
2,48
1,68
2,48
1,74
0,100
0,100
0,100
0,100
0,217
0,217
0,217
0,217
0,322
0,290
0,316
0,341
0,548
0,584
0,566
0,578
0,319
0,338
0,334
0,325
0,592
0,631
0,558
0,539
0,31
0,33
0,33
0,32
0,57
0,60
0,54
0,52
—
—
—
—
—
—
—
—
5,81
4,83
4,83
4,83
2,40
1,53
2,38
1,76
0,32
0,32
0,32
0,32
0,56
0,59
0,50
0,53
2-6
На
б
в
0,
0,
0,
27
32
39
0
0
0
,52
,44
,38
1
1
1
,30
,30
,30
2
3
3
,79
,07
,30
0
0
1
,76
,98
,29
5,
6,
6,
84
32
84
0,
0,
0,
207
207
207
0,
0,
0,
646
657
679
0,
0,
0,
568
566
568
0
0
0
,51
,50
,49
0
1
1
,80
,05
,34
4
5
6
,71
,66
,72
0
0
0
,49
,50
,51
12 | 0,24 10,251 1,28 | 2,84
0,68
5,02
0,083
0,992
0,920
0,78
0,68
5,48
0,80
13
14а
б
15а
б
16а
б
1,38
0,16
0,24
0,71
0,78
2,33
2,44
0,56
0,29
0,27
0,31
0,16
0,97
0,94
1,44
1,21
1,21
1,41
1,41
1,56
1,56
3,49
3,56
3,78
2,62
3,12
1,13
1,6.7
4,83
0,57
0,89
1,87
2,42
2,63
4,08
11,81
5,91
6,48
6,38
7,32
5,48
8,25
0,090
0,090
0,090
0,165
0,165
0,190
0,190
0,213
0,742
0,766
0,956
0,960
0,675
0,710
0,175
0,688
0,691
0,949
0,949
0,636
0,636
0,13
0,62
0,60
0,69
0,67
0,42
0,42
4,98
0,59
1,09
2,15
2,91
2,56
5,38
11,05
6,10
7,15
6,12
7,78
6,35
10,02
0,13
0,62
0,61
0,68
0,64
0,44
0,41
Примечание. Значения а'с
даны в радианах.
) Экспериментальные
величины, использованные в теоретических расчетах.
Продолжение табл. XV-3-3
о*
3 —б (а=£0, 6 = 0)
п/п
17
18
19а
б
0,29
0,10
0,06
0,08
0,07
0,31
0,31
0,31
1,19
1,18
1,18
1,18
Теория
нормальная сила
<а'ФкР
3,61
2,83
2,23
2,93
1,06
0,27
0,13
0,22
<a'cN>T.Kp
5,61
4,48
3,48
4,58
центр давления
/хд,д.\
1 *к )т
0,19
0,21
0,21
0,21
/*ц.д.а\
V *к )
т (кр)
0,954
0,548
0,525
0,545
/*ц.д.а\
V *к /
кр.(т)
0,954
0,457
0,460
0,475
/хцдЛ
V лк / т кр.
0,78
0,45
0,43
0,45
Эксперимент
нормальная сила
<а'Фкр. т
5,61
4,60
3,59
4,54
центр давления
/ХЦ.Д\
\ хк /кр.т
0,75
0,45
0,45
0,47
3 —в (а = 0, 6 ф 0)
п/п
17
18
19а
б
0,25
0,24
0,24
0,24
feKP
0,98
0,94
0,94
0,94
Теория
нормальная сила
(а'сЛГ>кр (т)
3,53
2,67
2,10
2,76
<а'Фкр. т
4,43
3,34
2,63
3,46
центр давления
/ХЦ.Д 6\
V х /т(кр)
0,954
0,548
0,525
0,545
/хц. дб\
V х„ /кр (т)
0,953
0,467
0,457
0,475
(хц. дб\
V хк /кр. т
0,96
0,47
0,44
0,46
Эксперимент
нормальная сила
<а'Фкр (т)
—
2,58
2,25
2,96
<а'Фкр. т
3,03
3,26
2,75
3,52
центр давления
/*Ц. Дб\
V хк /кр (т)
—
0,450
0,458
0,467
/*ц.д\
^ х„ /кр.т
0,98
0,48
0,46
0,48
Таблица XV-3-4
Теоретические и экспериментальные значения аэродинамических характеристик плоских комбинаций корпус—крыло—оперение
1 — а. Геометрические параметры комбинации, значения чисел М и Re
п/п
Схема комбинации
Re-10-6
'МИД
*вр
Поверхность
smax
Д, = -
'МИД
о
3
А
N
1,99
0,81
18,6
0,500
0,309
крыло
оперение
0,357
0,872
0,08
0,08
6,88
45,00
45,00
0,000
0,000
1,000
1,000
0,200
0,310
2а
26
2в
0,20
0,70
0,90
1,86
1,86
1,86
22,5
22,5
22,5
0,483
0,483
0,483
0,252
0,252
0,252
крыло
оперение
крыло
оперение
крыло
оперение
0,440
0,895
0,440
0,895
0,440
0,895
0,042
0,042
0,042
0,042
0,042
0,042
3,43
3,43
2,49
2,50
1,52
1,53
9,45
9,45
9,45
9,45
9,45
9,45
0,546
0,548
0,546
0,548
0,546
0,548
0,992
0,488
0,992
0,488
0,992
0,488
0,179
0,176
0,179
0,176
0,179
0,176
Ob
п/п
За
б
4
5
Схема комбинации
Л Л
VJ VJ
0,89
1,25
1,90
1,93
Re-10-е
6,0
9,2
1,51
0,33
гмид
32,6
32,6
31,8
21,9
хк
0,525
0,525
0,508
0,522
Son
«кр
9,00
9,00
0,392
0,839
Поверхность
крыло
оперение
крыло
оперение
крыло
оперение
крыло
оперение
или
0,226
0,597
0,226
0,597
0,389
0,809
0,486
0,869
Продолжен ие
smax
ИГ"
—
0,03
0,02
0,049
1,05
1,05
1,73
1,73
1,87
0,78
1,69
2,03
60,00
60,00
60,00
60,00
0,00
0,00
60,00
60,00
табл. XV-3-4
0,000
0,000
0,000
0,000
1,000
1,000
0,323
0,305
г
гмид
1,000
1,000
1,000
1,000
1,000
1,000
1,000
1,000
г
0,467
0,226
0,467
0,226
0,216
0,405
0,465
0,465
Оо
Продолжение табл. XV-B-4
п/п
Схема комбинации
Re •10-6
гмид
кр
Поверхность
smax
b
кр
Л
1,93
0,33
22,8
0,541
0,931
крыло
оперение
0,507
0,947
0,064
1,69
5,51
60,00
0,00
0,323
1,000
1,000
1,000
0,465
0,333
1,93
0,33
22,8
0,541
1,01
крыло
оперение
0,507
0,893
1,69
3,16
60,00
45,00
0,323
0,352
1,000
1,000
0,465
0,388
А
1,93
0,83
22,8
0,541
5,74
крыло
оперение
0,290
0,636
1,69
1,03
60,00
70,00
0,323
0,400
1,000
1,000
0,508
0,356
о*
Продолжение табл. XV-3-4
2
№
п/п
Схема комбинации
Re- 10-6
'МИД
Чкр
Поверхность
smax
кр
МИД
1,93
0,83
22,8
0,541
23,10
крыло
оперение
0,404
0,636
3,81
1,03
60,00
70,00
0,000
0,400
1,000
1,000
0,579
0,356
10
1,93
0,83
22,8
0,541
10,30
крыло
оперение
0,376
0,636
3,81
1,03
60,00
70,00
0,000
0,400
1,000
1,000
0,479
0,356
11
1,93
0,83
22,8
0,541
5,79
крыло
оперение
0,349
0,636
3,81
1,03
60,00
70,00
0,000
0,400
1,000
1,000
0,408
0,356
12
1,62
0,23
25,7
0,486
1,000
крыло
оперение
0,355
0,880
3,31
3,31
0,00
0,00
0,000
0,000
1,000
1,000
0,350
0,350
X
Продолжение табл. XV-3-4
и
1
2а
б
в
За
б
s
0,17
0,08
0,07
0,06
0,96
0,89
0,23
0,24
0,24
0,24
0,74
0,62
а
к
i,i6
1,14
1,14
1,14
1,42
1,42
9
О
Еч
0,12
0,24
0,24
0,24
0,32
0,27
в
1,27
1,14
1,14
1,14
1,19
1,19
1 — 6
Аэродинамические характеристики
Теория
а.
-?
о
4,00
3,47
2,83
2,02
1,32
2,34
нормальная
н
о
4,00
3,48
2,83
2,02
1,32
2,34
Еч
ъ
0,68
0,27
0,19
0,12
0,14
0,23
сила
* к
о
8,
7,99
6,45
4,70
3,60
2,51
4,17
о
8,
7,20
5,56
4,21
3,17
2,06
3,40
центр давления
Еч
н 1
0,154
0,229
0,229
0,229
0,104
0,104
н
0,558
0,480
0,478
0,474
0,257
0,281
&
X
у*"
н
Еч
К
0,500
0,485
0,485
0,485
0,261
0,267
(ПО
Я"
Еч
н
0,951
0,915
0,915
0,912
0,683
0,714
1ч
к
|
0,951
0,918
0,918
0,918
0,701
0,719
н
X
И
0,575
0,557
0,565
0,559
0,602
0,627
а-
н
X
н
0,535
0,521
0,525
0,510
0,581
0,607
Эксперимент
нормальная
сила
о
—
—
—
—
—
—
о
7,74
5,20
4,25
3,11
1,97
3,38
центр
давления
к
н
0,550
0,505
0,493
0,483
0,583
0,603
12 | (0,48)| 0,53 | 1,30 | 0,53 | 1,30 | 3,62 | 3,62 | 1,51 114,97 |
* Значения без учета влияния вихрей крыла.
( ) Экспериментальные значения, использованные в расчете.
[ ] Экспериментальные значения, нелинейные вблизи а = 0.
км — индекс относится к комбинации в целом.
Координата (х д/:ск)км отсчитывается от носка корпуса.
4| 0,08 | 0,31 | 1,18 | 0,62 | 1,36 | 2,93 | 1,50 | 0,22 | 5,74 | 5,19 | 0,182 | 0,547 | 0,475 | 0,931 | 0,864 | 0,559 | 0,5081 — | 5,00 | 0,485
5
6
7
(0,
(0,
(0,
82)
82)
82)
0
0
0
,63
,63
,63
1
1,
1,
41
41
41
0
0
0
,26
,06
,14
1
1
1
,41
,29
,34
2
2
2
,94
,94
,94
3
3
3
,12
,64
,67
2
2
1
,01
,01
,99
12
12
13
,77
,87
,81
8
11
10
,70
,73
,31
(0,
(0,
(0,
165)
118)
118)
0
0
0
,640
,655
,655
0,
0,
0,
574
591
591
0,
0,
о,
956
982
964
0,
0,
0,
948
973
959
0
0
0
,635
,647
,662
0
0
0
,488
,616
,561
2
2
2
,41
,41
,39
8,
и,
ю,
39
15
72
0,
0,
599
555
8| (1,15) | 0,69 |l,46|0,54| 1,31 | 2,94 | 1,94 | 0,49 | 4,98 | 4,26 | (0,118) | 0,431 | 0,361 | 0,868 | 0,830 | 0,666 | 0,625 | 0,59 | [3,90] | [0,595]
9
10
11
(3
(1
(0
,48)
,55)
,87)
0
0
0
,70
,54
,44
1
1
1
,54
,43
,36
0,
0,
0,
54
54
54
1
1
1
,31
,31
,31
3
3
3
,91
,91
,91
1
1
1
,94
,94
,94
0
0
0
,49
,49
,49
4,
4
5
54
,92
,39
4,
4,
4,
16
16
26
(0,
(0,
(0,
118)
118)
118)
0,
0,
0,
505
492
482
0
0
0
,440
,432
,431
0,
0,
о,
868
868
868
0,
0,
0,
830
830
830
0,
0,
0,
718
698
672
0,
0,
0,
705
675
629
0
0
0
,59
,59
,59
з,
з,
4,
77
82
00
0,
0,
[0,
683
663
604]
9,78 |(0,162)| 0,450 | 0,390 10,953 | 0,914 | 0,609 | 0,446 | 1,72 | 9,09 | [0,486]
о
3
о*
672
Глава XV
ческих и экспериментальных результатов косвенно подтверждает, что
распределение интерференционных составляющих нормальной силы между
корпусом и крылом вычислено правильно. Однако этот вопрос требует
дополнительного исследования.
При обработке опытных данных ([75], 1307) встречалась трудность
в определении наклона кривых момента, так как нелинейность, хотя и
незначительная, наблюдалась вблизи а = 0. Принималось, что линейность
имеется для а = ± 2° и выбирался средний наклон на этом участке.
Для некоторых комбинаций корпус — крыло — оперение моментные
характеристики оказывались настолько нелинейными, что невозможно
было точно определить положение центра давления при а — 0, и в этих
случаях соответствующие координаты центра давления в табл. XV-3-3
и XV-3-4 не указаны.
Углы наклона кривой нормальной силы для изолированных корпусов
в некоторых случаях также трудно определить вследствие очень малых
величин этих углов и ненадежности имеющихся экспериментальных данных.
Погрешность в определении углов наклона не превышает 10%.
Комбинация корпус — крыло. Сравнение с экспериментальными
данными показывает, что вычисленные наклоны кривых нормальной силы
-с
jt=
/
L
-м-
—<
с
f
<
и
о
£
Г"
.
4
,2
\
с
*s J
-—-
^»-"
3
hi
О
J
I °
I I
W 0,8 1,2 1,6
U о U3 2 б* Q 1
Рис. XV-3-14. Изменение производной с^ (а = 0)
комбинации корпус — крыло в зависимости от Мс»:
-расчет; П('); О (2У,
\
О {4) — экспериментальные
данные
для комбинации корпус — крыло отличаются от опытных ([75], 1307) в
пределах до 10%, причем, в среднем, их значения для комбинации с частью
корпуса за крылом больше, чем экспериментальные.
Наиболее надежными являются данные расчета нормальной силы для
корпуса с треугольным крылом. Рис. XV-3-14 показывает точность метода
определения наклонов кривых нормальной силы комбинации корпус —
крыло в зависимости от числа Моо. Хотя тенденция изменения расчетных
параметров предсказывается правильно, имеется различие в величинах,
в частности в трансзвуковом диапазоне расчетные величины меньше
экспериментальных.
Для расчета наклона кривой нормальной силы изолированных крыльев
применялась линейная теория, которая, в частности, для прямоугольных
крыльев обеспечивает хорошее совпадение с экспериментом в окрестности
Моо = 1, если некоторый условный параметр Якр (sm8LX/b)i/.s < 1. Однако
Стационарное обтекание
673
хорошей согласованности теоретических и экспериментальных наклонов
кривых нормальной силы для всех четырех форм комбинаций,
представленных на рис. XV-3-14, не наблюдается. Исследование данных, приведенных
на этом рисунке, показывает, что для комбинации в целом поведение кривой
нормальной силы в зависимости от числа Моо в окрестности Мто = 1 по своему
характеру будет таким, как для изолированного крыла малого удлинения.
Исследование влияния угла установки крыла на нормальную силу
показывает, что теоретические и экспериментальные значения а'с^
комбинаций корпус — крыло хорошо совпадают в тех случаях, когда величины
с^ для изолированных крыльев определены экспериментально.
В табл. XV-3-2 приведены для сравнения экспериментальные данные
о центрах давления, безразмерные координаты которых определялись по
формуле
"I Г" %U
(XV-3-47)
где mF и c<* — экспериментальные коэффициенты момента и нормальной силы;
^вр — расстояние от носка до центра вращения;
хк—длина комбинации.
Сравнение показывает, что когда используется теория, не
учитывающая влияние корпуса за крылом, теоретические и экспериментальные
данные согласуются лучше. Как и
в случае подъемной силы, влия- - °'68
ние части корпуса за крылом на
координату центра давления
может быть большим.
Анализ центров давления
показывает, что вычисленные их
координаты, отсчитываемые от
носка, будут по сравнению с
экспериментальными больше.
Причем для прямоугольных
крыльев центр давления
располагается ближе к корме, чем
для треугольных. Для
трапециевидной формы крыла ошибка
в вычислении координаты
центра давления будет
промежуточной. По опытным данным
([75], 1307) ошибка в
определении координаты центра
давления при наличии
прямоугольного крыла составляет 0,026 хК1
треугольного — 0,009 хк и
трапециевидного — 0,017 хк. Сравнение теоретических и экспериментальных
центров давления для дозвуковых и сверхзвуковых скоростей проведено на рис.
XV-3-15, где представлены данные для четырех комбинаций корпус — крыло.
Заметно небольшое изменение координаты центра давления по Моо, пока не
достигнуты трансзвуковые скорости. Экспериментальные и теоретические
величины (Дяц. д/як)б, найденные при условии, что 8е Ф 0, а = 0,
представлены в табл. XV-3-2.
Комбинация корпус — крыло — оперение. Установлено, что влияние
взаимодействия между оперением и крылом на суммарные аэродинамиче-
43-114
г
L
А-
1С
Г
~ь^<5
—«
/\~.
г
J
А
j
*^
,2
/
\-
/
/
\
'3
/
~1
j
/
—■
*—•
о
Л
А
0 0,4 0,8 1,2 1,6 2,0
1Д 2° 3D* 4 о
0,60
0,56
0,52
0,48
0,44
0,40
0,36
Рис. XV-3-15. Изменение координаты центра
давления комбинации корпус — крыло в
зависимости от числа Моо для а —►■ 0:
расчет; Л (1); О {2); □ (3); о— (4)
экспериментальные данные
674
Глава XV
ские характеристики может быть порядка 30-f-40%. Изложенный метод
учета влияния этого вида интерференции позволяет получить суммарные
характеристики с ошибкой до ±10%.
Изменение производной с^ при а ->• 0 для двух комбинаций корпус —
крыло — оперение в зависимости от Моо показано на рис. XV-3-16. Можно
—
EL
D
Й
, г
LL
u
у
,2
<*
о
2 |—
i
<9 ' ' [ I I I I I I I 1 I I iw I I I
^ /7,5 /,0 /^ /,5 М^
Рис. XV-3-16. Изменение производной с^ при а -> О
в зависимости от числа Моо для комбинации корпус —
крыло — оперение:
-— расчет; П (i); О (2) — эксперимент
видеть, что теория, учитывающая интерференцию между оперением и
крылом, находится в соответствии с экспериментом практически для всего
диапазона чисел Моо от дозвуковых до сверхзвуковых скоростей, включая
трансзвуковую область.
0,62
0fi6
о
—а«=
1
О
<=*
__с
<
9
0°
ГУ !■
о
V
п
г
ее
-0
V
0 0,2
0,6
1,8 Мо
Рис. XV-3-17. Изменение положения центра давления
в зависимости от числа Моо при а -> 0 для
комбинации корпус —- оперение:
. теория; О (*); О (2) — эксперимент
По теоретическим и опытным данным ([75], 1307) влияние
интерференции между оперением и крылом на положение центра давлений
комбинации обычно больше при сверхзвуковых, чем при дозвуковых скоростях.
Ошибки в теоретических расчетах составляют примерно 0,02 хк. Влияние
числа Маха и угла атаки на относительную координату центра давления
при а -> 0 у двух комбинаций корпус — крыло — оперение показано на
рис. XV-3-17 для до- и сверхзвуковых скоростей. Для комбинации с
трапециевидным крылом теоретические данные хуже согласуются с
экспериментальными результатами по сравнению с комбинацией, имеющей треуголь-
Стационарное обтекание
675
ное крыло. Это указывает на то, что для трапециевидной комбинации
существенными оказываются нелинейные эффекты.
При повороте крыла на положительный угол 8е создается
дополнительная нормальная сила, действующая вверх, но результирующие вихри крыла
вызывают обратную по направлению нормальную силу оперения. Вследствие
этого развивается значительный момент тангажа, способствующий
перемещению вперед центра давления. Это подтверждается теоретическими и
экспериментальными данными ([75], 1307) в табл. XV-3-2. На рис. XV-3-18
0,08
OfiU
0
-0,04
-0,08
-0,12
ГУ
\
\
\
(У
о о
■—«
—.
•9
—■
-—1—-
D
—о—
f
— —
ПО
J
8
10
12 /4 ссс
0 2 4
Рис. XV-3-18. Влияние угла поворота крыла комбинации
корпус — крыло — оперение на положение центра
давления:
— расчет; эксперимент:
аналогичные данные представлены для двух комбинаций, имеющих
различные по форме крылья. В диапазоне исследованных углов атаки
наблюдается хорошее совпадение теории с экспериментом для комбинации с
прямоугольными крыльями и менее удовлетворительное — для модели с
треугольным крылом, что объясняется недостаточностью принятой для этой
модели схемы одного вихря для крыла.
§ XV-4. Момент
демпфирования летательного
аппарата, обусловленный
движением топлива и
продуктов его сгорания
Вследствие вращения летательного аппарата вокруг центра массы
движущееся топливо (или продукты его сгорания) создает центробежные
и кориолисовы силы, что приводит к возникновению демпфирующего момента.
Как показывают исследования, центробежные силы пренебрежимо малы
по сравнению с кориолисовыми. Для летательного аппарата, схема которого
показана на рис. XV-4-1, боковая сила Rz и демпфирующий момент Муп,
вызванные вращением вокруг центра масс (оси ог/), могут быть определены
43*
676
Глава XV
соответственно по формулам
Qvm
-у (Zi + zlZo + z02)]} ,
(XV-4-1)
(XV-4-2)
где т — секундный массовый расход топлива двигательной установкой;
ха, хи Xq, za, zu z0 — координаты, показанные на рис XV-4-1.
Формулы (XV-4-1) и (XV-4-2) следует применять при условии, что
вращение равномерное (£iy = const). Эти формулы получены в предположении,
Рис. XV-4-1. Схема к расчету момента демпфирования от
движения топлива или продуктов сгорания относительно
летательного аппарата
что вращение летательного аппарата вокруг осей ох и oz не оказывает
влияния на момент демпфирования Мую а топливо или продукты его сгорания
движутся в направлении действия вектора тяги двигательной установки. Схема
сгорания, для которой производится расчет, соответствует схеме сгорания
твердого топлива, выполненного в виде шашек с центральным каналом,
горящих с обоих торцов.
§ XV-5. Расчет роллеронов
Расчет роллеронов (см. рис. П-3-4/) заключается в определении
геометрических параметров руля, размеров диска и его угловой скорости,
обеспечивающих потребную величину продольной угловой скорости летательного
аппарата Qxi при допустимом значении угла отклонения роллерона бр,
который должен быть меньше критического. Расчет может быть связан с
решением обратной задачи, а именно с вычислением значения бр и Qxl для
выбранных параметров роллеронов и заданных аэродинамических
характеристик летательного аппарата. Эти расчеты могут быть осуществлены в
результате решения следующей системы уравнений, описывающей возмущенное
движение по крену летательного аппарата, снабженного роллеронами,
(XV-5-1)
(XV-5-2)
.где Jxi, /рг1 —моменты инерции соответственно летательного аппарата
относительно оси Xi и роллерона относительно оси z4;
у и бр — соответственно углы крена и поворота роллерона;
Mxi~ момент крена, создаваемый роллеронами;
Стационарное обтекание 677
Мхд — момент демпфирования крена;
Мв — возмущающий момент крена;
Мг — гироскопический момент;
Мш — шарнирный момент роллерона.
Уравнение (XV-5-1) описывает вращательное движение летательного
аппарата вокруг оси х±, а уравнение (XV-5-2) — вращение роллерона вокруг
оси без учета его веса и трения в подшипниках. Моменты в этих
уравнениях^ заменяются выражениями
Мх1 - лдсоЯрГр^вр; (XV-5-3)
Mxi д = ?оАр ^- m£xQx; (XV-5-4)
MT = QyiQxiJvvi; (XV-5-5)
Мш = gooSp&cAx p4, (XV-5-6)
где п — число роллеронов;
5р — площадь роллерона в плане;
гр — расстояние от оси xi до центра давления роллерона;
сьу — статическая производная от коэффициента подъемной силы
роллерона по углу его поворота;
ж®* — вращательная производная от коэффициента момента демпфирования
крена по безразмерной угловой скорости крена
1 —момент инерции вращающегося с угловой скоростью Цд диска
роллерона относительно оси yi (см. рис. И-3-4');
р—средняя аэродинамическая хорда роллерона;
тш — статическая производная от коэффициента шарнирного момента
роллерона по углу его поворота.
Скоростные напоры q и #«> вычисляются соответственно для возмущенного
течения перед роллеронами и для набегающего потока. Возмущающий
момент Мв задается как функция времени MB(t).
После указанной замены система уравнений принимает вид
V + Ау + 5бр = J- MB (t); (XV-5-7)
бр + £6Р + Еу = О, (XV-5-8)
где
_
Е =
(XV-5-9)
Значения А, В, Е, D в первом приближении могут быть найдены
по данным расчета траектории поступательного движения центра массы
летательного аппарата без учета влияния крена. Решение уравнений (XV-5-7)
и (XV-5-8) существенно упрощается, если принять у = 0, что возможно для
многих классов летательных аппаратов. Для этого случая
=-^^в(0; (xv-5-Ю)
67S Глава XV
Примем параметры А, В, Е, D не зависящими от времени и равными
их средним значениям на некотором участке траектории, а момент Мв = const.
В этом случае решение уравнения (XV-5-10) получаем в следующем виде
[(D-EB)/A>0]:
^ (XV-5-12)
где
k* = D-^B\ F= —E(JxiAMB)~1 = const.
Постоянные интегрирования С и ср определяются из начальных данных
для бр и бр.
При установившемся вращении роллерона (бр = 0)
- (XV-5-13)
Угловая скорость по крену у = йа1 вычисляется непосредственно
из (XV-5-11).
Пример. Вычислим значения бр и у — пх\ по следующим данным: il/ooel,
= 540 м/сек); goo = l,3.104 кГ/м2;
^кр = 0,187 ж2; Z = 0,48 м\ Qyi = 2O90 1/сек; /л®*=— 0,19;
/Рг/1 = 0,2-10-3 кГ-сек2-м; Jxi = 0fi25 кГ'сек2-м\
^pzi = 0,18.10-3 кГ-сек*-м; Мв = 10 кГ-м.
Четыре прямоугольных роллерона (п = 4) помещаются на задней кромке
крестообразного оперения, расположенного за крылом, и имеют следующие размеры:
6р = 0,068 м; Zp = 0,064 м; гр^0,15 м; ^р = &ргр = 4,35• 10~3 м*.
Примем, что скоростной напор перед роллероном д = 0,85^оо и, следовательно,
М2^0,85 М^. Без учета влияния концов роллерона производная
^д 02
у УМ2 —1 1/1,82.0,85—1
Из формулы
где h — расстояние от центра давления роллерона до оси вращения, равное &р/2,
определяем
тш= — с = 1»51.
Далее подсчитываем
1,3-104.0,187.0,482-0,19
А
2-540-0,025
4,13-104.0,85.4,35.Ю-3-0,15.3,02
В== 0^25 = -3480;
л 1,3-104.0,85.4,35.10-3.0,068.1,51 97/пп
D = 0,18-Ю-з = 27 400.
По формуле (XV-5-13) определяем
2320-10 /ОГ7/ПП 2320-3480 \~
бР= 0,025.3,93 12/40°)
а из (XV-5-11) находим
( ) / 3,93 = 204
Стационарное обтекание
§ XV-6. Лобовое
сопротивление
Сопротивление при нулевой
подъемной силе
Общее сопротивление летательного аппарата определяется суммой
сопротивлений его отдельных элементов, вычисленных с учетом интерференции.
При дозвуковых и умеренных сверхзвуковых скоростях (М<х> < 5) полное
сопротивление можно расчленить на сопротивление, не зависящее от подъемной
силы и равное сопротивлению аппарата при су = 0, и на индуктивное
сопротивление, зависящее от подъемной силы. Сопротивление при су = 0 можно
представить в виде 128
Хо = Хт + Хкр + Хоп + АХТ(КР) + AXr(on) + Д-^кр(т) + Д^оп(т) + ДХ0П(кр)>
(XV-6-1)
где первые три составляющие представляют собой сопротивление
изолированных корпуса, крыльев и оперения; остальные компоненты в сумме дают
поправку на интерференцию. Индекс в скобке внизу справа у каждого члена
указывает элемент конструкции, в результате интерференции с которым
появляется дополнительное сопротивление корпуса, крыла и оперения.
Например, ДХТ(КР) представляет собой дополнительное сопротивление корпуса,
обусловленное интерференцией с крылом, AXT(On)— сопротивление корпуса,
обусловленное интерференцией с оперением, и т. д.
В первом приближении сопротивление можно определять без учета
интерференции как сумму сопротивлений изолированных корпуса, крыла и оперения:
Х0 = Хт + Хкр + Хоп. (XV-6-2)
Выделив из каждой составляющей сопротивление, вызванное разрежением
за задним срезом тела, напишем
Хо = Хт + Хкр + Хоп + Хт. дон + Хкр. дон ~\- -Хоп. дон» (XV-6-3)
где первые три величины представляют собой сопротивления от давления
и трения для корпуса, крыла и оперения, а вторые три компонента —
соответствующие составляющие донного сопротивления.
Корпус. Полное сопротивление корпуса определяется с учетом его формы,
которая в общем случае может отличаться от тела вращения. Если это
отличие невелико, то корпус рассматривается как тело вращения с распределением
радиусов вдоль продольной оси х, подчиняющимся закону
S(z), (XV-6-4)
где S (х) — площадь поперечного сечения корпуса заданной формы.
У такого тела вращения подъемная сила и моментные характеристики,
как показывают исследования, сохраняются такими же, как у корпуса
заданной формы. Различие в сопротивлении оказывается более существенным, и его
следует учитывать. Отклонение формы корпуса от формы тела вращения может
происходить из-за различного рода «надстроек», например обтекателей,
антенных устройств и т. д.
Аэродинамическое сопротивление корпуса зависит от расположения
надстроек. Исследования показывают, что наименьшим сопротивление будет при
среднем расположении надстроек на корпусе. При выносе вперед надстроек
сопротивление возрастает из-за повышенного давления на носовую часть,
а при заднем расположении оно увеличивается вследствие срыва потока
и повышения разрежения за дном.
680 Глава XV
Крылья и оперение. При расчете сопротивления изолированных крыльев
и оперения их можно рассматривать в наиболее простом виде как
соединенные вместе консоли. Соответствующее крыло (оперение) имеет ту же площадь,
но меньший размах, чем у реальных консолей. Наряду с этим
изолированное крыло можно сформировать из консолей, которые выступают над корпусом,
и фиктивных участков, расположенных внутри корпуса. У этого крыла
сохраняется прежним размах, но увеличивается площадь. Значение Хкр (или Хоп)7
учитываемое формулой (XV-6-2), равно сопротивлению крыла (оперения) минус
сопротивление, приходящееся на среднюю фиктивную часть площади, занятую
корпусом. И в том и в другом случае определение сопротивления носит
приближенный характер. Его величина должна быть уточнена экспериментально
или более строгим теоретическим расчетом. Имея в виду, что вертикальные
и горизонтальные консоли оперения могут быть неодинаковы, целесообразно
вести для них расчет сопротивления раздельно, определяя составляющие ХВш о
и Хг. о- В соответствии с этим формулу (XV-6-2) можно написать в виде
Хо = Хт + Хкр + Хв. о + ХР. о- (XV-6-5)
Обозначая через S характерную площадь для всего летательного аппарата,
получим выражение для суммарного коэффициента лобового сопротивления
^ *^КР SB 0 , Sv о /v-rr п еч
х кр —у- + Сх в. 0-f± + Сх г. о -^- , (XV-6-6)
где 5МИД, 5кр, 5В.О, 5Г. о —соответственно площадь миделевого сечения корпуса,
площади крыла в плане, вертикальных и горизонтальных консолей оперения.
Значения £кр, SBm0, STm 0 находят без учета площадей подкорпусных
участков крыла и оперения, а схт, схкр, схв.о, схг>0 представляют собой
коэффициенты сопротивления корпуса, крыла, вертикальных и горизонтальных
консолей оперения, рассчитанных соответственно по характерным параметрам
Без учета интерференции с корпусом коэффициент сопротивления крыла
СХкр = (СХ кр)из (1 - ^-) , (XV-6-7)
где S'Kp — площадь крыла с учетом части, занятой корпусом;
AS — площадь крыла под корпусом;
(с*кр)из—коэффициент сопротивления изолированного крыла с учетом площади
под корпусом.
Влияние интерференции на сопротивление можно учесть, введя поправку
к формуле (XV-6-7) в виде
СХ Кр = \Сх Кр)иЗ ( А ^ИНТ ~~а~' I » (XV-6-8)
4 °кр '
где Аинт — коэффициент интерференции, изменяющийся в широких
пределах в зависимости от расположения крыла на корпусе и характера их
сопряжения, а также формы и удлинения крыла. При небольшой стреловидности
и удлинении (А,кр > 2) крыльев, хорошо сопряженных с корпусом, величина
&инт мало отличается от единицы. При наличии положительной
интерференции, уменьшающей сопротивление, кинт >> 1.
Сопротивление горизонтального и вертикального оперения при су — О
вычисляется так же, как сопротивление крыла.
Полное сопротивление. Обычно влияние интерференции на полное
сопротивление аппарата, как показывают экспериментальные исследования,
оказывается небольшим и может быть учтено введением к сопротивлению
Хо некоторого суммарного поправочного коэффициента интерференции кс.
Стационарное обтекание 681
В соответствии с этим полное сопротивление
Xc = Xokc. (XV-6-9)
В зависимости от условий (скорость полета, конструкция летательного
аппарата и т. д.) коэффициент кс может быть больше или меньше единицы;
в большинстве случаев, представляющих практический интерес, величина
этого коэффициента мало отличается от единицы.
Приближенный расчет полного
сопротивления при су = 0. В практических случаях при вычислении полного
сопротивления можно принять, что сопротивление трения не зависит от
интерференции. Тогда следует учитывать изменение только сопротивления
от давления вследствие взаимного влияния крыльев и корпуса. Это
изменение пренебрежимо мало, если крылья установлены на цилиндрической
поверхности корпуса.
В том случае, когда крылья находятся на сужающихся или
расширяющихся участках корпуса, интерференционное сопротивление целесообразно
учитывать. Приближенно величину Хкр(т) можно найти, полагая, что
консоли расположены в поле давления изолированного корпуса, а значение
Хт(Кр) определить, исходя из предположения, что корпус находится в поле
давления изолированного крыла, которое вычисляется по сверхзвуковой
теории крыла.
Практический интерес представляет также расчет сопротивления с
учетом интерференции по методу эквивалентного тела [51].
В основе этого метода лежит следующее правило: сопротивление
комбинации корпус — крыло равно сопротивлению изолированного корпуса,
имеющего то же распределение площадей поперечного сечения, что и комбинация
корпус — крыло. Такой изолированный корпус называется эквивалентным
телом. Сформулированное правило известно в аэродинамике как правило
площадей.
В рассматриваемом методе существенным моментом расчета является
построение эквивалентного тела. Для этой цели комбинация корпус —
крыло рассекается поперечными плоскостями, перпендикулярными
продольной оси, и измеряется площадь в выбранном сечении комбинации.
Эта площадь считается принадлежащей эквивалентному телу, которое
отличается по внешнему виду от заданного корпуса тем, что начиная с
сечения, где расположены передние кромки крыла, такое тело приобретает
выпуклую форму. Если задние кромки крыла расположены перед концевым
сечением корпуса, то эквивалентное тело у кормы за пределами крыльев
не будет отличаться от корпуса.
Если известно эквивалентное тело, то определение сопротивления
комбинации корпус — крыло может быть осуществлено двумя способами.
Во-первых, можно применить формулы (IV-4-30). Находящиеся под
интегралами этих формул выражения для вторых производных S" (x), S" (г)
определяются для эквивалентного тела. Во-вторых, если известно
экспериментально определенное сопротивление эквивалентного тела, то его можно
использовать для определения сопротивления данной комбинации корпус —
крыло. В этом случае необходимо поступить следующим образом. По
экспериментальным данным строится кривая Асх = / (Moo), где Асх = сх —
— сх0 равно разности между сопротивлением сх при данном числе Моо и
постоянным сопротивлением сх0 при дозвуковой скорости. Полагая далее, что для
заданной комбинации корпус — крыло сопротивление с*0 известно, можно
для нее подсчитать полное сопротивление с учетом интерференции с" =
= скх0 + Асэх.
682
Глав
XV
7
п
Рис. XV-6-1. Построение оптимальной
формы комбинации корпус — крыло:
вверху — тело вращения минимального
сопротивления; внизу — соответствующая
оптимальная форма комбинации корпус —
крыло. Площади сечений 1 — 1 и II — II
равны
В сверхзвуковом диапазоне скоростей изложенный метод применим
только для очень тонких конфигураций, располагающихся вблизи оси
конуса Маха и имеющих, следова-
/ тельно, стреловидные крылья малого
удлинения. Метод можно применять
и для нестреловидных крыльев при
условии Моо<1.
Экспериментальные исследования
показывают, что правило площадей
можно использовать для получения
такой компоновки летательного аппарата,
которая бы обеспечила в области
трансзвуковых скоростей наименьшее
сопротивление. В соответствии с этим
правилом летательный аппарат
следует конструировать таким образом,
чтобы площади его поперечных
сечений, перпендикулярных к
направлению потока, изменялись вдоль оси
аппарата по тому же закону, что у
тела вращения с минимальным
сопротивлением (рис. XV-6-1).
На рис. XV-6-2 показана экспериментальная зависимость от чисел Моо
коэффициента сопротивления при су = 0, из которой видно, что
комбинация крыло — корпус, спроектированная по
правилу площадей, имеет меньшее
сопротивление по сравнению с комбинацией,
спроектированной без учета этого правила.
Метод эквивалентного тела может дать
удовлетворительные результаты для
околозвукового диапазона чисел Моо и, следовательно,
он ограничен для заданной комбинации неко-
торым предельным числом Моо > 1.
Сверхзвуковое правило
площадей [51]. Если число Моо превосходит
предельное число Моо и метод эквивалентного
тела неприменим, то для расчета
сопротивления можно использовать сверхзвуковое правило
площадей. В соответствии с этим правилом
определяется величина площади сечения данной
комбинации плоскостями, которые не перпен- о,84 0,92 1,00 Щ Ма
дикулярны продольной оси (как в методе
эквивалентного тела), а представляют собой
наклонные плоскости, касательные к конусу Маха
(рис. XV-6-3), с уравнением
х + a' (z sin у + у cos у) = х0. (XV-6-10)
'А
\
А
\ /
\|/
"хО
0,16
пня
и,ио
/^
3
'2
1
Рис. XV-6-2. Сопротивление
летательного аппарата,
спроектированного по «правилу
площадей»:
1 — корпус наименьшего
сопротивления; 2 — комбинация
корпус — крыло, спроектированная
по «правилу площадей»; 3 — такая
же комбинация, в компоновке
которой не учитывается «правило
площадей»
Площадь S(х0, у), отсекаемая этой
плоскостью от комбинации корпус — крыло, является
функцией меридионального угла у и координаты
#о начала конуса Маха (рис. XV-6-3). По величине
S (х0, у) можно вычислить проекцию этой площади на плоскость, нормальную оси х,
Sn (*о, У) - sin \iS (*„, V), (XV-6-11)
где sin \i = 1-i— .
«Стационарное обтекание
683
Для расчета сопротивления можно применить формулу (IV-4-30),
осуществив подстановку S" (х, у). При фиксированном значении угла у эти
формулы дадут для заданной комбинации величину с% = dcx/dy, равную
коэффициенту сопротивления
эквивалентного тела. Чтобы
получить коэффициент
сопротивления схвсей комбинации,
сопротивления эквивалент- \ \ \ /
ных тел осредняются по
углу у:
л
£х = А ^ сэ dy. (XV-6-12)
Рис. XV-6-3. Сверхзвуковое «правило площадей»:
1 — корпус; 2 — крылья; з — конус Маха с углом
(X = arc sin (1/Mqq); 4 — секущая площадь, наклоненная
под углом 7; 5 — площадь сечения, определяемая по
сверхзвуковому «правилу площадей»
Сопротивление при
Полное сопротивление X
летательного аппарата при
су Ф О может быть
представлено в виде суммы
сопротивления Хо при нулевой
подъемной силе, индуктивного
сопротивления Xt крыльев и
оперения, сопротивления АХа, включающего некоторые неучтенные
сопротивления (рост сопротивления от давления на корпус при а Ф 0,
увеличение сопротивления из-за срыва потока на крыле, оперении и корпусе
и т. д.). Таким образом,
X = Хо + Xt + АХа. (XV-6-13)
В соответствии с этой формулой выражение для полного коэффициента
сопротивления пишется в виде
— сх0 ~f~ схг
(XV-6-13')
где коэффициент индуктивного сопротивления cxi можно рассматривать как
сумму индуктивных сопротивлений крыла (СдОкр и оперения {cXi)T. 0, равных
соответственно
(СяОкр = (Схг)кр -о^~ ; (Схг)т. О = (Схг)т. о "7^" * (XV-6-14)
°мид °мид
Здесь 5кр и 5Г,о представляют собой площади изолированного крыла и
оперения с учетом площадей, занятых корпусом. Коэффициент Асха в (XV-6-13')
вычисляется по формуле Асха = AXaJqooSmvm, причем силу АХа можно
рассматривать как сумму трех слагаемых. Первое из них представляет
добавочное сопротивление корпуса при появлении угла атаки, второе
ж третье слагаемые равны соответственно неучтенным сопротивлениям
крыла или оперения. Таким образом, суммарный коэффициент сопротивления
= сх0 ~i~ (px
■ + (е«*)г. о-
Асх
(XV-6-15)
При дозвуковых скоростях коэффициенты индуктивного сопротивления
крыла и оперения можно вычислить соответственно по формулам
я (Хдф)
кр
' у \^xi)v. о —
я (^эф)г. о '
(XV-6-16)
684
Глава XV
в которых коэффициенты подъемной силы находятся для изолированных
крыльев и оперения по действительному размаху консолей. Для учета
интерференции введены эмпирические коэффициенты (А,Эф)кр и (А,Эф)г.О9.
эффективные удлинения, вычисляемые по формулам
где Якр и Яг.о — удлинения изолированных крыльев и оперения; (Si)KVr
(Si)r.o — площади крыла и оперения, занятые корпусом.
Практически индуктивное сопротивление оперения не вычисляется
и его величина для всего летательного аппарата принимается равной cxi =
= (ся0кр- Коэффициент подъемной силы, по которому вычисляется cxir
можно принять таким, как у аппарата в целом,
т. е. считать, что (cy)IiV = cy. Тогда суммарный
коэффициент сопротивления
0,03
0,02
^эф
+ Асха, (XV-6-18)
где АЭф=!
Рис. XV-6-4. Поправка к
сопротивлению за счет
больших углов атаки
Поправку Асха можно определить
экспериментально. На рис. XV-6-4 приведены опытные
данные [23] для величины Асха в зависимости
от отношения су/су тах. При пользовании графиком
можно считать, что у летательного аппарата
Су/Cymax практически такое же, как у крыла.
Формула (XV-6-18) дает зависимость для
коэффициента лобового сопротивления от
коэффициента подъемной силы. В графической форме эта
зависимость представляется полярой летательного аппарата, семейства
которых можно построить, задаваясь различными числами М<х>.
При сверхзвуковых скоростях в тех случаях, когда подсасывающие
силы отсутствуют, коэффициенты сопротивления, зависящего от подъемной
силы, будут равны для крыла и оперения соответственно
(СхОкр = (су)кр акр; (cxi)T, о = (су)г. о аГ. о (XV-6-19)
или
\Cy)V. О
[pxi)r. о —*
Юг.
(XV-6-19')
Подсасывающие силы, возникающие на дозвуковых передних кромкахт
уменьшают индуктивное сопротивление. Однако практически на тонких
крыльях подсасывающие силы реализовать не удается. Ввиду этого
формулы (XV-6-19) можно использовать и для дозвуковых передних кромок
стреловидных крыльев.
Углы атаки акр и аг. 0 включают углы атаки корпуса а и установочные
углы крыла бкр и оперения бг>0. Значения (cy)KV, (Су)г.о определяются
с учетом интерференции с корпусом; кроме того, коэффициент (су)т,0
должен вычисляться с учетом влияния крыла.
Величину Асха можно принять равной дополнительному
сопротивлению корпуса при появлении угла атаки. При небольших углах атаки эта
величина вычисляется по формуле
Асха = асут, (XV-6-20)
в которой коэффициент подъемной (или нормальной) силы может быть
вычислен с учетом интерференции с крылом и оперением. Вместо такой
Стационарное обтекание
685
схемы расчета можно применить следующую методику вычисления
суммарного сопротивления. Составляющая коэффициента сопротивления для
всего летательного аппарата, обусловленная углом атаки, принимается
равной
2
с2
= су(а — а0) или cxi = -£- .
с
(XV-6-21)
Здесь имеется в виду несимметричная схема летательного аппарата, у
которого подъемная сила равна нулю при некотором угле атаки корпуса а = а0.
Коэффициент подъемной силы су при малом а
может быть принят с известным
приближением равным его величине для крыла. Для
повышения точности расчетов коэффициент
су лучше вычислять с учетом влияния
корпуса и оперения. Имея в виду (XV-6-21),
можно написать уравнение для поляры в
следующем виде:
с, г
W
ьх —
- -Н- , (XV-6-22)
0,6
ОА
О
/
/^
/
/
-—■
^—
/
-ДО
3
0,02 0,0U
Рис. XV-6-5. Поляры
летательного аппарата
где с°х соответствует нулевой подъемной силе.
В качестве иллюстрации сетка поляр
приведена на рис. XV-6-5. Применение
стреловидных крыльев малых удлинений
позволяет уменьшить с£ в диапазоне чисел Моо =
= 1 -f- 3. Однако при этом ухудшаются
несущие свойства летательного аппарата, т. е.
снижается с® и тем самым возрастает общее
сопротивление аппарата. При больших су
величина cxi у аппарата со стреловидными крыльями малых удлинений настолько
возрастает, что их преимущество, связанное с уменьшением сх, теряется,
так как увеличивается суммарное сопротивление.
Указанная рекомендация по расчету поляры летательного аппарата
справедлива в том случае, когда можно расчленить общее сопротивление
на величину сх и сопротивление, зависящее от подъемной силы. При
больших Моо > 5 такое расчленение невозможно, и коэффициент
сопротивления надо находить отдельно для каждого угла атаки, пользуясь
рекомендациями, изложенными выше для крыльев и корпусов.
Аэродинамическое качество
Величина аэродинамического качества определяется отношением
С j,
Сх
Внося в эту формулу вместо сх выражение (XV-6-13') и пренебрегая
в нем величиной Дсха, получим
где А = 1/(пХЭф) — при дозвуковых и А = 1/с% — при сверхзвуковых скоростях.
Важной характеристикой летательного аппарата является максимальное
качество. При дозвуковых скоростях его величина
__ 1 Л
пХэ
(XV-6-24)
686
Глава XV
Соответствующий этой величине наивыгоднейший коэффициент
подъемной силы
^наив = 1/яХэф4. (XV-6-25)
При сверхзвуковых скоростях
V, (XV-6-26)
-Vе ус
y
угла стреловидности уменьшаются с°х и Су
(XV-6-27)
Применение стреловидных крыльев и крыльев малых удлинений
снижает значения су наив> так как с уменьшением удлинения и увеличением
Характер изменения су наив в
зависимости от стреловидности крыльев
виден из рис. XV-6-6.
При аэродинамической компоновке
аппарата необходимо обеспечить
повышение аэродинамического качества. С
этой целью, во-первых, следует
выбирать достаточно тонкие профили с малой
кривизной, обладающие малым
сопротивлением. Что касается формывпланег
то наивыгоднейшим с точки зрения
повышения качества является
треугольное крыло. Во-вторых, можно
варьировать углом стреловидности и
удлинением крыла. Увеличение угла % в
пределах чисел Моо, соответствующих
дозвуковой передней кромке, а также
уменьшение удлинения ведет к
снижению с°х. В современных аппаратах угол%
достигает 70°[23], а удлинение Хкр —2
и меньше. Следует, однако, иметь в виду,
что увеличение стреловидности и
уменьшение удлинения приводит к
ухудшению несущих свойств крыла, т. е. к
снижению Су. При аэродинамическом
проектировании необходимо определять
оптимальные величины удлинения и
стреловидности, при которых качество
получается наибольшим. Указанный
вывод относится в основном к
трансзвуковому диапазону чисел Моо. При
больших числах Моо > 3 форма крыла в
плане почти не влияет на аэродинамическое
качество, а решающим фактором
является толщина профиля.
Наконец, в-третьих, для получения
наибольшего аэродинамического
качества следует надлежащим образом выбрать форму корпуса и обеспечить
его сопряжение с крылом и оперением. Форма корпуса выбирается такой,
как у изолированного корпуса с минимальным сопротивлением при данном
Моо или, по крайней мере, близкой к наивыгоднейшей.
При компоновке всех элементов аппарата и, прежде всего, крыла
и корпуса необходимо стремиться к обеспечению положительной интерферен-
Рис
XV-6-6. Поляры летательных
аппаратов
/
s**z~—
2
\
0,0k
0,02
0,75 Щ 1,25 1,50 1,75 2,00 Ма
Рис. XV-6-7. Изменение сопротивления
у двух типов самолетов:
/ — дозвуковой самолет; 2 — сверхзвуковой
Стационарное обтекание
687
ции, ведущей к снижению сопротивления. На рис. XV-6-7 показано, что
выбором аэродинамической схемы, соответствующей современному
сверхзвуковому самолету (достаточно тонкое стреловидное крыло малого удлинения),
можно значительно снизить
сопротивление, особенно в условиях
трансзвуковых скоростей, что
вместе с тем ведет к повышению
аэродинамического качества. Однако
независимо от компоновки,
максимальное качество KmSiX при
сверхзвуковых скоростях всегда
значительно меньше, чем при
дозвуковых (рис. XV-6-8).
При дозвуковых скоростях
наибольшим качеством обладают
аппараты с крылом малой
стреловидности и большого удлинения.
"max
20
in
\
0
0,5
MQ
Рис. XV-6-8. Максимальное качество
летательных аппаратов
При приближении скорости полета
к скорости звука их качество резко падает. Менее значительно меняется
от числа Моо качество аппаратов, имеющих трапециевидные и треугольные
крылья. Причем треугольное крыло с малой относительной толщиной,
поставленное на аппарат типа «бесхвостка», обеспечивает некоторое
повышение качества благодаря большой стреловидности и малому удлинению.
Главка XVI
АЭРОДИНАМИКА
ОРГАНОВ
УПРАВЛЕНИЯ.
§ XVI-1. Силы,
создаваемые аэродинамическими
органами управления
Интерцепторы
Рассмотрим некоторые результаты экспериментальных исследований,
полученные по данным продувок интерцепторов, расположенных на конце
плоской пластинки ([76], 1962,
лс п ,0 № 4-5).
N '' хг ' На рис. XVI-1-1 приведены
данные для безразмерного
коэффициента AcN, равного
отношению нормальной силы AN,
создаваемой интерцептором, к
величине qh (q — скоростной
напор, h — высота
интерцептора). На рис. XVI-1-2 даны
экспериментальные графики для
величины AcNIAcR, где AcR =
=■- AR/qh (AR — осевая сила,
создаваемая интерцептором).
Расчеты коэффициентов AcN и AcR
велись для интерцептора
шириной 1 см и, следовательно,
площадью, равной h.
Эти данные указывают на
зависимость силового
воздействия для интерцепторов от его
длины 1И, высоты h и числа Mi
перед интерцептором.
Опыты показали ([76], 1962,
№ 4—5), что увеличение
положительных углов атаки
увеличивает значения AcN и AcR и,
наоборот, увеличение
отрицательных значений углов атаки
несколько уменьшает AcN. В этих
опытах скоростная киносъемка,
проводимая при выдвижении
интерцептора со скоростью 7 мм
за 5-10-3 сек при Mt = 2,21,
позволила установить, что в
каждый момент времени картина
течения около интерцептора соответствует картине течения при
установившемся потоке. После вдвижения интерцептора внутрь пластины скачки
уплотнения исчезали за 210~4 сек. Это дает основание проводить расчет
Рис. XVI-1-1. График зависимости коэффициента
нормальной силы &CN, создаваемой концевым
интерцептором, от числа Mi и размеров
интерцептора:
Знак
О
О
А
V
D
#
Ш
h, мм
2
3
3
о
8
2
6
8
ilV лш;
> 100
J
| 50
«а, _|_ с боковыми пластинами
Аэродинамика органов управления
689
колеблющихся интерцепторов, используя гипотезу стационарности. Для
таких интерцепторов нормальная сила определяется формулой
AN = AcNqhlmk, (XVI-1-1)
где k = (ti — t2)/(ti + t2) — так называемый коэффициент команды;
ti —время пребывания интерцептора в верхнем положении;
h — время пребывания интерцептора в нижнем положении.
Данные экспериментов показывают, что наличие пластин,
установленных параллельно потоку и препятствующих перетеканию воздуха через
/
\
▲
▼" ■*-
▼•
2,0
3,0 М1
Рис. XVI-1-2. График зависимости
отношения коэффициентов нормальной и
продольной сил, создаваемых концевым
интерцептором, от числа Mi и размеров
интерцептора:
///////////////^^^
Рис. XVI-1-3. Схема к расчету
интерцептора
боковые кромки интерцептора,
увеличивает AcN ([76], 1962, № 4—5).
При сверхзвуковых скоростях
потока, набегающего на интерцеп-
тор, его высоту следует выбирать
равной h > 56, где б — толщина
пограничного слоя перед интерцепто-
ром (рис. XVI-1-3). Может быть рекомендована следующая
последовательность расчета эффективности интерцептора.
1. По числу Mi потока перед интерцептором и значению числа Re,
определенного для расстояния от передней кромки крыла до интерцептора,
Знак
▲
V
h, мм
4
6
6
Примечание
с боковыми пластинами
без боковых пластин
с боковыми пластинами
}
0,2
0
-—
—,
—=
Р
-—.
■"—.
——
/
=
;/
■-—
—
*>,
——
2,0
2,5
Рис. XVI-1-4. График зависимости коэффициента
донного давления за пластинкой от числа Mi набегающего
на интерцептор потока и высоты его выдвижения h мм
рассчитывается коэффициент давления в срывной зоне за скачком уплотнения
перед интерцептором. Для ламинарного пограничного слоя
~- УЧпм. (XVI-1-2)
44—114
690 Глава XVI
а для турбулентного
Р2 = ——ттг . (XVI-1-3)
ReO,i(Mf —1)1/4 V Г
2. Полагая, что граница застойной зоны прямолинейна и проходит через
вершину интерцептора, определим
A<* = jp2/tgpo. (XVI-1-4)
Для вычисления осевой силы, создаваемой интерцептором, можно
использовать график на рис. XVI-1-4, где приведены результаты
экспериментального исследования коэффициентов донного давления рдон за интерцептором
в зависимости от числа М4 и высоты интерцептора h для случая, когда нет
боковых пластин. Зная коэффициент давления за интерцептором, можно
подсчитать коэффициент создаваемой им продольной силы
А Р2— Рдон А — —
Лсд = или AcR = р2 — ^дон.
Пример. Определить нормальную и осевую силы, создаваемые концевым
интерцептором, расположенным на расстоянии # = 0,140 м от передней кромки крыла и
обтекаемым потоком воздуха с числом Mi = 1,83. Высота интерцептора /& = 8 мм, длина
/и = 100 мм. Полет происходит на уровне моря (высота траектории i/^0).
По этим данным находим скорость полета У\ = М4а = 1,83*340 = 622 м/сек и число»
Re = 71a;/v = 622'0,140/l,46-10~5 = 6-106. Считая режим течения в пограничном слое
перед интерцептором турбулентным, найдем коэффициент давления в застойной зоне:
- 2,04 2,04
Р2 Re0'1 (Mf-l)1'4 (6-106)0'1 (1,832-D1/4 '
Отношение давлений
p2/Pi = l + kMlp2/2 = 1 + 1,40-1,832.0,346/2 = 1,81.
Угол наклона скачка
9С = arcsin
= arcsin У(1,81 + 0,167)/[(1 + 0,167) 1,832] = 45,5°,
=0'167-
Далее вычисляем угол поворота потока за скачком уплотнения:
tg (0с - рс) = {tp2/Pi+1) №+Р2/Р1Г1 tg ec=
= (0,167-1,81 + 1) (0,167 + 1,81)"! tg45,5° = 0,669;
tgpc = 0,2065.
Коэффициент нормальной силы
Aciv = ^2/tgPc = 0,346/0,2065 = 1,67.
Следовательно, нормальная сила
25;6222 8-10-3.0,1 = 32,4 пГ (318 н).
По графику на рис. XVI-1-4 для Mi = 1,83 и h = S мм находим р^ои^ — 0,3,
то т?2~0>346, опр
= 12,5 кГ (123 н).
Учитывая, что /?2~0,346, определяем коэффициент Дсд = 0,346+ 0,3 = 0,646 и силу
Аэродинамика органов управления
691
Увеличение подъемной силы
аэродинамических органов
управления путем вдувания газа
в пограничный слой
Вдувание в пограничный слой некоторого количества газа позволяет
сдвинуть точку отрыва к задней кромке руля и тем самым обеспечить
увеличение управляющего усилия ([70], 1965, № 5).
Определение необходимого количества вдуваемого газа связано с
вычислением коэффициента количества движения струи газа, вычисляемого из
выражения
_ 2,35А6** _ PcFc A
(XVI-1-5)
где рс, Fc— соответственно массовая плотность и средняя скорость газа в струе;
А — ширина щели;
Ъ — хорда руля.
Параметр Аб** представляет собой приращение толщины потери импульса
пограничного слоя при отсутствии вдувания на участке от точки отрыва S
до точки К на задней кромке руля (рис.
XVI-1-5). Этот параметр вычисляется
по формуле
Аб*
= 0,037 (У6К\
-з
Reo,2
X
Рис* XVI-1-5. График распределения
X
где xs^sj
F6 — скорость невязкого обтекания
безотрывным потоком;
Убк ~~ скорость в точке К.
Если аэродинамический руль поме-
щен на задней кромке крыла, то в фор-
мулах вместо Foo следует брать среднее
Значение СКОрОСТИ на руле. В качестве
примера определим коэффициент коли-
чества движения струи газа при
условии, что скорость потока вдоль элерона изменяется по линейному закону от
некоторого значения V6S до величины V6K = F6s/2, так что средняя скорость
Т^ср = (V6S + V6K)/2 = (3/2) V6K.
ничный слой:
V(у)-эпюра скорости потока в сечении*
перпендикулярном поверхности руля;
у () _ изменение скорости по длине руля
Средняя скорость в струе Fc =
(XVI-1-6) для этих данных:
число Re = 105. По формуле
Аб** 0,00967
[(-
6Kj
j г
0,8
5_ 1)0,8
/
V6K) \V6K
'»8 (105)0,2 (1-|_ 2)0,6 (2 — 1)0,8
-0,00583.
Соответствующее значение коэффициента количества движения
2 = 2,35-0,00583 (1-1)^ = 0,0548.
44*
692 Глава XVI
§ XVI-2. Расчет сил,
создаваемых
газодинамическими органами управления
Расчет силы тяги
газодинамических органов управления
с учетом потерь в воздухоза-
борных устройствах
Сила тяги, создаваемая при заборе воздуха из атмосферы и отбрасывании
массы продуктов сгорания топлива через сопловой аппарат, может быть
подсчитана по формуле
P = ^.Wa + ^-(wa-Va,) + (ра - Р») Л --f- , (XVI-2-1)
где Р — сила тяги;
GT — весовой секундный расход продуктов сгорания топлива;
GB — весовой секундный расход воздуха, забираемого из атмосферы;
Foo — скорость движения центра массы летательного аппарата;
wa — скорость истечения продуктов сгорания топлива из сопла;
ра — давление в струе в выходном сечении сопла;
Sa — площадь выходного сечения сопла;
Q — количество движения воздуха и продуктов сгорания топлива
относительно летательного аппарата.
Производная dQ/dt носит название вариационной силы.
Для ракетных двигателей, не использующих воздух атмосферы,
зависимость (XVI-2-1) упрощается:
P = ^JLWa + {Pa-Poo)Sa-§- (XVI-2-2)
При заборе воздуха лобовое сопротивление увеличивается на величину
АХВЗ добавочного сопротивления воздухозаборника, связанного с тем,
что во входном сечении воздухозаборника значения давления pi и скорости
воздуха Wi отличаются от соответствующих параметров в невозмущенном
набегающем потоке роо и Woo = Foo. Это добавочное сопротивление
АХВЗ = 5t (Pl - poo) —^ (Foo - wt). (XVI-2-3)
Зависимость (XVI-2-1) определяет силу тяги в условиях воздействия
на нее неподвижной атмосферы. Однако наличие воздухозаборных устройств,
сопловых аппаратов и струй продуктов сгорания топлива, истекающих из
них, изменяет картину обтекания летательного аппарата воздушным потоком.
Поэтому при определении аэродинамических коэффициентов необходимо
учитывать влияние скачка уплотнения перед воздухозаборником, усилий
на наружные поверхности воздухозаборников и сопел, интерференции между
воздухозаборниками и крылом или корпусом летательного аппарата и,
наконец, влияние струй на поток воздуха у поверхности летательного аппарата.
Коэффициент лобового сопротивления головной части корпуса
летательного аппарата или гондол его двигательных установок, в которых
расположены воздухозаборники, определяется зависимостью
Сх гол = {Сх гол)Ф=1 + (&Сх вз — Сп. вз) "7г^— , (XVI-2-4)
^мид
Аэродинамика органов управления
693
где ф = GB/(poogVooSi) — коэффициент расхода воздуха, равный отношению
действительного секундного расхода воздуха к
максимально возможному [21];
(£*гол)ф=1 —коэффициент лобового сопротивления головной части
при ф = 1;
&сх вз — коэффициент добавочного сопротивления
воздухозаборника;
Сп. вз — коэффициент подсасывающей силы воздухозаборника;
Si — площадь поперечного сечения входа в воздухозаборник.
Воздухозаборники без центрального тела. При <р = 1 и сверхзвуковых
скоростях коэффициент схтол = (схгол)ф=1 и его можно определить по
графикам, приведенным на рис. XVI-2-1 и XVI-2-2.
^ТОУ! СХГ0Л
0,2
Oft 0,8
Рис. XVI-2-1. График для определения Рис. XVI-2-2. График для определения
коэффициента лобового сопротивления па- коэффициента лобового сопротивления ко-
раболической головной части летательного нической головной части летательного
аппарата с протоком при ф = 1 (^тол — аппарата с протоком при ф = 1
= ^гол/^мид; Лгол = ^i/^мид)
При ф<1 и дозвуковых скоростях полета при условии, что наружная
поверхность у входного сечения воздухозаборника достаточно закруглена,
0,8
0,4
■ О
\
1—.
s
ч.
/
к
-—.
X
/
0,2
0,4 0,6
1,2
0,8
QM
О
\
S
>
/
- зр
//2,4
^1,0
0,2
0,6
Рис. XVI-2-3. График для определения
коэффициента подсасывающей силы
воздухозаборника
Рис. XVI-2-4. График для определения
коэффициента добавочного сопротивления
воздухозаборника
Глава XVI
можно считать cXT0Jl ж (схгол)ф=1- Это объясняется тем, что подсасывающая
сила достаточно велика и равна силе добавочного сопротивления
воздухозаборника. При ф<1 и сверхзвуковых скоростях расчет силы
сопротивления головной части усложняется, так как перед головной частью возникает
отсоединенный скачок уплотнения. Однако приближенно можно (сЗСГОл)ф=1
находить по тем же рис. XVI-2-1 и XVI-2-2, а для определения сПт вз
использовать график, показанный на рис. XVI-2-3 [21], справедливый для таких
воздухозаборников, у которых передняя кромка закруглена, а обвод
головной части криволинейный. Иначе величина сп.вз будет значительно меньше,
чем это следует из графика. Значение коэффициента Асхвз определяется
из графика на рис. XVI-2-4.
Пример. Найти коэффициент лобового сопротивления параболической головной
части летательного аппарата с воздухозаборным устройством без центрального тела
при следующих данных:
Моо = 2; Яоо = 340 м/сек\ роо «0,125 кГ* сек/м*;
вв = ШкГ/сек; da = 0f56 ж; <2мид = 0,80 Щ ^гол = 3.
Определяем:
<*аА*мид== 0,56/0,80 = 0,70; SMm
—1АГОЛ = У 2^1/3 = 0,577; 7оо = Моойоо = 2-340 = 680 м/сек.
По графику рис. XV1-2-1 находим
гол (°х гол)ф=1==0,22,
откуда
(с* гол)Ф=1 = 0,22/3* = 0,024.
Коэффициент
y = GB/(poogVooS1) = 1,44/(0,125.9,81.680.0,246) =0,70.
По графику рис. XVI-2-3 находим сп. вз — ^,06, а по графику рис. XVI-2-4
определяем Асхвз = 0,38.
В соответствии с этими данными
^ ^^
= 0,024 +(0,38-0,06)
Воздухозаборники с центральным телом. Их целесообразно применять
при скоростях полета, соответствующих числам Моо > (1,8 -f- 2,0). Ниже
приводятся данные для двухскачковых воздухозаборников. Расход воздуха
через такой воздухозаборник может быть рассчитан по зависимостям для
конических течений. Результаты расчетов приведены на рис. XVI-2-5 в виде
зависимости предельного коэффициента расхода Ф от числа М полета,
значений углов конуса центрального тела рк и угла выноса его относительно
передней кромки воздухозаборника |3Вын (Рис- XVI-2-6). Коэффициент
ф_ Ев max (XVI-2-5)
где GB max — максимально возможный секундный расход с учетом отклонения
струек воздуха системой скачков перед воздухозаборником,
a 51 = jtdJ/4.
В зависимости от значений ф и Ф возможны различные положения
скачков уплотнения, которые приведены на рис. XVI-2-6. При этом следует
учитывать, что воздухозаборные устройства рассчитывают на определенное
число Моо = Мрасч (случай а на рис. XVI-2-6).
При изменении числа Моо в полете необходимо регулировать параметры
воздухозаборника, иначе либо ф будет меньше 1 и возникнет добавочное
сопротивление Асхвз (случай виг); либо будут повышенные потери полного
давления за системой скачков (случай б). В случае г, который имеет место
при малой площади «горла» (сечение в самом узком месте входного канала
Аэродинамика органов управления
695
воздухозаборника), может возникнуть неустойчивая работа
воздухозаборника, связанная с периодическим перемещением скачков уплотнения вдоль
по центральному телу. Это явление, называемое помпажом, связано со еры-
а)
ш
1,3,
1,8,
\Уу
.—
К
у
1
I
ч
Ц2
о,г у о,б
зо
0,2
0,6 0,8
^—■
~ —
Si
у
——•
У
б<
у
</
\^
Рис. XVI-2-5. График для определения идеального
коэффициента расхода воздуха для следующих
значений углов центрального конического тела:
вом потока с центрального тела за скачком уплотнения, с пульсацией потока
ж приводит к тряске двигателя, к прекращению работы или даже к поломке
«его. Неустойчивая работа двигателя может иметь место в случае Мао > МраСч
г)
Рис. XVI-2-6. Различные виды скачков уплотнения перед' воздухозаборником
с центральным коническим телом:
а — расчетный режим Ф = ф = 1; нерасчетные режимы: б — Ф = ф = 1; в — ф = Ф < 1; г — ф < Ф ^ 1
(случай б), или когда площадь горла чрезмерно велика. Поток в
перерасширенном канале воздухозаборника отрывается от стенок, образуются вихри
и пульсации потока. Частота этих пульсаций выше, чем при помпаже
696
Глава XVI
поэтому они воспринимаются человеком как «зуд». Такой режим работы
также недопустим.
Если воздухозаборник находится в потоке воздуха под значительным
углом атаки а (или большим углом скольжения рск), то на входе в него
образуется сложная картина течения, плохо поддающаяся расчету
(рис. XVI-2-7). Характеристики работы двигателя при этом ухудшаются,
а Асхвз резко возрастает. Это накладывает ограничения на величины углов
ы и Рек? усложняет систему управления и увеличивает ее вес.
Зная параметры рк, рВын и Мое и определив на рис. XVI-2-5 значение
Ф, можно найти по данным рис. XVI-2-8 [21] Асхъг. Пунктирные линии
на этом рисунке показывают
минимально возможные значения
А^эсвз в случае, когда ф = Ф.
Величина коэффициента (сЛГОл)ф=1
в формуле (XVI-2-4) определяется,
как и в предыдущем случае, по
графикам рис. XVI-2-1 и XVI-2-2,
а коэффициент сп.вз в первом
приближении можно не учитывать,
так как при Моо > 1,8 -f- 2,0
передние кромки воздухозаборников
заострены и обводы их, как
правило, прямолинейны.
Расчет боковых
воздухозаборников с коническим центральным
телом, например полукруглых,
1 —косые скачки уплотнения; 2 — центральное
тело; з — обечайка; 4 — замыкающие скачки в гор- ПРОВОДИТСЯ анаЛОГИЧНО ПреДЫДу-
ловине; 5 — криволинейные скачки уплотнения щеМу. У боКОВЫХ ВОЗДуХОЗаборНИ-
ков с теми же исходными данными,
что у круглых, значения коэффициента ф и коэффициента восстановления
давления получаются на 3 -г- 6% менее, но зато постановка боковых
воздухозаборников увеличивает коэффициент лобового сопротивления
летательного аппарата на меньшую величину, чем постановка круглых.
Расчеты многоскачковых, кольцевых и других типов воздухозаборников
приводятся в специальной литературе.
Пример. Для данных предыдущего примера найти коэффициент лобового
сопротивления параболической головной части летательного аппарата, имеющего воздухоза-
борное устройство с центральным телом (двухскачковый диффузор) с параметрами
Рвын = 32°; рк = 20°.
По графику (см. рис. XVI-2-5, б) находим Ф = 0,75, тогда согласно формуле
(XVI-2-5) GBmax-0,75-0425-9,81.680-0,246 = 154 кГ/сек. По графику (рис. XVI-2-8, б)
находим Асх вз = 0,175. Далее по графику (см. рис. XVI-2-1) определяем, как и в
предыдущем примере (с# гол)ф==1 = 0,024. Полагаем сп. вз = 0, следовательно, по
формуле (XVI-2-4) находим
Рис. XVI-2-7. Схема обтекания
воздухозаборника потоком под значительным углом атаки:
Влияние работы воздухозаборника на величину подъемной силы
летательного аппарата. Это влияние сказывается вследствие изменения
направления струи воздуха на входе в канал воздухозаборника при угле атаки
а Ф 0. Коэффициент подъемной силы изменится на величину
Асу вз = 0,035фа, (XVI-2-6)
где а —угол атаки в градусах;
Ф — коэффициент расхода воздуха, проходящего через воздухозаборник.
Наличие на летательном аппарате воздухозаборных устройств
заставляет в процессе его проектирования тесно увязывать аэродинамические ис-
следоввния с расчетами двигательной установки ввиду их взаимного влияния.
Аэродинамика органов управления
69Г
0,5
0,5
Ofi
0,3
0,2
0,1
О
а)
я
0,7 0,8 0}9 (f
0,1
0,1+ 0,5 Op 0,7
1
\
Щ
\
\ \
V
V
\
Ьч1
\
\\
\\
\
\
л
у
X
\\\
N
^>
\
\
\
А
%
\
. \
\
\
\
\
\
\
\>
\
\
\\
V
V
-3
\Л8
А
Ч-
л
Oft 0,5 0,6 0,7
0,9 9
Рис. XVI-2-8. Графики для определения коэффициента
добавочного сопротивления воздухозаборника с центральным коническим
телом с углами:
698
Глава XVI
Неподвижные и поворотные
управляющие двигатели
В случае применения для управления полетом неподвижных
управляющих (как, правило, ракетных) двигателей, включаемых периодически,
расчет сил, создаваемых ими, сводится к определению сил тяги по
зависимости (XVI-2-1). Если время включения двигателей мало, то в период выхода
на режим и спада давления при выключении двигателя вариационная
составляющая силы тяги будет существенной и ею нельзя пренебрегать.
Если для управления полетом используется отклонение основного или
специальных поворотных верньерных двигателей, то управляющие силы,
создаваемые ими, рассчитываются путем определения проекции сил тяги
на рассматриваемое направление. Например, поворот основного двигателя
с тягой Р на угол бр создает управляющее усилие
Pyl = P sin бр, (XVI-2-7)
направленное по нормали к первоначальному положению продольной оси
двигателя и действующее в плоскости угла поворота.
Потеря тяги при повороте основного двигателя невелика, так как
проекция силы тяги на первоначальное направление продольной оси двигателя
(чаще всего это направление совпадает с продольной осью летательного
аппарата) будет
Pxl = Pcos6p. (XVI-2-8)
Поэтому в первом приближении при небольших углах поворота полагают,
что сила тяги не изменяется {Рх\ ~ P)i & управляющее усилие изменяется
линейно в зависимости от угла поворота, т. е. Pyi « P8V.
Линия действия управляющего усилия Pyi проходит через ось
вращения двигателя и это позволяет легко найти точку ее приложения и вычислить
момент относительно центра массы летательного аппарата.
Поворотные сопла
В случае, когда поворачивается все сопло, включая участок,
расположенный до критического сечения (рис XVI-2-9), расчет управляющих
Рис. XVI-2-9. Схемы поворотных сопел:
а— ось вращения лежит в плоскости, перпендикулярной оси
летательного аппарата; б — ось вращения лежит в плоскости,
перпендикулярной к линии, составляющей с осью аппарата
угол бп
усилий не представляет затруднений, поскольку с достаточной степенью
точности можно полагать, что при этом поворачивается весь вектор силы
тяги. Поэтому зависимости (XVI-2-7) и (XVI-2-8) оказываются справедли-
Аэродинамика органов управления
699
выми и в этом случае. Точку приложения управляющего усилия также
можно находить, считая, что линия действия его проходит через ось поворота
сопла. Потери тяги, связанные с поворотом сопла, могут быть больше, чем
при повороте двигателя, так как в последнем случае отсутствуют потери
в зазорах.
Расчет управляющих усилий значительно усложняется, если
поворачивается лишь некоторая часть сверхзвукового участка сопла (разрезное
сопло, рис. XVI-2-10). Дело в том,
что для поворота вокруг оси 4
необходимо обеспечить некоторые
зазоры между поворачивающейся 2
и неподвижной 1 частей сопла.
Это приводит к местному отрыву
потока от стенок сопла и к
образованию скачка уплотнения в месте
начала поворотной части сопла
даже при отсутствии поворота
(бр = 0). При повороте части сопла
картина течения изменяется: ин-
Рис. XVI-2-10. Схема течения в
сверхзвуковом сопле с поворотной частью
тенсивность скачка уплотнения 3
перед поворотной частью, надвинувшейся на поток, увеличивается, а в
диаметрально противоположном месте уменьшается, так что при некоторых
углах поворота там может возникнуть пространственная волна разрежения.
Приближенный расчет управляющих усилий, создаваемых разрезным
соплом, можно провести, используя некоторые опытные данные.
Управляющее усилие
Ур - Кэс6у pgpSp6p, (XVI-2-9)
где с6 —производная управляющего усилия по углу поворота сопла;
др — скоростной напор продуктов сгорания топлива в середине
поворотной части сопла;
Sp=Dcvlv — площадь продольного сечения поворотного сопла;
Dcv — внутренний диаметр в середине поворотной части сопла;
Zp —длина поворотной части сопла;
бр—угол поворота сопла в радианах;
Къ — коэффициент согласования с опытом.
Если число М определять в среднем сечении поворотной части сопла,
а для сь применять выражение
(XVI-2-10)
L/1 т \ ,
где X = Dcv/lv, то Кэ ж 1,24. Точкой приложения силы Ур считают
середину поворотной части сопла. Направление силы Ур в первом приближении
можно принять по нормали к оси симметрии поворотной части сопла,
проведенной в плоскости поворота.
Потери тяги при управлении поворотом сверхзвуковой части сопла
складываются из потерь при бр = 0 и потерь, вызванных поворотом части
сопла на угол бр Ф 0. Как правило, надежные данные о таких потерях
получают в результате проведения эксперимента.
Зависимости (XVI-2-9) и (XVI-2-10) позволяют выбрать длину
сверхзвуковой части сопла, необходимую для создания наибольшего заданного
усилия Ур. С этой целью выбирают, ориентируясь на экспериментальные
данные, наибольшее значение угла поворота бр тах, которое обеспечивает
примерно линейный характер зависимости Ур (бр) при 0<бр<бртах,
£р max ~ 15°. Тогда, задаваясь рядом значений Zp, определяют для выбран-
700 Глава XVI
ного целого сопла середину его поворотной части и все параметры для нее-
фср, др, М, X, £р). Это дает возможность по формулам (XVI-2-9) и (XVI-2-10)
найти соответствующие значения Fp/бр. Построив график зависимости
Ур/бр от Zp, по величине отношения Уртах/бртах находят необходимое
значение Zp.
Пример. Определить величину управляющей силы, создаваемой поворотом
сверхзвукового участка сопла на угол бр = 5°. В среднем сечении поворотной части сопла
параметры газа следующие: М = 2,43; р = 0,0822 кГ>сек2/м^; F = 1637 м/сек. Размеры
поворотной части сопла: /р = 0,0331 м; Z)cp = 0,057 м. По этим данным находим
0,057
"0,0331 ''
1=1,57;
2,432 — 1 V 2-1,722
= 1,1-105, кГ/м*;
0,0822-16372
11lU0 к!/м*
2
£р = А.р*р = 0.0331.0,057 = 0,001887 м*.
Приняв коэффициент -ЙГЭ = 1,24, подсчитываем управляющую силу:
Поворотные насадки
Для того чтобы управляющее усилие, создаваемое насадком, возникало
при минимальных значениях угла его поворота бр (чтобы не было «мертвых»-
зон), внутренняя поверхность насадка должна профилироваться в
соответствии с формой струи, истекающей из сопла. Однако необходимость поворота
насадка требует оставить между выходным сечением сопла и насадком неко-
торое пространство, что изменит форму струи и окажет определенное влияние
на течение по насадку. По выходе из сопла поток расширяется и
ускоряется, а затем, попадая на поверхность насадка, тормозится. Это
вызывает появление криволинейного отошедшего скачка уплотнения. Далее
за этим скачком происходит расширение потока в насадке. Картина течения
внутри поворотного насадка весьма близка к картине потока внутри сопла
с поворотной сверхзвуковой частью.
Сделав ряд допущений, можно упростить решение задачи об
определении управляющего усилия, создаваемого насадком. Главное из таких
допущений заключается в том, что вместо пространственной задачи течения
газа внутри насадка решается соответствующая плоская задача (в плоскости
угла поворота насадка). Криволинейные скачки уплотнения заменяются
прямолинейными косыми ударными волнами. Положение возможных точек
отрыва потока от стенок сопла можно определить по зависимостям теории
отрывных течений. Схема такого метода описывается далее применительно
к расчету усилий, создаваемых дефлектором. Применимость этого метода
для расчета поворотных насадков или поворотных сверхзвуковых частей
сопел требует экспериментального подтверждения.
Проводя расчеты по такому приближенному методу, необходимо
учитывать одну существенную особенность. Для сверхзвуковой части насадка
давление на стенки насадка будет переменным по его длине, даже если
скачок уплотнения прямолинейный. Это связано с расширением потока. Поэтому
более правильным будем считать давление на стенки насадка в
произвольном поперечном сечении равным давлению за скачком уплотнения в
соответствующей точке этого сечения.
Аэродинамика органов управления
701
Представляют интерес опытные данные по цилиндрическим насадкам
([74], 1958, № 565). Вид насадка и зависимость управляющей силы от угла
поворота, длины насадка и давления в камере двигателя приведены на
рис. XVI-2-11. Для исследуемой схемы поворотного насадка шарнирный
момент достигал 1,54 кГ-см на 1 кГ (1,54 к-см на 1 н) боковой
управляющей силы, в то время как для центрального газового руля эта величина
Ф
45
в)
\(Г/ 1<э
^
ю
го к
45
,- —
——
—«^
_____
$20
15
10
5
Щ
50,В1,
нас
Рис. XVI-2-11. Зависимость управляющей силы Ур поворотного
цилиндрического насадка (а) от угла поворота бр (б), а также от длины ZHac насадка (в):
1 — сопло, 2 —• насадок, з — положение насадка после поворота на угол бр
составляет 0,92 кГ-см/кГ. Потери тяги незначительны и мало зависят
ют конструкции входной части насадка. Можно ожидать, что от вида
конструкции в значительной степени зависит эрозионная стойкость насадка.
Опыты показывают, что оптимальная длина цилиндрического насадка
близка к 1,5 его диаметра.
Дефлекторы
При расчетах управляющих усилий возможны два случая.
Если угол поворота дефлектора бр мал, так что его поверхность
составляет с направлением потока газа из сопла угол (Зд = бр+ рсп, который
меньше критического (|3СП — угол сопла, рис. XVI-2-12, а), то перед
дефлектором возникает скачок уплотнения, близкий к прямолинейному. Зная
параметры потока в сопле перед дефлектором в плоскости его симметрии,
проходящей через ось сопла перпендикулярно оси поворота дефлектора
(Mi, р^ &i), можно по зависимостям для косого скачка уплотнения найти
для любого 8Р (при условии, что (Зд менее критического) угол скачка 0с.
Полагая далее, что закон распределения давления по поверхности будет
таким, как за косым скачком уплотнения АА' (например, давление в
поперечном сечении, проходящем через точку К, равно давлению р2 за скачком
в точке N этого же сечения), определим величину управляющего усилия:
(XVI-2-11)
(S)
где S — площадь проекции поверхности дефлектора, омываемой потоком
из сопла, на плоскость, проходящую через ось сопла и ось
поворота дефлектора.
Если угол Рд превышает некоторое критическое значение, то возникает
отрыв пограничного слоя в месте его взаимодействия со скачком
уплотнения. Повышенное давление в точке отрыва передается вверх по потоку
по дозвуковри части пограничного слоя. Это приводит к перемещению точки
702
Глава XVI
отрыва в глубь сопла. Картина течения будет такая, как на рис. XVI-2-12, а.
От точки А на внутренней поверхности сопла поток отрывается и, проходя
через скачок уплотнения АА', поворачивается на угол pci- Далее этот поток
присоединяется к поверхности дефлектора в точке В, в которой образуется
второй скачок уплотнения ВВ'. Ниже линии АВ находится застойная зона
(«жидкий клин»). За присоединенным скачком уплотнения с углом 0С2 в
точке В на поверхности дефлектора будет действовать давление р3.
АВ
2
flfi
у
/
/
/
/
/
/
/
' 1 2 3 M2
Рис. XVI-2-12. Схемы потока при малых и больших
углах поворота дефлектора (а); график зависимости числа
МАБ на линии А В от М2 (б)
Считая скачки АА', ВВ' и линию АВ прямыми, сделав допущение,,
что давление торможения р0 на линии АВ равно давлению р3 за скачком
ВВ' и применяя зависимости (XVI-1-2) или (XVI-1-3) для отрывных
течений, а также зависимости теории скачков уплотнения, можно найти
положения точек А и В и подсчитать величины давлений р2 и р3.
Последовательность расчета следующая. Задаемся положением точки А.
По величинам Мь Ret из формулы (XVI-1-2), если пограничный слой
ламинарный, или из формулы (XVI-1-3), если он турбулентный, находим
коэффициент давления р2 за скачком, а по формуле р2 — pi (1 + к1М21р2/2) —
величину абсолютного давления р2. При помощи зависимостей теории
скачков уплотнения по величинам Mi и р2 находят значения рс1, М2 и 6с1. Затем
проводят прямую АВ под углом РС1 к образующей сопла и определяют
положение точки В на поверхности дефлектора и угол рс2 поворота потока
за этой точкой. Используя те же зависимости для скачков уплотнения,
по известным величинам М2, рс2 находят значения 6с2, р3 и подсчитывают
давление торможения на линии АВ
Аэродинамика органов управления JQg
которое сравнивается с величиной р3. В этой формуле МАВ — число М
на линии АВ, которое находится по числу М2 с помощью графика (рис.
XVI-2-12, б), построенного по данным работы ([791, 1957, № 5). Положение
точек А, В и значения давлений р2, р3 будут считаться правильными, если
окажется, что р0 = р3.
Все расчеты следует проводить в плоскости симметрии дефлектора,
проходящей перпендикулярно оси его поворота. Считая, что давление
на поверхность сопла и дефлектора будет одинаковым в поперечных
сечениях (перпендикулярных оси сопла) и равно давлению за скачком
уплотнения А А' (или ВВ' соответственно) в этих же сечениях, можем определить
управляющую силу и потерю тяги:
-poo) dS2+ J J
(S3) (XVI-2-12)
II I (Pz—P°o)dS2x+ ^ ^ { )dS
(Six) (S2x) (Sax)
где S±, S2 — соответственно проекции поверхностей сопла и дефлектора,
на которые действует переменное давление р2;
S3 — проекция поверхности дефлектора с переменным давлениемр3
(проекция на плоскость, проходящую через ось сопла и ось поворота дефлектора);
SiX1 S2x, SBx — проекции рассматриваемых выше поверхностей на
плоскость, перпендикулярную оси сопла;
Рг, ср — среднее давление на участке AD сопла при условии его
безотрывного обтекания.
При определении S±, S2, S3i а также Six, S2x, S3x предполагается, что
они ограничены коническими скачками уплотнения с прямолинейными
образующими А А' и В В' и с осями симметрии, расположенными
соответственно на стенках сопла или дефлектора.
При определенных углах поворота дефлектора возможен случай, когда
линия АВ не попадает на стенку дефлектора. При этом положение точки
отрыва потока следует определять, исходя из того, что линия А В должна
проходить через край дефлектора. Задавшись рядом точек отрыва и
определив направление линий АВ, можно найти соответствующий каждой точке
отрыва угол поворота дефлектора.
Описанные выше методы расчета не учитывают некоторого уменьшения
управляющей силы и увеличения потери тяги, связанных с наличием
зазоров между соплом и дефлектором, которые необходимы для безотказной
работы.
Газовые рули
Для упрощения расчетов, излагаемых ниже, примем следующие
допущения.
1. Поток продуктов сгорания топлива в двигательной установке
считается равномерным на выходе из сопла.
2. Влияние щели между консолью руля и стенками сопла, пограничного
слоя у стенок сопла, а также профиля и формы руля в плане на подъемную
силу рулей учитывается косвенно с помощью эмпирического
коэффициента Kv.
3. Передняя кромка рулей сверхзвуковая.
Подъемная сила и лобовое сопротивление рулей определяются по
формулам
2 (XVI-2-13)
(XVI-2-14)
704
Глава XVI
где gp = 0,5раш| — скоростной напор в выходном сечении сопла;
Sv — площадь консолей рулей;
vx>
Производная
угол поворота рулей;
статическая производная коэффициента подъемной силы
рулей по углу их поворота;
— коэффициент лобового сопротивления рулей.
с
УР
кх]
(XVI-2-15)
огде Ма — число Маха в выходном сечении сопла.
В первом приближении для Ма>2,5 можно считать, что i£p « 0,7.
Для определения cxv рекомендуется следующая полуэмпирическая
зависимость, применяемая для крыльев малого удлинения, с формой в плане,
^близкой к прямоугольной:
. " _ 4бр
vx р ■
ScpO
где Яэ = Хр У Ml — 1; А,р = Zp/6cp. p — удлинение рулей;
Zp — размах консоли руля;
ЬСр. р^ средняя хорда консоли руля;
В = 2#4 — коэффициент, учитывающий форму профиля (см. табл. V-2-2);
с — относительная толщина профиля руля;
cXfV — коэффициент сопротивления трения рулей (см. § VI-1).
Формулы (XVI-2-15) и (XVI-2-16) справедливы для безотрывного
обтекания рулей (бр < 8р. кр), что имеет место при бр < 15°.
Необходимо экспериментально уточнить значения коэффициента Kv,
а также схр0 и схр& в формуле (XVI-2-16) для конкретных конструкций рулей
и соплового аппарата. Кроме того, ввиду высокой температуры потока,
омывающего поверхность рулей, они могут обгорать. Это может привести
к заметному изменению значений Ур
и Хр в процессе работы газовых рулей.
Лобовое сопротивление рулей
учитывается путем уменьшения
реальной силы тяги. В расчетах имеют
дело с эффективной тягой
Рэ = Р-Хр. (XVI-2-17)
В первом приближении можно
считать, что Yp и Хр приложены в
!
II
Рис. XVI-2-13.
Схема сопла
рулями
с газовыми
центре тяжести поверхности консоли
рулей.
Пример. Определить Хр и Ур для
рулей, размеры которых даны на рис. XVI-2-13.
й
р
Параметры газа в камере сгорания двигательной установки следующие: _ро =
<392 н/см2), ^0 = 2500° К, Л = 1,33, Л = 30,0 кГ-м/кГ град (30 нм/н-град).
В соответствии с рисунком сопла находим:
кГ/см*
itdl
я (6,4-10-2)2
= 3,22'10~3 ж2 —площадь выходного сечения сопла;
S* ==
d*^ л (3 6»10~2)2
.— = v * — = 1,02* 10~3
4 4
2 — площадь критического сечения сопла.
Определяем относительный расход
Sa 3,22-1и-з
"3
0316>
Аэродинамика органов управления - 705
По таблицам газодинамических функций для к = 1,33 [8] или по
соответствующим формулам одномерного установившегося изэнтропического потока идеальной
сжимаемой жидкости (II1-3-4) находим:
Ма = 2,60; Яа = 1,93; -^ = 0,472; -^- = 0,103;
то Ро
-^- = 0,0487; /а = 0,487.
Ро
Определяем по уравнению состояния плотность газа в камере сгорания:
^ ^0'544 ^се*/»* (5,33 ка/жЗ).
Подсчитываем температуру, давление и плотность в выходном сечении['сопла:
Та = Т0 (^-) =2500.0,472 = 1181° К;
V 1 0'
Ра = Ро (1±) =40-104.0,0487 = 1,948.104 кГ/м2 (19,1-104
v Ро /
ра = р0 (^Л =0,544-0,103 = 0,0560 кГ-сек*/м* (0,549
V Ро /
Подсчитываем силу тяги, развиваемую двигательной установкой в вакууме:
^тах = ^аРо/а = 3,22.Ю-з.40-104.0,487 = 627 кг (6150 н).
Тяга на уровне моря (для стандартной атмосферы)
Р = Ртах — Роо^а = 627 —1,033.104.3,22.10-3 = 594 кГ (5830 н).
Критическая скорость звука
= ]/kgRT0 щ^ = ]/ 1,33>9,81-30-2500 1
Скорость газов в выходном сечении сопла
м>а = Хаа* = 1,93-916 = 1768 м/сек.
Скоростной напор в выходном сечении сопла
=8,76.10* пГ1м> (86,0.104
Удлинение консоли руля (см. рисунок руля)
^ср.р 22
Подсчитываем значение Яэ:
Хэ = Хр УЩРЛ = 11/2,602-1 = 2,40.
Приняв число Re на поверхности руля равным 107 и считая поток
турбулентным, найдем, что при 6р = 10° (0,174 рад), с = 0,12 и J5 = 5,33, согласно (XVI-2-16):
/ 0,3 \ 5,33.0,12 2-0,074
СэсР~\ 2,40 + 0,3/ у2,602 — 1 1/1 + 0,12.2,602 (Ю7)°,2
4(0,174)2_ / 1 ) =2,83.10-2 + 0,44.10-2 + 4,01.10-2 = 7,28.10-2.
1/2,602 — 1 \ 2 1/2,602 — 1/
Согласно (XVI-2-15)
Площадь в плане двух консолей рулей
45-114
706
Глава XV1
Значения Хр и Ур при 6р = 10° будут следующими:
*p = 0o*Vxp = 8,76.104-9,68-10-4.7,28-10"2=:6,2 кГ(60,8 н).
Ур = да1УрС*бр = 8,76.10*.9,68.10-4.1,16.0,174 = 17,2 «Г (169 и).
Эффективная тяга (с учетом только одной пары рулей)
P3 = jp_Zp=:594-6 = 588 кГ(5760 н).
Управление вдуванием газа
в сверхзвуковую часть сопла
Вдувание газа или впрыск жидкости в сверхзвуковую часть сопла
производится чаще всего через круглые отверстия, расположенные по
периметру некоторого сечения сопла. Вдувание осуществляется навстречу потоку
и его направление составляет примерно 30° с нормалью к внутренней стенке
Рис. XVI-2-14. Схема расположения фронта скачка
уплотнения
сопла. Взаимодействие вдуваемой струи с расширяющимся осесимметрич-
ным потоком приводит к весьма сложной картине течения внутри сопла
([70], 1965, № 1).
Непосредственно за отверстием наддува вниз по потоку располагается
ядро вдуваемого газа, которое относительно слабо расширяется вниз по
потоку. За пределами ядра непосредственно после выхода из отверстия наддува
струя испытывает значительное расширение и при этом под воздействием
основного потока образуется вихревое течение, которое поворачивается
по направлению к стенкам сопла; давление в этих местах на стенке достигает
наибольшей величины. В вихревой зоне происходит смешение потока и
вдуваемого газа. На границе между вихревой зоной и ядром вдуваемого газа,
располагающейся на стенке сопла, давление сильно снижается и вследствие
этого происходит отрыв пограничного слоя.
Ядро вдуваемого газа и вихревая зона охватываются потоком,
прошедшим через Я-образный скачок уплотнения, который образуется перед
вдуваемой струей. На рис. XVI-2-14 виден фронт этого скачка 1 в
меридиональной плоскости, проходящей через отверстие наддува 3. Сечениями,
перпендикулярными оси сопла, фронт скачка пересекается по линиям 2,
близким к окружностям.
При исследовании величины, направления и точки приложения
управляющего усилия, обусловленного вдуванием газа в сверхзвуковую часть
сопла, одной из основных задач является определение конфигурации скачка
уплотнения, возникающего перед ядром вдуваемого газа. В первом
приближении для этого можно использовать формулу
этГ (ж)
'"
Аэродинамика органов управления 707
где R — радиус фронта Х-образного скачка уплотнения (не учитывая
передней ножки), измеряемый от оси х (ось х проходит параллельно оси сопла
в меридиональной плоскости, проведенной через центр отверстия наддува);
причем начало оси х расположено непосредственно перед этим отверстием
(рис. XVI-2-14); к — отношение теплоемкостей для газа, текущего по соплу;
/ и X — постоянные, зависящие от к (для к = 1,4 / = 0,88, X = — 1,989);
Ма — число М потока газа в сопле непосредственно перед отверстием при
отсутствии наддува, соответствующее скорости wa в этой точке;
Rc=
miWa )
a ) —характеристический радиус;
A '
mcwA ,
T)i = 1 ± (wt cos |3j) wa — поправочный коэффициент, учитывающий
угол |3С отклонения оси отверстия наддува от нормали к оси сопла (знак «+»
берется при вдувании газа против течения в сопле);
wt — скорость вдуваемого газа в выходном сечении отверстия наддува;
wa — скорость газа в выходном сечении сопла без учета влияния вдувания;
Sa, Wa — соответственно площадь поперечного сечения сопла и скорость
газа непосредственно перед отверстием наддува (без учета влияния
вдувания); тс, тг — соответственно секундный массовый расход газа через сопло
и отверстие наддува; т]2 = 1 ± Ah/(wAwa) — коэффициент, учитывающий
влияние испарения и химической реакции вдуваемой жидкости на
положение скачка уплотнения; ±ДА — энергия, выделяемая (знак +) или
поглощаемая (знак« —») единицей массы вдуваемой жидкости в процессе ее
испарения или химической реакции. Как показывают исследования ([70], 1965,
№ 2), формула (XVI-2-18) дает удовлетворительное совпадение с
экспериментом как при вдувании газа, так и при впрыске жидкости в
сверхзвуковую часть сопла.
Поскольку давление за скачком увеличивается, то можно предполагать,
что наибольшего значения боковая сила, возникающая от
перераспределения давления по внутренним стенкам сопла при вдувании газа, достигает
тогда, когда в выходном сечении сопла фронт скачка уплотнения попадает
в точки пересечения внутренней поверхности сопла и меридиональной
плоскости, перпендикулярной плоскости, проходящей через ось сопла и
отверстия наддува (точки С^ и С2 на рис. XVI-2-14). Соответствующее этому
оптимальное значение радиуса скачка уплотнения в выходном сечении сопла:
2, (XVI-2-19)
где D А — диаметр поперечного сечения сопла непосредственно перед
отверстием наддува.
Применяя зависимости (XVI-2-18) и (XVI-2-19), можно либо при
заданном положении отверстия наддува найти расход вдуваемого газа,
обеспечивающий наибольшее значение боковой силы, либо при заданном расходе
найти положение отверстия наддува, что позволит получить ту же силу.
Боковая управляющая сила образуется в результате повышения
давления на поверхности сопла в зоне отрыва потока между ножками Я-образного
скачка (а также за скачком уплотнения) и вследствие понижения давления
за отверстием наддува. Однако зависимость (XVI-2-18) не учитывает
влияния зоны повышенного давления между ножками Я-образного скачка (эта
зона увеличивает суммарную силу) и зоны пониженного давления за
отверстием наддува (эта зона уменьшает суммарную силу), что в известной мере
оправдано различным характером воздействия указанных факторов.
Для построения зоны отрыва и определения величины давления /?2, л,
за передней ножкой Я-образного скачка можно воспользоваться зависимостями
(XVI-1-2) или (XVI-1-3) для отрывных течений, а также формулами для
45*
708
Глава XVI
высоты эквивалентной преграды h и протяженности зоны отрыва I в
меридиональной плоскости сопла, проходящей через центр отверстия наддува
(рис. XVI-2-15).
Высота эквивалентной преграды
2кс
1/4
Ра
. ср
, (XVI-2-20)
/?/ — соответственно число М и давление во вдуваемой струе в
выходном сечении отверстия вдува;
кс — отношение теплоемкостей вдуваемого газа;
St — выходное сечение отверстия наддува;
В случае впрыска несжимаемой жидкости вместо формулы (XVI-2-20)
следует применять зависимость
h = , °'3"^a (XVI-2-21)
di (P2, К —Pi) V '
где di — диаметр выходного сечения отверстия наддува ([69], 1966, № 1).
Протяженность зоны отрыва, т. е. расстояние вдоль стенки сопла от
точки отрыва до кромки отверстия наддува
I = h [ctg pc + tg (pen + &)], (XVI-2-22)
где рс — угол отклонения потока за передней ножкой
i-образного скачка;
Реп — угол наклон астенки сопла к его оси.
Задача решается методом подбора. Задавшись
положением точки отрыва (а следовательно, величиной Z),
с помощью зависимостей (XVI-1-2) или (XVI-1-3)
находим давление^, %•> а по формулам теории скачков
уплотнения — угол рс. Затем по формуле (XVI-2-20)
определим высоту h. Это позволяет найти протяженность зоны
отрыва I по формуле (XVI-2-22) и сравнить ее с
первоначально выбранной. Следует добиться совпадения
этих величин.
Боковыми границами зоны отрыва являются линии
пересечения внутренней поверхности сопла с
конической поверхностью, образующей которой служит прямая линия передней
ножки Я-образного скачка, а осью симметрии — касательная к поверхности
сопла в точке отрыва.
Величину боковой силы за скачком уплотнения можно найти, считая,
что давление на стенки сопла будет в любом его поперечном сечении таким же,
как за скачком уплотнения:
Рис. XVI-2-15. Схема
к определению
давления и размеров зоны
отрыва перед
отверстием вдува в сопле
= 0,95
(р2 — р)
(S2)
p2t *,) St],
(XVI-2-23)
где множитель 0,95 учитывает уменьшение Yv из-за влияния зоны
пониженного давления за отверстием наддува; р2, Ср — среднее давление в зоне
отрыва, если бы в ней было безотрывное обтекание; «Si, S2 — проекции
соответственно площади зоны отрыва и поверхности сопла за скачком
уплотнения на плоскость, параллельную оси сопла и перпендикулярную мери-
Аэродинамика органов управления
709
pi
диональной плоскости, проходящей через ось отверстия наддува; р2, р —
давления соответственно за скачком и до скачка в рассматриваемом
поперечном сечении сопла; второе слагаемое — сила тяги, развиваемая струей
вдуваемого газа.
Дросселирование отдельных
сопел
Многосопловые устройства позволяют создавать управляющие усилия
путем дросселирования (частичного или даже полного перекрытия
критического сечения) отдельных сопел. С этой целью в критическое сечение
сопла вводится центральное тело («груша»), перемещением которого вдоль
оси сопла можно регулировать площадь его критического сечения, а значит,
и силу тяги, создаваемую этим
соплом. Если дросселируется
одно сопло или часть сопел,
расположенных несимметрично
вокруг продольной оси
летательного аппарата, то относительно
этой оси возникает момент,
стремящийся развернуть
летательный аппарат в соответствующую
сторону.
Пусть многосопловое
устройство состоит из п сопел,
каждое из которых создает
тягу Pt и расположено по окружности радиуса rt под углом 9^ к
продольной оси летательного аппарата. Тогда при /)гпроцентном
дросселировании каждого i-то сопла получим следующие величины моментов
относительно осей у± и Z\\
А /\
%гх cos Qt sin (yu rt); (XVI-2-24)
Рис. XVI-2-16. Схема обозначения параметров
i-ro сопла в многосопловой установке
АМУ - 10"2
1
г=1
гг cos Qi sin
zb r,)f
(XVI-2-25)
где (уи гг) и (zi, rt) — углы между соответствующими осями ^ и zj и
радиусом гг (рис. XVI-2-16).
Зависимости (XVI-2-24) и (XVI-2-25) предполагают, что в случае
полного открытия всех сопел АМУ1 = AMZl = 0, а также, что ось любого
i-то сопла находится в плоскости, проходящей через продольную ось
летательного аппарата х±.
Если все сопла имеют одинаковые Рг = Р, гг = г, 9^ = 9, то вместо
(XVI-2-24) и (XVI-2-25) можно написать:
АМУ = 10~2Рг cos
1
sin
(XVI-2-26)
AM21-10"2Prcos9 2j Dt sin (zt, n).
(XVI-2-27)
Рассмотренное расположение сопел позволяет управлять летательным
аппаратом по тангажу и рысканью. Для управления по крену необходимо
либо часть сопел расположить так, чтобы их оси с меридиональной
плоскостью летательного аппарата составляли некоторый угол, либо
предусмотреть специальные органы управления.
710
Глава XVI
Определение управляющих
усилий, создаваемых
газодинамическими органами в сопловых
аппаратах с центральным телом
Сопло с центральным телом хорошо работает в широком диапазоне
атмосферных давлений. Если рассмотреть отношение замеренной силы тяги
к силе тяги, полученной расчетом для условий изэнтропического
расширения до атмосферного давления, то, например, при давлении в камере
двигательной установки 35 кГ/см2 (343 н/см2) и Sa/S* = 16 это отношение для
сопла с центральным телом будет
изменяться от 0,95 на уровне моря
до 0,98 на высоте Н = 20 км
(расчетный режим), а для обычного
сопла в тех же условиях — от 0,80
до 0,98.
Несомненным преимуществом
сопла с центральным телом
является меньшая донная площадь Snoli,
что при прочих равных условиях
уменьшает коэффициент лобового
сопротивления летательного
аппарата. Сопловой аппарат с
центральным телом может быть как
кольцевым, так и многосопловым
(рис. XVI-2-17). При этом
центральное тело без значительного
уменьшения силы тяги может быть весьма коротким. Опыты показывают, что
укорочение на 75% практически не изменяет силы тяги, а при полном
отсутствии центрального тела уменьшение силы тяги составляет около 3%.
Следует отметить заметное
уменьшение силы тяги при увеличении рас-
стояния между выходными
сечениями сопел в многосопловом
Рис. XVI-2-17. Сопловой аппарат в
многосопловом варианте:
Lmax— максимальная длина центрального тела
Ь/р
0,05
0,04
0,03
0,02
0,01
О
1
1
1
1
1
1 /
\/
Y
-*-
\
0,020
•0,020
\
\
К
—
Ч
(
^\
-»—
россе/
г
"7
. • _
1 . 1
-*1
о
5
10
15
Ь град
0
0,2
0,6
Рис. XVI-2-18. Зависимость отношения
боковой составляющей силы тяги Yq к
осевой силе Р от угла поворота центрального
тела:
теория; эксперимент
Рис. XVI-2-19. Зависимость отношения
боковой составляющей силы тяги Yq к
осевой силе Р от длины укороченного
центрального тела при 12,5%-ном дросселировании
одного из сопел
варианте. Поэтому следует стремиться сделать это расстояние близким
к нулю, либо специально профилировать центральное тело. Известны
попытки создавать управляющие усилия поворотом центрального тела,
дросселированием отдельных сопел (или их поворотом) и выдуванием газа через
отверстия в боковой поверхности центрального тела.
Аэродинамика органов управления 711
Опыты показывают, что для создания достаточно больших значений
управляющих сил Y^ нужно центральное тело поворачивать на большие
углы б (рис. XVI-2-18), а при дросселировании отдельных сопел следует
считаться с влиянием длины центрального тела (рис. XVI-2-19). Удлиненное
центральное тело перестраивает асимметричное течение за соплами в почти
однородный поток. Именно поэтому при длинных центральных телах
управляющее усилие изменяет свое направление.
Данные на рис. XVI-2-18 и XVI-2-19 получены из эксперимента на
многосопловой установке со следующими характеристиками:
9 = 23°; п = 24; гс =
В литературе имеется указание, что управление вдуванием газа из
боковой поверхности центрального тела столь же эффективно, как и в обычных
расширяющихся соплах ([70], 1964, № 7).
В расчетах может оказаться полезной следующая зависимость между
характеристиками многосоплового варианта, полученная в предположении,
что выходные сечения сопел соприкасаются:
2- <XVI-2-28)
§ XVI-3. Расчет сил,
создаваемых
комбинированными органами управления
Органы управления с
неподвижным щелевым соплом на
задней кромке пластины
Рассмотрим опытные данные ([76], 1962, №4— 5), которые позволяют
провести расчет сил при взаимодействии струи, истекающей из щелевого
сопла на задней кромке пластинки перпендикулярно ее поверхности, и
невозмущенного потока воздуха, омывающего эту пластинку. Скорость
истечения струи в экспериментах звуковая; число Re, вычисленное по расстоянию
от передней кромки пластинки до щели, изменялось в диапазоне от 1,4-106
до 1,2-107 и заметного влияния на результаты не оказывало; длина щели
1Щ = 48 мм. Струя газа создавалась воздухом с нормальной температурой.
На рис. XVI-3-1 и XVI-3-2 приведены значения коэффициента
усиления Ку в зависимости от числа М набегающего потока воздуха и отношения
давлений торможения в струе poi к статическому давлению в набегающем
потоке роо, а также в зависимости от ширины щели 1Щ и наличия боковых
пластин, препятствующих перетеканию потока воздуха через боковые
кромки струи.
Коэффициентом усиления К7 называется отношение суммарной силы,
действующей в направлении нормали к пластинке, к силе тяги Pm3LX,
которую можно было бы получить, используя поток газа в сопле Л аваля,
работающем на расчетном режиме, т. е.
v AN + P
где AN — изменение силы нормальной к пластинке, расположенной перед
щелевым соплом;
Р —тяга, развиваемая потоком газа в щелевом сопле.
Определив значение KY и зная параметры щелевого сопла, а также
величины k, poi ж роо, можно подсчитать величину силы, создаваемой рас-
712
Глава XVI
сматриваемым органом управления:
■* р =
где
(XVI-3-1)
i/T"
-Э*]' <XVI-3-2>
[х = 0,90 -г- 0,99 — коэффициент расхода;
5Щ — площадь критического сечения щели.
Анализ графиков на рис. XVI-3-1 и XVI-3-2 показывает, что для
увеличения коэффициента усиления при заданном числе М и давлении роо
воздушного потока необходимо
Щ уменьшать давление
торможения в струе poi и ширину щели
Ьщ, а пластинки по бокам щели
ставить параллельно потоку
а)
з
It
1
1
*&-—
^-
-о-
—-о-о
8
•к
21
т.
глг—-
\
^, ■—
60 Рп.
2ft
3,0М,
5)
у
3
А
0
к
ЯГ"
т—•**
' ,.
^-—
Рис. XVI-3-1. Графики зависимости
коэффициента усиления Kj от отношения
давлений Рог/роо и числа М^
а — без боковых пластин; б — с боковыми
пластинами у щелевого сопла. Ширина щелевого сопла
1 мм; длина его — 48 мм
Боковые пластины
нет
О
д
V
D
есть
т
_
2,80
2,21
1,83
1,57
1,83*
Рис. XVI-3-2. Графики
зависимости коэффициента
усиления Ку от числа М4
и отношения давлений
P0i/P°°:
а — без боковых пластин; б —
с боковыми пластинами у
щелевого сопла. Размеры сопла:
ширина — 1 мм; длина —
48 мм. Сплошными линиями
показана зависимость
отношения коэффициентов
нормальной силы к осевой силе,
создаваемой интерцептором (см. рис.
XVI-1-2)
* ширина щелевого сопла 0,33 мм
воздуха. При этом уменьшение poi и Ьщ снижает Ртах и затрудняет
обеспечение заданного значения Ур. Действительно, из (XVI-3-1) и (XVI-3-2)
Аэродинамика органов управления
713
видно, что увеличить Ур можно только с помощью 5Щ при значительной
длине щели. Однако может оказаться, что на поверхности планера негда
будет разместить длинную щель.
Быстродействие рассматриваемого типа органа управления оценивается
по опытным данным. Для конкретного случая газопровода длиной 3 м
экспериментальные исследования
показали, что время от момента подачи
газа до появления силы Yv
составляло порядка 0,01 сек. ^
Приближенный расчет величины ^
силы AN может быть произведен
с помощью следующих зависимостей
([69], 1966, № 1):
AN = (р2 - рос) Ах, (XVI-3-3) ^
Ах
dr.
кр2М1У(кс-1)/2ксм
(XVI-3-4)
—_,
(XVI-3-5)
где Re = V2(L — Ax)/v, ReL =
5 6 7Mr
Рис. XVI-3-3. Изменение параметров воз-
kCM= 8,37/Re0'5— коэффициент ско- ДУха в застойной зоне и коэффициента
скорости смешения от числа Мао в случае-
турбулентного пограничного слоя
рости смешения на
границе застойной
зоны;
Ах — протяженность застойной зоны от места отрыва потока до
начала струи;
L — расстояние от передней кромки отверстия до начала струи;
р2, V2, М2 — соответственно давление, скорость и число М в застойной зоне,
которые могут быть определены из условий изэнтропическога
сжатия воздуха.
Эксп а
А
( Л
о 0,001
±0,003
о
о
о
о
д
8
о
\
\
Теория
>
йОЗ 0.05 0,1
10
50 100 Ро.
'/Pa,
Рис. XVI-3-4. Сравнение опытных и расчетных данных для ламинарного
(а) и турбулентного (б) пограничных слоев:
■^М— максимальная тяга, возникающая при истечении из щели в вакуум
Формула (XVI-3-5) является эмпирической и получена при Моо = 4
для случая ламинарного пограничного слоя. Если пограничный слой тур-
714 Глава XVI
булентный, то для определения кст М2 и р2/роо можно вместо формулы
(XVI-3-5) применять графики, изображенные на рис. XVI-3-3. Результаты
сравнения расчетных и опытных данных при числе Моо = 4 приведены
на рис. XVI-3-4 ([69], 1966, № 1). Некоторые дополнительные данные
показывают, что предлагаемые зависимости не следует использовать в случаях,
когда одновременно Моо > 5 и poi < 30.
Пример. Определить боковую управляющую силу при истечении газа через щель
в пластинке для следующих данных:
Моо = 1,83; Ft» = 622 ж/с**; роо = 1 кГ/см2]
Voo=: 1,45-10-5 м2/сек] ро. = 34,2 кГ/см2; к = 1,4; &с = 1,4;
Ма = 1; £ = 0,17 ж.
Ширина щели dc = 10~3 м, длина 10 мм. Этим данным соответствует число
ReL = F<x,L/Voo = 622-0,17/1,45.10-6 = 7,29-10е.
Рассмотрим случай, когда на пластинке образуется ламинарный пограничный
слой. Задавшись величиной Да; = 0,149 м, найдем
Следовательно,
p2=Ulpoo = Ui кГ/см*.
Из теории скачков уплотнения, зная Моо=1,83 и давление за скачком р2= 1Л кГ/см2,
найдем
М2 = 1,77 и F2=601 ж/сек.
Число Рейнольдса
Voo "~ 1,45-10-5
Далее определяем
*CM = 8,37/Re0,6 = 8,37/(8,7.106)0,5 = 8,1
и находим
1 + 1,4
4^ = ~ / ' = 0,148-103.
dc 1,4-1,1.1,772 У(1,4 —1)/2.8,97.10"3
Отсюда
Это значение мало отличается от заданной величины Ах = 0,149 ж, поэтому
дальнейшего приближения можно не делать. По полученным данным определяем искомую
боковую силу:
AN = (p2 — poo)Axl02 = (l,l —1)0,148-102 = 1,48 кГ.
Рассмотрим случай полностью турбулентного пограничного слоя. Из графика
на рис. XVI-3-3 по числу Моо = 1,83 находим:
Далее подсчитываем Аж/^с = 17,3 и находим:
A* = (A;r/dc)dc = 17,3-10-3 = 1,73-Ю"2 м.
Соответствующая полученным данным боковая сила
= (1,75 —1,0) 1,73-10-2-102=1,3 кГ.
Аэродинамика органов управления
715
Органы управления с
поворотным щелевым соплом на
задней кромке крыла при
дозвуковых скоростях
Во время старта летательного аппарата с неподвижной пусковой
установки скорости его движения малы, а поэтому малы управляющие усилия,
создаваемые аэродинамическими органами управления. Для увеличения
управляющих усилий применяют
комбинированные органы управ- Щ
ления со щелевым соплом на задней
кромке крыла — простым
струйным закрылком (рис. XVI-3-5, а).
Рис. XVI-3-5. Виды комбинированных
органов управления:
а — простой струйный закрылок; б —
закрылок, обдуваемый газом по верхней
поверхности; в •— закрылок, обдуваемый газом
по обеим поверхностям
Возможны варианты применения обычных
либо по верхней их поверхности (рис. XVI
закрылков, обдуваемых газом
-3-5, б), либо одновременно по
верхней и по нижней
поверхностям (рис. XVI-3-5, в).
Рассмотрим
экспериментальные данные, позволяющие
для крыльев с удлинением
Якр > 10 рассчитать указанные
выше разновидности
комбинированных органов управления.
1. Угол атаки
крыла а = 0. На графике рис.
XVI-3-6 приведены
зависимости для изменения
коэффициентов лобового сопротивления
Дсх, тяги крыла АсР = сР— Асх,
а также приращения
коэффициента подъемной силы крыла
Асу за счет воздействия струи
газа на поток воздуха. Эти
характеристики даны в
функции коэффициента количества
Дср=ср-Ас:
Рис. XVI-3-6. Графики зависимости изменения
коэффициентов лобового сопротивления (Лсх), тяги
(Лср) и подъемной силы крыла (Асу) при
различных значениях коэффициента количества
движения струи сР и угла поворота струи бс
движения струи сР = ?— ,
#°°^кр
где т — массовый расход газа
через сопло, wa — скорость на
выходе из сопла, #«> —
скоростной напор набегающего
невозмущенного потока, £кр —
площадь крыла в плане и угла
поворота струи бс ([70], 1964,
№ 1).
Этот график позволяет,
в частности, установить, что
достигнуть требуемого увели-
716
Глава XVI
чения коэффициента подъемной силы крыла можно при минимальных
значениях Асх и Ср.
Вид линий Асу = const показывает, что выполнить это требование
можно, выбирая нужные точки там, где линии Асу = const начинают идти
вверх. Геометрическое место
этих точек образует линию
рабочих режимов D. Ниже этих
линий происходит полное
восстановление тяги и независимо
от величины угла бс в тягу
крыла входит полностью реактивная
сила, создаваемая истечением
газа через сопло, а Асх остается
постоянным. За пределами этой
зоны Асх увеличивается, так
как начинает расти профильное
сопротивление крыла.
2. Угол атаки
крыла а Ф 0. Изменением угла
атаки крыла а можно улучшить
характеристики
комбинированных органов управления. С
ростом а у обычного крыла растут
су и сх, причем при небольших
значениях а рост сх
сравнительно мал. У крыла со щелевым
соплом рост а при бс = const
дополнительно увеличивает суг
так как возрастает
вертикальная составляющая реактивной
силы. При этом Асх в большом
диапазоне значений а остается
неизменным. Отсюда ясно, что
для достижения заданных вели-
Рис. XVI-3-7. Графики зависимости сх, су,
(ср— сх) от ср и угла атаки крыла а при бс = 55°
чин
Асу в случае а
можно уменьшить сР, что приведет в конечном
х по сравнению со случаем а = 0.
Асх
£0
итоге к уменьшению Ас
Однако при больших углах атаки наблюдается резкое увеличение сх (а)
крыла и происходит срыв потока. Все это приводит к значительному росту
Асх и к потере эффективности
комбинированного органа управления.
На рис. XVI-3-7 приведены
зависимости сх, су, сР — сх от сР
и а при бс = 55°.
Линией рабочих режимов
в этом случае будет геометрическое
место тех точек на линиях су =
= const, в которых касательные к
этим линиям параллельны линии
полного восстановления тяги.
Рис. XVI-3-8. Графики зависимости
изменения коэффициента лобового
сопротивления крыла (Ася) от ср и а для
б55°
/Л-
/
^—-
10°
"-8°
1,2
Аэродинамика органов управления
717
На рис. XVI-3-8 приведено изменение коэффициента лобового
сопротивления крыла в результате постановки на него органа управления при
различных углах атаки и коэффициентах сР для бс = 55°.
В области полного восстановления тяги справедливы зависимости
Асх = сР (Ct sin2 бс + С2 sin2 a); (XVI-3-6)
Лся = -^-Д4, (XVI-3-7)
где Си С2 и К — коэффициенты, получаемые экспериментальным путем.
Для простого струйного закрылка можно принять С± = 0,55; С2 = 7,7;
К = 3,65 + 0,35сР (или приближенно К = 4).
Для закрылков, обтекаемых газом, при а = 0 значение К = 5,3, а
отношения Ci/K равны 0,0270 (обтекание только сверху) и 0,0225 (обтекание
с обеих сторон).
Пример. Определить параметры простого струйного закрылка, обеспечивающего
коэффициент подъемной силы крыла Асу — 3,0.
В случае а —0 по графику рис. XVI-3-6 на пересечении линии рабочих режимов
с линией Асу — 3 берем точку А, координаты которой позволяют определить Дсх = 0,29,
АсР = 0,51, ср = 0,8, 6С = 55°. Для сравнения найдем аналогичные параметры для точек
В ж С, которые также обеспечивают крылу Асу=3. Соответствующие данные
приведены в табл. XVI-3-1.
Таблица XV1-3-1
Расчет параметров струйного закрылка при а = 0
Точка
А
В
С
Ас
з,
з,
з,
У
0
0
0
(
0
0
1
:р
,80
,67
,20
0
0
0
сх
,29
,38
,29
Аср
0,51
0,29
0,91
55°
71°
44°
лу
10
7
10
,3
,9
,3
лу,
4
4
3
Psin6c)
,58
,74
,64
а
0
0
0
Из табл. XVI-3-1 видно, что наиболее экономичным будет режим работы,
соответствующий точке Л, поскольку для условий, соответствующих точке В, резко
возрастает Асх и падает тяга крыла АсР\ третьей точке С соответствует, во-первых,
-большой расход газа (ср = 1,2 против сР = 0,8 в точке А), а значит, и больший вес
органа управления, и во-вторых, меньшие значения коэффициента усиления Асу/(ср sin 6C).
Для а^Ои заданного угла <5С = 55° по графику рис. XVI-3-7 для Асу = 3
определим параметры в точках А, В и С, а по графику рис. XVI-3-8 найдем Асх. Все
полученные данные приведены в табл. XVI-3-2.
Таблица XV1-3-2
Расчет параметров струйного закрылка при а^0 и 6С = 55°
Точка
А
В
С
с
3
3
3
У
,0
,0
,0
0
0
0
СР
,50
,42
,80
<
о,
о,
:х
296
350
312
Лср
0,204
0,07
0,488
с
55°
55°
55°
Vе*
10,1
8,57
9,61
V(cp
6,
7,
4,
sin 6C)
73
88
58
а
8
10
0
А
о,
о,
о,
28
29
29
Из табл. XVI-3-2 видно, что наиболее экономичным будет режим работы,
соответствующий точке А, которая лежит на линии рабочих режимов.
718
Глава XVT
Сравнение данных таблиц XVI-3-1 и XVI-3-2 показывает, что придание крылу
угла атаки а = 8° позволяет достигнуть ту же подъемную силу су = 3 со значительно
меньшим расходом газа (ср = 0,5 против ср—0,8 для а=0), а следовательно, и при
меньшем весе органа управления. Увеличение коэффициента лобового
сопротивления Асх из-за постановки на крыло органа управления в случае а=8° оказывается
меньшим, чем при а = 0 (соответственно Дсх=0,28 и Дсх = 0,29). Следует отметить
также большие значения коэффициента усиления при а Ф 0.
Органы управления в виде
неподвижного щелевого сопла
на цилиндрической
поверхности корпуса при
сверхзвуковых скоростях
Для расчета таких органов управления существуют лишь
эмпирические зависимости, не учитывающие влияние числа Рейнольдса для потока
воздуха, взаимодействующего со струями, истекающими из отверстий или
Число Ре
о 5040
□ 32 х Ю1
0 б*Ю*
*****
йнольдса
■ Re=
о-.
<>
10
20
U0 60 80100
200
чоо 600 юоо Рп}
Рис. XVI-3-9. Зависимость коэффициента усиления от
отношения давления торможения в струе к статическому
давлению в потоке воздуха при различных числах Re
и Mi = 6:
экстраполяция
щелей на кормовой части корпуса. На рис. XVI-3-9 показано влияние числа
Re на коэффициент усиления при различных величинах отношений давления
Струя боздуха
20 U0 60 80100
1—^
*-—
1—^
-^
-=;
1
Mf=W
—*J
•—«.
■—-«.
—■ .^
— —
— ■
—' —
7мге
Ш 600 1000 2000
Рис. XVI-3-10. Влияние угла атаки на коэффициент
усиления (Re = Foo#K/Voo = 6-10й; пограничный слой
турбулентный)
ротможения в струе к давлению в невозмущенном потоке воздуха PotlPi-
Эти данные получены из опытов в аэродинамической трубе при выдувании
Аэродинамика органов управления
719
перпендикулярно поверхности холодного воздуха из щели шириной 0,38 мм.
Щель располагалась на расстоянии 6,35 мм от дна параллельно донному
срезу между двумя стабилизаторами, выполненными по схеме «X».
Стабилизаторы препятствовали растеканию потока, взаимодействующего со струей,
и увеличивали управляющую силу. Скорость истечения из щели была
звуковой. Рис. XVI-3-9 показывает существенное
влияние чисел Re на коэффициент усиления
при Мое - 6 ([70], 1965, № 3).
На рис. XVI-3-10 приведены значения
коэффициента усиления при Re = 6-Ю6 для
различных углов атаки, а следовательно, чисел М±
воздушного потока перед щелью. Эти данные
получены при различных значениях pOi/pi для
условий, указанных ранее. Высокие значения
чисел Ку при малых pOt/pi и больших Mi
подтверждают тот факт, что комбинированные
органы управления могут быть такими же
эффективными, как аэродинамические органы
управления.
С помощью рис. XVI-3-11, на котором
представлены опытные данные, приведенные
в ряде опубликованных работ, можно
ориентировочно определять значения коэффициентов
усиления.
Зная величину Ку, можно найти по заданной величине управляющей
силы тягу, развиваемую щелевым соплом и рассчитать необходимые
параметры (размеры щели, расход газа и т. д.).
По экспериментальным данным ([76], 1962, № 4—5) форма и размеры щели
не оказывают существенного влияния на величину Ку, хотя отмечается
тенденция к росту Ку при уменьшении ширины щели.
/у
/
рф;
/,
/
у
-50J
/юо/
/
500/
О 4 8 Mf
Рис. XVI-3-11. Зависимость
коэффициента усиления от Mi
и Pot/pi
§ XVI-4. Определение
шарнирных моментов
газодинамических и
комбинированных органов
управления
Величина шарнирного момента Мт в общем случае может быть пред-
ставлена выражением
где МШ(№=о) — шарнирный момент при неподвижном органе управления;
Мш—шарнирный момент от демпфирования.
В свою очередь
э + Мш, вх,
=0) = Мш. и
где Мш. и — шарнирный момент, определяемый для условий течения газа по
соплу при отсутствии перекосов и погрешностей его изготовления
и при идеально выполненном входе в сопло;
Мт. э — шарнирный момент, возникающий от геометрического и
газодинамического эксцентриситета тяги;
Л^ш. вх — шарнирный момент, возникающий от влияния несимметрии входа
в сопло.
720 Глава XVI
Шарнирный момент от демпфирования возникает при вращении органа
управления с угловой скоростью (о. Главная составляющая часть момента
вызывается кориолисовыми силами. Рассчитывать величину Мщ следует
по формуле (XV-4-2), в которую необходимо подставить соответствующие
значения координат для входа и выхода газа в поворотную часть органа
управления.
При определении Мш для различных органов управления следует иметь
в виду некоторые особенности. Во-первых, отметим, что Мш = 0 для всех
тех органов управления, у которых отсутствуют вращающиеся части,
например у неподвижных управляющих двигателей, у органов управления
со вдуванием газа или впрыском жидкости в сверхзвуковую часть сопла,
у всех комбинированных органов управления (за исключением
изображенных на рис. XVI-3-5, б, в). Во-вторых, оказывается, что у поворотных
двигателей и сопел, как правило, МШтИ = 0. Исключение могут составлять
лишь конструкции неосесимметричных сопел, имеющих, например, косой
срез.
Теоретическое определение параметров некоторых органов управления
связано с расчетом пространственных течений газа внутри сопла,
омывающих элементы органов управления. Этот расчет весьма сложен, поэтому
допускают ряд упрощений. Как и при расчете управл^цогцих усилий, часто
рассматривают двухмерные течения в плоскости поворота органа
управления.
В случае поворота сверхзвуковой части сопла МШтИ = У^ц.д» гДе
^ц.д — расстояние от оси поворота до точки приложения боковой
управляющей силы Yv. В первом приближении можно считать, что сила Yp
приложена в середине поворотной части сопла.
Аналогично рассматривается Мш.и для дефлектора, однако в этом
случае необходимо определять величину 1Ц д путем непосредственного
определения точки приложения Ур по известным величинам и точкам
приложения ее составляющих.
Для поворотных насадков
■М ш. и. == * р «^ц. т — ДА Уц. т»
где Yv — боковая управляющая сила;
АХ — уменьшение осевой составляющей тяги из-за поворотного
насадка;
#ц.т> Уц.т — координаты центров тяжести проекций поверхности, от
давления на которую возникает боковая управляющая сила, на
плоскости, проходящие соответственно через ось сопла и
перпендикулярно к этой оси.
Глава XVII
НЕСТАЦИОНАРНЫЕ
ХАРАКТЕРИСТИКИ
ЛЕТАТЕЛЬНОГО АППАРАТА.
§ XVII-1. Определение
производных устойчивости по
аэродинамической теории
тонкого тела
Расчетные формулы [51]. Производные устойчивости летательных
аппаратов, представляющих собой комбинации весьма тонких корпусов и
хвостового оперения малого удлинения, можно рассчитывать при небольших
сверхзвуковых скоростях по формулам (IV-6-11)—(IV-6-45). Входящие в них
коэффициенты Aik, Eik зависят от
формы поперечного сечения ле-
тательного аппарата, а также
закона изменения этого сечения по
длине.
Каждому виду поперечного
сечения соответствует
определенный коэффициент присоединенной
массы Xih. Анализируя выражения
для производных устойчивости
(IV-6-U)-(IV-6-45), можно
заметить, что только производная
устойчивости т®х (коэффициент
демпфирования крена) зависит от
величины Я-зз, а все остальные
производные от нее не зависят.
Рассмотрим наиболее
распространенный вид поперечного
сечения, которое принадлежит
комбинации тонкого тела вращения
радиуса г и крестообразного
крыла, имеющего одинаковые по
величине консоли s в вертикальной и горизонтальной плоскостях (рис.
XVII-1-1, б). Коэффициенты присоединенных масс
Рис. XVII-1-1. Комбинация корпуса с]
крыльями:
а — корпус — плоское крыло; б — корпус —
крестообразное крыло; в — корпус — шесть лопастей;
г — корпус — симметричное горизонтальное и
несимметричное вертикальное оперения; д —
корпус — симметричное касательное горизонтальное
и несимметричное вертикальное оперения;
е—эллиптический корпус — симметричное
горизонтальное и несимметричное вертикальное оперения
= Х22 =
— r\
= ^13 = ^23 —
ч
(XVII-1-1)'
где rs = r/s.
Для более простой комбинации корпус — плоское горизонтальное крыло
(рис. XVII-l-l,a) соответствующие коэффициенты можно получить из
соотношений (XVII-1-1) в виде
= яРоо52 (1 - ri + ri)\ Xi2 - Я13 - Х23 = 0. (XVII-1-2)
46-114
722
Глава XVII
Приведем коэффициенты присоединенных масс для некоторых других форм
поперечного сечения. Для корпуса круглого сечения с тремя или большим
числом лопастей (на рис. XVII-l-l,e число лопастей п = 6), имеющих
одинаковый размах s,
2"J;
= ^13 = ^23 — 0,
где 7г — число лопастей.
Если корпус круглого сечения снабжен лопастями, расположенными
по схеме среднеплана и имеющими в верхней полуплоскости размах t^ а в
нижней— t2 (рис. XVII-1-1, г), то
Р)]1/2} ;
(XVII-1-4)
+ 2 [(1 + rlrl) (1 + *■) (1 + гУ2) (1 + Р2)]1/2}
где Г1 = г/1±; r2 = r/t2; rs = r/s; h^tjs; t2 = t2/s.
Коэффициент Xi3 определяется из работы [51]. Для корпуса круглого
сечения с горизонтальными лопастями, расположенными по касательной к
корпусу, вертикальными лопастями с размахом £4 в верхней полуплоскости * и t2
в нижней полуплоскости (рис. XVII-l-l,d) коэффициенты присоединенных
масс записываются в следующем виде:
(XVII-1-6)
sin Я cos2 А
cos2 A.
При использовании формул для Яи и Х22 следует иметь в виду следующие
вспомогательные соотношения:
= -{arcsh(TtgT)
М1/2
)
sinX
Коэффициенты присоединенных масс для комбинации, состоящей из
корпуса с эллиптическим сечением и хвостового оперения (рис. XVII-1-1, е),
имеют вид
%и = пРоо (4с2 - к2 - lab - б2); (XVII-1-10)
^22 = (д^)а [s2 («2 + Ь2) + 2ab (a-b)~ 2abs (s2 - а2 + Ь2)1/2]; (XVH-1-11)
^12 = ^13 = 0- (XVII-1-12)
Нестационарные характеристики летательного аппарата
723
В этих формулах введены обозначения:
r — Ъ
1- (XVII-1-13)
'• J
Для заданной формы сечения комбинации по известным коэффициентам
присоединенных масс определяют при помощи формул (IV-6-47) значения Aik,
включая Aik. Затем вычисляют коэффициенты Bik, Cik, Dik с использованием
формулы (IV-6-46). В этой формуле нижний предел интеграла равен
расстоянию от центра тяжести комбинации до задней кромки оперения, а верхний
предел — расстоянию до того сечения корпуса, где расположены передние
кромки консолей.
Чтобы получить суммарную величину производной устойчивости, надо
к значению производной для комбинации корпус — оперение, вычисленному
указанным методом, прибавить значение производной для оставшейся
передней носовой части корпуса.
§ XVII-2. Коэффициенты
демпфирования
Коэффициент демпфирования крена. В наиболее 'общем случае
движения под углами атаки и скольжения коэффициент демпфирования крена
некоторой комбинации вычисляется по формуле (IV-6-27) для т®х. В эту формулу
входит величина А33, зависящая от коэффи- 7 v
циента присоединенных масс Х33,
определяемого по параметрам в донном сечении. Для
одной из наиболее распространенных
комбинаций корпус — крестообразное оперение
коэффициент Х33 можно найти при помощи
графика на рис. XVII-2-1, где представлена кривая
изменения отношения ^4зз/(^зз)г=о = ^зз/(^зз)г=(ь
в знаменателе которого стоит величина
Йзз)г=о = (^зз)г=о = 2poos4/jx для чисто
крестообразного оперения. На том же рис. XVI1-2-1
показана кривая для комбинации корпус —
плоское оперение, соответствующая формуле 0,2
(Азз)г=о
10
0,6
V
V2
\
V
+ 2г. (1 - rl) (г* - 6г* + 1) arctg -J- -
rS
- яМ + rj (1 - rl)2]} . (XVII-2-1)
0,8 Л
Рис. XVII-2-1. Коэффициент,
применяемый для вычисления
производных устойчивости с
учетом интерференции:
1 — корпус — плоское крыло; 2 —
корпус — крестообразное крыло
Можно заметить, что коэффициенты Х33
для обеих комбинаций близки.
Следовательно, формула (XVII-2-1) с известным приближением применима и для
комбинации корпуса с крестообразным оперением.
Для расчета демпфирующего коэффициента можно применить и
упрощенный способ, основанный на предположении, что все другие виды
движения, кроме движения крена, отсутствуют, т. е. а = рСк = 0- В этом случае,
46*
724
Глава XVII
следовательно, coz =
= 0 и
т»*=-42зз. _ (XVII-2-2)
Для крестообразной и плоской комбинации значения Лъъ можно найти
при помощи графика на рис. XVII-2-1. При этом удобнее от формулы
(XVII-2-2) перейти к выражению
_ ^33
(XVII-2-3)
где (т®х)г==о — представляет собой коэффициент демпфирования «чистого»
оперения, т. е. когда радиус корпуса г = 0.
При помощи (XVII-2-3) и графика на рис. XVII-2-1 можно найти
коэффициент демпфирования в зависимости от величины радиуса корпуса
для случаев, когда число консолей п = 2 и А.
Практический интерес могут представить также
случаи, когда число консолей произвольное.
Анализ зависимости производных
устойчивости от числа консолей оказывается более
простым в предельном случае, когда радиус
г—>0. Исследования показывают, что эту
зависимость можно представить графически в виде
кривой (рис. XVII-2-2), изображающей
изменение величины
О
\
0,25 0,50 0J5 Ц
(XVII-2-4)
Рис. XVI1-2-2. Параметр
демпфирования при крене в
зависимости от числа консолей п
В этом выражении знаменатель
представляет параметры для двухконсольного
оперения (тг = 2), а числитель — соответствующие
параметры для многоконсольного оперения. Кривую на рис. XVII-2-2 можно
использовать для приближенной оценки влияния числа консолей на
коэффициент демпфирования и
в том случае, когда радиус
корпуса отличен от нуля,
но остается достаточно
малым.
Продольное
демпфирование. Рассмотрим
методы расчета
коэффициентов продольного
демпфирования в предположении,
что движение аппарата
-совершается в продольной
плоскости без крена и
скольжения. Полученные
цДкр
ц.5.оп
Рис. XVII-2-3. Движение комбинации корпус —
крыло — оперение по круговой траектории (Qz — угловая
скорость)
в результате такого расчета
частные характеристики
продольного
демпфирования оказываются
полезными для оценки динамических свойств летательного аппарата.
Демпфирование, обусловленное угловой скоростью Qz.
Предположим, что летательный аппарат движется по круговой траектории
(рис. XVII-2-3). При исследовании продольного демпфирования такое дви-
Нестационарные характеристики летательного аппарата
725
жение можно заменить вращением аппарата около центра тяжести с
некоторой угловой скоростью Qz, которую в дальнейшем примем постоянной.
Вследствие вращения оперение будет находиться под дополнительным углом
атаки, равным Да = Qzx^ д. 0JV^ где хп, д. оп — расстояние от центра тяжести
комбинации до центра давления оперения. Изменение угла атаки вызовет
приращение нормальной силы оперения
. д. on
(XVII-2-5)
где производную (dcNlda)on находят по местному числу М перед оперением
(q = О,5кМ2р — скоростной напор, вычисленный по этому числу М).
Приращение нормальной силы позволяет вычислить вращательные
производные для коэффициентов нормальной силы и демпфирующий момент
оперения:
dCN
q хц. д. оп
Qzl
Аналогично находим производные для крыла:
dcN \ хц. д. кр
- 2
dCN
I
Ц. Д. кр \ 2
)•
(XVII-2-6)
(XVII-2-7)
(XVII-2-8)
(XVII-2-9)
В этих двух формулах принято, что скоростной напор перед крылом
равен скоростному напору невозмущенного течения. Суммарное влияние
Рис. XVI1-2-4. Движение комбинации корпус —
крыло — оперение с постоянным а —
крыла и оперения на продольное демпфирование может быть выражено
суммой соответствующих производных.
Анализируя составляющие суммарной производной, можно оценить роль
в демпфировании крыла и оперения. Полная характеристика демпфирования
комбинации корпус —крыло —оперение может быть получена с учетом
производной изолированного корпуса.
Демпфирование, обусловленное производной а. Для
исследования демпфирования, обусловленного изменением по времени угла
атаки, воспользуемся схемой, изображенной на рис. XVII-2-4.
Рассматриваемое движение характеризуется значениями £2z = 0 и афО = const при
отсутствии вращения, но при наличии перемещения (свободного падения)
в направлении нормали к траектории с постоянным ускорением.
Демпфирование возникает вследствие появления добавочных моментов,
обусловленных изменением углов атаки оперения и крыла во времени. Пусть
— изменение угла атаки крыла. Тогда изменение угла атаки горизон
У26 Глава XVII
тального оперения, обусловленное скосом потока за крылом,
Даоп = _ (*L) г Дакр. (XVII-2-10)
Чтобы найти значение Аакр при заданной величине а, можно
воспользоваться принципом запаздывания вертикального скоса потока, в соответствии
с которым угол скоса у оперения отстает от угла атаки крыла на время,
затрачиваемое следом на прохождение расстояния от крыла до оперения
и равное t^x^lVoo. Подставляя это время в выражение Дакр = — at, получим
изменение угла атаки крыла Лакр = — а^ц/Foo. Таким образом, изменение
угла атаки горизонтального оперения Ааоп = (аХц/Voo) (de/da)ou, где хц —
расстояние от центра площади крыла до центра площади оперения.
Изменение угла атаки оперения на величину Ааоп приводит к
возникновению добавочной нормальной силы
зная которую, можно найти производные устойчивости
; (XVII-2-12)
)2; (XVII-2-13)
- 'al
a =
2Foo *
Демпфирование рысканья. Методика расчета продольного
демпфирования может быть использована для вычисления производных устойчивости
оперения при движении рысканья и при условии, что все другие виды
движения отсутствуют. Используя эту методику, можно получить следующие
значения для производных устойчивости:
(XVH-2-14)
(XVII-2-17)
рек / on ^oo «Рек II
где хц — расстояние между центрами площади крыла и оперения;
da/сфск — степень изменения угла бокового скоса по углу скольжения,
вычисляемая] аналогично степени изменения угла вертикального
скоса по углу атаки.
§ XVII-3. Анализ
производных устойчивости
оперенного тела
Расчленение заданной комбинации на отдельные элементы [51].
Изложенная методика расчета, основанная на применении коэффициентов
присоединенных масс, дает возможность вычислять суммарные значения производ-
Лестационарные характеристики летательного аппарата ?27
ных устойчивости. Вместе с тем представляет практический интерес оценить
вклад того или иного элемента хвостового оперения в общее значение
производной устойчивости в результате интерференции с корпусом, а также друг
€ другом. В частности, важно установить, как меняется величина
производной устойчивости корпуса от добавления к нему вертикальных и
горизонтальных консолей.
Приведенная методика не позволяет также учесть влияние интерференции
между оперением и крылом на производные устойчивости. Наконец, при
расчете суммарных характеристик не представляется возможным установить
зависимость этих производных от числа Мое. Излагаемый далее метод
исследования производных устойчивости позволяет устранить эти недостатки.
- -*>■]
тгвн - т = тг - т + тгв - тг + тгвн - тгв
Рис. XVII-3-1. Схема расчленения , комбинации корпус —
оперение на элементы
Важное преимущество этого метода состоит, прежде всего, в том, что он
дает возможность проанализировать отдельные составляющие, из которых
складывается суммарная величина производной устойчивости.
Для удобства исследования интерференции целесообразно расчленить
хвостовое оперение на отдельные элементы, имея при этом в виду, что
аэродинамические характеристики каждого такого элемента известны. Иными
словами, хвостовое оперение условно представляется в виде суммы отдельных
элементов, а суммарные аэродинамические характеристики — в виде суммы
соответствующих аэродинамических характеристик элементов,
скорректированных с учетом интерференции. Примем следующие обозначения: Т —
изолированный корпус; Г — изолированное горизонтальное оперение; В — верхнее
изолированное оперение; Н — нижнее изолированное оперение; ОП —хвостовое
оперение.
В соответствии с этими обозначениями комбинация корпус — оперение
будет иметь обозначение ТГВН, оперение — обозначение ТГВН —Т и т. д.
На рис. XVII-3-1 показана в качестве иллюстрации схема расчленения на
элементы комбинации корпус — оперение с неодинаковыми верхней и нижней
лонсолями. Первый член в правой части показывает влияние на силу или
момент добавления горизонтального оперения, второй и третий —
соответственно верхней и нижней консолей. Следует отметить, что расчленение
можно вести и по другой схеме, нежели показанной на рис. XVII-3-1.
Статические производные устойчивости. В качестве иллюстрации
изложенного метода рассмотрим определение производной устойчивости от
коэффициента боковой силы оперения по углу скольжения, учитывая при этом
только интерференцию корпуса и оперения. В соответствии с рис. XVII-3-1
^боковая сила хвостового оперения
ZH.
Интерференционные силы отнесены к силам для изолированных
элементов, причем изолированный корпус рассматривается как заостренное тело
у 28 Глава XVII
вращения с поперечным сечением у основания, равным сечению тела у
оперения. Боковая сила изолированной верхней или нижней консоли принимается
равной половине величины боковой силы оперения, сложенного из пары
одинаковых консолей.
Разности сил в правой части (XVII-3-1), отнесенные к силам для
изолированных элементов, представляют собой коэффициенты интерференции
ZTr —
(^h)t
—^тг (^и)тгв —
ZB
^тгв (^и)тгвн
(XVII-3-2)
Значения коэффициентов присоединенных масс Ли для различных
конфигураций были приведены ранее. Переходя в выражении (XVII-3-1) от сил
к коэффициентам и вычисляя производную по рск, найдем формулу для
статической производной от боковой силы по углу скольжения:
(фоп = Kit (®т + KiB (cf)B + Kiu (c%. (XVII-3-3)
Статическая производная от момента рысканья для оперения:
Аи = -^f- (cf)on, (XVII-3-4)
где хц, м — расстояние между центром моментов и точкой приложения
боковой силы оперения.
Особенность формул (XVII-3-3) и (XVII-3-4) состоит в том, что они
могут быть применены и для не очень тонких комбинаций. В этом случае
производные с$ для изолированных элементов вычисляются по
линеаризованной теории, т. е. с учетом влияния числа Моо, а коэффициенты
интерференции Кь не зависящие от М<х>, находятся по теории тонкого тела.
Изложенный расчет соответствует условию а —0. Если угол атаки
не равен нулю, то в общем случае в выражения для с$ и тР войдут члены,
пропорциональные а и отражающие взаимодействие между углами атаки
и скольжения.
Приведенные зависимости для с$ и т$ не учитывают влияния
интерференции оперения с крылом. При наличии крыла это влияние можно учесть
методами, изложенными ранее.
Демпфирование крена. В соответствии с рис. XVII-3-1 производная
устойчивости по крену для оперенного корпуса
«*)оп = «*)тгвн - «*)т = [«ж)тг - «ж)т1 +
+ [«*)тгв - «*)тг] + [«*)тгвн - «*)тгв]. (XVII-3-5)
Это выражение можно написать также в форме
«*)оп = Кгг «*)г + #зв «*)в + #зн «*)н, (XVII-3-6)
где величины К3 представляют собой следующие коэффициенты
интерференции:
Нестационарные характеристики летательного аппарата 729"
/VVTT Q 7\
(XVII-d-7)
(^зз)тгвн
"6П~ (^зз)н • J
Значения коэффициентов присоединенных масс Я33, от которых зависят
величины К3, приведены на рис. XVII-2-1.
Полученные результаты для т^.х относятся к случаю, когда а^=0. При
афО они могут быть уточнены, если учесть влияние вихрей от крыла
и корпуса. При этом система вихрей заменяется одним вихрем, сбегающим
с крыла, с координатами, определяемыми по изложенной ранее методике.
Хотя вихрь вследствие накренения крыла имеет тенденцию к вращению, этим
вращением можно пренебречь, рассматривая перемещение относительно вихря
только оперения. Тем самым влияние вихря будет рассматриваться, исходя
из предположения, что в каждый момент времени это влияние определяется
положением оперения относительно вихря. Результаты расчета могут быть
улучшены, если рассматривать некоторое среднее положение вихря. Вихрь,
возникающий от корпуса, сохраняет фиксированное положение, зависящее
только от угла атаки. В целях упрощения расчетов можно принимать, что
вихри от корпуса и крыла не взаимодействуют.
Пример расчета производных устойчивости. Вычислим производные
устойчивости для крестообразного оперения летательного аппарата, схема
которого изображена на рис. XV-2-13, при Моо = 2.
Производные (cf)on> (^)оп- При расчете производных будем
исходить из формул (XVII-3-3) и (XVII-3-4), а коэффициенты интерференции
определять из выражений (XVII-3-2) с учетом данных табл. XV-1-1.
Значения коэффициентов присоединенных масс следующие:
/Л \ /Л \ О.
V^iiJT==z \Au7Tr == зърооГ ;
(1 — 72"
(^ц)в = (^н)н = у ЯР~ (s — г)2-
После подстановки значений г и 5, указанных на рис. XV-2-13, получим:
(Яи)т = (кп)тт --= 0,316яроо; (^ц)тгв = 1,56яроо;
(^и)тгвн = Зяроо*, (А,ц)в = (^ц)н = 0,782яроо.
Внося эти значения в (XVII-3-2), найдем
#iT = 0; KiB = 1,602; Кш = 1,832.
Чтобы воспользоваться формулой (XVII-3-3), необходимо знать значения
(фв и (^)н, которые можно определить, полагая, что они равны — 0,5(с^)г
(имеется в виду, что верхние и нижние консоли оперения одинаковы). Относя
коэффициенты к площади крыльев б^р в плане, найдем
730 Глава XVII
После соответствующих подстановок в уравнение (XVII-3-3), получим
(фоп = 1,602 (-0,356) + 1,832 (-0,356) - -0,571-0,652 = -1,223.
По этим данным можно сделать вывод, что добавление нижней консоли
к трем другим увеличивает боковую силу оперения примерно на 14%.
Статическую производную (ттг^оп определим по формуле (XVII-3-4),
в которой #ц. м примем равным расстоянию между центрами площадей
консолей крыла и оперения. По данным рис. XV-2-13 #ц. м^ 4,74. Характерный
размер I равен средней аэродинамической хорде крыла Z = (2/3) ЬКр = 1,50.
После подстановки численных значений для (cf)on, хц,м и I в (XVII-3-4)
получим
К)оп = 4^1,223 = 3,87.
Значения (с^)оп и (tf^)on найдены без учета интерференции крыла и
корпуса, т. е. без учета влияния вихрей, возникающих при скольжении корпуса
и крыла.
Производная тгг®*. Для вычисления этой производной удобно
использовать графики на рис. XVII-2-1 и XVII-2-2. График на рис. XVI1-2-2
дает возможность оценить эффективность оперения при отсутствии корпуса,
когда число консолей отличается от двух. Из полученных данных следует,
что для рассматриваемого случая (п = 4) момент крена возрастает в 1,625
раза.
График на рис. XVII-2-1 фиксирует влияние корпуса на тот же момент,
определяемое в зависимости от параметра г Is. В нашем примере r/s = 0,31,
следовательно, как показывает график, добавление корпуса к паре
горизонтальных консолей увеличивает момент крена на 2%. В соответствии с этим
для четырехконсольного оперения
«*)оп = 1,625-1,02 (т°*)г,
где (тга®*)г — момент крена изолированного горизонтального оперения с
размахом, включающим часть корпуса.
Величину т®х изолированного горизонтального оперения, составленного
из пары консолей, можно определить по линеаризованной теории:
«*)г= —й-= -"к,-! = -0Д92.
да 6 yl
Учитывая площадь, расположенную под корпусом, и новый размах
крыла, найдем
1.812 /1,812\з
2^12 l2^50j =-
Таким образом, момент крыла от хвостового оперения
«*)оп = 1,625.1,02 (-0,080) =-0,133.
Производные (с®*)ош (™^)оп, (с%)оп, (^)оп- Величину (с%)оп будем
вычислять по формуле (XVII-2-6), в которой примем # = #«>. Имея в виду
найденные значения (с*)Оп= — (cf)on= —1,223 и хц, д. Оп = 4,74, получим
(с^Аптт — У.А 994 \ ^±1^ — 7 7е;
Нестационарные характеристики летательного аппарата
731
Полагая, что центр момента совпадает с центром тяжести, найдем
по (XVII-2-7):
«*)оп= -2-1,223 (£й)2= -24,5.
Найденные производные отнесены к величине Qz&cax/2Foo. Для вычисле-
еия остальных двух производных (с^)оп и (т%)ои применим формулы
(XVII-2-12) и (XVII-2-13), в которые входит производная d&/da,
определяемая из условия
V da ) г
Раньше мы нашли, что коэффициент эффективности т)г = 0,73,
следовательно, (de/da)r = 0,27. Имея в виду, что расстояние между центрами
площадей и оперением #ц — 4,74 и, полагая, что перед оперением число М
такое же, как в невозмущенном потоке, после подстановки этих значений
в (XVII-2-12) найдем
(4)оп = 2.1,223.0,27 iig. = 2,08.
Используя (XVII-2-13), получим
Й)оп= -2.2,08-^^ -6,59.
§ XVII-4. Эффекты Магнуса
Косо поставленное оперение. Вращение оперенного корпуса вокруг
продольной оси симметрии может быть обеспечено путем установки оперения
Рис. XVI1-4-1. Схема обтекания корпуса с косо
поставленным оперением
под некоторым углом бОп к этой оси (рис. XVII-4-1). В результате
вращения появляется дополнительный момент рысканья АМУ, обусловленный
действием [сил ДМагнуса на косо поставленное оперение. При отсутствии
скольжения у корпуса с плюсообразным оперением этот момент
'ОП/2
AMу =
c*bou (z) z dz,
(XVII-4-1)
732
Глава XVJ1
где боп(^) — хорда оперения на расстоянии z от оси корпуса;
dou^ диаметр корпуса в месте установки оперения;
^оп — размах оперения.
Зависимость между углом боп и угловой скоростью йх вращешш**лета-
тельного аппарата определяется из выражения
'ОП/2
'ОП/2
(XVII-4-2)
В частности, для прямоугольного оперения
(XVII-4-3)
где КОи = lou/dou — удлинение оперения.
При вращении четырехлопастного оперения с углом между лопастями
90° момент рысканья от силы Магнуса будет изменяться в зависимости от
угла поворота уи отсчитываемого от
Р/п горизонтальной плоскости, в
соответствии с выражением
AMу = А (Му)У1=о (sin у! + cos 71),
(XVII-4-4)
Qfi
1
f
J
f
J
)
1
f2'
,3
/,
Л
Re,
2.0
3.0 oi°
где A (My)Vl==o — момент рысканья,
соответствующий значению 7i — 0.
При движении под нулевым углом
атаки со скольжением (рск Ф 0)
вследствие вращения вокруг продольной
оси возникает дополнительный момент
тангажа, который можно подсчитать
по формуле, аналогичной (XVII-4-1).
Влияние отрыва потока. На
тонком оперении (s<0,05), обтекаемом
потоками с малыми числами Маха
и Рейяольдса, может возникнуть отрыв
пограничного слоя. Критическое
значение угла атаки, при котором
происходит отрыв, зависит от числа Re^FoAp/'v и для тонкой пластинки с
ламинарным пограничным слоем может быть определено по рис. XVI1-4-2. Отрыв
пограничного слоя обусловливает повышение давления и приводит
к появлению дополнительного момента.
По рис. XVI1-4-2 могут быть определены давления рлев и рПрав на
левой и правой консолях, обтекаемых под углами атаки
Рис. XVII-4-2. Влияние срыва потока на
давление при обтекании плоской
пластинки:
2_Reb = 0,5.106; 2-Reb = 0,7.106; 3-Reb =
= 0,9-106; 4~ Reb = l,3.10e
= ОС + Son —
Qxz
(XVII-4-5)
«прав
= a — °ОП
(XVII-4-6)
где z — расстояние от оси до центра тяжести консоли.
Нестационарные характеристики летательного аппарата 733
Момент тангажа, обусловленный разницей давлений на левую и правую
консоли,
AMz= (P^L_£^l\ SouPa*lon, (XVII-4-7)
\ Poo Poo I
где Хюп — расстояние от центра тяжести аппарата до центра тяжести
площади оперения.
Моментные характеристики летательного аппарата зависят от
интерференции оперения с корпусом. Однако, как показывают исследования, момент
ют интерференции мал и в приближенных расчетах суммарный момент от
юилы Магнуса можно определять по значению для изолированного косо
поставленного оперения.
Пример. Определим угол установки оперения боп, необходимый для сообщения
оперенному телу угловой скорости вращения Qx = b 1/сек, и момент рысканья АМу
от сил Магнуса при а = 5°.
Полет происходит со скоростью 7оо = 640,8ж/сек (Моо = 2) на высоте #=5 км.
Диаметр корпуса в месте установки оперения don = 0,25 м, удлинение оперения
прямоугольной формы Яоп = 3, хорда bou — d0IL. Из (XVII-4-3) находим
(+1) =0'00211
В соответствии с (XVI1-4-1) момент
Так как
с£ = 4(М2оо-1Г1/2; goo = 1,54.10* кГ/см*,
то
АМу= 1,54-104.0,00211-0,253-1- 3!l^_ = 0,204 кГ-м.
о<,д "1/4 — 1
Вычислим момент тангажа, вызванный отрывом пограничного слоя с консолей
стабилизатора, при условии, что
Qx = 5 1/сек; а = 2,5°; боп=10; 2 = 0,25 му Foo = 200 м/сек;
Reb = l,3.l0e (Ь = Ьср==0,25 м; Н ъ 10,7 км);
площадь оперения Son = 0,0625 ж2; расстояние между центрами тяжести аппарата
и оперения xion = 0,35 м; давление атмосферы ^ = 0,56 кГ/см2.
Из формул (XVII-4-5) и (XVII-4-6) находим
-^^5 57,3^3,14°;
Из рис. XVII-4-2 определяем рправ/роо = 0,47; рлев/Роо = 0,68 и по (XVII-4-7)
^вычисляем момент 168
AMZ = (0,47 — 0,68) 0,0625.0,56-104.0,35=—25,7 кГ-м.
734
3
ев
|
X
>*
5
О
S
к
В
>e<
a>
IS!
К
о
S
I
00 t>- Ю CM OJOrHri ^_ t,
CMt^Ovf Ю CO vf CM ОЭ <н О n
ю со ю ю оо о о о н t-^ ю чр
НчРСМОЭ Н^СМОЭ СМСОНОО
1>СО 0000 t» t^ L
ЮтНтН|> -НтНС
ОО^О) COCO С
чг со со nf st1 смс
!S
. _- CM ОЮСО
> Чр CO CM Ю 00
)4f vf CM l>- CO
■H ^^ <^) "H ч-ч ^^ <^> ■«
SfSfOfO ОЭ -гн -*ч СО Ю CM CO CD
CM CO CO t>- CM CO Ю Ю ОЭ n^ CM CD
о о оо оэ см со ю ю vji см н оэ
ЮСМСОСМ Ю н СО СМ ЮНСОН
v^ ОЭ Н 00 ЮчРСОчР
юсмоэю ооюоосо
t>» О CD CO OONsfO _ ^ - -.
Ю -ч-1 Ю н ЮОЮн СО О Ю О
н НОО*
н ООн
со
о"
00^
о
7756
t>-
со
t>. об со оэ о -н см чр -н оэ см со оо об о оо
со оэ со *<? со со со **Ф оо см см со ^гн t>" оэ оэ
оюсоо оюсоо оюсоо нч^смоэ
н Он СМ
1 Он СМ Н Он СМ
СОСЭ СО '
н О О ч
см оо н с
оэоэоэоо оэсочясм -
t- t>- CD ОЭ СМСМОООЭ OCOCOt^
.__ OOCOOt^ ЮООЭСО OOvft^CO
со*^оэю сочроэю со-ч^оою сооооою
гнООП тч О О н гнООп н О О ч
СО !>• ООО Н
Ю ** CD t— ОЭ
СО 00 vf !>• sf
•<J< СО t4- СО ЧН
s§
со юооюоэ
СМСМ Н Н NJ4 СМ СМ Ю СМ СМ
■ С— COOOOCD СОЧ^НСО
СО 4f СОС — •■--- —
тг1 ггН О О Н Н О О Н Н О О Н
00 СМН Ю
_. . оэ оо смео
СМ СО Н О 00 Н -чн ОЭ
CM CO т О
LQ СМ СО СМ
СМ СО Н Ю Н СОН
D ОЭ О чР СО СО 1^ н
эемюсо емюс^см
н 00 О 00 СО 00 00 СО
•н О О "Н тнООгн -гн О О н нООн
см
о"
о
О
«о
о
см
о
/
мл
Q
о
оо
см
о
/
мл
СМ 00 СО 00
00 ОЭ Ю СО
о со о ю
ООтнСО
н ОСМСО
со оэ t> см
СМ 00 СО СО
t** СМ с""} чР
СО I"* vP l>»
-НО н СМ
vF ОЭЮчР
СО Ю 00 О
н О О СМ
00 CM vt* СО
-^ О О н
см
о
9696
8136
1170
3696
оо см со
ОЭ ОЭ Н О
СОЮЮ 00
coS^S
н Он СМ
00 ЧР ЧР СМ
СО ОЭ чР СМ
сою ооо
н О О СМ
С- Н ОЭ 00
со см о- со
НООН
о
ОЭ OCD Ю-
СМ VJH СО СО
Vf СО t^ СМ*
о i> ооо
ноем со
г-ю ооэ
00 00 Ю Ю
со со со i>
Н Он СМ
ю оэ со оэ
союооо
н О О СМ
Ю t— vfi Ю
■sf l>- Ю 1>-
00 н Ю СМ
00 СМ чР СО
НО Он
о
9895
7905
1138
3660
оо см со
Nf -ЧРОЭОЭ
00 ^^ CM vf
СО t^4P С—
НОНСМ
Vt< СОЮ ОЭ
1>- Н СМ 00
со ю ооо
гнООМ
СО ЧР О О
СО ОЭ t--CO
00 CM v^ СО
н О О н
о
735
"Г
s^ СО СО С
ю см сое
СОЮ СО I
Ю СО Ю Ю
с^оо со ^
со со со см
N* 00 COCO
1>>СО С*- 00
с— о "4-1 со
-чч СО OS CO
СМ О 00 СО
OS ^н СО ^
со
о"
СО СО vf "чН
ЮСО 00 СМ
t> OCO t* Ot>*00CM
Ot^OCM гНСООМ
Vp СО СО СО
_ . СО СО СМ СО
юоюоо ^и см nf со
о со о ю cMCMt>*o
t>. Nf 00 OS t— "<tf t* OS
^гГо о"-ч-1
CO
о"
00
о
II
<за
о
о
со
о
<м
о
/
/
са
о
•«*
о
со
о
са
о
/
/
iXfl
СО СМ СО |>
юо^о
CMOS СОЮ
СО OS «чч О
со аэ со vF
СО 00 VF OS
Ю OS СО CM
Ю О СО Ю
as со t>* as
^ЧООСМ
о со as см
СО !>■ <О СМ
^ см со t>
СМОО^н
СО
о
coco t"- со
оо аэ ir^oo
-чч аэ сою
емю ооо
OS t>- OS Ю
00 тН OS 00
ю as vj< as
00 00 ■sH t-
"H OS OS CO
OS CO t- О
тн OOCO
'st1 CM 00 CO
OS !>• OS C\]
■tth COCO 00
СМОО^н
CM CM -чч LO
00 00 l>» Nf
CM 00 CM vf
1,6609
0,8038
1,4260
3,8460
ЮСО1>Ю
CO О CO 00
CO 00 XF OS
OS Ю t— 00
^.OOCM
t> t-cooo
со vf аэ со
^ч CM CM CO
<MOO^
CO
©"
CM -чЧСО О
OS t^» l>» OO
-чч as со ю
CO vp CO ^н
as о as oo
loasvtf as
о со
ю2со^
см оо as со
OS CO F- О
-еН О О СО
со !>• as as
■sf ю см as
"чЧ СО СО t^
СМОО^ч
^^ (^а н^н^ Gh Q
о
о
^ as оо "чч
со as ^н со
О Ю CM t—
со оо см со
■^ч О> CM ^vt*
о as sf vj^
as !>■ оо со
I>- !>> 00 !>•
CO !>• CO l>
см со см о
ЬЮтЧ(М
as ю t>« оо
^чООСМ
СМОО^ч
н^>- о* а,
о
ггЧ
Ю СО t*- 00
00 OS Ю СО
CM OS СО Ю
ОО^гН t>-CO
t^ СО СО Ю
ооо as t^
со оо^аэ
о со
9310
6659
7903
0268
^чОООО
ю t— аэ гн
СО 00 СО-гн
■sf СО CMOS
ггн СО СО t-
МООгн
л ^ ^ Он а.
см
о
00
о
■гч
• S
■чЧ
©
651
О
со
as
см
о
•чн 00 СО СМ
со со ^ ^
i>. чн аэ ю
Ю t*- 00 t^
сооо^аэ
о со
00 'гч СМ -^
СМ СО 0 05
as со i>» as
^оосм
1533
3060
3198
7632
СМОО^н
о
736
sPCOHvi О st CM s# COCO^HO
WpOlrH ^ v£ «*ф CO Ю CO 00 CO
CM l> CM sf ^ Ю
coos -4ft
„ 00 CO CO CO ч;н
CO OS CO О CO OS CO О
со о m со
i_O OS О О
, . „ _,._-. THOOt^OO
CM OS OS f- CO !>• CO CM Ю ЧР CO "SP
I- 00 Nf CO t>- 00 ^ CO l>OOSfiO
CO CO CO H CO t>> CO 00 чн CO OS О
vfN^cO'^ COCMOCM COOOSOO
vf CO Nf OS Ю vf CO CO CO CM О Ю
<O CO !>• !>• <O CO C4* l>» <O CO t>» CO
cm'oo'co'4 cnToo'co" cm~o~o~co~
coco coos
in см ю см „
CM CO CM CM CM COCM
~ CO
см
смоосм см о о см см о о см
CO
o~
00
CD
CM
CM vf Nf Ю CO CO ^ 00 О 00 CO OS CO С
- со оо in н — ■ -
, . 00 vf О CO _ .
-CM CO CO t>- CM !>• CM t^ чгч ОС
сможем сможем сможем сое
тгГ^Гсм^ш"
СО СО ^1 СО OS 00 Н СО 00C0OS00
н SP О 1> гН'Н t>O COO-vfCM
3 Ю СО Ю OS^fCMin О ^н ч-н СМ
SOSLOt>- COOSLOt- " — ■ - ^
5СО COOSCOCM OOOSCOO
• t-00 О tr^ t^ 00
ю со оо со
CO CO 00 Ю CO
-00 О CO !>• С
CMOOCO CMOOCO CMOOCO CMOOCO
s
gS?F^
. _J00rHiO 00-HOi
DOSOS N^TiOiCD COOS
sroiCOO vJ<00CO~ '""
CM CO CM CO CM CO CM
см о о* см см" о" о" см" cm" о о" cm" cm о" о" cm
•^ ^ sf 1Л
_ . _. -нЮСОгН
^cocoas mvj<cot>-
CMCOCMCM CMCOCMCM
CM
cT
н
сб
S
5
Я
О
о
к
со
о
м
&
и
я
ев
я
я
«
о
со
сб
LO СО 00 Г- тн
СО 00 СМ 00 NJH
t>> LQ СО СО t"»
4f CO тг1 СО СМ
OS OS 00 t>- СО
^н СО О СО О
Nf ГО 00 СО СО
vf СО чн Is- СО
!SS
NF СО -гн 00 Vf
ю см о см со
OS чН О СО СМ
COCO О 00 Ю
ю см о sf ^
CM t— О О OS
00 OS О Ю Nj«
"<Р СО О СО СМ
О5ЮСОЮ1>
NJ< СМ тп С-- О
СО OS Ю СО 1>-
v? СО тн СО СМ
OS CO OS OS 00
с^ см см о in
CM 00 OCO Ю
vji CO CM t> CO
!>• CM CM CO OS
CM CO Ю CM NJ<
OS t^ CO CM C*-
CO CO "чн 00 vjh
COsfO^W
00 OS О t-CM
l>- CO OCO CO
COCO O00 Ю
737
•-ч
- - w_ CDOOOCOCO
00 С- О 00 СО ^OOrHO
vF vt1 О 00 CD 1>тнОЮтн
LO CM О Ю -<г-< ЮСМОЮтн
t—CDCMC—LO ОЗ О t> CNIO
t>-vfv^oO-^H CMOOCMCMO
COCMOSOOS CD00OSC—■>■
_ _ .. sf оо со os -^ t-~
СО О О тн СО ООО^^ОО
*гн С— COCDCD СОСОСМСМО
Ю^^гнСОСМ LO <ч-« ^н CD CM
о
a,
OS 00 LO С— СО
LOCD 00 LO CM
тгн t— 00 С— 00
LO О О CD CM
?CD О
) OS v^
) OS "^
5 CD CO
0,0.
00
CD
о
СЛЮО
ЮтнОЮСО CM 00 1Л чн чi OSLO
OOCOCMCDCD О00О1ЛЮ -«rHLO
vf CO -rH CD CM Ю CM тн CD CM Ю CSI
CMJ
SCOCM
CD <M
С— Vf v^ OS ОС -, „ _ ~
CO ттн LO OS LO VF t— CDCOCO CO
Ю О CD CM LO l> vF *<Г m CO OS
*<F CO тН t— CO v^CM^Ht—"
4ft CM г-н CD CO
^н ООО^н
) ^н ^-i О О О тн
<H CO CD t> OS ОСО
CMCDCMCMCM COiM
C\jtCD ^
1>1> 00 vF 00 OS CD
NO t^-COCOCDO
OOCO CDCDOSIOOS
f ^OICO
COO
OS t—
5S
CD ^FOOOCOOS CMt—C
..см ^oogMsf t>coc
.^LOtH COOSOCNIC^- LOSfC
OOOLO sf-rHOOOsf ^тн(
О О О тн
^ thO OO^
а, а.
a< а,
a, cl
см
о"
CD
О
vF«r4COCD00 тчЬгЧОО^
CO t>- 00 CD t> vf тн CD CD -r-(
OS CD sj" OCD _ , .
11 >тн LO CO CM
^h <«-( О О О"
CM CM OS CO^
OS CM t— О О
CM О CM CM CM
vf CO CO t— CO
00 f- CO^r-f *
t>- ЧН OS OS С
s}< CM CM t>- С
тн О О О'
CM COCO •>* 00
00 LO CM CO CD
CM OSL
CO t- LOCD CO
CO CD тн О CM
OS 00 OS 00 Np
CO тгн ^ч 00 LO
^гн ^н О О О'
•чн СМ О О СО
S 00 bCOOCDsf
^ CD CO ^гн OOS CD
a,o.
а, о.
СМ
о"
о> t>» <о ■^-' см *<^ *^ о> см vf1
00 CD О CM vf CD CM О CM SF
ПОО00Ю НгНОООЮ
^нООО^н
тНСОООСМ^)4 I>-vJ<lOCOO
OSCD-^hlOCO 00 t-i I> Osf
t-OSCMOOLO 00 00I>Osf
^ГОООЮтн ^СОСМСО-ч-!
thCMlOvjhcO lOCMsf O«D
vf CD CM -4-1 OS 00 •>* OS CM CM
O> t*** <O OS O5 ■^н CO LO th (O
vfCO^CDCM ^СОСОС-СО
О CO CO OS LO C— CD Ю CM 00
I>OOOCOCO COOOOOOO
COCOCMOSLO CO CO CM OS LO
^OO~O~^h ^hOO^O^h
CQs^OOOt- QOONO
тн "чй <O lO OS 00 OS О OS CM
НЮО^О CM00OOO
со со о о t— со см о о t>
a,o.
а, о.
47—114
738
csi
00 ЧГ1 О 00 t^
Ю О О t- -*н
Is- СМ О "«ч CD
юсооюо
00 !>■ СО О СО
юю i>ooo
ю со оо ю о
Ю СМ -чч Ю чН
00 CD CD О 00
ОЮЮЮ\^
Ю тгн CM CD CM
sJOMni
СО vF -r-f vf
CD v^ I> CD
HOrHN
CM О CD CM
OO^CO
О О00 vf
Ю
Ю
t-
CD
ю
о"
CD
CO
CD
Ю
см см см см см
Ot>OCQLQ
CQO5 О5 00Ю
CM00C005O
OOOOLOOO CMCDCD^hvP
-НСОО'Н 0000Ю00О5
HCMCMt—CO vf-чЧСМСОСМ
1>^О5^^н OOCDI^OOt
LQ 4f O5 O5 Ю t-- O5 CO -чн 00
CD
О*
00
О
Г- СМ О СО С5 ОС5(
ЧР CO О СО Ю t- CM i
4fCOOb« ЧР СО <
CM G5 О О5 Ю
^>о^ч о съ о со со
> i> со ю см о со см
■i 00 О
D00 СО
СО СМ СО '^ ~~ ■ - -
CM 4F Г-СО 00 СО О СО СМ 00
СО ЧР О5 СО О5 i-O О> О5 СО ЬО
ЧР СО О> С^" СО чР СО О> 1^*" СО
. СМ О О^-
t- O5 G5 О
1 СМ О СО СО
ОСОСОСМЮ 'гчООС^
. , , „O5CD НЮЮ .
смсосмою юсмсмсо
тн О О О ^н
ООСООО COOSCOCDCO t-CMCMCOCM
СМЮО О^О^СОО^ Q5C5t>CMlO
05С0
см ю см ю о ~ — -« -- --
СОСОО^СОтН 00СМ00ОЗЮ пч
СОСМОО^СО СО ^ О 00 Ю ЧГ1
ЬОООСЛФ СОЮ
00 05ОЮ00 СО^
СОСМОСЛСО СОСМ
со
о
00
о"
00
о"
CM
о
о"
t-00OG5CM
OOhOCOCO
. . . . . осоосоюсосоосою
ООтнОСОСО гнСЛО^нСО СОСМОЮЮ ШС
г^оооосм оэсоооосм —
(М00Ю05
vf со О l> CO
ЮСООСМч^ СМ05000 НЮЮНС - ,
— ~ СОООЮтнО СОО5СОСОч^ О^СМЧ^ООтгн
" ^н со оо см тн о ю ооо ооосо
004f сОч^тнООчР ччсО^н^-кГ
00 -
о
. OOOSCD
СО NF тч 00 Ю
OOCMNtsv}^^LQ^0Q0ot>cO
00001>- Ю-нООСОт-i СМСОСОСМСО
CDOSCO ^ОЮОЗСО t^^^tO
тНООЮ СО^-ччСОЮ
vt<CMOOCOO ООСОЮ^О
ОО OliOOOCOt4- lOCOt>00 t>
05 00гнтчо05 Ot>OOiOO
О MJ<
nOOOn "чч
СМ^н О^ЮОСОСО ЮСООСМС
, — _ - ■ -,- _1>СО 05CDOCDC0 ОтнОЮС.
ЮЮОСОСО С—ООЮЮ 00c004f4r WOOthO
■ - ■■ смч^оос-смсос^-^ -----
) чР SP CM О О тч
)OI> COCO О О 1
см
о"
ГО СЛ О СЛ СО
СО СО О rfs J^.
^Л СО О 00 СО
ОО^О
to н-^ О О О
н^ 4N н^- СЛ СО
5O5 О СЛ O5
0 СП> СО 00
t*^ CD
5 О СЛ
Л СП> СО
^ t*^ C
соь-а. СЛ О
ь-* tO СЛ 00 t-^
СО tO СП> СП» СП>
СЛ СО "<1 СП) О
ha. ^OO на.
00 tO на. СП) О
СО !-*• СЛ СЛ СЛ
^ tO СО О tO
ЬС н* О О О
Ю СЛ О СЛ СО
C0N5OO4
to оо о сп> ел
•^ tO О rfN tO
h^- £ч M" СЛ СО
сп> О5 о to со
СО hfN Ox О СП>
СО О СП> СП» СО
О СО н СЛ О
to to сл ел ел
оо ьо со сп» »-^
^на, на. о О на.
СО на. на. СЛ на.
О СО на. сО О>
СЛ СО СО СО С
СО £s ^ ~ "
О н>» О О tO
СЛЧОО00
о
to
со1оосо »-^ со to о ^ н^
соосон а^ to о -а со сл со о to-j
О<|ООСЛ jscDOOi O5 O^OOOOi
to to О <IO CO-q О О 00 н^ 00 О tO СЛ
!-*• !-*• О О i-^ н-^
^Л О на. to [О 00 на. to CO tO OOHA-toCOtO 00 на. to JN tO
-sIOOOOOO-J OOOtfs^ ^^Hi.cotO OOtOCOO
СП» О CD CO СП» СЛ СЛ £» CO СЛ н^ОСЛОЧ СЛ 00 СО СО СП»
QOOCDH. tO tO СО на. на. ОСОСООСЛ СО ^ СО СО СО
на. О О О
СЛ 00 СО COCO
со -а н^ со to
СО 00 СО 00 to
к^ СО СО tO tO
СЛ 00 СО н
СО ^q CO С
*со сл оосо on t
Ю О СЛ СП» СП» С
5 *-Л СЛ СО tO 00 С
"СО СО hfN СП> О •
СО на. на. to tO нР>
СП» СЛ JS. СО СО tO
СО ^Л СО СП) tO rfN
СО на. СЛ -Л СО НА-О
-Л --Л СО СОСЛ на. 00
~ — ~~ "tO й^> СЛ
tO ^ CO
00 СО --J
CD СО СО
СЛ СО i4^-
i-^ОООь^
5 rfN ON tO СП» С
" "^ СЛ 00 -Л С
:> 4*ч ^j С" '
JtO 00С
»rf>» tO CD С
DCO СОООС . ._
)CO HA.HA.Oi4^tO COtOOCOCH)
Э ha. OOOOOha-co HA-QOOtOrfN
СП»
со
to
л
-Л
оо
8
о
Ъо
СП» CO н* ha. CO СП) О ha. ha. CO •<! О на. ю С
to^-л^чсп) ооо-лоосо --- ----
ЮСООСЛО й^. на. СО-Л на.
tOCOCHiHA.^ tO4^>^*^liiN
О О О н^
СЛ 00 t
„_.^--. ^ л -<1 СО на. сл с
tOHA.^000 «<1-^н1^н^СО О СОС
со-л-лсл>со -<itococoto
to
00
C0
tO
corf^ coqhcOht^
СП» СП» ь^ О СО СО £>
на. СЛО СО СЛ
СП»СО О -<1 на. ._ _
3
5
6SI
740
СМ чГ О О CD
«2
СО CM CD ЧР CD LO СО СО t- CM
CMiOOiOiOO LO CM Oi -sf1 CO
CM ЧР О О t>- CM 4F О О !>•
CD CM CO Г- LO CO th
l> ОСО О О © f-
tH^tHCMCD CM CO
h ^гн riOO'
О
СО
-*ч t^ LO LO CO^HCMCMOO
CMCMCDCO l0 05"HOh
LOOiCMCM CD-rHOit^CD
CO <O CO О1 '^ч CO <O CM Oi
CD CO О CO CO CM v -
(N -H О L^ CN COI>C
тч CO О N f" чГ* Oi C_ _
тнСООГОО HMOfOO
00
о"
Oi
о
CD
00
Si
LO
8
о
s
00
о
OiOOOCD^ t— О О CM 00 CO t-О СО 4f
О CM О CD ^h COQO^rH чР СО О 00 CO
Ю 00 О ЧГ LO OOCOOCMCM thOOOOoO
•~ - "~ -ilOOtHOO CMlOOOC^
S83S
ОО
ЮЮСМО00 OOOCOCMC
5 CM I> гнО^^(
. , н Oi Oi CD CM О CD t
JrHrHCO HLQHrHC
CO CD t>» Oi "*4
CO CO Oi CO CM
Oi 00 Oi CO CO
lOCMOOlOCD O^N^tH 00 00 4}^ 00 О
CM LO Oi ЧР -"гн О LO CM t"— CO CO LO l>- О CO
t>-CMvJH-rHCM ^rHt>-4tiOOOi vF CO CO LO Ю
ОЮ-гнСОО <н чР r-i CM Oi тн 4JH-гн CM Oi
О О
О О
CDCD-r-HCDO OOiOiOOO C0CDOiLO4P
OiCDCMCOOi OH^OCO CDO04TCDI>-
■ч-hoOOlOlO CDCOOiCMCM OiOOOit^F-
<O 4f rH 4f ^^ <O *^ C> 4f th <O CO О CO <O
CO "«"t C> Oi CO I4*" CO (
00 ^н f"*^ lO Oi Oi ЧГ^ С
01 l>* <O ^s"1 ^^ CO "
Oi 4f< О LO CM ~
5cooo oqcoooN
5 00 Oi t>» Oi O> тн Oi
- "" !>• CD О СО CM
ОООнМ ггч О О -<
G.Q.
f^Q.
см
о
CD
О
CDOOOLOCM 4f LO О •>■ CM
CD 4f О 00 LO 00 О О 00 LO
CM ЧР О Oi тч СО тн О 00 Oi
* - - " '• 00 чР ОЧР CO
^OOO^
8108
4347
1379
5300
4761
«*н ООО^ч
7734
4142
1822
6277
6578
^н ОО O^i
7379
3970
1207
7533
8781
^н ОО О^н
,7238
,3904
,0000
,8129
,9783
^н ОО О^н
8237
3971
1260
5216
4599
"гн О О О «чн
ЧР LO CM ^н 'гн
00 Oi Oi 00 т-i
00 CD CD тн 4f
t^ CO -r-i CD CD
^н О ООтн
7545
3456
1138
7372
8502
^ooo^
О СО О Oi чР
тн CD О CM CO
4t» CO О Oi чР
^н ^н о О О -чч
К (L. Ф
а, о.
CM
о"
ЮСМОч^СМ CDCOOsTO
чР CD О CM CO OsfO^^
-thOOOOCM CM CD О О CM
OOsfOiOsH 00 чр О LO чР
CD 4f тН
LO тгч 00
г* о t>
см ю см со см
CM Oi Oi CD CM
Ю CD Oi CM Ч)4
t>- ЧГ1 тгн CD CD
««4 vt< CO 00 С
LO О O00 С
CD чГ1 Oi CM l
CM 4t< LO !>• LO
■i CD CM LO 00
■■" rri l> 00
Oi 00 O4f t-
00 CD LO I> 4f
CM CM CM LO 00
Oi 00 О CO Oi
^CDOthCM
О lO О CM Oi
l> 4f О 00 Oi
CD CD О О Oi
4f г-н О Oi 00
-гн CM О'гн 00
" ~'00 Oi
Ci, O-
Н И. Ф
а, о.
741
II
8
ю
II
II
о
OS
ю
/
135
о
O5
о
/
CO О О Ю СО
00 'гн О СМ СО
00 СО О чР СМ
тн ООО-гн
СМ СО тн sf l>
00 Ю 00 ОЬ СО
СО О2 О Ю СО
00 СМ тН 4f СО
•чн ОО О^н
1>- "ч-ч О тн ч^
v^ t- O5 00 t-
СО Ю чГ ч^ О
00 СМ -^ Ю Ю
-чн ООО^н
О5 t- CO O2 СМ
vj* [>• СО LO 4f
О тн О vt1 00
00 СМ "^н СО СО
СОООнгн
СО тН О О2 00
©ОО00Ю
^н О ОО^н
о
со
см
ю
о
t-
о
ю
СО
t^
4f*
о
СО
г-
ч^
ч^
о
ЧР
00
СО
ЧР
о
t^i00^05 sfNOOOi
ОС^Очню ^ОООЮЮ
lOI^Ot^CO CO^OLOCM
ООСООЧ^СО ООСООЧ^СО
""НООО-чН ■^ООО'чн
8364
3641
1177
5076
4321
8503
3322
1119
4882
3928
^ООО"*н гчоООтн
8027
3311
1599
6016
6103
8175
2952
1533
5790
5674
^ОООО ^-ЮОО^н
чР СМ О5 00 Ю ^ОЮОЮ
О^нООСООО СООЮч^ч^
Г^» С"") f™*) ^—1 ("*) 00 СО С 00 *-О
Г^ООтнГ^ОО t^CM-^HCOt^
"^OOOr( тнОООт-f
CD СО О v^ ^ Ю СООЮ1>
h-ФОЮЮ sfiOO-H^
L000OC005 1>>Ч^ОСОСО
1>-СМО1^00 1ХМО1>00
^ООО^ -чн ОО О "чн
СО 00
о
о
CM LO О СО 00 ^
ttOsfC
СОЮ005С
00 vJH О СО -
COtH
-^ О О О ^н
5 СТЭ С- СМ 00
2 С"- СМ СО О
) Ntf< CM Nt СО 00 СО
й^
lOCOlOfr
-HiMOOOCO
COt^-тНСМЮ
00 СО CM N^ CM
ОСОС5 00Ю О00СМЮО
HlOCOt—Nt1 COCO^I^t
CMt
гнОО
t~-CMC
ОСОООЮ
vfOCMOO
CMCM00O2
^н ооосм тн о"о сГ^-Г
LQtaHO ЮОСМ
СООСОООЮ С005СМОСМ
CMvfOCMOO ^05005CM
tC
ОСООСОСМ СОСМОСМСО CD гч О СМ 00
l>-t-~OCOCO vfOOVOCO СОСООЮСО
ООЮООтн Ог^ОСО^ СМСООООСО
СОСМОСЪСМ Г--СМОС75тН ЬОООО
-^ОООСМ н
со
о"
00
о
СО
СМ
ю
ю
СО
СМ
СО
СМС00050 ONOt^OO CDCDO-HSf*
смсооюсо сосооюсм ^ооою-н assf
Ю0500СМ ЮО^ООСМ ЮООООСМ Ю t>
OOfO^CM OOFO^CM OO^O^CM OO^
> ОО'Н
^OVfCM
ОЮООСООО ^'СО
tr-^чСООСМ ^гн
CSOOCOCM-^ тн Ь^НГОСО
t^ ч^СО^СМ 00 Sf CO St1 CSI
COCOv^cOlO t-CSCDcOOO
CMC5^r-i00I>- OtCM^CM
СМЮО5СОС0
OOfCM^fCM
СОЮ^СО-Н О
COCOCMvPCO Ю"
cOCOt^OOi ^
<oOOO
МЮ^Ю 00I>lrCOt
"^СОСОСО ООСО-гНОСО
Oi ^тНЮНтН Ю1>»СОСМСО
C^vt<oOCOlO t-v^cOCOCO t-COCOCDCO
-^нООО-«н
OOt>-OOCMt-^ СО00!>-СЭ^ СМСОЮОЧ^ ЮСМО0500
LQ СО СО 00 00 t"** CJ5 CJ5 "тн СО t^- CJ5 СО ^н *^ ЧР t>* "^ 00 !>•
lO ^^^ СО 00 СО СО ^^ СМ О^ 00 С44* t^* СМ О^ 00 О^ СМ ^?ч t4^ СО
сочрсмооо сочг*смооо сососмооо сососмооо
■* О OO CM
tHOOOCM ^i
^ON4t CO ^H С
-H 1>ОСОгН О
CO CO O*^ CM f
СО ЧРООСО СО
см
о"
742
*чч О О О "^ ^н
CO CM CO CO CO CDObcMLOvti CD CO 00 СМ С
00 05гн bsf ЮЮ-нЮО t^ CM <Г ~~
l>S^^CDt^
^-i тн О О О *ir-i
СО О Ю 00 Ю СО -«Н Ю t>- CM С— Г— Ю СО L
Ю СМ 00 Г- 00 СО СО ^F О CM COCO-^hlOC
CO CO lO <O lO тн С4! lO 00 ^н СО 00 lO nj^ l
COsf-rHOOCO t^ vf< ггн t^ CO t—CO-rHt^-C
^"o o*o"« "
О О О ^ч тн О О О
- . сосм^-1-^о cocm^hooo
CO CM 00 vF 00 CO CM t^ О CO st^iMCDO-H
lO CO ^^ k-O Г4*"* t^~ O^ c^) C^\ C\l O^ ьО C^ t*4"* ^-O
CDsf tHOJtH CDCO-^CO'^h COCO^hOOO
О 00 О CO vf CD CO О «чн 00 I^OONfCD
l> CO О О CM t^t^OCMO СОСОО*^СО
СО^НОСМГ— Ю^ОООтН t^-OOOCOCO
CDNtOOCM CD CO О CO CM CO CO О СО тн
н ОО О CM
нОООСМ
c^ o-
СО
о"
00
о"
СОЮОСОЬ vt< 00 О CM гн СО 1> <
!>• ^н <О 00 *<Р СО t>- O> t*4» CM "^ CO <
OCMOCDCO т-iCOOCOCO СМГ
1>-CDOCDI>- " ■ ~ ~
5 LO CM СО ^н О 00 СО
5COLO ^СООО"^
>сосм ^«оюо
^COt^ t^iOC<Db
н ОООтн
C0IT^C0!>-lO COt^OOO'
CD CO t^"**> ^н cD lO ОО ^3 ^?^ *
cooco-thlo cooooO'^-i<;
COCO-^Ht^tr- СОЮтнЬС
COLOCMCMO CMCMCOt^LO
St^COI>O5^ М^^^тн
ococMOO cMCMCMCooo
") ^ t>QQ ОЮтНСО l>
""^ ■НОООП
COC5CDI>'H CO CO CM t-* tH t^COCO^'H CM "^ CO О 00
COHHr^O t^OO-^HCM-rH OOCOOOOO NOCOOO-H
CMCOt^NfOO vfCOI>»vF-^H LO^CD^f-rH t^OCOCMCO
CDLO'^OOCO COLO^OOO CO LO tH 00 О CDLO^HOOCO
^гнОООСМ <*н О О О СМ
О О О ^н
SCMCMvfCD t— CD t— CO
JOOCOvfCO CM CO CO CO , ,..,.,
DlO-чнОСМ cDlO-^OCM СОЮтч
l> t* CO CO vf тнООСОгНтН
COCMCMOOOO v3H-sfHO"^^H
CO «^ cOt-^HOOCM
CO CM CD Nf -гн CO CM
-nCNl тгнОООСМ
см
о
7167
6026
2762
^oo
5807
5537
О^ч
6176
5695
3371
8163
9329
^нОО
О^н
CM О О О CO
CM CO CO XP sP
CO CM "*h CO •«*
^O О
,4993
,5088
,0000
^н CM
,3396
,6843
00 СО CM LO СМ
nJi CO vf vf CO
t*- О 00 1> СО
СО CD M O f
СО Ю 00 СО О
со оо см со со
оо ^- ^ о со
LO Ю СО 00 00
LOCO 00 l> t>
LO ^Н СМ ^Н ЧР
^н LO <гн СО СМ
LOLO CM ^H VJ*
см со о со
!>• ^н О СМ
00 vf О ^f
•^ LO О СО С
743
CD LO O LO С
О CO ООО C_
00 LOO vF CO
t- 00 ЮСО*<Р
CD CD t- CD CM
CD О CM CD -^
t^ Ю CM Ю Ю
CD CD CM О CO
CM О 00 t> Ю
00 00 гн чР О
С- st* CM Ю lO
LO t~- -^ t~~ CO
ю со со оо t-
О СО О 00 vj<
CD CO CM О СО
СМ Ю СО ^н 4f
CD VF 00 CD CO
CM CM О v« 00
CD CO CM О CM
COCD О CM О CM CO С
CD CM О vfi Г- O500 С
t- CO О CM гн CDQOC
LO COO CM LO
00
о
CD
©~
00
CM
CO
oo
CM
CM
CO
;3g
CM 00 О CO 00 l> vf <
СЯЮОЮЬ -?н тн С
^ ■ -" as CD с
- Ю О Ю
l> CM vji vf cq , _
LO LO 00 t* LOCOCOt-CD
LOCMLOLO 1>ЮСМьОЮ
lO O> CD 00 "^sf vj^ O> 00 00 CM t^" CO lO CD ^r-i
ai00^H"rHCO 00OOC000 ^С^-^НСОСМ
СМСОСОСМЮ vfOCMCMCD COCD^-HCD
CDLOCOOOas CDLOCOOOOi CDn^COOOOS
LOCM
LOCOOOCMCD
00OOCMC5
LOvfCM^-iCO
н CM ^OOth
тН Г О CO
LO ^ О CO C
5 С- CD CD CD О О 1
5 CD t- s|*i>OOc
5 О CO lOt^O t^C
J CO CD Ю СО О CM i
см
CD
О О О 00 CO LO О О sf CD
СМ ^н О О LO CDLOOCOOO
lOOOO^FCO С-^ОСМО
CD CM CM 00 С
_ OOt^^^fLO
см со ^f1 sp ^st1 as vf as со lo
CD -CM LO O5 -4-1 0000LOl>>as
■ -^ ^ COCD'r-iCOCD
О О гн CM тн
!>• "<^ CO LO CD
CM LO LO -sf1 00
О 00 OO CO . _ .
COCD^rHCDOS C0CD-"
Н ft. Ф X
^^! а, а. ^
а, о.
см
о"
(M0005I> CM VF О CM Sf*
1>ФО1>^ ОНОСОСО
CMlOOOOOlO ^h^CMOO^h
OCDCM^Oi CM ^ ^ CO LO
Ю1>ОтН00 тнОО^тНгн
CO t* "чн CM CO •»* t-^гн CM Ю
гн О O^CSl ^''
LO SP ^н СО СМ
1>ЮО00"^
2647
7302
0950
6121
9248
CD 00 OCO CM
ЬООМО4^
OOOOth^
(Nt>-HCOO)
cpCMOCOOO
Н ft. <£>
744
l> V}* О vf CD
CD СО О LO CD
Ю СО О О СМ
CO^fs^O^
^ vt1 CD LO LO
(МСОтНф^
- со
CM CO ^
LO CD ^
LO CD CM 00 О
CO 00 CO CO LO
SfLOTHCNlLQ
00 00 00 ^H CO
^rH LO CO CM CM
CO ^н LO sfi
CD
3
CM
CO
H
vt* '-H О CD CD
_ CM CO О ЮОЭ
CO CM 00 О CD ^н
CO LO CO О О CO
OiCOrHCOO
COO
5гчО>
00СМ05С0 COCOI>-t>>O3
. Oth^CD 00 CO ггн С
СОСОтчЮОО cOlOtthl
OOMN _ .
.СООЮ^ CM050t>-CM
COCOOCOLO CDs^OOOOi
СОЮОСОСЭ С0ЮОЮ00
CD
О*
00
o"
мо^оою locmcococm
05 05"^ OliOm тнООЮОО
OOfHCOCM О'НгннО COCOCMOOCO
COCOCOCOCO ^COCOCOCO fOOMO
505tT-CO "^OCOt^'^H t—
)SfLQO5 N^LOOiCMO ^
00 O5
CO 00 CM NF CM
CO ЧР CM CD O5
OOhOCOO
СМЮ0 05СМ
CO Ю О О CM
o?coosg
h OOtho: th
H ^ Ф
CD
CM
00
00
О
O5
LO
LO
00
LO
CM
00
OOfOOOrH Oh
С0Ю 05^0005 OO-OCDCD
-чн ОООСМ^ОООСМ-^нОООСМ^нОООСМ
О* Ю О* ** Oi CMC
CMOCO CD I> CM 00 LO CMC
СМ^гнСМ ^ОСО-гнСМ СОС
CMOO РООМОМ ^ t
OCOCMt-CD CMCOO5C0CM
ООСООО'гнЮ OI>00CCM
LOCMOOtOOO
CMtCMCO^
CMOiO
COI>-CMCOC
СО М 1> <НСйО5О5Ю
C0O3CO05^ CMCOCOCOOO
СОООЮСМ CDI>^LOC0
COI>COCOCD COCDCOCOCD
CO O5 LO CO 00 , -
, , . . ОСОСОС^Ю bCOCMOCOO OOOi
м^ооою ciOQOoo гнсоофоо " —
rHCD-HOOO CNCDth XO CMCDCMC^O
CMOOCDCOCD
C0050500CO
)LOOI>CD
1 Ю О О5 CM
^нООСМСО тнООСМСО гнООМСО
см
о"
745
-«н СО О СО СО Ю LO С
OS СО , . . .
^н Ю COCO С
СО Г>- -чн^"<
> СО v
> О OS
>СО СО
МОООтн МОООгН
СО СМ СО 00 гн чР OS Ю Чр OS СО CM LQ 00 О
OS СО -ч-i CD LO lS* CM 00 CD £**• CO 00 LO rH 4f
OS t>- CO t"~ lO O> lO CM CO •^ "4—i CM CM lO CD
<O 4f ^ CO OS •^н 4f ^n CO OS 'г-' vf1 "чН CO CO
см"о"о"о"^-Г
-ч^соаэтн w^h^-hi
5COCOCDCO OS-4HLOLOC
)Ю^О^ COCOt-OSC
>4f<^HLOCO Ost^r^sfiC
О 4f -чН 4t^ CM
см"оо"о*~с\Г cvfo'o'ocM см" о" о о"* cm"
t4- CO CM OS CO
ч^ чг1 О 4t< CM
CM CO CM <" "
4f 4f "чгН СО О
COO CM ЧР OS
О Ч}1 -чти СО СО
ООО^н ^OS
LO ЧГ1 СО CM OS
4f С— СМ СМ -?н
О СО -ч-н СО СО
см о о о см см о о о см см о о о см
Nt< СМ О OS LO
о ю о со os
тн СМ О СО О
00 СО О OS С—
О СО О Ю v^
СМ СЛО т-( sj1
о со о t^ оо
О t- О 00 СО
СМ О О CD ^i
СО СО О 00 СО
о сое со с-
см о о о см смооосм см о о о см
а, о.
со
о
00
о
см
00
со
СО
о"
OS 00 О СО Ю
CMOObsf
OS CD О VF CO
О Ю О СО 00
CO
S4f
Ю
тОО 00 СО С
t>*CM ОСМС
vFCD OCOC
СООО ^ЮС
5 СО Ю СО 00 О "т-1 СО
) LQ СО ОО^ООЮ
> SF Ю ОО О "^ СО
> СО 00 «чн LO ОСООО
СМ О О О
СМОООгН МООО'Н МОООп
чсОСОСОСМ СОНЮОО
С5тн1>>^ 00 О Ю 00 ^
исооосо tvfeooooo
^ О> СО СО чР vj^ ^н lO OS СО
5COCDl>-CO "чНОч^СООО
) СМ СО 00 00 OS О СО 00 t—
JLO-^hcOOS OlO-4-icOOS
МОООтн СМ О О О
СО
00 C
смооосм смооосм смооосм смооосм
-- .-. ^ ^ - - LO 1> СО V
ocot-ooco oslocmoocd
OS СО О 00 СО OS^^OOOS
OSiO-^HCOI^ OSLO>4-<COI>-
О СО <
) "ЧН LO t^
j 00 00 00
тн CD гн t- t
ч-i О О О СМ г^ОООМ СМОООСМ СМОООСМ
. - os оооосоь
} CO 00 О LO О LQ LO
~-os O4fot--os
гнОООМ -«гчОООСМ СМОООСМ
а, о.
Н и. Ф
Он о.
см
о"
Ь О5 О Ч4* 00
OS СО О О5 О
см со о см о
iOOMf
SSS
00 4f OS СО 00
О LO CM CM v^
см о о о см
т^00ОЮ
CO OS О CD t-
os чр см со о
Ю
CO
о
os
1Л
о
CM OO О^н
0439
5477
3070
2623
2855
СМООО^н
^H CM CO t"- OS
LO OS чГ OS t-
t- CM CO CO О
OS LO CO 41^ О
rHOOO(N
9197
5144
2011
8668
0193
<чн О О ОСО
,8991
,5089
,0000
,0700
,5095
0,0.
746
l_O CO C^ t^* CO ЧР C**~ (~~j l-O CO
ЧР CM <O '^ч чР lO O3 О O> O3
■ч-н Ю О CM CO rH4fOCMCM
оГо^о^о*4^" ^"o^o^o"^
О t- CO CO чР CO CO CO <:
t— чР О ОЗ Ю ОЮОЗС
> COOO CO ^ <L , _ .
> CM CM CO -<H <P CM CM CO
CM О О О ^н
00 l> ОЭ ^н ^н чР 00 I> th ^h
■^н CnJ c~^ **^ CO t^ t*4"* ^^ ^^ ^3
СОЮЧ^СМСО COCOvHCMOO
ОЧ^СОЮСО О ЧР CO Ю СО
см о" о" о" см" см" о" о" о" см"
оз ю см см оо о "^ со оо о
00 СО Ю О5«н ОЗС^'гнсОСО
СОООСОСОСО С—ЮчГ'-^Н'гН
ОЗСОСМООО ОЗСОСМООО
nOOOCO ri
R.Q.
00
о"
со
о"
СО
о"
ьоооос
ч СО С
3 Ю С
-^ МОООтн СМООО'
5§ЗЙ^ ^^^^
чН О5 vf CO С
OS CO OS t>- С
о ю см см i
СМ Ю чР С
-ОЧ^СМС
CMOcSoO OthS00<h
Ю СМ СМ Ю ^гн Ю СМ СМ СО
СМОСО-н
СМ ^^ СМ чР "^ чР ^ч lO CO СО 1>" 00
00 00 00 Чр i-O 00 С*** <2^ чР (~~) i-O 00
ООСООтн ^H00vtl'r-Ha3 СМСОчРСМСО
ОЮСОЮСМ ОчРСОЮСМ ОчРСОЮСО
см"о о о см см о о"о см см~о"о"о"см
_ ■ аз со о> со оо
аз чр см оо о аз
чрооазс- ooooovfo
COthlocO ОЗЮООЮСМ
чр см со о ю гн см ю аз
чр см оо тн аз чр см оо о
тч ОО О СО
СМ
о"
СО
о"
ооооосмаз о-нослсм
СО СМ О1 4f >-O 4F t^~ <O CO CM
аз аз <о чр со cb со о> со чр
аз со о 1-О чр <о со о> ^-О vp
тгч СО СО чР LO СМ !>• 00 00 СО
noomoo5 ооюсмазоо
азсО'гнсою азсО""^
., . , _J СО
. , СМчРтНСОСМ
тНСОСОС—Ю СОСО1>-1>-Ю
азсо-^нс^аз азсО"чн1>-аз
^о'о'о'см*4 ^г"о"о"о''см"
чРтнОООСО ЮчРСОЮСО
гн (NOxMth чРОСОСМчР
i>- чр <о аз *-0 оо "г-н -^н оо со
оо со ^н аз со оо со-гн аз со
смоо оосм см
см со о см со ю
аз аз
00 Ю
<3 ^оос^аз
см
о"
HQOOrH СО ОЗ ^н
аз со ^н со со аз со
о t^ оо ^н оо
" ~ ~ 00
тн О О О СМ
аз о-^р о аз ю ю оо с^ со
^н о о о см
и О О О СМ
О 1>ЮЮ
тнсОГОЮ
lo !>• аз аз
оо со о аз
СО J-O !>• чР
СО 00 СО
аз со о оо '«н со см о ю со
оо аз о со с— ю ^н о ю ч^
сосооазсо чр ю о аз со
оо со о о ю оо со о о ю
а, о.
747
О
vt СО О 00 СО
CDs^oOO
СО О5 О О5 О5
ОЮО^М
см" о о~о~см"
. - - СО -.
тН 00 СОЮСО
О Ю тн Ю sf
(NOOO CM**
О5 LO O00 СО
СО СО ГО Ю ~н
СО Ю ОС' CM S?
- - t-oc
пООСМ
CM t^ СО ^гн LO
СО гн 00 СО Ю
СМ СМ СМ ^ С^
■пОООСО
00 ^гч О ^ О
ю со о со см
О О О О5 О
О5 Ю О О5 СО
^н О^о'о со"
СО
00
со
СО
CMOOt-00 ООСМОСОСО
^ЭТОЮЮ vfOSOOCO
thnPC CNO СМ-гчО^Ю
OCDO^O^ ОСООЮСО
см"о"о"о"см" см"о"о о"см
О О5 vt< 00 Ю
СО СМ О 00 О5
О5С0 СО 00 Ю
смооосм
9438
6076
1768
7627
9317
9552
5820
1804
7408
8947
О500СМСОО5
тнОООСО
0000ОС000 тн1>(
bCDOlOs^ O5 СОС
oomoosfi оо ю с
Йч Q.
СО
о"
со
о"
00 00 О О О5
Ю О5 О О5 СМ
Ю 1>- О vf СО
О СО О COCO
_ _> Ю ЮО5 О ^О
) <О СО СМ Г"— СО <О CM t>*
>осооо осоосос-
DCO СО тн
3 СО СО COVF
см о оосм смоо о см см ооо см
СМЮОО'гНСО
OOSO
чО^СОСО СМ00ЮСОО5
O5COCOt^00 O5LQ00C-00
^н О о"о"CM ■HOOON
СМС0^НСОО5 Г-00ОСМ05
ЮО5С0ЮСМ 00O5CMt>.CM
CO^COtfi ^00LOOO5
СО СО О 00 О5 СО С
- VfH СО !>• <:
. ,ч О5 i> со <:
. ) СО 00 НЮ(
) vjh О СО С^ ОО V? С
СО
о
оо
о"
S
о
о"
СМ
со
о"
< О5 О5 О О О5 СМ
> Ю Ь- 00 О Ю О5
. . _ 00ОЮО5
СО СМ О СО '«Н чР ^н О СО О ^05ОЮ00
Ot-OCOCS 0«>-ОС005 ОСООСООО
см"о"о"ю ^ смчо"о"о"*гн
t>- lO <О тн lO CM ^Ф <О СО !>■ CM O5
050СМСМ COt—О^нО OCD
- - — ■ -* см О со тч -" ■
D—
05-<И05С005 1>-СОСОО500
tFtOOO тгнСОСОСОО
СООЮСО
O5t-CM^
^n oo o^
ooocm th
cmooocm
*гнОООСМ Ч
5^ СМ Ю н -в О СО О5001>-000
Э О5 СО 1-О СО 00 ч^ СО О5 О5 СО <О СО
5COl>CD OOCDcOt^^- OOCOCOt-00
н" о" О" о" CM"
см
о
748
CMOSC
l> 00 С
doou:
DOSCC
DOC
D rHLC
) i> cmc
> со о с
> 4f t~- С
) !>• 00 С
DOS 00
ЭСОЧГ
D00LO
OS l>-
Ю ч*
t- 00
О 00 OS
oloco
О О CO
COMOJOt^ тн . .. . .
О СО гн CM CM CO О CD OS 00
O^COO^ -4HLQCOI>-CD
l>- 00 тн CM CO t- 00 гн тч Ю
CM t>- О гн о
00 гн гн Ю
о сГг-Гсо
>OSC04t< СОООСМООСО
СО 00 гн 4f 00
0 0 00
ООтнМ
^н NF 00
00 СМ СО Ю Ю
00 СО Ю t- СМ
CD Г- OS 00 t>
СО t> гн СО 1
СО чР OS О СМ
OS 00 VF СО ^н
СО 1>- СМ гн СМ
Ю1 t
00 О г
00 Ю СО
Ю1>
СО СО 00 vF О
см г- оо см соо оо
О СМ СОЧР OS
СО t"* rH CO OS
thst гн О О г
СО чР О О 00
СО GO О СО ЧР
чр Ю О СО СМ
Ю 1> О 00 СМ
1>ЬОСОЮ ЧР СО О t^- О
"OOOt-тн 4f* OS О OS CM
CM О OS CO 00 05 0 4^00
- с- гн юсоо^о
l>
СО
СО С
тг1 О О тН Sf rn
со
о"
00
о
СМ
О5
СО СО О О2 О5 CNJ
О О О СМ О О5
00 С-О Sf 00 00
CD O5 О тН Ю
*тн О О ^н СО гнООгн
OCOv^COCO t>-aSLOOOO СМСОСОЧ^Ч^ СОЧ^СОООСМ
ООЮ^СМОО t^COCMCMI^ t^COCMOSCO ЧР^^ООСМ
COOOOCOt^ ЮМОСО^ СОСМгнСМЮ ОООЭСМ-чНЧР
Ю OS О СМ гн CD OS rH CM CO CD OS rH CM CD CO CO rH CM СО
гнООгНСО гнОО-чНОО гнООгнеО
5t—«<pCM OSOI>-OCM rHCOCO00I>-
■|OSt>-0 СО О СМ Ю СО COCMOSCO"4H
5COI^-O0 OS00lOI>-O5 tHIOCOCOCS
"■ '" OOOrHSfOO С000гнч^00
гн о"о ггГсо** гн о'о гн со
00 CM Ю CM
CO^O
СО Ю OS СМ , .
гН Ю OS CD l>-
OS CO CD Ю OS rH
rH ЮООчН S ■И ЮООтН 1>тЧ
гН СО О 00 OS 4f !>■
со со о os см со оо
00 Ю О 00 гн OS СО
чР 00 О 00 СО Ч^ 00
. . . ЮГ-ОСОгн CDCMO00O
00О СО'^ОСОСМ COOSOvfCM
ООгН О СМ О 00 О CMOOOCOt^
0000 ЮОООООСО LOt^OOOCM
THOOrHsf "чн О О ^
а, о.
о, о.
а, о.
см
о"
O Vf Г O
CO OS CM "- 00
O5 Ю -H t^ 00
CO OS CM OS rH
Rococo
CD CD OS 00 LO
!>• CM 00 О CD
vtf t^ c^ CM OS
Ю 00 CM N? LO
^ OS О CM l>
CM CO l> CO CN1
CM OS 00 — CO
t<^OM
гн Ю О СО OS
sf !>• О О О
t^ CO О О t>-
со t- О со ю
OS СО О СО Ю
СО чР О СО Ю
Ю -чн О СО OS-
NOO00O
СО СМ 00 гн О
MCDlOOI>
Ю OS 00 t> СО
Ю00 HOS f
О О 00 СО CM
СО *чР Ю гн СО
ч^ оо см v? см
* Г~СО
СО 4f 00 ЮСО
гн СО Ч^ СМ чР
as о со гн ю
00
см с
О
00 00 О СО 00
см со о см со
СО СО О О С—
со г- о со ю
а, о.
749
-ч-н СО О СО О- Ю СО О ОЗ СО
■Н C<IO Oi 00 СМ О О 1>" СО
00 ОЭ О t— ОЗ 00 ОЗ О t>- ОЭ
СМ ^ 00 чР чР
СО ОЗ СО НЮ
Ю00 С- Ю СО
1> 00 CM ОЗ СМ
ОЗ ООЗ 00 СО
Ю СМ ^ч Г-СО
СО t» 00 СО -*ч
t- 00 СМ ОЗ СМ
пОООСО гнОООСО
MCOI>
CD C^ CO
чИ Ot> t"»
t>
t
OsfOI>l>
CO CM ЧР O3 4F
CO Г- 00 00 I>
CO t>- CO 00 t-
LO ЧР СО CM CO
CO CO LO CD О
■ ~ l>- © t-
CO O00
СО ОЗ
ОЭ Ю
00
о"
o"
СО
ю
см
|
о оо о <
см оо о о со
t- 00 О СО 00
t>- озо оо о
чр СМ О СО СО
LO !>• О -чч чР
00 СО О СМ СО
t^ оз о оо о
чр о о оо
..ООФО
ОЗ чР О О СО
гно оо со гнооосо Jdooco
00 v^ 00 D- С
СО О5 CM^ С
O^cot
Г"- ОЗ СМ ОЗ тН
^о"о"о оо"
О СО l> O5 00
Ю 00 Ю 00 СМ
см смю со со
Г^ О5 СМ ОЗ СМ
00 СО t> О СО
О5 00 00 СМ СО
СО О СО СО ч}Н
!>• ОЭ CM O5 СМ
ю оз см о о
СОтН ^н СОО
СО СО О СМ СО
Ю 00 СО vf СО
vF COCO 00 CM
СО 00 СМ СМ О
00 CO CO CM CO
Ю00 СО vf t—
00 СО v}H О чР
чгi lO г СО
00 00 NF t—
ц О О -
Ю О О5 О СО
Юнннн
тнтнгн
О тн 00
СМ О СМ
Ю 00 ^н СО О
00 О5 ЧГ 00 О
Ю Vt1 СМ ОЗ О5
vf !>. СМ ОЗ СМ
00 ОЗ CM vFCO
ОЗ ОО'гн Ю-sfi
чЛ t>- t^
СМ ОЗ CM
ЮОООчрСМ NCMOHO
00 ЧР О ОЭ СО О^ЮОСО
со i>- о см ю чр t>- о см ю
OvPONCO
СМЮОСМС0
CM CM О О О CM
О Ю
!>• ОЗ
СМ
смооосм смооосм
см
о"
со
о
00 CM LO 00 О
~ " " Р О Ю
> с— см „ _ .
■* чР <О "чч lO -чч ч^ О1
см о о"<о"со см о о о со
ОООСМСОСО O00OCMCD
МЮО5 1> -чч ООООСМчР
O00OL0O3 тн^-нЮОО
тн LO r^ CD Ю тн Югн СОЮ
СМ О О О fO СМ О о" о" 00
■н О ОООтн t^-CMOCO-чч
tT4* ОЗ С^1 t^* ОЗ чр СО С—' ОЗ ОЗ
ООСМОчРСО ОЗООСОО
сюоьоо сюо^оо
см о о о со см
а, о.
а, о.
СМ
о"
COCMOCOLO СО-^ООСО
Ю00ОСМ00 001>-ОСМСО
озооооосо озг—ооосо
^HLOOCMOO тнЮОС^о:
см" о" о" о" см" см о" о" о" см"
СО СО 00 l> CM t^ t
смоо о см смооосм
гМСЮС
СО СО СО ОЗ
■чч СО 4f СО
•чч 1П) -чН 4f !
■чч СО О LO ОЗ
СО ОЗ СО О ЧР
СО LO LO О- ОЭ
тН LO ^Н ЧР ОЭ
ОЗ 1>- Ю СО 00
00 ОЗ СМ 00 СО
00 Ю ОЗ >О О
о lo с со ю
СМ 00 ОЗ t^ LO
00 С— СМ ОО ОО
ОЗ чГ1 О Ю 00
СЮсСЮ
см о о о оо
СО СМ О СО СО
ОЗ Г- О О ОЗ
1> Ю О Ю sf
оюоьоо
СО 00 О ОЗ ОЗ
СО СО О ОЗ СО
00 ЧР О ЧР ЧР
С lOC 1>00
СМССССО (МО О О СО
750
CD О)
СО СО
CM n^O СМ ^н
см о" о" о" см
00 vfOO CO OS
LO О СО СО О5
005СОО^
00ОО^
CM -4t* -<Н СО *4t<
см" о" о" о" см
см о о о см
см о о о со
58
00 СО С_ _ .
тн СМ О 00 '.
•чч ЧР О СО СО
см" о" о" о" со"
а, о.
ю
СО
о"
со
OS
СМ
со
С0ЮОО00
tCOO^t
THCOOt-О ^птнОСОЮ
см ю о см со см ю о см см
смооосм смооосм
- ,
CD С
со с
5 t^ OS t>« О
> t>- СО ЧР "Чр
■ ОСОгН -
> О
JUO
СМОООСМ СМОООСМ
CDC0O00C5
fCCMfOO
■^н Ю тч чР О Hsf-п^С
см о" о" о" со" см" о" о" о" со
COCDLOt—O
tCO^CMI^
СМ СО СМ СМтгЧ
смооосо см"о"о"о со"
см
смооосо смоо осо
СО
о"
00
СОСМО'ОО^ L0 05COO СО "
сосооюоо ^юо^ю чрс
•rilO СМЮС -НЮ CMl.
СОСО
COCOO5VF00
OOLQt^OOCO
О5Ю1Ю
vfr-iO СП>^Ю^г-1СО
СОЮО О О t^ М 00
ОЮЬММ СЮСОСО1>
СМЮСМСМО СМЮСМСМО
о о"см" см о"о"о"см
смооосм см ооо"со смо^о о со
COCOOOOCM OCMOtCO
|>^О00 05 Ю00СМСОСМ
1-QvfLOCOOO СО^НСОСМСО
OFCMCMOO OtCMOOOO
см oooco смоо о со смооосо
CDO OhN OOlOOlOOS vPCOC
O> *^ C> O> CM O> "^sf О С> "ч~< C> CO С
см" О о" ^н" ^ см" о" О ^н •» "
SO
CD
о
00
о"
CD
CO
со
о
CO
o"
со
о"
СО ".
00 Г— С
CM OS С
см ю с
5 О CMC
5 00 СМ -
5 Ю О тн .
"> Ю -чн СО 00 О Ю
5 тн CD (МЮОтН
ГМООО^н СМОООгн
^н 05С005ОСМ COCMOt-CO -чн
Ь ОЮО-HOS ОО^НСО^Ю Ю
oot-t^oco oot^t-oco
^hilOCMCMCO ^-iiOCMCMC-
смоо о тгГ смооочтГ смооо^н смооо -th
t^ascooo th
cmoocoi^- о
fOC55
^cjoo
ооооо^
lOCOsflO -НЮСО^СО
см о о о см см о" о о см см о" о о см
j COt<FCOt
О5 СМСМ02Ю
СО ОЮнООО
CM CM^-CMCO
t-» CM sf Ю l>
О COOUO
thOOvF
ЮСМОООО
см о"о"о"со см"о"о"о"со см о"о"о*"со"
vfoO
00 00 О 00 СО О ^ч С
ю^ о аэ со о as с
01 COO t^ CD O^(
as ю о о со о ю с
50000 coi^ooco ascooasco
500CO NfCOOCOlH) CMCOOvfCO
> t>» CO ОООМЛ тн ^ОЮСМ
)OC0 ОЮООСО O^OOfO
MOOths? MOO<H^
Н ^ Ф
0,0.
CM
751
СМОООСО СМОООСО
G5 d Ю СО !>•
Чр 00 Ю СЛ СО
00 00 СО ЧР ^-н
о со ^н ю со
СМОООСО
СМОООСО
СЭ *^ СО ^ 00
СО СО СО ^н СМ
coco оо *^со
СМОООСО
О СО чн
см~о"о"о со"
со оо оо см ю
^ см ооюоо
Ю CM CJ5 -«гн СО
О СО *ri t- CO
СМОООСО
СМ ЧР СО t^ Sf
ю ю со о см
00 СО CM COCO
СЬ СО т-t О5 ■чн
СОЮО^О СОСОО-^СМ
ЮСООтн (М cOC^OOit^-
QCDOOM ОЮООМ
со
о"
00
о
00 ЮО СО О
со оо о ю ю
О Г- О ЧН СМ
смооосо смоосГсо см о о о со см о о о со
о t- со оо со со о оо с
см оо ^ О см cooot-c
->смслсоо сосоосоо
и со ю '«н оо ot^oocMt>.
Э1>1г-ОЮ 1>-Г-ООСОО
JCM'^CDCM 1>>ОСМЮСО
СМ О О О СМ СМОООСО СМОООСО СМОООСО
СМ 00 Ю чР СЛ
см i>-со см со
С- гН СМ ЮСО
CD t- ^H !>• СО
00С500Ю00 Oi О СО СО О
чр ю ю см «^ чр чн см оо i>
~ - ■ "» >чн CM00I>4t<CO
СМОООСО СМОООСО СМОООСО
тнОСОтНН СМ 00 О5 О5 СМ
Ю 00 СМ О СО О5 С— СО О5-^
ЧР О 00 О5 Ю Ю d <Jb 00 СО
СЛ t^> О Oi О О5 СО ОСЛт-1
> Ю СО rHCD
5 00 00 Ю05
5 СО Ю 4f
СО О5 СО
см
о
см о о о см
о t- см со^
csf о" о" о" см
СО О5 СО СО Ю
t>» см со со -^
СО О 00 тН СО
<Л £*• СМ 1>- СМ
чн" о" о" о" со"
О СО СО LO О
СО СО 1> СМ 00
г- со оо см с-
00 СО ^-i СМ СМ
^юоазю
00 СО О 4F t-
Ci, Q.
t0QO!>00
см со о см со
CONOOSrH
тн [г- О СМ чР
СО <О СО
CM LQ 00
CM t t
!>• СО CM L
00 CM CM t t
сэ t- см со t-
чР см чР тн ч^
LO t^> 00 СМ тН
-Н О5 СО тН тН
О5СО СМ 1>00
СО 00 СО -^н Ю
СОЮ1>тН(М
Ю !>• СО СМ СО
оо со «чн <rq -r-i
оо оо с
чр t- с
00 СО О чР 1>
^н О о"ггн чр"
752
> O3 "
) CM
) CO t^
> CM CM
смооосм смоо"о"см"
ЮЮОЮ1Г ОО
CO CO О С"— СО CO "чн
Ю ^гн О IT- CM СО О
-чн [>. О CM CO *чн t^
O3 ОЗ О CO С
OOOrHNC
О О 00 00 i
005Ю05
00 "*н СО 00
^ О3 00 00
гн СО СМ 00 t
смооосм смооосм
O3 t>- CO CO CM -чНСМСМОООО
t^ CO CM CO CM ЧР CO t— 00 00
О CO CO I>- CO OCDCOt^l>
смо"о"о"со см"о"о"о"оо"
fc3
Ю 00 О тн 00 4F00OCM00
00 СО 00 СМ Ю СМ тн СМ О СМ
тн^ЮФ^ СМ Ю О Г~~ тн
ОЗ Ю СМ тН 00 Ci Ю СМ 'гн СО
^ч-н О О -чн чР
'НООгн^ «чч О О *ч-<
а, а.
а, о.
00
о"
CO
o"
00
со
00
со
со
см о о о см смооосм см о о о см
ЭОЗ-ч-iOO rH"H|>COsf< 00 CO C— CM Ю
0COCDI> t- ЧР lO CM ЧР CO ^ Ю Ю CO
-ЗбОчРС^чР O3CMCO00LO _ . - -_.
О1>-СМ00Ю OIXNCOCD -чч l>- CM CO !>•
смо"о"осм" смо"о"о"см см"о"о"о"см"
3 СО СО t^ чР О СО CO С- Ю
гнОООСО тн О о"о"оо" NOOo"cO
00 ^-О с"^*> С^ ^^ О^1 С*^ О^ ^тн ^sj^ г^> с^) *^ (^, lO
ООСОСМСМОО ООСОСМСМСО О2СОСМСМ00
) t^ t— 00 00 О CM t— 4f t—О CM CM
)CM оОЮО^тн ОЮОЮ-чн
00ЮО sf l> оОЮОчрсо
см
о"
со
о"
t t^» ^_; uj tij k^j (JJ > ' ^T ^—J
•^^ОЗОСОСО hOOC^-H
000300000 O3l>-OCMCP
t^O3
7537
9804
-ЧНО
О тл 00
О^чН
1106
2359
4336
О^ч^
6806
9354
1506
5055
6262
^o
О^ЧР
CO CM t- ЧР 00
^ CM CO Ю 00
^гн аз о "чч аз
СО 00 тн 00 00
-нО
,5836
,8748
О-чР
,0000
,9553
,0191
!>• ОЗ О "чн 00
^ОО^ч.
аз ^ч со ю аз
с^ аз со t^ -чч
СО Ю СМ <7М СО
t^ аз «чч см чр
^ОО^нчР
6971
9121
1726
4966
6389
^ч О> О> ^ч чР
6286
8657
1188
8023
8821
^оо^чн
,6008
,8466
,0000
,9394
,9898
Q.Q.
см
о
со оо о аз t^
-«ч см о аз ю
с— <гм ооо аз
5 СМ
. -3 СО
5 оо аз
-г-. О "чч 4f
СО ЧР С^О тН
ЮтнЬООО
чр аз аз со см
£"*• аз о см 4f
-чнОО-ччсО ^нОО'^*
О О СМ чР 0
00
СМ
О
[>. Ю тч чР ОО
оо ^ чр аз г>
ю аз о оо с-
^ 00 ОС СО Г-
см ю см оо оо
з оо аз чр о ю !>•
5 аз чр аз о аз со
D СМ 1>00ОЮМ
-^ поооазо
Го"о"^"ю ^ч"
а, о.
753
OS OS О СО О
ЧРгНОтнЮ
COMORO
оо 02 о о см
(О "^н sf L.O -«тн
t>- о о см ю
О О Ю 1> н
00 О5 -4-1 -чн СО
СО СМ СМ тгн тгн
-in сГо-ч-Г^
00 СМ ^гн СМ 00
О5 ^Г1 "ч-i СО
ю ю о см оо
СО СО О СО 00
■ ~ СО О СО О2
tr- О 00 t-
Oi
со
О СО t— CD lO
OOCOOO^O OS'^Vf'OSC
МЮО^О О5 t— 00 CM тн
CMOSOOthCO COt^dO^
00 00 00 CNI CMCDO2COO5
Он Q.
СО
о"
00
^ оо о оо ю о см со
_51> ч}< СМЮОСМ00
50C003 О00ОЮС0
■ ~ - - 05 050IN
тн тн о ол ^н ^ноосо
^OOCMOO^ ^
СМ1>1>^О С0ЮО5С0СМ v^vOCMCM
0005СМО5О 00О5СМО2О OOOiCOOiO
СМ О 00 СМ СО
ООЬ-СО^СО CDUOOiCO^H THNji-rHCM^
О О
OOCOCOvfv^ "^HOS
О тн О5 Ю О OSNfi-OOO
t>-LOCOCOCM OOCMOOOi
lOh- CM О О5 LOt>-CMO5
CO^hOCDOO LOCOOOOxf S(OCOt
-~)CDOvf00 ОЮООО гнЮОЮСО
СООЮСО С^ООтн^ s}< l> О Ю 00
1>ОСОтн Ю h- О CO О ЮСООСМОЭ
« R. *>
00
о"
со
о"
СО
о"
см
о
о
тн тнОООО тНтнООСО "гн-чн
ООСМОО'^СО ЮСМСОтнО CDOiLOsfCD
02OCD05O MfOOQ ^COCDOOO
(MsfOOQ V^C
00 ^ О Ю 00 05
tOCMOit t^
CDOOO OO0000
<МЮ1> гн О5 LO sf* О
CMOSOO 00O5CMO5O2
CJCMOCO^-i CO
SOi ГНС0005М CO
ОО Ю00СМОО5 LQ
rr-ГоосМ ^
-чн Оо CM vjT
-пООМЮ
1/4 4 8-114
754
I
I
о
о
и
ф
ф
н
со см со со
СО LO !>• 00
о~о~о~о~ о
тЧ LO ЧГ СМ
1> ^О О
ос г- ю см
О тгн СМ СО
СП)
о
00
00
Ю СП;
1 t^LO
1 00 00
1 ОО
1 ^-i СМ
Sco
оо о оо ооо
СП) СМ
vf СП) СО СО
СП) -V? CM Г*-
СМ Ю С- С—
тч CM CO 4J*
о~о о о о
СП) С\1 СМ СО 'гН
СП> 00 00 СМ Г— <
СС^ О5 I 00l
Sft>-
OC!
CCCM
COCO
Он
оо о оо ооо
SJ* СО
СП) СЛ _
^ч CM LO
о см а: с
LO Vf "чН С
-^н «^ ОС
СО 00 vr
СМ^Г1 СО
О 00 СМ
ЧР LO СО
I 00 COvt^
I О -чч СМ
О00
СП) С—
СО СО
СП) СП>
СП)
о
осГ
I I
I I
00 СО
оо I
II ММ
I I
о
СО
OLC О (М LC С Ю С С М Ю С Л С
н НСМ НнСМ
о
X
ев
СС
ее
а,
а,
а.
аз
Я"
ф
о
ф
5-
а
с
аз
I
О
ОО
t^ 00 СО
СМ Ю О
00 СО LC
О ri СМ
см
о
ooo
оо оо о о
OOt^LO^rH v^iOOO COt^CMCM'iHOO COCO N00 ЮСМООЮ СМЮЮ 00
v^lOOOCO ^^^?О v?CJil>.N^00Cn) 00CO ЮС ОПт)^ тнОООС О
I>.t-~I>.00 00 CO lO LO О CD LO lO CO Юч On COCD l>00 lOOSCO О
0000 О'^СМ О чтн ттч «чч чгн >r-i тнСО -^СМСМСМСМСМ -rHCMvr ^н
о" о о" о" о о" о" о оо"оо о"о"о о о о" ооо о" о" о о оооо о о"
Ю СО "ч-i чгч LO vfcO СМСМч? ОСМ COLOCOCMCHiLO 'rH-eHvf ^н
t^-t>-00 ОСМ CO00 СОЮтН LO^t1 COCHi'^CO-^^-r-i I>-COI>» 00
0000001 00COI LO О I I>- t^» 00 Юч ОО0000СП>О vfC^CO OS
oo"o ооо ооо ооооооооо о о о" о оо'оо" о о
со о
IIII
CM СО СО ^Г1
III
, . , . - I СОЮ LO .
ООО ЮС ОО СМ СМ С\1 .
СМСМСМ 'гнсО <н (М СОСССО
LO 00
СО 1>
sf ОС
см
ООО ООО ООО
о о
СО СО
оюо оюо оюою ою
о
см
а,
05
Таблица IX-2-1
Газодинамические функции при осесимметричном обтекании химически реагирующим воздухом тела вращения,
составленного из конических элементов
0
0,2
0,4
0,6
У,
vr
р
р
ух
Vr
р
р
Ух
Vr
р
р
Ух
Vr
р
р
Углы полу раствора головного конуса |3 =40
X
1 ,0
1,377
1,156
2,524
10,757
1,388
1,143
2,521
10,747
1,398
1,131
2,513
10,719
1,408
1,120
2,500
10,674
1,24
1,748
0,830
0,745
4,001
1,636
0,946
1,159
5,729
1,570
1,002
1,487
7,013
1,524
1,035
1,765
8,053
1,88
2,031
0,355
0,160
1,075
2,033
0,330
0,167
1,123
1,978
0,435
0,260
1,634
1,904
0,566
0,437
2,566
5,8
2,028
0,354
0,163
1,090
2,035
0,352
0,164
1,105
2,100
0,359
0,164
1,208
2,262
0,350
0,151
1,626
28,52
2,053
0,358
0,193
1,305
2,263
0,378
0,192
2,228
2,362
0,377
0,188
4,975
2,372
0,361
0,178
5,212
°, основного конуса рк =
1
0,8
1,0
Ух
Vr
р
Р
Ух
Vr
р
р
W
wx
в
= 10°, число Mqo = 20
X
1,0
1,418
1,109
2,483
10,612
1,428
1,098
2,460
10,584
0,917
0,917
—
1 , 24
1,493
1,053
2,020
8,987
1,511
1,087
2,258
10,551
1,132
0,849
1,007
1 ,88
1,869
0,680
0,657
3,812
2,003
0,857
1,060
8,150
1,540
0,503
1,143
5,8
2,323
0,349
0,154
2,436
2,337
0,426
0,248
5,113
2,769
0,229
1,827
28,52
2,376
0,34 3
0,164
4,935
2,377
0,322
0,150
4,373
6,712
0,177
5,792
0
0,2
оо
46
Ух
Vr
п
г
Р
Ух
Vr
' Г
п
У
Р
Углы полураствора головного конуса Рк == 4(
X
i ,0
1,377
1,156
2,524
10,757
1,388
1,143
2,521
10,747
1,12
1,540
1,037
1,565
7,308
1,483
1,077
1,912
8,590
1,88
1,875
0,655
0,420
2,467
1,892
0,604
0,424
2,498
5,0
1,844
0,644
0,648
3,589
1,837
0,607
0,646
3,482
29,8
1,854
0,647
0,680
3,376
2,154
0,738
0,679
6,888
)ф, основного конуса рк =
П /.
и, <-±
П (К
U ,0
Ух
Vr
р
р
Ух
Vr
р
р
= 20°; число М№ =20
X
1 , 0
1,398
1,131
2,513
10,719
1,408
1,120
2,500
10,674
1 , 12
1,449
1,097
2,167
9,505
1,429
1,106
2,352
10,154
1,88
1,896
0,574
0,438
2,531
1,867
0,597
0,513
2,868
5,0
2,019
0,640
0,626
4,406
2,171
0,658
0,590
5,771
29,8
2,158
0,725
0,675
6,835
2,162
0,713
0,669
6,771
756
И
о
ч
о
х>
OS
СМ
ос
о
-
/
ил
Н
00
О5
СМ
-
00
см
о
/
ил
от
от
см
от
см
-^
1
ОТ
О
1
00
со
г—
■СО
о
см
5
о
от
о
от
о
со
см
см
см
см
1
1
«„„о ~о^
хтч !>• CD t~- *-гч CD CD CD
СМ О О СО СМ О О СО
О Ю ОТ CM t>-t>»COO
CM CD ПО О CM CD lQ -ч-ч
см о о t- см о о со
оо оо ю со ocoocm
•чн О ОТ СО CMNTiCMO
ОТ t^ СО СО О 00 О О
пОО^ СМ О -^ 00
СМ О lO CM CMOTCOCO
гЧтнМО гчгн СМО
00 ОТ СМ СМ ОООООчР
тчОХтг! СМ ОТ СО СО
ч? ^ч V? о vf О -С4 Ю
гНт-tMO -*ч тгн СМ О
Н к Н к.
00 О
о
30
(35
о
СМ
о
/
1
ил
н
30
ОЭ
СМ
о
оо
см
о
/
1
156
688
665
775
СМО О LO
t- t» CO 00
^н СМ СО СМ
CM CD LO !>•
СМ О OLO
СО !>- СО СМ
CD sf СО 00
оо г- оо о
^ч О О **
ОТ^нОТОО
О ОТ СО ^н
4f О 4f CO
т-1 ^гч СМ ОТ
О О^-^
-^гч ОТ 1>- СМ
ч}< о ч*ео
^н^нСМОТ
00
о
*vf t>» t— Sj1
CM CO 00 CO
00 CD CD ^ч
-гч ОО CM
О ОТ 4f ^
СО sf ОТ СО
00 CD LQ Г-
-гн О О СЧ1
!>. LO ОТ "чн
00 CD 4t* CO
^н ОО СМ
CM CM sf VT1
LQ О CD L.O
^н^ч^СО
СО N? 35 О
CD V? ^-н 00
^ч^ СМ ОТ
О
СО !>• LQ ОТ
^СОСОСО
см оо ю
CM LO ОТ ОТ
— О СМ 00
CM CD LO СО
см о о ю
t> Юч}« О
СО t- ОТ ^ч
ОТ 00 тч t>-
CM f- v^ О
CM t- v^ vf
•^ О vr CM
^ч — СМ ОТ
-гн -ч СМОТ
о
OrHLOOO
■sf CO 00 ^ч
^гч С^ СО ОТ
см о о lo
t^ О со ю
L.O ^н ОТ ОТ
00 СО Ю СО
^оосм
СО СО 00 t-
00 СО LOCO
^оосм
СО 00 СО -гн
СО СО 00 -?н
•ЧГ1 О ОТ !>•
^^^^
LO ОТ lO ОТ
t>» CM тгч СО
тЧтН (MOi
Н it.
см
о
1
см
734
см
см
со
LQ
от
СО
о
930
о
СО СО тн 00
тН t>- СО ОТ
см о о ю
ЮО^ч}1
о см оо о
ОИЮп
см о осо
О CM CO vF
ОТ СО СМ тн
00 lO lO *^
^О О СМ
со оо см см
V* О СМ Ю
-гч-гч СМ 00
t^ СО СО ОТ
00 ^гч О СО
СО ^ Ю v^i
-чн ^ч СМОТ
о
,388
'—'
со
со
о
»о
)О
LO
о
от
от
о
930
о
LO
,967
311
см
от
о S5
С^ СО 00
см о о ю
см
** оо от
СО Ю СМ
СО Ю vf
оо^
vf СМ СО
00 СО СО ОТ
оо см
СО-* Ч^СО
осоо
тп СМ ОТ
СО СО ^ч О
от о от от
СО ■^ч vf jvj
^ см от
и^ О, О.
со
о
Таблица IX-2-2
Сравнение газодинамических функций, рассчитанных с учетом и без учета химических реакций
Углы полураствора головного конуса Зк = 40°, основного конуса |3К — 0° (цилиндр); число М^ = 20
1
0
0,2
0,4
0,6
0
\
Vx
Vr
Р
Р
Vx
Vr
р
р
Vx
Vr
Р
Р
Vx
VT
Р
Р
\
vx
Vr
р
р
X
с учетом химических реакций
1,0
1,377
1,156
2,524
10,757
1,388
1,143
2,521
10,747
1,398
1,131
2,513
10,719
1,408
1,120
2,500
10,674
1,160
1,516
1,056
7,752
1,478
1,080
1,940
8,691
1,454
1,093
2,135
9,392
1,439
1,099
2,294
9,919
2,040
2,132
0
0,057
0,443
2,119
0,040
0,069
0,519
2,043
0,287
0,160
1,083
1,952
0,470
0,319
1,951
10,60
2,133
0
0,056
0,433
2,138
0,072
0,054
0,430
2,159
0,113
0,052
0,417
2,317
0,132
0,043
0,532
X
без учета химических реакций (k = 1,4)
1,0
1,329
1,115
2,591
6,065
1,16
1,486
1,035
1,865
4,796
2,040
2,207
0
0,091
0,660
10,60
2,239
0
0,056
0,399
0,8
1,0
\
vx
Vr
P
P
Vx
VT
p
p
W
wx
I
0,2
\
vx
Vr
p
p
X
с учетом химических реакций
1,0
1,418
1,109
2,482
10,612
1,428
1,098
2,460
10,534
0,917
0,917
j , 160
1,431
1,100
2,389
10,281
1,433
1,097
2,448
10,433
1,062
0,913
2,040
1,893
0,617
0,541
3,172
2,040
0,826
- 0,971
7,820
1,632
0,478
10.60
2,371
0,194
0,061
1,314
2,383
0,304
0,135
4,225
3,730
0,168
X
без учета химических реакций (ft= 1,4)
1,0
1,349
1,091
2,585
6,055
1,16
1,446
1,043
2,111
5,240
2,040
2,180
0,090
0,125
0,705
10,60
2,236
0,068
0,056
0,399
Продолжение табл. IX-2-2
3
Углы полураствора головного конуса Эк = 40°, основного конуса Эк = 0° (цилиндр); число М^ = 20
0,4
0,6
•0,8
\
vx
Уг
р
р
vx
Уг
р
р
Ух
Уг
р
р
X
без учета химических реакций (k = 1,4)
1,0
1,369
1,069
2,568
6,027
1,388
1,048
2,542
5,983
1,407
1,028
2,508
5,925
1,16
1,426
1,041
2,280
5,536
1,416
1,034
2,395 '
5,733
1,416
1,024
2,460
5,845
2,040
2,053
0,390
0,310
1,316
1,940
0,571
0,533
1,956
1,905
0,706
0,775
2,888
10,60
2,242
0,111
0,057
0,408
2,309
0,137
0,055
0,577
2,357
0,212
0,072
1,233
1
1,0
\
Ух
Уг
р
р
W
wx
X
без учета химических реакций (k = 1,4)
1 ,0
1,426
1,009
2,465
5,854
0,999
0,999
1,16
1,426
1,009
2,465
5,854
1,157
0,999
2,040
1,967
0,848
1,148
5,694
1,801
0,551
10,60
2,372
0,335
0,161
4,353
4,159
0,185
Газодинамические функции воздуха при осесимметричном обтекании тела вращения
Таблица IX2-3
—20, а~ 5°)
х= 1,2
I
0
Ух
Уг
V®
р
р
о*
0
1,047
0,984
0,000
3,095
9,990
45
1,077
1,012
0,039
2,937
9,681
90
1,156
1,086
0,054
2,575
9,061
135
1,247
1,172
0,038
2,237
8,688
180
1,290
1,212
0,000
2,101
8,676
х = 1,4
0
Ух
Уг
V®
р
р
0
1,309
0,840
0,000
1,705
5,951
45
1,342
0,862
0,041
1,578
5,652
90
1,430
0,918
0,057
1,291
5,018
135
1,531
0,983
0,039
1,018
4,535
180
1,576
1,012
0,000
0,907
4,393
OsfOOOO 00 CO С
н со о st* t4* со аз с
ОО(М t*OC
> t^ sfMOOO CD
:> СО СМ ЮЮО^н ^Н
5 l f CO^OOCO ^
-*н О -^ Ю тн -<Н О ^ !>• ^HthOCSJOO -г-н -<Н О СМ О
СО
СО
CD
(МООСМООЮ CM-
CO Ю ОЗ CM CO CDC
?ОО^О CO
CO Ю Ю ОЗ 00
COH^LOt
ННО-HCD
н О CM О
vp t>» ^ см t>» о аз ■<? см аз оосооазо ^ооосою
со аз -г-н со со
СО О
О t—
О О О ^ОООСОЮ
t— О Ю I>iMO(M-h
см '
о"
о"
00
о"
о
оо
о"
759
зсоазсм tooo
5 о i> со сч! аз о
5 оо см аз
н СО "гн О О СМ 00
О СМ •
о см с
■<азсмо азоазсосо
н со оо ^-i о см «^ аз со
ЗнСОСМ СОО<001>
но о см аз
аз
о"
о^осоьо смсмоюсо смсоососо смооазг- t-азе
■- -^ ооооо азооооою о^ооо^ азоос
^ о со
оо о аз
аз ю см оо о о о 'гн оо с
rHOOMt- ^чООСМОО
аз
со
аз
^ODJ М
гнОООСО Ь
смО'^аз смс
см t^ со оо тн со оэ rri о !>• »<р аз xf1 ю оо аз ю со аз гн о оо оо st< со
- -" *^ •*- • —~ по !>• аз аз lo cm i^*" см со io ^н t>» ^ф оо оо оо " -—■■—--
MrHOCOCSI (МтНтнЮОО CM-r-t-Н СО СМ СМ
со ^ч аз оо t— со см со ^ vf cdoocdv^ ^cmcnjoo3 соазо
ю аз аз v^ ч^ lo аз см ^ t>- vji аз t—1>- -^ ^оооон со оо см
тнООСОСО тнОтн^Ю -^О'^ОО-^ -гнОСМОЮ "гнОСМ
СО СМ 00 ^н С
ооо ос
о^
Г>.'гн00>ЮСО
ооооо
ocMt^-сочР
t>OH005
смсососмаз
ООЮф)!
тНт^ОСОО гНтн
оаз^1сооо ^но^нсосм
гн О О СО О ^т^ОоО^
СМ 1>-С
-^ t>» с
оазс
> ОСО Ос
) СМ СО ОС
5 СО СО OOJOnJC
аз аз о со о
ООЗОЮ^
<?н о О^со"^
49*
760
> СМ О СО СЪ 00 СО С
) СО О Ю О5 t>- vf с
5*>чГ|0"^н05 00 СО С
D CD v?OOO00 t>-OiC
ICO COOOOt^t- СООС
> vt ^н COO
2o СО 2
СМОООО ПОООО -^ О О О ^ -тн О О О СО
«2
CD rH 4f СО СО
O© lO CM Np 00 CM COC<|[>050 CO
00O5 ^rHOOMO Nf< ЮтН О5 00 ОЭ
^O OOCDOCOOO COOO-n^b» Ю
СМОООО 'гн
О О О СО r<OOncO тНтн
Ч^ООСО'чнОО СМСОООСЛ-чН СЛОгНООСЛ l>-vJ<00CMCO СООЮСОСМ
СО t**" OS СО CD t>» СО ^н CM vj< !>• СО СО -^ CM LO <О 00 1^н СО l>» Vt1 О) СО 1О
СОСООСМСО |>Югн^О lOI^-'^GSOii ЮОЗН^гН CDOCM00CM
СО
О
'^^HOS^vf ^vt^O^CDCO I^-IOCOCDCD CDGiCM
000*^0500 OOCMCDCD1^ OiCDOOiOCM rHCO'H
OOthO^Q t^COOCOCD СО^ОЮСО ЮСО^
5CMOCDt- СОСМОСМЮ
DCMCOCDO NCO^OiO
DOO^hiOCO
-«нОООСМ гн
гнООнсО >^н
CD
CD
со
со
о"
vf С
n^ С
00C
M30OON CMCM
OOCO C^-OOOt—CO CDO5C
sf^H CMOOOCQOO t—CM<
CM iOtOCDO COO5C
гнсО nOOMO
СО
о"
CM
cT
00
) CO <чН 00 Gi с
> vf ^ CD 00 <
t>sf
OOI
ЮО
5 00 CM
"^ОООСМ "гнОООСО
о
CM
00
00 OCO CD С
t^- I>- ^Ф Ю С
00ЮОМ4
юсп>а5^а5 гсмсм^гна^ смосмс—*
^СОГООСМ ЮЮООтНСО OOOCMCDC- ООСО^ЮС
С- £— О "^ Ю ©OOOt-st1 LOOSHCM^f ^О
5 CD CO CD ^H
) Ю Ю Ю >чн
D тН >чН О5 V^
пОООСМ тнОООСО гН
00
о*
. J *** ^Н Ч|Н <
_-COCDO500 CDOi<
1>ЮО00 00 СО СО "
5СМ00 t^CMCO
юю оосм
CO t-CMOOCD*
5со coascococ
riOOON -гнОООСО ^НОО^
OOiOO
l>COt^C
СМ СМ00ЮО-00 CM^COOvF тНСОЮ(Мт-1 ЮМЮгнЬ
00 ОООООО^1 OO^CDOQ OOiCOt^-CO ^OsfOiCO
СМ ЮС^-ОО"^ COOO^COOi sfOO-гнОЬ ЮОт^СОЮ
cTo OCM "^OOOCO
СО О5 О 1>» СО
H *<П as CO (
- О CO 00 <
^НОООСО
CO
00
CO
о
см
о
00
о"
R, Q. ^ н^ н^ С1н Q. н^ ^ н^. »ч О- ^ >- н^»
СМ
о"
ю
о"
00
о"
761
j
X
)Ю
8
OCM
CO Ю
00 CD OLO СМ О t> С
гнОООСО г^О(
CM О о"о о" CM О О O~O CM* О OOO СМОООО СМОООО CMOOOCD
Г1 О5 00ОООЮ vF О> О СМ Ю nFth
h CM COOOOrHfO Ю 00 ОЮ ^Р LO CM
>СО O(NOtH|> О Ю О CM 00 ОО
00
см
со"
1
00 iNo:00O5t^ COCOS^NtH ЮтНЬ-НО CDOOl>00 QOit^^-H t>« CO
-^ t>«OCMLOO t^ О CM LO О OiOrHiMt^ Sf1 LO CM CO О Ю t>« CM CD 00 l>»
ОЮтнМО SfLOCMCDO LOt
ОО^т-Ю^ О<МгНтН|> ОЮтН(М05 ^t
wo ooo wo о о о см" о" о" о" о"" см" о" о" о" о" см о'о'о"^ см o'o^o'cd" со о
о
о
00О0005СЛ OCMI>.05CD CMOOCDC
tOlOOJO OONOJ 00lC
) CM
5 чН
) CO
CMt>-CO00in
OOCOt-OCO
HCOHCDf1
thOOOO 'HOOOO ^hOOOO CMOOOCM CMOOOCD
со
о
OOi
гНОООО ^ОООО ^ОООО CMOOOCM CMOOOCD
00
см
О5
о"
00 С
1>- С
оос
) vf О СМ СЛ С
> 1> 1> 00 чН С
) "гч 00 00 О С
> СМ 1> 00 СО О 00 СО
> о- CD OisfO^-O
> -гн 00 00ОО 'НФ
5 00 L
:>оо с
ОЗ^НС
00 СОООгнОО ОбОО-нОО 00OOHQ ОСОС
" -г4<£<э<э<э ^н о о"о"о" ^*о'чо'*о'чоч см о" о" о" см см о" о" о" со"
LO
о
00
о"
со
н СМ С
00 00 О5 СО
О(М ОП
см о'о'о'о" см о" о" о" о" см о" о" о" о" Jooon no'o'o4^
5 СМ СО Н|>(
5 со ю -с-) оо <
Ofi ОСО<
> тн см оо i> с
> vt1 vf Oi CM С
> st* ** CDO> С
СООО О t> CO
©OOf
CO
оо
5C0O5CO
)OOCO
СОСООЗСМСМ CMOOO^CD
l>»CDt>-LOLO l>-O«H00CM
OSCOOrtO ^N
СМОООО СМОООО ^-«
ОО
см*
см
СО
о"
!> t>» CJ5 «^ О5 СО 00 ^Н ^н
Jt>-OOCD COOC5CMOO _
>ООЮ ОЗ^О-пЬ 00
О5 CO 0O 00 Sf CD v .
ОтНЮООЮ sfrHC
!>• CD "^н LO CD
'HOOOO ^h
-sh ^hoOOCM
LO
CD
о
1>-ОЮ00
ООЮЮ-
ОЮС_ ^ _. , -
t^OO^ CMCMOOOit- vt
O^OJ OOCMOCMCO СО
|<CD-HO5 CDCDSFCDC
] ОО CM CM CM CM Ю С
^h ^hOOOCM
5 t>- 00 CD
JrHCDO
00
о
Ю
о"
- ._ _
t>«OOOOCM iO^O^Hvt
OOOOnOl OOOOCMO
J-dOWCO OOC
?O LO
stC
t- С
OOC
) 00 LO
> NJ< О
^нОООСМ ^
CM
Ю
o*
762
Таблица IX-2-4
Функция Ф (а?, д) для определения координаты § по формуле (IX-2-1)
X
1,4
1,6
1,8
2,0
2,4
0
0,849
0,874
0,809
0,930
0,859
45
0,842
0,872
0,806
0,929
0,856
90
0,826
0,864
'0,799
0,927
0,850
135
0,811
0,856
0,790
0,924
0,843
180
0,800
0,839
0,776
0,917
0,837
ПРИЛОЖЕНИЕ№
Параметры воздуха на различных высотах (стандартная атмосфера)
Высота
Я, км
0
0,5
1
1,5
2
2,5
3
4
5
6
7
8
9
10
11
12
14
16
18
20
22
24
25
28
30
32
34
36
38
40
45
50
55
60
65
70
80
90
100
Температура
288,15
284,90
281,65
278,40
275,14
271,89
268,64
262,13
255,63
249,13
242,63
236,14
229,64
223,15
216,66
216,66
216,66
216,66
216,66
216,66
216,66
216,66
219,40
224,87
230,35
235,82
241,28
246,74
252,20
257,66
271,28
274,00
270,56
253,40
236,26
219,15
185,00
185,00
209,22
я
р
1,0000
9,4205-
8,8701
8,3460
7,8458
7,3716
6,9208
6,0850
5,3338
4,6595
4,0560
3,5182
3,0388
2,6144
2,2393
1,9137
1,3979
1,0213
ю-1'
7,4630-10-2
5,4546
3,9875
2,9155
2,1341
1,5736
1,1681
8,7337-
6,5820
4,9900
3,8042
2,9199
1,5436
8,3475
4,5166
2,3806
1,2006
5,7580
1,0995
1,8203
3,1987
ю-3
Ю-4
Ю-5
.10-6
• ю-7
Л гт
ря
р
1,0000
9,5282-Ю-1
9,0751
8,6384
8,2171
7,8127
7,4237
6,6891
6,0125
5,3895
4,8171
4,2931
3,8132
3,3761
2,9784
2,5453
1,8593
1,3584
9,9257-10-2
7,2547
5,3033
3,8776
2,8030
2,0164
1,4613
1,0676
7,8608-10"3
5,8276
4,3465
3,2656
1,6397
8,7788-10-4
4,8105
2,7071
1,4642
7,5712-Ю-5
1,7126
2,8354-10-6
4,4075-10-7
Скорость
звука
аЯ>
м/сек
340,28
338,36
336,43
334,48
332,52
330,55
328,56
324,56
320,51
316,41
312,25
308,05
303,78
299,45
295,07
295,07
295,07
295,07
295,07
295,07
295,07
295,07
296,93
300,61
304,25
307,84
311,38
314,89
318,36
321,78
330,17
331,82
329,74
319,11
308,13
296,76
272,66
272,60
Кинематическая
вязкость
м^/сек
1,4607-
1,5196
1,5812
1,6461
1,7146
1,7866
1,8624
2,0271
2,2103
2,4153
2,6452
2,9030
3,1942
3,5232
3,8966
4,5595
6,2420
8,5437
1,1694
1,5997
2,1883
2,9929
4,1842
5,9370
8,3565
1,1661
1,6135
2,2165
3,0248
4,0956
8,4977
1,5997
2,8903
4,8749
8,5151
1,5475
5,9202
3,5759
10-5
10"4
10"3
• 10-2
-ю-1
-10°
Ускорение
свободного
падения
тела
9,80665
9,80511
9,80357
9,80203
9,80049
9,79896
9,79742
9,79435
9,79128
9,78820
9,78514
9,78207
9,77900
9,77594
9,77287
9,76981
9,76369
9,75758
9,75146
9,74537
9,73927
9,73318
9,72710
9,72102
9,71494
9,70888
9,70282
9,69676
9,69071
9,68466
9,66957
9,65452
9,63950
9,62452
9,66957
9,59466
9,56494
9,53536
9,50591
Средний
молекулярный
вес,
28,
28,
28,
28,
28,
28,
28,
28,
28,
28,
28,
28,
28,
28,
28,
28,
28,
28,
28,
28
28
28
28
28
28
28
28
28
28
28
28
28
28
28
28
28
28
28
28
эЯ
966
966
966
966
966
966
966
966
966
966
966
966
966
966
966
966
966
966
966
966
966
966
966
966
966
966
966
,966
,966
,966
,966
,966
,966
,966
,966
,966
,966
,966
,962
763
Продолжение прил. № 2
Высота
Я, км
120
140
160
180
200
225
250
275
300
400
500
600
700
Температура
т°н к
332,24
768,00
1155,3
1193
1226,8
1269,9
1302,8
1334,6
1358,0
1480
1576
1691
1812
я
^3
2,5217-Ю-8
7,2887-10~9
3,7628
2,2199
1,3455
7,4584.10-ю
4,2900
2,5554
1,5731
5588-10~14
1566
5240-10~15
2011
"я
рз
1,0633-10"8
2,6748-Ю-9'
9,0457.10-1°
5,0883
2,9477
1,5404
8,3835-10-п
4,7024
2,7364
0,7342
0,1806
0,5402-10-12
0,1879-10-12
Скорость
звука
аЯ>
м/сек
Кинематическая
вязкость
мУсек
Ускорение
свободного
падения
тела
м/сек%
9,43288
9,38948
9,33205
9,27400
9,21750
9,14762
9,07850
9,01021
8,94270
8,680
8,428
8,187
7,957
Средний
молекулярный
вес,
28,624
28,314
27,950
27,476
27,000
26,348
25,577
24,672
23,731
19,56
18,28
17,52
17,03
Примечания:
1. Данные в приложении № 2 до высоты Н = 200 км взяты по ГОСТ 4401—64.
2. Данные в диапазоне высот от 225 до 300 км соответствуют рекомендациям, приводимым
в ГОСТ 4401—64.
3. Остальные данные (до Н = 700 км) взяты из работы [17].
П Я 0 25 /2 760 103323
3 н
При Я = 0
д (д ) р []
= V3 = 25 w/jw2 = 760 мм pm. cm. = 10332,3 кГ/м%;
1,225
= 0,12492
ПРИ ЛОЖЕН И Е № з
Таблица перевода единиц, применяющихся в аэродинамике для измерения различных
величин, из системы МКГСС в Международную систему единиц (СИ), ГОСТ 9867—61
Наименование
Старая единица
(система МКГСС)
Основные единицы
Длина
Масса
Время
Температура термодинамическая
Производные
Скорость
Ускорение
Ускорение силы тяжести
Сила
Давление
Динамическая вязкость
Кинематическая вязкость
Работа, энергия.
Количество теплоты
Термический эквивалент работы
Механический эквивалент теплоты
Удельная теплоемкость
Энтропия
Энтальпия
Удельный тепловой поток
Коэффициент теплообмена
Коэффициент теплопроводности
Коэффициент лучеиспускания абсолютно
черного тела
Газовая постоянная
4,
1 м
1 кг
1 сек
1°К
единицы
1 м/сек
1 м/сек2
9,8 м/сек2
1 кГ
1 кГ/см2
1 кГ/сек2
1 м2/сек
1 кГм
1 ккал
—г= ккал/кГм
427 кГм/ккал
1 ккал/кГ- град
1 ккал/кГ-град
1 ккал/кГ
1 ккал/м2-ч
1 ккал/м2-ч-град
1 ккал /м-ч- град
88 ккал/м2-ч-град4
1 кТм/кТ -град
Новая единица
(СИ)
1 м
1 кг
1 сек
1°К
1 м/сек
1 м/сек2
9,8 м/сек2
9,807 н
9,807-Ю4 н/м2
9,807 н-сек/м2
1 м2/сек
9,807 дж
4,187-103 дж
1 дж/нм
1 нм/дж
4,187-103 дж/кг-град
4,187-Ю3 дж/кг-град
4,187.103 дж/кг
1,163 ет/м2
1,163 ет/м2-град
1,163 ет/м-град
5,68 дж/м2-град4
9,807 дж/кг-град
Коэффициент температуропроводности
М2/Ч
2,778-10~4 м2/сек
ЛИТЕРАТУРА
1. Н. Аржаников С, Мальцев В.Н. Аэродинамика. Обо-
ронгиз, 1956.
2. Аржаников Н. С, Садекова Г. С. Аэродинамика
больших скоростей Изд-во «Высшая школа», 1965.
3. Аэродинамика разреженных газов. Сб. статей под ред. Валланде-
ра С. В. Изд-во Ленинградского университета, 1963.
4. Бабенко К. И., Воскресенский Г. П.,
Любимов А. Н., Русанов В. В. Пространственное обтекание гладких тел
идеальным газом. Изд-во «Наука», 1964.
5. Белоцерковский С. М. Тонкая несущая поверхность
в дозвуковом потоке газа. Изд-во «Наука», 1965.
6. Б у р а г о Г. Ф., Вотяков В. Д. Аэродинамика. Ч. П. Изд-во
ВВИА им. Жуковского Н. Е., 1961.
7. Вукалович М. П., Кириллин В. А., Ремизов С. А.,
Силецкий В. С, Тимофеев В. Н. Термодинамические свойства
газов, Гостехиздат, 1953.
8. Давидсон В. Е. Основы газовой динамики в задачах. Изд-во
«Высшая школа», 1965.
9. Гинзбург И. П. Аэрогазодинамика. Изд-во «Высшая школа»,
1966.
10. Дородницын А. А. Метод интегральных соотношений для
численного решения дифференциальных уравнений в частных производных.
Труды ин-та точной механики и вычислительной техники АН СССР,
1958.
11. Дракин И. И. Аэродинамический и лучистый нагрев в полете.
Оборонгиз, 1961.
12. Калихман Л. Е. Турбулентный пограничный слой на
криволинейной поверхности, обтекаемой газом. Оборонгиз, 1956.
13. Кибардин Ю. А., Кузнецов С. И., Любимов Л. Н.
Шумяцкий Б. Я. Атлас газодинамических функций при больших
скоростях и высоких температурах воздушного потока. Госэнергоиздат, 1961.
14. К о ч и н Н. Е., К и б е л ь И. А., Розе Н. В. Теоретическая
гидромеханика. Ч. I—II. Физматгиз. М., 1963.
15. Красильщикова Е. А. Крыло конечного размаха в
сжимаемом потоке. Госте хиздат, 1962.
16. Краснов Н. Ф. Аэродинамика тел вращения. Оборонгиз, 1958.
17. Краснов Н. Ф. Аэродинамика тел вращения. Изд-во
«Машиностроение», 1964.
18. К у з н е ц о в СИ. Диаграммы и таблицы течения
диссоциирующего воздуха около клина, конуса и выпуклой поверхности. Оборонгиз, 1962.
19. Л а н д а у Л. Д., Л и ф ш и ц Е. М. Механика сплошных сред.
Гостехиздат, 1954.
20. Л а н д а у Л. Д., Лифшиц Е. М. Статистическая физика.
М., ГИТТЛ, 1951.
765
21. Лебедев А. А., Чернобровкин Л. С. Динамика
полета. Оборонгиз, 1962.
22. Лойцянский Л. Г. Механика жидкости и газа. Гостехиз-
дат, 1950.
23. Мельник о^в А. П. Аэродинамика больших скоростей. Воен-
издат, Мин. обороны СССР, 1961.
24. О р л о в Б. В., М а з и н г Г. Ю. Газодинамические и
баллистические основы проектирования ракетных двигателей на твердом
топливе. Машиностроение, 1964.
25. Основы теплопередачи в авиационной и ракетной технике. Под
ред. проф. Кошкина В. К. Оборонгиз, 1960.
26. О с т о с л[а в с к и й И. В. Аэродинамика самолета. Оборонгиз,
1957.
27. П а н и ч к и н И. А., Ляхов А. В. Основы газовой динамики
и их приложение к расчету сверхзвуковых аэродинамических труб. Изд-во
Киевского университета, 1965.
28. Предводителев А. С, Ступоченко Е. В.,
Ионов В. П., Плешанов А. С, Рождественский И. В.,
Самуилов Е. В. Термодинамические функции воздуха для температур
от 1000 до 12 000° К и давлений от 0,001 до 1000 am (графики функций).
Изд-во АН СССР, 1960.
29. Предводителев А. С, Ступоченко Е. В.,
Самуилов Е. В., Стаханов И. П., Плешанов А. С,
Рождественски й И. Б. Таблицы термодинамических функций воздуха (для температур
от 6000 до 12 000° К и давлений от 0,0001 до 1000 am). Изд-во АН СССР
1957.
30. Мартынов А. К. Экспериментальная аэродинамика.
Оборонгиз, 1951.
31. Седов Л. И. Методы подобия и размерности в механике. Изд-во
«Наука», 1965.
32. Фабрикант И. Я. Аэродинамика. Изд-во «Наука», 1964.
33. Федоров В. И. Конструкция реактивных двигателей. Воен-
издат, 1960.
34. Ф е о д о с ь е в В. И., Синярев Г. Б. Введение в ракетную
технику. Оборонгиз, 1960.
35. Физическая газодинамика. Сб. статей. Изд-во АН СССР, 1959.
36. Ф р а н к л ь Ф. И., Карпович Е. А. Газодинамика тонких
тел. Гостехиздат, 1948.
37. Христианович С. А. Обтекание тел газом при больших
скоростях. Труды ЦАГИ, № 481, 1940.
38. Черный Г. Г. Течения газа с большой сверхзвуковой
скоростью. Физматгиз, 1959.
39. Численные методы в газовой динамике. Сб. статей под ред.
Рослякова Г. С. и Чудова Л. А. Изд-во Московского университета, 1963.
40. Широков М. Ф. Физические основы газодинамики.
Физматгиз, 1958.
41. Аэродинамика частей самолета при больших скоростях. ИЛ, 1959.
42. Б е р с Л. Математические вопросы дозвуковой и околозвуковой
газовой динамики. ИЛ, 1961.
43. Газовая динамика. Сб. статей. ИЛ, 1950.
44. Газодинамика разреженных газов. Сб. статей. ИЛ, 1963.
45. Г у д е р л е й К. Г. Теория околозвуковых течений, ИЛ, 1960.
46. Д о у Р. Б. Основы теории современных снарядов. Изд-во «Hay*
ка», 1964.
47. Исследование гиперзвуковых течений. Изд-во «Мир», 1964.
766
48. Курант Р., Фридрихе К. Сверхзвуковое течевие и
ударные волны. ИЛ, 1950.
49. Л и п п м а н Г. В., Р о ш к о А. Элементы газовой динамики.
ИЛ, 1960.
50. Научные проблемы искусственных спутников Земли, ИЛ, 1959.
51. Нильсен Д. Аэродинамика управляемых снарядов. Оборон-
гиз, 1962.
52. Общая теория аэродинамики больших скоростей. Под ред. проф.
Паничкина И. А. Воениздат Мин. обороны СССР, 1962.
53. Паттерсон Г. Н. Молекулярное течение газов. Физмат-
гиз, 1960.
54. Проблемы высоких температур в авиационных конструкциях.
ИЛ, 1961.
55. Проблемы движения головной части ракет дальнего действия
ИЛ, 1959.
56. Проблемы полета с большими скоростями. ИЛ, 1960.
57. Современное состояние аэродинамики больших скоростей, ИЛ,
т. 1—2, 1955—1956.
58. Ф е р р и А. Аэродинамика сверхзвуковых течений. Гостехиз-
дат, 1953.
59. Хейз У. Д., Пробстин Р. Ф. Теория гиперзвуковых
течений. ИЛ, 1962.
60. X и л т о н У. Ф. Аэродинамика больших скоростей. ИЛ, 1955-
61. Эткин Б. Динамика полета. Изд-во «Машиностроение», 1964.
62. Kopal Z, Tables of Supersonic Flow Around cones of Large Jaw,
Technical Report, No. 5, MIT, 1949.
63. Kopal Z., Tables of Supersonic Flow Around Jawing Cones, Technical
Report, No. 3. MIT. 1947.
64. Kopal Z. Tables of Supersonic Flow Around Cones, Technical Report,
No. 1. MIT, 1947.
65. Sigard F, Hoerner, Aerodynamic Drag, Ohio, USA, 1951.
66. Известия АН СССР. Механика и машиностроение. Известия АН
СССР. Механика жидкости и газа.
67. Инженерный журнал.
68. Прикладная математика и механика. АН СССР.
69. Вопросы ракетной техники. Изд-во «Мир».
70. Ракетная техника и космонавтика (AIAA Journal).
71. Jet Propulsion (ARS Journal).
72. Journal of the Aeronautical Sciences.
73. Journal of the Fluid Mechanics.
74. Journal of the Royal Aeronautical Society.
75. National Advisory Committee for Aeronantics (NACA).
76. Zeitschrift fur Flugwissenschaften.
77. Журнал вычислительной математики и математической физики.
78. М и е л е А. Механика полета. Изд-во «Наука», 1965.
79. Механика. Сборник сокращенных переводов и рефератов
иностранной периодической литературы, ИЛ.
80. Дмитриевский А. А., Кошевой В. Н. Основы теории
полета ракет. Военное изд-во МОСССР, 1964.
81. Л е б е д е в А. А., К а р а б а н о в В. А. Динамика систем
управления беспилотными летательными аппаратами. Изд-во
«Машиностроение», 1965.
ОГЛАВЛЕНИЕ
Предисловие 3
РАЗДЕЛ ПЕРВЫЙ. ОБЩИЕ ОПРЕДЕЛЕНИЯ АЭРОДИНАМИКИ
Глава I. Понятие о силах, моментах и аэродинамических коэффициентах
§ 1-1. Системы осей координат 9
§ 1-2. Силы, моменты и их аэродинамические коэффициенты 11
§ 1-3. Лобовое сопротивление 15
Крылатый летательный аппарат 15
Корпус 17
Крылья (несущая поверхность) 19
§ 1-4. Подъемная сила 23
Крылатый летательный аппарат 23
Корпус 25
Крылья (несущая поверхность) 26
§ 1-5. Момент 27
Крылатый летательный аппарат 27
Корпус 28
Крыло и профиль 29
§ 1-6. Применение аэродинамических характеристик для исследования
устойчивости тел в полете 30
Статическая устойчивость 30
Динамическая устойчивость 32
§ 1-7. Аэродинамические характеристики летательных аппаратов при
неустановившемся движении 37
Глава П. Формы летательных аппаратов и их элементов
§ П-1. Формы корпусов летательных аппаратов 45
§ П-2. Формы несущих, управляющих, стабилизирующих и вспомогательных ч
поверхностей 52 '
§ П-3. Органы управления 62
§ П-4. Аэродинамические схемы летательных аппаратов 70
§ П-5. Влияние назначения и тактико-технических требований на выбор
аэродинамических схем летательных аппаратов 76
Тип летательного аппарата и особенности аэродинамической схемы 77
Тип двигательной установки и особенности аэродинамической схемы .... 82
Глава III. Основные соотношения в теории газовых течений
§ II1-1. Особенности течения газа с очень большими скоростями 85
Изменение физико-химических свойств и термодинамических характеристик
воздуха с температурой 85
Диссоциация и ионизация 87
Основные зависимости для двухатомного диссоциирующего газа 93
Релаксационные явления '. 98
Диффузионные явления в пограничном слое 102
§ II1-2. Система основных уравнений 105
Уравнение движения 106
768
Уравнение неразрывности Ш
Уравнение диффузии 115
Уравнение количества движения * 116
Уравнение энергии 117
Уравнение состояния 120
Условие сохранения энтропии 121
Начальные и граничные условия 121
§ Ш-3. Изэнтропическое течение 123
§ III-4. Основные зависимости для определения параметров за скачком уплотнения 125
Уравнения косого скачка уплотнения 125
Расчет косого скачка уплотнения с помощью таблиц или графиков
термодинамических функций воздуха при очень высоких температурах 127
Скачок уплотнения в потоке газа с постоянными теплоемкостями 132
Эффекты релаксации в ударных волнах 137
Глава IV. Общие методы решения аэродинамических задач
§ IV-1. Метод характеристик 140
Общие уравнения для характеристик 140
Характеристики плоского потенциального потока 144
Схема решения задач по методу характеристик 147
Характеристики в диссоциирующем газе 151
§ IV-2. Конические течения 152
§ IV-3. Метод источников 153
§ IV-4. Теория сверхзвукового обтекания тонких тел с произвольным поперечным
сечением 155
Решение уравнения потенциала 155
Аэродинамические силы и моменты 159
Метод конформного преобразования 162
§ IV-5. Метод обратимости потока 165
§ IV-6. Общие выражения для производных устойчивости оперенного тела
вращения. Метод присоединенных масс 166
§ IV-7. Приближенные методы расчета обтекания поверхностей 173
§ IV-8. Аэродинамический нагрев 182
Параметры теплопередачи 182
Теплопередача в ламинарном пограничном слое на криволинейной поверхности 192
§ IV-9. Влияние вязкого взаимодействия на параметры обтекания 201
§ IV-10. Особенности обтекания тел с затупленной передней частью 203
РАЗДЕЛ ВТОРОЙ. АЭРОДИНАМИКА НЕСУЩИХ,
СТАБИЛИЗИРУЮЩИХ И УПРАВЛЯЮЩИХ ПОВЕРХНОСТЕЙ
Глава V. Расчет аэродинамических коэффициентов
§ V-1. Дозвуковые и околозвуковые скорости 209
Влияние сжимаемости на давление 209
Подъемная сила [6] 212
Лобовое сопротивление 222
Момент и фокус (центр давления) . » 227
§ V-2. Сверхзвуковые скорости 229
Обтекание тонкой пластинки 229
Профиль в сверхзвуковом потоке 233
§ V-3. Подъемная сила и момент тонких крыльев конечного размаха.
Сопротивление, зависящее от подъемной силы 241
§ V-4. Сопротивление крыльев конечной толщины 256
§ V-5. Нелинейная задача о сверхзвуковом обтекании крыльев 266
Применение метода характеристик 266
Аэродинамические характеристики при очень больших (гиперзвуковых)
скоростях 269
769
$ V-6. Донное сопротивление. Вязкое взаимодействие 284
| V-7. Аэродинамика затупленных крыльев при больших сверхзвуковых скоростях 288
Обтекание затупленной передней кромки профиля 288
Затупление в виде плоской пластинки 291
Профиль с малым затуплением 295
§ V-8. Кольцевые крылья 299
§ V-9. Крестообразные крылья 301
§ V-10. Нестационарная аэродинамика крыла 302
Пластинка в сверхзвуковом потоке 302
Крылья в дозвуковом потоке 305
Крылья в сверхзвуковом потоке (теория тонкого тела) 308
Влияние удлинения крыла и числа М<х> на производные устойчивости .... 312
Глава VI. Трение и теплопередача на крыльях
§ VI-1. Параметры трения при обтекании плоской пластинки 320
Однородный пограничный слой 320
Смешанный пограничный слой 332
Трение на пластинке, расположенной под углом атаки 336
§ VI-2. Теплопередача на плоской пластинке 338
Несжимаемый поток 338
Влияние больших скоростей 338
Теплопередача на пластинке, расположенной перпендикулярно к направлению
набегающего потока (ламинарный пограничный слой) 340
§ VI-3. Трение и теплопередача на крыльях конечной толщины 343
Крыло с заостренной передней кромкой 343
Теплопередача на затупленной поверхности крыла 348
§ VI-4. Температура стенки 350
Стационарный нагрев 350
Нестационарный нагрев 352
Температура стенки при солнечном нагреве 353
§ VI-5. Степень затупления передней кромки крыла, обеспечивающая
наибольшее снижение тепловых потоков 354
РАЗДЕЛ ТРЕТИЙ, АЭРОДИНАМИКА КОРПУСОВ
Глава VII. Аэродинамические коэффициенты при дозвуковых и околозвуковых
скоростях
§ VII-1. Дозвуковые скорости 359
§ VII-2. Околозвуковые скорости 362
Подобие околозвуковых потоков 362
Суммарное сопротивление различных тел вращения при трансзвуковых
скоростях 367
Глава VIII. Конус в сверхзвуковом потоке
§ VIII-1. Осесимметричное сверхзвуковое обтекание конуса 372
Система уравнений 372
Постоянные теплоемкости 373
Влияние диссоциации и ионизации 379
Влияние неравновесности 385
§ VIII-2. Конус под углом атаки 386
Некоторые результаты расчета сверхзвуковых конических течений 386
Анализ результатов расчета обтекания конусов 377
Таблицы Копала 390
Приближенный расчет обтекания при больших скоростях 391
Глава IX. Применение разностных методов для расчета, обтекания тел с
криволинейной образующей
§ IX-1. Расчет осесимметричного сверхзвукового обтекания заостренного тела
вращения по методу характеристик [17] 392
770
§ IX-2 Метод сеток 401
§ IX-3. Влияние угла атаки на лобовое сопротивление 403
Глава X. Гиперзвуковые скорости
§ Х-1. Обтекание тонких тел с очень большими скоростями 405
Система уравнений 405
Расчет обтекания 409
§ Х-2. Применение приближенных методов расчета обтекания тел вращения
потоками с очень большими скоростями 415
Метод «местных» конусов 415
Метод сочетания конических течений и течений разрежения 417
§ Х-3. Метод Ньютона 421
Давление 421
Коэффициент осевой силы 421
Форма головной части с минимальным сопротивлением 425
Коэффициент нормальной силы 429
Коэффициент момента и центра давления 435
Закон подобия при неосесимметричном обтекании 440
Оценка точности приближенных методов . 442
Глава XL Аэродинамика тонких корпусов в линеаризованном потоке
§ XI-1. Применение метода источников 443
§ XI-2. Осесимметричное обтекание 448
Расчет скорости и давления 448
Коэффициент волнового сопротивления 455
Весьма тонкий корпус 462
Форма тела вращения с минимальным волновым сопротивлением 463
§ XI-3. Обтекание тел вращения под углом атаки 464
Распределение давления при неосесимметричном обтекании 464
Коэффициент нормальной силы 469
Коэффициент момента сил 475
Коэффициент центра давления 477
Сопротивление, обусловленное подъемной силой 484
Глава XII. Аэродинамика затупленных тел вращения
§ XI1-1. Невязкое обтекание затупленного носка 485
Общее решение для носка произвольной формы 485
§ XI1-2. Приближенные методы расчета обтекания носков различной формы . . . 487
Сферический носок 487
Плоский торец 498
Другие формы затупленных ногков 500
Сферическая поверхность с «затупленной» передней частью 503
§ XI1-3. Обтекание потоками больших скоростей цилиндрических и конических тел
с малым затуплением 505
Аналогия с неустановившимся движением поршня 505
Обтекание затупленного цилиндра 508
Обтекание тонкого конуса с малым затуплением 511
§ XI1-4. Применение метода характеристик к расчету обтекания затупленных тел
вращения 515
§ ХИ-5. Влияние угла атаки 519
§ ХН-6. Метод Ньютона 520
§ ХИ-7. Обтекание затупленных тел криволинейной формы 524
§ ХП-8. Влияние неравновесности на параметры невязкого обтекания затупленных
тел 532
Неравновесное течение в областях с большим перерасширением и малыми
градиентами давления 532
Влияние неравновесности на положение и форму ударной волны 536
771
Глава XIII. Нестационарная аэродинамика корпусов
§ XIII-1. Линеаризованное обтекание тел вращения 539
Основные зависимости 539
Аэродинамические коэффициенты в условиях колебаний низкой частоты . . . 543
§ ХШ-2. Применение метода Ньютона 547
Заостренное тело вращения . . , 547
Затупленный конус 549
§ XII1-3. Дополнительное силовое воздействие, обусловленное вращением корпуса
вокруг продольной оси 553
Глава XIV. Трение и теплопередача при больших скоростях
§ XIV-1. Трение и теплопередача на корпусе 555
§ XIV-2. Влияние вязкости на сопротивление. Донное сопротивление 559
Влияние вязкого взаимодействия на параметры обтекания 559
Трение 562
Донное сопротивление 563
§ XIV-3. Определение степени затупления, обеспечивающей максимальное
снижение тепловых потоков 569
§ XIV-4. Теплопередача на корпусе 575
Поверхность криволинейной формы 575
Заостренный корпус 576
§ XIV-5. Точка полного торможения на затупленном носке 577
§ XIV-6. Криволинейная затупленная поверхность 531
Ламинарная теплопередача 581
Теплопередача через турбулентный пограничный слой 588
§ XIV-7. Сравнение трения и тепловых потоков на заостренном и затупленном
конусах 594
§ XIV-8. Влияние вязкости на внешний поток около затупленного тела .... 595
РАЗДЕЛ ЧЕТВЕРТЫЙ. АЭРОДИНАМИЧЕСКИЕ
ХАРАКТЕРИСТИКИ ЛЕТАТЕЛЬНОГО АППАРАТА
Глава XV. Стационарное обтекание
§ XV-1. Расчет аэродинамических коэффициентов с учетом интерференции для
комбинации, состоящей из тонкого корпуса и крыла 603
Общие определения 603
Зависимости для аэродинамического расчета с учетом интерференции . . . 605
Расчет интерференции «нетонких» комбинаций 614
§ XV-2. Изменение аэродинамических свойств оперения под влиянием крыла 622
Общее выражение для нормальной силы 622
Угол скоса потока за крылом 623
Несущая способность летательного аппарата с неподвижными крыльями и
оперением при сверхзвуковых скоростях 624
§ XV-3. Влияние интерференции на аэродинамические характеристики органов
управления 637
Полностью подвижные плоские органы управления 6^7
Полностью подвижные крестообразные органы управления 644
Взаимодействие между органами управления 644
Органы управления, расположенные вдоль задней кромки несущих
поверхностей 646
Нелинейные эффекты 649
Шарнирный момент полностью подвижных крыльев 651
Пример расчета аэродинамических характеристик комбинации корпус —
крыло — оперение. Экспериментальные данные 653
§ XV-4. Момент демпфирования летательного аппарата, обусловленный
движением топлива и продуктов его сгорания 675
§ Х.У--5Г"'Ря€«ает. роллеронов 676
772
§ XV-6. Лобовое сопротивление 679
Сопротивление при нулевой подъемной силе 679
Сопротивление при су Ф 0 683
Аэродинамическое качество 685
Глава XVI. Аэродинамика органов управления
§ |XVI-1. Силы, создаваемые аэродинамическими органами управления .... 688
Интерцепторы 688
Увеличение еподъемной силы аэродинамических органов управления путем
вдувания газа в пограничный слой 691
§ XVI-2. Расчет сил, создаваемых газодинамическими органами управления . . . 692
Расчет силы тяги газодинамических органов управления с учетом потерь в воз
духозаборных устройствах 692
Неподвижные и поворотные управляющие двигатели 698
Поворотные сопла 698
Поворотные насадки ? 700
Дефлекторы 701
Газовые рули 703
Управление вдуванием газа в сверхзвуковую часть сопла 706
Дросселирование отдельных сопел 709
Определение управляющих усилий, создаваемых газодинамическими органами
в сопловых аппаратах с центральным телом 710
§ XVI-3. Расчет сил, создаваемых комбинированными органами управления ... 711
Органы управления с неподвижным щелевым соплом на задней кромке
пластины 711
Органы управления с поворотным щелевым соплом на задней кромке крыла
при дозвуковых скоростях 715
Органы управления в виде неподвижного щелевого сопла на цилиндрической
поверхности корпуса при сверхзвуковых скоростях 718
§ XVI-4. Определение шарнирных моментов газодинамических и комбинированных
органов управления 719
Глава XVII. Нестационарные характеристики летательного аппарата
§ XVII-1. Определение производных устойчивости по аэродинамической теории
тонкого тела 721
§ XVI1-2. Коэффициенты демпфирования 723
§ XVI1-3. Анализ производных устойчивости оперенного тела 726
§ XVII-4. Эффекты Магнуса 731
Приложение № 1 734
Приложение № 2 762
Приложение № 3 763
Литература 764
ЗАМЕЧЕННЫЕ ОПЕЧАТКИ
Стр.
Строка
Напечатано
Следует читать
134
169
221
239
373
376
394
423
431
459
463
497
571
571
579
581
581
648
707
708
722
722
722
727
Формула (II1-4-34)
Формула (IV-6-21)
2 сн.
Формулы (V-2-33),
(V-2-36)
13 св.
Формула (VIII-1-19)
Формула (IX-1-1C)
4 св.
Формула (Х-3-50)
Формула (X1-2-40)
Формула (XI-2-48)
Формула (ХП-2-41')
Формула (XIV-3-9)
8 сн.
Формулы (XIV-5-6)
Формула (XIV-6-2)
Формула (XIV-6-3)
Формула (XV-3-35)
10 св.
Формула (XVI-2-20)
Формула (XVI1-1-4)
Выражение для t2fr
в формулах
(XVI1-1-9)
Формула (XVII-1-11)
Формула (XVII-3-1)
= 9.,95
Л-1
= (0,935 — 1,05р) Дт,
= Uxn tg PK
= 2,12-104 ...
= 89-106 ...
... sin2T][....r1/2-Z>
—-COS4T)) +
В третьем слагаемом
В четвертом слагаемом
± (Wi COS Pi) Wa
" V РА )
' " f/c — cosX ) '
....+8со2С12-...
= 0,95
Правые части в формулах
следует считать в степени — 1.
= (fc-l)/2
— I (dp — 0)fi; + -
"18
1
=2,12-107 ...
=89-109 ...
— cos 4т]) +
1-rJ
pA
sin X \ ~i .
" f/c + cosh)
+ 2аЪ*{а — Ъ) —
Зак. 114























































































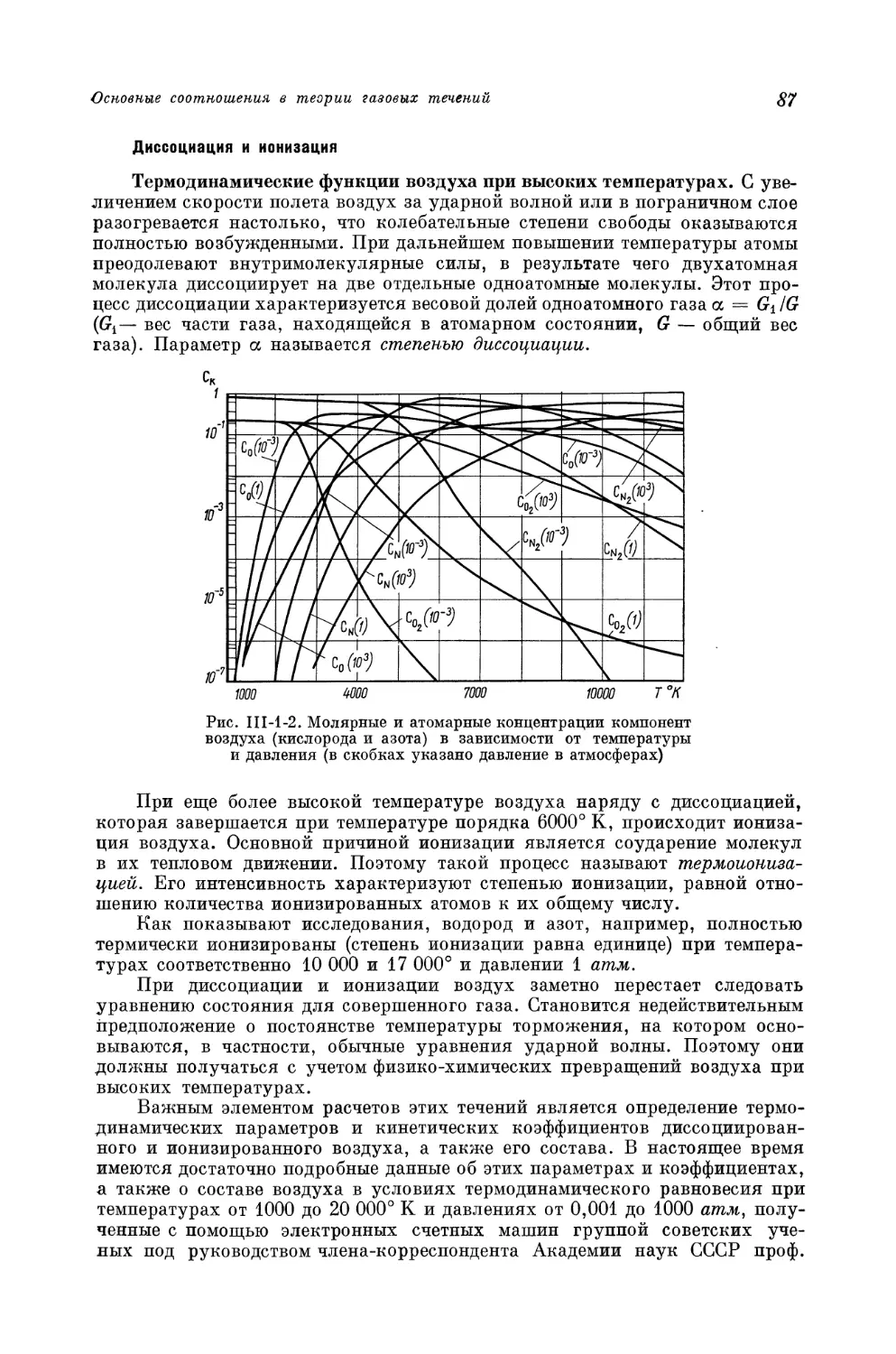




























































































































![Подъемная сила [6]](https://djvu.online/jpg1/Q/m/1/Qm108zHB1Iy3K/213.webp)