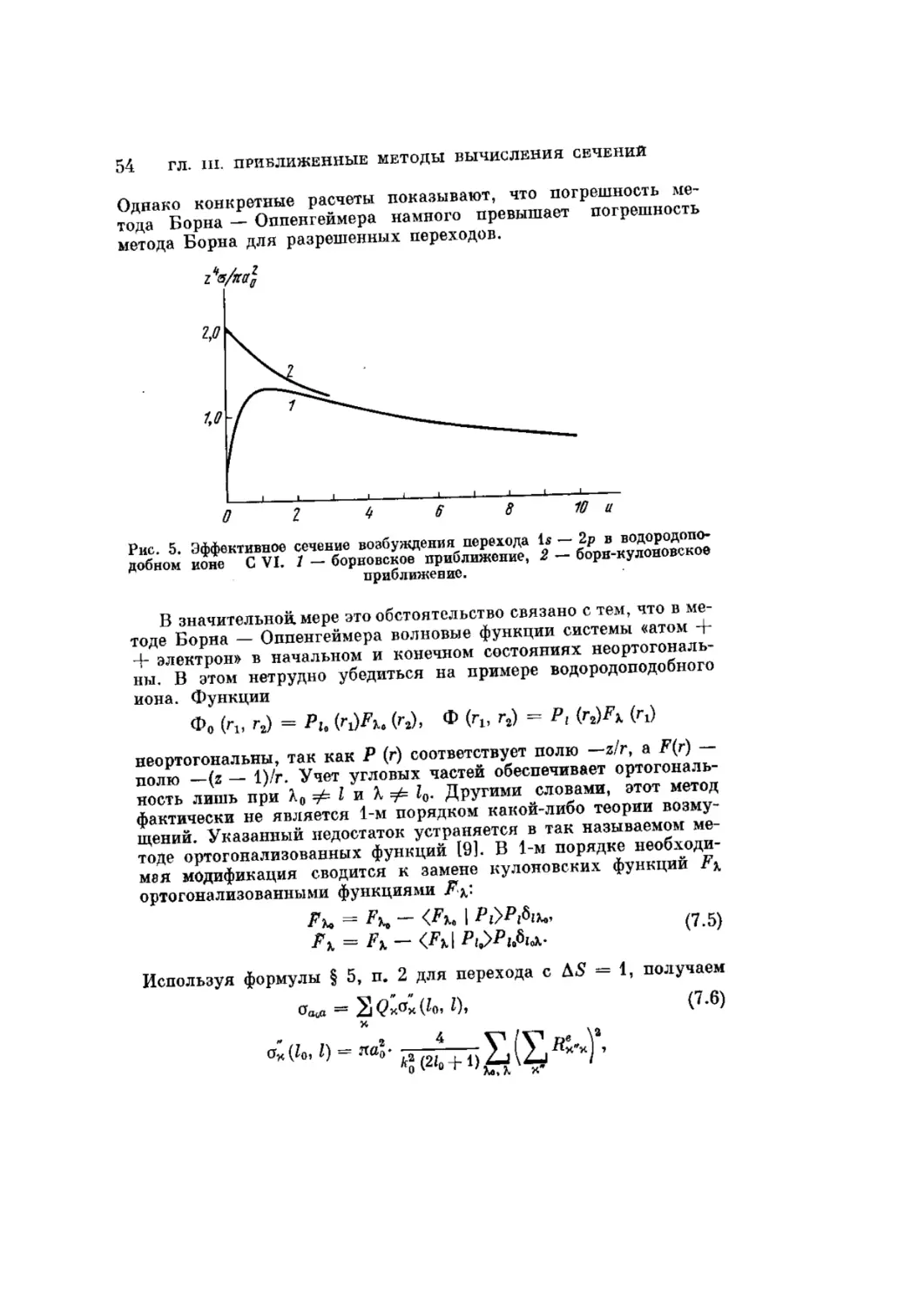
Text
ЛАВаинштейп
И.И.Собэдьман
ЕА.Юков
Возбуждение
атомов
и уширение
СПЕКТРАЛЬНЫХ
ЛИНИЙ
Л. А. Ва
5ЩЦ
тейн,
535, Г
В/
И. И. Собельман,
Е. А. Юков
Возбуждение
атомов
и уширение
спектральных
линий
Кввтятут Атаяве! 8пртм |
ве. й. В. Кдатов» 1
БИБЛИОТЕКА |
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1979
ОГЛАВЛЕНИЕ
Предисловие ..................................................... 6
Глава I. Элементарные процессы возбуждения спектров .... 7
§ 1. Сечения элементарных процессов........................... 7
§ 2. Населенности атомных уровней в плазме; соотношение ско-
ростей взаимно обратных процессов............................. 9
1. Термодинамическое равновесие (9). 2. Соотношение ско-
ростей взаимно обратных процессов (10). 3. Модель двух
состояний (12). 4. Корональный предел (13).
Глава II. Основы теории столкновений ........................... 15
§ 3. Основы теории рассеяния ................................ 15
1. Упругое рассеяние в центральном поле (15). 2. Волновые
функции ф£ и (17). 3. Квазиклассическое приближение (18).
4. Неупругое рассеяние (20). 5. Выражение эффективных
сечений через элементы 5-матрицы (21),
§ 4. Общие уравнения теории столкновений электронов с атомами 22
1. Введение (22). 2. Общие формулы для сечения (23). 3. 5-ма-
трица и сила столкновения (27). 4. Радиальные уравнения
(28). 5. Интегральные радиальные уравнения (31). 6. Вве-
дение поляризационного потенциала (32).
§ 5. Приближение 1-го порядка................................ 34
1. Общие формулы (34). 2. Сводка формул для сечений и
(^-факторов (36).
Глава III. Приближенные методы вычисления сечений .... 41
§ 6. Метод Борна............................................ 41
1. Столкновения быстрых электронов с атомами; разложение
по мультиполям (41). 2. Формула Бете (45). 3. Краткая
характеристика борновских сечений (46). 4. Ионизация
и трехчастичная рекомбинация (48).
§ 7. Некоторые уточнения метода Борна....................... 51
1. Введение (51). 2. Учет искажения падающей и рассеян-
ной волн, возбуждение ионов (52). 3. Учет обмена (53).
4. Нормировка (57), 5. Заключительные замечания; «обоб-
щенный метод Борна» (61).
§ 8. Более точные методы расчета сечений ................... 62
1. Переходы через виртуальные уровни (63). 2. Исполь-
зование К’-матрицы (66). 3. Использование поляризацион-
ного потенциала (67). 4. Метод сильной связи (68).
i § 9. Возбуждение многозарядных ионов......................... 71
1, Введение (71). 2. Кулоновская функция Грина (72).
3. Потенциальное и резонансное рассеяние (73). 4. Обсужде-
ние и примеры (76).
1*
4
ОГЛАВЛЕНИЕ
§ 10. Переходы между высоковозбужденными уровнями .... 78
1. Борновское приближение (78). 2. Переходы между высо-
ковозбужденными уровнями в квазиклассическом прибли-
жении (84). 3. Переходы с Ап = 1 (88).
Глава IV. Столкновения тяжелых частиц........................... 92
§ 11. Метод параметра удара.................................. 92
1. Общие формулы (92). 2. Приближение двух состояний
(94).
§ 12. Переходы, вызываемые мультипольным взаимодействием 98
1. Решение в приближении двух состояний (98). 2, Прибли-
жения двух уровней и «вращающейся оси» (104). 3. Учет
отталкивания ядер (107).
§ 13. Процессы перезарядки.................................. 108
1. Специфика задачи перезарядки (108). 2. Резонансная
перезарядка (109). jj. Приближение двух состояний (110).
4. Вклад внутренних оболочек (114). 5. Перезарядка много-
зарядных ионов на атомах (116).
Глава V. Некоторые вопросы кинетики возбуждения................ 118
§ 14. Скорости ялементарных процессов в плазме. Аппроксима-
ционные формулы для сечений и скоростей процессов ... 118
1. Возбуждение атомов и ионов (118). 2. Переходы между
близкими уровнями (122). 3. Ионизация (122). 4. Рекомбина-
ция (123). 5. Полуэмпирические формулы для скоростей возбуж-
дения, ионизации и диэлектронной рекомбинации (126).
§ 15. Диэлектронпая рекомбинация........................... 129
1. Захват электрона и допороговые резонансы. Упрощенная
модель (129). 2. Общий случай (133). 3. Формулы для вероят-
ности автоионизации (135). 4. Характер погрешности упро-
щенной модели (136). 5. Численные расчеты и аппроксимацион-
ные формулы (139).
§ 16. Сателлиты резонансных линий многозарядных ионов . . . 140
1. Возбуждение путем диэлектронной рекомбинации (140).
2. Прямое возбуждение внутреннего электрона (142).
§ 17. Населенности возбужденных состояний в плазме.......... 145
1. Введение (145). 2. Населенности уровней водорода в ко-
рональном пределе (146). 3. Плазма произвольной плотно-
сти (149). 4. Квазистационарное приближение для атрма
водорода (151). 5. Водородоподобные ионы (159). 6, Насе-
ленности высоковозбужденных уровней в плотной плазме;
режим стационарного потока (159).
Глава VI. Формулы и таблицы для оценки эффективных сечений 167
§ 18. Результаты численных расчетов сечений................. 167
1. Обзор содержания таблиц (167). 2. Борцовские сечения
возбуждения нейтрального водорода (171). 3. Таблицы
борновских сечений в приближении Бейтса — Дамгаард
(172). 4. Нормированные сечения возбуждения для конкрет-
ных атомов и ионов (173). 5. Переходы между близкими уров-
нями (180). 6. Сечения ионизации (180). 7. Скорость диэлек-
тронной рекомбинации (182).
§ 19. Формулы для (7-факторов............................... 239
1. Суммирование сечений по группам уровнем (239).
2. LS-связь; факторы Qv для переходов без изменения спи-
ОГЛАВЛЕНИЕ
5
на (240). 3. Интеркомбинационные переходы; угловые фак-
торы Q" (244). 4. /7-связь (245). 5. Зл/-символы и генеалоги-
ческие коэффициенты (246).
Глава VII. Уширение спектральных линий............................ 250
§ 20. Модель классического осциллятора......................... 250
1. Постановка задачи (250). 2. Ударное уширение (252).
3. Квазистатическое уширение (254). 4. Соотношение и
границы применимости ударного и квазистатического при-
ближений (255). 5. Эффект Доплера (258). 6. Свертка лорен-
цевского и доплеровского контуров (263).
§ 21. Общая теория ударного уширения......................... 265
1. Метод матрицы плотности в квазиклассическом прибли-
жении (265). 2. Вырождение уровней (270). 3. Квантовоме-
ханическое обобщение (273). 4. Метод квантового кинетиче-
ского уравнения (277). 5. Спектр поглощения (283). 6. Интер-
ференционные эффекты. Сужение спектральных линий (284).
§ 22. Уширение линий водородного спектра в плазме............ 289
1. Предварительные оценки (289). 2. Уширение ионами.
Теория Хольцмарка (289). 3. Учет теплового движения
ионов (294). 4. Уширение электронами (295). 5. Совместное
действие электрснов и ионов (299). 6. Высоковозбужденные
состояния (301).
§ 23. Уширение линий неводородоподобных спектров в плазме 302
1. Предварительные оценки (302). 2. Уширение электро-
нами (303).
§ 24. Уширение нейтральными частицами....................... 306
1. Возмущение атомами постороннего газа (306). 2. Уширение
в однородном газе (собственное давление) (307).
§ 25. Спектроскопический метод исследования упругого рассея-
ния медленных электронов.................................... 310
1. Возмущение высоковозбужденных состояний (310). 2. Ме-
тод Ферми определения сечений упругого рассеяния медлен-
ных электронов (314).
Литература..................................................... 315
ПРЕДИСЛОВИЕ
В последние годы получили широкое развитие новые прило-
жения спектроскопии, связанные с физикой газовых лазеров,
лазерной спектроскопией, лазерными стандартами частоты, фи-
зикой газовых разрядов, астрофизическими исследованиями,
диагностикой плазмы. Потребности этих приложений значитель-
но повысили интерес к таким проблемам теории атома, как при-
ближенные методы вычисления вероятностей и эффективных се-
чений возбуждения атомов и ионов. Одновременно возникли
новые задачи в теории уширения и сдвига спектральных линий —
форма нелинейных резонансов мощности, тонкие интерференци-
онные эффекты и т. п. Существенно повысились требования к
точности описания контуров спектральных линий в плазме.
Настоящая книга посвящена именно этим вопросам. Выбор
материала существенно отличается от традиционного для имею-
щихся в настоящее время книг по теории атомных столкновений.
Ставится задача — ознакомить читателя с наиболее эффектив-
ными и универсальными приближенными методами конкретных
вычислений и оценок сечений элементарных процессов. В книгу
включен большой табличный материал, содержащий результа-
ты численных расчетов для наиболее важных в практических
приложениях случаев. Общие вопросы теории атомных столк-
новений затрагиваются лишь в той мере, которая необходима
для изложения конкретных приближенных методов.
В части книги, посвященной теории уширения, выбор мате-
риала также диктуется наиболее интересными современными
приложениями.
Авторы рассматривают эту книгу как продолжение вышед-
шей в 1977 г. книги И. И. Собельмана «Введение в теорию атом-
ных спектров» [1], в которой изложены систематика атомных
спектров и теория радиационных переходов.
В работе над книгой большую помощь нам оказали И. Л. Бейг-
ман и Л. П. Пресняков: § 10 и часть § 17 написаны совместно
с И. Л. Бейгманом, а § 9, 11—13 совместно с Л. П. Пресняко-
вым. Ряд ценных замечаний по рукописи сделаны В. С. Лиси-
цей. Всем им мы хотим выразить свою искреннюю благодарность.
Л. А. Вайнштейн
И. И. Собелъман
Е. А. Юков
ЭЛЕМЕНТАРНЫЕ ПРОЦЕССЫ ВОЗБУЖДЕНИЯ СПЕКТРОВ
ГЛАВА I
§ 1. Сечения элементарных процессов
В этом параграфе дается перечень элементарных процессов,
ответственных за возбуждение и ионизацию атомов в плазме.
Обычно основную роль в этих процессах играют электроны.
Возбуждение тяжелыми частицами (ионами) существенно толь-
ко для переходов между очень близкими уровнями, а также в
случае нестационарной плазмы. Всюду ниже ион с зарядом Z =
= z — 1, где z — заряд атомного остатка, мы будем обозначать
посредством Xz. В ряде случаев термин атом будет использо-
ваться как для нейтрального атома (z = 1), так и для иона (z 1).
Наибольший интерес представляют следующие процессы.
Возбуждение и тушение возбуждения:
Xz-\- X* + е (1.1)
(звездочка означает возбужденное состояние).
Ионизация и трехчастичная рекомбинация:
Xz + е Х2+1 + е + е. (1-2)
Фотоионизация и излучательная рекомбинация:
Х2 -|- Йо) Х2+1 -f- е. (1-3)
Диэлектронная рекомбинация и автоионизация:
Xz+1 + е X** X,* + Йо). (1.4)
Тормозное излучение и поглощение:
Х2 + е Xz + е 4- Йо). (1.5)
Спонтанное излучение и поглощение кванта:
X* Х2 + Йо). (1.6)
Все процессы можно разбить на безызлучательные — (1-1),
(1.2) и излучательные — (1.3), (1.5), (1.6). Несколько особое место
занимает диэлектронная рекомбинация (1.4). Здесь на первой ста-
дии происходит безызлучательный процесс — захват электрона с
возбуждением иона. Далее возможны два пути: обратный про-
8 ГЛ. I. ЭЛЕМЕНТАРНЫЕ ПРОЦЕССЫ ВОЗБУЖДЕНИЯ СПЕКТРОВ
цесс — безызлучательный распад (автоионизация) или излучение
кванта с переходом в «устойчивое» состояние X*, которое уже не
подвержено автоионизации. Фактически рекомбинация имеет мес-
то лишь в последнем случае.
Число спонтанных радиационных переходов в единицу време-
ни на один атом X* дается вероятностью перехода W [с~Ч и не
зависит от характеристик плазмы. В случае столкновительных
процессов (1,1)—(1.5) число актов возбуждения в единицу време-
ни на один атом Xz пропорционально электронной плотности Ne
и скорости электронов v: W — Л\>1?ст[с-1], где ст[см2] — эффектив-
ное сечение возбуждения.
Пусть ($) — функция распределения электронов по энер-
гиям (скоростям). Тогда число электронов в интервале энергий $,
# + равно dNc = Nffi (&) d8, а вероятность возбуждения,
усредненная по распределению электронов, дается формулой
W — Ne <гст>, где
ОС оо_______
<РСТ> = J VO (£) F ($) = Jj ]/ ? а
ДЕ ДЕ
где АЕ — энергия возбуждения (пороговая энергия). Величину
обычно называют скоростью возбуждения. Аналогичным об-
разом определяются вероятности других процессов, для которых
в начальном и в конечном состояниях имеются две частицы. Так,
вероятность фотоионизации равна
оо
VT== XcoCO-jv dm,
Е^/П
где Na — плотность квантов на частоте <о.
В некоторых процессах в конечном состоянии имеются три
частицы, например, в процессе ионизации — ион и два электрона
(выбитый и рассеянный). Для приложений обычно представляет
интерес не дифференциальное сечение ионизации ст ($; 8', 8"),
соответствующее определенным значениям энергии обоих элек-
тронов 8', 8", а полное сечение, проинтегрированное по всем
возможным значениям энергии выбитого электрона 8":
8-Ez
Ст; (8) = j Ст; (8-, 8', 8") d8\ %'+ 8" = 8- Ez, (1.8)
о
где Ег — энергия связи атомного электрона в начальном состоя-
нии, т. е. энергия ионизации. Дифференциальное сечение иони-
зации Ui(8', 8', 8") имеет размерность см2/эрг, а полное сечение
Ст; (8) — размерность см2.
§ 2. НАСЕЛЕННОСТИ АТОМНЫХ УРОВНЕЙ В ПЛАЗМЕ
9
В ряде случаев в начальном состоянии имеются три частицы:
ион Хг и два электрона (трехчастичная рекомбинация) или элек-
трон и квант (тормозное поглощение). При этом вероятность пере-
хода пропорциональна произведению потоков двух частиц, на-
пример, для рекомбинации
Wr = №г, хг = П щг, Г (#2) (1.9)
При этом ог имеет размерность не см2, а см4 • с. Мы будем тем не
менее называть стг сечением.
Процесс захвата электрона при диэлектронной рекомбинации
(1.4) мы обсудим позднее (§ 15).
§ 2. Населенности атомных уровней в плазме;
соотношение скоростей взаимно обратных процессов
1. Термодинамическое равновесие. Если в некотором объеме
плазмы имеет место термодинамическое равновесие, то населен-
ности в этом объеме определяются следующими тремя функциями
распределения.
Распределение свободных электронов по энергиям (распределе-
ние Максвелла)
f (#) = 2п'^Т~^ ехр (-&/Т), (2.1)
где Т — температура электронов в энергетических единицах
(1 эрг = 7,243 • 10“ К, 1 эВ = И 605 К, 1 см’1 = 1, 439 К).
Распределение атомов по уровням (распределение Больцмана):
= А exp (- ₽w), ft™ = , (2.2)
60 1
где Nh, No и gh, g0 — населенности и статистические веса уровней
А: и 0. Индексом 0 обозначено основное состояние атома.
Распределение по кратностям ионизации (распределение Саха):'
Se-^
b 2nh^) Ne ~
R -
Pz — J» I
z30,/2
4л a^Ne ‘
(2.3)
(2.4)
Здесь и 7V<2+1> — плотность ионов Xz и Хг^; gz и gz+1 —
статистические суммы для Xz и Xz+1: gz = gk (z) exp (— ₽Ло);
Ez — энергия ионизации атома Xz; a0 = h2/me2=0,52Q • 10-8 cm—
боровский радиус; 0 = 77z2Ry, где Ry — единица Ридберга
lRy = те‘№ = 13,606 эВ - 157 894 К.
Распределения (2.1) — (2.3) целиком определяются температу-
рой Т и плотностью Ne. Порядок величины N& и 7У<2+1> существен-
10 гл. I. ЭЛЕМЕНТАРНЫЕ ПРОЦЕССЫ ВОЗБУЖДЕНИЯ СПЕКТРОВ
но зависит от множителя S в распределении Саха. Этот множитель
соответствует статистическому весу свободного электрона. Из
правой части (2.4) видно, что 5^*1. Действительно, его порядок
величины определяется фактором а$Хе ~ 10-8 — 10“12 для Nе ~
~ 1017 — 1013 см-3. В холодной плазме присутствуют в основном
нейтральные атомы Х\. Количество ионов Xz с z > 1 пренебре-
жимо (экспоненциально) мало при низких температурах, растет
с ростом Т, достигает максимума и затем убывает, уступая место
ионам Х2+1. Следовательно, ионы Xz существуют в плазме прак-
тически лишь в интервале температур Тг-.г Т Tz, где Tz тем-
пература, при которой N(z~> — N^t+1K Из (2.3) находим
= in >1. (2.5)
Тг X ё2 / v
При Ne ~ 1013—1017 величина EJTZ ~ 20.
Таким образом, мы приходим к важному выводу: ион Xz су-
ществует в плазме в заметных количествах лишь при T<^EZ. Для
большинства уровней энергия возбуждения Д£\.о ~ Ez, следо-
вательно, в формуле Больцмана рЛо^>1 и населенности возбуж-
денных уровней весьма малы.
В случае многозарядных ионов (практически для z 4) важ-
ное исключение из этого правила составляют уровни п01, где п0'—
главное квантовое число основного состояния п010. Расстояние
между уровнями п010 и nol /ХЕ{ t ~ EJz, поэтому при больших z
2. Соотношение скоростей взаимно обратных процессов. В ус-
ловиях термодинамического равновесия имеет место принцип де-
тального баланса; для любого типа столкновительного перехода
прямой и обратный процессы точно компенсируют друг друга.
Рассмотрим два атомных уровня к и i. Столкновения атома с элек-
тронами вызывают переходы к i (возбуждение) и обратные пе-
реходы i —к (тушение возбуждения). Согласно принципу деталь-
ного баланса
N*Ne <pOl!ly = NtNe <ycilty. (2.6)
Отсюда, используя соотношение (2.2), получаем
ёи <”&ы> = gt <™1кУ ₽ = ЛЕ/Т. (2.7)
В случае процесса ионизации аналогичные соображения дают
= 2 (эЯкГ к - EJT. (2.8)
Здесь величина — скорость прямой ионизации иона Xz,
хг — (Avivi°ryy—скорость трехчастичной рекомбинации. Двой-
ные угловые скобки означают усреднение по скоростям i>j и г2.
§ 2. НАСЕЛЕННОСТИ АТОМНЫХ УРОВНЕЙ В ПЛАЗМЕ
И
Соотношения (2.7), (2.8) не зависят от населенностей и, сле-
довательно, справедливы независимо от наличия термодинамичес-
кого равновесия. Единственное условие — наличие максвеллов-
ского распределения электронов по энергиям при температуре Т.
Запишем соотношение (2.7) в явной форме:
ДЕ
= «< I CT)’'’а“ (Л-х₽ (- ж'-т—)№'
о
или
gk jj № + (Г + ДЕ) ехр (- Ж =
о
= gi^raifc(nexp(-4-)dr-
о
Это соотношение справедливо при любой температуре. Поэтому
между Оки ajfr должно выполняться соотношение
g№ + ДЕНЖ + &Е) = ^Гоа-(^'). (2.9)
Эта формула называется соотношением Клейна — Росселанда.
Отсюда, в частности, [следует, что при <о ДЕ £ко>г — giOne
Формула (2.9) вообще не содержит каких-либо характеристик
плазмы и поэтому является совершенно общим соотношением
между сечениями возбуждения и тушения. Аналогичное соотноше-
ние можно получить между дифференциальным сечением иониза-
ции и сечением рекомбинации.
Для получения связи между скоростями и сечениями фотоио-
зации ff,v и излучательной рекомбинации arv надо предположить,
что атом находится в термодинамическом равновесии с электрона-
ми и с планковским полем излучения. При этом
«.<«*,> = 2 (2-Ю)
причем в левой части усреднение проводится по частотам w поля
излучения, xrV = (varv>. Далее, аналогично тому, как выводи-
лась формула (2.9), находим
&<?2<М<о) = g2+i*4v(#), Й® = Ez + S’ (2.11)
или
12 ГЛ. I. ЭЛЕМЕНТАРНЫЕ ПРОЦЕССЫ ВОЗБУЖДЕНИЯ СПЕКТРОВ
где q и к — волновые числа фотона и электрона, со — частота фо-
тона и $ — энергия выбитого электрона. Формулы (2.11), (2.12)
часто называют формулами Милна.
3. Модель двух состояний. Термодинамическое равновесие
реализуется лишь при достаточно высоких плотностях плазмы.
В условиях умеренной и низкой плотности условия термодинами-
ческого равновесия не выполняются. При этом перестает выпол-
няться и соотношение (2.6) для прямых и обратных процессов.
Населенность каждого уровня определяется балансом всех про-
цессов заселения. Общее решение задачи становится весьма гро-
моздким, так как оно должно включать бесконечную систему
уравнений для всей совокупности уровней и процессов.
В общем случае распределение населенностей может весьма
сильно отличаться от термодинамического. Следует, правда, от-
метить, что распределение свободных электронов по энергиям,
как правило, гораздо ближе к максвелловскому, чем распределе-
ние по уровням — к распределениям Больцмана и Саха. Всюду
в дальнейшем мы будем считать, что распределение электронов
максвелловское (2.1) и, следовательно, выполняются соотноше-
ния (2.7), (2.8). Чтобы дать качественное представление о перехо-
де от термодинамического к другим распределениям населенности,
мы рассмотрим простую двухуровневую модель, в которой помимо
процессов возбуждения (к -> г) и тушения (г —к) имеет место
излучательный переход i —> к. Добавим также возможность из-
лучательных переходов на другие уровни. Уравнение баланса
имеет вид
= NiNe <yol1c> + NtWi,
распада
(2.13)
где Wi = 2j^in — полная вероятность излучательного
п
уровня i. С учетом (2.7) отсюда получаем
дг. 1 W.
_Л = А. 'е-Р ____ R = г
г, 1 + я’
Формула (2.13) дает распределение населенностей в рамках
двухуровневой модели для любой плотности Ne. Фактор R в (2.12)
характеризует отступление от термодинамического распределения.
Нетрудно видеть, что <Р(Ую> сравнительно слабо зависит от Т.
Основная зависимость от температуры дается множителем
ехр (—Р) = ехр(—ЬЕ1Т) как в случае больцмановского распре-
деления, так и при нарушении его
Если в качестве уровня i прин-i гь границу ионизации, то по-
лучим уравнение для ионизационною равновесия. При этом надо
иметь в виду, что возможны три типа рекомбинации: трехчастич-
ная (вероятность которой пропорциональна Л^), радиационная
§ 2. НАСЕЛЕННОСТИ АТОМНЫХ УРОВНЕЙ В ПЛАЗМЕ
13
и диэлектронная (вероятности которых пропорциональны Ne).
В результате получаем
Мх+П _ ?2+1 ? -р, 1
М*> ~ 1 + Rz ’
(2.14)
(2-15)
где хг, Xv и — скорости трехчастичной, излучательной и диэ-
лектронной рекомбинации.
В случае R 1 распределения Ni/N^ и JV<z+1>/Ar<2'> сущест-
венным образом зависят от сечений элементарных процессов.
В этом принципиальное отличие общего случая от термодинамичес-
ких распределений.
4. Корональный предел. Как мы видели, в пределе большой
плотности имеет место термодинамическое равновесие с распреде-
лениями Больцмана и Саха. Рассмотрим теперь противоположный
предельный случай — низкие плотности. Такая ситуация осо-
бенно хорошо осуществляется в плазме солнечной короны, где
плотности Ne ~ 108—109 см-3 намного ниже, чем плотности, с
которыми приходится сталкиваться в лабораторной плазме. По-
этому предельный случай низких плотностей называется корональ-
ным пределом.
Из формул (2.13) при Ne -> 0, снова используя (2.7), получаем
(2-16)
При этом возбуждение всех уровней происходит из основного со-
стояния (А: = 0).
Для интенсивности линий i п имеем ,
W.
л„ = ад.<ии>л<»-^-. (2-17)
Отношение Win/Wi называется фактором ветвления. В отсутст-
вие ветвления, т. е. в случае единственного канала излучения
п — к, Wln = Wijf = интенсивность не зависит от величины
вероятности перехода. Это важная особенность коронального пре-
дела.
Условие применимости коронального предела согласно (2.13)
имеет вид
W
N.<N*, (2.18)
Известно, что Wt со Д£а со z4, со ЬЕГ*!* со z-3. Таким об-
разом, У? со Д-Е^’ со При z ~ I JVt ~ 101в см-’, при z 10
14 ГЛ. I. ЭЛЕМЕНТАРНЫЕ ПРОЦЕССЫ ВОЗБУЖДЕНИЯ СПЕКТРОВ
1023 см*3. Другими словами, в горячей плазме, когда преоб-
ладают ионы с большими z, практически всегда имеет место ко-
рональное распределение.
Аналогично выводу (2.16) нетрудно получить формулу для ио-
низационного равновесия в корональном пределе
/у(г+1} <у<54>
А<г> = *v + xd '
(2-19)
Как видно, степень ионизации не зависит от Ne в отличие от слу-
чая термодинамического распределения. С другой стороны, основ-
ные зависимости от температуры в обоих предельных случаях ана-
логичны: Ar<z+1)/7V<z> оо ехр (—pz).
Г Л А В A II
ОСНОВЫ ТЕОРИИ СТОЛКНОВЕНИЙ
В этой главе мы дадим краткие сведения по общей теории упру-
гих и неупругих столкновений, которые необходимы для дальней-
шего изложения. Основное внимание уделяется столкновениям
электронов с нейтральными атомами и ионами, приводящим к воз-
буждению последних. Начнем мы, однако, с краткого изложения
простейшей задачи о рассеянии в центральном поле.
§ 3. Основы теории рассеяния
1. Упругое рассеяние в центральном поле. Рассеяние частиц
принято характеризовать отношением числа частиц, рассеян-
ных в элементе телесного угла do в 1 с к плотности потока падающих
частиц (т. е. к числу частиц, падающих на 1 см2 в 1 с). Это отноше-
ние do [см2] называется дифференциальным сечением рассеяния.
Пусть частицы падают на рассеивающий центр вдоль оси z со
скоростью v. Свободное движение частиц описывается волновой
функцией ф = к = . Эта функция нормирована
так, что плотность потока частиц v | ф |2 -- 1. Рассеянным частицам
вдали от рассеивающего центра соответствует расходящаяся сфе-
рическая волна -Ц^-е1кг. Поэтому на больших расстояниях вол-
новую функцию можно записать в виде
(3.1)
у V у V г
Число частиц, рассеянных в элементе телесного угла do в 1 с,
равно
г2 do = | / (Ф) |2 .do.
Поскольку плотность потока падающих частиц равна единице,
do = | /(О) | 2do.
(3.2)
Таким образом, задача вычисления do сводится к нахождению
функции /(0j, входящей в асимптотику волновой функции (3.1).
Функция /(О') называется амплитудой рассеяния.
16
ГЛ. II. ОСНОВЫ ТЕОРИИ СТОЛКНОВЕНИЙ
Уравнение Шредингера для частицы в центрально-симметрич-
ном поле имеет решение вида Rt(r)Pt(cosfl), где — полином Ле-
жандра, a R{ — решение радиального уравнения:
[»_£/(,.)] л,= о, (3.3)
гЯ;(г)~ур sin (Аг--у- + Ч,|, г-ю». (3.4)
Фазы т)г в асимптотике 7?( определяются видом потенциала во
всей области 0 г < оо. Для определения этих фаз необходимо
найти решение (3.3) для всех г.
Волновые функции ф можно представить в виде разложения
по функциям RiPt:
Ф = У AtRi (г) Pi (cos fl) —-А- Р; (cos fl) у- sin (ftr — -у- + rjj) =
= 2f eikr У, pi (cos г<>) exp p hi - -r) -
- 27Г(cosexp [- * hi - -£)] • <3-5)
Это разложение называется разложением по парциальным волнам.
Выполним аналогичное разложение плоской волны в (3.1):
= %11 (21 + 1) Pt (cos fl) ц (кг), (3.6)
где it (кг) — сферические функции Бесселя:
Л (*) =)/"-£-J<+«/. (*) ~ sin (х — -у). (3.7)
Х-гоо
Подставляя (3.5) — (3.7) в (3.1) и сравнивая с (3.5), находим
Ч’~Ш'/’-2ЙГ^,г'(2г+1)Л(соз«)Х
X [—exp (- ikr + + е“"1 exp (ikr — , (3.8)
/ W - и* У, (21 + 1) [е»' - 1 ] Р, (cos «). (3.9)
I
§ 3. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ
17
Подставим (3.9) в (3.2) и выполним интегрирование по углам. По-
скольку
Р{ (cos ft) Ру (cos ft) sin ft dft = 2t 6ц>, (3.10)
для полного сечения упругого рассеяния получим
а = ^-У(2г + 1)зш’л,. (3.11)
I
Сравнивая (3.11) с (3.9), можно выразить полное сечение упру-
гого рассеяния через амплитуду рассеяния вперед /(0):
а=^-1ш/(0)--^-[/(0)-/‘(0)]. (3.12)
Это соотношение называется оптической теоремой. Оно имеет об-
щий характер и справедливо также в общем случае нецентрального
поля.
2. Волновые функции ф£ и фк. Введем волновую функцию ф£»
описывающую падающую плоскую волну eikr и рассеянную сфери-
ческую волну. В отличие от (3.1) нормируем фк условием
ф+ ~ eikr + 2Ж е<* г. (3.13)
При произвольном направлении волнового вектора к cos ft =
= (kr}jkr. Используя (3.8), находим
^ = -^Ei,(2Z + l)e4Pl(cos1&);?l(r)~2itEii(2i + 4)x
X Pi (cos ft) {— exp — i (кг-y-j J 4- exP (^r У~) ] j •
(3.14)
Заменяя в ф£ ехр(йр) наехр(—irji)» получим функцию ф*:
Ф; = 7=- £ (2* + D6-4 Р‘ R< ~
~ У*|С008 {“ ехР [— i (кг “ ~г) +
+ ехр —-у-)]} . (3.15)
Нетрудно видеть, что
% = ?ikr + = (ф+л)*. (3.16)
»МТп Йчзрги I
(Г?.. 8:. Ь. I
18
ГЛ. II. ОСНОВЫ ТЕОРИИ СТОЛКНОВЕНИЙ
Функции удовлетворяют интегральному уравнению
= gifcr J G±Jc (г, г') U (г') ф± (г') dr, (3.17)
где G±k (г, г') — функция Грина уравнения свободного движения:
(V2 -|- A2) G+)s (г, г') = 6 (г — г'),
G±t (г, >•') ~ II. . (3.18)
/ 4л | г — г' | '
При г г'
Gk(r, r')^~^exp(ikr— ik'r'), к'^к~. (3.19)
Поскольку -О' — кг -- кк', находим
/ (А) = - -2^Г j) ехР U (г) Фк Иdr- (3-20)
Уравнения (3.17), (3.20) удобны для решения задачи методом по-
следовательных приближений. В первом приближении в правую
часть вместо ф* подставляют eikr. В результате получаем первое
борновское приближение:
=: “ "2^ U СХР ~ ,С') Г1 dr‘ <3-21)
3. Квазиклассическое приближение. Как уже отмечалось
выше, нахождение точных фаз рассеяния в общем случае требует
численного решения радиального уравнения (3.3). Эта задача су-
щественно упрощается в квазиклассическом приближении. В этом
приближении функция R; для частицы с моментом I в поле U(f)
имеет вид
Л|~7Т81,1(т$Рг * + т)’ (3-22)
р? - 2т [4? - U (г)] -»’(! + '/•)*г'1- (3.23)
Для свободного движения
Г
~-L-sin [4 Jj + -J] . (3.24)
Го
Точки поворота гх, г0 определяются приравниванием нулю подко-
ренных выражений.
Сравнивая (3.22) — (3.24), нетрудно видеть, что наличие рас-
сеивающего потенциала U(r) приводит к появлению в аргументе
§ 3. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ
1»
синуса дополнительной фазы
60
Т]г = J к2тпЛ-1 2 [^ - £7 (Г)] - (Z + r*2 dr -
п
ос
- J + dr, (3.25)
Го
которая может быть отождествлена с фазой рассеяния.
Можно показать, что квазиклассическое приближение дает
хорошие результаты при вычислении сечения упругого рассеяния
при условии, что в это сечение дает существенный вклад большое
число парциальных волн фг. Это означает, что в сумме по I основ-
ную роль играют члены с большими значениями I.
Нетрудно видеть, что при больших значениях I нижние пре-
делы интегрирования в (3.25) также велики:
hl _ hl
Г1 /2т - U) ’ Г° ~ /2^ ’
Если U(r) убывает при увеличении г настолько быстро, что для
всей области интегрирования выполняется условие
U(r) < (3.26)
то » г0 ж Ик, где к — mvlh, и
оо
л _ V dr. (3.27)
В квазиклассическом приближении момент количества движения
частицы равен тир, где р — прицельное расстояние, поэтому
кУ 1(1 + 1) т HI ж тир, т. е.
I = кр.
(3.28)
Если принять, что движение частицы прямолинейно и равномерно,
то из (3.27), (3.28) находим
1 4 (•
- 2-п (р), ц(р) = — U(r)dt, (3.29)
Г2 = Р2 + v2t2.
В случае упругого рассеяния на атоме в состоянии а вместо U(r)
надо подставить (г). Но Uaa (г) есть не что иное, как поправ-
ка первого порядка к энергии Д£а за счет взаимодействия с рас-
сеиваемой частицей (в квазистационарном приближении).
20
ГЛ. II. ОСНОВЫ ТЕОРИИ СТОЛКНОВЕНИЙ
Следовательно,
ОО
л(р) = 4" jj bEa(t)dt.
—со
(3.29а)
Другими словами, в квазиклассическом приближении величина
—2т|; равна сдвигу фазы (по столкновению) за счет сдвига атомного
уровня. Отметим, что для поля U(r) = hCn/rn формула (3.29)
дает тот же результат, что и более точная формула (3.27):
п(р) = -2ч,--^=-, “» = г(4)г(^)г-'(^-). (3.30)
Заменим в формуле (3.11) для сечения упругого рассеяния
сумму по I на интеграл по р, используя соотношение
2(2Z + l)^2ZAZ»2fc2pdp.
д/
Тогда (3.11) приобретает вид
□О
ст = 4л [1 — cos т| (р)] р dp.
о
(3.31)
Как уже отмечалось, квазиклассическое приближение справед-
ливо в тех случаях, когда существенный вклад в сечение дают
парциальные волны с l^> 1. Это означает, что существенный вклад
в сечение (3.31) вносят прицельные расстояния
Р>^ = *- (3-32)
где X — длина волны де Бройля.
4. Неупругое рассеяние. В общем случае имеет место как
упругое рассеяние, так и неупругое — поглощение частиц или
изменение их энергии за счет передачи энергии рассеивающей
системе. Волновая функция помимо падающей плоской волны
должна содержать целый ряд расходящихся волн, соответствую-
щих различным типам или, как говорят, каналам рассеяния.
Если раньше в случае чисто упругого рассеяния интенсивности
сходящихся и расходящихся парциальных волн (Z-волн) были
одинаковы (см. (3.8)), то теперь интенсивность расходящейся
волны, описывающей упругое рассеяние, должна быть меньше,
чем сходящейся. Учитывая это волновую функцию ф, описываю-
щую упругое рассеяние, в общем случае можно записать в виде
*~ L 1‘ (2‘ + *>Р‘<cos<►) {- exp [- < (fa—£)] +
+ exp [- 2рг + 2Ц] exp [f (кг - -£)]}, (З'ЗЗ)
§ 3. ОСНОВЫ ТЕОРИИ РАССЕЯНИЯ
21
где Р/ > 0. Для амплитуды рассеяния получаем
V W = S У. (2i + 1ир (- 2₽1 + 2!Ч|) - 1) А (СОЗ »)• (3.34)
!
Это выражение отличается от (3.9) только тем, что вместо действи-
тельной фазы тр входит комплексная г|/ + ф,. Из (3.2) следует
Оупр = > У (2/ + «)| 1 - ехр(- 2Р, + 2Ц)|!. (3.35)
I
С помощью (3.33) можно найти также эффективное сечение
неупругих столкновений, которое дается разностью потоков в
сходящихся и расходящихся волнах:
ая.уда = >У](21 + 1)(1-е','9. (3.36)
I
Полное сечение равно
(Т = (ТуПр + «Тнеупр = У, (2Z + 1) (1 — соб2т]<). (3.37)
i
При р/ = 0 о = сгупр; при р; = оо (ехр (— 2р0 = 0) Oj,ynp =
= ff/.неупр = ^-(2Z + 1). Нетрудно заметить, что л (21 + 1)/к2 есть
число частиц с моментом I, падающих на рассеивающий центр за
1 с, если пучок нормирован на единичную плотность потока.
С помощью формул (3.35), (3.36), (3.37) легко установить пре-
делы изменения эффективных сечений:
0 (2(4-1), (3.38)
0 <»,<•£-(21-И).
Отметим, что неупругому рассеянию всегда сопутствует упругое.
Если ехр (— 2р;) =# 1, то при любом значении т)г, включая т|г —
~ 0,. Оупр =7^ 0-
5. Выражение эффективных сечений через элементы ^-ма-
трицы. Эффективные сечения упругого и неупругого рассеяния
кожно выразить через элементы матрицы рассеяния, которую
также называют просто 5-матрицей. Если рассеивающая система
вначале находилась в состоянии а, то, положив
ехр (—4- Зйр) = Slaa, (3.39)
22
ГЛ. II. ОСНОВЫ ТЕОРИИ СТОЛКНОВЕНИЙ
получим
l)|i-SL|!, (3.40)
I
<JHeynP = ^-^(2Z + 1)[1-|SLH’ (3.41)
I
° = йупр + йнеупр = ^2“ (2^4-1) Re [1 — 5аа]. (3.42)
Неупругое рассеяние связано с переходами рассеивающей системы
из начального состояния а во всевозможные энергетически дости-
жимые состояния b (т. е. в состояния, энергия которых не пре-
вышает суммы начальной энергии атома Еа и кинетической энер-
гии налетающей частицы #). Каждому такому каналу рассеяния
можно поставить в соответствие эффективное сечение перехода
ааЬ. Как будет показано в § 4, сечения ваЬ выражаются через не-
диагональные элементы 5-матрицы:
а"‘=^-Ц(2(+1)|л’»ь|’- (343)
I
Условие сохранения числа частиц, приводящее к неравенствам
(3.38), эквивалентно унитарности 5-матрицы:
Sl*Sib|1 2=l, 3 |5ib|a = 1-|5L|2. (3.44)
b b-^a
В соответствии с (3.44) модуль каждого из матричных элементов
5дЬ не может превышать единицу. Отсюда сразу следуют нера-
венства (3.38), причем
^<<4ynP<^(2J + l). (3.45)
§ 4. Общие уравнения теории столкновений
электронов с атомами
1. Введение. Рассмотрим общую задачу о рассеянии электро-
на на атоме или ионе. В общем случае мы имеем дело со сложной
системой «^электронный атом + внешний электрон». Взаимо-
действие электрона с атомом существенно зависит от состояния
атома. При этом необходимо учитывать также обменные эффек-
ты, т. е. описывать систему полностью антисимметричной функ-
цией. Результатом столкновения может быть возбуждение атома
в различные состояния — различные каналы рассеяния, между кото-
рыми может иметь место взаимодействие. Поэтому общие уравнения,
описывающие столкновение, имеют вид многоконфигурационных
уравнений Хартри — Фока.
§ 4. ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ СТОЛКНОВЕНИЙ 23
Сделаем ряд упрощающих предположений. Будем рассматри-
вать в основном неупругие столкновения, сопровождающиеся
возбуждением атома. (Мы не будем останавливаться на специфи-
ческих особенностях процесса ионизации (см., например, 12, 3]).)
Далее, ограничимся такими переходами, в которых изменяются
квантовые числа не более чем одного электрона. Будем предпо-
лагать, что этот электрон находится во внешней оболочке атома,
и назовем его оптическим электроном. Атом без оптического элек-
трона будем называть исходным ионом. Будем полагать, что атом
описывается волновыми функциями, построенными из одноэлек-
тронных в соответствии с определенной схемой сложения моментов.
Говоря об атоме, мы подразумеваем, что сказанное относится
и к положительным ионам. Обозначим — заряд ядра и
z = £ - N + 1 (4.1)
— спектроскопический символ иона. На больших расстояниях
на оптический электрон действует поле —z/r, на внешний элек-
трон — поле —(z — 1)/г.
Всюду ниже используется атомная система единиц с едини-
цей Ry = 13,6 эВ для энергии. Отметим, что в этих единицах
v = к — р = У %.
S
2. Общие формулы для сечения. Обозначим через Та# 0
полностью антисимметричную волновую функцию системы. Верх-
ние индексы описывают состояние системы до столкновения:
атом в состоянии а0М0 и налетающий электрон с волновым век-
тором fc0 и проекцией спина ms0. Разложим эту функцию по соб-
ственным функциям атома 'Гам:
аМтпа
А = S ( >-2- (4.2)
i /А 4-1 '
где А — оператор антисимметризации; Рц. — оператор переста-
новки £ — совокупность пространственных и спиновых
переменных.
В соответствии с общим определением дифференциальное се-
чение для перехода аоМотпо — аМта равно потоку электронов
с проекцией спина т* в телесном угле do при условии, что атом
оказывается в состоянии аМ, а поток падающих электронов ра-
вен 1. При этом скорость рассеянного электрона и — к удовлет-
воряет соотношению
к} 4- Е^ - к* + Еа.
(4.3)
24
ГЛ. II. ОСНОВЫ ТЕОРИИ СТОЛКНОВЕНИЙ
Учитывая антисимметрию функции % находим
da = v (N + 1) J | ЛТвМфаМтв |2 d £) г2 do, (4.4)
Г—>Оо
где d {%) означает интегрирование по всем переменным кроме
г, a do — по телесному углу. Асимптотика подынтегрального
выражения в (4.4) существенно зависит от того, относится ли со-
стояние аМ к дискретному или непрерывному спектру. Мы огра-
ничимся простейшим случаем дискретного спектра (о случае
непрерывного спектра см. [2]). При этом в (4.2) остается при
г оо лишь член с Р^, так как экспоненциально затухает.
Используя для асимптотическое выражение, аналогичное
(3.1),
а0М>’) + <Р) ] Хп16, (4.5)
где Хт* — спиновая функция, получаем
do (a0M0ms0, аМт“) = \faMms (й, cp)|2do. (4.6)
Проведем теперь разделение радиальных и угловых перемен-
ных. Для этого необходимо разложить волновую функцию внеш-
него электрона по парциальным волнам. Для упрощения формул
за ось z примем направление вектора к0. Формулу (4.2) перепи-
шем в виде
Ч'о,мл^ - А £|₽х.чГ.м(|1...6„)±/'’?(г)Гх»(«, <Р)Х„,, (4.7)
у = аМктт3, у0 = a0MoXo0/nJ. (4.8)
Здесь X, т — момент внешнего электрона и его проекция на ось
z (мы сохраняем букву I для оптического (атомного) электрона);
Уьп, (^, ф) — сферическая функция. Радиальные функции F^(r)
получаются в результате решения задачи о рассеянии. Они удов-
летворяют граничным условиям (для рассеяния на нейтральном
атоме)
₽?• (0) == О, F?~ *-{«„.sin tar - 4-) +
Г-ЮО У к I \ '
+ T’wo ехр [i (кг - . (4.9)
Сравнивая (4.7), (4.9) с (4.2), (4.5), находим
Г«»са.+1) , (410)
/»«„(*.<₽)= £ ^Г4я(2К, + 1) (4Л1)
Хо, X. т
§ 4. ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ СТОЛКНОВЕНИЙ
25
Таким образом, зная радиальные функции (г), а следователь-
но и матрицу Туу,, можно определить faMm» ($, ф) и затем сечение
рассеяния согласно формуле (4.6).
Представление у (4.8) пригодно лишь для расчетов в 1-м по-
рядке теории возмущений. Для получения общих уравнений ти-
па уравнений Хартри — Фока необходимо перейти к представле-
нию полных моментов. В схеме Л5-связи состояние системы ха-
рактеризуется набором квантовых чисел Г:
Г = qL^I^LtSt, и — clLS , (4.12)
где O.LS — набор квантовых чисел атома, Lt, St —полные мо-
менты системы «атом + электрон». Дальнейшие формулы не за-
висят от конкретного вида представления Г.
Обозначим матрицу преобразования у -> Г через (у | Г). То-
гда
= А V Рл,(V1 Г)Фг 7-Рг‘(г), (4ЛЗ)
Фг= 3(Г|у)ТвМГКмХж..
v/r
Используя унитарность преобразования, получаем
Fre~y^[Srrosin (ког — 4- Грговхр [г (*г —. (4.14)
= 2j (То I Го) (Г I у) Ггг,- (4.15)
Го/Vo, Г/т
Здесь и далее Г/у означает квантовые числа из Г, не входящие
в у. В схеме LS-связи Г/у = LtSt- Из (4.15), (4.6) и (4.11) полу-
чаем дифференциальное сечение в виде
d<j{a0MomaQ, аМшг) =
= Т | У, V <2Х" + (V. I Го) (Г I т) Ггг.п» («, Ф) f *>.
Го/cZr/a.m (4.16)
Обычно приходится иметь дело со столкновениями неполяри-
зованных электронов с атомами, ориентированными произволь-
ным образом. Ориентация возбужденных атомов (т. е. значение
М) определяет поляризацию испущенного после возбуждения
света. Чтобы получить соответствующее дифференциальное се-
чение, надо усреднить (4.16) по Мот‘п и просуммировать по тв.
Кроме того, удобно разложить содержащиееся в (4.16) произве-
дение по сферическим функциям от тех же углов.
Нетрудно показать, что при этом р, = 0, т. е. сечение не зави-
сит от ср, как и следовало ожидать. Окончательный результат
26
ГЛ. II. ОСНОВЫ ТЕОРИИ СТОЛКНОВЕНИЙ
представим в виде
do(a0’> аМ) — V* ВКРК (cos Ф) do. (4.17)
2&»*о V1
В случае схемы /5-связи
В, - 2 to til У.П (XoXiXV) IP(xLrL'r)X
/% X' x\ / X X' x\ //» LT \
X W 0 OH— m m О/ \MB 0 — mJ \M0 0 — Mo/ X
X V Lt VrrJr'r' (4.18)
л \м m —mJ \m m —mJ ° о v '
(суммирование no LTLTXJJX'mM0)-, П (/Ja-.-) — (2ji + IJ’/’X
x(2ja 4- !)*/«...
Перейдем к рассмотрению полного сечения. Формула (4.17)
после интегрирования по углам дает
о(а0, аМ) = ^Во.
(4.19)
Наконец, после суммирования по конечным ориентациям, т. е.
по М, получаем
°аоа —: ° (й<Ло> Я^),
Хо> X
а(а0Х0;а) = ла’4 У, f-Krr.P. (4.20)
г./Лг/.к S’
где g0 — статистический вес атома в состоянии а0, gr — стати-
стический вес состояния Г системы «атом + электрон».
Формула (4.20) дает простую связь между эффективным сече-
нием о и матрицей Т для произвольной схемы связи. Для удоб-
ства дальнейшего обсуждения введены парциальные сечения.
В случае /5-связи
, . . .. 2_L V (2Lr+l)(25r+l) |2
о (Я(Ло> а^) - ла0 Д2 2_j (2L0 + 1) (250 +1) । Ггг’ । ’
(l (%LS, Г := I^L^Sч**
Для переходов между /-уровнями в формуле (4.20) надо восполь-
зоваться Jj (или /Х)-связью: а = O.LSJ, Г — аХг/2 Если
в атоме соблюдается чистая Z-5-связь и магнитное взаимодействие
внешнего электрона с атомом не учитывается, то зависимость
от J чисто кинематическая и можно вернуться в Угг» к /5-связи.
§ 4. ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ СТОЛКНОВЕНИЙ
27
В результата получаем
о (я0Х0; яХ) = ла* • —V П2 (JT iojJ)] X
io
Sр Vj S,
Xo
i
V»
X
у
S у
LT
2
, (4.22)
о
о
Ъо
X У n2(Zr5T)
L^i Sy
a — aLSJ, Г = аЬ8\г1гЬт8т-
J-irp
т
S
L
Для промежуточной схемы связи в атоме явное выражение типа
(4.22) возможно лишь в 1-м порядке теории возмущений. Исполь-
зуя соотношения между Зн/-символами, можно формулу (4.22)
переписать в виде
о (ядХд, лХ) —• ЛЯд •
4 У. П2(ХХ1Х2У)
^2 Jо
So S
X
•Ь ^0 7 J Х1
л0 X f \sr 1/2 1/2 f x
Ж’ U4' (4.22a)
Это выражение более удобно для приложений в теории возмущений.
Полученные формулы сводят задачу вычисления эффективных
сечений к вычислению матрицы Тгго- Эта матрица определяется
согласно (4.14) асимптотикой радиальных функций Fp (г). Сле-
дующие разделы настоящей главы будут посвящены методам оп-
ределения этих функций.
3. 5-матрица и сила столкновения. Обычно в теории рассея-
ния используется 5-матрица, связанная с матрицей Т в (4.14)
и (4.20) простым соотношением
Srr, = бгг(“2гГгг0> о(я0Х0; яХ) = ляо • — У —-^-|<$гг» — ^rrj2-
(4.23)
Асимптотика радиальных функций представляется при этом в
виде
Ff°(r) — Аг^бтехр — i (к<г---—
— 5ГГв ехр р (kr--. (4.24)
Матрица 5 симметрична и унитарна
2lSrrJ!= 1.
г
(4-25)
28 ГЛ. II. ОСНОВЫ ТЕОРИИ СТОЛКНОВЕНИЙ
При использовании приближенных методов расчета определение
сечения через унитарную матрицу S или линейно связанную с
ней матрицу Т часто оказывается неудобным, так как приближен-
ное выражение для этой матрицы может быть уже неунитарным.
Это приводит к нарушению условия сохранения числа частиц,
причем даже отдельные слагаемые | jSttJ2 могут оказаться
сколь угодно большими. Чтобы избежать этого, часто использу-
ют Л-матрицу, связанную с матрицей S нелинейным соотношением
.S - , (4.26)
где I — единичная матрица: Угг» = бгг0-
Матрица К симметрична, эрмитова, но неунитарна. Соответ-
ствующие радиальные функции действительны и имеют асим-
птотику
?г° ~ k~'!t [бГГо Sin (/ссг - Лр) + Хгг. cos (fr - •
Их можно представить в виде линейной комбинации функций с
асимптотикой (4.14).
Независимо от вида приближенного выражения для К матри-
ца 5, вычисленная по формуле (4.26), унитарна, и приближенные
значения сечений удовлетворяют условию сохранения числа
частиц.
Иногда вместо сечения перехода оа#а используют безразмер-
ную величину — силу столкновения («collision strength»):
iU = -^-aeeS. (4.27)
Величина й((оа симметрична по отношению к прямым и обратным
процессам:
(*»; А) = tu (к-, к,), (4.28)
и аддитивна по структуре атомных уровней. При больших энер-
гиях о ~ ё"1 и, следовательно, й = const или очень медленно
(логарифмически) возрастает.
Выше (см. (3.38)) уже отмечалось, что полные парциальные
сечения неупругих процессов удовлетворяют определенным не-
равенствам. Поскольку сечение определенного перехода не может
превышать полное неупругое сечение, те же неравенства можно
записать в виде
2 Й (а0Х0; лк) < 2k0 + 1. (4.29)
%
4. Радиальные уравнения. Функции Ff* (г) являются ре-
шениями радиальных уравнений, которые можно вывести с
помощью вариационного принципа аналогично выводу уравнений
Хартри — Фока для состояний дискретного спектра. Хотя анало-
§ 4. ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ СТОЛКНОВЕНИЙ
29
гия с уравнениями Хартри — Фока довольно тесная, имеют
место и некоторые существенные отличия, на которых мы кратко
остановимся.
Прежде всего в задачах теории столкновений полная функция
системы Т принципиально является многоконфигурационной, так
как она должна содержать различные каналы рассеяния. Состоя-
ние внешнего электрона описывается системой функций Fr° (с),
удовлетворяющих соответственно системе (вообще говоря, беско-
нечной) иптегродифференциальпых уравнений.
С другой стороны, самосогласованное (т. е. усредненное по
движению) поле электрона в состоянии непрерывного спектра
равно нулю. Следовательно, атомные волновые функции можно
определить независимо от внешнего электрона, т. е. считать их
заданными заранее. На функции внешнего электрона обычно
не накладывается условий ортогональности с атомными функция-
ми. Уравнения выводятся с учетом возможной неортогональности.
Это, естественно, приводит к расширению класса допустимых
функций, но вид уравнений усложняется. Если сделать некото-
рые дополнительные, не очень сильные, допущения, то уравнения
существенно упрощаются и становятся аналогичными обычным
уравнениям Хартри — Фока.
Наконец, заметим, что энергия Е системы является заранее
заданной, в то время как в случае дискретного спектра она-'опре-
деляется как собственное значение задачи.
Мы не будем останавливаться на довольно громоздком выво-
де уравнений [4] и приведем окончательные формулы. Систему
интегродифференциальных уравнений можно записать в виде
[£г + &] Fp = 3' Urr- (г) Fr. (4.30)
rvr
Оператор Хр — обычный хартри-фоковский оператор:
2г = -^------t/rtr), Ur - t/г + t7rr, (4.31)
где Up описывает взаимодействие внешнего электрона с атомным
остатком, a Upp> — взаимодействие с оптическим электроном.
Потенциалы Upp’ (в частности, и при Г' = Г) являются интеграль-
ными операторами и выражаются через радиальные интегралы:
Uгг' (г) Ег'«= drr'Uii'Fг» — firryiK’Pi', (4.32)
к х"
Уп- (г) = 2 ( Р, (Г,) Рг (г,)
?, (4.33)
г гх“
Уы (г) = 2 \ - (1 — Сгг-бу/'оГ>) Pt (rj) Гг'(п) dri,
о r>
30
ГЛ. II. ОСНОВЫ ТЕОРИИ СТОЛКНОВЕНИЙ
Р; (г) = г Rt (г) — радиальные функции оптического nZ-элек-
трона атома в состоянии а,
Сгг- - 4- (- «. + И = 4- (-s»- + ft2)- (4.34)
Здесь еа и еа- — энергетические параметры оптического электрона
в состояниях а и а', вообще говоря, отличные от энергии уровня.
Однако, как правило, этой разницей можно пренебречь и считать,
что два выражения (4.34) совпадают.
Параметры аир зависят только от квантовых чисел угло-
вых моментов. В приближении генеалогической схемы а =
— ypLpSpnll/2.LiS:
«гг = &L L‘ 6spsp6ss'(— 1)Lt+L+L+Lpn (ZZ7A7J7) x
/I n' l'\ (k x' a'\ j x' L jL'Y ( и' L ЛД
X\0 0 oHo О 0П£г V I' I f’
₽ (4.35)
ftp, = 6 ' d > (- I)i+K+1-S-S'n (ZZ'XX'LL'SS') x
®p®p
iL L X
/I v." /X x" L I'
x W 0 о Ho 0 ojH S' i/2fj ,₽ „ ’
k P ’ ( k' I V. )
Если в исходном состоянии оптический электрон nl находится
в оболочке nlm, то вместо а и р из (4.35) надо писать
у, т агг'» У, ^LpSp V w Ргт'7 (4.36)
^р* ®р ‘^р* ®р
где GbpSp — генеалогические коэффициенты. Для переходов в
пределах одной конфигурации nlm а, р выражаются через коэф-
фициенты (||Е7Х’||) и (|| Ух"г||) [1].
Потенциал Urr выражается через радиальные интегралы ана-
логично (4.32).
В приведенных выше формулах для простоты не указываются
пределы суммирования по х. Эти пределы определяются условия-
ми треугольника и четности:
X = Xjnin, Xmin -}- 2, . . Xmax,
«inin = max {I I — V I, I X — X' [}, xmax = min { (Z + Z'), (k + X')},
(4.37)
Xmtn = max {| Z — X' |, | X — Z' |), x^ax = min {(Z + X'), (X + /')}•
Радиальные уравнения (4.30) надо дополнить граничными
условиями. При г — 0 все Fp (0) = 0. Что касается условий на
§ 4. ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ СТОЛКНОВЕНИЙ
31
бесконечности, то они зависят от знака /с2:
А2>0, F?— Аг’/« Гдгго sin —
Г—* ос L
+ Ггг.ехр i(kr~
(4.38)
F < 0, F? —► 0 при г -> оо.
(4.39)
В случае столкновений электрона с ионом Xz (z > 1) следует
заменить
(4.40)
где Г (х) — гамма-функция.
Величина к2 определяется условием сохранения энергии (4.3).
Для энергетически недостижимых уровней (к2 •< 0) на бес-
конечности отсутствует рассеянная волна. Включение этих уров-
ней в общую систему уравнений соответствует на языке теории
возмущений учету поляризации атома.
5. Интегральные радиальные уравнения. Для исследования
системы уравнений теории столкновений, а в некоторых случаях
и для ее численного решения можно перейти от уравнений (4.30)
к системе интегральных уравнений. Этот переход осуществляется
путем формального решения уравнений с помощью функции Гри-
на Gr (г — г'), удовлетворяющей уравнению
[2г + /са]£г (г, г') = 6 (г - г'). (4.41)
Функцию Грина можно выразить через два линейно независимых
решения F и Т соответствующего однородного уравнения
<?г(г, и == -Fr(r<)Fr(r>), (4.42)
[2г + W = [2Г + k2]Fr = 0, (4.43)
Fr (0) = 0, 7*г (г —0) = аг"1,
Fr ~ к~'/}е^ sin (Ат---~ + ц) , Fp — к~'к exp р (кг — ,
к2 > 0, (4.44)
Fp-----^-q~'/’eqr, Fp — q~'l*e-4r,k2 <0, q = ik. (4.45)
С помощью Gr (г, г') система интегральных уравнений для
Fp запишется в виде (см. [5]) *)
оо
Fr(r) = дГг/г.(г) 4- |бг(г,г') 2 ?7гг (И (г) dr'. (4.46)
о rvr
4 Следует заметить, что в [5] приведена функция Грина для однородных
граничных условий. Нетрудно показать, что те же формулы годятся и для
неоднородных граничных условий типа (4.38) при Г Ф Га. При Г = Го два
32
ГЛ. П. ОСНОВЫ ТЕОРИИ СТОЛКНОВЕНИЙ
Подставляя сюда (4.42) и (4.44) и сравнивая результат с (4.38),
получаем
оо
^гг0 — бгг^111 sin Л—У Рг 2 ^гг'^г'^’ (4.47)
о г>ьг
Мы исходили из решений однородных уравнений (4.43) с опе-
ратором Хг, определенным в (4.31). Этот оператор описывает
движение частицы в поле Up. Поэтому решение Р обычно назы-
вают искаженной волной. Возможны и другие представления.
В частности, можно опустить в Хг потенциал С7р, т. е. взять
за основу оператор свободного движения. Такое представление
естественно назвать борновским. При этом в (4.46) и (4.47) надо
снять ограничение Г' #= Г в У| и положить ц — 0. Приведем
г' _
явные выражения для функций Рг и Рр в борновском представ-
лении, которые понадобятся ниже:
рг = kl/>rjK(kr), Р= ik'l‘rh^ (кг), к2 > 0,
Рг = q'/triK (qr), F = ~ q'lrkK (qr), к2 < 0.
Jb
Здесь д и — сферические функции Бесселя и Ханкеля, г\
и к^ —те же функции для мнимого аргумента г).
6. Введение поляризационного потенциала. В предыдущих
пунктах было показано, что задача вычисления эффективных
сечений сводится к решению бесконечной системы интегродиф-
ференциальных или интегральных уравнений. Решая эту систему
методом последовательных приближений, можно получить другую
формулировку задачи, одним из преимуществ которой является
возможность наглядного физического истолкования.
Будем исходить из системы интегральных уравнений (4.46)
и примем, как обычно, за нулевое приближение свободный член
= бгг, Av (4.49)
решения однородного уравнения, из которых одно удовлетворяет граничным
условиям (4.38) при г = 0, а другое — при г—»оо, оказываются линейно
зависимыми. Поэтому второе решение при Г — Го надо выбирать так, чтобы
оно при г —► со удовлетворяло какому-то другому, например условию (4.38)
без стоячей волны (как это имеет место при Г =/= Го). Тогда в выражении
для Fr появляется дополнительный член — первое слагаемое правой части
(4.46). °
т) Сферические функции i^, к^ связаны с обычными функциями
Бесселя и Ханкеля 1^, соотношением
Г л
Ч = У ~2х Zk+l/2
§ 4. ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ СТОЛКНОВЕНИЙ 33
Тогда в первом приближении
= Frl) = f GrMUrrAr’)Fr^')drf. (4.50)
Г^Го J0
Переходя, далее, ко все более высоким приближениям, можно
получить
со
Fr. — Fr„ + J Gr„ (г, г') Vгог„ (г') Fг0 (г')Яг',
° (4.51)
Fг = f Gr (г, Н [?7гг»(г) + 7гг.(г')1/’гв(Н^г'
Г^Г« £
и для матрицы Т
Оо
ТГоГо = elT|° sin Т]о — РгУ VoVoF^dr,
(4-52)
Тгго ~ — Г ^г(^гг<>+ 7гг.)
Г>Г. Jo
Величина 7гг. называется поляризационным потенциалом.
Она является интегральным оператором типа
7 (г) ф (г) = J 7 (г, г') ф (г') dr'. (4.53)
о
Поляризационный потенциал определяется рядом
7 гг. = 21 7гг., 7^г. — 21 ^гГ1...гп_хГо, (4.54)
П=2 Гь.-Гп-! П 1
^ГГь-.Г^Г. (г, г') =
= у... $dri...drn-2 t/'гг. (r)Gr,(r, Г1)г7Г1г.(Г1)...
• • ’ Gl’n-i (гп-2, г') иГ^Го (г').
Последние формулы годятся как для Г #= Го, так и для Г = Го.
В сумме по 1\ . . .Гп-i необходимо опускать все члены, в которых
встречается хотя бы один диагональный потенциал #гйгк-
Таким образом, решение системы уравнений теории столкно-
вений выражено в замкнутой форме (4.51). Поправка к матрице
Тгг. дается матричным элементом от 7гг.- Из второй формулы
(4.52) видно, что 7 гг. представляет^ собой поправку к хартри-
фоковскому потенциалу С7гг0- Именно с этим^связано название:
поляризационный потенциал. Разумеется,' строго говоря, выше
получено лишь формальное решение, так как трудности решения
бесконечной системы уравнений перенесены на вычисление беско-
нечного ряда (4.54) сложной структуры. Кроме того, остается
2 Л- А. Вайнштейн и др.
34
ГЛ. II. ОСНОВЫ ТЕОРИИ СТОЛКНОВЕНИЙ
открытым вопрос о сходимости ряда. Однако если ряд сходится,
то использование поляризационного потенциала для получе-
ния приближенного решения обладает рядом очевидных пре-
имуществ. В частности, сформулировать приближенное выражение
для потенциала иногда значительно проще, чем для волновой
функции.
§ 5. Приближение 1-го порядка
1. Общие формулы. В предыдущем параграфе были получены
формальное решение интегрального уравнения и выражение
(4.52) для Т-матрицы. Здесь будет рассмотрено приближение 1-го
порядка, для которого можно написать явное выражение для
эффективного сечения через радиальные интегралы и угловые
факторы. Для последних приводятся выражения через Зп/-сим-
волы (в схеме £5-связи). Полученные в этом параграфе формулы
используются в гл. III при обсуждении конкретных приближен-
ных методов. Приближение 1-го порядка получается из решения
интегрального уравнения (4.52), если опустить поляризацион-
ный потенциал:
во
Т’гоГ, ” etT1’sin т}о, Тгг. == — $ ^г^ггв^г^г. (5.1)
о
На языке дифференциальных уравнений (4.30) это соответствует
замене полной системы связанных уравнений независимыми урав-
нениями:
(Zr, + k20)FT, = О, (Жг + k*)Fr = t/гг/г.- (5.2)
Сопоставляя граничные условия (4.38) при Го = Г и (4.44), не-
трудно видеть, что Fr» — Fr0-
В дальнейшем мы ограничимся рассмотрением неупругих
столкновений (Г =/= Го) и по-прежнему не будем учитывать маг-
нитное взаимодействие внешнего электрона с атомом. Начнем
с рассмотрения состояний в схеме ZS-связи; а = ypLpSpnlLSJ,
где VpLpSv — состояние атомного остатка. Подставляя (5.1) и
(4.32) в (4.22а), получаем
o<v = ла2 • У, п2 (XZ1X2J) | У (—If r+S’+Lr+L‘n2(LrST) х
х. Xi, хг Lr Sy
Хи, X
Г х L J Xj <£ Jxj JQ хП J J у
X \'LT Xo MVr V, VafVo S’ loftb Lo
x [У «ггХ- - £ WrX-] |2. (5.3)
x"
oo 00
Xr = 5 Fryu.Fr.dr, = f Fry^Pi'dr.
о 0
§ 5. ПРИБЛИЖЕНИЕ ПЕРВОГО ПОРЯДКА 35
Функции Fr зависят, вообще говоря, от всех квантовых чисел,
входящих в Г. Однако наибольший интерес представляет случай,
когда не зависит от полных моментов Lt, St- Всюду в даль-
нейшем это условие предполагается выполненным. В этом случае
формула (5.3) упрощается. Используя формулы (4.35) для а
и [3 и соотношения для Зге/’-символов, сечение можно представить
в следующей форме:
+ а”.,, - [<2хОх (?,„ I) (>хОх(/о, 01 - (5.4)
Здесь стх (Zo, I) и ст* (Zo, I) — сечения для одноэлектронного пере-
хода п010 — nl, которые фактически представляют радиальные
части сечения; QH и QK — угловые факторы, зависящие от кван-
товых чисел угловых моментов состояний ай, а. При этом о' вклю-
чает прямую и смешанную (интерференционную) части сечения,
а о* — чисто обменную часть. Фактор совпадает с угловым
фактором вероятности 2х-польного радиационного перехода (см.
[1], § 32, 35). Учет обмена в ст' на фактор никак не влияет (по-
этому мы сохраняем обозначение <?х вместо QH).
Отметим, что хотя пределы изменения х в двух членах в (5.4)
одинаковы, физический смысл х различен. В первом члене х со-
ответствует мультипольности взаимодействия, причем отличны
от нуля лишь стх с х одной и той же четности. Во втором члене
х является просто дополнительным индексом суммирования,
возникающим при преобразовании Зсту-символов; при этом отлич-
ны от нуля члены как с четными, так и с нечетными значениями
х. Разумеется, условия четности и пределы изменения вытекают
непосредственно из выражений для ст' и ст". Эти пределы, а также
формулы для стх, стх, Qn, Qn приведены в п. 2. Здесь мы отметим
лишь, что ^-факторы имеют вид
<2х = [Mflo5 а)]2, (?х= 2 («о! а)]2- (5.5)
Хъ X»
Рассмотрим теперь переходы между смешанными состояниями
а0, а. Через а0 и а обозначим по-прежнему одноконфигурацион-
ные состояния в схеме LS-связи:
ЧЪ = 2(я|а)фв. (5.6)
а/а
В случае промежуточной схемы связи для сечения о— сохраня-
ется форма (5.4), причем в (5.5) надо подставлять величины
Ьх (а0; ст) = («о | Оо) (а0, a) (a [ а),
г», Sj, l, s (5 7)
^xxix, (Йо> ст) = 21 (®о ] Сто) ^хх,х,(СТо» ст) (ст | ст).
JLo, Se, Lf S
2*
36
ГЛ. II. ОСНОВЫ ТЕОРИИ СТОЛКНОВЕНИЙ
Таким образом, радиальные части можно вычислить независимо
от схемы связи, меняются лишь угловые коэффициенты Ъ.
В случае взаимодействия конфигураций ситуация существен-
но сложнее, так как преобразуются и угловые и радиальные
части. При этом записать сечение в_форме (5.4) нельзя.
В зависимости от вида функций Fp различаются следующие
три приближенных метода.
1. Метод Борна — Оппенгеймера: функции Fp являются ра-
диальными функциями свободного движения, т. е. решениями
уравнения (4.43) при Ur — 0- Если в (5.3) и последующих форму-
лах опустить обменный член, то получим метод Борна.
2. Борн-кулоновское приближение (без обмена или с обменом):
Fp — радиальные функции в кулоновском поле, соответствующем
асимптотике Up, т. е. Up = — (z — 1)/г. Для нейтральных ато-
мов (z = 1) приближения 1 и 2 совпадают.
3. Приближение искаженных волн: Fp — решение (4.43) с
полным учетом Up — хартри-фоковского потенциала атома (иона).
Обсуждение этих приближений и их модификаций будет про-
ведено в гл. III. Для практических целей наибольший интерес
представляют приближения 1 и 2.
2. Сводка формул для сечений и Q-факторов. В произвольной
схеме связи для перехода й0 — а
& а^а
— 2 (ао> ®) (/о, О 4“ Qyl (Щ)> ®) (^0» 01’ (5.8)
и
Он (10; I) и Ox (Io'* 0 — одноэлектронные сечения, зависящие толь-
ко от квантовых чисел nolo, nl,
а« (?«'. 0 = • а У, (д» — У, >
2^ (5.9)
°’* (i’; г) = ла» ’ (2/о+ i)t; L (Е л“'“) '
' ° 1 ' 0 Ко, К V.”
Rx и — прямой и обменный радиальные интегралы:
nd II (IqIXqX) /х Iq 1\ /х Xq X\
4 Л (X) V) о 0Л0 0 (Vх
X 2^Р,(г-)Л(И-Д-^х.(г')Л.(г')*-<гг', (5.10)
£ *)(*' )}x
X 2^Р,(г')А(>л)-Д;(1-С'->^.-»)^.(Н^*.('-')*'*л. (5.11)
§ 5. ПРИБЛИЖЕНИЕ ПЕРВОГО ПОРЯДКА
37
множите-
(5.11)
(5.15)
с = 4- <- Е*+к^=-г (-
п (W2-) - (2/х + 1)*'’(2/2 +
Значения хих" согласно (5.10) и (5.11) лежат в пределах xmin ч-
~~ ^тах И Ит1п ^тах» ГДС
^min = max ( | I — I, | X ~~ Xfl |)> 'Ищах — ппп (Zo “Ь I, Хо Ч~Х),
(5.12)
^min = max (11 | X 10 |), хтах = min (Z ~Ь Xq, X Zo)
Из тех же формул видно, что х" принимает значения одной
четности; то же относится к х в первом члене в (5.8):
х" = x'roin + 2т, х = xmin + 2т, (5.13а)
где т — целое число. Индекс х во втором члене в (5.8) может
принимать целочисленные значения любой четности
х = xmin + гп. (5.136)
Угловые факторы и в произвольной схеме связи полу-
чаются путем преобразования «амплитудных» угловых
лей LS-связи:
Qu ~ 21 ^‘XXtXi'l
Х,Х,
(d0; d) = 21 (“»I «о) ЬК(а0\ а) (а | а),
£от So, S
Ьух,хг (a<>i — 21 («0 I ®o) ^XXiXs(®0> a) (® | ^),
La, So, L, S
где a0, a — состояния LS-связи. В случае чистой схемы связи
(например, jl, jj) коэффициенты (а; а) выражаются через Зп/-
символы. Для промежуточной связи (а; а) вычисляются численно.
Преобразование типа (5.15) можно использовать и в случае
изменения схемы сложения моментов. При этом суммировать
(5.15) надо по а/а, а0!а0, т. е. по всем квантовым числам из а0,
а, не входящим в а0, а. Например, при а = 1$2/> [L151]2sLSJ,
а = Is, 2s2p [WPjLSJ, а0 = а0 — ls22s£0S’0Z0 суммировать надо
по В дальнейшем случай изменения схемы связи специально
не рассматривается.
Для перехода типа l^1 — 1™~Ч имеем
а0 == %L0S0J0, а = 1Г1 ILPSPULSJ,
Ь» = 6аз.(-1/-',+£-«П(Мад{“ t
38
ГЛ. II. ОСНОВЫ ТЕОРИИ СТОЛКНОВЕНИЙ
= (- ^~s^/t+Ln+L-~n(i0JL0LS0Sxlxi)x
х/ J *^0 *^11 ^2 ] | *^2 ^0 1 J ^*0 z-iLoSo ‘l/~'wt
Х Но L LoJH ^0 L<\Sp 1/2J \Lp I Zof LpSp V ’
(5.16)
где Gl^sp — генеалогический коэффициент.
Приведем теперь совокупность формул для факторов QK и
Qy в случае чистой LS-свяэи для того же типа перехода I™ —
В аргументе факторов Qx, Q* будем писать лишь последние кван-
товые числа из а0, а. Из (5.16) и (5.14) имеем
л 4}‘{? '1 (;у<с^,)2т.
& >) = 4- У, П* (УХДЛ&г,!,) X (5Л7>
Xl, X»
. . f X Jq ^112 1 J *^2}^ I ^2 *0 1 ^0 -^'I^/ZtLqSo \2 т
Х Но L LJ И б’о bj Vp */« vj \Lp I Zof <Glpsp> m‘
Для перехода между термами L0S0 — LS надо просуммировать
(5.17) по J и усреднить по J0:
Qv. (Loso; LS) - <5Л8)
>1 qJ
и аналогично для Q„.
В результате получаются значительно более простые выра-
жения:
(?х (L050; LS) = <2х (Jo; LS) = (L0‘, L),
Qy. {LqSq'i LS) — Q* (Jo> LS) —
2^ + 1
2(2хУр+1)
Qy. (Lq‘, L),
(5.19)
где
(?X (b0; L) = П2 (l0L) { * £|s(GlX)2 in.
(5.20)
Другими словами, сечение перехода между термами записывает-
ся в виде
ow = £ gx (Z-0, L) [ 6g.s< fa 0 + 2^/+ i) a«fa!)]- <5'21)
X
Суммируя no L, имеем
3<?x(i».A) = (6%)2m-
Li
(5.22)
§ 5. ПРИБЛИЖЕНИЕ ПЕРВОГО ПОРЯДКА 39
Наконец, суммируя по S, Lp, Sp, получаем
<?« (С гг'о = <2» (ffiA. 1ГЧ) =
= I?; ((Г. Z"’1/) = <?; (l?L,Sa, I”-1;) = т, (5.23)
и, следовательно,
О (С, 1Гг0 = т 2 [< (Zo, I) + < Go, z)b (5.24)
X
Из (5.24) видно, что2<\ Go; I) и 2 о; (Zo; Z) соответствуют се-
X X
чениям одночастичных переходов. Физическая интерпретация
отдельных слагаемых требует, однако, специальных разъясне-
ний. Согласно (5.9) и (5.10)
3 <-3 3 о*.. (5.25)
X X XX
В первом слагаемом о! — сечение прямого взаимодействия муль-
типольности 2х, во втором слагаемом <Тхх" — интерференционный
член прямого и обменного взаимодействия мультипольности 2х
и 2х" соответственно; о* содержит сумму обменных членов всех
мультипольностей. Сумму 2 можно переписать в виде
X
2 Пх"’
л V.
. 2 4 \' П8 (101Х0л) /х" 10 К \ 3/х* 1\3
0 (2Z0 + l)^ AJ П3(х") '° 0 °' W 0
х^
х[2^Р,(г)Л(г')-^г(1 Р,.(ИЛ.(г')*'*-]‘, (5.26)
где Оу/ — сечение обменного взаимодействия мультипольности 2х".
Отметим, что явное суммирование по х и переход к2ах" воз-
х"
можен лишь для суммарного по конфигурации сечения, когда
Gx не зависит от х *).
В некоторых случаях необходимы парциальные сечения о (Го; Г)
для данных значений полных моментов LtSt- Ограничимся
случаем £5-связи и суммарного по Jo, J перехода между термами.
Используя (5.1), (4.32) и (4.35), получаем (Г = aX1/aLrSr)
9 II2 (LT St)
о (Го; Г) = ла3 (Lo^y-1 &sos f — Bs.sg |2,
f = 2 AKRl, g = 3 АЛ... (5'27)
X XX"
x) Суммирование по x можно выполнить также в случае Lp ~ 0.
40
ГЛ. II. ОСНОВЫ ТЕОРИИ СТОЛКНОВЕНИЙ
Здесь / и g — амплитуды прямого и обменного рассеяния, Rd
и Re — радиальные интегралы (5.10) — (5.11), к, х" определяют-
ся условиями (5.12) — (5.13). Коэффициенты Ая и Bs^ зависят
только от орбитальных и спиновых моментов. Для перехода
типа I™ — 1 имеем
а0 = 1™LOSO, а = 1Г1 ILPSP]ILS,
A^(~l)LT+La+L+Lpn(nL0L)^ L? Н{* ЛхС&иЧ (5-28)
58й = (-1)’-5’8,п(адГ'* M.
ч /2 pi
В частности, при == 0 Bs^ = (—l)Sr+1; при So = 0
^-(-1)1'S4(26’+1)'%t7..
ГЛАВА III
ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СЕЧЕНИЙ
§ 6. Метод Борна
1. Столкновения быстрых электронов с атомами; разложение
по мультиполям. В тех случаях, когда взаимодействие, ответствен-
ное за рассеяние, можно рассматривать в рамках теории возму-
щений и не учитывать обменное взаимодействие, оказывается воз-
можным получить простые общие формулы для эффективных се-
чений, не прибегая к разложению на парциальные волны фх.
Рассмотрим взаимодействие заряженной частицы произвольной
массы с атомом. Приведенную массу системы обозначим ц. Соглас-
но известной формуле теории возмущений вероятность перехода
атома между состояниями дискретного спектра а0М0 — аМ, со-
провождающегося изменением волнового вектора возмущающей
частицы к0 — jfc, определяется выражением
dW a0Mofco, аМк — "о" | aMk\4(80-$)dk, (6.1)
где
Uа^М^ко, аМк ~ J dr ф* (г) Uа.м^ ам (»’) Фа, (г),
и«м„ .„(«•) - <МЛ, | £ |r | аМ> , (6.2)
i
Л® к2
Н г
Множитель 2 в выражении для U связан с использованием еди-
ниц Ry; ф&0, фь — волновые функции свободного движения воз-
мущающей частицы. Волновая функция конечного состояния
нормирована па 5 (к — к'), т. с. ф^ (2л)“аА exp (ikr). Волновую
функцию фк„ начального состояния нормируем на единичную
плотность потока фЬ(г = —~ exp (ikor); тогда дифференциальное
У
эффективное сечение do совпадает с вероятностью перехода dW.
Из (6.1), интегрируя по к, получим
Jexp[-j(fc(|-fc)r]C7a.M.,aM(r)dr do, (6.3)
к2 = - Еа + fr2-
42 ГЛ. Ш. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СЕЧЕНИИ
Если мы не интересуемся изменением ориентации атома при рас-
сеянии, то надо просуммировать de по М и усреднить по Мо:
= Zj ISехр 1 “ *)r 3 u^i>’аМ dr do>
м, м.
где g0 — статистический вес состояния а0.
Формула (6.4) носит название формулы Борна. Случай а = а0,
к = к0 соответствует упругому рассеянию; случай а а0,
к к0 — неупругому.
Для применимости борновского приближения к электронам
достаточно, чтобы скорость налетающего электрона была велика
по сравнению со скоростями атомных электронов. Дальнейшие
формулы относятся к столкновениям с электронами; поэтому
полагаем ц = 1.
Выполнив интегрирование в (6.2) по dp с помощью формулы
Jexp(-iffr)-p^jjdr = exp (- iqr}),
получим
~ 77 Zl । помо, аМ (?) аМ I Тз >
(6.5)
(6-6)
(6.7)
q = к0 — к, q1 ~ к* + к2 — 2кк0 cos О.
Проведем теперь разделение радиальных и угловых переменных.
Разложим exp (—iqrj) в (6.7) по сферическим функциям (ср. (3.6)):
g-i®r _ ® YKjL (б'д» Фд) ф) К- (Цг)‘ (6.8)
X, Р-
Подставляя (6.7) и (6.8) в (6.6), используя формулу Эккарта —
Вигнера (см. [1], § 14)
<7/М|П„|Т./„Л/0> * j£) (6.9)
и правила суммирования Зу-символов и УИц, получаем
do”, “ I («И Ч ««) - I’ 7 • (6Л°)
где введен оператор
т”' - X (6Л1>
J
Рассмотрим сначала неупругое рассеяние а0 а. Тогда в при-
веденном матричном элементе в (6.10) возможен переход только
§ 6. МЕТОД БОРНА
43
одного электрона и формула (6.10) упрощается:
(6.12)
Для получения полного сечения надо проинтегрировать
в пределах от ?min = к0 — к до ?тах = к0 + к:
°' х ко—к
(6.12)
(6.13)
Здесь радиальный интеграл
оо
Л,_ (?) - П (xZZ0) (* £ § f Р, (г) Р,,(г) 1/К (?г) - 8„] dr (6.14)
О
отличается от соответствующего интеграла мультипольного излу-
чения лишь заменой гх на /х (qr). Отметим, что
'“*«г)-‘(27Т>)Нг’‘’ <615)
Множитель Qy (а0, а) в (6.13) определяет зависимость от угло-
вых моментов состояний а0 и а. Этот же множитель входит в вы -
ражение для силы линии электрического 2х-польного излучения
(см. [1], §32). Отметим, что в (6.13) и в (5.8) совпадают. Ради-
альные функции оптического электрона (г), вообще говоря,
зависят от всех квантовых чисел состояния а. В дальнейшем мы
предположим для простоты, что радиальные функции зависят
только от квантовых чисел nl, и будем, как ив § 4, 5, обозна-
чать их Р1 или Рп[.
Перепишем борновское сечение (6.13) в виде
= Ц<?к(ао,а)^х(/о, 0»
X
К = Xmhu ^min 2, . • 1 Iq |> ^min ” 1^0 I, (6.16)
аВ(;о,0 = ла;. - 8- - 1Я,(?)1»Д., (6.17)
°х Uo> О ~ сечение 2х-польного одноэлектронного перехода
neZe — nl. Выражение (6.16) называется разложением по мульти-
полям. Для перехода а0 = 1™L0S0J0, а = l™~1 [LpSp]lLSJ
?,(«*«)-e«n4WW){* J‘ '}’{2р (6.18)
где — генеалогический коэффициент.
44
ГЛ. Ш. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СЕЧЕНИЙ
Более полная сводка формул для фактора @х см. в § 5, п. 2,
и § 19.
Возможные значения х в (6.16) определяются 3/-символом
в (6.14) и соответствуют 2х-польному взаимодействию внешнего
электрона с атомом (а не какой-либо парциальной волне!). Все х
имеют одинаковую четность в соответствии с тем, меняется ли
четность при переходе 10 — I. Во многих случаях оказывается
достаточным ограничиться учетом низшей мультипольности
(х = xmin), так как ох довольно быстро убывает с ростом х.
Отметим, что для переходов между уровнями одной конфигурации
nlSQL0J0—nlS0LJ (jg = 0.
Следует подчеркнуть, что уменьшение ох с ростом х не связано
с наличием какого-либо малого параметра. Этим взаимодей-
ствие атома с электроном принципиально отличается от взаимодей-
ствия с полем излучения. В последнем случае высшие мультиполи
содержат множитель (ze2/fic)2*+1 = (z/137)2x+1, т. е. вклад каждого
следующего мультиполя примерно в 104/z2 раза меньше. В случае
Б
столкновении ох уменьшается с увеличением х на единицу всего
в несколько раз, и это уменьшение имеет скорее численный, чем
буквенный характер.
Из приведенных выше формул (см. (6.14), (6.18)) следует, что
правила отбора для х 0 такие же, как для соответствующего
электрического мультипольного перехода. Например, в схеме
LS-связи
при х — 1
М = ±1, Д£ = 0, ±1, AJ = 0, ±1,
L + LO>1, J4-JO>1, AS = 0, (6.19)
при х — 2
AZ ~ 0, Н-2, AL — 0, -4-1. 4-2, Д<7 = 0, il, -1-2,
I + Zo > 2, L 4- L9 > 2, J 4- > 2, AS = 0. (6.20)
При x — 0 в отличие от радиационных переходов о® 0 для пере-
ходов, в которых изменяется лишь главное квантовое число п и
не изменяется ни одно из квантовых чисел угловых моментов.
С помощью формул (6.13), (6.14) легко установить связь эффек-
тивных сечений прямого и обратного процессов. Поменяв в этих
формулах местами начальное и конечное состояния атома, а также
к0 и к, получим
(апк0, ак) = (ак, аоко). (6.21)
С учетом сохранения энергии (6.3) это соотношение совпадает
с (2.8), полученным из принципа детального баланса в § 2.
§ 6. МЕТОД БОРНА
45
Остановимся теперь коротко на упругом рассеянии, хотя рас-
смотрение его не входит в задачу книги. В общем случае вычисле-
ние ’^диагональных матричных элементов от представляет
собой более сложную задачу, чем вычисление недиагональных.
В ряде случаев эта задача упрощается, если выразить приведен-
ные матричные элементы Тл через приведенные матричные эле-
менты оператора Uy- (см. [1], § 18). Приведем окончательный ре-
зультат для электронной конфигурации, содержащей кроме за-
полненных оболочек одну незаполненную оболочку lm:
оо
<i<>B (6.22)
0 0 *5*0
где
Оо
p(r) = §pdr = N,
з о
»-•=
Число членов в сумме по х определяется условиями х 21,
х 2L. При I — 0 (сферически симметричное распределение
заряда) в (6.22) отличен от нуля лишь первый член. При Z 1,
L Ф 0 член х = 2 можно выразить через квадрупольный момент
атома.
2. Формула Бете. Разлагая в радиальном интеграле (6.14)
(qr) в ряд Тейлора и ограничиваясь первым неисчезающим чле-
ном, получаем
Л« (9) ~ Я. (?) ~ <? (6.23)
Отсюда видно, что в случае х = 1 (т. е. = +1) основной вклад
в интеграл (6.13) вносит область малых q, где это разложение пра-
вомерно, и можно получить простую приближенную формулу для
сечения. При этом следует верхний предел в интеграле (6.13)
заменить некоторой ограниченной величиной q0, так как при боль-
ших 5/х (qr) осциллирует и эта область фактически не дает вклада
в сечение. Получающееся таким образом выражение содержит
С 12 f
Ql^max >
о
гДе fata — сила осциллятора перехода а0 — а, &Е — Еа — Еаа —
энергия перехода. Учитывая все сказанное, получаем приближен-
ную формулу Бете (или «дипольное приближение»)
Оода ж ла® • 1п Ао!1 к • (6.24)
46 ГЛ. III. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СЕЧЕНИЙ
Как видно, сечение сравнительно слабо (логарифмически) зави-
сит от параметра q0. Для выбора q0 учтем, что величина 7?и (д)
определяется областью г ~ г0, где г0 ~ 1 1-,/’ — размер атома.
Поэтому можно положить
<7о = min {/с0 + к, У] £0 |}. (6.25)
При больших энергиях логарифм в (6.24) имеет вид
(6.26)
Формула Бете (6.24), очевидно, применима лишь к диполь-
ным (т. е. оптически разрешенным) переходам. Она часто исполь-
зуется для практических оценок благодаря ее простоте, хотя во
многих случаях ее погрешность значительно больше, чем погреш-
ность формулы Борна (6.13) или (6.16), (6.17).
Как видно из (6.22) и (6.13), в случае и У 1 приближение (6.22)
непригодно, так как величина q~ARn (g) при этом определяется
областью больших д. Другими словами, результат оказывается
весьма сильно зависящим от параметра д0.
3. Краткая характеристика борновских сечений. Сечения воз-
буждения атомов, вычисленные по формуле Борна (6.16), (6.17),
обладают рядом характерных свойств. Некоторые из этих свойств
можно получить в результате исследования общих формул; другие
вытекают из результатов конкретных численных расчетов. Под-
черкнем, что здесь, как и всюду в этом параграфе, рассматри-
ваются переходы без изменения спина.
При больших энергиях £ \Е для оптически разрешенных
переходов
х-1, А! = ±1, (6.27)
для оптически запрещенных переходов
х=#1, (6.28)
При малых энергиях борцовские сечения
ов сс к = У$ - ЬЁ. (6.29)
Конкретные расчеты, выполненные в борновском приближении,
показывают, что для различных атомов и переходов сечения, как
правило, ведут себя сходным образом, если выразить энергию
электрона в пороговых единицах:
$£ — ДЕ А2
7/ — - . —• .
ДЕ - ДЕ '
Обычно борновские сечения достигают максимального значе-
ния при u ~ 1. Для оптически запрещенных переходов максимум
§ 6. МЕТОД БОРНА
47
несколько сдвинут к меньшим энергиям. При малых Д£’ макси-
мум сдвинут к большим и.
В качестве иллюстрации на рис. 1 приводятся сечения для
ряда переходов атомов Н и Na. Для удобства сопоставления при-
Рис. 1. Борновские эффективные сечения для переходов в атоме Н (кривые
1—4) и в атоме Na (кривая 5). 1 — переход Is — 2s, 2 — переход Is — 2р,
3 — переход 2s — 5р, 4 — переход 4s — 5р, 5 — переход 3s — 4р.
Как правило, для переходов между соседними уровнями
tfmax CQ ДЕ"2. Для переходов между уровнями с сильно отличаю-
щимися главными квантовыми числами п0, п при ?г0 п сечение
примерно пропорционально п~3. Для оптически разрешенных пере-
ходов величина oaia сравнительно хорошо описывается формулой
(6-31)
Все сказанное требует уточнения в случае малых ДЕ <s^ | Ео |,
где Ео — энергия исходного уровня. Для таких переходов поро-
говые единицы становятся неудобными, а основной интерес пред-
ставляют энергии электрона $ ~ | Ео | ДЕ. Для этих энергий
сечение практически не зависит от ДЕ. В случае х — 1 (Д/ = ±1)
остается слабая логарифмическая зависимость сечения от ДЕ.
Отметим, что эти все особенности содержатся в формуле Бете
(6.24)—(6.26):
Отсюда при больших ДЕ следует (6.31), а при малых &Е п &Е
j со ДЕ, т. е. о со u-1 In (Си).
Надо подчеркнуть, что перечисленные общие свойства сечений
можно использовать лишь для ориентировочных оценок. Кроме
48 гл. III. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СЕЧЕНИЙ
того, их полезно иметь в виду при построении лолуэмпирических
формул.
Выше мы не рассматривали вопросов, касающихся примени-
мости борновского приближения, согласия с экспериментом и т. п.
Ограничимся двумя примерами. На рис. 2 и 3 показаны борнов-
ские и экспериментальные сечения для переходов 1s — 2s и
Is — 2р атома Н. Как видно, борновские сечения оказываются
завышенными в области максимума примерно вдвое. Кроме того,
Рис. 2. Эффективное сечение возбуждения перехода Is — 2$ в атоме водорода.
1 — эксперимент [6], 2 — борновское приближение, 3 — метод искаженных
волн без обмена, 4 — метод сильной связи трех уровней (1s — 2s — 2р) с уче-
том обмена [8].
максимум борновского сечения расположен слишком близко к'по-
рогу возбуждения. Подобное соотношение между борцовскими и
экспериментальными сечениями для переходов из основного со-
стояния нейтральных атомов является типичным.
4. Ионизация и трехчастичная рекомбинация.Формулу Борна
нетрудно обобщить на тот случай, когда одно из состояний атома,
начальное или конечное, является состоянием непрерывного
спектра. Переход из состояния дискретного спектра в состояние
непрерывного спектра означает ионизацию атома. Обратный про-
цесс носит название трехчастичной рекомбинации. Этот процесс
состоит в захвате электрона ионом при одновременном рассеянии
на этой системе второго электрона х).
Выражение для сечения ионизации можно получить непосред-
ственно из (6.16), (6.17), если состояние а отнести к непрерыв-
1) Присутствие третьей частицы необходимо для выполнения законов
сохранения энергии и импульса.
§ е. МЕТОД БОРНА
49
ному спектру: а — aitlLSJ, где е — энергия выбитого электрона.
При этом обычно полные моменты системы «атом + выбитый
Рис. 3. Эффективное сечение возбуждения перехода 1s — 2р в атоме водорода.
1 — эксперимент [6], 2 — борновское приближение, 3 — метод искаженных
волн без обмена, 4 — метод сильной связи трех уровней (1s — 2s — 2р)
с учетом обмена [8].
электрон» но представляют интереса и по ним надо просуммиро-
вать. Если волновая функция непрерывного спектра Р£1 нормиро-
вана на 6 (е — е'), то получаем дифференциальное сечение иони-
зации
doW (о0, = S Q*da<M (Zo, sZ),
X
= 8 de jj
/соИ'о+1) Ль 7
(6.32)
(6.33)
Радиальный интеграл RK вычисляется согласно (6.14) с функцией
Рц в качестве Рг (г). Для ионизации из оболочки I™ имеем (ср.
(5.22))
3 (flo, а) = Qi = т (G&ff, (6.34)
L, S,J 1
т. e. Qt не зависит от х. Если состояние а0 имеет определенную
генеалогическую схему а0 = ypLpSpL0S0J то = 1 (точнее,
50 ГЛ. III. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СЕЧЕНИЙ
В приложениях наибольший интерес имеет полное сечение
ионизации
ft) п V Е d°^ ei) я /й
= \ -----de—dE’ (6’35)
где Ег — энергия ионизации атома Xz.
Сечение обратного процесса — трехчастичной рекомбинации
определяется аналогичным образом, если поменять местами на-
чальное и конечное состояния. При этом волновая функция элек-
трона в непрерывном спектре нормируется не на б (е — е'), а на
Рис. 4. Эффективное сечение ионизации атома водорода из основного состоя-
ния. 1 — эксперимент [6], 2 — борцовское приближение.
единичный поток электронов. Кроме того, результат надо усред-
нить по направлениям движения этого электрона и по состояниям
системы «ион + электрон». В результате получаем соотношение
ds’ (<?о, гое/)
----= ek2giOr (a^l, g0). (6.36)
Напомним размерность сечений в системе единиц СГС: диффе-
ренциальное сечение ионизации d<54d& [см2/эрг]; полное сечение
ионизации oz [см2]; сечение рекомбинации стг (см4-с], так что
N^.vv'e' имеет размерность вероятности [с~х].
Формулы (6.32), (6.33) близки к соответствующим формулам
для переходов между состояниями дискретного спектра. Полное
сечение ионизации (6.35) отличается от сечения возбуждения
дискретного уровня наличием суммы по Z и интеграла по энергиям
вылетевшего электрона е. Тем самым расчет сечения ионизации
сложнее, чем сечения возбуждения. В конкретных расчетах
обычно приходится учитывать порядка 10 членов суммы по I.
§ 7. НЕКОТОРЫЕ УТОЧНЕНИЯ МЕТОДА БОРНА 51
Каждому значению I соответствует, вообще говоря, несколько
членов суммы по х.
Общий вид зависимости сечения ионизации от энергии пример-
но такой же, как и сечения возбуждения. При малых энергиях,
однако, о^) со и’/», где и — энергия рассеянного электрона в по-
роговых единицах г). Среди членов суммы по I, к всегда имеются
члены х = 1 и х 1, которые при больших энергиях ведут себя
соответственно как и ~ . Указать в общем случае, в какой об-
ласти энергий зависимость одного типа преобладает над другой, за-
труднительно.
Приведем в качестве примера борцовское сечение ионизации
атома Н и экспериментальные данные (рис. 4). Как видно из этого
рисунка, соотношение между борновским сечением ионизации и
экспериментальным примерно такое же, как и в случае сечений
возбуждения.
§ 7. Некоторые уточнения метода Борна
1. Введение. Метод Борна для вычисления сечений неупругих
столкновений существенно отличается своей простотой от всех
остальных методов, основанных на разложении по парциальным
волнам. Конкретные расчеты сечений в рамках этого метода сво-
дятся к вычислению нескольких определенных интегралов.
Вместе с тем метод Борна дает правильное качественное опи-
сание сечений и, как правило, не приводит к большим количест-
венным расхождениям с экспериментом. Для многих типов пере-
ходов из основного состояния типичным является 1,5—2-кратное
завышение сечений в области их максимума. Для переходов между
возбужденными состояниями экспериментальных данных недоста-
точно. Однако никаких указаний на то, что для таких переходов
метод Борна должен давать существенно худшие результаты,
тоже нет. Следует, правда, отметить, что это не относится к при-
менимости дальнейших упрощений метода Борна, например, ди-
польного приближения.
Тем не менее в ряде случаев метод Борна оказывается явно
неудовлетворительным или вообще не дает результата (например,
Шнтеркомбинационные переходы). Поэтому представляет интерес
рассмотреть возможные уточнения метода путем учета конкрет-
ных физических эффектов. При этом нашей целью является по
возможности расширить класс переходов, для которых можно
было бы обеспечить расчет сечения с точностью до множителя ~2
t области максимума. К таким эффектам относятся искажения
•ахающей и рассеянной волн полем атома, обмен и нормировка.
Ij^- х) Более детальное исследование, выходящее за рамки борновского
ирмажения, дает для сечения ионизации о(9 со и (см. [7, 3]).
52 гл. III. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СЕЧЕНИЙ
Все эти уточнения метода Борна возможно осуществить лишь
в представлении парциальных волн (§ 4). Поэтому приходится
отказаться от более простого (/-представления (§ 6). Мы будем
исходить из приближения 1-го порядка для решения общей си-
стемы уравнений теории столкновений (§ 5). Однако это прибли-
жение нуждается в некоторых уточнениях и модификациях, чтобы
обеспечить адекватный учет определенных физических эффектов.
Последующие разделы этого параграфа посвящены обсуждению
этих уточнений.
2. Учет искажения падающей и рассеянной волн, возбуждение
ионов. Простейшим уточнением метода Борна является прибли-
жение искаженных волн. Это приближение соответствует при-
ближению 1-го порядка без учета обмена (7?г = 0, § 5). Функ-
ции /г являются при этом решением радиального уравнения для
движения в поле притяжения атома Up. Следует, однако, разли-
чать эффекты притяжения электрона короткодействующим полем
нейтрального атома и дальподействующим кулоновским полем
иона. Первый эффект с избытком компенсируется поляризацией
атома, так что среднее расстояние между налетающим и атомным
электронами не только не уменьшается за счет притяжения к ато-
му, но даже увеличивается. Как уже отмечалось выше, борнов-
ское сечение, как правило, оказывается завышенным. Учет при-
тяжения электрона к атому естественно приводит к дальнейшему
увеличению сечения (это увеличение было бы еще больше, если бы
притяжение пе сопровождалось увеличением скорости электрона).
В действительности, внешний и оптический электроны испыты-
вают кулоновское отталкивание, что и приводит к уменьшению
сечения. Однако в рамках теории возмущений учет этого оттал-
кивания возможен лишь во 2-м порядке (ср. § 8, п. 3). Поэтому
метод искаженных волн дает для нейтральных атомов погреш-
ность большую, чем метод Борна.
Кулоновское притяжение электронов к иону приводит к увели-
чению потока электронов вблизи иона за счет дальних пролетов.
Этот эффект необходимо учитывать, так как он приводит к каче-
ственному изменению хода сечения; оно оказывается конечным
в пороге, в то время как в приближении Борна сечение в пороге
равно нулю.
Учитывая сказанное, для расчета возбуждения ионов вместо
борновского используется борн-кулоновское приближение. Сече-
ние определяется формулами (см. § 5, п. 2) без обменных членов,
причем в радиальный интеграл Rd (5.10) подставляются радиаль-
ные функции электрона в кулоновском поле. В результате получаем
— у1 Q-л(®о> а) сгх (Zo, Z), стх (Zo, 0 — ла®- # (-ZZ*)2’
AO(2ZO4-1)
(7.1)
х
§ 7. НЕКОТОРЫЕ УТОЧНЕНИЯ МЕТОДА БОРНА 53
,d II (L^tA) /К 1\ /X Aq Х\
х “ П (х) \0 о о/ \ О О о/ х
OQ СО
X 2 jj $ Л-' rfr' Fl, (г) Я,.(г') Р, (г") Fl (г'). (7.2)
0 0 >
Здесь Р[ — радиальные функции оптического nZ-электрона атома.
Функции определяются уравнением
’Л „ К^-|~ J 2 (z — 1)
dr2 г2 г
+ FK = О,
F\ (0) = О, Л к~'/г sin [кг - In (Ат) + П) .
(7.3)
Угловые факторы Q* — те же, что в методе Борна (см. § 5, п. 2,
и § 19).
Сумма по Хо, Л. в (7.1) сходится крайне медленно при больших
энергиях. С другой стороны, при Хо, Х> 1 стремится к бор-
новскому пределу Т?*- Поэтому сумму по Хо, X целесообразно вы-
числять следующим образом:
а« ((«./) - о® (/,. О + ,-J"- - У, |(7Й)! - (Я?)“|. (7.4)
Здесь определяется согласно (7.2), (7.3) при z = 1; О’® — бор-
новское сечение (6.17), вычисление которого не требует разложе-
ния по парциальным волнам. Сумма в (7.4) сходится достаточно
быстро.
Несмотря на внешнее сходство, борн-кулоновское приближение
принципиально отличается от метода искаженных волн. При z = 1
оно переходит в боряовское приближение. С помощью элементар-
ной замены переменных (zr г, k/z —> к) нетрудно показать, что
борн-кулоновское приближение является 1-м порядком теории
возмущений с малым параметром 1/z. С ростом z погрешность ме-
тода должна убывать.
На рис. 5 приведены сечения возбуждения водородоподобного
иона С VI, вычисленные в борновском и борн-кулоновском при-
ближении. В отличие от борцовского борн-кулоновское сечение
скачком возрастает в пороге до конечной величины. Как и следо-
вало ожидать, при S АЕ оба сечения совпадают.
3. Учет обмена. Интеркомбинационные переходы (AS = 1).
Такие переходы происходят целиком за счет обмена (в рамках
.LS-связи). Оставаясь на базе борновского приближения (для
ионов — борн-кулоновского), сечение можно вычислять с помощью
обменного члена в (5.8), подставляя в радиальный интеграл
(5.10) функции свободного электрона или кулоновские функции.
Это приближение называется методом Борна — Оппенгеймера.
54 гл. III. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СЕЧЕНИЙ
Однако конкретные расчеты показывают, что погрешность ме-
тода Борна — Оппенгеймера намного превышает погрешность
метода Борна для разрешенных переходов.
Рис. 5. Эффективное сечение возбуждения перехода 1s — 2р в водородопо-
добном ионе С VI. 7 — борновское приближение, 2 — борн-кулоновское
приближение.
В значительной, мере это обстоятельство связано с тем, что в ме-
тоде Борна — Оппенгеймера волновые функции системы «атом +
+ электрон» в начальном и конечном состояниях неортогональ-
ны. В этом нетрудно убедиться на примере водородоподобного
иона. Функции
Фо (О. га) = Рц (r^Fu (г2), Ф (гп г2) = Pt (r2)FK (гД
неортогональны, так как Р (г) соответствует полю —z/r, a F(r) —
полю — (z — 1)/г. Учет угловых частей обеспечивает ортогональ-
ность лишь при А0 =£ I и X Ф 10. Другими словами, этот метод
фактически не является 1-м порядком какой-либо теории возму-
щений. Указанный недостаток устраняется в так называемом ме-
тоде ортогонализованных функций [9]. В 1-м порядке необходи-
мая модификация сводится к замене кулоновских функций F%
ортогонализованными функциями
Pio = — <^0 I Pl)Pfil^ /7
Используя формулы § 5, п. 2 для перехода с Д5 == 1, получаем
См = (7.6)
X
I) - «4-
$ 7. НЕКОТОРЫЕ УТОЧНЕНИЯ МЕТОДА БОРНА 55
I 1 \х"+Х П 7<l»7 71 1 > ^0 Z \ (Х ^0 s ,
Лх"х — (—1) ГЦхЦМДо о оДо о о Дх л0 IJ А
Оо ОО у"
х 2 ^dr'dr’F^P^-^F^r-yPAr'). (7.7)
0 0 >
Формулы для углового фактора Qy_ и пределы изменения х, х*
приведены в § 5, п. 2.
Численные расчеты показывают, что метод ортогонализован-
ных функций (7.5)—(7.7) обеспечивает для интеркомбинационных
переходов точность того же порядка, что метод Борна для разре-
шенных переходов. Метод применим, вообще говоря, как для ней-
тральных атомов, так и для ионов, но фактически для ионов он
дает несколько лучшие результаты. В пределе больших z метод
ортогонализованных функций и метод Борна — Оппенгеймера
совпадают, так как функции и Pi становятся ортогональными
(их неортогональность —1/z).
Для нейтральных атомов существует другая модификация
метода Борна — Оппенгеймера — метод Очкура [10]. Область
применимости этого метода более ограничена, но он широко ис-
пользуется, в частности, благодаря простоте формул. Основная
идея метода состоит в том, что в разложении амплитуды обмен-
ного рассеяния по степеням 1/к при умеренных энергиях физиче-
ский смысл сохраняет лишь первый неисчезающий член. При этом
оказывается возможным получить выражение для обменного се-
чения в более простом ^-представлении аналогично выражению
(6.16), (6.17) для прямого перехода. Не останавливаясь на вы-
кладках, приведем результат:
О'€Ма = 2j@x(^0» ^) Ох (^0» (7.8)
S* Go, О = • — — \ [Ях (д)1г q dq,
Ао 0 + 1J ьДк
ОО
Л«(д) = П(иМ)(“ J? ‘0]$Л.(г)7>,('Ш<Г)*-. (79)
О
Как видно из (7.8), при больших # сечение обменного перехода
оо £“3, в то время как сечение прямого перехода со &-1 или
&-1 In $. Асимптотически (при больших $) метод Борна — Оппен-
геймера и обе его модификации совпадают. Однако выход на асимп-
тотическое значение происходит при столь больших энергиях,
что само сечение уже весьма мало.
Переходы без изменения спина (&S — 0). Такие переходы про-
исходят в основном за счет прямого взаимодействия; обменный
член дает обычно лишь сравнительно небольшую поправку.
56 ГЛ. HI. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СЕЧЕНИЙ
Однако в некоторых случаях (особенно для ионов) обменная по-
правка может оказаться существенной из-за частичной компен-
сации прямого и интерференционного членов (см. ниже). Анализ
показывает, что при AZ — ±1 это может иметь место тогда, когда
пороговая энергия &Е ~ | Ео | (Ео — энергия исходного уровня)
и только вблизи порога ($ — ДЕ ДЕ). Примером может слу-
жить сечепие возбуждения синглетных уровней ионов (Не]
из основного состояния. При | Д/ | 1 влияние обмена вблизи
порога может оказаться еще сильнее.
Для вычисления сечения нужно в формуле 1-го порядка (5.8)
сохранить как прямые, так и обменные члены. В радиальный ин-
теграл мы подставим кулоновские функции Е% (7.3), а в инте-
грал — ортогонализоваппые функции (7.5). Такой прием,
разумеется, не является вполне корректным, но он дает хорошие
результаты при умеренных z. (При больших z, как уже отмеча-
лось, и F% совпадают.) Таким образом, сечение определяется
формулами:
Оа0я = &аоа ! (fl0, ®) Их (Zq, Z) Д' Qх (^о> ®) Их (Zq> Z)],
X
(7.10)
(Zo> О — яао ,9. । ..Аг У ) [(^х)2 — 7?х У, 7?х"х ,
- а 1} ло2 4 У (У Re ? (7Л1)
oH(Z0, Z) - ла0 -’
' и к"
где 7?х и 7?х"х даются формулами (7.2) и (7.7), а угловые факторы
<2х и Q*. — формулами § 5 п. 2.
Как уже отмечалось выше, роль обмена оказывается сущест-
венной из-за компенсации прямого и интерференционного членов
в ст'. Рассмотрим в качестве иллюстрации сечение перехода между
термами LS. Используя (5.19), можно записать сечение (7.10)
в виде
(210 + 1) к* £ fg + 2 (2^+1) ' <7-12)
0 X®, X» х
где / — /?х» ё ~ S 7?х"х- Обычно обменная амплитуда g /.
Обмен оказывается существенным, если g / и спиновой фактор
в (7.12) мал. Так, например, для перехода Is2 'S — ls2p 1Р в ионах
(Не] х) в пороге g т 3/4/, (2S + 1)/2 (25Р + 1) — 1/i. Поэтому
выражение в квадратных скобках в (7.12) равно 0,4 /2, в то время
как без учета обмена было бы /2. При к j> 1 (| Д/ ] Ф 1) роль обме-
!) Для краткости записи ион изоэлектронной последовательности ато-
ма А будем обозначать (А].
§ 7. НЕКОТОРЫЕ УТОЧНЕНИЯ МЕТОДА БОРНА
57
на оказывается еще сильнее за счет членов с х* = 0 и х* = 1
в (7.11). При этом обмен может быть существенным даже при ма-
лых ДЕ | Ео |. При (S ДЕ всегда g <С / и Роль обмена несу-
щественна.
На рис. 6 в качестве иллюстрации приведены сечения возбуж-
дения уровней 2‘Ри23Рв ионе О VII. Как видно, вблизи порога
Рис. 6. Эффективные сечения возбуждения гелиеподобного иона О VII.
1 — борн-кулоновское приближение для перехода Is2 rS — is2p lP,
2 — борн-кулоновское приближение с учетом обмена (в рамках метода орто-
гонализованных функций) для перехода Is2 — ls2p 1Р, 3 — сечение об-
менного возбуждения для перехода 1s2 — ls2p SP.
сечения возбуждения 2 1Р и 2 3Р уровней близки. Этот факт на-
дежно подтверждается экспериментальными данными по рентге-
новским спектрам горячей лабораторной плазмы и солнечной
короны. Следует подчеркнуть, что если при расчете о (2 гР) не
учитывать обмен, то о (2 1Р) превосходит о (2 3Е) более чем
в 2 раза в противоречии с упомянутыми экспериментальными
данными.
Важно отметить, что для суммарного по S сечения множитель
в квадратных скобках в (7.12) равен
/2 - tg + g2,
т. е. слабо зависит от обмена при g / (см. рис. 6). В частности,
невелика роль обмена для [Н] и вообще при Sp = 0.
4. Нормировка. Эффективное сечение возбуждения атома долж-
но удовлетворять предельным неравенствам, вытекающим из
условия сохранения числа частиц. В случае рассеяния па силовом
центре эти неравенства имеют вид (3.38). Для неупругого рассея-
58 ГЛ. III. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СЕЧЕНИЙ
ния на реальном атоме предельные неравенства можно получить
из (4.23) и условия унитарности «S'-матрицы (4.25):
я П8(«УТЬГ) ___
<Г°’ Г) 2/с2 П2 (50£0) — <Г°’ Г)’
я ° (7ЛЗ)
о (oiAo, аХ) —у (2Х0 -|~ 1).
*0
Здесь ап>’ — предельная величина сечения.
В общем случае метод Борна не обеспечивает выполнения ус-
ловий (7.13); парциальные борновские сечения могут оказаться
большими, чем это следует из (7.13). В дальнейшем мы будем об
этом говорить как о нарушении нормировки. Сечения, исправлен-
ные за счет учета нормировки с помощью какого-либо приема,
будем называть нормированными. Примем для них обозначение й.
Рассмотрим метод нормировки, основанный на использова-
нии Х-матрицы. Матричное соотношение (4.26):
S = , (7.14)
где I — единичная матрица, обеспечивает унитарность 5-матрицы
независимо от приближения, использованного при вычислении
матрицы К. Для целей нормировки достаточно учесть в матри-
це К лишь переходы, включающие начальное состояние Го, т. с.
положить
/° ^Г.Г, ^ГоГ,
к _ I ^г«г» 0 0
“ *Г,Г. 0 0
(7-15)
При этом из (7.14) и (4.23) получаем следующее выражение для
нормированного сечения:
У о (Го. Г), а (Го, Г)- f, (7.16)
ui.77.sr г+ 2|, Агт.1
Здесь мы для простоты полагаем Г — aLSXLrSr- В случае пере-
ходов между состояниями LSJ Г == clLSJ, V/2 (f)Jr и суммировать
надо по ХоХ/о/А-
Нетрудно показать, что в приближении 1-го порядка
1 3(Го, Г') /7 17^
КГ Г>- 4 ' (7Л7)
Отметим, что суммирование в знаменателе (7.16) не распростра-
няется на квантовые числа Lt, St- Это означает, что нормировка
§ 7. НЕКОТОРЫЕ УТОЧНЕНИЯ МЕТОДА БОРНА 59
каждого канала рассеяния с данными LtSt проводится независи-
мо. Вследствие нелинейности связи а (Го, Г) с о (Го, Г) в (7.16)
нельзя выполнить суммирование по Lt, St в явной форме и ис-
пользовать формулы § 5, п. 2. Приближение 1-го порядка надо
писать в виде (см. (4.21), (4.32) и (5.1))
° (Го. Г) = | У «ГогЛх' - У, РгогЯх» |3 • (7-18)
° к' х"
В случае перехода между состояниями LSJ
о(Г„, Г) У, W(LTSr)x
° L.'p " S'p
Радиальные интегралы R’ и R" имеют вид (5.3), (4.33), но в каче-
стве функций Fr надо подставить соответственно (7.3) и
(7.5).
Расчеты с помощью формул (7.16)—(7.19) весьма громоздки.
Учитывая приближенный характер нормировки методом ^-ма-
трицы, целесообразно упростить (7.16), заменив Kt„v’ на среднее
по Lt$t значение:
„г V пг(^т^т) кг
= ) ( ---7-----J----. ЛГ'Го =
Lt,&t 2 )
А:2 А2
= У 4л (2^0 + 1) ° (Г°’ г ) = 4л (2Х0 + 1)“ а ^°^0’ а^' (7*20)
Подставляя в (7.16), получаем выражение для нормированного
сечения в виде
О (а^Ко, ак)
а°,а' М Ц '
1 + 4л(2Х0 + 1) 2-1 а(Яо?Ч>. а'к')
*- а'к' J
(7.21)
Формула (7.21) применима и к переходам между /-уровнями.
В качестве а (а0Х0, а'Х') мы можем теперь использовать формулы
§ 5, п. 2:
о (й(Л|ь а ) — S [(?xgx (/рХо, Z X ) -|- @х0х(^оХо, I X )], (7.22)
X
где Стх (/о^о, ГХ') и Ox (^Хо, Z'X') — парциальные сечения, т. е.
члены сумм в (5.9).
60 ГЛ. III. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СЕЧЕНИЙ
В знаменателе (7.21) сумма по X' содержит небольшое число
членов (~AZ). Сумма же по состояниям атома а', вообще говоря,
бесконечна. Однако, как правило, существенную роль в норми-
ровке играет один уровень а' (максимум два).
Следует подчеркнуть, что этим уровнем вовсе не обязательно
является конечный уровень а рассматриваемого перехода. Так,
например, для перехода 3$ —- 4р в атоме Na нормировка опреде-
ляется уровнем Зр, т. е. переходом 3s — З/j в сумме по а'. Другими
Рис. 7. Эффективное сечение возбуждения перехода 35 — Зр в атоме Na.
1 — борновское приближение, 2 — сечение, нормированное методом Х-ма-
трицы, 3 — метод сильной связи. 4 — эксперимент [11].
словами, тот факт, что борновское сечение для данного перехода
удовлетворяет условию (7.13), еще не означает, что нормировка
несущественна. Необходимо, чтобы условию (7.13) одновременно
удовлетворяли все прочие переходы из начального состояния.
Отметим, что метод нормировки, основанный на использова-
нии А’-матрицы, приводит к следующему результату: если бор-
новское сечение о (Го, Г) ппр (Го, Г), то нормированное сече-
ние о (Го, Г) <<о,1р (Го, Г).
Наиболее последовательный способ получения нормированных
сечений состоит в точном решении ограниченной системы урав-
нений типа (4.30) с учетом сильной связи рассматриваемых кана-
лов (см. § 8). Унитарность 5-матрицы при этом обеспечивается
во всех случаях, когда матрица U системы эрмитова. В системе
(4.30) следует, однако, опустить диагональные потенциалы
и {7Г#Г#, описывающие главным образом искажение падающей
и рассеянной волн. Этот эффект не имеет отношения к проблеме
нормировки.
§ 7. НЕКОТОРЫЕ УТОЧНЕНИЯ МЕТОДА БОРНА
61
Численные расчеты, проведенные этим методом, дают хоро-
шее согласие с методом Л’-матрицы в тех случаях, когда борнов-
ское сечение о не очень сильно превосходит онр. В тех случаях,
когда ст^> опр, метод сильной связи дает еще более сильное умень-
шение 5 по сравнению с оп₽, чем метод Л’-матрицы. В качестве
Рис. 8. Эффективное сечение возбуждения перехода 3s — 4р в атоме Na.
1 — борновское приближение, 2 — сечение, нормированное методом Л-ма-
трицы, 3 — метод сильной связи.
примера на рис. 7, 8 приведены результаты расчетов сечений для
переходов 3s — Зр и 3s — 4ц в атоме Na.
5. Заключительные замечания; «обобщенный метод Борна».
Борновское приближение с изложенными в настоящем параграфе
уточнениями позволяет получить сечение возбуждения с достаточ-
ной для многих приложений точностью. Характерная погрешность
метода Борна — завышенное в 1,5—2 раза сечение в области
максимума, уменьшение погрешности с ростом энергии. Типич-
ным примером может служить возбуждение резонансного уровня
в атоме II (см. рис. 2).
Эксперименты последних лет, а также астрофизические дан-
ные показывают, что аналогичную точность обеспечивает борн-
кулоновское приближение в случае ионов. Более того, с ростом z
погрешность борн-кулоновского приближения уменьшается х).
Однако для получения надежных результатов в ряде случаев
х) Исключение составляют резонансы, связанные с кулоновским взаимо-
действием и сосредоточенные обычно в узкой припороговой области. Их роль
может оказаться весьма существенной (см. § 9).
62 ГЛ. III. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СЕЧЕНИЙ
необходимо учитывать обмен (например, в случае возбуждения
синглетных уровней ионов [Не] из основного состояния).
Переходы с изменением спина происходят целиком за счет
обмена. Метод, изложенный в п. 3, обеспечивает для ионов ре-
зультат с погрешностью порядка характерной погрешности бор-
новского приближения. Для нейтральных атомов ошибка иногда
оказывается несколько больше.
Наконец, для переходов между близкими уровнями, чтобы не
выйти за рамки характерной погрешности, необходима нормиров-
ка сечений.
Борновское приближение с учетом аффектов кулоновского
поля, обмена, нормировки будем для краткости называть обоб-
щенным методом Борна. Область применимости этого метода зна-
чительно шире, чем область применимости обычного метода Борна.
При больших энергиях &Е оба метода дают одинаковые
результаты. Следует отметить, что обобщенный метод Борна не
охватывает случай, когда переходы происходят в основном через
промежуточный уровень (см. § 8). В вычислительном отношении
он более трудоемок, чем метод Борна. Тем не менее систематиче-
ские расчеты на обычных ЭВМ вполне реальны. В гл. VI будут
приведены результаты такого рода расчетов.
В данном параграфе речь шла о сечениях возбуждения. Для
расчета сечений ионизации из перечисленных выше эффектов су-
щественную роль играет лишь кулоновское поле. Более того,
влияние кулоновского поля меньше, чем в случае возбуждения:
сечение ионизации ионов в пороге остается равным нулю. В то же
время трудоемкость расчетов в рамках представления парциаль-
ных волн здесь возрастает чрезвычайно сильно. Поэтому часто
ограничиваются учетом кулоновского поля путем введения про-
стых полуэмпирических поправок к борновскому сечению.
§ 8. Более точные методы расчета сечений
В двух предыдущих параграфах рассматривались методы рас-
чета сечений, основанные на приближении 1-го порядка. Для по-
лучения более точных результатов нужно либо перейти к более
высоким порядкам теории возмущений, либо решать точную си-
стему (4.30), ограничив ее конечным числом уравнений. Оба под-
хода оказываются чрезвычайно громоздкими, и систематических
расчетов до настоящего времени не проводилось. Тем не менее
опубликован целый ряд работ по расчету сечений отдельных пере-
ходов. Анализ результатов и сопоставление их с эксперименталь-
ными данными показывает, что сходимость обоих методов (по чис-
лу включаемых состояний и порядку теории возмущений) обычно
плохая.
§ 8. БОЛЕЕ ТОЧНЫЕ МЕТОДЫ РАСЧЕТА СЕЧЕНИЙ
63
Одной из причин такой плохой сходимости являются «противо-
положные тенденции», возникающие от различных членов ряда
или различных членов в системе уравнений. Примером может
служить уже упоминавшаяся в § 7, п. 2 компенсация эффектов
притяжения электрона к нейтральному атому и поляризации
атома в случае неупругого рассеяния.
Характер уточнений результата в методах более высокого по-
рядка может быть двух типов. К первому относятся количествен-
ные уточнения, когда полностью или частично устраняется ха-
рактерная погрешность обобщенного метода Борна. Ко второму
типу отнесем случаи, когда этот метод по тем или иным причинам
дает неудовлетворительный результат, существенно выходящий
за рамки характерной погрешности. При этом использование
более точных методов особенно существенно. Однако целесообраз-
но вместо автоматического увеличения числа учитываемых членов
(или уравнений) ограничиться теми членами, которые устраняют
причину непригодности обобщенного метода Борна.
1. Переходы через виртуальные уровни. Формула Борна для
эффективного сечения возбуждения или ионизации соответствует
первому члену ряда теории возмущений. Последующие члены
этого ряда содержат бесконечные суммы по всевозможным вир-
туальным состояниям. Вообще говоря, выделять из этих сумм
небольшое число состояний нет оснований. Возможны, однако,
такие случаи, когда первый член ряда теории возмущений по тем
или иным причинам мал или вообще обращается в нуль. В этих
случаях приходится вычислять сечение с помощью первого не-
исчезающего члена ряда. Примером такого типа может служить
двухэлектронное возбуждение или ионизация с одновременным
возбуждением иона. Если все одноэлектронные атомные волно-
вые функции начального и конечного состояний, используемые
в расчете, ортогональны, то матричный элемент перехода в первом
борновском приближении равен нулю. Отличное от нуля сечение
можно получить лишь с учетом возможной слабой неортогональ-
ности одноэлектронных атомных функций. Во 2-м порядке такой
переход происходит через виртуальные уровни, соответствующие
возбуждению одного из электронов. Число подобных виртуальных
уровней, очевидно, не более двух. При этом свойства ортогональ-
ности волновых функций практически не играют роли, а сечение,
вообще говоря, может оказаться значительно большим, чем в пер-
вом борновском приближении.
Аналогичная ситуация может возникнуть и для некоторых
одноэлектронных переходов. Рассмотрим, например, квадруполь-
ные переходы (s — d и т. п.). Сечения таких переходов в борнов-
ском приближении обычно значительно меньше сечений диполь-
ных переходов. Во втором порядке переход может проходить
через виртуальный уровень как «последовательность» двух
64 ГЛ. III. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СЕЧЕНИЙ
дипольных переходов (s— р — d, . . .). Матричный элемент такого
перехода часто оказывается больше, чем матричный элемент
1-го порядка для квадрупольного перехода. Обычно можно выде-
лить один виртуальный уровень, дающий основной вклад во 2-м
порядке. Например, для перехода nos — nd таким уровнем явля-
ется пор: nos — пор — nd.
Для расчета сечения во 2-м порядке можно воспользоваться
формулами (4.52) — (4.54):
оо
r'^.= -^FlUrr,Fl.dr-
О
оо
- 2 И Gr> <г’г'> (r') dr'dr' <8Л>
01, Xi о
причем в обменных интегралах вместо следует подставлять
ортогонализованные функции (7.5). Функция Грина G^l для
нейтрального атома согласно (4.42), (4.48) равна
Gy, (г, г’) = — ikpr'h. (kp-^h^ (V>), (8.2)
кг — £ — Eaiao.
В соответствии со сказанным выше в сумме по промежуточным
состояниям можно ограничиться немногими членами. Обычно
достаточно сохранить одно состояние alt наиболее сильно
связанное с исходным состоянием а0 и конечным а.
В § 6 было получено выражение для борновского сечения
в ^-представлении, не требующем разложения на парциальные
волны. Получить столь же простое выражение во 2-м порядке
не удается. Можно, однако, получить приближенную формулу
для сечения во 2-м порядке. Для этого напишем выражение для
сечения возбуждения перехода а0 — а в трехмерной форме (ср.
(4.52) и (6.4)):
HISS ^aa^Waa.ir^Ua^r^e^dr^qdq, (8.3)
MM ai
где М0М — проекции полного момента на ось z, q — — к0,
W (г) = (г — х) Gj (x)Fkx dx.
(8-4)
Здесь G2 — трехмерная функция Грина. Вообще говоря, при
z > 1 следует в качестве Gj брать кулоновскую функцию Грина.
§ 8. БОЛЕЕ ТОЧНЫЕ МЕТОДЫ РАСЧЕТА СЕЧЕНИЙ
65
Мы, однако, приближенно заменим ее борновской:
С' W = - ж? к’ + = к' + =/с»' <8-5)
Даже в этом случае расчет Waai связан с серьезными трудностями.
Однако в предельном случае (к —> 0) выражение для W упро-
щается. Здесь и ниже предполагается, что уровень аг лежит ниже
уровня а. Рассмотрим сначала одноэлектронный атом и опустим
ядерный член 2/r: U = 2/ | г — | = 2/р.
Подставляя (8.5) в (8.4) и выполняя интегрирование по х
при к — 0, получаем
W = 2 [1 - exp (iр)], /с->0.
(8.6)
Можно показать, что при больших к W оо к"1 и мнимо. Простей-
шей экстраполяционной формулой, удовлетворяющей этому усло-
вию и (8.6), является
<-МУХ,р) _ . МуХ, р) ]_ (8 6а)
Ф *l/£aa,P J
к[ = к* + Еаа', р = I г — Гг |.
Наконец, для включения многих электронов и ядерного члена
достаточно заменить
-И'(г)]. (8.7)
3
Подставляя (8.6а), (8.7) в (8.3), получим приближенную формулу
для сечения во втором борновском приближении в д-представ-
лении.
Для проведения реальных расчетов необходимо в этой формуле
разделить радиальные и угловые переменные, т. е. разложить
потенциал (8.4)1 по мультиполям. Хотя W (р) в (8.6а) имеет
значительно более сложный вид, чем W (р) = 2/р — 2/г, раз-
ложение W (р) оказывается лишь незначительно сложнее.
Не останавливаясь на выкладках, приведем результат для воз-
буждения перехода
nol™.LoS — л0/0 [LpSplnlLS
с учетом виртуального уровня
-1+2 -„2
®aoa — ЛЛо •
0
/jgr)[4®+Л®1гМг|’, (8.8)
3 Л. А. Вайнштейн и др.
66 гл. III. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СЕЧЕНИЙ
где
= (/ II (Г, II у,
л® - xS. (2Х + 1) (*' »' 2 (I I К». I (t) ((, I Хх- II у,
Г _’2L + 1 fLo L * 1а (8.9)
Сх 2х +1 (J 1Л Lp] ’ '
и приведенный матричный элемент (Zt || VH || /2) определяется фор-
мул ОЙ
оо
(Z11 || 1г) = (- 1)<‘П (1,1г) 1'‘ £ J l‘i,(r,) P,,(r,) Mr, г,) dr,.
' ’ о
(8.10)
Радиальные операторы Ку, Их имеют вид
X
КЛг,г')^2^-^-^,
у'' • * Г
>
1 1/Е . 21 • (8.11)
Wx (г, Г) = к„ (г, г') + 2 Цр- шх,
«X (г, г) = (2х -|- 1)‘/х (х<) пу (х>) — бхО«о (я),
<0х (г, г) = (2х + 1) /х (х) /х (./) — дхо7о (*),
х = VEaai г, х' = VEaair'.
Следует подчеркнуть, что сумма по х', х" в (8.9) включает лишь
весьма небольшое число членов, так как х' и х" ограничены соглас-
но (8.9), (8.10) правилами треугольника
Н - h I < х' < | I + 1г |, - l0 |< х’ < | Zi + 10 | (8.12)
и сохранением четности.
2. Использование К-матрицы. Расчет переходов через проме-
жуточный уровень с помощью формул (8.1), (8.2) связан с серьез-
ными вычислительными трудностями. Значительно более простые
формулы в (/-представлении (8.8)—(8.12) являются приближенны-
ми, особенно при больших энергиях. Кроме того, они непригодны
для переходов с изменением спина (и вообще не допускают учета
обмена). В этой связи представляет интерес другой приближенный
метод, связанный с использованием /^-матрицы (4.26).
Элементы ЛГ-матрицы будем вычислять в 1-м порядке
Оо
/fp-р» = — Тр»р» dr, (8.13)
о
а эффективное сечение о — с помощью формулы (4.23) и матрич-
ного соотношения (4.26). Если включить в (4.26) элементы, свя-
§ 8. Г.ОЛЕЕ ТОПЙЫЕ МЕТОДЫ РАСЧЕТА СЕЧЕНИЙ
67
зывающие состояния а0Х0, лДц а'/-., то полученная таким образом
5-матрица будет включать прямые переходы а0 — а, переходы
через промежуточные уровни а0 — — а, а также эффекты
нормировки (см. § 7, п. 4). Последнее обстоятельство является
важным преимуществом метода Л’-матрицы.
Согласно (4.26) для перехода а0 — а
8гг. - [Кгг. + ‘ У, КггДгл + О (№)] , (8.14)
At
где О (№) включает члены не ниже 4-го порядка по Лгт"»
a D — детерминант матрицы I — iK:
D = || / - IK || = 1 + *гг.+ 2*г.г. + + 0(*3)- (8-15)
At А.
Если пренебречь членами 0(К2) в D и О (Л3) в числителе 5ГГо,
то сечение представляется в сравнительно простом виде
о<» (а0Х0, ab) + V । Ц ^ГГ^Г1Г» | *
L о Ly, Sy fa
(8.16)
Хотя этот метод значительно проще общего расчета согласно
(8.1), (8.2), он включает бесконечные суммы по парциальным вол-
нам Хо, Xt.
3. Использование поляризационного потенциала. Поляриза-
ционный потенциал Угг» (4.54) используется в основном в задачах
об упругом рассеянии, так как до сих пор не удалось сформулиро-
вать удовлетворительное приближение для недиагонального по-
тенциала Угг«> Сечение упругого рассеяния определяется диаго-
нальным потенциалом Угого- Для простоты ниже в этом разделе
индекс нуль опускается.
Целесообразно вместо использования формулы (4.52) ввести
Угг непосредственно в радиальное уравнение, что соответствует
частичному учету членов более высокого порядка. Ограничиваясь
для Угг 2-м порядком, получаем
[£г - Уг + Wr = 0, Угг = eiT1sin ц,
Лг — gin [kr — ~ + ц'') , (8-1?)
\ “ 1
ОО
угЛг = - S ^гг. $ СГ1 (г, г') 17Г1Г (г') dr'. (8.18)
Г1^Г О
В реальных расчетах часто используется так называемое адиа-
батическое приближение. В этом приближении в (8.18) опускают
обменный член, а функцию Грина записывают в виде
6('-И, де(8.19)
3*
68 ГЛ. III. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СЕЧЕНИЙ
где Eai и Еа — энергии атома (в единицах Ry). Потенциал Fr
при этом становится локальным. Если его усреднить по Lt по-
добно тому, как мы поступили в § 7, п. 4, суммирование по
выполняется явно. В результате получаем
х, at (8.20)
sx (a, at) = (а, аг) П2 (ZZX) *j2,
где Qy. — коэффициент в выражении для силы линии или сечения
мультипольного перехода.
Из (8.20) нетрудно получить предельные выражения для
Fe (г) при г -> 0 и г -> оо. В первом случае отличен от нуля член
с х = 0, т. е. Zj = Z, Lj = L, Qo (a, nJ = 1 и
CO
V.(0) - 5u-sr WЛи(г)£]‘. (8-21)
ni (J
При r -> оо основную роль играет член с х = 1, т. е. = I ± 1.
Из асимптотического поведения интеграла yh, (г) имеем
(8.22)
где Ъ — поляризуемость атома, а — сила осциллятора диполь-
ного перехода.
В практических расчетах часто используется простой поляри-
зационный потенциал вида
= (8.23)
к®+г;!2
где г0 — средний радиус атома в состоянии а. Это выражение
имеет правильную асимптотику и ограниченно при г —0.
Адиабатическое приближение справедливо при малых скоро-
стях внешнего электрона. Более точно: необходимо, чтобы
к2 <<: Д£. Можно показать, что, кроме того, необходимо, чтобы
/Д£г0<1.
4. Метод сильной связи. Под методом сильной связи обычно
подразумевают решение системы уравнений (4.30):
l2r + **)₽r“^arr'Fr'’
а2 1/г(г).
(8.24)
в которой набор состояний а («каналов») ограничен тем или иным
образом. Для определенности мы используем борновское пред-
§ 8. БОЛЕЕ ТОЧНЫЕ МЕТОДЫ РАСЧЕТА СЕЧЕНИЙ 69
ставлеиие, так что сумма в правой части включает диагональные
потенциалы U??.
Простейший случай метода сильной связи — приближение
двух состояний
[<^г0 + Fr0 = ^^г.г^’г,
* (8.25)
[£r + Aa]Fr = 3t/rr.Fi>
к#
Приближение 1-го порядка получается из (8.25), если в уравнении
для Ff' опустить правую часть, т. е. пренебречь обратным влия-
нием конечных состояний на начальные. Учет этого влияния,
т. е. связи каналов, и является основной особенностью метода.
Система уравнений (8.24), так же как (8.25), является эрмито-
вой. Поэтому ее решение автоматически оказывается нормирован-
ным — 5-матрица унитарна по учитываемым каналам.
Набор состояний Г включает энергетически достижимые со-
стояния а (открытые каналы < $, к2 0) и энергетически
недостижимые (закрытые каналы Д£ $, к2 < 0). В системе
(8.24) энергетически достижимые каналы а' а описывают воз-
буждение через промежуточный уровень а'. Энергетически не-
достижимые состояния описывают эффекты поляризации атома
внешним электроном. Разумеется, подобное деление является
достаточно приближенным, но оно полезно для качественного об-
суждения характера метода.
Как уже отмечалось в начале параграфа, сходимость решения
с увеличением числа уравнений оказывается медленной. Качест-
венно это можно объяснить следующим образом. Диагональные
потенциалы Z/гг в системе (8.24) описывают притяжение электро-
на к атому средним полем. Это притяжение определяет упругое
рассеяние электрона и в то же время приводит к уменьшению
среднего расстояния между внешним и атомным электронами.
Однако последний эффект в значительной мере компенсируется
отталкиванием электронов, т. е. поляризацией атома. Для эф-
фективного учета поляризации необходимо включить в ограничен-
ную систему много других состояний, в основном энергетически
недостижимых.
Во избежание недоразумений отметим, что диагональный поля-
ризационный потенциал Угг также описывает притяжение
внешнего электрона к центру атома. Увеличение среднего расстоя-
ния между электронами описывается недиагональными поляриза-
ционными потенциалами Угг'.
Учет энергетически достижимых состояний описывает, как
уже отмечалось, главным образом переходы через промежуточные
уровни. Очевидно, что этот эффект важен лишь тогда, когда речь
идет о влиянии сильных каналов на слабые. В частности, он мало
сказывается на сечениях возбуждения резонансных уровней.
70 ГЛ. Ш. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СЕЧЕНИЙ
Рассмотрим в качестве иллюстрации расчеты сечения возбуж-
дения 2s- и 2р-уровней атома Н. Результаты ряда расчетов и
экспериментальные данные приведены на рис. 2 и 3. Как уже отме-
чалось выше, борновское сечение оказывается завышенным в 1,5 —
2 раза в области максимума. Учет притяжения электрона к атому
(метод искаженных волн) приводит к дальнейшему увеличению
сечения, т. е. к еще большему расхождению с экспериментом
(особенно для 1s — 2«-перехода). Интересно отметить, что этот
эффект в значительной степени компенсируется при учете обмена.
Метод сильной связи трех состояний 1s — 2s — 2р (с учетом
обмена) для перехода 1s — 2р дает несколько лучший результат,
чем метод Борна, но это улучшение незначительно по сравнению
с общей погрешностью. В случае 1s — 2з-перехода этот метод
дает даже худшие результаты, чем метод Борна. Причина этого
как раз в том, что в расчет включены диагональные потенциалы,
учет которых «допустим» лишь при адекватном учете эффектов
поляризации. Характерно, что результаты метода сильной связи
оказываются весьма близки к результатам метода искаженных
волн с обменом.
Все сказанное о возможностях метода сильной связи не отно-
сится к припороговой области. В этой книге мы вообще не рассма-
триваем специфических эффектов, связанных с вырождением
/-уровней. Упомянем лишь, что это вырождение приводит к конеч-
ному в пороге сечению и осцилляциям в припороговой области.
Метод сильной связи хорошо описывает эти эффекты.
Методом сильной связи шести состояний (Is, 2s, 2р, 3s, Зр, 3d)
расчеты выполнены только до порога возбуждения уровня п — 3.
Учет состояний п = 3 до их порога позволяет частично учесть
поляризацию атома и сечение 1s — 25-перехода заметно умень-
шается, хотя и остается существенно выше эксперименталь-
ного.
Из сказанного следует, что при использовании метода сильной
связи выбор набора уровней и даже учитываемых потенциалов
требует предварительного анализа в соответствии с поставленной
задачей. В частности, для описания эффектов нормировки доста-
точно ограничиться приближением двух состояний (или даже двух
уровней, сняв суммирование в (8.25)). При этом следует опу-
стить диагональные потенциалы, за исключением кулонов-
ского поля. Диагональные потенциалы вообще целесообразно
опускать во всех случаях, когда не принимаются специальные
меры по учету поляризации атома.
Поскольку учет эффектов поляризации связан с необходи-
мостью решения большой системы уравнений, в [12] был предло-
жен специальный метод — так называемый метод псевдосостоя-
ний. Здесь мы не можем на нем подробно останавливаться, отсы-
лая читателя к обзорам [13, 14].
§ 9. ВОЗБУЖДЕНИЕ МНОГОЗАРЯДНЫХ ИОНОВ 71
§ 9. Возбуждение многозарядных ионов
1. Введение. В этом параграфе рассмотрены особенности не-
упругого рассеяния электронов на многозарядных ионах. Одна
из особенностей — конечное значение сечения в пороге, уже упо-
миналась в § 7, п. 2. Здесь мы подробнее остановимся на припоро-
говых особенностях, следуя работам [15, 16] 1). В § 15 будет рас-
смотрена диэлектронная рекомбинация, связанная с наличием
резонансов в рассеянии в допороговой области.
При рассмотрении многозарядных ионов (z^>l) удобно выде-
лить заряд z в явной форме. Для этого перейдем к так называе-
мой кулоновской системе единиц: единица длины a0/z, единица
энергии z2 Ry. Запишем систему уравнений (4.30), используя
кулоновские единицы, в виде
[5Sr + ^2] Fr = ^-^С/’гг'^’г'» (9.1)
г7
д> __ Х(Х-}-1) 2а . 1,
Urr> определяются формулами § 4, за исключением Urr, в кото-
рый включены члены Up + 2а/г. При z 1 ?7гг' почти не зави-
сят от z. Функции Fr согласно (4.14) и (4.40) удовлетворяют гра-
ничным условиям:
Fr(0) = 0, ^--^[бгг.вш^ог + ^ + Ггг.в^)], (9.2)
к "
d = - -Г- + -pn(2Ar) + argrh + 1-|i) ,
ft2 = г -
Системе (9.1), (9.2) соответствуют интегральные уравнения
(4.46), которые мы запишем, выделив в явной форме открытые
каналы Г = у (Аг2 0) и закрытые каналы Г = с (Аг2 < 0):
Fv — dvr„Fхв Ч——- у1 GyUfvl1 г',
! V - Г< (9-3)
г7"
где — регулярное решение однородного уравнения (см. (7.3)).
Интегральный оператор G определяется формулой
Gcp (г) = J G (г, г') ф (г') dr', (9.4)
О
*) См» также книгу [17].
72 гл. III. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СЕЧЕНИЙ
где G (г, г') — радиальная кулоновская функция Грина уравне-
ния (9.1).
В следующем разделе будет показано, что G? регулярна. По-
этому связь открытых каналов при слабая и к ним приме-
нима теория возмущений. В отличие от случая нейтральных ато-
мов теория возмущений содержит малый параметр 1/z и при
z 1 1-й порядок (борн-кулоновское приближение) дает хоро-
ший результат в отсутствие закрытых каналов. В отличие от Gv
функция Грина закрытых каналов Gr содержит полюсы, и теория
возмущений к ним непригодна. Эта ситуация будет рассмотрена
в п. 3.
2. Кулоновская функция Грина. Функция Грина G? определя-
ется формулами (4.42)—(4.45). Заменим F на С"1® и перепишем
Gp в виде
Gr (г, г') ---Ф (ц, к, r<) Р (р, к, г>), (9.5)
Ф (р, к, г) = ги+*/»7 г 0, р = % -Г 1/2,
причем С = С (р, к) не зависит от г и определяется формулой
= (9.6)
Вместо линейно независимых функций Ф (р, к, г), F (р, к, г)
можно ввести другую пару функций^ Ф± = Ф (±р, к, г). Исполь-
зуя (9.6) и известную асимптотику F (4.44), можно получить сле-
дующее выражение для Gr через Ф±:
2/
Gr(г, г ) = — k)C([L, — к) ф+ ф+ ) +
+ Т5Гф*<'<>Нч-М?ф*(г>)-ф-М • (9-7>
В случае кулоновского поля = —2а/г (9.7) приобретает вид
Gr (г, г') = ctg (jiv) F^ (г) Fvvl (г') + G? (г, г'),
G₽ (г, г ) = sjn (г<) [cos (2лр) FVfX (r>) Fv> (г>)], (9.8)
р = X + 1/2, v = ia/k, Im к 0.
Радиальные функции F^l выражаются через кулоновские функции
(7.3) для комплексного к — ia/v:
FV[l (г) = ay,Fk (г), av = [i ctg (nv) + !)]-'/=. (9.9)
В частности, для действительных к = j^cth -f- 1J * F\. Для
мнимых к, соответствующих целочисленным значениям, v = п
§ 9. ВОЗБУЖДЕНИЕ МНОГОЗАРЯДНЫХ ИОНОВ
73
(п = 1,2,..., оо), т. е. Е = —а2/п2,
Ав = 1-^-] Л Рпь v = п, ц = X + !/г. (9.9а)
Радиальная кулоновская функция Грина (9.8) состоит из двух
слагаемых. В случае закрытых каналов (к2 < 0) первое слагаемое
содержит сингулярный (по энергии) множитель ctg (jiv). Полюсы
при v — п соответствуют резонансам, сходящимся к порогу откры-
тия нового канала (А'2—>— 0). Второе слагаемое Gft как функция
энергии не имеет особенностей. При к —> 0 Gf не зависит от к
и является регулярной функцией от г, г'. Для приложений су-
щественно, что сингулярная часть Gr факторизована по перемен-
ным г, г'.
3. Потенциальное и резонансное рассеяние. Перепишем систе-
му интегральных уравнений (9.3), выделив в явной форме сингу-
лярную часть функции Грина закрытых каналов:
Fy — буГвЛо + — ^1 GyUyr'Fy', у — акк х/2 LTSr,
1 (9Л0)
Fc = F<Ae + -Л ) , GpcUcr>Fv, с = aovX Va LTST.
г
где Лс не зависят от координат и определяются уравнением
оо
zAc = ctg (лу) 2 $ FcUcr‘Fr' dr, (9.11)
Г' о
а функции Fe определяются (9.9). При v п можно применить
метод последовательных приближений. В результате получаем
для у #= Го (ср. (4.51))
Ру = — &у №?Го + VуГо) Л» Ч—— У\ &v (^?с 4- Vус) F<A0 (9.12)
с
и систему алгебраических уравнений для Лс:
2 [z tg (nv) dee' — Ясс'] лс = Ясг0, (9.13)
с'
оо
Ясс' = J Л (t^cc' + Усс') Л' dr. (9.14)
о
Йсг„ определяется (9.14) с заменой Яс- на Ло; поляризационные
потенциалы Угг' определяются формулами (4.53), (4.54), в кото-
рых Gr = Gy для открытых каналов, Gp = Gp — для закрытых
каналов. В отличие от стандартной теории возмущений здесь Угг'
не содержат сингулярностей. Выражения (9.12)—(9.14) справедли-
вы и при v — п, причем сингулярность выделена в явной форме.
ГЛ. Ш. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СЕЧЕНИЙ
Из (9.12) получаем
^гго = Пг, + 7гг„ (9.15)
оо
rfr. = - 4- ( Fl (Ггг. + Frr.) Fi,dr,
S (9.16)
CO
7гг. = - -±- У, Fi (Ur, + Кг.) Л dr.
с о
Величина Tjpr» совпадает с (4.52) и соответствует «обычному»
(потенциальному) рассеянию.* Т^г, описывает «дополнительное»
(резонансное) рассеяние, которое имеет место лишь в том случае,
когда имеются закрытые каналы. Каждому закрытому каналу
с (ас, к% = $ — Есаа) соответствует семейство резонансов вблизи
v = ia./kc = п (т. е. вблизи 8 = Ееа„ — а/п2). Ниже будем пола-
гать все резонансы «независимыми», т. е. пренебрежем в (9.13)
недиагональными матричными элементами Rcc>. Тогда
д e _____ с ztg(nv)-flec ’ zpiea 1 \ ^Гс^сГв *ГГо 2s / 1 1 c tg(nv) — ~RCC (9.17) (9.18)
Амплитуда Тут, как функция энергии проходит через резонан-
сы, положение $ (с, п) и ширина 6 которых определяются выраже-
ниями
£ (с, п) = Eeat — , tg (nvc) = Re Нсс,
" (9.19)
$ (с, п) — Ecat -Т s Re 7?сс, ~ nn8z
Каждому закрытому каналу с (т. е. энергетически недостижимо-
му состоянию ае) соответствует бесконечная последовательность
резонансов, сгущающаяся к точке $ = Есал. Все они сосредото-
чены в сравнительно небольшой области энергий от порога 8 =
— Еааа до 8 — Е^, так что п>—т^- и, как правило, п^> 1.
&са
При этом радиальные функции Рпк ~ т. в. практически
не зависят от v согласно (9.9а). Поэтому вся зависимость Трго (Ю
сосредоточена в функции tg (nv).
Сечение возбуждения перехода а0 — а в соответствии с (4.20)
равно
2
Е Г™.|!. (9.23)
Ч uMsT s‘
f 9. ВОЗБУЖДЕНИЕ МНОГОЗАРЯДНЫХ ИОНОВ
75
Очевидно, испытывает те же резонансы, что и Тгг», в точ-
ках $ — $ (с, и). Можно показать,' что в случае независимых
(неперекрывающихся) резонансов (9.17), (9.18) усредненное по
резонансам сечение равно
НМ
Ooyi — 2^ Gaga ($) d<o =
8-Ъ8
= У, [(Го, Г) + У а- (Г0Г, с) ]
[с
_ ла® о I дгЛг Is Г * ~ 0 (# — ^„ )
ог<* (ГоГ, с)= —2- — - Гс еГ‘- ’ - са’'
(9-21)
(9.22)
2
*2 z Im Rcc
Функция 0 (х) = ± 1 при х 0. При вычислении среднего (9.21)
мы предполагали, что в области усреднения 26$ изменяется толь-
ко tg (лу), а все матричные элементы 7?сг и Rcc постоянны. Отме-
тим, что в этом случае все интерференционные члены исчезают.
Это относится как к интерференции прямого и резонансного рас-
сеяния, так и к различным закрытым каналам с.
Рассмотрим теперь выражения для ТгГк и аад в приближении
1-го порядка. В формулах (9.16), (9.18) в 1-м порядке можно опус-
тить потенциалы Ргг0 всюду, кроме резонансного знаменателя
(9.18). В последнем необходимо дополнительно сохранить первый
неисчезающий член в мнимой части Rcc. Согласно (9.14) имеем
Я„ = jj Л +?! У|!/еГ.&Г,С7г,е + • .]
о Г ГТ
Согласно (9.9а) функции Fa действительны. Для выделения
мнимой части 9г (к2 >• 0) наиболее удобно прибегнуть к спект-
ральному представлению Gr:
Gt (г. г’) = 2^ f(И dk‘ ~iF*b W<r'>- (9-23)
где F^ = F\ — действительные функции; интеграл берется в
смысле главного значения. Определяя Im Rcc с помощью (9.23),
можно получить приближение 1-го порядка для Ггез. Таким обра-
зом, находим
W.= -7Я
_____________Д£еДсУ.______________
22 Л 18 («V) - т < + 7 Р ’
(9.24)
76 ГЛ. III. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СЕЧЕНИЙ
где введено обозначение
= J рк, Urr^ dr, (9.25)
о
причем для закрытых каналов Г — с вместо Гл следует подстав-
лять Гс —
Подставляя (9.24) в (9.22) и (9.20), получим выражения
для потенциальной и резонансной частей сечений в 1-м порядке:
2
<ТР« (Г., Г) - I I*, (9.26)
Z 50
-Гс,,гг ”» 2 £г. |ЛЙ1- <„• <-е(»-г«.)
а (ðÒ с) “ ~I। --------------------------2------ <9'27>
V
Выражение (9.26) совпадает с обычным выражением для парциаль-
ного сечения в 1-м порядке, полученным нами в § 5. Поскольку
мы здесь использовали кулоновские функции Гл, (9.26) совпадает
с борн-кулоновским сечением. В соответствии с (9.21) к ^2? ~
= У аР°1(Г0Г) добавляется вклад от резонансов, связанных
X, Lj> g j’
co всеми закрытыми каналами.
Вблизи порога перехода канала с в открытый канал у0 вели-
чина 7?сг. непрерывно переходит в Ry^Cf Поэтому вблизи порога
канала с
й'«(Го, Г, с) - аи*(Г,Тв) (£-> Е„.) (9.28)
zb I ™уе I
V
и, следовательно,
е) | ~ (9.29)
При достижении порога канала с в выражении (9.21) для ис-
чезают члены 3rcs (Г0Г, с), связанные с этим каналом. Одновремен-
но появляется новый открытый канал а0 — ас. Согласно (9.29)
вклад в полное (по всем а) сечение от резонансов за счет энерге-
тически недостижимого уровня ас непрерывно переходит во вклад
нового канала а0 — а0 при $ > ГСОо.
4. Обсуждение и примеры. В предыдущем разделе показано,
что сечение возбуждения перехода а0 — а в ионах помимо «обыч-
ной» потенциальной части содержит дополнительную часть
Это добавочное сечение связано с возможностью захвата
электрона в квазистационарное состояние иона Xz_i (ас пГ) с по-
следующим автоионизационным распадом на Хг (а) + е.
§ У. ВОЗБУЖДЕНИЕ МНОГОЗАРЯДНЫХ ИОНОВ
77
Из сравнения (9.20), (9.18) и (9.24) видно, что ширина резо-
нанса в 1-м порядке равна
а = <9-30)
V
Поскольку 6 равно вероятности автоионизации Wa в открытые
каналы у г), множитель в (9.27) и (9.28)
1Л&18 ^п(сГ)
(9.31)
т. е. он соответствует обычному ветвлению при наличии несколь-
ких каналов распада.
Сумма TVa(c) включает помимо канала у = Г исходное состоя-
ние у = Го, а также другие состояния Г', удовлетворяющие ус-
ловию сохранения энергии:
^->>0. (9.32)
Для данного п наиболее вероятны распады с наименьшим Еса>
и оптически разрешенным переходом: Хг — Хг = ± 1. С ‘другой
стороны, при очень малых Е^ возможны согласно (9.32) лишь
очень большие п и Wa~ 1/п3 может оказаться малой.
Помимо автоионизационного распада с — Г возможен и радиа-
ционный распад с— с' (с' — стационарное состояние иона Х/Д).
При этом обычно происходит переход типа аспк — ас> пк, т. е.
захваченный электрон остается на месте.
Для не слишком малых значений п можно воспользоваться
приближением (9.28). Добавляя вероятность радиационного рас-
пада W и используя (9.31), перепишем резонансную часть сечения
в виде
,,3
Х.Хо, Ly, Sf, с
_ W (сГ) (9.33)
(Тгез (Г0Г, с) = о^(Г0ус)
1
где oPot (Го ус) берется в пороге канала а0 — аг. Величина Wa —
вероятность радиационного распада W ~ z1 2 / (137)3 (в кулоновских
единицах) и не зависит от п. Поэтому W7Wa я? 10-9 z4n3. Обычно
радиационный распад сказывается лишь при очень больших п,
т. е. в чрезвьгчайно',узком"’энергетическом интервале."5
Важной особенностью <fres является то, что его относительный
вклад почти не зависит от z, если не считать роста W/Wa с ростом z.
1) Здесь 6 = Wa выражены в кулоновских единицах z2Ry; в единицах
Ry 6 и Wa практически не зависят от z.
78 ГЛ. Ш. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СЕЧЕНИЙ
Хотя резонансное возбуждение проявляется в сравнительно
небольшой энергетической области Еаа<) ч- Есал, в некото-
рых случаях его роль может быть весьма существенной. Это осо-
бенно относится к оптически запрещенным переходам а0 — а,
Рис. 9. Эффективное сечение возбуж-
дения перехода 2s — 3s в литиеподоб-
ном ионе О VI. 7 — борн-кулоновское
приближение; 2 — сечение с учетом
резонансов.
когда имеются вышележащие
уровни ас, для которых сече-
ние сгава велико. Например,
для перехода Is22s — ls23s в
ионе О VI (и любом ионе [Li])
при малых энергиях очень
велика роль закрытых кана-
лов пр (п > 3). Правда, с ро-
стом п ветвление в пользу
уровня 3s уменьшается. Се-
чение этого перехода с уче-
том резонансного вклада по-
казано на рис. 9.
Следует тем не менее под-
черкнуть, что резонансный
вклад оказывается существен-
ным лишь в тех случаях, ко-
гда потенциальное сечение
apot по тем или иным причи-
нам мало.
В заключение отметим,
что резонансное рассеяние
тесно связано с диэлектронной
рекомбинацией, рассмотренной в § 15. Фактически эти два про-
цесса являются альтернативными конечными каналами, сопро-
вождающими захват электрона на квазистационарное состояние:
(<*>*) +
Xt (®о) 4~ с Xz-i (gcmX)
Xz-i\arik) +
При этом среди каналов резонансного рассеяния есть канал
упругого рассеяния (а — а0) и различные неупругие каналы
(а' =#= а0).
§ 10. Переходы между высоковозбужденными уровнями
1. Борновское приближение. Для переходов между высоковоз-
бужденными уровнями п0, наибольший интерес представ-
ляют сечения, усредненные по Zo, и просуммированные по I, т.
В кулоновских единицах, с единицей расстояния a0/z и единицей
§ 10. ПЕРЕХОДЫ МЕЖДУ ВЫСОКОВОЗБУЖДЕПНЫМИ УРОВНЯМИ 79
энергии z2Ry,
2 fro—J-A
_ 8 Г . й
a"*n " 2* И2Й2 J ' W ?3 >
0 0 ко—к
/(?)= S | OoZoWo I eiqr I nlmy |2.
(10.1)
(10.2)
Для небольших n0, n суммирование в (10.2) обычно выполняют
численно. При больших п0, п такой путь становится слишком
трудоемким. В случае атома водорода, однако, суммирование в
(10.2) удается выполнить в общем виде (181. Кроме того, для п0,
п '>> 1 и п0, | п0 — п| возможны дальнейшие упрощения вы-
ражения для борцовских сечений. Полученные таким образом фор-
мулы для аПвП применимы и для переходов между сильновозбуж-
денными уровнями любых атомов и ионов, так как такие уровни
всегда водородоподобны.
Запишем (10.2) в следующем виде:
- lim (F - F \(F - F \ V <«" 1^ I
Z“ eJX (£° £n#) Fn) 2-1 (E0-En,)(E-En.) •
E-E** a'’a" (10.3)
-где a = n'l'm', a" = п"Гтп. Нетрудно видеть, что добавленные
в сумму (10.3) члены с п' п0, п" #= п после предельного перехода
Ео -> Ent, Е -> Еп обращаются в нуль. Используя далее извест-
ное спектральное представление функции Грина
Ge (г, г') -
а
Е — Е
и
(10.4)
получаем
/ (q) = lim (Ео — Еп,) (Е — Еп) f f GEt (г, г') X
Ег+ЕПл J J
E^En
X (r~r')GE (г, г') dr dr'.
(10.5)
Функция Грина для кулоновского поля имеет вид [191
И [”Mv) . (10.6)
X = г + г + — г’\, у = Г-г г' — [r — г'[, V = 1/У — Е,
С _д_______д_
дх ду ’
где W и М — функция Уиттекера первого и второго рода. Ис-
пользуя (10.6), удается свести вычисление / (q) к интегралу
q
/(9) = у $ A(q')dq,
о
(Ю.7)
80 ГЛ. III. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СЕЧЕНИЙ
где функция А (q) выражается через гипергеометрические функции
F (а, а', 1; z) и их производные. Приведем окончательный резуль-
тат [181:
A(q) = 777ЙГКе^(— п<> + + 1) — п) —
— 4(—«о + 1, —п)Гк (— п0, — п 4- 1) —
— ге° + — п + — «)—А(—«» + 1, — и)х
Х7*(-По, -п + 1)]}, (10.8)
где
Л («о, «) = Х»’-*-»-1 (X — р0)-«« (А — p)~aF (а0, а, 1; z), (10.9)
1 11
Ь =-НРо + р + ч), Ро = —. Р =
lln fb
Формулы (10.7), (10.8) являются точными. При их выводе не де-
лались какие-либо упрощающие предположения.
Рассмотрим теперь переходы между сильновозбужденными
уровнями. Используя известные асимптотические выражения ги-
пергеометричских функций через функции Бесселя J, удается
значительно упростить формулу (10.8). Таким образом, при
п0 1, п 1, Ап = | п — п0 | и0, п
Л<’> = ¥ ех₽ Н’ж+д] + <10-10)
М«)» ~^--^^-Ап(Дп-е) /Ап(Дп-г), (10.11)
Ь2 (в) = Дп р f3 (1 + Jln (Ди- в) —
(10.12)
с- [1+«!(-зг)7/'- (1013)
При выводе формулы (10.10) введен поправочный множитель
ехр {(Дп)2/2 (п0 + п)}[1 4~ (Дп)2/4н0и]_2, выбранный таким обра-
зом, чтобы в пределе q —0 величина / (д) из (10.7) давала бы
известное классическое выражение для силы осциллятора перехода
п0 — п [201:
Ип1/ПоП(д') — Ио/пвп
9-»0
“[щ5тч]1длЛ”(Лп)/;”(Дп)- <1014)
Как известно, (10.14) обеспечивает достаточно хорошее прибли-
жение даже при небольших значениях п0, п. Поправочный множи-
§ 10. ПЕРЕХОДЫ МЕЖДУ ВЫСОКОВОЗБУЖДЕННЫМИ УРОВНЯМИ 81
тель в (10.10) существен именно для таких главных квантовых
чисел. При Дп/гс—>-0 он стремится к единице.
Естественно ожидать аналогичных результатов и для сечений.
В качестве иллюстрации на рис. 10 приводятся сечения пере-
ходов 2—3, 5—6 и 4—7, вычисленные по формулам (10.1), (10.7)
Рис. 10. Борновские сечения переходов между высоковозбужденными уров-
нями. 1 — численный расчет но точным формулам борновского приближения»
2 — расчет по формулам (10.10).
и (10.10), а также результаты численных расчетов по исходным
формулам (10.1), (10.2). Как видно, (10.10) дает вполне удовлет-
ворительное приближение.
82 ГЛ. III. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СЕЧЕНИЙ
Для ряда .значений п0 и Ап выполнены численные расчеты се-
чений по формулам (10.1), (10.7), (10.10). Для удобства интерпо-
ляции по п удобно выделить основную зависимость сечения от п0,
п в. явном виде: ’
2
(10-15)
о
В табл. 1 приведены значения функции
Таблица 1
Функция ^П|((Дл, й’ц) для определения борновского сечения перехода
п0 —’ п по формуле (10.15); Дл = л — л0
П,= 10 50 100
^>1Еп Ди = 1 2 4 1 2 4 1 2 4
0,20 „ 0,01
0,28 — — — 0,03 0,01 — 0,04 0,03 0,01
0,40 — — — 0,10 0,07 0,03 0,11 0,09 0,07
0,57 0,18 0,05 0,24 0,22 0,16 0,24 0,24 0,20
0,80 0,40 0,36 0,19 0,43 0,46 0,40 0,43 0,47 0,44
1,13 0,64 0,64 0,50 0,66 0,71 0,69 0,66 0,71 олз
1,60 0,90 0,86 0,70 0,90 0,92 0,91 0,91 0,93 0,95
2,26 1,16 1,05 0,84 1,16 1,11 1,06 1,16 1,12 1,10
3,20 1,42 1,21 0,94 1,42 1,28 1,17 1,42 1,29 1,21
4,53 1,68 1,37 1,03 1,69 1,44 1,27 1,69 1,45 1,48
9,05 2,21 1,66 1,18 2,22 1,74 1,44 2,22 1,75 1,48
1,81.10* 2,74 1,96 1,33 2,75 2,04 1,59 2,75 2,05 1,64
3,62-101 3,27 2,25 2,53 1,48 3,28 2,33 1,75 3,28 2,34 1,79
7,24-Ю1 3,80 1,63 3,81 2,63 1,90 3,81 2,63 1,95
1,45-10* 4,33 2,83 1,78 4,34 2,92 2,06 4,34 2,93 2,10
2,90-10* 4,86 3,11 1,92 4,87 3,21 2,21 4,88 3,22 2>
5,79-10* 5,38 3,40 2,07 5,40 3,50 2,37 5,40 3,51 2,42
1,16-10» 5,87 3,66 2,20 5,89 3,77 2,52 5,89 3,78 2,56
Хорошую аппроксимацию функции & дает следующая анали-
тическая формула:
=-ртЖг (1 - %£) In (1+/ ад +
;(1 - ® [4 + • <«>•«»
В пределе больших значений An (1 Ап п0, п) использование
выражения (10.16) приводит к известной классической формуле
Стаблера для сечения [21].
§ 10. ПЕРЕХОДЫ МЕЖДУ ВЫСОКОВОЗБУЖДЕННЫМИ УРОВНЯМИ 83
Усредненную по максвелловскому распределению скорость
перехода п0 — п удобно представить в виде, аналогичном (10.15):
« ^7^’ (-ФТ' Ф-(ДЛ-П- 00.17)
о
Значения функции Ф„о приведены в табл. 2.
Таблица 2
Функция Ф„в(Дп, Т) для определения скорости перехода п0~>п
в борцовском приближении по формуле (10.17); Дл = л — л0
п»= 10 50 100
1оо;ея/т Дп = 1 2 4 1 2 4 1 2 4
0,01 8,34 5,55 3,57 8,36 5,75 4,17 8,17 5,77 4,26
0,02 7,76 5,24 3,41 7,78 5,43 4,00 7,78 5,45 4,09
0,04 7,18 4,92 3,25 7,20 5,11 3,83 7,20 5,13 3,92
0,08 6,61 4,61 3,08 6,63 4,79 3,66 6,62 4,81 3,75
0,16 6,03 4,29 2,92 6,05 4,47 3,49 6,05 4,49 3,58
0,32 5,46 3,97 2,76 5,47 4,14 3,31 5,47 4,16 3,40
0,64 4,88 3,65 2,59 4,89 3,82 3,13 4,89 3,84 3,22
1,28 4,31 3,33 2,42 4,32 3,49 2,94 4,32 3,50 3,03
2,56 3,75 3,00 2,23 3,75 3,15 2,73 3,75 3,16 2,82
5,12 3,19 2,67 2,04 3,19 2,79 2,51 3,18 2,81 2,59
1,02-101 2,65 2,32 1,83 2,64 2,43 2,25 2,63 2,44 2,32
2,05-101 2,13 1,97 1,60 2,11 2,04 1,95 2,10 2,05 2,01
4,10.101 1,65 1,61 1,34 1,61 1,64 1,60 1,60 1,64 1,64
8,19-Ю1 1,22 1,25 1,07 1,16 1,23 1,22 1,15 1,22 1,24
1,64-10» 0,86 0,92 0,80 0,78 0,84 0,84 0,77 0,83 0,84
3,28-10» 0,57 0,63 0,56 0,48 0,52 0,52 0,46 0,50 0,50
6,55-10» 0,36 0,41 0,37 0,36 0,29 0,30 0,25 0,26 0,27
На основе (10.16) можно построить аппроксимационную фор-
мулу для функции ФПо:
+ (‘ ~ [4 + и - Хф W1}, (10.18)
где
ф(х) - In [1 + • 1 = Е^Т' 7 = **” = 1’78- (10Л9>
В заключение раздела отметим, что при небольших энергиях
борновское приближение, вообще говоря, нарушает нормировку
сечения. Нормированные сечения можно вычислить в квазиклас-
сическом приближении.
84 ГЛ. Ш. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СЕЧЕНИЙ
2. Переходы между высоковозбужденными уровнями в квази*
классическом приближении. При больших значениях главного
квантового числа п движение атомного электрона квазиклассично.
Воспользуемся этим обстоятельством и рассмотрим задачу вы-
числения вероятности перехода п0 — п в квазиклассическом
пределе h —> 0. Квазиклассическая теория неупругих столкнове-
ний может быть развита различными способами. Можно исходить
из волновых пакетов стационарных состояний, которые при И —>
—>• 0 переходят в классическую траекторию — метод когерентных
состояний Глаубера. Ниже мы будем основываться на несколько
ином подходе, позволяющем наиболее просто учесть эффект ис-
кажения движения атомного электрона в процессе столкновения.
Будем исходить из следующего представления атомных вол-
новых функций:
Т„^ехр(4-5П), (10.20)
где 8а — функция действия. Вероятность перехода а0 — а запи-
сывается в виде
= lim|<H'?,(0|4'.,(0>|s~
~lim <%хр |exp (-i-(10.21)
где индекс 0 соответствует невозмущенному атому. В квазиклас-
сическом пределе (Й. -> 0) ряд полезных результатов относительно
функции действия Sa можно получить, воспользовавшись клас-
сическим уравнением Гамильтона — Якоби. Такой подход был
развит в работе [22]. Ниже изложение будет основываться на этой
работе х).
Запишем функцию Sa’ (0 в виде (0 = S<°> (0 + A.S (0,
где A<S[(i) — приращение функции действия в результате столкно-
вения. При t->- —оо Д5 —> 0. Для дальнейшего удобно вос-
пользоваться канонически сопряженными переменными действия
Ij и сопряженными им фазовыми переменными и/ область изме-
нения н;:0^ну-^2л. В этих переменных функция действия
невозмущенного атомного электрона [24]
= (10.22)
j
причем из условий квантования Бора следует
Ц = nh, 12 = lh, 13 — mh, (10.23)
1) Несколько иной подход, приводящий практически к тем же резуль-
татам, которые будут изложены ниже, разрабатывался авторами [23].
В этой же работе дан подробный обзор классических методов расчета сечений.
§ 10. ПЕРЕХОДЫ МЕЖДУ ВЫСОКОВОЗБУЖДЕННЫМИ УРОВНЯМИ 85
где п, I, т — главное, орбитальное и магнитное квантовые числа;
а = nlm. Используя (10.22), (10.23), получаем
We<a = lim|
(—►ос I
2Л 2Я 2Л
( Л1Л<2<газехр[-4-(5?’-5£,) + 4д5]|! =
ООО
= lim
i->eo
2Л
О
du exp
— iku 4- 4-AS
Л
(10.24)
где и — вектор с компонентами и2, и3; к — вектор с компо-
нентами Ан — п — п0, kl = I — 10, кт = т — т0. Множитель
(2л)-3 возникает вследствие нормировки волновой функции.
Нетрудно видеть, что формула (10.24) независимо от конкрет-
ного вида AS удовлетворяет условию унитарности. Поскольку
суммирование по конечным состояниям а эквивалентно суммиро-
ванию по к, имеем
2Л
Г ? 6 (w — и) ехр Г-j- AS (u) — AS (w')l du du' = 1.
a о
Воспользуемся теперь для вычисления AS классическим уравне-
нием Гамильтона — Якоби
dS . „ГПч/ dS\ , „ ( 3S \ п
"аГ + й(’’(“* а^) + v (“S’ 57 “ °’
(10.25)
где V (iij, I] = dSIdiij, t) — возмущение, создаваемое внешней
частицей. В 1-м порядке классической теории возмущения, при
AS S<°>, из (10.25) можно получить следующее приближенное
уравнение для AS:
Z-AS-^AS.-F
Uj,
^7’ /
(10.26)
В этом уравнении использовано то обстоятельство, что для куло-
новского поля Eat = Епл и Я<°> зависит только от ulf причем
дН^/ОЦ = ®п , где юПо = 2z2Ry/n^ — классическая частота дви-
жения электрона по орбите с энергией Еп . В член V (uj, dS/duj, t)
подставлены невозмущенные производные д8^/ди}.
Правая часть уравнения (10.26) может быть представлена в
виде разложения в ряд Фурье:
v = и (0 exp [i (gjUj + q2u2 + qsu9)] = 3 V4 (*) exP (^w)»
9 (10.27)
86 ГЛ. Ш. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СЕЧЕНИЙ
где величины д1гд2, д3 — целые числа. Используя (10.27),’решение
уравнения (10.26) можно записать следующим образом:
(t) = (t) exp (iqu + iqtf^t),
4 (10.28)
t
c«(C= J ^«(Cexp(~iqitonj'jdt'.
---------00
Таким образом,
ЗЯ
Wa<a = | exp — iku + 4~ У, 'cggiqM ] du (10.29)
о «
где
oo
c«^ce(“°°)= f 7g(f)exp( — iq^^dt. (10.30)
Формулы (10.29) и (10.30) позволяют вычислить вероятность
перехода а0 — а в квазиклассическом пределе в рамках класси-
ческой теории возмущений.
Необходимо подчеркнуть, что условие применимости-'формулы
(10.29) AS S<°> существенно отличается от условия применимо-
сти квантовой теории возмущений AS К. Действительно, из
(10.22), (10.23) следует, что Sa> ~ nh^>h при больших п. Поэ-
тому область применимости (10.29) AS nh значительно шире,
нежели AS Й. Формулу для И7^, соответствующую 1-му по-
рядку квантовой теории возмущений, получаем из (10.29), полагая
ехр Г 4- AS1 » 1 + 4-
L J п
оо
W7^ = -r|cfc|a = jj rfc(i)et(n-ne)w^di|2. (10.31)
В отличие от (10.31) формула (10.29) содержит сумму по q,
которая отражает вклад переходов через виртуальные уровни
а0 — а' — а и т. п.
Последовательный квазиклассический расчет сечения подфор-
мулам (10.29), (10.30) подразумевает использование фурье-раз-
/ \
ложения классического потенциала V (и;, , ^.Использование
классической механики требует чрезвычайно громоздких вычис-
лений (см. (231), практически исключающих возможность прове-
дения конкретных расчетов. Известно, с другой стороны, что в
квазиклассическом пределе квантовый матричный элемент воз-
мущения V (t) совпадает с компонентой Фурье Vk (t) (kt = п — nQ,
к2 ~ I — 10, к3 = т — пг0):
<n0Z07n0 [ V (/) | nlm> = Vk (t). (10.32)
§ 10. ПЕРЕХОДЫ МЕЖДУ ВЫСОКОВОЗБУЖДЕННЫМИ УРОВНЯМИ 87
При этом (10.31) совпадает с приближением 1~го порядка кванто-
вой теории возмущений для вероятности перехода п010т0 — nlm
под действием зависящего от времени потенциала V (i). Соотно-
шение (10.32) позволяет воспользоваться для вычисления прира-
щения действия и вероятности перехода квантовомеха-
ническим выражением для Vq, что оказывается значительно про-
ще, чем чисто классический расчет. При этом сумма по q =
= (<h, ?з) соответствует учету переходов через виртуальные уров-
ни, qx — п — n0, g2 = V — l0, q3 = т — т0.
Для вычисления вероятности перехода п0 — п необходимо
выполнить усреднение по 1йтй и суммирование по 1т\
= 2_| (1О-33)
0 n»o, I, т
Для квазиклассической вероятности (10.29) это эквивалентно сум-
мированию по к2 — I — 10, к3 — т — т0 и усреднению по 10т0.
Вычисление усредненной вероятности Wn<>n оказывается весьма
несложным, если распространить суммирование по к2, к3 на бес-
конечный интервал от —оо до -f-oo, предполагая, что Д5 не за-
висит от us и и3. Далее, используя усредненные величины не
зависящие от угловых моментов q2 = Г — 10 и q3 — т' — т0,
выражение для можно записать в виде
2Л
Ww = 14Д ехр Г— i (п — п0) и + V cqei(?ul |2 du. (10.34)
I ZlJl V L ” I I
О Ч
Здесь введены обозначения и = иг, q = qt. Процедуру усредне-
ния cq удобно ввести следующим образом:
— Сп*, n<r±q — л / I Т о+Ч, im |2i (10.35)
Г О т
оо
Cnjw, мч. Im = J <n0Z0Wo I V (£)1 По + q, 1т> е~№ dt.
— Оо
При таком определении с4 в 1-м порядке квантовой теории возму-
щений получается точное выражение для вероятности перехода
W1.
Задавая V (t) как функцию прицельного параметра р для се-
чения перехода п0 — п, имеем
оо
оп,п = 2л J Wntn (р, V) р dp. (10.36)
о
При использовании для вероятности Wnvn формулы (10.34) авто-
матически будет выполнена «нормировка» сечения.
88
ГЛ. III. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЙ СЕЧЕНИЙ
3. Переходы с Дп = 1. Если в формуле (10.34) ограничиться
учетом лишь членов с q = ±1, полагая с+1 = c_t = е15 то уда-
ется получить аналитическое выражение для вероятности пере-
хода W^n {25]:
1Уп.п=|/ап (4С1)|2’ (Ю.37)
где — функция Бесселя, Дп — | п — п0 [.
Для описания потенциала V (i) воспользуемся дипольным
приближением
Г=-^-. (10.38а)
Для того чтобы устранить полюс в потенциале, удобно определить
JR соотношением
+ f (/FFpj-p)- (Ю.386)
Здесь г — радиус-вектор внешнего электрона, d — дипольный
момент атома, р — вектор прицельного параметра р, перпенди-
кулярный скорости электрона v и лежащий в плоскости столкно-
вения. Параметр р0 ~ n2aQlz введен для устранения расходи-
мости при малых р. Его величину удобно подобрать таким об-
разом, чтобы сечение, вычисленное в 1-м порядке теории возму-
щений, совпадало с его квантовым борновским значением.
В области энергий внешнего электрона Е Епл как в случае
атомов, так и в случае ионов можно использовать приближение
прямолинейной траектории:
г (0 = р + vt. (10.39)
Используя (10.38) и (10.39) и определив <оПо в формуле (10.35)
симметричным соотношением:
П^-п0) = Еп-ЕПа, (10.40)
j
получим
с» = 4 (—V —— £ (₽), (10.41)
4 Xmvl <?4(pJ + ?2)
f G$
an n = r~l T — ’ q = Дп’ (10.42)
5 (₽) = ₽‘U5 (₽) + K? (₽)!. (10.43)
Д " «‘Sy тЛр1 . „1
P q (non)« hv V !o TP •
Здесь -Ko(P) и ^((3) — модифицированные функции Бесселя
(функции Макдональда), }П<)П — сила осциллятора перехода
§ 10. ПЕРЕХОДЫ МЕЖДУ ВЫСОКОВОЗБУЖДЕННЫМИ УРОВНЯМИ 89
п0 -> п. В приближении Крамерса для /П4п
о,*» 1,40 7 -Уд- •
(«о 4- п)2 г
(10.44)
Более точный расчет по формуле (10.14) в случае п = п0 ± 1 дает
значение численного коэффициента в (10.44), равное 1.31. Функция
Рис. 11. Сечения переходов между высоковозбужденными уровнями с An = 1
в квазиклассическом приближении. 1 — 1-й порядок квантовой теории воз-
мущений; расчет по квазиклассическим формулам (10.36), (10.38), (10.41):
2 — z = 1, 3 — z ~ i, 4 — 2 — 8.
| (0) с точностью не хуже 10% аппроксимируется простой фор-
мулой
В (Р) « (1+ лр)е-2Р. (10.45)
Формула (10.37) и дипольное приближение пригодны лишь для
переходов с Дп = 1. В случае Дп >> 1 выражение (10.37) учиты-
вает переходы через виртуальные уровни п0 —> п0 + 1 ->n0-j-
4- 2 . . . -> п, однако не учитывает прямые переходы п0 —> п и
поэтому не обеспечивает правильную асимптотику сечения при боль-
ших энергиях. Кроме того, в случае Дп >> 1 в области небольших
энергий внешнего электрона E<^z2 Ry в потенциале необходи-
мо учитывать высшие мультиполи [26]. Отметим, что для гармони-
ческого осциллятора формула (10.37) при п —>• оо является асимп-
тотически ^точной.
В случае Дп = 1 дипольное приближение (10.38) дает хорошие
результаты. Сравнение квазиклассических сечений переходов
10—11 и 100—101 для атома водорода и водородоподобных
90 ГЛ. III. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СЕЧЕНИЙ
ионов, вычисленных по формулам (10.36), (10.37), (10.41), с кван-
товым борновским сечением приведено на рис. 11. В области %
Ry борновское приближение дает сильно завышенную величи-
ну сечения. Это объясняется тем, что в области малых значений
йрицельного параметра р вероятность 1-го порядка теории воз-
мущений (10.31) оказывается много больше единицы. При ис-
пользовании формулы (10.37) максимальное значение И^р) ж 0,3.
В области больших энергий электрона результаты квазикласси-
ческих расчетов совпадают с квантовыми борновскими сечениями.
Таблица 3
Функция ^п<(^0) Для определения квазиклассического сечения переходов
по —’ ло + 1 в нейтральном водороде но формуле (10.15)
аъ/ву п.= 10 20 30 40 50 100 150 200 250
0,01 0,016 0,049 0,090 0,139 0,186 0,414 0,617 0,791 0,942
0,02 0,052 0,144 0,233 0,324 0,413 0,790 1,07 1,29 1,47
0,04 0,138 0,325 0,500 0,655 0,791 1,29 1,61 1,85 2,03
0,08 0,338 0,664 0,921 1,13 1,30 1,85 2,19 2,42 2,60
0,16 0,670 1,13 1,44 1,67 1,85 2,42 2,75 2,98 3,16
0,32 1,14 1,68 2,00 2,24 2,42 2,98 3,30 3,53 3,70
0,64 1,66 2,21 2,54 2,77 2,95 3,50 3,82 4,04 4,21
1,28 2,12 2,67 3,00 3,22 3,40 3,94 4,25 4,48 4,65
2,56 2,51 3,06 3,37 3,60 3,77 4,31 4,62 4,84 5,02
5,12 2,85 3,39 3,70 3,92 4,10 4,63 4,94 5,17 5,34
10,24 3,15 3,69 4,00 4,22 4,40 4,93 5,24 5,42 5,63
Таблица 4
функция ^По(^о) для определения квазиклассического сечения переходов
л0—в водородоподобных ионах по формуле (10.15)
п. = 10 50 100
z 2 4 ОО 2 4 ОО 2 4 8 ОО
0,01 0,06 0,14 0,41 0,41 0,79 1,65 0,79 1,29 1,81 2,22
0,02 0,15 0,33 0,65 0,79 1,29 1,94 1,29 1,85 2,28 2,52
0,04 0,33 0,64 0,92 1,29 1,82 2,23 1,85 2,38 2,67 2,79
0,08 0,67 1,01 1,21 1,85 2,28 2,52 2,42 2,84 3,01 3,07
0,16 1,11 1,38 1,50 2,39 2,67 2,80 2,95 3,22 3,31 3,34
0,32 1,56 1,72 1,79 2,85 3,01 3,07 3,39 3,55 3,60 3,61
0,64 1,95 2,04 2,07 3,23 3,31 3,34 3,77 3,85 3,88 3,88
1,28 2,29 2,34 2,36 3,56 3,60 3,62 4,09 4,14 4,15 4,15
2,56 2,60 2,53 2,64 3,86 3,88 3,89 4,39 4,41 4,42 4,42
5,12 2,89 2,91 2,91 4,14 4,15 4,16 4,68 4,69 4,69 4,69
10,24 3,18 3,18 4,42 4,42 4,42 4,95 4,96 4,96 4,96 4,96
§ 10. ПЕРЕХОДЫ МЕЖДУ ВЫСОКОВОЗСУЖДЕННЫМИ УРОВНЯМИ 91
Таблица 5
Функция Ф„о(7 ) для определения скорости возбуждения переходов
п0 —* ло + 1 нейтрального водорода в квазиклассическом приближении
по формуле (10.17)
T/Ry п0 = 10 20 30 40 50 100 150 200 250
0,01 0,052 0,130 0,21 0,30 0,37 0,78 1,09 1,34 1,56
0,02 0,12 0,29 0,46 0,62 0,76 1,35 1,75 2,14 2,42
0,04 0,29 0,61 0,89 1,13 1,35 2,15 2,69 3,10 3,43
0,08 0,62 1,14 1,54 1,87 2,14 3,11 3,72 4,17 4,53
0,16 1,15 1,87 2,38 2,78 3,10 4,17 4,93 5,30 5,67
0,32 1,87 2,77 3,36 3,80 4,15 5,28 5,94 6,42 6,79
0,64 2,72 3,75 4,38 4,85 5,21 6,35 7,02 7,49 7,85
1,28 3,62 4,71 5,37 5,84 6,20 7,34 8,00 8,46 8,83
Таблица 6
Функция ФПо(Т) для определения скорости переходов п0 —> n0 -f- 1 для
водородоподобных ионов (z > 1) в квазиклассическом приближении
по формуле (10.17)
п0= 10 50 100
T/z’Ry z = 2 4 ОО 2 4 ОО 2 4 8 СО
0,01 0,14 0,30 0,69 0,77 1,34 2,37 1,34 2,03 2,68 3,13
0,02 0,31 0,60 1,08 1,36 2,11 3,22 2,14 3,01 3,72 4,17
0,04 0,62 1,06 1,56 2,14 3,01 3,99 3,10 4,04 4,68 5,05
0,08 1,13 1,64 2,09 3,08 3,92 4,70 4,15 5,03 5,55 5,81
0,16 1,80 2,31 2,67 4,08 4,80 5,35 5,20 5,94 6,31 6,49
0,32 2,57 3,00 3,26 5,06 5,60 5,93 6,19 6,74 6,97 7,06
0,64 3,36 3,69 3,85 5,95 6,32 6,50 7,08 7,45 7,58 7,63
1,28 4,13 4,35 4,44 6,75 6,98 7,07 7,87 8,10 8,17 8,19
Результаты численных расчетов сечений переходов с Дп = 1
по формулам (10.36), (10.37), (10.41) для атома водорода и водо-
родоподобных ионов приведены в табл. 3 и 4. Аналогичные ре-
зультаты для усредненной по максвелловскому распределению
скорости даны в табл. 5 и 6. Подобно табл. 1 и 2 для
борновских сечений в табл. 3—6 приведены значения функций
?п, ($о) и Фпо (Л’ Сечение <т и скорость <гсг> определяются фор-
мулами (10.15), (10.17).
Отметим, что в кулоновских единицах cq ео 1/z. Поэтому при
z 1 эффект нормировки практически не играет роли и вычис-
ленные сечения приближаются к их борновским значениям.
ГЛАВА IV
СТОЛКНОВЕНИЯ ТЯЖЕЛЫХ ЧАСТИЦ
В этой главе, как правило, вместо атомной системы единиц
используется система единиц СГС.
§ 11. Метод параметра удара
1. Общие формулы. Столкновение атомов с тяжелыми части-
цами (атомами, ионами и т. п.) в широком интервале скоростей
можно описывать квазиклассически, считая расстояние R между
центрами инерции сталкивающихся частиц заданной функцией
времени. В простейшем случае прямолинейной траектории Ц —
= р + vt. При таком подходе эффективное сечение перехода си-
стемы из одного состояния в другое определяется формулой
оо
о (п) = 2л j W (р, v) р dp, (11.1)
о
где W (р, и) — вероятность перехода при столкновении с прицель-
ным параметром р и относительной скоростью V. Вычисление
вероятности перехода W (р, v) сводится к решению системы урав-
нений нестационарной теории возмущений, которую запишем в виде
(Ц-2)
Ц'Я' ” \ I
т
где х = vt', Ныкт = &Ект — разность невозмущенных уровней
энергии; = Ukm — матричные элементы взаимодействия,
зависящие, как от параметров, от р и v\ X — константа, характе-
ризующая величину взаимодействия.
Для вычисления вероятности перехода 0—1 нужно найти реше-
ние системы (11.2), удовлетворяющее начальным условиям
ак (— °°) = 6о,л- (И-З)
Искомая вероятность равна
= 1^(00)12. (11.4)
Матрица эрмитова. Поэтому амплитуды состояний ак и
вероятности переходов удовлетворяют условиям нормировки
3iv«=i. (И-5)
к к
§И. МЕТОД ПАРАМЕТРА УДАРА
93
Интегрируя систему (11.2) в 1-м порядке теории возмущений,
т. е. полагая в правой части ат (х) = 60, т, нетрудно получить
квазиклассическую формулу борновского приближения:
оо
= jj Ию (z) ехр (i-^2- (11.6)
—со
В ряде случаев приближение (11.6) оказывается совершенно
непригодным. Это приближение не удовлетворяет, вообще говоря,
условию нормировки (11.5), из-за чего И/Б может превысить еди-
ницу, что противоречит физическому смыслу этой величины.
Приближение (11.6) часто дает неверные (обычно завышенные)
результаты и при И7Б 1 в области малых скоростей. Это связано
с тем, что при решении системы (11.2) методом последовательных
приближений фактически используется разложение в ряд по па-
раметру Х/у, который может быть отнюдь не мал. Все эти дефекты
присущи, вообще говоря, и борновскому приближению для столк-
новений атомов с электронами. Однако в случае тяжелых частиц
тепловые скорости частиц намного меньше, и фактически погреш-
ность борновского приближения оказывается гораздо больше,
чем при столкновениях с электронами. Поэтому возникает необ-
ходимость решения системы (11.2), не прибегая к разложению по
параметру A/v.
Ниже мы будем рассматривать лишь такие случаи, когда
основной вклад в вероятность перехода дает взаимодействие на срав-
нительно больших расстояниях, превышающих атомные размеры.
При этом сечения в максимуме порядка и больше атомных разме-
ров. Для исследования свойств решения (11.2) мы ограничимся
рассмотрением системы из двух уравнений, что аналогично при-
ближению сильной связи двух состояний в общей теории неупру-
гих столкновений. Уже в этом приближении представляется воз-
можным установить ряд общих особенностей процесса, не описы-
ваемых 1-м порядком теории возмущений (11.6).
Решению системы двух уравнений (11.2) посвящено большое
число работ, основанных на двух дополняющих друг друга под-
ходах. Первый из них, начатый известной моделью Зинера — Ро-
зена, связан с использованием в качестве потенциалов V в (11.2)
таких элементарных функций, с которыми система из двух урав-
нений интегрируется точно. К настоящему времени исследована
совокупность таких моделей [27, 28].
Эти модели не описывают, однако, многих типов взаимодей-
ствий, встречающихся на практике. В частности, не существует
каких-либо модельных точных решений для мультипольных по-
тенциалов V оо R~n. В практических расчетах матричные элемен-
ты могут иметь весьма сложный аналитический вид или
могут быть получены в результате численного интегрирования.
94
гл. iv. столкновения тяжелых частиц
Поэтому представляет интерес и другой подход, основанный на
приближенном решении системы двух уравнений (11.2) при произ-
вольном виде коэффициентов. При этом оказывается возможным
получить результат, правильно описывающий оба предельных
случая Х/у -> 0, Х/у-> оо. Сравнение с имеющимися точными ре-
шениями показывает, что это приближение достаточно хорошо
описывает и промежуточную область 1/у ~ 1.
2. Приближение двух состояний 1). Рассмотрим переход 0—1
и сохраним в системе (11.2) лишь два уравнения, соответствующие
состояниям 0,1. Введем обозначения
=-LyM „ Ц. и»,
где V — действительная величина. Сделав замену переменных
а0 — Ьо ехр [— -г((р’+4гх)] » а1 = Ь1вх₽ +
получим систему двух уравнений:
(11.8)
с начальными условиями
Ьо (х) = ехр [ iх], bi(x) — 0 при —оо. (11.9)
Очевидно, вероятность перехода 0—1 W = | &i(oo) |2.
Для нахождения приближенного решения воспользуемся
асимптотическими методами теории дифференциальных уравне-
ний, которые позволяют надежно оценить фазы функций Ь0(х),
bi(x) в области малых скоростей. Значение этих фаз оказывается
достаточным для вычисления вероятности перехода, поскольку
в том случае, когда матрица коэффициентов эрмитова, модули
функций Ь0(х) и Ь^х) можно выразить через разность фаз этих
функций.
Преобразуем уравнения (11.8), введя функцию 2)
к (х) = р (х) ехр (i(й (х) - я/2]} - «<“(«>, (11.10)
X
а(а-) = Ja'(zi)djci = ах(л:) —Оо(х),
о (11.11)
а = «1 (я) — ао (х), ai,0 (х) = ± Vьо (х).
х) Дальнейшее наложение в этом параграфе основано на работе [29].
2) Функция К (х) является квазикласспческим аналогом ^-матрицы.
§11. МЕТОД ПАРАМЕТРА УДАРА
95
Здесь предполагается, что V (ж) — четная функция. Обобщение
на случай нечетных функций V (ж) будет дано ниже. Подставляя
(11.10) в (11.8), можно получить уравнение для функции К (х)
(уравнение Риккати) и следующую систему уравнений для ве-
щественных функций ц (ж) и Й (ж):
- - V v Wain l«(X) — О (*)] .
. . И (11.12)
-rfT = V v № cos 1а ~ Q ~
Система уравнений (11.12), очевидно, ничуть не проще системы
(11.8). Однако она обладает тем преимуществом, что позволяет
найти связь между функциями р (ж) и Й (ж) и выразить К (ж),
а также Ь0(х) и Ьг(ж) только через фазу Й (ж):
X
К (ж) — i tg V (ж') cos [а (ж') — О (ж')] е10<х\ (11.13)
—со
6о (®) =
X
= cos V (ж') cos [а (ж') — й (ж')] йж'| ехр {— i [a0 (ж) + »
(11.14)
bi (х) =
X
= i sin V (ж') cos [а (ж')— й (ж')] <2ж'} ех'р i Гах (ж) — 1|.
Фаза Й (ж) имеет простой физический смысл: ею определяется по-
правка к разности фаз величин Ьх(ж) и Ь0(х) за счет потенциала
V (ж). В соответствии с (11.10)
IМЛ) |а = i У | (].) |3 > I bo (ж) [2 = t + | Х |3 • (11.15)
Таким образом, независимо от приближения, используемого при
вычислении К (х), удовлетворяются условия нормировки (11.5).
Это видно и непосредственно из (11.14)—при любом виде функции
Q (ж) имеет место соотношение | b^x) |2 + I b0(x) |2 = 1.
Приближение Борна (11.6) получается из (11.14) при малых
Х/и, если в борновском пределе й (ж) —0.
В противоположном предельном случае малых скоростей (адиа-
батическое приближение) й (ж) можно найти из (11.10); решив
уравнения (11.8) для постоянных V и перейдя затем к квазиста-
ционарному случаю. В результате получаем
X ___________________________
dxv (11.16)
о
96
ГЛ. IV. СТОЛКНОВЕНИЯ ТЯЖЕЛЫХ ЧАСТИЦ
Используя асимптотические методы теории дифференциальных
уравнений, можно показать, что при Х/р > 1 с хорошей степенью
точности (см. 130])
^o,i (х) = /o,i X
X „__________________________________________
f, -Ст /7 ь т/V । 1 d Г 1 dV -г- • Я 1Г1 dV -т- • 'Гл !
хехр к)+ -Jd—LiT^+>0 J-т[г&;+ ,а J dx,±
1 о
±-£}, (11.17)
где /0, Д — некоторые вещественные функции. Отсюда следует
И, -l//?- tz\2 , 1 d 1 dV , • '1 1 Г1 dV , . ,12
а — I/ — 7) + --ттг- -На —
V \ v / 1 2 dii [ V dxt J 4 L V 1 J
0
- VTM’ +1А 1 - * [1 - fa-]n(11.18)
r \ v ] 1 2 dXi LdXi J 4 [V dXi J J ' '
Эта формула получена в предположении, что функция V (х)—чет-
ная. Если V (х) — нечетная функция, то к правой части (11.18)
следует прибавить л/2. При этом формулы (11.13), (11.14) сохра-
няют свой вид.
В предельном случае ——> <х> формула (11.18) переходит в
(11.16). В другом предельном случае больших скоростей (область
применимости борновского приближения), как уже отмечалось,
фаза Й (х) должна стремиться к нулю. Оба выражения (11.18) и
(11.16) удовлетворяют этому условию: при р->оо а —> О, Й (х)~->
-> 0. Таким образом, хотя формулы (11.18), (11.16) справедливы
в противоположном предельном случае малых скоростей, подста-
вив й (х) из (11.18) или (11.16) в (11.14), мы получим правильный
результат и при к-> со. Более того, можно показать, что в той
области, где фаза Й (х) мала, Ьг(х) вообще не зависит от й (х).
Ограничиваясь приближением (11.16) для Й (х), получим
| Ь-l (оо) | = | sin V (х) cos j/"(а')2 + 4 Vdx^ dx | ==
= |sinZ|. (11.19)
Поскольку (sup означает верхнюю грань)
/<4 sup
J + (т- v}2 cos[$ р4<а')2 +4 (“гv)2dxi] dx
— sup
оо . _ .
sin j/”(а')2 4- 4 dx
о
§ И. МЕТОД ПАРАМЕТРА УДАРА
97
в выражении (11.19) можно заменить sin I на I. Отметим, что ошиб-
ка, вносимая подобным упрощением, противоположна по знаку
ошибке, связанной с заменой более точной фазы (11.18) на (11.16).
Итак, примем для вероятности перехода W следующую при-
ближенную формулу:
оо X 2
W = [A- jj У (я) cos jj (а')2 + 4 (4" F)2 dx' dx ’
—оо О
которую для объединения обоих случаев четных и нечетных V (х)
удобно записать в виде
Оо X ____________________
W = I 4" $ V (*) ехр {« $ у (а')2 + 4 V)* ^1} | ’ • Щ.20)
—оо О
В случае X | Vj — То | со можно положить
[, ОО Х1
1 f Р Г/Р г-------------------- 'I 2
W = ~ \ V (х)ехр \ ]Ло2 4- 4лТ (xj dxAdx . (11.21)
—оо о
Из сказанного выше следует, что формула (11.20) в обоих пре-
дельных случаях и —> 0 и v —> оо совпадает с точным значением
вероятности W. Рассмотрение ряда различных частных случаев
показывает, что эта формула дает хорошие результаты и в про-
межуточной области.
Для проверки приближения (11.20) полезно рассмотреть два
примера, для которых можно найти точное решение системы (11.8).
1. Прямоугольная яма: V (х) = 1 при | х | р0 и V (х) — 0
при | х 1 > р0; V\ — Fo = 0. Формула (11.20) дает
W - sin’ 1У• <и-22)
2. Случай точного резонанса: са — 0, V\ — Ро — 0. Формула
(11.20) дает
оо
W = sin2 [2- И (х) dx j .
--оо
(11.23)
Точное решение системы (11 8) в обоих случаях приводит к тем
же результатам.
Система (11.8) может быть решена точно и в случае V\ — Fo =
= 0; V = 1/ch (ух); для вероятности перехода имеет место вы-
ражение
иг=[сЬ^Га1п’(^-)' (11-24)
4 Л. А. Вайнштейн и др.
98
ГЛ. IV. СТОЛКНОВЕНИЯ ТЯЖЕЛЫХ ЧАСТИЦ
Можно показать, что выражение для вероятности перехода W,
полученное с помощью (11.20), при < 1 совпадает с (11.24),
а при когда (11.24) экспоненциально мало, отличается
от (11.24) не более чем предэкспопенциальным множителем ж 1/4.
С помощью формул (11.20), (11.21) можно получить ряд извест-
ных приближений теории столкновений тяжелых частиц. Так,
если |
Бейтсом
Если
сечения
W =
то (11.20) переходит в выражение, полученное
131].
основной вклад в вероятность перехода дает «точка пере-
термов» а'(^о) = 0, то оценка интеграла в (11.20) дает
26 при 6<^1,
const -e-c при 6^*1,
Г X -]2
2л [— 7(х)
claidx
. (11.25)
X—Хо
Это выражение при малых 6 совпадает с формулой Ландау —
Зинера, а при больших 6 отличается от нее лишь постоянным
предэкспоненциальным множителем порядка единицы. Можно
показать, что в промежуточной области 0,2 <1. 6 5 рассматри-
ваемый здесь метод приводит к отличию от формулы Ландау —
Зинера не более чем на 20%.
При решении ряда задач о возбуждении атомов общая формула
(11.20) применялась наряду с точным численным решением си-
стемы из двух уравнений. При этом показано, что для столкновения
двух атомов водорода, сопровождаемого возбуждением одного из
них в состояние 2/>или2$, эффективное сечение, вычисленное с по-
мощью (11.20), отличается от полученного при помощи численного
интегрирования уравнений не более чем на несколько процентов.
При возбуждении атомов заряженными частицами это отличие не
превосходит 30%.
§ 12. Переходы, вызываемые мультипольным взаимодействием
1. Решение в приближении двух состояний. Предположим, что
выполняется одно из двух условий
w>MV>-Vo I. Г„|, (12.1)
и примем для вероятности перехода выражение (11.21). Второе из
условий (12.1) может выполняться в тех случаях, когда матрич-
ный элемент V убывает с увеличением R медленнее, чем Vlt Ео,
и основной вклад в вероятность перехода дает взаимодействие на
больших расстояниях, значительно превышающих размеры атомов.
Приближение (12.1) представляет интерес для целого ряда
приложений таких, как передача энергии возбуждения при столк-
§ 12. МУЛЬТИПОЛЬНЫЕ ВЗАИМОДЕЙСТВИЯ
99
новении атомов с совпадающими или близкими уровнями, воз-
буждение при столкновении с ионом и т. п.
Матричный элемент V можно вычислить точно только в слу-
чае столкновений двух атомов водорода или столкновений атома
водорода с бесструктурной заряженной частицей. Нетрудно по-
казать, что при столкновении двух атомов водорода, в результате
которого в общем случае меняются состояния обоих атомов, мат-
ричный элемент V имеет вид
£ £. (12.2)
к =—п+1 к—— п+1
Здесь п определяется мультипольностыо рассматриваемого пере-
хода: если один из атомов переходит из состояния ai в состояние
a't, а второй из состояния а2 в состояние а2, причем между состоя-
ниями йр а'х и а2, а-i разрешены мультипольпые электрические
переходы порядка и х2, то п — хх + х2 4-1. Константы Ьх и Ь2
выражаются через потенциалы ионизации I (в единицах Ry) со-
стояний flj, а" и а2, а2 : by = У1 у VIу, b2 = 4- V Ц- Кон-
станты С\, Ск выражаются через квантовые числа рассматри-
ваемых состояний, причем Ск, Ск и X связаны таким образом, что
при R —> О V (/?) —const.
В случае столкновения произвольных атомов матричный эле-
мент V должен обладать теми же основными свойствами, что и
(12.2). Положим поэтому
»ЧЯ) = А--<г»7(Я). (12.3)
где функция / (7?) представляет собой многочлен того же типа,
что и в (12.2), и удовлетворяющий условию: V (R) -> const при
7? ->0. Траекторию сталкивающихся частиц будем считать по-
прежнему прямолинейной: R2 = р2 4- у2 Z2 = ра 4~ х2.
Подставим (12.3) в (11.21), заменим величину р^со2 + 4Х2У2
на со + 2ХУ, сохраняющую основные аналитические особенности
и предельные случаи и отличающуюся от нее не более чем множи-
телем У2, и перейдем к интегрированию по комплексной пере-
менной z:
W = Re-£- jj У (р2 4-z2) ехр [§2ХУ (p24-z'2)dz' +az]|dz. (12.4)
—оо О
Предположим далее, что основной вклад в вероятность перехо-
да дают расстояния R > Ro = 1/b, для которых ХУ ж \lRn.
Для пояснения характера дальнейших приближений положим
сначала п = 2 и используем при интегрировании контур, замкну-
4*
100
ГЛ. IV. СТОЛКНОВЕНИЯ ТЯЖЕЛЫХ ЧАСТИЦ
тый в верхней полуплоскости г, с разрезом вдоль мнимой оси от
гоо до ip. При вычислении интеграла монотонную вдоль мнимой
оси функцию ехр (i ~ zj вынесем за знак интеграла в точке z15
в которой производная показателя экспоненты обращается
в нуль J):
г, = I }/-£-+р!. (12.5)
В случае п 2 вычисления можно провести аналогичным обра-
зом. Отличие состоит лишь в том, что линии разреза не лежат
вдоль мнимой оси, а составляют с ней угол л (т ~ • При этом
Im21 = /2«“(A)«"si„S^ + p!.
(12.6)
В результате для вероятности перехода получаем формулу
PV-exp[—2|22/npnsin2~1 [sin3 —- \ V (р, х)dx , (12.7)
I I Aifh I J | с/ g! _J
—ОС
где
Pn = 4" ^2/n«2(n’1,/n> X = T • (12-* 8>
Формула (12.7), очевидно, справедлива, если точка z1 лежит
вне круга радиусом /?0:
(4гГ8иа £-+₽’>«»• <12-9»
Таким образом, для всех прицельных расстояний р, удовлетво-
ряющих этому условию, вероятность перехода W ограничена со-
отношением
W ехр
(12.10)
При достаточно
больших X и малых со, когда
2Х \1/п
ш )
л
Sin -75—
2п
>Яй,
(12.11)
формулы (12.7), (12.9) справедливы при любых р. Из этих фор-
мул видно, что при уменьшении скорости, когда |3n > 1, вероят-
ность перехода экспоненциально убывает. При со = 0 (точный
резонанс) формула (12.7) совпадает с полученной выше для этого
случая формулой (11.23).
Точка находится до замены to2 + 4X2V2 на величину <о 4- 2X7.
В противном случае показатель экспоненциального спада сечения может
значительно отличаться от правильного.
§ 12. МУЛЬТИПОЛЬНЫЕ ВЗАИМОДЕЙСТВИЯ
101
Перейдем теперь к вычислению лредэкспопенциалыюго мно-
жителя в (12.7). Подставив в интеграл по х полюсной потенциал
XV (р, х) = Z (р2 + х2)-”72, получим
оо
4- jj F(P, x)dx = an4-|>-(“-u. rf(^2))'2j- <12-12)
— оо
При
. / % XV("-V
Р<Ро = (а>‘—)
(12.13)
аргумент sin во втором сомножителе (12.7) становится больше
единицы и sin2[...] начинает быстро осциллировать около сред-
него значения 1/2. Если
!»=(«.. 4-) (12.14)
то замена потенциала (12.3) потенциалом KR~n не сказывается
существенным образом на величине сечения, так как такая за-
мена приводит лишь к изменению характера осцилляций sin2 [...]
в той области, где аргумент велик. Поэтому для скоростей у, удов-
летворяющих соотношению (12.14), при вычислении or можно вос-
пользоваться приближением (12.12). При этом
W = sin2 ехр {— 2 Г2ЙХ sin2^- + X2 Т'Ч . (12.15)
\ у** *• / | J J
Интересно сравнить выражение (12.15) с борновским прибли-
жением:
„ оп/2 2
) е-2х. (12.16)
%
При 1 (12.15) практически совпадает с (12.16) при всех р,
для которых №Б <. 1/2, а при меньших р осциллирует около сред-
него значения, близкого к 1/2. Поэтому при 1 можно огра-
ничиться борновским приближением, дополнив его каким-либо
рецептом нормировки, например, положив
W =
Х/2
при
при
WB(p) = 1/2.
(12.17)
При 1 (12.15), очевидно, значительно отличается от (12.16)
даже в той области р, где WE мало. Максимальное значение W
ограничено условием (12.10). Поэтому при pn />> 1 формулу бор-
новского приближения (12.16) нельзя использовать даже для
грубых оценок.
102
ГЛ. IV. СТОЛКНОВЕНИЯ ТЯЖЕЛЫХ ЧАСТИЦ
Подставляя (12.15) в (11.1), можно получить следующее вы-
ражение для эффективного сечения перехода:
а = 2л (4-)“”’” ехр {- 2|п+,,/" /₽„ sin -i-} 1„ (Р„), (12.18)
\ U / 1 ыИ J
ОО
X ехр (- 2 )/рпГ(22/n sin2 + ^(n~1)y2)‘/t - 21/п sin-£-l|у dy. (12.19)
I \ /Lit |
При Рп ->0
/2(Р2) ->л21п1/р2, /3(Рз)+я/2,
П-2 2 о г
п — 3
п — 1’
(12.20)
При рп >> 1
In (₽.) = i (2 /2jMin -i. +1) [Г =51.
(12.21)
Значения 7п(рп) для п = 2 и 3 приводятся в табл. 7, 8.
При малых скоростях, когда рп велико, сечение очень быстро
(экспоненциально) убывает при уменьшении v. Подобное поведе-
ние сечения в области малых скоростей типично для неупругих
столкновений тяжелых частиц. Исключением является случай
малых значений о>, когда и при малых скоростях возможны зна-
чения pn 1.
Таблица 7
Интеграл 72(р2, у2)
₽ 7 = 0 0,064 0,128 0,256 0,512 1,024 2,048
0,00 0,02 21,6 21,6 21,5 21,5 21,5 21,2 19,3
0,04 15,9 15,9 15,9 15,9 15,8 15,5 13,9 8,43
0,08 10,7 10,7 10,7 10,7 10,5 10,1
0,16 6,25 6,24 6,23 6,20 6,06 5,60 3,96
0,32 2,94 2,93 2,92 2,88 2,73 2,29 1,14
0,64 1,01 1,01 0,996 0,956 0,826 0,546 0,126
1,28 0,268 0,264 0,253 0,217 0,137 4,73-2 2,03-3
2,56 8,29—2 7,88—2 6,82-2 4,28-2 1,09—2 5,76-4 6,69-7
5,12 2,73-2 2,29—2 1,52—2 4,92-3 2,42-4 1,44-7 8,5-14
10,24 8,83—3 5,13-3 1,69—3 9,51-5 1,47-7 1—14
Обозначение: 8,83 —3=8,83. Ю-*.
§ 12. МУЛЬТИПОЛЬНЫЕ ВЗАИМОДЕЙСТВИЯ
103
Интеграл /3(ря, у3)
Таблица 8
§ 7 = 0 0,064 0,128 0,256 0,512 1,024 2,048
0,00 1,57 1,57 1,56 1,50 1,32 0,463
0,02 1,42 1,42 1,41 1,40 1,34 1,11 0,324
0,04 1,32 1,31 1,31 1,30 1,22 0,984 0,255
0,08 1,16 1,16 1,15 1,14 1,06 0,803 0,170
0,16 0,954 0,951 0,943 0,923 0,833 0,574 8,76—2
0,32 0,699 0,695 0,686 0,662 0,567 0,330 2,92—2
0,64 0,436 0,433 0,422 0,396 0,306 0,132 4,72-3
1,28 0,224 0,220 0,210 0,184 0,115 2,92-2 2,28-4
2,56 9,80-2 9,41-2 8,45-2 6,24-2 2,49-2 2,40-3 1,44—6
5,12 4,24—2 3,84—2 3,01-2 1,48-2 2,37-3 3,71-5 2,94-10
Обозначение: 4,73 —2=4,73-10~2.
Рассмотрим зависимость с от и при фиксированной скорос-
ти и. При (0=0 (точный резонанс) 0П = 0 и
а = 2л (V02/<n-^ /п(0). (12.22)
При (о (г?Х"’* 1 * * * V/")'‘/(п-1) сечение остается близким к (12.22), а при
(L,’X~1/n)"'(n"O экспоненциально убывает с увеличением со.
При больших скоростях, когда 0n 1, формула (12.18) дает
и^2, <т~
1 2 <12-23)
п 2, In (const-р).
Эта зависимость, очевидно, справедлива лишь, если X настолько
велико, а со настолько мало, чтобы могло быть малым при ско-
ростях, удовлетворяющих условию (12.14).
При больших скоростях, когда условие (12.14) нарушается,
приближение (12.15), основанное на полюсном потенциале, ста-
новится незаконным. Можно показать, что потенциал
XV (/?) _------h----— (12.24)
V ’ (А2 4-ра + x2)n/2 ' ’
и вообще любой потенциал, убывающий на больших расстояниях
быстрее, чем Я-2 и не имеющий полюса при Я —>0, приводит при
больших скоростях (т. е. в борновской области) к зависимости
V
(12.25)
104
ГЛ. IV. СТОЛКНОВЕНИЯ ТЯЖЕЛЫХ ЧАСТИЦ
Выражение для вероятности (12.15) при этом сохраняется, если
положить
х - -£-((<’ + св)*.
В выражении для сечения интеграл 1п (Рп) заменяется на
со
Ы₽». »«) = $ч>(а)й. (12.26)
1/0
где <р (у) есть подынтегральное выражение в (12.19);
1
г/. - v= R.(х)”'1 • (12.27)
При у0 1 в полном соответствии с (12.14) фактор 7п(рп, У о)
практически совпадает с 1п (рп), т. е. различие между потенциа-
лами (12.24) и XV = lkR~n несущественно. При увеличении ско-
рости (и фиксированном X) становятся существенными все мень-
шие расстояния. При у0 > 1 7П (рп, у0) в отличие от 7П (0П) не
стремится к постоянной величине. В этой (борновской) области
2
(12.28)
Следует отметить, что при малых X, когда (12.14) может на-
рушаться уже при малых у, наличие полюса у потенциала V (R)
приводит к значительному сдвигу максимума сечения в область
малых скоростей. Таким образом, область применимости формулы
(12.18) для сечения ограничена условиями (12.9), (12.14). Вторым
из этих условий определяется интервал, в котором справедливо
(12.17), а первое не зависит от скорости и удовлетворяется тем
лучше, чем больше X и меньше со.
Случай малых значений со соответствует столкновениям, со-
провождающимся квазирезонансной передачей энергии возбуж-
дения. Пусть в результате столкновения первый атом переходит
с уровня Ег на уровень Е1У а второй атом — с уровня Е2 на уро-
вень Е2, причем Ех Elf Е„ <. Е2. При этом
Йсо = + Е2 - Е[ - Е2. (12.29)
В случае столкновения одинаковых атомов при Ех — Е2, Ег ~ Е2
о = 0 (точный резонанс). При столкновении разных атомов
также возможны случаи, когда | Ег — Ег\ + \ Е2 — Ег |.
2. Приближения двух уровней и «вращающейся оси». Обсудим
теперь применимость двухуровневого приближения. Очевидно,
что оно пригодно для переходов между двумя невырожденными
§ 12. МУЛЬТИПОЛЬНЫЕ ВЗАИМОДЕЙСТВИЯ
105
изолированными уровнями (например, ns — n's). Если же хотя
бы один из уровней является вырожденным, задача становится
принципиально многоуровневой. Для сведения такой задачи к
двухуровневой требуется ряд дополнительных допущений.
Наиболее простым и физически наглядным приемом является
использование системы координат, в которой ось квантования
атома все время направлена на возмущающую частицу. В процессе
столкновения ось квантования при этом поворачивается на угол л.
Из соображений симметрии нетрудно показать, что во враща-
ющейся системе координат электростатическое взаимодействие
приводит к переходам лишь между компонентами с одним и тем
же значением магнитного квантового числа т (Дш = 0). Тогда
для мультипольных переходов типа ns — n'l' получаем двух-
уровневую систему, описывающую переход ns — ril'ni = 0.
Такое описание не является полным. Вращение междуядерной
оси приводит к переходам nlm — п'1'т' с Дпг = -4- 1. Это экви-
валентно внешнему возмущению с оператором вращения вида
ГФ = -ФДС, (12.30)
где Ф — угловая скорость вращения междуядерной оси, Lx —
оператор х-компоненты углового момента. Легко видеть, что
7'ф ' и. Поэтому при и ->0 вращением оси можно пренебречь,
и задача сводится к двухуровневой с Дт — 0. С увеличением
скорости выражение (12.30) растет, поэтому использование адиа-
батической системы координат (приближения «вращающейся оси»)
становится неадекватным. В частности, для возбуждения опти-
чески разрешенного перехода бесструктурной заряженной час-
тицей в борновской области приближение «вращающейся оси»
дает результат, в л2/4 раза меньший точного значения.
Мы уже отмечалй (см. формулы (12.22) — (12.28)), что полюс
потенциала также может привести к отличиям написанных выше
формул от точных значений в борновской области. В связи с этим
обстоятельством целесообразно при использовании этих формул
в борновской области выбирать параметр /?0 (12.24) таким
образом, чтобы численная величина сечения совпадала с борнов-
ской асимптотикой, которую можно получить в рамках обычной
теории возмущений.
Тем не менее часто приходится ограничиваться простым двух-
уровневым приближением для случая перехода aJ — a'J' между
вырожденными уровнями. При этом следует подставлять в урав-
нение усредненный потенциал
7^,^.= (12.31)
ММ'
где матричные элементы потенциала должны быть вычислены в
106
ГЛ. IV. СТОЛКНОВЕНИЯ ТЯЖЕЛЫХ ЧАСТИЦ
неподвижной системе координат. В этом случае полученное сече-
ние следует рассматривать как усредненное:
CW, а'у = у £ О (aJM, a'J'M'). (12.32)
ММ’
При этом можно убедиться, что при v ->0 в области макси-
мума сечения результаты, полученные с усредненным потенциа-
лом (12.31), количественно близки к результатам решения систе-
мы уравнений сильной связи в неподвижной системе координат.
Для возбуждения зарядом Ze оптически разрешенного пере-
хода XV ~ "klR2
<12-33)
где 5 — сила линии электрического дипольного перехода и g —
статистический вес.
Пусть в результате столкновения двух атомов первый пере-
ходит с уровня Jу на уровень Jx, а второй с уровня J2 на уровень
J2, причем между уровнями Ji и Ji возможны электрические муль-
типольные переходы порядка хх и х2. В этом случае
А е2 Г S., S., -]Чг
= «1 + Х2 + 1, т[(2х1 + 1)(2х# + 1)?1й] ’
(12.34)
где SK — силы линий электрических мультипольных переходов.
Сила линии в (12.33), (12.34) равна
оо
(21'4-1) (J о ''f|$P,(r)Pl-(r)r’- dr|’. (12.35)
* о
В заключение дадим оценку сечений квазирезонансной пере-
дачи энергии возбуждения при взаимодействии (12.34), (12.35).
Условие квазирезонансности означает, что параметр Месси
2 У21/п$п sin ~ = 2(w+1)/wV/%(W~1)/n sin ~ < 1.
гг* 2п v 2п
При ЭТОМ
ехр {- /fesill » 1, 7„ (₽„) = /„ (0).
В этом случае формулы (12.22), (12.34) дают для сечения следую-
щее выражение:
/ ,1 х2/(п-1») ( Sv S.,
ст = 2л (4-) k—, o----- 4(0). (12.36)
\ hv 1 l(2xi+1)(2xj+1) ^,1 >' v ’ 1
§ 12. МУЛЬТИПОЛЬНЫЕ ВЗАИМОДЕЙСТВИЯ
107
При у ~ 105 см/с e4hv ~ 2-103 (легко проверить, что условие
(12.14) выполняется с большим запасом), т. е. эффективные се-
чения резонансной передачи энергии возбуждения могут быть
очень велики (для диполь-дипольных переходов порядка Ю4Яо),
причем повышение мультипольности переходов приводит к не
очень большому уменьшению сечения.
3. Учет отталкивания ядер :). Предыдущее изложение велось
в предположении прямолинейности траектории относительного
движения. Это предположение не является обязательным и никак
не используется при выводе общей формулы (11.20). Очевидно,
что при произвольной траектории R (t) — R (р, р, t) выражение
для вероятности перехода должно иметь вид
оо t 2
W = f W (R («)) exp j У [а' (Я (r))]2 + 4V [И (/? (r))]2 dr} dt .
— 00
(12.37)
При возбуждении ионов протонами и другими ионами междуядер-
ное расстояние R и время t связаны известными для кулоновского
поля отталкивания соотношениями
t 4r(Esh£ + 0»
~ Mv* ’
R = a [8chC + 1],
(12.38)
Zn Z2 — заряды сталкивающихся ионов.
В практически важном случае
I - Л l<®> W =
(12.39)
интеграл (12.37) может быть вычислен аналитически. Для эффек-
тивного сечения перехода получаем выражение, аналогичное
(12.18):
1 _1) с y
0 = 2я(4-) ехр{-2<’*«/’,УК»«п-Й] /»(₽„,!>«). (12.40)
\ У / I J
где рп по-прежнему определяется (12.8), но 1п уже зависит от до-
полнительного параметра и равно
In (Pn. Yn)
=j’*»’ [17»+2)(-1>Д ех₽ {- -
- 2arclg~)l] du. (12.41)
A/t’ A \ у / J J
Дальнейшее изложение основано на работе [32].
108
ГЛ. IV. СТОЛКНОВЕНИЯ ТЯЖЕЛЫХ ЧАСТИЦ
, v . 1/(п-1)
где уп — Ь~1 а, причем ап определено (12.12), а последний член
в показателе экспоненты связан с кулоновским отталкиванием
и обращается в нуль при переходе к прямолинейной траектории:
а ->0, ае —>р.
Нетрудно видеть, что с ростом параметра уп фактор 1п (Рп, уп)
экспоненциально убывает:
А(₽«. V„>1. (12.42)
В противоположном предельном случае
In (₽„, 7„) -Л (М. V» < 1. (12.43)
Таким образом, при возбуждении ионов, наряду с эффектом силь-
ной связи, существенным при 1, присутствует и эффект ку-
лоновского отталкивания, экспоненциальный по параметру Рп2?п =
= ыа/v. Сказанное иллюстрируется табл. 7 и 8, где даны значения
Zn (рп, уп) с учетом кулоновского поля и в его отсутствие (уп = О,
In (Pn, Тп) — In (Рп)) Для практически важных случаев п = 2 и
п ~ 3.
§ 13. Процессы перезарядки
1. Специфика задачи перезарядки. Перезарядка при атомных
столкновениях, т. е. процесс типа
А + В + ->Л+ 4- В, (13.1)
в котором электрон переходит от атома А к иону В+, является
примером процесса с перераспределением частиц. Волновые
функции электрона в начальном состоянии Т (г а) и конечном
Ф(гв), где Та, г в — радиус-векторы электрона относительно ядер
А и В соответственно пеортогональны. Они относятся к двум раз-
личным полным наборам атомных функций. Кроме того, переход
электрона сопровождается переносом импульса mv, где у — от-
носительная скорость движения ядер, т — масса электрона,
что существенным образом сказывается при больших v.
Все это резко отличает процесс перезарядки от процессов воз-
буждения тяжелыми частицами, рассмотренных выше в § 11, 12,
При малых скоростях относительного движения ядер у уо> где
v0 = e2lh — атомная единица скорости, наиболее простое и адек-
ватное приближенное описание задачи перезарядки достигается
разложением волновой функции системы по волновым функциям
квазимолекулы. Такой подход оказывается весьма эффективным
для анализа резонансной и квазирезонансной перезарядки при
медленных столкновениях (см. 133]).
В пределе больших скоростей может быть испльзована обычная
теория возмущений. Это позволяет сравнительно просто устано-
5 13. ПРОЦЕССЫ ПЕРЕЗАРЯДКИ
109
вить закон убывания сечения при больших v — формула Бринк-
мана — Крамерса 134]:
о (v) ~ v~n, v v0 (13.2)
(подробнее см. формулу (13.40)). Столь быстрое убывание при
больших скоростях связано с тем, что сечение определяется сверт-
кой двух Фурье-образов волновых функций электрона у пер-
вого и второго атомов. Для описания области промежуточных
скоростей ниже будет использован тот же подход, что и в § 11, 12
в случае возбуждения тяжелыми частицами.
2. Резонансная перезарядка. Рассмотрим процесс перезарядки
при столкновении атома А в состоянии у с ионом того же атома
А (у) + А + -+А+ + А (у). (13.3)
Пусть для определенности состояние у есть состояние ns, а ион
А+ содержит только заполненныо'электронные оболочки. При
малых скоростях относительного движения систему A (ns) + А +
можно рассматривать как молекулярный ион При R ->оо
основное состояние такой системы двукратно вырождено: электрон
может быть локализован на любом из двух центров А+. Обозна-
чим соответствующие функции и 4%. При сближении ядер вы-
рождение снимается, так как имеет место расщепление на два
терма—четный V (2Sg) = Vg и нечетный V (2SU) = Vu. Волновые
функции адиабатического приближения для этих термов выра-
жаются через Tj и 4% следующим образом:
t
T,(0 = -^(4'1 + T,)eip[-4- $ ^(«')Л'],
(13.4)
П (() = -1= (Т, - Y,) ехр Г - -L ( Г. ((') df' .
Волновая функция системы, удовлетворяющая начальному усло-
вию Т (t — оо) имеет вид
уГ{'Кг«)+(13.5)
Подставляя (13.4) в (13.5) и переходя к пределу t -> оо, получаем
оо
T(f)—> ехр Г — (7^ + Fu) dt'l {’Ficost] — i4%sinr|}, (13.6)
I - Alb J 4 J
—oo
oo
= $ l^(f')-Fs(OI*’. (13.7)
ИО ГЛ. IV. СТОЛКНОВЕНИЯ ТЯЖЕЛЫХ ЧАСТИЦ
Вероятность перехода электрона от первого центра ко второму,
очевидно, равна
W = sin2r|. (13.8)
Эффективное сечение соответствующего процесса получим, интег-
рируя W по прицельным параметрам:
о — 2л f sin2 т](р)рdp. (13.9)
6
При ц 1 sin2T] можно заменить средним значением 1/2. Поэтому
фактически надо знать функцию г) (р) на сравнительно больших
расстояниях, для которых ц<1.
В случае иона Н% обменное расщепление на больших расстоя-
ниях имеет вид [35]
~4-[уНЯ)~МЯ)1 - (13.10)
Здесь и в других разделах этого параграфа часть промежуточных
выкладок с целью упрощения записи дается в атомной системе
единиц. ________
В приближении прямолинейной траектории R = У"р2 v2t2,
т] = 2 )/2л -^-ж’/’в-1-3', я = р'а0- (13.11)
Поэтому из (13.9) следует
о = ло2а?о/2, (13.12)
где х0 находится из уравнения sin ц (я0) л (х0) = е“с/2 =
= 0,28 (С = 0,577 — постоянная Эйлера):
^«-*«0,15—. (13.13)
1’о
Общий анализ резонансной и квазирезонансной перезарядки при
малых скоростях содержится в [36]. Формула (13.12) дает сечение
в адиабатическом приближении, применимость которого ограни-
чена условием v < v0. Как показывается далее, при v/v0 1
о 2® / \2 Г 1 / F \а . j 1 ~5 2 218 / \12 / j о л / \
° = яо° 15 (~г) [тЬъ) + J • (13Л ‘)
3. Приближение двух состояний. Вернемся к общему процес-
су (13.1). Представим волновую функцию электрона в поле двух
центров А+ и В+ в виде разложения по полной системе волно-
вых функций атома В Фт (гв):
'F = 3 ауп (/) Фт {гв) ехр [— ie^J.
т
(13.15)
§ 13. ПРОЦЕССЫ ПЕРЕЗАРЯДКИ
111
Суммировании по т подразумевает также интегрирование по не-
прерывному спектру, Йе® — Ет — уровни энергии атома В. При
t -> — оо волновая функция (13.15) должна описывать атом А,
движущийся со скоростью v:
Т (t) То, (0 =
= То (ГВ —22(0) ехр ~ “г(^Л + f » (13.16)
где Т0(га) и Eq = h^Q — волновая функция и энергия началь-
ного состояния атома А, га = Гв —
Подставляя (13.15) в уравнение Шредингера системы А+, В+,
е, можно получить бесконечную эрмитову систему уравнений для
амплитуд am(t). Однако при t -> — оо вследствие неортогональ-
пости функций Т0(гв — -R) и Фт (гв) все эти амплитуды отличны
от нуля:
ат(£) Smo (0 елр(i«W), «то = е® — (13.17)
(-.—оо
Smo (0 = J То* (г — -у-) ехр (yjnw) ф (г + dr. (13.18)
Полученную бесконечную систему уравнений можно свести к двух-
уровневой, воспользовавшись следующим приемом. Положим
для всех т п
ат (t) = b ехр (iwmoi)(l - | 5п0 | 2)~*/« (13.19)
и просуммируем все уравнения с т п, используя условие пол-
ноты функций Фт (гв). Можно показать, что функция b (t) имеет
смысл амплитуды вероятности состояния
Ф = (1 - I Sn0 |2)-‘/г{То. - 5„ОФП}, (13.20)
которое при t — оо переходит в То® из (13.16). Амплитуды
a (t) = ап (Z) и b (Г) удовлетворяют следующей системе уравнений
с эрмитовой матрицей [37]:
iha = Vnna + Fn0 ехр (iwftOi)&,
iftb = F*o ехр (—iwnot) а + 700fe. (13.21)
Поэтому амплитуды a (t) и b (t) нормированы:
|«Ю l2 + 1М0 12 = 1.
Эрмитовость системы (13.21) следует из того, что функции Фп и Т
ортогональны при любых t. Матрица Г имеет вид
7 — Г* —
' on — ’по
= (1 - I v (rB - в) । ф„> -
- «КФ; I V (Гв - В)| ф„>), (13.22)
112
ГЛ. IV. СТОЛКНОВЕНИЯ ТЯЖЕЛЫХ ЧАСТИЦ
Гпп = <Ф*| V (гв - JR) | Фп>,
(13.23)
Гоо = (1 - I Sno I2)"1 {<П | U (гв) | Тов> -
- I ^о12<Ф*1 V (гв - Ж)[ Фп> +
+ S*o <Ф* | U (гв) | Yo„> - 5ПО<%* | V (гв - R) | Фп (гв)». (13.24)
Здесь V (га) — V (гв — R) — взаимодействие электрона с ионом
А+, U (гв)—с иопом В+. Можно убедиться, что в случае резонанс-
ной перезарядки V (г) = U (г) в пределе и ->0 Vnn = F00.
Выражения для матричных элементов (13.22) — (13.24) весьма
громоздки. Однако в различных предельных случаях они могут
быть значительно упрощены. Так, интегралы иеортогональности
существенны лишь в пределе больших скоростей, их учет дает
правильные значения константы в асимптотической формуле
(13.14). В области малых и средних скоростей v и0 можно по-
ложить S1l0 — 0. Недиагональные матричные элементы FOn, Рп0
экспоненциально убывают с увеличением междуядерного рас-
стояния R. Диагональные матричные элементы содержат степен-
ные члены по R.
Наиболее важные особенности зависимости = F*o от R
и v можно проследить, задав радиальные части атомных функций
в виде
'Fo (га) со Га ехр ( — у0
\ г° \ (13.25)
Фп (гв) СО Гвп ехр ( — уп -А)
и приняв, что потенциал взаимодействия электрона с ионом сфери-
чески симметричен
г оо
U(r)=J^-, C(r)--Z+J?(r')dr' +rj9(r')-^-. (13.26)
О г
Здесь Z — заряд ядра, q — электронная плотность иона.
В общем случае нерезонансной перезарядки решение системы
(13.21) с помощью тех же методов, что были использованы в § 11,
12, приводит к следующей формуле для вероятности процесса:
W = ехр [— 2Д (0, х)] sin2
со
[ j Pno (*, V, t) dt
—со
(13.27)
Здесь
д ” + [•’ + £<*’- + ₽+-£(*’-Х!)Г-
(13.28)
§ 13. ПРОЦЕССЫ ПЕРЕЗАРЯДКИ
113
P“(wa*)!- (13.29)
где 7n, 70 — потенциалы ионизации состояний Фп, 4%, выражен-
ные в атомных единицах, т. е. в единицах 2 Ry. Параметр Xi =
= RJao находится из решения уравнения
2 | Гп0 (X) | = 1 <о + Гпп (X) - Гоо (X) 1 (13.31)
и представляет собой междуядерное расстояние, на котором рас-
щепление термов равно удвоенному педиагональному потенциалу.
Интегрирование (13.2G) по прицельным параметрам дает
о — 2лао J ехр [— 2А (0, ж)] sin2
о
(13.32)
При малых скоростях быстро осциллирующий множитель sin2 I...]
можно заменить на 1/2. При этом
2/р>1,
(4-х?, х,>-Ьг\
— v-2 X <" —
( 8 V » Al 2 Y •
(13.33)
(13.34)
В противоположномпредельномслучае больших скоростей (р<</1)
выражение (13.31) дает первое приближение теории возмущений
ст со у-12.
В случае резонансной перезарядки со = 0, р — 0 и Д = 0
Оо
W = sin2 jj V (X, У) dt,
—<х>
х = j- /р2 + V42, (13.35)
где в приближении (13.25), (13.26)
U(X,v)---- 2 ХехрГ-Х]А+4-М-У1.
т/ 1 / у \2 L F 4 \ г о / J
"И' + тЫ
(13.36)
При v 0 величина U с точностью до множителя е/п да 0,86 дает
адиабатическое расщепление четного и нечетного термов. По-
этому (13.35) приводит к тому же результату, что и (13.8), т. е.
дает формулу (13.12).
114
ГЛ. IV. СТОЛКНОВЕНИЯ ТЯЖЕЛЫХ ЧАСТИЦ
При v vn из (13.35) следует
' (13.37)
Интегрируя (13.37) по р, получаем
аИсеЫ’Гц.Д-Ш’]”, -^>1. (13.38)
\ <> I L \ 2 о / J ’о
4. Вклад внутренних оболочек. Как было показано в преды-
дущем разделе при скоростях v г0Д//у ()Лр < 1), сечение пере-
зарядки быстро убывает с ростом энергии о со Е~6 (со у~1а).
Существует такая область скоростей, в которой для внешних элек-
тронов выполняется условие ]/ 0 <Z 1 и вместе с тем для электронов
внутренних оболочек вследствие больших значений А/ = | 1п —
— /0| имеет место обратное условие > 1. Поэтому при опреде-
ленных значениях скорости относительного движения захват из
внутренних оболочек может вносить основной вклад в сечение
перезарядки.
В рамках изложенного выше метода вычисления сечений нере-
зонансной перезарядки можно получить следующие результаты.
Рассмотрим перезарядку протона па атоме А, сопровождающую-
ся захватом электрона из оболочки па1а во все состояния nl с од-
ним и тем же главным квантовым числом п, т. е. процесс
A (nal”) + Р^А+ (nalNa-') + Н (п). (13.39)
Если относительная скорость v не слишком мала, сечение пере-
зарядки (13.39) дается элементарным обобщением формулы Брин-
кмана — Крамерса [38]:
/ 2st) N [2H”Ja)]11 I i’o \2
° (^t/a и) -- »а/(у) \ г’ / * (13.40)
где
(13.41)
В оригинальной формуле Бринкмана — Крамерса г) = 1. Бо-
лее аккуратный расчет в 1-м порядке теории возмущений [39]
дает в пределе больших и значение т] ж 1/3. В приведенных ниже
оценках мы примем т] = 1/3.
При малых скоростях сечение убывает быстрее, чем это следует
из (13.40), а именно, экспоненциально:
С («л — п) = Лй0- “8^-ехр -g—-JLJ , (13.42)
S 13. ПРОЦЕССЫ ПЕРЕЗАРЯДКИ
115
Обозначим через vc значение скорости, при которой кривые и (и),
определяемые формулами (13.40) и (13.42), пересекаются. При
v _> vc для оценки сечения необходимо использовать формулу
(13.40), а при и < v,. — формулу (13.42). При захвате из внутрен-
них оболочек при всех скоростях, для которых сечение не является
очень малым, оказывается справедливой формула (13.40). При
Рис. 12. Эффективное сечение перезарядки иона Н+ на атоме Ne. Сплошные
кривые соответствуют захвату электрона из различных оболочек, пунктир-
ная — сечению, суммарному по всем оболочкам; темные кружки — экспе-
римент {41 ], светлые — эксперимент [42].
этом / l/2/t2. Максимум сечения достигается при скорости
Ут = Ут М ~ ^0
а(рго)«т;- (13.43)
При v ит сечение быстро уменьшается (оо и’12). В области ско-
ростей vm <Z v < vm, где vm соответствует оптическим электронам,
a vm — оболочке 1s2, зависимость полного сечения перезарядки
(суммарного по всем оболочкам па1а) от энергии имеет вид
о (£) оо Е~р, 2,5 < р < 6.
(13.44)
Предельная зависимость р — 2,5 может реализоваться только для
самых тяжелых атомов.
В качестве примера на рис. 12 приведено сечение перезарядки
протонов на атомах Ne. До энергий ~100 кэВ основную роль иг-
рает захват из внешней оболочки. При дальнейшем повышении
энергии подключается захват электронов из внутренних оболочек.
116
ГЛ. IV. СТОЛКНОВЕНИЯ ТЯЖЕЛЫХ ЧАСТИЦ
Для атомов щелочных металлов захват из внутренних оболочек
становится решающим при энергии относительного движения
Е 20 кэВ [40].
5. Перезарядка многозарядных ионов на атомах. Формула
Бринкмана — Крамерса легко обобщается на случай перезарядки
произвольного иона на атоме [38] А 4- В2+1—>4+ Bz:
{na^a — HOq' $ A f (v) \ V ) ' *5)
Величина / (v) дается формулой (13.41) при А/ — I — /п, In —
= z2/2n2. Уровни n иона Bz предполагаются водородоподобными.
Рис. 13. Эффективное сечение перезарядки многозарядного иона на нейтраль-
ном атоме в зависимости от относительной скорости. 1 и 2 — приближение
Бринкмана — Крамерса для z = 20 и х = 10; 3 — 6 — сечения захвата
на различные возбужденные уровни: 3 — на уровень п0, 4 — на уровень
(п0 — 3), 5 — на уровень (п0 — 4), 6 — на уровень (п0 —5), п9— Z (Ry//
Светлые кружки — эксперимент для перезарядки Вг+1° 4* Нс —♦ Вг+9 +
+ Не+ [44].
Наибольшую величину имеет сечение квазирезонансной переза-
рядки в состояние с главным квантовым числом
n0 = z//27. (13.46)
Область применимости формулы (13.45) для резонансного случая
ограничена, однако, весьма большими скоростями vm. Ввиду
наличия сильно кулоновского возмущения термов в конечном ка-
нале экспоненциальное убывание сечения с уменьшением скорости
начинается при скоростях, значительно больших ve (см. (13.40) и
(13.42)).
В то же время кулоновское возмущение термов приводит к до_
полнительной специфике перезарядки на многозарядных ионах.
§ 13. ПРОЦЕССЫ ПЕРЕЗАРЯДКИ
117
Электронные термы системы А+ + Bz (п), для которых потенциал
ионизации 1п иона Bz больше потенциала ионизации /д атома А,
пересекают основной терм системы в точках Хп, удовле-
творяющих условию
(13.47)
В окрестностях точек пересечения Хп происходят неадиабатиче-
ские переходы типа Ландау — Зинера. В области малых скоростей
этот механизм переходов является определяющим. При увели-
чении скорости вклад в вероятность перехода начинают давать
также и другие области междуядерных расстояний, для которых
недиагональный потенциал (13.22) порядка расщепления между
термами.
Как показывают результаты расчета [43], при больших скоро-
стях эффективна перезарядка в состояния с п = п0 (квазирезо-
нансные условия при больших X, см. (13.47)). С уменьшением
скорости подключается и перезарядка на другие уровни с п <Z п0.
Для п < п0 сечение может иметь два максимума, что соответству-
ет изменению удельного вклада двух возможных механизмов,
упомянутых выше. В качестве примера на рис. 13 приведены ре-
зультаты расчета для z = 10 иг = 20. Полное сечение перезаряд-
ки во все возбужденные состояния иона Bz сравнительно слабо
зависит от скорости вплоть до скоростей, соответствующих мак-
симуму сечения перезарядки на уровне п0. Величина полного
сечения fftot быстро растет с увеличением z. Хотя различные мо-
дели дают несколько отличные значения ot0t, для оценки порядка
величины можно воспользоваться простой формулой
Qtotwna’.z®^8. (13.48)
Более подробное обсуждение см. в [45].
ГЛАВА V
НЕКОТОРЫЕ ВОПРОСЫ КИНЕТИКИ ВОЗБУЖДЕНИЯ
§ 14. Скорости элементарных процессов в плазме.
Аппроксимационные формулы для сечевий
и скоростей процессов
В этом параграфе приводится сводка формул для сечений о
и скоростей процессов через радиальные интегралы и угло-
вые ^-факторы. Для использования результатов в задачах кинетики
плазмы удобно использовать приближенные аналитические фор-
мулы. Здесь приводятся простые аппроксимационные формулы,
обеспечивающие правильную асимптотику б и <пб) и описывающие
результаты численного расчета с помощью двух подгоноч-
ных параметров. Кроме того, приводятся некоторые по-
лу эмпирические формулы, используемые в литературе. При на-
писании аппроксимационных формул основное внимание уделяется
области энергий $ Ez (Ez — энергия ионизации иона Xz, z —
спектроскопический символ иона), которая наиболее важна для
задач диагностики плазмы. В частности, асимптотическая зави-
симость сечений разрешенных переходов берется в виде М%, а не
In $/£. Поэтому применять приведенные формулы к задачам о воз-
буждении и ионизации в пучковых экспериментах следует с осто-
рожностью — фактор In $ в этих условиях может оказаться весьма
существенным.
В этом параграфе начальное состояние обозначается индексом
«О», конечное — индексом «1». Окончательные результаты приво-
дятся в системе единиц СГС.
1. Возбуждение атомов и ионов. Электроны в плазме распре-
делены по энергиям в соответствии с некоторой функцией распре-
деления f (£). Мы будем всюду считать это распределение мак-
свелловским (2.1).
Число актов возбуждения атома Xz в единицу Времени равно
(см. § 1)
оо
NzNe <woi> = NzNe f vo0& (8) d8, (14.1)
где 8 — энергия налетающего электрона, Д51 — пороговая энер-
гия. Подставляя сюда распределение (2.1), получим для скорости
§ 14. АППРОКСИМАЦИОННЫЕ ФОРМУЛЫ ДЛЯ СЕЧЕНИЙ
119
процесса:
<УО> - К ( ~ е~*!т
ЬЕ П°0
(14.2)
К = 2/лДао = 2,18-10-8см3/с.
т
Часто бывает удобно представить энергию и температуру в поро-
говых единицах. Обозначив
ц=—ДЁ •» Р = —’ (14-3)
можно переписать формулу (14.2) в виде
оо
<УЦО1> = К ( ( (Н - 1) е-^ du.
\ Ry I J4 ' ля?
о °
(14.4)
Скорости обратных процессов тушения возбуждения выражаются
через скорости возбуждения согласно (2.7).
В соответствии с результатами § 5—7 сечение для перехода
а о — «1 можно в общем случае записать в виде
= 2 [<?х («о, <h) Их (*о, к) -I- <?х («о, di) Он (^, *1)1, (14.5)
X
где ох и Ох зависят только от квантовых чисел п010, оптического
электрона, а вся зависимость от моментов атома в целом (J, L,
S, ...) сосредоточена в множителях Q* и QH. Для суммарного во
J, L, S, ... сечения перехода между конфигурациями —
— Q* = Q* = т, т. е.
и (гео^о, П0/0 1^i^i) — w X [<тх (^о, 11) 4" йх (^о, ^i)]. (14.6)
X
Таким образом, Ох и соответствуют сечениям одноэлектронного
перехода; Ох включает прямой и интерференционный члены:
(bi = <?х + <^нт, <?х («о, «1) <х> 6S1JSl; (14.7)
Ох представляет чисто обменный член. Выражения для Стх и бх че-
рез радиальные интегралы приведены в § 5. Очевидно, эти величи-
ны могут вычисляться лишь численно.
Индекс х принимает значения в интервале xmin4-xmaX:
ХпНп “ I ^1 |» ^шах “ 4“ 11' (14.8)
В соответствии с (5.9), (5.10) о* #= 0 лишь для х одной четности
0 XmjQ.
120 гл. V. НЕКОТОРЫЕ Л ОПРОСЫ КИНЕТИКИ ВОЗБУЖДЕНИЯ
Факторы Qyc и выражаются через Зп/-символы (см. § 5) и,
следовательно, могут вычисляться аналитически, либо с помощью
стандартных таблиц. В схеме Л5-связи для переходов между тер-
мами выполняется важное соотношение
<2и (а-о, ^1) = ^SqSiQx (Eq, ^i)>
2^ + 1
2 (2Sp + 1)
(Lo, Л),
(14.9)
— d,0LnS0, dy —•
t. e. Qv, и Qh отличаются лишь спиновыми множителями, не зави-
сящими от х. Qx (Lo, La) дается формулой (5.20).
Для представления результатов численного расчета восполь-
зуемся аналитическими аппроксимациями. Полагая, что о пред-
ставлено в форме (14.5) и учитывая характеристики ст, приведен-
ные в § 6, 7, запишем о^ и Сту, в виде
I Ry I Ej \',г
ДЕ J Ео j
Ф"(П),
" Пап
= 2Z0 + 1
$ — ЬЕ
и —
(14.10)
ДЕ
ДЕ = £i - Ео,
где Ео и Ei — энергии атомных уровней. Для функций Ф' и Ф"
воспользуемся следующими аппроксимациями:
Ф' (и) =
Ф"(и) =
/ и \*/» С' .
—гт —;—г при z = 1,
\ и -|- 1 j и + ф
Cf
------7 При Z >> 1,
« + Ф
I и у/. С
U + 1 I (« + 1)2(« + Ф') 14,11
С"
.(« + !)«(» + Ф") П₽И
2 = 1,
(14.11а)
(14.116)
Случай 2 = 1 соответствует нейтральным атомам, a z 1 — по-
ложительным ионам. Параметры С, ср подбираются по результа-
там численного расчета методом наименьших квадратов. Следует
отметить, что качество описания ст* с помощью функций Ф" ока-
зывается довольно низким, так как фактический ход функций
Стх (и) весьма разнообразен.
Скорость возбуждения <пст> можно записать аналогично (14.5):
'\уПаоа,)> = [<2х (Щ)! а1) (Ь’Щс (^0, Н- (?Х (а<н (^в> ММ*
" (14.12)
§ 14. АППРОКСИМАЦИОННЫЕ ФОРМУЛЫ ДЛЯ СЕЧЕНИЙ
121
Величины и [см3/с], используя (14.4) и (14.10), запи-
шем в виде
<№»>= Ю-’ 21^77
<w»> = 10” 27ГГГ
(14.13)
Учитывая асимптотику G (р) согласно (14.11), примем следующие
аппроксимационные формулы:
G'{₽) =
при Z = 1,
(14.14а)
^(p + l)‘z‘
Р + х'
р,/8 (Р+1)
Р + х'
при z 1;
<?"(£) =
(14.146)
Параметры А, % подбираются методом наименьших квадратов
по результатам численного расчета <уо'> и
Для переходов без изменения спина (AS = 0) часто достаточно
одной аппроксимационной функции вместо двух (Ф', Ф" или G',
G"). Для переходов между термами, используя (14.9), можно за-
писать сечение в виде
х (14 15)
<равЛ1> - 3<?x(Io,ii)<^OJIK(/oJi)>,
где Стх°лп — одноэлектроппое сечение для данного спина:
стГМк <£,. при = (14.16)
Величины Цк°Л11 и <глТк°ЛК> можно аппроксимировать функциями
Ф' или G':
ПОЛИ
1>х
(-sr №*-’•
<«““> = 10-^
(14.17)
Следует, однако, отметить, что для компонент тонкой структу-
ры такой способ аппроксимации непригоден, так как запись в виде
(14.9) и (14.15) невозможна.
В дальнейшем (§ 18) для лучшего описания результатов чис-
ленного расчета будут использоваться несколько модифицирован-
122
ГЛ. V. НЕКОТОРЫЕ ВОПРОСЫ КИНЕТИКИ ВОЗБУЖДЕНИЯ
ные формулы для функций Ф и G. В частности, в выражение для Ф'
и G' для случая Д/ = ± 1 можно вводить логарифмический фак-
тор, учитывающий правильную асимптотику о в этом случае.
Функции Ф и G симметричны относительно начального и ко-
нечного состояний. Поэтому для тушащего столкновения 1 —> 0:
<1’<Уа1ао> = V [<?х (<П, По) <^х {11, ^o)> + (?" (fll, «о) <™’ (Zr, Zo)>] =
X
= V-(Г1.18)
S1
<ро' (Zn Zo)> = 10- 1-^г ^\/г G' (р),
₽ £ (» (14.19)
<по; (Zb /„)> = 10- '* G" (Р).
2. Переходы между близкими уровнями. В случае переходов
между близкими уровнями с ДЕ ] Ео |, где Ео — энергия ис-
ходного состояния атома от границы ионизации, пороговые еди-
ницы неудобны. В частности, критерий большой температуры бу-
дет Т >>| Ео |, а не 7’^> \Е. В качестве безразмерного парамет-
ра можно использовать | Е^ | /Т или z2 Ry/E. При этом в наиболее
интересном случае Т &Е величина <уо> не зависит от &Е, ли-
бо зависит только логарифмически (для Д/ = ±1). Учитывая это
обстоятельство и полагая Т ДЕ, перепишем формулы (14.13),
(14.14) в виде
<УО-и> = 10- 2т ^г-7- Z 3Х 1 * , ,
р з/g
<ро-х> = 10- 1 z-А —,
(14.20)
где Pj = za Ry/71; параметры А',
(14.13), (14.14) соотношениями
Л", связаны с А', А", % из
л' _ Iz2Ry \
1 ~ х' \ Д£ I
Xi = X
I z®Ry \
\"А^/ '
(14.21)
Если для некоторого значения Ь.Е<^Т определены А и % соглас-
но (14.14а) (для или (14.146) (для <гчт">), то с помощью
(14.21) можно найти параметры At или ЛР пригодные для всех
ДЕ <<: Т. Эти параметры лишь весьма слабо (логарифмически) за-
висят от ДЕ в случае Д/ = ± 1. Что касается то они могут,
вообще говоря, зависеть от ДЕ, по, как правило, эта зависимость
достаточно слабая и к тому же обычно величина Рд/Хх < 1.
3. Ионизация. Сечение и скорость ионизации можно описать
способом, аналогичным изложенному в п. 1. Однако в этом случае
обменное взаимодействие не играет, как правило, существенной pq-
§ 14. АППРОКСИМАЦИОННЫЕ ФОРМУЛЫ ДЛЯ СЕЧЕНИЙ 123
ли. Кроме того, представляет интерес лишь суммарное по состоя-
ниям непрерывного спектра J 1} сечение. При этом фактор
не зависит от х. Для перехода типа nol™LoSo -> nJ^LtSi + е
фактор Q равен
Qi = zn(G^“)2. (14.22)
Учитывая сказанное, а также известную асимптотику сечения ио-
низации о;, имеем
ла2 /Rv\2 % — Е.
Oi = 2/0-|- 1 & ) Ф и Ё ’
1 /Ry V/, Z Е <14-23)
= 10 W+T^(|-^r) с(Р)е'3’
где Ez — энергия ионизации иона Xz. Функции Ф и G можно на-
писать в виде / и \’/« с
ф = с+” П1Ш ’ (14.24) I Р W* а .
G(P) = В 4-1 8 + у ПРИ Z-1' + Р + х (14.25) О1/2 \ л р + х при г>1.
следует отметить, что формулы для Ф и G при z = 1 написаны на
основе борновского приближения. В действительности поведение
сечений ионизации при и -> 0 для нейтральных атомов такое же,
как для ионов (см. примечание к стр. 51).
Скорость трехчастичной рекомбинации [см4 * * * 8 */с] определяется
формулой (2.7):
Иг
Хг = -п—
2^z+l
/2nh2\J/‘ л .
= 1О~84^а3о
Ry_\*/s Qi Sz
Ez / 2Z0 -f- 1 gz+1
(0).
(14.26)
4. Рекомбинация. В плазме высокой плотности основным про-
цессом рекомбинации является трехчастичная рекомбинация
(см. § 1). Число актов такой рекомбинации в единицу времени рав-
но Arz+i7VeXr, а скорость рекомбинации связана со скоростью
ионизации соотношением (14.26). В плазме умеренной и низкой
плотности преобладает двухчастичная рекомбинация — излуча-
тельная (или фоторекомбинация) и диэлектронная (см. (1.3), (1.4)).
Число актов двухчастичной рекомбинации в единицу времени
равно
Nz^Nen, х = xv + х^.
124 гл. V. НЕКОТОРЫЕ ВОПРОСЫ КИНЕТИКИ ВОЗБУЖДЕНИЯ
В двухчастичной рекомбинации участвует фотон, так что она яв-
ляется более слабым процессом, чем трехчастичная. Однако при не-
больших плотностях вероятность столкновения трех частиц су-
щественно меньше, чем двух, и это компенсирует слабость взаимо-
действия.
Диэлектронная рекомбинация будет подробно рассмотрена в
§ 15. Для скорости диэлектронной рекомбинации [см3/с] типа
Xz+1 («о) + е Xz (o^nZ) ~^XZ (aonl) + Йш (14.27)
аппроксимационная формула имеет вид
xd = 10~13(M/Vp4 р = ,(z-+paRy_ , (14.28)
где Ал и Xd — подгоночные параметры; Qd — фактор, завися-
щий от типа перехода а0 — «j. Для перехода а0 = —>• =
=
<14-29»
Для перехода Zj*ZJ — Z^^Zf*1
= 2/0 +1 f1 “ 2 (2/j 4-1)) ' (14.296)
В большинстве случаев рекомбинация происходит на высокие уров-
ни nl.
Перейдем к рассмотрению фоторекомбинации:
Хг+1 (а/) + е Хх (а) + Йо. (14.30)
Учитывая известные характеристики сечения фоторекомбинации
(см. [1], § 34), примем для скорости фоторекомбинации [см3/с] на
уровень а следующую аппроксимационную формулу:
(\Е 1 \*Z’ ЛВ7‘ |Я I
Xv(a) = (14.31)
где А и % — подгоночные параметры, Еа — энергия уровня а
(от границы ионизации). Фактор Qv зависит только от угловых
моментов состояния а.
Для а — a^nl L S, t-ц ^qZq LiS
q_________№ + 1) (2^ + 1) (14 32)
~ 2 (21 + 1) (2Si + 1) (2£i + 1) ’ V ’
Для суммарного по L, S сечения
nl) = (Мп^пГ) = 1. (14.33)
§ 14. АППРОКСИМАЦИОННЫЕ ФОРМУЛЫ ДЛЯ СЕЧЕНИЙ 125
Для а — nol™LS, at =• n^^LtSi
q _______(2.У 1) {2L Ч~ 1)_\2 _, И 4 341
2(2/0 + 1) (25i + l)(2Li4-i) ^Gbisi' (14.34)
Для суммарного по Д, 8г и L, S сечения
Q,(п,1?) - 1 - 2д,~Д> • (14.35)
Для полной скорости фоторекомбинации иона Xz+l Хг
можно принять формулу, аналогичную (14.31):
и. = Ух,(а) = «Г» М-) ..I.JL-, (14.36)
ЛшшЛ \ * У / Р "i Av 1
а
где Ег — энергия ионизации иона Xz. Факторы Qv должны учи-
тываться непосредственно при суммировании по а.
Можно показать, что фоторекомбинация происходит в основном
на уровни, для которых | Еа | > Т. Для этих уровней Xv (а)
медленно убывает со 1/п. Более высокие уровни с | Еа | < Т
практически не вносят вклада в xv, так как для них xv (а)оо 1/п3.
В случае больших температур Т Ег фоторекомбинация почти
целиком идет в состояние с минимальным п.
Приведем теперь для справок основные формулы для расчета
сечения и скорости фоторекомбинации (подробнее см. [1], § 34).
Скорость фоторекомбинации
xv (а) = К Ра7’ U du, (14.37)
' 14 У ' J па‘
о °
где и = ] Еа К — 2,18-10“8 см3/с; arV (а) — сечение фоторе-
комбинации на уровень а:
а„(а)-па;. (|£“' + 8)’ V Zmp>(^.n(),
1 ’ * iSi (14.38)
I Еа I + $ = ^(о, lm = max (I, A,).
Радиальный интеграл p (H, nl) равен
p (fcX, nl} = J Pnl (r} Pkx (r) r dr, (14.39)
0
где Pni и Pfcx — радиальные волновые функции оптического элек-
трона атома Хг в дискретном и непрерывном спектре. Функция
Pni нормирована, как обычно, на единицу, а функция Рк^ норми-
рована согласно (7.3):
T’fcx ~ у=- sin (Аг — In кг + г]). (14.40)
126 ГЛ. V. НЕКОТОРЫЕ ВОПРОСЫ КИНЕТИКИ ВОЗБУЖДЕНИЙ
В формулах (14.38) — (14.40) используются атомные единицы
с единицей Ry для энергии.
Рекомбинация на высокие уровни п 1 хорошо описывается
квазиклассической формулой
On,(п/) = ла5- зиз7^ ~/1 + 8?0(Дп,в,), (14.41)
О J /10
е(дп, „,) - /4»«)’- (Д'1)’~х‘ (Л„(х))!,
v 7 (14 42)
z-Mn, An--g£, е, = [1_<ЦЯ]'\ ( ’
Суммируя (14.41) по I, получаем известную формулу Крамерса для
фоторекомбинации на водородоподобные уровни:
Кр / \ „ 2 1Ьза Ry
O,y (п) — Лйа- ------у=----------г-~ .
v d 3^3 (137)3
(14.43)
Подставляя (14.43) в (14.37) и используя (14.2), находим
х?р w гК‘1 -л Ei W)’ (14-44)
3 у 6т (137)3
где pn = z2Ry/n2r, Ei (—Р) — интегральная экспонента. С по-
мощью (14.44) нетрудно показать, что
Ху (п) сю 1/п при pn >> 1, (14.45)
Ху (ге) сю 1/п3 при <С 1-
Используя (14.44) для уровней с п > пх и более точные методы
для Ху (а) при п < п15 можно записать суммарную скорость фото-
рекомбинации на все уровни в виде
Ху = У| xv (о) + х«₽ (п > гег), (14.46)
a(n<ni)
Х^Р(п > nj) =
32 лаой
3 /Зт (137)3
(14.47)
где pi = z3Ry/nJr.
5. Полуэмпирические формулы для скоростей возбуждения,
ионизации и диэлектронной рекомбинации. Возбуждение. При
больших значениях энергии электрона сечение возбуждения опти-
чески разрешенного перехода (Д£ = ± 1, Д5 = 0) выражается
через силу осциллятора этого перехода известной формулой Бете
(6.24). На основе формулы Бете построен ряд полуэмпирических
формул для оценки сечений. Здесь мы приведем наиболее употре-
§ 14. АППРОКСИМАЦИОННЫЕ ФОРМУЛЫ ДЛЯ СЕЧЕНИЙ
127
бительную в настоящее время формулу Ван Режемортера [46]
_ 2 8л , / Ry \2 у (и) ... /п.
Йаоа - ла0- у=- fwn и + 4 . (14.48)
Здесь faaat — сила осциллятора перехода а0 — «j. Множитель
у (и) подобран по экспериментальным данным и результатам теоре-
тических расчетов сечений. Его значения для нейтральных ато-
мов и ионов даны в табл. 9. При и оо
Y (“) = ln
и формула (14.48) переходит в формулу Бете.
Таблица 9
Фактор у(п) для атомов (z = 1) и попов (л>1)
Уй 0,0 0,2 0,4 0,6 0,8 1,0 2,0 3,0 4,0 5,0 6,0
VII 0,000 0,200 0,015 0,200 0,034 0,200 0,057 0,200 0,084 0,200 0,124 0,200 0,328 0,328 0,561 0,561 0,775 0,775 0,922 0,922 1,040 1,040
Используя для сечения формулу (14.48), скорость возбуждения
можно представить в виде
<»«,.> = 10->32/о.„, ₽'^-Sp (₽), р = С.Е/Т. (14.49)
При р 1
P(W~--0-Ei(-P).
Значения множителя р (Р) приведены в табл. 10.
Как уже отмечалось выше, для переходов между близкими
уровнями пороговые единицы неудобны. Кроме того, для таких
переходов нельзя использовать полюсный потенциал. Поэтому
мы приведем здесь также результаты квазиклассических расчетов
[97] с потенциалом Л/(г2 -}- которые в случае й’/Д£'^>1
можно представить в виде
2 8V, 1,4#’/2
СТ “ Ла°’ g П ДЕ./?0 ’
= ^°1 "ДЕ ’ Л° = ТЩ
(14.50)
<OT> = l,74-10-’^.p?ln—3,= ^-у, (14.51)
128
ГЛ. V. НЕКОТОРЫЕ ВОПРОСЫ КИНЕТИКИ ВОЗБУЖДЕНИЯ
Таблица 10
фактор р(Р) для атомов (z«= 1) и ионов (г>1)
0,01 0,02 0,04 о,1 0,2 0,4
ИА 1,160 1,160 0,956 0,977 0,758 0,788 0,493 0,554 0,331 0,403 0,209 0,290
₽ 1 2 4 10 >10
VII ►А- 0,100 0,214 0,063 0,201 0,040 0,200 0,023 0,200 0,066-р^1/* 0,200
где величины Д51, Ео, $ выражены в единицах Ry, a Ro — в еди-
ницах до- Отметим, что при <С | Ео | X2 оо z-2 и не зависит от
&Е. Формулы (14.50), (14.51) и (14.48), (14.49) при $ АЕ от-
личаются фактически лишь аргументом логарифма.
Ионизация. Известная классическая формула Томсона для се-
чения ионизации из оболочки n0Z™ соответствует (14.23) и (14.24)
при z ]> 1, <р = 1, С = 4 (2Z0 + 1):
<Ji = 4тп -{и 1)а.. (14.52)
Для оценки скорости ионизации атомов и ионов часто ис-
пользуется формула Ситона [47]
<гЮ1> — 4,3- 10“8/п(—У’ (14.53)
где Ez — энергия ионизации, р = EJT.
Эта формула соответствует (14.23), (14.25) для z > 1, % = 0,
А = 4,3 (2Z0 + 1).
В настоящее время широкое распространение получила фор-
мула Лотца [48]
<wt> - 10-e6m ? (14.54)
/ф) = -ИЕ1(-₽).
Эта формула отличается от формулы Ситона (14.53) фактором
1,4 / (Р) (табл. И).
Формула Лотца приблизительно соответствует (14.23), (14.25)
при z > 1, х = 0,4, А = 6 (2/0 + 1).
g 15. ДИЭЛЕКТРОННАЯ РЕКОМБИНАЦИЯ
Таблица 11
129
0,47 0,83 1,16 1,26
_Р_ 1/4 1 4 8
Диэлектронная рекомбинация. Берджесс [49] предложил полу-
эмпирическую формулу для расчета скорости диэлектронной ре-
комбинации. Ее можно переписать в виде (14.28):
%d(a) = 1(Г18ад’/* e~^d, • (14.55)
Bd - 480/^ Г ‘г Р (1 +0,105(2 + 1) % + 0,015(2 + 1)’х>]-1,
(14.56)
6 « <z + 1)aRy 7л = у Г1 + о 015__________—____Г1 у =________________
Р Т ’ Zd (г-bljaJ ’ Z (zH-i)2Ry •
§ 15. Диэлектронная рекомбинация
1. Захват электрона и допороговые резонансы. Упрощенная
модель. Выше уже отмечалось, что сечение возбуждения ионов
в пороге оказывается отличным от нуля благодаря наличию даль-
нодействующего кулоновского притяжения. С этим обстоятель-
ством связана возможность возбуждения иона Х2+1 при энергии
электрона ниже пороговой, сопровождающегося захватом нале-
тающего электрона на какой-либо уровень атома Xz. Например,
при энергии, меньшей порога возбуждения резонансного уровня
Не-подобного иона Ов+, возможен процесс
Oe+(ls2) + е —> О5+ (ls2pnZ).
Получающееся в результате захвата дважды возбужденное со-
стояние неустойчиво и может распадаться либо путем автоиони-
зации, либо путем излучения резонансного кванта 2р -* 1s. В по-
следнем случае атом Хг переходит в стационарное состояние, т. е.
происходит рекомбинация. Такой процесс называется диэлектрон-
ной рекомбинацией.
В общем случае процесс диэлектронной рекомбинации иона
Xz+1 через промежуточное (дважды возбужденное) состояние иона
Хг записывается в виде
*Х* (у') + Йсо,
Хх+1(ао)Ч-е-ХГ (у) (15.1)
Х2+1 (а ) +
у = а nlLSJ, у' a'nlL’S' J'.
5 Л. А. Вайнштейн и др.
130 ГЛ. V. НЕКОТОРЫЕ ВОПРОСЫ КИНЕТИКИ ВОЗБУЖДЕНИЯ
Ниже, если не оговорено обратное, предполагается схема LS-
связи. Кроме того, предполагается, что испускание кванта проис-
ходит при переходе «внутреннего» электрона (а — а'), а состояние
nl внешнего электрона не меняется. Радиационный переход внеш-
него электрона приводит к дополнительным сателлитам (см. § 16),
но не играет существенной роли в общем балансе диэлектронной
рекомбинации.
Отметим три наиболее существенных проявления процесса
диэлектронной рекомбинации.
А. Собственно диэлектронная рекомбинация — процесс, ко-
торый во многих случаях является определяющим в ионизацион-
ном равновесии.
Б. Сателлиты резонансной и других линий иопа Х2+1, возни-
кающие при излучательных переходах в (15.1).
В. Дополнительное возбуждение уровней а' при реализации
автоионизационного канала в (15.1) при а' Ф а0.
Последний процесс был детально рассмотрен в § 9, сателлитам
посвящен § 16. Здесь мы рассмотрим собственно диэлектроппую
рекомбинацию. В п. 1 мы ограничимся изложением упрощенной
модели, сделав следующие допущения:
а) состояние иона Xz описывается в виде anl без конкретиза-
ции терма;
б) п достаточно велико, так что можно пренебречь влиянием
электрона nl на состояние а; уровни nl можно считать водородо-
подобными, а сечение захвата можно-выразить через сечение воз-
буждения перехода а0 — ас помощью принципа соответствия;
в) в процессе излучения кванта электрон возвращается в ис-
ходное состояние а0.
При этом формулы для расчета сечения диэлектронной реком-
бинации оказываются достаточно простыми. Обсуждение погреш-
ностей, связанных с этими допущениями, отложим до п. 4.
В рассматриваемом случае процесс диэлектронной рекомбина-
ции записывается в виде
я X* (aonl) 4- Йю
Xz+1 (а0) + е^хГ («»П (15.2)
(«о) + <?>
причем нижняя ветвь (автоионизация) является конкурирующим
процессом. Поэтому сечение диэлектронной рекомбинации через
состояние anl равно
od (anl) = Od(a0, anl) w , (15.3)
где W (a, a0) — вероятность радиационного перехода a — «о в
ионе Xz+l, Wa (anl) — вероятность автоионизации уровня anl
атома Xz, od — сечение захвата электрона на уровень nl при воз-
§ 15. ДИЭЛЕКТРОННАЯ РЕКОМБИНАЦИЯ 131
буждении перехода а0 — а. Это сечение представляет собой со-
вокупность резонансов при энергиях
8 ж ДЕ-----< ДЕ, ДЕ = Е^, = Еа - Еае. (15.4)
В этом параграфе удобно вернуться к системе единиц СГС. Ширина
резонанса равна Г = hWa. Усредненное по резонансам сечение
можно получить с помощью принципа соответствия, экстраполи-
руя парциальное сечение возбуждения а0 — а в допороговую об-
ласть:
c'd («о» anZ) Г = о (а0, al) - (15.5)
Здесь о (u0, а/) — У о (а0Х0, al), а о(а0Х0, al)—парциальные се-
чепия возбуждения перехода а0 — а в пороге для значений
момента внешнего электрона Хо, I. В соответствие с указан-
ным выше условием б) берется суммарное по LTSr сечение. Оно
определяется формулами § 5 и 7. Разумеется, при этом в (5.9)
следует снять суммирование по X, положив X = Z.
Величины Wa и (или о) характеризуют взаимно обратные
процессы, и, следовательно, между ними существует простое со-
отношение. Его можно получить, учитывая, что при W = 0 меж-
ду Х2+1 (ао) и Xz (ап/) устанавливается распределение Саха.
Таким путем получаем
(2! + 1) g.VF.(ml) - <15'6’
где и £0 — статистические веса состояний а и а0. Скорость ди-
электронной рекомбинации, очевидно, равна
ха = 2jXa(a), xd(a) = ^vad(anl)r$\8), (15.7)
a nl
где Г — ширина резонанса, $X$) — функция максвелловского рас-
пределения электронов, дается выражением (15.4). Подставляя
(15.3), (15.5) в (15.7), получаем
м«>- Е a2) +(£•)*] *• (15-8>
n>nij<n
Величины п1 и п8 даются выражениями
z* Ry \ \3 !Ta(anZ,a0)
п2 V «/ ИЧа.ао) •
(15.9)
Очевидно, п-! определяет минимальное значение п, т. е. наиниз-
ший уровень, на который возможен захват в соответствии с ус-
ловием (15.4).
5*
132 гл. V. НЕКОТОРЫЕ ВОПРОСЫ КИНЕТИКИ ВОЗБУЖДЕНИЯ
Формулу (15.8) удобно переписать в несколько ином виде.
Подставим в (15.8) явное выражение для ($), выразим <з(а0, al) из
(15.6), и заменим W на силу осциллятора / согласно формуле
g.W (а, а,) = -pip- -bL gvfw \ (15.10)
Результат удобно записать, выделив основную зависимость
xd от температуры:
xd (а) = 10-135d (а)
о - (g + 1)aRy v = ЬЕ (15.11)
Р Т ’ Л (z+l)2Ry
Для величины Bd (а) получаем следующее выражение:
В. (а) = С- £ - ?'-h‘ £ вп^,
1 n»il 1<п 1 Т ( ~ ) 11>П1
(15.12)
Г> *0 = 4^, (15.13)
С' = 101Э-^?й = °’53 l—rv}3 •
(137)8 тп \ z + 1 ]
Значение пв делит все уровни п на две группы. При n j> n, (Z)
Wa < W и захват электрона на уровень nl приводит к диэлектрон-
ной рекомбинации. Вклад таких уровней в xd (а) согласно (15.8)
равен
ДЕ
xd(a)= V vo(a0, al)f(8)d$, Е,=--------2 *у-.
де-• । е9 । i “8
При п < nt (I) Wa > W, большая часть захватов сопровождается
автоионизацией и лишь небольшая доля их ~(пМ,)3 приводит к
диэлектронной рекомбинации. Тем не менее, как видно из (15.12),
именно уровни п <Z nt вносят основной вклад в xd. Действитель-
но, если в (15.12) опустить множитель то все уровни с п <
< п9 (I) при данном I будут давать одинаковый вклад в xd. По-
этому при 1 относительный вклад уровней с п <Z ntun)> пг
Учет фактора евР еще больше увеличивает долю xd, так как 60 ~
— 1/п2.
Уровни с п <Z n, (Z) иона Xz находятся в термодинамическом
равновесии с ионом Х2+1. При этом скорость диэлектронной рс-
§ 15. ДИЭЛЕКТРОННАЯ РЕКОМБИНАЦИЯ
133
комбинации пропорциональна вероятности излучательного пе-
реходаИл(а, а0)со Д£'2/а«ас<>—согласии с (15.12).
«1
Таким образом, диэлектронная рекомбинация происходит в
основном на уровни п в интервале — пв. Нетрудно видеть, что
в большинстве случаев пв 1, т. е. диэлектронная рекомбинация
происходит в основном через уровни п 1 в согласии с допуще-
нием б). Исключение составляет случай переходов 1s — 2р при
z 20. При этом оказывается па < п1г т. е. для всех п п пв.
Рассмотрим в качестве иллюстрации рекомбинацию иона [Li]
с возбуждением перехода 2s — 2р и рекомбинацию иона [Н] с воз-
буждением перехода 1s — 2р. В первом случае уровни очень
- ДЕ 1 / п
близки, т. е. х — --------<С 1 , а сечение о (а0, а/) ве
’ л (z-|~l)aRy z '
Поэтому фактор ехр (—Рх) в (15.11) не играет роли, пл пх
1.
Вклад в х^ вносит очень большое число уровней, сосредоточенных
в узком энергетическом интервале -—ДЕ. При этом вклад каждого
уровня мал ввиду малого значения W ~ х2/- Большое число
уровней лишь отчасти компенсирует эту малость W.
В случае рекомбинации иона [Н] (или [Не]) х » 3/4 и фактор
подавляет диэлектронную рекомбинацию при небольших
температурах. Величина пл сравнительно невелика, а для z
20 ne оказывается даже меньше х. 2. Поэтому в диэлектрон-
ную рекомбинацию вносит вклад сравнительно небольшое число
уровней, но вклад каждого достаточно велик ввиду большого зна-
чения W. Численный расчет показывает, что суммарный предэк-
споненциальный множитель при этом заметно больше, чем при
рекомбинации иона [Li].
2. Общий случай. Полученные в п. 1 формулы (15.11), (15.12)
позволяют рассчитать скорость диэлектронной рекомбинации
в рамках упрощенной модели. В этом разделе будет приведено об-
щее выражение, свободное от допущений упрощенной модели.
Рассмотрим снова процесс (15.1). Для получения общей фор-
мулы для скорости диэлектронной рекомбинации воспользуемся
методом, основанным на принципе детального баланса (см. § 2).
Полная скорость, очевидно, равна
Hd ~ V ।~ ^jxd(v) Дг(у) + РГа(у) ’ (15.14)
где xd (у) — вероятность захвата электрона в состояние у атома
Xz; W (у) - У W (у, у') и Wa (у) = Wa (у, у') — вероятности радиа
ционного и автоионизационного распадов. Автоионизационный рас-
пад происходит за счет внутреннего (электростатического) взаимо
действия; поэтому полные моменты LSJ нс меняются.
134 гл. V. НЕКОТОРЫЕ ВОПРОСЫ КИНЕТИКИ ВОЗБУЖДЕНИЯ
Если система находится в термодинамическом равновесии и
W — 0, выполняется принцип детального баланса:
N2+lNe х (у) = JVZ (у) Wa (у, а0),
Wa (у, а0) = 2^о(у, уо),
причем Nz+l/Nz дается распределением Саха — Больцмана (см.
§ 2). Разумеется, величина х не зависит от какого-либо допущения
о значении электромагнитной характеристики — вероятности
радиационного перехода W. Используя это обстоятельство для
определения х и подставляя результат в (15.14), находим
_ _1_ Г______2л?,‘ —Г’ «ММ»
2g0 L^+ l)»RyJ P ИЧу) + Жа(у)
(15.15)
где бр =----, Р и х определены в (15.11) , g0 и gv — статисти-
ческие веса состояний а0 (Xz+I) и у (Xz); Д£ = Еаа, и £Va„ —
энергии возбуждения уровней а и у. Эти энергии, очевидно, раз-
личаются на энергию б£, освобождающуюся при захвате элек-
трона:
ЬЕ = Е^- Е^^ . (15.16)
Суммарная вероятность перехода TV(y) фактически не зависит
от LSJ; в дальнейшем будем ее обозначать W (а). Величины р и
бр также практически не зависят от LSJ. Вероятность автоиони-
зации Wa в схеме LS-связи йе зависит от J, но существенно за-
висит от LS. Поэтому полная скорость диэлектронной рекомбина-
ции запишется в виде (15.11), причем коэффициент Bd (а) равен
Bd(a) = С 2 е6₽?(у),
nlLS
, ч gvW (a) Wa (у, cto)
1У(а) + Жа(у)
у = anlLS,
С = 1013
4л’^!а3
£o(s + l)8
(15.17)
Ввиду нелинейной зависимости Bd от Wa (у) выполнить анали-
тически суммирование по LS нельзя. Поэтому расчет Bd оказы-
вается весьма трудоемким. В большинстве случаев используется
приближенная формула, в которой Wa (у) в знаменателе q (у)
в (15.17) заменяется средним значением
,у"(отг)=(т)- (15Л8)
LS
§ 15. ДИЭЛЕКТРОННАЯ РЕКОМБИНАЦИЯ
135
После такой замены (15.17) перепишется в виде
Z?d(a) = (an/),
nl
2(2l + l)gaW(a)Wa(an],^
w (a) + Wa (ani)
(15.19)
Расчет по формуле (15.19) существенно проще, чем по (15.17).
Действительно, суммирование линейных выражений типа (15.18)
выполняется аналитически, так что остается лишь сумма по nl.
Кроме того, выражение для Wa(anl) значительно проще, чем для
И7a (у) (см. п. 3). Приближение (15.19) соответствует допущению
а) упрощенной модели.
Полагая п 1 (допущение б)), можно воспользоваться соот-
ношением (15.6) и выразить вероятность автоионизации Wa в
(15.19) через парциальное сечение возбуждения перехода а0 — al
в пороге. В результате получаем следующее выражение:
В‘ (а) - с -L. /ал £ е* £ • (15-20)
1 I <771
где
Н' = У 8<^ ( Е™' V В = w« {ап1)
& Sofaa \ £'аа0 ) ’ ’
(15.21)
С, пА и пв определены в (15.9) и (15.12).
Упрощенная модель (15.11), (15.12) получается из (15.20),
(15.21), если положить В = В' — 1. Это соответствует допущению
в) — все распады происходят в исходное состояние а0. Характер
погрешности упрощенной модели будет рассмотрен в п. 4.
3. Формулы для вероятности автоионизации. Здесь мы приве-
дем выражение для Wa, не прибегая к приближению (15.6). Рас-
смотрим сначала Wa (у) — вероятность распада уровня у —
= anlLSJ.
Выражение для вероятности автоионизации было получено в
§ 9 из общей теории возбуждения многозарядных ионов. Тот же
результат можно получить и непосредственно как вероятность пе-
рехода у — у0 в 1-м порядке теории возмущений аналогично вы-
воду формулы для парциального сечения у0 — у возбуждения иона
Хх+1. Существенное отличие состоит, однако, в том, что нас ин-
тересует ^(у) при заданных значениях LSJ, которые здесь играют
роль полных моментов системы LtStJt (по отношению к иону X’z+1).
Поэтому мы не можем воспользоваться более простыми формулами
типа приведенных в § 5, п. 2, где выполнено суммирование по
LtStJt- В рамках LS-связи W (у) не зависит от J, но зависимость
от LS остается. Используя формулы (5.27), (5.28), выражение для
136 ГЛ. V. НЕКОТОРЫЕ ВОПРОСЫ КИНЕТИКИ ВОЗБУЖДЕНИЯ
вероятности Wa можно представить в виде
Wa (v, ао) = У, У, Л (dSatsaR* - BSaj5a У1 Ях'х) | , (15.22)
к» X X*
Л = (- l)L+L«»+t“+L₽n (xLa^a) J Х La\\ К X
la 'a«J 1,ь I Ло f
Bsa,s^ _ (- i)i-s«-s«.n (S^SO) ('/’ £ 1. (15'23)
I '2 15a 6pJ
В радиальных интегралах R'1 и Re функции F^, (г) непрерывного
спектра заменены функциями Р, (г) дискретного спектра (Рг нор-
мированы на единицу, аналогично Pl9 и P,a). Функции Р1 и Р\о
в обменном интеграле Re — ортогонализованные функции, свя-
занные с Р( и Рхо согласно (7.5).
Для усредненной согласно (15.18) величины Wa (a nl) можно
воспользоваться процедурой, аналогичной использовавшейся в
§ 5 для получения формул для aa#a. В результате получаем вы-
ражения, аналогичные (5.8), (5.9):
Wa(anl, а0) =
= У, [<?Х (a, а0) Wv(lanl, lo) + <?х(а, «о) W^(lanl, Zo)],
К
W'^lanl, («) = ~ ’
Z„) = у, (£ .
Ко ' х"
(15.24)
(15.25)
X"
Формулы для (2-факторов и радиальных интегралов Rd и Re при-
ведены в § 5, п. 2. Однако в формулах для Q следует изменить нап-
равление перехода: a -*• а0 вместо а0 —> а; кроме того, вместо
функции F\ подставляется функция дискретного спектра Рп1.
В пределе п^>1 выражение (15.24) пропорционально парци-
альному сечению возбуждения перехода а0 — а в ионе Xz+l в по-
роге. Для получения явного соотношения используем известную
связь функций дискретного и непрерывного спектра:
(15.26)
В результате получаем соотношение (15.6).
4. Характер погрешности упрощенной модели. Погрешности,
возникающие при замене Wa (у) в (15.17) средним значением
Wa (a nl), существенно зависят от соотношения вероятностей
К 15. ДИЭЛЕКТРОННАЯ РЕКОМБИНАЦИЯ
137
Wa и W. В предельном случае Wa^W (большие z или п) имеем
q (а и/) = 2 (2Z -|- 1) gaWa (anl, а0),
S 9 (?) = g (у, a0) = q (anl). (15.27)
Последнее равенство следует из (15.18). Таким образом., в этом
случае замена Wa (у) на среднее значение не вносит дополнитель-
ной погрешности.
В противоположном случае Wa W ситуация сложнее. Если
неравенство Wa (у) W имеет место для всех LS, то q (у) —
= grW (а) и ^jq(y) — q (anl), т. е. замена Wa (у) средним значе-
LS
нием также оправдана. Может, однако, случиться, что для неко-
торых LS Wa (у) = 0 или аномально мало, так что соответствую-
щие члены не дают вклада в q(y).
v
Рассмотрим в качестве примера переход а0 — a = s — р
в ионе Хг+1 с одним электроном вне заполненных оболочек. Сна-
чала рассмотрим зависимость от орбитального момента. Имеем
у0 = sX0LS, у = plLS, причем из сохранения момента и четности
следует L = Хо = I ± 1, а при L — I Wa (у) — 0. Поэтому
3 « (Т) = а («) = (2S + i)(4Z + 2) W (a),
L L^l
q (anl) = £S-3 (21 + 1) W (a),
где gs — спиновая часть статистического веса gnnl. Следователь-
но, q (anl) дает результат, завышенный в 1,5 раза. Важно под-
черкнуть, что устранить этот недостаток нетривиально, так как
с ростом п А5-связь переходит в //-связь и запрет на L — I исче-
зает. Проследить количественно этот переход затруднительно.
Отметим, однако, что подобная погрешность имеет место лишь для
s — р-переходов. В остальных случаях замена Жа(у) на Wa(anl)
сказывается незначительно, кроме, быть может, самых нижних
значений п.
Если пренебречь упомянутым эффектом изменения схемы свя-
зи, нетрудно получить простое выражение для скорости диэлек-
тронной рекомбинации для случая s — р-перехода, свободное от
указанного недостатка. В этом случае полный момент системы L =
= Ао и вместо (15.18) достаточно провести усреднение Wa (у) по
S. Подставляя в знаменатель (15.17) вместо Wa(anl) величину
(15.28)
8
и проводя выкладки, аналогичные выводу формулы (15.20),
138 ГЛ. V. НЕКОТОРЫЕ ВОПРОСЫ КИНЕТИКИ ВОЗБУЖДЕНИЯ
находим (а0 = ns или ns2)
Bd(a) - V V • (15'29)
«? Z-J Z—I 1 + (n/n.)3
1 П>И1 1<п ' ' 3
Хо
Эта формула заменяет (15.12), причем п, отличается от nt заменой
о («о, aZ) = V a (a()X0, aZ) -> о (аДо, aZ). (15.30)
Хо
Рассмотрим теперь зависимость от спинового момента. Для
одного электрона вне заполненных оболочек согласно (5.27), (5.28)
Жа (у) со о (у0, у) со + ] [/ + (- l)s g]2,
где fug — амплитуды прямого и обменного рассеяния. Для пе-
реходов типа Is — 2р f т g (ср. § 7, п. 3) и Wa (3L) — весьма мало.
Если IVU(1L) W, имеем
S ? (Y) = (2Ь + 1) W (a), q (uni) = gL • 4W (a),
s
где gL — орбитальная часть статистического веса ganl. Следова-
тельно, в этом случае q (anl) дает результат, завышенный в 4 раза.
Этот вывод справедлив также лишь для Л5-связи и для переходов
с / — g-
Второе допущение упрощенной модели — использование эк-
страполяционной формулы (15.6) для Wa (anl). Это приближение
справедливо для п 4, но для п — 2 или 3 может давать серь-
езную погрешность. Как правило, основной вклад в полную ди-
электронную рекомбинацию вносят большие п. Однако для ре-
комбинации ионов [Н] и [Не] при z 15 основной вклад вносят
как раз уровни с п — 2 и 3. Численные оценки показывают, что
экстраполяционная формула при этом занижает результат.
Третье допущение упрощенной модели — учет переходов толь-
ко в основное состояние а0. Для резонансного уровня а другие
переходы, очевидно, невозможны. Для более высоких уровней
а дополнительные радиационные переходы a — а' приводят к не-
которому увеличению xd (фактора В в (15.20)). Как правило,
этот эффект невелик, так как W со Е2^ и Ет- Е^. С другой
стороны, дополнительный канал автоионизации у — а' может
существенно сказаться на величине фактора В в (15.20), так как
Wa (anl, а') быстро растет с увеличением Ет-. В результате
вклад в хй уровней nl, удовлетворяющих условию
z>Ry ,
сильно падает. Последовательный учет этого эффекта приводит к
серьезному усложнению расчетов. Приближенно его можно оце-
§ 15. ДИЭЛЕКТРОННЛЯ РЕКОМБИНАЦИЯ
139
нить, положив Wa W, если возможен автоионизационный рас-
пад на близкий уровень а'. Другими словами, целесообразно огра-
ничить суммирование по п в (15.12) условием
п < (z2 Ry/£aaJ’/-.
Примером подобной ситуации может служить процесс диэлектрон-
ной рекомбинации
Хг (2pfcnZ) + Й(о,
Хг+1 (2рк) + е -> Хг (Zp^dnl)/ (2pfc) + е,
\ Хг+1 (2рА’—1Зр) + е,
Хг+1 (2p*~13s) + е.
5. Численные расчеты и аппроксимационные формулы. Основ-
ная зависимость скорости диэлектронной рекомбинации от тем-
пературы дается формулой (15.11). Однако остаточная зависи-
мость Bd от температуры за счет фактора е°Р (см. (15.12)) в неко-
торых случаях может оказаться заметной. Чтобы отразить эту
зависимость в простой аналитической формуле, можно заменить
величину % = &EI (z + I)2 Ry в (15.11) на подгоночный параметр
Xd. Таким образом, получаем
xd = 10-135dp’/’^Pxd, Р = (z + I)2 RyIT,
= S Bn, и = х-Д, (15,31)
n>n,
t. e. Bd вычисляется для больших T (без учета е8^), а % подбирается
так, чтобы обеспечить правильное значение %d при некоторой тем-
пературе Тг. Очевидно, < %.
В рамках упрощенной модели Bd вычисляется через парци-
альные сечения перехода а0 — а в пороге. Берджес [49] предло-
жил простую эмпирическую формулу для скорости диэлектронной
рекомбинации. В наших обозначениях эта формула приведена
в § 14, п. 5 (формулы (14.55) — (14.56)). Формула Берджеса
для большинства случаев дает результаты, достаточно близкие
к результатам численного расчета, хотя она и не содержит подго-
ночных параметров. Успех подобной формулы связан со структу-
рой формулы (15.12). Если вынести среднее значение за знак
суммы, то сумма
S l + wv +
nl I
ZZ + 1\
Дп (I) = n.— max I.
ns»ni \ Ri /
Величина n, ~ т. e. сравнительно слабо зависит от иона
и перехода.
140 ГЛ. V. НЕКОТОРЫЕ ВОПРОСЫ КИНЕТИКИ ВОЗБУЖДЕНИЯ
§ 16. Сателлиты резонансных линий многозарядных ионов
1. Возбуждение путем диэлектронной рекомбинации. В про-
цессе диэлектронной рекомбинации (15.1) испускается фотон
Y — Yi — aonZx), энергия которого слегка отличается от энер-
гии перехода а — а0. Поэтому в спектре вблизи линии а — а„
возникают дополнительные линии, которые называются сател-
литами (часто — диэлектронными сателлитами). В этом параграфе
рассматривается наиболее простой и в то же время наиболее ин-
тересный случай сателлитов резонансных линий ионов [Н] и [Не].
Сателлиты линии 2р — 1s ионов [Н] связаны с переходами
2рп1— lsnlt в [Не]. (16.1)
Сателлиты линии ls2p — Is2 ионов [Не] связаны с переходами
\s2pnl — \s2nll в ILi], (16.2)
а также с переходами в ионах меньшей кратности ионизации:
\s2s2pnl — is^snl^ в [Be], (16.3)
ls2s32pfcnZ - is^s^p^n^ в [В], . . [Ne], к = 1, 2, 6,...
Сателлиты (16.1) — (16.3) в ионах с z Z>? 10 неоднократно на-
блюдались как в астрофизической, так и в лабораторной плазме.
Они очень удобны для диагностики плазмы, так как отношение ин-
тенсивностей сателлитов и резонансной линии существенно зави-
сит от температуры (см. ниже). В то же время сателлиты располо-
жены очень близко к резонансной линии и возбуждаются путем
диэлектронной рекомбинации из того же исходного состояния,
что сама резонансная линия (см. (15.1)). Поэтому такой метод
диагностики мало чувствителен к неоднородности плазмы.
В плазме с установившимся ионизационным равновесием са-
теллиты (16.3) обычно весьма слабы. Их интенсивность относитель-
но интенсивности резонансной линии становится заметной лишь
при столь низкой температуре, когда абсолютная интенсивность
становится весьма низкой. Однако в плазме с малым характерным
временем ионизационное равновесие не успевает установиться.
При этом сателлиты от ионов [Be], ..., [Ne] могут оказаться доста-
точно интенсивными. Они могут служить удобным инструментом
для оценки степени отклонения от ионизационного равновесия.
Смещение сателлитов относительно резонансной линии быстро
убывает с ростом п (приблизительно се 1/п3). Поэтому основной
интерес представляют сателлиты с п = 2 и 3. Сателлиты с п 4,
по-видимому, сливаются с резонансной линией и могут заметно
сказываться на ее интенсивности и контуре.
Помимо переходов «внутреннего» электрона 2р — 1s возможны
переходы внешнего электрона nl (правда, с меньшей вероятностью).
При этом возникают сателлиты линий пр — 1s или пр Is — Is2.
§ 16. САТЕЛЛИТЫ РЕЗОНАНСНЫХ ЛИНИЙ 141
Ниже рассматриваются лишь сателлиты (16.1) и (16.2) при
п = 2 и 3.
Как уже говорилось выше, основным механизмом возбуждения
сателлитов является диэлектронная рекомбинация иона Х1+1
(15.1). Кроме того, сателлиты (16.2) могут возникать при непосред-
ственном возбуждении электрона на ls-состояния иона Хг.
Перейдем к рассмотрению относительной интенсивности са-
теллитов.
Интенсивность сателлита у — ух относительно резонансной
линии а — а0 равна
I (v —V,)
i (Y — Yi) = Zf*g (a—a,,) = (V - Yi) + i'(Y — Yi)> (16.4)
где It и /rcs — абсолютные интенсивности сателлита и резонанс-
ной линии, I' и i” — вклады от двух механизмов: диэлектронной
рекомбинации и прямого возбуждения 1s электрона соответствен-
но. Для сателлитов линии 2р — Is IH1 i" = 0. Заметим, что уг —
Начнем с механизма диэлектронной рекомбинации. Очевидно,
. Kd(Y,Yi) к.
(16'5)
где х(( (у, Vj) определяется выражением (15.15), в числителе кото-
рого надо заменить вероятность радиационного перехода W (у) на
И7 (у, уД. Для интересующего нас случая a0 = 1s или 1s2, а = 2р
или ls2p, возможен только один канал автоионизационного распа-
да, так что Wa (у, a0) = Wa (у). Учитывая это и используя аппрок-
симацию (§ 14) для <waia>, получаем
i' (Y — Yi) = a'SPe6^'(Y, Yi),
X -in-13 8vW (V. Yi) Wa (y)
« (T, Vi) = 10 “ V(T) + TF„(T> ’ (16-6)
«о _ Еаал ___ 1 О О _ (г +1)8 Ry
Op — — ns pi P у
Множитель 10~13 введен для удобства: при z ~ 20 <?' порядка еди-
ницы. Коэффициент а лишь очень слабо зависит от р при р J> 1:
«Г’’ (16Л>
где р' = Ea(JT 3/4р, А' и %' —параметры аппроксимации
(§ 14)'для >, go— статистический вес состояния а0; при
z —> оо Е—>-1. Используя результаты расчета сечений в борн-
142
ГЛ. V. НЕКОТОРЫЕ ВОПРОСЫ КИНЕТИКИ ВОЗБУЖДЕНИЯ
кулоновском приближении с учетом обмена, получаем (при 0' — 3,
£ = 1)
а' — 0,75га2-10-3 для сателлитов резонансной линии [Не],
а = 0,47п2"10-3 для сателлитов резонансной линии [Н].
Важным для приложений обстоятельством является то, что за-
висимость i' от температуры Т для всех сателлитов практически
одинакова. Исходным состоянием как резонансной линии, так
и сателлитов является основное состояние иона Хг+1([Н] или
[Не] соответственно).
Порядок величины i'(y — Yi) определяется фактором д (у, yj.
При малых z вероятность автоионизации намного выше вероятно-
сти радиационного перехода (при z ~ 1 — в 10® раз):
W < Wa, q <у, Ti) ж Ю-^И7 (у, cq z4. (16.8)
При этом i' 1, но быстро растет с ростом z. При больших z
W^>wa. g(T,T1)«10-»gT(yoW-2^1L. (16.9)
т. e. i' практически не зависит от z. При этом если 60 1, i' ока-
зывается порядка единицы и даже больше. Переход от одного пре-
дельного случая к другому происходит при z ~ 20.
2. Прямое возбуждение внутреннего электрона. Рассмотрим
теперь механизм возбуждения сателлитов резонансной линии иона
Xz+i за счет прямого возбуждения внутреннего ls-электрона иона
Xz электронным ударом:
Xz (ls22Z0) -J- е Xz (lsnZ2Z0) + е. (16.10)
В плазме низкой плотности (например, астрофизической) ис-
ходным состоянием иона Xz [Li] является ls22s. В лабораторной
плазме высокой плотности, например в лазерной плазме с Ne ~
~ 1020 см-3, близкие состояния 2s и 2р заселены по Больцману, и
так как ЕЕ Т, то N (2p)/N (2s) gzplg2t ~ 3.
Очевидно, механизм прямого возбуждения эффективно рабо-
тает лишь для сателлитов резонансной линии иона [Не], когда
возбуждается ион [Li], Для сателлитов иона [Н] исходным со-
стоянием было бы is2l [Не], населенность которого в плазме весь-
ма мала.
Относительная интенсивность i" за счет прямого возбуждения
, = у! /УДто) <г^> W (у, Т1)
2-1 ZVz+1 <г>а^> 1^(у) + Жа(у)
То
зависит от отношения населенностей Xz [Li] и Xz+l [Не]. Для плаз-
мы низкой плотности
2V х х
+ = <16Л2>
§ 16. САТЕЛЛИТЫ РЕЗОНАНСНЫХ ЛИНИЙ
143
где xv и Xj - полпые скорости фоторекомбинации и диэлектрон-
ной рекомбинации, — скорость ионизации иона Хг. Исполь-
зуя аппроксимации § 14 для скоростей процессов и полагая
Ez = Е (ls22Z - Is2) » Е (Is 2Z2ZO - Is2) - Е (is2p - Is2) =
(16.13)
(ср. (16.6)), находим
= + <1вЛ4>
Подставляя это выражение в (16.11), получаем для низкой плот-
ности (у0 = ls22s)
i* (? — Yi) = а" И + D (71)] Sfk?6*3’ q" (y,Yi),
a" V У - А (Yo’ Т) W (V’ Y1)
Ч (Y, Yi) - w (v) _u Wa (Y) ’
n» _ /6^2 A- -I- Xi (2s) 0'+X'
~ { ’ A^As) 60 + Xv 0' + X' (Vo, Y) 2A' ’ (16.15)
(/?
<x Vo \ 2 O' CWXo др
’ P ~ ~1)E P’
«о T /
Здесь Av, Xv! Ai (y0), xz (Yo); A',^'\ A (y0, y), x (Yo, ?)—параметры
аппроксимаций (§ 14) для xv, <ко£ (y0)>, <waqa>, <ko-7oV>; g" 1
при z 1.
Легко видеть, что в этом случае возбуждаются лишь сателли-
ты ls2snZ, из которых заметную интенсивность могут иметь лишь
сателлиты Is2s2p (остальные связаны с двухэлектронпым радиа-
ционным переходом).
В случае плазмы высокой плотности заселены состояния ls22s
и ls22p. Поэтому
, Nz VI - <г?ру.7> W (т, Т1)
N~-Li8v° <г-0Иоа> Ж(т) + Жа(у) ’
То
Nz XV -
^z+l 2 S’Vo <yOi (Yo)> ’ V°
Vo Vo
(16.16)
и могут возбуждаться все сателлиты вида is2pnl. Используя снова
аппроксимации (§ 14), получаем те же формулы (16.15) с заменой:
^4 (То, Y) ~>2jgvo4 (Yo,Y).
Vo
(2s) yi Ai (2Z0)
60-ь Xf (2s) ^2j 4 [d₽ + X; (2Z0)J ’
(16.17)
144 ГЛ. V. НЕКОТОРЫЕ ВОПРОСЫ КИНЕТИКИ ВОЗБУЖДЕНИЯ
Таблица 12
Длина волн и относительные интенсивности сателлитов резонансной
линии Fe XXV
Эксперимент [50] Теория
X, А 1 X, А Переход V r
1,8510 100 1,8507 ls2p ipi — Is» hS1,, 100
1,8564 21 1,8557 is2p 3P2 — Is2 29
1,8571 15 1,8570 a2St/ -> m2Pt. h /» 4,7 —
—• — 1,8574 2pv, “* n 21У1/, 10,2 2,6
1,8579 23 1,8580 a2P,/t-> m 2Р,Д 0,18 —
1,8594 — 1,8597 игрзЛ-Их» АУ0 — 17
1,8608 12 1,8613 bt2pyt- n*S,/t 0,18 19,7
1,8618 22 1,8625 a2Pt/^ т2Рг/? 13 —
1,8634 47 1,8633 aWtlt^m*Pijt 32 —
— — 1,8638 WP^-. n*S4t 4,9 6
1,8660 47 1,8662 a 2D4t —m *руг 47 —
1,8674 | 38 1,8678 a2Dt/i^> тйР,и 3,8 —
1,8679 1,8685 is2s3S1—> Is» ASo 14
1,8700 21 1,8699 ls2p3 SP1)2^ ls»2p2»Pi .—
1,8729 — 1,8730 X a»P,/t^m»P,/s 7,7 127
8
Обозначения: а = 1s 2p*, b, = Is (2«2р.‘Р), Ь2 = 1s ,(2«2р >Р), т = is‘2p, п = ls!£
Подстановка численных значений показывает, что а" в обоих
случаях низкой и высокой плотности практически одинаково и
может быть записано в виде (для 50 — 1, 0' = 3, £* = 1)
/'«1,4.1(Г3
2-0,6 V
10п ]
(16.18)
Из сопоставления формул (16.15) и (16.6) видно, что если прене-
бречь величиной D (Т), то зависимость i' (Г) и i'(T) оказывается
одинаковой. D (Г) описывает влияние диэлектронной рекомби-
нации на ионизационное равновесие. В области температур
Т ~ Утах, где /Гез достигает максимума, D (Г) существенно
больше единицы и, следовательно, сильно влияет на i". Можно
показать, что D (Г) со e~3t&. Поэтому при меньших температурах
роль D (Г) убывает и температурный ход Г и Г сближается.
§ 17. НАСЕЛЕННОСТИ ВОЗБУЖДЕННЫХ СОСТОЯНИЙ В ПЛАЗМЕ 145
В равновесной плазме преобладающим механизмом возбужде-
ния сателлитов является диэлектронная рекомбинация. Воз-
буждение внутренних оболочек может оказатьсц преобладающим
в случае ионизующейся плазмы (т. е. при очень малых временах).
Как видно из (16.18), роль возбуждения внутренних оболочек
мала при z 15 и может стать существенной при z 20. Очень
важно, что время ионизации также быстро растет с ростом z.
В табл. 12 приведены значения i', i", а также эксперименталь-
ные значения i (в солнечной короне [50]) для сателлитов резонанс-
ной линии гелиеподобного иона Fe XXV. Значение бр (и, сле-
довательно, температура плазмы) находилось по эксперименталь-
ному значению интенсивности сателлита с X = 1,8662 А
7 = ls2pa 3Z)»/2.
Расчет длин волн и вероятностей осуществлялся методом тео-
рии возмущений с использованием разложения по степеням малого
параметра 1/Z. Интересно отметить, что при заряде Z = 26
необходимо учитывать не только все релятивистские эффекты, но
также и лэмбовский сдвиг для ls-электрона, который равен
0,0008 А.
§ 17. Населенности возбужденных состояний в плазме
1. Введение. Интенсивность линейчатого излучения I [эргх
Хсм-3-^1] в оптически тонкой1) плазме определяется насе-
ленностью верхнего уровня перехода i -* к, N (t) и вероятностью
радиационного перехода
Цк = Йй^(0 Wik. (17.1)
Вероятности W, как правило, являются атомными характеристи-
ками, а величины N (i) существенно зависят от условий, в кото-
рых находится излучающая среда. Таким образом, задача на-
хождения интенсивностей сводится к определению населенностей
атомных уровней.
В этом параграфе мы рассмотрим некоторые способы подхода
к расчету населенностей, а также коэффициентов ионизации S
и рекомбинации а плазмы. Определим эти коэффициенты так,
чтобы они имели размерность [см3-с'1]. Ниже на примере плазмы,
содержащей атомы водорода (или водородоподобные ионы), будут
изложены главным образом методы численного расчета г).
Обычно рассматривают три типа моделей плазмы: корональ-
ную модель в пределе малой плотности, модель локального тер-
Здесь мы будем рассматривать оптически тонкую плазму, в которой
излучение свободно выходит из объема и не влияет на населенности уровней.
а) Обзор аналитических методов вычисления коэффициентов рекомбина-
ции (ионизации) и населенностей уровней содержится в работе Л. М. Бибер-
иана и др. [51]. Подробное обсуждение проблемы спектральных интенсивно-
стей читатель может найти в книгах [52—54].
146 гл. V. НЕКОТОРЫЕ ВОПРОСЫ КИНЕТИКИ ВОЗБУЖДЕНИЯ
модинамического равновесия в пределе высокой плотности плазмы,
а модели плазмы в промежуточной области часто объединяют тер-
мином радиационно-столкновительная модель. (Условия приме-
нимости первой и второй моделей см. в § 2.)
Простые соотношения между населенностями уровней сущест-
вуют в пределе локального термодинамического равновесия,
когда вероятности столкновительных процессов значительно пре-
вышают вероятности радиационного распада любого из уровней,
а также характерные скорости изменения температуры и плот-
ности. При этом населенности уровней полностью определяются
температурой, плотностью и химическим составом плазмы (см.
формулы (2.2) и (2.3)) и не зависят от эффективных сечений эле-
ментарных процессов. Если же локальное термодинамическое
равновесие не имеет места, то населенности атомных уровней
определяются всей совокупностью радиационных и столкнови-
тельных процессов: возбуждением, рекомбинацией и каскадными
переходами на уровень г, его радиационным распадом, тушением
и ионизацией в результате столкновений. В плазме с не слишком
малой степенью ионизации обычно существенны лишь столкно-
вения с электронами.
2. Населенности уровней водорода в корональном пределе1).
В пределе малой плотности распад возбужденных уровней обус-
ловлен исключительно спонтанными радиационными переходами 2).
Это приводит к тому, что в плазме заселено только основное со-
стояние и метастабильные уровни, а населенности всех остальных
уровней очень малы. Заселение возбужденного уровня п может
происходить как за счет прямых процессов, так и в результате
каскадных радиационных переходов с вышележащих уровней
и т. п. Скорость прямого заселения qn (см-3-с'1] дается суммой
скорости возбуждения из основного состояния и скоростей фото-
рекомбинации и диэлектронной рекомбинации на уровень п.
Вклад каскадных переходов можно учесть, лишь решив систему
уравнений для населенностей.
Рассмотрим стационарные уравнения для атома водорода
(или водородоподобных ионов). Положим, что уровни nl с раз-
личными значениями орбитального момента I заселены пропор-
ционально их статистическому весу:
ЛГ. (»/) - N, (п). (17.2)
где Nz (и) — населенность всех уровней с главным квантовым
числом п.
х) В этом разделе изложение основано на работе М. Ситона [55].
2) Отметим, что распад метастабильяых уровней или уровней с очень
большими значениями главного квантового числа будет определяться столк-
новениями даже при очень малой плотности.
§ 17. НАСЕЛЕННОСТИ ВОЗБУЖДЕННЫХ СОСТОЯНИЙ В ПЛАЗМЕ 147
Уравнения для населенностей имеют вид
А. W Wn = 3 А. (»') «'»-„ +5». W„= 2 (17.3)
н’>П п"<п
qn = Nz (1) Nc <wJn> + У2+1Уеху (n). (17.4)
Здесь TV2+1 — плотность ядер атома X, <voln) — скорость воз-
буждения уровня п из основного состояния, xv (п) — скорость
фоторекомбинации на уровень п. Диэлектронная рекомбинация
в случае ионов [Н] отсутствует.
Решение системы (17.3) запишем в виде
Nz (») = У, Qn'C (п, п), С(п, тг) = 1. (17.5)
П
Элемент каскадной матрицы С (п , п) при п' п есть вероятность
того, что атом, возбужденный первоначально на уровень п ,
в результате одного или нескольких радиационных переходов
окажется на уровне п. Обозначим через Р (п, л) вероятность
перехода с уровня п на уровень п в результате лишь одного ра-
диационного перехода. Очевидно,
Р (п', п) - Wnn !Wn:
Элементы каскадной матрицы С (п , п) с п п выражаются через
эти величины следующим образом:
С (n + 1, л) — Р (п + 1, п),
С (п + 2, п) = Р (п + 2, п + 1) С (п + 1, л) + Р (п 4- 2, л),
........................................................(17.6)
С (п + т, ri) = Р (п + т, п + т — 1) С (тг + т — 1,п) +
4- Р (л 4~ лг, л 4- лг —• 2) С (л 4~ лг — 2, л) 4* ... 4- Р (п 4- лг, л).
Воспользовавшись тем, что С (л, тг) — 1, формулы (17.6) можно
объединить в одно рекуррентное соотношение
С(л4-лг, л) = У Р (л 4- лг, п')С(п’, т). (17.7)
п'=*п
Заметим, что по указанному рецепту можно построить каскадную
матрицу для любого атома, например, придавая л смысл номера
уровня в порядке возрастания энергии.
Значения элементов каскадной матрицы С (п т, п) для
п 10, т 10 приведены в табл. 13.
В интервале 5 т 10 С (п 4~ лг, л) хорошо аппроксими-
руется формулой
Д
С (л 4- лг, тг) = С (оо, п) 4—.
Значения С (оо, л) также приведены в табл. 13.
148 гл. V. НЕКОТОРЫЕ ВОПРОСЫ КИНЕТИКИ ВОЗБУЖДЕНИЯ
Величины С(п т, п)
Таблица 13
т п — 2 3 4 5 6 7 8 9 К)
1 0,4418 0,2978 0,2336 0,1975 0,1744 0,1581 0,1464 0,1369 0,1295
2 0,4105 0,2601 0,1947 0,1587 0,1361 0,1203 0,1093 0,1006 0,0939
3 0,3991 0,2454 0,1791 0,1430 0,1206 0,1052 0,0942 0,0858 0,0791
4 0,3934 0,2380 0,1710 0,1347 0,1120 0,0968 0,0858 0,0775 0,0711
5 0,3903 0,2336 0,1661 0,1294 0,1068 0,0916 0,0806 0,0723 0,0660
6 0,3833 0,2308 0,1627 0,1260 0,1033 0,0881 0,0771 0,0688 0,0624
7 0,3870 0,2289 0,1605 0,1236 0,1008 0,0854 0,0745 0,0662 0,0598
8 0,3860 0,2274 0,1589 0,1217 0,0990 0,08.35 0,0725 0,0642 0,0578
9 0,3853 0,2264 0,1575 0,1203 0,0975 0,0821 0,0710 0,0627 0,0563
10 0,3848 0,2255 0,1564 0,1191 0,0964 0,0809 0,0698 0,0615 0,0551
С (оо, л) 0,3796 0,2174 0,1468 0,1088 0,0860 0,0703 0,0590 0,0505 0,0441
В применении к еще более высоковозбужденным уровням
(п 10) можно использовать аналитическое выражение для кас-
кадной матрицы, полученное в работе 156] с помощью приближе-
ния Крамерса (формулы Крамерса для W см. в конце этого раз-
дела):
С(п', п) =
____2_. п» nW*
~~ ~п^ П 2 («' + »)(«' — л)
Го,5772 4- In . ,,п2'Г,----гГ2. (17.8)
L (л + л)(« — л) J ' '
Погрешность формулы (17.8) для п' — п = 1 не превышает 15%,
с увеличением (п — п) эта погрешность уменьшается (что соот-
ветствует характеру погрешностей приближения Крамерса).
Входящие в формулу (17.5) суммарные вероятности радиа-
ционного распада Wn запишем в виде
W„ - А, = - 0,789 • 10-V(с’Ч, (17.9)
оЛ у о (Zq
где а = e^lHc — постоянная тонкой структуры. Коэффициенты
т (п) для ряда значений п приведены в табл. 14. При п > 10
т (п) хорошо аппроксимируется формулой
т (п) » 31п п — 0,247,
В приближении Крамерса вероятность перехода п' — п равна
2А
W ' =_____________
пп п'3п(п'2-^) ’
§ 17. НАСЕЛЕННОСТИ ВОЗБУЖДЕННЫХ СОСТОЯНИЙ В ПЛАЗМЕ 149
Т а б л и п а 14
п 2 3 4 5 б 7 8 9
т(п) 1,911 3,084 3,929 4,589 5,132 5,590 5,989 6,389
п 10 и 12 13 14 15 20 25
Т(н) 6,657 6,943 7,205 7,442 7,668 7,876 8,740 9,410
а суммарную вероятность распада уровня п можно записать
в виде
пь 2
В соответствии с (17.4) и (17.5) населенности возбужденных
уровней в корональном пределе пропорциональны второй степени
плотности плазмы и пренебрежимо малы по сравнению с плот-
ностью атомов в основном состоянии. Суммарная населенность
всех возбужденных уровней также очень мала. Поэтому в плазме
низкой плотности ионизация атомов происходит в результате
прямой ионизации из основного состояния. Единственным про-
цессом рекомбинации в случае водорода и водородоподобных ионов
является фоторекомбинация. Определив коэффициент рекомби-
нации а таким образом, чтобы величина Nz+iN6a имела размер-
ность 1см“3-с-11, имеем
Оо
а = xv = У xv (и).
П=1
Для других атомов и ионов необходимо учесть также диэлектрон-
ную рекомбинацию:
а = -J- xd.
3. Плазма произвольной плотности. В общем случае наряду
с радиационными каскадными переходами необходимо учитывать
также каскадные переходы за счет столкновений. Так же как и
в предыдущем разделе, будем рассматривать водород или’водоро-
доподобные ионы, предполагая, что при данном п имеет место
полное перемешивание уровней с различными I, т. е. выполнено
условие (17.2).
150 ГЛ. V. НЕКОТОРЫЕ ВОПРОСЫ КИНЕТИКИ ВОЗБУЖДЕНИЯ
Уравнения для населенностей уровней п иона Xz ’) запишем
в виде
_L Nz (П) _ Nz гп + £ Nz гтп + Ni+1Hn. (17.10)
Здесь Гп 1с'1] — суммарная вероятность распада уровня п, вклю-
чающая в себя вероятность радиационного распада Wn, вероят-
ность переходов на другие дискретные уровни в результате столк-
новений с электронами We (л) — 2j We(n, n') = Ne <глТпп->,
n'^rl n'^kn
вероятность ионизации с уровня п Wt (и) и, вообще говоря, веро-
ятность рекомбинации в ион Xz_i (рекомбинация обычно суще-
ственна лишь для нижнего уровня иона);
fWe(m, n) + Wmn при лг>л,
1И7е (иг, л) при т<^п.
Вероятность рекомбинации на уровень п Rn равна сумме вероят-
ностей фоторекомбинации Wv (л) = Хеих (и) и тройной реком-
бинации Wr (л) — N2enr (п) 2).
В любом конкретном расчете количество рассматриваемых
уровней необходимо ограничить некоторым значением п0. Это
можно сделать, исходя из того, что уровни с достаточно большими
значениями главного квантового числа и должны находиться
в равновесии Саха с непрерывным спектром:
(n) = NE (л) = yz+1 NeBn (Т),
где множитель S дается формулой (2.4). Это объясняется следу-
ющим. Вероятности радиационного распада Wn быстро убывают
с ростом п. Вероятности переходов л -> л ± 1 при столкновениях
с электронами возрастают с увеличением п: We со л4 (см. § 10),
а вероятность ионизации (л) се л2 (см. ниже формулу (17.14)).
Поэтому заселение и распад уровней с большими п обусловлены
исключительно столкновениями с электронами. При п 1
(л, п ± 1) Wj (п), и движение электрона между высоко-
возбужденными уровнями имеет диффузионный характер [57,
58, 59], т. е. является медленным. Таким образом, при п больше
некоторого л0 населенности уровней практически полностью опре-
деляются балансом ионизации и тройной рекомбинации.
г) Как обычно, Nz — плотность ионов с зарядом z — 1, Xz —
г) В случае неводородоподобных атомов и ионов необходимо добавить
вероятность диэлектронной рекомбинации
§ 17. НАСЕЛЕННОСТИ ВОЗБУЖДЕННЫХ СОСТОЯНИЙ В ПЛАЗМЕ 151
Оценку величины п0 можно получить из условия
(n0)>W(n0).
(17.12)
Вероятность ионизации W( (п) оценим, используя для сечения
ионизации формулу Томсона (14.52). При этом
1Г,- (n) = N,S Vл 4
оо
( -4-г e~^'du
Ип r J '< + 1
О
= АД7-10-’
Ry
Л’п
|‘/‘р*-Ч1 + МЯ‘ (- ₽)Ь
(17.13)
где р = | Еп\ /Т = z^y/rfT.
Для возбужденных уровней с п Д> 1 р 1 и из (17.13) сле-
дует
[^г] ' (17.14)
Воспользовавшись для оценки W (п) формулой (17.9) (положив
в ней для простоты т («) — 10), из условия (17.12) получим
7? 0 .— Z
/ 10й [см-3] \177 / Т \’7”
k Ne ) U2 Ry ) '
(17.15)
В интервалах 0,01 эВ <4 Т <4 100 эВ и 108 см 3 < Ne < 1015см 3
из (17.15) следует, что
2^-^_^зо.
Для нахождения населенностей уровней и ионизационного
состояния плазмы необходимо решать совокупность уравнений
типа (17.10) для ионов нескольких кратностей ионизации при
условиях сохранения числа ядер каждого из химических элемен-
тов и электрической нейтральности плазмы. Если температура и
плотность плазмы изменяются не слишком быстро, то задача
допускает дальнейшее упрощение.
4. Квазистационарное приближение для атома водорода.
Малые отклонения от стационарного значения N (п) релаксируют
за время ~ 1/Гп. Анализ вероятностей элементарных процессов,
определяющих Гп, показывает, что релаксация любого из воз-
бужденных уровней водорода происходит значительно быстрее
(на несколько порядков величины), чем релаксация основного
состояния 1). Это обстоятельство позволяет считать, что населен-
ности возбужденных уровней в каждый момент времени соответ-
ствуют мгновенным значениям плотности атомов в основном
состоянии, плотности электронов и ионов Н+. При этом в системе
*) В певодородоподобных атомах релаксации может быть медленной для
метастабпльных уровней.
152
ГЛ. V. НЕКОТОРЫЕ ВОПРОСЫ КИНЕТИКИ ВОЗБУЖДЕНИЯ
уравнений (17.10) достаточно сохранить производную по времени
только для N (1), положив -Jj-W (п) = 0 для 2 п п0. Квази-
стационарное приближение для возбужденных уровней наряду
с упрощением вычислений позволяет составить универсальные
таблицы, пригодные для определения населенностей в стационар-
ной и нестационарной плазме в ши.роком диапазоне значений тем-
пературы и плотности [60—63].
Для расчета и табулирования населенностей удобно исполь-
зовать безразмерное отношение b(ri) = N (ii)/Ne («), где NE (л) —
значение населенности (17.11), соответствующее равновесию
Саха с непрерывным спектром (в случае водорода jVz+1 =
— N (Н+)). В этих обозначениях уравнения для уровней 2 п С.
н0 имеют вид
т^п Е \ f
Учитывая (17.11) и соотношение
Ne (1) We (1, n) = Ne (n) We (n, 1),
перепишем (17.16) в виде
m^n
b (n) Гп — V b (m) Bm ^T.L Г =________------1_ /n
V ’ n Ll V ' вп (T) mn NeBn(T) Ne (1) "«Г»1'*
(17.17)
Первый член в правой части (17.17) отвечает прямой рекомбина-
ции на уровень п и зависит только от Ne и Т. Второй член соот-
ветствует прямому возбуждению из основного состояния и про-
порционален N (1).
Решение (17.17) удобно представить в виде суммы двух слага-
емых:
Ь = AfJ(n) = Г° + Г1 NE(i) ’ (17.18)
из которых г0 (л) дает вклад рекомбинационного заселения (пря-
мого и каскадного), а второй член отвечает сумме прямого и сту-
пенчатого возбуждения из основного состояния.
С учетом (17.18) уравнение для N (1) запишем следующим
образом:
-^W(l) = W(H+)Wea-y(l)2VeS. (17.19)
1
а~ ”.
Величину а, определяющую приток атомов в основное состояние,
Го । V Nz(n) ,.г 1
n (Н+) г° ’
п>1 J
§ 17. НАСЕЛЕННОСТИ ВОЗБУЖДЕННЫХ СОСТОЯНИЙ В ПЛАЗМЕ 153
принято называть коэффициентом ударно-радиационной реком-
бинации, а величину S,
1 Гг V 1
15 - /V Г1 2-J ne (1) Г1^Гп1 ’
— коэффициентом ионизации.
Стационарное значение N (1) дается соотношением
АЦ1) = ЛГ(Н+)-£-. (17.20)
В большинстве случаев, представляющих практический ин-
терес,
Б Ar(n)<Ar(l),2Ve,7V(H+)1) (17.21)
п>1
и коэффициенты S, а определяют полные скорости ионизации и
рекомбинации. (Отметим, что в случае, противоположном одному
из условий (17.21), квазистационарное приближение вообще
неприменимо, так как малое изменение населенностей возбужден-
ных уровней будет приводить к значительному изменению Ne
или N (1).)
В пределе низкой плотности (Ne -> 0), очевидно,
S = Wi (i)/Ne = <уон>, а а = 2xv (п),
п
трр «V (п) — скорость фоторекомбинации па уровень п. При этом
величины гг (п), как нетрудно показать, определяются отно-
шением
а г0 (п) зависит только от температуры плазмы.
В пределе высокой плотности существенный вклад в коэффи-
циенты ионизации и рекомбинации, особенно при низкой темпе-
ратуре, вносят переходы через возбужденные уровни 2). Коэф-
фициенты г0 (п) и т\ (и) при этом от плотности не зависят.
Некоторые результаты расчетов величин r0, т\, S и а для атома
водорода, заимствованные из работы [63], приведены в табл. 15.
Исходными параметрами для определения с помощью этих таб-
лиц населенностей уровней и ионизационного состояния плаз-
мы являются температура Т, плотность электронов Ne, плот-
ность протонов N (Н+) и плотность атомов водорода в основном
*) Обсуждение вопроса о максимальном значении главного квантового
числа в сумме по п выходит за рамки нашего рассмотрения.
2) Оценка коэффициента рекомбинации а в пределе низкой температуры
и высокой плотности будет дана в п. 6.
Параметры г0(л), rj/i) и коэффициенты £, а для водородной плазмы
Таблица 15
—>о 10* 1010 10“ 10“ 10я 10м 10“ 10м ю” -*оо
ги (2) 4,9-6 6,2-6 7,6-6 1,1—5
Г! (2) 2,5—17/Ve 2,5—8 2,5—7 2,5—6
М3) 1,4-3 1,8-3 2,2—3 3,1-3
М3) 1,0-17АГе 1,0-8 1,0—7 1,0—6
М4) 1,1—2 1,5-2 1,8-2 2,8—2
М4) 7,2—18.Ve 7,2—9 7,2—8 7,1—7
го (5) 3,2-2 4,2-2 5,5-2 1,0—1
ri(5) 6,1—18Уе 6,0—9 6,0-8 5,7-7
Мб) 5,8-2 8,1—2 1,1—1 2,7-1
Мб) 5,5-18^ 5,4-9 5,2-8 4,3-7
5 1,2-26 1,6-26 2,1-26 3,2—26
а 7,9—13 1,0-12 1,2-12 1,7—12
Обозначение: 7,6—6—7,6-10-6.
Т = 4-103 К
сл о 1 1 сл Си 4,9-5 2,5-4 2,4—4 2,5-3 2,2—3 2,4—2 1,8-2 2,0-1 6,2—2 6,7-1 8,5—2 9,2—1
6,0-3 1,0-5 2,2—2 1,0—4 1,3-1 1,1—3 3,5-1 1,3-2 4,2-1 1,1—1 4,5—1 3,9—1 4,7-1 5,3-1
7,3-2 6,9—6 3,1—1 5,7—5 6,0—1 4,8—4 7,4-1 5,3-3 7,7—1 4,5-2 7,9—1 1,5—1 7,9-1 2,1—1
3,3—1 4,4—6 6,8-1 2,5—5 8,5-1 1,8-4 9,0—1 2,0-3 9,2-1 1,6-2 9,2-1 5,6-2 9,2—1 7,7-2
6,4—1 2,3-6 8,6-1 1,0-5 9,4—1 7,2-5 9,6-1 7,7-4 9,7—1 6,5-3 9,7—1 2,2-2 9,7—1 3,0-2
6,5-26 2,1-25 1,3-24 1,4-23 1,2—22 4,0-22 5,4-22
2,9-12 7,1-12 2,7—11 1,6—10 1,4—9 1,3-8 1,3-25 N
ГЛ. V. НЕКОТОРЫЕ ВОПРОСЫ КИНЕТИКИ ВОЗБУЖДЕНИЯ
§ 17. НАСЕЛЕННОСТИ ВОЗБУЖДЕННЫХ СОСТОЯНИЙ Б ПЛАЗМЕ 155
Таблица 15 (продолжение)
т4 ^Н 1 1 СМ 1 1 и см СО СО М« ян см ян см 1 1 ео | 1 1
и см Ю СМ 1 1 о ч? О со 1 1 СО О о н О СО о ю
Г. ГЧ Г" ♦* О со тН со г- ** *-
о. см ©5 ю ©5 тч тн со j тн см 05 4J1 тН LO тн ст> тН СЧ
1 2,2—1 9,5-1 К 1—9 9,9-1 1 9_9 J Cf 1 * -U'cr > СО 1 > О СЧ 5 ТН Т- 3 ’Г- 1 L с 2,4-9
^0 6 1 1-0 L 1 9,3—1 А 7_9 1 тчСМ ег 1 1 1 . ОО ТЧ О со 1 ОЗ т-ч -г-1 СТ > ес , о 1 G Н тг 1 9,5-15 Ч 9—10 > 1
1 1—0 1 i-i‘e 1 < яН сх 1 1 > U0 м < оо сх 1 тч W , ’ 1 1 со с 1 ОЗ 1Г D H cr 1 1 5 05 Г" 5 05т- J vt 1 • О О 4 я-4 1Г ч 1 1 с J 1Г > я-Ч ч Т-Ч 1 > Т4 Г г-
см сх 1 1 т*_а ] тН сг 1 1 ) см * Г 9,3-1 1,1—3 9,8-1 Ч 9 А Г тН 1 1 1 От 5 GTjt 9,4—16 1 А 11 i.
8-103 К 1,3—2 1,9-3 4,3-1 R 1 А 8,3—1 1 7 А f тЧ И 1 1 иэ с ч аз" ч 5 th 1Г 1 1 1 00^ 1> 5 оГт- 1,5-16 3,9-12 1,6-104 К
Т = I f’b3 Г *4 Щ тН 1/ III, 5 СМ Г- СО яг 4 ТН Г", LQ О' 5 ^4 1Г 1 ч Ч1 Т 5 00 - 1 * > * ! 9,4-1 4,0-6 7. Ч 17 -CM II 4 ягЧ 1 1 л Г TH
I 2,5-3 । -1 Q R. 5 СМ « 1 » ОС 4 та . ~ г* см 5 ТЧФ Т4ф Н0 тН ТН 1 II 1 1 1 1 1 1 > мн т г- о см о о э см т т см г— тн см тн
СО 1 Q0 С тн т 5 CM t- t- т, t— Tr- illi 1 1 1 1 5 со ян ям г- mi-<г тс 4 со оо ям т см sr хр с* 1 ’ 2 О' э * 1 7,3-13 I
1,5-3 1,9-7 2,6—2 Й О й 5 см а 1 1 1 см с з" GO н и , 1,5—1 Z Q Q 1- СО Э ^4 00 — н 1 1 1 1 1 Э ^яг4 О нН Г СЧ ХГ И о"
<Х> V Сй 05 01 к й» й* :> Г- СО _ 00 ОО 00 00 со СО тн СМ— СМ ^4 яН ^4 тн II II 1 1 1 1 1 1 1 1 см оз о см —' о -г- о иэ io иг оз н ян СМ 00 СО тн Ю Т<\Г Г- SF СМ СМ СОСО м* Ш U0 <© <©
TH см 1 1 CD О О vfT 1,0 5,1-3 l,o 9,6—4 •5» О io T, CM
тч CM I I th CO I 1 1 1
О 1 1 05 05 О хГ о m
** «ч м ir- *-
Oi co 05 4J* TH 05 TH CM
th CM I I ян CO 1 1 н-Sjl ! I 1
□0 CM Д th ! 1 05 00 о о
Or CO 03 vf 05 Гя. TH см
TH O] TH CO ! I TH Xtf I | н m 1 ।
CM TH 1 1 05 CD 1 1 00 о 1 1 05' th
T- #- T*
CO TH 00 T4 05 CO 05 00
CM co 1 1 hM* I I th m 1 t ТЧ LQ | I
c© m 00 co 1 1 CM TH CO 05
₽- V*- * *-
О ян CP CO 05 t-» 05 tH
CM stf 1 1 th m 1 I th m 1 I -и О I |
1 I 05 CO 1 1 О 05 1 1 Vf 05 H 05
*4 T* r- T- T*
*O< TH CO Ю t>. тгЧ C5 m
cm m t 1 ^4 & I I T- ZD I I TH CO 1 I
1 1 m cd CD 00 05 О 1 1 О co
CO" -Г4 нН О CQ St* b* TH
CM Ф 1 1 *T *7 ”7 *7
I 1 05 C© ГО О । i ST 05 о m
•» T- .- *-
CM TH TH Г-* CM чф CO
cm e* 1 I th 00 I t th O0 I 1 ЯН0О 1 1
1 1 о co 1 t tH ^-4 1 1 О TH 1 1 05 ТЧ
#« v* Г* T- T-
CM TH ЯН o* cm m CM Ttf
41 ф Щ
fe: £ fe:
00 CO co
CM TH I I CM ян I I TH tH 1 1 TH H 1 1
1. 1 CO (£> 00 см 1 1 00 CM f 1 v-r vr
CM' th 05 Гн нН LQ CM
CM CM^ OQ/O.
Ф H © H © iH e w
156 ГЛ. V. НЕКОТОРЫЕ ВОПРОСЫ КИНЕТИКИ ВОЗБУЖДЕНИЯ
Таблица 15 (продолжение) О.' < Ю S N -с III 1 О Щ О Ю © X ч-7 ОсГ 4 СО хГ U 1 1 Г ©СО О СО ОС *• * » *> е> Ч ^ч хн х-ч 04 чЧ С 1,0 2,0-5 Q О 4Л > с -1 г 4 С з" а | *-» у V т Q 9,9-1 7,3-3 1,0 а Л Z г 1 0 0
о -г-1 Г! Ц со s 7 7 7 и । о4 а о чч °.°г чр ** ** *• ** СЪ —1 ГЧ тК TH с ч-t с© чч Q0 1,0 6,0-5 1,0 2,0—5 Я 9 4П 1 9,0-12 9,9—1 7,3-3 1,0 СП Z г 0
itOl 1,0 Q Q d о а э Ч з о ч ч -1 — см м vr м ю 2 2 7е? 7 II 1 1 1 III сЦ ©4 , К \Г ОМ ОМ ОО ОО СМ Ю , 1 - . 4 г-*'»-»,»»*,»'»* (—рч , ff— * ©чЧхн^ч^чС4ччЮччС4ООчч
2 о wl —• СМ чч СМ чч Р 777 mi ! 1 1 сч со о о ООО Ю 00 - - * * - - © чч О ч хн СО чч хГ Э X 4 0- ч ~Ч О р Lf - О U- чч 1Г 5 U 5 о а £ ч ЪР и 01—9‘Л «-, М Ч 1 1 00^0 О СХ 7 © Г- ЧЧ W г
о тч 04 04 чч Г J 7 Т I. ~ *• «О t' чч 04 © еа 1 L - Of 1 1 V» 1 9,9—1 < Ч Z 1,0 3,4-5 1,0 1,1—5 4,9-10 Z R—1.4 чч Р 1 2.’ Г ©ir 0 чч SJ, I I Ч © Ю Э ©'хГ
о ч1 9,9—1 6,6—6 1,7-12 О 9 19 2-1СН К I 2,8-1 1 Я—Я 8,2—1 2,1-4 9,6—1 Z 9—5 О СГ. ) чгч Ю О чч X- II 111 © чч О 00 О X- <© х-ч хч CQ СМ ст 28-10* К 7,9-1 1,4-3 9,5—1 1 0 А I* >
ч-
8 о тЧ 2 2 II 7^ 1 1 1 1 Ьч О1/ Г* чч г- •. © с4 ь- to чЧ LT 1 о с Г IQxj ЧЧ LT 1 хг xj Г* ОО* ч ч-t С£ 1 Ю О' © х1 чч С£ 1 00 w © ч- 1,1—10 2 4—13 II 11 1 ео г Г* ч f 4110 1 1 Ч oo'io
О 8,7—1 7,7-7 4,4-13 /. Q ла !а Ъ 1 1~5*1 1 чн « 1 ХГ СГ СО С£ чч СГ 1 Ь- XI Ю ст чгч СС 1 © U- Г 00*4- 7 © С£ чч СС • чЧ X" I I © ч- ? 00 CN ч-I ХГ 1 о_°с t'- ч ч- С£ 1 r-CN > 1
7^ о о со о О’ 1 Г р СО чч СО чч Г- 7 ill I 1ГЗ CJ ь © - - - - чч хн 04 С£ СО 7Г ч-ч 1Г ХГ 71 Ю Г' ? 1ОСГ 7Г сч о t4- ч К1—б 1 И-2‘Д j - у -ч- 6,9-1 I 1 Я_R । Э чн (> 1
«01 чЧ« 1 00 *< СО О' СТ ч г с Г Р С»- ст Г р * 4.J •» ЧЧ ч- чч ОС 1 о ос 04 С£ тч a 1 t*-ОС Г 0OXJ -г- ОС 1 ю а Г хгог 5,3—1 3,1-8 К 7—11 сс ’i 7 х Г чч 7Ь о а С£?ч - чча 1 5 Mr 7 гч'ос г
1 fe а ЧЧ ч 1 © а сч сг er ,vr *SZ* 1 е 2,6-13 3,0-13 11,3—1 1 .4—17/V. ад : S 04 С£ 3,4-1 5,0—18Ле 4,0-1 Z 1—1RV ш ад fe; 00 TH сс Ч"Ч т—1 ЧЧ 1111 U0 © С4 ОС хГ СО © т- Й х-ч ч I 00 Р С£> т ад а 7’ 04 С\ * 1>ос ад ! Г
ад *5 S'S' сТсм* мр? х* У со_со. сГсм4 мм ''7>"7ч ® к*
§ 17. НАСЕЛЕННОСТИ ВОЗБУЖДЕННЫХ СОСТОЯНИЙ В ПЛАЗМЕ 157
Таблица 15 (продолжение)
1 Ч1 1 чч l,o 2,9—5 1,0 9,8-6 2,2-8 г, > со 1 о со 1 о о чч 05 1,0 7,9-4 1,0 1,5-4 1,0 4,0—5 1Г О_*5 ЧЧ Ч- 5 г 6,8-8 ЭЛ77£—0‘ 1
*ф О чч ю 1 о 05 -см* 1,0 9,8—6 00 1 см см 7,7-13 1 1,0 9,0-3 sr <Z> 05 1,0 1,5—4 Ю О о чч~хГ LT о < •—н Ч 5 г 00 1 оо СР 1,2-13
► «ф из со оо СО ЧЧ со •<г м< 1© Е" 00
М О W-I 1 о тЧ чЧ О 00 ’гч'сч* 1 о ос т-Гвз” 1 СМ СМ 1 хГ [ 1,0 9,0- О 03 - е» О 1© чЧ 1 -w sr °'а чч ч- г. 00 св 1 ХГ см*
10» 1,0 1,0-4 ю о СО тч см 1,0 9,5-6 СО см см 1 см V* СО 1 о г- «00 хГ О С© xF О ХГ T-* тЧ 1,0 3,9-5 1,о 1,4-5 6,7-8 хГ чч 1© тЧ
ю i© С© 00 ST со •tf ХГ ЕО 1© 00 М< чЧ
о чг* о чч 1 о м О 1© 1 С5 i© 1 rHCQ сз о О чч 1 О "W О ч 1 00 1 к©
чч 00 *ч см чч тН С© q© тЧ с© чЧ ЧЧ СО Ч-I чЧ 1©
О ю 1 1 С» CD 05 СО КО 1 о о чн 1,0 3,5-6 00 1 см чч Я-1‘9 к ю О см чЧ СО 1 г- чч чч М’ 1 О из ТЧ СМ 1© 1 о см ЧЧ 1© 1,0 1,5-5 1,0 5,3-6 00 SJ< 1,5-14
т- 1© тч С© *ч о 05 хГ ч“< к© II SJ< из 1© с© СР 00 чч
О тН ю ап чЧ 1 1 СЮ СО 05 ХГ 1 1 С5 СО ОЭ чЧ 05 00 1 05 *© 1 i© см ЧЧ см чч щ чЧ с© Ч-Н С5 чЧ ^4 1,0 6,2- чн v чЧ CS 1 ео со 1© чЧ
чч О -W 50 05 ХГ тЧ из с© с© с© оо ч< ^ч
О т-1 1 1 LO С— СО CQ СО с© аГч-Г 1 1 О 05 С© д. J. 1©* 1 l© со СМ* см оо w осГ 1,1 4,6- -ч СМ чч"сМ~ ок w'c 1 о со* 1 1© чч
ч-i О- 05 хГ чЧ из Г- о» о. 00 хГ чЧ
о чН 1 1 с» см 1© 1 1 Ч1 СО 00 03 1 1 о> -w сГсм см 1 из ю со см* ео ю чЧ О 1 ем со чЧ с© 1 о а ^Сч г 1 05 см* 1© чч
’Н 00 ^00 тч оо 05 sT о. 00 00 00 ос 00 хг
о тЧ 1 1 с- с© Ь-* 1© 1 1 О'» ОО*'*' 1 1 ем со оо со 05 С© 1 СО 1©* 1 из со w СМ 1 со Г* ч-Го? 1 ЧЧ с© 1 СМ со_ и\© *-1X3 чч'хГ °0, оТ L© ТЧ
о 1 QJ 00 чч чЧ | I ф < 00 чч I I •а й: 00 тч чч 05 ч* 1 ф < чЧ 1 ф > Гч. тч I Ф 00 чЧ I 00 т—< ОС 00 хГ тЧ 1
1 1 С© 05 Г^1© 00 ОО г* хг 1 1 05 СМ t^xjT «о" СО из 1 1DC0 *- СМ СО О чЧ чЧ СМ О см г* ^оо* 1 чч о ЧЧ ю 00 см* 1© чЧ
•— _. -Л -Л — j™™*
к хГ хГ ч Ю 1© £< с© С© 1? С- 41 а см см со со к? к4 ХГ хг к и1 1© 1© кг' ьГ* СР ср >с 4) о
158
ГЛ. V. НЕКОТОРЫЕ ВОПРОСЫ КИНЕТИКИ ВОЗБУЖДЕНИЯ
Таблица 15 (продолжение)
8 t п- СХ 1 1 О СХ о i О' О я- 14 V 1,0 9 1_А if о о яч 1Г 1Г О 1- 1 с\ а а i> й—7 (• 1—6‘6 1 э№8-z‘l ОТ О & ЧМ 4“ 1,0 9 7.Л 1Г о о 14 ь и- О ОС ч-4 СХ ОС 1 G С£ ст СТ 1 1
10» и с\ 1 СП сх Ci 1 СО Х1 1 О 14 О - 14 14 я— С\ W о а п 1Г ь 1 6 04 ос О' > 1,5—14.] I 9,9-1 I 1 А_ 9 СТ О о" 4—1 -г— 1,0 9 7—А Ю 1Г 1 он о ОС 14 1- ч—» сх ОС С С£ ю 14 1 о 14
ilOT сх о J 14 1 С* От- Ч-Ч яг 1,0 9 1—А 1Г СО о я- U" 1С О чг -и СХ ОС а г> 4,1-15 1 ' 1,0 1 1 А—9. 0“ О ст Я—| Я— •<} О С£ 1 СХ 1Г О С£ 14 Г* 1Г о а 14 сх ос 1 а сс 1
о ^ч СМ СО “М 1 1 и см о о ОС чн ч-ч чч is С\ Ю U0 ОС 1 1 ) QN О- Г 1 и 1/0 1* см Ь* ю -ч сх 1 -о см О- -СО 14 ЧТ а О сх 14 я₽1 м О 1Г 1Г О сх 1,о 9 й_=; ос ОС 1Г О 14 1 г* IQ
а о ч—* 7 У L Г1 г—Г1 5-4 Я О 1Г 14 1 1С о г1 чгчхЗ 5 и- ЗОЮ 1* яч я а V <ф V,. я 3,0-15 | £ 1 2,0 I i 7 9__3 •с ЯН С чгч а м о «: ) и 1 1Г о а in SJ 1Г о ос ’ 14 1 ОС с£ М 5,8—16
о я—’ 2,048-106 1,4 I 7 А_ .4 *С ом а и е- 1,1 К 3—R Ъ 0 V оЧ 1-М 1/0 ю СО 00 о 0* 111г 0 ОО t> CN м я- с- 1 СО СМ я м U7 Г- 14 с\ Ъ 7 У 1 1‘1 1,0 9 Л_К 1,0 7,5-6 .4 4—R 1 Сх СС э 5
о И т =: 2,1 1,7—3 1,6 й К_К 1Г см с» гч сх 1,1 7,6-6 1,0 Q Л Й 00 Ю ц > 00 II Ю ИО со о ОС 1 1 Г 1 1 1 1 1 а> со^счсо янсч юо см ш ж-я, <х 0 СО СО СО 41 СМ 1/0 чгчсм ч1 m чгч СО о СО 14 1 хГ 1 со
«lOV •< co^i см о ООО Г на СО « 1 ю о cov i М1 и 0 1,1 4 9 £ a э.г 1 ЕЕ Sl-£‘£ 8—9‘£ П Г9* Т СО э со О со СО 00 14 1 1 1 III 5М<^ч Oib- О’- СОИ СО *<Р ч СМ СО и СО и СМ 1ч и СМ СО
10*» | 1Q m г- г- оо or 1 1 1 1 I 1 1 1 sr я-ч Сгг- со СО Ю СО СО О чр -к? с© ч4< V СМ СМ —«00 и Ю —со со ОО СО ТМ СМ U и,Ч { 2,1 Z О 7 w о- г- а 1 1 q си см t> Г ЧП со 1 см с —м 6,5—16
о к ЧГ о см с 5 О! J Cj С 4 я, а и , и—и 11’1 0 Э 0 1 я ло а чя s 1/0 0 00 00 к Н- о Illi 1 б Ю О чф vf st< ф uo u Г Т- М1 СО СО СО i см <1 □ CI 0 14 S Э CM s 0 о 1 3< о U Г ЧЯ 0 0 о □ 00 С □ 14 С 0 о 1 Э Ч о с СО 0 14 1 1 ю М С0
кО с см о 0> 5 « - а 4 Ci С м г?, и— iu* ’ е 1,7 СО 4 О ЛГ <» ф z fe; < 0 оо а 1 1 0 Ф ТЧ LQ X 0 ИЛ их <и ?; 0 ч 0 1 г с Г с 0,0 — о 3,4-15 3,4 | ЛИ Л” ЛТ ф Ф Q) Ш Qi > > •< -< -< я 00 00 00 оо о 1 -ч яч ЯЯ ЯЧ 00 яя । । । 1 1 1 1 0 ШсОСЧьО ОС- о см ю ю я СМСО CM'tf СМ СО яч СО СМ Ф
5? NMCOnsf^lDincDtO МСЧМСОхГ^ЛЮШФ —— а х_х_ —— £4 £4 ^Ч ^яЧ
§ 17. НАСЕЛЕННОСТИ ВОЗБУЖДЕННЫХ СОСТОЯНИЙ В ПЛАЗМЕ 159
состоянии N (1). В чисто водородной плазме Ne = N (Н+). При
нахождении стационарного распределения по уровням не-
обходимо учесть соотношение (17.20).
5. Водородоподобные ионы. Как в корональном пределе, так и
в случае локального термодинамического равновесия температура
Т, при которой ион с потенциалом ионизации Е2 существует
в значительном количестве, примерно пропорциональна Ег.
В случае водородоподобных ионов Ег = z2Ry. Если Т <х> z2,
We (m, п) оо z-3. Вероятности радиационных переходов Wmn оо
оо z4. Поэтому при рассмотрении водородоподобных ионов (и
вообще многозарядных ионов) удобно использовать приведенные
значения плотности и температуры
)lt> = .Ve/z7 , й = 77z2.
В таком масштабе величины r0, гг, a/z и Sz3 не будут зависеть
от z.
Формулу Саха (17.11) запишем в виде
А’2 л3 / z2 Ry \’Д
ТУЕ (п) = (-?А) ех₽ ’ (17.22)
где X --= Ne/N2+1 — отношение плотности электронов к плот-
ности полностью ионизованных атомов (ядер). Из (17.18) и (17.22)
следует, что универсальный характер будет иметь также вели-
чина
Т) (и) = XNZ (n)/zn. (17.23)
Некоторые результаты расчетов величин r0, r15 a/z и Sz3
из работ [60,621 приведены в табл. 16. Для расчета населенностей
в формулу (17.18) необходимо подставлять Ne («) из формулы
(17.22), заменив в (17.18) N (Н+) на Nz+j,.
Различие в величинах г0, т\ для нейтрального водорода [63]
и водородоподобных ионов [62] весьма велико при T<^z2Ry.
Это объясняется различием в пороговом поведении сечений воз-
буждения и ионизации для атомов и ионов (сечение возбуждения
нейтральных атомов в пороге равно нулю, а в случае ионов —
константе (см. § 7)). В области Т ~ z2Ry, как и следовало ожидать,
результаты расчетов [62] и [63] дают близкие значения для г0
и гх.
6. Населенности высоковозбужденных уровней в плотной
плазме; режим стационарного потока. Для высоковозбужденных
уровней с п п0 ’) кинетика заселения уровней целиком обус-
ловлена столкновениями с электронами. Наиболее вероятны при
этом переходы между близкими уровнями, сопровождающиеся
небольшой передачей энергии. Поэтому движение электрона
х) Оценку п0 дает формула (17.15).
Таблица 16
Параметры r0(«), гг(п), коэффициенты £ и а для водородоцодобных ионов
Пе = Ne№ -*0 10* 10“ 10“ 10“ 10“ 10“ 10*’ 10“ -» оо
Т = 4-103-za К
г0(2) 4,7-6 5,9—6 8,8-6 3,6-5 1,6—4 1,4—3 1,3-2 6,1-2 1,1—1 8,9—1 1,1—1
П (2) 1,2—8 1,2—6 1,2-5 1,2—3 1,2—2 1,1—1 5,1—1 8,9-1
г о (3) 1,3-3 1,6—3 2,5-3 1,5-2 9,6—2 3,2-1 4,3-1 4,7—1 5,0—1 5,0—1
Гг(З) 5,5-9 5,5-7 5,5-5 5,7-4 6,4—3 6,0—2 2,9—1 5,1-1 5,1—1
г0(4) 1,0—2 1,4-2 2,2-2 2,1—1 5,2-1 6,9-1 7,5-1 7,7-1 7,8—1 7,8-1
гх(4) 5,1—9 5,0-7 4,2-5 2,9-4 2,9-3 2,7-2 1,3-1 2,2-1 2,2-1
Го (5) 2,9-2 3,9-2 7,0-2 5,5-1 7,8—1 8,7-1 8,9—1 9,0—1 9,0—1 9,0-1
ri (5) 4,3-9 4,1—7 2,3—5 1,3—4 1,3-3 1,2-2 5,8—2 1,0-1 1,0-1
г0(7) 7,9-2 1,1—1 3,2-1 8,8—1 9,5-1 9,7—1 9,8—1 9,8—1 9,8—1 9,8—1
ri(7) 3,4-9 2,7-7 6,3-6 3,0-5 3,0-4 2,8-2 2,4-2 2,4-2 2,4—2
5-гз 9,1-26 1,1-25 1,9-25 1,0—24 6,1—24 4,6—23 3,7—22 2,0—21 3,5-21 3,8-21
а/z 7,9—13 9,2-13 1,4-12 5,2-12 7 2,0—11 1 =8-103-zS 1,1—10 К 8,6-10 8,0-9 7,6-7 7,6—25г|е
га (2) 1,1-3 1,3-3 1,5-3 3,1—3 7,4-3 3,4-2 2,1-1 6,0-1 7,6-1 7,6-1
ri(2) 8,9-9 8,9—7 8,8-5 8,8-4 8,5-3 6,4-2 1,9—1 2,4-1 2,4-1
го(3) 1,9—2 2,2—2 2,7—2 6,9—2 2,5-1 6,1—1 7,7-1 8,9-1 9,4-1 9,4-1
гх(3) 4,2-9 4,1—7 4,0—5 3,6—4 2,6-3 1,8-2 5,1-2 6,5-2 6,5-2
г0 (4) 5,9-2 6,7-2 8,5—2 3,3-1 6,9-1 8,7-1 9,3-1 9,7—1 9,8-1 9,8-1
ri(4) 3,5-9 3,4—7 2,6—5 1,4-4 8,4-4 5,5—3 1,6—2 2,0-2 2,0-2
Го (5) 1,0—1 1,2—1 1,6—1 6,5-1 8,8-1 9,5—1 9,8—1 9,9—1 9,9—1 9,9-1
гх(5) 3,2—9 3,0—7 1,3-5 5,4—5 3,1-4 2,0-3 5,7-3 7,3-3 7,3-3
ГЛ. V. НЕКОТОРЫЕ ВОПРОСЫ КИНЕТИКИ ВОЗБУЖДЕНИЯ
§ 17. НАСЕЛЕННОСТИ ВОЗБУЖДЕННЫХ СОСТОЯНИЙ В ПЛАЗМЕ 161
Таблица 16 (продолжение)
8 t j 1,0 1 Z_4 4,5-14 1,0—26т)е I 9,4-1 fi .4—9 9,9-1 1 1—9 О' 1 <О ос Г ^"сх 1,о 9 1—4 1,0 1 R Л г Z 1 а и 1 е§ — г 1 1 Г- т- ео ст, т О- О S1 w М i 1,0 1 1 Л_3
"Н со 2 1 О IT чН чН sj (X с чН СХ 1 > vf а- 4 05 С£ 4- сх I С75 чт 05 ч- сс 1 о ОС чн СХ № О Ч- i ч-а 1,0 1,6-4 7,8-11 Я 1—19 1 V 1 1 1 9’7~1 1 4 1—9 1,0 А А_4 <т о с ? ч-< ч-
ч-м CO ч- 1 1 О ч-ч ОС Ч-Тч-I о* S 1 1 V- со с- -И 00 ч" ч* О' I X с > 05 с *7 7 05 1Г 05 СХ s О v ч-< X v 7 * 1,0 4 г С 5 CS сч 41 сх 1 1 05 оо С Г* 05 С< Ч-* СО *< 1 1 © ем О о( С5 •<* ч-ч О г
wl •< о а ч-< с* Si Г ’Г- 1 3 « —Ч с\ 1 1 г- сч сх со 1© ст О' I с-ОС С5 1Г X 00 1Г ) О5г 9,9—1 А 0—.4 1,о 8,5—5 4,3-11 .4 Л—19 чН сх I GO С с© СХ РО чч <г 1111 L© !©5 Q5 QQ С5 СЧ 05 с£>
я» ч-< 9,9-1 5,9-5 9 9_<=; 7,6-12 | ;2 К 1 1’5”1 1 й О 4 7,4—1 4 4 — 4 1 5 СО С£ " оГсг т *Я 1 5 СО СХ 5 05 4F ю * I О ЧТ* О т-< сч" Ч- 1,2-12 !2К 3,1-1 4,5-3 8,1-1 8,8-4 9,5—1 9 Q Z < э 4
8о •«И С© СЧ i СО -и О СЧ TH v II 1 1 г 1 1 1 ХО х л <D »• ©_ 00,'< С5 ci Sf СЧ 1Л ЦЭ СО С- 1! 7,6—1 Я й с 3i 6 ъ 1—V6 л ГЗ 1 f~t с 5 -т4 CD -ч I I J хь о > С5 1© *< q o’ j е* t< и Q ч-н чгч 1© г | | || || 3 N о М -Г-00 — VT > м л т, х to II
'о ч-Ч 9,2—1 3,3—6 1,7-16 4 О 4 0 Ч Ьч _1 СЧ Ю тч 1© чн 1© ч-4 « 1 1 1 1 1 1 1 1 q «О г- оо С> ео оо '-iff н ео со — ео ч-< t»d 9,3—1 2,1-6 О А 4 9 j co E*i - ч-1 UO чН 1/ 1 III Н со ю vj* ео < 4 4* Ю СО сх у г i-Ys о г
«ОТ 77 ’ оса Vt СЧ с М-13 | 2,6-2 6,8-7 1,1—1 Q О *7 2,0—1 2,5-7 2,9—1 О 9 7 сч со ‘ 77 7 7 77 77 77 4 оо л irt м ео-er г- >л г-оз 1 sr чЧ ТГ Lfi сч сч СО чН
ч-t 2,2—1 2,5-9 5,3-17 5,1-13 1 2’4“2 1 con Г5 чт< С5 ч-ч С 1111 о о см 00 сг ч-Гсо чтГе 5 чн С Э I/O С* <Г схГг с* , U 3,5—1 1,8—9 1,4—12 3,0-13 1 1’Н 1 5 чт* ^т< СГ5 1 1 1 1 1 J* С© е© Ю ©5 сч" сч" со" ’гч"
О t г* со ч-< СЧ СЧ ч- Ill II оо о 00 сч со ь ч-1 *<С* СЧ 05 •*’ сч со 7 7 7 7 со чн со С5 сх Г сч" со -г? с\Г Ч-< 1 1 1© со сч со
$• г: II tCtC- «, м SS n моГ 2-5- sS г с* ч s' гг гг гс ’к ч ~о ест гс
6 Л. А. Вайнштейн и др.
’’’е = Ne'zl — 0 1QS to10 10“
го(5) fl (5) 3,9-1
М7) М7) 4,6-1
S-z3 2,4—10
a/z 1,7—13
4,1—1
1,7-9
5,0—1
1,3—9
2,4—10
1,8-13
4,4-1
1,6—7
5,9—1
1,1—7
2,5—10
1,8-13
7,5-1
7,6-6
9,4-1
2,0-6
3,2-10
1,8-13
г0 (2) ri (2) 3,1-1 3,5-1 4,5-9 3,6—1 4,5—7 3,8—1 4,4-5
Го (3) М3) 4,6—1 4,8-1 2,1—9 4,9-1 2,1—7 5,3—1 1,9-5
Го (4) гх (4) 5,3-1 5,5—1 1,5—9 5,7-1 1,5-7 6,7-1 1,2-5
Го (5) Г1(5) 5,7-1 6,0-1 1,2-9 6,2-1 1,1—7 8,1-1 5,9—6
го (7) Г! (7) 6,2-1 6,6-1 9,2-10 7,1-1 7,9-8 9,6-1 1,3-6
Таблица 16 (продоллсение)
10“ !01‘ 10” 10м 10“ Г* 00
9,3-1 2,3-5 9,8-1 7,4-5 1,0 2,2—4 1,0 3,1-4 1,0 3,3-4 1,0 3,3-4
с© 1 1 О 1,0 1,2—5 1,0 3,6-5 1,0 5,1-5 1,0 5,4-5 1,0 5,4—5
4,4-10 8,5-10 2,0-9 2,8—9 2,9-9 2,9—9
2,0-13 2,4—13 3,3-13 5,0—13 2,9—11 2,9-2Л|е
= e,4-io*.z« к
4,2-1 4,3-4 5,2-1 3,6—3 7,8-1 1,5-2 04 1 [ Ю СО О 04 9,8—1 2,4-2 9,8-1 2,4-2
6,5—1 8,6-1 9,7—1 9,9—1 1,0 1,0
1,5-4 7,1-4 2,1—3 2,9-3 3,1—3 3,1-3
8,6—1 9,6-1 9,9—1 1,0 1,0 1,0
5,5—5 1,8-4 4,8-4 6,7-4 7,0—4 7,0—4
9,4—1 9,9-1 1,0 1,0 1,0 1,0
2,0—5 5,8-5 1,5-4 2,1-4 2,2—4 2,2—4
9,9—1 1,0 1,0 1,0 1,0 1,0
3,3-6 9,7-6 1Л см 3,4-5 3,5-5 3,5-5
ГЛ. V. НЕКОТОРЫЕ ВОПРОСЫ КИНЕТИКИ ВОЗБУЖДЕНИЯ
§ 17. НАСЕЛЕННОСТИ
ВОЗБУЖДЕННЫХ СОСТОЯНИЙ В ПЛАЗМЕ
163
Таблица 16 (продолжение)
6*
164 гл. V. НЕКОТОРЫЕ ВОПРОСЫ КИНЕТИКИ ВОЗБУЖДЕНИЯ
между возбужденными уровнями можно описывать как диффузию
в пространстве квантовых чисел и использовать для этого урав-
нения типа уравнения Фоккера — Планка 157—59].
Пренебрегая радиационными процессами, определим поток
электронов у (п) в пространстве квантовых чисел п выражением
/(«) = f 3 [7V(n + A:'+ 1Ж(п-И'+ 1,п~к)~
— N(n — k)We(n — k,n-\-k' + 1)]. (17.24)
Величина потока имеет размерность [см^-с”1]. Первый член
в (17.24) описывает поток электронов с уровней п' п на уровни
п" <4 п (т. е. поток, направленный к основному состоянию),
а второй член — поток электронов с уровней п' <4 п на все дис-
кретные уровни с п" п (поток, направленный к непрерывному
спектру). Как и в п. 4, введем безразмерную величину b (п) =
~ N (n)/Ns (п), определяющую отличие населенностей от термо-
динамически равновесных с непрерывным спектром (17.11). В этих
обозначениях
/(и) = Лг+1 -J- У, 1(" + к' + 1)а eEn+k'+l'Tb (п + к' + 1) х
fcir
XWe{n + k'^ 1, n — Л:) — (n — Л)аеЕ"-*/г X
X b(n — к) We (« — к, п 4- к' 4- 1)], (17.25)
Полагая b (п 4- к) ж b (п) 4~ к и ограничиваясь учетом
членов ~ к2, из (17.25) получим
<17'26>
1-J С/ / С
к
При рассмотрении высоковозбужденных уровней п^>1 сумми-
рование по к в (17.24) — (17.26) можно распространить до бес-
конечности. В величинах <уоп>п„л> выделим размерный множитель,
а также основную зависимость от п, к и температуры, определя-
ющие порядок <von>n_)f> (см. § 10):
о ,2 „
<pan,n-fc> = лао2~3&~'/т*к~а(р (п, к, 0), (17.27)
V л п
где функция (р (п, к, О) слабо зависит от своих аргументов. Далее
введем непрерывную переменную е = 1/п2. Используя (17.27),
запишем выражение для потока в виде
/ (е) - - aSe-’e-M/e L . (17.28)
§ 17, НАСЕЛЕННОСТИ ВОЗБУЖДЕННЫХ СОСТОЯНИЙ В ПЛАЗМЕ 165
Множитель L = — l/s'/*, £,©) весьма слабо зависит от 0
к
и е, и в дальнейшем мы положим L — 0,2 г).
В переменной е уравнение диффузии можно записать в виде
2«*4>(e) - (17-29)
Здесь q (е) [см-8*с-1] — скорость прямого заселения уровня е,
a W (е) [с-1] — вероятность ухода с уровня е в непрерывный спектр,
либо на нижние уровни. Величина W (е) не включает в себя столк-
повительных переходов между высоковозбужденными уровнями.
Влияние этих переходов уже учтено в выражениях для потока
(17.26), (17.28).
Для нахождения b (е) и / (е) уравнение (17.29) необходимо
дополнить граничными условиями. Условие на границе с непре-
рывным спектром можно легко сформулировать: в пределе е -► О
(п -> оо) функция b (е) должна переходить в соответствующую
функцию распределения электронов в непрерывном спектре. При
максвелловском распределении
limb(e) = l. (17.30)
е-»э
Второе граничное условие, вообще говоря, необходимо выбирать,
сшивая решение уравнения (17.29) с решениями системы уравне-
ний типа (17.10) для нижних уровней, где существенны радиа-
ционные процессы и дискретная структура. В ряде задач это
условие оказывается возможным задать в явном виде. Несколько
далее мы рассмотрим случай рекомбинирующей холодной плазмы,
когда в качестве второго граничного условия можно поставить
условие полного поглощения потока на некоторой границе ех.
В отсутствие какой-либо специфической накачки или опусто-
шения возбужденных уровней q (е) определяется тройной реком-
бинацией на уровень е, a W (е) есть вероятность обратного про-
цесса — ионизации. Полагая в нулевом приближении, что b (е)
мало отличается от термодинамического равновесного значения —
единицы, правую часть (17.29) можно положить равной нулю,
так как q (е) N (е) W (е). Таким образом, получаем приближе-
ние постоянного потока:
j (е) = const.
Далее из уравнения (17,28) с граничным условием (17.30) полу-
чаем
е
6(e)-l-j ( (ey-e-^e-, С = 32п* 4 4 (17.31)
х) Такое среднее значение для L принято в работе [51].
166
ГЛ. V. НЕКОТОРЫЕ ВОПРОСЫ КИНЕТИКИ ВОЗБУЖДЕНИЯ
При
zeL&
N N2C
/v?+rvev
8*/».
(17.32)
b (е) ~ 1 — j
Величина потока j должна быть определена из второго граничного
условия.
Рассмотрим теперь рекомбинирующую плазму. В этом случае
поток положителен и Ь (в) убывает с увеличением е. В качестве
второго граничного условия для уравнения диффузии можно
поставить условие полного поглощения потока на некоторой
границе ех:
Ь (8.) = 0. (17.33)
Если ограничить рассмотрение случаем низких температур,
0 ех, то величина потока, определенная из (17.31) и условия
(17.33), не зависит от е1т и можно положить ех — оо. При этом
7 = (17.34)
где
2'п* * я t/j _ N 4/2- L № ,17 35.
а - г« —3—L h ао° ~^е з L тЧ*т*Г U'-d5)
— есть коэффициент рекомбинации. Порядок величины и харак-
тер зависимости величины а из (17.35) от температуры при Т
8000z2 К согласуются с результатами численных расчетов
[62, 63].
Отметим, что формула (17.35) не содержит И, что вполне есте-
ственно, так как величина а определяется переходами между
высоковозбужденными уровнями, для которых справедливо ква-
зиклассическое рассмотрение.
ГЛАВА VI
ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ
ЭФФЕКТИВНЫХ СЕЧЕНИЙ
§18. Результаты численных расчетов сечений
В параграфе приводятся результаты численных расчетов
эффективных сечений о и усредненных по максвелловскому рас-
пределению скоростей возбуждения и ионизации, а также
скорости диэлектронной рекомбинации xd. Расчеты выполнены
с использованием метода Борна (см. § 6) и описанных в § 7 его
модификаций. При этом, так же как и в § 5—7, предполагалось,
что атомные волновые функции построены из одноэлектронных
функций в одпоконфигурациоином приближении с помощью
стандартных методов теории угловых моментов [1]. Радиальные
функции для всех уровней одной конфигурации и одной мульти-
плетности полагались одинаковыми. В таких предположениях
сечение может быть представлено в виде (5.4), (5.8). В этой главе,
однако, будет использована запись, несколько отличная от (5.8).
1. Обзор содержания таблиц. Сечение перехода а0 — без
изменения спина (AS — 0) представим в виде
= SCx(ao, ai)ox (l0, Zi). (18.1)
Всюду индекс «0» указывает начальный уровень, а индекс
«1» — конечный. Угловые коэффициенты Q* в (18.1) те же, что
и в § 5—7. Сводка необходимых для пользования таблицами фор-
мул для факторов Qv. приведена в § 19. Величина ох (l0, в раз-
личных разделах этого параграфа имеет несколько различный
смысл г).
Сечения иптеркомбипационных переходов (Д5 = 1) запишем
в виде
Caoa, = Q («0, #1) О’ Go, ^1). (18.2)
В отличие от (5.8) формула (18.2) не содержит суммы по к. Это
связано с тем, что в таблицах настоящего параграфа обменные
сечения о" приводятся только для тех случаев, когда суммиро-
вание по х можно выполнить аналитически, а именно, приведены
сечения для случая нулевого орбитального момента атомного
х) Отметим, что ни в одном из случаев ах (l0, не совпадает с введенной
в § 5 величиной °х (/«, Ij), содержащей прямой и интерференционный члены.
168 гл. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЁЧЕНИЙ
остатка (Lp = 0) и для переходов между двумя конфигурациями
в целом. Угловые факторы Q" (а0, at) для этих случаев также
даны в § 19.
Сечения ох, о" и соответствующие им скорости и
аппроксимируются несложными аналитическими формулами, со-
держащими два параметра, подобранные по результатам числен-
ных расчетов методом наименьших квадратов. В таблицах при-
водятся именно эти параметры аппроксимации1).
Приведем краткую сводку содержания таблиц и оценку ка-
чества использованных приближений.
1. В борновском приближении вычислены суммарные по Zo,
lr сечения возбуждения для атома водорода (см. п. 2, табл. 17),
таблицы сечений ох и скоростей в приближении Бейтса —
Дамгаард для атомных волновых функций (см. п. 3, табл. 18 и 19).
Борновское приближение использовано также для расчета се-
чений ионизации (подробнее см. п. 6).
Таблица 17
Борновскпе сечения возбуждения нейтрального водорода; параметры С, <р
и Л,% для суммарных по 10, сечений
Ап С ф
п0 = 1 2 3 4 Б 1 2 3 4 5
1 61 160 336 617 1020 5,0 4,6 5,4 6,8 8,5
2 43 86 155 254 — 3,7 2,7 3,0 3,6 —
3 38 69 114 175 -— 3,4 2,3 2,4 2,7 —
4 36 62 98 — — 3,2 2,1 2,1 — —
5 35 58 89 —— — 3,2 2,0 1,9 — —
6 35 56 — .— 3,1 2,0 ‘— — —
7 35 55 — .— .—. 3,1 1,9 — — —
8 35 55 .— — .— 3,1 1,9 — —
9 35 — — -— •— 3,1 — — — —
А X
Дп П, =-. 1 2 3 4 б 1 2 3 ь 5
1 24 67 124 185 249 0,28 0,30 0,26 0,21 0,16
2 22 58 101 142 -— 0,37 0,45 0,42 0,35 —
3 22 56 94 129 — 0,39 0,52 0,51 0,45 —
4 21 55 91 .— — 0,41 0,56 0,57 ,— —
5 21 54 90 — 0,42 0,59 0,61 —
6 21 54 — — — 0,42 0,61 — •—- —
7 21 54 — — —. 0,42 0,62 "II •— —
8 21 54 — 0,42 0,63 —— —
9 21 — — — — 0,43 — — ... - —
9 Об анпроксимации см. § 14.
§ IS. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
169
Наиболее существенным недостатком метода Борна является
нарушение нормировки (нарушение унитарности S'-матрицы).
В случае переходов между близкими уровнями борновское при-
ближение может сильно завышать величину сечения для ней-
тральных атомов и ионов малой кратности. Выполнить нормировку
сечений можно в представ-
лении парциальных волн.
Такие расчеты показывают,
что при больших энер-
гиях электрона (<§0
Т ДЕ) нормировка не-
существенна (см. рис. 7,14
и подробнее § 7). Проце-
дура нормировки практи-
чески не изменяет величи
ну сечения для возбужде-
ния из основного состоя-
Дамгаард, использованное
при составлении табл. 18
ния при условии пх п0. Рис. 14. Эффективное сечение возбуждения
Приближение Бейтса— перехода 3d — 4/ атома водорода. 1 — се-
чение, нормированное методом /^-матрицы;
2 — борновское приближение.
и 19, обосновано в тех слу-
чаях, когда главные максимумы радиальных функций лежат вне
атомного остатка. Обычно это условие формулируется в виде
= + =]/-^->Zi + 1/2, (18.3)
«о > «ост, «* > «ост, (18.4)
где ПоСТ — наибольшее из главных квантовых чисел электронов
атомного остатка, z — заряд атомного остатка (спектроскопиче-
ский символ иона). Условие (18.4) иногда оказывается более
жестким, чем (18.3), однако во многих случаях, когда выполнено
(18.3) и не выполнено (18.4), приближение Бейтса — Дамгаард
вносит сравнительно небольшую ошибку, в пределах фактора 2,
которая сравнима с погрешностью самого метода Борна.
2. При расчете сечений возбуждения для конкретных атомов
и ионов (табл. 20—24) выполнена нормировка за счет собственного
канала методом Е-матрицы (см. § 7). Вычисление радиальных
интегралов проводилось с помощью численных полуэмпириче-
ских волновых функций 164].
В случае нейтральных атомов для переходов без изменения
спина использовался метод Борна (с нормировкой), а для интер-
комбинационных переходов — метод ортогонализованных функ-
ций (см. § 7).
В случае ионов учитывалось искажение падающей и рассе-
янной волн кулоновским полем. Для переходов без изменения
170
ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
спина обменное взаимодействие, как правило, не учитывалось х).
Исключение составляет таблица для гелиеподобного иона Na X.
В расчете сечений для этой таблицы обмен в случае переходов без
изменения спина учитывался в рамках метода ортогонализованных
функций. Сечения интеркомбинационных переходов для ионов
вычислены с использованием метода ортогонализованных функций
и также с учетом кулоновского притяжения.
Ряс. 15. Эффективное сечение возбуждения перехода 2s — Зр для водорода
и водородоподобных ионов; для сравнения штрих-пунктиром приведено
борновское приближение.
Приведем краткую характеристику поправок к борновскому
приближению, которые вносят учет кулоновского притяжения,
учет обмена для переходов без изменения спина и нормировка
сечений. (Напомним, что интеркомбинационные переходы в при-
ближении LN-связи возможны только за счет обменного взаимо-
действия.)
Различие между борновскими и борн-кулоновскими сечениями
существенно лишь в сравнительно узкой припороговой области
энергий (рис. 15). Учет обмена также заметно изменяет величину
сечения только вблизи порога возбуждения (см. рис. 6). Поэтому
учет обмена и учет кулоновского притяжения существенны для
переходов из основного состояния. Нормировка при этом почти
не меняет величину сечения.
В случае переходов между близкими уровнями нейтральных
атомов и ионов невысокой кратности 1-й порядок теории возму-
’) Такое приближение в литературе принято называть борн-кулонов-
ским приближением.
§ 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
171
щений может сильно завышать величину сечения при энергиях
электрона $ <" Ry (см. рис. 7, 8, 11, 14). В случае многозарядных
ионов матричный элемент взаимодействия внешнего электрона
со связанным электроном содержит параметр малости 1/z. По-
этому при z 1 (практически при z > 4) нормировка несущест-
венна и для переходов между близкими уровнями.
Таким образом, при $ > ЛЕ (u > 1) и Т > ДЕ (Р< 1) для
оценки сечений и скоростей переходов без изменения спина в
многозарядных ионах можно использовать борновское прибли-
жение (рис. 15, 16).
Рис. 16. Скорость возбуждения перехода 2s — Зр для водорода и водородо-
подобных ионов.
В случаях, не охватываемых настоящими таблицами, можно
воспользоваться полуэмпирическими формулами, приведенными
в § 14.
2. Борновские сечения возбуждения нейтрального водорода1).
В случае водорода обычно наибольший интерес представляют сум-
марные по х сечения, усредненные по орбитальным квантовым
числам 10 нижнего уровня п0 и просуммированные по значе-
ниям орбитального момента 1г верхнего уровня nt. Сечение пере-
хода п0 —> представим в
% — ЬЕ
UsE
следующем виде:
(КуХЧЕа’Д Ф(«)
\ЬЕ) \Ej п2 ’
ф (и) = (—
4 ' \ и + 1 / « + ф
(18.5)
— ЭТО-д
и —
*) Для переходов между возбужденными уровнями при энергиях элек-
трона $ Ry борновское приближение дает завышенную величину сечения.
В этом случае необходимо использовать нормированные сечения, которые
даны в табл. 20. В случае переходов между высоковозбужденными уровнями
можно использовать табл. 3—6.
172
ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Скорость возбуждения запишется в виде
“о
₽ = ДЕ/Т, Gtf) = Л ¥'?Д+1> .
Параметры аппроксимации борновских сечений (С, ср) в ин-
тервале 0,01 и <1 80 и скоростей (Л, %) в интервале 1/16
Р 8 для переходов между рядом уровней водорода приве-
дены в табл. 17 (см. стр. 168). Экстраполяция сечений вне ука-
занных интервалов может привести к серьезным погрешностям.
3. Таблицы борновских сечений в приближении Бейтса —
Дамгаард. Использование кулоновского приближения для ради-
альных функций оптического электрона дает возможность зата-
булировать сечения сгх и скорости <wx)> (в см3/с) аналогично из-
вестным таблицам Бейтса — Дамгаард для сил осцилляторов.
Сечение и скорость перехода а0 —> задаются выражениями
o'a^i = ЛОо 2Z0 + 1 Vi Ф* (^.7)
“ = д/Е дя = £,-е„,
<»*-.> = £<?-<“" <18-8>
₽ = ЬЕ/Т, х = | /„ - I, |, | I, - + 2, . . I, + I,.
Функции Фк (и) и Gx (Р) аппроксимируются следующими фор-
мулами:
в случае х = 1
ф>(“) = с (гут)1'1 ‘‘“Ду’* • <18-9>
G1 (₽) - Л In (16 Ч- 1/₽). (18-10)
в случае х 1
ф«(“) = с(^ттГД-?’ <18Л1>
Сх(₽)-А-ЦЕНй (18.12)
Параметры С, <р приведены в табл. 18, параметры А, % —
в табл. 19 (см. стр. 206). Рассматриваемый переход характери-
зуется эффективными главными квантовыми числами начального
уровня п* и конечного уровня п^:
п* = /г2Яу/|^о|, n* = /z2 Ry/1^1.
§ 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
173
Энергии начального (£0) и конечного (2j\) уровней отсчиты-
ваются от границы ионизации, соответствующей состоянию атом-
ного остатка, z — спектроскопический символ иона, для нейтраль-
ного атома z — 1. Параметры С, ср и А, % подбирались методом
наименьших квадратов по результатам численных расчетов сече-
ний и скоростей. В таблицах они даются как функции п* и Дп* =
= га* — nJ. Принятый шаг по п* и Дп* в большинстве случаев
обеспечивает возможность линейной интерполяции. В таблицах
приводятся порядок и мантисса числа, например, 24 — 1, 47 — 0,
59 + 0, 42 + 1 и 12 + 2 означают соответственно 0,024, 0,47,
0,59, 4,2 и 12.
Эффективные сечения возбуждения аппроксимируются в ин-
тервале энергий 1 + и 128. Те случаи, когда погрешность
аппроксимации составляет более 10%, в табл. 18 помечены звез-
дочкой. Эта погрешность, однако, никогда не превышает фак-
тора 2.
Усредненные по максвелловскому распределению скорости
возбуждения аппроксимируются в интервале 1/32 р <^4.
Звездочки в табл. 19 указывают случаи, когда погрешность ап-
проксимации превышает 25%.
4. Нормированные сечения возбуждения для конкретных ато-
мов и ионов. Переходы без изменения спина. Результаты расчетов,
нормированных методом Л’-матрицы сечений о и скоростей <+сг>
для переходов без изменения спина, приведены в табл. 20, 21,
22 (см. стр. 228, 233) и на рис. 17—22. Величины и <Pdaq01>
задаются формулами
2 I Ry \2 / Ег \‘/. (й<” Л»> ч о d
(Jatat - ( де ) ( Ео ) 2l0 + 1 ф (18.13)
~ 10-» (ЗГ)1'- (4)’Л Q++",<11> <₽>• <18-14>
р = ДЯ/Л
Приведенные в указанных таблицах сечения соответствуют ми-
нимальному значению индекса мультипольности х = xmin1):
^min — I ^11-
Сводка формул для ^-факторов дана в § 19.
В борновском и борн-кулоновском приближениях, как показывают
результаты численных расчетов, основной вклад в сумму по х дает обычно
член с х = xmin.
Рис. 17. Скорости возбуждения ионов в борн-кулоновском приближении
(&S = 0); переход 2s — 3$.
Рис. 18. Скорости возбуждения ионов в борн-кулоновском приближении
(Д$ = 0); переход 2s — Зр.
ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
175
Рис. 19. Скорости возбуждения ионов в борн-кулоновском приближении
(AS = 0); переход 2s — 3d.
Рис. 20. Скорости возбуждения ионов в борн-кулоновском приближении
(AS — 0); переход 2р — 3s.
176
ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Рис. 21. Скорости возбуждения ионов в борн-кулоновском приближении
= 0); переход 2р — Зр, х = 0.
Рис. 22. Скорости возбуждения ионов в борн-кулоновском приближении
(Д5 = 0); переход 2р — 3J, х = 1.
§ 1Я. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
177
Формулы аппроксимации Ф и G в случае нейтральных атомов
(z = 1) приняты следующими:
ф(“) = Ьчй)’АТТФ (‘815)
С(Р) - А /^ + 1) , (18.16)
р I л
в случае ионов (z 1)
Ф(“) = ТТф' _ (‘8-1’)
+ (18.18)
Интервалы аппроксимации: для сечений 0,01 и 20, для
скоростей 1/4 р <7 8. Случаи, когда погрешность аппроксима-
ции превышает 25%, отмечены в таблицах звездочкой.
Интеркомбинационные переходы (Д5 = 1). Параметры ап-
проксимации для суммарных по х сечений и скоростей интерком-
бинационных переходов приведены в табл. 23, 24 (см. стр. 235)
и на рис. 23—27. Сечение о" и скорость <1ю"> даются формулами
" 2
— Я&о
1’* ф’ (“> (18Л9)
<ГО«.,> = 10~* &У- c-V (Р). (18.20)
178
ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Рис. 24. Скорости обменного возбуждения ионов; переход 2s — Зр.
Рис. 25. Скорости обменного возбуждения ионов; переход 2s — 3d.
§ 18, РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
179
Рис. 26. Скорости обменного возбуждения ионов; переход 2р — 3s.
Рис. 27. Скорости обменного возбуждения ионов; переход 2р — Зр, сечения
просуммированы по х.
180
ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Формулы для факторов Q" приведены в § 19, п. 3.
Формулы аппроксимации Ф" и G" имеют вид
в случае нейтральных атомов (z = 1)
(u + l)*/2(u+ ф") ’
G"(p) = ,
Vp + KP + x")
в случае ионов (z 1)
С"
v > (и + l)2(u+<р")
Л "На/г
G'® = TTr '
Интервалы аппроксимации:
(18.21)
(18.22)
(18.23)
(18.24)
0,01 < и <5, -А- < Р < 8.
Звездочкой помечены случаи, когда погрешность аппрокси-
мации составляет более 25%.
5. Переходы между близкими уровнями. В случае переходов
с ДЕ | Е | величина о ($) практически не зависит от ДЕ
(см. § 14, п. 2). Поэтому расчеты таких сечений были выполнены
с произвольно выбранными величинами ДЕ. Параметры С, (р
и Л, %, а также принятые значения ДЕ для ряда переходов без
изменения спина приведены в табл. 25 (см. стр. 236). Сечение
<тО0СТ1 и скорость <waoai> задаются формулами (18.13), (18.14),
а функции аналитической аппроксимации — формулами (18.15)—
(18.18). Интервал аппроксимации сечений $ 2 Ry, скоростей —
Т < 1/4zaRy.
Параметры аппроксимации скоростей для интерком-
бинационных переходов даны в табл. 26 (см. стр. 236). Скорости
определяются формулами (18.20), (18.22), (18.24). Интервал
аппроксимации
Т < V^Ry.
6. Сечения ионизации. Сечение ионизации нейтрального атома
в борновском приближении вычисляется аналогично сечению
возбуждения, однако, при атом необходимо добавить суммиро-
вание по орбитальным моментам и интегрирование по энергиям
выбитого электрона (см. формулу (6.35)). В результате расчет
сечений ионизации даже в борновском приближении значитель-
но сложнее, чем вычисление сечения возбуждения. Еще более
громоздкими вычисления становятся в борн-кулоновском прибли-
§ 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
181
жении. Влияние кулоновского поля на сечение ионизации суще-
ственно лишь вблизи порога и проявляется в изменении зависи-
мости сечения от энергии (см. § 7, п. 2). Результаты ряда конкрет-
ных расчетов борн-кулоновских сечений показывают, что для
определения сечений ионизации ионов можно использовать бор-
в
новские сечения ионизации ст, с поправочным множителем
[(и + 1)/и]*/2:
/ U 4- 1 \‘/« Б
Oi = (—) Hi при Z
(18.25)
Такой способ и был использован для табулирования сечений
ионизации. В этих расчетах использовались полуэмпирические
численные радиальные функции [64] как для состояний дискрет-
ного спектра, так и для состояний непрерывного спектра.
Сечение ог- и скорость ионизации запишем в виде
Oi — ла0 j ’ 2Z0 + 1 Ф*
'£-Ег
(18.26)
<ГО1> = 10-(-Й-)'7, (18.27)
Здесь Ez Ф; (U) И — энергия ионизации атома (или иона) Хг. Gi (Р) даются формулами: Функции
в случае нейтральных атомов (z — 1):
Ф|(«) = ( и \’/г С (18.28)
и -|- 1 / U -|- ф ’
с» да = ( р \*/= А (18.29)
₽ + 1 / Р + х’
в случае ионов (z 1)
Ф1(и) = и С (18.30)
и -f- 1 и 4- ф ’
<ч(Р) = Р + Х (18.31)
Если не интересоваться конечным состоянием образовавшегося
в результате ионизации иона, т. е. рассматривать суммарное по
LiSi сечение, то для ионизации из оболочки I™
Qi = т,
(18.32)
182 гл. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
где т — число эквивалентных электронов в оболочке. В случае
перехода
Xz (%L.S.) + е -> Х2+1 + е + е
угловой фактор Qt выражается через генеалогические коэффи-
циенты Gl°s° (см. § 19):
<2; (zl™L0S0, z + = т (Gjffi. (18.33)
Параметры С, ср и А, % для определения сечений ионизации
ряда нейтральных атомов даны в табл. 27; в табл. 28 приведены
параметры аппроксимации сечений и скоростей ионизации мно-
гозарядных водородоподобных и гелиеподобных ионов (см. стр.
237). Параметры А и % для ионизации из оболочек 2s и 2р [Li]-,
[Be]-, [В]-, [С]-, [N]-, [О]-, [F]- и [Nel-подобных ионов представ-
лены на рис. 28 и 29.
Пределы аппроксимации:
0,01 < и < 20, -1- < р < 8.
7. Скорость диэлектронной рекомбинации. Методы расчета
скорости диэлектронной рекомбинации
Хг+1 («о) + е -> Xz (fljnZ) -> Х2 (a.nl) + h®
описаны в § 15. Для расчета использовалась упрощенная модель
(15.12) с модификацией (15.29) для s — р-переходов. Сечение воз-
буждения а. — аг иона Xz+1 вычислялось в борн-кулоновском
приближении с учетом обмена (там, где он может быть сущест-
венным). Скорость xd диэлектронной рекомбинации, связанной
с переходом а0 — а1г можно представить в виде
Xd («О, «1) = Ю-13 Л^Рх<ф3/2,
Фактор Qd для наиболее интересных случаев:
Qd = т,
<2dWS'niff,= Nil- ,
N = 2 (21. + 1).
Параметры Ad и /d для ряда изоэлектронных последователь-
ностей приведены в табл. 29, 30 (см. стр. 238).
§ 1R. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИИ
183
Рис. 28. Скорости ионизации из оболочки 2s.
Рис. 29. Скорости ионизации из оболочки 2р.
184 гл. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Таблица 18
Сечения возбуждения нейтральных атомов б; переходы без изменения
спина (АД = 0). Параметры С и <р (метод Борна)
Эффективное главное квантовое число п*
Дп * 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0
Переход s — s г) параметр С
0,6 674-1 55+1 57+1 61+1 66+1 71+1 77+1 83+1 89+1 195+1
0,7 724-1 55+1 554-1 57+1 61+1 65+1 69+1 74+1 79+1 84+1
0,8 69 |1 49+1 48+1 49+1 51+1 54+1 57+1 60+1 64+1 67+1
0,9 584-1 39+1 37+1 37+1 38+1 40+1 42+1 44+1 46+1 49+1
1,0 424-1 26+1 25+1 24+1 25+1 26+1 27+1 28+1 30+1 31+1
1,1 164-1 15+1 14+1 14+1 15+1 15+1 16+1 16+1* 17+1* 18+1*
1,2 674-0 81+0 84+0 85+0 87+0 90+0 94+0 97+0 10+1* 10+1
1,3 60+0* 65+0* 68+0 69+0 70+0 72+0 75+0 77+0 80+0 83+0
1,4 13+1* 10+1 97+0 94+0 93+0 94+0 96+0 98+0 10+1 10+1
1,5 27+1 17+1 15+1 14+1 13+1 13+1 13+1 14+1 14+1 14+1
1,6 41+1 25+1 21+1 19+1 18+1 18+1 18+1 18+1 18+1 18+1
1,7 52+1 30+1 25+1 22+1 21+1 20+1 20+1 20+1 20+1 21+1
1,8 57+1 31+1 26+1 224-1 21+1 20+1 20+1 20+1 20+1 20+1
1,9 54+1 28+1 23+1 20+1 18+1 18+1 17+1 17+1 17+1 18+1
2,0 43+1 21 + 1 18+1 15+1 14+1 13+1 13+1 13+1 13+1 13+1
2,1 15+1 13+1 11+1 10+1 99+0 95+0 93+0 93+0* 93+0* 94+0*
2,2 71+0 78+0 73+0 68+0 64+0 63+0 62+0 61+0 61+0* 62+0*
2,3 57+0* 60+0* 58+0 54+0 52+0 50+0 49-0 49-0 49-0 49-0
2,4 12-41* 84+0 75+0 68+0 63+0 60+0 58+0 58+0 57+0 57+0
2,5 24+0 14+1 11+1 10+1 91+0 86+0 82+0 80+0 79+0 79+0
2,6 38+1 20+1 16+1 13+1 12+1 11+1 11+1 10+1 10+1 10+1
2,7 50+1 26+1 20+1 16+1 14+1 13+1 13+1 12+1 12+1 12+1
2,8 55+1 27+1 21+1 17+1 15+1 14+1 13+1 13+1 12+1 12+1
2,9 54+1 25+1 20+1 16+1 14+1 13+1 12+1 12+1 11+1 11+1
3,0 45+1 19+1 16+1 12+1 11+1 10+1 10+1 96+0 94+0 92+0*
3,1 15+1 12+1 10+1 91+0 82+0 76+0 72+0 69+0* 67+0* 66+0*
3,2 72+0 76+0 69+0 61+0 55+0 52+0 49-0 48—0 47-0* 46-0*
3,3 56+0* 58+0* 54+0 49-0 45-0 42-0 40-0 39-0 38-0 37-0
3,4 11+1* 79+0 684-0 59+0 53+0 49—0 46-0 44-0 43-0 42-0
3,5 23+1 13+1 10+1 87+0 76+0 69+0 64+0 61+0 59+0 57+0
3,6 37+1 19+1 14+1 12+1 10+1 93+0 86+0 81+0 78+0 76+0
3,7 49+1 24+1 18+1 14+1 12+1 11+1 10+1 98+0 93+0 90+0
3,8 55+1 26+1 19+1 15+1 13+1 11+1 11+1 10+1 98+0 95+0
3,9 54+1 24+1 18+1 14+1 12+1 11+1 10+1 96+0 92+0 88+0
4,0 46+1 19+1 15+1 11+1 10+1 91+0 84+0 79+0 75+0 72+0*
4,1 15+1 12+1 10+1 84+0 74+0 67+0 62+0 58+0* 55+0* 54+0*
4,2 72+0 76+0 66+0 57+0 51+0 47-0 43-0 41—0 39-0* 38-0*
4,3 56+0* 57+0* 52+0 46—0 42-0 38-0 35—0 33-0 32-0 31-0
4,4 11+1* 76+0 65+0 55+0 48-0 44-0 40-0 38—0 36—0 35-0
т) Этой таблицей можно пользоваться только для переходов между двумя
различными конфигурациями: либо между двумя конфигурациями в целом,
либо для переходов, в которых не изменяется ни одно из квантовых чисел
угловых моментов (х = 0, см. § 6).
§ 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
185
Табл и ц а 18 (продолжение)
Эффективное главное квантсвэе число п*
Дп*
0.5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0
Переход s — s, параметр <р
0,6 92+0 80+0 76+0 78+0 81+0 86+0 91+0 96+0 10+1 10+1
0,7 88+0 78+0 78+0 82+0 88+0 94+0 10+1 10+1 11+1 12+1
0,8 85+0 78+0 81+0 89+0 97+0 10+1 11+1 12+1 13+1 14+1
0,9 84+0 81+0 89+0 10+1 11+1 12+1 13+1 15+1 16+1 17+1
1,0 84+0 89+0 10+1 11+1 13+1 15+1 17+1 18+1 20+1 22+1
1,1 9340 10+1 12+1 14 1 1 16+1 19+1 21+1 24+1* 26+1* 29 pl*
1,2 15+1 15+1 15+1 16+1 18+1 20+1 23+1 25+1 27+1* 30+1*
1,3 20+1* 15+1* 12+1 11+1 12+1 12+1 13+1 13+1 14+1 14+1
1,4 13+1* Ю+1 77+0 69+0 67+0 66+0 64+0 64-f-0 63+0 62+0
1,5 10+1 784 0 62+0 564-0 55+0 53+0 52+0 52+0 52+0 52 40
1,6 91+0 7040 60+0 57+0 57+0 57+0 58+0 59+0 60+0 62+0
1,7 85+0 68+0 62+0 63+0 65+0 67+0 69+0 72+0 75+0 79+0
1,8 82+0 69+0 68+0 71+0 75+0 80+0 85+0 90+0 96+0 10+1
1,9 81+0 72+0 76+0 83+0 90+0 984-0 10+1 11+1 12+1 13+1
2,0 81+0 81+0 89+0 10+1 11+1 12+1 13+1 15+1 16+1 17+1
2,1 89+0 99+0 11+1 12+1 14+1 15+1 17-41 19+1* 21+1* 23+1*
2,2 13+1 13+1 13+1 14+1 16+1 18+1 20+1 21 + 1 23+1* 25+1*
2,3 20-1 1* 15+1* 12+1 12+1 12+1 13+1 14+1 15+1 15+1 16+1
2,4 13+1* 10+1 81+0 74+0 74+0 74+0 73+0 73+0 73+0 73+0
2,5 10+1 78+0 6140 56+0 55+0 53+0 52+0 51+0 51+0 51+0
2,6 91+0 68+0 57+0 55+0 54+0 53+0 53+0 53+0 54+0 55+0
2,7 85+0 66+0 59+0 59+0 60+0 61+0 63+0 64+0 67+0 69+0
2,8 82+0 67+0 65+0 67+0 70+0 73+0 77+0 81+0 86+0 90+0
2,9 81+0 70+0 73+0 78+0 84+0 90+0 97+0 10+1 11+1 12+1
3,0 81+0 78+0 85+0 95+0 10+1 11+1 12+1 13-41 14+1 16+1*
3,1 88+0 96+0 10+1 11+1 13+1 14+1 16+1 17+1* 19+1* 21+1*
3,2 13+1 13+1 13+1 14+1 15+1 17+1 18+1 20+1 22+1* 24+1*
3,3 20+1* 15+1* 12+1 12+1 12+1 13+1 14-1-1 15+1 15+1 16+1
3,4 13+1* 10+1 82+0 76+0 77+0 77+0 77+0 78+0 78+0 79+0
3,5 10+1 78+0 61+0 57+0 55+0 54+0 53+0 52-1-0 52+0 52+0
3,6 91+0 68 |-0 56+0 54-1-0 53+0 524-0 52+0 52+0 52+0 53+0
3,7 85+0 65+0 58+0 58+0 58 40 59+0 60+0 61+0 63+0 65+0
3,8 82+0 66+0 63+0 65+0 68+0 70+0 73+0 77+0 81+0 85+0
3,9 81+0 69+0 71+0 76+0 81+0 87+0 93+0 99+0 10+1 11+1
4,0 81+0 78+0 84+0 92+0 10+1 11+1 11+1 13+1 14+1 15+1*
4,1 88+0 95+0 10+1 11+1 12+1 14+1 15+1 16+1* 18+1* 19+1*
4,2 13+1 13+1 12+1 13+1 15+1 16+1 18+1 19+1 21+1* 22+1*
4,3 20+1* 15+1* 12+1 12+1 12+1 13+1 14+1 15+1 15+1 16+1
4,4 14+1* 10+1 82+0 77+0 79+0 79+0 7940 80+0 81+0 82+0
186
ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Таблица 18 (продолжение)
Эффективное главное квантовое число п*
Ап* 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0
Переход s — р; параметр С
0,1 0,2 0,3 0,4 0,5 11 + 1 27+1 49-41 73+1 96+1 16+1 37+1 59 4-1 80+1 97+1 21+1 44+1 67+1 86+1 10+2 25-1 504 73- 924 10- -1 -1 -1 -2 29+1 56+1 804-1 98+1 10+2 32+1 61+1 86 41 10+2 11+2 36+1 67+1 92+1 10+2 11+2 39 41 72 + 1 98+1 11-42 12+2
0,6 114-2 11+2 10+2 10+2 10J -2 10+2 10+2 11+2 114-2
0,7 144-2 11+2 10+2 98+1 96+1 95+1 96+1* 974-1* 99 4-1*
0,8 15+2 114-2 94+1 84+1 80+1* 77+1* 77+1* 77+1* 77-41*
0,9 15+2 93-41 75+1 63+1* 59+1* 55+1* 54+1* 53+1* 53+1*
1,0 13+2 69+1 524-1* 41-1-1* 37. -1* 34+1* 32+1* 31+1* 31+1*
1,1 304-2 10+2 464-1 30-41* 22+1* 194-1 16 + 1* 15+1* 14+1* 13+1*
1,2 254-2 61+1 23+1 12+1 86+0* 68+0* 58+0* 53+0* 50+0* 48—0*
1,3 184-2 27+1 74-40* 42—0 37—0 37- -0 38-0* 40—0* 43-0» 45—0*
1,4 104-2 71-40 43-0 554- 0* 63-40* 70- 0* 75+0* 80-40* 84+0* 88-40*
1,5 514-1 53+0* 11 + 1 13 + 1* 13+1* 14+1* 14+1* 14-|-1* 14+1* 15+1*
1,6 144-1 194-1* 244-1 24+1 22+1 21 -1 21+1 21+1* 20+1* 214-1*
1,7 10-0 42+1 38+1 34+1 29+1 27+1 25+1 25+1* 244-1* 24+1*
1,8 764-0 68+1 47-41 394-1 32+1 29+1 26+1* 25+1* 24-41* 23 + 1*
1,9 26 -1-1 87-41 49-41 38-41 29+1 26+1* 23+1* 21-41* 20+1* 194-1*
2,0 48-41 95+1 44+1 314-1 234-1* 20+1* 17+1* 15+1* 144-1* 13+1*
2,1 194-2 80+1 36+1 21+1* 15+1* 12+1 10+1 91+0 82+0 75+0
2,2 184-2 55+1 214-1 11+1 74+0 55+0* 45-0* 39-0* 35—0* 32-0*
2,3 144-2 29+1 87+0 42-0 30-0* 26- -0 24—0 24—0 24-0 24—0
2.4 10-42 10-f-l 34—0 34-0* 35—0* 37- -0* 38—0* 39-0 40-0 41-0
2,5 544-1 37-0 72+0 77+0 77+0* 76 -0* 75+0* 74-40* 744-0* 74+0*
2,6 204-1 11+1 16+1* 15+1 13+1 12+1 12+1* 11+1* 11+1* 11+1*
2,7 31—0 304-1 274-1 23-41 19+1 17+1 15+1 14+1* 14+1* 13+1*
2,8 28-0 52+1 36+1 29+1 22+1 19+1 17+1* 16+1* 14+1* 14+1*
2,9 15-41 73-41 40 4-1 30+1 22-41 18- л* 16-41* 14+1* 13+1* 124-1*
3,0 33-41 84+1 37+1 26+1 18-41* 1541* 12-41* 11+1* 104 1* 93+0*
3,1 164-2 73 + 1 32+1 18+1* 12-41* 10+1 814-0* 70+0 61+0 55+0
3,2 164-2 53-41 20 + 1 10+1 674-0 49- -0* 39-0* 32—0* 28-0* 25—0*
3,3 134-2 30+1 90+0 41—0* 28-0 23- -0 20-0 19-0 18—0 17-0
3,4 964-1 11+1 34—0 28-0* 28—0* 28- -0* 28-0* 27—0* 27—0* 28—0*
3,5 55-41 35-0 59+0 62+0 59+0* 57+0* 55+0* 53+0* 51+0* 50+0*
3,6 23-41 93+0 13+1* 12+1* 10+1* 10+1* 99+0* 90+0* 85+0* 77+0*
3,7 46-0 25+1 23+1 20+1 15+1 13-41 12+1 11+1 10+1 98+0
3,8 16-0* 47+1 32+1 25+1 18+1 16+1 13+1 12+1* 11+1* 10+1*
3,9 114-1 67+1 36+1 26+1 18+1* 15+1* 13+1* 11+1* 10+1* 97+0*
4,0 27-41 80+1 34+1 23-41 15+1* 13+1* 10+1* 93+0* 81+0* 74+0*
4,1 15+2 71+1 31+1 17+1 11+1* 89+0 71+0 59+0 51+0 46-0
4,2 15+2 52+1 20+1 99+0 62+0 45- -0* 35-0* 29-0* 25-0* 22—0*
4,3 13+2 30+1 92+0 41—0* 27-0 21- -0 18—0 16—0 15-0 14-0
4,4 94-41 11+1 34—0 26—0* 25-0 24- -0* 23-0* 22—0* 22—0* 22—0*
§ 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
187
Таблица 18 (продолжение)
Дн * Эффективное главное квантовое число п*
0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0
Переход s — р; параметр <р
0,1 0,2 0,3 о,4 0,5 10+1 14+1 17+1 21+1 25+1 11+1 16+1 21+1 25+1 30+1 12+1 18+1 24+1 29+1 36+1 13+1 20+1 27+1 34+1 41+1 15+1 22+1 304-1 38+1 46+1 16+1 24+1 33+1 42+1 52+1 17+1 26+1 36+1 46+1 57+1 18+1 28+1 39+1 50+1 62+1
0,6 22+1 29+1 36+1 43+1 49+1 56+1 63+1 70+1 76+1
0,7 25+1 34+1 42+1 51+1 60+1 68+1 77+1* 85+1* 94+1*
0,8 28-1-1 40+1 50+1 62+1 73-{-1* 84+1* 94+1* 10+2* 114-2*
0,9 32+1 47+1 61+1 76+1* 89+1* 10+2* 11+2* 12+2* 14+2*
1,0 37+1 58+1 75+1* 93+1* 11+2* 12+2* 14+2* 15+2* 17+2*
1,1 26+1 44+1 70+1 93+1* 1142* 12+2 12+2 13+2* 12+2* 11+2*
1,2 29+1 56+1 85+1 84+1 61 + 1* 40+1* 27+1* 19+1* 14+1* 10+1*
1,3 33+1 73+1 38+1* 49-0 10-0 10-0 10—0* 10-0* 10-0* 10—0*
1,4 38+1 37+1 10-0 10—0* 10—0* 10—0* 10—0* 10—0* 10—0* 10—0*
1,5 47+1 10—0* 10-0 13—0* 37-0* 59+0* 79+0* 98+0* 11+1* 13+1*
1,6 70+1 15-0* 74+0 И+1 14+1 18+1 21+1 24+1* 27+1* 30+1*
1,7 57+0 10+1 16+1 21 + 1 26+1 31+1 35+1 40+1* 45+1* 50+1*
1,8 45-0 17+1 25+1 31+1 38+1 45+1 52+1* 58+1* 65+1* 71+1*
1,9 16+1 23+1 34+1 43+1 53+1 62+1* 71+1* 79+1* 88+1* 96+1*
2,0 23+1 29+1 45+1 57+1 69+1* 81+1* 92+1* 10+2* 11+2 12+2*
2,1 24+1 37+1 56+1 73+1* 86+1* 96+1 10+2 10+2 10+2 10+2
2,2 28+1 48+1 71+1 78 4-1 68 41* 53+1 39+1* 30+1* 23+1* 19+2
2,3 32+1 64+1 56+1 17+1 44-0* 10—0 10—0 10-0 10-0 10—0
2,4 57+1 59+1 10-0 10—0* 10-0 10—0* 10—0* 10-0 10-0 10—0
2,5 46+1 10—0 10-0 10-0 10—0* 10—0* 23—0* 37-0* 50-0* 63-0*
2,6 63+1 10—0 33-0* 67+0 91+0 11+1 14+1* 16+1* 18+1* 21+1*
2,7 73+1 69+0 12+1 16+1 20+1 23+1 27+1 31+1* 35+1* 38+1*
2,8 10-0 14+1 21+1 26+1 32+1 37+1 43+1* 48+1* 53+1* 59+1*
2,9 11+1 21+1 30+1 38+1 46+1 53+1 61+1* 68+1* 75+1* 82+1*
3,0 20+1 27+1 41+1 51+1 62+1* 71+1* 80+1* 89+1* 97+1* 10+2*
3,1 23+1 35+1 52+1 67+1* 78+1* 86+1 92+1* 95+1 96+1 95+1
3,2 27+1 46+1 67+1 74+1 67+1 56+1* 44+1* 34+1* 27+1* 22+1*
3,3 32+1 61+1 59+1 23+1* 80+0 21—0 10—0 10—0 10—0 10-0
3,4 37+1 63+1 10-0 10—0* 10-0* 10—0* 10—0* 10—0* 10—0* 10—0*
3,5 45+1 10 0 10-0 10-0 10—0* 10—0* 10-0* 14-0* 24-0* 35-0*
3,6 61+1 10-0 18-0* 49-0* 69+0* 90+0* 11+1* 13+1* 15+1* 17+1*
3,7 88+1 54+0 10+1 14+1 17+1 20+1 24+1 27+1 30+1 33+1
3,8 10—0* 13+1 19+1 24+1 29+1 34+1 39+1 43+1* 48+1* 524-1*
3,9 91+0* 27+1 28+1 35+1 42+1 49+1* 56+1* 68+1* 68+1* 74+1*
4,0 19+1 27+1 38+1 48+1 58+1* 66+1* 74+1* 82+1* 89+1* 964-1*
4,1 23+1 34+1 57+1 63+1 73+1* 81+1 87+1 90+1 91+1 91+1
4,2 27+1 45+1 65+1 71+1 66+1 56+1* 45+1* 36+1* 29+1* 24 t-1*
4,3 31+1 60+1 61+1 25+1* 10+1 70-0 10-0 10—0 10—0 10-0
4,4 37+1 64+1 20-0 10-0* 10-0 10—0* 10-0* 10-0* 10-0* 10—0*
188 гл. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Таблица 18 (продолжение)
Дп* Эффективное главное квантовое число nJ
0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0
Переход s — d^параметр С
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 14+2 99+1 10+2 95+1 80+1 60+1 34+1 39+1 53+1 66+1 75+1 78+1 74+1 63+1 49+1 33+1 19+1 11+1 28—0 79+0 15+1 25+1 37+1 49+1 59+1 66+1 67 + 1 65+1 54+1 42+1 29+1 18+1 11+1 90+0 47-0 11+1 21+1 32+1 43+1 53+1 60+1 63+1 61+1 54+1 43+1 31+1 21+1* 13+1 93+0 96+0 63+0 15+1 26+1 37+1 48+1 57+1 62+1 62+1 57+1 51+1 37+1 26+1* 17+1 11+1 90+0 10+1 79+0 18+1 30+1 42+1 52+1 60+1 63+1 61+1 55+1 45+1 34+1* 23+1 15+1 10+1 92+0 11+1 93+0 21+1 33+1 46+1 56+1 62+1 64+1 61+1 53+1 48+1 31+1* 21+1* 13+1 99+0* 95+0 11+1 10+1 23+1 37+1 50+1 60+1 65+1 66+1 61+1 53+1* 41+1* 30+1* 20+1* 13+1 98+0* 99+0 12+1
1,7 11+2 16+1 89+0 11+1 13+1 14+1 14+1 15+1 15-j-l
1,8 75+1 91+0 13+1 17+1 18+1 18+1 18+1 18+1
1,9 40+1 12+1 21+1 24+1 22+1 21+1 20+1 20+1 19+1
2,0 16+1 23+1 31+1 29+1 25+1 23+1 20+1 20+1 18+1*
2,1 26+2 40—0 33+1 38+1 30+1 24+1 21+1 18+1 17+1* 16+1*
2,2 14+2 14+1 46+1 40+1 28+1 21+1 17+1* 15+1* 13+1* 12+1*
2,3 60+1 38+1 55+1 37+1 23+1 16+1 13+1 11+1* 10+1* 94+0*
2,4 15+1 62+1 57+1 29+1 16+1 11+1 95+0 83+0 75+0
2,5 83-1 79+1 51+1 20+1 11+1 83+0 72+0 67+0 65+0 64+0
2,6 29—0 83+1 35+1 12+1 80+0 71+0 70+0 71+0 72+0 73+0
2,7 11+1 75+1 20+1 84+0 83+0 85+0 88+0 90+0 91+0 92+0
2,8 19+1 58+1 10+1 90+0 11+1 11+1 11+1 11+1 11+1 ll-j-l
2,9 23+1 37+1 90+0 14+1 16+1 15+1 14+1 13+1 13+1 12+1
3,0 23+1 19+1 15+1 22+1 21+1 18+1 16+1 14+1 13+1 12+1*
3,1 12+2 50+0 22+1 29+1 23+1 18+1 16+1 14+1 12+1* 11+1*
3,2 78+1 85+0 34+1 33+1 23+1 17+1 14+1 12+1* 10+1* 98-j-O*
3,3 37+1 24+1 44-J-1 32+1 20+1 14+1 11+1 96+0* 84+0* 76+0*
3,4 11+1 43+1 49+1 27+1 15+1 10+1 85+0 72+0 64+0* 59-|-0
3,5 11-0 59+1 47+1 20+1 10+1 77+0 64+0 57+0 54+0 51+0
3,6 13-0 66+1 34+1 13+1 77+0 63+0 59+0 57+0 56+0 55+0
3,7 66+0 63+1 21+1 85+0 73+0 70+0 70+0 69+0 69+0 68+0
3,8 12+1 52+1 11+1 79+0 96+0 94+0 93+0 89+0 87+0 84+0
3,9 16+1 36+1 83+0 11+1 13+1 12+1 11+1 10+1 10+1 97+0
4,0 17+1 20+1 12+1 19+1 18+1 15+1 13+1 12+1 11+1 10+1
4,1 97+1 58+0 17+1 25+1 20+1 16+1 13+1 11+1 ю+i: 96+0*
4,2 61+1 66+0 28+1 29+1 21+1 15+1 12+1 10+1* 92+0* 83+0*
4,3 30+1 18+1 39+1 30+1 19+1 13+1 10+1 86+0 74+0* 66+0*
4,4 10+1 35+1 45+1 26+1 15+1 10+1 79+0 66+0 58+0 52+0
§ 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
189
Таблица 18 (продолжение)
Дп * Эффективное главное квантовое число
0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0
Переход s — d", параметр <р
0,1 81+0 70+0 64+0 62+0 60+0 60+0
0,2 62+0 61+0 62+0 64+0 66+0 69+0
0,3 63+0 66+0 70+0 74+0 79+0 83+0
0,4 68+0 74+0 80+0 86+0 93+0 99+0
0,5 74+0 83+0 91+0 99+0 10+1 11+1
0,6 72+0 82+0 92+0 10+1 11+1 12+1 13+1
0,7 78+0 90+0 10+1 11+1 13+1 14+1 16+1
0,8 84+0 10+1 11+1 13+1 15+1 17+1 19+1
0,9 91+0 11+1 13+1 15+1 17+1 20+1 22+1*
1,0 10+1 14+1 15+1 22+1 21+1 34+1 27+1*
1,1 85+0 11+1 14+1 17+1 21+1 25+1* 28+1* 32+1*
1,2 91+0 12+1 16+1 21+1 25+1* 29+1 33+1* 36+1*
1,3 99+0 14+1 19+1 24+1* 28+1 30+1 31+1 31+1
1,4 10+1 17+1 22+1 24+1 23+1 20+1 17+1* 15+1*
1,5 12+1 20+1 20+1 15+1 11+1 87+0 74+0 66+0
1,6 88+0 15+1 19+1 98+0 64+0 53+0 49-0 48—0 49-0
1,7 94+0 18+1 89+0 49-0 45-0 48—0 52+0 57+0 63+0
1,8 10+1 13+1 46-0 47—0 54+0 62+0 70+0 80+0 90+0
1,9 11+1 56+0 48-0 60+0 71+0 83+0 96+0 ll-j-l 12+1
2,0 14+1 50+0 61+0 77+0 93+0 11+1 12+1 15-j-l 16+1*
2,1 84+0 14+1 57+0 75+0 96+0 11+1 14+1 16+1 19+1* 21+1*
2,2 86+0 59+0 68+0 92+0 11+1 14+1 17+1* 20+1* 23+1* 26+1*
2,3 90+0 65+0 80+0 11+1 14+1 18+1 21+1 24+1* 26+1* 27+1*
2,4 98+0 71+0 92+0 13+1 17+1 21+1 22+1 22+1 21+1 20+1
2,5 16+1 77+0 10+1 16+1 19+1 18+1 15+1 13+1 11+1 97+0
2,6 66+0 84+0 12 |-1 18+1 14+1 10+1 76+0 63+0 56+0 53+0
2,7 78+0 92+0 16+1 14+1 67+0 52+0 47-0 46—0 48—0 51+0
2,8 85+0 10+1 16+1 62+0 45-0 46-0 50+0 55+0 62+0 68+0
2,9 90+0 11+1 83+0 44-0 50+0 58+0 66+0 76+0 86+0 97+0
з,о 96+0 13+1 48—0 52+0 65+0 76+0 92+0 10+1 12+1 13+1*
3,1 86+0 18+1 49—0 65+0 82+0 99+0 11+1 13+1 15+1* 17+1*
3,2 89+0 62+0 61+0 81+0 10+1 12+1 15+1 17+1* 20+1* 22+1*
3,3 94+0 59+0 73+0 99+0 13+1 16+1 18+1 21+1* 23+1* 24+1*
3,4 10+1 67+0 86+0 12+1 16+1 19+1 20+1 21+1 21+1 20+1
3,5 16+1 74+0 10+1 14+1 18+1 18+1 17+1 14+1 13+1 11+1
3,6 57+0 82+0 12+1 17+1 15+1 11+1 91+0 75+0 65+0 59+0
3,7 75+0 90+0 15+1 15+1 80+0 59+0 51+0 48-0 47-0 48—0
3,8 83+0 Ю+1 17+1 76+0 47-0 45—0 47-0 50+0 55+0 60+0
3,9 90+0 11+1 10+1 45-0 47-0 53+0 59+0 67+0 76+0 85+0
4,0 96+0 13+1 49-0 49-0 60+0 69+0 82+0 92+0 10+1 11+1
4,1 87+0 19+1 47-0 61+0 76+0 90+0 10+1 12+1 14+1 15+1*
4,2 90+0 68+0 57+0 76+0 97+0 11+1 13+1 16+1* 18+1* 20+1*
4,3 96+0 57+0 70+0 94+0 12+1 14+1 17+1 19+1 21+1* 23+1*
4,4 10+1 64+0 83+0 11+1 15+1 17+1 19+1 20+1 21+1 20+1
190 гл. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Тка блица 18 (продолжение)
Эффективное главное квантовое число п*
Дп ♦ 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0
П ереход р — $; параметр С
0,1 0,2 0,3 0,4 0,5 83+0 15+1 21+1 24+1 24+1 13+1 25 |-1 33+1 37+1 37+1 18+1 32+1 43+1 48 [-1 47-1-1 22+1 39+1 51+1 57+1 56+1 26+1 45+1 59+1 65+1 63+1 29+1 51+1 66+1 72+1 70+1 33+1 57-1-1 73+1 79+1 77+1 36+1 62+1 79-| 1 86+1 84+1
0,6 21+1 33+1 42+1 49+1 56+1 62+1* 67+1* 73+1*
0,7 16+1 26+1 33+1 39-1-1* 44+1* 48+1* 53+1* 57+1*
0,8 11+1 18+1 22+1* 27+1* 30+1* 33 -1-1* 36+1* 39+1*
0,9 58+0 10+1 13+1* 15+1 17+1 19+1 21+1* 23+1*
1,0 24-0 47-0* 58+0* 71+0* 80+0* 89+0* 97+0* 10+1*
1,1 15—0 21—0 26—0 30—0 33-0 36-0 39-0 42-0
1,2 21—0* 25-0* 27—0* 29—0* 31-0* 32—0* 33—0* 35-0*
1,3 41—0* 47-0* 51+0* 53+0* 55+0 56+0* 58+0* 60+0*
1,4 64+0* 77+0* 83+0* 87+0* 90+0* 93+0* 96+0* 99-1-0*
1,5 81+0 10+1* 11+1* H-j-l* 12+1* 12+1* 13+1* 13-1-1*
1,6 85+0 11+1 12+1 13+1 13+1* 14+1* 14+1* 15+1*
1,7 75+0 10+1 11+1 12+1* 13+1* 13+1* 14+1* 14+1*
1,8 53+0 83+0 91+0 10+1* 10+1* 11+1* 11+1* 12+1*
1,9 30—0 55+0 60+0 68+0 71+0 76+0 79+0 83+0
2,0 17—0 29-0* 31-0* 36-0* 38-0* 41—0* 42-0* 45-0*
2,1 12-0* 16-0 18—0 19-0 20-0 21-0 22-0 22—0
2,2 17—0* 18—0* 19-0* 19—0* 19—0* 19-0* 19—0* 19—0*
2,3 32-0* 33—0* 32—0* 32—0* 32-0* 31-0* 31-0* 31-0*
2,4 49-0* 53+0* 54+0* 52+0* 52+0* 51+0* 51+0* 51 + 0*
2,5 63+0 71+0* 73+0* 72+0* 71+0* 71+0* 70+0* 70+0*
2,6 66+0 81+0 83+0 83+0 83+0 83+0* 83-1-0* 83+0*
2,7 58+0 78+0 80+0 82+0* 82+0* 83+0* 83-1-0* 83+0*
2,8 41-0 63+0 65+0 69+0* 69+0* 70+0* 70+0* 72+0*
2,9 23-0 43-0 43-0 48—0 48-0 50+0* 50+0 51+0
3,0 15-0 24-0* 24-0* 27-0* 27-0* 28-0* 28-0* 29-0*
3,1 12—0* 14-0 15-0 15-0 15-0 16—0 16—0 16-0
3,2 16-0* 16-0* 16-0* 15—0* 15—0* 15-0* 14—0* 14-0*
3,3 29-0* 28—0* 27—0* 25—0* 24—0* 23-0* 23—0* 22-0*
3,4 44-0* 45-0* 44-0* 41-0* 41-0* 38-0* 37-0* 36-0*
3,5 56+0 61+0 60+0* 57+0* 55+0* 531-0* 51+0* 50+0*
3,6 59+0 70+0 68+0 67+0 64+0 63+0 61+0 60+0
3,7 51+0 68+0 66+0 66+0 64+0 63+0* 62+0* 61+0*
3,8 36-0 56+0 54+0 56+0 55+0* 55+0* 53+0* 53+0*
3,9 20-0 38-0 37-0 40-0 39-0 39-0 39-0 39-0
4,0 14-0 21-0* 21-0 23-0* 22-0* 23—0* 23-0* 23-0*
4,1 11—0* 13-0 14-0 14-0 13—0 13-0 13—0 13-0
4,2 15—0* 15-0* 15-0* 14-0* 13-0* 12-0* 12—0* 12-0*
4,3 27-0* 26-0* 25-0* 22—0* 21—0* 20—0* 19—0* 18-0*
4,4 42-0* 42-0* 40-0* 36-0* 34-0* 32—0* 30-0* 29-0*
§ 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
191
Таблица 18 (продолжение)
Эффективное главное квантовое число п*
Ап * 1,5 2.0 2,5 3,0 3,5 4,0 4,5 5,0
Переход р — s', параметр (р
0,1 10-и 11-1-1 124-1 144-1 15+1 16+1 17+1 18+1
0,2 14+1 174-1 19+1 21+1 23+1 25-|-1 27+1 29+1
0,3 19-L1 22+1 25+1 29+1 32+1 34+1 37+1 40+1
0,4 24-|-1 28 4-1 33+1 374-1 41+1 45+1 494-1 53+1
0,5 304-1 35-4-1 41+1 46+1 51+1 57+1 62+1 67+1
0,6 374-1 44! 1 51 L-1 58 |-1 644-1 71+1* 78+1* 84+1*
0,7 464-1 54+1 63-1 72+1* 80+1* 89+1* 97+1* 10+2*
0'8 554-1 66+1 78+1* 88+1* 99+1* 11+2* 12+2* 13+2*
0,9 52 |-1 74+1 87+1* 10+2 11+2 12+2 14+2* 15+2*
1,0 11-4-1 45+1* 49+1* 66+1* 72+1* 84+1* 90+1* 98+1*
1,1 10—0 10-0 29-0 52+0 70+0 864-0 99+0 11-}-1
1,2 10—0* 10—0* 10—0* 10-0* 10-0* 10-0* 10-0* 10-0*
1,3 10—0* 10—0* 10-0* 10-0* 10—0* 10-0* 10-0* 10-0*
1,4 674-0* 66+0* 69+0* 72+0* 77+0* 82+0* 88+0* 94+0*
1,5 14-И 15+1* 17+1 18+1* 20+1* 21+1* 23+1» 25+1*
1,6 234-1 25+1 28+1 31+1 34+1* 374 1* 40+1* 43+1*
1,7 32-j-l 36+1 41+1 46+1* 50+1* 55+1* 59+1* 64+1*
1,8 38+1 47+1 54+1 61+1* 67+1* 74+1* 80+1* 87+1*
1,9 274-1 514-1 57+1 68+1 75+1 85+1 924-1 10+2
2,0 10—0 274-1* 27+1* 40+1* 42+1* 51+1* 54-1-1* 60+1*
2,1 10-0* 10—0 10—0 28-0 42—0 57+0 68+0 79+0
2,2 10-0* 10-0* 10-0* 10-0* 10—0* 10-0* 10—0* 10—0*
2,3 10—0* 10-0* 10-0* 10-0* 10-0* 10-0* 10-0* 10—0*
2,4 49—0* 43-0* 41-0* 41-0* 42-0* 44-0* 46-0* 49—0*
2,5 12+1 12+1* 13+1* 14+1* 14+1* 15+1* 17+1* 18+1*
2,6 20+1 22+1 24+1 26+1 28+1 30+1* 32+1* 34+1*
2,7 28 | -1 32 ]-1 35+1 39] 1* 43+1* 46+1* 50+1* 53+1*
2,8 33-i 1 42+1 46 Н1 52+1* 57+1* 634-1* 68+1* 73+1*
2,9 194-1 44+1 47+1 57+1 62+1 704-1 76+1 834-1
3,0 10-0 224-1* 194-1* 33+1* 33+1* 41+1* 42+1* 484-1*
3,1 10—0* 10-0 10-0 17-0 30-0 43-0 53+0 63-1-0
3,2 10-0* 10—0* 10-0* 10-0* 10-0* 10-0* 10-0* 10—0*
3,3 10-0* 10—0* 10-0* 10-0* 10-0* 10-0* 10—0* 10—0*
3,4 42—0* 34—0* 32-0* 30-0* 30-0* 31-0* 32-0* 33—0*
3,5 11+1 11+1 12+1* 12+1* 13+1* 14+1* 14+1* 15+1*
3,6 194 1 20+1 22+1 23+1 25 |-1 27+1 29+1 30+1
3,7 27-1-1 зо-4-i 33+1 36+1 39-|-1 42+1* 45+1* 48+1*
3,8 304-1 39+1 43+1 48+1 53+1 57+1* 62+1* 66+1*
3,9 14+1 41+1 42+1 52+1 56+1 64+1 68+1 74-4-1
4,0 10-0 20+1* 16+1 29+1* 28+1* 36+1* 37+1* 43+1*
4,1 10—0* 10-0 10—0 12-0 23-0 35-0 45-0 54-j-O
4,2 10—0* 10—0* 10-0* 10—0* 10—0* 10—0* 10—0* 10-0*
4,3 10—0* 10—0* 10-0* 10—0* 10-0* 10-0* 10—0* 10-0*
4,4 39-0* 30-0* 27-0* 25-0* 24- 0* 24—0* 24-0* 25-0*
192 ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Таблица 18 (продолжение)
Дп* Эффективное главное квантовое число п*
1,5 2,0 2,5 3,0 3,5 4.0 4,5 5,0
Пер еход р— р !); х = ); параметр С
0,6 104-2 14+2 16+2 19+2 21+2 23+2 25+2 27+2
0,7 11+2 13+2 15+2 17+2 19+2 21+2 22+2 24+2
0,8 10+2 12+2 13+2 14+2 16+2 17+2 18+2 19+2
0,9 87+1 96+1 10+2 11+2 12+2 12+2 13+2 14+2
1,0 65+1 67+1 73+1 77+1 81+1 86+1 91+1 96+1
1,1 39+1 42+1 44+1 46+1 49+1 51+1 54+1 57+1
1,2 22+1 25+1 26+1 19+1 27+1 28+1 30+1 31+1 32+1
1,3 14+1 18+1 20+1 21+1 22+1 23+1 24+1
1,4 16+1 21+1 22+1 24+1 25+1 27+1 28+1 29 + 1
1,5 26+1 31+1 33+1 35+1 36+1 38+1 40+1 41+1
1,6 39+1 43+1 45+1 47+1 48-1-1 50+1 52+1 54+1
1,7 51+1 52+1 54+1 55+1 56+1 58+1 59+1 61+1
1,8 58+1 55+1 56+1 56+1 57+1 58+1 59+1 61+1
1,9 57+1 51+1 51+1 51+1 51+1 51+1 52+1 53+1
2,0 49+1 41+1 41+1 40+1 40+1 40+1 41+1 41+1
2,1 31+1 30+1 29+1 28+1 28+1 28+1 28+1 29+1
2,2 20+1 20+1 19+1 19+1 19+1 19+1 19+1 19+1
2,3 13+1 15+1 14+1 14+1 14+1 14+1 14+1 14+1
2,4 13+1 16+1 15+1 16+1 15+1 16+1 16+1 16+1
2,5 20+1 22+1 22+1 22+1 22+1 22+1 22+1 22+1
2,6 31+1 31+1 30+1 30+1 29+1 29+1 29+1 29+1
2,7 42+1 39+1 38+1 36+1 35+1 35+1 35+1 35+1
2,8 49+1 43+1 41+1 39+1 38+1 37+1 37+1 36+1
2,9 50+1 41+1 39+1 36+1 35+1 34+1 34+1 34+1
3,0 45+1 34+1 33+1 30+1 29+1 28+1 28+1 27+1
3,1 29+1 26+1 24+1 22+1 21+1 21+1 20+1 20+1
3,2 19+1 18+1 16+1 16+1 15+1 14+1 14+1 14+1
3,3 13+1 14+1 12+1 12+1 11+1 11+1 11+1 11+1
3,4 12+1 14+1 13+1 13+1 12+1 12+1 12+1 11+1
3,5 18+1 19+1 18+1 17-1-1 17+1 16+1 16+1 16+1
3,6 28+1 27+1 25+1 24+1 23+1 22+1 21+1 21+1
3,7 39+1 34+1 32+1 29+1 28+1 27+1 26+1 25+1
3,8 46+1 38+1 35+1 32+1 30+1 29+1 28+1 27+1
3,9 48+1 37+1 34+1 31+1 29+1 27+1 27+1 26+1
4,0 44+1 31+1 29+1 26+1 25+1 23+1 22+1 22+1
4,1 28+1 24+1 21+1 20+1 18+1 17+1 17+1 16+1
4,2 19+1 17+1 15+1 14+1 13+1 12+1 12+1 12+1
4,3 13+1 13+1 11+1 11+1 10+1 10+1 96+0 93+0
4,4 12+1 13+1 12+1 11+1 11+1 10+1 10+1 99+0
1) Этой таблицей можно пользоваться только для переходов между дву-
мя различными конфигурациями: либо между двумя конфигурациями в
целом, либо для переходов, в которых не изменяется ни одно из квантовых
чисел угловых моментов (х = 0, см. § 6).
§ 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
193
Таблица 18 (продолжение)
Ап* Эффективное главное квантовое число п*
1,5 2,0 2,5 3,о 3,5 4,0 4,5 5,0
Переход р — р\ х — 0; параметр <р
0,6 90+0 77+0 78+0 83+0 88+0 94+0 99+0 10+1
0,7 84+0 77+0 82+0 90+0 97+0 10+1 11+1 12+1
0,8 81+1 80+0 90+0 10+1 11+1 12+1 13+1 14-[-1
0,9 80+0 87+0 10+1 11+1 13+1 14+1 16+1 18+1
1,0 82+0 10+1 12+1 14+1 16+1 19+1 22+1 24+1
1,1 94+0 12+1 15+1 18+1 22+1 26+1 29+1 34+1
1,2 13+1 16+1 18+1 21+1 25+1 28+1 31+1 34+1
1,3 20+1 15+1 14+1 14+1 14+1 14+1 13+1 13+1
1,4 17+1 92+0 74+0 70+0 67+0 64+0 61+0 59+0
1,5 11+1 64+0 56+0 54+0 53+0 52+0 51+0 52+0
1,6 85+0 57+0 55+0 56+0 57+0 58+0 60+0 62+0
1,7 74+0 58+0 60+0 63+0 67+0 71+0 75+0 80+0
1,8 70+0 62+0 69+0 75+0 81+0 88+0 96+0 10+1
1,9 69+0 71+0 81+0 91+0 10+1 11+1 12+1 13+1
2,0 72+0 84+0 99+0 Н+1 13+1 15+1 17+1 19+1
2,1 82+0 10+1 12+1 15+1 17+1 20+1 23+1 26+1
2,2 11+1 13+1 15+1 18+1 21+1 24+1 27+1 30+1
2,3 17+1 14+1 14+1 15+1 15+1 16+1 16+1 16+1
2,4 17+1 96+0 83+0 81+0 77+0 74+0 72+0 70+0
2,5 11+1 64+0 57+0 56+0 53+0 51+0 50+0 50+0
2,6 86+0 55+0 53+0 52+0 52+0 52+0 53+0 55-j-O
2,7 73+0 54+0 56+0 58+0 60+0 63+о 66+0 70+0
2,8 68+0 58+0 64+0 68+0 73+0 79+0 85+0 92+0
2,9 67+0 66+0 75+0 83+0 92+0 10+1 11+1 12+1
3,0 69+0 79+0 92+0 10+1 12+1 13+1 15+1 17+1
3,1 78+0 10+1 11+1 13+1 16+1 16+1 21+1 23+1
3,2 10+1 13+1 14+1 17+1 19+1 22+1 25+1 27+1
3,3 16+1 13+1 13+1 15+1 15+1 16+1 17+1 17+1
3,4 17+1 97+0 87+0 86+0 83+0 80+0 78+0 76+0
3,5 12+1 65+0 59+0 57+0 54+0 52+0 51+0 50+0
3,6 87+0 54+0 52+0 51+0 51+0 51+0 51+0 52+0
3,7 73+0 53+0 55+0 56+0 57+0 59+0 62+0 65+0
3,8 67+0 57+0 62+0 65+0 69+0 74+0 80+0 86+0
3,9 66+0 64+0 73+0 80+0 87+0 11-1-1 96+0 10+1 11+1
4,0 68 j-О 76+0 89+0 10+1 12-|-1 14+1 16+1
4,1 76+0 97+0 11+1 13+1 15+1 17+1 19+1 22+1
4,2 10+1 12+1 14+1 16-1-1 19+1 21+1 234-1 26+1
4,3 15+1 13+1 13+1 15-1 1 15+1 16+1 17+1 17+1
4,4 17+1 97+0 88-|-0 89+0 85-1-0 83+0 81+0 80+0
7 Л. А. Вайнштейн и др.
194 гл. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Таблица 18 (продолжение)
Дп* Эффективное главное квантовое число п*
1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0
Переход р — р ; х = 2; параметр С
0,1 19—0 42-0 59+0 76+0 91+0 10+1 12+1 13+1
0,2 47—0 93+0 12-1-1 15+1 18+1 21 + 1 24+1 26+1
0,3 83+0 14+1 19+1 23+1 27+1 31+1 35+1 38+1
0,4 124-1 19+1 25-4-1 30+1 34+1 38+1 43+1 47+1
0,5 15+1 23+1 29+1 34+1 38-1-1 43+1 47+1 51+1
0,6 18+1 25+1 30+1 35+1 39+1 43+1 47+1 51 + 1
0,7 19+1 25+1 29+1 33+1 37+1 40+1 43+1 47+1
0,8 18+1 22+1 264-1 294-1 31+1 34+1 37+1 39 + 1
0,9 15+1 19+1 21+1 23+1 25+1 27+1 29+1 31+1
1,0 12+1 14+1 16+1 17+1 18+1 19+1 21+1 22+1
1,1 84+0 10+1 11+1 12+1 12+1 13+1 14+1 15+1
1,2 57+0 73+0 84+0 86+0 91+0 95+0 10+1 10+1
1,3 43-0 60+0 67+0 72+0 76+0 81+0 84+0 88+0
1,4 44-0 64+0 72+0 78+0 83+0 87+0 92+0 96+0
1,5 59+0 79+0 88+0 94+0 10+1 10+1 11+1 11+1
1,6 79+0 99+0 10+1 11+1 11+1 12+1 12-f-l 13+1
1,7 994 0 11+1 12+1 12+1 13+1 13+1 14+1 14+1
+8 11+1 12+1 12+1 12+1 13+1 13+1 144-1 14+1
1,9 10+1 11 + 1 11+1 11+1 12+1 12+1 12+1 13+1
2,0 96+0 97+0 10+1 10+1 10+1 10+1 10+1 11+1
2,1 70+0 78+0 80+0 82+0 83+0 84+0 86+0 87+0
2,2 52+0 62+0 63+0 65+0 65+0 66+0 67+0 68+0
2’3 40-0 52+0 55+0 56+0 57+0 57+0 58+0 59+0
2’4 39-0 534 0 56+0 58+0 59+0 49+0 60+0 61+0
2,5 50+0 64+0 66+0 67+0 68+0 69+0 70+0 71+0
2,6 67+0 76+0 80+0 80+0 81+0 81+0 82+0 83+0
2'7 84+0 91+0 91+0 91+0 91+0 90+0 91 + 0 91+0
2,8 96+0 98+0 97+0 95+0 94+0 94+0 94+0 94+0
2'9 98+0 954 0 94+0 91+0 90+0 89+0 89+0 89+0
3,0 90+0 84+0 83+0 81+0 80+0 79+0 78+0 78+0
3,1 66+0 70+0 69+0 68+0 67+0 66+0 65+0 65+0
3,2 58+0 57+0 56+0 56+0 55+0 54-1-0 53+0 53+0
3 3 39+0 49-0 49-0 49-0 48-0 48-0 47-0 47-0
34 38-0 50+0 5,0+0 50-1-0 49+0 49+0 48-0 48-0
3,5 47-0 58+0 58+0 57+0 56+0 56+0 55+0 55+0
3,6 63+0 71+0 694-0 68+0 66+0 65+0 64+0 63+0
3 7 79+0 83+0 80+0 77+0 75+0 73+0 72+0 71+0
38 92+0 89+0 85+0 81+0 79+0 76+0 75+0 74+0
39 95+0 87+0 84+0 79+0 77+0 74+0 72+0 71+0
4’о 87+0 78+0 76+0 72+0 69+U 67+0 65+0 64+0
4 1 64+0 664-O 63+0 61+0 59+0 57+0 55+0 54+0
4 9 49-0 54+0 53+0 51+0 49—0 48-0 46-0 45-0
39-0 47—0 47-0 45-0 44-0 42-0 41-0 40-0
4,4 37—0 48-0 47-0 46-0 45-0 43-0 42-0 41—0
§ 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
195
Таблица 18 (продолжение)
Дп* Эффективное главное квантовое число п?
1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0
Переход р — р\ х = 2; параметр ф
о,1 18+1 13+1 98+0 81+0 71-1-0 66+0 62+0 60+0
0,2 10+1 75+0 64+0 61+0 61+0 63+0 65+0 68+0
0,3 79+0 64+0 63+0 66+0 70+0 75+0 79+0 84+0
0,4 70+0 65 ]-0 70+0 76+0 83+0 89+0 97+0 10+1
0,5 68+0 71+0 79+0 88+0 98-Hi 10+1 11+1 12+1
0,6 70+0 79+0 91+0 10+1 11+1 12+1 14+1 15+1
0,7 75+0 91+0 10+1 12+1 13+1 15+1 17+1 19+1
0,8 84+0 10+1 124-1 14 + 1 16+1 19 + 1 22+1 24+1
0,9 96+0 12+1 14+1 17+1 20+1 23 + 1 27+1 30+1
1,0 11+1 14+1 17+1 20+1 24+1 27+1 32+1 35+1
1,1 14+1 16+1 18+1 21 + 1 24+1 26+1 29+1 32+1
1,2 16+1 14+1 14+1 15+1 16+1 17+1 17+1 17+1
1,3 12+1 87+0 84+0 83+0 82+0 80+0 79+0 78+0
1,4 72+0 51+0 49-0 48-0 47—0 47—0 47-0 48-0
1,5 49-0 42-0 43-0 43-0 45-0 47—0 49-0 52+0
1,6 46-0 47-0 49-0 53+0 57+0 61+0 66+0 72+0
1,7 51+0 58+0 63+0 69+0 77+0 85+0 94+0 10+1
1,8 61+0 72+0 80+0 91+0 10+1 11+1 13+1 14+1
1,9 73+0 90+0 10+1 11+1 13+1 15+1 17+1 19+1
2,0 90+0 10+1 12+1 14+1 16+1 18+1 21+1 23+1
2,1 11+1 12+1 14+1 16+1 18+1 20+1 22+1 24+1
2,2 13+1 12+1 12 + 1 13+1 14+1 15+1 I64-1 16+1
2,3 12+1 88+0 88+0 89+0 90+0 89+0 89+0 88+0
2,4 78+0 56+0 55+0 54+0 53+0 524-0 52 4-0 51+0
2,5 50+0 43-0 43-0 43-0 43—0 44-0 45-0 46—0
2,6 44-0 44-0 45-0 47—0 49-0 52+0 56+0 59+0
2,7 48-0 52+0 55 4-0 60+0 65+0 71+0 77+0 84+0
2,8 56+0 65+0 70+0 78+0 87+0 97+0 10+1 11+1
2,9 68+0 81+0 89+0 10+1 11+1 12+1 14+1 16+1
з,о 83+0 98+0 11+1 12+1 14+1 16+1 18+1 20+1
3,1 10+1 11+1 12+1 14+1 15+1 17+1 19+1 21+1
3,2 12+1 11+1 12+1 13+1 13+1 14+1 15+1 16+1
3,3 12+1 87+0 88 f0 90 ТО 91+0 91+0 92+0 91+0
3,4 79+0 58+0 57+0 56+0 55+о 55+0 54+0 54+0
3,5 51+0 44-0 43-0 43-0 43-0 44-0 44—0 45-0
3,6 44-0 43-0 44-0 45—0 47-0 49—0 52+0 55+0
3,7 47-0 50+0 52+0 56+0 60+0 65+0 70+0 76+0
3,8 54+0 62+0 66+0 734-0 81+0 89+0 98+0 10+1
3,9 66+0 77+0 84+0 95+0 10 +i 11+1 13+1 14+1
4,0 80+0 94+0 10+1 11+1 13+1 14+1 16+1 18+1
4,1 10+1 10+1 11+1 13-f-l 14+1 16+1 17+1 19+1
4,2 12+1 10+1 11+1 12+1 13+1 14+1 14+1 15+1
4,3 11+1 86—0 87+0 90+0 92+0 92-| 0 92+0 93+0
4,4 80+0 58+0 58+0 58+0 57+0 56+0 55+0 55+0
7*
196
ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Таблица 18 (продолжение)
Ьп* Эффективное главное квантовое число п*
1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0
Переход р — d; х=1; параметр С
0,1 0,2 0,3 0,4 0,5 24+1 58+1 104 2 15+2 20+2 37+1 80+1 134 2 17+2 224-2 47+1 98+1 15+2 194 2 23+2 57+1 11+1 16+2 21+2 24+2 65+1 12+2 18+2 23+2 264 2 734-1 15+2 19+2 24-1-2 274 2
0,6 224-2 23+2 244-2 25+2 26+2 264-2 27+2*
0,7 27+2 25+2 25+2 25+2 25+2* 25+2* 25+2*
0,8 30+2 25+2 24+2 22+2* 21+2* 21+2* 20+2*
0,9 30+2 23+2 20+2* 18+2* 17+2* 15+2* 14+2*
1,0 28+2 19+2 154-2* 13+2* 11+2* 99+1* 894-1*
1,1 344-2 23+2 14+2* 10+2* 79+1* 67+1* 61+1* 56+1*
1,2 31+2 16+2 86+1* 55+1* 39+1 26+1* 16+1* 15+1*
1,3 26+2 94+1* 40+1 17+1* 10+1* 91+0* 87+0 89+0
1,4 19+2 40+1 10+1* 83+0* 96+0* 114-1* 13+1* 14+1*
1,5 12+2 10+1 10+1* 16+1* 20+1* 23+1* 25+1* 27+1*
1,6 50+1* 14+1* 25+1* 34+1* 374-1 40+1 41+1 43+1*
1,7 99+0 38+1* 49+1 55+1 55+1 56+1 55+1* 55+1*
1,8 76+0* 73+1* 73+1 74+1 68+1 66+1* 62+1* 61+1*
1,9 31+1 11+2 89+1 82+1 714-1* 66+1* 59+1* 55+1*
2,0 68+1 13+2 93+1 78+1 63+1* 55+1* 47+1* 42+1*
2,1 13+2 13+2 86+1* 63+1 48+1* 39+1* 33+1* 30+1*
2,2 16+2 11 + 2 64+1* 414-1 29+1* 22+1 16+1* 12+1*
2,3 16+2 80+1* 37+1* 19+1 10+1* 76+0* 62+0* 56+0*
2,4 14+2 44+1* 13+1* 67+0* 57+0 58+0* 62+0* 66+0*
2,5 10+2 14+1 65+0* 79+0* 944-0* 10+1* 11+1* 12+1*
2,6 58+1 79+0* 12+1* 18+1* 20+1* 20+1* 20+1* 21+1*
2,7 20+1* 19+1* 27+1 31+1 30+1 31+1 30+1* 30+1*
2,8 41-0 43+1 45-|-1 46+1 41+1 39+1* 37+1* 35+1*
2,9 13+1* 74+1 61+1 56+1 47+1* 43+1* 38+1* 35+1*
3,0 39+1 10+2 69+1 57+1* 45+1* 39+1* 33+1* 29+1*
3,1 94+1 10+2 69+1 49+1* 37+1* 30+1* 25+1* 22+1*
3,2 12+2 98-1 55+1* 35+1* 24+1 19+1 14+1 10+1*
3,3 13+2 74+1 35+1* 18+1 10+1* 71+0* 54+0 46+0*
3,4 12+2 45+1 15+1 65+0* 48-0 45-0* 44-0* 45-0*
3,5 10+2 18+1 57+0 59+0* 66+0* 73+0* 78+0* 82+0*
3,6 61+1 70+0 92+0* 12+1* 13+1* 14+1* 14+1* 14+1*
3,7 24+1* 13+1* 20+1* 24+0 22+1 22+1 214-1* 21+1*
3,8 47-0 33+1 36+1 36+1 31+1 30+1 27+1 26+1*
3,9 88+0* 61+1 50+1 46+1 37+1* 34+1* 29+1* 27+1*
4,0 28+1 89+1 59+1 484-1 374 1* 32+1* 27+1* 23+1*
4,1 77+1 97+1 62+1 43+1* 32+1* 25+1* 21+1* 18+1*
4,2 18+2 91+1 51+1* 31+1* 22+1* 174-1* 12+1 99+0*
4,3 12+2 71+1 34+1* 18+1 10+1 68+0* 50+0* 41-0*
4,4 11+2 45+1 15+1 64+0* 45—0 39-0 37-0* 37-0*
§ 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
197
Таблица 18 (п родолжение)
Эффективное главное квантовое число п0*
Дп* 1,5 2,0 2,5 з,о 3,5 4,0 4,5 5,о
0,1 Иерел •мд р — d 13+1 'll + параметп 15+1 Р <Р (316+1 17+1 18+1
0,2 0,3 0,4 0,5 0,6 24+1 16+1 204-1 24+1 28+1 33+1 19+1 24+1 29+1 35+1 41 | 1 21+1 27+1 34+1 414-1 50-1 1 ’23+1 30+1 38+1 48+1 59+1 25+1 34+1 43+1 55+1 684-1 27+1 37+1 48+1 62+1 78+1*
0,7 28+1 39+1 50+1 52+1 73+1* 86+1* 98+1*
0,8 32+1 464-1 60+1 76+1* 92+1* 10+2* 12+2*
0,9 36+1 56+1 74+1* 96+1* 11+2* 12+2* 13+2*
1,0 42+1 69+1 94+1* 11+2* 13+2* 15+2* 16+2*
1,1 28+1 52+1 87+1* 11+2* 14+2* 17+2* 20+2* 22+2*
1,2 32+1 66+1 11+2* 14+2* 14+2 93+1* 54+1* 35+1*
1,3 37+1 88+1* 12+2 49+1* 16+1* 70+0* 35-0 22—0
1,4 43+1 98+1 15+1* 12-0* 10—0* 10—0* 22-0* 36—0*
1,5 54+1 10+1 10-0* 24-0* 52+0* 81+0* 11+1* 14+1*
1,6 83+1* 10-0* 56+0* 10+1* 15+1 19+1 24+1 28+1*
1,7 57+1 67+0* 14+1 20+1 27+1 33+1 40+1* 47+1*
1,8 10-0* 14+1 23+1 31+1 41+1 52+1* 61+1* 70+1*
1,9 85+0 21+1 33+1 45+1 59+1* 72+1* 85+1* 96+1*
2,0 15+1 29+1 46+1 62+1 81+1* 97+1* 11+2* 12+2*
2,1 21+1 38+1 61+1* 85+1 10+2* 12+2* 14+2* 16+2*
2,2 26+1 50+1 83+1* 11+2 13+2* 12+2 92+1* 63+1*
2,3 32+1 68+1* 10+2* 91+1 42+i* 20+1* 11+1* 67+0*
2,4 39+1 88+1* 47+1* 90+0* 21—0 10—0* 10-0* Ю-0*
2,5 49+1 40+1 11—0* 10-0* 14-0* 33-0* 53+0* 73+0*
2,6 69+1 10-0* 17-0* 55+0* 87+0* 12+1* 15+1* 19+1*
2,7 96+1* 25-0* 90+0 14+1 19+1 24+1 29+1* 35+1*
2,8 28—0 98+0 17+1 24+1 31+1 39+1* 47+1* 56+1*
2,9 34-0* 17+1 27+1 37+1 48+1* 50+1* 70+1* 80+1*
3,0 11+1 25+1 39+1 52+1* 68+1* 82+1* 95+1* 10+2*
3,1 18+1 34+1 53+1 73+1* 92+1* 10+2* 12+2* 14+2*
3,2 24+1 45+1 73+1* 98+1* 11+2* 12+2 10+2 79+1*
3,3 30+1 61+1 95+1* 98+1 57+1* 30+1* 16+1* 10+1*
3,4 37+1 81+1 64+1 15+1* 48-0 15-0* 10-0* 10—0*
3,5 46+1 58+1 35-0 10-0* 10-0* 17-0* 32-0* 49—0*
3,6 65+1 25-0 10-0* 36-0* 63+0* 92+0* 12+1* 15+1*
3,7 93+1* 10-0* 69+0* 11+1 15+1 20+1 24+1* 29+1*
3,8 12+1 78+0 15+1 21+1 27+1 34+1 41+1* 48+1*
3,9 13-0* 15+1 24+1 33+1 42+1* 52+1* 62+1* 71+1*
4,0 94+0 23+1 36+1 48+1 62+1* 75+1* 874-1* 96+1*
4,1 17+1 32+1 49+1 67+1* 85+1* 10+2* И+2* 12+2*
4,2 23+1 43+1 68+1* 91+1* Ю+2* 11+2* 10+2 87+1*
4,3 29+1 58+1 90+1* 98+1 66+1 36+1* 21+1* 13+1*
4,4 36+1 77+1 71+1 20+1* 68+0 25-0 10-0* 10-0*
198
ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Таблица 18 (продолжение)
Эффективное главное квантовое число п*
Дп* 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0
Переход р — d‘, х = 3; параметр С
0,1 0,2 0,3 0,4 0,5 0,6 95+0 10-0 26-0 47—0 73+0 10+1 12+1 16-0 38—0 64+0 93+0 11+1 14+1 22—0 48—0 78+0 10+1 13+1 15+1 27—0 57+0 91+0 12+1 15+1 16+1 31-0 66+0 10+1 13+1 16+1 17+1 35-0 74+0 11+1 14+1 17+1 18+1
0,7 12+1 14+1 15+1 16+1 17+1 18+1 18+1
0,8 14+1 15+1 15+1 15+1 16+1 16+1 17+1
0,9 15+1 14+1 14+1 14+1 14+1 14+1 15+1
1,0 15+1 13+1 12+1 12+1 12+1 12+1 12+1
1,1 134-1 13+1 11+1 10+1 98+0 97+0 97+0 98+0
1,2 12-|-1 10+1 88+0 79+0 76+0 75+0 75+0 76+0
1,3 11+1 82-j-O 66+0 60+0 59+0 59+0 бо+о 62+0
1,4 90+0 58+0 50+0 49-0 50+0 51+0 53+0 55+0
1,5 63+0 42-0 44-0 46—0 49—0 51+0 54+0 57+0
1,6 37-0 36-0 46—0 50+0 54+0 57+0 59+0 62+0
1,7 20-0 41—0 54+0 59+0 61+0 64-j-0 66+0 68+0
1,8 15-0 54+0 65+0 68+0 68+0 70+0 70+0 72+0
1,9 21-0 70+0 74+0 73+0 72+0 71+0 71+0 72+0
2,0 34-0 84+0 79+0 73+0 70+0 69+0 68+0 67+0
2,1 59+0 88+0 77+0 68+0 64+0 62+0 61+0 60+0
2,2 71+0 83+0 68+0 60+0 56+0 54+0 52+0 52+0
2,3 76+0 71+0 57+0 50+0 47-0 46-0 45—0 45—0
2,4 71+0 56+0 46-0 42-0 41—0 41-0 40-0 41-0
2,5 60+0 42-0 40—и 39-0 39-0 40-0 39-0 41-0
2,6 40-0 35-0 39-0 40-0 41-0 42-0 42-0 44-0
2,7 24-0 35-0 43-0 45-0 45-0 46-0 46-0 47-0
2,8 16-0 43-0 51+0 52+0 51+0 51+0 49—0 50+0
2,9 16-0 56+0 59+0 57+0 54+0 53+0 51+0 52+0
3,0 24-0 70+0 65+0 59+0 55+0 53+0 51+0 504-0
3,1 44-0 75+0 66+0 57+0 53+0 50+0 48-0 46-0
3,2 57+0 74+0 61+0 52+0 47-0 45-0 42-0 42-0
3,3 64+0 66+0 52+0 45+0 41-0 40-0 38-0 38—0
3,4 65+0 54+0 44-0 39-0 37—0 36-0 34-0 33-0
3,5 57+0 42—0 38-0 35-0 34-0 35-0 33-0 34-0
3,6 41—0 34-0 36-0 36-0 35-0 36-0 33—0 37-0
3,7 26-0 33-0 39-0 40-0 39-0 39-0 38-0 40-0
3,8 17-0 38-0 46-0 45—0 43-0 44-0 41—0 40-0
з]э 15-0 50+0 53+0 50+0 47—0 46-0 41-0 43-0
4,0 20-0 63+0 59+0 52+0 48-0 46—0 43—0 43-0
4,1 38-0 70+0 61+0 51+0 47—0 44-0 41—0 39-0
4,2 50+0 70+0 57+0 47-0 43—0 41-0 37-0 37-0
4,3 59+0 64+0 50+0 42-0 38-0 36-0 33-0 33-0
4,4 61+0 54+0 42-0 37-0 34—0 34-0 30-0 28-0
§ 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
199
Таблица 18 (л родолжение)
Ап* Эффективное главное квантовое число п*
1.5 2,0 2,5 3,0 3,5 4,0 4.5 5,0
Переход р — <7; х = 3; параметр ф
0,1 35+1 23+1 17+1 13+1 11+1 92+0
0,2 13+1 90+0 68+0 57+0 51+0 47-0
0,3 81+0 58+0 49-0 45-0 44-0 44-0
0,4 60+0 48-0 45-0 45—0 45-0 46-0
0,5 51+0 45-0 45-0 46-0 48-0 49-0
0,6 64+0 47—0 45-0 47—0 49-0 51+0 53+0
0,7 56+0 46-0 47—0 49-0 52+0 55+0 58+0
0,8 51+0 46-0 49-0 52+0 56+0 60+0 64+0
0,9 49-0 48-0 52+0 56+0 61+0 67+0 73+0
1,0 48-0 51+0 5б-|-0 62+0 68+0 76+0 84+0
1,1 62+0 48-0 55+0 61+0 68+0 77+0 86+0 94+0 95+0
1,2 56+0 51+0 60+0 67+0 75+0 84+0 10+1
1,3 53+0 57+0 66+0 71+0 79+0 86+0 92+0 98 j-0
1,4 51+0 67+0 69+0 70+0 73+0 75+0 77+0 78+0
1,5 51+0 78+0 63+0 60+0 60+0 60+0 59+0 57+0
1,6 56+0 78+0 53+0 50+0 49-0 48-0 47-0 46-0
1,7 76+0 63+0 45-0 44-0 43-0 43—0 42-0 42—0
1,8 10+1 51+0 42-0 42-0 42-0 42—0 43-0 44-0
1,9 89+(. 45—0 42-0 42—0 43-0 45-0 46-0 49-0
2,0 67+0 43—0 43-0 45-0 47-0 49-0 53+0 56+0
2,1 60+0 43-0 46-0 48-0 52-1-0 56+0 61+0 66+0
2,2 53+0 45—0 49-0 53+0 58+0 64+0 70+0 77+0
2,3 49—0 49—0 54+0 58+0 65+0 70+0 77+0 85+0
2,4 48—0 56+0 58+0 62+0 67+0 71+0 75+0 78+0
2,5 48-0 65+0 59+0 60+0 62+0 63+0 64+0 65+0
2,6 51+0 70+0 54+0 54+0 54+0 53+0 54+0 54+0
2,7 63+0 64+0 48-0 47-0 47-0 46-0 45-0 43-0
2,8 86+0 53+0 43-0 43-0 43-0 42-0 42—0 42—0
2,9 90+0 45—0 42-0 42-0 42-0 42-0 43-0 44-0
3,0 70+0 42—0 42-0 43-0 44-0 45-0 48-0 49—0
3,1 60+0 42—0 44-0 45-0 47-0 50+0 53+0 59+0
3,2 52+0 44—0 47+0 49-0 53+0 57+0 62+0 68+0
3,3 48—0 47—0 50+0 54+0 59+0 64+0 69+0 86+0
3,4 46-0 53+0 55+0 58+0 63+0 67+0 69+0 77+0
3,5 47-0 60+0 56+0 59+0 62+0 62-+0 59+0 77+0
3,6 49-0 66+0 54+0 55+0 55+0 52+0 48-0 73+0
3,7 59+0 63+0 53+0 46 0 49—0 48-0 48-0 46—0 48—0 56+0
3,8 78+0 44-0 44-0 44-0 43-0 44-0 39-0
3,9 88+0 42-0 42-0 42-0 43-0 40-0 37-0
4,0 71+0 42—0 42—0 42-0 43—0 45-0 44-0 46-0
4,1 60+0 42 0 43-0 44-0 46-0 48-0 50+0 47—0
4,2 52+0 48 0 45-0 48-0 51+0 55+0 59+0 60+0
4,3 48-0 46 0 49-0 52+0 56+0 57+0 61+0 67+0 63+0
4,4 46-0 51+0 53+0 61+0 64+0 71+0 68+0
200
ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Таблица 18 (продолжение)
Дп* Эффективное главное квантовое число п* 0
2,5 3,0 3,5 4,0 4,5 5,0
Переход d — s', параметр С
0,1 17-0 33+0 48-0 62+0 76+0 89+0
0,2 31—0 60+0 88+0 11+1 14+1 16+1
0,3 41—0 79+0 11+1 15+1 18+1 21+1
0,4 45-0 88+0 12+1 16+1 20+1 24+1
0,5 45—0 87+0 12+1 16+1 20+1 24+1
0,6 41-0 79+0 11+1 15+1 18+1 22+1
0,7 34—0 66+0 97+0 12+1 15+1 18+1
0,8 27-0 52+0 76+0 99+0 12+1 14+1
0,9 21—0 40—0 57+0 74+0 90+0 Ю+1
1,0 30—0* 31—0 13+1* 55+0 16+1* 76+0
1,1 16-0 26—0 36—0 44-0 51+0 58+0
1,2 16—0 26-0 34—0 41—0 47-0 52+0
1,3 17-0 28-0 36—0 43-0 49-0 54+0
1,4 19-0 31-0 40-0 48-0 54+0 60+0
1,5 19—0 33—0 43—0 51+0 59+0 66+0
1,6 19-0 33-0 43-0 52+0 60+0 67+0
1,7 18—0 31—0 41—0 50+0 57+0 65+0
1,8 16—0 28—0 37—0 44-0 51+0 58-0
1,9 14-0 24—0 32—0 38-0 44-0 49—0
2,0 25-0* 21-0 33—0* 33-0 44-0* 41—0
2,1 13-0 20-0 25-0 29-0 33—0 36—0
2,2 13—0 20—0 25-0 29-0 31—0 34—0
2,3 14-0 22—0 26-0 30-0 33—0 35—0
2,4 15-0 23-0 29—0 33-0 36-0 38—0
2,5 16—0 24-0 31—0 35-0 39-0 42—0
2,6 16-0 25—0 31-0 36-0 40-0 43—0
2,7 15-0 24-0 30-0 35-0 39-0 42—0
2,8 14-0 22—0 28-0 32-0 36-0 39-0
2,9 13-0 20-0 25-0 29-0 32—0 35—0
3,0 14-0* 18-0 23-0 26—0 29-0 30-0
3,1 12—0 18-0 21-0 24-0 26-0 27—0
3,2 12-0 18—0 21-0 24-0 26—0 27—0
3,3 13—0 19—0 23-0 25-0 27-0 28-0
3,4 14-0 20—0 24—0 27-0 29-0 30-0
3,5 14-0 21—0 26-0 29-0 31-0 32-0
3,6 14-0 21-0 26-0 29-0 32-0 34-0
3,7 14-0 21—0 26—0 29-0 31-0 33-0
3,8 13-0 20-0 24—0 27-0 29-0 31-0
3,9 12-0 18—0 22—0 24-0 26-0 28-0
4,0 13-0* 17—0 21—0 22—0 25-0 25-0
4,1 11-0 16—0 19-0 21-0 22-0 23-0
4,2 12-0 17—0 19-0 21—0 22—0 23-0
4,3 12—0 18—0 20-0 22—0 23—0 24-0
4,4 13-0 19—0 22-0 24-0 25-0 26-0
§ 1R. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
201
Таблица 18 (п родолжепие)
Эффективное главное квантовое число п*
&п* 2,5 3,0 3,5 4,0 4,5 5,0
Переход d — $; параметр <р
0,1 764-0 68+0 63+0 61+0 59+0 59+0
0,2 634-0 62+0 63+0 66+0 68+0 714-0
0,3 704-0 724-0 75+0 79-1-0 84+0 88+0
0,4 804-0 84+0 89+0 95+0 10+1 10+1
0,5 924-0 98+0 10+1 11+1 12+1 13+1
0,6 104-1 11+1 12+1 13+1 14+1 16+1
0,7 114-1 13+1 14+1 16+1 17+1 19+1
0,8 124-1 14-|-1 16+1 18+1 20+1 23+1
0,9 134-1 14+1 17+1 19+1 22+1 25+1
1,0 10-0* 12+1 93+1* 17+1 87+1* 22+1
1,1 814-0 90+0 10+1 11+1 13+1 75+0 15+1
1,2 614-0 59+0 63+1 69+0 81+0
1,3 524-0 47-0 47-0 48—0 49—0 51+0
1,4 53+0 47—0 47—0 48-0 48-0 49-0
1,5 59+0 56+0 57+0 59+0 61+0 63+0
1,6 68+0 69+0 73+0 77+0 82+0 86+0
1,7 79+0 84+0 91+0 99+0 12+1 10+1 11+1
1,8 92+0 96+0 10+1 13+1 14-J-1
1,9 10 |-1 10+1 11+1 13+1 14+1 16+1
2,0 58+1* 92+0 22+1* 12+1 24+1* 15+1
2,1 71+0 73-40 82+0 93+0 10+1 11+1
2,2 59+0 55+0 59+0 64+0 68+0 734-0
2,3 52+0 46-0 47-0 48—0 49-0 51+0
2,4 51+0 46-0 46-0 46—0 47—0 47—0
2,5 54+0 52+0 53+0 54+0 55+0 57+0
2,6 62+0 62+0 65-0 68—0 71+0 754-0
2,7 72+0 74+0 80+0 86+0 92+0 98 4-0
2,8 85+0 85+0 95+0 10+1 11+1 12+1
2,9 97+0 89+0 10+1 11+1 12+1 13+1
3,0 21+1* 82+0 12+1 10+1 144-1 13+1
3,1 68+0 68+0 75+0 84+0 92+0 10+1
3,2 58+0 53+0 57+0 61+0 65+0 69+0
3,3 51+0 46-0 46-0 48-0 49-0 50+0
3,4 50+0 45-0 45-0 46-0 46-0 47-0
3,5 53+0 50+0 514-0 52+0 53+0 54+0
3,6 60+0 60+0 62+0 65+0 67+0 70+0 914-0
3,7 70+0 71+0 76+0 814-0 86+0
3,8 82+0 80+0 89+0 96+0 10+1 11+1
3,9 964-0 84+0 96+0 10+1 11+1 12+1
4,0 25+1* 78+0 11+1 98+0 794-0 13+1 И4-1
4,1 66+0 65+0 72+0 87+0 95+0
4,2 57+0 52+0 56+0 59+0 63+0 67+0
4,3 51+0 45-0 46-0 47-0 49-0 50 +0
4,4 49-0 45-0 45-0 45-0 46-0 46 — 0
202
ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Таблица 18 {продолжение)
Дп* Эффективное главное квантовое число п*
2,5 3,0 3,5 4,0 4,5 5,0
Переход d — р\ х — 1; параметр С
0,1 0,2 0,3 0,4 0,5 16+1 25-1-1 304-1 31+1 27+1 27+1 44+1 54+1 57+1 53+1 37+1 62+1 75+1 79+1 74+1 46+1 76+1 944-1 99+1 93+1 55+1 90+1 11+2 11+2 11+2 62+1 10+2 12+1 13+2 12+2*
0,6 22+1 44+1 62+1 78+1* 93+1* 10+2*
0,7 13+1 33+1 46+1* 59+1* 69+1* 79+1*
0,8 87+0 21+1 29+1* 38+1* 46+1* 53+1*
0,9 44—0 10+1 14+1 19+1 22+1 26+1*
1,0 30—0 45-0* 59+0 74+0 85+0* 97+0*
1,1 27—0* 34-0* 43-0 49-0 55+0 60+0
1,2 37-0* 47-0* 60+0 66+0* 73+0* 78+0*
1,3 58+0 73+0 92+0 10+1* 11+1* 12+1*
1,4 59+0 98+0 12+1 14+1 16+1 17+1*
1,5 61+0 11+1 14+1 17+1 19+1* 21+1*
1,6 56+0 11+1 14+1 17+1* 20+1* 22+1*
1,7 43-0 99+0 12+1 15+1* 18+1* 20+1*
1,8 31-0 72+0 92+0 11+1 13+1 15+1*
1,9 24—0 43-0 53+0 68+0 77+0 88+0*
2,0 24-0 26-0 32-0 37-0* 41-0* 45-0*
2,1 21-0* 23-0* 28-0* 30-0* 32-0* 34-0*
2,2 27-0* 31-0* 37-0* 39—0* 42-0* 43-0*
2,3 34-0* 45-0* 54+0* 59+0* 63+0* 65+0*
2,4 39—0* 60+0 73+0 81+0 87+0 92+0*
2,5 39-0 70+0 86+0 98+0 10+1 11+1*
2,6 35-0 72+0 88+0 10+1 11+1* 12+1*
2,7 28-0 63+0 77+0 94+0 10+1* 11+1*
2,8 22-0 48-0 57+0 73+0 79+0 89+0*
2,9 20—0 31-0 36-0 45-0 48-0 54+0*
3,0 23-0 20-0 24-0 27-0 29—0 31—0*
3,1 19-0 19—0* 22-0* 23-0 24—0* 25-0*
3,2 24-0 25-0* 29-0* 30-0* 31-0* 31-0*
3,3 29-0 36-0* 42—0* 44-0* 46-0* 47-0*
3.4 32—0 47-0 56+0* 60+0* 63+0 65+0*
3,5 31-0 55+0 65+0 73+0* 77+0 81+0*
3,6 28-0 57+0 67+0 78+0 87+0 87+0*
3,7 23—0 50+0 59+0 71+0 76+0 82+0*
3,8 19+0* 38-0 44-0 55+0 59+0 65+0*
3,9 19—0* 26-0 29-0 35-0 37-0 40-0*
4,0 24—0* 18-0 21-0 22-0 23-0 24-0*
4,1 18-0* 17—0* 20-0* 20-0* 21-0 21-0*
4,2 23—0* 22-0* 26-0* 26-0* 26-0* 26-0*
4,3 27—0 31-0* 36-0* 37-0* 38-0* 38-0*
4,4 29-0 41-0 48-0 51+0* 52+0 53+0*
§ 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
203
Таблица 18 (продолжение)
Ап* Эффективное главное квантовое число п*
2,5 3,0 3,5 4,0 4,5 5,0
Переход d — р', х = 1; параметр Ф
0,1 13-j-l 14+1 15+1 16+1 17+1 19+1
0,2 184-1 20+1 23+1 25+1 27+1 29+1
0,3 244-1 27+1 31+1 34+1 37+1 41+1
0,4 314-1 36+1 41+1 46+1 51+1 56+1
0,5 404-1 46+1 53+1 61+1 68+1 75+1*
0,6 504-1 60+1 70+1 80+1* 90+1* 10+2*
0,7 564-1 76+1 904-1* 10+2* И+2* 12+2*
0,8 434-1 85+1 10+2* 12+2* 14+2* 15+2*
0,9 14+1 55+1 64+1 88+1 10+2 11+2*
1,0 13-0 12+1* 12+1 18+1 19+1* 23+1*
1,1 10-0» 10—0* 10-0 11—0 15-0 21—0
1,2 15—0* 10—0* 11-0 12—0* 15-0* 17—0*
1,3 61+0* 61+0* 68+0 74+0* 80+0* 87+0*
1,4 11+1 13+1 15+1 16+1 18+1 20+1*
1,5 18+1 22+1 26+1 29+1 32+1* 36+1*
1,6 22+1 33+1 39+1 45+1* 51+1* 56+1*
1,7 28+1 44+1 52+1 62+1* 70+1* 79+1*
1,8 11+1 45+1 53+1 70+1 80+1 94+1*
1,9 25—0 26+1 27+1 42+1 46+1 56+1*
2,0 10-0 67+0 61+0 10+1* 11+1* 14+1*
2,1 10-0* 10-0* 10-0* 10-0* 10—0* 13—0* .
2,2 13-0* 10—0* 10-0* 10-0* 10—0* 10-0*
2,3 48-0* 46-0* 51+0* 54+0* 59+0* 64+0*
2,4 92+0* 10+1 12+1 13+1 14+1 15+1*
2,5 13+1 18+1 21+1 24+1 26+1 29+1*
2,6 15+1 27+1 32+1 37+1 41+1* 46+1*
2,7 12+1 35+1 41+1 50+1 57+1* 65+1*
2,8 52+0 34+1 38+1 54+1 61+1 72+1*
2,9 10-0 19+1 19+1 31+1 33+1 41+1*
3,0 10—0 51+0 41—0 83+0 83+0 11+1*
3,1 10-0 10-0* 10—0* 10-0 10—0* 10—0*
3,2 14-0 10-0* 10—0* 10-0* 10-0* 10—0*
з,з 43—0 40-0* 45-0* 48—0* 52+0* 56+0*
3,4 83+0 96+0 10+1* 11+1* 13+1 14+1*
3,5 11+1 16+1 19+1 21+1* 23+1 26+1*
3,6 12+1 24+1 28+1 33+1 37+1 41+1*
3,7 87+0 31+1 36+1 45+1 50+1 58+1*
3,8 30-0* 29+1 32+1 46+1 51+1 62+1*
3,9 10—0* 16+1 15+1 26+1 27+1 35+1*
4,0 10—0* 43-0 31-0 72+0 694-0 96+0*
4,1 10—0* 10-0* 10—0* 10-0* 10-0 10—0*
4,2 14—0* 10—0* 10-0* 10-0* 10—0* 10-0*
4,3 44—0 37—0* 42-0* 44-0* 48—0* 51+0*
4,4 78+0 90+0 10+1 11+1* 12+1 13+1*
204
ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Таблица 18 (продолжение)
Дп* Эффективное главное квантовое число п*
2,5 3,0 3,5 4,0 4,5 5,0
Переход d — р\ х = 3; параметр С
0,1 74-1' 13-0 18-0 23-0 27-0 32-0
0,2 13-0 24-0 34-0 48-0 51+0 59+0
0,3 18-0 33-0 46-0 59+0 70+0 82+0
0,4 22—0 39-0 55+0 70+0 83+0 96+0
0,5 23-0 42-0 59+0 74+0 88+0 10+1
0,6 23-0 42-0 58+0 72+0 86+0 99+0
0,7 22—0 39-0 53+0 66+0 78+0 90+0
0,8 20-0 34-0 46-0 57+0 68+0 77+0
0,9 17—0 29-0 39-0 48-0 56+0 64+0
1,0 15-0 25-0 33-0 40-0 46-0 52+0
1,1 13-0 22-0 28-0 34-0 39-0 44-0
1,2 13-0 20-0 26—0 31-0 35-0 39-0
1,3 13-0 20-0 26—0 30-0 34—0 38—0
1,4 13—0 21—0 27-0 31—0 35-0 39-0
1,5 14-0 22—0 28-0 33-0 37—0 40-0
1,6 15-0 23-0 29-0 34-0 37-0 41—0
1,7 15-0 23-0 27-0 33-0 37-0 41-0
1,8 14-0 22-0 27-0 32-0 36-0 39—0
1,9 14-0 20-0 25-0 29-0 33-0 36—0
2,0 13-0 19-0 23-0 27—0 30-0 32—0
2,1 12-0 18-0 22—0 25-0 27-0 29-0
2,2 12-0 17—0 21—0 24-0 26-0 28—0
2,3 12—0 17-0 21—0 24—0 26—0 28—0
2,4 12-0 18-0 21—0 24—0 26-0 28-0
2,5 12-0 19—0 22-0 25—0 27-0 29-0
2,6 13-0 19—0 23-0 26-0 28-0 29-0
2,7 13-0 19-0 23-0 26—0 28-0 29-0
2,8 13-0 19—0 22-0 25-0 27-0 29-0
2,9 13-0 18-0 21—0 24-0 26-0 27-0
3,0 12-0 17-0 20-0 23—0 24-0 24-0
3,1 11-0 16-0 19-0 21-0 22-0 23-0
3,2 11-0 16-0 19-0 21-0 21-0 23-0
3,3 11-0 16—0 18-0 21—0 21-0 23-0
3,4 12—0 16—0 19-0 22-0 22-0 23-0
3,5 12-0 17—0 20-0 22-0 23-0 24-0
3,6 12—0 17—0 20—0 23-0 23-0 24-0
3,7 12—0 17-0 20—0 23—0 24-0 25—0
3,8 12-0 17-0 20-0 23-0 24-0 23-0
3,9 12-0 16—0 19-0 21—0 22-0 24-0
4,0 12-0 16-0 18-0 20-0 22-0 22-0
4,1 11-0 15-0 18-0 20-0 21-0 20-0
4,2 11-0 15—0 17-0 20—0 20—0 19—0
4,3 11-0 15-0 17-0 20-0 19—0 18-0
4,4 11-0 16-0 17-0 20-0 20-0 18-0
§ 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
205
Таблица 18 (продолжение)
in* Эффективное главное квантовое число п*
2,5 3,0 3,5 4,0 4,5 5,0
Переход d — р; х = 3; параметр
0,1 33+0 22+0 16+0 12+0 10+1 89+0
0,2 11+1 81+1 63+1 54+1 49-0 46-0
о,з 67+0 52+0 46-0 45-0 44-0 45-0
0,4 52+0 47-0 46-0 46-0 47-0 47-0
0,5 51+0 49-0 48-0 49-0 49-0 51+0
0,6 57+0 53+0 52+0 52+0 53+0 55+0
0,7 66+0 58+0 55+0 55+0 58+0 61+0
0,8 76+0 60+0 58+0 60+0 64+0 69+0
0,9 80+0 62+0 61+0 65+0 71+0 77+0
1,0 77+0 61+0 63+0 69+0 76+0 83+0
1,1 68+0 59+0 62+0 68+0 75+0 82+0
1,2 58+0 56+0 58+0 62+0 67+0 72+0
1,3 53+0 52+0 52+0 54+0 57+0 59+0
1,4 53+0 50+0 47-0 47-0 48-0 48-0
1,5 57+0 48—0 44-0 43-0 43-0 43—0
1,6 62+0 47-0 42—0 42-0 42—0 43-0
1,7 66+0 47-0 43—0 43-0 44-0 44-0
1,8 68+0 47-0 45-0 47-0 48—0 51+0
1,9 66+0 48-0 48-0 51+0 54+0 57+0
2,0 61+0 49—0 51+0 55+0 59+0 61+0
2,1 55+0 51+0 53+0 57+0 61+0 63+0
2,2 52+0 52+0 53+0 56+0 59+0 64+0
2,3 52~|-0 51+0 50+0 52+0 55+0 60+0
2,4 54-j-O 50+0 47-0 48-0 49-0 51+0
2,5 59+0 48-0 43-0 43-0 44-0 45-0
2,6 63+0 46—0 42—0 42—0 43-0 42-0
2,7 66+0 45-0 42-0 43-0 42-0 43-0
2,8 65+0 44-0 44-0 45-0 46-0 48-0
2,9 62+0 45-0 46-0 47-0 51+0 49-0
3,0 57+0 47-0 49-0 51+0 53+0 52+0
3,1 52+0 49-0 51+0 53+0 54+0 57+0
3,2 50+0 51+0 51+0 53+0 54+0 62+0
з,з 51+0 50+0 49-0 50+0 53+0 71+0
3,4 55+0 49-0 46-0 48-0 48-0 54+0
3,5 60+0 47-0 44-0 44-0 41-0 53+0
3,6 64+0 45-0 42-0 41-0 38—0 52+0
3,7 65+0 44-0 42-0 42-0 45-0 50+0
3,8 64+0 43-0 43—0 44-0 45-0 44—0
3,9 60+0 44-0 45-0 47-0 48-0 53+0
4,0 55+0 46—0 48-0 50+0 54+0 60+0
4,1 50+0 48—0 50+0 54+0 59+0 54+0
4,2 49-0 50+0 50+0 55+0 58+0 39-0
4,3 51+0 50+0 50+0 53+0 53+0 41-0
4,4 55+0 49-0 47-0 47-0 52+0 41-0
206
ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Таблица 19
Скорость возбуждения нейтральных атомов <гг>; переходы без
изменения спина (Дб1 — 0). Параметры А и % (метод Борна)
Дп* Эффективное главное квантовое число
0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0
Переход s — s 1); параметр А
0,6 0,7 0,8 0,9 1,0 10+2 12 |-2 12+2 10+2 80+1 10+2 11+2 10+2 80+1 51+1 11+2 11-| 2 10+2 72+1 41+1 13+2 12+2 94+1 62+1 32+1 13+2 11+2 88+1 54+1 26+1 14+2 1142 81+1 47+1 22+1 14+2 11+2 75+1 42+1 18+1 14+2 10+2 70+1 37+1 16+1 144-2 104-2 65+1 34+1 14+1 14+2 10+2 61+1 31+1 12+1
1,1 29+1 23+1 17+1 12+1 10+1 83+0 70+0 61+0 54+0 49-0
1,2 67+0 65+0 54+0 50+0 49-0 504-0 51+0 53+0 54+0 55-+0
1,3 21-0 32-0 54+0 80+0 10+1 12+1 144-1 15+1 16+0 17+1
1,4 11+1 11+1 17+1 23+1 28+1 32+1 35+1 36+1 36+1 36+1
1,5 35+1 29+1 37+1 44+1 48+1 49+1 49+1 47+1 45+1 43+1
1,6 64+1 52+1 57+1 60+1 59+1 55+1 51+1 47+1 44+1 40+1
1,7 91+1 69+1 68+1 64+1 57+1 51+1 45+1 40+1 36+1 33+1
1,8 10+2 74+1 66+1 56+1 47+1 394 1 34+1 2941 25+1 23+1
1,9 10+2 65+1 53+1 41+1 32+1 25+1 21+1 17+1 15+1 13+1
2,0 85+1 45+1 34+1 23+1 17+1 13+1 10+1 88+0 74+0 63+0
2,1 30+1 22+1 15+1 10+1 78+0 60+0 48-0 40-0 34-0 29-0
2,2 80+0 74+0 56+0 46-0 41-0 38-0 35-0 33-0 32—0 30—0
2,3 19-0 30-0 45-0 60+0 70+0 77+0 804 0 82+0 82+0 81—0
2,4 94+0 84+0 12+1 16+1 19+1 20+1 20+1 20+1 19+1 18+1
2,5 30+1 23+1 29+1 33+1 35+1 34+1 31+1 29+1 26+1 24+1
2,6 59+1 44+1 47+1 47+1 44+1 39+1 35+1 30+1 27-11 24+1
2,7 86+1 61+1 58+1 52+1 44+1 37+1 31+1 27+1 23+1 20+1
2,8 10+2 67+1 59+1 47+1 37+1 29+1 24+1 20+1 17+1 14-j-l
2,9 10+2 61+1 48+1 35+1 26+1 20+1 15+1 12+1 104-1 89+0
3,0 88+1 43+1 32+1 20+1 15+1 10+1 84+0 66+0 54+0 45—0
3,1 30+1 22+1 14+1 97+0 69+0 51+0 40-0 32-0 26-0 22-0
3,2 84+0 76+0 56+0 44-0 38-0 33-0 29-0 26-0 24—0 22—0
3,3 19—0 30—0 42-0 53+0 60+0 62+0 62+0 60+0 58+0 56+0
3,4 87+0 76+0 11+1 14+1 16+1 16+1 16+1 15+1 14+1 13+1
3,5 28+1 21+1 26+1 29+1 30+1 28+1 25+1 22+1 20+1 184-1
3,6 57+1 41+1 43+1 42+1 38+1 33+1 2841 24+1 21+1 18+1
3,7 84+1 58+1 55+1 47+1 39+1 31+1 26+1 21+1 18+1 15+1
3,8 10+2 65+1 55+1 43+1 33+1 25+1 20+1 16+1 13+1 11+1
3,9 10+2 59+1 46+1 32+1 23+1 17+1 13+1 10+1 86+0 71+0
4,0 90+1 42+1 31+1 19+1 13+1 97+0 73+0 56+0 45-0 37-0
4,1 30+1 22+1 14+1 93+0 64+0 47—0 35-0 28—0 22-0 19-0
4,2 85+0 77+0 56+0 43-0 36—0 30—0 26—0 23—0 20—0 19—0
4,3 19-0 30—0 41—0 51+0 55+0 55+0 53+0 50+0 47-0 44—0
4,4 84+0 72+0 10+1 13+1 14+1 14+1 13+1 12+1 11+1 10+1
^Этой таблицей можно пользоваться только для переходов между двумя
различными конфигурациями: либо между конфигурациями в целом, либо
для переходов, в которых не изменяется ни одно из квантовых чисел
угловых моментов (и — 0, см. § 6).
§ 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
207
Таблица 19 (продолжение)
Эффективное главное квантовое число п0*
Дп* 0,5 1,0 1,5 2,0 2,5 з,о 3,5 4,0 4,5 5,0
Переход s — s; параметр %
0,6 0,7 0,8 0,9 1,0 13Н-1 14+1 154-1 15+1 16+1 15+1 16+1 17+1 17+1 16+1 17+1 17+1 17+1 16+1 14+1 17+1 17+1 16+1 14+1 11+1 17+1 16+1 14+1 12+1 90+0 16+1 15+1 13+1 10+1 72+0 15+1 13+1 11+1 87+0 58+0 14+1 12+1 10-1-1 74+0 47-0 13+1 11+1 88+0 63+0 39-0 12+1 10+1 78+0 54+0 32-0
1,1 15+1 13+1 99+0 74-1-0 57+0 44-0 35-0 29—0 24—0 20—0
1,2 88+0 68+0 53+0 48-0 47-0 48—0 49-0 50+0 50+0 50+0
1,3 26-0 39-0 64+0 98+0 13+1 15+1 17+1 18+1 19+1 Л9+1
1,4 72+0 91+0 14+1 20+1 25+1 28+1 30+1 30+1 29+1 28+1
1,5 10+1 14+1 20+1 25+1 28+1 29+1 28+1 27+1 25+1 23+1
1,6 13+1 17+1 22+1 25+1 26+1 25+1 23+1 21+1 19+1 17+1
1,7 14+1 18+1 22+1 23+1 22+1 20+1 18+1 16+1 14+1 12+1
1,8 15+1 19+1 21+1 20+1 18+1 16+1 13+1 11+1 10+1 90+0
1,9 16 + 1 19+1 19+1 17+1 14+1 12+1 10+1 83+0 70+0 60+0
2,0 16+1 18+1 16+1 13+1 10+1 82+0 66+0 53+0 43-0 36-0
2,1 16+1 14+1 11+1 86+0 66+0 52+0 42-0 34-0 28-0 23—0
2,2 99+0 81+0 63+0 56+0 54+0 52+0 50+0 48-0 46-0 45-0
2,3 26-0 40-0 62+0 93+0 11+1 13+1 14+1 15+1 15+1 15+1
2,4 65+0 82+0 13+1 20+1 25+1 28+1 30+1 29+1 28+1 27+1
2,5 10+1 13+1 20+1 27+1 31+1 32+1 31+1 29+1 27+1 24+1
2,6 13+1 17+1 23+1 27+1 28+1 27+1 25+1 23+1 20+1 18+1
2,7 14-4-1 19+1 23+1 25+1 24+1 22+1 19+1 17+1 15+1 13+1
2,8 15+1 20+1 22+1 22+1 19+1 17+1 14+1 12+1 10+1 95+0
2,9 16+1 19+1 20-1-1 18 |-1 15+1 12+1 10+1 87+0 74+0 63+0
3,0 16+1 18+1 16+1 13+1 10+1 86+0 69+0 56+0 46-0 38-0
3,1 16+1 15+1 11+1 90+0 70+0 55+0 44-0 36-0 30-0 25-0
3,2 10+1 86+0 68+0 60+0 57+0 54+0 51+0 48-0 46—0 23-0
3,3 26-0 41-0 63+0 93+0 11+1 13+1 14+1 14+1 14+1 14+1
3,4 63+0 79+0 13+1 20+1 25+1 28+1 29+1 29+1 27+1 26+1
3,5 10+1 13+1 20+1 28+1 32+1 33+1 32+1 30+1 27+1 25+1
3,6 12+1 17+1 23+1 28+1 30+1 28+1 26+1 23+1 21+1 19+1
3,7 14+1 19+1 24+1 26+1 25+1 23+1 20+1 17+1 15+1 14+1
3,8 15+1 20+1 23+1 22+1 20+1 17+1 15+1 13+1 11+1 98+0
3,9 16+1 20+1 20+1 18+1 15+1 13+1 10+1 90+0 76+0 64+0
4,0 16+1 18+1 17+1 14+1 11+1 884-0 71+0 57+0 47-0 39-0
4,1 16+1 15+1 12+1 93+0 72+0 57+0 46-0 37-0 31—0 26-0
4,2 10+1 88+0 70+0 62+0 58+0 55+0 52+0 48-0 46-0 43-0
4,3 26-0 41-0 63+0 93+0 11+1 12+1 13+1 13+1 13+1 13+1
4,4 62+0 78+0 13+1 20+1 25+1 28+1 28+1 28+1 27+1 25+1
208 гл. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИИ
Таблица 19 (продолжение)
Эффективное главное квантовое число п0
Дп* 0,5 1,0 1,5 2,0 2,5 з,о 3,5 4,0 4,5 5,0
Переход s — р\ параметр А
0,1 0,2 0,3 0,4 0,5 14+1 30+1 4641 58+1 64+1 20+1 37+1 48 |-1 52+1 51+1 25+1 40+1 46+1 46+1 41+1 28+1 41+1 44+1 41+1 34+1 31+1 41+1 42-|-1 37+1 30+1 33+1 41+1 40+1 34+1 26+1 35+1 41+1 37+1 31+1 23+1 36+1 40+1 35+1 28+1 20+1
0,6 89+1 62+1 44+1 33+1 26+1 21+1 18+1 15+1 13+1*
0,7 95+1 53+1 34+1 23+1 17+1 14+1 11+1* 97+0* 84-j-O*
0,8 91+1 40+1 23+1 14+1 10+1* 81+0* 66+0* 55+0* 48—0*
0,9 77+1 25+1 13+1 79+0* 57+0* 44-0* 37—0* 33—0* 30—0*
1,0 57+1 13+1 66+0* 41-0 33-0 30-0 28—0 28—0 27—0*
1,1 19+2 32+1 66+0 34-0 31-0 33-0* 36-0* 38-0* 40—0* 41—0*
1,2 14+2 13+1 32-0 43-0* 64+0* 86+0 10+1 10+1 10+1 97+0
1,3 89+1 37-0* 73+0 21+1 22+1 18+1 15+1 13+1 11+1 94+0
1,4 44+1 52+0 29+1 28+1 22+1 17+1 13+1 11+1 94+0 80+0
1,5 15+1 29+1 37+1 27+1 19+1 14+1 11+1 92+0 76+0 64+0
1,6 21-0 45+1 36+1 24+1 16+1 12+1 90+0 71+0 58+0 49—0*
1,7 34-0 56+1 33+1 20+1 12+1 89+0 65+0 51+0* 41-0* 34—0*
1,8 14+1 61+1 27+1 15+1 88+0 60+0 43-0* 34—0* 27—0* 23—0*
1,9 25+1 58+1 19+1 99+0 54+0 37-0* 27—0* 22—0* 19—0 17—0
2,0 34+1 49+1 11+1 55+0 32-0 24-0 20-0 18—0 17—0 16—0
2,1 13+2 30+1 66+0 31-0 24—0 23-0* 23—0* 23—0* 23—0* 22—0*
2,2 10+2 14+1 32—0 31-0 39-0* 46-0* 52+0 53+0 52+0 48—0
2,3 73+1 46-0 44-0 11+1 15+1 13+1 10+1 84+0 67+0 55+0
2,4 41+1 32-0 23+1 22+1 17+1 12+1 97+0 75+0 60+0 49—0
2,5 16+1 22+1 32+1 23+1 15+1 11+1 82+0 63+0 50+0 41—0
2,6 37—0 39+1 32+1 20+1 13+1 91+0 65+0 50+0 39-0 32-0*
2,7 75-1 49+1 29+1 17+1 10+1 69+0 49-0 37—0* 29—0* 23—0*
2,8 10+1 54+1 24+1 13+1 72+0 48-0 33-0* 25—0* 20—0* 16—0*
2,9 18+1 54+1 17+1 88+0 46-0 31-0* 22—0* 17—0* 14—0* 12—0*
3,0 26+1 46+1 10+1 51+0 28-0 21—0 17—0 14—0 13—0 12—0
3,1 11+2 29+1 66+0 29-0 22-0 20-0 19—0* 18—0* 17—0* 16—0*
3,2 96+1 14+1 32-0 28-0 32-0* 36—0* 38-0 38—0 36—0 34—0
3,3 68+1 50+0 38-0 87+0 12+1 11+1 86+0 66+0 52+0 42—0'
3,4 39+1 29-0 21+1 20+1 15+1 11+1 81+0 61+0 47—0 38—0
3,5 17+1 19+1 30+1 21+1 14+1 96+0 69+0 52-J-0 40—0 32—0
3,6 44-0 36+1 30+1 19+1 11+1 79+0 55+0 41-0 32-0 25-0*
3,7 65—1 46+1 27+1 16+1 91+0 61+0 42-0 31—0* 24—0* 19—0*
3,8 82+0 51+1 22+1 12+1 65+0 43-0 29—0* 22—0* 17—0* 14—0*
3,9 15+1 51+1 16-f-l 84+0 42—0 28-0* 20—0* 15—0* 12—0 10—0
4,0 23+1 45+1 10+1 49-0 26-0 19—0 15—0 12—0 11—0 10—0
4,1 10-1-2 29+1 66+0 28-0 20-0 18-0 16—0* 15—0* 14—0* 13—0*
4,2 91+1 14+1 33-0 27-0 29—0* 31—0 32—0 31—0 30—0 27—0
4,3 65+1 52+0 35-0 76+0 10+1 97+0 76+0 57+0 45—0 35—0
4,4 38+1 28-0 19+1 19+1 14+1 10+1 72+0 53+0 41—0 32—0
§ 1Я. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
209
Таблица 19 (продолжение)
Эффективное главное <вантово е число п *
Дп* 0,5 1,0 1.5 2,0 2,5 3,0 3,5 4,0 4,5 5,0
0,1 Пе 10+1 реход s 10+1 — р\ fl to+i а рам ст 10Ц1 Р X 97+0 93+0 89+0 85+0
0,2 0,3 0,4 0,5 0,6 71+0 99+0 87+0 75+0 64+0 54+0 92+0 76+0 62 +0 51+0 40-0 84+0 66+0 52-1-0 40-0 30-0 77+0 58+0 44-0 32—0 23—0 70+0 51+0 37—0 26—0 18-0 64+0 45-0 31-0 22-0 14-0 59+0 40-0 27-0 18—0 11—0 54+0 35-0 23-0 15-0 10-0*
0,7 63+0 44—0 31-0 22-0 16-0 12-0 10-0* 10-0* 10-0*
0,8 56+0 35-0 23—0 15-0 10—0* 10-0* 10—0* 10—0* 10-0*
0,9 48—0 26—0 16-0 10—0* 10-0* 10—0* 10-0* 10-0* 10—0*
1,0 41—0 18-0 10-0* 10—0 10—0 10—0 10—0 10-0 10—0
1,1 61+0 31—0 12—0 10—0 15-0 23-0* 30—0* 37—0* 43-0* 47-0*
1,2 55 | -0 20—0 13—0 44-0* 96+0* 15+1 19+1 21+1 20+1 17+1
1,3 48-0 11—0 11+1* 42+1 39+1 30+1 23+1 18+1 14+1 11+1
1,4 40-0 81+0 38+1 30+1 21+1 16+1 12+1 93+0 73+0 59+0
1,5 29-0 31+1 21+1 15+1 10+1 81+0 62+0 48—0 38—0 30-0
1,6 12-0 18+1 12+1 86+0 62+0 46—0 35-0 27-0 21—0 16—0*
1,7 26 4-1 11-1-1 78+0 54 4-0 38-0 27-0 20—0 15—0* 12—0* 10-0*
1,8 14+1 82+0 53+0 35-0 23-0 17-0 12-0* 10-0* 10-0* 10—0*
1,9 87-1-0 63+0 36-0 23-0 15-0 11-0* 10—0* 10—0* 10—0* 10-0*
2,0 67+0 50+0 24-0 14-0 11—0 10-0 11—0 11-0 12-0 12—0
2,1 65+0 36-0 16-0 12-0 16-0 22-0* 29—0* 34—0* 38-0* 41—0*
2,2 57+0 24—0 13-0 34-0 68+0* 10+1* 13+1 15+1 15+1 15+1
2,3 49-0 13-0 61+1 27+1 41+1 35+1 27+1 21+1 16+1 13+1
2,4 40—0 36-0 45+1 37+1 27+1 20+1 15+1 11+1 90+0 72+0
2,5 30—0 35+1 28+1 20+1 14+1 10+1 78+0 60+0 47-0 37-0
2,6 16-0 23+1 15+1 10+1 77+0 56+0 42-0 33-0 26-0 20-0*
2,7 27-0 13+1 92+0 64+0 45-0 33-0 24-0 19-0* 14—0* 11—0*
2,8 23 |-1 92+0 60+0 40—0 27-0 20-0 15-0* 11—0* 10—0* 10-0*
2,9 10+1 69+0 40—0 26—0 17—0 13—0* 10—0* 10-0* 10—0 10-0*
3,0 73+0 53+0 26-0 16—0 13-0 11-0 12-0 12-0 13-0 13-0
3,1 66+0 39-0 17—0 13-0 17-0 23-0 28-0* 33-0* 37—0* 40-0*
3,2 57+0 25-0 14—0 32—0 61+0* 92+0* 11 + 1 13+1 14+1 13+1 ,
3,3 49-0 14-0 50+0 22+1 37+1 36+1 28+1 22+1 17+1 14+1
3,4 40-0 28-0 45+1 40+1 30+1 22+1 16+1 12+1 99+0 78+0
3,5 30—0 35+1 31+1 22+1 16+1 11+1 87+0 67+0 52+0 42—0
3,6 17—0 25+1 17+1 11+1 85+0 62+0 47-0 36-0 28-0 23-0*
3,7 13-0 14+1 10+1 69 4-0 49—0 36-0 27-0 21—0* 16-0* 13-0*
3,8 28 [1 97+0 64+0 43-0 30—0 22—0 16—0* 12-0* 10—0* 10-0*
3,9 11+1 71+0 42-0 27-0 18-0 14-0* 11—0* 10—0* 10-0 10-0
4,0 78+0 54+0 27-0 17-0 14-0 12-0 13-0 13—0 14—0 14-0
4,1 67+0 40-0 18-0 14—0 17—0 23-0 28-0* 32-0* 36-0* 38-0*
4,2 57+0 26-0 14-0 31-0 59+0* 86+0 11 + 1 12+1 13+1 13+1
4,3 49-0 15-0 45-0 19+1 35+1 35+1 29+1 23+1 18+1 14+1
4,4 40-0 25—0 43+1 42+1 32+1 23+1 17+1 13+1 10+1 83+0
210
ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Таблица 19 (продолжение)
Дп* Эффективное главное квантовое число п*
0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0
Переход s — d\ параметр А
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 27+2 19+2 18+2 16+2 11+2 74+1 30+1 93-1-1 12+2 13+2 14+2 13+2 Ю+2 76+1 45+1 22+1 97 4 0 84+0 36-0 16-1-1 38+1 64+1 894-1 10+2 114-2 11 + 2 97+1 74+1 50+1 29+1 14+1 84+0 10+1 30+1 73+0 28-1 55+1 79+1 964-1 10+2 96+1 82+1 63+1 43+1 26+1 14+1 86+0 91+0 20+1 46+1 11 + 1 384-1 66+1 86+1 94+1 91+1 80+1 63+1 45+1 28+1 16+1 96+0 80+0 12+1 30+1 46+1 15+1 47-!-1 744-1 884-1 89+1 80+1 66+1 49+1 33+1 20+1 11+1 804-0 88+0 17+1 34+1 40+1 20-|-1 55 |-1 794-1 87+1 834-1 71+1 56+1 39+1 25+1 154-1 94+0 75+0 10+1 20+1 33+1 34+1 24+1 61 + 1 81 + 1 84+1 77+1 634-1 47+1 32+1 20+1 12+1 81+0 76+0 11+1 22+1 30+1 28+1
1,7 19+2 89+0 264-1 60+1 56+1 46+1 36+1 29+1 23+1
1,8 11+2 86+0 61 + 1 70+1 53+1 39+1 29+1 22+1 17+1
1,9 55+1 364-1 84+1 68+1 44+1 31+1 21+1 16+1 12+1
2,0 15+1 79+1 924 1 58+1 34+1 22+1 15+1 17+1* 86+0
2,1 49+2 31—0 10+2 85+1 43+1 23+1 14+1 97+0 73+0 60+0
2,2 264-2 36+1 12+2 68+1 29+1 14+1 89+0 66+0 56+0 51+0
2,3 104-2 91+1 114-2 47+1 164-1 87+0 65+0 61+0 61+0 63+0
2,4 25+1 14+2 10+2 27+1 93+0 70+0 76+0 89+0 10+1 10+1
2,5 66—1 16+2 754-1 13+1 77+0 10+1 144-1 17+1 18+1 17+1
2,6 69+0 16+2 37+1 754-0 15+1 25+1 29+1 274-1 23+1 19+1
2,7 24+1 13+2 13+1 12+1 39+1 42+1 35+1 27+1 21+1 17+1
2,8 384-1 93+1 65+0 394-1 58+1 43+1 32+1 23+1 17+1 13+1
2,9 43+1 51+1 19+1 68+1 59+1 38+1 26+1 18+1 13+1 10+1
3,0 40+1 19+1 55+1 81+1 53+1 30+1 19+1 12+1 93+0 70+0
3,1 23+2 24-0 79+1 78+1 40+1 21+1 13+1 87+0 64+0 50+0
3,2 14+2 20+1 10+2 65+1 28+1 13+1 84+0 60+0 48-0 42—0
3,3 63+1 62+1 10+2 47+1 17+1 86+0 60+0 51+0 49-0 48-0
3,4 17+1 10+2 96+1 29+1 98+0 64+0 624-0 67+0 72+0 75+0
3,5 91—1 13+2 754-1 14+1 71+0 84+0 10+1 12+1 13+1 12+1
3,6 35-0 134-2 40+1 79+0 114-1 18+1 22+1 21+1 18+1 15+1
3,7 14+1 11+2 16+1 97+0 31+1 35+1 30+1 23+1 18+1 14+1
3,8 24+1 85+1 67+0 29+1 51+1 39+1 28+1 20+1 15+1 11+1
3,9 30+1 49+1 13+1 60+1 55+1 35+1 23+1 16+1 11+1 87+0
4,0 29+1 21+1 444-1 75+1 50+1 28+1 17+1 11+1 84+0 62+0
4,1 17+2 28-0 694-1 74+1 39+1 20+1 12+1 81+0 58+0 45—0
4,2 10+2 14+1 90+1 63+1 27+1 13+1 80+0 56+0 44-0 37—0
4,3 50+1 51+1 98+1 47+1 17+1 84+0 57+0 47-0 42-0 40-0
4,4 144 1 90+1 92 + 1 29+1 10+1 61+0 56+0 574-0 59+0 60+0
§ 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
211
Таблица 19 (продолжение)
Эффективное главное квантовое число 4
Дп* 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 15+1 Пе 16+1 15+1 14+1 12+1 10+1 77+0 ’реход s 19+1 18+1 17+1 16+1 14+1 12+1 10+1 81+0 57+0 41-0 68+0 — d', п 10+1 17+1 20+1 20+1 20+1 18+1 16+1 14+1 12+1 104-1 80+0 59+0 42-0 39-0 90+0 29+1 арамет 12+1 19+1 21 + 1 20+1 18+1 16+1 134 1 11+1 91+0 70+0 51+0 37—0 34-0 66+0 21+1 40+1 Р X 14+1 20+1 21+1 19+1 16+1 13+1 11+1 884-0 67+0 49-0 36-0 29—0 42-0 11+1 30+1 36+1 15+1 21+1 20+1 17+1 14+1 11+1 91+0 69+0 51+0 36-0 27—0 29-0 58+0 16+1 32+1 28+1 17+1 21+1 19+1 16+1 12+1 98+0 744-0 55+0 39-0 28-0 23—0 31—0 74+0 19+1 29+1 22+1 18+1 21+1 18+1 14+1 11 + 1 83+0 62+0 44-0 31—0 23—0 21-0 36-0 89+0 21+1 25+1 18+1
1,7 14+1 44-0 25+1 41+1 34+1 25+1 19+1 14+1 11+1
1,8 13+1 82+0 37+1 32+1 23+1 17+1 12+1 97+0 76+0
1,9 11+1 24+1 31+1 23+1 16+1 11+1 85+0 65+0 50+0
2,0 85+0 27+1 24+1 16+1 11+1 79+0 58+0 10—0* 35—0
2,1 15^1 64+0 24+1 18+1 12+1 79+0 54+0 41-0 33—0 28-0
2,2 15+1 19+1 21+1 14+1 86+0 55+0 40-0 35-0 34-0 35—0
2,3 15+1 19+1 18+1 10+1 60+0 42-0 41-0 48-0 57+0 66+0
2,4 13+1 18+1 15+1 78+0 46-0 52+0 76+0 10+1 13+1 14+1
2,5 70+0 17+1 12+1 53+0 61+0 12+1 19+1 24+1 25+1 24+1
2,6 19+1 16+1 93+0 50+0 17+1 32+1 36+1 32+1 26+1 21+1
2,7 17+1 15+1 58+0 13+1 404-1 40+1 31+1 24+1 18+1 14+1
2,8 16+1 13+1 51+0 36+1 39+1 29+1 21+1 15+1 12+1 93+0
2,9 15+1 11+1 17+1 37+1 28+1 20+1 14+1 10+1 79+0 61+0
3,0 14+1 90+0 29+1 29+1 204-1 13+1 96+0 70+0 53+0 42—0
3,1 15+1 40-0 28+1 22+1 14+1 94+0 65+0 49-0 39-0 33—0
3,2 15+1 19+1 23+1 16+1 10+1 65+0 47—0 39-0 36-0 36—0
3,3 14+1 21+1 19+1 12+1 70+0 48-0 43-0 47+0 53+0 59+0
3,4 13+1 19+1 16-f-l 88+6 51+0 51+0 68+0 89+0 10+1 12+1
3,5 71+0 18+1 13+1 60+0 57+0 10+1 15+1 20+1 22+1 21+1
3,6 21+1 17+1 10+1 49-0 14+1 26+1 32+1 31+1 26+1 22+1
3,7 18+1 15+1 64+0 10+1 36+1 41+1 34+1 26+1 20+1 15+1
3,8 16+1 13+1 48-0 31+1 42+1 33+1 24+1 17+1 13+1 10+1
3,9 15+1 11+1 14+1 40+1 31 + 1 22+1 16+1 11+1 88+0 68+0
4,0 14+1 92+0 29+1 31 + 1 22+1 15+1 10+1 78+0 59+0 46—0
4,1 15+1 39—0 30+1 23+1 15+1 10+1 72+0 54+0 42-0 36—0
4,2 15+1 17+1 25+1 17+1 10+1 71+0 51+0 42-0 38-0 36—0
4,3 14+1 21+1 20+1 13+1 76+0 524 0 45-0 46—0 51+0 56+0
4,4 12+1 204 1 17+1 94+0 54+0 51+0 64+0 82+0 99+0 11+1
212 гл. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Таблица 19 (продолжение)
Дп* Эффективное главное квантовое число п*
1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0
Переход р — s; параметр А
0,1 10+1 17+1 21+1 25+1 28+1 30+1 32+1 33+1
0,2 16+1 24+1 28+1 31+1 32+1 33+1 33+1 33+1
0,3 18+1 24+1 27+1 28+1 28+1 28+1 27+1 27+1
0,4 16+1 21 + 1 22+1 22 + 1 21 + 1 21 + 1 20+1 19+1
0,5 12+1 15+1 15+1 15+1 14+1 14+1 13+1 12+1
0,6 84+0 99+0 99+0 95+0 89+0 84+0* 79+0* 74+0*
0,7 45-0 55+0 55+0 53+0 50+0» 48—0* 45-0* 43-0*
0,8 21—0 29-0 30—0 31—0 31-0 30—0 30—0 29-0*
0,9 16-0 21-0 26-0 27-0 28-0* 28—0* 28—0* 28—0*
1,0 51+0 37-0 49-0 45-0* 48—0* 45-0* 45-0* 43-0*
1,1 92+0 13+1 15+1 14+1 13+1 11+1 10+1 94+0
1,2 12+1 15+1 15+1 14+1 12+1 11+1 98+0 86+0
1,3 12+1 13+1 12+1 11+1 99+0 87+0 77+0 68+0
1,4 10+1 10+1 96+0 84+0 74+0 65+0 58+0 51+0
1,5 75+0 76+0 69+0 60+0 53+0 46—0 41—0 37-0*
1,6 48—0 51+0 46-0 40-0 36—0 32—0 29-0* 26—0*
1,7 27—0 31—0 29-0 27-0 24-0 22—0 20—0 19-0
1,8 15—0 20-0 21-0 20-0 19-0 18-0 17—0 16—0
1,9 19-0 20-0 23-0 22-0* 21-0* 20-0* 19—0* 17—0*
2,0 71+0 39-0 51+0 39-0 39-0* 33—0* 31—0* 28—0*
2,1 85+0 11+1 12+1 10+1 89+0 74+0 62+0 53+0
2,2 11+1 12+1 11+1 99+0 83+0 69+0 58+0 49—0
2,3 11+1 11+1 97+0 80+0 67+0 56+0 47-0 40—0
2,4 89+0 85+0 73+0 60+0 50+0 42-0 36-0 31-0
2,5 65+0 61+0 52+0 43-0 36-0 31-0 27-0 23-0*
2,6 41-0 41-0 35-0 30-0 26-0 22—0 19—0* 17—0*
2,7 23-0 26-0 24-0 21-0 18-0 16—0 14—0 13-0
2,8 14—0 18-0 18-0 17-0 16—0 14-0 13—0 12-0
2,9 22-0 19—0 23-0 19-0* 19-0* 16—0* 15—0* 14-0*
3,0 79+0 39-0 53+0 36-0 36-0 28-0 26-0 22-0
3,1 83+0 10+1 10+1 87+0 72+0 58+0 47—0 39-0
3,2 10+1 11+1 10+1 83+0 67+0 54+0 44-0 37—0
3,3 10+1 10+1 85+0 68+0 55+0 44-0 36-0 30-0
3,4 85+0 77+0 64+0 51+0 41-0 34-0 28-0 24-0
3,5 61+0 56+0 46-0 37—0 30-0 25-0 21-0 18-0*
3,6 38-0 38-0 31-0 26-0 21-0 18-0 15-0 13-0*
3,7 21-0 24-0 21-0 19-0 16-0 14—0 12-0 11—0
3,8 14-0 17-0 17-0 16-0 14-0 12-0 11—0 10-0
3,9 24-0 19-0 22—0 18-0* 17—0* 15-0* 13-0* 12—0*
4,0 83+0 39-0 55+0 35-0 34-0 25—0 23-0 19-0
4,1 81+0 10+1 10+1 82+0 64+0 50+0 40-0 33-0
4,2 10+1 10+1 95+0 75 -j-0 59+0 47-0 38-0 30-0
4,3 10+1 96+0 79+0 62+0 49-0 38-0 31-0 25-0
4,4 82+0 73+0 59+0 46—0 37—0 30-0 24-0 20-0
§ 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
213
Таблица 19 (продолжение}
Дп* Эффективное главное квантовое число * по
I,5 2,0 2,5 3,о 3.5 4,0 4,5 5,0
0,1 104-1 10+1 Перех 10+1 од р — s 10+1 парамет 97+0 пр X 93+0 62+0 89+0 85+0
0,2 97+0 89+0 82+0 75+0 68+0 57+0 52+0
0,3 81+0 71+0 62+0 54+0 47-0 41—0 37-0 33-0
0,4 66+0 54+0 45-0 38-0 32-0 27-0 24-0 20-0
0,5 514-0 40—0 32—0 26-0 21-0 18-0 15-0 12—0
0,6 37-0 28-0 22-0 17-0 13-0 11-0* 10-0* 10-0*
0,7 25—0 19-0 14-0 11—0 10—0* 10—0* 10—0* 10-0*
0,8 17—0 13-0 11—0 10—0 10—0 10-0 10-0 10-0*
0,9 29-0 21-0 23-0 20-0 19—0* 18-0* 17-0* 15-0*
1,0 18+1 93+0 10+1 844-0* 81+0* 71+0* 66+0* 60+0*
1,1 39+1 46+1 45+1 39+1 33+1 28+1 24+1 20+1
1,2 33+1 34+1 31+1 27+1 23+1 19+1 16+1 13+1
1,3 21+1 19+1 17+1 14+1 12+1 10+1 85+0 71+0
1,4 12+1 11+1 91+0 76+0 63+0 52+0 44-0 37—0
1,5 81+0 65+0 53+0 43-0 35-0 29-0 24-0 20—0*
1,6 51+0 40-0 32-0 26—0 21—0 17-0 14-0* 12—0*
1,7 32-0 26-0 22-0 18—0 15-0 13-0 11—0 10—0
1,8 26-0 22-0 22-0 19—0 17—0 15-0 14—0 12-0
1,9 64+0 39—0 45-0 38-0* 37—0* 32—0* 30-0* 27-0*
2,0 30+1 14+1 17+1 12+1 12+1* 10+1* 93+0* 80+0
2,1 42+1 50+1 49+1 42+1 35+1 28+1 23+1 19+1
2,2 36+1 37+1 34+1 29+1 24+1 20+1 16+1 14+1
2,3 24+1 22+1 19+1 16+1 13+1 11+1 92+0 77+0
2,4 14+1 12+1 10+1 86+0 71+0 59+0 49-0 41-0
2,5 89+0 72+0 59+0 49-0 40—0 33-0 28-0 23-0*
2,6 55+0 45-0 36-0 30-0 25-0 21—0 17—0* 15-0*
2,7 35-0 30—0 26-0 22-0 19—0 16-0 14—0 12-0
2,8 31—0 27-0 28—0 24-0 23—0 20-0 18—0 16-0
2,9 89+0 48-0 59+0 47-0* 47—0* 40-0* 37-0* 33-0*
3,0 34+1 16+1 22+1 14+1 14+1 11+1 10+1 90+0
3,1 43+1 52-1 50+1 43+1 35+1 29+1 23+1 19+1
3,2 37+1 39-1 35+1 29+1 24+1 20+1 17+1 14+1
з,з 25+1 23-1 20+1 16+1 13+1 11+1 95+0 80+0
3,4 154-1 13-1 10+1 90+0 75+0 62+0 52+0 44-0
3,5 92+0 76+0 63+0 52+0 43-0 36-0 30-0 25-0*
3,6 57+0 47-0 39—0 32-0 27—0 23-0 19—0 16-0*
3,7 36—0 32—0 28—0 24-0 21-0 18-0 16-0 14-0
3,8 34-0 29—0 32-0 27-0 26-0 23-0 21—0 18-0
3,9 4,0 10+1 53+0 68+0 53+0* 53+0* 44-0* 42-0* 36—0*
35+1 18+1 25+1 16+1 16+1 12+1 11+1 97+0
4,1 43+1 53+1 51+1 43+1 36+1 29+1 24+1 19+1
4,2 4,3 38+1 39+1 35+1 30+1 24+1 20+1 17+1 14+1
25+1 24+1 20+1 17+1 14+1 11+1 97+0 82+0
4,4 154-1 13+1 11+1 93+0 77+0 64+0 54+0 45-0
214 гл. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Таблица 19 (продолжение)
Дп* Эффективное главное квантовое число п*
1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0
Переход р — р1)'. х = 0; параметр А
0,6 18-1-2 294 2 36-| 2 39+2 41+2 42+2 42 Н 2 41+2
0,7 20+2 294-2 33+2 33+2 33+2 32+2 31- Н2 30+2
0,8 20+2 254-2 26+2 24+2 234-2 214 2 20- 2 18- -2
0,9 18+2 18+2 17+2 924-1 15+2 13+2 11+2 10 -2 97 -J -1
1,0 13+2 11+2 75+1 62+1 53+1 46- -1 40+1
1,1 71+1 50+1 37+1 29+1 23+1 20+1 17+1 15+1
1,2 27+1 174-1 15+1 14-1-1 14+1 14+1 15+1 15+1
1,3 79+0 124-1 19 |-1 264-1 334-1 39-|-1 43+1 464-1
1,4 97+0 32+1 56+1 75+1 89+1 97+1 10+2 10+2
1,5 31+1 77+1 И+2 12+2 13+2 13+2 13+2 12+2
1,6 65+1 12+2 15+2 15+2 154-2 14+2 13+2 12+2
1,7 10+2 15+2 16+2 15+2 13+2 12+2 11+2 10+2
1,8 13+2 15+2 14+2 12+2 10+2 92+1 81+1 71+1
1,9 13+2 12+2 10+2 85+1 69+1 57+1 49+1 42+1
2,0 11+2 83+1 64+1 47+1 37+1 29+1 24+1 20+1
2,1 67-|-1 43+1 30-1-1 21 J-1 16+1 134-1 И -1 95 0
2,2 30+1 17+1 13+1 11+1 10+1 97+0 91+0 88- -0
2,3 97+0 Ю+-1 14+1 17+1 19+1 20+1 21 + 1 21- -1
2,4 74+0 22+1 364-1 464-1 51+1 53+1 54-j-l 52 -1
2,5 22+1 56+1 77+1 87+1 88+1 84+1 78+1 72+1
2,6 53+1 98+1 11+2 11+2 10+2 92+1 82+1 74-{-1
2,7 98+1 12+2 12+2 11+2 97+1 83+1 64+1 72+1 63+1
2,8 11+2 13+2 114-2 94+1 77+1 54+1 46+1
2,9 12+2 11+2 88+1 66+1 52+1 41+1 34+1 28+1
3,0 11+2 74+1 55+1 38+1 29+1 22+1 18+1 14+1
3,1 66+1 39+1 26+1 18+1 14+1 10+1 88+0 73+0
3,2 31+1 17+1 12+1 10+1 88+0 78+0 71+0 65+0
3,3 10+1 104-1 12+1 14+1 14+1 15+1 15+1 14+1
3,4 69+0 20+1 30+1 36+1 39+1 39+1 38+1 36+1
3,5 19+1 49+1 65+1 98+1 71+1 69+1 644-1 59+1 53+1
3,6 48+1 88+1 93+1 83+1 73+1 63+1 56- -1
3,7 83+1 11+2 114-2 95+1 804-1 674-1 57+1 484-1 36-|-1
3,8 11+2 12+2 10+2 81+1 65+1 52+1 43+1
3,9 12+2 10+2 80+1 58+1 45+1 34+1 28+1 234-1
4,0 11+2 70+1 50+1 34+1 25+1 19+1 15+1 12- 1-1
4,1 65+1 38+1 25+1 17+1 12+1 964-0 76+0 62+0
4,2 32+1 16+1 124-1 964-0 80+0 69+0 60+0 54 0
4,3 11+1 10+1 11+1 12+1 12+1 12+1 12+1 11+1
4,4 67+0 18+1 27+1 31 + 1 33+1 32+1 31+1 29+1
. *) Этой таблицей можно пользоваться только для переходов между дву-
мя различными конфигурациями: либо между двумя конфигурациями в
целом, либо для переходов, в которых не изменяется ни одно из квантовых
чисел угловых моментов (х = О, см. § 6).
<18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
215
Таблица 19 (продолжение)
Ди* [Эффективное главноз квантовое число п*
1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0
Переход р —х — 0; параметр %
0,6 14+1 17+1 18+1 17+1 16+1 15+1 14+1 13+1
0,7 15+1 17+1 17+1 16+1 14+1 13+1 11+1 10+1
0,8 16+1 17+1 16-1-1 14+1 12+1 10+1 94+0 82+0
0,9 17+1 16+1 14+1 11+1 96+0 80+0 68+0 58+0
1,0 17+1 14+1 11+1 85+0 67+0 53+0 43-0 35-0
1,1 15+1 10+1 73+0 54 1-0 41-0 32-0 26—0 21-0
1,2 18+1 59+0 48-0 44-0 44-0 45-0 45-0 46-0
1,3 45-0 55+0 88+0 11+1 14+1 16+1 30+1 28+1 17+1 18+1
1,4 49—0 12+1 20+1 25 М 28+1 29+1 28+1
1,5 18+1 20+1 27+1 29-1-1 29+1 26+1 24+1
1,6 14+1 23+1 27-1-1 26+1 25-| 1 22 ]-1 20 (-1 184-1
1,7 17+1 24+1 24+1 22+1 20+1 15+1 17-1--1 15-1-1 13+1
1,8 19+1 23+1 21+1 18+1 13+1 11+1 97-j-O
1,9 19+1 20+1 17-1-1 14-1-1 11+1 94+0 78+0 65 1-0
2,0 19+1 17+1 13+1 10+1 78+0 61+0 49-0 40-0
2,1 17+1 12+1 87+0 58+0 64+0 49-0 38-0 31—0 25—0
2,3 12+1 73+0 51+0 47—0 45-0 43—0 41-0
2,3 61+0 58+0 83+0 10+1 12+1 13+1 13+1 14+1
2,4 44-0 11+1 19+1 24+1 27-4-1 28+1 28+1 27+1
2,5 93+0 20+1 28+1 32+1 29+1 32+1 30+1 28+1 26+1 20+1
2,6 14+1 25+1 29+1 27+1 25+1 22+1
2,7 17+1 26+1 27+1 25+1 22-(-1 19+1 164 1 144-1
2,8 19+1 24+1 23+1 19+1 16+1 14+1 12+1 10+1
2,9 20+1 22+1 18+1 15+1 12+1 ю+1 82+0 69+0
3,0 20+1 18+1 14+1 10+1 83+0 65+0 52+0 42—0
3,1 18+1 13+1 94+0 69+0 53+0 41—0 33-0 27-0
3,2 з,з 13+1 79+0 63+0 54+0 49—0 45-0 43-0 40-0
68+0 61+0 84+0 10+1 11+1 12+1 12+1 12+1
3,4 44-0 11+1 19+1 23+1 26+1 27+1 27+1 26+1
3,5 89+0 20+1 29+1 32+1 33+1 31+1 29+1 23+1 26+1
3,6 14+1 25+1 31+1 31+1 29+1 26+1 20+1
3,7 17+1 27+1 28+1 26+1 23+1 20+1 17+1 15+1
3,8 19+1 25+1 24+1 20+1 17+1 14+1 12-1-1 10+1
3,9 20+1 23+1 19+1 15+1 12+1 Ю+1 85+0 71+0
4,0 20+1 18+1 14+1 11+1 86+0 67+0 54| 0 44-0
4,1 19+1 13+1 97+0 72+0 55+0 43-0 35-0 28—0
4,2 14+1 82+0 66+0 56-1-0 50+0 46—0 43-0 40-0
4,3 72+0 62+0 85+0 99-1-0 11+1 11+1 11+1 12+1
4,4 44-0 11+1 18+1 23+1 25+1 J 26+1 26+1 25+1
21(4 ГЛ. VT. ФОРМУЛЫ И ТАЛЛИНЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Таблица 19 (продолжение)
Эффективное главное квантовое число ♦ %
Ь.Г\* 1,5 2,0 2,5 З.о 3,5 4,0 4,5 5,0
0,1 13-0 42—0 Переход 77+0 х 11+1 — 2‘, па pi 16+1 гметр А 21+1 254-1 30+1
0,2 634-0 16 |-1 27- -1 384-1 474-1 56|-1 63+1 69+1
0,3 154-1 33+1 494-1 614-1 69 |-1 75|-1 79|-1 814-1
0,4 254-1 48+1 63+1 71+1 75+1 76+1 754-1 74+1
0,5 364-1 57+1 65+1 68+1 67+1 644-1 61+1 58+1
0,6 424-1 56+1 58+1 56+1 52+1 48+1 45+1 41+1
0,7 42+1 48+1 45+1 40+1 36+1 32+1 29+1 27+1
0,8 37+1 35+1 30+1 26+1 22+1 20+1 18+1 16+1
0,9 28+1 22+1 18+1 15+1 13+1 12+1 11+1 10+1
1,0 17+1 12+1 10+1 95+0 91+0 904-0 89+0 88+0
1,1 78+0 67+0 73+0 83+0 92+0 99+0 10+1 10+1
1,2 36-0 61+0 95+0 12+1 15+1 16+1 17+1 18+1
1,3 34-0 11 + 1 19+1 264-1 414-1 30+1 31 + 1 31-1-1 29-(-1
1,4 82+0 244-1 36+1 41+1 38+1 34+1 31-; 1
1,5 18+1 37+1 43+1 424-1 37+1 334-1 29+1 254-1
1,6 28+1 41+1 40+1 35+1 29+1 25+1 214-1 194-1
1,7 33+1 37+1 31+1 26+1 21+1 18+1 15+1 13+1
1,8 32+1 28+1 22+1 17+1 14+1 12+1 104-1 94+0
1,9 26+1 18+1 14- -1 11+1 99+0 87+0 77+0 70+0
2,0 17+1 11+1 92- -0 82+0 75+0 70+0 66+0 63+0
2,1 83+0 68+0 70- -0 74+0 77+0 78+0 77+0 76+0
2,2 41-0 60+0 854 -0 10+1 11+1 114-1 11+1 11+1
2,3 33—0 98+0 15- -1 19+1 20+1 20+1 19+1 17+1
2,4 66+0 20+1 28- -1 314-1 29+1 26+1 23+1 19+1
2,5 15+1 32+1 364 И 334 1 28+1 24+1 20+1 17+1
2,6 25+1 37-1-1 34+1 28+1 23+1 19+1 15+1 13+1
2,7 31+1 33+1 27+1 21+1 17+1 14+1 11+1 98+0
2,8 31+1 26+1 19+1 15+1 12+1 10+1 84+0 72+0
2,9 26+1 17+1 13+1 104-1 86+0 73+0 63+0 56+0
з,о 18+1 10+1 87+0 75+0 67+0 61+0 56+0 52+0
3,1 86+0 67+0 68+0 70+0 69+0 67+0 65+0 61+0
3,2 43-0 60+0 81+0 94+0 99+0 98+0 95+0 90+0
3,3 32-0 93+0 14+1 16+1 17+1 16+1 14+1 13+1
3,4 60+0 18+1 254-1 26+1 24+1 21+1 18+1 15+1
3,5 14+1 30+1 33+1 30+1 24+1 20+1 16+1 13+1
3,6 24+1 35+1 31+1 25+1 20+1 16+1 13+1 10+1
3,7 30+1 32+1 25+1 19+1 15+1 12+1 99+0 82+0
3,8 31+1 25+1 18+1 14+1 11+1 88+0 73+0 61+0
3,9 26+1 16+1 12+1 97+0 79+0 66+0 56+0 49-0
4,0 18+1 10+1 84+0 72+0 62+0 56+0 50+0 46—0
4,1 87+0 67+0 66+0 67+0 65+0 61+0 88+0 58+0 54+0
4,2 44-0 59+0 78+0 88+0 90+0 83+0 77+0
4,3 32-0 90+0 13+1 23+1 15+1 15+1 14+1 12+1 11+1
4,4 58+0 17+1 24+1 22+1 18+1 15+1 13+1 S
5 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
217
Таблица 19 (продолжение)
Ап* Эффективное главное квантовое число п*
1,5 2,о 2,5 3,0 3,5 4,0 4,5 5,0
о,1 63+0 84+0 Переход 10+1 р — р< > 12+1 — 2; naj. 14+1 шметр % 16+1 17+1 18+1
0,2 11+1 14+1 17+1 19+1 20+1 21+1 21+1 21+1
0,3 14+1 18+1 20+1 21+1 21+1 20+1 19+1 17+1
0,4 17+1 20+1 20+1 19+1 18+1 16+1 15+1 13+1
0,5 18+1 20+1 18+1 16+1 14+1 12+1 11+1 98+0
0,6 19+1 18+1 16+1 13+1 11+1 96+0 82+0 70+0
0,7 18+1 16+1 13+1 10+1 85+0 70+0 58+0 49-0
0,8 17+1 13+1 10+1 78+0 61+0 5040 41-0 34-0
0,9 15+1 10+1 734-0 56+0 46-0 38-0 33-0 29-0
1,0 12+1 71+0 54+0 47-0 42-0 40-0 38-0 37-0
1,1 80+0 54+0 56+0 62+0 67+0 71+0 73+0 73+0
1,2 52+0 71+0 10+1 13+1 15+1 16+1 17+1 16+1
1,3 66+0 16+1 25+1 31+1 33+1 33+1 31+1 28+1
1,4 15+1 31+1 40+1 42+1 39+1 35+1 30+1 25+1
1,5 24+1 37+1 39+1 35+1 30+1 25+1 20+1 17+1
1,6 28+1 33+1 30+1 24+1 20+1 16+1 13+1 11+1
1,7 27+1 26+1 21+1 16+1 13+1 10+1 89+0 74+0
1,8 24+1 19+1 14+1 11+1 91+0 74+0 62+0 52+0
1,9 20+1 13+1 10+1 81+0 67+0 57+0 50+0 44-0
2,0 15+1 94+0 76+0 67+0 62+0 58+0 48-0 52+0
2,1 10+1 71+0 74+0 80+0 85+0 86+0 86+0 84+0
2,2 65+0 82+0 11+1 14+1 16+1 16+1 16+1 16+1
2,3 66+0 15+1 24+1 29+1 31+1 30+1 28+1 26+1
2,4 13+1 30+1 41+1 43+1 40+1 35+1 30+1 26+1
2,5 24+1 40+1 43+1 39+1 33+1 27+1 22+1 18+1
2,6 29+1 37+1 34+1 28+1 23+1 18+1 15+1 12+1
2,7 2,8 29+1 29+1 24+1 19+1 15+1 12--1 10+1 84+0
26+1 21+1 16+1 13+1 10+1 86--0 71+0 60+0
2,9 22+1 15+1 11+1 93+0 78+0 67—0 58+0 51+0
3,0 17+1 10+1 86+0 77+0 71+0 67--0 62+0 58-рО
3,1 11+1 78+0 83+0 89+0 93+0 94--0 92+0 89+0
3,2 71+0 87+0 12+1 15+1 16+1 16-1 16+1 1541
3,3 67+0 15+1 24+1 29+1 30+1 29—1 27+1 24+1
3,4 13+1 30+1 41+1 43+1 40+1 35--1 30+1 264-1
3,5 23+1 40+1 45+1 41+1 34+1 28+1 23+1 19+1
3,6 30+1 39+1 36+1 30+1 24+1 19+1 16+1 13+1
3,7 30+1 31+1 25+1 20+1 16--1 13+1 10+1 90+0
3,8 27+1 23+1 17+1 14+1 11-1 92+0 77+0 65+0
3,9 22+1 16+1 12+1 10+1 84--0 72+0 63+0 56+0
4,0 17+1 10+1 91+0 83+0 76--0 72+0 66+о 62+0
4,1 11+1 82+0 88+0 94+0 98--0 98+0 96+0 92+0
4,2 74+0 90+0 12+1 15+1 16-1 16+1 16+1 15+1
4,3 67+0 16+1 24+1 28+1 30--1 29+1 26+1 24+1
4,4 12+1 30+1 41+1 43+1 40+1 35+1 30+1 25+1
218
ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Таблица 19 (продолжение)
Дп* Эффективное главное квантовое число п*
1,5 2,0 1 2’5 3,0 3,5 4,0 | 4,5 | 5,0
Переход р—<Г, х = Г, параметр А
0,1 30+1 43+1 53+1 59+1 65 |-1 68+1
0,2 60+1 73+1 79+1 82+1 82+1 82+1
0,3 86+1 91 + 1 90+1 86+1 82+1 78+1
0,4 10+2 99+1 894-1 81+1 74 + 1 67+1
0,5 11+2 96+1 81+1 69+1 60+1 534-1
0,6 15+2 10+2 85+1 66+1 54+1 45+1 38+1*
0,7 16+2 96+1 68+1 49+1 38+1 30+1* 25+1*
0,8 15+2 76+1 49+1 32+1 24+1* 18+1* 15+1*
0,9 12+2 53 + 1 31+1 19+1* 13+1* 10+1* 84+0*
1,0 97+1 32+1 16+1* 10+1* 74+0* 61+0 54+0
1,1 19+2 59+1 17+1* 83+0* 6ОТО 54+0 54+0 55+0
1,2 15+2 29+1 79+0* 57+0 65+0* 78+0* 93+0* 10+1
1,3 10+2 11+1* 64+0 11+1 19+1 25+1 24+1 21+1
1,4 64+1 65-1-0 23+1 41+1 34+1 28+1 23+1 194-1
1,5 29+1 29+1 52+1 42+1 32+1 25+1 20+1 17 + 1
1,6 66+0* 68+1 53+1 39+1 28+1 21+1 17+1 13+1
1,7 38-0 79+1 49+1 34+1 23+1 17-|-1 13+1* 10+1*
1,8 34+1 83+1 43+1 28+1 17+1 12+1* 93+0* 73+0*
1,9 56+1 80+1 344 1 20+1 12+1* 83+0* 60-40* 48-0*
2,0 724-1 69+1 24+1 12+1* 73+0* 51+0* 39—0* 33-0
2,1 10+2 48+1 15+1 71+0* 46—0 36-0 33-0 31-0
2,2 98+1 27+1 79+0* 45-0 41—0 42-0 45-0 48-0
2,3 79+1 12+1 50+0 57+0* 78+0* 10+1 11+1 11+1
2,4 54+1 61+1 87+0* 21+1 23+1 18+1 14+1 12+1
2,5 30+1 10+1 39+1 31+1 23+1 174-1 13-|-1 10+1
2,6 97+0 50+1 42+1 30+1 21+1 15+1 11+1 93+0
2,7 26-0 65+1 39+1 27+1 17+1 12+1 94+0* 73+0*
2,8 20+1 68+1 35+1 22+1 13+1 97+0* 69+0* 53+0*
2,9 41+1 67+1 29+1 17+1 98+0* 67+0* 47-0* 36-0*
3,0 54+1 61+1 21+1 11+1* 62+1* 43-0* 32-0* 26-0*
3,1 84+1 44+1 14+1 664-O* 40—0* 30-0 26—0 23-0
3,2 81+1 27+1 79+0* 41-0 33-0 32-0 33-0* 33-0
3,3 68+1 13+1 47-0 44-0 54+0 66+0 75+0 75+0
3,4 50+1 63+0 65+0 13+1 17+1 14+1 11+1 92+0
3,5 30+1 73+0 32+1 27+1 19+1 14+1 11+1 86+0
3,6 11+1 42+1 37+1 26+1 17+1 13+1 96+0 74+0
3,7 29-0 58+1 35+1 24+1 15+1 10+1 78+0 60+0*
3,8 10+1 62+1 31+1 20+1 12+1 84+0* 59+0* 45-0*
3,9 35+1 61-1-1 26+1 15+1 87+0* 59+0* 41—0* 31-0*
4,0 47+1 57-И 19+1 10+1 57+0* 39-0* 28-0* 22-0*
4,1 74+1 42+1 13+1 63+0* 37-0* 27-0 22—0 20—0
4,2 73+1 26+1 78+0* 38—0 30-0 28-0 27—0 26-0
4,3 63+1 13+1 46—0 39-0 45-0 52+0 58+0 58+0
4,4 48+1 65+0 56+0 10 И 14-| 1 12+1 99+0 78+0
§ 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
219
Таблица 19 (продолжение)
Эффективное главное квантовое число * 71 0
Дп* 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,(1
Переход р — (Г, > = 1; параметр X
0,1 10+1 10+1 10+1 76+0 96+0 69+0 92+0 88 +0
0,2 94+0 84 -1-0 63+0 57+0
0,3 79+0 67+0 58+0 50+0 44—0 38—0
0,4 66+0 53 |-0 44-0 37-0 31-0 26—0
0,5 55+0 42-0 33-0 27-0 22-0 18-0
0,6 65-|-0 45 - 0 33 0 25—0 19—0 15-0 12 0*
0,7 57-1-0 36-0 25-0 18 -0 13—0 10-0* 10—0*
0,8 49—0 28-0 19—0 12—0 10-0* 10-0* 10—0*
0,9 41 -0 21-0 13—0 10—0* 10-0* 10-0* 10-0*
1,0 33-0 15—0 10-0* 10—0* 10—0* 10-0 10—0
1,1 56+0 25-0 10-0* 10-0* 10-0 10-0 11-0 14-0
1,2 48-0 16-0 10—0* 11—0 23-0* 40—0 59+0* 77+0
1,3 41-0 10—0* 19-0 76+0 18+1 24+1* 21+1 17+1
1,4 33-0 18-0 21 |-1 36+1 24+1 16-| 1 12+1 92-1-0
1,5 24—0 26+1 32 j-1 19-[-1 12+1 84-1-0 61+0 46-0
1.6 11—0* 32+1 16+1 95+0 63+0 45-0 33-0 25—0
1,7 44-0 16+1 87+0 55+0 37-0 26-0 19—0* 14-0*
1,8 30+1 10+1 54+0 34-0 22-0 15—0* 11—0* 10—0*
1,9 15+1 67+0 35—0 22-0 13-0* 10-0* 10-0* 10—0*
2,0 95 +0 48-0 23-0 13-0* 10-0* 10-0* 10—0* 10—0
2,1 73+0 34-0 15—0 10-0* 10-0 10—0 10—0 12-0
2,2 58+0 22—0 10—0* 10-0 16-0 25-0 36-0 46-0
2,3 47—0 13-0 13-0 37-0* 82+0* 13+1 17+1 16+1
2,4 36-0 12—0 76+0* 29 |-1 30+1 21+1 15 +1 11+1
2,5 27—0 76+0 43+1 26+1 17+1 И |-1 834-0 62 |-0
2,6 14-0 43+1 23+1 13+1 87+0 60-1-0 44-0 33-0
2,7 12-0 25+1 11+1 72+0 48—0 33-0 24-0* 18—0*
2,8 37+1 13+1 68 ; о 43-0 28-0 19—0* 14-0* 10-0*
2,9 22+1 81+0 42-0 26-0 17-0* 11—0* 10-0* 10-0*
3,0 12+1 55+0 27—0 16-0* 10—0* 10-0* 10-0* 10-0*
3,1 82+0 38-0 18-0 10-0* 10—0* 10-0 10-0 11—0
3,2 63+0 25-0 11-0* 10-0 14-0 21—0 30—0* 38-0
з,з 49-0 15—0 12-0 30—0* 61+0 10+1 13+1 14+1
3,4 38-0 12-0 53+0 20+1 29+1 23+1 17+1 13+1
3,5 28-0 47—0 44+1 30+1 19+1 13+1 96 +0 71+0
3,6 16—0 45+1 28+1 15+1 10+1 70+0 51+0 38-0
3,7 10—0 30+1 13+1 82+0 55+0 38-0 28—0 21—0*
3,8 20+1 15+1 76+0 48—0 32-0 22-0* 16-0* 12-0*
3,9 28+1 90+0 47-0 29-0 19—0* 13—0* 10—0* 10-0*
4,0 14+1 59+0 30—0 18-0 11—0* 10-0* 10—0* 10-0*
4,1 88 +0 41-0 19—0 11-0* 10-0* 10-0 10—0 10—0
4,2 66+0 27—0 12—0* 10-0 14—0 20-0 27—0 34-0
4,3 51+0 17--0 12—0 26-0 52+0 85+0 11+1 13+1
4,4 39—0 12—0 44-0 16+1 27-+1 24+1 18+1 14 | 1
220 гл. vr. формулы и таблицы для оценки сечений
Таблица 19 (продолжение)
Ьп* Эффективное главное квантовое число п*
1,5 2,0 3,5 3,0 3,5 4,0 4,5 5,0
Переход р — d, к = 3; параметр А
0,1 27-1 66-1 11-0 18-0 26-0 36-0
0,2 19-0 42-0 72+0 10+1 14+1 19+1
0,3 63+о 12+1 19+1 27+1 34+1 42+1
0,4 144-1 25+1 254-1 364 1 464-1 54+1 61+1
0,5 40+1 514-1 60+1 65+1 68+1
0,6 19+1 38+1 53+1 614-1 65 |-1 654-1 G3+1
0,7 29+1 494-1 59+1 62+1 59+1 56+1 51+1
0,8 40+1 56+1 58+1 54+1 48+1 42+1 37+1
0,9 48+1 55+1 49+1 4141 344 1 29+1 254-1
1,0 51+1 47+1 36+1 28+1 22+1 18+1 15+1
1,1 31+1 48+1 35+1 23+1 17+1 13+1 11+1 10+1
1,2 34+1 38+1 22+1 14-j-l 10+1 95+0 91+0 92+0
1,3 33+1 254-1 12+1 86+0 83+0 92+0 10+1 11+1
1,4 28+1 13+1 69+0 774 0 10+1 13+1 16+1 19+1
1,5 21+1 59+0 65+0 11+1 174-1 23+1 27+1 29+1
1,6 11+1 38-0 10+1 21+1 294-1 34+1 34+1 33+1
1,7 40-0 61+0 20+1 32+1 38+1 37+1 34+1 30+1
1,8 13-0 13+1 31+1 39+1 38+1 33+1 28+1 24+1
1,9 22-0 23+1 39+1 39+1 32+1 26+1 21+1 17+1
2,0 62+0 33+1 39+1 32+1 24+1 18+1 15+1 12+1
2,1 13+1 38+1 33+1 23+1 16+1 12+1 10+1 88+0
2,2 20+1 36+1 23+1 14+1 11+1 92+0 80+0 74+0
2,3 24+1 27+1 14+1 96+0 83+0 81+0 81+0 83+0
2,4 25+1 17+1 84+0 76+0 85+0 10+1 10+1 11+1
2,5 21+1 86+0 65+0 92+0 124-1 15+1 16+1 17+1
2,6 14+1 46-0 85+0 15+1 20+1 23+1 23+1 22+1
2,7 65+0 48-0 154-1 24+1 28+1 28+1 25+1 22+1
2,8 2,9 21-0 92+0 24+1 32+1 31+1 27+1 22+1 19+1
15-0 17+1 33+1 34+1 28+1 22+1 17+1 15+1
3,0 37—0 28+1 36+1 29+1 22+1 16+1 13+1 10+1
3,1 99+0 34+1 32+1 22+1 15+1 11+1 95+0 78+0
3,2 16+1 34+1 23+1 14+1 10+1 88+0 71+0 68+0
3,3 21+1 28+1 15+1 98+0 80+0 76+0 71+0 69+0
3,4 23+1 18+1 91+0 75+0 78+0 87+0 89+0 93+0
3,5 21+1 99+0 66+0 84+0 10+1 12+1 13+1 14+1
3,6 15+1 52+0 78+0 12+1 16+1 19+1 19+1 19+1
3,7 78+0 45-0 13+1 21+1 24+1 24+1 21+1 19+1
3,8 28-0 79+0 22+1 28+1 27+1 24+1 19+1 16+1
3,9 14-0 15+1 30+1 31+1 26+1 20+1 15+1 13+1
4,0 29-0 26 |-1 34+1 27+1 20+1 15+1 11+1 10+1
4,1 83+0 33+1 31+1 21+1 15+1 11+1 87+0 79+0
4,2 14+1 34+1 23+1 14+1 10+1 86+0 66+0 69+0
4,3 20+1 28+1 15+1 98+0 79+0 75+0 62+0 63+0
4,4 22+1 19+1 94+0 75+0 74+0 85+0 76+0 73+0
§ 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ 221
Таблица 19 (продолжение)
Дп* Эффективное главное квантовое число п*
1,5 2,0 2,5 з.о | 3,5 4,0 4,5 5,0
0,1 0,2 0,3 0,4 0,5 п ере ход / 19-0 59+0 10+1 15-|-1 201 1 — d‘, х 30-0 88+0 15+1 21 + 1 26+1 —— 3, пира 41-0 11+1 19+1 26+1 30+1 метр % 54+0 14+1 23+1 294-1 324-1 66+0 17+1 26+1 31-|-1 32-|-1 79+0 20+1 294-1 32-}-1 31+1
0,0 16+1 24 |-1 29+1 31+1 31+1 29+1 274-1
0,7 19+1 27+1 31+1 30+1 28+1 25+1 22+1
0,8 22+1 29+1 30+1 27+1 23+1 20+1 17+1
0,9 25+1 30+1 27+1 23+1 23+1 194-1 15+1 13+1
1,0 27+1 28+1 18+1 14-|-1 12+1 10+1
1,1 19+1 28+1 25+1 18+1 14+1 11+1 974-0 864-0
1,2 21+1 28+1 20+1 14+1 11+1 10+1 99+0 10+1
1,3 24+1 25+1 14+1 11+1 11+1 12+1 14+1 16+1
1,4 25+1 18+1 10+1 12+1 17+1 22+1 26+1 284-1
1,5 26|-1 11+1 11+1 20+1 294-1 37+1 41+1 42+1
1,6 24+1 82+0 18+1 33+1 44+1 48+1 47+1 43+1
1,7 16+1 11+1 29+1 44+1 49+1 46+1 41+1 35+1
1,8 68+0 19+1 38+1 46+1 44+1 38+1 31+1 26+1
1,9 84+0 14+1 26+1 41-4-1 42+1 35+1 29+1 23+1 19+1
2,0 31+1 404-1 344-1 27+1 21+1 17+1 14+1
2,1 18+1 34+1 34+1 26+1 20+1 16+1 13+1 11+1
2,2 22+1 34+1 27+1 19+1 15+1 13-| 1 12+1 11+1
2,3 26+1 31+1 20 4-1 15+1 13+1 144-1 14+1 15+1
2,4 28+1 24+1 14+1 14+1 16+1 204-1 22+1 24+1
2,5 29+1 16+1 12+1 18+1 26+1 32+1 34+1 35+1
2,6 28+1 10+1 17+1 30+1 40+1 45+1 45+1 42+1
2,7 21-| 1 10+1 27-J 1 43+1 50+1 49+1 44+1 37+1
2,8 10+1 17+1 38+1 49+1 49+1 434-1 35+1 29+1
2,9 72+0 25+1 44+1 47+1 41+1 33+1 26+1 22+1
3,0 12+1 32+1 44+1 39+1 31+1 25+1 20+1 16+1
3,1 17+1 36+1 38+1 30+1 23+1 18+1 15+1 13+1
3,2 22+1 37+1 31+1 22+1 17+1 15+1 13+1 13+1
з,з 26+1 34+1 224-1 17+1 15+1 15+1 15+1 15+1
3,4 29+1 27+1 16+1 15+1 17+1 19+1 21+1 23+1
3,5 30+1 18+1 13+1 18+1 24+1 30+1 32+1 35+1
3,6 29+1 11+1 16+1 28+1 37+1 42+1 45+1 43+1
3,7 23+1 10+1 26+1 42+1 494-1 49+1 45+1 41+1
3,8 13+1 16+1 37+1 50+1 51+1 45+1 37+1 31+1
3,9 75+0 24+1 45+1 49+1 43+1 35+1 27+1 24+1
4,0 11 + 1 32+1 45+1 42+1 34+1 26+1 214-1 18+1
4,1 17+1 37+1 41+1 32+1 25+1 20+1 16+1 15+1
4,2 22+1 38+1 33+1 24+1 19+1 16+1 13+1 14+1
4,3 27+1 35+1 24+1 18+1 16+1 16+1 14+1 15+1
4,4 29+1 28+1 17+1 16+1 17+1 20+1 20+1 21+1
222
ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Таблица 19 (продолжение)
Дп* Эффективное главное квантовое число па
2,5 3,0 3,5 4,0 4,5 5,0
Переход d — s; параметр Л
0,1 24-0 54 -0 90+0 12+1 16 |-1 204-1
0,2 71+0 15+1 23-|-1 30-|-1 364-1 42+1
0,3 10+1 20- 1 28+1 354-1 40+1 444-1
0,4 10+1 19- -1 25+1 30-4-1 33 {-1 35+1
0,5 83+0 14+1 18-J-1 21 + 1 234-1 24+1
0,6 56+0 96 -4 о 12+1 1341 14 + 1 15+1
0,7 34-0 59+0 75+0 86+0 92+0 96+0
0,8 21-0 38- -0 51 +‘» 59+0 65+0 68+0
0,9 17-0 35- -0 47-0 56+0 62 4-0 66+0
1,0 11-0* 49- -0 57+0 78+0 78-рО 89+0
1,1 44-0 85+0 11+1 13+1 14+1 14+1
1,2 67+0 12+1 17+1 19+1 20+1 20+1
1,3 74+0 13+1 17+1 18+1 18+1 18+1
1,4 65-1-0 11+1 13+1 14+1 14+1 14+1
1,5 49—0 80+0 97-4-0 10+1 10+1 10+1
1,6 34-0 56 -0 68+0 73+0 744-0 734-0
1,7 24-0 41- -0 50+0 55 4-0 564-0 55+0
1,8 19-0 35- -0 43-0 48-0 49-0 49-0
1,9 18-0 38- -0 47-0 53+0 54+0 55+0
2,0 18-0 53+0 62+0 74+0 — 73+0
2,1 45—0 81+0 10+1 11+1 11+1 10+1
2,2 59+0 10+1 13+1 13+1 13+1 124-1
2,3 61+0 10+1 12+1 13+1 12+1 11+1
2,4 52+0 86+0 10+1 10+1 99+0 93+0
2,5 40-0 64+0 75+0 76+0 74+0 70+0
2,6 29-0 47- -0 55+0 57+0 56+0 53+0
2,7 22-0 37- -0 44-0 46-0 45-0 44-0
2,8 18-0 34- -0 40-0 44-0 43-0 42-0
2,9 18-0 39- -0 46-0 50+0 49—0 48—0
3,0 18-0 54+0 59+0 69+0 64+0 63+0
3,1 44—0 77+0 94+0 97+0 93+0 87+0
3,2 55+0 95+0 11+1 11+1 11+1 10+1
3,3 55+0 92+0 10+1 10+1 10+1 92+0
3,4 47-0 76+0 86+0 86+0 81+0 74+0
3,5 36-0 57+0 65+0 65+0 62+0 57+0
3,6 27-0 43- -0 50+0 50+0 48-0 45-0
3,7 21—0 35- -0 41-0 42—0 40-0 38-0
3,8 18-0 33- -0 39-0 41—0 39—0 37-0
3,9 17—0 39- -0 44—0 48—0 45—0 43-0
4,0 17—0 53+0 57+0 65+0 59+0 57+0
4,1 43-0 75+0 89+0 90+0 84+0 76+0
4,2 52+0 90+0 10+1 10-4-1 96+0 86+0
4,3 52+0 86+0 98+0 96+0 88+0 79+0
4,4 44-0 70+0 79+0 77+0 714-0 64+0
§ 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
223
Таблица 19 (продолжение)
Ди* Эффективное главное квантовое число п*
2,5 3,0 3,5 4,0 4,5 5,0
Переход d—s; параметр %
0,1 11+1 13+1 14+1 16+1 17+1 18+1
0,2 18+1 20+1 21+1 21+1 21+1 21+1
0,3 21+1 21+1 20+1 19+1 18-|-1 17+1
0,4 19+1 18+1 16+1 15+1 13+1 12+1
0,5 15+1 14+1 12+1 11+1 97+0 86+0
0,6 11+1 10+1 90+0 78+0 67+0 59+0
0,7 84+0 74+0 65+0 57+0 49-0 43-0
0,8 64+0 61+0 56+0 51+0 45—0 41—0
0,9 68+0 76+0 73+0 70+0 64+0 59+0
1,0 27—0* 14+1 11+1 13+1 10+1 11+1
1,1 23+1 27+1 28+1 27+1 25+1 23+1
1,2 34+1 39+1 41+1 39+1 36+1 32+1
1,3 34+1 37+1 36+1 34+1 30+1 27+1
1,4 27+1 28+1 264-1 23+1 21+1 18+1
1,5 20+1 19+1 18+1 15+1 13+1 12+1
1,6 14+1 13+1 12+1 11+1 98+0 85+0
1,7 10+1 10+1 99+0 90+0 79+0 70+0
1,8 93+0 10+1 98+0 91+0 82+0 73+0
1,9 10+1 13+1 12+1 12+1 11+1 10+1
2,0 10+1 21+1 19+1 20+1 — 16+1
2,1 28+1 33+1 34+1 32+1 29+1 26+1
2,2 35+1 41+1 42-1-1 39+1 35+1 31+1
2,3 34+1 38+1 37+1 34+1 30+1 26+1
2,4 27+1 28+1 27+1 24+1 21+1 18+1
2,5 20+1 20+1 19+1 17+1 15+1 13+1
2,6 14+1 15+1 14+1 12+1 11+1 97+0
2,7 11+1 12+1 11+1 10+1 95+0 84+0
2,8 10+1 12+1 12+1 11+1 10+1 91+0
2,9 11+1 16+1 15+1 15+1 13+1 12+1
3,0 12+1 24+1 22+1 23+1 20+1 18+1
3,1 30+1 36+1 37+1 34+1 31+1 27+1
3,2 35+1 42+1 43+1 40+1 35+1 31+1
3,3 33+1 38+1 37+1 34+1 30+1 26+1
3,4 27+1 29+1 27+1 24+1 21+1 18+1
3,5 20+1 21+1 19+1 17+1 15+1 13+1
3,6 15+1 15+1 15+1 13+1 11+1 10+1
3,7 12+1 13+1 12+1 11+1 10+1 93+0
3,8 11 н 1 13+1 13+1 12+1 И+1 10+1
3,9 12+1 18+1 17+1 17+1 15+1 13+1
4,0 13+1 26+1 24+1 25+1 21+1 20+1
4,1 30+1 37+1 38+1 35+1 32+1 28+1
4,2 35+1 42+1 43+1 40+1 35+1 30+1
4,3 33+1 38+1 37+1 34+1 29+1 25+1
4,4 26+1 29+1 27+1 25+1 22+1 19+1
224
ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Таблица 19 (продолжение)
Дп Эффективное главное квантовое число п*
2,5 3,0 3,5 4,0 4,5 5,0
Переход d — р', х=1; параметр А
0,1 19+1 31+1 41+1 48+1 53+1 58+1
0,2 24+1 37+1 46+1 51+1 55+1 57+1
0,3 21 + 1 32 4-1 38+1 41+1 43+1 43+1
0,4 15+1 23+1 27+1 29+1 29+1 29+1
0,5 94+0 15+1 17+1 18+1 18+1 18+1
0,6 52+0 87+0 99+0 10+1* •10+1* 10+1*
0,7 32-0 50+0 58+0 63+0 65+0 66+0
0,8 35-0 38-0 47—0 49—0 52+0 52+0
0,9 77+0 50+0* 63+0* 60+0* 63+0* 62+0*
1,0 18+1 12+1 15+1 13+1 13+1 11+1
1,1 16+1 20+1 23+1 21+1 20+1 18+1
1,2 14+1 17+1 18+1 17+1 16+1 14+1
1,3 99+0 12+1 13+1 12+1 11+1 11+1
1.4 63+0 87+0 92+0 89+0 85+0 79+0
1,5 39-0 59+0 62+0 62+0 59+0* 56+0*
1,6 28-0 40-0 43-0 43—0 42—0 40-0
1,7 31-0 31-0 35-0 35-0 34-0 32-0
1,8 57+0 33-0 39-3 35-0 35-0 33-0
1,9 13-И 51+0 64+0 50+0 50+0 44-0*
2,0 17-j-l 12+1 15+1 10+1 10+1 81+0
2,1 13+1 14+1 15+1 13+1 12+1 10+1
2,2 11+1 12+1 12+1 10+1 96+0 84+0
2,3 75+0 89+0 89+0 81+0 73+0 65+0
2,4 47-0 63 |-0 63+0 58+0 53+0 48—0
2,5 31—0 44-0 44-0 42—0 39—0 36—0
2,6 26-0 32—0 33—0 32-0 30-0 27-0
2,7 36-0 28—0 30—0 28-0 26-0 24-0
2,8 75+0 32—0 37-0 30-0 29—0 26—0
2,9 14-|-1 52+0 65+0 45-0 44-0 36-0
3,0 17+1 И+1 14+1 924-0 86+0 65+0
3,1 12+1 12+1 12+1 10+1 91+0 77+0
3,2 10 |-1 10+1 10+1 85 |-0 74-1-0 63 |-0
3,3 67+0 75 j-О 73+0 64-0 56+0 49—0
3,4 42-0 53+0 52+0 47-0 42—0 37-0
3,5 28-0 38-0 38—0 35-0 31—0 28—0
3,6 26-0 29-0 29-0 27-0 25-0 22-0
3,7 40-0 26-0 28—0 25-0 23-0 20-0
3,8 86+0 31-0 36-0 28-0 27-0 23-0
3,9 14+1 52+0 66+0 42-0 41-0 32—0
4,0 17+1 10+1 13+1 84+0 77+0 57+0
4,1 12-И 11+1 11+1 91+0 77+0 64+0
4,2 95+0 92+0 88+0 74+0 63+0 52+0
4,3 63+0 68+0 65+0 56+0 48-0 41—0
4,4 39-0 49-0 47-0 41-0 36-0 31-0
§ 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
225
Таблица 19 (продолжение)
Дп* Эффективное главное квантовое число п*
2,5 3,0 3,5 4,0 4,5 5,0
Переход d — р; х = 1; параметр %
0,1 10+1 10+1 99+0 95+0 90+0 86+0
0,2 88+0 79+0 71+0 64+0 59+0 53+0
0,3 67+0 57+0 49-0 43-0 38-0 33- -0
0,4 48-0 40- -0 33—0 28-0 24-0 20- -0
0,5 32—0 27- -0 21-0 18—0 15-0 12- -0
0,6 21—0 17- -0 14-0 11-0* 10-0* 10- -0*
0,7 19-0 13- -0 11-0 10-0 10-0 10- -0
0,8 42-0 19- -0 18-0 14-0 12-0 10- -0
0,9 16+1 57+0* 55+0* 42—0* 38—0* 32- -0*
1,0 44-J-1 26+1 25+1 18+1 15+1 12Н Н1
1,1 40+1 41+1 36+1 31+1 26+1 22- Н1
1,2 27+1 25+1 21+1 17+1 15+1 12- -1
1,3 15+1 13+1 11+1 93+0 78+0 66+0
1,4 88+0 74+0 61+0 50+0 42-0 35- -0
1,5 54+0 45- -0 36-0 30-0 25—0* 20- -0*
1,6 44—0 31- -0 26-0 21-0 17-0 14- -0
1,7 65+0 30- -0 27-0 21-0 18-0 15- -0
1,8 16+1 49- -0 48-0 34-0 31-0 25- -0
1,9 41+1 12Н (-1 12+1 84+0 75+0 60+0*
2,0 46-j-1 40- -1 39+1 26+1 23+1 17+1
2,1 42+1 42- -1 36+1 31+1 26+1 21+1
2,2 28+1 26- -1 22+1 18+1 15+1 12+1
2,3 16+1 14- -1 12+1 10+1 85+0 71+0
2,4 98+0 85- -0 70+0 57+0 47-0 40- -0
2,5 65+0 53Н НО 44-0 36-0 29-0 24- -0
2,6 63+0 40- -0 34-0 27-0 23-0 19- -0
2,7 11+1 42- -0 39-0 29-0 25-0 21- -0
2,8 27+1 70+0 70+0 47—0 43-0 34- -0
2,9 47+1 16+1 18+1 11+1 10+1 76+0
3,0 45+1 45+1 45+1 29+1 26+1 19+1
3,1 42+1 42+1 36+1 30+1 25+1 21+1
3,2 29+1 27+1 22+1 18+1 15+1 13+1
3,3 17+1 15+1 12+1 10+1 88+0 73+0
3,4 10+1 91+0 74+0 61+0 51+0 42- -0
3,5 72+0 58+0 48-0 39-0 33-0 27- -0
3,6 77+0 46- -0 39-0 31—0 26-0 22- -0
3,7 14+1 50+0 47—0 34-0 30-0 24- -0
3,8 33+1 84+0 86+0 56+0 51+0 40- -0
3,9 47+1 19+1 21+1 12+1 11+1 87+0
4,0 45+1 48+1 47+1 31+1 27+1 20+1
4,1 42+1 42+1 36+1 30+1 25+1 21+1
4,2 29+1 27+1 22+1 19+1 15+1 13+1
4,3 17+1 16+1 13+1 10+1 90+0 75+0
4,4 10+1 94+0 77+0 64+0 53+0 44- -0
8 Л. А. Вайнштейн и др.
226
ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Таблица 19 (продолжение)
Дп* Эффективное главное квантовое число п*
2,5 3,0 3,5 4.0 4,5 5,0
Переход d — р\ и — 3; параметр А
0,1 20—1 55-1 10- -0 16-0 24-0 33-0
0,2 11-0 30-0 55+0 85+0 12+1 15+1
0,3 29-0 74+0 12+1 19+1 25+1 31+1
0,4 534-0 12+1 20+1 27+1 34+1 39+1
0,5 734-0 15+1 23+1 29+1 34+1 37+1
0,6 80-рО 15+1 21+1 25+1 27+1 29+1
0,7 70+0 12+1 16 |-1 18+1 19+1 20+1
0,8 51+0 88+0 11+1 12+1 12+1 13+1
0,9 32-0 55-j-О 71+0 80+0 87+0 90+0
1,0 20-0 37—0 51+0 62+0 70+0 76+0
1,1 15-0 32-0 49- -0 65+0 78+0 89+0
1,2 17-0 41-0 67+0 92+0 11+1 13+1
1,3 26—0 62+0 10+1 14+1 16+1 19+1
1,4 40-0 91+0 14+1 18+1 21+1 22+1
1,5 53+0 11+1 16+1 19+1 20+1 21+1
1,6 58+0 11+1 15+1 16+1 17+1 17+1
1,7 51+0 93+0 11+1 12+1 12+1 12+1
1,8 39-0 69+0 85+0 93+0 94+0 92+0
1,9 27-0 49—0 62+0 70+0 73+0 73+0
2,0 20—0 38-0 52+0 61+1 66+0 67+0
2,1 17-0 36-0 53+0 66+0 74+0 76+0
2,2 20-0 44-0 67+0 87+0 96+0 10+1
2,3 27—0 60+0 93+0 11+1 13+1 13+1
2,4 38-0 82+0 12+1 15+1 15+1 16+1
2,5 48-0 97+0 13+1 15+1 15+1 15+1
2,6 51+0 96+0 12 л И 13+1 13+1 12+1
2,7 45-0 81+0 10- -1 10+1 10+1 99+0
2,8 34-0 62+0 76- 1-0 82+0 81+0 76+0
2,9 25-0 46-0 584 -0 64+0 65+0 63+0
3,0 19-0 38-0 51- -0 58+0 62+0 59+0
3,1 18-0 37-0 52- -0 64+0 69+0 65+0
3,2 20-0 44-0 654 НО 83+0 84+0 92+0
3,3 28-0 59+0 87п -0 11+1 11+1 11+1
3,4 38-0 77+0 И- -1 13+1 13+1 13+1
3,5 46-0 90+0 124 Н1 13+1 13+1 13+1
3,6 48-0 88+0 11+1 12+1 11+1 11+1
3,7 42-0 75+0 92+0 98+0 93+0 85+0
3,8 32—0 58+0 71+0 76+0 74+0 69+0
3,9 24-0 45-0 56+0 62+0 62+0 58+0
4,0 19-0 37—0 50+0 56+0 61+0 50+0
4,1 18-0 37-0 52+0 64+0 68+0 57+0
4,2 21-0 44-0 63+0 83+0 75+0 82+0
4,3 28-0 58+0 83+0 11+1 98+0 98+0
4,4 37-0 75+0 10+1 12+1 12+1 11+1
§ 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИИ
227
Таблица 19 (продолжение)
Ап* Эффективное главное квантовое число п*
2,5 3,0 । 3,5 4,0 4,5 5,0
Переход d, — р: X — 3; параметр %
ОД 21-0 32-0 43-0 56+0 69+0 82+0
0,2 68+0 97+0 12+1 15+1 18+1 21+1
0,3 12+1 17+1 21+1 25+1 28+1 30+1
0,4 19+1 24+1 28+1 31+1 32+1 32+1
0,5 24+1 29+1 31+1 31+1 31+1 29+1
0,6 27+1 29+1 29+1 28+1 26+1 23+1
0,7 26+1 26+1 24+1 22+1 20+1 18+1
0,8 21+1 20+1 19+1 17+1 15+1 13+1
0,9 14+1 15+1 14+1 13+1 12+1 11+1
1,0 10+1 11+1 12+1 12+1 12+1 11+1
1,1 86+0 11+1 13+1 15+1 16+1 16+1
1,2 10+1 15+1 20+1 24+1 26+1 27+1
1,3 15+1 24+1 31+1 37+1 40+1 41+1
1,4 23+1 33+1 42+1 47+1 48+1 46+1
1,5 30+1 39+1 45+1 46+1 45+1 41+1
1,6 32+1 38+1 40+1 39+1 36+1 32+1
1,7 28+1 32+1 32+1 30+1 27+1 24+1
1,8 21 + 1 24+1 24+1 22+1 20+1 18+1
1,9 15+1 18+1 19+1 18+1 17+1 16+1
2,0 11+1 15+1 17+1 17+1 17+1 16+1
2,1 10+1 15+1 18+1 21+1 21+1 20+1
2,2 12+1 19+1 25+1 29+1 30+1 30+1
2,3 17+1 27+1 35+1 40+1 41+1 41+1
2,4 24+1 36+1 44+1 48+1 48+1 46+1
2,5 30+1 41+1 47+1 48+1 45+1 41+1
2,6 32+1 39+1 42+1 41+1 37+1 33+1
2,7 28+1 33+1 34+1 32+1 29+1 25+1
2,8 21+1 25+1 26+1 25+1 23+1 20+1
2,9 15+1 20+1 21+1 20+1 19+1 18+1
3,0 12+1 17+1 19+1 20+1 20+1 18+1
3,1 11+1 17+1 21+1 23+1 24+1 22+1
3,2 13+1 21+1 27+1 31+1 31+1 33+1
з,з 18+1 28+1 37+1 41+1 42+1 44+1
3,4 25+1 37+1 46+1 49+1 48+1 47+1
3,5 31+1 41+1 48+1 48+1 46+1 43+1
3,6 31+1 40+1 43+1 42+1 39+1 34+1
3,7 27+1 33+1 35+1 33+1 30-4-1 27+1
3,8 21+1 26+1 27+1 26+1 24+1 22+1
3,9 15+1 20+1 22+1 22+1 21+1 20+1
4,0 12+1 18+1 20+1 21+1 22+1 19+1
4,1 12+1 18+1 22+1 25+1 26+1 22+1
4,2 14+1 22+1 29+1 33+1 31+1 31+1
4,3 19+1 29+1 38+1 43+1 39+1 43+1
4,4 26+1 37+1 46+1 49+1 47+1 49+1
8*
228
ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Таблица 20
Переходы без изменения спина. Нормированные борновские
и борн-кулоновские сечения
Атом Переход C <p A X
HI 1 .S'—2.S’ 2,52 0,862 5,13 1,05
—2/7 51,4 5,62 18,2 0,226
-3s 2,03 0,757 4,74 1,19
—Зр 33,5 4,10 16,1 0,308
-3d 1,68 1,82 1,78 0,579
—4s 1,89 0,730 4,58 1,23
—4/> 29,4 3,75 15,4 0,334
-4d 1,98 1,72 2,22 0,610
-4/ 0,0309 1,07 0,0546 0,902
2s—3s 2,38 1,66 2,53 0,568
—dp -Ы 7,67 1,18 11,5 0,780
—4s 1,54 1,18 2,38 0,817
—4/> — — 1,41* 0,085
-4d 3,03 0,587 8,86 1,44
-4/ 1,66 0,723 4,10 1,23
2p~ 3s 0,913* 1,01 1,41 0,961
—3p 7,29* 2,20 5,53 0,386
—3d 132 12,5 20,2 0,077
—4s 0,625* 0,688 1,42 1,33
—4p 4,88 1,12 7,48 0,793
—4d 51,2 4,75 21,0 0,259
-4/ 7,35 2,05 6,99 0,520
3s—4s 2,95 4,22 1,40 0,270
— 4/7 — — 0,944 0,085
—4d 6,12 3,25 3,83 0,316
-4/ 2,69 0,695 6,70 1,24
3/>—4s 1,10* 1,03 1,46 0,812
—4p 10,6* 7,14 3,09 0,158
—4d — — 5,86 0,0378
-4/ 19,5 2,78 12,7 0,342
3d—4s 0,291 1,02 0,526 0,979
-4/7 1,40* 0,892 2,44 0,928
—4d 12,9 6,90 3,81 0,224
-4/ — — 12,8 0,051
Не I ls2—ls2s ‘5 1,77 0,93 3,3 0,94
— 2/7 *P 48,9 6,64 15,0 0,20
—3s IS 1,61 0,89 3,21 1,00
—3/AP 43,0 5,87 14,7 0,22
—4s 15 1,57 0,86 3,17 1,00
—4/7 iP 41,2 5,63 14,7 0,23
Hell Is—2s 2,63 1,19 4,63 0,817
-2/7 54,1 7,15 16,4 0,188
—3s 2,09 1,11 3,93 0,862
—3/7 36,3 5,87 13,4 0,227
—3d 1,82 3,68 1,06 0,282
§ 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
229
Таблица 20 (продолжение)
Атом Переход C Ф A X
НеП Is—4s 1,94 1,09 3,71 0,875
—4p 32,1 5,54 12,5 0,240
—4J 2,15 3,55 1,30 2,93
-4/ 0,0327* 2,39 0,0292 0,394
2s—3s 2,42 1,32 3,84 0,753
—3p 20,9* 14,8 2,92 0,0378
—3d 7,72 1,89 8,63 0,580
—4s 1,53 1,20 2,66 0,808
—4p 13,1 12,4 2,21 0,0576
—id 3,14 1,42 4,63 0,714
-if 1,68 1,40 2,55 0,721
2p—3s 1,21* 3,87 0,644 0,367
—3p 8,17 1,65 10,4 0,624
—3d 104 6,69 33,7 0,218
—4s 0,775* 2,78 0,572 0,496
—ip 5,19 1,33 8,22 0,740
-id 46,5 3,99 25,0 0,336
-4/ 7,32 3,07 5,19 0,385
3s—4s 2,46 1,42 3,63 0,718
—ip — 1,30 -0,0180
-id 4,81 2,18 4,68 0,568
—if 2,56 0,982 5,47 1,00
3p—is 1,60* 4,86 0,680 0,328
—ip 9,02 2,15 8,92 0,515
—id 58,1 11,3 11,3 0,137
-if 17,5 2,16 17,5 0,553
3d—is 0,277 1,40 0,418 0,778
—ip 1,59 2,27 1,51 0,567
—id 11,9 2,31 11,1 0,498
-if 214 13,8 33,7 0,121
Lil 2s—2p 22,0 4,90 7,35 0,15
—3s 2,35 1,21 3,30 0,71
-3p 1,67 0,48 5,70 1,62
2p—3s 8,99 7,51 2,35 0,088
—3p 7,25 2,07 5,71 0,389
3s—3p — — 2,77 -0,013
Bel 2s« tf—2p IP 50,6 4,27 21,4 0,24
-,3s 2,29 1,17 3,47 0,77
—3/jiP 2,58 0,55 7,78 1,14
Bell 2s—2p 12,4 3,12 8,29 0,389
—3s 2,50 1,37 3,81 0,722
-3p 6,11 17,9 0,72 0,084
-3d 8,08 2,28 7,52 0,484
ВИ 2s2 'S—2p 4> 8,18 2,75 6,20 0,430
CI 2p—3s 10,3 8,31 2,56 0,119
—3p 7,55 1,01 12,7 0,845
230
ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Таблица 20 (продолжение)
Атом Переход C ф A X
NI 2jP4>—2psapi) 0,12 4,24 0,049 0,221
2p—3.? 10,6 8,40 2,62 0,120
—3p 6,70 0,99 11,7 0,882
—4s — 1,71 0,113
—3d 29,1 9,94 6,09 0,131
01 2p4iD-2p* 1) 0,44 2,33 0,18 0,40
2p—3s 9,66 8,60 2,35 0,135
-3p 5,45 0,97 9,64 0,893
—4s 5,83 7,24 1,68 0,143
-3d 23,6 9,92 4,96 0,132
FI 2p—3s 8,84 8,47 2,16 0,118
-3p 5,07 0,98 9,05 0,904
-3d 19,3 9,03 4,42 0,148
Nal 3s—3p 34,5 6,07 9,91 0,144
—3d 7,45 1,27 10,6 0,740
3p—3d 142 14,8 17,9 0,064
Mgl 3s® lJ—Зр ip 60,8 6,15 18,8 0,188
-4s 1*9 2,26 1,37 2,99 0,688
—3d 11,3 1,04 19,1 0,862
-4p IP 10,2 1,57 11,5 0,611
Mg II 3s—3p 24,8 3,99 13,0 0,318
—4s 2,41 1,42 3,55 0,703
-3d 8,46 2,01 8,88 0,538
—4p 2,09 1,03 4,19 0,926
AU 3p—4s 18,3 8,99 4,26 0,140
Al И 3s2 ’5—3p 36,8 4,49 17,3 0,288
KI 4s—4p 34,7 7,52 ; 8,00 0,105
—5s 2,22 1,48 2,64 0,620
-3d 7,95 1,05 13,2 0,836
—5p 4,83 1,05 7,82 0,827
4p—5s 18,1 11,9 3,16 0,090
-3d 125 22,1 10,6 0,031
—5p 8,25 3,27 4,74 0,316
5s—3d 0,122 2,15 0,101 0,484
3d—5p 19,3 13,2 2,77 0,083
Cal 4s® i$-3d lD 3,05 0,821 6,41 1,04
—ЬрЧ> 59,2 7,86 14,3 0,143
-5s1 J 2,78 1,72 3,03 0,582
Call 4s—3d 0,360 1,02 0,732 0,908
—4p 26,3 4,54 12,2 0,289
—5s 2,27 1,50 3,17 0,673
—4d 5,48 2,54 4,59 0,452
х) х = 2
f 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
231
Таблица 20 (продолжение)
Атом Переход C Ф A X
Gul 4s—ip 36,6 4,18 15,3 0,226
—5s 2,10 1,14 3,22 0,783
—5p 8,14 1,20 H,7 0,756
—4d 5,69 1,39 7,55 0,696
ip—5s 14,6 7,68 3,80 0,165
—5p 6,34 1,87 5,75 0,461
-id 121 10,4 22,9 0,120
5s—5p 50,7 18,7 5,06 0,026
—4d 4,58 1,34 5,79 0,627
Znl 4s«iS-ip'P 63,9 5,28 22,9 0,217
—5s iS 1,99 1,33 2,72 0,711
—id 4) 8,7 1,20 13,1 0,778
—Ър1Р 16,3 1,97 14,9 0,510
Znll is—ip 27,8 4,06 14,4 0,312
Gal ip— 5s 17,3 7,78 4,57 0,169
—5p 6,28 1,47 7,46 0,611
-id 141 7,42 37,1 0,167
-6s 7,54 5,94 2,66 0,210
Gall 4s2 is—ip ip — — 18,6 0,283
-5s IS — — 2,63 0,616
—idlD — — 10,6 0,525
ВЫ 5s—5p 37,5 8,17 8,07 0,099
—id 6,89 0,990 12,0 0,870
—6s 2,16 1,57 2,47 0,599
—6p 5,73 1,26 7,87 0,718
5p—id 74,4 20,2 6,64 0,014
—6s 19,6 12,7 3,20 0,085
—&p 8,35 3,50 4,58 0,307
id—fys 0,144 1,68 0,153 0,583
—6p 13,9 12,2 2,37 0,112
6s—6p — — 3,27 —0,016
Sr I 5s2 IS—id 4) 4,51 0,867 8,87 0,971
—5p4> 68,5 10,3 13,2 0,120
-6s IS 3,16 2,03 3,01 0,517
-6p 2,89 0,688 7,14 1,20
Sr II 5s—id 0,627 1,09 1,19 0,868
—5p 28,9 4,81 12,7 0,277
—6s 2,20 1,54 2,99 0,659
—5rf 4,08 2,85 3,05 0,414
Agl 5s—5p 40,8 4,56 15,7 0,210
—6 s 2,21 1,22 3,20 0,746
—&p 8,26 1,26 11,4 0,726
—5d 6,39 1,43 8,26 0,680
232
ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИИ
Таблица 20 (продолжение)
Атом Переход C ф A X
Agl 5p—6s 16,5 8,56 3,89 1,152
-6p 6,65 1,97 5,81 0,448
-5d 129 10,8 23,4 0,115
6 s—&p 47,7 18,2 4,78 0,018
—5d 4,26 1,37 5,24 0,610
Cdl 5s2 IP 72,0 6,11 22,7 0,194
—6s> V 2,34 1,45 2,98 0,668
—5d iD 9,94 1,32 13,8 0,723
—6p LP 14,7 2,03 13,2 0,502
Cd II 5s—5p 29,8 4,25 14,8 0,302
Ini 5p—6s 20,9 9,22 4,75 0,136
—6p 7,78 1,60 8,50 0,565
—5d 172 8,56 39,7 0,148
In II 5s2 15—5p lP — — 18,9 0,271
—6s 15 *—• — 2,79 0,600
CsI 6s—6p 39,4 9,26 7,54 0,085
—5d 3,86 0,914 7,22 0,927
—7s 2,14 1,73 2,27 0,565
-7P 5,90 1,36 7,58 0,676
6p-5d 15,9 15,0 1,81 0,0071
-7p 8,80 3,83 4,47 0,288
M-7s 0,368 0,784 0,796 1,06
-7p 1,58 2,05 1,25 0,428
Bal 6s2 i5-5rf XD 1,53 0,926 2,87 0,938
—6p *P 63,0 10,2 11,9 0,110
—7s 15 2,26 2,83 1,66 0,369
Ball 6s—5d 0,242 1,01 0,498 0,916
—&p 29,6 4,96 12,6 0,269
-7s 2,14 1,58 2,84 0,645
—6d 4,71 2,69 3,72 0,436
5d-6p 14,1 3,58 8,11 0,344
-7s 0,207 1,19 0,363 0,840
-6d 7,80 1,77 9,32 0,593
Qp—7 s 13,8 6,80 4,38 0,212
6p—&d 94,3 8,79 23,4 0,172
7s—6rf 1,19 1,21 2,05 0,828
Hgl 6s2 15—6pl P 69,5 6,38 20,8 0,181
—7s IS 3,04 1,63 3,51 0,613
6p 3P—7s aS 23,8 9,43 5,25 0,136
6p>P—7s IS 18,4 7,01 4,78 0,141
$ 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
233
Таблица 21
Сечения и скорости возбуждения водородоподобного Ne X в
борн-кулоновском приближении
Переход C ч> A X
is—2s 2,65 1,05 5,23 0,890
-2Р 45,9 4,82 20,4 0,288
-3s 2,12 1,02 4,29 0,911
-Эр 31,7 4,18 16,2 0,323
—3d 1,71 2,97 1,23 0,388
—4s 1,97 1,01 4,03 0,917
—4р 28,3 4,01 15,2 0,335
-4d 2,02 2,88 1,51 0,397
-4/ 0,0316 1,92 0,0351 0,534
2s—3s 2,42 1,03 4,89 0,907
-Зр 17,1 8,30 4,43 0,182
—3d 7,14 1,52 9,90 0,725
—4s 1,52 0,987 3,19 0,937
—4p 10,8 7,06 3,31 0,209
—4d 3,01 1,27 4,98 0,805
-4/ 1,58 1,19 2,78 0,849
2p—3s 1,27* 4,48 0,599 0,333
-3p 8,17 1,15 14,8 0,825
-3d 81,3 3,26 53,1 0,418
—is 0,821* 3,37 0,513 0,411
—ip 5,18 1,11 9,75 0,850
—id 41,1 2,69 32,6 0,483
-if 6,57 2,33 6,10 0,528
3 s—4s 2,45 0,990 5,15 0,939
—4/? 0,80* 8,64 2,39 0,200
-id 4,05* 1,57 5,29 0,782
-if 2,38 0,913 0 >42 1,10
3p—is 1,46* 4,59 0,654 0,364
—ip 8,90 1,18 15,7 0,812
-id 37,1* 4,08 19,4 0,374
-if 15,2* 1,45 22,2 0,811
3d—is 0,255 1,15 0,460 0,928
—ip 1,52* 2,33 1,43 0,589
-id 12,2 1,08 23,7 0,868
-if 123* 2,50 98,7 0,538
Примечание. Параметры С, <р и А, X из табл. 21 можно использо-
вать для любого водородоподооного иона с г^>3.
234
ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Таблица 22
Сечения и скорости возбуждения гелиеподобного иона Na X
в борн-кулоновском приближении с учетом обмена; переходы
без изменения спина
Переход C ч> A X
ls21S—2sxS 2,72 1,92 2,99 0,55
—2р1Р 54,1* 10,3 10,7 0,048
—3s 1-5 2,24 2,10 2,26 0,510
—Зр ХР 33,8* 8,23 7,99 0,039
—3d Ч) 1,00* 3,61 0,44* 0,025
—is lS 2,10 2,17 2,06 0,49
—iplP 28,6* 7,51 7,26 0,035
-id lD 1,18* 3,44 0,53 0,024
-4/xF 0,21* 1,58 0,024 0,55
2s XS—3s iS 2,41 1,37 3,67 0,73
—3p XP 20,9 16,7 2,67 0,057
—3d ID 8,02 2,98 5,78 0,42
2s aS—3s »S 2,38 1,27 3,90 0,770
—3p3P 19,3 13,5 3,07 0,0106
-3d»D 7,27 2,08 7,39 0,58
Примечание. Параметры С, ф и А, х из табл. 22 можно использо-
вать для любого гелиеподобного иона с 3.
Таблица 23
Скорости интеркомбинационных переходов
Atom Переход A" X" Atom Переход A" X*
He I tz. tZ) Co ftq C| J OS co OS % eo co ^.'43 СЧ OJ CQ CQ 1 1 1 1 1 H «о 5» 0,93 11,0 1,5 13,0 1,1 14,0 1,7 0,53 0,71 0,90 0,88 1,10 0,94 0,93 Al II 3s2 2s-3p 3P 3,40 0,32
Cal 4s2 XS—ip 3P -3d*D —5s 3S 2,33 7,59 1,46 0,085 0,37 0,40
Znl “ nJ n » Illi яЧ СЧ 5 3,46 0,80 5,74 18,4 0,11 0,31 0,50 0,77
Bel £ £ Illi CO CO OO № w и M 2,48 0,81 3,06 17,8 0,220 0,27 0,35 0,80
Ga II 4s2xS—ip3P -5s »S —id 3D 4,43 2,00 16,9 0,35 0,98 0,98
В П 2s2 lS—2p 3P 5,15 0,32 Sri 3s^S—3p3P —id *D —6s «S 2,61 7,31 2,17 0,097 0,31 0,52
Mg I ^czs^ej OS M OS os a.’ts co vr Illi 2? 4, co 2,69 0,86 4,90 24,5 0,10 0,28 0,51 0,70
Cd I Сл % Co Illi СП 05 05 CO £.•« «»Чз 3,48 0,98 9,89 21,5 0,091 0,35 0,43 0,88
$ 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
235
Таблица 23 (продолжение)
Атом Переход А" X* Атом Переход A" x'
In II 5s» 15—5рЗ р 4,66 0,44 Hgl 6s2 6р »Р —7s»S Ър Зр—Qp ip —7s IS epip-7s*S 7saS—7s1S 5,04 1,60 1,46 3,25 2,17 0,10 0,13 0,47 0,031 1,11 0,47 —0,030
Bal №'S—bd*D —Ьр3Р —7s aS 1,62 2,43 2,17 0,097 0,089 0,55
Таблица 24
Сечения и скорости возбуждения гелиеподобного иона NaX;
интеркомбинационные переходы (АкУ = 1). Интервалы аппроксимации
0,01 < и <5, 1/4<(3<8
Переходы C Ф" A" X"
isaiS—2s«£ 4,62 5,72 1,77 0,522
—2p »P 7,01* 1,12 11,1 0,877 .
—3saS 3,56 3,46 1,87 0,592
-3psP 5,89 0,892 11,6 0,970
—3d aD 0,438* 0,218 2,82 1,45
—isaS 3,24 2,93 2,02 0,638
—ipaP 5,58 0,830 11,7 0,983
—id aD 0,54* 0,209 3,60 1,45
—ifaF — — 0,24* 2,21
2s—3s 0,83 3,08 0,49 0,635
—3p 1,22* 1,84 1,12 0,611
—3d 3,29* 1,48 3,73 0,683
2s—is 0,48 1,57 0,56 0,863
—ip 0,81* 1,02 1,28 0,755
-id 2,06 2,06 3,12 0,723
-if — — 2,69 1,21
2p—3s 1,38* 2,93 0,81 0,546
—3p 5,82* 2,20 4,68 0,629
—3d 8,92* 1,16 13,4 0,820
—is 0,84* 1,45 0,99 0,750
—ip 3,57* 1,23 4,95 0,769
—id 5,95* 0,706 14,1 0,956
-if — — 6,89 1,44
3p—is 0,35 1,27 0,47 0,723
—ip 2,07* 2,14 1,73 0,637
—id 2,10* 0,937 3,75 0,830
-if —. — 5,35 0,696
3d—is 0,61 1,39 0,73 0,676
—ip 1,41* 0,947 2,41 0,760
—id 5,68 1,35 7,56 0,816
-if 9,74* 1,24 13,5 0,782
Примечание. Параметры С, <р" и А", Iя из табл. 24 можно ис-
пользовать для любого гелиеподобного иона с 3.
236
ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Таблица 25
Переходы между близкими уровнями (AS — 0)
Атом Переход AE/z’, Р СМ-1 ° ч> А X X Метод расчета
Не1 2s—2р 4530 13,0 14,1 1,78 0,0784 1 Борновское приближение с нормиров- кой
Li II 2s—2 р 3560 8,57 5,33 2,03 0,119 1 Борн-кулонов- ское прибли- жение с нор- мировкой
ВIV 2р—2р 200 0,0258 15,4 0,00227 0,0421 2 Борновское приближение
2р—2р 20 0,00258 149 0,229.10-* 0,00424 2 То же
2s—2р 500 1,56 5,36 0,183 0,0547 1
2s—2р 100 0,386 14,5 0,0129 0,0155 1 » >
NaX 2s—2р 850 2,32 4,47 0,356 0,0720 1 > »
3s—Зр 234 4,20 10,0 0,218 0,0419 0,0240 1 » >
3s—3d 280 0,116 1,06 0,167 2
Зр—3d 46 1,39 28,5 0,0205 0,00679 1 > »
CV Зр—Зр 20 0,0164 8,75 0,511 ЛО-3 0,0143 2 Борновское приближение
3d—3d 20 0,0150 27,6 0,343.10'3 0,0106 2 То же
Fe XXV 2s—2р 500 1,66 13,4 0,108 0,0308 1 Борн-кулонов- ское прибли- жение
2s—2р 500 1,66 5,38 0,193 0,0541 1 Борновское приближение
2р—2р 180 0,023 17,0 0,00184 0,0379 2 То же
Таблица 26
Скорости интеркомбинационных переходов между
близкими уровнями, вычисленные для гелиеподобного
иона NaX
Переход ДЕ/z», см~* А" X*
2s—2s -2р 2р—2р 3s—3s -Зр -3d Зр—Зр —3d 3d—3d 200 747 200 20 210 252 20 42 20 0,0096 0,047 0,087 9,7.10-* 0,015 0,028 0,0067 0,013 0,029 0,0050 0,017 0,0057 1,2.10-» 0,013 0,017 0,0012 0,0029 0,00135
§ 18. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ СЕЧЕНИЙ
237
Таблица 27
Сечения и скорости ионизации нейтральных атомов
Атом Уровень (оболоч- ка) C A X Atom Уровень (оболоч- ка) C Ф A X
HI is 9,3 2,5 9,7 0,73 CI 2p2 36 8,0 12 0,27
2s 6,4 1,2 12 1,2 2s» 5,1 2,1 5,9 0,78
2p 3s 23 5,5 1,9 0,90 31 14 0,91 1,6 NI 2p8 34 10 9,0 0,21
3p 17 1,2 33 1,2 0 I 2pi 31 11 7,6 0,22
3d 35 1,9 50 0,92 FI 2p8 30 13 6,1 0,18
Hel Is»’5 2s 3S 3,4 6,0 4,1 1,3 7,1 11 0,48 1,2 Nel 2p* 28 11 5,1 0,16
2p3P° 26 2,2 29 0,80 Na I 3s 5,3 0,84 17 1,8
Lil 2s 5,1 1,0 12 1,5 KI 4s 5,7 1,1 15 1,5
2p 25 2,2 30 0,82 Rbl 5s 5,7 1,3 13 1,3
Bel 2s» 5,8 1,6 9,1 1,0 CsI 6s 5,7 0,92 17 1,7
BI 2p 2s» 34 5,4 5,6 1,8 17 7,3 0,35 0,90 Ar I 3p6 36 2,8 37 0,71
...... Mg I 3s» 5,4 0,88 15 1,7
Таблица 28
Сечения и скорости ионизации ионов [Н] и [Не]
Ион Оболочка c Ф A X
NeX [H] Is 9,3 2,5 8,1 0,57
О VII [He] is» 9,6 2,6 7,9 0,53
2s 6,5 1,3 10 1,0
2p 23 1,9 26 0,68
3s 5,3 0,87 12 1,3
3p 17 1,2 27 1,0
3d 34 1,9 40 0,65
238
ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Таблица 29
Скорость диэлектронной рекомбинации ионов [Н]
и [Не]
*4-1 [Н] 1» - 2р [Не] 1 *S — 2 «’•Р
Ad *d Ad xd
4 36,7 0,72 23,6 0,90
7 28,3 0,68 18,2 0,77
10 21,0 0,65 15,0 0,71
15 13,0 0,62 7,8 0,66
20 7,8 0,59 5,3 0,63
25 4,9 0,58 3,8 0,62
30 3,1 0,57 2,6 0,61
Таблица 30
Скорость диэлектронной рекомбинации ’ионов от [Li] до [Ne]
*4-1 2» —2р 2» — Зр 2p — 3d
Ad Xd Ad *d Ad Xd
Ион [Li]
4 6,75 0,04 6,52 0,16 — —
7 2,73 0,02 6,88 0,14 —
10 1,43 0,02 6,35 0,13 —. —
15 0,65 0,01 — — — —
20 0,37 0,01 3,54 0,11 —— ——
30 0,16 0,004 1,70 0,10 — —
Ион [Be] •
4 16,8 0,08 7,0 0,19
7 6,70 0,04 8,4 0,16 —
10 3,67 0,03 7,7 0,14 —
15 1,63 0,02 — — — a—
20 1,04 0,01 4,1 0,11 —-
30 0,57 0,01 1,95 0,10 — —
Ион [В]
2 17,5 0,14 1,70 0,36 54,3 0,24
5 7,27 0,05 5,26 0,21 93,1 0,18
12 1,78 0,02 5,25 0,14 66,5 0,14
20 0,70 0,01 3,32 0,12 41,7 0,12
30 0,28 0,006 1,70 0,10 23,1 0,10
§ 19. ФОРМУЛЫ ДЛЯ Q-ФАКТОРОП
239
Таблица 30 (продолжение)
z + l 2s — 2р 2s — Яр 2p - 3d
Ad Xd Ad *d Ad *d
Ион [С]
2 21,9 0,19 1,42 0,44 41,1 0,29
5 8,91 0,06 4,71 0,24 83,3 0,20
12 2,17 0,02 4,93 0,15 63,8 0,14
20 0,91 0,012 3,11 0,12 40,5 0,12
30 0,38 0,007 1,63 0,11 22,3 0,10
Ион [N]
2 25,9 0,25 1,25 0,53 55,3 0,33
5 10,5 0,07 4,15 0,27 74,6 0,22
12 2,64 0,03 4,62 0,16 61,0 0,15
20 1,10 0,014 2,92 0,13 39,5 0,12
30 0,48 0,009 1,53 0,11 21,8 0,11
Ион [0]
2 30,4 0,32 1,13 0,63 25,3 0,36
5 12,0 0,09 3,79 0,30 63,9 0,24
12 з;о2 0,03 4,30 0,17 59,0 0,16
20 1,23 0,02 2,76 0,13 38,1 0,13
30 0,58 0,01 1,45 0,11 21,2 0,11
Ион [F]
2 35,0 0,39 1,00 0,73 20,5 0,39
5 13,4 0,10 3,39 0,33 34,5 0,26
12 3,55 0,03 3,94 0,18 56,5 0,17
20 1,39 0,02 2,65 0,14 36,3 0,13
30 0,68 0,01 1,39 0,12 20,7 0,11
Ион [Ne]
2 - 0,83 0,83 16,9 0,42
5 - - — 2,99 0,36 50,0 0,28
12 3,66 0,19 53,4 0,17
20 — 2,51 0,14 35,4 0,14
30 — — 1,31 0,12 19,8 0,12
§ 19. Формулы для Q -факторов
1. Суммирование сечений по группам уровней. В различных
приложениях возникает потребность в определении сечений для
переходов между отдельными уровнями, между двумя группами
близких уровней, для переходов с одного уровня на группу уров-
ней или переходов с данной группы уровней на один уровень
другой группы. Например, можно интересоваться переходами
между отдельными компонентами тонкой структуры двух термов
L0S0J0 — LiSiJt или переходами между термами Lo£o —
240 гл. VI. ФОРМУЛЫ И ТАБЛИЦЫ для оценки сечений
Сечение перехода с уровня а группы уровней А на все уровни
Ь группы уровней В естественно определить формулой
о (Аа, В) = 2 ° (Аа, ВЬ), (19.1)
ь
где о (Аа; ВЬ) — сечение перехода между уровнями а и Ь. В том
случае, когда каждый уровень а группы А заселен пропорцио-
нально его статистическому весу, сечение переходов А -> ВЬ
определяется усреднением по группе начальных уровней
о (Л, ВЬ) = -~у ^g{a)o {Аа, ВЬ), (19.2)
а
а сечение перехода между группами А и В — суммированием по
конечным уровням Ъ и усреднением по всем начальным уровням а:
°в> = ттч У.««° <Ла’ вьу <19-3>
ab
В формулах (19.2) — (19.3) g {а) — статистический вес уровня а,
g (А) = ^g {а) — статистический вес группы уровней А.
а
В принятых в этой главе приближениях эффективные сечения
выражаются в виде (18.1), (18.2) так, что зависимость от кванто-
вых чисел угловых моментов задается фактором Q или Q". Поэтому
суммирование сечений по компонентам тонкой структуры или по
термам, принадлежащим одной электронной конфигурации, сво-
дится к суммированию этих угловых факторов. В последующих
разделах этого параграфа будут приведены формулы для (?-фак-
торов и свойства их суммируемости.
2. Ь$-связь; факторы Qx для переходов без изменения спина.
Для краткости записи совокупность всех квантовых чисел, ха-
рактеризующих терм, в некоторых случаях мы будем обозначать
одной буквой у, а компоненту тонкой структуры терма — двумя
буквами yJ. Из набора квантовых чисел у удобно выделить
квантовые числа моментов атомного остатка Lp, Sp, орбитальный
момент оптического электрона I, полный спин S и полный орби-
тальный момент L. В каждом конкретном выражении мы будем
опускать те квантовые числа, которые не входят непосредственно
в данную формулу.
Индекс мультипольности х, вообще говоря, пробегает значе-
ния X = Xmjn» ^min “Ь 2, . . ., Zo -|- Zj, Hjnin ~ I Zq •— Zj |.
Для перехода между компонентами тонкой структуры термов
L0S и LiS фактор Qy. равен
Сх (Yo-^о» Т1А) = (2Ь0 + 1) (2Ji-J-1) | “ | <2x(Yo»Yi)- (19.4)
t 1 J-'l Л J
§ 19. ФОРМУЛЫ»ДЛЯ Q-ФАКТОРОВ 241
Сумма по Ji (см. формулу (19.42)) не зависит от Jo:
SCMYoJo, YiJi) = (М?о, Ti), (19.5)
Ji
(7-фактор, усредненный по компонентам Jo терма у0, пропорцио-
нален статистическому весу уровня J\:
(2L0 + 1) (2S + 1) Ц (2/о + Till) =
J О
e (2Li + 1) (2Л- + 1) ^°’ '*’9* (19-6)
Формулы, определяющие (7-факторы для переходов между тер-
мами в целом (у0, Yi), в соответствии с определением (19.3)),
приводятся ниже.
I. Один электрон сверх заполненных оболочек. В этом случае
L = I, S = г/2 и
<?x(Zo, /i) = l. (19.7)
II. Переходы, не затрагивающие группы эквивалентных элек-
тронов
У о ~ [J'piSp] IqLqS, Yi — [Z/p5p] IjLjS ,
<?«(?», ?l) = (2i. + l)(2L, + !){'• L.’ (19.8)
t *1 ** I
Суммируя no Li, получим QH(L0S, L^S) — 1. Усреднение no Lo
T-i
дает Qy. ([ZpSp] l0S, [LP5P] liLrf) = (2^4-1)\^ +i) • Для перехода
co всей группы термов конфигурации 10 на группу термов конфи-
гурации 1г с той же мультиплетностью в соответствии с (19.3)
<?х ([LPSP] l0S, [LpSp] ltS) = Q* {lLpSp] l0, [LpSp] ZJ = 1. (19.9)
III. Переходы из оболочки с эквивалентными электронами.
у0 = l^L0S, Y1 = 1Г1 [LpSp] hL.S,
<?x (Yo, Yi) = m (G^Sp)2 (2Z0 + 1) (2M 4-1) { ь?}2, (19.10)
где GLpSp — генеалогический коэффициент. Таблицы генеалоги-
ческих коэффициентов для конфигураций рт приведены в п. 5
этого параграфа.
В результате суммирования по Lx имеем
(19.11)
242 ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ для оценки сечений
Суммируя далее (19.11) no LPSP, получим
QML.S, ir\S) = =
(19.12)
IV. Переходы между конфигурациями'. IqI™ —- Z^-1Z™+1. В слу-
чае переходов между конфигурациями Z^ZP -> Z^-1Z^+1 общие
формулы весьма громоздки, поэтому мы ограничимся рассмотре-
нием заполненных оболочек N — 2 (2Z0 + 1). Для подавляющего
большинства приложений это оказывается достаточным. Итак,
Yo = Z0NzrL05, V1 = Z^’1 [Zo, Va] ZF+1 UpSJ LtS,
где Sp и Lp — соответственно полный спин и полный орбиталь-
ный момент оболочки Z”+1;
Qx(?o, ?1) =
_ {т , n ,rLpSpi2 + D (2lp + D (2г<> + П (2Ьх +1)
- И + 1) (G^P) ---------(25 + l)(2Z0 + l)-----
l0 Li Lpy
Lo lt x J ’
(19.13)
Между генеалогическими коэффициентами для конфигураций
jm+i и /R-m} где r = 2 (2Z + 1), имеет место следующее соотно-
шение:
(_ l)-5'1 /(Я - ш) (25 + 1) (2£ + 1) Gfyr (ZB~”) -
= (- /(m + 1)(25p + 1)(2L„ + 1) Gjf’(/”"). (19.14)
Поэтому выражению (19.13) эквивалентна формула
<2х(Уо, Т1) =
= (4Z1 + 2-m)(G^
Zo Li Lp
Lq Zj x
2
Суммирование no Lx дает
<2x(Z^r*bo5, l^l^lLpSpjS) =
__ (m , n zpbpS (2Ур + 1)(2£р + 1)(22о + 1) __
- {m ± i) (.^LoS ) (2iy + (2Lo _j_ (2Zj +
= (4Z, + 2 - m) (GiJp)> • («1(i)
Усреднение (19.16) no Lo приводит к следующему:
О (lNlmS <7 1 <71 m + 1 ^p + l)(2Lp + l)(2Zo + l)
Vx(Zo4 Zo Zj [Lp»Sp]5)= 2^-f-l
(19.17)
§ 19. ФОРМУЛЫ ДЛЯ Q-ФАКТОРОВ
243
где g (Z™) — статистический вес конфигурации I™, равный числу
сочетаний из 2 (2^ + 1) по тп, т. е.
) = ml (41х + 2 — m)l ’ (19.18)
и, наконец, суммирование (19.16) по Lp и Sp дает
QK(l^^L„S, = (МЧ?. = («, + 2 - m)|£±T.
(19.19)
V. Переходы между термами одной конфигурации.
Yo = l?L0S, У1 = l^L.S.
В этом случае
Т») - -ЙЙт 1 II и" II 17L.S) |>. (19.20)
Приведенные матричные элементы (1™LOS в формуле
(19.20) имеют четные значения х. При х = 0
(l?L,S || U° || Сад = т У <19'21)
Из (19.4) следует также, что
Qy 0> У1/1) 0x3 ftjoJe
т. е. не должно изменяться ни одно из квантовых чисел угловых
моментов. Это означает, что случай х = 0 без учета обмена не
соответствует какому-либо неупругому переходу х).
Наибольший практический интерес представляет случай х =
= 2, соответствующий квадрупольным переходам. Для конфи-
гураций где N = 2 (2Z0 4- 1), и I™ имеет место следующее
соотношение:
(tf'” L„S || £7>||iJ'-’”Z,1S) = —(СМ |0* II CM). (19.22)
В общем случае приведенный матричный элемент можно вы-
числить по формуле
(lmL0S || U* || lmLtS) =
= »3 Gi&fity (- + 1)(2Л + 1) { ' L° Ч.
Р Р Р Р I I X J
(19.23)
где LPSP — термы конфигурации Z™-1.
х) С учетом обмена при х = 0 возможны переходы с изменением спина.
244
ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
Для конфигураций р3 и р3 значения приведенных матричных
элементов приведены в табл. 31.
Таблица 31
(p»LoSo||U«||p»L,S1)
IS »р 1£> *S 2Р 2Р>
0 0 2 Уз- *s 0 0 0
3Р 0 —1 0 *Р 0 0 — Уз
Ч) 2 УТ 0 1/" 7 И "з 2D 0 ут 0
3. Интер комбинационные переходы; угловые факторы Q"*
Сечения и скорости возбуждения интеркомбинационных перехо-
дов, приведенные в § 18, вычислены методом ортогонализованных
функций (см. § 7). Здесь мы приведем формулы для атомов с ос-
новным состоянием ns3, т. е. для гелия, элементов второй группы
периодической системы, а также их изоэлектронных последова-
тельностей.
Для переходов из основного состояния
То = nos* 15, Yi = n^nrl^^LY
угловой фактор пропорционален статистическому весу уровня
<?'(?./.!= о, Wi) = т-ёйт <19-24)
Для суммарного по сечения
Q'№,liS!)= 2%+1 . (19.25)
В случае переходов между возбужденными состояниями таких
атомов То = ns [0, V2] n0l0S0i Yi = ns [0, V2] n^S»
Q’il., Vi) = (2У й (19.26)
В случае переходов с синглетов
Q"{1А = О, W,/,) - 4^X1) ' (19-27)
В случае произвольных Sp и Lp =# 0 в виде (18.2) можно предста-
вить суммарное по сечение о". При этом
Q" (l^LA, 1Г1 [Зд.1 W = т (0^,)* . (19.28)
§ 19. ФОРМУЛЫ ДЛЯ Q-ФАКТОРОВ
245
4. J/-связь. Ниже приводятся формулы для угловых факторов
в двух случаях: 1) оба уровня, начальный и конечный, описы-
ваются в схеме /7-связи; 2) один уровень описывается в схеме
Ь£-связи, а другой — в схеме /7-связи.
1) Для перехода между компонентами тонкой структуры двух
дублетов имеем
г v т 1/12
(ад, ад) - (2я0 +1) (2л +1) {е° 7 " I Q. (к0,
I J1 Л. 1 л J
(19.29)
Суммирование по дает
Q. (K0J0, KJ = QK (Ко, KJ. (19.30)
Усредняя выражение (19.29) по Jo, получим
(Ко, ад) = Q* kj. (19.31)
Схема /7-связи внутри оболочки эквивалентных электронов
не имеет смысла. Поэтому следует рассматривать лишь один слу-
чай, а именно, переходы, не затрагивающие группы эквивалент-
ных электронов (это соответствует случаю II в п. 2). Для пере-
хода между дублетами у0 = [Z,P5P/] l0K0, = [LPSP/]
в целом фактор Q» равен
Q* (То, Тх) - (2/о + 1) (2Х, + 1) { £ *•'}’. (19.32)
Суммирование (19.32) по Кг дает
Go Ко, li) = Q* Go, li) = 1, (19.33)
а усреднение по Ко —
= (19.34)
2) Если начальный уровень Т0/0 описывается в схеме LS-
связи, а конечный уровень — в схеме /7-связи, т. е.
То = [£р£Р1 /о^о^о, У1 = tLpSyj] то угловой фактор
ФхСМо, ?1Л) равен1)
(МтоЛ, TiA) =
= (2Z0 +1) (2Л +1) (250 +1) (2Lo+1) (2/ +1) (2Kt +1)
Lq Sp x К i ®
lo Jo 1 l/t
,Lp So ./j_
(19.35)
Усредняя no Jo и суммируя затем no Jlt для перехода между
1) Определение 12/-символа 2-го рода дается формулой (19.53).
246
ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ ДЛЯ ОЦЕНКИ СЕЧЕНИЙ
термами в целом получим
<м?.. г.)- (2*.
x$>+i){tp £;}*{£ i;}'- («-Зв)
г
Суммирование (19.36) по Кх дает
Q* ИЗД,] WoSo, [LpSpj] h) = (2Zp+2^p + 1) • (19.37)
Далее, суммируя по у, получим
([LPSP] l0L0S0, [ад] /,) = 1. (19.38)
Усреднение (19.36) по Lo дает
<?H([LpSp] l0S0, [LpSpj] hKi) — ^2ij} д_ j) (2Jp +1) (2Ii +1)' (19.39)
Для переходов из группы эквивалентных электронов I™ -►
-> Щ формулы (19.35) — (19.38) следует умножить на
5. 3 nJ-символы и генеалогические коэффициенты. Формулы
для угловых факторов QM приведенные в пп. 2—4, содержат бу-сим-
волы, 9/-символы, 12/-символы и генеалогические коэффициенты
^LpSp. Подробное описание их свойств, формулы и таблицы чис-
ленных значений содержатся в книге [65]. Здесь будут приведены
некоторые формулы, численные значения и правила сумм, бу-
{Gl 1
. к и г удовлетворяют следующим соотношениям
О, 03 J
симметрии: бу-символ остается неизменным при любой переста-
новке его столбцов, а также при одновременной перестановке
нижних и верхних аргументов в каждом из любых двух столбцов.
Например,
{^1 ®2 ^'3*1 Г ^3 1 С Я3 ^2 "1
b3J &3 J J
( а1 а2 а31 _ f ^1 &8 “3 1
I b2 b3 j [ аг а2 b3 J
бу-символ ( ,1 ) отличен от нуля при выполнении следующих
I "г °з J
условий треугольников:
{bibjfls}.
Условие треугольника {а Ъ с) означает, что сумма любых двух
аргументов из а, Ъ, с должна быть больше или равна третьему,
§ 19. ФОРМУЛЫ ДЛЯ Q-ФАКТОРОВ
247
а модуль разности любой пары аргументов должен быть меньше
или равен третьему аргументу.
Приведем ряд формул суммирования произведений 6у-символов.
а) Суммы бу-символов.
3(2ж + 1){“ " '}=(-1)к{«М. (19.40)
X V J
3(~1)-(2х+1){“ ‘ сх] - (- 1)‘"V(2I. + l)(2d + l)dK. (19.41)
б) Суммы произведений двух бу-символов.
2(-1гих(2х+1){: *;}{> ‘ ;}={“ “ ’}. (19.43)
3 (2х + 1)(2у 4-l)(2z + 1)|‘ I Ч’ = (2а + 1)(26 + 1)(2с+1).
(19.44)
в) Суммы произведений трех бу-символов.
Уд_Пв+х/о . лЛа ь d xUe 1 х\-$р q q rl
2j( ) (2x-|-l)[c d. pj (e / qj (b a rj [e a d][f b cj'
(19.45)
R — a + & + c + Oe + /+ /’+? + r)
3(2х+1)(2У+1){» ‘ ;}{’ { ;}{“ J ’} = {« ‘ ’},(19.46)
£(-ir-(2x+i)(2S+i){: ;»}{: * j}=
XV
= 2ПТ{“Й ₽}{'«₽} (19.47)
г) суммы произведений четырех 6/-символов,
248 ГЛ. VI. ФОРМУЛЫ И ТАБЛИЦЫ для оценки сечений
У| (— 1) ’c+v+z+ai+a«+a»+b1+b2+b«+c + 1)(2у + 1) (2z -f- 1) X
xyz
ai аг «з! Га1 Ьа 631 Саг b3 6,) |«з Ъх Ь2] л \ (а1
,х у z J [с Z у J |с X z J (с у Z J ' ' ' |&1
Часто бывает полезна
новки аргументов:
формула, позволяющая делать переста-
3(2*+1)1 3 ^(М?* 1 "г ®l?3 4 ®12 =
х | Ь',с' 1Л1 b2 ^ij 1Л1 Ь2 с2/
= 3(2*+1)1 «3 ®1Г«2 «4 *1 2
х |bV (с2 Сх М (с2 q 6J
а2 аз1
&2 63/
(19.50)
(19.51)
где F — произвольная функция любой комбинации аргументов bt,
CJ (i, 7 — 1, 2). Выбор переменных суммирования Ь'с' также про-
изволен.
Формулы для 6/-символов, один из аргументов которых не
превышает единицы, даны в табл. 32.
Формулы для 67-символов
Таблица 32
{о с £} = (—П’ [(2*4-l) (2c-Fl)] ,Л.
а b с 1__ ,_Г (а-]-с — Ь) (а —f-& — с + 1) "1*^
5a с -1/2 Ь + 1/J * } L (26 +1) (26 + 2) 2с(2с + 1) J ’
а Ь с I__ ,_ns Г (л + Ь + с-|-1) (Ь + с — а) 1^*
Vac — х/г b — VaJ J L 26 (26 + 1) 2c (2c + 1) J ’
(a b c|_______j.e 2 [а (a + 1) — b(6 + l) — c(c-|-l)]
I1 c N [2b (26 +1) (26 + 2) 2c (2c + 1) (2c + 2)]*^ ’
a 6 с 1___________.__Г s(s4-l)(s — 2a — 1) (s — 2a) "1 l^2
1 c — 1 b — 1 J 1 ’ L (2b —1)26 (26 + 1) (2c —1) 2c (2c + 1) J ’
fa 6 cl , Г 2 0 +1) (s — 2a) (s — 26) (s—2c + 1)
(1 c — 1 6J 1 ' |_26 (26 + 1) (26 + 2) (2c — 1) 2c (2c + 1) J ’
a b c I . j.» r(s — 26) (s — 26 —l)(s — 2c + l)(s — 2c + 2)l1/1
1 c — 1 6 + 1 J 1 ' L (2b + 1) (26 + 2) (26 + 3) (2c -1) 2c (2c + 1) J
Обозначение: s = a + &+c.
§ 19. ФОРМУЛЫ ДЛЯ Q-ФАКТОРОВ
249
Таблица 33
Генеалогические
коэффициенты
(ра [Грб'р] pLS} р3 LS)
Таблица 34
Генеалогические
коэффициенты
(p3[Lplyp]pL1S}p4 LSy
Таблица 35
Генеалогические
коэффициенты
(Р1 [ад,]р«Р}рзаР)
9у-символы и 12/-символы выражаются через 6/-символы
следующим образом:
'а Ь с]
dp; J=?(-i)“(2^+d{“ ‘ :}{t: yg»g,
aj a3
ba b3 bt =
_C1 Cj Cg Ci
= (_ i)b1-b1-b»+b4 ^2x + 1)JC1
x las
<2*1 fa c<
ai bjJ [«3
*1 fa c2 xl fc3
МИ4 «2 b3jla4
C4 X 1
«2 bi J
(19.53)
Используемое нами обозначение генеалогических i “
ентов Gl^sp соответствует книге [1]. В обозначениях Рака
= (Г-1 [ад,] ILS) Г£5).
коэффици-
Значения генеалогических коэффициентов для конфигураций
рт (тп = 3, 4, 5), приведены в табл. 33—35. Для конфигураций s2,
ра и р6 генеалогические коэффициенты равны единице.
ГЛАВА VII
УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
§ 20. Модель классического осциллятора
1. Постановка задачи. Современная теория уширения спек-
тральных линий, вызываемого взаимодействием атома с окружа-
ющими частицами, тесно связана с общей теорией атомных стол-
кновений. В наиболее интересной для приложений области не
очень больших давлений, когда уширение определяется ударным
механизмом, вычисление контуров спектральных линий включает
в себя вычисление амплитуд или фаз рассеяния возмущающих
частиц на атоме. Тем не менее изложение теории уширения по-
лезно начать с рассмотрения задачи о спектре излучения клас-
сического осциллятора, испытывающего внешние возмущения.
В рамках такой модели наиболее просто выясняются как сам под-
ход к проблеме уширения спектральных линий, так и характер
тех основных приближений, которые используются в теории уши-
рения.
Сделаем вначале следующие упрощающие предположения:
1) относительное движение атома и возмущающей частицы ква-
зиклассично, что позволяет пользоваться понятием траектории
возмущающей частицы;
2) эта траектория прямолинейна;
3) основную роль в уширении играют взаимодействия с бли-
жайшей возмущающей частицей (бинарные взаимодействия), по-
этому тройными и другими многочастичными взаимодействиями
можно пренебречь;
4) возмущение адиабатично, т. е. не вызывает переходов между
различными состояниями атома.
В рамках этих предположений механизм уширения спектраль-
ных линий рисуется следующим образом. При пролете возмущаю-
щей частицы на атом накладывается внешнее поле
V (Я) = V (/р2 + v*(t- i0)2), (20.1)
где R — расстояние до возмущающей частицы в данный момент
времени t, р — прицельное расстояние, t0 — момент наибольшего
сближения и v — относительная скорость. В результате уровни
энергии атома и, следовательно, частота колебаний атомного
осциллятора меняются во времени. Поэтому колебание атомного
§ 20. МОДЕЛЬ КЛАССИЧЕСКОГО ОСЦИЛЛЯТОРА
251
осциллятора можно записать в виде
/(«) =ехр
idiot -4- i
(20.2)
где со0 — невозмущенная частота и х (£) — сдвиг частоты, обус-
ловленный взаимодействием. Нарушение монохроматичности ко-
лебаний приводит к уширению соответствующей спектральной
линии. При заданном законе изменения частоты осциллятора
х (i) форма линии определяется разложением функции j(t) в ин-
теграл Фурье
I ((о) = lim
Т->оо
Т/2
1 С
/2лТ J,
-Т/2
= lim
Т—со
1
2лГ
Т/2
\ ехр [ — i (о — соо) t + й] (01 dt
-Т/2
t
ц(0 = J x(f)df,
—оо
(20.3)
(20.4)
где т] (/) — фаза колебаний осциллятора, обусловленная взаимо-
действием.
Если отсчитывать частоту со от невозмущенной частоты осцил-
лятора ю0, то в (20.2) надо опустить множитель При этом
/(ш)= г™
Т/2
ехр [— id)t 4- гт](£)] dt
-Т/2
(20.5)
Ниже, как правило, будет использоваться именно такое оп-
ределение (D.
В теории уширения спектральных линий обычно рассматри-
ваются такие условия, когда давление и температура, химический
состав, состояние ионизационного равновесия и т. п. не меняются
со временем. При этом функции ц (/) и / (i) — ехр [— гц (£)]
представляют собой стационарные случайные процессы. В этом
случае спектр I (со) можно выразить через функцию корреляции
Ф (т):
СО
I (со) = — Re С е-«отф (20.6)
л j
о
Т/2
Ф(г)=Ит± \ /*(*)/(* + т)^ = /*(0/(^4-т). (20.7)
Т—»оо -* d
Усреднение по времени в (20.7) можно заменить усреднением по
статистическому ансамблю величин, определяющих функцию
252 ГЛ. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ линий
/ (£). Обозначим такое усреднение угловыми скобками:
Ф (т) = </* (0) / (т)>. (20.8)
Для / (i) = ехр lit] (/)] имеем
Ф (т) = ехр {— i [ц (i) — т| (t + т)]} = <ехр [it] (т)]>. (20.9)
2. Ударное уширение. Вычисление спектра I (со) по общим
формулам (20.5) — (20.9) значительно упрощается, если восполь-
зоваться приближением, получившим название ударного. В осно-
ве этого приближения, развитого в работах Лоренца, Ленца и
Вейскопфа, лежит допущение, что решающим фактором уширения
линии является нарушение когерентности колебаний атомного
осциллятора при столкновениях. Другими словами, если длитель-
ность столкновения мала по сравнению со временем свободного
пробега атома между двумя столкновениями, то излучением в те-
чение столкновения можно пренебречь, считая столкновение
мгновенным. Столкновение проявляется лишь в сдвиге фазы атом-
ного осциллятора. Принимая столкновения мгновенными, можно
вычислить функцию корреляции (20.9) следующим простым спо-
собом. Образуем разность АФ = Ф (т + Ат) — Ф (т). В соответ-
ствии с (20.9)
АФ = <e»n(T+At)> _ = <^егт1(т)егДг1> —
где через Ат] обозначен сдвиг фазы за время Ат. Если столкнове-
ния мгновенны, то Ац не зависит от значений фазы в предыду-
щие моменты времени. Поэтому ц (т) и Ац статистически незави-
симы и, следовательно,
АФ = <gin(t)> -1] = _ ф (Т) <1 _ е1Дп>. (20.10)
Согласно (20.1) столкновение характеризуется параметрами р и v.
Обозначим число столкновений с параметрами р и v в единицу
времени через Р (р, v) dp dv. Тогда число таких столкновений за
время Ат равно Р (р, v) dp dv Ат и
<1 _ е1Дл> = 0 дт, 0 = J <1 _ еЫ> р (р, у) dp dv, (20.11)
где ц — приращение фазы в результате столкновения с параметра- •
ми р, v. Число возмущающих частиц, пролетающих в единицу вре-
мени через кольцевой элемент 2лр dp, очевидно, равно JVv2np dp,
где N — плотность. Поэтому
0 = N f pF (v) dv 2л J (1 — eiT>) p dp. (20.12)
Положим
o' = 2л j (1 — cos ц) p dp, (20.13)
0
oo
о" = 2л Jsinrjpdp. (20.14)
0
§ 20. МОДЕЛЬ КЛАССИЧЕСКОГО ОСЦИЛЛЯТОРА
253
Тогда
0 = N <у (o' - io")>. (20.15)
Из (20.10), (20.11) легко получить уравнение
т£ = -М>. (20.16)
Поэтому
Ф = ехр [- 0т]. (20.17)
Подставляя (20.17) в (20.6), получаем
1 = 2л (со —Д)2 + (у/2)2 > (20.18)
у = 2N <ро'>, А = N <ро«>. (20.19)
Формула (20.18) дает спектр излучения при ударном уширении.
Распределение интенсивности такого типа обычно называют ло-
ренцевским. Ширина распределения (расстояние между симмет-
ричными точками о)1, со2, для которых I (со) = 1/2 7тах) равна у.
Максимум сдвинут на величину А. Величины а' и ая носят назва-
ние эффективных сечений ширины и сдвига.
Предположим, что возмущающая частица, находящаяся на
расстоянии R от атома, приводит к сдвигу частоты х = CnR~\
Тогда для столкновения с параметрами р, v
х (/) = Сп [р2 + р2 (/ - i0)2]^, (20.20)
г) (р, v) = Сп J [р2 + р2 (i - f0)2]-n/2 dt = anCn/pp-i, (20.21)
—оо
an = /лГ / Г (-Й • (20.22)
Для n = 2, 3, 4, 5, 6 имеем соответственно an = л, 2, л/2, 4/3,
Зл/8. Подставив (20.21) в (20.13), (20.14), нетрудно получить сле-
дующие значения у и А, которые понадобятся нам в дальнейшем
для приближенных оценок:
п = 3,
у = 2л2С3А\
п — 4,
у = Г c*l*v4*N ~ IMCjWV, А = -^ у, (20.23)
п = 6,
у = 8,16 А = 0,36 у.
Нетрудно также показать, что основной вклад в (20.13) дают
столкновения, для которых т] 1, т. е. прицельные расстояния
254
ГЛ. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
Р Ро, гДе Ро определяется условием т| (р0) = 1,
г. _ I П П \
Ро -
(20.24)
Прицельное расстояние р0 обычно называют радиусом Вейскопфа.
По порядку величины сечение уширения, таким образом, равно
о' « про- (20.25)
Сдвиг линии (см. (20.14)) определяется в основном более далекими
пролетами р р0.
В случае п — 2 фаза ц (р) оо р-1. Поэтому интегралы (20.13)
(20.14) расходятся, первый как In pm, а второй как рт, где рт —
верхний предел интегрирования. Эта расходимость означает не-
применимость бинарного распределения.
Квазистатическое уширение. В случае очень медленного из-
менения возмущения можно найти спектр излучения, приняв,
что I (co)dco просто пропорционально статистическому весу кон-
фигурации возмущающих частиц, при которой частота атомного
осциллятора заключена в интервале со, со + day. В бинарном
приближении сдвиг частоты создается ближайшей частицей. Сле-
довательно, для вычисления I (со) необходимо найти вероятность
W (7?) dR того, что ближайшая частица находится на расстоянии
R, R + dR от атома. Эта вероятность равна
W(R)dR =
= 4n7?2JV ехр [- NR3] dR = ехр [- d (А)8 , (20.26)
где Ro = (3/4n2V)*/». Подставив в (20.26) х = со — <оо = CnR~n,
получим распределение вероятности для сдвига частоты атомного
осциллятора. В соответствии с основным допущением квазистати-
ческого приближения этим распределением и определяется форма
спектральной линии. Если ввести обозначение Дсо — CnR~^,
то из (20.26) следует
7 (со) dco = АГС8/П (со - co0)-(s+n)/n ехр
(Дм
dco. (20.27)
со — <00 / 4 '
Выражение (20.27) имеет смысл лишь для достаточно больших
значений (со — соо), для которых 7? = (со — coo)-1/TtCi/n значитель-
но меньше 7?0. При 7? 7?0 бинарное приближение незаконно.
Таким образом, выражением (20.27) заведомо не описывается
внутренняя часть линии. Условие R 7?0 означает, что Дсо
<С со — соо. Поэтому в (20.27) можно опустить экспоненциальный
множитель, после чего получим 7
7 (со) dco = JVC8/n (со - coo)-(3+n)/n dco. (20.28)
§ 20. МОДЕЛЬ КЛАССИЧЕСКОГО ОСЦИЛЛЯТОРА
255
4. Соотношение и границы применимости ударного и квази-
статического приближений. Вернемся к общим соотношениям
(20.3), (20.4). Рассмотрим сначала (20.3) для больших значений
До> = <о0 — со. Если А со велико, подынтегральное выражение в
(20.3) сильно осциллирует всюду, кроме окрестности точек tk,
в которых
(^),,=х(« = дт-
Поэтому основной вклад в (20.3) дают малые области вокруг
этих точек и вместо (20.3) можно записать
/(«) =
У, ехр {Цц (£) + («о—w) (f — fft) +(ю0—со)М} dt 2.
к Atfc
(20.29)
Разложим функцию т] (i) в ряд вблизи tk по степеням t — tk.
Так как (dv\/dt)ik — Дсо, то члены, линейные относительно t— tk,
в показателе экспоненты в (20.29) сокращаются, и ряд начинается
с члена
1 /
2 \dfi
При интегрировании существенна область Дт^, где этот член
меньше единицы (дальше начинаются сильные осцилляции).
Отсюда легко получить размеры этой области
~ /21 (•»„ Г’ -- | (£),, Г'’ • <20-з°)
Если в пределах этой области следующий член разложения
для чего необходимо выполнение неравенства
(20.32)
то ряд можно оборвать на члене, пропорциональном (t — tk)2,
и в каждом члене суммы (20.29) пределы интегрирования распро-
странить от — оо до оо (вне Дт^ из-за осцилляций подынтеграль-
ного выражения интегрирование дает нуль); при этом х)
0 Здесь предполагается, что фазы ак — [ц (tk) + (<о0 — независи-
мы. Ниже будет показано, что это предположение выполняется.
256
ГЛ. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
у1, exp {i [ц (tk) + (®о — о) м} X
к
X J ехр (i [4- - ^)2]} dt f =
—00
lim-l-
Т—со У
У|ехр {i [т] (М + («О -®Hfc ч--£-]}
2
(20.33)
Легко видеть, что
V4 ! dx\-l j
/_1 ("dF/ da) есть вРемя> в течение которого
к к
х (i) заключено в интервале ю — со0, со — соо 4- doi. Действитель-
но, dxk и da> на рис. 30 связаны соотношением (dx/di)/fcdrfc = dco,
поэтому (20.33) является не чем иным, как квазистатическим рас-
пределением интенсивности W (со — (о0) d<x>. Заменим суммирова-
ние в (20.33) интегрированием. Число пролетов через кольцевой
элемент 2лр dp за время Т будет равно 2лр dpNvT, где N — плот-
ность возмущающих частиц. Учитывая, что каждое столкновение
/ С \1/п
при хтах = Спр п До, р < рдю = (-д^-1 дает две точки tk и tfr+1
(рис. 30), получим
Рдш
I (со) d(a = do 4лр 1 Nv dp =
о
(20’34)
т. е. квазистатическое распределение в крыле линии.
Если опустить из рассмотрения малую окрестность вокруг мо-
мента наибольшего сближения t0, то
dz _ cnv
dt рП+1 ’
d«x _
<№ ' „п+2 ’
г
(20.35)
§ 20. МОДЕЛЬ КЛАССИЧЕСКОГО ОСЦИЛЛЯТОРА
257
и соотношение (20.32) принимает вид
Сп
гр"'1
(20.36)
Как легко увидеть из рис. 30, точки tk, в которых = Дю,
дают лишь те пролеты, для которых Спр~п Дю, другими сло-
вами, нас интересуют столкновения с р рДо — (Сп/
Учитывая это, (20.36) можно переписать в другом виде:
vn/(n-l)
С1/(п-1)
п
(20.37)
Соотношение (20.37) является условием применимости квазиста-
тического приближения. Из него следует, что это приближение
применимо для больших Дю, т. е. в крыле линии.
Рассмотрим теперь (20.3) в предельном случае малых Дю.
Если Дю мало настолько, что Дю-1 много больше длительности
столкновения
(20.38)
то изменение фазы при столкновении можно считать мгновенным.
Но мгновенность столкновения как раз и является исходной пред-
посылкой ударной теории, позволяющей крайне просто вы-
числить I (ю) <2ю. Основную роль в ударном уширении линии иг-
рают столкновения с р ~ р0 = (апСп/и)1^п~г>. Подставляя р0
в (20.38), получаем соотношение, обратное (20.37),
рп/(п-1)
Д®—^<1/(п-1) = О.
Таким образом, в центре линии Дю Q справедливо ударное
(лоренцевское) распределение интенсивности. Для больших же
значений Дю, Дю^>О, ударное распределение сменяется квази-
статическим. Квазистатическое крыло может располагаться как
с длинноволновой, так и с коротковолновой стороны в зависимости
от направления сдвига термов. В области частот Дю, противо-
положных по знаку квазистатическому крылу, лоренцевское рас-
пределение сменяется экспоненциальным.
Выясним теперь, при каких условиях большая часть инте-
гральной интенсивности линии сосредоточена в ударной области.
Легко видеть, что для этого необходимо, чтобы Q значительно
превышало ударную ширину у. Учитывая, что у ш 2np^Nv =
= 2jiNv (апСп/к)2/(п-1), получим
2лр^Ур<<й = —,
Рп
9 Л. А. Вайнштейн и др.
258
ГЛ. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
откуда
(20.39)
Таким образом, для малых давлений и больших скоростей, пока
выполняется неравенство (20.39), ударный механизм уширения
играет решающую роль. На долю квазистатического крыла при-
ходится относительно ничтожная часть общей интенсивности.
При больших давлениях и малых скоростях, когда неравенство
(20.39) нарушается, т. е. когда
h = ~ 1,
(20.40)
ударная теория неприменима даже к внутренней части линии.
Отметим, что если условие (20.39) не выполняется, то, вообще
говоря, нет никаких оснований использовать бинарное прибли-
жение. Действительно, соотношение (20.40) означает, что эффек-
тивный радиус р0 примерно равен среднему расстоянию между
возмущающими частицами. Хотя при P87V 1 квазистатическое
приближение применимо практически по всему контуру, выраже-
ния (20.27), (20.28) не описывают центральной части линии.
Они применимы лишь к крылу линии, так как большие сдвиги
частоты создаются наиболее сильными возмущениями, т. е. би-
нарными взаимодействиями.
Выше при выводе формулы (20.33) фазы считались независи-
мыми. Поскольку согласно (20.36) основную роль в образовании
квазистатического крыла играют сильные столкновения, для ко-
С □
торых —— — 2>1, причем эта разность раз-
pn v
лична для разных столкновений.
5. Эффект Доплера. Частота осциллятора, составляющая
скорости которого в направлении луча зрения равна V, в соот-
ветствии с принципом Доплера смещена на величину (ооп/с. Пусть
распределение излучающих атомов по v определяется функцией
W (v). Тогда и = «о + (£>ov/c, v = с (ы — со0)/ю0 и
1 (со) d(d = W ~ dw. (20.41)
При максвелловском распределении
W И*> = [- (-£-)*] % , (20.42)
где v0 = У2кТ/тп, получаем
1
/ (w) do = ехр
Д(ор = ЮоЛ. (20.43)
С
§ 20. МОДЕЛЬ КЛАССИЧЕСКОГО ОСЦИЛЛЯТОРА
259
Распределение интенсивности (20.43) симметрично относительно
частоты осциллятора <о0. Величина уширения определяется пара-
метром Дсор. На расстоянии Дсор от соо интенсивность убывает в
е раз. Через параметр Дыд выражаются ширина линии, которую
мы обозначим посредством 6, и интенсивность в максимуме I (ю0).
Определим ширину линии аналогично тому, как это было сделано
выше в случае ударного уширения, т. е. как расстояние между
точками контура coj, <оа, для которых I (сог) = I (ю2) = г/2/(<в0).
В соответствии с (20.43)
6 = 2 ^ЙГ2Д(ор, (20.44)
I (о,) = 1 . (20.45)
у л Дсор
Обычно доплеровской шириной линии называют непосредственно
величину Дсод.
При выводе формул (20.41), (20.43) неявно используется пред-
положение, что в спектре осциллятора с лучевой скоростью v
содержится только одна частота соо (1 + vic). Это действительно
так, если v не меняется во времени или остается постоянной вели-
чиной в течение достаточно большого интервала времени. Если
скорость остается неизменной в течение времени т, то вместо од-
ной частоты соо (1 -|- vic) в спектре осциллятора содержится целый
интервал частот ширины 1/т. Формула (20.41) остается справед-
ливой, если для характерных величин пит выполняется неравен-
ство (&avlc 1/т. Подставляя для т среднее время свободного про-
бега т = L!v, где L — длина свободного пробега, получаем
2я-г>1- (20.46)
В общем случае доплеровское уширение определяется разло-
жением в интеграл Фурье функции
t
f (£) = ехр р -у- х (t) , х (t) — v(t')dt'. (20.47)
—оо
Подставляя (20.47) в (20.6), (20.7), получаем
I (<в) = Re ф
о
Ф (т) = <^ехр р ~~х (f) ^> . (20.48)
При вычислении функции Ф (т) можно воспользоваться методом
кинетического уравнения х).
х) Дальнейшее изложение в этом параграфе основано на работе [66].
9»
260 ГЛ. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
Запишем Ф (т) в виде
ф (т) = <ехр [ikr (т)]>, г (х) = J v (t) dt (20.49)
о
и введем функцию распределения / (г, v, t), задающую относи-
тельное число осцилляторов, которые в момент времени t нахо-
дятся в точке г и имеют скорость V, при условии, что в момент
t = 0 все эти осцилляторы находились в точке г = 0. Эта фун-
кция распределения удовлетворяет обычному кинетическому урав-
нению
= = (20.50)
dt 1 1 \ dt / ст \ /ст
и начальному условию
/ (г, v, 0) = W (у) 6 (г). (20.51)
Здесь (д//д£)ст — так называемый столкновительный член, или ин-
теграл столкновений, G — линейный оператор столкновений,
W (у) — распределение по скоростям. Для функции корреляции
(20.49) и спектра I (со) имеем
Ф (т) = j dv $ ехр (ikr) f (г, v, х) dr, (20.52)
Z (со) = — Re dv exp [— i (cor — for)] f (r, v, t) dr dx. (20.53)
Л t) t)
Здесь для упрощения формул со — со0 заменяется на со, т. е. час-
тота со отсчитывается от несмещенной частоты соо. Согласно (20.53)
спектр I (со) определяется пространственно-временной компонен-
той Фурье Fa (v, к) функции / (г, v, t):
I (ц>) = JL Re £ Fa (v, к) dv, (20.54)
Fa (v, k) = f exp [— i (сот — kr)] / (r, v, x) dr dx. (20.55)
Выполняя фурье-преобразование по т и г в уравнении (20.50) и
учитывая начальное условие (20.51), нетрудно получить следую-
щее уравнение для Fa (v, к):
— W (у) + i (со — kv) Fa (у, к) = (GF)wk- (20.56)
В дальнейшем индекс со у функции F® и (GF)ak будет опускаться.
Как будет видно из дальнейшего, функцию F (vk) в ряде случаев
найти значительно проще, чем саму функцию распределения /.
В отсутствие столкновений (df/dt)cv — 0, (GF)к — 0
г, / > \ (^) г / \ 1 D С (^) &V /ЛА С7\
F (у, к) — т-.—~-г, I (со) = — Re \ .. , <, (20.57)
' ’ ' i (со — kv) 4 ' л J i (со — kv) ' '
i 20. МОДЕЛЬ КЛАССИЧЕСКОГО ОСЦИЛЛЯТОРА
261
что для максвелловской функции W приводит к обычному доп-
леровскому распределению (20.43). Действительно, W (v) dv =
= W (у) w (г?j) dv dv±, где v — проекция скорости на направле-
ние Aj, v± перпендикулярно к. Интегрирование по Vj_ дает едини-
цу, после чего
1 (ю) = S $ Т = $ 6 (“ - fo)wИ*’ =
1 Г / (О \21
= _____---ехр _ / ---\
/л Д(0п /
Рассмотрим теперь влияние столкновений, принимая модель
броуновского движения (см. [67]). Эта модель может быть исполь-
зована в случае слабых столкновений, сопровождающихся рас-
сеянием на малые углы. Примером может служить рассеяние тя-
желого излучающего атома на легких возмущающих частицах.
В модели броуновского движения столкновительный член в (20.50)
имеет вид
v div„ (v/) 4- ~ vkvf.
dt j а
(20.58)
Здесь принято, что эффективная частота столкновений v не зави-
сит от скорости и у® = 2кТ/т. По своему физическому смыслу v
есть величина, обратная времени тг, за которое частица теряет
память о своей первоначальной скорости. С помощью решения
(20.50), (20.58), удовлетворяющего начальному условию (20.51),
можно получить
Ф (т) = ехр
ДсОп
, Дсор = kv0, (20.59)
/ (to) = _L Re 2v-------------------
11 Д(0д — i2vco
, (20.60)
_ -г — » -2^2“
где Ф (а, у; z) — вырожденная гипергеометрическая функция:
ф (а V 54 = 1 4- — 4- а(а + 1) 28 I <х(а + 1)(«4-2) z3 ,
( > Y> 2) + ? ц + ? (? + 2! + у (у -j-1) (у 4- 2) 31 + ' •'
(20.61)
Если положить v — 0, то снова получим обычное доплеровское
распределение. При у =/= 0, но у Дсор (редкие столкновения)
для центра линии ю = 0 и далекого крыла со Дсор имеет место
/(0) =
_4____Ц + =______
Кл Дсор \ 3 У"л ’
1 тДсор
У л Дсор 2 У л со4
(20.62)
262
ГЛ. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
Таким образом, наличие редких столкновений приводит к увели-
чению интенсивности в центре линии о — 0 и появлению степен-
ного крыла оо со-4. В предельном случае больших плотностей,
когда v Дюп,
„ 1 Vj v2 1
I (со)де 4- —... * , yd = 4-----------. (20.63)
4 ' П 0)2 у2 и2 -f- № •“ 2 v ' '
Центральная часть линии (о2<^ v2 описывается лоренцевским кон-
туром
7<ш> = 4—JTT (20.64)
я w2 + Yd
с шириной 2yd = ДсоЬ/v. Поскольку v де v0IL, то 2yd ж Дсор х
X 2л£/Х, т. е. ширина уменьшается при повышении плотности про-
порционально длине свободного пробега L(oo./V~1).
При больших частотах со v выражение (20.63) совпадает с
распределением в крыле (20.62).
Качественные особенности влияния столкновений на допле-
ровское уширение не связаны с конкретной моделью столкнове-
ний, использованной выше. Примем, что после каждого столкно-
вения вероятность различных значений скорости атома, независи-
мо от того, какова была его скорость до столкновения, опреде-
ляется равновесным распределением W (v). В этом случае (модель
сильных столкновений) столкновительный член в (20.50) можно
записать в виде
(^)ст = — v/ + vTF («) J f (г, v', f) dv'. (20.65)
Для (GF)fc в (20.56) имеем
(GF)k = — vF (v, fc) + vW (v) j* F (v', k) dv'. (20.66)
Подстановка (20.66) в (20.56) дает
F («, fc) = , v7(r)b X F (”'> *)H--------гЛ —b < • (20.67)
4 ' v -J- i (to — kv) J ' ' v -J-1 (<d — kv) ' '
Интегрируя правую и левую части этого уравнения по и, найдем
j F (v, к) dv и затем с помощью (20.54) спектр
1 (* W (v)dv
I (со) = Re я • (20.68)
' ’ ( IV (v) dv ' ’
1 — V \ " * -------
J v -f- i (<d — kv)
При v Дсоп второй член в знаменателе имеет порядок величины
v/Дсод. Если пренебречь этим членом по сравнению с единицей, то
§ 20. МОДЕЛЬ КЛАССИЧЕСКОГО ОСЦИЛЛЯТОРА
263
(20.68) дает обычное доплеровское распределение. Для интенсив-
ности в центре линии I (0) и далеком крыле со Дсор можно по-
лучить
I (0) -----I 1 .— -т---| , I (со) ------------.
Ул Д®р \ Ул А®г> / Ул Д®п 2 Ул
(20.69)
Отличие от (20.62) состоит только в другом численном множителе
при параметре v/Дсор в формуле для I (0). В предельном случае
v Дсод формула (20.68) также, как и (20.60), дает для централь-
ной части линии лоренцевское распределение с шириной Дюр/v.
При со v лоренцевское распределение сменяется крылом
/ (со) се со"4.
Таким образом, независимо от конкретной модели столкновений
при повышении давления, когда длина свободного пробега L
Х/2л, столкновения приводят к сужению центральной части ли-
нии и появлению степенного крыла се со-4. При больших давле-
ниях, когда L < Х/2л, контур сужается пропорционально L се
се Л"1, и в пределе L <<; Х/2л центральная часть описывается ло-
ренцевским распределением, причем ширина этого распределения
в 2л£/Х раза меньше Дсор.
Подобное сужение, очевидно, может наблюдаться только в тех
случаях, когда отсутствует или мало уширение из-за взаимодей-
ствия. В общем случае нет никаких оснований разделять эффекты
взаимодействия и доплер-эффект. Одни и те же столкновения мо-
гут вызывать изменение фазы, а также затухание колебаний ос-
циллятора и изменение его скорости. Таким образом, уширение
из-за взаимодействия и доплеровское уширение, вообще говоря,
не являются статистически независимыми. Надо отметить, что в
оптической области спектра доплеровское уширение обычно пред-
ставляет интерес именно при условии L Х/2л. Действительно,
условие Дсор у, где у — ударная ширина, можно переписать
в виде 2лу/Х Nva' = Nva • о'/в — , где сг' — эффективное
сечение ударного уширения, о — сечение упругих столкновений.
В оптической области спектра, как правило, о' ст и, следова-
тельно, Дсоо У при L Х/2л.
Тем не менее статистическая зависимость ударного уширения и
доплеровского уширения (с учетом влияния столкновений) в
определенных условиях может оказаться существенной. По-
этому этот вопрос будет рассмотрен более детально в следующем
параграфе, в рамках квантовомеханической теории уширения.
6. Свертка лоренцевского и доплеровского контуров. Если
L Х/2л, то совместный учет ударного и доплеровского уширений
(статистически независимых) приводит к свертке лоренцевского
и доплеровского контуров. Распределение интенсивности в удар-
264
ГЛ. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
но уширенной линии излучения атома с лучевой скоростью v
имеет вид
1л ’ (со - А - соог>/с)2 + (Т/2)2 ’ (20.70)
Для того чтобы получить контур линии излучения совокупности
атомов, надо просуммировать (20.70) по всем атомам. Обозначим
опять нормированную на единицу функцию распределения излу-
чающих атомов по лучевым скоростям v через W (у). Тогда
I ((0) = _Г С_____________________W^dv___________________
{ > 2л J (со - А - соог>/<92 + (?/2)2
При максвелловском распределении
у 1 Г ехр [— (г?/г0)2] dv
2л (со —А —со0г>/с)а + (у/2)2 '
(20.71)
(20.72)
При Асор <<! у/2 в знаменателе в (20.72) можно пренебречь
членом d)ov/c, после чего интегрирование по и, выполняемое с
учетом нормировки функции распределения W (у), дает лорен-
цевское распределение с шириной у. Следовательно, при Асор
у/2 доплеровским уширением можно пренебречь. При Асор ^>
у/2 существенный вклад в интеграл (20.72) могут дать две об-
ласти значений v: и ~ 0 и v ~ с (со — А)/со0- В первой из этих
областей можно пренебречь членом G)ov/c в знаменателе, а во вто-
рой заменить в числителе v на с (со — А)/соо. После этого легко
получить два приближенных выражения для / (со), справедливых
для центра линии со — A йр и крыла со — А йр, где йр
определяется условием
йр — Асор In
ДсОп / йп \2
2л*/« . (20.73)
У \ д“р J
В области со — А йр I (со) совпадает с обычным доплеровским
распределением. В крыле линии I (со) — у/2лсо2. Таким образом,
при любом соотношении Асор и у/2 при достаточно больших зна-
чениях со доплеровское распределение сменяется лоренцевским
крылом.
Запишем (20.72) в виде
(20-74)
IV = | ”Р+7у - Г ° Ug | ехр [- ^ + i (х + iy) *1 <&,
— оо О
(20.75)
где х — ю. ~~ - , у = ТГ5Г-— , t = — т”- - • Функция W (х, w) может
м Atop J 2AcoD с Acod j \ > »/
быть выражена через интеграл вероятности от комплексного
§ 21. ОБЩАЯ ТЕОРИЯ УДАРНОГО УШИРЕНИЯ
265
Г 9
W (х, у) = ехр [ — (z -J- iy)2] 1 — —
аргумента *)
i(.x+iv)
e~t2 dt
о
(20.76)
С помощью этого представления можно вычислить Z (со) при любом
соотношении параметров у и Дссщ.
§21. Общая теория ударного уширения
1. Метод матрицы плотности в квазиклассическом приближе
нии. В квазиклассическом приближении воздействие на атом ок-
ружающих частиц можно описать введением зависящего от вре-
мени возмущения V (0. В этом случае координаты возмущающих
частиц можно считать заданными функциями времени, а не дина-
мическими переменными, что позволяет перейти от возмущения
V (У?) к возмущению V (0. Поэтому в этом, разделе будет показа-
но, каким образом вычисляется форма линии в том случае, если
атом подвергается произвольному возмущению V (0.
Используя общие методы теории возмущений, нетрудно пока-
зать, что распределение интенсивности в линии, соответствующей
переходу между состояниями а, р атома, определяется выражением
I (со) оо | Рар (0 | 2, (21.1)
где Рар (0 — матричный элемент дипольного момента атома, вы-
численный с помощью возмущенных волновых функций Ta (0,
Тр (0. Эти функции являются решением уравнения Шредингера
для гамильтониана
Н = + V (0. (21.2)
Формула (21.1) представляет собой естественное обобщение клас-
сической формулы (20.3). Для дальнейшего ее удобно записать
в виде, аналогичном (20.6),
оо
I (со) = Re г-‘“тФ (т) dr, (21.3)
о
где
ф (Т) = Pap (* + г) Р'^ (0 - Рар (i 4- т) Рра (0, (21.4)
или
Ф(Т) - <Ра₽ (Т) Рра (0)>. (21.5)
Рассмотрим далее переход между двумя вырожденными уровня-
ми а, Ь, причем индексами аир пронумеруем состояния, относя-
0) Детальный анализ свойств этой функции и ее таблицы содержатся
в работе [68].
266
ГЛ. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
щиеся соответственно к начальному и конечному уровням. Будем
считать, что все состояния а заселены с равной вероятностью.
В этом случае
lab (<*) = S Лф (®),
a, p
поэтому вместо (21.4), (21.5) надо положить
Ф (т) = 3^(Ht)PJ(0, (21.6)
ар
= (21.7)
ар
Формулы (21.6), (21.7) можно обобщить на тот случай, когда ли-
ния образована совокупностью переходов между двумя группами
близко расположенных уровней. Пронумеруем индексом а сос-
тояния, относящиеся к начальным уровням, и индексом р — к ко-
нечным, и обозначим через Wa населенность состояния а,
3^а=1. Тогда
Ф(Т) = 2^aPap(f + T)Ppa(O = 2vra<Pap(T)Ppa(O)>. (21.8)
ap ap
Разложим функции Т"» (£) и Тр (t) по независящим от времени
волновым функциям стационарных состояний изолированного
атома
^а (О = У, «а'а (О Фа' ехр (-- Ea't) ,
а'
ТР (0 = У, ар'рфр' ехр (- Ep-t\ ,
tv
<Рар (Т) Рра (0)> = 3 <«а'а (1) Яр'Р (т)> Ра'р'Рра =
а'Р'
а'Р'
где р^р' = <«а'айр'р> — матрица плотности атома, матричные
элементы Pa»p', Рра не зависят от t. Верхние индексы «(ар)» ука-
зывают начальные условия р£?{у (0) — 6aa-6pp'- Изменение мат-
рицы плотности со временем дается уравнением
4р“4-<ЯР-РЯ)> »=H. + V(t). (21.9)
Для функции корреляции Ф (т) теперь имеем
Ф(Г)= 3 Wap^l (Г) Pa.f.P^. (21.10)
aPa'P'
§ 21. ОБЩАЯ ТЕОРИЯ УДАРНОГО УШИРЕНИЯ 267
Предполагая, что уширение определяется ударным механизмом,
можно записать уравнение для матрицы плотности р в виде
4-р = 4-(я«₽-₽я«)+(>)„•
Последний член в правой части (21.11) дает изменение оператора
р, вызываемое столкновениями. Пусть атомные волновые функции
до столкновения Т и после столкновения Y' связаны соотношением
= S4, (21.12)
где S — оператор, или матрица, столкновения. Матрица плот-
ности р в результате столкновения с параметрами v (прицельное
расстояние, скорость и т. п.) преобразуется по общему правилу
преобразования матриц следующим образом:
р S+pS,
т. е. испытывает приращение
Др = S+pS - р, (21.13)
где S+ik = Ski. Поэтому
= $ |S’ (V) (V) - p] P (V) dy, (21.14)
где P (v) dv — число столкновений с параметрами v в интервале
v, v + dv в 1 с. Если в качестве этих параметров задаются при-
цельное расстояние р и скорость, то
Р (у) dv = Nvf (у) • 2npdp dv,
где N — плотность возмущающих частиц, / (у) — функция рас-
пределения по скоростям.
Подставив (21.14) в (21.11) и выполнив преобразование Фурье,
нетрудно получить систему алгебраических уравнений для мат-
ричных элементов р£/[Р (ю) с фиксированными индексами а,
Дха'ЗрР' — i (<о — <оаГ) р£$ (to) =
= 2 РаЧ" (®) J IWW - P (v) dv. (21.15)
a"P"
Из (21.3) и (21.10) имеем
/(М) = -М1е У, WaPa.p.Paf>p<S)(«>). (21.16)
ар, a'P'
Формула (21.16) подразумевает излучение определенной поляриза-
ции. В общем случае надо заменить Ра^' Рар на Ра'р' Р’р. Вообще
говоря, суммирование по а'р', а"0" в (21.15) и (21.16) распростра-
няется на все стационарные состояния атома. Однако в интере-
268
ГЛ. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
сующей нас задаче вычисления интенсивности в узком частот-
ном интервале, соответствующем переходам между двумя груп-
пами близко расположенных, или вырожденных, уровней а, р,
индексы а', а" принимают те же значения, что и а, а индексы
Р', Р’ — те же значения, что и р.
Таким образом, если известна 5-матрица столкновений, то,
определив с помощью (21.15) элементы матрицы плотности
Рс?р' (со), можно найти спектр I (<в).
Для одной изолированной линии из (21.15) следует
1 — i (ft) — (Oq) р<х|3 “ Pap $ [1 — 5аа5рр] Р (v) dv
и из (21.16)
'<•> = ‘• (21.17)
(21.18)
o' — io" = J [1 — ‘SaaSppl 2лр dp. (21.19)
В общем случае элементы 5-матрицы комплексны: 5^ =
= ехр (— Га 4- *Па), 5рр = ехр (— Гр + й]р). Поэтому ширина
линии уар и сдвиг Дар определяются выражениями
Yap = J [1 — ехр [— (Га 4- Г₽)] cos (т]а — Пр! Р (v) dv,
(21.20),
Дар = S ехр I— (Га + Гр)] sin (т]а ~ Т]р) Р (v) dv.
Рассмотрим также распределение интенсивности в крыле линии
образованной совокупностью переходов а—р. Если разности
со — соа'р' достаточно велики, в правую часть (21.15) можно
подставить нулевое приближение р«“р» = — боа’ брр- (со — со о)'1,
где со0 — среднее значение частот соа'р'. После этого нетрудно
получить
(21.21)
аР
?= (ЗЖа|Рар|а)_12Ве 3 ТУаРаЛ J [баа'брр'- 5^'5ppd X
ар ара'Р'
xP(v)dv. (21.22)
Центральная часть линии в этом случае имеет более сложную
структуру, нежели лоренцевский контур (21.17).
Спектр излучения I (со) в общем виде можно вычислить еще
для одного частного случая, а именно, когда 5-матрица диагональ-
§ 21, ОБЩАЯ ТЕОРИЯ УДАРНОГО УШИРЕНИЯ
269
на, например, при адиабатическом возмущении V (t). Действитель-
но, в этом случае система (21.15) расщепляется на независимые
уравнения для каждого из Подставляя соответствующие
выражения для нетрудно получить
(21.23)
Это распределение имеет вид суперпозиции независимых лорен-
цевских контуров 7ар (со), каждый из которых такой же, как и для
изолированной линии (21.17).
Вычисление спектра I (щ) по формулам (21.15), (21.16) требует
вычисления S'-матрицы и затем решения системы алгебраических
уравнений. Второй этап, очевидно, не связан с какими-либо прин-
ципиальными трудностями. При вычислении элементов 5-матри-
цы можно использовать различные приближенные методы и ре-
зультаты общей теории атомных столкновений. В частности, мож-
но определить S-матрицу с помощью ряда теории возмущений.
Волновая функция T (i) гамильтониана Но + V, удовлетво-
ряющая начальному условию 4е (i0) — — Фп (£0), где Фге — невоз-
мущенная волновая функция, имеет вид
*7 ~ $тп Ф”1 ехР ( h~ i Smn (fo) =
m
где коэффициенты разложения Smn (i) удовлетворяют системе
уравнений
i^5mn — V mkSkn @Хр £ (Ет 7s\-)ij .
к
Величины Ут/с ехр — £\) J можно рассматривать как матрич-
ные элементы оператора
7 = е*Р (-£- Hot) V ехр (---------Hot) ,
так как ехр
уравнений для Smn можно записать в виде
Поэтому систему
iAS'jnn — ^l^mk^kn
к
или в операторном виде
ihS = 75.
270
ГЛ. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
Решая это уравнение методом последовательных приближений
S (t) = + <S(1) + 5(2) + . . получим
t t t-
5(<) = 1+(--т)$Г('')^' + (-4-П V‘~t">dt' S F<n*”+ •••
to to to
(21.24)
Для определения 5-матрицы столкновения с параметрами v на-
до подставить в (21.24) причем Vv (£) —► 0 при t -> ± оо, и
положить t0 = — оо, t = оо, тогда
оо оо t
5(v) = l+(—у) jj rv(«)^+ (~4*)2 $ Fv(<)^$ WG-
—оо —оо —оо
(21.25)
Если ограничиться членами 2-го порядка по Г включительно,
то для параметров Г и ц в формулах для ширины у и сдвига А
(21.20) нетрудно получить
OO
Re yi| <a{Pv[s> exp (i<dasi) di ,
Г_____
la- 2h2
8 — ОО
оо
4 (•
% =-----j- J <a]7v(f)|a>^ —
—оо
оо
<a|Pv(Ols>exp(i©aef)d/X
t
X <s|7v(^)|a>exp(i(o3ai')df.
S —oo
(21.26)
Величина 2Га равна полной вероятности переходов из состоя-
ния а во все другие состояния атома. Такие переходы приводят
к сокращению жизни атома в состоянии а, что эквивалентно уши-
рению соответствующего уровня. Величина ца есть сдвиг фазы,
возникающий вследствие сдвига уровня, создаваемого взаимо-
действием Vv (I). Увеличение Га, Гр приводит к увеличению ши-
рины и уменьшению сдвига (см. (21.20)). Об уширении вследствие
переходов, индуцированных столкновениями, обычно говорят
как об уширении вследствие неупругости, или из-за неупругих
столкновений.
2. Вырождение уровней. Рассмотрим изолированную спектраль-
ную линию, соответствующую переходу между состояниями ато-
ма с угловым моментом jlt j2. Поскольку и начальный и конечный
уровни вырождены, по магнитным квантовым числам т1, т2,
§ 21. ОБЩАЯ ТЕОРИЯ УДАРНОГО УШИРЕНИЯ
271
такая линия образована совокупностью переходов /j/nj -> j2m2.
Запишем уравнение для матрицы плотности р (i) (21.11) в виде
_ЗгРтП1ТП1= —^оргщтг + У Р ' ’' ' „ „ ’ (21.27)
Q't Trt-j^TXl2 ^71 > TTliTTlj
тп1тп2
где (Oq = о)/,/, и в соответствии с (21.14) и (21.15)
G ' = ( [д ' • - S* • S > ] Р (у) dv.
mjrn2, тп|Ш2 J т^тП1 т2тг т2т2
Преобразуем систему уравнений (21.27) так, чтобы в нее входили
линейные комбинации pmirn„ обладающие трансформационными
свойствами неприводимого тензорного оператора Tsa. Поскольку
~ ( l)J,+mi'4,j1 -тЛРлтП.»»
искомое преобразование имеет вид
Рза = У, (— 1)->‘-т‘(— [ SO) pm.m. =
7П17П1
= £ (- +1 (Д * д р™.
ГП17П»
(21.28)
Pm.m, = У (~ 1^‘+7П1 т1ТП2 । SCF) PsCT =
за
= У (— iy.+”b+4/2s+ 1
за
71
.— тпх
7*2
S ’
—5,
Psa,
где (— ] so) — коэффициенты Клебша — Гордана. Умно-
жим левую и правую части (21.27) на (— 1)-л-т* (— трп^ | so),
просуммируем по mlf т2 и, кроме того, выразим рт'т' в столкно-
1 2
вительном члене через psa- В результате получим
Рза = — itBopsa Н- 1| Ра'а'^з'о', so,
s'a'
<?8'о',8а= 3 (— l)“m,+wi(— mX|s'o')G , , (—пг^ | SO),
nijmt mimt
П>17П2
В столкновительном члене (21.14) подразумевается усреднение
по направлениям скоростей возмущающих частиц v и прицельных
параметров р в пространстве. Поэтому в среднем воздействие на
атом возмущающих частиц изотропно. Это означает, что уравне-
ние для неприводимых тензорных величин psa должно быть ин-
вариантным относительно вращений, а матрица G должна быть
272
ГЛ. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
диагональной по $ и о, и кроме того, не должна зависеть от а:
Gs'o',»o = 6sS'6oa'Gs.
Таким образом, система уравнений для pgo имеет вид
Pso = i<j>oPso 4“ GsPsu’ (21.29)
Ее преимущество перед исходной системой для величин pmimi
заключается в том, что эта система распадается на независимые
уравнения для величин ps0.
Диагональность матрицы G нетрудно проверить прямым вычис-
лением. После усреднения по направлениям р и v подынтеграль-
ное выражение в (21.14) должно иметь вид
У, <трн21 (— i)qUqV-q | тцпг) =
XQ
- £<- ; Д)(Д \ §
XQ 12
где Uq и Vq — неприводимые тензорные операторы, действующие
соответственно на функции %imi и ф?-2т2. Подставляя это выраже-
ние в формулу для GS'0', go и выполняя суммирование приведе-
ний четырех Зу-символов по mv т2, тх, т2, можно получить
GS'a', so = 63S'SoO-G4, Gs = 2 Gs (x).
X
Перейдем теперь к вычислению спектра I (со). Из (21.16) имеем
/(ffl)=XRe £
77117712
mjmgX
где Р\ — сферические компоненты вектора Р. Будем считать, что
тх — компоненты уровня у‘г равнозаселены и Wmi = (2у\ + I)-1.
Повторяя для системы уравнений (21.15) те же преобразования,
что и при выводе (21.29), получаем
р<?->(<0) = (-!)-»-•«.-«/2Г+Т( '* *)— J .
\ ТП-у 777 g <5/ I ^(0 — COqJ -J-
Величины P^',™',)(co) находятся с помощью (21.28).
Для матричных элементов имеем
V1’”'(Л; L Д) (А ИII «• -
§ 21. ОБЩАЯ ТЕОРИЯ УДАРНОГО УШИРЕНИЯ
273
Поэтому при вычислении I (св) возникает следующая сумма про-
изведений четырех 3/-символов
ш17П2А,
71 1 h\ = у ( 71
— тг X те2/ / । \—
х f /1 /2 » \/ 71
\—тп. тп_ —а/\—т'
7» 5 W Z1 in X
т?г2 — о/ \— т2 м
Напомним, что 2]\ — 2т1 — всегда четное число. Окончательно
1 (м) = Шу _LRe - ' =
2/Х“Ь1 л i (ю — <Оо)
_ (71II РII/2)2 Не G, _____1__________ /п4 w
2/i+l л (w-w04-ImG1)2+(ReG1)2 •
Для ширины у и сдвига Д линии имеем
у = 2 Re Gi, Д = — Im Gv (21.31)
Хотя возможные значения s равны s = Д + j2, j2 — 1, . . .
• • -»l 71— /г 1> уширепие полностью определяется только вели-
чинами р1О, а ширина и сдвиг линии выражаются только через
величину Gv Таким образом, в общем случае линии, образованной
совокупностью переходов а —[3 между двумя группами близко
расположенных уровней, спектр I (о) из (21.16) не описывается
единой лоренцевской формулой. Лишь в крыльях линии распреде-
ление интенсивности определяется простой формулой (21.21)
с единой константой уширения у из (21.22).
Однако в случае изолированной спектральной линии, соот-
ветствующей переходу между уровнями /х, /2, несмотря на вы-
рождение этих уровней по mv т2, формула (21.16) для I (со) дает
распределение интенсивности (21.30), т. е. единый лоренцевский
контур. Для вычисления ширины и сдвига этого контура доста-
точно найти лишь одну из величин^, а именно Gv Таким образом,
уширение линии, соответствующей дипольному переходу, описы-
вается лишь одним из уравнений системы (21.29), т. е. неприводи-
мым представлением s = 1.
Если повторить вывод формулы (21.30) для квадрупольного
перехода, то нетрудно показать, что в этом случае уширение оп-
ределяется другим уравнением этой системы — уравнением для
рв0 при s = 2, причем у = 2Re 6?2, Д = — Im G2.
3. Квантовомеханическое обобщение. Выше было показано,
что в тех случаях, когда относительное движение атома и воз-
мущающих частиц можно описывать классически, теория ушире-;
ния спектральных линий является естественным обобщение^
274
ГЛ. VII, УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
классической теории, основанной на модели осциллятора. Теперь
мы перейдем к построению последовательной квантовомеханиче-
ской теории ударного уширения, в которой и движение атомных
электронов, и движение атома и возмущающих частиц описы-
ваются уравнением Шредингера. Начнем рассмотрение с макси-
мально упрощенной задачи: масса атома много больше массы воз-
мущающей частицы, поэтому движением атома можно пренеб-
речь; имеет место лишь упругое рассеяние.
Определим матрицу плотности атома с помощью общего пра-
вила (см. [35])
р (г, г') = §¥* (г, R) Т (rz, R) dR, (21.32)
где R — координата возмущающей частицы.
Будем описывать стационарные состояния системы «атом 4-
возмущающая частица» волновыми функциями
(г, Ж) = Фа (г)-Х Ге»» + , (21.33)
где Фа (г) — атомная волновая функция, /а (0) — амплитуда рас-
сеяния, к — волновой вектор возмущающей частицы, V — нор-
мировочный объем.
Разложим волновые функции системы в правой части (21.32)
по волновым функциям (21.33):
Т(г,Л) =
а
Разложим также оператор р (г, г') по стационарным состояниям
атома
Р (г, г') = 2j РофФа (г) Фр (г'),
ар
(21.34)
В результате получаем следующее выражение для элементов мат-
рицы плотности атома:
* i
pap — &aOp ~y~
f*
e-ikR [ , 2» g-ifcR
eikR + A giftR dR =
* I. . 1
fla^p ] 1 4—p-
exp (— ikR 4- ikR) +
f* f*f '
4- exp {ikR — ikR) -|—
Здесь экспоненциальные множители exp [— ikR 4~ ikR] =
= exp [— ikR cos 0 4~ ikR] быстро осциллируют всюду, за исключе-
нием области cos 0 ~ 1, 0 = 0. Поэтому при вычислении первого и
второго интегралов в (21.35) можно вынести значения амплитуд
§ 21. ОБЩАЯ ТЕОРИЯ УДАРНОГО УШИРЕНИЯ
275
/*, /р при 6 — 0 .за знак интеграла. После этого
{i - -4 4 <°) - /₽ (°) 1+4 $ 1* <е>do} •
(21.36)
где R — радиус шарового объема V; fa (0), /р (0) — амплитуды
рассеяния вперед. Если в (21.33), (21.35) оставить лишь плоские
волны, положив fa — /р = 0, т. е. пренебречь взаимодействием,
то рар — й«ар. Таким образом, последние два члена в (21.36)
дают приращение матрицы плотности атома в результате акта
рассеяния
Драр = рар А {_ 2А. (/* (0) _ (0)] 4 J /*/pdo} . (21.37)
Это выражение является квантовым обобщением квазиклассиче-
ского выражения (21.13).
Для того чтобы перейти от (21.37) к столкновительному члену
(dp/dt)CT в общем уравнении для матрицы плотности в ударном
приближении (21.11), надо учесть, что при принятой в (21.32)
нормировке волновой функции па объем V приходится одна воз-
мущающая частица, а время, приходящееся на один акт рассея-
ния, равно R/v, где v — hk/m — скорость, тп — масса возмущаю-
щей частицы. Умножив Драр на NVv/R и усреднив по скоростям
V, получим
(“йЧог = - А' <г(а' - /О’)) Рсф, (21.38)
а - ia" = i 4 If* (0) - /о (0)1 - J (21.39)
Представим амплитуды рассеяния fa, в виде разложения по
парциальным волнам
/“4r£j(2i+1)l‘s’-1lpi<cos0)' = (21.40)
Я'-ш"=4^(2!+1){1- ЙХ). (21-41)
- 4 Е <2! + 11 - C0S 2 (’|“ ~ Лз))' <21-42)
--4Е(2г + 1)3‘п2<’1““’|’)- <21-43)
Таким образом, сечения уширения о' и сдвига сг" выражаются че-
рез амплитуды рассеяния или фазы рассеяния г). Тем самым ус-
танавливается связь между ударным уширением и упругим рас-
х) Формулы (21.39), (21.42) и (21.43) были получены несколько другим
способом в работах [69, 70].
276
ГЛ. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИИ
сеянием. Если возмущением одного из уровней можно пренебречь,
то ст' — 1/2 и, где о — сечение упругого рассеяния (напомним, что
ширина линии у = 2Nva'). При переходе к квазиклассическому
пределу hl -+mvp, (21 + 1) —> 2пр dp, 2 — т]р) —> т](р) и фор-
мулы (21.42), (21.43) совпадают с (21.19).
Формула (20.21) для ц (р) является предельным выражением
общей квазиклассической формулы для фазы 2 (д« — лр), справед-
ливым (в случае рассеяния на потенциале hDnR~n) при условии
mD кп~2
-------->1«
Л
которое можно также записать в виде
= <21-44)
где р0 — радиус Вейскопфа (20.24).
Для тяжелых возмущающих частиц это условие практически
всегда выполняется. Оно может нарушаться только в случае уши-
рения электронами.
Рассмотрим, какой вид имеет зависимость о' от скорости элект-
ронов v при больших v, т. е. в борновском пределе. Сечение б'
(21.42) можно также записать в виде
1 г1
|/«(0)-/ц(1Э)|2<Ю. (21.45)
В борновском приближении
где & — полное число электронов в атоме, F (q) — атомный форм-
фактор, q =-^-siny. Подставляя это выражение для f (0)
в (21.45), получаем
, 4лт2е4 f 7 о (д)
° = ~т~ J---------------—q iq- (21'46>
о
При больших скоростях рассеяние происходит в основном на ма-
лые углы. Это означает, что подынтегральное выражение в ин-
теграле (21.45) отлично от нуля только для малых значений 0
и, следовательно, этот интеграл не зависит от верхнего предела
(q — 2к при 0 = л/2). Поэтому интегрирование в (21.46) можно
распространить до q — оо. После этого интеграл в (21.46) уже не
зависит от к и
ст' оо к~2 оо у-2, у оо и-1.
§ 21. ОБЩАЯ ТЕОРИЯ УДАРНОГО УШИРЕНИЯ
277
Таким образом, при больших скоростях ширина линии обратно
пропорциональна скорости, причем это имеет место для потенциа-
лов любого типа. Необходимо только, чтобы интеграл (21.46)
СХОДИЛСЯ.
Выше мы ограничились случаем чисто упругого рассеяния.
Если повторить вывод выражения для столкновительного члена
(<9р/с?£)ст, учитывая также неупругое рассеяние, то нетрудно по-
казать, что формулы (21.39) и (21.41) сохраняют прежний вид. Те-
перь только величины S1 — ехр [— 2Г1 + i2iqz], поэтому
°' = 4 Е(2Z + l1 - ехр I- 2 (Г« + 4)1 cos [2 (т]4 - 4)]},
(21.47)
о" = — У, (2Z + 1) ехр [— 2 (Г« + Гр)] sin 2 (4 — рр).
(21.48)
Если возмущением одного из состояний можно пренебречь, то
о = t (2Z + 1) {1 — ехр [— 2Гг] cos 2р1} — — (оуП1) 4- оНеупр)»
“ (21.49)
где аупр и Онеупр — сечения упругого и неупругого рассеяния
соответственно.
4. Метод квантового кинетического уравнения. В этом разделе
мы обобщим уравнение для матрицы плотности и метод кинети-
ческого уравнения (20.50), перейдя к последовательному квантово-
механическому описанию движения атома и возмущающих частиц.
Такое обобщение необходимо для выяснения ряда принципиаль-
ных вопросов, связанных в первую очередь со’ статистической
зависимостью ударного и доплеровского уширений. Интере-
сующее нас уравнение для матрицы плотности атома р имеет
ту же структуру, что и (21.11):
-4=4-(я"р-ря") + Ш„,- <21-50>
Теперь, однако, невозмущенные волновые функции атома должны
быть взяты в виде
ФтР = Ф,п (Г)^Л, (21.51)
где JR — координата центра инерции атома, т — квантовые числа,
характеризующие внутренние состояния атома, р — волновой
вектор движения атома как целого, Ир — импульс атома. В фор-
муле (21.16) для I (со) в случае одной изолированной спектральной
линии m надо сделать замены
а->тр0, р->пх0, а' -+тр, |3'->пх, ТУа -* РГ(_р0),
Р -^deikR,
278
ГЛ. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
где к — волновой вектор фотона, d — электрический дипольный
момент атома, и заменить суммирование по оф, а'р' интегриро-
ванием по р0, р, х0, х. Поскольку
(пир | пх> оо с4«п6 (— р + к + х),
<пх01 de~ikB [ тр0У оо d^n6 (— х0 — к + р0),
нетрудно получить
I Л 12 р
/ (со) = Re jj dp0 dpW (p0) p^W” =
Irf |* 2 c
= Re dpF (p, p - fc), (21.52)
где через/1 (p, p — k) — §dp0 W (p0) p(mp,n(P-k)k)) обозначен соот-
ветствующий элемент матрицы плотности, усредненный по на-
чальному распределению волновых векторов р0. Всюду в даль-
нейшем в этом разделе мы будем опускать множитель j dmn \ 2-
Введем обозначение (dp/dt)CT = Gp, где G — оператор, задающий
изменение р за счет столкновения. Из уравнения (21.50) можно
получить следующее уравнение для F (р, р — к):
— W (р) 4- i (со — рк) F (р, р — к) = (GF)P, р~к, (21.53)
где т — масса атома, со отсчитывается от невозмущенной частоты
comn г). Формула (21.52) и уравнение (21.53) имеют точно такой
же вид, как и (20.54), (20.56). Теперь, однако, используя квантовое
описание движения атома и возмущающих частиц, оказывается
возможным значительно детальнее исследовать структуру столкно-
вительного члена (GF). В частности, его удается выразить через
точные амплитуды рассеяния возмущающих частиц на атоме а).
Общее выражение для столкновительного члена (GF) оказывается
довольно громоздким, причем в основном это связано с тем, что
матрица р определяется в лабораторной системе координат, а ам-
плитуды рассеяния вычисляются в системе центра инерции. Мы
приведем ниже соответствующие выражения для двух предельных
случаев легких и тяжелых возмущающих частиц, тр т и
/Ир тп, где тр — масса возмущающей частицы, т — масса
атома.
В первом случае, в пределе т(11т ->0,
(GF)?,p_fc = _ FptP_k, (21.54)
4 В этом уравнении опущен член со к2’. (Нор — рН0) п к =
( , Я2 1 ( Я2 1
Ртр, np-k + 2т ^)2Jj— Ртр, np-к |^ю0 + т pkj .
2) Вывод общего выражения для столкновительного члена дается в ра-
боте [71].
§21. ОБЩАЯ ТЕОРИЯ УДАРНОГО УШИРЕНИЯ
279
где-т>--iA = N <рр(о'—- io")>, ст', ст" — сечения ширины и сдвига,
определяемые полученными выше формулами (21.39) — (21.43),
ир — скорость возмущающих частиц. Подставляя (21.54) в (21.53),
нетрудно получить, что спектр I (©) имеет вид свертки доплеров-
ского контура с обычным лоренцевским контуром ударной теории
уширения, имеющим ширину у и сдвиг А:
I (со) = — Re \ —-----,W , /9 , (21.55)
' ' л J i (со — A —pkh/m)у/2 v '
где pkh/m — vk, v — скорость атома.
В другом предельном случае легкого атома и тяжелых возму-
щающих частиц тр т, рр и
(GF)P, P_k=-N-^- [ст' (р) - io" (р)] F (р, р - к) -
_ дг М о (р) р (р, р - к) +
+ ^-^-J^°e/m(ff,J>)/n(«,Jp)F(®,^-JP), (21.56)
где ст', о" — те же, что и прежде, сечения ширины и сдвига, за-
висящие, однако, от р, т. е. от волнового вектора атома, а не воз-
мущающей частицы:
г (р) = (<г, Руп (9, р) = V (2i +1) [5,1, -1] [si, -1]*.
(21.57)
Если бы эта формула вместо /*/п содержала | fm | 2 (или | fn | 2),
то сечение ст (р) совпало бы с обычным сечением упругого рассея-
ния ст в состояниях т (или п). В данной задаче именно сечение ст
играет роль сечения упругих столкновений. В отличие от ст се-
чение ст в общем случае комплексно.
Если рассеяние близко к изотропному, то ст (р) » 4л/£/п.
Вынося в этом случае произведение из-под знака интеграла
в (21.56), получим
(GF)p, = — Nv [o' (г) — io" (p)] F (p, p — k) —
r dQ„
— Nvo (p) F (p,p — k) + Nvo (p) \ F (q,q — k). (21.58)
Уравнение (21.53) приобретает следующий вид (ср. с (20.67)):
i (со — kv) + Nv (□' — is" + г) — Р (Р^Р ~ —
NV'S Г
i (со — kv) 4- Nv (s' — is" -J- S) J in
280 гл. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
Интегрируя правую и левую части по dOp и учитывая, что
W = ’ w dp = w dv' dOp = dOv'
легко найти j F (р, р — к) dOp и затем с помощью (21.52) спектр
(• dOv____________1_____________
/(ш) „ J_Не f-------J —‘s" + ^>----w(„)dv.
' 7 Л I (• dov 1 4 7
J 1 — NvZ J _ kv^ Nv _ i(5„ + ~y
(21.59)
Этой формулой обобщается формула (20.68) на тот случай, когда
одни и те же столкновения возмущают и внутреннее движение
электронов в атоме, и его движение как целого.
Все сечения о', о", а в этом выражении являются функциями
скорости атома. Легко видеть, что при N 0 (21.59) переходит в
обычное доплеровское распределение интенсивности (20.57). При
достаточно больших плотностях, когда можно пренебречь членом
kv, (21.59) принимает вид
I (со) — — ----лг N„^. —мт w (у) &v- (21.60)
' 7 nJ (to — Nvs")2 (Nv<3 ')2 v 7
• Вместо единого лоренцевского контура формула (21.60) дает супер-
позицию лоренцёвских контуров, каждый из которых характери-
зуется шириной 2Nvo,' сдвигом Nvo" и весом w (у). Если положить
о = 0, то (21.59) принимает вид
I (со) = _L Re С —--- . (21.61)
' 7 л J I (и — kv)-[-Nvz—iNvs 4 7
Это выражение отличается от обычной свертки доплеровского и
ударного контуров тем, что в знаменателе содержатся Nvq' (у)
и Nvo" (у) вместо усредненных по у величин у/2 = N <(уо'> и
Д = N (уо"у. Распределения интенсивности (21.60), (21.61) асим-
метричны.
Если положить о' — о" = 0, то (21.59) дает распределение
интенсивности того же типа, что и (20.68), описывающее эффект су-
жения доплеровского контура столкновениями. Параметр ТУуп
играет ту же роль, что и частота газокинетических столкновений v
в (20.68).
Рассмотрим случай больших давлений и воспользуемся разло-
жением (о' = о" == 0, Nvd^> kv):
С 7?0„ 1______ 1 _ kW 1
j 4л i (и —> kv) Nv5 ito ф- Nve 3 (sw ф- Nv5)a
21. ОБЩАЯ ТЕОРИЯ УДАРНОГО УШИРЕНИЯ
281
Для области частот ы <^ Nvd из (21.59) следует
I (Ш) = JL Re (j--------.
ico + -я- kzv2 (ЛГг><5)-1
О
1 V
Введем обозначение D = — -ft- • Тогда
/ _ С Не D w (v) dv
J я (co +A2ImZ>)2-|- (А2НеЙ)2 ‘
(21.62)
Если f m — tn и 5 совпадает с сечением упругого рассеяния а,
то Im D = 0, a Re Л — D есть коэффициент диффузии, зависящий,
однако, от v, а не от средней скорости и. В общем случае комплекс-
ных о и Л действительной частью D определяется ширина, а мни-
мой — сдвиг. Ширина 2к2 Re Л оо 1/N, таким образом, при
Nvo kv столкновения приводят к сужению доплеровского кон-
тура.
Результирующий контур линии согласно (21.61) представляет
собой суперпозицию лоренцевских контуров с ширинами 2к2 Re Л
и сдвигами к2 Im Л. Этот контур асимметричен.
Если о', о" не равны нулю, по меньше чем д, то сначала при
увеличении N имеет место сужение доплеровского контура до ши-
рины ~ Nvo', а затем уширение.
Результаты вычисления спектра I (со) с помощью метода кван-
тового кинетического уравнения, позволяющего учесть все аспекты
влияния столкновений на спектр излучения (ударное уширение и
компенсация доплер-эффекта с учетом их статистической зависи-
мости), содержат ряд новых элементов, наиболее интересными из
которых представляются следующие. Уже при рассмотрении
чисто ударного уширения (o', п"^> о) возникают качественные от-
личия от обычных формул ударного уширения. Только в случае
уширения такими легкими частицами, как электроны, возникает
единый лоренцевской контур с шириной 2N <гро')>, и сдвигом
N <црст">, где — скорость электронов; угловыми скобками
обозначено усреднение по vp. R общем случае тр ~ т после ус-
реднения по скоростям возмущающих частиц vp в столкновитель-
ный член входят сечения о' (г), а" (г), зависящие от скорости ато-
ма. В результате
Г((Л\ = С Nvs> (г;> ____w (г’)dv_____ /91 Г 9а
Этот контур в отличие от обычного лоренцевского асимметричен.
Наибольшее отличие возникает в случае рассеяния легкого ато-
ма на тяжелых (почти неподвижных возмущающих частицах).
Совершенно по-разному происходит сложение возмущений со
стороны возмущающих частиц разного сорта. Если возмущающие
282 гл. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
частицы сорта 1 и 2 легкие, то имеет место сложение ширин и
сдвигов
---iA = Nt <г-Х> 4- 7V2 <ЗД> + iNi (Mi> + <р2<Т2>-
Если же возмущение создается тяжелыми частицами (1) и электро-
нами (2), то при о=0
/(ш) =
= 1 Re С ________________________w (v) dv_____________________
Л’ J i (<0 — kv) (®1) 4” iNjVjfS" (Vj) ^2 (^2)^ 4" i^2
(21.64)
Все это является отражением статистической зависимости допле-
ровского и ударного уширений.
Второй характерной особенностью является комплексность
параметра о, ответственного за компенсацию доплеровского уши-
рения столкновениями и играющего в данной задаче роль сечения
упругого рассеяния. Интересно, что столкновения сказываются
на доплер-эффекте, только если амплитуды рассеяния для обоих
атомных состояний т и п отличны от нуля. Если /т = 0 (или fn —
= 0), то о = 0.
Перечисленные особенности влияния столкновений, вытекаю-
щие из статистической зависимости доплеровского и ударного
уширений, как правило, не очень сильно сказываются на ширине
результирующего контура. Поэтому в приближенных оценках
обычно их можно не учитывать. Однако в некоторых определен-
ных ситуациях они могут оказаться существенными. Примером
такого типа являются нелинейные резонансы мощности в спектре
газовых лазеров. Форма и положение этих резонансов, как пра-
вило, очень чувствительны к ряду тонких деталей механизма
столкновений и, в частности, к эффектам, обсуждавшимся в этом
разделе [72].
Для квантового кинетического уравнения также можно про-
вести разложение по неприводимым тензорам того типа, что рас-
сматривалось в п. 2 настоящего параграфа. Однако столкновитель-
ный член этого уравнения после усреднения по направлениям
движения возмущающих частиц в общем случае зависит от им-
пульса атома 1гр (ср. (21.56)). Поэтому он не является диагональ-
ным. Диагонализация столкновительного члена в уравнениях
(21.29) возникала именно из-за того, что все рассмотрение относи-
лось к неподвижному в пространстве атому. Поэтому единый
лоренцевский контур с шириной и сдвигом (21.31) возникает толь-
ко при условии, что при рассмотрении ударного уширения дви-
жением атома как целого можно пренебречь. Как было показано
выше, для этого необходимо, чтобы скорость атома была много
меньше скорости возмущающих частиц — легкие возмущающие
§ 21. ОБЩАЯ ТЕОРИЯ УДАРНОГО УШИРЕНИЯ 283
частицы, в частности электроны. В случае тяжелых возмущающих
частиц недиагональность столкновительного члена GS'0^aa яв-
ляется еще одним проявлением статистической зависимости удар-
ного и доплеровского уширений.
5. Спектр поглощения. Если система зарядов находится в поле
Е (R, t) = {Ео ехр [г (cof — fcJR)] + Е* ехр [— i (ю£ — кJR)]},
то энергия, поглощаемая системой в единицу времени (мощность
поглощения), в дипольном приближении равна
<2 = —Ed = Re {i(dE*dM ехр (ikR)},
где
d = da (R) + d* (R)e~iM
есть дипольный момент, наведенный в системе полем Е (R, t).
Квантовое обобщение формулы для Q имеет вид
Q — Re {г<в Sp E*d ехр (ikR) р (си)}. (21.65)
Здесь d — оператор дипольного момента атома, R — координата
центра инерции атома, к — волновой вектор фотона, р (со) — ком-
понента Фурье матрицы плотности, удовлетворяющей уравнению
~ (Нор - рН0) - £р = -L (Edp - pEd). (21.66)
R, R,
Это уравнение в отличие от (21.50) содержит член взаимодействия
атома с полем. Решая это уравнение методом последовательных
приближений по внешнему полю, можно с помощью (21.65) найти
мощность Q, поглощаемую, или излучаемую, атомом в данном
поле в различных приближениях по Е.
Если поле возмущает группу переходов атома а -+ [3 (частоты
<вар близки к частоте со), то из (21.65) нетрудно получить
<2 = Re йаЕ* 2 ^ар f <Рррр, а^+fc (w), (21.67)
ар
где р — импульс атома.
Покажем, каким образом из (21.66), (21.67) получается спектр
линейного поглощения. Опустим для простоты столкновительный
член и будем решать уравнение (21.66) в линейном приближении
по полю. Подставим в правую часть (21.66) матрицу плотности
нулевого приближения, диагональную по индексам а, (3 и р, р':
Р®, Рр = ^рЖ (р), pS+fc, a2)+fc = NaW (р + к) ж (р),
где Na, TVp — населенности состояний а, 0; W (р) — функция
распределения атомов по импульсам р. Поскольку к р, можно
284
ГЛ. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
принять, что W (р 4* Л) ж W (р). В этом приближении имеем
1 ъ
Ppp, ay+fc — *2 (TVp — 7Va)
W (р)
? “TTL^-y“>l I21 <“>’
ap
W (p) dp= ].m e C W (p)dp
e->0 Л
i w = M -
i
h \2
2
>2
А \
Рис. 31. Схема уровней
и рассматриваемые ра-
диационные переходы.
типа возникают при
Таким образом, мощность поглощения Q пропорциональна разно-
сти населенностей атомных состояний JVp — Na и функции I (со),
которая дает доплеровское распределение
интенсивности. В общем случае, когда ре-
шается уравнение (21.66) со столкнови-
тельным членом, функция I (со) описывает
контур линии (как поглощения, так и
спонтанного излучения) с учетом допле-
ровского и ударного уширений. Все полу-
ченные выше результаты для спектра
спонтанного излучения можно получить
также из (21.65), (21.66).
Как уже говорилось выше, решая урав-
нение (21.65) в следующем приближении
по полю -Е, можно найти мощность не-
линейного поглощения Q. Задачи такого
описании резонансов мощности газовых
лазеров [72].
6. Интерференционные эффекты. Сужение спектральных ли-
ний 1). В тех случаях, когда частоты двух или нескольких атомных
переходов совпадают или настолько близки, что возникает пере-
крытие спектральных линий, возможны своеобразные интерферен-
ционные эффекты, приводящие к качественному изменению харак-
тера уширения. В некоторых специальных случаях роль подоб-
ных интерференционных эффектов настолько велика, что картина
уширения полностью меняется. В частности, при увеличении дав-
ления может иметь место не уширение, а сужение спектра. Пояс-
ним сказанное на примере четырехуровневой системы, показанной
на рис, 31. Примем, что частоты переходов ым — &г и атп = ю2
близки, а частоты всех других переходов в этой системе лежат
в другой области спектра. При этом в формуле (21.16) для распре-
деления интенсивности в спектре, а также в системе уравне-
ний (21.15) для элементов матрицы плотности индексы а, а', а"
принимают значения к, т, а индексы р, |3', р" принимают значе-
т) В этом пункте изложение основано на работе [73].
§ 21. ОБЩАЯ ТЕОРИЯ УДАРНОГО УШИРЕНИЯ
285
ния I, п. Обозначим для упрощения записи пару индексов к, I
через 1, а пару индексов т, п через 2. Введем также обозначение
Wk = Wlt Wm — W2. Решая систему (21.15), получаем
r/ х 1 „ W^P^G^^ W2] P^G^-W^P^-W.^P^
/ (со) = Re-------------- ----- ------------J----,
Л ^11V22 — ^21^12
(21.68)
где
Gn = i (q - W1) + j (1 - SkkS^P (v) dv,
G22 — i (ft) (02) ~f“ j (1 $mmSnn)P (v)
G12 = -$S*mkSnlP(y)dv, (21.69)
G2i = - J S*mSln P (v) dv.
Примем далее, что элементы S-матрицы столкновений удовлетворя-
ют соотношениям
$кк Sтт — Snn, Skm Sin, Sтк — Snii
= *Smn ~ Skn — Sml — 0. (21.70)
Это означает, что столкновения приводят лишь к взаимному воз-
мущению состояний к и т, а также I и п, причем это возмущение
одинаково. Ниже будет показано, что имеется целый класс систем,
для которых возникает именно такая ситуация.
Используя (21.70), а также условие унитарности S-матрицы
2IW-1,
ь
получим
S^kSnl - I Smk I2 - 1 - I Smm I2,
SkmSin = I Skm I2 — 1 — | $kk I2-
Наконец, из общего определения эффективного сечения неупру-
гих столкновений о через соответствующие элементы S-матрицы
следует
S I Stm |! Р № = N <Wlra>, f I Smt I’ P (v) dv = V<Wral>.
(21.72)
где N — плотность возмущающих частиц, v — относительная
скорость, угловыми скобками обозначено усреднение по скоростям.
В стационарных условиях населенности уровней W и вероятно-
сти переходов должны быть связаны соотношениями
Wk (ивкт) = Wzrn<POmfr>. Поэтому
N<vohm> = , N(vomk> = ->, ЖгТх = W2y2. (21.73)
286
ГЛ. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
Таким образом,
Сц — i (со — coi) + -у-, G22 = i (со — со2) + -ну- у
с _ wi 7’1 г — 71
Ь12 jy2 2 ’ Gai ~ 2 '
Для частот Oi и w2 введем обозначения
wi — юо — б>2 = со0 4-6, 26 = Д.
(21.74)
(21.75)
Частоту оо будем отсчитывать от w0. В итоге из (21.68) для интен-
сивности линии I (со) получим
Т ((Л\ = 1 (^iTi + ^2Т2) I (о) - 6) Л - (о 4- 6) Р2 I2 7Р.
2л 1(м + б)(Ш-б)]2 + [у1(“-6)4-Т2(0) + 6)]2 •
Рассмотрим предельные случаи малых и больших у.
В первом предельном случае, когда величина отношения
Y1,г/в*С1, второй член в знаменателе выражения (21.76) мал и
интенсивность I (со) имеет два острых максимума в окрестности
со = ± 6. Выражение (21.76) можно переписать в виде
Z(co)
1
H\Yi I Л I2
(СО + 6)2 + у2
W2I ++ '
(CO -б)2 4-
(21.77)
В другом предельном случае Ух,2/6 1, выражение (21.76) имеет
один острый максимум при
(О^СОт =
Y1-Y2 s
71 + 72
В этой области (21.76) принимает вид
(ТУ171 + ТУ 2Y2) I 7 г 1 + Vi-Р а I2 1_______Г________ . 7q\
2717г (71 4- 72) л (СО - <0^)2 + 1’2 ’ • °'
где
^717г62
(71 +7г)3 '
Формулой (21.78) описывается лоренцевский контур с шириной
Г со UN.
Таким образом, общая картина уширения имеет следующий
вид. При малых давлениях, когда у1>2/6 обе компоненты ли-
нии уширяются независимо, причем их ширины у2 со N.
При дальнейшем увеличении давления, когда начинается перекры-
тие компонент, характер уширения меняется, и в предельном слу-
чае у1>2/6 1 обе компоненты стягиваются в один лоренцевский
контур, ширина которого убывает с ростом давления со 1/N.
В далеком крыле линии се ух, у2, 6 из (21.76) следует
^71 + ^7, |о(Р1-р2)-б(Р1 + Л)|2
2л со4
(21.79)
Заметим, что в частном случае Pr — Р2, I (со) со со~4.
§ 21. ОБЩАЯ ТЕОРИЯ УДАРНОГО УШИРЕНИЯ
287
Все качественные особенности рассматриваемого примера выте-
кают из условий (21.70), наложенных на элементы 5-матрицы
столкновений. Эти условия могут реализоваться в целом ряде
конкретных физических систем. Рассмотрим две подсистемы I
и II с уровнями А, В и а, b соответственно, показанными на
рис. 32. Предположим, что
подсистема I возмущается
столкновениями, а на подси-
стему II столкновения не
влияют (или влияют в значи-
тельно меньшей степени).
Система в целом, очевид-
но, имеет 4 уровня: 1 (Аа);
2 (Ва); 3 (АЬ); 4 (В&), при-
веденных на рис. 32.
Переходу а — b подсисте-
мы II теперь будут соответ-
ствовать два перехода 3 — 1
Рис. 32. Схема уровней подсистем I и
II (а) и всей системы (б).
и 4 — 2. Если взаимодействие между подсистемами I и II неве-
лико, то в достаточно хорошем приближении можно считать, что
оно приводит к различию частот w31 — о42 — Л 0, но не ска-
зывается на переходах в подсистеме I вследствие столкновений.
В этом случае 5-матрица столкновений имеет вид
5п
^21
^31
‘^22
532
^42
^13
*^23
^33
^43
*^24
^34
^44
tSAA SAB 0 0
$ВА SBB ° °
0 0 SAA SAB
0 SBA SBB
(21.80)
Но это в точности соответствует условиям (21.70). Таким обра-
зом, рассмотренный нами пример соответствует ситуации, которая
в принципе может возникнуть во всех случаях, когда ставится
вопрос о влиянии релаксационных переходов в подсистеме I на
спектр излучения подсистемы II. При этом естественно предпола-
гается, что между этими подсистемами имеется взаимодействие.
Если это взаимодействие, а следовательно, и связанное с ним рас-
щепление А, достаточно велико, т. е. у/А <С1, то, как показывает
проведенное выше рассмотрение, релаксация в подсистеме I
приводит к уширению спектральной линии, соответствующей ра-
диационному переходу в подсистеме II.
Если же взаимодействие стремится к нулю (у/А —> оо), то
контур этой спектральной линии приобретает вид б-функции
(ср. (21.78)). Другими словами, в этом случае возмущение под-
системы I не сказывается на спектре излучения подсистемы II.
Характерным параметром, показывающим, когда наступает раз-
вязывание подсистем I и II, является отношение у/Д. Поскольку у
288 гл. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
зависит от давления, при любом фиксированном значении Д су-
ществует область давлений, в которой у/Д <^1 и подсистемы I и II
связаны (в том смысле, что релаксация в подсистеме I дает ушире-
ние линии излучения подсистемы II). При повышении давления,
когда у/Д становится много больше 1, эта связь нарушается и
рассматриваемая линия начинает сужаться. Сужение линии, про-
порциональное N, обязано интерференции амплитуд излучения
смежных (перекрывающихся) переходов.
Рассмотрим в качестве конкретного примера, в котором могут
реализоваться подобные интерференционные эффекты, расщепле-
ние терма 2Р в сильном магнитном поле Н (эффект Пашека — Бака)
(см. [1]):
ЛЕ = ц0Я (ML + 2 Ms) + AMLMS, (21.81)
где ц0 — магнетон Бора, Ml и Ms — магнитные квантовые числа
орбитального момента и спина, А — константа тонкой структуры.
В этом случае мы имеем две подсистемы. Орбитальный момент
электрона в магнитном поле — уровни [i0HMl, Ml — 0, ±1 и
спин электрона в магнитном поле — уровни 2р,0 HMs. Рассмо-
трим магнитные дипольные переходы Ms — 1/2 -*-Ms — —1/2.
Очевидно, имеем три перехода соответственно трем возможным
значениям Ml = 0, ±1. Частоты этих переходов ~ 2р,077 рас-
щеплены на величину ~А. Сечение переориентации орбитального
момента в результате столкновения <3l значительно больше сече-
ния переориентации спина Os- Поэтому можно принять
у = N(vCl>.
Если у А, то переориентация орбитального момента проявля-
ется в уширении спектра переходов Ms — Ч2 —Ms — —1/2.
Если же у>Л, то релаксационные переходы Ml -*-Ml пере-
стают давать вклад'в уширение. Больше того, при увеличении N
должно наблюдаться сужение линии Ms -+Ms, пропорциональ-
ное 1/JV, причем в пределе у А ширина линии оказывается
меньшей первоначального расщепления Следует отметить,
что условие у А может быть реализовано лишь для самых лег-
ких атомов, для которых тонкое расщепление невелико. Напри-
мер, для Li тонкое расщепление основного уровня составляет
0,34 см-1.
Интерференционные эффекты могут проявляться в заметной
компенсации уширения и в ряде других случаев. Например,
в уширении электронами спектральных линий, образованных
переходами между сильновозбужденными состояниями атома во-
дорода (см. § 22).
§ 22. УШИРЕНИЕ ЛИНИЙ ВОДОРОДНОГО СПЕКТРА В ПЛАЗМЕ 289
§ 22. Уширение линий водородного спектра в плазме
1. Предварительные оценки. Основной причиной уширения
линий водородного спектра в плазме является линейный штарк-
эффект в полях электронов и ионов. Характер уширения в соот-
ветствии с (20.39), (20.40) зависит от величин безразмерных пара-
метров
h. = N (22.1)
где Са — константа линейного штарк-эффекта, ие и — скорос-
ти электронов и ионов соответственно. Для уровня с глав-
ным квантовым числом п константа С2 имеет порядок величи-
е2д 11
ны Zn(n — 1) —— ^Zn(n—1)[см2/с], Z — заряд возмущающей
частицы. Для большинства приложений наибольший интерес
представляет такая ситуация, когда 1, ahe 1, т. е. ионное
поле квазистатично, а электроны создают ударное уширение.
2. Уширение ионами. Теория Хольцмарка. При условии
hi 1 число уширяющих ионов в вейскопфовской сфере велико
и бинарное приближение уже неприменимо. Таким образом, пер-
вая задача, которая возникает при рассмотрении уширения иона-
ми, состоит в нахождении квазистатического распределения интен-
сивности с учетом одновременного воздействия на атом большого
числа ионов.
Если воздействие ионного поля <S на атом квазистатично, то
оно вызывает расщепление верхнего и нижнего уровней на от-
дельные штарковские компоненты, уширяющиеся независимо
друг от друга. Рассмотрим компоненты линии а — р и обозначим
через
X — Ва$,
яар = = 4- п' ИГ (22-2)
сдвиг этой компоненты в ионном поле # (а и р обозначают совокуп-
ность параболических квантовых чисел пх, и2, т и п[, т; ось
OZ |] #). Распределение интенсивности при фиксированном ионном
поле дается выражением
1ар (£, Дсо)dco = 6 ( Ай)~^ dm. (22.3)
•°ар \ Лхр /
Усреднив это выражение по распределению ионного поля W ($),
можно найти квазистатическое распределение интенсивности для
компоненты линии а — р:
7а₽ (со) Jco = W (Jo. (22.4)
"ар \ "ар /
Ю Л. А. Вайнштейн и др.
290
ГЛ. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
Функцией W (8) определяется вероятность данного значения
модуля поля %, являющегося векторной суммой полей отдельных
ионов
Таким образом, задача вычисления контура (со) сводится к на-
хождению функции распределения W ($). Эта функция была вы-
числена Хольцмарком в приближении идеального газа 1). В рам-
ках этого приближения вероятность нахождения иона к в эле-
менте объема Rjf, R* + dR\ равна dR-jV. Поэтому вычисление
функции распределения Хольцмарка Wh($) проводится следую-
щим образом:
WV
TVh (g) d$ = <6 - Ze =
fc=i
vv
fc=l *
NV
= $ ф- $ • • • $ exp П ex₽ (-z d® •
Здесь мы воспользовались известным представлением б-функции,
введя дополнительное интегрирование по р. Меняя порядок ин-
тегрирования по Rk и р, получаем в пределе V
= —jrjrfp ехр (ipg) 11-4-х
1 — ехр
/ е ZepRk \
I 1 R2 3 )
\ /
NV 1 (*
= -(25ij5"JdPexP(W Х
X ехр N dR £ 1 — ехр (— i •
Интегрирование по R удобно выполнить в сферических координа-
тах с осью OZ вдоль вектора р:
J dR [1 - ехр (- I = A(2nZep)'/..
Затем можно выполнить интегрирование по угловым переменным
вектора р. В результате получаем
WH (£) d8 = ^f-, (22.5)
©о j \ ©о/
2) Подробное изложение теории Хольцмарка, а также общих методов
решения ряда аналогичных задач см. в [67].
§ 22. УШИРЕНИЕ ЛИНИЙ ВОДОРОДНОГО СПЕКТРА В ПЛАЗМЕ 291
Таблица 36
Распределение Хольцмарка
₽ й?(₽) ₽ э? (₽) ₽ й?(Р)
0,0 0,00000 2,6 0,238221 7,0 0,015165
0,1 0,0042245 2,8 0,205563 7,2 0,013981
0,2 0,016665 3,0 0,176063 7,4 0,012922
0,3 0,036643 3,2 0,150242 7,6 0,011974
0,4 0,063082 3,4 0,128118 7,8 0,011120
0,5 0,094596 3,6 0,109422 8,0 0,010350
0,6 0,129587 3,8 0,093753 9,0 0,007438
0,7 0,166360 4,0 0,080674 10,0 0,005561
0,8 0,203233 4,2 0,069765 11,0 0,004289
0,9 0,238641 4,4 0,060654 12,0 0,003392
1,0 0,271221 4,6 0,053023 13,0 0,002739
1,1 0,299870 4,8 0,046604 14,0 0,002249
1,2 0,323782 5,0 0,041180 15,0 0,001875
1,3 0,342461 5,2 0,036573 17,0 0,001351
1,4 0,355702 5,4 0,032640 20,0 0,0008856
1,5 0,363566 5,6 0,029263 24,0 0,0005537
1,6 0,366334 5,8 0,026349 28,0 0,0003733
1,7 0,364456 6,0 0,023822 33,0 0,0002457
1,8 0,358502 6,2 0,021619 38,0 0,0001718
1,9 0,349109 6,4 0,019690 43,0 0,0001256
2,0 0,336939 6,6 0,017993 48,0 0,0000952
2,2 0,306821 6,8 0,016494 53,0 0,0000741
2,4 0,272746
ОО
2 (*
ИМ = "пф" J ж#ехР
о
где
dx,
= 2я (Ау/а£еЛ+* = 2,603ШУл.
(22.6)
(22.7)
Значения функции № (0) для широкого интервала значений 0
приводятся в табл. 36. Кроме того, график функции &С (0)показан
на рис. 33. Максимуму функции (0) соответствует точка
0 = 1,607. В двух предельных случаях, больших и малых значе-
ний 0, функция Ж (0) может быть аппроксимирована рядами
1,4960-‘А(1 + 5,1070-’/» + 14,930"3 + ...), 0> 1, (22.8)
А 02 (1 - 0,46302 + 0,12270*+...), 0<1. (22.9)
W)~
Если в выражении для (0) переопределить поле $0, положив
$0 = ZeR^, где Ro = (3/4n7V)’/», то вместо (22.8) получим
Ж (0) ж 1,5 0~’7’, что совпадает с бинарным распределением, кото-
Ю*
292
ГЛ. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
рое следует из (20.26). Отметим, что с практической точки зрения
отличие в обоих определениях $0 несущественно.
Для крыла линии из (22.8) получаем
I (со)«(со - (Оор». 1,5 3 /ар(5ар)‘/«(^0)*/., (22.10)
ар
что находится в полном согласии
Рис. 33. Распределение Хольцмарка
^(₽).
с бинарным распределением
(20.28). Это связано с тем, что
наиболее сильные поля созда-
ются в основном ближайшим
ионом. Надо отметить, что во-
обще функция распределения
бинарного приближения до-
вольно близка к Ж (Р) всюду,
за исключением области ма-
лых значений р. Последнее
также ясно: слабые поля
создаются большой совокуп-
ностью сравнительно удален-
ных ионов. Формулу (22.10)
удобно переписать, введя эф-
фективную константу Штарка В для линии в целом:
(В®,)-/., (22.11)
ар
где в соответствии с (22.1)
5’/а = Лхр Ш /2[заа - zpp]sA, (22.12)
ар
zaa, zpp — матричные элементы координаты атомного электрона.
Сравнение с результатами точных численных расчетов показы-
вает, что для водородоподобного иона с зарядом ядра & величи-
на В может быть аппроксимирована формулой
(22.13)
п, п — главные квантовые числа начального и конечного уров-
ней.
Аналогичным образом для контура линии I (со) = 2-^ар (со)
ар
также можно воспользоваться приближенным выражением [74]:
= (22.14)
Зависимость Гн от р определяется табл. 37. При больших
значениях р Тн (Р) ~ 1,5р~“К Поскольку контур линии (22.4),
а также (22.14) симметричен относительно <о0, хольцмарковская
§ 22. УШИРЕНИЕ ЛИНИЙ ВОДОРОДНОГО СПЕКТРА В ПЛАЗМЕ 293
Таблица 37
0 0,5 1 2 3 5 7 10 15 20
т л н 0,1 0,1 0,098 0,086 0,070 0,039 0,02 0,0072 0,0023 0,00099
ширина линии Дсон примерно равна 8В$0. Используя (22.13),
получим для линий водородного спектра
Дон ж 12,5 (и2 - п,2)У2\ (22.15)
Формула (22.14) достаточно хорошо описывает большую часть
квазистатического контура линии, за исключением его централь-
ной части.
Уточнение квазистатической теории Хольцмарка связано
с учетом взаимной корреляции положений ионов. Действительно,
в теории Хольцмарка для вероятности данной конфигурации
ионов .Вр -К2, • •.,-В/с не учтен множитель ехр [—У(-Вх, _В2,...)/?’],
связанный с энергией взаимодействия ионов. Таким образом,
в этой теории оказываются завышенными относительные вероят-
ности таких конфигураций, которым соответствуют большие по-
ложительные значения V, т. е. малые расстояния между ионами.
В частности, теория Хольцмарка дает слишком высокие вероят-
ности больших сдвигов частоты х, т. е. больших значений $ и
заниженные вероятности малых х.
Взаимодействие ионов V в плазме должно вычисляться с уче-
том дебаевского экранирования. Как известно, поле иона в плазме
на больших расстояниях убывает как ехр [—RIRd], где радиус
Дебая Rd определяется выражением
йл = 4лЛгеа (1 _|_ 22) 1 (22.16)
Отличие функции распределения ($), вычисленной с учетом
дебаевского экранирования, от функции Хольцмарка Ж (0), зави-
сит от величины безразмерного параметра
(22.17)
Величина а-3 равна числу частиц Nd в сфере дебаевского ра-
диуса. При а ->0 (Rd -> оо) функции Ж d (Р) и Ж (р) совпадают.
Графики функции $%d (Р), вычисленные в [75], для ряда зна-
чений а приводятся на рис.'34. Видно, что отличие &d (Р) от (Р)
становится заметным уже при а ж 0,4 (Nd ~ 16).
294
ГЛ. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
Таким образом, критерием применимости хольцмарковского
распределения является требование
а-з = дгп = Г__________L______Т1г (22.18)
a -Ivo- 3 |_ 4jre2(1-рZ2) J '
При рассмотрении уширения в спектрах водородоподобных
ионов типа Не+, Li++ и т. п. необходимо также учитывать влия-
ние заряда излучающего иона на возмущающие ионы (см. [75]).
Рис. 34. Распределение (Р) для нейтральной точки [75].
3. Учет теплового движения ионов. Тепловое движение ионов
приводит к тому, что поле $ в данной точке меняется как по вели-
чине, так и по направлению в пространстве. Изменение модуля £
приводит к изменению величины расщепления уровней, т. е.
к фазовой модуляции излучаемой волны.
Если переориентация вектора 8 происходит достаточно мед-
ленно, то угловой момент атома адиабатически следует за полем %.
При такой переориентации атома изменяется проекция его ди-
польного момента d на направление распространения световой
волны к, т. е. возникает амплитудная модуляция.
Расщепление уровня по магнитным квантовым числам М во
вращающейся вместе с полем системе координат имеет порядок
величины В%. Медленность переориентации означает, что
В% 1/т, где т — характерное время изменения направления
вектора <S. В обратном случае (В% <</ 1/т) возникающее во вра-
щающейся системе координат магнитное поле вызывает переходы
между M-компонентами. В результате связь между угловым мо-
ментом атома и полем разрывается.
§ 22. УШИРЕНИЕ ЛИНИЙ ВОДОРОДНОГО СПЕКТРА В ПЛАЗМЕ 295
Поправки на тепловое движение ионов, учитывающие как
эффекты фазовой и амплитудной модуляции, так и эффекты не-
адиабатичности (разрыв связи между угловым моментом атома J
и полем <9), были вычислены в работе [76].
Из этих вычислений следует, что тепловое движение ионов
наиболее сильно проявляется в центральной части контура. Крыло
контура, для которого Д<в Дсо0 = В$о и Д<в Q = vNBeZ
(см. (20.37)), описывается хольцмарковским приближением и при
hi > 1 и при При поправки на тепловое движение
пренебрежимо малы.
4. Уширение электронами х). Последовательная теория удар-
ного уширения линий водородного спектра электронами должна
учитывать неадиабатичность воздействия электронов на атом.
Основной вклад в уширение вносят вызываемые столкновениями
переходы между состояниями, относящимися к одному и тому же
уровню.
Рассмотрим спектральную линию, соответствующую радиа-
ционному переходу между уровнями а (состояния а, а', . . .) и b
(состояния р, Р', . . .).
Вычисление спектра I (со) может быть выполнено с помощью
общей формулы (21.16). Для этого необходимо определить эле-
менты матрицы S и решить систему (21.15). Для дальнейшего
удобно записать столкновительный член в (21.15) в виде
3 (22.19)
а"|з* ' '
где Ф — оператор столкновений, равный
Ф = АГ j v/(p) dv J {1 - S*Sb}• 2лр dp, (22.20)
о о
/ (р) — максвелловская функция распределения электронов по
скоростям; фигурными скобками обозначено усреднение по ориен-
тациям векторов риг; для краткости использовано обозначение
OP" I 5*5,1 а'Р'» = <а« | 5* | а'ХР" | 5 | р'>. (22.21)
Для определения 5 воспользуемся рядом теории возмущений
(21.29). Возмущение V (t), создаваемое пролетом электрона, имеет
вид
V (£) = е2 -Г-(Р+Т*) , (22.22)
(р2 + VW)'2 V ’
где г — радиус-вектор атомного электрона.
г) Детальное изложение теории уширения линий водородного спектра
электронами см. [77—80].
296
ГЛ. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
Ранее при анализе формул (20.13), (20.14) уже отмечалось, что
в случае взаимодействия V се R~2 основной вклад дают столкно-
вения с прицельным параметром р р0, где р0 — радиус Вейс-
конфа. Это позволяет ограничиться первым неисчезающим чле-
ном ряда (21.29). При усреднении по ориентациям векторов р
и v возмущение V обращается в нуль. Усреднение произведения
V(t)V(f) дает
{У (t) V (*')} = -------Р1+_^------ . (22.23)
Поэтому
оо оо
{1 - = 4 («')<«' +
—оо —оо
оо t со t
+ J Va(t)dt J va(t')dt'+ $ Vb(t)dt J Vb^df]. (22.24)
Первый член в квадратных скобках выражения (22.24) равен
ОО оо
е4 С С j, j*/ Р2 + v2tt'
-г-ГаГь \ \ dtdt ------------------4---------------гп- =
3 “ ° J J (р2 2,2^2)’/® (р2 V2t'2)Чг
— 00 — оо
= гл4^, (22.25)
второй и третий можно вычислить следующим образом:
«аТ
t
Va^dt Va(t')dt' а'Р) =
оо t
^‘^Да"а'7*аа'
а •—оо —оо
ехр (ian„nt) ехр „ „ , „„
aas — т2 , р2 + v2tt'). (22.26)
(р2 r2f2)’/2 (р2 _|_ V2t'2)’/2 4
Если ввести безразмерные переменные
Z1 = Z2 = -£- С0а'а, Хг = -у , Т2 = -у , [(22.27)
то (22.26) можно выразить через интеграл
Л (zi, zs) + iB (zi, z2) =
oo Xi
J dxi J dxt exp [Z (z^i — z2.r2)] • <22-28)
—oo —oo 4 2
Суммирование по а в (22.26) распространяется только на состоя-
ния уровня а. Возмущающим влиянием всех других уровней
§ 22. УШИРЕНИЕ ЛИНИЙ ВОДОРОДНОГО СПЕКТРА В ПЛАЗМЕ 297
пренебрегается. Матричные элементы ?’а"а отличны от нуля толь-
ко для соседних штарковских компонент а", а. Поскольку рас-
щепление эквидистантно, то при а" = а' zY = z2 = z и при
а" =/= а' zr = —z2 = z. Обозначим соответствующие интегралы
через А+ (z), В+ (z) и (z), В- (z). Все они могут быть выражены
через модифицированные функции Бесселя (функции Макдо-
нальда):
„ „ (jt I z I e-3lz|, z>l,
^±(2) = z’[X?W±X!(2))~| * , (22'.29)
B±(z) =
Z2 - Z'’
Л
17 ПРИ
—» 0 при
(22.30)
При интегрировании по р в (22.20) нижний предел интегрирова-
ния надо положить равным радиусу Вейскопфа р0, поскольку для
р р0 нет оснований ограничиться первым неисчезающим при-
ближением теории возмущений. Как уже говорилось выше, при
анализе формул (20.13), (20.14) область р < р0 дает сравнительно
малый вклад, который можно учесть, положив
СО оо
J {1 - S*Sb} 2лр dp « лро 4- J 2лр dp {1 - S*Sb}.
0 Ро
В качестве верхнего предела интегрирования следует принять
р = BD (см. (22.16)). Нетрудно убедиться, что для типичных пара-
метров плазмы величина zmax = RD®a."aJv, где иа»а — расщепле-
ние уровня в ионном поле $ = 2,6 ZeN*1*, много меньше единицы.
Поэтому в задаче электронного уширения линий водородного
спектра А = 1, 5=0*). В результате получим
ф = - 2r“r*} $ f1 +1,1• (22-31>
Относительно выбора верхнего предела интегрирования по р
надо сделать следующее замечание. Спектр I (со) в области частот
Д<о в основном определяется поведением функции корреляции на
временах t — 1/Дсо. Поэтому ударное приближение, основанное
на модели мгновенных столкновений, заведомо не может быть ис-
пользовано для столкновений с длительностью р/v > 1/Дсо. Отсю-
да возникает верхний предел интегрирования рт ~ vlДо. Поэтому
в качестве рт надо использовать наименьшую из двух величин
Rd и и/Дш.
При интегрировании по v в (22.24) нижний предел интегриро-
вания i;min должен быть выбран из условия р0 (pmm) < Rd-
х) Те же интегралы А и В возникают и в задаче уширения линий неводо-
родоподобного спектра (§ 23).
298
ГЛ. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
В результате нетрудно получить следующее выражение для Ф:
ф = 4 N (4Г lr°r°+r‘r“ - 2r"r»i (|n +°-215) • <22-32»
Здесь использовано соотношение = 4/<г>л, константа 0,215
ответственна за сильные столкновения р < р0. Определение ра-
диуса Вейскопфа р0 точно таким же образом, как это делалось
в § 20, дает
= ,22-33>
I (и, п) = I2)'1 S I ГаГа 4- ГЬГЬ —
а(3 ара'0'
-2гХ|аО«о2- (22.34)
Здесь п, п' — главные квантовые числа рассматриваемых уров-
ней а, Ь,
С помощью (22.32)—(22.34) нетрудно определить эффективную
константу ударного уширения электронами у, определяющую рас-
пределение интенсивности в крыле линии (21.21), (21.32):
? = N W1 -5- (in 4s + 0.215) I (п, п). (22.35)
О iftr \ [Jq /
Этой же величиной определяется масштаб уширения электронами.
Запишем фактор I (п, п) из (22.34) в виде
I («, п’) = I (n) + I (п') — 2К (п, п'). (22.36)
Поскольку (гаГа) а%п4, факторы I (п), I (п) имеют порядок
величины I (п) ~ пл, I (п) ~ п’* (для водородоподобного иона
с зарядом ядра z соответственно n4z“2, n/4z-2). Если пп , то
К (п, п') по порядку величины равен I (n), I (п'). Например,
для перехода п = 3 = 2: I (п) — 56, I (п) + I (п') = 68,
I (п, п') = 27. Для перехода п — 4 ->п' — 2: I (и) = 359,
I (п, п’) = 291. Тем не менее, имея в виду оценочный характер
формулы (22.36), для переходов между нижними возбужденными
уровнями атома водорода можно принять I (п, п') п\ где п —
наибольшее из главных квантовых чисел, или 1/2 (и4 + п'4).
Для переходов между близкими сильновозбужденными уровня-
ми п 1, n'^> 1, \ п — п’ |<^ п, п' член 2К (п, п') приводит
к сильной компенсации уширения. Этот эффект будет рассмотрен
в п. 6 настоящего параграфа.
Вычисление всего контура ударного уширения электронами
(при заданном ионном поле) требует трудоемкой численной про-
цедуры, связанной с решением системы уравнений (21.15) или диа-
гонализацией резольвенты этой системы. Поскольку гамильтониан
атома в электрическом поле диагоналеп в параболических коорди-
§ 22. УШИРЕНИЕ ЛИНИЙ ВОДОРОДНОГО СПЕКТРА В ПЛАЗМЕ 299
патах с осью z, направленной вдоль поля, вычисление матричных
элементов Ф должно проводиться с помощью параболических
атомных функций.
Результирующую картину электронного ударного уширения
в ионном поле схематически можно представить следующим обра-
зом. Ионное поле расщепляет водородную линию на отдельные
штарковские компоненты, которые уширяются вследствие столк-
новений с электронами. Электронный контур линии при фиксиро-
ванном ионном поле имеет весьма сложный характер. Если ионное
поле сравнительно мало и расщепление в этом поле меньше или
сравнимо с ударной шириной В<§ у, то отдельные штарковские
компоненты перекрываются. При этом существенную роль играют
недиагональные матричные элементы Ф. В результирующий кон-
тур линии, однако, основной вклад вносят ионные поля $ ~ $0)
для которых расщепление В<о0 превышает ударную ширину у.
В целом, в той области частот, где применимо ударное приближе-
ние, удается достаточно хорошо описать уширение электронами.
Расчет контура в промежуточной области, где ударное ушире-
ние сменяется квазистатическим, в случае водородного спектра
существенно усложняется тем обстоятельством, что вследствие
вырождения уровней эффекты неадиабатичности заведомо не
являются малыми. Тем не менее такие вычисления удается про-
вести, используя дополнительную симметрию кулоновского поля,
с которой связано присущее водороду вырождение уровней [81].
Оказывается, что сильные столкновения р < р0 отвечают кванто-
ванию по электрическому полю, а слабые столкновения р р0 —
по эффективному магнитному полю ЯЭфф. Последнее возникает
вследствие вращения электрического поля. Таким образом, уда-
ется найти процедуру диагонализации оператора Ф, применимую
ко всем водородным линиям.
5. Совместное действие электронов и ионов. Результирующий
контур, создаваемый возмущающим воздействием электронов и
ионов, можно получить, вычислив контур электронного уширения
при фиксированном ионном поле и усреднив результат по распре-
делению ионных полей W ($). Простейшее выражение для I (<в)
можно получить, описывая уширение электронами лоренцевским
контуром с шириной у из (22.35), а уширение ионами — прибли-
женным выражением (22.14) и вычисляя свертку обоих распреде-
лений. Результат таких вычислений представляется в виде
1 = ~в^ Т ( вад ’ “Йг) • (22.37)
Функция Т (х, у) определяется выражением
_ , _ f и (* Tw (»')
=. 2л j — а/р+О//2)2 • (22 •33)
300
ГЛ. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
1g т (X, у)
Таблица 38
X V 0 0,5 1 2 3 5 7 10 15 20
0,0 1,004 1,000 2,992 2,936 2,846 2,591 2,292 3,860 3,370 4,996
0,5 2,963 2,958 2,943 2,912 2,828 2,579 3,313 3,975 3,455 3,159
1,0 2,912 2,911 2,905 2,862 2,794 2,588 2,356 3,050 3,580 3,252
1,5 2,874 2,872 2,864 2,826 2,768 2,592 2,385 2,092 3,666 3,354
2,0 2,837 2,834 2,826 2,794 2,742 2,588 2,402 2,123 3,729 3,434
3,0 2,768 2,766 2,759 2,734 2,692 2,570 2,415 2,175 3,822 3,550
4,0 2,706 2,704 2,699 2,678 2,645 2,545 2,417 2,208 3,888 3,663
5,0 2,651 2,649 2,646 2,628 2,600 2,518 2,410 2,228 3,938 3,698
Значения логарифма функции Т (х, у) приводятся в табл. 38.
При у ->0 Т (х, у) -+Тн (х). Формула (22.37) описывает контуры
водородных линий в их центральной части с точностью порядка
20%.
В крыле линии (большие значения ж)
(22.39)
Уточнения этих результатов связаны с учетом двух обстоятельств:
1) в далеком крыле ударное уширение электронами переходит
в квазистатическое; 2) в центре линии уширение ионами должно
вычисляться с учетом поправок на тепловое движение ионов.
Кроме того, функция распределения ионных полей должна
учитывать эффекты экранировки.
Детальные расчеты контуров водородных линий были прове-
дены Кеплем, Гримом [82] и Видалем, Купером, Смитом [83].
Расчетные и наблюдаемые контуры в целом хорошо совпадают.
Расхождение с теорией заметно лишь в центральной части, осо-
бенно для линий с несмещенными центральными компонентами
(£а, На, Ну). Для таких линий контур содержит интенсивную
центральную компоненту, уширение которой целиком обусловлено
электронами. Для линий без центральных компонент (Lp, Г/р, Н^)
роль электронов в образовании центральной части контура мень-
ше. Она сводится в основном к сглаживанию провала в квазистати-
ческом ионном контуре.
Контуры линий в плотной плазме обладают заметной асим-
метрией, создаваемой неоднородностью поля и соответствующим
квадрупольным взаимодействием. Учет этого взаимодействия дает
поправки к хольцмарковскому контуру, величина которых'опре-
деляется параметром aon2/Ro, где п — главное квантовое
§ 22. УШИРЕНИЕ ЛИНИЙ ВОДОРОДНОГО СПЕКТРА В ПЛАЗМЕ 301
число, Ro — (3/4л7У)‘/’. Учет этих эффектов накладывает ограни-
чения на применимость хольцмарковского распределения со сто-
роны больших значений р = &а)/В80; Р (7?0/3п2а0)2. При
N ~ 1017 см-3 и п = 4 это неравенство выполняется до |3 ~ 30
[84].
6. Высоковозбужденные состояния. Компенсация электрон-
ного уширения за счет члена К (п, п') в (22.36) связана с обсуж-
давшимися в § 21 интерференционными эффектами. Элементы
5-матрицы 5nz,n(i±1) и 5n'z,n'(z±i)> которыми определяется уши-
рение, при больших п и ri = п — 1 почти одинаковы
*^nZ,n(Z±l) ^n'Z,n'(l±l) ^nl,n(l±i)-
Кроме того, матричные элементы дипольного момента Pni,(n-i)i
при замене I на I ± 1 также меняются очень мало. Поэтому воз-
никает ситуация, близкая к той, которая была рассмотрена в п. 6
§ 21 применительно к четырехуровневой системе. Можно показать
(см. [85]), что для переходов п -> п’ между близкими сильновоз-
бужденными уровнями 1, n' 1, \п — п' \ п, п' имеет
место неравенство
I (п, п') << I (п), I (п').
Так, для переходов п -> п — 1, п 1
Цп,п-1)~ Д- 1(п). (22.40)
rb
Выше было показано, что для переходов пп', п п' электрон-
ная ширина растет с ростом п, как п4. В соответствии с (22.40)
для переходов п п— 1, п^>1 имеет место зависимость
уе со п2. Это означает, что для таких переходов, а также любых
других переходов между близкими сильновозбужденными уров-
нями п 1, п' 1, | п — п' | п, п' необходимо учитывать
не только взаимное возмущение состояний Z, относящихся к од-
ному уровню, но также и возмущающее влияние на уровни п, п'
всех других уровней. Другими словами, для таких переходов имеет
место уширение такого же типа, как для неводородоподобных
атомов с квадратичным по полю эффектом Штарка. Уширение
неводородоподобных спектров рассматривается в следующем пара-
графе.
Как правило, задача вычисления ширины линий с n, п' 1
возникает в тех случаях, когда плотность плазмы невелика г).
При этом и для электронов и для ионов выполняются критерии
ударного уширения: he 1, hi 1.
4) Типичным примером являются спектры атомарного водорода эмис-
сионных туманностей. В таких спектрах наблюдаются дискретные линии
п —* п — 1 при п ~ 100. Соответствующие значения N примерно равны
102 -т- 104^см~®.
302
ГЛ. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
Для ширины линии п — п' поэтому имеем
Т = Те + Ть
Ve = Ne [<уие (n)> + <we («')>], (22.41)
Yi = Nt (n)> + <yoi (n')>],
гдеое(п)= У anin+fe— сечение неупругого рассеяния электрона
М >0
(иона) на атоме водорода в сильновозбужденном состоянии п.
Для величины (у<зе (п)У на основе описанных в § 10 квазикласси-
ческих расчетов сечений для высоковозбужденных уровней можно
построить следующую аппроксимационную формулу, аналогич-
ную формулам (10.17)—(10.19):
<щуе (п)> = 10 8 Ф (ж) /г (0),
z30 12
где
0 = T/z2 Ry, х = Еп/Т = z2 Ry/n2T,
(22.42)
Ф (x) = 2,18 {0,82<p (x) + 1,47 [1 - xy (x)]},
Ф (x) == — e5CEi(—x)^ In [14-] » у = 1,78,
T' v 7 L yx(l 4-l,4x) J ’ ‘
- h{‘+xa+wra;} /ln 11 + n (22'43>
fz (®) 1 при z оо или 0 r~i~ 00 •
В случае, если возмущающими частицами являются протоны,
в формулах (22.42), (22.43) величину Т необходимо заменить па
величину Тт/М, где m — масса электрона, а М. — приведенная
масса сталкивающихся частиц.
§ 23. Уширение линий
неводородоподобных спектров в плазме
1. Предварительные оценки. Спектральные линии неводородо-
подобных атомов в присутствии постоянного и однородного элек-
трического поля испытывают смещение (а также расщепление),
пропорциональное $2,— квадратичный штарк-эффект. Предполо-
жим, что поле $ — QR~2, создаваемое зарядом Q, мало меняется
на протяжении атома (это справедливо для достаточно больших
значений R). Тогда в выражении (20.20) для сдвига частоты ос-
циллятора п = 4 и х = С4Т?-4. Оценим величины параметров he
(уширение электронами) и hi (уширение ионами):
‘ = л'(тт)' hi = N(-T^\- <23Л>
\ 4 ve. / \ л vi /
§ 23. УШИРЕНИЕ ЛИНИЙ^НЕВОДОРОДОПОДОБНЫХ СПЕКТРОВ 303
Константы квадратичного штарк-эффекта С4, как правило,
имеют порядок величины 10-12 -j- 10-16 см4/с, хотя встречаются
и значения < 10-15 и С4 ~ 10-11 -н 10'10 см4/с. Подставляя
С4 = 10-12 -j- 10-15 см4/с в (23.1) и принимая ve — 5-107 см/с и
Vi = 2 -105 см/с, получаем
he = 3-(10~19— 10~22)jV, hi = 0,75-(10-17 - 1O~2O)7V.
При не очень больших значениях концентрации заряженных
частиц N < 1016 см~3 Ле<^1, ^<^1 и, следовательно, и электро-
ны и ионы создают ударное уширение.
Согласно (20.23) у4, Д4 со z/A. Таким образом, основную роль
в уширении линии играют электроны. Взаимодействие с ионами
лишь немного увеличивает ударную ширину и сдвиг линии —
примерно на 15—20%, так как (velvi)'l* — 5 -н 6. По-
скольку х со Q2, направление сдвига линии одинаково для ионов
и электронов.
2. Уширение электронами. Воспользуемся для описания удар-
ного уширения электронами результатами, полученными в § 21.
В случае изолированной спектральной линии контур является
лорепцевским, т. е. описывается формулой (21.17) с шириной и
сдвигом из (21.18), или (21.19), (21.20). В эти формулы необходимо
подставить усредненные по М-компонентам уровней элементы
5-матрицы. Как правило, основной вклад в ширину у и сдвиг Д
вносит область больших значений прицельного параметра р,
в которой можно ограничиться первыми членами разложения 5
по Г ищ. Поэтому для вычисления у и Д можно воспользоваться
усредненными по М фазами Г и г].
Рассматривая дипольное взаимодействие V — d%, можно опре-
делить 5 (v) с помощью формулы (21.25), сохранив в ней только
второй член (квадратичный штарк-эффект). Первый член, линей-
ный по V, равен нулю.
Предположим далее, что возмущением одного из уровней мож-
но пренебречь. Тогда для перехода к1), считая, что уровень к
не возмущается, можно получить
где функции А, В совпадают с функциями А+, В+ (22.29), (22.30)
(значения функций А и В приведены в табл. 39), Д^гз = Es — Еп,
fna — сила осциллятора перехода п->$2). Суммирование по s
г) Уровень п расположен выше уровня к.
fns > 0 при Es > Еп.
304
ГЛ. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
Таблица 39
Функции А (г), В (z)
Z А в Z А В
0,0 1,000 0,000 1,8 0,177 0,507
0,2 1,035 0,160 2,0 0,130 0,467
0,4 0,962 0,359 2,4 0,0688 0,393
0,6 0,829 0,498 2,8 0,0355 0,331
0,8 0,680 0,576 3,2 0,0181 0,283
1,0 0,540 0,606 3,6 0,0090 0,245
1,2 0,418 0,603 4,0 0,0045 0,216
1,4 0,318 0,580 5,0 0,00075 0,166
1,6 0,239 0,546 —* оо nze-2z л/4г)
распространяется на все уровни атома, связанные с уровнем п,
электрическими дипольными переходами. Как правило, однако,
основной вклад в сумму по s дают несколько ближайших из таких
уровней или даже один ближайший возмущающий уровень. В этом
последнем случае вычисления значительно упрощаются. Такие
вычисления, включающие усреднение по максвелловскому рас-
пределению скоростей электронов, приводят к следующим выра-
жениям для ширины и сдвига:
у = 2ДГ<р>о; «у»/' (Р), (23.4)
А = JV<p>ao (Р), (23.5)
где Сто, Но — сечения ширины и сдвига из (20.13), (20.14),
а« = НгГГ Ш (23.6)
йо ~ VЗн0,
(у) — среднее значение скорости электронов, константа С4 в дан-
ном случае определяется формулой С4 = 2е^а° / . Факторы
J' (р), J" (Р) являются функциями безразмерного параметра
I , Ry 1*/« ЬЕ
|' &Е I т(г>>2
(23.7)
При Р —» оо J', J" —> 0,97. Этот случай соответствует чисто адиа-
батическому возмущению, когда уширение целиком определяется
набегом фазы т]. При Р<^1, наоборот, основную роль играют не-
упругие столкновения и уширение определяется величиной Г.
§ 23. УШИРЕНИЕ ЛИНИЙ НЕВОДОРОДОПОДОБНЫХ СПЕКТРОВ 305
При этом
<-> - (/-&) <? >" [лщ (' &)']> •
<ш'> = - 2па (/ <» (^)’> - Д . (23.9)
Результаты численных вычислений факторов J' (0), J" (0) приво-
дятся в табл. 40.
Таблица 40
Значения интегралов J' (§), J" (Р)
₽ J'(P) J"(₽) 6 J'(P) J’(₽)
64 0,97 0,97 0,156-10-1 0,594 0,151
32 0,97 0,97 0,78-10-2 0,451 0,094
16 1,02 0,97 0,39-10-2 0,334 0,063
8 1,03 0,96 0,195-10-2 0,239 0,0405
4 1,06 0,94 0,97-10-з 0,171 0,0245
2 1,12 0,90 0,48-10-з 0,119 0,0167
1 1,17 0,861 0,24-Ю-з 0,0824 0,0103
0,5 1,20 0,746 0,12-Ю-з 0,056 0,0065
0,25 1,15 0,604 0,61-10-1 0,038 0,004
0,125 1,09 0,455 0,305-10-4 0,024 0,0026
0,625-10-1 0,927 0,326 0,15-10-1 0,017 0,0016
0,312-10-1 0,764 0,223
Рассмотрим теперь, в какой мере полученные выше результаты
можно обобщить на случай нескольких возмущающих уровней.
Этот вопрос, очевидно, возникает лишь в том случае, когда для
одного или нескольких возмущающих уровней параметр р по-
рядка или меньше единицы. Действительно, в адиабатической
теории у и Д выражаются через постоянную квадратичного штарк-
эффекта для данной линии. Величина этой постоянной определя-
ется суммарным возмущающим влиянием всех атомных уровней.
Если для нескольких ближайших возмущающих уровней
Р<С 1, то ширину у можно вычислить, суммируя (23.4)
у = 2ZV<p>3'q^«p»J'(P). (23.10)
8
Это связано с тем обстоятельством, что неупругие ширины адди-
тивны. Что касается сдвига, то здесь ситуация сложнее. Соглас-
но (23.9) вклад одного возмущающего уровня в не зависит
от величины ] ДЕ |. Поэтому несколько возмущающих уровней
могут давать вклад одного порядка величины, причем разного
знака. По этой причине оценка сдвига с помощью суммирования
(типа (23.10)) может дать совершенно неверный результат.
306 гл. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
Условия, допускающие суммирование вкладов отдельных воз-
мущающих уровней в неупругую ширину (23.10), могут реализо-
ваться, например, для линий, соответствующих переходам типа
ns — п'р. В этом случае основную роль, как правило, играет
возмущение уровня п'р ближайшими уровнями п's и п'd, причем
соответствующие параметры 1.
В общем случае, когда возмущаются оба уровня п, к и при-
мерно одинаковую роль играют несколько возмущающих уровней,
причем параметры |3 не удовлетворяют ни условию [3^>1, ни
условию р<^1, необходимо проводить численные вычисления
по общим формулам для у и А (21.20), в которых Г = Гп + 1\,
т] — т|п — т]Л., а величины Гп, 1\, цп, щ вычисляются по форму-
лам (23.2), (23.3).
Результаты расчетов параметров уширения для большого
числа линий конкретных атомов и ионов приведены в книге
Грима [77].
§ 24. Уширение нейтральными частицами
1. Возмущение атомами постороннего газа. Ван-дер-ваал ьсов-
ское взаимодействие нейтральных атомов на больших расстояниях
имеет вид V (7?) со R~6. Поэтому обычно полагают
х = C6R~6. (24.1)
Сравнительно простая оценка константы Св дается формулой
С6^еа<^., (24.2)
где \г2> ж 6/an*4a2 — среднее значение г2 для возбужденного со-
стояния излучающего атома, п* — эффективное главное кван-
товое число, а ?=? (4/3)ша0<г2> (Ry/Z)2 — поляризуемость возму-
щающего атома, I — потенциал ионизации, т — число эквива-
лентных электронов. Константа С6 имеет порядок величины
С6 ~ 10-30 п*4. Следовательно, при v ~ 106 см/с
h = Г* N ~ W21W- (24.3)
Эта оценка показывает, что в области не очень больших давлений,
порядка и меньше атмосферного, основную роль играет ударный
механизм уширения. Сравним также величины Й = v'kC^1* и
Асор. Поскольку й ~ 1012, а Дсод ~ 1010, имеем й Асор, и
поэтому область ударного уширения простирается далеко за пре-
делы доплеровской ширины. В соответствии с (20.23) для оценки
ширины и сдвига линии можно воспользоваться формулами
у = 8,16^’у’/. ДГ, А у/2,8. (24.4)
Типичные значения ширины имеют порядок у ~ 10-8 N. При по-
строении более точной теории следует учитывать два обстоятель-
§ 24. УШИРЕНИЕ НЕЙТРАЛЬНЫМИ ЧАСТИЦАМИ 307
ства. Прежде всего закон взаимодействия V (2?) на расстояниях
порядка атомных размеров имеет существенно более сложный
вид, нежели со R~6. В зависимости от типа и состояний взаимодей-
ствующих атомов на больших расстояниях может иметь место
как притяжение, так и отталкивание; на малых расстояниях
всегда имеет место отталкивание. В ряде случаев возможно обра-
зование квазиустойчивых связанных состояний атом — возму-
щающая частица. Кроме того, вычисления должны проводиться
с учетом угловой зависимости взаимодействия и вырождения
уровней х). Результаты таких расчетов не сводятся к простым
универсальным формулам типа (24.4). Они зависят, в частности,
от типа рассматриваемого перехода J — J'.
Приближения, на которых основаны оценочные формулы
(24.4), особенно сильно сказываются на сдвиге А и отноше-
нии у/ А.
Экспериментальные данные по уширению линий атомов ще-
лочных металлов посторонними газами (Не, Ne, Аг, Кг, Хе, Н2, N2
и т. п.) при давлениях, меньших 10 атм, т. е. в области примени-
мости ударной теории, показывают, что для начальных членов
главной серии, как правило, наблюдается красный сдвиг, причем
отношение у!А близко к 2,8. В ряде случаев (обычно для высших
членов главной серии) наблюдается синий сдвиг. Сдвиг одной и
той же линии может иметь различный знак для разных возму-
щающих частиц.
Параметр h достигает значений порядка единицы лишь при
N 1021 см-3, т. е. при давлениях в десятки атмосфер. При этом
среднее расстояние между частицами сравнимо с атомными раз-
мерами, когда взаимодействие V (2?) уже заведомо нельзя описы-
вать простой формулой V (R) оо R~e.
Расчет потенциала V (R) на расстояниях порядка атомных раз-
меров связан с целым рядом трудностей. Поэтому часто данные по
уширению используют для выяснения особенностей взаимодей-
ствия нейтральных атомов, т. е. вида V (R).
2. Уширение в однородном газе (собственное давление).
При увеличении плотности однородного газа резонансные линии
уширяются значительно сильнее, чем при добавлении посторон-
него. Это связано с тем, что при столкновении двух одинаковых
атомов, один из которых возбужден, возможна резонансная пере-
дача энергии возбуждения, причем эффективные сечения таких
столкновений весьма велики. Они могут значительно (на несколько
порядков) превосходить газокинетические.
Оценим уширение резонансной линии, возникающее из-за
сокращения времени жизни возбужденного состояния. Эффектив-
ные сечения резонансной передачи возбуждения ст вычисляются
х) Расчеты такого типа для взаимодействия со R~e см. в работах [86, 87],
308 ГЛ. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
в § 12. Для электрического дипольного перехода передача возбуж-
дения определяется диполь-дипольным взаимодействием V со R~s,
а сечение о и ширина у имеют следующий порядок величин (см.
(12.36)):
е2 6" 2 е2 , е2 ... г,
о----т------а0---------/, у---------fN, (24.5)
Йу Зе2а2 пгсо0» ' 1 та>0 ‘ '
где S — сила линии, / — сила осциллятора перехода. Принимая
/ 1, 1015 с-1 получаем у ~ 10-7 N, тогда как для ван-дер-
ваальсовского взаимодействия типичны значения у — 10~8 N.
Эффективные сечения передачи энергии возбуждения могут
быть весьма велики не только при точном резонансе, но и в об-
щем случае столкновений атомов с близкими уровнями. Так, при
вычислении ширины компоненты 2Pi/t — 2Si/t резонансного дуб-
лета щелочного атома помимо передачи энергии в процессах
2Pi/226'1д (излучающий атом) и 25i/2-> 2Р1д (возмущающий
атом) надо, вообще говоря, учитывать процесс возбуждения
2Si/t -> 2Р>/г возмущающего атома. В § 12 показывается, что
сечение второго процесса имеет тот же порядок величины, что и
чисто резонансного при выполнении условия
где \Е — дублетное расщепление. Из всех атомов щелочных ме-
таллов этому условию удовлетворяет лишь атом Li, для которого
ДЕ мало (0,34 см-1).
Оценка ширины (24.5) основана на вычислении сечений пере-
дачи возбуждения в приближении вращающейся оси столкнове-
ния. Уточнение этой оценки требует учета угловой зависимости
взаимодействия и вырождения уровней рассматриваемой системы
двух сталкивающихся атомов. Приведем окончательные результа-
ты наиболее детальных из имеющихся расчетов [88, 89]. Эти рас-
четы показывают, что в рамках ударного механизма возникает
как уширение, так и сдвиг спектральной линии того типа, что
приводит к хорошо известной формуле Лоренц — Лоренца в тео-
рии дисперсии.
Для атомов щелочных металлов ширина у и сдвиг Д компонент
тонкой структуры резонансных линий 25i/2 — 2Л/2, 25i/2 — 2А/2
определяются формулами
А- + .Д = (1,16 -10,48) fN, ’Л/, - »/>.,„ (24.6)
А- + 1Д = (1,86- 10,79) -^fN, гЗч,-гР.„. (24.7)
§ 24. УШИРЕНИЕ НЕЙТРАЛЬНЫМИ ЧАСТИЦАМИ
309
Для лития с учетом обоих возможных процессов возбуждения воз-
мущающего атома 251/г — 2Р*/г, 2P»/t имеем
+ <Д - (2,33 -10,37) fN, *S./t - (24.8)
+1Д> (2,33-10,74)^-/W, (24.9)
В этих формулах / — суммарная сила осциллятора дублета
2Si/2 — 2Pi/2is/2, т. е. сила осциллятора перехода ns — п'р. Для
перехода ns — пр / 1.
В крыльях линии со — со0 и’/* (/е2/тсо)“^г ударное рас-
пределение должно сменяться квазистатическим крылом. В данном
случае взаимодействия распределение интенсивности в кры-
ле также имеет вид (со — соо)’2 (см. (20.28)), но с другим коэффи-
циентом. Вместо распределения у/2л(со — соо)2 с величиной у из
(24.6), (24.7) имеем
/>2 4
(24.10)
Ца) я; 2,15—1—2$1/,-’Р./>. (24.11)
' ' 2та0 ' (со —<й0)2 '* ,г ' '
Для резонансных линий атомов, у которых угловой момент
в основном состоянии Jo — 0, в возбужденном J = 1 (атомы
гелия, ртути ит. п.):
1 + *А = (2,.33-11,11) ^-/W. (24.12)
В квазистатическом крыле
Р2 4
I (со) « 2,79 fN 7—.
' ' 2гм)0 7 (со — со0)
(24.13)
Здесь / — сила осциллятора перехода Jo = 0 -> J = 1. Ушире-
ние вследствие резонансной передачи энергии возбуждения имеет
место также и для линий, соответствующих переходам на резо-
нансный уровень. Для таких линий ширины у совпадают с шири-
нами соответствующих резонансных линий, а сдвиг А — 0.
Условия оптически тонкого слоя для центральной части резо-
нансной линии могут реализоваться только при достаточно малой
плотности, когда у, А <<; Acdd. Действительно, коэффициент по-
глощения в центре резонансной линии имеет порядок величины
W
4
Рг
—fN
mr z
1 ___ у 1
AcOj-) Дсо^ X
где W — вероятность спонтанного перехода. Поэтому для слоя тол-
щины L условие kL 1 1\ можно выполнить лишь при
310 гл. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
у <<! сор. При больших N, когда у контур линии, неиска-
женный эффектами самопоглощения, может наблюдаться лишь
при | со — соо | Дсор. С учетом сказанного совместное действие
доплеровского и ударного механизмов уширения можно описы-
вать обычной сверткой доплеровского и ударного контуров, от-
влекаясь от таких эффектов, как статистическая зависимость
обоих механизмов уширения.
Для линий, оканчивающихся на резонансном уровне, условия
оптически тонкого слоя могут быть выполнены при любом соотно-
шении у и Дсои- В этом случае, однако, эффекты статистической
зависимости доплеровского и ударного уширений вообще не игра-
ют существенной роли, так как в выражении для о (21.57) одна из
амплитуд рассеяния много меньше другой и о<^о' (диполь-ди-
польное взаимодействие V оо R~3 имеет место лишь для одного
из состояний, участвующих в радиационном переходе). Кроме
того, в данном случае о' со р-1 и Nvo вообще не зависит от v.
§ 25. Спектроскопический метод исследования
упругого рассеяния медленных электронов
1. Возмущение высоковозбужденных состояний. Уширение
спектральных линий, соответствующих переходам между основ-
ным состоянием и высоковозбужденными состояниями, практиче-
ски полностью определяется возмущением возбужденных состоя-
ний. В случае уширения нейтральными частицами для состояния
с достаточно большим главным квантовым числом п может иметь
место такая ситуация, когда среднее расстояние атомного элек-
трона от ядра ~а0п2 настолько велико, что возмущающая частица
или взаимодействует с электроном и не взаимодействует с атомным
остатком, или, наоборот, взаимодействует только с атомным
остатком.
В этом случае уширение линии будет определяться двумя ста-
тистически независимыми эффектами — рассеянием атомного
электрона на возмущающих частицах и рассеянием возмущающих
частиц на атомном остатке.
Начнем с рассмотрения первого из этих эффектов. Как следует
из (21.39), в тех случаях, когда возмущением одного из состояний
можно пренебречь, эффективные сечения ширины и сдвига опре-
деляются формулами
а'=-£-1ш/(0), О”=_ JiRe/(0), (25.1)
где / (0) —- амплитуда рассеяния вперед возмущающей частицы
на атоме, Тгк — импульс возмущающей частицы (для простоты
предполагается, что масса атома больше массы возмущающей ча-
стицы). Если а0^2^>Ррэфф~ гДе Рэфф — эффективный
§ 25. УПРУГОЕ РАССЕЯНИЕ МЕДЛЕННЫХ ЭЛЕКТРОНОВ
311
радиус взаимодействия электрона с возмущающей частицей, а — по-
ляризуемость возмущающей частицы, то в области взаимодействия
электрона с возмущающей частицей потенциал, создаваемый атом-
ным остатком, практически не меняется. Следовательно, во всей
этой области остается постоянной и скорость электрона ve, имею-
щая порядок величины v0/n, где v0 = e* 2/h — атомная единица
скорости. Если вместе с тем скорость возмущающей частицы
vp — ПкМ, где М — ее масса, мала по сравнению со скоростью
электрона ve ~ v0/n, то амплитуду рассеяния / (0) в (25.1) оказы-
вается возможным выразить через амплитуду рассеяния (0)
электрона на возмущающей частице х)
/ (°)=4 S । ° (п1т । «> Is л (°) <25-2>
Здесь т — масса электрона, hq — импульс электрона, G (nlm/q) —
коэффициенты разложения атомной электронной функции фпг7п
по плоским волнам:
G (nlm | q) = Gnl (q)Ylm (0e, <pe). (25.3)
Поскольку состояния с большими значениями п водородоподоб-
ны, в качестве коэффициентов G(nlm\q) можно использовать
известные выражения для водородных функций в импульсном
представлении через полиномы Гегенбауэра 2).
Подставляя (25.2) в (25.1) и выполняя интегрирование по углам
и усреднение по ориентациям углового момента возмущающей
частицы, можно получить следующие формулы для ширины и
сдвига:
= (25.4)
A=_№^^(?)Re4(°)</?, (25.5)
w (9) = 9s I <?„, (9) р, J W (q)dq = 1. (25.6)
Из сказанного выше следует, что эти формулы для ширины и
сдвига, обусловленные эффектом рассеяния сильновозбужден-
ного атомного электрона на возмущающих частицах, применимы
при выполнении следующих условий:
п'/. > (25.7)
_т е2
п<ИГТ^;- (25.8)
г) Эта и последующие формулы этого раздела были получены в рабо-
те [90].
2) См., например, [91].
312
ГЛ. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
Перейдем теперь ко второму эффекту — взаимодействию воз-
мущающих частиц с атомным остатком. Поскольку атомный оста-
ток имеет заряд е, это взаимодействие на расстояниях, больших
размеров атомного остатка и возмущающей частицы, имеет вид
U = (25.9)
Оно приводит к поляризации возмущающей частицы атомным
остатком и сдвигу частоты рассматриваемого атомного перехода
х (0 = ~ 2д g2 [я (f)j4 • (25.10)
Уширения из-за взаимодействий такого типа рассматривались
в § 23. Если
*, = ₽?Л<1, (25.11)
где N и vp — плотность и скорость возмущающих частиц, то цен-
тральная часть линии | со — соо | Q = (2ЙРр/ае2)1/* имеет ло-
ренцевский контур с шириной у' и сдвигом Д':
/«lugff’w, = (25.12)
В том случае, еслиДг 1, взаимодействие (25.9) приводит к ква-
зистатическому уширению. Можно показать, что при этом ширина
и сдвиг имеют порядок величины 10
Наибольший интерес представляют такие условия, когда
hi <<; 1. В этом случае величины у' и Д' можно вычислить весьма
надежно. Для этого необходимо знать лишь поляризуемость воз-
мущающих частиц. Поэтому вычитая из измеренных значений
ширины и сдвига величины у' и Д', можно найти у и Д, определяе-
мые формулами (25.4), (25.5). Тем самым оказывается возможным
получить информацию об упругом рассеянии электронов со ско-
ростями ~v0/n на возмущающих частицах.
Выразив амплитуду рассеяния (0) через фазы рассеяния тц,
запишем у и Д из (25.4), (25.5) в следующем виде:
" = Пт £|!; +1' si“! ч, 1W (?) <г? = jv 4 («а w <«>
гГД у ***' л)
(25.13)
(2Z + l)sin2n,] W(q)dq. (25.14)
Здесь о (q) — эффективное сечение упругого рассеяния электрона
с импульсом q.
§ 25. УПРУГОЕ РАССЕЯНИЕ МЕДЛЕННЫХ ЭЛЕКТРОНОВ
313
Нетрудно показать, что если учесть обменное рассеяние, то
в формулах (25.13), (25.14) надо сделать замену
sin2 тр -> С+ sin2 т|)+) 4- С~ sin2 цг-), (25.15)
sin 2т)г -> С+ sin 2Лг+) + С~ sin 2т]^, (25.16)
где T]t+), r|j_) — фазы рассеяния, вычисленные с учетом обмена
для состояний системы «возмущающая частица + электрон» с пол-
ным спином S = Sp ± х/2, Sp — спин возмущающей частицы,
Рассмотрим серию поглощения щелочных металлов, т. е. переходы
s-p1). В этом случае [91]
W = 2л (п2 - Г) ) Х
X [(и + 1) sin (п— 1) ср — (п — 1) sin (п + 1) ф]2 а0, (25.18)
п2<?2а2 — 1
cos ф = ———5. (25.19)
Y п2?2а2+1 \ /
Функция W (?) имеет п максимумов, причем п/2 максимумов рас-
положены в области 0 < q <Z 1/па0. В этой области огибающая
приближенно ведет себя как (1 4- п2(ра%)~2. При q 1/тга0 W (q)
монотонно убывает:
W (?) (—L_V. (25.20)
3 л \ nqaQ J ' '
Таким образом, основной вклад в интегралы по q в (25.13), (25.14)
дает область 0 < q < 1/па0. Если п настолько велико, что основ-
ную роль в сумме по Z в этой области играет член 1 = 0 (s-pac-
сеяние)ти, кроме того, (1/?) sin 2тц мало отличается от своего
предельного значения
lira (-J-sin2Y]() = A а (°), (25.21)
TO
(25.22)
Здесь а (0) — предельное значение сечения упругого рассеяния
при’? -> 0; под т]0 понимается та часть фазы, которая после вы-
читания рл, где р — целое число, лежит в интервале —л/2, л/2.
*) Щелочные металлы наиболее удобны для эксперимента, так как их
спектры поглощения расположены в видимой и ближней ультрафиолетовой
областях спектра.
314 ГЛ. VII. УШИРЕНИЕ СПЕКТРАЛЬНЫХ линий
Поскольку при q —> 0 qa (q) -> 0, то в области применимости
(25.22) | Д Г).
2. Метод Ферми определения сечений упругого рассеяния
медленных электронов. Формула (25.22) была получена в работе
Ферми [93]. В соответствии с этой формулой по эксперименталь-
ному значению Д можно определить эффективное сечение упругого
рассеяния очень медленных электронов (в пределе q —0) на воз-
мущающих частицах. Так, по сдвигу линий поглощения Cs в атмо-
сфере благородных газов были найдены сечения о (0) для атомов
Не, Ne, Аг, Кг и Хе. Тем же методом исследовались и некоторые
другие газы (см. [93], а также [94]). Метод Ферми позволяет полу-
чить информацию об упругом рассеянии электронов при очень
малых энергиях, т. е. в области, наиболее трудно доступной для
других экспериментальных методов. Существенно, что сдвиг Д
чувствителен не только к абсолютной величине, но и к знаку фазы
рассеяния ц0.
В общем случае, когда в у и Д из (25.13), (25.14) дают вклад
несколько членов суммы по Z, определить фазы рассеяния по из-
вестным значениям у и Д нельзя. Знание этих величин, однако,
позволяет контролировать качество приближенных расчетов фаз
рассеяния * 2).
Некоторые дополнительные механизмы уширения рассмотрены в [92].
2) Экспериментальные исследования сдвига и ширины высших членов
резонансной серии поглощения атомов щелочных металлов и сопоставление
с теорией см. в работах [95, 96].
ЛИТЕРАТУРА
1. Собельман И. И. Введение в теорию атомных спектров. — М.: Физмат-
гиз, 1963; 2-е изд.— М.: Наука, 1977.
2. Budge М. В. Н. Theory of the ionization of atoms by electron impact.—
Rev. Mod. Phys., 1968, v. 40, p. 564.
3. Петеркоп P. П. Теория ионизации атомов электронным ударом.— Рига:
Зинатне, 1975.
4. Вайнштейн Л. А., Собельман И. И. Вывод радиальных уравнений тео-
рии столкновений электронов с атомами.— ЖЭТФ, 1960, т. 39, с. 767.
5. Курант Р., Гильберт Д. Методы математической физики.— М.: Гос-
техиздат, 1961, т. 1.
6. Файт В. Измерение сечений возбуждения и ионизации при столкнове-
ниях.— В сб.: Атомные и молекулярные процессы: Пер. с англ./Под ред.
Д. Р. Бейтса.— М.: Мир, 1964, с. 367.
7. Wannier G. Н. Threshold law for multiple ionization.— Phys. Rev., 1955,
v. 100, p. 1180.
8. Burke P. G., Schey H. M. Collisions of slow electrons and positrons with
atomic hydrogen.— Phys. Rev., 1963, v. 129, p. 1258.
9. Бейгман И. Л., Вайнштейн Л. А. Эффективные сечения обменного воз-
буждения атомов и ионов электронным ударом.— ЖЭТФ, 1967, т. 52,
с. 185.
10. Очкур В. И. О методе Борна — Оппенгеймера в теории атомных столкно-
вений.— ЖЭТФ, 1963, т. 45, с. 735.
И. Запесочный И. П. Абсолютные сечения возбуждения уровней атомов
щелочных металлов электронами малых энергий.— Теплофизика вы-
соких температур, 1967, т. 5, с. 7.
12. Damburg В., Karule Е.— A modification of the close-coupling approxima-
tion for e — H scattering allowing for the longrange interactions.— Proc,
Phys. Soc., 1967, v. 90, p. 637.
13. Geltman S.— In: Proc. VII Int. Conf, on Phys, of Electron, and Atom Col-
lisions. Physics of Electronic and Atomic Collisions.— North—Holland,
1972.
14. Burke P. G., Bobb W. D.— Adv. Atom. a. Molec. Phys., 1975, v. 11, p. 144.
15. Пресняков JI. П., Урнов A. M. Возбуждение многозарядных ионов элек-
тронным ударом.— ЖЭТФ, 1975, т. 68, с. 61.
16. Presnyakov L. Р., Urnov А. М. Asymptotic approach to the theory of
excitation of multiply-charged ions by electron impact.— J. Phys., Atom.
Molec. Phys., 1975, v. B8, p. 1280.
17. Базь А. И., Зельдович Я. Б., Переломов А. М. Рассеяние, реакции и
распады в нерелятивистской квантовой механике.— М.: Наука, 1971.
18. Бейгман И. Л., Урнов А. М. Борновские сечения переходов между
высоковозбужденными состояниями атомов при столкновениях с элек-
тронами.— J. Quant. Spectrosc. Radiat. Transf., 1974, v. 14, p. 1009.
19. Hostler L., Pratt В. H. Coulomb Green’s function in closed form. Phys.
Rev. Letters, 1963, v. 10, p. 469.
20. Буреева Л. А. О квазиклассическом приближении для сил осцилляторов
и эффективных сечений радиационных переходов.— Астр, ж., 1968,
т. 45, с. 1215.
316
ЛИТЕРАТУРА
21. Stabler R. C. Classical impulse approximation for inelastic electron—atom
collisions.— Phys. Rev., 1964, v. A133, p. 1268.
22. Бейгман И. Л., Вайнштейн Л. А., Собелъман И. И. О классическом
приближении в теории неупругих столкновений высоковозбуждепных
атомов с заряженными частицами.— ЖЭТФ, 1969, т. 57, с. 1703.
23. Percival I. С., Richards D. The theory of collisions between charged particles
and highly excited atoms.— Adv. Atom. a. Molec. Phys., 1975, v. 11, p. 2.
24. Борн M. Лекции по атомной механике.— Харьков — Киев: ОНТИ,
1934, т. 1.
25. Presnyakov L. Р., Urnov А. М. Quantum Transitions between highly exci-
ted atomic levels induced by external time-dependent forces.— J. Phys.,
Atom. Molec. Phys., 1970, v. B3, p. 1267.
26. Бейгман И. Л. Сечения переходов между высоковозбужденными уров-
нями при столкновениях с заряженными частицами.— ЖЭТФ, 1977,
т. 73, с. 1729.
27. Никитин Е. Е. Теория элементарных атомно-молекулярных реакций.—
Новосибирск: Изд. НГУ, 1970.
28. Никитин Е. Е., Смирнов Б. М. Квазирезонансные процессы при медлен-
ных соударениях.— УФН, 1978, т. 124, с. 201.
29. Вайнштейн Л. А., Собелъман И. И., Пресняков Л. П. О возбуждении
атомов тяжелыми частицами.— ЖЭТФ, 1962, т. 43, с. 518.
30. Де Брейн Н. Г. Асимптотические методы в анализе.— М.: ИЛ, 1961.
31. Bates D. R.— Proc. Phys. Soc., 1959, v. A73, p. 227.
32. Пресняков Л. II., Уланцев A. Д. Возбуждение многозарядных ионов про-
тонами.— Краткие сообщения по физике (ФИАН СССР).— М., 1973,
№ 8, с. 42.
33. Фирсов О. Б. Резонансная перезарядка ионов при медленных столкнове-
ниях.- ЖЭТФ, 1951, т. 21, с. 1001.
34. Brinkman Н. С., Kramers Н. А.— Proc. Acad. Sci. Amsterdam, 1930,
v. 33, p. 973.
35. Ландау Л. Д.. Лифшиц Е. М. Квантовая механика.— М.: Наука, 1974,
§ 81.
36. Смирнов Б. М. Асимптотический метод в теории атомных столкновений.—
М.: Наука, 1973.
37. Полуэктов И. А., Пресняков Л. П., Собелъман И. И.
О столкновениях, сопровождающихся перезарядкой.— ЖЭТФ, 1964,
т. 47, с. 181.
38. Shevelko V. Р. One-electron Capture in Collisions of Fast Ions with
Atoms.— Zs. Physik, 1978, Bd. A 287, s. 19.
39. Бродский A. M., Потапов В. С., Толмачев В. В. Асимптотическое пове-
дение сечения перезарядки.— ЖЭТФ, 1970, т. 58, с. 264.
40. Виноградов А. В., Пресняков Л. П., Шевелъко В. П. О перезарядке про-
тоновна атомах щелочных элементов.— Письма в ЖЭТФ, 1968, т. 8, с. 449.
41. Афросимов В. В., Ильин Р. Н., Соловьев Е. С., Захват электронов прото-
нами в инертных газах.— ЖТФ, 1960, т. XXX, с. 705.
42. Schryber U. Elektroneneinfang schneller Protonen in Gasen.— Helv. Phys.
Acta, 1967, v. 40, p. 1023.
43. Пресняков Л. П., Уланцев А. Д. Перезарядка многозарядных ионов на
атомах.— Квантовая электроника, 1974, т. 1, с. 2377.
44. Betz Н. D. Charge states and charge-changing cross-sections of fast heavy
ions penetrating through gaseous and solid media.— Rev. Mod. Phys.,
1972, v. 44, p. 465.
45. PresnyakovL. P. Charge-exchange of highly charged ions in neutral atoms.—
In: Proc. X Int. Conf, on Phys, of Electron, and Atom. Collisions. Elec-
tronic and Atomic Collisions, North — Holland, 1978, p. 407.
46. Van Regemorter H. Rate of collisional excitation in stellar atmospheres.—
Astrophys. J., 1962, v. 132, p. 906.
ЛИТЕРАТУРА
317
47. Seaton М. J. The spectrum of the solar corona. Planet. Space Sci., 1964,
v. 12, p. 55.
48. Lotz W. Electron-impact ionization cross-section for atoms up to z — 108.—
Zs. Physik, 1970, Bd. 232, s. 101.
49. Burgess A. Dielectronic recombination and the temperature of the solar
corona.— Astrophys. J., 1964, v. 139, p. 776.
50. Grineva Yu. I., Karev V. I., Korneev V. V., Krutov V. V., Mandelstam S. L.,
Vainstein L. A., Vasilyev B. N., Zhitnik I. A. Solar X-ray spectra, observed
from the «Intercosmos-4» satellite and the «Vertical-2» rocket.— Solar
Physics, 1973, v. 23, p. 441.
51. Биберман Л. M., Воробьев В. С., Якубов H. Т. Кинетика ударно-радиа-
ционной ионизации и рекомбинации.— УФН, 1972, т. 107, с. 353.
52. Грим Г. Спектроскопия плазмы.— М.: Атомиздат, 1969.
53. Диагностика плазмы: Сб. статей / Под ред. Р. Хаддлстоуна и С. Лео-
нарда.— М.: Мир, 1967.
54. Методы исследования плазмы: Сб. статей / Под ред. В. Лохте-Хольт-
гревена.— М.: Мир, 1971.
55. Seaton М. J. The solution of capture-cascade equations for hydrogen.—
Monthly Not. Roy. Astron. Soc., 1959, v. 119, p. 90.
56. Бейгман И. Л., Михалъчи Е. Д. О населенности высоковозбужденных
уровней в разреженной плазме.— J. Quant. Spectr. Radiat. Transf.,
1969, v. 9, p. 1365.
57. Беляев С. T., Будкер Г. И., Многоквантовая рекомбинация в ионизован-
ном газе.— В сб.: Физика плазмы и проблема управляемых термоядер-
ных реакций.— М.: Изд-во АН СССР, 1958, т. 3, с. 41.
58. Питаевский Л. П. Рекомбинация электронов в одноатомном газе.—
ЖЭТФ, 1962, т. 42, с. 1326.
59. Гуревич А. В., Питаевский Л. П. Коэффициент рекомбинации в плотной
низкотемпературной плазме.— ЖЭТФ, 1964, т. 46, с. 1281.
60. Bates D. В., Kingston А. Е., McWhirter R. W. Р. Recombination between
electrons and atomic ions. I. Optically thin plasmas.— Proc. Roy. Soc.,
1962, v. A267, p. 297.
61. Bates D. B., Kingston A. E., McWhirter B. W. P. Recombination between
electrons and atomic ions. II. Optically thick plasmas.— Proc. Roy. Soc.,
1962, v. A270, p. 155.
62. McWhirter B. W. P., Hearn A. G. A calculation of the instantaneous popu-
lation densities of the excited levels of hydrogenlike ions in a plasma.—
Proc. Phys. Soc., 1963, v. 82, p. 641.
63. Johnson L. C., Hinnov E. Ionization, recombination and population of
excited levels in hydrogen plasmas.— J. Quant. Spectr. Radiat. Transf.,
1973, v. 13, p. 333.
64. Вайнштейн JI. А. Вычисление волновых функций и сил осцилляторов
сложных атомов. — В сб.: Тр. ФИАН. — М.: Наука, 1961, т. 15,
с. 3.
65. Варшалович Д. А.» Москалев А. Н., Херсонский В. К. Квантовая теория
углового момента.— Л.: Наука, 1975.
66. Раутиан С. Г., Собелъман И. И. Влияние столкновений на доплеровское
уширение спектральных линий.— УФН, 1966, т. 90, с. 209.
67. Чандрасекар С. Стохастические проблемы в физике и астрономии.— М.:
ИЛ, 1947, с. 49.
68. Фаддеева В. Н., Терентьев Н. М. Таблицы значений интеграла вероятно-
стей от комплексного аргумента.— М.: Гостехиздат, 1954.
69. Собелъман И. И. Уширение спектральных линий вследствие уширения
электронами. Оптика и спектроскопия, 1956, т. I, с. 617.
70. Baranger М. Simplified quantum-mechanical theory of pressure broadening.
Problem of overlapping lines in the theory of pressure broadening.— Phys.
Rev., 1958, v. Ill, p. 481; v. Ill, p. 494; v. 112, p. 855.
318
ЛИТЕРАТУРА
71. Алексеев В. А., Андреева Т. Л., Собельман И. И. Метод квантового кинети-
ческого уравнения для атомов и молекул и его приложения к вычисле-
нию оптических характеристик газов.— ЖЭТФ, 1972, т. 62, с. 614.
72. Алексеев В. А., Андреева Т. Л., Собельман И. И. К теории нелинейных
резонансов мощности газовых лазеров.— ЖЭТФ, 1973, т. 64, с. 813.
73. Алексеев В. А., Собельман И. И. О влиянии столкновений на вынужден-
ное комбинационное рассеяние в газах.— ЖЭТФ, 1968, т. 55, с. 1974.
74. Griem Н. R. Stark broadening of higher hydrogen and hydrogenlike lines
by electrons and ions.— Astrophys. J., 1960, v. 132, p. 883.
75. Hooper C. F., Jr. Electric microfield distribution.— Phys. Rev., 1968,
v. 165, p. 215.
76. Шолин Г. В., Лисица В. С., Коган В. И. Амплитудная модуляция и не-
адиабатичность при штарковском уширении водородных линий в плазме.—
ЖЭТФ, 1970, т. 59, с. 1390.
77. Грим Г. Уширение спектральных линий в плазме. — М.: Атомиздат,
1978.
78. Лисица В. С., Штарковское уширение линий водорода в плазме.— УФН,
1977, т. 122, с. 449.
79. Deutsch С., Herman L., Drawin Н. W. Electron impact broadening of over
lapping He I lines in plasmas.— Phys. Rev., 1968, v. 178, p. 261.
80. Green R. L., Cooper J., Smith E. W. A unified theory of stark — broade-
ning for hydrogenic ions. I. A general theory.— J. Quant. Spectr. Radiat.
Transf., 1975, v. 15, p. 1025; II. Line wings.— J. Quant. Spectr. Radiat.
Transf., 1975, v. 15, p. 1037; III. Results for He II Lymana.— J. Quant.
Spectr. Radiat. Transf., 1975, v. 15, p. 1045.
81. Лисица В. С., Шолин Г. В. Точное решение задачи об уширении водо-
родных спектральных линий в одноэлектронной теории.— ЖЭТФ, 1971,
т. 61, с. 912.
82. Kepple Р., Griem Н. R. Improved stark profile calculations for the hydro-
gen lines Ha, Hp, Hv and Phys. Rev., 1968, v. 173, p. 317.
83. Vidal C. R., Cooper J., Smith E. W. Hydrogen stark broadening calcula-
tions with the unified classical path theory.— J. Quant. Spectr. Radiat.
Transf., 1970, v. 10, p. 1011; Unified theory calculations of stark broade-
ned hydrogen lines including lower state interactions.— J. Quant. Spectr.
Radiat. Transf., 1971, v. 11, p. 263.
84. Демура А. В., Шолин Г. В. Теория асимметрии штарковских профилей
водородных линий в плотной плазме.— J. Quant. Spectr. Radiat. Transf.,
1975, т. 15, p. 881.
85. Минаева Л. А., Собельман И. И. Об уширении спектральных линий высо-
ковозбужденных атомов водорода в плазме.— J. Quant. Spectr. Radiat.
Transf., 1968, v. 8, p. 783.
86. Ребане В. II. О связи между оптическим уширением, сдвигом и деполяри-
зацией спектральных линий под действием столкновений.— Оптика и
спектроскопия, 1969, т. 26, с. 673.
87. Мацкевич В. В. Деполяризующие столкновения атомов и уширение спек-
тральных линий.— Оптика и спектроскопия, 1974, т. 37, с. 411.
88. Вдовин Ю. А., Галицкий В. М. Диэлектрическая проницаемость газа
резонансных атомов.— ЖЭТФ, 1967, т. 52, с. 1345.
89. Вдовин IO. А., Добродеев Н. Н. Диэлектрическая проницаемость паров
щелочных металлов и водорода на резонансных частотах.— ЖЭТФ,
1968, т. 55, с. 1047.
90. Алексеев В. А., Собельман И. И. О спектроскопическом методе исследова-
ния упругого рассеяния медленных электронов на атомах цезия и ар-
гоне.— ЖЭТФ, 1966, т. 50, с. 343.
91. Бете Г., Солпитер Э. Квантовая механика атомов с одним и двумя элек-
тронами.— М.: Физматгиз, 1960.
ЛИТЕРАТУРА
319
92. Presnyakov L. P. Broadening of highly excited atomic levels in an atmo-
sphere of alcali metal vapor.— Phys. Rev., 1970, v. A2, p. 1720.
93. Chen S., Takeo M. Broadening and shift of special lines due to the presence
of foreign gases.— Rev. Mod. Phys., 1957, v. 29, p. 20. (Перевод:
УФН, 1958, т. 66, c 391.)
94. Месси Г., Бархоп E. Электронные и ионные столкновения.— М.: ИЛ,
1958.
95. Мазинг М. А., Врублевская М, А. Спектроскопическое исследование
упругого рассеяния медленных электронов на атомах цезия и аргона.—
ЖЭТФ, 1966, т. 50, с. 343.
96. Мазинг М. А., Серапинас П. Д. Уширение и сдвиг высоковозбужденных
атомов калия и цезия.— ЖЭТФ, 1971, т. 60, с. 541.
97. Shevelko V. Р., Urnov А. М., Vinogradov А. V. Inelastic Transitions Bet-
ween Closed Atomic Levels Induced by Electrons and Protons.— J. Phys.,
1976, v. B9, p. 2859.
Леонид Абрамович Вайнштейн
Игорь Ильич Собельман
Евгений Александрович Юков
ВОЗБУЖДЕНИЕ АТОМОВ
И УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ
М., 1979 г., 320 стр. с илл.
Редактор Д. А. Миртова
Техн, редактор И. Ш. Аксельрод
Корректор 3. В. Автонеева
ИБ № 11279
Сдано в набор 29.01.79. ,
Подписано к печати 11.04.79.
Т-08908. Бумага 60х90«/м. Тип. № 1.
Высокая печать. Обыкновенная гарнитура.
Условн. печ. л. 20. Уч.-изд. л. 21,79.
Тираж 3700 эка. Заказ № 1512
Цена книги 2 р. 40 к.
Издательство «Наука»
Главная редакция
физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
2-я типография издательства «Наука»
Москва, Шубинский пер., д. 10