Author: Бендат Дж. Пирсол А.
Tags: теория вероятностей и математическая статистика теория вероятностей математическая статистика комбинаторный анализ теория графов математика математический анализ информатика
ISBN: 5-03-001071-8
Year: 1989
i
Дж. Бендаi. А. Пирсол
Прикладной анализ
случайных данных
Прикладной анализ случайных данных
RANDOM DATA
Analysis and Measurement Procedures
Julius S. Bendat
Mathematical Consultant in Random Data Analysis
Allan G. Piersol
Senior Scientist, Astron Research and Engineering
A Wiley-Interscience Publication
JOHN WILEY & SONS
New York • Chichester • Brisbane • Toronto • Singapore
Дж.Бендат, А.Пирсол
Прикладной анализ
случайных данных
Перевод с английского
д-ра физ.-мат. наук В. Е. Привальского
и А. И. Кочубинского
под редакцией
акад. И. Н. Коваленко
Москва «Мир» 1989
Scan AAW
ББК 22.172
Б 46
УДК 519.2
Бендат Дж., Пирсол А.
Б 46 Прикладной анализ случайных данных: Пер. с англ.— М.:
Мир, 1989.— 540 с., ил.
ISBN 5-03-001071-8
Монография известных специалистов из США, посвященная проблемам
сбора и предварительной обработки данных, оценке спектральных плотно-
стей, ковариационных и передаточных функций, использованию этих характе-
ристик для решения прикладных задач, в частности идентификации систем,
определения числа трактов распространения случайных сигналов, выделения
периодических составляющих.
Книга написана ясно и доступно, не перегружена математическими выво-
дами, и в то же время имеет достаточный уровень строгости. Теоретические
положения иллюстрируются многочисленными практическими примерами и
задачами.
Для инженеров и научных работников, а также студентов и аспирантов,
интересующихся практическим анализом случайных данных.
Может служить учебным пособием.
1602090000 — 083
Б-------------------16—89,4.1
041(01) — 89
ББК 22.172
Редакция литературы
по новой технике и космическим исследованиям
ISBN 5-03-001071-8(русск.)
ISBN 0-471-04000-2(англ.)
© 1986 by John Wiley & Sons, Inc.
All rights reserved. Authorized translation from
English language edition published by John Wiley
& Sons, Inc.
© перевод на русский язык, «Мир», 1989
ОТ РЕДАКТОРА ПЕРЕВОДА
Книга известных американских специалистов в области прикладного
анализа случайных процессов посвящена подробному разбору основных
практических методов анализа случайных данных, которые могут исполь-
зоваться для решения очень широкого круга прикладных задач в самых
разных областях науки и техники. Последовательно и на высоком научном
и методическом уровне излагаются все основные этапы анализа случайных
данных: сбор и предварительная обработка, оценивание спектральных ха-
рактеристик, ковариационных функций и частотных характеристик линей-
ных систем, оценка надежности полученных результатов. Подробно о со-
держании и целях книги говорится в предисловии авторов, однако некото-
рые ее разделы заслуживают особого упоминания. Прежде всего отметим
итерационные методы вычисления частотных характеристик линейных си-
стем с коррелированными входными процессами, позволяющие избежать
обращения матриц большой размерности. Несомненный интерес представ-
ляют спектральные методы анализа ряда важных классов нестационарных
случайных процессов. Отметим, наконец, последнюю главу, посвященную
применениям преобразований Гильберта к анализу случайных данных.
Этот предмет вообще редко излагается в литературе прикладной направ-
ленности, вследствие чего, вероятно, преобразования Гильберта совершен-
но недостаточно используются на практике.
В книге приводятся основные сведения из теории вероятностей, матема-
тической статистики и теории случайных процессов; все главы снабжены
задачами, поэтому она может служить прекрасным учебным пособием для
первоначального знакомства с предметом. В то же время широта охвата
материала и хорошо продуманная структура книги позволяют использо-
вать ее как справочник по данной тематике.
Авторы не стремились дать полное математическое обоснование всех
излагаемых ими методов, поэтому изложение порой оказывается поверх-
ностным; иногда без пояснений используются довольно сложные матема-
тические понятия. В тех случаях, когда это препятствует пониманию основ-
ного текста, такие понятия разъясняются в примечаниях. Заметим, однако,
что на практике по имеющейся реализации случайного процесса обычно не
представляется возможным проверить выполнение довольно сложных ус-
ловий, гарантирующих применимость того или иного метода; это чаще
6
От редактора перевода
всего делается по косвенным признакам. Некоторые рекомендации на этот
счет приводятся в данной книге.
Авторы не исчерпывают всего многообразия существующих методов
анализа случайных данных, да и вряд ли это возможно. Заметим все же,
что интенсивно развиваемые в настоящее время параметрические методы,
особенно полезные при анализе коротких реализаций, заслуживают хотя
бы краткого описания.
Параметрический, особенно авторегрессионный спектральный анализ
может служить, по меньшей мере, эффективной заменой описанных в этой
книге традиционных непараметрических методов во многих ситуациях, в
частности при малой длине реализации и наличии априорной информации о
процессе. Таким путем можно анализировать.и многомерные линейные си-
стемы со случайными процессами на входе и выходе. Одно из важных до-
стоинств этого подхода — возможность получать аналитические выраже-
ния для всех оцениваемых спектральных характеристик, одновременно
представив анализируемый процесс разностным стохастическим уравнени-
ем. Подробная информация о параметрическом спектральном анализе со-
держится в работе [11.13], а краткое описание метода и его геофизические
приложения — в [11.14]. Способы построения доверительных интервалов
для авторегрессионных оценок автоспектров описаны в работах [11.14,
11.15], а приближенные результаты для линейной системы с одним вход-
ным и одним выходным процессами с относительно гладкими спектраль-
ными характеристиками дан в работе [11.16]. При достаточно длинных ре-
ализациях точность параметрических и авторегрессионных оценок, по-
видимому, одинакова.
Не вызывает сомнений, что эта книга, как и предыдущие монографии
тех же авторов, окажется полезной специалистам самого разного профиля,
использующим в своей работе методы теории случайных процессов, а так-
же студентам и аспирантам, специализирующимся в этой области, и бу-
дет способствовать внедрению эффективных методов прикладного анализа
случайных процессов в практику научных и инженерных исследований.
И. Н. Коваленко
ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
Эта книга — четвертая наша работа, опубликованная издательством
«Мир» в переводе на русский язык. Ей предшествовали два более ранних
варианта, вышедшие на английском языке в 1966 и 1971 гг., и дополняю-
щая их книга по приложениям корреляционного и спектрального анализа
(1980 г.). Мы глубоко признательны издательству «Мир» и советским спе-
циалистам, которые взяли на себя труд перевода и редактирования наших
работ. Нам хочется особо отметить вклад сотрудника Института водных
проблем АН СССР В. Е. Привальского, участвовавшего в переводе всех че-
тырех книг. Многие его замечания профессионального характера включа-
лись в более поздние допечатки англоязычных публикаций наших книг и
значительно способствовали их улучшению.
Мы, как и прежде, надеемся, что это издание окажется полезным не
только советским, но и другим читающим по-русски ученым и инженерам,
которые работают в области измерения и анализа случайных процессов са-
мого различного типа.
Лос-Анджелес, Калифорния,
1 декабря 1987 г.
Алан Дж. Пирсол,
Джулиус С. Бендат
ВВЕДЕНИЕ
Эта книга представляет собой существенно переработанное и расширен-
ное издание нашей книги, вышедшей в 1971 г.*\ которая, в свою очередь,
является значительно переработанным вариантом нашей книги «Measu-
rement and Analysis of Random Data», впервые опубликованной в 1966 г.* 2) В
данное издание вошли более совершенные и современные методы измере-
ния и анализа случайных процессов, в которых отражены последние дости-
жения в области построения моделей, оценки статистических ошибок, ме-
тодов сбора данных и вычислительных алгоритмов. Первые четыре главы
содержат основные сведения, необходимые для чтения книги, и охватыва-
ют интуитивные предпосылки теории, свойства линейных систем, основы
теории вероятностей и математической статистики и в целом совпадают
по содержанию с аналогичным материалом, имеющимся в издании 1971 г.
В гл. 5 подробно обсуждаются стационарные случайные процессы, причем
основные понятия излагаются более полно и включены новые разделы, на-
пример раздел, посвященный производным от случайных процессов. В гл.
6 и 7 выводятся и детально анализируются соотношения, связывающие
входные и выходные процессы одномерных и многомерных линейных си-
стем. Особое внимание здесь уделяется современным методам анализа, ко-
торые появились за время, прошедшее с момента выхода предыдущего из-
дания книги. Далее в гл. 8 и 9 выводятся формулы для статистических
ошибок, присущих разнообразным оценкам параметров, в том числе и тем
довольно сложным оценкам, для которых такие формулы в 1971 г. еще не
были получены. Гл. 10 и 11 посвящены изложению современных методов
сбора и цифровой обработки данных с включением дополнительного мате-
риала, относящегося к обработке входных и выходных процессов много-
мерных линейных систем с помощью эффективных итерационных алгорит-
мов. Гл. 12, посвященная нестационарным процессам, полностью перера-
ботана и значительно расширена. Особое внимание в ней уделяется различ-
ным способам спектрального описания нестационарных процессов и выво-
Имеется перевод: Бендат Дж., Пирсон А. Измерение и анализ случайных про-
цессов: Пер. с англ.— М.: Мир, 1974. — 464 с.— Прим, перев.
2) Имеется перевод: Бендат Дж., Пирсон А. Измерение и анапиз спучайных про-
цессов: Пер. с ангп. — М.: Мир, 1971. — 408 с.— Прим, перев.
Введение
9
ду соотношений, связывающих вход и выход линейных систем в случае не-
стационарных входных процессов и(или) линейных систем с зависящими от
времени параметрами. Гл. 13 содержит совершенно новый материал, каса-
ющийся преобразования Гильберта и его применений, который вообще от-
сутствовал в предыдущих изданиях. Для удобства читателя в книгу вклю-
чены приложения А и Б. В приложении А приводится ряд статистических
таблиц, облегчающих пользование книгой, а приложение Б содержит крат-
кие определения основных понятий, относящихся к области анализа случай-
ных процессов, что может способствовать стандартизации терминологии в
этой области.
Как и издание 1971 г., данная книга задумана прежде всего как справоч-
ное пособие для практически работающих инженеров и ученых. Кроме то-
го, авторы стремились дать полное теоретическое введение к своей книге
«Engineering Applications of Correlation and Spectral Analysis», вышедшей в
1980 г.1), имеющей прикладную направленность. Вторая наша цель — дать
учебное пособие студентам, специализирующимся в данной области, поэто-
му в конце каждой главы помещены задачи. Предполагается, что читатель
знаком с основами математического анализа и прикладными аспектами те-
ории преобразований Фурье. Желательно также знакомство с основными
понятиями теории линейных систем, теорци вероятностей и математичес-
кой статистики, хотя в первых главах книги и дается краткий обзор этих
предметов.
Хочется выразить признательность многим нашим коллегам и сотруд-
никам за помощь в работе над книгой. Мы особенно благодарны Дж. Рич-
ману, просмотревшему часть, рукописи и сделавшему полезные замечания.
Мы благодарим также правительственные учреждения и частные компа-
ний, оказавшие поддержку нашей работе, а также Калифорнийский универ-
ситет, Институт повышения квалификации и другие организации, которые
поддержали наши семинарские занятия по данной тематике. Наконец, мы
признательны Б. Кларк, И. Салазер и Ф. Паррис за их тщательную работу
по оформлению рукописи.
Лос-Анджелес, Калифорния,
январь 1986 г.
Джулиус С. Бендат,
Алан Дж. Пирсол
Имеется перевод: Бендат Дж., Пирсол А. Приложения корреляционного и
спектрального анализа: Пер. с англ.— М.: Мир, 1982. —312 с. — Прим, перев.
СПИСОК ОБОЗНАЧЕНИИ
с.к.о. ФКИПФ ФБИПФ а, b — среднеквадратичное отклонение — фильтры с конечной импульсной переходной функцией — фильтры с бесконечной импульсной переходной функцией — выборочные коэффициенты регрессии; произвольные постоян- ные
А Ь[ ] В — амплитуда; число инверсий — смещение величины [ ] — ширина полосы частот в герцах
с С схх(т) СхУТ) Сху(П e(Z ) f[ ] f Xf FT [ ] Gxv(/) G (f) xy^' G (Л yy x v f Gx.y x (/) W)' h (r) IW(/)I ] i — затухание механической системы; произвольная постоянная — электрическая емкость — ковариация — корреляционная функция — взаимная корреляционная функция — коспектральная плотность (односторонняя) — разность потенциалов — математическое ожидание величины [ ] — циклическая частота — разрешение по частоте — преобразование Фурье функции [ ] — спектральная плотность (односторонняя) — взаимная спектральная плотность (односторонняя) — условная спектральная плотность (односторонняя) — условная взаимная спектральная плотность (односторонняя) — спектральная плотность «энергии» — импульсная переходная функция — частотная характеристика — амплитудная характеристика системы — преобразование Гильберта функции [ ] — индекс
Im[ ] J — ток — мнимая часть [ ] — V — 1; индекс
к К log L L (f) /77 — коэффициент жесткости пружины; индекс — следовое волновое число; число интервалов группировки — натуральный логарифм — электрическая индуктивность; длина — условная частотная характеристика — механическая масса; максимальный сдвиг
"’f — индекс модуляции
Список обозначений
И
п N Р U) р (х У ) Р {х) р (X, у ) Prob [ ], Р Q Q (' ) г г ху R Rxx <г> Rxy <» в ('|.'2), & (т, 1 ) Re [ ] 5 5 2 — число степеней свободы; индекс — размер выборки — плотность вероятности — совместная плотность вероятности — функция распределения — совместная функция распределения — вероятность события [ ] — число входов; число реализаций — электрический заряд — квадратурная спектральная плотность (односторонняя) — число серий; число выходов — выборочный коэффициент корреляции — электрическое сопротивление — ковариационная функция — взаимная ковариационная функция — двойная по времени ковариационная функция — действительная часть [ ] — выборочное стандартное отклонение — выборочная дисперсия — выборочная ковариация
v(/) — спектральная плотность (двусторонняя) — взаимная спектральная плотность (двусторонняя) — условная спектральная плотность (двусторонняя) — условная взаимная спектральная плотность (двусторонняя)
/(/) stfvf2), X (f- g) S/N — спектральная плотность «энергии» (двусторонняя) — двойная по частоте спектральная плотность (двусторонняя) — отношение сигнал/шум
t — время; случайная величина с /-распределением Стью- дента
Д/ T T r Un U (J), V(t ) Var [ ] W 0 — интервал дискретности — длина реализации; период — суммарная длина реализации — исходные значения случайного процесса — величины, зависящие от времени — дисперсия [ ] — ширина интервала — нестационарная частотно-временная спектральная плотность, определенная как для отрицательных, так и для положитель- ных частот (двусторонняя)
x (/ ), у (t ) .V — величины, зависящие от времени — выборочное среднее х
X X(f) X(f, T) z К ]l И Q — амплитуда гармонического процесса х (1 ) — преобразование Фурье функции х (1 ) — преобразование Фурье реализации х (t ) длиной Т — стандартная нормальная случайная величина — абсолютная величина [ ] — оценка [ ] — малая вероятность; уровень значимости; связанная переменная
12
Список обозначений
0 У 1(f) УуХ(/) 5( ) A £ Г е м р Р(т) (J а2 — вероятность ошибки второго рода; связанная переменная — функция обычной когерентности — функция множественной когерентности — функция частной когерентности — дельта-функция — малое приращение — нормированная ошибка — коэффициент механического затухания — фазовый угол — аргумент Gху (f ) — среднее значение — коэффициент корреляции — нормированная корреляционная функция — стандартное отклонение — дисперсия
т Ф(П Ф х2 Ф ф2 — сдвиг времени — фазовая характеристика — произвольный статистический параметр — случайная величина с распределением хи-квадрат — среднеквадратичное значение — средний квадрат
Глава 1
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И МОДЕЛИ
Данная глава содержит основные определения и модели детерминиро-
ванных и случайных процессов и имеет целью описать интуитивные пред-
посылки теории, составляющей предмет этой книги. Отличительные
свойства стационарных, эргодических и нестационарных случайных процес-
сов поясняются с помощью классификации по простым признакам наличия
или отсутствия тех или иных свойств. Дается неформальное определение
основных статистических характеристик, описывающих обобщенные
свойства отдельных реализаций стационарных случайных процессов и пар
таких реализаций, а также их свойства во временной и частотной областях.
Формулируются основные типы задач анализа линейных систем, решаемых
в этой книге, а также основные критерии оценки ошибок, свойственных
анализу случайных данных, которые лежат в основе планирования экспери-
ментов и сравнения разных методов анализа.
1.1. Детерминированные и случайные процессы
Любые данные, полученные в результате наблюдения реального физиче-
ского явления, можно отнести, вообще говоря, к детерминированному или
недетерминированному типу. Детерминированные процессы — это процес-
сы, которые можно описать явными математическими формулами. Рас-
смотрим, например, жесткое тело, подвешенное к неподвижной опоре с по-
мощью линейной пружины (рис. 1.1). Пусть т — масса тела (предполага-
ется, что оно неупругое), к — коэффициент жесткости пружины (предпола-
гается, что она не имеет массы). Пусть тело смещено от положения равно-
весия на расстояние X и освобождается в момент времени t = 0. С по-
мощью основных законов механики или на основе многократных наблюде-
ний можно установить, что имеет место следующая зависимость:
t
Уравнение (1.1) позволяет точно определять положение тела в любой буду-
щий момент времени. Следовательно, этот процесс, описывающий движе-
ние тела, является детерминированным.
На практике часто встречаются физические явления, протекание кото-
рых с разумной точностью можно описать явными математическими зави-
симостями. Например, движение спутника по околоземной орбите, измене-
ние потенциала между обкладками конденсатора по мере его разряда через
резистор, колебания несбалансированного вращающегося механизма, изме-
нение температуры воды по мере ее нагревания по сути своей являются де-
терминированными процессами. Однако многие другие физические явления
порождают процессы, которые нельзя считать детерминированными. На-
пример, высота волн при морском ветровом волнении, акустическое давле-
14
Глава 1
|| к
Положение
---1-- равновесия
Рис. 1.1. Простая система, состоящая из тела и
x(t) пружины.
ние, производимое потоком воздуха при его движении по трубе, и электри-
ческий сигнал на выходе генератора шума — это процессы, которые невоз-
можно описать во всех деталях. Совершенно невозможно предсказать точ-
ное значение таких процессов в будущие моменты времени. Эти процессы
случайны по своей сути, и для их описания требуются вероятностные поня-
тия и статистические характеристики.
Отнесение тех или иных физических процессов к детерминированному
или случайному типу зачастую не бесспорно. Например, можно утверж-
дать, что встречающиеся на практике физические процессы вообще не мо-
гут быть в полной мере детерминированными, поскольку никогда нельзя
исключить возможности того, что в будущем произойдет какое-нибудь со-
бытие, которое повлияет на явление, порождающее процесс, совершенно
непредсказуемым образом. С другой стороны, можно утверждать, что нет
и истинно случайных процессов, поскольку может оказаться, что при до-
статочно полном знании основных механизмов явления порождаемый этим
явлением процесс удастся описать точными математическими формулами.
С практической точки зрения решение о случайности или детерминирован-
ности конкретного физического процесса обычно основывается на нашей
способности воспроизвести процесс в ходе контролируемого эксперимента.
Если многократное повторение эксперимента, в ходе которого получается
интересующий нас процесс, приводит к одним и тем же результатам (в
пределах ошибок эксперимента), то этот процесс обычно можно считать
детерминированным. Если же невозможно указать эксперимент, который
давал бы при его повторении идентичные результаты, то такой процесс
обычно считается случайным по своей сути.
Сейчас мы обсудим несколько способов классификации детерминирован-
ных и случайных процессов. Заметим, что принципы классификации выби-
рались с точки зрения удобства анализа и не всегда являются наилучшими
с других возможных точек зрения. Заметим также, что обычно предполага-
ется, что физические процессы представляют собой функции времени, так
что далее для удобства будем пользоваться именно такой интерпретацией.
При желании вместо времени можно взять любую другую независимую пе-
ременную.
1.2. Классификация детерминированных процессов
Процессы, описывающие детерминированные явления, делятся на пе-
риодические и непериодические. В свою очередь периодические процессы
Основные определения и модели
15
Рис. 1.2. Классификация детерминированных процессов.
можно разделить на гармонические и полигармонические. Непериодические
процессы делятся на «почти периодические» и переходные. Такая классифи-
кация детерминированных процессов схематически представлена на рис.
1.2. Разумеется, может встретиться и любое сочетание этих типов. Перей-
дем к краткому обзору всех этих типов детерминированных процессов и
дадим ряд практических примеров.
1.2.1. СИНУСОИДАЛЬНЫЙ ПЕРИОДИЧЕСКИЙ ПРОЦЕСС
Синусоидальный процесс — это периодический процесс, поведение кото-
рого во времени математически выражается следующей формулой:
x(t) = Xsin(2w/Oz + в), (1.2)
где А' — амплитуда,/0 — циклическая частота в герцах, в — начальный фа-
зовый угол в радианах, х (I ) — мгновенное значение в момент t.
Синусоидальный процесс, определенный формулой (1.2), обычно назы-
вается гармоническим. При практическом анализе гармонических процессов
фазовый угол 0 часто игнорируется. В этом случае
х(/) = JfsinZTr/oZ. (1.3)
Уравнение (1.3) графически можно изобразить либо в виде зависимости
мгновенного значения от времени, либо в виде зависимости амплитуды от
частоты (частотного спектра), см. рис. 1.3.
Интервал времени, на котором происходит одно полное колебание или
цикл гармонического процесса, называется периодом Т . Число циклов в
единицу времени называется частотой /0. Частота и период связаны соот-
ношением
1
Тр = 7- (1-4)
JQ
Заметим, что частотный спектр, изображенный на рис. 1.3, состоит из
единственной амплитуды, расположенной на определенной частоте, и этим
16
Глава 1
Рис. 1.3. Реализация и спектр гармонического процесса.
отличается от спектров, задающих непрерывную зависимость амплитуды
от частоты. Такие спектры называются дискретными или линейчатыми.
Известно много примеров физических явлений, которые на практике
приближенно описываются гармоническими процессами. Примером может
служить напряжение на выходе электрического генератора. Другой пример
дают колебания несбалансированного вращающегося груза. Гармонические
процессы являются с точки зрения анализа простейшим видом процессов,
протекающих во времени.
1.2.2. ПОЛИГАРМОНИЧЕСКИЕ ПРОЦЕССЫ
К полигармоническим процессам относятся периодические процессы, ко-
торые математически представляются функцией времени, точно повторяю-
щей свои значения через одинаковые интервалы времени, т. е.
x(t) = x(t + пТр) п = 1,2,3,... . (1-5)
Как и в случае гармонических процессов, интервал времени, в течение кото-
рого происходит одно полное колебание, называется периодом Тр. Число
циклов в единицу времени называется фундаментальной частотой J\. Гар-
монические процессы представляют собой частный случай полигармониче-
ских процессов при j\ = /0.
За редкими на практике исключениями, полигармонические процессы
разлагаются в ряд Фурье по формуле
а0 £
x(t) = — + д, (ancos2irnf1t 4- bnsin2trrnflt)f (1.6)
И=1
где/j = \/Тр и
2 ст
ап = — I px(t)cos2irnfltdt1 п = 0,1,2,...;
тр Jo
2 fT
bn = — I px(t)sin2irnf1tdt, n = 1,2,3,... .
Гр-'о
Другое представление полигармонических процессов рядом Фурье дает
формула
Основные определения и модели
17
х(‘) = хо + Е - 0„), (1.7)
Л = 1
где Хо = а 0/2 и
Хп - ^ап + » п ~ 1’ 2, 3, ... ;
Ь„
6п = arctg —, п = 1, 2, 3, ... ;
ап
иначе говоря, формула (1.7) утверждает, что полигармонический процесс
есть сумма постоянной составляющей XQ и бесконечного числа гармониче-
ских составляющих, называемых гармониками и имеющих амплитуды Хп и
фазы 0п . Все частоты гармонических составляющих кратны фундаменталь-
ной частоте f j.
При практическом анализе периодических процессов фазовые углы 0п ча-
сто игнорируются. В этом случае формулу (1.7) можно охарактеризовать
дискретным спектром, как показано на рис. 1.4. Иногда полигармонические
процессы содержат только конечное число составляющих. В других случаях
может отсутствовать фундаментальная составляющая. Например, пусть
периодический процесс образован суммой трех гармонических процессов с
частотами 60, 75 и 100 Гц. Наибольший общий делитель этих частот равен
5 Гц, т. е. период этого процесса равен 0,2 с. Поэтому при разложении в
ряд Фурье все величины Хп равны нулю, кроме соответствующих значени-
ям п = 12, 15 и 20.
Физические явления, описываемые полигармоническими процессами,
встречаются намного чаще, чем явления, порождающие простые гармони-
ческие процессы. Фактически многие полигармонические процессы рассмат-
риваются как простые только приближенно. Например, детальный анализ
напряжения на выходе электрического генератора может выявить неболь-
шие составляющие на высших гармониках. В других случаях физические пе-
риодические процессы имеют много мощных гармоник. Например, вибра-
ция многоцилиндрового двигателя внутреннего сгорания обычно содержит
значительное число мощных гармоник.
18
Глава 1
1.2.3. ПОЧТИ ПЕРИОДИЧЕСКИЕ ПРОЦЕССЫ
В разд. 1.2.2 было отмечено, что периодический процесс обычно пред-
ставляется в виде ряда, состоящего из гармонических процессов с соизме-
римыми частотами. И наоборот, любой процесс, образованный суммой
двух и более гармонических процессов с соизмеримыми частотами, будет
периодическим. Однако если процесс образован суммой двух и более гар-
монических процессов с произвольными частотами, то он, как правило, не
будет периодическим. Точнее говоря, сумма двух и более гармонических
процессов будет периодическим процессом тогда и только тогда, когда от-
ношение любых двух частот есть рациональное число. В этом случае су-
ществует фундаментальный период, который удовлетворяет уравнению
(1.5). Поэтому процесс
х(/) = A^sin^Z + #i) + Jf2sin(3/ + 02) + Jf3sin(7/ 4- 03)
периодический, так как 2/3, 2/7 и 3/7 — рациональные числа (фундамен-
тальный период Тр = 1). С другой стороны, процесс
x(t) = X1sin(2/ + 4- Jf2sin(3z 4- в2) 4- Jf3sin(\/5O t 4- 03)
не периодический, так как 2/V50 и 3/V5O не рациональные числа (фундамен-
тальный период бесконечно велик). Реализация такого процесса носит
почти периодический характер, но соотношение (1.5) не выполняется ни
при каком конечном значении Тр .
На основании этих соображений почти периодические процессы опреде-
ляются математически как функция времени вида
00
х(г) = £ X„sin(2w/„r + 0„), (1.8)
п = 1
причем fn/fm не для всех значений индексов являются рациональными чис-
лами. На практике почти периодические процессы порождаются физически-
ми явлениями, в которых одновременно действуют гармонические процес-
сы, не связанные между собой. Хороший пример дает вибрация многомо-
торного винтового самолета, в котором двигатели не синхронизированы.
Почти периодические процессы обладают следующим важным свойст-
вом. Если исключить из рассмотрения фазовые углы Оп, то формулу (1.8)
Рис. 1.5. Спектр почти периодического процесса.
Основные определения и модели
19
можно охарактеризовать дискретным спектром, подобным спектру поли-
гармонического процесса. Единственное отличие состоит в том, что отно-
шения частот составляющих не являются рациональными числами (рис.
1.5).
1.2.4. ПЕРЕХОДНЫЕ НЕПЕРИОДИЧЕСКИЕ ПРОЦЕССЫ
По определению, переходные процессы — это все непериодические про-
цессы, за исключением почти периодических процессов, определенных в
разд. 1.2.3. Другими словами, к переходным относятся все процессы, кото-
рые можно задать какой-либо функцией времени, за исключением рассмот-
ренных выше.
К переходным процессам приводят многочисленные и самые разно-
образные явления. Например, процесс, показанный на рис. 1.6, а, может
представлять температуру воды в чайнике (по отношению к температуре
помещения) после выключения нагревателя. Процесс, изображенный на
рис. 1.6,6, может характеризовать свободные колебания демпфированной
механической системы после прекращения действия вынуждающей силы.
Процесс, представленный на рис. 1.6, в, может описывать напряжение в
тросе с нагруженным концом, который разрывается в моменте.
Важная особенность переходных процессов, отличающая их от периоди-
ческих и почти периодических, состоит в том, что их нельзя охарактеризо-
вать дискретным спектром. В большинстве случаев для переходных процес-
сов можно получить непрерывное спектральное представление, используя
преобразование Фурье вида
/00
x^e-^f'dt. (1.9)
- 00
Вообще говоря, преобразование Фурье X (f) является комплексной величи-
ной, которая записывается в полярной форме:
*(/) = |Д/ЖА/)-
Рис. 1.6. Примеры переходных процессов.
20
Глава 1
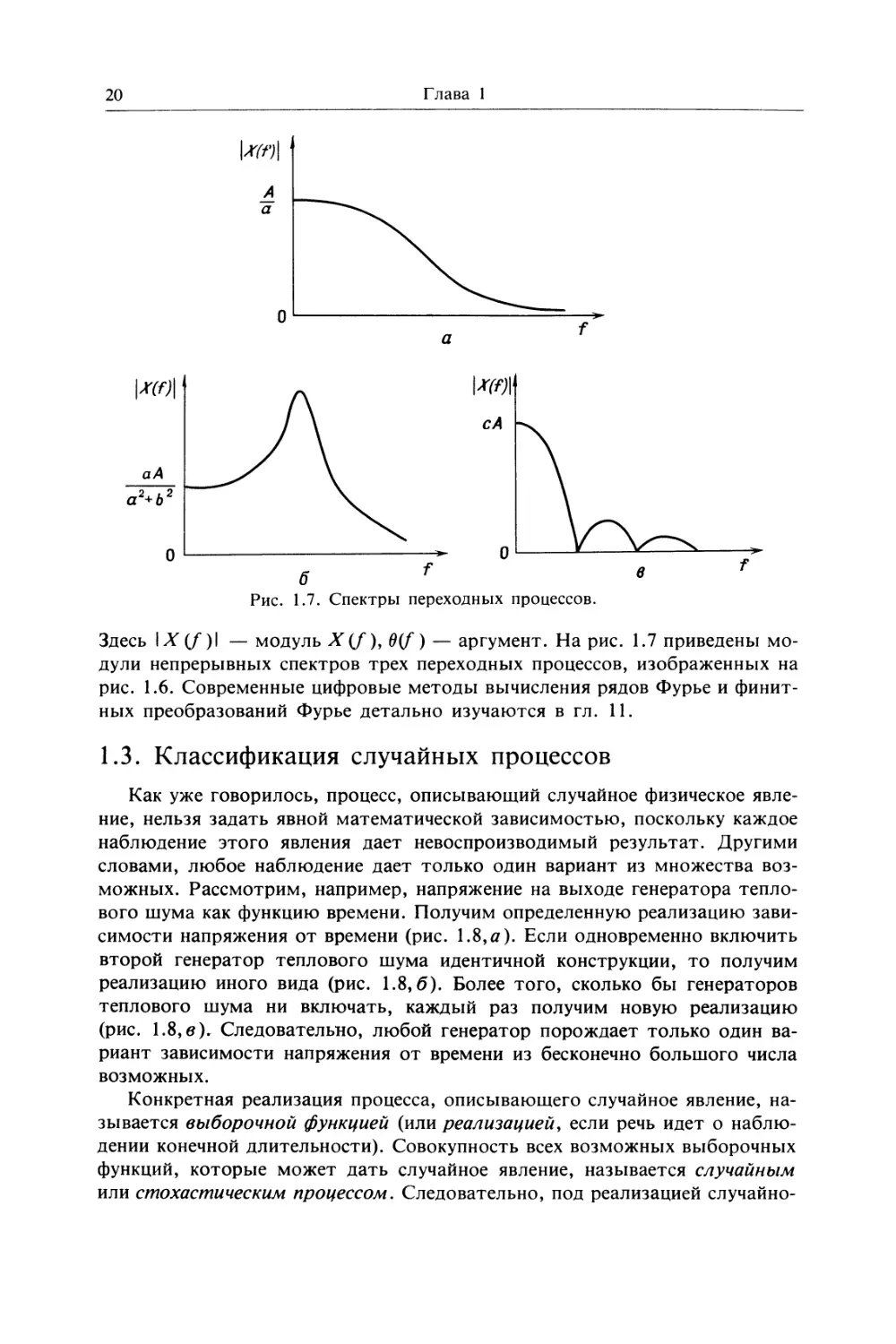
Рис. 1.7. Спектры переходных процессов.
Здесь IJV(/)I — модуль X(f), 6(f) — аргумент. На рис. 1.7 приведены мо-
дули непрерывных спектров трех переходных процессов, изображенных на
рис. 1.6. Современные цифровые методы вычисления рядов Фурье и финит-
ных преобразований Фурье детально изучаются в гл. 11.
1.3. Классификация случайных процессов
Как уже говорилось, процесс, описывающий случайное физическое явле-
ние, нельзя задать явной математической зависимостью, поскольку каждое
наблюдение этого явления дает невоспроизводимый результат. Другими
словами, любое наблюдение дает только один вариант из множества воз-
можных. Рассмотрим, например, напряжение на выходе генератора тепло-
вого шума как функцию времени. Получим определенную реализацию зави-
симости напряжения от времени (рис. 1.8,а). Если одновременно включить
второй генератор теплового шума идентичной конструкции, то получим
реализацию иного вида (рис. 1.8, б). Более того, сколько бы генераторов
теплового шума ни включать, каждый раз получим новую реализацию
(рис. 1.8,в). Следовательно, любой генератор порождает только один ва-
риант зависимости напряжения от времени из бесконечно большого числа
возможных.
Конкретная реализация процесса, описывающего случайное явление, на-
зывается выборочной функцией (или реализацией, если речь идет о наблю-
дении конечной длительности). Совокупность всех возможных выборочных
функций, которые может дать случайное явление, называется случайным
или стохастическим процессом. Следовательно, под реализацией случайно-
Основные определения и модели
21
а
Время
в
Рис. 1.8. Выборочные функции на выходе генератора теплового шума.
го физического явления понимается один из возможных исходов случайно-
го процесса.
Случайные процессы делятся на стационарные и нестационарные. В
свою очередь стационарные случайные процессы делятся на эргодические и
неэргодические. Дальнейшая классификация нестационарных случайных
процессов проводится по особенностям их нестационарностей. Классифика-
ция случайных процессов схематически показана на рис. 1.9. Рассмотрим
Рис. 1.9. Классификация случайных процессов.
22
Глава 1
более подробно содержание и физический смысл всех этих понятий. Точ-
ные определения и соотношения приведены в гл. 5 и 12.
1.3.1. СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
Если физическое явление описывается случайным процессом, то свой-
ство этого явления в принципе можно оценить в любой момент времени
путем усреднения по совокупности выборочных функций, образующих слу-
чайный процесс. Рассмотрим, например, совокупность выборочных функ-
ций (называемую также ансамблем), определяющую случайный процесс,
изображенный на рис. 1.10. Среднее значение (первый момент) этого слу-
чайного процесса в момент времени t j можно вычислить, взяв мгновенные
значения всех выборочных функций ансамбля в момент времени t j, сложив
эти значения и разделив на число выборочных функций. Аналогичным об-
разом ковариацию (смешанный момент) значений случайного процесса в
два различных момента времени (эта величина называется ковариационной
функцией) вычисляется путем усреднения по ансамблю произведений мгно-
венных значений в моменты времени^ и/j 4- т. Следовательно, среднее
значение рх (t j) и ковариационная функция Rxx (t t { 4- т) случайного про-
цесса {х(О], где символ [ ] обозначает ансамбль выборочных функций,
определяется формулами
= lim 77 Е (1.10а)
N->oo /V /r = 1
1 N
+ t) = lim — £ xk(ti)xk(tl + t), (1.106)
У-* 00 /V £ = !
в которых суммирование производится в предположении равновероятности
всех выборочных функций.
В общем случае, когда (t j) и Rxx (t \ 4- т), определенные уравнени-
ями (1.10), зависят от момента времени t и случайный процесс [х (t )j назы-
вается нестационарным. В том частном случае, когда fix(tx) и R^tt 4- т)
не зависят от момента времени t j, случайный процесс называется слабо
стационарным или стационарным в широком смысле. Среднее значение
слабо стационарного процесса постоянно, а ковариационная функция зави-
сит только от сдвига времени т, т. е. mx(zi) = 1*х и ^rx(G» G + т) =
= *хх (г)-
Для определения полного набора функций распределения, задающих
структуру случайного процесса [х (t)], нужно вычислить бесконечное число
моментов и смешанных моментов высших порядков. В том случае, когда
все моменты и смешанные моменты инвариантны во времени, случайный
процесс [х (t)] называется строго стационарным или стационарным в уз-
Основные определения и модели
23
Рис. 1.10. Ансамбль реализаций, задающих случайный процесс.
ком смысле1). Во многих приложениях проверка слабой стационарности
позволяет обосновать строгую стационарность.
1.3.2. ЭРГОДИЧЕСКИЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
В разд. 1.3.1 было показано, как можно определить характеристики слу-
чайного процесса путем усреднения по ансамблю в определенные моменты
времени. Однако в большинстве случаев характеристики стационарного
случайного процесса можно вычислить, усредняя по времени в пределах от-
дельных выборочных функций, входящих в ансамбль. Возьмем, например,
к-ю выборочную функцию ансамбля, изображенного на рис. 1.10. Среднее
значение (к) и ковариационная функция Rxx (т, к), вычисленные по к -й
Авторы не рассматривают случай, когда некоторые моменты распределения
могут не существовать.— Прим. ред.
24
Глава 1
реализации, равны
1
MxU) = lim / ХМ dt,
Т —» оо Г •'о
1 гТ
lim — xk(t)xk(t + т) dt.
Т-* оо Г •'о
(1.11а)
(1.116)
Если случайный процесс [ х(Г)] стационарен, а рх(к) и Rxx(t, к), вычислен-
ные по различным реализациям согласно формулам (1.11), совпадают, то
случайный процесс называется эргодическим. Для эргодических процессов
средние значения и ковариационные функции, полученные усреднением по
времени (как и другие характеристики, вычисленные усреднением по време-
ни), равны аналогичным характеристикам, найденным усреднением по ан-
самблю, т. е. рх(к) = 1лх и Rxx(t, к) = /^(т). Отметим, что свойством
эргодичности могут обладать только стационарные процессы.
Очевидно, что эргодические случайные процессы образуют очень важ-
ный класс случайных процессов, поскольку все свойства эргодических про-
цессов можно определить по единственной выборочной функции. К счас-
тью, на практике стационарные случайные процессы обычно оказываются
эргодическими. Именно по этой причине свойства стационарных случай-
ных явлений часто можно определить по одной наблюдаемой реализации.
Подробное изложение свойств эргодических случайных процессов дается в
гл. 5.
1.3.3. НЕСТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
К нестационарным процессам относятся все случайные процессы, не
удовлетворяющие условиям стационарности, сформулированным в разд.
1.3.1. Если не наложены дополнительные ограничения, то свойства неста-
ционарных случайных процессов обычно зависят от времени и могут быть
установлены только путем усреднения в отдельные моменты времени по
ансамблю выборочных функций, образующих процесс. На практике часто
не удается получить достаточное для точной оценки свойств процесса чис-
ло реализаций. Этим фактом объясняется отставание в развитии практиче-
ских методов измерения и анализа нестационарных случайных процессов.
Во многих случаях нестационарные случайные процессы, отвечающие
реальным физическим явлениям, имеют особенности, упрощающие их ана-
лиз и измерение. Например, иногда случайные данные удается представить
в виде случайного процесса [х(0], все выборочные функции которого име-
ют вид x(t) = a(t)u(t). Здесь u(t) — выборочная функция стационарно-
го случайного процесса [и (О), a a(t) — детерминированная функция. Дру-
гими словами, данные представляются нестационарным случайным процес-
сом, все выборочные функции которого имеют общий детерминированный
тренд. Если нестационарный случайный процесс имеет такой вид, то для
описания его свойств не всегда требуется усреднение по ансамблю. Иногда
Основные определения и модели
25
многие важные свойства удается оценить по единственной выборочной
функции, как и в случае эргодических стационарных процессов. Подробно
такие задачи изучаются в гл. 12.
1.3.4. СТАЦИОНАРНОСТЬ ВЫБОРОЧНЫХ ФУНКЦИЙ
Понятие «стационарность», введенное и рассмотренное в разд. 1.3.1,
относится к средним по ансамблю свойствам случайного процесса. Однако
на практике часто говорят о стационарности или нестационарности дан-
ных, представляющих собой единственную реализацию случайного явле-
ния. В этом случае стационарность понимается в несколько ином смысле.
Если о единственной реализации говорят как о стационарной, то обычно
имеют в виду, что ее свойства, определенные на коротких интервалах вре-
мени, существенно не изменяются от интервала к интервалу. Слово «су-
щественно» означает здесь, что наблюдаемые колебания превосходят от-
клонения, которые можно объяснить обычной выборочной изменчивостью
статистических оценок.
Чтобы пояснить это соображение, рассмотрим одну реализацию хк (t),
являющуюся к-й выборочной функцией случайного процесса (х (t )]. Пусть
среднее значение и ковариационная функция оценены по небольшому интер-
валу длиной Т с началом в точке t j, т. е.
М'р к) = ~ р + Тхк(1) dt, (1.12а)
1 \
Rjji> li + тД) = rf''l + Txk(t)xk(t + r)dt. (1.126)
В общем случае, когда выборочные величины, определенные формулами
(1.12), сильно изменяются с изменением начального момента t выбороч-
ная функция называется нестационарной. В том частном случае, когда вы-
борочные свойства величин (1.12) не изменяются существенно с изменением
начального момента ti9 реализация называется стационарной. Заметим,
что реализация эргодического случайного процесса стационарна. В то же
время выборочные функции большинства практически интересных неста-
ционарных случайных процессов не стационарны. Поэтому при выполне-
нии свойства эргодичности (что справедливо для большинства стационар-
ных физических явлений) проверка стационарности одной реализации явля-
ется эффективным методом проверки в целом предположения стационарно-
сти и эргодичности случайного процесса, из которого эта реализация полу-
чена. Методы проверки стационарности отдельных реализаций изучаются в
гл. 4 и 10.
1.4.. Анализ случайных данных
Анализ случайных данных основан на иных соображениях, чем анализ
детерминированных данных, описанных в разд. 1.2. В частности, в силу
26
Глава 1
того что реализацию случайного процесса нельзя задать явной математи-
ческой формулой, для оценки свойств таких данных должны использовать-
ся статистические методы. Тем не менее случайные процессы удовлетворя-
ют вполне определенным соотношениям, описывающим преобразования
этих процессов; эти соотношения играют ключевую роль во многих прило-
жениях. В таких приложениях важно уметь выявлять и учитывать стати-
стические ошибки, связанные с оценками параметров и соотношениями
между входными и выходными процессами преобразований.
1.4.1. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Основные статистические характеристики, имеющие важное значение
для описания свойств отдельных реализаций стационарных случайных про-
цессов, таковы:
1) средние значения и средние квадраты;
2) плотности вероятности;
3) ковариационные функции;
4) функции спектральной плотности.
При обсуждении интуитивных предпосылок теории поучительно дать
описательные определения этих величин, не прибегая к математическим
формулам. Затем в качестве примеров будут рассмотрены некоторые осо-
бенно интересные частные случаи.
Среднее значение и дисперсия ах2 стационарной реализации случайного
процесса характеризуют соответственно центр рассеяния и величину рассея-
ния данных. Средний квадрат ^А2, равный сумме дисперсии и квадрата сред-
него значения, является мерой того и другого одновременно. Среднее зна-
чение оценивается простым усреднением всех значений реализации. Анало-
гичным усреднением квадратов значений реализации оценивается средний
квадрат. Если перед возведением в квадрат из значений реализации вычи-
тать среднее значение, то такое усреднение даст оценку дисперсии.
Плотность вероятности р (х ) стационарной реализации задает скорость
изменения вероятности в зависимости от значения реализации. Функция
р (х) обычно оценивается путем вычисления вероятности того, что мгно-
венное значение отдельной реализации заключено в узком интервале, центр
которого пробегает область значений процесса, с последующим делением
на ширину интервала. Общая площадь, ограниченная графиком плотности
вероятности по всей его области определения, равна единице, что просто
свидетельствует о достоверности события, заключающегося в том, что
значения реализации содержатся между — оо и +оо. Часть этой площади,
лежащая левее данного значения х, определяет функцию распределения,
обозначаемую Р (х). Часть площади, ограниченная графиком плотности
между произвольными двумя значениями хг их2 и равная Р(х2) — Р (хг),
задает вероятность того, что значения реализации в наугад выбранный мо-
мент времени попадут в этот интервал значений процесса. Плотности веро-
ятности и функции распределения подробно изучаются в гл. 3 и 4.
Ковариационная функция Rxx (т) стационарного процесса задает меру за-
висимости его значений, сдвинутых относительно друг друга на определен-
Основные определения и модели
27
б
г
Рис. 1.11. Четыре примера реализаций случайных процессов: а — гармонический
процесс; б — гармонический процесс плюс случайный шум; в — узкополосный слу-
чайный шум; г — широкополосный случайный шум.
ный интервал времени. Чтобы оценить ковариационную функцию, следует
сдвинуть реализацию на время т, перемножить исходную и сдвинутую реа-
лизации и усреднить полученные произведения по всей реализации или по
некоторому ее отрезку. Эта процедура выполняется для всех требуемых
значений сдвига времени.
Спектральная плотность (иначе, спектр мощности) Gxx(f) стационар-
ной реализации задает скорость изменения среднего квадрата в зависимо-
сти от частоты. Для оценивания спектра вычисляется средний квадрат в
28
Глава 1
узкой полосе частот при разных центральных частотах, а затем полученное
значение делится на ширину этой полосы. Общая площадь, лежащая под
графиком спектральной плотности по всей полосе частот, равна суммарно-
му среднему квадрату реализации. Часть этой площади, заключенная меж-
ду частотами j\ и /2> равна среднему квадрату, сосредоточенному в этой
Рис. 1.12. Плотности вероятности: а — гармонический процесс; б — гармониче-
ский процесс плюс случайный шум; в — узкополосный случайный шум; г — широко-
полосный случайный шум.
Основные определения и модели
29
полосе частот. Ковариационные функции и спектральные плотности изуча-
ются в гл. 5.
На рис. 1.11 показаны типичные реализации гармонического процесса,
гармонического процесса в случайном шуме, узкополосного шума и широ-
кополосного шума. На рис. 1.12—1.14 приводятся вычисленные теоретиче-
ски соответственно плотности вероятности, ковариационные функции и
КХХМ
АЛ » г
Рис. 1.13. Ковариационные функции: а — гармонический процесс; б — гармони-
еский процесс плюс случайный шум; в — узкополосный случайный шум; г — широ-
ополосный случайный шум.
30
Глава 1
спектральные плотности этих процессов. Формулы, по которым были по-
строены эти графики, выводятся наряду с другими в гл. 5.
Для пар реализаций, принадлежащих двум разным стационарным слу-
чайным процессам, важное значение имеют совместные статистические ха-
рактеристики, а именно:
1) совместные плотности вероятности;
2) взаимные ковариационные функции;
Gn(f)
О
Рис. 1.14. Спектральные плотности: а — гармонический процесс; б — гармони-
ческий процесс плюс случайный шум; в — узкополосный случайный шум; г — широ-
кополосный случайный шум.
Основные определения и модели
31
3) взаимные спектральные плотности;
4) частотные характеристики;
5) функции когерентности.
Первые три функции описывают основные свойства пары реализаций по
принимаемым ими значениям и по их свойствам во временной и частотной
областях. По известным взаимной спектральной плотности и спектраль-
ным плотностям реализаций можно теоретически вычислить линейные ча-
стотные характеристики (амплитудные и фазовые характеристики), связы-
вающие эти две реализации. В этом случае реализации считаются входом и
выходом некоторой линейной системы. Функция когерентности характери-
зует точность принятой линейной модели и тоже может быть вычислена
по измерениям спектральной и взаимной спектральной плотностей. Де-
тально этот предмет рассматривается в гл. 5—7.
Плотности вероятности и функции распределения обычно применяются,
помимо описания вероятностной структуры процесса, с целью:
1) проверки нормальности;
2) выявления нелинейностей;
3) анализа экстремальных значений.
Основные применения ковариационных функций охватывают:
1) выявление периодичностей;
2) выделение сигналов из шума;
3) измерение запаздываний;
4) локализацию источников помех:
5) идентификацию трактов и скоростей распространения сигналов.
В число типичных применений спектральных плотностей входят:
1) определение свойств систем по наблюдениям входных и выходных
процессов:
2) предсказание выходных процессов по входным процессам и свойст-
вам системы;
3) идентификация входных процессов по выходным процессам и свойст-
вам системы;
4) задание динамических данных для тестовых программ;
5) идентификация источников энергии и шума;
6) оптимальный линейный прогноз и фильтрация.
1.4.2. СООТНОШЕНИЯ МЕЖДУ ВХОДНЫМИ И ВЫХОДНЫМИ
ПРОЦЕССАМИ
Большинство задач преобразования входного процесса в выходной мож-
но сформулировать в виде одной из следующих моделей или их комбина-
ций:
1) модель с одним входом и одним выходом;
2) модель с одним входом и несколькими выходами:
3) модель с несколькими входами и одним выходом;
4) модель с несколькими входами и несколькими выходами.
Во всех случаях сигналы от каждого входа к каждому выходу проходят по
одному или нескольким параллельным трактам, имеющим разные запаз-
32
Глава 1
n(t)
Рис. 1.15. Система с одним входом, одним выходом и шумом на выходе.
дывания. В системах с несколькими входами входные процессы могут кор-
релировать или не коррелировать между собой. Если процессы не стацио-
нарны, то анализ проводится специальными методами, которые рассмат-
риваются в гл. 12.
Простая система с, одним входом и одним выходом изображена на рис.
1.15. Здесь х (t) и у (t) — наблюдаемые входные и выходные реализации
стационарных процессов, п (t) — ненаблюдаемый внешний шум. Величина
Hxy(f) — частотная характеристика линейной системы с постоянными па-
раметрами, преобразующей x(t) в у (/). На рис. 1.16 показана система с
одним входом и несколькими выходами, представляющая собой простое
обобщение системы, изображенной на рис. 1.15; здесь входной сигнал x(t)
вызывает несколько выходных сигналов y^t) (i = 1, 2, 3, ... , г). Выход-
ной сигнал у, (t) является результатом преобразования x(t) линейной си-
стемой с постоянными параметрами, задаваемой частотной характеристи-
кой Шумовые процессы л, (О описывают влияние внешнего шума
на соответствующие выходные сигналы. Из рис. 1.16 понятно, что такая
система может рассматриваться как комбинация отдельных систем с од-
ним входом и одним выходом.
Методы изучения систем с одним выходом излагаются в гл. 6 в терми-
нах оценок спектральных и взаимных спектральных плотностей. Там же
определены функции обычной когерентности, играющие ключевую роль
как в задачах идентификации систем, так и в задачах идентификации источ-
ников. Для определения амплитудной и фазовой составляющих искомой ча-
стотной характеристики необходимо знать взаимную спектральную плот-
ность между входным и выходным процессами. Хорошую оценку только
ni(t)
Рис. 1.16. Система с одним входом и несколькими выходами.
Основные определения и модели
33
амплитудной характеристики можно построить, зная лишь оценки входной
и выходной спектральных плотностей при условии, что внешним шумом на
входе и выходе можно пренебречь.
Если в модели с одним входом и одним выходом стационарные входной
и выходной сигналы полностью определены, система линейна и имеет по-
стоянные параметры, на входе и выходе отсутствует внешний шум, то
функция обычной когерентности тождественно равна единице на всех ча-
стотах. Любое отклонение от этих идеальных условий приводит к тому,
что значение функции когерентности будет меньше единицы. На практике
оценки функции когерентности часто меньше единицы; эти функции играют
важную роль при оценке статистической надежности измерений частотных
характеристик.
Все эти понятия можно перенести на более общие системы с нескольки-
ми входами и выходами, при этом потребуется определить и соответству-
ющим образом истолковать функции множественной и частной когерент-
ности. Такие общие схемы представимы в виде комбинации систем с не-
сколькими входами и одним выходом при заданных входных стационарных
процессах и различных частотных характеристиках, определяющих систе-
мы с постоянными параметрами, как показано на рис. 1.17. Современные
методы анализа систем со многими входами и выходами, в которых ис-
пользуются условные (остаточные) процессы, рассматриваются в гл. 7.
Рис. 1.17. Система с несколькими входами и одним выходом.
34
Глава 1
Эти методы представляют собой обобщение классических регрессионных
методов, описанных в гл. 4. В частности, строится разложение спектраль-
ной плотности выходного процесса, показанного на рис. 1.17, которое по-
казывает вклад любого входного сигнала в выходной спектр на данной ча-
стоте при некоторых условиях, наложенных на остальные входные сигна-
лы, упорядоченные определенным образом.
Основные понятия математической статистики, используемые при оцен-
ке случайных данных, рассмотрены в гл. 4. В гл. 8 и 9 выводятся формулы
для систематических и случайных ошибок, присущих различным оценкам,
используемым при анализе одномерных и многомерных случайных процес-
сов. В их число входят формулы для случайных ошибок, появляющихся
при оценивании частотных характеристик (как амплитудных, так и фазо-
вых) и функций когерентности (обычной, множественной и частной). Эти
формулы удобны в вычислительном отношении и безусловно полезны для
правильной интерпретации полученных результатов.
1.4.3. ХАРАКТЕРИСТИКИ ОШИБОК
В качестве введения в материал гл. 8 и 9 рассмотрим сейчас некоторые
характеристики ошибок оценивания. Оценку величины ф обозначим через ф,
т. е. с помощью символа ( у. Величина ф — это оценка ф, построенная по
наблюдению на конечном интервале времени или по конечному числу вы-
борочных точек.
Предположим, что оценка ф (хотя бы умозрительно) может быть полу-
чена многократно путем повторения эксперимента или выполнения опреде-
ленной программы измерений. Тогда в^ принципе можно оценить матема-
тическое ожидание ф, обозначаемое £ [ф]. Например, если эксперимент по-
вторяется многократно и дает оценки ф, (/ = 1, 2, ... , TV), то
£[ф] = ^Еф,- (113)
Это математическое ожидание может совпасть или не совпасть с истин-
ным значением ф. В случае совпадения оценка ф называется несмещенной.
В противном случае оценка называется смещенной. Смещение оценки, обо-
значаемое b [ф], равно математическому ожиданию оценки минус истинное
значение параметра:
&[ф] = £[ф] - ф. (1.14)
Следовательно, смещение оценки — это систематическая ошибка, которая
всегда имеет одну и ту же абсолютную величину и один и тот же знак, ес-
ли измерения проводятся при неизменных условиях.
Дисперсия оценки, обозначаемая Уаг[ф], определяется как математиче-
ское ожидание квадрата разности между оценкой и ее средним значением.
Формально
Уаг[ф] = Е [(ф - £[ф])2] .
(1-15)
Основные определения и модели
35
Дисперсия характеризует случайную ошибку оценки, т. е. ту часть общей
ошибки, которая не является систематической и может иметь разные знаки
и разные абсолютные значения от измерения к измерению.
Суммарная ошибка оценивания характеризуется средним квадратом
ошибки, который определяется как математическое ожидание квадрата
разности между оценкой и ее истинным значением. Средний квадрат
ошибки оценки ф равен
£[(ф-ф)2]. (1.16)
Легко проверить, что
я[(ф-ф)2] = Уаг[ф]+(*[ф])2. (1.17)
Иначе говоря, средний квадрат ошибки равен сумме дисперсии и квадрата
смещения. Если смещение равно нулю или пренебрежимо мало, то средний
квадрат ошибки и дисперсия совпадают.
Рис. 1.18 иллюстрирует смысл смещения (систематической ошибки) и
дисперсии (случайной ошибки) на примере пристрелки двух винтовок.
Рис. 1.18, а показывает, что винтовка А обладает большим смещением и
малой случайной ошибкой. Рис. 1.18,6 показывает, что винтовка Б имеет
малое смещение, но большую случайную ошибку. Очевидно, из винтовки А
никогда нельзя попасть в цель, в то время как из винтовки Б можно слу-
чайно поразить ее. Однако большинство стрелков предпочтет винтовку А,
поскольку систематическую ошибку можно исключить (если известно, что
она есть) путем регулировки прицела винтовки, а случайную ошибку устра-
нить нельзя. Следовательно, винтовка А потенциально имеет меньший
средний квадрат ошибки.
2*
Рис. 1.18. Случайные и систематические ошибки при стрельбе из винтовки по
мишени: а — винтовка А, большая систематическая ошибка и малая случайная
ошибка; б — винтовка Б, малая систематическая ошибка и большая случайная
ошибка.
36
Глава 1
Наконец, важной величиной является нормированная среднеквадратич-
ная ошибка оценки, обозначаемая £[ф]. Эта безразмерная ошибка равна
квадратному корню из среднего квадрата ошибки, деленному на истинное
значение параметра (разумеется, в предположении, что оно не равно
нулю). Формально
е[ф] =
/е (ф - ф)2
ф
(1-18)
На практике стараются уменьшить нормированную среднеквадратичную
ошибку в максимально возможной степени. В этом случае появляется уве-
ренность в том, что произвольная оценка ф близка к истинному значе-
нию ф.
1.4.4. МЕТОДЫ АНАЛИЗА ДАННЫХ
Рекомендуемые методы анализа данных детально обсуждаются в
гл. 10—13. В гл. 10 рассматриваются задачи сбора данных, включая их на-
копление, запись, передачу, подготовку и предварительную оценку. Описы-
ваются общие подходы к анализу отдельных реализаций и их совокупно-
стей, которые могут применяться в разнообразных приложениях. Основное
внимание уделяется эффективным методам анализа свойств стационарных
случайных процессов. Методы анализа цифровых данных обсуждаются в
гл. 11, в том числе вычислительные процедуры для исключения тренда и
цифровой фильтрации, ряды Фурье, быстрое преобразование Фурье дис-
кретных временных рядов, представляющих реализации стационарных (эр-
годических) случайных процессов. Выведены численные формулы для по-
строения оценок плотностей вероятности, ковариационных функций и
спектральных плотностей по отдельным реализациям и парам реализаций.
Кроме того, подробно описаны цифровые процедуры получения оценок
всех величин, изученных в гл. 6 и 7 при решении разных задач, связанных с
одномерными и многомерными линейными системами. Гл. 12 посвящена
специальным методам анализа нестационарных процессов, а в гл. 13 рас-
сматриваются методы преобразования Гильберта.
Задачи
1.1. Определите, какие из перечисленных ниже функций являются периодически-
ми, а какие непериодическими:
а)х(/) = 3sinZ 4- 2sin2/ 4- sin3/;
б)х(Г) = 3sin/ 4- 2sin2r 4- sin7r/;
в)х(Г) = 3sin4r 4- 2sin5r 4- sin6/;
r) x (t) = e sin/.
1.2. Определите период функции x (t) = sin 111 4- sin 12/.
В задачах 1.3—1.6 требуется установить, какие из перечисленных свойств всегда
справедливы.
Основные определения и модели
37
1.3. Стационарный случайный процесс должен
а) быть дискретным;
б) быть непрерывным;
в) быть эргодическим;
г) иметь не зависящие от времени средние по ансамблю характеристики;
д) иметь средние по времени характеристики, совпадающие с соответствующи-
ми средними по ансамблю.
1.4. Эргодический процесс должен
а) быть дискретным;
б) быть непрерывным;
в) быть стационарным;
г) иметь не зависящие от времени средние по ансамблю характеристики;
д) иметь средние по времени характеристики, совпадающие с соответствующи-
ми средними по ансамблю.
1.5. Все статистические свойства случайного процесса можно установить по его
единственной реализации, если процесс
а) детерминированный;
б) эргодический;
в) стационарный;
г) обладает всеми перечисленными свойствами.
1.6. Ковариационная функция стационарного случайного процесса должна
а) убывать с возрастанием I т I;
б) зависеть только от сдвига времени;
в) стремиться к постоянной с возрастанием I т I;
г) всегда быть неотрицательной.
1.7. Как изменятся ответы на вопросы задачи 1.6, если стационарный случай-
ный процесс не содержит периодической составляющей?
1.8. Выведите формулу (1.17).
1.9. Известно, что средний квадрат оценки равен 0,25, а смещение равно 0,40.
Вычислите дисперсию оценки.
1.10. Пусть в условиях задачи 1.9 истинное значение параметра равно ф = 5.
Вычислите нормированную среднеквадратичную ошибку оценки.
Глава 2
ЛИНЕЙНЫЕ ФИЗИЧЕСКИЕ СИСТЕМЫ
До детального обсуждения процедур измерения и анализа случайных
физических данных желательно пояснить некоторые важные понятия и ос-
новные определения, относящиеся к динамике физических систем. В этой
главе дается обзор теоретических формул, описывающих характеристики
отклика идеальных линейных систем; основные представления иллюстри-
руются простыми примерами из физики.
2.1. Линейные системы с постоянными параметрами
Идеальная система — это система, которая имеет постоянные пара-
метры и в которой две четко определенные фиксированные характеристи-
ки, именуемые входными (возбуждение) и выходными (отклик), линейно
связаны между собой. Система имеет постоянные параметры, если все ее
основные свойства неизменны во времени. Например, простая пассивная
электрическая цепь будет системой с постоянными параметрами, если зна-
чения сопротивления, емкости и индуктивности всех элементов одинаковы
в разные моменты времени. Система линейна, если ее реакция аддитивна и
однородна. Термин «аддитивна» означает, что реакция на сумму двух вход-
ных сигналов равна сумме реакций на каждый сигнал в отдельности. Тер-
мин «однородна» означает, что реакция на произведение постоянной и
входного сигнала равна произведению этой постоянной и реакции, вызыва-
емой одним лишь сигналом. Формально, если f(x) обозначает реакцию на
входной сигнал х, то система линейна в том случае, когда для любых двух
входных сигналов х j, х 2 и постоянной с имеют место свойство аддитивно-
сти
/(%! + Х2) = /(*1) + /(*2) (2’1а)
и свойство однородности
/(<•%) = с/(х). (2.16)
Предположение о постоянстве параметров на практике выполняется с
разумной точностью для многих физических систем. Например, основные
свойства электрической цепи или механической конструкции обычно не ис-
пытывают существенных изменений на протяжении промежутков времени,
представляющих практический интерес. Разумеется, есть и исключения.
Параметры электрического сопротивления могут измениться под взаимо-
действием высокой температуры, а жесткость конструкции — из-за накоп-
ления усталости, вызванной постоянной вибрацией. Кроме того, в некото-
рые физические системы зависимость параметров от времени заложена
конструктивно и необходима для выполнения системой ее функций. Оче-
видный пример дают электронные системы связи. Однако подобные случаи
являются скорее исключениями и легко выявляются на практике.
С предположением о линейности дело обстоит сложнее. Все физические
Линейные физические системы
39
системы становятся нелинейными при экстремальных значениях входных
сигналов. Например, в электрическом конденсаторе в конце концов проис-
ходит пробой при нарастании напряжения, и, следовательно, проходящий
через него ток уже не будет пропорционален приложенному напряжению;
металлический трос в конце концов оборвется при увеличении нагрузки, и,
следовательно, напряжение уже не будет пропорционально нагрузке. Труд-
ности усугубляются тем, что обычно нелинейные эффекты проявляются
постепенно, начиная с некоторого момента времени. Например, связь меж-
ду нагрузкой и напряжением в металлическом тросе обычно начинает от-
клоняться от линейной задолго до момента обрыва. Тем не менее характе-
ристики отклика многих физических систем можно считать линейными, во
всяком случае в некоторой ограниченной области значений входных сигна-
лов, не рискуя совершить серьезных ошибок.
ПРИМЕР 2.1. НЕЛИНЕЙНАЯ СИСТЕМА. Рассмотрим простую систему с
квадратичной реакцией, в которой выходной сигнал имеет вид
У = /(*) = ах2.
Для любых двух входных сигналов х{ и х2
f(xx + х2) = a(xi + х1)2 = axi + laxix2 + ах2
а свойство аддитивности из соотношения (2.1а) требует, чтобы
/(%! + Х2) = ах\ + ах2 •
Далее, для произвольной постоянной с
f(cx) = а(сх)2 = с2ах2у
а свойство однородности из соотношения (2.16) требует, чтобы
f(cx) = сах\
Следовательно, эта система нелинейна, поскольку она не обладает ни
свойством аддитивности, ни свойством однородности.
2.2. Основные динамические характеристики
Динамические характеристики линейной системы с постоянными пара-
метрами можно описать с помощью весовой функции h (т), иногда называ-
емой импульсной переходной функцией, которая определяется как реакция
в произвольный момент времени на импульсное воздействие, поступившее
40
Глава 2
на вход системы за г единиц времени до этого момента. Полезность весо-
вой функции для описания такой системы связана со следующим обстоя-
тельством. Для произвольного входного сигнала x(t) выход системы у( t)
задается интегралом свертки
/♦00
y(t) = [ h(r)x(t - г) dr, (2.2)
•'-00
т. е. значение выходного сигнала у (t) является взвешенной линейной
(бесконечной) суммой по всей реализации входного сигнала х( /).
Для того чтобы линейная система с постоянными параметрами была
физически осуществимой (причинно-обусловленной), необходимо, чтобы
система реагировала только на прошлые значения входного сигнала. Это
означает, что
й(т) = 0, т < 0. (2.3)
Следовательно, в физических системах нижний предел интегрирования в
уравнении (2.2) фактически равен нулю, а не — оо.
Линейная система с постоянными параметрами называется устойчивой,
если любая допустимая ограниченная входная функция приводит к ограни-
ченной выходной функции. Из уравнения (2.2) имеем
/оо
|А(т)| |x(z - т)| dr. (2.4)
- nr
Если входная функциях (О ограничена, то существует некоторая конечная
постоянная А такая, что для всех t
|x(z)| < А.
(2-5)
Из соотношения (2.4) следует, что
/00
|й(т)|<7т. (2.6)
- 00
Поэтому, если весовая функция Л (т) линейной системы с постоянными па-
раметрами абсолютно интегрируема, т. е. если
f |Л(т)| dr < оо , (2.7)
•'-00
то выходная функция тоже ограничена, а система устойчива.
ПРИМЕР 2.2. НЕУСТОЙЧИВАЯ СИСТЕМА. Рассмотрим простую систему,
импульсная переходная функция которой имеет вид
Поскольку h (т) = 0 для т < О, то, согласно определению, система физиче-
ски осуществима. Однако
Линейные физические системы
41
г00 z х г00 А
/ |А(т)|</т = / |Леат| dr = -(е000 - 1).
— ос •'о а
Отсюда следует, что система неустойчива при а 0 и устойчива
при а < 0. В частности, если а = — b < 0, то
/•ОО Л Л
I \Ae-h'\dT = — = - •
•'о ~~ b b
На этом пример 2.2 заканчивается.
Линейную систему с постоянными параметрами можно охарактеризо-
вать также передаточной функцией Н (р), которая определяется как преоб-
разование Лапласа функции h (т), т. е.
Н(р)={ h(r)e~pr dr, p = a+jb. (2.8)
•'о
В терминах передаточной функции Н (р) можно придать интересный вид
критерию устойчивости линейной системы с постоянными параметрами
(в предположении, что она физически осуществима). Именно, если Н(р) не
имеет полюсов в правой полуплоскости комплексной плоскости р, включая
мнимую ось (отсутствуют полюса с а 0), то система устойчива. Обрат-
но, если Н (р ) имеет хотя бы один полюс в правой полуплоскости ком-
плексной плоскости р или на ее мнимой оси, то система неустойчива.
Важное свойство линейных систем с постоянными параметрами — со-
хранение частот. Более подробно, рассмотрим линейную систему с посто-
янными параметрами, имеющую весовую функцию h (г). Уравнение (2.2)
показывает, что при произвольной входной функции х (t) п-я производная
по времени выходной функции у (О равна
гоо dnx(t — т)
(2-9>
Пусть теперь на вход поступает гармоническая функциях (Г), т. е.
х(/) = Xsmtynft + 6) . (2.10)
Вторая производная х (t) равна
dt1
-47r2f2x(t).
(2.11)
Из уравнения (2.9) следует, что вторая производная выходной функции(t)
имеет вид
~^ = ~^2f2y(t). (2.12)
42
Глава 2
Следовательно, у (t) — гармоническая функция с той же частотой, что и
х (t). Этот результат показывает, что линейная система с постоянными па-
раметрами не меняет частоты, а воздействует только на амплитуду и фазу
сигнала, подаваемого на вход.
2.3. Частотные характеристики
Если линейная система с постоянными параметрами физически осущест-
вима и устойчива, то ее динамические свойства можно описать посредст-
вом частотной характеристики которая определяется как преобра-
зование Фурье функции h (г), т. е.
/♦00
h(r)e ~j2,r/r dr. (2.13)
Отметим, что нижний предел интегрирования равен нулю, а не — оо, по-
скольку h (т) = 0 при т < 0. По существу, частотная характеристика — это
частный случай передаточной функции, когда в показателе экспоненты р =
= а + jb величина а = 0, a b = 2тг/. В случае физически осуществимых
устойчивых систем частотная характеристика содержит ту же информа-
цию, что и передаточная функция.
Можно получить важное соотношение, содержащее частотную характе-
ристику, взяв преобразование Фурье от обеих частей уравнения (2.2). Пусть
X(f) — преобразование Фурье входного сигналах (О» a Y(f) — преобразо-
вание Фурье соответствующего выходного сигнала у (О, при этом предпо-
лагается, что оба эти преобразования Фурье существуют; тогда из уравне-
ния (2.2) следует, что
У(/) = Я(/)Х(/). (2.14)
Итак, в терминах частотной характеристики системы и преобразований
Фурье входного и выходного сигналов интегралу свертки из уравнения (2.2)
соответствует простое алгебраическое выражение (2.14).
Как правило, частотная характеристика — это комплекснозначная функ-
ция, поэтому удобно представить ее через модуль и аргумент. Для этого
запишем H(f) в полярной форме:
Я(/) = |Я(/)|е-^>. (2.15)
Модуль \H(f)\ называется амплитудной характеристикой, а соответству-
ющий аргумент </>(/') — фазовой характеристикой. В этих терминах частот-
ная характеристика интерпретируется следующим образом. Предположим,
что входным сигналом системы служит гармоническая функция с частотой
f (считаем, что она определена на всей оси времени); эта функция вызыва-
ет выходной сигнал, являющийся, как было показано в разд. 2.2, тоже гар-
монической функцией с той же частотой. Отношение амплитуд выходного
и входного сигналов равно амплитудной характеристике системы I
а сдвиг фазы между выходным и входным сигналами задается фазовой ха-
рактеристикой </>(/*) системы.
Линейные физические системы
43
Из условий физической осуществимости следует, что частотная, ампли-
тудная и фазовая характеристики линейной системы с постоянными пара-
метрами обладают следующими свойствами симметрии:
я(-/) = я*(/),
|Я(-/)| = |Я(/)|, (2.16)
Ф(-/) = -Ф(/).
Далее, если последовательно с системой, описываемой частотной характе-
ристикой включена вторая система с частотной характеристикой
причем между двумя системами отсутствует обратная связь или
связь через нагрузку, то частотная характеристика H(f) новой системы
имеет вид
Я(/) = Я1(/)Я2(/),
\Н(П\ = \НАП\\НАП\, (2.17)
Ф(/) = Ф1(/) + Фг(/)-
Следовательно, при последовательном соединении двух систем с соблюде-
нием указанных выше условий амплитудные характеристики перемножают-
ся, а фазовые складываются.
Важно помнить, что частотная характеристика H(f) линейной системы
с постоянными параметрами зависит только от частоты и не зависит ни от
времени, ни от вида входного сигнала. В случае нелинейной системы H(f)
может зависеть от входного сигнала системы. Если же параметры системы
не постоянны, то H(f) зависит от времени.
2.4. Примеры частотных характеристик
Для лучшего понимания частотных характеристик рассмотрим несколь-
ко примеров распространенных физических систем. Приводимые ниже при-
меры относятся к простым механическим и электрическим системам, по-
скольку они более наглядны. Проводится аналогия между свойствами ме-
ханических, электрических и ряда других систем.
2.4.1. МЕХАНИЧЕСКИЕ СИСТЕМЫ
Рассмотрим простую механическую конструкцию, которую можно
представить в виде системы с сосредоточенными параметрами, состоящей
из массивного тела, пружины и демпфера, причем масса может смещаться
только в одном направлении (рис. 2.1). На этом рисунке к — коэффициент
жесткости пружины (Н/м), с — затухание (Нс/м), ат — масса (кг).
44
Глава 2
Рис. 2.1. Простая механическая система.
Перед определением частотной характеристики следует выяснить, какие
входные и выходные параметры системы нас интересуют. Как будет пока-
зано ниже, для системы, изображенной на рис. 2.1, возможно несколько
вариантов выбора таких параметров.
Сила как входной процесс и смещение тела
как выходной процесс. Допустим, что в качестве входного сиг-
нала нас интересует сила, приложенная к телу, а в качестве выходного сиг-
нала — вызванное силой смещение тела (рис. 2.2). Здесь F(t) — приложен-
ная сила в ньютонах, y(t) — соответствующее смещение тела в метрах.
Для определения частотной характеристики этой системы в первую оче-
редь следует вывести уравнение движения. Для этого воспользуемся одним
из основных положений механики, согласно которому сумма всех сил,
действующих на массу, должна равняться нулю:
F(t) + Fk(.t) + Fc(z) + Fm(t) = 0, (2.18)
где
Fk(t) = — ky(t) — упругая сила пружины, (2.18а)
Fc(t) = — cy(t) — демпфирующая сила, (2.186)
= -my(t) — сила инерции, (2.18в)
t) =----------скорость,
dt
y(t)
F(t)
Рис. 2.2. Механическая система, входом
которой служит сила.
Линейные физические системы
45
y(t) =
d2y(t)
dt2
— ускорение.
Следовательно, уравнение движения Системы имеет вид
my(t) + cy(t) + ky(t) = F(t). (2.19)
В разд. 2.3 частотная характеристика системы была определена как пре-
образование Фурье реакции системы на импульсное воздействие. В данном
случае реакция системы — это смещение у (t); его преобразование Фурье
дается формулой
г(/) = ry(t)e-^'dt = H(f). (2.20)
•'о
Тогда преобразования Фурье имеют вид
[j(0] (2.20а)
[j>(0]= -(2^)2Я(/). (2.206)
Переходя к преобразованиям Фурье в обеих частях уравнения (2.19) с уче-
том того, что преобразование Фурье импульсного воздействия силы
F(t) = 6(0 равно единице, получим следующее выражение:
[-(2tt/)2W + j2irfc + Л] H(f) = 1. (2.21а)
Поэтому
[k-(2vf)2m+j2vfc]~\ (2.216)
где индекс f—d указывает, что рассматриваемая функция H(f) связывает
силу на входе и смещение на выходе системы.
Уравнение (2.21) целесообразно переписать в другой форме, введя обо-
значения
с
ly/km
fn = ^4- ’ (2.226)
2 77 V т
Величина f из формулы (2.22а) безразмерная и называется коэффициентом
затухания. Величина fn из формулы (2.226) называется собственной часто-
46
Глава 2
той незатухающих колебаний и измеряется в герцах. Подставив эти вели-
чины в уравнение (2.21), получим следующее выражение:
1A
(2.23)
1-(///J2+W//„
Переписав выражение (2.23) в показательной форме, получим выражение
для частотной характеристики в терминах амплитудной (Iи фазовой
(0(f)) характеристик:
(2-24)
где
1/Л
\H(f)\f.d= -/f . =====
+[2с///„]2
ф(/)/-</ = arctg
2С//А
1 - (//А)2
(2.24а)
(2.246)
Отметим, что размерность \H(f)\f_d совпадает с размерностью 1/Хг, т. е.
измеряется в м/Н. Эта функция иногда называется коэффициентом дина-
мического усиления.
Графики \H{f)\j_d и </>(/* задаваемых выражениями (2.24а) и
(2.246), представлены на рис. 2.3. Особый интерес вызывают три свойства
этих графиков. Во-первых, при f 1/V2 амплитудная характеристика име-
ет максимум на частоте, несколько меньшей собственной частоты fn . Ча-
стота, на которой достигается максимум амплитудной характеристики, на-
зывается резонансной частотой системы. В частности, минимизируя зна-
менатель \H(f)\j_d из уравнения (2.24а), можно показать, что резонансная
частота (обозначим ее fr) равна
(2-25)
а максимальное значение амплитудной характеристики, достигаемое на
этой частоте, есть
1Д
2(71 - с2
Во-вторых, если определить ширину полосы пропускания по уровню по-
ловинной энергии амплитудной характеристики системы как Br = f 2 — f j,
где
(2.26)
|//(Л)Г = |//(/2)Г = 2Ч//(Л)Г,
Линейные физические системы
47
а
Рис. 2.3. Частотная характеристика механической системы, входом которой слу-
жит сила: а — амплитудная характеристика; б — фазовая характеристика.
48
Глава 2
то эта величина для рассматриваемой амплитудной характеристики при-
ближенно выражается в предположении малости затухания через резонанс-
ную частоту как
Br = 2tfr, f < 0,1 . (2.27)
В-третьих, фазовая характеристика меняется от 0° на частотах, много
меньших fn , до 180° на частотах, много больших fn . Вид кривой </>(/) меж-
ду этими крайними значениями фазового угла зависит от коэффициента за-
тухания f. Однако при f = fn фаза равна 90° независимо от вели-
чины f.
ПРИМЕР 2.3. РЕЗОНАНСНАЯ СИСТЕМА. Простая механическая система,
подобная изображенной на рис. 2.1, имеет следующие параметры:
т = 1,79 кг, с = 35,72 Н-с/м, к = 17 857,88 Н/м.
Определим собственную частоту незатухающих колебаний, коэффициент
затухания, резонансную частоту и максимум амплитудной характеристики
системы.
Собственную частоту незатухающих колебаний и коэффициент затуха-
ния находим по формулам (2.22):
1 Д' с
A = :pV~ =15’9 Гц’ ^77Г=0Л
2тг V т ly/km
Резонансная частота определяется по формуле (2.25):
/г=//1-2£2 = 15,7 Гц,
а максимум амплитудной характеристики — по формуле (2.26):
1/Л
|Я(/ )| = — = 0,0003 м/Н.
пК^Т2
На практике принято амплитудную характеристику физических систем
представлять в безразмерном виде, умножая ее на коэффициент жесткости:
1
к\Н( Л)| =---. = 5,0.
Эта величина часто называется добротностью системы и обозначается
буквой Q. Величина, обратная к Q, обычно называется коэффициентом по-
терь и обозначается буквой т/. Для рассматриваемой системы Q = 5,0,
i] = 0,2. На этом пример 2.3 заканчивается.
Линейные физические системы
49
Возвращаясь к сказанному в разд. 2.3, можно следующим образом
интерпретировать частотную характеристику Пусть к телу
(рис. 2.2) приложена сила, изменяющаяся по гармоническому закону:
F(t) = Fosin 2тг/7. Тогда смещение на выходе системы имеет вид
y(t) = F0\H(f)\f_dsin[2^ft - (2.28)
Эта интерпретация подсказывает иной метод определения частотной ха-
рактеристики. Именно по гармоническому входному сигналу находим вы-
ходной сигнал, тогда частотная характеристика определяется по измене-
нию амплитуды и сдвигу фазы выходного сигнала относительно амплиту-
ды и фазы входного сигнала. Проиллюстрируем этот подход на примере
рассматриваемой системы.
Реакция системы, изображенной на рис. 2.2, на гармонический входной
сигнал задается решением уравнения (2.19); когда F(t) — гармоническая
функция, имеем
my(t) + cy(t) + ky(t) = Fosin2Tr/Z = Im[Foey2,r/'], (2.29)
где Im[ ] обозначает мнимую часть [ ]. Запишем теперь решение уравнения
(2.29) в виде выходной гармонической функции общего вида:
,у(0 = Ysm(2irft - ф) = 1т[Уе7(2’г/'-ф>]. (2.30)
После подстановки выражения (2.30) в уравнение (2.29) получим следующее
соотношение: .
1т[(-(2тг/)2т + jlirfc + к) Уе7(27г/Г-Ф)] = 1т[Гое72,г/']. (2.31)
Решение уравнения (2.29) находим из уравнений (2.30) и (2.31):
Я') = Im
FQell~fl
к ~(2irf)2m + j2irfc
(2.32)
Используя обозначения, введенные в (2.22), и переходя к тригонометриче-
скому представлению, получаем выражение для выходного сигнала у (I):
Fosin[2w/r - ф(/)]
y(t) = —......... ==г ,
W -(//А)Т + IW/J2
(2.33)
где
<#►(/) = arctg
1-(//А)2
50
Глава 2
Следовательно, выходной сигнал получается путем умножения амплитуды
входного сигнала на амплитудную характеристику системы, определенную
формулой (2.24а), и сдвига по фазе на величину, равную фазовой характе-
ристике системы, определенной формулой (2.246).
Смещение основания как входной процесс и
смещение массы как выходной процесс. Рассмотрим
теперь другой случай, когда нас интересует воздействие смещения основа-
ния на смещение тела (рис. 2.4). Здесь х (О — исходное смещение основа-
ния, измеренное в метрах относительно среднего положения основания, а
у (t) — результирующее выходное смещение тела, измеренное в метрах от-
носительно положения равновесия.
Как и ранее, исходя из основных законов механики, выводим уравнение
движения системы
ГД/)+ ГС(/)+ £„,(/) = 0,
(2-34)
где
Fk(t) = “MHO “ *(0]— УпРУгая сила пружины, (2.34а)
Fc(t) = — с[Н0 “ *(0] — Демпфирующая сила, (2.346)
Fw(/) = -my(t) —сила инерции. (2.34в)
Следовательно, уравнение движения этой системы имеет вид
my(t) + cy(t) + ky(t) = kx(t) + cx(t). (2.35)
Как и ранее, частотная характеристика системы определяется преобразова-
нием Фурье смещения у (t), вызванного импульсным смещением основания
х [t) = d(t). Беря преобразование Фурье от обеих частей уравнения (2.35) с
учетом того, что преобразование Фурье функции ) равно j 2irf, получим
следующее выражение:
^y(t)
Рис. 2.4. Механическая система,
входом которой служит смещение
основания.
Линейные физические системы
51
[~(2irf)2m +j2irfc + &] У(/) = [fc + j2irfc].
Следовательно,
(2.36а)
к + jlnfc
Y(f) = H(f)d_d = 2
к - ybrf) m + jlirfc
где индекс cf—d означает, что данная частотная характеристика связывает
смещения на входе и выходе системы.
С учетом обозначений, введенных в (2.22), выражения (2.36) можно пе-
реписать в следующем виде:
(2.366)
1 + №f/fn
(2.37)
В полярных обозначениях формула (2.37) записывается через амплитудную
и фазовую характеристики:
Ш) = l#(/)KW), (2.38)
где
\H(f)\d_d =
I 1 +1W/J2 j1/2
I [1 -(//А)2]2 +РШ]2/’
ф(/Ъ-</ = arctg
2П//А)3
1-(//А)2 + 4Г(///„)2
(2.38а)
(2.386)
Заметим, что 1Н(/')1б/_б/ — безразмерная величина. Эта функция часто на-
зывается коэффициентом динамичности. Графики IH(f)\d_d и <b(f)d_d
представлены на рис. 2.5. Отметим, что амплитудная характеристика име-
ет один максимум подобно амплитудной характеристике системы, изобра-
женной на рис. 2.3. Однако детальный анализ амплитудной и фазовой ха-
рактеристик, представленных на рис. 2.5, показывает, что они существенно
отличаются от аналогичных характеристик, изображенных на рис. 2.3.
Другие сочетания входных и выходных сигна-
лов. Приведенные выше два примера показывают, что в зависимости от
типа исследуемого входного сигнала одна и та же простая механическая си-
стема описывается разными частотными характеристиками. На самом деле
любое новое сочетание входных и выходных параметров, какое только
может встретиться, приводит, как правило, к иной частотной характери-
стике. Например, в некоторых приложениях интересуются относительным
смещением на выходе системы z (О = у (I ) - х (/), вызываемым смещени-
ем основания х (t) на входе, в то время как в других случаях важно знать
52
Глава 2
Отношение частот f/fn
б
Рис. 2.5. Частотная характеристика механической системы, входом которой слу-
жит смещение основания: а — амплитудная характеристика; б — фазовая характери-
стика.
Таблица 2.1. Амплитудные характеристики механической системы, показанной на
рис. 2.1.
Входной про- цесс — сила (см. модель на рис. 2.2)
Амплитудная характери- стика простой механичес- кой системы как функция от входных и выходных параметров Входной процесс — смещение основания (см. модель на рис. 2.4) Сила (в еди- ницах сме- щения), м x(t) = F(t)/k
Смещение яо, м Скорость *(0, м/с Ускорение x(t), м/с2
Абсолютное смещение ЯО £1 Я Я
В терминах смещения на выходе, м Я 2я/Я 4v2f2D2 1
Относитель- ное смеще- ние f2 ' f 1 т2
40 = Я') - Я') f2D2 ^f2D2 4^2ЯЯ
Абсолютная скорость y(t) я Я
В терминах скорости на выходе, м/с Я D2 2irfD2 Ът/
Относитель- ная ско- рость ZU) = ЯО - ЯО 2тт/3 f2 f р2
Яя f.;D2 ^f2D2
В терминах Абсолютное ускорение я о 4ir2f2Dl d2 d2 —< I ri 4тг2/2
ускорения на выходе, м/с2 Относитель- ное ускоре- ние 2(0 = у(‘) - ЯО 4тг2/4 /,,2Я 2irf' f2D2 f2 f2D2 р2
£>1 = yi + f„ = 7- \ 2тт V Т я = 4^ с у _ ______ (f/f,,)2]2 + [2К//А)]2
m 2^ кт
54
Глава 2
абсолютное ускорение^ (t) на выходе в зависимости от скорости смещения
основания х (t) на входе. В каждом случае получится несколько иная ча-
стотная характеристика. Для иллюстрации сказанного в табл. 2.1 приведе-
ны разнообразные амплитудные характеристики простой механической си-
стемы, изображенной на рис. 2.1, соответствующие 21 разному сочетанию
входных и выходных параметров.
ПРИМЕР 2.4. РЕАКЦИЯ СИСТЕМЫ НА УСКОРЕНИЕ ОСНОВАНИЯ. Про-
стая механическая система, подобная показанной на рис. 2.4, подвергается
смещению основания, измеряемому в единицах абсолютного ускорения.
Полагая, что коэффициент затухания системы равен f = 0,7, определим
смещение массы относительно основания на частотах, меньших частоты
собственных незатухающих колебаний.
Соответствующую амплитудную характеристику возьмем из табл. 2.1:
lW)l =---------/г 1 э12 •
+[W//„]2
Значения нормированной естественным образом амплитудной характери-
стики при///л 1 таковы:
f/fn 0 0,2 0,4 0,6 0,8 0,9 1,0
[W)J
0,0253
1,00 1,00 0,99 0,95 0,87 0,79 0,72
Заметим, что значения амплитудной характеристики примерно постоянны
на частотах, существенно более низких, чем частота собственных незатуха-
ющих колебаний системы. По этой причине такая система лежит в основе
одного из типов датчиков ускорения, называемых сейсмическими акселеро-
метрами, последние будут рассмотрены в гл. 10.
2.4.2. ЭЛЕКТРИЧЕСКИЕ СИСТЕМЫ
Рассмотрим простую электрическую цепь, которая представляется в ви-
де системы с сосредоточенными параметрами, состоящей из индуктивно-
сти, сопротивления и конденсатора. Предположим далее, что входом си-
стемы служит разность потенциалов, как показано на рис. 2.6. На этом ри-
сунке С — емкость в фарадах, R — сопротивление в омах, L — индуктив-
ность в генри, e(t) — приложенный потенциал в вольтах, i(t) — резуль-
тирующий ток в амперах. Заметим, что i (t) = dq (t )/dt, где q (t) — заряд
в кулонах.
Предположим, что в качестве входного сигнала нас интересует прило-
Линейные физические системы
55
Рис. 2.6. Электрическая цепь, на
вход которой подается напряжение.
женное напряжение, а в качестве выходного — результирующй заряд. Как
и при анализе механической системы (разд. 2.4.1), для определения соот-
ветствующей частотной характеристики сначала нужно вывести дифферен-
циальное уравнение, описывающее систему. Согласно основным положени-
ям теории электрических цепей, сумма всех разностей потенциалов на эле-
ментах цепи должна равняться нулю. Следовательно,
e(0 + ec(z) + eR(/) + eL(/) = 0, (2.39)
где
(/) = “ —#(/)—разность потенциалов на конденсаторе,(2.39а)
ес
eR(t) ~ —разность потенциалов на сопротивлении,(2.396)
eL(z) = —Lq(t)— разность потенциалов на индуктивности.(2.39в)
Поэтому дифференциальное уравнение системы имеет вид
+ Rq(t) + = e(t). (2.40)
Отметим сходство между уравнением (2.40) и уравнением движения меха-
нической системы под воздействием силы (2.19). Используя тот же метод
анализа, который был описан в разд. 2.4.1, непосредственно получаем, что
частотная характеристика этой простой электрической системы имеет вид
Н(Пе-Ч
^-^f)2L+j2irfR \
(2.41)
где индексе—q означает, что данная//(/) связывает напряжение на входе
и заряд на выходе. Заметим, что измеряется в кулонах на вольт.
График H(J) e_q идентичен графику частотной характеристики механи-
ческой системы представленному на рис. 2.3, если только в ка-
честве коэффициента затухания f и частоты fn собственных незатухающих
56
Глава 2
колебаний электрической цепи взять величины
(2.42а)
(2.426)
Совершенно ясно теперь, что между механической и электрической систе-
мами существует прямая аналогия (табл. 2.2).
Обычно для описания электрических систем применяется частотная ха-
рактеристика, связывающая напряжение на входе и ток на выходе. Эта ча-
стотная характеристика имеет вид
/ 1 \ 1
R + j\lirfL - —- ,
\ 2w/C/J
(2-43)
где измеряется в амперах на вольт. Функция, обратная к функции
(2.43) (обозначим ее Я(/)/_е), называется полным сопротивлением (импе-
дансом):
= • (2.44)
\ 2itjC J
Заметим, что механическим аналогом величины (2.44), согласно табл. 2.2,
служит
с + - — Г (2.45)
\ 2тг//
Таблица 2.2. Аналогия между механическими и электрическими системами
Электрическая система с напря- Механическая система с силой жением на входе на входе
Вход Напряжение е (t) Сила F (t)
Выход Заряд q (t) Смещение у (1 ) Ток i (t ) = dq/dt Скорость v (t) = dy/dt
Постоянные параметры Индуктивность L Масса m Сопротивление R Затухание с Емкость С Податливость \/к
Линейные физические системы
57
Таблица 2.3. Аналогия между различными физическими системами
Система Вход Выход Постоянные параметры
Электрическая Напряжение Ток Индуктив- ность Сопротив- ление Емкость
Механическая (смещение) Сила Скорость Масса Затухание Податли- вость
Механическая (вращение) Вращающий момент Угловая скорость Момент инерции Угловое затухание Угловая податливость
Акустическая Давление Скорость частиц Акустическая Акустическое Акустическая масса затухание емкость
Тепловая Температура Тепловой поток — Тепловое сопротивле- ние Теплоем- кость
Магнитная Магнито- движущая сила Магнитный поток — Магнитное сопротивле- ние —
Функция (2.45) часто называется механическим импедансом по аналогии с
обычным электрическим импедансом.
2.4.3. ДРУГИЕ СИСТЕМЫ
Аналитические методы, описанные в разд. 2.4.1, позволяют (по крайней
мере в принципе) найти частотную характеристику любой четко заданной
линейной системы с постоянными параметрами, если она физически осу-
ществима и устойчива. Более того, частотные характеристики разных фи-
зических систем часто имеют сходный вид, как мы только что видели в
разд. 2.4.2 на примере механической и электрической систем (см. табл. 2.2).
В табл. 2.3 дается сводка аналогичных характеристик некоторых распро-
страненных физических систем.
2.5. Практические соображения
В разд. 2.4 был продемонстрирован аналитический подход к определе-
нию частотных характеристик физических систем. Для простоты выкладок
и с целью выявления основных идей в качестве примеров были взяты про-
стые механические и электрические системы. Поэтому на основании этих
примеров не следует делать вывода, что определение частотных характери-
стик физических систем аналитическими методами всегда легко выпол-
нимо.
Рассмотрим, например, механическую систему в виде непрерывной
58
Глава 2
упругой конструкции, в которой различные параметры (масса, затухание и
жесткость) распределены, а не сосредоточены, как предполагалось в приме-
рах разд. 2.4.1. У такой механической системы может быть несколько
представляющих интерес входных и выходных точек. Кроме того, в отли-
чие от единственной резонансной частоты, свойственной системам из разд.
2.4.1, частотная характеристика для каждого сочетания входов и выходов
может иметь несколько максимумов, соответствующих нескольким резо-
нансным частотам. Для относительно простых непрерывных конструкций,
таких как балки, плиты и оболочки, частотные характеристики еще можно
найти с разумной точностью с помощью аналитических методов [2.1, 2.2].
Для оценки частотных характеристик и других свойств более сложных
структур, например жидкостей и других физических систем, можно исполь-
зовать машинные методы моделирования, такие как метод конечных эле-
ментов [2.3]. Если изучаемая физическая система представляет собой гото-
вую конструкцию, с которой можно экспериментировать, то частотную ха-
рактеристику можно оценить эмпирически. Простейший эмпирический под-
ход заключается в воздействии на систему гармоническим входным сигна-
лом и измерении амплитуды и частоты выходного сигнала для различных
частот. Согласно разд. 2.3, отношение амплитуд выходного и входного
сигналов на данной частоте равно амплитудной характеристике на этой ча-
стоте, а сдвиг фазы выходного сигнала по отношению к фазе входного сиг-
нала дает значение фазовой характеристики на этой же частоте. Однако та-
кие же результаты можно получить с существенно меньшими затратами
времени, если на вход системы подавать случайные или переходные про-
цессы естественного или искусственного происхождения и измерять реак-
цию системы. Оценивание частотных характеристик по случайным и пере-
ходным входным и выходным процессам подробно рассматривается в
гл. 6 и 7.
Задачи
2.1. Запишите в виде одного уравнения условия, определяющие линейность фи-
зических систем.
2.2. Какие из перечисленных ниже требований должны выполняться для того,
чтобы динамические свойства системы можно было задать весовой функцией h (7),
зависящей только от параметра 7? Система должна:
а) иметь постоянные параметры;
б) быть линейной;
в) быть физически осуществимой;
г) быть устойчивой.
2.3. Покажите, что если входной сигнал % (/) вызывает выходной сигналу (/) =
= х (t )1х (/ )1, то вход и выход связаны нелинейно.
2.4. Определите весовую функцию механической системы, изображенной на
рис. 2.2, «входом» которой служит сила.
2.5. Определите частотную характеристику физической системы с весовой функ-
цией h (7) = А ехр(— ат), где а > 0.
2.6. Механическая система, изображенная на рис. 2.2, имеет коэффициент жест-
Линейные физические системы
59
кости к = 180 Н/м, затухание с = 3,7 Нс/м и массу т = 1,8 кг. Найдите:
а) частоту собственных незатухающих колебаний fn;
б) коэффициент затухания
в) резонансную частоту /г;
г) максимальное значение амплитудной характеристики I//(/*)!.
2.7. Тело механической системы, изображенной на рис. 2.1, выведено из положе-
ния равновесия, а затем освобождено. Покажите, что в результирующих колебаниях
последовательные прохождения через положение равновесия происходят с пе-
риодом Т = (1/2)[/л^1 - Г2]- 1 при f2 1,0.
2.8. Покажите, что резонансная частота механической системы, изображенной
на рис. 2.2, равна fr = — 2f2 (f2 0,5), в согласии с уравнением (2.25).
2.9. Ширина полосы пропускания по уровню половинной энергии резонанс-
ной системы определяется как Вг = /2 - j\, где I H(J\) 12 = I Я(/2) 12 =
= (1/2)\Н(fr)2. Покажите, что в случае механической системы, изображенной на
рис. 2.2, Вr » 2tf при малых f, как утверждается в формуле (2.27).
2.10. Начертите электрическую схему, аналогичную механической системе с под-
вижным основанием, изображенной на рис. 2.4. Определите параметры аналогичной
электрической цепи, соответствующие механическим параметрам к, с и m.
Глава 3
ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Эта глава содержит обзор основных принципов теории вероятностей,
которые в последующих главах используются для введения понятий теории
случайных процессов. Материал главы охватывает случайные величины,
функции распределения, математические ожидания, замену переменных,
производящие функции моментов и характеристические функции одномер-
ных и многомерных случайных величин. Более детальное изложение тео-
рии вероятностей с инженерной точки зрения можно найти в книгах
[3.1—3.3].
3.1. Одномерные случайные величины
В основе теории вероятностей лежит понятие множества, понимаемого
как совокупность объектов (именуемых также точками или элементами),
причем относительно каждого конкретного объекта можно сказать, при-
надлежит он этой совокупности или нет. В частности, возможные исходы
некоторого эксперимента (или измерения) представляют собой множество
точек, которое называется выборочным пространством. Эти точки мож-
но сочетать самыми разными способами; такие сочетания называются со-
бытиями. При соответствующих условиях каждому событию можно при-
писать некоторую вероятность. Вероятность всегда заключена между ну-
лем и единицей, причем вероятность невозможного события равна нулю, а
вероятность достоверного события равна единице. Выборочное простран-
ство может быть конечным или бесконечным.
Рассмотрим точечное выборочное пространство, которое описывает все
возможные исходы некоторого эксперимента (или измерения). Случайная
величина х(к) — это функция множеств, определенная в точках к выбороч-
ного пространства; следовательно, случайная величина — это действитель-
ное число, заключенное между — оо и + оо, которое сопоставляется каждой
возможной выборочной точке. Иными словами, случайный исход некото-
рого эксперимента, отмеченный индексом к, представляется действитель-
ным числом, которое называется случайной величиной. Все события, кото-
рые могут произойти в эксперименте, образуют вполне аддитивный класс
множеств1), и любому из них можно приписать вероятностную меру.
3.1.1. ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
Пусть х (к) — некоторая случайная величина. Тогда для любого фикси-
рованного значения х случайное событие х (к) х определяется как мно-
жество всех возможных исходов к таких, что х(к) х. В терминах исход-
ной вероятностной меры, заданной на выборочном пространстве, функция
11 Более часто употребляется термин «а-алгебра множеств (событий)». — Прим,
ред.
Основы теории вероятностей
61
распределения Р (х) определяется как вероятность, приписанная множеству
точек А:, удовлетворяющих неравенствух (к ) х. Заметим, что множество
точек А:, удовлетворяющих неравенству х (к ) х, является подмножеством
совокупности точек, которые удовлетворяют неравенству х (к ) оо. Фор-
мально
Р(х) = Prob[x(fc) < х] . (3.1)
Очевидно, что
Р(а) < Р(Ь) при а < b , (3.2)
Р(-оо) = 0, Р(оо) = 1. (3.3)
Если область значений случайной величины непрерывна, что и предпо-
лагается в дальнейшем1^, то плотность вероятности (одномерная) р( х)
определяется дифференциальным соотношением
р(х) = lim
Дх->0
Prob[x < х(к) < х + Дх]
Дх
(3-4)
Следовательно,
/>(х)>0, (3.5)
( р(х) dx = 1 , (3.6)
~~ ОС
гх dP(x)
р(х) = f p(i-) di-, —— = р(х) . (3.7)
— оо @Х
Для того, чтобы можно было рассматривать дискретные случаи, подобные
примеру 3,1, следует допустить наличие в составе плотности вероятности
дельта-функций.
ПРИМЕР 3.1. ДИСКРЕТНОЕ РАСПРЕДЕЛЕНИЕ. Допустим, что эксперимент
заключается в однократном бросании монеты, причем предполагается, что
оба возможных исхода — герб и решетка — случаются с одинаковой веро-
ятностью (1/2). В этом примере случайная величина х (к) принимает толь-
ко два дискретных значения, х (герб) и х (решетка), в качестве которых
можно взять произвольные действительные числа, скажем х (герб) = а и
х (решетка) = b, где а и b — действительные числа, причем b > а. При та-
11 Как видно из примера 3.1, это предположение соблюдается не всегда.—
Прим, перев.
62
Глава 3
ком построении случайной величины х (к) ее функция распределения имеет
вид
/О х < а ;
Р(х) = И а < х < Ь;
11 х > b ,
а плотность вероятности задается формулой
р(х) = |S(x - а) + |S(x - b),
где д(х — а) и д(х — Ь) — дельта-функции (рис. 3.1).
3.1.2. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
Пусть случайная величина х (к ) принимает значения из области от — оо
до 4-ос. Среднее значение (иначе, математическое ожидание или ожидае-
мое значение) х (к) вычисляется с помощью соответствующего предельно-
го перехода в сумме произведений значений х (к ) на вероятности наступле-
ния этих событий:
£[%(£)] = ( xp(x)dx = nx, (3.8)
* — 00
а
Р(х)
1,0
0,5
а b х
б
Рис. 3.1. Дискретные плотность вероятности и функция распределения: а —
плотность вероятности; б — функция распределения.
Основы теории вероятностей
63
где Е [ ] — математическое ожидание выражения в квадратных скобках по
индексу к. Аналогично определяется математическое ожидание действи-
тельной однозначной непрерывной функции g (х) от случайной величины
Х(М
£[g(x(&))] = ( g(x)p(x)dx, (3.9)
J - оо
гдер (х) — плотность вероятности случайной величины х (к). В частности,
взяв g (х ) = х2, получим средний квадрат х (к):
f[x2(A:)] = ( х2р(х) dx = ф2 . (3.10)
J -00
Дисперсия х (к) определяется как средний квадрат разностих (к ) и ее сред-
него значения, т. е. в этом случае g(x) = (х — /лх)2 и
£[(%(£) - Ах)2] = f (х - Мх)2р(*) = ’/'х - Ах = ах- (3.11)
J — 00
По определению, стандартное отклонение случайной величины х (к ), обо-
значаемое ох, есть положительное значение квадратного корня из диспер-
сии. Стандартное отклонение измеряется в тех же единицах, что и среднее
значение.
ПРИМЕР 3.2. РАВНОМЕРНОЕ (ПРЯМОУГОЛЬНОЕ) РАСПРЕДЕЛЕНИЕ.
Допустим, что эксперимент состоит в случайном выборе точки из интерва-
ла [а, д], включая его конечные точки. В этом примере в качестве значения
случайной величины х(к) можно взять числовое значение выбранной точ-
ки. Соответствующая функция распределения имеет вид
Р(х) =
О,
х — а
b - а
1,
х < а ;
а < х < b;
х > Ь.
Поэтому плотность вероятности задается формулой
9 u \ л Ь ’
в остальных случаях.
В данном примере вычисление среднего значения и дисперсии по формулам
(3.9) и (3.11) дает
а 4- b 2 (Ь - а)2
Графики функций Р(х) ир(х) приводятся на рис. 3.2.
64
Глава 3
р(х)
1
(б-а)
Рис. 3.2. Равномерные плотность вероятности и функция распределения: а —
плотность вероятности; б — функция распределения.
3.1.3. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Пусть x(t) — случайная величина с плотностью вероятности р(х), и
пусть g(x) — однозначная действительная непрерывная функция от х. Рас-
смотрим сначала случай, когда обратная функция x(g) тоже является
действительной однозначной непрерывной функцией от g. Плотность веро-
ятности p(g), соответствующую случайной величине g(x(к)) = g(k), мож-
но определить по плотности вероятности р(х) случайной величины х(к) и
производной dg/dx в предположении, что производная существует и от-
лична от нуля, а именно:
Prob[g < g(x(ky) < g + Ag] Prob[x < x(k) < x + Ax]
kg kg
Prob[x < x(k) < x + Дх] Дх
Дх Д#
(3.12)
Поэтому в пределе при dg/dx Ф О
Jx .
Ts (злз)
Основы теории вероятностей
65
Используя эту формулу, следует в ее правой части вместо переменной х
подставить соответствующее значение g.
Рассмотрим теперь случай, когда обратная функция х (g) является
действительной п -значной функцией от g, где п — целое и все п значений
равновероятны. Тогда
Р g) = гЯп • (3-14)
ПРИМЕР 3.3. РАСПРЕДЕЛЕНИЕ ГАРМОНИЧЕСКОЙ ФУНКЦИИ. Гармо-
ническая функция с фиксированными амплитудой X и частотой /0 будет
случайной величиной, если ее начальный фазовый угол 0 = 0(к) — случай-
ная величина. В частности, пусть t фиксировано и равно /0, и пусть гармо-
ническая случайная величина имеет вид
х(к} = х(0) = %sin[27T/0Z0 + #(&)].
Предположим, что 0(к) имеет равномерную плотность вероятности р (0)
вида
^(0)= 0<«?<2ir;
\о, в остальных случаях.
Найдем плотность вероятности р (х) случайной величины х (к ).
В этом примере прямая функция х (0) однозначна, а обратная функция
0(х) двузначна. Из формулы (3.14), подставив вместо х величину 0, а вме-
сто g величину х, получим
2 р (0 ) dx
где
= Xcos(2w/0r0 + 0) = X/1 - sin2(2ir/0Z0 + 0) = ^Х2 - х2.
du
Поэтому
Соответствующая функция распределения имеет вид
/О, х < -X;
Р(х) = { Г p«)^ = -(^+arscin^, -Х<х<Х;
J-X 77 \ 2 л /
U, х > X.
Графики функций Р(х) ир(х) показаны на рис. 3.3.
3-953
66
Глава 3
Рис. 3.3. Плотность вероятности и функция распределения гармонической слу-
чайной величины: а — плотность вероятности; б — функция распределения.
3.1.4. ПРОИЗВОДЯЩИЕ ФУНКЦИИ МОМЕНТОВ И ХАРАКТЕРИСТИЧЕСКИЕ
ФУНКЦИИ
Производящая функция моментов т (s ) случайной величины х (к) опре-
деляется формулой (3.9), если положить g(x) = exp(sx):
m(s) = E[eIX] = f esxp(x)dx. (3.15)
- 00
Тогда
w(0) = f P(x) dx = 1 .
- 00
Считая, что все производные существуют, имеем
dm(s) с , ч
ш'(^) = —j— = 1хе™р(х)dx ’
as J
Основы теории вероятностей
67
z ч d2m(s) с
m"(s) = —71— = x2esxp(x) dx
ds J
и т. д. Поэтому при 5 = 0
Е[х] = fxp(x) dx =
(3.16)
Е[х2] = Jx2p(x) dx = >n"(0)
и т. д. Для любого целого п моменты равны
Е[хл] = Г хпр(х) dx = (3.17)
J - 00
где обозначают п-ю производную функции т(5).
Характеристическая функция С (f) случайной величины х (к ) определя-
ется формулой (3.9), если положить g(x) = ехр(/2тг/х):
С(/) = E[eJ2,r/x] = Г р{х}еМх dx. (3.18)
* ~' 00
Следовательно, С(/) по виду совпадает с обратным преобразованием
Фурье р (%), ар(х) есть преобразование Фурье C(f). В предположении,
что соответствующие интегралы существуют, имеем
р(х) = Г C(f)e-J2”fxdf' (3.19)
- 00
Если р (х) = д(х) — дельта-функция, то
С(/) = Г 8(x)ej2”fx dx = 1,
- 00
5(х)= Г e~J2*fxdf. (3.20)
* — 00
Заметим, что C(f) совпадает с т (s), если 5 = jlirf:
C(f)= (3.2!)
3.1.5. НЕРАВЕНСТВО ЧЕБЫШЕВА
Пусть х (к) — произвольная случайная величина с средним значением рх,
средним квадратом ф2 и дисперсией а2. Предположим, что она имеет плот-
ность р(х), которая может быть и неизвестной1^. Тогда
d2m(s) г
m"(s) = —75— = fx2esxp(x) dx ,
___________ ds J
Это предположение вводится лишь для упрощения записи и не является необ-
ходимым.— Прим. ред.
з*
68
Глава 3
7 ?
поскольку подынтегральное выражение неотрицательно их £ во всех
точках области интегрирования в правой части. Отсюда следует, что
Г Г '/'г
РгоЬ[|х(/:)|.> е] = I p(x)dx<—. (3.22а)
J\x\>e Е
Заменим теперь х (к) нах (к) - . Тогда 1Д2 обратится в а2 и неравенство
(3.22) примет вид
о2
Prob[|x(fc) - рх\ > е] < . (3.226)
В частности, при £ = сох имеем
РгоЬ[|х(/с) - рх\ > coj < > (3.22в)
что эквивалентно
Prob[|x(&) - рх\ < coj > 1 - . (3.22г)
Любое из неравенств (3.22) называется неравенством Чебышева.
ПРИМЕР 3.4. ОЦЕНКА ВЕРОЯТНОСТЕЙ УКЛОНЕНИЙ. Рассмотрим слу-
чайную величину х(к) с неизвестной плотностью вероятности. С помощью
неравенства Чебышева (3.226) при с = 2 и с = 3 можно сделать следую-
щие вероятностные утверждения:
РгоЬ[|х(/с) - рх\ > 2ах] < 0,250 ,
Prob[|x(/c) - jux| > 3qJ < 0,111 .
Эти относительно слабые утверждения полезно сравнить с результатами,
справедливыми в том случае, когда х (к ) имеет гауссово распределение. Из
табл. А.2 в гауссовом случае получим более сильное утверждение
РгоЬ[|х(/с) - jux| > 2ох] < 0,050.
РгоЬ[|х(/с) - jll^I > Зох] < 0,003.
Следовательно, можно утверждать, что отклонения гауссовой случайной
величины от среднего значения в 95 % случаев не превышают ±2а, в то же
время относительно случайной величины с произвольным распределением
можно утверждать, что доля таких значений составляет лишь 75%.
3.2. Двумерные случайные величины
Рассмотрим теперь две случайные величины х(к) и у (к), где к обозна-
чает точки в подходящем выборочном пространстве. Пусть Р(х) и
Основы теории вероятностей
69
Р(у) — две различные функции распределения, задающие соответственно
х(к) и у (к). По определению, совместная функция распределения Р(х, у) —
это вероятность, приписанная подмножеству точек к выборочного про-
странства, одновременно удовлетворяющих неравенствам х(к) х и
у (к) < У- Совокупность всех точек к удовлетворяет неравенствам
х(к) У (к) оо. В формальной записи имеем
Р(х, у) = РгоЬ[х(Л) < х and у(к) < . (3.23)
Очевидно, что
Р(-оо, у} = 0 = Р(х, - оо), Р(оо,оо) = 1. (3-24)
Как и ранее, в предположении непрерывности случайных величин со-
вместная плотность вероятности р(х, у) определяется как
РгоЬ[х < х(к) < х + Дх and у < у{к) < у + Д^]
р(х, у} = lim
Дх—>0
Ду-0 L
Дх Д^
(3-25)
Следовательно,
р(х, у) > 0, (3.26)
00 //р(х, у) dxdy = — 00 1, (3.27)
P(x,y) = f Iх - <X)J - д pU,ri) d^dtj , — 00 9 у ' дР(х,у) дх = Р(х, у).
(3.28)
Плотности вероятности случайных величин х (к) и у (к) выражаются через
совместную плотность по формулам
p(x)=f p(x,y)dy, (3.29) р(у) = [ p(x,y)dx. — 00
Если теперь р(х, у) ^р(х)р(у), (3.30)
то две случайные величины х (к) иу (/с) называются статистически незави-
симыми. Для статистически независимых случайных величин
Р(х, у) = Р(х)Р(у). (3.31)
70
Глава 3
3.2.1. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ И КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ
Математическое ожидание произвольной однозначной непрерывной
функции g (х, у) от двух случайных величин х (к) и у (к) определяется фор-
мулой
00
E[g(x, у)] = If g(x, у)р(х, у) dxdy. (3.32)
— 00
Например, если g (х, у) — (х (к) - ^х)(у (к) - д ), где дх и цу — средние
значения х (£) пу(к) соответственно, то получаем определение ковариации
Сху случайных величин х (к) и у (к), т. е.
\у = £[(*U) - Mx)(j(^) - mJ] = Е[х(Л)^(Л)] - £[x(£)]£[j(A:)]=
00
= ff (х - MJ(7 - Ру)р(х, у) dxdy . (3.33)
- 00
Заметим, что Схх = ах — дисперсия случайной величины х (к), определен-
ная в (3.11).
Ковариация случайных величин х (к) иу (к) связана с их стандартными
отклонениями простым неравенством
1^у| <аЛ . (3.34)
Следовательно, абсолютная величина ковариации случайных величин х (к)
nj(Zr) не превышает произведения их стандартных отклонений. Этот факт
будет доказан в разд. 5.1.3.
Из приведенного выше неравенства следует, что нормированная ве-
личина
Рху = — . (3.35)
называемая коэффициентом корреляции, заключена между — 1 и +1. Слу-
чайные величины х (к) иу(к), коэффициент корреляции которых равен ну-
лю, называются некоррелированными. Это понятие следует отличать от
приведенного выше понятия независимости случайных величин. Заметим,
что если х (к) ну (к) — независимые случайные величины, то из формул
(3.30) и (3.32) имеем
00
£[х(&)Д&)] = ff хур(х, у) dxdy=
— 00
= / xp(x)dxf ур(у) dy = £[x(&)]£[j(fc)].
J -00 J - 00
Основы теории вероятностей
71
Следовательно, Сху, а значит, и рху равны нулю; таким образом, независи-
мые случайные величины не коррелированы^. Обратное утверждение, во-
обще говоря, неверно, т. е. некоррелированные случайные величины не
обязательно независимы. Однако в практически важных случаях, где часто
встречаются две и более нормально распределенные (гауссовы) случайные
величины, взаимная некоррелированность означает и независимость. Дока-
зательство будет дано в разд. 3.3.4.
3.2.2. РАСПРЕДЕЛЕНИЕ СУММЫ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН
Пусть х (к) и у (к) — случайные величины, имеющие совместную плот-
ность вероятностир(х, у). Найдем плотность вероятности суммы случай-
ных величин
z(k) = х(к) +у(к).
При фиксированном х имеем у = z — х. Поэтому
р(х, у) = p(x,z - х).
При фиксированном z значения х пробегают интервал от -- оо до + оо. Поэ-
тому оо
p(z) = p(x,z-x)dx1 (3.37)
- 00
откуда видно, что для вычисления искомой плотности суммы нужно знать
исходную совместную плотность вероятности. Если х (к) пу(к) — незави-
симые случайные величины, имеющие плотности р j (х) ир2(У) соответст-
венно, тор(х, у) = Р[(х)р2(у) = Pi(x)p2(z - х) и
p(z)= f P!(x)p2(z - х) dx. (3.38)
- 00
Пример 3.5. Сумма двух независимых, равномерно распределен-
ных случайных величин. Пусть две независимые случайные величины
имеют плотности вида
Pi(*) = -, 0^х<а;
а
Р1(у) ~ ~ > 0 < у < а .
а
Точнее, если случайные величины с конечными дисперсиями независимы, то
они некоррелированы.— Прим. ред.
72
Глава 3
В остальных случаяхPj(г) = р2(У) = 0- Найдем плотность вероятности
р (z ) их суммы z = х + у.
Плотность вероятности/? 2 (V) — ~ х) Для 0 а, т. е. для
z — а х z. Следовательно, х не превышаете. Кроме того, р{(х) не
равно нулю для 0 х а. По формуле (3.38) находим, что
Графики функций р ),/?2(у) np(z) показаны на рис. 3.4. Заметим, что
сумма двух независимых, равномерно распределенных случайных величин
имеет треугольную плотность вероятности. Нетрудно убедиться, что плот-
ность суммы четырех независимых, равномерно распределенных случайных
величин близка к нормальной плотности, как и должно быть согласно
центральной предельной теореме, которая будет сформулирована в следу-
ющем разделе.
PiW
1/а
АДО
1/а
О
а у
Рис. 3.4. Плотность вероятности суммы двух независимых, равномерно рас-
пределенных случайных величин.
Основы теории вероятностей
73
3.2.3. ПРОИЗВОДЯЩИЕ ФУНКЦИИ МОМЕНТОВ И ХАРАКТЕРИСТИЧЕСКИЕ
ФУНКЦИИ
Совместная производящая функция моментов m(s, t) случайных вели-
чин х(к) и у (к) определяется формулой (3.32) при g(x, у) = exp(sx + ty):
00
m(s, t) = Е[е'л + ,>] = esx+'yp(x, у) dxdy . (3.39)
Очевидно, что
00
m(0,0) = p(x, y} dxdy = 1 .
— 00
Считая, что все частные производные существуют, имеем
dm(s, t)
ds J dm(s, z) dt ~ J d2m{s,t) ds2 J d2m(s, t) dt2 ~J d2m(s,t) ds dt J и т. д. Поэтому При 5 = 0 и t = £[*] = / j*p(x, = / fyp(x, £h2] = / fx2p(* = / fy2p(x 1 J xe fyp(x, y) dxdy , f f yesx+typ(x, y} dxdy, { jx2esx+typ(x, y} dxdy, Jy2esx+typ(x, y) dxdy, Г Jxyesx+typ(x, y) dxdy - 0 имеем dm(s, t) y)dxdy = ds (3.40) dm(s, t) y)dxdy= - > dt d2m(s, t) 3tl (3.41) d2m(s, t) :,y)dxdy=
74
Глава 3
г г d2m(s, t)
= f (хур(х, у) dxdy = — (3.42)
J J OS Ol
и т. д. И вообще при s, t = 0 смешанные моменты
7r dr+nm(s,t)
£[х>"] = If хгупр(х, у) dxdy = —- ............ (3.43)
OS Ol
— оо
Совместная характеристическая функция C(f, g) случайных величин
x(k) и у (к) определяется по формуле (3.32) при g(x, у) = ехр[/2тг(/х +
+ ЗУ)]'-
00
С(/, g) = E[ej2,,(/x+gy)] = JJ р(х, y)eJ2<fx+gy)dxdy. (3.44)
— 00
Поэтому C(f, g) является двойным обратным преобразованием Фурье
плотности, ар(х, у) есть двойное преобразование Фурье функции C(f, g).
Если соответствующие интегралы существуют, то
00
р(х,у)= ff C(f,g)e-J2^x+gy>dfdg. (3.45)
— 00
Заметим, что C(f, d) совпадает с m(s, t) при 5 = у2тг/ и t = j2ng'.
C(f, g) = mfjlirf, jlng).
(3-46)
3.3. Гауссово (нормальное) распределение
Будем говорить, что случайная величина х(к) подчинена гауссову (или
нормальному) распределению, если ее плотность имеет вид
р(х) = (Ьу/2чг) 'ехр
(х - а)2
2Ь2
(3-47)
где а — произвольная постоянная, а b — произвольная положительная по-
стоянная. Можно убедиться, что а и b представляют собой соответственно
среднее значение и стандартное отклонение случайной величины х(к).
Действительно,
Е[х(&)] = f хр(х) dx = а = [лх у
- 00
е[(х(&) - л)2] = f (х - а)2р(х) dx = b2 = о2 .
- 00
Таблица 3.1. Плотности вероятности, часто используемые в исследовательской
работе
Тип Функция распределения
Дискретная />(г) = А$(х — а) + Вд(х — Ь) + • • + N д(х — n)f а Ь п гае А + В + • • + N = 1
Равномерная (прямоуголь- ная) f ч f в остальных» р(х) = (Ь — а)-1, а <> X <. Ь\ а случаях р = 0
Г армоническая р(х) = ( „у/X2 - х2 ) Л |х| < X; в остальных ' ' случаях р = 0 -X X
Гауссова (нормальная) р(ж) = (<txV27t ) е-Ся-д»)1/2*»1
Рэлея р<х) = ® e-x'ltc2 х > 0; в °стальных г сг случаях р = 0 0
Максвелла р(г) = ~.Ле-хЧгс\ х £ 0; в остальных г п случаях р = 0 0
Усеченная Пусть исходная Pj (х) определена на (-оо, оо) Р' Усеченная в остальных р(х) = Ср/х), а £ х <£ Ь; случаях р = 0 a b j\p^dx=cjbapAx)dx = l
Срезка Пусть исходная рх(х) определена на (—оо, оо) . Срезка р(х) = pi(x), а < х < b; = А д(х — а), х = а; = В д(х — />), х = Ь \ = 0, х < а или х > Ь, а Лоо гь J = J ^Х + 1
76
Глава 3
Таким образом, нормальную плотность вероятности можно переписать в
виде
р(х) = (oxJ2tt) Техр
(3.48а)
По определению, нормальная функция распределения есть
Р(х) = (ох]/2тт) 1У ехр
G-mJ2
2а2
(3.486)
Без потери общности предположим теперь, что все средние значения
равны нулю. Для одной случайной величины х(к) нормальная плотность
примет вид
р(х) = (oxJ2it} Техр
х2 \
2 о2 у ’
(3.49а)
а соответствующая нормальная функция распределения равна
1 м е \
Р(х) = (а^Г1 [ exp \d£. (3.496)
* — ОС I 2 Y I
Более подробное изложение свойств нормального распределения и истори-
ческие сведения можно найти в книге [3.4]. Применения нормального рас-
пределения в задачах анализа статистических данных кратко рассмотрены в
гл. 4. Графики стандартных нормальных плотности вероятности и функ-
ции распределения приведены на рис. 4.1. Сводка других часто встречаю-
щихся в исследовательской работе плотностей вероятности содержится в
табл. 3.1.
3.3.1. ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА
Важность нормального распределения в практических задачах частично
объясняется центральной предельной теоремой [3.2, 3.5], которая утверж-
дает, что это распределение вполне естественно появляется в результате
суммарного действия большого числа независимых случайных величин.
Точнее, пусть хДАг), х2(к), ..., xN(k) есть N взаимно независимых случай-
ных величин с произвольными и, возможно, различными функциями рас-
пределения. Пусть gz и — среднее значение и дисперсия случайной вели-
чины Xj(k) (J = 1, 2, ..., N). Рассмотрим сумму случайных величин
х(к) = 22 а1х,(к) > (3.50)
/ = 1
Основы теории вероятностей
77
где ai — произвольные фиксированные постоянные. Тогда среднее значение
и дисперсия случайной величины а* имеют вид
Е «,*,(*)
/ = 1
рх = Е [х(&)] = Е
= Е а,£[%,(£)] = £ a,fl, ,
/=1 Z = 1
(3-51)
°х = Я [(*(*)
Последнее равенство справедливо в силу взаимной независимости х^к) и
Xj(k) при i Ф j. Центральная предельная теорема утверждает, что при до-
вольно общих условиях распределение суммарной случайной величины х(к)
при N — оо стремится к нормальному распределению с приведенными вы-
ше средним рх и дисперсией
3.3.2. СОВМЕСТНОЕ ГАУССОВО (НОРМАЛЬНОЕ) РАСПРЕДЕЛЕНИЕ
Совместная гауссова (нормальная) плотность вероятности случайных
величин х(к) и у (к) с нулевыми средними значениями и одинаковыми дис-
персиями aj = 02 = о2 определяется формулой
1 I - [х2 - 2рху -1- у2] \ )’ (3'52)
где £[ху] Е [ху] Р = = 2 V3’53) а1а2 0
Полезно убедиться с помощью формул (3.29) и (3.52), что плотность веро-
ятности каждой случайной величины в отдельности имеет вид (3.49а).
Действительно,
/00 1
р(х, у) dy = ,
-00 2 770 yl — р
х2 - 2рху + у2] \
2а2(1 - р2)
Далее имеем
х2 - 2рху + у2 = (1 - р2)х2 +G - рх)\
так что экспоненту под интегралом можно записать в виде
/ - [х2 - 2рху + у2]
ехр “7(7-7)
/ х2 \
= ехР “ ехР
\ 2о /
-(у - рх)2
2а2(1 - р2)
78
Глава 3
Поэтому
ехр(—х2/2а2) ,«
Р(х) = „ 2/-. 2 J еХР
2тто2у1 — р2
~(у ~ Р*)2
2о2(1 - р2)
dy-
Пусть теперь
у- рх dy
и = —. - , аи = —г—.......- .
0^2(1 - р2) <^2(1 - р2)
Тогда
ехр(-х2/2а2) гоо
р(х) =---------j=---( exp(-u2)du =
<нту2 J-vo
ехр(-х2/2а2)
Оу/2тТ
что совпадает с формулой (3.49).
3.3.3. ПРОИЗВОДЯЩИЕ ФУНКЦИИ МОМЕНТОВ И ХАРАКТЕРИСТИЧЕСКИЕ
ФУНКЦИИ
Согласно формулам (3.15) и (3.49), производящая функция моментов га-
уссовой случайной величины с нулевым средним есть
m(s) = exp(a2s2/2). (3.54)
Из формулы (3.17) находим
Е[х2”-1] = О,
п = 1,2,3,... . (3.55)
Е[х2”] = 1 • 3 • 5 ••• (2л - 1)о2",
Итак, все моменты нечетного порядка равны нулю, а моменты четного по-
рядка имеют вид
Е[х2] = о2, Е[х4] = За4,
(3.56)
£[х6] = 15а6, £[х8] = 105а8
И т. д.
По формуле (3.21) характеристическая функция гауссовой случайной ве-
личины с нулевым средним значением есть
С(/) = ехр(-2тт2а2/2) . (3.57)
По формуле (3.39) совместная производящая функция двумерной гауссо-
вой случайной величины с нулевым средним и плотностью вида (3.52) рав-
на
m(s, /) = exp
о
у (s2 + 2pst + /2)
(3.58)
Основы теории вероятности
79
Непосредственно по формуле (3.43) находим
Е[хтуп] = 0, если г + п нечетно,
£[х2] = Е[у2] = а2, £[х.у] = ра2, (3.59)
£[-Х3>'] = £[•*/] = Зра4,
£[х2у2] = а4(1 + 2р2)
и т. д.
Согласно формуле (3.46), характеристическая функция двумерной гауссо-
вой случайной величины с нулевым средним и плотностью вида (3.52) име-
ет вид
C(f, g) = ехр{-2w2a2[/2 + 2pfg + g2]} . (3.60)
3.3.4. TV-МЕРНОЕ ГАУССОВО (НОРМАЛЬНОЕ) РАСПРЕДЕЛЕНИЕ
Рассмотрим N случайных величин х{(к)9 х2(к)9 ..., xN(k), возможно,
коррелированных. Введем следующие обозначения для средних значений,
дисперсий и ковариаций:
р, = £[х,(Л)‘] ,
о2 = £ [(х, (Ar) - |и,)2] , (3.61)
С,7 = £[(х((Л)-р,)(ху(£)-р7)]> С„ = о2 .
Будем говорить, что их совместное распределение является TV-мерным га-
уссовым (нормальным), если соответствующая TV-мерная плотность веро-
ятности имеет вид
ехр[(-1/2|С|)Е^_1|С,.Дх/-р;)(х7.-ру)]
...’ (3'‘
где С — ковариационная матрица, элементы которой Су определены ниже,
ICI — определитель С, a IСуI — алгебраическое дополнение Су. В явном
виде, если
^12 ’ ’ * Cin
с- с“ , (3.63)
Cn2 ’ * * CNN
80
Глава 3
то алгебраическое дополнение I Су I произвольного элемента Су есть умно-
женный на (- 1)/+у определитель матрицы порядка N - 1, которая получа-
ется из матрицы С путем вычеркивания в ней z-й строки и у-го столбца.
Замечательная особенность /V-мерн о го нормального распределения за-
ключается в том, что все его свойства определяются исключительно сред-
ними значениями и ковариациями Су. При N = 1 эта функция принима-
ет вид
р(хг) = (а^) ^хр
(*1 ~ Mi)2
2 о2
(3.64)
т. е. представляет собой нормальную плотность, заданную выше форму-
лой (3.48).
При N = 2 получаем совместную двумерную нормальную плотность
вероятности
(3.65)
где р12 = “ коэффициент корреляции случайных величин х{(к)
и х2(к). Заметим, что при некоррелированных хх(к) и х2(к), т. е. при
012 = 0,
р(*1,х2) = р(х1)р(х2),
(3.66)
откуда следует, что хх(к) и х2(к) одновременно независимы. Этот резуль-
тат не имеет места для произвольных распределений.
Аналогичные формулы можно выписать для распределений высших раз-
мерностей (А = 3, 4, 5, ...). Для произвольного N легко убедиться, что ес-
ли все различные пары нормально распределенных случайных величин
взаимно не коррелированы (т. е. ру = 0, если только i Ф j), то эти случай-
ные величины взаимно независимы в статистическом смысле, т. е.
p(xl,x2,...,xN) = р(х^р(х2) p(xN) . (3.67)
Важность A-мерного нормального распределения в практических задачах,
как и одномерного нормального распределения, частично объясняется мно-
гомерной центральной предельной теоремой (см. работы [3.2, 3.5]). Эта
Основы теории вероятности
81
теорема утверждает, что при довольно общих условиях векторная сумма
большого числа взаимно независимых N-мерных случайных величин приб-
лиженно распределена согласно N-мерному нормальному распределению.
Произвольная N-мерная гауссова плотность, определенная формулой
(3.62), удовлетворяет равенству
00
f p(xd х2> • > xn) dxi dx2 ” * dxN = 1 • (3.68)
— 00
Кроме того, математическое ожидание любой однозначной непрерывной
действительной функции g(x{, х2, ..., хп) от N случайных величин имеет
вид
00
£[g(x1)x2,...,xy)] =//•• fg(x1,x2,...,xN)p(xl,x2,...,xN)x
— 00
Xdxxdx2 ••• dxN . (3.69)
Если g(Xj, х2» •••» XN> = ехР(51^1 + S2X2 + ••• + SNXN>' T0 C Уче’
том (3.62) получаем производящую функцию моментов N-го порядка:
m(sx, 52,..., 5У) = Е[ехр(51х1 + s2x2 + • • • Н-^Хд^)] . (3.70)
Рассмотрим случай четырех гауссовых случайных величин Xj, х2 , х3 и х4
с нулевыми средними значениями и одинаковыми дисперсиями а2 = а2. Их
ковариации Су имеют вид Су = Ру о1, где
С\2 ~ £[%1Х2] 5 ^23 = £[%2Хз] >
С13 = ^[хЛ], С24 = [*2*4] > (3-71)
С14 = Е[х1х4] э С34 = Е[х3х4].
Пусть р(х{, х2, х3, х4) задана формулой (3.62). Тогда производящая функ-
ция моментов четвертого порядка есть
n?(515 52, 53, 54) = Е[ехр(51х1 + S2x2 + S3X3 + ^4^4)] =
= exp
— (>S|2 + 4 + sj + si + lp22s2s2 + 2px2s2s3 +
+ 2p14i^4 + 1p22s2s2 + 2p24s2s4 + 2p34i3i4)
82
Глава 3
Непосредственно можно убедиться, что момент четвертого порядка опре-
деляется смешанной частной производной четвертого порядка:
a4w(i1,i2,53,54)
Е ХуХ^х^Хл ---------------------
1 1 2 3 4J dSlds2ds3ds4
S i — 5 2 — ^3 — ^4 — О
Простые, хотя и утомительные вычисления частных производных при =
= s2 = 53 = s4 = 0 дают
£^[х1Х2Х3Х4] ~ ^12^34 + ^13^24 + ^14^23 • (3.72)
Отсюда следует, что момент четвертого порядка равен сумме 3-1 = 3 раз-
личных произведений пар моментов второго порядка (ковариаций).
Аналогичные вычисления момента шестого порядка гауссовых случай-
ных величин с нулевыми средними показывают, что момент шестого по-
рядка есть сумма 5-3-1 = 15 произведений троек моментов второго по-
рядка:
Е [х1Х2Х3Х4Х5Х6] = ^12 [^34^56 + ^*35Об + ОбОб] +
+ Оз1О4Об + ОбОб + ОбОб] +
+ С14[С23С56 + с25с36 + С26С35] +
+ О5[ОзОб + ОдОб + ОбОд] +
+ С16[с2зс45 + С24С35 + С25С34]. (3.73)
В общем случае, если п — четное целое число, то E[XjX2 ... xN] состоит из
суммы (N — 1)-(7V — 3)... 3-1 различных произведений, включающих все-
возможные Су,
С другой стороны, все моменты нечетного порядка гауссовых случай-
ных величин с нулевыми средними равны нулю, т. е.
Е\х3х2 = 0 , (3.74)
если N — нечетно. Все эти соотношения верны не только для собственно
случайных величин х«, но и для любых их линейных преобразований, на-
пример преобразований Фурье.
Если средние значения не равны нулю, то аналогичные выражения име-
ют более сложный вид. Для примера рассмотрим четыре гауссовы случай-
ные величины Xj, х2, х3, х4 с одинаковыми ненулевыми средними /х =# 0 и
одинаковыми дисперсиями а2. Тогда вместо формул (3.71) ковариация Су
при i Ф j задается формулой
С'У = Е [(•*' - ^XJ ~ ^)] • (3.75)
Основы теории вероятности
83
Если i = j, то
Q = £[(х, - м)2]-= о2 =’Z'2 - м2- (3.76)
Формула (3.72) верна для четырех случайных величин (Xj — /г), (х2 — ц),
(х3 - /г), (х4 — /г). Поэтому из формул (3.72) и (3.74) имеем
Е [х^х2х^х4] С?|2С^4 ^13^'24 ^14^'23 М
+ M2[^i2 + Q3 + С14 + Q3 + Q4 + Q4] • (3.77)
В частности,
Е [x2xj] = ф4 + 2СЪ + 4/?С12 . (3.78)
Ковариация
С12 = £[(%! - д)(х2 - м)] = £[*гХ2] - м2 =
= *12 - м2 , (3.79)
где
Я12 = Efx^J . (3.80)
Поэтому формулу (3.78) можно записать в виде
е[х2х22] =,// +2[Я22-М4] , (3.81)
а формула (3.77) принимает вид
Е[х1х2х3х4] = *12А34 + *13*24 + *14*23 _ 2М4. (3.82)
Аналогичным образом вычисляются и моменты шестого порядка при
1л Ф 0.
Задачи
3.1. Случайная величина х имеет функцию распределения вида
Р(х) =
(°’
' хл,
1,
х < 0;
0 < х < 1;
х > 1.
а) Найдите плотность вероятности р(х).
б) Вычислите среднее значение и дисперсию случайной величины х.
84
Глава 3
3.2. Случайная величина х имеет плотность вероятности вида
4х3, 0 < X < 1;
О, в остальных случаях.
а) Найдите функцию распределения Р(х).
б) Вычислите среднее значение и дисперсию случайной величины х.
3.3. Случайная величина х распределена равномерно с плотностью
/ х / 1, 0 < X < 1;
р(х) = 1 л
\0,в остальных случаях.
Найдите плотность вероятности случайной величины у = 2х + 1.
3.4. Случайная величина х имеет нормальное распределение с нулевым средним
значением и единичной дисперсией. Найдите плотность вероятности случайной вели-
чины у = х2.
3.5. Компьютер генерирует случайные цифры (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) с равны-
ми вероятностями. Пусть Т — случайная величина, равная сумме N цифр. Найдите
среднее значение и дисперсию Т.
3.6. Предприятие производит оси и подшипники, которые затем поступают на
сборку, где подшипник устанавливается на ось. При изготовлении осей их внешний
диаметр s имеет нормальное распределение с средним значением д = 25 мм и стан-
дартным отклонением as = 0,007 мм. Внутренний диаметр b производимых под-
шипников тоже имеет нормальное распределение средним значением = 25,01 мм
и стандартным отклонением оь = 0,009 мм. Если сборщик наугад выбирает ось и
подшипник, то с какой вероятностью взятая ось не войдет в подшипник (считается,
что оси и подшипники имеют идеальную круговую форму и сборка возможна, если
s < Ь).
3.7. Пусть в условиях задачи 3.6 требуется, чтобы при сборке зазор между осью
и подшипником составлял не более 0,05 мм. Стандартное отклонение диаметра оси
s изменить нельзя, однако можно менять стандартное отклонение внутреннего диа-
метра b подшипников. Каким должно быть стандартное отклонение диаметра b для
того, чтобы сборка была успешной в 99% случаев.
3.8. Случайная величина х подчиняется пуассоновскому распределению, т. е.
р(х) = g*exp(—д)/х!. Найдите среднее значение и дисперсию х, используя произво-
дящую функцию моментов.
3.9. Предприятие изготавливает шайбы толщиной d, имеющей среднее значение
fjLd = 5 мм и стандартное отклонение Oj = 0,005. Если выбрать наугад N = 25 шайб
и сложить их стопкой, то какова вероятность того, что высота образовавшейся
стопки заключена между 120 и 130 мм в предположении, что
а) толщина d имеет нормальное распределение;
б) толщина d имеет неизвестную функцию распределения.
3.10. Независимые случайные величины х и у имеют плотности вида
Н*) = 2^е <Х1)2/4’ = 2^е~{У+1)2/4 '
Найдите плотности вероятности случайных величин
а) и = х + у\
б) v = х — у.
Глава 4
ОСНОВНЫЕ ПОНЯТИЯ
МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Наряду с основными понятиями теории вероятностей, введенными в
гл. 3, при измерении и анализе случайных данных для определения их до-
стоверности и оценки возможных ошибок используются статистические ме-
тоды. В этой главе даются обзор и примеры использования основных ста-
тистических понятий, широко применяемых во многих задачах анализа дан-
ных. Цель главы — дать читателю минимум основных сведений по терми-
нологии и некоторым методам инженерной статистики, существенных для
понимания последующих глав. Более детальное изложение прикладной ста-
тистики и ее инженерных применений можно найти в книгах [4.1—4.4].
4.1. Выборочные значения и оценивание параметров
Рассмотрим случайную величинух в смысле определения разд. 3.1; ар-
гумент к, указывающий на принадлежность к исходному выборочному про-
странству, опущен для упрощения обозначений. Рассмотрим далее две ос-
новные характеристики случайной величины х, описывающие ее центр рас-
сеяния и величину рассеяния, а именно среднее значение и дисперсию. Сог-
ласно формулам (3.8) и (3.11), среднее значение и дисперсия равны
/00
xp(x)dx, (4.1)
- 00
0Л2 = £[(х - Мл)2] = ( (* “ Мл)2р(Х)
J — оо
(4-2)
где р (г ) — плотность вероятности случайной величины х. На практике,
разумеется, эти две характеристики величины х нельзя определить точно,
поскольку обычно плотность вероятности полностью не известна. Поэтому
приходится довольствоваться оценками среднего значения и дисперсии, по-
лученными по конечному числу наблюдений.
Один из возможных методов (есть и другие) оценивания среднего значе-
ния и дисперсии случайной величины х noN независимым наблюдениям та-
ков:
1 N
х = = — Е , (4.3)
1 N
s2h = ^ = -^(x-xf .
(4-4)
Здесь х и 5^ — выборочное среднее и выборочная дисперсия соответствен-
но. Знак над и указывают на то, что эти выборочные значения ис-
86
Глава 4
пользуются в качестве оценок среднего значения и дисперсии х. Подстроч-
ный индекс в означает, что это смещенная оценка дисперсии (определе-
ние будет дано ниже). Число наблюдений, по которым вычисляются оцен-
ки (выборочные значения), называется размером выборки.
Оценки, введенные формулами (4.3) и (4.4), не являются единственно
возможными оценками среднего значения и дисперсии случайной величины
х. Например, впрлне разумные оценки среднего и дисперсии можно полу-
чить, если деление наТУ сумм в формулах (4.3) и (4.4) заменить делением на
N—1. Об оценках никогда нельзя определенно сказать, что они верны или
неверны, поскольку они задаются в некотором смысле произвольно. Тем
не менее некоторые оценки можно считать “хорошими” или “лучшими” по
сравнению с другими.
Для установления качества или “правильности” оценки используются
три основных свойства. Во-первых, желательно, чтобы математическое
ожидание оценки равнялось оцениваемому параметру, т. е.
£[ф] = Ф, (4.5)
где $ — оценка параметра ф. Если это свойство имеет место, то оценка на-
зывается несмещенной. Во-вторых, желательно, чтобы среднеквадратичная
ошибка данной оценки была наименьшей среди всех возможных оценок,
т. е.
£[(ф1-ф)2] <£[(ф,-ф)2] , (4.6)
где фх — исследуемая оценка, a ф — любая другая оценка. Если это свой-
ство имеет место, то оценка называется эффективной. В-третьих, жела-
тельно, чтобы оценка сходилась к оцениваемому параметру с вероятнос-
тью, стремящейся к единице по мере увеличения размера выборки, т. е.
для любого е > О
lim РгоЬ[|ф - ф| > е] = 0 . (4.7а)
7V-> оо
Если это так, то оценка называется состоятельной. Из неравенства Чебы-
шёва (3.22) следует, что достаточным (но не необходимым) для выполне-
ния (4.7а) является условие
lim £ [(ф — ф)2] = 0. (4.76)
» 00
Заметим, что условия, задаваемые соотношениями (4.7), представляют со-
бой определения сходимости по вероятности (а) и среднеквадратичной схо-
димости (б), которые будут даны в разд. 5.3.4.
В качестве примера рассмотрим оценку среднего значения по формуле
(4.3). Математическое ожидание выборочного среднего х равно
£[J] = Е
1
-ne
N
Ex,.
= ^(^х) = Мх-
(4-8)
1 Г
Основные понятия математической статистики
87
Следовательно, согласно определению (4.5), оценка ftx = х несмещенная.
Среднеквадратичная ошибка выборочного среднего х равна
1
= 1ёЕ
2
Поскольку наблюдения х, независимы, то в силу результатов разд. 3.2.1
математические ожидания членов, содержащих смешанные произведения,
равны нулю. Поэтому
Следовательно, согласно определению (4.76), оценка цх = х состоятельна.
Можно также показать, что эта оценка эффективна.
Рассмотрим теперь оценку дисперсии, задаваемую формулой (4.4). Ма-
тематическое ожидание оценки дисперсии s2h равно
1
£ (*. ~ х)2
/ = 1
1
N
я И
Однако
Е (х, - х)2 = У. (х, - цх + цх- х)2 =
= 1 1 = 1
= Е (х, - МЛ)2 - 2(х - цх) У (х, - Мх) + Е (х - Мх) =
1=1 1=1 1=1
= Е (х, - Мх)2 - 2(х - Mx)^x - Мх) + N(x - Мх)2=
1=1
= Е (х, - Мх)2 ~ N(x - цх)2. (4.10)
/ = 1
Поскольку E[(xi - gx)2] = ахиЕ[(х - /лх)2] = —, то
N
- Дх2) = ..^х2 • (4-11)
Следовательно, оценка а2 = смещена. Хотя выборочная дисперсия 52 и
является смещенной оценкой, эта оценка состоятельна и эффективна.
88
Глава 4
Из формулы (4.11) понятно, что для получения несмещенной оценки о х
следует взять несколько видоизмененную выборочную дисперсию:
1 N
s2 = °х = Ё (х, - х)2 (4.12)
Величина, определенная формулой (4.12), представляет собой несмещенную
оценку о*. По этой причине выборочная дисперсия из формулы (4.12) часто
считается “лучшей” оценкой по сравнению с выборочной дисперсией из
формулы (4.4). В дальнейшем в качестве оценки дисперсии случайной вели-
чины будет использоваться выборочная дисперсия вида (4.12).
4.2 . Важнейшие функции распределения
Несколько примеров функций распределения было дано в гл. 3. Важней-
шей из них с точки зрения прикладной статистики является гауссова (нор-
мальная) функция распределения. Широкое применение в статистике нахо-
дят и другие функции распределения, тесно связанные с нормально рас-
пределенными случайными величинами. Это х2-распределение, / -распреде-
ление и F-распределение. Сейчас мы определим и обсудим наряду с нор-
мальным каждое из этих трех распределений. Их применение в статистике
будет описано в последующих разделах.
4.2.1. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Плотность вероятности и функция распределения нормальной случай-
ной величины х определены в разд. 3.3 (формула (3.48)). Удобнее пользо-
ваться стандартной нормальной случайной величиной z вида
Если это выражение подставить в формулу (3.48), то получим стандартные
плотность и функцию распределения с нулевым средним значением и еди-
ничной дисперсией (^ = 0, aj = 1):
p(z) = (У2тг )-1e”z2/2, (4.14а)
P(z) = (?27)-1Г e~e/2d£. (4.146)
~ 00
Для дальнейшего удобно обозначить через z а значение z, соответствующее
данной вероятности Р (z) = 1 - а, т. е.
( ° ?(*) dz = Prob[z < za] = 1 - а (4.15а)
* — 00
p(z) dz = Prob[z > za] = a (4.156)
l-P(ze) = J
Основные понятия математической статистики
89
б
Рис. 4.1. Стандартные нормальные плотность вероятности и функция распреде-
ления: а — плотность вероятности; б — функция распределения.
Значение za, удовлетворяющее уравнению (4.15), называется 100а-
процентной точкой нормального распределения. Стандартная нормальная
плотность вероятности р (z) унимодальна, монотонно изменяется по обе
стороны моды1) и симметрична с точками перегиба ± 1 (рис. 4.1, а). Соот-
ветствующая функция распределенияР (z ) приведена на рис. 4.1, б. Неболь-
шая сводка значений стандартной нормальной плотности дана в табл. А.1,
а табл. А.2 содержит процентные точки стандартного нормального рас-
пределения.
0 Модой называется точка максимума плотности вероятности. Унимодальная
плотность имеет одну моду. — Прим, перев.
90
Глава 4
4.2.2. ХИ-КВАДРАТ РАСПРЕДЕЛЕНИЕ
Пусть zpz2 zn есть п независимых случайных величин, каждая из
которых имеет нормальное распределение с нулевым средним и единичной
дисперсией. Определим новую случайную величину вида
X2 = 2124- + z32 + • • • + z2. (4.16)
Случайная величина называется хи-квадрат случайной величиной с п сте-
пенями свободы. Число степеней свободы п определяет число независи-
мых, или “свободных”, квадратов, входящих в сумму. Плотность вероят-
ности х% имеет вид [4.2]
Их2) = [2'-/2Г(«/2)]’1(х2)<<"/2,-1)е-х2/2> х2 0, (4.17)
где Г(д /2) — гамма-функция. Соответствующая функция распределения х2,
равная интегралу от плотности (4.7) по интервалу от — оо до данного зна-
чения х^, называется хи-квадрат распределением с п степенями свободы.
100а-процентные точки х2-распределения обозначим через хп.а2, т. е.
/ р(х2) ^х2 = Рг°ь[х2 > х2.«] = « • (4.18)
Среднее значение и дисперсия х% равны
^[х2] = Мх2 = п , (4.19)
^[(х2 - Мх2)2] = ах2 = 2л • (4-20)
Небольшая таблица процентных точек хи-квадрат распределения приводит-
ся в табл. А.З.
Следует отметить несколько особенностей хи-квадрат распределения.
Во-первых, хи-квадрат распределение фактически является частным случа-
ем более общего гамма-распределения. Во-вторых, важную роль играет
распределение случайной величины, равной квадратному корню из случай-
ной величины, имеющей хи-квадрат распределение с двумя степенями сво-
боды (х2), которое называется распределением Рэлея. Распределение Рэлея
широко применяется при решении задач, связанных с попаданием в двумер-
ную мишень; кроме того, оно служит предельным распределением экстре-
мальных значений узкополосного гауссова случайного сигнала при стремле-
нии ширины полосы сигнала к нулю. В-третьих, с ним связано еще одно
важное распределение, отвечающее случайной величине, равной квадратно-
му корню из хи-квадрат случайной величины с тремя степенями свободы
(Хз), называемое распределением Максвелла. Распределение Максвелла при-
меняется при решении задач, связанных с попаданием в трехмерные мише-
ни. В-четвертых, хи-квадрат распределение приближается к нормальному
по мере увеличения числа степеней свободы. Именно, для п > 30 величина
Основные понятия математической статистики
91
приближенно нормальна со средним /х = 72д — 1 и дисперсией
а2 = 1.
4.2.3. t-РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА
Пусть у и z — независимые случайные величины, при этом у имеет
Х2-распределение, a z — нормальное распределение с нулевым средним и
единичной дисперсией. Определим новую случайную величину
v67«
(4-21)
Случайная величина tn имеет t -распределение Стьюдента с п степенями сво-
боды. Известно [4.2], что плотность вероятности случайной величины tn
имеет вид
(4-22)
Соответствующая функция распределения вычисляется интегрированием
плотности (4.22) от — оо до данного значения tn и называется t -распределе-
нием сп степенями свободы. 100а-процентная точка t-распределения обо-
значается tn .а, причем
( р(/) Ж = Prob[/„ > = а .
а
(4-23)
Среднее значение и дисперсия tn равны
= М, = 0,
£[('п ~ М,)2] = а,2 = —
* J и
п > 1;
п > 2.
(4-24)
(4-25)
Небольшой набор процентных точек t -распределения представлен в табл.
А.4. Отметим, что t -распределение стремится к стандартному нормально-
му распределению с увеличением числа степеней свободы п.
4.2.4. ^-РАСПРЕДЕЛЕНИЕ
Пусть у1 и у 2 — независимые случайные величины такие, что у j имеет
Х2-распределение сп{ степенями свободы, aj2 есть х2-Распределение сп2
степенями свободы. Определим новую случайную величину
У1/«1 _ У1Пг
Уг/пг Угп1
(4-26)
92
Глава 4
Случайная величина Fnun2 — это ^-распределенная случайная величина с пх
и п2 степенями свободы. Известно, что плотность вероятности Fn „ равна
[4.2]
Г[(П1 +
М Г(Я1/2)Г(и2/2)[1 +(W1F/«2)]("'+"2,/2
Соответствующая функция распределения Fni,n вычисляется интегрирова-
нием плотности (4.27) от — оо до данного значения F„lt„ и называется
F-распределением с п{ и п2 степенями свободы. 100а-процентная точка
F-распределения обозначается Fnyn^a9 причем
/°° p(F)^=Prob[F„i,„2>F„i,„2.a] = а .
С4-28)
Среднее и дисперсия Рп^п равны соответственно
п2 >2; (4.29)
2п2(п1 + п2- 2)
«1(«2 - 2)2(п2 - 4)
п2 > 4 . (4.30)
Небольшой подбор процентных точек F-распределения представлен в
табл. А.5а—А.5в. Отметим, что статистика равная квадрату случайной
величины, определенной формулой (4.21), имеет F-распределение с = 1 и
п2 = п степенями свободы.
4.3 Выборочные распределения и примеры
Рассмотрим случайную величину х с функцией распределения Р (г).
Пусть•••,*?/ — выборка изА^ наблюденийх. Любая величина, вы-
численная по этим выборочным значениям, тоже будет случайной. Рас-
смотрим, например, среднее значение* выборки. Если взять несколько вы-
борок размеромN из одной и той же случайной величины*, то значения*,
вычисленные по разным выборкам, будут, вообще говоря, различными.
Следовательно,* тоже случайная величина с некоторой функцией распреде-
ления Р(*). Эта функция распределения называется выборочным распреде-
лением х.
Сейчас мы рассмотрим несколько выборочных распределений, часто ис-
пользуемых на практике. Среди них встретятся и функции распределения,
определения и некоторые свойства которых были рассмотрены в разд. 4.2.
Применение этих выборочных распределений к построению выборочных
интервалов и испытанию гипотез описывается в разд. 4.4—4.8.
Основные понятия математической статистики
93
4.3.1. РАСПРЕДЕЛЕНИЕ ВЫБОРОЧНОГО СРЕДНЕГО ПРИ ИЗВЕСТНОЙ
ДИСПЕРСИИ
Рассмотрим выборочное среднее выборки из N независимых наблюде-
ний случайной величины х:
- 1 г
(4-31)
Пусть сначала случайная величина х распределена нормально с средним
и известной дисперсией о^. Согласно разд. 3.3.1, выборочное распределение
выборочного среднего х тоже нормально. Формула (4.8) показывает, что
среднее значение выборочного распределения величины х равно
Мл = Мх >
(4-32)
а из формулы (4.9) следует, что дисперсия выборочного распределения ве-
личины х есть
2
°* = V (4-33)
Следовательно, в силу (4.13) распределения обеих частей следующего соот-
ношения, содержащего х, совпадают:
(х -
------------ = z .
°х
(4-34)
Здесь z — стандартная нормальная случайная величина, описанная в
разд. 4.2.1. Поэтому относительно возможных значений выборочного сред-
него можно утверждать, что
Prob
= а.
(4.35)
Пусть теперь распределение случайной величины х отлично от нормаль-
ного. Применяя центральную предельную теорему, получаем следующий
результат. С увеличением размера выборки N выборочное распределение
выборочного среднего х стремится к нормальному распределению незави-
симо от вида распределения исходной случайной величины х. Практически
во многих случаях выборочное распределение х можно считать нормаль-
ным уже приТУ > 4, а приТУ > 10 приближение будет очень хорошим. По-
этому при достаточно большом размере выборки формула (4.35) примени-
ма к выборочному распределению х, вычисленному для случайной величи-
ны с произвольным распределением.
94
Глава 4
4.3.2. РАСПРЕДЕЛЕНИЕ ВЫБОРОЧНОЙ ДИСПЕРСИИ
Рассмотрим дисперсию выборки из N независимых наблюдений случай-
ной величины х:
S2 = —у Е (*, - х)2 . (4.36)
Если случайная величинах распределена нормально с средним и диспер-
сией а2, то, как показано, например, в работе [4.1], распределения правой и
левой частей соотношения
Е (-Х, - х)2 = ах2х2„ , п = N - 1,
/ = 1
совпадают. Здесь х* имеет хи-квадрат распределение с п = N — 1 степеня-
ми свободы согласно определению разд. 4.2.2. Следовательно, выборочное
распределение выборочной дисперсии s2 определяется из соотношения
ns2
— = х2 , п = N — 1 . (4.37)
Поэтому относительно возможных значений выборочной дисперсии S2
можно утверждать, что
= « . (4.38)
4.3.3. РАСПРЕДЕЛЕНИЕ ВЫБОРОЧНОГО СРЕДНЕГО ПРИ НЕИЗВЕСТНОЙ
ДИСПЕРСИИ
Рассмотрим среднее значение выборки из N независимых наблюдений
случайной величины х, определенное формулой (4.31). Еслих распределена
нормально с средним цх и неизвестной дисперсией, то из соотношений
(4.21) и (4.37) следует, что
(* - Мх)
s/yfN
axz/y[N
^2Х2/п /№
Z
7= = t
Х2/п
где tn имеет -распределение с п = N — 1 степенями свободы согласно
определению разд. 4.2.3. Следовательно, выборочное распределение выбо-
— -2
рочного среднего х при неизвестной of задается соотношением
(х - iix)Jn
s
п = N - 1.
(4-39)
Основные понятия математической статистики
95
Поэтому относительно возможных значений выборочного среднего х мож-
но сделать следующее вероятностное утверждение:
Prob х >
(4.40)
4.3.4. РАСПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ДВУХ ВЫБОРОЧНЫХ ДИСПЕРСИЙ
Рассмотрим дисперсии двух выборок, одна из которых состоит из Nx
независимых наблюдений случайной величины х, а другая из Ny независи-
мых наблюдений случайной величины^ (см. формулу (4.36)). Если случай-
ная величина х распределена нормально с средним и дисперсией ох, а
случайная величина м распределена нормально с средним цу и дисперсией
ау, то из соотношений (4.26) и (4.37) следует, что
= ахХ2Пх/Пх°х
Sy/Oy ОуХ2„/Пу°у
где Fn п имеет F-распределение с пх = Nx — 1 и пу = Ny — 1 степенями
свободы согласно определению разд. 4.2.4. Следовательно, выборочное
распределение отношения выборочных дисперсий sx и sy задается соотно-
шением
Sx/ax пх = Nx ~ 1 >
ny = Ny-l. (4.41)
Поэтому относительно возможных значений отношения выборочных дис-
персий si и si можно сделать следующее вероятностное утверждение:
л у
Prob
5; аг
— > — F
-2 2',Их.'>>.;“
^у °у
(4-42)
Заметим, что если обе выборки сделаны из одной и той же случайной вели-
чины х = у, то соотношение (4.41) превращается в следующее:
S1=F «1 = М - ь,
_у2 nt.n2, 1.
(4.43)
4.4 Доверительные интервалы
В разд. 4.1 обсуждалось использование выборочных значений в качестве
оценок параметров случайных величин. Однако такие процедуры дают
только точечные оценки интересующих нас параметров; они не позволяют
96
Глава 4
судить о степени близости выборочных значений к оцениваемому парамет-
ру. Более содержательны процедуры оценивания параметров, связанные не
с получением точечного значения, а с построением интервала, который на-
крывает оцениваемый параметр с известной степенью достоверности.
Пусть, например, выборочное среднеех, вычисленное по N независимым
наблюдениям случайной величины х, используется в качестве оценки сред-
него цх. Обычно представляет интерес оценить в терминах некоторого
интервалах ± d, в который попадает с заданной степенью достоверно-
сти. Такие интервалы можно построить, если известны выборочные рас-
пределения рассматриваемой оценки.
Продолжим пример оценивания среднего значения. В разд. 4.3 было по-
казано, что относительно значений выборочного среднего х можно сделать
следующее вероятностное утверждение:
Prob
(4.44)
Формально это утверждение верно до получения выборки и вычислениях.
После получения выборки значениех становится вполне определенным чис-
лом, а не случайной величиной. Следовательно, можно сказать, что веро-
ятностное утверждение, содержащееся в формуле (4.44), теряет смысл, по-
скольку величина (х — /ох либо попадает в указанные границы, либо
не попадает. Другими словами, после получения выборки формально пра-
вильным будет следующее утверждение:
(4-45)
Обычно истинное значение вероятности (4.45), равное либо нулю, либо
единице, неизвестно. Однако по мере уменьшения а (увеличения интервала,
заключенного между z1_a/2 и za/2) разумно считать, что эта вероятность
скорее равна единице, чем нулю. Иначе говоря, если производится много
выборок и для каждой из них вычисляется значение х, то можно ожидать,
что участвующая в формуле (4.45) величина будет попадать в указанный
интервал с относительной частотой, примерно равной 1 — а. При таком
подходе можно утверждать, что существует интервал, в который величина
(х — /ох попадает с большой степенью достоверности. Такие утверж-
дения называются доверительными. Интервал, относительно которого дела-
ется доверительное утверждение, называется доверительным интервалом.
Степень доверия, сопоставляемая доверительному утверждению, называет-
ся уровнем доверия.
При оценивании среднего значения доверительный интервал для средне-
го цх можно построить по выборочному значению х, перегруппировав чле-
Основные понятия математической статистики
97
ны в формуле (4.45):
(4.46а)
Далее, если ах неизвестна, то доверительный интервал для можно по-
строить по выборочным значениям* иs, перегруппировав члены в форму-
ле (4.39):
х —
Stn \ а/2
y/N
п ’, а/2
~Ж~
п = N - 1. (4.46 б)
< < х +
В формулах (4.46) использованы свойства —«/2 = ~ za/2 и
~ ~ (п‘,а/2- Этим интервалам соответствует уровень доверия
1 — а. Следовательно, доверительное утверждение звучит так: истинное
значение попадает в указанный интервал с доверительной вероятностью
1 — а или (в общепринятых терминах) с доверительной вероятностью
100(1 — а)%. Подобные утверждения можно делать относительно любых
оценок параметров, лишь бы были известны соответствующие выбороч-
ные распределения. Например, формула (4.37) позволяет построить довери-
тельный интервал с уровнем доверия 1 — а для дисперсии ах по выбороч-
ной дисперсии 52, вычисленной по выборке ’размером N:
2 2
ns „
—— <, < —---------
Хи; а/2 Хи;1— а/2
(4-47)
п = У - 1 •
ПРИМЕР 4.1. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ. Пусть
выборка содержит N = 31 независимое наблюдение нормально распреде-
ленной случайной величины х:
60 61 47 56 61 63
65 69 54 59 43 61
55 61 56 48 67 65
60 58 57 62 57 58
53 59 58 61 67 62
54
Найдем 90%-доверительные интервалы для среднего значения и дисперсии
случайной величины*.
Согласно формуле (4.466), доверительный интервал с уровнем доверия
1 — а для среднего значения строится по выборочному среднему * и
4-953
98
Глава 4
дисперсии s’2 при размере выборки N = 31:
Из табл. А.4 для а = 0,1 находим t 30;а/2 = * ЗО;О,О5 = 1,697, поэтому интер-
вал имеет вид
[(х - 0,30485) < цх < (х + 0,30485)].
Согласно формуле (4.47), доверительный интервал для дисперсии ах с
уровнем доверия 1 - а строится по выборочной дисперсии s2 при размере
выборки N = 31:
3052 . 3052
—------< <тЛ2 < —------- •
ХзО; <х/2 ХзО;1-а/2
Из табл. А.З ДЛЯ а = 0,1 находим ХзО;а/2 = ХЗО;О,О5 = 43>77 и ХЗО;1-а/2 =
= Хзо-0 95 = 18,49, поэтому интервал принимает вид
[0,685452 < ох2 < 1,62252 ] .
Остается вычислить выборочное среднее и выборочную дисперсию и под-
ставить эти значения в формулы для доверительных интервалов. Выбороч-
ное среднее вычисляем по формуле (4.3):
1 Д
х = — У х, = 58,61 .
N ,=i
Выборочную дисперсию находим по формуле (4.12):
52 = —Д У (х,- - х)2 = Ду/ У xf - N(x)2! = 33,43.
N — 1 / = i N - 1 / = 1 j
Итак, доверительные интервалы с уровнем доверия 90% для среднего зна-
чения и дисперсии случайной величины х таковы:
[56,85 < цх < 60,37],
[22,91 < ах2 < 54,22] .
Основные понятия математической статистики
99
4.5. Проверка гипотез
Пусть дана некоторая оценка ф, построенная по выборке изТУ независи-
мых наблюдений случайной величины х. Предположим, что есть основания
считать истинное значение оцениваемого параметра равным ф0. Однако да-
же если истинное значение параметра ф равно ф0, выборочные значения ф,
вероятно, не будут в точности равняться ф0 из-за выборочной изменчиво-
сти, присущей ф. Поэтому возникает следующий вопрос. Если предполо-
жить, что ф = ф0, то при каком отклонении ф от ф0 эта гипотеза должна
быть отвергнута как несостоятельная? На этот вопрос ответ можно дать в
статистических терминах, вычислив вероятность любого значимого откло-
нения ф от ф0 по выборочному распределению ф. Если вероятность такого
отклонения мала, то отличие следует считать значимым, и гипотеза
ф = ф0 должна быть отвергнута. Если же вероятность такого отличия ве-
лика, то отклонение следует приписать естественной статистической измен-
чивости, и гипотеза ф = ф0 может быть принята.
Это рассуждение представляет собой простейший вид статистической
процедуры, называемой проверкой гипотез. Для уяснения общего подхода
предположим, что выборочное значение ф, являющееся оценкой параметра
ф, имеет плотность вероятности/? (ф). Теперь, если гипотеза ф = ф0 верна,
тор (ф) должна иметь среднее значение ф0 (рис. 4.2). Вероятность того, что
ф окажется меньше нижней границы Ф1_а/2> равна
РгоЬр < ф1 _а/2] = [Фг~‘/2р(ф) с!ф = ^- , (4.48а)
J — 00
а вероятность того, что ф превзойдет верхнюю границу фа/2, равна
РгоЬ[ф > фа/2] = ( р(ф)<1ф = - (4.486)
Га/2
4*
100
Глава 4
Следовательно, вероятность того, что ф окажется вне интервала, заклю-
ченного между </>i-a/2 и фа/2, есть а. Пусть теперь а настолько мало, что
представляется крайне неправдоподобным выход ф за пределы интервала,
заключенного между Ф1-а/^и фа/2. Если бы выборка была такой, что вы-
численное по ней значение ф оказалось вне интервала, заключенного между
Ф1-а/2 и Фа/2» т0 появились бы серьезные основания сомневаться в истин-
ности исходной гипотезы ф = ф0, поскольку в случае ее истинности такое
значение ф было бы крайне неправдоподобным. Следовательно, гипотезу
ф = ф0 нужно отвергнуть. С другой стороны, если значение ф попадает в
интервал, заключенный между Ф\_а/2 и фа/2, то нет никаких серьезных ос-
нований ставить под сомнение истинность исходной гипотезы. Поэтому ги-
потеза ф = Фо может быть принята.
Вероятность а, использованная при испытании гипотез, называется
уровнем значимости критерия. Область значений ф, при которых гипотеза
должна быть отвергнута, называется областью отклонения гипотезы или
критической областью. Область значений ф, при которых гипотеза прини-
мается, называется областью принятия гипотезы. Описанный выше про-
стой критерий испытания гипотез называется двусторонним критерием,
так как в том случае, когда гипотеза неверна, значение ф может быть либо
больше ф0, либо меньше. Следовательно, нужно проверять значимость от-
клонений ф от ф0 в обе стороны. В других случаях достаточно бывает од-
носторонних критериев. Например, пусть гипотеза состоит в том, что
ф > ф0. В этой ситуации гипотеза будет неверна только тогда, когда ф
меньше ф0. Следовательно, в критерии должна использоваться только ниж-
няя граница, определяемая по плотности вероятности р ($).
При проверке гипотез возможны два типа ошибок. Во-первых, гипотеза
может быть отклонена, хотя фактически она верна. Такая ошибка называ-
ется ошибкой первого рода. Во-вторых, гипотеза может быть принята, хо-
тя фактически она неверна. Такая ошибка называется ошибкой второго ро-
да. Из рис. 4.2 видно, что ошибка первого рода происходит в том случае,
когда при справедливости гипотезы ф попадает в область ее отклонения.
Следовательно, вероятность ошибки первого рода равна а, т. е. уровню
значимости критерия.
Для определения вероятности ошибки второго рода следует уточнить
каким-то образом отклонение истинного значения параметра ф от постули-
руемого гипотезой и подлежащего проверке значения ф0. Предположим, к
примеру, что истинный параметр равен либо ф = ф0 + б/, либо
ф = ф0 — d, как показано на рис. 4.3. Если гипотеза состоит в том, что
ф = ф0, тогда как на самом деле ф = ф0 ± d, то вероятность того, что ф
попадет в область принятия гипотезы, заключенную между Ф\_а/2 и фа/2,
равна /3. Следовательно, вероятность ошибки второго рода равна /3 при
выявлении отклонений величиной ± d от гипотетического значения ф0.
Вероятность 1 — 0 называется мощностью критерия. Очевидно, что
при любом данном размере выборки N вероятность ошибки первого рода
может быть сделана как угодно малой за счет уменьшения уровня значимо-
сти а. Однако при этом возрастет вероятность 0 ошибки второго рода
Основные понятия математической статистики
101
(уменьшится мощность критерия). Единственный способ одновременно
уменьшить и а, и /3 состоит в увеличении размера выборки N, используе-
мой для вычисления оценки ф. Такие соображения лежат в основе выбора
нужного размера выборки в статистических экспериментах.
ПРИМЕР 4.2. ПОСТРОЕНИЕ КРИТЕРИЯ ПРОВЕРКИ ГИПОТЕЗ. Предпо-
ложим, что есть основания считать, что среднее значение случайной вели-
чины х равно = 10. Предположим далее, что дисперсия х известна и
равна ах = 4. Найдем размер выборки, позволяющей построить критерий
проверки гипотезы цх = 10 с 5 % -уровнем значимости и 5 %-ошибкой вто-
рого рода для выявления 10%-отклонений от гипотетического значения.
Построим также область принятия гипотезы для данного критерия.
Выборочное среднее х, определенное формулой (4.3), является несме-
щенной оценкой ilx. Соответствующее выборочное распределение* опреде-
ляется из соотношения (4.34):
о*
X = .
где z — нормальная случайная величина с нулевым средним значением и
единичной дисперсией. Отметим, что такое выборочное распределение х
будет точным, еслих распределена нормально, и приближенным, если рас-
ределениех отлично от нормального.
Верхняя и нижняя границы области принятия гипотезы в данном крите-
рии соответственно равны
Уу z“/2 +м
ах
Если теперь истинное среднее значение равно на самом деле /4 = ц,х ± d,
то с вероятностью /3 произойдет ошибка второго рода, если выборочное
102
Глава 4
значение* окажется меньше верхней границы или больше нижней. В тер-
минах выборочного распределения х с средним /4 = 4- d или
— d имеем соответственно для верхней и нижней границ
°Х , °х
+ + а + дх- d .
Итак, справедливы следующие равенства:
°х °х
-^^/2 + ^x = -^^_p + nx + d,
°х °х
+ Mr = ~~i=ZR + Mr ~ d .
1—а/2 Ух Jn р Гх
Оба эти соотношения дают
Ту Ту
za/2 = 4- d = —Zp + ~^~~d .
Отсюда находим требуемый размер выборки
У =
gx(Za/2 + ^)l2
d
При конкретных значениях, принятых в данном примере (ах = 2,
za/2 = 1,96, Zp = 1,645, d = 0,1-10 = 1), требуемый размер выборки равен
N = 52. Область принятия гипотезы в данном критерии определяется со-
ответственно следующими верхней и нижней границами:
+ fjL х = 10,54
oY
~j=fZ\-a/2 + ^х= ^,46 *
4.6. Критерий согласия хи-квадрат
Для проверки эквивалентности плотности вероятности выборочных
данных некоторой гипотетической плотности часто используется особый
критерий, называемый критерием согласия хи-квадрат. Общая идея крите-
рия заключается в использовании в качестве меры расхождения наблюдае-
мой плотности вероятности и гипотетической плотности некоторой стати-
стики, приближенно подчиняющейся распределению хи-квадрат (^-распре-
делению). Затем гипотеза относительно их эквивалентности проверяется
путем изучения выборочного распределения этой статистики.
Основные понятия математической статистики
103
Пусть, например, дана выборка из N независимых наблюдений случай-
ной величины х с плотностью/? (х). Сгруппируем N наблюдений по/С ин-
тервалам, называемым интервалами группировки, которые в совокупности
образуют гистограмму частот. Число наблюдений, попавших bz-й интер-
вал, называется наблюденной частотой z-ro интервала; обозначим ее
Число наблюдений, которые могли бы попасть bz-й интервал, если бы ис-
тинной плотностьюх была/?(х), называется ожидаемой частотой z-ro ин-
тервала; обозначим eeFz. Далее, расхождение между наблюденной и ожи-
даемой частотами в каждом интервале равно /,• — Для того чтобы из-
мерить общее расхождение по всем интервалам, нормируем квадраты рас-
хождений соответствующими ожидаемыми частотами и просуммируем их:
получим выборочную статистику
к
х2= £
/=1
(Z - Ъ)2
F,
(4.49)
В работе [4.1] показано, что распределение величины X2 из формулы
(4.49) приближенно совпадает с ^-распределением, изученным в разд.
4.2.2. Число степеней свободы п в этом случае равно К минус число раз-
личных независимых линейных ограничений, наложенных на наблюдения.
Существует одно такое ограничение, связанное с тем, что частота в по-
следнем интервале группировки полностью определяется частотами всех
остальных интервалов. Если при сравнении плотностей одновременно под-
бираются параметры гипотетического распределения с целью достижения
наилучшего согласия с гистограммой частот, построенной по выборочным
данным, то добавляется по одному ограничению на каждый независимый
параметр гипотетической плотности, который будет определяться для до-
стижения этого согласия. Например, если гипотетическая плотность —
нормальная, с неизвестными средним значением и дисперсией, то появятся
два дополнительных ограничения, поскольку для подбора нормальной
плотности придется оценить два параметра (среднее значение и
дисперсию). Следовательно, в том обычном случае, когда критерий согла-
сия хи-квадрат применяется для проверки нормальности, число степеней
свободы вХ2 из формулы (4.49) равной = К — 3.
После выбора числа степеней свободы величины X2 проверка гипотезы
проводится следующим образом. Предположим, что случайная величинах
имеет плотность р (х). Сгруппировав выборочные значения по К интерва-
лам и вычислив ожидаемую частоту для каждого интервала группировки в
предположениир (х) = /?0(х), найдем %2 по формуле (4.49). Поскольку лю-
бое отклонение р (х) от/?0(х) вызовет увеличение %2, то используем одно-
сторонний критерий (по верхней границе). Область принятия гипотезы
имеет вид
Хг<х1,а. (4.50)
где значение берется из табл. А.З. Если выборочное значение^2 пре-
вышает ^2;а, то гипотеза о том, что/?(х) = /?0(х), отвергается с уровнем
104
Глава 4
значимости а. Если X2 меньше то гипотеза принимается с тем же
уровнем значимости а.
Известны два основных способа применения критерия согласия хи-
квадрат. Первый заключается в выборе таких интервалов группировки, ко-
торые обеспечивают равенство ожидаемых частот для всех интервалов. За
исключением гипотезы о равномерности распределения, такой способ при-
водит к интервалам группировки различной длины. Второй способ состоит
в выборе интервалов одинаковой длины. Опять-таки за исключением гипо-
тезы о равномерности распределения, в этом случае разными окажутся ча-
стоты попадания в тот или иной интервал. Для проверки нормальности с
помощью критерия согласия хи-квадрат обычно используются интервалы
равной длины. Если стандартное отклонение выборочных данных равное,
то часто берут интервалы группировки длиной Дх » 0,4 5. Более сущест-
венное требование заключается в том, что ожидаемые частоты для каждо-
го интервала группировки должны быть достаточно большими, с тем что-
бы Хп с приемлемой точностью приближала величину из формулы (4.49).
Обычно рекомендуется добиваться выполнения условия F, > 3 для всех ин-
тервалов. При проверке нормальности, когда частоты, соответствующие
хвостам распределения, быстро убывают, обычно в качестве первого и по-
следнего интервалов выбирают интервалы, простирающиеся соответствен;
но до — оо и 4- оо, причем должно выполняться указанное выше требова-
ние F^Fk > 3.
Таблица 4.1. Выборочные значения, упорядоченные по возрастанию
- 7,6 - 3,8 - 2,5 - 1,6 - 0,7 0,2 1,1 2,0 3,4 4,6
- 6,9 - 3,8 - 2,5 - 1,6 - 0,7 0,2 1,1 2,1 3,5 4,8
- 6,6 - 3,7 - 2,4 - 1,6 - 0,6 0,2 1,2 2,3 3,5 4,8
- 6,4 - 3,6 - 2,3 - 1,5 - 0,6 0,3 1,2 2,3 3,6 4,9
- 6,2 - 3,5 - 2,3 - 1,5 - 0,6 0,3 1,3 2,3 3,6 5,0
- 6,1 - 3,4 - 2,3 - 1,4 - 0,5 0,3 1,3 2,4 3,6 5,2
- 6,0 - 3,4 - 2,2 - 1,4 - 0,4 0,4 1,3 2,4 3,7 5,3
- 5,7 - 3,4 - 2,2 - 1,2 - 0,4 0,4 1,4 2,5 3,7 5,4
- 5,6 - 3,3 - 2,1 - 1,2 - 0,4 0,5 1,5 2,5 3,7 5,6
- 5,5 - 3,2 - 2,1 - 1,2 - 0,3 0,5 1,5 2,6 3,7 5,9
- 5,4 - 3,2 - 2,0 - 1,1 - 0,3 0,6 1,6 2,6 3,8 6,1
- 5,2 - 3,1 - 2,0 - 1,1 - 0,2 0,6 1,6 2,6 3,8 6,3
- 4,8 - 3,0 - 1,9 - 1,0 - 0,2 0,7 1,6 2,7 3,9 6,3
- 4,6 - 3,0 - 1,9 - 1,0 - 0,2 0,8 1,7 2,8 4,0 6,5
- 4,4 - 2,9 - 1,8 - 1,0 - 0,1 0,9 1,8 2,8 4,2 6,9
- 4,4 - 2,9 - 1,8 - 0,9 - 0,0 0,9 1,8 2,9 4,2 7,1
- 4,3 - 2,9 - 1,8 - 0,9 0,0 1,0 1,8 3,1 4,3 7,2
- 4,1 - 2,7 - 1,7 - 0,8 0,1 1,0 1,9 3,2 4,3 7,4
- 4,0 - 2,6 - 1,7 - 0,8 0,1 1,1 1,9 3,2 4,4 7,9
- 3,8 - 2,6 - 1,6 - 0,7 0,2 1,1 2,0 3,3 4,4 9,0
Основные понятия математической статистики
105
Таблица 4.2. Вычисления, выполняемые при построении критерия согласия
Номер интервала Верхняя граница интервала Р F = NP f 1^-/1 (F ~Л2
Za X ~ SZa + Х
F
1 - 2,0 - 6,36 0,0228 4,5 4 0,5 0,06
2 - 1,6 - 5,04 0,0320 6,4 8 1,6 0,40
3 - 1,2 - 3,72 0,0603 12,1 10 2,1 0,36
4 - 0,8 - 2,40 0,0968 19,4 21 1,6 0,13
5 - 0,4 - 1,08 0,1327 26,5 29 2,5 0,24
6 0 0,24 0,1554 31,1 31 0,1 0,00
7 0,4 1,56 0,1554 31,1 27 4,1 0,54
8 0,8 2,88 0,1327 26,5 25 1,5 0,08
9 1,2 4,20 0,0968 19,4 20 0,6 0,02
10 1,6 5,52 0,0603 12,1 13 0,9 0,07
11 2,0 6,84 0,0320 6,4 6 0,4 0,03
12 оо оо 0,0228 4,5 6 1,5 0,50
1,000 200 200 2,43
N = 200 х = 0,24 5 = 3,30 п =К - 3 = 9 X2 = 2,43
ПРИМЕР 4.3. ПРОВЕРКА НОРМАЛЬНОСТИ. В табл. 4.1 представлена вы-
борка изА" = 200 независимых наблюдений преобразованного к числовому
виду выхода генератора теплового шума. Для удобства выборочные значе-
ния упорядочены по возрастанию. Проверим выход генератора шума на
нормальность с помощью критерия хи-квадрат с уровнем значимости а =
= 0,05.
Все вычисления, необходимые для построения критерия, сведены в
табл. 4.2. При длине интервалов Дх = 0,4 5 границы интервалов группи-
ровки, определенные по стандартному нормальному распределению, приве-
дены в столбце, отмеченном символом za. Следующий столбец содержит
те же величины после преобразования в вольты. По табл. А.2 определим,
используя значения za, вероятность Р попадания выборочных значений в
каждый из интервалов группировки. Произведение Р на размер выборки N
даст ожидаемые частоты для каждого интервала; эти частоты представле-
ны в столбце, отмеченном символом F. Заметим, что первый и последний
интервалы выбраны так, что/7 > 3. В результате получилось 12 интерва-
лов. Подсчитаем затем наблюденные частоты, используя границы интерва-
лов (табл. 4.1). После этого вычислим и просуммируем нормированные
квадраты расхождений ожидаемых и наблюденных частот; получим
X2 = 2,43. Отметим, что в данном случае число степеней свободы равно
п = К — 3 = 9. Область принятия гипотезы находим из табл. А.З; получа-
106
Глава 4
ем^2 Х9 0 05 = 16,92. Следовательно, гипотеза о нормальности прини-
мается с уровнем значимости а = 0,05.
4.7 Статистическая независимость и выявление тренда
При анализе случайных данных часто возникают ситуации, когда требу-
ется выяснить, являются ли наблюдения или оценки параметров статисти-
чески независимыми или же они подвержены тренду. Особое значение эта
задача приобретает при анализе нестационарных данных, изучению кото-
рых посвящена гл. 12. Поскольку наблюдения или оценка параметров мо-
гут иметь самые разнообразные функции распределения, то удобно такие
исследования проводить на основе свободных от распределений или непа-
раметрических методов, в которых относительно функции распределения
исследуемых данных не делается никаких предположений. Критерий серий
и критерий инверсий дают два примера таких процедур, весьма полезных
для установления статистической независимости и выявления тренда.
4.7.1. КРИТЕРИЙ СЕРИЙ
Рассмотрим последовательность N наблюденных значений случайной
величины х, причем каждое наблюдение отнесено к одному из двух взаим-
но исключающих классов, которые можно обозначить просто как (+) или
(-). Простейший пример дает последовательность бросаний монеты, в ко-
торой каждое наблюдение — это либо герб (+), либо решетка (-). В ка-
честве второго примера можно привести последовательность измереннных
значений xi (i = 1, 2, ..., N) с средним значением х, где каждое наблюде-
ние — это х- х (+) или X; < х (—). Третий пример — последователь-
ность одновременных измерений двух случайных величин х, иу1- (i = 1, 2,
...,2V), где каждое наблюдение — этох, > (+) илих, <у{ (-). В любом
случае образуется последовательность вида
+ +-++- -h + + + -- +------
2 3 4 5 6 7 8 9 10 11 12
Серией называется последовательность однотипных наблюдений, перед и
лосле которой следуют наблюдения противоположного типа или же вооб-
ще нет никаких наблюдений. В данном примере в последовательности
из N = 20 наблюдений имеется г = 12 серий.
Число серий, появившихся в последовательности наблюдений, позволя-
ет выяснить, являются ли отдельные результаты независимыми наблюде-
ниями одной и той же случайной величины. Именно, если последователь-
ность?/ наблюдений состоит из независимых исходов одной и той же слу-
чайной величины, т. е. если вероятность отдельных исходов ((+) или (—))
не меняется от наблюдения к наблюдению, то выборочное распределение
числа серий в последовательности является случайной величиной г со сред-
ним значением и дисперсией [4.1]
2Л\#2
lir =------
(4.51)
N
Основные понятия математической статистики
107
2 = 1NXN2(1N^2 - У)
°г N2(W-1)
(4-52)
Здесь/V] — число исходов (+), aN2 — число исходов (—). В частном слу-
чае = Л^2 = N/2 выражения (4.51) и (4.52) принимают вид
= - + 1 .
2
Mr
(4.53)
Небольшая табл. А.6 дает 100а-процентные точки функции распределения
числа серий.
Вероятно, самое непосредственное применение критерий серий находит
в задачах оценки данных, связанных с выявлением тренда в анализируемой
последовательности. Предположим, что есть основания подозревать, что в
последовательности наблюдений имеется тренд, т. е. есть основания счи-
тать, что вероятности появления (4-) или (—) меняются от наблюдения к
наблюдению. Существование тренда можно проверить следующим обра-
зом. Примем в качестве гипотезы, что тренда нет, т. е. предположим, что
N наблюдений являются независимыми исходами одной и той же случай-
ной величины. Предположим также, что число исходов (4-) равно числу ис-
ходов (—). Тогда число серий в последовательности будет иметь выбороч-
ное распределение, протабулированное в табл. А.6. Для проверки гипотезы
с любым требуемым уровнем значимости а надо сравнить наблюденное
число серий с границами области принятия гипотезы, равными гл;1_а/2 и
гл а/2» гДе п — N/2. Если наблюденное число серий окажется вне этой обла-
сти, то гипотеза должна быть отвергнута с уровнем значимости а. В про-
тивоположном случае гипотезу можно принять.
ПРИМЕР 4.4. ПРИМЕНЕНИЕ КРИТЕРИЯ СЕРИЙ. Пусть имеется следую-
щая последовательность N = 20 наблюдений некоторой случайной величи-
ны: 1. 5,5 6. 5,7 11. 6,8 16. 5,4
2. 5,1 7. 5,0 12. 6,6 17. 6,8
3. 5,7 8. 6,5 13. 4,9 18. 5,8
4. 5,2 9. 5,4 14. 5,4 19. 6,9
5. 4,8 10. 5,8 15. 5,9 20. 5,5
Проверим независимость наблюдений, подсчитав число серий в последова-
тельности, полученной путем сравнения наблюдений с медианой1) исходной
последовательности. Применим критерий с уровнем значимости а = 0,05.
Из анализа данных видно, чтох = 5,6 является медианой 20 наблюде-
ний. Наблюдения, превышающие 5,6, классифицируем как (4-), а наблюде-
ния, меньшие 5,6, классифицируем как (—). В результате получим
(Выборочная) медиана — это число, правее и левее которого лежит равное
число наблюдений.— Прим, перев.
108
Глава 4
Таким образом, в последовательности из 20 наблюдений имеется 13 серий.
Предположим, что наблюдения независимы. Область принятия этой гипо-
тезы имеет вид
[Г10;1-а/2 < Г — Г10;а/2] *
Из табл. А.6 для а = 0,05 находим гЮ;1_а/2 = г1О;О>975 = 6, г10;а/2 =
= г10; о о25 = 15. Гипотеза принимается, ибо г = 13 попадает в интервал,
заключенный между 6 и 15. Это означает, что нет оснований сомневаться в
независимости наблюдений, т. е. свидетельства в пользу тренда нет.
4.7.2. КРИТЕРИЙ ИНВЕРСИЙ
Рассмотрим последовательность H3N наблюдений случайной величины
х, обозначенных х, (1 = 1, 2, ...,2V). Подсчитаем теперь, сколько раз в по-
следовательности имеют место неравенства xz > ху при i <j. Каждое та-
кое неравенство называется инверсией. Обозначим через А общее число ин-
версий.
Формально А вычисляется следующим образом. Определим для мно-
жества наблюденийхj,х2, ...jX^y величины
h = fl,'x,>xj'> (4.55)
,J 10, х,- Xj.
Тогда
N~1 N
A=YlAi , £ hu . (4.56, 4.57)
i-l y-, + 1
Например,
N N N
~ 2 — ^2j i 3 = 22 3j > • ’ •
j-2 7=3 y=4
Для уяснения понятия инверсии рассмотрим такую последовательность
из 8 наблюдений:
xi = 5, х2 = 3, х3 = 8, х4 = 9, х5 = 4, х6 = 1, х7 = 7, х8 = 5.
В этой последовательностихj > х2,х { > х5 ихх > хв, т. е. — 3 — чис-
ло инверсий дляхр Возьмем теперьх2 и сравним его с последующими наб-
людениями (т. е. i = 2 и i <j = 3, 4, ..., 8). Обнаруживаем, что только
х2 > х6, так что число инверсий длях2 равно А2 = 1. Продолжив эту про-
цедуру, найдем что Л3 = 4, Л4 = 4, Л5 = 1, Л6 = 0 и Л7 = 1. Следова-
тельно, общее число инверсий равно
А = Аг 4- А2 + • • • +Л7 = 3 + 1 + 4 + 4 + 1 + 0 + 1 = 14,
Если последовательность из N наблюдений состоит из независимых ис-
ходов одной и той же случайной величины, то число инверсий является
случайной величиной А с средним значением и дисперсией
Основные понятия математической статистики
109
N(N - 1) - 4 " > (4.58)
2N3 + 3N2 - _2 5W N(2N + 5)(N - 1) (4-59)
А 72 72
Небольшая табл. А.7 содержит 100а-процентные точки функции распреде-
ления А.
Критерий инверсий применяется примерно так же, как и критерий се-
рий. Вообще говоря, этот критерий более мощный по сравнению с крите-
рием серий при обнаружении монотонного тренда в последовательности
наблюдений. Однако этот критерий не столь эффективен при выявлении
тренда типа флуктуаций.
ПРИМЕР 4.5. ПРИМЕНЕНИЕ КРИТЕРИЯ ИНВЕРСИЙ. Проверим наличие
тренда в последовательности из N = 20 наблюдений из примера 4.4 при
уровне значимости а = 0,05. Подсчитаем число инверсий в последователь-
ности
А == 8 А = 6 А1 = 7 Аб = 0
А = 3 А = 1 Аг — 6 Аг = 2
А = 8 А = 8 Аз = 0 As = 1
А = 3 А = 1 Ад = 0 Л19 = 1
А == 0 Ао = 4 As = 3
Общее число инверсий А = 62.
Пусть гипотеза заключается в том, что наблюдения представляют со-
бой независимые исходы случайной величины х, т. е. тренда нет. Область
принятия этой гипотезы имеет вид
[ А();1-а/2 Ао; а/2] •
Из табл. А.7 при а = 0,05 находим ^420;1 — «/2 = Ао;О,975 = 64 и ^20;а/2 =
= Л 2оо 025 = *25. Следовательно, гипотеза должна быть отвергнута с
уровнем значимости 5%, так как А = 62 не попадает в интервал, заклю-
ченный между 64 и 125. Напомним, что гипотеза о независимости этой же
последовательности была принята при использовании критерия серий в
примере 4.4. Этот факт иллюстрирует различную чувствительность этих
двух методов проверки.
4.8. Корреляционные и регрессионные методы
Методы корреляционного и регрессионного анализа играют фундамен-
тальную роль во многих разделах этой книги. Понятие корреляции двух
случайных величин было введено в гл. 3 и получит дальнейшее развитие в
по
Глава 4
гл. 5. Понятие «линейная регрессия» лежит в основе методов оценивания
частотной характеристики по входным и выходным данным (см. гл. 6 и 7).
Однако материал этих глав излагается в терминах частот, что может “за-
темнить” его связь с более известными традиционными представлениями.
Поэтому краткий обзор понятий «корреляция» и «регрессия» с точки зре-
ния элементарной статистики будет полезным введением в данную тема-
тику.
4.8.1. ЛИНЕЙНЫЙ КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
Исключительный интерес для широкого класса задач представляет об-
наружение взаимных связей между двумя и более случайными величинами.
Например, существует ли связь между курением и ожидаемой продолжи-
тельностью жизни или между умственными способностями и успеваемос-
тью. В инженерных применениях такие задачи обычно сводятся к установ-
лению связи между некоторым предполагаемым возбуждением и наблюда-
емым откликом изучаемой физической системы. Существование таких вза-
имосвязей и их относительную силу можно измерить коэффициентом кор-
реляции р, определенным в разд. 3.2.1. В простом случае двух случайных
величиях и у коэффициент корреляции задается формулой (3.35):
. (4.60)
°х°у
где Су, — ковариациях иу, определенная формулой (3.33).
Пусть теперь из случайных величин х и у получена выборка, состоящая
из N пар наблюденных значений. Коэффициент корреляции можно оценить
по выборочным данным следующим образом:
= « = = 1(х< ~ *)(z -J)
Гху Рху -М, [е*Лх, - х)2ЕГ=1(л - я2]1/2
- Nxy
!(&- '
Как и рху, выборочный коэффициент корреляции лежит между — 1 и + 1 и
принимает одно из граничных значений только при наличии идеальной ли-
нейной связи между наблюдениями. Нелинейная связь и (или) разброс дан-
ных, вызванный ошибками измерения или же неполной коррелированнос-
тью случайных величин (рис. 4.4), приводит к уменьшению абсолютного
значения гху.
Для оценки точности выборочного значения гху удобно использовать не-
которую функцию от г :
Основные понятия математической статистики
111
Рис. 4.4. Различные степени корреляции: а — точная линейная корреляция; б —
умеренная линейная корреляция; в — нелинейная корреляция; г — отсутствие корре-
ляции.
W = |1п
1 + Гху
1 - гху
(4-62)
В работе [4.2] показано, что распределение случайной величины w можно
аппроксимировать нормальным распределением с средним значением и
дисперсией вида
М. = |1п
1 3" РХу
1 - Рхр
(4.63, 4.64)
N - 3
На основе этих соотношений легко построить доверительные интервалы
для рху по выборочной оценке гху в соответствии с рекомендациями
разд. 4.4.
Из-за выборочной изменчивости оценок корреляции обычно приходится
проверять, свидетельствует ли ненулевое значение выборочного коэффици-
112
Глава 4
ента корреляции о существовании статистически значимой корреляции
между изучаемыми случайными величинами. Сделать это можно, проверив
гипотезу pxv = 0, причем отклонение гипотезы будет говорить о значимо-
сти корреляции. Из формул (4.63) и (4.64) следует, что при рху = 0 выбо-
рочное распределение w будет нормальным с средним = 0 и дисперсией
а? = 1/(7V - 3). Поэтому область принятия гипотезы о нулевой корреля-
ции будет иметь вид
y/N -3
~Za/2 2
(4-65)
где z — стандартная, нормально распределенная случайная величина. Если
значение окажется вне этого интервала, то это будет признаком наличия
статистической корреляции с уровнем значимости а.
ПРИМЕР 4.6. ЛИНЕЙНЫЙ КОРРЕЛЯЦИОНЫЙ АНАЛИЗ. Табл. 4.3 со-
держит данные о росте и массе N = 25 выбранных наугад студентов. Есть
ли основания считать, что рост и масса студентов коррелированы при
уровне значимости а = 0,05?
Пусть х — рост, а у — масса. По табл. 4.3 вычислим величины, нужные
для применения формулы (4.65):
N N N
= 344 493, £ х,2 = 806 105, £ у} = 148 918,
1-1 i - 1 i - 1
1 N 1 -1 4485 _ 1 Д 1916 тал л= 25 1 - 1
Подставив эти значения в формулу (4.61), получим оценку коэффициента
корреляции:
'аблица 4.3. Данные о росте и массе студентов (х — рост в сантиметрах, .у — масса
килограммах)
X 178 188 178 165 175185 183 175 183 193 188 183
У 63 95 67 66 83 75 70 77 79 70 84 84
X 173 178 180 173 185165 185 188 163 183 183 170 185
У 75 100 84 82 77 61 79 82 68 77 75 66 77
Основные понятия математической статистики
113
344 493 - 25-179,4-76,64
г = ----------------------------------------г—— = 0,43.
ху [(806 105 - 25-179,42)(148 918 - 25-76,642)]1/2
По формуле (4.62) величина ич= 0,460; поэтому w VN - 3 = 2,16. Гипоте-
за рху = 0 должна быть отвергнута с уровнем значимости 5%, поскольку
w \!n — 3 = 2,16 не попадает в область принятия гипотезы, ограниченную
величинами ± za/2 = ± 1,96. Следовательно, есть основания считать, что
между ростом и массой студентов существует значимая корреляция.
4.8.2. ЛИНЕЙНЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ
Корреляционный анализ позволяет установить степень взаимосвязи
двух и более случайных величин. Однако наряду с этим желательно иметь
модель этой связи, которая дала бы возможность предсказывать значения
одной случайной величины по конкретным значениям другой. Например,
корреляционный анализ данных из примера 4.6 установил значимую линей-
ную связь между ростом и массой студентов. Логичен следующий шаг:
конкретизировать эту связь так, чтобы по данному росту можно было бы
предсказать массу студента. Методы решения подобных задач носят наи-
менование «регрессионный анализ».
Рассмотрим простой случай двух коррелированных случайных величин*
иу. В условиях примера 4.6* может быть ростом, а у — массой студента.
Линейная связь между двумя случайными величинами означает, что про-
гноз значения величины^ по данному значению* имеет вид
у = А + Вх , (4.66)
где Л и В — это соответственно отрезок оси ординат, отсекаемый прямой,
и ее наклон. Если данные связаны идеальной линейной зависимостью
(rxy = 1), то предсказанное значение у{ будет в точности равняться наблю-
денному значению^, при любом данном*,. Однако на практике обычно от-
сутствует идеальная линейная зависимость между данными. Как правило,
внешние случайные воздействия приводят к разбросу данных, и, кроме то-
го, возможны искажения за счет присутствия нелинейных эффектов (см.
рис. 4.4). Тем не менее, если все же предположить существование линейной
связи и наличие неограниченной выборки, то можно подобрать такие зна-
чения Л и В, которые дадут возможность предсказать ожидаемое значение
У1 для любого данного*,. Это означает, что .у, не обязательно совпадает с
наблюденным значением^,, соответствующим данному*,, однако оно бу-
дет равно среднему значению всех таких наблюденных значений.
Общепринятая процедура определения коэффициентов уравнения (4.66)
состоит в выборе таких значений Л и В, которые минимизируют сумму
квадратов отклонений наблюденных значений от предсказанного значения
114
Глава 4
у. Эта процедура называется методом наименьших квадратов. Точнее, по-
скольку отклонения наблюденных значений от предсказанных равны
у,Я = у> ~(А + Bxi) ’ (4-67)
то сумма квадратов отклонений имеет вид
Q = Е (л - л - BxiY
/ = 1
(4.68)
Следовательно, наилучшее согласие в смысле наименьших квадратов обес-
печивают значения А и В, для которых
9Q
дА
9Q
~ = о .
дв
(4.69)
На практике обычно имеется ограниченная выборка из?/ пар наблюден-
ных значений х и у. Это означает, что уравнение (4.69) даст всего лишь
оценки Л и В; обозначим их через а мЬ соответственно. Подставляя (4.68)
в уравнение (4.69) и решая его относительно оценок величин Л и В, полу-
чим
а = у - Ьх , (4.70а)
EfLi(x, - x)yt Е^Х'У, - Nxy
Е/=1(х, - х)2 Е/=1*,2 - Nx2
(4.706)
Эти оценки можно теперь использовать для построения модели, позволяю-
щей предсказывать у по данномух:
у = а + Ьх = (у - Ьх) + Ьх = у + Ь(х - х) . (4.71)
Прямая линия, задаваемая уравнением (4.71), называется прямой линей-
ной регрессии у нах. Поменяв ролями зависимую и независимую перемен-
ные в уравнении (4.70), получим прямую регрессии х на .у:
X = X + Ь'(у - у) , (4.72)
Л ~ Nxy
Ь L^jj,2 - Ny2
Сравнение произведения формул (4.706) и (4.73) с формулой (4.61) показы-
вает. что наклоны прямых регрессии у нах их на у связаны с выборочным
Основные понятия математической статистики
115
коэффициентом корреляции соотношением
(4.74)
Займемся теперь точностью оценок а иЬ, определенных формулами
(4.70). Как показано в книге [4.2], в предположении нормальности распре-
деления у при данном х оценки а и b являются несмещенными оценками А
и В соответственно. Их выборочные распределения связаны с t -распределе-
нием соотношениями
а — А
~ ГТ = 5у|х^-2 ’
1 х2 |
N + £"=1(х,-х)2/
b - В
~Т = Sy\xlN-2 '
1 V
E^U-x)2/
(4.75)
(4.76)
Особый интерес представляет выборочное распределение у при конкретном
значении х = х0. Оно имеет вид
У ~У
' ГТ ~ ^1x^-2
J_ + (-Хо~х) V
N + Е/=1(х,-х)2
(4-77)
В формулах (4.75)—(4.77) величина syix — это выборочное стандартное от-
клонение наблюденного значения от предсказанного У; = а + bxh равное
^|Х =
Е*1(у,-Л)2
N - 2
(4-78)
Приведенные выше соотношения дают возможность построить довери-
тельные интервалы для Л, В и у по оценкам а, b и у.
ПРИМЕР 4.7. ЛИНЕЙНЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ. Определим по
данным, содержащимся в табл. 4.3 из примера 4.6, прямую регрессии, за-
дающую линейный прогноз средней массы студента по его росту. Найдем
также 95 %-доверительный интервал для средней массы студентов, имею-
щих рост 178 см.
Пусть, как и в примере 4.6, х обозначает рост, а у — массу. Величины,
116
Глава 4
необходимые для определения наклона и отрезка, отсекаемого прямой на
оси ординат, уже были вычислены в примере 4.6. Подставив иХ в формулы
(4.70), найдем
344 493 - 25-179,4-76,64
b =---------------------’ = 0,51 ,
806 105 - 25-179,4 ’
а = 76,64 - 0,51-179,4 = - 14,854.
Следовательно, прямая регрессии, оценивающая среднюю массу студента
по его росту, имеет вид
у = - 14,85 4- 0,51х,
откуда для ростах = 178 см получаем массу у = 75,9 кг.
Для построения< доверительного интервала для средней массы у по
оценке у = 75,9 кг следует вычислить s (л, по формуле (4.78). С вычисли-
тельной точки зрения удобнее воспользоваться формулой
1 N
н—у L(z-j')2-
N~ 2\,-i
расчеты по которой можно упростить еще больше, заметив, что
Е (^ -”)2 = L A - N»2 > *)(/, - /) = L х)У. - N*y
i=i /=1 i-i /-1
Подставив нужные значения в эти выражения, получим
— ( 2075,76
23 \
762,62\
1496 /
8,56.
Тогда по формуле (4.77) 95 %-доверительный интервал для средней массы
студента, имеющего рост 178 см, имеет следующий вид:
У i Sy\x^N-2; а/2
— 75,9 ± 8,56-^23; 0,025
1 (178 - 179,4)2
25 1496 .
= 75,9 ± 3,6, т. е. от 72,3 до 79,5 кг.
На этом пример 4.7 заканчивается.
Описанные выше методы корреляционного и регрессионного анализа
легко обобщаются на случай более двух случайных величин. Как указыва-
лось ранее, такие обобщения играют фундаментальную роль в задачах ана-
лиза систем со многими входными и выходными процессами, изучаемых в
Основные понятия математической статистики
117
гл. 7. Поэтому дальнейшее обсуждение этого предмета откладывается до
этой главы.
Задачи
4.1. Пусть плотность вероятности случайной величины х имеет вид
Найдите среднее значение и дисперсию х.
4.2. Даны две независимые случайные величины х и у с средними значениями /хх и
/Ху и дисперсиями аi 2 и of. Найдите:
а) среднее значение произведения ху;
б) дисперсию разности х — у.
4.3. Дана случайная величина у = сх, где с — постоянная, ах — случайная вели-
чина с средним значением /хх и дисперсией а2. Докажите справедливость следующих
соотношений:
а) Му = с/хх;
б) Оу2 = с2а2.
4.4 Даны четыре независимые стандартные нормально распределенные случай-
ные величины z р z 2, z3 nz4. Найдите функции распределения указанных ниже комби-
наций этих случайных величин. В каждом случае определите в зависимости от харак-
тера распределения либо число степеней свободы, либо среднее значение и диспер-
сию.
(a) zj2 + zf + z} + zj. ;
(6) Zj + z2 - z3 - z4. ;
izi2+л+а ]/з
u
4.5. Какие функции распределения следует использовать при построении довери-
тельных интервалов для следующих параметров двух независимых нормально рас-
пределенных случайных величин х и у 1
а) Интервал для /хх по выборочному среднему х и известной дисперсии стх2.
б) Интервал для а2/а2 по отношению выборочных дисперсий $2/$2.
2 У j У
в) Интервал для ах по выборочной дисперсии s^.
г) Интервал для /хх по выборочному среднему х и выборочной дисперсии s 2.
4.6. Дана временная последовательность из N = 100 измерений случайной вели-
чины х. Постройте область принятия следующих гипотез с 2%-уровнем значимости:
а) случайная величина содержит тренд;
б) 100 измерений х статистически независимы.
4.7. Дана выборка изЛ^ независимых наблюдений случайной величины х с извест-
118
Глава 4
ным нулевым средним значением. Тогда эффективной оценкой дисперсии % окажется
величина
1 N
s2 = — У х2
N ,=i ‘
а) Докажите, что эта оценка не смещена.
б) Выпишите выражение, связывающее эту оценку со случайной величиной хи-
квадрат, выбрав подходящее число степеней свободы.
в) Какова дисперсия этой оценки? (Указание: дисперсия х„ равна 2л.)
4.8. Нормированная случайная ошибка (коэффициент вариации) ег несмещенной
оценки параметра ф определяется как отношение стандартного отклонения оценки к
ее математическому ожиданию, т. е. ег = оф/цф. Используя формулу (4.12), найдите
нормированную случайную ошибку оценки дисперсии s2, вычисленной по N = 200
выборочным значениям.
4.9. Исследуется корреляция выборки из N = 7 пар наблюдений (х}у}, х2у2, ...
... , х7т7). Вычислен коэффициент корреляции гху = 0,77. Проверьте гипотезу о том,
что рху больше нуля с уровнем значимости а = 0,01.
4.10. Выборочные средние двух коррелированных случайных величин равны
х = 1 и у = 2, выборочный коэффициент корреляции гху — 0,5. Если прямая регрес-
сии у на х есть у = 1 + х, то получите:
а) угол наклона Ь' прямой регрессии х на у;
б) уравнение регрессии х на у (х = а' + Ь'у).
Глава 5
СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ
ПРОЦЕССЫ
В этой главе обсуждаются элементарные и более сложные понятия тео-
рии стационарных случайных процессов, образующие основу для решения
задач измерения и анализа таких процессов; изложение следует книгам [5.1,
5.2]. В главе приводятся формальные определения из теории стационарных
случайных процессов, а также основные свойства ковариационных функций
и спектральных плотностей. Формулируются результаты, относящиеся к
эргодическим случайным процессам и производным от случайных процес-
сов. Нестационарные случайные процессы рассматриваются в гл. 12.
5.1. Основные понятия
Случайный процесс — оо < / < оо (иначе, временной ряд или
стохастический процесс), обозначаемый символом [ ], — это совокупность
действительнозначных (или комплекснозначных) функций, которую можно
охарактеризовать ее вероятностной структурой. Для удобства в последую-
щем изложении переменная t будет интерпретироваться как время. Каждая
отдельная функция х^(/), где t — переменная, а к фиксировано, называется
выборочной функцией. С практической точки зрения выборочную функцию
(или некоторый отрезок выборочной функции конечной длины) можно счи-
тать наблюдаемым результатом отдельного эксперимента. Возможное чис-
ло экспериментов определяется выборочным пространством индексов к,
причем последнее может быть счетным или несчетным. Для любого N и
любых фиксированных моментов времени г2, ... , tN значения процесса
^(^), xk(t£, ... , xk(tN) представляют собой N случайных величин, зави-
сящих от индекса к. Предполагается, что для любого N существует полно-
стью определенная N-мерная плотность вероятности. Пример совокупно-
сти выборочных функций, образующих случайный процесс, показан на
рис. 1.10.
Отдельная выборочная функция хк( t) случайного процесса, вообще го-
воря, не характеризует случайный процесс [л^( г)} в целом. Однако ниже
будет показано, что при определенных условиях в особом классе эргодиче-
ских случайных процессов необходимую статистическую информацию о
случайном процессе в целом можно получить с помощью соответствующе-
го анализа единственной выборочной функции. Для двух случайных процес-
сов [хдХ г)} и [ук( t)] аналогичная задача заключается в оценке совместных
свойств двух случайных процессов путем соответствующего анализа произ-
вольной пары выборочных функций хк( t) и ук( t).
Рассмотрим два произвольных случайных процесса [х^( /)] и [ук( /)]. В
первую очередь представляют интерес средние значения по ансамблю в
произвольный фиксированный момент времени t, где хк( t) и ук( t) — слу-
120
Глава 5
чайные величины от аргумента к. Такие средние значения определяются
формулой (3.8):
Мх0) = £[хЛ(0], ny(t) = £[п(0]. (5Л)
Вообще говоря, эти средние значения зависят от времени и должны оцени-
ваться особо для каждого момента t. Поэтому при Ф t2 имеем
MxOi) * М'г). MyOi) * М'г).
Следующие важные статистические характеристики — это корреляционные
функции, определенные для произвольных фиксированных моментов време-
ни ty — t и t2 = t + т:
cxxU/ + т) = £[(**(') - +т) - Мх(? + т))]>
Cyy(t> t + т) = £[(л(0 - + т) - мДг + т))], (5.3)
СХЛ,(/,Г + т) = £[(хДг) -^х(г))(^(/ + т) -ny(t + т))].
В общем случае эти величины различны для различных комбинаций tx и t2.
Заметим, что при т = 0 ( = t2 = t)
схх(^‘) = -Мх(0)2] =
Cyy(t, t) = я[(л(') - M'))2] = <\2(0» (5.4)
cxy(h t) = я[(**(0 - Мх(0)(л(0 - МО)] = cxy(t) •
Следовательно, корреляционные функции СХ¥( Z, г) и С ( t, t) совпадают с
обычными дисперсиями процессов [хк( /)] и [yk( t)] в фиксированный мо-
мент t, в то время как С ( t, t) представляет собой ковариацию случайных
величин [хк( /)} и [ук( /)]. Как и выше, результат зависит от t.
По ансамблю реализаций можно определить и другие статистические
характеристики, зависящие от трех и более моментов времени. Тем самым
вероятностная структура случайных процессов1) будет описываться все бо-
лее детально. Если [хк{ /)] и {ук{ /)] имеют для фиксированного момента t
двумерное гауссово распределение, то каждая из величин [хк( /)] и [ук{ /)}
тоже подчиняется гауссову распределению. В этом случае определенные
выше средние значения и ковариационные функции полностью описывают
вероятностную структуру процесса. По этой причине в данной главе основ-
11 В отечественной литературе используется термин «совокупность конечномер-
ных распределений случайного процесса». — Прим. ред.
Стационарные случайные процессы
121
ное внимание уделено этим двум статистическим характеристикам и их свя-
зи со спектральными плотностями.
Если средние значения дх( /) и цу( t) вместе с корреляционными функ-
циями С( t, t + т), Си1?( /, t + т) и С (t, t + т) принимают одинаковые
лл у у лу
значения при всех фиксированных значениях t (т. е. не зависят от выбора
начала отсчета), то случайные процессы [хк( /)} и [ук( /)} называются сла-
бо стационарными. Если всевозможные распределения, связанные с
[хк( /)} и [ук( /)], не зависят от выбора начала отсчета времени, то такие
процессы называются строго стационарными. Поскольку средние значе-
ния и корреляционные функции определяются только одномерными и дву-
мерными функциями распределения, то отсюда следует, что класс строго
стационарных случайных процессов входит в класс слабо стационарных
случайных процессов1^. Однако в случае гауссовых случайных процессов
слабая стационарность влечет строгую, поскольку все характеристики этих
процессов определяются средним значением и корреляционной функцией.
Следовательно, для гауссовых случайных процессов оба понятия стацио-
нарности совпадают.
5.1.1. КОВАРИАЦИОННЫЕ (КОРРЕЛЯЦИОННЫЕ) ФУНКЦИИ
Для стационарных случайных процессов [хк( /)] и [ук( /)}, которым по-
священа эта глава, средние значения постоянны и не зависят от времени /,
т. е. для всех t
Мх = = [ xp(x)dx,
J - 00 . .
(5.5)
/S = £[л(0] = [ УР(у)^у,
- 00
где р(х) и р(у)— плотности вероятности случайных величин хк( t) и
ук( t) соответственно. Корреляционные функции стационарных процессов
также не зависят от t.
Определим для произвольных фиксированных t и т функции
Лхх(Т) = Е1Хк(‘)Хк({ + Т)] >
Ryy(-r) = -Е[л(0л(? + т)] > (5-6)
ЯхДт) = Е [хДг)л(/ + т)],
где вместо С используется символ R для того, чтобы отличать эти величи-
ны от корреляционных функций, введенных формулами (5.3). При ненуле-
вых средних R отличны от С, Величины R^fj) и Ryy(r) называются авто-
корреляционными или ковариационными функциями процессов [xk( /)} и
11 Предполагается, что существует второй момент процесса. — Прим, перев.
122
Глава 5
[ук( О) соответственно, a Rxy{r) называется взаимной ковариационной
функцией [*t( О) и
Для того чтобы Rxx(t) была ковариационной функцией слабо стацио-
нарного случайного процесса [xk(J)], необходимо и достаточно, чтобы
R^r) = R^- т) и Rxx(r) была неотрицательно определенной функцией.
Можно также показать, что Rxx(r) — непрерывная функция от т, если она
непрерывна в нуле. Аналогично Rxy(r) — непрерывная функция во всех
точках т, если Rxx(r) и Ryy(r) непрерывны в нуле [5.3].
Для двух стационарных случайных процессов [хк( /)] и {ук( /)] совмест-
ная плотность вероятности р( х2) пары случайных величин х{ = хк( t) и
х2 = хк{ t + т) не зависит от t. Совместная плотность вероятности р(ух,
у2), относящаяся к паре случайных величин yt = уk(t) и у2 = ук( t 4- т),
тоже не зависит от t. Этим же свойством обладает совместная плотность
вероятности р( у2), характеризующая случайные величины хг = хк( t) И
у2 = Ук( t 4- т). В терминах этих плотностей имеем
00
Лхх(т) = ff xlx2p(xl,x2)dx1dx2,
— 00
00
Ryy(P = ff УгУгР^У^ У2) dyrdy2 , (5.7)
— 00
00
Rxy(r) = ff y2) dxx dy2 .
— 00
При произвольных усх и ру ковариационные функции связаны с корреляци-
онными функциями соотношениями
Сх(Т) = - Рх , Суу(т) = Яуу(т)-р2у,
(5.8)
Сху(т) = Кху(т)-рхру.
Следовательно, корреляционные функции совпадают с ковариационными,
если средние значения равны нулю. Заметим, что, по определению, два
стационарных случайных процесса не коррелированы, если Сх (т) = 0 для
всех т. В силу формул (5.8) это имеет место, если только Rxy(r) = nxfiy для
всех 7. Следовательно, если Rxy(r) = 0, то два процесса не коррелированы
только тогда, когда хотя бы одно из средних цх или цу равно нулю.
Из предположения стационарности следует, что ковариационные функ-
ции Ryy(t) и R„v(t) — четные функции от 7, т. е.
лл у у
^(-т) = Лхх(т), у-т) = ут). (5.9)
В то же время взаимная ковариационная функция не обладает свойством
Стационарные случайные процессы
123
четности или нечетности, но удовлетворяет соотношению
ЛхД-т) = ^х(т). (5.10)
Соотношение (5.10) доказывается следующим образом. По определению,
RXy(~T) = £[*(')/(' - т)] >
где зависимость от к опущена для простоты обозначений. Поскольку ре-
зультат не зависит от сдвига начала отсчета, t можно заменить на t 4- т до
взятия математического ожидания. Поэтому
= £[%(/ + т)^(г + т - т)] =
= + т)] = Ryxh),
что завершает доказательство. При х = у получаем
Rxx(~'r) = Rxxi-r), Ryy(-r) = Ryy(r) ,
т. e. формула (5.9) — частный случай формулы (5.10).
Корреляционные свойства стационарных случайных процессов [хк{ t)] и
[yk(t)} описываются четырьмя функциями Rxx(t), Куу(т), Rxy(r) и Ryx(r),
которые можно вычислять только для значений т > 0, поскольку из соот-
ношений (5.9) и (5.10) легко получить их значения для т < 0.
5.1.2. ПРИМЕРЫ КОВАРИАЦИОННЫХ ФУНКЦИЙ
В табл. 5.1 приведены примеры ковариационных функций, находящих
применение в теоретических исследованиях.
ПРИМЕР 5.1. КОВАРИАЦИОННАЯ ФУНКЦИЯ ГАРМОНИЧЕСКОГО ПРО-
ЦЕССА. Пусть [хк( t)] = { %sin [2тг/0 t 4- в( £)]] — гармонический процесс,
причем Хи f$ — постоянные, а в( к) — случайная величина с равномер-
ной плотностью р(0), заданной на (0, 2тг). Найдем его ковариационную
функцию Rxx(t).
Здесь для любого фиксированного t случайные величины имеют вид
xk(t) = Arsin[27r/O/ + #(£)] = *i(0) ,
xk(t 4- т) = Xsin[2Tr/0(t 4- т) 4- #(&)] = х2(0) •
По формуле (5.6) получим
Лхх(т) = Е + т)] = Е hl(0)*2(0)] >
Таблица 5.1. Ковариационные функции, часто используемые в теоретических
исследованиях
Тип Ковариационная функция
Постоянная Яхх(т) = С2 0
Гармоническая \ f *\ /\ У 2 Y / Rxx ( Т ) = Т cos 2w/oT 0
Белый шум Л.л(т) = а«(т) 0
Низкочастотный белый шум п z \ sin 2тгВт \ 2,8, )
Ограниченный по частоте белый шум jcos2w/0T 0
Экспоненциальная ЛлДт) = е-"1’1 0
Экспоненциально- косинусоидальная Rxx (т ) = e~a|T| cos 2тг/от 0
Экспоненциально- косинусоидально- синусоидальная Rxx(T) = e~ ( b cos 2 ITf0T + c sin 2tt/0|t|) 0
Стационарные случайные процессы
125
где р(6) = (2тг) 1 при 0^0^ 2тг и р(0) = 0 в остальных случаях. Поэто-
му величина
Rxx(r) = ( sin(2Tr/0Z + в)sin[2Tr/0(t 4- т) 4- 0] dO =
2тг •'о
X2
= — cos2tt/0t
дает ковариационную функцию стационарного случайного гармонического
процесса; ее график изображен в табл. 5.1.
ПРИМЕР 5.2. КОВАРИАЦИОННАЯ ФУНКЦИЯ ТЕЛЕГРАФНОГО СИГНА-
ЛА. Рассмотрим теперь физический эксперимент, порождающий случайный
телеграфный процесс [хк( /)] , представляющий собой совокупность прямо-
угольных волн, принимающих два значения (с и — с), причем перемены
знака внутри интервала (Z, t 4- т) происходят в случайные и независимые
моменты времени с интенсивностью X. Предположим также, что события
внутри интервала (Z, t 4- т) не зависят от событий, происходящих вне это-
го интервала. Определим событие Ап*.
Ап = Событие [Внутри интервала (Z, t 4- т) происходит
ровно п перемен знака].
Такой физический эксперимент описывается пуассоновским распределением
[5.1], в котором вероятность события Ап равна
Найдем ковариационную функцию процесса {хк( /)).
Ковариационная функция вычисляется следующим образом. Каждое от-
дельное произведение хк{ t) хк( t 4- т) равно либо с2, если xk(t) и
xk{t 4- т) имеют одинаковые знаки, либо -с2, если их знаки противопо-
ложны. СуммарнаяНзероятность того, что это произведение есть с2, равна
сумме Р(А$) 4- Р(А2) 4- Р(Л4) 4- ... , а суммарная вероятность того, что
это произведение есть -с2, равна сумме Р( А{) 4- Р( А3) 4- Р( Л5) 4- ... .
Следовательно,
RXX(T) = £[**(')**(' + т)] = с2 £ (-1)"р(я„)=
п = 0
= с2е-Х|,|£ (_1)"к_12_ = с2е-2Х|т|ф
и = о «!
Эта экспоненциальная функция изображена в табл. 5.1 при а = 2Х и
с2 = 1.
126
Глава 5
ПРИМЕР 5.3. КОВАРИАЦИОННАЯ ФУНКЦИЯ СУММЫ ДВУХ
СТАЦИОНАРНЫХ ПРОЦЕССОВ. Пусть случайный процесс [yk(t)] равен
сумме двух стационарных процессов {хх к{ t)] и [х2 к( /)Ь Любая его
выборочная функция имеет вид
Ук<А = a1xKk(t) + a2x2j!(t),
где ах и а2 — постоянные. Допустим также, что [ х} к( t)] и [х2 к( /)]
могут коррелировать между собой. Вычислим ковариационную функцию
Ryy(r). По формуле (3.44) получим
Ryyir) = + т)]
= £[(*1*1, k(t) +в2^л(0)(М1д(< + т) + a2x2tk(t + т))] =
= *1£[*1д(0*1,Д' + т)] + a1a2£[x1Jl(/)x2Jt(/ + т)] +
+ *1*2£[*2д(0*1,*(' + т)] + alE[x2'k(t)x2tk(t + т)] =
= яМх.х.И +М2|МТ) +Лх2х1(т)] + *^х2х2(т).
Следовательно, для определения ковариационной функции суммы нужно
знать ковариационные функции исходных процессов, а также их взаимную
ковариационную функцию.
ПРИМЕР 5.4. НЕКОРРЕЛИРОВАННЫЕ ЗАВИСИМЫЕ СЛУЧАЙНЫЕ ВЕЛИ-
ЧИНЫ. Пусть х и у — случайные величины вида х = cos ф и у = sin ф, где
ф — случайная величина, распределенная равномерно на (0, 2тг). В этом
случае существует связь между х и у, поскольку у = V1 — х2. Поэтому
р(х, у) Ф р(х) р(у), что говорит о статистической зависимости между х
и у. Однако ковариация х и у равна
Сху = £[*у] - £[*]£[Я =
= E[cos</>sin</>] - E[cos</>]£[sin</>] =
= |E[sin 2ф] = 0.
Следовательно, х и у не коррелированы.
5.1.3. НОРМИРОВАННАЯ КОВАРИАЦИОННАЯ ФУНКЦИЯ
Для взаимной ковариационной функции справедливо неравенство
|ЯхДт)|2 < Лхх(0)ЯЛУ(0), (5.11)
Стационарные случайные процессы
127
называемое неравенством для взаимных ковариационных функций. Дока-
зать его можно следующим образом. Для любых действительных чисел а и
b математическое ожидание
E[(ax(f) 4- by(t 4- т))2] > 0 ,
поскольку в нем участвуют только неотрицательные величины. Это нера-
венство эквивалентно следующему:
а2Яхх(0) + labR^) + b2Ryy^ > 0 .
Поэтому в предположении b Ф О
/ а \2 / а \
- Яхх(0) + 2 - (т) 4-Я (0) > 0 .
\ Ь ) \Ь)
Левая часть этого неравенства представляет собой квадратный трехчлен
относительно а/b, не имеющий в силу последнего неравенства различных
действительных корней. Поэтому дискриминант этого трехчлена не превос-
ходит нуля, т. е.
Дискриминант = 4Е2Дт) — 4Лхх(0)Л^(0) < 0 .
Следовательно,
Л2/т) = |ЕхДт)|2</?хх(0)Луу(0),
что завершает доказательство.
Рассматривая x(t) — цх п у (t + т) — ц,у вместо x(t) и y(t 4- т), тем же
способом получаем неравенство для взаимных корреляционных функций:
|Сх/т)|2< Схх(0)С,,(0). (5.12)
Заметим, что
|Яхх(т)|</?хх(0), |Схх(т)| < Схх(0), (5.13)
поэтому максимальные значения Кхх(т) и Схх(т) достигаются в т = 0 и
равны соответственно среднему квадрату и дисперсии процессов, т. е.
Яхх(0) = ф2(г)] =^2 , Qx(0) = ax2,
(5-14)
/?,„(()) = е[л2(0] = , СД0) = < .
Следовательно, неравенство (5.12) можно записать как
1С„(г)|!<аХ. (5.13)
128
Глава 5
Определим теперь коэффициент корреляции {нормированную взаимную
корреляционную функцию)
* Cxv (т)
Мт) = ’ (516)
который для всех т удовлетворяет неравенствам
-1<рх/т)<1. (5.17)
Если одна из величин или равна нулю, то
л у
так как в этом случае Сху{т) = Rxy{r). Функция рху(т) характеризует сте-
пень линейной зависимости между [ атАг( Z)} и [ук{ /)} при данном сдвиге т
процесса [ук{ /)} по отношению к процессу {хк{ /)]. По сути дела, это —
обобщение коэффициента корреляции, используемого в классической стати-
стике и изученного в разд. 3.2.1 и 4.8.1.
5.1.4. ВЗАИМНАЯ КОВАРИАЦИОННАЯ ФУНКЦИЯ
ПРИ НАЛИЧИИ ЗАПАЗДЫВАНИЯ
Пусть передаваемый сигнал представляет собой стационарный случай-
ный процесс x{t) с нулевым средним значением. Предположим, что прини-
маемый сигнал тоже стационарен и имеет нулевое среднее:
y(t) = ax(t - т0) + n(t). (5.19)
Величина а — это постоянный коэффициент затухания, величина
т0 = d/c — постоянное запаздывание, равное частному от деления расстоя-
ния d на скорость распространения сигнала с, а п{ t) — некоррелирован-
ный шум на выходе с нулевым средним (рис. 5.1).
В этой задаче взаимные ковариационные функции x{t) и y{t) имеют
вид
^x.v(T) = E[x(t)y(t + т)] = Е[х(/)(ах(/ + т - т0) + n(t + т)}] =
= а£[х(г)х(/ + т - т0)] = aRxx(r - т0). (5.20)
Следовательно, Rxy{r) попросту равна ковариационной функции /^(т),
сдвинутой на величину запаздывания т0 и умноженной на коэффициент за-
тухания а. Максимальное значение Rxy{r) приходится на т = т0, так что
ЯхДт)реак = Ях/т0) = аЯхх(0) = а<тх • (5.21)
Стационарные случайные процессы
129
n(t)
Рис. 5.1. Схема распро-
странения сигнала в задаче
определения запаздывания.
*(У)
Запаздывание
ax(t-т0)
Этот результат иллюстрирует рис. 5.2. Заметим, что, определив значение
т0 по положению максимума и зная одну из величин — расстояние d или
скорость распространения с — можно найти другую, так как d = ст0.
Практические примеры задач измерения запаздывания рассматриваются в
книге [5.2].
Считая по-прежнему, что x(t) и n(t) имеют нулевые средние значения,
определим значение коэффициента корреляции при т = т0 по формуле (5.18)
РХУЫ = = «- • (5.22)
°х°у °у
Поэтому, зная Pvv(^0), можно найти коэффициент затухания а:
а = РхЛто)[°/а*]- (5-23)
Рис. 5.2. Типичная взаимная ковариационная функция в задаче определения за-
паздывания.
5-953
130
Глава 5
Следовательно, дисперсия у( t) при некоррелированных x(t) и n(t) равна
= Е [/2(0] = «Ч2 + *2 (5.24)
и имеет две составляющие: вклад x(t) в дисперсию y(t) и вклад n(t) в дис-
персию y(t), которые соответственно равны
«Ч2 = Р2Ч’ ап = (1 - Рху) °2- (5-25)
Формула (5.24) — частный случай соотношения
куу(т) = + т)] = a2Rxx(r) + Я„„(т) (5.26)
При 7 = 0.
5.2. Функции спектральной плотности
Функции спектральной плотности можно определять тремя различными
эквивалентными способами, которые будут описаны в последующих разде-
лах:
а) с помощью ковариационных функций;
б) с помощью финитного преобразования Фурье;
в) с помощью фильтрации, возведения в квадрат и усреднения.
Будут также получены важные соотношения для этих функций, кото-
рые используются во многих приложениях.
5.2.1. ОПРЕДЕЛЕНИЕ СПЕКТРОВ С ПОМОЩЬЮ
КОВАРИАЦИОННЫХ ФУНКЦИЙ
Исторически первый способ определения спектральной плотности поя-
вился в математике. Он состоит во взятии преобразования Фурье от пред-
варительно вычисленной ковариационной функции. После вычитания сред-
них такие (бесконечные) преобразования Фурье обычно существуют, даже
если (бесконечное) преобразование Фурье исходного стационарного случай-
ного процесса не существует. Этот подход дает двустороннюю спектраль-
ную плотность, обозначаемую S (/) и определенную для f из ( — оо, оо).
Пусть существуют ковариационные и взаимная ковариационная функции
/?хх(т), Ryy(r) и Rxy(r), задаваемые формулами (5.6). Предположим дЬлее,
что конечны интегралы от их абсолютных величин:
[ |Я(т) | dr < оо .
00
На практике это условие всегда выполняется для реализиций конечной дли-
ны. Тогда преобразования Фурье функций R(t) существуют и определяют-
ся формулами
Стационарные случайные процессы
131
Zoo
Rxx(^-^dr,
- 00
/00
Ryy(r)e-^ dr , (5.27)
- 00
sxy(f)= Г Rxy{^e-W dr.
J - 00
Такие интегралы по конечным реализациям существуют всегда. Величины
5^(7) и 5(7) называются функциями спектральной плотности процес-
сов [xk(t)\ и [yk(t)] соответственно или просто спектральными плотно-
стями, а 5(7) называется взаимной спектральной плотностью {хк( /)] и
Обратные преобразования Фурье от формул (5.27) дают
U') = Г Sxx(f)e^df,
•'-00
/00
Syy(f)e™'df, (5.28)
- 00
Rxy(r)={XSxy(f)e^df.
J - 00
При решении практических задач приходится допускать наличие в /?(т) и
5(7) дельта-функций. Соотношения (5.27) и (5.28) часто называются фор-
мулами Винера — Хинчина в честь математиков Н. Винера из США и
А. И. Хинчина из СССР, которые в начале 30-х годов независимо устано-
вили связь между ковариационными функциями и спектральными плотно-
стями через преобразование Фурье.
Из свойств симметрии стационарных ковариационных функций, описы-
ваемых формулами (5.9) и (5.10), следует, что
sxx(-f) = sx*x(f) = sxx(f), (5 29)
syy(-f) = s*(/) = syy(/) ,
Sxy(-f) = Sx*y(f) = Syx(f). (5.30)
Следовательно, спектральные плотности 5^(7) и Syy(f) — действитель-
ные четные функции от 7, а взаимная спектральная плотность — ком-
плексная функция от 7- Позже будет доказано также, что S(f) и 5WW(7)
ЛЛ уу
неотрицательны для всех f.
5
132
Глава 5
Формула (5.30) доказывается следующим образом. По определению,
М~/) = Г Rxy^)e^dr,
J - 00
/00 „ Z
- 00
sxy(f)= Г Ryx(r)e~^ dr.
* — 00
Сразу видно, что S (- f) = S*y(f). Выполним теперь замену переменных
в первом интеграле, положив, т = —uf dr = —du. Тогда
/00
Rxy(-u}e-^udu.
- 00
Но R(-u) = RvAu) согласно формуле (5.10). Поэтому
луv ул
/ОС
RYX(u)e~j2”fu du = Syx(f),
- 00
что завершает доказательство. Формулы (5.29) — частный случай форму-
лы (5.30) при x(t) = y(t).
Спектральные соотношения из формул (5.27) можно преобразовать к
виду
sxx(f)=f Rxx(r)cos2irfTdT = 2 f Rxx(r)cos27rfrdT,
•'-oo A)
(5.31)
Syy(f)=[ Ryr(r)cos2irfTdr = 2 ( R (t)cos2tt/t Jt.
•'-oo •'o
Обратные преобразования имеют вид
Rxx('r) = 2f Sxx(f)cos2irfrdf,
Jo
(5.32)
Ryv(r) = 2 f S (/)cos2w/rJ/.
Jo
Односторонние спектральные плотности G^f) и G (f)9 где f изме-
няется только в пределах интервала (0, оо), определяются формулами
Gxx{f) = 2Sxx(J\ 0<f<ao-
(5.33)
Gyy(f) = 2Syy(f), 0 </<оо,
а вне указанной области значений f имеем Gvv = Gvv - 0. Именно эти ве-
уу
Стационарные случайные процессы
133
Рис. 5.3. Односторонняя и двусторонняя спектральные плотности.
личины измеряются на практике с помощью прямой фильтрации. Однако
использование в математических расчетах функций S^f) и Syy(f), опреде-
ленных на ( — оо, оо), и показательных функций с мнимым аргументом ча-
сто упрощает анализ. Большое значение имеет возможность свободно опе-
рировать с обоими представлениями, и оба они будут использоваться в
этой книге. Рис. 5.3 иллюстрирует связь между этими функциями.
Односторонние спектральные плотности Gxx(f) и Gyy(f) связаны со
стационарными ковариационными функциями RXX(T) и Ryy(r) соотно-
шениями
Gxx(f) = 4 Г Rxx(T)cos27rfrdr, 0 </< оо ;
•'о
(5.34)
GZ(,(/) = 4y Ryy(r)cos2irfrdT , 0 < / < оо .
Обратные преобразования имеют вид
RXX(T) = f Gxx(f)co$2irfrdf ,
00 (5-35)
Ryy(T) = fQ Gyy(f)cos2irfrdf .
В частности, при т = 0 получаем
Rxx(0) = Е[х2(0] = ^ = Гсхх(/) df,
•'о
(5.36)
Ryy(0) = £[/(r)] = е = J^Gy.Af) df .
Односторонняя взаимная спектральная плотность Gvv(/), где f изменя-
Л/ v
134
Глава 5
ется на (0, оо), определяется как
Gx//) = 2^(/), 0</<оо, (5.37)
а в остальных случаях Gvu = 0. Из формулы (5.27) имеем
Gxy(f) = 2 Г Rxy(r)e-^ dr = Cxy(f) ~jQxyU), (5-38)
J 0
где C (f) называется коспектралъной плотностью (коспектром), а
0^(7) — квадратурной спектральной плотностью (квадратурным
спектром). В терминах С (f) и Qxy(f) взаимная ковариационная функция
имеет вид
Rxyb} = Jo [Cxy(f)cos2irfT + Qxy(f)sin2irfr] df. (5.39)
Заметим, что C (f) и Qxy( t) выражаются через Gxy(f), а не через
5^(7)* Отметим также, что при т = 0
Rxy(0) = Е [х(0 ЯО] = f°CXy(f) df. (5.40)
•'о
Величину Rxy(O) можно определить, зная С (f) = Re[G (/)].
Одностороннюю взаимную спектральную плотность можно предста-
вить в комплексной полярной форме:
Gxv(/) = l^,(/)KA‘<Z>, 0 </<оо, (5.41)
где модуль и фазовый угол определяются формулами
\Gxy(f) | = fCx2y(f) + Q2xy(f), (5.42)
OXy(f) = аг^ (5.43)
^xy\J /
Знаки членов Cxy(f) и Qxy(f) могут быть как положительными, так и от-
рицательными, и их сочетание определяет квадрант, в котором располага-
ется фазовый угол. Эти знаки определяют также частоты, на которых
функция у( t) опережает x(t) или х( t) опережает у( t). Если реализация
у( t) опережает х( /), то это означает, что у( t) = х( t — т0), где т0 > 0 и
0^(7) = 2тг/т0- Связь фазового угла с Cxy(f) и Qxy(f) показана на
рис. 5.4. Аналогично двусторонняя взаимная спектральная плотность в
комплексной полярной форме имеет вид
М/) = 1М/)1<?’АЛ/),
(5-44)
Стационарные случайные процессы
135
-Cxy(f)
V2 < QxAf) < *
y(t) опережает x(t)
на частоте f
О < Qxy{f) < ,7/2
y(t) опережает x(t)
на частоте f
< Qxy(f) < -w/2
x(t) опережает y(t)
на частоте f
-v/HQxy(D£O
x(t) опережает y(t)
на частоте f
+ cxy(f)
Рис. 5.4. Связь между фазовым углом и составляющими взаимной спектральной
плотности.
где 15^(7)! = I Gxy(f)\/2, a &ху(Л то же, что и в формулах (5.41) и
(5.43).
Из формулы (5.38) следует, что
Cxy(f) = 2/о°°[Ях,(т) + Ryx(T)]cos2irfTdT = Cxy(-f) ,
(5-45)
Qxy(f) = 2fo [лх>,(т) - A/X(r)]sin2w/TJT = -Qxy(-f)-
Поэтому Cx (f) — действительнозначная четная функция /, a Qxy(f) —
действительнозначная нечетная функция f. Итак,
Сху(П = 1[.GX,(/) + ^х(/)] = |Gx//)|cos^(/),
(5.46)
QXy(f) = 0/2)[<л,(/) - <М/)] = |Gx,(/)|sin вху(/).
Спектральные характеристики стационарных случайных процессов
[хк( /)] и [^( /)], описываемые тремя функциями S^C/), Syy(f) и Sxy(f)
или четырьмя функциями 5^(7), 5^(7), Cxy(f) и Q (/), достаточно вы-
числять только для / > 0, поскольку соотношения (5.29), (5.30) и (5.45) по-
зволяют вычислить их для f < 0. Очевидно, соответствующие функции G
должны вычисляться только для / > 0.
При выполнении операций над спектральными плотностями, включаю-
щими дельта-функции в f = 0, удобно считать, что нижний предел инте-
грирования понимается как предел слева в нуле. В частности, если
R(t) = с2, то отсюда следует, что G(f) = с26(/). В этой ситуации S (f)
тоже имеет вид S(f) = с26(/), т. е. множитель 2 в формуле (5.37) в случае
Таблица 5.2. Функции спектральной плотности, применяемые в теоретических
исследованиях
Тип (Односторонние) спектральные плотности
Постоянная Gxx(/)-C2S(/) 0
Г армониче- ская 0 f0
Белый шум 2а 1 Gxx(f) = f > 0; в остальных случаях Gxx ^f0 0
Низкочастотный белый шум а Gxx(f) ayQ < f < В\ в остальных случаях 0 В Gxx = °
Ограниченный по частоте белый шум в GXK(/) = a, 0 </0 - ( В/2) < / </0 + (В/2); в остальных случаях G =0 о f0
Экспоненциальная Gxx(f)= 2 22 0 а+ 4тг72
Экспоненциально- косинусоидальная G„(/) = 2a - + i [а2 + 4w2(/ + /0) а1 + 4тг2 (/-/0) 0
Экспоненциально- косинусоидально- синусоидальная G z f Л _ 2а6 + 4”с(/ + /о) + - 4те(/-/о) 0 а2 + 4w2 (/+/0)2 а2 + 4тт2(/-/0)2
Стационарные случайные процессы
137
дельта-функции в f = 0 отсутствует. Это рассуждение не имеет силы для
ковариационных функций, содержащих дельта-функцию в т = 0, поскольку
ковариационные функции определены для всех т. Поэтому 7?(т) = аб(т) со-
ответствует как плотности S(f) = а для всех /, так и G(b) = 2а для
0.
В табл. 5.2 приводятся примеры функций спектральной плотности, при-
меняемых в теоретических исследованиях.
Ограниченный по частоте белый шум. По определению, ограниченный
по частоте белый шум — это стационарный случайный процесс с постоян-
ной спектральной плотностью вида
С„(/)-Ь °^»-(*/2)</</о+(В/2); (54?)
(0, в остальных случаях.
Здесь /0 — центральная частота прямоугольного фильтра с шириной поло-
сы В. Процесс этого вида называется также узкополосным белым шумом.
По формуле (5.35) находим, что соответствующая ковариационная функция
есть
7 х Г/о + (^/2) / SH1 ТТ2?Т \
^(T) = / acos2w/r dr = аВ\—-— cos2tt/0t. (5.48)
Jf0-(B/2) \ чтВг )
В частном случае /0 = В/2 процесс называется низкочастотным белым
шумом и имеет спектральную плотность вида
GxAf)={a' (5.49)
в остальных случаях.
с ковариационной функцией
I sin2irBr\
КхАт) = ’ (5.50)
\ IttBt /
Соответствующие графики изображены в табл. 5.1 и 5.2. Узкополосный
белый шум, в том числе и низкочастотный, имеет конечный средний
квадрат вида
Г^х(/)^=^ = ЛЛЛ(0). (5.51)
•'о
Такими плотностями иногда аппроксимируют спектры реальных про-
цессов.
Предельный случай низкочастотного ограниченного по частоте белого
шума, именуемый белым шумом, по определению, имеет спектр, равный
постоянной для всех частот. Такой процесс на практике встретиться не
может. Именно в случае белого шума при / > 0
GxAh = a-
(5.52)
138
Глава 5
Поэтому
Sxx(f) = (a/ty Для любых значений/, (5.53)
Ахх(т) = (а/2)5(т), (5.54)
/“<U/H=oo = W (5.55)
Jo
откуда видно, что белый шум имеет бесконечный средний квадрат. Такой
чисто теоретический белый шум не может быть гауссовым процессом, по-
скольку для корректного определения гауссова процесса его средний ква-
драт должен быть конечным.
ПРИМЕР 5.5. СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ ГАРМОНИЧЕСКОГО ПРО-
ЦЕССА. Ковариационная функция гармонического процесса, описанного в
примере 5.1, имеет вид
X2
Rxx(t) = —cos2w/0T.
Подстановка в формулу (5.27) дает двустороннюю спектральную плот-
ность
X2
Sxx(/)= Т[5(/-/о) + 5(/ + /о)Ь
состоящую из двух дельта-функций, локализованных в f = /0 и f = — /0.
Поэтому односторонняя спектральная плотность равна
X2
GJJ)=
График этой функции изображен в табл. 5.2. Заметим, наконец, что
у-2
f°Gxx(ndf= — = ЯЛХ(0).
•'О 2
ПРИМЕР 5.6. СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ ТЕЛЕГРАФНОГО СИГНАЛА.
Телеграфный сигнал, описанный в примере 5.2, имеет ковариационную
функцию экспоненциального вида
Лхх(т) = с2е-2Х^.
Подстановка в формулу (5.27) дает двустороннюю спектральную плот-
ность
Стационарные случайные процессы
139
X2 + 7Г2/2 ’
Поэтому односторонняя спектральная плотность имеет вид
2Хс2
GxxW) = Л2 + ^2 •
График этой функции приведен в табл. 5.2 для а = 2Х и с2 = 1. Заметим,
что
Гехх(/)^=с2 = Лхх(0).
Jo
ПРИМЕР 5.7. СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ СУММЫ ДВУХ ПРОЦЕССОВ.
Ковариационная функция суммы двух стационарных случайных процессов,
описанных в примере 5.3, равна
Ryyk'r) = ^Кхл(т) + <2^2[т) + ЯХ2Х,(т)] + alRX2X2(T) .
Подстановка в формулу (5.27) дает двустороннюю спектральную плот-
ность
Syy(f) = a2SXiXi(f) + ^a2[SX2X2(f) + SX2X1(/)] + a2SX2X2(f) .
Однако SX2Xi(f) = S*iX2(f), поэтому
S„x2(/) + $x2x,(/) = 2Re[5XiJJ/)] = CXtX2(f) .
Следовательно, S (f) — действительная функция и может быть записана
в виде
Syy(f) = a2SXiXi(f) + aia2CXiX2(f) + a2SX2X2(f) .
Соответствующая односторонняя спектральная плотность имеет вид
Gyy(f) = alGx^f) + 2aia2CXiX2(f) + a2GX2Xi(f) .
5.2.2. ОПРЕДЕЛЕНИЕ СПЕКТРОВ ЧЕРЕЗ ФИНИТНОЕ
ПРЕОБРАЗОВАНИЕ ФУРЬЕ
Второй способ определения спектральных плотностей по своему харак-
теру тоже является математическим. Он основан на финитном преобразо-
вании Фурье реализаций исходного процесса. Именно этот способ в настоя-
щее время используется для вычисления спектральных плотностей.
140
Глава 5
Рассмотрим пару реализаций хк( t) и ук( t) стационарных случайных
процессов [xk(t)\ и Определим на конечном интервале времени
0 t С Т функцию
\,.(/,ТД)= |хЛ/,Т)П(/,Т), (5.56)
где
Х.(/,Т)= jTxk^e-^dt,
•'о
(5.57)
У.(/,Т)= jTyk(t)e-^ dt.
Величины Xk(f, Т) и Yk(f, Т) — это финитные преобразования Фурье ре-
ализаций хк( t) и ук( t) соответственно, а %£(/, Г) — величина, комплекс-
носопряженная Xk(f, Т). Такие преобразования Фурье по конечному ин-
тервалу существуют для реализаций широкого класса случайных процессов,
в то время как преобразования Фурье по бесконечному интервалу обычно
не существуют, поскольку теоретически стационарный процесс определен
на всей оси времени.
Распространенная ошибка состоит в том, что по аналогии с периодиче-
скими процессами взаимную спектральную плотность определяют по фор-
муле
sxy(f,k)= lim S(f,T,k). (5.58)
Г—» ос
Это определение не годится в случае стационарных случайных процессов
общего вида, поскольку при стремлении Т к бесконечности оценка S (f,
Т, к) величины S (j\ к) не становится лучше в статистическом смысле,
т. е. она не состоятельна (по определению разд. 4.1). Вспомним теперь,
что левая часть зависит еще и от индекса к. Правильное определение
Дает следующее выражение:
Sxy(f)~ Um E[Sxy(J,T,k)], (5.59)
где E[Sxy(f, Т, £)] — это, разумеется, математическое ожидание, взятое
по множеству индексов к. Спектральные плотности S^f) и Syy(f) — это
просто частные случаи формулы (5.59). Докажем эквивалентность опреде-
лений (5.59) и (5.27).
Обозначив во избежание недоразумений переменные интегрирования
разными символами, перепишем формулу (5.56) следующим образом:
Sxy(f, Т,к)=^~ (TxMe^ada [Tyk^)e~^dp =
1 •'о •'о
= 7ГГхМук(^)е-^^~а> dad/З . (5.60)
2 •'О •'О
Стационарные случайные процессы
141
Преобразуем теперь область интегрирования путем замены переменных (а,
0) на (а, т), где т = 0 — а, dr = d(3. Приведенный ниже чертеж показыва-
ет, как изменятся пределы интегрирования.
Интегрируя по паре переменных (а, т) вместо пары переменных (а, 0), по-
лучим
(T(Tdad/3= (° (Т dadr + Г Г 'dadr . (5.61)
Л) Л) J-TJ-t •'О
Легко убедиться, что обе части соотношения (5.61) равны Т2. Поэтому та-
кое преобразование области интегрирования позволяет переписать формулу
(5.60) в виде
dr +
e-'2”/TdT. (5.62)
По определению, взаимная ковариационная функция Rxy(r) равна мате-
матическому ожиданию
= Е\хк(а)ук(а + т)] . (5.63)
Взяв математическое ожидание от обеих частей формулы (5.62), получим
E[Sxy(f,T,k)] =
тГ 1
е
Rxy(r) da е j27TfT dr—
= Г(1 -
J -Т\ 1 /
(5.64)
142
Глава 5
В пределе, когда Т стремится к бесконечности, имеем
lim Т, Лг)] = Г Rxy(r)e-^dT. (5.65)
Т-* оо J — оо
Это и есть искомое утверждение (5.59), поскольку правая часть формулы
(5.56) равна Sxy(f) согласно определению (5.27).
Заметим, что замена S(f) на соответствующие G(f) приводит к
следующим формулам:
Gxy(f) = 2 lim ~E[Xk*(f, T)Yk(f, T)J, (5.66)
G„(/)-2ta ^£[|Л-Д/, Г)Р] G„(/)-2 lim ^[iW. П12].
/-♦ooi J > Г-+001
(5.67)
Для вычислений по этим формулам применяются реализованные на ЭВМ
процедуры быстрого преобразования Фурье, описанные в гл. 11. На прак-
тике длина реализации Т всегда конечна, так как предельный переход
Т — оо осуществим только теоретически. Математическое ожидание Е [ ]
также всегда берется только по конечному ансамблю, поскольку невозмож-
но получить бесконечный набор реальных данных.
5.2.3. ОПРЕДЕЛЕНИЕ СПЕКТРОВ С ПОМОЩЬЮ ФИЛЬТРАЦИИ
Третий способ вычисления-спектральной плотности подразумевает при-
менение аналоговых устройств и включает следующие операции, схемати-
чески представленные на рис. 5.5:
1) частотную фильтрацию сигнала x(t) с помощью узкополосного
фильтра с полосой пропускания Д f и центральной частотой /0; в результа-
те этой операции получается величина х(/0, Д /, Z);
2) возведение в квадрат мгновенного значения отфильтрованного сиг-
нала;
3) усреднение квадрата мгновенного значения по реализации длины Т; в
результате этой операции образуется оценка среднего квадрата отфильтро-
ванного сигнала;
4) деление на ширину полосы пропускания фильтра Д /, в результате че-
го получается оценка скорости изменения среднего квадрата в зависимости
от центральной частоты /0.
Следовательно, оценка спектральной плотности имеет вид
<L(/) = /оГх2(/о, Д/, 0 dt . (5.68)
Для вычисления взаимной спектральной плотности аналоговыми мето-
дами применяется прямое обобщение описанной процедуры на случай двух
сигналов x(t) и у( t), которое включает следующие операции:
1) раздельную частотную фильтрацию обоих сигналов с помощью узко-
полосных фильтров, имеющих одинаковые полосы пропускания Д f и одну
Стационарные случайные процессы
143
Рис. 5.5. Измерение спектральной плотности аналоговыми методами.
и ту же центральную частоту /0; в результате получаются х(/0, Д/, t) и
2) перемножение мгновенных значений двух отфильтрованных сигналов
при отсутствии сдвига фазы между ними с целью получения синфазных
членов, необходимых для вычисления коспектра;
3) перемножение мгновенных значений двух отфильтрованных сигналов,
причем j(/0, Д /, t) сдвигается по фазе на 90° по отношению к х(/0, Д /,
/), с целью получения смещенных по фазе членов, что нужно для вычисле-
ния квадратурного спектра;
4) усреднение каждого из этих произведений по реализации длиной Т с
целью построения оценок средних произведений синфазных и смещенных
по фазе членов;
5) деление каждого из средних произведений на ширину полосы пропу-
скания Д f для получения оценок Cxy(fQ) и QXJ(/0). Тогда оценка взаимной
спектральной плотности имеет вид
вхуШ = 4,(/о) - jQx,M , (5.69)
где 1
4//о) = /о^(/о, А/, А/. 0 dt,
° (5.70)
А А ГТ
<2хуШ = /о х(/0, А/, А/, /) dt.
Здесь у°(/0, Д /, t) — сдвинутый по фазе на 90° отфильтрованный сигнал
y(f0, bf, t).
Эквивалентность этого третьего, аналогового определения спектраль-
ных плотностей предыдущим двум математическим определениям из
разд. 5.2.1 и 5.2.2 не очевидна и требует доказательства. Приведем такое
доказательство для автоспектров. Эквивалентность обоих определений вза-
имной спектральной плотности доказывается аналогично.
Рассмотрим определение спектральной плоскости из формулы (5.67),
где
Gxx(/) = 2 1im -£[|ХД/, Т)|2]. (5.71)
/-*оо 1
Величина
\Xk(J,T)\2 =
I xk(t)cos2irftdt
о
2 fT
+ / (z)sin 2тг/гdt
(5.72)
144
Глава 5
действует как фильтр, выделяющий значение среднего квадрата хк( t) в уз-
кой полосе частот, окружающей центральную частоту f. Чтобы доказать
это неочевидное утверждение, определим для любой реализации xk(t) про-
цесса [хк( г)] величину
X (t Т}= ® < t < Т; / ч
в остальных (э./З;
случаях.
Тогда средний квадрат конкретной реализации xk(t) можно выразить фор-
мулой
$2х(к) = lim - fTxt(t) dt = lim - f x2k(t,T)dt. (5.74)
T-*oo/*0 T —> ос / — oo
Если F (/) — преобразование Фурье /(Г), то по теореме Парсеваля
Г f\t)dt= Г \F(f)\2df. (5.75)
J — 00 J — 00
Доказательство этого соотношения оставим в качестве простого упражне-
ния. Поскольку Xk(j\ Т) — это преобразование Фурье хк{ t, Т), т. е.
XkU,T) = [Txk(t)e ^1 dt = Г xk(t,T)e-Wdt, (5.76)
J0 J-<x>
TO
^U) = lim \Xk(f,T)\2df=2 lim F\Xk(f, T)\2 df.
1 00 1 — оо T —» оо 1 J 0
(5-77)
Тогда, взяв математическое ожидание от фх(к) по всевозможным реализа-
циям xk(t) процесса [xk(t)}, получим уже знакомую формулу
^ = E[^U)] = f°°Gxx(f) df, (5.78)
•'о
где Gxx(f) определено формулой (5.71).
Предположим теперь, что xk(t) проходит через узкополосный фильтр с
центральной частотой /0 и полосой пропускания Д /, имеющий частотную
характеристику Н (/) вида
OS/o-W/2)S/S/o + (A//2); (5 79)
( 0 f в остальных случаях.
Стационарные случайные процессы
145
Тогда преобразование Фурье процесса на выходе фильтра равно
H(f) Xk(f, Т), где Xk(f, Т) — преобразование Фурье входного процесса.
Поэтому вместо формулы (5.77) для среднего квадрата отдельной от-
фильтрованной реализации хк( t) получим выражение
1 fOC
ф2(/0,Д/Д) = 2 Um -/ |//(/)|2|%A(/,T)|2t//. (5.80)
Г —* оо 1 •'О
Взяв математическое ожидание от обеих частей формулы (5.80), получим
«Ш0,Д/) = Г|Я(/)|2(7ЛЛ(/)#= (5.81)
0 А) </0-(Д//2)
Таким образом, формула (5.81) утверждает, что Gxx(f) есть скорость из-
менения среднего квадрата в зависимости от частоты. Кроме того, опе-
ратор \Xk(j\ Т)\2 действует на реализацию xk(t) как фильтр, который
пропускает только те ее составляющие, что лежат в узкой полосе частот, а
затем возводит в квадрат значения на выходе до выполнения соответству-
ющих операций усреднения. Именно на таком принципе действуют анало-
говые спектральные анализаторы.
5.2.4. ФУНКЦИИ КОГЕРЕНТНОСТИ
Сейчас мы дадим простое прямое математическое доказательство нера-
венства для взаимной спектральной плотности:
\Gxy(f)\2 Gxx(f)Gyy(f). (5.82)
Этот результат значительно сильнее аналогичного неравенства (5.11) для
взаимных ковариационных функций, в котором I 7? (т)12 оценивается про-
изведением (0) ДО), содержащим значения Ryy(t) и RvAt) в точке
хх уу лл уу
т = 0.
Для любого значения f функцию GY(f) можно представить как
Gxy(f) =
через модуль \Gxy(f)\ и фазу 6xy(f). Известно также, что
Gyx(f) = G*y(f) = \Gxy(f)\eM)^
Рассмотрим теперь величины Xk(f) и Yk(f) exp[j0XJ(/)]> где Xk(f) и
Yk(f) — финитные преобразования Фурье реализаций xk(t) и yk(t) соот-
ветственно. Для любых действительных чисел а и b справедливо нера-
венство
|аХЛ/) + />Ш)е^</)|2>0.
146
Глава 5
a W/)|2 + ab[Xk^f)Yk(f)e^ + Xk(f)YW)e-*„<'>]+
+ b2\Yk(f)\2 > 0.
Перейдем в этой формуле к математическому ожиданию по индексу к; ум-
ножив обе ее части на 2/Г и устремив Т к бесконечности, получим
a2Gxx(f) + аЬ\вху(Пе^ + Gyx(f)+ b2Gyy(f) > 0.
Здесь были использованы определения автоспектров и взаимных спектров
(5.66) и (5.67). Согласно формуле (5.41),
Gxy(f)e^n + Gyx(f)e~W> = 2|GX,(/)|,
следовательно,
a2Gxx(f) + 2ab\Gxy(J)\ + b2Gyy(f) > 0.
В точности повторяя рассуждение, использованное при доказательстве не-
равенства для взаимных ковариационных функций, убеждаемся в справед-
ливости неравенства (5.82), т. е.
\Gxy(f)\2<Gxx(f)Gyy(f).
Отсюда следует одновременно неравенство для двусторонних взаимных
спектров: для всех f
|SX//)|2 < Sxx(f)Syy(f) . (5.83)
Теперь можно определить функцию когерентности (называемую иног-
да квадратом когерентности)
, . |G,,(/)|2 _ |S„(/)I;
' s,,(nsn(f)
которая для любых f удовлетворяет неравенствам
0 < у2//) < 1 . (5.85)
Комплексная функция когерентности yxy(f) определяется формулой
Ухуи) = , (5.86)
где
|УхЛ(/)| = +^Yxy(f)
(5.87)
Стационарные случайные процессы
147
а 0*//) — фазовый угол Gxy(f). Всюду в этой книге под функцией коге-
рентности будет пониматься действительная функция (5.84), a
всегда будет пониматься как квадратный корень из у* (/).
5.2.5. ВЗАИМНАЯ СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ
ПРИ НАЛИЧИИ ЗАПАЗДЫВАНИЯ
Согласно формуле (5.20), взаимная ковариационная функция в задаче
определения запаздывания (см. рис. 5.1) равна
Rxy(T) = aRxxb - То) • (5.88)
Подставив в формулу (5.27), получим двустороннюю взаимную спектраль-
ную плотность
Sxy(f) = aSxx(f)e-W° . (5.89)
Соответствующая односторонняя взаимная спектральная плотность имеет
вид
Gxy(f) = aGxx(f)e-J2”^ . (5.90)
Поэтому в силу формулы (5.41)
1<М/)1 = а(М/), (5.91)
^(/) = 2^/т0. (5.92)
Следовательно, сдвиг времени т0 участвует только в фазовом угле 0xy(f).
Измерение 0ху(Ь) позволяет определить сдвиг времени, поскольку 0xy(f) —
линейная функция от f с наклоном, равным 2тгт0 (рис. 5.6). Коэффициент
затухания а на всех частотах f равен
« = [lM/)l/Gxx(/)]. (5.93)
Рис. 5.6. Типичный график зависимости фазового угла от частоты в задаче
определения запаздывания.
148
Глава 5
Односторонние спектральные плотности передаваемого сигнала x(t) и
принимаемого сигналаy(t) для схемы, изображенной на рис. 5.1, равны со-
ответственно G(f) и Gvv(/), где
ЛЛ уу
Gyy(f) = a2Gxx(f) + G„„(f). (5.94)
Этот результат также непосредственно следует из формулы (5.26). Для лю-
бого значения /, согласно формулам (5.84) и (5.91), функция когерентности
равна
2(П 1^(/)Г
Ух^}) Gxx(f)Gyy(n а [с,//)
Заметим, что Gyy(f) имеет две составляющие — соответственно вклад
x(t) в спектр y(t) и вклад n(t) в спектр y(t):
a2<U/) = Yx2//)^(/X GJJ) = [1 - У2,(/)К(/). (5.96)
Эти результаты более содержательны по сравнению с усредненными по
всем частотам результатами, приведенными в (5.25), где отсутствует зави-
симость от частоты.
С учетом выражения (5.94) для Gyy(f) функция когерентности из фор-
мулы (5.95) принимает вид
у2 (/) = ----- _____
У a2Gxx(f) + G„„(f) ’
где все члены в правой части неотрицательны. Очевидно, что для всех зна-
чений f y*y(f) 1, поскольку знаменатель не может быть меньше числи-
теля. В эквивалентной форме
ч . = [«2^(/) + G„H(/)]-Gn„(/) = Gyy(f)-Gnn(n =
' a2Gxx(f) + GJJ) Gyy(f)
= l-K(/)/G,,(/)]. (5-97)
И здесь очевидно, что т^(/) 1 для всех /, так как Gnn(f) Gyy(f). Ес-
ли впп(Л = 0, то т^(/) = 1, если же Gnn(f) = Gyy(f), то т^(/) = 0.
Определение положения максимума. Из формул (5.21) и (5.28) следует,
что максимум RyAt) равен
/ОО
SxvU)e^df. (5.98)
- 00
Обозначим оценки /?rv(rn) и S(f) соответственно через /?(тп) и £,(/).
___ V Ху vz Ху
Тогда
Стационарные случайные процессы
149
Sxy(f) = \SxyU)\e~A'(f} . (5-99)
Уравнение (5.98) перепишем в виде
Rxy(r0) = Г df~
J — оо
= Г |^(/)|cos[2w/T0 - $xy(f)] df,
J - 00
поскольку &ху(т^ принимает только действительные значения. В точке
максимума т0
= 0 = Г (-2w/)|Sx//)|sin[2^T0 - ^(/)] df .
OTq •'-00
По формуле (5.92) Qxy(f) » 2тгf т0, так что
sin[27r/r0 - 0Х>,(/)] = 2тт/т0 - 0^(/).
Отсюда следует приближенная формула
Г (-27г/)|^г(/)|[2тг/т0 - ^(/)] df* 0.
J — 00
Решив это уравнение относительно т0, получим
Г (2W/)|^(/)|^(/)#
J — 00 (С Л
Используя односторонние спектральные плотности <5 (/) вместо двусто-
ронних £(/), придем к эквивалентной формуле
/J(2W/)|GX//)|^(/)^
Т°" y°°(2w/)2|d ' (5Л01)
5.2.6. СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТИ
Рассмотрим стационарный случайный процесс {у(0] с нулевым сред-
ним значением, ковариационной функцией Куу(т) и соответствующей дву-
сторонней спектральной плотностью S (f) согласно определениям (5.6) и
150
Глава 5
(5.27), где
Syy(f) = Г Rvv(r)e~j2vfr dr = 2 (°°Ryy(r)cos2irfTdT,
J - оо •'о
(5.102)
Мт) = fKJyy(f)e^df= 2 ^S^n^lirf-rdf.
Известно также, что
ЛГДО) > ЯДт) для любых т,
(5.103)
Syy(f) >0 для любых f.
Вместо S (f) можно использовать одностороннюю спектральную плот-
ность Gyy(f), равную
Gyy(f) = [2Syy^’ ’ (5.104)
( 0 , /< 0 .
Следовательно,
Gyy(f^=4f0 Ryy(.'r)cos2‘rrfTdT , Ryy(r) = f Gyy(f)cos2vfTdf.
(5.105)
Сейчас мы дадим определения эффективной шумовой ширины спектра и
эффективного шумового времени корреляции. Для произведения этих вели-
чин будет установлено полезное соотношение неопределенности.
Эффективная шумовая ширина спектра по определению равна
В. - я„(0)/с,,(/)[„. (5.106)
Эффективное шумовое время корреляции определяется как
/ОО / /’ОС /
|7?>>>,(т)| Jt/я (т)|макс= 2J |Я (т)|</тR (0). (5.107)
- 00 / ' •'О /
Из этих соотношений следует, что
ВпТ„ = 2 Г|^(т)| dJGvv(n\макс (5.108)
•'О /
Оценка этого произведения и дает соотношение неопределенности', для
любой Ryy(r) и соответствующей G (f) произведение Вп и Тп удовлетво-
Стационарные случайные процессы
151
ряет неравенству
ВпТп>^2- (5.109)
Следовательно, с уменьшением Вп величина Тп растет и, наоборот, с
уменьшением Тп растет Вп.
Доказывается соотношение неопределенности следующим образом. Из
формулы (5.105) имеем для любого f
/•ОО fOC
G^(/)<4JT |^(t)cos2,7/t|Jt<4Jo |^(t)|Jt . (5.110)
Поэтому
С,//)1макс^4/Х,(т)Ит. (5.111)
•'о
Подставив неравенство (5.111) в формулу (5.108), немедленно получаем со-
отношение (5.109). Заметим, что в этом доказательстве неравенство
Коши — Буняковского — Шварца не используется.
ПРИМЕР 5.8. НИЗКОЧАСТОТНЫЙ БЕЛЫЙ ШУМ. В случае низкочастот-
ного белого шума имеем
S\,v(/) = я/2? ~B<f<B. в остальных случаях Syy = 0;
G (f) = 0 </< В; в остальных случаях Gyy = 0;
Луу(т) = аВ {8т(27гВт)/(2тгВт)}.
Для этого процесса эффективная шумовая ширина спектра равна
B„ = ^(0)/G^(/)|MaKC=B,
а эффективное шумовое время корреляции равно
/•ОО
^/0 \Ryy^dT 1 /-оо sinw
Следовательно, ВпТп = оо, что, конечно, удовлетворяет соотношению нео-
пределенности (5.109). Форма Ryy(T) подсказывает, что в этом случае удоб-
нее задать Тп как ширину главного максимума, в котором сосредоточена
основная часть энергии, а именно Тп = 1/В. Тогда Вп Тп = 1, т. е. соотно-
шение неопределенности выполняется и в этом случае.
152
Глава 5
ПРИМЕР 5.9. СПЕКТР ГАУССОВА ШУМА. Для этого процесса имеем
Ryyh) = “е
Syy(f) = (a/aj2ir)e f2''2”2, - оо </< оо;
Gyy(f) = (ay/l/o^e-f2^2, />0;
/•°° а 6уу(0)
/о ^(Т)1</Т= = ’
В этом случае эффективная шумовая ширина спектра равна
В„ = -^- = 1,25а.
Gyy(B„) = Gyy(0)e~”/4 0,456(7^(0) .
Эффективное шумовое время корреляции есть
1 0,40
Т = —1= =------- ,
<зу/1~*тг о
поэтому
Ryy(T„) = Ryy(0)e~” = 0,043Я,Д0) .
Заметим, что в случае гауссова шума соотношение неопределенности прев-
ращается в равенство ВпТп = 1 /2.
ПРИМЕР 5.10. ШУМ С ЭКСПОНЕНЦИАЛЬНОЙ КОВАРИАЦИОННОЙ
ФУНКЦИЕЙ. Для шума с экспоненциальной ковариационной функцией
имеем —
^(т)=Ле-“1т1, а>0;
Syy(f) = 2Аа/{а2 +(2тг/)2} , -оо</<со;
(?,//) = 4Ла/{ а2+(2^/)2}, />0;
г00 z G (0)
/0
Эффективная шумовая ширина спектра равна Вп = а/4. Тогда
Стационарные случайные процессы
153
Gyy(B„) = <7^(0)[1/{1 + (тг/2)2}] = 0,2886^,(0) .
Эффективное шумовое время корреляции есть Тп = 2/а. Следовательно,
Ryy{Tn} = Куу^е~г 0,10ЯЛ.Д0) .
В этом случае соотношение неопределенности тоже превращается в равен-
ство ВпТп = 1/2. Другие примеры, иллюстрирующие соотношение неопре-
деленности, можно построить, используя Rxx(r) и Gxx(f) из табл. 5.1 и
5.2.
5.3. Эргодические и гауссовы случайные процессы
С практической точки зрения важнейшими классами стационарных слу-
чайных процессов являются:
а) эргодические процессы с произвольной вероятностной структурой;
б) гауссовы процессы, эргодические или неэргодические.
Сейчас мы изучим эти два класса случайных процессов, а также линей-
ные преобразования случайных процессов.
5.3.1. ЭРГОДИЧЕСКИЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
Рассмотрим два слабо стационарных случайных процесса [хк( /)] и
\ Ук( /)] и две их произвольные выборочные функции хк( t) и yk(t). Эти
стационарные случайные процессы называются слабо эргодическими, если
их средние значения и ковариационные (корреляционные) функции, которые
в разд. 5.1.1 были определены путем усреднения по ансамблю, можно вы-
числить с помощью усреднения по времени любой пары выборочных функ-
ций. Таким образом, исходная вероятностная структура таких слабо стаци-
онарных случайных процессов легко определяется по любой паре реализа-
ций, и, следовательно, отпадает необходимость накопления большого чис-
ла данных.
Например, средние значения конкретных выборочных функций хк{ t) и
ук( (), вычисленные путем усреднения по времени, можно представить как
= l>m - f\(‘) dt,
T-*oo 1
(5.112)
1 rT
р. (к) = lim - / yk(t)dt.
Т-* оо 1 •'О
Заметим, что результат уже не зависит от (, поскольку по t было выполне-
но усреднение. Однако в общем случае результат зависит от выбора кон-
кретной выборочной функции, что отмечено индексом к.
Взаимные корреляционная и ковариационная функции реализаций хк( t)
и ук( t + т), вычисленные путем усреднения по времени, определяются вы-
154
Глава 5
ражением
Сх„(т,Л)= Нт + т) dt =
Т->оо 1 •'О
1 т
= lim - / xk(t)yk(t + т) dt - ух(к)цу(к) =
Г—оо Т •'о
= Rxy(r,k) - MxUW*:) • (5.113)
Ковариационная и корреляционная функции имеют вид
С(т,к) = Hm Hxk(t) -Цх(к)][хк(1 + т) -дДЛ)] dt =
Т-00 Т Jq
= Rxx(-r,k)- pW ,
(5.114)
С^(т, к) = ^lim^ у^Г[л(0 “ М.Л^)][л(< + т) - dt =
= Л^(т, к) - ц2у(к) .
Сравним теперь эти величины с ранее определенными средними значе-
ниями /хх, цу и корреляционными функциями Cvy(t), Суу(т), С (т), вычис-
ленными путем усреднения по ансамблю в предположении стационарности
соответствующих процессов (см. разд. 5.1.1). Если окажется, что независи-
мо от значения к
= Мх >
Му(*) = .
Схх(т,к) = Схх(т) , (5.115)
Суу(т,к) = Суу(т),
= Сху^)>
то случайные процессы [ хк( t)} и [yk(t)] называются слабо эргодически-
ми, Если все статистические характеристики [хк( Г)] и [ук( г)], определен-
ные путем усреднения по ансамблю (а не только средние значения и кова-
риационные функции) совпадают с соответствующими величинами, полу-
ченными с помощью усреднения по времени, то такие случайные процессы
называются строго эргодическими. Следовательно, строгая эргодичность
Стационарные случайные процессы
155
влечет слабую1), но не наоборот. Для гауссовых случайных процессов оба
понятия совпадают.
Для эргодичности некоторого процесса прежде всего требуется, чтобы
он был стационарным. Каждая выборочная функция в равной степени
представляет весь процесс в указанном выше смысле, так что выбор какой-
либо конкретной реализации для выполнения усреднения по времени не
имеет никакого значения. В случае эргодических процессов x(t) и y(t) для
определения их ковариационной и взаимной ковариационной функций вме-
сто формулы (5.6) можно использовать следующие формулы:
КХЛ(т) = lim - (Tx(t)x(t + т) dt,
Т-*оо 1 •'о
1 гТ
Ryy^)= lim - y(t)y(t + т) dt, (5.116)
Г—>оо 1 •'О
Ях^(т)= lim - (Tx(t)y(t + т) dt.
ПРИМЕР 5.11. НЕЭРГОДИЧЕСКИЙ СТАЦИОНАРНЫЙ СЛУЧАЙНЫЙ
ПРОЦЕСС. Приведем простой пример неэргодического стационарного слу-
чайного процесса. Рассмотрим случайный процесс состоящий из
гармонических выборочных функций вида
{**(')} = {^*sin[2w/i + 0J).
Пусть амплитуды Хк и фазовые углы 6к — случайные величины, принима-
ющие разные значения в разных реализациях (рис. 5.7). Если 0к распределе-
ны равномерно, то характеристики процесса, вычисленные путем усредне-
ния по ансамблю в фиксированные моменты времени, не зависят от време-
ни; следовательно, процесс стационарен. Однако характеристики, вычис-
ленные усреднением по времени отдельных выборочных функций, могут и
не совпасть. Например, ковариационная (или корреляционная) функция, вы-
численная по произвольной выборочной функции, равна
Схх(т, Л) = —8т2тг/т .
Поскольку Хк зависит от к, то СлЛ.(т, к) Ф С/т). Следовательно, этот слу-
чайный процесс не эргодичен.
Предположим теперь, что вместо случайных амплитуд [л^] в определе-
нии процесса взяты неслучайные амплитуды, т. е. не зависящие от к. Тог-
1)
Если существует момент второго порядка. — Прим, перев.
156
Глава 5
Рис. 5.7. Пример неэргодического стационарного гармонического процесса.
Рис. 5.8. Пример эргодического гармонического процесса.
Стационарные случайные процессы
157
да случайный процесс будет состоять из выборочных функций вида
= {Xsin(2TT/Z + 0*)} .
Такой случайный процесс эргодичен, каждая его реализация статистически
эквивалентна любой другой реализации с точки зрения операции усредне-
ния по времени, что иллюстрирует рис. 5.8. На этом пример 5.11 заканчи-
вается.
5.3.2. ДОСТАТОЧНЫЕ УСЛОВИЯ ЭРГОДИЧНОСТИ
Известны два важных класса заведомо эргодических случайных процес-
сов. Первый класс состоит из стационарных гауссовых процессов с абсо-
лютно непрерывными спектральными плотностями, т. е. в их спектре нет
дельта-функций, соответствующих бесконечным значениям плотности сред-
него квадрата на фиксированных частотах. Второй класс эргодических про-
цессов (входящий в первый) — это стационарные гауссовы марковские про-
цессы; марковский процесс — это процесс, будущие значения которого за-
висят только от одного непосредственно предшествующего значения. Мож-
но показать, что ковариационная функция стационарного гауссова марков-
ского процесса имеет простой экспоненциальный вид [5.3].
Достаточные условия эргодичности произвольного случайного процесса
таковы.
I. Для слабой эргодичности произвольного случайного процесса доста-
точно, чтобы процесс был слабо стационарным и его цх(к) и Схх(т, к),
вычисленные усреднением по времени, были одинаковыми для всех выбо-
рочных функций к.
Докажем это утверждение. По определению,
Мх(^)= lim -fTxk(t)dt.
Т->оо 1 •'о
По предположению рх(к) не зависит от к. Следовательно, математическое
ожидание по к совпадает с оценкой по одной реализации, а именно
Е[рх(к)] = рх(к). Ниже будет показано, что математическое ожидание
перестановочно с линейными операциями. Следовательно,
Е [М^)] = Jim - dt =
Т-*оо 1 •'О
1 [Т
= Нт - / dt = рх.
Т-+0О Т •'Q
В силу предположения о слабой стационарности £[хАг( /)] = Поэтому
/хг( к) = рх. Аналогично Сл.¥(т, к) = С (т)9 поскольку предположение не-
зависимости Схх(т, к) от к влечет за собой равенство Е \Схх(т,
158
Глава 5
£)] = С (т, к), в то время как из предположения стационарности следует,
что Е [Схх(т, £)1 = Схх(тУ
Утверждение доказано.
II. Для эргодичности гауссова случайного процесса достаточно, чтобы
он был слабо стационарным, а его ковариационная функция облада-
ла следующими четырьмя свойствами интегрируемости:
/ |Схх(т)|4/т < оо , ( СЛ(т) dr < оо ,
(5.117)
/ 1тСхх(т)1 Лт < 00 , f |т|Сх\(т) dr < 00 .
Четыре условия (5.117) можно заменить единственным требованием
7/r|Qx(r)|rfT-0, (5.118)
1 j-т
Это утверждение будет доказано в разд. 8.2.1 и 8.2.2, где показано, что
оценки среднего значения и ковариационной функции, полученные усредне-
нием по времени, при выполнении условия (5.117) не зависят от выбора
конкретной реализации. Поэтому утверждение II следует из утверждения I.
Эти условия часто выполняются на практике, оправдывая предположение
эргодичности.
5.3.3. ГАУССОВЫ СЛУЧАЙНЫЕ ПРОЦЕССЫ
Дадим формальное определение гауссова случайного процесса. Случай-
ный процесс \хк( г)] называется гауссовым, если для любого набора фикси-
рованных моментов времени {случайные величины xk(tn) подчиняются
многомерному нормальному распределению, определенному формулой
(3.62). Гауссовы случайные процессы преобладают в практических задачах;
часто наличие гауссова свойства можно предсказать на основании много-
мерной центральной предельной теоремы. Можно показать также, что в
результате линейного преобразования гауссова процесса снова получается
гауссов процесс. Это свойство играет важную роль во многих практических
и теоретических применениях теории случайных процессов.
Рассмотрим реализацию x(t) эргодического гауссова процесса с нуле-
вым средним значением. Заметим, что индекс к можно уже не указывать,
поскольку свойства любой выборочной функции характеризуют все осталь-
ные выборочные функции. В силу эргодического свойства поведение x(t) на
большом временном интервале обладает теми же статистическими свойст-
вами, что и аналогичные средние по ансамблю в фиксированные моменты
времени. В качестве следствия получаем, что плотность вероятности, свя-
занная с мгновенными значениями x(t) на большом интервале времени,
является гауссовой с нулевым средним значением:
Стационарные случайные процессы
159
р(х) = (ах\/2т7) 1е *2/2о\
(5.119)
Когда x(t) имеет нулевое среднее, дисперсия равна
ох2 = Е [х2(0] = f х2р(х) dx
* — 00
и не зависит от t. Для больших Т
°гх а ~r£x2^dt =
= Г Sxx(f) df- 2 (°°SJJ) df — Гвхх(П df. (5.120)
•'-00 •'о •'о
Следовательно, гауссова плотность р(х) полностью характеризуется функ-
циями 5^(7) или 0^(7), так как по каждой из них можно определить а2.
Это важное свойство выдвигает определение 5^(7) или Gxx(f) в число
первостепенных задач анализа случайных процессов. Заметим, что на вид
спектральных плотностей или соответствующих ковариационных функций
не накладывается никаких ограничений.
Если среднее значение х( t) не равно нулю, то исходная плотность явля-
ется гауссовой общего вида:
р(х) = (<тУ2тг) 1е“(х"^)2/2а?, (5.121)
где среднее значение равно
рх = Е[х(г)] = Г хр(х) dx
- 00
и не зависит от t. Для больших Т
»x~^fTx(t)dt, (5.122)
7 •'О
а дисперсия равна
°* = Е [(x(z) - fix)2] = Е [х2(/)] - Мх. (5.123)
Пусть х{ t) — стационарный гауссов случайный процесс (индекс к опу-
щен для простоты обозначений). Рассмотрим две случайные величины
xl = x(t) их2 = x(t -I- т) для двух произвольных фиксированных момен-
тов времени t и t + т. Предположим, что хх и х2 подчиняются двумерному
(совместному) гауссову распределению с нулевыми средними значениями и
одинаковыми дисперсиями а2. Тогда, по определению,
ох — е[х2(г)] = Е[х2(г + т)] = { х2р(х) dx , (5.124)
J - 00
160
Глава 5
00
Лхх(Т) = Е [*(')*(' + 0] = Рхх(Т)°х2 = // *1*2Р(*1> *2) dxxdx2.
— 00
(5.125)
Величина Рхх(т) — это коэффициент корреляции из формулы (5.16) при
Сх^ = Rxx^ И % = % = ах'
Р„(г)-М^ • <5Л26>
°х
Если положить р = рхх(т) и р = 0, то совместная гауссова плотность веро-
ятности есть
р(*1, х2) = - Р2) Техр 2q2^ _ р2)(Л12 “ 2P*i*2 + х£) .
(5.127)
Все свойства, перечисленные в гл. 3, справедливы для гауссовых случайных
процессов, рассматриваемых на наборе фиксированных моментов времени.
Рассмотрим четыре случайные величины хр х2, х3, х4 с нулевыми сред-
ними значениями, которые имеют четырехмерное гауссово распределение.
По формуле (3.72)
Е'[х1х2х3х4] =
= £[*1*2]£[*3*4] + £[х!х3]£[х2х4] + ffx^J£[х2х3]. (5.128)
В частности, пусть хх = х(и), х2 = У (и + т), х3 = x(v), х4 = y(v + т), а
Я (т) — стационарная взаимная ковариационная функция вида
Л/
ЯхДт) = £[х(г)у(г + т)]. (5.129)
Из формулы (5.128) непосредственно следует, что
£[*(m)^(w + r)x(v)y(v + т)] = Я2/т) + Rxx(v - u)Ryy(v - и) +
+ £х>,(и - и + r)Ryx(v - и - т).
(5.130)
Этот результат используется в гл. 8 (формула (8.94)).
5.3.4. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
Динамическое поведение типичных линейных физических систем было
проанализировано на примерах в гл. 2. Полезно очень кратко рассмотреть
Стационарные случайные процессы
161
сейчас математические свойства линейных преобразований случайных про-
цессов. Эти сведения используются в гл. 6 и 7 при выводе важных соотно-
шений, связывающих вход и выход линейных систем, на вход которых по-
ступают случайные процессы.
Рассмотрим произвольный случайный процесс [xk(t)]. Оператор/4,
преобразующий выборочную функцию хк (t) в другую выборочную функ-
цию ук (v), можно записать как
_y*(t>) = Л[хА(0], (5.131)
где А обозначает функциональную операцию над членом, заключенным в
квадратные скобки. Аргумент v может совпадать или не совпадать с t. На-
пример, если рассматривается операция дифференцирования, то v = t и
ук (t) будет выборочной функцией производной [хк (t)] случайного процес-
са при условии, разумеется, что эта производная существует. Иной пример
дает операция интегрирования с конечными пределами интегрирования. В
этом случае v и Ук(и) — случайная величина, зависящая от индекса к и
определяемая реализацией хк (t) и конечными пределами интегрирования.
Оператор Л может иметь самый разнообразный вид. В дальнейшем индекс
к, указывающий на выборочное пространство, будет опускаться для прос-
тоты обозначений.
Оператор А называется линейным, если для любого набора допусти-
мых значений хр х2, •••» хм и любых постоянных яр а2, aN имеет место
соотношение
(5.132)
Иначе говоря, такая операция одновременно аддитивна и однородна. Допу-
стимыми значениями могут быть значения разных выборочных функций в
один и тот же момент времени t или же значения одной и той же выбороч-
ной функции в разные моменты времени t.
Оператор А называется инвариантным во времени, если любой сдвиг
/0, переводящий входной процесс х( t) в процесс х( t + Zo), вызывает такой
же сдвиг выходного процесса, переводящий у (Г) в у (Г 4- Го). В формаль-
ной записи для любого tQ
y(t + t0) = A[x(t + t0)]. (5.133)
Если не будет сказано противное, то в дальнейшем все линейные системы
будут считаться инвариантными во времени. Такие системы представляют
собой линейные системы с постоянными параметрами в смысле определе-
ния гл. 2.
Операция взятия математического ожидания от случайных величин пе-
рестановочна с любой линейной операцией, если только все участвующие
величины существуют, т. е. для фиксированных t и v имеем
£[^(t>)] = Е [ A [x(z)] ] = Я[Е[х(/)]]. (5.134)
6-953
162
Глава 5
Это соотношение легко доказывается следующим образом. Пусть х (Г)
принимает N дискретных значений хр х2, ...,xN, aj(y) принимает соот-
ветствующие им N дискретных значений ylf у2, •••> где Л = [*/]•
Тогда
I N i N 1 N
Ел = ЕЖ], яМО] = Е*. •
Поскольку/! — линейный оператор, то
1 N Г 1 w
= А[Е[%(/)]] .
Поэтому
Е[Я")] =Л[Е[х(0]]. (5-135)
В непрерывном случае утверждение доказывается путем устремления N к
бесконечности с использованием того или иного понятия сходимости, на-
пример приведенного ниже определения (5.138). Доказательство закончено.
Основной результат, справедливость которого непосредственно следует
из определений, гласит: если x(t) — выборочная функция слабо (строго)
стационарного случайного процесса, а оператор А линейный и инвари-
антный во времени, то у (v) — А [х (г)] является слабо (строго) стацио-
нарным случайным процессом. Очень важен еще один результат [5.4]: если
x(t) имеет гауссово распределение, а оператор А линейный, то
у (у) = А [х (О] тоже подчиняется гауссову распределению.
Интегральное преобразование любой выборочной функции х (t) произ-
вольного случайного процесса (х (t)] по определению есть
/ = /\(/)ф(/) dt, (5.136)
J а
где 0(0 — произвольная заданная функция, для которой этот интеграл су-
ществует. При данных ф(О и пределах интегрирования (а, Ь) величина/
случайна и зависит от выбора реализации х (t). Для изучения статистиче-
ских свойств случайной величины / обычно интервал интегрирования (а, b )
разбивают на подынтервалы Дг и рассматривают приближение интеграла
линейной суммой
N
iN= Е хОМфОДО • (5-137)
<«1
Сходимость //у к / можно определять по-разному. Говорят, что последова-
тельность [IN] сходится к /
1) в среднеквадратичном, если
lim Е[|4 - 7|2] = О ; (5.138)
N —» оо
Стационарные случайные процессы
163
2) по вероятности, если для любого е > О
lim Prob[|4 - /| > е] = 0 .
N—> оо
Из неравенства Чебышева (3.22) немедленно следует, что сходимость в
среднеквадратичном влечет сходимость по вероятности. На практике боль-
шинство интегральных выражений, содержащих случайные величины, су-
ществуют в смысле среднеквадратичной сходимости.
5.4. Производные случайных процессов
Производная любой данной выборочной функции х (t) произвольного
случайного процесса [x(t)] определяется как
Существование этого предела можно понимать по-разному. Говорят, что
производная х (t) существует
1) в обычном смысле, если предел существует для всех реализаций x(t)
процесса [х (t)];
2) в среднеквадратичном смысле, если
lim£
£ О
x{t + е) ~x(t)
---------------x(t)
(5.140)
Для стационарных случайных процессов х (t) существует в среднеквадра-
тичном смысле тогда и только тогда, когда ковариационная функция
Rxx(t) имеет производные первого и второго порядков, т. е. существуют
R'xx(t) иЩт) [5.4].
5.4.1. КОВАРИАЦИОННЫЕ ФУНКЦИИ
Рассмотрим следующие производные, предполагая, что они существуют
и непрерывны:
^хх(Т) =
4/?ЛХ(т)
dr
d2Kxx(r)
dr2
R"x(T) =
x(t) =
dt
(5-141)
По определению, для стационарных случайных процессов
Лхх(т) = £[jc(z)x(f + т)] = £[х(г - т)х(г)],
= E[x(t)x(t + т)] = £[х(/ - т)х(/)], (5.142)
164
Глава 5
7?^(т) = E[x(r)x(f + т)] = Е[х(/ - т)х(/)].
Тогда
й'«(т) = у-Е[х(/)х(г + т)] = Е[х(г)х(/ + т)] = Axi(r), (5.143)
ат
поэтому
d
R'xx^) = -r£tx('_ T)x(r)l = - т)*(0] = -Rxx^Y
dr
Следовательно,
R'xxW = Rxx(9) = -*xx(0) = 0 , (5.144)
поскольку RXX(O) должна одновременно быть и положительной, и отрица-
тельной. Соответствующее значение ^хх(0) = шах Rxx(t)- Отсюда следует,
что для стационарных случайных процессов
Е[х(г)х(г)] = 0 . (5.145)
Иначе говоря, формула (5.145) указывает, что в любой момент t производ-
ная (x(Z)j случайного процесса [х(Г)] с равной вероятностью принимает
положительные и отрицательные значения. Из формулы (5.143) следует,
что производная Я(т) ковариационной функции Rxx(r) по т совпадает со
взаимной ковариационной функцией (x(Z)j и [х(О]. Максимум ковариаци-
онной функции Rxx(t) соответствует пересечению оси абсцисс функцией
Rхх (т), т. е. взаимной ковариационной функцией процессов [х (/)] и (х (Г)].
Пересечение оси абсцисс функцией Rхх(т) происходит с отрицательным
наклоном (рис. 5.9), т. е.
Л;х(0-)>0, К'хх(0+)<0. (5.146)
На практике определять положение точки пересечения обычно проще, чем
определять положение максимума.
Покажем теперь, что/?^х(т) — нечетная функция от т; напомним, что
ЯХЛ.(т) — четная функция т. По определению,
Л«(-т) = Е[х(г)х(г - т)] = Е[х(г + т)х(г)], (5.147)
поэтому
d
R'xxi-'r) = -T-E[x(t + т)*(')] = E[x(r + т)х(г)] = Rix(r). (5.148)
dr
Но по формуле (5.143) Rxx(t) = — Rxx(t). Поэтому соотношение (5.148)
принимает вид
R'xx(-r)= -R'xx(r). (5.149)
Отсюда следует, что Rxx(t) — нечетная функция от т.
Стационарные случайные процессы
165
Рис. 5.9. Примеры производных ковариационных функций: а — исходная функ-
ция; б — первая производная; в — вторая производная.
Вторая производная равна
d d d
Л"х(т) = = j~RXx(T) = тЕ1х(‘ ~ Ф(0] =
ат ат ат
= -£[х(г - т)х(г)] = -Я^(т), (5.150)
поэтому
d d d
= J~E[x(t)x(t + т)] =
ат ат ат
= £[х(г)х(* + т) = Я^(т). (5.151)
Непосредственная проверка показывает, что^^-Ст) — четная функция от т,
а именно
Я"х(-т) = Я"х(т). (5.152)
При т=0 имеем
Е [х2(Г)] = КЛА(0) = -Ях4(0) = -Я"х(0). (5.153)
166
Глава 5
Ранее было показано, что
d
R^t) = —RxAt) = R'xAt). (5.154)
ат
Типичные графики 7?^ (т), Rxx(t) kRxx(t) показаны на рис. 5.9 для гармо-
нического процесса1^, где
Лхх(т) = Xcos2w/0t,
R'XX(T) = - y(27r/0)sin2w/0T, (5.155)
RXX(T) = -%(2w/0)2cos2tt/0t .
Полученные результаты обобщаются на производные высших поряд-
ков. Например,
d
RM = TRM= (5.156)
ат
= (5-157)
ат
При т=0 имеем
£[x2(r)] = Яи(0) = Л""(0). (5.158)
Таким образом, зная/?хх(т) и ее последовательные производные, можно
делать выводы о свойствах ковариационных и взаимных ковариационных
функций процесса [х(О] и его последовательных производных {*(/)},
[x(Oj и т. д.
5.4.2. СПЕКТРАЛЬНЫЕ ПЛОТНОСТИ
Несложно установить аналогичные свойства спектральных и взаимных
спектральных плотностей процесса [х (t)] и его последовательных произ-
водных [x(Oj и [x(t)]. Обозначим преобразование Фурье [х(О]:
Х(/)=^[х(0]. (5.159)
&[*(t)] = (j2irf)X(f), (5.160)
^[x(t)]= -(2nf)2X(f). (5.161)
11 На самом деле на рис. 5.9 изображены ковариационные функции узкополосно-
го шума и его производных (см. рис. 1.13,в). — Прим, перев.
Стационарные случайные процессы 167
Из формул (5.66) и (5.67) сразу следует, что
GJJ) =J(2*f)Gxx(f), (5.162)
Gjj) = (2W/)2GXX(/), (5.163)
<?«(/) =Л2^)Чх(/)’ (5-164)
Gxx(f) = (2vf)4Gxx(f) (5.165)
и т. д. Точно такие же формулы имеют место для двусторонних спектраль-
ных плотностей.
Эти результаты можно получить и с помощью соотношения Винера —
Хинчина (5.28). Возьмем в качестве исходного соотношение
/00
Sxx(f)e^df. (5.166)
-- 00
Последовательно дифференцируя, получим
Zoo
(2irf)Sxx(f)e^df, (5.167)
- 00
/00 -
(2vf)2Sxx(f)e^df, (5.168)
- 00
Л"Ят) = -j(°° (2W/)4x(/)^7Wt df, (5.169)
* — 00
/00 л
{l-nf}4Sxx{f)e^^ df. (5.170)
- 00
Из соотношений Винера — Хинчина и формул предыдущего разд. 5.4.1 сле-
дует, что эти четыре производные равны
/•00
А'хх(т) = ЛхЛ(т) = / Sx\f}e^dft (5.171)
- 00
Л'Л(т) = -АЛЛ(т) = - Г S^e^df, (5.172)
•'- 00
/00
(5.173)
- 00
/00
S^f}e^df. (5.174)
- 00
168
Глава 5
Сравнивая аналогичные члены в последних восьми формулах, приходим к
формулам (5.162) — (5.165).
5.4.3. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ЧИСЛА
ПЕРЕСЕЧЕНИЙ ОСИ АБСЦИСС
Рассмотрим реализацию стационарного случайного шума х (t), имею-
щего производную х (t). Пусть р (а, /3) — совместная плотность х (!) и х (t)
при x(t) = а и x(t) = /3. По определению, для всех Г
р(а, /?) Да ДД = Prob [а <%(/)< 4-а 4- Да, /?<£(/)</? +Д/?]>,
(5-175)
Иначе говоря, р (а, /3)ДаД/3 оценивает вероятность того, что в тот мо-
мент, когда x(t) лежит в интервале [а, а 4- Да], ее производная x(t) за-
ключена между /3 и /3 4- Д/3. Эта вероятность равна доле единичного интер-
вала времени, которую x(t) проводит внутри интервала [а, а 4- Да], при-
чем значение производной заключено между /3 и /3 4- Д/3. Если Д/3 прене-
брежимо мало по сравнению с /3, то последнее означает, что производная
просто равна /3.
Для определения математического ожидания числа пересечений реализа-
цией x(t) интервала [а, а 4- Да] надо время, проведенное x(t) внутри это-
го интервала, разделить на время, нужное для пересечения этого интерва-
ла. Если/^ — время пересечения интервала при данном значении производ-
ной /3, то
tp = Да/1/31, (5.176)
где стоит абсолютное значение /3, так как время пересечения — положи-
тельная величина. Следовательно, математическое ожидание числа прохож-
дений x(t) через интервал [а, а 4- Да] в единицу времени при данном зна-
чении х (I) = /3 равно
р(а, /?) &а&/3
= |Д|р(а,Д)ДД.
(5.177)
В пределе при Д/3 — 0 получаем, что математическое ожидание общего чис-
ла пересечений в единицу времени реализацией х (t) линии х (t) = а при
всех возможных значениях /3 есть
*« = Г \P\p(a,P)dp. (5.178)
J - 00
Эта величина задает математическое ожидание числа пересечений уровня а
в единицу времени как снизу вверх, так и сверху вниз. Предполагая, что по-
ловина пересечений уровня а реализацией х (t) происходит снизу вверх, а
половина — сверху вниз, jioлучим, что реализация x(t) пересекает уровень
а снизу вверх в среднем /2 раз в единицу времени.
Стационарные случайные процессы 169
Математическое ожидание числа нулей реализации х( t) на единичном
интервале времени равно общему числу пересечений уровня х( t) = 0 как
снизу вверх, так и сверху вниз. Эта величина равна Na при а = 0, т. е.
2V0 = J00 |Д|р(О, Д) 4/Д. (5.179)
J -00
Значение No можно истолковать как удвоенную «кажущуюся» частоту реа-
лизации шума. Например, если бы реализация представляла собой идеаль-
ный гармонический процесс с частотой /0 герц, то No равнялось бы 2/0
нулей в секунду (скажем, гармонический процесс с частотой 60 Гц имеет
120 нуль/с). Для случайного шума ситуация более сложная, тем не менее
знание No и ряда других величин дает возможность охарактеризовать шу-
мовой процесс.
Для произвольной реализации х (t) стационарного случайного процесса
с нулевым средним и ее производной x(t) имеем из формул (5.145) и
(5.150): . г . 1
ах2 = £[х2(г)] =Ялл(0), (5.180)
о/ = Е (х2(г)] = ЯАЛ(0) = -А'Л(О), (5.181)
= £[*(')*(')]= 0- (5.182)
Из формул (5.166) и (5.168) следует также, что
<\2 = Г Sxx(f)df= (°°Gxx(f)df, (5.183)
7-оо
ZOO 9 /• 00
(2ir/)\x(/)# = / (2w/)4x(/)< (5.184)
- oo •'o
Предположим теперь, что x(t) и x (t) имеют нулевое среднее и подчи-
няются двумерному нормальному распределению с указанными выше дис-
персиями и нулевой ковариацией. Тогда
р(а.0)=р(а)р(0), (5.185)
где
/’(«)= —/х=ехр(-а2/2ах2), (5.186)
ох\
р(0)= —5=ехр(-02/2а/), (5.187)
Подставляя выражение (5.185) в формулу (5.178), находим, что
_ ехр(-а2/2о2) гоо . „
Na = ----( |0|ехр -072а2 J0 =
.'-оо
1 / а • \
= — — 1ехр(-а2/2ох2). (5.188)
170
Глава 5
В частности, при а = 0 имеем
А)
-7S5--------
/ GxAf)df
А)
(5.189)
Используя Nq, можно записать
Na = #оехр(-а2/2<тЛ2) .
(5.190)
Эти результаты заимствованы из книги [5.1], впервые они были получены
Райсом [5.5], который пользовался другим методом доказательства.
ПРИМЕР 5.12. ЧИСЛО ПЕРЕСЕЧЕНИЙ ОСИ АБСЦИСС НИЗКОЧАСТОТ-
НЫМ БЕЛЫМ ШУМОМ. Для иллюстрации приведенных выше формул рас-
смотрим низкочастотный белый шум, сосредоточенный в полосе частот от
0 до В герц, т. е. Gxx(f) = К при в остальных случаях
G = 0. Тогда
ХХ 4 77 2
ох2 = (BKdf = КВ, = fB(2irf)2Kdf = ——КВ3.
•'о •'О J
По формуле (5.189) имеем
2
No = д Я « 2(0,585).
Детерминированный гармонический процесс с частотой В герц имел бы
= 2 В нуль/с. Поэтому можно заключить, что низкочастотный белый
шум с полосой частот, ограниченной В герц, имеет кажущуюся частоту,
составляющую примерно 0,58 граничного значения В.
Задачи
5.1. Корреляционная функция случайного процесса равна
Яхх(т) = 25е-41т1 cos 4тгт 4- 16. Найдите:
а) среднее значение и дисперсию процесса;
б) соответствующую одностороннюю спектральную плотность.
5.2. Какие из перечисленных ниже свойств всегда справедливы для кова-
риационной функции стационарного случайного процесса:
а) эта функция четная;
б) неотрицательная;
в) ограничена значением в нуле;
Стационарные случайные процессы
171
г) позволяет найти среднее значение процесса;
д) позволяет найти дисперсию процесса.
5.3. Какие из свойств, перечисленных в задаче 5.2, всегда справедливы
для взаимной ковариационной функции стационарных случайных про-
цессов?
5.4. Двусторонняя спектральная плотность случайного процесса равна
5 (z)./16S(/) + 20[l- Щ), |/|< 10;
XX\J / \ \ IV /
I о, |/| > ю.
Вычислите:
а) среднее значение и дисперсию процесса;
б) соответствующую ковариационную функцию.
5.5. Какие из свойств, перечисленных в задаче 5.2, всегда справедливы
для следующих двусторонних величин:
а) спектральной плотности;
б) взаимной спектральной плотности.
5.6. Какие из следующих свойств всегда справедливы для пары эргоди-
ческих процессов:
a) RXy (°° )
б) Rху (0) = 0, если /гЛ. = 0 или ру = 0;
в)Яху(т) = 0, если7?хд.(т) = 0 или 7?^ (т) = 0;
г) I Rxy (т)1 2 sg Rxx(T)Ryy(r)-,
д) Gxy (0) = 0, если р,х = 0 или р = 0;
е) I Gx//)l2 G^(0)G^(0);
ж) Gxy(f) = 0, если Gxx(f) = 0 или G^/> 0.
5.7. Односторонняя взаимная спектральная плотность двух случайных
процессов равна Gxy(f ) = 6/У 2 4- j (8/У3). Вычислите двустороннюю
взаимную спектральную плотность Sxy(f) через
а) действительную и мнимую части;
б) модуль и фазовый угол.
5.8. Реализация х (t) эргодического случайного процесса имеет ковариа-
ционную функцию вида Rxx(т) = cos 2тг/0т при а > 0. Найдите ко-
вариационную функцию первой производной по времени х (t) процесса
X (Г).
5.9. Реализация x(t) эргодического процесса имеет одностороннюю
спектральную плотность вида
1
G (Л = ---------г , 0 </< 25 .
^xxxJ / 25 + у2 1 J
В остальных случаях Gxx = 0. Определите среднее число пересечений оси
абсцисс в секунду реализацией x(t).
5.10. Выведите соотношение (5.30) из формулы (5.59).
Глава 6
СООТНОШЕНИЯ ДЛЯ ЛИНЕЙНЫХ
СИСТЕМ С ОДНИМ ВХОДНЫМ
ПРОЦЕССОМ
Эта глава посвящена теории систем с одним входом и ее применениям.
Предполагается, что на вход системы поступают реализации стационарно-
го случайного процесса с нулевым средним, а система линейная и имеет по-
стоянные параметры. Рассматриваются модели с одним входом и одним
выходом, а также модели с одним входом и несколькими выходами. Для
этих моделей определяется функция обычной когерентности. Системы с не-
сколькими входами изучаются в гл. 7.
6.1. Системы с одним входом и одним выходом
Пусть линейная система с постоянными параметрами задается весовой
функцией/? (т) и частотной характеристикой//^), которые были определе-
ны и исследованы в гл. 2. Предположим, что воздействие на систему одно-
го вполне определенного входного сигнала х (t), являющегося реализацией
стационарного случайного процесса )], вызывает один вполне опреде-
ленный выходной сигнал у (!) (рис. 6.1). Этот выходной сигнал представля-
ет собой реализацию стационарного случайного процесса [у (/))•
6.1.1. КОРРЕЛЯЦИОННЫЕ И СПЕКТРАЛЬНЫЕ СООТНОШЕНИЯ
При идеальных условиях выходной сигнал системы, изображенной на
рис. 6.1, задается сверткой
ЯО = h(r)x(t - T)dr, (6.1)
где h (т) = 0 при т < 0, если система физически осуществима. Произведе-
ние у (t )у (t + т) равно
y(t)y(t + т) = f h(a)h(/3)x(t - ft)x(t + т - a) dadfi . (6.2)
Взяв математическое ожидание от обеих частей этого равенства, получим
соотношение, устанавливающее связь между ковариационными функциями
выходного и входного процессов'.
00
Мт) = ^h(a)h(^Rxx(T + /}-a)dad0. (6.3)
Аналогично определяется произведение х (t )у (t + 7):
x(t)y(t + г) = f h{a)x(t}x(t + т — a) da . (6.4)
Jo
Линейные системы с одним входным процессом
173
*(t)---------H(f) ---------------------y(t)
Рис. 6.1. Идеальная система с одним входом и одним выходом.
Взяв математическое ожидание от обеих частей этого равенства, получим
взаимную ковариационную функцию входного и выходного процессов:
Rxy(T) = fo h(a)Rxx(T - a) da . (6.5)
Заметим, что свертка в формуле (6.5) имеет тот же вид, что и в (6.1).
Применение преобразования Фурье к соотношениям (6.3) и (6.5) после
ряда алгебраических преобразований позволяет показать, что двусторонние
спектральные плотности Sxx(f), Syy(f) и Sxy(f) удовлетворяют следую-
щим важным соотношениям:
syy(n = \H(f)\2Sxx(f) , Sxy(f) = H(f)Sxx(f) . (6.6, 6.7)
Здесь частота/ может быть как положительной, так и отрицательной. За-
метим, что выражение (6.6) действительное и содержит только амплитуд-
ную характеристику системы IН (f)l. В то же время выражение (6.7) ком-
плексное и может быть разбито на две формулы, содержащие соответст-
венно амплитудную \Н (f)\ и фазовую ф(/) характеристики системы. Фор-
мула (6.6) называется соотношением между спектрами входного и выход-
ного процессов, а формула (6.7) — соотношением для взаимного спектра
входного и выходного процессов. Эти формулы применимы только в иде-
альном случае — при отсутствии шума на входе и выходе, когда характе-
ристики системы линейны и не меняются во времени. Интерпретировать
эти спектральные соотношения в частотной области значительно проще,
чем соответствующие корреляционные соотношения во временной области.
Соотношения (6.6) и (6.7) можно записать через физически измеримые
односторонние спектральные плотности Gxx(/), Gyy(f) и Gxy(f), где
G (f) = 2S(f) при/ 0 и G/) = Ов остальных случаях. Соотношения
(6.6) и (6.7) принимают вид
Gyy(f) = |Я(/)|Чх(/), Gxy(f) = H(f)Gxx(f\ (6.8, 6.9)
Пусть
Gxy(f) = \Gxy(f)\e~^f\ = (6.10,6.11)
Тогда уравнение (6.9) эквивалентно следующим двум
IM/)I = IW)|(U/), М/) = Ф(/). (6.12, 6.13)
На этих результатах основаны многочисленные инженерные применения
функций спектральной плотности. Практические примеры можно найти в
174
Глава 6
Выход Gyy(f)
б
Рис. 6.2. Соотношения между спектрами входных и выходных процессов линей-
ных систем: а — спектры; б — взаимные спектры.
книге [6.1]. На рис. 6.2 показано изменение спектра входного процесса
Gxx (f) после прохождения через линейную систему с частотной характери-
стикой Н (f).
Формула (6.8) дает возможность вычислить средний квадрат выходного
процесса:
= (°°G (f) df- (°°\H(f)\2Gxx(f) df. (6.14)
•'о •'о
Формула (6.8), кроме того, позволяет определить Gxx(f) по известным
Gyy(f) и I H(f)\ или же 1/7(01 по известным Gxx (f) и Gyy(f), но из фор-
мулы (6.8) нельзя найти полностью частотную характеристику Н (f) систе-
мы, так как эта формула не содержит информации о фазе. Полностью вос-
становить амплитудную и фазовую характеристики системы можно из
формул (6.9)—(6.13), когда известны как Gxy(f), так и Gxx(f).
Формулы (6.8) и (6.9) можно вывести и без предварительного нахожде-
ния корреляционных соотношений (6.3) и (6.5). Для любой пары достаточ-
Линейные системы с одним входным процессом
175
но больших, но конечных реализаций длины Т соотношение (6.1) эквива-
лентно следующему равенству:
ПЛ = #(/)%(/), (6Л5)
где X (f) и Y (f) — финитные преобразования Фурье х (t) и у (I) соответст-
венно. Тогда
У*(Л = Я‘(/)Р(/), |У(/)|2 = |Н(/)|2|Х(/)|2,
Х*(/)У(/) = Я(/)|Х(/)|2 .
Если теперь последние два равенства усреднить по ансамблю реализаций,
умножить на 2/Г и устремить Т к бесконечности, то из соотношений (5.66)
и (5.67) получим, что
Gyy(f) = \H(f)\2Gxx(f) , Gxy(f) = H(f)GjJ) . (6.16, 6.17)
Обратим внимание на простоту непосредственного вывода этих соотноше-
ний. Этот метод будет использован в разд. 6.1.4 и гл. 7.
Переходя в формуле (6.17) к комплексно-сопряженным величинам, полу-
чим
<?;//) = Gyx(n = H*(f)Gxx(f), (6.18)
где
Gyx(f) = \Gxy(f)\e^\ (6.19,6.20)
Следовательно, для определения фазовой характеристики можно использо-
вать формулу
Gxy(J)
Gyx(f)
---— = е-у2ф(/)
я*(Л
(6.21)
Имея целью определение
что из формул (6.16) и (6.18)
полной частотной характеристики, заметим,
следует соотношение
GyyU) = H(/)[H*(/)GXX(/)] = H(f)Gyx(f\ (6.22)
Поэтому для идеальной системы с одним входом и одним выходом Н (f)
можно найти из соотношения (6.17):
а формула (6.22) дает я(/) = ^xy\J 7 Gjj) ’ (6-23)
Я(Л = Gyy(f) Gyx(fV (6-24)
Следовательно, Gxy(f) Gyy(h (6-25)
GJJ) ' Gyx(f) ’
176
Глава 6
что эквивалентно
IM/)I2 = GxAf)Gyy(f). (6.26)
При анализе переходных процессов, изучаемых в гл. 12, вместо спект-
ральных плотностей «мощности», определенных в гл. 5 и 6, используются
спектральные плотности «энергии». Эти два типа спектров связаны соот-
ношением ^ху (f)—TGxy (f), где -^ху (f) описывает взаимную спектраль-
ную плотность «энергии». Предполагается, что переходные процессы х (t)
и у (t) существуют только в интервале 0 t Т. Полученные в этой главе
и гл. 7 соотношения между входными и выходными процессами верны и
для таких переходных процессов после простой замены спектральных плот-
ностей «мощности» спектральными плотностями «энергии».
ПРИМЕР 6.1. РЕАКЦИЯ НИЗКОЧАСТОТНОГО ФИЛЬТРА НА БЕЛЫЙ
ШУМ. Предположим, что на вход низкочастотного RC-фильтра с постоян-
ной времени К = RC поступает белый шум. Найдем спектральную плот-
ность, средний квадрат и ковариационную функцию выходного процесса.
Частотная характеристика этого низкочастотного фильтра имеет вид
H(f) = (1 +;2^/)-1 = ,
причем ей соответствует весовая функция
т>о;
й(т) = <К
\ 0 , т < 0 .
Здесь г
|Я(/)|= [1 +(2^/)2]- /2Л ф(/) = arctg (2irA/) .
Если Gxx(f) — спектральная плотность белого шума (т. е. Gxx(f) = А ) и
постоянна для всех / > 0, то
G„(/) - |Я(/)|2С„(/) - --у-, ,
э г00 / х /оо А А
«И = / G (f) df= I -------------df= — ,
Jo 'о 1 + (2irKf) 4K
Ryy(r) = J™Gyy(f)cos2‘!rfTdf= y~|T|/* .
ПРИМЕР 6.2. РЕАКЦИЯ НИЗКОЧАСТОТНОГО ФИЛЬТРА НА ГАРМОНИ-
ЧЕСКИЙ ПРОЦЕСС. Предположим, что на вход низкочастотного RC-
фильтра, описанного в примере 6.1, поступает гармонический процесс с
спектральной плотностью
Gxx(/) = (X2/2)6(/-/0) .
Линейные системы с одним входным процессом
177
Найдем спектральную плотность, средний квадрат и ковариационную
функцию выходного процесса. В данном случае
^(/) = |я(/)|ЧЛ/) =
(Х2/2)б(/-/0)
1 + (2wA/)2
%2/2
1 + (2irKf)2 ’
roo Х2/2
Ryy(r) = / Ga,f(/)cos2i7/tJ/= -————2COS27T/0T.
•'о 1 +(2wX/o)
ПРИМЕР 6.3. СИСТЕМА С СИЛОЙ НА ВХОДЕ И СМЕЩЕНИЕМ НА ВЫХО-
ДЕ. Вычислим спектральную плотность, ковариационную функцию и сред-
ний квадрат выходного процесса системы, изображенной на рис. 2.2, в
предположении, что на ее вход поступает белый шум. Результаты справед-
ливы и для других аналогичных систем, как указывалось в гл. 2.
Пусть Gxx(f) = G, где G — постоянная. Тогда по формуле (2.24а) или
табл. 2.1 в предположении, что сила выражена в единицах смещения, т. е.
х (I) = F(t )/к, находим спектральную плотность выходного процесса:
Gyy(f) — \H(f)\2_dG —
G
[1-(//А)Т +(Ш)2
О < / < оо .
Соответствующая ковариационная функция выходного процесса равна
Girf e-WJhl
Ry)M =----------------cos(277/„ j/1 - f2 |т|) +
Средний квадрат выходного процесса есть
Следовательно, если на вход поступает белый шум, то средний квадрат
обратно пропорционален f.
Если входной процесс гармонический, то, как мы сейчас увидим, макси-
мальное значение фу обратно пропорционально f2. Пусть сигнал
F(t) = kx(t) = kXcos2irf0t, f0 = (1/T),
178
Глава 6
проходит через систему, задаваемую частотной характеристикой H(j)
(рис. 2.2). Тогда выходной процесс y(t) есть
y(t) = kX\H(fe)\cos[2irf0l - ф(/о)] ,
причем
= 7 dt = Р(Х2/2)|Я(/0)|2 .
1 •'о
По формуле (2.26) для малых f
шах|Я(/0)| = |Я(/Г)| ~ ,
2Ц
следовательно,
max^v = ^2 >
что и утверждалось.
ПРИМЕР 6.4. СИСТЕМА СО СМЕЩЕНИЕМ НА ВХОДЕ И ВЫХОДЕ. Вычис-
лим спектральную плотность, ковариационную функцию и средний квадрат
выходного процесса в том случае, когда на вход системы, изображенной на
рис. 2.4, поступает белый шум. Эти результаты справедливы и для других
аналогичных систем, как указывалось в гл. 2.
Пусть Gxx(f) = G, где G — постоянная. Тогда по формуле (2.38а) или
табл. 2.1 спектральная плотность выходного процесса есть
СЛГ(/) = |Я(/)|2_^ =
с[1 +(Ш)2]
[i -(//А)Т +(W/J2
Соответствующая ковариационная функция выходного процесса равна
Яд/т) =
G<(1 + 4f2)
---------е
Ф - 4£2)
1/1 - Г2(1 + 4f2)
sin(27r/Jl - £2 |т|)
Средний квадрат выходного процесса есть
= /о Gyy(H df=Ryy(0) =--------.
Последние два примера показывают важность экспоненциально-
косинусоидальной и экспоненциально-синусоидальной ковариационных
функций'для многих практических задач. Если f < 1, то можно обойтись
только экспоненциально-косинусоидальными ковариационными функциями.
Линейные системы с одним входным процессом
179
6.1.2. ФУНКЦИИ ОБЫЧНОЙ КОГЕРЕНТНОСТИ
Если Gxx (f) и Gyy (f) отличны от нуля и не содержат дельта-функций,
то функция когерентности входного процесса х (t) и выходного процесса
y(t) — действительная величина вида
гдеО — односторонние спектры, aS — двусторонние теоретические спект-
ры, определенные выше. Из формулы (5.85) следует, что для всех f функ-
ция когерентности удовлетворяет неравенствам
0<уД,(/)<1. (6.28)
Для исключения дельта-функций на нулевой частоте перед использованием
последних двух формул из случайных процессов следует вычесть их ненуле-
вые средние. Заметим, что функция когерентности аналогична квадрату
коэффициента корреляции РхУ(т) из формулы (5.16).
Линейные системы с постоянными параметрами удовлетворяют форму-
лам (6.16) и (6.17); после подстановки в формулу (6.27) получаем
„ |H(/)|2GX2X(/)
v2 ( f) =---!—___!— 1
xyU) Gxx(f)\H(f)\2Gxx(f) ’
(6-29)
Следовательно, в идеальном случае линейной системы с постоянными па-
раметрами и полностью определенными входом и выходом функция коге-
рентности равна единице. Еслих(/) и у (t) совершенно не связаны, то функ-
ция когерентности равна нулю. Если же функция когерентности больше ну-
ля, но меньше единицы, то на практике возможны следующие три ситуа-
ции:
а) в измерениях присутствует внешний шум;
б) система, связывающая х (t) и у (I), не является строго линейной;
в) выход у (t) зависит помимо х (t) и от других входных процессов.
Для линейных систем функцию у^у (f) можно интерпретировать как от-
носительный вклад входного процесса х (t) в средний квадрат выходного
процессаy(t) на частоте /. С другой стороны, величина 1 — у27(А) задает
долю среднего квадрата y(t) на частоте /, не связанную сх(О-
ПРИМЕР 6.5. ИСПОЛЬЗОВАНИЕ ФУНКЦИИ КОГЕРЕНТНОСТИ. Рассмот-
рим самолет, пролетающий через зону атмосферной турбулентности
(рис. 6.3). Пусть входной процесс x(t) — это вертикальные пульсации ско-
рости потока в метрах в секунду, измеряемые датчиком, который располо-
жен в носовой части самолета, а выходной процесс у (I) — вертикальное
ускорение в долях g, измеряемое акселерометром, расположенным в центре
тяжести самолета. Результирующая функция когерентности и спектраль-
ные плотности реальных данных показаны на рис. 6.4 и 6.5. В данном слу-
180
Глава 6
Выход:/^-вертикальное ускорение ЦТ
У(х)
Вход:x(t) -вертикальные пульсации потока
Рис. 6.3. Пролет самолета через зону атмосферной турбулентности.
чае спектры вычислялись в полосе частот от 0,1 до 4,0 Гц с разрешением
0,05 Гц при длине реализации около 10 мин.
Рис. 6.4. показывает, что скорость пульсаций на входе и ускорение са-
молета на выходе обладают относительно большой когерентностью, рав-
ной 0,8...0,9 в полосе частот примерно от 0,3 до 2,0 Гц. Однако правее и
левее этой полосы функция когерентности убывает. На низких частотах
вертикальное ускорение самолета в основном определяется нагрузками, вы-
Рис. 6.4. Функция когерентности между скоростью пульсаций воздуха и резуль-
тирующим ускорением. Эти данные были получены в исследованиях, проведенных в
исследовательском центре NASA в Лэнгли (Хэмптон, Вирджиния) по контракту
NAS-I-8538.
Линейные системы с одним входным процессом
181
званными действиями пилота, управляющего самолетом, а не влиянием ат-
мосферной турбулентности. Поэтому убывание функции когерентности на
низких частотах отражает, вероятно, вклад в выходной процесс у (I)
других входных процессов, отличных от наблюдаемого входного процесса
х (t). На высоких частотах выходной спектр резко убывает за счет характе-
ра реакции самолета, подобной действию низкочастотного фильтра, а так-
же из-за убывания в этой полосе частот спектра входного процесса, как
видно из рис. 6.5. С другой стороны, фоновый шум оборудования сбора и
регистрации данных обычно не уменьшается с ростом частоты. Поэтому
уменьшение функции когерентности на высоких частотах определяется, ве-
роятно, наличием в наблюдениях постороннего шума. На этом пример 6.5
заканчивается.
По любым двум реализациям х (I) и у (t) всегда можно вычислить функ-
цию обычной когерентности, используя Gxx (f),Gyy (f) nGxy(f). Значения
этой функции указывают на степень линейной зависимости одной реализа-
ции от другой. Однако это не обязательно означает, что между двумя реа-
лизациями существует причинно-следственная связь. О причинности будет
сказано в разд. 6.2.1.
В применениях функции когерентности к задачам оценки линейных ча-
стотных характеристик ее можно рассматривать как отношение двух раз-
личных оценок квадрата амплитудной характеристики системы. Одна из
них задается формулой (6.16):
= (6.30)
а другая — формулой (6.17):
|я(/)|^ = |^(/)‘ • (6.31)
^xx\J )
Их отношение и равно функции когерентности
\Н{П\21 \Gxy{n\2 г
Слл(/)^(/) Уху
(6.32)
На практике вычисленные по формуле (6.32) значения всегда будут ле-
жать между нулем и единицей. Оценка амплитудной характеристики по
формуле (6.30), использующая значения автоспектров выходного и входно-
го процессов, всегда смещена, за исключением того случая, когда функция
когерентности равна единице. В то же время оценка амплитудной характе-
ристики по формуле (6.31), использующая значения спектра входного про-
цесса и взаимного спектра входного и выходного процессов, смещена толь-
ко при воздействии постороннего шума на входной процесс, однако если
посторонний шум воздействует только на выходной процесс, то эта оценка
несмещенная. В частности, формула (6.31) дает несмещенную оценку ам-
182
Глава 6
Рис. 6.5. Спектральные плотности скорости пульсаций потока и результирую-
щего ускорения. Эти данные были получены в исследованиях, проведенных в ис-
следовательском центре NASA в Лэнгли (Хэмптон, Вирджиния) по контракту
NAS-I-8538.
плитудных характеристик системы с несколькими входами, если, входные
процессы не коррелированы. Такие задачи рассматриваются в гл. 9, где
также показано, что точность оценок частотных характеристик увеличива-
ется по мере приближения значения функции когерентности к единице.
Линейные системы с одним входным процессом
183
Функции когерентности сохраняются при линейных преобразованиях.
Именно, предположим, что требуется вычислить функцию когерентности
процессов х (О и у (t), причем эти процессы непосредственно не наблюда-
ются. Допустим, однако, что наблюдаются два других процесса х} (t) и
у j (О, относительно которых на основании физических соображений можно
утверждать, чтох^О связан точной линейной зависимостью cx(Z), а
у 1 (О — с у (t). Тогда функция когерентности между Xj (Г) и у равна ис-
ходной функции когерентности междух (О и_у(/)« Докажем это.
Наличие точной линейной связи означает, что существуют такие гипо-
тетические частотные характеристики A (f) и В (f), возможно, неизвест-
ные, что Yx(f) = Тогда при любом
значении f имеем Gy у = \А l2Gyy, Gv v = IBI2GVV,
Л1Л1 ЛЛ у у
Gy w = A*BG. Следовательно,
л 1 ЛУ
2 l^l2 |GXJ2 2
GXiXGyiyi \A\2Gxx\B\2Gyy GxxGyy
Этот результат важен для многих приложений [6.1].
6.1.3. МОДЕЛИ С ПОСТОРОННИМ ШУМОМ
Рассмотрим модели линейных систем с частотной характеристикой
H(f), на вход и выход которых воздействует посторонний шум. Пусть
u (I) и v (г) — истинные сигналы, а т (t) и п (t) — шумы, воздействующие
соответственно на u (t) и v (t) (рис. 6.6). Предположим, что через систему
проходит только и (Г) и вызывает выходной сигнал v (t), однако наблюда-
ются реализации вида
x(t) = u(t) + т(Х) , y(t) = v(t) + n(t). (6.33)
При произвольной корреляции между сигналами и шумами спектраль-
ные и взаимные спектральные плотности процессов х (t) и у (t) равны
Gjj) = Guu{h +Gmm(f) + Gum(J) + Gmu(f),
Gyy(h = Gjj) + <?„„(/) + <U/) + Gjj) , (6.34)
Gxy(P) = Gjj) + Gun(H + Gmv(f) + Gmn(/),
m(t)
Рис. 6.6. Система с одним входом и одним выходом при наличии постороннего
шума.
y(t)
184
Глава 6
где
<?Д/) = |Я(/)|ЧИ(/), (6.35)
(6.36)
В зависимости от степени коррелированное™ т (t) и п (I) между собой и с
сигналами возможны самые разные ситуации. Особый интерес представля-
ют три из них.
Случай 1. Шум на входе отсутствует; на выход воздействует некоррели-
рованный шум.
Случай 2. Шум на выходе отсутствует; на вход воздействует некоррели-
рованный шум.
Случай 3. Шумы воздействуют и на вход, и на выход, причем они не
коррелированы как между собой, так и с сигналами.
СЛУЧАЙ 1. ШУМ НА ВХОДЕ ОТСУТСТВУЕТ; НА ВЫХОД ВОЗДЕЙСТ-
ВУЕТ НЕКОРРЕЛИРОВАННЫЙ ШУМ:
W------------- Ht(f) — > 2 ---------------------------^y(t)
V(l>)
x(z) = и(г),
Я0 = u(r) + n(t), Gv„(f) = 0,
Gxx(f) = GUU(D,
Gyy(f) = Gvv(f) + Gnn(f\
Gxy(f) = <U/) = ^(/)GXX(/),
= (6.37)
Gjj) = l^(/)|2G„„(/) = • (6.38)
Заметим, что Gvv (f) можно оценить no x (t) и у (t), даже если v(f) не наб-
людается. Следовательно, можно определить и Gnn (/), не наблюдая п (t).
В практических применениях это, несомненно, важнейший случай, посколь-
ку часто удается точно определить входной сигнал и минимизировать влия-
Линейные системы с одним входным процессом
185
ние шума на входе. Однако о шуме на выходе этого сказать обычно нельзя,
поскольку он может быть вызван нелинейностью системы или воздействи-
ем каких-либо ненаблюдаемых входных сигналов.
В случае 1 функция обычной когерентности равна
2, lM/)l2 = l<W)l2 =
УхЛ/) Gxx(f)Gyy(J) Guu(f)[Gvv(f) + Gnn(f)]
=--------Д-------’ (6.39)
1 + G„„(/)/Gpy(/)
поскольку
тЧ/)= |С"(/)|2 =!.
Заметим, что у^(/) < 1, если Gnn (f) > 0 и
= (6.40)
Это произведение у*у (f) на Gyy (f) называется когерентным спектром вы-
ходного процесса. Заметим также, что спектр шума на выходе равен
g„„(/) = [i-y2,(/)]g,//).
(6.41)
Следовательно, в этом случае можно интерпретировать как относи-
тельный вклад х (О BGyy(f) на частоте/, а 1 - т^(/) — как относитель-
ный вклад BGvy(f) отличных отх(О процессов на частоте/. Следователь-
но, функция обычной когерентности разбивает наблюдаемый спектр вы-
ходного процесса на некоррелированные составляющие, соответствующие
входному сигналу и постороннему шуму. Формула (6.40) лежит в основе
решения многих задач идентификации источника, в которых используются
функции обычной когерентности [6.1].
СЛУЧАЙ 2. ШУМ НА ВЫХОДЕ ОТСУТСТВУЕТ; НА ВХОД ВОЗДЕЙСТВУЕТ
НЕКОРРЕЛИРОВАННЫЙ ШУМ:
u(th-------- H2(f) ----------^y(t)
m(t)-------- I -----^X(t)
186
Глава 6
х(г) = u(t) + m(t) , Gum(J) = O, y(t) = u(t),
Gjf) = Guu(f) + Gmm(f),
Gjj) = Gjf) = \H2(J)\2GJJ) = H2(f)[H*(J)Gjf)],
Gjf) = Gjf) = H2(f)Gjf),
Gjf) = H2Jf)Gjf),
= (6-42)
^yx\J )
r ,,, G„(/) 1МЛ12 |C„(/)I!
c-(/)‘iW)F‘^(7r’X(7r' (6'43>
В этом случае Gnn (f) и Gmrn(f) можно определить nox(O ny(t). Такая
ситуация встречается в некоторых специфических приложениях [6.2]. Одна-
ко эти соотношения нельзя использовать, если выход подвержен воздейст-
вию шума, связанного с нелинейностью системы, вкладом других входных
сигналов и (или) инструментальным шумом на выходе. В этих ситуациях
предпочтительнее использовать результаты, полученные при анализе слу-
чая 1.
В случае 2 функция обычной когерентности равна
2( } = 1<М/>12 = KU/)!2 =
УхЛ Gjf)Gjf) [Gjf) + Gmm(f)]Gjf)
1
= l+Km(/)/G„„(/)] * (6>44)
Следовательно, < 1, ес л и Gm m (f) > 0 и
Gjj) = yJjGjf), (6.45)
GmJf)= [1-Yx2,(/)]Gxx(/). (6.46)
Поэтому в случае 2 функция обычной когерентности разбивает наблюдае-
мый спектр входа на некоррелированные составляющие, соответствующие
сигналу и шуму.
Если разделить частотную характеристику определенную в слу-
Линейные системы с одним входным процессом
187
чае 1 формулой (6.37), на частотную характеристику определенную
в случае 2 формулой (6.42), то в результате получим функцию когерентно-
сти
НАП Gjf)/Gjf) 2
H2(f) Gjf)/Gjf) УхуЧ)'
(6-47)
СЛУЧАЙ 3. НА ВХОД И ВЫХОД ВОЗДЕЙСТВУЮТ ШУМЫ, НЕКОРРЕЛИ-
РОВАННЫЕ МЕЖДУ СОБОЙ И С СИГНАЛОМ-.
x(t) = u(t) + m(t), Gjf) = Gjf) = 0,
y(t) = v(t) + n(t), Gjf) = 0,
Gjf) = Gjf) + Gjf), Gjf) = Gjf) + Gjf),
Gjf) = Gjf) = H(f)Gjf),
Gjf) = \H(f)\2Gjf). (6.48)
В этом случае H(f) нельзя определить по наблюдениям х (t) и^(/), если
неизвестен или не наблюдается шум
я(/) = =
^ии\1 )
1Я(П|!=ё<7Г
на входе. Точнее,
Gjf)
Gjf) ~ Gjf) ’
Gjf)-Gjf)
Gjf) ~ Gjf)
(6.49)
(6.50)
Заметим, что, согласно формуле (6.49), H(f) зависит от Gmm (/), но не за-
висит от Gnn (f). Формула (6.50) для определения IН (/)12 показывает, что
\Н (f)l2 зависит как от Gmm (f), так и от Gnn(f).
В случае 3 функция обычной когерентности равна
2 1^,(/)12 =________________KU/)!2______________=
Уху U) Gjf)Gjf) [Gjf) + Gmm(f)][Gjf) + Gjf)]
1
= 1 +а(/) + Д(/) + а(/)А(/) ’
(6.51)
где a(f) и @(f) — отношения шума к сигналу, равные
»(/) = [G„jf)/Gjf)] , Kf) = lGjf)/Gjf)] . (6.52)
188
Глава 6
Очевидно, что уху (f) < 1, если только a(f) > 0 или (3(f) > 0. В этом слу-
чае невозможно разложить Gxx (f) или Gyy (f) на отдельные составляющие,
соответствующие сигналу и шуму, если известны только х (t) и у (t).
6.1.4. ОПТИМАЛЬНЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
Вернемся к исходной системе с одним входом и одним выходом, в кото-
рой шум воздействует только на выход (случай 1, рис. 6.7). Откажемся те-
перь от предположения о некоррелированности п (I) и v (t), и пусть Н (f) —
произвольная линейная частотная характеристика, задающая преобразова-
ние х (t). Найдем такую H(f), которая минимизирует шум на выходе, при
этом оптимальность оценки Н (f) понимается в среднеквадратичном смыс-
ле. Заметим, что если между выходным сигналом и шумом есть корреля-
ция, например если выход содержит зависящий от сигнала инструменталь-
ный шум или вклад ряда других входных сигналов, коррелированных с наб-
людаемым сигналом х (t), то результирующая оптимальная//^) вовсе не
будет описывать фактически имеющийся тракт между точками, в которых
наблюдаются х (t) иу(1). Кроме того, преобразование входного сигнала в
выходной может быть нелинейным. В любом случае H(f) просто является
функцией, которая формально задает наилучшую в среднеквадратичном
смысле линейную связь между х (t) и у (t).
Для любого набора реализаций достаточно большой длины Т поведе-
ние системы, изображенной на рис. 6.7, описывается соотношениями
У(/) = Я(/)Х(/) + Я(/), (6.53)
где прописными буквами обозначены финитные преобразования Фурье со-
ответствующих реализаций во временной области. Очевидно, что
^(/) = г(/) - #(/)*(/), Я*(/) = У*(/) - Я*(/)Х*(/).
Следовательно,
И/)12 = |Г(/)!2 - я(/)у*(/)%(/)-
-Я*(/)Х*(/)У(/) + Я(/)Я*(/)|Х(/)|2. (6.54)
Взяв математическое ожидание от обеих частей равенства (6.54), умножив
их на 2/Г и устремив Т к бесконечности, получим
H(f)
«я;
I--------^y(t)
Рис. 6.7. Система с одним входом и одним выходом при наличии шума на
выходе.
Линейные системы с одним входным процессом
189
<?„„(/) = (6.55)
= Gyy(f) - H(f)Gyx(f) - H*(f)Gxy(f) + H(f)H*(f )Gxx(f\
Это выражение для Gnn (f) справедливо при произвольной H(f). По опре-
делению, оптимальная частотная характеристика H(f) это такая частот-
ная характеристика, которая минимизирует Gnn(f) по всем возможным
H(f). Эта оценка называется оценкой по методу наименьших квадратов
(см. разд. 4.8.2).
Минимизируем теперь Gnn(f) как функцию от H(f). Для упрощения
обозначений зависимость от f указываться не будет. Таким образом,
Gnn = Gyy - HGyx - H*Gxy + HH*GXX. (6.56)
Представим комплексные величины через их действительные и мнимые ча-
H = HR- jH„ H* = HR+ JH,,
Gxy = GR-jGlt Gyx = GR+jG,.
Тогда
G„„ = Gyy ~(HR — jH,)Gyx—(HR + jH,)Gxy +(HR + H?)GXX.
Для нахождения вида частотной характеристики Н, минимизирующей Gnn ,
нужно приравнять нулю частные производные Gnn по HR и Hj и решить
полученную таким образом систему уравнений. Имеем при этом
— -С„-С„ + 2ЯА,-0,
dGnn
=JGyx ~jGxy + 2H,GXX = 0 ,
откуда
_ Gxy + Gyx _ Gr = j(Gxy - Gyx) Gj_
R ~ 2G ~ Gxx ’ ' 2GXX G '
Следовательно, оптимальная характеристика H равна
Gn — jGj G
H = HR -jH, = 7 = • (6.57)
Gxx Gxx
Оптимальная характеристика H, вычисляемая по произвольным реализаци-
ям согласно формуле (6.57), носит теоретический характер и не обязатель-
но физически осуществима.
Подстановка оптимальной частотной характеристики//^) из (6.57) в
190
Глава 6
формулу (6.55) позволяет обнаружить еще одно ее важное свойство. Имен-
но, спектр шума на выходе равен
<?„„(/) =[1-гЛ(/)]^(/), (6.58)
откуда получаем выражение для когерентного спектра на выходе:
Gjj) = Gyy(f) - G„„(/) = Yxy(f)Gyy(f) . (6.59)
Кроме того, для оптимальной частотной характеристики Н (f) справедли-
вы соотношения
Gjj) = H(f)GjJ) ,
Gxn(f) = Gxy(f)-H(f)Gxx(f) = O. (6.60)
Следовательно,
<?,„(/) = tf*(/)Gxn(/) = 0. (6.61)
Таким образом, если для оценки линейной системы (рис. 6.7) используется
оптимальная частотная характеристика Н (f), то п (Г) и v (t) автоматиче-
ски не коррелированы.
Заметим также, что специальный вид уравнений (6.56) позволяет просто
найти ту же оптимальную Н путем приравнивания нулю или частной про-
изводной Gnn по Н (при фиксированном Н *) или частной производной Gnn
по Н * (при фиксированном Н). Этим способом получаем
= ~Gyx + H*G = 0,
дН у
G Gx v
= Н = -^- (6.62)
^ХХ ^хх
Обоснуем этот метод. Уравнение (6.56) показывает, что Gnn — действи-
тельная функция от (HR, Hj) или от (Я, Н *). Обозначим ее как
G„„=f(HR,Hf) = g(H,H*),
причем эта функция имеет вид
g(H, Н*) = АН + А*Н* + ВНН* + С, (6.63)
где А — комплексная величина, а В, С — действительные. Величина
HR(f} — это действительная часть H(f), a Hj(f) — мнимая часть H(f),
причем выполняются следующие соотношения: Н = HR - jHp Н* =
= HR + jHr Далее,
dGnn dg дН dg дН* dg dg
dHR ~ ~dH ~dlTR + dH* dHR~~dH dH* ’
Линейные системы с одним входным процессом
191
<?g ! ag <?я* /dg dg \
дН, ЭН дН,+ дН* дН, J[dH дН*]'
(6.64)
Следовательно, условия минимума, состоящие в том, что соотношения
dG„„ dHR Жпп дН, = 0 (6.65)
эквивалентны условиям — = дН А + ВН* = 0, ^--0. дН* (6.66)
Согласно формуле (6.63), эти равенства имеют место, если
---= А + ВН* = 0, откуда имеем Я* =-------;
дн в
д (6-67)
dg А*
----= А* + ВН = 0, откуда имеем Н =----------
ая* в
Поэтому оба условия (6.66) выполняются, если
(6.68)
Заметим, что это решение получено либо из равенства dg/ dH = 0 (при
Н * фиксированной), либо dg/дН * = 0 (при Я фиксированной) без исполь-
зования HR nHj. Из соотношения (6.56) находим, что Л = — Gyx(f) и
В = Gxx(f). Поэтому
Я(/) = Ми' <6-69)
GXX\J /
что совпадает с выражением (6.57).
6.2. Системы с одним входом и несколькими выходами
Опишем теперь модели, полезные при изучении свойств систем переда-
чи сигналов по нескольким трактам, соединяющим один источник с не-
сколькими точками на выходе. Предполагается, что системы, описываю-
щие передачу сигналов по таким трактам, линейны и имеют постоянные
параметры и что все неизвестные отклонения от этого идеального случая
включены в некоррелированный шум на выходе.
6.2.1. МОДЕЛЬ С ОДНИМ ВХОДОМ И ДВУМЯ ВЫХОДАМИ
Рассмотрим частный случай, когда система имеет один вход и два вы-
хода (рис. 6.8). Если предположить, что шумы п j(r) и n2(t) не когерентны
192
Глава 6
Рис. 6.8. Система с одним входом и двумя выходами.
(не коррелированы) между собой и с входным процессом х (t), то получим
приведенные ниже спектральные соотношения (зависимость от частоты f
не указывается для простоты обозначений):
Gxnx = GVxnx = Gxn2 = Gv2n2 = Gnxn2 = 0 >
Gyxyx = G^x + = l^|4x + G„x„x , (6.70)
Gy2y2 = GV2«2 + G"2"2 = \H2\1Gxx + G„2n2 2
Gxyx = Gxo, = Hfixx , Gxy2 = GXV2 = H2Gxx , (6.71)
Gyxy2 = G^2 = H*H2Gxx (6.72)
Функция когерентности между двумя выходными процессами в этом
случае равна
2 |С„.1; , 2
^y\yi G G G G ^ху^хуг * (6.73)
у\у\ у2у2 у\у\у2у2
Последнее равенство следует из того, что
IG^J2 = \h^h2gxx\2 = (|Я1|ЧХ)(|Я2|ЧХ) = GViVGV2V2,
2 IGxJ2 |Я^|2
GxxGytyi GxxGy2y2 Gy,yi
г IG..I' I//A.I1 G,,.,
”• a,fim Gnn
Применение этих результатов зависит от возможности измерения входного
сигналах (О одновременно с измерениями двух выходных сигналов —y{(t )
И ?20 )•
Линейные системы с одним входным процессом
193
СЛУЧАЙ 1. x(j), yx(t) И y2(t) НАБЛЮДАЮТСЯ ОДНОВРЕМЕННО,
В этом случае формула (6.71) дает следующие выражения для//! и //2:
н2 = ^.
Gxx Gxx
Тогда из формул (6.70) и (6.74) можно определить величины
G„tVl = |^l4x = y^Gyiyi, Gn^ = (1 - 7^yi)Gyiyi,
GV2v2 ~ 1#г1 Gxx — УХурУ2У21 Gn2n2 — (1 — yxy2)Gy^y^.
Следовательно, все величины, входящие в формулы (6.70)—(6.74), могут
быть вычислены.
СЛУЧАЙ 2. ОДНОВРЕМЕННО НАБЛЮДАЮТСЯ ТОЛЬКО у x(t) И y2(t). В
этом случае//! и//2 нельзя найти по формуле (6.71). Однако если//! и//2
известны из других соображений, скажем теоретических, то можно вос-
пользоваться формулой (6.72) для определения Gxx, т. е. Gxx =
= Gy /(Н ХН2). По известным//! и Н2 и вычисленной Gxx определяются
все остальные величины, входящие в формулы (6.70)—(6.74).
Если неизвестные Н х и Н2 нельзя определить из других соображений,
то все же можно вычислить Gy, „ , Gy, w и Gy, „ , а затем воспользоваться
У1У1 У2У2 У1У2 2
формулой (6.73) и найти функцию когерентности Уу^2 • Большие значения
тДу2 Указывают на то, что J 1(0 иу2(О, возможно, представляют собой
неизвестные линейные преобразования ненаблюдаемого общего источника
х (I), при этом посторонний шум на выходе мал по сравнению с сигналами.
Следует подчеркнуть, что большие значения когерентности не означают,
что между у x(t) и у2(1) существует причинная связь. Действительно, в
рассмотренной модели между выходными процессами нет причинной свя-
зи. Применение модели с двумя выходами к задаче локализации источника
энергии подробно рассмотрено в книге [6.1].
6.2.2. МОДЕЛЬ С ОДНИМ ВХОДОМ И НЕСКОЛЬКИМИ ВЫХОДАМИ
Рассмотрим систему (рис. 6.9), на единственный вход которой поступа-
ет стационарный случайный сигнал х (О, а на г выходах наблюдаются вы-
ходные сигналы у^ (t) (/ = 1, ... , г). В данном случае спектральные соот-
ношения для / = 1, ... , г имеют вид
у;(/) = я,(/)х(/) + а;.(/), (6.75)
где прописными буквами обозначены финитные преобразования Фурье со-
ответствующих реализаций во временной области, обозначенных строчны-
ми буквами. Для простоты и без потери общности предположим, что сред-
ние значения всех реализаций равны нулю. Предположим также, что каж-
7-953
194
Глава 6
Рис. 6.9. Система с одним входом и несколькими выходами.
дый шумовой процесс на выходе я ДО не коррелирован сх(/)и что все они
не коррелированы между собой.
СЛУЧАЙ 1. ОДНОВРЕМЕННО НАБЛЮДАЮТСЯ ВХОДНОЙ И ВСЕ ВЫХОД-
НЫЕ ПРОЦЕССЫ. По одновременным наблюдениям х (t) и всех выходных
процессов(О (i = 1, 2, ... ,г) можно определить
Gxy(J) = Я,.(/)СХХ(/).
(6.76)
Эти формулы совпадают с аналогичными формулами для рассмотренных
ранее моделей с одним входом и одним выходом. Тогда любую мож-
но вычислить по формуле
(6.77)
Иначе говоря, Hi (f) равна взаимной спектральной плотности входного
процесса х (/) и соответствующего выходного процесса (t), деленной на
спектральную плотность входного процесса. Функция обычной когерентно-
сти междух (Z) и .у, (t) есть
G„(/)G„,(/)
(6-78)
Любой выходной процесс легко разбивается на составляющие, соответст-
вующие сигналу и шуму.
Во временной области взаимная ковариационная функциях (t) и yt(I) за-
дается формулой
Rxy,('r)=f hi('r)Rxx(r - a) da, (6.79)
Линейные системы с одним входным процессом
195
где hi(r) — обратные преобразования Фурье 77, (О, т. е. импульсные пере-
ходные функции i -го тракта.
СЛУЧАЙ 2. НАБЛЮДАЮТСЯ ТОЛЬКО ВЫХОДНЫЕ ПРОЦЕССЫ. Рас-
смотрим теперь случай, когда наблюдаются только выходные процессы
y^t). Для каждого i = 1, 2, ... , г можно вычислить автоспектры
Gy.y,(f) = |Я,(/)|Чх(/) + (?„,„,(/). (6.80)
Соответствующие ковариационные функции равны
00
Ry,y,(r) = */(“)А^)йхх(т + a- 0)dadfi + /?„„(t). (6.81)
Для любых пар различных выходных процессов можно также найти
взаимные спектральные плотности и взаимные ковариационные функции.
При i Ф j в силу того, что Rn п (т) = 0 и Gn п (f) = 0, взаимная ковариа-
ционная функция задается формулой 1 J
Ry,yST) = £[z(')jy(' + т)] =
00
= t>i(a)hj(P)E[x(t - a)x(t + т - Д)] dadfi =
00
= ff+ a - Д) dadfi , (6.82)
так как математические ожидания всех остальных членов равны нулю.
С другой стороны, взаимную спектральную плотность любых двух выход-
ных процессов можно представить в виде
<?,.,,(/) = Я,.*(/)Я,(/)СХХ(/) . (6.83)
Из этого результата следует, что при известных 77, (/) и наблюдае-
мой Gy у (f) с помощью простых алгебраических операций легко найти
6^(7*), если Gxx(f) не наблюдается непосредственно.
Из формул (6.80) и (6.83) следует, что функция когерентности для лю-
бых двух выходных процессов равна
[|Я,.(/)126ХХ(/) + сп,и,(/)][|я7(/)|Чх(/) + <?„,„,(/)]
(6.84)
196
Глава 6
Различные частные случаи формулы (6.84), представляющие практический
интерес, исследуются в гл. 7 книги [6.1].
6.2.3. ИСКЛЮЧЕНИЕ ПОСТОРОННЕГО ШУМА
Предположим, что три или более наблюдаемых выходных процесса,
скажем .у! (О, .У и^3(О, суть искаженные шумом измерения исследуе-
мых выходных сигналов v ), v 2(t) и v 3(t) (рис. 6.9). Предположим так-
же, что шумы пх(1), n2(t) и n3(t) не коррелированы между собой и с 1^(0,
v2(t) и v3(t). Основываясь на идеях работы [6.3], покажем, что свойства
спектральных плотностей истинных выходных процессов v^t) можно уста-
новить, анализируя наблюдения
Величины, входящие во все последующие соотношения, зависят от ча-
стоты /, однако для простоты обозначений эта зависимость не указывает-
ся. Автоспектры наблюдаемых выходных процессов имеют вид
Gn = Gyiyi = 6^ + G„ini = <^„,(1 +
G22 = Gy2y2 = Gv2„2 + Gn2n2 = СР2Р2(1 + C2), (6.85)
G33 = Gy,y, = GViVi + G„3„3 = + C3),
где ci 0 обозначают отношение шума к сигналу на выходе i:
^1 ~ "> С2 ~ ^n2n2/^v2v2^ С3 ~ (6.86)
Наблюдаемые взаимные спектры выходных процессов таковы:
<?12 = Gyty2 = (713 = Gyiy} = GViU3, G23 = Gy2y3 = GV2U3. (6.87)
Предполагается, что vx(t), v2(t) и v3(t) порождаются общим ненаблю-
даемым источником х (t) (см. рис. 6.9). Поэтому функция обычной коге-
рентности между парами v^t) должна равняться единице, т. е.
2 _ 2 _ । _ 2 _ _
^^1^2 Л'’ S'"* ^1^3 S'"* S'"* ^^2^3 *
^JVlViJV2V2 ^3Р3 ^^2и2иЗиЗ
(6.88)
Поэтому
|G12|2 = |G„it,2|2 = GViUGV2V2 , |G13|2 = |GP1„3|2 = GUiVGV3V3,
|G23|2 = |G„2„3|2 = GV2VGV3V} . (6.89)
Из формул (6.85) и (6.89) следует, что
Линейные системы с одним входным процессом
197
2 = lGn!2 = 1 2 = 1<?1312 = 1
712 GUG22 (1 + q)(l + с2) ’ Y13 GUG33 (1 + q)(l + c3) ’
7 iW 1 (6’90)
^22^33 (1 + Сг)(1 + сз)
Разумно считать, что ни одна из наблюдаемых функций когерентности в
формуле (6.90) не обращается в нуль, поэтому
(1 + С1) Ti>(l + с2) ' (1 + Сг) " 72!,(1 + с,) ’(1+С5)’ъгз(1+С,) '
Отсюда получаем
, ч Т22з(1 + С3) = У23
С1 Уп YnYiV1 + ci)
(6.91)
(6-92)
Аналогичные формулы справедливы и для 1 + с2, 1 + с3. Следовательно,
, X |Т231 „ , ч 1Т1з1 ,л , . |У121
(1 + Сз ) = -------------- , (1 + С? ) = --------------- ) (1 + Со ) — -----------------
IY12I 1Т1з1 IY12I 1^231 |У1з1 1^231
Из уравнений (6.85) получаем требуемый результат:
" (1 + q) " |у23| 11 “ |G23|
_ @22 _ IT12I IT23I „ _ l^nl 1^2з1 ,
(TT7J“n^rG22- |G13| ’
(6.93)
(6.94)
_ G33 _ |Yi3| |y23I _ l<Jj3| |G23|
(TT7J"~Ы~ 33~1^Г‘
Поскольку GH, Gv^2 sj G22 и Gv^3 G33, то для
функций когерентности справедливы неравенства
V2V2 < V2 . v2v2 < v2 v2v2 < v2 (6.95)
Y12Y13 Y23, Y12Y23 T13; Y13Y23 — Г12. V 7
Уравнения (6.85) и (6.94) позволяют определить также и Gn п , Gn п
/-> 112 2
Gni'i'
ПРИМЕР 6.6. ИСКАЖЕННЫЕ ШУМОМ НАБЛЮДЕНИЯ. Вычисления пока-
зали, что спектральные плотности трех выходных наблюдаемых процессов
198
Глава 6
равны Gп(/) = G22(f) = 633(f) ~ 6, где 6 — постоянная, а функции
когерентности между выходными процессами равны 7J2 = 0» 5, 7J3 = 0,5 и
723 = Определим отношения сигнала к шуму и спектральные плотно-
сти сигналов, содержащихся в наблюдаемых выходных процессах.
Отношения шума к сигналу находим по формуле (6.93):
0,4 0,5
С1 = (0,5)(0,5) " 1 = °’60; Сг = (0,5)(0,4) “ 1 = 1’50’’
0,5
Сз ' (0,5)(0,4) 1'1’50-
Следовательно, отношения сигнала к шуму в наблюдаемых выходных про-
цессах равны
( W)i = 1,67; ($/ЛГ)2 = 0,67; (S/W)3 = 0,67,
а спектральные плотности сигналов, содержащихся в наблюдаемых выход-
ных процессах, таковы:
6,,,. = 0,6256 ; GV2V2 = 0,406; 6^ = 0,406.
6.3. Модели линейных решеток
Интересный частный случай системы с одним входом и несколькими
выходами дает модель, изображенную на рис. 6.9, если под входом x(t) по-
нимать точечный источник, излучающий энергию (например, акустический
шум) в однородной среде (например, в воздухе или воде), а под выходами
ум
yt(i)
УМ
УМ
Элементы
решетки j
Рис. 6.10. Линейная дискретная решетка.
Линейные системы с одним входным процессом
199
Л (О 0 = 1, 2, ... , г) — точечные приемники излучения, расположенные в
этой среде. В простейшем варианте такой модели приемники излучения
расположены на прямой линии, удаленной от источника (рис. 6.10). Конфи-
гурация приемников излучения, изображенная на рис. 6.10, обычно называ-
ется линейной дискретной решеткой, а приемники излучения называются
элементами решетки. В простой модели такой решетки предполагается,
что частотные характеристики /7z(f) (/ = 1, 2, ... , г) (рис. 6.9) практиче-
ски одинаковы с точностью до сдвига времени. Суммирование выходных
измерений дает два преимущества: а) увеличение отношения сигнала к шу-
му на выходе (усиление) и б) направленность, которая позволяет выделять
отдельные источники, имеющие разные углы падения в по отношению к
решетке (6 = 0, если источник находится на нормали к оси решетки).
6.3.1. КОЭФФИЦИЕНТ УСИЛЕНИЯ РЕШЕТКИ
Возвращаясь к модели с одним входом и несколькими выходами,
изображенной на рис. 6.9, предположим, что импульсные переходные
функции, задающие преобразование входного процесса х (Z) в выходные
процессы y.(t) (j = 1, 2, ... , г) одинаковы, т. е.
й.(т) = Л(т), / = 1,2,...,г. (6.96)
Линейная дискретная решетка, изображенная на рис. 6.10, будет довольно
точно отвечать этому предположению, если: а) источник находится доста-
точно далеко от решетки, так что падающую на решетку волну можно счи-
тать плоской; б) источник находится на нормали к оси решетки (в = 0°);
в) среда однородна. Предположим также, что шумы, присутствующие в
наблюдениях выходных процессов, имеют нулевые средние значения и рав-
ные дисперсии; кроме того, будем считать, что они статистически незави-
симы между собой и не зависят от входного сигнала, так что
£[и,(г)] = 0,
£[и,2(0] = а„2, • i,j = 1,2,..., г,
£[«,(/)%(/)] = опх = 0,
(6-97)
£[и,(фу(г)] = <jn nj = 0, z *j.
Следовательно, выходные наблюдения равны
л(0 = / й(т)х(г-т) dr+ «,(/) =
•'о
= и(/) + nz(/), i = 1,2,..., г. (6.98)
200
Глава 6
Среднее значение наблюдаемых выходных процессов есть
у = - t Ж + ",(')] = "(t) + - t (6.99)
r ,-i r <=i
Согласно формуле (4.33), дисперсия суммарного выходного процесса равна
°-у = °v +(Оп/г). (6.100)
Следовательно, если определить отношение сигнала к шуму на входе как
(S/N)in = (6.101)
то на выходе решетки отношение сигнала к шуму будет равно
(S/N )out = г = г (S/N )in. (6- Ю2)
Формула (6.102) показывает, что отношение сигнала к шуму на выходе ре-
шетки прямо пропорционально числу отдельных наблюдений на выходе
(числу элементов решетки). Поэтому это число обычно называют коэффи-
циентом усиления решетки. Коэффициент усиления решетки часто выра-
жается в децибелах, т. е. коэффициент усиления в децибелах равен lOlgr.
6.3.2. НАПРАВЛЕННОСТЬ РЕШЕТКИ
Если источник (рис. 6.10) смещается по отношению к нормали к оси ре-
шетки, то сигналы vi (t), содержащиеся в выходных наблюдениях у, (t)
Рис. 6.11. Определение запаздывания между элементами линейной дискретной
решетки.
Линейные системы с одним входным процессом
201
(/ = 1, 2, ... ,г), уже не будут синфазны, и, следовательно, чувствитель-
ность решетки к сигналу источника будет уменьшаться с ростом угла паде-
ния; это означает, что решетка обладает направленностью. Для оценки на-
правленности предположим, что скорость распространения энергии в среде
равна с, шаг решетки (расстояние между соседними элементами) равен d, а
угол падения энергии от источника равен 0 (рис. 6.11). Заметим, что для
удобства выбрано нечетное число элементов решетки, положение элемен-
тов по отношению к центру решетки определяется величинами nd (п =0,
± 1, ± 2, ... , ±т ), так что г = 2т 4- 1. Кроме того, пусть по-прежнему
выполняются все предположения, обеспечивающие справедливость формул
(6.97).
Предположим, что на центральный элемент решетки от источника па-
дает гармонический сигнал с единичной амплитудой, т. е.
t?0(z) = sin2тт/к . (6.103)
Из рис. 6.11 легко видеть, что на другие элементы решетки сигналы от ис-
точника попадают с запаздыванием тп = (nd/с) sin0 (п = 0, ±1,
±2, ... ,±пг). Поэтому
v„(t) = smfyrft + Кп d), (6.104)
где величина А', именуемая следовым волновым числом, равна
К= (2я//с>т0. (6.105)
Суммарный выход решетки тогда равен
Т = 22 sin(2w/Z + Knd) =
n=« — m
m
sin 2 я/z 22 cos Knd
n** —m
m
sin Kn d
(6.106)
+ CQSlirft
n= —m
Поскольку фаза суммарного выхода особого интереса не представляет, то
найдем модуль выражения (6.106):
m 12 Г m 12\
£ wsKnd + £ sintfnJ >. (6.107)
п= — m J Ln——m J /
|T| = Z>(*) =
Однако в силу симметрии относительно центрального элемента решетки
второй член в формуле (6.107) равен нулю, так’что
m
D(K) = 22 cos Knd =
n~ —m
sin( rKd/2)
sin(/W/2) ’
r = 2m + l. (6.108)
Последнее равенство получено с помощью известной формулы для суммы
202
Глава 6
конечного числа косинусов [6.4]
” cos[mx/2]sin[(m + 1)х/2]
2, cos их =------------ ------------- (6.109)
„-0 sm(x/2) v 7
и тригонометрического тождества
2 cos a sin b = sin(a + &) + sin(Z> — а) . (6.110)
Величина D (К ) из формулы (6.108) называется характеристикой на-
правленности и представляет собой зависимость коэффициента усиления
решетки от числа элементов решетки г и, следовательно, от волнового числа К,
которое в свою очередь зависит от частоты f и угла падения 0. Нормиро-
ванная характеристика направленности, максимальное значение которой
равно единице, определяется формулой
z ч sin(rXJ/2)
r-2m + 1 (6Л11>
Величина 10 lgD0(X^ называется коэффициентом направленного действия.
График типичной D 0 (К ) линейной дискретной решетки в полярных ко-
ординатах изображен на рис. 6.12. Главный лепесток характеристики на-
правленности называется лучом решетки. Заметим, что на характеристике
направленности видны несколько боковых лепестков, которые тесно связа-
ны с боковыми максимумами, свойственными спектральным окнам финит-
ных преобразований Фурье реализаций случайных процессов, о чем подроб-
но говорится в гл. 11. Действительно, формула (6.107) определяет модуль
дискретного преобразования Фурье в пространстве волновых чисел. Поэто-
Рис. 6.12. Характеристика направленности линейной дискретной решетки.
Линейные системы с одним входным процессом
203
му многие процедуры и проблемы, изучаемые в гл. 10 и 11, в том числе эф-
фекты маскировки частот и применение сглаживания для подавления боко-
вых максимумов, имеют прямое отношение к линейным решеткам.
ПРИМЕР 6.7. ШИРИНА ЛУЧА ДИСКРЕТНОЙ РЕШЕТКИ ПО УРОВНЮ ПО-
ЛОВИННОЙ МОЩНОСТИ. Ширина луча решетки иногда характеризуется
углом между прямыми, исходящими из центра решетки и проходящими че-
рез точки половинной мощности характеристики направленности решетки,
т. е. через точки характеристики направленности, в которых коэффициент
усиления составляет 50% его максимального значения. При фиксированном
расстоянии от источника угловая мера (ширина луча) может быть выраже-
на в линейных единицах. Для примера рассмотрим акустическую линейную
дискретную решетку в воздухе (с = 341 м/с), состоящую из г = 50 элемен-
тов с шагом d = 0,03 м. Найдем ширину луча решетки по уровню поло-
винной мощности в случае акустического источника с частотой 1000 Гц,
расположенного на расстоянии 300 м от решетки.
При указанных значениях параметров Kd /2 = O,28sin0. Следовательно,
по формуле (6.111) угловая ширина луча решетки по уровню половинной
мощности равна удвоенному углу, удовлетворяющему уравнению
Р„(Я _ 0,5 , sin(14-Qsinl?)
0 5Osin(O,28sin0)
Решая это уравнение методом последовательных приближений, получим
Q = 5,70°, поэтому угловая ширина луча решетки по уровню половинной
мощности равна 20 = 11,4°. Тогда при расстоянии источника от решетки
300 м ширина луча по уровню половинной мощности в метрах составляет
2-300 tg0 = 82 м.
Задачи
6.1. Рассмотрим простую механическую систему, изображенную на рис. 2.2, ча-
стотная характеристика которой, связывающая силу в единицах смещения на входе
х (t) = F (t )/к и смещение у (I) на выходе, имеет вид
H(f)--------------ч---------- •
1 -(///„) +JW/f„
Пусть f = 10 Гц и f = 0,01; найдите среднеквадратичное значение результирующе-
го смещения, вызванного белым шумом на входе, имеющим нулевое среднее значе-
ние и спектральную плотность Gxx(f) = 0,1 для всех частот.
6.2. Для механической системы из задачи 6.1 найдите максимум среднеквадра-
тичного значения смещения на выходе, вызванного гармоническим процессом
х (О = 2sin(207r/) на входе.
6.3. Предположим, что в условиях задачи 6.1 на выходной процесс воздействует
посторонний шум с спектральной плотностью Gnn (f) =0,1 для всех частот. Опре-
204
Глава 6
делите функцию когерентности между х (t) и у (t) на частотах:
а)/ = 0 Гц;
б)/ = 10 Гц;
в)/ = 100 Гц.
6.4. В условиях задачи 6.3 определите частотную характеристику по формулам
(без учета ошибок оценивания)
а)//.(Г) = G
б) Я#) = Gyy{f)/Gyxif).
6.5. Входной сигнал физической системы имеет спектральную плотность
Gxx (f) = 2/f 2. Взаимная спектральная плотность входного и выходного процессов
равна Gxy(f) = 4//3 - j (4/f2). Определите
а) амплитудную характеристику системы;
б) фазовую характеристику системы;
в) величину запаздывания, вызываемого системой.
6.6. На вход трех идентичных физических систем с равномерной амплитудной
характеристикой IН (f )1 = 10 поступают статистически независимые процессы ти-
па белого шума с спектральными плотностями - 1» GX2x2^ = 2 и
^х3х3(/) = Системы имеют общий выход, на который накладывается внешний
шум с спектральной плотностью Gnn (/*) = 100. Определите функцию когерентности
между каждым входным процессом и выходом.
6.7. Даны две физические системы с частотными характеристиками
= (1 + H2(f) = (1 + /в/)’1,
имеющие общий входной сигнал с спектральной плотностью Gxx (f)= 10, а на вы-
ходные сигналы систем накладываются посторонние шумы с одинаковыми спект-
ральными плотностями Gn i(/) = Gny2(f) = 0,1. Определите для частоты 1 Гц:
а) функцию когерентности между входным процессом и каждым из выходных
процессов;
б) функцию когерентности между выходными процессами.
6.8. Требуется построить решетку для обнаружения удаленных акустических ис-
точников. Предположим, что для надежного обнаружения сигнала требуется отно-
шение сигнала к шуму (5/7V)0Ut = 1,5, а ожидаемое отношение сигнала к шуму в
отдельном измерении (S/7V)in = 0,1. Определите:
а) сколько элементов должна иметь решетка;
б) функцию когерентности между выходными процессами любых двух элемен-
тов.
6.9. Подводная линейная дискретная решетка состоит из г = 100 элементов и
имеет шаг d = 0,3 м. Чему равен коэффициент усиления решетки для удаленного
акустического источника, расположенного под углом 10° по отношению к нормали к
оси решетки на частоте/ = 1000 Гц? (Скорость звука в воде принять равной с =
= 1500 м/с.)
6.10. Подводная линейная дискретная решетка должна иметь ширину луча по
уровню половинной мощности 60 м на частоте 5000 Гц, источник удален на 300 м,
шаг решетки равен d = 0,06 м. Сколько элементов должна иметь решетка?
Глава 7
МНОГОМЕРНЫЕ СИСТЕМЫ
В этой главе результаты гл. 6 обобщаются на системы с несколькими
входами. Как и ранее, предполагается, что все реализации принадлежат
стационарным случайным процессам с нулевыми средними значениями, а
системы линейны и имеют постоянные параметры. Изучаются системы с
несколькими входными процессами и одним или несколькими процессами
на выходе. Для этих систем определяются функции множественной и част-
ной когерентности. Приводятся итерационные вычислительные методы,
обладающие большей эффективностью по сравнению с матричными мето-
дами и позволяющие естественным образом раскладывать такие системы
на элементарные подсистемы. Разнообразные системы, изученные в гл. би
7, образуют набор элементарных моделей, дающий возможность сводить
анализ сложных реальных систем к анализу комбинаций элементарных
подсистем.
7.1. Системы с несколькими входами и одним выходом
Этот раздел основан на работах [7.1—7.3] и посвящен выводу основных
соотношений для систем с несколькими входами и одним выходом. Ниже
предлагается ряд подходов к анализу таких систем и интерпретируются по-
лученные результаты. Рассмотрим q линейных систем с постоянными па-
раметрами, задаваемых частотными характеристиками Hi (f)(i =
= 1, 2, ... , q ). На входы систем поступают полностью определенные наб-
людаемые входные процессы(t) (/ = 1, 2, ... tq ), которые преобразуют-
ся в один наблюдаемый выходной процесс y(t) (рис. 7.1). Относительно
коррелированности входных процессов не делается никаких предположе-
ний. В шум на выходе п (t) включены все отклонения от этой идеальной
модели, в том числе ненаблюдаемые входные процессы, нелинейные и не-
стационарные эффекты и инструментальный шум. Предполагается, что
наблюдаются реализации стационарных (эргодических) случайных процес-
сов, из которых предварительно исключены ненулевые средние значения и
периодические составляющие. Системы с несколькими входами и несколь-
кими выходами сводятся к комбинации систем с несколькими входами, но с
одним выходом типа изображенной на рис. 7.1.
7.1.1. ОБЩИЕ СООТНОШЕНИЯ
Для корректного определения системы с несколькими входами, изобра-
женной на рис. 7.1, нужно потребовать выполнения следующих условий:
1) функция обычной когерентности для любой пары входных процессов
не равна единице; в противном случае такие два входных процесса несут
избыточную информацию и один из них следует исключить из модели; это
условие позволяет сводить изучение систем с распределенным входом к
анализу систем с дискретными входами;
206
Глава 7
Рис. 7.1. Система с несколькими входными и одним выходным процессами.
2) функция обычной когерентности любого входного процесса и процес-
са на выходе не равна единице; в противном случае остальные входные
процессы не влияют на выходной процесс и систему можно считать про-
стой системой с одним входом и одним выходом;
3) функция множественной когерентности между любым входным про-
цессом и остальными процессами не равна единице; в противном случае
этот входной процесс является линейной комбинацией остальных входных
процессов; такой входной процесс не несет новой информации и должен
быть исключен из модели;
4) значение функции множественной когерентности между выходным
процессом и данными входными процессами должно быть достаточно
большим, скажем более 0,5, для того чтобы выполнялись теоретические
предпосылки и вытекающие из них выводы; в противном случае может
оказаться, что не учтены какие-то существенные входные процессы или не-
линейные эффекты; порог 0,5 выбран произвольно, практически он должен
выбираться исходя из инженерного и статистического анализа конкретных
условий и всего объема имеющихся данных.
Предположим, что в данной системе можно одновременно наблюдать
реализации входных и выходного процессов. Предположим также, что все
ошибки выбора модели и статистические ошибки, присущие вычисляемым
величинам, минимизированы с помощью тщательной калибровки и выбора
Многомерные системы
207
параметров процедур обработки данных. В частности, требуются хорошие
оценки действительных спектральных плотностей всех процессов и ком-
плекснозначных взаимных спектральных плотностей для любых пар про-
цессов. Эти спектральные величины используются для решения таких за-
дач:
1) разложения спектра выходного процесса на составляющие, имеющие
физический смысл и задающие вклад наблюдаемых входных процессов;
2) определения оптимальных линейных систем с постоянными парамет-
рами, связывающих каждый входной процесс с выходным и минимизирую-
щих долю спектра выходного процесса, не обусловленную линейными опе-
рациями над наблюдаемыми входными процессами.
Выходной процесс у (t) представляется в виде суммы q ненаблюдаемых
выходных процессовyi(t) (i = 1, 2, ... , q) и шума л (t):
q
y(t) = Е уМ + «(0 • (7.1)
/=1
В терминах финитных преобразований Фурье имеем
q
r(/)=EW) + M/). (7.2)
/ = 1
Каждая выходная функция У,- (f) удовлетворяет при i = 1, 2, ... ,q соотно-
шению . . Z \ Z \ Z
Ш) = #,(/)*,(/)• (7.з)
Следовательно, для системы, изображенной на рис. 7.1, основное соотно-
шение в частотной области имеет вид
q
+ (7.4)
7 = 1
где любые Xj(f) и Y (f) можно вычислить по наблюдениям xz (O и y(t).
По этим данным требуется вычислить частотные характеристики систем
//,(/*) и другие их параметры, причем все операции выполняются в частот-
ной области.
Финитные преобразования Фурье Х.(/) и У(/) отдельных реализаций
(О и у (t) длины Т равны
Xt(f) = dt, Y(f) = fTy(t)e~j2^‘dt. (7.5)
A)
Согласно формулам (5.66) и (5.67), односторонние спектральные и взаим-
ные спектральные плотности определяются как
<Ш) = Gx,x,(/) = lim ^[|^,(/)Г],
г (7.6)
<?,;(/) = сх,х//) = Нт [Х*(/Ч(Л],
Т —* оо 1
208
Глава 7
Gyy(f)= Нт |£[|Г(/)|2],
2 (7’7)
<?,>(/) = <?,,//) = Jim -E[Х*(/)У(/)].
T-*oo 1
Вместо односторонних спектров G (f), для которых G (f) = 0 при f < 0,
можно использовать двусторонние спектры S (f) (см. разд. 5.2.1). Все фор-
мулы, приведенные в этой главе, верны как для G (/*), так и для S (/). От-
ношение двух величин типа G (f) совпадает с аналогичным отношением
двух величин типа S (/). Ниже, как и в гл. 6, используются односторонние
спектры G (f).
На практике приходится иметь дело с оценками величины (7.6) и (7.7),
поскольку Т конечно, а математическое ожидание Е [ ] вычисляется по ко-
нечному набору реализаций. Далее, при цифровой обработке реализаций
(см. гл. 10 и 11) вычисления дают результаты только для определенных
дискретных частот. Для любой такой частоты/ оценка величины Gxy(f)
(обозначим ее Gvv(/)) обычно вычисляется по формуле
лу
2 nd
Gxy(f) = —£Xk*(f)Yk(f), (7.8)
ndi к=\
где nd — число различных (непересекающихся) реализаций x(t ) иу(1) дли-
ной Т каждая, так что общая длина реализации равна Tr = ndТ. В гл. 8
доказывается, что для уменьшения систематической ошибки значение Г
должно быть по возможности большим, а для уменьшения случайной
ошибки следует увеличивать nd. Поэтому при фиксированном Тг приходит-
ся искать компромисс между этими двумя ошибками.
В случае необходимости можно выписать аналогичные соотношения во
временнбй области через свертки весовых функций Л/т) (/ = 1, 2, ... , q),
соответствующих величинам //(/). Вместо уравнения (7.3) будем иметь
J/*OO
' Л,(т)х,(/ - т) dr , (7.9)
о
где нижний предел интегрирования равен нулю, если только системы физи-
чески осуществимы. Такие свертки и их аналоги для ковариационных функ-
ций значительно сложнее соответствующих спектральных соотношений и
поэтому в дальнейшем использоваться не будут. Ковариационные соотно-
шения не содержат в явном виде информации о зависимости искомых ха-
рактеристик от частоты. Хотя такая информация неявно присутствует в
ковариационных функциях, вряд ли будет оправдано вычисление их без
особой на то необходимости, тем более что прямое вычисление спектраль-
ных характеристик гораздо эффективнее.
7.1.2. ОБЩИЙ СЛУЧАЙ ПРОИЗВОЛЬНЫХ ВХОДНЫХ ПРОЦЕССОВ
Рассмотрим общий случай произвольных входит процессов. Из урав-
Многомерные системы
209
нения (7.4), заменив индекс суммирования i на у, имеем
<7
ПЛ = Е #,(/)*,(/) + *(/)• (7.10)
7=1
Умножив обе части этого уравнения на %/*(/’) при i = 1, 2, ... , q, получим
я
= Е Н,(/)Л,*(Л*,(Л + X*(f)N(f).
7 = 1
Возьмем математическое ожидание от обеих частей этого равенства:
я
E[X*(f)Y(f)] = ЕЯ,.(/)£[Х*(/)ХУ(/)] +Е[Х,*(/)У(/)]
/=1
Умножив обе части на 2/Г и устремив Тк бесконечности, получим, соглас-
но формулам (7.6) и (7.7),
я
Gjj)= Е Я,(/)6„(/) + Gin(f) ’ ,
7 = 1
где взаимные спектральные плотности Gin (f) равны нулю, если п (t) не
коррелирован ни с одним изхДО- При этом предположении получаем си-
стему уравнений q
z = 1,2,...,<?. (7.П)
7 = 1
В этой системе q уравнений с q неизвестными //•(/) (/ = 1, 2, ... , q) все
спектральные плотности можно вычислить по реализациям входных и вы-
ходного процессов. Если модель выбрана правильно, то систему можно ре-
шить относительно Н^) с помощью правила Крамера или любыми дру-
гими матричными методами.
Суммарная спектральная плотность выходного процесса Gyy(f) выра-
жается через (f), найденные из системы (7.11), и имеет вид
Gyy(f) = Е Е Я,*(/)НУ(/)С17(/) + Gnn(f) (7.12)
/=17=1
в предположении, что п(t), как и ранее, не коррелирован ни с одним x^t).
Формула (7.12) получена из соотношений
Y*(f) = Е #*(/)*,*(/)+ 7V*(/);
7=1
я
Y*(f)Y(f) = Etf,*(/)W) + tf*(/) Е «,(/)%//) +И/) =
.7=1 7=1
= Е Ея,*(/)я7(/)х,*(/Ц(/) + ЛГ*(/)М/)+
'=1 /=1
+ EW)WW) + Ея;(/)Н/)^(/).
210
Глава 7
Если обе части последнего равенства умножить на 2/Г и перейти к преде-
лу, то получим
q q
Gyy(f) = Е Ея,*(/)яу(/)с,7(/)+ (?„„(/)+
'=17=1
q q
+ EW)g,(/) + Е
i-l у=1
Отсюда следует формула (7.12), если взаимные спектральные плотности
Gin(f) = 0 для всех f и i. При q различных входах, если Gzy(/) * 0
для i Ф j, спектр выходного процесса Gyy(f) из формулы (7.12) содержит
q2 + 1 составляющих. Разложение Gyy(f) на эти составляющие и их ин-
терпретацию оставляем в качестве полезного упражнения.
7.1.3. ЧАСТНЫЙ СЛУЧАЙ ПОПАРНО НЕКОРРЕЛИРОВАННЫХ ПРОЦЕССОВ
Рассмотрим важный частный случай, когда не только п (t) не коррели-
рован ни с одним из (О, но и входные процессы попарно не коррелирова-
ны. В этом частном случае уравнения (7.11) и (7.12) приводятся к виду
= i=l,2,...,q (7.13)
ч ,
Gyy(f)= Е |Я,(/)| Gu(f) + G„„(/). (7.14)
/=1
Эти соотношения имеют очень простой смысл: исходная модель распалась
на совокупность отдельных моделей с одним входом и одним выходом.
Для определения 77z(/) решать систему уравнений не надо. По формуле
(7.13) любая //,(/) задается отношением
Я//) = Т?Т7Т’ (7.15)
\f)
Спектр выходного процесса Gyy(f) из формулы (7.14) в отличие от спектра
из формулы (7.12) содержит теперь только+ 1 составляющих. Любая из
q составляющих представляет собой когерентный спектр выходного про-
цесса отдельной системы с одним входом и одним выходом:
|Я,(/)|2С,,(/) = 7^(/)^(/) • (7.16)
Эти величины задают вклад реализации xz (7) входного процесса bj(Z), при
этом х, (4) проходят только через систему с частотной характеристикой
//, (/’). Никакая часть xz(f) не проходит через другие системы с частотными
характеристиками Hj (f), поскольку xz (t) не коррелирован с ху (t) при i Ф j.
В общем случае входных процессов с произвольными корреляционными
Многомерные системы
211
соотношениями между ними любая входная реализация xi (t) может по-
пасть на выход у (t) через любую из систем с частотными характеристика-
ми //,.(/) (i = 1, 2, ... , q). В этом случае довольно трудно определить
вклад в Gyy(f) каждой из входных реализаций, если для решения этой за-
дачи использовать «грубые» матричные методы. Кроме того, матричные
методы ничего не говорят о физическом смысле проводимых преобразова-
ний, что не позволяет судить о согласии математических результатов с
практическим положением дел. В этой главе показано, что для решения
этих и многих других задач существуют более эффективные методы.
7.2. Системы с двумя входами и одним выходом
Для того чтобы лучше понять основные этапы анализа систем с произ-
вольным числом входных процессов, рассмотрим частные случаи систем с
двумя и тремя входами. Общий случай исследуется аналогично с очевидны-
ми изменениями. В этом разделе подробно изучены системы с двумя вхо-
дами. Соотношения для систем с тремя входами и одним выходом будут
выведены в разд. 7.3.
7.2.1. ОСНОВНЫЕ СООТНОШЕНИЯ
Рассмотрим систему с двумя входами и одним выходом (рис. 7.2), в ко-
торой входные процессы могут быть коррелированы. Предположим, что
Х1(О, ) и^(О доступны наблюдению. Такая система описывается сле-
дующим соотношением в терминах преобразований Фурье:
У(Л = ЯЖ(/) + Я2(/)Х2(/) + Я(/). (7.17)
При произвольном n(t), которое может коррелировать с xx(t) и(или)
х2(О, односторонняя спектральная плотность процесса у (t), вычисляемая
согласно формулам (7.5)—(7.8) по достаточно длинной реализации конеч-
ной длины Г, равна
2
2
= у Е [ { Н?Х* + Я2*Х2* + N* } { Н1Х1 + Н2Х2 + N) ], (7.18)
Рис. 7.2. Система с двумя входными и одним выходным процессами.
212
Глава 7
где зависимость от / и предельный переход по Т не указаны для упроще-
ния обозначений. Из (7.18) имеем
Gyy = + H?H2Gl2 + HjH2*G21 + |H2|2G22 + G„„ +
+ H^Gln + H2Gnl + H2*G2n + H2Gn2, (7.19)
где последние четыре слагаемых в правой части присутствуют только в
том случае, когда n(t) коррелирован с Xj(O и x2(Z).
При произвольном л (t) взаимные спектральные плотности х j (t) и у (О,
как и x2(t) и j (О, вычисляются аналогично:
2 2
Gly = + Н2Х2 + ЛГ)] =
= HlGn + H2G12 + Gln ; (7.20)
2 2
G2y = = ~Е[Х{(НгХ2 + H2X2 + tf)] =
= Hfi22 + H2G22 + G2n. (7.21)
Здесь зависимость от / и предельный переход по Т тоже не указаны для
простоты обозначений. Члены G 1л и G присутствуют только тогда, ког-
да п (t) коррелирован с Xj(Z) и x2(Q.
По известным хj(О, x2(t) их (О можно найти следующие односторон-
ние спектральные характеристики:
Gn = Gn(/) = Спектр Xj (О,
G22 = G22^) = Спектр х2(О,
Gyy = Gyy^ = Спектр х (О,
G12 = С12(/) = Взаимный спектр х^ (О их2(О,
G ij = G iy ) = Взаимный спектр х j (О и у (О,
G2y ~ G2y^^ = Взаимный спектр х2(О их (О,
G2i = С *2(/) = Величина, комплексно-сопряженная G12.
Все спектральные характеристики, связанные сп (Z), неизвестны. В частно-
сти, уравнения (7.20) и (7.21) нельзя решить относительно Н х и Н2, за ис-
ключением случая, когда G Хп = ОиС^ = 0, где
G \п = G in ) = Взаимный спектр х j (t) и п (г),
G2n = G2n^^ = Взаимный спектр x2(t) и п (t).
Если n(t) не коррелирован сх^) их2(Г), то уравнения (7.20) и (7.21)
принимают вид
Gly(f) = H1(/)Gn(/) + H2(/)G12(/) ,
G2y(f) = ^(/)G21(/) + H2(f)G22(f) . (7 22)
Многомерные системы
213
Решив эти уравнения относительно Hx(f) и H2(f) в предположении
Т12(/) * 1, получим
Я2(/)=
n G12(/)C2//)
Л[ С22(/)<?1,(/)
Gn(/)[1 " Yi22(/)]
GiyU)
G2i(f)Gly(f)
Gn(OG2y(f)
G22(/)[1-Yi22(/)]
(7.23)
где величина
7 ( f\ lGl2(/)l /7 -дх
Y12(/) Gu(/)G22(/)
является обычной функцией когерентности. В частном случае некоррелиро-
ванных входных процессов, когда 712(f) — 0, члены G n(f) и G2i(f) равны
нулю и формулы (7.23) сводятся к формулам для систем с одним входом и
одним выходом:
(7'25’
Случай 712(f) = 1 требует осдбого рассмотрения. Если функция коге-
рентности равна единице, то отсюда следует, что между х1 (t) и x2(t) су-
ществует строго линейная зависимость. Поэтому должна существовать ли-
нейная система, связывающая эти процессы (рис. 7.3). Следовательно, пер-
вый входной процесс х} (t) фактически поступает на выход у (t) по двум
разным трактам. В этом случае преобразование х j (t) в у (I) описывается
одной частотной характеристикой Н (f):
Ж/) = Я1(/) + Я2(/)Я3(/).
Если л (О не коррелирует cXj(O их2(О, но 612(/*) =# 0, то формула
(7.19) принимает вид
Gyy(f) =|h1(/)|2g11(/) + я1*(/)я2(/)с12(/)+
+Я2*(/)Я1(/)С21(/) + |я2(/) |2G22(/) + G„„(/). (7.26)
Перепишем ее иначе:
Gyy(f) = GJJ) + GJJ) = Gyx(f) + Gy .„(/), (7.27)
где Gnn ) = Gy:n (f) — вклад шума в автоспектр выходного процесса, а
214
Глава 7
Рис. 7.3. Система с двумя полностью коррелированными входными процессами.
Gvv(f) = — идеальный спектр на выходе системы, определяемый
первыми четырьмя членами формулы (7.26), зависящими от двух входных
процессов. Точйее говоря, Gvv(f) вычисляется по известным ОцСЛ),
С?12(/*), ^22^)’ а также по и найденным по общей формуле
(7.23). Наконец, даже еслии(/) не наблюдается, спектральную плотность
Gnn (f) можно найти по формуле
Gjf) = Gjf) - Gjf) . (7.28)
В частном случае некоррелированных входных процессов, когда
G12(/) = 0, идеальный спектр выходного процесса равен
Gjf) =\HAf)\2GJJ) + \H2(J) \2GJJ), (7.29)
где Hx(f) и H2(f) задаются формулами (7.25),
\HAn\2Gjf) = yJf)Gjf),
(7.30)
\HAf)\2Gjf) = yJf)Gjf).
Здесь 7iy(f) и — функции обычной когерентности:
уЧ/). ,, 1М/)1г ,731)
Для некоррелированных входных процессов имеем
Gjf)= [yJf) + yJf)]Gjf) , (7.32)
Gjf) = [1 - yjf) ~ yJf)]Gjf) . (7.33)
Величина задает спектральную плотность выходного процесса
системы с частотной характеристикой Н i, входом которой служит только
х{. Аналогично \Н212G н задает спектральную плотность выходного про-
Многомерные системы
215
цесса системы с частотной характеристикой Н2, входом которой служит
только процессх2. Эти две величины представляют собой обычные коге-
рентные спектры выходного процесса и соответственно для
входного процесса Xj и выходного процесса у и входного процесса х2 и вы-
ходного процесса у.
7.2.2. ОПТИМАЛЬНЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
Уравнения (7.22) и (7.26) выведены в предположении некоррелированно-
сти п (t) с Xj(О их2(О- Если отказаться от этого предположения, то при
прохождениих j (О их2(О через произвольную пару линейных систем с по-
стоянными параметрами и частотными характеристиками Нx(f) и H2(f)
соответственно имеет место соотношение (7.17), утверждающее, что
М/) = Л/) -
Следовательно, для произвольных Нx(f) и H2(f) спектр шума на выходе
равен
2
= Gyy(f) - - H2(f)Gy2(f)-
-Hr(f)Gly(f) + H*(/)^(/)Gu(/) + Я1*(/)Я2(/)С12(/)-
-H2*(f)G2y(f) + ^(/)^*(/)G21(/) + H2(/)^2*(/)G22(/)_
Оптимальными частотными характеристиками называются такие ча-
стотные характеристики Hx(f) и H2(f), которые минимизируют Gnn(f)
для всех f по всем возможным парам Hx(f) и H2(f). Такие функции зада-
ют оптимальный в среднеквадратичном смысле прогноз у (t) по х j (t) и
х2(О.
Как указывалось в гл. 6, для получения оптимальных//^) и H2(f) до-
статочно приравнять нулю следующие частные производные:
dGnn(f) п А
------—- = 0 при фиксированном
Яа"<-п п
———Г = 0 при фиксированном H2(f).
^"2 U )
Эти равенства приводят к системе уравнений
-Gly(f) + ^(/)Gn(/) + H2(f)G12(f) = О,
- G2y(f) + H1(/)G21(/) + H2(/)G22(/) = 0,
идентичной системе (7.22).
216
Глава 7
Для любой пары Hi(f) и H2(f) взаимные спектральные плотности
61„(Л И G2n(f) равны
2
= Gly(J) ~ - H2(f)G12(f)-
2
G2Af) = ^E[X2*(f)N(f)] =
= G2y(f) - ^(/)G21(/) - H2(f)G22(f).
Если H{(f) и H2(f) — оптимальное решение, удовлетворяющее уравнени-
ям (7.22), то эти взаимные спектральные плотности тождественно равны
нулю для всех/. Следовательно, оптимальные и H2(f), минимизи-
рующие Gnn (/*), автоматически обеспечивают некоррелированность п (t) с
X, (О и Xj(t): z ч .
<?1и(/) = о, g2„(/) = o.
Следует отметить, что оптимальные//^) и H2(f), удовлетворяющие
уравнениям (7.22), не обязательно физически осуществимы. Это означает,
что соответствующие весовые функции hx(r) и h2(r) могут отличаться от
нуля при т < 0. В самом деле, если реальные системы нелинейны, то такое
оптимальное решение представляет собой всего лишь численное оптималь-
ное линейное приближение и соответствующие линейные системы никогда
не совпадут с истинными нелинейными системами. Разумеется, если реаль-
ные системы — это физически осуществимые линейные системы с постоян-
ными параметрами, в которых учтены все входные сигналы, влияющие на
выходной сигнал, то теоретические результаты будут отвечать реальным
условиям, если только шум на выходе не коррелирован со всеми входными
процессами, а шумом на входе можно пренебречь. В дальнейшем будем
считать, чтоHx(f) nH2(f) определены по формулам (7.23). Эти результа-
ты следуют либо а) из предположения о некоррелированности п (t) с xx(t)
и х2(О, либо б) из требования, что//x(f) nH2(f) задают оптимальные ли-
нейные системы с постоянными параметрами, оптимизирующие Gnn(f),
при этом n(t) автоматически не коррелирован cXj(O и x2(t).
7.2.3. ФУНКЦИИ ОБЫЧНОЙ И МНОЖЕСТВЕННОЙ КОГЕРЕНТНОСТИ
Вернемся к общему случаю коррелированных входных процессов, когда
У 12(f) — любое положительное число, меньшее единицы. Функции обыч-
ной когерентности между каждым входным процессом и выходным про-
цессом равны
|Я1(/)611(/) + Я2(/)С12(/)|2
GnU)GyyU)
У22,(/) =
I^(/)g21(/) + Я2(/)С22(/)Г
(7-34)
б2АПбУЛП
Многомерные системы
217
где числители — это G^(f) и определенные из уравнений (7.22).
Произведение 7^,6^, задает когерентный спектр выходного процесса, рав-
ный вкладу Xi в выходной процессу. Однако х{ влияет на выход не только
через систему с частотной характеристикой Н j. В силу того что уf2
часть х j влияет на выход и через систему с частотной характеристикой Н 2.
Аналогично х 2 попадает на выход как через систему с частотной характери-
стикой Н j, так и через систему с частотной характеристикой Н 2, если
712 =# 0; обычный когерентный спектр выходного процесса У2у^уу учиты-
вает все способы, какими х2 влияет на выходной процесс у. Вообще говоря,
при малой G„„(/) сумма yly(f) и у^(/) превосходит единицу, если вход-
ные процессы коррелированы.
Функция множественной когерентности — это сравнительно простое
понятие, непосредственно обобщающее функцию обычной когерентности.
По определению, функция множественной когерентности равна отношению
идеального спектра выходного процесса, обусловленного наблюдаемыми
входными процессами при отсутствии шума, к суммарному спектру выход-
ного процесса, включая вклад шума. Формально функция множественной
когерентности есть
2 ,,2 G^f> ,
(7-35)
поскольку Gvv(f) = Gyy(f) — Gnn(f). Для системы с двумя входами об-
щего вида Gvv(f) определяется формулой (7.26). Множественный коге-
рентный спектр выходного процесса определяется как произведение функ-
ции множественной когерентности и спектра выходного процесса:
<?„„(/) = уДх(/ЧД/). (7.36)
Очевидно, из формулы (7.35) следует, что для любых f
0^2:х(/)^1. (7.37)
Эта функция равна 1, если Gnn(f) = 0, что соответствует идеальной ли-
нейной системе, и равна нулю, если Gyy (f) = Gnn (f). Последнее равенство
означает, что выходной процесс не обусловлен какими-либо линейными
операциями над наблюдаемыми входными процессами.
Для системы с одним входом и одним выходом, когда x2(t) = 0 и
H2(f), идеальный спектр выходного процесса, как показывает формула
(6.59), равен
<U/) =I#(/)|2(U/) = Y2,(/)G,//), (7.38)
где х,(Г) = x(t) и H(f) = Gxy(f)/ Gxx(f). Тогда
у,2:л(/) = т47Т = ^(/)- (739)
Uy у'J '
Следовательно, функция множественной когерентности в этом случае со-
впадает с функцией обычной когерентности.
218
Глава 7
Для системы с двумя входами и одним выходом при некоррелирован-
ных входных процессах идеальный спектр выходного процесса в соответст-
вии с формулой (7.32) имеет вид
Gvv(f)= ,У12Л/) + ъ2Л/)]^(/)-
В этом случае функция множественной когерентности равна
У2л(/) = У12Д/) + У22,(/)- (7-40)
Это означает, что при некоррелированных входных процессах функция
множественной когерентности равна сумме функций обычной когерентно-
сти между каждым входным процессом и выходным процессом. Для кор-
релированных входных процессов такой простой зависимости нет.
ПРИМЕР 7.1. МНОЖЕСТВЕННАЯ КОГЕРЕНТНОСТЬ ДЛЯ НЕКОРРЕЛИРО-
ВАННЫХ ВХОДНЫХ ПРОЦЕССОВ. Рассмотрим пример системы с двумя
некоррелированными процессами на входе и одним выходным процессом;
действием шума на выходе можно пренебречь. Предположим, что эти два
входных процесса порождают одинаковые спектры на выходе. В данном
случае
Уу-.xU) = ylyU) + y///) = i,o ;
Y?//) = Y22//) = 0,50 .
Здесь каждый вход и выход соединены линейными системами с постоянны-
ми параметрами и частотными характеристиками Hx(f) и H2(f)\ yXy(f) =
= 0,5 в силу наличия второго входного процесса. Если бы он не наблюдал-
ся и система рассматривалась как система с одним входом и одним выхо-
дом, то это привело бы к ложным выводам.
7.2.4. УСЛОВНЫЕ СПЕКТРАЛЬНЫЕ ПЛОТНОСТИ
Если некоторая пара входных процессов коррелирована, то для пра-
вильного математического описания реальных систем следует по возмож-
ности выяснить степень влияния одного процесса на другой. Если это мож-
но сделать, то исключение первого процесса приведет к вычитанию из вто-
рого процесса вклада первого за счет корреляции, так что останется только
та часть второго процесса, которая никак не связана с первым. Более точ-
но, если исходя из инженерных соображений можно утверждать, что кор-
реляция между х j (I) и х2(О заключается во влиянии xx(t) наx2(t), то сле-
дует определить оптимальный линейный вкладxx(t) вх2(О; обозначим его
х2:1 (О- Вычтя его изх2(О, получим условный (иначе говоря, остаточный)
процесс х2-1(О> представляющий часть x2(t), не связанную с Xj(O- Фор-
мально x2(t) раскладывается в сумму двух некоррелированных членов
(РИС-7'4): x2(t) = x2.A(t) + х2.^) • (7.41)
Переходя к преобразованиям Фурье, получим
Многомерные системы
219
X,(t)
-r2.iW
Рис. 7.4. Выделение вкладах^/) в х2(/).
Х2(/) = Х2:1(/) + Х21(/), (7.42)
где
Х2:1(/) = Ь12(/)Х1(/). (7.43)
Последнее соотношение определяет оптимальный в среднеквадратичном
смысле линейный прогноз х2(О по Xj(/). Преобразование Фурье х2>1(/)
равно
Х2.1(/) = Х2(/)-£12(/)Х1(/). (7.44)
Линейная система с постоянными параметрами и частотной характеристи-
кой£ 12(f) — это оптимальная линейная система, прогнозирующая x2(t) по
Xj(Z), взятым именно в этом порядке. Как показано в гл. 6, L 12(f) задается
отношением взаимной спектральной плотности входного и выходного про-
цессов к спектральной плотности входного процесса:
(7-45)
Формула (6.61) показывает также, что такой выбор обеспечивает некорре-
лированность х2. j(О hXj(O и приводит к разложению спектрах2(t):
С22(/)= С22:1(/) + <?221(/)» С7’46)
гдеО22:1(/*) — когерентный спектр выходного процесса:
G22:1(f) =1^12(7) Г<?п(/) = 7122(/)<?22(/), (7-47)
а ^22-— спектр шума на выходе:
<?22 i(/) = [1 - Yi22(/)]G22(/). (7.48)
Отметим, что следует строго различать индексы 22:1 и 22-1.
ПРИМЕР 7.2. ЛОЖНАЯ СИЛЬНАЯ КОГЕРЕНТНОСТЬ. На рис. 7.5 приво-
дится пример ложной сильной когерентности. Предположим, что функция
обычной когерентности процессов х j (t) иу(1) близка к единице. Отсюда
можно было бы заключить, что существует реальная линейная система, ко-
торая связывает эти два процесса как входной и выходной. Пусть, однако,
имеется третий процесс х2(Г), сильно когерентный cXj(O, который преоб-
разуется линейной системой в у (О- Тогда сильная когерентность х j (t) и
220
Глава 7
Рис. 7.5. Пример ложной сильной когерентности.
у (I) отражает только тот факт, 4T0Xj(Z ) их2(О сильно когерентны их2(О
связан линейной системой cy(t). В действительности может оказаться, что
х j (t) и (О вообще не связаны никакой реальной системой. Вычисление
функции частной когерентности (которая будет определена ниже) показало
бы, что ее значение очень мало и близко к нулю. На этом пример 7.2 за-
канчивается.
В тех случаях, когда причинно-следственные связи между входными
процессами не ясны, следует вычислять взаимную ковариационную функ-
цию этих двух процессов для определения относительного запаздывания,
которое покажет, какой из процессов опережает другой. Как отмечалось в
разд. 6.2.1, между двумя процессами, вызванными общим источником,
может существовать сильная взаимная корреляция и сильная когерент-
ность, хотя ни один из процессов не является причиной другого.
Если нет естественных причин для упорядочения процессов, а относи-
тельное запаздывание, определенное по взаимной ковариационной функ-
ции, незначительно, то рекомендуется вычислять функции обычной коге-
рентности между каждым входным процессом и выходом. Процессы сле-
дует упорядочивать в соответствии со значениями функции обычной коге-
рентности на особо важных частотах, скажем соответствующих максиму-
мам спектра выходного процесса, где передается большая часть мощности
или энергии. Например, если на некоторой частоте значения функции
обычной когерентности для входных процессов x^t) и x2(t) равны у^уС/])
и t2j(/2), то в качестве первого следует выбирать процесс с бдлыпим зна-
чением функции обычной когерентности. Аналогичное сравнение значений
функций обычной когерентности у^,(f2) и (f2) на другой частоте f2
может привести к иному упорядочению входных процессов. Таким обра-
зом, на разных частотах могут быть выбраны разные модели.
Для определенности будем считать, что процесс х j (t )предшествует
x2(t). Вместо рис. 7.2 следует взять соответствующий ему рис. 7.6, на ко-
тором Нх = НХу иН2 = Н2у. Рис. 7.6 показывает, что входной процесс
х j (О проходит на выход по двум параллельным трактам, в то время как
условный входной процесс x2-1(Z) проходит по одному тракту. В явном ви-
де эта ситуация изображена на рис. 7.7.
На исходном рис. 7.2 два наблюдаемых входных процессах^ ) их2(О
коррелированы, полученные линейным преобразованием выходные процес-
Многомерные системы
221
Рис. 7.6. Система, эквивалентная системе, изображенной на рис. 7.2.
сы у j(t) и^2(О тоже коррелированы. На эквивалентном рис. 7.7 входные
процессы хг (О их2-1(О Уже не коррелированы, что следует из способа их
построения. Выходные процессы v j (t) и и2(О, полученные линейным пре-
образованием входных процессов, тоже не коррелированы. Рисунок 7.7 эк-
вивалентен рис. 7.8, если в качестве частотных характеристик взять L j (f)
hL2 (f) вида
Lly(f) = Hly(f) + L12(f)H2y(f),
L2y(f) = H2y(f) .
(7-49)
На рис. 7.8 изображена система с двумя входами и одним выходом,
причем выходной процесс у (t) и шум и (t) те же, что и на рис. 7.2. Однако
входные процессы теперь не коррелированы, так что система, показанная
на рис. 7.8, эквивалентна двум отдельным системам с одним входом и од-
ним выходом, которые сейчас будут описаны. Линейная система с постоян-
ными параметрами и частотной характеристикой Lly — это оптимальная
линейная система, осуществляющая прогноз у (/) пох^О, а линейная си-
стема с постоянными параметрами и частотной характеристикой L 2у — оп-
тимальная линейная система, осуществляющая прогноз у (!) пох2>1(О-
Рис. 7.7. Система, эквивалентная системе, изображенной на рис. 7.6.
222
Глава 7
Рис. 7.8. Система, эквивалентная системе, изображенной на рис. 7.7.
В формальной записи основное соотношение в частотной области, описы-
вающее систему, изображенную на рис. 7.8, для стационарных случайных
процессов имеет вид
У(/) = L1//)X1(/) + А2Д/)Х24(/) + N(f), (7.50)
где
v(/) " ’ 1у{П~ G221U) ' ( ' }
Здесь Giy(f) — взаимный спектр*^) и y(t); — спектр Xj (О;
^71(f) — взаимный спектрx2.j(О ny(t); G— спектрх2. j(Z).
Величина G2y.x(f) называется условной (остаточной) взаимной спект-
ральной плотностью, а величина G22.x(f) — условной (остаточной)
спектральной плотностью.
Эти условные спектральные плотности можно вычислить по заранее
определенным спектральным плотностям исходных наблюдаемых процес-
сов с помощью простых алгебраических операций. Никакого усреднения ус-
ловных преобразований Фурье не требуется, разве что для вывода соот-
ветствующих алгебраических соотношений. По определению, после взятия
математических ожиданий для конечного Т имеем
2 2
= -Е [ X^(f)Y(f)] , G12.sn = -Е [ХЫПХ2.АП] •
Согласно формулам (7.43) и (7.45)
rne£12(f) = G 12(f)/G n(f). Следовательно, для любых трех реализаций
х 1 (Г), х2(О и у (t) имеем
2
G2y.l(f) = у£[{ W) - ^2(/) W) W)] =
2 fl 1
= ^E[X2^f)Y(f)] - £?2(/)|у£[Х*(/)П/)]} =
Многомерные системы
223
= G2v{f) ~[G2l(f)/Gn(f)\Giy(J). (7.52)
В частности, подставляя х2(О вместо ^(Z), получаем
<?22.1(/) = G22U) - [б21(/)/С11(/)]б12(/) =
= [1-712(/)]G22(/), (7.53)
т. е. G22- i(f) — спектр шума на выходе для системы с одним входным
процессом х j (t )и одним выходным процессом х2(О (см. рис. 7.4). Анало-
гично замена x2(Z) naj(Z) дает
Gyy 1(/) = I1 - ГьХ/)]^//), (7.54)
что определяет спектр шума на выходе системы с одним входным процес-
сом х^Ои одним выходным процессом^ (Z). Формулы (7.52)—(7.54) — это
алгебраические уравнения, позволяющие вычислить условные спектральные
и взаимные спектральные плотности по спектрам исходных процессов.
Модель, изображенная на рис. 7.9, иллюстрирует формулу (7.54) и пока-
зывает разложение у (t) на сумму двух некоррелированных членов, пред-
ставляющих часть у (t), линейно обусловленную оптимальным линейным
преобразованием входного процесса x{(t), и часть у (t), не связанную с
Xj(Z). В частотной области эта модель описывается соотношением
Y(f)=Yyl(f) + Yyl(f), (7.55)
где
ГУ:1(/) = М/)У1(/)» (7‘56)
М/Л = [С1Д/)/Сц(/)] , (7.57)
МЛ = ПЛ-МЛШ). (7-58)
Г,(У
Рис. 7.9. Выделение вклада (/) в y(t).
y(t)
224
Глава 7
Отметим, что по сути дела эти формулы совпадают с формулами
(7.42)—(7.45).
7.2.5. ФУНКЦИИ ЧАСТНОЙ КОГЕРЕНТНОСТИ
Вернемся к рис. 7.8. Поскольку выходные процессы v j (t), v2(t) ип (t) не
коррелированы, то наблюдаемый спектр выходного процесса Gyy (f) равен
сумме спектральных плотностей этих трех процессов, причем в этой сумме
не участвуют взаимные спектры, а именно
Gjf) = GvJf) + GvJf) + Gjf) . (7.59)
Здесь
GvJf)=\Ljf)\2Gjf), (7.60)
G„Jf)-\Ljf)\2G22Jf), (7.61)
Gjf) = Gyy.Jf). (7.62)
Символом Gyy. i 2(f) обозначена часть спектра^ (t), не связанная ни ex j(О,
ни сх2(О. Заметим также, что первый выходной процесс v x(f) на рис. 7.8
совпадает с выходным процессом уу: j (t) на рис. 7.9. Первая спектральная
плотность
GvJf) =
Gjf)
Gjj)
Gn(f) = yJf)Gjf)
(7.63)
есть обычный когерентный спектр выходного процесса системы с одним
входным процессом xx{t) и одним выходным процессом y(t) (рис. 7.9).
Здесь
г , п _ |G.,(/)I
' G„(/)G„(/)
(7-64)
есть функция обычной когерентности между хх (t) ny(t).
Вторая составляющая спектральной плотности
где
GvJf) =
G2Jf)
G22 1(f)
G22.i(f) = lJi(f)GyyJf) ,
(7.65)
G22.Af)GyyJf)
(7.66)
Т2У1(/) =
|<?2,.1(/)Г
называется функцией частной когерентности условных процессов х2. j (Г) и
у^.](Г), показанных соответственно на рис. 7.4 и 7.9. Поэтому GV^VJ) на-
Многомерные системы
225
ГГ1,2^
^2-]
L2y(f)
Уу.^>
—Z------- v2(t)
Рис. 7.10. Система с одним условным входным процессом и условным процес-
сом на выходе.
зывается частным когерентным спектром выхода системы с условным
входным процессом х2-i(O и условным выходным процессом уу ч (О (рис.
7.10), где^7.12(О соответствует л (О (рис. 7.8).
Рис. 7.10 полностью совпадает с рис. 7.9, за исключением того, что:
1) исходные процессы Xj(Г) и у (I) заменены условными процессам!.
x2.j(O и77Ч(О;
2) исходные спектральные плотности G п (/*), Gyy (f) nG iy(f) заменены
условными спектральными плотностями G 22. j (f), Gyy и j(/*);
3) функция обычной когерентности 7^y(f) заменена функцией частной
когерентности 72>,. j (f).
Это сопоставление показывает, что функции частной когерентности
играют такую же роль, как и функции обычной когерентности с тем толь-
ко отличием, что первые определяются по условным процессам, а вто-
рые — по исходным. Из неравенства для взаимных спектральных плотно-
стей (5.82) следует, что для всех f
О < < 1.
(7-67)
Система с двумя входами, на которые поступают некоррелированные
процессы Xj (О их2<1(О, и одним выходом, изображенная на рис. 7.8, экви-
валентна двум отдельным системам с одним входом и одним выходом, по-
казанным на рис. 7.9 и 7.10. Заметим, в частности, что входной процесс
Xj(O (рис. 7.9) преобразуется в выходной процесс .у (О, а условный входной
процесс х2. j (О (рис. 7.10) преобразуется в выходной процесс уу. j (О- Этот
входной процесс не влияет на выходной процесс у (О- Еще одно важное
замечание заключается в том, что взаимный спектр х2. j(Z) и у (t) совпада-
ет с взаимным спектром х2. j (t) и у. j (О. Другими словами, если из х2(О
исключен вклад х}(/) за счет корреляции, что дает процесс x2>1(Z), то при
определении G2y. i (/) не обязательно исключать вклад х j (t) в у (Г) за счет
корреляции, т. е. не обязательно строить процесс уу ч (Г). Для того чтобы
убедиться в этом, докажем соотношение
=£[Х2*1У].
(7.68)
Из соотношений (7.44) и (7.58) имеем
Х2*1 = Х2* -(G21/Gn)y*>
Гг1= r-(Glj/Gu)X1.
8-953
226
Глава 7
Тогда
£[ед.1] = *[*2*1П - •
EfX/iXj = Е[{Х2* - (G^/Gj^jxj =
= Е[ВД] - (G2l/Gn)E[X^] =
= 2TG21-(G21/G11)2TG11 = 0.
Этим соотношение (7.68) доказано.
Выведем формулу для спектра шума на выходе системы, изображенной
на рис. 7.10, совпадающего с искомым спектром шума Gnn(f) на выходе
системы, показанной на рис. 7.8. Этот спектр имеет вид
^.1,2(/) = Gyy.Af) -|Е2//)Гс22.1(/) =
= [1-Т22г.1(/)]^1(/)- (7.69)
Подставив вместо Gyy. j (f) его выражение из формулы (7.54), получим
С^.1,2 = [1 - Y12//)] [1 - Т2У1(/)]Gyy(f) . (7.70)
Функция множественной когерентности yy:x(f), определенная формулой
(7.35), для двух коррелированных входных процессов равна
= 1-[1 - У12//)][1!(/)]• (7.71)
Эта формула устанавливает связь функции множественной когерентности с
функциями обычной и частной когерентности при данном упорядочении
двух процессов, т. е. еслих^Г) предшествуетх2(О-
Описанный подход будет обобщен на системы с тремя произвольными
коррелированными процессами на входе и одним процессом на выходе,
причем аналогичные процедуры можно построить для анализа общих си-
стем с несколькими входами и одним выходом. Следует отличать исход-
ные модели с неупорядоченными входами от условных моделей с упорядо-
ченными входами, которые строятся при обработке данных. В примерах
7.3 и 7.4 анализируются результаты наблюдений системы с тремя входами
и одним выходом. Соответствующие формулы выводятся в разд. 7.3.
ПРИМЕР 7.3. ВЫЧИСЛЕНИЕ ФУНКЦИИ ЧАСТНОЙ КОГЕРЕНТНОСТИ.
Рассмотрим систему с тремя входами и одним выходом, на который на-
Многомерные системы
227
кладывается шум. Тракты системы представляют собой низкочастотные
/?С-фильтры (рис. 7.11). Заметим, что входной процесс x2(t) коррелирован
как с Xj(Z), так исх3(/). В какой степени входной процесс х2(Г) когерентен
с выходным процессом y(t) по своему тракту?
Для того чтобы ответить на этот вопрос, в полосе частот примерно от
О до 1000 Гц были вычислены функции обычной и частной когерентности
между входным процессом х2 (О и выходным процессом y(t) с разрешени-
ем 32 Гц по реализации длиной 1 с. Результаты этих вычислений представ-
лены на рис. 7.12. Рис. 7.12,я показывает, что когерентность междух2(О и
у (О довольно высокая по всей полосе частот, она близка к единице на низ-
ких частотах, а на высоких частотах равна примерно 0,95. Однако частично
это связано с тем, что и%|(/), их3(/) когерентны с x2(t) и вносят свой
вклад в выходной процесс y(t) непосредственно по своим собственным
трактам. Функция частной когерентности x2(t) иу(1) указывает на мень-
шую когерентность (до 0,75), как видно из рис. 7.12, б.
ПРИМЕР 7.4. ВЫЧИСЛЕНИЕ ФУНКЦИИ МНОЖЕСТВЕННОЙ КОГЕРЕНТ-
НОСТИ. Рассмотрим снова систему с тремя входами и одним выходом,
описанную в примере 7.3 и показанную на рис. 7.11. На рис. 7.13 изображе-
на функция множественной когерентности, вычисленная для выходного
процесса y(t) и трех входных процессов xz(/) (i = 1, 2, 3). Заметим, что
функция множественной когерентности принимает большие значения (более
0,96) во всей полосе частот, но с ростом частоты несколько уменьшается.
Единственная причина, по которой функция множественной когерентности
не равна единице во всей полосе частот,— наличие инструментального шу-
ма на выходе. Поскольку инструментальный шум имеет равномерный
спектр, а входные процессы проходят через фильтры низких частот, то
относительный вклад инструментального шума в суммарный выходной
сигнал растет с увеличением частоты. Об этом отчетливо свидетельствует
уменьшение функции множественной когерентности по мере увеличения
Рис. 7.11. Система с тремя входными и одним выходным процессами и шумом
на выходе.
8
228
Глава 7
б
Рис. 7.12. Функции когерентности между входным процессом x2(t) и выходом
системы, изображенной на рис. 7.11: а — функция обычной когерентности; б —
функция частной когерентности.
7.3. ОБЩИЕ И УСЛОВНЫЕ МОДЕЛИ С НЕСКОЛЬКИМИ ВХОДАМИ
Модель общей системы с несколькими входами и одним выходом с про-
извольными входными процессами изображена на рис. 7.14, где X^f) (i =
= 1 , 2, ... , q) обозначают финитные преобразования Фурье, вычисленные
по входным реализациям x^t). Финитное преобразование Фурье выходного
процесса у (t) обозначено через Y(f) = XqJri(f). Подлежащие определению
частотные характеристики линейных систем с постоянными параметрами
обозначены (i = 1, 2, ... , q), причем индекс, указывающий
входной процесс, предшествует индексу, обозначающему выход. Все откло-
нения от суммарной идеальной модели включены в финитное преобразова-
ние Фурье N(f) неизвестного независимого шума на выходе. Аналогичные
Многомерные системы
229
Рис. 7.13. Функция множественной когерентности между тремя входными про-
цессами и выходным процессом системы, изображенной на рис. 7.11.
модели можно строить, меняя порядок входных процессов или выбирая
другой выходной процесс. Предполагается, что входные и выходной про-
цессы наблюдаются одновременно в единой системе отсчета времени.
Предполагается также, что ненулевые средние значения вычтены, а воз-
можные систематические ошибки, связанные с запаздыванием сигналов, ис-
правлены до вычисления Xtf) и Y (/’).
На рис. 7.15 изображена альтернативная условная модель с несколькими
входами и одним выходом, где исходные процессы (рис. 7.14) заменены
Рис. 7.14. Система с несколькими входами в случае произвольных входных про-
цессов.
230
Глава 7
Рис. 7.15. Система с несколькими входами в случае
упорядоченных условных
входных процессов.
упорядоченным набором условных входных процессов; Y (f) и N (f) остав-
лены без изменения. После этого вычисляются финитные преобразования
Фурье ^/.(/-1)1 U = 1, 2, ... , #), упорядоченные согласно рис. 7.15. При
произвольном i подстрочный индекс /*(/ — 1)! означает, что z-й входной
процесс обусловлен предшествующими i — 1 процессами, т. е. линейные
вклады Xj(z), x2(t), ... вплоть до x^^t) исключены из x^t)с помощью оп-
тимального в среднеквадратичном смысле линейного прогноза. Такие упо-
рядоченные условные входные процессы оказываются попарно некоррели-
рованными; последнее свойство, вообще говоря, не имеет места для исход-
ных процессов. Определяемые при этом частотные характеристики линей-
ных систем с постоянными параметрами обозначены Liy (f)
(z = 1, 2, ... q), где индекс, обозначающий вход, предшествует индексу,
указывающему выход.
При q входных процессах всего можно построить q ! различных упоря-
доченных условных моделей с несколькими входами и одним выходом, по-
скольку любой из q исходных процессов можно взять в качестве первого,
любой из q - 1 оставшихся — в качестве второго, любой из q - 2 остав-
шихся — в качестве третьего и т. д. Невозможно, да и нет смысла анали-
зировать все q! вариантов, если q — достаточно большое число. Напри-
мер, при# = 5 возможно 120 различных моделей. К счастью, на практике
лишь немногие варианты упорядочения имеют физический смысл, о чем го-
ворилось в разд. 7.2.4. Там же даны рекомендации относительно того, как
упорядочивать входные процессы.
Отметим, что при данном наборе входных процессов системы [Hiy] или
[Liy] применимы только к одному конкретному выходному процессу. Для
Многомерные системы
231
разных выходных процессов потребуются разные наборы [Hiy] и [Liy], По-
этому для упрощения представления уравнений для систем с несколькими
входами и несколькими выходами полезны матричные обозначения. Одна-
ко при рассмотрении систем с несколькими входами и одним выходом мат-
ричные обозначения не нужны и пока использоваться не будут.
Из сказанного в разд. 7.1 понятно, что анализ систем с частотными ха-
рактеристиками [Ну], изображенных на рис. 7.14, существенно сложнее
анализа систем с частотными характеристиками [Liy] (рис. 7.15). Из урав-
нений (7.12) и (7.14) ясно также, что выражение для спектра выходного
процесса Gyy (f) системы, изображенной на рис. 7.14, содержит# 2 + 1 сла-
гаемых, в то время как выражение для спектра выходного спектра систе-
мы, показанной на рис. 7.15, состоит всего лишь из q + 1 слагаемых.
В дальнейшем преобразования Фурье исходных и условных процессов
будут обозначаться прописными буквами, а зависимость от частоты не
указывается. Будут построены оптимальные частотные характеристики
[Hiy j и [Liy j, показанные как на рис. 7.14, так и на рис. 7.15, а также уста-
новлена связь между ними. Для этого нужно уметь вычислять условные
преобразования Фурье и условные спектральные плотности; об этом и пой-
дет речь в следующих разделах.
7.3.1. УСЛОВНЫЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
Система, изображенная на рис. 7.15, определяется соотношением в ча-
стотной области у
г= Еь,Л,.(7.72)
/=1
Если выходной процесс Y рассматривать как (# + 1)-й процесс X (С{ + а
шум N — как (# + 1)-й процесс, обусловленный предыдущими# процесса-
ми, то N = и уравнение (7.32) преобразуется к виду
Q
X(q+1) = 52 + X(q+V) q'. . (7.73)
( = 1
Здесь +! рассматривается как (# + 1)-й процесс, обусловленный все-
ми предшествующими # процессами.
Важное значение имеют различные подмножества условий. Для первых
г условных входных процессов при г # можно написать
^(</+1) = 52 ^(<7+1)^ (/-1)! + X{q+l) r\ . (^-74)
/ = 1
Здесь X+ есть (# + 1)-й процесс, обусловленный первыми г процесса-
ми, где г = 1, 2, ... , #. Подставив вместо Х^ произвольный процесс
Xj {j > г), получим более общее соотношение
(7.75)
7 = 1
232
Глава 7
Здесь вместо частотных характеристик (£/(<?+р] использованы частотные
характеристики [2Lry]. Если теперь г заменить наг — 1, то соотношение
(7.75) примет вид
г— 1
*,= L 4^0-1)! + • (7-76)
/=1
Последние два соотношения дают алгоритм вычисления условного преоб-
разования Фурье
= ^/ (г-1)! “ Лу^г-(г-1)! * (7.77)
Следовательно, PQ.r!] можно вычислить по известным и частот-
ным характеристикам [Lrj] для у > г. В частности, соотношение (7.77) по-
казывает, что [Xj. j j можно найти по известным PQ j и частотным характе-
ристикам [Liyj. Затем [Xj.2\\ вычисляются по известным [Xj. J и частот-
ным характеристикам [Lrj] и т. д.
7.3.2. УСЛОВНЫЕ СПЕКТРАЛЬНЫЕ ПЛОТНОСТИ
Исходные спектральные и взаимные спектральные плотности определя-
ются по исходным реализациям [Xj]^ (i = 1, 2, ... ,q) и Y = Xq + x следу-
ющим образом:
2 2
Gn = , GtJ = -£[X,*Xy],
(7.78)
2 2
= Grv = -£[y*y].
Аналогично по условным реализациямXj,r, (j > г) определяются условные
спектральные плотности:
2
= (7.79)
Условные взаимные спектральные плотности реализаций ХГг} и Xj.rl,
когда i Ф j и одновременно i > г nj > г, определяются формулой
2
Gtj.r, = -£[Х*нХ7,г!]. (7.80)
Формулы (7.78) — частный случай формул (7.79) и (7.80) при г = 0. Заме-
тим также, что
2 2
G,.7..r, = -£[ХД,Х7] = -£[Х,*Х7,г!] . (7.81)
Напомним, что речь идет о преобразовании Фурье исходных реализаций.—
Прим, перев.
Многомерные системы
233
Для вычисления условных спектральных плотностей по исходным
спектральным плотностям воспользуемся рекуррентной формулой (7.77).
Умножим обе части этой формулы на X возьмем математическое ожида-
ние и умножим на масштабный коэффициент 2/Т. После перехода к преде-
лу от Т получим алгоритм вычисления условных спектров:
=GV(r-1)!-^A(-1)-. (7.82)
Следовательно, можно вычислить по известным и ча-
стотным характеристикам [Lrj] для всех/ > г и j > г.
Соотношение (7.82) лежит в основе алгоритма анализа систем с не-
сколькими входами и одним выходом. В частности, соотношение (7.82) по-
казывает, что [G-. и ] определяются по известным [Gg] и частотным харак-
теристикам [L у}. Далее, [Gij.2\] вычисляются по известным и ча-
стотным характеристикам [Ly] и т. д. Применение этого алгоритма в ре-
шающей степени зависит от умения определять частотные характеристики
[Lrj] для всех г = 1, 2, ... ,q и всех j > г. Об этом сейчас и пойдет речь.
7.3.3. ОПТИМАЛЬНЫЕ СИСТЕМЫ ДЛЯ УСЛОВНЫХ ВХОДНЫХ ПРОЦЕССОВ
Системы с частотными характеристиками \Ljy] (i = 1, 2, ... ,#), пока-
занные на рис. 7.15, оптимальны в классе линейных систем с одним входом
и одним выходом, поскольку входные процессы этих систем попарно не
коррелированы. Следовательно, как было показано в гл. 6, каждая частот-
ная характеристика Ljy равна отношению взаимной спектральной плотно-
сти входного и выходного процессов к спектральной плотности соответст-
вующего входного процесса. Если Ljy вычисляются таким образом, что
шум п (t) автоматически не коррелирован ни с одним из входных процес-
сов, поэтому это свойство можно не включать в число предположений.
Следовательно, для условных входных процессов имеем
= / = (7.83)
Формулу (7.83) можно вывести прямо из соотношения (7.72), если пред-
варительно предположить, что п (I) не коррелирован ни с одним из вход-
ных процессов системы, изображенной на рис. 7.15. Для этого перепишем
соотношение (7.72), изменив индекс суммирования:
я
Y= +
7 = 1
Умножим обе части наХД^.^ (/ = 1, 2, ... ,#). Получим
я
7 = 1
Взяв математическое ожидание от обеих частей этого соотношения и умно-
234
Глава 7
жив на 2/Т, получим формулу (7.83), т. е.
поскольку
, ДЛЯ/ =# у;
-1)!#] = о, ДЛЯ любого /.
Выпишем частные случаи формулы (7.83):
т _ ^1у Т — ^2уЛ г _ ^Зу-2\
iy~ G ’ 2у G ’ Зу~ ~Г.
и11 °22-1 °33-2!
(7.84)
и т. д. Частотная характеристика последней системы, т. е. при/ = q, име-
ет вид
^qy G
Каковы отдельные подсистемы с одним входом и одним выходом, образу-
ющие систему, изображенную на рис. 7.15? Для того чтобы ответить на
этот вопрос, заметим, что спектр выходного процесса, полученного преоб-
разованием процесса ^/.(/-1)! системой с частотной характеристикой Liy
при / = 1, 2, ... , q, задается формулой
IД>|2^й (/-1)! = > (7.86)
где — спектр входного процесса, а
,у ° °'
есть функция частной когерентности между и Yy,^_^. Далее из
формулы (7.82) при / = j = у иг = i имеем
Gyy • /! — Gyy '(j-1)! LiyGyi. (/-1)!
= [1 “"%>•(/-!)!]Gyy.(/-I)? • (7.88)
Здесь 6уу.ц — спектральная плотность условной реализации Yy.n. Далее
имеем _
l^i>l ^// (/-1)! + Gyy.a = Оуу.^_^. (7.89)
Отсюда следует, что система с одним условным входным процессом и од-
ним выходом для любой условной реализации должна иметь вид,
показанный на рис. 7.16.
Набор оптимальных систем с одним входом и одним выходом, эквива-
лентный системе, изображенной на рис. 7.15, показан на рис. 7.17. Заме-
тим, что входная реализация X j преобразуется в выходную реализацию Y,
условная входная реализация Х2. j преобразуется в условную выходную реа-
Многомерные системы
235
%1*(1 -1 )i
Рис. 7.16. Оптимальная система с одним условным входным процессом и одним
условным выходным процессом.
лизацию Y, j, условная входная реализация % 3.2| преобразуется в услов-
ную выходную реализацию Yy,2i и т. д. Было бы ошибкой считать, что
какой-либо из этих условных процессов влияет на суммарный выходной
процесс Y.
Рис. 7.17. Системы с одним входом и одним выходом, эквивалентные системе,
изображенной на рис. 7.15.
236
Глава 7
7.3.4. АЛГОРИТМ ВЫЧИСЛЕНИЯ УСЛОВНЫХ СПЕКТРОВ
Алгоритм вычисления условных спектров содержится в формуле (7.82),
в которой частотные характеристики [Lrj] пока не определены. Сейчас эти
характеристики будут найдены путем обобщения оптимальных характери-
стик заданных формулой (7.83) для входных реализаций Х{, X2. i,
Х3.2! вплоть ДО^.^-щ и выходного процесса. Возьмем вместо Y в ка-
честве выходной реализации любую реализацию Xj (j = 1, 2, ... , q 4- 1).
Пусть входными процессами будут , Х2. j, Х3.2! вплоть Д° где
г — любое целое число такое, что г < j, т. е. г = 1, 2, ... , j — 1. Фор-
мально это означает, что строятся новые модели с несколькими условны-
ми входными процессами и одним выходным процессом, оптимальные ли-
нейные характеристики ] которых определяются по той же схеме, что и
оптимальные характеристики [Liy ] с заменой у на у и / наг, т. е.
г _ Grj (r-iy.
Lrj G
^гг. (г— П1
г = l,2,...,(y — 1),
7 = 1,2,...,(9 + 1).
(7.90)
Заметим, что Lrj определяются по условным процессам порядка (г — 1)!.
В частности, при г = 1, 2, 3 имеем
II »—k II II 2,3,.. +1; (7.91)
G2.4 Г = 2: L2j = -y±, j = °221 3,4,-. .,?,? +1; (7.92)
II II II 4,5,.. +1 (7.93)
и т. д. Если г=^иу = ^4-1,то Lq{q + = Lqy9 как и в формуле (7.85).
Вернемся к итерационному алгоритму вычисления спектра (7.82) и вме-
сто Lrj- подставим выражение для нее (7.90). Получим окончательную фор-
мулу
Gij r< - СО (г-1)!
Grj(r-iy.
6>г(г-1)!
(7.94)
Gir(r-1)!
7
которая полностью задает способ вычисления спектральных величин по-
рядка г! по ранее вычисленным условным спектральным величинам порядка
(г — 1)! для любых г = 1, 2, ... 9q и любых/, j вплоть до# 4- 1, где/ > г
nj > г.
Для лучшего понимания этого результата рассмотрим частные случаи
при г = 1, 2, 3. Для г = 1 из формулы (7.94) получаем
^7-1 ^ij
gg
<?n
(7-95)
Многомерные системы
237
В правой части этой формулы стоят только исходные спектральные и вза-
имные спектральные плотности, вычисленные по данным реализациям
входных и выходного процессов. Условные спектры G-. j определяются по
формуле (7.95) с помощью алгебраических операций, при этом не требуется
выбирать разрешение по частоте или прибегать к усреднению. При i Ф j
получаем действительные условные спектры Gu. j, а при i Ф j — комп-
лексные условные взаимные спектры GtJ. j. Индексы i и j обязательно
больше 1.
При г = 2 по формуле (7.94) находим
(^2/1
G,7.2. = G,7.i-7^-G,2i- (7.96)
а22 1
В этом случае все величины в правой части являются условными спектра-
ми, вычисленными на предыдущем шаге. Формула (7.96) позволяет опреде-
лить условные спектры [G-.2!] с помощью алгебраических операций, при
этом не требуется выбирать разрешение по частоте или прибегать к усред-
нению. При i = j получаем действительные условные спектры G/7.2!, а при
i Ф j — комплексные условные взаимные спектры. Теперь индексы i и j
должны быть больше 2.
При г = 3 формула (7.94) дает возможность алгебраическим путем вы-
числить условные спектры по ранее вычисленным условным спект-
рам [G,y.2!] и т. д. Эта итерационная процедура изображена на рис. 7.18,
где Lrj — величины, определенные формулой (7.90). В этой процедуре сна-
чала выполняется внутренний цикл, а затем последовательно выполняются
остальные циклы. Изображенная на рис. 7.18 схема вычислений в равной
Рис. 7.18. Алгоритм вычисления условных спектральных плотностей (алгоритм
обобщается на любое число входов).
238
Глава 7
Рис. 7.19. Частный случай вычисления условных спектральных плотностей (ал-
горитм обобщается на любое число входов).
степени применима как к условным автоспектрам, если i = j, так и к ус-
ловным взаимным спектрам, если i #= j. Однако при вычислении условных
автоспектров можно использовать несколько видоизмененный алгоритм.
При / = j формула (7.94) сводится к виду
Gjj-r\ ~ ~ l^rj|2^rr (r-l)! • (7.97)
Эта процедура изображена на рис. 7.19.
7.3.5. ОПТИМАЛЬНЫЕ СИСТЕМЫ ДЛЯ ИСХОДНЫХ ВХОДНЫХ ПРОЦЕССОВ
Оптимальные частотные характеристики [Hiy] линейной системы, изо-
браженной на рис. 7.14, для исходных входных процессов вычисляются
сложнее, чем оптимальные характеристики [Liy] системы, показанной на
рис. 7.15. Эти \Hiy] удовлетворяют системе уравнений (7.11) q уравнений с
q неизвестными. Однако не представляет труда вывести соотношение, свя-
зывающее частотные характеристики и [L ,•>,]. Покажем это.
Основное соотношение для системы, изображенной на рис. 7.14, имеет
вид q
Y= Xj + N. (7.98)
j=i
Умножим обе части наХ,*^..^ для/ = 1, 2, ... ,q и возьмем математиче-
ское ожидание от обеих частей. Умножив затем это равенство на масштаб-
ный множитель 2/Ти перейдя к пределу, получим
я
>(,-!)!= (7.99)
j = i
Многомерные системы
239
где индексу пробегает значения, начиная су = / , поскольку = О
для у < i. Разделив обе части на получим соотношение
я
L,y = 'LHjyLij; i = 1,2,..., q; j > i, (7.100)
J = l
где в силу формулы (7.83)
^iy =
Формула (7.100) и дает
ристиками [Hiy] и [Liy].
Для лучшего понимания формулы (7.100) рассмотрим несколько част-
ных случаев. Поскольку Lqq = 1, при / = j = q имеем
_ Gij(j-1)\
G
(7.101)
искомое соотношение между частотными характе-
^ЯУ НЯУЬЯЯ НЯУ
(7.102)
Поэтому оптимальная частотная характеристика Hqy, как и
(7.85), равна
= иду(д-1у = идуЛ,2,...,(Я-У
яу G G
^ЯЯ'(Я~^У идд1,2,- • ,(<?-!)
в формуле
(7.103)
Оптимальная частотная характеристика Hiy теперь получается простой за-
меной Xq на Xj и равна
Н,у = ^>i.2„..,(,-i).(,+i)....ч . (7.104)
G»l,2...(i-l),(i + l).q
В частности,
Hiv _ W. , И2у = S1-3.4..................Я t Нзу _ ^.Х.2,4.5. : (7105)
^11-2,3,...,? ^221,3,4,..., д U33 1,2,4,5,..., д
и т. д. Сравнение формул (7.84) с формулами (7.105) показывает, что ча-
стотные характеристики [Liy] всегда имеют более простой вид, чем соот-
ветствующие характеристики [Hiy] для всех / = 1, 2, ... ,q — 1, за ислюче-
нием случая / = q, когда Lqy = Н.
Для системы с двумя входами и одним выходом, изображенной на рис.
7.2, где НХу 1лН1у задаются формулами (7.23), формула (7.105) позволяет
записать эти характеристики в более кратком виде:
Н1у =
Gly-2
G112
н2у =
G2yA
G22 1
(7.106)
Соответствующие характеристики L х и L2y задаются формулами (7.51).
Заметим, что связь между этими! и Н, выраженная формулой (7.49), на-
ходится в согласии с формулой (7.100).
Формула (7.100) дает общий метод вычисления частотных характери-
240
Глава 7
стик [Hiy] по частотным характеристикам [Liy] путем их последовательно-
го вычисления в обратном порядке:
Hqy = Lqy , Н1У = L,
<7
Е L4Hjy ’
(7.107)
где i = q — 1, q — 2 , ... , 2, 1. Например, если q = 3, то
^Зу >
^2у ^2 у L23H3y у
(7.108)
^12^2у ^13^3у *
На практике для нахождения частотных характеристик [Hiy\ вместо прямо-
го вычисления их удобнее определять в два этапа, т. е. сначала найти ча-
стотные характеристики [Liy], а затем уже по формуле (7.107) вычислять
соответствующие частотные характеристики [Hiy].
7.3.6. ФУНКЦИИ ЧАСТНОЙ И МНОЖЕСТВЕННОЙ КОГЕРЕНТНОСТИ
Функции обычной когерентности для произвольного входного процесса
xi (i = 1, 2, ... , q) и выходного процесса у задаются формулой
(7.109)
- G.fiyy
Функции частной когерентности для произвольного условного входного
процессах,. j (/ = 2, 3, ... , q) и выходного процесса^ определяются фор-
мулой 2
1^7 11
2
Gn.Gy
(7.110)
Функции частной когерентности для условного входного
i = 3, 4, ... , q и выходного процесса^ имеют вид
2 |6,,.2!|2
%У2! = 7-----г-----
процесса хг2! при
(7.111)
и т. д. вплоть до
2 _ • (<7— 1)?1
lqy(q-\)\ г
^qq^q-V^yy (<?-!)!
(7.112)
Спектр шума на выходе системы с одним входом
определяется выражением
G„„ , = G.J1 - тЛ
и одним выходом
(7.113)
в системе с двумя входами и одним выходом
Gvv о» = Gv„ Ji - Уэ2,, J = 6L.(I
(7.П4)
Многомерные системы
241
в системе с тремя входами и одним выходом
Gvy 3' = Gyy 2'(1 - Y32v 2') = Ч.Д1 - YbJO ~ У2у 1)(1 - Тз2х 2')
(7.115)
и т. д. Спектр шума на выходе системы с q входами и одним выходом
есть q
г» (7116)
I = 1
Эти результаты обобщают формулу (7.88).
На основании формулы (7.35) легко теперь найти соответствующие
функции множественной когерентности для произвольной системы с не-
сколькими входами и одним выходом. Для системы с одним входом и од-
ним выходом имеем
> (7-117)
для системы с двумя входами и одним выходом
Y,22l = 1 - = 1 -(1 - Yi2J(1 - YzVi) > (7-118)
для системы с тремя входами и одним выходом
7,2 = I - | - 1 -0 - 7,2 )(1 - JO ’ ..) (7.119)
\ ^УУ /
и т. д. Для системы с q входами и одним выходом функция множествен-
ной когерентности имеет вид
Y2 = 1 - = 1 - П(1 - Y,2. O-D-) . (7.120)
Изящные формулы (7.117)—(7.120) верны для произвольных входных
коррелированных процессов, поступающих на вход системы со многими
входами и одним выходом. Эти формулы устанавливают связь функций
множественной когерентности с соответствующими функциями обычной и
частной когерентности. Отметим, что эти формулы зависят от способа
упорядочения входных процессов. В частном случае взаимно некоррелиро-
ванных входных процессов формула (7.120) сводится к уже известной про-
стой формуле
у,2 „=£?,2 , (7.1..1-
т. е. в этом случае функция множественной когерентности равна сумме
242
Глава 7
функций обычной когерентности между каждым из входных процессов и
процессом на выходе.
7.4. МАТРИЧНЫЕ ФОРМУЛЫ ДЛЯ МНОГОМЕРНЫХ СИСТЕМ
Рассмотрим теперь общие системы с несколькими входами и нескольки-
ми выходами, причем число входов равно числу выходов. Приводимые ре-
зультаты легко обобщаются на тот случай, когда число входных процессов
не равно числу выходных процессов. Для лучшего понимания физической
сути этих задач рекомендуется разбивать такие системы на подсистемы с
несколькими йХодами и одним выходом и анализировать их алгебраически-
ми методами, описанными в разд. 7.2 и 7.3. При желании системы с не-
сколькими входами и несколькими выходами можно исследовать и матрич-
ными методами, на этот случай в данном разделе приводятся все необхо-
димые определения'и формулы. Матричные методы не позволяют раскла-
дывать естественным образом наблюдаемые спектры выходных процессов
на составляющие, соответствующие наблюдаемым входным процессам.
Кроме того, анализ ошибок по матричным формулам значительно сложнее
анализа ошибок по формулам, приведенным в разд. 7.3, где система с не-
сколькими входами и одним выходом преобразуется в совокупность упоря-
доченных условных систем с одним входом и одним выходом. Относитель-
но простые оценки ошибок для таких условных систем выводятся в гл. 8.
7.4.1. СИСТЕМА СО МНОГИМИ ВХОДАМИ И МНОГИМИ ВЫХОДАМИ
Пусть X — вектор-столбец, представляющий преобразования Фурье q
входных процессов = %(/) (/ = 1, 2, ... , q), a Y — вектор-столбец,
представляющий преобразования Фурье# выходных процессов Yk = Yk(f)
(к = 1, 2, ... ,#),
X*, Y*— векторы, комплексно-сопряженные к X, Y; X', Y' — транспониро-
ванные векторы (строки) для X, Y.
Входная матричная спектральная плотность равна
2
Gxx = -E{X*X'}. (7.123)
Выходная матричная спектральная плотность равна
2
Gvv = -£{¥*¥'}. (7.124)
Многомерные системы
243
Взаимная матричная спектральная плотность между входными и выходны-
ми процессами равна
Gxf = y£{X*Y'}. (7.125)
Строго говоря, в формулах (7.123)—(7.125) должен стоять предельный пе-
реход по Т -* оо, но для упрощения обозначений этот предельный переход,
как и зависимость от частоты, не указывается. На практике этот предель-
ный переход никогда не выполняется в силу конечности имеющихся реали-
заций.
Определим теперь основные матричные величины:
2 г
G„ - ,
2 r
(7.126)
(7.127)
(7.128)
Gv V
У 1Уд
G
У2Уд
G v
С с
С С
^УгУх ^УгУг
G v Gv v
УдУ\ УдУ2
(7.130)
244
Глава 7
Отметим, что Gxx и Gyy — эрмитовы матрицы, т. е. G- = G* для всех/ и
/’. Для эрмитовых матриц G* = G' и G* = G'. Имеем
лл хх уу у у
*1*
х2*
•••
G2yt G2y2 ’ ’ ’ G2y„
Gqy> Gqyi ' ’' Gqy<<
(7.131)
Во всех этих выражениях Giy = Gx y , причем индекс, обозначающий вход-
ной процесс, предшествует индексу, Обозначающему выходной процесс.
Обозначим матричную частотную характеристику, задающую преобра-
зование X в Y, через Нх>, = HXJ(/), где, как и выше, индекс, обозначающий
вход, предшествует индексу, обозначающему выход. Элементы матрицы
Hiyk = Тогда
^у. • • • H\yq
нх = Н2у> Н2уг ••• Н2У< (7.132)
J^qyi Hqy2
Из этого определения следует, что
Y = Щ,х, (7.133)
где HXJ, — матрица, транспонированная по отношению к матрице Hxv. По-
этому
< = Н2у. • ' Н2уг • НЧУ! Hqy2 • 1 (7.134)
V а. Н2у, • Hqyg _ ХЯ.
Заметим, что в алгебраической форме это эквивалентно формуле
я
k = (7.135)
Многомерные системы
245
Эта формула естественным образом устанавливает связь между выходным
процессом Yk и входными процессами причем^ проходит через
Н. , проходит через Н^, и т. д. вплоть до X. которое проходит че-
рез НЯук • Схематически это можно представить так:
Используя эти определения, выведем теперь матричные формулы для
систем общего вида с несколькими входами и несколькими выходами в том
случае, когда число выходов равно числу входов. Предполагается, что все
требуемые обратные матрицы существуют.
Определение Grv и Hrv :
АЛ АЛ
Y = ЩГХ ,
(7.136)
У = (Н^Х)' = Х'Н„ , (7.137)
X*Y' = Х*ХН .
л У
(7.138)
Взяв математическое ожидание от обеих частей последнего соотношения и
умножив на 2/Г, получим
Gx, = GXXHXV . (7.139)
Эта формула выражает GXJ через Gxx и НЛ>. Умножив обе части формулы
(7.139) на G^1, получим
G;;GXV = G^G^HJ, (7.140)
где
G^.1 — матрица, обратная по отношению к Gxx. (7.141)
Формула (7.140) эквивалентна формуле
нху = gx;gx>
(7.142)
246
Глава 7
и выражает Hvv через Gxx и Gxv. Формула (7.139) показывает, что матрица
Gxy равна произведению матриц Gxx и Нху размерностью q х q.
Определение Gyy и Gxx:
Y = Н^Х, (7.143)
n = (н;,х)' = хнхи, (7.144)
у* = (н;,х)* = н;;х* (7-145)
Y*Y' = (Щ*Х*)(Х'Н (7.146)
Взяв математическое ожидание от обеих частей последнего соотношения и
умножив на 2/Т, получим
= (7.147)
Следовательно,
(7.148)
при условии, что соответствующие обратные матрицы существуют. Фор-
мула (7.147) показывает, что (луу равна произведению трех матриц размер-
ностью q х q: Нх *, Gxx и HXJ,. Комплексно-сопряженная транспонирован-
ная матрица имеет вид н* П^У1 н*
Н'* = ху н* П1У2 Н2У2 • •• (7.149)
и* •• • Ня\_
Соотношения (7.139), (7.142), (7.147) и (7.14$) — это основные матричные
формулы, используемые при анализе систем со многими входами и выхо-
дами.
Выведем теперь матричные формулы для системы общего вида со мно-
гими входами и одним выходом. Как и выше, входные процессы не упоря-
дочены и не обусловлены.
7.4.2. СИСТЕМА С МНОГИМИ ВХОДАМИ И ОДНИМ ВЫХОДОМ
Система с многими входами и одним выходом имеет вид
Х = 1 1 ’ Нх,= 1 , Y = У,
(7.150)
Многомерные системы
247
'1, "1,
2
(7.151)
У' = У=Х'Н v
Hly
H2y
(7.152)
Х* =
(7.153)
В данном случае входная матричная спектральная
плотность равна
2
Gxx = -£{X*X'} =
Gu
G2i
Gi2
622
G24
(7.154)
G4i
Вектор-столбец взаимных спектральных плотностей
вид
входа и выхода имеет
2
Gx, = -£{X*Y} =
G'y
G2y
(7.155)
х2
2
Я
2
<7^
Я
М
Выходная матричная спектральная плотность есть
2 2
G„--Z{r-r')-y£(H;«,X«X'H„)-H;‘G„H„. (7.156)
248
Глава 7
Формула (7.156) эквивалентна формуле
Gyy=[tb Н?у
<?12 • • Glq-
я* 1 (э21 G22 G2q n2y
Al А •• Gqq _ Hqy
(7.157)
Далее
Л*1 * U *
(7.158)
G* — G' .
(7.159)
Для системы с несколькими входами и одним выходом
(7.160)
6,, = 6*=^
(7.161)
(7.162)
Gv)=GvxHxv. (7.163)
Соотношение (7.163) эквивалентно формуле
(7.164)
Заметим также, что равенство
Hv = G^G,
(7.165)
следует непосредственно из формулы (7.163), где Gxx' — матрица, обрат-
ная по отношению к матрице G^. Здесь предполагается также, что систе-
ма определена корректно и что все обратные матрицы существуют.
Многомерные системы
249
7.4.3. СИСТЕМЫ С ШУМОМ НА ВЫХОДЕ
Рассмотрим теперь более реалистическую модель системы с нескольки-
ми входами и одним выходом, в которой учитывается наличие посторонне-
го некоррелированного шума на выходе системы. Вместо идеального соот-
ношения (7.151) для Y имеет место формула
У=Н^Х + #, (7.166)
rji,eN = N (f) — преобразование Фурье шума на выходе п (Z). Вместо фор-
мулы (7.156) получаем
Gyy = H'-GxxHxy + Gnn. (7.167)
Формула (7.163) не изменяется, так что GXJ и при наличии шума имеет вид
Gxy = GXXHX, . (7.168)
Следовательно, G можно представить как
Gyy = H£GX, + Gnn . (7.169)
Входная матричная спектральная плотность Gxx из формулы (7.154) есть
эрмитова матрица размерностью q х q. Определим расширенную матрич-
ную спектральную плотность выходного процесса у (О при входных про-
цессах xz(Z) как эрмитову матрицу размерностью (<? 4- 1) х (д 4- 1)
Gyy Gyl • Gyq
gg Gn ^12 Glq
р — G2y G2i ^22 • G24
G4y G44
(7.170)
Покажем, что определитель I Gvxx I этой расширенной матрицы равен нулю
для всех f в идеальном случае отсутствия шума, т. е. при Gnn = 0 в фор-
муле (7.169).
Для i = 1, 2, ... , q элементы Giy первого столбца (стоящие под элемен-
том Gyy) представляют собой линейные комбинации элементов G^-, стоя-
щих в соответствующей строке, т. е. в силу формулы (7.164)
<7
/ = 1,2,..., </. (7.171)
7=1
В идеальном случае отсутствия шума спектр выходного процесса есть
Gyy = H'*GX>. = H;„Gyx ,
(7.172)
250
Глава 7
причем последнее равенство следует из равенств Gyy = Gyy и Gx^ = GJX.
Формула (7.172) эквивалентна формуле
я
Gyy = Е HlvGyi . (7.173)
/ = 1
Следовательно, Gyy — линейная комбинация элементов Gyi первой строки
GJXX. Поэтому в матрице Gyxx весь первый столбец состоит из линейных
комбинаций элементов соответствующих строк. По известной теореме
(см., например, работу [7.4]) определитель такой матрицы равен нулю,
т. е.
|G^X| = °, если G„„ = 0. (7.174)
Вернемся теперь к модели, учитывающей шум, в которой Gyy задается
формулой (7.169) при Gnn Ф 0. Как уже отмечалось, формула (7.163) имеет
одинаковый вид как при наличии шума, так и при его отсутствии. Поэтому
в силу результатов, справедливых при отсутствии шума, определитель
IGJXXI матрицы GJXX для любого f выражается формулой
|G,xxl = ^JGxxl, (7.175)
где I Gxx I — определитель матрицы Gxx. Заметим: из этой формулы следу-
ет, что I Gyxx I = 0, если Gnn = 0.
Функция множественной когерентности, задаваемая формулой (7.35),
может быть выражена через определители:
Yv:x= 1
I |GyXX| )
\ G>TlGxxl /
(7.176)
Проверим эту формулу при q —
ним выходом. Имеем
1 т. е. для системы с одним входом и од-
Gyy Gyx
Gxy Gxx
(7.177)
В данном случае, определители равны
\Gyxx\ = GxxGyy-\Gxy\2, |GXX| = GXX. (7.178)
Подставив эти выражения в формулу (7.176), получаем
2 _ 1 _ | ^хх^уу 1^,1
у:х GG
IGxyl2 ,
GxxGyy
(7.179)
т. е. выражение для функции обычной когерентности такой системы.
Многомерные системы
251
7.4.4. СИСТЕМА С ОДНИМ ВХОДОМ И ОДНИМ ВЫХОДОМ
В этом случае
Х = Х'=Х, Y = Y' = y, (7.180)
Нху = Н^ = Я, (7.181)
Y=HX, (7.182)
2
Gxx = -E[X*X] = G?x , (7.183)
2
Gyy = ~E{Y*Y] = G;y> (7.184)
2
Gx, = -£[X*Y], G*y = Gyx. (7.185)
Из формул (7.182)—(7.185) следует, что
Gxy = HGXX , (7.186)
где
G
Н=~ > Gyy = H*GXXH = \H\2GXX , (7.187, 7.188)
^xx
причем
= • (7.189)
xx \H\2
Приведенные выше соотношения уже были получены в гл. 6 при изучении
систем с одним входом и одним выходом. Они представляют собой част-
ные случаи матричных формул, выведенных в разд. 7.4.1 и 7.4.2, и показы-
вают, что использованные там определения пригодны для анализа систем
со многими входами и одним или многими выходами.
Задачи
g22 А
7.1. Рассмотрим следующую систему с двумя входами и одним выходом при на-
личии некоррелированного шума на выходе:
G„ = 2A
252
Глава 7
Найдите спектральную плотность G выходного процесса. Какова будет спект-
ральная плотность выходного процесса для некоррелированных входных процессов
(Я12 = 0)?
7.2. В условиях задачи 7.1 вычислите когерентность входных процессов, а
2 2 12
также когерентности у*у и у? каждого из входных процессов и процесса на выходе.
7.3. В условиях задачи 7.1 вычислите функцию множественной когерентности
между двумя входными процессами и выходным процессом.
7.4. Рассмотрим систему с двумя входами и одним выходом, а которой значе-
ния спектральных плотностей на некоторой частоте таковы:
Gn = 3, G22 = 2, Gyy = 10,
G12 = 1 + Ij, Giy = 4 + \j, G2y = 3 - Ij.
Найдите условные спектральные плотности:
а) G22 i» б) G2y, j; в) Gyy. j.
Вычислите также оценку частотной характеристики Н2.
7.5. Используя данные задачи 7.4, вычислите функцию множественной когерент-
ности между двумя входными процессами и выходным процессом.
7.6. Идеальная система с двумя входами и одним выходом имеет следующие ча-
стотные характеристики:
2 3
Пусть
Яп(т) = 35(т), (722(/) = 12, G12(/) = 8.
Вычислите следующие величины:
а) 7?2(/); б) Ryy(r) и Gyy(f)\ в) Л17 (г) и Giy(f); y2ly(f).
7.7 Рассмотрим линейную систему с несколькими входами, в которой q вход-
ных процессов не коррелированы, однако имеют ненулевые средние значения. Выве-
дите следующие формулы:
а) формулу для взаимной спектральной плотности z-ro входного и выходного
процессов, аналогичную формуле (7.13);
б) формулу для спектральной плотности выходного процесса, аналогичную фор-
муле (7.14).
7.8. Используя данные задачи 7.1, найдите частотные характеристики L}y и L2y,
задающие преобразование некоррелированных входных процессов с спектральными
плотностями Gj и G22'lt в выходной процесс на основе формулы (7.51).
7.9. В системе с трепля входами и одним выходом на некоторой частоте были
измерены следующие величины:
GH = 10, G 22 = 8, G 33 = 6,
G12 = 2 + V, G32 = 1 - 2j, G13 = 3 + Зу.
Упорядочите три входных процесса таким образом, чтобы анализ с использованием
условных процессов по схеме, изображенной на рис. 7.15, дал результаты, в наи-
большей степени согласующиеся с физическим смыслом задачи.
7.10. Предположим, что в задаче 7.1 Н п = 0,2 + 0,2у на некоторой частоте.
Вычислите спектральную плотность Gyy в том случае, когда спектральная плот-
ность второго процесса G22 = 0.
Глава 8
СТАТИСТИЧЕСКИЕ ОШИБКИ ПРИ
ОЦЕНИВАНИИ ОСНОВНЫХ ПАРАМЕТРОВ
Как отмечено в гл.4, точно определить характеристики случайных вели-
чин по выборочным данным невозможно. По выборке конечной длины
можно найти лишь оценки интересующих исследователя параметров. В
гл.4 приведены сведения о точности определения ряда основных парамет-
ров случайного процесса по выборке независимых измеренных значений
этого процесса. В настоящей главе рассматривается вопрос о точности оце-
нок параметров для непрерывной реализации процесса длиной Т. Предпо-
лагается, что анализируемые реализации принадлежат стационарному (эр-
годическому) случайному процессу с непрерывным временем и произволь-
ными средними значениями. Получены формулы для статистических оши-
бок следующих параметров:
среднее значение,
средний квадрат,
плотность вероятности,
ковариационная функция,
функция спектральной плотности.
Основное внимание в этой и следующей главах уделено ошибкам, кото-
рые возникают по причинам чисто статистического характера. Ошибки,
связанные с получением и обработкой данных, рассмотрены в гл. 10.
8.1. Понятие о статистических ошибках
Точность оценки некоторого параметра случайного процесса, получен-
ной на основании выборки, характеризуется, как указано в разд.4.1, сред-
ним квадратом ошибки, равным
^[(ф-ф)2], (8.1)
где $ — оценка параметра ф. Равенство (8.1) можно представить в виде
2?[(ф — ф)2] = £[(ф - £[ф] + £[ф] ~ ф)2] =
= Е[(ф - Е[ф])2] + 2Е[(ф - Е[ф])(Е[ф] - ф)] +
+е[(е[ф] - ф)2] •
Заметим, что среднее слагаемое приведенного выражения содержит
множитель, равный нулю
£[ф-Е[ф]] = Е[ф]-Е[ф] = 0.
254
Глава 8
Следовательно, средний квадрат ошибки равен
£[(ф-£[ф])2] + £[(£[ф]-ф)2]. (8.2)
Таким образом, средний квадрат ошибки состоит из двух частей. Первая
часть — это дисперсия оценки, характеризующая долю «случайности» в ве-
личине ошибки
Уаг[ф] = £[(ф - £[ф])2] = Е[ф2] - £2[ф] • (8.3)
Вторая часть есть квадрат смещения оценки, характеризующий ее систе-
матическое отклонение:
&2[ф] = Е [&2[ф]] = Е [(£[ф] - ф)2] - (8.4)
Итак, средний квадрат ошибки равен сумме дисперсии оценки и квадра-
та смещения оценки:
Е [(ф - ф)2] = Var[ ф ] + Ь2[ф] . (8.5)
На практике удобнее представить ошибку оценки в тех же единицах из-
мерения, что и оцениваемый параметр. Для этого можно вычислить поло-
жительное значение корня квадратного из величин ошибок, описываемых
формулами (8.3)—(8.5). Квадратный корень из величины (8.3) определяет
среднеквадратичное отклонение оценки, называемое стандартной (или слу-
чайной) ошибкой
а[ф] = /Е[ф2] - £2[ф] • (8.6)
Квадратный корень из суммы квадратов ошибок (8.5) определяет ошибку
смещения:
Ь[ф] = £[ф]-ф. (8.7)
Квадратный корень из суммы квадратов ошибок (8.5) определяет средне-
квадратичную ошибку:
^е[(ф - ф)2] = Уо2[ф] + г>2[Ф]. (8.8)
Для удобства желательно представить ошибку в долях от оцениваемого
параметра. Для этого ошибку делят на величину оцениваемого парметра и
получают нормированную ошибку. При ф Ф 0 нормированные стандартная
ошибка, ошибка смещения и среднеквадратичная ошибка выражаются со-
ответственно формулами
.it] ;ен-е![ф] .
е =------=----------------у (о. 9а)
Ч = —----------1 > (8-96)
Ф
Статистические ошибки при оценивании основных параметров
255
А2[ф] + *2[ф]
е =-------------
Ф
/Ё (ф - ф)2
Ф
(8.9в)
Заметим, что нормированную стандартную ошибку ег часто называют ко-
эффициентом вариации.
В случаях, когда ег мало, можно положить ф2 = ф2(1 + £г) , так что
Ф = ф(1 ± ег)1/2 ~ ф(1 ± у);
таким образом, имеем
сДф2] » 2еДф].
(8.10)
А7
Иными словами, при малом ег нормированная случайная ошибка оценки ф
квадрата параметра ф примерно равна удвоенной нормированной ошибке
оценки самого параметра ф.
Если смешение оценки $ пренебрежимо мало, т. е. b [$] = 0, и нормиро-
ванная среднеквадратичная ошибка £ = £[ф] = а[ф]/ф также мала, скажем
£ 0,2, то плотность вероятности этой^оценки можно приближенно счи-
тать гауссовой со средним значением Е[ф] » ф и среднеквадратичным от-
клонением а[ф] = еф:
1
Р(ф) = /т~ ехР
£фу2т7
-(ф - ф)2
2(еф)2
(8.П)
Отсюда следуют такие утверждения относительно вероятности получения
других значений того же параметра:
РгоЬ[ф(1 - е) < ф < ф(1 + е)] ~ 0,68 ;
(8Л2)
РгоЬ[ф(1 - 2е) < ф < ф(1 + 2г)] « 0,95.
При этом доверительный интервал для неизвестного истинного значения
параметра ф, определенный по любой индивидуальной оценке ф, принима-
ет вид
Ф Ф
-----< ф <--------
1 + £ 1 - £
ф
1 + 2е
с доверительной вероятностью 68%;
(8.13)
1 - 2е
с доверительной вероятностью 95%.
При малом £, скажем £ 0,1, эти выражения сводятся к виду
[ф(1 - е) < ф < ф(1 + е)] с доверительной вероятностью 68%;
[ф(1 - 2е) < ф < ф(1 + 2е)] с доверительной вероятностью 95%.
256
Глава 8
Эти утверждения остаются справедливыми при малом с даже в тех случа-
ях, когда неизвестное истинное распределение оценки ф есть хи-квадрат, F
или любое другое, более сложное распределение из тех, что описаны в
гл. 4.
Доверительные интервалы для оценок можно построить и в случаях,
когда нормированную среднеквадратичную ошибку нельзя считать малой
(см.разд.4.4). В данной главе подобная задача будет рассмотрена для оце-
нок спектральной плотности. Помимо вывода формул для ошибок здесь
будет обсужден и вопрос о состоятельности оценок (см.формулы (4.7)).
ПРИМЕР 8.1. ПРИБЛИЖЕННЫЕ 95%-ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ ДЛЯ
ОЦЕНОК СРЕДНЕГО КВАДРАТА И СРЕДНЕКВАДРАТИЧНОГО ЗНАЧЕНИЯ.
Пусть оценка среднего квадрата сигнала x(Z) есть = 4, а ее нормирован-
ная среднеквадратичная ошибка ег = 0,05. Определим приближенные 95 % -
доверительные интервалы для среднего квадрата и среднеквадратичного
значения ф
Согласно формуле (8.14), приближенный 95%-доверительный интервал
для фх есть
[4(0,90) < ^ < 4(1,10)] = [3,6 < ^ < 4,4] .
Из формулы (8.10) следует, что для оценки = 2 величина ег — 0,025, так
что приближенный 95 %-доверительный интервал для фх есть
[2(0,95) £ фх < 2(1,05)] = [1,9 <^х< 2,1].
Заметим, что значения границ доверительного интервала для оценки фг
примерно равны корню квадратному из значений границ доверительного
интервала для оценки
8.2. Оценки среднего значения и среднего квадрата
8.2.1. СРЕДНЕЕ ЗНАЧЕНИЕ
Предположим, что отдельная реализация х (I), принадлежащая стацио-
нарному (эргодическому) случайному процессу [*(/)) , определена на конеч-
ном интервале времени длиной Т. Выборочное среднее значение можно вы-
числить по формуле
1 гТ
^x=TJ0X^dt' (8-15)
Истинное среднее значение
Ах = £[-х(0] (8.16)
не зависит от времени/, если процесс {*(/)] стационарен. Математическое
ожидание оценки равно
(8.17)
Статистические ошибки при оценивании основных параметров
257
поскольку оператор математического ожидания коммутативен с линейны-
ми операторами. Следовательно, независимо от длины реализации gx есть
несмещенная оценка величины gx. Так как — несмещенная оценка, то
средний квадрат ошибки оценки равен дисперсии
Var[Ax] = я[(Ах - Мх)2] =£[Ах] “Ах. (8.18)
где из формулы (8.15) следует, что
£[Мх] = ^2 ГГЕ1Х(^ХМ] di)d^. (8.19)
1 •'О •'о
Автокорреляционная функция 7?хх(т) стационарного случайного процесса
{x(t)) , определяемая формулой (5.6), есть
Лхх(т) = £[*(')*(* +т)]. (8.20)
Согласно гипотезе о стационарности,Rxx(t) не зависит от временив и явля-
ется четной функцией аргумента т с максимумом в точке т = 0. Будем счи-
тать, что функция Rxx(t) непрерывна и ограничена при всех значениях т и
что все периодические составляющие функции Кхх(т) заранее исключены.
Автокорреляционная функция Схх(т), определяемая формулой (5.8), имеет
вид
Схх(т) = *хх(т)-М2х • (8.21)
Оказывается, что в случае, когда р.х Ф 0, удобнее пользоваться функцией
Схх(т), а не Яхх(т). Будем полагать, что функция Схх(т) интегрируема
(см.формулу (5.117)) и, следовательно, процесс (х(О) обладает свойством
эргодичности.
Дисперсию оценки (средний квадрат ошибки), определяемую соотноше-
ниями (8.18) и (8.19), можно выразить через автокорреляционнцую функ-
цию схл.(т): 1 _
Var[£x] = ГfCxxt'n “ О dyd% = fTfT *Схх(т) =
1 •'о •'о 1 •'о •'-£
1 ГТ I |тП
= т/ 1-у Cxx(t)Jt. (8.22)
1 J-т\ * )
Последнее выражение получено изменением порядка интегрирования по
переменным т, £ и интегрированием по переменной £. По этой причине ме-
няются пределы интегрирования по переменным т и £, как показано на схеме
9-953
258
Глава 8
и поэтому
Г Г (CXx(T)dTd£= (° fTCxx(r)didr + Г Г TCxx(r)d^dr =
•'()•'-£ J-TJ-r •'О •'О
= Г (Г + т)схх(т) dr + (\т - r)Cxx(r) dr =
J-T 'о
= Г (Т - \r\)Cxx(r) dr .
J-T
Устремляя теперь T к бесконечности, можно переписать формулу (8.22) в
виде оо
lim ТУаг[Дх] = / Схх(т) dr < оо . (8.23)
Г—* оо ^-00
Здесь использованы соотношения (5.117), из которых следует, что функции
Схг(т) и тСхг(т) абсолютно интегрируемы на интервале (— оо, оо), и поэто-
му можно перейти к пределу под знаком интеграла. Равенство (8.23) пока-
зывает, в частности, что при больших Г, когда Iт1 < Г, дисперсия равна
Var[Aj«4f° Cxx(r)dr. (8.24)
1 ~ 00
Следовательно, в тех случаях, когда интеграл сходится, дисперсия Var[/2j
стремится к нулю при стремлении Т к бесконечности. Это значит, что
есть состоятельная оценка параметра ^х.
Рассмотрим важный частный случай, когда процесс (х (/)) есть ограни-
ченный по частоте белый шум, имеющий среднее значение #= 0 и дис-
персию ах. Предположим, что спектральная плотность имеет вид
{q2
У + 0</<В; (8 25)
О, в остальных случаях,
где В — ширина полосы частот. Соответствующая корреляционная функ-
ция равна
/ к г00 , ч о JsinlirBrX
exx(r) = f Gxx( f )cos2rrfг dr - цх = а/ ——— . (8.26)
•'О \ Z771JT /
Заметим, что С^ДО) = ах и Схх(т) = 0 при т = п /(2В), где п — целое чис-
ло. Таким образом, значения процесса в точках, разделенных промежутка-
ми 1/(25), некоррелированы. В случае гауссова процесса [х(0) они будут
статистически независимыми. В этом случае из формулы (8.24) следует
приближенная формула при ВТ>5:
о2
Уаг[Дх] » —- - (8.27)
Статистические ошибки при оценивании основных параметров 259
При 1лх Ф 0 нормированная среднеквадратическая ошибка равна
1 / ох \
(828)
Заметим, что, согласно (8.3),
я[Ах] = Var[£j + ц2 * *х. (8.29)
Следовательно, в соответствии с равенством (8.27) для ограниченного по
частоте белого шума имеем
2
£[4]=^ + мЬ (8-30)
ZjD 1
В гауссовом случае и при 0 четвертый момент, согласно формуле
(3.82), равен
£[Д1] = 3{£[Д2]}2 - 2/4 . (8.31)
Пренебрегая членами порядка 1/(ВГ)2, получаем
Var[4] = £[4] - {£[Д2]}2 = . (8.32)
D1
Таким образом, нормированная среднеквадратическая ошибка оценки зада-
ется выражением
Сопоставление с уравнением (8.28) показывает, что
«г2[Мх] s 4е2[Дх], еДд2] « 2е[Дх] »—, (8.33)
у ВТ \ Мх /
что согласуется с общим соотношением (8.10)
ПРИМЕР 8.2. СЛУЧАЙНАЯ ОШИБКА ОЦЕНКИ СРЕДНЕГО ЗНАЧЕНИЯ. Рас-
смотрим ограниченный по частоте белый шум хЦ) со спектральной шири-
ной В = 100 Гц, средним значением = 0 и стандартным отклонением
ох = 2. Пусть среднее значение оценивается усреднением по реализации
длиной Т = 2 с. Определим ширину доверительного интервала, в пределах
которого оценка среднего значения окажется с вероятностью около 95%.
Согласно формуле (8.27), случайная ошибка оценки имеет среднеква-
дратическое отклонение
2
a[Aj = - = 0,10 .
1/2(100)(2)
9*
260
Глава 8
При этом из соотношений (8.12) следует, что с вероятностью около 95%
оценка окажется внутри интервала [ — 0,2 < < 0,2] .
8.2.2. СРЕДНИЙ КВАДРАТ
Пусть, как и в разд.8.2.1, x(t) есть отдельная реализация стационарного
эргодического случайного процесса (х(О) . Средний квадрат процесса
(x(t)) можно найти путем осреднения в пределах конечного интервала вре-
мени Т следующим образом:
А 1 сТ
^х = TJox2(t) dt' (8.34)
Истинный средний квадрат
^ = £[х2(/)] (8.35)
не зависит от времени так как процесс (x(t)) стационарен. Математиче-
ское ожидание оценки составляет
- 1 р[х!(<)] Л - 1 Л-*}. (8-36)
Следовательно, независимо от длины реализации Т величина есть несме-
щенная оценка величины фх.
Средний квадрат ошибки этой оценки равен дисперсии
Var[^] = £[(^ - ^)2] = £[ЭД - Ф4 =
= 72 /Г/Г(£[х2(О^2(ч)] - Ф4) dv di. (8.37)
Т Jq
Предположим теперь, что (x(f)) — гауссов случайный процесс со средним
значением рх Ф 0. В этом случае математическое ожидание в формуле
(8.37) запишется с учетом соотношения (3.81) в ином виде
E[x2(£)x2(i})] = 2(Я2Х(Ч - £) - ц4) + (8.38)
Из основного соотношения (8.21) следует, что
*х(ч - О - /4 = СЛ(1) - О + 2|и2СХх(ч - <). (8.39)
Таким образом,
VarH2] = 72 Jrfr(RxX(v - О - ft) dv di =
1 Jo Jo
= т1-Г(У ~ 7" Ml) dr =
_ ^fT ( M) /
гЛД1 " 7 j(Cx2x(T) + 2д2СХЛ(т)) dr. (8.40)
Статистические ошибки при оценивании основных параметров
261
При больших Т, когда I т1 < Т, дисперсия становится равной
Var[^] = |/°° (сА(т) + 2м2Ах(т)) dr . (8.41)
1 ~ ОО
Следовательно, величина есть состоятельная оценка параметра так
как дисперсия Var[i^] стремится к нулю при Г — оо и при условии, что
функции с£(т) и Схх(т) абсолютно интегрируемы на интервале (-оо, оо),
как это устанавливается соотношениями (5.117).
Рассмотрим важный частный случай ограниченного по частоте гауссова
белого шума, определенного формулой (8.25). Тогда, согласно (8.26),
Схх(т)
/ sinhrBr
х \ ЪпВг
Из формулы (8.41) видно, что ,
^4 2
Varfi^l « —4- —^2 2
LYxJ вт ВТ
(8.42)
(8.43)
Эта величина представляет собой дисперсию оценки среднего квадрата,
причем В есть полная спектральная ширина процесса, а Г — полная длина
реализации. В общем случае при ф 0 нормированная среднеквадратич-
Рис. 8.1. Нормированная случайная ошибка оценок среднего квадрата и средне-
квадратичного значения.
262
Глава 8
ная ошибка есть
ф* jBTX'I'J /ВТ \ I
(8.44)
При /л.х = 0 величина 1Д2 = ах и последнее равенство сводится к виду
так что
е$] » 1/V5T.
(8.45)
(8.46)
При = 0 соответствующий результат для среднеквадратичной ошибки
оценки ане $ есть, согласно равенству (8.10),
£[фх] « 1/(2VBT). (8.47)
Графики, отвечающие формулам (8.46) и (8.47) при различных значениях
ВТ, представлены на рис.8.1.
8.2.3. ДИСПЕРСИЯ
Оценка дисперсии может быть получена как
ох2 = - Д2 , (8.48)
Очевидно, что
Var[ox2] = Е[а4] ~(£[ох2]), (8.49)
где
£[ах2] =£[Й-£[Д2], (8.50)
£[б4] =Е[&-2£2Д2 + Д4] =
= £[ЭД - 2£[.р2Д2] + £[A4J. (8.51)
Поэтому
Уаг[ол2] = Var[i£2] + Var[g2] - 2(£[^2Д2] - £[^2]£[Д2]). (8.52)
В отличие от оценок среднего значения и среднего квадрата, оценки диспер-
сии, полученные в виде (8.48), будут смещены. В частности, в случае огра-
ниченного по частоте гауссова белого шума подстановка уравнений (8.36) и
(8.30) в (8.50) показывает, что
Е [ d2] ~ ~ ~—И Мх ~
L х J \ 2ВТ х)
Статистические ошибки при оценивании основных параметров
263
Следовательно, систематическая ошибка равна
Фх] = £[ах2] - о2 ~ (8.54)
Этот результат согласуется с формулой (4.11) приТУ = 2ВТ.
Вернемся теперь к важному частному случаю ограниченного по частоте
гауссова белого шума, для которого дисперсии оценок и Д2 определены
формулами (8.43) и (8.32) соответственно. В гауссовом случае при =# О
выражение для четвертого момента имеет, согласно (3.82), вид
£[Й&2] ~ Е [ф2] Е [Д2] + 2(£[Д2])2 - 2/?Л . (8.55)
При этом принято, что » Е[Д^]. Пренебрегая членами порядка ве-
личины 1/(ВГ)2, из формулы (8.30) получаем, что
/ 2 \2 22
(£[м2])2я: + + (8-56)
Следовательно, _ 2 2
£[^2Д2] -£[^]£[Д2] - (8.57)
D1
Подстановка формул (8.32), (8.43) и (8.57) в (8.52) дает
г ?!
Varta ] * ^7 • (8.58)
Di
Этот результат не зависит от ц.х.
Нормированная случайная ошибка есть
Этот результат справедлив и при Ф 0, в то время как формулой (8.46)
для оценки среднего квадрата можно пользоваться лишь при Ф 0. Оба
утверждения справедливы для процессов типа ограниченного по частоте га-
уссова белого шума. Из соотношения (8.10) можно теперь получить соот-
ветствующий результат для оценки среднеквадратичного отклонения ах, а
не дисперсии
£r[ax] « 1/(2V5T). (8.60)
Заметим, что рис.8.1 отвечает также формулам (8.59) и (8.60) для нормиро-
ванных случайных ошибок оценок дисперсии и среднеквадратичного откло-
нения при произвольном !1Х.
8.3. Плотность вероятности
Рассмотрим задачу оценивания плотности вероятности отдельной реа-
лизации х (г) стационарного эргодического случайного процесса (х (t)) . Be-
264
Глава 8
роятность того, что ординатах (О примет некоторое значение в интервале
от х — W /2 до х 4- W /2 за время Т, можно оценить выражением
Р{х, W] =РгоЬ
1 тх
(8.61)
где Тх — промежуток времени, в течение которого ординаты х (/) находят-
ся в пределах указанного интервала при /-м попадании в этот интервал;
Тх = £ Atj. Отношение Тх/Т представляет собой суммарную долю време-
ни, в течение которого ординаты x(t) находятся в интервале [x — W/2,
x + W/2]. Следует отметить, что величина Тх обычно зависит от ординаты
х. Оценка вероятности Р[х, W ] стремится к истинной вероятности Р\х, W ]
при Т — оо. Кроме того, она является несмещенной оценкой истинной ве-
роятности. Следовательно,
Т
P[x,lF] = £[P[x,fF]] = lim Р[х, IP] = lim —. (8.62)
Т-*оо Г-»оо Т
Одномерная плотность вероятности равна, по определению,
Р[х, W] р(х) - hm Р[х, Ж] = lim = lim р (х), (8.63)
и/-о W Г—»оо W
И/-*0 ГТ—0
где
Р[х,1У] Тх
р(х) = W ~ TW (8.64)
есть выборочная оценка величины р (х). Вероятность того, что ордината
реализациих(Z) попадает в интервал междуXj их2, можно выразить через
плотность вероятности р (х) следующим образом:
Prob[xj < х(/) < х2] = У dx .
х\
(8.65)
В частности,
Р[х, И7] = Prob
W W
х “ у x(t) ^х + —
= Г+<и//2)Н£) (8-66)
Jx-(W/2)
Тогда из формулы (8.64) следует, что
£[Р[х,Ж]] Р[х,1К]
*+(И//2)Н^.(8.67)
с-(^/2)
Таким образом, вообще говоря,
Статистические ошибки при оценивании основных параметров
265
£[р(х)] *р(х), (8.68)
и, следовательно, р(х) в общем случае представляет собой смещенную
оценку функции р(х).
Средний квадрат ошибки оценки р(х) находят по формуле (8.5):
^[(М*) “/’(•’О)2] = Var[p(x)] + b1 [р(х)], (8.69)
где Var[p(x)] — дисперсия оценки, определяемая формулой
Var[/>(x)] = £[(£(%) - £[£(х)])2], (8.70)
а b [р (х)] — смещение оценки, определяемое формулой
/>[р(х)] = £[р(х)]-р(х). (8.71)
8.3.1. СМЕЩЕНИЕ ОЦЕНКИ
Найдем теперь выражение для ошибки смещения, входящей в соотноше-
ние (8.71). С учетом истинной плотности вероятности из формулы (8.67)
находим, что
E[p(x)]=^-r+<tV/2)pU)dC (8.72)
W Jx-(W/T)
Разложим р(£) в ряд Тейлора в точке £ = х и оставим только три первых
члена: п
(£ ~ *)
р(О = />(х) +« - х)р'(х) +---------р"(х). (8.73)
Последние два соотношения дают
Г+<И//2,а-х)^ = 0, (8.74)
Jx-(W/T)
х + (и//2) (£ - *)2 W3
й я* = ‘ЧТ’ ’
-(И72)-------2-24
Следовательно,
W1
я [£(•*)] ==/>(*)+ -^-Т"(*)- (8-76)
Таким образом, в первом приближении ошибка смещения равна
г , W2
(8.77)
гдер"(х) — вторая производная функции р(х) по аргументу х.
ПРИМЕР 8.3. СМЕЩЕНИЕ ОЦЕНКИ ПЛОТНОСТИ ВЕРОЯТНОСТИ ГАУССО-
ВА СЛУЧАЙНОГО ПРОЦЕССА. Оценки плотности вероятности обычно
ищут при ширине коридора W 0,2ах. Рассмотрим все же случай построе-
266
Глава 8
ния грубой оценки плотности вероятности при ширине коридора W = ох.
Пусть анализируемые данные принадлежат гауссову случайному шуму с ну-
левым средним и единичной дисперсией. Согласно формуле (8.67), матема-
тическое ожидание оценки есть
£[£(*)] ='/у=- [X+O,5e~x2/2 dx.
У 2/П <С-О,5
Значения интеграла приведены в табл.А.2. Например, в точке, совпадаю-
щей со средним значением (х = 0), Е[р(0)] = 0,3830. Однако, согласно
табл. А.1, р(0) = 0,3989. Следовательно, смещение такой оценки гауссовой
плотности вероятности в точке, совпадающей со средним значением, со-
гласно формуле (8.71), равно
М^(О)] = 0,3830 - 0,3989 = -0,0159,
а знак минус означает, что оценка плотности вероятности оказывается ни-
же истинного значения.
Рассмотрим теперь в первом приближении систематическую ошибку,
определенную равенством (8.77). Для гауссова процесса с нулевым средним
и единичной дисперсией имеем
7=---
^77
Следовательно, в точке х = 0 смещение приближенно задается формулой
что всего на 5% отличается от истинного смещения, подсчитанного выше.
8.3.2. ДИСПЕРСИЯ ОЦЕНКИ
Для того чтобы найти дисперсию оценкир (х), необходимо знать стати-
стические свойства промежутков времени A/z, которые в сумме дают ин-
тервал Тх. К сожалению, получить такую временную статистику для слу-
чайного процесса очень трудно. Однако соответствующее выражение для
дисперсии величины р(х) в общем виде все же можно получить, исходя из
следующих эвристических соображений.
Как видно из соотношения (8.64), дисперсия оценки равна
Var[p(x>] = -^Var[P(x, Ж)] , (8.78)
гдеР[х, W] — оценка величины Р[х, W]. Дисперсия оценки этой доли вре-
мени, полученной по выборке объемом А независимых значений случайной
величины, имеет вид [8.3]
гл п Р(х, РГ)[1 - Р(х, И")]
Var[P(x, IF)] = —----------—-------— . (8.79)
Статистические ошибки при оценивании основных параметров
267
Подставляя выражение (8.79) в (8.78) и полагая, что Wp(x) < 1, можно по-
лучить приближенную формулу для дисперсии оценки плотности вероятно-
сти Z ч
Var[p(x)] ~ ^7’ (8.80)
где число N должно быть определено. Далее, как следует из доказанной в
разд. 10.3.1 теоремы о дискретном представлении процесса во временной
области, реализацию х (t) случайного процесса с полосой частот В, задан-
ную на интервале времени Т, можно полностью описать N = 2ВТ дискрет-
ными значениями. ЭтиТУ дискретных значений не обязательно, разумеется,
будут статистически независимы. Тем не менее для любого данного стаци-
онарного случайного процесса, обладающего свойствами эргодичности,
каждая его реализация содержите = N/с2 независимых выборочных значе-
ний (степеней свободы), где с — постоянная. Таким образом, из формулы
(8.80) следует, что
г , с2р(х)
Varlf(x)1 * 2B7W ' (8И>
Постоянная с зависит от вида ковариационной функции процесса и от ве-
личины интервала дискретности. Для ограниченного по частоте непрерыв-
ного белого шума, как показывают результаты расчетов, с » 0,3. Если из
ограниченного по частоте белого шума производится выборка N = 2ВТ
дискретных значений, то результаты расчетов дают для этого случая по-
стоянную с = 1, как это и следовало ожидать на основании соотношения
(8.26).
8.3.3. НОРМИРОВАННАЯ СРЕДНЕКВАДРАТИЧНАЯ ОШИБКА
Суммарный средний квадрат ошибки для оценки р (х) плотности вероят-
ности р(х) получается как сумма дисперсии (8.81) и квадрата смещения
(8.77):
г.А. . . ч.2] с2р(х) fw2p"(x)l2
El(p(x) -р(х)) ] = + I 24' (8.82)
Следовательно, нормированный средний квадрат ошибки равен
с2 W4 Гр"(х) I2
S 2BTWp{x) + 576 р(х)
(8.83)
Корень квадратный из выражения (8.83) дает нормированную средне-
квадратичную ошибку е.
Как следует из соотношения (8.83), при измерении плотности вероятно-
сти к ширине коридора W предъявляются противоречащие друг другу тре-
бования. С одной стороны, для уменьшения случайной ошибки желательно
задаваться большими значениями W. С другой стороны, чтобы снизить
ошибку смещения, необходимо сузить интервал W. Однако при Т — оо сум-
268
Глава 8
марная ошибка стремится к нулю, если величина W ограничена таким об-
разом, что W — 0, a WT — оо. На практике при W 0,2ах нормированная
ошибка смещения не превышает 1%. Это утверждение справедливо пото-
му, что выражение для этой ошибки (8.83) содежит производную/?" (%), а
плотности вероятности обычных (приблизительно гауссовых) случайных
процессов не содержит крутых и острых пучков, которым соответствуют
большие числовые значения второй производной.
8.3.4. ОЦЕНКИ СОВМЕСТНОЙ ПЛОТНОСТИ ВЕРОЯТНОСТИ
Оценки совместной плотности вероятности Двух реализаций % (О и у (I)
стационарных эргодических случайных процессов {x(t)) и |j>(0) можно
найти следующим образом. Аналогично соотношению (8.61) положим, что
величина
P[x,Wx;y,Wy]=^ (8.84)
дает оценку вероятности того, что ординаты x(t) попадают в интервал Wx
с центром в точке х и ординаты y(t) одновременно попадают в интервал
Wy с центром в точке^. Эта оценка определяется отношением Тх у/Т, где
Тх у — суммарное время, в течение которого эти два события наблюдают-
ся одновременно в пределах интервала Т. Очевидно, что величина Тх в
общем случае зависит и от х, и от у. Эта оценка совместной вероятности
приближается к истинной. вероятности Р [%, Wx; у, Wy ] при стремлении
времени Т к бесконечности, т.е.
ф, Wx, у, Wy] = lim ф, Wx; у, Wy] = lim . (8.85)
Т —* оо Т—* оо /
Совместную плотность вероятности р (%, у) можно теперь определить как
величину
Р(х,у) =
где
ф,^;Ь^]
lim —-----—
и;—о WXWV
ч P[x,Wx;y,Wy] Тх у
Р^Х,У^ WxWy TWxWy '
lim р(х, у),
Т оо
ИС->0
(8.86)
(8.87)
Предположим, что интервалы Wx и Wy настолько малы, что ошибками
смещения можно пренебречь. Тогда средний квадрат ошибки, связанной с
оценкой/?(%, у), определяется дисперсией оценки. Как и в случае оценки од-
номерной плотности вероятности, найти точное значение дисперсии, по ль
зуясь лишь теоретическими соображениями, весьма трудно. Однако с по-
мощью эвристических рассуждений, которые позволили получить соотно
шение (8.81), можно приближенно найти общий вид дисперсии А именно г
Статистические ошибки при оценивании основных параметров
269
частном случае, когда nx(t) ny(t) представляют собой белый шум с огра-
ниченной полосой частот шириной В, дисперсия равна
Var[p(x,y)] « 2/^^/ (8 88)
где с — неизвестная постоянная
8.4. Оценки ковариационных функций
Рассмотрим теперь две реализации x(t) и y(t) стационарных эргодиче-
ских случайных процессов [%(/)] и {МО)- Определим другие характеристи-
ки процессов — стационарные автоковариационные функции и R (т)
и взаимную ковариационную функцию Rxx(j)- Чтобы упростить последую-
щие выкладки, примем, что средние значения цх и д равны нулю. Оценку
взаимной ковариационной функции /^(т), связывающей заданные на конеч-
ном интервале Т реализации %(/) и у(I) с непрерывным временем, можно
записать в виде
О < т < Т;
-Т< т < 0.
(8.89)
Чтобы избежать использования знака модуля, будем в дальнейшем считать
величину т положительной, так как для отрицательных значений т справед-
ливы те же выводы. Оценки ковариационных функций Rxx(t) и Ryy(r) пред-
ставляют собой частные случаи оценки взаимной ковариационной функции,
когда обе реализации совпадают, т.е. при 0 т < Т
Кхх(т) = --------fT Tx(t)x(t + т) dt,
1 — Т Jo
(8.90)
Л (т) = --------- Г Ty(t)y(t + т) dt,
7 — Т •'о
Таким образом, путем анализа оценки взаимной ковариационной функции
можно получить результаты, применимые к оценкам автоковариационной
функции.
Если процессы заданы на интервале Т 4- т, а не Т, то можно дать дру-
гое определение функции Rx (fy.
А. 1
^xy(r) = - x(i)y(i + r) di, 0 < т < 7\ (8.91)
270
Глава 8
В эту формулу входит фиксированный интервал интегрирования Т вместо
переменного интервала интегрирования в формуле (8.89). Именно в таком
виде выше было дано определение ковариационных функций. Отметим,
что оценки средних значений квадратов функций x(t) или y(t) представля-
ют собой просто частные случаи соотношения (8.89) или (8.91) при ъ = 0.
Для упрощения обозначений в последующих выкладках вместо формулы
(8.89) будет использоваться формула (8.91). В обоих случаях окончательные
результаты будут одинаковы, если считать, что процессы заданы на интер-
вале Т + т.
Математическое ожидание оценки
Е[^х?(т)] = J+ т)] т/оКху^ dt = Rxy^'
° ° (8.92)
Следовательно, независимо от длины реализации Т величинаRxy(j) есть не-
смещенная оценка функции Яху(т). Средний квадрат ошибки определяется
дисперсией
Var[Ax/r)] = Е |(Ях/т) - /Цг))2] = Е [яЦ т)] - Я^(т) =
7 •'О •'О
- Лх/Т)) dvdu.
(8.93)
Чтобы упростить последующие преобразования и согласовать результаты
со многими физическими приложениями, представляющими наибольший
интерес, будем считать, что совместная плотность распределения случай-
ных процессов {x(t)] и {7 (О) Для любой совокупности фиксированных мо-
ментов времени есть функция Гаусса. Этого ограничения можно избежать,
вводя некоторые условия интегрируемости для негауссовых частей случай-
ных процессов и не меняя при этом существенным образом окончательные
выводы. В случае, когда совместная плотность вероятности процессов
{х(О) и [^(О) нормальна, сами процессы [х(О) и {j(f)J порознь также
подчиняются нормальному распределению.
Для гауссовых стационарных случайных процессов с нулевыми средни-
ми значениями формула (5.130) дает следующее выражение для четвертого
смешенного момента:
E[x(m)j(m + t)x(d)^(u + т)] = Яху(т) + Rxx(v - u)Ryy(v - и) +
+ ЯХ>,(1> - и + r}Ryx(v - и - т).
(8.94)
Следовательно, дисперсия
Статистические ошибки при оценивании основных параметров
271
Уаг[Л (т)] = frfT(Hxx(v - u)R {v - и) +
1 I •'О •'о
+ Rxy(v — и + r)Ryx(v - и - т)) dvdu =
1 J _ уд 1 ]
+RXy(i + r)Ryx(i-r))di. (8.95)
Второе равенство можно получить из первого, используя подстановку
£ = v — и, d% = dv и меняя затем порядок интегрирования по переменным
$ им. Если считать, что произведенияRxx(%)Ryy($) nRxy(£)Ryx(£) абсолютно
интегрируемы в промежутке (— оо, оо), то
lim Т Varfft (т)1 =
Т-оо 1 J
= Г (RxM)Ryy(l) + Rxy(l + r)Ryx(i - т)) di < оо. (8.96)
J - 00
Этим доказывается, что величинаRxy(r) представляет собой состоятельную
оценку функции Rxy (т). При больших Т оценка имеет дисперсию
Уаг[ЬхДт)] « (Rxx(i)RyyW + Rxy(i + r)Ryx(i - т)) di.
1 •'-00
(8.97)
Заслуживают внимания несколько частных случаев соотношения (8.97).
Дисперсия оценки ковариационной функции равна
1 00
Уаг[Ахх(т)] (R^ + RAi + ^R^i-^di. (8.98)
1 •'-00
При нулевом сдвиге (т = 0)
2 /»00
Var[*xx(O)] = -( R2J^di. (8.99)
•'-00
Из предположения, что при больших значениях т функция Кхх(т) стремится
к нулю, следует неравенство
R2xx(i)»Rxx(i + r)Rxx(i-T).
Таким образом, при больших т
Уаг[Л„(г)1-^Г К2„Ш<И. (8.100)
i •'-00
что составляет половину величины (8.99).
272
Глава 8
8.4.1. ОГРАНИЧЕННЫЙ ПО ЧАСТОТЕ БЕЛЫЙ ШУМ
Для ограниченного по частоте гауссова белого шума с полосой частот
В, имеющего среднее значение = 0 и наблюдаемого на интервале Т [см.
формулы (8.25) и (8.26)], дисперсия при всех значениях т не превышает, со-
гласно (8.98), величины
Уаг[Лхл(т)] = — [Я^(0) + *L(t)] • (8.101)
При т = 0 это соотношение переходит в равенство (8.45). Аналогично в
случае, когдах(Г) hj(O — реализации длины Т ограниченного по частоте
белого шума, имеющие средние значения /^ = ^ = 0 и одинаковую шири-
ну полосы частот В, из формулы (8.97) следует, что дисперсия равна
Уаг[Ях/т)] *^;[Л„(О)^(О) + Я2,(т)]. (8.102)
Соотношение (8.102) справедливо при достаточно большом Т, таком, что
формулой (8.97) можно пользоваться вместо (8.95). Практически это усло-
вие удовлетворяется при Т 101 т1 к ВТ 5.
равен
При цх = /Ху = 0 и Rxy Ф 0 нормированный
средний квадрат ошибки
е2[*^(т)]
Уаг[Ях/т)] 1
Я2,(т) * 2ВТ
R хх(0) R уу(0)
Я2/т)
(8.103)
1
+
Корень квадратный из выражения (8Л03) дает нормированную среднеквадра-
тичную ошибку £, которая включает в себя только случайную ошибку, так
как при длине реализации более Т 4- т смещение равно нулю.
Таким образом, для оценок взаимной ковариационной функции имеем
где
4*ЛтЯ= + р^2(т)Г/2>
(8.104)
, (т)- '
Ху /Яхх(0)Я,Д0)
(8.105)
есть нормированная взаимная корреляционная функция. Заметим, что
= ПРИ Рх = Ру — 0- Если % (Z) = у (I), то в точке т = 0 имеем
^xv<0) = и Рлх(°) = ь так что
е[Ялх(0)] =£[^] (8.106)
что согласуется с формулой (8.46). В общем случае оценивания ковариаци-
онной функции ошибка равна
Статистические ошибки при оценивании основных параметров
273
Рис. 8.2. Нормированная случайная ошибка оценок ковариационной функции.
Рхх(Т) =
(8.107)
где
RxAt)
Яхх(0)
(8.108)
График, отвечающий уравнению (8.107), приведен на рис.8.2.
8.4.2. ОБ ОТНОШЕНИИ СИГНАЛ/ШУМ
Отметим некоторые приложения формулы (8.104). Пустьх(/) и у (Г) за-
даются в виде
х(/) = s(t) + w(0,
y(t) = S(t) + n(t), (8.109)
где$(О, /w(r) и n(t) попарно некоррелированы. Тогда
Мт) = Я„(т) = Я„(0)р„(т) = Spss(r),
Лхх(0) = Я„(0) + RmJ£) = S + M, (8.110)
Я?Д0) = Я„(0) + Япп(0) = .$ + АГ.
274
Глава 8
Из уравнения (8.104) следует, что нормированная среднеквадратичная
ошибка равна
е2[^х>.(т)] ~ 2ВТ
(S + M)(S + 2V)
(8.111)
Учитывая, что рхх(0) = 1, имеем при т = 0:
е2[ЯЛ/0)] = ^[2 + (M/S) +(N/S) +(M/S)(N/S)]. (8.112)
Эти соотношения полезны для анализа систем с двумя детекторами, на вы-
ходе которых наблюдаются заданные формулами (8.109) последовательно-
сти x(t) и у (t), содержащие один и тот же сигналя (О и некоррелированные
помехи m (t) и n(t).
Случай 1.
М = 0 при N /S >
1
Случай 2.
М = N wlN/S >
1:
(8.113)
(8.114)
Эти два случая могут иметь важные физические приложения. Например, в
случае 1 x(t) может быть опорным сигналом, для которого строится
взаимная корреляция с последовательностью у (t), представляющей собой
смесь принятого сигнала помехи. Во втором случае строится корреляция
искаженного помехой сигнала у (О с самим собой. При любом отношении
N /S > 1 получение одной и той же заданной среднеквадратичной ошибки
требует во втором случае гораздо большей величины ВТ.
Дальнейшее осуждение этих вопросов содержится в работе [8.1]. Прило-
жения формул, приведенных в этом разделе, даны в книге [8.2].
8.4.3. ЛОКАЛИЗАЦИЯ ЭКСТРЕМУМОВ КОВАРИАЦИОННОЙ ФУНКЦИИ
Результаты, приведенные выше в разд.8.4, содержат формулы для
определения случайных ошибок при оценивании эстремальных значений
функций Rxy(r) hRxx(t). Однако при этом остается пока нерешенной важная
проблема точной локализации таких экстремальных значений ковариацион-
ных функций. Предположим для определенности, что ковариационная
функция имеет форму, отвечающую ограниченному по частоте белому шу-
му, т.е.
^хх(т) = *хх(0)(
8т2тгВт
(8.115)
'I'itB't
Статистические ошибки при оценивании основных параметров
275
Максимальное значение Rxx(т) наблюдается в точке т = 0. Разлагая Rxx(t) в
ряд в окрестности т = 0, имеем
(2ттВт) 8т2тгВт » (2ттВт) . 6 Таким образом, вблизи т = 0 оценка Rxx(t) имеет вид 2(тгЛт)2 Яхх(т) » 1 - „ *хх(0), Л Л \ z ЛЛ \ z г (8.116) (8.117)
и ее математическое ожидание
£[Лхх(0)]=Яхх(0). (8.118)
Следовательно, 7?ГЛ.(0) есть несмещенная оценка Rxx(0). Ее дисперсия
Var[Axx(0)] = £[{Яхх(0) " Лхх(0)}2] « |(W5)4A2xx(0)£[t4]. (8.119)
Поэтому нормированная среднеквадратичная ошибка равна
е2[*хх(°)] = в К^)4^4]. <812°)
Предположим теперь1^, что значения т описываются гауссовым распре-
делением с нулевым средним значением и диперсией а2(т):
М1(т) = = 0, <>12(т) = £[т2]. (8.121)
В этом случае четвертый момент распределения, входящий в формулу
(8.120), равен
Е[т4] = Зо4(т) , (8.122)
следовательно,
е2[«хх(0)] «И^)Ч4(т). (8.123)
Таким образом, имеем
0,93 , г А
<>i(t)»-He[*xx(0)]} Z . (8.124)
95 %-доверительный интервал для оценки местоположения экстремума ко-
вариационной функции есть
[-2а1(т)^т^2а1(т)] . (8.125)
О Это можно сделать, поскольку речь идет о локализации случайного положе-
ния экстремума ковариационной функции. — Прим, перев.
276
Глава 8
ПРИМЕР 8.4. ОЦЕНКА ЗАПАЗДЫВАНИЯ ПО ВЗАИМНОЙ КОВАРИА-
ЦИОННОЙ ФУНКЦИИ. Пусть наблюдаемые реализации x(t) и у (г) со-
держат общий сигнал s(t) и некоррелированные помехи m(t) и n(t):
x(r) = s(t) + m(t), y(t) = s(t + т0) + n(t).
Согласно разд.5.1.4, максимальное значение взаимной ковариационной
функции Rxy(т) = Rss(t — т0) будет наблюдаться при сдвиге т = т0, опреде-
ляющем относительное запаздывание в поступлении сигнала s (О в реализа-
ции x(t) ny(t). Предположим теперь, что$(О — ограниченный по частоте
белый шум со спектральной шириной В = 100 Гц, а отношения шума к
сигналу вх(1) и у (t) суть М/S = N /S = 10. Имея реализации % (О и у (О
длиной Т = 5 с, определим точность оценивания запаздывания т0 по оцен-
ке положения максимума ковариационной функции Rxy(r).
Согласно уравнению (8.114), нормированная случайная ошибка оценки
максимума ковариационной функции дается приближенным соотношением
4^(то)]=е[Я„(О)] =
102 ]1/2
(2)(100)(5)
= 0,32
Заметим, что из формулы (8.112) следует более точная оценка £ = 0,35.
В соответствии с формулой (8.124) приближенное значение для среднеква-
дратичного отклонения оценки есть
Я1(т) =
0,93(0,35)1/2
тг(ЮО)
= 0,0017 с.
Из соотношения (8.125) следует, что приближенный 95%-доверительный
интервал для оценки т0 (в секундах) есть
[т0 - 0,0034 < т0 < т0 + 0,0034].
8.5. Оценки спектральных плотностей
Блок-схема стандартного фильтрующего устройства для оценивания
спектральной плотности реализациих (I) приведена на рис.8.3. Предполага-
ется, что подаваемая на вход фильтра реализациях^) характеризует стаци-
онарный (эргодический) случайный процесс с нулевым средним значением,
а усреднение производится в пределах интервала времени Т. Считается да-
лее, что настраиваемый узкополосный фильтр имеет постоянную полосу
пропускания Ве, отличную от нуля, с центральной частотой /, которую
можно изменять в исследуемом диапазоне частот. Эту полосу пропускания
частотВе не следует путать с полной полосой частот, содержащихся в реа-
лизации х(/). Оказывается, что для получения состоятельной оценки функ
ции Gxx(f) необходимо осуществить операцию фильтрации, позволяющую
проводить усреднение в пределах некоторой полосы частот. Окончательная
Статистические ошибки при оценивании основных параметров
277
Рис. 8.3. Полосовой фильтр с постоянной полосой пропускания для измерения
спектральной плотности.
оценка Gxx(f) характеризует усредненную по времени величину xfy), кото-
рая содержит составляющие с частотами в полосе от f - Ве/2 до / + Ве/2
и отнесена к ширине полосы Ве. Отметим следующее обстоятельство. Так
как отличное от нуля среднее значение соответствует наличию дикретной
составляющей с нулевой частотой, то предположение о равенстве среднего
значения нулю существенно в дальнейшем лишь в том случае, когда полоса
Ве содержит частоту/ = 0. Во всех дргуих случаях, когда Ве не включает в
себя частоту/ = 0, полученные ниже выводы применимы ко всем процес-
сам с произвольным средним значением.
Средний квадрат функции х (t) в пределах полосы частот Ве с централь-
ной частотой/ определяется выражением
^f,Be) = \jTx\t,f,Be)dt, (8.126)
1 •'О
где х(t, f, Ве) — реализация на выходе узкополосного фильтра, а Г — ин-
тервал усреднения. В разд.8.2.2 показано, что величина (8.126) представля-
ет собой несмещенную и состоятельную оценку истинного среднего квадра-
та при Т, стремящемся к бесконечности. Это означает, что
Ве) = E[^x(f, Bj] = lim fTx\t,f, Be) dt, (8.127)
T-»oo 1 •'О
где i/^(/, Ве) — средний квадрат реализации х (I) на выходе фильтра с поло-
сой пропускания Ве и центральной частотой /.
По определению, спектральная плотность
1 гТ
Gxx(f) = lim -----------= lim ~^J x2(t,f,Be)dt = lim Gxx(f),
ве^о Be т^х В.Г Jq t—x
e Be-*0 e Be^0
(8.128)
где величина
1 rr l2Af,Be)
Gxx(f) = X f’ dt = (8-129)
Bel De
представляет собой оценку функции Gxx(i), определяемую методом, кото-
рый поясняется на рис.8.1. Средний квадрат функциих(/) в полосе частот
278
Глава 8
от/j до/2 можно выразить через истинную спектральную плотность Gxx(f)
В частности, /2) = j Gjf) df . Jh (8.130)
rAf,Bejf/+(B'/2) Gjl) . (8.131)
Из формул (8.129) и (8.131) следует, что
r(f.B) 1 (/>l= \ -B. j'^Gj^. (8.132)
Таким образом, для большинства значений Gxx(f)
E{Gjf)\*Gjf), (8.133)
т.е. Gxx(f) в общем случае представляет собой смещенную оценку функции
G^tfY
Средний квадрат ошибки оценки Gxx(f) вычисляют из соотношения
(8.5):
Е [(<L(/) - <U/))2] = Var[4x(/)] + > (8.134)
где дисперсия оценки равна
Уаг[СЛХ(/)] = Е|(<7ХХ(/) - £[<L(/)])2], (8-135)
а смещение оценки равно
b [<L(/)] = £[^х(/)1 - Gjf). (8136)
8.5.1. СМЕЩЕНИЕ ОЦЕНКИ
Выражение для ошибки смещения (8.136) можно получить тем же спосо-
бом, что и при оценивании плотности вероятности в разд.8.3.1. Разлагая
величину Gxx(g) в ряд Тейлора в точке £ = / и оставляя только три первых
члена, из формулы (8.132) можно найти, что
2? 2
Е[<L(/)] « Gjf) + -^GJJ). (8.137)
Таким образом, ошибка смещения равна
M<L(/)] =^G*"(/), (8.138)
где G^f) — вторая производная функциии G^f) по аргументу /, связан-
ная с ковариационной функцией Rxx(r) соотношением
Gjf) = ~8w2y JRjJe~jlr,fr dr. (8.139)
Статистические ошибки при оценивании основных параметров
279
Рис. 8.4. Пример ошибки смещения при сглаживании оценок спектральной плот-
ности по частоте.
Следует подчеркнуть, что формула (8.138) дает только первое прибли-
жение для ошибки смещения, которое применимо в тех случаях, когда
B2eG^f) < СхАП- Так как на практике спектры зачастую содержат ост-
рые пики, которым соответствуют большие числовые значения второй
производной, то использование формулы (8.138) может привести к получе-
нию неверных представлений об ошибке смещения. Соотношение (8.138)
будет давать завышенные значения ошибки смещения, если произведение
G^if) велико.
Уравнение для ошибки смещения (8.138) получено в предположении, что
оценка спектральной плотности найдена, как показано на рис.8.4, при ис-
пользовании идеального прямоугольного спектрального окна, заданного
формулой (8.131). В разд.11.5 будет показано, что практические методы
спектрального оценивания предполагают использование спектральных
окон, форма которых существенно отличается от точного прямоугольника.
Тем не менее формула (8.138) представляет собой полезное первое прибли-
жение, дающее верные и важные качественные результаты. В частности,
ошибка смещения возрастает при фиксированном Ве с ростом <7^(/) или с
ростом Ве при фиксированном значении G^if). Кроме того, из рис.8.4 яс-
но видно, что ошибка смещения всегда ведет к уменьшению размаха значе-
ний спектральной плотности: ее максимумы занижаются, а провалы завы-
шаются.
ПРИМЕР 8.5. СМЕЩЕНИЕ СПЕКТРАЛЬНОЙ ОЦЕНКИ. Пусть на вход систе-
мы с одной степенью свободы, описанной в разд. 2.4.1, поступает белый
шум. Согласно примеру 6.3, функция спектральной плотности смещения
массы задается в этом случае формулой
где G — выраженная в единицах смещения массы спектральная плотность
280
Глава 8
возмущения, поступающего в систему, fn — собственная частота незатуха-
ющих колебаний, f — коэффициент затухания системы. Согласно уравне-
нию (2.25), максимальное значение G (f) достигается на резонансной ча-
стоте fr = — При 2f2 < 1 вторая производная функции G (f) в
точке f = fr есть
G"(/r)e(-8/Br2)^a) ,
гдеВг — полоса пропускания по уровню половинной энергии в области ре-
зонансного максимума спектра, задаваемая формулой (2.27), т.е. Вг » 2f/r.
В соответствии с равенством (8.138) нормированная систематическая ошиб-
ка есть теперь
М<Ш)] =
М<Ш)].
Gyy(fr) ~ 3 у )
Этот результат часто используется для оценивания максимального смеще-
ния оценок спектральной плотности процессов на выходе механических и
электрических систем с небольшим затуханием. Очевидно, что для получе-
ния небольшого смещения разрешение по частоте Ве должно быть меньше
полосы пропускания Вг. Обычно принимают Ве » ВЛ/4, что дает пренебре-
жимо малую систематическую ошибку еь ® — 2%.
8.5.2. ДИСПЕРСИЯ ОЦЕНКИ
Для того чтобы непосредственно получить выражение для дисперсии
оценки спектральной плотности, воспользуемся выводами разд.8.2.2. Как
следует из соотношения (8.129), величина
Bfixx(f) = Ш Ве) (8.140)
есть несмещенная оценка, характеризующая средний квадрат функции х (I) в
полосе частот Ве с центральной частотой /. Если спектральная плотность
Gxx(f) постоянна в пределах полосы частот Ве, то истинный средний ква-
драт равен x//x(ff Ве) = BeGxx(f). Это условие выполняется приближенно
при достаточно малых значениях Ве. Теперь можно использовать формулу
(8.45), положив в ней/?ХЛ.(0) = BeGxx(f)\
дХ2х(/)
Var[2?Ax(/)] =
вет
Так как Ве — постоянная, то
Уаг[вДх(/)] =B/Var[GXA.(/)]_
Отсюда можно получить дисперсию оценки
GU
Var[(L(/)]~ RT
L).J
(8.141)
(8.142)
(8.143)
Статистические ошибки при оценивании основных параметров
281
Другие сведения о дисперсии оценок спектральной плотности приведены в
разд.8.54.
Соотношение (8.143) получено в предположении, что отфильтрованный
процесс ведет себя как ограниченный по частоте белый шум. На практике
такое предположение вполне приемлемо при узкой полосе пропускания
фильтра Ве. Согласно центральной предельной теореме, процесс на выходе
фильтра должен быть ближе к гауссову, чем входной процесс, и тот факт,
что ширина Ве мала, означает, что спектр выходного процесса должен, по
существу, почти не зависеть от частотыСледовательно, при малой ши-
рине Ве можно с большой степенью уверенности утверждать, что нормиро-
ванная случайная ошибка оценки есть
M<L(/)] = • (8.144)
Заметим, что эта величина не зависит от частоты.
8.5.3. НОРМИРОВАННАЯ СРЕДНЕКВАДРАТИЧНАЯ ОШИБКА
Суммарный средний квадрат ошибки, характеризующий оценку Gxx(f),
равен сумме выражения (8.143) и квадрата выражения (8.138):
E{(Gxx(f)-Gxx(nY]^^~p- +
B&'x(f) j2
24
(8.145)
Следовательно, нормированный средний квадрат ошибки можно приб-
лиженно представить в виде
£[(<L(/)-Gxx(/))2] 1 Г <?"(/) I2
Gxx(f) ~ ВеТ+ 57б[схх(/)
(8.146)
Квадратный корень из величины (8.146) дает нормированную среднеквадра-
тичную ошибку £.
Следует отметить две важные особенности выражения для ошибки, ха-
рактеризующей оценку спектральной плотности. Во-первых, к разрешаю-
щей способности Ве предъявляются два противоречащих друг другу требо-
вания: для уменьшения ошибки смещения необходимо задаваться малым
значением Ве, тогда как для уменьшения случайной ошибки разрешающую
способность следует увеличивать. Это противоречие аналогично описанной
Имеется в виду область частот вне полосы пропускания фильтра. Более под-
робно вопрос о приближенной нормализации процесса на выходе узкополосного
фильтра рассмотрен, например, в книге: Б.Р.Левин. Теоретические основы статисти-
ческой радиотехники. Т.1.—М.: Сов.радио, 1974, с.241. — Прим.перев.
282
Глава 8
в разд.8.3.3 ситуации, связанной с выбором ширины коридора W при изме-
рении плотности вероятности. Однако в данном случае вопрос стоит еще
более остро, так как на практике кривая спектральной плотности зачастую
содержит резко выраженные пики (которым соответствуют большие чис-
ловые значения второй производной), что делает затруднительным сниже-
ние ошибки смещения. Во-вторых, случайная ошибка включает в себя толь-
ко полосу пропускания Ве, а не всю полосу частот В, присутствующих в
процессе. Следовательно, случайная ошибка в большей степени зависит от
параметров схемы анализа, чем от неизвестных параметров процесса. Это
обстоятельство еще раз подчеркивает практическое значение формулы
(8.146) для планирования эксперимента и анализа процессов. Затронутые
здесь вопросы рассматриваются также в разд.8.6.
8.5.4. ОЦЕНКИ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ, ПОЛУЧЕННЫЕ ФИНИТНЫМ
ПРЕОБРАЗОВАНИЕМ ФУРЬЕ
В разд.8.5.2 приведено выражение для дисперсии оценок спектральной
плотности, которые получают путем фильтрации, возведения в квадрат и
усреднения. Эти операции обычно осуществляются с помощью аналоговой
аппаратуры. Можно найти также выражение для дисперсии оценок спект-
ральной плотности, полученные путем непосредственного преобразования
Фурье. Эту операцию осуществляют с помощью цифровых вычислитель-
ных машин, используя описанный в гл. 11 алгоритм быстрого преобразова-
ния Фурье. Краткое описание второго способа вычисления спектра может
облегчить задачу определения ошибок, характеризующих оценки спектраль-
ной плотности.
Рассмотрим вычисляемую по формуле (5.67) спектральную плотность
стационарного (эргодического) гауссова случайного процесса х (I). В част-
ном случае реализации неограниченной длины Т спектр имеет вид
Gxx(f) = 2 lim Ь?[|Х(/, Г)|2], (8.147)
Т -+ оо 1
где X(f, Т) — финитное преобразование Фурье функции х(1):
X(f,T)= (Tx(t)e-J2^'dt. (8.148)
«Несглаженную» оценку величины G^it) можно теперь получить, просто
опуская в формуле (8.147) знаки предела и математического ожидания:
2
6j/) = ^(/J)|2. (8.149)
При этом обеспечивается максимально высокая разрешающая способность
А/ = 1/Т.
Для того чтобы найти дисперсию этой оценки, заметим, что финитное
Статистические ошибки при оценивании основных параметров
283
преобразование Фурье X(f, Т) дает ряд составляющих с частотами
f = к /Т, vjxzk — 1, 2, 3 и т.д. Отметим также, что%(/, Т) есть комплекс-
ная величина, действительная XR(f, Т) и мнимая Х/(Л Т) части которой
представляют собой, как можно показать, некоррелированные случайные
величины с нулевыми средними-значениями и одинаковыми дисперсиями.
Так как преобразование Фурье есть линейная операция, то очевидно, что в
том случае, когда процесс*(О подчиняется нормальному распределению,
функцииXR(f, Т) nXjif, Т) будут нормальными случайными величинами.
Отсюда можно заключить, что величина
|Х(/, Г)|2 = Х2(/, Т) + X](f, Т) (8.150)
есть сумма квадратов двух независимых величин. Следовательно, как выте-
кает из определения (4.16) с учетом выражения (4.37), каждая частотная со-
ставляющая оценки Gxx(f) имеет выборочное распределение
Gxx(f) = Хг
Gxx(f)
где *2 — величина, подчиняющаяся ^-распределению с п = 2 степенями
свободы.
Необходимо подчеркнуть, что величина (8.151) не зависит от длины реа-
лизации Т. Поэтому при увеличении длины реализации функция распреде-
ления, которая описывает случайную ошибку полученной оценки, не меня-
ется, а только возрастает число частотных составляющих оценки. Если
длину реализации интерпретировать как меру объема выборки, характери-
зующего данную оценку, то отсюда следует, что формула (8.149) дает несо-
стоятельную оценку спектральной плотности (что отмечалось еще в
разд.5.2.2). Кроме того, случайная ошибка такой оценки достаточно вели-
ка. Обращаясь к соотношениям (4.19) и (4.20), можно видеть, что среднее
значение и дисперсия величины, подчиняющейся х -распределению, состав-
ляют п и 2п соответственно. Поэтому нормированная стандартная ошиб-
ка, определяющая случайную погрешность полученной оценки, будет иметь
вид
'|c"(/,l = “h7F=~=v; (8Л52)
В рассматриваемом случае п = 2 и £r = 1, т.е. среднеквадратичная
ошибка оценки равна оцениваемой величине. В большинстве случаев такая
ошибка неприемлема.
На практике случайную ошибку спектральной оценки, получаемой по
уравнению (8.149), уменьшают путем вычисления оценок по nd различным
(неперекрывающимся, отдельным) участкам реализаций длиной Т каждая и
их последующего усреднения, что приводит к «сглаженной» оценке
а 2 nd
Gxx(/) = -^ElX(/,7’)|2- (8153)
ndT
284
Глава 8
Поскольку каждое слагаемое в правой части равенства (8.153) дает две ста-
тистические степени свободы, сглаженная оценка имеет ошибку
(8.154)
Очевидно, что минимальная общая длина реализации, необходимая для по-
лучения оценки спектра, есть
Tr = ndT, (8.155)
а разрешение спектральной оценки по частоте задается приближенным ра-
венством
\/Т. (8.156)
Таким образом, nd = Тг/Т и формула (8.154) эквивалентна соотношению
(8.157)
что совпадает с (8.144) при замене Т наТг.
Возвращаясь к формуле (8.151), заметим, что выборочное распределение
оценки спектральной плотности можно теперь записать в виде
4х(/) х2%
Gxx(f) « ’
п = 2nd.
(8.158)
В соответствии с равенством (4.47) доверительный интервал для спектраль-
ной плотности Gxx(f), основанный на оценке Gxx(f), с вероятностью 1 — а
есть
nGxx(f)
Хи; а/2
nGxx(f)
V2
X п; 1 — а/2
n = 2nd.
(8.159)
^Gxx(f)<
Как и прежде, при сравнительно небольшой случайной ошибке е (скажем,
£ 0,1) приближенный 95 %-доверительный интервал для спектральной
плотности может быть получен в соответствии с формулами (8.14) и
(8.154) в виде
2 К / 2 \ А
1 - 7- К(/) GJJ) < 1 + к(/)
/
(8.160)
Следует отметить, что случайные ошибки при вычислении спектральных
плотностей будут в действительности несколько больше в зависимости от
детальных особенностей метода. Этот вопрос рассмотрен в разд. 11.5.1.
Статистические ошибки при оценивании основных параметров
285
8.6. Выбор длины реализации
Выражения для ошибок, приведенные в разд.8.2—8.5, позволяют оце-
нить статистическую точность оценок различных параметров, полученных
после завершения эксперимента. Желательно также уметь использовать
эти формулы для предсказания точности оценок, которые предполагается
получить в планируемых экспериментах, и, в частности, для того, чтобы
выбрать длину реализации, необходимую для получения оценки с заданной
степенью точности. Действительно, приведенные выше формулы связыва-
ют длину реализации с ошибкой оценки каждого параметра. Однако они
содержат обычно и другие величины, которые до завершения эксперимента
остаются неизвестными. Поэтому непосредственное использование этих
формул как основы для выбора длины реализаии неоправданно. Придется
сделать некоторые допущения, основанные на априорном знании свойств
процессов и (или) на инженерной интуиции.
Например, дисперсия оценки среднего квадрата гауссова процесса связа-
на формулой (8.41) с длиной реализации Т через ковариационную функцию
и среднее значение процесса. Если бы можно было допустить, что все на-
ши процессы ведут себя как ограниченный по частоте белый шум со спект-
ральной шириной В и нулевым средним значением, то длина реализации,
необходимая для получения оценки с заданной нормированной среднеква-
дратичной ошибкой определялась бы по формуле (8.46) в виде
Т = (Be2)-1. К сожалению, такое допущение практически мало пригодно
даже в качестве первого приближения.
Все же существует один параметр, при оценивании которого можно за-
частую сделать разумные допущения и получить практически приемлемую
формулу, связывающую длину реализации и ошибку оценки. Это — оценка
спектральной плотности. Из формулы (8.146) видно, что случайная часть
нормированной среднеквадратичной ошибки спектральных оценок зависит
лишь от длины реализациии Г и от разрешения по частоте Ве (в предполо-
жении, что спектральная плотность мало меняется в пределах полосы ча-
стот шириной Ве и что процесс является гауссовым). Это означает, что
длина реализации, требуемая для получения такой спектральной оценки с
заданной нормированной случайной ошибкой, определяется в виде
Т = (Bee^)~ii гдеВе — известный параметр расчетного метода, а не под-
лежащий определению параметр процесса. Остается лишь правильно вы-
брать разрешение по частоте Ве.
Возвращаясь к формуле (8.146), видим, что систематическая часть
ошибки спектральной оценки зависит в первую очередь от разрешения по
частоте Ве. Однако существенную роль в определении смещения играет и
величина О^(/), определяющая «изрезанность» спектра в пределах полосы
Ве. Поэтому можно выбрать некоторое предельное значение производной
О^.(/) и затем связать ошибку смещения с шириной полосы Ве. Это дела-
ют обычно на основе общих физических соображений относительно ре-
286
Глава 8
шаемой задачи. Рассмотрим, например, частный случай процесса, пред-
ставляющего собой реакцию некоторой резонирующей физической системы
при условии, что каждое решение, дающее резонанс, можно описать про-
стой системой второго порядка, заданной уравнением (2.19). Если предпо-
ложить, что в пределах полосы шириной Ве относительно каждой резо-
нансной частоты спектр входного процесса почти постоянен, то следует
ожидать, что спектр реакции системы вблизи каждой резонансной частоты
будет иметь вид Gxx(f) = с где с — некоторая постоянная, &H(f)
задается в механических единицах формулой (2.24). Ошибку смещения оцен-
ки спектральной плотности на резонансных частотах можно тогда вычис-
лить, как показано в примере 8.5, через отношение разрешения по частоте
Ве к полосе пропускания по уровню половинной энергии Вг частотной ха-
рактеристики H(f).
Приведенное выше обсуждение вопроса о выборе длины реализации при
оценивании функции спектральной плотности особенно важно по двум при-
чинам. Во-первых, во многих инженерных приложениях спектр представля-
ет собой наиболее важный параметр случайного процесса. Во-вторых, в
сравнении с оценками других параметров, рассмотренными в этой главе,
Таблица 8.1. Длина реализации и число усреднений для основных оценок
Необходимая
Оценка
длина реализации
Необходимое
число усреднений
Ах 1 1 О.\2 1 / О \2 Т = 1 — 1 N = — — 1 €2\/ал/
Ах .4 II to I х——— У l*Q II У 1>Я
°х> lx 1 1 ' 4Ве2 Л 2е2
®х2> 1 2 Тг = -—г N = — Be2 е2
Р(х) 1 2 Г = v = WBp(x)e2 И7?(х)е2
Ях>(т) = тк[1 + Рх7(т)] N = 4 [1 + Рх?(т)] /ле е
Gxx(f) 1 1 Тг ° V п“= 7
Статистические ошибки при оценивании основных параметров
287
получение спектральной оценки с заданной величиной ошибки предъявляет
наиболее жесткие требования к длине реализации. Это последнее обстоя-
тельство легко проверить, сопоставив выражения для ошибок, относящие-
ся к оценкам спектральной плотности и к оценкам других параметров. Лег-
ко видеть, что знаменатели формул, определяющих ошибки оценок других
параметров, обычно содержат множители, превышающие величину Ве, не-
обходимую для получения спектральной оценки с приемлемым разрешени-
ем.
Различные формулы для ошибок оценок, приведенные в этой главе, со-
держат либо произведение ВТг, либо произведение ВеТг, где Тг (вместо
Т) — общая длина реализации, В — общая спектральная ширина процесса
(по аналогии с ограниченным по частоте белым шумом с заданной диспер-
сией), а Ве — разрешение по частоте при вычислении оценки спектра. Вме-
сто использования произведения ВеТг оценки функций частоты можно ха-
рактеризовать числом усреднений nd = ВеТг, что и сделано при описании
методов вычисления в гл.11. Используя числовой параметр N = ВТг для
числа независимых оценок, можно переписать и другие формулы, приве-
денные в этой главе.
В табл. 8.1 даны выражения для минимальной длины реализации Тг или
минимального числа независимых усреднений N = ВТГ или nd = ВеТг, не-
обходимые для получения оценок с заданной ошибкой £, выраженные через
другие параметры самого процесса или метода анализа. Предполагается,
что ошибки смещения пренебрежимо малы, так что нормированная случай-
ная ошибка совпадает с нормированной среднеквадратичной ошибкой, при-
водимой в табл. 8.1.
Задачи
8.1. Какая из указанных ниже оценок параметров содержит обычно как случай-
ную, так и систематическую ошибку:
а) среднее значение;
б) средний квадрат;
в) плотность вероятности;
г) кавариационная функция;
д) функция спектральной плотности.
8.2. Среднее значение ограниченного по частоте белого шума x(t) оценивается по
реализации длиной Т. Пусть среднеквадратичное отклонение процесса x(t) есть
ох = 1, а среднеквадратичная ошибка оценки среднего значения (4/zJ = 0,1. Опреде-
лите нормированную случайную ошибку оценок следующих параметров, получае-
мых по данной реализации:
а) средний квадрат
б) среднеквадратичное значение
в) среднеквадратичное отклонение.
8.3. Пусть x(t) — реализация ограниченного по частоте гауссова белого шума, и
пусть цх = 0,1, ах = 0,2, В = 200 Гц, Т = 2 с. Вычислите нормированную средне-
квадратичную ошибку для оценок:
а) среднего значения
б) среднего квадрата.
288
Глава 8
8.4. Оценка плотности вероятности гауссова процесса x(t) ищется при ширине ко-
ридора W = 0,25 о*. Определите нормированную ошибку смещения оценки р(х) в
точке х = цх + 2,5ах:
а) точным расчетом,
б) в первом приближении по формуле (8.77).
8.5. Оценка функции распределения (а не плотности вероятности) гауссова слу-
чайного процесса {%(/)) вычисляется путем усреднения по ансамблю, состоящему из
N = 100 независимых реализаций. Определите нормированную случайную ошибку
оценки Р(х) в точке х = /г. Смещена ли эта оценка?
8.6. Рассмотрим две реализации длиной Т ограниченных по частоте белых шумов
x(t) и у(t) с шириной полосы частот В:
x(t) = s(t) + Л1(?), y(t) = $(/) + И2(г).
Пусть s(t), n2(t) — попарно некоррелированные процессы с нулевыми средни-
ми и средними квадратами ^2 = °п2 = Определите:
а) нормированную среднеквадратичную ошибку оценок ковариационных функций
^(т), Ryy(r) в точке т = 0;
б) нормированную среднеквадратичную ошибку оценки взаимной ковариационной
функции Рху(т) в точке т = 0;
в) то же, что в пункте б), но при > S и N2 > S;
г) то же, что в пункте б), но при = 0 и N2 > S.
8.7. Для двух ограниченных по частоте белых шумов из задачи 8.6 определите
приближенный 95%-доверительный интервал для оценки запаздывания т, отвечаю-
щей максимальному значению оценки взаимной ковариационной функции Вху(т).
8.8. Пусть Х(/) = I Gxx(f)/G^fY'71, a Xm— максимальное значение функции
8.8. Пусть Х(/) = I Gxx(f)/ G'Gtfy'71, a Xm — максимальное значение функции
Х(/). Определите требования, предъявляемые к параметрам Ве и Т как функциям \т
при условии, что нормированные систематическая и случайная ошибки оценки спект-
ральной плотности не должны, превышать 5%.
8.9. Рассмотрим оценку функции спектральной плотности, вычисляемую, как
описано в разд. 8.5.4, путем финитного преобразования Фурье и последующего ус-
реднения по ансамблю. Исходная реализация длиной Т = 60 с разделяется на 12
смежных отрезков. Найдите 95%-доверительный интервал для истинного значения
6хх(/) при = 0,3 (Условная единица)2/Гц. Какова нормированная случайная
ошибка этой оценки?
8.10. Функция спектральной плотности случайного процесса имеет вид
Gxx(f) = т-------------~Я2—:--------------
[1-(//100)2] + [0,1//100]2
Определите разрешение по частоте Ве и общую длину реализации Тг, необходимые
для получения выборочной оценки такого спектра, имеющей нормированную систе-
матическую ошибку еь 0,05 и нормированную случайную ошибку ег = 0,1.
Глава 9
СТАТИСТИЧЕСКИЕ ОШИБКИ
ПРИ ОЦЕНИВАНИИ БОЛЕЕ
СЛОЖНЫХ ПАРАМЕТРОВ
В этой главе продолжается начатое в гл. 8 обсуждение ошибок, возни-
кающих при анализе случайных процессов. Основное внимание уделено
здесь функциям частоты, характеризующим зависимости между двумя ста-
ционарными (эргодическими) случайными процессами. К числу рассматри-
ваемых здесь оценок сравнительно сложных параметров относятся оценки
модуля и аргумента функций взаимной спектральной плотности, а также
характеристики, возникающие при анализе систем с одним или многими
входными и выходными процессами (гл. 6 и 7). В частности, получены
формулы для статистических ошибок оценок следующих параметров:
частотная характеристика (амплитудная и фазовая);
функция когерентности;
когерентный спектр выходного процесса;
функция множественной когерентности;
функция частной когерентности.
9.1. Оценки взаимной спектральной плотности
Рассмотрим определенную формулой (5.66) функцию взаимной спект-
ральной плотности, связывающую два стационарных (эргодических) гауссо-
вых случайных процесса [х (t)} и {.у (/)]. Если реализации х (t) и у (t) имеют
неограниченную длину Г, то односторонний взаимный спектр задается в
виде
2
Gxy(f) = lim —E[X*(f, T)Y(f, Г)] , (9.1)
/ ~► ОС 1
где X (f, Т ) и У (/, Т ) — финитные преобразования Фурье последова-
тельностей х (Г), у (t):
X(f) = X(f, Т) = fTx(t)e-^'dt,
Jo
(9-2)
У(/)= Y(f,T) = f y(t)e-Wdt.
Таким образом, «несглаженная» (т. е. без усреднения) оценка взаимного
спектра, получаемая по реализациям конечной длительности Г, есть
2
<Ц/) = ^*(/)Г(/)]. (9.3)
а ее разрешение по частоте имеет вид
5е«Д/=(1Д). (9.4)
10-953
290
Глава 9
Это означает, что спектральные компоненты оцениваются только на дис-
кретных частотах
fk = (k/T), к = 0,1,2,... . (9.5)
Как указано в разд. 8.5.1, разрешение по частоте Ве » \/Т в формуле (9.4)
определяет потенциальную ошибку смещения спектральной оценки. Однако
в дальнейшем в этой главе будет предполагаться, что длина реализации Т
достаточно велика, так что возможной ошибкой смещения можно прене-
бречь.
Как и в случае оценивания автоспектра (разд. 8.5.4), «несглаженная»
оценка взаимного спектра обладает в большинстве реальных ситуаций не-
приемлемо большой случайной ошибкой. На практике эту случайную
ошибку уменьшают путем вычисления ансамбля оценок по nd различным
(неперекрывающимся, несовместным) реализациям длиной Т каждая и по-
следующим усреднением результатов. Это дает окончательную сглажен-
ную оценку:
2
—М/Ш (9.6)
ndT i=l
Таким образом, минимальная общая длина реализации, необходимая для
получения оценки взаимного спектра, есть Tr = ndT. Оценки автоспектров
Gxx(f ), Gyy(f ) получаются из выражения (9.6) при x(t) = y(t).
Функции X(f) и У(/), входящие в формулу (9.6), можно записать че-
рез их действительные и мнимые части:
ГДе ГТ
XR(f) = / x(t)cos2irftdt,
Jo
YK(f) = (Ty(t)cos2irftdt,
Y(f) = YR(f) -jY,(f),
Xr(f) = [Tx(t)sin2nftdt, (9.8)
Jo
YiU)= [Ty(t)sm27rftdt.
Jo
(9-7)
(9.9)
Если последовательности x (t) и у (t) распределены нормально и имеют ну-
левые средние значения, то функции, заданные формулами (9.8) и (9.9),
также будут иметь нормальные распределения с нулевыми средними значе-
ниями. Опуская для упрощения обозначений индекс / и зависимость от ча-
стоты /, можно записать «несглаженные» оценки спектральной плотности
(9.3) в виде
2 2
Gxx = ~(X* + X?), Gyy =—(Yr + Yr2), (9.10)
Gxy = Сху - jQxy = \Gxy\e~J^ , (9.11)
где
2 . 2
C=-(XRYR + XrYr), Qx=—(XRY, — XrYR). (9.12)
X у rji \ К К //// Xy rji УК/ 1 I\ J 7 \ /
Ошибки при оценивании более сложных параметров
291
l<V = сх\ + Q*xy , tg ёху = Qxy/Cxy . (9.13)
Нетрудно убедиться, что для частот f = fk, определяемых формулой
(9.5), из соотношений (9.8) и (9.9) следует, что
Е[ад] = £[УЛУ,] = О, £[%*] = £[%;] = (T/f)Gxx ,
£[ул2] = £[у/] = (T/4)Gyy , £[ХЯУЯ] = E[X,Y,] = (Т/4)СХК,
£[ад] = -£[Х,УЯ] = (Т/4)^ . (9.14)
Поэтому Е[Сху] = Сху , E[Qxy\ = Qxy и
M<L] = GXX) £[G„] = G„, (9.15)
£ [GxJ = £ [СхJ - jE [0 J = Cxy - jQxy = Gxy . (9.16)
Согласно соотношению (3.72), из предположения о гауссовости для любых
четырех случайных величин а р а2, а3 иа4 следует, что
£[а1а2а3а4] = £[а1а2]£[аза4] + Е [ а1аз ] Е [ «2^4] + £[а1а4]£[а277з].
(9-17)
Применяя эту формулу, находим, что
Ж\] = 72 £[(*« +*?)2] =
4
= 72£[^я + + *74] = 2G2X. (9.18)
Этот результат полууен с учетом равенств
£[*;*] = 3(£[x2])2 = 3(T/4)2Gi,
Е[Х}Х1\ =£[У2]£[Х2] = (T/4)2GX2X, (9.19)
£[У,4] =,3(£ [ Х]\ )2 = 3(7’/4)2G2x.
Действуя подобным образом, можно убедиться, что
£[(%] =2G^y, (9.20)
10*
292
Глава 9
е [сд.] = \(GxxGyy + зса - еА)- (9-21)
е\&у\ = \(GxxGyy + ЗбА - CX2J. (9.22)
9.1.1. ФОРМУЛЫ ДЛЯ ДИСПЕРСИИ ОЦЕНОК
Получим теперь основные формулы для дисперсии оценок. По опреде-
лению (8.3), дисперсия любой несмещенной (Е\А ] = А ) «несглаженной»
оценки параметра А есть
Уаг[Л] = Е[А2] - А2. (9.23)
Следовательно,
Var[Gxx] = Gxx , Var[Gj = GA, (9.24)
Var[CxJ = \{Gxfiyy + C2xy - Q2xy\ (9.25)
Var[£xJ = \(GxxGyy + Q2xy - C2J. (9.26)
Заметим, что из формул (9.13), (9.21) и (9.22) следует, что
£[|GX,|2] = Е [Сх2,] +£[&,] = GxxGyv + |GX J2. (9.27)
Поэтому
Var[|Gxj] = GxxGzv = ^-, (9.28)
I ху
vne у2у — обычная когерентность, задаваемая уравнением
В соответствии с формулой (4.9) дисперсия ошибки «сглаженных» оце-
нок, полученных усреднением по nd статистически независимым «несла-
женным» оценкам, уменьшится в nd раз:
Var[Gxx] = Gxx/nd , Var[Gj = G2y/nd , (9.30)
Var[|Gxj] = \Gxy\2/y2ynd .
(9.31)
Согласно (8.9), нормированные среднеквадратичные ошибки (совпадающие
в этой главе с нормированными случайными ошибками) имеют вид
г-н 1 г а i 1
£[^хх] - Г- > e[GpJ = Г~ ’
\nd Vnd
(9.32)
Ошибки при оценивании более сложных параметров
293
'[Iй-II - i77c= (’«>
Здесь I yvv I есть квадратный корень из 7Л2,. Заметим, что для оценки моду-
ля взаимного спектра I Gxy\ ошибка изменяется обратно пропорционально
17VVI и с приближением к единице стремится к 1 />[nd. Эти
результаты и некоторые другие формулы, приведенные в этой главе, со-
держатся в работе [9.1].
В табл. 9.1 дана сводка основных формул, определяющих нормирован-
ные случайные ошибки оценок спектральных плотностей. Число усредне-
ний nd означает число различных (неперекрывающихся) реализаций, кото-
рые, как предполагается, содержат статистически независимую информа-
цию. Эти реализации можно получить, разбивая длинную реализацию ста-
ционарного эргодического процесса на nd частей или повторяя эксперимент
nd раз при одинаковых условиях. Ошибки оценок всех характеристик, кро-
ме автоспектра, представляют собой функции частоты. При использовании
этих формул для определения случайных ошибок реальных оценок неиз-
вестные истинные значения характеристик, входящие в формулы, заменя-
ются соответствующими оценками.
Таблица 9.1. Нормированные среднеквадратичные ошибки спектральных оценок1^
Оценка Нормированная среднеквадратичная ошибка £
ълпЛлп 4
J п
1
\G„(J)\ lYo(/)lA'
QAf) + СД(/) - g2,.(/)]1/2 cxAf)}/^
Q.Af) [GxAf)GVy(f) + QlU) ~ G2.(/)]I/2
Заметим, что эти формулы не пригодны в случае некоррелированных последо-
вательностей %(/) и у(1). Для дисперсий оценок С (f) и Qxy(f) справедливы со-
отношения Var [ С (/)] G^f )Gyy(f )/^, Var [ Qxy | < G^f) Gyy(
(см. также [9.2] и Бендат Дж. и Пирсол А. Измерение и анализ случайных процес-
сов: Пер. с англ. — М.: Мир, 1974. — 464 с.). Это же замечание относится и к оцен-
кам функции когерентности и частотной характеристики. — Прим, перев.
294
Глава 9
9.1.2. ФОРМУЛЫ ДЛЯ КОВАРИАЦИЙ ОЦЕНОК
Получим теперь некоторые основные формулы для ковариаций оценок.
По определению (3.33), ковариация двух несмещенных (Е[А] = А и
Е [ В} = В) «несглаженных» оценок параметров А и В есть
Cov(/T, В) = Е[(ДЯ)(ДВ)] = Е[(Л - А)(В - Я)] =
= Е[АВ]-АВ. (9.34)
Приращения А и В равны Д Л = Л — А, АВ = В — В. Оценки А и В на-
зываются некоррелированными, если Cov (Л, В ) = 0. Применяя формулу
(9.17), получаем
г ~ ~ 1 4 г
Е1с*ув*у] = 72£[(ВД + хл)(ад- Х7УД)] = lCxyQxy. (9.35)
Следовательно, согласно (9.34), на каждой частоте
Cov(Cx/,exJ = C^. (9.36)
Подобным же образом нетрудно убедиться, что
Cov(<L, Сху} = GxxCxy, Cov(Gxx, Qxy) = GxxQxy,
(9.37)
Соу((5^, Cxy) — GyyCxy , Cov(g>v, Qxv) = GyyQxy .
Кроме того,
4
E[GxxGyy] = + У'2)1 = G^Gyy + |G^2- (938)
Следовательно,
Cov(Gxx, Gyy) = |GJ2 = yxyGxxGyy . (9.39)
Докажем теперь следующие формулы для ковариаций:
Cov(Gxx, = 0 , Cov(G„, Ъху) = 0 , (9.40)
Cov(|GJ,0j = O. (9.41)
Иными словами, оценка 0ху некоррелирована с Gxx, G и I Gxy I на лю-
бой частоте /. Для доказательства формул (9.40) заметим, что
tg Qxy = Qxy/Cxy. Аппроксимируя производные обеих частей этого равенст-
ва конечными разностями, получаем
^Ху
Ошибки при оценивании более сложных параметров
295
где
sec20xv
От/
Таким образом,
Л. с,„ле„-е„дс..
Д9" *
Положив
Мху = 6ху-0ху, LQxy = Qxy- Qxv,
(9-42)
^х у Осу Осу
и пользуясь формулой (9.37), получим, что
Cov(Gaa,^) = £[(AGaa)(A^)]«
с Q
= —^Cov(Gxx,Qx}---------^Cov(Gaa,C J = 0.
|GJ2 ' xx'*xv> |GAJ2 V '
Очевидно и величина Cov (Gyy, &ху) — 0. Формула (9.40) доказана.
Для доказательства соотношения (9.41) заметим, что
| G |2 = С 2 + Q 2 Аппроксимация производных конечными разностями
ЛУ лу лу
дает
\Gxy\L\Gxy\~Cxy\Cxy + QxybQxy.
Таким образом,
Air I ^ху ^ху + ®ху к®
Д|^1 =--------—
(9-43)
Из формул (9.42) и (9.43) следует, что
Cov(|GxJ,^) = £[(A|Gxy|)(A^)]«
« -Д-у£[(С^ ЬСху + Qxy^Qxy^CxyKQxy - Qxl ДСХ>.)]
1'Лх у I
= ^р{(сЛ - et)cov(cxv.,e4>.)+
+ CAveAv.(Var[exJ-Var[CV)])}=0.
Соотношение (9.41) доказано.
296
Глава 9
Пользуясь равенством (9.43), можно получить также следующие форму-
лы для ковариаций:
Cov(Gxx, |Gxj) = Е [(AGXX)( 4|GX j)] « GXX|GXJ ,
(9.44)
Cov(G>ir, |Gj) = E[(bGyy)(A|G^|)] « ,
Cov(C,„ |G,,|) £[(ДС.,)(Ж,1)] - С-'|С-’!<7ТЛ) •
Z • xy
(9-45)
Cov(6xr, |GX>,|) = £[(4exJ(A|Gxj)] = + Tv>) .
L ixy
Формула (9.43) позволяет получить следующий приближенный результат
для дисперсии Var [ I Gxy I ] оценки Gxy\
Va4=
- E [(A|G„|)2] - -^£[(C„ AC,, + е,,де„)’]=>
« IG^TVar^ + 2^A.vCov(c^’ QXy) + Qiy MO*
Эта приближенная формула, полученная в работе (9.2) путем аппроксима-
ции производной конечной разностью, уступает более точной формуле
(9.28), полученной прямым путем:
(9-47)
Поскольку ху
1.1 + Ух2,
Уху Ьху
при всех ууу < 1, дисперсия, задаваемая формулой (9.47), всегда превышает
дисперсию, определяемую по формуле (9.46).
Рассмотрим функцию когерентности
2 1°-/
т" ‘ ' (9'48’
Ошибки при оценивании более сложных параметров
297
После логарифмирования имеем
log Уху = 2 logical - log Gxx - log Gyy ,
а конечно-разностная аппроксимация производных дает приближенное ра-
венство
&у?у _ 2A|GJ bGxx bGyy |
Уху 1^1 Gxx Gyy
^Уху = Уху - Уху , Д 1<Лу1 = -|Gj,
&GXX = Gxx - Gxx , &Gyy = Gyy - Gyy,
Таким образом,
кУху ~ Yxvj
2A|G^|
IGJ
bGxx
№yy\
Gyy )
(9.49)
С учетом соотношений (9.40) и (9.41) отсюда сразу следует, что
= °-
Таблица 9.2. Формулы для ковариаций различных оценок
Соу(Сл,„2хг)= CxrQ„
Cov(G„, СЛ.Г) = СДЛСУ,
Cov(G„, Qxr) = GXXQXV
Cov(Gxx, Gvl.) = |GK,.|2 = ^VGXXGV<
Cov(G„, 04l.) = 0
Cov(|dvl.|, 0XV) = 0
Cov(V,., 0V>.) = 0
Cov(G„,|Gx>|)= GXY|GJ
Cov(Cv,,|Grl.|) =
+ y2,)
2yv2,.
Cov(ex>.,|G4l.|) =
gA,.|Gt,|(l+Y2,)
2r2,.
298
Глава 9
Иными словами, оценки уху и 6Х не коррелированы на всех частотах f.
Наиболее важные формулы для ковариаций приведены в табл. 9.2.
9.1.3. ОЦЕНКИ ФАЗОВОГО УГЛА
Формула для дисперсии «несглаженной» оценки 6 (выраженной в ради-
анах) может быть получена из равенства (9.42) следующим образом:
уаг[^] = £[(a<U2| « - Qxy ДСХ,)2] =
= Me j - 2CxyQxyCov(Cxy,Qxy) + Q2xy Var(cJ} =
1 fIGxy)2
2
(9.51)
Для «сглаженной» оценки, полученной усреднением по nd величинам, сред-
неквадратичная ошибка равна
с.к.о.
(9-52)
Эта формула задает среднеквадратичное отклонение оценки 0ху фазового
угла. Нормированной случайной ошибкой в этом случае пользоваться не
следует, поскольку величина 0ху может быть равна нулю. Как и ошибка
оценки абсолютного значения взаимного спектра, заданная формулой
(9.33), ошибка оценки его фазы (9.52) зависит от частоты. Заметим, что
при любом nd > 1 величина с. к. о. [0XJJ стремится к нулю при у*у 1.
ПРИМЕР 9.1. СЛУЧАЙНЫЕ ОШИБКИ ОЦЕНКИ ВЗАИМНОЙ СПЕКТРАЛЬ-
НОЙ ПЛОТНОСТИ. Рассмотрим пару реализаций х (I), у (t), представляю-
щих гауссовы стационарные случайные процессы с нулевыми средними зна-
чениями. Пусть значение функции когерентности между этими процессами
на некоторой частоте уху = 0,25. Определим нормированную случайную
ошибку оценки абсолютного значения и с. к. о. оценки фазы взаимного
спектра, полученной при nd = 100.
Согласно формуле (9.33), нормированная случайная ошибка оценки мо-
дуля взаимной спектральной плотности есть
г . . 1
е |G I =----- =0,20.
1 0,5/100
Заметим, что это значение вдвое больше нормированной случайной ошибки
Ошибки при оценивании более сложных параметров 299
автоспектра, заданной формулой (9.32). Среднеквадратичное отклонение
оценки фазового угла определяется по формуле (9.52):
. (0,75)1/2
1 “ I’-i ‘ (адЖ ‘0,12 рад'
9.2. Оценки для моделей с одним входом
и одним выходом
Рассмотрим показанную на рис. 9.1 модель системы с одним процессом
на входе и одним процессом на выходе. Здесь
X(f) — преобразование Фурье измеренного входного сигнала х( /),
который, как предполагается, не содержит помехи;
Y ( f) — преобразование Фурье измеренного на выходе сигнала
у( t) = v( t) + п( t);
V ( f) — преобразование Фурье расчетного выходного сигнала v( t);
N ( f ) — преобразование Фурье расчетного шума на выходе п( Г);
Нху (f)~~ частотная характеристика оптимальной линейной системы с
постоянными параметрами, связывающей y(t) с х( t).
Пусть для анализа имеется лишь одна пара реализаций x(t) и y(t), с
достаточной полнотой описывающая свойства соответствующих гауссовых
случайных процессов с нулевыми средними значениями. Эти процессы мо-
гут быть как стационарными, так и переходными. Для определенности бу-
дем считать их стационарными, а результаты выразим через односторон-
ние спектры. Формулы для нормированных случайных ошибок одинаковы
для односторонних и двусторонних спектров.
Искомые оценки параметров модели, представленной на рис. 9.1, опре-
деляются, согласно разд. 6.1.4, приводимыми ниже формулами. Оценка оп-
тимальной частотной характеристики есть
GxAf)
= 7m <9-53)
^хх\/ )
X(f)---------НХу f
Рис. 9.1. Модель системы с одним входом и одним выходом.
300
Глава 9
где Gxx(f ) и Gxy(f) — «сглаженные» оценки функций спектральной плот-
ности входного процесса и взаимной спектральной плотности входного и
выходного процессов соответственно. Оценка функции обычной когерент-
ности имеет вид
ХУ GxxU)GyyU)
(9-54)
где Gyy(f) — «сглаженная» оценка спектра процесса на выходе системы.
Оценка когерентного спектра выходного процесса Gvv(f) есть
<U/) = \Hxy(f)\2Gxx(f) = у///)^(/), (9.55)
а оценка спектра шума на выходе имеет вид
G„Af)= [1 -Ух2//)] Gyy(f). (9.56)
Из формулы (6.61) следует также, что
Gyy(f) = GJJ) + GJJ), (9.57)
поскольку при расчете Н (f) по соотношению (9.53) и при некоррелиро-
ванных процессах х( t) и п( t) взаимный спектр Gvn(f) = 0.
При записи в полярных координатах частотная характеристика имеет
ЯЛ,(/) = |ЯЛ//)|е-^</> (9.58)
где оценка амплитудной характеристики системы равна
GXxU )
а оценка фазовой характеристики системы представлена в форме
Фх//) = arct8
(9.60)
Функция $xy(f) совпадает с фазовым углом 0xy(f) взаимного спектра, а
также с фазой, которая в дальнейшем будет отвечать комплексной функции
7xy(f), определенной в полярных координатах в виде
Ух//) = |Ух//)к’Ад/) = + Д2//) (9-61)
Заметим, что все приведенные здесь «сглаженные» оценки можно вычис-
лить по «сглаженным» оценкам функций Gxx(f), Gyv(f) и Gxy(f).
Формулы для случайных ошибок оценок всех этих характеристик будут
содержать неизвестную истинную функцию когерентности yxy(f) и число
независимых оценок nd, по которым производится усреднение. Для их при-
Ошибки при оценивании более сложных параметров
301
менения к реальным данным нужно заменить y^y(f) ее оценкой y^y(f) при
соответствующем значении числа независимых слагаемых nd.
Это даст практически приемлемые результаты, особенно в случаях, ког-
да полученная таким путем нормированная случайная ошибка не превыша-
ет 20 <7о.
9.2.1. СМЕЩЕНИЕ ОЦЕНОК ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ
Оценки частотной характеристики и функции когерентности обычно
содержат систематическую ошибку, источником которой могут быть ука-
занные ниже факторы:
1. Смещение, свойственное методу оценивания;
2. Смещение, связанное с запаздыванием при распространении входного
процесса в системе.
3. Нелинейность системы и (или) зависимость ее параметров от вре-
мени.
4. Смещение оценок спектральной и взаимной спектральной плотностей.
5. Измерительные шумы на входе (присутствие некоррелированного шу-
ма на выходе не создает смещения оценок).
6. Наличие других входных процессов, коррелированных с измеряемым
(наличие других некоррелированных с данным входных процессов не со-
здает смещения, поскольку по отношению к измеряемому входу их можно
рассматривать как дополнительный некоррелированный шум на выходе).
Первый источник смещения обязан своим существованием тому факту,
что, вообще говоря,
Следовательно, Е[Нху\ Ф Нху9 £[т^] Ф у^у. Эти ошибки смещения обыч-
но малы сравнительно с другими типами ошибок, возникающими при
практическом анализе, и в этих случаях, когда сочетание величин nd и у^у
таково, что соответствующая нормированная случайная ошибка мала, ими
можно пренебречь. При nd -* 00 или у^у — 1 эти систематические ошибки
стремятся к нулю.
Второй источник ошибки смещения связан с тем, что при измерении
х (О и у (t) в одной системе отсчета времени необходимо вводить поправ-
ку на запаздывание при преобразовании системой процесса x(t) в y(t);
это нужно делать в случаях, когда задержку ту нельзя считать пренебрежи-
мо малой по сравнению с длиной реализации Т. Пусть
х(/) = х(/) , 0 < t < Т ;
(Произвольная функция, 0 < t < ;
302
Глава 9
В этом случае оценку Rxy(r) взаимной ковариационной функции можно за-
писать в первом приближении в виде
^(т) « (1 - (9.64)
откуда видно, что£ [ЯЛ>, (г)] Ф Вху(т) и, таким образом, Кху(т) — смещен-
ная оценка. Следовательно,
Gxy(H * (1 - ,
ЯхД/)»(1-у)ях//), (9.65)
/ Т. \ 2
Yx,(/) s I1 - у) УхД/)
Поэтому оценки Gxy(f), Hxy(f) и yxy(f) также смещены. Для того чтобы
избавиться от возможной ошибки смещения, сигнал у (t) следует сдвинуть
по времени на тх так, чтобы сдвиг по времени между ними стал равным
нулю. Запаздывание т1 можно оценить либо из физических соображений,
зная скорость распространения сигнала в системе, либо оценивая функцию
Rxy(r) и локализуя ее первый экстремум [9.3]^.
Третья причина, вызывающая ошибку смещения, это нарушение основ-
ных допущений о линейности системы и независимости ее параметров от
времени. Даже в тех случаях, когда предположение о постоянстве парамет-
ров в достаточной степени оправданно, свойство линейности зачастую ока-
зывается нарушенным, если диапазон изменений процессов достаточно ши-
рок. Следует, однако, отметить, что применение формул (9.53) к нелиней-
ным системам даст при заданных условиях на входе и выходе системы наи-
лучшее (в смысле метода наименьших квадратов) линейное приближение
для частотной характеристики системы. Это обстоятельство составляет
важное преимущество прямого способа оценивания частотной характери-
стики по реальным данным, а не по результатам лабораторных экспери-
ментов или искусственным данным, которые не способны воспроизвести
действительные условия на входе реальной системы.
Четвертый источник ошибок смещения связан со смещенностью оценок
спектральной плотности. Как показано в разд. 8.5.1, эта ошибка может
быть довольно значительной на частотах максимумов спектральной плот-
ности. Ошибку этого рода можно уменьшить, правильно подбирая разре-
шающую способность оценок спектра и взаимного спектра, т. е. принимая
Ве достаточно малым, так чтобы правильно локализовать спектральные
максимумы. Количественная формула приведена в примере 8.5 для спект-
ральных оценок, описывающих резонирующую систему.
Точнее, не первый, а главный экстремум (см. также: Неппап Е., Tompson Р.,
Estimating group delay, Biometrika, 60, 2, 241—253 (1973)). — Прим, перев.
Ошибки при оценивании более сложных параметров
303
Измерительный шум т (t), наблюдающийся на входе системы, но не
проходящий через нее, представляет собой пятый источник ошибок смеще-
ния. Если истинный процесс на входе есть и (I), то спектр измеренного
входного процесса имеет вид Gxx = Guu + Gmm. Равенства (9.53) и (9.54)
принимают теперь вид
А = ^ху Л 2 = ______ /Q
Нху а । а ’ Уху । а \ л (9.66)
^ии + ^тт Wuu + ^тт)^уу
(зависимость от частоты опущена для сокращения записи). При отсутствии
прочих ошибок смещения имеем Е [Gxy ] = Guy и
Guu
G I G
'J и и ' m
(9-67)
(9.68)
Поскольку Gmn > 0, все эти математические ожидания будут занижены
сравнительно с истинными значениями, т. е. оценки имеют отрицательное
смещение. Нормированная ошибка смещения (8.96) принимает в этом слу-
чае вид
(9-69)
Например, при Gmm = 0,1 Guu отрицательное смещение получаемых оце-
нок составит 0,1/1,1 ~ 9 %.
Шестой источник систематической ошибки, указанный выше, связан с
присутствием других входных процессов, коррелированных с измеряемым
входом. Появление этой ошибки легко видеть, добавляя в разд. 7.2 еще
один входной процесс, коррелированной с первым входом. В частности,
можно показать, что при аккуратном решении этой задачи частотная ха-
рактеристика Нj (/ ) будет определяться формулой (7.23). С другой сторо-
ны, если считать, что система имеет по одному процессу на входе и выхо-
де, то оценку Н) следует искать с помощью формулы (9.53). Ее мате-
матическое ожидание не совпадает с истинным значением т. е.
оценка смещена. Далее, оценку функции когерентности между и выход-
ным процессом^ при наличии коррелированного cXj входах2 следует ис-
кать в виде (7.34). Если же считать, что на входе присутствует толькох^,
то оценка ixy(f ) определяется формулой (9.54). Математическое ожидание
этой оценки также не дает верного результата.
Рассмотренные здесь ошибки смещения появляются и в более общем
случае систем со многими входными и выходными процессами, и их оце-
нивание требует более сложных формул.
304
Глава 9
9.2.2. ОЦЕНКИ КОГЕРЕНТНОГО СПЕКТРА ВЫХОДНОГО ПРОЦЕССА
Считая оценки Gvv и Gnn статистически независимыми, из соотношения
(9.57) можно получить, что
Var[G„] = Var [Gw] + Var[Gnn] , (9.70)
где зависимость от частоты f опущена для упрощения обозначений. Со-
гласно соотношению (9.30), дисперсии оценок равны
С2
Var[G,,] - Var[G„] - . (9.71)
”d nd
Отсюда после подстановки Gnn = (1 - y2y)Gyy и Gvv = у2у Gyy имеем
G2 - G2 (2 - у2 }G2
Var[G„J = 1 (9.72)
nd 7xynd
Окончательно нормированная случайная ошибка равна
Конечно-разностная аппроксимация при этом выводе не используется. За-
метим, что e(Gvv] = e[Gyy ] = l/V^ ПРИ Уху ~ L Кроме того,
. (9.74)
График зависимости ошибки (9.73) от у2у при nd — 100 представлен на
рис. 9.2. На рис. 9.3 ошибка (9.73) дана для различных значений nd и у2у. В
табл. 9.3 приведены соответствующие формуле (9.73) соотношения между
у2у nnd, необходимые для получения ошибки e[Gvv ] = 0,1.
ПРИМЕР 9.2. СИСТЕМАТИЧЕСКАЯ И СЛУЧАЙНАЯ ОШИБКИ ОЦЕНКИ
КОГЕРЕНТНОГО СПЕКТРА ВЫХОДНОГО ПРОЦЕССА. Рассмотрим случай,
когда несколько независимых источников акустического шума в воздухе со-
здают в приемнике акустического давления сигнал у (t). Когерентный
спектр выхода оценивается на основе измеренного входа х (t), представля-
ющего собой источник, удаленный от приемного устройства на 10 м.
Пусть число усреднений nd = 400, а длина участков, на которые разбивает-
ся запись, есть Т = 0,1 с (Ве ® 10 Гц). Предположим также, что x(t) и
у (t) регистрируются и анализируются одновременно, т. е. предполагается,
что запаздывание отсутствует. Считая, что истинные значения функции ко-
герентности и спектра выходного процесса суть у2у = 0,4 и Gyy = 10, най-
дем основную систематическую и случайную ошибки оценки когерентного
спектра выходного процесса.
Рис. 9.2. Нормированная случайная ошибка оценок когерентного спектра выход-
Рис. 9.3. Нормированная случайная ошибка оценки когерентного спектра выход-
ного процесса как функция числа усреднений.
306
Глава 9
Таблица 9.3. Условия, необходимые для достижения ошибки £[6р1?] = 0,1
у2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
nd 567 400 300 234 186 156 123 100
Обращаясь вначале к систематической ошибке, заметим, что время
необходимое для распространения акустического шума в воздухе на рассто-
яние 10 м (при скорости звука с ® 330 м/с), составляет около 0,03 с. Со-
гласно (9.65), оценка когерентности будет смещена и составит в среднем
п I 0,03 \2
U = (1 - ) (0Л) = 0,2 ,
что отличается от правильного значения у* = 0,4; средняя оценка коге-
рентного спектра выхода 6 = 0,2-10 = 2 при истинном значении
Gvv = 4. В рассмотренном случае ошибка смещения, связанная с запазды-
ванием, приходит к занижению когерентного спектра выходного процесса
на 50 %.
Обращаясь теперь к случайной ошибке, заметим, что ее величина опре-
деляется в первую очередь систематической ошибкой оценки когерентно-
сти. Из соотношения (9.73) следует, что нормированная случайная ошибка
оценки когерентности спектра выходного процесса на интересующей нас
частоте есть
[2 - 0,2]1/2
- (о,45)(2О) " 0,15 ’
9.2.3. ОЦЕНКИ ФУНКЦИИ КОГЕРЕНТНОСТИ
Приближенная формула для систематической ошибки оценки функции
когерентности получена в работе [9.4]. Она имеет вид
(9-75)
nd
Например, при часто встречающемся в практике случае пи = 100 имеем,
2
что при всех значениях у* смещение равно
ф2,] < 0,01 .
Ошибка смещения стремится к нулю при nd — оо или у*у — 1.
Вывод формулы для случайной ошибки начнем с равенства
Gvv = l2xyGyy . (9.76)
Строя конечные разности для обеих частей этой формулы, получаем
Ошибки при оценивании более сложных параметров
307
ДСГ1, ~ у2ху bGyy + Gyy ДуД. (9.77)
&GVV = Gvv - Gvu, &Gyy = Gyy-Gyy, ДуД = уД-уД (9-78)
и имеются в виду «сглаженные» оценки. Для несмещенных оценок имеем,
по определению,
Var[drp] = £[ДС(,„ Д6„„], Var[GzJ = Е [Д(^ Д^.],
г , г , (9-79)
V аг [ У* у ] = Е [ ДуД ДуД ].
Кроме того,
Cov(G„„, Gyy) = £ [Д^ AGj = Var[GJ, (9.80)
поскольку
ЛСД, = ДСГГ + ДС„„, £[AGP(, AG„„] = 0.
Решая уравнение (9.77) относительно С^ДуД, находим
G Ду2 = ДС - у2 ДС
ТУ ' ху I ху у У •
Возводя обе части в квадрат и находя математические ожидания, получаем
СДУаг[уД] « Var[Gj - 2уДСоу((Д„, Gj + уДУаг[(ДД.
Подставляя сюда формулы (9.71), (9.72) и (9.80), имеем
Окончательно имеем
(9-81)
(9.82)
При малом £ формула (9.82) дает тот же результат, что и соответствую-
щая формула в работе [9.4]. Заметим, что £ [у* ] стремится к нулю при
nd — оо или у*у — 1. Если значение у*у близко к единице, то при любом
nd > 1 оценки функции когерентности могут оказаться более точными, чем
используемые для их расчета оценки спектра и взаимного спектра. Ограни-
чение nd > 1 очевидно, поскольку при nd = 1 значения у*у = 1 на всех ча-
стотах, т. е. соответствующие этому случаю оценки когерентности бес-
смысленны.
График зависимости ошибки (9.82) от у* прии^ = 100 представлена на
рис. 9.4. На рис. 9.5 ошибка (9.82) дана для различных значений nd и у*у. В
табл. 9.4 приведены соответствующие формуле (9.82) соотношения между
и Уху» необходимые для получения ошибки £ \у% ] = 0,1.
ПРИМЕР 9.3. ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ ДЛЯ ОЦЕНКИ ФУНКЦИИ
КОГЕРЕНТНОСТИ. Пусть оценка функции когерентности случайных сигна-
308
Глава 9
Рис. 9.4. Нормированная случайная ошибка оценок функции когерентности при
nd = 100.
лов х( t) и y(t) ищется при nd = 100. Требуется найти приближенный
95%-интервал для истинной когерентности у* при условии, что ее оценка
на соответствующей частоте у?у = 0,5.
Приближенное значение нормированной случайной ошибки для оценки
функции когерентности находится из соотношения (9.82) при подстановке в
него оценки у* вместо неизвестного истинного значения у* . В рассматри-
ваемом случае получаем
... 72(1-0,5)
- (о>71)Доо - °'1 •
Поэтому в соответствии с формулой (8.14) приближенный
95%-доверительный интервал для истинного значения когерентности на
данной частоте есть
[0,4 < у*ху < 0,6].
Таблица 9.4. Условия, необходимые для достижения ошибки ^[у^у] = 0,1
у£, 0,3 0,4 0,5 0,6 0,7 0,8 0,9
nd 327 180 100 54 26 10 3
Ошибки при оценивании более сложных параметров
309
Рис. 9.5. Нормированная случайная ошибка оценок функции когерентности как
функция числа усреднений.
9.2.4. ОЦЕНКИ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ
Поскольку мы уже знаем, как находить случайные ошибки для оценок
параметров Gxx и Gvv, построение формул для случайной ошибки оценок
амплитудной характеристики можно начать с соотношения
GVV = \HXV\2GXX. (9.83)
Вычисляя конечные разности для обеих частей этого'равенства, имеем
Д6О4, = |ЯХ/ДСХХ + GXX\\H^\2. (9.84)
Величины & GXX и Д Gvv заданы формулами (9.78), а
Д|ЯХ,|2 = |ЯХ,12 - |НХ,|2.
Считая оценки несмещенными, имеем
Уаг[|Яху|2] =£[Д|ЯХГ|2Д|ЯХ>,|2] .
Кроме того, поскольку I Gxv I2 = GXXGVV, согласно формуле (9.39) находим
G G
Cov(Gxx, Gvl>) = £[Дбхх AGJ = . (9.85)
nd
310
Глава 9
Решая уравнение (9.84) относительно GXXA I Нху I2, получаем
6ххД|Ях/ = Д6„„-|ЯХ,|2Д6ХХ .
Математическое ожидание квадрата обеих частей последнего равенства
имеет вид
Var[|ЯХ/] « Var[G„J - 2|Ях/|2Соу(6хх, Gvv) + |ЯХ/Var[<7ХХ],
и подстановка дает
г А 2(1 - у2 )|Я I4
Уаг[|Ях>,|2] « —---. (9.86)
Уху” d
Для любой оценки А имеем в первом приближении ДД2 = 2ДДД,
где
ДЛ=Л-Л, дл2 = л2-л2,
£[ДЛ]=0, Е[ДЛ2]=0.
Нетрудно заметить, что
(ДЛ2)2 « 4Л2(ДЛ)2,
£[ДЛ2ДЛ2] « 4Л2Е[ДЛ ДЛ],
что эквивалентно уравнению
Уаг[Л2] ~ 4Л2Уаг[Л ]. (9.87)
Поделив обе его части на Л 4, получаем
2Г/21 М^2] 4Уаг[Л]
е [Л2] = —~4— =------------= 4е [Л ],
следовательно,
е[Л2] « 2е[А]. (9.88)
Этот полезный результат позволяет сопоставлять случайные ошибки оце-
нок среднего квадрата и среднеквадратичного значения, что было показано
ранее уравнением (8.10).
Имея в виду соотношение (9.87), получаем из выражения (9.86)
(9.89)
Окончательно
е||н„ц ,С1°ЛМ1. <] -^/г.
11 <rlJ \HXV\ \yxy\^Td
(9.90)
Ошибки при оценивании более сложных параметров
311
Нормированная случайная ошибка оценок амплитудной характеристи-
100.
Рис. 9.6.
ки при па =
Заметим, что этот результат оказывается таким же, как и в формуле
(9.52). Видно, что при уху -* 1 ошибка £ [ I Нху I ] стремится к нулю незави-
симо от nd, а с ростом пd она стремится к нулю независимо от Эти
результаты в принципе согласуются с полученными в работе [9.5] более
сложными формулами, в которых ошибки оценок связаны с параметрами
F-распределения.
График зависимости ошибки (9.30) от уху прии^ = 100 представлен на
рис. 9.6. На рис. 9.7 ошибка (9.30) дана для различных значений nd и уху.
Таблица 9.5. Условия, необходимые для достижения ошибки s[l Нху I ] — 0,1
7* 0,3 0,4 0,5 0,6 0,7 nd 117 75 50 34 22 0,8 0,9 13 6
В табл. 9.5 приведены соответствующие уравнению (9.30) соотношения
между yxv и nd, необходимые для получения ошибки £[l Нху I ] = 0,1.
Следует помнить, что эта и подобные ей формулы — приближенные, и ими
вряд ли можно пользоваться при ууу 0. — Прим, перев.
312
Глава 9
9.2.5. ОЦЕНКИ ФАЗОВОЙ ХАРАКТЕРИСТИКИ
Оценки фху(Л фазовой характеристики, заданные формулой (9.60), сов-
падают с оценками фазового угла 6xy(f), среднеквадратичное отклонение
которых находится из равенства (9.52). Поэтому
(1 - у2 )1/2
Г 7 1 ~ А—_
с.к.о. [фху] ~ г-—
Сопоставление с формулой (9.30) показывает, что
с.к.о. [фх,] « •
(9-91)
(9.92)
Иными словами, среднеквадратичное отклонение оценки фазовой характе-
ристики Фху(/), измеряемой в радианах, оказывается примерно таким же,
как и нормированная случайная ошибка оценки амплитудной характеристи-
ки \Нху\. Как показано в работе [9.6], это утверждение можно считать
приемлемым во всех случаях, когда ошибка £[1#^,!] мала, скажем
£ 0,2. Поэтому можно считать, что на рис. 9.6 представлена зависи-
мость, связывающая выраженное в радианах среднеквадратичное отклоне-
ние с. к. оДф^] с функцией уху при nd = 100, а табл. 9.5 содержит приме-
ры соотношений между уху и nd, которые должны быть выполнены для
получения с. к. о.[фху ] ® 0,1 рад.
Рис. 9.7. Нормированная случайная ошибка оценок амплитудной характеристи-
ки как функция числа усреднений.
Ошибки при оценивании более сложных параметров
313
ПРИМЕР 9.4. СЛУЧАЙНАЯ ОШИБКА ОЦЕНКИ ЧАСТОТНОЙ ХАРАК-
ТЕРИСТИКИ. Пусть оценка частотной характеристики системы, связываю-
щей сигналы х (t) и у (t), ищется при nd = 50, а значения функции коге-
рентности на двух интересующих нас частотах суть т^(/1)= 0,1 и
Уху (А) = Требуется определить случайные ошибки оценок амплитуд-
ной и фазовой характеристики на этих частотах.
Согласно формуле (9.90), нормированные случайные ошибки оценок ам-
плитудной характеристики на частотах J\ и /2 равны
Г. л z Х|1 (1 - 0Д0)1/2
|] - (О>32)(1О) ~ °’30’
Г. A z Ч|1 (1 - 0,90)1/2
41ялЛ/2)|] - (0f95)(10) = °>°33-
Как следует из выражения (9.91), эти равенства дают также приближенные
значения среднеквадратичного отклонения (не нормированного) для оценки
фазовой характеристики:
с-к-°- [ФхДЛ)] рад = 17%
с.к.о. [фху(/2)] рад = 169°-
Как видно, оценка, получаемая при когерентности у*у (f2) = 0,9, почти в
Таблица 9.6. Случайные ошибки оценок для системы с одним входным и одним вы-
ходным процессами
Оцениваемая функция Нормированная случайная ошибка е
у2,(/) Д[1 -Ул2,(/)]
[2-уЛ(/)]1/2
[I -уЛ(/)]1/2 |Ух> (/)
Кг(/) 1Го(/)1у2"</
314
Глава 9
десять раз точнее оценки, которой отвечает когерентность = 0,1.
Это замечание завершает пример.
В табл. 9.6 приведена сводка основных формул для нормированных слу-
чайных ошибок, отвечающих оценкам параметров моделей с одним вход-
ным и одним выходным процессом. Некоторые инженерные приложения
описаны в работах [9.6, 9.7], а общая теория систематических ошибок, за-
висящих от выбора разрешения по частоте, развита в работе [9.8].
9.3. Оценки для моделей с многими
входными процессами
Рассмотрим более сложную модель с многими входными процессами и
одним процессом на выходе (рис. 9.8). Все реализации должны измеряться
одновременно в единой системе отсчета времени. На первом этапе анализа
следует заменить эту модель показанной на рис. 9.9 моделью с условными
входными процессами (см. гл. 7). Соответствующие итерационные вычис-
лительные алгоритмы описаны в разд. 7.3. Операция усреднения необходи-
ма только для расчета «сглаженных» оценок спектров и взаимных спектров
Gjj(f) по исходным данным. Все прочие характеристики вычисляются по
описанному ниже алгоритму (для простоты обозначений зависимость от
частоты f в дальнейшем опущена).
Вначале вычислим исходный набор оценок условных спектральных
плотностей
дил = , (9.93)
Рис. 9.8. Многомерная система с произвольными входными процессами и одним
процессом на выходе.
Ошибки при оценивании более сложных параметров 315
где
Рис. 9.9. Многомерная система с условными входными процессами и одним
процессом на выходе.
L
17 <?и
(9.94)
Исходные оценки G- нужны только на этом этапе. Полученные результаты
используем для вычисления второго набора оценок спектральных плотно-
стей которые находятся тем же способом, что и ранее:
Aj-2! = l ~ (9.95)
Здесь
L = ^-
27 g22.2
(9.96)
Оценки Gjj. 2J используются для получения аналогичным способом третьего
набора оценок спектральных плотностей G^.2\ и операция повторяется до
тех пор, пока не будут найдены все нужные оценки спектральных плотно-
стей. Оценки функций частной и множественной когерентности и связан-
ных с ними характеристик ищутся путем алгебраических операций над
оценками спектров.
Оценку функции множественной когерентности можно искать в виде
у2
ГУ
Gvy
Gyy Gnn^ _ | _ Gnn
Gyy
(9.97)
316
Глава 9
Здесь символом х обозначены все входные процессы от х ] до xq. Спектр
шума на выходе системы есть
Gnn = Gyy q, = G,,(l - у2„)(1 - Yf,. J • • • (1 - D-)' (9‘98)
Он содержит вычисленные ранее оценки обычной и частной когерентности.
Следовательно,
Уу-х = 1 - [(1 - Y12, )(1 - У2у-1) •••(!- Уду («,-!>.)] • (9.99)
Оценка множественного когерентного спектра выходного процесса опреде-
ляется как сумма процессов, поступающих на выход системы (см. рис. 9.9):
= yy.xGyy = + \12у\2С22Л + • • . (9.100)
Заметим, что эта формула дает еще один способ оценивания у2.у:
Yy:x = Л" • (9.101)
'Jyy
Значение Gvv задается здесь правой частью формулы (9.100).
9.3.1. ОЦЕНКИ ФУНКЦИИ МНОЖЕСТВЕННОЙ КОГЕРЕНТНОСТИ
Оценка уу.х функции множественной когерентности уу,х описывает обе
системы, представленные на рис. 9.8 и 9.9. Если сглаженные оценки авто-
спектров и взаимных спектров вычисляются по исходным данным при чис-
ле усреднений, равному, то по аналогии с уравнением (9.82) имеем
е[Ъ2 х] =
^[1~У2:х]
\Уу-.х\^ + 1 - Я
(9.102)
Эта формула отличается от (9.82) лишь заменой обычной функции коге-
рентности у2у на у 2 .х и nd на nd + 1 - q.
9.3.2. ОЦЕНКИ
МНОЖЕСТВЕННОГО КОГЕРЕНТНОГО СПЕКТРА
ВЫХОДНОГО ПРОЦЕССА
Пусть G„„ = Gvv — оценка множественного когерентного спектра
г- ~
выходного процесса, вычисленная либо как произведение на Gvw, либо
У УУ
в соответствии с формулой (9.100). По аналогии с (9.73) имеем
[2-/:х]1/2
\yy -.x\^d+ 1 - Я
(9.103)
Это равенство отличается от аналогичного ему для системы с одним вход-
ным процессом лишь заменой у2у на уу.х и nd на nd + 1 — q.
Ошибки при оценивании более сложных параметров
317
9.3.3. МОДЕЛИ С ОДНИМ УСЛОВНЫМ ВХОДНЫМ ПРОЦЕССОМ и
ОДНИМ ВЫХОДНЫМ ПРОЦЕССОМ
Модель, показанную на рис. 9.9, можно разбить на последовательность
простых моделей с одним условным входным процессом и одним выход-
ным процессом. Спектральная интерпретация такого представления дана
на рис. 9.10. Первая модель на этом рисунке совпадает с моделью с одним
входом и одним выходом, рассмотренной в разд. 9.2. Последующие систе-
мы представляют собой ее непосредственное развитие, причем их связь с
первой системой очевидна. Вычисление «сглаженных» оценок условных ха-
рактеристик на каждом последующем этапе требует вычитания оценок, по-
лученных на предыдущем этапе, так что число независимых усреднений nd
на каждом последующем шаге уменьшается на единицу. Таким образом,
если оценка Gyy находится при числе усреднений nd, то оценкам &уу.\ и
Gyy.2\ отвечают числа усреднений nd - 1 и nd - 2, и вообще, оценке
соответствует nd + 1 - / усреднений. Ниже приведены формулы
Gu
Gyy 2'.
Gyy2\
^3y2\Gyy2\
Gyy(i-\)\
Рис. 9.10. Системы с одним условным входным процессом и одним процессом
на выходе.
318
Глава 9
для случайных ошибок, отвечающих оценкам параметров простых систем с
условными процессами на входе и выходе при таком уменьшении числа ус-
реднений.
9.3.4. ОЦЕНКИ ФУНКЦИЙ ЧАСТНОЙ КОГЕРЕНТНОСТИ
По аналогии с соотношением (9.82) имеем
(9.104)
В общем случае при i = 1, 2, ... , q
efy2 U
1)! 1 - ‘
(9.105)
9.3.5. ОЦЕНКИ ЧАСТНЫХ КОГЕРЕНТНЫХ СПЕКТРОВ
ВЫХОДНОГО ПРОЦЕССА
Формулы, подобные (9.73), описывают и ошибки оценок частных коге-
рентных спектров выходного процесса, изображенных на рис. 9.10. В част-
ности,
h - 2 11/2
«[li.J’c..] - «(Ж,) - |Y1J^
[2 - 2 11/2
414^224] = 4Y2V Дк-1) * 7----------> (9-106)
U2v 1
4l4l43 2?] = е(?з2р 2'6vv-2<) * 7 . Y 2 ] -
1ТзР.2'1у"^- 2
и т. д.
Ошибки при оценивании более сложных параметров
319
9.3.6. ОЦЕНКИ АМПЛИТУДНЫХ ХАРАКТЕРИСТИК
ДЛЯ УСЛОВНЫХ МОДЕЛЕЙ
По аналогии с соотношением (9.90) можно получить следующие резуль-
таты:
e(lZ ,1..
11 ”'11'
е'|£г,|1 * ItL.W”-'- 1) ’
t|lz я.
11 ,'11 |г„.„|/2(Л^-2)
(9.107)
и т.д.
9.3.7. ОЦЕНКИ ФАЗОВЫХ ХАРАКТЕРИСТИК ДЛЯ УСЛОВНЫХ МОДЕЛЕЙ
Приводимые ниже формулы, построенные на аналогии с (9.92), опреде-
ляют погрешности выраженных в радианах оценок фазовых характеристик,
отвечающих показанным на рис. 9.10 системам:
с.к.о. [ф1л.] « e[|bj],
(9.108)
с.к.о. [ф2л] ~ £[|^2у|]
и т. д. В общем случае при i = 1, ... , q имеем
с.к.о. -е[|М. (9.109)
Заметим, что эти оценки не нормированы и что ошибки будут малы при
малых с [ I Liy I ].
Задачи
9.1. Рассмотрим два случайных" сигнала х (t) и у (t), описывающие стационарные
случайные процессы. Пусть оценки их автоспектров и взаимных спектров вычислены
при nd = 100. Считая, что значение функции когерентности (связывающей x(t) и
у (t) на заданной частоте) уху = 0,5, определите нормированные ошибки оценок сле-
дующих параметров:
а) автоспектров Gxx и Gyy;
б) модуля взаимного спектра I G I.
320
Глава 9
9.2. Значения автоспектров случайных сигналов х( /) и у( t) на заданной частоте
суть = G = 1, а коспектра и квадратурного спектра — Сху = Qxy - 0,5. Опре-
делите нормированные случайные ошибки оценок коспектра и квадратурного спект-
ра плотностей при nd = 100.
9.3. Определите для случайных сигналов из задачи 9.2 приближенный
95%-доверительный интервал для оценки фазы на той же частоте.
9.4. Определите для случайных сигналов из задачи 9.2 приближенный
95%-доверительный интервал для оценок:
а) функции когерентности уху\
б) когерентного спектра выходного процесса Gvv = yxyGyy на то^ же частоте-
9.5. Рассмотрим два ограниченных по частоте белых шума:
х(/) = и(г) + w(/) } y(t) = 10u(r - Tj) + «(/),
где т( t) и п( t) — статистически независимые помехи. Пусть для входного процес-
са спектральные плотности сигнала и шума на заданной частоте одинаковы, т. е.
Guu = Gmm, а запаздывание = 0,1 с. Укажите основные источники ошибок сме-
шения и определите величины этих ошибок для оценки частотной характеристики,
связывающей x(t) и y(t), считая, что она вычисляется при некотором большом
числе усреднений и при длине индивидуальных реализаций Т = 0,5 с.
9.6. Ограниченные по частоте белые шумы из задачи 9.5 имеют на заданной ча-
стоте спектральные плотности Gmm = 0 и6лл = 100 Guu. Считая, что спектральная
плотность выходного процесса на этой частоте Gyy = 1, определите:
а) истинное значение когерентного спектра выходного процесса Gvv = уху Gyy;
б) систематическую ошибку оценки Gvv ;
в) случайную ошибку оценки Gvv при nd = 400.
9.7. Рассмотрим систему с одним процессом на входе и одним процессом на вы-
ходе, которой на заданной частоте отвечает значение функции когерентности, связы-
вающей вход x(t) и выход y(t), равное 0,75. Спектры входного и выходного про-
цессов суть соответственной^ = 2,1, G = 0,8. Каково минимальное число усред-
нений пd, нужное для получения оценки 1 Нху I амплитудной характеристики, гаран-
тирующей отклонение от истинного значения I Н I не более чем на ± 10% с веро-
ятностью 95 %?
9.8. Какое значение функции когерентности необходимо в случае системы с од-
ним входом и одним выходом (задача 9.7) для получения оценок амплитудной ха-
рактеристики и автоспектров с одной и той же нормированной случайной ошибкой?
9.9. Рассмотрим показанную на рис. 7.2 систему с входными процессамих (Г) и
x2(t) и выходным процессом Д'(О- На некоторой частоте и прил^ = 100 получены
следующие оценки: = 20, G 22 = 25, Gyy = 40, G12 = 15 и
G {у = G 2у = 16 — 12у . Определите 95%-доверительный интервал для оценок ам-
плитудной и фазовой характеристик функции Н2у , связывающей процессы х2( t) и
9.10. Используя данные из задачи 9.9, определите математическое ожидание и
нормированную случайную ошибку оценки функции множественной когерентности
уу.х, связывающей процессы на входе и выходе системы.
Глава 10
СБОР И ОБРАБОТКА ДАННЫХ
Выбор методов сбора и обработки данных наблюдений над случайными
процессами в значительной степени зависит от того, какое физическое явле-
ние представляет изучаемый процесс, и от целей, которые достигаются об-
работкой. Однако в самом общем виде можно выделить пять основных
этапов, связанных с этой процедурой:
а) сбор данных;
б) регистрация (в том числе передача);
в) подготовка;
г) оценивание основных свойств;
д) анализ.
Каждый из этих этапов требует выполнения ряда последовательных
операций, схематически изображенных на рис. 10.1. Цель главы состоит в
кратком изложении основных соображений во всех перечисленных ключе-
вых этапах анализа. При этом особое внимание уделяется вероятным ис-
точникам ошибок (помимо статистических ошибок, рассмотренных в гл. 8 и
9). Алгоритмы численного анализа данных наблюдений обсуждаются в гл. 11.
10.1 . Сбор данных
Первым шагом при сборе данных является преобразование исследуемо-
го процесса с помощью специального устройства. Вообще говоря, преоб-
разователем следует считать любое устройство, преобразующее энергию
из одной формы в другую. Однако в технике под преобразователем пони-
мают устройство, позволяющее количественно оценить изучаемый физиче-
ский процесс путем преобразования его в аналоговый^ сигнал с взаимно
однозначным соответствием между входными и выходными величинами.
Согласно рис. 10.1, а, это преобразование может потребовать выполнения
трех операций: 1) механического преобразования изучаемой физической ве-
личины в некоторую промежуточную механическую величину; 2) преобра-
зования промежуточной механической величины в промежуточную электри-
ческую величину; 3) промежуточной электрической — в электрическую вели-
чину, обычно в напряжение. Некоторые преобразователи могут выполнять
две или все три описанные операции в зависимости от того, какая физиче-
ская величина измеряется с их помощью, в зависимости от конструкции и
принципа действия самого преобразователя. Например, широко известный
преобразователь температуры — термопара — производит непосредствен-
но преобразование разности температур в электрическое напряжение без
каких-либо промежуточных операций. С другой стороны, такой широко
применяемый преобразователь, как термометр сопротивления, вначале
производит преобразование изменения температуры в изменение электриче-
Существуют и преобразователи неэлектрических величин в цифровые
сигналы. — Прим. Г.Я. Мирского.
11-953
322
Глава 10
Ввод данных Сбор данных Регистрация Подготовка Оценивание свойств Анализ Вывод
Сбор данных
I________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________I
а
Регистрация
Подготовка
I-----------------------------------------------------1
в
Оценивание свойств
2
Анализ
д
Рис. 10.1. Основные этапы сбора и обработки данных.
ского сопротивления, которое затем преобразуется в изменение электриче-
ского напряжения. В этом случае имеет место двухступенчатая операция
без промежуточного преобразования в механические величины. Преобразо-
ватели типа сейсмометров, которые часто применяются для измерения
смещения, скоростей и ускорений, требуют выполнения всех трех опера-
ций, указанных на рис. 10.1,а. Движение на входе преобразуется в относи-
тельное смещение, которое при помощи чувствительного элемента преоб-
разуется в промежуточную электрическую величину, например в изменение
сопротивления. Наконец, изменение сопротивления преобразуется в измене-
ние электрического напряжения, величина которого пропорциональна ин-
тенсивности входного процесса.
Сбор и обработка данных
323
В идеальном случае перечисленные выше операции должны выполнять-
ся без каких-либо искажений измеряемой величины как функции времени.
Иными словами, если реализация входного процесса есть x(t), а
выходного — у (Г), то в случае идеального преобразователя зависимость
между ними имеет вид y(t) = cx(t)t где с — постоянная калибровки. К со-
жалению, такая ситуация практически недостижима. При работе преобра-
зователей происходят, как правило, изменения амплитуд и фаз, а также и
другие искажения, приводящие к нелинейным эффектам. Это обстоятель-
ство делает преобразователь потенциальным источником ошибок при лю-
бом способе сбора и обработки данных.
ПРИМЕР 10.I. СЕЙСМИЧЕСКИЙ АКСЕЛЕРОМЕТР БЕЗ ОБРАТНОЙ СВЯЗИ.
Рассмотрим идеальный сейсмический акселерометр без обратной связи,
схема которого изображена на рис. 10.2,а. В этом устройстве механическое
преобразование осуществляется при помощи массивного тела, амортизиро-
ванного пружиной, — входное ускорение у основания преобразуется в отно-
сительное смещение тела. В качестве чувствительного элемента использует-
ся потенциометр. Окончательное электрическое преобразование осущест-
вляется путем измерения напряжения на потенциометре. Используя описан-
ные в разд. 2.4.1 методы, легко показать, что частотная характеристика
Рис. 10.2. Схема и частотные характеристики сейсмического акселерометра без
обратной связи: а — упрощенная схема; б — амплитудная характеристика; в — фа-
зовая характеристика.
324
Глава 10
этой системы, связывающая напряжение на выходе с ускорением на входе,
описывается выражением
с
(10.1)
где с — постоянная калибровки, a f nfn — соответственно коэффициент за-
тухания и частота собственных незатухающих колебаний (см. формулу
(2.22)). Заметим, что в данном случае амплитудная и фазовая характери-
стики совпадают по форме с соответствующими величинами для простой
механической системы с вынуждающей силой на входе (рис. 2.3).
Рассмотрим сначала изображенную на рис. 10.2,6, в амплитудную ха-
рактеристику. Как видно из рисунка, на частотах, существенно более низ-
ких, чем частота собственных колебаний системы, акселерометр обладает
довольно постоянной амплитудной характеристикой. С приближением к
частоте собственных колебаний амплитудная характеристика в зависимо-
сти от коэффициента затухания либо возрастает до пиковых значений и по-
том убывает, либо сразу убывает. Постоянство амплитудной характери-
стики в наиболее широком диапазоне частот достигается при коэффициенте
затухания f = 0,7. Показанные на рис. 10.2,6 характеристики имеют верх-
нюю границу частотного диапазона сейсмического акселерометра несколь-
ко ниже частоты собственных колебаний системы, а более точно положе-
ние этой границы определяется допустимой ошибкой (т. е. отклонением ам-
плитудной характеристики от постоянного уровня). Показанные на
рис. 10.2,6 величины ошибок для различных условий могут быть либо
уменьшены путем калибровки, либо просто полагаться допустимыми. Во
всяком случае, чтобы избежать неопределенных и, возможно, больших
ошибок при окончательной обработке данных, необходимо иметь доста-
точно четкое представление о величинах ошибок.
Рассмотрим теперь фазовую характеристику, изображенную на
рис. 10.2, в. Акселерометр сдвигает регистрируемый сигнал по фазе, при-
чем сдвиг изменяется от 0° на нулевой частоте до 180° на очень высоких
частотах. Точное значение фазового сдвига зависит от величины коэффици-
ента затухания. Здесь важно подчеркнуть, что на каждой данной частоте
фазовый сдвиг соответствует запаздыванию и, следовательно, может при-
вести к искажению распределения фаз в результирующем процессе. Эти ис-
кажения обусловливают ошибки при анализе одномерных процессов, имею-
щих полигармоническую или переходную форму, а также любых многомер-
ных процессов, для которых ищут различные совместные характеристики.
Ошибки в случае одномерного процесса могут быть сведены к минимуму
путем выбора преобразователя, обладающего фазовой характеристикой ви-
да « 0. Для рассматриваемого сейсмического акселерометра это усло-
вие выполняется, если частота f гораздо выше максимальной частоты ис-
следуемого диапазона. В многоканальной системе, предназначенной для
сбора данных о многомерных процессах, можно уменьшить ошибки, ис-
пользуя преобразователи с соответствующим образом подобранными фа-
зовыми характеристиками. На этом пример 10.1 заканчивается.
Сбор и обработка данных
325
Подводя итог сказанному, можно утверждать, что выбор и использова-
ние преобразователей для сбора данных требуют осторожного подхода.
Преобразователи промышленного изготовления обычно снабжаются опи-
санием, в котором указана область возможного применения данного уст-
ройства. Как правило, эти спецификации достаточно точны, но следует по-
мнить, что фирмы-изготовители вряд ли относятся к своей продукции пес-
симистично. Поэтому неразумно пользоваться промышленно изготовлен-
ным преобразователем вне пределов, указанных в его спецификации, если
допустимость использования прибора не подтверждается соответствующи-
ми исследованиями. Более детально различные системы преобразователей
и вопросы сбора данных рассмотрены в работах [10.1, 10.2].
10.2 . Регистрация данных
В некоторых практических приложениях можно выполнять всю необхо-
димую обработку данных, используя непосредственно сигналы преобразо-
вателя, поступающие в реальном масштабе времени. Однако в большинст-
ве случаев такой подход непрактичен, и поэтому требуется запоминание в
той или иной форме или, возможно, передача сигналов, поступающих с
преобразователя. Наиболее желательный и удобный тип системы для запо-
минания данных — магнитофон. Можно пользоваться и другими запоми-
нающими устройствами, но преимущество магнитофона состоит в возмож-
ности запоминания данных в форме электрического сигнала. Предпочти-
тельный способ передачи данных — по электрическому кабелю. Существу-
ют, очевидно, и ситуации, когда это нереализуемо, например при передаче
данных с находящегося на орбите искусственного спутника Земли. Обычно
в таких случаях необходима передача по радио сигналов, поступающих с
преобразователя (телеметрия).
Запись данных на магнитную ленту и радиотелеметрия сами по себе
представляют предметы большого специального исследования, которое,
вообще говоря, лежит вне пределов данной книги. Фундаментальные сведе-
ния по этим вопросам содержатся в работах [10.3—10.5]. Однако два этапа
применения этих методов следует рассмотреть, поскольку они непосредст-
венно связаны с основными положениями обработки данных. Как показано
на рис. 10.1,6, эти этапы представляют собой: 1) операцию записи сигнала
на магнитную ленту и его воспроизведение при использовании магнитофо-
на и 2) операцию модуляции и демодуляции сигнала при магнитной записи
его и телеметрии.
10.2.1 . ЗАПИСЬ СИГНАЛОВ НА МАГНИТНУЮ ЛЕНТУ
И ИХ ВОСПРОИЗВЕДЕНИЕ
Последовательность операций при регистрации и воспроизведения дан-
ных на магнитной ленте для большинства магнитофонов серийного типа
показана на рис. 10.3,а. Пластмассовая пленка с магнитным покрытием пе-
ремещается относительно головки записи. При прохождении электрическо-
го тока через эту головку в ней возникает магнитный поток, намагничива-
326
Глава 10
Усилитель
воспроизведения
Усилитель
записи
Записывающая
головка
Воспроизводя-
щая головка
Направление__
движения
ленты
Пластмассовая пленка
Магнитное покрытие
Спектр
входного
процесса
Спектр
выходного
процесса
Рис. 10.3. Принципы и характеристики записи на магнитную ленту: а — прин-
цип действия магнитофона; б — частотная характеристика записи; в — затухание в
зазоре воспроизводящей головки. </>(/) — изменение магнитного потока во времени,
W — ширина зазора, е(/) — изменение напряжения во времени, X — длина волны,
i(t) — изменение силы тока во времени, eQ — фактическое напряжение на выходе,
Cj, с2 — константы, — идеальное напряжение на выходе.
ющий покрытие. При движении пленки относительно головки воспроизве-
дения появляется электрический сигнал, интенсивность которого пропорци-
ональна скорости изменения потока.
Использование системы регистрации и воспроизведения такого типа
связано с некоторыми трудностями, к числу которых относятся принципи-
ально нелинейный характер процесса намагничивания, обрывы ленты и
другие побочные эффекты, вызванные конструктивными недостатками
магнитной ленты. Однако, имея в виду основные свойства регистрирующе-
го устройства, следует учитывать два важных обстоятельства. Во-первых,
головка воспроизведения реагирует на скорость изменения магнитного по-
тока и поэтому воспроизводит сигнал скорее в продифференцированной
форме, чем в его истинном виде. Во-вторых, головка воспроизведения ос-
редняет изменение потока по ширине зазора. Первое обстоятельство ведет
к ухудшению частотной характеристики регистратора на низких частотах,
как показано на рис. 10.3,а, б, второе приводит к ухудшению частотной ха-
Сбор и обработка данных
327
рактеристики на высоких частотах (рис. 10.3,в). Заметим, что частотная
характеристика регистратора на высоких частотах может быть улучшена
путем уменьшения зазора головки воспроизведения, однако такое решение
приводит к уменьшению чувствительности головки. Чтобы добиться преж-
него уровня чувствительности, можно уменьшить зазор между головкой и
магнитной лентой, но это приводит к сокращению срока службы головки
воспроизведения. Чувствительность можно повысить также, увеличив чис-
ло витков обмотки на головке воспроизведения, но это ведет к ухудшению
частотной характеристики на высоких частотах.
В серийно выпускаемых магнитофонах эти две трудности устраняются
применением корректирующего контура, выравнивающего частотную ха-
рактеристику в пределах возможно более широкой полосы частот. Серий-
ные магнитофоны со скоростью движения ленты 3 м/с имеют постоянную
с точностью до ±3 дБ частотную характеристику в диапазоне частот от
400 Гц до 2 МГц. Однако отношение сигнал/шум на выходе составляет все-
го около 28 дБ. Такие свойства регистрирующего и воспроизводящего уст-
ройств, как правило, неудовлетворительны для аппаратурного анализа по
двум причинам: во-первых, регистрирующее устройство не реагирует на
постоянный ток; во-вторых, отношение сигнал/шум в нем недостаточно
велико. С другой стороны, регистрирующее устройство все же обеспечива-
ет получение записи в достаточно широком частотном диапазоне. Таким
образом, задача состоит в том, чтобы за счет сужения полосы пропускания
добиться желаемой реакции на постоянный ток и улучшить отношение сиг-
нал/шум. Это достигается при помощи модуляции и демодуляции записы-
ваемого сигнала.
10.2.2 . МОДУЛЯЦИЯ И ДЕМОДУЛЯЦИЯ
Для передачи и (или) записи данных наблюдений наиболее широко ис-
пользуются два метода модуляции и демодуляции: частотная и кодово-им-
пульсная.
Частотная модуляция (ЧМ) чаще всего применяется при аналоговой те-
леметрии и записи сигнала на магнитную ленту. Принципиальная сущность
ЧМ состоит в том, что частота несущего сигнала превращается в аналог
амплитуды входного сигнала, как это показано на рис. 10.4,а. Когда моду-
лирующее напряжение отсутствует, модулированный сигнал просто пред-
ставляет собой колебание с несущей частотой. При наличии на входе стро-
го постоянного тока (постоянная составляющая) модулированный сигнал
есть сигнал чистого тона, частота которого выше несущей на величину де-
виации, вызываемой постоянной составляющей. Если модуляция осущест-
вляется синусоидальным сигналом, то модулированный сигнал теоретиче-
ски выглядит как синусоида переменной частоты. В случае записи на маг-
нитную ленту модулированный сигнал напоминает скорее прямоугольную
волну переменной ширины, поскольку ЧМ-сигнал записывается обычно при
уровне насыщения. Важный параметр ЧМ — отношение девиации частоты
Д/ к частоте модуляции fd. Это отношение называется индексом модуля-
328
Глава 10
Исследуемый сигнал
Рис. 10.4. Основные методы модуляции: а — частотная модуляция (ЧМ); б —
кодово-импульсная модуляция (КИМ).
ции nif и тесно связано как с полосой пропускания, так и с отношением сиг-
нал/шум, которые обеспечиваются при ЧМ-передаче и записи сигнала. Со-
ответствующие зависимости приведены в табл. 10.1, где указаны также ос-
новные достоинства и недостатки ЧМ.
Из рассмотрения табл. 10.1 видно, что ЧМ особенно чувствительна к
изменениям скорости движения магнитной ленты (временные ошибки), по-
скольку эти искажения немедленно переходят в ошибки регистрации ампли-
туд. Особенно важную роль играют динамические временные ошибки. Ча-
ще всего рассматривается динамическая временная ошибка в одноканаль-
ной системе, называемая флаттером. Флаттер можно определить как от-
клонение скорости движения магнитной ленты от нормы1). Он играет осо-
бенно важную роль при частотной модуляции, когда аналогом амплитуды
сигнала является масштаб времени или частота. Интеграл от флаттера и
есть динамическая временная ошибка. Величина флаттера у высококачест-
11 В отечественной терминологии английскому термину flutter соответствует
термин коэффициент колебания скорости и в частном случае для звукозаписываю-
щей аппаратуры термин коэффициент детонации. Коэффициент колебания скорости
представляет собой отношение отклонения от средней скорости к значению средней
скорости и выражается в процентах. Если скорость записи непостоянна, то шкала
времени сигналограммы по сравнению с реальным временем, в течение которого
происходило изменение регистрируемого сигнала, имеет мгновенную временную
ошибку. Более подробно см., например: Дэвис Г.Л. Применение точной магнитной
записи. — М.: Энергия, 1967, или Атей С. Устройства записи на магнитную ленту.
— М.: Энергия, 1969. — Прим. Г.Я. Мирского.
Сбор и обработка данных
329
Таблица 10.1. Основные характеристики методов модуляции
Вг — требуемая полоса пропускания магнитофона и пере-
дающего устройства, Гц;
с — число мультиплексируемых каналов;
fd — наибольшая частота сигнала, Гц;
nij — индекс модуляции;
п — число импульсов на группу кодов при КИМ;
Sj/Nj — исходное отношение сигнал/шум;
S0/2V0 — отношение сигнал/шум после модуляции
Характеристика
Частотная модуляция
Кодово-импульсная модуляция
Требования к полосе про-
пускания
Отношение сигнал/шум
Достоинства
Недостатки
вг = 2fd(i + my)
So/No ~ 6m2jSi/Ni
Возможность передачи
сигналов постоянного то-
ка, существенный рост от-
ношения сигнал/шум
Большая чувствительность
к изменению скорости
магнитной ленты, умень-
шение полосы пропуска-
ния
Вг = ncfd
= 22"
Возможность передачи
сигналов постоянного то-
ка, очень сильный рост
отношения сигнал/шум,
легко осуществить муль-
типлексирование каналов
Сильное уменьшение по-
лосы пропускания
венных магнитофонов промышленного производства составляет — 0,25%.
Как правило, спектр флаттера практически постоянен на всех частотах до
некоторой граничной частоты, которая при высокой скорости движения
ленты равна обычно примерно 100 Гц. Наиболее неприятная динамическая
временная ошибка между каналами появляется вследствие динамического
перекоса, определяемого как изменение угла, под которым лента проходит
магнитную головку. Это явление, очевидно, влияет на результаты взаим-
ного анализа сигналов в многоканальных системах, например на взаимные
корреляционные и спектральные функции. Динамический перекос можно
минимизировать, по возможности записывая предназначенные для взаим-
ного анализа данные через различные головки.
При кодово-импульсной модуляции (КИМ) аналоговый сигнал на входе
немедленно преобразуется в цифровой и затем записывается (рис. 10.4,5).
Поскольку цифровой код состоит из последовательности импульсов, при
его снятии с магнитной ленты с частотами вплоть до постоянной составля-
ющей не возникает никаких трудностей. Существует верхний предел часто-
ты регистрируемых данных, который определяется частотой съема во
330
Глава 10
входном аналого-цифровом преобразователе (АЦП). Вопрос о предельной
частоте рассмотрен в разд. 10.3.2. Требования к ширине полосы пропуска-
ния и к отношению сигнал/шум указаны наряду с основными достоинства-
ми и недостатками записи и передачи информации с помощью КИМ в
табл. 10.1.
Из табл. 10.1 видно, что отношение сигнал/шум при КИМ зависит
лишь от числа бит в принятом цифровом коде и никак не связано с непо-
средственным отношением сигнал/шум в записи. Это обстоятельство слу-
жит основным преимуществом КИМ сравнительно с методами аналоговой
модуляции, в том числе ЧМ. Кроме того, мультиплексирование нескольких
каналов, по которым поступают данные, в единый канал осуществляется
при КИМ особенно легко, поскольку кодированные сигналы разных преоб-
разователей нетрудно передавать одновременно в общей системе отсчета
времени. При ЧМ такое уплотнение достигается лишь за счет того, что
различным сигналам отводятся неперекрывающиеся полосы частот, пред-
ставляющие собой участки общей полосы пропускания канала телеметрии
или записи на магнитную ленту. Более подробное обсуждение этих вопро-
сов содержится в работе [10.5].
ПРИМЕР 10.2. ПАРАМЕТРЫ СТАНДАРТНОЙ ЗАПИСИ С ЧМ. Как прави-
ло, передача и регистрация научной информации с ЧМ осуществляется по
стандартам, разработанным Inter-Range Instrumentation Group (IRIG) и
подробно описанным в работе [10.6]. В соответствии с этими стандартами
значение индекса модуляции принимается равным 2,16, а выраженная в
процентах девиация несущей частоты сигнала во всем диапазоне его изме-
нений составляет ±40%. Одна из многих стандартных центральных несу-
щих частот сигнала равна 108 кГц. Определим максимальную частоту сиг-
нала fd, которую можно зарегистрировать на ЧМ-магнитофоне при несу-
щей частоте 108 кГц. Найдем также получаемое при этом отношение сиг-
нал/шум в записи.
При относительной девиации ±40% максимальное отклонение несущей
частоты сигнала Д/ = 43,2 кГц. По определению максимальная частота ре-
гистрируемого сигнала fd = Af/m, — 20 кГц. Из табл. 10.1 следует, что
отношение сигнал/шум S0/2V0 » 2&S/N-. Принимая характерное значение
отношения сигнал/шум в прямой записи Si/Ni = 630 (28 дБ), получим, что
отношение сигнал/шум в выходной записи Sq/Nq ® 17 640 (42,5 дБ). В ре-
альной ситуации магнитофоны с ЧМ способны обеспечить в зависимости
от их устройства отношения сигнал/шум, превышающие указанное значе-
ние на величину до 6 дБ.
10.3. Подготовка данных
Следующая важнейшая фаза сбора и обработки данных заключается в
подготовке собранного материала к детальному анализу. Исходные данные
обычно представляют собой непрерывные изменения электрического напря-
жения, снимаемые с датчиков или поступающие с магнитной ленты, на ко-
торую они были предварительно записаны. На этой стадии необходимо
Сбор и обработка данных
331
произвести ряд операций, с помощью которых сигналы с датчиков перево-
дятся в форму, удобную для дальнейшего анализа (см. рис. 10.1).
Первая из этих операций называется редактированием. Этот термин от-
носится к последовательности операций, применяемых до начала анализа с
целью выявить и исключить аномальные и (или) искаженные сигналы, кото-
рые могли возникнуть при сборе и регистрации данных, например, за счет
высокого уровня помех, снижения уровня сигнала и его исчезновения при
плохой работе датчика. Редактирование обычно сводится к визуальному
анализу реализаций сигнала опытным специалистом до перевода данных в
цифровую форму.
Следующая и наиболее важная стадия подготовки данных заключается
в преобразовании аналогового сигнала в цифровую форму (дискретизация).
Процесс дискретизации состоит из двух отдельных и не связанных друг с
другом операций: а) собственно дискретизации; б) квантования. Собствен-
но дискретизация есть процесс определения моментов времени, в которые
должны быть произведены отсчеты; квантование есть перевод этих от-
счетов в цифровую форму. Прежде чем переходить к обсуждению практи-
ческих проблем дискретизации, полезно обратиться к теоремам о дискрет-
ном представлении случайных процессов. После этого будут обсуждаться
вопросы, связанные с аналого-цифровыми преобразователями и с метода-
ми предварительной обработки данных.
10.3.1. ТЕОРЕМЫ О ДИСКРЕТНОМ ПРЕДСТАВЛЕНИИ СЛУЧАЙНЫХ
ПРОЦЕССОВ
Пусть реализация x(t) случайного процесса задана в интервале времени
от 0 до Т. Преобразование Фурье этой реализации имеет вид
X(f) = dt . (10.2)
•'о
Для того чтобы получить периодическую функцию времени с периодом
Г, положим, что реализация x(t) непрерывно повторяется. Основное при-
ращение частоты f = 1/Т. Разлагая функцию в ряд Фурье, находим
об
x(t)= £ Anej2”n,/T , (Ю.з)
где -оо
An = ^ [Tx(t)e^n^Tdl . (10.4)
1
Из формулы (10.2) следует, что
(И \ />'г
- = / x(t)e~j2™,/Tdt = ТА„ . (10.5)
Г/ •'о
Таким образом, величина Х(п/Т) определяет значения коэффициентов Ап
и, следовательно, ординаты x(t) при всех t. Вид функции x(t) в свою оче-
редь определяет величины X(f) при всех значениях /. Этот вывод составля-
332
Глава 10
ет содержание теоремы о дискретном представлении процесса в частот-
ной области. Основное приращение частоты \/Т называется коинтерва-
лом Найквиста.
Пусть преобразование Фурье X(f) некоторой реализации x(t) задано в
интервале частот от — В до В Гц и равно нулю вне этого интервала. Ин-
тервал физически осуществимых частот составляет 0...В Гц. Обратное пре-
образование Фурье имеет вид
x(z)= fB df . (10.6)
Для того чтобы получить периодическую функцию частоты с периодом
2В Гц, положим, что функция X(f) непрерывно повторяется. Основное
приращение времени составляет t = 1/(2В). Теперь
00
%(/) = Е C„e~J,rnf/\ (10.7)
- 00
где
Af)e^df. (Ю.8)
2.В J-в
Из формулы (10.6) следует, что
(п \ rR
— = f X(f)e^Bdf= 2ВСп . (10.9)
ZB / J-В
Таким образом, величина х(п/2В) определяет значения коэффициентов
Сп и, следовательно, функцию X(f) при всех значениях /. Вид этой функции
в свою очередь определяет ординаты x(t) при всех значениях t. Этот вывод
составляет содержание теоремы о дискретном представлении процесса во
временной области. Основное приращение времени 1/(2В) называется ин-
тервалом Найквиста.
Предположим теперь, что реализация x(t) задана только в интервале
времени от 0 до Г, а ее преобразование Фурье X(f) — в интервале частот
— В...В Гц. Это двойственное предположение теоретически невозможно в
силу принципа неопределенности [10.7]. В действительности, однако, оно
может быть приближенно справедливым для конечных интервалов времени
и для полосовых фильтров. Полагая, что на функции x(t) и X(f) наложены
ограничения, касающиеся интервалов времени и частот, можно установить
теперь число дискретных значений, нужное для того, чтобы установить
вид функции x(t) при всех значениях t.
Согласно формуле (10.5), снимая дискретные значения функции X(f) в
точках, разделенных на шкале частот коинтервалом Найквиста 1/Гв про-
межутке от —В до В, можно найти число дискретных значений, необходи-
мое для описания функции x(Z):
N = 2В/(1/Т) = 2 ВТ. (10.10)
Снимая дискретные значения x(t) в точках, разделенных на шкале времени
Сбор и обработка данных
333
интервалом Найквиста 1/(2В) в промежутке от 0 до Г, можно найти, что
N = 77(1/2В) = 2 ВТ. (10.11)
Таким образом, требуется одинаковое число дискретных значений при вы-
борке их через коинтервал Найквиста по шкале частот и при выборке через
интервал Найквиста по шкале времени.
10.3.2 . МЕТОДЫ ДИСКРЕТИЗАЦИИ И ОШИБКИ МАСКИРОВКИ ЧАСТОТ
Перевод аналогового сигнала в дискретную форму для численного ана-
лиза производится обычно через равные интервалы времени, как показано
на рис. 10.5. Задача заключается в правильном выборе величины интервала
дискретности Д/. Согласно формуле (10.11), минимальное число отсчетов,
нужное для описания реализации длиной Т при ширине спектра В, есть
N = 2ВТ. Поэтому при постоянном шаге по времени максимальный ин-
тервал дискретности Д/ = 1/(2В). С одной стороны, при выборках (отсче-
тах) в точках, отстоящих друг от друга менее чем на 1/(2В), будут полу-
чаться коррелированные данные, число которых будет избыточно велико,
что неизбежно вызовет увеличение как объема, так и стоимости расчетов.
С другой стороны, при выборках в точках, отстоящих друг от друга более
чем на 1/(2В), возможно перепутывание низко- и высокочастотных состав-
ляющих исходного процесса. Это явление называется маскировкой (подме-
ной) частот. Оно представляет собой источник ошибок, которые отсутст-
вуют при обработке аналогового сигнала; при цифровой обработке, когда
сигнал предварительно преобразуется из аналоговой формы в дискретную,
проблемы, связанные с маскировкой частот, могут играть важную роль.
Так, например, все, кто видел классические фильмы «вестерны», обращал,
несомненно, внимание на то, что при изменении скорости кареты кажется,
что меняется и направление вращения ее колес. Это и есть простейший
пример ошибок маскировки, вызванных преобразованием непрерывного
процесса в дискретный, которое осуществляется съемочной камерой.
Чтобы пояснить явление подмены частот, рассмотрим иллюстрируе-
мый рис. 10.5 случай преобразования непрерывного сигнала в дискретную
форму; интервал времени между последовательными отсчетами составляет
Д/ секунд. Следовательно, скорость дискретизации равна 1/Д/ отсчетов в
Рис. 10.5. Дискретное представление непрерывной реализации.
334
Глава 10
секунду. Для того чтобы дискретная реализация содержала все те же час-
тоты, что и исходный непрерывный сигнал, на каждый цикл соответству-
ющего колебания должно приходиться по меньшей мере два отсчета. Поэ-
тому наиболее высокая частота, которая может быть выделена при дис-
кретизации со скоростью 1/ДГ отсчетов в секунду, равна 1/(2AZ) Гц. Содер-
жащиеся в исходном сигнале более высокие частоты будут свернуты в диа-
пазон О...1/(2ДГ) Гц и будут неотличимы от более низких частот этого
диапазона (рис. 10.6). Граничная частота
fc = 1/(2Д/) (10.12)
называется частотой Найквиста или частотой свертывания (наложения).
Свертывание составляющих исходного процесса в диапазоне частот [0, fc\
представляет собой нечто вроде гофрирования частот, как показано на
рис. 10.7. В частности, для любой частоты /, принадлежащей диапазону
замаскированными под частоту f являются высокие частоты
(2/с±/),(4/с±(2л/с±
(10.13)
Для доказательства этого факта заметим, что при t = 1/(2/с)
cos2t7/z = cos2tt(2m/c + /)
— = cos —
2/с Л
(10.14)
Таким образом, при снятии отсчетов с интервалами 1/(2/с) значения коси-
нуса для частот/и 2nfc±f одинаковы. Например, если fc = 100 Гц, то со-
ставляющие с частотой 30 Гц будут неотличимы от составляющих с часто-
тами 170, 230, 370, 430 Гц и т. д. Аналогичным образом энергия колебаний
Рис. 10.6. Пример маскировки частот.
Сбор и обработка данных
335
J________I________I________I_______I________I________I________L
О ' fc 2fc 3fc 4fc 5fc 6fc 7fc
Исходные частоты
Маскированные частоты
Рис. 10.7. Свертывание частот относительно частоты Найквиста fc.
с такими высокими маскирующими частотами будет неотличима от энер-
гии колебаний с более низкими частотами. Это объясняется тем, что при
t = 1/(2/с) характеризующие энергию величины sin2(27r/Z) и cos2(2tt/Z) оди-
наковы для частот f и 2nfc±f. Следовательно, если граничная частота fc
такая, как показано на рис. 10.8, то истинная спектральная плотность
(рис. 10.8, а) будет искажена (рис. 10.8,6).
Единственный практический способ избавиться от ошибок маскировки
частот при цифровом анализе данных заключается в том, чтобы еще до
аналого-цифрового преобразования информации подавить в исходной ана-
логовой записи ту ее часть, которая может содержать частоты, превыша-
ющие частоты Найквиста f Это делают, ограничивая диапазон частот ис-
ходных данных с помощью аналогового низкочастотного фильтра, уста-
навливаемого перед аналого-цифровым преобразователем. Такие низкоча-
стотные фильтры, применяемые на АЦП, называются противоподменны-
ми. Поскольку ни один низкочастотный фильтр не может иметь вертикаль-
но спадающую частотную характеристику, принято задавать вырезываю-
щую частоту фильтра равной примерно 0,7...0,8 частоты f. Этот прием
обеспечивает сильное подавление всех колебаний с частотами, превышаю-
щими f
Рис. 10.8. Искажение спектральной плотности при свертывании частот: а — ис-
тинный спектр; б — искаженный спектр.
336
Глава 10
10.3.3 . ОШИБКИ КВАНТОВАНИЯ
Рассмотрим теперь операцию квантования. Поскольку числовое значе-
ние каждого отсчета должно быть выражено некоторым конечным числом
цифр, континуум значений непрерывного процесса можно описать с по-
мощью конечного числа уровней квантования лишь приближенно. Как бы
ни была точна шкала, необходимо сделать выбор между двумя ее соседни-
ми значениями (рис. 10.9). Если квантование выполнено верно, то истин-
ным значениям исходного непрерывного сигнала будут соответствовать на-
иболее близкие к ним уровни квантования. Точность приближения к непре-
рывному процессу зависит от числа уровней квантования. Поскольку в
большинстве современных аналого-цифровых преобразователей сигнал на
выходе дается в двоичном коде, что позволяет непосредственно вводить
его в ЭВМ, число уровней квантования также удобно представлять в двоич-
ном коде. Типичные преобразователи аналогового сигнала в цифровой да-
ют от 6 до 16 бит информации, что соответствует диапазону от 64 до
65 536 уровней квантования. При идеальном преобразовании ошибка кван-
тования распределена равномерно со стандартным отклонением, прибли-
женно равным 0,29Дх, где Дх — шаг квантования. В этом легко убедиться.
Пусть р(х) — плотность вероятности ошибки квантования:
р(х\ = I Ь -0,50 < х < 0,50 ;
10, в остальных случаях.
Очевидно, что среднее значение ошибки равно нулю, поскольку кривая
зависимости р(х) симметрична относительно х = 0. Дисперсия ошибки
равна 1
°х2 = / (* - Рх)2р(х) dx = Г’5 х2 dx = —,
-оо •'-0,5 12
так что среднеквадратичное отклонение равно
Рис. 10.9. Ошибка квантования.
Сбор и обработка данных
337
Это и есть среднеквадратичное значение ошибки квантования, которое
можно рассматривать как среднеквадратичное значение помехи, наложен-
ной на полезный сигнал. Предположим, например, что весь диапазон зна-
чений сигнала разбит на 256 уровней (8 бит). В этом случае отношение пи-
кового значения сигнала к среднеквадратичному значению помехи составит
256Дл7(0,29Дх) » 1000, т. е. около 60 дБ.
На практике ошибка квантования обычно пренебрежимо мала по срав-
нению с другими ошибками, возникающими в процессе сбора и обработки
данных. Однако следует всегда стремиться к тому, чтобы диапазон измене-
ний исходного непрерывного процесса занимал возможно большую часть
шкалы квантования. В противном случае разрешающая способность ока-
жется малой, а ошибка квантования — существенной.
10.3.4 . АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
Аналого-цифровые преобразователи (АЦП) промышленного производ-
ства обычно представляют собой двоичные либо двоично-десятичные
(ДД) системы. Двоичная система преобразует непрерывные изменения
электрического напряжения в двоичный цифровой код, а ДД-система — в
цифровой код, который может быть представлен десятью различными ци-
фрами. Конструкция двоичной системы сравнительно проще, но для обра-
ботки данных приходится составлять, как правило, программы в машин-
ном коде. Двоично-десятичная система сложнее и относительно менее на-
дежна, но она позволяет производить непосредственно обработку данных
наблюдений по программам, написанным на обычном алгоритмическом
языке, например на Фортране. Кроме того, ДД-системы могут непосредст-
венно взаимодействовать с терминалом или дисплеем.
Помимо уже рассмотренных ошибок дискретизации и квантования не-
обходимо указать еще и другие наиболее существенные ошибки, возникаю-
щие в системах АЦП. К ним относятся:
1) апертурная ошибка, которая возникает за счет того, что каждый от-
счет выполняется на протяжении некоторого отрезка времени, а не мгно-
венно;
2) дребезжание или неустойчивая синхронизация — ошибка, возникаю-
щая в результате того, что интервал времени между соседними отсчетами
может меняться случайным образом;
3) нелинейные эффекты, которые появляются в результате самых раз-
личных причин, например плохой подгонки деталей системы, неточной гра-
дуировки, разрыва в нуле и т. д.
Как правило, скорость преобразования в существующих АЦП составля-
ет до 108 отсчетов в секунду при 8-битном слове и до 107 отсчетов при 12-
битном слове. Однако на практике ограничения, налагаемые цифровыми
магнитными устройствами и требуемой разрешающей способностью, при-
водят к уменьшению скорости квантования. Кроме того, скорость снятия
отсчетов в АЦП следует уменьшить во столько раз, сколько каналов опра-
338
Глава 10
шивается одновременно, и этот результат даст истинную скорость снятия
отсчетов для каждого канала.
Необходимо отметить еще одно обстоятельство, касающееся аналого-
цифровых преобразователей. При одновременном преобразовании в не-
скольких каналах наличие интервала времени между опросами в различных
каналах приводит к появлению межканальной временной ошибки в отсче-
тах, которая для быстро меняющихся сигналов может оказаться весьма за-
метной. Ее появления можно избежать, используя в системах АЦП запо-
минающие схемы, в которые данные из всех каналов поступают одновре-
менно и хранятся там до момента опроса соответствующего канала комму-
татором.
ПРИМЕР 10.3. ДИСКРЕТИЗАЦИЯ ДАННЫХ. Случайные вибрации кон-
струкции измеряются датчиком, который преобразует механическое ускоре-
ние в аналоговую форму колебаний электрического напряжения. Получае-
мую запись предполагается перевести в цифровую форму для последующе-
го анализа в диапазоне частот от 0 до 2000 Гц при отношении сигнал/шум
не менее 80 дБ. Требуется определить частоту опроса и число бит на один
отсчет, необходимые для аналого-цифрового преобразования сигнала.
Прежде всего для получения данных в диапазоне частот до 2000 Гц без
ошибок маскировки частот аналоговый сигнал следует пропустить через
фильтр низких частот с вырезывающей частотой 2000 Гц. Поскольку ча-
стотные характеристики противоподменных фильтров не могут спадать
строго вертикально, следует принять несколько более высокую частоту
Найквиста, скажем 2500 Гц. В соответствии с формулой (10.12) необходи-
мый для этого интервал дискретности Д/ = 1/(2/с) = 0,2 мс, так что ча-
стота съема должна составить 5000 отсчетов в секунду.
Для получения максимальной величины отношения сигнала к среднеква-
дратичному уровню шума около 80 дБ (104 по амплитуде) необходимо в со-
ответствии с формулой (10.15), чтобы выполнялось условие 2п/0,289 = 104,
где п — число бит на один отсчет. Логарифмируя обе части этого равенст-
ва по основанию 10, получаем равенство 0,301 п — 3,46. Следовательно,
п = 11,5, так что нужное при преобразовании число бит на один отсчет
равно 12.
10.4. Оценивание основных свойств процесса
Корректность методов анализа случайных процессов, а также интерпре-
тации результатов анализа в значительной степени зависят от некоторых
основных свойств анализируемого процесса. К их числу в первую очередь
относятся стационарность, присутствие периодических составляющих и
нормальность процесса. Стационарность процесса играет важную роль по-
тому, что методы анализа нестационарных процессов существенно более
громоздки, чем в стационарном случае. Если установлено, что в процессе
содержатся периодические составляющие, то это позволяет избежать в
дальнейшем ошибок при интерпретации результатов анализа. Предположе-
Сбор и обработка данных
339
ние о нормальности позволяет существенно упростить аналитическое ис-
следование свойств случайного процесса (не содержащего периодических со-
ставляющих), поэтому желательна проверка этой гипотезы. На рис. 10.1
оценивание основных свойств процесса, т. е. этих трех фундаментальных
характеристик, указывается как отдельная операция, выполняемая до нача-
ла детального анализа. Однако на практике она зачастую осуществляется
как составная часть общего анализа. Ниже рассмотрены практические со-
ображения, касающиеся оценивания основных свойств процесса.
10.4.1. ПРОВЕРКА СТАЦИОНАРНОСТИ
По-видимому, наиболее простой способ оценивания стационарности ре-
ализации заключается в рассмотрении физической природы процесса, кото-
рому эта реализация принадлежит. Если основные физические факторы,
определяющие процесс, не зависят от времени, то можно без дальнейшего
исследования полагать изучаемый процесс стационарным. Рассмотрим, на-
пример, случайный процесс изменения давления в турбулентном погранич-
ном слое, возникающем при полете самолета с большой скоростью. Если
очертания самолета, его высота и скорость остаются во время полета не-
изменными, то справедливо допустить, что рассматриваемый случайный
процесс обладает свойством стационарности. С другой стороны, если вы-
сота, скорость и (или) конфигурация самолета быстро изменяются, то сле-
дует ожидать, что колебания давления в пограничном слое нестационарны.
На практике такие простые соображения, позволяющие проверить спра-
ведливость гипотезы о стационарности, обычно отсутствуют. В подобных
случаях эта гипотеза должна быть проверена путем анализа имеющихся ре-
ализаций. Способы проверки могут быть различными — от визуального
просмотра реализаций опытным специалистом до детального статистиче-
ского оценивания различных параметров процесса. Во всяком случае, если
исследователь намеревается установить стационарность процесса по его
отдельной реализации, необходимо сделать существенные допущения. Во-
первых, следует предположить, что любая реализация правильно отражает
нестационарный характер изучаемого процесса. Это допущение вполне при-
емлемо для нестационарных процессов, содержащих детерминированный
тренд (см. гл. 12). Во-вторых, нужно допустить, что длина данной реализа-
ции существенно больше периода самой низкочастотной составляющей
процесса. Иными словами, длина реализации должна быть настолько боль-
шой, чтобы можно было разделить нестационарный тренд и низкочастот-
ные случайные колебания1).
Помимо этих допущений, удобно (но не обязательно) предположить,
что любые представляющие интерес нестационарные свойства процесса
полностью описываются медленными изменениями во времени среднего
квадрата процесса. Нетрудно, конечно, построить нестационарный процесс
со стационарным средним квадратом. Примером может служить синусои-
11 Строго говоря, в общем случае эта задача неразрешима, поскольку процесс
может содержать составляющие со сколь угодно низкой частотой. — Прим, перев.
340
Глава 10
дальное колебание постоянной амплитуды, но с непрерывно возрастающей
частотой и со случайной начальной фазой. Все же на практике такие случаи
встречаются редко, поэтому маловероятно, чтобы нестационарный случай-
ный процесс обладал ковариационной функцией, зависящей от времени т
при всех значениях т, кроме т = 0. Поскольку /?(0) = ^2, то переменный
средний квадрат случайного процесса обычно означает, что его ковариаци-
онная функция зависит от времени. Аналогичные рассуждения справедливы
и для моментов более высокого порядка.
Имея в виду эти допущения, можно предложить такую последователь-
ность действий для проверки стационарности случайного процесса по от-
дельной его реализации x(t).
1. Реализация разделяется на N равных интервалов, причем наблюдения
в различных интервалах полагаются независимыми.
2. Вычисляются оценки среднего квадрата (или отдельно средних значе-
ний и дисперсий) для каждого интервала, и эти оценки располагаются в по-
рядке возрастания номера интервала:
2 2 2 2
Х[,Х2,Хз, • • • 9XN .
3. Эта последовательность оценок среднего квадрата проверяется на на-
личие тренда или других изменений во времени, которые не могут быть
объяснены только выборочной изменчивостью оценок.
Окончательная проверка реализаций на наличие трендов может быть
выполнена различными способами. Если известно выборочное распределе-
ние оценок, то можно воспользоваться статистическими критериями, опи-
санными в гл. 4. Однако, как отмечалось в разд. 8.2.2, знание выборочного
распределения оценок среднего квадрата требует знания частотной струк-
туры процесса. Обычно при проверке стационарности эти сведения от-
сутствуют. Поэтому более желательно применение непараметрических кри-
териев, при использовании которых не требуется знать выборочные рас-
пределения оценок. Два таких непараметрических критерия, которыми
можно воспользоваться для решения данной задачи, описаны в разд. 4.7.
Это критерий серий и критерий инверсий. Последний представляет собой
более мощное средство для обнаружения монотонных трендов в данных
наблюдений. Критерий инверсий может быть непосредственно использован
для проверки гипотезы о стационарности следующим образом.
Предположим, что последовательность оценок среднего квадрата (х^,
х%,..., x2N) есть выборка, составленная из независимых наблюдений над
стационарной случайной последовательностью со средним значением ф2.
Если эта гипотеза верна, то изменения последовательности средних значе-
ний будут носить случайный характер и не будут содержать тренда. Следо-
вательно, вероятное число инверсий будет таким же, как и для последова-
тельности независимых наблюдений над рассматриваемой случайной вели-
чиной, т. е. будет определяться формулой (4.56). Если же число инверсий
окажется существенно иным, то гипотеза стационарности должна быть от-
вергнута. В противном случае гипотезу можно принять. Заметим, что опи-
Сбор и обработка данных
341
санный метод проверки стационарности не требует знания спектральной
ширины рассматриваемого процесса или длины интервала усреднения, по
которому определены оценки среднего квадрата. Понятно, что его приме-
нение не ограничено оценками среднего квадрата. Метод будет работать
столь же эффективно и для оценок среднего или среднеквадратичного зна-
чения, среднеквадратичного отклонения, среднего абсолютного значения
или любых других оценок. Более того, анализируемые данные не обяза-
тельно должны быть свободны от вклада периодических компонент. По-
лезные выводы могут быть получены и при наличии периодичностей, если
только их максимальный период мал по сравнению с интервалом усредне-
ния, по которому получают выборочные оценки параметров.
ПРИМЕР 10.4. ПРОВЕРКА СТАЦИОНАРНОСТИ. Для того чтобы показать
применение критерия инверсий для проверки гипотезы стационарности,
рассмотрим показанную на рис. 10.10 последовательность из 20 оценок
среднего квадрата. Измерения производились на выходе аналогового гене-
ратора случайного шума при постепенном повышении усиления примерно
на 20%. Число инверсий, определенное для этой последовательности в со-
ответствии с разд. 4.7.2, оказалось следующим:
А = 7 А = 4 А1 = 7 Аб = 0
^2 = 2 А = 0 Аг = 6 Л17 = 2
А3 = 6 А = 8 Аз = 3 As ~ 0
А4 = 2 А = 0 Л14 = 0 Л19 = 1
А5 = 0 Ао = 2 As = 2
Общее число инверсий А = 52.
Предположим теперь, что эта выборка принадлежит стационарному
процессу. Согласно табл. А.7, эта гипотеза была бы принята при уровне
значимости а = 0,01, если бы последовательность, состоящая из N = 20
измерений, содержала не менее Л20; 0 >001 = 59 инверсий. Поскольку в дейст-
5
О
20
10 15
Номер измерения
Рис. 10.10. Последовательность измерений среднего квадрата.
342
Глава 10
вительности выборка содержит А = 52 инверсий, гипотеза стационарности
должна быть отвергнута при 1%-ном уровне значимости; иными словами,
эту выборку следует признать нестационарной. На этом пример 10.4 закан-
чивается.
Заметим в заключение, что предположение о стационарности может
быть зачастую подтверждено (или опровергнуто) при помощи простого не-
параметрического критерия среднего квадрата (или других связанных с ним
оценок характеристик), рассчитываемых по отдельным отрезкам имеющей-
ся реализации. Однако если исследователь не считает постоянство во вре-
мени среднего квадрата достаточным доказательством стационарности ав-
токорреляционной функции, то следует использовать и другие методы про-
верки, при которых производится разбиение процесса по отдельным диапа-
зонам частот. В частности, можно разделить процесс на несколько смеж-
ных частотных диапазонов при помощи полосового фильтра и отдельно
проверить на стационарность оценки среднего квадрата в каждом интерва-
ле частот. Поскольку спектральная плотность и автокорреляционная функ-
ция представляют собой пару преобразований Фурье, постоянство во вре-
мени одной функции означает, что и другая функция обладает тем же
свойством1 \
10.4.2. ПРОВЕРКА ПЕРИОДИЧНОСТИ
Теоретически наличие периодических и (или) почти периодических со-
ставляющих в случайном процессе проявляется в виде дельта-функций в его
спектральной плотности. На практике оказывается, что спектральная плот-
ность содержит острые пики, которые можно ошибочно приписать узкопо-
лосному случайному шуму. Желательно поэтому установить наличие пери-
одических составляющих, чтобы не путать их с узкополосным случайным
шумом, спектральная плотность которого конечна. Если периодические со-
ставляющие имеют большие амплитуды, то их наличие совершенно оче-
видно. Однако при малых амплитудах периодические компоненты не про-
являются столь отчетливо. Их присутствие устанавливается наиболее эф-
фективно при помощи методов, тесно связанных с методами анализа чисто
случайных процессов. Поэтому практически методы выделения скрытых
периодичностей представляют собой развитие методов анализа случайных
процессов. В частности, периодические составляющие можно зачастую об-
наружить в случайном процессе в результате визуального анализа оценок
спектральной плотности, плотности распределения и (или) ковариационной
функции, рассчитанных по данным наблюдений над стационарным процес-
сом. Для решения этой задачи чаще всего используют оценки автоспектра.
Делают это таким образом. В оценке спектральной плотности, вычис-
ленной при высоком разрешении по частоте, периодические составляющие
даже небольшой амплитуды проявятся в виде острых максимумов. Однако
11 Следует все же помнить, что проверка гипотезы никогда не может ее дока-
зать: результаты проверки либо не противоречат гипотезе, либо указывают на то,
что ее следует отвергнуть. — Прим, перев.
Сбор и обработка данных
343
острый максимум оценки автоспектра может отвечать и узкополосному
случайному шуму. Различить эти две ситуации можно, строя оценки авто-
спектра с все более высоким разрешением по частоте. Если максимум отве-
чает гармоническому колебанию, то его ширина всегда будет совпадать с
шириной полосы пропускания используемого для построения оценки
фильтра, сколь бы малой она ни была. Кроме того, высота максимума
будет расти всегда пропорционально уменьшению полосы пропускания.
Очевидно, что такой метод детектирования даст иные результаты, если
ширина элементарной полосы частот при спектральном анализе меньше
возможной ширины спектра узкополосного случайного процесса1).
ПРИМЕР 10.5. СПЕКТР СМЕСИ ШУМА И ГАРМОНИЧЕСКОГО КОЛЕБА-
НИЯ. Чтобы показать, как по энергетическому спектру можно обнаружить
наличие периодической составляющей в случайном процессе, обратимся к
рис. 10.11. В этом примере процесс на выходе генератора случайного шума
смешивается с гармоническим сигналом. Среднеквадратичное значение ам-
плитуды гармонического сигнала задано равным 1/20 соответствующего
среднеквадратичного значения случайного сигнала. На графике рис. 10.11,6/,
полученном при использовании фильтра с относительно широкой полосой
пропускания, наличие синусоиды почти незаметно. График на рис. 10.11,6,
построенный при использовании фильтра с шириной полосы пропускания,
составляющей 1/5 ширины предыдущего фильтра, показывает, что перио-
дическая составляющая, по-видимому, присутствует. График на
рис. 10.12, в, полученный при использовании фильтра, ширина полосы про-
пускания которого еще в 5 раз меньше, достаточно четко свидетельствует о
наличии синусоидальной составляющей.
10.4.3. ПРОВЕРКА НОРМАЛЬНОСТИ
Наиболее просто проверить, подчиняются ли реализации стационарного
случайного процесса нормальному закону, можно, измерив плотность веро-
ятности значений процесса и сравнив ее с теоретическим нормальным рас-
пределением. Если длина реализации достаточно велика и ошибки измере-
ния малы по сравнению с отклонениями функции от нормальной кривой,
то несоответствие ее нормальному распределению будет очевидно. Если
выборочное распределение оценки плотности вероятности известно, можно
применить критерии нормальности даже в том случае, когда статистиче-
ские ошибки велики. Однако, как и в случае проверки стационарности
(см. разд. 10.4.2), при нахождении выборочного распределения оценки
плотности вероятности необходимо знать частотную структуру процесса.
Такого рода сведения на практике получить трудно. Следовательно, более
желательно применять непараметрические критерии. Один из наиболее
Строго говоря, никакие статистические методы анализа не позволяют с пол-
ной уверенностью доказать наличие периодических компонент в конечной реализа-
ции случайного процесса. Поэтому тесты целесообразно сочетать с априорными
данными и физическими соображениями. — Прим, перев.
344
Глава 10
Рис. 10.11. Оценки автоспектра смеси гармонического сигнала и шума.
Рис. 10.12. Общая схема анализа отдельных реализаций.
346
Глава 10
удобных непараметрических критериев нормальности распределения — это
критерий согласия хи-квадрат, описанный в разд. 4.6.
10.5. Анализ данных
Методы, при помощи которых изучаются свойства случайных процес-
сов, логично разделить на две группы: методы анализа отдельных реализа-
ций и методы анализа ансамбля реализаций при известных статистических
свойствах каждой отдельной реализации. Ниже описываются практические
приемы анализа для каждой группы.
10.5.1. АНАЛИЗ ОТДЕЛЬНЫХ РЕАЛИЗАЦИЙ
Схема оценивания статистических характеристик отдельных реализаций
представлена на рис. 10.12. Заметим, что многие из рекомендуемых этапов
обработки могут быть при необходимости исключены; возможно также
осуществление дополнительных операций. Отметим еще, что в приводи-
мую здесь схему включены этапы определения основных свойств процес-
сов, рассмотренные в разд. 10.4; это поможет лучше понять связь обеих
стадий анализа данных. Обратимся теперь к рассмотрению блоков схемы,
приведенной на рис. 10.12.
Определение среднего значения и среднего квадрата (блок А). Первый
этап заключается в вычислении среднего значения и среднего квадрата (или
дисперсии). Необходимость этих вычислений практически во всех случаях
диктуется следующими важными соображениями. Во-первых, среднее зна-
чение и средний квадрат определяют некоторый средний уровень и диспер-
сию процесса; поэтому вычисление этих величин необходимо для решения
даже самых простых прикладных задач. Во-вторых, вычисление средних
значений и среднего квадрата по коротким интервалам времени позволяет
проверить стационарность процесса (см. рис. 10.12 и разд. 10.4.1). Вычис-
ление среднего значения и среднего квадрата рассмотрено в разд. 11.1, а
статистическая точность соответствующих оценок — в разд. 8.2.
Оценивание ковариационной функции (блок Б). Ковариационная функ-
ция стационарного процесса представляет собой обратное преобразование
Фурье его спектральной плотности и потому не содержит никакой допол-
нительной информации о процессе, помимо той, что дает его автоспектр.
Однако оценку спектра легче вычислить и, как правило, проще интерпрети-
ровать, и потому оценивание ковариационных функций часто пропускают.
Могут, однако, существовать ситуации, когда эта оценка представляет ин-
терес. В таких случаях ее обычно вычисляют по оценке спектральной плот-
ности, как описано в разд. 11.4.2. Статистическая точность оценивания ко-
вариационных функций рассмотрена в разд. 8.4.
Оценивание спектральной плотности (блок В). Наиболее важная одно-
мерная характеристика стационарных случайных процессов — спектральная
Сбор и обработка данных
347
плотность, описывающая частотный состав процесса. Для линейных физи-
ческих систем с постоянными параметрами спектр выходного процесса
может быть найден как произведение спектра процесса на входе на квадрат
амплитудной характеристики системы. Результаты измерения спектра да-
ют информацию о динамических характеристиках системы. Общая пло-
щадь для кривой спектральной плотности как функция частоты равна сред-
нему квадрату В более общей формулировке среднее значение квадрата
процесса в некотором рассматриваемом интервале частот определяется
площадью под кривой спектра в пределах этого интервала. Очевидно, что
данные измерений спектральной плотности представляют значительную
ценность для большинства приложений анализа.
В гл. 6 и 7 было показано, насколько велико физическое значение функ-
ции спектральной плотности при анализе соотношений на входе и выходе
линейной системы. Другие инженерные приложения этой характеристики
рассмотрены в работе [10.8]. Способ вычисления оценки спектральной
плотности описан в разд. 11.5, а ее статистическая точность — в разд. 8.5.
Оценивание плотности вероятности (блок Г). Последний основной
этап рассматриваемой процедуры анализа заключается в определении
плотности вероятности. При анализе процессов плотность вероятности ча-
сто не оценивают, так как принято считать, что все случайные явления
подчиняются нормальному закону. Все же в некоторых случаях распределе-
ние процесса может существенно отличаться от гауссова. Это бывает пре-
жде всего, когда рассматриваемый процесс представляет собой результат
нелинейного преобразования некоторого другого процесса. Способ вычис-
ления оценки плотности вероятности рассмотрен в разд. 11.3, а ее стати-
стическая точность — в разд. 8.3.
Анализ реализаций нестационарных и переходных процессов (блок Д).
Все рассмотренные до сих пор методы могут быть применены только для
анализа реализаций стационарных процессов. Если в результате оценива-
ния основных свойств процесса установлено, что рассматриваемая реализа-
ция принадлежит некоторому нестационарному процессу, то для ее анализа
необходимо использовать специальные методы. Задача анализа нестацио-
нарных и переходных процессов рассмотрена в гл. 12. Заметим, что для
анализа некоторых классов нестационарных процессов можно иногда ис-
пользовать ту же аппаратуру или программное обеспечение, что и в стаци-
онарном случае. Однако интерпретация результатов такого анализа требу-
ет особой осторожности (см. разд. 12.5 и 12.6).
Анализ реализаций периодического или почти периодического процесса
(блок Е). Если в результате оценивания основных свойств процесса уста-
новлено, что рассматриваемая реализация содержит периодические или по-
чти периодические составляющие, то анализ несколько усложняется. В
частности, для решения задачи можно воспользоваться одним из двух опи-
санных ниже приемов. Во-первых, можно разделить случайную и периоди-
348
Глава 10
ческую части путем фильтрации и рассматривать их раздельно. Во-вторых,
можно совместно анализировать периодическую и случайную части процес-
са, учитывая присутствие периодических составляющих при интерпретации
результатов. Например, если построен спектр процесса, содержащего гар-
монические колебания, то около максимумов спектральной плотности на
соответствующих этим гармоникам частотах можно изобразить символ
дельта-функции и указать значение среднего квадрата гармоники. Послед-
няя оценка находится как произведение спектральной плотности на частоте
соответствующего гармонического колебания на разрешение по частоте.
Если этого не сделать, то можно, как уже отмечалось в разд. 10.4.2, дать
неверную физическую интерпретацию таким максимумам спектральной
плотности.
Специальные методы анализа (блок Ж). В зависимости от конкретных
целей исследования возможно применение различных специальных приемов
анализа отдельных реализаций. Например, как показано в работе [10.9],
при исследовании усталости различных механических конструкций прихо-
дится строить оценки плотности распределения вероятности экстремаль-
ных значений нагрузки. Некоторые вопросы теории связи, касающиеся
проблемы шумов, требуют исследования пересечений нулевого или некото-
рого другого произвольного уровня (см. разд. 5.4.3 и работу [10.7]). Для
решения некоторых специальных задач может потребоваться преобразова-
ние Гильберта, описанное в гл. 13. Необходимость проведения специаль-
ных видов анализа, указанных в блоке Ж, устанавливается при решении
конкретных инженерных задач.
10.5.2. АНАЛИЗ СОВОКУПНОСТИ РЕАЛИЗАЦИЙ
В предыдущем разделе были описаны методы анализа отдельных реа-
лизаций, полученных в результате эксперимента. Процедура определения
наиболее важных статистических характеристик совокупности реализаций
изображена схематически на рис. 10.13. Как и в случае анализа отдельных
реализаций (рис. 10.12), при решении конкретных физических задач некото-
рые из рекомендованных на рис. 10.13 этапов обработки могут быть ис-
ключены и заменены при необходимости дополнительными видами обра-
ботки. Следует иметь в виду, что описываемые ниже приемы выполняются
в предположении стационарности отдельных реализаций. Рассмотрим те-
перь каждый из блоков, показанных на рис. 10.13.
Анализ отдельных реализаций (блок А). Этот первый этап заключается
в анализе необходимых статистических свойств отдельных реализаций
(рис. 10.12). Поэтому блок А на рис. 10.13 должен содержать соответству-
ющую часть схемы, изображенной на рис. 10.12.
Проверка коррелированности реализаций (блок Б). На следующем эта-
пе анализа выясняется вопрос о существовании корреляции между отдель-
Рис. 10.13. Общая схема анализа совокупности реализаций.
350
Глава 10
ними реализациями совокупности. Во многих случаях для решения этой за-
дачи достаточно беглого оценивания основных физических свойств процес-
сов. Например, если ансамбль реализаций образован в результате наблюде-
ний некоторых физических явлений и интервалы времени между получени-
ем отдельных реализаций достаточно велики, то можно без дальнейшего
исследования считать эти реализации некоррелированными. С другой сто-
роны, если совокупность представлена результатами одновременных изме-
рений процессов на входе и выходе некоторой физической системы, то сле-
дует ожидать, что корреляция между реализациями существует. В тех слу-
чаях, когда отсутствие связи не вытекает с очевидностью из элементарных
физических соображений, необходимо проведение специальной проверки,
состоящей в вычислении взаимных корреляционных функций или функций
когерентности (рис. 10.13).
Проверка эквивалентности некоррелированных реализаций (блок В).
Если реализации признаны некоррелированными (блок Б), то следует про-
верить эквивалентность их статистических свойств. На этот важный этап
анализа случайных процессов часто не обращают внимания. Нередко при-
ходится встречать такие случаи, когда результаты анализа большой сово-
купности реализаций представляют в виде отдельных графиков, тогда как в
действительности различия в результатах, полученных для отдельных реа-
лизаций, полностью можно объяснить дисперсией оценок. Формальное
представление таких избыточных сведений обычно не приносит никакой
пользы; оно скорее даже вредит исследованию. Действительно, излишне
большой объем анализированного материала может без всякой необходи-
мости усложнить интерпретацию результатов. Кроме того, неопытный ис-
следователь может ошибочно придать физический смысл случайному раз-
бросу отдельных оценок. Наконец, если результаты анализа статистически
эквивалентных данных объединены до стадии интерпретации, то, как пока-
зано ниже, точность полученных оценок возрастает. Заметим, что для
большинства прикладных задач эквивалентность оценок спектров может
служить достаточным критерием эквивалентности реализаций, по которым
построены эти оценки. Способ проверки эквивалентности спектральных
оценок описан в разд. 10.5.3.
Объединение эквивалентных некоррелированных реализаций (блок Г).
Результаты анализа отдельных реализаций, для которых установлена ста-
тистическая эквивалентность, должны быть объединены. Это делают пу-
тем расчета соответствующих средних взвешенных величин из оценок, по-
лученных при анализе отдельных реализаций. Пусть, например, по двум
некоррелированным реализациям получены оценки спектральной плотно-
сти, которые представляют статистически эквивалентные процессы. Если
исходным оценкам Gx(f) и G2(f) соответствуют ndx и nd2 усреднений, то
новая, объединенная оценка спектральной плотности находится в виде
А / n + nd2^2(f)
(jp \j)
"<п + ”</2
(10.16)
Сбор и обработка данных
351
причем число усреднений для этой оценки составит ndp = ndx 4- nd2. Равен-
ство (10.16) легко распространить на случай q оценок некоррелированных,
но эквивалентных выборок:
£,(/) =
Функции Gp(f) отвечает теперь эквивалентное число усреднений
q
nd=
1 = 1
(10.17)
(10.18)
Согласно разд. 8.5.4, приближенное значение случайной ошибки оценки
спектральной плотности есть е = l/Vn^, и потому из формулы (10.18) сле-
дует, что операция объединения приводит к оценке автоспектра, обладаю-
щей меньшей случайной ошибкой.
Однако нужно также отметить, что операция объединения не приводит
к уменьшению систематических ошибок (смещения) при оценке спектраль-
ной плотности (определение и анализ этих ошибок даны в разд. 8.5.1). Это
обстоятельство зачастую вынуждает производить новую обработку реали-
заций, обладающих статистически эквивалентными свойствами, причем
способы обработки строятся таким образом, чтобы уменьшить ошибки
смещения. Для оценок спектральной плотности такая новая обработка
может заключаться в пересчете оценок спектральной плотности по исход-
ной реализации, но со значительно увеличенной разрешающей способнос-
тью по частоте. Это приводит к росту дисперсии оценки и уменьшению
ошибки смещения. Последующее усреднение позволяет уменьшить диспер-
сию оценки.
Оценивание взаимных ковариационных функций (блок Д). Подобно ав-
токовариационной функции и спектральной плотности, взаимная ковариа-
ционная функция и взаимная спектральная плотность представляют собой
пару преобразований Фурье. Следовательно, получение взаимной ковариа-
ционной функции фактически не дает никакой новой информации о процес-
се, кроме той, которую содержит взаимный спектр. Однако эта функция
позволяет иногда получить требуемую информацию в более удобной фор-
ме. В качестве примера можно привести определение задержки по времени
между процессами, измеряемыми в двух точках. Такие измерения лежат в
основе многих применений, описанных в работе [10.8]. Измерение взаим-
ной ковариационной функции как отдельная стадия анализа представлено
блоком Д. Заметим, что оценка взаимной ковариационной функции может
служить показателем коррелированности двух отдельных реализаций; ее
вычисление является иногда промежуточным этапом при расчете взаимной
спектральной плотности.
Оценку взаимной ковариационной функции ищут обычно как обратное
преобразование Фурье оценки взаимной спектральной плотности
(см. разд. 11.6.2). Их статистическая точность рассмотрена в разд. 8.4.
352
Глава 10
Оценивание взаимных спектральных плотностей (блок Е). Наиболее
важная часть анализа совместных характеристик совокупности коррелиро-
ванных реализаций — это измерение взаимной спектральной плотности.
Взаимная спектральная плотность содержит сведения о линейных зависи-
мостях, которые могут наблюдаться между отдельными реализациями,
принадлежащими данной совокупности. Физическая интерпретация этой
информации часто непосредственно ведет к решению поставленных задач
(см. гл. 6 и 7 и работу [10.8]).
Вычисление оценок взаимной спектральной плотности рассмотрено в
разд. 11.6.3, а их статистическая точность — в разд. 9.1.
Оценивание функций когерентности (блок Ж). Оценки функций коге-
рентности находят косвенным путем — по оценкам спектральной и взаим-
ной спектральной плотностей. Различные типы этой функции (обычная,
множественная и частная) применяются для разных целей. Во-первых,
функции когерентности могут быть использованы как показатели коррели-
рованности отдельных реализаций. Во-вторых, они играют весьма сущест-
венную роль при определении точности оценок частотных характеристик.
И, во-вторых, с их помощью возможно иногда непосредственно решить не-
которые задачи.
Вычисление функций когерентности рассмотрено в разд. 11.6.6, а их
статистическая точность — в разд. 11.7. Примеры использования функции
когерентности при решении инженерных задач содержатся в работе [10.8],
а статистической точности ее оценок посвящены разд. 9.2.3 и 9.3.
Оценивание частотных характеристик (блок 3). Часто конечной целью
анализа совокупности является установление линейных зависимостей меж-
ду процессами, к которым принадлежат рассматриваемые реализации. Су-
ществование таких линейных соотношений может быть установлено по
оценкам взаимных корреляционных функций, спектральных плотностей
или функций когерентности. Однако вычисление частотных характеристик
позволяет наилучшим образом описать линейные зависимости.
Формулы для вычисления частотных характеристик и их применения
рассмотрены в разд. 11.4 и 11.7, а статистическая точность оценок этих
функций — в разд. 9.2.4, 9.2.5 и 9.3.
Другие методы анализа совокупности реализаций (блок И). При сов-
местном анализе совокупности реализаций в зависимости от целей конкрет-
ного исследования вычисляют и другие совместные характеристики. Сюда
относятся такие более сложные спектральные характеристики, как обоб-
щенные спектры, которые используются при анализе нестационарных про-
цессов (см. гл. 12), а также преобразования Гильберта (см. гл. 13).
10.5.3. ПРОВЕРКА ЭКВИВАЛЕНТНОСТИ СПЕКТРОВ
В предыдущем разделе отмечалось, что при расчете оценок спектраль-
ной плотности по двум или более статистически независимым реализациям
Сбор и обработка данных
353
следует проверять эквивалентность этих оценок. Ниже показано, каким об-
разом может быть выполнена эта проверка.
Если число усреднений nd достаточно велико, например nd 30, то
оценка G(f) спектральной плотности G(f) имеет приблизительно нормаль-
ное распределение. В разд. 8.5 показано, что среднее значение оценки и ее
дисперсия соответственно равны
W)M(/), (10.19)
Var[G(/)] =-G2(/). (10.20)
nd
Следовательно, соответствующий доверительный интервал для функции
G(f) с уровнем доверия 1 — а, который можно найти при измерении вели-
чины (5(/), приближенно выражается в виде
£(/)( 1 - ^/21/- <?(/) < G(n 1 + za/2
\ V nd ) \
(10.21)
где za/2 — 100а/2 %-ная точка нормированного гауссова распределения.
При выводе соотношения (10.21) предполагалось, что za/2 < 1, и по-
этому
Логарифмическое преобразование оценки G(f), т. е. величина logG(/)
имеет распределение, более близкое к нормальному, чем исходное распре-
деление. Среднее значение и дисперсия величины logG(/) составляют
£[logG(/)] =logG(/), (10.23)
Varflog G(/)] ---- (10.24)
"d
Таким образом, дисперсия в этой формуле не зависит от частоты. Теперь
доверительный интервал для величины logG(/), соответствующий уровню
доверия 1 - а, приближенно можно выразить в виде
logG(/) + zo/2
<logG(/)<
(10.25)
12-953
354
Глава 10
Это соотношение можно получить непосредственно из формулы (10.21) и
найти таким образом эвристическое объяснение зависимостей (10.23) и
(10.24)._
Za/2^4/
При
< 1,
(10.25) предполагалось, что
выводе неравенства
и поэтому
(10.26)
±2"/гд-
Рассмотрим теперь две различные оценки спектральной плотности
Gx(f), G2(f), полученные при различных условиях, например по двум раз-
ным реализациям или по двум разным участкам одной и той же реализа-
ции. Требуется определить, эквивалентны ли в статистическом смысле эти
два спектра в одной и той же полосе частот (fQi fb) шириной В = fb — f
Предположим, что каждая из двух оценок спектральной плотности по-
лучена при разрешающей способности Д/, так что ширина спектра В де-
лится на Nj- полос, т. е.
Nf = B/Af. (10.27)
Будем считать далее, что число усреднений для этих оценок равно соот-
ветственно ndi и nd2, причем время усреднения (длина записи) для каждой
оценки может быть различным, хотя разрешение по частоте будет одним и
тем же. С учетом соотношений (10.23) и (10.24) выборочные распределения
логарифмов оценок в z-й полосе частот можно приближенно выразить с по-
мощью формул
log <?!(/,) =У
logGj/,),—
п dl
(10.28)
^G2(fi)=y logG2(/J, — ,
L nd2]
где у[у, a2] — нормально распределенная случайная величина со средним
значением /г и дисперсией а2. Теперь если две исследуемые реализации об-
ладают одинаковой спектральной плотностью G(f) = Gl(f) = G2(f), то из
формулы (10.28) следует, что
log
1
о, — +
i
nd2
Следовательно, статистика
Х2 =
1 1 Г1 v ^а)]2
----- + - L log/, / ,ч
п dl-nd2] / = 1 [ ^2\fi) _
(10.29)
(10.30)
<Ш)
подчиняется х^распределению с Лу степенями свободы, т. е.
*2 = X2, n = Nf . (10.31)
Сбор и обработка данных
355
Используя формулу (10.30), можно проверить гипотезу о том, что
Gx(f) = G2(f). Область принятия гипотезы есть
X2 < х2;а , п = Nf (10.32)
где а — уровень значимости критерия (см. разд. 4.6).
10.5.4. СООБРАЖЕНИЯ О МЕТОДАХ ВЫЧИСЛЕНИЙ
До 1950 г. практически все задачи, связанные с анализом временных ря-
дов, решались с помощью специальной аналоговой аппаратуры. С развитием
вычислительной техники произошел сдвиг в сторону цифровых методов
анализа. Первыми переход на численные методы осуществляли, как прави-
ло, специалисты, интересующиеся относительно низкими частотами; сюда,
в частности, относятся некоторые типы экономических и биологических ис-
следований, анализ океанографических данных и исследования атмосферной
турбулентности. Анализ высокочастотных явлений (на акустических
частотах и выше) по-прежнему осуществлялся в основном с помощью анало-
говой аппаратуры, что было связано с необходимостью обеспечить очень
высокую частоту съема данных и с относительно высокой стоимостью опе-
раций фильтрации данных на цифровых ЭВМ. В 1965 г. ситуация изменилась
радикальным образом благодаря появлению одного нового приема — алго-
ритмов быстрого вычисления коэффициентов Фурье на цифровой ЭВМ.
Эти алгоритмы, называемые обычно методами быстрого преобразования
Фурье (БПФ), обеспечили разительное снижение затрат времени и стоимо-
сти операций фильтрации, необходимых для вычисления спектральных
плотностей.
Сегодня практически весь анализ случайных процессов до частот не ме-
нее 100 кГц осуществляется численными методами. Для анализа в области
ниже 25 кГц существует, в частности, широкий набор стандартно выпуска-
емой цифровой аппаратуры, которая позволяет чрезвычайно быстро осу-
ществлять различного типа вычисления, основанные на использовании
БПФ. Имея в виду эти соображения, авторы сочли целесообразным исклю-
чить из этой главы детальное рассмотрение аналоговых методов анализа,
содержавшееся в первом ее издании1 \ Современные численные методы ана-
лиза случайных процессов рассмотрены в гл.11.
Задачи
10.1 Произведены измерения ускорения при помощи сейсмического акселерометра
(см. рис. 10.2), причем £ = W,fn = 100 Гц. По результатам измерений рассчитана
оценка спектральной плотности для диапазона частот 0...100 Гц. Определите ошиб-
ку смещения в оценке спектральной плотности на частоте 100 Гц, возникающую за
счет отличия частотной характеристики акселерометра от П-образной формы.
О См.Бендат Дж., Пирсол А. Измерение и анализ случайных процессов. Гл. 8.:
Пер.с англ. — М.: Мир, 1974. — 464 с. — Прим, перев.
12
356
Глава 10
10.2. По данным предыдущей задачи получена также оценка автоковариационной
функции. Возникают ли и здесь ошибки за счет отличия частотной характеристики
акселерометра от П-образной формы и, если да, то какие?
10.3. Предполагается запись 10 реализаций случайного процесса в частотном диа-
пазоне 0...1000 Гц с использованием кодово-импульсной модуляции при 12 импуль-
сах на кодовую группу. Если требуется передавать все 10 сигналов по одному ре-
гистрирующему каналу, то
а) каким должен быть частотный диапазон регистрирующего устройства;
б) чему равно отношение сигнал/шум?
10.4. Если приходится производить запись случайного сигнала магнитофоном с
сильной детонацией, то какой тип модуляции следует предпочесть — ЧМ или КИМ?
10.5. Требуется найти цифровым методом оценку спектральной плотности реали-
зации. Известно, что спектральная плотность отлична от нуля только в диапазоне
частот ниже 500 Гц. Установите:
а) какова наименьшая скорость дискретизации при обработке исходной реализа-
ции;
б) чему равна эта величина при расчете ковариационной функции;
в) чему равна эта величина при расчете плотности вероятности?
10.6. Сколько нужно задать уровней квантования при преобразовании аналогово-
го сигнала в цифровой, если известно, что в результирующей дискретной последова-
тельности потенциальный динамический диапазон (отношение пикового значения
сигнала к среднеквадратичному значению шума) должен быть 100:1 (т.е. 40 дБ)?
1С.7. В случайном процессе содержится гармоническое колебание со среднеква-
дратичным значением 1 В. Измерена спектральная плотность этого процесса
при разрешающей способности Ве = 10 Гц. Какова (в среднем) оценка спектраль-
ной плотности на частоте гармонического колебания, если известно, что вблизи
этой частоты оценка спектральной плотности случайной части процесса равна
G = 0,1 В2/Гц?
10.8 Какая потребуется разрешающая способность по частоте, если при оценке
спектральной плотности той же суммы случайного и гармонического сигналов, что
и в задаче 10.7, необходимо получить спектральную плотность на частоте гармони-
ческого сигнала в среднем в 10 раз большую, чем на других частотах?
10.9. Воспользовавшись представленной на рис. 10.12 общей схемой анализа от-
дельных реализаций, объясните, почему проверка стационарности осуществляется
прежде, чем проверка периодичности и (или) нормальности.
10.10. Воспользовавшись представленной на рис. 10.13 общей схемой анализа со-
вокупности реализаций, объясните, почему при расчете частотной характеристики
всегда необходимо находить и оценку функции когерентности.
Глава И
ЦИФРОВЫЕ МЕТОДЫ АНАЛИЗА
В этой главе дано подробное описание методов, необходимых для вы-
числения различного рода характеристик при анализе временных рядов.
При этом предполагается, что анализируемые данные представляют собой
дискретные по времени выборки из стационарных (эргодических) случай-
ных процессов. Методы анализа нестационарных процессов рассмотрены в
гл. 12, а преобразование Гильберта — в гл. 13.
11.1. Подготовка данных
В ряде случаев изучаемое физическое явление имеет дискретное время по
самой своей природе. Примерами могут служить эмиссия нейтронов или
многие типы экономических данных. Однако в большинстве случаев про-
цесс имеет непрерывное время, и его следует вначале преобразовать во вре-
менной ряд, сделав это с учетом соображений относительно дискретизации
и маскировки частот, детально рассмотренных в разд. 10.3. Во всяком слу-
чае, предполагается, что дискретные данные состоят из N равноотстоящих
отсчетов с интервалом дискретности At секунд, как было показано ранее
на рис. 10.5. Пусть величины
и = 1,2,...,АГ, (11.1)
отвечают моментам времени
Г„ = Г0 + иДг, и = 1,2,..., W . (11.2)
причем момент /0 выбирается произвольно и в случае стационарного про-
цесса в дальнейшие формулы не входит. Таким образом
ип = w('o + п » n = l,2,...,N. (11-3)
Общая длина реализации есть, очевидно, Tr = NAt. Согласно разд. 10.3,
частота Найквиста, отвечающая этой выборке, есть
f =— • (11.4)
л 2 Дг v
Как указано в разд. 10.3, исходные данные должны быть подвергнуты
различного рода предварительной обработке. При этом наиболее часто вы-
полняются следующие операции: а) приведение к нулевому среднему значе-
нию и единичной дисперсии; б) удаление тренда; в) фильтрация.
11.1.1. ПРИВЕДЕНИЕ К НУЛЕВОМУ СРЕДНЕМУ ЗНАЧЕНИЮ И ЕДИНИЧНОЙ
ДИСПЕРСИИ
Выборочное среднее значение последовательности отсчетов [ип] (и = 1,
2, ..., N) определяется в виде
1 N
й = -Е«и. (П-5)
А Л7= 1
358
Глава 11
В случае стационарного и эргодического процесса величина й представляет
собой несмещенную оценку среднего значения /г (см. разд. 4.1). Для после-
дующих расчетов удобно преобразовать последовательность [ип] в новую
последовательность [хл], имеющую нулевое выборочное среднее заначение:
х„ = *0о + п Дг) = “л - n = l,2,...,N. (11.6)
Все последующие формулы относятся к преобразованным таким образом
данным \хп}, для которых х = 0.
Среднеквадратичное отклонение преобразованной выборки \хп] имеет
вид
1 У 1/2
' 7—Г -- <п-7’
L7V 1 m=i J
Величины $ и s2 представляют собой несмещенные оценки среднеквадра-
тичного отклонения ах и дисперсии ах соответственно (см. разд. 4.1). Если
дальнейшие расчеты предполагается вести на ЭВМ с фиксированной, а не
плавающей запятой, то [хп] следует преобразовать в новую последователь-
ность [zn], определенную в виде
zn = \ п = 1, 2.....N. (11.8)
5
11.1.2. УДАЛЕНИЕ ТРЕНДА
В некоторых случаях исходные данные могут содержать посторонние
случайные тренды или низкочастотные компоненты, период которых пре-
вышает длину реализации Tr = N At. Обычными источниками таких слу-
чайных трендов служат дрейф нуля регистрирующей аппаратуры и опера-
ции интегрирования сигнала. Если такие тренды не исключить из исходных
данных, то при их последующем анализе могут возникнуть значительные
искажения оценок плотности вероятности, ковариационных и спектральных
характеристик. Однако здесь нужно проявлять известную осторожность и
удалять тренд лишь в том случае, если его присутствие очевидно или сле-
дует из априорных физических соображений.
Наиболее распространенный способ удаления тренда заключается в под-
гонке к данным многочлена невысокого порядка с помощью метода наи-
меньших квадратов (см. разд. 4.8.2). Пусть исходный ряд наблюдений [ип]
приближается многочленом степени К:
к
й„ = Ybk{n\t)k, n = l,2,...,N. (11.9)
k = 0
В рамках метода наименьших квадратов подгонка осуществляется путем
минимизации квадрата разностей исходной последовательности и значений
многочлена:
Q= Е («„- «и)2 = Е ип- Y,bk(nbt)
п=1 и=1L к = 0
(11.10)
Цифровые методы анализа
359
Искомая последовательность коэффициентов Ьк(к = 0, 1, К) получает-
ся путем приравнивания нулю частных производных функции Q по пере-
менным Ьк. Это дает систему из К 4- 1 уравнений
Е Е (иДг)/:+'"= E»n(«AOm, w = o, 1,2,..., К. (11.11)
к=0 п=1 п=1
В частности, при К = 0 уравнение (11.11) принимает вид
г>0 Е (« Д?)0 = Е «Дя Д0°> п=1 п —1 (И-12)
откуда имеем 1 N ь0 = -Цип = й. 1 ’ п = 1 (11.13)
При К = 1 уравнение (11.11) запишется в виде
/>о 52 (п Е (п = W = 0,1. (11.14)
н = 1 п = 1 п = 1
Имея в виду, что
Д N(N+V) " N(N + l)(2tf + 1) Е«= » ’ Е« = , и = 1 2 „ = 1 6 (И-15)
получим решение
2(2У + 1&1И„ - 6Е^1ЯИя Ь° У(ДГ-1) (11.16а)
12^.1Пип - 6(# + 1&1«я 1 Д/У(У - 1)(W + 1) (11.166)
Формулы (11.16) определяют линейную регрессию со свободным членом Ьо
и углом наклона Ь}. Величины, отвечающие этой прямой, следует вычесть
из исходных данных [ип]. Заметим, что при ип = yjt n&t = хр bQ = А и
b j = В равенства (11.16) эквивалентны равенствам (4.70). Пример исключе-
ния линейного тренда показан на рис. 11.1. Тренды более сложной формы
удаляются подгонкой многочленов более высокого порядка, однако прини-
мать значение К > 3, как правило, не рекомендуется.
360
Глава 11
11.1.3. ПРИМЕНЕНИЕ ЦИФРОВЫХ ФИЛЬТРОВ
Фильтрация данных, предшествующая их детальному анализу, может
выполняться для различных целей, например для выделения периодических
компонент, как основной элемент «наплывающего» преобразования Фурье
(см. разд. 11.5.4) или для исключения ошибок маскировки частот до «про-
реживания» исходных данных. Последнее приложение особенно важно, по-
скольку операция прореживания выполняется во многих случаях для умень-
шения объема данных, подлежащих дальнейшему анализу. По определе-
нию, прореживание порядка d заключается в сохранении в исходной после-
довательности каждого tf-го наблюдения при игнорировании всех прочих.
Таким образом, последовательность, имевшая прежде интервал дискретно-
сти ДГ, преобразуется в последовательность с интервалом дискретности
d&t. При этом новая частота Найквиста равна f'c = 1/(2<УД0, а составляю-
щие с более высокими частотами преобразуются (маскируются) переходом
в диапазон частот от 0 до 1/(2с?Д/). Чтобы избежать ошибок маскировки
t
Рис. 11.1. Удаление линейного тренда.
t
Цифровые методы анализа
361
частот, исходные данные следует предварительно пропустить через низко-
частотный фильтр, подавляющий компоненты с частотами выше
1 /(2dA t).Заметим, что эта операция не исключает необходимости фильтра-
ции из исходного ряда составляющих с частотами выше fc = 1/(2Дг) при
помощи низкочастотного аналогового фильтра.
Цифровым фильтром можно пользоваться как во временной, так и в
частотной области. Фильтрация в частотной области соответствует умно-
жению преобразования Фурье исходной реализации x(t) на частотную ха-
рактеристику фильтра H(f) и выполнению затем обратного преобразова-
ния Фурье. Если х (Z) — исходный ряд, то отфильтрованная последователь-
ность есть
ЯО = пт[я(/)Х(/)] , (11.17)
где IFT означает обратное преобразование Фурье, a X(f) — преобразование
Фурье реализации x(t). Такой способ фильтрации обладает рядом досто-
инств, к числу которых относятся простота понимания и отсутствие необ-
ходимости задавать аналитическое выражение для частотной характеристи-
ки фильтра. Однако он может оказаться громоздким и неэкономичным в
вычислительном отношении, если, как это часто бывает, длина исходного
временного ряда настолько велика, что его неудобно держать полностью в
памяти ЭВМ. В этих случаях фильтрацию приходится осуществлять по-
этапно для отдельных смежных отрезков исходного ряда.
Фильтры, применяемые во временной области, можно разбить на два
типа:
а) нерекурсивные фильтры, или фильтры с конечной импульсной пере-
ходной функцией (ФКИПФ)1).
б) рекурсивные фильтры, или фильтры с бесконечной импульсной пере-
ходной функцией (ФБИПФ).
Нерекурсивные фильтры (ФКИПФ) имеют вид
л/
У, = Е hkxi-k. (11.18)
* = 0
Эта формула представляет собой дискретный аналог уравнения свертки
(6.1) -оо
y(t) = h(r)x(t - т) dr, (11.19)
где h (т) — импульсная переходная (весовая) функция фильтра. Подобным
же образом [hk] есть импульсная переходная функция цифрового фильтра.
Примерами ФКИПФ могут служить классические приемы сглаживания, ин-
терполяции, экстраполяции, дифференцирования и интегрирования времен-
ных рядов.
Рекурсивным (ФБИПФ) называется цифровой фильтр, для которого
значение последовательности на выходе определяется не только конечным
числом прошлых значений исходного ряда, но также и предшествующими
11 Имеется в виду длина интервала, на котором импульсная переходная функция
отлична от нуля. — Прим, перев.
362
Глава 11
значениями выходного процесса, которые также рассматриваются как вход
фильтра (в технике это называется обратной связью). Простейшая запись
рекурсивного фильтра имеет вид
м
Уп = сх„+ £ hkyn_k, (11.20)
к=1
т. е. фильтр использует М значений выходного процесса и только одно
входного. В более общем случае число значений выходного процесса не ме-
няется, а число значений входного процесса возрастает. Формула (11.20)
иллюстрируется рис. 11.2, где треугольники обозначают операцию умноже-
ния на соответствующие величины, квадраты — задержку по времени на
Д/ между смежными точками и, наконец, окружность соответствует опе-
рации суммирования.
Преобразование Фурье равенства (11.20) дает
л/
У(/) = cX(f) + У(/) Е hke~^f^‘ , (11.21)
к = 1
причем сумма содержит многочлен по степеням экспоненты ехр(—у 2тг/Д/).
Обозначая последнее выражение символом z, можно воспользоваться для
изучения свойств цифровых фильтров теорией z -преобразований. Как сле-
дует из формулы (11.21), частотная характеристика всей системы имеет
ВИД y(f) с
~ 1(7) ” 1 - ’ (1L22)
Таким образом, изучение свойств частотной характеристики H(f) сводится
к определению положения и характера полюсов в знаменателе последнего
выражения.
Рассмотрим в качестве примера рекурсивный цифровой фильтр
Рис. 11.2. Схема простого рекурсивного фильтра.
Цифровые методы анализа
363
где а — ехр(— Д/ /RC). В непрерывном случае это выражение эквивалентно
низкочастотному ЯС-фильтру. Чтобы убедиться в этом, заметим, что, со-
гласно формуле (11.22),
1 — a z
Здесь квадрат амплитудной характеристики равен
|Ш)Р = 7Г1 24 о ЭМ,
(1 + а ) - 2ясо82тт/Д/
(11.25)
Отметим, что если RC > Д/, то а = ехр( — &t/RC) » 1 — Ы/RC и
1 — а » &t/RC. Если, кроме того, < 1, то справедливо приближен-
ное равенство ехр(—у2тг/Д/) » 1 — В этом случае
, |Н(/)|2«----------------7, (11.26)
’ \ + jlirfRC 1 4-(2w//?C)2
что соответствует обычному низкочастотному 7?С-фильтру.
Синтез рекурсивных цифровых фильтров, дающих хорошее приближе-
ние к фильтрам Баттерворта, может быть выполнен при помощи формулы
(11.22) путем нахождения последовательности весов [hk] и коэффициента с,
таких, что соответствующая им величина IH(f)\2 имеет вид
|Я(/)|2 =--------------------------— , 0 </< -Д- • (11.27)
1 + (sin77/Ar/sin?r/0 Д/)2 2 Д/
Заметим, что при/ = 0 значение \Н(/")12 = 1, а при/ =/0 квадрат модуля
частотной характеристики равен 1/2. На частоте Найквиста/ = 1/(2ДГ) ве-
личина Htf) при больших М стремится к единице. Таким образом, в интер-
вале (0, 1/2Дг), наиболее важном в дискретном случае, фильтр, описывае-
мый уравнением (11.27), ведет себя как низкочастотный фильтр Баттервор-
та:
|Н(/)|2 =------------г* (11.28)
1 + (///оГ
где /0 — частота, соответствующая половинной энергии, а величина К
определяет наклон кривой \H(f)\2. Более детальное описание математиче-
ских основ синтеза рекурсивных цифровых фильтров содержится в работах
[11.1 — 11.4].
ПРИМЕР 11.1. РЕКУРСИВНЫЙ ЦИФРОВОЙ ФИЛЬТР. Пусть исходный
временной ряд получен при скорости дискретизации, равной 1000 отсчетов
в секунду. Предполагается выполнить его низкочастотную фильтрацию с
помощью простого RC -фильтра с частотой пропускания по уровню поло-
винной энергии, равной/0 = 10 Гц. Требуется построить необходимый для
этой цели рекурсивный цифровой фильтр.
364
Глава 11
Согласно соотношению (11.26), частота пропускания по уровню поло-
винной энергии соответствует значению частотной характеристики
' W/ = тах 1//г' = ’/2 I/7(10)12 = 0,5. Поскольку в этом случае
RC > А/ = 10“3, имеем
1 + (20ттЯС)2
Таким образом, RC = 0,016 и а = ехр( —0,063) » 0,94. Этот результат
можно проверить подстановкой а = 0,94 в выражение (11.25), что дает
1/7(10)12 = 0,5. В соответствии с формулой (11.23) искомый низкочастот-
ный фильтр задается уравнением
У„ = 0,06х„ + 0,Муп_х.
11.2. Ряд Фурье и быстрое преобразование Фурье
Построение ряда и преобразования Фурье теоретически представляют
собой различные операции, но в большинстве практических приложений
численная реализация этих операций осуществляется одинаковым образом.
Это объясняется тем, что для дискретной реализации можно построить
ряд или преобразование Фурье только в конечном диапазоне частот, и этот
диапазон определяется значением периода при вычислении соответствую-
щего ряда Фурье. Как уже отмечалось в разд. 5.2.2, одна из основных при-
чин использования быстрого преобразования Фурье состоит в том, что оно
позволяет получить оценки спектральной плотности и ковариационной
функции. Прежде чем излагать алгоритм быстрого преобразования Фурье,
полезно рассмотреть, каким образом вычисляется обычный ряд Фуфье.
11.2.1. РЯД ФУРЬЕ
Если предположить, что реализациия x(t) — периодическая с периодом
Тр и фундаментальной частотой J\ = UTp, то ее можно представить ря-
дом Фурье
ао 00
х(‘)=~^ + И (aqcos2irqfxt + bqsm'l'nqfxt'), (11.29)
2 </=i
где
2 /’7
а = — / x{t)cos2irqfxtdt, ^ = 0,1,2,...;
/ •'о
2 7.7
bq = - J x(t)sm2-nqfxtdt, q=l,2,3,....
Пусть реализация x(t) имеет конечную длину Тг = Т, равную фунда-
ментальному периоду. Предположим также, что она состоит из четного
числа N эквидистантных наблюдений с интервалом дискретности Д/, кото-
Цифровые методы анализа
365
рый выбран таким образом, что частота Найквиста fc = 1/(2ДГ) достаточ-
но высока. Будем считать, что начальный момент реализации равен нулю, и
обозначим, как и прежде, преобразованную последовательность следую-
щим образом:
х„ = х(лДт), n = l,2,...,N. (11.30)
Вычислим теперь по всем N значениям реализации конечный ряд Фурье.
Для любой точки t, принадлежащей интервалу (0, Тр), этот ряд имеет вид
/ч Д2 (2irqt\ l2irqt\
x(t~) = A0 + E^os -— + Е ^sinl —- • (11.31)
<7=1 \ 1Р / q=l \ У I
В точках t = nbt (п = 1, 2, TV) где Т = пЫ, получим
Д2 (2irqn\ [2irqn\
Х„ = х(п bt) = Ао+ E^?c°s -— + Е —Г- • (11-32)
<?-! \ Л / Ч=1 \ " I
Коэффициенты Aq и Bq определяются выражениями
1 £
Ао = Е х„ = X = о?
7V М=1
2 2^ 'lirqn N
Aq= ~ E^os—, <7 = 1,2,—lj
1 £
AN/2 = E X „COS П1Т,
7V M=1
2 Д 'I'rrqn N
"‘'2.... 2'1'
Программа для расчета величин Aq и Bq должна содержать следующие
операции:
1) определение величины 6 = I'wqn/N при фиксированных значениях q и п;
2) вычисление cos0, sin0;
3) вычисление xncos0, хл8Ш0;
4) вычисление суммы для каждого из этих выражений при п = 1, 2, ..., N;
5) приращение аргумента q на единицу и повторение всех перечисленных
действий.
Такой способ требует выполнения примерно N2 операций умножения и
сложения действительных чисел.
Поскольку затраты машинного времени и стоимость расчетов зависят
366
Глава 11
от N2, при больших N такой стандартный метод вычисления коэффициен-
тов A q nBq может оказаться дорогостоящим и потребовать значительного
времени. Чтобы существенно снизить затраты машинного времени, были
разработаны и введены в практику другие способы расчета, получившие
название «быстрое преобразование Фурье» (БПФ). Рассмотрим детально
эти важные методы, применяемые для цифрового анализа случайных про-
цессов.
11.2.2. БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
Преобразование Фурье действительной или комплексной функции х(/),
заданной на бесконечном интервале, представляет собой комплексную ве-
личину
/•00
*(/)=/ x(t)e~^f'dt. (11.34)
- 00
Если область интегрирования не ограничена, то, как уже отмечалось ранее,
преобразование X(f) не существует, когда реализация x(t) обладает всеми
свойствами стационарного случайного процесса. Ограничив интервал зада-
ния функции х(Г), скажем приняв его равным [О, Г], можно построить фи-
нитное преобразование Фурье
%(/,Г) = (Tx(t)e~Wdt. (11.35)
Л)
Предположим теперь, что функция x(t) представлена N эквидистантны-
ми наблюдениями с интервалом дискретности ДГ, который выбран таким
образом, что частота Найквиста достаточно высока. Поскольку /0 = О,
моменты tn = п At (в данном случае удобно начать с п = 0). Формула
(11.30) запишется в виде
хп = х(п kt), и = 0,1,2,..., TV — 1 .
Дискретная аппроксимация выражения (11.35) при произвольном значении
f есть V-1
%(/, Г) = Д/ Е х„ехр[-у2я-/лД/] . (11.36)
и = 0
Для расчета функции X(f, Т) обычно выбираются дискретные значения ча-
стоты
к к
fk = - = —r, к = 0,1,2,..., N - 1 . (11.37)
Jk Т Nbt ’ v '
Преобразованная последовательность дает на этих частотах составляющие
Фурье
, = *(Л)
к Д/
У-1
Е
/? = ()
2тткп
к = 0,1,2,..., N - 1, (11.38)
причем интервал дискретности At внесен в значение X(fk), чтобы перед
Цифровые методы анализа
367
знаком суммы не было множителя. Заметим, что преобразование одно-
значно только до значений к = N/2, поскольку этой точке соответствует
частота Найквиста. Быстрое преобразование Фурье применяется для вы-
числения последовательности Xki но может быть также использовано для
нахождения коэффициентов Фурье Aq и Bq из формул (11.33).
Упростим обозначения, положив
2тги1
Ж(и) = ехр (11.39)
Заметим, что W(N) = 1 и при всех и и v справедливо равенство
Ж(и + и) = Ж(и)Ж(и).
Положим также Х(к) = Хк, х(п) = хп. Формула (11.38) примет теперь вид
N-1
%(Л)= ^х(«)Ж(Ь), к = ОДЛ---,#- 1- (11-40)
и = 0
Следует внимательно рассмотреть равенства (11.38) и (11.40), представляю-
щие собой не что иное, как преобразования Фурье последовательности
х(п), содержащей конечное число N членов. Для расчета всех значений
Х(к) по этим формулам необходимо выполнить примерно N2 операций ум-
ножения и сложения комплексных чисел (одна такая комплексная операция
эквивалентна четырем операциям умножения и сложения действительных
чисел).
‘ Идея быстрого преобразования Фурье. Быстрое преобразование Фурье
основывается на представлении величины N в виде ряда (отличных от еди-
ницы) сомножителей и в выполнении обычного преобразования Фурье для
более коротких последовательностей, число членов в которых определяется
соответствующими сомножителями. Если N может быть представлено в
виде произведения р целых и больших единицы чисел:
р
N = ГЕ = гл • • • rPi (и-41)
то, как доказано ниже, входящая в соотношение (11.40) последовательность
Х(к) может быть найдена итеративно путем расчета суммы р слагаемых:
N/ т\ — преобразований Фурье, каждое из которых требует 4/*j
операций с действительными числами;
N/г2 — преобразований Фурье, каждое из которых требует 4г^
операций с действительными числами; (П-42)
N/rp— преобразований Фурье, каждое из которых требует
4г^ операций с действительными числами.
Таким образом, общее число операций над действительными числами со-
368
Глава 11
ставляет
Р
4(Угх + Nr2 + Nr3+ ••• +Nrp) = 4N^r,. (П.43)
/ = 1
В результате при использовании БПФ, а не стандартного метода получаем
коэффициент ускорения вычислений (к.у.в.)
ДГ2 N
к.у.в. = ---------- = -------- •
4NLf=1r, 4'Lf’,lrl
ПРИМЕР 11.2. КОЭФФИЦИЕНТ УСКОРЕНИЯ ВЫЧИСЛЕНИЙ ДЛЯ N = 2Р,
ГДЕ р — ЦЕЛОЕ ЧИСЛО. Если N = 2Р, то
р
rt = 2р = 21og2N.
/=1
В этом случае, согласно формуле (11.44),
2V2 N
к.у.в. = --- = --- •
8Np Ър
Однако скорость вычислений можно увеличить еще вдвое, используя следу-
ющее свойство: при N = 2р все значения W(kn) равны либо 1, либо — 1,
так что соответствующие операции умножения заменяются сложением и
вычитанием. Таким образом,
N
к.у.в. = — • (11.45)
В частности, при N = 213 = 8192 из формулы (11.45) получаем:
к.у.в. = 8192/52 » 158. Но и этот результат представляет собой лишь кон-
сервативную оценку; в действительности можно добиться нового двукрат-
ного увеличения скорости, разделив исходную реализацию пополам и про-
изводя расчет, как указано в разд. 11.24.
Построение метода. Для получения результата, постулированного в
(11.42), представим индексы к и п из формулы (11.40) в виде
^+1 -1,
(11.46)
Рр — V 1 >
Отметим, что теперь индексы к и п заменены индексами kv и nv. Послед-
ние формулы можно переписать в виде
Цифровые методы анализа
369
к = к0 + кхгх + k2rxr2 + • • • + kp_l(rlr2 ,
(11.47)
n = n0 + nxrp + n2rprp_l + • • • + np_1(rprp_1 r2),
k0 = 0,1,2,..., i\ - 1 , n0 = 0,1,2,..., rp - 1,
kx = 0,1,2,..., r2 - 1, = 0,1,2,..., rp l - 1,
^_1 = 0,1,2,...,^- 1, np_x = 0,1,2,..., f! - 1.
Фиксируя поочередно kv и nv, можно непосредственно убедиться в том, что
величины кип принимают значения от 0 до N — 1, где N есть произведе-
ние всех значений г, (см. равенство (11.41)). Перепишем теперь формулу
(11.40) в виде
Х(к) = Х(к0, кх,... ,kp-J =
= У Е1 х(п0,П1,...,Пр.2,пр_^(кп),
И0 = 0 И!=0 '’r2=0"r-l=0
где (11.48)
Jk'(kn) = w(k [л0 + пхгр+ ••• +пр_„(гргр~х • r,+i) + ••• +
+ пр-1(гргр-1 гг)])» (П.49)
а величина к определена равенством (11.46).
Другой способ представления величины к заключается в следующем:
к = (к0 + кхгх + • • • + к„_хгхг2 +
+ (''1'2 ••• г^(к> + *г+Л+1 + •• +kp-ir, + 1r„+2 rp_l).
Следовательно, в формуле (11.49)
кпр-ЛГрГр-1 Г- + 1) = (ко + к1г1 + ••• +к„-1Гхг2 ••• Г„_!)Х
*”р-ЛГрГр_х ••• г,+ 1) +
+ Nnp_„(k,. + ^.+1^4 1 + ••• +
+ кр-1г,+Л+2 • • rp-ih (11-50)
370
Глава 11
Далее величина W для любого аргумента, кратного 7V, равна единице, поэ-
тому при v = 1, 2, ... р
W(knp_vrprp^x r„+1) = W[(к0 + к{гг + • • • +к„_гг1г2 • • r^-Jx
Xnp_,rprp_1 ••• r„+1].
(И-51)
Рассмотрим последнее равенство подробнее. При v = 1 имеем
••• гг)= ^(^0Пр-1Гргр-1 г2) =
TJ konP-iN\
= W\--------- = ехр
2irkonp^l
(U-52)
Мы получили экспоненциальное выражение для преобразования Фурье
функции х(пр_х), состоящей из а не из N членов (см. формулы (11.36) и
(11.40)). Заметим, что переменные kQ и пр_{ принимают значения от 0 до
— 1, и потому для расчета каждого значения X (к 0) нужно всего rf опера-
ций умножения и сложения. Имея в виду равенство W(u + v) = W(u)W(v),
нетрудно показать, что при v = 2, 3, ... р формула (11.51) принимает вид
произведения
1Г[(^0 + к1Г1 + • • • + к,-2Г1Г2 • • Гг+1] X
^(k^iV2 ••• ••• 'V+i), (11-53)
в котором только второй сомножитель содержит величину kv_{. Этот со-
множитель представляет собой выражение
(11-54)
т. е. экспоненту, необходимую для преобразования Фурье функции x(np_v),
состоящей из rv членов. Заметим, что переменные кр_х и пр_р принимают
значения от 0 до гv — 1. Следовательно, для вычисления каждого значения
X(kv_x) нужно всего г2р операций умножения и сложения.
Алгоритм БПФ. С учетом преобразований (11.50)— (11.52) уравнение
(11.49) можно записать в виде
-Д- / kv-\nn-vN
W(kn) = ---------
»=i \
(И-55)
где
Цифровые методы анализа
371
Т(/с0, • • • > kv-i)
f 1, v = г,
^[(^0 + кру + • • • + k,_2r1r2 • • • г„_2)х
x(nP-,VP-l ••• r,+i)] ,
< v = 2,3,..., р .
(11.56)
Величины типа Т часто называют «ориентирующими коэффициентами».
Подставив выражение (11.55) в формулу (11.48), получим
«о = 0 \ Гр j
Г'’^1 / х
X Е Т(к0,к3,...,к 3 1Г -^--1 Х...Х
«1=0 \ гР-1 /
Г2 1 ( kxnn_2N \
X Е Ш0М X
"„-2 = ° V Г2 /
r'-1 / knnn-iN \
X Е x(n0,nl,...,np_2,np_1)W\------------- . (11.57)
"Р-!=о \ ri /
Таким образом, согласно формуле (11.57), искомое преобразование Фурье
может быть построено за р итераций. Теперь следует остановиться на
этом итеративном методе более подробно.
Рассмотрим последнюю внутреннюю сумму в формуле (11.57). Пусть
/ \ lko”P-iN\
по> np-2j= Е х(п0, «!,•••, пр_2, .
»,-1=0 \ Г1 /
(11.58)
Имея в виду все возможные значения, которые могут принимать величины
и0, ..., ир_2, найдем, что уравнение (11.58) дает N/r2 преобразований
Фурье функции х(пр_ j), каждое из которых требует rj операций. Рассмот-
рим теперь следующую внутреннюю сумму в формуле (11.57). Пусть
А2(к0,к1,п0,п1,...,пр_3) =
/ х (kinn.N\
= Е Al(k0,n0,nl,...,np_2)T(k0)W\ -1 р 2 (11.59)
"„-2 = 0 \ Г2 /
372
Глава 11
Тогда, имея в виду все возможные значения, которые могут принимать ве-
личины kQ, п0, nif ..., пр_3, найдем, что уравнение (11.54) дает N/r2 преоб-
разований Фурье функции х(Ир_2)5 каждое из которых требует г2 операций.
Продолжая эти рассуждения до р-го шага, где v = 2, 3, ...,р — 1, поло-
жим
= Е Л-iUo-^-2> «о, "п---
I kv_,nn__vN \
ХГ(А:0Др...Ду_2)И . (11.60)
\ Гр )
И вновь, имея в виду все возможные значения, которые могут принимать
величины kv ..., kv_2, nQ, nv ..., np_v_v получим N/rv преобразова-
ний Фурье функции x(np_v)9 каждое из которых требует rj операций. На
последнем шаге формула (11.57) дает
%(Zcq, fcp ..., ZCp.j) = Ap(kQ, kx,..., kp-^ =
rp~ 1
= 52 ^-1(^0’ • • • ’ По)Х
z?o = O
X т(к0, kx,..., kp_2)w\ -p-1 (11.61)
\ rp /
откуда, имея в виду все возможные значения величин kQ, к р ..., кр_2, по-
лучим N/rp преобразований Фурье функции х(и0), каждое из которых тре-
бует гр операций. Последовательность действий, определенная равенствами
(11.58) — (11.61), приводит к результату, постулированному в (11.42), при-
чем комплексные числа теперь заменены действительными.
Выражение (11.60) и есть алгоритм быстрого преобразования Фурье; оно
служит основой для многих применяемых сейчас численных методов расче-
та преобразования Фурье. Более детальное рассмотрение содержится в кни-
ге (11.5).
11.2.3. МЕТОД КУЛИ — ТЬЮКИ
Описанный в 1965 г. в работе [11.6] метод Кули — Тьюки представляет
собой вариант алгоритма (11.60); этот метод особенно удобен для реализа-
ции на ЭВМ с двоичной системой счисления. В частности, он применим в
случаях, когда число анализируемых ординат равно
N = 2Р. (11.62)
Чтобы удовлетворить этому требованию, можно при необходимости до-
Цифровые методы анализа
373
полнить последовательность нужным числом нулей. Определяющая итера-
ционную процедуру формула (11.57) содержит теперь р сумм, каждая из
которых дает N/2 преобразований Фурье, и для расчета каждого преобра-
зования нужны четыре операции. Таким образом, всего необходимо произ-
вести 2Np операций умножения и сложения комплексных чисел.
Желательно теперь отдельно выписать уравнения для этого весьма важ-
ного частного случая. Это делается просто подстановкой нужных величин
в предыдущие формулы. Формула (11.47) принимает вид
k = kQ + 2k1 + 22к2 + • • • + 2p~1kp_i,
п = nQ + 2п1 4- 22п2 4- • • • + 2р~1пр_1, (11.63)
где величины кип могут иметь только значения 0 и Для всех v =
= 1, 2, ...» р2 уравнение (11.54) переписывается в виде
кг-\.пр,\ = CXp(-jvkr_xn ), (11.64)
\ /
причем эта экспонента может быть равна только 1 или — 1. Вместо форму-
лы (11.56) имеем
Г 1, V= 1;
Т(к0,кх,...,к^2) = \ w[(k0 + 2k} + +Т-2к,_2)2р-рпр_^
L v = 2,3,..., р. (11.65)
Итерационное преобразование Фурье (11.57) можно записать для этого
частного случая следующим образом:
Х(Л0Л1,...,^_1) =
= Е L ••• L Е x(n0,nx,...,np_2,np~x)W(kn), (11.66)
И0 = 0Л1=° пр-2 = () Пр-1 =
где
р
W(kn) = П kx,...,kv_2Yxp(-jnk,,_xnp_,,).
V = 1
Согласно уравнению (11.58), первая итерация дает
1
Ах{к0,п(х,пх,...,пр_2) = £ *(«о- пх,..., пр_2. np_l)exp(—jirkonp_l
В правой части уравнения.— Прим, перев.
374
Глава 11
На р-м шаге (при v = 2, 3, ...,р — 1) уравнение (11.60) запишется следую-
щим образом:
А„(к0, кх,...,кр_х, п0, Лр..., =
1
= Е Аг_1(к0,к1,...,кр_2, и0, Пр..., пр_р)х
np_v = Q
ХТ(к0, Л15... Д,_2)ехр(-Л^г_1л/,_г). (11.68)
Это и есть алгоритм быстрого преобразования Фурье по Кули — Тьюки.
Последняя итерация (уравнение (11.61)), принимающая вид
%(Л0, ..., ^_х) = ^1» • • • > кр-1) =
1
= И ^р-1(^0> ^1’’ •• по)х
z?o = O
X r(fc0,£1,...,£p_2)exp(-j^p_1«0)> (11.69)
завершает последовательность действий для этого частного случая. Более
подробное обсуждение метода содержится в работах [11.2 — 11.6].
11.2.4. ПРИМЕНЕНИЕ К ДЕЙСТВИТЕЛЬНЫМ ПОСЛЕДОВАТЕЛЬНОСТЯМ
Если даны две действительные реализации х(п) и у (и), то их преобразо-
вание Фурье можно вычислить одновременно, приравняв одну реализацию
действительной, а другую мнимой частям некоторой комплексной реализа-
ции
г(и) = х(и) + /у(л) ? п = 0,1,..., N - 1 . (11.70)
Согласно формуле (11.38), преобразование Фурье функции z(n) имеет вид
W-1
Е [*(”) +7>(«)]ехр
/7 = 0
2 77 кп
~J N
к = 0,1,2,..., У - 1,
(11-71)
и может быть рассчитано по алгоритму БПФ. В формулах (11.70) и (11.71)
обычно преполагается, что N ординатам реализаций х(и) и j(/?) соответст-
вует N значений частот, отстоящих друг от друга на величину \/Т. При
этом частоте Найквиста отвечает значение к = 7V72. Поэтому при N чет-
ном однозначные результаты получаются только для значений к = 0, 1, 2, ...,
N/2 - 1. Для получения функций Х(к) и Y(k) заметим, что
2irn(N — к)
exp j
= ехр
2тгпк
N
N
Цифровые методы анализа
375
поскольку ехр(/2тгл)= 1 при любых п. Следовательно, комплексно-сопря-
женная функция равна
Z*(2V-fc) = £ [х(и) -;>(и)]ехр -j—jj-
л = 0 N
Тогда
W-1
Z(k) + Z*(W - к) = 2 £ х(и)ехр
Л7 = 0
2ъпк
~J N
= 2Х(к),
N-1
Z(k) - Z*(N - к) = 2j У. j(n)exp
п — 0
2чтпк
~J N
= 2;У(Л).
Таким образом, преобразования Фурье Х(к) и Y(k) двух действительных
реализаций х(п) и у(п) имеют вид
, ч Z(k) + Z* (N — к)
Х(к) = ———----
Z(k) — Z*(N - к) ^0,1,...,N-1. (11.72)
Тем же приемом можно воспользоваться для расчета преобразования на
интервале вдвое большей длины. Для этого вещественная реализация v(n)
(п = 0, 1, ..., 2N — 1) разделяется на две части, и одна часть состоит из
значений v(n) при четном п, другая — при нечетном п. Иными словами,
х(п) = р(2л), у(п) = v(2n + 1),
п = 0,1,2,..., N-1.
(11.73)
Пользуясь теперь формулой (11.71), вычислим преобразование Фурье по-
следовательности z(n) = х(п) + jy(n) (п = 0, 1, ..., N — 1), а затем по
формуле (11.72) найдем преобразования Фурье последовательностей х(п) и
у(п). Их объединение дает искомое преобразование Фурье последователь-
ности v(n) в виде
V(k) = Х(к) + У(^)ехр -j— ,
V(N + к) = Х(к) - У(^)ехр[-7^],
к = 0,1,..., N - 1.(11.74)
Заметим, что этот способ позволяет выполнить преобразование Фурье 2N
действительных чисел путем преобразования комплекснозначной последо-
вательности, состоящей из N чисел.
376
Глава И
11.2.5. НЕКОТОРЫЕ ДРУГИЕ ФОРМУЛЫ
В соответствии с (11.34) обратное преобразование Фурье имеет вид
*(') = Г X(f)e^‘df.
J - 00
(И-75)
Аналогичная формула для дискретного обратного преобразования Фурье
есть
1 2ккп'
Е **ехр J —
J’ А=0 L ,у
п = 0,1,2,..., N - 1. (11.76)
где заданные равенством (11.38) коэффициенты Фурье вычисляются с по-
мощью процедуры БПФ. Постоянная 1/N в формуле (11.76) представляет
собой лишь масштабный множитель и не имеет другого смысла. Это об-
ратное преобразование Фурье можно выполнить с помощью тех же мето-
дов БПФ, что и ранее, для чего нужно поменять местами символы к и п и
заменить хп наА^, a W(kn) на W(—kn).
В заключение этого раздела следует отметить, что БПФ всегда осу-
ществляется над функциями с неотрицательным значением независимой пе-
ременной, а его результат также есть функция неотрицательного аргумен-
та. В частности, исходная функция x(t) всегда определяется на интервале
от 0 до Г, а не на интервале от —Т/2 до 772. Аналогичным образом пре-
образование X(J) задается на интервале 0 f 2/с, а не — fc f fc.
В дискретной форме хп = x(n^t) (п = 0, 1, ..., N - 1) и Х(к) =
/X(k/NAt)/At (к = 0, 1, ..., N - 1) причем значение к — N/2 соответст-
вует частоте Найквиста /, определенной равенством (10.12). Однако из
(11.72) видно, что
Х(к) = X*(N - к), к = 0,1,..., N - 1, (11.77)
и потому частоты выше N/2 можно при желании рассматривать как от-
рицательные и получить таким образом двустороннюю спектральную
функцию (рис. 11.3).
11.2.6. ПРЕОБРАЗОВАНИЕ ВИНОГРАДА
Способы дискретного преобразования Фурье постоянно обновляются.
Большинство модификаций БПФ подстроено под решение специальных за-
дач или аппаратурную реализацию. Особого упоминания заслуживает раз-
работанный Виноградом (см. работу [11.7]) новый метод, основанный на
совершенно ином подходе. По сути дела, он заключается в преобразовании
одномерной последовательности в многомерный массив, каждая компонен-
та которого совпадает с одним из N значений исходной последовательно-
сти. Затем этот массив подвергается преобразованию Фурье и вновь преоб-
разуется в одномерную последовательность как функция частоты. Преоб-
разование последовательности в массив осуществляется на основе пред-
ставлений, заимствованных из теории чисел с использованием так называв-
Цифровые методы анализа
377
Рис. 11.3. Пример поведения коэффициентов Фурье, вычисленных методом БПФ
при N = 16: а — вычисленные значения коэффициентов; б — транспонированные
значения, задающие двусторонний спектр.
мой китайской теоремы об остатках. Теория и реализация преобразования
Фурье методом Винограда существенно сложнее, чем в случае использова-
ния БПФ, описанного в разд. 11.2.2. Кроме того, процесс преобразования
последовательности в массив требует расширения объема памяти, в кото-
рой хранятся данные, и получить преобразованный ряд на месте исходного
378
Глава 11
в рамках этого алгоритма невозможно. Несмотря на эти недостатки, алго-
ритм Винограда приобретает все большую популярность, поскольку он, во-
первых, позволяет существенно сократить расход машинного времени и,
во-вторых, легко обобщается на алгоритмы с основанием более 2 и на ал-
горитмы со смешанным основанием1^ Более подробно о методе Винограда
см. в работе [11.7].
11.3. ПЛОТНОСТЬ ВЕРОЯТНОСТИ
Рассмотрим N значений [хл] (п = 1, 2, ..., N) преобразованной реали-
зации x(t) стационарного случайного процесса с нулевым средним значени-
ем х. Согласно уравнениям (3.4) и (8.64), плотность вероятности функции
x(t) можно оценить в виде
р(х) = NX/(NW), (11.78)
где W — узкий интервал, симметричный относительно точки х, Мх — чис-
ло значений реализации, попадающих в интервал х ± W72. Таким обра-
зом, численную оценку плотности вероятности р(х) находят путем разбие-
ния всего диапазона значений функции х на соответствующее число равных
по величине интервалов, табулирования величин х по интервалам и делени-
ем на ширину интервала IF и объем выборки N. Заметим, что оценка р(х)
не однозначна, поскольку она зависит, очевидно, от числа интервалов и их
ширины.
Дадим теперь формальное описание метода. Пусть К — число интерва-
лов, которые охватывают весь диапазон [a, Z?] изменения функции. Ширина
каждого интервала
И^=—, (11-79)
К
а верхняя граница /-го интервала равна
dt = а + iW, i = 0,1,2,..., К. (11.80)
Заметим, что dQ = а и dK = b. Определим теперь последовательность из
К 4- 2 чисел [Nj] (i = 0, 1, 2, ..., К 4- 1) из условий
NQ = число значений х, удовлетворяющих неравенству х dQ;
= число значений х, удовлетворяющих неравенству d0 < х df,
— число значений х, удовлетворяющих неравенству dt_ j < х df, (11.81)
NK — число значений х, удовлетворяющих неравенству dK__ }<х dK;
= число значений х, удовлетворяющих неравенству dK < х dK+v
11 Имеются в виду случаи, когда длина ряда N есть целая степень числа, боль-
шего 2, или представляет собой произведение целых степеней различных чисел. —
Прим, перев.
Цифровые методы анализа
379
В результате N значений последовательности х будут отсортированы та-
ким образом, что последовательность чисел будет удовлетворять усло-
вию
К+1
N = (11.82)
/ = 0
Один из способов выполнения этой сортировки на ЭВМ состоит в рассмот-
рении последовательных значений хп (и = 1, 2, ..., 7V) следующим обра-
зом:
1. Если хп а, то прибавить единицу к N0.
2. Если а < х Ь, то вычислить I = (хп - a)/W. Затем выбрать i как
наибольшее целое цисло, меньшее или равное I, и прибавить единицу к Nz .
3. Если хп > Ь, прибавить единицу к NK+V
Можно пользоваться четырьмя различными итоговыми формами после-
довательности [Nj]. Первая форма представляет собой гистограмму, т. е.
просто последовательность без всяких изменений. Вторая форма —
выборочные процентные значения процесса в каждом интервале, определя-
емые для / = 0, 1, 2, ..., К 4- 1 в виде
7V.
Р, = Р k,-1 <*<<]= ~ (11.83)
Третья форма — последовательность выборочных значений плотности ве-
роятности IpJ, определенных в виде
A к \
-----------------Ь /= 1,2,..., К. (11.84)
W \N )\b — aj v 7
Четвертая форма — последовательность выборочных значений функции
распределения определенных для концевых точек интервалов в виде
/ Z
P(z) = P[-00 <х<<]= £р7= . (11.85)
7=0 у=0
11.4. Ковариационные функции
Существует два способа вычисления ковариационных функций. Прямой
способ заключается в вычислении среднего значения произведений случай-
ных переменных, образующих выборку. Косвенный прием требует вычис-
ления вначале оценки спектральной плотности с помощью БПФ и ее после-
дующего обратного преобразования. Прямой способ проще для програм-
мирования и логичнее с точки зрения основных определений. Преимуще-
ство второго подхода заключается в возможности существенно повысить
экономичность расчетов путем использования БПФ и потому обходится за-
метно дешевле.
380
Глава 11
11.4.1. НЕПОСРЕДСТВЕННОЕ ОЦЕНИВАНИЕ КОВАРИАЦИОННОЙ ФУНКЦИИ
Рассмотрим N значений случайной переменной [хп] (п = 1, 2, ...,?/),
выбранных через одинаковый промежуток времени Az из реализации
x(t) = х(пМ), принадлежащей стационарному процессу и имеющей среднее
значение х = 0. Согласно основному определению (8.90), оценка ковариа-
ционной функции реализации x(t) при задержке по времени г Az вычисляется по
временному ряду хп в виде
^хл(гД/) = Е х„х„+г , г = 0,1,2,..., т , (11.86)
Г И = 1
где г называется сдвигом, ат — максимальным сдвигом (т < N)*\ Заме-
тим, что число возможных произведений при сдвиге г в уравнении (11.86)
есть N — г. Следовательно, для получения несмещенной оценки ковариаци-
онной функции деление в правой части уравнения следует производить на
N — г. Число операций умножения и сложения действительных чисел, нуж-
ное для получения ковариационной оценки, равно примерно Nm (предпола-
гается, что т <с N).
11.4.2. ОЦЕНИВАНИЕ КОВАРИАЦИОННОЙ ФУНКЦИИ МЕТОДОМ БПФ.
Косвенный способ оценивания ковариационной функции основан на ис-
пользовании соотношений Винера — Хинчина (5.28). Оценка ковариацион-
ной функции находится как обратное преобразование Фурье оценки спект-
Рис. 11.4. Пример эффекта цикличности при вычислении ковариационной функ-
ции методом БПФ.
Точнее, т < N. Более подробно см., например: Яглом А.М. Корреляционная тео-
рия стационарных случайных функций. — М.: Гидрометеоиздат, 1981, с. 65—77. —
Прим, перев.
Цифровые методы анализа
381
ральной плотности. Поскольку в основе финитного преобразования Фурье
лежит допущение о периодичности, получаемая таким путем ковариацион-
ная функция имеет «циклический» характер. Это присходит потому, что в
алгоритме БПФ исходная последовательность длиной Т = N&1 рассматри-
вается по сути дела как реализация одного периода периодической функ-
ции. Потому, как показано на рис. 11.4, вычисляемая таким путем ковариа-
ционная функция как бы представляет собой ковариационную функцию пе-
риодической последовательности. Для момента времени t} и запаздывания
Тр удовлетворяющих условию Т — tx < тр произведение x(t^x(tx 4- Tj) =
= x(tx)x(tx - Т + Tj). Следовательно, получаемая таким образом оценка
будет содержать вклад как от /^(т), так и от R^T — т).
Для количественной оценки этих вкладов поступим следующим обра-
зом. Пусть X(f) и %*(/) — преобразование Фурье реализации x(t)
(О Т), и его комплексное сопряжение равно
У*(/) = frx(a) е'2*/а da , X(f) = Cxtfi) е~>2”№ d/3. (11.87)
•'о Jo
Очевидно, что
1*(/)|2= Г fTx(a)x(0)[e^l3-a>]d0da. (11.88)
Jo Jo
Произведя замену переменных т = /3 — а, так что dr = d0 и 0 = а + т,
перепишем равенство (11.88) в виде
|^(/)|2 = [Г °х(а)х(а + т) е-72я/т drda . (11.89)
•'О J-a
Согласно (5.67), оценка двусторонней функции спектральной плотности ре-
ализации х(() ищется в виде
Sxx(f) = --U[|*(/)|2] = 7fTfT~aRxx(T)e-^dTda. (11.90)
J 1 J-a
Меняя порядок интегрирования (см. рисунок ниже), получим
382
Глава 11
sxx(f) =^f Г kA?) e-^dadr +
1 J - T
+ ~ Г Г Xx(T) da dr =
1 ‘'о ‘'O
I/O A
= -/ (T+r)Rxx(r)e~^dr +
1 J -T
+ ^jT{T-r)Rxx(r)e~^dr. (11.91)
1 Jo
Положив и = — т и du = — dr в первом слагаемом правой части (11.91),
получим
f (Т+т)Лхх(т)е->2^^т= fT(T-u)RxAu)e^udu,
J -т •'О
где вместо Rxx(-u) подставлено Кхх(ц)> Произведя еще одну замену
т = Т — и, dr = —du, получим
[\т - u)Rxx(u) е^“ du = ГrRxx(T - т) е->^ dr.
•'о уо
При получении этого равенства использован тот факт, что для любого зна-
чения/ = fk = к Af = к /Т и целого к величина ехр(/2т/Т) = 1. Таким об-
разом, формула (11.91) эквивалентна равенству
кАП = 7 (TrRxAT-r) e-^dr + 1 (Т(Т- r)Rxx(r) dr =
1 •'О 1 Jo
= №хх(т) е->^ dr, (11.92)
где
кМ = -^^-Лхх(т) + уЛхх(Т - т). (11.93)
Отсюда следует, что обратное преобразование Фурье функции ^(У), заданной
соотношением (11.92), даст функцию /?^(т), определенную формулой (11.93). В
случае дискретной последовательности [xj (п — 0, 1, ..., N - 1) отвечающая
формуле (11.93) циклическая ковариационная функция принимает вид
Л N - г г - г
Я<хх(гД/)= —Лхх(гД/)+ -/?хх[(у_г)Дг]. (11.94)
Поведение слагаемых в первой части этого равенства показано на рис. 11.5.
При быстро затухающих ковариационных функциях эффект цикличное-
Цифровые методы анализа
383
Рис. 11.5. Пример циклической корреляционной функции.
ти не играет особенно важной роли в практических расчетах для значений
максимального сдвига порядка т < О, 12V. Во всяком случае, этого ослож-
нения можно избежать, дополняя исходный временной ряд нулями. В ре-
зультате этого происходит разделение обеих частей циклической оценки ко-
вариационной функции. В частности, при добавлении N нулей к исходному
временному ряду той же длины N происходит полное разделение.
(N - г) „
——Rxx(r^)>
(г - N) Л _
——Rxx[(2N-r)bt],
r = 0,l,...,N - 1,
г = N,N + 1,...,2W - 1.
(И.95)
Обе части соотношения (11.95) показаны на рис. 11.6. Заметим, что первая
половина этой оценки (при 0 г N — 1) представляет собой значения
ковариационной функции при положительных значениях сдвига (0 г т),
а вторая (при TV г 2/V — 1) — при отрицательных значениях сдвига
(—т г 0). Но поскольку ковариационная функция есть всегда четная
Рис. 11.6. Изменение ковариационной функции при добавлении нулевых значе-
ний к исходному ряду.
384
Глава 11
функция г, вторую половину можно отбросить, и окончательно несмещен-
ная оценка ковариационной функции находится в виде
N А
^-(^0= г = 0,1,...,N-1. (11.96)
Оценка (11.96) статистически эквивалентна прямой оценке (11.86). Одна-
ко в зависимости от величины максимального сдвига т такой косвенный
метод с использованием БПФ может потребовать заметно меньшего объе-
ма вычислений. Действительно, косвенный метод требует нахождения вна-
чале оценки спектральной плотности, для чего осуществляется БПФ по nd
независимым реализациям, каждая из которых содержит N отсчетов и до-
полнена N нулями, так что БПФ производится для реализаций длиной 2N.
Затем 2N значений сглаженной спектральной оценки подвергаются обрат-
ному преобразованию Фурье, что в общей сложности дает nd -I- 1 быстрых
преобразований Фурье, каждое из которых требует 4Np операций над дей-
ствительными числами (см. разд. 11.2.2). Для реализации эквивалентного
объема ndN прямой метод расчета требует примерно mndN операций. Сле-
довательно, при одном и том же максимальном сдвиге т = N коэффици-
ент ускорения вычислений равен
ndN2 N
к.у.в. = 7----- — (11.97)
(nd + l)47V/> 4р
Например, при = 1024 = 210 имеем к.у.в. = 1024/40 « 26. На практике
же благодаря тому, что оценки автоспектра и автоковариационной функ-
ции строятся для последовательностей действительных чисел, применение
БПФ позволяет повысить скорость расчета еще вдвое (см. разд. 11.2.4).
Рекомендуемая последовательность операций для получения оценки ко-
вариационной функции методом БПФ описана ниже в предположении, что
длина исходной реализации есть Nnd и N = 2Р.
1. Выбирается максимальный сдвиг т и исходная реализация разбивает-
ся на nd отрезков, каждый из которых состоит из N т отсчетов.
2. Каждый отрезок (л = 1, 2, ..., N) дополняется N нулями, в ре-
зультате чего новая последовательность содержит 2N членов.
3. По формуле (11.36) при замене N на 2N рассчитывается 2/V значений
последовательности X(fk) (к = 0,1, ..., 2N — 1).
4. По приводимой ниже формуле (11.101) рассчитывается оценка двусто-
ронней спектральной плотности ^(Д) к = 0,1, ..., 2N - 1.
5. По соотношению (11.76) при замене N на 2N, Хк на и хп на
/?^(гД/) осуществляется обратное БПФ последовательности даю-
щее оценку /?^(гД/) (г = 0, 1, ..., 2/V - 1).
6. Вторая половина значений Я^^-Дг) отбрасывается, и сохраняются
лишь результаты для г = 0, 1, ..., N — 1.
7. Искомая оценка R^r&t) находится умножением 7?^(гД/) (г = 1, 2, ...,
N - 1) на масштабные коэффициенты N/(N — г).
Цифровые методы анализа
385
Следует отметить, что обратное преобразование, выполняемое на ша-
ге 5, требует использования всех значений спектральной оценки ^XX(J^
{к = 0, 1, ..., 2N — 1), несмотря на то, что частота Найквиста отвечает
значению к = N. Дальнейшее обсуждение этого вопроса содержится в
разд. 11.5.1. Следует также иметь в виду, что, согласно разд. 8.4, диспер-
ция оценки ковариационной функции обратно пропорциональна величине
2BeTr = Nnd. Поэтому при достаточно большом N приемлемую оценку ко-
вариационной функции можно получить, выполнив БПФ лишь однажды
(nd = 1). Наконец, при вычислении оценки автоспектра на шаге 4 опера-
цию сглаживания, рассмотренную в разд. 11.5.2, выполнять не следует.
11.5. Функция спектральной плотности
Прежде оценки спектральной плотности строились обычно с помощью
методов, основанных на формуле (5.34), т. е. вначале по соотношению
(11.86) рассчитывалась оценка ковариационной функция, а затем оценка
спектральной плотности вычислялась как ее преобразование Фурье при со-
ответствующем значении максимального сдвига. Такой подход, называе-
мый обычно методом Блэкмана — Тьюки, требует гораздо большего числа
операций, чем прямой метод расчета с помощью БПФ, основанный на
определении спектра формулой (5.67). Поэтому теперь его рекомендовать
нельзя. В принципе ход вычислений при непосредственном использовании
БПФ очевиден, однако при этом требуется ряд «улучшающих» операций,
которые часто осуществляют дополнительно для повышения качества оце-
нок. Эти вопросы обсуждаются ниже.
11.5.1. ОСНОВЫ ОЦЕНИВАНИЯ АВТОСПЕКТРОВ
Рассмотрим реализацию x(t) длиной Тг, принадлежащую стационарно-
му случайному процессу и имеющую нулевое среднее значение х = 0. Разо-
бьем ее, как показано на рис. 11.7, на nd смежных отрезков длиной Т каж-
дый и обозначим эти отрезки через ((/ — 1)Т t С iT), где i = 1, 2, ..., nd.
Разделив соотношение (8.153) справа и слева на 2, получим оценку $^(/) двусто-
ронней спектральной плотности Sxx(f) на произвольной частоте f в виде
4х(/) = -Д=Е|^((ЛП|2, (11.98)
nd1 / = 1
Рис. 11.7. Разбиение реализации на nd отрезков длиной Т.
13-953
386
Глава 11
где
Xj/, Т) = /\(0 dt .
JQ
Приближение к математическому ожиданию (5.67) получается усреднением
nd индивидуальных оценок Т)\2/Т.
При дискретном временнбм параметре каждая реализация х, (/) пред-
ставлена N значениями временного ряда |х/л] (п = 0, 1, ... ,N — 1; i =
= 1, 2, ...» nd). Финитное преобразование Фурье, отвечающее формуле
(11.98), даст значения спектральной плотности на дискретных частотах
к к
T~NAt ’
к = 0,1
.,N - 1.
(11.99)
При этом коэффициенты Фурье для каждого отрезка определяются ра-
венством (11.38) в виде
N—1
x.Uk) = &tX,k = Д' Е х<иехР
п = 0
—jlirkn
(11.100)
Оценка двусторонней спектральной плотности (11.98) принимает вид
1 ”d э
ЯХХШ = = 0,1,..., ЛГ - 1. (11.101)
п<1 <-1
Как отмечалось в разд. 11.2.4, частоте Найквиста при использовании БПФ
отвечает значение индекса к = N /2. Поэтому первые 2V/2 + 1 значений
спектральной плотности при Аг = 0, 1, ... , N /2 задают оценку спектра в
диапазоне частот fk от 0 до fc, а остальные N /2 — 1 значений (при к =
= N/2 4- 1, N/2 4- 2, ... , N — 1) можно рассматривать как оценку спект-
ра в интервале частот —fc < fk < 0. Поскольку функция спектральной
плотности вещественна, из формулы (11.77) следует, что §xx(fk) =
= S** (2fc — fк\
Односторонняя функция спектральной плотности оценивается непо-
средственно по соотношению (11.101) как
2 . .2 #
А) = Е I *,( А) I, к = 0,1,..., - . (11.102)
Число отсчетов N в формулах (11.101) и (11.102) при каждом БПФ часто
называют размером блока, и оно служит ключевым параметром, определя-
ющим разрешающую способность по частоте:
Д/ = 1/Т= 1/(^г) . (11.103)
С другой стороны, от числа усреднений nd зависит случайная ошибка оцен-
ки спектра (см. разд. 8.5.4). Заметим, что при осуществлении БПФ по алго-
ритму Кули — Тьюки размер выборки удобно выбирать как целую степень
числа 2, т. е. принимать N = 2Р (см. разд. 11.2.3).
Цифровые методы анализа
387
11.5.2. ПОДАВЛЕНИЕ ПРОСАЧИВАНИЯ ЧЕРЕЗ БОКОВЫЕ МАКСИМУМЫ
Определенное формулой (11.98) финитное" преобразование Фурье функ-
ции х (t) можно рассматривать как преобразование Фурье заданной на бес-
конечном интервале функции v (t), умноженной на прямоугольное «времен-
нбе окно» и( /), имеющее вид
м(,)=/1. 0</^Г; (ПЛО4)
v \0, в остальных случаях.
Иными словами, реализацию х (Г) можно рассматривать как произведение
(рис. 11.8):
x(t) = . (11.105)
Следовательно, преобразование Фурье функции x(t) есть свертка преобра-
зований Фурье функций и (t) и v (Г):
X(f) = Г <7(а)К(/- a) da . (11.106)
00
Преобразование Фурье «прямоугольной» функции и (f), заданной формулой
(11.104), есть
I sin тг/Т\
u(f) = г е • (п.ю7)
у 1TJ1 j
График функции IU (/)1 показан на рис. 11.9. Заметим, что первый боко-
вой максимум составляет около 13 дБ от главного максимума, а в дальней-
шем боковые максимумы спадают со скоростью 6 дБ на октаву. Описанная
функция представляет собой основное «спектральное окно», используемое
при анализе. Большие боковые максимумы функции IU (/*)! обусловлива-
ют большое просачивание энергии с частот, далеких от главного максиму-
ма спектрального окна, и могут привести к сильным искажениям спект-
ральной оценки, особенно заметным для процессов с узкополосным спект-
ром. Проблема просачивания не возникает при анализе периодических
(с периодом Тр) процессов, если принять длину реализации Т равной цело-
му числу периодов, т. е. выбрать Т = кТр (к = 1, 2, 3, ...). В этом случае
коэффициенты Фурье, отвечающие частотам/ = kfp — k/Tpi не могут
Рис. 11.8. Временнбе окно при спектральном анализе.
13*
388
Глава 11
U(t)
1
Рис. 11.9. Прямоугольное окно: а — временнбе; б — спектральное.
«проникнуть» в главный максимум, поскольку заданная равенством (11.107)
функция U(/*) обращается на этих частотах в нуль. Однако при Т ± кТр
просачивание энергии происходит и при анализе периодических процессов.
Временное сглаживание. Для подавления просачивания обычно исполь-
зуют временные окна, сглаживающие исходную реализацию таким обра-
зом, чтобы подавить резкие вариации на ее начальном и конечном участ-
ках. Существует множество таких окон, но одно из наиболее ранних и ши-
роко используемых — косинусоидальное сглаживающее окно, называемое
окном Ханна:
( I \ J nt \
(11.108)
/ I 1 “ cos---- = 1 - cos
«л(О = < 2\ т /
\0, в остальных случаях.
Эта функция показана на рис. 11.10, а. Ее преобразование Фурье
tfA(/) = W) - W-/1) - W+/1),
где/! = 1/Г, a U (f) задана формулой (11.107). Заметим, что
sinw(/- Л)Г
J17 ,
т ’
-Т
1меет вид
(11.109)
u(f+fi) = - т
+ f,)T
-----li__717 e-j«fT
(11.110)
”4/ +/1
График функции I (/")! показан на рис. 11.10, б. Первый боковой макси-
Цифровые методы анализа
389
Рис. 11.10. Окно Ханна: а — временное; б — спектральное.
мум спектрального окна Ханна примерно на 32 дБ ниже главного максиму-
ма, а скорость спадания боковых максимумов равна 18 дБ на октаву.
Рассмотрим теперь произвольную функцию v (t), такую, что Т не явля-
ется ее периодом, и пусть
x(t) = Uh(t)v(t) . (11.111)
Ее преобразование Фурье есть
Х(/) = fTx(t)e-J2”f,dt = Г Uh(a)V(f- a) da . (11.112)
A) * — оо
Для дискретных значений частоты fk = к/Т получаем при к =
= 0, 1, 2, ... , N/2
X(fk) = WJ - ИА-О - (11-113)
ГДе V(fk)= fTv(t)e~j2,rk'/Tdt. (11.114)
•'о
Предположим теперь, что в пределах каждой полосы частот шириной
Д/ = 1/Г функция v(t) ведет себя как ограниченный по частоте белый
шум. Тогда математическое ожидание произведения V*(f) и V(g), вычис-
ленное для любых частот / и g из набора к= к/Т, равно
Е[И/)И(8)]-{"’ (ПП5)
С учетом этого свойства из (11.113) получаем
Е [| X(fk) |2] = (I)2 + (|)2 + (i)2 = | (11.116)
при любых Д = к/Т (к = 0, 1,2,..., 2V/2). Эта величина характеризует
потери, вызванные использованием спектрального окна Ханна (11.108) для
оценки спектральной плотности при помощи финитного преобразования
390
Глава 11
Фурье. Поэтому при оценивании спектров по формулам (11.101) и (11.102)
выражение (11.100) нужно умножить на масштабный множитель V8/3.
В частности, при вычислении спектральной плотности по формулам
(11.101) и (11.102) и использовании окна Ханна следует принимать
flirkn
N
1 - cos — ехр -
«=о v .
(11.117)
где fk = k/(NM ) (к = 0, 1, ... , N/2). Более подробно вопросы сглажива-
ния разбираются в работах [11.8, 11.9].
ПРИМЕР 11.3. ОШИБКА СПЕКТРАЛЬНОЙ ОЦЕНКИ ЗА СЧЕТ ПРОСАЧИ-
ВАНИЯ ЧЕРЕЗ БОКОВЫЕ МАКСИМУМЫ. Для иллюстрации проблемы про-
Спектральная плотность, м2/(с2Гц)
Рис. 11.11. Сглаженная и несглажен-
ная оценки автоспектра скорости частиц
в моделируемом ветровом волнении.
Исследование финансировалось фирмой
«Шелл Интернейшнел Петролеум Матс-
хапей» (Гаага, Нидерланды).
сачивания через боковые максиму-
мы при оценивании спектральной
плотности рассмотрим две оценки
спектра, показанные на рис. 11.11.
Они получены по одному и тому же
ряду наблюдений над скоростью ча-
стиц в лотке, измеренной с по-
мощью лазерного измерителя ско-
рости при возбуждении в лотке ста-
ционарных волн в масштабе 1:10
реального времени. Спектры рас-
считывались прил^ = 400 и разре-
шение по частоте Д f = 0,0488 Гц
( Т = 20,49 с) при частоте дискре-
тизации 50 отсчет/с ( fc = 25 Гц).
Единственное отличие этих двух
спектральных оценок заключается в
том, что оценка, представленная
сплошной линией, рассчитана после
предварительного сглаживания ряда
квадратичной косинусоидальной ве-
совой функцией (окно Ханна), а
штриховая — без такого сглажива-
ния.
Из рис. 11.11 ясно, какие ошибки
в оценках спектральной плотности
может создавать просачивание энер-
гии через боковые максимумы. Вид-
но, в частности, что значения спект-
ральной плотности на частотах вне
спектрального максимума завыше-
ны за счет просачивания через боко-
вые максимумы вблизи частоты
максимума спектра. Заметим, что
принятое здесь разрешение по ча-
Цифровые методы анализа
391
стоте (Д f = 0,0488 Гц) обеспечивает малость ошибки смещения в соот-
ветствии с требованиями, поставленными в разд. 8.5. Таким образом,
ошибки просачивания могут создавать серьезные проблемы даже при по-
давлении обычных ошибок смещения, связанных с конечной разрешающей
способностью оценок.
Расчет по перекрывающимся отрезкам. Из рис. 11.9 и 11.10 видно, что
сглаживание реализации для подавления просачивания через боковые мак-
симумы увеличивает одновременно ширину главного максимума спектраль-
ного окна, что приводит к уменьшению разрешающей способности анали-
за. При использовании окна Ханна ширина полосы пропускания по уровню
половинной энергии возрастает примерно на 60%. Обычно такое ухудше-
ние разрешающей способности вполне компенсируется подавлением проса-
чивания энергии с частот, лежащих вне главного максимума. Вместе с тем
временное сглаживание приводит также к росту изменчивости спектраль-
ных оценок. Если анализируемый процесс имеет примерно постоянный по
частоте спектр, то сглаживание реализации окном Ханна увеличивает дис-
персию получаемой таким путем спектральной оценки примерно вдвое
[11.10]. Иными словами, ошибка оценки спектральной плотности, найден-
ной при использовании окна Ханна, есть е = ^2/ndi а не е = \/yJnd, как
было показано в гл. 8.
Чтобы уменьшить рост изменчивости оценки за счет временного сгла-
живания, производимого для подавления просачивания через боковые мак-
симумы, иногда используют прием анализа по перекрывающимся отрезкам
реализации. При этом реализация делится не на nd независимых отрезков
хД/) (0 - 1)Г t iT\ i = 1, 2, ... ,nd), а на перекрывающиеся интер-
валы
k(/- 1)]Т</< [q(i- 1)4-117’, / = q < 1.
(11.118)
Значение <7 обычно принимают равным 0,5, что приводит, как показано на
рис. 11.12, к 50%-ному перекрытию отрезков. Этот прием позволяет вос-
становить до 90% устойчивости оценки, потерянной при временном сгла-
живании, но ведет при этом к удвоению числа БПФ, нужных для построе-
ния оценки. Более детальное обсуждение этого вопроса содержится в рабо-
те [11.10].
Сглаживание корреляционной функции. Другой способ подавления про-
сачивания через боковые максимумы заключается в сглаживании оценки ко-
вариационной функции, а не исходной реализации. Такой подход, называе-
мый иногда корреляционным сглаживанием, почти не увеличивает выбо-
рочную изменчивость спектральной оценки и потому позволяет избежать
392
Глава 11
Рис. 11.12. Последовательность временных окон
50%-ным перекрытием.
при анализе по отрезкам с
оценивания по перекрывающимся интервалам. Кроме того, он требует
меньшего объема вычислений. Его основные этапы состоят в следующем.
а) По длинной и несглаженной реализации вычисляется оценка Sxx(f)
двухсторонней спектральной плотности (11.101).
б) С помощью обратного преобразования Фурье вычисляется, как опи-
сано в разд. 11.4.2, оценка ковариационной функции Rxx(j). (При этом
можно пользоваться циклической оценкой.)
в) Эта оценка ковариационной функции сглаживается некоторым окном
с весовой функцией и (г), удовлетворяющей условиям и (г) = 1 при т = 0 и
и (?) = 0 при 7 = 7тах < Т.
г) Сглаженная оценка односторонней спектральной плотности Gxx(f)
вычисляется по формуле (5.34) как БПФ функции w(r) Rxx(r) при 0 т
Tmax (результат следует умножить на 4). Поскольку средний квадрат реа-
лизации совпадает со значением ковариационной функции при т = 0, опи-
санная выше операция не меняет среднего квадрата и потому не приводит
к уменьшению значений спектра. Кроме того, при rmax < Т дисперсия
спектральной оценки практически не растет, и потому нет необходимости в
ее расчете по перекрывающимся интервалам.
При построении спектральной оценки с ковариационным сглаживанием
исходный автоспектр приходится вычислять по формуле (11.101) при длине
реализации, превышающей величину, необходимую для получения оконча-
тельной оценки с заданным разрешением по частоте. Значения Д/ ип(/ ока-
зываются меньшими заданных. Но поскольку окончательная оценка полу-
чается как БПФ функции и (r)R п (т), ее разрешение равно
1 1
Д/ =— = —- ,
(11.119)
где m < N — максимальный сдвиг ковариационной функции. Что же каса-
ется нормированной случайной ошибки окончательной оценки, то она
приближенно описывается формулой
(11.120)
Таким образом, окончательная оценка спектра имеет практически такую же
дисперсию, как и оценка, полученная при том же разрешении по частоте
Цифровые методы анализа
393
путем временного сглаживания и дальнейшего расчета по перекрывающим-
ся отрезкам.
Как и для временного сглаживания, оценку ковариационной функции ча-
сто сглаживают полным1) косинусоидальным окном Ханна
/ 1 / 77 Т \ 1/ 77 Г \
I — 1 + cos---- = — 1 + cos— ь г = 0,1,2,..., m \
uh(T)={2\ ттах/ 2\ m)
I О, r>m. (11.121)
Применение окна Ханна к оценке ковариационной функции подавляет про-
сачивание через боковые максимумы в меньшей степени, чем при аналогич-
ном сглаживании исходной реализации. Такая операция над ковариацион-
ной функцией отвечает спектральному окну, в котором первый боковой
максимум на 16 дБ ниже главного максимума, а скорость спадания после-
дующих боковых максимумов равна 9 дБ на октаву. Однако существуют и
корреляционные окна, обладающие существенно меньшими боковыми мак-
симумами [11.10].
11.5.3. РЕКОМЕНДУЕМАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫЧИСЛЕНИЙ
Рекомендуются следующие этапы вычисления оценки спектральной
плотности.
1. Имеющаяся реализациях;, (п = 0, 1, ... , Nnd) разбивается на nd от-
резков, каждый из которых содержит N отсчетов.
2. При необходимости подавить просачивание энергии через боковые
максимумы каждый отрезок [хп ] (п = 0, 1, ... , N — 1) сглаживается в со-
ответствии с формулой (11.108) фильтром Ханна или любым другим под-
ходящим образом выбранным фильтром (можно, например, использовать
описанное в разд. 11.5.2 ковариационное сглаживание).
3. Для каждого отрезка реализации вычисляется N значений БПФ X (fk)
(к = 0, 1, ... , N - 1). При необходимости уменьшить рост дисперсии
оценки за счет сглаживания БПФ выполняются по перекрывающимся от-
резкам (см. формулу (11.118)).
4. Значения X (fk) умножаются на масштабный коэффициент для ком-
пенсации изменений, внесенных сглаживанием (при использовании окна
Ханна этот коэффициент равен V 8/3).
5. По формулам (11.101) или (11.102) вычисляется оценка двухсторонней
или соответственно односторонней спектральной плотности для nd
отрезков.
Имеется в виду, что длина весовой функции uh равна периоду ш Д/.— Прим,
перев.
394
Глава 11
11.5.4. НАПЛЫВАЮЩИЕ ПРЕОБРАЗОВАНИЯ
Одна из основных проблем спектрального анализа связана с расчетом
значений спектральной плотности на высоких частотах при высоком разре-
шении, т. е. в случаях, когда отношение fc/Af очень велико. Понятно, что
если объем данных, приходящийся на один отрезок реализации, подвергаю-
щийся преобразованию Фурье, может быть выбран произвольно большим,
то и разрешающую способность оценки по частоте можно „сделать доста-
точно высокой, так как
//А/ =
1/(24/ )
—-------- = N /2.
1/(77 4/)
(11.122)
Однако в действительности число отсчетов 7V, по которым выполняется
преобразование Фурье, ограничено (даже при использовании ЭВМ с вирту-
альной памятью), и число операций, необходимое для вычисления преоб-
разования Фурье по алгоритму Кули — Тьюки, растет пропорционально
Np, где N = 2Р . Поэтому целесообразно пользоваться методами вычисле-
ний, допускающими получение оценки автоспектра с частотой Найквиста fc
и разрешением по частоте 4/ по числу точек, меньшему, чем следует из ус-
ловия (11.122). Такие приемы называют обычно наплывающим преобразо-
ванием.
Существует несколько вариантов наплывающего преобразования, но ча-
ще всего исходная реализация подразделяется на ряд последовательностей,
каждой из которых отвечает определенная полоса частот, а затем нижняя
граница полосы частот каждой последовательности смещается в нуль с
помощью метода комплексной демодуляции^. Пусть исходная реализация
x(t) пропускается через полосовой фильтр и процесс у (I) на выходе фильт-
ра есть
fo- (В/2) <f <f0+ (В/2)-, (11.123)
\ 0, в остальных случаях.
Умножив y(t) на экспоненту, получим модулированный сигнал
v(t) = y(t)ej2”fp, (11.124)
где — частота модуляции. Его преобразование Фурье имеет вид
И(/) = dt =
= dt = (11.125)
•'o
1 ’ Более подробно о комплексной демодуляции и ремодуляции и ее применении
для анализа случайных процессов, в том числе для осуществления полосовой фильт-
рации, см. в книге: Гренджер К., Хатанака М. Спектральный анализ временных ря-
дов в экономике: Пер. с англ.— М.: Статистика, 1972.— Прим, перев.
Цифровые методы анализа
395
так что автоспектр функции v {t) есть
2
<U/) = I™ -Е[|И(/)|21 = Gjf-Л) • (11126)
Т —* оо 1
Из равенств (11.126) следует, что если частота модуляции f j = /0 - В/2,
то автоспектр исходной последовательности с ограниченной полосой ча-
стот передвинется, как показано на рис. 11.13, от исходного диапазона
/0 — В /2 f /0 + В/2 в диапазоне 0 f В. Теперь минимальную
скорость дискретизации можно принять равной 2В отсчетов в секунду, не
опасаясь маскировки частот; эта величина всегда меньше минимальной ско-
рости дискретизации 2(/0 + В/2), необходимой при отсутствии модуля-
ции. Поэтому при том же объеме выборки N можно получить гораздо бо-
лее высокое разрешение по частоте:
в исходной последовательности: Д/ > 2(/0 4- В /2)/N\
(11.127)
в преобразованной последовательности: Д/ > 2B/N.
При этом, разумеется, весь расчет приходится вести для каждого нап-
лывающего преобразования на всех заданных частотах.
На практике операции полосовой фильтрации и демодуляции, необходи-
мые при наплывающем преобразовании, выполняются иногда с помощью
аналоговой аппаратуры до перевода данных в дискретную форму. Это по-
зволяет использовать аналого-цифровые преобразователи (АЦП) с неболь-
шим быстродействием для анализа данных, диапазон частот которых рас-
положен существенно выше максимальной частоты съема АЦП. Использо-
вание современных высокоскоростных АЦП (см. разд. 10.3.4) позволяет,
как правило, осуществлять дискретизацию с шагом по времени, необходи-
мым для анализа непосредственно исходной реализации х (О, а наплываю-
щее преобразование выполнять затем в цифровой форме. В этом случае ис-
ходная реализация х(дД/) (д = 1, 2, ... , N) вначале пропускается через
полосовой фильтр (см. разд. 11.1-3), на выходе которого получается функ-
ция _у( дД/) (д = 1, 2, ... , принадлежащая диапазону частот
kx/NAt fk kz/NA t. Затем последовательностьу(пМ) модулируется:
v(n М) = у(п bpexpl-jlirnkJN], п = 1,2,..., N. (11.128)
Теперь можно произвести прореживание функции v (п At), уменьшив таким
образом число ее значений в d раз, где
d = к2/(к2 - kJ (11.129)
Эта операция дает последовательность v {nd At ) (д = 1, 2, ... , TV). Заме-
тим, что теперь длина реализации, необходимая для получения отдельного
Следует помнить, что отфильтрованная реализация всегда короче исходной.—
Прим, перев.
396
Глава 11
Gyy(f)
_______I ________________________I____________►
0 (f0-f,) В f0-% f0 f0+& t
Рис. 11.13. Сдвиг частот при комплексной демодуляции.
отрезка, есть Т = Nd At секунд. Прореженная реализация подвергается
преобразованию Фурье:
/ fc \ N
j = и(”^А/)ехР[-jlnkn/Nd}, к = 0,1,..., N/2.
(11.130)
Эти операции повторяются для каждой из nd независимых реализаций по-
следовательности х (/), и оценка автоспектра вычисляется по формуле
(11.102). Результирующий спектр имеет разрешение по частоте Д/ =
= U (Nd At) и определен в диапазоне частот к X/(N At ) fk k2/(N At),
где fk = к /(Nd At ) и индекс к меняется от dk х до dk2.
ПРИМЕР 11.4. ВЫБОР ПАРАМЕТРОВ ДЛЯ НАПЛЫВАЮЩЕГО ПРЕОБРА-
ЗОВАНИЯ. Пусть спектр стационарной последовательностих (t) нужно оце-
нить с нормированной случайной ошибкой е = 0,1 при разрешающей спо-
собности Af = 1 Гц в полосе частот от 0 до 5120 Гц. Расчет ведется при
фиксированной длине отрезков N = 1024 отсчета. Требуется определить
объем выборки, необходимой для получения такой оценки.
Из формулы (11.102) следует, что для получения разрешающей способ-
ности Af = 1 Гц при N = 1024 нужен интервал дискретности
Дг = 1/(W) = 0,000977 с,
что отвечает частоте Найквиста fc = 1/(2Д/) = 512 Гц. Следовательно,
для анализа в диапазоне частот от 0 до 5120 Гц исходную реализацию нуж-
но подвергнуть наплывающему преобразованию для 10 смежных частот-
ных интервалов шириной В = 512 Гц каждый. Согласно формуле (8.154),
для получения оценки с ошибкой е =• 0,1 потребуется/?^ = 100 усреднений
для каждого диапазона частот. Поэтому общая продолжительность запи-
си, необходимая для анализа в каждом диапазоне, равна
Tr = ndNAt = 100 с.
Цифровые методы анализа 397
Если исходная реализация хранится в памяти ЭВМ, то для анализа во всех
10 диапазонах достаточно длины записи 100 с. Если же анализ осуществля-
ется в реальном времени, то общая длина записи, нужная для анализа по
каждому из 10 диапазонов, составит 1000 с.
11.5.5. ДРУГИЕ СПОСОБЫ СПЕКТРАЛЬНОГО АНАЛИЗА
В этой главе дается сводка лишь обычных способов спектрального ана-
лиза, основанных на преобразовании Фурье и обеспечивающих получение
спектральных оценок с разрешением по частоте до Д/ = 1/Г. Однако на
практике часто возникают ситуации, когда получение реализации, длина
которой достаточна для обеспечения таким путем заданной разрешающей
способности, оказывается очень сложным или вообще невозможным де-
лом. Это в особенности относится к таким областям, как сейсмология,
океанография, теория атмосферной турбулентности, и к некоторым видам
биомедицинских исследований. За последние годы для преодоления этой
трудности был разработан ряд методов спектрального оценивания, осно-
ванных на модельных представлениях о процессах. Такие методы спект-
рального оценивания часто называют параметрическими.
По сути дела этот подход заключается в построении на основе данных
наблюдений некоторой модели анализируемого процесса. В этой модели
анализируемый процесс рассматривается как процесс на выходе линейной
системы с частотной характеристикой Н (/*), на вход которой поступает
белый шум. Частотная характеристика задается в виде
N
Е
= , (11.131)
Е bkzk
л=о
где z = ехр(—у 2тг/Д/) есть z -преобразование, упомянутое в разд. 11.1.3.
Модель процесса описывается в этом случае разностным уравнением
N М
Л = Е aixt-i + L Ьку^к. (11.132)
/=0 А>-=1
Если все коэффициенты Ьк равны нулю, то получается модель скользящего
среднего (СС), а если равны нулю все коэффициенты at, кроме я0, то мо-
дель называют авторегрессионной (АР). В случае когда и я, и Ьк отличны
от нуля, получается модель типа АРСС. Тип модели следует выбирать на
этапе, предшествующем спектральному анализу. Обычно это делают на ос-
нове сведений о физической природе анализируемого процесса. При невер-
ном выборе оценка спектра будет совершенно ошибочной и, скорее всего,
будет обладать худшими свойствами, чем оценка, полученная с помощью
стандартных методов.
После выбора модели оценивание ее коэффициентов производится мето-
дом наименьших квадратов. В случае модели авторегрессии такой способ
398
Глава 11
называется спектральным анализом по методу максимальной энтропии.
Это название связано с тем, что в рамках этого метода ищется спектраль-
ная оценка, которая была бы наиболее случайной (по терминологии теории
связи — «обладала бы максимальной энтропией») среди всех возможных
спектров, не противоречащих данным наблюдений. Модель СС приводит к
спектральным оценкам максимального правдоподобия, а метод, основан-
ный на использовании коэффициентов модели АРСС, не имеет специально-
го названия. Наиболее сложный этап параметрического спектрального ана-
лиза — выбор порядка модели. Для выбора оптимального в статистиче-
ском смысле порядка модели разработаны специальные критерии. Более
детальное обсуждение этих методов содержится в работах [11.11, 11.12]^.
11.6. Расчеты для двух реализаций
В последующих выкладках предполагается, что реализации и (t) и v (t)
принадлежат стационарным* 2^ случайным процессам и заданы на конечном
интервале времени Zo t tQ + Т, где^0 — произвольное начало отсчета
(в стационарном случае). Пусть интервал дискретности равен Д/ и, следо-
вательно, частота Найквиста fc = 1/(2ДГ). Реализации и (t) и v (t) пред-
ставлены дискретными последовательностями
ий = и(/0 + иА/), п = 1,2,..., N,
(11.133)
vn = + п ~ N&t .
Прежде всего рассчитываются средние значения
IV 1 V
“ = v = (11.134)
* = 1 7V И = 1
а затем производится центрирование
хп = ип “ й > Уп = vn ” й > л == 1,2,..., У, (11.135)
так что полученные последовательности соответствуют новым реализаци-
ям x(t) = и (t) — и, у (t) = v (t) — v с нулевыми средними значениями.
Могут также выполняться другие операции предварительной обработки,
указанные в разд. 11.1.
11.6.1. СОВМЕСТНАЯ ПЛОТНОСТЬ ВЕРОЯТНОСТИ
Как следует из соотношений (3.25) и (8.87), оценку совместной плотно-
сти вероятности двух стационарных реализаций х (t) иу (Z) можно найти по
дискретным выборкам из этих реализаций в виде
См. также предисловие редактора перевода.— Прим, перев.
2) И стационарно связанным.— Прим, перев.
Цифровые методы анализа
399
NWW
(11.136)
где Wx и Wy — узкие интервалы с центральными значениями х и у соот-
ветственно, a Nxfy — число пар отсчетов, которые одновременно попадают
в эти интервалы. Таким образом, оценкур (х, у) получают следующим об-
разом. Прежде всего разбивают диапазоны изменения переменных х и у на
интервалы равной ширины, образующие в совокупности таблицу с двумя
входами. Затем подсчитывают число точек, попадающих в каждую клетку
таблицы, и это число делят на площадь клетки WxWy и объем выборки N.
Программа для рассортировки данных по соответствующим клеткам ана-
логична программе, используемой для получения оценок одномерной плот-
ности (см. разд. 11.3).
11.6.2. ВЗАИМНЫЕ КОВАРИАЦИОННЫЕ ФУНКЦИИ
Оценки взаимных ковариационных функций, так же как и оценки авто-
ковариационных функций, могут быть получены двумя основными спосо-
бами: непосредственным вычислением и с использованием БПФ. Ниже рас-
смотрены оба способа.
Непосредственное вычисление. Несмещенные оценки взаимных ковариа-
ционных функций при сдвигах г = 0, 1, ... , т (т < N) находятся в виде
ът _ lb хпУп + г f
Г Л? = 1
Ryx(^t) = _ £ УпХп+г.
г И = 1
(11.137)
(11.138)
Заметим, что взаимные ковариационные функции Rxy(rAt), Ryx(rAt) раз-
личаются порядком сомножителей хп и уп .
Выборочную взаимную ковариационную функцию Rxy (г At) можно нор-
мировать так, что значения ее будут находиться между — 1 и +1, для чего
нужно разделить ее на величину R^t®) VRyy(0). Таким образом получает-
ся нормированная взаимная корреляционная функция
R(rkt)
которая теоретически должна удовлетворять неравенству — 1
pxy(rAt) 1. Аналогичным образом определяется функция pyx(rAt).
Вычисление при помощи БПФ. Для получения взаимной ковариацион-
ной функции при помощи БПФ, как и в разд. 10.4.2, можно рекомендовать
следующую последовательность вычислений. Пусть объем каждой выборки
400
Глава 11
из реализаций х (О иу(1) составляет N = 2Р чисел. Взаимную ковариаци-
онную функцию в этом варианте находят по спектральной плотности про-
цесса, для чего дважды применяют БПФ — к функции х (t) и к функции
у (t). Оба преобразования можно находить одновременно, используя метод,
описанный в разд. 11.2.4.
Рекомендуемая в итоге последовательность операций для получения
оценки взаимной ковариационной функции описана ниже в предположении,
что длина исходных реализаций х (п At) и у (п At) есть ndN и N = 2Р .
1. Выбирается максимальный сдвиг т и исходные реализации разбива-
ются на nd отрезков, каждый из которых состоит из N > т отсчетов.
2. Каждый отрезок {хп}, \уп} (п = 1, 2, ... , N) дополняется N нулями,
в результате чего новый отрезок содержит 2N отсчетов.
3. По отрезкам, содержащим по 2N точек, в соответствии с форму-
лой (11.71) методом БПФ вычисляются коэффициенты Z(k) (к =
= 0, 1, ... , 2/V - 1).
4. По формулам (11.72) вычисляются величины X (к) и Y (к) (к =
= 0, 1, ... , 2N - 1).
5. По методу, описанному в разд. 11.6.3, вычисляется оценка ^(/^)
двухсторонней спектральной плотности.
6. По формуле (11.76) вычисляется обратное БПФ последовательности
дающее оценку Rsxy(r At) (г = 0, 1, ... , 2N - 1).
7. Несмещенная оценка Rxy(r At) взаимной ковариационной функции при
положительном сдвиге г = 0, 1, ... , N — 1 находится умножением
Rxy(rAt) на масштабные коэффициенты N/(N — г).
8. Несмещенная оценка Rxy (г At) взаимной ковариационной функции при
отрицательном сдвиге находится умножением R ху (г At) (г = N + 1, N +
+ 2, ... , 2N — 1) на масштабные коэффициенты?//(г — N).
Соображения, положенные в основу этой методики, аналогичны обосно-
ванию способа оценивания автоковариационной функции (см. разд. 11.4.2).
11.6.3. ФУНКЦИИ ВЗАИМНОЙ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ
По аналогии с оцениванием автоспектров (разд. 11.5) можно рекомендо-
вать следующие этапы оценивания функции взаимной спектральной плот-
ности.
1. Имеющиеся реализации разделяются на nd отрезков хп, уп, каждый
из которых содержит N отсчетов.
2. При необходимости подавить просачивание энергии через боковые
максимумы каждый отрезок хп, уп (п = 0, 1, ... , N - 1) сглаживается
фильтром Ханна (см. разд. 11.5.2) или любым другим подходящим обра-
зом выбранным фильтром (можно использовать описанное в разд. 11.5.2
корреляционное сглаживание).
3. Сглаженные значения хп запоминаются как действительная часть, а
сглаженные значения уп — как мнимая часть последовательности zn =
= хп + jyn (п = 0, 1, ••• - О-
4. По формуле (11.71) для каждого отрезка вычисляется N значений
БПФ Z (к) (к — 0, 1, ... , N - 1). При необходимости уменьшить рост
Цифровые методы анализа
401
дисперсии оценки за счет сглаживания БПФ выполняются по перекрываю-
щимся отрезкам (см. разд. 11.5.2).
5. По формулам (11.72) для каждого отрезка вычисляются коэффициен-
ты X (к) и Y (к) (к = 0, 1, ... , N — 1).
6. Значения X (к), Y (к ) умножаются на масштабный коэффициент для
компенсации внесенных сглаживанием изменений (при использовании окна
Ханна этот коэффициент равен V 8/3).
7. Для каждой пары отрезков по значениям X *(fk) = AtX*(k),
Y(fk) = AtY(k) вычисляется несглаженная оценка двухсторонней взаимной
спектральной плотности
Ш = £ = 0,1,..„АГ-1,(11.140)
или односторонней взаимной спектральной плотности
а„Ш = с - о.'.....«/2.(11.141)
8. Осреднение несглаженных оценок по nd парам отрезков дает оконча-
тельную сглаженную оценку 4л№) & = О, 1, ... , W - 1) или Gxy(fk)
(к = 0, 1, ... , 7V/2). Сглаженная оценка может быть представлена в виде
бхуШ = СХУШ -jQxyUk) =\Gxy(fk)\e-*^\
11.6.4. ЧАСТОТНАЯ ХАРАКТЕРИСТИКА
Оценку частотной (амплитудной и фазовой) характеристики линейной
системы с одним процессом на входе и одним процессом на выходе при на-
личии помехи только на выходе рекомендуется вычислять по формуле
|9-!3): с m
(11.142)
GXX\J )
Таким образом,
(U143)
GXX\J )
Следовательно, численные оценки амплитудной и фазовой характеристик
на частотах fk = к /(N&t) (к = 0, 1, ... , 7V/2), определяются в виде
|Я(Д)| = , (Ц.144)
^xx\Jк)
4>(fk) = arctg[ex/A)/Cx/A)]. (11.145)
Здесь Gxx(fk) — оценка автоспектра, вычисленная в соответствии с
402
Глава И
разд. 11.5 по отрезкамхл (л = 0, 1, ... ,7V - 1); Cxy(fk), Qxy(fk) — дейст-
вительная и мнимая части оценки взаимной спектральной плотности
вычисленной в соответствии с разд. 11.6.3 по парам отрезков
хп> Уп (п = °, Ь - 1).
11.6.5. ИМПУЛЬСНЫЕ ПЕРЕХОДНЫЕ (ВЕСОВЫЕ) ФУНКЦИИ
Подобно тому как обратное преобразование Фурье функций §xx(f) и
Sxy(f) дает циклические смещенные оценки Rxx (т) иКху(т), обратное преоб-
разование Фурье функции Н (у) позволяет получить циклическую смещен-
ную оценку импульсной переходной (весовой) функции h (т). При необходи-
мости оценить Л (т) по Н (f) функции Gxx(f) и Gxy(f) в формуле (11.142)
следует заменить двухсторонними оценками, полученными, как описано в
разд. 11.4.2 и 11.6.2, добавлением N нулевых значений к исходной последо-
вательности. Обратное преобразование Фурье этой новой последовательно-
сти, представляющей собой отношение соответствующих оценок взаимной
спектральной и спектральной плотности, даст последовательность ds(rAt)
(г = 0, 1, ... , 27V — 1); вторую половину ее следует отбросить. После ум-
ножения на масштабные множители /V/(N — г) получается искомая оценка
h (г At) (г = 0, 1, ... , TV - 1).
11.6.6. ФУНКЦИЯ ОБЫЧНОЙ КОГЕРЕНТНОСТИ
Согласно формулам (9.54), функцию обычной когерентности уху (f), свя-
зывающую последовательности х (t) иу((), записывают в виде
|<У/)|
Gxx(f)Gyy(f) ’
(11.146)
где Gxx (f) и Gyy (f) — оценки автоспектров последовательностей х (t) и
У (t) соответственно, a Gxy(f) — оценка взаимной спектральной плотности
последовательностей х (t) и у (t). Поэтому численная оценка функции обыч-
ной когерентности на частотах fk = к /(NAt) (к = 0, 1, ... , 7V/2), нахо-
дится в виде
Л2 ( f \ = |^хЛ(А) |
У к Gxx(fk)Gyy(fk) ’
где Gxx(fk) и Gyy(fk) — оценки автоспектров, вычисленные в соответствии
с разд. 11.5 по отрезкамхл, уп (п = 0, 1, ... , TV - 1), a Gxy(fk) — соот-
ветствующая оценка взаимного спектра (см. разд. 11.6.3).
11.7. Описание систем со многими входными
процессами
В этом разделе описаны итеративные алгебраические процедуры, с по-
мощью которых по формулам, приведенным в разд. 7.3, вычисляются
оценки характеристик систем со многими входными процессами и одним
Цифровые методы анализа
403
процессом на выходе. Эти процедуры основаны на приведенном в
разд. 7.3.4 алгоритме оценивания условной взаимной спектральной плотно-
сти по оценкам спектров и взаимных спектров. Система со многими вход-
ными и многими выходными процессами описывается путем последова-
тельного рассмотрения систем со многими входными процессами и одним
процессом на выходе.
Модель системы со многими произвольными входными процессами и
одним процессом на выходе и модель системы с упорядоченными условны-
ми входными процессами показаны соответственно на рис. 11.14 и 11.15.
Исходный набор входных процессов следует по возможности упорядочить
в соответствии с причинно-следственными соображениями физического ха-
рактера. Если этого сделать нельзя, то входы нумеруются, как описано в
разд. 7.2.4, в соответствии со значениями обычной функции когерентности,
связывающей каждый входной процесс с выходом системы. Вполне доста-
точно произвести такое упорядочивание лишь на отдельных наиболее инте-
ресных частотах (обычно на частотах максимумов автоспектра выходного
процесса).
11.7.1. ПРЕОБРАЗОВАНИЯ ФУРЬЕ И СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ
Каждая стационарная реализациях, (г) (z = 1, 2, ...,<? ) входных процес-
сов и стационарная реализация у (t) = xq + i(t) процесса на выходе разбива-
ются на nd неперекрывающихся отрезков длиной Т каждый, так что общая
длина каждой исходной реализации есть Tr = ndT. Затем для каждого от-
резка этих q 4- 1 реализаций входных и выходного процессов выполняются
преобразования Фурье на частотах fk = к (к = 1, 2, ... , 7V/2), где
Д/ = 1/(УД/) — разрешающая способность по частоте. Понятно, что при
Рис. 11.14. Система со многими произвольными входными процессами и одним
процессом на выходе.
404
Глава И
Рис. 11.15. Система со многими упорядоченными входными процессами и од-
ним процессом на выходе.
этом получается (q 4- V)nd преобразований Фурье, каждое из которых со-
держит N/2 коэффициентов, относящихся к несовпадающим частотам. Эта
информация служит основой для получения оценок функций спектральной и
взаимной спектральной плотностей, вычисляемых как среднее из nd оценок
соответствующих характеристик HaN/2 частотах. В дальнейшем для одно-
сторонних функций спектральной плотности будут использованы такие
обозначения:
С,У(Л) = ^(Л), i,j=l,2,...,q,q + l;
(11.148)
l,2,...,(N/2).
Функции вида Giy (fk) получаются при подстановке j = q + 1 = у. В ре-
зультате получается расширенная матрица [Gy] спектральных плотностей
входных и выходного процессов размерностью (q 4- 1)х(<7 4- 1), значения
которой можно запомнить, как показано на рис. 11.16, последовательно на
частотахД (к = 1, 2, ... ,7V/2). Заметим, что эта матрица эрмитова, т. е.
на главной диагонали она содержит действительные числа, а элементы,
симметричные относительно главной диагонали, комплексно сопряжены.
Свойство эрмитовости сохраняется и для матрицы условных спектральных
плотностей, рассматриваемой в следующем разделе.
11.7.2. ФУНКЦИИ УСЛОВНОЙ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ
Полученный в разд. 7.3.4 алгоритм оценивания функций условной спект-
ральной плотности с помощью только алгебраических операций реализует-
ся следующим образом. Для любых значений j i иг < j, где i =
= 1, 2, ... , q, q 4- 1; г = 1, 2, ... , q, и на любой фиксированной частоте
Цифровые методы анализа
405
Рис. 11.16. Расширенная спектральная матрица jG ].
fk имеем
<?,, Л Л) = - Lrj(fk)Gir (Г_1);(Л)>
r (f} Ъ.-М (1Ы49)
rAfk):= Grr(r_lvM
Результат для выходного процесса^ (О получается при замене xq + }(/) на
у (/). Для сокращения записи зависимость от частоты в дальнейшем опу-
скается.
Начиная со значения г = 1, каждый последующий член рассчитывается
по предыдущим. При г = 1 формула (11.149) дает для каждой частоты
^ij l = Gij ~ = -~~9
Оц
. . , , . (11.150)
z, j = 2,3,..., q, q + 1.
Заметим, что члены вида L- вычисляются по элементам первой строки
матрицы, показанной на рис. 11.16. Равенства (11.150) определяют функции
вида через [G^]. При у = q + 1 = у имеем
Giv 1 = Giy ~~ Д1’
Glv (11.151)
406
Глава 11
В результате для каждой частоты fk получается условная спектральная
матрица [Gy, J размерностью qxq; эти матрицы можно запоминать, как
показано на рис. 11.17.
При г = 2 для каждой частоты fk имеем
^7-2! Gijl ^2jGi21f L2j —
i, j = 3,4,..., q, q + 1 .
^2у-1
^22 1
(11.152)
Заметим, что члены вида вычисляются по элементам первой строки
матрицы, показанной на рис. 11.17. Равенства (11.152) определяют функции
вида [Gy .2!] через [Gy. При у = q 4- 1 = у получаем
Giy2\ ~ Giyl ^2yGi2A >
2у ~ G
v22-l
(11.153)
В результате для каждой частоты fk получается условная спектральная
матрица [Gy,2]\ размерностью (<? - 1)х (<у — 1); эти матрицы можно запо-
мнить, как показано на рис. 11.18.
При г = 3 для каждой частоты fk имеем
_ бу2! т
Gij.y. = Gjj.2, - L3jGi3.v., L3j- '
332! (11.154)
i, j = 4,5,...,q,q + 1.
В этом случае члены вида L вычисляются по элементам первой строки
матрицы, показанной на рис. 11.18. Функции вида [Gy .у] определяются че-
рез lGij • 2.’] и т- Д-
Вычисления повторяются, и через q — 2 шагов получаем в соответствии
с (11.149) функции
Gij.(4-2y. - Gij.iq_3), L(q_2)jGl((l_2) (.q-3y. f
2)(q —2) (^-3)!
(11.155)
G22 1 G23-1 G2(q-l)l G2qt G2y-1
G32-1 G331 G3(q-1)-1 G3?l G3yl
G(q-l)2 1 G(4-1)(q-l)-1 ^(^-l)q-1 a(4-i)yi
Gq2 1 Gq3\ Gq(q-l)l Gwl Gqy-\
Gy2i Gy3\ Gy(q-i)-1 Gyq i Gyy.]
Рис. 11.17. Условная спектральная матрица
Цифровые методы анализа
407
{*33 2! G3(<7-l)-2! g3<?-2! aiy-2'.
G(g-1)3-2! Gfg-1)(g-1)-2! G(g-1)g-2! G(q-1)y2!
Gg32! Ggfg-l)-2! Gqq-2\ Gqy-2!
G/3-2! Gy(g-1)-2! Gyq-Z\ 1 i Gyy. 21
Рис. 11.18. Условная спектральная матрица [ Gjy z, ].
При этом на каждой частотеД получается условная спектральная матрица
размерностью (3x3) (рис. 11.19).
На (q - 1)-м шаге из формулы (11.149) имеем
G.j(q~^ = Gij(q-2)'. ~ L(q-l)JGi(q-l)(q-2y ,
_ 2[д-1)г(д-2у i, j = q,q+ 1. (11 156)
Заметим, что члены вида L( вычисляются по элементам первой стро-
ки матрицы, показанной на рис. 11.19. Равенство (11.156) дает на каждой
частоте fk показанную на рис. 11.20 условную спектральную матрицу
размерностью (2x2).
Наконец на^-м шаге получаем в соответствии с формулой (11.149) для
каждой частоты fk скалярную функцию, показанную на рис. 11.21:
Gyy -q\ ^yy(q-\y LqyGyq.(q-\)\ 1
G (11.157)
bqv G
Uqq{q~\y
Заметим, что Gyy , есть спектр выходного шума в показанной на
рис. 11.14 и 11.15 модели с q процессами на входе и одним процессом на
выходе. Таким образом, оценка функции Gnn , которую нельзя получить не-
посредственно, может быть найдена по исходным данным при выполнении
описанной выше процедуры.
Представленная на рис. 11.16—11.21 информация служит основой для
идентификации и интерпретации различных полезных характеристик и со-
G(f-1)(q-1)-(q-2)! G(q-\)y(Ч-2У
Gq(q-l)(q~2)t Gqq (q~2)! Gqy(q-2)l
Sylq-l)(q-2)l Gyq (q-2)\ Gyy(q-2)\
Рис. 11.19. Условная спектральная матрица [G^
408
Глава 11
Рис. 11.20. Условная спектральная матрица
Gqq(q-\)\ Gqy(q-i)\
Gyq(q-\y. Gyy(q-\)\
отношений по измерениям процессов на входе и выходе системы. Эти во-
просы рассмотрены в последующих разделах.
11.7.3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ И ФУНКЦИИ КОГЕРЕНТНОСТИ
Оптимальные частотные характеристики L- = вычисляются на
каждой частоте fk по формулам
i, j = l,2,...,q,q + 1. (11.158)
Gii (/-1)!
Приу = q -I- 1 = у имеем (см. рис. 11.15):
Ч = г V ’ z = 1,2,...,<7 +1 . (11-159)
Ч/•(/-!)»
Подставляя/ = 1, 2, ... в равенство (11.158), получаем соотношения
II j = 1,2,.. -,q +1 ; (11.160)
_ G2/ i 21 , 1 J = 2,3,. ...,^ + 1 ; (11.161)
_ G^.2! 37 “ G ^33-2! J = 3,4, • • •, q +1; (11.162)
и т. д. Заметим, что Lt, = 1, i = 1,2,... ,? + !• (11.163)
Функции обычной когерентности вычисляются для каждой частоты fk
по формулам
i,j= \,2,...,q + 1- (11.164)
" G^J
Рис. 11.21. Условный спектр G
Цифровые методы анализа
409
При i = 1 имеем
= 7 = 1,2....,<7+1> (11-165)
а при j = q + 1 = У IG р У.у- ’ / = 1,2,...,<7 +1. (11.166) GnGyy
В частности, 7^ = ^^- (И-167)
Заметим, что у2 = 1 (11.168)
при всех i.
Функции частной когерентности yj.(fk) вычисляются
для каждой частоты fk по формулам
у,2у <,_w = _ ’ / = 1,2,+1, j>i. (11.169)
(,-lfyj 0-1)!
При j = q + 1 = у имеем
тЛ((’ / = 1,2,..., <7 + 1. (11.170)
Заметим, что — j)i = 1 при любых/.
Функции множественной когерентности ур.^_= yj\(i-\y(fk) для си-
стем су — 1 входным процессом вычисляются для каждой частоты fk по
формулам
(Hl’»
7 GJj
При j = q + 1 = у получаем функцию множественной когерентности для
полной системы с q входными процессами:
Уу-.ч< = ^ (11.172)
Gyv
11.7.4. КОГЕРЕНТНЫЙ СПЕКТР ВЫХОДНОГО ПРОЦЕССА
Обычные когерентные спектральные функции Gy ;1 выходного процесса
показывают, какая доля спектра последовательности Xj (t) обусловлена по-
следовательностью Для каждой частоты fk эти функции вычис-
Здесь и в аналогичных ситуациях ниже в этом разделе имеется в виду лишь линей-
ный вклад.— Прим, перев.
410
Глава 11
ляются по формулам
Ч:1 = ^Ч7 = 1Ч12(;и» J = l,2,...,? + 1 . (11.173)
При j = q + 1 = у формула (11.173) принимает вид
<?У:1 = У12Аг = |Ь1/<?11 • (11.174)
Частные когерентные спектры Gj.2.x показывают, какая часть спектра
последовательности Ху (Z) обусловлена последовательностью х2. i (О- Для
каждой частоты fk эти функции рассчитываются по формулам
С/ :2.1 = У2У1Ч71 = 1Ч|2С221 ’ J = 2, 3,..., 9 + 1 . (11.175)
При j = q + 1 = у равенство (11.175) принимает вид
<V24 = У1у-fiyyl = 1^2,1421 • (И^б)
Частные когерентные спектры Gj.i.^_iy (i = 2, 3, ...» q) показывают, ка-
кая доля автоспектра последовательности Ху (t) обусловлена последователь-
ностью xi (t) при исключении из xi (t) линейных вкладов последовательно-
стей Xj(Z), х2(О, ... , xz_i(r). Эти спектры вычисляются для каждой часто-
ты Д по формулам
= 1Ч12(7-«-1)! ’ / = 2,3,...,9 + 1. j>i. (11.177)
Заметим, что соотношения (11.173) и (11.175) представляют собой частные
случаи формулы (11.177) при/ = 1 и / = 2 соответственно.
При у* = q 4- 1 = у формула (11.177) принимает вид
= / = 2,3,...,? + Ь (11.178)
так что при / = q имеем
Gy:q(q-l)\ ~ ~ l^qyl ^qq (q-l)'.- (11.179)
Эта функция задает вклад последовательности xq (t) в спектр Gyy при ис-
ключении из y(t) линейных вкладов последовательностей х^г),
... ,^(О.
Множественный когерентный спектр Gy.^_pj выходного процесса пока-
зывает, какая доля автоспектра последовательности Xj(t) обусловлена
предыдущими входными процессамиXj(t), х2(t), ... ,Xj_i(t). Эти спектры
вычисляются по формулам
=
= ^-^••(>-1)!, 7 = 2,3,. ...9 + 1. (11.180)
Цифровые методы анализа
411
При У = q 4- 1 = у имеем
Gy..q, = ^:^yy = Gyy-Gyy.4X. (11.181)
Эта функция задает вклад входных последовательностей %i(O, х2(О,
... , xq(t) в спектр Gyy.
11.7.5. РАЗЛОЖЕНИЕ ОЦЕНОК СПЕКТРАЛЬНЫХ ФУНКЦИЙ
Все измеренные автоспектры Gjj (j = 1, 2, ... ,q 4- 1) могут быть пред-
ставлены на каждой частоте fk в виде имеющих самостоятельный физиче-
ский смысл функций:
I4I2G,, -
/ = 1
7-1
= Е I4I2G,7 (/-D! + Чу 0-1)1, J = 1,2,...,? + 1. (11.182)
/ = 1
При У = q 4- 1 = у формула (11.182) принимает вид
<7
Gyy = Е 1^,|2Ч/.</-1). + Gyy.q,. (11.183)
(=1
В правые части уравнений для G- и Gqq входят те же частные когерентные
спектры выходного процесса, что и в формулы (11.177) и (11.178) соот-
ветственно. При любом значении У уравнение (11.182) представляет спектр
процесса Xj(t) в виде
GjJ = Gj-l + Gj.^.y + 4:3-2! +
+ • ‘ ’ +G7:(J-1) (7-2)! + 4 (7-1)! • (П.184)
Аналогичным образом переписывается и уравнение (11.183):
Gyy = 4:1 + 4:2 1 + 4:3-2! +
+ • • • +4:(«-1) (?-2)! + Gyy.q, . (11.185)
Интегрируя Gyy(f), можно в соответствии с постановкой задачи вычис-
лить средний квадрат процесса для заданного диапазона частот от fa до fb.
Например, при q = 3 имеем
АУУ = jfkGyy(f)df, (11.186)
fa
АуЛ= (/kGy:1(f)df, (11.187)
412
Глава И
АУ11= Gy.2 AT) df, Jfa ' (11.188)
^у 3 2’=/ &у 3 2! (/) ? fa (11.189)
Ayy^.=ffhGyy3Af)df. fa (11.190)
Нетрудно видеть теперь, что
Ауу = АуЛ + Ау.2 1 + АуЗ 2! + АууУ. • (11.191)
Иными словами, Ауу есть средний квадрат последовательности у (!) для
диапазона частот отfa nfb. ВеличинаАу:1 задает долюЛ^, обусловлен-
ную последовательностью Xj(r); Л есть доля Ауу, обусловленная
х2.1(/); Л^.3.2! — доля Ауу, обусловленная x3.2!(Z); наконец, последнее сла-
гаемое Ayy'V определяет долю Ауу, не связанную с последовательностями
*1(0, X2(t) И Х3(Г).
ПРИМЕР 11.5. СИСТЕМА С ТРЕМЯ ПРОЦЕССАМИ НА ВХОДЕ И ОДНИМ
ПРОЦЕССОМ НА ВЫХОДЕ. Рассмотрим частный случай системы с тремя
процессами на входе и одним выходным процессом. Построим вначале в со-
ответствии с рис. 11.16 расширенную матрицу спектральной плотности, а
затем трижды применим формулу (11.149) для получения условных спект-
ральных характеристик на каждой частоте Д, как показано на рис. 11.22.
Члены вида [Gzy. j ] вычисляются по формулам
Gn <*13 Gly
^21 &22 G23 &2y
G31 G32 <*33 &3y
Gyj ^/2 Gy3 Gyy
Gyy-3!
^33 2! ^3/-2«
^Зу-2! ^уу2\
Рис. 11.22. Последовательность спектральных матриц при анализе системы с
тремя входными процессами и одним процессом на выходе.
Цифровые методы анализа
413
&22 1 “ ^22 ^12^21 9 ^12 = (^12/^11)9
^23 1 = G23 — ^13^219 ^13 = (^1з/^п)?
&2у 1 = G2y * ^1^21, ^\у = (^ц/^11).
^33 1 = &33 ~ ^13^31 9
G3y 1 = ^з,- ^1/^319
Gyy 1 = Gyy - LlyGyl j
G32 ! = ^2*3 1, ^у2Л II N>* II h—‘
Члены вида вычисляются по формулам
^33 2» = ^33 1 “ ^23^32 1 г ^23 ~ (^23 1/^22 1) 9
^Зу-2! = ^З.у-1 “ ^2у^32 1, ^2у ( G2y • 1/^22 • 1) 9
^уу-2! Gyyl ^2у(?у2 1)
<Л’3 -2! ~ ^*г2!‘
Наконец, функция Gyy.3, находится в виде
Gyy-3\ ” Gyy*2\ ~ ^з/ЛЗ-2! f
где г
j _ ^-2?
Зу~~ G
°33-2!
Теперь для каждой частоты fk можно вычислить обычные и частные
когерентности:
Y2 = i£k!t .
" GnGyy ’
2 1<?2,.!|2
У2,1 = 7—’
G12
Тз^-2! =
1^-2.|2
G33-2'Gyy2l
414
Глава 11
Функция множественной когерентности определяется уравнением
2 = I _ Gyy*
Уу-у. G
УУ
Когерентные спектры вычисляются по формулам
G =v2g
Угу^уу q 9
2
G>:21 Y2j1G^1 ’
2 r
G>:3-2! “ УЪу Т@уу '1\
V33-2!
Суммарный спектр Gyy = Gyy(fk) представляется в этом случае четырьмя
слагаемыми-
Gyy = Gy l + Gy.2.1 + :з-2? + Gyy.3} .
При у = х4 последнее равенство можно записать в виде
G44 = G4:1 4- G4.2.i + G4:3.2! 4- G^.31.
Аналогичные формулы можно было выписать и для предыдущих этапов,
рассматривая спектр G22 как спектр выходного процесса х2 (О системы с
одним входом Xj(/):
G22 = ^2:1 + G22 4 = Yl22^22 + ®22Л*
Аналогичным образом спектр G33 представляется как спектр выходного
процесса x3(t) системы, на вход которой поступают последовательности
*1(0 их2(Г):
G33 = (*3:1 + G3:21 + G33 2! =
= Тв^ЗЗ + 723 1^33 1 + ^33 -2! •
Для проверки правильности алгоритма заметим, что сумма членов, входя-
щих в правые части трех последних равенств, должна совпадать со значе-
ниями непосредственных оценок автоспектров, стоящих в левой их части.
Задачи
11.1. Выборка [мл] (п = 1, 2, ... , N) имеет среднеквадратичное отклонениеsu .
Найдите среднеквадратичное отклонение последовательности {*_ ] = fw ~ w J (Л = 1,
2, ... , N).
Цифровые методы анализа
415
11.2. Из последовательности ju^] (п — 1, 2, ... ,7V) удаляется полиномиальный
тренд со степенью К = 2. Определите коэффициенты ф b j, b 2) соответствующего
многочлена, подгоняемого к исходной последовательности методом наименьших
квадратов.
11.3. Постройте уравнение для фильтра первого порядка с бесконечной импульс-
ной переходной функцией (рекурсивный ФБИПФ), который ведет себя как высокоча-
стотный RC -фильтр.
11.4. Анализируемая последовательность комплексных величин состоит из?/ =
= 16 384 отсчетов. Сколько операций над действительными числами требуется для
ее преобразования Фурье:
а) обычным методом;
б) методом БПФ по алгоритму Кули — Тьюки?
11.5. По реализации х (t) стационарного случайного процесса строится оценка
автоковариационной функции, приближаемая формулой
/?хх(т) = е-2|т| cos 18,85т ,
причем длина реализации составляет Т = 1 с. Напишите уравнение для циклической
ковариационной функции, получаемой путем обратного преобразования Фурье оцен-
ки автоспектра, к которой не добавляются нулевые значения.
11.6. Оценка автоковариационной функции строится по реализации стационарно-
го случайного процесса, содержащей N = 8192 отсчета. Расчет предполагается вести
косвенным методом с использованием БПФ и при максимальном сдвиге m = 256.
Есть два варианта расчета: по всей реализации длиной N = 8192 отсчета или по
nd = 32 отрезкам длиной по N = 256 отсчетов. Какой вариант требует меньшего
числа операций?
11.7. Непрерывная реализация длиной Т = 4 с дискретизируется со скоростью
4096 отсчетов в секунду и полученный временной ряд используется для построения
оценки спектральной плотности при разрешающей способности Д/ = 16 Гц. Опреде-
лите:
а) примерное число операций над действительными числами, нужное для вычис-
ления искомой оценки;
б) нормированную случайную ошибку оценки.
11.8. По выборке длиной Т = 1,015 с, принадлежащей процессу x(t) =
= A sin IOOttZ , вычислены коэффициенты Фурье. Считая скорость дискретизации
очень высокой, определите максимально возможное значение коэффициента Фурье,
которое можно получить по этой выборке при осуществлении преобразования:
а) с прямоугольным временным окном;
б) с окном Ханна.
11.9. Взаимная ковариационная функция оценивается по одной паре реализаций,
каждая из которых содержит N = 4096 отсчетов. Определите коэффициент ускоре-
ния вычислений, отвечающий прямому и косвенному (с использованием БПФ) спосо-
бам расчета при максимальном сдвиге m = 256.
11.10. Шумовая ширина определяется как полоса пропускания идеального пря-
моугольного полосового фильтра, дающего на выходе то же значение среднего ква-
драта процесса, что и при фильтрации белого шума. Определите шумовую ширину
спектрального окна, отвечающего временнбму сглаживанию прямоугольным окном
шириной Т.
Глава 12
АНАЛИЗ НЕСТАЦИОНАРНЫХ ПРОЦЕССОВ
Предшествующие главы посвящены прежде всего измерению и анализу
стационарных случайных процессов, т. е. процессов, статистические
свойства которых не изменяются при переносе начала отсчета времени (или
другого аргумента, от которого зависит рассматриваемый процесс). При-
веденные в этих главах теоретические выводы, формулы для ошибок оце-
нок и методы анализа, как правило, не применимы для нестационарных
процессов. Их анализ требует специального рассмотрения и специальных
методов, чему и посвящена данная глава.
12.1. Классы нестационарных процессов
Большинство случайных процессов, встречающихся на практике, имеют
в общем нестационарный характер. И все же для целей измерения и анали-
за довольно часто удается «вынудить» процесс по крайней мере к кусочно-
стационарному поведению. Так, возвращаясь к примеру, приведенному в
разд. 10.4.1, заметим, что флуктуации давления в турбулентном погранич-
ном слое, возникающие при обычном полете высокоскоростного самолета,
следует, вообще говоря, считать нестационарным процессом, так как они
зависят от скорости воздушного потока и от высоты, а эти параметры ме-
няются в течение одного полета. Однако для целей измерения легко осу-
ществить полет при заданных условиях и обеспечить стационарность вари-
аций давления. Затем полетное задание можно менять по определенной
программе от эксперимента к эксперименту, получая каждый раз стацио-
нарную запись. В результате достаточно детальное описание всевозмож-
ных условий полета получается в виде набора кусочно-стационарных реали-
заций. Такие приемы описания в целом нестационарных явлений при помо-
щи стационарных процессов используются довольно часто и настоятельно
рекомендуются, поскольку они позволяют избежать применения методов,
необходимых при анализе нестационарных процессов.
Существуют ситуации, когда описанный подход к сбору и анализу дан-
ных нецелесообразен или нереален, так что индивидуальные реализации
приходится анализировать как реализации нестационарного процесса. С чи-
сто вычислительной точки зрения наиболее удачна ситуация, когда экспери-
мент, дающий реализацию изучаемого нестационарного процесса, допуска-
ет повторение при статистически идентичных условиях. Таким путем мож-
но, как показано на рис. 12.1, получить ансамбль реализаций в единой си-
стеме отсчета времени. Однако чаще бывает так, что изучаемое нестацио-
нарное явление уникально и его нельзя повторить при статистически сход-
ных условиях. Примерами могут служить нестационарные волны в океане,
атмосферная турбулентность, различные временные ряды в экономике. Ос-
новные силы, создающие процесс, настолько сложны, что повторные экс-
перименты при сходных условиях не осуществимы. Во всех этих случаях
анализ приходится осуществлять лишь по одной реализации процесса.
Анализ нестационарных процессов
417
12 i
Рис. 12.1. Реализации нестационарного случайного процесса.
Не существует единой методологии, в рамках которой можно анализи-
ровать свойства нестационарного случайного процесса любого типа, поль-
зуясь индивидуальной его реализацией. В известной мере это связано с тем,
что вывод о нестационарности изучаемого процесса имеет чисто негатив-
ный характер, означая просто отсутствие свойства стационарности. Пози-
тивного определения точной природы нестационарности такой вывод не
содержит. Поэтому для анализа нестационарных процессов приходится
разрабатывать специальные методы, приложимые только к отдельным
классам нестационарных процессов. Обычный подход состоит во введении
гипотезы о специфическом характере нестационарности изучаемого процес-
са, который рассматривается как результат воздействия некоторых детер-
минированных факторов на стационарный случайный процесс. Три приме-
ра, показанные на рис. 12.2, представляют собой реализации нестационар-
ных процессов вида
a) x(r) = a(t) + u(t),
б) x(z) = (12.1)
в) x(r) = u(tn),
где u(f) — реализация стационарного случайного процесса {«(/)], a a(t) —
14-953
418
Глава 12
Время
Время
Рис. 12.2. Примеры нестационарных процессов: а — с переменным во времени
средним значением; б — с переменным во времени средним квадратом; в — с пере-
менной во времени частотной структурой.
заданная функция, в точности повторяющаяся для каждой реализации. Та-
кие элементарные нестационарные модели можно комбинировать или
обобщать, добиваясь лучшего соответствия реальным физическим условиям.
12.2. Вероятностная структура нестационарного процесса
Как показано на рис. 12.1, статистические свойства нестационарного
случайного процесса [х(0], определенные усреднением по ансамблю в мо-
мент времени г, не инвариантны относительно переноса момента t. Следо-
вательно, при любом t = tx вероятностная структура случайной величины
x(zp зависит от tv Точнее говоря, нестационарная плотность вероятности
р(х, /р случайной величины [х(/р] имеет вид
Р[х < х(л) < х + Дх]
р(х, *1) = lim -----------X----------
Дх-»О Дх
(12-2)
Анализ нестационарных процессов
419
и при любом t обладает следующими основными свойствами:
/•00
1 = / р(х,/) dx,
' - 00
= £[x(z)] = f xp(x,t)dx,
(12.3)
г 1 /*0С
ф*(/) = f[x2(r)] = ( x2p(x,t)dxt
J - 00
Ox2(z) = f[(x(r) - M')}2] = ’Рл(') -
В стационарном случае функция р(х, t) = р(х), т. е. не зависит от t. Не-
стационарная функция распределения есть
P(x,tO = р[-оо < x(zj < х]. (12.4)
Для Р(х, zp справедливы соотношения, подобные рассмотренным в гл. 3
соотношениям для стационарной функции распределения Р(х).
Если при t = tx нестационарный случайный процесс (х(/)) гауссов, то
функция р(х, /р имеет вид
р{х, tr) = [ох(^)^]-1ехр/—!—к (12.5)
( )
т. е. полностью определяется нестационарным средним и нестационарным
средним квадратом функции x(t) в момент t = tx. Отсюда видно, что, как
и в рассмотренном ранее случае стационарных процессов, измерение этих
двух характеристик весьма важно во многих приложениях к нестационар-
ным задачам.
12.2.1. РАСПРЕДЕЛЕНИЯ БОЛЕЕ ВЫСОКОГО ПОРЯДКА
Для двух моментов времени tx и t2 двумерная нестационарная плот-
ность вероятности случайных величин xfq) и x(t2) определяется выражени-
ем
р(*и х2> h)=
P[xj < x(fj) < Xj + Дх/ И X2 < x(/2) < x2 + Дх2]
" Ax.-o (Дх2)(Дх2)
Дх2-*0
(12.6)
14:
420
Глава 12
и при любых Zj и t2 обладает такими основными свойствами:
Я 00
р(х15 х2, /2) dxx dx2 >
—
p(x1,t1; x2,t2) dx2 ,
J - oo
p(x2,t2)=( p(x1,tl;x2,t2)dxl>
J - 00
(12.7)
Яхх('1, *2) = E [*01)*( l2)] = ff x1x2p(xl, ZiJ x2, t2) dx2 dx2
J J - 00
В случае стационарного процесса p(xv tx*9 x2, t2) = p(xp 0, x2; t2 — rp.
Двумерная нестационарная функция распределения может быть определена
по аналогии с формулой (12.4):
Р(хр 1г; х2, /2) = р[-оо < x(t2) < и -оо < х(/2) < х2]. (12.8)
Продолжая таким образом, можно строить нестационарные функции
распределения и плотности вероятности более высоких порядков, получая
все более детальную информацию о нестационарном случайном процессе
[х(0]. Такой подход дает вполне строгое описание нестационарного процес-
са.
Рассмотрим теперь два различных нестационарных процесса [x(Z)} и
[j(Z)]. Совместная (двумерная) плотность вероятности случайных величин
x(t}) и j(G) есть
р(х, у, t2) =
Р[х < х(?1) < X + Дх и у < y(t2) <у + Aj/]
lim -------------------—---------------------
д^о (Д*)(Лр)
(12-9)
Эта функция обладает теми же основными свойствами, что и плотность
вероятности (12.7). В частности, нестационарная взаимная ковариационная
функция, рассматриваемая в разд. 12.5, удовлетворяет соотношению
Лху('1> *2) = £[Л(?1)/(^)] = (( хур(х, t2; у, t2) dxdy. (12.10)
J J — oo
В случае стационарного процесса p(xlf у, t2) = р(х, 0; у, t2 - гр.
Измерение нестационарных плотностей вероятности может оказаться
весьма трудоемкой задачей. Даже в случае одномерной плотности, задан-
ной формулой (12.2), нужно рассматривать все возможные сочетания х и
tv Для этого нужно анализировать большой ансамбль реализаций процес-
са. Если гауссово приближение приемлемо, то, согласно (12.5), задача из-
мерения р(х, zp сводится к измерению только Mx(zp и ax2(zp, что сущест-
венно проще. И все же, как показано в разд. 12.3 и 12.4, усреднение по ан-
самблю остается обычно необходимым. Ф'
Анализ нестационарных процессов
421
12.2.2. СРЕДНИЕ ПО ВРЕМЕНИ РАСПРЕДЕЛЕНИЯ
На практике для анализа нестационарного процесса имеется часто лишь
одна или несколько реализаций. В таких случаях появляется соблазн анали-
зировать процесс путем вычисления средних по времени характеристик, как
это делается в случае стационарных (эргодических) процессов. Как будет
показано ниже, такое усреднение по времени может дать осмысленные ре-
зультаты для некоторых параметров и при некоторых специфических усло-
виях. Однако при оценивании плотности вероятности такое усреднение по
времени ведет, как правило, к сильно искаженным оценкам. В частности,
при вычислении плотности вероятности процесса с нестационарным сред-
ним квадратом путем усреднения по времени плотность вероятности боль-
ших и малых величин будет завышена за счет уменьшения плотности веро-
ятности умеренных величин (см. пример ниже).
ПРИМЕР 12.1. СРЕДНЯЯ ПО ВРЕМЕНИ ПЛОТНОСТЬ ВЕРОЯТНОСТИ. Пусть
первая половина реализации принадлежит гауссову стационарному случай-
ному процессу с нулевым средним значением и дисперсией aj, а вторая —
такому же процессу, но с дисперсией
О < t < Т/2;
T/2<t < Т,
Рис. 12.3. Прих плотности вероятности нестационарного процесса.
422
Глава 12
так что плотность распределения реализации x(f) есть
Т/2. < t < т.
О < t < Т/2;
Если теперь игнорировать это свойство нестационарности при вычислении
плотности вероятности функции x(t) на интервале от 0 до Г, то при лю-
бом значении х плотность вероятности будет определяться как среднее из
плотностей, отвечающих двум отрезкам реализации, т.е.
Я%) 2^2?
O1 о2
Пусть, например, = 1 и = 16. Получаемая в этом случае средняя по
времени плотность вероятности показана на рис. 12.3. Заметим, что для
этой оценки а = 2,9, поскольку + а2) = 8,5. На рис. 12.3 показана
также эквивалентная гауссова плотность вероятности при а = 2,9.
12.3. Среднее значение нестационарного процесса
Рассмотрим задачу оценивания переменного во времени среднего значения
нестационарного процесса. Располагая ансамблем реализаций хДг)
(О t Т, i = 1,2, нестационарного процесса [х(0], оценку средне-
го значения в момент времени t получают усреднением по ансамблю:
= (12-11)
Оценки Дх(г) будут различаться при различном выборе N реализаций xz(z).
Следовательно, при каждом t необходимо изучить степень приближения
оценки к истинному среднему значению. Математическое ожидание оценки
Мх(0 равно
х 1 л
Е[МО] = Е £[*,(')] = МО, (12.12)
где
М0 = £[М0] (12.13)
есть истинное среднее значение рассматриваемого нестационарного процес-
са в момент t. Таким образом, мх(0 есть несмещенная оценка при
всех t независимо от N. Дисперсия оценки £Х(Г) есть
Var[M0] = Е[{) - МО}2]. (12.14)
Анализ нестационарных процессов
423
х\(1) ---------Устройство
г . для
л2 запоминания
: ансамбля
xN(i) ---------► реализации
Устройство
для усреднения
----по ансамблю -
(суммирование
и деление на А')
P*(i)
Рис. 12.4. Измерение нестационарного среднего значения.
Среднее значение нестационарного случайного процесса можно оценивать с
помощью специальной аппаратуры или на ЭВМ (рис. 12.4). Построение
этой оценки требует двух основных операций. Первая — получение и запо-
минание каждой реализации x^f) как функции t. Реализация может быть
записана в аналоговой форме при всех t в диапазоне 0 t Т или дис-
кретно с помощью того или иного способа дискретизации. После выполне-
ния этой операции для всех N реализаций выполняется вторая операция —
усреднение по ансамблю, для чего реализации суммируются и делятся на
N. Если каждая реализация состоит, скажем, из М отсчетов, то общее чис-
ло содержащихся в памяти машины величин равно MN.
12.3.1. НЕЗАВИСИМЫЕ РЕАЛИЗАЦИИ
В большинстве практических приложений N выборочных функций, ис-
пользуемых для расчета Дх(/), статистически независимы. Поэтому и здесь
реализации полагаются независимыми. Раскрывая скобки в равенстве
(12.14), как при выводе соотношения (4.9), найдем, что дисперсия оценки
gv(Z) в момент t есть
a2(z)
Var[/ix(/)] =, (12.15)
где — дисперсия нестационарного процесса {*(/)]. Таким образом,
дисперсия оценки стремится к нулю при стремлении N к бесконечности, так
что /^(Ц есть состоятельная оценка px(t) при всех t.
Доверительный интервал для нестационарного среднего значения цх(1)
можно построить по оценке дх(0, пользуясь методом, описанным в
разд. 4.4.
Для момента времени t доверительный интервал с уровнем доверия
1 — а есть
<(0^;а/2
МО МО +
М0'П;а/2
(12.16)
Здесь ax(t) — несмещенная оценка среднеквадратичного отклонения ax(t)
процесса {%(/)} в момент /, определяемая в соответствии с формулой (4.12)
в виде
1
W -1
МО =
Е [МО - МО]2
(12.17)
424
Глава 12
и t есть 100а/2%-ная точка /-распределения Стьюдента с п = N — 1
степенями свободы (см. разд. 4.2.3). Заметим, что при достаточно боль-
шом размере ансамбля (скажем, N = 10) формула (12.16) справедлива и
для негауссовых процессов. Это утверждение следует из центральной пре-
дельной теоремы (см. разд. 3.3.1), которая прямо относится к вычислению
среднего значения нестационарного процесса по формуле (12.11).
12.3.2. КОРРЕЛИРОВАННЫЕ РЕАЛИЗАЦИИ
Рассмотрим общий случай, когда выборочные функции хДГ) (/ = 1,
2, ..., 7V) нестационарного случайного процесса попарно коррелированы,
так что при любом Z1)
E[x,.(r)x/z)] = ЯХХ(М), k=j-i. (12.18)
Величина Rxx(k, t) называется нестационарной пространственной взаим-
ной ковариационной функцией в момент Г, связывающей все пары реализа-
ций х(Г) и х (Г), удовлетворяющие условию к = j - Z. Как следует из фор-
мулы (12.18), замена i на j дает
Rxx(-k,t) = Rxx(k,t), (12.19)
При независимых выборочных функциях хДг) и Xj(f) и при i Ф j (что со-
ответствует к Ф 0)
Rxx(k, t) = Е[x,(z)xy(/)] = E[x,(z)]E[x7(0] = ц2(г), к * 0.
(12.20)
При к = 0 формула (12.18) принимает вид
Яхх(0, о = Е[x,2(z)] = ax2(z) + м2(/)_ (12.21)
Эти соотношения охватывают и рассмотренный в предыдущем разделе
случай независимых реализаций.
При коррелированных реализациях формула (12.15) в общем виде запи-
шется следующим образом:
о ) 1
VarlM')] = £ £{[*,(')-мх(0][*7(0-МХ(О]) =
лу=1
ох2(/) 1 Д
= + ~ '> - Мх(0]. (12.22)
i*j
Здесь принята иная система обозначений, чем в предыдущей части книги. —
Прим, перев.
Анализ нестационарных процессов
425
Теперь попытаемся избавиться от двойной суммы в формуле (12.22). Ин-
декс к — j — i принимает значения к = 1, 2, ..., N — 1. Всего имеется
N2 - N слагаемых. Так как R^ — k, t) = R^ik, t), то N2 — N слагаемых
в этой двойной сумме можно расположить в таком порядке, чтобы выде-
лить два члена вида R^tN — 1, 0, для которых к = N — 1; четыре члена
вида R^N — 2, Г), для которых к = N - 2, ...; 2(N — 1) членов вида
^(1, 0, Для которых к = 1. Таким способом можно получить более про-
стое выражение:
Е АХЛ(у-/,/) = 2N^\N-k)Rxx(k,t). (12.23)
/,;=1 £ = 1
Для проверки заметим, что
7V-1
2 X (N - к) = N2 - N . (12.24)
А: = 1
Подстановка формулы (12.23) в (12.22) дает
Var[Ajr)] =^ + -л Е (У-Л)[Лхх(^0-Мх(0] (12.25)
Я к=1
Из равенства (12.20) следует, что при независимых реализациях формула
(12.25) сводится к виду (12.15), что может служить дополнительным под-
тверждением справедливости равенства (12.25). Формула (12.25) представ-
ляет собой важное обобщение равенства (12.15), и ее следует использовать
вместо (12.15) при коррелированных реализациях.
Следует упомянуть частный случай полной зависимости между всеми ре
ализациями. Тогда для любых к
Rxx(k, Г) = Яхх(0,1) = ох(/) + /х2(г) . (12.26)
Формула (12.25) принимает вид
VarfMO] = ^ + ^(tf2-tf)ax2(z) = ax2(0. (12.27)
Таким образом, при полностью коррелированных реализациях дисперсия
оценки не уменьшается.
В тех физических ситуациях, когда между отдельными реализациями су-
ществует частная корреляция, количественные результаты можно полу-
чить, основываясь на приводимом ниже примере.
ПРИМЕР 12.2. ДИСПЕРСИЯ ОЦЕНОК СРЕДНЕГО ЗНАЧЕНИЯ ПРИ ЭКС-
ПОНЕНЦИАЛЬНОЙ КОРРЕЛЯЦИИ МЕЖДУ РЕАЛИЗАЦИЯМИ. Предполо-
жим, что взаимные ковариационные функции Rxx(k, t) имеют экспоненци-
альный вид. Получим для этого случая некоторые результаты, характери-
426
Глава 12
зующие различные степени корреляции. Итак, пусть
t) = g2(0 + o^(t)e~kc,
где кис — положительные постоянные. Определим соответствующую
выборочную дисперсию оценок нестационарного среднего значения.
Согласно формуле (12.25), эта выборочная дисперсия имеет вид
Var[£x(0] = ~^ +
7V2
у-1
У. (# - к)е~кс.
к = 1
Для подсчета суммы в правой части положим
N—l j _
/W - I
к — 1 е 1
Тогда
N—1
f'(c) = - L ке~к
к = 1
Теперь
^-(y-2>c — (ЛГ - 1)е-<Л,-1)с - ес
(е‘-1)2
W-1 _ N + е-^-1)с
F(c) = Е (N - к)е~кс = W) +/'(с) = ----------------~2------
к = \ [е с-1)
Подстановка этого выражения в формулу для дисперсии дает
ох2(/)
Уаг[ДЛ(г)] =—— +
2ах2(г)
7V2
(N - Г)ес - N + e~{N~l)c
(е‘-1)2
Этот результат можно использовать для построения семейства кривых, от-
вечающих различным значениям aJ(Z), W и с. Постоянную с для практиче-
ского использования этих кривых можно оценить экспериментально.
12.3.3 . АНАЛИЗ ИНДИВИДУАЛЬНЫХ РЕАЛИЗАЦИЙ
Как уже отмечалось в разд. 12.1, на практике для анализа нестационар-
ного процесса зачастую имеется всего одна реализация. В таких случаях не-
стационарное среднее значение оценивают обычно по одной реализации с
помощью той или иной операции, эквивалентной фильтрации низких ча-
стот. Для некоторых классов нестационарных процессов такой прием мо-
жет дать полезные результаты. Пусть, например, [х(0] — нестационарный
процесс вида
(х(0) =а(г) +{«(0), (12.28)
где a(t) — детерминированная функция и — случайный процесс с не
Анализ нестационарных процессов
427
зависящим от времени нулевым средним значением. Тогда среднее значение
в момент времени t есть
Е [{ х(/)}] = Е[а(г) + {«(0)] = £[«(')] + £[{«(')}] = «(0- (12-29)
Если предполагается, что функция a(t) меняется медленнее низкочастотных
составляющих процесса (u(Z)], то ее можно отфильтровать из смеси с [u(t)
низкочастотным фильтром по одной реализации x(t). Такую операции
можно осуществить несколькими способами, в том числе:
а) рекурсивным или нерекурсивным низкочастотным фильтром (см.
разд. 11.1.3);
б) подгонкой к x(t) степенного многочлена (см. разд. 4.8 и обсуждение
задачи удаления тренда в разд. 11.1.2);
в) оцениванием среднего по отдельным отрезкам реализации (усреднени-
ем по коротким интервалам).
Получаемые таким путем оценки среднего будут в любом случае со-
держать систематическую ошибку, зависящую от вырезывающей частоты
низкочастотного фильтра (степени подгоняемого многочлена или длины
интервала усреднения) и от скорости изменения функции a(t).
Рассмотрим, например, оценку среднего значения, полученную усредне-
нием по короткому интервалу:
Mx(z) = f'+T/2x(t) dt = f^T/2[a(() + M(z)] dt, (12.30)
Jt-T/2 Jt-T/2
где T — время усреднения. Легко показать, что
/+Г/2[«(0 + «(О] dt
Jt- Т/2
£[М0] = £
Г7'/2{£[а(/)]+Е[М(/)]}^ =
t-T/2
= Г T/2a(t) dt Ф a(t). (12.31)
J t-T/2
Следовательно, оценка дх(0, вообще говоря, смещена. Рассуждая таким же
образом, как и в разд. 8.3.1, можно получить первое приближение для
ошибки смещения в момент t в виде
Т2
ММ')]=^-«"(Ф (12.32)
где a"(t) — вторая производная функции a(t) по t. Из формулы (12.32) сра-
зу видно, что ошибка смещения уменьшается по мере уменьшения интерва-
ла усреднения Т. Однако, как и в случае стационарного процесса, рассмот-
ренном в разд. 8.2.1, случайная ошибка смещения возрастает с уменьшени-
ем Т. Таким образом, при выборе длины интервала усреднения нужно ис-
кать компромиссное решение с учетом систематической и случайной оши-
бок оценки. Наилучшее решение, как правило, находится методом проб и
ошибок.
428
Глава 12
12.4. Средний квадрат нестационарного процесса
Теперь по аналогии с разд. 12.3 проанализируем, как зависит от време-
ни средний квадрат процесса. Такую информацию можно получить при по-
мощи специальной аппаратуры или вычислительной машины, которая рас-
считывает оценку среднего квадрата по N реализациям следующим путем.
Значение квадратов N выборочных функций хДг) (j = 1, 2, ..., N) нестацио-
нарного процесса [x(/)j при фиксированном t усредняются по ансамблю:
^(0 = Е>.2('). (12.33)
Величина ifyf) представляет собой при любом t несмещенную оценку ис-
тинного среднего квадрата процесса xfyt) при любом /, поскольку ее мате-
матическое ожидание равно
£[^(0] = Е £[*,2(0] = ^(0. (12-34)
Величина 1~1
^(/) = Е [х,2(г)] = /4(0 + <4(0 (12.35)
есть истинный средний квадрат нестационарного процесса в момент t. Из
рис. 12.4 видно, как можно измерить ^(/), просто заменив хД/) на х?(Г).
12.4.1. НЕЗАВИСИМЫЕ РЕАЛИЗАЦИИ
Допустим теперь, что N реализаций хД/) попарно, независимы, так что
при любых i и j
Е [*,(0*7(0] = Е [х,(0] Е [х/о] = /4(0- (12.36)
Найдем дисперсию оценки ^(/). По определению
Var[^(0] = я[Ш0 - *2(0}2] = £[{<И(0}2] - V4(0, (12.37)
где величина определяется формулой (12.35) и
£[{^(0}2] = Е 1£[^,2(0^;2(0] =
-у E£h, (0] + Е е[х,(0-4(0]
V < = 1 <.у=1
1*7
(12.38)
Таким образом, согласно соотношению (12.38), задача сводится к оценке
математического ожидания.
Анализ нестационарных процессов
429
Для получения разумных решений в замкнутой форме допустим теперь,
что случайный процесс [хД0] при любом t подчиняется нормальному рас-
пределению со средним значением мЛ(0 и дисперсией (fyt). Можно пока-
зать, что тогда
£[x,4(O] = 3^(z)-2g4(z), (12.39)
£[x2(z)x2(z)] = «p4(z),
i *j-
(12.40)
Вывод формул (12.39) и (12.40) основан на соотношении для четвертых мо-
ментов нестационарных нормальных случайных величин (формула (3.82):
£[x,(z)xy(z)xm(z)x„(z)] = £[x,(z)xy(z)]£[xm(z)x„(z)] +
+ £[x,(z)x„,(z)]£[x,(z)x„(z)] +
+ £[x,(z)x„(z)]£[xy(z)xm(z)] - 2g4(z).
(12-41)
Подстановка этого соотношения в формулы (12.37) и (12.38) дает
2
Var[^(z)] = -№(0-M4x(')L (12-42)
Следовательно, дисперсия оценки стремится к нулю при N -* оо, так
что ^(z) — состоятельная оценка для всех t.
Чтобы получить доверительный интервал для ^(0, удобнее работать с
оценкой нестационарной дисперсии, которая, согласно выражению (12.35),
имеет вид ~ ?2 л2 ч
оЛ2(/) = ^х~ Рх- (12.43)
Если величины хДг) (z = 1, 2, ..., N) распределены нормально, то оценка
о^(/) имеет при каждом t определенное в разд. 4.3.2 выборочное распреде-
ление, где аэ/ х о/ х о z
°х(0 = ах^)хп/п> п = N - 1, (12.44)
Хп2 — случайная величина, имеющая ^-распределение с п = N - 1 степе-
нями свободы (см. разд. 4.2.2). Таким образом, при любом t доверитель-
ный интервал для о^(0 с уровнем доверия 1 — а есть
И«х2(0 2/ ч »®х2(0
—------< Ox2(z) < —--------
Хи; а/2 Хи;1-а/2
п = N - 1.
(12.45)
12.4.2. КОРРЕЛИРОВАННЫЕ РЕАЛИЗАЦИИ
Для случая коррелированных реализаций примем, как и в разд. 12.3.2,
что функции хДг) удовлетворяют соотношению
£[x,(z)x,(z)] = z), к =j - i. (12.46)
430
Глава 12
Теперь при i Ф j формула (12.40) принимает вид
Е [x2(z)x2(/)] = ^(z) + l[R2xx(k, z) - /(z)], (12-47)
где к = j — i Ф 0. При i = J равенство (12.46) перепишем в виде
я[х,2(/)] = ЯЛД0,0 = ^(0- (12.48)
Способ включения в анализ функций R^k, t) описан в разд. 12.3.2.
Здесь аналогичный прием ведет к соотношению
2 4 N-i
Var[^2(/)] = — [ 1/4(0 - /(0] + Е (^ - k)[R2xx(k, z) - /(z)],
(12.49)
что служит полезным обобщением формулы (12.42).
ПРИМЕР 12.3. ДИСПЕРСИЯ ОЦЕНОК СРЕДНЕГО ЗНАЧЕНИЯ КВАДРАТА
ПРИ ЭКСПОНЕНЦИАЛЬНОЙ КОРРЕЛЯЦИИ МЕЖДУ РЕАЛИЗАЦИЯМИ. Для
Получения некоторых соответствующих формуле (12.42) количественных
выражений, которые отвечали бы различной степени корреляции, предпо-
ложим, что Rxx(k, t) имеет вид
Rxx(k, t) = /(z) + o2(t)e~k\
где кис — положительные постоянные. Определим соответствующую вы-
борочную дисперсию для оценок среднего значения квадрата.
Выборочная дисперсия определяется выражением (12.49). Для нахожде-
ния этой оценки, как и в примере 12.2, воспользуемся функциями /(с) и
f (с). Имеем
R2xx(k, t) ~ /(z) = ox2(z)[2/(z)e~*c + o2(t)e~2kc]
Следовательно, второе слагаемое в правой части выражения (12.49) есть
(W - фу*-*' + <ФФ~2‘']-
w *-1
= ^1[2/(z)F(c) + /(z)F(2<
N
Итак, искомая дисперсия определяется последней формулой и первым чле-
ном формулы (12.49).
12.4.3. АНАЛИЗ ИНДИВИДУАЛЬНЫХ РЕАЛИЗАЦИЙ
В некоторых случаях оценка переменного во времени среднего квадрата
может быть получена путем низкочастотной фильтрации всего одной реа-
Анализ нестационарных процессов
431
лизации (см. разд. 12.3.3). При этом удобно иметь дело с мультипликатив-
ной моделью нестационарного процесса вида
{x(z)} = <z(z){M(z)}, (12-50)
где a(t) — детерминированная функция, a [u(/)J — случайный процесс с не
зависящими от времени нулевым средним значением и единичной дисперси-
ей. Таким образом,, средний квадрат процесса в момент t есть
Var[{x(z)}] = Var[a(z){w(z))] = а2(t)Var[{w(z)}] = a2(z). (12.51)
Как и при оценивании среднего значения, заметим, что если a(t) меняется
медленнее низкочастотных составляющих процесса [«(О), то a2(t) можно
отфильтровать по одной реализации x(t). Это можно осуществить, приме-
няя к квадрату х2(/) сигнала x(t) один из методов, рассмотренных в
разд. 12.3.3. Конечно, получаемая таким путем оценка среднего квадрата
будет смещена. Например, при оценивании усреднением по короткому ин-
тервалу имеем
f,+r/2a2(z)w2(z) dt
t-T/2
(>+Г/2Е[а2(/)] £[w2(z)] dt =
t-T/2
('+T/2a2(t)dt * a2(t).
t-T/2
(12.52)
ПРИМЕР 12.4. ОЦЕНКА СРЕДНЕГО КВАДРАТА, ПОЛУЧЕННАЯ УСРЕД-
НЕНИЕМ ПО КОРОТКОМУ ИНТЕРВАЛУ ВРЕМЕНИ. Рассмотрим вибрации
конструкций стартующего космического корабля. Естественно ожидать,
что в любой точке корабля вибрация образует нестационарный случайный
процесс, поскольку вынуждающие силы во время взлета (прежде всего, аку-
стический шум, создаваемый турбулентным перемешиванием выхлопных
газов ракетного двигателя с окружающим воздухом) зависят от быстро ме-
няющихся параметров, в частности от скорости корабля и от расстояния
до точки отражения струи на поверхности земли. Измерение переменного
во времени среднего квадрата путем усреднения по ансамблю в соответст-
вии с формулой (12.33) в этом случае нереально экономически, поскольку
для получения нужных для операции усреднения N реализаций придется N
раз запускать космический корабль. Можно ли получить приемлемое реше-
ние этой задачи, пользуясь усреднением по коротким интервалам времени?
При любой заданной конфигурации космического корабля характер ви-
брации его конструкций будет в общем повторяться, поскольку параметры,
от которых зависят вынуждающие силы, меняются от запуска к запуску
одним и тем же образом. Кроме того, такой временной тренд будет отно-
сительно медленным (несколько секунд на полуцикл) по сравнению с мини-
мальной частотой энергетически значимых возмущений (несколько герц).
Поэтому для решения задачи в первом приближении можно воспользовать-
ся моделью (12.50).
Для демонстрации конкретного приложения рассмотрим данные реаль-
ных измерений, показанные на рис. 12.5. Здесь даны полученные усреднени-
432
Глава 12
Время с момента отрыва,с
Рис. 12.5. Переменные во времени среднеквадратичные значения вибрации кос-
мического корабля во время старта. Данные Лаборатории реактивного движения в
Пасадене, Калифорния.
ем по коротким интервалам оценки среднеквадратичного значения вибра-
ций одной и той же конструкции при взлете трех космических кораблей
примерно одинаковой конфигурации. Время усреднения в каждом случае
составляет около 1 с, а ширина спектра процесса — несколько сотен герц.
Хорошее согласие результатов для всех трех запусков показывает, что по-
следовательность оценок среднего квадрата, вычисленных усреднением по
коротким интервалам, служит неплохим приближением зависимости сред-
него квадрата ^(/) от времени. При этом нужно, конечно, помнить, что,
согласно соотношению (12.52), все эти оценки смещены.
12.5. Корреляционная структура нестационарных
процессов
Рассмотрим вещественные нестационарные случайные процессы [*(/)] и
[у(ОЬ В произвольный момент t их средние значения определяются мате-
матическими ожиданиями
МО = £[*(0],
(12.
М') = Е [/(г)].
Исходные процессы можно теперь привести к нулевым средним значениям,
заменяя x(t) на x(t) — nx(t) и y(t) на y(t) — ny(t). В дальнейшем предпола-
гается, что эта операция выполнена.
Анализ нестационарных процессов
433
12.5.1. ДВОЙНЫЕ ПО ВРЕМЕНИ КОВАРИАЦИОННЫЕ ФУНКЦИИ
Ковариационные функции при произвольных фиксированных значениях
Zj и /2 определяются математическими ожиданиями
Rxx^i) = Е [х(/1)х(г2)] ,
(12.54)
Ryykh, h} = Е [Я'ЛЯ'г)] >
Rxy(tvti) = £[x(G)j(r2)] • (12.55)
Величины Rxx(tj, Z2) и Ry(tv Z2) называются нестационарными ковариаци-
онными функциями, a Rxy(tv t2) — нестационарной взаимной ковариацион-
ной функцией. Как показано в разд. 5.1.1, в стационарном случае эти функ-
ции зависят не от и Z2, а только от разности — t2.
Действуя по аналогии со стационарным случаем (см. разд. 5.1.3), мож-
но показать, что при любых tx и Z2 верхняя граница нестационарной взаим-
ной ковариационной функции определяется неравенством для взаимной ко-
вариации:
|АхД/1,/2)|2<Лхх(г1Л1)М?2,/2). (12-56)
Из основных определений сразу следует, что
(12.57)
RyyUl’ *1) = RyyUl’ h),
MW1) = M'!’'2)- С12’58)
Рассмотрим задачу измерения Rxx(t\, t?) по совкупности из N выбороч-
ных функций xz(Z) (/ = 1, 2, ..., 2V), принадлежащих нестационарному слу-
чайному процессу. Вместо формулы (12.54) нужно найти среднюю по ан-
самблю оценку
RxxUi’ h) = Е (12.59)
Рекомендуемый прием — фиксирование tx при переменном z2. Пусть tx = Z
и Z2 = Z — т, где т — фиксированная величина сдвига во времени. Тогда
функция N
Rjj, ‘ - т) = 77 Е ^,(0х,(г - т) (12.60)
™ i-1
в случае стационарного процесса является только функцией 7, а в случае не-
стационарного процесса — функцией Z и т. Для каждого фиксированного
значения сдвига т и каждой реализации xz(z) рассчитываются и запомина-
ются произведения xf.(Z)xz(Z — 7). Эта операция повторяется для всех N реа-
лизаций, а последующее усреднение по ансамблю дает оценку (12.60). Вся
434
Глава 12
Xi(t)
Умножающее
устройство
Запоминание
ансамбля
реализации
Генератор
времени
задержки
Xi(t-T)
Блок
усреднения
по ансамблю
Рис. 12.6. Схема измерения нестационарной автоковариационной функции.
последовательность вычислений должна повторяться для всех значений N.
Метод измерения нестационарных автоковариационных функций иллюст-
рируется на рис. 12.6. Аналогичный метод можно применить и для измере-
ния нестационарных взаимных ковариационных функций.
12.5.2. ДРУГОЙ СПОСОБ ПРЕДСТАВЛЕНИЯ ДВОЙНЫХ ПО ВРЕМЕНИ
КОВАРИАЦИОННЫХ ФУНКЦИЙ
Двойную по времени ковариацйонную функцию можно определить и
иначе — с помощью описанных ниже преобразований. Пусть
= t2 = t + v (12-61)
тогда 2
+ G
т = G ~ h > * = —— • (12.62)
Здесь т есть длина интервала между tx и t2, a t — средняя точка этого ин-
тервала. Очевидно, что
= + j) =
(12.63)
0 = Е
2
2
(12.64)
^(т, z) = Е у
Символ 3? использован здесь вместо R для функции, заданной на плоско-
сти с координатами (т, /), а не (Zp /2). Заметим, что при т = 0 (и
Анализ нестационарных процессов
435
мх(0 = м/0 = °)
0 = £[*2(0] = Ox(Z) >
(12.65)
%(о, 0 = £[/(*)] = «’ДО,
^ху(°’ t) = ^[^(0/(0] = %Х') , (12.66)
где и — дисперсии последовательностей x(t) и y(t) в момент /, а
axy(t) — ковариация последовательностей x(t) и y(t) в момент t. Для всех
функций вида ^(т, /) справедливы равенства вида
^хх(т,0) = Е х{~ (12.67)
L \ 2 / \ 2 / J
Кроме того,
(12.68)
%Д-т,0 =%(т,/),
^(-т,г) = ^(т,/)- (12.69)
Формулы (12.68) означают, что ^^(т, t) — четная функция т.
На плоскости (т, /) можно иногда разделить стационарную и нестацио-
нарную части нестационарной ковариационной функции. В частности, мо-
жет оказаться справедливым равенство
^(т, г) = Л(г)А(т) = /?(/2 - (12.70)
где A(t) — медленно меняющаяся неотрицательная функция момента вре-
мени /, отвечающего середине интервала между tx и /2, a R(t) — стацио-
нарная ковариационная функция, зависящая только от разности /2 — В
случаях, когда такое представление ковариационной функции возможно, со-
ответствующий случайный процесс называют локально стационарным. По-
добные ситуации рассмотрены в разд. 12.6.4. _
Средняя по времени взаимная ковариационная функция Rxy(r) определя-
ется через &ху(т, t):
Rxy(r)= lim ^f\y(r,t)dt, (12.71)
7’—» оо 1 •'О
а средняя по времени автоковариационная функция Rxx(t) — в виде
/Мт)= lim ^(T<%xx(r,t)dt. (12.72)
Т —»оо 1
Поскольку /) = ^-(7, /), имеем
Ллл(-т) = Аха(т). (12.73)
436
Глава 12
Таким образом, Rxx(t) есть действительная и четная функция аргумента т,
представляющая обычную автоковариационную функцию стационарного
случайного процесса. Имея в виду, что ^.„( —т, t) — t), получаем из
(12.69): _ _ У У
Ях/-т) = Я,х(т), (12.74)
так что Rxy(r) представляет обычную взаимную ковариационную функцию
стационарного случайного процесса.
ПРИМЕР 12.5. ДВОЙНАЯ ПО ВРЕМЕНИ АВТОКОВАРИАЦИОННАЯ ФУНК-
ЦИЯ ПЕРИОДИЧЕСКОГО СИГНАЛА. Рассмотрим периодическую функцию
x(z) = A cos27t/0Z,
где А и bQ — постоянные. Согласно формуле (12.54),
Rxx(ti, G) = = ^2cos2tt/0Z1 cos2tt/0Z2 =
Л2 / + t2 \
= — cos277/0(/2 - Zj + cos477/0I—-— I ,
а из (12.69) следует, что
A2
&xx(-r, t) = У [cos277/0t + cos4tt/0z],
где т = t2 - tx и t = (Z} + z2)/2. В этом примере ^^(т, Z) представляет
собой сумму стационарного слагаемого (Л2/2)со82тг/0т и нестационарного
слагаемого (H2/2)cos47r/0Z.
ПРИМЕР 12.6. ДВОЙНАЯ ПО ВРЕМЕНИ КОВАРИАЦИОННАЯ ФУНКЦИЯ
МОДУЛИРОВАННОГО СЛУЧАЙНОГО ПРОЦЕССА. Рассмотрим модулиро-
ванный случайный процесс
(x(z)} = [cos2w/0z]{w(z)} ,
где /0 — постоянная, [u(Z)J — стационарный случайный процесс с нулевым
средним значением. Из соотношений (12.54) и (12.64) следует, что
RxAt^ '2) = £[*('1)*('г)] = [cos2w/0z1cos2t7/0z2]A„„(z2 - zj;
= f[cos2w/0r + cos 4w/0z] Ruu( t) .
В этом примере нестационарная часть ^^.(т, Z) распадается на произведе-
ние функции Z и т на функцию только одного аргумента т. Заметим, что
при всех Z
0 = £[*20)] = И1 + cos477/0z]Aum(0) > 0.
Анализ нестационарных процессов
437
Однако при т Ф 0 функция ^хх(т, t) может быть как положительной, так и
отрицательной.
12.6. Спектральная структура нестационарного процесса
Здесь будут рассмотрены два различных теоретических подхода к описа-
нию спектральной структуры нестационарного процесса. Каждый из них
приводит к вполне определенным соотношениям и свойствам, которые мо-
гут оказаться более или менее полезными в зависимости от рассматривае-
мой задачи. Этим подходам отвечают два типа спектров:
а) двойные по частоте (обобщенные) спектры;
б) частотно-временные (мгновенные) спектры.
Двойные по частоте (обобщенные) спектры рассматриваются в
разд. 12.6.1 и 12.6.2. Частотно-временные (мгновенные) спектры, называе-
мые также распределением Вигнера, обсуждаются довольно детально в
разд. 12.6.3. Физическая интерпретация частотно-временных спектров дает-
ся в разд. 12.6.4 на примере мультипликативного нестационарного процесса.
12.6.1. ДВОЙНЫЕ ПО ЧАСТОТЕ СПЕКТРАЛЬНЫЕ ФУНКЦИИ
Пусть реализациям x(t) и y(t) стационарных случайных процессов {%(/)}
и {/(/)] отвечают финитные преобразования Фурье
Х(/,Т) = (Tx(l)e-J2”f'dt,
‘'О
(12.75)
Y(f,T)= f y(t)e~^'dt,
т. e. предполагается, что вне интервала (О, Т) реализации x(t) и y(t) обра-
щаются в нуль. Для простоты обозначений зависимость от Т в дальнейшем
опускается:
%(/) = %(/, Т), Y(f)=Y(f,T). (12.76)
Кроме того, в приводимых далее интегралах вида (12.75) будут опущены
пределы интегрирования.
Функции спектральной плотности для любых двух фиксированных ча-
стот /р /2 определяются математическими ожиданиями
5хл(/1,/2) = £[%*(/1)%(/2)],
(12.77)
5,,(/1,/2) = £[у*(/1)П/2)],
М/1’А) = £[**(А)Г(/2)], (12.78)
438
Глава 12
где X* и У* — величины, комплексно-сопряженные с X и У. Величины
/2) и Л) называются двойными по частоте (обобщенными)
функциями спектральной плотности, a Sxy(fv f2) — двойной по частоте
(обобщенной) взаимной спектральной плотностью. Заметим, что эти функ-
ции комплексные, а /р /2 МОГУТ принимать любые значения в интервале
( — оо, оо).
Рассуждая примерно таким же образом, как и в разд. 5.2.4, можно по-
казать, что при любых значения и /2 верхняя граница этой двойной по
частоте функции взаимной спектральной плотности определяется нера-
венством для взаимных спектров
М/1’ А) Г Ж(/р А). (12.79)
Из исходных определений следует, что
Sxx(fi, /1) = 5Л (/1, /2), Syy(f2, Л) = /2), (12.80)
Sxy(f2,fi) = S*(fl,f2). (12.81)
Из формул (12.77) и (12.80) следует, что 5^(7, f) есть действительная, по-
ложительная и четная функция частоты /.
Согласно соотношению (12.75), имеем
X*(fi)Y(fi)=
Jy(l2)e j2^dt2
(12.82)
Применяя к обеим частям этого равенства оператор математического ожи-
дания, получаем
SxyUi,fi) = / fRxy(tl,t2)e^^-^dtldt2. (12.83)
Следовательно, функция S (J\, f2) не совпадает с двойным преобразовани-
ем Фурье функции Rxy(tv имеющим вид
DFT[/?xv(/1,/2)] = / jRxy{tx,t2)e-^l'+f^dtxdt2. (12.84)
Напротив, она получается обратным преобразованием Фурье функции
/^(/р ^2) по переменной tv а затем прямым преобразованием результата
по переменной t2. Замена y(t) на x(t) в определении (12.83) показывает, ка-
ким образом можно получить Sxx(fvf2) по Rxx(tv t2).
Пара обратных преобразований Фурье, отвечающих равенствам (12.75),
имеет вид
x(t)= Jx(f)e^'df , y(t)=fY(f)e^'df, (12.85)
причем пределы интегрирования здесь бесконечны. Поскольку x(t) — дей-
ствительная функция, можно написать также
%(/)= (X*(f)e~^'df. (12.86)
Анализ нестационарных процессов
439
Из формул (12.85) и (12.86) следует, что
Применяя к обеим частям этого равенства оператор математического ожи-
дания, получаем
Rxy(t„t2) = j (12.88)
что не совпадает с двойным обратным преобразованием Фурье функции
^(/р/гЬ имеющим вид
IDFT[Sxy(/1, /2)] = jf df, df2. (12.89)
Напротив, функция Rxy(tv t2) получается прямым преобразованием Фурье
S (fv Л) по переменной /р а затем обратным преобразованием результа-
та по переменной /2. Замена y(t) на x(t) в определении (12.88) показывает,
каким образом можно получить Rxx(tv t2) по S^C/p /2).
12.6.2. ДРУГОЕ ПРЕДСТАВЛЕНИЕ ДВОЙНОЙ ПО ЧАСТОТЕ СПЕКТРАЛЬНОЙ
ФУНКЦИИ
Двойную по частоте спектральную функцию можно определить и
иначе — с помощью описанных ниже преобразований. Пусть
£ £
Л=/-|’ А = /+у <12-90)
Тогда
/-^' (1291)
Двойной по частоте взаимный спектр можно записать теперь в виде
/ g g\
/ £ \ / £ V
= £[%*(/- -)У+ -jj =^Д/, g). (12.92)
Символ / использован здесь вместо 5 для функции, заданной на плоскости
с координатами (/> g), а не (Д, /2). Для двойных по частоте автоспектров
имеем
(12.93)
я) = Е
/ g \ / g \
^v(/,g) = £[y*(/-y)y(/+-]
440
Глава 12
Заметим, что в точке g = 0 функции
^(/,0) = е[|%(/) I2] ,
(12.94)
у;д/,о) = £[|у(/)|2],
^„(/,0) = £[**(/)У(/)] (12.95)
представляют собой функции спектральной плотности энергии последова-
тельностей x(t) и y(t) и функцию взаимной спектральной плотности энер-
гии, связывающую х(0 и y(t) на частоте /. Поскольку
^x(-/,g) = £
/ g\ / Q \ "
= £[%*(/- г)*(/+ у)] (12-96)
то g) есть четная функция частоты /. Кроме того,
%*(/+ I)] = ^(Л -g)’ (12_97)
так что —g) есть комплексно-сопряженное g). Для произволь-
ных последовательностей x(Z) и y(t) справедливы равенства
g) =^х(/, g) >
^*(Л g) =^х(/, -g) •
(12.98)
При x(r) = y(t) отсюда получаются формулы (12.96) и (12.97).
Возвращаясь к равенству (12.75) и производя замену tx = t — т/2,
dt{ = -dr/2f получаем
= p(z1)^2’7,/~g/2)'1 dtr=
— — fx( t — — } ej2,r^~g/'2^'^T'/2)( —
J \ 2/ ( 2
Аналогичным образом замена u = f + g/2, du = dg/2 в формуле (12.85)
дает
•F(r + i)=lY(u^ej2,r('+r/2)u du =
— } ej2n(/+^/2^, + T/2'>( —
2/ \ 2
Анализ нестационарных процессов
441
Поскольку
/ %\/ т \ ( 8\/ т \
(/+d(' + ir (/-2.1(' “ 2)+/т + s'-
Умножая обе части последнего равенства на x(t — т/2) и интегрируя по т,
получаем
Математическое ожидание обеих частей уравнения имеет вид
УХ,.(т, t)e~^ dr = f^xy(f, g)e^‘dg. (12.99)
Частные случаи этого уравнения при y(t) = x(t) показывают связь функций
.^(т, /) и g).
Левая часть формулы (12.99) представляет собой преобразование Фурье
функции ^ху(т, I) по переменной т при фиксированных f и t. Правая же
часть есть обратное преобразование Фурье функции g) по перемен-
ной g при фиксированных f и t. Каждая из этих операций приводит к функ-
ции, заданной в частотно-временной области:
= jdixy{r,t)e-^dr. (12.100)
Ее рассмотрению будет посвящен следующий раздел. Функцию ^xy(f, t) ни
в коем случае не следует смешивать с ^xy/J, g)- Из формулы (12.99) следу-
ет, что
j^xy(r,t)e-^+^dTdt. (12.101)
Иными словами, ^xy(f, g) есть двойное преобразование Фурье функции
^L(r, t) по переменным т и t.
В частном случае стационарного случайного процесса приведенные вы-
ше равенства связи характеристик нестационарных процессов упрощаются,
так как заданные формулами (12.55) и (12.63) ковариационные функции, за-
висящие от двух аргументов, становятся функциями лишь одного аргумен-
та:
М'1’'2) = М'2-'1)> (12-102)
^x/r,t) = Rxy(r). (12.103)
442
Глава 12
При замене x(t) = y(t) отсюда получаются и соответствующие частные
случаи. Из соотношения (12.88) следует, что
(12.104)
(в правой части зависимость от t входит в экспоненту). Для стационарного
процесса имеем
Rxy(t,t) = Rxy(O) = f Js^^f^df.df^
= fs^df, , (12.105)
где
^(/1) = pU/1,/2)J/2. (12.106)
Следовательно, в стационарном случае
5лу(/1,/2) = \ДА)51(/2-/>)1 (12.107)
где 6j(/) — финитная дельта-функция:
ац)=(Г’ (-1/2Г) </< (1/2Т); (12.108)
\ 0 , в остальных случаях.
Таким образом, если частоты fx и /2 различаются на 1/Т, то функция
S^C/p /2) существует на плоскости (/р /2) только вдоль линии j\ = f2. По-
этому
£[Х*(Л)У(/2)] = 0,
£[^*(/1)y(/1)] = rsx>.(/1), (12Л09)
откуда следует, что
МЛ) = 7£[%*(/1)у(/1)] . (12.1Ю)
Эти выкладки показывают, что для получения устойчивых результатов
функцию взаимной спектральной плотности стационарных случайных про-
цессов следует определять в виде (12.110), как и было сделано ранее в фор-
муле (5.59).
Обращаясь теперь к равенству (12.92) для двойного по частоте спектра,
видим, что
^(Ag) = M/)Mg), (12-in)
где 6j(g) задана выражением (12.108). Это означает, что при шаге по часто-
те g, равном 1/Т, функция g) существует на плоскости (/, g) только
вдоль линии g = 0. Таким образом, в случае стационарного процесса
Уху(/, g) = |)у(/+ |)] = 0, g * 0;
(12.112)
^(/,0) = £[У*(/)У(/)] = TSxy(f), g = 0.
Анализ нестационарных процессов
443
Отсюда
5ХЛ(/) = у£[%*(/)У(/)], (12.113)
что совпадает с функцией (12.110). Частный случай этого уравнения опреде-
ляет спектральную плотность стационарного процесса:
Sxx(/) = ^£[X*(/)X(/)] = [| %(/) |2]. (12.114)
ПРИМЕР 12.7. ДВОЙНОЙ ПО ЧАСТОТЕ АВТОСПЕКТР ПЕРИОДИЧЕСКО-
ГО СИГНАЛА. Рассмотрим периодическую функцию x(t) = A cos 2%/0Z,
где А и /0 — постоянные. Ее преобразование Фурье имеет вид
АГ(/) = у[3(/-/о) + 5(/ + /о)],
где 5(f) — обычная дельта-функция. Согласно формулам (12.77), имеем
^(АА) = е[х*(Л)х(/2)] =
Л2
= у [«(А - /о) + «(А + /о)] [5(А - /о) + 5(Л + /о)] =
Л2 л2
= ув(/2 - А) + у R(A - А - 2/о) + «(А - А + 2/о)].
Функция Sxx(fv f2) существует на плоскости (/р /2) только вдоль линий
/2 = /р Л = Л 2/0- Соответствующий спектр имеет вид
^A(/,g) = £
а2
= y3(g)[S(/-/o)+S(/ + /o)] +
А2
+ y3(/)[3(g-2/0)+a(g + 2/0)].
444
Глава 12
Заметим, что g) существует на плоскости (ft g) только вдоль линий
g = О и g = ± 2/0.
ПРИМЕР 12.8. ДВОЙНОЙ ПО ЧАСТОТЕ СПЕКТР МОДУЛИРОВАННОГО
СЛУЧАЙНОГО ПРОЦЕССА. Рассмотрим модулированный случайный про-
цесс вида
{*(')} = [cos2tt/oz]{«(г)) ,
где /0 — постоянная, a [u(t)] — стационарный случайный процесс с нуле-
вым средним значением. Согласно примеру 12.6, имеем
Я«(Т>0 = HCOs2,T/oT + C°s4l7/odKu«(T) ,
а из формулы (12.101) следует, что
g) = ур?хх(т, t drdt «
= 2S(g) / (COs2”7oT)^««(T) +
+ |J(cos47r/Oz)e72’'g' dt f Кии(т)е~ dr =
= |S(g)[Su„(/-/o) + ^M(/ + /o)] +
+ HS(g-2/0) + «(g + 2/0)]S„„(/)-
Рис. 12.7. Пример двойного по частоте автоспектра: узкополосный случайный
шум, модулированный косинусоидой.
Анализ нестационарных процессов
445
Таким образом, функция g) существует на плоскости (f, g) только
вдоль трех линий: g = 0 и g = ±2fQ. Автоспектр Suu(j) оказывается сме-
щенным на ±/() вдоль линии g = 0 и остается прежним вдоль линий
g = ±2/0. На рис. 12.7 приведен график функции g) в положитель-
ной полуплоскости частот / > 0 для случая, когда [w(/)j — узкополосный
шум.
12.6.3. ЧАСТОТНО-ВРЕМЕННЫЕ СПЕКТРАЛЬНЫЕ ФУНКЦИИ
Рассмотрим пару нестационарных случайных процессов [х(0], [7(0] с
нулевыми средними значениями. Предположим, что для них вычислены не-
стационарные ковариационные функции t), &л,Ат, t), t), тд$
хх у ух ху v
(см. разд. 12.5.2)
t) = Е
(12.115)
и нестационарные функции спектральной плотности g), ^yy(f, g),
g)> w (см. разд. 12.6.2)
Az
/ я \ / я V
yxy(f, g) = £[%*(/- -)r(/+ I)]- (12.116)
Преобразование Фурье нестационарной взаимной ковариационной функции
<^L.(r, /) по аргументу т при фиксированном t имеет вид
Л/
С/Л 0 = /С/т, dr. (12.117)
Это уравнение определяет частотно-временную спектральную плотность,
которую часто называют также мгновенным спектром (мощности). Функ-
ция ^xy(f, t) совпадает с распределением Вигнера (см. работу [12.1]). Из
формулы (12.99) следует, что
0 = /С/Л dg , (12.118)
так что Txy{f, t) представляет собой и обратное преобразование Фурье
функции (f, g) по переменной g при фиксированном /.
Согласно равенствам (12.117) и (12.118), обратные преобразования име-
ют вид
Яху(т, t) = faytf, df , (12.119)
С/Л g) = Jdt. (12.120)
Подставляя выражение (12.177) в (12.120), a (12.118) в (12.119), получаем
С/Л g) =/f®Xy(r, t)e-^+^drdt, (12.121)
С/т’ 0 = J g)e^T+g,) dfdg . (12.122)
446
Глава 12
Следовательно, ^xy[f9 g) действительно является двойным преобразова-
нием Фурье функции жху(т, t), а <^L,(r, t) — двойным обратным преобразо-
ванием Фурье функции g). Эти утверждения следует сопоставить с
приведенными выше равенствами (12.83) и (12.88).
В частном случае нестационарной автоковариационной функции t)
имеем
О-') = dr =
= z)cos2tt/tdr . (12.123)
Последнее равенство справедливо, поскольку ^хх(т, t) — четная функция т.
Отсюда следует, что
(12.124)
т. е. ^xx(f, t) есть действительная и четная функция /. Благодаря этому
свойству обратное преобразование, отвечающее формуле (12.123), есть
= t)e^df =
= f^xx(f,t)coS2nfTdf. (12.125)
Для случая нестационарной спектральной плотности ^xx(f, g) соот-
ветствующее уравнение получается из (12.118) с учетом (12.96) и (12.97) в
0-0 = Г ^Af,g)ej2ng‘dg =
J - 00
= Г [«^(.Ag) + ^(Л g)]cos277gzdg +
•'о
+j( g)g)]sin2fl-gr4/g. (12.126)
Обратное преобразование имеет вид
Og) = ji^xx(f,t)e-^dt =
= /^х(Л t)c.os2irgt dt - jУ#;х(/, t)sin2irgt dt, (12.127)
где t задано на всем интервале от — оо до оо.
Анализ нестационарных процессов
447
Из формул (12.124) и (12.127) следуют соотношения
,Ухх(—•/» S) = xx^f ' ~ ^xx^f* ~8)i
которые совпадают с равенствами (12.96) и (12.97).
Следует заметить, что, пользуясь частотно-временными спектрами и
производя замену переменных, можно переписать нестационарные форму-
лы, переходя из временной области от двумерных ковариационных функ-
ций в частотную область к двумерным спектрам. Переход можно осущест-
влять в обоих направлениях (табл. 12.1).
Рассмотрим теперь некоторые свойства частотно-временного спектра
t). Из формул (12.65) и (12.125) следует, что в частном случае г = О
^(0,z) = j^xx(f,t)df=E[x2(t)]. (12.129)
Таким образом, интегрирование ^х(/*, t) вдоль всей оси f дает нестацио-
нарный средний квадрат (мгновенную мощность) сигнала (х(/)] в момент
времени t. Кроме того, при g = 0 из формул (12.94) и (12.127) имеем
= = (12.130)
Таким образом, интегрирование ^.(Д t) вдоль всей оси t дает функцию
спектральной плотности энергии последовательности [х(0] на частоте /.
Пусть t и f меняются от — оо до оо. Тогда энергия, содержащаяся в
(х(г)] за время от ta до tb, есть
ifxAf,t)df dt . (12.131)
1а
Таблица 12.1. Нестационарные ковариационные и
спектральные функции
Функция
Аргументы
(Время, время)
ф
^vr(T, t) (Время, время)
Ф ф
(Время, время)
Ф ф
g) (Частота, частота)
Ф Ф
(Частота, частота)
448
Глава 12
С другой стороны, энергия, содержащаяся в интервале частот от fa до Д,
равна
(fhE[\X(f)\2]df= /Л[/°° ^xx(f,t)dt]df.
Jfa Jf. Г-ОО J
(12.132)
Полная энергия последовательности МО) на всей плоскости (f, t) задается
в виде
Г fvjj,t)dfdt = f f^xx(f,t)dtdf. (12.133)
•'-оо*' *'-00*'
Эти соотношения демонстрируют физический смысл частотно-времен-
ного спектра ^.(Л О как характеристики свойств последовательности
МО).
Рассмотрим теперь частотно-временной спектр ^XJJ\ t)» Согласно
(12.66) и (12.119), имеем
^(0,0 = fay(f,t)df=<>xy(t). (12.134)
Иными словами, интеграл от ^xy(f, t) по всей оси f дает ковариацию по-
следовательностей [х(0] и \y(t)} в момент t. Кроме того, из формул (12.95)
и (12.120) следует, что
•^ДЛО) = /^xy(f, г) dt = Е[Х*(/)У(/)]. (12.135)
Иными словами, интеграл от ^xy(f, t) по всем t дает функцию взаимной
спектральной плотности энергии, связывающую процессы (х(/)] и [МО] на
частоте /.
Заменяя функции, входящие в равенство (12.118), их комплексными сопря-
жениями и имея в виду (12.98), получим
о = j^*(f,g)e-^‘dg =
= dg =
= j^yx(f,g)e^‘dg= ^yx(f,t).
Кроме того, из формул (12.98) и (12.118) следует, что
^Xy(-f, t) = pXy(-f, g)e^‘dg =
= f^yAf,g)e^ldg=irvx(f,t).
При x(t) = y(t) эти соотношения принимают вид
откуда, как и из (12.134), видно, что ^.(Л О — действительная и четная
(12.136)
(12.137)
(12.138)
Анализ нестационарных процессов
449
функция аргумента /. Заметим, что функция /) не обязана быть не-
отрицательной. Более того, ниже показано, что 0 может принимать
отрицательные значения.
Средняя по времени функция взаимной спектральной плотности Sxy(f)
определяется через ЗГ(Л 0 выражением
Л/
Sxy(f)= lim ^fTKyU,t)dt. (12.139)
Т-оо Г •'о
а средний по времени автоспектр имеет вид
Sxx(f) = lim fTWxx(f, /) dt. (12.140)
Т-оо Т •'о
Поскольку ^xy(f, t) есть преобразование Фурье &ху(т, /), то, полагая воз-
можным изменение порядка операций предельного перехода, получаем
SX7(/) = FT[Ax/t)],
(12.141)
\л(/) = ^[Яхх(т)],
где средние по времени ковариационные функции заданы равенствами
(12.71) и (12.72).
Из формулы (12.130) следует, что функция S^ij) неотрицательна при
всех /, так как при достаточно больших Т
S„(/) = y£[|2f(/)|2] >0. (12.142)
Это совпадает с обычным определением автоспектра стационарного слу-
чайного процесса. Аналогичным образом из формул (12.135) и (12.139)
можно получить, что при больших Т
= (12.143)
что совпадает с обычным определением взаимной спектральной плотности
стационарных случайных процессов. Как и ранее, односторонние средние
по времени спектральные плотности имеют вид
(12.144)
У (0, /<0; v
Gjj) = (12.145)
( V, J < U.
В частном случае стационарных процессов нестационарные ковариаци-
онные функции обращаются в стационарные:
^xj(t,z) = Rxy(r), (12.146)
15-953
450
Глава 12
следовательно,
= f^y(^‘^-^dr = Sxy(f). (12.147)
Иными словами, в этом случае частотно-временнбй взаимный спектр
t) не зависит от t и совпадает с обычной стационарной взаимной
спектральной плотностью Sxy(f). Аналогичным образом в стационарном
случае справедливо равенство
^y(f,g) = Sxy(f)8(g). (12.148)
Как и прежде,
Ky(f,') = /^(Л g)eJ2”8'dg = Sxy(f). (12.149)
Таким образом, стационарный взаимный спектр Sxy(f) есть частный
случай нестационарного спектра e/L,(f9 g).
лу
ПРИМЕР 12.9. МГНОВЕННЫЙ СПЕКТР ПЕРИОДИЧЕСКОГО СИГНАЛА.
Рассмотрим периодический сигнал вида x(t) = Лсо82тг/0г, где А и/0 — по-
стоянные. Согласно примеру 12.5,
А2
= — [cos2tt/0t + cos4tt/0z].
Частотно-временной спектр находится из формулы (12.117) в виде
^(/.') = /^(T,0e-yWT^ =
А2
= y[«(/-/o) + «(/ + /o) + 2S(/)cos4^].
Заметим, что
а) ^.(А, 0 содержит стационарные компоненты при f = ±fQ плюс не-
стационарную компоненту при f = 0, которая является периодической
функцией с частотой 2/0;
б) спектр 3^(4 t) может быть отрицательным.
Мгновенная мощность этого сигнала определяется формулой (12.65):
А1
^хх(0, z) = Е [х2(/)] = — [1 + cos4tt/0z] = ^2cos22tt/0Z ,
что согласуется с выражением (12.129):
/*^(Л 0 df = A2cos,2lirf0t.
Из равенств (12.72) и (12.140) следует, что средние по времени функции в
Анализ нестационарных процессов
451
рассматриваемом примере имеют вид
1 гт А2
Rxx(r) = 1™ ~ 0 dt = —cos2w/0T ,
т-оо Т 'о 2
- 1 гТ А2
Sxx(f)= lim -f Kx(f,‘)dt = -[8(f-f0) + 8(f + f0)],
T-*oo / •'О 4
что согласуется с рассмотренными выше примерами 5.1 и 5.5. Заметим,
что
_ _ А2
Sxx(n = FT[Rxx(r)], Rxx(O) = — =[sxx(f)df.
Z J
ПРИМЕР 12.10. МГНОВЕННЫЙ СПЕКТР МОДУЛИРОВАННОГО ПРОЦЕС-
СА. Рассмотрим модулированный процесс вида
{х(г)} = [cos2w/0z]{u(z)} ,
где /0 — постоянная, а (и(/)] — стационарный случайный процесс с нуле-
вым средним значением. Согласно примеру 12.6, имеем
^хх(т> 0 = I[cos2w/0T + cos477/0Z]Rии(т),
и потому из формулы (12.123) следует, что
ОЗ)=/^(М)е^Г =
= ![$««(/-/о) + \u(/ + /o)] + Mcos4^0z)S„„(/).
Заметим, что
а) стационарная компонента Suu(f) смещается по частоте на ±/0;
б) нестационарная компонента функции t) является периодичес-
кой функцией с частотой 2/0;
в) функция ^(/, 0 может принимать отрицательные значения.
Мгновенная мощность этого процесса определяется по Формуле (12.65):
= £[*2(0] = /?„„(0)cos22w/0z,
что совпадает с интегралом от ^.(А, 0 по переменной /. Функция спект-
ральной плотности энергии процесса задана формулой (12.130):
^(7,о) = е[|х(/)|2],
где .
Следовательно, при Ер C/(/)l2] = TSuu(j) имеем при конечном Г, что
•^х(Л 0) = £ [5ИИ(/ - /0) + Sjj + /0)],
15*
452
Глава 12
что совпадает с интегралом от ЗГД/*, t) по переменной t при конечном Г.
График функции t) на положительной полуплоскости частот показан
на рис. 12.8 для случая, когда SUU(J) — спектр узкополосного случайного
шума.
Средние по времени функции имеют в этом случае вид
Кхх(т) = - £&хх(т, t) dt = |(cos2w/0t)«„u(t),
Sxx(f) = frjj, t) dt = + Suu(f + /о)].
I •'o
Заметим, что
SJJ) = , RXX(Q) = |Яви(0) = fsxx(f) df.
12.6.4. МУЛЬТИПЛИКАТИВНАЯ МОДЕЛЬ НЕСТАЦИОНАРНОГО ПРОЦЕССА
Рассмотрим нестационарный случайный процесс {*(/)], представляющий
собой произведение детерминированного сигнала a(t) на стационарный слу-
Рис. 12.8. Пример частично-временнбго спектра для модулированного по коси-
нусоидальному закону узкополосного случайного шума.
Анализ нестационарных процессов
453
чайный процесс (м(0):
{%(,)} = a(/){u(z)} . (12.150)
Такой простой нестационарный процесс, называемый обычно мультипли-
кативным, служит приемлемым приближением для некоторых нестацио-
нарных явлений, в частности для атмосферной турбулентности и для тур-
булентных движений в пограничном слое [12.2, 12.3].
Из формулы (12.64) следует, что нестационарная ковариационная функ-
ция процесса {%(/)], заданного соотношением (12.150), имеет вид
^хх(т> 0 = Е
где
х('" + i)]= Ааа(т’ (12-151)
Каа(т.') = + 2)’
(12.152)
/ т \ / т
u\t - — U Z + —
\ 2/ \ 2
(12.153)
(12.154)
При фиксированном t двусторонний частотно-временной спектр определя-
ется по формуле (12.117):
= f^xx(r,t)e~J2^dT.
Введем функции
SaAf,t) = fRaa(T,t)e-^dr,
Suu(f)= jRMe-^dr.
Поскольку «^(т, t) есть произведение функций Каа(т, t) и /?мм(т), спектр
^xx(f, t) представляет собой свертку функций Saa(f, t) и SMM(/):
О-') = fsaa(a,t)SjJ-a) da. (12.155)
Это соотношение справедливо при произвольной функции a(t).
В тех частных случаях, когда функция а(/) из формулы (12.150) меняется
заметно медленнее наиболее низкочастотных составляющих процесса {м(0},
равенство (12.151) можно заменить приближенным соотношением
^(т,г) = а2(г)Яии(7). (12.156)
При этом частотно-временной спектр принимает вид
^(Л') = «2(')5МЫ(Л, (12-157)
где а2(/) — медленно изменяющаяся неотрицательная функция t.
454
Глава 12
Нестационарный случайный процесс, ковариационная функция и спект-
ральная плотность которого могут быть аппроксимированы соответствен-
но формулами (12.156) и (12.157), часто называют локально-стационарным
или равномерно-модулированным случайным процессом [12.4]. Для таких
процессов удобно пользоваться в выражении (12.156) нормированной функ-
цией Ruu(t) (т. е. RUU(Q) = 1), так что
(12.158)
Г (12.159)
•'-оо Jo
Здесь Guu(f) — односторонняя функция спектральной плотности, равная
2S (/) при / > 0 и нулю при f < 0. Отсюда получается односторонний за-
висящий от времени автоспектр
где
(/ (12.161)
Если a(t) меняется существенно медленнее u(t), то
С..(/)-С„(/), (12.162)
где GYY(f) — средний по времени автоспектр, заданный формулами (12.140)
и (12.145).
Из выражения (12.160) следует, что переменный во времени спектр
локально-стационарного случайного процесса можно оценивать по одной
реализации процесса двумя различными способами:
а) оценивая ф2(1) усреднением по коротким интервалам или при помощи
другого подходящего приема для всего диапазона частот (см. разд. 12.4.3);
б) оценивая Guu(f) путем вычисления G^tf) по всей реализации, т. е.
при высокой разрешающей способности по частоте (как делается в стацио-
нарном случае).
Поскольку любой из этих приемов возможен при относительно боль-
шом значении произведения ВТ (эквивалентного числа усреднений), иско-
мый нестационарный спектр оценивается с относительно небольшой слу-
чайной ошибкой даже при анализе по единичной реализации.
ПРИМЕР 12.11. ОЦЕНКА УСРЕДНЕННОГО ПО ВРЕМЕНИ СПЕКТРА. Рас-
смотрим вибрации космического корабля на старте при прохождении обла-
сти максимального динамического давления (VipV2, где р — плотность
воздуха, V — скорость воздушного потока). В этой фазе запуска вибрации
создаются главным образом колебаниями давления в турбулентном погра-
ничном слое, возникающем при движении корабля в атмосфере. Поскольку
и скорость, и высота корабля меняются во времени, следует ожидать, что
колебания давления в пограничном слое и, следовательно, вибрации кон-
Анализ нестационарных процессов
455
струкций корабля образуют нестационарные случайные процессы. Допу-
стим, что процесс, описывающий вибрации конструкций в любой точке,
локально-стационарен. В таком случае зависящий от времени автоспектр
вибраций можно оценить по одной реализации процесса усреднением по
отдельным временным интервалам (рис. 12.9).
На рис. 12.9,а показана оценка функции полученная при усредне-
нии по двухсекундным отрезкам 20-секундного интервала, отвечающего
максимальному динамическому давлению. Заметим, что в течение этого
интервала значение среднего квадрата меняется в четыре раза. На
рис. 12.9,6 представлена оценка спектра Guu(f), полученная усреднением по
всему 20-секундному интервалу. Если гипотеза локальной стационарности
этого процесса верна, то показанная на рис. 12.9 оценка переменного во
времени спектра f) вполне приемлема. Значение произведения ВТ для
каждой части этой оценки заметно превышает 200, а разрешение по време-
ни и частоте вполне достаточно для того, чтобы избежать больших оши-
бок смещения.
Пригодность гипотезы локальной стационарности в этой задаче можно
проверить, сопоставляя независимые оценки функции Guu(f), полученные
усреднением по пятисекундным отрезкам полного 20-секундного интервала
записи. Соответствующие результаты представлены на рис. 12.10. Имея в
виду, что для каждой из этих оценок ВТ ~ 70 (т. е. ег « 0,12), можно ви-
Рис. 12.9. Переменный во времени автоспектр вибраций стартующего космиче-
ского корабля: а — переменный во времени средний квадрат; б — средний авто-
спектр. Интервал усреднения 20 с, разрешающая способность спектра по частоте
14 Гц; t = 0 совпадает с моментом максимума вибраций. Исследование финансиро-
валось Годдардовским центром космических полетов NASA, Гринбелт, шт. Мэри-
ленд (контракт NAS5-4590).
456
Глава 12
Рис. 12.10. Автоспектры вибраций космического корабля на старте, рассчитан-
ные по отдельным отрезкам реализации (интервал усреднения 5 с, разрешающая
способность спектра по частоте 14 Гц): а — -5...0 с; б — 0...5 с; в — 5... 10'с;
г — 10... 15 с. Исследование финансировалось Годдардовским центром космических
полетов NASA, Гринбелт, шт. Мэриленд (контракт NAS5-4590).
деть, что представленные на рис. 12.10 результаты не отличаются сущест-
венно от общей оценки Guu(j), показанной на рис. 12.9. На этом пример
12.11 заканчивается.
Мультипликативная модель (12.150) представляет собой очевидное об-
общение модулированного процесса, рассмотренного в примере 12.10. Из
этого примера видно, что роль модуляции заключается прежде всего в уве-
личении ширины среднего по времени спектра 5^(7) на величину ±/0, т. е.
на значение частоты модулирующего колебания. Следовательно, при
стремлении верхней частоты функции a(t) к нижней частоте спектра про-
цесса u(t) приближение S^C/) ~ перестает быть справедливым, так
что описанная выше процедура анализа, проиллюстрированная примером
12.11, будет давать искаженные результаты. Если, однако, можно считать,
что функция a(t) неотрицательна, a — гауссов процесс, то мульти-
пликативную модель можно аккуратно разделить на стационарное и неста-
ционарное слагаемые при любой скорости вариаций a(t). Соответствую-
щий прием, детально описанный в работе [12.2], кратко излагается ниже.
Пусть в формуле (12.150) a(t) — зависящее от времени среднеквадратич-
ное отклонение (которое не может быть отрицательным), a — стаци-
онарный гауссов случайный процесс с нулевым средним значением и еди-
ничной дисперсией. Пользуясь нестационарной реализацией х(/), построим
новую стационарную реализацию y(t) по такому правилу:
'«И-5:3')^' (12Л63)
Операцию преобразования, заданную условиями (12.163), часто называют
идеальным ограничением, и после ее выполнения сохраняется, по существу,
Анализ нестационарных процессов
457
только информация о пересечении нулевого уровня исходной нестационар-
ной реализацией x(t). Полагая, однако, что a(f) — неотрицательная функ-
ция, легко видеть, что пересечения нулевого уровня последовательностями
x(f) и y(t) совпадают (рис. 12.11). Поэтому y(t) представляет собой идеаль-
но ограниченную версию u(f). Полагая (м(/)) гауссовым, можно показать
[12.5], что ковариационная функция процесса имеет вид
л„и(т) =sin
77
(12.164)
где Ryy(r) — ковариационная функция идеально ограниченного процесса
y(f), вычисляемая по всей реализации длиной Т в виде
/МТ) = 77---------С Г Ty(t)y(t + т) <Л . (12.165)
уу (Т - т) jo
Окончательно, автоспектр процесса есть
Guu(f) = 4 /"т“лии(т)со8 27т/т</т, (12.166)
•'о
Рис. 12.11. Пересечения нулевого уровня мультипликативным нестационарным
процессом.
458
Глава 12
и разрешение результирующей спектральной оценки по частоте равно
АА = 1/ттах.
12.7. Соотношения между входом и выходом линейной
системы в нестационарном случае
Рассмотрим реализацию нестационарного случайного процесса [%(/)],
поступающую на вход линейной системы с зависящими от времени весовой
функцией Л(т, /) и частотной характеристикой
(12.167)
При произвольной входной реализации х(/), принадлежащей процессу
МО), реализация на выходе y(t), принадлежащая процессу [XOJ, есть
y(t) = fh(r, t)x(t - т) dr . (12.168)
Ясно, что в общем случае процесс МО) нестационарен, поскольку его ста-
тистические характеристики зависят от t как при нестационарном входном
процессе [х(0], так и ПРИ зависящей от t функции Л(т, /). Для линейной си-
стемы с постоянными параметрами равенства Л(т, /) = Л(т), H(f, t) = H(f)
справедливы при всех t. Соотношения между процессами на входе и выходе
линейных систем будут рассмотрены ниже как во временндй области для ко-
вариационных функций двух аргументов, так и в частотной области для спект-
ральных функций двух аргументов для следующих четырех случаев:
1) нестационарный процесс на входе системы с зависящими от времени
параметрами;
2) нестационарный входной процесс на входе системы с постоянными
параметрами;
3) стационарный процесс на входе системы с зависящими от времени
параметрами;
4) стационарный процесс на входе системы с постоянными параметра-
ми.
Последний случай сводится к модели с ковариационной функцией одно-
го временного аргумента и спектральной плотностью, зависящей от одной
частоты (см. гл. 6).
12.7.1. НЕСТАЦИОНАРНЫЙ ПРОЦЕСС НА ВХОДЕ СИСТЕМЫ С ЗАВИСЯЩИ-
МИ ОТ ВРЕМЕНИ ПАРАМЕТРАМИ
Произведение значений М^), y{t^) в моменты времени и t2 имеет вид
y(ti)Ah') = //Л(«- f2)*('i - а)х(г2 - Д) dad[S.
Математическое ожидание обеих частей этого уравнения дает соотношение
Анализ нестационарных процессов
459
между ковариационными функциями процессов на входе и выходе системы:
f fh(a,tl)h(P, t2)Rxx(t1-a,t2-p)dadp. (12.169)
Аналогично
= /Л(Д, G)*('1)x(*2 - А)
так что математическое ожидание равно
M'i> t2) = fh(P, t2)Rxx(‘i, t2 - P) dp. (12.170)
Равенства (12.169) и (12.170) представляют собой общий результат, спра-
ведливый для вещественных функций временнбго аргумента.
Для перехода к комплексным функциям частоты положим сначала
J(/,g) = fH(J,t)e-№dt. (12.171)
Тогда из формулы (12.167) следует равенство
ЛЛк) = У fh(T,t)e~j27r(/T+g,) drdt, (12.172)
т. е. J(f, g) — двойное преобразование Фурье весовой функции Л(т, Г). Оче-
видно, что
й(т, t) = У fd(f, g)e>2^T+«'> dfdg. (12.173)
Таким образом, равенство (12.168) эквивалентно равенству
Я') = УУУ^Л g)e>2^T+«')x(r - т) drdfdg. (12.174)
Пусть теперь g = j\ - /, а = t - т, da = -dr. Тогда
Я')= У У УЛЛ/1-/)еу2’г/,'е-22’/вх(а) dadfdf^
= УУдлл-/)^(/)е72,г/1'« =
= УЯЛ)^2’71'^» (12.175)
W X(f) = jx(a)e~j2^tt da , (12.176)
Я/i) = УЯЛ/i ~f)X(f)df. (12.177)
Формула (12.177) играет ключевую роль при получении искомых соот-
460
Глава 12
ношений между спектральными плотностями процессов на входе и выходе
линейной системы в нестационарном случае. В частности, произведение
на У(/2) Для частот /р /2 имеет вид
У*(Л)У(/2) = f jj^X,fl-\)J^,f2-^X^X)X(v)dXdv,
и математическое ожидание обеих частей этого равенства приводит к соот-
ношению
SyyUi,f2)= f (12178)
Аналогичным образом получаем
Х*(Л)У(/2) = - ч)х*(/м^ dv ,
так что математическое ожидание имеет вид
М/1’/2)= р(ч,/2-ч)\х(/1,ч)^- (12.179)
Формулы (12.178) и (12.179) представляют собой общий результат, спра-
ведливый для комплексных функций частоты. Назовем их случаем 1.
12.7.2. РЕЗУЛЬТАТЫ ДЛЯ НЕКОТОРЫХ ЧАСТНЫХ СЛУЧАЕВ
Рассмотрим теперь некоторые частные случаи, отвечающие получен-
ным в разд. 12.7.1 формулам для случая 1.
Случай 2. Нестационарный процесс на входе системы с постоянными
параметрами. Для линейной системы с постоянными параметрами имеем
A(t,z) = A(t), J(/,g) = H(/)S(g),
(12.180)
я(/,0 = я(/), у(/1) = я(/1)х(/1).
Формулы (12.169) и (12.170) принимают вид
Ryy{h,t2)= ffh(a)h(P)Rxx(ti-a,t2-p)dadp, (12.181)
Rxy(ti, t2) = fh(p)Rxx(t1, t2 - p) dp, (12.182)
а формулы (12.178) и (12.179) — вид
Syyifi, f2) = H*Ui}HU2)Sxx(fx, f2), (12.183)
Sxy(fM = H(f2)Sxx(f2, f2). (12.184)
Заметим, что последнее равенство содержит величину а не
Анализ нестационарных процессов
461
Случай 3. Стационарный процесс на входе системы с зависящими от
времени параметрами. В случае стационарного входного процесса имеем
V/i>/2) = V/1W2-/1). (12.185)
Следовательно, формулы (12.169) и (12.170) принимают вид
Ryy(A, '2) = f tjhfji, t2)Rxx(t2 - 'i + « - Ю dadfi, (12.186)
Rxy(tlf t2) = t2)Rxx(t2 -ti-P) W, (12.187)
а формулы (12.178) и (12.179) — вид
\»(/1>/2) = рш-лш-шм (12.188)
Sxy(fi,f2) = Л/1,/2 ~/i)V/i)- (12.189)
Заметим, что последнее равенство содержит величину а не
Случай 4. Стационарный процесс на входе системы с постоянными па-
раметрами. В случае стационарного процесса на входе линейной системы с
постоянными параметрами справедливы все соотношения, заданные фор-
мулами (12.180) и (12.185). В конечном итоге они приводят к хорошо из-
вестным результатам, представляющим собой простейшую форму уравне-
ний (12.169), (12.170), (12.178) и (12.179):
Мт) = / /й(а)й(Д)Ахх(т + а - Д) da df! , (12.190)
Мт)= fh(Ji)Rxx(T-l3)df!, (12.191)
SyyU)=\H(f)\2Sxx(f), (12.192)
Sxy(f) = H(f)Sxx(f). (12.193)
Основные формулы для рассмотренных четырех случаев сведены в
табл. 12.2.
12.7.3. СВЯЗЬ ЧАСТОТНО-ВРЕМЕННЫХ СПЕКТРАЛЬНЫХ ФУНКЦИЙ ВХОД-
НОГО И ВЫХОДНОГО ПРОЦЕССОВ
Рассмотрим случай 2 из предыдущего раздела — прохождение нестаци-
онарного процесса через систему с постоянными параметрами. Получим
теперь соотношения между частотно-временными спектрами входного и
462
Глава 12
выходного процесса, начав с соотношений (12.183) и (12.184) для двойных
по частоте спектров.
Пусть р- а
Л=/-|> /2=/+2- (12.194)
Тогда Syykfl' fl) = &yy(f’ g) ’ (12.195)
sxv(f^fi) = ^f^g)- (12.196)
Вместо формул (12.183) и (12.184) получаем следующие результаты:
^yy(f, g) = Я*(/- ()#(/ + g), (12.197)
^//,g) = #(/+ |)^(/,g). (12.198)
Частотно-временные спектры находим теперь из уравнений (12.118) и
(12.126) в виде
(12.199)
^,(/,0 = f^yy(f,g)eJ2^dg,
Ky(f^) = fyxy(/,g)eJ2”g‘dg- (12.200)
Введем функции
yHH(f,g) = H*[f- |)я(/+ I), (12.201)
^hhU, t) = g)ej2vgl dg • (12.202)
Формула (12.197) принимает вид
yyy(f, g) = g^Af, g), (12.203)
так что соотношение между частотно-временными спектрами процессов на
входе и выходе системы есть
^(/. ') = /«)#;,(/, t - a) da . (12.204)
Таким образом, t) представляется сверткой функций t) И
Таблица 12,2, Соотношения между входом и выходом линейной системы
Процесс Соотношения между ковариационными _ Соотношения между спектральными плотностями функциями
Нестационарный процесс на входе си- стемы с зависящи- ми от времени пара- метрами ‘г) = ffh(a,tl)h(p, t2)Rxx(tt -a,t2- Р) dadp Syv{f.J2} - / }J*(X, j\ - X)J(i),f2 - V) Sxx(X, q) dX di) '2) = fh(P, t2)Rxx(tl, t2 - p) dp Sxv(f2,f2) = fJ(i),f2 - i))Sxx(f2,i)) di)
Нестационарный процесс на входе си- стемы с постоянны- ми параметрами R„(h, t2) - ffh(a)h(p)Rxx(tx — a, t2 — P) dadp Syy(fltf2) = Н'ЦРЩШМ) R^ti) = fh(p)Rxx{t2,t2 - p)dp Sxy(fx,f2) = Я(/2)5д,((/1(/2)
Стационарный про- цесс на входе систе- мы с зависящими от времени пара- метрами = Sfh(a,tx)h(P,t2)Rxx(t2 — tx + a — p)dadp Syy(Jx,f2) = //*(/./, -/)/(/,/2 - f)Sxx(f) df R^,t2) = jh{p,t2)Rxx(t2 -tl- P)dp S*AfxJ2) = JUxJ2
Стационарный про- цесс на входе систе- мы с постоянными параметрами Ryy('r) = ffh(a)h(P)Rxx(T + a - P)dadp Syy(f) = \H(f)\2Sxx(f) RXy<T) = fh(p)Rxx(T - P) dp sxy(f) = H(f)Sxx(f)
464
Глава 12
t). При некоторых значениях f и t функция, заданная равенством
(12.204), может быть отрицательной.
12.7.4. СВЯЗЬ СПЕКТРАЛЬНЫХ ФУНКЦИЙ ЭНЕРГИИ ВХОДНОГО И ВЫХОД-
НОГО ПРОЦЕССОВ
Рассмотрим частный случай нестационарных входных процессов, кото-
рые существуют физически лишь на протяжении конечных и измеримых
интервалов времени, т. е. случай, когда входной процесс [x(r)j и выходной
процесс (y(OJ отличны от нуля лишь при 0 t Т. Такие процессы, назы-
ваемые обычно переходными, допускают использование существенно более
простых методов анализа, поскольку в этом случае для любых двух после-
довательностей x(t) и y(t) с нулевыми средними значениями справедливы
равенства
*(/) = Сх^е-'2”'1 dt = Г x(t)e~Wdt,
А) •'-00
(12.205)
У(/) = dt = f y(t)e~J2,rf‘dt,
•'О J - 00
Согласно равенству (12.135) математическое ожидание произведения вели-
чин X*(f) и Y(f) задает функцию взаимной спектральной плотности энер-
гии
^(/) = Е[Х*(/)У(/)] = t) dt. (12.206)
Аналогичным образом определяются и функции спектральной плотности
энергии
^(/) = Е[Х*(/>Х(/)1 = fTKAf, 0 dt,
Jo
(12.207)
^(/) = £[У*(/)У(/)] = f\y(f,t)dt.
При g = 0 из соотношений (12.197) и (12.198) для входного и выходного
процессов следует, что
^(/)=|Я(/)|Чх(/), (12.208)
•^,(/) = Я(/)^х(/). (12.209)
Для односторонних спектральных плотностей энергии, существующих
только при / > 0, эти уравнения имеют вид
^(/)=|Я(/)|ЧХ(/), (12.210)
^(/) = Я(/)^Х(/). (12.211)
Анализ нестационарных процессов
465
Заметим, что приведенные соотношения между входными и выходными
характеристиками в случае переходных процессов идентичны соотношени-
ям (6.6) — (6.9) для стационарных процессов; отличие состоит лишь в том,
что спектры «мощности» заменяются на спектры «энергии». Теоретически
в случае переходных процессов операция усреднения, необходимая для полу-
чения оценок спектров энергии ^xy(f) и Л подразумевает, что экспери-
мент, в результате которого получены записи процессов, может быть по-
вторен многократно. Однако при практическом анализе систем с переход-
ными случайными процессами отношение сигнал/шум часто бывает доста-
точно большим, что позволяет, как показано ниже (пример 12.12), полу-
чить значимые результаты при единичном эксперименте.
ПРИМЕР 12.12. ОЦЕНКА СПЕКТРА ЭНЕРГИИ. Рассмотрим лобовое
столкновение автомобилей, движущихся со скоростями 13,4 м/с. В одном
из автомобилей установлена модель пассажира, закрепленная на правом пе-
реднем сиденье обычным поясом безопасности и плечевым поясом. На
рис. 12.12 показана зависимость ускорения от времени; измерения произво-
дились а) на корпусе автомобиля непосредственно справа от пассажирского
сиденья и б) на груди модели пассажира. Энергетические спектры этих реа-
лизаций представлены на рис. 12.13. Спектры вычислялись без разбиения
реализаций на отрезки и при разрешающей способности Д/ = 1,16 Гц.
Согласно формуле (12.210), амплитудная характеристика, связывающая
ускорения корпуса автомобиля и модели пассажира, есть
!#(/)! = \^yy(f)/xxU)]172’ где ^(/)» ^хх^~ спектры энергий ускоре-
Время от момента контакта,мс Время от момента контакта, мс
а б
Рис. 12.12. Реализации ускорений во времени столкновения автомобилей: а — на
корпусе автомобиля; б — на груди модели пассажира на переднем сиденье.
466
Глава 12
Рис. 12.13. Энергетические автоспектры столкновения автомобилей.
ний модели и корпуса соответственно. Результат такого расчета показан
на рис. 12.14. Из сопоставления с амплитудной характеристикой, показан-
ной на рис. 2.5, видно, что модель пассажира ведет себя во время столкно-
вения примерно так же, как и сильно демпфированное пружиной массивное
тело с собственной частотой колебаний около 10 Гц.
Рис. 12.14. Амплитудная характеристика модели пассажира во время столкнове-
ния автомобилей.
Анализ нестационарных процессов 467
Задачи
12.1. Нестационарный случайный процесс имеет вид
{*(')} = a(t) + b(t){u(t)} ,
где <z(Z), b(l) — детерминированные функции, [w(r)J — стационарный случайный про-
цесс с нулевым средним значением и единичной дисперсией. Определите для момен-
та времени /:
а) среднее значение процесса;
б) дисперсию;
в) средний квадрат.
12.2. Считая процесс [w(/)J из предыдущей задачи гауссовым, выпишите уравне-
ние для плотности вероятности процесса {%(/)] в момент t.
12.3. Нестационарный случайный процесс имеет вид
771
{%(/)}= Л sin—+ (w(/)}, 0<z<7;,
* Г
где А — постоянная, [«(/)] — стационарный случайный процесс с нулевым средним
значением и единичной дисперсией. Оценка среднего значения процесса [х(0] ищется
методом усреднения по коротким интервалам длиной Т = 0,1 Тг. Найдите а) точное
и б) приближенное по формуле (12.32) значения для ошибки смещения оценки средне-
го значения в момент t = 0,5 Тг,
12.4. Нестационарный случайный процесс имеет вид
{x(z)} = Ae~a'(u(t')} ,
где Айа — положительные постоянные, [u(/)J — стационарный случайный процесс
с нулевым средним значением и единичной дисперсией. Определите двойную по вре-
мени ковариационную функцию процесса {%(/)], выразив ее через:
а) г2), заданное формулой (12.54);
б) ^.(т, 0> заданное формулой (12.64).
12.5. Считая ^.(т, /) из предыдущей задачи четной функцией т, определите двой-
ной по частоте автоспектр, выразив его через:
a) SXXU\, f2)> заданный формулой (12.77);
б) /^.(f, g), заданный формулой (12.93).
Указание: воспользуйтесь равенствами (12.83) и (12.101).
12.6. Для нестационарного случайного процесса из задачи 12.4 определите задан-
ный формулой (12.123) частотно-временндй спектр ^(Д /)•
12.7. Двойной по частоте автоспектр нестационарного случайного процесса имеет
вид
g) =
где А и а — положительные постоянные. Определите
а) частотно-временндй автоспектр ^.(f, /);
б) функцию спектральной плотности энергии.
12.8. Определите двойную по времени автоковариационную функцию /^хх(т, I)
нестационарного случайного процесса из предыдущей задачи.
468
Глава 12
12.9. Нестационарный случайный процесс задан мультипликативной моделью ви-
да
{х(0} = c°s2w/oz {и(/)},
где /0 — постоянная, [u(t)] — стационарный случайный процесс с нулевым средним
значением и единичной дисперсией. Считая, что односторонний автоспектр процесса
имеет вид
\ О, в остальных случаях,
определите средний по времени автоспектр процесса [х(0] ПРИ /0 = 5/2 и В.
12.10. Система с зависящими от времени параметрами имеет частотную характе-
ристику
Я(/, 0 = ; •
1 + jlirft
На вход системы поступает стационарный белый шум с автоспектром Gxx(f) = G.
Определите двойной по частоте автоспектр на выходе системы.
Глава 13
ПРЕОБРАЗОВАНИЕ ГИЛЬБЕРТА
Преобразованием Гильберта действительного сигнала х(Г), определен-
ного во временной области, называется определенный во временной же об-
ласти действительный сигнал х(Г), такой, что сигнал z(t) = x(t) 4- jx(t)
является аналитическим1). Преобразование Фурье x(t) — комплексная функ-
ция X(f), определенная в частотной области, которая, очевидно, отличает-
ся как от преобразования Гильберта x(t), так и от функции z(t). По сигна-
лу z(t) можно вычислить его модуль A(t) и аргумент 6(t), причем A(t)
описывает огибающую исходной функции x(t), a задает мгновенную
фазу х(0 в зависимости от времени. В разд. 13.1 даются три эквивалент-
ных математических определения преобразования Гильберта, а также при-
водятся примеры преобразований Гильберта и его основные свойства. Опи-
сана также характеризация причинно-обусловленных функций и физически
осуществимых систем в терминах преобразований Гильберта. В разд. 13.2
приводятся формулы для преобразований Гильберта ковариационных
функций и их огибающих. Описаны применения к задачам дисперсного и
бездисперсного распространения сигналов. В разд. 13.3 вычисляются огиба-
ющие двух сигналов, а затем ковариационные функции этих огибающих.
Более полные сведения о преобразованиях Гильберта и их применениях
можно найти в работах [13.1 — 13.6].
13.1. Преобразование Гильберта процессов общего вида
Преобразование Гильберта произвольных процессов можно определить
тремя разными способами. Все они будут представлены в этом разделе. За-
метим, что в практических задачах все встречающиеся ниже интегралы
обычно существуют.
1. Определение через свертку
Преобразование Гильберта действительной функции х(/), определенной
во всей области — оо<г<оо, это действительная функция х(г), задаваемая
формулой2)
лоо х(и) / ч
(13.1)
J - 00 и “ и )
Следовательно, x(t) есть свертка x(t) и 1/(тгГ), т. е.
x(z) = x(t) . (13.2)
*) Аналитическим называется комплексный сигнал, зависящий от действительно-
го аргумента и равный пределу некоторой аналитической функции при стремлении
мнимой части ее аргумента к нулю. — Прим, перев.
2) Интеграл (13.1) следует понимать в смысле главного значения. — Прим. ред.
470
Глава 13
Как и преобразование Фурье, преобразование Гильберта — линейный one-
^[a^t) + a2x2(t)] = a1Jf[x1(t)] + a2^[x2(t)] (13.3)
для любых постоянных alf а2 и любых функций х/Г), x2(t).
2, Определение через сдвиг по фазе на к/2
Пусть X(f) — преобразование Фурье х(7):
%(/) = ^[x(r)] = Г00 x^tje-w dt. (13.4)
00
Тогда из формулы (13.2) следует, что X(f) равно преобразованию Фурье
X(f) функции х(Г), умноженному на преобразование Фурье функции 1/(тгГ).
Преобразование Фурье функции 1/(тг/) имеет вид
^[I/tt/J = -jsgn/ = ( у* /<о’ (13.5)
При f = 0 функция sgn/ = 0. Поэтому формула (13.2) описывает преобра-
зование сигнала x(t) системой с частотной характеристикой —jsgn/ и экви-
валентна формуле
X(/) = (-jsgn/)X(/). (13.6)
Эта комплексная функция X(f) не является преобразованием Гильберта
комплексной функции X(f). Она связана с x(t) соотношением
х(г)= Г X(f)e^df, (13.7)
J — 00
т. е. x(t) есть обратное преобразование Фурье X(f).
Преобразование Фурье вида —jsgn/ можно представить как
7 X l е~Л”/2) , f > Л *
Bifl- ^да/-(еЛ./г, , ’ (13.8)
и В (О) = 0. Следовательно, 1
5(/)=|В(/)|е-^> (13.9)
Поэтому B(f) задает систему, сдвигающую входной сигнал по фазе на тг/2,
т. е.
7*0; (13.10)
Ш)-( ^,2’ дп,{> ( -77/2, ДЛЯ / < 0; : 0. (13.11)
Если положить , ,/ч Х(/)=|Х(/)|е-^</>, ТО (13.12)
Х(/) = | Х(/) le-X-M/H-M/)] (13.13)
Преобразование Гильберта
471
зг/2
0 f* -17/2
Итак, преобразование Гильберта состоит в преобразовании сигнала х( t) си-
стемой, которая оставляет модуль X(J) неизменным, а аргумент из-
меняет на 4- где <t>b(f) определяется формулой (13.11), т. е.
Фх(/)-Фх(/) + «2), />0;
(13.14)
<Ш) - <Ш) ~ (V2), /<0.
Другими словами, происходит сдвиг по фазе на тг/2 на положительных ча-
стотах и сдвиг по фазе на —тг/2 на отрицательных частотах, что иллюст-
рирует приведенный выше рисунок.
3. Определение через мнимую часть аналитического сигнала
Третий способ определения преобразования Гильберта, проясняющий его
смысл и позволяющий практически вычислять x(t) по x(t), состоит в исполь-
зовании аналитического сигнала z(t), связанного с x(t) соотношением
z(t) = x(t)+jx(t), (13.15)
Можно написать также
z(t) = A(t)eje(,), (13.16)
где A(t) называется огибающей сигнала x(t), a 0(t) называется мгновенной
фазой сигнала x(t). Очевидно, что в терминах x(t) и x(t)
Л(7) = [x2(z) + х2(г)]1/2, (13.17) (13.18)
6(t) = arctg *(0 = 2ir/07.
«Мгновенная» частота /0 равна 7 -1 1 \ ° \2ir/dt (13.19)
Пусть Z(f) — преобразование Фурье z(0, т. е. Z(/)=^[z(7)] =^[х(7)+ух(/)] = = ^[x(t)] + j^[x(t)] = X(f) + jX(f). (13.20)
472
Глава 13
Выполнив обратное преобразование Фурье Z(/), получим
z(z) = = x(z) + 7x(z), (13.21)
где
x(z) = = Im[z(z)] . (13.22)
13.1.1. ВЫЧИСЛЕНИЕ ПРЕОБРАЗОВАНИЯ ГИЛЬБЕРТА
Для того чтобы вычислить Z(f), заметим, что из формулы (13.6) следу-
ет равенство
X(/) = (-7sgn/)X(/).
Поэтому формула (13.20) принимает вид
Z(/) = [l + sgn/]X(/) = JB1(/)X(/),
где, как видно из рисунка, В{(0) = 1 и
(13.23)
(13.24)
B/f)
2
Таким образом, Z(f) получается из x(f) очень просто. Надо вычислить
X(f) для всех f и затем определить Z(/), положив Z(0) = %(0) и
г(/)НоЖ)’Г<о’
Тогда обратное преобразование Фурье Z(f) даст z(t), причем
x(t) = Im[z(Z)]. Именно так и рекомендуется вычислять преобразование
Гильберта. Из формулы (13.25) следует
x(z) = Re 2 ЕX(f)ej2^'df ,
•'о
x(z) = Im|2 Р Х(/)е'2^' df
(13.26)
ПРИМЕР 13.1. ДИСКРЕТНЫЕ ФОРМУЛЫ ДЛЯ x(t) и x(t). В численных расче-
тах используются следующие формулы, получаемые из формул (11.76) и (11.77)
(п = 0, 1, 2, ..., N - 1):
Преобразование Гильберта
473
'N/1 I 2тгкп
х{п &t) = 2 Д/ Re £ Х(&Д/)ехр у-------
_*-i \ N
+ X0Af,
х(п A/) = 2 Д/ Im
7, , I 2-nkn
E X(£A/)exp y——
k-i \ N
Здесь множитель Д/ = l/(7VAt), а величина X равна
/ Ъпкп \
Х(ЛД/) = Az £ х(п Az)exp ~j—^~ •
л=0 \ N I
Заметим, что для получения дискретных значений сигнала x(wAt) и его
преобразования Гильберта x(nkt) требуются значения X(k&f) только для
к от к = 0 до к = 7V/2, соответствующего частоте Найквиста. Огибающая
сигнала x(t) имеет вид
А(п At) = [х2(и At) 4- х2(п At)] 1/2
13.1.2. ПРИМЕРЫ ПРЕОБРАЗОВАНИЙ ГИЛЬБЕРТА
В табл. 13.1 приводится ряд функций x(t) и их преобразований Гильбер-
та x(t), а также огибающие A(t). Эти преобразования получены непо-
средственно из данных выше определений. Соответствующие графики изо-
бражены на рис. 13.1. Последняя строка в табл. 13.1 представляет собой
частный случай общей теоремы, утверждающей, что
J^[m(z)cos2w/0z] = M(z)sin2w/Oz (13.27)
для любой четной функции w(t).
13.1.3. СВОЙСТВА ПРЕОБРАЗОВАНИЯ ГИЛЬБЕРТА
Перечислим теперь ряд свойств преобразования Гильберта, часть кото-
рых легко следует из основных определений, а остальные доказаны в ука-
занной выше литературе. Пусть x(t) = ^[x(t)], y(t) = ^ly(t)] — преоб-
разования Гильберта функций x(t) и у(t), имеющих преобразования Фурье
X(f) и Y(f) соответственно.
а) Линейное свойство:
Jf[ax(t) + frv(z)] = ax(z) + by(t) (13.28)
для произвольных функций x(t) и у(t) и любых постоянных а и Ь.
б) Свойство сдвига:
^[x(t - а)]= x(t - а). (13.29)
474
Глава 13
Таблица 13.1. Примеры преобразований Гильберта
x(Z) x(t) л(0
COS277/or sin2tf/or 1
sin2Tr/0 -cos2fl/0r 1
sin t 1 - cos t sin( t/2)
t t G/2)
1 t 1 11/2
1 + t2 1 + r2 1 +t2
e~r|z|sin2fl-/or
в) Преобразование Гильберта преобразования Гильберта:
= “*('), (13.30)
т.е. последовательное применение двух преобразований Гильберта дает ис-
ходную функцию с обратным знаком.
г) Обратное преобразование Гильберта x(t):
x(z) = -f°° -,X^ du. (13.31)
•'-00 n(t - u)
Следовательно, x(t) есть свертка x(t) и -1/(тгГ)- Кроме того, x(t) можно
найти как
x(Z)=^-1[(7sgn/)i(/)], (13.32)
где
X(/)=^[x(z)]. (13.33)
д) Свойство четности и нечетности:
Если x(t) — четная (нечетная) функция от г, то x(t) — нечетная (четная)
функция от t:
x(t) четна - x(t) нечетна,
x(t) нечетна — x(t) четна. (13.34)
е) Свойство подобия:
[х(а/)] = x(at) .
(13.35)
Преобразование Гильберта
475
x(t) x(t) A(t)
cos(2nf0t)
sin(2irf0t)
Рис. 13.1. Примеры преобразований Гильберта.
t
ж) Энергетическое свойство:
(13.36)
476
Глава 13
Это тождество следует из теоремы Парсеваля, поскольку
f?(/)<* = f\x(f)\2df,
(13.37)
Гх2(/)<й = Г
J-CX) ?-оо
и из, свойства
|*(/)|2=1*(/)Г- (13.38)
з) Свойство ортогональности:
( dt = 0 . (13.39)
- 00
Это свойство следует из теоремы Парсеваля, так как
Г x(t)x(t) dt = Г %*(/)%(/) df, (13.40)
J - 00 J - 00
И ИЗ ТОГО, ЧТО
^*(/)^(/) = (-7'sgn/)|X(/)|2 (13.41)
есть нечетная функция от /, поэтому правая часть формулы (13.40) равна
нулю.
и) Свойство модуляции:
^[x(z)cos27t/0z] = x(z)sin27r/oz , (13.42s)
если x(t) — сигнал с ограниченным по частоте преобразованием Фурье
X(f), т.е.
х(/) = / 1^1 - F> (13.43)
в остальных случаях;
причем /0 такова, что /0 > F. Аналогично
Ж [x(/)sin2tt/oz] = -x(z)cos2tt/0Z. (13.44)
к) Свойство свертки:
тфОМО] = *(')*j(0 = ^(0*^(0- (13.45)
Это свойство следует из того, что
•Нх(/)*Я0] = Х(/)У(/), (13.46)
[( -J sgn/)Х(/)] У(/) = Х(/)У(/) =
= Х(/)[(-j sgn/)У(/)] = Х(/)У(/). (13.47)
Преобразование Гильберта
477
л) Отсутствие коммутативности:
(13.48)
т.е. преобразования Фурье и Гильберта не коммутируют,
13.1.4. СВЯЗЬ С ФИЗИЧЕСКИ ОСУЩЕСТВИМЫМИ СИСТЕМАМИ
Физически осуществимая линейная система с постоянными парамет-
рами задается весовой функцией й(т), удовлетворяющей свойству (2.3), т. е.
й(т) = О для Т < 0. (13.49)
Соответствующая частотная характеристика H(f) задается формулой (2.13)
и равна
Н(/)=^[Л(т)] = ( h(r)e-^Tdr =
Jo
= НЛ(/)-jHAf). (13.50)
Здесь HR(f) — действительная часть H(f), a Hj(f) — мнимая часть H(f),
т. е.
нк(Л=( h(r)cos2irfTdr,
.. (Ч-Я)
I Л(т)8ш2тг/тdr .
уо
В этом разделе будет доказано, что линейная система физически осущест-
вима тогда и только тогда, когда Hj(f) есть преобразование Гильберта
Этот факт является частным случаем более общей теоремы, которая
верна для любых причинно обусловленных функций. По определению, дей-
ствительная функция y(t) называется причинно обусловленной, если
y(t) = 0 для t < о . (13.52)
Любую функцию y(t) можно представить в виде суммы четной функции
ye(t) и нечетной функции y0(t):
y(t) = ye(j) + yo(t) , (13.53)
полагая
Уе(0 = ИЯ') +Я-')]> л(') = НЯ')-Я-')] • (13.54)
Отсюда следует, чтоye(-t) = ye(t) ny0(-t) = -y0(t). Разложение произ-
вольной причинно обусловленной функции на четную и нечетную составля-
ющие иллюстрирует рис. 13.2.
Пусть теперь ХО — причинно обусловленная функция. Тогда по форму-
478
Глава 13
Рис. 13.2. Четная и нечетная составляющие причинно обусловленной функции.
лам (13.52) и (13.54) при t > О
л(') = 2y(t)>
yo(j) = 1/(0 = ye(j),
а для t < 0
л(0 = 1/(-0,
/Л0 = -1/(-0 = -/е(0,
Следовательно, для причинно обусловленной функции
/о(0 = (sgn/)/e(0,
где
(13.55)
(13.56)
(13.57)
(13.58)
Преобразование Фурье Y(f) любой причинно обусловленной функции
y(t) должно удовлетворять соотношению
Г(/)=^[/(0]=^[/е(0+/о(0] = YR(f)-jY,(f), (13.59)
где
•Н/,(01 = Ш).
(13.60)
^[/о(0] = -jYf(f).
Из формулы (13.57) имеем
Преобразование Гильберта
479
•^[уЛ')1 =^l(sgnt)ye(O] = ^'[sgnz]*^'[^(z)],
где
•И sgn И = -у.
Следовательно, ( ч
, гоо -/Ур(м)
откуда получаем
Zoo Y»(u) _
к ’ du =^{YR(h], (13.61)
-оо 77 V/ ~ и)
т. е. Yj(f) является преобразованием Гильберта YR(f), если y(t) — причин-
но обусловленная функция, что и требовалось доказать.
Доказанное утверждение дает возможность проверить, является ли дан-
ная H(f) частотной характеристикой физически осуществимой системы.
Система физически осуществима, если Hj(f) есть преобразование Гильбер-
та поскольку формула (13.61) эквивалентна формуле (13.57). Поэто-
му формула (13.61) дает необходимое и достаточное условие линейности и
физической осуществимости системы. В формальной записи имеем
Я(/) = ЯД/) -/ЯД/) при H,U) = HR(n- (13.62)
Следовательно,
ЯД/) = ЯД/)= -ЯД/), (13.63)
Я(/) = ЯД/) = ЯД/) +/ЯД/) = /Я(/) . (13.64)
Отклонения от этих соотношений можно использовать для изучения нели-
нейных систем.
ПРИМЕР 13.2. ПОКАЗАТЕЛЬНАЯ ПРИЧИННО ОБУСЛОВЛЕННАЯ ФУНК-
ЦИЯ. Рассмотрим причинно обусловленную функцию
y(t) = 7ге“2,г', t > 0.
При t С 0 имеем y(t) = 0. Здесь для
= (тг/2)ехр( — 2тг I /1) и
любых t функция ye(t) =
— е“2,г/
2
__Д*'
2
z>0;
t < 0.
480
Глава 13
Взяв преобразование Фурье, получим
r'(/)=W)=2(rb)
Г»(/>=Ш) = ^(ГТ7Т
Следовательно, YR(f) — четная функция от /, a Yf(f) — нечетная функция
от f и
Полное преобразование Фурье y(t) есть
П/) = yRU)-HjU) = •
ПРИМЕР 13,3. ПОКАЗАТЕЛЬНО-КОСИНУСОИДАЛЬНАЯ ПРИЧИННО
ОБУСЛОВЛЕННАЯ ФУНКЦИЯ. Рассмотрим причинно обусловленную функ-
цию
y(t) = e"flfcos27rZ>r, а > 0, t > 0.
При t = 0 имеем y(t) = 0. В этом случае преобразование Фурье y(t) имеет
вид
/ . а + jlvf
YU} = 7~TTTTTTTv = Ш)
(а + jlirf) + (2ttZ>)
где выражения для YR(f) и У;(/) в отдельности довольно сложны. Однако
поскольку у(t) — причинно обусловленная функция, то должно выполнять-
ся соотношение
у7(/) = ^[ул(/)],
где YR(f) — четная функция от /, a Yf(f) — нечетная функция от f.
13.2. Преобразование Гильберта и ковариационные
функции
Одним из важнейших применений преобразований Гильберта является
вычисление огибающих ковариационных функций с целью оценки запазды-
вания в задачах распространения энергии. Сейчас будут рассмотрены тео-
ретические основы таких применений как для без дисперсного, так и дис-
персного распространения сигналов.
13.2.1. ОПРЕДЕЛЕНИЕ КОРРЕЛЯЦИИ И ОГИБАЮЩЕЙ
Пусть x(t) и у(t) — стационарные случайные процессы с нулевым сред-
ним значением, ковариационными функциями RyAt) и RvAt) и взаимной ко-
хх у у v
Преобразование Гильберта
481
вариационной функцией Rxy(r). Пусть Sxx(f) и Syy(f) — соответствующие
двухсторонние спектральные плотности, a Sxy(f) — двухсторонняя взаим-
ная спектральная плотность. Как отмечалось в разд. 5.2, ковариационные
функции и соответствующие спектральные плотности образуют пары вза-
имных преобразований Фурье. Пусть x(t) = и y(t) = —
преобразования Гильберта стационарных случайных процессов х(Г) и y(t).
Поскольку преобразование Гильберта — линейная операция, то x(t) и
y(t) — тоже стационарные случайные процессы. Поэтому для них совер-
шенно так же, как и для x(t) и у(t), можно определить ковариационные
функции и спектральные плотности (обозначим их через 7?^(т), R~~(t),
Rxy(r) и причем соответствующие ковариационные
функции и спектральные плотности образуют пары взаимных преобразова-
ний Фурье. Приведем точные определения:
Л«(т) = £[x(/)x(z + т)],
Ryy(r) = E[y(t)y(t + т)], (13.65)
Rxy(T^ = £[*(0 y(t + т)].
Применяя преобразование Фурье, получим
5^(т) = ^[Л«(т)] ,
S^(/)=jr[/?..(T)]> (13.66)
С точностью до масштабного множителя (который в теоретических по-
строениях значения не имеет, поскольку он участвует в обеих частях соот-
ношений и, следовательно, сокращается) можно пользоваться определения-
ми
^(/) = £[Х*(/)Х(/)] = £[|У(/)|2] ,
^(/) = £[у*(/)у(/)] = е[|у(/)|2] , (13-67)
£,//) = £[Х*(/)У(/)].
Смешанные характеристики процессов и их преобразований Гильберта, а
именно RyAt), RyAt), S-Jf), определяются следующим образом:
Az Ал
£^(т) = £[x(/)J(z + т)] ,
Яху(т) = £[x(0j>(' + т)], (13.68)
16-953
482
Глава 13
5х//)=^[/?хДт)],
5^(/)=^[7?^(т)].
Функции Rxx(r), Rxx(t), Sxx(f) и S~x(f) — частные случаи этих определений.
Как и выше, с точностью до масштабного множителя Sx~(f) и S*y(f) мож-
но определить непосредственно
5х//) = £[Х*(/)Г(/)],
(13.70)
^(/) = £[Х*(/)Г(/)].
Огибающие функций /?хх(т), Ryy(j) и Rxy(r) определяются через их преоб-
разования Гильберта RyAt), Rvv(f) и R~(t) следующим образом. Огибаю-
щая RXX(T) есть У
= [«2х(т) + Л2х(т)]1/2 (13.71)
Огибающая Ryy(j) имеет вид
Л/т) = [СЫ + ^(т)]1^ (13.72)
Огибающая RyAt) равна
А,И = |л2хДт) + Л2/т)]1/2 (13.73)
В следующем разделе будут установлены свойства введенных выше вели-
чин и связь между ними.
13.2.2. СООТНОШЕНИЯ ДЛЯ ПРЕОБРАЗОВАНИЙ ГИЛЬБЕРТА
В табл. 13.2 дана сводка полезных соотношений, которым удовлетворя-
ют ковариационные и взаимные ковариационные функции, а также спект-
ральные и взаимные спектральные плотности. Доказательство этих соот-
ношений оставляем в качестве простых упражнений.
Некоторые из соотношений, включенных в табл. 13.2, заслуживают
особого внимания. В частности,
Яхх(т)=^[Яхх(т)] = Ях,(т), (13.74)
т. е. преобразование Гильберта Rxx(j) есть взаимная ковариационная функ-
ция x(t) и его преобразования Гильберта x(t). Заметим далее, что Rxx(t) —
нечетная функция от т, поскольку Rxx(r) — четная функция от т. Поэтому
^хх(О) = Лх,(0) = 0. (13.75)
Преобразование Гильберта
483
Таблица 13.2. Соотношения для ковариационных и взаимных ковариационных функ-
ций при преобразованиях Гильберта
Л;;(т)= 7?vv(t) Sxx(f) = Sxx(f)
R~~( — т) = R~~(r), Четная функция от т
о-} = Я;;(0) = ЯХ¥(0) = о2
Л„(т) = Rx,(r) = -R-X(r) Sxx(f) = Sx-x(f) = -S-xx(f)
Rxx( — t) — ~Rxx(r), Нечетная функция от т
Я„(0) = Ях-(0) = Яь(0) = О
Ли.(т) = Яо(т) S-x.(f)=Sxv(f)
= Як(0) = ЯЛДО) = <ухг
*<..(0 = Лл-(т) = -Л;,.(т) Sxt,(f) = SxJ.(f) = -S-xr(f)
Ль(т) §*,(/) = S-vx(f)
£U0) = RX1(O) = 0 (13.75)
Следовательно, Rxx(r) пересекает ось абсцисс в точке т = 0, соответствую-
щей положению максимума Rxx(t), достигаемого в точке т = 0; Rxx(j)
пересекает ось абсцисс снизу вверх, т. е.
кЛХ(о-)<О; яЛХ(о+)>о. (13.76)
в чем можно убедиться на примерах из табл. 13.1. Таким образом, Rxx(t) и
производная Rxx(t) пересекают ось абсцисс в противоположных направле-
ниях (ср. с соотношениями (5.146)).
13.2.3. АНАЛИТИЧЕСКИЕ СИГНАЛЫ ДЛЯ КОВАРИАЦИОННЫХ ФУНКЦИЙ
Аналитический сигнал zx(t), соответствующий стационарному случайно-
му процессу х(1), определен формулой (13.15):
гх(0 = 40 +740»
гдех(Г) - ^(х(Г)]. Комплексная ковариационная функция Rz^ (т), по опре-
делению, есть х
RZ<JT) = ^[ОЧОМ'+0] = Е [{х(0 - jx(0) {x(t + т) +jx(t + т)}]=
= Rxx(r) + R-x-x(t) +j[Rxi(r) ~ Rxx(r)].
16*
484
Глава 13
Но, согласно табл. 13.2,
Л«(т) = Яхх(т), ЛЯх(т)= -Axi(r),
поэтому
Rz,Jt) = 2[ЯХЛ(т) +jRxx(r)] = 2[Rxx(т) +jRxx(r)].
Отсюда следует, что функция
R..(т) ~ , ч
-^-Л„(т)+7«„(т) (13 77)
является аналитическим сигналом для Rxx(f).
Преобразование Фурье R „ (т) равно ST т (/), где
SZxdf) =^[AzJt)] = 2[5ХХ(/) +Дх(Л1 =
= 2[1+ sgn/]5xx(/>.
Поэтому спектральная плотность имеет вид
S22(/)=(!5^^’ ^°’ (13.78)
2'гД77 (0, /<0. v
Из формулы (13.77) имеем
^[s^(f)/2] = Яхх(т) +JRxx(r). (13.79)
Поэтому имеют место формальные соотношения
Rxx(T) = 2/ 5xx(/)cos2w/tdf,
0 (13.80)
RM = 2rSxx{f^2^Tdf.
•'о
Для определения аналитического сигнала для RyAt) рассмотрим аНаЛИ-
ЛУ
тические сигналы, соответствующие стационарным случайным процессам
*х(0 = x(t) +jx(t), zy(t) = y(t) +jy(t).
Комплексная взаимная ковариационная функция, по определению, есть
^z,zv(T) = £[z*GK(Z + т)] = £[{*(0-./*(')} (Я' + т) + Т)}] =
= Rxy(r) + А„(т) + j[ЯхР(т) - /?v(t)].
Преобразование Гильберта
485
Но, согласно табл. 13.2,
Я„(т) = АхДт), Яху(т) = -Ях?(т).
Поэтому
Jr) = 2[ ЯхДт) + 77?х-(т)] = 2[ях/т) +дх,(т)].
Отсюда следует, что функция
Лгг(т)
-^— = Rxy(r)+jRxy(r) (13.81)
является аналитическим сигналом для Rxy(r).
Преобразование Фурье R. „ (т) есть S, „ (/), где
ZxZy
=^[/?zJt)] = 2[5ХД/) + jSxy(f)] =
= 2[1 + sgn/]5Х?(/).
Поэтому взаимная спектральная плотность имеет вид
|о, /<о- <13-82)
Из формулы (13.81) имеем
=Rxy(r)+jRxy(r). (13.83)
Отсюда получаем формальные выражения
Rxy(T) = Re2(°°Sxy(f)e^df
•'о
(13.84)
~ У00 г
А (т) = Im 2j Sxy(f}e™'df .
. *'0
ПРИМЕР 13.4. ДИСКРЕТНЫЕ ВЫРАЖЕНИЯ ДЛЯ Rxy(r) и Rxy(r). При чис-
ленных расчетах дополним, согласно рекомендациям разд. 11.4.2 и 11.6.2,
каждую из последовательностей длиной N {х(иД/)} и \y(n&t)} N нулями;
в результате получим реализацию длиной 2N. При Д/ = 1/(22УД/) для
к = 0, 1,2, ... , N вычислим
N~x / <пкп\
X(kkf) = Дг £ х(дД/)ехр -7—• Ь
л = 0 \ Л '
/ тткп \
У(&Д/) = Дг ^(иДг)ехр -j-тг ,
л-о \ N I
2
Gxy(k Д/) = [ %*(к Д/)У(к Д/)] •
486
Глава 13
Далее имеем для г = 0, 1,2, ... , N — 1
/ Л/Д f \ г N / к кг \
= Т7— Re Сх>.(^Д/)ехр J— »
\2V Г) |_АМ) \ 1У /J
/ Л^Д/ \ Г Д / irkrX
Rxy(rb‘) = —— Im Е Gx/fcA/)exp I/— .
\ yv '/ |_£ = О \ yv /.
Квадрат огибающей Ryv(t) есть
лу
Л^.(гДг) = А^.(гДг) + А^(гДг).
Ковариационные функции вычисляются как частные случаи указанных со-
отношений:
ЛхДгДг) =
/ ЛГДУ \Г N
----- Е Gxx (к )cos( nkr/N)
\ N - r/[*=0
N
I Nif\ Д
Rxx(rkt) = ——- E Gxx(k&f)sin(irkr/N) ,
_k = 0
А2хх(Г^) = R2xx(r^{) + R2xx(rbt).
13.2.4. ЗАДАЧИ БЕЗДИСПЕРСНОГО РАСПРОСТРАНЕНИЯ
Рассмотрим простейший вариант бездисперсного распространения сиг-
нала, описываемый формулой (5.19). Для простоты будем считать, что
n(t) отсутствует, так что
y(t) = ax(t - т0), (13.85)
Лхг(т) = а2Лхх(т),
Rxy(.T) = «Лхх(Т - То),
< > *<'-> < > (13'86)
т /«„(0)Я„(0) То)'
Пусть x(t) — ограниченный по частоте белый шум, определенный форму-
лой (5.48), т. е.
sinirBr
тгВт
Rxx(T) = аВ
cosl-nf^ . (13.87)
Преобразование Гильберта
487
Тогда
Rxx(0) = аВ,
Ryy(Q) = a1{aB),
(13.88)
Рх/Т)
8Ш7гВ(т — То)
1т5(т - т0)
cos2tt/0(t - т0).
(13.89)
Здесь /0 — центральная частота идеального фильтра с полосой пропускания
В, причем спектральная плотность Gxx(f) постоянна в этой полосе и равна
нулю вне ее. Запаздывание т0 — постоянная величина. График функции
(13.89) показан на рис. 13.3.
Следует отметить несколько особенностей формулы (13.89), верной в
случае бездисперсного распространения сигнала.
1. Косинусоида со8(2тг/0т) с центральной частотой /0 модулируется огиба-
ющей 8т(7гВт)/тгВт, которая определяется шириной полосы пропускания В.
2. Максимальное значение огибающей соответствует запаздыванию
т0 = d/c, которое постоянно и не зависит от частоты.
3. Пики косинусоиды соответствуют запаздываниям тп = т0±л//0, где
п — произвольное целое число. В частности, положение максимального
значения косинусоиды совпадает с положением максимального значения
огибающей.
4. Главный максимум огибающей заключен между точками т0 — \/В и
т0 4- \/В и имеет ширину 2/В. В главном максимуме содержится 2/0/В ко-
лебаний косинусоиды.
Рху(Т)
Рис. 13.3. Типичная нормированная взаимная ковариационная функция при без-
дисперсном распространении сигнала по одному тракту.
488
Глава 13
Три важных класса задач бездисперсного распространения сигналов, в
которых требуется вычислять огибающие взаимных ковариационных функ-
ций, иллюстрируются приведенными ниже примерами. Как и во всех инже-
нерных задачах, при планировании экспериментов и вычислении оценок
нужных величин требуются формулы для оценки статистических ошибок.
В частности, нужны формулы для оценки статистических ошибок, связан-
ных а) с определением абсолютной величины максимального значения оги-
бающей и б) с определения запаздывания, т. е. локализации максимального
значения огибающей. Эти вопросы рассматриваются в работе [13.1] на ос-
нове результатов, изложенных в разд. 8.4.
ПРИМЕР 13.5. БЕЗДИСПЕРСНОЕ РАСПРОСТРАНЕНИЕ ПО НЕСКОЛЬКИМ
ТАРКТАМ. На рис. 13.4 показано распространение одного входного сигнала
по нескольким трактам, выходы которых суммируются и дают один вы-
ходной сигнал. Для простоты на рисунке показаны только три тракта, од-
нако их число может быть произвольным. Эта модель описывается уравне-
нием
ЯО = «!%(/ - Tj) + a2x(r - т2) + a3x(t - т3) + «(/),
где а. — постоянные коэффициенты затухания в каждом тракте, а т. — со-
ответствующие запаздывания. Предполагается, что шум n(t) не коррелиро-
ван с x(t). Одновременно наблюдаются x(t) и y(t). Требуется определить
относительный вклад каждого тракта в мощность выходного сигнала и со-
ответствующие запаздывания г, в каждом из трактов. Для этого оценива-
ется взаимная ковариационная функция x(t) и у(1), а затем для определения
огибающей вычисляется преобразование Гильберта этой взаимной ковариа-
ционной функции. В данном случае
МТ) = «1Лхх(т - т1) + «2Лхх(т - т2) + «3Лхх(т - тз)-
ПРИМЕР 13.6. БЕЗДИСПЕРСНОЕ РАСПРОСТРАНЕНИЕ СИГНАЛОВ, ИС-
ХОДЯЩИХ ИЗ НЕСКОЛЬКИХ НЕКОРРЕЛИРОВАННЫХ ИСТОЧНИКОВ. На
рис. 13.5 показано распространение нескольких сигналов по разным трак-
там, выходы которых затем суммируются и дают один выходной сигнал.
Одновременно наблюдаются все входные и выходные сигналы. Для про-
стоты показаны только три источника и соответствующие тракты, однако
число некоррелированных источников может быть произвольным. Требу-
Рис. 13.4. Бездисперсное распространение сигнала по нескольким трактам.
Преобразование Гильберта
489
Рис. 13.5. Без дисперсное распространение сигналов из нескольких некоррелиро-
ванных источников.
ется определить относительный вклад каждого из источников в мощность
выходного сигнала и соответствующие запаздывания в каждом тракте.
Предполагается, что шум на выходе n(t) не коррелирован с входными сиг-
налами хДг), а источники не коррелированы между собой. Эта модель опи-
сывается уравнением.
y(j) = «лО - Ti) + «2хг(г - тг) + a3x3(t - т3) + и(/),
где ai — постоянные коэффициенты затухания в каждом тракте, a Ti — со-
ответствующие запаздывания в каждом тракте. Вычисляются взаимные ко-
вариационные функции для каждой пары хД/) и а затем для определе-
ния их огибающих вычисляются преобразования Гильберта. В данном слу-
чае
Rxiy(T) = aiRxx(r - Ti)
ПРИМЕР 13.7. БЕЗДИСПЕРСНОЕ РАСПРОСТРАНЕНИЕ СИГНАЛА ИЗ ОД-
НОГО НЕНАБЛЮДАЕМОГО ИСТОЧНИКА ПО НЕСКОЛЬКИМ ТРАКТАМ С
НАБЛЮДАЕМЫМИ ВЫХОДНЫМИ СИГНАЛАМИ. На рис. 13.6 показано рас-
пространение сигнала из одного ненаблюдаемого источника по нескольким
Рис. 13.6. Без дисперсное распространение сигнала из ненаблюдаемого источника
по нескольким трактам с наблюдаемыми выходными сигналами.
490
Глава 13
трактам. Одновременно наблюдаются все выходные сигналы. Для просто-
ты показаны только три выходных сигнала, однако их число может быть
произвольным. Требуется определить относительные запаздывания между
любыми двумя выходными сигналами, при этом фактическое запаздывание
выходных сигналов по отношению к входному сигналу x(t) неизвестно, по-
скольку по предположению сигнал x(t) не наблюдается. Предполагается,
что посторонние шумы иДг) не коррелированы между собой и с x(t). Эта
модель описывается следующими уравнениями, задающими вид выходных
сигналов для i = 1, 2, 3:
л(0 = VM + л>(0 = - т<)+ "АО
Определяются взаимные ковариационные функции для пар выходных сиг-
налов с последующим вычислением огибающих с помощью преобразования
Гильберта. В данном случае
Ry,yST^ = aiaJRxx(T + Т< ~ Т7).
13.2.5. ЗАДАЧИ ДИСПЕРСНОГО РАСПРОСТРАНЕНИЯ СИГНАЛОВ
В разд. 13.2.4 рассматривались задачи бездисперсного распространения
сигналов, когда скорость распространения сигналов постоянна и не зависит
от частоты. Рассмотрим теперь случай, когда характеристики трактов рас-
пространения сигналов зависят от частоты [13.7, 13.8]. В частности, «кажу-
щаяся» скорость распространения волн изгиба в конструкциях на данной
частоте называется групповой скоростью cg. Эта скорость cg связана с фа-
зовой скоростью ср, но не равна ей. Известно, что для групповой скоро-
сти волн изгиба в тонких балках имеет место соотношение
cg = 2ср - ff, (13.90)
т. е. cg равна удвоенной ср, причем обе эти скорости пропорциональны ква-
дратному корню из частоты.
В задачах дисперсного распространения сигналов, описываемых в пер-
вом приближении соотношением (13.90), взаимная ковариационная функ-
ция, аналогичная функции (13.89), имеет, как показано в работе [13.8], сле-
дующий вид:
[sinw50(T-т2)1 /поп
РХ(,(т)=» -----------— cos2w/0(t - tJ, (13.91)
У L Wj5o(T-T2)
где
Т1 = (d/cp) (13.92)
ь = (^)~Л;1/2> (13.93)
причем тх = 2т2, поскольку с — 2с . График функции (13.91) показан на
рис. 13.7.
Преобразование Гильберта
491
Рис. 13.7. Типичная нормированная взаимная ковариационная функция при дис-
персном распространении сигнала по одному тракту.
Отметим, что график функции (13.91) похож на график функции (13.89),
но имеет отличительные особенности:
1) максимальное значение огибающей приходится на запаздывание
т2 = d/cg, которое в данном случае зависит от частоты, так как cg ~ V/o;
2) пики косинусоиды соответствуют запаздываниям тп = ± где
п — произвольное целое число; вообще говоря, положение максимального
значения косинусоиды не совпадает с положением максимального значения
огибающей.
Из формулы (13.91) видно, что «кажущаяся» скорость распространения
для огибающей на данной частоте определяется в основном групповой ско-
ростью cg, а не фазовой скоростью с . При таком дисперсном распростра-
нении сигнала положение максимального значения рху(т), определенное по
ее тонкой структуре, задаваемой косинусоидой, входящей в формулу
(13.91), может не совпасть с положением максимального значения огибаю-
щей, приходящимся на запаздывание т2. Для определения т2 нужно вычис-
лить огибающую рху(т), для чего удобно использовать преобразование
Гильберта.
Вывод формулы (13.91) основывается на следующих соображениях.
Возьмем исходное соотношение
*» = Г Sxy(J)ej2”/Tdf. (13.94)
-со
В случае дисперсного распространения, приводящего к формуле (13.91), со-
ответствующая функция £(/) есть
sxv(f) = «М/К'2*',
(13.95)
где запаздывание тр = d/cp зависит от частоты, поскольку фазовая ско-
492
Глава 13
рость ср - \[f. В данном случае значение тр = т (f) на частоте f равно
d а ^ = - = -75=7’ <13’96) Р Ср f^f
где а — некоторый коэффициент пропорциональности. Подстановка фор-
мулы (13.95) в выражение (13.94) дает
ЛЛДт) = аГ Sxx(He^-^df =
J - 00
/•ОО
= «/ Gxx(/)cOS2w/(t - Т ) J/.
Л)
(13.97)
где односторонняя спектральная плотность Gxxif) — lSxx(f) при / > 0 и
равна нулю в остальных случаях. Для ограниченного по частоте белого шу-
ма
Gxx(f) = (К, 0 \ 0, в < /0 - (Ло/2) < / < /о + (*о/2); (13 98) остальных случаях.
Поэтому Далее R ху(т) = aKJ *хх(0) = r° + <Bo/2)cos27r/(T - т ) df. (13.99) /о-(Во/2) К (fo+( B°/2)df= КВ0, (13.100)
RyyW = а2ЯЛЛ(0) = а2О0-
Следовательно, нормированная взаимная ковариационная функция имеет
вид
PxJ(T) = -Z-//o + <B°/2>cos277/(t - т ) df. (13.101)
»о •'/»-( »о/2)
Рассмотрим теперь случай, когда ширина полосы пропускания BQ менее
одной октавы, так что для любого е < 1 вместо f можно подставить вы-
ражение
/ = /о(1+е)> df = fode. (13.102)
После такой замены переменных получаем
/ \ f3 f^o/2/o nz/li \f \ J
РхуЬ) = -Z-j cos2tt/0(1 + е)(т - т ) de ,
O0J-Bn/2fn
а г из формулы (13.96) принимает вид
а а
Р 'i^f ^2тг/0(1 + е)
(13.103)
(13.104)
Преобразование Гильберта
493
Для малых е, пренебрегая членами порядка е2, имеем
2тг/0(1 + е)(т - тр) = 2тг/0(1 + е)т - + е) *
« 2тт/0(1 4- е)т - а
/ а \ / а \
2тг/0 т----г 4- 2тг/0 т--------;--
\ /2^/ '°1 2^Л /
Тогда, отбрасывая члены, содержащие синусы, получим
cos27t/0(1 + е)(т - tJ » cos[2w/0(t - tJ + 2тг/0(т - т2)е] ~
« [cos2tt/0(t - tJ] [cos2tt/0(t — т2)е]. (13.106)
где
a d
ср
(13.107)
a d
т2 = = —
(13.108)
Здесь ср и cg — фазовая и групповая скорости на частоте /0, причем
cg = 2ср. Наконец, подставив выражение (13.106) в формулу (13.103) и ин-
тегрируя полученное выражение справа и слева по £, получим
Рху(т) ~ (^-|cos2ir/o(
\ "о /
। cos2t7/0(t - т2)еае
-^о/2/о
sin тгВ0(т — т2)
тгВ0(т-т2)
cos2tt/0(t — Tj)
(13.109)
что совпадает с искомой формулой (13.91).
13.3. Выделение огибающей с последующим
вычислением корреляции
Рассмотрим рис. 13.8, на котором функции
(13.110)
обозначают квадраты огибающих составляющих x(t) и y(t). Взаимная ко-
494
Глава 13
Рис. 13.8. Выделение квадрата огибающей с последующим вычислением корре-
ляции.
вариационная функция Ruv(t) этих квадратов огибающих задается форму-
лой
= E[w(z)t>(z + т)] = Е[{х2(?) + x2(t)}{y2(t + т) + y2(t + т)}] =
= E[x2(t)y2(t + т)] + E[x2(t)y2(t + т)] +
+ Е[х2(г)/(г + т)] + f[x2(z) j2(/ + т)]. (13.111)
Предположим, что х(/), x(Z), y(t) и y(t) имеют совместное нормальное
распределение с нулевым средним значением. Тогда
E[x2(z)/(z + т)] = 02о2 + 2А2,.(т),
£[x2(z).y2(z + т)] = о2а-2 + 2Л2Р(т),
(13.112)
e[x2(z)/(z + т)] = а?а2 + 2А?Дт),
E[x2(z)J2(z + т)] = 0?о? + 2Я?-(т).
Подставляя выражения (13.112) в (13.111) и используя соотношения из
табл. 13.2, получим
+ 4[л2„(т) + Ё2/т)] . (13.113)
Далее
и = £[м(/)] = 2ох2 , и = £[у(/)] = 1Оу , (13.114)
Преобразование Гильберта
495
поэтому
ЯИ(,(т) - (й)(й) = 4[я2Дт) + Я2у(т)] = 4Л^(т), (13.115)
где, как следует из формулы (13.73), величина Л^(т) есть квадрат огибаю-
щей функции Я (т). Тогда
Лии(0) = Е [м2(/)] = Е [ (x2(z) + x2(z)}2] =
= Е [x4(z)] + 2£[x2(z)x2(z)] + £[x4(z)] =
= Зох + 2o2o~2 + Зо/ = 8о* . (13.116)
Поэтому
Лии(0)-(й)2 = 4ах4 (13.117)
и аналогично
/и0)-(*)2 = 4< (13.П8)
Полученные соотношения позволяют утверждать, что коэффициент корре-
ляции puv(t) квадратов огибающих функций u(t) и v(t) имеет вид
, . _ Л™(т) - («)(”) _ Л2г(т)
РиЛт) rf уГТ yj- 22
4МоР(й)2][лр1,(О) - (о)2] W
Сравним выражение (13.119) с обычным коэффициентом корреляции
Рху(т) исходных сигналов x(t) и определенным формулой (5.16), т. е.
^(r)-(x)(j) = £ЛДт)
Рху Т УКГ(О) - (x)2][av/0) - (J)2]
Вычислив преобразование Гильберта, получим
. (13.120)
(13.121)
Из формулы (13.73) следует, что
р«Лт) = р2>,(т) + р2Лт)-
(13.122)
Следовательно, если перед вычислением функции puv(t) исключить средние
значения, то этот коэффициент корреляции будет задавать квадрат огиба-
496
Глава 13
ющей Рху(т). Величина puv(t) является коэффициентом корреляции, соот-
ветствующим выражению
СшХт) = - (й)(и) = £[{«(/) - U} {v(t + т) - v}], (13.123)
где w(Z), v(t), и и v определены формулами (13.110) и (13.114). Схема вы-
числения величины Cuv(t) изображена на рис. 13.8.
Отметим три особенности формулы (13.122), касающиеся характера по-
ведения коэффициента корреляции puv(t) огибающих по сравнению с пове-
дением исходной величины Rxy(r) и ее огибающей Аху(т):
1) величина puv(t), как и Аху(т), не зависит от тонкой структуры 7?XJ(r);
2) величина puv(t) имеет более острый максимум по сравнению с величи-
нами Rxy(r) и рху(т) в окрестности значения т, определяющего положение
этого максимума;
3) величина puv(t) имеет более острый максимум по сравнению с ковари-
ационной функцией Аху(т) в окрестности т, определяющего положение мак-
симума.
Следовательно, puv(t) превосходит как рху(т), так и Аху(т) в том, что ка-
сается эффективности определения положения максимума.
ПРИМЕР 13.8. ПОКАЗАТЕЛЬНО-КОСИНУСОИДАЛЬНАЯ ВЗАИМНАЯ КО-
ВАРИАЦИОННАЯ ФУНКЦИЯ. Рассмотрим нормированную взаимную кова-
риационную функцию вида
РхДт) =---------= e-z,|T|cos277/0T.
Ее преобразование Гильберта есть
РХу(т) = ~ = e“ft|T|sin27r/0T.
ахау
Тогда
Ри„(т) = —= e-2fclTl .
°хау
Заметим, что puv(t), и Аху(т) не зависят от частоты модуляции /0. Далее в
окрестности точки т = 0, определяющей положение максимума рху(т), обе
величины, рху(т) и Аху(т), ведут себя как ехр(-#1т1), а соответствующая
Puv(t) ведет себя как ехр( — 2b 1т1). Очевидно, что puv(t) имеет более резко
выраженный максимум в т = 0 по сравнению с Аху(т). На этом пример за-
канчивается.
Рассмотрим теперь взаимные спектральные плотности и автоспектры
квадратов огибающих функций u(t) и r(Z), заданных формулами (13.110).
Согласно формуле (13.115), взаимная спектральная плотность огибающих
есть
5ие(/) =^[/?и„(т) - «*] = 4^[л^(т)] . (13.124)
Преобразование Гильберта
497
Квадрат огибающей 7?vv(t), т. е.
А2ху(т) = R2xy(r) + R*xy(j), (13.125)
можно вычислить способом, намеченным в примере 13.4. Тогда
•НАх/т)1 = Г Sxy(a)Sxy(f- a) da , (13.126)
^[^Ь)]= Г Sxy(a)Sxy(f-a) da =
J - 00
у ОС
= / B(a)B(f-a)Sxy(a)Sxy(f-a) da, (13.127)
- 00
где B(f) = —Jsgn/, как в формуле (13.8). Поэтому
U/НГ [1 + B(a)B(f - a)]Sxy(a)Sxv(f - a) da. (13.128)
J - 00
При любом f > 0 имеем
I 1, а < 0 ;
B(a)B(f—a) = -1, 0<«</; (13.129)
I 1, а> f.
Аналогично определяются автоспектры огибающих:
SUUU) = + B^B(f-a)]Sxx(a)Sxx{f- a) da,
(13.130)
^„(/) =4Г [1 + B(a)B(f — a)]Svy(a)SYy(f — a) da.
Следовательно, по известным спектральным плотностям исходных сигна-
лов x(t} и у(/) можно вычислить соответствующие спектральные плотно-
сти квадратов огибающих функций u(t) и v(t).
Задачи
13.1. Какие из следующих утверждений верны?
а) Преобразование Гильберта — линейный оператор.
б) Преобразование Гильберта функции, зависящей от времени, тоже является
функцией, зависящей от времени.
в) Если x(t) и ее преобразование Гильберта x(t) имеют преобразования Фурье
X{f) и X(f) соответственно, то X(f) есть преобразование Гильберта X(f).
т) Модули преобразований Фурье x(t) и ее преобразования Гильберта x(t) равны.
д) Еслц преобразование Фурье х(Г) — действительная величина, то преобразова-
ние Фурье ее преобразования Гильберта х(Г) — тоже действительная величина.
498
Глава 13
13.2 Вычислите преобразование Гильберта функции
x(t) = ae~h^,) b > 0.
13.3. Вычислите преобразование Гильберта
t - а
x(z) = ------------г -
1 + (/- а)2
13.4. Функция x(t) имеет преобразование Фурье вида
*</)=. А л
1 + jZnf
Вычислите преобразование Фурье преобразования Гильберта x(t).
13.5. При каких условиях преобразование Гильберта комплексной функции
z(t) = %(/) + jy(t) (обозначим его z(t)) будет равно jzit)!
13.6. Действительная часть частотной характеристики физически осуществимой
линейной системы с постоянными параметрами имеет вид
1 -/2
HR(f) =------------5--------7 •
(1-Г)2 + (а/)2
Вычислите мнимую часть частотной характеристики.
13.7. Взаимная ковариационная функция возбуждения и отклика физической си-
стемы имеет вид
I 8Ш7ГВ|Т - Т2| \
Кху\Т) аВ I ТГ, j I cos 2 | т — f
у 77£>|T — T2| /
где В < /0. Если = т2, то чему равно время прохождения сигнала через систему
на частоте f = fQ + В?
13.8. Пусть в задаче 13.7 ф т2. Чему равно время прохождения сигнала через
систему на частоте f = j\ + В, если групповая скорость распространения волн рав-
на с ~ V/.
я
13.9. Пусть имеется модулированный сигнал y(t) = x(r)cos 2тг^Г, причем в
спектр %(/*) не входят частоты, превышающие F < /0. Вычислите следующие величи-
ны:
а) преобразование Гильберта y(t) сигнала _у(Г);
б) ковариационную функцию R (т) сигнала y(t) через ковариационную функцию
в) преобразование Гильберта Ryy(r) ковариационной функции Ryy(f);
г) огибающую ковариационной функции Rvy(r).
13.10. Рассмотрим аналитическую функцию z(t) = x(t) + jx(t), причем двухсто-
ронняя спектральная плотность х(/) имеет вид
Sxx(f^ = a2 + 4^2f2 •
Вычислите спектральные плотности функций: a) x(t); б) z(t).
Приложение А
Статистические таблицы1*2’
Таблица А. 1. Значения плотности стандартного нормального распределения
р (г ) = -------------е ~z 2/2
V 2 7Г
Z 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09
0.0 0.3989 0.3989 0.3989 0.3988 0.3986
0.1 0.3970 0.3966 0.3961 0.3956 0.3951
0.2 0.3910 0.3902 0.3894 0.3884 0.3876
0.3 0.3814 0.3802 0.3790 0.3778 0.3765
0.4 0.3683 0.3668 0.3653 0.3637 0.3621
0.5 0.3521 0.3503 0.3485 0.3467 0.3448
0.6 0.3332 0.3312 0.3292 0.3271 0.3251
0.7 0.3123 0.3101 0.3079 0.3056 0.3034
0.8 0.2897 0.2874 0.2850 0.2827 0.2803
0.9 0.2661 0.2637 0.2613 0.2589 0.2565
1.0 0.2420 0.2396 0.2371 0.2347 0.2323
1.1 0.2179 0.2155 0.2131 0.2107 0.2083
1.2 0.1942 0.1919 0.1895 0.1872 0.1849
1.3 0.1714 0.1691 0.1669 0.1647 0.1626
1.4 0.1497 0.1476 0.1456 0.1435 0.1415
1.5 0.1295 0.1276 0.1257 0.1238 0.1219
1.6 0.1109 0.1092 0.1074 0.1057 0.1040
1.7 0.0940 0.0925 0.0909 0.0893 0.0878
1.8 0.0790 0.0775 0.0761 0.0748 0.0734
1.9 0.0656 0.0644 0.0632 0.0620 0.0608
2.0 0.0540 0.0529 O.O5I9 0.0508 0.0498
2.1 0.0440 0.0431 0.0422 0.0413 0.0404
2.2 0.0355 0.0347 0.0339 0.0332 0.0325
2.3 0.0283 0.0277 0.0270 0.0264 0.0258
2.4 0.0224 0.0219 O.O2I3 0.0208 0.0203
2.5 0.0175 0.0171 0.0167 O.OI63 O.OI58
2.6 0.0136 0.0132 0.0129 0.0126 0.0122
2.7 0.0104 0.0101 0.0099 0.0096 0.0093
2.8 0.0079 0.0077 0.0075 0.0073 0.0071
2.9 0.0060 0.0058 0.0056 0.0055 0.0053
3.0 0.0044 0.0043 0.0042 0.0040 0.0039
3.1 О.ООЗЗ 0.0032 0.0031 0.0030 0.0029
3.2 0.0024 0.0023 0.0022 0.0022 0.0021
3.3 0.0017 0.0017 0.0016 0.0016 0.0015
3.4 0.0012 0.0012 0.0012 0.0011 0.0011
3.5 0.0009 0.0008 0.0008 0.0008 0.0008
3.6 0.0006 0.0006 0.0006 0.0005 0.0005
3.7 0.0004 0.0004 0.0004 0.0004 0.0004
3.8 0.0003 0.0003 0.0003 0.0003 0.0003
3.9 0.0002 0.0002 0.0002 0.0002 0.0002
0.3986 0.3982 0.3980 0.3977 0.3973
0.3945 0.3939 0.3932 0.3925 0.3918
0.3867 0.3857 0.3847 0.3836 0.3825
0.3752 0.3739 0.3725 0.3712 0.3697
0.3605 0.3589 0.3572 0.3555 0.3538
0.3429 0.3410 0.3391 0.3372 0.3352
0.3230 0.3209 0.3187 0.3166 0.3144
0.3011 0.2989 0.2966 0.2943 0.2920
0.2780 0.2756 0.2732 0.2709 0.2685
0.2541 0.2516 0.2492 0.2468 0.2444
0.2299 0.2275 0.2251 0.2227 0.2203
0.2059 0.2036 0.2012 0.1989 0.1965
0.1826 0.1804 0.1781 0.1758 0.1736
0.1605 0.1582 0.1561 0.1539 0.1518
0.1394 0.1374 0.1354 0.1334 0.1315
0.1200 0.1282 0.1163 0.1145 0.1127
0.1023 0.1006 0.0989 0.0973 0.0957
0.0863 0.0848 0.0833 0.0818 0.0804
0.0721 0.0707 0.0694 0.0681 0.0669
0.0596 0.0584 0.0573 0.0562 0.0051
0.0488 0.0478 0.0468 0.0459 0.0449
0.0396 0.0387 0.0379 0.0371 0.0363
0.0317 0.0310 О.ОЗОЗ 0.0297 0.0290
0.0252 0.0246 0.0241 0.0235 0.0229
0.0198 0.0194 0.0189 0.0184 0.0180
0.0154 0.0151 0.0147 0.0143 0.0139
0.0119 0.0116 0.0113 0.0110 0.0107
0.0091 0.0088 0.0086 0.0084 0.0081
0.0069 0.0067 0.0065 0.0063 0.0061
0.0051 0.0050 0.0048 0.0047 0.0046
0.0038 0.0037 0.0036 0.0035 0.0034
0.0028 0.0027 0.0026 0.0025 0.0025
0.0020 0.0020 0.0019 0.0018 0.0018
0.0015 0.0014 0.0014 0.0013 0.0013
0.0010 0.0010 0.0010 0.0009 0.0009
0.0007 0.0007 0.0007 0.0007 0.0006
0.0005 0.0005 0.0005 0.0005 0.0004
0.0004 0.0003 0.0003 0.0003 0.0003
0.0002 0.0002 0.0002 0.0002 0.0002
0.0002 0.0002 0.0002 0.0001 0.0001
Таблицы А.2 — А.6 заимствованы из книги: Owen D.B. Handbook Statistical
Tables с согласия издательства Addison-Wesly Publishing Company, Reading, Mass.
2) В табличных данных запятая в десятичных дробях заменена точкой. — Прим,
ред.
500
Приложение А
Таблица А.2. Вероятность того, что наблюденное значение стандартной нормальной
случайной величины превысит заданную величину
Значение а =
е Z1/2dz = Prob [г >za]
Площадь=а
zd
ze 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09
0.0 0.5000 0.4960 0.4920 0.4880 0.4840 0.4801 0.4761 0.4721 0.4681 0.4641
0.1 0.4602 0.4562 0.4522 0.4483 0.4443 0.4404 0.4364 0.4325 0.4286 0.4247
0.2 0.4207 0.4168 0.4129 0.4090 0.4052 0.4013 0.3974 0.3936 0.3897 0.3859
0.3 0.3821 0.3783 0.3745 0.3707 0.3669 0.3632 0.3594 0.3557 0.3520 0.3483
0.4 0.3446 0.3409 0.3372 0.3336 О.ЗЗОО 0.3264 0.3228 0.3192 0.3156 0.3121
0.5 0.3085 0.3050 0.3015 0.2981 0.2946 0.2912 0.2877 0.2843 0.2810 0.2776
0.6 0.2743 0.2709 0.2676 0.2643 0.2611 0.2578 0.2546 0.2514 0.2483 0.2451
0.7 0.2420 0.2389 0.2358 0.2327 0.2296 0.2266 0.2236 0.2206 0.2177 0.2148
0.8 0.2119 0.2090 0.2061 0.2033 0.2005 0.1977 0.1949 0.1922 0.1894 0.1867
0.9 0.1841 0.1814 0.1788 0.1762 0.1736 0.1711 0.1685 0.1660 0.1635 0.1611
1.0 0.1587 0.1562 0.1539 0.1515 0.1492 0.1469 0.1446 0.1423 0.1401 0.1379
1.1 0.1357 0.1335 0.1314 0.1292 0.1271 0.1251 0.1230 0.1210 0.1190 0.1170
1.2 0.1151 0.1131 0.1112 0.1093 0.1075 0.1056 0.1038 0.1020 0.1003 0.0985
1.3 0.0968 0.0951 0.0934 0.0918 0.0901 0.0885 0.0869 0.0853 0.0838 0.0823
1.4 0.0808 0.0793 0.0778 0.0764 0.0749 0.0735 0.0721 0.0708 0.0694 0.0681
1.5 0.0668 0.0655 0.0643 0.0630 0.0618 0.0606 0.0594 0.0582 0.0571 0.0559
1.6 0.0548 0.0537 0.0526 0.0516 0.0505 0.0495 0.0485 0.0475 0.0465 0.0455
1.7 0.0446 0.0436 0.0427 0.0418 0.0409 0.0401 0.0392 0.0384 0.0375 0.0367
1.8 0.0359 0.0351 0.0344 0.0336 0.0329 0.0322 0.0314 0.0307 0.0301 0.0294
1.9 0.0287 0.0281 0.0274 0.0268 0.0262 0.0256 0.0250 . 0.0244 0.0239 0.0233
2.0 0.0228 0.0222 0.0217 0.0212 0.0207 0.0202 0.0197 0.0192 0.0188 0.0183
2.1 0.0179 0.0174 0.0170 0.0166 0.0162 0.0158 0.0154 0.0150 0.0146 0.0143
2.2 0.0139 0.0136 0.0132 0.0129 0.0125 0.0122 0.0119 0.0116 0.0113 0.0110
2.3 0.0107 0.0104 0.0102 0.00990 0.00964 0.00939 0.00914 0.00889 0.00866 0.00842
2.4 0.00820 0.00798 0.00776 0.00755 0.00734 0.00714 0.00695 0.00676 0.00657 0.00639
2.5 0.00621 0.00604 0.00587 0.00570 0.00554 0.00539 0.00523 0.00508 0.00494 0.00480
2.6 0.00466 0.00453 0.00440 0.00427 0.00415 0.00402 0.00391 0.00379 0.00368 0.00357
2.7 0.00347 0.00336 0.00326 0.00317 0.00307 0.00298 0.00289 0.00280 0.00272 0.00264
2.8 0.00256 0.00248 0.00240 0.00233 0.00226 0.00219 0.00212 0.00205 0.00199 0.00193
2.9 0.00187 0.00181 0.00175 0.00169 0.00164 0.00159 0.00154 0.00149 0.00144 0.00139
Статистические таблицы
501
Таблица А.З. Процентные точки распределения хи-квадрат.
Значение х^. а такое, что Prob[x^ > х„. а] = Для п > 120 х^. а в
Г. 2 ПГ 1 3
/— I , где z — соответствующая процентная точка
\9л J
~ п
9п
стандартного нормального распределения
. Площадь=ot
*2л;о1
а
п 0.995 0.990 0.975 0.950 0.900 0.10 0.05 0.025 0.010 0.005
1 0.000039 0.00016 0.00098 0.0039 0.0158 2.71 3.84 5.02 6.63 7.88
2 0.0100 0.0201 0.0506 0.103 0.211 4.61 5.99 7.38 9.21 10.60
3 0.0717 0.115 0.216 0.352 0.584 6.25 7.81 9.35 11.34 12.84
4 0.207 0.297 0.484 0.711 1.06 7.78 9.49 11.14 13.28 14.86
5 0.412 0.554 0.831 1.15 1.61 9.24 11.07 12.83 15.09 16.75
б 0.676 0.872 1.24 1.64 2.20 10.64 12.59 14.45 16.81 18.55
7 0.989 1.24 1.69 2.17 2.83 12.02 14.07 16.01 18.48 20.28
8 1.34 1.65 2.18 , 2.73 3.49 13.36 15.51 17.53 20.09 21.96
9 1.73 2.09 2.70 3.33 4.17 14.68 16.92 19.02 21.67 23.59
10 2.16 2.56 3.25 3.94 4.87 15.99 18.31 20.48 23.21 25.19
И 2.60 3.05 3.82 4.57 5.58 17.28 19.68 21.92 24.73 26.76
12 3.07 3.57 4.40 5.23 6.30 18.55 21.03 23.34 26.22 28.30
13 3.57 4.11 5.01 5.89 7.04 19.81 22.36 24.74 27.69 29.82
14 4.07 4.66 5.63 6.57 7.79 21.06 23.68 26.12 29.14 31.32
15 4.60 5.23 6.26 7.26 8.55 22.31 25.00 27.49 30.58 32.80
16 5.14 5.81 6.91 7.96 9.31 23.54 26.30 28.85 32.00 34.27
17 5.70 6.41 7.56 8.67 10.08 24.77 27.59 30.19 33.41 35.72
18 6.26 7.01 8.23 9.39 10.86 25.99 28.87 31.53 34.81 37.16
19 6.84 7.63 8.91 10.12 11.65 27.20 30.14 32.85 36.19 38.58
20 7.43 8.26 9.59 10.85 12.44 28.41 31.41 34.17 37.57 40.00
21 8.03 8.90 10.28 11.59 13.24 29.62 32.67 35.48 38.93 41.40
22 8.64 9.54 10.98 12.34 14.04 30.81 33.92 36.78 40.29 42.80
23 9.26 10.20 11.69 13.09 14.85 32.01 35.17 38.08 41.64 44.18
24 9.89 10.86 12.40 13.85 15.66 33.20 36.42 39.36 42.98 45.56
25 10.52 11.52 13.12 14.61 16.47 34.38 37.65 40.65 44.31 46.93
26 11.16 12.20 13.84 15.38 17.29 35.56 38.88 41.92 45.64 48.29
27 11.81 12.88 14.57 16.15 18.11 36.74 40.11 43.19 46.96 49.64
28 12.46 13.56 15.31 16.93 18.94 37.92 41.34 44.46 48.28 50.99
29 13.12 14.26 16.05 17.71 19.77 .39.09 42.56 45.72 49.59 52.34
30 13.79 14.95 16.79 18.49 20.60 40.26 43.77 46.98 50.89 53.67
40 20.71 22.16 24.43 26.51 29.05 51.81 55.76 59.34 63.69 66.77
60 35.53 37.48 40 48 43.19 46.46 74.40 79.08 83.30 88.38 91.95
120 83.85 86.92 91.58 95.70 100.62 140.23 146.57 152.21 158.95 163.65
502
Приложение А
Таблица А.4. Процентные точки /-распределения Стьюдента
Значение tn. а такое, что Prob[/n > = а. Для а = 0,995, 0,990, 0,975,
п 0.10 0.050 0.025 0.010 0.005
1 3.078 6.314 12.706 31.821 63.657
2 1.886 2.920 4.303 6.965 9.925
3 1.638 2.353 3.182 4.541 5.841
4 1.533 2.132 2.776 3.747 4.604
5 1.476 2.015 2.571 3.365 4.032
6 1.440 1.943 2.447 3.143 3.707
7 1.415 1.895 2.365 2.998 3.499
8 1.397 1.860 2.306 2.896 3.355
9 1.383 1.833 2.262 2.821 3.250
10 1.372 1.812 2.228 2.764 3.169
11 1.363 1.796 2.201 2.718 3.106
12 1.356 1.782 2.179 2.681 3.055
13 1.350 1.771 2.160 2.650 3.012
14 1.345 1.761 2.145 2.624 2.977
15 1.341 1.753 2.131 2.602 2.947
16 1.337 1.746 2.120 2.583 2.921
17 1.333 1.740 2.110 2.567 2.898
18 1.330 1.734 2.101 2.552 2.878
19 1.328 1.729 2.093 2.539 2.861
20 1.325 1.725 2.086 2.528 2.845
‘ 21 1.323 1.721 2.080 2.518 2.831
22 1.321 1.717 2.074 2.508 2.819
23 1.319 1.714 2.069 2.500 2.807
24 1.318 1.711 2.064 2.492 2.797
25 1.316 1.708 2.060 2.485 2.787
26 1.315 1.706 2.056 2.479 2.779
27 1.314 1.703 2.052 2.473 2.771
28 1.313 1.701 2.048 2.467 2.763
29 1.311 1.699 2.045 2.462 2.756
30 1.310 1.697 2.042 2.457 2.750
40 1.303 1.684 2.021 2.423 2.704
60 1.296 1.671 2.000 2.390 2.660
120 1.289 1.658 1.980 2.358 2.617
Статистические таблицы
503
Таблица A. 5(a). Процентные точки F-распределения
Значения п*от такие, что Prob[Fnj > -Г „2; о>о51 = °-05
Площадь=0,05
^ЛцЛз’О.ОБ
Vi Я2\ 1 2 3 4 5 6 7 8 9 10 И 12 13 14 16
1 161 200 216 225 230 234 237 239 241 242 243 244 245 245 246
2 18.5 19.0 19.2 19.2 19.3 19.3 19.4 19.4 19.4 19.4 19.4 19.4 19.4 19.4 19.4
3 10.1 9.55 9.28 9.12 9.01 8.94 8.89 8.85 8.81 8.79 8.76 8.74 8.73 8.71 8.69
4 7.71 6.94 6.59 6.39 6.26 6.16 6.09 6.04 6.00 5.96 5.94 5.91 5.89 5.87 5.84
5 6.61 5.79 5.41 5.19 5.05 4.95 4.88 4.82 4.77 4.73 4.70 4.68 4.66 4.64 4.60
6 5.99 5.14 4.76 4.53 4.39 4.28 4.21 4.15 4.10 4.06 4.03 4.00 3.98 3.96 3.92
7 5.59 4.74 4.35 4.12 3.97 3.87 3.79 3.73 3.68 3.64 3.60 3.57 3.55 3.53 3.49
8 5.32 4.46 4.07 3.84 3.69 3.58 3.50 3.44 3.39 3.35 3.31 3.28 3.26 3.24 3.20
9 5.12 4.26 3.86 3.63 3.48 3.37 3.29 3.23 3.18 3.14 3.10 3.07 3.05 3.03 2.99
10 4.96 4.10 3.71 3.48 3.33 3.22 3.14 3.07 3 02 2.98 2.94 2.91 2.89 2.86 2.83
11 4.84 3.98 3.59 3.36 3.20 3.09 3.01 2.95 2.90 2.85 2.82 2.79 2.76 2.74 2.70
12 4.75 3.89 3.49 3.25 3.11 3.00 2.91 2.85 2.80 2.75 2.72 2.69 2.66 2.64 2.60
13 4.67 3.81 3.41 3.18 3.03 2.92 2.83 2.77 2.71 2.67 2.63 2.60 2.58 2.55 2.51
14 4.60 3.74 3.35 3.11 2.96 2.85 2.76 2.70 2.65 2.60 2 57 2.53 2.51 2.48 2.44
16 4.49 3.63 3.24 3.01 2.85 2.74 2.66 2.59 2.54 2.49 2.46 2.42 2.40 2.37 2.33
18 4.41 3.55 3.16 2.93 2.77 2.66 2.58 2.51 2.46 2.41 2.37 2.34 2.31 2.29 2.25
20 4.35 3.49 3.10 2.87 2.71 2.60 2.51 2.45 2.39 2.35 2.31 2.28 2.25 2.22 2.18
22 4.30 3.44 3.05 2.82 2.66 2.55 2.46 2.40 2.34 2.30 2.26 2.23 2.20 2.17 2.13
24 4.26 3.40 3.01 2.78 2.62 2.51 2.42 2.36 2.30 2 25 2.21 2.18 2.15 2.13 2.09
26 4.23 3.37 2.98 2.74 2.59 2.47 2.39 2.32 2.27 2.22 2.18 2.15 2.12 2.09 2.05
28 4.20 3.34 2.95 2.71 2.56 2.45 2.36 2.29 2.24 2.19 2 15 2.12 2.09 2.06 2.02
30 4.17 3.32 2.92 2.69 2.53 2.42 2.33 2.27 2.21 2.16 2.13 2.09 2.06 2.04 1.99
40 4.08 3.23 2.84 2.61 2.45 2.34 2.25 2.18 2.12 2.08 2.04 2.00 1.97 1.95 1.90
50 4.03 3.18 2.79 2.56 2.40 2.29 2.20 2.13 2.07 2.03 1.99 1.95 1.92 1.89 1.85
60 4.00 3.15 2.76 2.53 2.37 2.25 2.17 2.10 2.04 1.99 1.95 1.92 1.89 1.86 1.82
80 3.96 3.11 2.72 2.49 2.33 2.21 2.13 2.06 2.00 1.95 1.91 1.88 1.84 1.82 1.77
100 3.94 3.09 2.70 2.46 2.31 2.19 2.10 2.03 1.97 1.93 1.89 1.85 1.82 1.79 1.75
200 3.89 3.04 2.65 2.42 2.26 2.14 2.06 1.98 1.93 1.88 1.84 1.80 1.77 1.74 1.69
500 3.86 3.01 2.62 2.39 2.23 2.12 2.03 1.96 1.90 1.85 1.81 1.77 1.74 1.71 1.66
оо 3.84 3.00 2.60 2.37 2.21 2.10 2.01 1.94 1.88 1.83 1.79 1.75 1.72 1.69 1.64
504
Приложение А
Таблица А.5(а) (продолжение)
18 20 22 24 26 28 30 40 50 60 80 100 200 500 ОС 7 /п2
247 248 249 249 249 250 250 251 252 252 252 253 254 254 254 1
19.4 19.5 19.5 19.5 19.5 19.5 19.5 19.5 19.5 19.5 19.5 19.5 19.5 19.5 19.5 2
8.67 8.66 8.65 8.64 8.63 8.62 8.62 8.59 8.59 8.57 8.56 8.55 8.54 8.53 8.53 3
5.82 5.80 5.79 5.77 5.76 5.75 5.75 5.72 5.70 5.69 5.67 5.66 5.65 5.64 5.63 4
4.58 3.56 4.54 4.53 4.52 4.50 4.50 4.46 4.44 4.43 4.41 4.41 4.39 4.37 4.37 5
3.90 3.87 3.86 3.84 3.83 3.82 3.81 3.77 3.75 3.74 3.72 3.71 3.69 3.68 3.67 6
3.47 3.44 3.43 3.41 3.40 3.39 3.38 3.34 3.32 3.30 3.29 3.27 3.25 3.24 3.23 7
3.17 3.15 3.13 312 3.10 3.09 3.08 3.04 3.02 3.01 2.99 2.97 2.95 2.94 2.93 8
2.96 2.94 2.92 2.90 2.89 2.87 2.86 2.83 2.80 2.79 2.77 2.76 2.73 2.72 2.71 9
2.80 2.77 2.75 2.74 2.72 2.71 2.70 2.66 2.64 2.62 2.60 2.59 2.56 2.55 2.54 10
2.67 2.65 2.63 2.61 2.59 2.58 2.57 2.53 2.51 2.49 2.47 2.46 2.43 2.42 2.40 И
2.57 2.54 2.52 2.51 2.49 2.48 2.47 2.43 2.40 2.38 2.36 2.35 2.32 2.31 2.30 12
2.48 2.46 2.44 2.42 2.41 2.39 2.38 2.34 2.31 2.30 2.27 2.26 2.23 2.22 2.21 13
2.41 2.38 2.37 2.35 2.33 2.32 2.31 2.27 2.24 2.22 2.20 2.19 2.16 2.14 2.13 14
2.30 2.28 2.25 2.24 2.22 2.21 2.19 2.15 2.12 2.11 2.08 2.07 2.04 2.02 2.01 16
2.22 2.19 2.17 2.15 2.13 2.12 2.11 2.06 2.04 2.02 1.99 1.98 1.95 1.93 1.92 18
2.15 2.12 2.10 2.08 2.07 2.05 2.04 1.99 1.97 1.95 1.92 1.91 1.88 1.86 1.84 20
2.10 2.07 2.05 2.03 2.01 2.00 1.98 1.94 1.91 1.89 1.86 1.85 1.82 1.80 1.78 22
2.05 2.03 2.00 1.98 1.97 1.95 1.94 1.89 1.86 1.84 1.82 1.80 1.77 1.75 1.73 24
2.02 1.99 1.97 1.95 1.93 1.91 1.90 1.84 1.82 1.80 1.78 1.76 1.73 1.71 1.69 26
1.99 1.96 1.93 1.91 1.90 1.88 1.87 1.82 1.79 1.77 1.74 1.73 1.69 1.67 1.65 28
1.96 1.93 1.91 1.89 1.87 1.85 1.84 1.79 1.76 1.74 1.71 1.70 1.66 1.64 1.62 30
1.87 1.84 1.81 1.79 1.77 1.76 1.74 1.69 1.66 1.64 1.61 1.59 1.55 1.53 1.51 40
1.81 1.78 1.76 1.74 1.72 1.70 1.69 1.63 1.60 1.58 1.54 1.52 1.48 1.46 1.44 50
1.78 1.75 1.72 1.70 1.68 1.66 1.65 1.59 1.56 1.53 1.50 1.48 1.44 1.41 1.39 60
1.73 1.70 1.68 1.65 1.63 1.62 1.60 1.54 1.51 1.48 1.45 1.43 1.38 1.35 1.32 80
1.71 1.68 1.65 1.63 1.61 1.59 1.57 1.52 1.48 1.45 1.41 1.39 1.34 1.31 1.28 100
1.66 1.62 1.60 1.57 1.55 1.53 1.52 1.46 1.41 1.39 1.35 1.32 1.26 1.22 1.19 200
1.62 1.59 1.56 1.54 1.52 1.50 1.48 1.42 1.38 1.34 1.30 1.28 1.21 1.16 1.11 500
1.60 1.57 1.54 1.52 1.50 1.48 1.46 1.39 1.35 1.32 1.27 1.24 1.17 1.11 1.00 00
Статистические таблицы
505
Таблица А.5(б). Процентные точки F-распределения
Значения Fn| такие, что Prob[F„i; „2 > F^ ода1 = 0,025
Площадь=0,025
F/ibn2; 0,025
\Л1 «X 1 2 3 4 5 6 7 8 9 10 11 12 13 14 16
1 648 800 864 900 922 937 948 957 963 969 973 977 980 983 987
2 38.5 39.0 39.2 39.2 39.3 39.3 39.4 39.4 39.4 39.4 39.4 39.4 39.4 39.4 39.4
3 17.4 16.0 15.4 15.1 14.9 14.7 14.6 14.5 14.5 14.4 14.4 14.3 14.3 14.3 14.2
4 12.2 10.6 9.98 9.60 9.36 9.20 9.07 8.98 8.90 8.84 8.79 8.75 8.72 8.69 8.64
5 10.0 8.43 7.76 7.39 7.15 6.98 6.85 6.76 6.68 6.62 6.57 6.52 6.49 6.46 6.41
6 8.81 7.26 6.60 6.23 5.99 5.82 5.70 5.60 5.52 5.46 5.41 5.37 5.33 5.30 5.25
7 8.07 6.54 5.89 5.52 5.29 5.12 4.99 4.90 4.82 4.76 4.71 4.67 4.63 4.60 4.54
8 7.57 6.06 5.42 5.05 4.82 4.65 4.53 4.43 4.36 4.30 4.24 4.20 4.16 4.13 4.08
9 7.21 5.71 5.08 4.72 4.48 4.32 4.20 4.10 4.03 3.96 3.91 3.87 3.83 3.80 3.74
10 6.94 5 46 4.83 4.47 4.24 4.07 3.95 3.85 3.78 3.72 3.66 3.62 3.58 3.55 3.50
11 6.72 5.26 4.63 4.28 4 04 3.88 3.76 3.66 3.59 3.53 3.47 3.43 3.39 3.36 3.30
12 6.55 5 10 4.47 4.12 3.89 3.73 3.61 3.51 3.44 3.37 3.32 3.28 3.24 3.21 3.15
13 6.41 4.97 4 35 4.00 3.77 3 60 3.48 3.39 3.31 3.25 3.20 3.15 3.12 3.08 3.03
14 6.30 4.86 4.24 3.89 3.66 3 50 3.38 3.29 3.21 3.15 3.09 3.05 3.01 2.98 2.92
16 6.12 4 69 4 08 3.73 3.50 3.34 3.22 3.12 3.05 2.99 2.93 2.89 2.85 2.82 2.76
18 5.98 4.56 3.95 3.61 3.38 3.22 3.10 3.01 2.93 2.87 2.81 2.77 2.73 2.70 2 64
20 5.87 4.46 3.86 3.51 3 29 3.13 3 01 2 91 2.84 2.77 2.72 2.68 2.64 2.60 2.55
22 5.79 4.38 3.78 3.44 3 22 3.05 2.93 2.84 2.76 2.70 2.65 2.60 2.56 2.53 2.47
24 5.72 4.32 3 72 3.38 3.15 2.99 2.87 2.78 2.70 2.64 2.59 2.54 2.50 2.47 2.41
26 5.66 4.27 3 67 3.33 3.10 2.94 2.82 2.73 2.65 2.59 2 54 2.49 2.45 2.42 2.36
28 5.61 4.22 3 63 3.29 3.06 2.90 2.78 2.69 2.61 2.55 2 49 2.45 2 41 2.37 2.32
30 5.57 4.18 3.59 3.25 3.03 2.87 2.75 2.65 2.57 2.51 2.46 2.41 2.37 2.34 2.28
40 5.42 4.05 3.46 3.13 2.90 2.74 2.62 2.53 2.45 2.39 2.33 2.29 2 25 2.21 2.15
50 5.34 3.98 3.39 3.06 2.83 2.67 2.55 2.46 2.38 2.32 2.26 2.22 2.18 2.14 2 08
60 5.29 3.93 3 34 3 01 2.79 2.63 2.51 2.41 2.33 2.27 2.22 2.17 2.13 2.09 2.03
80 5.22 3 86 3.28 2.95 2.73 2.57 2.45 2.36 2.38 2.21 2.16 2.11 2.07 2.03 1.97
100 5.18 3 83 3.25 2 92 2.70 2.54 2.42 2 32 2.24 2.18 2.12 2.08 2.04 2.00 1.94
200 5.10 3 76 3 18 2 85 2.63 2 47 2.35 2 26 2.18 2.11 2.06 2.01 1.97 1.93 1.87
500 5 05 3.72 3 14 2 81 2 59 2 43 2.31 2.22 2.14 2.07 2.02 1.97 1.93 1.89 1.83
со 5.02 3 69 3.12 2.79 2.57 2 41 2.29 2.19 2.11 2.05 1.99 1.94 1.90 1.87 1.80
506
Приложение А
Таблица А.5(б) (продолжение)
18 20 22 24 26 28 30 40 50 60 80 100 200 500 00 «1/ /П2
990 993 995 997 999 1000 1001 1006 1008 1010 1012 1013 1016 1017 1018 1
39.4 39.4 39.5 39.5 39.5 39.5 39.5 39.5 39.5 39.5 39.5 39.5 39.5 39.5 39.5 2
14.2 14.2. 14.1 14.1 14.1 14.1 14.1 14.0 14.0 14.0 14.0 14.0 13.9 13.9 13.9 3
8.60 8.56 8.53 8.51 8.49 8.48 8.46 8.41 8.38 8.36 8.33 8.32 8.29 8.27 8.26 4
6.37 6.33 6.30 6.28 6.26 6.24 6.23 6.18 6.14 6.12 6.10 6.08 6 05 6.03 6.01 5
5.21 5.17 5.14 5.12 5.10 5.08 5.07 5.01 4.98 4.96 4.93 4.92 4.88 4.86 4.85 6
4.50 4.47 4.44 4.42 4.39 4.38 4.36 4.31 4.28 4.25 4.23 4.21 4.18 4.16 4.14 7
4.03 4.00 3.97. 3.95 3.93 3.91 3.89 3.84 3.81 3.78 3.76 3.74 3.70 3.68 3.67 8
3.70 3.67 3.64 3.61 3.59 3.58 3.56 3.51 3.47 3.45 3.42 3.40 3.37 3.35 3.33 9
3.45 3.42 3.39 3.37 3.34 3.33 3.31 3.26 3.22 3.20 3.17 3.15 3.12 3.09 3.08 10
3.26 3.23 3.20 3.17 3.15 3.13 3.12 3.06 3.03 3.00 2.97 2.96 2.92 2.90 2.88 11
3.11 3.07 3.04 3.02 3.00 2.98 2.96 2.91 2.87 2.85 2.82 2.80 2.76 2.74 2.72 12
2.98 2.95 2.92 2.89 2.87 2.85 2.84 2.78 2.74 2.72 2.69 2.67 2.63 2.61 2.60 13
2.88 2.84 2.81 2.79 2.77 2.75 2.73 2.67 2.64 2.61 2.58 2.56 2.53 2.50 2.49 14
2.72 2.68 2.65 2.63 2.60 2.58 2.57 2.51 2.47 2.45 2.42 2.40 2.36 2.33 2.32 16
2.60 2.56 2.53 2.50 2.48 2.46 2.44 2.38 2.35 2.32 2.29 2.27 2.23 2.20 2.19 18
2.50 2.46 2.43 2.41 2.39 2.37 2.35 2.29 2.25 2.22 2.19 2.17 2.13 2.10 2.09 20
2.43 2.39 2.36 2.33 2.31 2.29 2.27 2.21 2.17 2.14 2.11 2.09 2.05 2.02 2.00 22
2.36 2.33 2.30 2.27 2.25 2.23 2.21 2.15 2.11 2.08 2.05 2.02 1.98 1.95 1.94 24
2.31 2.28 2.24 2.22 2.19 2.17 2.16 2.09 2.05 2.03 1.99 1.97 1.92 1.90 1.88 26
2.27 2.23 2.20 2.17 2.15 2.13 2.11 2.05 2.01 1.98 1.94 1.92 1.88 1.85 1.83 28
2.23 2.20 2.16 2.14 2.11 2.09 2.07 2.01 1.97 1.94 1.90 1.88 1.84 1.81 1.79 30
2.11 2.07 2.03 2.01 1.98 1.96 1.94 1.88 1.83 1.80 1.76 1.74 1.69 1.66 1.64 40
2.03 1.99 1.96 1.93 1.91 1.88 1.87 1.80 1.75 1 72 1.68 1.66 1.60 1.57 1.55 50
1.98 1.94 1.91 1.88 1.86 1.83 1.82 1.74 1.70 1.67 1.62 1.60 1.54 1.51 1.48 60
1.93 1.88 1.85 1.82 1.79 1.77 1.75 1.68 1.63 1.60 1.55 1.53 1.47 1.43 1.40 80
1.89 1.85 1.81 1.78 1.76 1.74 1.71 1.64 1.59 1.56 1.51 1.48 1.42 1.38 1.35 100
1.82 1.78 1.74 1.71 1.68 1.66 1.64 1.56 1.51 1.47 1.42 1.39 1.32 1.27 1.23 200
1.78 1.74 1.70 1.67 1.64 1.62 1.60 1.51 1.46 1.42 1.37 1.34 1.25 1.19 1.14 500
1.75 1.71 1.67 1.64 1.61 1.59 1.57 1.48 1.43 1.39 1.33 1.30 1.21 1.13 1.00 00
Статистические таблицы
507
Таблица А.5(в). Процентные точки F-распределения
Значения F . такие, что Prob[F > F „ ,nnl] = 0,01. Числа из
rij, П2, 0,01 nl’n2 п 1 ’ п2' 0,01
первой строки (п2 = 1) следует умножить на 10
Площадь = 0,01
F nJtn2;0,01
1 2 3 4 5 6 7 8 9 10 11 12 13 14 16
*1 405 500 540 563 576 586 593 598 602 606 608 611 613 614 617
2 98.5 99.0 99.2 99.2 99.3 99.3 99.4 99.4 99.4 99.4 99.4 99.4 99.4 99.4 99.4
3 34.1 30.8 29.5 28.7 28.2 27.9 27.7 27.5 27.3 27.2 27.1 27.1 27.0 26.9 26.8
4 21.2 18.0 16.7 16.0 15.5 15.2 15.0 14.8 14.7 14.5 14.4 14.4 14.3 14.2 14.2
5 16.3 13.3 12.1 11.4 11.0 10.7 10.5 10.3 10.2 10.1 9.96 9.89 9.82 9.77 9.68
6 13.7 10.9 9.78 9.15 8.75 8.47 8.26 8.10 7.98 7.87 7.79 7.72 7.66 7.60 7.52
7 12.2 9.55 8.45 7.85 7.46 7.19 6.99 6.84 6.72 6.62 6.54 6.47 6.41 6.36 6.27
8 11.3 8.65 7.59 7.01 6.63 6.37 6.18 6.03 5.91 5.81 5.73 5.67 5.61 5.56 5.48
9 10.6 8.02 6.99 6.42 6.06 5.80 5.61 5.47 5.35 5.26 5.18 5.11 5.05 5.00 4.92
10 10 0 7.56 6 55 5.99 5.64 5.39 5.20 5.06 4.94 4.85 4.77 4.71 4.65 4.60 4.52
11 9.65 7.21 6.22 5.67 5.32 5.07 4.89 4.74 4.63 4.54 4.46 4.40 4.34 4.29 4.21
12 9.33 6.93 5.95 5.41 5.06 4.82 4.64 4.50 4.39 4.30 4.22 4.16 4.10 4.05 3.97
13 9.07 6.70 5.74 5.21 4.86 4.62 4.44 4.30 4.19 4.10 4.02 3.96 3.91 3.86 3.78
14 8.86 6.51 5.56 5.04 4.70 4.46 4.28 4.14 4.03 3.94 3.86 3.80 3.75 3.70 3.62
16 8.53 6.23 5.29 4.77 4.44 4.20 4.03 3.89 3.78 3.69 3.62 3.55 3.50 3.45 3.37
18 8.29 6.01 5.09 4.58 4.25 4.01 3.84 3.71 3.60 3.51 3.43 3.37 3.32 3.27 3.19
20 8.10 5.85 4.94 4.43 4.10 3.87 3.70 3.56 3.46 3.37 3.29 3.23 3.18 3.13 3.05
22 7.95 5.72 4.82 4.31 3.99 3.76 3.59 3.45 3.35 3.26 3.18 3.12 3.07 3.02 2.94
24 7.82 5.61 4.72 4.22 3.90 3.67 3.50 3.36 3.26 3.17 3.09 3.03 2.98 2.93 2.85
26 7.72 5.53 4.64 4.14 3.82 3.59 3.42 3.29 3.18 3.09 3.02 2.96 2.90 2.86 2.78
28 7.64 5.45 4.57 4.07 3.75 3.53 3.36 3.23 3.12 3.03 2.96 2.90 2-84 2.79 2.72
30 7.56 5.39 4.51 4.02 3.70 3.47 3.30 3.17 3.07 2.98 2.91 2.84 2.79 2.74 7.66
40 7.31 5.18 4.31 3.83 3.51 3.29 3.12 2.99 2.89 2.80 2.73 2.66 2.61 2.56 2.48
50 7.17 5.06 4.20 3.72 3.41 3.19 3.02 2.89 2.79 2 70 2.63 2.56 2.51 2.46 2.38
60 7.08 4.98 4.13 3.65 3.34 3.12 2.95 2.82 2.72 2.63 2.56 2.50 2.44 2.39 2.31
80 6.96 4.88 4.04 3.56 3.26 3.04 2.87 2.74 2.64 2.55 2.48 2.42 2.36 2.31 2.23
100 6.90 4.82 3.98 3.51 3.21 2.99 2.82 2.69 2.59 2.50 2.43 2.37 2.31 2.26 2.19
200 6.76 4.71 3.88 3.41 3.11 2.89 2.73 2.60 2.50 2 41 2.34 2.27 2.22 2.17 2.09
500 6.69 4.65 3.82 3.36 3.05 2.84 2.68 2.55 2.44 2.36 2.28 2.22 2.17 2.12 2.04
оо 6.63 4.61 3.78 3.32 3.02 2.80 2.64 2.51 2.41 2.32 2.25 2.18 2.13 2.08 2.00
508
Приложение А
Таблица А.5(в) (продолжение)
18 20 22 24 26 28 30 40 50 60 80 100 200 500 00 я1/
619 621 622 623 624 625 626 629 630 631 633 633 635 636 637 1
99.4 99.4 99.5 99.5 99.5 99.5 99.5 99.5 99.5 99.5 99.5 99.5 99.5 99.5 99.5 2
26.8 26.7 26.6 26.6 26.6 26.5 26.5 26.4 26.4 26.3 26.3 26.2 26.2 26.1 26.1 3
14.1 14.0 14.0 13.9 13.9 13.9 13.8 13.7 13.7 13.7 13.6 13.6 13.5 13.5 13.5 4
9.61 9.55 9.51 9.47 9.43 9.40 9.38 9.29 9.24 9.20 9.16 9.13 9.08 9.04 9.02 5
7.45 7.40 7.35 7.31 7.28 7.25 7.23 7.14 7.09 7.06 7.01 6.99 6.93 6.90 6.88 б
6.21 6.16 6.11 6.07 6.04 6.02 5.99 5.91 5.86 5.82 5.78 5.75 5.70 5.67 5.65 7
5.41 5.36 5.32 5.28 5.25 5.22 5.20 5.12 5.07 5.03 4.99 4.96 4.91 4.88 4.85 8
4.86 4.81 4.77 4.73 4.70 4.67 4.65 4.57 4.52 4.48 4.44 4.42 4.36 4.33 4.31 9
4.46 4.41 4.36 4.33 4.30 4.27 4.25 4.17 4.12 4.08 4.04 4.01 3.96 3.93 3.91 10
4.15 4.10 4.06 4.02 3.99 3.96 3.94 3.86 3.81 3.78 3.73 3.71 3.66 3.62 3.60 И
3.91 3.86 3.82 3.78 3.75 3.72 3.70 3.62 3.57 3.54 3.49 3.47 3.41 3.38 3.36 12
3.72 3.66 3.62 3.59 3.56 3.53 3.51 3.43 3.38 3.34 3.30 3.27 3.22 3.19 3.16 13
3.56 3.51 3.46 3.43 3.40 3.37 3.35 3.27 3.22 3.18 3.14 3.11 3.06 3.03 3.00 14
3.31 3.26 3.22 3.18 3.15 3.12 3.10 3.02 2.97 2.93 2.89 2.86 2.81 2.78 2.75 16
3.13 3.08 3.03 3.00 2.97 2.94 2.92 2.84 2.78 2.75 2.70 2.68 2.62 2.59 2.57 18
2.99 2.94 2.90 2.86 2.83 2.80 2.78 2.69 2.64 2.61 2.56 2.54 2.48 2.44 2.42 20
2.88 2.83 2.78 2.75 2.72 2.69 2.67 2.58 2.53 2.50 2.45 2.42 2.36 2.33 2.31 22
2.79 2.74 2.70 2.66 2.63 2.60 2.58 2.49 2.44 2.40 2.36 2.33 2.27 2.24 2.21 24
2.72 2.66 2.62 2.58 2.55 2.53 2.50 2.42 2.36 2.33 2.28 2.25 2.19 2.16 2.13 26
2.65 2.60 2.56 2.52 2.49 2.46 2.44 2.35 2.30 2.26 2.22 2.19 2.13 2 09 2.06 28
2.60 2.55 2.51 2.47 2.44 2.41 2.39 2.30 2.25 2.21 2.16 2.13 2.07 2.03 2.01 30
2.42 2.37 2.33 2.29 2.26 2.23 2.20 2.11 2.06 2.02 1.97 1.94 1.87 1.83 1.80 40
2.32 2.27 2.22 2.18 2.15 2.12 2.10 2.01 1.95 1.91 1.86 1.82 1.76 1.71 1.68 50
2.25 2.20 2.15 2.12 2.08 2.05 2.03 1 94 1.88 1.84 1.78 1.75 1.68 1.63 1.60 60
2.17 2.12 2.07 2.03 2.00 1.97 1.94 1.85 1.79 1.75 1.69 1 66 1.58 1.53 1.49 80
2.12 2.07 2.02 1.98 1.94 1*92 1.89 1.80 1.73 1.69 1.63 1.60 1.52 1.47 1.43 100
2.02 1.97 1.93 1.89 1.85 1.82 1.79 1.69 1.63 1.58 1.52 1.48 1.39 1.33 1.28 200
1.97 1.92 1.87 1.83 1.79 1.76 1.74 1.63 1.56 1.52 1.45 1.41 1.31 1.23 1.16 500
1.93 1.88 1.83 1.79 1.76 1.72 1.70 1.59 1.52 1.47 1.40 1.36 1.25 1.15 1.00 00
Статистические таблицы
509
Таблица А.6. Процентные точки распределения серий
Значения гп. а такие, что РгоЬ[гп : > гп- cJ = а, где п = N, = N2 = N
а
п = N/2 0.99 0.975 0.95 0.05 0.025 0.01
5 2 2 3 8 9 9
6 2 3 3 10 10 И
7 3 3 4 11 12 12
8 4 4 5 12 13 13
9 4 5 6 13 14 15
10 5 6 6 15 15 16
11 6 7 7 16 16 17
12 7 7 8 17 18 18
13 7 8 9 18 19 20
14 8 9 10 19 20 21
15 9 10 11 20 21 22
16 10 11 11 22 22 23
18 11 12 13 24 25 26
20 13 14 15 26 27 28
25 17 18 19 32 33 34
30 21 22 24 37 39 40
35 25 27 28 43 44 46
40 30 31 33 48 50 51
45 34 36 37 54 55 57
50 38 40 42 59 61 63
55 43 45 46 65 66 68
60 47 49 51 70 72 74
65 52 54 56 75 77 79
70 56 58 60 81 83 85
75 61 63 65 86 88 90
80 65 68 70 91 93 96
85 70 72 74 97 99 101
90 74 'll 79 102 104 107
95 79 82 84 107 109 112
100 84 86 88 113 115 117
510
Приложение А
Таблица А. 7. Процентные точки распределения числа инверсий
Значения Ап.а такие, что РгоЩЛ^ > AN. а] = а, где N— общее число наб-
люденных значений.
N а
0.99 0.975 0.95 0.05 0.025 0.01
10 9 11 13 31 33 35
12 16 18 21 44 47 49
14 24 27 30 60 63 66
16 34 38 41 78 81 85
18 45 50 54 98 102 107
20 59 64 69 120 125 130
30 152 162 171 263 272 282
40 290 305 319 460 474 489
50 473 495 514 710 729 751
60 702 731 756 1013 1038 1067
70 977 1014 1045 1369 1400 1437
80 1299 1344 1382 1777 1815 1860
90 1668 1721 1766 2238 2283 2336
100 2083 2145 2198 2751 2804 2866
Приложение Б
Основные определения
Амплитудная характеристика (см. Частотная характеристика)
Взаимная ковариационная функция
Взаимной ковариационной функцией Rxy(j) двух последовательностей
x(t) и y(t) называется среднее за интервал времени Т значение произведе-
ния величин x(t) в момент времени t и y(t) в момент времени t 4- т:
1 гТ
Кху(т) = - + т) dt.
1 •'о
Для эргодических процессов x(t) иу(1) величина Т должна стремиться к
бесконечности; на практике Т всегда конечно.
Ковариационная функция Вхх(т) представляет собой частный случай
функции Rxv(t) при x(t) = y{t)x\
Гауссов процесс
Гауссовым называется стационарный* 2^ случайный процесс х (/), значе-
ния которого в любой момент времени t имеют плотность вероятности
где g — истинное среднее значение процесса, ох — истинная дисперсия.
Распределение, описываемое приведенной формулой, называется гауссо-
вым.
Гистограмма
Гистограммой называется график, на котором по оси ординат отложе-
но число значений функции х (Г), попадающих в заданные интервалы, а по
оси абсцисс — границы этих интервалов, называемых интервалами группи-
ровки.
Дисперсия
Дисперсией s2 функции x(t) называется средний за интервал времени Т
квадрат отклонения значений х (t) от среднего значения х:
г/) •
На самом деле здесь и далее определены не сами статистические характери-
стики случайных величин и процессов, а их выборочные значения. — Прим.перев.
2) Гауссовым (нормальным) может быть и нестационарный случайный процесс;
в этом случае его моменты распределения зависят от времени. — Прим.перев.
512
Приложение Б
В случае эргодического процесса истинная дисперсия получается перехо-
дом к пределу при устремлении Т к бесконечности. При х = 0 величина
sx — %2-
Импульсная переходная (весовая) функция
Импульсная переходная функция линейной системы с постоянными па-
раметрами h (т), называемая также весовой функцией, описывает реакцию
системы на единичный импульс (дельта-функцию). Она равна обратному
преобразованию Фурье от частотной характеристики системы.
Ковариационная функция
Ковариационной функцией Rxx(т) последовательности х (Z) называется
среднее за интервал времени Т значение произведения величин, принимае-
мых последовательностью в моменты времени/ и / + с:
1 /*г
Лхх(т) = 7 / + т) dt.
1 Jq
Сдвиг т может быть положительным или отрицательным.
Для эргодического процесса Т должно стремиться к бесконечности; на
практике Т всегда конечно. ____
Суммарный средний квадрат х2 последовательности оценивается в виде
*2 = Лхх(0) = 7 fTx2(t)dt.
1 JQ
Когерентный спектр выходного процесса
Когерентный спектр Gvv(f) выходного процесса для системы с одним
процессом x(t) на входе и одним процессом у(() на выходе есть произведе-
ние функции когерентности последовательностей x(t) и y(t) на функцию
спектральной плотности выходного процесса
Gvv(f) = Yxy(f)Gyy(f) .
Соответствующий спектр шума на выходе равен
[1-Yx2//)]S>(/)-
Линейная система
Аддитивная и однородная система называется линейной. Пусть вход-
ным значениям Xj их2 отвечают выходные значения иу2; система адди-
тивна, если входу %! + х2 отвечает выход .у j -I- у 2, и однородна, если вход
сх! генерирует на выходе значение су р где с — произвольная постоянная.
Основные определения
513
Линейчатый спектр
Линейчатым называется спектр, значения которого отличаются от нуля
лишь на дискретных частотах, как, например, при представлении функции
ее рядом Фурье.
Нелинейная система
Нелинейной называется система, которая не обладает свойствами адди-
тивности и однородности или хотя бы одним из этих свойств (см. Л иней-
ная система).
Нестационарный процесс
Нестационарным называется любой процесс, не обладающий свойством
стационарности (см.соответствующее определение). Статистические харак-
теристики такого процесса, определенные усреднением по ансамблю его ре-
ализаций, не являются инвариантными по отношению к переносу начала
отсчета на временнбй оси и зависят от времени.
В общем случае результаты усреднения по любой отдельной реализации
процесса не характеризуют свойства ни одной из его реализаций, поскольку
информация о зависимости свойств процесса от времени в результате тако-
го усреднения утрачивается.
Нормированная взаимная корреляционная функция
Нормированной взаимной корреляционной функцией рху(т) двух после-
довательностей х (I) и у (I) называется отношение взаимной ковариацион-
ной функции Rxy (т) к квадратному корню из произведения ковариационных
функций последовательностей при нулевом сдвиге
/ х =
Рху Т) ^х(0)Я,,(0) ’
Величина рху(т) удовлетворяет при всех т неравенству — 1 Pxy(j) 1.
Нормированная взаимная корреляционная функция и функция обычной
когерентности не образуют пару взаимных преобразований Фурье.
Переходный процесс
Переходным называется детермированный или случайный процесс, име-
ющий конечную продолжительность.
Передаточная функция
Передаточная функция линейной системы с постоянными параметрами
есть преобразование Лапласа импульсной переходной функции системы.
Значения передаточной функции на мнимой оси определяют частотную ха-
рактеристику системы (см. соответствующее определение).
17-953
514
Приложение Б
Плотность вероятности
Плотность вероятности/? (х) величиных([) в момент времени/ задается
отношением
, . Р(х,Ж)
р (х) =--------- ,
7 W
где Р(х, W) — вероятность попадания значениях (О в интервал шириной W
с центром в точке х. Иными словами, р (х) есть оценка интенсивности из-
менения вероятности значения функции х (Г).
В случае стационарного процесса ширину интервала W следует устре-
мить к нулю; на практике она всегда конечна. Функция р(х) удовлетворяет
при всех х условию р(х) > 0, а площадь под кривой р(х) равна единице.
Преобразование Гильберта
Преобразование Гильберта действительной функции х(/), заданной на
оси — оо < t < оо, называется вещественная функция х(/), определенная ра-
венством
x(t) =Jf[x(t)] = [ —у du.
J-Kv(t - и)
Таким образом, преобразование Гильберта есть свертка исходной функции
х(/) с функцией 1/(тг/).
Преобразование Фурье
Преобразование Фурье % (О функции х(/), называемое также спектром
Фурье, есть комплексная функция частоты f, определяемая в виде
/00
x(t)e~j2”fl dt.
- 00
Предполагается, что функция х(Г) такова, что % (О существует. Функция
времени х(() определяется из %(/*) в виде
х(0 = Г X(f)ej2”f,df.
J - 00
Функции X (f) их (Г) называются соответственно прямым и обратным пре-
образованиями Фурье.
Функция % (f) выражается через свои действительную и мнимую части в
виде
X(/) = Re[X(/)]-jIm[X(/)],
Re[X(/)] = f x(t)cos2irftdt, Im[%(/)]= f x(z)sin 2тг/г .
На практике x(t) задается на интервале конечной длины Г, так что % (О
оценивается по финитному преобразованию Фурье
Основные определения
515
ХГ(/) = Х(/,Т)= frx(t)e
•'о
Такие финитные интегралы существуют всегда.
Реализация
Реализацией функции называется ее представление в зависимости от
временного параметра, причем сама функция может быть детермирован-
ной или случайной. Если реализация является периодической, то величина,
обратная периоду, называется частотой реализации. Вместо времени мож-
но использовать любую другую независимую переменную, изменив соот-
ветствующим образом определение частоты.
Ряд Фурье
Ряд Фурье представляет периодическую функцию x(t) как сумму индиви-
дуальных гармоник. Если*(Z) — периодическая функция с периодом Г, так
чтох(О = x(t 4- Г), то
а оо оо
x(z) = — + 52 ajx^lirnft + 52 bn&a24rnft.
2 1 п=1
Частота f = 1/Т называется фундаментальной частотой. Коэффициенты
Фурье равны
2 ут 2 ут
ап = — х (и )cos 2^ nfи du, bn = — x(u)sin2irnfudu,
T Jq T Jq
h = 0,1,2,...>
где и — переменная интегрирования.
Случайный процесс
Случайным процессом называется ансамбль реализаций, который мож-
но описать с помощью соответствующих статистических характеристик,
задающих, например, средние свойства этих реализаций в фиксированные
моменты времени.
Спектр
Спектром любой величины называется ее описание как функции часто-
ты. Спектр может быть линейчатым, непрерывным или кусочно-
непрерывным.
Спектральная плотность (см. Функция спектральной плотности и
Функция взаимной спектральной плотности)
17*
516
Приложение Б
Среднее значение
Средним значением х функции x(t) называется величина, получаемая
при усреднении по времени t значений х (t) на некотором интервале усред-
нения Т:
X = - fTx(j) dt
1 •'о
В случае эргодического процесса истинное среднее значение х получается
переходом к пределу при устремлении Т к бесконечности.
Среднеквадратичное значение
Среднеквадратичное значение есть положительный квадратный корень из
среднего квадрата. Если среднее значение равно нулю, то среднеквадратич-
ное значение совпадает со среднеквадратичным отклонением.
Среднеквадратичное отклонение
Среднеквадратичное отклонение есть положительный квадратный ко-
рень из дисперсии. При нулевом среднем значении среднеквадратичное от-
клонение равно среднеквадратичному значению.
Средний квадрат
Средним квадратом х2 функции х (I) называется величина, получаемая
усреднением по времени t значений квадрата х 2(t) на некотором интервале
усреднения Т:
x2=-T=fTx2(t)dt
1 Jq
В случае эргодического процесса истинный средний квадрат получается пе-
реходом к пределу при устремлении Т к бесконечности (см. также замеча-
ния в определениях ковариационной функции и функции спектральной
плотности).
Стационарный процесс
Стационарный случайный процесс есть ансамбль реализаций, статисти-
ческие свойства которого инвариантны по отношению к переносу начала
отсчета времени. Стационарный процесс может быть эргодическим или не-
эргодическим.
Узкополосный случайный процесс
Узкополосным называется случайный процесс, спектральная плотность
которого существенно отлична от нуля лишь в пределах узкой полосы ча-
стот, сосредоточенной вблизи некоторой центральной частоты. Если мгно-
венные значения процесса имеют гауссовское распределение вероятностей,
Основные определения
517
то его экстремальные значения приближенно подчиняются распределению
Рэлея.
Фазовая характеристика (см. Частотная характерстика')
Функция взаимной спектральной плотности
В рамках методов, основанных на финитном преобразовании Фурье,
функция взаимной спектральной плотности определяется для частот/ в ин-
тервале от/ = 0 до/ = оо в виде
2 г
М/) = 7£1^*(/)гг(/)]
где Е [ ] означает усреднение при фиксированной частоте / по ансамблю из
п функций А^(/) и Yjif), вычисленных по имеющимся парам реализации
х(() и y(t), заданным на интервале длиной Т каждая. Величина X^(f) есть
комплексное сопряжение финитного преобразования Фурье Xjff) функции
x(t), a Y(f) — финитное преобразование Фурье функции y(t). Функция
G(f) = 0 при / < 0, и именно ее измеряют на практике.
В теоретических исследованиях используется двухсторонняя функция
взаимной спектральной плотности Sxy(f), существующая при всех значени-
ях/ от/ = -оо до/ = оо:
sxy(f) = L2Gxy(f), f>0-,
sxy(-f) = sx*y(f).
В стационарном случае функция взаимной спектральной плотности Gxv(f)
равна удвоенному преобразованию Фурье взаимной ковариационной функ-
ции Яху(т).
Функция взаимной спектральной плотности энергии
В рамках методов, основанных на финитном преобразовании Фурье,
функция взаимной спектральной плотности энергии определяется для ча-
стот / в интервале от/ = 0 до/ = оо в виде
^(/) = 2£[ХГ*(/)УГ(/)],
где Е [ ] означает усреднение при фиксированной частоте / по ансамблю из
nd имеющихся пар финитных преобразований Фурье (переходных) реализа-
ций, заданных на интервале времени длиной Т каждая. Функция ^xy(f) — О
при / < 0, и именно ее измеряют на практике.
Функция взаимной спектральной плотности энергии переходных случай-
ных процессов связана с обычной функцией взаимной спектральной плотно-
сти тех же процессов соотношением
«МЛ = 74//),
518
Приложение Б
где Т — длина реализаций.
В теоретических исследованиях используется двусторонняя функция вза-
имной спектральной плотности энергии, существующая при всех значениях
f отf = —оо до/ = оо:
= />0,
Функция когерентности
Функцией когерентности y*y(f) двух последовательностей x(t) и y(t) на-
зывается отношение квадрата модуля функции взаимной спектральной
плотности к произведению функций спектральной плотности
Величина yxy(f) удовлетворяет при всех / неравенству 0 7^(/) 1-
Эта функция обычной когерентности служит мерой точности оптималь-
ного линейного прогноза последовательности у (t) по значениям последова-
тельности х (t
Функция множественной когерентности
Функция множественной когерентности yy:x(f), связывающая последова-
тельность 7 (/ ) и набор отличных от нее последовательностей xt(t) (i = 1,
2, задает достижимую точность оптимального в среднеквадратичном
смысле прогноза значений ) по значениям xt(t) с помощью уравнений ли-
нейной регрессии. Значения yy:x(f) удовлетворяют при всех / неравенству
О yy:x(f) 1- Функция обычной когерентности есть частный случай
функции множественной когерентности.
Функция распределения
Функцией распределения Р (х) называется вероятность того, что в лю-
бой момент временив значение* (Z) удовлетворяет условию* (t) *. Функ-
ция распределения связана с плотностью вероятности соотношением
р(х) = [ Р(«)du,
- 00
Точнее, значения функции когерентности на всех частотах определяют точ-
ность восстановления значений y(f) по значениям х(Г) во все моменты времени
( — оо < t < оо). См. также Гельфанд И.М., Яглом А.М. О вычислении количества
информации о случайной функции, содержащейся в другой такой функции, УМН,
1957, т.12 (1), с.З—52: функция обычной (множественной, частной) когерентности
определяет количество информации i относительно гауссовой последовательности
7(/), содержащееся в гауссовой последовательности x(t). — Прим.перев.
Основные определения
519
гдем — переменная интегрирования. Заметим, чтоР(—оо) = 0 иР(оо) = 1.
Функция спектральной плотности
В рамках методов, основанных на конечном преобразовании Фурье,
функция спектральной плотности (называемая также функцией спектраль-
ной плотности мощности) Gxx(f) определяется для частот/ в интервале от
/ = 0 до/ = оо в виде
<и/) = |я[|Хт(/)|2],
где Е[ ] означает усреднение по ансамблю из имеющихся nd выборочных
реализаций I 12 при фиксированной частоте /. Величина A'yV) есть фи-
нитное преобразование Фурье последовательности x(t), заданной на интер-
вале времени длиной Т. Функция Gxx(f) = 0 при / < 0, и именно ее измеря-
ют на практике.
В теоретических исследованиях используется двухсторонняя функция
спектральной плотности, существующая при всех значениях/ от/ = — оо
до/ = оо:
Sxx(f) = ^Gxx(f), /^0,
Sxx(~f) = Sxx(f).
В случае стационарного процесса функция спектральной плотности
Gxx(f) равна удвоенному преобразованию Фурье ковариационной функции
RXXG)- —
Суммарный средний квадрат % последовательности х (t) может быть
получен интегрированием функции Gxx.(f) или Sxx.(f):
-- /00 /00
х2=/ Gxx(f)df=[ Sxx(f)df.
А) •'-00
Функция спектральной плотности энергии
В рамках методов, основанных на конечном преобразовании Фурье,
функция спектральной плотности энергии определяется для частот/ в ин-
тервале от/=Одо/=оов виде
ЪАП = 2£[|ХД/)|2] ,
где Е[ ] означает усреднение при фиксированной частоте по имеющемуся
ансамблю из nd (переходных) реализаций \XT(f)\2 при фиксированной ча-
стоте/. Величина XT(f) есть финитное преобразование Фурье функции х(Г),
заданной на интервале времени длиной Т. Функция -^xx(f) = 0 при / < 0, и
именно ее измеряют на практике.
Функция спектральной плотности энергии переходного случайного про-
цесса связана с функцией спектральной плотности «мощности» того же
520
Приложение Б
процесса соотношением
^л(/)=ГСхх(/)>
где Т — длина (переходных) реализаций. Заметим, что в случае переходно-
го процесса функция Gxx (f) должна стремиться к нулю при стремлении Т к
бесконечности.
В теоретических исследованиях используется двухсторонняя функция
спектральной плотности энергии, существующая при всех значениях/ от
/ = -оо до/ = оо:
= />о;
Функция частной когерентности
Функция частной когерентности, связывающая последовательность y(t)
с любым подмножеством из набора заданных последовательностей хДг)
(/ = 1, 2, ..., q) задает достижимую точность оптимального в среднеква-
дратичном смысле прогноза значений y(t) по значениям соответствующего
подмножества из набора xz(Z) с помощью уравнений линейной регрессии1).
Значение функции частной когерентности изменяется от нуля до единицы.
Частотная характеристика
Частотной характеристикой///) линейной системы с постоянными па-
раметрами называется преобразование Фурье импульсной переходной функ-
ции h (т), отвечающей этой системе. Соответствующая связь имеет вид
HU)= Г Л(т)е’>2’/Тdr
- оо
Инженеры часто называют H(f) передаточной функцией системы, хотя
в действительности этот термин относится к преобразованию Лапласа от
импульсной переходной функции.
При записи в полярных координатах имеем
где I H(f)\ — амплитудная характеристика системы, ф(/) — фазовая харак-
теристика системы.
В случае линейной системы функцию H(f) можно оценивать для детер-
мированных, переходных или стационарных случайных процессов, посколь-
ку ее свойства не зависят от типа процесса, проходящего через систему.
11 См. примечание на с.518. — Прим.перев.
Основные определения
521
Широкополосный случайный процесс
Широкополосным называется случайный процесс, спектральная плот-
ность которого существенно отлична от нуля в пределах широкой полосы
частот относительно некоторой центральной частоты.
Экстремальное значение
Экстремальным значением последовательности х (t) называется ее мак-
симальное или минимальное значение. Число экстремумов в единицу вре-
мени может относится только к ее максимумам или минимумам, либо к
тем и другим одновременно.
Эргодический случайный процесс
Эргодическим называется случайный стационарный процесс, для кото-
рого результаты усреднения по времени в пределах отдельной реализации
одинаковы для всех реализаций. Таким образом, усреднение по времени
для любой отдельной реализации эквивалентно соответствующему усредне-
нию по ансамблю реализаций.
Чтобы легче понять это определение, рассмотрим стационарный слу-
чайный процесс {xk (I)) , где £ = 1, 2, 3, ... — номер реализации. Для лю-
бой реализации хк (Z) среднее по времени значение статистической характе-
ристики, например, средний квадрат, определяется равенством
Х2к= lim - (Tx2k(t)dt.
Т —* ос 1
Если процесс эргодический, то этот результат не должен зависеть от £ и
будет одним и тем же для всех реализаций. Соответствующее среднее по
ансамблю значение определяется равенством
£[х2] = lim — £ x2k(t)
К к = 1
и в случае стационарного процесса не зависит от t. Для эргодического про-
цесса оба усреднения дают одинаковый результат.
Литература
К главе 2
2.1.Stokey W.F., Vibration of systems having distributed mass and elasticity, Chap-
ter 7, in: Shock and Vibration Handbook, 2nd ed., C.M. Harris and C.E. Cre-
ed (eds.), McGraw-Hill, New York, 1976.
2.2.Hurty W.G., Rubinstein M.F., Dynamics of structures, Prentice-Hall, Englewood
Cliffs, New Jersey, 1964.
2.3.Oden J.I., Reddy J.N., An introduction to the mathematical theory of finite
elements, Wiley-lnterscience, New York, 1976.
К главе 3
3.1. Papoulis A., Probability, random variables, and stochastic processes, McGraw-
Hill, New York, 1965.
3.2. Loeve M.M., Probability theory, 4th ed., Springer-Verlag, New York, 1977.
[Имеется перевод 2-го издания: Лоэв М. Теория вероятностей: Пер. с
англ. — М.: ИЛ, 1962. — 720 с.]
3.3. Laha R.G., Rohatgi V.K., Probability theory, Wiley, New York, 1979.
3.4. Patel J.K., Read C.B., Handbook of normal distribution, Dekker, New York,
1982.
3.5. Laning J.H. (Jr.), Battin R.H.,Random processes in automatic control, McGraw-
Hill, New York, 1956. [Имеется перевод: Лэнинг Дж.Х., Бэттин Р.Г. Случай-
ные процессы в задачах автоматического управления: Пер. с англ. — М.:
ИЛ, 1958. — 387 с.]
К главе 4
4.1. Brownlee К.A. Statistical theory and methodology in science and engineering,
2nd. ed.,Wiley, New York, 1965.
4.2. Guttman I., Wilks S.S., Hunter J.S., Introductory engineering statistics, 3rd ed.,
Wiley, New York, 1982.
4.3. Johnson N.L., Leone F.C., Statistics and experimental design in engineering and
physical sciences, 2nd ed., Wiley, New York, 1977.
4.4. Kendall M.G., Stuart A., The advanced theory of statistics, Vol.2, Hafner, New
York, 1961. [Имеется перевод: Кендалл М.Дж., Стьюарт А. Статистические
выводы и связи: Пер. с англ. — М.: Наука, 1973. — 900 с.]
К главе 5
S.l. Bendat J.S., Principles and applications of random noise theory, Wiley, New
York, 1958. Reprinted by Krieger, Melbourne, Florida, 1977. [Имеется перевод:
Бендат Дж. Основы теории случайных шумов и ее применения: Пер. с
англ. — М.: Наука, 1965. — 463 с.]
5.2. Bendat J.S., Piersol A.G., Engineering applications of correlation and spectral
analysis, Wiley-lnterscience, New York, 1980. [Имеется перевод: Бендат Дж.,
Пирсол А. Приложения корреляционного и спектрального анализа: Пер. с
англ. — М.: Мир, 1982. — 312 с.]
5.3. Doob J.L., Stochastic processes, Wiley, New York, 1953. [Имеется перевод:
Дуб Дж. Вероятностные процессы: Пер. с англ. — М.: ИЛ, 1956. — 605 с.]
5.4. Papoulis A.,Probability, random variables, and stochastic processes, McGraw-
Hill, New York, 1965.
5.5. Rice S.O., Mathematical analysis of random noise, in: Selected Papers on Noise
and Stochastic Processes, N.Wax, (ed.), Dover, New York, 1954.
Литература
523
К главе 6
6.1. Bendat J.S., Piersol A.G., Engineering applications of correlation and spectral
analysis, Wiley-Interscience, New York, 1980. [Имеется перевод: Бендат Дж.,
Пирсол А. Приложения корреляционного и спектрального анализа: Пер. с
англ. — М.: Мир, 1982. — 312 с.]
6.2. Upton R., Innovative functions for two-channel FFT analyzers, J.Sound and
Vibration, 18, 18, March(1984).
6.3. Chung J.Y., Rejection of flow noise using a coherence function method,
J. Acoustical Society of America, 62, 338 (1977).
6.4. Adams E.P., Smithsonian mathematical formulae and tables of elliptic functions,
Smithsonian Institution, Washington, D.C., 1947.
К главе 7
7.1.Dodds C.J., Robson J.D., Partial coherence in multivariate random processes,
J. Sound and Vibration, 42, 243 (1975).
7.2.Bendat J.S., Piersol A.G., Engineering applications of correlation and spectral
analysis, Wiley-Interscience, New York, 1980. [Имеется перевод: Бендат Дж.,
Пирсол А. Приложения корреляционного и спектрального анализа: Пер. с
англ. — М.: Мир, 1982. — 312 с.]
7.3.Bendat J.S., Modern analysis procedures for multiple input/output problems,
J. Acoustical Society of America, 68, 498 (1980).
7.4.Liebeck H.,Algebra for scientists and engineers, Wiley, New York, 1969.
К главе 8
8.1.Bendat J.S., Principles and applications of random noise theory, Wiley, New
York, 1958. Reprinted by Krieger, Melbourne, Florida, 1977. [Имеется перевод:
Бендат Дж. Основы теории случайных шумов и ее применения: Пер. с
англ. — М.: Наука, 1965. — 463 с.]
8.2.Bendat J.S., Piersol A.G., Engineering applications of correlation and spectral
analysis, Wiley-Interscience, New York, 1980. [Имеется перевод: Бендат Дж.,
Пирсол А. Приложения корреляционного и спектрального анализа: Пер. с
англ. — М.: Мир, 1982. — 312 с.]
8.3.Dixon W.J., Massey F.J. (Jr.), Introduction to statistical analysis, 3rd ed.,
McGraw-Hill, New York, 1969.
К главе 9
9.1.Bendat J.S. Statistical errors in measurement of coherence functions and
input/output quantities, J. Sound and Vibration, 59, 405 (1978).
9.2.Jenkins G.M., Watts D.G., Spectral analysis and its applications, Holden-Day,
San Francisco, 1968. [Имеется перевод: Дженкинс Г., Ватте Д. Спектраль-
ный анализ и его приложения: Пер. с англ. — М.‘: Мир, вып.1, 1971, 316 с;
вып.2, 1972, 288 с.]
9.3.Seybert A.F., Hamilton J.F., Time delay bias error in estimating frequency re-
sponse and coherence functions, J. Sound and Vibration, 60, 1 (1978).
9.4.Carter G.S., Knapp C.H., Nuttall A.H., Estimation of the magnitude-squared
coherence via overlapped fast Fourier transform processing, IEEE Transactions
on Audio and Electroacoustics, AU-21, 337, August (1973).
9.5.Goodman N.R., Measurement of matrix frequency response functions and mul-
tiple coherence functions, AFFDL TR 65-56, Air Force Flight Dynamics Labora-
tory, Wright-Patterson AFB, Ohio, February, 1965. [Имеется сокращенный пе-
ревод: Гудмен Н. Вычисление матрицы частотных характеристик и функ-
524
Литература
ции множественной когерентности. — В кн.: Бендат Дж., Пирсон А. Изме-
рение и анализ случайных процессов. М.: Мир, 1974, с.448—463.]
9.6.Bendat J.S., Piersol A.G., Engineering applications of correlation and spectral
analysis, Wiley-Interscience, New York, 1980. [Имеется перевод: Бендат Дж.,
Пирсол А. Приложения корреляционного и спектрального анализа: Пер. с
англ. — М.: Мир, 1982. — 312 с.]
9.7.Herlufsen Н., Dual channel FFT analysis (parts I and II), Bruel and Kjaer
Technical Review, Nos. 1 and 2, 1984.
9.8.Schmidt H.,Resolution bias errors in spectral density, frequency response and
coherence function measurements, J. Sound and Vibration, 101, 347 (1985).
К главе 10
lO.l. Doeblin E.O., Measurement systems: application and design, McGraw-Hill, New
York, 1966.
10.2. Beauchamp K.G., Yuen C.K., Data acquisition for signal analysis, Allan and
Unwin, London, 1980.
10.3. Davies G.L., Magnetic tape instrumentation, McGraw-Hill, New York, 1961.
10.4. Gregg W.D., Analog and digital communication, Wiley, New York, 1977.
10.5. Fitzgerald J., Eason T.S., Fundamentals of data communication, Wiley, New
York, 1978.
К главе 11
11.1. Hamming R.W., Digital filters, 2nd ed., Prentice-Hall, Englewood-Cliffs, New
Jersey, 1983.
11.2. Rabiner L.R., Gold B., Theory and applications of digital signal processing,
Prentice-Hall, Englewood Cliffs, New Jersey, 1975.
11.3. Oppenheim A.V., Schafer R.W. Digital signal processing, Prentice-Hall, Eng-
lewood Cliffs, New Jersey, 1975.
11.4. Otnes R.K., Enochson L., Applied time series analysis, Vol.l, Wiley, New York,
1978. [Имеется перевод: Отнес P., Эноксон Л. Прикладной анализ времен-
ных рядов. Основные методы: Пер. с англ. — М.: Мир, 1982. — 428 с.]
11.5. Brigham Е.О., The fast Fourier transform, Prentice-Hall, Eriglewood Cliffs,
New Jersey, 1974.
11.6. Cooley J.W., Tukey J.W., An algorithm for the machine calculation of complex
Fourier series, Mathematics of Computation, 19, 297, April (1965).
11.7. Winograd S.,On computing the discrete Fourier transform, Mathemathics of
Computation, 32, 175, January (1978).
11.8. Harris F.J., On the use of windows for harmonic analysis with the discrete
Fourier transform, Proc. IEEE, 66, 51, January (1978).
11.9. Nuttall A.H., Some windows with very good side lobe behavior, IEEE Trans-
actions on Acoustics, Speech, and Signal Processing, ASSP-29, 84, February
(1981).
11.10. Nuttall A.H., Carter G.C., Spectral estimation using combined time and lag
weighting, Proc. IEEE, 70, 1115, September (1982).
11.11. Childers D.G., Modern spectral analysis, IEEE Press, New York, 1978.
11.12. Robinson E.A., Treitel S., Geophysical signal analysis, Prentice-Hall, Englewood
Cliffs, New Jersey, 1980.
Литература
525
Дополнительная литература к главе 11
11.13. Спектральное оценивание. — Труды Института инженеров по электротехни-
ке и радиотехнике. 1982, т.70, №9, с. 307.
11.14. Привальский В.Е. Климатическая изменчивость (стохастические модели,
предсказуемость, спектры). — М.: Наука, 1985. — 184 с.
11.15. Koslov J., Jones R.H.H., A unified approach to confidence bounds for autoreg-
ressive spectral estimator, J. Time Series Analysis, 6, 141 (1985).
11.16. Burstein D., Weinstein E. Confidence intervals for the maximum entropy spe-
ctrum, IEEE Transactions on Acoustics, Speech, and Signal Processing, ASSP-
35, 504 (1987).
11.17. Privalsky V.E., Protsenko I.G., Fogel G.A. The sampling variability of autoreg-
ressive spectral estimates for hydrometeorological processes, Transactions of the
1st World Congress of the Bernouilli Society for Mathematical Statistics and
Probability, Tashkent, September 1986, VNU Science Press, Utrecht, 1987, 1,
651.
К главе 12
12.1. Claasen T.A.C.M., Mecklenbrauker W.F.G., The Wigner distribution — a tool
for time-frequency signal analysis, Philips Journal of Research, 35, Nos. 3 — 6
(1980).
12.2. Mark W.F., Fischer R.W., Investigation of the effects of nonhomogenous (or
nonstationary) behavior on the spectra of atmospheric turbulence, NASA CR-
2745, NASA Langley Research Center, Virginia, February 1976.
12.3. Piersol A.G., Power spectra measurements for spacecraft vibration data, J. Spa-
cecraft and Rockets, 4, 1613, December (1967).
12.4. Silverman R.A., Locally stationary random processes, Trans. IRE, Information
Theory. IT-3, 182, September (1957).
12.5. Lawson J.I., Uhlenbeck G.E., Threshold signals, McGraw-Hill, New York, 1950.
К главе 13
13.1. Bendat J.S., The Hilbert transform and applications to correlation measure-
ments, Bruel and Kjaer, Denmark, 1985.
13.2. Bracewell R., The Fourier transform and its applications, McGraw-Hill, New
York, 1965.
13.3. Oppenheim A.V., Shafer R.W., Digital signal processing, Prentice-Hall, New
Jersey, 1975.
13.4. Thrane N., The Hilbert transform, Bruel and Kjaer Technical Review, No.3,
1984.
13.5. Herlufsen H., Duel channel FF1 analysis (parts 1 and 2), Bruel and Kjaer
Technical Review, Nos. 1, 2, 1984.
13.6. Dugundji J., Envelopes and pre-envelpoes of real waveforms, Trans. IRE,
Information Theory, IT-4, 53, March (1958).
13.7. Cremer L., Heckl M., Unger E.E., Sructure-Borne Sound, Springer-Verlag, New
York, 1973.
13.8. White P.H., Cross-correlation in structural systems: dispersive and nondispersive
waves, J. Acoustical Society of America, 45, 1118, May (1969).
Предметный указатель
Автоковариационная функция (см. Ковариа-
ционная функция)
Авторегрессионная модель 397
Автоспектр (см. Функция спектральной плот-
ности)
Акселерометр сейсмический 54, 323
Алгоритм БПФ 372, 374
— вычисления условного преобразования
Фурье 231
----условного спектра 232, 236, 237, 238
Амплитудная характеристика (см. также Фа-
зовая характеристика) 42, 53
----акселерометра 323
----вычисление 401
----оценка 181, 300
----случайная ошибка 309, 310, 319
----смещение 301
----системы с силой на входе 47
----со смещением основания на
входе 52
----примеры 47, 52, 466
Аналитическая функция (см. Аналитический
сигнал)
Аналитический сигнал 471
----для автоковариационной функции 484
----взаимной ковариационной функции
484, 485
Аналого-цифровой преобразователь 335
Ансамбль реализации 22, 416
Белый шум 137
----гауссовость 138
----низкочастотный 137, 151
----пересечения оси абсцисс 170
----ограниченный по частоте 137
----дисперсия оценки автоспектра
280
----ковариационной функции
272, 275
----среднего значения ква-
драта 261
----применение окна Ханна 389
----распространение бездис-
персное 487
---- дисперсное 492
----узкополосный 137
Блэкмана — ТЪюки метод 385
Вероятностное утверждение 96, 255
Весовая функция (см. Импульсная переходная
функция)
Взаимная ковариационная функция (см. также
Ковариационная функция)
-------аналитического сигнала 485
-------вычисление 399
-------комплексная 484
-------локализация максимума 148, 274
-------нестационарная 420, 433,434, 447
-------огибающая 482, 486
-------оценивание через взаимный спектр
131, 134
-------оценка 269, 272, 351
-------математическое ожидание 270
-------ошибка систематическая за-
паздывания 302
------------случайная 272, 274
-------преобразования Гильберта от случай-
ного процесса 481, 483
-------при наличии запаздывания 128
-------стационарная 121, 155, 511
Взаимный спектр (см. Функция взаимной
спектральной плотности)
Вигнера распределение (см. Частотно-времен-
ной спектр)
Винера — Хинчина формулы 131
Винограда преобразование 376
Волновое число следовое 202
Временной ряд (см. Процесс случайный)
Выборочная функция (см. Реализация)
Гауссов случайный процесс 158, 511
----линейное преобразование 160
----моменты распределения 159
----связь с белым шумом 138
----эргодичностью 158
Гауссово распределение 74, 88
----совместное 77
----моменты 81, 83
----нестационарное 419
----таблица 499, 500
----N-мерное 79
Гильберта преобразование 469, 514
----вычисление 472, 473
----и ковариационные функции 480, 483,
486
---- обратное 474
----примеры 473, 474, 480, 496
----свойства 473 — 477
----связь с физически осуществимыми сис-
темами 477
Гистограмма 103, 379, 511
Двойная по времени ковариационная функция
433
----альтернативное представление
434
----примеры 436, 437
----частоте спектральная функция 437
----альтернативное представление
439
----примеры 443, 444
Дельта-функция 62, 137
— финитная 442
Детерминированный процесс 13, 14
----переходный непериодический 19
Предметный указатель
527
----полигармонический 16
----почти-периодический 18
----синусоидальный периодический
15
Диаграмма направленности 202 (?)
Дискретное распределение 61
Дисперсия 63, 85, 511
— оценка 34, 87, 254, 262
----доверительный интервал 97, 98
----ошибка систематическая 263
------- случайная 263
Добротность системы 268
Запаздывание 128
— оценка 276
Идеальное ограничение 456
Импульсная переходная функция 39, 512
-------вычисление 402
-------системы с переменными параметра-
ми 458
Инвариантный во времени оператор 161
Интеграл свертки 40
----для системы с постоянными парамет-
рами 172
----для преобразования Гильберта 469
---------Фурье 387
Интервал доверительный 95, 255
----для оценки автоспектра 284
---------дисперсии 97, 98
---------среднего значения 96
— группировки 103, 378, 511
Испытания космических аппаратов 432, 455
456
Квадратурная спектральная плотность 134
------- оценка 291
---------случайная ошибка 293
Ковариационная функция 26
----взаимная 30
-------пространственная нестационарная
424
---- графики 29
----идеально ограниченного процесса 457
----комплексная 483
----нестационарная 420, 433, 435, 447
----огибающая 483, 486
----оценка 269, 275, 276
-------дисперсия 270
-------ошибка систематическая 270, 275
-------по автоспектру 131
-------через преобразование Фурье 380,
384
----сглаживание 391, 393
----стационарная 24, 155, 512
----циклическая 380, 382, 383
Ковариация 70
— нестационарная 448
— оценок 297
Когерентный спектр выходного процесса 184,
190, 512
----вычисление 409
----множественный 217
----вычисление 410
----оценка 300, 304, 305
----случайная ошибка 316
----частный 225
----вычисление 409
----случайная ошибка оценки 318
Комплексная демодуляция 394, 395
Корреляционная функция 120
---- нестационарная 120
----стационарная 122, 155
Коспектральная плотность (см. также Функ-
ция спектральной плотности) 134
----оценивание 290, 293
Коэффициент вариации (см. также Ошибка
оценки случайная) 255
— динамического усиления 46
— затухания 45
— корреляции (см. также Нормированная
взаимная корреляционная функция) 70,
ПО, 160
— ориентирующий 371
— потерь 48
Критерии сходимости 162, 163
Критерий двусторонний 100
— инверсий 108, 334
----распределение 109
---- таблица 510
— односторонний 100
— серий 105
----распределение 106
---- таблица 509
— согласия хи-квадрат 102
Кули — Тьюки метод 372
Линейная решетка 198
----коэффициент усиления 200
----направленность 200
— система (см. также Система линейная)
39, 512
----с зависящими от времени параметрами
458
----с постоянными параметрами 39
Линейное преобразование случайного процесса
160
---------и функция когерентности 183
Линейный корреляционный анализ ПО
— оператор 160
Локально-стационарный процесс 435, 454
Магнитофон 325
Максвелла распределение 75
Марковский процесс 157
Математическое ожидание (см. Среднее значе-
ние)
528
Предметный указатель
Матричная формула 242
— для системы со многими входными
процессами 242, 246, 248
---------с одним входным процессом 250
Мгновенная фаза 471
Мгновенный спектр (см. Частотно-временной
спектр)
Метод максимального правдоподобия 397
— максимальной энтропии 397
— наименьших квадратов 114, 189, 358, 397
Множественный когерентный спектр выход-
ного процесса 217
------------вычисление 411
------------случайная ошибка оценки
316
Модель авторегрессии 397
— линейной решетки 198
— мультипликативная нестационарного про-
цесса 452
---------частотно-временной автоспектр
453
— скользящего среднего 397
Модуляция кодово-импульсная 327, 328
— частотная 327, 328
Момент распределения 67, 73, 81, 82
Мощность критерия 100
Найквиста интервал 332
— коинтервал 332
— частота 334, 335, 338
Наплывающее преобразование 394, 396
Неравенство для взаимного спектра 146
---в нестационарном случае 438
--- взаимной корреляции 127
---в нестационарном случае 433
Нормальное распределение (см. Гауссово рас-
пределение)
Нормированная взаимная корреляционная
функция 128, 160, 513
---------вычисление 399
---------при бездисперсином распростра-
нении 487
---------при дисперсном распространении
490
---------квадрат огибающей процесса 495
Область отклонения гипотезы 100
— принятия гипотезы 100
Объединение реализаций 350
Огибающая взаимной ковариационной функ-
ции 482, 486
— ковариационной функции 482
— нормированной взаимной корреляционной
функции 495
— сигнала 471
---вычисление 472, 473
Окно временное 387, 388
— прямоугольное 387
— спектральное 387, 388
— Ханна 388, 389, 391, 393
Оценка 34, 86, 253, 289
— квадрат 255
— несглаженная 282, 289
— несмещенная 86
— сглаженная 284, 290
— состоятельная 86
— эффективная 86
Ошибка квантования 336
— маскировки частот 333
— оценки 34
---нормированная 36, 253, 254
---систематическая 34, 254
-------взаимного спектра 290, 302
-------взаимной ковариационной функции
27, 301
-------дисперсии 262
-------за счет входного шума 303
------------запаздывания 302
------- источники 301
-------ковариационной функции 270
-------когерентного спектра 306
-------плотности вероятности 264, 265
-------пример 279
-------связь с разрешением по частоте
278, 280, 314
-------спектральной плотности 279, 280
------- среднего значения 256
------------ квадрата 260
-------функции когерентности 301, 302,
306
-------частотной характеристики 301,
302, 303
---случайная 35, 254, 255
-------амплитудной характеристики 309,
311, 313
-------взаимного спектра 292
-------взаимной ковариационной функции
272, 274
-------диаграмма 261, 273, 305, 308,
309, 311, 312
-------дисперсии 261, 262
—- ----квадрата оценки 254
------- квадратурной спектральной плот-
ности 293
-------кавариационной функции 273
-------когерентного спектра 304, 306,
313
------------множественного 316
------------частного 318
-------коспектральной плотности 293
-------плотности вероятности 266, 269
-------связь с длиной реализации 286
Предметный указатель
529
-------спектральной плотности 278, 280,
292, 293
-------среднего значения 257, 258
------------ квадрата 262
-------среднеквадратичного значения 262,
263
-------фазового угла 298
-------фазовой характеристики 311, 313
-------функции когерен±ности 306, 307,
308, 313
------------множественной 316
--------------- частной 318
----смещения (см. Ошибка оценки систе-
матическая)
---- среднеквадратичная 254
----плотности вероятности 264
----средний квадрат 35, 253
— первого и второго рода 100
Передаточная функция (см. также Частотная
характеристика) 41, 513
Плотность вероятности 26, 29, 61, 514
----вычисление 378, 379
----гармонической функции 269
---- гауссова 74, 88, 159
-------/V-мерная 79
----график 28, 75
----нестационарная 418
----нормальная (см. Гауссово распределе-
ние)
---- оценка 263
-------ошибка систематическая 264, 265
--------- случайная 267
----преобразованной случайной величины
64
----проверка нормальности 343
----совместная 30, 69, 67
-------вычисление 398
------- гауссова 77, 160
------- оценка 268
---------случайная ошибка 269
Подавление боковых максимумов 387
-------прямоугольное окно 387
-------окно Ханна 388
Полоса пропускания по уровню половинной
энергии 46, 280
Преобразователь 321
Принцип неопределенности 332
Причинно обусловленная система (см. Систе-
ма физически осуществимая)
----функция 477, 478
-------и преобразование Гильберта 479
-------пример 479, 480
-------связь с функцией когерентности 193
Проверка гипотез 99
— нормальности 105, 343
— периодичности 342
— стационарности 339
— эквивалентности автоспектров 352
Производная случайного процесса 163
-------ковариационная функция 163
-------функция спектральной плотности 166
Производящая функция моментов 66, 73, 81
------- гауссова 78
-------четвертого порядка 81
Прореживание 360, 395
Процентная точка 89, 90, 91, 92
Процесс гармонический 15
— детерминированный 13
— переходный 19
— периодический 14, 15
----двойная по времени ковариационная
функция 436
----------спектральная плотность 444
----мгновенный спектр 450, 451
----ряд Фурье 166, 515
— полигармонический 16
— почти-периодический 18
— случайный 13, 20, 22, 119, 515
---- гауссов 153
----гармонический 65, 155
------- автоспектр 136
-------ковариационная функция 125
-------плотность вероятности 61
-------смесь с шумом 27 — 30, 344
----нестационарный 24, 416, 513
------- вероятностная структура 418
------- корреляционная структура 432
-------мультипликативная модель 452
-------примеры 417, 418
-------равномерно модулированный 454
------- спектральная структура 437
------- среднее значение 422
---------- квадрата 428
-------стационарный результат 442, 443
450
----переходный 176, 513
-------соотношения между процес-
сами на входе и выходе
системы 465
----стационарный 22, 25, 121
-------линейное преобразование
162
-------неэргодический 155
-------эргодический 23, 153, 521
---------- достаточное условие 157
-------условный (см. Реализация остаточная
----узкополосный 27, 516
----широкополосный 27, 521
Пуассона распределение 125
530
Предметный указатель
Разложение системы со многими входами 235
— спектра выходного процесса 411
Размер блока 386
— выборки 86
Распределение выборочное 92
— выборочного среднего 93
— выборочной дисперсии 94
— гармонической функции 65
— дискретное 61
— нормальное (см. Гауссово распределение)
— равномерное (прямоугольное) 63
— Рэлея 75
— Стьюдента (/) 91
— суммы двух случайных величин 71
— хи-квадрат 90
Распространение бездисперсное 486
----из нескольких источников 486
----ошибка в связи с задержкой по вре-
мени 302
----по нескольким трактам 488, 489
----по одному тракту 129, 486
— дисперсное 490
Расчет по перекрывающимся отрезкам 391
Реализация 515
— анализ 25, 321, 346, 348
— нестационарная коррелированная 424, 429
----независимая 423, 428
— остаточная (условная) 218
----спектр 222, 232
---- упорядочивание 220, 230'
Рэлея распределение 75
Сглаживание временное 398
— ковариационной функции 391
Сдвиг 380
Система линейная 38, 512
----зависящая от времени 458
---------идеальная 38, 173, 179
---------со многими входами и многими выхо-
дами 205, 242
---------одним выходом 33, 205, 206
--------------вычисление 404
--------------матричная формула
246, 248
--------------множественная коге-
рентность 217, 241,
250
--------------при условных входах
225, 235, 315, 404
------------------- оценка 314
-------------------разложение 235, 411
-------------------с некоррелированными
входами 210
-------------------с произвольными вхо-
дами 208, 229, 314,
403
-----с нестационарными входны-
ми процессами 458, 463
-----со стационарными входны-
ми процессами 461, 463
-----с тремя входами и одним выходом
227
----- условная 412
— механическая 43, 50, 56
— нелинейная 39, 513
— неустойчивая 40
— резонансная 50
— устойчивая 40
— физическая 38, 57
-----с одним входом 31, 32
-----и двумя выходами 192
-----многими выходами 31, 194
-----одним выходом 31, 172
-----вычисление 401
-----соотношение для кова-
риаций 173
-----спектральных
плотностей 173,
175, 250
----- оценка 299
-----с шумом на выходе
183 — 188
-----со многими входами 31, 205, 206, 242
— физически осуществимая 40, 477
----- преобразование Гильберта 479
— электрическая 54
Скорость групповая 490
— фазовая 490
Случайная величина 60, 68, 71
-----некоррелированная 70, 80
-----статистически независимая 69
Соотношение неопределенности 149
Соотношения между процессами на входе и
выходе системы 31
-----с двумя входными про-
цессами 211
-----с нестационарными
входными процессами
458, 461, 463,
-----с одним входным про-
цессом 173, 193
-----со многими входами
208, 210
-----с переходными вход-
ными процессами 176,
464
Спектр (см. также Функция спектральной
плотность) 515
— двойной по частоте 437, 439, 444
— двухсторонний 131, 133, 140, 386
— гауссового шума 152
— линейчатый 512
Предметный указатель
531
— мгновенный (См. также Частотно-времен-
ной спектр) 445, 450, 451
— односторонний 131, 140, 186
— средний по времени 449
— шума на выходе линейной системы 183,
512
--------------- оценка 300
---------------со многими входами 226, 241
— частотно-временной (см. Частотно-времен-
ной спектр)
Спектральная матрица расширенная405, 412
-----условная 406, 407, 408, 412
Спектральный анализ авторегрессионный 6
-----методом максимального правдоподобия
397
-----максимальной энтропии 397
-----непараметрический 6
-----параметрический 6, 397
Среднее значение 26, 62, 85, 516
-----квадрата 26, t ’>
-----выходного процесса 174, 176, 177,
178
-----нестационарное 428, 431, 447
----- оценка 256
-----ошибка систематическая 262
262
----- случайная 263
----- стационарное 340, 512
-----нестационарное 120, 422, 427
----- оценка 256
-----доверительный интервал 98
-----ошибка систематическая 257
----- случайная 256
----- стационарное 121, 153
Среднеквадратичное значение 516
-----вычисление 358
-----нестационарное 432
-----оценки фазовой характеристики 311
-----случайная ошибка оценки 263
— отклонение (с.к.о.) 53, 516
Средний квадрат ошибки 35, 257
Средняя по времени взаимная ковариационная
функция 435
-----спектральная плотность 449
-----ковариационная функция 435, 452
-----плотность вероятности 421, 422
-----спектральная плотность 449
Стандартное отклонение (см. также Средне-
квадратичное отклонение) 63
-----оценки фазового угла 298
Статистическая независимость 69, 106
Стохастический процесс (см. Процесс случай-
ный)
Стьюдента ^-распределение 91
----- таблица 502
Сходимость с среднеквадратичном 162
— по вероятности 163
Телеграфный сигнал 125
Теорема о дискретном представлении процесса
332
Требования к длине реализации 285
Удаление тренда 106, 359
— шума на выходе 196
Уровень значимости 100
Фаза сигнала мгновенная 471
Фазовая характеристика (см. также Амплитуд-
ная характеристика) 42
----акселерометра 323
----вычисление 401
---- оценка 300
-------среднеквадратичное отклонение 311,
313, 319
----примеры 46, 52
Фазовый сдвиг 470
— угол 134, 135
----при задержке по времени 147
Фильтр низкочастотный 176
— числовой нерекурсивный 361
----рекурсивный 362
Функция взаимной спектральной плотности
(см. также Функция спектральной плот-
ности 31
---------для преобразований Гильберта
481, 483
--------- квадратурная 144
---------нестационарная 437,439, 447
---------огибающих 496
оценивание 289
-----------------------путем------------------аналогбвой фильтрации
142
-----------------------через взаимную ковариацион-
ную функцию 130
---------преобразование Фурье 139,
142, 207
---------ошибка оценки систематическая
291, 301
---------случайная 292
---------при наличии запаздывания 147
---------разрешающая способность 290
---------стационарная 130, 134, 1406,
142, 517
---------энергии 117, 440, 448, 464,
517
Функция когерентности (см. также Функция
множественной когерентности, Функция
частной когерентности) 31, 146, 518
----вычисление 402, 408
----идеальной системы 179
532
Предметный указатель
----и причинная обусловленность 193
----комплексная 146
------- оценка 300
----оценка 300, 308, 309
-------ложная 219
-------ошибка систематическая 301, 302,
306
---------случайная 307, 308, 309
----при двух выходных процессах 191, 193
----при задержке по времени 148
----при линейном преобразовании 183
----примеры 180, 228
Функция множественной когерентности 217,
518
-------вычисление 250, 409
-------для системы с двумя входами 218,
226
------------со многими входами 241, 250
-------пример 229
-------случайная ошибка оценки 316
Функция распределения 60, 61, 518
----вычисление 379
----гармонической функции 365
---- гауссова 76, 88
---- нестационарная 420
----равномерная 63
----совместная 69
Функция спектральной плотности (см. также
Функция взаимной спектральной плотнос-
ти) 26, 31
-------вычисление 385, 393
---------с помощью аналоговой фильтра-
ции 142, 276
---------через преобразование Фурье 139,
207, 281
-------график 30, 136
-------нестационарная 437, 440, 447
-------односторонняя 132, 142, 386
------- оценка 276
---------ошибка систематическая 278, 279
------------случайная 281, 285
-------примеры 182, 344, 390, 466
-------проверка эквивалентности 352
-------разрешение по частоте 276
-------условная 222, 232
---------вычисление 236, 404
-------энергии 176, 440, 447, 451, 464,
466, 519
Функция частной когерентности 34, 520
-------вычисление 409
-------для системы со многими входами
234, 240
-------примеры 227
-------случайная ошибка оценки 318
Фурье преобразование 19, 514
----алгоритм 372
-------Кули — ТЬюки 374
----быстрое 366
-------вычисление 366, 374, 376, 377
-------коэффициент ускорения вычислений
368
----двойное 438, 441, 446
----для оценивания автоспектра 385, 393,
396
---------взаимного спектра 400
---------взаимной ковариационной функции
399
---------ковариационной функции 380, 384
----обратное 361, 376
---- условное 231
-------алгоритм 232
----финитное 139, 142, 366, 515
-------вычисление 366, 376, 386
-------применение для спектрального оцени-
вания 140, 142, 207, 208, 283, 519
Фурье ряд 16, 515
----вычисление 364
Характеристическая функция 66
— гауссова процесса 79
— совместного распределения 74, 79
Центральная предельная теорема 77
-------многомерная 80
Частота «мгновенная» 471
— Найквиста 334, 335, 338
— собственная незатухающих колебаний 45
Частотная характеристика (см. также Ампли-
тудная характеристика, Фазовая характе-
ристика) 31, 42, 520
----вычисление 401, 480
-------по гармоническому входному сигналу
49
-------по импульсной переходной функции
45, 51
----оптимальная 189
-------многомерной системы 233, 238
-------системы с двумя входами 215
----оценивание 58, 300, 301
----примеры 47, 52
----системы с зависящими от времени па-
раметрами 458
----физическая осуществимость 188, 189,
217
Частотно-временной спектр 440, 445
-------связь с ковариацией 448
---------с автоспектром энергии 447
---------с взаимным спектром энер-
гии 449
---------со средним значением ква-
драта 447
-------примеры 450, 451
-------соотношения между процессами на
входе и выходе 460
Предметный указатель
533
------- локально стационарного процесса
454, 455
-------стационарного процесса 450
Чебышева неравенство 67
Число пересечений оси абсцисс 164
----------определение по ковариационной
функции 164
---------------идеально ограниченному сиг-
налу 456
---------------преобразованию Гильберта
483
---------------реализации 168
— степеней свободы 90
— усреднений 283, 290
Шум на выходе системы 183, 184, 186, 191
---------спектр 190, 223, 240, 241
Экстремальное значение 521
---- ковариации 274
----локализации 148, 274
----частотной характеристики 46
Эффективная шумовая ширина спектра 150
Эффективное шумовое время корреляции 150
Оглавление
От редактора перевода.................................................... 5
Предисловие к русскому изданию .......................................... 7
Введение ................................................................ 8
Список обозначений ....................................................... 10
Глава 1. Основные определения и модели ................................... 13
1.1. Детерминированные и случайные процессы ................ 13
1.2. Классификация детерминированных процессов.............. 14
1.2.1. Синусоидальный периодический процесс ................. 15
1.2.2. Полигармонический процесс ............................ 16
1.2.3. Почти периодические процессы ......................... 18
1.2.4. Переходные непериодические процессы .................. 19
1.3. Классификация случайных процессов ..................... 20
1.3.1. Стационарные случайные процессы ...................... 22
1.3.2. Эргодические случайные процессы..................... 23
1.3.3. Нестационарные случайные процессы .................... 24
1.3.4. Стационарность выборочных функций..................... 25
1.4. Анализ случайных данных.............................. 25
1.4.1. Основные характеристики случайных процессов........... 26
1.4.2. Соотношения между входными и выходными процессами .... 31
1.4.3. Характеристики ошибок................................. 34
1.4.4. Методы анализа данных ................................ 36
Глава 2. Линейные физические системы ...................................... 38
2.1. Линейные системы с постоянными параметрами .............. 38
2.2. Основные динамические характеристики .................... 39
2.3. Частотные характеристики ................................ 42
2.4. Примеры частотных характеристик ......................... 43
2.4.1. Механические системы ................................... 43
2.4.2. Электрические системы .................................. 54
2.4.3. Другие системы ......................................... 57
2.5. Практические соображения ................................ 57
Глава 3. Основы теории вероятностей....................................... 60
3.1. Одномерные случайные величины ........................... 60
3.1.1. Функции распределения .................................. 60
3.1.2. Математическое ожидание................................. 62
3.1.3. Преобразование случайной величины ...................... 64
3.1.4. Производящие функции моментов и характеристические
функции ................................................. 66
3.1.5. Неравенство Чебышева ................................... 67
3.2. Двумерные случайные величины ............................ 68
3.2.1. Математическое ожидание и коэффициент корреляции..... 70
3.2.2. Распределение суммы двух случайных величин.............. 71
3.2.3. Производящие функции моментов и характеристические
функции ................................................. 73
3.3. Гауссово (нормальное) распределение ..................... 74
Оглавление 535
3.3.1. Центральная предельная теорема.......................... 76
3.3.2. Совместное гауссово (нормальное) распределение ......... 77
3.3.3. Производящие функции моментов и характеристические
функции ....................................................... 78
3.3.4. /V-мерное гауссово (нормальное) распределение........... 79
Глава 4. Основные понятия математической статистики..................... 85
4.1. Выборочные значения и оценивание параметров ............. 85
4.2. Важнейшие функции распределения ......................... 88
4.2.1. Нормальное распределение ............................... 88
4.2.2. Хи-квадрат распределение ............................... 90
4.2.3. /-распределение Стьюдента............................... 91
4.2.4. F-распределение ........................................ 91
4.3. Выборочные распределения и примеры ...................... 92
4.3.1. Распределение выборочного среднего при известной диспер-
сии ........................................................... 93
4.3.2. Распределение выборочной дисперсии ..................... 94
4.3.3. Распределение выборочного среднего при неизвестной дис-
персии ........................................................ 94
4.3.4. Распределение отношения двух выборочных дисперсий..... 95
4.4. Доверительные интервалы ................................. 95
4.5. Проверка гипотез ........................................ 99
4.6. Критерий согласия хи-квадрат ........................... 102
4.7. Статистическая независимость и выявление тренда......... 106
4.7.1. Критерий серий ........................................ 106
4.7.2. Критерий инверсий ..................................... 108
4.8. Корреляционные и регрессионные методы .................. 109
4.8.1. Линейный корреляционный анализ ......................... ПО
4.8.2. Линейный регрессионный анализ ......................... 113
Глава 5. Стационарные случайные процессы .............................. 119
5.1. Основные понятия ....................................... 119
5.1.1. Ковариационные (корреляционные) функции................ 121
5.1.2. Примеры ковариационных функций ........................ 123
5.1.3. Нормированная ковариационная функция .................. 126
5.1.4. Взаимная ковариационная функция при наличии запаздыва-
ния .......................................................... 128
5.2. Функции спектральной плотности ......................... 130
5.2.1. Определение спектров с помощью ковариационных функций 130
5.2.2. Определение спектров через финитное преобразование
Фурье................................................... 139
5.2.3. Определение спектров с помощью фильтрации ............. 142
5.2.4. Функции когерентности ................................. 145
5.2.5. Взаимная спектральная плотность при наличии запаздыва-
ния .......................................................... 147
5.2.6. Соотношение неопределенности .......................... 149
5.3. Эргодические и гауссовы случайные процессы.............. 153
5.3.1. Эргодические случайные процессы ....................... 153
5.3.2. Достаточные условия эргодичности ...................... 157
536
Оглавление
5.3.3. Гауссовы случайные процессы .............................. 158
5.3.4. Линейные преобразования случайных процессов............... 160
5.4. Производные случайных процессов............................ 163
5.4.1. Ковариационные функции................................... 163
5.4.2. Спектральные плотности ................................... 166
5.4.3. Математическое ожидание числа пересечений оси абсцисс .... 168
6. Соотношения для линейных систем с одним входным про-
Глава
Глава
Глава
цессом ............................................... 172
6.1. Системы с одним входом и одним выходом .........,..... 172
6.1.1. Корреляционные и спектральные соотношения .......... 172
6.1.2. Функции обычной когерентности......................... 179
6.1.3. Модели с посторонним шумом ......................... 183
6.1.4. Оптимальные частотные характеристики ............... 188
6.2. Системы с одним входом и несколькими выходами......... 191
6.2.1. Модель с одним входом и двумя выходами .............. 191
6.2.2. Модель с одним входом и несколькими выходами......... 193
6.2.3. Исключение постороннего шума ....................... 196
6.3. Модели линейных решеток .............................. 198
6.3.1. Коэффициент усиления решетки ....................... 199
6.3.2. Направленность решетки.............................. 200
7. Многомерные системы .................................. 205
7.1. Системы с несколькими входами и одним выходом......... 205
7.1.1. Общие соотношения ................................... 205
7.1.2. Общий случай произвольных входных процессов.......... 208
7.1.3. Частный случай попарно некоррелированных входных про-
цессов ..................................................... 210
7.2. Системы с двумя входами и одним выходом .............. 211
7.2.1. Основные соотношения ................................ 211
7.2.2. Оптимальные частотные характеристики ................ 215
7.2.3. Функции обычной и множественной когерентности ....... 216
7.2.4. Условные спектральные плотности ..................... 218
7.2.5. Функции частной когерентности ....................... 224
7.3. Общие и условные модели с несколькими входами ........ 228
7.3.1. Условные преобразования Фурье........................ 231
7.3.2. Условные спектральные плотности ..................... 232
7.3.3. Оптимальные системы для условных входных процессов .. 233
7.3.4. Алгоритм вычисления условных спектров ............... 236
7.3.5. Оптимальные системы для исходных входных процессов.. 238
7.3.6. Функции частной и множественной когерентности ....... 240
7.4. Матричные формулы для многомерных систем ............. 242
7.4.1. Системы с многими входами и многими выходами......... 242
7.4.2. Система с многими входами и одним выходом............ 246
7.4.3. Системы при наличии шума на выходе................... 249
7.4.4. Система с одним входом и одним выходом............... 251
8. Статистические ошибки при оценивании основных парамет-
ров ........................................................ 253
Оглавление 537
8.1. Понятие о статистических ошибках .......................... 253
8.2. Оценки среднего значения и среднего квадрата............... 256
8.2.1. Среднее значение ......................................... 256
8.2.2. Средний квадрат .......................................... 260
8.2.3. Дисперсия ................................................ 262
8.3. Плотность вероятности ..................................... 263
8.3.1. Смещение оценки .......................................... 265
8.3.2. Дисперсия оценки ......................................... 266
8.3.3. Нормированная среднеквадратичная ошибка .................. 267
8.3.4. Оценки совместной плотности вероятности................... 268
8.4. Оценки ковариационных функций ............................. 269
8.4.1. Ограниченный по частоте белый шум......................... 272
8.4.2. Об отношении сигнал/шум................................... 273
8.4.3. Локализация экстремумов ковариационной функции....... 274
8.5. Оценки спектральных плотностей............................. 276
8.5.1. Смещение оценки .......................................... 278
8.5.2. Дисперсия оценки ......................................... 280
8.5.3. Нормированная среднеквадратичная ошибка .................. 281
8.5.4. Оценки спектральной плотности, полученные финитным пре-
образованием Фурье .......................................... 282
8.6. Выбор длины реализации .................................... 285
Глава 9. Статистические ошибки при оценивании более сложных па-
раметров ........................................................ 289
9.1. Оценки взаимной спектральной плотности .................... 289
9.1.1. Формулы для дисперсии оценок .............................. 292
9.1.2. Формулы для ковариаций оценок ............................. 294
9.1.3. Оценки фазового угла ...................................... 298
9.2. Оценки для моделей с одним входом и одним выходом ......... 299
9.2.1. Смещение оценок частотных характеристик ................... 301
9.2.2. Оценки когерентного спектра выходного процесса............. 304
9.2.3. Оценки функции когерентности .............................. 306
9.2.4. Оценки амплитудной характеристики.......................... 309
9.2.5. Оценки фазовой характеристики.............................. 312
9.3. Оценки для моделей с многими входными процессами...... 314
9.3.1. Оценки функций множественной когерентности ................ 316
9.3.2. Оценки множественного когерентного спектра выходного
процесса ......................................................... 316
9.3.3. Модели с одним условным входным процессом и одним вы-
ходным процессом........................................... 317
9.3.4. Оценки функций частной когерентности................ 318
9.3.5. Оценки частных когерентных спектров выходного процесса . 318
9.3.6. Оценки амплитудных характеристик для условных моделей . 319
9.3.7. Оценки фазовых характеристик для условных моделей ......... 319
Глава 10. Сбор и обработка данных.......................................... 321
10.1. Сбор данных......................................... 321
10.2. Регистрация данных ........................................ 325
10.2.1. Запись сигналов на магнитную ленту и их воспроизведение .. 325
538
Оглавление
10.2.2. Модуляция и демодуляция ............................. 327
10.3. Подготовка данных ..................................... 330
10.3.1. Теоремы о дискретном представлении случайных процессов . 331
10.3.2. Методы дискретизации и ошибки маскировки частот ..... 333
10.3.3. Ошибки квантования .................................. 335
10.3.4. Аналого-цифровые преобразователи .................... 337
10.4. Оценивание основных свойств процесса................... 338
10.4.1. Проверка стационарности ............................. 339
10.4.2. Проверка периодичности .............................. 342
10.4.3. Проверка нормальности ............................... 343
10.5. Анализ данных.......................................... 346
10.5.1. Анализ отдельных реализаций ......................... 346
10.5.2. Анализ совокупности реализаций ...................... 348
10.5.3. Проверка эквивалентности спектров................... 352
10.5.4. Соображения о методах вычислений..................... 355
Глава 11. Цифровые методы анализа..................................... 357
11.1. Подготовка данных ..................................... 357
11.1.1. Приведение к нулевому среднему значению и единичной дис-
персии ...................................................... 357
11.1.2. Удаление тренда ..................................... 358
11.1.3. Применение цифровых фильтров......................... 360
11.2. Ряд Фурье и быстрое преобразование Фурье............... 364
11.2.1. Ряд Фурье ........................................... 364
11.2.2. Быстрое преобразование Фурье......................... 366
11.2.3. Метод Кули—Тьюки..................................... 372
11.2.4. Применение к действительным последовательностям ..... 374
11.2.5. Некоторые другие формулы ............................ 376
11.2.6. Преобразование Винограда............................. 376
11.3. Плотность вероятности ................................
11.4. Ковариационные функции................................. 379
11.4. 1. Непосредственное оценивание ковариационных функций . 380
11.4. 2. Оценивание ковариационных функций методом БПФ...... 380
11.5. Функции спектральной плотности ........................ 385
11.5.1. Основы оценивания автоспектров ...................... 385
11.5.2. Подавление просачивания через боковые максимумы..... 387
11.5.3. Рекомендуемая последовательность вычислений ......... 393
11.5.4. Наплывающие преобразования .......................... 393
11.5.5. Другие способы спектрального анализа................. 394
11.6. Расчеты для двух реализаций............................ 397
11.6.1. Совместная плотность вероятности .................... 398
11.6.2. Взаимные ковариационные функции ..................... 398
11.6.3. Функции взаимной спектральной плотности ............. 399
11.6.4. Частотная характеристика............................. 400
11.6.5. Импульсные переходные (весовые) функции.............. 401
11.6.6. Функция обычной когерентности ....................... 402
11.7. Описание систем со многими входными процессами ........ 402
11.7.1. Преобразования Фурье и спектральные характеристики .. 403
11.7.2. Функции условной спектральной плотности ............. 404
11.7.3. Частотные характеристики и функции когерентности .... 408
Оглавление
539
11.7.4. Когерентный спектр выходного процесса ............... 409
11.7.5. Разложение оценок спектральных функций .............. 411
Глава 12. Анализ нестационарных процессов ............................ 416
12.1. Классы нестационарных процессов ....................... 416
12.2. Вероятностная стурктура нестационарного процесса ...... 418
12.2.1. Распределения более высокого порядка................. 419
12.2.2. Средние по времени распределения .................... 421
12.3. Среднее значение нестационарного процесса ............. 422
12.3.1. Независимые реализации .............................. 423
12.3.2. Коррелированные реализации .......................... 424
12.3.3. Анализ индивидуальных реализаций .................... 426
12.4. Средний квадрат нестационарного процесса .............. 428
12.4.1. Независимые реализации............................. 428
12.4.2. Коррелированные реализации .......................... 429
12.4.3. Анализ индивидуальных реализаций..................... 430
12.5. Корреляционная структура нестационарных процессов..... 432
12.5.1. Двойные по времени ковариационные функции............ 433
12.5.2. Другой способ представления двойных по времени ковариа-
ционных функций ............................................ 434
12.6. Спектральная структура нестационарного процесса........ 437
12.6.1. Двойные по частоте спектральные функции.............. 437
12.6.2. Другое представление двойной по частоте спектральной
функции ...................................................... 439
12.6.3. Частотно-временные спектральные функции.............. 445
12.6.4. Мультипликативная модель нестационарного процесса... 452
12.7. Соотношения между входом и выходом линейной системы в
нестационарном случае ...................................... 458
12.7.1. Нестационарный процесс на входе системы с зависящими от
времени параметрами ........................................ 458
12.7.2. Результаты для некоторых частных случаев............. 460
12.7.3. Связь частотно-временных спектральных функций входного
и выходного процессов....................................... 461
12.7.4. Связь спектральных функций энергии входного и выходного
процессов .................................................... 464
Глава 13. Преобразование Гильберта ................................... 469
13.1. Преобразование Гильберта процессов общего вида ........ 469
13.1.1. Вычисление преобразования Гильберта ............... 472
13.1.2. Примеры преобразований Гильберта..................... 473
13.1.3. Свойства преобразования Гильберта ................... 473
13.1.4. Связь с физически осуществимыми системами............ 477
13.2. Преобразования Гильберта и ковариационные функции ..... 480
13.2.1. Определение корреляции и огибающей .................. 480
13.2.2. Соотношения для преобразований Гильберта ............ 482
13.2.3. Аналитические сигналы ковариационных функций......... 483
13.2.4. Задачи бездисперсного распространения ............. 486
13.2.5. Задачи дисперсного распространения .................. 490
540
Оглавление
13.3. Выделение огибающей с последующим вычислением корре-
ляции ................................................ 493
Приложение А. Статистические таблицы ................................ 499
Приложение Б. Основные определения.................................. 570
Литература .......................................................... 522
Предметный указатель ................................................ 526
Научное издание
Джулиус Бендат, Алан Пирсол
ПРИКЛАДНОЙ АНАЛИЗ СЛУЧАЙНЫХ ДАННЫХ
Зав. редакцией Пропой В. И.
Ст. научный редактор Кирий А. Ю.
Мл. научный редактор Тарасова Л. В.
Художник Потапов В. С.
Художественные редакторы Иванов Н. М., Адаскина О.Н.
Технический редактор Анциферова М. А.
Корректор Куликова Т. Б.
ИБ № 6801
Подписано к печати 23.06.89.
Формат 60х90Иб Бумага офсетная № 1
Гарнитура тайме. Печать офсетная.
Объем 17,00 бум.л.Усл.печ.л. 34,00
Усл. кр.-отт. 37,00 Уч.-изд.л. 32,00
Изд. № 7/5948 Тираж 19000 экз. Зак.953,
Цена 2 р. 80 к.
Издательство «МИР»
В/О «Совэкспорткнига» Государственного комитета СССР
по делам издательств, полиграфии и книжной торговли.
Набрано в межиздательском фотонаборном центре
издательства «Мир»
129820, ГСП, Москва, И-110, 1-й Рижский пер., 2.
Можайский полиграфкомбинат В/О «Совэкспорткнига»
Государственного комитета СССР по делам издательств,
полиграфии и книжной торговли.
143200, Можайск, ул. Мира, 93.
УВАЖАЕМЫЙ ЧИТАТЕЛЬ!
Ваши замечания о содержании книги, ее
оформлении, качестве перевода и другие просим
присылать по адресу: 129820, Москва, И-110,
ГСП, 1-й Рижский пер., д. 2, изд-во «Мир».
Издательство «Мир» выпустит в 1990 году
Оран Э., Борис Дж. Численное моделирование реагирующих
потоков: Пер. с англ. — 39 л., ил. — (В пер.): 3 р. 20 к.
Книга авторов из США посвящена численным методам, используемым для
расчетов химически реагирующих потоков в различных технических устройст-
вах. Рассмотрены случаи до- и сверхзвуковых течений, однофазные и много-
фазные системы, детонация, моделирование турбулентного горения.
Для специалистов, аспирантов и студентов в различных областях приклад-
ной математики, авиационной, ракетно-космической техники, энергомашино-
строения и химической технологии.
Издательство «Мир» выпустит в 1990 году
Громадка Т.(П), Лей Ч. Метод комплексных граничных эле-
ментов для инженеров: Пер. с англ. —16 л., ил. — (В пер.): 1 р. 90 к.
Книга авторов из США, в которой излагаются методы граничных элементов
в комплексной плоскости для решения двумерных задач течения жидкости,
распространения тепла, теории упругости и др. Рассмотрены классические за-
дачи, допускающие аналитическое решение. Приведены соответствующие про-
граммы для расчетов на ЭВМ. Материал изложен просто и доступно, книга
может быть использована в качестве учебного пособия. Дополнена новыми
разработками в области методики и программами для расчетов на ЭВМ, в том
числе и созданными отечественными учеными.
Для специалистов в области численных расчетов физических и инженер-
ных задач, инженерно-технических работников, студентов и аспирантов соот-
ветствующих специальностей.
2р.80к: