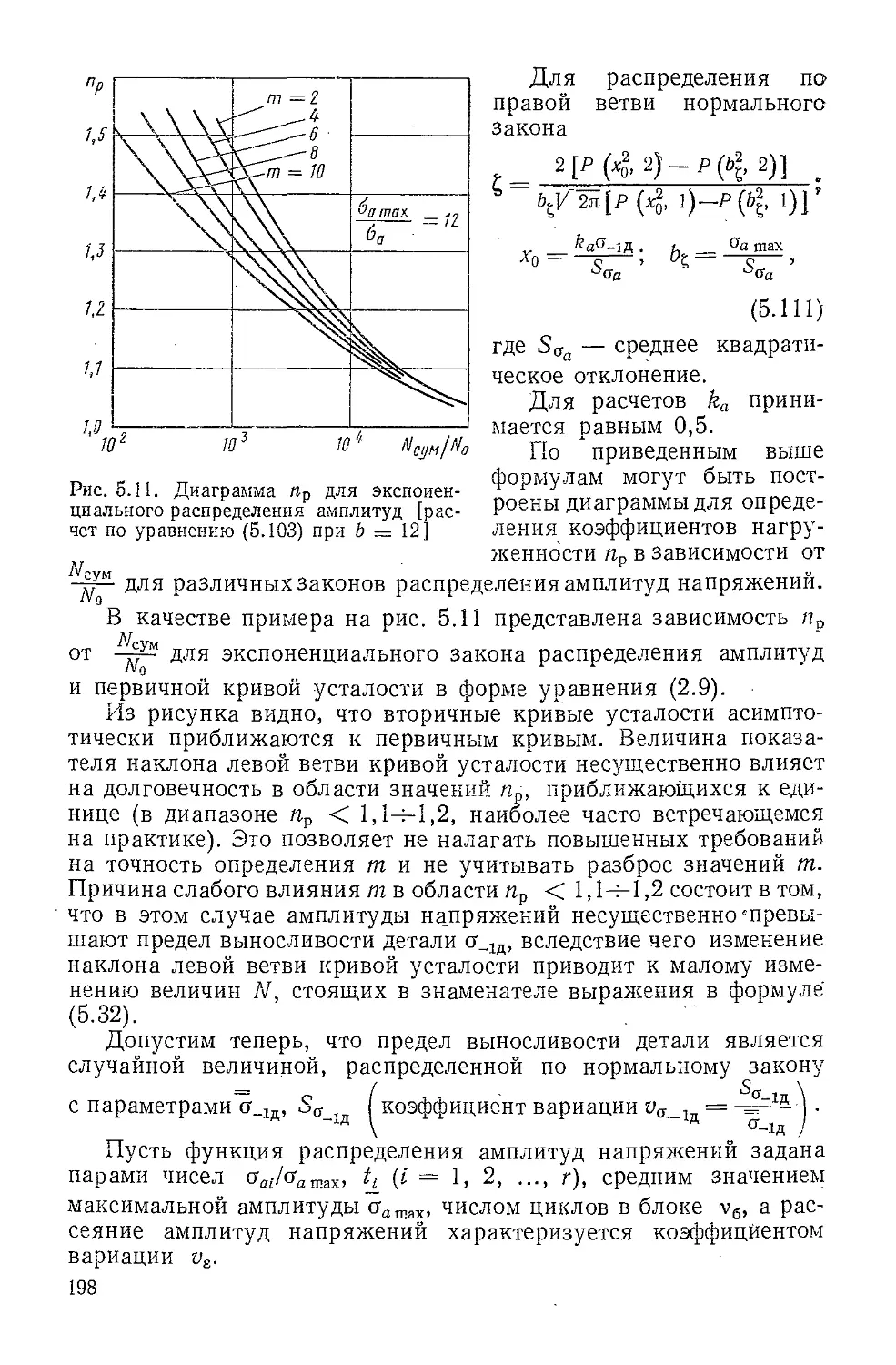
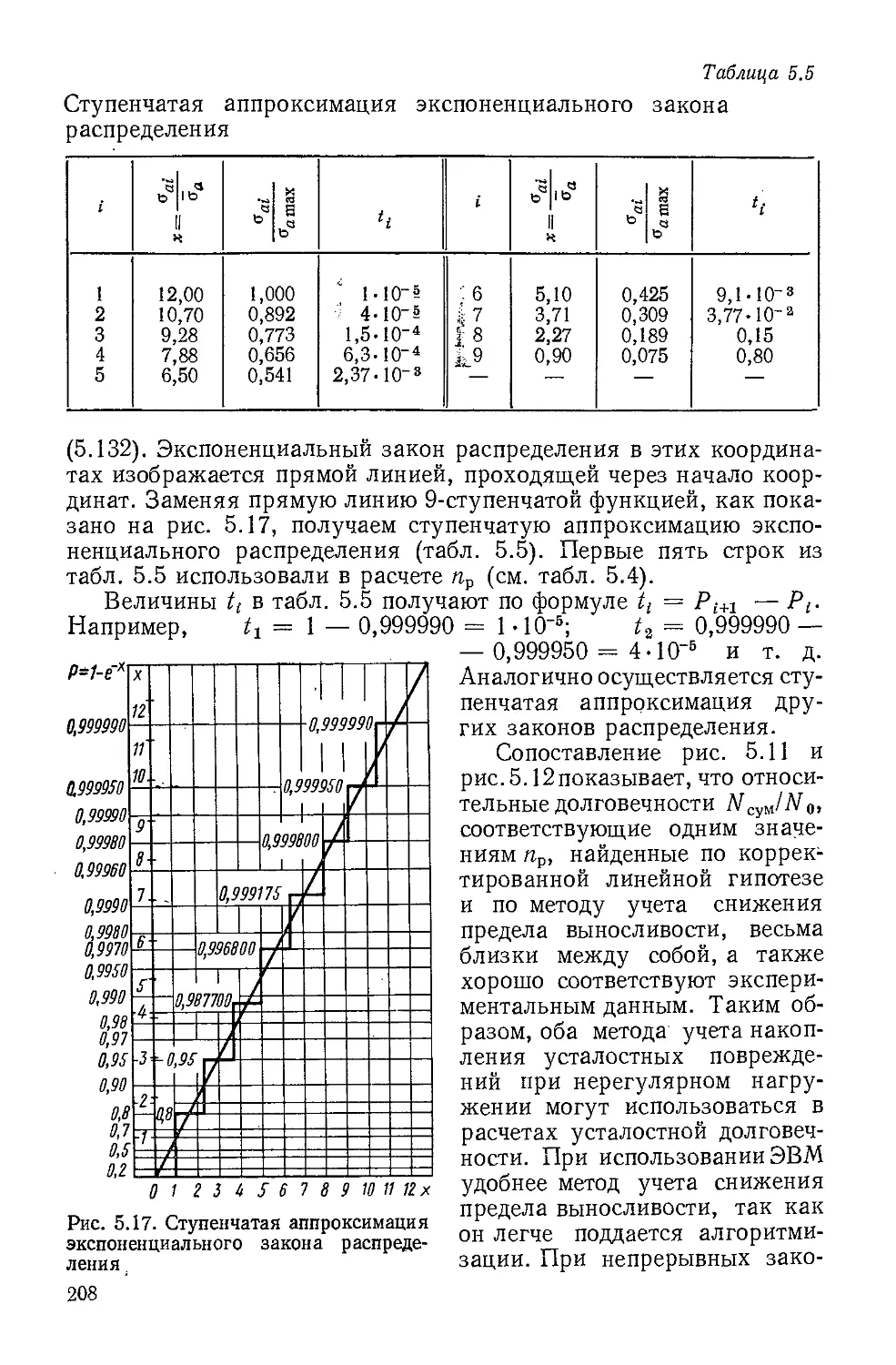
Author: Когаев В.П.
Tags: общее машиностроение технология машиностроения машиностроение машиностроительные нормативы
Year: 1977
Text
В.П.КОГАЕВ
Расчеты на прочность
при напряжениях,
переменных
во времени
БИБЛИОТЕКА
РАСЧЕТЧИКА
Редакционная
коллегия:
лауреат Ленинской премии,
заслуженный деятель науки и техники
РСФСР '
д-р техн. наук проф. С. Д.
Пономарев (председатель);
д-р техн. наук проф. Н. А. Алфутов;
лауреат Ленинской премии д-р техн.
наук проф. В. Л. Бидерман;
д-р техн. наук проф. В. П. Когаев;
лауреат Ленинской премии
заслуженный деятель науки и техники
РСФСР д-р техн. наук проф.
Н. Н. Малинин; д-р техн. наук
проф. В. А. Светлицкий
В.П.КОГАЕВ
Расчеты на прочность
при напряжениях,
переменных
во времени
V. J
МОСКВА «МАШИНОСТРОЕНИЕ» 1977
6П5.1
К57
УДК 621.01 : 539.4
Рецензент д-р техн. наук проф. И. А. БИРГЕР
Когаев В. П.
К57 Расчеты на прочность при напряжениях, переменных
во времени. М., «Машиностроение», 1977 (Б-ка
расчетчика).
232 с. с ил.
В книге изложены закономерности усталостного разрушения и методика
усталостных испытаний. Показано влияние конструктивных,
технологических и эксплуатационных факторов на выносливость. Описаны методы
расчета деталей машнн на прочность при напряжениях, переменных во
времени, как в детерминистической постановке, так и в .вероятностном аспекте.
Приведены примеры расчета.
Книга предназначена для научных работников и инженеров НИИ н КБ,
занимающихся вопросами прочности и надежности, она также может быть
использована студентами и аспирантами, которые изучают вопросы
прочности.
Kii3°?:°f? 29-78 6П5.1
038@1)-77
1-029
k 038@1)- 77
31301-029
Kn„»fnn 77 29-78 (§> Издательство «Машиностроение», 1977 г.
ИБ № 835
ВЛАДИМИР ПЕТРОВИЧ. КОГАЕВ
РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ НАПРЯЖЕНИЯХ,
ПЕРЕМЕННЫХ ВО ВРЕМЕНИ
Редактор издательства Т. Д. Онегина Технический редактор Н. В. Тимофеенко
Корректоры: В. А. Воробьева, Н. И. Шарунииа
Переплет художника А. Я- Михайлова
Сдано в набор 16/V 1977 г. Подписано к печати 6/IX 1977 г.
Т-16221 Формат 60X90 1/16
Бумага типографская № 2 Усл. печ. л. 14,5
Уч.-изд. л. 15,95 Тираж 14 000 экз. Заказ 220 Цеиа 1р. 10 к.
Издательство «Машиностроение»
107885, Москва, Б-78, 1-й Басманный пер., 3
Ленинградская типография № б Союзполиграфпрома прн Государственном комитете
Совета Министров СССР по делам издательств, полиграфии и книжной торговли
193144, Ленинград, С-144, ул. Моисееико, 10
Предисловие
Напряжения, возникающие в деталях машин в процессе
эксплуатации, в большинстве случаев переменны во времени, причем
они часто являются случайными функциями времени. Если уровень
переменных напряжений превышает определенный предел, то
в материале детали' протекает процесс постепенного накопления
повреждений, приводящий к образованию трещины, ее развитию
и окончательному разрушению детали. Этот процесс условно
называют усталостью металла, а соответствующее разрушение —
усталостным.
Проблема предотвращения усталостных разрушений весьма
актуальна во всех отраслях машиностроения, особенно в таких,
где аварии вследствие разрушения ответственных деталей""ведут
к катастрофическим последствиям (авиация, железнодорожный
транспорт и т. д.). Эта проблема приобретает еще большее значение
в связи с быстрым ростом мощностей в одном агрегате (без
существенного изменения габаритов), увеличением скоростей, _сил и
других параметров рабочих процессов машин.
Первоначально расчеты на прочность деталей машин при
напряжениях, переменных во времени, проводили по таблицам
допускаемых напряжений (Баха, Ретшера и пр.), в которых не
учитывался ряд факторов, оказывающих существенное влияние на
сопротивление усталости.
Исследования влияния на сопротивление усталости
концентраций напряжений, масштабного фактора, качества поверхности,
асимметрии цикла, вида напряженного состояния и других
факторов позволили предложить формулы для расчета коэффициентов
запаса прочности при переменных нагрузках [53], которые вошли
в практику расчета деталей во всех отраслях машиностроения и до
настоящего времени используются в нормативных расчетах,
основанных на детерминистических представлениях [43, 52].
Дальнейший прогресс в развитии методов расчета деталей
машин на прочность при переменных напряжениях связан с
внедрением вероятностных представлений в практику расчетов [6, 7, 33,
24, 34, 52, 59, 62].
Эффективность и перспективность применения вероятностных
методов расчета на усталость связаны с тем, что на основе учета
5
рассеяния характеристик прочности и нагруженности они
позволяют рассчитывать функцию распределения ресурса детали до
возникновения усталостной трещины, являющуюся важнейшей
характеристикой долговечности, надежности детали и ее поведения в
процессе эксплуатации. Эмпирическую оценку функции распределения
ресурса получают статистической обработкой данных о количестве
случаев появления усталостных трещин в условиях эксплуатации
в зависимости от ресурса деталей серийного и массового
производства. Близость эмпирической и расчетной функций распределения
ресурса является критерием правильности применяемых
вероятностных методов расчета и исходных данных о нагрузках и прочности.
Достоверность получаемых расчетом оценок функций
распределения ресурса определяется объемом экспериментальной
информации о характеристиках прочности и нагруженности. При этом,
чем больше вероятность безотказной работы, которую нужно
оценить расчетом, тем больше при этой же точности оценок требуемый
объем экспериментальной информации. В настоящее время
возможна оценка расчетом с удовлетворительной точностью
вероятностей безотказной работы до Р = 0,990-^0,999. При более высокой
требуемой вероятности Р соответствующие расчеты носят
сравнительный характер и должны быть дополнены нормативными
расчетами по запасам прочности, определяемым по нижней границе
(с учетом рассеяния) пределов выносливости и верхней границе
амплитуд напряжений [3].
В настоящей книге изложены основные понятия о
характеристиках сопротивления усталости, методах их определения,
факторах, влияющих на сопротивление усталости и традиционных
детерминистических методах расчета на усталость по коэффициентам
запаса прочности; приведены методы статистической интерпретации
случайной переменной нагруженности деталей и вероятностные
методы расчета их на усталость. Эти методы касаются расчетов
ресурса до появления первой макроскопической трещины
усталости в тех деталях, которые испытывают за срок службы суммарное
число циклов повторения амплитуд напряжений NcyK > 105
циклов, т. е. расчетов на многоцикловую усталость. Даны примеры,
поясняющие использование изложенных методов расчета.
Глава 1
Образование
и развитие усталостных
повреждений металла
1. Механизм усталостного разрушения
и характер
усталостных изломов деталей машин
Большинство деталей машин (валы, шестерни, болты, рамы,
упругие элементы и т. д.) в процессе работы подвергаются
воздействию напряжений, переменных во времени. Если уровень
переменных напряжений превосходит определенный предел, то в
материале деталей происходит процесс постепенного накопления
повреждений, который приводит к образованию
субмикроскопических трещин. Длина этих трещин увеличивается, затем они
объединяются, образуя первую макроскопическую трещину, под которой
понимается трещина протяженностью 0,1—0,5 мм. У корня этой
трещины возникает местное увеличение напряжений, называемое
концентрацией напряжений, которое облегчает ее дальнейшее
развитие. Трещина, постепенно развиваясь и ослабляя сечение,
вызывает в некоторый момент времени внезапное разрушение детали,
которое нередко бывает связано с авариями и весьма тяжелыми
последствиями. Указанный процесс постепенного накопления
повреждений в материале детали под действием переменных
напряжений, приводящих к изменению свойств материала, образованию,
развитию трещин и разрушению детали называют усталостью
материала.
Для изучения физической природы процесса усталостного
разрушения применяют микроскопические, электроноскопические,
рентгеновские, калориметрические и поляризационно-оптические
методы, а также измеряют твердость материала в процессе усталости,
рассеяние энергии, плотность дислокаций и т. д. [1, 19, 66,
67, 76].
Механизм процесса усталостного разрушения металлов
неразрывно связан со структурной неоднородностью, заключающейся
в случайных вариациях размеров и очертаний отдельных
кристаллитов (зерен) металла, направлений их кристаллографических
плоскостей, в наличии различных фаз, включений, дефектов
кристаллической решетки (вакансий, дислокаций) и т. д. Вследствие
указанной неоднородности при переменных напряжениях, даже
не превосходящих предел пропорциональности, в отдельных небла-
7
гоприятно ориентированных зернах начинается циклическая
пластическая деформация, которая связана с циклическими
деформациями сдвига по определенным кристаллографическим плоскостям.
Результаты этих сдвигов можно наблюдать с помощью
металлографического микроскопа. На рис. 1.1 можно видеть развитие следов
сдвига на разных стадиях циклического нагружения образцов из
. чистого никеля. Первые линии сдвига появляются в отдельных
зернах уже на ранних стадиях нагружения, составляющих по
числу циклов 1—10% от общей долговечности образца до
разрушения.
По мере накопления числа циклов количество линий сдвига
увеличивается, они расширяются, переходят на другие зерна,
что показано на рис. 1.1 (здесь образец нагружался амплитудами
переменных напряжений, превосходящими предел выносливости).
При этом циклическая пластическая деформация и образование
линий сдвигов происходит почти во всех зернах металла. На
рис. 1.2 показано развитие следов сдвига по мере накопления числа
циклов на образцах из мягкой стали при амплитудах напряжений
ниже предела выносливости. Характерным для этого случая
является то, что следы сдвига образуются лишь в отдельных
неблагоприятно ориентированных зернах и не переходят на другие зерна
даже после значительного количества циклов (например, после
4,6-107 циклов, см. рис. 1.2, г). Образования макроскопической
трещины усталости и разрушения при этом не происходит.
На циклическую пластическую деформацию в отдельных
зернах металла при напряжениях, не превосходящих пределы
выносливости и пропорциональности, затрачивается определенная
энергия, и образуется петля упругого гистерезиса (рис. 1.3). Площадь
петли, пропорциональная энергии, затрачиваемой за один цикл на
пластическую деформацию в отдельных зернах, характеризует
рассеяние энергии в материале при циклическом нагружении.
Изучение зависимости площади петли гистерезиса от. уровня
амплитуды напряжений, числа циклов, состояния материала,
температуры и других факторов позволяет глубже понять механизм
усталостного разрушения и создает предпосылки для разработки
энергетических трактовок закономерностей усталостного разрушения
[19, 40].
Образование первых следов сдвига начинается, как правило,
на поверхности образца вследствие облегченных условий
деформирования зерен в этой зоне и наличия концентрации напряжений от
микронеровностей поверхности. В работе Томпсона [66]
приведены результаты испытаний на усталость образцов из чистой меди.
На различных стадиях испытания образцы подвергались
электрополировке со снятием слоя толщиной около 2 мкм.
Электрополировка после 0,27 >106 циклов G,5% от общей долговечности
образца) привела почти к полному удалению линий сдвига. Это
свидетельствует о том, что на данной стадии деформирования глубина
проникновения следов сдвига не превышала 2 мкм. После 1,54 X
8
,1 »*
Рис. 1.1. Развитие следов сдвига на разных стадиях циклического нагружения
образцов из чистого никеля при амплитуде напряжений, превышающей
предел выносливости:
а — после 10* циклов; б — после 5-10* циклов; в ^-. после 27-10* циклов [66]
Рис. 1.2. Развитие следов сдвига на разных стадиях циклического
нагружения образцов из мягкой стали при амплитуде напряжений, не
превышающей предел выносливости:
а — после 5-10* циклов; б — после 5-Ю5 циклов; в — после 6,5.10»
циклов; г —. после 4,6-10' циклов [66]
Рис. 1.3. Петля гистере- Рис. 1.4. Схема образования экструзий
зиса при циклическом
деформировании в ко- х 106 циклов многие следы сдвига при
ординатах напряжения удалении электрополировкой слоя тол-
р ' щиной 2 мкм исчезли, однако ряд ли-,
^ ~ а "^<7пд; 2 ~ ° > ний сдвига, названных устойчивыми,
т сохранился. Их глубина превышала
2 мкм. После 2,8 • 106 циклов
некоторые устойчивые следы сдвига переходят на соседние зерна и при
окончательном разрушении при 3,65 X 106 циклов сильно
разрастаются, превращаясь в усталостную трещину. Эти испытания
показывают, что начальные усталостные повреждения
концентрируются в тонком поверхностном слое. Было проведено
исследование, в котором через каждые 25% долговечности исходного
образца электрополировкой удалялись все устойчивые следы
сдвига, после чего испытание образца продолжалось. В результате
суммарная долговечность образцов значительно превысила исходную.
Форсайтом [66] были обнаружены поверхностные повреждения
металла при циклическом нагружении, названные экструзиями и
интрузиями. Экструзии представляют собой выдавленные выступы
в виде тонких лепестков (рис. 1.4); интрузии — тонкие щелеоб-
разные углубления (впадины), проникающие внутрь металла по
мере накопления числа циклов и постепенно превращающиеся
в зародыш усталостной трещины. Продольный разрез
образца с экструзиями и интрузиями на поверхности дан на рис. 1.5.
Таким образом, из-за устойчивых следов сдвига, экструзий и
интрузий, а также вследствие других механизмов, как правило, на
поверхности образца зарождается начальная макроскопическая
трещина усталости. Весьма малую локальную зону, близкую
к точке, в которой образуется первая трещина и откуда начинается
ее развитие, называют фокусом усталостного излома [68]. На
рис. 1.6 приведена схема усталостного излома шатунной шейки
коленчатого вала, на которой показаны основные характерные
зоны и признаки, позволяющие отличить усталостный излом от
других видов излома (хрупкого, вязкого в условиях статического
10
•'*.
1 §'■'*"..
^ ■•■
и,
Рис. 1.5. Экструзии и интрузии на поверхности образца, образовавшиеся в
результате циклического нагружения [66]
разрушения и др.). Обычно фокус излома располагается на
поверхности в местах концентрации напряжений или поверхностных
дефектов в виде царапин, трещин, неметаллических включений
и т. п. При наличии внутренних дефектов или при поверхностном
упрочнении (например, при цементации, азотировании и т. д.)
фокус излома может располагаться и на некоторой глубине от
поверхности образца.
Очагом разрушения называют
весьма малую зону, прилегающую к
фокусу излома и соответствующую
начальной макроскопической
трещине усталости. Зона излома в
области очага разрушения обычно
характеризуется наибольшим блеском и
наиболее гладкой поверхностью по
сравнению с другими участками
излома. Усталостные линии на
поверхности очага разрушения обычно
отсутствуют. На усталостном изломе могут
быть и несколько очагов разрушения.
Одновременное возникновение
нескольких таких очагов свойственно
большим напряжениям,
соответствующим ограниченной
долговечности по кривой усталости. Правиль-
Рис. 1.6. Схема усталостного
излома шейки коленчатого вала:
1 — фокус излома и очаг
разрушения; 2 — вторичные ступеньки
и рубцы; 3 — усталостные лннин;
4 — зона ускоренного развития
излома; 5 — зона долома
11
йое выявление очагов разрушения при анализе усталостных
изломов имеет важное значение при установлении причины
разрушения.
Участок избирательного развития соответствует зоне
развившейся трещины усталости. Эта зона имеет гладкую блестящую
поверхность, на которой видны характерные признаки излома.
Степень блеска и шероховатость поверхности усталостной трещины
бывают различными. Более блестящая (наименее шероховатая)
поверхность получается при малых перегрузках, при которых
скорость распространения трещины мала, а время ее развития велико.
Гладкий и блестящий вид поверхности усталостной трещины
возникает не от трения и наклепа вследствие притирания смежных
поверхностей трещины, как полагали ранее, а связан с
микроизбирательностью распространения усталостной трещины [68]. В зоне
избирательного развития обычно видны характерные усталостные
линии, имеющие волнообразный вид и расходящиеся от очага
разрушения как из центра. Усталостные линии являются следами
фронта продвижения трещины. Появление этих линий часто
связано с некоторым изменением направления развития трещин,
вследствие чего образуется небольшой уступ, выявляемый только
при профилографировании. Другой причиной появления
усталостных линий является изменение шероховатости поверхности
излома при изменении степени перегрузки в процессе эксплуатации.
Форма усталостных линий зависит от формы детали и характера ее
нагр ужения.
Часто в деталях может зарождаться несколько трещин
усталости из разных фокусов. В этом случае начальные трещины
располагаются параллельно одна другой. В результате последующего их
слияния на поверхности излома образуются ступеньки и рубцы.
Чем выше уровень действующих напряжений, тем большее
количество очагов зарождения трещин усталости, тем большее число
ступенек и рубцов появляется на поверхности излома.
Направление развития первоначальной трещины может
измениться (см. рис. 1.6), при этом образуются зародыши пасынковых
трещин, развивающихся в другом направлении. От слияния
пасынковых трещин образуются вторичные ступеньки и рубцы 2.
Участок ускоренного развития 4 является переходной зоной
между участком собственно усталостного развития трещины и
зоной долома. Эта зона образуется в течение нескольких циклов,
предшествующих окончательному разрушению.
Зона долома 5 образуется на последней стадии излома и
обладает признаками макрохрупкого разрушения. Изучение формы и
свойств поверхности усталостных изломов дает возможность в ряде
случаев судить о характере усилий, вызвавших разрушение, о
степени перегруженности сломавшейся детали и т. д., что позволяет
правильно определить причину, вызвавшую разрушение детали и
наметить мероприятия по предотвращению повторных разрушений.
Развитие трещины после образования ее зародыша зависит от ха-
12
а
-=*с?-
-<
Усталостная
трещит
рактера распределения напряжении.
Если условия возникновения трещины
зависят в основном от касательных
напряжений, то ее развитие связано в
большинстве случаев с влиянием
нормальных напряжений. При действии
переменного напряжения (растяжения-
сжатия или изгиба) трещина
развивается по поверхности действия
наибольших нормальных напряжений. На
рис. 1.7 показана трещина усталости
по месту сопряжения стержня и головки
болта. Нормали к поверхности трещины
приблизительно совпадают с
направлениями наибольших нормальных напряжений. Так, при кручении
трещина развивается под углом 45° к образующей~цилиндра, т. е.
перпендикулярно к направлению максимальных растягивающих
напряжений.
При анализе усталостных изломов широко применяют фракто-
графические методы исследования их поверхности [19, 76].
Рис. 1.7. Трещина усталости
у головки болта
2. Закономерности развития усталостных трещин
Опыт эксплуатации самых разнообразных машин (подвижного
состава железных дорог, автомобилей и тракторов,
сельскохозяйственных и строительно-дорожных машин и т. д.) показывает, что
в процессе работы могут появляться усталостные трещины в их
элементах. Дефекты, заложенные в элементах машин еще при их
изготовлении (трещины, непровары в сварных соединениях,
неметаллические включения и рыхлоты в отливках и т. п.), могут играть
роль начальных трещин. Начальные трещины развиваются под
действием эксплуатационных нагрузок до тех пор, пока не
достигают критических размеров, при которых происходит внезапное
разрушение детали. Период работы конструкции (измеренный в
километрах пробега, часах или годах работы, количестве полетов и
т. п.) от момента возникновения первой макроскопической
трещины усталости (протяженность которой обычно принимается
равной 0,1 -г-0,5 мм) до окончательного разрушения называют
живучестью элемента конструкции или детали машины.
Знание живучести элемента имеет большое практическое
значение, так как срок между детальными профилактическими
осмотрами конструкции должен устанавливаться в зависимости от
живучести, оцениваемой в статистическом аспекте с введением запаса
по ресурсу.
При изучении роста трещин используют методы и понятия
механики разрушения, в частности понятие коэффициента
интенсивности напряжений К\ (кгс/мм3/2). В простейшем случае тонкой
пластины бесконечно большой ширины с трещиной длиной 21,
13
растягиваемой напряжением а (рис. 1.8), Кг находят следующим
образом. Распределение напряжений в пластине на продолжении
трещины (вдоль оси х) определяют по формуле Ирвина [32, 41]:
1 + г
Vx* — /2
V2lr + r2'
A.1)
г -- расстояние от начала координат до текущей точки
- расстояние от вершины трещины до этой же текущей
где л: = / -
на осих; г
точки.
При приближении текущей точки к вершине трещины
напряжения возрастают согласно решению теории упругости до
бесконечности, так как при х —»/ или г —*0 из (формулы 1.1) следует, что
а,,—>оо. Поэтому выразить какие-либо характеристики прочности
тел с трещинами через напряжения у конца трещины не
представляется возможным. Чтобы обойти эту трудность, можно поступить
следующим образом. Умножим обе части уравнения A.1) на ]/2яг
и перейдем к пределу при г—*0. Имеем
lim]/2nr^ = lim а(г+^
V2.
ш
г->0
г->о Vllr + г2
■ а]/"я/.
A.2)
Таким образом, указанный предел существует. Его обозначают
К\ и называют коэффициентом интенсивности напряжений. Для
бесконечно широкой пластины с трещиной длиной 2/ при плоском
напряженном состоянии, растягиваемой напряжением а в
направлении, перпендикулярном трещине (см. рис. 1.8), согласно
формуле A.2) коэффициент интенсивности напряжений
/Ci=xr/n£ A.3)
Заменив приближенную функцию, стоящую слева под знаком
предела в формуле A.2), ее предельным значением Ki (кгс/мм3/2),
получим приближенную формулу для ау, которая в окрестности
трещины практически совпадает с точной формулой A.1):
t \ t t 11
ГГГГГГГГТТГПТТТТ
Рис. 1.8. Пластина бесконечно
большой ширины с трещиной при
растяжении
14
_,- ^=. A.4)
V 2лг
Индекс I введен для
характеристики первого вида
деформации (нормальный разрыв
трещины, см. рис. 1.8) в
отличие от двух других
рассматриваемых в механике
разрушения видов деформаций
(сдвиговых) [41, 71].
Для пластины ограниченной
ширины В с трещиной длиной 21,
растягиваемой напряжением а (рис. 1.8), Кг находят следующим
образом. Распределение напряжений в пластине на продолжении
трещины (вдоль оси х) определяют по формуле Ирвина [32, 41]:
1 + г
Vx2 — /2
V2lr + r2'
A.1)
г -- расстояние от начала координат до текущей точки
- расстояние от вершины трещины до этой же текущей
где л: = / -
на осих; г
точки.
При приближении текущей точки к вершине трещины
напряжения возрастают согласно решению теории упругости до
бесконечности, так как при х —»/ или г —*0 из (формулы 1.1) следует, что
а,,—>оо. Поэтому выразить какие-либо характеристики прочности
тел с трещинами через напряжения у конца трещины не
представляется возможным. Чтобы обойти эту трудность, можно поступить
следующим образом. Умножим обе части уравнения A.1) на ]/2яг
и перейдем к пределу при г—*0. Имеем
lim/2nray = lim а{1+!-
V2.
ш
г->0
г->о Vllr + г2
■ а]/"я/.
A.2)
Таким образом, указанный предел существует. Его обозначают
К\ и называют коэффициентом интенсивности напряжений. Для
бесконечно широкой пластины с трещиной длиной 2/ при плоском
напряженном состоянии, растягиваемой напряжением а в
направлении, перпендикулярном трещине (см. рис. 1.8), согласно
формуле A.2) коэффициент интенсивности напряжений
/Ci=>a/n£ A.3)
Заменив приближенную функцию, стоящую слева под знаком
предела в формуле A.2), ее предельным значением Ki (кгс/мм3/2),
получим приближенную формулу для ау, которая в окрестности
трещины практически совпадает с точной формулой A.1):
t \ t t 11
ГГГГГГГГТТГПТТТТ
Рис. 1.8. Пластина бесконечно
большой ширины с трещиной при
растяжении
14
_,- ^=. A.4)
V 2лг
Индекс I введен для
характеристики первого вида
деформации (нормальный разрыв
трещины, см. рис. 1.8) в
отличие от двух других
рассматриваемых в механике
разрушения видов деформаций
(сдвиговых) [41, 71].
Для пластины ограниченной
ширины В с трещиной длиной 21,
Обобщение результатов ряда исследований позволило [41 ]
предложить следующую формулу для коэффициента
интенсивности напряжений для трещин, размеры которых малы по
сравнению с остальными размерами тела:
#! = С4а/я/, A.8)
где а — номинальное напряжение по брутто-сечению в плоскости
2
трещины; С4 — коэффициент, принимающий значения от — (для
дискообразной трещины радиусом /) до 1,12 (для поверхностной
трещины или трещины на кромке листа глубиной /). Типичные
дефекты, представляющие опасность, начинаются, как правило, на
поверхности, причем их относительные размеры обычно сходны.
Поэтому в первом приближении для таких дефектов могут быть
приняты указанные значения С4.
Изучению закономерностей развития усталостных трещин было
посвящено значительное количество работ [42, 71, 72, 96]. Для
описания развития усталостных трещин в весьма широких тонких
пластинах со сквозной трещиной длиной 21 в большом количестве
работ были предложены различные формулы, которые могут быть
приблизительно аппроксимированы следующей зависимостью:
w = A(snlm' (L9>
где -jKr— скорость развития трещины (мм/цикл); а — переменное
номинальное напряжение по брутто-сечению пластины (кгс/мм2);
/ — половина длины трещины; А, т, п — константы.
Если принять /п = -у- и учесть формулу для коэффициента
интенсивности напряжений Кг A.3), то в правой части выражения
A.9) получим функцию от Ki- С учетом этого Пэрисом была
предложена следующая формула для скорости роста усталостной
трещины:
^ = С(А^Г- A-10)
где AK'j = Ki щах — Ki „,!„ — размах (кгс/мм3/2) колебания
коэффициента интенсивности напряжений; lKimax,
Kimla—вычисляются по формулам типа A.3), A.5)—A.8), если в них вместо о
подставить соответственно максимальное ашах и минимальное 0min
напряжения цикла при условии, что эти напряжения
растягивающие, т. е. коэффициент асимметрии R > 0 (знакопостоянный цикл
напряжений)].
Если минимальное напряжение amln отрицательное
(знакопеременный цикл напряжений, R < 0), то при подсчете AK\ в формуле
A.10) принимается Kimin = 0. В работе Ирвина и Пэриса [42]
приведены следующие значения констант: п = 4 для всех сталей
при испытании на воздухе при комнатной температуре; С1 = 1,6 X
X Ю-13 мм7/кгс4 — для средней скорости роста трещины в сталях
16
Рис. 1.10. Зависимость скоростей
развития усталостных трещин от размаха
коэффициент! интенсивности
напряжений A/(i:
0,40-10-8 (A/<C,J.25; 2 ~*
1
dl
dl
dN
-3^= 0.97.10- (AKj)
2.25
Л К, ,кгс/мм3Ь
10J
5
J
2
Wz
5
J
г
w
-4f[f/
11II
/
-4Ц-
'
1
|W
nfl
~"Hf
Tff
-1
Tf
|
W~S234S 10'f
1Г dl/dN.MM/цикп
средней и малой прочности; С2 = 2,6-10~13 — для средней
скорости во всех сталях; С3 = 3,2-103 мм7/кгс4— для максимальной
границы зоны разброса опытных точек на графике в координатах
lg-7TT—- IgA/Ci, соответствующей оценке максимальной скорости
роста трещины во всех сталях.
Уравнение A.10) при указанных значениях констант
дает удовлетворительную оценку скоростей роста трещин от
2,5-10 мм/цикл (и выше) до скорости в момент окончательного
разрушения при условии, что значение К\ останется ниже
критического значения коэффициента интенсивности КХй
(соответствующего хрупкому разрушению) для данного материала, а
номинальное напряжение не превысит предела текучести.
В статье Бэрсома [72] приведены результаты обработки
опытных данных по скорости развития усталостных трещин по 19 типам
сталей, полученных различными авторами при испытании на
воздухе при знакопостоянных циклах растяжения (R > 0). Опытные
точки укладываются в зону разброса, заштрихованную на рис. 1.10.
По оси абсцисс на этом рисунке отложены скорости ^развития
трещин -TTj (мм/цикл) в логарифмическом масштабе, по оси
ординат— АК1 (кгс/мм3/2) в том же масштабе. Верхняя и нижняя
границы зоны разброса описываются уравнением A.10) при п =
= 2,25, С = 0,40-10-8 — для верхней линии и С = 0,97-Ю-8 —
для нижней линии.
выразить в дюймах за цикл, a'AKi в ksi У in
{lksi l/"JnT == 3,543 кгс/мм3/2), где ksi — одна тысяча фунтов на
квадратный дюйм, то уравнения для верхней и нижней линий будут
иметь вид
-^^О^-Ю-^А^J-25; A.11)
т, dl
Если w
dN'
0,66-lO-8^J-25.
A.12)
17
Нетрудно видеть, что при переходе от дюймовой системы к
метрической коэффициент С в уравнении A.10) умножается на 1,47,
an — остается без изменения.
Уравнение Пэриса A.10) не учитывает степень асимметрии
цикла. Для этого фактора Форманом [71 ] была предложена
следующая формула:
где
dl __ C(AKi)n
dN~ A —i?) /Cc — А/С '
A — —T? ", A Ai —■ A] max Al mln-
A.13)
Ku
Один из вариантов теории роста усталостных трещин был
разработан Г. П. Черепановым [71 ]. В простейшем случае из этой
теории вытекает следующее уравнение, хорошо соответствующее
опытным данным при надлежащем подборе параметров:
^ = -P(^-«-^^ + ln|^L). A.14)
\ Лс Лс Л1 min '
В работе Бэрсома [72] приводится формула, которая
одинаково хорошо описывает рост усталостных трещин для материалов
с различными модулями упругости, а именно:
|i = DAGI( A.15)
где AG, = Gj max — Gj m!n — размах величин энергий на
продвижение трещины в пластине на единицу длины. Размах AGj (кгс/мм)
связан с К\ следующими соотношениями:
при плоском напряженном состоянии
AGI==^; A.16)
при плоском деформированном состоянии
AGI = i^L(A^1J> A.17)
где Е, ц — соответственно модуль упругости и коэффициент
Пуассона. При подсчете AG, в уравнении A.15), как и в формуле
Пэриса, предполагается, что трещина растет только при
растягивающих напряжениях. Поэтому при cmln < 0, т. е. при R < 0,
принимается Gj max = 0.
Уравнение A.15) практически идентично уравнениям A.11),
A.12), если пренебречь небольшой разницей в значениях я. На
рис. 1.11 представлены экспериментальные данные по развитию
трещин в пластинах из высокопрочной стали, титанового и
алюминиевых сплавов.
18
Значение константы D равно 5 • Ю-7, если / выражено в дюймах,
a G: в psi-in (psi — фунт на квадратный дюйм). Если / выражено
в мм, a Gl имеет размерность кгс/мм, то D = 0,351 • 10~9.
При подсчетах ординат модули упругости были взяты: для стали"
Е = 2,Ы04 кгс/мм2, для алюминиевых сплавов Е = 0,74 X
X 104 кгс/мм2, для титанового сплава Е = 1,1 -Ш4 кгс/мм2.
Несмотря на существенное различие модулей упругости указанных
материалов, уравнение A.15) хорошо соответствует опытным
данным для сталей, алюминиевых и титановых сплавов при общем для
всех материалов значении константы D.
Величина энергии на продвижение трещины Gt, а следовательно,
и ее размах связаны следующими соотношениями с раскрытием
трещины б и пределом текучести ат:
G: = бтат и AGl = (Абт) ат. A.18)
На рис. 1.12 показано раскрытие трещины б и пластическая
зона (заштрихованная) у края трещины протяженностью 2гу.
Подставляя выражение A.18) в уравнение A.15), получаем
dl
Ж, = П(АЬ)вт
dN
A.19)
Таким образом, скорость роста трещины пропорциональна
раскрытию трещины и пределу текучести материала.
Уравнения A.15) и A.18) справедливы только в области низких
значений коэффициентов интенсивности К\ и номинальных
напряжений, низких по сравнению с пределом текучести. Для сталей
с высоким значением ат эта область соответствует значениям
Ki< 100 ksi]/"in = 354,3 кгс/мм3/2.
По мере приближения Ki к критическому значению К\с
(соответствующему хрупкому разрушению в условиях плоского
деформированного состояния) ско-
Mi ^KZCiHH рость развития трещин су-
/F ' щественно возрастает,
причем на графиках в
координатах -Tj- — AKi имеется
/ -
OS
Пй -
П ? -
П 9 -
U,L
,'''
QXT*
.'Г"
7^
#*
-*тл
3*:
J US
10
г з 6
Ж
dN
, мм/цикл
Рис. 1.11. Зависимость скоростей разви- Рис. 1.12. Пластическая зона и рас-
тия усталостных трещин от отношения крытие трещины у ее края
I^KilVE в пластинах из высокопрочной
стали, алюминиевых и титановых сплавов
19
200
700
I
III 1 III
LSr = 0,041мм
--
:;
—4
i
■•rrtl
40
30
£0
10
В
4
3 45 W~* 2 3 4S W'3 2 3 ^-,мм1и,икп
dN
Рис. 1.13. Зависимость скоростей развития
усталостных трещин от размаха
коэффициента интенсивности АК\
перелом, как показано на
рис. 1.13. На этом рисунке
представлены
экспериментальные данные Кларка,
приведенные в статье
Бэрсома [72] по
развитию трещин в листах
из алюминиевого сплава
5456-H32L_ При A*d «s
<25ksi]/in=88,5 кгс/мм3/2
показатель степени в
уравнении A.10) «s2,a при
А.К1 больше этого
значения, nsz 5,5. Таким
образом, переход от одной
интенсивности роста
скоростей развития трещин с
увеличением A.Ki к другой, существенно большей, происходит
при A.Ki = 88,5 кгс/мм3^ (или AGt =1,1 кг/мм). Подставляя это
значение (AGj) и значение предела текучести для данного
материала (стт = 26 кгс/мм2) в уравнение A.18), получаем значение
приращения величины раскрытия трещины Абт, соответствующее
переходу от меньшей интенсивности роста скоростей развития
трещин с увеличением Л/Ci к большей, а именно, Дбт = 1,6-Ю-3
in = 0,041 мм.
В статье Бэрсома [72] показано, что значение Абт,
соответствующее точке перелома на графике типа рис. 1,13, является
общим для высокопрочных сталей, алюминиевых и титановых
сплавов. Таким образом, основным фактором, определяющим скорость
развития усталостной трещины, по мнению Бэрсома, является
размах величины энергии на продвижение трещины AGj, связанный
с размахом коэффициента интенсивности напряжений Л/Сг
соотношениями A.15), A.16), и с размахом величины раскрытия трещины
Абт соотношением A.18).
Имея зависимость для скоростей развития усталостных трещин
dl
•jjj и интегрируя ее, можно найти зависимость для числа циклов
Np, необходимого для развития трещины от ее начальной длины /0
до конечной /р, соответствующей окончательному разрушению.
Так, на основании соотношений A.8) и A.10) при п = 4
A.20)
где
С = Ся Сц.
Разделяя переменные и интегрируя, получаем
Nn
J|- = C'(ActL \dN,
20
где /0, /р — длины трещин соответственно начальной и в момент
разрушения; Np — число циклов, необходимое для развития длины
трещины от 10 до 1Р (живучесть элемента). В результате Ирвином и
Пэрисом получено [42]
*p=w(i4)- (L2I)
Если принять п = 2 в уравнении A.10) и Т^ представить в виде
уравнения A.8), то
ln-^ = C"(Ao?Np, A.22)
где
С" = СС\ п.
В уравнениях A.21), A.22) при 10 -> 0 Np -»- оо, что является
чисто математической особенностью этих функций в точке £0 = 0,
не имеющей физического смысла, так как сама модель
предусматривает только развитие трещины, а не ее начальное образование.
Поэтому функциями A.21) A.22) следует пользоваться только при
10, превышающем некоторое определенное значение (например,
10 > 0,1-е-0,5 мм). Формула A.21) имеет тот недостаток, что при
малом 10 и большом 1р последняя величина практически не влияет
на Np (например, при 10 = 0,1 мм изменение 1р в пределах от 1 до
100 мм и более изменяет Np только на —10%, а в пределах от 5 до
100 мм только на 2% и т. п.). Этот недостаток не свойственен
формуле A.22), которая должна лучше отвечать опытным данным [ибо
значение показателя п = 2 в формуле Пэриса A.10) является более
оправданным, как уже отмечалось, чем п = 4 для малых
значений АК\]-
Описанные методы оценки распространения усталостных
трещин применяются на практике для прогнозирования роста трещин
в реальных конструкциях. Так, например, с использованием
выражения A.7) для К\ и формулы Пэриса A.10) при постоянных Сип,
характерных для реакторных сталей с учетом радиации и
воздействия воды под давлением в работе Рикарделла и Мэгера [96] было
найдено, что за 40 лет эксплуатации рост трещин в наиболее
опасном месте корпуса атомного реактора будет следующим:
Начальная длина
трещины /„, мм- . 3,18 '6,35 12,6 19,1 25,4
Рост трещины (/р—/0) за
40 лет, мм 0,105 J),254 0,87 2,49 9,75
По этим данным, зная возможную протяженность критических
трещин, которые могут привести к внезапному хрупкому разруше-
21.
нию, можно найти допустимую протяженность начальных трещин
или подобных им дефектов, определяющую требования к
дефектоскопии и приемке готовых корпусов реакторов.
Для определения живучести конструкции и размеров
допустимых начальных дефектов необходимо знание зависимости между
длиной трещины и остаточной прочностью, т. е. нагрузкой или
соответствующим номинальным напряжением, которые приводят
к разрушению тела с заданной трещиной при их однократном
приложении. Эту задачу рассматривают в механике разрушения [32,
42, 71].
Глава 2
Экспериментальное определение
характеристик
сопротивления усталости
3. Характеристики сопротивления усталости
при симметричных и асимметричных циклах
Для определения характеристик сопротивления усталости
лабораторных образцов или деталей из данного материала
проводят их усталостные испытания. Основные понятия,
определения и методика усталостных испытаний регламентированы
ГОСТ 2860—65.
Характер изменения напряжений во времени при стандартных
усталостных испытаниях показан на рис. 2.1. В общем случае
напряжения меняются периодически (по закону, близкому к
гармоническому) и являются суммой постоянного (среднего) напряжения
от и напряжения, меняющегося по синусоиде с амплитудой оа
(рис. 2.1, а).
Циклом напряжений называют совокупность последовательных
значений переменных напряжений за один период процесса их
изменения.
Различают максимальное стшах и минимальное стш1п напряжения
цикла, под которыми понимают наибольшее и наименьшее по
алгебраической величине напряжения цикла (см. рис. 2.1, г). В
качестве среднего напряжения ат и амплитуды напряжений аа цикла
принимают соответственно полусумму и полуразность стшах и стш1п:
_ ^тах ~Ь gmln . _ <Jmax gmln - /9 1 \
°т — £ ' а 2 ' \z,1>
Отсюда следует
<W = Gm. + Оа! tfmln = ат ~ <V B-2)
Размахом напряжений называют разность максимального и
минимального напряжений цикла, т. е.
2аа = стшах — стш1п. B.3)
Все понятия и формулы, приведенные в настоящем параграфе,
справедливы и для кручения, если в них а заменить на т.
Цикл, в котором максимальное и минимальное напряжения по
абсолютной величине различны, называют асимметричным
(рис. 2.1, а, б, г).
Симметричным циклом (рис. 2.1, е) называют цикл, у
которого максимальное и минимальное напряжения равныпо абсо-
23
Рис. 2.1. Схемы изменения напряжений во
времени при различных циклах: .
а — асимметричном, со средним растягивающим
напряжением; б — отнулевом; в —
симметричном; г — асимметричном, со средним сжимающим
напряжением
лютнои величине, но
противоположны по знаку.,
В этом случае
®а == °шах == ' ' °ш1п>
0т = О. B.4)
Для характеристики
степени асимметрии цикла
напряжений вводится
коэффициент асимметрии
цикла, под которым
понимается отношение
минимального напряжения
цикла °rmin K максимальному
R = -
Omax
B.5)
Очевидно, что с учетом формулы B.4) коэффициент асимметрии
для симметричного цикла R = —1, поэтому в обозначения
величин, соответствующих симметричному циклу, вводят индекс «—1».
Частным случаем асимметричного цикла является отнулевой
(или пульсационный) цикл, у которого минимальное напряжение
цикла 0ш1п, а следовательно, и коэффициент асимметрии R равны
нулю (рис. 2.1, б):
■"mln
0; Я = 0; оа
■ ОГ„
^тах
B.6)
Подобными называют циклы с одинаковыми коэффициентами
асимметрии; отношение их максимальных напряжений равно
отношению соответствующих средних и амплитудных напряжений:
СГшах
Omax
От
От
При этом
R' =
Omin
Omax
Ртах ■— 20а
СГтах
==1
Оа
Оа
Omax
-=1-2
Оа
= #".
Omax
Для проведения усталостных испытаний используются
специальные усталостные машины. По способу возбуждения нагрузок
в испытуемом объекте усталостные машины можно разделить на
механические, гидравлические, электромеханические,
пневматические, по виду нагружения образца —машины для испытаний при
изгибе, кручении, растяжении-сжатии, сложном напряженном
состоянии, а также универсальные.
Испытания при переменном изгибе осуществляют по
нескольким схемам: изгиб с вращением (консольный или чистый изгиб)
24
и изгиб в одной плоскости. По характеру изменения во времени
напряжений в образце различают усталостные испытания при на-
гружении гармоническом (по симметричному или асимметричному
циклу), бигармоническом (наложение двух гармоник),
программном (изменение амплитуды напряжений по определенной прог-
грамме) и случайном.
Размеры испытуемых образцов и соответственно развиваемые
в машинах усилия изменяются в весьма широких пределах
(например, диаметры образцов варьируются от 1 до 300 мм, усилия
от нескольких килограммов до нескольких тыс. тонн). Существуют
машины для испытаний в различных эксплуатационных условиях
(пониженные и повышенные температуры, коррозионные среды,
включая жидкие расплавленные металлы, вакуум и др.), при
частотах, изменяющихся от нескольких циклов в минуту до 10—20 кГц.
Читатель может ознакомиться с разнообразными типами и
размерами машин по специальной литературе [50].
На рис. 2.2 для пояснения методики усталостных испытаний
приведена схема простейшей усталостной машины,
предназначенной для испытания лабораторных образцов при консольном изгибе
с вращением. Образец 1 круглого поперечного сечения
закрепляется в патроне шпинделя 2 машины, вращающемся с
определенным числом оборотов (чаще всего п = 3000 об/мин). На
конце.образца смонтирован подшипник 3, через который на испытуемый
образец передается сила Р постоянного направления. В наиболее
напряженном сечении /•—/ образца возникают напряжения изгиба'
о = Р//0,Ы3, изменяющиеся вследствие вращения по
симметричному циклу (один цикл напряжений соответствует одному полному
обороту образца). Со шпинделем машины соединен счетчик
накопленного числа оборотов, регистрирующий общее количество
циклов нагружения до разрушения образца (при разрушении образца
машина автоматически выключается).
Для получения характеристик сопротивления усталости
согласно ГОСТ 2860—65 необходимо провести испытания не менее 10
одинаковых образцов из деформируемых. и не менее. 15 образцов
из литейных сплавов. Последнее связано с тем, что литейные сплавы
дада
Рис. 2.2. Схема машины Для испытаний при
консольном изгибе с вращением:
1 *— испытуемый образец; 2 — шпиндель; 3
«-[подшипник; 4 — счетчик числа, циклов
25
ба,кгс/ммг
SO
SO
40
30
10"
t_
4
10"
i_
a)
6a, кгс/ммг
^
о*
Г
I
III
0 „"
9 :
7 =
III
Л7
4/7
30
^
•,
s\
II
1L
in
^
/0J
w4
fl
J, 80
1,1 S
J, 70
1,65
1,60
1.S0
N
IgN
Рис. 2.3. Кривые усталости лабораторных образцов из
легированной стали при изгибе с вращением {а_г = 37,8 кгс/мм2; N0 —
— 106 циклов; аБ = 85 кгс/мм2)
обладают повышенной неоднородностью и разбросом
характеристик сопротивления усталости, вследствие чего для получения
той же точности необходимо испытание большего количества
образцов. Результаты испытаний изображают или в
полулогарифмических координатах аа — lg N (амплитуда напряжений аа по оси
ординат в равномерном масштабе, логарифм числа циклов до
разрушения lg N по оси абсцисс в равномерном масштабе, см.
рис. 2.3, а), или в двойных логарифмических координатах lg aa —
lg N (см. рис. 2.3, б).
Первый образец испытывают обычно при амплитуде
напряжений аа, составляющей @,65—0,75) ав, и при этом фиксируют число
циклов до его разрушения.
На рис. 2.3 представлены результаты усталостных испытаний
образцов из легированной стали, имеющей предел прочности ав =
= 85 кгс/мм2. Образец № 1, испытанный при амплитуде аа —
= 0,7ав = 59 кгс/мм2, проработал до разрушения 2-104 циклов (что
соответствует ординате и абсциссе точки 1 на рис. 2.3, а). Образец
№ 2, испытанный при амплитуде аа = 55 кгс/мм2, разрушился при
числе циклов N = 5 • 104. Постепенное снижение амплитуды
напряжений приводит к повышению долговечности образца, под которой
понимается число циклов до разрушения образца (или до
появления трещины заданных размеров). Испытания при изгибе с
вращением в большинстве случаев проводят до окончательного
разрушения образца. Так, образец № 5 при амплитуде аа = 40 кгс/мм2
проработал до разрушения N = 5-105 циклов (точка 5).
Следующий образец № 6 при амплитуде аа = 35 кгс/мм2 проработал без
разрушения 107 циклов (чему соответствует непрерывная работа
усталостной машины в течение 56 ч при частоте вращения шпин-
26
деля п = 3000 об/мин.) В процессе более длительных испытаний
было установлено, что в условиях нормальных температур и
отсутствии коррозии (при обычных атмосферных условиях) образцы из
сталей малой и средней прочности (ав < 100-И20 кгс/мм2),
титановых сплавов, не разрушившихся при N = 107 циклов, не
разрушаются и далее. Поэтому испытания этих образцов можно
прекращать при N = Ю7 циклов в том случае, если они не разрушались.
Соответствующая точка на графике в этом случае снабжается
стрелкой (точка 6 на рис. 2.3, а).
Предварительно задаваемое число циклов напряжений, до
которого образцы испытывают на усталость, называют базой
испытания и обозначают N6. В данном случае N6 = 107 циклов.
Оставшиеся образцы № 7, 8, 9, 10 испытывают в интервале между
амплитудами напряжений, при которых испытывались образцы № 5
и 6, причем таким образом, чтобы сузить интервал между
амплитудами, соответствующими сломавшимся и несломавшимся
образцам. Так, образец № 9 при амплитуде аа = 37,6 кгс/мм2 не
сломался до базы испытания, а образец № 10 при амплитуде аа—
= 38,0 кгс/мм2 сломался при числе циклов N = 106.
Амплитуда аа = 37,8 кгс/мм2, соответствующая середине
интервала, обладает тем свойством, что при аа < 37,8 кгс/мм2
образцы не разрушаются до базы испытания, а при аа> 37,8 кгс/мм2—
разрушаются. Такое значение амплитуды напряжений при
симметричном цикле называют пределом выносливости при
симметричном цикле и обозначают а_г (индекс «—1» указывает значение
коэффициента асимметрии цикла). Таким образом, по результатам
описанных испытаний найдено, что предел выносливости при
симметричном Цикле для гладкого лабораторного образца из данной
стали при изгибе с вращением составляет а_г = 37,8 кгс/мм2 (—— =
= -85- = 0'45)-
Согласно ГОСТ 2860—65 при испытании ограниченного числа
образцов предел выносливости определяется как наибольшее
значение максимальных (по величине) напряжений цикла, при
действии которого еще не происходит образование усталостных
трещин заданной протяженности или полного усталостного
разрушения образцов до заданного числа циклов.
Через экспериментальные точки на рис. 2.3, а проведены
наклонная и горизонтальная линии, которые в совокупности
образуют кривую усталости, или кривую Веллера *.
Уравнение левого наклонного участка кривой усталости,
изображаемой в полулогарифмических координатах прямой линией,
имеет вид
аа + К lg N = ff_x + К lg NQ, B.7)
* По имени немецкого ученого А. Веллера, впервые построившего усталост»
ные машины в середине XIX в. и проведшего усталостные испытания.
27
где а_г — предел выносливости; /V0 — число циклов,
соответствующее точке перелома кривой усталости (на рис. 2.3, a N0 =
= 106 циклов, о_г = 37,8 кгс/мм2); К — коэффициент,
характеризующий наклон левого участка кривой усталости.
Для определения коэффициента К необходимо знать кроме а_г
и JV0 координаты одной точки наклонной линии. Например, на
■ рис. 2.3, а в качестве таких координат могут быть взяты оа =
= 59 кгс/мм2, N = 2-Ю4 (точка 1). Тогда из уравнения B.7)
к __ Од — g.j _ 59 — 37,8 _ 19 -
А \gN0 — \gN lg 10е — lg2-104 1Z'0<
Те же самые результаты усталостных испытаний могут быть
изображены в двойных логарифмических координатах, как
показано на рис. 2.3, б. Прямая линия, проведенная на рис. 2.3, а,
переходит в кривую, изображенную пунктиром на рис. 2.3, б.
Однако (вследствие разброса точек) кривая усталости в двойных
логарифмических координатах также может быть изображена
в виде прямой линии (сплошная линия на рис. 2.3, б), которая мало
отклоняется от пунктирной. Уравнение этой линии имеет вид
/ralgffe+lg^ = mlgff_1 + Ig^0- B-8)
Уравнение кривой усталости имеет вид
{ „ при а„ > а,;
a?iV = \<£iNo -^ B.9)
[ со ПрИ ОГа<ОГ_1.
Значения а_г и JV0 остаются прежними, а величину т
определяют по уравнению, вытекающему из выражения B.8):
ё N-
Подставляя в это уравнение значения: аа = 59 кгс/мм2, N =
= .2-104 и а_! = 37,8 кгс/мм2, N0 = 106, получаем т = 8,8.
Значение /V0 колеблется в пределах A-^—3) • 10е циклов.
Величину т для деталей можно определить по формуле
т~&- BЛ°>
где Kod — суммарный коэффициент, учитывающий влияние всех
факторов на сопротивление усталости (см. гл. III); с = 12 — для
сварных соединений (по предложению М. М. Гохберга); с = 12—f-
ч-20 — для деталей из углеродистых сталей; с = 2СН-35 — для
деталей из легированных сталей. •
Горизонтальный участок кривой усталости, соответствующий
неограниченной долговечности, имеет место, как уже отмечалось,
у сталей малой и средней прочности, титановых сплавов при испы-
28
тании без воздействия коррозии и при нормальной температуре.
В других случаях кривая усталости не имеет горизонтального
участка и. непрерывно снижается (легкие сплавы и высокопрочные
легированные стали во всех случаях, стали малой и средней
прочности и титановые сплавы при повышенных температурах и в
условиях коррозии и т. д.). При этом сопротивление усталости
характеризуют пределом ограниченной выносливости a_lN, под которым
понимают максимальное напряжение цикла, соответствующее по
кривой усталости числу циклов N. Кривую усталости
аппроксимируют тогда двумя наклонными прямыми линиями в двойных
логарифмических координатах, описываемыми уравнениями
o™lN = a1\NoN0 при аа > <г_ш,; 1
o^N = aHlNoN0 при aa<cr_Wo, J
где а_щ0 — предел ограниченной выносливости, соответствующий
числу циклов N0, причем lg в-ш,, и lgN0 являются координатами
точки пересечения указанных прямых; т1, т% — соответственно
показатели углов наклона верхней и нижней частей кривых
усталости.
Для описания указанных кривых усталости используют также
уравнения Вейбулла [10]:
(Ga-a-i^iN + N^^B, B.12)
где Nu C, В — параметры уравнения; a_i m— предел
выносливости, соответствующий неограниченной базе (N — оо).
Для этой же цели предложено уравнение обобщенной кривой
усталости [60], которая является общей для деформируемых
алюминиевых сплавов при изгибе с вращением:
5a = a_1 + 4jlg(iV + iV1)ra) B.13)
где аа = -^г~; ог_х — "Г1""'; Nlf A, a — параметры- уравнения;
а—г а—г
all — предел выносливости, соответствующий базе N6 = 107
циклов.
На рис. 2.4 [60] представлена обобщенная кривая усталости,
которая является единой для деформируемых алюминиевых
сплавов (марок В95, Д16, АВ, АДЗЗ и др.). Линия на рис. 2.4
рассчитана по уравнению B.13) при следующих значениях параметров:
all = 0,46; А = 31,9; a = 2,1; N1 *« 5-103. Параметр Nx
оказывает влияние лишь на ту часть кривой усталости, которая
соответствует N < 10Б циклов. При N > 10Б можно принять N1 = 0.
Из рисунка видно: увеличение базы с 107 до 109 циклов приводит
к дополнительному снижению предела выносливости
приблизительно на 20%, что имеет существенное значение в расчетах на
прочность.
29
'10s 10s JO7 JO8 N
Рис. 2.4. Обобщенная кривая
усталости для деформируемых
алюминиевых сплавов
Рис. 2.5. Диаграмма
максимальных предельных
напряжений при асимметричных циклах
Для получения характеристик сопротивления усталости при
асимметричных циклах нагружения проводят усталостные
испытания при различных асимметриях и по их результатам строят
диаграмму предельных напряжений (рис. 2.5), характеризующую
зависимость между .максимальными предельными напряжениями
ашах> равными пределам выносливости при асимметричных циклах
aR (откладываемыми по оси ординат) и средними напряжениями
цикла ат (откладываемыми по оси абсцисс).
Эти же результаты часто представляют в виде диаграммы
предельных амплитуд напряжений, показанной на рис. 2.6 и
характеризующей зависимость между предельными амплитудами аа
(откладываемыми по оси ординат) и средними напряжениями цикла
ат (откладываемыми по оси абсцисс). Построение этих диаграмм
можно производить двумя способами. При первом способе
сохраняют постоянным среднее напряжение цикла ат для всех образцов
данной серии, а меняют амплитуду напряжений при переходе от
одного образца к другому. Кривую усталости при этом строят,
откладывая значения амплитуд напряжений по оси ординат и число
циклов до разрушения (или до появления трещины заданных
размеров) по оси абсцисс. В результате находят предельную амплитуду
напряжений при асимметричном цикле ат, под которой понимается
то наибольшее значение амплитуды, которое при заданном среднем
напряжении ат не вызывает еще разрушения до базы испытания.
При втором способе сохраняют постоянным для всех образцов
данной серии коэффициент асимметрии цикла R, меняя при
переходе от образца к образцу аа и ат, но так, что циклы остаются
подобными (R = const). Под предельной амплитудой а^ в данном
случае понимают то наибольшее ее значение, которое при заданном
коэффициенте асимметрии не вызывает разрушения до базы
испытания. Под пределом выносливости при асимметричном цикле aR и
в том и в другом случае понимают наибольшее значение максималь-
30
ного напряжения цикла, не
вызывающего разрушение от
усталости до базы испытания:
<*А = <*т + <*<ш- B-14)
При этом способе находят
вначале предел выносливости
при симметричном цикле ©_1;
откладывая соответствующую
ему точку Л на рис. 2.5 и 2.6
(приат= 0). Следующую серию
из 10 образцов испытывают
при отнулевом (пульсирующем)
цикле, определяя
соответствующий предел выносливости при
Рис. 2.6. Диаграмма 'предельных
амплитуд напряжений при
асимметричных циклах
отнулевом цикле а0 (индекс
указывает значение коэффициента асимметрии R = 0).
Предельная амплитуда напряжений при этом в соответствии с
выражением B.6) равна ааи = -у. Следует отметить, что подобным
циклам (R = const) на рис. 2.5 и 2.6 соответствуют лучи ОС,
проходящие через начало координат под углом р иак оси абсцисс
(на рис. 2.5 и 2.6 соответственно). Так, для текущей точки на
рис. 2.5 с учетом зависимостей B.1) и B.5) имеем
tfmax tfmax 2
te
l
(tfmax + CTmln)
l+R1
B.15)
При R = const C = const. Иначе говоря, точки,
расположенные на луче ОС, соответствуют подобным циклам с заданным
коэффициентом асимметрии R.
Аналогично на рис. 2.6 с учетом формулы B.1)
{~R B.16)
tea =
CTmax — tfmln
l+R'
СТтах + CTmln
Таким образом, отнулевым циклам на рис. 2.5 соответствует луч
ОВ, для которого tg р0 = 2 [из уравнения B.15) при R = 0], а на
рис. 2.6 луч, для которого tga0 = 1 (a0 = 45°). Следовательно,
точки В, соответствующие отнулевому циклу, имеют координаты
—■, а0 — на рис. 2.5 и -у-, ~ — на рис. 2.6.
Третья серия из 10 образцов испытывается по второму способу
при коэффициенте асимметрии 0 < R < 1 (значение R = 1
является наибольшим возможным значением R и соответствует
статическим напряжениям, при которых ашах = ап
= ст„
и аа = 0),
например, при R = +0,333, как на рис. 2.5 и 2.6. В результате
находится третья точка диаграммы предельных напряжений (см.
рис. 2.5) или предельных амплитуд (см. рис. 2.6) — точка С. ■
Проведя испытания при нескольких значениях коэффициента
асимметрии цикла R, нанося соответствующие точки на графики
31
и соединяя их плавной линией, получаем диаграммы предельных
напряжений и предельных амплитуд при асимметричных циклах.
Указанные диаграммы, найденные двумя способами, практически
совпадают. Проведение усталостных испытаний до базы 107 циклов
при асимметричных циклах растяжения с весьма большими
значениями средних напряжений ат, приближающихся к пределу
прочности ав, весьма затруднено тем, что на образце образуется шейка
и наблюдается накопление пластических деформаций.
Экстраполяция линий ABC обычно приводит к точке D, имеющей координаты
огв, ав на рис. 2.5 и ав, 0 на рис. 2.6. Некоторая область на этих
диаграммах, прилегающая к точке D, является нерабочей, так как
в условиях эксплуатации деталей машин средние напряжения
цикла, близкие к ав, не допускаются [максимальные напряжения
цикла ашах почти во всех случаях меньше @,5—0,6) ав]. Поэтому
на рис. 2.5 и 2.6 диаграмма в области, прилегающей к точке D,
проведена штрихпунктиром.
Для расчета на усталость диаграмму предельных амплитуд
напряжений ABC схематизируют, а именно заменяют ее прямой
линией, проходящей через точки А я В, как показано пунктиром
на рис. 2.6. На рабочем участке диаграммы прямая АВ весьма мало
отклоняется от действительной диаграммы ABC, так что
погрешность, вносимая в расчет вследствие схематизации, пренебрежимо
мала. Записывая уравнение прямой, проходящей через две точки
с координатами А @, а_г), В (-у-, ~) на рис. 2.6, получаем
<Тд — P-I __ От — 0
Т "-1 ^Г °
Отсюда находим уравнение схематизированной диаграммы
предельных амплитуд напряжений при асимметричных циклах:
oa = o.i — ^ifim, BЛ7)
где
Коэффициент/фд характеризует влияние асимметрии цикла на
предельную амплитуду напряжений и, как легко показать,
равняется tg 7 (см. рис. 2.6). Для углеродистых сталей Ира — 0,1-ь0,2,
для легированных сталей и легких сплавов Ира = 0,15-Ю,30.
Аналогичные коэффициенты Ирх при кручении имеют меньшие
значения, а именно а|эг = 0—=—0,1 для углеродистых сталей, 'ipr—
= 0,05-f-0,15 для легированных сталей и легких сплавов.
В области сжимающих средних напряжений циклов (слева от
точки 0 на рис. 2.6) предельные амплитуды вначале увеличиваются,
что особенно 'заметно у хрупких материалов, например у серого
чугуна, у которого предел прочности при сжатии авсж значительно
32
Рис. 2.7. Диаграмма
предельных амплитуд напряжений при
асимметричных циклах для
серого чугуна
6а кгс/мм ?
40
-60 -чо -го о
го dm,Kc/m2
превышает предел прочности при растяжении авр. Типичная
диаграмма предельных амплитуд напряжений для серого чугуна
представлена на рис. 2.7. Из рисунка видно, что в области
растягивающих средних напряжений циклов диаграмма может быть
представлена прямой линией, проходящей через точки А @, а_г) —
.симметричный цикл, D (авр, 0) — статический разрыв. Уравнение
линии AD имеет вид
<*а=?0-1--%£От- * B.19)
Сравнивая выражение B.19) и B.17), получаем для этого случая
tyo = а~г • В области средних сжимающих напряжений
предельные амплитуды вначале существенно увеличиваются, а далее после
точки Е (соответствующей приблизительно отнулевому циклу
сжатия) снижаются до нуля при ат = — авсж. Аналогичные диаграммы
предельных амплитуд напряжений для ряда конструкционных
сталей представлены на рис. 2.8, для свободного цементованного
слоя и ложноцементованной стали — на рис. 2.9 и для
алюминиевых сплавов — на рис. 2.10. Под ложноцементованной
сталью понимается сталь, прошедшая такую же термическую
обработку, как и при цементации, но без науглероживания
поверхности. Кривая / на рис. 2.9 получалась путем испытания микрообраз-
цов, вырезанных целиком из цементованного слоя, т. е.
образцов, представляющих «свободный» цементованный слой. Из
рис. 2.8 —2.10 видно, что у азотированной и цементованной
стали предельные амплитуды напряжений особенно резко
возрастают с ростом средних сжимающих напряжений цикла. Несколько
в меньшей степени это же наблюдается у алюминиевых сплавов и
80
40
©«^
;
In
3
н
Р=8
о
-200 -160 -ПО -ВО -40
Сжатие
0 40 80 6т
Растяжение
Рис. 2.8. Диаграммы
предельных амплитуд напряжений при
асимметричных циклах для
конструкционных сталей
1,2 — высокопрочная
легированная сталь соответственно
азотированная и улучшенная; 3 — сталь
18Х2Н4МА; 4 — сталь 25
2 В. П. Когаев
33
бд,кгс/мм2
6а, kzc/mm1
150
ПО
90
60
30
6т,кгфмг-60-30 0- 30 60 90
Рис. 2.9. Диаграммы
предельных амплитуд напряжений для
свободного цементованного
Слоя A) и ложноцементован-
ной стали B)
ч
'J
X
/
•**
*>*
N
2
Js^
1tf^
-10-ZS-ZQ-15-10 -5 0 56т,кгс/ммг
Рис. 2.10. Диаграммы предельных
амплитуд напряжений при асимметричных
циклах для алюминиевых сплавов:
/ — АК4-1 (полирование); 2 — АК4-1
(обкатка роликами); 3 — ВД-17 (полирование);
4 — ВД-17 (обкатка роликами)
конструкционных сталей. Указанное повышение предельных
амплитуд является одной из основных причин существенного
увеличения пределов выносливости деталей машин при поверхностном
упрочнении (см. разд. 10).
4. Рассеяние характеристик
сопротивления усталости
и построение полных вероятностных диаграмм
усталости
Такие характеристики сопротивления усталости, как число
циклов до разрушения N и предел выносливости а_г являются
случайными величинами, которым свойственно большое рассеяние
даже при условии испытания идентичных образцов, изготовленных
из материала одной плавки. Для совокупности всех плавок
металла данной марки это рассеяние становится еще большим, так
как добавляется межплавочное рассеяние механических свойств
металла, связанное со случайными вариациями химического
состава металла различных плавок и металлургических факторов,
влияющих на свойства [10, 13, 26—28, 34, 60, 76].
С одной стороны, причинами рассеяния характеристик
сопротивления усталости образцов, изготовленных из металла одной
плавки, являются различия в условиях термической и
механической обработки образцов, точности назначения нагрузок на
усталостной машине во время испытания и т. п. Эти факторы в
значительной мере могут быть устранены путем ужесточения требований
к технологии изготовления и испытания образцов, к точности
измерения нагрузок в машине.
34
С другой стороны, причинами рассеяния являются факторы,
связанные с различиями в микроструктуре, степени дефектности,
в микрогеометрии и свойствах поверхностного слоя и т. п. Так как
зарождение и развитие усталостной трещины начинается от
дефектов, имеющих различную степень опасности и неравномерное
распределение по объему, и связано с микроструктурной
неоднородностью, то говорят о статистической природе процесса усталости
металла, которая и является одной из основных причин рассеяния
характеристик выносливости.
При изучении закономерностей рассеяния характеристик
выносливости обычно изготовляют из металла одной плавки
достаточно большое число образцов, которые испытывают на усталость
при нескольких уровнях амплитуд напряжений.
Логарифмы полученных чисел циклов до разрушения
располагают в возрастающем порядке, образуя таким образом
вариационный ряд, служащий исходной информацией для статистической
обработки и графического изображения функции распределения
случайной величины X = lg N, а именно
Хг<Х2« ••• <.Х{*£ • • • <£Хп.
Эмпирическая функция распределения долговечности строится
обычно на логарифмически нормальной вероятностной бумаге.
По оси абсцисс откладываются значения Xt = lg Nt в
равномерном масштабе, по оси ординат — оценки вероятности разрушения
(накопленные частоты), вычисленные по формуле Р =
= —100%, где п число образцов, испытанных при данном
уровне напряжения.
В качестве примера на рис. 2.11 представлены функции
распределения долговечности образцов с глубокими гиперболическими
надрезами из стали 40Х при изгибе с вращением, испытанных при
ряде значений сгшах = aRaa [34] (cfmaXi стн — соответственно
максимальное и номинальное напряжения в зоне концентрации;
аа — теоретический коэффициент концентрации напряжений).
Этот график называют полной вероятностной диаграммой
усталости Р — N.— с?шах (в координатах Р — N с параметром стшах).
Так как точки располагаются по кривой, то можно говорить о
существовании в данном случае порога чувствительности по циклам
N0, т. е. такого значения числа циклов, вероятность разрушения
раньше которого равна нулю. В этом случае нормально
распределенной оказывается величина X = lg (N — N0) [26]. Для
получения параметров функций распределения долговечности
производят статистическую обработку исходной информации по методам,
изложенным в работах [18, 26, 61, 76].
Полная вероятностная диаграмма усталости может быть также
представлена в координатах сгшах — N с параметром Р, т. е. в виде
семейства кривых усталости, соответствующих различной
вероятности разрушения Р (рис. 2.12). Этот график строится по рис. 2.11
.2* 35
99
98
95
90
70
60
50
40
30
20
10
5
1
0,5
*
^
1
X
1
#^
Qvx ■
о/
X J^
£ У
у /" /
Г-ЗЙ2
—-Ш-
ц к
ТГ7
ь ^
у'
>
1-"
- _i С-
izi'L
„Э^*^
f/A
- i/ift
/,—-—
-87
■ °""
Тд~
—J~~
\~
•-U-
2 3 4561810s 2 3 4561810s Z 3 4 5б78107Н,цим
Рис. 2.11. Функции распределения долговечности образцов с
глубокими гиперболическими выточками из стали 40Х при изгибе с
вращением [а„ = 3,4; г = 0,2 а= t= 3,76 мм; lg — = 0,36 (см. разд. 7)]
G
ffmax- кгс/мм2
путем его сечения горизонтальными линиями, соответствующими
различным значениям Р, и фиксации значений сгшах и N,
соответствующих точкам пересечения. Например, проводя горизонталь
на рис. 2.11, соответствующую Р = 70%, получаем следующие
значения сгшах и N для точек пересечения с линиями распределений:
140 127,5 114
8-10* 1,8-105- 2-Ю6
По этим данным нанесены точки (крестики) на рис. 2.12, по
которым проведена кривая усталости, соответствующая
вероятности разрушения Р = 70%. Аналогично построены и другие
кривые усталости.
Те же экспериментальные данные могут быть изображены
в координатах Р — сгшах с параметром N, как показано, на
рис. 2.13. Построенные на этом рисунке линии являются
функциями распределения пределов выносливости, соответствующих
различным значениям долговечности. Построение этих линий
производится следующим образом. Проводя вертикальную линию
на рис. 2.11, соответствующую N = 4-Ю5 циклов, получаем по
точкам пересечения следующие значения crmax и Р:
127,5 114 100 87
92 60 13 4
36
0"шах. кгс/мм2
Р, %
Рис. 2.12. Кривые усталости,
соответствующие различным
вероятностям разрушения
образцов из стали 40Х при изгибе
с вращением (аа = 3,4; г =
= 0,2 мм; а = t =» 3,76 мм;
lg|-=0,36)
<W, кгс/мм
ISO
г ь Ш7ios г з ts67 ws
3 i S 518 N, цикл
По этим данным на рис. 2.13 нанесены треугольники,
обведенные кружками. Проведя на рис. 2.12 вертикальную линию,
соответствующую N = 4-105, получаем координаты точек,
обозначенных треугольниками на рис. 2.13. Эти точки (треугольники)
практически совпадают с прямой линией на рис. 2.13, что говорит о
возможности описания функции распределения пределов
выносливости, выраженных через сгшах при N = 4-105 циклов, нормальным
законом распределения. Среднее (совпадающее с медианным в
данном случае) значение сгшах получаем при Р = 50%, а именно
сгшах = 113 кгс/мм2. Для нахождения среднего квадрэтического
отклонения Sa фиксируем значение сгшах при Р = 84,1%
(tip = 1), в результате получаем crmax84,i
Sa определяется как разность:
123 кгс/мм2. Значение
Р,%
98
95
90
80
70
50
30
20
10
' 80 85 90 95 100 105 110 Ш6тх,кгфмг
Рис. 2.13. Функции распределения
максимальных разрушающих напряжений в зоне
концентрации crmax, соответствующих
различным долговечностям
S
<г
d
">Т
' <ЩУ
1
У.
^"VS
-
S-*
<
ФУ*
с^
^
Uk
jjE^
А
W7
^
Л
Л
s
i
,<#
S-Ws\
ffmax = 123 - 113 = 10 кгс/мм2.
Коэффициент вариации
^22=-^- = 0,088.
^ашах '
Аналогично построена на
рис: 2.13 функция
распределения пределов
выносливости, соответствующих базе
N = 107 циклов.
То
обстоятельство, что линии на
рис. 2.13, соответствующие
различным базам испытания,
параллельны, говорит о
совпадении значений Sa max для
различных баз в данном
случае. Описанный метод
37
V IB
Щ9
Щ2
4S.S-
6,кгс]ммг J
mt
я_х
-*-o-o—X-M-
—X X X X o-X-
-0~X—О—O-O—X~О !<
—-*-X X-—
-о—о—к—o—*-
-o X-*~
И того '
J
J
7
5
2
24
3
3
7
6
S
z
26
m
■3
6
10
11
10
7
2
50
Рис. 2.14, Диаграмма испытаний образцов по методу «лестницы»
построения функций распределения пределов выносливости
соответствует «пробит»-методу [25, 61 ]. Значения всех параметров
(и их доверительных интервалов) полных вероятностных диаграмм
усталости могут быть рассчитаны аналитически на ЭВМ
современными методами математической статистики.
Для построения полной вероятностной диаграммы усталости
(см. рис. 2.11—2.13) было испытано 125 образцов E уровней атах
по 25 образцов на уровень). На практике во многих случаях
оказывается невозможным провести испытание столь большого
количества образцов. В этом случае можно рекомендовать
комбинированный метод, заключающийся в нахождении функции
распределения пределов выносливости методом «лестницы» по 15—20
образцам и параметров левой ветви кривой усталости методом
регрессионного анализа по результатам испытания 10—15 образцов, что
в общем требует проведения испытания 25—35 образцов.
Метод «лестницы», предложенный Диксоном и My дом [73],
состоит в последовательном испытании на усталость до базы
испытания серии из 15—50 образцов по схеме, показанной на рис. 2.14
[25, 61 ]. Горизонтальные линии соответствуют различным
уровням амплитуд напряжений, написанным слева. Расстояние между
линиями соответствует ступеньке d, которая должна иметь
значение, близкое к стандартному отклонению предела выносливости
Sai (допускается 0,5<^—<2,oV
Первый образец испытывается при амплитуде напряжений ал,
как можно более близкой к среднему значению предела
выносливости а_г Так как вначале испытания величины а_ъ Sa_x
неизвестны, то для сталей можно принять
а_! == оа1& @,55 — 0,001 ofB) aB; d sz 0,05^. B.20)
Формулы B.20) получены исходя из корреляционной
зависимости G_2 ш @,4-^0,5) ав, где 0,4 взято для ав = 150 кгс/мм2,
0,5 -=- для Cg ~ 50 кгс/мм2, и d — SQ_^ = Pff^oLr (коэффициент
вариации предела выносливости для лабораторных стальных
образцов принят va = 0,05). Для других материалов и
типоразмеров образцов предварительные приближенные значения о_г и
va_x следует находить по справочным данным.
Допустим, что первый образец сломался до базы испытания
при испытании с амплитудой оа1 = 46,2 кгс/мм2 (на диаграмме
рис. 2.14 отмечается крестиком). В этом случае второй образец
испытывается при амплитуде напряжений аа2 = аа1 — d, т. е.
на одну ступеньку меньшей, чем' оа1. Пусть второй образец не
сломался до базы испытания (на рис. 2.14 отмечено кружком). Если
предыдущий образец не сломался до базы испытания, то
последующий образец испытывается при амплитуде напряжений на одну
ступеньку большей, чем предыдущий, т. е. в общем случае
<*ai = <'a,l-l±d, B.21)
где знак «+» берется в случае отсутствия разрушения, а знак «—»
в случае разрушения (г — 1)-го образца. В правой части графика
выписывается таблица количества образцов сломавшихся (rt),
несломавшихся {т.-) и общего (nl = rt + rnv), испытанных при
амплитуде аа1.
Для дальнейших вычислений берется общее количество
сломавшихся, или несломавшихся, образцов (лучше брать меньшее
количество). Среднее значение а_г и среднее квадратическое
(стандартное) отклонение Sa^ предела выносливости находят по
формулам [73]
a_i = а'а + d {■— ± ^-) 5 B.22)
Sa^ = l,62d (RB^A2 + 0,029) , B.23)
где
А = £ irii В = £ »% R = S П. . B.24)
j=0 i=0 i=l
Здесь знак «-(-» берется в том случае, если расчет ведется по
неразрушенным образцам, знак «—» — по разрушенным; о'а —
амплитуда напряжений, соответствующая наименьшему уровню,
при котором имелись несломавшиеся, или сломавшиеся, образцы.
Для подсчета стандартного отклонения выборочного среднего
So х и стандартного отклонения выборочного значения Sa_v
обозначаемого 5S, предлагаются формулы
S;,^; B-25)
-i
VR
HSn -
S*--yf> B-26)
39
V"
VJ
Q
"ZZSa^c**
V.\
д
'
/
/
/
'^*~'
Рис. 2.15. Функции. О и Н к
по методу «лестницы»
расчетам
$,н | 1 1 П ] ~~] 1'Де G и // — функции отноШё-
3 I 1 —I (/ 1 i ния-^—, представленные на
^-х
рис. 2.15. Сплошные линии
определяют значения G и Н
для случаев, когда а_х равен
одному из испытательных
уровней, пунктирные— когда
ff_j находится посредине
между двумя уровнями.
Кривые для других положений
среднего значения лежат
между ними. По значениям
Sa_i и Ss могут быть
найдены доверительные области для функций распределения
пределов выносливости, соответствующих генеральной совокупности.
При оценке сопротивления усталости натурных деталей часто
бывает затруднительным проведение испытаний 25—35 деталей
вследствие их большой стоимости, тихоходности крупных
испытательных машин и т. п. В этом случае ограничиваются испытаниями
10—15 деталей. Для приближенной оценки среднего значения сг_]Д
и среднего квадратического отклонения Sa предела
выносливости детали в этом случае может быть использован метод, описанный
в работе [39], или аналогичный метод, основанный на
использовании уравнений кривой усталости Вейбулла B.12) или B.9)
и сводящийся к следующему. Пусть в результате испытания
п образцов получены значения aal, Nt (i = 1, 2, ..., я), где
eai, N[ — амплитуда напряжений и число циклов до разрушения
i-ro образца.
Воспользуемся для простоты уравнением кривой усталости
в форме B.9). В результате регрессионной обработки [61, 70]
определяются параметры уравнения B.9), а именно т, N0. Считая
приближенно эти параметры фиксированными, можно найти
предел выносливости а_и, как бы соответствующий t-му образцу,
из уравнения
a?tNt = aluNo,
откуда
-Xi
т Г
ваг У ■
No
B.27)
B.28)
Приближенные значения а_г и Sa находятся по формулам
- 1 "
S--1 = \/r-K=rt(a.u-aJf.
B.29)
40
Аналогично используется для этой цели уравнение Вейбулла
B.12). Проверка применения указанного способа показывает, что
если аа[ ненамного превышают а_х (aai < 1,5а_г), то получаются
оценки величин о_г и Sa_ , близкие к оценкам, определяемым по
методу «лестницы».
5. Оценка характеристик сопротивления
усталости
при сложном напряженном состоянии
В связи с тем, что во многих деталях машин в местах
повышенной напряженности, в которых образуется очаг усталостного
разрушения, возникает плоское (или объемное) напряженное
состояние, необходимо ""'использовать условия прочности при сложном
напряженномгсостоянии для расчета на усталость [1, 14, 43, 57,
74, 76, 85, 86]. Условия прочности при переменных напряжениях
аналогичны следующим условиям пластичности:
Треска—Сен-Венана (гипотеза максимальных касательных
напряжений)
Тшах = а1~2аз = тт = -у- (ПРИ ог>а3> <х3); B.30)
Губера—Мизеса—Генки (гипотеза энергии формоизменения)
(ог - a2f + (cr3 - азJ + fas - Oif = 2a\\ B.31)
Геста—Мора
а1-а3 = 2тт-Я((У1 + аз). B.32)
Здесь тт, ат соответственно пределы-текучести при чистом сдвиге и
растяжении; аг, а2, as — главные напряжения (индексы
расставляют таким образом, чтобы обеспечить выполнение неравенств
с?! > сг2 > °з в алгебраическом смысле). Применяя условие B.32)
к одноосному растяжению (а1 — ат, а3 = 0)> получаем
% = ^L—\. B.33)
Из выражений B.32) и B.33) следует, что условие пластичности
Геста—Мора может быть представлено в следующем виде:
^-(-g-- l) а,■= а,. B.34)
Наиболее распространен в деталях машин случай плоского
напряженного состояния, который характеризуется
возникновением нормального напряжения а и касательного напряжения т
41
по одной из площадок (как, например, при совместном изгибе и
кручении бруса). В этом случае сг2 = 0 и
*i,s="f ±]/т- + т2. B.35)
Подставляя зависимость B.35) в выражения B.30) и B.31),
получаем соответствующие условия пластичности для данного
частного случая плоского напряженного состояния:
гипотеза максимальных касательных напряжений
]/оа + 4т2 = ат; B.36)
гипотеза энергии формоизменения
уа2 + 3т2 = 0т. B.37)
а2 ст2
Если учесть, что по условию B.36) —|- = 4, а по B.37) —f- = 3,
тт тт
°?
то, подставляя вместо этих цифр отношения —■*■ и делая эле-
ментарные преобразования, получаем следующее эллиптическое
условие пластичности:
4 + 4=1- B.38)
0Т тт
Подстановка выражения B.35) в B.34) приводит, как показано
С. В. Серенсеном [57], к следующему условию пластичности
Геста—Мора, записанному для данного случая плоского
напряженного t состояния:
(£)'(:*- l)+£ B - Д)+(£)•-1. B.39)
При —- = 2 из условия Геста—Мора B.39) получается
выражение B*38).
В связи с тем, что накопление усталостных повреждений
связано с протеканием циклических пластических деформаций,
следует ожидать, что условия прочности при переменных нагрузках
и сложном напряженном состоянии должны иметь выражения,
аналогичные B.30)—B.39), если в них заменить тт на т_1; сгт на а_х
и считать, что компоненты тензора напряжений изменяются
синхронно и синфазно по симметричному циклу. Под величинами аг,
а2, а3, а, т, входящими в эти выражения, следует понимать тогда
их амплитудные значения а1а, а2а, о3а, аа, ъа соответственно.
Синхронным и синфазным изменением компонент тензора напряжений
называют такое, при котором совпадают частоты и фазы их
изменения. Эксперименты, проведенные в соответствующих условиях,
подтверждают высказанное предположение. Таким образом, усло-
42
вия прочности при переменных нагрузках и плоском напряженном
состоянии при изменении напряжений о и т по симметричному
циклу можно записать в следующем виде:
(■г-),(^-о+-ё-(!-^)+(^-)'-1- <2-41»
Условие прочности B.41) было предложено Г. Гафом [74] как
эмпирическое. В работе С. В. Серенсена [57] было показано, что
это условие вытекает из гипотезы Геста—Мора B.39), примененной
для расчета на усталость.
Экспериментальная проверка условий B.40) B.41) была
осуществлена Г. В. Ужиком, Г. Гафом, В. Финдли, П. Фритом [43,
74, 76].
Испытания производили на специальной усталостной машине
[74], схема которой представлена на рис. 2.16. В этой машине
неподвижный образец /, закрепленный с помощью зажимов 2 в
суппорте 3, нагружается одновременно изгибающим и крутящим
моментами, изменяющимися по симметричному циклу синхронно и
синфазно. Нагружение осуществляли с помощью рычага 7, жестко
соединенного с зажимом 5, в котором укреплена вторая головка
образца. При установке образца он может быть повернут
относительно рычага 7 за счет цапф 6 так, что ось образца будет
составлять угол а с плоскостью рычага, в которой он и совершает
вертикальные колебания под действием центробежной силы от
неуравновешенной массы 10, вращающейся вместе с диском 9. Поворот
образца на угол а осуществляется вместе с суппортом 3 и контроли-
Рис. 2.16. Схема машины Гафа для испытания образцов на усталость при
одновременном действии изгибающего и крутящего моментов:
/ — образец; 2, 5 — зажимы;- 3 — суппорт; 4 — шкала; 6 — цапфы; 7 —
нагружающий рычаг; 8 -=■ тяга; 9 — диск; 10 — неуравновешенная масса
43
руется по шкале 4. Полный момент в опасном сечении изменяется
по симметричному циклу. Вследствие наличия угла а этот момент
дает две составляющие, а именно изгибающий момент Мтг =
= М cos а и крутящий момент Мкр — М sin а, изменяющиеся
синхронно и синфазно по симметричному циклу. При а = 0 имеет
место только изгиб образца, при а = 90° — только кручение,
а в промежуточных положениях — совместный изгиб и кручение.
Испытания на усталость проводят, как и ранее, с построением
кривой усталости при определенном угле а = const путем
постепенного уменьшения момента М. В результате находят момент M_v
соответствующий пределу выносливости при симметричном цикле,
а затем по моменту М_г определяют предельные амплитуды
нормальных оа = М_г cos a/0,Id3 и касательных ха = Atj sin a/0,2d3
напряжений, соответствующих пределам выносливости. Такие
испытания повторяют при различных углах а, включая а = 0 и
а,= 90° (при а = 0 получают a_lt при а = 90° —■ т^).
На рис. 2.17 в координатах -^-; -^-представлены
эксперименту a-i
тальные данные, полученные путем указанных испытаний при
совместном изгибе и кручении гладких образцов (симметричный
цикл). Из рис. 2.17 видно, что экспериментальные точки
располагаются близко к кривой 1, рассчитанной по уравнению B.40).
Для хрупких материалов (например, чугуна) лучше
согласуется с опытными данными уравнение B.41) [линия 2 на рис. 2.17].
Как видно из рис. 2.17, расхождение между линиямиУ и2 невелико.
При асимметричных циклах синхронного и синфазного
изменения касательных и нормальных напряжений условия прочности
B.40) и B.41) могут быть записаны в виде [43, 57, 74]
Ш+Ш-ь <2-42>
Ш & - >)+-£ B - ^)+(тгУ - '• <2-43»
где ааэ, хаэ —■ эквивалентные амплитуды напряжений, приведенные
к симметричному циклу и вычисляемые по формулам (см. разд. 3)
Оаэ = Яа+№т, B-44)
Ъаэ^^а + ^т- B-45)
Здесь ф0, г|)х — коэффициенты, характеризующие влияние
среднего напряжения цикла на предельную амплитуду.
Экспериментальное исследование сопротивления усталости при
совместном изгибе и кручении при синхронном изменении
касательных и нормальных напряжений по асимметричным циклам
было проведено Г. Гафом [74] на машине, аналогичной
изображенной на рис. 2.16, но с добавлением нагружающей системы для
наложения статической составляющей силы. Результаты испытания
44
гладких образцов из легированной стали представлены на рис. 2.18
для трех уровней средних значений касательных и нормальных
напряжений. Как следует из этого рисунка, экспериментальные
точки располагаются достаточно близко к дугам эллипсов.
Для проверки выполнения условия прочности B.42) по
результатам испытания [74] были оценены величины я|)а и фт, которые
получились равными i[H = 0,11, г|)т = 0,19. По данным рис. 2.18
и формулам B.44), B.45) при указанных ч|H и ч|)т были подсчитаны
значения т^/т^ и ою1о_л, соответствующие точки нанесены на
рис. 2.19. Экспериментальные точки располагаются близко к дуге
окружности, рассчитанной по уравнению B.42).
Следует отметить, что значение я|H = 0,11 для высокопрочной
легированной стали, полученное по данным работы [74], занижено.
Если принять ч|H = 0,2 (в соответствии с рекомендациями разд. 3),
то соответствующие экспериментальные точки сдвинутся вправо.
С учетом указанной поправки можно утверждать, что
экспериментальные данные Г. Гафа хорошо соответствуют условию прочности
B.42) с учетом уравнений B.44) и B.45).
В ряде работ влияние асимметрий цикла учитывалось по Гуд-
ману, т. е. принималось ч|H = -^З- = 0,4 ч- 0,5. Однако столь боль-
0*в
шие значения ij)a приводят к заметным погрешностям (в безопасную
сторону).
В общем случае трехосного напряженного состояния при
синхронном и синфазном изменении главных напряжений по
асимметричным циклам условия
прочности при переменных
нагрузках могут быть записаны по
аналогии с условиями пластич-
W 6a>MC/MMz
Рис. 2.17. Диаграмма предельных
амплитуд напряжений при
одновременном изгибе и кручении
цилиндрических образцов:
Расчетные кривые: / — по уравнению
B.40); 2 — по уравнению B.41)
Рис. 2.18. Результаты испытаний
гладких образцов из легированной стали
при асимметричных циклах:
' ~ °т = °: хт ■= О: 2 - от =
= 26,8 кгс/мм2; хт = 17,1 кгс/мм2; 3 —
ат = 53,6 кгс/мм2; %т = 34,6 кгс/мм2
45
^аэ/^-1
1,0
0,8
0,6
0,4
0,2
О
в А Д
,
К'
\
с
Рис. 2.19. Результаты испытаний
гладких образцов при совместном
изгибе и кручении с асимметричными
циклами изменения а и т в
относительных координатах:
@—от=26,8 кгс/мм* Тт=17,1 кгс/мм2;
А — от=53,6 кгс/мм2; Тт =34,6 кгс/мм8;
ф0 = 0,11; А— От = 53,6 кгс/ммг;
тт = 34,6 кгс/мм2; ф0 = 0,2
0,2
0,4 0,6 0,8 6a3f6_,
ности B.30), B.31), B.34), а именно [43, 57, 76]: по гипотезе
максимальных касательных напряжений
Стюэ — «Гвоэ = 2т_х; B.46)
по гипотезе энергии формоизменения
@1аэ — СГ2аэJ + (а2аэ — ОзаэУ + (<ТЗаэ — <3\аэТ = 2oi-i', B.47)
по гипотезе Геста—Мора
°1оэ — (7 — Ч °3аэ = а-1-
B.48)
Здесь а1аэ, а2аэ, а3аэ — эквивалентные амплитуды главных
напряжений, приведенных к симметричному циклу,, вычисляемые по
формуле
°tm = °t* + Wm (i = 1. 2, 3), B.49)
где <X;a, oim — амплитуда и среднее напряжение цикла t'-ro
главного напряжения.
Испытания трубок при пульсирующем внутреннем давлении
с наложением переменного растяжения с известным приближением
подтверждают применимость указанных гипотез прочности
[43, 85, 86].
Глава 3
Факторы,
влияющие на сопротивление
усталости деталей машин
6. Концентрация напряжений и абсолютные
размеры
поперечного сечения
Предел выносливости а_г при симметричном цикле изгиба
гладкого (с плавными очертаниями) лабораторного тщательно
полированного образца диаметром d0 = 7,5 составляет для
сталей @,4—0,5) <тв. Мощные усталостные машины позволяют
производить испытания на усталость деталей натуральной величины
(натурных деталей), например, валов диаметром до d = 300 мм.
Предел выносливости натурной детали при симметричном цикле,
найденный по описанной выше для образцов методике и
выраженный в номинальных напряжениях, обозначают <т_гд. Под
номинальными напряжениями в дальнейшем будем понимать
напряжения, вычисленные по следующим формулам сопротивления
материалов:
<тн = -=*- — при изгибе,
W х
р
ан = -р при растяжении или сжатии, C.1)
тн = -—■— при кручении,
W р
где Wx, Wp — осевой и полярный моменты сопротивления
сечения (например, для круга Wx =s 0,ld3; WV =ё 0,2d3); Мх, Мкр —
изгибающий и крутящий моменты; Р, F — сила и площадь
поперечного сечения.
Опыты показывают, что величины <т_1д могут быть в 2—6 раз
меньше _ с,!. Например, предел выносливости гладких
лабораторных образцов из стали, идущей на изготовление осей подвижного
состава железных дорог, в среднем равен а_г = 30 кгс/мм2.
В то же время предел выносливости натурной оси по
разрушению "составляет <т_1д = 7 кгс/мм2, т. е. в 4,3 раза меньше о_г.
Предел выносливости а_х лабораторных образцов из СтЗ в
среднем равен 22 кгс/мм2, а предел выносливости некоторых типов
сварных соединений крупных сечений из этой стали а_г = 3-г-
-г- 4 кгс/мм2; т. е. в 5,5—7 раз меньше.
47
Указанное снижение
предела выносливости, является
следствием влияния ряда
следующих факторов [1, 51, 52,
66, 67, 761:
1) концентрации
напряжений;
2) абсолютных размеров
поперечных сечений (масштабный
,,, фактор);
3) качества обработки
поверхности;
4) эксплуатационных
факторов (коррозия, повышенная и
пониженная температура,
радиация, частота переменной
г, о , ir ' - нагрузки и т. д.).
Рис. 3.1. Концентрация напряжении £У " '
в пластине с боковыми надрезами при 5) технологических методов
растяжении поверхностного упрочнения
деталей (наклеп поверхностного
слоя роликами, дробью и т. п., химико-термические методы —
азотирование, цементация, нитроцементация и др.,
поверхностная закалка с нагрева токами высокой частоты,
комбинированные методы и т. д.).
Примем, что коэффициент, учитывающий суммарное влияние
всех факторов на предел выносливости деталей,
Кпп = -
-1Д
C.2)
Далее поясним влияние каждого из указанных факторов на
сопротивление усталости, причем в данном разделе рассмотрим
влияние концентрации напряжений и абсолютных^, размеров
поперечного сечения.
Под концентрацией напряжений понимают местное увеличение
напряжений по сравнению с номинальными напряжениями в
местах резкого изменения очертаний детали (у канавок, отверстий,
резьбы, в местах перехода от одного сечения к другому по
галтели и т. д.).
Рассмотрим в качестве примера распределение напряжений
в пластине с двумя боковыми вырезами глубиной t и радиусом
закругления на дне выреза р при растяжении (рис. 3.1).
Распределение номинальных напряжений <тн = Р/Яб показано
пунктирной линией п—п. Действительная эпюра напряжений показана
сплошной линией ABC (здесь предполагают, что напряжения по
всему сечению не превышают предела пропорциональности
материала, т. е. возникают только упругие деформации). Из рис. 3.1
видно, что у дна надреза в точке О (и 0{) действительные напря-
48
жения ашах существенно превышают номинальные напряжения qH.
Это превышение оценивают теоретическим коэффициентом
концентрации напряжений, соответствующим упругим деформациям
Оа=^Ш-. C.3)
В тонкой пластине, показанной на рис. 3.1, возникает плоское
напряженное состояние. Эпюра ABC является эпюрой первого
(наибольшего) главного напряжения ох в сечении OOt,
направленного вдоль направления действия силы Р. В этом сечении
возникает также и второе главное напряжение <т2> направленное
вдоль оси X и равное нулю в точках О и Ог.
В случае растяжения круглого стержня с кольцевой канавкой
в поперечном сечении возникает объемное напряженное состояние
(на поверхности у дна канавки плоское).
Часто пренебрегают влиянием второго <т2 и третьего os
компонент напряженного состояния на сопротивление усталости и
учитывают только первое главное напряжение ог. Это допущение
оправдывается тем, что зарождение трещины начинается, как
правило, с поверхности, где имеет место линейное напряженное
состояние с главным напряжением ог (в случае пластины) или
плоское напряженное состояние с главными напряжениями ог
и 0а одного знака (в случае круглого образца), вследствие чего,
по гипотезе максимальных касательных напряжений, <та также
не влияет на сопротивление усталости. Поэтому в дальнейшем
учитывается только первое главное напряжение ах.
Действительное распределение напряжений в деталях и
элементах сложной конфигурации находят методами теории
упругости [36] или экспериментально (методами тензометрирования,
поляризационно-оптическим [90] и др.). В последнее время для
этой цели широко применяют численные методы решения задач
теории упругости (и пластичности) на ЭВМ (метод' конечных
элементов, вариационно-разностные методы и др.).
Величины а'а и ах для элементов различной конфигурации
и схем нагружения приведены в работах [36, 52, 80, 90]. Они
зависят от относительных размеров деталей. Например, в случае
пластины с вырезами при растяжении аа зависит от отношений
plh и H/h, причем с уменьшением относительного радиуса
закругления коэффициент а0 резко возрастает (см. разд. 17).
Как будет видно из дальнейшего, важную роль играет также
другая характеристика распределения напряжений, а именно
тангенс угла 8 (см. рис. 3.1) наклона касательной к эпюре первого
главного напряжения в точке А, т. е. у дна надреза.
Тангенс угла 8 равен абсолютному значению производной -^-
при х —J), где х — расстояние текущей точки поперечного^сече-
49
ния от точки О, которая называется градиентом напряжения
кгс/мм^
(
G = K*e»= [-£],_• C.4)
где К — масштабный коэффициент.
В расчетах на усталость далее используется относительный
градиент первого главного напряжения G( J, определяемый
по формуле
Г—1 •
C.5)
Например, в пластине, изображенной на рис. 3.1, при Hlh >
> 1,5, как вытекает из решения Нейбера [36],
G = ~. C.6)
Формулы для определения G в элементах различной
конфигурации приведены в табл. 3.1.
Чтобы оценить влияние концентрации напряжений на
сопротивление усталости, проводят усталостные испытания образцов
без концентрации и с концентрацией напряжений. Допустим, что
путем испытания серии пластин, показанных на рис. 3.1, нашли
их предел выносливости, обозначенный далее (ст_1к)й, выраженный
в номинальных напряжениях. Обозначим предел выносливости
гладких пластин такой же ширины h через (О-^н (имеются в виду
пластины без вырезов, не имеющие концентрации напряжений).
Индексы h показывают, что пластины с концентрацией напряжений
и без нее должны иметь один и тот же абсолютный размер
поперечного сечения, в данном случае ширину пластины h. Фактическое
снижение предела выносливости деталей вследствие концентрации
напряжении характеризуется отношением , *" , называемым
эффективным коэффициентом концентрации напряжений:
K" = l^t- C-7)
Значение Ко, как правило, меньше, чем сс0, и приближается
к сс0 при уменьшении уровня концентрации напряжений, с ростом
абсолютных размеров поперечного сечения и увеличением предела
прочности стали.
В качестве примера на рис. 3.2 приведены зависимости
теоретических сс0 и эффективных коэффициентов концентрации
напряжений Ко для ступенчатых валов с галтелью при изгибе с вра-
50
щением от p/d при —т- = 2. На рис. 3.2 нанесены точки,
соответствующие экспериментально найденным значениям Ка для таких
валов из углеродистой стали (<тв = 50 кг/мм2) диаметром d =
= 40-йЮ мм (линия 2) и d = 7ч-15 мм (линия 3) [51 ]. Линии 2
и 3 рассчитаны в соответствии с теорией, изложенной в разд.'7
[по уравнению C.68) при va = 0,1].
На рис. 3.2 видно, что Ка < аа- При увеличении диаметра
образцов с 7—15 до 40—50 мм значения Ка заметно увеличиваются.
Это же можно видеть и на рис. 3.3, где представлена зависимость
Ка от диаметра образцов с глубокой кольцевой выточкой из
осевой стали при изгибе с вращением. Экспериментальные точки
нанесены по данным работы [65]. Линия рассчитана по
уравнению C.68) при va — 0,1 (см. разд. 7).
Для установления связи между Ка и аа используют
коэффициент чувствительности металла к концентрации напряжений [90]
Ча =
1
C-8)
Тогда
#<Т= 1+<7а («*-!)•
При Ка — 1. Яа = 0 металл не чувствителен к концентрации
напряжений. Такое положение наблюдается на небольших
образцах из серого чугуна и объясняется тем, что графитовые,
включения в чугуне являются внутренними источниками концентрации
напряжений, определяющими уровень предела выносливости как
гладких, так и надрезанных образцов.
При Ка — аа> с/о = 1 металл обладает полной
чувствительностью к концентрации напряжений. Первоначально
предполагалось, что qa зависит только от свойств материала и радиуса
закругления в зоне концентрации напряжений р. Пример такой
зависимости приведен на рис. 3.4. Однако позднее была
установлена неоднозначность подобной зависимости (qa от р) и
возможность получения заметных ошибок при использовании зави-
Рис. 3.2. Зависимость
коэффициентов аа и Ка для
ступенчатых валов с
галтелью из углеродистой стали
при изгибе с вращением от p/d
[ -rj- = 2; о-в = 50 кгс/мм2 ,
[90]; 2 — i = 40-
\
1 — а.
- 50 мм; 3 — d = 7 +15 мм
0,15 p/d
4*
51
[енш
(Г
>>
§
\о
и
S
СУ
н
Й
е-сд
:ени
О
СЪ
Я
а
СУ
Е
от
Й
а
СУ
ГЬНЬ
)CHTej
Отнс
HIT
:из дета
со
1
1
, _
'
<N Ut
+
1
см о.
II
Ю
, ^
SS
см|о.
II
Ю
ю
~-"
л\
аз|^
si
1
i
, ^
СО
4—'
см
"&■
+
>—>,
(М
JS
о.
II
га
, ч
^
^.^
э-
+
<м
о.
II
га
ю
.-*'
V
аз|^
И
\
п
I
.У
р^"
<м]-а
+
~|о.
II
, _
Ю
'
<N
+
1
сМ О.
II
га
, ч
<£>
<м о.
II
Ю
ю
1-Г
л\
С||чЗ
V-
о
см|"а
+
—1 О.
II
, ^
со
^-^
СХ1
S?
+
С
СМ
43
о.
II ■
га
, ^
22-
,__^
э-
+
см
о.
II
Ю
ю
«
V
C||ts
iH®i
а
т
1
Ly
1
1
, _
>—>,
<N Vst
+
СО
3|°-
II
га
^
см
~-*-
.
II
га
ю
.-Г
л\
азН
%
к
V.
\\
.1,
^7
52
I
1
CO
■—'
CM |JS
^
Э-
+
CO
CM
Q.
II
Ю
, ^
^f
S
+
CO
CM
Q.
- II
ra
V
аз]-*
t~-
-cM ra -
+
Ю 1
—J o.
II
itf
Ю
CM
CO
CM
■a
Q.
II
ra
t ^
CD
см-|°-
II
Ю
л\
q|^
О
CM
см Its
+
in |
" Q-
II
itf
CO
■—'
см [-a
Э-
+
CO
CM
Q.
II
1<Э
, ^
CT>
&
+
CO
CM
Q.
II
Ю
in
V
q|^3
■ л
«3
V
;1
' и
4
I»
|
I
I
, _
SI
■ «L
II
lO
I
5>L
X
•^
X
u®
^
m cj '
?! &>■
О 5, ft
ft ft
Я ^
ч я
Ж m t i
4
в sg
и ftg
3* о ^
>> «.«
4
о в -
S 3^o
w of4
^ Д 4)
a Й 5
со <J G
1-1 в?
rt И О
ft t; И
<u oB
\D Ч О
m В cf
*~ g§
a* G ft
s* а ч
go | о
4) Ч 0 С
ft >> я
«ft § Я
«о ra§
$3 о о >■
si csi 4
»B ""g
Eh В » G
юответс
аналог
.8), A9)
ла B)
" 2 з>-м
соВ .: S Ч
Г-Р- + 2
7) получены и
, (9) записаны
К- Прейссом
15), A6), A7),
зами. 5. Фор
шения Гоулан
11 -SSSb'S
в „©„-. о ч
-w -w—- Еч о
А <? ГС Л >,м
р и м е ч
Формул
:я Нейбер
Формул
Формул
ой или дв
лизкие к
в IS
ft И Ен
53
Кб
2,S
2,5
2А
2,3
/
/
©
(
\-^^"^
мизг Мизг
1 i
го
40
so
d,MM
О
Рис. 3.3. Зависимость эффективных
коэффициентов концентрации Кд от
диаметра геометрически подобных
валов с кольцевой канавкой
(выточкой) из осевой стали при изгибе с
вращением I -у— = 35; аа = 3,35;
D/d= 2
1,5 р,мм
Рис. 3.4. Зависимость коэффициентов
чувствительности металла и
концентрации напряжений от радиуса
закругления в зоне концентрации
напряжений:
/ — высокопрочные стали после нормали- .
зации; 2 — стали средней прочности после
нормализации
симости C.8) для определения Ка по величинам аа и qa. Поэтому
рекомендации определять Ка по зависимости C.8), встречающиеся
в литературе, следует использовать лишь в тех случаях, когда
нет возможности определить Ка другими более точными методами.
При этом следует иметь в виду возможность получения ошибок
в оценке Ка до 20% и более.
На рис. 3.4 видно, что с ростом предела прочности стали
увеличивается чувствительность к концентрации напряжений,
т. е. для образцов одной и той же конфигурации и размеров
эффективные коэффициенты концентрации увеличиваются в
большинстве случаев с ростом предела прочности стали.
Наряду с формулой C.8) некоторые авторы предлагали другие
формулы для подсчета Ка по известным значениям аа. Нейбер
[36], рассматривая задачи теории упругости для тел с
остроугольными выточками, ввел поправку, осредняя напряжения у дна
выточки на весьма малом конечном участке длины
протяженностью, соизмеримой с размерами зерна или блока зерен,
получил формулу для «технического» коэффициента концентрации ак:
а.
1
«я— 1
1
Я l/ Р'
C.9)
где р —■ константа материала; г — радиус закругления и со
угол раствора выточки.
54
Куном [52] было предложено принять Ка = сск по формуле
C.9). Были найдены значения р' в зависимости от предела
прочности стали. Формулы типа C.9) приводят к ошибкам до±20%
в определении Ка, не позволяют описать зависимость Ка от
абсолютных размеров поперечного сечения и не отражают
статистических закономерностей совместного влияния концентрации
напряжений и масштабного фактора на сопротивление усталости.
Поэтому формулы типа C.8), C.9) могут использоваться лишь для
весьма приближенных предварительных оценок.
Влияние концентрации напряжений на сопротивление
усталости при асимметричных циклах во многих случаях
характеризуется следующей закономерностью, установленной на основе
обработки многих экспериментальных данных [52]: отношение
предельных амплитуд гладких образцов и образцов с
концентрацией напряжений, соответствующих одному и тому же среднему
напряжению цикла ат, не зависит от асимметрии цикла. Иначе
говоря, эффективные коэффициенты концентрации напряжений
при асимметричных циклах, найденные по отношению указанных
предельных амплитуд при одном ат, не зависят от асимметрии
цикла, вследствие чего можно принять
(Ко)г = (Ко)-ъ (ЗЛО)
где (Ка)г = —— ; (Ka)-i — -^ эффективные концентрации
при асимметричном и симметричном циклах соответственно (аа,
аак — предельные амплитуды напряжений для образцов
гладких и с концентрацией напряжений соответственно, найденные
при одном среднем напряжении от).
Существенное влияние на сопротивление усталости оказывает
также масштабный фактор, под которым понимают влияние
абсолютных размеров поперечного сечения (диаметра вала, высоты
и ширины пластины и т. п.).
С ростом абсолютных размеров поперечного сечения гладких
образцов пределы выносливости их снижаются. При изгибе с
вращением при увеличении диаметра с d0 = 7,5 мм до 200—300 мм
это снижение доходит до 30—45%. Для оценки влияния
масштабного фактора вводится коэффициент влияния абсолютных
размеров поперечного сечения на величину предела выносливости
% = ^> C.11)
a-i
где a_ld — предел выносливости гладкого вала диаметром d
при изгибе с вращением; а_х — предел выносливости гладкого
лабораторного полированного образца при изгибе с вращением
диаметром d0 = 7,5 мм.
На рис. 3.5 представлены экспериментальные данные ряда
исследований [23, 65, 66, 67, 83, 88, 91 ], характеризующие мас-
55
9) 1
3
^ ф ♦ 4 ST
i
1
\
0
-at
i
i
IW-
*
<
<
Г
¥
1,5 10 20 30 40 SO 70 100 150d,MM
Рис. 3.5. Зависимость коэффициентов влияния абсолютных
размеров поперечного сечения га при изгибе с вращением гладких
образцов (валов) из углеродистых сталей от диаметра образца
штабный эффект при изгибе с вращением валов из углеродистых
сталей. На рис. 3.5 видно, что еа = 0,6-МЗ,7 при d = 100-;-150 мм
[65, 66], и в,, = 0,88 при d = 100 мм [88], т. е. имеет место
заметный разброс, что объясняется различием материалов,
условий обработки и испытания образцов. Из рис. 3.5 видно, что
масштабный фактор оказывает сильное влияние на предел
выносливости. Аналогично влияние масштабного фактора у
легированных сталей при изгибе, и у всех материалов при кручении. При
растяжении-сжатии масштабный эффект до d = 40 мм
проявляется очень слабо.
Основными причинами проявления масштабного эффекта
являются металлургический, технологический и статистический
факторы.
Металлургический фактор связан с ухудшением механических
свойств металла с ростом размеров отливки или поковки, так как
при этом увеличивается неоднородность металла, уменьшается
степень деформации при ковке, затрудняется качественное
проведение термической обработки по всему объему металла. Все это
приводит к снижению пределов прочности ов, пределов
выносливости а_г и других характеристик, определенных на
лабораторных образцах малых размеров, вырезанных из заготовок
различных размеров. Согласно данным справочной литературы
по сталям величины пределов прочности, определенные на
лабораторных образцах, снижаются в среднем на 10% у углеродистых
и марганцовистых сталей и на 15—20% у легированных сталей
56
при увеличении диаметра заготовки с 10 до 500 мм. При этом
предел прочности уменьшается по мере смещений от периферии
заготовки к центру. Аналогичную зависимость получают для
пределов выносливости образцов, твердости и характеристик
пластичности. Чтобы исключить влияние металлургического
фактора при исследовании зависимости абсолютных размеров
деталей от сопротивления усталости, большие и малые образцы
изготовляют из одной заготовки или из нескольких заготовок одной
плавки металла, образцы при этом располагают так, как показано
на рис. 3.6. На рисунке изображено поперечное сечение заготовки
диаметром D, из которой изготовляют образцы наибольшего
в рабочем сечении диаметра d. Образцы малого диаметра d0 и
промежуточного диаметра d1 располагают так, что
соответствующие окружности касаются окружности диаметра d. При этом
обеспечивается наличие в поверхностных слоях образцов
различного диаметра зон с одинаковыми механическими свойствами,
соответствующими удалению от центра заготовки на расстоя-
d •
ние т.
Для учета влияния металлургического фактора в расчетах
на прочность исходные механические свойства металла (схв, а_х)
должны определяться на лабораторных образцах, вырезанных
из заготовок, соответствующих по размерам натурной детали.
Влияние второго (технологического)'фактора связано с тем,
что при механической обработке образцов в их поверхностных
слоях создается наклеп и остаточные напряжения, которые по-
разному влияют на величину предела выносливости больших
и малых образцов. Для исключения влияния этого фактора при
исследовании масштабного эффекта пользуются! или_. отжигом
в вакууме, снимающим наклеп
и остаточные напряжения без
окисления поверхности, или
применяют много проходов при
обточке образцов с постепенным
уменьшением глубины резания и
подачи для существенного
уменьшения наклепа и остаточных
напряжений.
В исследованиях, результаты
которых приведены на рис. 3.5,
применялись указанные меры для
исключения влияния
металлургического и технологического
факторов. Поэтому величины га, пред- Рис. 3.6. Схема расположения
ставленные на рис. 3.5, характе- образцов в объеме заготовки
ризуют влияние третьего, стати- 7ри исслеД°вании масштабного
Г „ j. фактора, исключающая влияние
стического фактора на сопроти- £азличИя механических свойств по
вление усталости, связанного со радиусу заготовки
57.
статистической природой процесса усталостного
разрушения.
Объяснение влияния этого фактора вытекает из статистической
теории подобия усталостного разрушения (см. разд. 7).
Влиянием длины образца на сопротивление усталости можно
пренебречь, так как оно невелико. В большинстве случаев детали
имеют концентрацию напряжений, приводящую к локализации
места разрушения и исключению влияния длины вследствие
этого.
7. Статистическая теория подобия
усталостного разрушения
Вводные замечания. Для расчета деталей машин на усталость
конструктор должен располагать характеристиками
сопротивления усталости натурных деталей. Наибольшую информацию об
указанных характеристиках можно получить по полной
вероятностной диаграмме усталости (см. разд. 4), для построения которой
требуется провести испытание не менее 50—100 деталей, что во
многих случаях осуществить невозможно. Для расчета на
усталость вероятностными методами, как будет показано далее,
можно ограничиться меньшим объемом информации, а именно,
знать параметры уравнения кривой усталости, соответствующего
вероятности разрушения 50%, в форме
a%N = 0^1ДМ) при аа > о_1Д;
N =zoo при аа < о_1д
и коэффициент вариации предела выносливости va . В
уравнении C.12) Л^0 — абсцисса точки перелома кривой усталости;
т — показатель угла наклона левой ветви кривой усталости;
сГ1д — медианное (соответствующее вероятности разрушения 50%)
значение предела выносливости детали на множестве всех плавок
металла данной марки, возможных отклонений размеров от
номинальных в пределах допуска, всех возможных внутриплавоч-
ных отклонений свойств, а также технологических отклонений.
Отметим, что в дальнейшем будем использовать также
величину сг_1д, являющуюся медианным значением предела
выносливости деталей с возможными отклонениями размеров и
технологии, но изготовленных из металла одной плавки. Иначе говоря,
переход от о_1д к о_1д связан с дополнительным осреднением
величин о_1д по множеству всех плавок металла данной марки.
Аналогично а_г — медианное значение предела выносливости
гладких, тщательно полированных лабораторных образцов при
изгибе с вращением диаметром 7,5 мм, изготовленных из металла
одной плавки; а_г — то же для образцов, изготовленных из
металла различных плавок данной марки.
58
C.12)
Для получения параметров уравнения C.12) необходимо
проводить испытания меньшего количества образцов, т. е. для
получения приемлемых результатов можно ограничиться-
натурными испытаниями 15—25 деталей. Однако и такое испытание
выполнить трудно или практически невозможно (для деталей
с размерами поперечных сечений >400—500 мм). Как будет
видно далее, можно не требовать большой.точности в оценке
параметров N0 и т, которые могут быть найдены на основе испытаний
ограниченного числа деталей с использованием статистических
осреднений указанных величин, ранее полученных по результатам
испытаний однотипных деталей.
Таким образом, основное значение имеет точное
определение а_1д и уа_г . Возникает необходимость разработки метода,
позволяющего по результатам испытания малых образцов и
моделей средних размеров находить указанные величины для
натурных деталей. Для этого необходимо отыскать такой критерий
подобия усталостного разрушения, соблюдение постоянства
которого у модели и детали обеспечивало бы совпадение функций
распределения пределов выносливости и их параметров о~_1д и Va_x .
Для решения этой задачи большую роль сыграли различные
варианты статистических теорий прочности [1, 4, 14, 97].
Статистическая теория прочности «наиболее слабого звена»,
предложенная Вейбуллом [97], позволила описать влияние
абсолютных размеров образцов и неоднородности распределения
напряжений на характеристики сопротивления хрупкому разрушению.
Статистическая теория прочности Н. Н. Афанасьева [1] дала
возможность охарактеризовать влияние конструктивных факторов
на средние значения пределов выносливости деталей машин.
Использование и развитие идей, содержащихся в указанных
работах, позволило сформулировать статистическую теорию
подобия усталостного разрушения [23], которая дает
удовлетворительное описание влияния конструктивных факторов на
параметры функций распределения пределов выносливости. Эта теория
послужила основой для создания новой системы справочной
информации, предназначенной для определения расчетных
статистических характеристик сопротивления усталости деталей
машин.
Статистическая теория подобия усталостного разрушения
в изложенной далее форме дает описание влияния концентрации
напряжений, масштабного фактора, формы поперечного сечения
и вида нагружения на характеристики сопротивления усталости,
определяемые по условию появления первой макроскопической
трещины усталости. Характеристики прочности на стадии
развития усталостной трещины и окончательного разрушения
описываются методами механики разрушения (см. разд. 2).
Под первой макроскопической трещиной усталости понимается
трещина протяженностью до 0,1—0,5 мм, обнаруживаемая при
59
Itt
m
a)
Рис. 3.7. Схемы к выводу фор<
мул статистической теории
прочности наиболее слабого звена
усталостных испытаниях
визуально, с помощью лупы, или по
началу снижения частоты
собственных колебаний при
испытаниях на резонансных
усталостных машинах. Некоторая
неопределенность в указании размера
начальной трещины не имеет
практического значения, так как
у деталей с умеренной
концентрацией напряжений (аа < 2-=-3)
пределы выносливости по началу
образования трещины и
окончательному разрушению почти
совпадают [8 ].
В основе этой теории лежит
статистическая теория прочности
«наиболее слабого звена». Допустим, что имеется цепь из я звеньев
(образцов), соединенных последовательно и нагруженных
напряжением а (рис. 3.7, а). События, заключающиеся в разрушении
отдельных звеньев, будем считать независимыми, т. е. вероятность
разрушения r'-го звена не зависит от факта наступления
разрушений в каком-либо другом звене или в группе звеньев.
Обозначим вероятность разрушения г-го звена при действии
напряжения а—Рi (а). Эту функцию от а можно рассматривать так же,
как функцию распределения характеристики прочности звена,
например, предела прочности ав, если речь идет о статической
прочности, ибо Рi (а) — это одновременно вероятность того, что
прочность ав меньше или равна а, т. е.
/>,(*) = Вер {а,<а}. C.13)
Вероятность неразрушения i-то звена
Qt (а) = 1 - Pt (а).
Вероятность неразрушения всех звеньев, т. е. цепи, по теореме
о вероятности одновременного наступления я независимых
событий
Q(cr)=fl[l-P,(cr)].
t=i
Вероятность разрушения цепи имеет вид
P(cr)=l-Q(cr)=l- П[1-Р,(°-)]-
C.14)
Выражение C.14) определяет функцию распределения
прочности цепи. Если все звенья одинаковы, то вероятность
разрушения единичного звена Рь (а) не зависит от i, вследствие чего
6Q
ее можно обозначить Р1 (а). В этом случае уравнение C.14)
принимает вид
Р (а) - 1 — [1 —Рг (а)]". C.15)
Уравнение C.15) уже как бы отражает влияние «масштабного
фактора», ибо из этого уравнения следует, что с ростом
количества звеньев я вероятность разрушения цепи при том же <з
увеличивается. Пусть, например, вероятность разрушения единичного
звена Р1 (а) = 0,0001; тогда при я = 10 по уравнению C.15)
Р (а) = 1 — A — 0,0001I0 = 0,001, а при я = 1000 Р (а) =
= 1 — A —• 0,0001I000 =g 0,095.
Допустим теперь, что деталь имеет неравномерное
распределение напряжений по объему, заданное функцией (рис. 3.7, б)
о = <W(*. У; г). C-16)
где ашах — максимальное напряжение в некоторой точке детали;
0 < / (х, у, z) s^ 1 — безразмерная функция координат
(рассматривается случай только положительных напряжений а; если
в части объема детали действуют отрицательные напряжения, то
объем разбивается на две части, рассматривается вероятность
разрушения каждой из частей, и затем находится общая
вероятность разрушения).
Возьмем некоторый объем детали AVt достаточно малый для
того, чтобы считать напряжения в нем равномерно
распределенными и равными а,-, однако состоящий из некоторого количества nt
единичных объемов Vg (я,- = AF,-/V0). Предположим, как и
ранее, независимыми события, заключающиеся как в
разрушении единичных объемов в пределах ЛУ,-, так и в разрушении
этих последних в пределах всего тела. Тогда вероятность
разрушения г'-го объема AV,- согласно выражению C.L5) будет
иметь вид
Pt(at)= 1-[1-Pa (a,)] \ C.17)
где Рп (а;) — вероятность разрушения единичного объема,
входящего в объем ЛУ,- и нагруженного напряжением а,-. Примем,
что эта вероятность распределена по закону Вейбулла:
. Ра(а^\1~М~{^Т] при а, > и; J
I 0 при а,- < и.!
Здесь и, а0, т — параметры распределения. Подставляя
выражение C.18) в формулу C.17), получаем
р,<«,>=('-ехрн^га ^,нC.ш>
( 0 при at < и. )
61
Полагаем, что разрушение любого из объемов AVlt входящих
в состав тела, означает разрушение всего тела, что эквивалентно
рассмотрению всех ДУг, как образующих цепь последовательно
соединенных звеньев. Подставляя выражение C.19) в формулу
C.14) вместо Р( (а), получаем вероятность разрушения детали
при максимальном напряжении ашах:
р ы =
_ |, - ехр {- 2 [^^ „)-.]■ т. j при Сш„ „ к I
I 0 при отах<и. ]
C.20)
Суммирование в уравнении C.20) осуществляется только по
тем объемам AVt, в которых а,- > и.
Полагая, что возможен переход к пределу в формуле C.20)
при АУ(- -э- 0, в результате которого сумма заменяется
интегралом, получаем вероятность разрушения детали при действии
ашах в виде
Р (Ртах) =
при агаах > и; }
C.21)
при агаах < 0. J
Обозначим интеграл, входящий в выражение C.21), через /:
/= | ^ОщЯХЦх^у,г)-иу^_^ C22)
и
В выражениях C.21) и C.22) Vu — часть объема детали,
в которой а = amax/ (х, у, z) > и. Из зависимости C.21) имеем
^ = ^(стшах)=1-е^ C.23)
или / = ji-lgA _/>) = _2,3lg(l-/>).
Уравнение типа C.21), приведенное в работе [97], послужило
основой для трактовки закономерностей влияния конструктивных
факторов на пределы прочности хрупких тел.
Статистическая теория подобия усталостного разрушения.
Рассмотрим теперь использование уравнения C.21) для вывода
основных соотношений статистической теории подобия
усталостного разрушения [23, 52]. Для получения достаточно простых
соотношений, удобных для практического использования,
целесообразно пренебречь влиянием второстепенных факторов, сделав
некоторые допущения. Первое допущение, сделанное уже при
62
fl —ехр/— [[•^»/(^У,г)-и]т-^
1 Vu
о
выводе уравнения C.21), заключается в пренебрежении влиянием
второго и третьего компонента главных напряжений. Аналогичное
соотношение, записанное с учетом всех компонент, дано в [25].
Второе допущение состоит в пренебрежении влиянием длины
и в замене интегрирования по объему в выражении C.21)
интегрированием по площади поперечного сечения, а именно, с учетом
уравнения C.22) и C.23)
/ 2,31g(l —/>)= J [ашшГ%У)~и]'
dF
F0
C.24)
где Р = P (ашах) — вероятность разрушения при максимальном
предельном напряжении в зоне концентрации, не превышающем
атах при ашах > Щ Fu — та часть площади поперечного сечения,
в которой ап
> и. Если по всей площади сечения сшах < и,
то принимается Р (ашах) = 0. Второе допущение было предложено
Н. И. Афанасьевым [1] и мотивировалось тем, что переход от
одного сечения к другому не приводит к новой комбинации в
распределении дефектов по сечению при волокнистой структуре
с волокнами вдоль образца.
Под величиной ашах в уравнении C.24) понимается
максимальное напряжение в зоне концентрации, соответствующее пределу
выносливости детали а_1д, а именно
C.25)
: = С-1Яав>
где а,д — теоретический коэффициент концентрации напряжений.
Рассмотрим брус прямоугольного поперечного сечения с двумя
боковыми надрезами глубиной t и радиусом закругления на дне
надреза р. На рис. 3.8 представлена эпюра распределения первого
главного напряжения аг
(направленного вдоль
вертикальной оси а) по поперечному
сечению в месте надрезов. Ось х
направлена вправо с началом
координат в центре сечения.
При х = а (на дне надреза)
напряжение равно сшах. На
участке, прилегающем к точке В,
действительную эпюру
напряжений можно заменить
отрезком прямой линии, являющейся
касательной к эпюре
напряжений в точке В. Тангенс угла
наклона этой касательной к оси
абсцисс, т. е. tg 6, как уже от- Рис- 3-8- Распределение первого глав-
,,^,то,т,-™ „ „ г- л ного напряжения в призматическом
мечалось в разд. 6, равен абсо- (fl) и цилиндрическом (б) брусах с
лютному градиенту напряже- надрезами при растяжении-сжатии
63
ний G, определяемому по формуле C.4). Точка А, которая также
лежит на касательной, имеет абсциссу х = а0 и ординату 0=
= и, т. е. абсцисса этой точки ограничивает область
интегрирования в выражении C.24).
Легко проверить, что уравнение линии АВ, заменяющей
действительную эпюру на участке а0 ^ х ^ а, имеет вид
0 — и = G (х — а0), C.26)
где
G= а™*~и . C.27)
Интеграл / в уравнении C.24) получает вид
F.
К^гГ-й-'П0-^]'
_ 2bGm(ct — a0)m+l
Выражая а—а0 из уравнения C.27) и принимая
C.28)
g = _£m-L; G=-A_; L = 2fr, C.29)
и °max
после элементарных преобразований из последнего выражения
получаем
/ = ■
_L 1_ f U \m {I— \)m+l
GFn («+
W(iT^FL=-2-3^-^ <3-3°>
Выражение C.30) является по существу функцией
распределения величины £, а следовательно, и предела выносливости
0_1д = -^- [см. формулы C.25) и C.29)] бруса, показанного на
рис. 3.8, ибо каждому значению g соответствует определенная
вероятность разрушения Р.
Множитель -=—■ может быть назван критерием подобия уста-
GF0
лостного разрушения, а выражение C.30) — уравнением
подобия, ибо если деталь и модель имеют различные абсолютные
размеры а, Ъ, р и различные относительные размеры а/р, гУр
и т. п., но имеют одинаковое значение L/GF0, то функции
распределения их пределов выносливости, выраженных через 0шах =
= 0_1дао или £ = отах/и, должны согласно формуле C.30)
совпадать. Эта закономерность, справедливость которой
подтверждена экспериментами, проведенными в разных странах многими
исследователями, как будет показано далее, имеет большое прак-
64
тическое значение, ибо она дает возможность находить в первом
приближении функции распределения натурных деталей на основе
испытаний образцов и моделей.
Величина Р0, имеющая размерность площади в выражении
критерия подобия, является произвольной и может быть принята
равной F0 = 1 мм2. В этом случае критерий подобия принимает
вид -=-, где L — следует подставлять в мм, a G в 1/мм (в дальней-
G
шем во всех уравнениях принято .F0 = 1 мм2).
Легко установить, что все формулы и рассуждения остаются
без изменений, если вместо растяжения бруса, показанного на
рис. 3.8, а, нагружать его знакопеременным изгибом относительно
оси z, перпендикулярной к передней плоскости бруса.
Следовательно, формула C.30) распространяется на случай изгиба при
L = 26.
В случае круглого бруса с кольцевой канавкой при
растяжении-сжатии или изгибе с вращением элементарную площадку dF
в интеграле C.24) следует выбирать в виде кольца с внутренним
радиусом г и наружным г + dr, как показано на рис. 3.8, б,
т. е. dF = Inrdr. В этом случае вычисление интеграла / в фор-,
муле C.24) приводит к следующему выражению, аналогичному
зависимости C.28):
/' 1 —-^
j _2яо_ _G^_ (а~а0)т+г . _ о_
~~ F0 af m+l V т + 2
Г Значения а0 обычно весьма близки к а, т = 6ч-10, так что
вторым слагаемым в скобках можно пренебречь, в результате чего
последнее выражение приводится к формуле C.30) при L =
= 2па = nd, где d — диаметр бруса по дну надреза. Все
сказанное справедливо и для круглого ступенчатого бруса с переходом,
от одного сечения к другому по галтели при растяжении-сжатии
или изгибе с вращением, причем в этом случае также справедливо,
уравнение C.30) при L = nd. Таким образом, уравнение C.30)
применимо для всех деталей, показанных на рис. 3.9 и им
аналогичным. Значения параметра L указаны на этом рисунке.
Параметр L равен периметру рабочего сечения, если
максимальные напряжения одинаковы по всему периметру (круглые, брусья
при растяжении-сжатии или изгибе с вращением, для которых
L = nd), или части периметра, прилегающей к зоне повышенной
напряженности для других случаев, как показано на рис. 3.9.
Если взять любые две различные детали из изображенных на
рис. 3.9 и нагруженных различными способами (например,
пластина с отверстием при растяжении-сжатии и круглый
ступенчатый брус при изгибе с вращением), но имеющие одно. ито. же
значение критерия подобия -=г-, то согласно уравнению C.30) эти
3 В. П. Когаев
65?
L = l(n-d)
Рис. 3.9. К определению параметра L для деталей различных форм и схем нагру-
жения
детали будут иметь совпадающие функции распределения пределов
выносливости, выраженных в максимальных напряжениях 0гаах.
Эта закономерность подобия усталостного разрушения хорошо
подтверждается экспериментальными данными (как будет
показано ниже) и является основой для моделирования при
усталостных испытаниях.
Рассмотрим теперь детали, изображенные на рис. 3.10:
пластины с отверстиями (д), с боковыми надрезами (а), с переходом
от одной ширины к другой (г), цилиндрические образцы с
отверстиями: сплошные (б) и полые (в), изгибаемые относительно оси х.
На рис. 3.10, а изображено распределение первого главного
напряжения в такой пластине, действующего вдоль оси z.
Максимальное напряжение стшах действует в точке О на дне выреза
пластины, на верхней (и нижней) плоскости пластины. Очевидно,
таких точек максимальной напряженности в пластине имеется
четыре. Неравномерность распределения напряжений здесь
характеризуется двумя градиентами напряжений, один из которых
г да 1 „
-з— характеризует скорость падения напряжении
■в плоскости хОо от точки С, второй Ga = -£- — в вертикаль-
«1
ду
20л
-, т. е.
ной плоскости уОо. В качестве Ga можно принять G2
такое же значение, как при изгибе гладкого бруса высотой h.
Рассечем эпюру напряжений плоскостью а = и, г. е. плоскостью,
параллельной плоскости хОу и отстоящей от нее на расстояние и
(в масштабе а). Эта плоскость пересекает эпюру напряжений
в точках А' (Ь, О, и) и В' (О, а, и), где в скобках указаны коорди-
66
наты точек в системе х—у—0. Реальную эпюру (поверхность)
напряжений заменим плоскостью, касательной к поверхности
в точке С. Эта плоскость пройдет через точки А' и В', и ее
уравнение в системе координат х—у—0 имеет вид
' = и + (<W — и) (l — -b
C.31)
Отрезки а и b определяются градиентами напряжений Gx
и G2 = 2omJh:
b =
а =
tfmax — U
:Goi
(l --"-)• C-32)
\ umax /
Интегрирование в уравнении C.24) осуществляется по площади
Fu, которая в данном случае представляет собой площадь четырех
изе
а м,т
П'Ъ
'изг
Рис. 3.10. Детали с двумя учитываемыми градиентами напряжений
3*
'изг
67
Треугольников типа ОАВ (в точках этого треугольника 0 > и).
вычисление интеграла C.24) осуществляется следующим образом:
0 ° °
В результате вычислений получаем
т _ 4аЬ ((тшах — и)т ,, оо\
(сомножитель 4 введен потому, что при изгибе деталей,
показанных на рис. 3.10, имеется четыре одинаковых зоны
концентрации, т. е. четыре треугольника типа ОАВ).
Обозначая £ = —SS- , G\ =—— и учитывая выражения C.32),
и tfmax
Получаем
j _ 2ft / и у A-1)т+2 ,оШ
G± Wo/ ?2 (m+l)(m +2) ' . ^"^
При известных параметрах и, о0 n m по уравнению C.34)
мэжно найти функцию распределения пределов выносливости
деталей, показанных на рис. 3.10. Для< практического
использования целесообразно получить соотношение, позволяющее по
функции распределения предела выносливости 0_1гл гладкой
пластины высотой h и шириной b (без концентрации напряжений)
найти функцию распределения предела выносливости пластины
с концентрацией напряжений нетто-сечением h x b — ст_1д.
Обозначим
t 1 gmax 2 Р-1гл . е tfmax l T-iA^c
62 — - — " .
Sill
Где crmax2 и crmaxi — максимальные напряжения соответственно
для, гладких пластин и пластин с концентрацией напряжений.
Для гладкой пластины при изгибе, как следует из
выражения. C.30) при F0 = 1 мм2, имеем
, = jb /« \m(£,-i)m+1 1 C.35)
G2 V <*о/ Ь (т+1) '
Соотношение между £2 и £i получим, приравнивая / по
уравнениям C.34) и C.35):
2 (?1-1)т+2 _6(|s-l)m+1
G, E!(m+2)
C.36)
|при этом каждой паре значений £2 и £х, удовлетворяющей
уравнению C.36), соответствует общая вероятность
разрушения].Зависимость -между £2 и ^.подсчитанная по формуле .C.36) для
68'
ряда значений т и произведения bG = 50 представлена на рис." 3.11.
Следовательно, зная функцию распределения пределов
выносливости гладкой пластины, сечением hxb, определяемой
уравнением C.35), по рис. 3.11 можно найти функции распределения
деталей, показанных на рис. 3.10. При этом ширина гладкой
пластины, с которой сравнивается заданная деталь, определяется
соотношением Ь = ~^-. В случае изгиба круглых стержней
(сплошных или полых) с поперечным отверстием, изображенных
на рис. 3.10, процедура определения функций распределения
пределов выносливости остается" такой же, причем следует
полагать h = D.
Зависимость C.36) между £а и \х при bG1 = 50,
представленную графически на рис. 3.11, можно для удобства заменить
следующей приближенной линейной зависимостью, ошибка которой
не превышает 1 % в практическом диапазоне изменения т и £4:
% _ £а + 0.557 lgm — 0,991
й 0,587 lgm — 0,028 '
C.37)
Как будет видно из дальнейшего, для сталей в среднем ш=8.
При т = 8 зависимость C.37) имеет вид
£i = 2S, - 1
или
'lg (ёх — 1) = lg (£*-!) +0,301.
C.38)
C.39)
Величина \% может быть найдена из уравнения C.35) при
заданной Р, а следовательно, и / при
Т)гл= l| = Ж = bh = 10,87Ы°™ s 11Ы0ТВ, C.40)
так как
50
50do
Gi 2,3/p
= .10,87dOTB,
Для .пластины
4;6
C.41)
с отвер-
— 05
стием значение G, = ——■ =
* п
4,6
в соответствии с
теоретическим решением Гоу-
ланда для растягиваемой
пластины, в предположении,
что для изгиба градиент
такой же. Зная ga, по
уравнениям C.36) или C.37),
V
1,6
1А
1,3
1,2
1,1
1,0
^
г
s
/
^Л
т_2
V
6
3;
1,0 1,1 1,2 1,3 1,i 1,5 1,6 1,1 1,8 1,9 2,0 2,1 ^
Рис. 3.11. Зависимость %ъ = / (|х, т) для
расчета деталей, изображенных на
рис. 3.15
69
бтах
Рис. 3.12. Схема к
выводу формулы для круглого
„ гладкого бруса при изги-
ч чтшд бе в одной плоскости
C.38) находим |х и о_1д = -^- для деталей, показанных на
(Хо-
РИС. 3.10; экспериментальное подтверждение этих соотношений
дано ниже.
Рассмотрим отдельно случай переменного изгиба в одной
полоски круглого гладкого бруса. Эпюра распределения
напряжений в этом случае и необходимые обозначения показаны на
рис. 3.12. Областью интегрирования являются два сегмента, для
которых у > а0 и а > и; элементарной площадью <£F являются
две полоски, одна из которых показана на рис. 3.12, причем
dF = 2ЪУ dy = 4 У а2 — у2, dy, где а = -д- ■— радиус бруса.
Вычисление интеграла C.24) сводится к следующему:
/ =
а I У
I °"шах —— ■
4 Va2 — у2 dy
о о
(Л-У^&т), C.42)
а0
где
(&г — 1)У 1 —2«dz;
i/l
У . р ffmax
а ' " и '
C.43)
z = -
Соотношение между пределами выносливости круглых гладких
образцов при плоском изгибе <т_1пл и при изгибе с вращением
(или круговом изгибе) о_1кр получается, если выражение C.42)
приравнять уравнению C.30), приняв для гладкого бруса при
круговом изгибе
L \ nd nd2
кр
Тогда
AКР-1Г+1 _ 2(m+l) г № шч
C.44)
Здесь |кр = а_1кр/м; £пл = °-W«-
70
Зависимость
у = -|2i = -^1™.
5кр °"-1кр
от £кр или £пл и /п, подсчитанная по уравнению C.44) с учетом
зависимости C.43), представлена на рис. 3.13, из которого
следует, что отношение предела выносливости круглого гладкого
бруса при изгибе в одной плоскости к пределу выносливости при
изгибе с вращением лежит в пределах 1,05—1,20; это
соответствует опытным данным при определенных значениях тми.
Рис. 3.13, а или 3.13, б используются в зависимости от того,
какая величина известна: £кр или |пл.
Для цилиндрических брусьев с концентрацией напряжений
(с канавками, галтелями и т. п.) при изгибе в одной плоскости
может быть выполнено аналогичное вычисление интегралов /
типа C.42) и соотношений типа C.44). Однако при этом областью
интегрирования являются уже не сегменты, а более сложные
фигуры. В первом приближении уравнение C.44) можно
распространить и на случай брусьев с концентрацией напряжения.
Аналогичное вычисление интегралов C.24) и соотношений
для пределов выносливости может быть проведено и для других
форм поперечных сечений.
Переход к нормальному распределению величины X =
= Ig (сгшах— и). Уравнение подобия C.30) является уравнением
семейства функций распределения пределов выносливости деталей
машин (выраженных через £) с различными значениями критерия
г
подобия ~. Эти функции распределения по форме очень близки
G
к распределению Вейбулла, с' которым они совпали бы, если
исключить %, стоящую в знаменателе уравнения C.30).
Незначительное изменение формы функции распределения не имеет суще-
11> = £пл/Ькр
' 1,1 1,2 1,3 1AWM1 ^кр V 1,2 1.3 1,4 1,51,61,1 ^пл
а) 5)
Рис. 3.13. Зависимость между %ил и |кр для расчета круглых
брусьев при изгибе в одной плоскости
71
ственного значения в том смысле, что надлежащий подбор
параметров видоизмененного распределения обеспечивает, как правило,
хорошее соответствие опытным данным. Поэтому, если
исключить I , стоящую в знаменателе в формуле C.30), и ввести £ =
= 0шах , то после элементарных преобразований получим
(приняв F0 = 1 мм2)
= lg[—2,3 lg(l-/>)].
Это выражение может быть приведено к виду
lg((Xmax-M)=^L-S'lg-|- + /(P), C.45)
Q
' где /(Р) = {lg[-2,3lg(l-P)] +0,159}^;
5* = 1Гй; ^ = ^rr{ig[(«+i)^]-o,i59};
P — вероятность разрушения (при Р = 0,5 f (P) = 0).
Выражение C.45) является уравнением семейства функций
L
распределения величин 0тах для деталей с различными. ~-,
G
выраженных законом Вейбулла.
При Р = 0,5 (f (P) = 0) получаем выражение для медианных
значений <ттах (соответствующих вероятности разрушения 50%),
обозначенных 0щах'.
lg (amax -u) = A'L~B'lg-~. C.46)
G
Экспериментальные исследования показывают [23, 60], что
в диапазоне вероятностей 0,01 < Р < 0,99 для описания
функций распределения пределов выносливости, выраженных через
tfmax, с одинаковым успехом могут быть использованы нормальный
закон распределения величин 0шах [23, 25, 52], X = lg (crmax — и)
gmax
величины 0тах [25, 52] и др. Здесь и — минимальная граница
[23, 25, 52] или у = тах [34], распределение Вейбулла
СТК СТщах
ства 0тах < и принимается равной нулю; 0К — максимальная
граница величин 0тах (Вер |0тах > ок\ = 0).
Против использования нормального распределения величины
°тах есть два возражения. Во-первых, нормальное распределение
случайной величины z соответствует ее изменению в пределах
всей числовой оси, т. е. от —со до' + сх>,. в то время как 0шах > 0.
72
Во-вторых, с ростом абсолютных размеров поперечного сечения
уменьшается среднее значение 0шах, но одновременно уменьшается
и среднее квадратическое отклонение этой величины Scmax,
т. е. функция распределения атах на нормальной вероятностной
бумаге будет изображаться прямой линией, проходящей с
большим наклоном к оси абсцисс у больших образцов по сравнению
с малыми. При нормальном распределении величин 0шах
получается пересечение соответствующих линий на нормальной
вероятностной бумаге при достаточно малых вероятностях
разрушения, что противоречит представлениям о влиянии
масштабного фактора. Поэтому при анализе закономерностей подобия
усталостного разрушения целесообразно пользоваться нормальным
распределением величины X = lg @max — и), которому не
свойственны" указанные особенности. Однако указанные соображения
против использования нормального распределения 0шах
несущественны. С другой стороны, это распределение весьма удобно
при практических расчетах на прочность. Поэтому в дальнейшем
с целью упрощения расчетов нормальное распределение
величины X = lg @max — и) будет аппроксимировано нормальным
распределением величины 0шах.
Заменяя распределение Вейбулла C.45) нормальным
распределением величины X = lg @max — и), получаем уравнение
подобия усталостного разрушения
lu(Om**-u) = AL-Blg± + UpS. C.47)
и
В этом уравнении иР — квантиль нормального
распределения, соответствующий вероятности разрушения Р; S — среднее
квадратическое отклонение случайной величины X = lg @шах —
— и); остальные величины имеют тот же смысл, что и в
уравнении C.45).
Медианное значение 0шах, обозначенное ашах, соответствует
среднему значению величины X — lg @max — и) и получается
из выражения C.47) при иР = 0:
^ = lg((Tmax-«)-lg(amax-") = ^L-Slg^-. C.48)
Таким образом, уравнение C.47) эквивалентно соотношению,
определяющему нормированное значение случайной величины X
(квантиль):
иР = ^^, C.49)
где X определяется выражением C.48).
В дальнейшем предлагается описывать семейство функций
распределения пределов выносливости для образцов и деталей
73
L
с различными значениями критерия — с помощью уравнения
G
C.47), а соотношения между пределами выносливости деталей
различных форм поперечных сечений при разных видах нагру-
жения определять с помощью формул типа C.30), C.33), C.34),
C.44) и им подобных, как будет показано далее. Уравнение C.47)
является уравнением подобия усталостного разрушения,
определяющим семейство функций распределения пределов
выносливости деталей с различными значениями критерия подобия —,
G
выраженных нормальным распределением величин X =
= lg (<W — и)-
Легко найти связь между величинами S и —, входящими
соответственно в уравнения C.47) и C.45) и характеризующими
рассеяние пределов выносливости.
В выражении C.47) S может быть определена как разность
величин X = lg (ашах — и), соответствующих вероятностям
разрушения 84,1% (иР = 1) и 50% (иР = 0), т. е.
5 = lg (<W 84, i — и) — lg (<W — и), C 50)
где amax 84>1, ашах — значения ашах, соответствующие вероят- '
ностям разрушения 84,1% и 50%.
Из уравнения C.45) при Р = 84,1% получим
/ (^)={lg [-2,3 lg(l_P)] + 0,159} jjrlT = |^-
lg (Omax 84,1 - «) = Л2 - Б'lg ^ + -^ ,
G ' т-\-1 '
при Р = 50%
/ (Р) = 0 и lg (amax - и) = A'L - В lg-^-.
Подставляя найденные величины в уравнение C.50), находим
с 0,423
т-\- 1
или
т=_04|3__1 C51)
Если воспользоваться исходным уравнением C.30) для
аналогичного вычисления т, то получим соотношение [23]
ms^i_l, C.52)
т. е. разница получается практически незначимой.
74
В уравнение C.47) входят четыре параметра: и, AL, В, S,
которые должны определяться по опытным данным. Три из них
являются параметрами логарифмически нормального
распределения с пороговым значением и случайной величины сгшах, и один
параметр характеризует влияние концентрации напряжений и
масштабного фактора, так что количество параметров в
уравнении подобия C.47) является минимально возможным.
В ряде случаев бывает удобно воспользоваться другой формой
уравнения подобия усталостного разрушения, которая
получается из уравнения C.47) путем следующих преобразований.
Параметр и, определяющий нижнюю возможную границу
величин ашах, может трактоваться как значение предела
выносливости гладкого круглого бруса бесконечно большого диаметра
при изгибе с вращением. В самом деле для гладкого круглого
бруса диаметром d при изгибе с вращением, предел выносливости
которого обозначим a_ld, имеем
а„ = 1; сгшах = 0_1(г;
lgT = Ig-2-
Таким образом при d-*oo, lg -=—мх> и согласно уравнения
G
C.47) lg (ашах — и) = lg (а_и — и) ->- —оо, т. е. a_ld ->• и.
Примем, что коэффициент влияния абсолютных размеров
поперечного сечения ест определяется отношением
&а — ~ »
O-l
где а_!— среднее значение предела выносливости гладкого
лабораторного образца диаметром 7,5 мм при изгибе с вращением
для образцов из материала данной плавки.
Обозначим
б», = lim ест = lim -~^- = -=—; C.53)
Б ffmax __ G-ip&o
С учетом этих обозначений уравнение C.47) представим в виде
lg(£-l) = .4L-lg(a_ie..)-51g-J- + "pS. C.54)
75
Для гладкого лабораторного образца диаметром d0 = 7,5 мм
при изгибе с вращением при иР = О (Р = 50%)
lg—= lg_JL = lg 88,3 =1,946;
ige_„_,g(iL_ ,) = „(-!._,)_■
= AL - lg (а^ей) - 1,9465. C.55)
Вычитая из уравнения C.54) выражение C.55) и обозначая
В = vCT, получаем
lg(i_l) = lg|_L- ij_Ve(lg-|--l,946J + «PS. C.56)
Выражение C.56) является новой формой уравнения подобия
усталостного разрушения, в которое входят четыре параметра:
<7_i, era, v<j = В и 5. Два.из этих параметров (\>ст = В и S)
остались прежними. Два других (AL и и) заменены на о_х и ет.
Последние параметры являются более удобными по следующим
причинам. Значение а_г может быть найдено непосредственно' по
результатам испытаний гладких лабораторных образцов
диаметром d0 = 7,5 мм при изгибе с вращением. Параметр е„, как
величина относительная, более устойчив и может быть принят
одинаковым для большой группы конструкционных материалов.
Так, по рекомендации [52] для конструкционных сталей,
алюминиевых деформируемых сплавов и модифицированных чугунов
с шаровидным графитом можно принять е„ = 0,5. Для литейных
легких сплавов, серых чугунов и других материалов, весьма
чувствительных к влиянию абсолютных размеров, рекомендуется
значение е„ = 0,4.
Уравнения C.47), C.56) описывают семейство функций
распределения пределов выносливости деталей из металла одной
плавки с различными значениями критерия LIG, изображенных
на рис. 3.9. Однако эти уравнения можно применить и для
деталей с двумя учитываемыми градиентами напряжений,
изображенных на рис. 3.10, если определить для них параметр L/G исходя
из следующих соображений, основанных на использовании
уравнений C.37)—C.41). Рассмотрим вначале случай т = 8 (к
которому можно приближенно свести случаи с т = 6-ь-Ю, наиболее
часто встречающиеся на практике). Величина lg (£2 — 1) в C.39)
может быть найдена- по уравнению C.56) при (-=-) = llhd0Ta
[см. формулу C.40)]. С учетом зависимостей C.39) и C.56) по-
76
лучаем для lg (^ — 1) выражение для деталей, изображенных
на рис. 3.10:
lg (Si - 1) = 0,301 + lg(g8 - 1) = 0,301 +
l)-v°[lg(TL-i'946]+"pS
или
lg&-l) = lg(-£-- 1
0,301 MJM _1)946
Q /гл
+ uPS C.57)
Сравнивая зависимости C.57) и C.56), получаем для деталей
с двумя учитываемыми градиентами напряжений (см. рис. 3.10)
значение критерия подобия LIG при т = 6-т-Ю:
[gi=_M+igfi) =igi^. C;58)
Во многих случаях можно в среднем принять для подсчетов по
формуле C.58) va = 0,1, вследствие чего для деталей по рис. 3.10
-4 = 0,01ШОТВ. C.59)
О
Для значений т, отличных от т = 6-т-Ю, аналогичное
вычисление Si по |2 осуществляется по формуле C.37).
Вернемся теперь к. рассмотрению соотношения между
пределами выносливости круглых образцов при круговом и плоском
изгибах с целью приведения ранее полученных, соотношений
C.42)—C.44) к виду, более удобному для практического
использования. Для этого найдем приведенное значение lg(~=H для
\ G /пл
круглых брусьев при переменном изгибе в одной плоскости с целью
подсчета функций распределения пределов выносливости этих
деталей по уравнениям подобия C.47), C.56).
Обозначим f^=r-\ = ^г- где L = nd; с @ < с < 1) — коэф-
\ О /пл ■ G '
фициент, показывающий какую часть периметра L следует взять,
чтобы по уравнениям C.47) или C.56) получить функцию
распределения предела выносливости круглого бруса при изгибе в одной
плоскости.
Запишем уравнение C.56) применительно к плоскому и
круговому изгибу круглого бруса, используя те же обозначения, что
и в уравнении C.44):
lg(S™-l) = lg(-£-- l)-v0(lg-^-l,946) + HpS;
lg(SKP-l) = lg(^r- l)-vJlg4--l,946J + aPS.
77
\а
\
N
N
ч
N
\
\
V
\
8
18
b
0,06
0,04
0,02
О
Рис. 3.14. График va lg с для подсчета Рис. 3.15. Зависимость коэффициентов
пределов выносливиости круглых а и Ь от т
брусьев при изгибе в одной плоскости
Вычитая из второго уравнения первое, получаем
vCTlgc = lg
=кр
— 1
: — 1
C.60)
Величины vCT lg с, подсчитанные по формуле C.60) с
использованием рис. 3.13, представлены на рис. 3.14 для практического
диапазона изменения т и £пл. Криволинейные зависимости
с весьма малыми отклонениями могут быть аппроксимированы
прямыми линиями, как показано пунктиром. Уравнение семейства
этих линий имеет вид
va\gc = a+ b\g(lnjl- l), " C.61)
где а и b — коэффициенты, зависящие от т (рис. 3.15).
Например, при т = 6 имеем а = —0,108, b = 0,068.
Следовательно, уравнение C.61) принимает вид
vclgc = -0,108 + 0,068 lg(iM- 1),
при lg (£пл — 1) = —0,25 и vCT = 0,1 имеем
lgc = :
-0,108 — 0,068-0,25
= —1,25 = 2,75
0,1
откуда с = 0,056.
Таким образом, для подсчета пределов выносливости в данном
случае следует использовать значение критерия подобия
L \ __ 0,056Jirf
G /пл G
Уравнения подобия усталостного разрушения C.47), C.56)
хорошо описывают влияние концентрации напряжений и мас-
78
штабного фактора на сопротивление усталости деталей машин.
Найдем из C.56) выражения для соответствующих
коэффициентов Ка1&о, Ка, еа, имея в виду определение этих величин через
медианные значения пределов выносливости, получаемые из
уравнения C.56) при иР = 0. После элементарных преобразований
из выражения C.56) получаем
g-iflgg __
е-+A ~8~Hw
— р ( 8со, -=-, Vc
C.62)
Суммарный коэффициент Коо> учитывающий влияние
концентрации напряжений и масштабного фактора, из уравнения
C.62) получает вид
KoD =
Ка
0-1
СХ-1Д
<%
e-+A-e-)(-g§J-g-
L \-v„
C.63)
Коэффициент влияния абсолютных размеров поперечного
сечения на величину пределов выносливости гладких круглых
брусьев при изгибе с вращением диаметром d получается из
уравнения C.62), если принять
«а=1. ог_1д = <з_ы, -=- =
-Ш =
nd2
Тогда
80 =
0)гл~ 2
1 / L
~ ТГ ~6" + (I ~8оо) Ы* (т)
C.64)
Эффективный коэффициент концентрации напряжений Ка
получается из выражений C.63) и C.64):
1 / L
Ка = KaD^a = —
(Т-1д
аи 6„ + A-s»)
8-3 ( 0 )r
+A-6-)(wir
. C.65)
В большинстве случаев для пластичных конструкционных
металлов можно принять е,*, = 0,5 [52], в результате чего
уравнения C.63)—C.65) приобретают вид
К — Ag —
1
1 + ( 88,3 а )
—w<1 + [w(t)„]"
L \ -va
1 +
Ка = аа-
3 \ G /гл
8,3 I в
г л.
1 +
1
88,3 q
C.66)
C.67)
C.68)
79
Приведенные выше уравнения теории подобия усталостного
разрушения записаны для случаев возникновения в деталях
нормальных напряжений а (при изгибе или растяжении-сжатии).
Однако все формулы остаются справедливыми и при
возникновении в деталях касательных напряжений при кручении, если
в них а заменить на т. Так, например, основное уравнение
подобия C.56) в этом случае имеет вид
lg (i - 1) = lg (-£- - 1) - vt (lg ±- - 1,946) -f UpSx, C.69)
где
Т-1ДКТ
T_lSoo
значение е„ = -~ может быть принято для касательных напря-
жений таким же, как и для нормальных. Значения vt обычно
в 1,5—2 раза выше, чем vCT:
vt = (l,5-*-2)v0. ■ C.70)
Формулы C.62)—C.68) преобразуются в соответствующие
выражения для касательных напряжений путем замены о на т.
Например, формула C.66) преобразуется к виду
*&) = •£- = , ,2KT,.,-v_ • C-71)
1 +
3,3 qx
Приведенные выше уравнения теории подобия усталостного
разрушения применимы для радиусов закругления в зоне
концентрации напряжений р > рпред и не применимы при р '< рпред,
где рПред — предельное значение радиуса, кривизны,
ограничивающее область применимости описанной теории подобия.
Значение рпред обычно достаточно мало (лежит в пределах 0,1 —
0,3 мм) и несколько увеличивается с ростом размеров. Характерно
также, что при уменьшении радиуса кривизны в зоне
концентрации (р) значения эффективных коэффииентов концентрации
увеличиваются, но только до р = Рпред, после чего они остаются
практически постоянными и равными Каар&А, что соответствует
постоянству значений пределов выносливости деталей: о_1д =
= ог_1дПред с предельно острыми надрезами, т. е. при изменении р
в пределах 0 < р <р пред. Это свойство рпред и лежит в основе
методики их определения.
Определение коэффициентов вариации пределов выносливости
деталей машин. Под коэффициентом вариации предела
выносливости детали понимается отношение:
falA = i< C.72)
1Д ст-1д
80
где Sct^ и а_1д — соответственно среднее квадратическое
отклонение и среднее значение предела выносливости детали ст_1д.
Рассеяние характеристик сопротивления усталости может
порождаться следующими факторами:
а) статистической природой процесса усталости металла,
связанной со структурной неоднородностью металла (наличием
различных фаз, включений, искажений кристаллической решетки
и т. д.). Влияние этого фактора приводит к тому, что при
испытании совершенно идентичных (по технологии и размерам) деталей,
изготовленных из металла одной плавки, получают существенное
рассеяние характеристик усталости. Влияние этого фактора
учитывается с помощью коэффициента вариации va —
максимальных разрушающих напряжений в зоне концентрации,
соответствующих пределам выносливости деталей (при испытании
идентичных деталей, изготовленных из одной плавки);
б) межплавочным рассеянием механических свойств металла,
влияние которого учитывается коэффициентом вариации ьъ_г
средних (в пределах одной плавки) значений пределов выносливости
гладких лабораторных образцов диаметром 7,5 мм. Вариации
рассматриваются на множестве всех плавок металла данной
марки. Если обозначить о_и величину о_г для i-й плавки, то
среднее значениеcLi стандартное отклонение Sb^ и коэффициент
вариации vb_t величины а_г можно определить по следующим
формулам:
<7-1 = — S O-iP C-73)
п
=1
^^/dnl^b-^J;
C.74)
^=5f- ' C-75)
Если данных по межплавочному рассеянию величин о_г нет,
то, учитывая практически линейную зависимость между
пределами прочности и выносливости; можно в первом приближении
принять
в) отклонением фактических размеров деталей (особенно в
зонах концентрации напряжений) от номинальных (в пределах
допусков). Этот фактор учитывается с помощью коэффициента
вариации vaa теоретического коэффициента концентрации <ха;
81
г) вариацией технологических параметров, приводящей к
дополнительному рассеянию пределов выносливости.
Выражение для коэффициента вариации famax получается
из уравнения C.56) на основании следующих соображений. Для
упрощения расчета на усталость целесообразно заменить
нормальное распределение величины lg (£ — 1) = lg [—?^ 1 \
нормальным распределением величины атах = а_1яаа,
осуществив совпадение этих распределений в двух точках,
соответствующих иР = 0 и иР = —2 (или иР — —3). При этом в области
иР > (—5)ч-(—6), имеющей практическое значение, различие
в величинах ашах для натурных деталей, соответствующих одной
и той же вероятности разрушения, по двум распределениям
настолько мало, что не отражается сколь-нибудь заметно на
вычисленных вероятностях разрушения. В этом легко убедиться путем
проведения сравнительных расчетов.
Чтобы вывести формулу для va , преобразуем уравнение
C.56) к виду
Отах —" ёоо(Т_
или, обозначив
^ 8„ ( 88,3 о )
C.76)
■'-■^(жтГ'.- <>
получаем
amax = eOoa_1(l+M0"Ps). C.78)
Тогда величины атак и о'тах, соответствующие иР = 0 и
иР = —2, равны
^ = 8-0,A + 0; } C79)
amax = 8coa_i A + М0 ). J
Среднее квадрэтическое отклонение S0max величины атах
в предположении нормального распределения
с ffmax сттах 1 - ,/, , А—2S\
. S%ax= 2 = -2-e.a_i/(l- 10 )•
Коэффициент вариации va с учетом уравнения C.79)
выражается формулой
Va а,^ = A-Д'< C.80)
(Ттах 2A+/)
где / — находится из выражения C.77).
82
Отметим, что S в формулах C.56) или C.76) зависит от
принятого значения £„. При е» = 0,5, характерном для большинства
конструкционных металлов, по опытным данным получается [52]
S = 0,045-=-0,05 для сталей, 0,05—0,06 для легких
деформируемых сплавов. Для магниевого литейного сплава Мл5 при е„ = 0,4
S = 0,16, что соответствует значительном}/ рассеянию пределов
выносливости.
Зависимость C.80) хорошо подтверждается опытными данными,
как будет показано'ниже. Согласно этой зависимости va
уменьшаются с ростом отношения -=- от значений 0,05—0,10 при lg -=- =
G G
= 1 до 0,02—0,04 при lg-Ь- = 4 (при S з* 0,045^0,06 ?и va =
G
— 0,08^-0,14). Для магниевого литейного сплава Мл5 при S =
= 0,16 значения va возрастают до 0,10—0,18.
Определение коэффициентов вариации vag сводится к
следующему. Отклонение фактических размеров деталей машин от
номинальных в пределах допусков может порождать
дополнительное рассеяние пределов выносливости деталей, которое
необходимо учитывать в расчетах на прочность вероятностными
методами.
Относительные колебания основных абсолютных размеров
деталей (например, диаметров, валов) невелики, и, как
показывают расчеты ими можно пренебречь при оценке vag.
Сильное влияние на vag оказывают случайные колебания
радиусов кривизны в зоне концентрации напряжений, которые
можно охарактеризовать коэффициентами вариации vp. Значения
этих коэффициентов должны находиться по результатам
измерения партии деталей (не менее 30—50 шт.) в условиях производства.
Допустим, что в результате п измерений получены следующие
значения радиусов р:
Pi < р2 < • • • < р/ < • • • < р„.
Среднее значение р и среднее квадратическое отклонение
радиуса кривизны Sp находят по формулам
p = -i-tPj.; C.81)
Sp = y t^J^-PJ. C-82)
о
Коэффициент вариации vp определяют по формуле vp = ~-.
Как показывают результаты измерений, коэффициенты вариации
радиусов перехода в деталях машин могут изменяться в пределах
vp = 0,05-s-0,25.
83
Зависимость аа от р. может быть представлена функцией
ав = Ф (р). C.83)
Дисперсию ав—S«a можно определить по приближенной
формуле, известной из математической статистики:
si ^
дер
до
где Sp — дисперсия р; значение производной
при р = р.
В этом случае коэффициент вариации
дер
др
р
0 ас
<3<р
dp
берется
C.84)
— — д<х>
где аст — среднее значение аст, соответствующее р = р; -т3-
абсолютное значение производной, которое берется при средних
значениях определяющих параметров.
Вид функции C.83) обычно бывает весьма сложным, а иногда
и неизвестным (если значения аа находились экспериментально,
например поляризационно-оптическим методом). Поэтому для
нахождения производной в выражении C.84) целесообразно
осуществить линейную аппроксимацию функции C.83) в окрестности
заданных значений параметров, используя уравнение прямой,
проходящей через две точки:
0^0 — OT0J
а02 — aai
C.85)
где -^— заданное значение отношения параметров р и d (вместо
p/d может быть р/£ и т. п.); (-^-j > -j- и (-^-J <-^ значения
отношений -^-, близкие к заданному значению; аа2 и а01 —
значения аа, соответствующие
JL\ (JL
d Л W /1
Примеры определения коэффициентов вариации va(S даны ниже.
Формулу для результирующего коэффициента вариации
предела выносливости детали у^ , учитывающего все указанные
возможные источники рассеяния, можно получить исходя иа
следующих соображений. Выразим а_1д из формулы C.62) и
прологарифмируем:
In сг_1д = In а_! — In a„ -j- In F.
C.86)
84
Здесь F = F [в
L
T
Vn = 80
A
•)
88,3
функция, слабо зависящая от радиуса кривизны в зоне
концентрации, так что можно пренебречь влиянием рассеяния р на
рассеяние F и считать дисперсию величины In F равной нулю. а_1д —
медианное значение предела выносливости деталей из металла
данной плавки при номинальных ее размерах. Рассеяние этой,
величины на множестве всех плавок металла данной марки к
возможных случайных отклонений радиусов кривизны от
номинальных характеризуется коэффициентом вариации уъ ■
Заметим, что дисперсия D {In х\ натурального логарифма:
некоторой случайной величины х может быть найдена по
следующему приближенному выражению для дисперсии функции
случайной величины:
D-{lnx\^[^}2D{X\ = ^ = vl C.87>
где vx — коэффициент вариации случайной величины х; значение
производной берется при. среднем значении х = х. Учитывая,
что а_1 и аа — некоррелированные случайные величины,.
a D {In F\ ss 0, и определяя дисперсию величины In а_1д как;
дисперсию суммы двух случайных величин по формуле C.86).
с учетом выражения C.87), находим
C.88)
2
V- =* V-
СТ-1Д °-1
vl
В пределах одной плавки и при отсутствии отклонений в
размерах величину ог_1д, как уже отмечалось, можно принять
нормально распределенной со средним значением а_1д и
коэффициентом вариации va . Величина а_1д может быть принята также,
нормально распределенной (на множестве всех плавок и
возможных отклонений размеров) со средним значением а_1д и
коэффициентом вариации иъ , определяемым по формуле C.88).
Тогда [23] величина а_1д может быть принята нормально,
распределенной со средним значением а_1д и коэффициентом
вариаций ve , определяемым по формулам [с учетом уравнения
C.62)-] "Д
0-1Д =
о-г
е. + A-
= I! F (гя
= v2- -\-v2
ст-1д ^ атах
-»(wtP]
'Т' V(J);
-v2^+vK+vk
=
C.89)
C.90)
г
85
о/
10
W
J\ ^
чО 46 48 51 60,кгфмг
Рис. 3.16. Полигон частот
распределения пределов прочности
углеродной стали
Рис. 3.17. Функции распределения
пределов прочности осевой стали:
/ — оси паровозов; 2 — оси вагонов
Известно небольшое количество экспериментальных данных
о коэффициентах вариации пределов выносливости натурных
деталей с учетом влияния технологических факторов. Обычно
изменение коэффициентов вариации va_x наблюдается в пределах
0,05^0,30. Величины va > 0,20 характеризуют недостаточно
хороший уровень технологии изготовления деталей, так как
в-этом случае по правилу трех сигм пределы_выносливост-и могут
меняться случайным образом в интервале а_1д =*= 0,6а_]д (т. е.
в интервале ±60% от среднего значения) и более широком, чего
ле должно быть при стабильной и контролируемой технологии.
Порядок отдельных слагаемых, входящих в формулу C.90),
можно охарактеризовать следующими данными. Из-за отсутствия
данных о ve_v как уже говорилось, можно принять va ss v„B>
гДе Щв — коэффициент вариации предела прочности материала
на множестве всех плавок, характеризующий межплавочное
рассеяние свойств. На рис. 3.16 приведен построенный Н. П.
Щаповым полигон частот пределов прочности образцов из
углеродистой стали одной марки, изготовленных из 4000 рам паровозов.
На рис. 3.17 показаны построенные В. Н. Маховым функции
распределения пределов прочности образцов из осевой стали
одной марки, но многих плавок. В обоих случаях наиболее
вероятный диапазон колебания ав составляет 40—60 кгс/мма при
среднем значении ов s 50 кгс/мм2 и коэффициентах вариации v„B ss
^0,06-^0,08, что соответствует отклонениям крайних значений
от средних до =*= B0 ч-25)%. Аналогичные данные по весьма
большой номенклатуре конструкционных сталей и легких
сплавов приводятся в справочнике [13], из которого следует, что v„
может изменяться в большинстве случаев в пределах 0,04—0,12.
S6
Зависимости v„max, найденные по опытным данным для ряда-
конструкционных металлов, от lg ^- приведены на рис. 3.18.
о
Эти данные хорошо соответствуют величинам, определяемым по
уравнению C.80), как указано выше.
Как будет видно из приведенных ниже примеров, выражение
C.84) обычно имеет вид va<J = @,3-5-0,4) vp. Значения ур в
зависимости от уровня технологии и контроля изготовления деталей,
могут изменяться в довольно широких пределах, а именно ур=
= 0,05^-0,25.
Таким образом, значение va<J может изменяться в пределах-
0,02—0,10. Расчеты деталей автомобилей и самолетов [6]
показывают, что несоблюдение допусков на радиусы закругления р,.
а иногда и отсутствие самих допусков на р в чертежах, являющееся
причиной повышенных значений vp, а следовательно и vaar
может приводить к заметному увеличению рассеяния ресурса
деталей и снижению ресурса, отвечающего достаточно малой
вероятности разрушения. Поэтому. ужесточение требований на
соблюдение допусков на радиусы закруглений деталей является
важным мероприятием, позволяющим повысить их долговечность
и надежность.
С учетом трех указанных составляющих [формула C.90)]
суммарные коэффициенты вариации пределов выносливости
деталей машин изменяются в пределах va = 0,05-s-0,15.
Формула C.90) не учитывает влияния некоторых
технологических факторов на рассеяние пределов выносливости деталей.
Это влияние должно оцениваться на основании усталостных
испытаний натурных деталей или путем анализа влияния
отдельных факторов на рассеяние, связанных с технологией.
Чтаж
0,25
Рис. 3.18. Зависимость v„ от lg-=r
G
87
На сопротивление усталости сварного соединения кроме
масштабного фактора, концентрации напряжений и состояния
поверхности влияют также механические свойства металла шва,
■околошовной зоны и основного металла, распределение
остаточных напряжений, дефекты сварки (непровары, неметалллические
включения, сварочные трещины и т. д.). Эти факторы, в свою
очередь, зависят от материала электродов и обмазки, от
оборудования и режимов сварки, от квалификации сварщика, от методов
контроля готовых сварных соединений и выбраковки
дефектных и т. д. Влияние этих факторов на va может быть
оценено по результатам усталостных испытаний сварных
соединений.
Экспериментальное подтверждение статистической теории
■подобия усталостного разрушения. Определение параметров
уравнения подобия. Экспериментальные исследования, по
результатам которых могут быть проверены уравнения подобия
усталостного разрушения, делят на две группы. К первой группе
относят те исследования, в которых пределы выносливости
находились обычным методом путем испытания 6—10 образцов
данного типоразмера. В этом случае считают, что найденное значение
предела выносливости является приближенной оценкой
медианного значения о х (с возможной ошибкой до ±10%). Функция
распределения предела выносливости и характеристики
рассеяния [например, 5 в формуле C.56)], в этом случае найдены быть
не могут. По этим данным закономерности подобия могут быть
проверены только по средним значениям [при иР = 0 в
уравнении C.56)]. Ко второй группе относят те исследования, в которых
закономерности подобия изучались в статистическом аспекте
-<; построением функций распределения пределов выносливости
деталей на основе испытания достаточно большого количества
образцов каждого типоразмера (необходимого для применения
методов «лестницы» «пробитов» и др.).
Вначале рассмотрим некоторые результаты экспериментальных
исследований первой группы. Обширные исследования
закономерностей подобия усталостного разрушения на образцах
различных типов из среднеуглеродистой стали @,35% С) были
предприняты Массоне [82]. Испытывали при растяжении-сжатии
плоские образцы с отверстиями различных диаметров (табл. 3.2),
круглые гладкие образцы различных диаметров при растяжении-
сжатии (табл. 3.3), круглые образцы диаметром 16 мм с глубокими
гиперболическими надрезами различных радиусов при
растяжении-сжатии (табл. 3.4). При знакопеременном изгибе в одной
плоскости испытывали образцы прямоугольного сечения (табл. 3.5)
Образцы круглого сечения различных диаметров (от 4 до 56 мм)
испытывали также при изгибе с вращением (табл. 3.6).
Приведенные в таблицах результаты соответствуют мелкозернистой
-структуре и механической полировке образцов. В таблицах даны
38
Таблица 3.2
Параметры плоских образцов с отверстием и результаты их
испытаний на растяжение-сжатие [82]
р, мм
0,25
0,5
1,0
2,0
4,0
8,0
16,0
В, мм
45
45
50
60
64
64
70
Приме'
ав
2,97
2,96
2,92
2,88
2,77
2,56
2,24
в,
1/мм
9,35
4,68
2,35
1,18
0,614
0,311
0,174
•-«.
^кгс/мм2
14,8
13,7
13,1
12,3
11,8
13,2
14,0
1*-^
в
—0,19
0,1
0,41
0,71
0,99
1,29
1,54
i а н и е. р — радиус отверстия; £
amaxi
кгс/мм2
44,1 .
40,6
38,2
35,4
32,7
33,8
31,5
— ширина
=~2f, где t — толщина пластинки (принято t = 3 мм).
атах р>
кгс/мм2
-44,0
40,6
37,7
' 34,9
32,7
31,0
29,2
б, %
—0,22
0
—1,2
—1,3
0
-8,2
-7,3
пластинки; L =
Таблица 3.$
Параметры круглых гладких образцов и результаты их испытаний.
на растяжение-сжатие [82] ,
d, мм
5
6
16
32
в, 1/мм
0,067
0,067
0,067
0,05
.**.
2,37
2,45
2,87
3,30
сттах>
кгс/мм2
24,2
25,0
23,7
22,9
Примечание. При подсчете L/в принято L =
радиус перехода к головкам образца (принято R — 30
R = 40 мм для d = 32 мм).
сттах р>
кгс/мм2
24,7
24,5
22,-9
21,5
б, %
+2,0
—1,9
—3,5
—6
= 7id; G = 2/R, где R —
мм для d =. 5,6 и 16 мм и
' " ■ Таблица 3.4'
Параметры круглых образцов с глубокими гиперболическими
выточками диаметром в рабочем сечении d = 16 мм и результаты
их испытаний при растяжении-сжатии
р, мм
3,125
2,000
0,889
0,320
0,125
t, мм
8
8
6
4
. 4
V
1,842
2,257
3,027
4,600
.7,06 .
в,
1/мм
0,64
1,00
2,25
6,25
16
в
1,89
, 1,70
1,34
0,90
0,49
СТ-1Д. „
кгс/мм2
14,0
12,2
11,1
8,8
9,3
сттах>
кгс/мм2
25,8
27,5
33,6
.40,5
. 65,6
сттах р>
кгс/мм2
27,0
28,2
30,5
6, %
+4,5
+2,5
—9,1
П р им ечание. р, t. — радиус иглубина надреза; значения а брались
по-Нейберу; в = 2/р, L = ad = 50,2 мм; для р < рпред =0,40 мм отклонения
б не определялись.
89»
Таблица 3.5
Параметры образцов прямоугольного поперечного сечения и
результаты их испытаний при переменном изгибе в одной
плоскости [82]
■ 4
8
16
s 32
5
10
■ 20
32
16
8
4
5
10
20
*-f
в
2,11
2,11
2Д1
2,11
1,40
2,0
2,6
сттах.
кгс/ммг
25,2
26,4
24,5
25,3
27,6
27,6
25,3
"max р.
кгс/ммг
25,8
25,8
25,8
25,8
29,8
26,6-
.-■•24,0
б, %
+2,5
—2,1
+5,3
+2,0
+8,0
—3,5
—5.L
3 Vr '"'
Таблица 3.6
Параметры гладких круглых образцов и результаты их испытаний
при изгибе с вращением [82]
d, мм
\ 4
8
: 16
32
3 56 ■
в, 1/мм
С, 564
0,314
0,187
0,096
0,069
»т
1,35
1,90
2,43
3,02
3,41
CT-i = ffmax,
кгс/ммг
27,0
26,2
24,7
22,4
23,0
"max p,
кгс/мм2
30,0
26,9
24,6
22,4
21,2
б, %
+ 11,0
+2,5
—0,5
0
—7,5
— 22
Примечание. в= j—-г-, где р — радиус перехода к головкам
образца (принимался равным 32 мм для образцов d = 4,8 и 16 мм; 60 мм — для
'; d = 32 и 56 мм); L = nd; результаты испытаний образцов d = 2 мм исключены
J из рассмотрения как недостоверные.
.характерные размеры образцов, значения величин lg -^=- и 0шах =
G
— ааа_]д. __
Чтобы исключить случайные ошибки в определении а_г (для
.лабораторного образца d0 = 7,5 мм), зададимся вначале
ориентировочным значением oLi = 28 кгс/мм2 и построим зависимость
3g (omax — и') от lg-=-, где 0тах = ог_1даст, и' = ъ^о'-х = 0,5 X
и
X 28 = 14 кгс/ммг. Эта зависимость изображена на рис. 3.19, а.
Точки на рис. 3.19, а отвечают данным, приведенным в табл. 3.2—
:3.6 в соответствии с обозначениями, указанными на рис. 3.19, б.
Из рис. 3.19 видно, что отклонения точек от прямой линии
.невелики. Однако нахождение о_г, а следовательно, и и = 0,5а_г
дао осредненной линии является более точным, так как при этом
•90
1д{Ьтп~л')
IJ
i,t
1,}
иг
V
¥
0,9
ft»
-US 0 ftf 1,0 1,S 2,0 Z,5 lff±
a) 0
\
\
\
\
\
1 «b'
9
t
34J
1
s
л*0
,p=ftZT-ff
l/= ^ Л
old*/
fP-e/zr-j./zr
о{Сп.таШ.2) .л-w. AfCMmaSs.SJl o{Cn.mah.3A]
~"^ d=b-SS
г(См mad/i.J.S)
4 i c»o„)
OfC«. msS/i.J.S)
Рис. 3.19. Зависимость Ig (стШах — «') от lg — для образцов из углеродистой
[G
стали (а) и эскизы испытанных образцов (б)
практически исключается случайная ошибка в определении 5_t
по опытным данным. Этим оправдывается построение
промежуточного графика, подобного изображенному на рис. 3.19.
Осредненная линия проводится или по методу наименьших
квадратов или просто графически, после чего по очевидным
соотношениям аналитической геометрии находятся параметры
уравнения прямой линии.
Параметры уравнения C.47) при и' = 14 кгс/мм2 равны:
AL= 1,
В = 0,17.
Для
v о J™
ЯЙп
88,3 по формуле G.36)"находим а_х =
= ог„
= 26,9 и и = 0,5-26,9 = 13,45 кгс/мм2.
Существует, как указывалось в работе [23], такое предельное
значение радиуса кривизны в надрезе рпред, что при р < рпреД
значения Ка не увеличиваются, а остаются практически
постоянными и равными До пред- а пределы выносливости а.
•1Д
-1д пред-
г - ■» j—гл -■ —д.,ц —л,ц пред
При р < рпред уравнения подобия уже не применимы. В данном
случае для образцов d = 16 мм с надрезом (см. табл. 3.4) имеем
Рпред = 0,5 ММ; 0Г_1дпред =8,3 КГС/ММ2; Капред = 2,6. ПО ЭТИМ
данным построена пунктирная линия на рис. 3.19^-Далее, опре-
Рщах _ Р-1Яаа ^„„„ i^ /К i4._i„ L
и и
деля я
, строим зависимость lg (I — 1) от lg-^-,
G
представленную на рис. 3.20. Значения, необходимые для
построений, даны в табл. 3.2—3.6. В них же приведены значения
полученные расчетом по-
: р = О^др^ст == O-iF (г«
9L
формуле C.62), и 6 =
Ртах р — Q"max
100% (отклонения расчетных
.-значений пределов выносливости от экспериментальных). Значе-
0 27
ние V(j = 0,14 было найдено, как отношение . ' , где 0,27 —
это значение lg (£— 1) по прямой линии при lg-=r-=0, что
о
шытекает из формулы C.56).
Значения отклонений б из табл. 3.2—3.6 были объединены
в один статистический коллектив, и на рис. 3.21 на нормальной
вероятностной бумаге построена функция распределения б. (не-
залитые треугольники и линия 2). Из рис. 3.21 видно, что
распределение б близко к нормальному, средняя ошибка 6 = 0.
С вероятностью 95% ошибка в опасную сторону не превышает
7,5%, что соответствует точности определения предела
выносливости стандартным методом (по испытанию 6—8 образцов для
построения всей кривой усталости).
к
На рис. 3.22, а показаны зависимости —2- от радиуса кри-
визны в надрезе круглых образцов при растяжении-сжатии (см.
табл. 3.4) и для пластинок с отверстием при растя жени и-сжатии
ют радиуса отверстия (см. табл. 3.2). На рис. 3.22, б представлены
зависимости ест от диаметра гладких образцов при растяжении-
сжатии (см. табл. 3.3) от d при изгибе с вращением гладких
образцов (см. табл. 3.6). Под ест в данном случае понимается отношение
лредела выносливости образца диаметром d при растяжении-
вжатии или изгибе к пределу выносливости а_х = 26,9 кгс/мм2,
гладкого образца диаметром d0 = 7,5 мм при изгибе с вращением.
К
Экспериментальные значения — находили по формуле
Ка 0_! 26,9 ° л
= —- = ——, где а_1л — пределы выносливости
образец 0_1д о-1д
дав с концентрацией напряжений, представленные в табл. 3.2—
Хд&-1)
.0,4
.0,3
.в,г
.о,1 V
. о
г 0,1
'0,1
-0,3
ч
\с
0>.
fe&U
s*0
-0,1
lj.L/q
Рис. 3.20. Зависимость lg (g — 1) от
lg -^ для углеродистой стали (у„ =
О
= 0,14; 8оо = 0,5; ~о_х = 26кгс/мм2)
?92
3.4. Расчетные значения (орди-
наты кривых) —£- находили по
формуле C.63), ест—по
формуле C.64) при vCT = 0,14. Из
рис. 3.22 видно, что уравнения
C.63), C.64) хорошо описывают
влияние концентрации
напряжений и масштабного фактора
на сопротивление усталости.
Отклонения экспериментальных
точек от расчетных кривых
только в трех случаях из 20
доходят до 9—11%, в
остальных случаях не превосходят
цог
15 20 С/о
Рис. 3.21. Функция распределения отклонений б расчетных значений
пределов выносливости от экспериментальных:
J _"б = 0; Sfi = 2%; 2 - <Г= 0; S. = 4,3%
Рис. 3.22, Зависимость -^2
%
от lg р и еа от d (б) для
углеродистой стали:
/ — изгиб; 2 — растяжение-
сжатие
-п к
"-"-л
г—"^ 7_
—»- (Г
"-•
zK
£0
W
0,9
0,8
0,7
-0,S
а)
0,5
10
20
30
В)
40
1 Iff?
в ^V
\ е
^■■Д-.
1.
"' У—
Z
в
SO d.MM
93
7%, что соответствует функции распределения отклонений б,
представленной на рис. 3.21.
Таким образом, пределы выносливости образцов различных
размеров, форм и видов нагружения, указанных на рис. 3.19, б,
описываются одним уравнением C.56) при ея = 0,5, va = 0,14,
O-i = 26,9 кгс/мм2 с погрешностью, не превышающей 7,5%
(с вероятностью 95%). Сопоставляя данные табл. 3.2—3.6, можно
видеть, что значения пределов выносливости, выраженных через
0шах, практически совпадают у образцов различных типоразмеров
при совпадении критерия -=■. Например, это вытекает из сравне-
О
ния первых двух строк табл. 3.3 итретьей строки табл. 3.6 (lg-^- =
= 2,37-7-2,45, ашах = 24,2 — 25,0J или из сравнения
предпоследней строки табл. 3.5 и второй строки табл. 3.6 (lg-^=- = 1,9 — 2,0,
0^ = 26,2-27,6).
о 1 г ю з 4 iff 0 1 г е) з * i9j
Рис. 3.23. Зависимости Ig (| — I) от lg -=-
Результаты ряда других исследований первой группы (т. е.
выполненных не в статистическом аспекте) представлены в виде
зависимостей lg(£ — 1) от Ig-^- на рис. 3.23. Прямые на этом
G
рисунке рассчитаны по уравнению C.56) при еет = 0,5, иР = 0
и значениях о_г и va ила vx, представленных в табл'. 3.7.
В исследованиях,' результаты которых отражены на рис. 3.23
и в табл. 3.7, испытано более 1200 образцов и моделей сечением
от 7 до 300 мм. Отклонения б расчетных значений 0шах р от
экспериментальных оггаах, определенные по описанной выше методике,
были объединены в один статистический коллектив, и построена
функция распределения б на рис. 3.21 (прямая 2, точки ф).
Таким образом, проверка по всей этой большой совокупности
экспериментальных данных показала, что уравнение подобия
усталостного разрушения C.56) обеспечивает вычисление
пределов выносливости с погрешностью, не превышающей 7,5% с
вероятностью 95%.
На рис. 3.23 (линии 17, 18) и в табл. 3.7 приведены также
данные, полученные при кручении [уравнение подобия C.69)].
По этим ограниченным данным можно сделать вывод, что в
среднем vx = A,5-^2) vc.
Ш
OS
О,}
цг
0,1
о
-0,1
0,1
0,1
о
-0,1
-0,1
Ш
0,1
0,1
о
-0,1
ч%
нЛ
ЛЗ
X
Ж)
лл «"
x^S^
- *»
^v
Ч^*
16
W»
is
151
0,1
-0,1
-0,1
-0,3
-0,4
-0,S
~o,s
-o,i
чн
0,1
-0,1
-0,1
-0,3
-OS
-OS
-0,6
\
\
V
V
\"
\r77
»
к)
\
\
4 *
%?
fl
k
\A
• fc x
*• ^
?v"w
x\
г
a)
3 Iff-
г з
a)
4 Ig-
для различных материалов (см. табл. 3.7)
95
Таблица 3.7
Значения параметров уравнения подобия усталостного разрушения
C,56) при 8„ = 0,5
Материал
Изгиб
Осевая сталь
Углеродистая сталь
SAE 1035
Углеродистая сталь
SAE 1020
Сталь 45*, /= 20° С
Сталь 45* t= —60° С
Углеродистая сталь
Сталь 45
Легированная сталь
CNCM
Легированная сталь
SAEX 4130
Сталь 40Х
Сталь 40ХН
Легированная сталь
SAE 2345
Легированная сталь
Коррозионностойкая
сталь 18-8, t= 450° С
Коррозионностойкая
сталь 18-8, /= 630° С
Углеродистая сталь **
Кручение
Легированная сталь
Углеродистая сталь ***
* Тибаиов В. П. Иссле;
турах. Автореферат диссе рта
МВТУ, 1970.
** См. рис. 3.20.
*** Дори и Шмидлей [76]
Ъ-1 (?-!)-
кгс/ммг
25,2
27,4
23,2
44,2
46,0
25,3
27,2
30,9
35,2
48,8
43,7
25,0
38,5
24,0
26,9
32,7
16
^вание про
ции на соис
vo(\)
0,18
0,10
0,11
0,19
0,23
0,10
0,11
0,04
0,05
0,10
0,07
0,06
0,30
0,27
0,14
0,29
2
чиоети вале
кание учен<
Литературный
источник
[65]
[83]
[83]
[91]
[8]
[34]
[88]
[83]
[29]
[84]
[89]
[95]
[82]
[81]
в и осей п
эй степени ъ
Номер
линии на
рис. 3.23
1
3
4
9
10
12
15
16
•» 2
5
6
7
8
11
13
14
—
17
18
5И НИЗКИХ Т
сайд. техн.
Вид на
рис. 3.23
а
б
б
д
д
е
3
и
а
в
в
в
г
д
ж
—
№ . .
(л)
емпера-
наук М,
Сопоставим теперь с опытными данными зависимости C.58),
C.59), которые позволяют распространить уравнение подобия
C.56) на случай расчета деталей с двумя учитываемыми
градиентами напряжений, показанных на рис. 3.10.
В табл. 3.8 приведены значения пределов выносливости
пластин из стали 22К шириной Ь = 85 мм с поперечным отверстием
диаметром dOTB = 14 мм (don/b = 0,165) различной толщины h
при пульсационном цикле растяжения-сжатия и изгибе [64].
Значения теоретических коэффициентов концентрации аа
находили в работах [52, 90].
Таблица 3.8
Параметры пластин разной толщины h из стали 22К и результаты
их испытаний при растяжении-сжатии и изгибе [64]
ft, мм
15
25
40
15
25
40
60
°-1Д',
кгс/мм2
14,5
14,5
14,5
27
20,6
18
18
%
2,58
1,97
2,13
2,27.
2,38
-т
ь
*ip
Растяжение-сжатие
1,96
2,18
2,38
1,96
Изгиб
0,36
0,58
0,78
0,96
2,80
2,31
2,15
2,25
2
1,95
1,90
2,45
2,36
2,30
2,26
«*-*
14,7
14,4
14,0
23,7
21,1
19,2
18,1
Ошибка
6, %
—1,5
+0,5
+3,5
+ 11,4
—2,5
—6,5
—0,5
Значения -=- для пластин при изгибе подсчитывали по урав-
G
нениям C.58), при растяжении-сжатии по формуле
T = f = —-0,435МОТП.
Вычисляя ашах «= oLi^e, откладывая соответствующие точки
на графике в координатах сгшах — lg-=-n проводя осредненную
G
линию, ' получаем при lg-^=r- = 1,946 значения а_г — <тшах ==
О
= 38 кгс/мм2 и и = О.ба,! = 19 кгс/мм2. Значения |1э,
соответствующие экспериментальным данным, находили по формуле C.59).
Зависимость lg A1э — 1) от lg -=- показана на рис. 3.24, а. На ри-
G
суике видно, что экспериментальные точки достаточно хорошо
ложатся на прямую линию, уравнение которой имеет вид C.59)
при v0 == 0,1.
4 В. П. Когаев 97
ы-п
0,2
0,1
о
-0,1
0,5
О А
0,3
0,2
0,1
О
-0,1
№-1)
ОА
0,3
0,1
0,1
О
-0,1
-0,2
А
Р>Ы
*v
^
"^Se
А
""*>
А
^L
eri
^
^»
b*^f
Т*"ч> "^
— ii ^*^^*^" ~—
Рис. 3.24. Зависимости lg (|х —
— 1) от lg-4-:
О
а — пластины с отверстием при
растяжении-сжатии (в) и изгибе (А)
из стали, v = 0,1 (см. табл 3.8);
б — пластины с отверстиями при
симметричном изгибе из стали 45,
9 — h — 10 м; А — ft = 24 мм;
v = 0,1 (см. табл. 3.9); в—
цилиндрические образцы с поперечным
отверстием при изгибе с вращением
из стали 45, v„ = 0,09, 9 — D =
о
— 9 мм, д — D = 15 мм
-г -1
3 1д 4
Расчетные значения пределов выносливости находили по
формуле, вытекающей из уравнения C.56):
р
;iPeoo °_i
C.91)
при ех = 0,5, а_! = 38 кгс/мм2, а значения lip по формуле C.56)
при Vo- = 0,1 и значениях-^-, указанных в табл. 3.8. В табл. 3.8
О
приведены найденные
ошибки
таким способом значения 11р и
р
<Г-1д
6 =
J-lfl-
-1д
<*-1д
100%.
На рис. 3.25 приведены
значения сг_1д в зависимости от h.
Кривые рассчитаны по
уравнению C.56) при Vq- = 0,1, е„ =
= 0,5; а_г = 38 кгс/мм2.
Из табл. 3.8 и рис. 3.24, 3.25
виднО| что отклонения
расчетных значений пределов
выносливости от экспериментальных
невелики и соизмеримы с
погрешностью эксперимента.
98
6 _1}, кгс/мм2
2S
U
U
22
10
18
15
U
12
о
ff^
- А
L
Ми3г М^г
10
20 30 40 SO 60 h.MM
Рис. 3.25. Зависимость пределов
выносливости пластин с отверстиями при
растяжении-сжатии (Д) и изгибе (О)
Таблица 3.9
Параметры пластин толщиной h = 10 мм и 24 мм с различными
значениями dOTB и Ь из стали 45 и результаты их испытаний
при симметричном изгибе
ft, мм
10
22
"оТВ,
мм
Гладкий
32,5
- 24
12
6
3
1,5
1
0,7
0,5
Гладкий
50
34
22
12
6
2
1
* Гальпериь
отверстиями. — «
Ь, мм
35
65
59
47
41
38
36,5
36
35,7
35,5
50
99
84
72
62
56
52
51
%
1
1,35
1,50
1,80
2,14'
2,46
2,72
2,82
2,87
2,91
1
1,42
1,60
1,82
2,11
2,46
2,81
2,90
М. Я. Сопрот!
Вестник машии
*
кгс/мм2
27,5
23,8
22,5
19,5
17,5
16,5
16,0
15,5
15,7
16,5
26,0
22,0
19,8
18,2
17,0
16,3
15,8
16,5
шленйе уст
остроения»
»Т
2,54
0,55
0,42
0,12
—0,19
—0,49-
—0,79
—0,96
-1,12
—1,27
3,08
1,11
0,95
0,76
0,50
0,19
—0,28
—0,58
алости плас
1976, №
S»
1,90
2,22
2,33
2,42
2,58
2,80
3,00
3,01
3,10
3,31
1,79
2,17
2,18
2,28
2,48
2,76
3,06
*1Д
27,0
25,8
23,4
20,3
17,7
16,2
15,4
15,2
15,3
15,4
26,0
22,9
20,5
18,5
16,5
14,6
13,8
Ошибка
6, %
—1,9
—7,6
—3,9
—3,9
-1,0
—2,0
+3,9
+2,0
+2,5
+6,8
0
-4,0
—3,5
+ 1,8
+ 3,0
+ ПД
+ 14,0
3,30 13,9 +18,5
тии и валов со сквозными
1, с.
27 — 31.
В качестве другого примера в табл. 3.9 представлены
результаты усталостных испытаний при симметричном изгибе пластин
толщиной 10 и 24 мм с различными значениями й0тв и Ь. Ширина
пластин изменялась таким образом, что величины разности Ъ — d
оставались постоянными C5 и 50 мм) за исключением самых
широких пластин, где это условие выполнялось приблизительно.
Значения-=-для пластин с отверстием подсчитывали по уравнению
о
L 26
C.59), >для гладких пластин — по -=^ = -—-= Ыг. Значениям
G ^i"
приведены в работах [52, 90]. Путем построения осредненной
прямой в координатах 0 • \а -=- были определены значения
о_х = 29 кгс/мм2 и и = 0,5 ■о_1 = 14,5 кгс/мм2. Значения |1э
находили по уравнению C.56). Экспериментальные точки
представлены графически в координатах lg(^i3— 1) — lg~^~ Ha
L_
G
рис. 3.24, б. Прямая на этом рисунке соответствует уравнению
C.56) при vff =0,1. Значения а£лд находили по формуле C.91),
4* 99
а |1р — по C.-56) при v0 = 0,1;
800=0,6; ир = 0. Из рис. 3.24, б
и табл. 3.9, в которой
представлены численные значения
ошибок б (%), следует, что
расчетные и экспериментальные
значения пределов
выносливости имеют весьма хорошее
соответствие. Только в двух
случаях из 18 ошибка составляет
14 и 18,5%, вследствие чего
отклонения следует считать
статистически незначимыми.
Аналогичная обработка
результатов испытаний
цилиндрических образцов из стали 45
диаметром D =9 и 15 мм с
отверстиями различных диаметров dOTB при
изгибе с вращением, приводит
к зависимости, показанной на рис. 3.24, в. На рис. 3.26
представлена зависимость эффективных и теоретических коэффициентов
концентрации для цилиндрических образцов с поперечными
отверстиями при изгибе с вращением. Значения аа взяты из работ [52,
90], значения Ка подсчитаны по формуле Ка=~ ~lD
Рис. 3.26. Зависимость эффективных Kg
и теоретических аа коэффициентов
концентраций от d0TJD для
цилиндрических образцов с отверстием при
изгибе
-1Д
где
1D>
а_1д — пределы выносливости образцов гладких и с отверстием
одинакового диаметра. Кривые рассчитаны по уравнению C.56)
при v0 = 0,09, а_х = 29 кгс/мм2 (&х = 0,5; иР = 0). Из рис. 3.25
и 3.26 видно, что экспериментальные точки хорошо соответствуют
зависимости C.56) при указанных значениях параметров.
Значения -^ для этих образцов подсчитывали по уравнению C.59)
о
с заменой h на D.
Таким образом, уравнение подобия усталостного разрушения
применимо также к деталям, изображенным на рис. 3.10.
Рассмотрим теперь экспериментальные данные,
характеризующие влияние концентрации напряжений и масштабного фактора
на сопротивление усталости, полученные путем испытания
большого числа образцов, достаточного для оценки рассеяния пределов
выносливости. Одновременно будет проиллюстрирована и
методика определения параметров уравнения подобия в форме C.47)
или C.56).
Для решения указанной задачи необходимо проведение
усталостных испытаний образцов нескольких типоразмеров с
различными значениями критерия подобия -=-. Методика будет проиллю-
G
стрирована на примере испытания образцов из стали 40Х (ав =
= 202 кгс/мм2) при изгибе е вращением. Испытанию подвергали
100 -
Таблица 3.10
Параметры образцов и результаты усталостных испытаний
образцов из стали 40Х при изгибе с вращением
№
образцов
1
2
3
4
5
6
7
8
d.
ММ
7,52
7,52
7,52
7,52
8,6
8,6
13,0
15,0
Р.
мм
75,0
2,0
1,22
0,2
2,05
од
1,345
0,169
%
1,00
1,46
1,67
3,40
1,50
5,00
2,00
5,0
G,
1/мм
0,29
1,27
1,91
10,27
1,23
20,23
1,64
11,97
1.4-
в
1,91
1,27
1,09
0,36
1,34
0,13
1,40
0,60
°шах>
кгс/мм2
85
94
97
105
93,5
112
92,5
99
°тах р>
кгс/мм2
85,6
93,3
95,7
105
92,8
109
92,5
101
б, %
+0,7
—0,6
-1,2
0
—0,7
—2,7
0
+2,6
образцы гладкие и с глубокими надрезами, имеющими форму
спрямленных гипербол, диаметром 7,5 и 15 мм [34]. Размеры
испытанных образцов (диаметр d и радиус закругления в вершине
надреза р), аа, G и lg ^ (L~nd для изгиба с вращением) даны
G
в табл. 3.10.
Количество испытанных образцов каждого типоразмера
колебалось в пределах от 130 до 185 шт. Для каждого типоразмера
строились полные вероятностные диаграммы усталости (Р — о —
./V-диаграммы).
Пример подобной диаграммы для образцов № 4 (табл.'3.10,
аа = 3,4) был приведен в разд. 4. На рис. 3.27 на нормальной
вероятностной бумаге приведены функции распределения
максимальных разрушающих напряжений в зоне концентрации ашах =
= ст_1да0, построенные по методике, описанной в разд. 4. На
рис. 3.27 каждой линии' соответствуют две группы точек: необ-
веденные и обведенные кружками. Точки второй группы
получались путем нахождения ординат Р точек пересечения кривых
распределения долговечности (см. рис. 2.11) с вертикальной
линией, соответствующей N = 107 циклов. Так, для образцов № 4
по табл. 3.10 (аа = 3,4; lg-=- = 0,36) и по рис. 2.11 находим, что
ПРИ tfmax = 114 КГС/ММ2 Р — 73%, при СГшах = 100 КГС/ММ2 —
Р = 32% и при ашах = 87 кгс/мм2 — Р = 15%. Эти данные
определяют координаты черных круглых точек, обведенных
кружками на рис. 3.27, соответствующих линии lg -=- = 0,36. Точки
G
первой группы (не обведены кружками) получались путем
экстраполяции кривых усталости, соответствующих различным
вероятностям разрушения, до N = 107 циклов и определения ординат
точек пересечения этих кривых с вертикальной линией, соответ-
101
80 85
95 WO 105 110 115 6тах,кгс/ммг
S)
Рис. 3.27. Функции распределения
максимальных разрушающих напряжений в
зоне концентрации стшах образцов из стали
40Х на базе 107 циклов
ствующей N = 107. Средние
значения crmax, найденные
по кривым распределения на
рис. 3.27 при Р=50%, даны
в табл. 3.10.
Для определения
величины и = 8„а_х = 0,5а_х,
входящей в уравнение
подобия C.47), выбирают
предварительное значение и' и
строят зависимость lg (ашах—
— и') от lg-=-. По осреднен-
G
, L
ной зависимости при lg-=r- =
G
= 1,946 находится стшах = а_х
и и = 0,5а_х. Так было
найдено значение а_1=84кгс/мм2
и и = 0,5 ■о_1 = 42 кгс/мм2.
Из зависимости C.56) при
ем = 0,5 и иР = 0 следует
ig(!-i) =
_va(lg-|-- 1,94б),C.92)
_ gmax 'Jmax /o nq\
U ~~ O,50_i
где
На рис. 3.28 представлена зависимость lg (|
1) OTlg^,
о
подсчитанная по данным табл. 3.10 с учетом уравнения C.93).
Из рисунка видно, что экспериментальные точки хорошо
соответствуют линейной зависимости C.92) при va = 0,11. Это
значение находится после проведения осредненной линии,
вычисленной по формуле, вытекающей из уравнения C.92) при
1§4г = 0: ,
Iig(I-
в
1,946
C.94)
Ртахр В Табл. 3.10
Расчетные значения ашах, обозначенные
находят по следующей формуле, вытекающей из уравнения- C.92)
102
(при -найденных выше значениях а_г = 84 кгс/ммй, va
= 0,11):
•'шах р '
0,5ст_
+ (-
1 L \~\
.3 G
C.95)
В последнем столбце табл. 3.10 приведены численные
значения отклонений g — атюр~<?шах iqqo/oi которые ' в данном
Umax
случае не превышают 2,7%.
Столь же высокая точность уравнения C.92) получена и в
других исследованиях закономерностей подобия усталостного
разрушения, проведенных в статистическом аспекте на достаточно
большом количестве образцов [6, 23, 27, 28, 34, 60]. В эту группу
исследований включены также и те, в которых образцы каждого
типоразмера испытывались в количестве 20—30 шт. с
определением предела выносливости методом «лестницы».
Результаты этих исследований приведены в виде зависимости
lg (£ — 1) OTlg-^r- на рис. 3.29 для ряда материалов при изгибе
G
и кручении. Параметры прямых линий а_ъ va, входящих в
уравнение C.92), приведены в табл. 3.11. Параметры уравнения
подобия, представленные в табл. 3.7 и 3.11, являются справочной
Таблица 3 .11
Параметры уравнения подобия C.92), найденные по результатам
экспериментов, проведенных в статистическом аспекте
Материал
Сталь 45 (кручение)**
Сталь 45
Сталь 40Х
АВТ
В95
АДЗЗ
Д16*
.ВМ65
Мл5
Модифицированный
чугун **
Модифицир ов энный
чугун (кручение) **
ЗОХГСНА
* Данные получены ]\
ав>
кгс/ммг
66,0
202
36,4
61,8
33,3
55,4
26,7
22,1
83,0
83,0
кгс/мм2
19,6
30,7
84,0
13,5
17,4
12,7
16,6
11,3
7,3
35,0
26,2
- 1 73,0
1. Я- Гальпериным.
** Данные получены совместно с М. Э. Гарфо»
лаковским, М. Я. Гальпериным.
va (\)
0,19
0,10
0,11
0,08 ,
0,09
0,09
0,20
0,10
0,30
0,15
0,28
0,10
I, О. К. Кр
№ линии
на рис.
3.29 -
8
4
2
3
5
5
6
7
1
11
10
9
амаренко, С
Литературный
источник
[34]
[34]
[27, 34]
[60]
[60]
—■
[34]
[34]
—
—
[6]
). Б. Ба-
103
Ig(j-1) Рис. 3.28. Зависимость lg(f —
— 1) от lg^^ для образцов из
G
стали 40Х:
с_г = 84 кгс/мм2; vg = 0,11
' О 12 3 - Lgk
S
информацией, которая может быть^использована для определения
средних значений пределов выносливости деталей машин.
По группе данных, полученных в статистическом аспекте и
представленных на рис. 3.29 (с параметрами в табл. 3.11) находили
отклонения б (%) расчетных значений 0тахр от
экспериментальных 0шах так же, как это пояснялось применительно к табл. 3.10.
Указанные значения б (%) были объединены в один
статистический коллектив, и по ним построена функция распределения
ошибки б, показанная на рис. 3.21 линией 1, построенной по
точкам, обозначенным крестиками. В этом случае, как и ранее,
средняя ошибка равна нулю, а стандартное отклонение ошибки
5в существенно меньше, чем в случае линии 2 на рис. 3.21, и со-
ставлят 2%.
Абсолютное значение ошибки б с вероятностью 95% не
превышает 4%, что говорит о весьма высокой точности уравнения
подобия усталостного разрушения.
До сих пор рассматривалась зависимость средних значений
0шах от lg -^г-. Однако уравнение подобия усталостного разрушения
G
в форме C.47) или C.56) "хорошо описывает также семейство
функций распределения пределов выносливости для образцов
и деталей с различными значениями критерия подобия -=-. На
G
рис. 3.30 представлены функции распределения величин lg @max —
— и) и при и = 42 кгс/мм2 для образцов из стали 40Х различных
типоразмеров, параметры которых указаны в табл. 3.10.
Экспериментальные точки нанесены по данным рис. 3.27, линии
рассчитаны по уравнению C.56) при е» = 0,5 va = 0,11; a_x =
= 84 кгс/мм2; S = 0,045. Из рис. 3.30 видно, что образцы,
имеющие близкие значения критериев -=-, например lg -=-= 1,27
G G
B-я строка табл. 3.10) и lg -=-= 1,34 E-я строка), имеют практи-
G
чески совпадающие функции распределения lg (amax — и), а
следовательно, и пределов выносливости ст_1д.
В этом проявляется важная закономерность подобия
усталостного разрушения, вытекающая из уравнений подобия C.47),
104
0,1
О
-п 1
в
C.56). Эта закономерность лежит в основе методов моделирования
при усталостных испытаниях. 5 — это среднее квадратическое
отклонение нормально распределенной случайной величины X =
= lg (tfmax —-и). Таким образом, на графике рис. 3.30 величина
5 определяется по каждой линии как разность:
5 = [lg (а™* - m)W - lg (<W - и), C-96)
где [lg (amax — и)]o,84i — значение X = lg (amax — и),
соответствующее вероятности Р = 84,1% (ир = 1); lg (amax — и) —
среднее значение X (соответствующее вероятности Р = 50% или
ир = 0).
Величина 5 пропорциональна котангенсу угла наклона линии
распределения на рис. 3.30 к оси абсцисс. Чем круче линия,
т. е. чем больше угол наклона к оси абсцисс, тем меньше
рассеяние величин X = lg (amax — и), а следовательно, и а_1д. То
обстоятельство, что линии распределения на рис. 3.30,
соответствующие различным значениям lg -=- параллельны, говорит
G
О
-0,1
Ы-1)
U
0,1
о
-0,1
-и
0,1
0,1
о
-0,1
ОЛ
0,3
0,1
0,1
о
-0,1
-0,1
"W
•*-<
ч^
<9
>**.
4
^
О
Ь)
\,
н>г
"•^^
©
0,3
0,1
0,1
о
-0,1
-0,1
-0,3
-0А
щн
лз
0,1
0,1
о
-0,1
-0,2
-0,3
^Ofi
~o,s
Ig-k
. s
^^"-3
d)
\
4. '
//
\
^\10
•^д\
V^
x>
\
V.
\ '
\
0
Рис.
e)
У-
3.29.
L
Зависимости lg (| — 1)
от lg -^r- для образцов из различных
G
материалов при изгибе и кручении
105
99
98
95
90
80
70
60
SO
40
30
20
10
S
2
0,5\
lg-j=-=l,91 1,40 1,34 1,27 1,09
i/fri
4
°/ J
7 .J8
Ж И
м
7т®П
р " /$
/Ул/ *
А©
/
fflfflitffc)/ $>)
rraxi
///§
в
/
у/щ
)£.0fJff
-0,/J
Обозначения
в
Д
X
в
о
▼
D
УQ
0,13
0,36
0,60
1,09
1,27
1,34
1,40
1,91
Рис. 3.30. Функции
распределения величин
lg (ffmax — и) для
образцов из стали 40Х с
различными значениями кри-
L
терия -тг-
0
1,4 1,5 1,6 1,7 1,8 1,9 lgFmx-u)
о независимости 5 от lg^=-. Величины 5 для сталей равны 0,045—
G
0,05, для алюминиевых и магниевых деформируемых сплавов 0,05—•
0,06 (при е„ = 0,5); для сплава Мл5 (при ем = 0,4) 5 = 0,16.
Процедура определения параметров уравнения подобия по
результатам испытаний сводилась к определению о_х по осредненной
кривой в координатах lg (amax — и') — lg^=- и проведению пря-
G
мой линии по экспериментальным точкам на графике в
координатах lg (| — 1) — lg-=-,' по которой определяется значение va
G
(см. рис. 3.28, 3.29). Последняя операция может выполняться
графически или аналитически по методу наименьших квадратов.
Величина е„ при этом для пластичных конструкционных сплавов
была рекомендована постоянной и равной 0,5. Величину 5
находят по графикам типа рис. 3.30 с использованием уравнения
C.96). Значение е„ = 0,5 соответствует пределу выносливости
гладкого образца весьма большого диаметра (в пределе d->oo)
а-и = и = 0,5о_х, где и — минимальная граница сгшах
(вероятность того, что ашах может быть меньше и, принимается равной
нулю). Однако удовлетворительные результаты в смысле
аппроксимации опытных распределений получаются и при других
значениях е», а следовательно, и и = е„ст_1. При этом
естественно получаются другими значения остальных параметров v0,
106
5, причем, как показывают опытные данные, величина 5 стано-
L
вится зависящей от -=г-.
G
Для достаточно надежного определения порогового значения и
случайной величины, распределенной по логарифмически
нормальному закону с минимальной границей (например, при
нормальном распределении величины X = lg (amax — и) или X =
= lg (N — A/q), требуется весьма большое количество опытных
точек, которое обычно не достижимо при оценке параметров
распределения пределов выносливости. Но известная
произвольность в выборе sM и а = е„о_х не вносит погрешностей в
аппроксимацию опытных распределений, так как эта аппроксимация
получается удовлетворительной при изменении и в достаточно
широких пределах. На основании анализа большого количества
опытных данных поэтому и рекомендуется для конструкционных
сталей, деформируемых легких сплавов и модифицированных
чугунов принимать е„ = 0,5.
Для литейных сплавов это значение должно быть снижено,
учитывая их существенно большую неоднородность и зависимость
от абсолютных размеров.
8. Фреттинг-коррозия
В местах напрессовки на вал деталей (шестерен, колец
подшипников и т. п.), а также в других случаях контакта сопрягаемых
деталей возникает резкое снижение (в 3—6 раз) пределов
выносливости детали. При этом зарождение усталостной трещины
начинается, как правило, у края напрессованной детали. После рас-
прессовки соединяемых деталей на поверхности можно обнаружить
следы коррозии в виде затемненных пятен, каверн, а также
красный порошок, частицы которого в большинстве случаев
представляют собой окислы железа (Fe203) при сопряжении стальных
деталей.
Причинами столь резкого снижения пределов выносливости
деталей в зонах контакта являются, с одной стороны,
концентрация напряжений у края контакта, и с другой стороны, сложные
механические и физико-химические процессы (фреттинг-процессы),
протекающие на стыке двух сопрягаемых деталей при малых
взаимных циклических смещениях.
При переменных деформациях деталей, неподвижно
соединенных между собой, например валов с напрессованными ступицами
шестерен, неизбежно возникает весьма малое (от Ю-6 до 0,25 мм)
циклическое скольжение, которое является необходимым
условием протекания фреттинг-процессов. Если при этом не
происходят химические процессы (контакт благородных металлов, на-
107
пример золота и платины, Или контакт абсолютно сухих
поверхностей в среде инертных газов), то повреждения поверхностей
за счет износа называют просто фреттингом."
Но, как правило, механические процессы износа при фреттинге
сопровождаются химическими процессами взаимодействия
поверхностных слоев и отделившихся частиц износа с окружающей
средой, чаще всего с кислородом воздуха,- водой и т. п. Кроме
того, в местах контакта протекают и процессы электроэрозион-
ного разрушения. Совокупность этих процессов называют фрет-
тинг-коррозией.
Результаты многих исследований показывают, что степень
повреждения при фреттинге, выражаемая, например, потерей
массы образца вследствие отделения частиц износа, возрастает
с увеличением амплитуды проскальзывания во многих случаях
по линейному закону. Повреждение поверхностных слоев от
фреттинга возникает при весьма малых контактных давлениях
и возрастает с ростом давления до определенных пределов, после
чего происходит стабилизация или даже уменьшение
повреждений. Степень повреждения растет приблизительно по линейному
закону с увеличением числа циклов относительных скольжений,
несколько уменьшается с ростом частоты смещений (при одном
числе циклов) в случае стальных образцов. Определенную роль
играет также температура, среда, материал трущихся пар и
другие факторы [52, 69]. Трещины.усталости при фреттинг-корро-
зии образуются при весьма малых напряжениях (для
углеродистой стали при о = 3-=-5 кгс/мм2). При низких напряжениях
скорость развития поверхностных трещин усталости настолько мала,
что не приводит к увеличению их размера до критического при
весьма большом числе циклов. Поэтому сопротивление усталости
деталей с напрессовками можно характеризовать двумя пределами
выносливости: по разрушению и по началу образования
неразвивающихся трещин.
На рис. 3.31 показана кривая усталости железнодорожной
оси с напрессованным колесом при консольном изгибе с
вращением. Материал осей — сталь, близкая по свойствам к стали
марки Ст5; механические свойства: ав = 64 кгс/мм2, ат =
= 35 кгс/мм2, 1];=48%; оси проходили нормализацию и отпуск.
По поверхности А колесо болтами прикрепляется к
планшайбе, соединенной со шпинделем усталостной машины. Черные
точки на графике соответствуют результатам испытаний осей,
сломавшихся в процессе испытания, белые точки — несломав-
шихся осей, но имеющих трещины усталости. Цифры около белых
точек означают глубину трещин в мм. Следовательно, даже при
весьма низких напряжениях C,5 кгс/мм2) образуются трещины
усталости, не развившиеся до опасных размеров по достижении
85 млн. циклов. Предел выносливости по разрушению равен
7,7 кгс/мм2, а предел выносливости по началу образования
трещин около 3,5 кгс/мм2. Максимальная глубина трещин (в мм)
108
6,кгс/им*
20
is
кгс/мм'
2 3 4 SB
ZO 30 Ы N-10
Рис. 3.31. Кривая усталости
железнодорожной оси при изгибе с вращением
Рис. 3.32. Зависимость глубины
усталостной трещины / от
напряжений при испытании на усталость:
/ — оси d = 241 мм без обкатки после
85 млн. циклов; 2 — оси d = 241 мм с
обкаткой после 85 млн циклов; 3 —
модели осей; d = 55 мм, сталь-40Х по-
вле 250 мли. циклов с обкаткой
после 85 млн. циклов действия
переменных напряжений в
зависимости от напряжения при
испытании показана на рис. 3.32.
Все точки на графике (кроме черных ромбов) соответствуют
результатам испытаний осей из различных сталей [75]. Точки
в виде белых ромбов — результатам испытаний осей, обкатанных
роликом, черные точки — осей, прошедших специальную
термическую обработку, в'результате которой в поверхностных слоях
осей действовали значительные сжимающие остаточные
напряжения. Пунктирная линия характеризует оси, имеющие в
поверхностном слое остаточные напряжения сжатия, а сплошная
линия —=- оси без остаточных напряжений.
Черными ромбами и штрихпунктирной линией обозначены
результаты испытаний моделей осей, обкатанных роликами и
испытанных А. М. Усовым до 250 млн. циклов [52]. Диаметр
моделей осей равнялся 55 мм, материал — сталь 40.
У осей без специальной поверхностной обработки (линия 1
на рис. 3.32) при приближении напряжений к уровню 8,0—
8,5 кгс/мм2 глубина трещины становится настолько большой, что
это напряжение соответствует пределу выносливости по
разрушению. При наличии остаточных сжимающих напряжений в
поверхностном слое глубина трещин при том же напряжении
значительно меньше, чем при отсутствии их. Для получения
расчетных характеристик сопротивления усталости валов с
напрессованными деталями при изгибе с вращением были обобщены
исследования различных авторов и построены графики,
изображенные на рис. 3.33, 3.34, 3.35. На рис. 3.33 отложены значения
(—— ) = -^i- в зависимости от диаметра стального вала d (aB =
= 50 кг/мм2) при давлении в месте запрессовки р > 3 кгс/ммл.
Здесь o_i, а_1Д — соответственно пределы выносливости глад-
109
(А)
Еб">
If
3
г
п\
Мизг
\шж
.fr~^
\шш
1
2
ч
■*t шъ
ТЕ
т
1И
20 30 40 50 10 100 150 200 300d, мм
Рис. 3.33. Зависимость коэффициентов
\8сгУС
от диаметров валов с
напрессованными деталями при изгибе (ств =
= 50 кгс/мм2, Р > 3 кгс/мм2):
/ — через напрессованную деталь
передается сила или момент; 2 — через
напрессованную деталь не передается усилий
кого лабораторного полированного образца диаметром 7,5 мм
и вала с напрессовкой диаметром d. Кривая 1 соответствует
случаям, в которых через напрессованную деталь передается
поперечная сила, или изгибающий момент или то и другое одновременно.
Кривая 2 соответствует случаям, в которых через напрессованную
деталь не передается ни сил, ни моментов. Коэффициенты—^-,
учитывающие одновременное влияние концентраций напряжений
и масштабного фактора, получаются при этом несколько
меньшими, чем в первом случае, что объясняется меньшими
контактными давлениями и амплитудами проскальзывания во втором
случае по сравнению с первым.
На рис. 3.34 и 3.35 даны поправки |' и |", учитывающие
влияние предела прочности материала вала и давления напрессовки
на величину —2-
8а
С учетом поправок
соответственно
К
для валов с напрессовками при изгибе
с вращением определяется по формуле
8а \ 8а Л S S -
C.97)
Из рис. 3.35 видно, что с ростом предела прочности стали
значение -£. возрастает на 80%, с увеличением ов с 50 до
0 0,5 1,0 1,5 1,0 2,5 р, кгс/мм2
Рис. 3.34. Зависимость
коэффициента %" от давления напрессовки
ПО
90 6S,кгс/мм2
Рис. 3.35. Зависимость
коэффициента \' от предела прочности
110кгс/мм2. При давлении р<3 кгс/мм2 значения —-
небо
сколько снижаются, как следует из рисунка 3.34. Однако и при
давлениях, близких к нулю, остается.значительный эффект
снижения сопротивления усталости вследствие фреттинг-коррозии.
В работе [69] приведены результаты испытаний валов из
стали 30, прошедших нормализацию (ав = 52-^-53 кгс/мм2)
(рис. 3.36). Испытания проводили на машине резонансного типа
с частотой — 1000 циклов/мин с поддержанием постоянства
амплитуды деформации до базы 107 циклов. Соотношения размеров,
конического сопряжения выбирали так, чтобы моделировать
сопряжения судового гребного вала с винтом. Муфты для насадки
на конические хвостовики отливали из стали. Конические
отверстия в них после расточки проходили шабровку по калибру-
пробке. Сборку соединений производили запрессовкой на
ручном прессе с контролем натяга по перемещению муфты.
Валы типа VI вследствие утолщения до диаметра 60 мм в
месте напрессовки разрушались в цилиндрической части,
поэтому предел выносливости их t_i = 15 кгс/мм2 можно
рассматривать как предел выносливости гладкого вала диаметром 55 мм
при кручении.
Валы типа / не имели
шпоночного паза, и крутящий момент
передавался за счет сил трения в
запрессовке. Пределы выносливости в этом
случае получились равными: по
разрушению т_1д =12,5 кгс/мм2, по
началу образования трещин tLia=
= 11,8 кгс/мм2.
Пределы выносливости валов,
изображенных на рис. 3.36, и
эффективные коэффициенты концентрации
напряжений Кт = ■
1-1Д
(при Т_х
= 15 кгс/мм2) приведены в табл. 3.12.
В вале типа // врезная шпонка
имела полную длину. При этом
коэффициент К.% получился наибольшим
B.21). Наилучший результат
получился при использовании
укороченной врезной шпонки (тип V), для
которой Кх = 1,27. Конструкция паза
в образце типа IV характеризуется
ложкообразной разделкой выхода
лыжеобразного шпоночного паза и
рекомендуется при изготовлении
новых гребных валов. Предел
выносливости при этом получается до-
Рис. 3.36. Типы образцов-валов,
применявшихся при испытаниях
на усталость при
знакопеременном кручении с передачей
момента через коническое
сопряжение
111
статочно большим (9,9 кгс/мм2),
однако он меньше, чем у валов
с укороченной шпонкой. В
валах со шпонками полной длины
при кручении усталостные
трещины возникают в районе
выхода шпоночного паза при
небольших натягах (характерных
для глухой посадки). При
значительных натягах,
характерных для прессовых посадок,
значительная часть крутящего
момента передается за счет сил
трения. При этом уменьшается
роль концентрации
напряжений от шпоночного паза, и
трещины образуются в местах
наиболее интенсивного фреттинга
у края напрессованной втулки.
В работе [69] приведены результаты испытаний Е. Корне-
лиуса и А. Е. Рогожкиной, характеризующие влияние фреттинг-
коррозии на сопротивление усталости при кручении.
В работе Е. Корнелиуса приведены результаты исследования
влияния натяга на сопротивление усталости валов диаметром
60 мм из стали St50 при знакопеременном кручении
(бесшпоночное соединение). Предел выносливости гладких валов при
кручении составлял т_х = 20,7 кгс/мм2. Изменение натяга в пределах
от 0,127 до 0,303 мм не привело к закономерному изменению
пределов выносливости. При этом эффективные коэффициенты
концентрации напряжений Кх — 1,6-4-1,77.
А. Е. Рогожкиной испытывались при знакопеременном
кручении валы диаметром 65 мм из различных сталей -с
напрессованными втулками, через которые передавался знакопеременный
крутящий момент, без упрочнения и обкатанные роликами.
Значения пределов выносливости на базе 3-Ю7 циклов, эффективных
коэффициентов концентрации Kz = т_х/т_1д и коэффициентов
упрочнения |Зупр = т_1дупр/т_1д приведены в табл. 3.13 (т_1дупр —
Таблица 3.13
Характеристики сопротивления усталости валов диаметром 65 мм
с напрессованными втулками при знакопеременном кручении
Марка стали
Сталь 45
40Х
15Х2Г2СВА
ffB,
кгс/мм2
137
т-1>
кгс/мм2
11
14,5
21,6
кгс/мм2
7,0
7,0
4,0
Т-1Д упр>
кгс/мм2
11,0
13,2
*т
1,57
2,07
5,4
Рупр
1,57
1,89
Таблица 3.12
Пределы выносливости
и эффективные коэффициенты
концентрации валов
с напрессовками и шпонками
при кручении
Тип
вала
по рис.
3.36
/
II
III
IV
V
VI
кгс/мм2
12,5
6,8
8,7
9,9
11,8
15,0
\
1,20
2,21
1,73
1,52
1,27
1
112
предел выносливости валов с напрессовкой, упрочненных
обкаткой роликами).
Анализ данных табл. 3.13 показывает, что с ростом предела
прочности стали резко возрастают эффективные коэффициенты
концентрации от напрессовки при кручении. Вследствие этого
применение высокопрочных сталей для валов с напрессовками
оказывается малоэффективным, а может даже привести и к
снижению предела выносливости в сравнении с. углеродистой сталью,
[например, т_1д = 4 кгс/мм2 (для стали 15Х2Г2СВА) и т_1д =
= 7 кгс/мм2 (для стали 45)].
Поверхностный наклеп (как вытекает из табл. 3.13) повышает
предел выносливости валов с напрессовками при кручении на
60-90%'
Зависимость эффективных коэффициентов концентрации для
валов с напрессовками при кручении от предела прочности стали,
построенная по описанным результатам, приведена на рис. 3.37.
Значение Кх = 5,4, полученное для легированной стали с сгв =
= 137 .кгс/мм2, является весьма высоким и нуждается в
последующей дополнительной проверке. В связи с этим линия на рис. 3.37
правее абсциссы сгв = 100 кгс/мм2 проведена пунктиром, и ее
положение следует рассматривать в этой области как
ориентировочное.
Представляют интерес данные об одновременном влиянии
фреттинг-коррозии и коррозии в 3%-ном растворе поваренной
соли на сопротивление усталости образцов из стали 35 диаметром
d =12 мм и 50 мм с насаженными жесткими (D=2d, L=2d)
неразрезными стальными и латунными втулками, не передающими
изгибающего момента или поперечной силы [69]. Испытания
на усталость производились
при изгибе с вращением с пол- Krt
ным погружением рабочей части,
цилиндрического образца с на-
раженной втулкой в проточную
соленую воду на базе 50 млн.
циклов (частота ЗОООцикл/мин).
Значения пределов
выносливости образцов с
напрессованными втулками приведены в
табл. 3.14.
Из анализа данных табл. 3.14
следует, что воздействие жидкой
коррозионной среды приводит
к резкому снижению пределов
выносливости образцов с
напрессованными втулками (в 3,6—
3,8 раза на образцах d = 12 мм
Г
j*
v MjtpS~\
J
ш
^
<s
*г
/
У
о
/
/
/
/
/
(
40 S0
so
100 ПО 6а,кгс/мм2
Рис. 3.37. Зависимость эффективных
коэффициентов концентрации валов
диаметром 65 мм с напрессованными
втулками при знакопеременном
кручении при передаче момента за счет сил
и в 1,6—1,8 раза на образцах трения (без шпонки) от ав
ИЗ
d = 50 мм). Таким образом, можно сказать, что в 3%-ном растворе
NaCl определяющую роль играет не фреттинг-коррозия, а
коррозия от жидкой среды, усиленная щелевым эффектом в зазоре
между образцом и втулкой.
Если оценить пределы выносливости гладких образцов из
стали 35 при испытании на воздухе величинами а_х = 26 кгс/мм2
при d = 12 мм и ст_! = 22 кгс/мм2 при d = 50 мм, то суммарный
коэффициент Kod> характеризующий одновременно влияние фрет-
тинга и коррозии в жидкой среде, равен:
26
при d= 12 мм Kqd = -t- = 6,5;
при d= 50 мм /Сад = g-g- = 3,4.
Таким образом, с ростом размеров происходит ослабление
суммарного влияния двух указанных факторов на сопротивление
усталости, т. е. как бы инверсия масштабного фактора [21, 69].
Из анализа данных табл. 3.14 следует также, что с ростом
диаметра вала с напрессованной втулкой предел выносливости его
существенно снижается. Например, при увеличении диаметра
с 12 до 50 мм в стальной втулке снижение получается на 30%
(с 15,3 до 10,6 кгс/мм2).
Повышение пределов выносливости деталей с напрессовками,
в которых возникает фреттинг-коррозия, может осуществляться
конструктивными и технологическими методами.
Конструктивные мероприятия сводятся к созданию выточек на торце ступицы
(рис. 3.38, а), введению утоненного пояска у края ступицы
(рис. 3.85, б), утолщения подступочной части (рис. 3.38, б),
разгружающих выточек на валу (рис. 3.38, г) и других
конструктивных изменений, уменьшающих концентрацию контактных
давлений и напряжений в вале у края напрессованной ступицы и
вследствие этого приводящих к повышению сопротивления усталости.
Так, введение разгружающей выточки на торце ступицы (см.
Таблица 3.14
Пределы выносливости образцов из стали 35 с напрессованными
втулками при испытании в соленой воде
Материал втулки
Латунь
Сталь
Диаметр образцов, мм
<* =12
Воздух
14,5
15,3
3%-ный
раствор NaCl
4,0
4,0
d = 50
Воздух
11,5
10,6
3%-ный
раствор NaCl
7,0
6,0
114
рис. 3.38, а) приводит к повы-
metmicf предела выносливости до
30%. Изменение предела
выносливости валов диаметром 50 мм
с напрессованной ступицей из
углеродистой стали ов =
= 55 кгс/мм2 в зависимости от
размеров утоненного пояска у
края ступицы можно
проследить по данным в табл. 3.15, в
которой приведены результаты
исследования К- Нишиока и
Г. Коматсу [69]. Предел
выносливости гладких образцов
диаметром 45 "мм равнялся
27,5 кгс/мм2. Испытания
производились при изгибе с
вращением на базе 20 млн. циклов, так что через напрессованную
втулку передавались изгибающий момент и поперечная сила.
Из анализа данных табл. 3.15 видно, что при длине пояска
/ = 4-f-8 мм и толщине t = 2ч-3,75 мм предел выносливости вала
с напрессованной ступицей повышается на 26—31%. Утолщение
пояска до t = 6 мм приводит к исчезновению эффекта упрочнения.
Положительное влияние утоненного пояска связано (так же как
и влияние канавки на торце ступицы) с уменьшением
концентрации контактных давлений и напряжений в вале у края ступицы.
Очаг зарождения усталостной трещины при этом смещается на
Рис. 3.38. Конструктивные схемы валов
с напрессовками
Таблица 3.15
Зависимость предела выносливости валов 0 50 мм
с напрессованной ступицей от размеров утоненного пояска
(см. рис. 3.38, б)
Размеры пояска, мм
1
1,5
4,0
8,0
4,0
4,0
t
3,75
3,75
3,75
2,0
6,0
■ °-1Д>
кгс/мм2
9,7
10,4
12,2
12,7
12,5
10,0
Примечание. (ivnD = —~1^упр — t
а-1Д
тивного упрочнения на предел выносливости; G
вости деталей с конструктивными улучшениями
ственно; а<_ = 9,7 кгс/мм2.
кс
2,84
2,65
2,25
2,17
2,20
2,75
коэффициент
1дупр' а-1Д
I (С ПОЯСКОМ)
Рупр
1,00
1,07
1,26
1,31
1,29
1,03
влияния конструк-
— пределы выносли-
и без них, соответ-
115
1,5—2,5 мм от края ступицы,' а ширина зоны фреттинг-коррозии
увеличивается до 3—6 мм (против 1,6 мм без пояска).
К- Нишиока и Г. Коматсу исследовали влияние утолщения
подступичной части на валах диаметром 50 мм из углеродистой
стали (ав = 55 кгс/мм2, а_2 = 27,5 кгс/мм2 при d = 45 мм) при
изгибе с вращением на базе 20 млн. циклов. При Did = 1,046
предел выносливости вала с напрессовкой увеличился на 29—34%
(по сравнению со случаем Did = 1, т. е. без утолщения, для
которого tf-in = 9,7 кгс/мм2). При Did = 1,07 это увеличение
составило 31— 48%, при Dld= 1,09-н1,12 — 48-г-51%. В
указанных пределах сопротивление усталости увеличивается с
уменьшением радиуса, но только до тех пор, пока разрушение не
переходит из подступичной части в зону галтели. При дальнейшем
уменьшении радиуса предел выносливости падает в соответствии
с закономерностями подобия, описанными выше.
По данным работы [75], аналогичный результат был получен
при испытаниях крупных осей диаметром 241 мм из осевой стали
(ств = 64 кгс/мм2) с напрессованной деталью фупр = 1,36).
Влияние разгружающих выточек (см. рис. 3.38, г) на
сопротивление усталости валов с напрессовками было рассмотрено
в работе [69]. Валы из стали 38ХНМА (сгв = 71—74 кгс/мм2)
с напрессованными жесткими втулками (Did — 2), через
которые не передавались силы и моменты, испытывали при изгибе с
вращением на базе 50 млн. циклов с частотой 3000 об/мин. Предел
выносливости (<х_1д) вала без канавки составил 10,3 кгс/мм2
f —- = ' ю'з '" ~ 3'^) ' с канавк°й — 13,3 кгс/мм2, т. е. эффект
упрочнения получился равным 28%.
Введение аналогичной канавки на валах из осевой стали
диаметром 241 мм с напрессовкой повысило предел выносливости
на 36% [75].
Важное значение для повышения сопротивления усталости
деталей с фреттинг-коррозией имеют методы поверхностного
упрочнения (наклеп поверхности роликом, дробью и т. п.'; химико-
термические методы: цементация, азотирование, нитроцемента-
ция и т. д.; поверхностная закалка с нагрева токами высокой
частоты; комбинированные методы), которые при правильной и
рациональной технологии обеспечивают повышение пределов
выносливости до 1,5—3 раз (см. табл. 3.13).
Одним из способов повышения сопротивления усталости
деталей с напрессовками и фреттинг-коррозией является введение
между контактирующими поверхностями пленок из
неметаллических материалов, препятствующих развитию фреттинг-коррозии.
Так, в работе [69] приведены результаты испытаний валов
диаметром 30, 90 и 178 мм с напрессованными деталями на базе 108
циклов, полученные В. А. Веллером.
Это исследование показало, что введение полимерных пленок
между валом и напрессованной деталью приводит к повышению
116
пределов выносливости их на 20—40 %. Сочетание накатки роликом
и покрытия вала диаметром 30 мм полимерной пленкой приводит
к повышению предела выносливости в 1,8 раза.
Фреттинг-коррозия оказывает существенное влияние на
сопротивление усталости и в других случаях, когда имеется контакт
двух деталей, например в замковых, болтовых и других
соединениях.
9. Качество обработки поверхности, коррозия
и частота испытания
Качество обработки поверхности оказывает весьма сильное
влияние на сопротивление усталости, что связано с влиянием
концентрации напряжений вследствие микронеровностей
поверхности, а также остаточных напряжений и наклепа тонкого
поверхностного слоя, возникающих при механической обработке.
С ухудшением качества поверхности, с ростом высоты
микронеровностей увеличивается концентрация напряжений и
снижается предел выносливости. Это снижение более резко выражено
у высокопрочных сталей вследствие их большей чувствительности
к концентрации напряжений.
Для характеристики влияния качества обработки поверхности
на сопротивление усталости на рис. 3.39 показаны
экспериментально найденные кривые, характеризующие снижение предела
выносливости образцов, имеющих различное качество обработки
поверхности [51]. По оси абсцисс на графике отложен предел
прочности стали сгв, по оси ординат — коэффициент р,
характеризующий влияние качества обработки поверхности на предел
выносливости и равный отношению
Р =
u_i
C.98)
где all — предел выносливости образцов с данным качеством
обработки поверхности; а_г — предел выносливости тщательно
полированных образцов.
Снижение предела выносли- ^
вости оказывается тем большим,
чем больше предел прочности W
стали. В случае грубого точе- gS
ния снижение предела вынос- '
ливости оказывается очень боль- 0,4
шим, до 40% при пределепроч- .„
ности ав =' 125 кгс/мм2. Нали- ' tg so SO W0 б^кгфм2'
чие окалины приводит к еще .
более резкому снижению а_х.
Поэтому в случае
использования высокопрочных легирован-
—
г
~-2И
4
s
Рис. 3.39. Зависимость Р от ав стали:
/ — полирование; 2 — шлифование; 3 —
тонкое точение; 4 — грубое точение; 5 —
наличие окалины
117
ных сталей детали должны иметь тщательно шлифованную или
полированную поверхность; в противном случае теряется смысл
применения дорогих легированных сталей. Чтобы в этом
убедиться, найдем пределы выносливости образцов из сталей с
пределами прочности сгв1 = 80 кгс/мм2 и сгв2 = 140 кгс/мм2,
имеющих на поверхности окалину. С учетом уравнений C.98) и
B.20) имеем
а11 = |3@,55-0,001ав)ав; C.99)
По рис. 3.39 (кривая 5) при указанных значениях ав имеем
р\.= 0,54 (<тв1 = 80 кгс/мм2) и |32 = 0,3 (ав2 = 140 кгс/мм2).
По формуле C.99) получим oLi, i = 20,7 кгс/мм2; crLi,2 =
= 17 кгс/мм2. Таким образом, при наличии окалины предел
выносливости образцов из более прочной стали (сгв = 140 кгс/мм2)
оказался ниже предела выносливости образцов из стали средней
прочности.
В работе [80] приведена следующая формула Нимана и Гла-
убитца для определения значений отношения пределов
выносливости образцов о_ъ х, 0_Xi 2 с высотами микронеровностей
поверхности соответственно Rz± и Rz2:
&=йНж-Г (ЗЛ00)
По результатам усталостных испытаний было найдено, что
для стали с сгв = 70 кгс/мм2 п = 0,079, а для стали с сгв =
= 100 кгс/мм2 п = 0,102.
С учетом этих данных построена зависимость |3 от сгв и Rz,
представленная на рис. 3.40 [80]. Влияние качества обработки
поверхности на величину пределов выносливости гладких
образцов из алюминиевых деформируемых сплавов характеризуется
данными, приведенными в табл. 3.16 [60].
Для образцов, точеных из магниевых сплавов, |3 = 0,7-Ю,8;
для деталей из легких сплавов, содержащих на поверхности
литейную корку, окалину и другие дефекты литья, прессования или
прокатки, |3 = 0,5-=-0,75. При обдувке дробью таких деталей |3 =
= 0,8-Я,0.
Особенно чувствительны к качеству обработки поверхности
титановые сплавы [52]. Снижение предела выносливости точеных
образцов по сравнению со шлифованными у этих сплавов доходит
до 30%.
Предел выносливости может существенно снизиться из-за
повреждений поверхности в процессе шлифования (ожоги и
шлифовочные трещины).
Заметное снижение пределов выносливости получается в тех
случаях, когда на поверхности детали в результате каких-либо
технологических процессов при обработке создается мягкий,
пусть даже весьма тонкий слой (обезуглероживание, омеднение
118
и т. п.). В этом случае усталостная
трещина, зародившись в мягком
поверхностном слое, легко
распространяется на все сечение детали. При
обезуглероживании поверхности
стальных образцов при термической
обработке в среднем |3 = 0,6 при
0В = 90 кгс/мм2 и р = 0,3 при
рв = 150 кгс/мм2.
Приведенные выше значения
коэффициентов |3 соответствуют
гладким образцам (без концентрации
напряжений). Для оценки пределов
выносливости деталей с
концентрацией напряжений и различным
качеством обработки поверхности может быть использована
формула для эффективного коэффициента концентрации
напряжений Ком, соответствующего комбинированному надрезу
(глубокому с наложенным на него мелким надрезом), полученная в
работе [9] на основе поляризационно-оптических измерений
напряжений и усталостных испытаний:
коы^к0 + кж-1, C.101)
100 6g,KiclMriz
Рис. 3.40. Зависимость Р от
предела прочности и параметра
шероховатости поверхности Rz
где Ко, Кш — соответственно эффективные коэффициенты
концентрации напряжений для основного (глубокого) и мелкого
(наложенного) надрезов.
Положим
-Ко = KaD =
Ко
СТ-1д
C.102)
где K'cd — суммарный коэффициент, учитывающий влияние
концентрации напряжений и абсолютных размеров для полированной
детали, равен отношению предела выносливости полированного
Таблица 3.16
Значения коэффициентов |3 для деформируемых алюминиевых
сплавов
Окончательная обработка
Полирование
Шлифование
Чистовое точение
Точение
Грубое точение
Очень грубое точение
Высота неровностей
Rz, мкм
0,5—1
1,5—2
4—10
10—15
20—30
50—100
Р
1,00
0,96—0,98
0,87—0,94
0,84—0,88
0,78—0,83
0,70—0,75
119
гладкого лабораторного образца а_г к пределу выносливости
натурной полированной детали <т—1Д.
Рассматривая влияние шероховатостей поверхности как
влияние наложенных надрезов принимаем Кы = 1/р. В результате
получаем
^-■^- = -^ + -1-1, (злоз)
где сг_1д — предел выносливости натурной детали с заданным
качеством обработки поверхности.
Влияние коррозии. Резкое снижение пределов выносливости
получается при воздействии коррозионной среды (например,
пресной или морской воды) на металл детали или образца в процессе
их усталостных испытаний. Явление постепенного накопления
повреждений в металле под воздействием переменных напряжений
и коррозионной среды называется коррозионной усталостью.
При этом в поверхностных слоях металла возникают трещины
коррозионной усталости, в основном внутрикристаллитные. Около
небольших местных коррозионных повреждений поверхности,
образующихся вначале, создается концентрация напряжений,
причем на дне коррозионной полости возникают максимальные
напряжения. Это приводит к более интенсивному развитию
коррозии на дне полости и к постепенному углублению трещины
коррозионной усталости.
Чем больше время пребывания детали в коррозионно-агрес-
сивной среде и чем больше число циклов переменных напряжений
в условиях коррозии, тем глубже будут трещины коррозионной
усталости, тем меньше будет сопротивление усталости. В связи с
этим кривая коррозионной усталости все время снижается, и
предел выносливости, в обычном смысле слова, не существует. В
качестве примера на рис 3.41 представлены кривые коррозионной
усталости трех марок сталей, применяемых в гидротурбостроении,
из которой следует, что почти до 1 млрд. циклов наблюдается
систематическое падение кривой усталости, которое, однако, до
некоторого числа циклов является более интенсивным, чем после
него. Поэтому под пределом коррозионной выносливости
понимается ограниченный предел выносливости, соответствующий
определенному числу циклов по кривой коррозионной усталости.
Из рис. 3.41 видно, что с увеличением базы испытаний с 10' до
109 циклов предел выносливости гладких образцов из стали 20ГСА
снижается на 27%, из стали 0Х12НДЛ— на 42% и из стали
00Х12НЗД —на 18%.
С ростом предела прочности стали резко усиливается
отрицательное влияние коррозии на сопротивление усталости, что
связано с большей чувствительностью высокопрочных сталей
к концентрации напряжений, возникающей у коррозионных
повреждений. В результате с ростом предела прочности стали пре-
120
6а, кгс/мм*
чи
iff
32
28«
24
tQ
16
12
I
\
}
III
II
||
I I
I
I I
J
4\
f
I
I
r*«
ГГ
I
f tj
ТГ
П
T|
"I "J
Tf
|Р
ti
it
:f 4» IB
ТИ
;: :n
no"
a)
107 10s N 10s 107 10s N 10s W7 10
S)
8)
Рис. 3.41. Кривые коррозионной усталости образцов из сталей 20ГСА (а).
0Х12НДЛ (б) и 00Х12НЗД (в) без концентрации напряжений (темные точки)
и с надрезом (светлые точки); по данным Г. 3. Зайцева и др. [20].
Примечание. Испытания при круговом изгибе с частотой 2800 об.'мин в пресной
проточной воде
делы коррозионной выносливости не увеличиваются, оставаясь
на том же уровне, что и у сталей малой прочности. Из рис. 3.42
видно, что если при сгв = 60 кгс/мм2 пределы выносливости
снижаются в 2—3 раза вследствие коррозии в пресной воде, то при
сгв = 100 кгс/мм2 — в 3,5—5 раз; коррозия в морской воде
приводит к еще более резкому снижению пределов выносливости,
а именно в 3,5—6 раз при сгв = 60 и в 7—11 раз при сгв =
= 100 кгс/мм2.
Аналогичная зависимость 6.икгс/мм2
для алюминиевых сплавов пред- 70
ставлена на рис. 3.43. во
Пределы выносливости
магниевых сплавов на базе 10'-—• so
5-10' циклов при испытании в 40
пресной и морской воде имеют }д
весьма низкие значения в
диапазоне 1—2 кгс/мм2 [60]. го
Так как степень развития да
коррозионных повреждений су- д
щественно зависит от времени
пребывания образца в
агрессивной среде, положение кривых
коррозионной усталости зависит
от частоты испытания, как
показано на рис. 3.44. Например, для
'//4
У/л
\Ш
ш
у77л
1
2
W>
3
I
щ
ш
*>-
щ
77%.
К
__
i0 SO SO 70 80 90 100 110 6е,кгс/мм2
Рис. 3.42. Зависимость предела
выносливости от предела прочности для
различных сталей в разных средах:
/ — на воздухе; 2 — в пресной воде; 3 —
в морской воде
121
6ij ,кгс/мм2
О 10 20 дО 40 SO д0бд,кгс/ммг
Рис. 3.43. Зависимость предела выносливости для базы 107 циклов от предела
прочности алюминиевых сплавов:
/ — на воздухе; 2 — в 3% -ном растворе NaCl
наработки 105 циклов при частотах 5 и 1450 об/мин требуется
время соответственно 333 и 1,2 ч. За 14 суток непрерывной
работы C33 ч) развитие коррозионно-усталостных повреждений
будет значительно большим, чем за 1,2 ч, что и приводит к
снижению предела выносливости в условиях коррозии более чем
в 2 раза на данной базе (с 54 до25кгс/мм2) при снижении частоты
с 1450 до 5—8 об/мин. Поэтому при оценке сопротивления
усталости деталей в условиях коррозии необходимо учитывать
частоту и базу испытания.
В расчетах на усталость влияние коррозионной среды учиты;
вается с помощью коэффициента
РкоР = ^, C.104)
где а_1кор, о_х — пределы выносливости гладких образцов в
условиях коррозии и на воздухе соответственно. Следует иметь
в виду, что а_1кор, а следовательно, и ркор зависят от частоты
и базы испытания, которые должны учитываться при определении
Ркор. На рис. 3.45 представлены зависимости |Зкор от предела
прочности стали. Эти данные соответствуют испытаниям при
изгибе с вращением гладких лабораторных образцов на базе
107 циклов при частоте п = 2000-ьЗООО об/мин. При переходе
122
к базе 109 циклов, как следует из рис. 3.41, эти коэффициенты
Ркор должны быть дополнительно умножены на коэффициент
0,6—0,8, что соответствует дополнительному снижению предела
выносливости в условиях коррозии в среднем на 20—40%.
Для расчета пределов выносливости деталей с концентрацией
напряжений в условиях коррозии может быть использована
следующая формула, аналогичная уравнению C.103):
KoD кор
Ко
СТ-1Д кор
+
JKOp
■-1,
C.1.05)
где о_1ДКОр— предел выносливости натурной детали в условиях
коррозии при той же частоте и базе испытания, при которых
определялся ркор; -^ находится по формулам разд. 7; ркор
определяется по уравнению C.104).
Опытные данные, подтверждающие зависимость C.105),
приведены в работах [52, 60].
При исследовании влияния масштабного фактора на
сопротивление усталости гладких образцов в условиях коррозии в
работе [87] было получено снижение пределов коррозионной
выносливости на 15—20% при увеличении диаметра образцов с 12
до 60 мм. Однако в работах [21, 31] было получено увеличение
предела выносливости в условиях коррозии на 26% при
увеличении диаметра образцов с 16 до 40 мм. В других работах получалось
как снижение, так и повышение пределов коррозионной
выносливости образцов с увеличением размеров. Так, в работе Г. 3.
Зайцева и др. [12] для стали 0Х12НДЛ получено более резкое
проявление масштабного фактора в условиях коррозии, чем на воз-
6, кгс/ммг
100
духе, в то время как для стали
00Х12НЗД масштабный фактор,
весьма существенный на воздухе,
не проявился совсем в условиях
коррозии. Поэтому вопрос о ВЛИЯ-
мгор
0Л
0,2
10° 10°
Число циклов
Рис. 3.44. Кривые
коррозионной усталости
образцов из кремниеникеле-
вои[стали для разных
частот испытаний
;
г
0'
40 60
W0 6в,кгс/ммг
Рис. 3.45. Зависимость
коэффициентов влияния коррозии ркор от
предела прочности стали (частота
2000—3000 об/мин;база 107 циклов):
1— в пресной воде; 2^» в морской воде
123
нии масштабного фактора на
сопротивление усталости в
условиях коррозии подлежит
дальнейшему изучению. В
расчетах на усталость для
получения дальнейшей более
полной информации
масштабный фактор в условиях
коррозии целесообразно
принимать таким же, как и на
воздухе.
В условиях воздействия
коррозионной среды
усиливается влияние асимметрии
цикла на сопротивление усталости, что иллюстрируется данными,
приведенными в табл. 3.17 [15]. Наложение средних
сжимающих напряжений весьма благотворно действует на
сопротивление коррозионной усталости, вследствие чего предел
выносливости в воде только на 5% ниже предела выносливости на
воздухе.
Однако растягивающие средние напряжения цикла весьма
резко снижают сопротивление усталости, вследствие чего предел
выносливости при отнулевом цикле растяжения в 10 раз ниже
аналогичного предела при сжатии.
Коэффициенты влияния асимметрии цикла tya для гладких
образцов в условиях коррозии могут возрастать для легированных
сталей до значений 0,3-^-0,6 [20].
Наиболее эффективными средствами повышения пределов
выносливости деталей в условиях коррозии являются такие методы
поверхностного упрочнения, как наклеп поверхности,
поверхностная закалка с нагревом т. в. ч., азотирование и др. Так,
обкатка роликами или обдувка дробью повышают предел
выносливости образцов из стали 45 в морской воде в 2—2,5 раза,
поверхностная закалка с нагревом т. в. ч. — в 3,5 раза,
кратковременное азотирование — в 2 раза [49]. Причиной столь эффективного
положительного влияния указанных методов являются
значительные остаточные сжимающие напряжения в поверхностном
слое детали, возникающие в результате их применения,
препятствующие образованию и развитию усталостны'х повреждений (см.
табл. 3.17).
Электролитические покрытия хромом, никелем, кадмием и
т. п. сами по себе неэффективны. В результате их применения
снижается предел выносливости как на воздухе, так и в коррозионной
среде, причем это снижение может доходить до 30% и более.
Причиной снижения пределов выносливости в этом случае
являются значительные растягивающие остаточные напряжения в
поверхностном слое, возникающие в результате нанесения
электролитических покрытий, снижающих предельную амплитуду. Од-
124
Таблица 3.17
Пределы выносливости (кгс/мм2)
гладких образцов при отнулевых
циклах растяжения и сжатия на
воздухе и в коррозионной среде
[15]
,. „ Растя-
Условия испытаний жение
На воздухе
В пресной воде
120
15
Сжатие
165
157
Таблица 3.18
Результаты усталостных и коррозионно-усталостных испытаний
хромированной стали 45 с предварительной поверхностной
электрозакалкой и без нее [49]
Вид обработки образцов
Нормализация
(исходное состояние)
Электролитическое
хромирование
Электролитическое
хромирование с
предварительной поверхностной
электрозакалкой
Предел выносливости при базе испытаний 10' циклов
иа воздухе
кгс/мма
25,7
20,3
34,6
%
100
79
134
в 3°/„-ном растворе NaCl
кгс/мм2
10,0
8,7
30,0
%
100
87
300
нако весьма эффективно электролитическое хромирование в
сочетании с предварительной поверхностной закалкой с нагревом
т. в. ч., что следует из данных, приведенных в табл. 3.18.
Закалка с нагревом т. в. ч. создает в поверхностном слое
значительные сжимающие остаточные напряжения, "которые
компенсируют затем растягивающие остаточные напряжения от
хромирования.
В результате происходит значительное повышение пределов
выносливости образцов, полученных на воздухе и в коррозионной
среде.
Дополнительные данные о влиянии коррозии на
сопротивление усталости и средствах защиты от нее приведены в работах [15,
21, 49, 51, 87].
Влияние частоты испытания. Частота испытаний не
оказывает существенного влияния на сопротивление усталости при
нормальной температуре и
без воздействия коррози- y_(°-i)r
онных сред. Как видно из F-,)fiso
рис. 3.46 [52], на котором 1^
представлены обобщенные 7г
данные о влиянии частоты
на пределы выносливости /,;
в указанных условиях,
повышение частоты с 5—10 Ь0
до 200 Гц (рабочий
диапазон частот в большинстве "" w zo зо 40S0
машин) приводит к
увеличению пределов
выносливости на 2—8%, а до
1000 Гц— на 5—15%.
0,9 ILL
i%
л
'' l/Z2k$ark-
i
1
к
i
■t
щ
I
%
щ
100 200 300 S00 f, Гц
Рис. 3.46. Зависимость пределов
выносливости при испытании в условиях нормальной
температуры и отсутствии коррозии от
частоты испытаний
125
Это позволяет для ускорения усталостных испытаний в
указанных условиях повышать частоты до 200—300 Гц, что существенно
сокращает время испытаний. При снижении частоты испытаний
в этих же условиях с 50 Гц C000 циклов в минуту) до 6—8 циклов
в минуту пределы ограниченной выносливости снижаются в
среднем на 10%, а долговечность в 4—8 раз.
В тех же случаях, когда при испытаниях протекают активные
химические и физико-механические процессы, связанные с
изменением свойств металла во времени (испытания при коррозии,
повышенной температуре), частота испытаний оказывает
существенное влияние, и ее необходимо учитывать в расчете на
усталость.
10. Технологические методы поверхностного
упрочнения деталей машин
К технологическим методам поверхностного упрочнения
деталей машин относят следующие:
наклеп поверхности путем обкатки роликами, обдувки дробью,
алмазного выглаживания, чеканки и т. п.;
поверхностную закалку с нагрева токами высокой частоты
(т. в. ч.);
химико-термические методы (цементацию, азотирование,
цианирование и др.);
- комбинированные методы (например, цементацию с
последующей обдувкой дробью и т. п.).
Эти методы являются мощным средством повышения несущей
способности, долговечности и надежности деталей машин,
вследствие чего они нашли-широкое применение во всех отраслях
машиностроения. Эффект упрочнения оценивается коэффициентом
Рупр = ^> C-Ю6)
0-1Д
где а_1д, а_1д упр — пределы выносливости натурной детали
соответственно до и после поверхностного упрочнения.
С учетом упрочнения и выражения C.103) коэффициент
При правильной и оптимальной технологии поверхностного
упрочнения коэффициенты рупр могут иметь значения, равные
2—3, что соответствует 2—3-кратному увеличению пределов
выносливости. Особенно эффективны эти методы для деталей
с резкой концентрацией напряжений или деталей, работающих
в условиях коррозии (в среде) или фреттинг-коррозии (см. разд. 8,
9). Однако при неправильной технологии (например, при обрыве
поверхностного закаленного слоя в зоне концентрации
напряжений, при возникновении шлифовочных трещин и т. п.) пределы
126
выносливости могут даже снижаться. Поэтому весьма важно
установить причины, вызывающие повышение пределов
выносливости, и провести исследования по выявлению оптимальных
параметров технологии поверхностного упрочнения [12, 35, 38,
22, 52]. Основными причинами увеличения пределов выносливости
деталей вследствие поверхностного упрочнения являются
повышение механических свойств металла упрочненного
поверхностного слоя и положительное влияние сжимающих остаточных
напряжений, возникающих в этом слое, связанное с характером
диаграмм предельных амплитуд напряжений при асимметричных
циклах, приведенных на рис. 2.7—2.10.
Если в поверхностном слое детали имеется остаточное
напряжение аост и возникает рабочее напряжение от внешних нагрузок,
изменяющееся по симметричному циклу с амплитудой аа, то
результирующее напряжение будет изменяться по
асимметричному циклу Со средним напряжением от — сгост и амплитудой
оа. Если напряжение аост сжимающее, то, как следует из рис. 2.7—
2.10, предельная амплитуда существенно возрастает, что и
является одной из причин повышения предела выносливости детали
вследствие упрочнения. Однако при наличии остаточных
растягивающих напряжений в поверхностном слое (это возможно при
неправильной технологии упрочнения) предельная амплитуда
падает (см. рис. 2.7—2.10), так как рабочая точка на диаграмме
предельных амплитуд сдвигается вправо от точки,
соответствующей симметричному циклу (от = 0). Возникновение остаточных
растягивающих напряжений в поверхностном слое, снижающее
предел выносливости детали, получается при обрыве
поверхностного закаленного слоя, при обезуглероживании поверхности
при химико-термической обработке, при наличии в слое
остаточного аустенита, при наличии шлифовочных прижогов и в
некоторых других случаях. Дробеструйная обработка, проведенная
после химико-термической обработки, увеличивает сжимающие
остаточные напряжения в поверхностном слое до 70—150 кгс/мм2
[35]. В этом состоит большое преимущество использования
комбинированных методов упрочнения.
На рис. 3.47 представлены эпюры остаточных напряжений
в образцах из легированных сталей 25Х2ГНТА и 20Х2НЧА после
цементации и последующей обдувки дробью. По оси абсцисс на
этом рисунке отложено расстояние от поверхности внутрь
металла. Как видно, в слое глубиной —0,15 мм возникают
сжимающие остаточные напряжения, максимальное значение которых
80—100 кгс/мм2. Далее эти сжимающие напряжения переходят
в растягивающие.
Глубина залегания и величина остаточных сжимающих
напряжений, а также характер их распределения по сечению детали,
существенно влияющие на сопротивление усталости, зависят от
режимов химико-термической обработки, обдувки дробью
(скорости полета дробинок, вида и размеров дроби, длительности на-
127
6, KlCJf,
40
го
о
-20
-40
-60
-80
-100
о
L
1
Ц
4
«
VZ
ч
s^
2
\
^
Ья=
щ
Й^
60cm,Kc/MM>Jy°P-1'28
-i№-20-WD
10 20 0,8Щ2ЦЩ8б/6-,
Рис. 3.48. Схема упрочнения при
обкатке шариками (глубина упрочнен-
0,2 0,4 0,6 0,8 1,0 АЬ.мм ного слоя Д =1 мм, р:
упр
1,27):
Рис. 3.47. Эпюры остаточных
напряжений в цементованных слоях
сталей 25Х2ГНТА (сплошные
линии) и 20Х2Н4А (штриховая линия)
при наклепе дробью [35]:
/ — глубина цементованного слоя 1,4 —
1,5 мм; 2 — глубина цементованного
слоя 1,6—1,7 мм
/ — эпюра распределения твердости н
пределов выносливости зон слоя без учета
остаточных напряжений (выраженных в
относительных единицах по отношению к
соответствующим свойствам в сердцевине); 2 —
эпюра остаточных напряжений; 3 — эпюра
предельных амплитуд напряжений с учетом
остаточных напряжений; 4 — эпюра
предельных рабочих напряжений в
относительных единицах (по отношению к пределу
выносливости нёупрочненной сердцевины)
клепа, расхода дроби) и т. п. Для объяснения и количественной
оценки эффекта упрочнения, определяемого коэффициентом р упр,
в работе [22] предложена методика, основанная на анализе
расположения эпюр изменения по сечению детали механических
свойств, остаточных и рабочих напряжений. Рассмотрим
применение этой методики на примере анализа эффекта упрочнения
вследствие обкатки роликами гладких образцов диаметром 10,5 мм
из стали 45. На рис. 3.48 и 3.49 представлены эпюры,
соответствующие различным-глубинам упрочненного (наклепанного) слоя Д,
полученным изменением усилия обкатки.
Кривые / характеризуют распределение пределов
выносливости по поперечному сечению без учета влияния остаточных
напряжений (имеется в виду, что пределы выносливости
определены как бы на микрообразцах, вырезанных из различных зон
по высоте поперечного сечения образца). Эти графики построены
по кривым распределения твердости в предположении, что ~1накл =
•J-1 нсх
гт
= накл , т. е. предел выносливости микрообразцов повышается
" исх
от наклепа пропорционально увеличению твердости (сх_1накл,
#накл — предел выносливости и твердость образцов,
подвергнутых равномерному по всему объему наклепу; а_г исх, Яисх —
то же, для образцов из исходного ненаклепанного металла).
Кривые 2 показывают распределение остаточных напряжений от
обкатки, найденные экспериментально. Для оценки влияния оста-
128
точных напряжений на сопротивление усталости необходима
диаграмма предельных амплитуд напряжений при асимметричном
цикле. В этом случае можно использовать для сталей средней
прочности диаграмму, которая в относительных координатах
представлена на рис. 3.50 (эта диаграмма построена по рис. 2.8).
Если значения пределов выносливости по кривым 1 на рис. 3.48,
3.49 умножить на отношение
0-1
найденное по рис. 3.50 в
зависимости от величины остаточного напряжения, соответствующего
данному расстоянию от поверхности, то получим кривые 3 (см.
рис. 3.48, 3.49). Кривые 3 характеризуют распределение
пределов выносливости отдельных слоев по поперечному сечению с
учетом влияния остаточных напряжений и упрочнения от наклепа.
В поверхностном слое, в котором действуют сжимающие
напряжения, кривые 3 оказываются правее кривых 1, вследствие того,
что остаточные сжимающие напряжения увеличивают предельные
амплитуды. В зоне, где действуют растягивающие остаточные
напряжения, кривые 3 расположены левее кривых /, так как
растягивающие средние напряжения снижают предельную
амплитуду. Кривые 1 и 3 пересекаются на таком расстоянии от
поверхности, на котором остаточные напряжения равны нулю.
При изгибе гладких образцов предельная эпюра
распределения рабочих напряжений, соответствующая разрушению от
усталости, представлена на рис. 3.48, 3.49 линиями 4. Эти линии
должны быть касательными к кривым 3, так как разрушение от
усталости начинается только тогда, когда рабочие напряжения
достигнут предела выносливости в какой-либо точке поперечного
сечения. Рабочее напряжение на поверхности по линии 4,
отнесенное к пределу выносливости неупрочненного образца (шкала
определяет эффект упрочнения, характеризуемый
расчетным коэффициентом эффектив-
0
J>ynp ~h$
ности упрочнения (ЗуПР.
^
6а
fa
- 1fS
-
Рис. 3.49. Схема упрочнения
при обкатке шариками (глубина
упрочненного слоя Л = 2 мм,
P^p=l,45).
Примечание. Наименование
кривых то же, что и на рис. 3.48
5 В. П. Когаев
6т,кгс/ммг -10 -10 0 10 20 30
■а
Рис. 3.50. Диаграмма
относительных предельных амплитуд
напряжений при асимметричных циклах
для улучшенных сталей средней
прочности
129
Сопоставляя коэффициенты рупр и рупр, найденные по схемам
(см. рис. 3.48 и 3.49) и экспериментально, можно сделать вывод,
что указанные схемы дают весьма удовлетворительное
объяснение эффекта упрочнения. Из этих схем следует, что разрушение
гладких образцов, наклепанных роликами или шариками, должно
получаться подслойным. Из опыта следует, что подслойное
разрушение от усталости наблюдается в ряде случаев на гладких
образцах из стали при наклепе роликом и обдувке дробью.
Схемы, подобные приведенным на рис. 3.48, 3.49, позволяют
проанализировать влияние различных факторов (глубины
упрочненного слоя, абсолютных размеров, уровня концентрации
напряжения и т. д.) на эффект упрочнения. Так как разрушение в
описанном выше случае является подслойным, то твердость и
остаточные напряжения у поверхности не влияют на эффект упрочнения.
Основную роль при подслойном разрушении играют глубина
наклепанного слоя и распределение остаточных напряжений в
зоне перехода от слоя к неупрочненной сердцевине. Эффект
упрочнения растет с увеличением глубины слоя до определенного
предела, а также с увеличением глубины проникновения остаточных
сжимающих напряжений.
При дальнейшем увеличении глубины упрочненного слоя,
не сопровождающемся увеличением твердости на поверхности,
разрушение (из подслойного) может перейти на поверхность.
В этом случае дальнейшее увеличение глубины слоя не приводит
к повышению эффекта упрочнения, и основную роль играют
твердость и остаточные напряжения на поверхности. Эти
закономерности подтверждаются экспериментально.
В работе [35] по описанной методике проанализирован эффект
упрочнения при нитроцементации на различную глубину и при
наклепе дробью. Соответствующие эпюры представлены на
рис. 3.51. При нитроцементации на глубину 0,4 мм (рис. 3.51, а)
на поверхности возникают остаточные сжимающие напряжения
оост s—10 кгс/мм2. Расчетное значение коэффициента
упрочнения (оцененное на схеме по линии 4, касательной к кривой 3)
Рупр = 1,18 при экспериментальном значении (Зупр = 1,28.
Увеличение глубины слоя нитроцементации с 0,4 до 0,9 мм приводит
к возникновению в поверхностном слое растягивающих
остаточных напряжений с наибольшим значением —20 кгс/мм2 (линия 2
на рис. 3.51, б). Поэтому кривая 3 предельных амплитуд с учетом
остаточных напряжений в поверхностном слое лежит левее
кривой 1, и эффект упрочнения снижается (рупр = РУпР = 1,06).
Введение обдувки дробью после нитроцементации создает
в поверхностном слое значительные сжимающие напряжения
( 50 кгс/мм2 при глубине слоя 0,4 мм— рис. 3.51,6, —70 кгс/мм2
при глубине слоя 0,9 мм — рис. 3.51, г). Эффект упрочнения при
этом несколько снижается при глубине слоя 0,4 мм и возрастает
при глубине 0,9 мм. Характерно, что в обоих случаях линии 4
1Я0
боап'Мф
кгс/нм2
1,2 ?,46/6_,(ti*!0J -ГО О
Рис. 3.51. Схемы упрочнения при нитроцементации на глубину 0,4 мм (а), 0,9 мм
(б) и при наклепе дробью нитроцементованных образцов на глубину 0,4 мм (в)
и 0,9 мм (г). Наименование кривых то же, что и на рис. 3.48
касаются линий 3 в той зоне по сечению, в которой действуют
остаточные растягивающие напряжения. Таким образом, добившись
уменьшения растягивающих напряжений в подслойной области,
можно дополнительно повысить эффект упрочнения. Для всех
случаев на рис. 3.51 характерно подслойное разрушение.
Необходимо отметить, что переход очага разрушения с
поверхности в подслойную область сам по себе должен вызывать
некоторое повышение сопротивления усталости, так как зерна металла,
выходящие на поверхность, находятся в облегченных условиях
для накопления усталостных повреждений. Кроме того, при
указанном переходе перестают влиять на возникновение трещины
поверхностные дефекты (микронеровности и т. п.).
Дополнительное повышение сопротивления усталости не учитывается схемами
типа рис. 3.48, 3.49, 3.51, что является одной из причин того, что
на схемах рис. 3.51 j3ynp > рупр. Однако близость величин рупр
и РуПр подтверждает целесообразность использования описанного
метода для объяснения и оценки зависимости эффекта упрочнения
от многих технологических и конструктивных факторов.
Представляет интерес анализ"'влияния абсолютных размеров
поперечного сечения на эффект упрочнения, который может быть
5* 131
Рис. 3.52. Зависимость Рупр для
гладких образцов различных
диаметров от относительной
глубины - упрочненного слоя при
обкатке роликами:
/ — й = 6,5 мм; 2 — й = 36 мм
(сталь 12ХНЗА); 3 — й = 6,5 мм;
4 — d = 35 мм (сталь 38ХНЗМА);
б — d = 6,5 мм (сталь 18Х2Н4МА)
''" О 0,05 0,10 0,15 А/Я
проведен по аналогичной схеме [52]. Из анализа следует, что при
изгибе гладких образцов одинаковый эффект упрочнения на валах
различного диаметра должен получаться в том случае, если
относительная глубина упрочненного слоя одинакова. Этот вывод
в некоторых случаях подтверждается экспериментальными
данными (рис. 3.52). На этом рисунке видно, что при одинаковом
отношении -Q- на образцах разного диаметра эффект упрочнения
практически один и тот же. Однако вследствие дополнительного
эффекта упрочнения от перехода разрушения в подслойную
область, который, очевидно, не зависит от размеров, указанная
закономерность несколько корректируется, и эффект упрочнения
остается заметным и на деталях больших размеров.
При наличии резкой концентрации напряжений с большим
градиентом напряжений у поверхности очаг разрушения
переходит на поверхность. При этом увеличение глубины упрочненного
слоя не приводит к повышению эффекта упрочнения [22, 52].
Влияние абсолютных размеров поперечного сечения на эффект
упрочнения образцов с концентрацией напряжений зависит от
расположения очага зарождения трещины усталости. Если
трещина зарождается у поверхности (например, в образцах с
повышенной концентрацией напряжений), то эффект упрочнения,
очевидно, не зависит от относительной толщины упрочненного слоя
и, следовательно, от размеров образца. При средних же уровнях
концентрации напряжений эффект упрочнения определяется
взаимным расположением эпюр распределения пределов
выносливости по сечению (с учетом влияния остаточных напряжений) и
распределения рабочих напряжений.
Вследствие указанного выше характера диаграмм предельных
напряжений при асимметричном цикле в области средних
растягивающих напряжений цикла эффект упрочнения снижается с
ростом асимметрии цикла, особенно при химико-термических
обработках. Коэффициенты влияния асимметрии цикла для
образцов, подвергнутых цементации, достигают значений i|>ff = 0,5-г-
-^-0,6 [52]. В случае поверхностного наклепа влияние асимметрии
цикла сказывается в меньшей степени.
Технологические методы поверхностного упрочнения деталей
.машин широко применяют в промышленности [12, 20 и др,].
132 . .
Рупр
1,2
U
1 п
У
*
&.
£»,,,.
&
#
^р.
■^s^
t
t^
^"^fk
=~—&
Z
1
5
J
Глава 4
Статистическая оценка
характеристик
переменной нагруженности
деталей машин
11. Методы схематизации случайных
процессов изменения
нагрузок
С целью расчета на выносливость случайные процессы
нагруженности деталей в условиях эксплуатации заменяются некоторыми
схематизированными процессами, которым соответствуют
определенные функции распределения амплитуд напряжений.
Известно большое число методов схематизации, обоснованием
которых до сих пор служили лишь логические рассуждения [17,
24, 55]. Вместе с тем, различные методы могут приводить к весьма
существенной разнице в расчетных долговечностях.
Интерпретация случайных процессов нагруженности с целью расчета на
выносливость осуществляется также методами теории случайных
функций, с использованием в основном теории Раиса [44].
Для апробирования указанных методов необходимы прямые
экспериментальные исследования на усталость при случайном
нагружении с различными типами процессов.
На рис. 4.1 представлена осциллограмма изменения
напряжений в детали в зависимости от времени t в интервале ti
Назовем блоком нагружения 1б совокупность
последовательных значений переменных напряжений, возникающих в детали
за какой-либо характерный период эксплуатации, по отношению
к которому вычисляется ресурс детали (например, 1 км пробега
транспортных машин, 1 полет самолета, 1 ч работы машины и т. п.).
Тогда ti — время (в с), соответствующее 16.
Возникает -вопрос, как получить из этой осциллограммы
количественную информацию об уровне напряженности детали,
необходимую для расчета на выносливость. Ответ на этот вопрос
не однозначен. Существует довольно много методов решения
указанной задачи, которые в общем приводят иногда к заметной
разнице в получаемых расчетом ресурсах деталей. Сравнение
различных методов и практические рекомендации будут даны после
изложения самих методов.
Все известные методы получения количественных расчетных
характеристик нагруженности деталей основываются на замене
реального случайного процесса некоторым схематизированным
133
Ь,кгс/мн2
?
1
г
А
- 3
%
U\
Ч\
j V
, 1 ,
в
а
{■'
ч-
-«
уЗ
у
V
:
_А
?
Ц
/
_i_
-М
•^ 1
,
ч
//
^/7
10
_|_
1
г/
./? X'
/2Т1
/z"
i
:/ji
i
\%
И
\р
н'
1
16
4]
^i
j7
?
77
^%-
м
4±
RT
Е
1_
W
Г1£~±
t^
к
у
~T1t>"
W-
i
!
\
/9
U
-я7
.. 1
1.
л
Р1
?'-
i i
"г
/
2
3
3
*
9
11
9
№
Ш
11
9
4
S
4
г
О
"ли
/
/
/
0
1
i
J
в
7
4
1
1
0
1
0
0
0
а
nmin
0
0
0
0
в
О
1
1
1
0
4
3
4
0
1
г
г
0
3 S 7 9 11 131517 mi 23 25 П 29 3133 35 37 39 4143 4Sm9S153 55 37 S9 SI m
У
6
5
4
3
•1
1
и
-1
-2
1.
17
и
и
11
-
V
7
5
3
-
1
L
О f ~~М fi ОА tj tic
Рис. 4.1. Осциллограмма случайного процесса изменения напряжений
в детали
процессом, который по уровню вносимого усталостного
повреждения должен быть эквивалентен реальному.
Методы схематизации случайного процесса можно разделить
на одномерные и двухмерные (в принципе можно говорить и о
многомерной схематизации, которая, однако, на практике не
применяется из-за чрезмерной сложности обработки и трактовки
накопления повреждений). Одномерные методы схематизации
сводятся к нахождению функции распределения одной случайной
величины — амплитуды переменных напряжений оа. Среднее
напряжение от при этом считается неизменным во времени и
детерминированным. Двухмерные методы схематизации сводятся
к нахождению функции распределения двух случайных величин —
амплитуды оа и среднего напряжения цикла ат (или однозначно
связанной с ней функции распределения величин максимумов
0шах и минимумов cfmln процесса).
Для нахождения функции распределения амплитуд оа при том
или ином методе схематизации процесса применяют два способа:
непосредственный подсчет числа амплитуд различных уровней,
выделяемых тем или иным методом из процесса;
использование математического аппарата теории случайных
функций.
Наиболее известные методы схематизации основываются на
использовании экстремумов (методы максимумов, экстремумов,
учета одного экстремума между двумя соседними пересечениями
среднего уровня), размахов (методы размахов, укрупненных раз-
махов, полных циклов и др.) и числа пересечений заданного уровня.
Рассмотрим сущность этих методов. В'"качестве примера для
иллюстрации процедуры обработки осциллограммы различными
134
методами используем рис. 4.1. Этот пример будет носить*~чисто
методический характер, так как при обработке реальных
процессов длительность обрабатываемой осциллограммы должна быть
значительно большей.
В рассматриваемом примере ti = 0,64 с (по оси абсцисс
отложено время). По оси ординат отложено напряжение о. Кроме
того, для облегчения обработки весь рабочий диапазон изменения
напряжений разбит на 18 разрядов, отмеченных горизонтальными
линиями. Протяженность одного разряда соответствует
напряжению 0,5 кгс/мм2. Напряжение, равное нулю, соответствует
уровню i = 4, ниже которого напряжения сжимающие, выше —
растягивающие.
При обработке методами, основанными на использовании
экстремумов процесса, вначале требуется найти среднее
напряжение, которое вычисляется по формуле
огп=(Х-Х0)Аа, D.1)
где
—среднее арифметическое значение Хг; Х0—номер разряда,
соответствующего нулевому напряжению, на рис. 4.1 Х0 = 4;
Xt — значение ординаты процесса в точке i, выраженной в
количестве разрядов; п — общее количество точек по оси абсцисс,
по которым находится от\ До = 0,5 кгс/мм2 — цена одного
разряда в напряжениях.
Среднее напряжение процесса ат= 2,25 кгс/мм2, найденное
по формуле D.1), предполагается постоянным во времени.
Экстремумы процесса пронумерованы на рис. 4.1: максимумы —
арабскими цифрами от 1 до 20, минимумы — арабскими цифрами со
штрихами от Г до 20'.
Метод максимумов. В этом методе в качестве амплитуд напряжений
принимают разности между максимумами процесса ашах i и средним Напряжением
процесса ат, причем принимают во внимание только те максимумы, которые лежат
выше среднего напряжения ат-
Таким образом, максимумы 3,4 и 20 исключаются из рассмотрения, так как
они лежат ниже уровня ат. Вычитая из максимумов ашах / среднее напряжение
ат = 2,25 кгс/мм2, получаем набор амплитуд напряжений сгаг. Если эти
амплитуды расположить в возрастающем порядке, то получим вариационный ряд
распределения амплитуд, из которого путем статистической обработки может быть
найдена функция распределения амплитуд, необходимая для расчета на
выносливость.
s- В методе максимумов предполагается, что распределение минимумов
симметрично распределению максимумов относительно уровня оп, причем за
максимумом некоторого уровня amaxt следует сразу же минимум ошт/. дающий ту же
амплитуду что и сгшаХ1-, так что пара этих экстремумов образует один полный цикл
изменения напряжений с амплитудой aai = сгшах г- — ат = ] crmin ,- — от \.
При этом игнорируется тот факт, что после некоторых максимумов напряжения
135
Рис. 4.2. Схемы к пояснению метода
максимумов (а) и метода учета одного экстремума
между двумя соседними пересечениями среднего
уровня (б)
непосредственно не доходят до
уровня ат и полный полуцикл
напряжений не образуется (как
например, после максимумов 6,
8,13,17). Число
зарегистрированных указанным образом
амплитуд vg дает общее число
/<У_У_^_^/ W \В циклов в блоке нагружения.
Метод максимумов приводит
к схематизированному процессу,
обладающему большим
повреждающим действием, чем
реальный процесс. При этом
расчетные оценки долговечности
должны получаться более низкими,
чем фактические. Указанное
свойство метода максимумов
легко уяснить из рассмотрения
рис. 4.2, а. Пусть процесс имеет
характер, изображенный на
рис. 4.2, а, причем колебания а
вблизи максимумов /—7 невелики. Если амплитуды этих колебаний
напряжений, т. е. величины полуразмахов о±—а{/2, а2—a'J2 и т. д. не превышают
половины предела выносливости детали, то, как показывают опытные данные, они
практически не оказывают повреждающего действия до появления трещины, и
. их можно было бы из рассмотрения исключить. Однако в методе максимумов мы
полагаем, что каждому максимуму соответствует амплитуда колебаний amaxi —
— ат, т. е считаем, что напряжения изменяются, как показано пунктиром на
рис. 4.2, а. Это приводит к более повреждающему процессу (по сравнению с
реальным).
Метод экстремумов. Этот метод аналогичен во многом методу максимумов.
В методе экстремумов принимаются в рассмотрение максимумы, лежащие выше
среднего уровня, и минимумы, лежащие ниже среднего уровня; т. е. применительно
к процессу, показанному на рис. 4.1, следует исключить из рассмотрения
максимумы 3, 4, 20, как лежащие ниже ат, и минимумы 6', 8', 13', 17', как лежащие
выше ат. За амплитуды напряжений принимаются значения разностей
0'ai = amaxi — От (t'=l, 2, . . ., йщахб); \ ,,,,
Oaj = От ~ Omin / (/ = !'. 2', . . ., «'mm б)- J
Здесь nmax б, «min б— соответственно количество учитываемых максимумов
и минимумов процесса в блоке нагружения. Полученные амплитуды объединяются
в один статистический коллектив, по которому находится функция
распределения амплитуд напряжений. При достаточно большой длине обрабатываемой
реализации процесса nmax6 =s n'mia6.
Общее количество циклов в блоке нагружения v6 = nmax б = nmin б, так как
каждый цикл образуется комбинацией одного максимума и одного минимума.
На практике в большинстве случаев распределение максимумов симметрично
распределению минимумов относительно среднего уровня ат. В этом случае
методы максимумов и экстремумов приводят к весьма близким функциям
распределения амплитуды.
Метод учета одного экстремума между двумя соседними пересечениями
среднего уровня. Этот метод похож на метод экстремумов, однако на каждом участке
осциллограммы между двумя соседними пересечениями процессом среднего уровня
учитывается только один экстремум, дающий наибольшую амплитуду. Так, для
процесса на рис. 4.2, а между точками А я В учитываем максимум 4, который
дает амплитуду аа = а4 — от, на участке ВС — учитываем минимум 7', дающий
амплитуду аа= ат — а7, и т. д. Применительно к процессу, показанному на
136
рис. 4.1, мы должны принять во внимание для подсчета амплитуд максимумы 1, 2,
5,6, 8, 10, И, 12, 14, 15, 16, 17, 19 и минимумы Г, 4', 5', 7,9', 10', IV, 12', 14',
15', 16', 18', 19' при обработке этим методом. Максимумы 3, 4, 20, как и раньше,
не учитываются потому, что лежат ниже ат. Максимумы 7, 9, 13, 18 не
учитываются потому, что они находятся рядом с максимумами, дающими большую
амплитуду и лежащими на тех же интервалах между двумя соседними
пересечениями уровня ат. Например, максимумы б и 7 лежат на одном интервале между
соседними пересечениями уровня от, вследствие чего максимум 6 учитывается,
а 7 — отбрасывается. Из пары максимумов 8, 9 максимум 8 учитывается, а 9
отбрасывается, и т. п. Аналогично поступают и с минимумами.
26
Число циклов в блоке нагружения составляет vg = -„- = 13, так как 26 —•
это общее число всех учитываемых максимумов и минимумов, а каждый цикл
образуется одним максимумом и одним минимумом.
Если метод максимумов в случае процесса, показанного на рис. 4.2, а
приводит к схематизированному процессу более повреждающему, чем реальный,
как пояснялось выше, то метод учета одного экстремума между двумя соседними
пересечениями дает в этом случае более хороший результат, так как мелкие
наложенные колебания не будут учтены. Однако в случае процесса, показанного на
рис. 4.2, б, последний метод приведет к процессу менее повреждающему, чем
реальный, так как здесь учтется только одна амплитуда, определяемая
максимумом М, и не учтется ряд других достаточно больших колебаний напряжения.
Метод размахов. .Размахом называют абсолютное значение разности между
напряжением в точке максимума и напряжением в точке минимума,
непосредственно следующего за максимумом или непосредственно предшествующего
максимуму. В первом случае размах называют нисходящим 1 (рис. 4.3, а), во втором—
восходящими. Размах равен 2аа = ашах — ат1п, где аа — max ——
амплитуда напряжений. При одномерной схематизации, которая здесь
рассматривается, находятся только амплитуды напряжений, а средние напряжения
каждого полуцикла omi во внимание не принимаются.
В методе размахов при одномерной схематизации принимают следующие
допущения. Полагают, что распределение нисходящих размахов симметрично
распределению восходящих, что за нисходящим размахом некоторой величины
сразу же следует восходящий размах той же величины, образуя один цикл
(пренебрегаем влиянием последовательности чередования восходящих и нисходящих
размахов различной величины, полагая, что их можно переставлять, не изменяя
накопленного усталостного повреждения). Кроме того, при одномерной
схематизации пренебрегают влиянием изменения средних напряжений отдельных
полуциклов.
Метод размахов приводит к схематизированному процессу, обладающему
меньшим повреждающим действием, чем ёреальный процесс, что поясняется
рис. 4.3, б. Применяя метод размахов, учтем размахи 1—1', 1'—2, 2—2' 2'—3,
3—3', 3'—4, но не учтем размах
/'—4. .Может оказаться так, что
перечисленные мелкие размахи не
вызовут усталостных повреждений
(если соответствующие амплитуды
меньше половины предела
выносливости детали), в то время как
неучтенный размах }'—4 вызывает
усталостное повреждение. Поэтому
расчетные оценки ресурса детали
при использовании метода
размахов обычно превышают
фактические ресурсы, что является
недостатком метода.
Выше был рассмотрен метод Рис. 4.3.
учета всех размахов. Однако ис- размахов
Л а.
Г
1.
i?
g
хэ
2
f VL
/з1
ho
j
J
ч
•о
.
•^3
J
'
3
zN
1 Л/,
A
/у
ч
' \
V'
а.)
б) t
Схема к пояснению метода
137
пользуют также метод учета только
восходящих размахов, при этом
количество циклов в блоке нагру-
жения Vg принимается равным
количеству зарегистрированных
восходящих размахов п. Так как
распределение восходящих размахов
обычно почти симметрично
распределению нисходящих, то
указанные разновидности -метода
размахов приводят к весьма близким
результатам (в смысле расчетной
оценки ресурса детали).
Метод размахов, превышающих
заданное значение. Этот метод
полностью аналогичен методу
размахов, с той лишь разницей, что
малые размахи, значения которых
меньше некоторой заранее
принятой величины, исключаются из
рассмотрения, как не оказывающие
повреждающего действия.
Недостатком этого метода является то,
что при отбрасывании малых
размахов (в предположении, что они не
вызывают накопления
повреждений) существенно изменяется
функция распределения амплитуд
напряжений.
!Шетод укрупненных размахов
[17]. В этом методе сравнивается
по линейной гипотезе накопленное
повреждение от серии
промежуточных мелких размахов с
повреждением Г°т одного более крупного
охватывающего размаха, и
учитываются те размахи, которые
вызывают большее повреждение. Например, для процесса, показанного на
рис. 4.3, б, необходимо сравнить повреждение от совокупности размахов/'—2,
2—2', 2'—3, 3—3', 3'—4 с повреждением от одного охватывающего
размаха /'—4 и принять для учета тот вариант, который дает наибольшее
повреждение. Указанная обработка возможна при применении ЭЦВМ.
Метод полных циклов. Полагают, что этот метод дает наилучшее соответствие
по повреждающему действию между схематизированным и реальным случайным
процессом по сравнению с другими методами.
Поясним этот метод, используя рис. 4.1, 4.4. Анализируя осциллограмму на
рис. 4.1, вначале отмечаем циклы с наименьшими размахами, а именно размахи
5—5', 17'—18, 20—20', имеющие величину, равную одному разряду. Амплитуда,
им соответствующая, равна половине размаха, т. е. 0,25 кгс/мм2. Число
повторения таких амплитуд в блоке нагружения v;-g равно 3. Записываем эти данные в 1-ю
строку табл. 4.1 и затем исключаем указанные размахи из процесса (эти размахи
заштрихованы, на рис. 4.1). В результате приходим к новому процессу,
изображенному на рис. 4.4, а. В этом процессе отмечаем размахи величиной, равной
двум разрядам (размах 1 кгс/мм2, амплитуда — 0,5 кгс/мм2). Указанные размахи
заштрихованы на рис. 4.4, а и имеют номера 1—Г, 2'—3, 3'—4, 6'—7, 8'—9,
9'—10, 11'—12, 14'—15, 18'—19. Таким образом, число повторения амплитуды
оа = 0,5 кгс/мм2 в блоке нагружения равно v;6 = 9. Записываем эти данные во
2-ю строку табл. 4.1, затем исключаем перечисленные размахи из процесса, в
результате чего приходим к процессу, показанному на рис. 4.4, б. Далее продолжаем
Рис. 4.4. Схема
полных циклов
к пояснению . метода
138
указанный процесс последовательного подсчета и исключения все больших раз-
махов.
Из рис. 4.4, б видно, что размах 13—13' пересекает три линии, т. е. три
разряда (цифра, написанная в кружке), а следовательно, равен 3-0,5=1,5 кгс/мм2,
так. как цена разряда на рис. 4.4 составляет 0,5 кгс/мм2. Следовательно, соответ-
1 5
ствующая амплитуда оа = -~ = 0,75 кгс/мм2 повторяется один раз, что
записано в 3-й строке табл. 4.1.
Аналогично фиксируем размах 16—16' E разрядов) с амплитудой 1,25 кгс/мм2,
размах 11—12' F разрядов) с амплитудой 1,5 кгс/мм2, размах 6—Т G разрядов)
с амплитудой 1,75 кгс/мм2. Все эти амплитуды повторяются по одному разу, что
отражено в строках 5, 6. 7-й табл. 4.1 соответственно. Исключение этих размахов
приводит к процессу, показанному на рис. 4.4, в сплошной линией. Фиксируем
размахи 2—4' A0 разрядов, аа = 2,5 кгс/мм2) и 10'—14 A2 разрядов, аа =
= 3 кгс/мм2), отраженные в 8 и 9-й строках табл. 4.1. Исключение этих размахов
приводит к процессу, показанному на рис. 4.4, в пунктирной линией. В этом
процессе имеем два размаха 8—15' и 17—19' по 15 разрядов с амплитудой оа =
= 3,75 кгс/мм2.
Схематизируя случайный процесс^указанным образом, мы получили данные,
представленные в табл. 4.1 и характеризующие повторяемость амплитуд
напряжений различных уровней в блоке нагружения vj6> а также накопленные числа
циклов N. = 2 v;6- По этим данным может быть построена функция
распределения амплитуд напряжений [24].
Таким образом, в отличие от метода размахов в методе полных циклов не
выпадают из рассмотрения большие размахи, внутри которых имеются размахи
меньшей величины. Как показывает практика, метод полных циклов обычно
приводит к расчетным оценкам ресурса, которые занимают промежуточное
положение между оценками, полученными с использованием методов максимумов и
размахов.
Процессы, показанные на рис. 4.1 и 4.2 обладают тем свойством, что число
пересечений процессом среднего уровня заметно меньше общего числа экстрему- .
мов, так как имеется много участков, на которых между двумя соседними
пересечениями среднего уровня имеется по 3—5 и более экстремумов (например,
участок, включающий экстремумы 2', 3, 3', 4, 4', или участок с экстремумами 8, ■
9 и т. д. на рис. 4.1). Такое
свойство характерно для процессов с
достаточно широкой полосой частот.
В этом случае получается заметная
разница в оценках ресурса при
использовании различных методов
схематизации.
При случайном процессе,
показанном на рис. 4.5, число пересечений
среднего уровня примерно равно числу
экстремумов (для гармонического
процесса имеется точное равенство этих
величин). Таким свойством обладают
процессы с узкой полосой частот (узко-
полосные процессы, см. ниже), для
которых различные методы схематизации
приводят к весьма близким оценкам
ресурса.
Двухмерная схематизация по
методу всех размахов. Рассмотрим
построение корреляционной таблицы
максимумов ашах и минимумов аШ1п>
представленной на рис. 4.6 и
отображающей корреляционную связь между
этими величинами. Эта таблица содер-
Таблица 4.1
Распределение амплитуд
напряжений при одномерной
схематизации процесса методом
полных циклов
1
1
2
3.
4
5
6
7
8
9
10
°аЬ
кгс/мм2
0,25
0,50
0,75
1,00
1,25
1,50
1,75
2,50
3,00
3,75
v<6
3
9
1
0
1
1
1
1
1
2
Накопленные
числа
циклов
3
12
13
13
14
15
16
17
18
20
139
6кгфм\
A>Oi
JA^-i
knmax
rJ
V^-
\mtn
.1
2 ^>4
17
i i i —
О Ч- 8 JZ 16 20 Zf
6)
Рис. 4.5. Реализация узкополосного случайного процесса (а) и результаты его
статистической обработки (б):
1,2 — соответственно, полигон частот н выровненная функция распределения числа
пересечений отдельных уровней; 3, 4 — соответственно распределения числа максимумов
и минимумов процесса
жит исходную информацию для™получения совместной плотности
распределения / (o"max, crmm) или связанной с ней совместной плотности распределения
амплитуд аа и средних напряжений цикла от — /i (o"a, от).
На рис. 4.6 по горизонтальной оси отложены значения максимумов jio
правилу
[<^<z2, п0 вертикальной оси — минимумовj|no правилу Ьх
=^crmm<62, 'где (dlt а2) и (Ьъ
62) — интервалы изменения
соответствующих величин. Возьмем
размах /—/.' (см. рис. 4.1), для
которого Стягах = 2,25 кгс/мм2 и
о"шш = 1,25 кгс/мм2. Этот размах
попадает в заштрихованную для
наглядности на рис. 4.6 клетку,
для которой 2г^ашах<;2,5 и
1 =^°"min <C 1.5 кгс/мм2. Наряду с
/—/' имеются еще два размаха,
попадающих в эту же клетку, а
именно размахи //'—12 и 14'—15,
Других таких же размахов нет,
поэтому в этой клетке записана цифра 3.
Переходим к размаху 2—2',
попадающему в клетку, для
которой 3,5^атах<4иО,5^Тт1п<1-
Сюда же попадает еще только один
размах, а именно 7—Т, вследствие
чего в этой клетке записана цифра 2.
Аналогичным образом заполняются
остальные клетки таблицы.
Эти же данные могут быть
представлены в виде
корреляционной таблицы, выражающей связь
между амплитудами оа и средними
напряжениями циклов ат. Корре-
ГУ
ОтиК
V-HI
1-ОЯ
HS-0
0-0,5
0-1
1-1,5
1,5-1
1-2,5
2,5-3
3-3,5
3,5-k
i-i,5
1,5-5
5-5,5
5,5-6
6-6,5
6fi-l
3-
\
I
\
4
\
\ s'o-o
1
1
\
J»
\
Wi-i
1
1
\
/
/
N
г
1
Ъ
1
\
/
/
2
\
f-1
\
/
2
2
1
\
4
/
4
1
1
1
\
/
/
\
s-s.5
1
\
/
\
/
/
\
4a
/
1
^
Рис. 4.6., Корреляционная таблица
совместного распределения максимумов и
минимумов процесса, представленного
на рис. 4.1
140
ляционная таблица аа — ат может или непосредственно использоваться
в расчете или быть сведена к одномерному распределениюэквивалентных амплитуд.
Предельная амплитуда напряжений в детали аол при асимметричном цикле
[см. B.17)]
Сад = а_1д — ^вр?т, D.4)
где о_1Д —-г предел выносливости детали; г|зад — коэффициент влияния
асимметрии цикла на величину предельной амплитуды (разд. 14).
Расчет на усталость можно производить, сравнивая рабочие амплитуды аа
с предельными аод или эквивалентные амплитуды аа ЭкВ, ^приведенные к
симметричному циклу, с пределом выносливости о"_1Д. При этом
Оа экв = Оа + %лат. D.5)
По формуле D.5) двухмерное распределение аа и ат может быть сведено к
одномерному распределению эквивалентных амплитуд.
Двухмерная схематизация по методу полных циклов. Двухмерная
схематизация с построением корреляционной таблицы может быть осуществлена и при
использовании метода полных циклов. Рассмотрим снова рис. 4.1. Как и раньше
мы вначале фиксируем три размаха 5—5', 17'—18 и 20—20' с амплитудой
0,25 кгс/мм2, однако теперь отмечаем также и средние напряжения этих
полуциклов, а именно 2,4 и —1 кгс/мм2, соответственно, и заносим эти данные в
корреляционную таблицу. Далее принимаем во внимание девять размахов с
амплитудами 0,5 кгс/мм2 (заштрихованы на рис. 4.4, б) и различными средними
напряжениями ат. Отмечая ат для этих размахов, заносим данные в корреляционную
таблицу. Этот процесс продолжается до окончания подсчета всех полуциклов.
Метод пересечений. Метод пересечений заключается в подсчете числа
пересечений процессом отдельных уровней напряжений (разрядов) и в нахождении
на основе этой информации функции распределения амплитуд напряжений.
На рис. 4.1 точками отмечены пересечения восходящих ветвей процесса
с разрядными линиями. Число пересечений на уровне i процесса на интервале t[Q
обозначено щ. Величины щ даны справа от рис. 4.1; справа.даны также числа
максимумов п\ тах и минимумов я,- шщ процесса, попадающих в интервал от i —1-й
до i-й разрядной линии. Аналогичные цифры даны для другого процесса на
рис. 4.5. Легко убедиться в справедливости соотношения
Щ — П1_г — Щ Шах — Щ mm, D.6)
т. е. разница в числе пересечений восходящими ветвями процесса г'-го и (t — 1)-го
уровней равна разности между числом максимумов щ шах и числом минимумов
Щ mm процесса, попадающих в t'-ю полосу, т. е. в полосу, заключенную между
(i — 1)-й и i-й линиями разрядов.
Цифры, представленные справа от рис. 4.1 и 4.5, являются исходными
данными для построения функций распределения числа пересечений процессом
уровней а, а также функций распределения максимумов и минимумов процесса. Эти
функции распределения представлены на нормальной вероятностной бумаге на
рис. 4.7 (применительно к процессу, изображенному на рис. 4.1) и на рис. 4.8
(применительно к процессу, приведенному на рис. 4.5). Гистограммы, а также
функции с точностью до постоянного сомножителя, равные плотностям
распределения числа пересечений, максимумов и минимумов процесса, представлены
на рис. 4.5. Из рис. 4.5, 4.7, 4.8 следует, что для рассматриваемых процессов
распределение числа пересечений, максимумов и минимумов достаточно хорошо
соответствует нормальному закону. Это соответствие лучше всего выявляется при
изображении интегральных функций распределения на нормальной
вероятностной бумаге (рис. 4.7, 4.8).
В табл. 4.2 даны средние значения i и средние квадратические отклонения Si
рассматриваемых величин, выраженных в разрядных единицах i, a также в
напряжениям а и Sa [а = (t — 4) 0,5 кгс/мм2 —для процесса рис. 4.1; а'= (i —
— 6) 0,5 кгс/мм2 — для процесса рис. 4.5; Sa = 0,5S,- — для обоих процессов].
141
р,%
99,5
99
I 98
95
90
80
70
60
V 50
40
30
20
10
5
V г
1
0,5
О I 4 6 8 10 11 14 16 18 I
i i i i i ' ' ' ' ' i
-l-101li4 56,кгс/ммг
Рис; 4.7. Функции распределения
числа пересечений A), максимумов
B) и минимумов C) процесса,
представленного иа рис. 4.1
Г
к
/
Л
/
/я,
J
/
/л
*А
/
&{
/
/
' ?
1
]/•
А
/t\
t
/
г
s\
>
У
7
/
1i
/
д~
/
Kj
Г
f
f
/д
--г
/
*
Up
-I
-3
Hh
99,5
98
95
90
60
70
60
SO
48
30
10
10
с
0,5
ОД
X
/
I
1 ,
J
'A
/^
&
4
■
X
1
i-~
t.
1
i
1
A
»t
J
/
i
1
«
¥>
i-
A
A
/
f
/1
/
VA
1
A
j
/
/a
i
/
k
i
G
V
/
r
' V
/
14
A
?
i
■3
0
11
16
Рис. 4.8. Функции распределения
числа пересечений A), минимумов
B) и максимумов E) процесса,
представленного на рис. 4.5
Ниже будет показано, что для стационарного нормального
процесса
IcL—l = f(a)
No %V*i TKh
D.7)
где Na — среднее в единицу времени число пересечений процессом
уровня a; N0 — то же, среднего уровня; а5 — среднее квадрати-
ческое отклонение величины i; f (a) = —-— ехр / а
плотность нормального распределения случайных ординат
процесса, выраженных в виде а = i—i. Таким образом, по кривой
числа пересечений N (X) для стационарного случайного процесса
может быть найдена функция распределения случайных ординат
и ее параметры, а также среднее число нулей процесса ЛГ0,
характеризующее эффективную частоту.
Выражая приращение функции N (i) через производную из
уравнений D.6), находим
<7-1 =
dN(i)
da
Дст(
-щ
mlir
D.8)
142
Таблица 4.2
Параметры функций распределения числа пересечений,
максимумов и минимумов процессов
Параметры
i
st
а
Sa
Функции распределения
пересечения
max
fflin
Процесс на рис. 4.1
8,5
3,5
2,25
1,75
11,5
3,5
3,75
1,75
6,3
3,5
1,15
1,75
пересечения
max
min
Процесс на рис. 4.5
9,5
3,5
1,75
1,75
14,5
2
4,25
1,00
4,5
2
—0,75
1,00
Таким образом, дифференцированием N (t) может быть
построена кривая, характеризующая разность между числом
максимумов и минимумов, попадающих в интервал (а, а + Да). Для
процесса, показанного на рис. 4.5, плотности распределений
максимумов и минимумов практически не перекрываются.
Поэтому для такого процесса указанные плотности вероятности
max и min с точностью до постоянного множителя совпадают с
производной . , что позволяет по кривой N (г) найти
распределения max и min.
Для процесса, показанного на рис. 4.1, плотности
вероятностей max и min существенно перекрываются, вследствие чего эти
плотности по кривой N (г) найдены быть не могут с достаточной
точностью.
Для статистической обработки результатов измерений
эксплуатационной нагруженности, представленных в виде вариационных
рядов тех или иных случайных величин (мгновенных значений,
числа пересечений, амплитуд напряжений и т. д.), полученных путем
схематизации осциллограмм случайных процессов одним из
перечисленных методов, применяют методы математической
статистики [18, 70].
Для узкополосных случайных процессов (см. рис. 4.5), у
которых число пересечения нулевой линии примерно равно числу
экстремумов, все указанные методы схематизации дают
практически одинаковый результат, вследствие чего выбор метода
схематизации определяется лишь соображениями удобства
обработки.
Для широкополосных процессов наиболее оправданным в
настоящее время считается метод полных циклов.
143
12. Применение теории случайных функций
для оценки
расчетных характеристик нагруженности
Для описания эксплуатационных напряжений применяют
спектральную теорию случайных процессов [2, 4, 30], основные
понятия которой, используемые далее, изложены в работах [2,
11, 30]. Важное значение для оценки расчетных характеристик
нагруженности имеет теория выбросов, разработанная С. Райсом
и др. [2, 44, 63, 30].
Далее изложено решение некоторых основных задач по Раису.
Ожидаемое число нулей в единицу времени. Пусть случайная
функция | (t) представляет собой дважды дифференцируемый
стационарный случайный процесс с нулевым средним, дисперсией
S2 и автокорреляционной функцией
К (т) = S*R (т), D.9)
где R (г) — нормированная автокорреляционная функция.
Как известно, связь между функциями автокорреляции К (т)
и спектральной плотности 5 (со) устанавливается формулами
Винера—Хинчина
со
К(х) = -L J S(a)eiaxda;
5(со)= [ K(t) e-iax dx.
— oo
)
Требуется найти математическое ожидание числа пересечения
процессом нулевой линии (числа нулей) в единицу времени,
определяющее эффективную частоту процесса. Эта задача решена
Райсом [44].
Для вывода формулы Раиса обозначим через р (§, т], f) —
совместную плотность вероятности значений процесса | (t) и его
производной т] (t) = °/, ' =,| (t) в совпадающий момент
времени t (не предполагая пока, что процесс является стационарным).
Получим вначале формулу для числа пересечений нулевой линии
восходящими участками процесса, т. е. теми участками, на
которых производная т] (/) положительна (т] (t) > 0).
Рассмотрим интервал времени (t, t + dt), на котором процесс
пересекает нулевую линию с положительной производной (рис. 4.9).
Вследствие малости интервала dt кривую процесса на этом
участке можно заменить прямой и считать, что здесь имеется только
одно пересечение процессом нулевой линии. Из рис. 4.9 видно,
144
D.10)
что для пересечения процессом нулевой линии на участке dt
должно выполняться условие
О < А < dt,
причем ~l(t) = т] (t + А) & т] (t), или А = — ^-(^
dl
4@
Здесь т] (t) =-~-={g а; минус поставлен потому, что | (t) < О,
аД>0иг]>0.
Таким образом:
D.11)
о<—Щ<я
ч@
или
-т] (t) dt <Ъ (t) < 0.
Вероятность того, что восходящая ветвь процесса пересечет
нулевую линию на интервале времени (t, t + dt), равна
вероятности одновременного выполнения неравенств D.11) и л (^)>0:
P\-T){f)dt<t{t)<0; Л @ > 0} =
X 0 X 0
= j J p(g, т], *)d£<tn = J ^ j P(S, Л. *)<& D.12)
0 —Т](^)Л 0 —mt)dt
Учитывая малость интервала времени dt, можно для
вычисления внутреннего интеграла в выражении D.12) применить теорему
о среднем, заменив р (|, л> t) на р @, т|, ^). Тогда
о
j p(g, т], *)dg = p@, л. *)[<>-(—Л #I = ЛР@, л. *)#■
-Т1(<)Л
D.13)
Таким образом, вероятность прохождения процесса через
нуль с положительной производной на интервале (t, t + dt)
00
gldt=dt\ лр@, л. /)^Л- D-14)
о
Аналогично доказывается, что
вероятность прохождения
процесса через нуль с
отрицательной производной на интервале (t,
t+ dt)
о
g2dt = - dt J лр@, Л, 0 ЙЛ-' Рис. 4.9. Схема к выводу формулы
м для ожидаемого числа нулей процес-
D.15) са в единицу времени
145
Объединяя уравнения D.14) и D.15), получаем вероятность
пересечения процессом нулевой линии на участке dt:
оо
gdt = di J |т,|р@, т], t)di\. D.16)
Если процесс стационарный, то плотность вероятности р
(О, т], t) не зависит от t; интегрируя уравнение D.16) по t в
пределах одной секунды, получаем- математическое ожидание числа
нулей процесса в единицу времени (формула Раиса)
^о = J hlp@, Л)*!- D.17)
СО
Также можно прийти к формуле D.17), рассуждая следующим
образом [2]. Вероятность того, что случайная функция | (t)
принадлежит интервалу (а, а + da), a | (t) интервалу (т|, т] + fify)
Р {а < £ (£)< a -f- da, т] < | (?) < т] -f- dx\) = р (а,т]) ^а df].
Это же выражение определяет в среднем относительное время
пребывания | и | в указанных интервалах. Среднее число
пересечения процессом | (t) полосы (а, а +. da) в единицу времени
равно отношению относительного времени пребывания \ (t) в этой
полосе на время, необходимое для пересечения этой полосы, рав-
• dec
ное при скорости \ (t) = г] величине т = -:—р. Таким образом,
ожидаемое число пересечения процессом | {t) уровня а в единицу
времени
оо оо
к_ J Р(«,т.)*»*|= J I т, | „ («. Л) rfT,. D.18)
Для определения математического ожидания числа нулей
процесса необходимо в выражении D.18) принять а = 0. Тогда
можно записать
оо
N0= jh|p@, Ti)dn, D.19)
—оо
что совпадает с формулой D.17).
Для нормального стационарного процесса совместная
плотность вероятности [30]
р& ^ = -ш^;е^
2о| 2а\
D.20)
146
(так как величины 1 и т] некоррелированы для такого процесса).
Подставляя выражения D.20) в формулу D.19) при 1 = 0,
получаем
Nn
Г i i dv 2al If to?, j
5 'I « ' . 0
Путем интегрирования по частям находим
г]е "л <iirj = а2
Таким образом, математическое ожидание числа нулей в
единицу времени нормального стационарного процесса с нулевым
средним
N,
0 ял я К /С @) я
f aAS(co)
do
J 5(ш)
<2ш
, D.21)
где
— со
о«=_/С'@) = -^г J co25(co)rfco;
— со
оо
og = i((IV,@)=-ir J co4S(co)dco.
Следует заметить, что величина /С" @) отрицательная, так
как корреляционная функция в начале координат имеет
максимум.
Формулы D.21) вытекают из зависимости D.10) : К @), К" @)
и iC(IV) @) — значения автокорреляционной функции и ее второй
и четвертой производной в начале координат, т. е. при т = 0
[формула для iC(IV) @) понадобится в дальнейшем].
Следовательно, зная корреляционную функцию К (т) или
спектральную плотность 5 (со) стационарного нормального
147
процесса, можно по формуле D.21) найти эффективную частоту
процесса, определяющую эффективное число циклов в единицу
времени:
' — ' 2 '
так как каждому циклу изменения напряжений в среднем
соответствуют два нуля процесса. Отметим, что если р (£, т]) при \ = а
I a2 \
подставить в выражение D.18), то, так как ехр ( 2"\ не
зависит от переменной интегрирования, этот сомножитель выйдет
за знак интеграла. Путем аналогичных выкладок можно
получить формулу для среднего числа пересечения процессом уровня
| = а в единицу времени:
я as
Отсюда
Na = ^Le ** =Жпе Ч
No ag V 2я a^V 2я
Здесь / (а) представляет собой плотность вероятности случайных
ординат процесса, которая с точностью до постоянного
сомножителя равна плотности вероятности относительного числа
пересечений процессом заданного уровня а, что равносильно
совпадению функций распределения числа пересечений и случайных
ординат процесса [см. D.7)].
Функция распределения и среднее число максимумов в
единицу времени нормального стационарного процесса. Предположим,
как и прежде, что \ (t) — это центрированный случайный
стационарный процесс изменения напряжений в детали во времени,
т. е.
l(t) = a (t) - am,
где a (t) —• случайный процесс изменения напряжений; ат —
математическое ожидание этого процесса.
Математическое ожидание | (t) равно нулю, а дисперсия \ (t)
равна дисперсии величины a (t). Максимумы процесса Мг, 7И2
М3, ■ • ■ определяются соответствующими ординатами |т1, 1т2,
1т3, ••• (рис. 4.10).
Если каждому максимуму М.ь поставить в соответствие один
полуцикл изменения напряжений с амплитудой \mi (как
показано пунктиром на рис. 4.10), то получится схематизация
случайного процесса по методу максимумов. Следовательно, если найти
плотность вероятности распределения максимумов, т. е. вели-
148
чин \mi, а также среднее число максимумов в единицу времени,
то можно рассчитать долговечность детали (при этом
предполагается, что распределение минимумов симметрично
распределению максимумов, так что каждый максимум, дополненный
симметричным ему минимумом, образует один полный цикл
изменения напряжений).
Райсом [44] получены формулы для плотности вероятности
и среднего числа максимумов в единицу времени, которые могут
быть использованы для расчета на усталость деталей машин
при случайном нагружении. Как известно из математического
анализа, в точке максимума функции ее первая производная равна
нулю, а вторая производная отрицательная. Поэтому для
дальнейших выводов понадобится совместная плотность вероятности
значений самого процесса | (t), его первой производной ц (t) =
= dt =i{t) и второй производной £ (t) = -п§- = \ (t) в
совпадающий момент времени t, которую обозначим, р (|, ц, £, t).
В случае стационарного процесса р не зависит от времени,
вследствие чего для стационарных процессов будем писать р (|, ц, Q.
Вероятность того, что процесс % (t) на интервале времени
(t, t + dt) будет иметь максимум, попадающий в интервал а —
— da < \т < а, равна вероятности одновременного выполнения
следующих неравенств:
а — da < | (t) < a;
_d4<i^L<0;
Ш = ^><0.
Второе неравенство связано с требованием равенства нулю
первой производной с точностью до бесконечно малых величин,
третье неравенство очевидно.
Рис. 4.10. Схема к выводу формулы для среднего числа
максимумов процесса
149
Для получения указанной вероятности необходимо
проинтегрировать плотность вероятности р (|, г], £, t), умноженную
на дифференциалы аргументов по областям изменения
аргументов, определяемым указанными неравенствами, т. е.
p{a-da<Ut)<a, -^<4г<0' ^Ж < °} =
О а О
= I 1 j р(£> ть £> 0 ^^4 =
—со а—ice—от)
О
= =—tfl J di\p(a, О, £, t)d%. D.23)
Два внутренних интеграла (учитываем малость разности
пределов интегрирования) заменены выражениями, вытекающими из
теоремы о среднем для определенных интегралов. Зная, что
di\ = £Ш dt = £ А,
преобразуем выражение D.23) к виду [30]
P^m-dlm<l<im,-dy\<^<0, -|i<o} =
о
= — d%dt \ lp (lm, 0, I, t) dl D.24)
■—oo
Для получения среднего числа максимумов, которые лежат
в пределах от \т — d\m до \м на интервале времени от tx до t2,
выражение D.24) необходимо проинтегрировать по t в указанных
пределах. В случае стационарных случайных процессов
подынтегральное выражение не зависит от t, и среднее число максимумов
в единицу времени, лежащих в интервале (|m — d%m, |m),
определяется выражением
о
g (U dl = -dl\ lp (%m, 0, £) d%. D.25)
Среднее число всех максимумов в единицу времени iVmax
получается путем интегрирования выражения D.25) по \ в
пределах от —оо до +оо, так как возможны максимумы и с
отрицательными значениями \т.
150
Таким образом:
\ со О
' max "
-oi .«-oo
= JK|P@, £)#, D-26)
—"oo
где p (tj, £) — совместное распределение первой и второй
производных процесса.
Плотность вероятности максимумов процесса равняется
отношению g (|m) к Nn
" max-
О
f IC[p(£m.o,C)dC
/(U = ^o = фй. D.27)
j IClP@,OdC
iVn
Для дальнейших вычислений необходимо знание совместной
плотности вероятности р (|, tj, Q случайного процесса |, его
первой производной tj и второй производной £.
Как известно [30], первая производная от стационарного
случайного процесса в совпадающие моменты времени не коррели-
рована как с самим процессом, так и со второй производной, т. е.
взаимные корреляционные функции iCg^ (т), K4i{t) при т = 0
равны нулю, т. е.
К1ц @) = 0, Кц1 @) = 0. D.28)
В этом случае плотность распределения
Р (!, ЧЛ) = Р (л) Р A. £),
где р (tj) — плотность распределения первой производной;
р (|, Q — совместная плотность распределения процесса и его
второй производной.
Для нормальных стационарных процессов [30]
/,(т,)в-^"еХр(—2%
X ехр
где
рE, £) = Л. х
_S OP «. Sb i b
20-4e)
D.29)
/?ffi = —— = ^_^_ D.30)
151
—коэффициент корреляции | и £ (математические ожидания | и
С равны нулю).
Здесь
^2 _ J. <PR (T) | _ 2n(IV).
Кк @) = оЙо-
D.31)
Вычислим вначале среднее число всех максимумов в 1 с по
формуле D.26), имея в виду, что уравнение совместной плотности
распределения первой и второй производных нормального
стационарного процесса имеет вид
pOl,Q = p(Ti)p(E) = -fc—s-exp
Vi°t
?2
_rf
2ff2 2of
D.32).
Полагая в выражении D.32) т] = 0 и подставляя в уравнение
D.26), получаем, с учетом зависимостей D.30), D.31) и D.22),
о о
Л^шах= |£|р@,£) d£ =
Ч
1
2яаТ| 2я
2ясТ|СГ£
2я^/
J
£ехр
С2
2о|
d£ =
d(IV)
к0
или, с учетом выражения D.21),
JVmax 2ЖТ,, 2я у
D(IV)
2я
[ co*S(co)
— оо
00
[ o2S((fl)
dco
dm
D.33)
Вычислим теперь выражение g (|m) по формуле D.25), с
учетом уравнения D.29), при ц — О
о
1
g(U = - \ Sp(Sm.O, Qd£ =
о
X [ Sexp
2 0- «le)
BяK/2а§а11а£1/г1-^
* 6 ffE°t
152
Для вычисления интеграла в этом выражении может быть
использована следующая формула:
о
— J £ехр(— р£2__ qrg -f- /■)rfg = Jxexp(— px2 + qx-{-r) dx =
e'
2p
+ «/f
e4p ф [_^_
j^Wj
D.35)
где Ф (x) = -^- j e 2 dt — интеграл вероятностей (интегральная
.00
функция распределения нормального закона). Формула D.35)
получается путем вынесения за знак интеграла сомножителя ег
и дополнения оставшегося показателя степени у экспоненты до
полного квадрата суммы. Сопоставляя интегралы в выражениях
D.34) и D.35), имеем
" - <...</ —■'
4A-4) '
(l-Rk)aiat '
р =
1
4l~Rk)ol
D.36)
На основании уравнений D.34), D.35), D.36) получаем
окончательную формулу Раиса для плотности вероятности максимумов
нормального стационарного процесса [63], выраженных через
безразмерную величину h = |m/oy.
m~7S
Здесь
v2= 1
ve
ft'
2v2
°H
_J£_ , r
-V2n{l-v2)he 2 Ф1 Ki-va
. D.38)
Таким образом,
плотность распределения
максимумов зависит лишь от
одного параметра v,
который может изменяться
от 0 до 1. При v -* О,
Ф
V~-
•/ij->l и/(A)-
h?_
2
•/i exp f 2~j ,
получается закон
распределения Рэлея для ft = -l2L.
D.37)
0,5
С1,4
О, J
0,2
0,7
/4
^
■ J7
j/=7^
=0
-0,2
,0,4
,0,6
0,8 -
-1
о
1
Рис. 4.11. Графики ^плотностей
распределения максимумов процесса • по Раису:
h — —; v — параметр, определяемый по
формуле D.38)
153
При v ->■1 второе слагаемое [см. D.37)] в квадратных скобках
стремится к нулю h/(/i)—» ,_ехр ( „-), т. е. получается
нормальный закон распределения относительных максимумов
процесса. Плотности вероятностей максимумов при различных
значениях v, вычисленные по формуле D.37), представлены на
рис. 4.11 [63].
Выясним физический смысл параметра v. Заметим, что
среднее число нулей процесса в 1 с определяется выражением D.21),
а среднее число экстремумов в 1 с с учетом зависимости D.33)
*«« = 2AW = -^ =" i У-ЪГ' D9)
Последнее выражение справедливо потому, что
распределение минимумов может быть принято симметричным распределению
максимумов, так что число всех экстремумов равно удвоенному
числу максимумов.
Найдем отношение % среднего числа нулей процесса к среднему
числу экстремумов:
K = J1_^^L = A.. D.40)
Сопоставляя выражения D.38) и D.40), имеем
v2 = 1 —к\ D.41)
Для детерминированного синусоидального процесса % = 1
и v = 0. Для узкополосного случайного процесса, показанного
на рис. 4.12, а, к е* 1 и v ^ 0. Такой процесс близок к
гармоническим колебаниям с фиксированной частотой и случайными
амплитудой и фазой, причем каждому циклу изменения
напряжений соответствуют примерно два нуля и два экстремума (такие
процессы называют также квазигармоническими).
Для процесса, показанного на рис. 4.12, б, число нулей
процесса существенно меньше числа экстремумов, так что к «^ 1
и v приближается к единице (например, на отрезке осциллограммы,
показанной на рис. 4.1, JV0 = 8, Жэкст = 39, т. е.
и =-^- = 0,16 и v = 0,988.
Такая ситуация обычно характерна для широкополосных
процессов, так что величина v может рассматриваться как
характеристика ширины энергетического спектра, т. е. как показатель
широкополосное™. Однако величину v нельзя считать
однозначным показателем широкополосности процесса, так как само
понятие широкополосности не является достаточно определенным.
Так, в работе [30] шириной полосы Ап энергетического спектра
называют отношение площади под кривой энергетического спектра
154
(кривой спектральной плотности) к спектральной плотности на
некоторой характерной черте а0:
А^=-2Щ^]8^^-Ш- D-42)
о
Площадь под кривой спектральной плотности равна значению
корреляционной функции в начале координат и дисперсии
процесса сг§. Таким образом, величину Ап можно трактовать как
ширину равномерного в полосе энергетического спектра процесса,
эквивалентного данному по средней мощности (рис. 4.13).
Случайный процесс с непрерывной функцией спектральной
плотности называется узкополосным [30], если Дп <^ (о0.
т. е. если график спектральной плотности располагается в узкой
полосе вблизи частоты а0, как показано на рис. 4.13, а. Если
указанное условие не выполняется, то процесс называется
широкополосным (рис. 4.13, б).
На практике во многих деталях различных машин
преобладающими являются случайные процессы, спектральная
плотность которых имеет вид, показанный на рис. 4.13, в, т. е. процессы,
в которых энергетический спектр сосредоточен вблизи двух или
трех частот, и процесс является как бы комбинацией двух или
трех узкополосных процессов в указанной выше трактовке.
Подводя итоги изложенной теории Раиса, можно сделать
следующие выводы. Если случайный процесс изменения напряжений
во времени является стационарным, нормальным, с четырежды
дифференцируемой корреляционной функцией в начале
координат, и нам известны корреляционная функция К (т) или
функция спектральной плотности S (со),
то по формулам D.21) можно S(u)
Рис. 4.12. Типы случайных процессов: Рис. 4.13. Схема к определению по-
a^x^l, v ~ 0; б — х s 0, v^l нятия широкоплосности процесса
155
найти дисперсии процесса а§ и его двух первых производных
а^ и а|, по формулам D.21), D.33) — среднее число нулей и
максимумов в единицу времени соответственно и по уравнению
D.37) — функцию распределения максимумов. Если считать, что
каждому максимуму \mi соответствует один полуцикл
напряжений с амплитудой \т1 (т. е. ■ применить метод схематизации
случайного процесса, названный выше методом максимумов), то
уравнение D.37) дает функцию распределения амплитуд
напряжений / (оа) = / (!т). По / (Оа) И Л/щах МОЖНО рЭССЧИТЭТЬ ДОЛ-
говечность детали. Таким образом, теория Раиса применима
только к ограниченному кругу случайных процессов, ибо часто
процессы не являются стационарными, нормальными и с
дифференцируемой корреляционной функцией. Кроме того, метод
максимумов схематизации случайного процесса, на котором основано
применение формулы D.37) для расчета на усталость, приводит
как. отмечалось выше, к процессу более повреждающему, чем на
самом деле, в результате чего расчетная долновечность
получается заниженной.
Возникает некоторая трудность в применении изложенной
теории из-за погрешностей в статистической оценке параметров
корреляционных функций и спектральных плотностей. Дело в том,
что истинная корреляционная функция процесса является, как
правило, неизвестной, а имеется лишь ее статистическая оценка,
полученная по ограниченному числу реализаций процесса.
Поэтому вопрос о получении необходимой точности статистических
оценок значений производных от корреляционной функции
становится трудноразрешимым. В этом случае удобнее пользоваться
формулами для определяющих величин ffg, оц и as, в которых
они выражаются через функции спектральной плотности.
Несмотря на эти трудности, теория Раиса может
использоваться для оценки уровня случайной переменной нагруженности
при расчетах на усталость на стадии проектирования новой
машины, когда отсутствует опытный экземпляр и невозможно
произвести тензометрирование в условиях эксплуатации или на
полигоне. В этом случае спектральная плотность процесса может быть
найдена методами статистической динамики, и по приведенным
выше формулам оценена нагруженность для расчета на
выносливость.
Нахождение функции распределения амплитуд напряжений
методами теории случайных функций применительно к другим
способам схематизации процесса. В работе [94] дано приближенное
численное решение задачи о распределении разностей двух
последовательных экстремальных значений непрерывного
случайного процесса, т. е. фактически о распределении размахов (что
соответствует методу размахов) при некоторых частных видах
функций спектральной плотности. Общее точное решение в
замкнутом виде для любых функций спектральной плотности, как
156
это было сделано для максимумов f(h/6)
С. О. Райсом, для размахов полу- о, 4
чить не удалось из-за чрезмерных
математических трудностей.
Вычисления проведены для функ
ций спектральной плотности, имею
щих уравнение
_2
0,3
0,2
S (а)-
'%
(Г^р)Шс приР(ос<(о<сос;
О в прочих случаях,,
D.43)
0,1
О
Л—*
V
1
■
щ
fi = 0
,0,2$
^0,50
fl=0,77
1 2 3 4 5 В h/6
Рис. 4.14. Графики плотностей
распределения размахов
процесса по Раису и Биру
где 0--^ р г=с 1; параметр ас—
наибольшая частота интервала, в
котором S (со) постоянна; Р©?
—наименьшая частота интервала.
Плотности вероятностей распределения размахов для
четырех значений р приведены на рис. 4.14. При р = 0,75 процесс
является достаточно* узкополосным. При этом вычисленная в
работе [94] функция распределения размахов хорошо соответствует
распределению Рэлея.
Таким образом, в принципе возможно определение функции
распределения амплитуд напряжений при схематизации по
способу размахов методами теории случайных функций по известной
функции спектральной плотности. Однако при этом возникают
математические трудности. Кроме того, как уже отмечалось,
метод размахов приводит к процессу, менее повреждающему,
чем реальный процесс, вследствие чего расчетные оценки
долговечности оказываются завышенными.
В работе [16] на основе ряда допущений найдено
приближенное распределение амплитуд напряжений методами теории
случайных функций при схематизации процесса по методу полных
циклов.
13. Статистическая оценка расчетных
характеристик нагруженности
Применяя тот или иной метод схематизации случайного
процесса изменения напряжений в детали (см. разд. 11), получают
функцию распределения амплитуд напряжений, которая в
исходном виде задается в виде таблицы, содержащей пары чисел
(fffl». vi6)< t = 1, 2, • • •, г, как, например, показано в табл. 4.1.
Напомним, что оа1 — это амплитуда t-ro уровня, vi6 — число
циклов повторения амплитуды oai в одном блоке нагруженйя.
Общий ресурс детали (в км или ч и т. п.)
L = U6, D.44)
157
где 'К — общее число блоков нагружения до появления
усталостной трещины в детали; 1б — блок нагружения (см. разд. 11).
Общее число циклов повторения амплитуд всех уровней в
одном блоке нагружения v6 и за весь срок службы до появления
трещины NcyM определяется следующими формулами:
т
v6 = Ъ v/6; D-45)
> 1=1
ЛГсум = Н, D-46)
где г —■ число уровней амплитуд в блоке при ступенчатой
аппроксимации функции распределения амплитуд.
В ряде случаев бывает удобно данные в исходной таблице (оа[,
Vj6) (например, табл. 4.1) задать в относительных величинах
CTat , tt, где аашах = аа1 — максимальная из зарегистрирован-
®а max
ных амплитуд напряжений, а
ii = ~- D-47)
Наряду со ступенчатой формой представления функций
распределения амплитуд напряжений для их описания применяют
аналитические выражения известных законов распределения
случайных величин (нормального, экспоненциального, Рэлея,
логарифмически-нормального и др.).
Методика определения параметров этих законов и их
графическое изображение на вероятностной бумаге по исходной
информации, заданной в виде таблиц типа 4.1, изложена в
ГОСТ 11.008—75 и ГОСТ 17509—72, а также в руководствах
по математической статистике (см. разд. 11) [18, 70].
Различие условий эксплуатации учитывается при
планировании тензометрических измерений путем разбивки этих условий
на некоторое число групп по определенным регламентируемым
параметрам. Например, применительно к автомобилям такими
параметрами являются тип дороги (асфальт, булыжник, грунт
и т. п.), скорость движения и груз в кузове.
Однако на величину эксплуатационных напряжений могут
влиять другие (случайные) факторы, которые не отражаются
обычно в данных тензометрирования. Например, применительно
к автомобилю такими - факторами являются состояние, погоды,
квалификация водителя, индивидуальные особенности дороги
(в пределах данного типа дорог) и экземпляра машины и т. д.
Повторяя многократно замеры и подсчеты функций
распределения амплитуд напряжений в пределах данного сочетания
регламентируемых факторов, получают различные функции
распределения. Однако опытные данные показывают, что при этом
меняются только параметры функций распределения амплитуд, а
закон распределения амплитуд остается практически неизменным,
158
т. е. имеет место подобное преобразование функций
распределения.
Пусть, например, закон распределения амплитуд оказался
нормальным с параметрами оа (среднее значение амплитуды)
и Saa (стандартное отклонение). Вследствие влияния случайных
нерегламентируемых факторов величины оа и S0a будут иметь
также случайные вариации. Но при подобном преобразовании
закон распределения будет оставаться нормальным, а коэффи-
ч
циент вариации va = —— неизменным.
а Оа
Если в результате п повторных измерений нагруженности
в условиях заданного сочетания регламентируемых
эксплуатационных условий работы получены п значений средних амплитуд
оаг (г = 1, 2, • • •, п), то среднее значение оа, среднее квадрати-
ческое отклонение So и коэффициент вариации Va =Sa/aa
величины оа можно определить по следующим формулам:
= 1 " —
Ofl = — X Car'.
п r=l
V~o„
S-
D.48)
Если закон распределения амплитуд представлен в виде
ступенчатого графика со ступенями оа[, то указанные выше
случайные вариации функций распределения амплитуд при их
подобном преобразовании могут быть описаны соотношением
°al = ~Gafi, ■ D-49)
где oai — среднее значение амплитуды t'-й ступени блока; е =
= 1 + uPv£ — нормально распределенная случайная величина,
имеющая среднее значение, равное единице, и коэффициент
вариации v£, характеризующий случайные отклонения уровня
нестационарной нагруженности. При ступенчатой аппроксимации
нормального закона распределения амплитуд w6 = ьъ (uP —■
квантиль нормального распределения).
Предположение о нормальном распределении величины vs
оправдывается результатами непосредственных измерений
напряжений в рамах тележек локомотивов [33, 34], электровозов
[52], в полуосях автомобилей [34] и некоторых других случаях.
Нормальность распределения е можно объяснить на основе
центральной предельной теоремы теории вероятностей, так как на
159
величину е влияет большое количество случайных нерегламен-
тируемых факторов, каждый из которых воздействует
незначительно.
Параметры функций распределения амплитуд напряжений
более существенно зависят от регламентируемых условий работы.
Поэтому функции распределения амплитуд находят при
различных режимах эксплуатации (при различных сочетаниях
регламентируемых условий работы). Для получения результирующего
смешанного закона распределения амплитуд привлекаются
статистические данные о долях времени работы машины при
различных режимах. В результате плотность распределения
смешанного закона и его параметры могут быть найдены по
соотношениям
/@"а)'= S Pftfft(CTa);
к
Оа = Zi Pkaak\
k > D.50)
Sa= liPk Oak A + Oft) — CTa =
a к
= SPft[SL + ^aft-aaJ].
где oak= M {оак\ = j ofk(o)da; рк — относительное время ра-
о
боты машины в условиях с номером k; fk (aa) — плотность
распределения амплитуд напряжений в условиях k; aak, vk —
математическое ожидание и коэффициент вариации амплитуды в
условиях k, aa, Saa — среднее значение и дисперсия амплитуды
смешанного закона распределения.
Глава 5
Методы расчета
на прочность деталей
машин при нагрузках,
переменных во времени
14. Методы расчета по коэффициентам
запаса прочности
Рассмотрим вначале случай регулярного изменения
нагрузок по асимметричному циклу при линейном напряженном
состоянии. Под регулярной нагруженностью понимают периодический
закон изменения напряжений во времени с периодом,
соответствующим одному циклу, при неизменности во времени характеристик
цикла напряжений. Во всех остальных случаях процесс нагру-
жения называют нерегулярным. Вывод формулы коэффициента
запаса прочности при асимметричном цикле регулярного нагру-
жения поясняется рис. 5.1, на котором представлены диаграммы
предельных амплитуд напряжений при асимметричных циклах
для гладких лабораторных полированных образцов (прямая 1)
диаметром d0 = 7,5 мм и для натурных деталей прямая B).
Уравнения для прямых 1 к 2 соответственно имеют вид
Оа = (Т-1 — -фоСГт", E-1)
а'а О-^оо'тя __ , /С ОЧ
<5аЯ— К D ~~ К~Ъ _ СТ_1Д Ч'ОД^Д' \Р-*)
где
<>-*=-&■> ^-Ь- ' E-3)
Уравнение E.1) совпадает с уравнением B.17).
Ординаты точек прямой 2 получаются делением ординат
точек прямой / на одно и то же число Кар при сохранении абсцисс
в соответствии с установленной ранее закономерностью влияния
концентрации напряжений на сопротивление усталости при
асимметричном цикле (см. разд. 6).
Пусть рабочие напряжения в детали определяются
координатами точки М на рис. 5.1, т. е. амплитуда напряжений равна оа,
среднее напряжение цикла ат. Допустим, что в процессе
работы переход к предельному состоянию возможен путем
возрастания напряжений оа и от, а следовательно, и crmax = от +
+ оа пропорционально одному параметру. При этом коэффи-
V26 В. П. Когаев 161
бцрад
циент асимметрии цикла
напряжений R
0"min
будет
Рис. 5.1. Схема к выводу формулы для
коэффициента запаса прочности
оставаться постоянным, а
точка М, изображающая
уровень напряжений, будет
двигаться по лучу OMN.
Циклы напряжений с
одинаковыми коэффициентами
асимметрии R называются
подобными. При подобном
нагружении (при котором'
R = const) предельные
напряжения определяются
координатами точки N, а
коэффициент запаса
прочности
°"тд Q"max д
ат Сщах
E-4)
асимметричном цикле.
(Хгд — предел выносливости детали при
Из уравнения E.4) находим aaR = оапа, 0тд = стпа.
Подставляя' эти величины в формулу E.2), получаем
Пп =
OaK0D + ^п.
E.5)
Формула E.5), предложенная С. В. Серенсеном [53], лежит
в основе детерминистических методов расчета на усталость при
регулярном переменном нагружении деталей машин во всех
отраслях машиностроения.
Наряду с расчетом на выносливость необходимо проверить
также выполнение условия статической прочности, которое для
пластичных металлов имеет вид
>[я]т=1,2-н1,5.
т 0"тах От + СГа
Формулу E.5) можно представить в несколько ином виде/
Представим яр0 согласно выражению E.3) в виде % = т!раяКоо
И подставим в уравнение E.5). Тогда получим
п„ = -
KaD (Оа + %яат)
Или с учетом зависимости E.3)
1%с,
где
162
и-1Д
Оа эк
Ga эк = °а + ty<Jp?m
E.6)
E.7)
E.8)
— эквивалентная амплитуда симметричного цикла,
равноценная по своему повреждающему действию асимметричному циклу
с параметрами аа и от.
Зависимость E.3) в большинстве случаев подтверждается
опытными данными. Так, например, для болтовых [52] и
сварных соединений с резкой концентрацией напряжений [64], как
правило, 1]>ад s 0, что получается и по формуле E.3), так как
для этих случаев KoD = 3-4-6. Это же справедливо и для
большинства деталей с умеренной концентрацией напряжений. Однако
в отдельных случаях диаграмма предельных амплитуд для
детали (прямая 2 на рис. 5.1) оказывается почти параллельной
диаграмме для лабораторного образца, а г[>Сд остается достаточно
большим и близким к-г|?а. Такое положение правомерно для
поверхностно упрочненных деталей, для литых деталей из
малопластичных металлов (серый чугун) и в некоторых других случаях.
Однако остается справедливым уравнение
СГад = СГ-1д — Ч'одаягд- E-9)
Подставляя сюда сад = оап.(, и отл = отп0, получаем снова
формулы E.6), E.7), которые таким образом справедливы во всех
случаях, если в качестве %я подставлять значение, найденное
для деталей опытным путем.
Формула E.5) выведена для случая перехода к предельному
состоянию путем возрастания напряжений по подобному циклу.
Известны также и другие формулы, относящиеся к случаям
возрастания только амплитуд напряжений при постоянном среднем
напряжении, или такого возрастания ат и аа, при котором
остается неизменным минимальное напряжение цикла ат1п и т. п. [52 ].
Выражение для коэффициента запаса прочности при плоском
напряженном состоянии, при котором возникают нормальное а
и касательное т напряжения, при симметричном цикле их
изменения вытекает из формулы B.40), которая может быть
представлена в виде
1/"<т|д + £Мд = (г_1д, ■ E.10)
где
fc = -5=ii. E.11)
Т-1Д
Здесь (тод., тод — предельные амплитуды напряжений
в детали при совместном действии нормальных . и касательных
напряжений.'
Пусть аа, ха — рабочие амплитуды нормальных и касательных
напряжений.' В соответствии с общим понятием коэффициента
запаса прочности полагаем
п = а~1Д = р-дд
арасч ]/Ч+А|'
V26*
E.12)
163
Введем также коэффициенты запаса отдельно по нормальным
и касательным напряжениям:
ла=-^=^-; n, = iii. E.13)
Подставляя выражение E.13) в уравнение E.12), получаем
формулу для коэффициента запаса прочности:
папх EЛ4)
f < '
или
•4
Формула E.14) распространяется также и на общий случай
плоского напряженного состояния с компонентами о и т,
изменяющимися регулярно по асимметричным циклам без соблюдения
требования синхронности и синфазности. Величина я0 при этом
находится по формуле E.5) [или E.6)], величина ят — по
аналогичной формуле
пх = и T-i , . E.16)
Деталь считается работоспособной, если я, определенное по
уравнению E.14), не ниже минимально допустимого значения
коэффициента запаса прочности [я], т. е. условие прочности
имеет вид я > [я]. В большинстве случаев в машиностроении
[я] = 1,5-^-2,5. С другой стороны, если я > [я], т. е. я намного
превышает минимально допустимое значение, то деталь имеет
завышенные размеры и может быть облегчена, если ее размеры
определяются условиями прочности, а не условиями жесткости,
конструктивными, технологическими соображениями и т. п.
Величина [я] зависит от точности определения нагрузок и
характеристик сопротивления усталостному разрушению (зависящей
от объема экспериментальной информации), от уровня технологии
изготовления и контроля дефектности, ответственности
конструкции, однородности материала.
При высоком уровне технологии изготовления, применении
современных средств дефектоскопии, при проведении
фундаментальных исследований эксплуатационных нагрузок,
распределения напряжений и характеристик сопротивления усталости, при
применении высококачественных сталей даже для ответственных
конструкций допускаются небольшие значения, я при условии
строгого ограничения ресурса эксплуатации и текущего контроля
за состоянием детали. Такое сочетание условий характерно для
коленчатых валов, шатунов и некоторых других деталей
поршневых авиационных двигателей, для расчета которых принимают
[я] = 1,3-5-1,5.
164
При среднем уровне технологии изготовления, применении
таких процессов как сварка, которые могут приводить к
появлению дефектов и повышенному разбросу механических свойств
(особенно характеристик сопротивления усталости), при
невозможности проведения усталостных испытаний достаточно
большого числа натурных деталей вследствие больших габаритов и
потребных затрат, однако при соблюдении определенных
требований к технологии изготовления, величины [я] принимаются
средними из указанного выше интервала. Указанные условия
характерны, например, для тележек локомотивов подвижного
состава железных дорог, в расчете которых по формулам типа
E.5) принимается [я] = 2 [33].
С увеличением габаритов и ответственности конструкции,
с возрастанием убытков от аварии, особенно при опасности для
жизни людей, связанной с возможным разрушением детали,
величины [я ] должны повышаться.
Ранее предлагался так называемый дифференциальный способ
определения минимально допустимого значения коэффициента
запаса [я], согласно которому эта величина представлялась как
произведение большого числа сомножителей (до 12), каждый из
которых варьировался в определенных пределах и
предназначался для учета того или иного фактора (однородности материала,
ответственности конструкции и т. д.). Этот метод себя не оправдал
и не получил распространения, так как, варьируя сомножителями,
можно было получать значения [я] в достаточно широких
пределах на основе волевых решений и без достаточной связи с
практикой.
Наиболее правильным путем выбора [я] является метод,
применяемый в настоящее время во многих отраслях
машиностроения и основанный на сопоставлении результатов расчета сданными
об отказах в условиях эксплуатации, обобщении опыта
конструирования, расчетов и указанных сопоставлений с практикой.
Величина [п.] неразрывно связана с методом расчета, включающим
расчетные формулы, правила выбора расчетных величин
нагрузок и характеристик сопротивления усталости. Поэтому изменение
метода расчета в какой-либо части может приводить и к
изменению [я 1, который находится на основе опыта практического
применения вполне определенной методики расчета.
Формулы E.5), E.14), E.16) широко применяют в расчете
деталей машин на прочность при переменных нагрузках. Однако
сейчас назрела необходимость дальнейшего развития методов
расчета, требующего выхода за рамки условных допущений,
положенных в основу вывода формулы E.5). Это связано с
необходимостью учета случайного характера изменения
эксплуатационных напряжений, рассеяния характеристик сопротивления
усталости, с необходимостью оценки ресурса по параметру
вероятности разрушения.
6 В. П. Когаев 165
Формулы E.5) не дают возможности рассчитать ресурс
детали в зависимости от вероятности разрушения, т. е. оценить
характеристики долговечности и надежности детали, имеющие
первостепенное значение в современном машиностроении.
Свободными от указанных допущений и ограничений являются
вероятностные методы расчета на усталость, изложенные далее.
Следует заметить, что применение вероятностных методов
расчета не всегда возможно из-за недостатка экспериментальной
информации о нагрузках и характеристиках прочности. Особенно
это относится к деталям, вероятность безотказной работы которых
должна быть весьма высокой (> 0,9990-М),9999). В этих случаях
детерминистические методы расчета на усталость, основанные
на использовании формул E.5), E.14), E.16), сохранят свое
значение и в дальнейшем как нормативные с введением ряда
усовершенствований (учета нерегулярного характера нагрузок,
рассеяния характеристик нагруженности и прочности и др., как
будет поясняться далее).
Учет нерегулярного характера нагруженности может быть
осуществлен на основе использования корректированной
линейной гипотезы суммирования усталостных повреждений, условие
прочности согласно которой имеет вид
N;
= а
■pi
E.17)
(<W сг_]Д)
где nt — число циклов повторения амплитуды аа1 за весь срок
службы; Nt — число циклов по кривой усталости, полученной
при регулярном нагружении, соответствующее амплитуде аа1\
ар = 0,1-М :— корректированное значение суммы
относительных долговечностей N ~Tf~> соответствующее предельному
повреждению (формула для ар будет дана в разд. 16). Известно, (см.
разд. 13), что
n[ = %vi6 = %v6ti:
E.18)
где X — число блоков нагружения за весь срок службы; vi6 —
число циклов повторения амплитуд oai в блоке; 2jVt-6 = v6 —
общее число циклов в блоке.
Запишем уравнение кривой усталости в виде [см. B.9I
N,=
ЗД,
<t
при аа
->-1Я,
. оо при oai < 0_]д.
166
E.19)
Подставляя выражения E.18), E.19) в уравнение E.17),
получаем формулу для ресурса детали, выраженного числом
блоков X до появления трещины:
%=■
(%£ > а-1д)
или условие прочности:
^~^Й7' E-20)
'{УЖГ S <#* = *-*. E.207)
Индекс (оа[ > сг_1д) под знаком суммы в уравнениях E.17),
E.20) и A5.20') показывает, что суммирование в этих выражениях
следует производить только по амплитудам аа(, превышающим
предел выносливости детали а_1д, ибо при аа1 < в_1д согласно
зависимости E.19) NL — ©о, и соответствующие слагаемые в
выражении E.17) обращаются в 0.
Если деталь имеет запас прочности па, то согласно
предположению о переходе к предельному состоянию путем увеличения
всех оai в па раз, получаем условие прочности [56]
г-
2 {Oatna)mil = 0-
•1д-
Отсюда
па = -^, E.21)
иэкв
где
-,"•/",&•, S ->»■ ("?>
У
at■— п_
[В выражении E.22) у величин т, N0, v6, ap, ^ дополнительно
введен индекс a, чтобы отличить их от соответствующих величин
для касательных напряжений, используемых далее].
Величина па по уравнению E.21) находится методом
последовательных приближений, так как она входит также в выражение
"экв-
Если в детали возникают нормальные а и касательные т
напряжения, изменяющиеся во времени нерегулярно, то
вычисляется коэффициент запаса прочности по нормальным напряжениям
«а по формулам E.21), E.22), а коэффициент запаса по
касательным напряжением по формуле
пх = iii , E.23)
6*
167
где
7& 2 С%, E.24,
Общий коэффициент запаса прочности
E.25)
Учет потребного срока службы детали и нерегулярности
режима ее работы на основе линейной гипотезы суммирования
повреждений осуществлялся в работах А. И. Петрусевича, Д. Н. Ре-
шетова [45], С. В. Серенсена [58], Майнера и др. Так, в работе
[45] предлагается вести расчет на усталость по амплитуде Коашх,
где oamax — максимальная амплитуда напряжений, К < 1 —
коэффициент долговечности, определяемый по формуле,
вытекающей из линейной гипотезы, сводящейся к уравнению E.17)
при ар = 1:
где Qh nit Tt — соответственно нагрузка, число нагружений
в минуту и время работы в часах при режиме i (i = 1, 2, 3, • • •)'>
Qx — максимальная нагрузка (по отношению к которой
вычисляется коэффициент долговечности), действующая при числе
оборотов /гх; Т — общее расчетное время, в ч; N0 — число
циклов, соответствующее точке перелома кривой усталости
(рекомендуется для сталей М0 = 107).
В работе [47] рекомендуется за расчетную принимать
максимальную рабочую нагрузку, а нерегулярность режима
учитывать корректировкой допускаемых напряжений по формуле
f[*bfjf приЛ^<Л^ E2?)
[a]D при Ne^N0,\
где
£**i \ °а max /
[в] о— допускаемое напряжение при длительной работе
регулярного режима; [а] — допускаемое напряжение при
нерегулярном режиме и расчете по 0max; oai, oamax — сооответственно
амплитуды напряжений t'-ro режима и максимальная; остальные
обозначения те же, что и в формуле E.26).
Для высокоответственных деталей, вероятность безотказной
работы которых должна быть выше 0,9990 — 0,9999, предлагается
168
расчет на прочность выполнять по коэффициентам запаса прочности,
определяемым с учетом рассеяния характеристик прочности и
нагруженности по формуле , [3 ]
п = -£™Д_ 2£ [П]> E.29)
•^тах
где Qmta, Lfflax — соответственно минимально возможные значения
прочности и максимально возможные значения нагрузки,
определяемые статистическими .методами с учетом возможных
случайных вариаций Q и L. Можно, например, принять по правилу
трех сигм, известному из математической статистики, что
Qma = Q_-3SQ; J Eзо)
где Q, L — соответственно средние значения нагрузки и прочности;
Sq, Sl — средние квадратические отклонения величин Q и L
(согласно правилу трех сигм принимается, что выход случайной
величины Q за пределы интервала Q ± 3SQ является событием
практически невозможным; аналогично и для L).
Применение метода расчета на прочность, основанного на
использовании уравнения E.29), имеет значение для
сравнительных расчетов, причем значение [я] определяется на основе опыта
эксплуатации выполненных конструкций.
15. Экспериментальное обоснование
методов расчета
на выносливость при нерегулярной
переменной нагруженности
Под нерегулярной переменной нагруженностью понимают
такой характер изменения напряжений во времени, при котором
амплитуды переменных напряжений или средние напряжения
цикла изменяются во времени по некоторой программе или
случайным образом. Для расчета деталей машин на усталость при
нерегулярной напряженности необходимо применять
определенные условия суммирования усталостных повреждений. Одним
из наиболее простых условий является линейная гипотеза
накопления усталостных повреждений E.17).
Учитывая рассеяние долговечности при усталостных
испытаниях как при регулярном, так и при нерегулярном нагружении,
испытывают в каждом варианте от 5 до 20 (и более) образцов и
подсчитывают сумму относительных долговечностей по средним
значениям:
169
где tt = ——— относительное число циклов действия амплитуды
аа, в программном блоке; vc6, v6 — те же, что и в формулах E.17),
E.18); N,: — среднее арифметическое значение числа циклов до
разрушения при испытаниях с постоянной амплитудой aai (иногда
в качестве Nt берут медианное значение числа циклов при
амплитуде oai); NcyM — среднее арифметическое значение
суммарного числа циклов при испытаниях с программным изменением
амплитуды напряжений.
Результаты многих исследований показывают, что даже при
испытании достаточно большого количества образцов в каждом
варианте величина а отклоняется от единицы [23, 34, 40, 46,
52, 56, 66, 67, 76—79]. Эти отклонения имеют детерминированную
и случайную составляющую. Детерминированная составляющая
возникает из-за того, что действительные закономерности
накопления усталостных повреждений более сложны, чем простое
линейное суммирование относительных долговечностей. Так,
например, вполне отчетливо проявляется «тренировка» (при оп <
< 0К) и разупрочнение (при ан > ак) при одноступенчатом
однократном изменении амплитуды напряжений (ан — амплитуда
начальной тренировки; 0К — амплитуда напряжений при
испытаниях образцов после тренировки). Заметные отклонения от
линейной гипотезы получаются при наличии в программном блоке
амплитуд, которые меньше предела выносливости и амплитуд оа > а_1д
наряду с большими кратковременными перегрузками. В этих
случаях сумма относительных долговечностей а может снижаться
до значений а = 0,05-4-0,10. Случайная составляющая связана
со значительным рассеянием как самих долговечностей Nt и iVcyM,
так и их средних значений N£ и JVcyM (при числе образцов п =
= 5-4-20), входящих соответственно в выражения E.17) и E.31).
Поэтому при исследовании закономерностей накопления
усталостных повреждений при меняющихся амплитудах необходим
статистический подход, позволяющий выявить соотношение между
детерминированной и случайной составляющими величины а,
и тем самым получить более обоснованные выводы о
действительных закономерностях накопления усталостных повреждений.
Неучет случайной составляющей, имевший место во многих работах,
в ряде случаев приводил к недостаточно обоснованным выводам.
Приближенная оценка доверительных интервалов для суммы
относительных долговечностей а показывает [23], что при средне-
квадратическом отклонении логарифма долговечности SigN= 0,2
и справедливости линейной гипотезы в среднем (медианное
значение а = 1) 95% доверительный интервал для а составляет 0,6 <
<а < 1,6 при условии вычисления а по формуле E.31) по
средним значениям iVcyM и N[t найденным по" результатам испытания
15—20 образцов на каждый вариант; при 'Si^N — 0,6
аналогично
ный интервал получается 0,25 < а < 4, что и подтверждается
опытными данными [25].
В ряде работ были предложены нелинейные гипотезы
суммирования повреждений, которые, однако, не нашли
практического применения вследствие громоздкости вычислений и
отсутствия убедительных доказательств их точности в применении
к многоступенчатым программным испытаниям. Введение
факторов взаимодействия между уровнями напряжений [76] или
измененного наклона левой ветви вторичных кривых усталости
[54, 56] требует экпериментального определения
соответствующих характеристик применительно к конкретным случаям
практики, что также затрудняет использование указанных подходов.
В работе [23] была предложена следующая формула,
корректирующая линейную гипотезу суммирования усталостных
повреждений: .
Sf=^ E-32)
где
„ °а maxfa ~ &ap-i д
°а max — ^a^-ip,
т
<4ст/ "a max
Здесь tfamax — максимальная амплитуда программного блока;
Goi — t-я амплитуда программного блока; 0 < ka < 1 —
постоянное число, определяющее нижнюю границу повреждающих
напряжений; амплитуды аа[ < kaa_lR не оказывают влияния на
процесс усталостного разрушения и не учитываются при
вычислении сумм, входящих в формулы E.33), E.34) (по опытным
данным можно принять ka = 0,5).
Формулой E.33) можно пользоваться при Ратах > 1 и до тех
СТ-1Д
значений £ = £*, для которых ар =0,1; при £ < с* следует
полагать ар = 0,1.
Формула E.33) была получена на основе анализа ряда
экспериментальных данных. Из этих данных следует, что сумма
относительных долговечностей а имеет тенденцию к уменьшению при
увеличении разницы между наибольшей oamsx и наименьшей
оатп амплитудами блока и при уменьшении относительного
времени tt действия амплитуд высоких уровней.
Испытания при однократной смене амплитуд проводились
в большинстве случаев на сравнительно небольшом числе
образцов (т. е. не в статистическом аспекте). При этом установлены
171
т
— z ; E.33)
°а шах KaG~in
следующие закономерности. При ан < сгк наблюдается
упрочнение, при котором а > 1 [в этом случае долговечность,
полученная экспериментально, оказывается в 1,4—2 раза более высокой,
чем вычисленная по линейной гипотезе по формуле E.31)]. При
сгн > сгк наблюдается, как правило, разупрочнение, при котором
а < 1. Как показывают опытные данные, более интенсивное
накопление усталостных повреждений получается в начальной
стадии циклического нагружения.
Проведение испытаний на достаточно большом количестве
образцов в статистическом аспекте позволяет сделать более
обоснованные выводы о закономерностях накопления усталостных
повреждений.
Известно большое число исследований при двухступенчатом
многократном изменении амплитуды напряжений [10, 23, 25, 40,
54, 66, 67, 76]. Исследования показывают, что при переходе от
однократного изменения амплитуды к многократному величины
сумм относительных долговечностей а приближаются к 1, если
оба уровня амплитуд напряжений превышают предел выносли-
васти и отсутствуют кратковременные резкие перегрузки.
Значения а в этих условиях находятся, как правило, в пределах
0,5 < а < 2,0, хотя наблюдаются и отдельные более
существенные отклонения. Отмечается тенденция к уменьшению а с увели-
чением отношения —=±- и уменьшением отношения гх = -±~ =
_ %
«! + «2 '
Исследования закономерностей накопления усталостных
повреждений при двух ступенчатых программных блоках,
проведенные в статистическом аспекте на большом числе образцов,
описаны в работах [23, 76—79]. Большое исследование
предпринято Кортеном и Доланом [76]. Результаты подсчета а для
различных сочетаний ал — сга2 и t1 — t2 показывают, что если брать
варианты сочетания напряжений, в которых все амплитуды были
больше предела выносливости, то а колеблется в пределах 0,75—
1,06. Даже в тех вариантах, в которых сга2 = 32,2 < а_г при
длительностях t > 0,04, имело место 0,66 < а < 1,19. И только при
весьма кратковременных перегрузках (tt = 1-^1,3%) и при
основном времени работы на напряжении ниже предела
выносливости а = 0,35.
Обобщение ряда исследований различных авторов,
охватывающих испытание большого числа образцов при
многоступенчатом программном нагружении, дано на рис. 5.2 [23], на котором
на логарифмически нормальной вероятностной бумаге
представлены функции распределения величин 1/аэ и ар/аэ. Здесь аэ =
= S tiilNt — суммы относительных долговечностей, найденные
экспериментально по медианным значениям п{ и Nt (обобщению
подвергались в основном данные, полученные в статистическом
аспекте [23, 25, 34, 46, 76]; ар — расчетные значения суммы от-
172
носительных долговечностей найденные по формуле E.33) при
ka = 0,5.
Величины \1аэ характеризуют ошибку не в запас
долговечности, получающуюся при оценке долговечности по линейной
гипотезе без корректировки (Ор = 1).' Например, при вероятности
Р si 95% по рис. 5.2 имеем —е=;5, т. е. линейная гипотеза
аэ
без корректировки может приводить к завышению расчетной
долговечности по сравнению с фактической до 5 раз и более (~5%
случаев). В среднем (при Р = 50%) линейная гипотеза приводит
к 1,5-кратной ошибке не в запас долговечности.
Величина ^- = ;..сум;р характеризует ошибку в оценке
"э (Лсум)э
долговечности при использовании корректированной линейной
гипотезы [уравнения E.32) — E.34)], так как (#сум)р —
расчетное суммарное число циклов, (NcyMK — суммарное число
циклов, найденное при программных испытаниях. Из рис. 5.2, видно,
что в среднем (при Р = 50%) корректированная линейная
гипотеза практически не дает ошибки в оценке долговечности. С
вероятностью 95% корректированная линейная гипотеза приводит
к ошибке в оценке долговечности, не превышающей 2,5-кратную,
что следует признать приемлемым для практики [23]. Последнее
вытекает из того, что вследствие пологого характера левой ветви
кривой усталости изменение напряжений на 5—10% приводит
к изменению долговечности в 2—3 и более раза (в зависимости
от угла наклона кривой усталости). Ошибки же в определении
предела выносливости и уровня напряженности имеют именно
такой порядок и больше. Вследствие этого, а также в связи с
рассеянием характеристик нагруженности и сопротивления усталости
практически нельзя оценивать долговечности и ресурсы деталей
с погрешностями, меньшими
чем 2—3-кратные.
Таким образом, проведенное
обобщение показывает
целесообразность использования
корректированной линейной
гипотезы для подсчета ресурса
деталей в условиях эксплуатации,
что подтверждается также
практикой расчетов по этой гипотезе
в промышленности.
Указанные выше
исследования проводились, как
правило, на базе испытания N6 <S
«S 107 циклов. Однако
суммарное число циклов А/сум,
нарабатываемое деталью за срок
службы, обычно превышает
99,9
99,5
SO
30
го
10
5
г
0,5
0,1
о,ог
i
,'
s'
' /
7
- f - ар/о3
у л
♦ \
-Цвз
0,1 0,2 0,3 0,5 1 2 S i56?8910ap/ay;l/a}
Рис. 5.2. Функции
величин 1/аэ и ар/аэ
распределения
173
Ю8 — Ю9 циклов. Поэтому возник вопрос об асимптотическом
характере статистических закономерностей накопления
усталостных повреждений при нерегулярном переменном нагру-
жении. Для изучения этих закономерностей были проведены
программные усталостные испытания на базе 5-Ю8 циклов при
ступенчатых законах изменения амплитуд напряжений в блоках,
полученных путем аппроксимации экспоненциального,
нормального и равномерного распределений, представленных в табл. 5.1
[40] *.
Таблица 5.1
Функции распределения амплитуд при программных испытаниях
1
1
2
3
4
5
6
Закон распределения амплитуд
экспоненциальный
Б
ь3
1
0,866
0,737
0,608
0,477
h
4,7-10-3
0,0111
0,0512
0,193
0,74
нормальный
«
Б
1
0,88
0,82
0,76
0.71
0,66
h
0,0037
0,0163
0,030
0,045
0,060
0,09
равномерный
X
«
Б
а
ь3
1
0,95
0,90
0,85
0,80
0,75
h
0,0435
0,0869
0,0869
0,0869
.0,0869
'0,0869
t
7
8
9
10
11
12
Закон распределения амплитуд
нормальный
«
Б
'3
0,61
0,55
0,50
0,44
0,36
0,30
h
:о,п
0,15
0,15
0,15
0,10
0,10
равномерный
«
Б
а
о
'а
0,70
0,65
0,60
0,55
0,50
0,45
h
0,0869
0,0869
0,0869
0,0869
0,0869
0,0869
Испытания с распределением амплитуд, являющимся
пятиступенчатой аппроксимацией экспоненциального распределения,
производили на гладких образцах из стали 45 (сгв = 66 кгс/мм2)
диаметром d0 = 7 мм при изгибе в одной плоскости на
программных электромагнитных резонансных машинах. Предел
выносливости определяли испытанием 20 образцов на базе 107 циклов
по методу «лестницы» (см. разд. 4). Соответственно среднее
значение и среднее квадратическое отклонение предела выносливости
получили равными: а_1 = 29,9 кгс/мм2 и S0_1 = 1,4 кгс/мм2.
Испытания с распределениями амплитуд, являющимися
12-ступенчатой аппроксимацией нормального и равномерного
законов распределения, производили на машинах типа МИП-8 [50]
при консольном изгибе с вращением гладких образцов диаметром
8 мм из стали 45 (ств = 72 кгс/мм2, а_г — 28 кгс/мм2, S0_1 =
= 0,41 кгс/мм2).
Для построения первичной (исходной) кривой усталости,
соответствующей испытаниям при регулярном нагружении, т. е.
* Испытания проведены автором совместно с И. М. Петровой и В. П. Ванды-
шевым.
174
с постоянными амплитудами, проводили испытания при
нескольких уровнях амплитуд по 15—20 образцов на каждом уровне.
В качестве примера на рис. 5.3 кривыми /, 2, 3 представлены
полученные таким образом функции распределений
долговечности образцов при регулярном нагружении при испытании на
плоский изгиб при трех уровнях амплитуд напряжений.
На рис. 5.4 показаны в двойных логарифмических координатах
кривые усталости при регулярном нагружении, соответствующие
вероятности разрушения 50%. По оси ординат на рис. 5.4 в
случае программного нагружения отложены значения максимальной
амплитуды программного блока оа1 = cramax, по оси абсцисс —
суммарное число циклов до появления трещины:
# сун = Xv6
к S v,-
E.35)
где Я — число блоков нагружения до появления трещины при
программных испытаниях (по обеим осям взяты логарифмические
шкалы). Уравнение кривой усталости при регулярном нагружении
(кривая / на рис. 5.4) имеет вид
E.36)
<« = *™iA.
где а_1д = 29,9 кгс/мм2; N0 = 2,28-10е; т = 5,7.
Кривая 2 на рис. 5.4, характеризующая зависимость между
ffamax и А/сум ПРИ программных испытаниях, называется вторич-
%
9i
80
10
40
40
10
г
i
-/-
«?
\
■
- ,
р
я
/of
'
1~/о
&
<£'
?>
Р
г А
' ./О V
/°
~>i
5/
¥
V ■
■Л
о
л
1
6
З.о^
И
Л
.
АА -^ /
*■ J&
/ V
* S
/*/
ш/
*■
/
'
s*
>
п
5~
/
~~\s
s
X
V
<р
?''
У
V
•X' 1
-7<
I
Г"
2 3 4 5 678106
2 3
55 7810'
2 3 4 5S78106
2 3 4N,NCI
Рис. 5.3. Функции распределения долговечности при испытании на изгиб в одной
плоскости с постоянными амплитудами (линии 1, 2, 3) и при программном
нагружении с экспоненциальным распределением амплитуд (линии 4, 5, 6, 7):
1 — о„ = 34 кгс/мм2; 2 — 0
"a max
а
32 кгс/мм2; 3 — О = 30 кгс/мм8; 4
°ашах/°-1= L3;
5 - о„ „,.,/0^ = 1,2; 6 - аа ^/о^ =1.1; 7
"а шах/0
1,05
175
6;6атах,кгс/мм
44
4Z
40
38
36
34
32
30
Z8
\Л
\
\
ii-3
i к
2\
1
1
Г ^"^t
10 *
10'
пр--
1,5
1,1
W
'-19
и-1д
^
W
I
к
к
I I
]
10 е N,NcyM
10
N N,
100 — ,
N„
сум
N„
Рис. 5.4. Первичная A) и вторичная B) Рис. 5.5. Первичная {1) и вторичная B)
кривые усталости: кривые усталости, выраженные в от-
J и 2 - экспериментальные; 3 - расчет- НОСИтельных координатах
ная кривая
ной кривой усталости. Кривая 5, являющаяся вторичной кривой
усталости, рассчитана по уравнениям E.32) — E.34). Из рис. 5.4
видно, что до базы испытания Ncyw = 5-Ю8 циклов
экспериментальные и расчетные долговечности находятся в хорошем
соответствии, причем вторичные кривые усталости асимптотически
приближаются к горизонтальному участку первичной кривой при
увеличении iVCyM.
Для дальнейшего удобно первичную и вторичную кривые
усталости представить в относительных координатах, как показано
на рис. 5.5. На рисунке по оси ординат отложены в
логарифмическом масштабе величины -^- и gQmax для регулярных и прог-
сг_
Ч
-1Д
раммных усталостных испытании соответственно, по оси абсцисс—
JL
N0
N,
величины -ГГ-, - * также в логарифмическом масштабе (N0
— 2,28 • 10е циклов — абсцисса точки перелома первичной кривой
усталости).
Значение отношения максимальной амплитуды программного
блока аашах к пределу выносливости сг_1д, отложенное по оси
ординат на рис. 5.5, обозначим через
°"атах
а-1Я
E.37)
и назовем предельным коэффициентом нагруженности. Таким об-
разом, зависимость пр от —^—, показанная на рис. 5.5 кривой 2,
представляет собой не что иное, как вторичную кривую
усталости, выраженную в относительных величинах; построение
176
этой кривой является приведением результатов программных
испытаний к координатам аа — N. Зависимости пр = / (-тр~х
далее, будут играть основную роль в расчетах на усталость при
программном и случайном нагружении. Зависимость предельного
Мсум
коэффициента нагруженности пр от
Nn
представленная на
сум
рис. 5.5, справедлива только для ступенчатого распределения
амплитуд, данного в табл. 5.1. При переходе к полному
экспоненциальному распределению без усечения снизу (как сделано в
табл. 5.1 и при испытаниях с целью сокращения времени)
необходим соответствующий пересчет по числам циклов N
(разд. 17).
Аналогичные усталостные испытания при регулярном и
программном нагружении были проведены с использованием
нормального и равномерного распределения амплитуд напряжений на
базе 5-Ю8 циклов. Первичная и вторичные кривые усталости
представлены на рис. 5.6. Из рисунка видно, что и в этих случаях
вторичные^кривые усталости асимтотически приближаются к
горизонтальной ветви первичной кривой, причем расчетные
долговечности по уравнениям E.32)—E.34) удовлетворительно
соответствуют опытным значениям (расхождения не превышают
2-кратных). Последнее подтверждается также значениями сумм
относительных долговечностей, полученных экспериментально (аэ) и
расчетом (Ор) по формуле E:33), представленных в табл. 5.2.
Из табл. 5.2 видно, что Ор и аэ зависят от вида распределения
амплитуд напряжений; для экспоненциального распределения
ар — 0,12-^-0,30 (в среднем 0,2), для нормального ар = 0,2-=-
-Я),6 (в среднем 0,4), для равномерного ар = 0,26-^0,92 (в
среднем —0,6). Указанные осредненные значения ар могут
использоваться в приближенных
расчетах долговечности.
В дальнейшем (разд. 18)
предлагается также метод
суммирования усталостных
повреждений при нерегулярном
нагружении, основанный на учете
постепенного снижения предела
выносливости вследствие
предварительного циклического на-
гружения. В качестве примера
на рис. 5.7 [25] представлены
экспериментальные данные ряда
авторов, характеризующие
снижение предела выносливости
вследствие предварительного
циклического нагружения при
6,кгс/'имг
Рис. 5.6. Первичная A) и вторичные
B и 2', 3, 3') кривые усталости 2, 3 —
нормальное распределение; 2', 3' —
равномерное распределение; 2, 2' —
экспериментальные кривые; 3, 3' —
расчетные кривые
177
У =
о
0,1
М
0,6
о, в
6.
1UCX
-6.
■ 1 ПОВ
-1 исх
^
^
6н
6-1 исх
1 7,/
^Ччц4 ',2
XI»
■=',s
амплитуде сгн до числа циклов пи
(число циклов до разрушения
по исходной кривой усталости
при амплитуде сгн составляет NH).
По оси ординат отложены значе-
i/=l
-) где сг_1пов,
и-з исх
пределы выносливости
(циклическим
исходного ме-
0,2
ОЛ
0,6
0,8 С =
Ни
ния
'-'-l исх '
поврежденного
нагружением) и
талла.
Линии на рис. 5.7
рассчитаны по уравнению, которое
является частным случаем
уравнения, предложенного С. В. Серен-
сеном [58],
от с для сред-
Рис. 5.7. Зависимость
неуглеродистых сталей.
Примечание. Прямые рассчитаны по
уравнению E.38) при К. = 1,65.
а
хК-
: = СТ
Сн
"О]
X
E.38)
Здесь К — параметр уравнения, характеризующий интенсивность
снижения предела выносливости вследствие циклических
перегрузок.
Таким образом, для среднеуглеродистых сталей в
соответствии с опытными данными рис. 5.7 можно принять К = 1,65.
Аналогично найдено значение для малоуглеродистых сталей
К = 1,33, для легированных К = 1,80 [25].
Таблица 5.2
Экспериментальные аэ и расчетные ар значения сумм
относительных долговечностей при программных испытаниях
на базе 5-Ю8 циклов
°а max
G-1
2,0
1,5
1,3
1,2
1,15
1,10
1,05
1,02
Закон распределения амплитуд
экспоненциальный
йэ
0,13
0,29
0,14
0,2!
аР
0,13
0,30
0,23
0,19
нормальный
аэ
0,55
0,40
0,29
аР
0,31
0,26
; 0,23
1
1
равномерный
аэ
0,92
0,71
0,26
0,28
0,29
Р
0,50
0,49
0,35
0,51
0,48
Важное значение для выявления закономерностей накопления
усталостных повреждений, апробирования методов
схематизации случайных процессов изменения напряжений (см. разд. 11)
и гипотез накопления повреждений имеют результаты
усталостных испытаний при случайном нагружении. Обзоры
соответствующих исследований приведены в работах [77-^-79, 59, 92, 93].
Ряд указанных исследований проводился на
электродинамических или электромагнитных вибраторах без обратной связи
и без надлежащей стабилизации параметров случайного процесса,
поэтому результаты этих исследований не могут считаться вполне
достоверными. Появление электрогидравлических машин с
обратной связью позволило проводить усталостные испытания при
случайном нагружении с обеспечением заданных параметров
процесса и его стационарности. Однако соответствующих
результатов имеется пока ограниченное количество. Рассмотрим в
качестве примера результаты работы Пфайфера [93], в которой
при регулярном и случайном нагружении испытывались на
электрогидравлической машине с обратной связью при растяжении-
сжатии плоские образцы с надрезами (а0 = 2,44) из трех типов
углеродистых сталей. На рис. 5.8 представлены четыре типа
использованных при испытании случайных процессов,
характеризующихся различными значениями г ил. Здесь г —
коэффициент корреляции между минимумами и непосредственно
следующими за ними максимумами процесса [55], получающийся при
статистической обработке данных, представленных в
корреляционной таблице (см. рис. 4.6); i — фактор нерегулярности
процесса (обозначение и название по данным работы [93]),
представляющий собой отношение среднего числа пересечения процессом
нулевой линии к среднему числу экстремумов [величина i
совпадает с к, определяемой соотношением D.40) ]. Процесс F1 является
узкополосным процессом, для которого все методы схематиза-
■ ции дают практически одинаковые результаты; процесс F4 — -
достаточно широкополосен, процессы F2 и F3 имеют
промежуточный характер. Применяли схематизацию процесса' по методу
экстремумов. Распределение экстремумов, максимумов и
минимумов процессов было близким к нормальному.
F3,r=*0,4-6; 1 = 0,48;
F1,r=-0,98; 1*0,99;
FZ, р = ->-0,15; i=0,7Z;
#У w^^^^^W^^v^
FV, f =+0,80:1=0,4-5
Рис. 5.8. Реализации четырех типов случайных процессов, применявшихся
при усталостных испытаниях
179
40
30
20
IS
12
W
N
4
N
ч
7s
V
\
I
\-i
i
V.
4
6
*4
&g.
i
На рис. 5.9 представлены
первичная (линия 5), а
также вторичные кривые
усталости при программном
блочном нагружении (линия 6) и
при случайном нагружении
(линии /—4). Кривые
соответствуют вероятности
разрушения 50%. Функцию
распределения амплитуд на- -
пряжений при программном
нагружении получали путем
ступенчатой аппроксимации
распределения амплитуд,
найденного с использованием
схематизации случайных
процессов методом экстремумов (см. разд. 11).
Суммы относительных долговечностей, подсчитанные по
формуле линейного суммирования E.32) применительно к
результатам программных испытаний (по линии 6), изменялись в пределах
а = 0,6-ь0,8. Из рис. 5.9 следует, что долговечности при
случайном нагружении с узкополосным процессом (линия /) Ыслуч ■—•
получились в 4 раза меньшими, чем при программном нагружении
Л^прогр при той же функции распределения амплитуд напряжений.
Для учета этой разницы в работе [93 ] вводится фактор
»я = "^2г- E-39)
W* 2 5 W5 2 5 10s 2 5 107 N;NCyM
Рис. 5.9. Первичная E) и вторичные
кривые усталости при случайном (/, 2, 3, 4)
и программном F) нагружениях [93];
П р и м е ч а н и е. 1 — F1; 2 — F2; 3 — F3;
4 — F4
"прогр
Для узкополосного процесса (F1) величины aR для трех ти-
1 1
пов испытанных сталей изменялись в пределах aR = -^- -=- -^ —
= 0,2-Н),263. Таким образом, экспериментальные значения аэ
для испытаний при случайном нагружении с узкополосным
процессом получаются равными аэ = aRa = @,2-^-0,263) -@,6-=-0,8) =
= 0,12-Ю,21, что подтверждает существенное значение
корректировки линейной гипотезы. Аналогичные результаты получены
в работе [773, в которой найдены значения aR = 0,16-Ю,25.
Из рис. 5.9 видно, что с увеличением широкополосности
(снижении i) при переходе от линии / к линии 4 фактор aR
приближается к единице, т. е. вторичная кривая при случайном
нагружении приближается к соответствующей кривой при
программном нагружении. Такой характер расположения линий / — 4
связан с тем, что при одинаковом распределении экстремумов
процесса узкополосный процесс F1 является более
повреждающим, чем широкополосный F4, что пояснялось в разд. 11 при
рассмотрении метода максимумов.
Однако у Линсли и Хиллберри [92] получилось практическое
совпадение усталостных долговечностей для двух процессов с раз-
180
личной широкополосностью при трех значениях дисперсии процесса,
но при совпадающих функциях распределения экстремумов.
Поэтому вопрос о накоплении повреждений при случайном на-
гружении процессами различной широкополосности требует
дальнейшего изучения с целью апробирования методов схематизации
случайных процессов и гипотез накопления повреждений при
расчетах на усталость в случае широкополосных процессов. Тем
не менее, уже накопленные результаты испытаний при случайном
нагружении [77—79, 93] показывают, что переход от
программного к случайному нагружению приводит к дополнительному 4—6-
кратному снижению долговечности при той же функции
распределения амплитуд напряжений, что требует "обязательной
корректировки линейной гипотезы. Указанная-^корректировка может
быть достигнута использованием уравнений E.32)—E.34).
\-fi Возможно также использование количественной трактовки
накопления повреждений, предложенной О. Ф. Трофимовым [591
и основанной на сопоставлении энергетической структуры
случайных процессов. Эта трактовка приводит к следующему
соотношению долговечностей двух процессов при их равной дисперсии:
JL JL .L
Г ^ / mj \ 2 ( д« \ 2 я0* / 1 - е! \ 2 E,40)
Г* \т2 ) \mi ) п0 \ 1 — е2 ) '
где тк= akS(a)da—моменты спектра; 8= 1/1'— (~) — па"
о
раметр широкополосности процесса; п0, пх — число нулей и
максимумов процесса.
Экспериментальная проверка этого соотношения на
электрогидравлической машине «Щенк» с обратной связью при испытании
образцов из различных материалов с различными процессами (по
степени широкополосности, виду распределения, дисперсии)
подтвердила применимость этого соотношения [59].
1.6. Вероятностные методы расчета
на прочность
при нагрузках, переменных во времени
Так как нагрузки в условиях эксплуатации носят, как
правило, случайный характер, а характеристики
сопротивления-усталости являются случайными величинами, то трактовка условий
прочности должна основываться на вероятностных
представлениях. Ниже изложены вероятностные методы расчета деталей
машин и элементов механических систем на усталость при много-
цикловом|нагружении Н23, 24, 34, 52]. Особенностью
описываемых далее методов является то, что расчет заканчивают определе-
18 1
нием функции распределения ресурса детали, выражающей связь
между ресурсом и вероятностью разрушения. Эта функция
является характеристикой надежности и долговечности детали и
необходима при решении таких важных задач, как определение
среднего и гарантийного (Y-процентного) ресурса, обоснование
сроков профилактических осмотров и ремонтов, планирование
объема выпуска запасных частей и т. д. Эти методы широко
используют в автомобильном, тракторном, сельскохозяйственном,
строительно-дорожном, металлургическом, транспортном,
авиационном машиностроении и в других отраслях [6, 7, 23, 24, 33,
34, 40, 52, 59, 62]. Опыт применения этих методов показал их
эффективность и перспективность.
Вероятностные методы расчета на прочность эффективны и
могут рассматриваться и применяться как нормативные при
требуемой вероятности безотказной работы Рт < 0,99-М),999. При
Рт > 0,999 вследствие ограниченной информации о нагрузках
и прочности нормативные расчеты на прочность целесообразно
строить на основе нормирования допустимых значений
коэффициентов запаса прочности, вычисляемых с учетом рассеяния
характеристик нагруженности и прочности. Вероятностные методы
расчета на прочность в этом случае могут быть использованы для
обоснования нормативных значений коэффициентов запаса.
Расчет на прочность при регулярной
переменной нагруоюенности
Вероятностная трактовка условий прочности деталей машин
и элементов конструкций при регулярной переменной
напряженности основывается на статистической оценке возможных
случайных отклонений амплитуды переменных напряжений и величины
предела выносливости или его значений, ограниченных по числу
циклов, если рассматриваются условия прочности для данного
ресурса по числу циклов [55].
Случайные отклонения амплитуды регулярной переменной
напряженности деталей порождаются как случайными
нарушениями режима работы, связанными с воздействием регулирующих
и управляющих данной машиной систем (флуктуации мощности,
числа оборотов, технологических сопротивлений- и т. д.), так и
случайными отклонениями нагруженности одинаковых деталей
машин вследствие производственных и эксплуатационных
влияний (допуска на точность изготовления, частотной отстройки,
регулировки, вариации в условиях нагруженности деталей
стационарно работающих машин данного типа, поставленных в разные
эксплуатационные условия по используемым мощностям, изно-
сам, режимам ремонта и т. д.).
Расчет вероятности разрушения по напряжениям наиболее
просто получается при использовании нормального закона рас-
182
пределения пределов выносливости и амплитуд напряжений.
Условием разрушения в этом случае будет соотношение
М = а_1я-аа<0. E.41)
Если ст_1д и аа распределены нормально и некоррелированы,
то согласно известным положениям теории вероятностей М также
распределена нормально с параметрами (М, 5М), где среднее
значение М и стандартное отклонение 5М определяются
соответственно соотношениями
М = о_1я-оа; E.42)
S3k = S5_M + S&e. E.43)
Выражение E.43) справедливо при некоррелированности
величин а_1д и аа. Значение М, отвечающее некоторой вероятности Р,
определяют из выражения МР = М + г;Р5м, где иР —
квантиль, отвечающий вероятности Р. Значение М = 0
разграничивает области отрицательных и положительных величин М, так
что вероятность разрушения определяется из условия
МР = Ж + «р5м = 0. E.44)
Из уравнений E.42), E.43), E.44) находим,
М
-1Д •
5м iAc2 , оя
VSKK + S°a
E.45)
Назовем п = о_1р1аа условным коэффициентом запаса
прочности по средним значениям.
Тогда
иР= г Х~п=, E.46)
где
У*_1Д = 5а_1Д/а_1д; o„a = Sffa/aa.
Соотношение, подобное E.46), использовал А. Р. Ржаницын
[48] при статическом расчете на прочность конструкций.
Зная коэффициенты va , v0a и п по уравнениюE.46), можно
определить квантиль иР, по которому, по таблицам нормального
распределения [5], находится вероятность разрушения Р.
Зависимость квантилей иР и соответствующих им
вероятностей разрушения Р (%) от п. и vaa для va_x = 0,04 и 0,08,
построенная по уравнению E.46), показана на рис. 5.10.
В случае каких-либо других законов распределения а_1д и
аа вычисление вероятности разрушения можно произвести
следующим образом. Вероятность разрушения, эквивалентная
вероятности осуществления неравенства а_1д — аа < 0, находится
183
р,%
на основе известного соот-
10-о ношения теории вероятно-
Щ_1д-$ стей, связанного с
функцией распределения разности
двух случайных величин (с
учетом реальных пределов
J-10~1 изменения величин z = с_1д
■' и у = аа) [11]:
разр
= P(z-y<0) =
1,0 1,5 1,0 2,5 3,0 3,5 п
= J Шфг0/)^,E-47)
—-со
где 1У (у) — плотность
распределения величины у =сха;
Фг (у) — интегральная
функция распределения величины
г = а_1д, взятая при значе-
Рис. 5.10. Диаграмма для определения нии z = у = Ga, т. е.
вероятности разрушения: а
Vi = °'04; Vi = °'08
Фг(У) = ФгЫ=\ L(t)dZ.
Здесь fz (z) — плотность распределения величины г = а_1д.
Вычисление интеграла E.47) удобнее производить численным
способом, как показано далее на примере.
Пример вычисления вероятности разрушения. Пусть амплитуды
эксплуатационных напряжений для данной детали в процессе работы не меняются, но на
совокупности всех деталей амплитуды распределены нормально со средним
значением аа = 9,3 кгс/мм2 и коэффициентом вариации %а = 0,3. Распределение
пределов выносливости деталей на основании экспериментальных данных примем
логарифмически нормальным с нижней пороговой границей и = 26,3 кгс/мм2,
т. е. будем считать, что величину х = lg (ст_1Да(У — и) распределена нормально
со средним значением х = lg (а11Яа-а — ") и стандартным отклонением S =
= 0,07. Здесь о"_1д = 18,6 кгс/мм3 — медианное значение предела выносливости
детали в номинальных напряжениях (соответствующее вероятности разрушения
Р = 50%). с% = 2—теоретический коэффициент концентрации напряжений.
Вычисления сведены в табл. 5.3. В 1-й и 2-й графах приведены значения
квантилей upi и соответствующих им значений плотностей вероятностей f {upi),
выписанные из таблиц нормального закона распределения [5]. Значения —=—
Ста
C-я графа) получаются по очевидному соотношению
о~ог
= !+«=
Для определения значения Фг (у) = Ф (u'pi) найдем квантиль upi из
следующего выражения:
lg (oi,i„aff — и) = lg G_1даа — «) + u'pt S^ E-48)
184
со
СО
t-
■чр
СО
(М
о
о
3
*^~s
•&
а
-~^
ч а.
^
•&
v £
а
V.
ъо
V.
а
1»
^•~
о
3
сС
a
.„
со
о
о
о
о
со
1
о
со
in^
см"
о
со
ю.
1
а>
со
о
1
оо
•^
о
см
t>-
(М
1
о
а>
со
°i
см"
•*
см
-
см
о
см
о
«
i
о
со
■*.
о
(^
СП
см
1
оо
о
см
о
1
см
со
о
оо
IS.
м
1
о
оо
ю
со
со
см
см
1П
о
оо
in
см
Si
ок
о"
о
о
о
см
1
о
■*
1—1
9
1
см
t~-
о
-*
оо
w
1
О
см
а>
t--"
оо
см
со
о
ts.
•*
in
•*
со
см
о"
оо
in
7
_
оо
о
о
.1
со
со
о
о
ст>
«
j
о
со
■#
•*"
о
со
•*
о
см
[~-
t~-
оо
со
см
со_
о"
[~-
1П
■*
о
1
см
со
о
о
1
со
а>
о
со
о
W
1
о
со
со_
см"
см
со
in
о
ю
со
о
о
о
ю
о"
о
о
о
о
о
о
о
о
о
о
см
о
см
W
I
о
со
CN_
•*
со
со
о
со
*ч
со"
ю
см
со
1П
о"
см
оо
о
о
[-■
ю
о
о
-*
оо
о
см
т*
ь
см
СО
СО
со
[-■
о
1П
со
см
со
со
о
а>
о"
о
см
со
со
а>
о
о
•*
см
•*
1—1
см
^1
1
о
см
а>
см"
оо
со
оо
о
а>
см
а>
■*
со
а>
о"
о
со
о
со
о
in
со
о
см
см
^1
ь
•*
со_
о
•*
а>
•*
со
ю
о
со
а>
со
°i
о"
о
со
СМ
_ч
со
о
ю
•*
со
см
СМ
ю
1
О
а>
in
°i
^f"
о
ст> о
-* о
см —■
о" о"
t~- см
со а>
СП СГ>
а> а>
о" о"
см •*
i> —_
см" со
§ см
— см
о о
1Л СО
Ю СО
см оо
со со
см см
ю ю
1 1
О О
ю о
см —*
•* со
•* •*
— см
о
•*
о
о
оо
СП
ст>
°1
о"
см
LO
со
со
■*
°1
сГ
со
[~-
•*
•ф
см
to
1
о
о_
*ф
со
•*
со
in
о
о
а>
а>
СП
°\.
о"
а>
оо
со
см
г~
см
о
t~-
со
о
in
см
to
[
о
ю
о
in
•*
1
о
со
со
"Я.
а>"
см
II
2
■&
^—-^
^
**■—
W
185
откуда
црг = -4-'е = 1дК°~~"- E.49)
^ ст_1Дс%—и
Так как значение интегральной функции распределения Фг (у) следует.взять
при у = aai, то в выражении E.49) вместо ст_1Д следует подставить ста,-, в
результате чего получим
где
aaiaa — U 0а Ста ,ст
rt = щ— = . E.50)
ct_i пап- — и
СТа
Здесь принято
ст_1Д __ 18,6 и _ 26,3 _
—— —-Q-s- = i, q-5- — 2,84.
СТа y>d Ста y>d
Oal
Таким образом, имеем при принятых исходных данных: г; = 1,725 -z~ 2,45.
Ста
По этому выражению найдены значения, приведенные в 4-м столбце. Далее
определяются значения lg rt- и и'р[ = ' (столбцы 5 и 6-й) и по таблице нормального
закона распределения находятся значения интегральной функции
распределения Ф ("р;)- В 8-м столбце вычислены произведения f (upi) Ф (u'pi)- Суммируя их
по г", находим
Sf("p;H("p;) = 29>535-10-
i
Вероятность разрушения определяем из уравнения
00
J 0<га Ста «а ;
О
В результате получаем
0,06
0,3
рразР = -7Г7Г- 29,535-Ю-4 = 5,91 ■ 10"
АСТа
( _ " =0,06, что следует из 3-го столбца табл. 5.3]
\ Ста /*
При работе деталей в условиях коррозии (в воде или даже во
влажной атмосфере) и повышенной температуры (для деталей из
легких сплавов и высокопрочных сталей — при любых условиях
работы) кривая усталости при регулярном нагружении не имеет
горизонтального участка, соответствующего неограниченной
выносливости, а имеет все время ниспадающий характер. В этих
186
случаях кривую усталости можно аппроксимировать двумя
прямыми линиями в двойных логарифмических координатах,
имеющими уравнения
o1\ANN = <£1ддг0ЛГо при а_1Д^ а_1д#0; J
o!\rNN = al\ANaN0 при o_iAiV < o_Wo. J
Здесь ст_1дЛг и (Т_1длг0 — пределы ограниченной выносливости
натурной детали, соответствующие числам циклов N и N0,
соответственно, где N — текущее значение, NQ — число циклов,
соответствующее точке перелома кривой усталости; тг, т2 —
соответственно показатели углов наклона верхней и нижней ветвей
кривой усталости.
Если режим работы регулярный со случайной амплитудой оа,
которая не изменяется во времени, то вероятность того, что
деталь не разрушится до числа циклов N, равна вероятности того,
что аа < g_1rN или М = аа — а_1дЛг < 0.
Рассуждая так же, как при выводе уравнения E.46),
получаем, что квантиль нормального распределения, соответствующий
вероятности разрушения Р до числа циклов N, выражается
формулой
up = / (N) = ,^. 'Г"" , E.53)
lfv% +n\Tv% '
(/ аа т N a-mN
где с учетом уравнении кривых усталости
1
а
пы
nN
1P.N
Оа
п^[~Ж) ПРИ N^>N*
= ^==^(*Г при N<N0;
E.54)
"iV„ =
а -,
ДЛ^о
E.55)
Полученная формула для иР дает возможность рассчитать
функцию распределения ресурса детали, т. е. зависимость
вероятности разрушения Р от ресурса детали, выраженного числом
циклов нагружения детали за срок службы N.
Так как испытаний на усталость в вероятностном аспекте
при базах N > NQ = B-=-4) 106 циклов проводилось крайне мало,
можно в первом приближении принять va_lRN£i va N при N >N0.
Рассмотрим теперь случай плоского напряженного состояния
с нормальным напряжением а и касательным напряжением т
(например, сочетание изгиба и кручения вала) при синхронном
и синфазном изменении этих компонентов. Как известно (см.
j 87
разд. 5), условие прочности в этом случае может быть выражено
уравнением
]/"^ + й2т' = а_1д, E.56)
где ф
/г =
ст.
1Д
Условие разрушения можно представить в виде
М = а_1Д — Y<& + kSl < 0. E.57)
Величины а_1д, ха, аа являются случайными. Предположим,
что они распределены по нормальному закону со средними
значениями а_1д, аа, ха и средними квадратическими отклонениями
^<y_i > S°a' S*a соответственно. Коэффициенты вариации величин
равны
Ъ№ = Ы, %а = Ь-; ща = Ь-. E.58)
-1Д СТ_1Д а СТд а Ха
Величина k обычно меняется незначительно, вследствие чего
пренебрежем ее рассеянием для металла данной марки и примем
ее как детерминированную величину.
Если рабочие напряжения изменяются по асимметричному
циклу, то в качестве аа и ха следует принимать амплитуды,
эквивалентные по своему действию амплитудам симметричного цикла
[см. E.8)]:
°а эк == °а ~\- 'фо-дО'т'
Та эк = та ~Т г1'тдтт> E.59)
где -фад, я|5тд •— коэффициенты влияния асимметрии цикла,
определение которых пояснено в разд. 3.
На основании известных формул теории вероятностей среднее
значение М и дисперсия 5м величины М могут быть найдены по
приближенным формулам в предположении некоррелированности
аргументов, от которых зависит М:
М = о_1Д — ]Лта + k^xl;
s^\™LTsl + \^-Tsl + \^]2sl ] E'60)
L da_1A Jo -1Д ' L daa Jo "a r [ dxa Jo «
Индекс «ноль» у квадратных скобок обозначает, что
производные берутся при средних значениях аргументов.
В предположении нормальности распределения величины М
с параметрами М и 5М получим значение М, соответствующее
вероятности Р:
MP=M + uPSn. E.61)
Приравнивая МР = 0 и введя обозначения
na = ^is-; пх = ±&-, E.62)
получаем с учетом выражений E.56), E.57), E.58), E.60) квантиль
нормального распределения иР, соответствующий вероятности
разрушения Р (%):
V 4 + А
E.63)
Если £ детали возникают только одни нормальные
напряжения, т. е. %а = 0 и пх = оо, то формула E.63) превращается в
прежнюю формулу E.46) для иР.
Формула E.63) получена в предположении, что кривые
усталости как по нормальным, так и по касательным напряжениям
имеют горизонтальные участки, соответствующие неограниченной
долговечности, что можно принять для конструкционных сталей
с ав < 150 кгс/мм2 при работе на воздухе при нормальной
температуре. В других случаях кривые усталости можно
аппроксимировать двумя наклонными линиями в двойных логарифмических
координатах для нормальных и касательных напряжений:
«О&Л = а^ NM при N < N0a, E.64)
el?ANN = o^.tfoa при N > N0a, E.65)
■C&ff - *3bA при N < ^ E-66)
^ГдлД = т^Л^ при N > Л^. E.67)
Здесь величины ти т2, N0 приняты в общем случае разными
для нормальных и касательных напряжений, в связи с чем введены
дополнительные индексы а и т у них. Однако существенное
упрощение расчета получается в случае Noa = N^ = NQ, что
подтверждается также и экспериментальными данными.
189
В этом случае рассуждая так же, как и при выводе уравнений
E.53), E.63), получаем
"l/l
ON ,lxN
ON
i + -F
2
noN
lxN
1
и2 »2
1 + 2
E.68)
где
'■ON '
Q-irN
Oa
ll<sNo
N )
lxN ■
No
nr», = 1fZ- = ntlfa[jfrV"«
„ _ СГ-1ДЛГ __
'«■irw = — "-(Wo
'■ON ■
HN-
^ Т-1ДЛГ __
Та
iV
^olf)m";
при Л/ > Л/'о E.69)
i
при N < /V0 E.70)
^(ГЛГ,
__ СГ-1Д iVp
Ста
птЛГ0 —
Т-1Д iVo
E.71)
В уравнении E.68) величина иР, а следовательно, и
вероятность разрушения зависят от числа циклов нагружения за срок
службы N, вследствие чего может быть построена функция
распределения ресурса детали.
Расчет на прочность при нерегулярной погруженности
по корректированной линейной гипотезе
суммирования повреждений
Расчет на усталость при нерегулярной переменной нагружен-
ности удобно вести, используя понятие вторичной кривой
усталости, представленной, например, на рис. 5.4 и 5.6. Применяя те или
иные гипотезы накопления повреждений при нерегулярном нагру-
жении, можно построить вторичные кривые усталости расчетным
путем.
Подсчет ресурса по корректированной линейной гипотезе
суммирования усталостных повреждений сводится, как известно
[52], к подсчету числа блоков нагружения % до появления
трещины по формуле E.20) и вычислению ар по формуле E.33).
190
Уравнения E.20), E.32)—E.34) справедливы в том случае, когда
кривая усталости имеет горизонтальный участок, соответствующий
пределу выносливости детали. Однако при работе деталей в
условиях коррозии и повышенной температуры (для деталей из легких
сплавов и высокопрочных легированных сталей при ав >
> 150 кгс/мм2 — даже при нормальной температуре и отсутствии
коррозии) кривая усталости не имеет горизонтального участка,
ее характер ниспадающий. Для простоты расчетов такие кривые
усталости можно схематизировать двумя прямыми линиями в
двойных логарифмических координатах. Эти линии пересекаются
в точке с координатами lg N0, lg а_]д#0, где o_1rNo — предел
ограниченной выносливости, соответствующий числу циклов N0
(абсцисса точки перелома кривой усталости). Уравнение
указанной кривой усталости можно записать в форме [см. формулу B.11)]
. « = <йд*.*0 ПРИ °at > '«-UN.' E-72)
aZ?Ni = <S1\rn0N0 при .aat < <г-1длг„. E.73)
Условие прочности по-корректированной линейной гипотезе
в этом случае имеет вид
S "$7 + ' 2 Ж = ар ПрИ °a™*>a-^»;E-74)
ieai > о_1д No) (<rat- < <т_1д n0)
~ = ар при сгашах < a_iANo. E.75)
Ni
Подставляя в выражение E.75) nt = %vl6 и Nh найденное из
уравнений кривой усталости, получаем
. _Я_
+ ~^7 2j ^N«1 = aP при (ramax> (Г_1д^0; E.76)
-bw. «та(.<<г_1дЛ,о)
т2
£ а>гб+
^o0^f„jv
cC2v«5 = aP при аатах<а__1дЛ?0- E.77).
о (<Т„,<<Т_
Из этих выражений может быть найден ресурс детали по
условию усталостного сопротивления, выраженный числом блоков до
разрушения К.
Так как в рассматриваемом случае все амплитуды напряжений
являются повреждающими, то в формуле E.33) следует принять
ka — 0, в результате чего получаем
г
аР = ^=У1Тз£~^ E-78)
r i=J <J<z шах
1=1
191
При подсчете ар в данном случае принимают во внимание все
амплитуды в блоке нагружения без отбрасывания малых значений.
Формулы E.74)—E.78) соответствуют функции распределения
амплитуд напряжений, заданной в дискретной ступенчатой форме.
Функция распределения амплитуд напряжения может быть
задана и в непрерывной форме, например в виде плотности
вероятности распределения амплитуд / (аа) в сочетании с числом циклов
действия всех амплитуд в блоке нагружения v6 или суммарным
числом всех амплитуд за срок эксплуатации NcyM = Xv6, где как
и раньше, X — количество блоков нагружения за срок
эксплуатации до появления усталостного повреждения.
Количество циклов действия амплитуд, лежащих в интервале
от аа до аа + daa, за срок службы
dn = уйЦ (аа) doa. E.79)
Условие прочности по корректированной линейной гипотезе
суммирования усталостных повреждений в этом случае имеет вид
аа max °-1Д N0
1 ¥" + 1 "F = aP ПРИ аатах><идлг0; E-80)
| ~Т =GP ПРИ °аша<^-±ЛЫа- E-81)
О
С учетом выражений E.72)—E.73) и E.79) из уравнения E.80)
получим
°а max
1
No
-1Д No
} о?'/(оаLг„ +
1
-1д#о
Xv6
J <fi*Hpa)doa
= Op при aamax> aliAAT0; E.82)
/Voo?
1Д^о 0
: шал.
| Oa'f (<Ja) doa = ap при oaшах<<Т-1Длг„, E.83)
где
} oJ{aa)daa. E.84)
Здесь аашах — максимальная амплитуда, которая ограничивает
интервал учитываемых в расчете на усталость амплитуд
(амплитуды <ха > аа max не учитывают в расчете на усталость, но они имеют
существенное значение для расчета на прочность при возможных
192
перегрузках весьма малой кратности, т. е. расчета,
выполняемого по критериям прочности при однократном нагружении).
Если эмпирическая функция распределения амплитуд
аппроксимирована каким-либо теоретическим законом распределения,
например нормальным, экспоненциальным, рэлеевским и т. д., то
формально аашах = оо. Однако на практике амплитуды
напряжений ограничены некоторым предельным значением, определяемым
или предохранительными устройствами (предельными муфтами,
штифтами и т. п.) или какими-либо другими факторами,
связанными с работой машины. С другой стороны, предельное значение
аашах может устанавливаться из самого расчета на усталость, как
величина, удовлетворяющая условию, что амплитуды аа >'<ташах
практически не вносят усталостного повреждения вследствие
малого количества их повторений.
Уравнение E.82) соответствует случаю кривой усталости без
горизонтального участка в форме E.72)—E.73). Если кривая
усталости имеет горизонтальный участок, то второе слагаемое в
квадратных скобках в уравнении E.82) обращается в нуль, так как
в этом случае числа циклов по кривой усталости N = со. В
результате имеем
°а max
_U6_ J ^(„j^»^, E.85)
""=» «->»
где
а = °а шах^ ^-чл /5 85)
Р Оа шах — kaQ_m ' \ ■ I
£=-т^ f <yaf(<ya)daa. E.87)
лоа шах J
Здесь
А= J f(oa)daa E.88)
— нормирующий множитель.
Если функции распределения амплитуд напряжений
аппроксимированы какими-либо теоретическими законами распределения,
то интегралы, входящие в выражения E.82)—E.88), могут быть
выражены [4] через табулированную функцию интеграла
вероятностей %2 [5]:
Р{х. п) =-й-1 \ У2 е 2 *УШ> E-89)
193
Интеграл, входящий в правую часть равенства E.89), может
быть выражен так:
J у2 е 2 dy = 2ф (ft) Р (х, п),
E.90)
гдеф(п) = 22 Т(И-\ • Г (а) — гамма-функция Эйлера [5].
Значения г|э (ft) могут быть найдены по формулам
4>(я) =
(п — 2)!! 1/ у при нечетном п\
— 1I при четном ft.
22' V-^
2
E.91)
Здесь (ft - 2) !!= 1 -3-5 ... (ft - 4) (ft — 2);
гИ1) = гИЗ)= j/|; *B)=1; фD) = 2; ф E) = 3 |/-J и т. д.
Покажем, как вычисляются интегралы, входящие в равенство
E.82), на примере распределения амплитуд по закону Рэлея:
/>«) =
"# еХр V 2^"/ ПРИ а° > °'
0 при ста < 0.
Вычислим интеграл с заменой переменной:
а| J. sa
-трг =■ г/; оа = Sy2; oadea= — dy;
оо со
} а?/ (Сто) ^ста = } ст'ап -^f- ехр (— ^ ) daа =
E.92)
-Y J г/2 е 2 dr/.
a2/S2
E.93)
Сопоставляя выражение E.93) с E.90), находим п = т + 2.
Следовательно,
со
J <#/ К) йста = ^ 2ф (т + 2) Р (J, m + 2) . E.94)
а
Имея в виду, что
Ь со со
J f(x)dx=j f (x) dx — J / (x) dx,
194
получаем для закона Релея при аашах > сг_1дЛг0 («р > 1)
N,
где
f(m2+2)ft;?
6 = ^
&2
я„
р
1-Р
, т2 + 2 -/>(&■,/^ + 2)
, щ-\-'2
= а
р>
E.95)
Од шах
а_
1Д^о
При аашах < а_1дл/0 («р < 1) на основании выражения E.83)
имеем
A.V6 i(nv\m'
No
{(^)% К + 2) [1 - Р (б2, т2 + 1)]} = flp. E.96)
Уравнение E.95) по существу представляет собой уравнение
вторичной кривой усталости в относительных координатах ftp —
— -^сум, соответствующей первичной кривой в форме E.72), E.73),
ибо оно может быть представлено (с учетом Kv6 = NcyM) при
Ga max > <7_1ДЛГ0 («р > 1) В ВИДе
м
сум
Nn
= с
Л И+ 2)
р
1-Р
+
E.97)
P\j> m1 + 2j-PF2,m1 + 2)
ПРИ aamax < а-1дЛ/0 (ftp < 1) аналогично имеем
"/сум = «р{(?)'ПЖ + 2) [l - Р(Ь2, т, + I)]}-1. E.98)
М,
Если кривая усталости имеет горизонтальный участок, то
второе слагаемое в скобках в уравнении E.82), а следовательно, и
в фигурных скобках в выражении E.97), как уже отмечалось,
обращается в ноль (этому соответствует значение т2 — оо). В этом
. случае уравнение вторичной кривой усталости для распределения
Рэлея имеет вид
-1
М.ум_ /лрХт + 2)
= «п
P[^-,m + 2)-PFa, т + 2)
E.99)
Принимая.в уравнении E.99) ар = 1 и пренебрегая вторым
слагаемым в квадратных скобках, получаем выражение,
представляющее в других обозначениях формулу В. В. Болотина [4] для
усталостной долговечности.
Определение ар при непрерывных законах распределения
амплитуд будет рассмотрено далее.
195
Аналогичные формулы могут быть выведены и для других
законов распределения амплитуд напряжений.
Плотность вероятности экспоненциального закона
распределения амплитуд имеет вид
ехр (
0
-~\ при аа>0;
при аа<0.
/Ы = \°а ч °а ' E.100)
Уравнение вторичной кривой усталости на основании
уравнения E.82) для экспоненциального закона и первичной кривой
усталости в форме E.72)—E.73) [две наклонные прямые в двойных
логарифмических координатах] при аашах > а_1длг0 (пр > 1) имеет
вид
Ncvu /<4>Bmi+2) г Bb
^ = ап
-N7 - -р 1~ -рт,2"» fP (v 2nh + 2
//». Х
-РBЬ, 2/п1 + 2)] + -^
♦i?u±a.[l-p(|>ufIl + 2)]p E.101)
при ffamax < <?_1дд/, (ftp =^1) на основании уравнения E.83)
^-^{(трГ^(У2)[1-р^ 2^+2)Г- EЛ02)
Для кривой усталости с горизонтальным участком
^сум_ „ КЧB/И1 + 2) х
#0 "p ii«i
Г_ /2ft
X
Р(|, 2m1 + 2)->B6, 2mi+2)]J . E.103)
В уравнении E.101) принято
Оа max . 1. Оа max
я "а шах . t vg г
ff_
1WV,, аа
В уравнении E.103) <т_1длг0 заменяется на а-1д.
Иногда для описания распределения амплитуд напряжений
удобно использовать правую ветвь нормального закона.
В этом случае плотность вероятности имеет вид
0 при аа<0.
196
E.104)
Уравнение вторичной кривой усталости на основании
уравнения E.82) при первичной кривой в форме E.72)—E.73) при
оаШах > с_1длг„ («р > 1) имеет вид
j/it bm>
Na
з-' mi +
2ф(/я,+ 1)яр'
j/n б2
й2
1-Р(—,m2+l
1)-Р(Ь2, щ+1)
1
E.105)
ПРИ ^ашах < g-irn0 (пр < 1) на основании уравнения E.83)
-1
Nn
= ап
iVcyM_/y j24>(/n,+ l)V
j/x
[l-P(b\ /na+l)]
E.106)
Для первичной кривой с горизонтальным участком
М
сум
N„
= ап
2ty (т + 1) V
1/я Ь
, т+ 1 -Р (Ь2, т+1)
В уравнении E.105) принято
„ Ста max . и °а шах
СТ-1Д ЛГ„ ba
E.107)
В выражении E.107) а_1длг0 заменяется на а_1д.
Аналогичные формулы для нормального закона распределения
амплитуд получаются весьма громоздкими и неудобными для
пользования. В этих случаях интегралы следует определять
численно.
Расчет ар может быть выполнен по уравнениям, полученным
путем вычисления интегралов в уравнениях E.84), E.87) и E.88).
В результате получим -
. hi — ч
ап
bi~xu '
E.108)
где для экспоненциального закона с параметром оа
Р B*ь, 4) - р Bйс, 4) .
£ =
Ьг,{РBх0, 2)~Р Bйе, 2)]'
„ Ка<7_1д . , аа шах.
Х0 — —= , Or = ,
Оа Ста
E.109)
для распределения Рэлея с параметром S
_У^[рD.з)-р(%з)]
S~ ug[PD 2)-PD 2)]
-1Д . и CTQ шах
E.110)
197
rip
1,S
i A
1,3
12.
1,1
1,0
>\A\v
^
■
m =Z
^
^lk~
J а так
6a
к
= 11
Для распределения по
правой ветви нормального
закона
2 [Р D 2) -Р (Ь\, 2)] ^
fc u£K2S[pD i)-pF|, or
,. 1гаР~\А. и. ®а шах
JOa
=
Joa
W2
70J
Мсум/No
N,
ум
M,
ОТ
E.111)
где Saa — среднее квадрати-
ческое отклонение.
Для расчетов ka
принимается равным 0,5.
По приведенным выше
формулам могут быть
построены диаграммы для
определения коэффициентов нагру-
женности ftp в зависимости от
для различных законов распределения амплитуд напряжений.
В качестве примера на рис. 5.11 представлена зависимость пр
Рис. 5.11. Диаграмма пр для
экспоненциального распределения амплитуд
[расчет по уравнению E.103) при 6 = 12]
М
сум
М,
для экспоненциального закона распределения амплитуд
и первичной кривой усталости в форме уравнения B.9).
Из рисунка видно, что вторичные кривые усталости
асимптотически приближаются к первичным кривым. Величина
показателя наклона левой ветви кривой усталости несущественно влияет
на долговечность в области значений пр, приближающихся к
единице (в диапазоне яр < 1,14-1,2, наиболее часто встречающемся
на практике). Это позволяет не налагать повышенных требований
на точность определения т и не учитывать разброс значений т.
Причина слабого влияния т в области пр < 1,14-1,2 состоит в том,
что в этом случае амплитуды напряжений несущественно
"превышают предел выносливости детали а_1д, вследствие чего изменение
наклона левой ветви кривой усталости приводит к малому
изменению величин N, стоящих в знаменателе выражения в формуле
E.32).
Допустим теперь, что предел выносливости детали является
случайной величиной, распределенной по нормальному закону
коэффициент вариации va_l = =~1д
°-1Д ,
Пусть функция распределения амплитуд напряжений задана
парами чисел oai/aamsx, tt (i — 1, 2, ..., г), средним значением
максимальной амплитуды <хашах, числом циклов в блоке v6, а
рассеяние амплитуд напряжений характеризуется коэффициентом
вариации и8.
198
Условие прочности при заданном ЛГсум = h/6, как следует из
изложенного выше, имеет вид
gamax .-
а-1Д ,
ИЛИ
°а шах — 'V-lA ^ О.
Условие разрушения можно записать в виде
М = пР(Т_1д-аашах<0.
В силу принятых допущений М является нормально
распределенной случайной величиной, имеющей следующие выражения
для среднего значения и дисперсии:
М = Яр<Т_1„ - CTe max! E-112)
S^ = Sa +«pSa . . E.113)
"' "а шах ' Р °-1д v '
Вероятность разрушения определяется из соотношения
Mp = M + HPSM = 0, E.114)
где иР — квантиль нормального распределения, отвечающий
вероятности разрушения Р.
Подставляя выражения E.112), E.113) в уравнение E.114),
получим
_ 1—^р.
иР = — —= • п =' E.115)
5м - Г <vl
„2 , Р °-1Д
V-i-
где /г = -i-^5 отношение соеднего значения максимальной
°-1Д
амплитуды блока к медианному значению предела выносливости..
Этот коэффициент может быть назван предельным коэффициентом
нагруженности по средним. Выражение E.115) можно
представить также в следующем виде, удобном для составления номограмм
и вычислений:
иР= г *""- , E.116)
где п — —^ относительный коэффициент запаса.
Таким образом, процедура определения вероятности
разрушения при случайном нагружении сводится к следующему. По
заданным величинам ЛГсум, N0 и т по диаграмме (типа изображенных
на рис. 5.11) определяют величину пР. Далее по известным <хпП1ах,
199
С-1Д, v&, va_lA определяют значения n = статах/а_1д, п = npln
и по формуле E.116) квантиль иР, соответствующий вероятности
разрушения Р.
Расчет функции распределения ресурса по корректированной
линейной- гипотезе можно выполнить также следующим способом.
Заменяя <х_1д и оа1 в формуле E.20) их средними значениями,
находим, с учетом выражения D.44), медианный ресурс детали,
выраженный количеством километров пробега, часов работы и т. п.:
L^l^-^Щ-. EЛ17)
Величина ар находится по формуле E.33).
Пренебрегая рассеянием величин v6, ар, m, N0, можно найти
среднее квадратическое отклонение S!g L по формуле [52 ]
Slg l = SlsX = 0,434m ]Л4_1д + у2е. • E.. 118)
По величинам lg L и SigL в предположении справедливости
логарифмически нормального закона распределения ресурса
строится его функция распределения, как показано на примерах
в разд. 17.
Из формулы E.20) после элементарных преобразований с
учетом уравнения D.44) вытекает также следующее выражение для
ресурса, выраженного отношением NcyJN0:
<- У
... Y
а ) vi6
иа max/
где яр = °а шах; суммирование в знаменателе выражения E.119)
осуществляется только по амплитудам aai > <т_1д, что равносильно
условию —^—^ —. По величинам п0, наиденным в ЗаВИСИМО-
Оа шах «p p
сти от долговечности -^ по выражению E.119), по формуле E.116)
находим иР и по таблицам нормального закона распределения
вероятность разрушения Р.
На основе уравнения E.20) и метода статистических испытаний
можно учесть влияние рассеяния всех величин, входящих в
формулу E.20), на рассеяние ресурса детали.
Расчет ,на прочность при нерегулярной погруженности
методом учета снижения предела выносливости
вследствие перегрузок
В соответствии с уравнением E.38)
^»в1 = <т.111ех[1-^-^(^-1)], E.120)
200
где <т_1исх 1— предел выносливости исходного металла, не.
подвергавшегося предварительному нагружению; К — параметр
уравнения, характеризующий интенсивность снижения предела
выносливости от предварительного нагружения; N1 — число циклов по
кривой усталости^исходного металла, соответствующее амплитуде
а л-
Как показывает опыт использования уравнения E.120) в
практических расчетах для всех материалов можно принять осреднен-
ное значение К = 1,65.
В первом приближении (согласно опытным данным) можно
принять, что абсцисса точки перелома кривой усталости N0 и
показатель угла наклона левой ветви кривой усталости т не изменяются
от циклического нагружения. В этом случае при
предварительном циклическом нагружении кривая усталости будет опускаться
по вертикали без изменения наклона левой ветви в соответствии
с изменением предела выносливости согласно уравнению E.120).
Указанное явление может быть положено в основу метода
суммирования усталостных повреждений при нерегулярном
нагружении для расчета на выносливость. Примем следующие
допущения. Будем считать, что циклическое нагружение образцов, уже
поврежденных ранее, приведет к новому снижению предела
выносливости по зависимости, аналогичной уравнению E.120), т. е.
если образец нагружается циклически второй ступенью с
амплитудой аа2 и числом циклов я2, то предел выносливости металла после
воздействия двух ступеней нагружения
-1 пов 2
= 0
•-"['-^«(загт-')]"•*■
После приложения i-й степени нагружения предел
выносливости поврежденного металла
-1 ПОВ ( 0-1 ПОВ, 1-1
1-ж(^ 01- EЛ21)
iVj \ CF_X пов, l-l /J
Здесь a_ln0Bi(-_j — величина предела выносливости
поврежденного металла после приложения (i — 1)-й ступени нагружения;
Nt — число циклов по кривой усталости поврежденного металла
после приложения (i — 1)-й ступени при амплитуде аа1.
Для упрощения записей обозначим
Xi = <т_1 пов;! £/ = g °ai . =^- E.122)
0_! ПОВ, 1-1 К1-.\
Из уравнения кривой усталости
^i-^o—1- , E.123)
7 В. П. Когаев 201
С учетом указанных обозначений и выражения E.123)
уравнение E.121) приобретает вид
1-&, . E-124)
X. ,
1-1
где
Здесь принято
fi = l?{li~\). E.126)
Щ = *,#«.„, = *М, = Ь;б, ' E.127)
где iVcyM — суммарное число циклов повторения всех амплитуд
за срок службы детали; X — количество блоков нагружения за
срок службы. Примем также, что все амплитуды напряжений,
возникающих в детали за срок службы, расположены в
убывающем порядке, что может привести к погрешности в оценке
долговечности лишь в безопасную сторону (опыт расчетов показывает,
что эта погрешность мала, и ею можно пренебречь).
На основе принятых допущений и соотношений E.124)—E.126)
можно рассчитать деталь на выносливость.
Введем предельный коэффициент нагруженности
^пах^ o2L_> E.128)
«-1Д «-1Д
являющийся ординатой вторичной кривой усталости,
соответствующей заданной величине -~р* (см. рис. 5.5).
При определенном значении относительной долговечности
NcyJN0 существует такое предельное значение пр, превышение
которого приводит к разрушению до числа циклов iVcyM.
Рассчитывать предельный коэффициент нагруженности пр удобно методом
последовательных приближений (табл. 5.4).
Расчет производится для определенного закона распределения
амплитуд, заданного в ступенчатой форме в виде пар чисел4
(aai/aa mam ^)> как показано в первых трех строках табл. 5.4.
Приведенный здесь пример соответствует ступенчатой
аппроксимации экспоненциального закона распределения амплитуд. В 4-й
строке даны значения KntIN0, входящие в уравнение E.125).
В рассматриваемом примере расчет ведется для случая NcyjN0 =
= 103, т = 6; К= 1,65.
В 5-й строке даны значения
Ogj = Oai qamax= Ogi > E.129)
xo Gg max %a ®g max
202
Таблица 5.4
Данные к подсчету пр для экспоненциального распределения
амплитуд напряжений при —~^- = 103, т — 6; К = 1,65
1
2
3
4
5
6
7
8
9
10
11
■12
13
14
15
16
17
18
{
Gai/Ga max
'«
Ktit KtiNcyu
N0 N0
- /Zp
■^0 Ga max
/f = cf(c{-0
2/1 - ' • Na
1 xi
xl-l
xi xi-i %i
Xq Xq X(^i
Hi У1
Nt K&i-l)
<W*0
c<
h
Vi
l-VI
Xj_
A'q
Щ
Ni
1
1
1 -10-^
0,0165
1,3500
1
i
1,3500
I
2,1187
\
0,0350
|
1
0,9650
i
1
I
0,9650 -
<1
Яр =
1,3300
1,3300
1,8265
0,0301
0,9699
0,9699
<1
2
0,892
4-10"?
0,0660
1,35
1,2042
1,2479
\
0,9360
\
0,0618
!
1
0,9382
1
1
I
-> 0,9054
<1
1,33
1,1864
1,2232
0,7477
0,0493
0,9507
0,9221
<1
3
0,773
1,5-10-*
0,2475
1,0435
1,1525
0,3574
0,0885
0,9115
0,8253
<1
1,0281
1,1150
0,2209
0,0547
0,9453
0,8717
<1
4
0,656
6,3-10-*
1,0395
0,8856
1,0731
0,1116
0,1160
0,8840
0,7296
<1
0,8725
1,00092
0,00092
0,00096
0,99904
0,87086
<1
5
0,541
2,37-10-3
3,9105
0,7303
1,00096
0,00097
0,00378
0,99622
0,7268
>1 разр.
0,7195
0,8262
(нет
разрушения
7*
203
т. е. числа 5-й строки получаются путем умножения чисел 2-й
строки на принятое на данном этапе расчета значение п~. В 6-й
строке приведено значение £,-, входящее в выражение E.126):
Zl=s^aL==£alJ^t EЛ30)
*i-l Xi-l/X0
где значения aallxQ берутся из 5-й строки, a xt_t /xQ из 10-й строки
предыдущей графы.
Далее, в 7-й строке, приводятся значения /,-, вычисленные по
уравнению E.126), в 8-й строке у{ по зависимости E.125)
(путем умножения чисел из 4-й строки на /,-)> в 9-й' строке
х.
1 — yt = —— [согласно уравнению E.124)]. В 10-й строкепри-
xi-i
X • X. X.
ведены отношения —- = -±±—Ц как произведение чисел 9-й
Xq Xq X[_i
строки i-ой графы и 10-й строки (г — 1)-ой графе. Например, число
0,9054, стоящеев 10-йстрокеиграфег=2, получается как
произведение чисел 0,9382 (9-я строка при i = 2) и 0,9650 A0-я строка при
i = 1).
Числа 10-й строки являются отношениями предела
выносливости поврежденного металла после очередной ступени нагруже-
ния Xi к пределу выносливости исходного металла х0.
Расчет выполняют последовательно, от графы к графе, как
показано стрелками. Очередное значение £, получается путем
деления соответствующего числа из 5-й строки на число из 10-й строки
предыдущей графы. Например, число 1,2479 F-я строка при i = 2)
получается от деления числа 1,2042 E-я строка при I = 2) на число
0,9650 A0-я строка при i = 1).
При последовательном подсчете, отражающем постепенное
снижение предела выносливости, могут встретиться лишь следующие
два результата:
п.
а) при некотором значении i окажется t,i > 1, а —■ > 1, что
означает разрушение. Это видно из того, что при £г = — > 1,
Ощ > #/-i > т. е. амплитуда напряжения очередной г'-й ступени
выше предела выносливости поврежденного металла, получивше-
п,
гося после действия (i — 1)-й ступени. Если при этом -jj- > 1,
то число циклов tii действия амплитуды аа1 превышает
соответствующее число циклов по кривой усталости NI, что приводит к
разрушению.
Величины ~ вычисляются в 11-й строке по формуле
Nt
E.131)
N' Щ^-xKi K($i-1)
204
При ручном счете на малых ЭВМ величину —- можно не вы-
числять, ограничиваясь установлением факта превышения
единицы.
Данный исход получился при пр — 1,35, так как при i — 5
оказалось 1,1 = 1,00096 > 1, в то время как -J- > 1, что отвечает раз-
рушению при данном значении пр до относительного числа циклов
N,
сум
ЛГ„
103
б) при некотором-1 окажется, что £,- < 1, т. е. амплитуда
следующей f-й ступени aai оказалась меньше предела выносливости
#;_! , в результате чего дальнейшее накопление повреждений
прекращается (при наличии горизонтального участка кривой
усталости), и деталь не разрушается. Такое положение получилось
в табл. 5.4 при пр = 1,33, так как при i = 5 t,i = 0,8262, что
означает отсутствие разрушения.
Таким образом, в результате вычислений в данном случае
N,
сум .
получено, что при пр = 1,35, получается разрушение до
= 103, при ир = 1,33 — разрушение отсутствует. Следовательно,
предельное значение коэффициента нагруженности пр при
экспоненциальном распределении амплитуд, соответствующее
относительной долговечности
Л/,
сум
Nn
представленную для
= 103, может быть принято равным
1,34. Проделав указанные вычисления для различных значений
■Л'с'ум 1 1
—~ и т, можно построить диаграмму предельных коэффициентов
нагруженности пр в зависимости от —гр*,
экспоненциального закона
распределения на рис. 5.12.
Следует отметить, что
значение коэффициента К,
входящего в выражение E.120)
и характеризующего
интенсивность снижения пределов
выносливости в зависимости
от относительного числа
циклов и амплитуды начального
циклического нагружения,
по опытным данным Травно
1,33 — для малоуглеродистых
сталей; 1,65 — для сталей
средней прочности; 1,80 —
для высокопрочных сталей.
В работах [23, 24, 52]
рекомендовалось использовать эти
1,5 -
1Л
1,3
1,2
1,1
1,0
\ \Х\\Г
I I I I I ILL
^/77 = 2
i i i i, in
1 1 1 1 1 Ml
W2 2 3 45 10д 2 3 45 Wk
Nr,
сум/No
Рис. 5.12. Диаграмма гер для
экспоненциального распределения
20S
"«,-«*
L^
йГЧц,
/
«a
^^Ss
7.7
w w' wJ w*
Рис. 6.13. Диаграмма пр для нормального распределения
Нсдн/Но
10 10l WJ W4 10s NCy„IN0
Рис. 5.14. Диаграмма пр для нормального распределения
206
№
сум
значения, и диаграммы для пр строились в зависимости от N
Однако опыт расчетов показывает, что можно для всех материалов
принять осредненное значение К — 1,65, что несколько упрощает
процедуру расчета.
На рис. 5.13, 5.14, 5.15, 5.16 представлены рассчитанные
указанным образом при К — 1,65 диаграммы для пр в зависимости от
N.
сум
NB
и т Для распределений амплитуды нормального, по Рэлею
и описываемого правой ветвью нормального распределения.
Замена непрерывного распределения амплитуд ступенчатым
законом поясняется для экспоненциального распределения
рис. 5.17 и данными табл. 5.5.
Как известно, интегральная функция экспоненциального
закона распределения случайной величины оа имеет вид
ФШ
1 — ехр
О
при аа^гО;
при <га<0, ,
E.132)
где аа — параметр распределения, характеризующий значение
случайной величины аа, соответствующее вероятности Р = Ф =
= 1 = 0,632.
е
На рис. 5.17 изображена вероятностная бумага,
соответствующая экспоненциальному закону. По оси абсцисс и ординат в
равномерном масштабе (не обязательно одинаковом) отложены величины
о„
х = -=-; на второй шкале по оси ординат отложены величины
Оа
вероятности Р = Ф = 1 — е-х, соответствующие х по формуле
'Л
V
1,1
ы
ЬО
10
10'
4—лЗ
/77=70- '
l "ати
s
т=5
-¥<
пи
а
10'
"сум/Но ' г lose W3 ZUS6 ю^ г 5ts6 w%.„///a
Рис. 5.15. Диаграмма пр для распре- Рис. 5.16. Диаграмма пр для
распределения Релея деления амплитуд, описываемого
правой ветвью нормального распределения
207
Таблица 5,5
Ступенчатая аппроксимация экспоненциального закона
распределения
1
2
3
4
5
bS|it?
II
12,00
10,70
9,28
7,88
6,50
1 *
1,000
0,892
0,773
0,656
0,541
h
МО"?
-< 4-10-§
1,5-10
6,3-10
2,37-Ю-3
:б
17
|8
*9
ь8||ьа
II
5,10
3,71
2,27
0,90
—
а
Е
а
ь
0,425
0,309
0,189
0,075
li
9,Ы0-3
3,77-Ю-2
0,15
0,80
E.132). Экспоненциальный закон распределения в этих
координатах изображается прямой линией, проходящей через начало
координат. Заменяя прямую линию 9-ступенчатой функцией, как
показано на рис. 5.17, получаем ступенчатую аппроксимацию
экспоненциального распределения (табл. 5.5). Первые пять строк из
табл. 5.5 использовали в расчете пр (см. табл. 5.4).
Величины tt в табл. 5.5 получают по формуле tt = Pi+1 — Pt.
Например, tx = 1 — 0,999990 = МО; t% = 0,999990 —
— 0,999950 = 4-10 и т. д.
Аналогично осуществляется
ступенчатая аппроксимация
других законов распределения.
Сопоставление рис. 5.11 и
рис. 5.12 показывает, что
относительные долговечности NcyJNo,
соответствующие одним значе-
тированнои линейной гипотезе
и по методу учета снижения
предела выносливости, весьма
близки между собой, а также
хорошо соответствуют
экспериментальным данным. Таким
образом, оба метода учета
накопления усталостных
повреждений при нерегулярном нагру-
жении могут использоваться в
расчетах усталостной
долговечности. При использовании ЭВМ
удобнее метод учета снижения
предела выносливости, так как
он легче поддается
алгоритмизации. При непрерывных зако-
S б 7 8 9 w и к х
Рис. 5.17. Ступенчатая аппроксимация
экспоненциального закона
распределения
208
нах распределения амплитуд и ручном счете удобнее использовать
формулы типа E.97)—E.107). Функция распределения ресурса
детали по известным значениям пр находится по формуле E.116).
Расчет на прочность нерегулярной переменной
погруженности при сложном напряженном состоянии
Если в детали возникает плоское напряженное состояние
с компонентами а (нормальное напряжение) и т (касательное
напряжение), причем аит являются случайными функциями
времени, то расчет функции распределения долговечности может быть
основан на следующих предпосылках.
На основе критерия прочности при плоском напряженном
состоянии в виде эллиптической зависимости E.10) и понятия об
эквивалентном напряжении [E.22), E.24)] можно записать
Ш2+Ш2=1> EЛЗЗ)
где
apaNo<j
' Ь>бт
ЯртЛ'от
S
S
ai la
ai lT
E.134)
•*™ = Y£fcbW«- E.135)
Здесь v6, m, N0, ap, tt — величины в общем случае различные для
нормальных и касательных напряжений (поэтому введены
дополнительные индексы а и т у этих величин); X — долговечность детали
при совместном возникновении в ней нормальных и касательных
напряжений, выраженная в количестве блоков нагружения.
Обозначим Хд — долговечность детали, вычисленную при
условии, .что в ней возникают только нормальные напряжения.
Из уравнения E.20)
a jV ome
Ъ = VV" • EЛ36)
со *J ш га
В этом случае из выражений E.134) и E.136) имеем
2
Аналогично
Ш2~Шт°- <М37>
209
Подставляя выражения E.137) и E.138) в формулу E.133),
получаем
Если та и тх равны и т„ = тх — т, то из уравнения E.139)
Я = ЯстЯт д . E.140)
/ _2_ jixTT
Медианная долговечность X при сложном напряженном
состоянии определяется по формуле
U*
E.141)
2\ 2
_2_ _2\
Для подсчета дисперсии логарифма долговечности при
случайном нагружении Sig% прологарифмируем уравнение E.140) и
обозначим
lg ^ = У, Ы К = *i*. lg ?Ч '= *2->
/ _2fi_ _2*Л
Дисперсию величины г/ находим по следующей приближенной
формуле, известной из математической статистики, полагая
случайные величины хх я х2 некоррелированными:
Вычислив производные, окончательно получим
S2
\е% =
1 -
,+t£
—2 2
1 -
1 +
х\
S?eV E.142)
Величины 5fgA(j и 5fg^ находятся по уравнениям
s2lg%a- (o,434mJ D_1Д + «2Е);
■SJUT = @,434mJ К_1д + и2).
E.143)
Определив lg L = lg (W6) и 5teL = Sig*, = l/"Sfga,, можем
построить функцию распределения долговечности по уравнению
lgLP=\gL + uPSlgL.
E.144)
210
Вместо формулы _E.141) можно использовать формулу для
медианного ресурса L, получающуюся путем элементарных
преобразований с учетом выражения D.44)
Т — La
1 + 'ff
Tr^/m
от/2"
E.145)
Дисперсия S?gL вычисляется по формуле E.142), если учесть,
С? . С2 Q2 . Q2 С 2
■big*.. ^igLa — ^>1еХ(,> ^lgLr — ^iev
что 5fgL
17. Практическое применение вероятностных
методов
расчета на выносливость деталей машин
Изложенные в разд. 16 вероятностные методы расчета на
усталость применяют в транспортном машиностроении [33, 34, 52, 59],
автотракторном [7, 24, 59, 62], авиационном [6, 62],
сельскохозяйственном, металлургическом, строительно-дорожном и в
других отраслях [24].
Функции распределения ресурса деталей, рассчитанные этими
методами, достаточно хорошо соответствуют эмпирическим
функциям распределения, найденным путем статистической обработки
данных о долговечности деталей до появления усталостных
трещин в условиях эксплутации. Указанные функции являются
объективными характеристиками долговечности и надежности деталей
и имеют важное значение для установления средних и
гарантийных ресурсов, планирования выпуска запасных частей,
установления периодов „между капитальными ремонтами и т. д.
Ниже приводятся примеры расчета деталей на выносливость
вероятностными методами, имеющие целью пояснение
последовательности и методики расчета.
Пример 1. Рассчитать функцию распределения долговечности вала (рис. 5.18)
в сечении /—/, нагруженного изгибающим Мизг и крутящим Мкр моментами,
случайно изменяющимися во времени.
Исходные данные. Характеристики механических свойств
материала, качество обработки поверхности вала. Материал вала — сталь 45, среднее
значение 0В и коэффициент вариации % предела прочности стали на множестве
всех плавок равны соответственно
66 кгс/мм2 и 0,66; среднее значение
средних пределов выносливности гладких
лабораторных образцов при изгибе с
вращением eix=Z\ кгс/мм2, при
знакопеременном кручении тГ1= 18 кгс/мм2.
Параметры уравнения подобия
усталостного разрушения va и vT,
характеризующие чувствительность к
концентрации напряжений и масштабному
фактору соответственно равны 0,11, Рис. 5.18. Эскиз вала:
0,22 (табл. 3.7). Окончательная обра- D = но мм; d — 100 мм
'изг
211
2,8
2,6
2 A
2,2
2,0
1,8
1,6
1Л
1,1 -
1,0
1
1
1
1
1
vS
D/u--
\
\
w
§
1
1,03-
1,02-
=1,01-
^i§
{
Mu
"*№ J-
r~
n
"t~
"tJ
Bid=6
^
',i
',07
,05
Мизг
—
0 0,04 0,08 0,12 0,16 0,20 0,24 <?/d
Рис. 5.19. Зависимость коэффициентов
концентрации напряжений <ха для
ступенчатых валов с галтелью при изгибе
от p/d и Did
ботка поверхности — чистовое
точение, высота неровностей профиля
по 10 точкам Rz■ = 5,5;
поверхностному упрочнению и воздействию
коррозионных сред вал не
подвергается. Вал работает при
нормальной температуре.
Характеристики
эксплуатационной напряженности. Ресурс
вала измеряется в часах работы.
Блок нагружения /б = 100 ч,
среднее значение случайного процесса
изменения нормальных
напряжений ат = 0. Амплитуды
нормальных напряжений распределены по
нормальному закону с
параметрами ~да = 6 кгс/мм2, %а = ОД;
общее число циклов амплитуд
нормальных напряжений в блоке Vfa =
= 1,5-106; коэффициент вариации
средних амплитуд va = vs = 0,08.
Эквивалентные амплитуды
касательных напряжений,
приведенные к симметричному циклу,
распределены по нормальному закону
с
параметрами ха = 4 кгс/мм2;
= 0,3; v-a = ,Е = 0,08; vgT =
= 1,2.10е циклов.
Расчет
характеристик сопротивления
усталости при изгибе.
1. Находим значение теоретического
коэффициента концентрации напряжений аа по рис. 5.19 [52, 90] для -=г =
d
Тоо=1'1и1- = Тоо = 0,05:
а„= 1,85
(черточками" вверху отмечены средние значения размеров и аа).
2. Определяем относительный градиент первого главного напряжения по
формуле A8) табл. 3.1:
П D~d к
t = тг = 5 ММ;
~т = 1--
ф =•
Vi
= 0,167;
+ 2
5=2,3<1_+Ф) ,2- = 2,3A+0,167) 2 =0556 1/ы
о d 5 100
3. Подсчитываем значение lg "-=*, где L = nd = 314 мм,
212
4. Определяем значение —- по формуле C.66) при va = 0,11
Ка
аа
1,85
4 '(**).'
'-'(i*)-«[i+Uir-
= 2,04,
= 0,91.
5. Находим для чистового точения при о"в = 66 кгс/мм2 и i?2 = 5,5 по
рис. 3.40 значение коэффициента влияния качества обработки поверхности |3 =
= 0,88; Рупр = 1, так как упрочнение поверхности по условию задачи отсутствует.
Определяем значение KaD по формуле C.107):
^ = ($+T-1)iiP=B'04+w-1I=2'18-
6. Рассчитываем среднее значение предела выносливости вала
<*-1Д =
ff_t 31-
KoD ~ 2,18
= 14,2 кгс/мм2.
7. Определяем коэффициент вариации %шах по формуле C.80), находя
вначале / по уравнению C.77) при ё^ = 0,5:
1
(miP'—D^h
lg I = lg
= —0,11 B,75—1,946) = —0,089; I = 0,82.
Значение среднего квадратического отклонения S величины lg (ашах — и),
входящего в выражения C.56) и C.80), принимаем для стали согласно
рекомендации на с. 83 равным 0,05. Тогда
_ A — ю—а») / A-10-2-°-05)о,82 пп,е
. "вшах 2A+/) ~ 2A+0,82) -°'045-
Такое же значение получается по рис. 3.18.
8. Находим линеаризованную зависимость аа от -~ по формуле C.85), для
чего определяем по рис. 5.19 значения .
D
аа при -j- = 1,1 и двух —:
при (-£-\ =0,04 ат= 1,95;
при (-J-) = 0,06 aai = 1,75.
Подставляя эти значения в формулу C.85), получаем
аа = 2,35 — 10
др
0
д9
d'
213
Из уравнения C.84) следует,
О 0,04 0,08 ОД 0,16 0,20 0,U y/d
Рис. 5.20. Зависимость коэффициентов
концентрации напряжений ат для
ступенчатых валов с галтелью при
кручении от p/d и Did
"аа
= io-§-i-0p=
= 10-0,05-щ-ор = (),271»р.
Для определения коэффициента
вариации vp радиуса галтели р
примем, что поле допуска на
радиус ± 2 мм соответствует по
«правилу трех сигм» шести средним квад-
ратическим отклонениям Sp
радиуса р, т. е.
2
3Sn
2; V--g-,
следовательно:
2/3
Ур = 4?-=^ = 0,133.
м п 5
В результате имеем vag =
= 0,27.yp=: 0,036.
9. Принимаем коэффициент
вариации v- равным коэффициенту
0,06. В результате по формуле C.90) находим суммарный коэффициент
вариации предела выносливости детали при изгибе:
va = у J _■_ »1 + „2 = ]/0,0453 + 0,036а + 0,06а = 0,083.
— 1д ' "max "-1 a(j
10. Выбираем параметры уравнения кривой усталости в форме C.12) в
соответствии с рекомендациями на с. 28:
16
16
KeD 2,18
= 7,3; Мои = 2- 10е циклов.
Расчет характеристик сопротивления усталости
при кручении производим в той же последовательности, что и при изгибе.
1. Находимо,; по рис. E.20) [52, 90] -=- = 1,1;
Р _
d d
2. Определяем GT по формуле B0) табл. 3.1:
1,15 , 2 1,15 , 2
0,05; ат= 1,3.
GT =■
100'
0,25 1/мм;
о it . L , JtlOO . ,„
3. Находим lg — = Ig-jr-—- = 3,13.
Gr °>25
214
4. Вычисляем
К% ах 1,3
L \ 0,775
—0,22
= 1,68,
= 0,775.
где, (A, Vt)=0,5[. + (^^)-
5. Принимаем значение [3 такое же, как и при изгибе, т. е. E = 0,88. Тогда
Jynp
6. Находим
^д="й=тж = 9,9кгс/мма-
7. Принимаем значение %шах таким же, как и при изгибе, т. е. Щшах =
8. Определяем по рис. 5.20 оц^ = 1,38 при (-^-) =0,04 и 0Ц;3 = 1,26 при
(-^-) =0,06; по формуле C.85) получаем ат = 1,62 — 6-=-.
Из уравнения C.84) при vp = 0,133 имеем va = 6 -=- -=— v0 = 6 X
'da,
X 0,05-^0,133 = 0,03.
9. Вычисляем
ут_1д = ]/" 0,0452 + 0,033 + 0,06s" = 0,08.
10. Принимаем mx = ma = т = 7,3; Л^0О = Л^от == Л^о = 2 • 10е циклов.
Расчет функции распределения ресурса валапри
■действии только нормальных напряжений. Расчет ведется
по формуле E.116). Величины предельных коэффициентов нагруженности пр
определяем для нормального закона по диаграмме рис. 5.13, 5.1,4. Величину
°а тах> входящую в выражение п = — - , определяем по соотношению
О а шах = О a + 5<ja«P шах = Oa A + Up max%a),
где up max = 5,5 — квантиль нормального распределения, соответствующий
максимальной амплитуде aa max, учитываемой при расчете диаграмм рис. 5.13,
5.14.
При указанных выше значениях исходных данных имеем
„ Окатах 6A + 5,5-0,4)
п = — = YA2 = '-35.
Значения пр находим по рис. 5.13 при % = 0,4, т = 7,3 и различных
значениях %£. Так, при ^pt = 103, пр = 1,29, га = njn = -ЬЦ- = 0,955.
215
й
95
/
/
/ /
П 11
„_
.
»^-
S.&
3 11
4
_ V
У
' 1
If '
f I
1
V
л
t
i 1
у
-
.A |
1
r
7*
«
Iе 1
-^
77 11
_J
J^'
^
J* rt
2
1*1 „
По формуле E.116) находим
квантиль нормального
распределения Ир, соответствующий
вероятности разрушения Р,
1—гс
р у™а_№+*
1 — 0,955
V@,955-0,083J + 0,082
^0,4.
L ±
Ьдь6 tgL6+Si3L6
По таблице нормального закона
распределения этому квантилю соот-
Рис. 5.21. Функции распределения ре- ветствует вероятность разрушения
сурса>ала: Р = 0,655 F5,5%).
Мсум
Аналогично, при
N0
1 — La; 2j—"Lx ' при Ха = 4 кгс/мм2; 3 —
— L при Ч„ = 4 кгс/мм2; 4 — L при тя = 1п . 1п ~ , „„ iv°
= 5 кгс/мм» " = Ю пР= 1,42; п = 1,05; иР
= —0,435; Р= 0,331.
При f
i n,
сум
N,
N0
= 30. np = 1,55; п= 1,15; йр = —1,2; Р = 0,115. По вели-
сум
чине —тг- можно вычислить ресурс работы вала в часах по формуле, вытекаю-
щей из уравнений D.44), D.45),
\ No I V6<j
(индекс о" указывает на то, что вычисляемые здесь долговечности соответствуют
действию только нормальных напряжений). Так, при 1?м = 10s имеем
No
2.10°
L«=108w100:
1,33-Ю5 ч.
Таким образом, получено соответствие между ресурсом La работы вала (ч)
под воздействием только нормальных напряжений и вероятностью
разрушения Р (табл. 5.6).
По данным этой таблицы на рис. 5.21 на логарифмически нормальной
вероятностной бумаге нанесены три расчетные точки и проведена линия 1, являющаяся
расчетной функцией распределения
ресурса вала при действии только
нормальных напряжений. С достаточной
для решения данной задачи точностью
можно полагать, что распределение
ресурса подчиняется логарифмически
нормальному закону, которому
соответствует прямая линия 1 на рис. 5.21.
При Р = 50% имеем ср_еднее значение
логарифма ресурса lg La = 4,64 и
медианное значение ресурса La =
=4,37-10*4. При Р = 84,1%(ир =
1) имеем (см. рис. 5.21) lgi-ff+S]g£.ff=
Таблица 5.6
Зависимость Р от ресурса La
= 5,54, вследствие
=5,54 — 4,64 =- 0,9;
216
чего Sig £.„ =
*сум
10s
102
30
V4
1,33-Ю5
1,33-Ю4
4-Ю8
р. %
65,5
33,1
11,5
Расчет функции распределения ресурса вала при
действии только касательных напряжений. Расчет
производят по той же методике, что и при изгибе, а именно по формуле E.116)
определяют квантили up; nv находят по рис. 5.14. Значение
%а A + 5,5y%) 4A+5,5-0,3)
-1Д
9,9
= 1,07.
Результаты вычисления сведены в табл. 5.7.
Зависимость Р от ресурса Lx
Таблица 5.7
N
сум
No
10s
105
5-105
LT> Ч
1,67-105
1,67-107
8,35-107
nP
1,266
1,09
1,04
n
1,18
1,02
0,97
"p
—1,45
—0,1.8
0,25
P. %
7,35
42,9
59,9
lgLT
5,22
7,22
7,92
По этим данным на рис. 5.21 нанесены крестики и по ним проведена линия 2,
по которой определены значения lg L% = 7,4; Sig г. = 1,7; LT = 2,5-107 ч.
Расчет функции распределения ресурса вала, при
одновременном действии нормальных и касательных
напряжений. Медианный ресурс определяем по формуле E.135)
4,37-104
1 + (^2
i +
4,37-104'
2,5-107 ,
2
= 25 300 ч;
lgL = 4,4.
Дисперсию логарифма L вычисляем по формуле E.142)
S „ , =
1-
1
1 +
2,5-107 \ 2/7,3
4,37-104/
@,9J+
1-
1
1 +
4,37-10* \ 2/7,3
2,5-107/
1,73= 1,12.
Среднее квадратическое отклонение логарифма L
SigL = Vrni2=l>06.
По lg L = 4,4 и Sig l = 1>06 на рис. 5.21 построена линия 3, являющаяся
функцией распределения ресурса вала при совместном изгибе и кручении.
Указанная линия проведена через две точки, обозначенные треугольниками и имеющие
координаты lgT= 4,4; Р = 50% и lg L = 4,4 + 1,06; Р = 84,1%. Из рис. 5.21
видно, что так как ресурс Lx существенно превышает ресурс La, то добавление
касательных напряжений привело к несущественному уменьшению ресурса L
по сравнению с Ls. _
Однако аналогичные подсчеты при ха = 5 кгс/мм2 и сохранении остальных
величин без изменения приводят к следующим результатам: lg LT = 5,57; L% =
= 37 400 ч; S\g i = 1,4. Функция распределения ресурса L, соответствующая
одновременному действию нормальных и касательных напряжений (при %а =
217
= 5 кгс/мм2_)_показана линией 4 на рис. 5.21. Таким образом, в данном случае
ресурсы ~Ъа иТ.т оказались соизмеримыми, а результирующий ресурс L стал на
порядок меньше La и LT.
Пример 2. Найти функцию распределения ресурса пластинки с отверстием
при знакопеременном изгибе, изготовленной из стали 40Х (рис. 5.22).
И с х о д н ы е д а н н ы е. ов = 82 кгс/мма; %в = 0,06; о_х = 42 кгс/мма;
поверхности пластины шлифованы; обработка поверхности отверстия —
развертка. Деталь работает при нормальной температуре без коррозионных
воздействий.
Функция распределения относительных амплитуд напряжений в одном блоке
нагружения задана в ступенчатой форме (табл. 5.8)
Число циклов в блоке нагружения
vg = ^ v.- = 2,1 • 10е циклов.
Нагружениость характеризуется также следующими данными:
% = 0-аШах = 28 кгс/мм2; %а шах = vs = 0,07.
Определение характеристик сопротивления
усталости детали.
1. Определяем величину теоретического коэффициента концентрации аа по
рис. 5.23: 4- = -£=2;-5- = 4?- = 0,2; аа = 1,72.
Я
80
2. Находим lg-5T по формуле C.58)
lg-=-=lg-
Utd
G - ю0'3^
lg11'^16 = 0,16; L/G= 1,45.
Здесь принято по данным табл. 3.7, что va = 0,1.
3. Определяем по формуле C.66) при v0 = 0,1:
Ка
1,72
0,5 1 +
ЗодТ"=-1'38-
\—0,11
1,45) ]
4. Получаем по рис. 3.39 для ав = 82 кгс/мм2 по кривой 3 6 = 0,83
(шероховатость поверхности при развертывании здесь приравнена шероховатости поверх-
ности при тонком точении). * Таблица 5.8
Функция распределения
амплитуд напряжений
Рис. 5.22. Эскиз пластины с
отверстием: Н = 80 мм; d = 1 6+0'01 мм;
t = 8 мм
1
2
3
4
а
О
н
о
1,0
0,9
0,8
0,7
о
2 я
Ч
5
10
35
100
5
6
7
8
^
о
н
0,6
0,5
0,4
0,2
о
а я
,. ч
!2§
f 150
250
650
900
218
5. Находим суммарный коэффи- d
циент влияния всех факторов на ве- 6
личину предела выносливости по
формуле C.107)
-A'38+ois-1)'1-1'69-
6. Подсчитываем среднее
значение предела выносливости
-1Д—
g_! 42
Ksd~ 1,59
= 26,4 кгс/мм2.
7. Определяем коэффициент
вариации %шах для стали 40 по рис. 3.18 1,6
nPHlg^-=0,6 t/cmax = 0,055.
Коэффициент вариации vaa
принимаем равным нулю, так как коэффи- Ы
циент вариации радиуса отверстия vp
пренебрежимо мал. Принимаем ? д
и- = vaB = 0,06. Суммарный коэффи- 0 0,1
0,3 0,4 0,5 0,Sa/H
Рис. 5.23. Зависимость коэффициентов
концентрации напряжений аа для
тонкой пластины с отверстием при
изгибе
_ бМизг \
0н - w^rt2)
циент вариации %_1д = Vo,0552 -4- "*
^+0 + 0,062 = 0,081.
8. Выбираем параметры кривой
усталости в форме C.12) в соответствии
с рекомендациями на с. 28
25 25
т^-К^^Т59 =16;^„-2.10-.
Расчет функции распределения ресурса ведем по
корректированной линейной гипотезе суммирования усталостных повреждений, что
можно осуществить двумя способами.
J-й способ. Проиллюстрируем вначале использование формулы E.119).
Вычисляем ар по формуле E.33). Суммирование в формуле E.34) для £
осуществляется только для амплитуд оа( > 0,5а_1Д, что равносильно условию
ggf ^ 0.5
0*<2 тлях fir,
где
-1Д
При яр = 1,25-5-1,3 ПОЛучаем-
Оо/
при вычислении t, используются отношения
показано в табл. 5.9.
7 6
Здесь v'6 = ^ vM;
=1
0,5
E.146)
= 0,385 -*- 0,4, т. е.
1,25 ~ 1,3
——— до 0,4 включительно, как
Од шах
219
Данные к подсчету ресурса
Таблица 5. 9
i
1
2
3
4
5
6
7
Итого
aal
ffamax
1,0
0,9
0,8
0,7
0,6
0,5
0,4
—
vi6>
тыс.
циклов
5
10
35
100
150
250
650
1200
«;-^
чб
0,0042
0,0083
0,0292
0,0833
0,1250
0,2080
0,5420
1,000
Jai и
a max
0,0042
0,0075"
0,0234
0,0582
0,0750
0,1040
0,2168
0,489
и=^
чб
0,0091
0,0182
0,0636
0,1818
0,2727
0,4545
1
/"' *'t
иа шах
0,0091
0,0164
0,0509
0,1273
0,1636
0,2273
0,595
Для этих значений получено £ = 0,498. При лр<1,25
>0,4,
аа шах
т. е. значение 0,4 не учитывается. В результате получаются новые значения U,
как показано в предпоследнем столбце таблицы, и новое значение £, = 0,595,
равное сумме чисел, стоящих в последнем столбце.
Величины ар подсчитываем по формуле E.33), которая легко преобразуется
к виду (при ка = 0,5)
ар =
гср£ — 0,5
яр — 0,5
Значение ар для различных пр даны в табл. 5.10.
Gal С-1Д = 1
"a max Cfl max np
Зависимость —^L от п
N» р
Выражение E.119) представим в виде
N,
сум
N0
«pV6
«р'к
E.147)
E.148)
Таблица 5.10
"р
1,001
1,02
1,06
1,10
1,12
1
0,595
°Р
0,19
0,22
0,24
0,26
0,27
N
сум
No
79,5
67,3
38,7
23,8
13,4
"р
1,20
1,24
1,25
1,30
1
0,595
0,595
0,489
0,489
аР
0,31
0,32
0,15
0,17
N
сум
No
5,3
3,2
1,11
0,69
E.149)
220
где
- 2 Ойг)*~
ео/>в-1д)
Вычисления сведены в табл. 5.11.
E.150)
Таблица 5.11
Данные
i
1
2
3
к подсчету ресурса
uoi
aamax
1,0
0,9
0,8
/ "at У6
V^amax/
1,0
0,185
0,0282
v*6
5 000
10 000
35 000
Wamax/ 1б
5000
1850
985
"p
1,001—1,10
1,11—1,24
1,25—1,42
X.
5000
6850
7835
При tin > 1,25 в расчет принимают все три строки (для i = 1, 2, 3), т. е.
х = 5000 + 1850 + 985 = 7833, так как для них аа!/аа шах > 0,8.
При 1,11:
1,24 включительно в расчет должны приниматься только
:0,9. В этом случае х = 5000 + 1850 =
1,10 х = 5000. Используя значение ар (из
N,
сум
две строки, так как 0,8 < oai/aa
= 6850. Наконец, при 1,001
табл. 5.10) их (из табл. 5.11) по формуле E.149) получаем значения
висимости от пр, представленные в табл. 5.10 и на рис. 5.24. Из рисунка видно,
что при яр = 1,25 получается ступенька вследствие скачкообразного изменения х
и ар, при яр = 1,11 получается ступенька вследствие скачкообразного
изменения х.
По найденным значениям яр в зависимости от ^м ■ (см. табл. 5.10) по фор-
муле E.116) находим квантили up и соответствующие им значения вероятности
разрушения Р (по таблицам нормального закона распределения). При этом
Од шах
СТ-1д
28
26,4
= 1,06.
Nc
Так, например, при ' д°гУМ = 74, яр=1,01 имеем
1,01
,06
= 0,953;
1 — 0,953 .
]^@,953-0,081J +@,07J
= 0,452;
Р = 67,4°/0.
При
N,
сум
"Ж"
= 22,4 яр =1,1; п =1,038; иР = — 0,347; Р = Ж,4%.
При
N,
сум
N„
= 5,3 яр = 1,2; я= 1,13; иР =
13; Р = 12,9%.
221
lip
1,1
ы
1,1
1,0
0,1
X
\
Ч
\
\
\
X
\
10 NCyr,/NB
P°lo
95
90
W
SO
SO
iO
30
20
10
S
1
1
/'
/
/
/
/
x"
A<
/
/
/
/
/
_p
-fr
Рис. 5.24. Зависимость пр от
ресурса
N,
сум
Nn
0,1 1 Ю 100NcyM/No
Рис. 5.25. Функции
распределения ресурса пластины с
отверстием:
!_ ~ °а шах = 28 кгс/мм^: 2 -
°атах = 24 кгс/мм2
По этим данным на рис. 5.25 на логарифмически нормальной вероятностной
бумаге нанесены крестики, через которые проведена линия /, соответствующая
функции распределения ресурса при оа шах = 28 кгс/мм2.
Следует отметить, что при пр = 1 по рис. 5.24 получаем Ncyu/No = 80.
При яр< 1, NcywINo = оо, так как все амплитуды аа;. становятся меньше
предела выносливости о_т. Поэтому линия 1 на рис. 5.24 при NCYaINo >80
переходит в . горизонтальную прямую.
2-й способ. Этот способ заключается в применении уравнений E.117) и E.118).
Медианное значение ресурса NcyJNo можно найти также по уравнению E.119)
[или E.149)] при яр = п = ^шах , что следует и из выражения E.116), ибо при
СТ-1Д
яр = п имеем я = 1, up = 0, Р = 50%. Таким образом, по уравнению E.149)
при я = 1,06 и % = 5000 (см. табл. 5.11) получаем
N,
сум 0,24-2,1-10е
No
A,06)" 5000
= 38,7; lg.
N,
сум
Ж"
= 1,59.
По формуле E.118) находим
Slg % — S
lg
NcyM =0,434-16 ]/"@,081)a + @,07J =0,74.
По этим значениям на рис. 5.25 нанесены круглые залитые точки, которые
также ложатся на линию / (т. е. оба способа приводят практически к одинаковым
результатам). _
_Представляет интерес расчет функции распределения ресурса при аа шаХ <3
<5 о_1д, например, при сгаП1ах = 24 кгс/мм2. В этом случае второй способ,
основанный на использовании уравнений E.117) и E.118), применен быть не может, так
как все амплитуды меньше предела выносливости и выражение E.117) теряет
смысл. Расчет функции распределения ресурса производим по уравнению E.116)
222
с использованием зависимости яр от
N,
сум
Tv7
> представленной в табл. 5.10.и на
рис. 5.24. Предельный коэффициент нагруженности по средним я =
24
26,4
При
ватах
СТ-1д
= 0,91.
N,
сум
N0
= 74 имеем: я„ = 1,01; in = — =
Р= 16,7%. При
/V,
1,01
0,91
= 1,11; ир = —0,965;
сум
= 39 яр = 1,06; я = 1,165; ив = —1,4; Р = 8,1%
По этим данным построена функция распределения ресурса на рис. 5.25
Nc.
(линия 2). В точке с абсциссой
"сум
"Ж"
= 80 линия 2 так же как и линия 1,
переходит в горизонтальную линию, так как ресурс становится неограниченным.
Пример 3. Рассчитать функцию распределения ресурса рычага при изгибе
(рис. 5.26), изготовленного из легированной стали.
Исходные данные. Механические свойства стали: ав = 120 кгс/мм2;
va = 0,07. Рычаг работает на воздухе при нормальной температуре.
Поверхностному упрочнению рычаг не подвергается, окончательная обработка поверхнос-
сти — тонкое шлифование.
Характеристики эксплуатационной напряженности заданы в виде функции
спектральной плотности S (ш), представленной на рис. 5.27. Коэффициент ва-
5с
риации Vе = vs = -=?- случайной величины S равен vs = 0,08 (здесь S =
о
= 1/G? где а|-—дисперсия случайного процесса изменения напряжений).
Расчет характеристик сопротивления усталости
приизгибе. 1. Определяем ад по рис. 5.28 [52, 90] для -=- = -sjr = 1,2;
d J"
% = 1,99.
M,
'изг
Рис. 5.26. Эскиз рычага:
D = 36 мм; ~d = 30 мм; р = 1,8±0'6 мм; Ь =
= 10 мм
Рис. 5.27. Функция спектральной
плотности случайного процесса изменения
напряжений в рычаге
1,4-
1.1
1,0
0,8
0.6
04
0.2
-
-
-
\
so
Г\
S,
и0 100
А
*<•
*:
\ ♦
110
CJ, '/С
223
2. Находим G по формуле A3) табл. 3.1 для
D — dQ t 3 . ._ 1
= 3мм; — = -rpg- = 1,67; q> = -г= = 0,14;
-g--.™, y--rj
? 2,3A+Ф) 2 2,3-1,14 ,2
G= ^_*_+ _. = ___ + -.= 1,53 1/mm.
3. Вычисляем значение
lg¥=lgT==lgT53- = 1,12: T = 13>2™2-
4. Определяем по формуле C.66) —2-. Для этого вначале выбираем значе-
Ёв
ние va по табл. 3.7. Так как для легированных сталей va = 0,04ч-0,11, примем
= 0,08.
Тогда
К- 1 QQ
= 1,84.
Kg _ ЦЮ
* "«■»['+(«*•"■*)"*"]
5. По рис. 3.39 для шлифования стали с ав = 120 кгс/мм2 находим E = 0,83.
По формуле C.107) определяем
^ = A.84+^-1). 1 = 1.98.
6. Вычисляем среднее значение средних пределов выносливости гладких
лабораторных образцов по формуле B.20)
a_i= @,55—0,001 ав)ав = @,55 — 0,001-120I20 = 51,6 кгс/мм2.
Среднее значение предела выносливости рычага
^1д = ^ = т!Й- = 26*1кгС/мм2-
7. Находим коэффициент v0 по рис. 3.18 по кривой для стали 40Х
(полагая, что для данной стали он будет таким же) va = 0,05.
8. Линеаризируем зависимость аа от -j- в окрестности точки с абсциссой
p/d = 0,06, принимая по рис. 5.28 : ад = 1,89 для (p/d)i = °,07 и аа = 2,°9
для (p/.di) = 0.05.
В результате по формуле C.85) получаем
аа = 2,59 — 10 -^- ; откуда
10
d ' —*"*' ар" о"" Ж о~Т
Из уравнения C.84) имеем
дф
аР
0
ааст
vaa = 10-0,06 -yig- Op = 0,301i>p= 0,033,
где ,p = W =0,111.
224
9. Принимаем v-„ = v„ =0,07. .
Тогда
? 8
ve_ls = ]/,052 + 0,0332 + 0,072 =
= 0,092. . Z'S
10. Выбираем в соответствии с ре- '>*
комендациями на с. 28 No= 2 ■ 106 цик-
лов т = тж = 13-
Оценка характеристик уровня 2,0
напряженности рычага производится
по функции спектральной плотности 1,8
(рис. 5.27) и формулам разд. 12.
1. Находим дисперсию ст| процес- j g
са изменения напряжений, дисперсию
его первой производной а2 и второй ; ^
производной ag по формулам D.21).
В первом приближении заменяем 1,1
действительную функцию
спектральной плотности функцией ; д
S (Q) =
1
1
1
7 /?2~~^
Л/d =1,01-
Ми
У
( *,: дЗ
зг -ю
■B/d=6
-—J
г-—2 "
7,3
7,7
1,01
1,05
1 >
У
"иг
0 0,04 0,00 ОД 0,П 0,16 0,18 y/d
H при a>0 ^ w <^ o0 -\- До;
. 0 при и < <в0 и со > <в0 -[- До,
E.151)
Рис. 5.28. Значение коэффициента
концентрации напряжений оса при изгибе
ступенчатой пластины
где Н = 1,33 кгс2-с.мм-4; а>0 = 90 1/с; До = 18 1/с.
В результате имеем
» соо+Асо
4 = ^(°) = i | W> = ^ | **> = *£> =
—~ ' coo
1,33-18
= -Ц^— = 38 кгса.мм;
соо+Асо
—» COo
Ясо§
6я
E.152)
где принято Ди/ио = 0,2;
4_9Ясо|_
10я
В том случае, когда функция спектральной плотности имеет более сложную
форму и не может быть аппроксимирована функцией E.151), интегралы,
входящие в выражения D.21), могут быть найдены методами численного
интегрирования.
225
2. Находим по формуле D.38) параметр v2, характеризующий сложность
структуры процессаа(после сокращения Я, о>о, я):
„4
о|о?
= 1
0,732-2-10
:0,0065;
1"Ч
36-0,2.1,49
v = 0,0806.
Находим отношение среднего числа нулей процесса к среднему числу
экстремумов из формулы D.41): к = ]/*1 — v2 ±= ]Л — 0,0065 = 0,997.
Близость % к единице и v к нулю показывает, что процесс является достаточно
узкополосным (что видно качественно и из рис. 5.27).
Вследствие малости v2 выражение D.37) для плотности вероятности
максимумов процесса преобразуется в распределение Рэлея
/ (А) ==; he
E.153)
где h = -S2L .
Выражение E.153) является распределением амплитуд в форме Рэлея с
параметром S = а| = ]/*38 =6,17 кгс/мм2.
3. Находим эффективную частоту процесса /, как половину среднего числа
нулей в секунду No по формулам D.21) и E.152):
1
' 2 2яаЕ
2я
К'
0,73Яю%2я
6яО,2#а>о
= -^1 1
2я
E.154)
Таким образом, эффективная круговая частота процесса и = 2я/ = 1,1а>0,
т. е. соответствует середине интервала, на котором спектральная плотность
S (и) = Н.
Подставляя в формулу E.154) значение о>о = 90 1/с, получаем значение
эффективной частоты f = 15,8 Гц.
Расчет функции распределения ресурса рычага может быть выполнен по
формулам разд. 16 для закона распределения амплитуд в форме Рэлея.
1. Подсчитаем ар по формулам E.108) и E.110), имея в виду, что
-Ь£ = 6 =
(принято ka = 0,5).
■ = 5:
°~g max
^-1Д
Х„
о,5А = М
Таблица 5.12
Данные к подсчету величин
N*
Ум
Nn
о.
1,1
1,18
-1,25
ю р.
cn й
II
2,27
2,12
2,00
(NO
X
5,15
4,50
4,00
со
CNO
X
а,
0,1612
0,2125
0,2615
CN
NO
х ■
а,
0,0763
0,1055
0,1353
ЬЛ
0,528
0,504
0,483
О.
а
0,138
0,138
0,137
-к
4,54
4,24
4,00
(М
+
S
л| й
а,
0,15323
0,26267
0,38205
СО
•=|й°"
3,4-108
1,41-108
6,61.10'
s
>>
о
г:
s;
2680
538
161
226
Здесь 6 = 5, так как предварительные
подсчеты показывают, что учет величин о"атах>
превышающих 5 S, практически не влияют
на вычисленные ресурсы.
Для подсчета функции распределения
ресурса необходимо задаться несколькими
значениями яр. Данные для подсчета ар для
трех значений пр сведены в табл. 5.12.
Величины £ определяются по формуле,
вытекающей из выражения E.110) при
V-
-f-1.26;
3) = 0,00002 ;
£ =
bg =5; Р (bf, 3) = Р B5,
0; Р B5, 2) = 0
0.25Р (*§, 3)
Я № 2)
E.155)
Здесь Р (*, я) — значения интеграла
вероятностей ха, определяемые по табл. 2.1, а в
справочнике [5]. Подсчет ар выполняем по
формуле E.108) при bg = 5
4%
9S
90
111
60
SO
40
30
20
10
S
г
/
'
/
У
/~
J
-J~
/
/
/
f
10'
1,ч
Рис. 5.29. Функция
распределения ресурса рычага
2. Находим зависимость сум от я„ по формуле E.99) при от = 13; я|) (от -
+ 2) = я|; A5) = 1,696-105; Р (б2! от + 2) = Р B5, 15) = 0,04994
N,
сум
1,696-105
F/ярI3
P'-V' 15
0,0499
E.157)
Величины, входящие в формулу E.157), и результаты подсчета све-
0
дены в табл. 5.12.
3. Находим ресурс работы рычага L (ч) по формуле L = Л?сум//-3600-
Результаты подсчета L в зависимости от яр при /= 15,8 Гц, No = 2-Ю6
представлены в табл. 5.13.
Таблица 5.13
Зависимость ресурса L и вероятности разрушения Р от пр
"р
1,1
1,18
1,25
N
сум
Wo
2680
538
161
L, ч
1,13- 10е
2,27-10^
6,78-10*
h
0,932
1,000
1,06
Up
0,58
0
-0,49
Р, %
71,9
50
31,2
4. Определяем квантили ир, соответствующие вероятности разрушения Р,
по формуле E.116) при п = 1,18; t>e = 0,08.
На рис. 5.29 показана функция распределения ресурса рычага .
227
Список литературы
1. Афанасьев Н. Н. Статистическая теория усталостной прочности металлов.
Киев, Изд-во АН УССР, 1953. 123 с.
2. Бендат Дж. Основы теории случайных шумов и ее применение. М.,
«Наука», 1965. 463 с.
3. Биргер А. И. Проблемы механики твердого деформированного тела. —
В кн.: «Вероятность разрушения, запасы прочности и диагностика. Л.,
«Судостроение», 1970. с. 71—82.
4. Болотин В. В. Статистические методы в строительной механике. М.,
Стройиздат, 1965. 279 с.
5. Большее Л. Н., Смирнов Н. В. Таблицы математической статистики.
М., «Наука», 1965. 464 с.
6. Бойцов Б. В. Надежность шасси самолета. М., «Машиностроение», 1976.
216 с.
7. Бухарин Н. А., Прозоров В. С, Щукин М. М. Автомобили. М.— Л.,
«Машиностроение», 1973. 504 с.
8. Вагапов Р. Д., Шишорина О. И., Хринина Л. А. Моделирование при
испытаниях на усталость. — В кн.: Испытание деталей машин на прочность. Под
ред. С. В. Серенсена. М., Машгиз, 1960. с. 24—66.
9. Вагапов О. Д., Шишорина О. И. Эффект положения концентрации
напряжений при действии переменных нагрузок. — В кн.: «Вопросы прочности
материалов и конструкций. М., Изд-во АН СССР, 1959, с. 36—51.
10. Вейбулл В. Усталостные испытания и анализ их результатов. М.,
«Машиностроение», 1964. 275 с.
11. Вентцель Е. С. Теория вероятностей. М., «Наука», 1969. 576 с.
12. Вопросы прочности крупных деталей машин. [Сборник статей]. Под
ред. И. В. Кудрявцева, М., «Машиностроение», 1976. 320 с.
13. Вероятностные характеристики прочности авиационных материалов и
сортамента. Справочник. М., «Машиностроение», 1970 г. 576 с. Авт.: А. А.
Кузнецов, О. М. Алифанов, В. И. Ветров и др.
14. Волков С. Д. Статистическая теория прочности. М., Машгиз, 1960. 176 с.
15. Гликман Л. А. Коррозионно-механическая прочность металлов. М.—
Л., Машгиз, 1955. 176 с.
16. Гусев А. С. Основы оценки нагруженности и расчета долговечности
деталей мобильных машин. Автореферат диссертации на соискание ученой степени
д-ра техн. наук. Челябинск, ЧПИ, с. 33.
17. Дмитриченко С. С. Методы оценки и повышения долговечности несущих
систем тракторов и других машин. Автореферат диссертации на соискание
ученой степени д-ра техн. наук. М., МВТУ, 1970. 36 с.
18. Дунин-Барковский И. В., Смирнов Н. В. Теория вероятностей и
математическая статистика в технике (общая часть). М., Гостехтеориздат, 1955. 556 с.
19. Иванова В. С, Терентьев В. Ф. Природа усталости металлов. М.,
«Металлургия», 1975. 455 с.
20. Исследования по упрочнению деталей машин [Сборник статей]. Под
ред. И. В. Кудрявцева. М., «Машиностроение», 1972. 328 с.
228
21. Карпенко Г. В. Влияние активных жидких сред на выносливость стали.
Киев, Изд-во АН УССР, 1955. 208 с.
22. Когаев В. П. Вопросы поверхностного упрочнения в проблеме
конструирования. — В кн.: Теоретические основы конструирования машин. М.,
Изд-во АН СССР, 1958. с. 210—230.
23. Когаев В. П. Статистические закономерности усталости металлов.
Автореферат диссертации на соискание ученой степени д-ра техн. наук. М., ИМАШ,
1968. 55 с.
24. Когаев В. П. Определение надежности механических систем по условию
прочности. М., «Знание», 1976, вып. 1, 2, 48 с.
25. Когаев В. П. Усталость и несущая способность узлов и деталей машин
при стационарном и нестационарном переменном нагружениях. М.,
«Машиностроение», 1968. 134 с.'
26. Когаев В. П. Методы статистической обработки результатов усталостных
испытаний. — «Заводская лаборатория», 1957, № 5, с. 612—620.
27. Конструкционная прочность легких сплавов и сталей. Труды МАТИ.
Под ред. С. В. Серенсена [Сборник статей]. Вып. 61, М., «Машиностроение»,
1964. 168 с.
28. Конструкционная прочность авиационных сплавов. Труды МАТИ.
Вып. 54, М., Оборонгиз, 1962. 102 с. Авт. С. В. Сервисен, Е. В. Гиацинтов,
Е. В. Когаев, М. Н. Степнов.
29. Кудрявцев И. В., Белкин М. Я- Влияние поверхностного наклепа на
сопротивление усталости круглых валов из легированной стали. — В кн.: Вопросы
механической усталости. М., «Машиностроение», 1964. с. 285—299.
30. Левин Б. Р. Теоретические основы статистической радиотехники. М.,
«Советское радио», 1969. 751 с.
31. Масштабный эффект при коррозионной усталости стальных валов с
насаженными деталями. — «Физико-химическая механика металлов», 1970, т. 6.,
№ 2, с. 7—10. Авт. Г. В. Карпенко, Р. Г. Погорецкий, Я- М. Сирак, Я- М.
Филимонов.
32. Махутов Н. А. Сопротивление элементов конструкций хрупкому
разрушению. М., «Машиностроение», 1973. 200 с.
33. Мейснер Б. А. Прочность и надежность рам локомотивных тележек
(оценка и прогнозирование). Автореферат диссертации на соискание ученой
степени д-ра техн. наук. М., ЦНИИ МПС, 1973. 43 с. .
34. Механическая усталость в статистическом аспекте. [Сборник статей].
М., «Наука», 1969. с. 174.
35. Морозов В. И., Шубина Н. Б. Наклеп дробью тяжелонагруженных
зубчатых колес. М., «Машиностроение», 1972. 104 с.
36. Нейбер Г. Концентрация напряжений. М., Гостехиздат, 1947. 204 с.
37. О расчете усталостной долговечности при плоском напряженном
состоянии. — «Машиноведение», 1977, № 2, с. 27. Авт.: А. С. Гусев, В. В. Никонов,
С. С. Дмитриченко, И. М. Илинич.
• 38. Повышение прочности и долговечности деталей машин [Сборник статей].
Под ред. И. В. Кудрявцева. М., «Машиностроение», 1969. 312 с.
39. Почтенный Е. К. Кинетическая теория механической усталости и ее
приложения. Минск. «Наука и техника», 1973. 213 с.
40. Прочность материалов и конструкций. [Сборник статей]. Киев. «Наукова
думка», 1975. 384 с.
41. Пэрис П. С, Си Дж. Анализ напряженного состояния около трещин. —
В кн.: Прикладные вопросы вязкости разрушения. М., «Мир», 1968. с. 64—142.
42. Разрушение [Сборник статей]. М., «Мир», Т. I, 1973, 616 с; т. II, 1975,
763 с; т. III, 1976, 796 с; т. IV, 1976, 496 с.
43. Расчеты на прочность в машиностроении. Справочник. В 3-х т.'^Т. III.
М., Машгиз, 1959. 1118 с. Авт.: С. Д. Пономарев, В. Л. Бидерман, К. К°
Лихарев и др.
44. Райе С. Теория флуктуационных шумов. — В кн.: Теория передачи
электрических сигналов при наличии помех. ML, Изд. иностр. лит. 1953. 157 с.
45. Решетов Д. Н. Расчет деталей станков. М., Машгиз, 1945. 138 с.
229
46. Решетов Д. Н., Чатынян С. М. Расчет деталей машин на прочность при-
переменных режимах нагружений. — «Вестник машиностроения», 1965, № 8,
с. 11—14.
47. Решетов Д. Н. Детали машин. М., «Машиностроение», 1974. 655 с.
48. Ржаницын А. Р. Расчет сооружений с учетом пластических свойств
материалов. М., Стройиздат, 1949. 236 с.
49. Рябченков А. В. Коррозионно-усталостная прочность стали. М., Машгиз,
1953. 179 с.
50. Серенсен С. В., Козлов Л. А., Гарф М. Э. Машины для испытаний на
усталость. М., Машгиз, 1957. 404 с.
51. Серенсен С. В., Козлов Л. А., Когаев В. П. Концентрация напряжений
в деталях машин (применительно к расчету на выносливость). Листки для
конструктора. — «Вестник машиностроения», 1949, № 10, с. 23—28; № 11, с. 27—30,
№ 12, с. 19—20; 1950, № 3, с. 21—24, № 4, с. 23—26; № 6 с. 20—21.
52. Серенсен С. В., Когаев В. П., Шнейдерович Р. М. Несущая способность
и расчеты деталей машин на прочность. М., «Машиностроение», 1975. 488 с.
53. Серенсен С. В. Определение запаса прочности при расчете деталей
машин.— «Вестник машиностроения», 1943, № 6, с. 5.
54. Серенсен С. В., Козлов Л. А. Линейная интерпретация накопления
повреждения и характеристики сопротивления усталостному и длительному
статическому разрушению — «Заводская лаборатория», 1958, № 11,- с. 1378.
55. Серенсен С. В., Буглов Е. Г. О вероятностных представлениях
переменной нагруженности деталей машин. — «Вестник машиностроения», 1960, № 10,
с. 10—17; № 11, с. 23—32.
56. Серенсен С. В., Козлов Л. А. Характеристики нестационарной
нагруженности и определение запаса прочности. — «Вестник машиностроения», 1964,
№ 6, с. 5—10. '
57. Серенсен С. В. Об условиях прочности при переменных нагрузках для
плоского и объемного напряженного состояния. — «Инженерный сборник»,
Т. I, вып. 1, 1941. с. 3—12.
58. Серенсен С. В. Об оценке долговечности деталей — «Вестник
машиностроения», 1944, № 7—8, с. 1—7.
59. Статистические вопросы прочности и динамики машин. [Тезисы докладов
совещания]. Рига, РПИ, 1976. 259 с. :
60. Степнов М. Н., Гиацинтов Е. В. Усталость легких конструкционных
сплавов. М., «Машиностроение», 1973. 317 с.
61. Степнов М. Н. Статистическая обработка результатов механических
испытаний. М., «Машиностроение», 1972. 232 с.
62. Тезисы докладов Всесоюзного научно-технического совещания
«Совершенствование расчетов прочности и надежности машин на основе
статистических методов». М., «Знание», 1972. 187 с.
63. Тихонов В. И. Выбросы случайных процессов. М., «Наука», 1970. 392 с.
64. Труфяков В. И. Усталость сварных соединений. Киев, «Наукова думка»,
1973. 216 с.
65. Ужик Г. В. Об эффекте масштаба при переменных напряжениях. В кн.:
«Symposium о unave», cs. VTS, Прага, 1960. с. 493—502.
66. Усталость металлов. Под ред. Г. В. Ужика [Сборник статей]. М., Изд.
иностр. лит. 1961. 378 с.
67. Усталость и выносливость металлов. Под ред. Г. В. Ужика [Сборник
статей]. М., Изд. иностр. лит., 1963, 497 с.
68. Фридман Я. Б., Гордеева Т. А., Зайцев А. М. Строение и анализ изломов
металлов. М., Машгиз, 1960. 128 с.
69. Филимонов Г. Н., Балацкий Л. Т. Фреттинг в соединениях судовых
деталей. Л., «Судостроение», 1973. 296 с.
70. Хальд А. М. Математическая статистика с техническими приложениями.
М., Изд. иностр. лит. 1956. 664 с.
71. Черепанов Г. П. Механика хрупкого разрушения. М., «Наука», 1974.
640 с.
72. Damage Tolerance in Aircraft structures. — «ASTM STP 486», '1971.
p. 251.
230
73. Dixon W. J., Mood A. M. A method for obtaining and analysing
sensitivity data. —«Journal Amer. Statist. Ass.», 1948, Vol. 43, p. 109—126.
74. Gough H. J. Engineering Steels Under Combined Cyclic and Static
Stresses. — «Proc. J. Mech. Eng.», London, 1949, Vol. 160, p. 417.
75. Horger 0. J. Fatigue of Large Shafts by Fretting Corrosion, — «Proc.
Intern. Conf. on Fatigue of Metals», London, 1956, p. 352—360.
76. Proc. of the Intern. Conf. on Fatigue of Metals. — «Inst, of Mech. Eng.»,
London, 1956, 961 p. '
77. Jacoby G. Beitrag zum Vergleich der Aussagefahigkeit von Programm und
Random — Versuchen. Z. Flugwiss, 1970, Bd. 18, N 7, s. 253—258.
78. GaGner E. Zur experimentellen Lebensdauerermittlung von Konstruk-
tionselementen mit zufallartigen Beanspruchungen. Materialprufung, 1973, Bd.
15, N 6/ s. 197—228.
79. Kowalewski J. Uber die Beziehungen zwischen der Lebensdauer Von Bau-
teilen bei unregelmafiig schwankenden und bei geordneten Belastungsfolgen.
DVL — Bericht, 1963, s. 249.
80. Laszlo Sors. Berechnung der Dauerfestigkeit von Maschinenteilen, —
«Verlag der Ungarischen Akademie der Wissenschaften», Budapest, 1963, s. 194.
81. Mailander R., Bawersfeeld W. Einfluss der Probengrosse und Probenform
auf die Dreh—Schwingunsfestigkeit von stahl. — «Technische Mitteilungen Krupp»,
1937, H. 5, s. 143.
82. Massanet С Revue Universelle des Mines de la Metallurgie. Paris, 1955,
Ser. 9, t. XI, pp. 203—232.
83. Moore H. F., Morkovin D. Second Progress Report on the Effect of Siz e of
Specimen on Fatigue Strength of Three Types of Steel. — «Proc. ASTM». Philadel-
fia, Vol. 43, 1943, p. 109; Vol. 44, 1944, p. 137.
84. Moore H. F., Jordan R. L. Stress Concentration in Steel Shafts with
Semi—Circular Notches. — «Proc. 5th Intern. Congress for Applied Mechanics»,
New York, Willey, 1939, p. 188.
gj 85. Marin J. Engineering Materials. New York, Prentice — Hall, 1952, p. 164.
86. Marin J. Biaxial tention—tention fatigue strengths of metals. — «Journal
of applied mechanics», Vol. 16, N 4, 1949, p. 55.
87. Mc Adam. D. I. Proc. ASTM. Philadelfia, Vol. 26, 1926, p. 11; Vol. 27,
1927, p. 11; Vol. 28, 1928, p. 11; Vol. 30, p. 11; Vol. 31, 1931, p. 11.
88. Ouchida H. A Study of Size Effect on Fatigue Strength of Steel. — «Proc.
of the Second Japan Congress on Testing Materials», 1959, p. 14.
89. Peterson R. E., Wahl A. M. Two and Three Dimensional Cases of Stress
Concentration and Comparison with Fatigue Tests. — «Trans. ASME», 1936, Vol. 58,
p. A—15.
90. Peterson R. E. Stress concentration factors. New York, Welley, 1974,
p. 317.
91. Peterson R. E. Model Testing as Applied to strength of materials». ASME,
Paper АРМ 55—11, —«Journal of Applied Mechanics», 1933, Vol. 1, No 2, p. 55.
92. Probabilistic Aspects of Fatigue. —ASTM STP 511, p. 203.
93. Pfeiffer F. Mitteilungen aus dem Institut fur Leichtbau und б ton. Ver-
wendung von Werk, 1976, No 1/2, s. 19—30.
94. Rice {. R., Beer R. P. On the distribution of rises and falls in a continuous
random process.—«Journal of Basic Engineering», 1965, N 2, p. 154—161.
95. Sakurai Т., Masaki I., Kitamoto I., Proc. of the ninth Japan Congress on
Testing Materials. Kyoto. Un. Japan, 1976, p. 7.
96. Stress Analysis and Growth of Cracks. — «ASTM STP 513», 1972, p. 25.
97. Weibull W. A. A statistical theory of the strength of materials. —«Proc.
Royal Swedish Institute for Engineering Research». Stockholm, 1939, N 151,
p. 45.
Оглавление
Предисловие 5
Глава 1. Образование и развитие усталостных повреждений
металла 7
1. Механизм усталостного разрушения и характер усталостных изломов
деталей машин 7
2. Закономерности развития усталостных трещин 13
Глава 2. Экспериментальное определение характеристик
сопротивления усталости 23
3. Характеристики сопротивления усталости при симметричных и
асимметричных циклах 23
4. Рассеяние характеристик сопротивления усталости и построение полных
вероятностных диаграмм усталости . . . . 34
5. Оценка характеристик сопротивления усталости при сложном
напряженном состоянии 41
Глава 3. Факторы, влияющие на сопротивление усталости
деталей машин 47
6. Концентрация напряжений и абсолютные размеры поперечного сечения 47
7. Статистическая теория подобия усталостного разрушения 58
8. Фреттинг-коррозия 107
9. Качество обработки поверхности, коррозия и частота испытания 117
10. Технологические методы поверхностного упрочнения деталей машин 126
Глава 4. Статистическая оценка характеристик переменной
нагруженности деталей машии 133
11. Методы схематизации случайных процессов изменения нагрузок . . 133
12. Применение теории случайных функций для оценки расчетных
характеристик нагруженности 144
13. Статистическая оценка расчетных характеристик нагруженности . . . 157
Глава 5. Методы расчета на прочность деталей машин при
нагрузках, переменных во времени 161
14. Методы расчета по коэффициентам запаса прочности 161
15. Экспериментальное обоснование методов расчета на выносливость при
нерегулярной переменной нагруженности 169
16. Вероятностные методы расчета на прочность при нагрузках,
переменных во времени 181
17. Практическое применение вероятностных методов расчета на
выносливость деталей машин 211
Список литературы 228