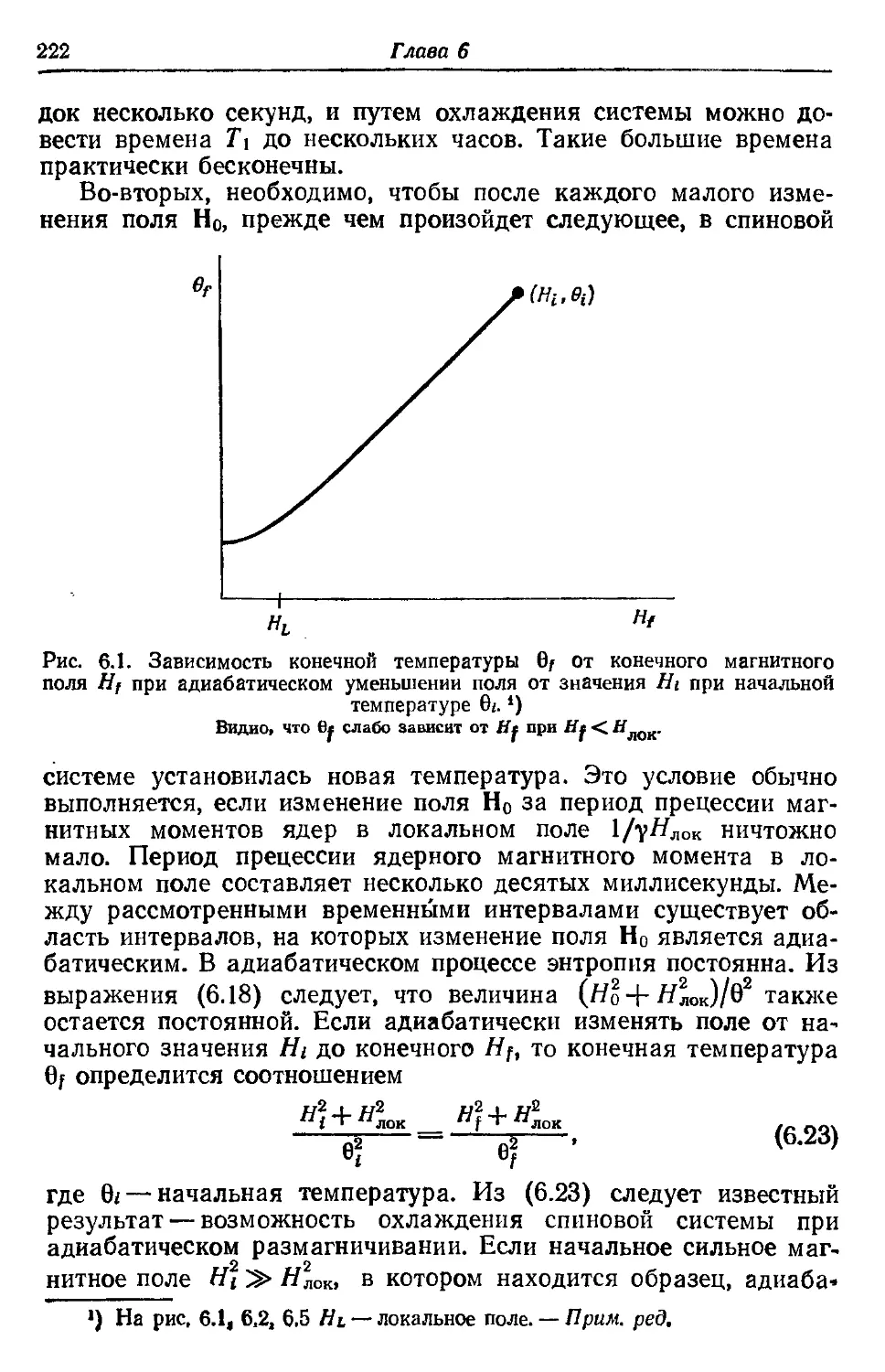
Author: Сликтер Ч.
Tags: ядерная, атомная и молекулярная физика свойства и структура молекулярных систем физика магнитный резонанс
Year: 1981
Text
Ч.СЛИНТЕР
ОСНОВЫ
ТЕОРИИ
МАГНИТНОГО
РЕЗОНАНСА
Springer Series in Solid-State Sciences
Editors: M. Cardona, P. Fulde, H.-J. Queiseer
Volume 1. Edited by P. Fulde
C. P. SLICHTER
PRINCIPLES OF
MAGNETIC RESONANCE
Second Revised and Expanded Edition
Corrected Second Printing
Sprlnger-Veriag
Berlin Heidelberg New York
1980
Ч.СЛИНТЕР
ОСНОВЫ
ТЕОРИИ
МАГНИТНОГО
РЕЗОНАНСА
Второе, пересмотренное,
дополненное и исправленное издание
Перевод Н. Н. КОРСТА, Б. Н. ПРОВОТОРОВА
и А. П. СТЕПАНОВА
под редакцией д-ра физ.-мат. наук,
проф. Г. В. СКРОЦКОГО
Издательство «Мир»
Москва 1981
УДК 539.1+539.2
Книга Ч. Сликтера (США) содержит ясное и доступное изло-
жение основных идей и результатов современной теории магнит-
ного резонанса, включая ядерный магнитный резонанс и элек-
тронный спиновый резонанс с примерами их применения в каче-
стве методов исследования физических свойств вещества, особен-
но твердых тел. Она представляет собой учебный курс теории
магнитного резонанса, основанный на лекциях автора, прочитан-
ных физикам, химикам и исследователям в области прикладных
наук.
Настоящее, второе издание (первое издание вышло в русском
переводе в 1967 г.) значительно расширено, так что книга отра-
жает современное состояние теории магнитного резонанса. Вклю-
чены три новые главы, посвященные спиновой температуре, двой-
ному резонансу и импульсному сужению линий в твердых телах.
Добавлено много оригинальных задач, способствующих усвоению
материала, п ряд приложений.
Книга представляет интерес для всех специалистов, применяю-
щих методы магнитного резонанса в своих исследованиях, и осо-
бенно для преподавателей и студентов физических и физико-
химических специальностей.
Редакция литературы по физике
Чарльз Сликтер
ОСНОВЫ ТЕОРИИ МАГНИТНОГО РЕЗОНАНСА
Второе, пересмотренное, дополненное и исправленное издание
Научн. редактор Е. И. Майкова. Мл. научн. редакторы В. Цлаф, В. И. Аксенова.
Художник Е. К. Самойлов. Художественный редактор Л. Е. Безрученков.
Технический редактор 3. И. Резник. Корректор В. И. Постнова.
ИБ Ks 2481
Сдано в набор 20.06.80. Подписано к печати 02.04.81. Формат 60Х90/,в. Бумага типограф-
ская № 2. Гарнитура литературная. Печать высокая. Объем 14 бум. л. Усл. печ. л. 28,
усл. кр. отт.28. Уч.-изд. л. 26.89. Изд. Кя 2/0982. Тираж 4500 экз. Зак. 727. Цена 4 р. 10 к.
ИЗДАТЕЛЬСТВО «МИР» 129820, Москва, И-ИО, ГСП, 1-й Рижский пер., 2.
Ленинградская типография *й 2 головное предприятие ордена Трудового Красного Зна-
мени Ленинградского объединения «Техническая книга» им. Евгении Соколовой Союз-
полиграфпрома прн Государственном комитете СССР по делам издательств, полиграфии
и книжной торговли. 198052, г. Ленинград. Л-52, Измайловский проспект. 29.
©by Springer-Verlag Berlin Heidelberg 1978
and 1980 All rights reserved.
Authorized translation from English langua-
1704060000 ge edition published by Springer-Verlag
20403—063 Berlin — Heidelberg — New York
C 041@1)—81 63~81' ч" 1 ©Перевод на русский язык, «Мир», 1981
Предисловие редактора перевода
К явлениям магнитного резонанса обычно относят широкий
класс явлений, в котором можно выделить следующие самостоя-
тельные разделы: 1) ядерный магнитный резонанс, 2) электрон-
ный парамагнитный резонанс (называемый также электронным
спиновым резонансом) в ионных кристаллах, парамагнитных со-
лях, полупроводниках и т. п., 3) ферромагнитный резонанс (сюда
включают явления магнитного резонанса в спиновых системах
ферромагнетиков, антиферромагнетиков и ферритов). К тому же
классу явлений можно отнести и разнообразные эффекты в ме-
таллах, полупроводниках, в жидкостях и газах, связанные с их
поведением в переменных электромагнитных полях различной
частоты.
Каждый из указанных выше трех разделов довольно по-
дробно освещен в книгах и обзорах, имеющихся на русском
языке. Можно, например, указать фундаментальный труд А. Аб-
рагама «Ядерный магнетизм» (М.: ИЛ, 1963) и оригинальную
монографию С. А. Альтшулера и Б. М. Козырева «Электронный
парамагнитный резонанс соединений элементов промежуточных
групп» B-е изд., перераб. — М.: Наука, 1972). Однако упомяну-
тые книги рассчитаны на подготовленных читателей и трудны
для тех, кто впервые приступает к изучению этой большой об-
ласти физики.
Предлагаемая вниманию советского читателя книга извест-
ного американского ученого, профессора Иллинойсского универ-
ситета Чарльза П. Сликтера «Основы теории магнитного резо-
нанса» как по форме изложения, так и по подбору и расположе-
нию содержащегося в ней материала представляет собой учебное
руководство по физике магнитного резонанса. Все важные для
понимания предмета специфические вопросы теории излагаются
в ней значительно подробнее, чем в специальных монографиях и
журнальных статьях, приводится много иллюстраций и приме-
ров, даны задачи ^упражнения. Читатель без особого труда мо-
жет выполнить все рассматриваемые р книге вычисления,
освоить методы решения и анализа конкретных физических
задач.
в Предисловие редактора перевода
Читателю, который овладеет материалом этой книги, будет
значительно легче изучать специальные монографии (типа ука-
занных выше) и оригинальные научные статьи.
Книга содержит много удачных педагогических находок и
примеров, позволяющих просто, строго и без большой затраты
времени излагать некоторые трудные вопросы теории магнитного
резонанса. В ней можно найти ценный материал для курсов лек-
ций по физике твердого тела и электронике, радиоспектроскопии,
теории электромагнитного поля в среде, физике магнетизма
и т.п.
В книге приведена библиография, включающая учебники, об-
зоры и некоторые основные статьи, в которых можно найти до-
полнительные сведения по различным вопросам, изложенным в
основном тексте. С большинством из рекомендованных автором
книг можно познакомиться в русском переводе. Редактор все же
счел целесообразным несколько дополнить библиографию ссыл-
ками на имеющиеся на русском языке руководства и обзоры.
При подготовке второго английского издания книги A978 г.)
первое издание A963 г.) было полностью пересмотрено автором.
В ряд старых глав включен новый материал, например по во-
просу о спиновом эхе (§ 9, гл. 2), добавлены три главы F—8)
и приложения (Е и Ж), расширена библиография, помещенная
в конце книги. В новых главах рассматриваются представления
о спиновой температуре, двойном магнитном резонансе п методы
сужения линий в твердом теле. Эти методы находят все возрас-
тающее применение в физике и химии твердого тела, так как с
их помощью можно изучать очень тонкие эффекты и слабые
взаимодействия. В 1980 г. автор внес ряд исправлений в издание
1978 г. и таким образом появилось второе исправленное издание
1980 г., перевод с которого мы и выносим на суд читателей. При
переводе были исправлены (без специальных оговорок) опечат-
ки, а также устранены некоторые неточности в тексте.
Книга вполне доступна для аспирантов и студентов старших
курсов университетов и физико-технических вузов. Она, несом-
ненно, будет полезна как для теоретиков, так и для эксперимен-
таторов, которым по характеру работы необходимо познако-
миться с основами теории магнитного резонанса. Особенно инте-
ресной она будет для тех, кто занимается применениями методов
магнитного резонанса (электронного и ядерного) в физике твер-
дого тела.
В. Скроцкий
Предисловие автора ко второму
исправленному изданию
После распродажи первого тиража книги «Основы теории
магнитного резонанса», выпущенной издательством Шпрингер, я
получил возможность внести изменения, улучшающие текствто-
рого издания:
1) поправил ряд фраз и добавил несколько новых ссылок;
2) исправил типографские и другие опечатки;
3) добавил таблицу перевода единиц (приложение 3), кото-
рая поможет научным работникам при желании перевести вели-
чины, содержащиеся в тексте, в систему СИ.
Я нахожусь в долгу перед рядом ученых, приславших мне
замечания по предыдущему изданию, и я благодарен издатель-
ству Шпрингер за предоставленную мне возможность внести
исправления.
Урбана, Иллинойс
Январь 1980 г.
Чарльз П. Сликтер
Предисловие автора
ко второму изданию
Автору доставляет большое удовольствие внести свой вклад
в выпуск новой серии (издательства Шпрингер) по физике твер-
дого тела. Несколько лет назад я написал книгу «Основы теории
магнитного резонанса». Я очень хотел опубликовать новую кни-
гу, в которой рассматривались бы спиновая температура, двой-
ной резонанс и импульсное сужение линий магнитного резонанса.
Эти темы являются важнейшими направлениями развития совре-
менного магнитного резонанса. Они совсем не рассматривались
в моей первой книге. Приглашения прочесть лекции в Осаке
(Япония), Лёвене (Бельгия) и Лозанне (Швейцария) побудили
меня приготовить первые наброски новых тем н получить на них
отзывы студентов. Однако мои планы изменились, когда я узнал,
что книга «Основы теории магнитного резонанса», став библио-
графической редкостью, более не доступна читателю. Доктор
Лоч, возглавляющий редакцию физики издательства Шпрингер,
и я решили, что имеет смысл объединить новую книгу с пересмо-
тренной старой и тем самым предложить читателю полный текст
по основам магнитного резонанса, содержащий подробный ана-
лиз небольшого числа концепций, которые являются основой для
больших областей магнитного резонанса. Кроме трех новых
глав, в текст предыдущего издания включен новый материал.
Написаны также два новых приложения (одно по применению
уравнений Блоха для анализа кинетических процессов, другое
по влиянию диффузии на спиновое эхо) и добавлен ряд задач.
Урбана, Иллинойс
Январь 1978 г.
Чарльз П. Сликтер
Глава 1
Понятие о магнитном резонансе
§ 1. Введение
Магнитным резонансом называют явление, которое наблю-
дается в системах частиц, обладающих как магнитными, так и
механическими моментами. Как будет видно из последующего,
термин резонанс означает, что при экспериментальном наблюде-
нии явления производится настройка на собственную частоту
магнитной системы, соответствующую в рассматриваемом слу-
чае частоте гироскопической прецессии магнитного момента си-
стемы во внешнем постоянном магнитном поле. Поскольку эта
частота аналогична характеристическим частотам атомных
спектров и находится обычно в высокочастотной (для ядерных
спинов) или сверхвысокочастотной (для электронных спинов)
областях, мы будем часто пользоваться в дальнейшем терми-
нами высокочастотная или сверхвысокочастотная спектроскопия.
Достоинство резонансного метода заключается в том, что он
позволяет обнаруживать и выделять из полной магнитной вос-
приимчивости очень небольшие ее изменения, обусловленные
различными причинами. Наиболее эффектным примером, несом-
ненно, является наблюдение очень слабого ядерного парамагне-
тизма железа на фоне электронного ферромагнетизма. Резонанс-
ные методы дают возможность получать такую точную и деталь-
ную информацию о магнитных свойствах вещества, которую едва
ли можно получить какими-либо другими методами.
Одна из причин интенсивного проникновения методов маг-
нитного резонанса в различные области физики заключается в
том, что они позволяют получать информацию о процессах на
атомном уровне. В этой книге мы стремимся дать некоторые
сведения, необходимые или полезные с точки зрения применения
магнитного резонанса для изучения твердого тела. Большая
часть книги посвящена рассмотрению явления ядерного магнит-
ного резонанса, однако в последних главах в центре внимания
стоят некоторые проблемы, особенно важные при изучении элек-
тронного спинового резонанса. Большинство положений, разви-
тых в первых главах книги, конечно, в равной степени примени-
мо как к ядерному, так и к электронному магнитному резонансу.
Наша цель состоит не в том, чтобы рассказать, как при-
менять магнитный резонанс для исследования твердого тела.
10 Глава 1
Интерес к магнитному резонансу возрос до такой степени и вы-
лился в такое количество новых концепций и результатов, что
всякий автор или лектор сталкивается с большими трудностями
при отборе материала. В данной книге, обращаясь к изучению
твердого тела, мы преследовали цель на этом примере поставить
основные физические вопросы, требующие обсуждения в про-
блеме магнитного резонанса, а также получить наибольшее чис-
ло конкретных примеров, иллюстрирующих формальные методы.
Как отмечено выше, мы рассматриваем магнитные системы,
обладающие механическими моментами. Примерами таких си-
стем могут служить электронные спины или ядра атомов. Такая
система, как ядро, может состоять из большого количества час-
тиц, связанных вместе таким образом, что в любом возможном
состоянии она обладает полным магнитным моментом fi и пол-
ным механическим моментом J. Эти векторы можно считать па-
раллельными, вследствие чего можно написать
H = \J, A.1)
где у — скалярная величина, которая называется «гиромагнит-
ным отношением». Для любого состояния ядра задание волно-
вой функции в принципе дает возможность вычислить обе вели-
чины ji и J. Эти расчеты показывают, что гиромагнитное отно-
шение у зависит от состояния ядра. Вычисления такого рода
выходят за рамки данной книги.
В квантовой теории величины ц и J представляют собой век-
торные операторы. Смысл утверждения о «параллельности» двух
операторов может быть выяснен при рассмотрении матричных
элементов этих операторов. Предположим, что мы определили
безразмерный оператор механического момента J соотношением
J=M; A.2)
вдесь I2 имеет собственные значения /(/ -j- 1), где / является це-
лым или полуцелым числом. Любая компонента I (например,
Iz) коммутирует с I2, поэтому мы можем одновременно опреде-
лить собственные значения операторов I2 и /г. Обозначим эти
собственные значения соответственно через / и т. Величина т
может принимать 2/+1 значение: /,/ — 1, ..., —/. Соотноше-
ние A.1) теперь можно записать в развернутом виде:
Aт | iv 11т') = уП Aт \ 1Х. \ 1т'), A.3)
где (V и 1Х' — проекции операторов ц и I на произвольное на-
правление х'. В справедливости этого равенства можно убедить-
ся, воспользовавшись теоремой Вигнера — Эккарта, которая рас-
сматривается в гл. 9.
Понятие о магнитном резонансе 11
В этой вводной главе кратко рассматриваются основные по-
ложения магнитного резонанса и без доказательства принимают-
ся некоторые существенные положения и выписываются некото-
рые уравнения, обоснование которых дано в последующих гла-
вах.
§ 2. Элементарная теория резонанса
В последующих главах явление магнитного резонанса рас-
сматривается как с классической, так и с квантовомеханической
точки зрения. Классическое описание оказывается особенно по-
лезным при обсуждении динамических или переходных эффек-
тов. В качестве введения в физику магнитного резонанса мы
рассмотрим вначале элементарную квантовомеханическую тео-
рию этого явления.
При включении магнитного поля Н каждое ядро приобретает
дополнительную энергию —ц-Н, которую называют зеемаиов-
ской. Гамильтониан в этом случае имеет очень простой вид:
^ = _,i.H. A.4)
Направляя ось г вдоль приложенного постоянного магнитного
поля Но, получаем
Ж ПН1 A.5)
Собственные значения этого гамильтониана являются произве-
дениями величины ytlHo на собственные значения оператора /2.
Поэтому возможные значения энергии равны
m = I, /-1 -/. A.6)
Схема уровней энергии для случая / = 3/г. который имеет
место для ядер Na и Си, приведена на рис. 1.1, где уровни экви-
дистантны и расстояние между ними равно уНН0.
m
—з/г —
Рис. 1.1. Уровни энергии для спина — jfz
'-''* иг
з/г
Существование такой системы уровней энергии можно обна-
ружить по появлению избирательного поглощения. Для этого не-
обходимо включить взаимодействие, которое могло бы вызвать
переходы между уровнями. Для удовлетворения закона сохра-
нения энергии необходимо, чтобы это взаимодействие изменя-
лось во времени с угловой частотой ю, определяемой соотноше-
нием
Й<о = Д?, A.7)
12 Глава 1
где Л? — разность энергий между начальным и конечным уров-
нями зеемановского энергетического спектра. Более того, ма-
тричный элемент этого взаимодействия, связывающий начальное
и конечное состояния системы, должен быть отличным от нуля.
Чаще всего для наблюдения магнитного резонанса приме-
няют переменное магнитное поле, направленное перпендику-
лярно постоянному полю. Если амплитуду переменного поля обо-
значить через Н°х, то часть полного гамильтониана, приводящая
к переходам, т. е. гамильтониан возмущения, будет иметь вид
Жози = - \hH°Jx COS (О/. A.8)
Оператор /* имеет отличные от нуля матричные элементы
(m'\Ix\tn), связывающие состояния т и т', только в случае вы-
полнения равенства т' = т± 1. В соответствии с этим разре-
шены переходы только между соседними уровнями, что дает
/гсо = Л?==уВДъ A.9)
или
(й = уН0. A.9а)
Заметим, что постоянная Планка не входит в последнее соот-
ношение, определяющее условия резонанса. Это обстоятельство
указывает на возможность классической интерпретации явления.
Ниже будет показано, что классическое описание действительно
также приводит к соотношению A.9а). Рассмотрение обоих под-
ходов, классического и квантовомеханического, позволяет более
глубоко понять изучаемые явления.
Соотношение A.9а) позволяет вычислить частоту, при кото-
рой можно наблюдать резонанс, если известно, каким образом
можно определить у. Методы вычисления этой величины для
ядер лежат вне области наших интересов, хотя они и имеют
очень большое значение в теории структуры ядра. Однако пра-
вильно оценить порядок величины у можно на основе простой
классической модели.
Вычислим магнитный и механический моменты частицы мас-
сы т и заряда е, движущейся по окружности радиуса г с перио-
дом Т. В этом случае механический момент
а магнитный момент
ц = М A.11)
(мы рассматриваем систему как контур тока I, охватывающий
площадь А). Поскольку i = (е/с) A/Т), получаем
Понятие о магнитном резонансе 13
Сравнение вычисленных значений ц и J дает у = [i/J =
= e/2tnc. Помимо оценки порядка величины у эта формула по-
зволяет сделать еще один важный вывод о том, что величина у
для ядер должна быть на три порядка меньше величины у для
электронов. Действительно, для магнитных полей Н от 3 • 103 до
104 Гс резонанс в электронных системах наблюдается в области
частот ю/2я» 104 МГц (диапазон СВЧ), в то время как ядерный
резонанс наблюдается на частотах ~ 10 МГц (высокочастотный
диапазон). Конечно, всегда можно изменить ю, изменив Но, од-
нако в большинстве случаев предпочтительнее пользоваться са-
мыми сильными магнитными полями, какие могут быть получены
в лабораторных условиях, так как при этом возрастает величина
поглощаемых квантов и сигнал резонанса увеличивается.
Типичные экспериментальные устройства будут описаны
ниже.
§ 3. Поглощение энергии
и спин-решеточная релаксация
Сделаем теперь следующий шаг и выясним особенности пове-
дения макроскопического образца в условиях магнитного резо-
нанса. Для простоты рассмотрим систему, содержащую ядра со
— г/г /V
Рис. 1.2. Уровни энергии для спина уЫ10
1"" Ч» +7/2 /V+
спином х/2 (рис. 1.2). Поскольку в макроскопическом образце
много ядер, удобно ввести населенности N+ и N-, которые озна-
чают числа спинов в состояниях m = '/г и гп=* — '/г соответ-
ственно.
Под воздействием переменного поля населенности N+ и iV_
изменяются в результате вынужденных переходов; при этом, ко-
нечно, общее число спинов Xf остается постоянным. Пусть
№{+)+.{-) — вероятность перехода в единицу времени спина с
уровня m = '/г на уровень m = —'/г. a lF(_)->(+) — вероятность
обратного перехода. Тогда можно написать следующее диффе-
ренциальное уравнение для изменения населенности N+ со вре-
менем:
^ . A.13)
Не делая пока никаких предположений относительно вычис-
ления №(+).>.(_) и W(_)^.(+), заметим, что известная формула для
вероятности перехода в единицу времени Ра-*ь, следующая из
14 Глава 1
нестационарной теории возмущений, имеет вид
% A.14)
где V(t) — возмущение, вызывающее переход из состояния а с
энергией Еа в состояние Ь с энергией Еь. Поскольку
| (a|K|6)|2= |F|K|a)|2, вероятности переходов Ра-+ь и Рь-*а
равны. Это обстоятельство приводит в данном случае к условию
W W W. Следовательно,
^ A.15)
Удобно ввести переменную п — N+— N- (избыток населен-
ности), представляющую собой разность населенностей двух
уровней. Тогда две переменные N+ и ./V- можно выразить через
п и N, пользуясь уравнениями
N=*N+ + N_, n = N+-N_, A.16)
N+=z±.(N + n), N_ = ±-(N-n). A.16а)
Подставляя A.16а) в A.15), получаем уравнение
•§- = -2Wn, A.17)
решение которого имеет вид
n = n@)e-2wt, A.18)
где п@) — значение п при t = 0. Из решения видно, что если
вначале населенности уровней были различными, то в конце кон-
цов в результате вынужденных переходов они сравниваются и
разница в населенности исчезает.
Скорость поглощения энергии высокочастотного поля dE/dt
определяется разностью между числом квантов tta>, которые
поглощаются при переходе спинов с нижнего уровня энергии на
верхний, и числом квантов, которые испускаются при обратном
переходе. Таким образом,
-^ = N+Wh(o - N_Wha> = ha>Wn. A.19)
Следовательно, чтобы имело место поглощение энергии, чи-
сло п не должно равняться нулю, т. е. должен существовать из-
быток населенности на верхнем или нижнем уровне. Если верх-
нее состояние населено больше, чем нижнее, результатирующее
поглощение отрицательно, т. е. система отдает энергии больше,
чем получает. Эта возможность послужила основой для созда-
Понятие о магнитном резонансе 15
ння квантовых генераторов и усилителей, известных под назва-
нием мазеры1).
Таким образом, если приведенные выше уравнения правильно
описывают процесс, резонансное поглощение энергии в конце
концов должно прекратиться п сигнал резонанса не будет на-
блюдаться, что противоречит опыту. Еще более серьезное проти-
воречие возникает, если принять W = 0 (что означает отсутствие
внешнего переменного поля). При этом из наших уравнений сле-
дует, что dN+/dt = 0, т. е. населенности не изменяются со вре-
менем. Однако если поместить ненамагниченный образец в по-
стоянное магнитное поле, то он намагнитятся. Иными словами,
направление ядерных моментов, параллельное полю, является
предпочтительным, т. е. N+ больше N- (N- = 0 соответствует
состоянию полной поляризации, которое возможно только при
абсолютном нуле температуры). Следовательно, для процесса
намагничивания образца необходимо, чтобы скорость переходов
из верхнего состояния в нижнее была больше скорости обрат-
ных переходов. При таком процессе спиновая система теряет
энергию, иначе говоря, происходит отвод тепла. Для этого необ-
ходимо, чтобы существовала некоторая другая система, способ-
ная поглощать энергию. Окончательная разность населенностей
уровней спиновой системы зависит от способности другой систе-
мы поглощать энергию. Говоря на языке термодинамики, пере-
дача тепла будет продолжаться до тех пор, пока отношение на-
селенностей N-/N+ не будет соответствовать равновесному зна-
чению для температуры Т резервуара, в который передается
энергия. Окончательные равновесные населенности №+ н N-
в этом случае удовлетворяют соотношению
A20)
Таким образом, необходимо предположить существование ме-
ханизма, вызывающего переходы между уровнями спиновой си-
стемы с населенностями N+ и N- и обусловленного взаимодей-
ствием с другой системой. Пусть И?^ — вероятность перехода в
единицу времени из состояния (+) в состояние (—) под влия-
нием такого взаимодействия, a W+ — вероятность обратного пе-
рехода. Тогда в отсутствие высокочастотного поля
A.21)
Введем опять переменные ./V и п. Теперь уже нельзя считать ве-
роятности перехода вверх я вниз одинаковыми, так как это не
') Maser (microwave amplification by stimulated emission of radiation) —
сверхвысокочастотный усилитель на основе вынужденного излучения.
16 Глава 1
давало бы преимущества переходам вниз и не приводило бы
к намагничиванию образца. В самом деле, в стационарном со-
стоянии dN+/dt = 0, и из уравнения A.21) мы получаем
«V
A.22)
откуда с помощью уравнения A.20) находим
117.
A.22а)
Естественно задать вопрос, почему здесь не применимы аргу-
менты, приводящие к равенству №(+).>(_) = W(_»(+). Решение
Резервуар Ядро Резервуар
а г * х
а 6
Рис. 1.3. Переходы: а — разрешенный, б — запрещенный.
этого парадокса состоит в том, что для термического перехода,
помимо взаимодействия с другой системой, требуется существо-
вание определенного энергетического состояния этой системы,
при котором возможен переход. Это можно проиллюстрировать,
предположив, что резервуар имеет только два уровня энергии,
расстояние между которыми точно такое же, как у ядерной си-
стемы. Если ядро и резервуар вначале находятся в противопо-
ложных состояниях (рис. 1.3, а), то одновременный переход, ука-
занный стрелками, удовлетворяет закону сохранения энергии.
Следовательно, ядро может отдавать энергию решетке. С дру-
гой стороны, если обе системы находятся в верхнем состоянии
(рис. 1.3, б), то одновременный переход невозможен, так как при
этом не сохраняется энергия. В результате скорость ядерного
перехода зависит не только от матричных элементов, но также
и от вероятности того, что резервуар находится в состоянии, при
котором возможен переход.
Таким образом, если мы обозначим населенности ядерных со-
стояний 1 и 2 через Л^ и N2, а населенности состояний а и Ь
через Na и Nt, то число указанных на рис. 1.3, а переходов будет
равно
NiNbWib+K, A.23)
где W\b+2a — вероятность такого перехода за единицу временя
при условии, что ядро и решетка действительно находятся в со-
Понятие о магнитном резонансе 17
стояниях 1 и b соответственно. Стационарное состояние удовле-
творяет условию, которое мы найдем, приравняв скорость такого
перехода скорости обратного перехода:
A.24)
Поскольку из квантовой теории следует равенство Wi&-*2a
WW&t мы видим, что при тепловом равновесии
Поэтому ядерные уровни будут характеризоваться таким же от-
ношением населенностей, как и решеточные, т. е. населенности
ядерных уровней будут находиться в тепловом равновесии с ре-
шеткой. Кроме того, для этой простой модели мы можем срав-
нить Wjt-и W+i
Wt = NaW2a + lb, W+ = NbWlb + 2a = NbW2a+lb A.26)
и убедиться в том, что они не равны друг другу.
Оставим теперь нашу специальную модель и вернемся к урав-
нению A.21). После подстановки A.16а) для N+ и N- получим
уравнение
Z A.27)
которое можно записать также в виде
d,l flQ-П п
где
(ДО7. ЦТ . N 1
wl + wj' тг==(^ + ^)- (К29)
Из решения уравнения A.28)
л = /ю + Ае-*!** A.30)
(где А — постоянная интегрирования) видно, что п0 — равновес-
ная разность населенностей, скорость установления которой ха-
рактеризуется промежутком времени Т\, так называемым «вре-
менем спин-решеточной релаксации». Например, процесс намаг-
ничивания первоначально не намагниченного образца происхо-
дит по экспоненциальному закону возрастания п до равновесного
значения п0:
п = поA-е-"г0. A.31)
Таким образом, Т\ представляет собой время, необходимое для
намагничивания образца.
18 Глава 1
Объединив два уравнения для dn/dt, найдем полную скорость
перехода, обусловленную тепловыми процессами и внешним пе-
ременным полем:
-g. = _2№n + -^=-^. A.32)
Из уравнения A.32) следует, что в стационарном состоянии
Следовательно, до тех пор пока 2WTi «С 1, п = По и поглощение
энергии внешнего переменного поля практически не нарушает
равновесных населенностей. Скорость поглощения энергии dE/dt
определяется следующим выражением:
4f = nh(»w = "«л* l+w2WTi. A.34)
Ниже мы увидим, что вероятность W пропорциональна квад-
рату амплитуды переменного магнитного поля. Тогда из A.34)
следует, что, повышая амплитуду переменного поля, можно уве-
личивать поглощаемую ядрами мощность до тех пор, пока
2WTi <^; 1. Однако это утверждение оказывается неверным, как
только W становится порядка Уг^ь При дальнейшем увеличении
W поглощаемая мощность остается постоянной. Этот эффект
называется насыщением. Наблюдая эффект насыщения, можно
измерять Т\, если только имеется достаточная информация для
вычисления W (часто встречающаяся ситуация).
Мы познакомились с несколькими величинами, необходи-
мыми для описания магнитного резонанса. При этом выяснилось,
что Ти очевидно, связано с микроскопическими деталями строе-
ния как ядерной системы, так и резервуара. Мы рассмотрим в
дальнейшем различные механизмы спин-решеточной релаксации
и покажем, каким образом можно вычислить Ti для некоторых
из них. В ранних работах по ядерному резонансу высказывались
опасения по поводу того, что процесс спин-решеточной релакса-
ции может оказаться очень медленным и поэтому за разумный
промежуток времени трудно достигнуть заметной разности насе-
ленностей. Известный голландский физик Гортер, сделавший
много предсказаний и открытий в области магнитной релакса-
ции, первый пытался наблюдать магнитный резонанс в макро-
скопическом образце [1]. Его постигла неудача, по-видимому
связанная с тем, что он выбрал вещество, обладающее большим
значением Тх и, следовательно, легко насыщающееся.
Когда Пёрселл, Торри и Паунд [2] впервые наблюдали ре-
зонанс на протонах в парафине, они помещали ядра в магнитное
поле Но задолго до начала резонансного поглощения. При этом
они применяли слабое переменное поле, чтобы избежать насы-
Понятие о магнитном резонансе 19
щения и успеть наблюдать резонанс, хотя Ti составляло несколь-
ко секунд. Их работа, а также работы Блоха, Хансена и Пакар-
да [3] были выполнены независимо от работы Гортера.
Как мы видели, скорость поглощения энергии связана со ско-
ростью перехода W. Оценка величины резонансного поглоще-
ния играет основную роль при решении вопроса о том, может ли
наблюдаться резонанс. Ниже мы увидим, как вычисляется W.
Кроме того, поскольку резонансная линия всегда в той или иной
мере размыта, важно рассмотреть причины, вызывающие ее
уширение. Сюда же примыкает вопрос о том, какое значение
магнитного поля нужно подставлять в соотношение со = уН0,
поскольку около каждого ядра всегда находятся близкие со-
седи. В самом деле, благодаря присутствию электронов и сосед-
них ядер всегда имеются магнитные поля, которые должны до-
бавляться к внешнему полю. Эти поля вызывают очень интерес-
ные эффекты, например расщепление сигнала протонного резо-
нанса в этиловом спирте (СН3СН2ОН) на три линии с соотно-
шением интенсивностей 3:2:1. Они ответственны также за то,
что ядерный резонанс в ферромагнетиках наблюдается даже при
отсутствии внешнего постоянного магнитного поля.
ЛИТЕРАТУРА
1. Gorier С. J., Broer L. J. F., Physika, 9, 591 A942).
2. Purcell Е. М., Тоггеу Н. С, Pound R. V., Phys. Rev., 69, 37 A946).
3. Block F., Hansen W. W., Packard M., Phys. Rev., 69, 127 A946).
Глава 2
Основы теории
§ 1. Движение невзаимодействующих спинов.
Классическое рассмотрение
Изложение основ теории мы начнем с классического описа-
ния движения спина во внешнем магнитном поле Н, которое,
вообще говоря, может зависеть от времени. В поле Н на маг-
нитный момент ц действует момент сил цХ Н. Если в магнитное
поле поместить намагниченный стерженек, установленный в под-
шипниках таким образом, что он может свободно ориентировать-
ся в пространстве, то момент сил будет стремиться установить
его параллельно направлению Н. В случае когда поле Н не за-
висит от времени и трение в подшипниках отсутствует, стерже-
нек будет колебаться около положения равновесия. При нали-
чии трения в подшипниках колебания стерженька будут зату-
хать до тех пор, пока он не установится параллельно Н; затуха«
ние обусловлено передачей энергии колебаний подшипникам.
Если намагниченный стерженек обладает моментом количе-
ства движения, то ситуация изменяется, так как стерженек будет
двигаться подобно гироскопу. Как будет показано ниже, при от-
сутствии трения в подшипниках угол между магнитным момен-
том и полем Н, если последнее не зависит от времени, будет
оставаться неизменным и магнитный момент будет прецессиро-
вать вокруг направления Н. Энергия будет по-прежнему сохра-
няться, но превращения кинетической энергии в потенциальную
и обратно уже не будет происходить. Однако и в этом случае
при наличии трения в подшипниках магнитный момент будет
ориентироваться параллельно постоянному полю Н. Ниже мы
увидим, что трение соответствует релаксационному процессу, ко-
торый характеризуется временем релаксации Т\.
Уравнение движения магнитного стерженька мы получим,
приравнивая момент сил скорости изменения механического мо-
мента J:
-ЗГ~1*ХН. B.1)
Учитывая, что ц = yi, и исключая из этого уравнения J, полу-
чаем
§ B.2)
Основы теории 21
Как следует из этого уравнения, в каждый момент времени при-
ращение ц перпендикулярно как ц, так и Н независимо от того,
изменяется ли поле Н со временем или нет. Обратимся к рис. 2.1.
Если начальную точку вектора ц считать неподвижной, то его
конец будет двигаться от плоскости чертежа. Угол G между ц
и Н не изменяется. Если Н не зависит от времени, то вектор ц
описывает конус.
Решение уравнения B.2) при различных предположениях
о характере зависимости Н от времени можно получить обыч-
ными методами решения дифференциальных уравнений. Однако,
Рис. 2.1. Относительное положение
векторов |i и И.
как будет видно из дальнейшего, в этом случае удобнее всего
применить специальный прием, который заключается во введе-
нии вращающейся системы координат.
Рассмотрим векторную функцию времени F(/), проекции ко-
торой на соответствующие оси прямоугольной системы коорди-
нат обозначим через Fx(t), Fy(t) и Fz(t). Если через i, j, k обо-
значить единичные векторы, направленные вдоль этих осей, то
величину F можно записать в виде
F = iFx + iFy + kFz. B.3)
Обычно i, j и к считают не зависящими от времени. Мы рассмо-
трим более общий случай, когда длины этих векторов фиксиро-
ваны, но векторы могут вращаться. Предположим, что они вра-
щаются с мгновенной угловой скоростью Q. Тогда
B-4)
При этом производная от F по времени равна
dF« . P di JЬ
= -S- + fiXF. B.5)
Здесь символ 6F/6? введен для обозначения скорости изменения
вектора F во времени в системе координат, определяемой векто-
22 Глава 2
рами i, j и к. Например, когда 6F/6t = 0, проекции вектора F на
направления i, j и к не меняются во времени.
С учетом B.5) уравнение движения для вектора ц в системе
координат, вращающейся относительно лабораторной системы
координат с произвольной угловой скоростью Q, можно записать
в следующем виде:
^ B.6)
или
-?•-цХ(?Н + О). B.7)
Из уравнения B.7) видно, что движение вектора ц во вращаю-
щейся системе координат будет таким же, как в лабораторной
системе при замене магнитного поля Н эффективным полем НЭфф:
НН
Теперь легко решить уравнение движения для ц в постоян-
ном поле Н = к#о, если выбрать Q таким образом, чтобы поле
НЭфф было равно нулю. Для этого нужно положить Q = — уНок.
Поскольку в этой системе отсчета 6ц/Ы = 0, вектор ц фиксиро-
ван по отношению к осям i, j n k. Следовательно, вектор ц будет
неподвижен относительно системы осей, которые сами вращают-
ся с угловой скоростью Q = — v#ok в лабораторной системе ко-
ординат. Другими словами, вектор ц вращается с угловой ско-
ростью Q = —уНок относительно лабораторной системы коор-
динат. Угловая частота уН0 называется ларморовской частотой.
Подчеркнем, что классическая частота прецессии Q равна по
величине угловой частоте, необходимой, согласно элементарной
квантовой теории, для наблюдения магнитного резонансного по-
глощения. Перейдем теперь к более подробному рассмотрению
квантовомеханического описания.
§ 2. Квантовомеханическое описание спина
в постоянном поле
Как было показано выше, квантовомеханическое описание
спина в постоянном поле приводит к выражению для энергии,
зависящему от квантового числа гп, которое представляет собой
собственное значение проекции спина 1г, параллельной постоян-
ному полю Но. Выражение для энергии имеет вид
Em = -yhHom. B.9)
Соответствующие собственные функции не зависящего от вре-
мени уравнения Шредингера обозначим ш, т. Тогда зависящее
Основы теории 23
от времени решение, соответствующее данному значению т, мож-
но записать в виде
^t. т (О = «/. те~ (т Ет*- B.10)
Следовательно, наиболее общее решение имеет вид
4(t) = ]tiCmul,me-m)B'"t, B.11)
где Cm — комплексные постоянные. С помощью W(t) можно рас-
считать средние значения любых наблюдаемых величин. В каче-
стве примера вычислим среднее значение проекции магнитного
момента на ось х:
B.12)')
Необходимо подчеркнуть, что среднее значение величины цх,
обозначаемое <цж>, зависит явно от времени, поскольку в него
входят зависящие от времени функции. Учигывая, что ц* = уЫх,
определено выражением B.11), находим
(Hx(t))= X yfic*m,c(mr \lx\m)em) {-Em'~E^t, B.13)
ffl, ftl'
где
B.14)
представляет собой не зависящий от времени матричный эле-
мент. Выражение, подобное B.13), можно получить для произ-
вольного оператора. Отметим, что средние значения величин, во-
обще говоря, зависят от времени; в них входят гармонически
осциллирующие члены, возможные частоты которых
3z? B.15)
соответствуют частотам поглощения или излучения при перехо-
дах между состояниями m и т'. Здесь мы встречаемся с основ-
ным предположением, сделанным Гейзенбергом и Борном при
формулировке квантовой теории в матричной форме, согласно
которому наблюдаемые величины должны определяться выра-
жениями типа B.13).
') Здесь переменные интегрирования обозначены через dx, подобно тому
как это делается для пространственных координат х, у, г или угловых коор-
динат G, ф. Для спина это представление должно рассматриваться как сим-
волическая запись скалярного произведения двух функций xV(t) и ЧЦЦ
24 Глава 2
Поскольку матричные элементы (т'\1х\т) равны нулю для
всех т', кроме m' = m± 1, в выражении B.13) остаются лишь
члены с угловыми частотами, равными -f- уН0 или — уН0. Сумма
их также включает только частоты уН0. Таким образом, среднее
значение <ц*@> осциллирует во времени с классической часто-
той прецессии.
Здесь удобно ввести хорошо известные «повышающие» и «по-
нижающие» операторы /+ и /-, определяемые равенствами
I+ = Ix + iIy, r = Ix-Hy. B.16)
Операторы Ix и 1У можно выразить через /+ и /~, пользуясь ра-
венствами B.16):
/*=4(/+ + Г), Iy^~r(l+-r). B.17)
Операторы 1Х и 1У называются «повышающими» и «понижаю-
щими» в зависимости от результата их действия на функцию
Ш, т.
1+uj, m — У/ (/ + 1) — m (m + \)uh т+и
B1)
l) — m(m—
Оператор /+ переводит «/, т в функцию, у которой индекс увели-
чивается на единицу. Очевидно, величина (т'|/+|ш) обращается
в нуль, если не выполняется соотношение т =т + 1, а вели-
чина (т'\1~\т) обращается в нуль, если нарушается соотноше-
ние т' ~ т — 1. Эти правила отбора Ван Флек [1] назвал «бо-
лее жесткими» правилами отбора, чем правила отбора для опе-
раторов 1х и 1У, которые могут переводить состояние Ui, m как
в состояние ш, т+и так и в состояние ш, т-\.
Чтобы лучше понять физический смысл общего выражения
B.13) для <ц*@>, рассмотрим форму, которую оно принимает
для спина 1/2. Учитывая, что диагональные матричные элементы
1Х равны нулю, получаем
- \IX I - у) е-
Для удобства введем в рассмотрение величину соо = уН0. Мы
видели выше, что соо — угловая частота, при которой в системе
возникает резонанс; она совпадает с классической частотой пре-
цессии. Принимая во внимание, что матричный элемент
Основы теории
25
(xh\l*\—lh) является величиной, комплексно-сопряженной ма-
тричному элементу (—'AU'I'A)» и вводя символ Re для обо-
значения действительной части, получаем
<рх @)= 2YA Re[c\rf_ll2 A1 /я| - 1)е-*»*]. B.20)
Вычисляя матричный элемент с помощью равенств B.17) и
B.18), находим
Величины с удобно выразить через две действительные поло-
жительные величины а и Ь и через две другие действительные
величины аир, которые могут принимать как положительные,
так и отрицательные значения:
B.21)
¦-1/2
¦ ае
la
Условие нормировки волновой
функции дает с2 + 62= 1. Отсю-
да имеем
(V'x (Ф — Y^afe cos (a — р + ©оО-
B.22а)
Подобным же образом получаем
(\ху (()) = — yhab sin (a — Р -f- cooOi
(Рг @> = YА f-^-тг— ) • B.226)
Рис. 2.2. Связь проекций Ах, Аи
Заметим, что величины <цх> и Аг вектора А с углами е_ \
<Ц{,> осциллируют во времени с модулем А
ларморовской частотой yHOl а ве-
личина <[хг> не зависит от времени. Более того, максимальные
значения <^> и <f%> одинаковы. Если определить
<M>> = i<Hx) + j<Hv) + k<Hz) B.23)
и использовать соотношение <ц*J + <Цг/J = const, которое сле-
дует из B.226), то нетрудно видеть, что <ц> ведет себя как век-
тор, направленный под определенным углом к оси z и прецесси-
рующий вокруг этой оси.
В полярных координатах G, <р (рис. 2.2) проекции любого
вектора А можно записать в виде
Ах = A sin G cos <p,
АУ = А sin G sin <p, B.24)
Аг — А cos 6.
26 Глава 2
С помощью алгебраических преобразований можно показать да-
лее', что
W*> = — sm6 cos ф,
(Vy) = -у- sin 6 sin ф, B.25)
<(*г) = "У" COS6,
если
Ф = р-а-шо*, a^H^ii. B.26)
Соотношения B.26) можно рассматривать, конечно, как фор-
мальную замену переменных, однако выражения B.25) допус-
кают простое физическое истолкование, которое заключается
в том, что среднее значение оператора (д, можно рассматривать
как вектор длиной yh/2, ориентация которого задается углами 6,
ф. Если задана ориентация <fi> в некоторый момент времени, то
ее можно найти для всех последующих моментов времени, ис-
ходя из допущения, что <ja> прецесспрует с угловой скоростью
соо в направлении уменьшения угла ф. Следует особо подчерк-
нуть, что ориентацию можно задать произвольно (путем выбора
а или Ь и р — а), так как иногда приходится сталкиваться с
ошибочным мнением, что спины могут быть направлены только
параллельно или антипараллельно направлению поля квантова-
ния. Одно из достоинств квантовой теории заключается в том,
что она может описывать как дискретные, так и непрерывные
свойства. С помощью двух квантовых состояний с т = ± '/г
можно описать все средние значения намагниченности, заклю-
ченные между параллельной и антипараллельной ориентациями.
Так, волновая функция с а = Ь дает среднее значение вектора
намагниченности, соответствующее его положению в плоскости
(х, у), что отвечает равной нулю г-компоненте. Направление
вектора в этой плоскости определяется комплексной фазой
а — р, а также временем наблюдения ориентации.
Рассмотрим вкратце, как должна выглядеть волновая функ-
ция образца, содержащего большое количество невзаимодей-
ствующих спинов, находящихся в состоянии теплового равно-
весия. Каждому спину в этом случае будет отвечать волновая
функция, вообще говоря, не совпадающая с волновой функцией
какого-либо одного состояния (с т = + 1/2 или с т = — у2);
она будет представляться некоторой линейной комбинацией вол-
новых функций возможных состояний. Каждый спин характери-
зуется определенным набором величин а, Ъ, а, р. Эти величины
различны для разных спинов.
В качестве примера рассмотрим распределение величин
а — Р, определяющих ориентацию проекций спинов на плоскость
Основы теории 27
(х, у) в начальный момент времени t = 0. Если спины находятся
в состоянии теплового равновесия, то среднее значение вектора
полной намагниченности должно быть направлено параллельно
магнитному полю. Отсюда следует, что нельзя отдавать предпо-
чтение какому-либо одному значению а — р по сравнению с дру-
гими значениями этой величины, т. е. спины характеризуются
случайным распределением а — р. С другой стороны, поскольку
спины в какой-то степени поляризованы, значения а, большие
чем значения Ь, должны встречаться чаще, чем значения Ъ,
большие чем а. Иными словами, среднее значение величины а
должно быть больше среднего значения величины Ь. Из выраже-
ния B.13) видно, что наблюдаемые величины можно определить,
либо просто задав значения ст, либо задав комплексные произ-
ведения с*т?т, которые ради удобства мы будем обозначать
СИМВОЛОМ Ртт''-
tntnr tnr tn*
В данном случае
Р\/21/2 = а2,
Величины Ртт' можно рассматривать как матричные элементы
комплексной матрицы Р. Отметим, что диагональные матричные
элементы (т = т') определяют вероятности нахождения спинов
в различных состояниях т, в то время как недиагональные эле-
менты связаны с компонентами магнитного момента, перпенди-
кулярными постоянному полю. В следующем параграфе мы бу-
дем пользоваться матрицей Р, усредненной по статистическому
ансамблю. Утверждение, что в состоянии теплового равновесия
вектор намагниченности параллелен полю, равносильно утвер-
ждению, что усредненные по ансамблю величины Ртт- для
т'' ф т равны нулю, в то время как для т = т' вероятности
нахождения спинов в различных состояниях т определяются
распределением Больцмана1).
§ 3. Уравнения движения для средних значений
Тесная взаимосвязь между классическим и квантовым рас-
смотрением становится особенно ясной при исследовании диффе-
ренциального уравнения, описывающего изменение во времени
') Само собой разумеется, что в квантовой теории даже для нескольких
спинов с одинаковыми волновыми функциями любой эксперимент по опре-
делению количества спинов в состоянии т будет создавать статистическое
распределение, которое, однако, не связано с температурой.
28 Глава 2
средних значений <ц,*>, (\ху} и <ц,г>. Это уравнение получается
с помощью хорошо известной формулы, вывод которой мы при-
ведем в несколько сокращенной форме.
Пусть W(t) и Ф(г')—две волновые функции, являющиеся
решениями одного и того же уравнения Шредингера
JL-
B.27)
Рассмотрим оператор F, который не зависит явно от времени.
Тогда
~ J QfFW dx = -L J Ф* (Ж? — FM) W dx. B.28)
Это уравнение легко вывести, используя соотношение
?- \ <3fFWdx=\^FWdx + J VF^dx. B.29)
в котором производные по времени выражаются с помощью
уравнения B.27)').
Уравнение B.28) удобно записать в оперативной форме. Пра-
вую часть этого уравнения можно записать в виде (l/h) X
Х(^^ — FM). Для левой части введем некоторые новые обо-"
значения. Определим оператор dF/dt с помощью равенства
\ф* 4г ^dx=
Таким образом, символ dF/dt не означает взятие производной от
F по времени. Такая производная равна нулю, поскольку F не
зависит явно от времени; dF/dt представляет собой просто
оператор, смысл которого определяется равенством B.30). Из
B.30) следует
2L = -L[X,F], B.31)
где \М, F] — обычный коммутатор d&F — F2/G. Этим формализ-
мом можно воспользоваться для вычисления производных по
времени от средних значений \хх, \iv, \kz. Введем фиксированную
в пространстве систему осей х, у, z с осью г, направленной па-
раллельно направлению магнитного поля в данный момент вре-
мени. (Таким путем мы в.члючаем в рассмотрение как постоян-
ное, так и переменное поля.) Тогда
B.32)
Воспользуемся коммутационными соотношениями для ком-
понент момента количества движения. Их все можно получить
') При выводе уравнения B.28) необходимо учитывать эрмитовость
оператора F (см. § 5 этой главы).
Основы теории 29
циклической перестановкой из соотношения
[1х,1у] = *7г. B.33)
Тогда
Точно так же находим
dI dK - B.346)
Эти уравнения являются компонентами векторного операторного
уравнения
5==|XyH, B.35)
Л ~~ ' df + 3 df + K dt ¦
Далее, поскольку (д, = уН1, производя усреднение, получаем
уравнение для среднего значения магнитного момента
»XyH, B.37)
которое представляет собой классическое уравнение движения
магнитного момента. Уравнение B.37) показывает, что среднее
значение магнитного момента удовлетворяет - классическому
уравнению движения. Оно выведено для среднего значения маг-
нитного момента отдельного спина. Если имеется группа спинов
с моментами \ik для &-го спина, то полный магнитный момент
И==Е^- B,38)
Если спины не взаимодействуют друг с другом, легко показать,
что уравнение B.37) справедливо и для среднего значения пол-
ного магнитного момента. Поскольку на опыте всегда прихо-
дится иметь дело с большим количеством спинов одновременно,
то, измеряя намагниченность, находим среднее значение различ-
ных компонент полной намагниченности. Иначе говоря, экспери-
ментально наблюдаемая величина намагниченности образца
представляет собой просто среднее значение полного магнитного
момента. Поэтому классическое уравнение правильно описывает
динамику намагниченности, если спины могут считаться не вза-
имодействующими друг с другом.
Важно помнить, что уравнение B.37) справедливо не только
для постоянных полей, но и для полей, зависящих от времени.
Поэтому оно позволяет пользоваться классической схемой для
изучения эффектов, связанных с переменными магнитными по-
лями. Эти эффекты рассматриваются в следующем параграфе.
30
Глава 2
§ 4. Эффекты, связанные с переменными
магнитными полями
Движение магнитного момента в переменном магнитном поле
Hx(t) — Нхо cos at удобнее анализировать, если разложить поле
на две составляющие с одинаковыми амплитудами Н\, одна из
которых вращается по часовой стрелке, а другая — в противопо-
ложном направлении (рис. 2.3).
Обозначим эти вращающиеся составляющие через Нд и Hz.:
= Н\ (i cos со/ + j sin со/),
, — Hi (i cos со/ — j sin at).
B.39)
Отметим, что Hz. и Ня отличаются только знаком величины со.
Одна из них вращается в том же направлении, что н прецесси-
рующий момент, а другая —
в противоположном направ-
лении. Можно показать, что
вблизи резонанса состав-
ляющей, вращающейся в
противоположном направ-
лении, можно пренебречь.
Ниже мы всюду будем поль-
зоваться этим допущением.
Однако это допущение де-
лается ненужным, если соз-
давать сразу вращающееся
магнитное поле. В этом по-
следнем случае задачу мож-
но решить точно. Такое поле
можно получить, например,
с помощью двух одинаковых
катушек, расположенных под прямым углом друг к другу, пере-
менные токи в которых сдвинуты по фазе на 90°.
Не уменьшая общности рассмотрения, можно решить задачу
только для поля Нд, так как, меняя знак перед со в решении для
поля HR, можно перейти к решению для поля Hz.. Чтобы сохра-
нить символ со для обозначения положительной величины, вве-
дем символ сог, обозначающий проекцию вектора to на направ-
ление оси г. Составляющая сог может принимать ц'оложнтельные
или отрицательные значения. Следовательно, можно написать
общее выражение
Рис. 2.3. Разложение линейно-полярнзо-
ванного поля на две вращающиеся со-
ставляющие.
Ht = Hi (i COS СОг/ + j Sin &J),
B.40)
которое допускает любое направление вращения в зависимости
от знака сог.
Основы теории 31
Уравнение движения спина, включающее действие как пере-
менного поля Н^), так и постоянного поля Но = ktf0, имеет вид
TJHfiXYlHo + H^]. B.41)
Зависимость величины Hi от времени можно исключить, если
воспользоваться системой координат, вращающейся вокруг оси z
с угловой скоростью coz. В такой системе координат поле Hi не
зависит от времени. Поскольку ось вращения совпадает с на-
правлением Но, поле Но также не будет зависеть от времени.
Тогда вместо уравнения B.41) получим
¦Йг=и х lk <ю*+?я°) + Wi- B-42а)
При преобразовании уравнения B.41) в уравнение B.42а) вы-
являются два эффекта. Первый связан с изменением единичных
векторов во времени и приводит к появлению члена, пропорцио-
нального шг. Второй связан со способом выражения векторов Но
и Hi через их компоненты во вращающейся системе координат
и отражает превращение поля Hi из переменного в постоянное.
Чтобы подчеркнуть, что вблизи резонанса сог + уН0 ~ 0, пере-
пишем уравнение B.42а), принимая во внимание соотношение
&>z = — со, где частота со теперь положительна (здесь предпола-
гается, что величина y положительна). Тогда
= И X Y [(# о - f) к + Я,1] = .и X Нзфф, B.426)
где
Физический смысл уравнения B.426) состоит в том, что во вра-
щающейся системе координат магнитный момент движется так,
как если бы на него действовало магнитное поле НЭфф. Таким об-
разом, он прецесснрует вокруг направления НЭфф с угловой ча-
стотой уНэфф, описывая конус с фиксированным углом при вер-
шине. Это показано на рис. 2.4 для магнитного момента, кото-
рый в начальный момент / = О был направлен вдоль оси г.
Заметим, что это движение момента периодично. Если момент
вначале был направлен вдоль оси г, то он будет периодически
возвращаться к этому направлению. Увеличению угла между
магнитным моментом и осью г соответствует изменение потенци-
альной энергии в лабораторной системе координат1). Однако
вся энергия, которая затрачивается на отклонение вектора ц от
') В лабораторной системе координат магнитная энергия, обусловлен-
ная Но, намного больше магнитной энергии, связанной с Ни поэтому по-
следней обычно можно пренебречь.
32
Глава 2
Но, возвращается обратно в течение цикла вращения ц. Поэтому
поглощения энергии переменного магнитного поля наблюдаться
не будет; система спинов будет лишь отдавать и получать обрат-
но ту же энергию.
Отметим, что в случае, когда Но «выше резонанса»
(Но > о»/у), эффективное поле имеет положительную г-состав-
ляющую, когда же Но «ниже резонанса» (Но <. (а/у), z-состав-
ляющая эффективного поля отрицательна.
Если условие резонанса выполняется точно (со = V^o), то эф-
фективное поле равно просто i#i. В этом случае магнитный мо-
Рис. 2.4, Эффективное поле (а) и движение момента ц во вращающейся си-
стеме координат (б).
мент, ориентированный в начальный момент времени парал-
лельно постоянному полю, будет прецессировать в плоскости
(у, г). Иначе говоря, он будет прецессировать, оставаясь ориен-
тированным перпендикулярно полю Нь Он будет также перио-
дически принимать направление, антипараллельное Но. Если
поле Hi включить на короткий промежуток времени (т. е. воз-
действовать цугом волн длительностью tw), то момент будет по-
ворачиваться на угол 6 = yHitw. Если же интервал времени tw
выбрать таким, чтобы выполнялось равенство G = п, то импульс
будет просто переворачивать момент. Такой импульс принято на-
зывать «180-градусным». При 6 = я/2 (90-градусный импульс)
магнитный момент будет ориентироваться параллельно оси у.
После выключения поля Hi момент перестает двигаться во вра-
щающейся системе координат; следовательно, в лабораторной
системе он будет прецессировать, сохраняя ориентацию, перпен-
дикулярную постоянному полю.
Эти замечания подсказывают очень простой метод наблюде-
ния магнитного резонанса, который иллюстрируется на рис. 2,5,
Основы теории
33
Поместим образец из исследуемого вещества в катушку, ось
которой ориентирована перпендикулярно Но. При тепловом рав-
новесии будет существовать избыток моментов, ориентирован-
ных параллельно Но. При приложении к катушке переменного
напряжения возникает переменное магнитное поле, перпендику-
лярное Но. При соответствующим образом подобранных Н\ и tw
можно получить 90-градусный импульс. После такого импульса
избыточная намагниченность будет прецессировать с угловой ча-
стотой уН0. В результате в катушке возникнет магнитный поток,
jj I 4-H St.
а
Рис. 2.В. Катушка с образцом в поле Нэ.
В состоянии теплового равновесия 1а) магнитные моменты ориентированы преимущественно
вдоль направления поля Но. После 90-градусного импульс: \)ае) магнитные моменты
ориентированы преимущественно перпендикулярно направлению поля Н
меняющийся вследствие прецесош^спинов. Индуцируемую при
этом электродвижущую силу можно наблюдать.
Из этого объяснения следует, что индуцированная электро-
движущая сила должна существовать неограниченно долго, од-
нако практически взаимодействие спинов со средой приводит
к затуханию прецессии. Это затухание в жидкостях происходит
в течение многих миллисекунд, а в твердых телах — обычно за
время порядка 100 мкс. Однако даже такой короткий промежу-
ток времени во много раз больше периода прецессии. Описан-
ный способ наблюдения спада свободной индукции (в отсут-
ствие поля Н\) часто применяется для наблюдения резонанса.
Его большим достоинством является то, что он позволяет изу-
чать резонансный сигнал в отсутствие напряжения, создающего
поле Hi. Поскольку генератор всегда генерирует шумы, такой
способ может оказаться в ряде случаев наиболее удобным.
Метод вращающейся системы координат позволяет легко до-
казать интересную теорему, лежащую в основе другого способа
наблюдения резонансных сигналов. Предположим, что имеется
магнитное поле Нй постоянной величины, направление которого
можно изменять (прочие магнитные поля отсутствуют). Пусть
о Зак. У'^
34
Глава 2
м
намагниченность М параллельна Но при / = 0. Изменение на-
правления Но можно характеризовать угловой скоростью со. То-
гда теорему можно сформулировать следующим образом. Если
\Н0»со,
то при вращении поля Но намагниченность М будет поворачи-
ваться вместе с полем Н0) оставаясь все время параллельной
ему.
Чтобы доказать эту теорему, предположим, что вектор со на-
правлен вдоль оси Z перпендикулярно Но (параллельная Но ком-
понента вектора со интересующе-
го нас эффекта не дает). На
рис. 2.6 показано расположение
векторов в момент времени t — 0
для случая, когда М и Но в лабо-
раторной системе координат на-
правлены параллельно друг дру-
гу и оси X. Если перейти к си-
стеме координат х, у, г, вращаю-
щейся с угловой скоростью
С*я = со, то в этой системе коор-
динат вектор Но будет неподвиж-
ным, но к полю Но необходимо
добавить эффективное поле fi^/v-
Для случая, когда оси г и Z
параллельны друг другу, а ось х совпадает с осью X при t = 0,
эффективное поле и намагниченность при / = 0 показаны на
рис. 2.7.
Эффективное поле во вращающейся системе координат не-
подвижно и определяется выражением
Нэфф = Но-
Намагниченность М прецессирует вокруг НЭфф под углом 6, опре-
деляемым соотношением
B.43)
Рис. 2.6. Магнитное поле Но, на-
магниченность М и угловая ско-
рость со при t = 0.
Следовательно, вектор М будет оставаться в пределах угла 26,
биссектриса которого направлена вдоль Но. Таким образом, если
со/у#о ¦С 1, то векторы М и Но будут оставаться параллельными.
Если при достаточно медленном изменении направления поля
намагниченность следует за ним, то мы будем говорить в даль-
нейшем, что изменение поля происходит адиабатически.
С помощью аналогичных рассуждешиг можно рассмотреть и
случай магнитного поля Hi, вращающегося в плоскости, перпен-
Рис. 2.7. Намагниченность М и эффективное поле Нэфф во вращающейся
системе координат х, у, г.
Намагниченность прецессирует вокруг направления аффективного поля, образуя коиуо
с углом в
м
о
Рис. 2.8. Ориентация намагниченности М во вращающейся системе координат.
Намагниченность М и эффективное поле Нэ. . параллельны (а). Намагниченность М па-
раллельна Н- при значениях Яо много выше резонанса; при медленном уменьшении Wo
намагниченность в момент резонанса параллельна Я] F).
2*
36 Глава 2
дикулярной постоянному магнитному полю Но, с частотой со. Ко-
гда напряженность поля Но значительно выше резонансного зна-
чения, намагниченность во вращающейся системе координат на-
правлена практически параллельно эффективному полю
V#i + («>/Y — Hof- В области резонанса изменяются как вели-
чина, так и направление эффективного поля, но если приближе-
ние к резонансу происходит достаточно медленно, то намагни-
ченность М во вращающейся системе координат будет оста-
ваться параллельной НЭфф согласно доказанной выше теореме.
Таким образом, при резонансе намагниченность будет направле-
на вдоль Нь образуя прямой угол с Но (рис. 2.8).
При дальнейшем прохождении через резонанс намагничен-
ность в конце концов окажется направленной в сторону отрица-
тельных значений г. Этот метод переворачивания М часто ока-
зывается полезным при проведении экспериментов и называется
адиабатической инверсией.
§ 5. Экспоненциальные операторы
Полезно рассмотреть, какое преобразование в квантовой ме-
ханике соответствует переходу к вращающейся системе коорди-
нат в классической механике. Однако для этого необходимо ис-
пользовать несколько соотношений, которые мы здесь приведем
для удобства читателя.
Пусть имеются две волновые функции Ф и Ч7, которые удо-
влетворяют соответствующим граничным условиям и обладают
необходимыми аналитическими свойствами в некоторой области
пространства; пусть имеется также некоторый оператор F, ко-
торый может быть, например, спиновой компонентой. Этот опе-
ратор называется эрмитовым, если
= J (FG>Y W dt, B.44)
где интегрирование проводится в определенной области про-
странства. Чтобы доказать эрмитовость оператора, необходимо
сформулировать условия, которым должны удовлетворять XV
и Ф, а также определить область интегрирования. Например,
если оператор F содержит производные, то доказательство его
эрмитовости может включать преобразование объемного инте-
грирования в интегрирование по поверхности и требование, что-
бы подынтегральное выражение в интеграле по поверхности
исчезло на границах заданной области.
Собственные и средние значения эрмитовых операторов пред-
ставляют собой действительные величины. Поэтому любой опе-
ратор, соответствующий физически наблюдаемой величине, дол-
жен быть эрмитовым. Так, операторы /д, /„ и /г являются эрми-
Основы теории 37
товыми. Учитывая эрмитовость этих операторов, нетрудно пока-
зать, пользуясь соотношением B.44), что операторы /+ = Ix+tly
и 1~ = 1Х — Ну не эрмитовы.
В теории функций экспоненциальная функция комплексной
переменной z определяется следующим образом:
этот степенной ряд сходится при всех г. Для оператора F подоб-
ным же образом определим функцию
е^=1 4-F4-4-4-—-4-
е- i-t-r-r-jp-t-gj-t-....
Особый интерес представляет функция
)l+.... B.45)
Применяя разложение в ряд, можно показать, что если оператор
F эрмитов, то оператор e'F не является эрмитовым. Действи-
тельно,
J )*Ч dx = J Ф*е~1РЧ dx. B.46)
Экспоненциальная функция операторов подчиняется тем же ал-
гебраическим правилам, что и функция обычных переменных, за
исключением тех случаев, когда встречаются два некоммути-
рующих оператора. Так, если А и В — два оператора, то нетруд-
но проверить с помощью разложения в ряд, что
AeiB=*eiBA B.47а)
только в том случае, если операторы А и В коммутируют. По-
добным же образом
е1(А+в)^е1Ае1В B.476)
только в том случае, если А и В коммутируют.
Если Л и Б не коммутируют, то может быть справедливо
другое полезное соотношение. Обозначим коммутатор операто-
ров А а В через С:
[А, В] = АВ — ВА=зС.
Пусть оператор С коммутирует как с А, так и с Б:
[Л,С] = 0, [В, С] = 0.
Тогда
Доказательство этой теоремы дано в приложении А.
Применение экспоненциальной функции дает очень простой
метод нахождения формального решения уравнения Шредин-
гера, если гамильтониан не зависит явно от времени. Так, если
88 Глава 2
4r(t) —решение уравнения
-у-Т- = ^(/), B.48)
то функцию W(t) можно выразить через ее значение W@) при
/ = 0 в виде
()*«-<«» **?(()). B.49)
Соотношение B.49) можно проверить, непосредственно подста-
вив в уравнение B.48). Например, если рассматривается движе-
ние спина в магнитном поле, так что Ж = — yflH0]z, то
«Vz) V @) = eta°u*W @), B.50)
где ©о = у Но.
Известно, что поле Но вызывает вращение магнитного момен-
та с угловой скоростью fi, определяемой соотношением Q =
= — уНок. Назовем такое вращение «отрицательным», посколь-
ку составляющая угловой скорости по оси г отрицательна. Есте-
ственно предположить, что функция *?Ц) должна соответство-
вать функции Ч^О), отнесенной к осям, повернутым в отрица-
тельном направлении на угол <оо*. Таким образом, функция
e~l ^W @) должна соответствовать функции 4^@), отнесенной к
осям, повернутым в положительном направлении на угол q>.
Если вычислить среднее значение матричного элемента, напри-
мер 1х, то получим
х = \ [(>о«гЧг (О)]*/^"^ @) dx =
W* @) е-Щ'ч^'тр @) dx = ^ Ч1" @) 1Х. (/) W @) dx, B.50а)
5 ЧГ @1
где
1Х. (/) = е-Щ'Чге1***1'. B.506)
Последнее равенство определяет оператор Ix\
Равенство B.50а) нетрудно интерпретировать следующим об-
разом. Первый интеграл, определяющий величину </*(*)). опи-
сывает прецессию вектора момента количества движения, обу-
словленную действием не зависящего от времени оператора 1Х
на зависящую от времени функцию W(t). Последний интеграл
в B.50а) описывает действие зависящего от времени оператора
IX'(t) на не зависящую от времени функцию ^(О). Поскольку
прецессия происходит в отрицательном направлении, первый ин-
теграл содержит оператор, определенный в лабораторной системе
координат, и волновую функцию, определенную в системе коор-
динат, вращающейся в отрицательном направлении. Поэтому по-
следний интеграл должен содержать оператор в системе коор-
динат, вращающейся в положительном направлении относитель-
Основы теории 89
но неподвижной системы координат, в которой определена функ-
ция ^@).
Легко показать, что операторы /*< и 1Х связаны между со-
бой поворотом координатных осей. Рассмотрим оператор
е - ixe —/ щ>). ^s.oi;
Чтобы выяснить его смысл, вычислим величину /(ф). Для этого
можно разложить экспоненты в ряды, воспользоваться комму-
тационными соотношениями и
попытаться свести операторную М \У
функцию к более простому виду.
Однако той же цели можно до-
стигнуть более простым путем,
написав и решив простое диффе-
ренциальное уравнение для функ-
ции /(ф). Это уравнение имеет V——-~~~~НУ
вид х
df -М2Ф/ -I г _1_ •/ М "W Рнс- 2"®" Относительное положе-
7?ф" е ' 1'г*х~т~ tlxlz)V » ние осей координат х, у и х', у'.
B.52)
или, после учета соотношения [/*, /*]= Ну,
df -lljfi iljf /о еоч
—~- = е 'ив ar« iz.oo)
d<p * У"
Аналогичным образом можно получить
d2f —Ujfi :т i I :т t \„НгР ^~H^lt \ n'^zf f (О КЛ\
= g V у—1/г/„т11|,/гN ="—в г \1х)в == —/» ^/.0^
ИЛИ
откуда находим
f (ф) = A cos ф + В sin Ф-
Необходимо определить постоянные интегрирования (как мы
увидим, эти постоянные являются операторами). Очевидно,
Л = Д0), но из уравнения B.51) следует тогда, что f@) = Ix.
Подобным же образом с помощью уравнения B.53) получаем
В = f(O)=s Iy. Аналогично можно найти и другие соотношения:
e11^ = /х cos ф + 1У sin ф,
1^ = - 1Х sin Ф + /„ cos ф, B.55)
40 Глава 2
Величины 1Х', 1у> и /^ представляют собой компоненты вектора
момента количества движения вдоль осей х', у' и zr, вращаю-
щихся относительно осей х, у, г (рис. 2.9). Таким образом, экс-
поненциальный оператор eir^ представляет собой оператор по-
ворота.
§ 6. Квантовомеханическое рассмотрение
движения магнитного момента
во вращающемся магнитном поле
Применим теперь экспоненциальные операторы для вы-
полнения квантовомеханического преобразования, аналогичного
классическому переходу к вращающейся системе координат.
Наряду с постоянным полем кЯ0 будем рассматривать магнит-
ное поле Hi, вращающееся с угловой скоростью сог. Тогда пол-
ное магнитное поле
Н (/) = !//, cos co^ + jtf, sin еМ + кЯо. B.56)
а уравнение Шредингера имеет вид
-4-^ = - И • H^= -\h[H0Iz+ HX(IX cosaj + Iy sin e>J)] W.
B.57)
С учетом соотношений B.55) гамильтониан уравнения B.57)
можно записать в виде
Ш = - yh (#0/г + Н &-"»*" *1хе1а*"*). B.58)
Попытаемся «отделить» оператор ela>z г от 1Х и перенести его
действие на W, т. е. предпримем шагн, противоположные тем, ко-
торые выполнены в B.50). Для этого положим
или
V^e-'^'V. B.59)
Физический смысл соотношений B.59) состоит в том, что функ-
ции W и Ч" переходят друг в друга при повороте осей координат
на угол со2< (преобразование поворота осей координат).
Тогда
4J '-Л "** *?. B 60)
Подставляя B.59) и B.60) в B.57) н умножая обе части равен-
ства слева на оператор е{<Лг"г, получаем
ь ami
~ ТЧг в ~ tft &* + ^Я°) *' + ?ЙВД Ч". B.61)
Основы теории 41
В уравнении B.61) Hi (t) не зависит от времени. Это обстоятель-
ство связано с появлением эффективного постоянного поля
совпадающего с эффективным полем в классических уравнениях.
В соответствии с этим спины можно считать квантованными
вдоль направления эффективного поля во вращающейся системе
координат с расстояниями между уровнями энергии состояний,
равными уННэфф.
Волновая функция Ч", определяемая соотношением B.59),
связана с функцией W оператором поворота осей координат, при-
чем «прямое» вращение 1Х относительно неподвижной Ч? эквива-
лентно «обратному» вращению W при неподвижном h. Как
обычно, резонанс имеет место при <о2 « —т^о- Если преобразо-
ванный гамильтониан Ж' во вращающейся системе координат
определить формулой
х], B.62)
то формальное решение уравнения B.61) будет иметь вид
ху' (t) = e-WWtxy @)j B.63a)
откуда при учете B.59) получим
у (?) = е~ш*"*е~т) *" V @); B.636)
заметим, что ?@) = W@) при t = 0.
Выражение B.636) представляет собой компактную запись
решения уравнения Шредингера для случая вращающегося
поля.
В качестве иллюстрации применения волновой функции
B.636) вычислим зависимость от времени среднего значения ве-
личины [кг- Конечно, результат уже известен из классического
рассмотрения, справедливость которого была доказана выше.
Для простоты будем считать, что условие резонанса выполняется
точно. Тогда из B.62) найдем
x, B.64)
что при учете равенства B.636) даст
»Vip @)]* /.[r^V^*? @)] dx. B.65)
Если ввести обозначение
cois=y#i B.66)
42 Глава 2
и воспользоваться эрмитовостью операторов 1Х и lz, то получим
<И* @> = Ф \ *?* @)e-to'"^"^-^V'"^ @) dx =
¦= Yft J V @) е" WxljWxyg @) dr. B.67)
Применяя соотношение B.55), мы можем записать
e-WxI^W* = -1у sin со|* + /« cos ©,*. B.68)
Подставляя это равенство в B.67), находим
<И* @> = - W @)> sin со,/ + <цг @)> cos ©if. B.69)
Если намагниченность в момент времени t = 0 направлена вдоль
оси z, так что <1%@)> = 0, то
B.70)
Отсюда следует, что z-компонента намагниченности осцилли-
рует во времени с частотой yHlt как это и должно быть вслед-
ствие наличия прецессии вектора <|л) во вращающейся системе
координат. Важно отметить, что приведенные рассуждения, не
учитывающие взаимодействия спинов с решеткой и друг с дру-
гом, приводят к выводу, что намагниченность осциллирует меж-
ду значениями + <Мг@)> и — <м*@)> неограниченно долго. Этот
вывод существенно отличается от вывода, к которому можно
прийти с помощью рассуждений гл. 1, основанных на понятии
не зависящей от времени вероятности перехода. Переходы с не
зависящими от времени вероятностями происходят только тогда,
когда некоторые другие физические процессы нарушают коге-
рентность прецессии вокруг направления Hi во вращающейся
системе координат.
§ 7. Уравнения Блоха
Как квантовомеханическое, так и классическое описания дви-
жения невзаимодействующих спннов приводят к выводу о суще-
ствовании периодического движения во вращающейся системе
координат. Например, если y^o = to и намагниченность парал-
лельна полю Но при t — 0, то вектор намагниченности будет
прецессировать вокруг направления Hi во вращающейся системе
координат, ориентируясь попеременно параллельно и антипарал-
лельно постоянному магнитному полю. В этом случае в лабора-
торной системе координат намагниченность будет непрерывно
изменять свою ориентацию по отношению к большему по вели-
чине постоянному магнитному полю. При этом энергия, затра-
чиваемая на поворот спинов от параллельной постоянному полю
ориентации к антипараллельной, будет периодически возвра-
Основы теории 43
щаться обратно. В соответствии с этим при увеличении времени
наблюдения не будет наблюдаться увеличения поглощенной
энергии, а будет иметь место попеременно поглощение и возвра-
щение энергии. Такая ситуация напоминает случай, описанный
в гл. 1 перед введением связи спинов с тепловым резервуаром.
(Подчеркнем, что в гл. 1 в системе просто выравнивались насе-
ленности уровней, в то время как в рассматриваемом здесь слу-
чае получаются населенности, изменяющиеся во времени. По-
этому эти две модели основываются на различных допуще-
ниях.)
При отсутствии контакта с решеткой отсутствует и меха-
низм, обеспечивающий установление равновесного значения на-
магниченности. По аналогии с уравнением
йп _ ПВ — П
ЧГ~ Г,
естественно ожидать, что равновесное значение Мг будет уста-
навливаться по закону
dt ~ Г, ' V-1*)
где Mz — yhn/2, а Мо — равновесное значение намагниченности.
Последнюю величину можно выразить через магнитную воспри-
имчивость %о и амплитуду постоянного магнитного поля Яо:
М0 = ъН0. B.73)
Объединяя уравнение B.72) с уравнением, определяющим изме-
нение М под действием момента сил, получаем
^^ B.74)
Теперь учтем тот факт, что в состоянии теплового равновесия
при наличии постоянного магнитного поля намагниченность
должна устанавливаться параллельно Но, что соответствует ис-
чезновению х- и у-компонент. В соответствии с этим
dMx Mx dMy My
Мы ввели здесь одно время релаксации Г2 для х- н у-компонент
намагниченности, однако необходимо помнить, что это время
релаксации отличается от Т\. Отличие скорости затухания по-
перечных компонент от скорости затухания колебаний продоль-
ной компоненты становится понятным, если вспомнить о том,
что в противоположность релаксации продольной компоненты
релаксация поперечных компонент не сопровождается измене-
нием энергии магнитного момента в постоянном магнитном
44 Глава 2
поле. Поэтому при релаксации поперечных компонент не про-
исходит передачи энергии в тепловой резервуар. (Последнее
утверждение не вполне точно при насыщении магнитного резо-
нанса в твердых телах. В этом случае, как показал Редфилд,
учет передачи энергии в тепловой резервуар может привести к
появлению важных эффектов. Теория насыщения Редфилда
рассматривается в гл. 6, начиная с § 5.)
С другой стороны, принятый нами постулат о существовании
данного (экспоненциального) закона релаксации является весь-
ма произвольным. Он очень полезен при описании ряда важных
эффектов, но его не следует понимать слишком буквально. Со-
гласно уравнениям B.75), при наличии постоянного магнитного
поля релаксация поперечных компонент происходит по экспо-
ненциальному закону. (Этот результат легко усмотреть, если
перейти к системе координат, вращающейся с угловой ско-
ростью уН0 вокруг направления постоянного магнитного поля;
в этой системе эффективное поле равно нулю.)
В твердом теле, в котором вблизи каждого ядра располо-
жены другие ядра, один из возможных простых механизмов ре-
лаксации поперечных компонент возникает вследствие разброса
значений скорости прецессии для магнитных моментов отдель-
ных ядер. Этот разброс обусловлен магнитными полями, дей-
ствующими со стороны магнитных моментов одних ядер на маг-
нитные моменты других ядер. При этом на магнитный момент
ядра действует дополнительное локальное поле Ялок ~ р/r3, где
г — расстояние между соседними ядрами. Это поле склады-
вается с постоянным магнитным полем или вычитается из него.
В результате когерентность фаз прецессирующих магнитных мо-
ментов, имеющих одинаковые фазы в момент времени t = 0, в
последующие моменты времени будет нарушаться. К моменту
времени т, определяемому равенством уН„ОкТ « 1, расфазировка
достигнет значительной степени, вследствие чего векторная сум-
ма моментов значительно уменьшится. Поскольку т должно быть
равно по порядку величины времени релаксации Т2, для Т2 в
рассматриваемой модели получаем
в большинстве случаев для ядерных магнитных моментов это
значение составляет приблизительно 100 мкс.
Уравнения B.74) и B.75) впервые были предложены Бло-
хом, и их называют обычно уравнениями Блоха. Хотя область
их применимости ограничена, они сыграли очень важную роль
при исследовании магнитного резонанса, так как в очень про-
стой форме учитывают релаксационные эффекты.
Основы теории 45
§ 8. Решение уравнений Блоха
в случае малых Hi
Рассмотрим теперь решение уравнений Блоха в случае ма-
лых переменных полей Н\, при которых отсутствует насыщение.
Переходя к системе координат, вращающейся с угловой ско-
ростью со2 вокруг направления постоянного магнитного поля, в
которой Н\ направлено вдоль оси х, и обозначая величину
Но + (g>z/y) через Ло> получаем
*§l+M^, B.77а)
*k = + YAyt0-TT' B-776)
^ ^B.77в)
Из уравнения B.77а) легко видеть, что в стационарном состоя-
нии величина Мг отличается от своего равновесного значения
Мо на величину порядка Hi. Это обусловлено тем, что компо-
ненты Мх и Му стремятся к нулю при Н\ ->- 0. В соответствии с
этим заменим в уравнении B.77в) Мг на Мо. Для дальнейшего
упрощения решения введем величину М+ = Мх -f- iMy. Умно-
жая уравнение B.77в) на i и складывая его с уравнением
B.776), получаем
% и B.78)
где
a = TT + Y%"- B.79)
Поэтому
Пренебрегая здесь членом, описывающим процесс установления
стационарного состояния, после подстановки Мо = Хо^о нахо-
дим
B81)
му=ъ (щт2) 1 ни
1 + (со — соо) Т2
где ю0 = y^o. а (о2 = —ю.
Равенства B.81) показывают, что намагниченность не зави-
сит от времени во вращающейся системе координат, и, следова-
тельно, в лабораторной системе координат она вращается со
46
Глава 2
скоростью со. Обычно экспериментальное определение намагни-
ченности связано с измерением э.д. с, создаваемой намагни-
ченностью в неподвижной относительно лабораторной системы
координат катушке. Если в лабораторной системе координат
ось катушки направлена вдоль оси X, то для вычисления э. д. с.
необходимо знать только зависящую от времени компоненту на-
магниченности Мх вдоль оси X.
Используя рис. 2.10, можно выразить компоненту Мх, отно-
сящуюся к лабораторной системе координат, через компоненты
Мх и Му во вращающейся системе
координат:
Мх = Мх cos at + Му sin at. B.82)
Если переменное магнитное поле
рассматривать как линейно-поляри-
зованное поле
Их (О = #хо cos at, 2Я, = Ях0,
B.83)
то легко видеть, что величины Мх
Рис. 2.10. Положение осей х, и Му пропорциональны Нх0. Тогда
у вращающейся системы ко- мы можем написать равенство
ординат относительно осей X,
Y лабораторной системы коор- Мх (t) = (у/ cos at + X sin at) Hx0,
дииат. B.84)
определяющее величины у/ и %". С помощью равенств B.81) и
B.84) получаем
(сор — со)
B.84а)
Величины Mx(t) и Hx(t) удобно представить в виде действи-
тельных частей комплексных функций Mx(t) и Hx(t). Опреде-
ляя далее комплексную восприимчивость % соотношением
% = %'-i%" B.85)
и записывая
Ях(/) = Яхое'ш', B.86)
находим
MCx(t) = %Hcx(t), B.87)
или
Mx(f)^=Re(%Hx^). B.87а)
Несмотря на то что соотношения B.83) и B.87а) получены
с помощью уравнений Блоха, они справедливы и в общем слу-
Основы теории 47
чае. Любой резонанс можно описать с помощью комплексной
восприимчивости, отражающей линейный характер зависимости
намагниченности от приложенного магнитного поля.
Известно, что при заполнении катушки индуктивности Lo
магнитным материалом с магнитной восприимчивостью %0 ее
индуктивность возрастает до значения Z.0(l + 4язсо), так как
магнитный поток увеличивается в 1 + 4п%0 раз при неизменном
токе. Аналогичным образом комплексная магнитная восприим-
чивость вызывает изменение магнитного потока. При этом маг-
нитный поток изменяется не только по величине, но также и по
фазе. С помощью уравнений B.84) —B.87) легко показать, что
индуктивность на частоте со изменяется и становится равной1)
1 = 1о[1 + 4лк(в>)], B.88)
где
В теории электрических цепей для обозначения V— 1 приме-
няют символ /. Для устранения недоразумений, связанных с при-
менением двух различных символов для обозначения одной и
той же величины, мы будем пользоваться только символом i.
Обозначая активное сопротивление катушки без образца че-
рез Ro, для импеданса катушки Z получаем
Z = Щи A + 4ях' - *W) + Ro =
= iL&> A + 4«хО + L^W + Ro- B.89)
Отсюда видно, что действительная часть восприимчивости %' из-
меняет индуктивность, в то время как мнимая часть %" изме-
няет сопротивление. Относительное изменение сопротивления
. B.90)
Здесь мы ввели в рассмотрение добротность Q, принимающую
значения от 50 до 100 для радиочастотных катушек и от 1000 до
10000 для сверхвысокочастотных резонаторов.
Если принять, что магнитное поле постоянно в пределах
объема V, то для максимальной величины запасаемой в этом
объеме магнитной энергии, создаваемой переменным током,
максимальное значение которого равно i0, получим
±/ 2 B.91)
') Практически образец никогда не заполняет всего пространства, поэто-
му необходимо вводить в рассмотрение «фактор заполнения» q. Для его вы-
числения необходимо знать, как распределено магнитное поле в пространстве.
В этом случае выражение B,88) принимает вид L «= L0[l + 4()]
48
Глава 2
Средняя мощность, рассеиваемая на ядрах,
С учетом равенства B.91) находим
B.92)
B.93)
Это равенство устанавливает простую связь между поглощае-
мой мощностью, восприимчивостью х" и амплитудой перемен-
ного магнитного поля. Мы используем его в качестве основы
- w)Tt
Рис. 2.11. Зависимость полученных из уравнений Блоха величин 5с' и %" от
(со0 — ю) Т2.
для определения %" с помощью микроскопической теории, так
как поглощаемая мощность может быть выражена через веро-
ятности переходов. Поскольку, как мы увидим ниже, величины
X' и %" связаны друг с другом, то, зная величину %", можно вы-
числить и %'. Отметим также, что B.93) справедливо и в тех
случаях, когда допущения, сделанные при выводе уравнений
Блоха, становятся незаконными.
Функции х' и %", удовлетворяющие уравнениям Блоха, встре-
чаются часто. Они показаны графически на рис. 2.11; их часто
называют лоренцевыми линиями.
Здесь необходимо отметить, что до сих пор вычислялась
компонента намагниченности вдоль оси X, создаваемая пере-
менным полем, направленным вдоль той же оси. Ввиду того что
вектор намагниченности вращается вокруг оси Z, будет отлична
от нуля также компонента намагниченности вдоль оси Y. Что-
бы описать такую ситуацию, величину х необходимо рассматри-
вать как тензор, а это можно записать в следующем виде:
<(О = Х„А/И( (а = Х, У, Z, a'*=X,Y,Z).
В дальнейшем нас будет интересовать величина %Хх.
Основы теории 49
§ 9. Спиновое эхо
Еще студентом Эрвин Хан [2] вошел в мировую науку, от-
крыв замечательное явление — спиновое эхо. Его открытие мо-
жно отнести к наиболее значительным вкладам в магнитный ре-
зонанс; оно положило начало развитию импульсных методов в
ЯМР. Что такое спиновое эхо и чем оно так замечательно?
Предположим, что к группе спинов прикладывается импульс
я/2 для наблюдения следующего за ним сигнала свободной ин-
дукции. Согласно уравнениям Блоха, сигнал свободной индук-
ции экспоненциально затухает с постоянной времени Т2. Для
твердых тел Т2 составляет доли миллисекунды, что соответ-
ствует ширине резонансной линии в несколько гаусс. Для
жидкостей линии обычно значительно уже и возможные вре-
мена имеют порядок нескольких секунд. Ширины таких линий
много меньше величины обычной неоднородности поля магнита
в объеме образца. Вызванный неоднородностью поля разброс
частот прецессии спинов в различных частях образца приводит
к расфазировке прецессии спинов. Сигнал свободной индукции
определяется суммой вкладов от всех частей образца. Так как
отдельные группы спинов выходят из синхронной прецессии, то
сигнал затухает. Постоянная времени затухания по порядку
величины равна 1/(уАН), где Д#— неоднородность постоянного
поля по образцу.
Открытие Хана состояло в том, что он возбудил спины вто-
рым импульсом я/2, приложенным вслед за первым через ин-
тервал времени т, и спустя время 2т после первого импульса
наблюдал другой сигнал свободной индукции. Этот удивитель-
ный сигнал Хан назвал спиновое эхо. Чтобы он возник, спины
должны были каким-то образом снова сфазироваться и прецес-
сировать все в фазе. Это казалось загадкой. Не противоречит
ли это основным принципам необратимости? Не демон ли Мак-
свелла фазирует спины? Хан открыл спиновое эхо эксперимен-
тально, однако вскоре он теоретически из уравнений Блоха под-
твердил его существование. Из решений уравнений следовало,
что при увеличении т амплитуда спинового эха экспоненциаль-
но уменьшается с постоянной времени Т2. Таким образом, на-
блюдая эхо, можно измерять ширины резонансных линий, много
меньшие неоднородности поля магнита. Понимание физической
основы образования эха привело к более глубокому проникно-
вению в сущность явления резонанса в целом и в импульсный
метод в частности.
Основные физические принципы перефазировки легче всего
рассмотреть на примере импульсной последовательности, в ко-
торой первый импульс производит поворот намагниченности на
л/2, а второй — на п. Такую импульсную последовательность
60
Глава 2
М,
rt/Z
a t=o~
6 t=o+
T-V
/
a:
Рис. 2.12. Процесс формирования спинового эха во вращающейся системе
координат импульсной последовательностью я/2 — я.
а—при t*=0~ равновесная намагниченность Мо направлена вдоль оси г. б—положение
намагниченности непосредственно после импульса л/2. в—отклонение элемента намагни-
ченности 6М на дополнительный угол 6 вследствие неоднородности магнитного поля.
г—влияние импульса л на 6М. д—в момент времени 2т все элементы намагниченности
сфазированы вдоль направления +у.
обозначим через п/2—п. Рассмотрим группу спинов, первона-
чально находящуюся в тепловом равновесии в постоянном маг-
нитном поле Н, направленном вдоль оси г. Равновесная намаг-
ниченность Мо параллельна Н, как показано на рис. 2.12, а.
Предположим, что по образцу существует разброс магнитных
Основы теории 61
полей около среднего значения Но. Проанализируем сначала
явление, пренебрегая процессами релаксации с постоянными
времени Т\ и 7V
Пусть в момент времени t = О включается магнитное поле
Н\, вращающееся с частотой <о, настроенной точно в резонанс
при среднем постоянном поле Но.
а = уН0. B.94)
Точный импульс я/2 можно получить, регулируя его длитель-
ность tP. Полагаем здесь, что амплитуда #i достаточно велика,
чтобы длительность импульса tP была пренебрежимо мала. Обо-
значим моменты времени непосредственно перед и после им-
пульса через 0~ и 0+.
Поведение спинов удобно рассматривать во вращающейся с
частотой уН0 системе координат, ось которой х совпадает с на-
правлением поля Hi. В этой системе импульс я/2 поворачивает
намагниченность Мо так, что она оказывается совпадающей с
отрицательным направлением оси у (рис. 2.12,6). В случае аб-
солютно однородного постоянного магнитного поля все спины
образца прецессируют с равными частотами уН0 и намагничен-
ность каждой части образца остается ориентированной вдоль
оси —у. Неоднородность магнитного поля приводит к распреде-
лению скоростей прецессии и расфазировке спинов. Рассмот-
рим, что произойдет за интервал времени т после первого им-
пульса я/2. Поскольку мы пренебрегаем процессом продольной
релаксации, то в любой малой области образца элементарная
намагниченность 6М будет оставаться в плоскости (х, у).
В конце интервала времени т направление 6М в плоскости
(х, у) отклонится от оси —у на некоторый угол 6, который
определяется выражением
Q = yt>Hr, B.95)
где величина
6Н = Н-НО B.96)
— неоднородность магнитного поля Н. Эта ситуация показана
на рис. 2.12,е. (Заметим, что величина &Н и соответствующее
отклонение намагниченности могут быть положительными или
отрицательными).
Предположим, что мы можем управлять фазой переменного
напряжения второго импульса так, чтобы во вращающейся си-
стеме координат поле #i было вновь направлено вдоль осп
+ х1). Пусть теперь в момент времени ^ = т действует импульс
') В так называемой когерентной импульсной аппаратуре высокостабнль-
ный по частоте генератор выдает стационарное переменное напряжение, кото-
рое поступает в усилитель мощности через ключевую схему. Ключевая схема
S2 Г/iaea 2
л, длительностью которого снова можно пренебречь. Моменты
времени непосредственно перед импульсом и после него обозна-
чим через т~ и т+. Ситуация, возникающая сразу после импульса
л, показана на рис. 2.12, г. Мы видим, что после импульса л в те-
чение второго интервала времени длительностью г элементарная
намагниченность 61W повернется на тот же угол 6 в том же на-
правлении и в момент времени t = 2т совпадет с положитель-
ным направлением оси у. Это рассуждение справедливо для всех
элементарных намагниченностеи образца независимо от величин
неоднородностей поля б#, которые их разворачивают, поскольку
конечный результат — выстраивание 6М вдоль оси +у — не за-
висит от угла поворота 6.
После совпадения фаз всех спинов в момент времени t = 2x
снова происходит их расфазировка, вызванная неоднородностью
поля, поэтому сигнал свободной индукции снова затухает. Заме-
тим, что его форма как функция времени в процессе расфази-
ровки начиная с момента времени / = 2т должна совпадать с
формой затухания сигнала свободной индукции после первого
импульса я/2 (см. рис. 2.13). Нарастание сигнала эха перед мо-
ментом времени t = 2т представляет собой зеркальное отобра-
жение во времени затухания сигнала эха после t — 2т.
Теперь нетрудно представить себе влияние членов уравнений
Блоха, содержащих Т\ и Г2- В течение первого временного ин-
тервала т составляющие 61W в плоскости (х, у) будут экспонен-
циально затухать с постоянной времени Г2, а составляющая z
будет экспоненциально расти с постоянной времени Т\. Импульс
п инвертирует составляющую z элементарной намагниченности,
которая затем изменяется так, что не влияет на составляющие
6М в плоскости (х, у) в момент t = т+. В течение интервала вре-
мени т после импульса л составляющие намагниченности 61W
в плоскости (х, у) продолжают затухать с постоянной времени Г2.
В результате величина намагниченности МBт), определяющая
пропускает РЧ-сигнал, и он усиливается усилителем лишь в течение про-
межутка времеви, когда эти схемы открываются стробнруюшим импульсом.
Таким образом, мощные РЧ-импульсы на выходе усилителя во времени сов-
падают со стробнрующими импульсами. Выходное напряжение усилителя при-
кладывается к катушке с образцом, в которой создается РЧ-поле Яь Если
частота генератора <о настроена точно в резонанс, <о = Мо, то фаза РЧ-поля
Н\ всегда одна и та же в системе координат, вращающейся с частотой соО-
Такой метод работы, а также применение фазочувствительного детекти-
рования затухающего сигнала свободной нндукцин впервые предложили Спо-
кас н Сликтер [3]. В их статье разъяснены выгоды использования фазочув-
ствительного детектирования. В известной статье по ядерной релаксации в
щелочных металлах их коллеги Холкомб и Норберг [4] описали применение
метода усреднения сигнала для улучшения отношения сигнал/шум в импульс-
ных экспериментах. Оии показали, что фазочувствительное детектирование
необходимо для достижения максимально возможного интегрирования шума.
Основы теории
сигнал эха, описывается выражением
Если второй импульс взять л/2, как в оригинальном экспери-
менте Хана, то в момент времени t = т он повернет г-составляю-
щую бМ в плоскость (х, у). Интересно выяснить, не будет ли
сигнал эха в этом случае включать экспоненциальную зависи-
мость с постоянной времени Т\. Анализ показывает, что такой
зависимости нет. Этот результат легко понять, представив себе,
что намагниченность, нарастающая вдоль оси г, связана с неза-
1 Импульс я/В
Сигнал свободной
индукции
Импульс л
О X ZX
Рис. 2.13. Затухание сигнала эха начиная с момента времени 2т совпадает
по форме с затуханием сигнала свободной индукцнн начиная с момента вре-
мени t = 0+. Нарастание сигиала эха до момента времени t = 2т является
зеркальиым отображением во времени затухаиия сигиала после 2т. Заметим,
что сразу за импульсом я никакого сигнала свободной индукции не возни-
кает.
висимой группой спинов, которая не имеет составляющей намаг-
ниченности в плоскости (х, у). Непосредственно перед вторым
импульсом намагниченность бМ этой группы спинов направлена
вдоль оси г, как изображено на рис. 2.12, с Импульс л/2 повора-
чивает намагниченность в плоскость (х, у). В момент времени
t = 2т все спины расфазируются, как показано на рис. 2.12, в.
Таким образом, спин-решеточная релаксация, ответственная
за появление составляющей z намагниченности, после первого
импульса не влияет на сигнал эха. Для наблюдения такого влия-
ния необходимо произвести перефазировку спинов рассмотрен-
ной группы. Для перефазировки необходим еще один дополни-
тельный импульс. Влияние спин-решеточной релаксации на сиг-
нал эха можно наблюдать с помощью трех РЧ-импульсов.
Хан действительно обнаружил такие сигналы эха. Он наблю-
дал, что если приложить третий импульс в момент времени Т
(т. е. спустя Т — т после второго импульса), то спустя 2(Г — т)
после второго импульса или в момент времени t = 2T — т инду-
цируется сигнал эха. Кроме того, Хан обнаружил сигналы эха в
моменты времени Т -\- т, 2Т — 2т и 27\ Эха, индуцированные
третьим импульсом, обычно называют стимулированными.
В жидкостях диффузионное движение приводит к перемеще-
нию ядер между различными частями образца, в которых ско-
рости ядерной прецессии могут отличаться. В результате расфа-
зировка в течение первого интервала времени т может отли-
чаться от фазировки в течение второго интервала времени т и
сигнал эха уменьшается. Этот эффект имеет большое практиче-
ское значение. Он дает способ измерения скоростей диффузии
в жидкостях. Эффект был обнаружен Ханом и описан в его пер-
вой статье по спиновому эху. Хан показал, что диффузия приво-
дит к затуханию пика намагниченности М в момент эха согласно
формуле
[(^J^] B.98)
где
(Ц) B.99)
т. е. имеется в виду случай аксиально симметричного поля во-
круг оси z. Вывод этого результата приведен в приложении Ж.
Предварительно, в приложении Е, рассматривается более про-
стой случай влияния физического движения на структуру спек-
тра ядерного магнитного поглощения.
§ 10. Соотношения между переходным
и стационарным откликами системы
и между действительной и мнимой частями
восприимчивости
Чтобы избежать насыщения, предположим, что переменное
магнитное поле достаточно мало. В таком случае магнитную
систему можно считать линейной. Это означает, что намагни-
ченность, создаваемая двумя одновременно действующими сла-
быми полями, будет равна сумме намагниченностей, создавае-
мых каждым полем в отдельности. (Постоянное поле Но нельзя
рассматривать в качестве одного из таких полей, но этим спосо-
бом удобно рассматривать эффекты, обусловленные небольшими
изменениями постоянного поля). В этом же смысле обычные
электрические цепи можно считать линейными, так как в них
ток, создаваемый двумя источниками напряжения, равен сумме
токов, создаваемых каждым источником напряжения в отдель-
ности.
Рассмотрим намагниченность АЛ4 (/) в момент времени t, воз-
никающую благодаря действию магнитного поля H(t') в преды-
дущий момент времени ? в течение промежутка времени А/'
Основы теории Б5
(рис. 2.14). Вследствие линейности системы величина AM(t)
будет пропорциональна H(t'). При выполнении условия Ы' «С
«С t — V величина ДМ(/) будет пропорциональна также Ы', по-
скольку два импульса, разделенные небольшим промежутком
времени, должны давать такой же эффект, какой они дали бы
будучи приложенными к системе одновременно. Эту пропорцио-
нальность можно записать в виде соотношения
AM @ = m(t — f)H (/') At', B.100)
где m(t— t') — «константа» для заданных значений t и t', кото-
рая, однако, может изменяться при изменении промежутка вре-
мени t — t', отделяющего момент рассмотрения намагниченное
*' «
Рис. 2.14. Импульс магнитного поля.
ста от момента действия поля. Полную намагниченность в мо-
мент времени t можно получить, интегрируя B.100) по всем пред-
шествующим моментам времени, в течение которых действовало
поле Я (Г)
М
@= J m(t-t')H(t')dt'. B.101)
Заметим, что m(t — *') = 0 при f > /, так как следствие не мо-
жет предшествовать причине.
Чтобы выяснить смысл величины m(t—f), предположим,
что Н(?) представляет собой 6-функцию времени Ь{(') в момент
времени t = 0. Тогда намагниченность для t > 0 (которую мы
будем обозначать М6) будет равна
t
M6(t)= J m(f —Ов(ОЛ'="и@- B.102)
— oo
Таким образом, m(t) представляет собой реакцию (отклик) на
возмущение вида b(t'), возникающее в момент времени t = 0.
Знание величины m\t) позволяет определять по формуле B.101)
намагниченность, обусловленную магнитным полем, произволь-
ным образом зависящим от времени.
56 Глава 2
Если магнитное поле, величина которого равна единице, скач-
кообразно возникает в момент времени t — О (рис. 2.15), то воз-
никающая при этом намагниченность, которую мы обозначим
Мск, будет равна
t t
Мск (/) = J т (/ - /') Л'=\т (т) их; B.103)
о о
дифференцируя это выражение, находим
«W = -^(AU B.104)
Из уравнения B.104) видно, что если известна величина MCK(t),
то можно вычислить m(t).
HU)
о t
Рис. 2.15. Ступенчатая функция.
В качестве примера исследуем намагниченность образца,
возникающую после включения единичного постоянного магнит-
ного поля вдоль оси z для системы, подчиняющейся уравнениям
Блоха. Из этих уравнений находим
Мг (/) = Хо A - е-«ТЧ = Мск, B.105)
или
,„(/) = |1е-'/п. B.106)
Заметим, что в любой реальной системе намагниченность, возни-
кающая после скачкообразного изменения поля, ограничена по
величине, так что величина
m(x)dx B.107)
не обращается в бесконечность.
Перейдем теперь к случаю переменного магнитного поля.
Запишем его для простоты в комплексном виде:
. B.108)
Основы теории 57
Тогда
t
A«?(/) = ,j m(t-
— оо
t 00
= НхОеш \ m(t — t')e'att'-odt' — НхОеш ^ т(т)е~Шхdx. B.109)
-оо б
Сравнивая эти выражения с выражениями B.87), получаем1)
оо
Х= \ т{х)е~Шхйх,
о
00
х' = \ т (т) cos шт dx, B.110)
о
оо
X" = \ т (т) sin шт dx.
') При строгом выводе B.110) переменное поле необходимо включать
адиабатически и переходить в пределе к бесконечно медленному включению.
Для этого можно принять
ctt, s>0.
При I-*-—оо эта функция обращается в нуль. Мы находим предельное зна-
чение при s-»-0. В результате имеем
t
Мсх (/) = J m (/ - /') Нхое"»*'е°" dt' -
Нхйеше* J m (/ - Г) еш «'~ V (''-« Л'
m (т)
ОС (со) = lim ^ m (т)
Преимущество такого определения состоит в том, что оно справедливо н для
«резонатора без потерь» (магнитного аналога незатухающего гармониче-
ского осциллятора), в котором при скачкообразном приложении поля долж-
ны возникать незатухающие переходные эффекты.
58 Глава 2
Легко показать далее, используя интегральное представление
6-функции
— 00
что
+
+00
B.112)
Таким образом, функции т(х) и х(ю) являются фурье-образами
друг друга. Задание одной из этих функций полностью опреде-
ляет другую. Свойства резонансных линий можно предсказы-
вать, анализируя либо отклик на переменный сигнал, либо пере-
ходный отклик. Кубо и Томита [5], например, свою общую тео-
рию магнитного резонанса основывают на переходных откликах,
вычисляя отклик системы на скачкообразное изменение поля.
Выражения B.110) дают некоторую информацию о значе-
ниях величин х' и х" ПРИ нулевой и бесконечно большой часто-
тах. Очевидно, при со = 0 величина %" также равна нулю, так
как в этом случае sin шт обращается в нуль, но величина %' от-
лична от нуля при со = 0. Более того, если функция т(х) непре-
оо
рывна и ограничена, так что величина V т (т) dx конечна, то
о
обе величины %' и %" обращаются в нуль при ш ->• оо; это свя-
зано с быстрыми осцилляциями функций sin шт и cos ©т, благо-
даря которым подынтегральные выражения «усредняются» до
нуля.
Вообще говоря, функция т{х) может обращаться в бесконеч-
ность при т = 0. В этом можно убедиться, рассмотрев отклик на
скачкообразное изменение поля \m(x)dx. В данном случае, ко-
о
нечно, нельзя считать, что функция т(х) будет иметь разрывы
в моменты времени, отличные от момента времени t = 0, когда
происходит скачкообразное изменение поля. Вследствие ограни-
ченности отклика при интегрировании функции т{х) вблизи
t = 0 должна получаться конечная величина, несмотря на то что
/п@)= оо. Для описания этой ситуации введем 6-функцию, т. е.
предположим, что
m(t) = m,(T)+c,fi(t), B.113)
где функция mi (т) не содержит 6-функции. Тогда
00
X' (а) == [ mi (т) cos шт dx + су. B.114)
Основы теории 59
Здесь интеграл стремится к нулю при to—*- tx>, вследствие чего
можно написать ci=%'(oo). Поэтому полезное в ряде случаев
отделение 6-функции от т(т) эквивалентно записи
х Н — х' (°°) = $ m ^
о
где функция т(х) теперь не содержит 6-функции.
[Конечно, ни одна физическая система не может иметь от-
личную от нуля намагниченность, следующую за полем при
ю —»¦ оо, поэтому х'(°°) —0- Однако, если рассматривать анало-
гичную теорему для магнитной проницаемости ц, то величина
ц(оо) будет отлична от нуля. Мы сохранили здесь величину
%'(°°) для того, чтобы указать способ, которым должна вводить-
ся в рассмотрение подобная величина.]
Докажем теперь теорему, устанавливающую связь между yf
и %", — так называемую теорему Крамерса — Кронига. Для это-
го будем считать х функцией комплексной переменной z =
= х + iy- Действительная часть z совпадает с частотой со, од-
нако мы сохраним обозначение х, так как при этом формулы
имеют более привычный вид. Таким образом,
X (г) — %' (со) = J m (т) е~ lzxdx = J m (т) е^е~ш dx. B.116)
о о
Поскольку любой интеграл в определенном смысле представляет
собой сумму, величина %(z) может рассматриваться как сумма
экспоненциальных функций. Каждая экспонента является ана-
литической функцией 2, поэтому интеграл будет также аналити-
ческой функцией, если только интегрирование не приводит к ка-
ким-либо особым эффектам.
Аналитичность функции %(z) — х'(°°) можно доказать с по-
мощью условий Коши. Функция
X(z)-X'M = " + ">, B.117)
где и и v — действительные функции, является аналитической
функцией 2, если выполняются условия Коши
дх ~~ ду и дх — ду ¦ 12.II8)
Из B.116) находим
оо
и = \ m (т) cos xxeyx di,
B.119)
v = — ^ m (т) sin хте«х dx.
о
60
Глава 2
откуда получаем
ди
_=_$m(T)TSi
о
оо
-?- = \ т (т) % cos
до
-—.
B.120)
Таким образом, условия Коши удовлетворяются в предположе-
нии, что дифференцирование можно выполнять под знаком ин-
теграла. Последнее допустимо при соблюдении ряда условий,
Рнс. 2.16. Контур интегрирования.
которые рассматриваются в книге Гобсона [6]. Для наших це-
лей вполне достаточно потребовать, чтобы интегралы в B.119) и
B.120) не расходились. Этого достаточно для рассмотрения об-
ласти отрицательных значений у. Для любых достаточно хоро-
ших функций га(т), например для функций, определяемых вы-
ражением B.106), интеграл будет сходиться в области у ^ 0,
так что функция %(z) — х'(°о) будет аналитической на действи-
тельной оси и в нижней полуплоскости комплексных значений г.
В тех случаях, когда функции т(т) не являются достаточно
хорошими, мы будем считать, что их можно рассматривать как
предельные значения достаточно хороших функций. (Так, не
имеющую физического смысла линию поглощения нулевой ши-
рины можно рассматривать как предельное значение очень уз-
кой линии.)
Вследствие присутствия множителя еут
1%(г) — х'(°°I-*-0, если у-*- — оо.
Выше было показано также, что
— %'(оо)\-*-0, если х->±оо.
Основы теории 61
Поэтому функция %{г)—%'(оо) является аналитической в обла-
сти (/<0и обращается в нуль при |г|->- оо в нижней половине
комплексной плоскости.
Рассмотрим интеграл от функции
% (О - %' (°°)
г' — а
по контуру, изображенному на рис. 2.16. По теореме Коши этот
интеграл равен нулю, так как функция %(z) не имеет полюсов
внутри контура:
$(г]гХ(ОО)^'-0- B-121)
Интеграл по дуге большого круга радиуса р равен нулю, по-
скольку Ix(z') — %'(°о)| равно нулю на этой дуге. Остаются ин-
тегралы по действительной оси и по дуге радиуса R, где
z' — со = Re'v. Таким образом,
Т "ТХ" ? *"'?'¦'
+ 00
* {<*!~Л(ОО) d®' + ™ h N - %' (оо)]. B.122)
Здесь символ Р означает, что необходимо брать интеграл в смы-
сле главного значения (т. е. рассматривать интеграл как предел
<i)-R +oo
суммы интегралов \ и \ при одновременном стремлении к
и+
нулю величины R в обоих интегралах). Для действительной и
мнимой частей отсюда находим известные соотношения Кра-
мерса — Кронига
+ОО
-*M-ip \ ?^
—о»
\
B.123)
62
Глава 2
Подобные соотношения можно получить и для таких величин,
как диэлектрическая проницаемость или диэлектрическая вос-
приимчивость.
Смысл этих соотношений заключается в том, что они нала-
гают ограничения, например на свойства дисперсии, если изве-
стно поглощение. Нельзя задавать %'(со) и х"(со) независимо
друг от друга. Иначе можно сказать, что задание значений %"
для всех частот позволяет вычислить значения %' для любой ча-
стоты. Отметим, в частности, что для узких резонансных линий
X"
т
Я
Рис. 2.17. Спектр поглощения (а) и соответствующий ему спектр диспер-
сии (б).
при выполнении соотношения %'(°о) = 0 статическая восприим-
чивость
Основной вклад в интеграл от функции %"{ы') вносит область
под кривой поглощения. Очевидно, он может быть вычислен,
если известна статическая восприимчивость1).
В качестве примера рассмотрим случай, когда
= с [б (ш - Q) - б (- ш - Q)].
B.125)
Первый член соответствует поглощению на частоте Q. Второй
член добавлен для того, чтобы сделать функцию %" нечетной
') Конечно, если говорить об экспериментах по магнитному резонансу,
в которых постоянное и переменное поля направлены вдолТь осей г и х соот-
ветственно, то нужно рассматривать величину зс**- Тогда величина %'@) в
выражении B.124) равна %хх @), в то время как через хо обычно обозначают
отношение намагниченности Мо к создающему эту намагниченность полю Но,
т. е. %гг @). Однако слабое магнитное поле Нх, направленное вдоль оси х,
приводит просто к повороту вектора Мо, откуда следует Мх<= M
¦= ^О0) н *• Таким образом. %'хх @) - ггг @) = хо-
Основы теории 63
функцией со. Вычислим %'(ы), соответствующее этой функции:
= i:\Q=^~ - Q - m) = 7Г
Здесь мы воспользовались равенством 6(х) = б(— хI).
Конечно, вблизи резонанса (со л; Q) существен только пер-
вый член. Эта функция представлена на рис. 2.17.
§11. Микроскопическая теория поглощения
и дисперсии
Перейдем теперь к определению выражений для поглощения
и дисперсии, содержащих атомные характеристики, такие, как
волновые функции, матричные элементы и уровни энергии рас-
сматриваемой системы. Непосредственно мы будем вычислять
величину /'i а величину /' определим с помощью соотношений
Крамерса — Кронига.
Связь между микроскопическими и макроскопическими свой-
ствами можно установить, вычисляя среднее значение погло-
щаемой в единицу времени энергии F переменного магнитного
поля Нхо cos at. Согласно B.93), для объема V имеем
Р = -%-7СН%у. B.127)
В дальнейшем ради удобства объем V мы будем принимать рав-
ным единице. (Об этом нужно помнить при вычислениях по фор-
мулам микроскопической теории в различных частных случаях.)
С другой стороны, переменное магнитное поле оказывает дей-
ствие на магнитный момент k-то спина ц**. В соответствии с
этим в гамильтониане появляется зависящий от времени возму-
') В том, что б-функция Дирака является четной функцией аргумента х,
+ СО
можно убедиться, вычисляя \ f (х) б (— х) их. После замены переменной
— оо
интегрирования х' = —х такое вычисление дает
')dA:'=K0)= J f(x)b(x)dx,
-00 _00
откуда следует 6 (х) = б (— х))
64 Глава 2
щающий член
= ~ 2j ЦхкНх0 COS CO/ = — Цх^хО COS Си/, B.128)
где [ix представляет собой х-компоненту полного магнитного мо-
мента:
E B.129)
Если возмущение отсутствует, то гамильтониан включает в себя
обычно взаимодействие Ж,к между спинами / и k и взаимодей-
ствие спинов с внешним постоянным магнитным полем. Следо-
вательно,
Ш = - ? \хгкИ, + I Ж1к. B.130)
ft / fc
Обозначим через Еа и ?ь собственные значения энергии много-
спинового гамильтониана, а через \а) и |6) соответствующие
S Рис. 2.18. Уровни энергии.
= Еь,р(Еъ)
собственные функции (рис. 2.18). Вследствие большого числа
степеней свободы энергетический спектр этого гамильтониана
будет квазинепрерывным.
Волновая функция наиболее общего вида представляется в
виде линейной комбинации собственных функций гамильтониана
\а) и |6):
V=Ece|a)e-(lw4 B.131)
а
где са — комплексные постоянные. Квадрат модуля величины са
определяет вероятность р(а) нахождения системы в собствен-
ном состоянии а:
р(а) = \са\2.
Если система находится в состоянии теплового равновесия,
то в какой-то мере будут осуществляться все состояния, причем
вероятность нахождения системы в состоянии а будет опреде-
ляться законом Больцмана
р(Еа)= J Ес/кТ. B-132)
е
где индекс суммирования Ес пробегает значения, соответствую-
щие всем уровням спектра. Знаменатель представляет собой
классическую статистическую сумму Z и обеспечивает равенство
Основы теории 6S
единице полной вероятности нахождения системы в какой-либо
из возможных квантовых состояний, т. е.
Z
Поглощаемую в единицу времени энергию Раь при переходах
между состояниями а и 6 можно выразить через величину Wab,
представляющую собой вероятность перехода в единицу времени
между состояниями а и 6 в случае, когда система первоначаль-
но находилась в состоянии а:
Pab = ti<>>Wab[p(Eb)-p{Ea)]. B.133)
Величины р(Еь) и р{Еа) входят в это выражение потому, что
состояния \а) и \Ь) заполнены только частично.
Методы вычисления вероятностей переходов Wab хорошо из-
вестны из элементарной квантовой теории. Рассмотрим случай»
когда зависящее от времени возмущение 5#Возм имеет вид
B.134)
где F и G — операторы. Чтобы оператор 36-возп был эрмитовым,
операторы F и G должны подчиняться соотношению
(a\F\b) = (b\G\aY, B.135)
где |а) и \Ь) могут соответствовать любым состояниям. Для та-
кого возмущения величина Wab не зависит от времени и опреде-
ляется выражением
Wab=*\{a\F\b)fb{Ea-Eb-h<b), B.136)
если выполняются некоторые условия. Мы не будем интересо-
ваться деталями, проявляющимися в течение промежутков вре-
мени, малых по сравнению с некоторым характеристическим вре-
менем т. Тогда эти условия можно сформулировать следующим
образом: можно найти такой интервал времени т, что 1) в тече-
ние времени т населенности уровней меняются только на малые
величины и 2) состояния, ответственные за поглощение, непре-
рывно распределены в интервале энергии &Е ^> %/%.
Эти условия нарушаются, когда матричный элемент
|(a|.F|&)| становится по величине больше ширины линии, как
это имеет место в случае приложения очень сильных перемен-
ных полей. Это утверждение можно пояснить следующим обра-
зом. Величину Д? можно принять равной ширине линии. Тогда
получаем ДЕ < | (a j F| 6) |. Можно показать, что при этом насе-
ленности будут существенно изменяться за время порядка
Й/| (a|.F|&) |. Отсюда следует, что для выполнения первого усло-
вия, требующего небольшого изменения населениостей в течение
66 ^ Глава 2
времени т, необходимо, чтобы т было меньше, чем h/\ (a\F\b) \,
или
Но в соответствии со сделанным выше предположением
A?<|(
Поэтому
что противоречит приведенному выше второму условию. Таким
образом, оба условия становятся несовместимыми, вследствие
чего вероятности не будут не зависящими от времени.
Этот пример объясняет, почему в § 6 настоящей главы мы
не получили процесса, протекающего с не зависящей от времени
скоростью. В этой задаче в отсутствие поля Н\ уровни энергии
были бесконечно тонкими (Д? = 0) и поэтому | (o|F|6) | > АЕ.
В выражение для Wab входит б-функция. При этом подразу-
мевается, что должно проводиться суммирование по всему ква-
зинепрерывному спектру. Вероятности переходов лучше записы-
вать в форме, содержащей б-функции, чем в интегральном виде,
включающем плотность состояний, так как при этом явно входят
квантовые числа отдельных состояний.
Производя суммирование по всем состояниям с Еа > Еь, по-
лучаем
= Y%"Hlo- B.137)
Откуда
Х"(со)=я S [р{Еь)-р{Еа)]\{а\цх\Ь)?Ъ(Еа-Еь-Ы).BЛЗ&)
Еа>4
Если Еа>Еь, то поглощение будет происходить только при поло-
жительных частотах со вследствие наличия б-функции в B.138).
При отказе от ограничения Еа> Еь величину х"(ю) формально
можно рассматривать и в области отрицательных значений со:
X" (а) = я S [р (Еь) - р (Еа)] | (а | \ix 16) р б (Еа - Еь - Щ. B.139)
Еа-ЕЬ
Функция х"(ю) здесь, так же как и в предыдущем параграфе,
является нечетной функцией со, поскольку величина р(Еь) —
— р(Еа) изменяет знак при перестановке индексов а и Ъ. Пред-
полагая, что в рассматриваемом случае %'{°°)=0, можно без
Основы теории 67
труда вычислить %'(&), поскольку
[p\tb)— P\pa)\\ \a\ nx\ b) p—f \ —i-2—r-2 -da,
B.140)
или после вычисления интеграла
Учитывая далее, что индексы а и Ъ под знаком суммы можно
менять местами, получаем
B.141а)
Величина кванта Тш примерно равна энергии, затрачиваемой на
переворачивание спина в постоянном магнитном поле. Эта энер-
гия обычно много меньше kT. Для ядерного магнитного момен-
та в сильном постоянном поле (~ 104 Гс) величина Т должна
быть порядка 10~~3 К для того, чтобы энергия На была порядка
kT. Это приводит к некоторым трудностям при получении поля-
ризованных ядер. Для электронов kT ~ hu> при 1 К в полях
~ 104 Гс. Поэтому в большинстве рассматриваемых случаев мы
будем приближенно принимать
Ea — Eb<:kT. B.142)
Этот случай называют «высокотемпературным приближением».
Из соотношений B.132) и B.142) получаем
B. ИЗ)
Подставляя выражение B.143) в B.139) и учитывая равенство
Еа — Еь = ftco, обусловленное присутствием б-функций, находим
B.144)
Часто применяют другое выражение для %"(со). Например,
оно используется в теории Андерсона сужения резонансных ли-
ний, вызванного молекулярным движением [7]. Мы рассмотрим
68 Глава 2
его в приложении Б, так как строгое рассмотрение требует зна-
ния некоторого материала, изложенного в гл. 3 и 5.
Важно обсудить роль множителя e~EdkT. Известно, напри-
мер, что в воде линия поглощения протонов существенно изме-
няется при изменении температуры. Для достаточно хорошо
охлажденного льда ширина резонансной линии равна несколь-
ким килогерцам, в то время как для резонанса протонов в воде
она равна примерно 1 Гц. Очевидно, это изменение связано толь-
ко с изменением подвижности молекул Н2О при переходе из
твердого состояния в жидкое. Отсюда следует, что простран-
ственные координаты протонов играют важную роль в резонансе.
Формально это обстоятельство можно учесть, включая в гамиль-
тониан наряду с энергиями спинов кинетическую и потенциаль-
ную энергию атомов. Тогда величины Еа и Еь будут содержать
вклады как от спиновых, так и от пространственных степеней
свободы. Одни состояния | а) будут соответствовать твердому
состоянию, а другие — жидкому. Множитель e~EalkT фиксирует
тип «решеточных» волновых функций или соответствующих им
состояний, осуществляющихся при данной температуре. Иначе
говоря, он определяет, в какой фазе — жидкой, твердой или газо-
образной— находятся молекулы воды. Обычно в выражении для
%" экспоненциальный множитель опускают, но состояния |а) и
\Ь) должны быть выбраны тогда таким образом, чтобы они со-
ответствовали рассматриваемому состоянию вещества. Такой
прием применен в классических работах Гутовского и Пейка
[8], в которых они исследовали влияние заторможенных моле-
кулярных движений на ширину резонанса.
Для вычисления х" по формуле B.144) требуется знать вол-
новые функции и уровни энергии системы. Как мы увидим ниже,
такая информация имеется лишь в редких случаях. Однако фор-
мула B.144) позволяет рассчитывать так называемые моменты
линий поглощения. Из этой формулы видно также, что частоты,
при которых наблюдается сильное поглощение, должны соответ-
ствовать переходам между состояниями для которых матричные
элементы магнитного момента велики.
ЛИТЕРАТУРА
1. Van Vleck J. H., Phys. Rev., 74, 1168 A948).
2. Hahn E. L., Phys. Rev., 80, 580 A950).
3. Spoka? 1 J., Slichter C. P., Phys. Rev., 113, 1462 A959).
4. Holcomb D. F., Norberg R. E., Phys. Rev., 98, 1074 A955).
5. Kubo R., Totnita K., Journ. Phys. Soc. Jap., 9, 888 A954).
6. Hobson E. W., The Theory of Functions of a Real Variable and the Theory
of Fourier's Series, Cambridge University Press, Cambridge, 1926, p. 353.
7. Anderson P. W., Journ. Phys. Soc. Jap., 9, 316 A954). .
8. Outowsky H. S., Pake G. E., Journ. Chem. Phys., 16, 1164 A948); 18, 162
A950).
Глава 3
Магнитное дипольное уширение
резонансных линий в жесткой решетке
§ 1. Введение
Уширение резонансных линий обусловлено целым рядом фи-
зических причин. Самой простой из них является неоднородность
приложенного постоянного магнитного поля. В обычных магни-
тах, создающих магнитные поля ~ 104 Гс, отклонение магнит-
ного поля от среднего значения составляет несколько десятых
гаусса; при помощи специальных сложных приспособлений это
значение может быть снижено до нескольких миллигаусс. Одно-
родность поля в пределах магнитного образца зависит от раз-
меров образца. Обычно используются образцы, объемы которых
лежат в пределах от 0,1 см3 до нескольких кубических санти-
метров. Применение полей очень высокой однородности нала-
гает, конечно, жесткие ограничения на стабильность частоты
генератора, создающего переменное магнитное поле. Мы не бу-
дем рассматривать здесь детали такого рода, хотя они и важны
с технической точки зрения.
Для ядер, обладающих электрическими квадрупольными мо-
ментами, может наблюдаться несколько резонансных линий. По-
явление таких линий связано со взаимодействием ядерного ква-
друпольного момента с электрическим полем кристалла. Это
приводит к существенному уширению резонансных линий. Уста-
новление равновесных значений населенностей зеемановских
уровней системы связано с переходами между этими уровнями
под влиянием спин-решеточного взаимодействия. Благодаря та-
ким переходам время жизни системы на каком-либо одном уро-
вне будет ограничено, что приводит к дополнительному ушире-
нию линии на величину %/Т\ в энергетических единицах.
В этой главе мы пренебрежем всеми перечисленными выше
эффектами и сосредоточим внимание на механизме уширения ре-
зонансных линий, связанном с диполь-дипольным взаимодей-
ствием между магнитными моментами различных ядер. Такое
пренебрежение во многих случаях вполне допустимо. В частно-
сти, оно вполне оправдано в тех случаях, когда спины отдельных
ядер равны '/2 (в этом случае квадрупольные моменты ядер
равны нулю), а время спин-решеточной релаксации достаточно
велико.
70 Глава 3
Вклад диполь-дипольных взаимодействий в ширину резонанс-
ных линий легко оценить по порядку величины. Если расстояние
между соседними ядрами, обладающими магнитными момента-
ми ц, равно г, то каждое ядро будет создавать в точке, где нахо-
дится соседнее ядро, магнитное поле НЛОК, по порядку величины
равное
#лок —тг- C-1)
Если принять, что г = 2 А и ц= 10~23 эрг/Гс A0-3 магнетона
Бора), то Ялок да 1 Гс. Так как это поле может иметь различную
ориентацию относительно постоянного поля Но, резонансные ча-
стоты отдельных ядер будут распределены в области шириной
примерно 1 Гс. В этой же области будет наблюдаться резонанс-
ное поглощение энергии. Из этих рассуждений следует, что ши-
рина резонансной линии не зависит от Но. Этот вывод согла-
суется с экспериментальными данными, полученными при иссле-
довании магнитного резонанса в полях ~104 Гс. Поскольку ши-
рина линии значительно превышает степень неоднородности маг-
нитного поля, при анализе формы линии можно не учитывать по-
правки, связанные с техникой наблюдения резонанса.
§ 2. Основное взаимодействие
Классическое выражение для энергии взаимодействия двух
магнитных моментов fij и |j,2 имеет вид
р_ Hi-Иг 3 (Ц, • Г) (цг • г)
С -р ^5
где г — радиус-вектор, проведенный от \х\ к м-2- (Выражение не
изменится, если вектор г заменить вектором, проведенным от
ц2 к ц\.) Для получения квантовомеханического гамильтониана
взаимодействия необходимо подставить в C.2) вместо векторов
\х\ и |Л2 соответствующие операторы
Здесь мы предполагаем, что как спины, так и гиромагнитные от-
ношения ядер могут быть различными. Гамильтониан диполь-ди-
польного взаимодействия для N спинов будет иметь вид
Л N
»in~'-kWk-rik)i C4)
где множитель '/г введен потому, что при суммировании по / и k
каждая пара спинов считается дважды; члены с у = k, конечно,
не входят в гамильтониан^
Магнитное дипольное уширение резонансных линий 71
Выражая операторы щ и цг через их компоненты и опуская
индексы у г, получаем из общего выражения C.2), что гамиль-
тониан содержит члены типа
YiY2U2Ii*I2*7f. УхЪП\х\2и^г. C.5)
Выражая Ii* и \\и через понижающий и повышающий операторы
I* и 1Г и записывая х, у, г в сферической системе координат г,
G, ф (рис. 3.1), запишем гамильтониан в более удобной для вы-
числения матричных элементов форме:
f C.6)
где
л=/1г/2Л1-Зсо82е),
В = -1 (Itla + /Г/г+) (l ~ 3 cos2G),
С = - 4 (/Г/2г + /l2/2+) sin G cos Be-**,
d=-1 (/г/г, + /l2/2~) sin e cos еЛ C)
? =-1 It It
Как было показано выше, величина {ухуЖ2)/!* представляет
собой энергию взаимодействия магнитного момента ядра с по-
лем, равным примерно 1 Гс, в то время как зеемановский гамиль-
тониан (Mz = —V\tiH0I\z — V2ftH0Iiz) представляет собой энер-
гию взаимодействия того же момента с полем, равным Ю4 Гс. По-
этому можно сначала решить задачу с зеемановским гамильто-
нианом, а затем учесть дипольный член как малое возмущение.
(Для двух спинов, каждый из которых равен у2, задачу можно
решить точно.)
Для выяснения роли различных членов А, В, С и др. рассмот-
рим простой случай, когда оба магнитных момента одинаковы
и оба спина равны 1/2. Зеемановские уровни и соответствующие
им волновые функции полностью определяются заданием кван-
товых чисел гп\ и тг, представляющих собой собственные зна-
чения операторв hz и /22- Зеемановская энергия равна
Ez = — уПНот{ — уПНот2. C.8)
Определяемые этим выражением уровни энергии изображены
на рис. 3.2. Введем сокращенное обозначение состояний. На-
72
Глава 3
пример, состояние cffl|= +'/2 и m2 = — !/2 будем обозначать
символами (-1 ). Состояния Ц ) и |— +) вырождены, так
как для обоих состояний Ez — 0. Зеемановские энергии для со-
стояний |+ +) и | ——) равны —Нщ и -f ftcoo соответственно,
где соо = т^о- Выясним теперь, какие пары состояний связывают-
ся различными членами выражения для диполь-дипольного вза-
имодействия. Пропорциональ-
ный hzhz оператор А, очевид-
но, диагоналей. Он связывает
\тхт2) с (mim2|. В противо-
положность этому оператор В,
пропорциональный/i ЛГ +/Г/^»
связывает состояние | mim2)
только с состояниями (mi-)-1,
m2—1| или (гп\ — 1, т2+1|.
Иначе говоря, оператор В од-
новременно переворачивает в
разные стороны оба спина. По-
этому В связывает только со-
стояния
)
и |
Рис 3.1. Связь между прямоуголь- Связь между состояниями, об-
условленная операторами А и
В, показана схематически на
рис. 3.3.
Заметим, что оператор В
не имеет отличных от нуля
диагональных матричных элементов в представлении m\tn% но
он имеет отличные от нуля недиагональные матричные элементы
между двумя вырожденными состояниями. Это означает, что со-
у ру
ными координатами х, у, г (харак-
теризующими положение ядра 2 от-
носительно ядра 1) и сферическими
координатами г, в, <р.
-+
Рис. 3.2. Уровни энергии двух одинаковых спинов.
стояния |н ) и | 1-) не являются правильными волновыми
функциями в нулевом порядке теории возмущений. Поэтому
оператор В играет важную роль при определении правильных
функций нулевого порядка теории возмущений. Если в качестве
базисных функций выбрать правильные функции, то оператор. В
в этом представлении будет диагональным. Ниже мы вернемся
к этому вопросу.
Каждый из операторов С и D переворачивает только по од-
ному спину. Поэтому они связывают состояния, изображенные
Магнитное дшюльное уширение резонансных линий 73
на рис. 3.4, которые отличаются по энергии на величину /коо.
Наконец, операторы Е и F переворачивают по два спина сразу
вверх или вниз; они связывают состояния, отличающиеся по
энергии на величину 2Нщ (рис. 3.5).
Таким образом, операторы С, D, Е и F являются недиагональ-
ными. Они приводят к появлению слабой примеси целого ряда
Рис. 3.3. Состояния, связанные операторами А к В.
Пунктирные линии проведены между связанными состояниями.
/C,D \С,
ч /
\C,D /C,D
Рис. 3.4. Состояния, связанные операторами С и D.
Рис. 3.5. Состояния, связанные операторами Е н F.
функций нулевого порядка теории возмущений в точных волно-
вых функциях. Степень примешивания можно определить при
помощи формул первого порядка теорий возмущений. Выраже-
ние, определяющее волновую функцию в первом порядке теории
возмущений, имеет вид
(nX-^] ^- C-9)
n'
где ип — исправленная волновая функция, и°п — волновая функ-
ция нулевого порядка теории возмущений, соответствующая
энергии Еп, Жъоък — оператор возмущения, (д'1Жзозм1п)—ма-
74 Глава 3
тричные элементы переходов между невозмущенными состояния-
ми м°, и и°п.
Из выражения C.9) видно, что состояние |++) имеет ма-
лую примесь состояний |4 ), | h) и | ). Степень при-
мешивания определяется величинами (п'\ЗёВозм\п) и Еп — Еп
Первая величина равна произведению у2^2/^ на спиновый ма-
тричный элемент. Поскольку спиновый матричный элемент по
¦- +
Рис. 3.6. Сильный переход (обозначен двойной стрелкой) и переход, соот-
ветствующий матричному элементу, отличному от нуля вследствие дипольного
примешивания.
порядку величины всегда равен единице, а Ялок = \ti/r3, то
(я' | «Завозы | п) « уйЖло*. С другой стороны, Еп — Еп- = йсоо = \hfio.
Поэтому
(п71 Жвозы \п) _ Ялок _. 1 п-4 C ю)
Еп — Еп,
что соответствует очень малой степени примешивания. Конечно,
такое примешивание состояний приводит к появлению поправок
к уровням энергии лишь во втором порядке теории возмущений.
Однако более важен другой эффект: при примешивании состоя-
ний переменное поле будет возбуждать такие переходы, которые
без примешивания запрещены. Так, например, переходы между
состояниями | ++) и |——), которые запрещены для чистых
состояний, будут происходить за счет того, что исправленные
волновые функции этих состояний содержат примеси состояний
I + -) и |-+) (рис. 3.6).
Матричный элемент этого перехода в Н0/Нлок раз меньше
матричного элемента нормального перехода, например между
состояниями |++) и |-| ), а поглощение, соответствующее
этому переходу, пропорциональное квадрату матричного элемен-
та, в (Яо/ЯлокJ раз слабее поглощения, сязанного с нормаль-
ными переходами. Этот переход происходит на частоте со = 2соо.
Вследствие примешивания состояний могут происходить также
переходы на частоте, близкой к со = 0. [На самом деле такие пе-
реходы запрещены для двухспиновой системы, каждый спин
которой равен '/2, так как ее волновые функции при М =
— п%\ -\- т2 = 0 обладают различной симметрией по отношению
к перестановке индексов частиц (синглетное и трнплетное СО-
Магнитное диполтое уширение резонансных линий 75
стояния), а оператор возмущения симметричен по отношению к
такой перестановке. В системе, содержащей более двух одина-
ковых спинов, такие переходы разрешены.]
Таким образом, полный эффект от членов С, D, Е и F заклю-
чается в появлении поглощения вблизи частот 0 и 2соо, показан-
ного на рис. 3.7. Дополнительные пики при со = 0 и со = 2соо
очень слабы, и ими можно пренебречь в нашем рассмотрении.
Поэтому с хорошей степенью точности операторы С, D, Е и F
можно исключить из гамильтониана. Ниже мы увидим, что в
некоторых расчетах присутствие членов С, D, Е и F приводит к
ошибочным результатам. Сумму оставшихся членов А 4- В обо-
значим через
= у ^ О - 3 cos2 6) C/,Лг - I. • Ь). C.11)
Упрощенный гамильтониан имеет вид
) +
k I-* r/k C.12)
Операторы 3$z и Жг коммутируют друг с другом. В этом
можно убедиться, рассматривая гамильтониан для двух спинов
1 и 2. Очевидно, 1г = I\z + I-zz коммутирует с З/^/гг. Что можно
сказать по поводу произведения Irh? Оператор /г коммутирует
также с оператором A| + ЬJ, поскольку оператор I] -(- Ь = I
представляет собой оператор полного момента количества движе-
ния (любая компонента полного момента количества движения
1
OJq ZU)g Ш
Рис. 3.7. Зависимость поглощения от частоты при учете яипольного взаимо-
действия.
Три пика поглощения нмеют ширину ~У#ЛОК. но интенсивность пнков при частотах О
н 2и0 в (w0/WqoKJ раз меньше интенсивности пика при частоте esg.
коммутирует с квадратом полного момента количества движе-
ния). Выписывая оператор I2 = (Ii + ЬJ в виде
I2 = I? + l2+2Ii-h, C.13)
мы видим, что оператор hz -\- Ы коммутирует с левой частью и
двумя первыми членами правой части этого равенства. Следова-
тельно, он должен коммутировать и с Irb-
76 Глава 3
Если два оператора коммутируют, то для них можно выбрать
систему таких собственных функций, которые будут собствен-
ными функциями каждого из операторов. Обозначим индексом а
собственные функции и собственные значения оператора Ш&> Тог-
да можно написать
или
= Va. MztiM=-(yhH0M)uM, C.14)
+ Ж а) | Ma) = (- yhH0M + Ea) \ Ma). C.15)
Определяемые этими равенствами квантовые числа будут по-
лезны в дальнейшем. К сожалению, мы знаем лишь, что кванто-
вые числа а существуют; сами квантовые числа и соответствую-
щие им собственные функции нам еще не известны. Если бы опе-
ратор Зёв. содержал только члены вида hzhz, то задачу о вычис-
лении формы резонансной линии можно было бы решить точно.
Ее можно было бы решить точно и в том случае, если бы опера-
тор Ж d включал в себя только члены вида Irb- Вследствие не-
коммутативности операторов первого и второго вида при одно-
временном присутствии этих членов в гамильтониане эти реше-
ния становятся непригодными. В этом случае для решения за-
дачи приходится пользоваться методом моментов, разработан-
ным ван Флеком. Этот метод позволяет вычислять различные
характеристики резонансных линий в тех случаях, когда соб-
ственные волновые функции и собственные значения неизвестны.
§ 3. Метод моментов !)
Прежде чем начинать изложение метода моментов, рассмо-
трим полученное выше выражение для %"((?>):
C.16)
а.Ь
Переменные решетки мы будем рассматривать как параметры,
поэтому единственными переменными в рассматриваемой задаче
будут переменные спинов. Иначе говоря, квантовые числа а и Ъ
относятся к спинам. Следовательно, можно положить Еа <? КГ
и заменить экспоненту единицей.
Доказательство правильности этого предположения требует
дополнительного рассмотрения, поскольку величины Еа пред-
<) См. в библиографии, помещенной в конце книги, раздел «Второй мо-
мент».
Магнитное дипольное уширение резонансных линий 77
ставляют собой уровни энергии гамильтониана для N спинов.
Если оставить в гамильтониане только зеемановский член и счи-
тать спины всех ядер равными '/2, то энергия отдельного спина
будет равна ± ynhH0/2, а энергия Еа будет лежать в области,
ограниченной значениями ± NyntiH0/2. Поскольку величина N
может быть очень большой, могут быть такие значения Еа, для
которых условие \Ea\<g.kT не выполняется. Самое большое зна-
чение энергии, соответствующее параллельной ориентации всех
спинов, равно NyntiH0/2. Ближайшее к нему значение энергии
Еа= (N — 2)yhH0/2 соответствует состоянию, получающемуся
в результате переворачивания одного спина в рассмотренной
выше конфигурации. Такое состояние можно получить, перево-
рачивая любой из N спинов, поэтому оно будет Af-кратно вырож-
дено. Можно ожидать, что распределение состояний по энергии
будет описываться гауссовой функцией распределения. В этом
случае среднее значение Еа будет равно по порядку величины
*JWytlHo/2. Это значение существенно больше зеемановской
энергии отдельного спина. Известно, однако, что резонансные
частоты поглощения получаются с высокой точностью при рас-
смотрении зеемановских уровней отдельного спина. Можно ожи-
дать поэтому, что появление множителя <\/ТГ в неравенстве,
определяющем справедливость высокотемпературного прибли-
жения, ошибочно. Это доказывается в приложении Д, где в ка-
честве условия применимости высокотемпературного приближе-
ния получено неравенство yhH0I «С kT.
В этом приближении форма линии определяется множителем
со и функцией f (со), определяемой выражением
f (©)= Е I («I \ix\b)?6{Ea-Eb-tta). C.17)
а, Ь
На практике экспериментальное измерение величины %"(со)
позволяет определять функцию f (со) из C.17) и, обратно, теоре-
тическое вычисление функции f (со) дает возможность определить
%"(со). Рассмотрим функцию f (со). Отметим, что функция f(co)'
является четной функцией частоты со, поскольку функция %'''(со)
представляет собой нечетную функцию частоты со. [Этот факт
становится очевидным также при точном исследовании функции
f(co).] Определим теперь я-е моменты функции /(со) выраже-
ниями
со
[ anf (a) da
- (ЗЛ8)
((со) da
78 Глава S
(ЗЛ9)
о
Выражение C.19) для n = 2 называется вторым моментом. Оче-
видно момент <Дсо2> по порядку величины равен квадрату ши-
рины линии, так что
<Д2>(ЯкJ. C.20)
Определяемые выражениями C.18) и C.19) моменты тесно свя-
заны друг с другом. Эту связь в случае п = 2 можно установить
следующим образом. Выписывая (со — <со>J = со2 — 2со <со>-|-
+ <со>2 и учитывая C.18) и C.19), получаем
<Дсо2) = <сй2)-<№>2. C.21)
Очевидно, величину <Дю2> можно рассчитывать либо непо-
средственно, либо выражать ее через предварительно вычислен*-
ные значения <со2> и <со>. Мы воспользуемся последним спо-
собом.
В качестве иллюстрации общего метода рассчитаем сначала
оо
интеграл \ f (co)dco, пропорциональный площади, ограниченной
о
кривой поглощения. Затем мы вычислим величины <со> и <Дсо2).
Поскольку функция /"(со) является четной функцией,
ОО +ОО
СО)ЛО = 4 \ f(©)rf<D =
о —°°
+ ОО
= 1 5 Х(а1МЬ)(Ь|Ыа)б(?а-Еь-/гсо)Ло. C.22)
—оо а, Ь
Вследствие наличия б-функции в подынтегральном выражении
этот интеграл отличен от нуля только в том случае, когда
Йа = Еа — Еь. Но для любой пары состояний \а) и \Ь) имеется
некоторое значение со в области между —оо и +°°. которое удо-
влетворяет условию /ш = Еа — Еь. (Отметим, что при интегри-
ровании от 0 до оо в интеграл не давали бы вклада состояния,
для которых величина Еа — Еь отрицательна. По этой причине
область интегрирования была распространена на всю область
изменения частоты от — оо до -f- оо.) Заменяя переменную инте-
Магнитное дипольное уширение резонансных линий 79
грирования со на /ко, получаем
5 / (ю) d<o = -^j-J] (о| ця |6) (b\ цх |о). C.23а)
О о, &
Применяя основную теорему квантовой механики
Ф\А | Р') Ф'I В |П = (Р\АВ |П. C.236)
справедливую для произвольных операторов Л и В и для любого
полного набора функций |{3'), находим
|^|a) = 4rSp^ C.24)
Здесь символ Sp означает след, или сумму диагональных ма-
тричных элементов. Другая важная теорема утверждает, что при
замене полного набора ортогональных функций |{3) другим пол-
ным набором функций |?) [функции |{3) могут быть представ-
лены в виде линейных комбинаций функций |?)] величина следа
не меняется. Поэтому для вычисления следа можно пользовать-
ся любым полным набором функций. Выберем в качестве такого
набора произведения iV собственных функций отдельных спинов,
собственные квантовые числа которых равны гп\, т%, тг, .,., ты.
Тогда
/ (со) dco = -jj- ]Г (т^^з ... | ц^ | т1т2т3 ...). C.25)
Отсюда при учете равенства nx = Xi V-xi находим
HS-Z *„¦**. C-26)
В этом выражении содержатся члены двух типов с \ф k и с
/ = k. Рассмотрим сначала члены первого типа. Положим / = 1,
k = 2. Фиксируя значения т2, тз, ша, получаем
• • •) = {rn\. I Hi* I mi) (tn21 Vhx I '«2). C.27,
или после суммирования по т\
fl C.28)
E
Но J] (trii \^1х \ffii) = O. В этом можно убедиться, если заметить,
/Ml
что функции \trii) являются собственными функциями оператора
1\г, а диагональные матричные элементы операторов /и и ^iu?
80 Глава 3
вычисленные с этими волновыми функциями, равны нулю. В про-
тивоположность такому выбору в качестве собственных значе-
ний Ш\ можно было бы выбрать собственные значения операто-
ров 1\х. Но тогда каждому значению + т будет соответствовать
точно такое же отрицательное значение, что дает
Е (т, | ни I т,) = ф Z (т, 11и | т,) = 0. C.29)
Таким образом, вклад от членов с / ф k будет равен нулю. Для
членов с / = k, полагая / = 1, находим
C.30)
Входящий в это выражение матричный элемент не зависит от
m<i, т3 и т. д. Поэтому сумма будет состоять из множества оди-
наковых слагаемых. Так как имеется B/+ 1) квантовых чисел
m<i, B/ + 1) квантовых чисел т3 и т. д., то матрица, матричные
элементы которой зависят от т\, будет встречаться при сумми-
ровании B/ 4- l)w-1 раз. С другой стороны, учитывая, что сим-
вол Spi обозначает след по квантовым числам спина 1, находим
SPi'xL== SpiH'ij/. Это равенство легко проверить непосредствен-
ным вычислением. С помощью собственных функций оператора
1уХ находим
+/
sPi^u = Y^2 Z т2. C.31а)
т— -I
Применяя собственные функции оператора hy, можно найти ана-
логично
SPi^ = Y2U2 I m\ C.316)
Следовательно,
sp, ixf, = sPl 11^=sPl i*L=-|- sp ^?- C-31в)
Оператор и, имеет B/+1) диагональный матричный элемент,
каждый из которых равен -fti^lij +1). Поэтому
Учитывая, что имеется N одинаковых членов с / = k, получаем
-1-
f (со) rfco = -1- fh*-t«±± N B/ + l)-v. C.32)
Магнитное дипольное уширение резонансных линий 81
Вычислим теперь изменение средней частоты линии поглоще-
ния <со>, обусловленное дипольным взаимодействием. Существо-
вание такого сдвига средней частоты предполагает, что созда-
ваемые соседними магнитными моментами локальные магнитные
поля направлены преимущественно параллельно приложенному
полю. Этот эффект связан с лоренцевым локальным полем ДЯ,
которое должно быть равно по порядку величины %пН0, где
%п — статическая магнитная восприимчивость ядер. Величину
%п можно определить по формуле Ланжевена — Дебая
Ny44 (I + 1)
где N— число ядер в единице объема. Если расстояние между
ближайшими ядрами равно а, то N « 1/а3. Следовательно,
Этой величиной в большинстве случаев можно пренебречь, так
как она очень мала по сравнению с шириной линии Ялок вслед-
ствие того, что зеемановская энергия ядра yhH0 во много раз
меньше величины kT. Физический смысл полученного выражения
для ДЯ состоит в- том, что магнитные моменты соседних ядер,
хотя и в слабой степени, но все же ориентируются преимуще-
ственно параллельно постоянному полю, входящему в аргумент
болыдаановского множителя (yhH0/kT). Среднее значение Ялок
отличается от нуля на величину yhH0/kT. Вычисленные с по-
мощью равенства C.17) величины ДЯ и <ю> должны равняться
О и соо соответственно, поскольку C.17) соответствует случаю
бесконечно большой температуры.
Строгое вычисление средней частоты, или первого момента
if (ю) da
<<o>=-°«— .
\ i (ю) dco
представляет собой более сложную задачу, чем вычисление ин-
оо
теграла \ /(co)d<o. В C.22) удобно было перейти к интегрирова-
о
нию от — оо до + оо. После такого изменения пределов интегри-
рования каждой паре уровней энергии всегда можно было сопо-
ставить такое значение частоты со, чтобы равенство Еа — Еь =
= /ico выполнялось как для положительных, так и для отрица-
тельных значений Еа — ?&. В выражении для величины <со) та-.
82 Глава 3
кого преобразования сделать нельзя, так как
cu/(co)dco = O C.33)
вследствие нечетности подынтегральной функции. Поэтому мы
оо
вынуждены вычислять \ со/ (со) dco:
о
5 со/ (со) Ло = -р- ? 5 (с | ц, 16) F1 ц, | с) (Йсо) б (?0-?6-Йсо) d (Йсо)=
О а.ЬО
E (°ll*)Fl^la)(f?) C-34)
Как было отмечено выше, энергии Еа и f'b равны суммам зеема-
новских и дипольных вкладов (—yhH0M + Еа). Предположим,
что при приводящих к поглощению переходах изменение диполь-
ной энергии всегда много меньше изменения зеемановской энер-
гии, соответствующего поглощению на частоте, равной примерно
соо (это следует из проведенного выше анализа различных чле-
нов А, В, ..., F). Поскольку Еа > Еь, мы можем написать
Еъ = — уПНо (М + 1) + Еа', C.35)
Еа — Еь = Йсоо -\- Еа — Еа'.
С помощью этих соотношений перепишем равенство C.34) в
виде
оо
\ cof (со) d(n ==
S
= "F Z (Mv\ »xl M+la')W+la'\iix\ Ma) (hm + Ea-Ea').
'"•«•«' C.36)
Рассмотрим сначала в этом выражении член, пропорциональный
ж IЛ1 + 1аО (ЛЦ- 1а' | |хх | Ма). C.37)
М. а, а'
Это выражение можно было бы записать в виде следа, если бы
не была фиксирована величина М -f- 1. От этого ограничения мо-
жно избавиться, если воспользоваться свойствами повышающих
Магнитное дипольное уширение резонансных линий 83
и понижающих операторов и учесть равенство
цх = 1(ц+4-ц-). C.38)
Тогда
(М + la'l Их | Afa) == -g- (M + la' I V+ I Ma).
Поскольку оператор ц+, связывающий состояния М' и М, имеет
отличные от нуля матричные элементы (M'a'\\i+\Ma) только
для переходов, при которых выполняется условие M'=M-f- 1,
выражение C.37) можно записать в форме, где суммирование
проводится по всем значениям величины М':
^Р- 2, (Ма|ц-|М'а')(М/а'|^+|Ма) =
М, М'
а. а'
Здесь мы воспользовались равенствами Spn^ = Spn2 и
Sp (|1,ц„ - Ц„|1Я) = Y%2 Sp (/»/„ - 7„/я) = y2ft4 Sp /г = 0 C.40)
До сих пор рассматривался только член в C.36), пропорцио-
нальный ftcoo. Легко рассмотреть член этого равенства, пропор-
циональный Еа — Еа: Известно, что Жг! Ма') = Еа-1 Ма'). По-
этому для произвольного оператора Р справедливо равенство
(MV | РЖа | Ма) == ^ «l,vP4«Ma ^т =
им'а'РЕаиМа dx = ?„ (М'a' | P | Ma). C.41)
При учете эрмитовости оператора Ж% далее находим
(MV 15»ЗР | Mo) = J «'и'а'^Р«Ма dx = ^ (^i«M'a')* Р«-Иа ^Т =
= ^а- ^ и'м'а'РиМа dx = Еа- (AfV | Р| Мо). C.42)
84 Глава 3
Поэтому
? (Ma | ц~ | М'а') (MV | ц+ | Ма) (?„ - ?„<)
л*, м'
а, а'
- ? (Мх |[Я#, ц-]| ЛГа') (MV| ц+ | Ма) =
^^' C.43)
Детальное вычисление следа в C.43) показывает, что он равен
нулю. Поэтому из C.36), C.39) и C.43) получаем
$f(<a)*a = -g-SPn2. C.44)
Но, согласно C.24),
поэтому
оо
\ ю/ (ю) dco
C.45)
Следовательно, «среднее» значение частоты не изменяется в при-
сутствии дипольного взаимодействия.
Для вычисления упомянутой выше поправки, обусловленной
локальным полем, необходимо было бы вернуться к выражению
C.17) и включить в него экспоненциальный множитель, опушен-
ный при переходе от C.16) к C.17). (Необходимость включения
такого множителя вытекает из того, что выражение ДЯ«
f& Hj,OK(yhHo/kT) зависит от температуры, а в выражение C.17)
температура входит только через экспоненциальный множитель.)
Второй момент <ю2> можно вычислить аналогичным образом:
\ со2/ (со) dco
(«?> = ^ • C.46)
В выражении C.46) необходимо вычислить только числитель,
так как знаменатель уже вычислен выше:
Магнитное дипольное уширение резонансных линий 85
+00
О —°°
+ОО
== " \ / о (я | и* [ 6) F1 Ид | а) б (?"а — Е^ — ft©) do =
—«o a, b
= irj(?a- ?ЬJ (а I цж 16) F1 (i, | a). C.47)
а, Ь
Так же, как это было сделано при выводе равенств C.42) и
C.43), при учете уравнения Ж\а) = Еа\а) находим
1 V
ю2/ (ю) dv> == — -яр- > (а | ^(лх — Цх^1 Ь) (ft I °@Px — №Х3@ \а) =
C.48)
а.Ь
1
Учитывая, что ^ = ^z + ^d> далее получаем
со
<о2/ (©) rf© - —зр- Sp [Жг, nJ2 - -2F Sp [5»z, ця
2^. C-49)
Здесь при преобразовании перекрестных членов, включающих
операторы [<№z, Ц*] и \_Ж\, |лх], было использовано справедливое
для пары любых операторов An В равенство
C.50)
которое легко проверить при помощи C.236).
Если исключить из рассмотрения дипольное взаимодействие,
то в правой части равенства C.49) остается только первый член
и величина <©2> будет равна ©о В этом случае форма линии бу-
дет описываться б-функцией. Точный расчет подтверждает этот
вывод. Второй, или «перекрестный», член в правой части C.49)
равен нулю в силу того, что он содержит множитель Spini*. По-
оо
оо
следний член в правой части C.49), деленный на \ /(©)rf©, дает
°
i /*
Отсюда с помощью C.21)
8В Глава 3
и с учетом равенства <со> = соо получаем
1 — 3 cos2 6„,Л2
g • (с.ог)
Чтобы лучше уяснить себе смысл равенства C.52), рассмот-
рим случай, когда спины занимают эквивалентные положения
в решетке. В этом случае величина
(l-3cos»e/ft)a
не зависит от /. Поэтому сумма содержит N эквивалентных сумм,
каждая из которых соответствует определенному значению /.
Таким образом,
^Z('-!T'e>8 C.53)
Каждый член суммы в C.53), очевидно, равен по порядку вели-
чины (уНлок) , где Нлок представляет собой локальное поле,
создаваемое k-м спином в точке, где находится /-й спин. Важный.
смысл равенства C.53) состоит в том, что оно позволяет выяс-.
нить точный смысл понятия локального поля, давая возможность
сравнить теоретические значения с экспериментально измеряе-
мыми значениями.
До сих пор вычислялся второй момент для систем, состоя-
щих из одинаковых спинов. Несколько иные результаты полу-
чаются в случае, когда в кристалле содержатся различные сорта
спинов. Основное отличие этого случая от рассмотренного выше
состоит в изменении роли члена типа В в дипольном взаимодей-
ствии, связывающего состояния \-\ ) и | \-).
Если эти состояния вырождены, как это имеет место в случае
одинаковых спинов, то оператор В приводит к изменению уров-
ней энергии в первом порядке теории возмущений. Если же со-
стояния не вырождены, то оператор В вызывает лишь сдвиг уро-
вней энергии на величину второго порядка и обусловливает сла-
бые запрещенные переходы. Поэтому в случае неодинаковых
спинов оператор В можно исключить ').
') Ван Флек указал, что отбрасывание этого члена в случае неодинако-
вых спинов, так же как отбрасывание членов С, D, Е и F в случае одинако-
вых спинов, играет очень важную роль при вычислении второго момента
(Дш2). Причина заключается в том, что слабые по интенсивности сателлиты
[их интенсивность в (Н0/НткJ раз меньше интенсивности основной линии],
расположенные на частотах ю = 0 и ю = 2юо, сдвинуты на ю0 от центра
основной резонансной линии. Второй момент определяет средний квадрат
отклонения частоты поглощения от центра основной линии. Поэтому сагел-
Магнитное дипольное уширение резонансных линий 8Г
Взаимодействия между одинаковыми и неодинаковыми спи-
нами могут давать сравнимые по величине вклады во второй мо-
мент. Эти вклады легко вычислить. Если спины одного сорта обо-
значить через /, а спины другого сорта — через S, то дииольное-
взаимодействие между одинаковыми спинами можно записать,
в виде
A—3 cos2 в. л
1 з -(ЗУг(-1*-1/). C.54>
к. I Гк1
В случае одинаковых спинов члены вида 1*-1/ не дают вклада во
второй момент, так как они коммутируют с цх [см. C.49)]. Га-
мильтониан, описывающий взаимодействие между неодинако-
выми спинами, имеет вид
d)is = yi\sti }_,- -р —1г^г1- C.55)
Выражения C.54) и C.55) различаются в основном численными
множителями гг-членов, причем в C.55) подобный множитель в
3/г раза меньше, чем в C.54). В соответствии с этим в выраже-
нии для второго момента появляется множитель 4/э. Оконча-
тельно получаем
^ № <S + 0 ! ? ^'Г^ • C.56)
Отметим, что в это выражение входит множитель S(S + О. а не
/(/ -f 1). входивший в C.52). Это соответствует тому, что на
спины / теперь действует локальное магнитное поле, пропорцио-
нальное магнитному моменту ysh V-S(S + 1) ядер другого сорта.
Полный второй момент резонансной линии получается при сум*
мировании вкладов от одинаковых и неодинаковых спинов.
§ 4. Пример применения вторых моментов
После появления первой работы Пейка и Гутовского было
опубликовано много работ, в которых изучались вторые моменты.
В качестве очень интересного примера мы опишем исследование,
которое провели Эндрю и Идее [1] на твердом бензоле. Изучая
различные молекулы, получающиеся при замещении водорода
дейтроном, они смогли определить расстояние между смежными
протонами бензольного кольца и показать, что при температурах
литы, несмотря на малую интенсивность, могут вносить большой вклад в ве-
личину второго момента. Поскольку нас интересует ширина основной липни
поглощения, вклад сателлитов следует исключить. Для этого в гамильтониане
необходимо отбросить члены, связанные с сателлитам».
88
Глава 3
выше 90 К молекулы бензола могут относительно свободно вра-
щаться вокруг оси, перпендикулярной плоскости молекулы.
Три типа молекул, изученные Эндрю и Идесом, показаны на
рис. 3.8. По структуре кристаллы бензола очень похожи на гра-
нецентрированные кубические кристаллы с молекулами бензола
н
\
с—с
//
н—с
\
с=с
/
н
н
ч
с—н
\
н
D
\
н
/
с—с
f
н—с
\
X
С—D
/
с=с
/
D
\
н
н
\
с—с
//
н—с
\
с=с
/
н
н
/
X
С—D
/
\
н
с,
Рис. 3.8. Три разновидности молекул бензола, исследованные Эндрю и Идесом.
в вершинах и центрах граней куба. Ребра элементарной ячейки
кристалла взаимно перпендикулярны, но имеют разную длину.
Ребра, параллельные осям а, Ь и с, равны 7,44, 9,65 и 6,81 А со-
ответственно. Плоскости всех
молекул параллельны кристал-
лической оси Ь. Если смотреть
на кристаллическую решетку
в направлении оси Ъ, то распо-
ложение молекул будет иметь
вид, схематически изображен-
ный на рис. 3.9; сплошными
линиями обозначены положе-
ния молекул, атомы которых
расположены в плоскости
у = 0, пунктирными — молеку-
лы, атомы которых лежат над
\
Рис. 3.9. Элементарная ячейка кри-
сталла бензола.
Сплошными линиями обозначены молекулы,
расположенные в плоскости j/»=0; пунктир-
ными—молекулы, расположенные в пло-
скости j/=b/2.
плоскостью у = 0 на расстоя-
нии Ь/2. (Поскольку изучались
поликристаллические образцы,
влияние ориентации магнитного поля по отношению к кристал-
лическим осям не было исследовано.)
Вклад в величину второго момента, очевидно, будут вносить
как ядра, расположенные внутри молекулы бензола, так и ядра,
расположенные вне молекулы. В принципе, если положения и
ориентации всех молекул в кристалле заданы, единственной не-
известной величиной будет расстояние R между соседними про-
тонами бензольного кольца. Замещая протоны дейтронами, Эн-
дрю и Идее смогли экспериментально определить вклады во вто-
рой момент от внутренних и внешних ядер в отдельности. В воз-
можности такого определения легко убедиться, если заметить,
Магнитное дипольное уишрение резонансны): линий
что при замещении протона, расположенного в определенном
узле решетки кристалла, дейтроном вклад во второй момент от
этого узла становится в 1/а раз меньше, причем
н
Здесь индексы PhD относятся к протону и дейтрону. Учитывая
далее, что /D=l, h = 'А, Суе/2я)= 6,535-102, Gр/2я) =
= 42,57-102, находим а = 0,0236.
Рассмотрим Si — вклад во второй
момент от ядер, расположенных вне
молекулы. Для СбНзОз в любом узле
кристалла с равной вероятностью мо-
жет находиться как протон, так и дей-
трон. Поэтому вклад во второй мо-
мент от протонов в этом кристалле
уменьшается в 2 раза. Если бы во
всех узлах решетки находились дей-
троны, то второй момент уменьшился
бы в 1/а раз. Однако, поскольку в рас-
сматриваемом случае только полови-
на узлов занята дейтронами, вклад от
них будет равен oSi/2. Таким обра-
зом, полный вклад во второй момент от внешних ядер будет
D
//'
/77?
V "
У/
\
\
D
г к
**\
\
\
Л
- 1 п
1
/
•' н
Рис. 3.10. Положения про-
тонов и дейтронов в мо-
лекуле и расстояния ме-
жду ними.
определяться выражением
C.58)
в котором величина а известна.
Анализ вклада во второй момент от ядер, расположенных
внутри молекулы, проводится аналогичным образом. Обозначим
через S2 и S% вклады от внутренних ядер для молекул С6Н6 и
С6Н3Оз соответственно. Величина Si меньше S2, так как в дей-
терированном соединении узлы 2, 4 и 6 дают в 1/а раз меньший
вклад во второй момент. Обращаясь к рис. 3.10 и замечая, что
вклад во второй момент зависит от расстояния как 1/г6, находим
27
j-^-=6. C.59)
128
Отсюда для второго момента в кристаллах
ветственно получаем
S' = S\ + S'2 = (~^) S, + 6S2,
S ==¦ S\ -f- S2,
и С6Н6 соот-
C.60)
Глава S
где а и 6 — известные величины. Таким образом, измеряя вели-
чины S и S', можно определить вклады Si и 5г от внутренних и
внешних по отношению к молекуле ядер. Данные для кристал-
лов СбН5О позволяют независимым путем проверить эти резуль-
таты.
Таким методом Эндрю и Идее нашли, что расстояние между
соседними протонами R в бензольном кольце равно 2,495 ±
± 0,018 А. Это значение близко к значению 2,473 ± 0,025 А, по-
лученному на основе измеренного рентгенографическим спосо-
1,6 Гс'
240
280
160 200
Температура, К
Рис. 3.11. Зависимость второго момента от температуры для бензола.
бом расстояния между соседними атомами углерода и извест-
ного значения длины связи С—Н. Можно конечно, использовать
рентгенографические данные и данные по измерению магнитного
резонанса для определения длины связи С—Н. В принципе, ис-
следуя резонанс на ядрах С13, можно также непосредственно
определить длину связи С—Н.
Приведенные выше данные получены при измерениях в обла-
сти температур ниже 90 К. Другой важный результат Эндрю и
Идее получили, исследуя зависимость второго момента от темпе-
ратуры (рис. 3.11). Резкое уменьшение второго момента свя-
зано с вращением молекул бензола вокруг оси симметрии шес-
того порядка. Рассмотрим этот эффект.
Эффект вращения очень просто учесть, если ввести в рассмо-
трение углы, показанные на рис. 3.12. Рассмотрим ядра / и k мо-
лекулы. Пусть ось вращения молекулы составляет угол 6' с на-
правлением постоянного поля Но, а угол между радиусом-векто-
ром, проведенным от ядра / к ядру к, и осью вращения равен 7/ft-
При вращении молекулы угол G/л (между Но и вектором, соеди-
няющим ядра / и k), входящий во второй момент в виде множи-
Магнитное дипольное уширение резонансных линий
91
теля A—3cos20/ft), изменяется во времени. Поскольку частота
вращения велика по сравнению с характерными частотами резо-
нанса, во второй момент будет входить усредненное по времени
значение величины A —3cos20/ft). Если предположить, что дви-
жение определяется потенциалом, характеризующимся осью сим-
метрии третьего или более высокого порядка, то это усредненное
по времени значение не будет зависеть от деталей движения и
будет равно
C cos2 v,u — П
A-3 cos2 0/ft>cp = A-3 cos2 0') ± p >- . C.61)
Из этого выражения видно, что при вращениях молекулы вокруг
оси, параллельной вектору, соединяющему два ядра (v/ft = 0),
при которых относительное поло-
жение этих двух ядер не меняется, ли°
угловой множитель не изменяется.
В противоположность этому при
A-3 cos2 0/ft>cp = \ A - 3 cos2 0').
C.62)
В порошковом образце отдель-
ные кристаллы ориентированы слу-
чайным образом по отношению к
полю Но. Поэтому для жесткой ре-
шетки необходимо усреднять величину A—3cos20/fcJ по слу-
чайному распределению ориентации кристаллов. При наличии
движения нужно сначала усреднить величину A — 3cos20y-ft) по
движению, чтобы получить второй момент, соответствующий
данной ориентации осей кристаллов, а затем уже полученную
величину усреднить по различным ориентациям кристаллов.
Пара взаимодействующих магнитных моментов в случае
жесткой решетки дает вклад во второй момент
Рис. 3.12. Углы, характеризую-
щие вращение молекулы.
W2. C.63)
где черта сверху означает усреднение по случайным значениям
величины 0/А.
При наличии вращения второй момент для пары взаимодей-
ствующих моментов определяется выражением
/пращ
(<l-3cos20/ft>cpJ,
C.64)
где индекс «ср» означает усреднение по вращению, а черта свер-
ху означает усреднение по случайным ориеитацням оси враще«
92 Глава 3
ния относительно направления Но. Из C.61) находим
<Ао2)вращ - A-3 cos2 б'J CCOS22/fe~1J. C.65)
Поскольку кристаллические оси случайным образом ориентиро-
ваны относительно Но, ось вращения, направление которой ха-
рактеризуется углом 0', также будет ориентирована случайно.
В результате получим
A-3 cos2 0ikf = A - 3 cos2 О'J.
Если v/ft = я/2 (пара вращается вокруг оси, перпендикуляр-
ной межъядерному вектору), то вклад во второй момент от вза-
имодействующей пары уменьшается в 4 раза •).
Для бензола Эндрю и Идее нашли, что второй момент для
внутримолекулярных протонов уменьшается от значения 3,10 Гс2,
соответствующего низким температурам, до значения 0,77 ±
± 0,05 Гс2 при высоких температурах. Если предположить, что
сужение линии обусловлено вращением молекул вокруг оси сим-
метрии шестого порядка, т. е. y,-k = я/2 (все протоны находятся
в плоскости, перпендикулярной оси вращения), то второй момент
будет уменьшаться до значения 3,10/4 = 0,78 Гс2, что прекрасно
согласуется с экспериментальными данными.
ЛИТЕРАТУРА
1. Andrew E. R., Eades R. О., Proc. Roy. Soc, A218, 537 A953).
') В том, что по движению должна усредняться перед возведением в
квадрат величина A—3cos26,*), а не A—3cos26/*J, можно убедиться при
рассмотрении общего выражения для х"(ю), которое пропорционально ве-
личине
? е~ЕкТ (я | Цж | Ь) (Ь | ц* \а) 6 (Еа -?ь- йсо).
а, Ь
В этом выражении состояния |а) и \Ь) должны рассматриваться как состоя-
ния, зависящие от спиновых и вращательных квантовых чисел. Однако, по-
скольку величина Еа — Еь соответствует частоте ларморовской прецессии, со-
стояния \а) и \Ь) будут характеризоваться одинаковыми вращательными
квантовыми числами. Поэтому при вычислении второго момента след нужно
брать только по спиновым переменным. Зависящий от углов множитель пред-
ставляет собой диагональный оператор относительно переменных «решетки».
Это означает, что классическую величину A — 3 cos26;*) мы заменяем вели-
чиной \ u'L (l — 3 cos 6yft) «? dx, где uL — собственная функция состояния
решетки (в данном случае вращения). Это равносильно усреднению величины
A — 3cos26,/;) no движению до возведения в квадрат.
Глава 4
Магнитные взаимодействия ядер
с электронами
§ 1. Введение
До сих пор мы не учитывали взаимодействия ядер с окружаю-
щими их электронами. В этой главе рассматриваются магнит-
ные взаимодействия между ядрами и электронами. Сильные элек-
тростатические взаимодействия, обусловленные квадрупольными
моментами ядер, будут рассмотрены в гл. 9. Магнитные взаимо-
действия ядер с электронами обусловлены магнитными полями,
возникающими либо благодаря движению электрических заря-
дов, либо вследствие наличия магнитных моментов, связанных
со спином электронов. Первая причина приводит к появлению
так называемых химических сдвигов, вторая — к появлению най-
товских сдвигов.
Некоторые свойства химических и найтовских сдвигов по-
хожи друг на друга. Полный гамильтониан для ядер и электро-
нов можно записать в виде суммы четырех членов:
Ш^ (Я) + Ше @) + Mei (Я) + Жеп,
где Жпг(Н) — зеемановский гамильтониан взаимодействия ядер
с приложенным магнитным полем Н, Жеф) — гамильтониан
электронов в отсутствие поля Н (этот гамильтониан включает
в себя пространственные и спиновые переменные электронов),
Mez(H}—зеемановский гамильтониан электронов в поле Н, а
Шеп — зависящий от пространственных и спиновых переменных
гамильтониан взаимодействия между ядерными спинами и элек-
тронами.
Если<3^еи=0, то ядерная спиновая система не связана с элек-
тронами и ее уровни представляют собой просто зеемановские
уровни ядер в приложенном поле Н. Член Жеп соответствует до-
полнительному магнитному полю, действующему со стороны
электронов на ядра. В диамагнитных и парамагнитных веще-
ствах среднее значение этого поля приближается к нулю при
стремлении к нулю поля Н. Если поле Н не равно нулю, то элек-
троны будут поляризоваться под влиянием взаимодействия
Жег(Н), поэтому среднее значение поля Шеп, действующего на
ядро со стороны электронов, будет отлично от нуля. Мы можем
сказать, что ядра испытывают как прямое взаимодействие с по-
94 Глава 4
лем Н, описываемое 36nz{H), так и косвенное взаимодействие,
обусловленное совместным действием Жег(Н) и Жеп- Эта задача
очень похожа на задачу о вычислении электрического поля в
диэлектрике, в котором на каждый атом наряду с внешним элек-
трическим полем действует еще электрическое поле со стороны
индуцированных электрических моментов других атомов.
В магнитных системах ферромагнитного типа полный магнит-
ный момент электронов отличен от нуля даже при Н = 0. В та-
ких системах поле, обусловленное взаимодействием Жеп, отлично
от нуля и в отсутствие приложенного поля Н.
Мы рассмотрим вначале эффекты, связанные с движением
электронов. Для этого прежде всего дадим обзор основных дан-
ных по химическим сдвигам.
§ 2. Экспериментальные данные
по химическим сдвигам
Наиболее известным и часто цитируемым примером химиче-
ских сдвигов могут служить химические сдвиги в этиловом спир-
те СН3СН2ОН1). Резонансный сигнал протонов в этом веществе
состоит из трех линий, интенсивности которых относятся друг к
другу как 3:2:1. Если проводить измерения в очень однородном
магнитном поле, то можно обнаружить тонкую структуру у каж-
дой из этих линий, обусловленную взаимодействием протонов с
электронными спинами (см. ниже). Ясно, что эти три линии со-
ответствуют протонам трех «типов». К первому, второму и тре-
тьему типу относятся соответственно три протона группы СНз,
два протона группы СНг и один протон группы ОН. Очевидно, на
ядра этих трех типов действуют различные локальные поля, обу-
словленные различным молекулярным окружением. Сопоставле-
ние постоянных магнитных полей, при которых наблюдаются от-
дельные линии, с частотой переменного магнитного поля пока-
зывают, что расстояние между отдельными линиями (расщепле-
ния) линейно зависят от частоты. Если расщепление приписать
действию поля Но и некоторого магнитного поля ДЯ, то для ре-
зонансной частоты ш можно написать выражение
где АН пропорционально Но. Таким образом, можно ввести в
рассмотрение не зависящую от Н величину с, определяемую ра-
венством
= — аН0. D.2)
') См. в библиографии, помещенной в конце книги, раздел «Химические
СДВШ Ц».
Магнитные взаимодействия ядер с электронами 95
Если величина а положительна, то сигнал магнитного резонанса
от атомов будет наблюдаться при больших значениях поля Но,
чем сигнал от ядер, лишенных электронных оболочек. Конечно,
экспериментально исследуют всегда ядра, окруженные электрон-
ными оболочками. Поэтому наблюдаются изменения величины
с, связанные с различным молекулярным окружением. Для про-
тонов вся область изменения величины а составляет Ю-5. Для
атомов фтора эта величина равна 6-10~4, т. е. на два порядка
больше. Вследствие малой величины сдвигов обычно их изучают
в жидкостях, в которых резонансные линии очень узки. По-
скольку величина сдвига зависит от ориентации молекулы по от-
ношению к постоянному магнитному полю, было бы интересно
получить возможность исследовать сдвиги в монокристаллах.
(См. гл. 8.)
Как было отмечено выше, химические сдвиги связаны с ор-
битальным движением электронов. Важно выяснить отличие ор-
битального движения электронов в твердых телах или молекулах
от движения электронов в свободных атомах. Этот вопрос рас-
сматривается в следующем параграфе.
§ 3. Замораживание орбитального движения
Из классической теории электричества и магнетизма изве-
стно, что движущийся со скоростью v электрический заряд q со-
здает на расстоянии г' от заряда магнитное поле
Если же положение заряда задать Ёектором г й искать создавае-
мое им поле в начале координат, то это поле получается при за-
мене в D.3) г' на —г:
с г3 тс г3 тс г3 v*-T/
Где L — орбитальный момент количества движения частицы от-
носительно начала координат. Как мы увидим ниже, формула
D.4) имеет аналогичный вид и в квантовой механике. Из нее
немедленно следует, что в атомах, электроны которых находят-
ся в s-состоянии, действующее на ядро поле равно нулю, по-
скольку в s-состоянии момент количества движения электрона
равен нулю. В то же время Н ф 0 для р-, й- и других электро-
нов, для которых момент количества движения не равен нулю.
По порядку величины поле Н равно
#«•?. D.5>
96 Глава 4
где р—магнетон Бора A0~20 эрг/Гс). Для фтора среднее значе-
ние величины \/гъ в случае 2р-электронов равно
где й0 — боровский радиус. Таким образом, среднее расстояние
электрона от ядра равно 1/4 А, что соответствует магнитному
полю, равному примерно 600 000 Гс.
Казалось бы, такие огромные поля должны полностью пре-
обладать над внешним полем Но и резонанс должен наблюдаться
на частотах yti1), значительно превышающих частоту уН0, на
которой обычно наблюдается резонанс. Следует понять, почему
большие поля таких свободных атомов не существуют в молеку-
лах и твердых телах. Исчезновение этих полей связано с тем, что
в большинстве веществ атомы не обладают постоянными элек- ¦
тронными магнитными моментами, т. е. большинство веществ
диамагнитны. При описании этого явления часто применяется
термин замораживание орбитального момента. Проиллюстри-
руем это явление на очень простом примере.
Рассмотрим атом, обладающий одним электроном в незапол-
ненной оболочке, находящимся в р-состоянии. Для удобства
пренебрежем спином электрона. Ниже при анализе так называе-
мых ^-сдвигов мы рассмотрим эффекты, связанные со спином.
Три р-функции, соответствующие одной и той же энергии атома,
можно записать либо в виде
xf (r), yf(r), zf(r), D.7)
либо в виде
±J zf(r). ^f-f(r). D.8)
Здесь f(r) —сферически симметричная функция.
Функции D.8) являются обусловленными функциями г-ком-
поненты оператора момента количества движения Lz, соответ-
ствующими собственным значениям этого оператора 1, 0 и —1.
Волновые функции D.7) можно рассматривать как линейные
функции D.8). Оба набора функций одинаково применимы для
описания свободного атома. Однако если на атом действует на-
правленное вдоль оси z постоянное магнитное поле Яо, то удоб-
нее пользоваться набором функций D.8).
Если теперь выключить постоянное поле и окружить атом за-
рядами так, как показано на рис. 4.1, то вырождение состояний
снимается. Если обусловленную зарядами потенциальную энер-
гию рассматривать в качестве возмущения, то правильными фун-
') Такой резонанс можно наблюдать в экспериментах с атомными пуч-
ками.
Магнитные взаимодействия ядер с электронами
97
кциями будут функции D.7). Это связано с тем, что недиаго-
нальные матричные элементы возмущения, вычисленные с волно-
выми функциями D.7), равны нулю в силу симметрии энергии
возмущения (см. рис. 4.1). С другой стороны, диагональные ма-
тричные элементы будут иметь равную величину для различных
состояний D.7), поскольку в состояниях xf(r) и yf(r) электроны
Рис. 4.1. Четыре заряда, расположенные около атома (а), и волновая функ-
ция xf(r) (б).
Атом находится в начале координат; заряды расположены на одинаковых расстояниях от
начала координат. Заряды +q находятся на оси х, заряды —q — на оси у. На любом
расстоянии г от начала координат волновая функция xf (r) максимальна на оси х.
расположены преимущественно около положительных и отрица-
тельных зарядов соответственно. Очевидно, что при наличии воз-
мущения уровень энергии состояния xf(r) будет расположен
ниже уровня состояния yf(r), а уровень состояния zf (r) будет
находиться между уровнями состояний xf(r) и yf(r) (в первом
Рис. 4.2. Расщепление р-уровня атома в кри-
сталлическом поле зарядов, изображенных на
рис. 4.1,о.
t
й
I
¦ г((г)
¦хГ(г)
порядке теории возмущений положение уровня состояния zf (r)
не меняется). Расположение уровней энергии показано на
рис. 4.2.
Волновую функцию основного состояния xf(r) можно запи-
сать в виде линейной комбинации собственных функций опера-
тора Lz, собственные значения которого т — + 1 и т — — 1 со-
ответствуют вращению электрона вокруг оси z в противополож-
ных направлениях:
D.9)
V2" '
Поскольку в эту волновую функцию состояния с т = + 1 и
т = —1 входят с одинаковым весом, она будет соответствовать
состоянию, в котором вращение электрона отсутствует.
Л Зяк. 727
98 Глава 4
Этот результат можно получить более строгим способом, про-
водя вычисление <LZ> — среднего значения г-компоненты момен-
та количества движения. Приведем общее доказательство для
любой волновой функции, зависящая от пространственных ко-
ординат часть которой действительна. Оператор Lz имеет вид
Для произвольной волновой функции w0 можно написать равен-
ство
\?(§) D.11)
которое для действительных функций и0 можно переписать в
виде
j\(^) D.12)
Здесь все величины под знаком интеграла действительны. По-
этому отсюда следует, что <LZ> либо равно нулю, либо пред-
ставляет собой чисто мнимую величину. С другой стороны, диа-
гональные матричные элементы эрмитовою оператора должны
быть действительными. Следовательно,
@|1г|0) = 0. D.13)
Очевидно, подобное доказательство можно провести для лю-
бой компоненты момента количества движения. Если
@|/.,|0) = @]^|0) = @|?г|0) = 0, D.14)
то говорят, что орбитальный момент количества движения замо-
рожен.
Выясним теперь, при каких обстоятельствах происходит за-
мораживание орбитального момента. Очевидно, для этого необ-
ходимо, чтобы волновая функция могла быть действительной.
Если действительная функция является собственной функцией
гамильтониана в отсутствие магнитного поля (в этом случае
спины можно не рассматривать), то действительным должен
быть и гамильтониан. Более того, если какое-либо собственное
состояние такого гамильтониана не вырождено, то его собствен-
ная функция, соответствующая данному состоянию, действитель-
на (с точностью до постоянного комплексного множителя, не
влияющего на средние значения), поскольку она является реше-
нием действительного дифференциального уравнения. Следова-
тельно для таких состояний @1 Lx | 0) = 0. Резюмируя, можно
сказать, что в тех случаях, когда электрическое поле зарядов
приводит к появлению невырожденных состояний, орбитальный
момент в них заморожен. Физическая причина замораживания
Магнитные взаимодействия ядер с электронами 99
состоит в том, что под действием внешних зарядов плоскость ор-
биты электрона начинает прецессировать. При полном перевора-
чивании плоскости орбиты электрона направление его вращения
меняется. Грубо говоря, траектория электрона перестает быть
плоской и электрон начинает двигаться по траектории," напоми-
нающей путь нитки в клубке.
При включении магнитного поля положение, конечно, меняет-
ся. Интуитивно очевидно, что в магнитном поле, направленном
вдоль оси 2, вращение в одном из направлений должно преобла-
дать по сравнению с вращением в другом направлении. В соот-
ветствии с этим волновая функция основного состояния должна
быть исправлена таким образом, чтобы в ней была отражена
предпочтительность одного из вращений (состояние с m = — 1
должно войти в волновую функцию с ббльшим весом). Вводя в
рассмотрение малую величину е, запишем волновую функцию
основного состояния в виде
' D.15)
Из этого выражения видно, что изменение основного состояния
xf(r) связано с появлением небольшой примеси состояния yf(r).
Ниже будет показано, что характеризующая степень примеши-
вания величина е пропорциональна Но. Поэтому вращение элек-
трона линейно зависит от Но.
Перейдем теперь к более детальному рассмотрению химиче-
ских сдвигов.
§ 4. Формальная теория химических сдвигов 1)
Химические сдвиги возникают при одновременном взаимо-
действии ядер с электронами и электронов с внешним полем Но.
Общая теория химических сдвигов была дана Рэмси [1]. Мы
изложим ее несколько иначе, чем в работе [1], разбив выкладки
на две части. Сначала вычислим токи, появляющиеся в молекуле
при включении постоянного магнитного поля, а затем рассчи-
таем магнитные поля, создаваемые этими токами в местах, где
расположены ядра. Мы рассмотрим теорию для случая одного
электрона. Выведем гамильтониан для электрона. Введем в рас-
смотрение два векторных потенциала Ао и А„, один из которых
связан с магнитным полем Но, а другой — с действующим со сто-
роны ядра полем Нп:
Ho = VXAo, Hn = VXAft. D.16)
') См. в библиографии, помещенной в конце кингн, раздел «Химические
сдвиги».
100 Глава 4
Хорошо известно, что данное магнитное поле можно описать при
помощи различных векторных потенциалов. Так, например, одно
и то же магнитное поле Н можно задать как потенциалом А, так
и потенциалом А' = А + Уф (где ф — произвольная скалярная
функция), поскольку ротор градиента любой функции всегда ра-
вен нулю. Преобразование от А к А' называется калибровочным
преобразованием. Необходимо проверить, что физические ре-
зультаты после проведения любого вычисления не зависят от
выбора калибровки, т. е. калибровочно инвариантны. Магнитное
поле учитывается в уравнении Шредингера путем замены опе-
ратора (ft/t)V оператором (ft/t)V — (q/c)A, где q— заряд части-
цы (величина q может быть положительной или отрицательной
в зависимости от знака заряда частицы). После такой замены
гамильтониан будет иметь вид
где р =='(ft/t) V. Если выбрать другую калибровку А'=А4^ф(г)',
то гамильтониан изменится и его собственная волновая функция
1|/ будет связана с собственной функцией первоначального га-
мильтониана ф унитарным преобразованием
D.18)
Если сравнить теперь средние значения (ft/OS, (^i (Й/?)У-ф) и
0Ф'. (Й/0^')> то они окажутся не равными друг другу. По-
скольку наблюдаемые значения физических величин не должны
зависеть от выбора калибровки, отсюда следует, что (ft/i)V не
может представлять собой оператора импульса mv в присут-
ствии магнитного поля. Импульсу в этом случай будет соответ»
ствовать оператор (h/i)\ — (q/c)A, инвариантный относительно
калибровочного преобразования:
По аналогичным причинам моменту количества движения г X mv
в присутствии магнитного поля будет соответствовать оператор
Отличие между величинами mv и p(=(ft/t)V) существует и в
классической механике. Так, в классической механике канониче-
ский импульс рх равен дЬ/дх, где L — функция Лагранжа, в то
время как обычный импульс равен тх. При наличии магнитного
поля эти величины связаны соотношением
Магнитные взаимодействия ядер с электронами 101
Введем в рассмотрение очень важную для дальнейшего вели-
чину — плотность тока
НО = Ж Т №** - Wtf) ~ -? А*Ч- D.20)
Отметим, что j(r) представляет собой действительную функцию
координат (иначе говоря, мнимая часть этой функции равна
нулю). Величина j(r) отличается только множителем q от кван»
товомеханической плотности тока. Подставляя в D.20) сначала
•§ и А, а затем ¦$' и А', можно убедиться, что плотность тока j (г)
не зависит от выбора калибровки. Более того, если Ф представ-
ляет собой решение зависящего от времени уравнения Шредин»
rep а, можно показать, что
divj + |f- = O, где р — «Я>Ч. D.21)
т. е. функция j удовлетворяет классическому уравнению нераз-
рывности. Для стационарных состояний величина ip*t]) не зависит
от времени и div j = 0. Вектор j можно рассматривать как клас*
сическую плотность тока. Из последующего будет видно, что та-
кая интерпретация очень полезна при рассмотрении химических
сдвигов.
Таким образом, гамильтониан электрона, взаимодействую-,
щего с двумя магнитными полями, можно записать в виде
Здесь V — полная потенциальная энергия, включающая в себя
поля, которые могут приводить к замораживанию орбитального
момента.
Удобно теперь ввести в рассмотрение оператор я, определяе-
мый равенством
я = Р_-1а0. D.23а)
Оператор я эрмитов в силу того, что эрмитовы операторы р и Ао.
Теперь D.22) запишется в виде
D.236)
Вектор An можно выбрать равным
А„—?$±. D.24)
где (л — ядерный магнитный момент, так как рассматриваемый
векторный потенциал характеризует поле диполя. Величина ц
очень мала по сравнению с магнитным моментом электрона. По-
102 Глава 4
этому ее можно рассматривать как малый параметр, что позво-
ляет пренебречь членом, пропорциональным Ап- После этого
получаем
я^ + у&(«•** + *»•«')• D-25)
В отсутствие связи между электроном и магнитным моментом
ядра величина A/2/п)л2+ V представляет собой гамильтониан
электрона в постоянном магнитном поле. Рассматривая завися-
щие от А„ члены в качестве возмущения, вычислим энергию
электрона в первом порядке теории возмущений.
Определим изменение энергии состояния, волновая функция
•ф которого является точным решением уравнения Шредингера,
учитывающего действие потенциала V и постоянного магнитного
поля Но в первом порядке теории возмущений. Энергия возмуще-
ния в этом случае равна
Явозм = —2~ $ Ф* (« • А„ + А„ • я) ф dx. D.26)
В формуле D.26) интегрирование выполняется по координатам
электрона. (В действительности А„ содержит оператор ядерного
магнитного момента (i, вследствие чего величина Ев0зм должна
рассматриваться как оператор, действующий на переменные
ядерного спина. Мы включаем ее в спиновый гамильтониан
ядра.)
При учете эрмитовости оператора я выражение D.26) можно
записать в виде
\- [(*¦)*¦ + ?Щ]dx. D.27)
Учитывая определения величины я D.23а) и плотности тока
D.20), находим
^г [¦(*¦)•+*•*¦] =
где jo(r)—плотность тока появляющегося при включении по-
стоянного магнитного поля. Следовательно, величина jo(r) опре-
деляет ток, возникающий при действии на электрон потенциаль-
ной энергии V и поля Но (но без учета поля, создаваемого яд-
ром). Следовательно,
Явоэм = - 7 S Ап ¦ Jo (r) dx. D.29)
Между прочим, D.29) представляет собой общее выражение, ха-
рактеризующее изменение энергии электрона ЬЕ при изменении
Магнитные взаимодействия ядер с электронами 103
магнитного поля, определяемом изменением векторного потен-
циала 6А через токи j(r), существовавшие в системе до измене-
ния магнитного поля
6Е = - -i J 6A • j (r) dr. D.30)
Полагая
А„ = ^, D.31)
находим
где, как уже отмечалось выше, ц представляет собой оператор
yti\, a jo(r) —векторная функция координат. Необходимо иметь
в виду, что величина jo (г) не должна зависеть от калибровки
векторного потенциала постоянного поля Ао. Выражение D.32)
имеет вид, аналогичный виду классического выражения, опре-
деляющего взаимодействие магнитного момента ц с плотностью
тока jo(r), поскольку величина, стоящая в квадратных скобках,
представляет собой магнитное поле Н, создаваемое токами. Оно
очень похоже также на выражение, определяющее магнитный
момент М электронов
^$r)dT. D.33)
Из выражения D.32) следует, что должны существовать хи-
мические сдвиги. Если величина jo (г) известна, то можно вычис-
лить магнитное поле, действующее на ядро со стороны электро-
нов. Таким образом, задача о вычислении химических сдвигов
действительно может быть разбита на две части: 1) определение
плотности токов jo(r) и 2) вычисление интеграла в D.32). По-
следняя задача, по существу, является классической и включает
разложение в ряд по мультипольным моментам. Действие токов
на какое-либо достаточно удаленное от них ядро во многих слу-
чаях может быть приближенно определено дипольным магнит-
ным моментом атома.
Вообще говоря, ток jo (г) возникает в результате действия
постоянного поля Но. Поэтому для строгого определения вели-
чины jo (г) необходимо решать квантовомеханическую задачу о
движении электрона в электростатическом поле и постоянном
магнитном поле. Однако во многих случаях можно угадать вид
функции jo (г) и оценить ее величину при помощи эксперимен-
тальных данных по магнитной восприимчивости. Такой метод
применялся для объяснения химических сдвигов для протонов
в молекулах, содержащих бензольные кольца. В этих соедине-
ниях протекающие в кольцах токи можно определить при по-
104 Глава 4
мощи экспериментальных (или теоретических) значений магнит-
ных моментов колец. Можно решить и обратную задачу и ис-
пользовать экспериментальные данные по химическим сдвигам
для получения информации о магнитной восприимчивости ато-
мов, молекул или химических связей. Кроме того, из-за наличия
в выражении D.32) под интегралом функции 1/г3 химические
сдвиги наиболее чувствительны к токам, протекающим вблизи
ядра. Ниже будет показано, например, что химические сдвиги
для протонов малы по сравнению с химическими сдвигами для
атомов фтора вследствие того, что токи вблизи протонов отно-
сительно слабы. Во всяком случае, выражения D.32) и D.33) по-
зволяют точно выяснить, какую информацию об индуцированных
внешним полем в молекуле токах можно получить из экспери-
ментальных данных по восприимчивости и химическим сдвигам.
§ 5. Вычисление плотности тока
Перейдем к вычислению плотности тока jo (г). Для этого не-
обходимо воспользоваться волновой функцией г]), описывающей
движение электронов в электростатическом поле и постоянном
магнитном поле. Эта функция удовлетворяет уравнению
5&4> = ?я|>, D.34)
где
(*У+У. D.35)
Раскрывая скобки, получаем
^l D.36)
Предположим, что известны собственные волновые функции га-
мильтониана Жо, не учитывающего внешнего поля:
^^Ш+У> а?оФп = ?пф,.. D.37)
В гамильтониане D.36) зависящие от Ао члены можно рассма-
тривать в качестве возмущений. Для учета влияния магнитного
поля на плотность тока вычислим возмущенные волновые функ-
ции. Величину А0) исчезающую при стремлении На к нулю, запи-
шем в виде
A0 = YH°Xr- D.38)
Хотя это выражение и соответствует определенному выбору ка-
либровки векторного потенциала, величина Ао остается пропор-
циональной Яо при произвольном выборе калибровки. При по-
Магнитные взаимодействия ядер с электронами 105
мощи выражения
можно вычислить величину jo(r) в первом приближении с точ-
ностью до членов, пропорциональных Яо. Для этого в первый и
второй члены правой части D.39) необходимо подставить волно-
вые функции я|) и я))*, определенные с точностью до членов, про-
порциональных Яо, но в последний член можно подставить вме-
сто я|) невозмущенную волновую функцию ty0- Поскольку во всех
случаях
можно сохранить только такие возмущения, которые пропорцио-
нальны Яо. При этом, согласно D.36) — D.38), имеем
= - i (Р • Ао + Ао • р). D.41)
Введем обозначение
«„о-Ч^Т101- D.42)
Тогда
^о^^о+^^о^- D.43)
п
С помощью этого равенства находим
п
Е 5г№^о - *oV<] <„ - ? А,«Ь. D.44)
n
Член
^¦[¦^¦b-^V*a-J(r) D-46)
представляет собой ток для случая, когда Яо = 0. Если орби-
тальный момент заморожен, так что волновая функция г^о дей-
ствительна, то J(r)= 0, т. е. при Но = 0 плотность тока во всех
точках молекулы равна нулю.
Величина J(r) характеризует плотность тока, возникающего
при вращении молекулы как целого. Она дает дополнительный
вклад в действующее на ядро магнитное поле, обусловленный
взаимодействием спина с вращением молекулы, проявляющимся
в экспериментах с молекулярными пучками.
Полезно вычислить величину jo (г) для свободного атома,
находящегося в р-состоянии в случае, когда m = + 1, а Яо = 0.
106 Глава 4
В этом случае jo(r) = J(r), так что
jp frj = —2_ IM) Yib — ib V^n 1. D.46)
Но
поэтому
jo (г) = $L (xj - yl) f* (r) = -^ k X rP (r). D.48)
Таким образом, ток течет по кругу в плоскости, перпендикуляр-
ной оси г. Если скорость v(r) определить выражением
v М = J°fr) (а лд\
где величина qty*ty представляет собой плотность заряда, то мы
найдем
Из этого выражения видно, что вектор v(r) направлен по каса-
тельной к окружности в плоскости, перпендикулярной оси г, а
его модуль
|v(r)| *! D.51)
|v(r)| 7==!=.
Отсюда находим, что г-компонента орбитального момента равна
mv^/x2 + y2 = h; D.52)
это находится в соответствии с тем, что в рассматриваемой по-
луклассической модели электрон в состоянии т = + 1 обладает
одним квантом орбитального момента.
Таким образом, существует близкая связь между плотностью
тока, «скоростью» и полуклассической моделью квантованных
орбит.
Если функции фо и г))п действительны (орбитальный момент
заморожен), то J (г) = 0 и
*» <р> = Ш Ч Z (в«° - <о) (Wn - Wo) - ¦? Ао^- D.53)
п
Для справедливости выражения D.53) фактически необходимо
лишь, чтобы орбитальный момент в основном состоянии был за-
морожен, хотя относительно волновых функций возбужденных
состояний и было предположено, что они действительны.
Приведем несколько примеров. Рассмотрим s-состояние и
р-состояние и покажем, что химический сдвиг в s-состоянии на
Магнитные взаимодействия ядер с электронами 107
два порядка величины меньше химического сдвига в р-состоянии
и что это различие обусловлено в основном неполным заморажи-
ванием орбитального момента в р-состоянии в присутствии маг-
нитного поля.
Для наших целей удобно ввести векторный потенциал в виде
Ао=уНоХг==УЯокХг'
соответствующий определенному выбору калибровки. Вектор-
ный потенциал можно также задать в виде
A0 = YH°X(r-R>' D.55а)
где R — постоянный вектор. Проекции векторного потенциала
равны
Д,2 = 0, Асх = Ноу, Асу = 0. D.556)
Потенциал D.54) удовлетворяет равенству
div Ао = 0. D.56)
Из D.41) получаем
—2"Ь- [Ао • Р + (Р • Ао) + Ао • р]. D-57)
Здесь скобки в выражении (р'Ао) указывают, что оператор р
действует только на Ао. Однако, поскольку р = H/)
(p-Ao) = f(V-Ao) = O. D.58)
Учитывая D.54), получаем
^ D.59а)
Оператор гХр представляет собой оператор орбитального мо-
мента количества движения в отсутствие поля Но. При вычисле-
нии матричных элементов удобно пользоваться безразмерным
оператором момента количества движения (l//)rXV. Обозна-
чая его через L, перепишем выражение D.59а) в виде
^ D.596)
Если бы мы выбрали калибровку, соответствующую D.55а), то
получили бы
i "о • (г - R) X Р = —^ Я012 (R). D.59в)
Здесь оператор Lz(R) представляет собой оператор г-компонен-
ты орбитального момента, определенного относительно точки R.
Следовательно, изменение калибровки соответствует изменению
точки, относительно которой отсчитывается входящий в возму-
108 Глава 4
щение орбитальный момент. Поскольку волновые функции атома
выбираются в виде линейных комбинаций s-, р-, й- и т. д. функ-
ций, естественно определять орбитальный момент относительно
ядра, что можно сделать, положив R = 0. Когда электронная
орбита охватывает несколько атомов, на электрон действуют
силы со стороны всех атомов. В этом случае выбор калибровки
становится более трудным. С этим вопросом тесно связана за-
дача об определении ^-сдвигов в электронном спиновом резо-
нансе, которая рассматривается в гл. 10.
Рассмотрим сначала s-состояние, волновая функция которого
сферически симметрична:
*.« = *. (г). D.60)
В этом случае
0, D.61)
поскольку Lztys = 0. Следовательно, величины епо Для всех воз-
бужденных состояний равны нулю. При этом весь ток jo (г) опре-
деляется последним членом в правой части выражения D.44):
Jo М " ~ -Ш кЛ = --&Но^Х ntf (r). D.62)
Этот ток, очевидно, течет по окружностям, центры которых рас-
положены на оси 2. Направление тока таково, что он создает
магнитный момент, направленный антипараллельно Но, т. е. диа-
магнитный момент. Этот магнитный момент создает на ядре
поле, направленное противоположно Но (рис. 4.3).
Интересно отметить, что в атоме, находящемся в s-состоянии,
может течь ток. Появление тока свидетельствует о наличии ор-
битального момента, который мы привыкли считать равным
нулю в s-состоянии. Возникает парадокс: если в s-состоянии ор-
битальный момент равен нулю, то как он может возникнуть в
первом порядке теории возмущений, в котором вычисления про-
водятся с невозмущенными волновыми функциями? Ответ на
этот вопрос легко найти, если вспомнить о том, что оператор ор-
битального момента, равный rX(ft/i)V в отсутствие магнитного
поля, при наличии магнитного поля, имеет вид rX[(h/i)V —
— (ч/с)А]. Вычисление среднего значения последнего опера-
тора с невозмущенными волновыми функциями показывает, что
орбитальный момент не равен нулю в s-состоянии. Этот орби-
тальный момент появляется в результате действия электриче-
ского поля, индуцируемого при включении магнитного поля, по-
скольку электрическое поле создает момент сил. При этом та-
кой же момент сил противоположного направления действует на
магнит, создающий магнитное поле. Мы замечаем, что вычислен-
ный орбитальный момент может непрерывно изменяться, так как
величина А изменяется непрерывно. Для типичных значений Но
Магнитные взаимодействия ядер с электронами
109
и г мы получили орбитальный момент намного меньший, чем Ь.
На первый взгляд это противоречит известному положению о
том, что орбитальный момент может изменяться только на вели-
чину п%, где п — целое число. На самом деле, здесь никакого
противоречия нет, поскольку рассматривается полный момент си-
стемы, состоящей из атома и магнита. Полный момент такой
замкнутой системы действительно может изменяться только на
величину п%, но изменение момента количества движения отдель-
ных частей системы может и не быть равным rih.
Рис. 4.3. Диамагнитный ток в s-состоя-
нии атома и создаваемое им магнитное
поле.
Рис. 4.4. Заряды
= z = 0) и — q{y — ±а, х =
= 2 = 0), создающие кристалли-
ческое поле.
Рассмотрим теперь р-состояние xf(r); изменение свойства
этого состояния в кристаллическом поле исследовано в § 3. Для
удобства читателя мы воспроизведем здесь снова рис. 4.1, а и 4.2
(см. рис. 4.4 и 4.5), характеризующие кристаллическое поле и
Рис. 4.5. Уровни энергии в присутствии
кристаллического поля, создаваемого за-
рядами, изображенными на рис. 4.4.
I
zf(r)
xf(r)
положение уровней энергии. Рассмотрим случай, когда поле Но
направлено вдоль оси z. В отличие от случая, когда атом нахо-
дится в s-состоянии, матричные элементы, связывающие р-со-
стояния с возбужденными состояниями, не всегда равны нулю.
С этим связано частичное размораживание орбитального момен-
та в постоянном поле. Для рассматриваемой ориентации поля
Но матричный элемент перехода между состоянием г](г) и ос-
новным состоянием равен нулю, а матричный элемент перехода
между состоянием yf (r) и основным состоянием отличен от нуля
и равен
D.63)
110 Глава 4
При получении окончательного результата в этом равенстве мы
учли» что функция yf(r) нормирована. Из D.63) находим
_ (п | з^возм 10) .• дЛНр 1 ,. Л..
е«о— Ей-Еп 1~ШГТ- ^'т>
Легко видеть, что входящий в D.53) член $оЩп — tynS/tyo равен
D.65)
Зависящий от возбужденных состояний член в формуле
D.44) мы назовем парамагнитным током и обозначим его через
jp. Этот член удобно так называть потому, что он, как это будет
видно из дальнейшего, приводит к появлению парамагнитного
момента. Последний член в правой части D.44) мы назовем диа-
магнитным током и обозначим через jo- Для величины jp в на-
шем примере из D.44), D.64) и D.65) находим
Ь-^Т^Х-Иг). D.66)
а для величины ]d из D.44) и D.54) получаем
i^ D.67)
Очевидно, токи jP и jo текут по концентрическим окружностям
в противоположных направлениях. Однако если div jP = 0, то
}d Ф 0. Поскольку в стационарном состоянии должно выпол-
няться равенство div j = 0, где j = jp + jo, то получается про-
тиворечие. Это противоречие связано с применением для вычис-
ления токов jp и ]d не точных волновых функций, учитывающих
влияние электрического поля кристалла, а функций нулевого
порядка по отношению к возмущению, создаваемому кристалли-
ческим полем. Заряды, которые приводят к смещению атомных
уровней, также, конечно, вызывают изменение вида волновых
функций. Например, в состоянии xf(r), в котором электрон рас-
пределен преимущественно вдоль линии, проходящей через по-
ложительные заряды, область, в которой находится электрон, бу-
дет удлиняться в присутствии внешних зарядов. Та же область
для состояния yf (r) будет сжиматься. В результате у тока по-
явится радиальная компонента, которая будет усиливать теку-
щий вдоль окружности диамагнитный ток. Однако этот радиаль-
ный ток не будет влиять ни на величину химического сдвига
(радиальная компонента тока не создает магнитного поля на
ядре), ни на величину атомного магнитного момента. Поэтому
мы не будем вводить в рассмотрение другие, более точные на-
чальные волновые функции.
Соотношение между парамагнитными и диамагнитными то-
ками изменяется при переходе к другим векторным потенциалам
Maammbie взаимодействия ядер с электронами 11Г
Ао, соответствующим другому выбору калибровки. Однако полу-
ченное нами выражение для полного тока jo (г) является точным^
(точность его определяется величиной, пропорциональной Но) и:
инвариантным относительно калибровочного преобразования..
Поэтому так полезно полученное в § 4 выражение D.32), по-
скольку оно справедливо при любой калибровке векторного по-
тенциала Ао и любом способе деления тока jo на парамагнит-
ную и диамагнитную части.
Интересно сравнить величины ]р и jo. Из D.66) и D.67) по-
лучаем
Jc — — }р -дГ **Л = — 1р (д2/тх2) • D.68);
Здесь величина Н2/тх2 имеет размерность энергии и сравнима по-
величине с кинетической энергией электрона, дебройлевская дли-
на волны которого равна х. После подстановки численных зна-
чений находим
В этом выражении величина х измеряется в ангстремах. Если
принять, что А = 8 эВ (это типичное значение химического сдви-
га) , то jp будет больше jD при значениях х, меньших 1 А; при зна-
чениях х, больших 1 A, \D будет больше jP. Типичные значения
химического сдвига соответствуют величине х = 'ДА, таким об-
разом, преобладает парамагнитный ток. Однако при вычислении
магнитных моментов величину х нужно брать равной 1А или
больше. В этом случае трудно установить, какой из токов яв-
ляется более важным.
Вычислим теперь поля НР и HD> соответствующие токам jP
. D.70,
Непосредственный расчет показывает, что х- и у-компоненты
поля Нр равны нулю, а г-компонента не равна нулю:
Для любой функции "ф (г) среднее значение величины 1/г3 опре-
деляется выражением
Таким образом,
\^f^{^)\^f^- D.73)
112 Глава 4
С учетом этого соотношения находим
Нр-к^Л-^Г?)- D-74)
Мы замечаем, что поле Нр направлено вдоль поля Но и пропор-
ционально ему, что соответствует экспериментальным данным.
Диамагнитное поле
& $ ^9^ ^ D-75)
также направлено вдоль оси г:
HD= - -gr Но J -^^ *2/2 (г) Л. D.76)
Удобно усреднить поле HD по различным ориентациям Но от-
носительно осей координат. Можно показать, что такое усред-
нение эквивалентно усреднению значений HD, соответствующих
ориентациям поля Но вдоль осей х, у и г. С учетом этого нахо-
дим
<4'77>
Из выражения D.77) видно, что HD — —oDH0, где величина oD
представляет собой диамагнитный вклад в константу химиче-
ского сдвига а, равный
&О) D-78>
Это выражение впервые получил Лэмб [2] при рассмотрении
экранирующего эффекта заполненных оболочек атомов.
Аналогичным образом можно усреднить НР. Однако НР равно
нулю, когда поле Но направлено вдоль оси х, так как цилиндри-
чески симметричное относительно оси х состояние не возмущает-
ся. Состояния yf(r) и zf(r) можно считать вырожденными и
расположенными на расстоянии Д выше основного состояния
xf(r), поскольку это соответствует типичному случаю химиче-
ской связи. С учетом этого находим
Парамагнитный вклад в константу химического сдвига сР равен
Н-&Ш-
Магнитные взаимодействия ядер с электронами 113
Если принять А = 4,3 эВ и A/г3) = 8,89/а^, где ао — боровский
радиус (эти значения соответствуют 2р-электронам фтора в мо-
лекуле F2), то получим аР = —20 ¦ 10~4. Величина aD обычно
равна 10~5. Мы видим, что значение аР сравнимо с изменениями
о, наблюдаемыми в соединениях фтора, в то время как значение
oD слишком мало по сравнению с наблюдаемыми изменениями.
Именно вследствие этого область изменения химического сдвига
для фтора значительно больше, чем для протонов.
Большие химические сдвиги для фтора связаны с размора-
живанием орбитального момента магнитным полем. Чем меньше
значение Д, тем эффективнее происходит размораживание.
Поясним теперь причину возникновения химических сдвигов
в s-состояниях. Этим состояниям соответствуют не зависящие от
углов радиальные волновые функции. Поскольку сила, действую-
щая на электрон со стороны магнитного поля, перпендикулярна
направлению его движения, она вызывает медленное вращение
электронной оболочки, подобное вращению плоскости колебаний
маятника Фуко под действием кориолисовой силы.
Из вышеизложенного видно, что при любых разумных значе-
ниях Д диамагнитный член дает лишь очень небольшой вклад
в величину сдвига.
Рассмотрим теперь парамагнитный и диамагнитный вклады
в магнитный момент атома
XhdT. D.81)
Сравним его с экранирующим полем
Благодаря наличию множителя 1/г3 поле Н очень чувствительно
к токам, протекающим вблизи ядра. Формулы для экранирую-
щего поля отличаются от формул для усредненной восприимчи-
вости зс только радиальными средними. Обозначим вклады пара-
магнитных и диамагнитных токов в магнитную восприимчивость
X через %Р и %d- Тогда
D.83)
После усреднения по всем возможным ориентациям находим
%р 3 m me2 Д •
1 q2
114 Глава 4
Анизотропия обусловливает существенную часть средних значе-
ний величин %Р и y_D. Сравнивая %Р и %D, получаем
где г измеряется в ангстремах, а А — в электронвольтах. В ти-
пичных случаях V7 ** lA и А»8 эВ. Отсюда следует, что
%D ж —1Р. Какой из этих членов больше, можно определить
только при проведении дополнительного исследования. Отметим,
в частности, хотя ток \Р и дает преобладающий по величине
вклад в константу химического сдвига, он не всегда является
главным фактором, определяющим магнитную восприимчивость.
Магнитная восприимчивость зависит от токов, протекающих на
больших расстояниях от ядра. Поэтому она в значительно боль-
шей степени, чем химический сдвиг, определяется диамагнит-
ными токами, которые наиболее сильны на больших расстояниях
от ядра.
Важно иметь в виду, что выбранная нами калибровка при-
водит к зависимости Жюзм от начала координат, в которых за-
писан орбитальный момент. При точном решении задачи эта
калибровка не имеет никаких преимуществ по сравнению с дру-
гими возможными калибровками. Однако с точными решениями
приходится иметь дело очень редко. При вычислениях с прибли-
женными решениями с физической точки зрения кажется более
разумной калибровка, соответствующая отсчету входящего в воз-
мущение орбитального момента от наиболее существенного в
рассматриваемой задаче центра сил. Поскольку вычисление про-
водится с приближенными волновыми функциями, такая кали-
бровка позволяет точнее учесть сильное взаимодействие элек-
трона с атомом и приводит к ошибкам только при учете более
слабого взаимодействия электрона с кристаллическим полем.
Вычисление химических сдвигов в молекулах представляет
собой очень сложную задачу вследствие трудностей учета хими-
ческих связей, характеризуемых двумя центрами сил (в случае
парной связи), по одному на каждое ядро. Единственный про-
стой приближенный способ решения этой задачи основан на
рассмотрении атомов в первом приближении как невзаимодей-
ствующих и отождествлении энергий возбуждения связей с энер-
гиями возбуждения молекулы. При этом эффекты ионного харак-
тера могут быть учтены путем применения ненормированных
атомных волновых функций. Попл [3] исследовал эту задачу
методом Лондона. Его результат можно получить также при
помощи теории возмущений. Аналогичная задача, возникающая
при вычислении g-сдвигов, рассмотрена ътп. 10.
При исследовании таких молекул, как молекула бензола,
важную роль играют межатомные токи. В этих задачах выделяют
Магнитные взаимодействия ядер с электронами 115
центр молекулярных сил, т. е. калибровку выбирают таким обра-
зом, чтобы величина Lz представляла собой орбитальный момент
относительно цилиндрической оси симметрии молекулы. Для
бензола эта ось совпадает с осью симметрии шестого порядка.
Вокруг такой оси течет только диамагнитный ток. Этот ток про-
текает по бензольному кольцу и создает магнитное поле в точ-
ках, где находятся протоны; оно приводит к появлению химиче-
ских сдвигов. Это поле неэквивалентно, конечно, полю диполя,
так как расстояния протонов от бензольного кольца сравнимы
по величине с радиусом кольца. С другой стороны, когда токи
j(r) локализованы на атомах или на связях, размеры которых
малы по сравнению с расстояниями от них до рассматриваемого
ядра, магнитное поле, создаваемое этими токами на ядре, можно
рассматривать как поле диполя. В жидкостях после усреднения
по случайным ориентациям молекул химические сдвиги исче-
зают, если только сами атомные восприимчивости не зависят от
ориентации молекул относительно постоянного поля.
Важный вклад в химический сдвиг вносят замкнутые атомные
оболочки внешних по отношению к рассматриваемому ядру ато-
мов. Этот вклад в жидкостях равен нулю. Можно показать, что
такой результат обусловлен тем, что токи заполненных оболочек
не зависят от ориентации молекул относительно поля Яо. Необ-
ходимо подчеркнуть, что при применении приближенных методов
вычисления экранирующего поля замкнутых оболочек нужно со-
блюдать особую осторожность, поскольку в этом случае пара-
магнитный и диамагнитный вклады могут оказаться большими.
Их алгебраическая сумма (которая при точном решении равна
нулю для жидкостей) при приближенном вычислении может ока-
заться не равной нулю. Поэтому при вычислениях всегда полезно
1) оценивать токи ]0.(г) на основе физических соображений;
2) выбирать калибровку для каждого атомного тока так, чтобы
вызывающее его возмущение Жюзм содержало момент количе-
ства движения, определенный относительно наиболее важного
центра атомных сил; 3) исключить из расчетов все токи, которые
должны давать результат, строго равный нулю.
В заключение подчеркнем еще раз, что для удаленного атома
невозможно заранее установить, диамагнитен или парамагнитен
его момент; необходим точный учет энергии возбуждения атома
и его среднеквадратичного радиуса. Более того, например, пара-
магнитный момент внешнего атома может создавать как пара-
магнитное поле, так и диамагнитное экранирующее магнитное
поле, в зависимости от того, какой ориентации соединяющего
два ядра вектора относительно поля Но соответствует наиболь-
шее значение анизотропного момента — параллельной или пер-
пендикулярной.
116 Глава 4
Все приведенные выше выражения получены для одного элек-
трона. Чтобы перейти к более общему случаю N электронов, при-
пишем всем зависящим от координат электрона величинам ин-
декс /, принимающий значения от 1 до N. При этом величины
А0/ и А„/ будут определяться теперь уравнениями
^Ho, УУХА„,-Н„. D.85)
Обычно эти величины равны
К, = -^4^. Ao/ = -iHoX(r/-R). D.86)
г, 2
Здесь вектор R определяет начало отсчета. Если определить да-
лее величину я/ выражением
то гамильтониан, учитывающий внешнее магнитное поле и маг-
нитное поле ядер, будет иметь вид
D-88>
Введем теперь в рассмотрение точную волновую функцию W за-
дачи для N электронов в отсутствие взаимодействия с ядрами,
удовлетворяющую уравнению
Эта функция зависит от координат г;- всех N электронов. Опре-
делим через нее обусловленный /-м электроном ток в виде
T, ... </т,_, dri+l ... drN. D.90)
Функция Jo/ зависит только от одного вектора г/, так как в пра-
вой части D.90) интегрирование выполняется по координатам
всех остальных электронов. С учетом равенства D.90) находим
D.91)
Магнитные взаимодействия ядер с электронами
117
Необходимую для вычисления тока функцию Ч* можно получить
при помощи теории возмущений. Если ввести в рассмотрение
функции Wo и Wn, являющиеся собственными функциями га-
мильтониана Жй в отсутствие внешнего поля и соответствующие
собственным значениям Ео и Еп:
(?
2т
<4-92)
то с- точностью до членов первого порядка по Но функцию
можно записать в виде
¦Ч'п»
где
2тс
D.93)
D.94)
здесь P/==(fi/t)V/.
Для получения решения необходимо выбрать электронные
волновые функции ^о, ^п в удобном виде. Обычно их выбирают
в виде произведений одноэлектронных или (для учета ковалент-
ных связей) двухэлектронных функций. Хотя индекс / нумерует
электроны, равенство D.91) во многих случаях можно записать
в таком виде, в котором суммирование по электронам заменяет-
ся суммированием по орбитам, что позволяет разделить вклады
от электронов замкнутых оболочек и от валентных электронов.
Рассмотренная выше формальная теория очень полезна для
выяснения физического смысла химических сдвигов. Конечный
результат можно выразить более компактно одной формулой,
как это сделал Рэмси [4]. Для этого выделим из D.91) выраже-
ние, определяющее магнитное поле:
D.95)
Подставляя сюда Jo/ из D.90), Ч^ из D.93) и D.94) и учитывая,
что div/Ao/ = 0, после соответствующих алгебраических выкла-
док получаем
D.96)
118
Глава 4
или, полагая АОй =
и Но = Яок, находим
Вместо того чтобы вычислять сначала зависимость плотности то-
ков от координат, как мы делали выше в рассмотренных приме-
рах, можно сразу вычислить химические сдвиги, используя вы-
ражение D.97).
§ 6. Взаимодействие электронных спинов
В случае, когда спины отдельных атомов не равны нулю (в
парамагнитных и ферромагнитных веществах), взаимодействие
между спинами .приводит к эффектам в первом порядке теории
возмущений. Примером может служить найтовский сдвиг (изме-
нение резонансных частот в металлах по сравнению с изолято-
рами) '). В диамагнитных веществах взаимодействие между спи-
нами проявляется лишь во втором порядке теории возмущений.
Это взаимодействие обусловливает связь между ядрами через
электроны (косвенную связь). Оно приводит также к появлению
тонкой структуры резонансных линий в жидкостях и к сужению
или уширению резонансных линий в твердых веществах. Напри-
мер, косвенная связь в 10 раз уширяет резонансную линию в
металлическом индии по сравнению с шириной линии, рассчи-
танной с учетом только прямого диполь-дипольного взаимодей-
ствия. Однако вклад в химические сдвиги от спинов электронов
в диамагнитных веществах равен нулю. Мы рассмотрим этот
вопрос в конце § 8 этой главы.
Рассмотрим магнитную связь между электроном и ядром.
Если электронный и ядерный магнитные моменты ще и щ„ доста-
точно удалены друг от друга, то можно ожидать, что их вза-
имодействие будет хорошо описываться гамильтонианом для
двух магнитных диполей
г6
D.98)
') См. в библиографии, помещенной в конце книги, раздел «Ядерный маг-
нитный резонанс в металлах».
Магнитные взаимодействия ядер с электронами 119
где г — радиус-вектор, проведенный от ядра к электрону. Мож-
но ожидать, что для р-, d- и других состояний электрона, обла-
дающих отличным от нуля орбитальным моментом, выражение
D.98) будет давать хорошее приближение. Однако в случае
s-состояний электронная волновая функция не равна нулю на
малых расстояниях от ядра. Для таких малых расстояний при-
менимость дипольного приближения сомнительна. Детальные ис-
следования подтверждают правильность этого вывода. Для про-
ведения вычислений в первом порядке теории возмущений усред-
ним Ж по волновой функции электрона в s-состоянии и(г). По-
сле такого усреднения в выражении D.98) появятся члены, ана-
логичные членам А, В, С, D, Е и F, рассмотренным при анализе
уширения линии в жесткой решетке (см. гл. 3, § 2). Исследуем
сначала член, аналогичный А, зависимость которого от угла и
расстояния имеет вид A—Зсоб'ЧЭ)//-3. Среднее значение такого
члена с точностью до постоянного множителя равно
-^7^- 0 - 3 cos2 e)r*dr dQ' D-99)
где Q — телесный угол. Если в этом выражении выполнить сна-
чала интегрирование по углам, то оно обратится в нуль. С дру-
гой стороны, при выполнении сначала интегрирования по г инте-
грал логарифмически расходится при г—>-0, т. е. при г ж О
и2 (г) = и2@) ф 0. Поскольку интеграл обращается либо в нуль,
либо в бесконечность в зависимости от способа интегрирования,
очевидно, нельзя просто пренебрегать вкладом в интеграл от об-
ласти малых значений г.
Из изложенного очевидно, что дипольное приближение, во-
обще говоря, несправедливо. Оно не учитывает двух важных эф-
фектов. Во-первых, ядро имеет конечные размеры. Магнитный
момент ядра частично обусловлен вращением ядра как целого;
этому магнитному моменту соответствуют ядерные токи, распре-
деленные по всему объему ядра. Поскольку частицы в ядре дви-
жутся со скоростями, значительно превышающими скорости
атомных электронов (уровни энергии ядра распределены в бо-
лее широком интервале, чем уровни энергии атомных электро-
нов) , с точки зрения электронов спиновые моменты ядерных час-
тиц также распределены непрерывно по всему объему ядра. Во-
вторых, вычисления, проводимые с помощью релятивистской тео*
рии (уравнение Дирака), показывают, что на расстоянии от ядра
ё?/тс? (эта величина представляет собой классический радиус
электрона го и равна 3-1(Н3 см) взаимодействие электрона с яд-
ром существенно изменяется. Электрон не может сблизиться с
ядром на расстояние меньше го- Радиусы ядер приближенно
определяются формулой
г =1,5- 10~иЛ|/3см, D.100)
120 Глава 4
из которой видно, что размеры ядра сравнимы с размерами элек-
трона.
Независимо от всех этих замечаний необходимость приме-
нения релятивистской теории, конечно, следует из того факта,
что потенциальная энергия электрона вблизи ядра ~тс2.
Мы рассмотрим сначала взаимодействие электрона с ядром
с классической точки зрения, а затем дадим краткое пояснение,
как эту задачу можно решить при помощи уравнения Дирака.
Полученную при рассмотрении химических сдвигов теорему о
связи между токами и магнитными полями можно применить
для вычисления вклада во взаимодействие между ядром и элек-
троном, обусловленного вращением ядра как целого. Наконец,
поскольку распределение магнитного момента в объеме ядра (со-
здаваемое спиновыми моментами ядерных частиц) эквивалентно
распределению токов, в классическом рассмотрении можно учесть
и вклад в магнитное взаимодействие от спина ядра. Таким обра-
зом, этот простой подход в действительности является строгим
в нерелятивистском случае.
Заменим ядро частицей с зарядом q, движущейся по окруж-
ности радиуса а со скоростью v. Эта частица эквивалентна витку
тока, величина которого равна (q/c)A/T), где Т — период вра-
щения. Усредненное по пространственному распределению элек-
трона |«(л)|2 значение z-компоненты создаваемого ядром поля
Яг будет равно
\ D.101)
где Я2(г)—поле витка тока. Ось z направлена перпендикулярно
плоскости витка. Можно показать, что другие компоненты поля Н
исчезают при усреднении, так как в s-состоянии величина \и(г) |8
сферически симметрична. Если провести сферу радиуса а вокруг
центра витка, то поле #2(г) можно выразить через скалярный
потенциал как в области г < а, так и в области г > а. Легко
показать, что вклад в интеграл от внешней по отношению к этой
сфере области исчезает при интегрировании по углам. Если пред-
ставить скалярный потенциал внутри сферы в виде суммы произ-
ведений сферических гармоник на радиальные функции, то вклад
в интеграл от всех членов суммы, за исключением первого (ко-
торому соответствует постоянное поле внутри сферы), будет ра-
вен нулю. Этот первый член легко определить, если учесть, что
только он отличен от нуля при л=0. Поэтому выражение D.101)
можно записать в виде
D.102)
Магнитные взаимодействия ядер с электронами 121
где Нс — поле в центре сферы. Выражение D.102) можно упро-
стить, если учесть, что в пределах ядра функция и(г) изменяется
очень мало. Тогда получим приближенное выражение
^3. D.103)
Поле в центре витка тока
He = -f"^ = -h?-k. D-104)
Магнитный момент ядра цп равен та2, где /—«ток», поэтому
|i|eli«A«kf. D.105)
Таким образом,
Нс = ^. D.106)
Подставляя это значение в D.103), находим
^0). D.107)
Тогда эффективная энергия взаимодействия между магнитным
моментом це электрона и ядерным магнитным моментом равна
Е=-^11е-11пиЦ0). D.108)
Для описания этого взаимодействия удобно ввести в гамильто-
ниан член
Я?=—тр|1.-ц„в(г), D.109)
где вектор г определяет положение электрона относительно ядра,
а б (г) — б-функция Дирака. Входящие в D.109) величины маг-
нитных моментов можно выразить через ядерный и электронный
спины I и S. Гиромагнитное отношение для электрона обозна-
чим уе; для ядер уп может принимать положительные и отрица-
тельные значения. В соответствии с этим можно написать
Мв = — Ye^,
D.110)
Тогда выражение D.109) принимает вид
A2ISe(r). D.111)
В выражение D.108) не входит радиус ядерной орбиты. Оче-
видно, оно справедливо также в тех случаях, когда круговые
токи распределены в объеме. Более того, поскольку распределе-
122 Глава 4
ние спина внутри ядра эквивалентно распределению токов в
объеме ядра, при подстановке экспериментальных значений уп
й I это выражение будет автоматически учитывать внутренний
спин ядра. Поэтому выражение D.111) является вполне общим.
Если нельзя пренебречь изменением величины ы(г) в пределах
ядра, то получится несколько иной результат. Поэтому отноше-
ние энергии взаимодействия для двух изотопных ядер, в которых
распределение токов различно, не будет точно равно отношению
магнитных моментов этих ядер. С этим связаны так называемые
сверхтонкие аномалии.
При помощи уравнения Дирака можно получить более точ-
ное выражение для энергии взаимодействия магнитных момен-
тов ядра и электрона. Мы приведем лишь основные этапы вы-
вода, предоставив читателю возможность самостоятельно разби-
раться в деталях. Дираковский гамильтониан электрона (заряд
электрона равен —е) имеет вид
5^ = — о • (ср + еА) — Ртс2+ V, D.112)
где о и р — четырехрядные матрицы, V—потенциальная энергия
электрона, А — векторный потенциал. Матрицы о и р можно вы-
разить через двухрядную матрицу Паули а и двухрядную еди-
ничную матрицу 1:
/О а\ /1 0\
вЧо о)' Ко -J- <4Л13>
Волновые функции Ч?, являющиеся решениями уравнения
D.112), можно записать в виде столбца, состоящего из двух
функций Ч*! и Чгг:
D.114)
каждая из которых в свою очередь также является столбцом,
состоящим из двух обычных функций.
Собственные значения гамильтониана Ж можно представить
в виде
Е = Е' + тс2. D.115)
Для неподвижной свободной частицы Е' = 0. Если теперь ввести
в рассмотрение оператор
я = ср + еА D.116)
и величину V/e обозначить через <р, то релятивистские уравне-
ния для движущегося в кулоновском поле электрона можно за-
Магнитные взаимодействия ядер с электронами 123
писать в виде
(?" + еф + 2тс2) ?i + а • я?2 = О,
2 + а • я?, = О,
где ф = е/г — потенциал поля ядра.
Хорошо известно, что в нерелятивистском случае W\ много
меньше Ч2. Поэтому Ч^ обычно называют «большой компонен-
той». В s-состоянии атома водорода функция 4*2 много больше,
чем Чи даже вблизи ядра. Чтобы получить гамильтониан Ж
для 4% с хорошей степенью точности, можно исключить Wj и по-
ложить
Ж'Ч2^Е'Ч2. A.118)
После соответствующих выкладок находим
— lee div A + ehca • V X А) +
D.119)
где Е — действующее на электрон на стороны ядра электриче-
ское поле. В данном случае нас интересуют только два члена:
' D.120а)
D.121а)
В рассматриваемой задаче связь с ядром можно задать с по-
мощью векторного потенциала А = цп X г/г3. Следовательно,
величина V X А представляет собой просто магнитное поле ядра,
рассчитанное в дипольном приближении. До тех пор пока
еф <С 2тс2, выражение D.120а) совпадает с D.98) и зависит от
расстояния как 1/г3. Однако если г настолько мало, что
еф ~ 2тс2, то положение меняется. Заменив еф на е2/г, умножив
числитель и знаменатель в D.120а) на г и используя обозначе-
ние е2/тс2 = го (классический радиус электрона), получаем,
пренебрегая величиной Е',
)S D.1206)
Теперь при расчете поля Нг вычисление радиального интеграла
не приводит к бесконечности, а при интегрировании выражения
D.1206) по углам получается, очевидно, нуль.
124 . Глава 4
Выражение D.121а) можно переписать в виде
D.1216)
Множитель в квадратных скобках зависит от расстояния как
1/г4. Можно показать, что при г Э- г0 выражение D.1216) будет
в r/го раз меньше, чем D.1206). Однако при г ^ го выражение
D.1216) зависит от расстояния более слабо (вблизи г = 0 оно
зависит от расстояния как 1/г). Поэтому при интегрировании
этого члена по г получается конечное выражение. Этот член не
обращается также в нуль при интегрировании по углам для
s-состояния и обусловливает появление энергии взаимодействия
вида D.108).
Обусловленные членами вида D.1206) и D.1216) эффекты
можно получить и в нерелятивистском рассмотрении, вводя в
гамильтониан взаимодействие вида D.108) и обрывая интегри-
рование в радиальном интеграле D.99) на расстояниях, равных
классическому радиусу электрона (это необходимо для устране-
ния расходимости интеграла при г->0). Для соблюдения послед-
него требования можно умножить взаимодействие на 2r/Br+r0)
и проводить интегрирование по г от 0.
Перейдем теперь к рассмотрению некоторых важных эффек-
тов, обусловленных взаимодействием между спинами электронов
и ядрами. Сначала рассмотрим эффекты, возникающие в пер-
вом порядке теории возмущений, а затем эффекты второго по-
рядка теории возмущений. Дальнейшее обсуждение эффектов
первого порядка теории возмущений дано в гл. 10.
§ 7. Найтовский сдвиг')
Найтовский сдвиг назван по имени впервые наблюдавшего
его профессора У. Найта. Найт нашел, что резонансная частота
ядер Си63 в металлической меди на 0,23% выше резонансной ча-
стоты этих же ядер в диамагнитном CuCl при условии, что оба
резонанса наблюдаются в одном и том же постоянном поле. Этот
сдвиг на порядок величины больше химических сдвигов в раз-
личных диамагнитных веществах, поэтому его разумно связать
со свойствами металла. Дальнейшие исследования показали, что
подобные сдвиги наблюдаются во всех металлах, и выявили
основные свойства найтовских сдвигов. Для характеристики этих
свойств удобно ввести следующие обозначения: сот и cod — резо-
нансные частоты в металлах и диамагнетиках при одинаковом
постоянном магнитном поле; изменение резонансной частоты Дсо
') См. в библиографии, помещенной в конце книги, раздел «Ядерный
магнитный резонанс в металлах».
Магнитные взаимодействия ядер с электронами 126
определяется равенством
cum = cud + Aco. D.122)
Обнаружены следующие свойства найтовских сдвигов:
1. Величина Асо положительна (было найдено несколько ис-
ключений из этого правила, но мы не будем их рассматривать).
2. При изменении юй (которое осуществляется путем соот-
ветствующего изменения постоянного поля) относительный сдвиг
Aco/(Od не изменяется.
3. Относительный сдвиг почти не зависит от температуры.
4. Относительный сдвиг обычно увеличивается с увеличением
заряда ядра Z.
Металлы обладают слабыми парамагнитными свойствами.
Поэтому сдвиг резонансной частоты можно было бы попытаться
объяснить втягиванием магнитных силовых линий внутрь об-
разца. Однако магнитная восприимчивость металлов слишком
мала ("^Ю-6 ед. СГС на единицу объема), чтобы объяснить та-
кой большой эффект. Кроме того, как будет видно из дальней-
шего, обычное вычисление внутренних полей в твердом теле пу-
тем усреднения по объему локального магнитного поля не даст
правильного значения найтовского сдвига, так как ядра зани-
мают определенные места в кристаллической решетке, вблизи
которых электроны проводят большую часть времени под влия-
нием сильного потенциала притяжения ядерных зарядов.
Для правильного объяснения найтовских сдвигов необходимо
рассматривать магнитные поля на ядрах, обусловленные сверх-
тонким взаимодействием ядер с электронами проводимости, на-
ходящимися в s-состоянии по отношению к данному ядру. Мы
можем считать, что в металле каждый электрон непрерывно пе-
рескакивает с атома на атом, так что данное ядро испытывает
взаимодействие со многими электронами. Поэтому магнитное
поле на ядре определяется усредненным по ориентации элек-
тронных спинов сверхтонким взаимодействием. В отсутствие
внешнего поля спины электронов ориентированы хаотически и
магнитное поле на ядре равно нулю. При наложении постоян-
ного поля #о электронные спины поляризуются, и обусловленное
сверхтонким взаимодействием магнитное поле на ядре отлично
от нуля. Поскольку сверхтонкое взаимодействие ядра с s-элек-
троном приводит к появлению магнитного поля на ядре, парал-
лельного электронному магнитному моменту1), а суммарный
магнитный момент электронов металла направлен параллельно
Но, действующее на ядро со стороны электронов магнитное поле
будет направлено параллельно Яо. Поэтому фактически дей-
•) Зависимость взаимодействия от взаимной ориентации ядерных а элек-
тронных спинов легко определить, если заменить ядро витком тока.
126 Глава 4
ствующее на ядро магнитное поле будет больше чем Яо. Так
как сдвиг частоты пропорционален степени поляризации элек-
тронных спинов, он пропорционален также Яо или со<*. Более
того, поскольку поляризация электронов не зависит от темпера-
туры (спиновый парамагнетизм сильно вырожденного электрон-
ного газа не зависит от температуры), и сдвиг частоты не зави-
сит от температуры. Наконец, увеличение сдвига с увеличением
Z обусловлено тем, что плотность волновой функции на ядре воз-
растает с увеличением Z, как хорошо известно из данных по
сверхтонкому расщеплению атомных уровней.
Из проведенного выше анализа видно, что сверхтонкое вза-
имодействие обладает всеми свойствами, необходимыми для
объяснения основных свойств найтовских сдвигов. Перейдем те-
перь к более детальному рассмотрению найтовских сдвигов.
Рассмотрим систему ядерных магнитных моментов, связан-
ных сверхтонким взаимодействием с электронами. Вследствие
относительной слабости этого взаимодействия его можно учесть
на основе теории возмущений, выбирая в качестве невозмущен-
ных волновых функций волновые функции не связанных между
собой ядерных спинов и электронов. В действительности можно
обойтись без определения явного вида волновых функций ядер-
ных спинов, так как взаимодействие приводит просто к появле-
нию действующего на ядро эффектного магнитного поля, парал-
лельного приложенному полю. Определение невозмущенных вол-
новых функций электронов представляет собой очень трудную
задачу. Эту задачу строго решить невозможно, так как каждый
электрон сильно связан с другими электронами дальнодействую-
щим кулоновским взаимодействием. Поэтому мы вынуждены
решать задачу приближенным методом, предполагая, что элек-
троны не взаимодействуют (или по крайней мере слабо взаимо-
действуют) друг с другом.
Бом и Пайнс (см. [5]) показали, что такое предположение в
значительной степени теоретически обосновано. С помощью ка-
нонического преобразования им удалось показать, что главный
эффект кулоновского взаимодействия состоит в появлении кол-
лективных, или плазменных, колебаний электронов, обладающих
настолько высокими основными частотами, что систему электро-
нов при обычных условиях можно считать находящейся в основ-
ном плазменном состоянии. Однако каждая частица может со-
вершать еще индивидуальное движение. Взаимодействия же ме-
жду частицами в основном плазменном состоянии можно рассма-
тривать как слабые, экспоненциально уменьшающиеся с увели-
чением расстояния между частицами. Поэтому при рассмотре-
нии низкоэнергетических процессов, при которых плазменные
колебания не возбуждаются, электроны можно считать слабо
взаимодействующими друг с другом,
Магнитные взаимодействия ядер с электронами 127
Таким образом, рассматриваемую систему можно описать га-
мильтонианом
где Же — гамильтониан слабо взаимодействующих электронов,
Жп — гамильтониан, включающий в себя зеемановскую энергию
ядер в постоянном поле Hj> и энергию магнитного дипольного
взаимодействия между ядрами, а 9ёеп — гамильтониан магнит-
ного взаимодействия между ядерными и электронными спинами.
Мы не учитываем взаимодействие ядер с орбитальным дви-
жением электронов, так как он приводит к эффектам, сравни-
мым по порядку величины с химическими сдвигами. (Вообще
говоря, эффект орбитального движения электронов в металле
должен несколько отличаться от такого же эффекта в диэлек-
трике, так как в металле электроны почти свободны, а в диэлек-
трике они связаны.)
Можно показать, что вклад в найтовский сдвиг обычного ди-
польного взаимодействия между ядерными и электронными спи-
нами [см. D.98)] равен нулю для металлов с кубической решет-
кой. Для некубических металлов этот вклад не равен нулю и за-
висит от ориентации поля Но относительно кристаллографиче-
ских осей. Поскольку магнитный резонанс в металлах обычно
наблюдается на порошкообразных образцах (для обеспечения
достаточно глубокого проникновения переменного магнитного
поля в глубь образца), это анизотропное взаимодействие приво-
дит к уширению резонансной линии. Для простоты предположим,
что электроны и ядра связаны взаимодействием вида
R/), D.124)
где и — радиус-вектор 1-го электрона, a R/ — радиус-вектор /-го
ядра.
Выражение D.124) можно переписать в более удобном виде.
При квантовомеханическом описании электрических зарядов
вводят оператор зарядовой плотности р<ор)(г), определяемый вы-
ражением
Р(орЧг)=]?<7/6(г,-г), D.125)
где qi — заряд 1-й частицы, а суммирование проводится по всем
частицам.
Аналогичным образом введем оператор плотности спиновой
намагниченности для электронов
M(op)(r)=- ZyenSfi(ri-r), D.126)
128 Глава 4
среднее значение которого равно классическому значению плот-
ности спиновой намагниченности. Используя это определение,
получаем
*-» = ~ Z ТГ М<ОР> (R/> • <Y»fiI/)- D-! 27)
Поскольку мы приняли, что электроны и ядра лишь слабо
связаны, полную волновую функцию я]) можно записать в виде
произведения многочастичной волновой функции электронов я]зе
и волновой функции ядер t])n:
я|> = яМз„. D.128)
(Эта волновая функция, конечно, является точной, когда Жеп
равно нулю.) Вычислим теперь поправку к энергии Ееп в пер-
вом порядке теории возмущений
3®en№edTa. D.129)
Здесь d%e и dxn обозначают, что интегрирование выполняется по
электронным и ядерным (пространственным и спиновым) коорди-
натам. Конечно, нас интересует влияние энергии D.129) на пере-
ходы ядерной системы из одного состояния Црп в другое состоя-
ние i]>n/. Поскольку это переходы в ядерной системе, электронное
состояние t])e не изменяется. Чтобы определить энергию ядерного
перехода Ееп — Ееп>, нужно вычислить как Ееп, так и Ееп'\ по-
следнее связано с интегрированием по электронным координа-
там. Поэтому мы сначала вычислим интеграл по электронным
координатам
что является, конечно, первым шагом при вычислении интеграла
D.129), поскольку волновая функция -ф представляется произве-
дениями фефп и 'Фе'Фп' Для состояний, соответствующих энергиям
Ееп и ?е„'. Интеграл D.130) мы обозначили Жеп, чтобы подчерк-
нуть, что по отношению к ядерным координатам он должен рас-
сматриваться как оператор.
Используя D.127), представим D.130) в виде
УпН1„ D.131)
где M(R,-) — классическое значение плотности спиновой намаг-
ниченности на /-м ядре.
Если считать, что электроны не взаимодействуют (или слабо
взаимодействуют) друг с другом, то электронные волновые фун-
кции -фе можно представить в виде произведения одноэлектрон-
Магнитные взаимодействия ядер с электронами 129
ных волновых функций. В качестве одноэлектронных волновых
функций воспользуемся так называемыми блоховскимн волно-
выми функциями. Напомним кратко основные свойства блохов-
ских функций. Если рассматривать электрон, движущийся в по-
тенциальном ящике, ширина которого равна а (рис. 4.6), и коор-
динату электрона обозначить через х, то волновая функция элек-
трона будет зависеть от х как sin kx или cos kx, где k опреде-
ляется исходя из граничных условий на стенках ящика х =¦ 0 и
х = й. Для описания состояний, соответствующих отличному от
нуля току, удобно вместо этих функций воспользоваться реше-
ниями вида eikx, в которых k определяется исходя из условия,
чтобы значения волновой функции при х = а и при х = 0 были
Рис. 4.6. Потенциальный ящик глубиной Vo, характеризующий потенциальную
энергию электронов в металле.
равны. В трехмерном потенциальном ящике волновые функции,
удовлетворяющие подобным граничным условиям, имеют вид
¦ф = е'к'г. D.132)
Чтобы учесть увеличение потенциальной энергии электронов
вблизи ядер, необходимо несколько изменить вид этих волновых
функций. Такие волновые функции называются блоховскими
функциями и имеют вид
%=-мк(г)е'кг. D.133)
Здесь величина к по-прежнему определяется исходя из условия,
чтобы волновая функция имела одинаковые значения на стенках
Ящика, а модулирующая функция «k(r) обладает симметрией
решетки. Индекс к указывает, что функция ык (г), вообще говоря,
зависит от к. Функция wk(r) принимает большие значения вбли-
зи ядер.
С учетом спиновых координат волновую функцию электрона
можно записать в виде
Фк."^""'*,. D-134)
где t])s — спиновая волновая функция.
Волновую функцию ./V электронов i]>e можно записать как
произведение волновых функций tyks. После антисимметризации
в соответствии с принципом Паули эта волновая функция имеет
130 Глава 4
ВИД
Здесь Р — оператор, перестанавливающий координаты электро-
нов и ядер в произведении одноэлектронных функций [6]; вели-
чина (—1)р равна +1 или —1 в зависимости от четности или
нечетности числа перестановок; l/V^T — нормировочный мно-
житель.
Вычислим теперь вклад в выражение D.130) /-го ядерного
спина Ж'еп1- Полагая, что этот спин находится в начале коор-
динат (R/ = 0), получаем
W*V S«Z V(O %dr D.136)
Поскольку оператор S/б (г/) зависит от пространственных и спи-
новых координат только одного электрона, выражение D.136)
не содержит членов, соответствующих обмену электронами. По-
этому правую часть D.136) можно записать в виде
,{Z)...-]dTldTa.... D.137)
Предположим далее, что электроны квантованы вдоль оси г, па-
раллельной постоянному полю Но. В этом случае в выражении
D.137) останутся только члены, пропорциональные Szi- [Можно
было бы, конечно, предположить, что ядерные спины квантованы
вдоль оси г; в этом случае в выражении D.137) остались бы
только члены, пропорциональные /z/. Конечный результат при
этом не изменился бы.] Выражение D.137) можно записать те-
перь в виде
k. s
Здесь суммирование проводится по всем значениям к и s, a
д(к, s) равно единице, если состояние к, s занято электроном, и
равно нулю в противном случае; ms представляет собой проек-
цию спина в состоянии tyk s, которая может принимать значения
± 72; uk, s@) ~ плотность волновой функции на /-м ядре.
Усредняя выражение D.138) по соответствующим данной
температуре вероятностям нахождения электронов в состояниях
k, s, получаем
X Y.Vn»8'./ Е К • М I' mJ <к> *>' <4'139>
к. s
Магнитные взаимодействия ядер с электронами
131
где f(k, s)—функция распределения Ферми. При абсолютном
нуле для электронов, полная энергия которых (пространствен-
ная и спиновая) меньше или больше энергии Ферми ?V, вели-
чина Дк, s) соответственно равна единице или нулю. При тем-
пературах, отличных от нуля, функция /(k, s) изменяется в ин-
тервале энергий, примерно равном ht вблизи энергии ?V
(рис. 4.7). В этом случае функция f(k, s) имеет вид
f(E) =
D.140)
Здесь мы обозначили функцию /(k, s) через f(E), имея в виду,
что Е — энергия электрона в состоянии, характеризуемом волно-
ПЕ)
в
а
Рис. 4.7. Функция Ферми f(E) при абсолютном нуле (а) и функция Ферми
при температуре Т (б).
вым вектором к и спиновой координатой s. Обычно ?=J
где ?Спин — энергия, зависящая от ориентации спина, а ?к —
сумма кинетической и потенциальной энергии электрона (в даль-
нейшем эту энергию мы будем называть трансляционной энер-
гией). Энергия ?Спнн, например, может представлять собой зее-
мановскую энергию электронного спина в постоянном поле Яо.
Однако в нее могут давать вклад и электростатические взаимо-
действия между электронами, зависящие от взаимной ориента-
ции их спинов.
Рассмотрим теперь член суммы D.139), соответствующий
определенному значению к и двум значениям ms:
— hi
3 'ft ¦
D.141)
В этом выражении величина в квадратных скобках, очевидно,
представляет собой средний вклад состояния к в z-компоненту
намагниченности электронов рассматриваемого образца (с точ-
ностью до знака минус, поскольку |ше = — Ve^S). Обозначим
этот вклад через Дгк. Тогда z-компонента полной намагниченно-
132
Глава 4
сти электронов будет равна
D.142)
Если ввести в рассмотрение полную спиновую восприимчивость
электронов %se:
Йг = з?#о DЛ43)
и величину %1'.
Kv = %tHo> D-144)
то выражение D.142) будет эквивалентно выражению
D.145)
Поэтому выражение D.141) теперь можно записать в виде
8я л. т i
D.146)
и полную эффективную энергию взаимодействия ядерного спина
/ с электронами можно представить в виде
D.147)
Задача сводится теперь к вычислению суммы. Эта задача
просто решается для невзаимодействующих электронов. Ее не-
Рис. 4.8. Сечеиие двух поверхностей равной энергии плоскостью kg = 0.
с—для свободных электронов, б—для гипотетического «реального» вещества.
трудно решить и при наличии взаимодействия между электро-
нами. Мы рассмотрим последний случай, поскольку получаю-
щиеся при этом выражения позволяют провести интересное срав-
нение теории с экспериментом.
Магнитные взаимодействия ядер с электронами
138
Площадь ?А
Если пренебречь спиновыми эффектами, то энергия электро-
нов будет зависеть только от к. Для свободных электронов эта
зависимость имеет вид
*~йг. <4Л48>
т. е. все электроны, для которых концы векторов к в к-простран-
стве расположены на сфере радиуса k, обладают одинаковой
энергией (рис. 4.8). При учете потенциала решетки поверхности
постоянной энергии будут от-
личаться от сфер.
Предположим, что функция
| ык @) |2 5Сь достаточно медлен-
но изменяется при переходе от
одного разрешенного значения
к к другому ближайшему раз-
решенному значению к в
к-пространстве, т. е. мы мо-
жем определить функцию плот-
ности, чтобы найти число раз-
решенных значений к в любой
области.
Обозначим через g{Ek, A)dEkdA число разрешенных значе-
ний к, лежащих в некоторой области ^-пространства. В качестве
этой области выберем малый параллелепипед, заключенный ме-
жду поверхностями равной энергии, соответствующими значе-
ниям энергии ?к и Ek~\-dEk (рис. 4.9). Грани этого параллеле-
пипеда, лежащие на поверхностях постоянной энергии, имеют
площадь dA и являются элементами поверхности постоянной
энергии. От координаты точки на этой поверхности А зависит
функция g{Ek, А). Полное число состояний dN в объеме, огра-
ниченном поверхностями Ек — const и Ек + dEv. = const, можно
найти, суммируя вклады по всем точкам поверхности Еи = const:
Рис. 4.9. Элемент объема в к-про-
страистве dEdA.
dN -=dEk
, A) dA = p (Ek) dEk. D.149)
к—const
Мы можем использовать функции |«k@)|2%k, чтобы сумму в
D.147) заменить интегралом:
?k, A)dEkdA. D.150)
Величина %к зависит от функций распределения Ферми f (k, 1/2)
и f(k,—'/2) и, следовательно, зависит от энергии Еь и от раз-
ности спиновых энергий электрона в состоянии к, соответствую-
щих двум различным ориентациям спина электрона. (Эта раз-
134 Глава 4
ность для невзаимодействующих электронов равна уеКН0.) По-
этому величина хк будет одинаковой для всех k-состояний, обла-
дающих одинаковой трансляционной энергией ?к. Даже при на-
личии электростатического взаимодействия между электронами,
изменяющего разность энергий электронов, спины которых ори-
ентированы параллельно и антипараллельно друг другу, вполне
разумно считать, что эта разность энергий зависит в основном
от ?к- Поэтому можно принять, что х? зависит только от ?к-.
D.151)
Учитывая это, перепишем D.150) в виде
» A)dAdEk. D.152)
k
Для любой функции F, зависящей от Е, среднее значение
(F(k))?k на поверхности постоянной трансляционной энергии
Ей определяется выражением
\8(Ek,A)dA p(?") J
Пользуясь этим определением, перепишем интеграл по dA в
D.152) в виде
<||V D.154)
откуда следует
ZIЧ @) |2 Х{ = J < | ик @) ft t (Ek) p (Ек) dEk. D.155)
ь
Но функция Xs(Ей) равна нулю для всех значений Ей, кроме
тех, которые лежат внутри интервала, примерно равного kT,
вблизи энергии Ферми EF (рис. 4.10), так как при малых Е^ в
каждом состоянии находится по два электрона с противополож-
но ориентированными спинами, а при больших Еь, наборот, на-
селенности этих уровней равны нулю.
Поэтому, предполагая, что функция (|«к@)|2)? достаточно
медленно меняется при изменении ?к вблизи поверхности Фер-
ми, мы можем (| ик @) \2}Ер вынести из-под знака интеграла:
D.156)
Магнитные взаимодействия ядер с электронами 135
Из соотношения D.145) имеем
S я* (?*л) dEkd
D.157a)
откуда после выполнения интегрирования по А находим
D-1576)
Учитывая далее D.147), D.156) и D.157), для взаимодействия
/-го ядра с электронами получаем
] D-158)
Таким образом, рассматриваемое взаимодействие эквива-
лентно действию дополнительного магнитного поля АН, парал-
лельного полю Но, которое определяется формулой
<К(°I2>Х D-159)
Эта формула обладает всеми свойствами, необходимыми для
объяснения экспериментальных данных. Она приводит к следую-
щим выводам.
Рис. 4.10. Зависимость %s от Е*.
1. Резонансная частота увеличивается при переходе от диа-
магнитного вещества к металлу.
2. Относительный сдвиг ие зависит от со.
3. Поскольку A"к@)|2)р и Xs не зависят от температуры,
АН/Но также не зависит от температуры. При увеличении Z
ядра плотность волновой функции на ядре (I^CO)^ увеличи-
вается за счет притяжения электронов ядром, и, следовательно,
величина найтовского сдвига возрастет.
Полученную формулу для найтовского сдвига можно прове-
рить, измерив независимо величины АН/Н0, (| Uk @) J2^ и j?.
Такие измерения были проведены только для металлического
136 Глава 4
лития. Спиновая восприимчивость лития была измерена Шу-
махером и Сликтером [7] способом, который кратко описан
ниже. Величину (| ик @) |2^? определил Райтер [8] по сдвигу ре-
зонансной частоты электронного резонанса, обусловленному вза-
имодействием между ядрами и электронами. Этот сдвиг Д#«
определяется формулой
^Л> <4Л60>
гДе %п~~ восприимчивость ядер Li7. Если количество ядер в еди-
нице объема обозначить через N, то
Если известно %sn, то, измерив АЯе, можно определить
(| ик @) j2^ . Чтобы увеличить наблюдаемый сдвиг, Райтер по-
ляризовал ядра, используя для этого эффект Оверхаузера.
В этом случае формулы несколько изменяются, но в основном
метод расчета остается без изменений.
Для сравнения с экспериментом удобно вычислять
(I "к @) l2^ , пользуясь волновыми функциями, нормирован-
ными на атомный объем. Вычисленные таким образом значения
(|ык@)|^? мы обозначим через РР, а через РА обозначим плот-
ность волновой функции на ядре свободного атома. Рассмотрим
отношение Pf/Pa для лития и натрия.
Данные Райтера, теоретические значения и значения, полу-
ченные из экспериментальных значений %se Шумахера в сочета-
нии с экспериментальными данными по найтовским сдвигам,
приведены в табл. 4.1. Из этих данных видно, что значения, по-
Таблица 4.1
Отношение Рр/Рд для лития
Теоретические значения Кона и Кьелдаса
Экспериментальное значение (/* и найтовский
сдвиг)
Экспериментальное значение Райтера
0,49±0,5
0,45±0,03
0,442 ±0,015
лученные тремя различными способами, прекрасно совпадают
друг с другом. Для натрия Кон и Кьелдас [9, 10] нашли Pf/Pa =
= 0,80 ± 0,03. Используя это значение и экспериментальные
данные по найтовскому сдвигу, можно найти значение у?е. Полу--
Магнитные взаимодействия ядер с электронами 137
ченное таким способом значение %* приведено ниже. Опишем те-
перь прямой метод измерения %se, предложенный Шумахером.
Основная трудность при измерении восприимчивости j? свя-
зана с отделением ее от других вкладов в полную восприимчи-
вость, которые (для металлов) сравнимы по величине с %se. Шу-
махер использовал для этого метод магнитного резонанса. Из
соотношения Крамерса — Кроиига для %se имеем
«-¦^"-Цг1' <4162>
о
где Хе — мнимая часть спиновой восприимчивости электронов
проводимости. Если резонансная линия достаточно узка, можно
пренебречь изменением величины со в пределах резонансной ли-
нии и вынести со из-под интеграла. Заменяя переменную инте-
грирования со на уН, получаем
оо
D.163)
Таким образом, для определения %se достаточно провести абсо-
лютное измерение площади под резонансной кривой. (В действи-
тельности в этом случае линию нельзя считать узкой; можно по-
казать, однако, что это обстоятельство не влияет на окончатель-
ную формулу. Этот вопрос рассматривается в статье Шумахера
и Сликтера [7]. Отметим также, что может наблюдаться обус-
ловленное циклотронным резонансом поглощение энергии на ча-
стотах, совпадающих с частотой электронного резонанса. Од-
нако линия циклотронного резонанса настолько сильно уши-
ряется вследствие частых столкновений электронов, что стано-
вится ненаблюдаемой. Поэтому можно быть уверенным в том,
что измеряется только величина /"•)
Абсолютные измерения площади под резонансной кривой все-
гда очень трудны. Шумахер обошел эти трудности, измеряя
ядерный резонанс на ядрах Li7 или Na23 в тех же образцах, в
которых измерялся резонанс на электронах проводимости. Спи-
новая восприимчивость ядер xsn определяется выражением
D.161). Для нее мы получаем
DO
Stf*"- <4Л64>
На частоте щ/2п « 10 МГц Шумахер в одном и том же образ-
це наблюдал как электронный, так и ядерный резонанс, изменяя
138
Глава 4
поле Но. Ядерный резонанс наблюдался при полях, равных
104 Гс, в- то время как электронный резоиаис наблюдался при
полях, равных нескольким гауссам.
Если обозначить площади под резонансными кривыми для
электронного и ядерного резонанса через Ае и Ап соответственно,
то можно написать следующее соотношение:
Величину %п можно вычислить; поэтому соотношение D.165)
позволяет определить %se. При этом площади под резонансными
кривыми можно измерять в любых единицах (например, в квад-
ратных сантиметрах иа экране осциллографа1) при условии, что
эти единицы одинаковы для любых кривых. При этом не нужно
даже определять объем образца, так как ои одинаков для ядер
и электронов.
Экспериментальные и теоретические значения % приведены
в табл. 4.2. Во втором столбце') приведены теоретические зна-
Таблица 4.2
Значения восприимчивости X* A0е ед. СГС)
Теоретическое
значение
для свободных
электронов
Теоретическое
значение
Семпсоиа и
Зейтца
Теоретическое ВДниг
значение
ПаЙнса
Найтовский
и теоре-
тическое
значение
PFIPA
Значение
Шумахера
Литий
Натрий
1,17
0,64
2,92
1,21
1,87
0,85
1,85 ±0,20
0,83 ±0,03
2,08±0,10
0,95 ±0,10
чения для невзаимодействующих электронов. При этом взаимо-
действие электронов с потенциалом решетки учитывалось путем
введения эффективной массы электрона; эффективные массы вы-
числил Брукс по методу квантового дефекта. В третьем столбце
приведены теоретические значения, полученные Семпсоном и
Зейтцем с помощью интерполяционной формулы Вигнера. В чет-
вертом столбце приведены теоретические значения, полученные
Пайнсом на основе коллективного описания электронов по ме-
тоду Бома — Пайиса. В пятом столбце приведены значения, по-
лученные с использованием экспериментальных данных по най-
товским сдвигам и вычисленных Коном и Кьелдасом теоретиче-
ских значений отношения Pf/Pa- В последнем столбце приведены
данные Шумахера. Более поздние результаты см. в [22].
•) Приведенные здесь различные экспериментальные и теоретические зна-
чения рассмотрел Пайяс [Б].
Магнитные взаимодействия ядер с электронами 139
Отметим, что при использовании полученных Райтером зна-
чений Рр/Ра найтовские сдвиги увеличиваются и вычисленные
значения прекрасно согласуются с данными Шумахера.
Задача о вычислении найтовских сдвигов тесно связана с тео-
рией ядерного резонанса в веществах, в которых намагничен-
ность электронов отлична от нуля при #о = 0 (т. е. в ферромаг-
нетиках или антиферромагнетиках). Рассмотрим кратко ферро-
магнитный случай1). Взаимодействие между электронами и яд-
рами можно записать в виде суммы обычного диполь-дипольного
взаимодействия Ж& и взаимодействия в s-состоянии Ж*:
2een = Md + 2%s. D.166)
Если усреднить это взаимодействие по волновой функции элек-
тронов ij)e, как это сделано выше при рассмотрении найтовского
сдвига, то мы получим эффективный гамильтониан Ж'еп, завися-
щий от операторов ядерных спинов:
+ Я.)*вс1хв. D.167)
Здесь die обозначает интегрирование по всем (пространствен-
ным и спиновым) координатам электронов, а символ G означает,
что интегрирование по пространственным координатам выпол-
няется по всему объему образца.
Разобьем объем G на атомные ячейки d, G2, .... Gn, каж-
дая из которых соответствует одному из N атомов кристалла.
Распределение магнитного момента электронов в каждой атом-
ной ячейке определяется волновой функцией г|зе. Поэтому вклад
взаимодействия Жа в D.167) можно определить, вычисляя сум-
марное локальное магнитное поле от всех электронов на различ-
ных ядрах. Предположим, что намагниченность в различных
ячейках образца одинакова. В этом случае в кубической решет-
ке учет взаимодействия Жа приведет к появлению эффективного
поля, аналогичного лоренцевскому локальному полю
^М-а-М. D.168)
Здесь М — магнитный момент единицы объема, а а—размагни-
чивающий фактор (вообще говоря, эта величина представляет
собой тензор), учитывающий действие «магнитных зарядов», по-
являющихся на поверхности образца при включении постоянного
магнитного поля. Для сферы, например, а = Dя/3) (ii + jj + kk).
Взаимодействие Ж* приводит к появлению дополнительного
•) См. в библиографии, помещенной в конце книги, раздел «Ядерный
резонанс в ферромагнетиках».
140 Глава 4
поля Hs/, действующего на /-е ядро:
Н./ в —Т Уе* ? S ^S'6 (Г' ~ R/) ¦• d\- D« 169>
Если волновую функцию электронов выбрать в виде произведе-
ния одноэлектронных функций |Р), задаваемых набором кван-
товых чисел р, то получим
Hs)=-^yeh ? (p|S6(r-R;)|p), D.170)
Р
занятые
где суммирование ведется только по тем состояниям |р), кото-
рые заполнены электронами. В этом выражении мы опустили
индекс / при S и г.
Учитывая, что ц* = — YeftS, находим
Суммирование по / в D.169) сводится к суммированию по за-
полненным одноэлектронным состояниям в D.170) и D.171), так
как каждый член суммы зависит от координат только одного
электрона. В таком веществе, как железо, некоторые значения р
будут соответствовать заполненным оболочкам, некоторые 3d-
слою и некоторые 4в-слою. Вклады от подобных электронов кра-
тко рассмотрены ниже.
Вклад члена 2/ва несколько изменяется при переходе от пара-
магнетиков к ферромагнетикам. В парамагнетиках намагничен-
ность одинакова по величине и направлению в каждой точке эл-
липсоидального образца, вследствие чего размагничивающие
поля можно определить обычным образом. В ферромагнетиках
намагниченность постоянна в пределах домена, но другие до-
мены характеризуются другими векторами намагниченности.
Так, в мягких ферромагнитных материалах в отсутствие внеш-
него поля значение намагниченности, усредненное по объему,
большему по сравнению с объемом домена, равно нулю. Поэтому
плотность магнитных зарядов на внешней поверхности равна
нулю. Вычисление дипольного вклада в магнитное поле в этом
случае можно провести следующим образом.
Проведем вокруг рассматриваемого ядра сферу достаточно
малого радиуса, чтобы поверхность сферы была расположена
в пределах одного домена. Магнитное поле, действующее на
ядро со стороны атомов, находящихся внутри сферы, можно вы-
числить, суммируя вклады в это поле от всех расположенных
внутри сферы атомов. Атомы, находящиеся вне сферы, можно
Магнитные взаимодействия ядер с электронами 141
рассматривать как равномерно распределенные по объему,
В кубической решетке вклад атомов, расположенных внутри
сферы, равен нулю. Вклад от внешних атомов эквивалентен
полю, создаваемому магнитными зарядами, расположенными нд
поверхности образца. Первое поле равно 4лМ/3, где М — намаг-
ниченность внутри домена. Второе поле равно —а-М', где М' —
намагниченность, усредненная по объему, во много раз боль-
шему объема домена. Полное магнитное поле на ядре /
Hr/ = H0 + -f-M-a.M/ + Hs/, D.172)
где Но — внешнее поле.
Если внешнее поле Но равно нулю, то намагниченность М'
также равна нулю, однако поле Нг/ не равно нулю. В этом слу-
чае, следовательно, можно наблюдать резонанс в нулевом внеш-
нем поле. Такой резонанс впервые наблюдали Госсард и Портис
[11] в гранецентрированных кубических кристаллах кобальта.
Исследуя резонанс на ядрах Со59, они нашли, что Hsl =?=•
= 213400 Гс. В железе Hsi равно 330 000 Гс. Поле Hs, можно
определить также, используя эффект Мессбауэра. Было обна-
ружено, что включение поля Но приводит к понижению резонанс-
ной частоты. Это означает, что векторы Hs/- и М направлены в
противоположные стороны.
Вклады Ы- и 45-электронов, согласно данным Маршалла
[12], должны давать параллельное локальной намагниченности
магнитное поле от 105 до 2-Ю5 Гс. Поэтому поле от внутренних
электронов направлено антипараллельно локальной намагничен-
ности и составляет примерно 4-Ю5 Гс (см. также [13]).
Это явление, названное поляризацией остова, хорошо изве-
стно из наблюдений парамагнитного резонанса ионов, не содер-
жащих 45-электронов. В принципе Зй-электроны не должны при-
водить к появлению изотропного сверхтонкого взаимодействия,
поскольку плотность d-функций на ядре равна нулю. Однако эти
электроны связаны электростатическим взаимодействием с элек-
тронами внутренних оболочек. Электростатическое взаимодей-
ствие при параллельной спину d-электрона ориентации спина'
внутренней оболочки отличается от взаимодействия, соответ-
ствующего антипараллельной ориентации этих двух спинов. По-
этому пространственные волновые функции таких электронов,
как Зя-электроны, различны в этих двух спиновых состояниях и
сумма намагниченностей двух s-электронов не равна нулю во
всех точках электронного облака. Как видно из D.171), в том
случае, когда плотности каждого из двух Зя-электронов на ядре
различны, эти электроны будут давать отличный от нуля вкла<ц
в поле Hs/-, несмотря на то что спины 3s-электронов направлены
антипараллельно.
142 Глава 4
§ 8. Эффекты второго порядка.
Косвенная ядерная связь
Мы рассмотрели роль взаимодействий между ядрами и элек-
тронами в парамагнитных и ферромагнитных веществах. В диа-
магнитных веществах в отсутствие внешнего поля электроны и
ядра не взаимодействуют в первом порядке теории возмущений,
поскольку в этом случае полный спин электронов равен нулю.
Однако это взаимодействие в диамагнетиках появляется во вто-
ром порядке теории возмущений') и приводит к возникновению
так называемой косвенной связи.
а б
Рис. 4.11. Спектр Ps» (о) и спектр F" (б).
Линии в спектре Р81 расположены на одинаковых расстояниях друг от друга всор, а их ин-
' тевсивиости относятся как 1:3:3:1;
Косвенная связь была открыта Ханом и Максвеллом [14] и
независимо от них Гутовским и Мак-Коллом [15]. Рассмотрим
это явление на примере молекулы PF3, спины всех ядер которой
равны '/г- В жидком PF3 быстрые вращения молекул приводят
к сужению резонансной линии. Было обнаружено, что резонанс-
ные спектры от ядер Р31 и F19 состоят из нескольких линий
(рис. 4.11). Поскольку все ядра F химически эквивалентны, это
расщепление резонансной линии не может быть связано с хими-
ческим сдвигом. Тем более нельзя объяснить химическим сдви-
гом появление четырех резонансных линий в спектре единствен-
ного в молекуле атома Р. Молекулы в рассматриваемом случае
движутся достаточно быстро, так как отдельные линии в спектре
очень узки; поэтому прямое диполь-дипольное взаимодействие
неэффективно. Кроме того, экспериментальные наблюдения по-
казывают, что расстояния между отдельными линиями не зави-
сят от температуры и напряженности постоянного поля. Числа и
относительные интенсивности линий в спектрах получаются та-
кими, как если бы на ядра каждого сорта в молекуле действо-
вало магнитное поле, пропорциональное г-компоненте полного
спина ядер другого сорта. Было найдено также, что 6mf =
') См. в библиографии, помещенной в конце книги, раздел «
Магнитные взаимодействия ядер с электронами 143
= бюр^/тр (см. рис. 4.11), где 6<оР и 6(uf — расстояния между
соседними линиями в спектрах фосфора и фтора соответственно.
Эти факты показывают, что приводящее к появлению подобных
спектров взаимодействие каким-то образом связано с ядерными
магнитными моментами.
Предложенное первоначально объяснение рассматриваемого
явления было основано на предположении о том, что каждое
ядро возбуждает токи в электронном облаке, которые взаимо-
действуют с другими ядрами. При качественном рассмотрении
действие токов можно заменить действием индуцированного маг-
нитного момента электронов. Если этот момент изотропен (т. е.
не изменяется при изменении ориентации молекулы относитель-
но ядерного магнитного момента), то взаимодействие рассматри-
ваемого ядра с другими ядрами при усреднении по случайным
вращениям молекулы в жидкости будет стремиться к нулю. Од-
нако, как это отмечалось при рассмотрении химических сдвигов,
индуцированный магнитный момент, вообще говоря, не изотро-
пен. В этом случае взаимодействие между двумя ядрами можно
оценить, рассматривая второй порядок теории возмущений. Дей-
ствие первого ядра можно характеризовать магнитным полем
y\ti(l/r3), где AД3)—среднее значение величины, обратной кубу
расстояния между электроном и первым ядром. Это поле приво-
дит к частичному размораживанию орбитального момента, свя-
занному с появлением примеси возбужденного состояния. Сте-
пень примешивания равна y\yeti2(l/r3)/AE, где Д? — энергия воз-
бужденного состояния. При полном размораживании магнитное
поле на другом ядре равно yeti/R3, где R—расстояние между
ядрами (мы рассматриваем магнитное поле, связанное с орби-
тальным движением электрона, как поле диполя). Поэтому энер-
гия взаимодействия ядер Ei2 по порядку величины равна
Р ПА"8) Yeft ft (. ,7оч
12 А! ^rY2«- D.17.3)
Эта формула дает результат, отличающийся на порядок вели-
чины или более от экспериментальных значений. Тем не менее
она правильно отражает факт увеличения взаимодействия при
переходе от молекулы РН3 к молекуле PF3, который тесно свя-
зан с увеличением химического сдвига при переходе от водорода
к фтору.
Хан и Максвелл, а также Гутовский и Мак-Колл указали,
что любой механизм, который, подобно рассматриваемому выше,
приводит к билинейной зависимости взаимодействия от ядерных
магнитных моментов, должен характеризоваться очень простой
формулой. Поскольку взаимодействие жидкости усредняется по
всем ориентациям молекулы, оно может зависеть только от вза-
144 Глава 4
имной ориентации спинов и его можно записать в виде
АцЩ • М2. D.174)
где Л12 не зависит от температуры и магнитного поля.
Эти исследования отметили также, что взаимодействие вида
D.174) объясняет парадоксальный на первый взгляд факт отсут-
ствия расщепления резонансной линии фтора, обусловленного
взаимодействием между ядрами фтора в молекуле PF3. Мы не
будем приводить здесь подробного объяснения, отметим лишь,
что оно связано с инвариантностью взаимодействия D.174) отно-
сительно поворота обоих спинов на один и тот же угол. В моле-
АтомА Атом В
9 • Состояние!
¦ Состояние!!
Рнс. 4.12. Механизм косвенного взаимодействия, предложенный Рэмси н
Пёрселлом.
При наличии взаимодействия межцу атомами А к В в электронную волновую функцию
состояния I и II входят с одинаковым весом. В состоянии I электронный момент атома Л
направлен вверх, а электронный момент атома В—вниз; в состоянии II электронные мо
менты атомов А к В имеют обратные направления.
куле PF3 все три ядра F химически эквивалентны и поэтому на-
ходятся в одинаковых постоянных и переменных магнитных по-
лях. В этой молекуле невозможно повернуть спин одного из ядер
F, не поворачивая на такой же угол спины других ядер F. Та-
ким образом, взаимодействия между эквивалентными ядрами
не влияют на резонансные частоты.
Рэмси и Пёрселл [16] предложили другой механизм взаимо-
действия, учитывающий электронные спины, который приводит
к существенно большему взаимодействию между ядрами. Это
связано с тем, что в этом механизме оба ядра одновременно вза-
имодействуют с близлежащими электронами, в то время как в
рассмотренном выше орбитальном механизме ядро каждого ато-
ма взаимодействовало только с электронами того же атома.
Схематически этот механизм показан на рис. 4.12.
В отсутствие ядерных моментов волновая функция связан-
ных атомов содержит с одинаковым весом волновые функции
состояний lull. Если ядро атома А обладает спином, направ-
ленным вверх, то состояние / будет входить в волновую функцию
связи с несколько большим весом, чем состояние //. В этом слу-
чае электронный магнитный момент атома А будет слабо поля-
ризован и направлен вверх, а электронный магнитный момент
атома В будет направлен вниз. Вследствие этого на ядро атома
Магнитные взаимодействия ядер с электронами 145
В будет действовать отличное от нуля магнитное поле со сто-
роны его же собственных электронов. Поскольку это поле меняет
знак при переворачивании магнитного момента ядра А, возни-
кает эффективное взаимодействие между ядрами. Легко оценить
порядок величины этого взаимодействия. Относительное увели-
чение веса состояния / по сравнению с весом состояния // равно
3 '''е л энергия сверхтонкого взаимодействия
Д? энергия электростатического взаимодействия '
D.175)
где | и @) fA — плотность волновой функции электронов на ядре
атома А, а АЕ— энергия соответствующего возбужденного со-
стояния. Таким образом, взаимодействие между электронами и
ядром атома В равно произведению взаимодействия ядра ато-
ма В с параллельно ориентированными электронными спинами
(8я/3) Y2Ye^21u @) || на относительное увеличение веса состоя-
ния /s
-о" YiYeA2 I « @) U) ( -о" Y2Y*ft21« @) \В )
-Л ^_i L. D.176)
Это выражение дает правильный порядок величины энергии вза-
имодействия. Если волновые функции электронов не содержат
примеси s-состояний, то в выражение D.176) войдет обычное ди-
поль-дипольное взаимодействие между ядерными и электрон-
ными спинами.
Эти идеи были распространены на твердые тела Бломберге-
ном и Роуландом [17] и независимо от них Рудерманом и Кит-
телем [18]. Рассмотрим эту задачу для металлов, предполагая,
что электроны в s-состоянии связаны с ядрами сверхтонким
взаимодействием. Поскольку металл не является диамагнетиком,
мы должны помнить о связанных с найтовским сдвигом эффек-
тах первого порядка теории возмущений. Подобный механизм
взаимодействия был предложен Фрелихом и Набарро [19]. Од-
нако, как показал Иосида [20], эффект Фрелиха — Набарро в
действительности является эффектом второго порядка. Рассмот-
рим кратко физическую природу косвенного взаимодействия,
пренебрегая пока эффектами первого порядка теории возмуще-
ний. Последние также рассмотрел ван Флек [21].
Влияние магнитного момента ядра, находящегося в опреде-
ленной области кристаллической решетки, проявляется в том,
что в эту область легче проникают электроны, магнитные момен-
ты которых параллельны магнитному моменту ядра, чем элек-
троны с антипараллельными магнитными моментами. При этом
волновые функции электронов, обладающих магнитными момен-
146
Глава 4
тами, параллельными магнитному моменту ядра, искажаются и
увеличиваются вблизи ядра. Это искажение осуществляется за
счет примешивания к k-состоянию электрона других состояний
с той же поляризацией спина электрона, но с другими значе-
ниями к. В результате, как будет видно из дальнейшего, проис-
ходит примешивание состояний, расположенных выше поверх-
ности Ферми. К иевозмущенной волновой функции будут при-
мешиваться блоховские волновые функции других состояний та-
ким образом, что их фазы на ядре будут совпадать с фазой не-
возмущенной волновой функции, представленной на рис. 4.13,
Рис. 4.13. Невозмущенная волновая функция (б) н волновые функции двух
состояний с более высокой энергией (а).
Ядро расположено в точке х=0, поэтому в этой точке фазы волновых функций совпа-
дают. Между примешиваемыми волновыми функциями возникают биения.
вследствие чего эти волновые функции будут сильно интерфери-
ровать вблизи ядра. Благодаря разбросу длин волн различных
блоховских функций по мере удаления электрона от ядра будет
происходить быстрая расфазировка примешанных состояний.
В результате биений между возмущенными и невозмущенной
волновыми функциями первоначально равномерное распределе-
ние плотности заряда электрона в состоянии со спином, направ-
ленным вверх1), вблизи ядра будет иметь осциллирующий ха-
рактер. Осцилляции плотности заряда исчезают на расстояниях
от ядра, примерно равных длине волны электрона на поверхно-
сти Ферми. Распределение плотности заряда электрона, магнит-
ный момент которого параллелен магнитному моменту ядра, по-
казано на рис. 4.14.
Перейдем теперь к вычислению этого эффекта. Для простоты
мы не будем вычислять изменение плотности распределения
электронных спинов в пространстве, а сразу рассчитаем взаимо-
действие между двумя ядрами. Наличие осцилляции можно бу-
дет усмотреть в конечном результате вычисления.
') Мы пренебрегаем здесь изменениями плотности заряда, обусловлен-
ными зарядами решетки.
Магнитные взаимодействия ядер с электронами
147
Рассмотрим электронно-ядерное взаимодействие Шеп для
двух ядер, спины которых равны Ii и Ь. Для простоты будем
предполагать также, что электроны в s-состоянии связаны с яд-
рами сверхтонким взаимодействием. В этом случае
z6 (г, - R2) =
D.177)
Здесь мы предположили, что ядра могут иметь различные спины
Ii и Ь и различные гиромагнитные отношения vi и уч.
Рис. 4.14. Плотность заряда электронов, магнитные моменты которых парал-
лельны магнитному моменту ядра.
Ядро расположено в точке х=0; р3—плотность заряда в отсутствие ядерного магнитного
момента При х=х, плотность р<ро*. в этом случае полный электронный момент напра-
влен противоположно ядерному моменту. •**
Необходимо учесть принцип Паули для электронов. Это мо-
жно сделать, либо определяя сначала возмущенные одноэлек-
тронные волновые функции и строя затем из них антисимметрич-
ные многоэлектронные волновые функции, либо сразу же поль-
зуясь в нулевом порядке теории возмущений антисимметрич-
ными многоэлектронными волновыми функциями. Мы применим
второй способ.
Рассмотрим многоэлектронное состояние |0), соответствую-
щее энергии Ец, и возбужденное состояние \п), соответствующее
энергии Еп, и вычислим изменение уровней энергии системы во
втором порядке теории возмущений, принимая за возмущение
взаимодействие Шеп- Будем считать, как обычно, что волновые
функции в нулевом порядке теории возмущений представляют
собой произведения электронных и ядерных волновых функций.
Обозначим ядерную волновую функцию, соответствующую уро-
вню энергии Еа через я]за> где а — квантовые числа ядерного спи-
на, и вычислим Д?оа— изменение энергии состояния |О)яра во
втором порядке теории возмущений:
(Оа | Звеп I ли') (па' | Жеп \ Оа) ,
п,а'
148
Глава 4
Поскольку величина Ео — Еп значительно больше разности
Еа — Еа,г последней можно пренебречь в знаменателе1). Пола-
гая Шеп = Ш\-\- Жъ, получаем
= У р ' Р [(Оа | Шх | па') (па' 15», | Оа) +
и, а'
+ (Оа 1302 I па') (па' | Ж2 | Оа) + (Оа 1ЗД \ паГ) (па' | ЗД I Оа) +
+ (Оа | Зв2 | па') (па' | 2вх | Оа)]. D.179)
Первые два члена в фигурных скобках отличны от нуля при уда-
лении одного из ядер. Последние два члена представляют собой
дополнительную энергию, не равную нулю только при одновре-
менном присутствии ядер, т. е. энергию взаимодействия ядер.
Поскольку нас интересует взаимодействие ядер, рассмотрим два
последних члена. Их можно записать в виде
компл>
л, а'
Величины Ж\ и Ж2 запишем в виде
¦3#i = Ij'GI= 2-( Лв ' Gig,
P"tr D.181)
где G( и G2 не зависят от переменного ядерного спина. С уче-
том соотношения D.181) получаем
a'
+ компл. сопр. =
Е Е@' ^вЧ-еУ '0) <а'1^'' а>+компл• сопр- <4Л82>
РР'
Р.Р' "
Для вычисления энергии D.182) необходимо задать волновые
функции |а). Вид этих функций определяется полным ядерным
гамильтонианом, включающим взаимодействие ядер с постоян-
*) Такой расчет можно рассматривать, по существу, как расчет в нуле-
вом внешнем поле. В действительности зависимость от поля очень слаба. Это
обусловлено тем, что спектр величин Еп непрерывен и начинается с Ео. Пре-
небрежение величиной Еа — Еа, лишь незначительно искажает спектр воз-
бужденных состояний и матричные элементы. Дальнейшее обсуждение этого
вопроса даио сразу после выражения D.195).
Магнитные взаимодействия ядер с электронами 149
ным внешним полем Но, диполь-дипольные взаимодействия
между ядерными спинами и т. д. Полезно заметить, что незави-
симо от вида функций |а) величину ДЯоа можно рассматривать
как поправку к энергии в первом порядке теории возмущений,
если в качестве возмущения принимается ядерный гамильтониан
Е0-Еп ) + компл• СОПР- D-183)
Подставляя в это выражение величины G\ и G2 в явном виде,
получаем
+ компл. сопр., D.184)
где
Выберем теперь волновую функцию |0) в виде произведений
блоховских функций. Обозначим произведение спиновой и бло-
ховской функций отдельного электрона через А, В, С и т. д.
Тогда
1 1 <4Л85)
1 п)" Z р
Очевидно, оператор перестановок будет обращать в нуль любую
функцию вида D.185), у которой А и В тождественно равны.
Рассмотрим матричные элементы симметричного относительно
перестановок координат электронов оператора возмущения V:
X[A(l)BB)CC)...]dx. D.186)
Удобно ввести новый оператор перестановок Р". Он опреде-
ляется как такой оператор, который, действуя после оператора
Р, дает тот же порядок расположения индексов электронов, что
и один оператор Рг, т. в. его можно определить равенством
150 Глава 4
Р"Р = р\ Подставляя в D.186), находим
ХИ'A)В'B) ...]*VP[A(l)BB)CC) ...]dx =
(-if" ^P"P[A'(l)B'B) ...]* УР[ЛA)ВB) ...]dT==
p.p"
>"[Л'A)В'B) ...]*V[A(l)BB) ...]dr. D.187)
При переходе к последней строке мы учли, что оператор V не
меняется при переобозначении электронов. Рассмотрим теперь в
качестве оператора V оператор, представляющий собой сумму
одноэлектронных операторов:
V=ZV(Q> D.188)
где оператор V(l) зависит только от координат /-го электрона.
Вычислим, например, вклад в матричный элемент от члена, со-
ответствующего / = 1:
(n\Vl\0)=YJ(-l)P"\P"lA'(l)B'B)...YVl[A(l)BB)CC)...]dT.
р" D.189)
Этот матричный элемент не равен нулю только в том случае,
если состояние \п) включает член вида ВB)СC)... .
Такое возбужденное состояние можно записать в виде
DЛ90)
Откуда получаем
(и IV, 10) =
{
р"
0, если А' совпадает с одной из функций В, С, D и т.д.,
(Л'| Vt | А) в противном случае. ' '
Очевидно, разные значения / в сумме D.188) просто выделяют
различные состояния А, В, С в волновой функции |0), а сумма
по возбужденным состояниям \п) выделяет состояния А', В'
и т. д., которые не заполнены в состоянии |0). Поэтому выраже-
Магнитные взаимодействия ядер с электронами 151
ние D.184) можно записать в виде
^эфФ = С X I, • (Eks - Ewyl (ks IS6 (г — R,) | k's') X
kt s заполненные
V, 5' незаполненные
X (k's' i S6 (г - Ra) | ks) • I2 + компл. conp. D.192)
Здесь мы заменили Ео — ?„на Eks — fkv, поскольку состояния,
соответствующие энергиям ?о и Еп, отличаются по энергии толь-
ко из-за того, что один из электронов переходит из состояния
(k, s) в состояние |к', s'). Термины «к, s заполненные», «к', s'
незаполненные» означают, заполнены или не заполнены электро-
нами эти состояния в волновой функции |0).
Вводя в рассмотрение функцию p(k, s), определяемую равен-
ствами
Р (к, s) =
1, если состояние к, s представлено
в основном состоянии 10),
0, если состояние к, s не представ-
лено в основном состоянии | 0),
D.193)
в сумме D.192) можно перейти к суммированию по всем состоя-
ниям:
^эфФ = С Z Ii • (Eks - Ek>s>yl (ks | S6 (r - R,) | k's') X
k, s
k'.s'
X (k's' IS6 (r—Ra) | ks) p (k, s) [1 — p (k', s')] • 12+компл. сопр. D.194)
Для определения зависимости эффективного взаимодействия
<^Эфф от температуры электронов усредним его по статистиче-
скому ансамблю, что эквивалентно замене p(k, s) на функцию
распределения Ферми f(k, s):
= С Z I, • (Eks - fikv) (ks | S6 (г — RO | k's') X
k,s
k'.s'
X (kV | S6 (r - R2) |ks) / (k, s) [1 - / (k', s')] • I2 + компл. сопр. =
^C ? I, • (s|S |s')(s' |S |s) • MEks-Ewy^k |6(r- RO |k')X
k,s
k'.s'
X(k'|6(r-R2)|k)/(k, s)[l-/(k', в'Я + компл. сопр. D.195)
В этом выражении энергии Eks и функции Ферми зависят от спи-
новых квантовых чисел. Например, зеемановская энергия элек-
тронных спинов изменяется при изменении s. Однако уровни
Ферми для электронов с противоположно направленными спи-
нами совпадают. Поэтому при абсолютном нуле в сумму войдут
152 Глава 4
состояния с энергиями Eks меньшими энергии Ферми, и состоя-
ния с энергиями Ем; ббльшими энергии Ферми. Матричные эле-
менты 6-функций медленно меняются при изменении спиновой
энергии. Поэтому Жфф очень мало меняется при изменении спи-
новой энергии электронов, и этим изменением энергии можно
пренебречь с хорошей степенью точности и записать D.195) в
том виде, который оно имеет в нулевом магнитном поле:
= С ? (?к - ВД-fli • (s\ S| sr)(s' |S| s) • I2(k |6(r - Ri) |k') X
k.k'
s.s'
X (k' 16 (r - Ra) | k) / (k) [1 - f (к')] + компл. сопр. D.196)
Мы можем провести теперь суммирование по s и s':
I(O)
s.s' P'.P~*.0.z
s.s'
E D.197)
Учитывая далее (см. гл. 3), что
Sp 5p5p- = з" 5 (S + 1) B5 + 1) бар- = -f1. так как 5 = т, D.198)
находим наконец
-« , t с (у (к|а(г-к,)|кО(к'[а(г-112)|кЖкН1-Нк')] ,
^эфф— hh-2< Zj ?ь - Ew г
I к. к' к к
+ компл. сопр. > = Ai2li • Ь, D.199)
где Л12 — постоянная, не зависящая от спинов. Вычислим теперь
матричные элементы при помощи блоховских волновых функций
i>k=«k(iVk'r. D-20°)
Здесь, как и раньше, функции Мк(г) обладают симметрией ре-
шетки. Таким образом,
(k'|6(r- R2)|k) = «k,(R2)«k(R2)e'№-k')* \ D.201)
так что
(k|6(r-R1)|k/)(k'|6(r-R2)|k) =
= «L' (R2) «к- («О «к («О «к («О е1 <к-к° • (Rj'Rl). D-202)
Если предположить, что узлы решетки Ri и R2 эквивалентны
(это имеет место в простых металлах) и ввести
Ri2 = R2-Rb D.203)
Магнитные взаимодействия ядер с электронами 163
то получим
* CI w V I и* @) f I «к @) f 2 «к [(к - к') • R,2]
k.k'
к. к' к k'
Эту сумму невозможно вычислить, если нет более точной
информации о зависимости волновых функций и энергии от к
Рис. 4.15. Относительная ориентация векторов к,
к' н Ri2.
или если не сделать дадьнейших упрощений. Предполагая, что
поверхность Ферми имеет вид сферы, а
Ev—~k\ D.205)
где т* — эффективная масса электрона, и заменяя вблизи по-
верхности Ферми |ык'@)|2 и | ми @) |2 на [ Ык^ @) |2^ получаем
**ф - VI2T *ФЛ* К@) Г Х
Z fe; D.206)
к. к'
В /г-пространстве число состояний dN в пределах телесного угла
dQ между сферическими поверхностями радиусов k и k + dk
равно
Обозначая угол между к и Ri2 через 6, угол между векторами к'
и Ri2 через 6' (рис. 4.15) и величину |Ri2| через R, получаем
V cos [(к - к') ¦ Rl2] f (к) [1 - f (kQ] _
к, к'
( \ Лб Г Г [cos (kR cos 6) cos (k'R cos в') + sin (fej? cos 6) sin (k'R cos 6') v
"* Kin) ) ) ft2-*'2 X
X / (k) [1 — / (k')J k2k'2 du du' dk dk\ D.208)
154 Глава 4
После интегрирования по dQ = — 2:rcd(cos6) и du' =— 2яХ
X d(cosB'), которое выполняется без труда, находим, что сумма
D.208) равна
W"F"H ""йУ-У M7(k)[l -f (kOlrfferffe'. D.209)
Этот интеграл можно вычислить при абсолютном нуле, если
учесть, что интегрирование по k' можно проводить не от kp до
оо, а от 0 до оо, так как при k' < kF для k = Aj, k' = k2 и для
& = &2, k' = ^i подынтегральная функция отличается только зна-
ком. В рассматриваемом интеграле по к' область интегрирования
можно расширить от — оо до оо, после чего он легко сводится
к интегралу по замкнутому контуру. Для устранения расходимо-
сти при k' = k интеграл берется в смысле главного значения.
В итоге получаем
D.210)
Из этого выражения видно, что взаимодействие осциллирует при
изменении величины R. Для больших расстояний взаимодействие
изменяется как
=?* («id
Множитель |ы@)|4 обусловливает увеличение взаимодействия
при увеличении Z. В случае тяжелых атомов это взаимодействие
значительно больше прямого диполь-дипольного взаимодействия.
Если волновые функции электронов не содержат примеси
s-состояний, то взаимодействие между электронами и ядрами
осуществляется через диполь-дипольное взаимодействие. В этом
случае эффективное взаимодействие
ye Pi I 3 (I, 'R|2) (h- R12) 1 г, i, n\n\
<^»ФФ = I M * '2 -\ гг 1 fii2- D.212)
L ^12 J
Функция fii2 имеет сложную структуру. Эта функция обращает-
ся в нуль, если волновые функции электронов не содержат со-
стояний, отличных от s-состояний. При больших расстояниях
Б,2 ~ \1Щ2. Функция fii2 исследована в работе Бломбергена и
Роуланда [17].
Гутовский и др. [15] рассмотрели эффективное взаимодей-
ствие, обусловленное прямым диполь-дипольным взаимодей-
ствием в молекулах, аналогичных PF3. Предполагая, что элек-
троны атомов Р и F находятся в р-состояниях, и проводя усред-
нение по всем возможным ориентациям молекул относительно
Магнитные взаимодействия ядер с электронами 155
внешнего поля, они получили для эффективного взаимодействия
выражение
Л121,.12. D.213)
Это взаимодействие обращается в нуль при усреднении по ориен-
тациям молекулы, так как обусловленная спинами намагничен-
ность сама зависит от ориентации молекулы относительно ядер-
ного спина.
Взаимодействие D.212) зависит от спинов так же, как обыч-
ное прямое диполь-дипольное взаимодействие. Чтобы подчерк-
нуть это сходство, такое взаимодействие часто называют «псев-
додипольным». С другой стороны, взаимодействие A^Irh имеет
Рис. 4.16. Форма резонансной кривой в пренебрежении псевдообмеиным
взаимодействием (сплошная линия) и с учетом псевдообменного взаимодей-
ствия (пунктирная линия).
вид, аналогичный виду электростатического обменного взаимо-
действия. В рассмотренном случае взаимодействие не зависит
от обменного интеграла, поэтому это взаимодействие часто назы-
вают «псевдообменным».
Влияние псевдообменного н псевдодипольного взаимодей-
ствий на форму и ширину резонансных линий можно учесть, до-
бавляя эти взаимодействия к прямому диполь-дипольному вза-
имодействию между ядерными спинами. При учете этих вза-
имодействий возникает много интересных случаев. В жидкостях
при усреднении по различным ориентациям молекул относи-
тельно постоянного поля псевдодипольное взаимодействие обра-
щается в нуль, а псевдообменное взаимодействие приводит
к расщеплению резонансных линий.
В твердых телах необходимо учитывать оба взаимодействия.
Псевдообменный член, коммутирующий с оператором 1Х =
=1\х + /2*. не дает вклада во второй момент резонансной ли-
нии, но существенно изменяет величину четвертого момента.
Ван Флек показал, что в этом случае центральная часть резо-
нансной линии сужается, а крылья линии повышаются
(рис. 4.16) в соответствии с тем, что четвертый момент более
чувствителен к крыльям линии, чем второй момент. Подобное
сужение центральной части резонансной линии называется об-
менным или псевдообменным сужением. В электронном резо-
156 Глава 4
нансе при наличии реального обменного взаимодействия обмен-
ное сужение может быть значительным.
Если два ядра не одинаковы, то псевдообменное взаимодей-
ствие между ними можно записать в виде А^Ытг. Это взаимо-
действие не коммутирует с оператором 1\х + /г*, поэтому оно
дает вклад во второй момент резонансной линии. В этом случае
резонансная линия уширяется; подобное явление называют «об-
менным уширением». При наличии квадрупольного взаимодей-
ствия, приводящего к изменению расстояний между различны-
ми ближайшими m-уровнями, обменное взаимодействие может
приводить к уширению линий даже в случае одинаковых ядер.
В заключение отметим, что эффект Фрелиха — Набарро со-
стоит в том, что взаимодействие ядра с электронами приводит
к изменению населенностей спиновых состояний электронов,
вследствие чего возникает магнитное поле на других ядрах,
аналогично тому как постоянное магнитное поле обусловли-
вает появление найтовских сдвигов. Иосида рассмотрел эту за-
дачу, разлагая взаимодействие между ядрами и электронами в
интеграл Фурье. Он указал, что эффект Фрелиха — Набарро ха-
рактеризуется членом, волновой вектор которого q = 0 (этому
члену соответствует бесконечно большая длина волны). Во вто-
ром порядке теории возмущений компоненты с q ф 0 связывают
электронные состояния к и к', для которых выполняется соот-
ношение
D.214)
Поскольку при вычислениях во втором порядке теории возму-
щений основное и возбужденное состояния должны быть различ-
ными, из соотношения D.124) мы видим, что компоненты с
q = О следует опустить. Иосида учитывал компоненты с q = 0 в
первом порядке теории возмущений, а компоненты с q ф 0 — во
втором порядке теории возмущений и складывал полученные
результаты. Окончательный результат, полученный Иосидой,
аналогичен результатам Бломбергена — Роуланда и Киттеля —
Рудермана, исключавшим из рассмотрения члены с к' = к путем
взятия интеграла в смысле главного значения [см. вывод выра-
жения D.210) ]. Для выявления этого сходства рассмотрим по
существу аналогичный вопрос о возникновении найтовских сдви-
гов.
Найтовские сдвиги можно вычислить двумя различными спо-
собами. В первом способе предполагается, что постоянное маг-
нитное поле однородно и вычисляется энергия взаимодействия
поляризованного электрона в первом порядке теории возмуще-
ний. Второй способ более сложный. При вычислениях по вто-
рому способу предполагается, что постоянное магнитное поле
осциллирует в пространстве с волновым вектором q. В таком
Магнитные взаимодействия ядер с электронами 157
поле полная намагниченность электронных спинов в образце
равна нулю, поскольку магнитное поле в одних точках образца
направлено вверх, а в других вниз.
В этом случае взаимодействие в первом порядке теории воз-
мущений равно нулю. Если во втором порядке теории возмуще-
ний в качестве одного матричного элемента возмущения взять
матричный элемент взаимодействия между электронами и ядра-
ми, а в качестве другого — матричный элемент взаимодействия
электронов с внешним полем, то получается отличный от нуля
результат. Таким образом, постоянное поле обусловливает изме-
няющуюся в пространстве поляризацию электронных спинов.
В качестве постоянного поля можно взять такое поле, которое
имеет максимальное значение на ядре. В этом случае при очень
малых q (большие длины волн) можно ожидать, что результат
получится таким же, как и в случае строго однородного поля.
Следовательно, при переходе к пределу при q -*- 0 в вычислениях
во втором порядке теории возмущений должно получиться обыч-
ное выражение для найтовского сдвига. Этот результат под-
тверждается строгим расчетом.
Взятие интеграла в смысле главного значения при получении
выражения D.210) эквивалентно предельному переходу k'->-k.
Так же как при вычислении найтовского сдвига, эта процедура
учитывает возникающее в первом порядке теории возмущений
изменение населенностей спиновых уровней электронов, или эф-
фект Фрелиха — Набарро.
Прежде чем закончить эту главу, выясним влияние электрон-
ных спинов на химические сдвиги в диамагнитных веществах.
В отсутствие внешнего магнитного поля диамагнитные вещества
характеризуются равным нулю квантовым числом полного спи-
на S. При включении внешнего магнитного поля Но вдоль оси z
электронные спины будут взаимодействовать с полем. Гамильто-
ниан этого взаимодействия имеет вид
N
0esz=yehHo ? S2/ = VebHoS» D.215)
Здесь индекс / нумерует электроны, а
N
S2^ES2/. D.216)
Поскольку волновая функция основного состояния |0) соответ-
ствует спину, равному нулю, можно написать
S2|0) = 0. D.217)
Поэтому все матричные элементы, связывающие основное со-
стояние с возбужденными состояниями \п), будут равны нулю:
(п 126SZ10) = yehH0 (п | Sg |0) = 0. D.218)
158
Глава 4
Таким образом, зеемановское взаимодействие D.215), строго
говоря, не связывает основное состояние с возбужденными со-
стояниями. Это означает, что внешнее поле не может приводить
к возникновению отличного от нуля полного спина в диа-
магнетике и явления, подобного размораживанию орбиталь-
ного момента под влиянием магнитного поля, не должно наблю-
даться.
В действительности спины связаны с внешним магнитным по-
лем. Поэтому такой результат кажется странным. Интуитивно
мы ожидаем, что в достаточно сильных магнитных полях спины
в диамагнетиках должны
быть поляризованы. Разъ-
ясним этот парадокс на
примере молекулы водо-
рода. Основное состояние
молекулы водорода син-
глетное, но возбужденное
состояние триплетное.
В присутствии постоянно-
го магнитного поля уров-
ни молекулы водорода
расщепляются. Это рас-
щепление показано на
рис. 4.17, где видно, что
в достаточно сильных
магнитных полях Яо со-
стояние с 5=1, Ms =
= — 1 пересекается с со-
стоянием S = О, Ms = 0.
В этом случае основным
состоянием может стать
обладающее отличным от нуля спином триплетное состояние.
Такая ситуация, однако, не осуществляется в достижимых в ла-
бораторных условиях полях, поскольку разность энергий три-
плетного и синглетного состояний в нулевом внешнем поле рав-
на нескольким электронвольтам.
Предположим теперь, что к основному состоянию примешано
триплетное состояние. В результате примешивания будет проис-
ходить одинаковое по величине, но противоположное по знаку
изменение полных спинов на двух атомах молекулы водорода.
Вследствие этого изменение спиновой зеемановской энергии мо-
лекулы будет равно нулю. Поскольку предположенное нами из-
менение спинового состояния молекулы не приводит к пониже-
нию полной энергии молекулы, оно не будет возникать.
Отметим, однако, что в том случае, когда два атома моле-
кулы не одинаковы, магнитное поле может возбуждать на этих
Энергия J
Триплет
Синглет
ч.
\в-/, ма
S-U
= -7
X
,м
ма
ш
$ = + /
-0
>-
Рис. 4.17. Зависимость уровней сииглетно-
го и триплетного состояний молекулы во-
дорода от приложенного магнитного поля
Но.
При достаточно большом поле //о трнплетнос со-
стояние лежит ниже сннглетного и основное со-
стояние будет обладать магнитным моментом.
Магнитные взаимодействия ядер с электронами 159
атомах различные орбитальные моменты, которые вследствие
спин-орбитального взаимодействия индуцируют спиновую поля-
ризацию. Так, в молекуле HI орбитальный момент атома иода
будет индуцировать спиновую поляризацию в связи, обусловли-
вающую возникновение химических сдвигов как у водорода, так
и у иода.
ЛИТЕРАТУРА
1. Ramsey N. F., Phys. Rev., 78, 699 A950); Phys. Rev., 86, 213 A952).
2. Lamb W., Phys. Rev., 60, 817 A941).
3. Pople J. A., Proc. Roy. Soc., A239, 541, 550 A957).
4. Ramsey N. F., Phys. Rev., 86, 243 A952).
5. Pines D., Solid State Physics, Vol. 1, Academic Press, New York, 1955,
p. 38.
6. Pauling L., Wilson E. В., Jr., Introduction to Quantum Mechanics, McGraw-
Hill Book, New York, 1935, p. 232.
7. Schumacher R. Т., Slichter С. Р., Phys. Rev., 101, 58 A956).
8. Ryter Ch., Phys. Rev. Lett., 5, 10 A960).
9. Kohn W., Phys. Rev., 96, 590 A954).
10. Kjeldaas Т., Jr., Kohn W., Phys. Rev., 101, 66 A956).
11. Gossard A. C, Portis A. M., Phys. Rev. Lett., 3, 164 A959); J. A. P. Suppl.
31, 2055 A960).
12. Marshall W., Phys. Rev., 110, 1280 A958).
13. Watson R., Freeman A., Phys. Rev., 123, 2027 A961).
14. Hahn E. L, Maxwell D. E., Phys. Rev., 88, 1070 A952).
15. Gutowsky H. S., McCall D. W., Slichter С. Р., Journ. Chem. Phys., 21, 279
A953).
16. Ramsey N. F., Purcell ?. AJ., Phys. Rev., 85, 143 A952).
17. Bloembergen N., Rowland T. J., Phys. Rev., 97, 1679 A955).
18. Ruderman M. A., Kittel C, Phys. Rev., 96, 99 A954).
19. Frdhlich F., Nabarro F. R. N., Proc. Roy. Soc. (London), A175, 382 A940).
20. Yosida K., Phys. Rev., 106, 893 A957).
21. Van Vleck J. H., Rev. Mod. Phys., 34, 681 A962).
22. Whiting B. R., Van der Ven N. S., Schumacher R. Т., Phys. Rev., B18, 5413
A978).
Глава 5
Спин-решеточная релаксация
и сужение линий,
обусловленное
молекулярным движением
§ 1. Введение
Обратимся теперь к вопросу о том, каким образом ядерная
намагниченность в процессе спин-решеточной релаксации прихо-
дит к значению при тепловом равновесии. Рассмотрим два спо-
соба вычисления Тх.
Первый способ применим в тех случаях, когда взаимодей-
ствие ядер друг с другом намного сильнее, чем с решеткой.
В этом случае попытка вычислить изменение населенности инди-
видуального ядра за счет взаимодействия с решеткой услож-
няется благодаря наличию очень сильной связи между ядрами.
Данный способ основан на предположении о том, что сильная
связь только устанавливает общую для всех спинов темпера-
туру, а взаимодействие с решеткой вызывает изменение этой
температуры. Процесс аналогичен процессу теплообмена между
газом и стенками сосуда, при котором роль столкновений внутри
газа состоит в сохранении теплового равновесия среди молекул.
При этом мы считаем, что распределение скоростей молекул,
сталкивающихся со стенками, соответствует тепловому равно-
весию. Как мы увидим, первый способ приводит к выражению
для Ти особенно пригодному в тех случаях, когда можно дать
квантовомеханическое описание решетки. Например, релакса-
ция в металле включает переход энергии к электронам проводи-
мости, которые хорошо описываются с помощью функций Бло-
ха и принципа Паули.
Второй способ называется методом матрицы плотности. Хотя
это вполне общий метод, его большей частью применяют для
систем, для которых решетку естественно рассматривать с клас-
сической точки зрения и для которых ширина резонансной ли-
нии существенно сужается за счет движения ядер. Кроме того,
если имеет место движение ядер, то время релаксации Т2, ха-
рактеризующее взаимодействие между ядрами, увеличивается,
и предположение о том, что спиновая температура устанавли-
вается за время более короткое, чем Т\, становится неверным.
Таким образом, второй способ наиболее полезен в тех случаях,
когда первый способ не применим.
Спин-рсшеточная релаксация и сужение линий 161
Ввиду большой массы ядер классическое описание их дви-
жения часто дает вполне удовлетворительные результаты. Дей-
ствительно, попытка дать квантовомеханическое описание дви-
жения молекул в жидкости привела бы к большим трудностям.
Поэтому метод матрицы плотности удобен в тех случаях, когда
имеет место сужение линии, обусловленное молекулярным дви-
жением. Кроме того, при наличии сужения линии вследствие
молекулярного движения метод матрицы плотности позволяет
единым образом рассматривать как релаксацию компоненты
спина /2, так и релаксацию 1Х или 1У с относящимся к ним вре-
менем релаксации Т1 и Т2 соответственно.
Метод матрицы плотности тесно связан с общепринятой не-
стационарной теорией возмущений. По существу они совершенно
эквивалентны. Однако метод матрицы плотности позволяет полу-
чать результаты в очень удобной форме. Это идеальный метод
для решения задач, в которых важен учет фазовой когерентно-
сти. Более того, при рассмотрении таких задач необходимо ис-
пользовать матрицу плотности или ее математический эквива-
лент. Во всяком случае, формализм данной главы в значитель-
ной степени применим к другим системам, отличным от спинов.
Например, этими методами может быть рассмотрена диэлектри-
ческая релаксация.
Как мы видим, оба подхода дополняют друг друга: один при-
меняется в случае широких резонансных линий в твердой решет-
ке, а другой наиболее полезен, если резонансная линия сужается
благодаря движению ядер.
§ 2. Релаксация системы,
описываемой спиновой температурой ')
Если система, имеющая энергетический спектр Еа, Еъ и т.д.,
находится в тепловом равновесии с резервуаром, имеющим тем-
пературу Т, то ее уровни населены с вероятностями р{Еа), р(Еь)
и т. д., которые определяются соотношением
р (Еа) _
Р (Еь) е ь
Поэтому, поскольку существуют условия
Zp (?«)-=!, E.2)
Z
') См. в библиографии, помещенной в конце книги, раздел «Спиноваи
температура»
в Зак. 72?
162
Глава 5
мы имее;.1
где
I
_Е ,kT
E.3)
E.4)
— статистическая сумма, пли «сумма состояний».
Соотношения E.1), E.3) можно интерпретировать двумя
способами. Проиллюстрируем это, рассматривая Л' одинаковых
Энергия
-'Л
+ '/*
+3/г
Огибающая
а
Рис. 5.1. Уровни энергии для ядра со спином 3/г (а) и графическое изобра-
жение зависимости населенности от энергии (б).
Ллииа полосок, соответствующая населенности, меняется но экспоненциальному закону.
спинов. В первой интерпретации спины рассматриваются как не-
взаимодействующие друг с другом. Тогда «система» состоит из
одного спина н энергии Еа относятся к уровням энергии одного
спина. Во второй интерпретации полагают, что систему образуют
все А/ спинов. В этом случае Еа представляет собой общую энер-
гию всех А/ спинов. Нам будет удобно использовать обе интер-
претации. Однако следует заметить, что первая интерпретация
справедлива только в том случае, если можно считать, что спины
подчиняются статистике Максвелла — Болышана; в то же время
вторая интерпретация всегда верна, независимо от того, подчи-
няются ли отдельные частицы статистике Максвелла—• Больц-
мана, Ферми — Дирака или Бозе — Эйнштейна. Различия, вно-
симые статистикой, появляются только тогда, когда мы строим
волновую функцию общей системы с помощью волновых функ-
ций индивидуальных спинов.
Мы будем говорить, что любую систему, для которой на-
селенности удовлетворяют соотношению E.1), можно описать
с помощью температуры Т даже в том случае, если система не
Спин-решеточная релаксация и сужение линий 163
находится в равновесии с каким-либо резервуаром. Соотношение
E.3) позволяет дать простую картину распределения населен-
ностей уровней. Рис. 5.1 иллюстрирует случай, относящийся к
первой интерпретации. В данном случае рассматриваются на-
селенности энергетических состояний одного спина / = 3/г, поме-
щенного в постоянное магнитное поле.
Система уровней, показанная на рис. 5.2, очевидно, не соот-
ветствует тепловому равновесию, поскольку огибающая полосок
на рисунке ие является экспонентой.
На рис. 5.2, б показаны возможные переходы, при которых
сохраняется общая энергия спинов. Два спина, состояния кото-
рых обозначены крестиками, одновременно переходят в состоя-
Чь
Энергии
-x—x-
'/• -1 ¦*-
Населенность
a 6
Рис. 5.2. Распределение населенностей, которое нельзя описать с помощью
температуры (а), и разрешенные переходы двух спинов из состояний, обозна-
ченных крестиками, в состояния, обозначенные кружками (б).
ния, обозначенные кружками; один спин переходит на более вы-
сокий уровень энергий, другой — на более низкий. (Такой пере-
ход описывается членом диполь-дипольного взаимодействия
вида I*Ij.) Число переходов в единицу времени спинов из со-
стояний, обозначенных крестиками, в состояния, обозначенные
кружками, (dN/dt)x_>0) равно произведению вероятности нахож-
дения двух спинов в начальном состоянии на вероятность пере-
хода Wx_>Ot если спины находятся в начальном состоянии. Та-
ким образом,
Обратный переход из состояний, обозначенных кружками, в со-
стояния, обозначенные крестиками, будет иметь скорость
l определяемую выражением
Dг) ^Р-зЛ^о*. E-6)
При равновесии эти скорости должны быть равны. Таким обра-
зом, мы предполагаем, что выполняется принцип детального рав-
6*
164 Глава 5
новесия. Так как W0_>x = Wx_>0, находим
или -^==^1. E.7)
Но это соотношение представляет собой условие теплового рав-
новесия среди состояний, поскольку отвечающие им уровни энер-
гии эквидистантны.
Таким образом, мы видим, что тепловое равновесие насту-
пает в результате таких процессов, которые показаны на
рис. 5.2, б. Обычно скорость такого процесса порядка обратной
величины ширины линии в твердой решетке, т. е. от 10 до
100 мкс для типичных ядер. Следовательно, если значения Т\ со-
ставляют от миллисекунд до секунд, то спиновые уровни ядер
будут населены в соответствии с больцмановским распределе-
нием.
Теперь мы перейдем к рассмотрению релаксации системы
ядерных спинов, гамильтониан которой 36 имеет собственные
значения Е„, а населенность данного состояния п равна />я.
(Здесь через п обозначено состояние всей системы, а не энергия
отдельного спина.) По условию нормировки
п
В этом случае среднее значение энергии системы
!-• == 2—1 Prfin' E.9)
п
Примем далее, что энергии Е„ отсчитываются от такого уровня,
что имеет место условие
^?B=Sp^ = 0, E.10)
п
которое выполняется для зеемановской и диполь-дипольной
энергий.
Для определения процесса релаксации рассмотрим изменение
средней энергии. Если вместо спиновой температуры ввести ве-
личину р = \/kT, то мы получим
Поскольку Ё—sZpnEn, мы также имеем
п
d~E с
Спин решеточная релаксация и сужение линий 165
Предположим, что вероятности рп подчиняются простым линей-
ным уравнениям движения. Определяя величину Wmn как веро-
ятность перехода в системе в единицу времени под влиянием ре-
шетки из состояния m в п, если система находилась в состоянии
in, уравнение движения можно записать в виде
™W>"» ~ P-Wnm)- E.13)
Это уравнение часто называют основным кинетическим уравне-
нием.
Подставляя dpn/di из E.13) в E.12), находим
!§-=¦? (PmWmn - PnWnm) Я„ =4 ? (pmWmn - pnWnm) (En - Em),
m.n т.п.
E.14)
где вторая форма суммы приведена ввиду того, что индексы т
и п входят в нее более симметрично. С помощью уравнений
E.11) и E.14) можно получить дифференциальное уравнение,
определяющее поведение спиновой температуры. Имеются две
задачи: 1) вычисление dE/dfi и 2) определение формы уравне-
ния E.14) для случая, когда справедливо требование, что поня-
тие спиновой температуры применимо в любой момент времени.
Обратимся сначала к вычислению dE/d$. Имеем
Найдем сначала приближенное выражение для 2. Считая опять
температуру достаточно высокой для того, чтобы условие $Еп<.1
выполнялось для большинства состояний, разложим е~ Еп в
степенной ряд и оставим только первые члены разложения:
Z = ? (l - р?Г„ + Р~ + ...). E.17)
п
Очевидно, это приближение, заключающееся в разложении
в степенной ряд при сохранении лишь первых членов, применимо
только в том случае, если |?n|<C kT для характерных энергий.
Однако законность этого приближения можно показать и при
более слабых условиях. Для этого здесь и при выводе уравнений
E.19) — E.26) можно применить метод, использованный в при-
ложении Д.
166 Глава б
Ввиду соотношения E.10) второй член в правой части обра-
щается в нуль. Если пренебречь членом, пропорциональным Р2,
то Z станет равным полному числу состояний. Поскольку это
совпадает со значением при бесконечно большой температуре
Zco, МОЖНО ПОЛОЖИТЬ
Z = ZTO. E.18)
Учитывая данное обстоятельство и воспользовавшись форму-
лами E.15) и E.16) в приближении высоких температур, полу-
чаем
dE 1 V с2 -Р?я
y]i E.19)
ч и
Таким образом,
У 2
Ё ^L
dt — dt
Вернемся теперь к уравнению E.14). Поскольку рассматривае-
мой системе всегда можно приписать температуру, имеем
<?«-?»)р. E.21)
Примем далее, что, когда система находится в тепловом равно-
весии с решеткой, переходы между каждой парой уровней также
должны находиться в равновесии, т. е. что выполняется так на-
зываемый принцип детального равновесия. Обозначим через р^
значение вероятности рп для случая, когда спины находятся в
тепловом равновесии с решеткой. Тогда из принципа детального
равновесия следует
PmW,nn — PnWnm' E-22)
ИЛИ
т __ vw fjL — т р(Ет~ьп) f/. /к ооч
" тп — " пт I — "' пте » {О./.О)
Рщ
Подставляя E,21) и E.23) в уравнение E.14), находим
i~_— _ V4 „ П7 fi р(Ет~Еп)Ф~^1)Л1р р \ /г пл\
dt 2 Zj "m mn L ЛУ-'п ^ml- [.O.zi)
т. п
Разлагая далее экспоненту в ряд, получаем
т,п
Спин-решетбчная релаксация и сужение линий 16?
Здесь
рт « ^— « ^ fi- « J-. E.26)
ЛОО Л«! ZOO
Подставляя E.26) в E.25) и сравнивая результат, получающий-
ся для dE/dt, с формулой E.20), находим
2
-Jf — (Pz. — P)
где
ZW IF —
TT = Ym-ra ^E2 • E.28)
в
Формула E.28) сначала была получена Гортером [1] при усло-
вии, что |р — Pi.|<C P- Как мы видим, в таком ограничении нет
необходимости.
Большое преимущество формулы E.28) состоит в том, что,
постулируя понятие спиновой температуры, мы тем самым учи-
тываем спин-спиновое взаимодействие. На основании уравнений
движения E.14) нужно было бы предположить наличие боль-
шого числа постоянных времени, описывающих спин-решеточную
релаксацию, однако постулат о спиновой температуре приводит
к тому, что релаксация всей системы описывается одной экспо-
нентой.
Рассматриваемые состояния п можно считать почти точными
решениями ядерного спинового гамильтониана, между которыми
(поскольку они не являются точными состояниями) происходят
быстрые переходы, гарантирующие тепловое равновесие. Однако
переходы между этими состояниями, которые возбуждаются ре-
шеткой, происходят очень редко. После каждого индуцирован-
ного решеткой перехода, нарушающего ядерное распределение,
приближенные уровни восстанавливаются, так что, когда проис-
ходит следующий спиновый переход, индуцированный решеткой,
спины уже оказываются в распределении, описываемом некото-
рой температурой. Здесь предполагается, что ошибкой, связан-
ной с рассмотрением состояний п как точных решений, можно
пренебречь.
§ 3. Ядерная релаксация в металле
Теперь обратимся к примеру применения формулы E.28).
Рассмотрим ядерную релаксацию в металле, вызываемую вза-
имодействием со спиновыми магнитными моментами электронов
проводимости. Это основной релаксационный механизм.
168 Глава б
В процессе спин-решеточной релаксации ядро совершает пе-
реходы, поглощая или отдавая энергию. Чтобы энергия сохраня-
лась, в решетке должны происходить компенсирующие измене-
ния. Поскольку существует связь с электронами проводимости,
можно считать, что одновременно с ядерным переходом происхо-
дит электронный переход из некоторого состояния с волновым
вектором к и ориентацией спина s в состояние с к', s'. Можно
представить этот процесс как задачу рассеяния. Обозначив ядер-
ные квантовые числа начального и конечного состояний тип
соответственно, найдем, что число переходов в единицу времени
Wmks, nVs' из начального состояния ядра и электрона | mks) в
конечное состояние |nk's') определяется формулой
Wmks. nW = Щ-\ (mks | V\ пкУ) |2б (?„ + Eks -Еп- Ew), E.29)
где V—взаимодействие, вызывающее рассеяние. При этом в
E.29) предполагается, что в состоянии |ks) электрон есть, а в
состоянии |kV) нет электрона. Полная вероятность ядерного
перехода в единицу времени получается путем суммирования
Wmks.nVi' по всем начальным и конечным электронным состоя-
ниям. Имеем
¦Wmn= Z Wm^nv*. (В.80)
ks заполненные
kV незаполненные
Сумма по заполненным состояниям ks, конечно, эквивалентна
суммированию по электронам. Можно отбросить ограничения на
ks и kV, введя величину pks, которая равна единице, если со-
стояние ks заполнено, и равна нулю, если ks не заполнено. Это
позволяет представить E.30) в виде
Wmn = Z Wmks. nkWPks [ 1 — Pk's']. (B.31)
ks
kV
При усреднении E.31) по ансамблю электронных систем нужно
лишь заменить pks на функцию Ферми f(Eks), которую мы со-
кращенно обозначим f(k, s):
Wmn = ? Wmks, пЫ (k, s) [1 - / (k'( 8% F.32)
ks
k's'
Теперь нужно получить явное выражение для Wmks, nk's1- Для
этого необходимо конкретизировать взаимодействие V. Для ме-
таллов, волновая функция которых вблизи поверхности Ферми
в основном определяется s-состоянием, главный вклад во вза-
имодействие вносит связь ядерного и электронного спинов в
s-состоянии электрона
^. E.33)
Спин-решеточная релаксация и сужение линий 169
Здесь мы считаем, что ядро со спином I находится в начале ко-
ординат. Волновую электронную функцию возьмем в виде про-
изведений спиновой функции и функции Блоха ик (г) elk'r. Сле-
довательно, начальная волновая функция имеет вид
| mks) = \m)\s) ukelkr. E.34)
Теперь легко вычислить матричный элемент, входящий в E.29):
(mks | V | лкУ) = ~ yeynti2 (/и 111 п) • (s | S | s') uk @) uk- @), E.35)
отсюда получаем
{m\Ia\n)(n\b\m)X
а, а'"Х, у, z
X(s\Sa\s') (s' 15a-1s)| uk @) |21 u*@) |2б (Em+Eks~En~-Ek>S'). E.36)
Подставляя это выражение в E.32), можно вычислить Wmn-
Здесь опять встречается суммирование по к и к' медленно ме-
няющейся функции. Как и выше, заменим суммирование инте-
гралом, пользуясь плотностью состояний g(?k, А), введенной в
гл. 4, § 7. Это дает
"* I' J ») (n I 'a-1 m) (s | Sa | sO (s' | SJ s) X
aa'ss'
X \ I «к @) P| uk- @) P / (k, s) [ 1 - / (k', s')\ g (Ek, A) X
X g (Ev, А') б (Em - En + ?k, - ?k'S>) rf?k ЙЛ rf?k- dA'. E.37)
Сначала интегрируем по dA и <i4', используя соотношения
D.153) и D.154) и вводя опять среднее от |«к@)|2 по энергети-
ческой поверхности Ек, т. е. (|«k(O)p)fik. Предполагаем также,
что энергия Eks, входящая в функции Ферми, остается постоян-
ной на поверхности постоянной энергии Ек. Это предположение
должно выполняться, если спиновая энергия не зависит от поло-
жения на поверхности Ек. Тогда легко проинтегрировать по
dEk', используя наличие б-функции. Имеем
Eks + Em = Ek'S' + En E.38)
и, принимая Eks — ?k -f- Es, получаем
a, a'
(\uk< @) \%k, f (Eks) [1 - f (Eks + Em- En)]X
X9{Ek)p(Ek')dEk, E.39)
Ev = Ek + E,-E, + Em-En. E.40)
170 Глава 5
Так как изменение ядерной энергии Ет — ?„ очень мало по
сравнению с kT, функцию Ферми / (Ей -f Em — Еп) можно заме-
нить на f(Eks). Это приводит к равенству Wтп = Wnm. На са-
мом деле между Wmn и Wnm существует небольшое различие.
Именно это малое различие приводит к установлению населенно-
сти ядерных уровней, соответствующей тепловому равновесию.
Однако здесь при вычислении Wmn мы можем пренебречь этим
различием, поскольку его влияние уже учтено в соотношении
E.23).
Кроме того, поскольку как р (Як')> так и < |ик @) p)fi t пред-
ставляют собой медленно меняющиеся функции ?V, можно по-
ложить их равными своим значениям при ?k = ?k'- Мы будем
оценивать р (Еу) и т.д. по их значениям при Ей. Это ласт нам
следующее выражение для интеграла E.39):
\ < 1 «к@) ffBр2(Е) f(E)\l-f (?)]dE. E.41)
о
Здесь нижний предел интегрирования мы положили равным
нулю, поскольку существенный вклад в интеграл вносит только
область вблизи поверхости Ферми Е — ?>.
Поскольку E.41) не зависит от спиновых квантовых чисел s
и s', теперь можно вычислить сумму по спиновым состояниям
в E.39):
S \Sa \s')(s'\Sa' ^) = 2, (S iSaSa' |S) ^
s. s1 s
= Sp(SuSa') = 6a«'4-S(S+1H25+l)=^»l. E.42)
3 2
так как 5 == ]/2. Отсюда получаем
X U l«k @) P>! p2 (E) f (E) [1 - / (?)] d?. E.43)
Ho J
-ЛГ-^, E.44)
что непосредственно следует из вида функции f(E):
Поэтому f(?) [1 —/.(?)] имеет резкий пик (рнс. 5.3) при Е « ?,,
Спин-решеточная релаксация и сужение линий
171
Поскольку /@)=1, /(оо)=0, а функция Д?)[1--/(?)]
имеет пик только внутри интервала порядка kT, эта функция
близка к 6-функции, если только другие функции под интегралом
медленно меняются в этом интервале, т. е.
E.45) ')
E.46)
Заметим, что Wmn пропорционально температуре Т. Этот
факт имеет простую физическую интерпретацию. Совершая
кТ
f(E)\l-f (?I =Ш(Е- EF).
Используя этот результат, мы окончательно получаем
\/
X
/\
I,
Рис. 5.3. Функции /(?), 1-/(?) и /(Е)[1 -/(?)]-
Сплошной линией изображена функция I lE)ll — nF.)\.
ход, ядра передают электронам очень незначительную энергию
по сравнению с kT. Поэтому большинство электронов не может
принять участие в релаксации, так как близкие по энергии со-
') Равенство E.45) легко получить. Пусть С (?)—медленно меняющаяся
функция времени. Тогда, поскольку функция /(?) [1—/(?)] не р.авна нулю
лишь внутри интервала kT вблизи точки Ер, можно разложить G{E) в сте-
пенной ряд в окрестности Ef:
(E~EFf
21
Таким образом,
OO
\ G(E)f(E)ll-f(E)]dE=G(Ep) J f (E) [1 - /
F-F
dE +
Первый член, согласно E.44), дает G{EF)kT. Второй равен нулю, так как
подынтегральная функция нечетна относительно Е — EF, а третий член дает
172 Глава 5
стояния, в которые они могут переходить, заполнены. Участвует
в релаксации лишь небольшая часть электронов, относящаяся
к определенной части распределения. Число этих электронов
пропорционально ЬЛ.
Выражение E.46) можно написать в виде
а
где величина аоо не зависит от ядерных состояний п и т. Если
имеется не одно, а несколько ядер, то можно показать [2], что
Wmn принимает вид суммы по индексам i и j ядер N (i, j =
= 1.2, ..., N):
Wmn = Latl L (m I /lo I n) (n | I,a | ra), E.48)
l.l a
где ац = aoo при t=/, а а/,- при ?=^/ быстро уменьшаются с
увеличением расстояния между ядрами i и /. Эти члены возни-
кают вследствие размазанности волновой функции электрона по
многим ядрам, так что не одно, а много ядер участвует в рас-
сеянии электрона из данного начального состояния в данное ко-
нечное состояние.
Пользуясь нашей формулой для 7\ и выражением E.47), на-
ходим
1 1 т.п. а
-#я— — МОП *К" ^т о ' ==Л
J1 х \ р*
т
L (™ I W> Ia] I п) (я | [Ж /а] | т) L SP t^. ^al2
Qqo m, n. a Ooo а=дг. |/, z
E.49)
Подобное выражение получается и при использовании выраже-
ния E.48). Важно отметить, что здесь нет необходимости поль-
зоваться явным видом собственных функций и собственных зна-
чений, достаточно выполнить диагональное суммирование в ка-
ком угодно удобном представлении.
В случае одного спина квантовые числа тип относятся к
2/ -\-1 собственным состояниям оператора /2. Тогда, учитывая
E.50)
вклад, пропорциональный (kTK, что видно при замене переменной интегри-
рования Е на х ев E/kT. Если пренебречь третьим и более высокими членами
Fизложения, то результат совпадет с тем, который получается при замене
A—/) на kTb(E — Ef). Поправка по порядку величины меньше, чем
(kTIEJ. Точное значение интеграла зависит от вида функции G(?).
Спин-решеточная релаксация и сужение линий 173
и
Uг. 1х] = Ну И Т. Д., E.51)
находим
? Sp [Ж, /а]2 = - ч1&Н1 Sp (Рх + Ру),
E.52)
а поскольку
получаем
Z SP \Ж, /J*
- = -2, E.53)
7Г = "оо =» т-я3^ Y« < I""«@) 12>2^ р2 (?^) *г- E-54)
Величина (|Ык@) l2)^, которая входит в это выражение,
имеется также в выражении для найтовского сдвига АН/Н:
^^^- E-55)
Следовательно, можно использовать E.55) для оценки (| Uk@) \2)ef',
в результате получим
Г) = l^ J "SF ^F- E-56)
Для ферми-газа невзаимодействующих спинов можно показать,
что %se определяется выражением
П = ^Ро(Ер), E-57)
где индекс нуль у %s и p(EF) соответствует приближению не-
взаимодействующих электронов. В этом приближении получаем
соотношение
которое обычно называют соотношением Коррингп по имени ав-
тора, впервые его опубликовавшего [3]. Это соотношение очень
174
Глава 5
удобно использовать для того, чтобы по измеряемым значениям
найтовского сдвига находить времена спии-решеточной релакса-
ции. Более точное соотношение получается из E.56) и E.57) и
имеет вид
Время Th входящее в соотношение Корринги, представляет
собой только один вклад во время релаксации, а именно вклад,
обусловленный взаимодействием ядер с магнитными моментами
электронов в s-состоянии. Поэтому можно ожидать, что экспе-
риментальное значение Тх будет меньше теоретического. В связи
с этим интересно рассмотреть таблицу, составленную Пайнсом
[4] (табл. 5.1). В табл. 5.1 приведены экспериментальные зна-
Таблица 5.1
Экспериментальные и теоретнческие значення Г, (в мс)
Экспериментальное
значение
Значение Коррннги
Значение Пайнса
Li
Na
Rb9S
Си
AI
150+5
15,9+0,3
2,75 ±0,2
3,0 ±0,6
6,3 ±0,1
10,3
2,1
2,3
5,1
232
18,1
2,94
4,0
6,5
чения Т\, значения, вычисленные с помощью соотношения Кор-
ринги E.58), и значения, вычисленные с помощью соотношения
E.59) с использованием полученных Пайнсом теоретических ве-
личин х'/Хо и 9Q(EF)/p(EF).
Мы замечаем, что значения Т\, вычисленные с помощью со-
отношения Корринги, всегда меньше экспериментальных значе-
ний. Это несоответствие нельзя отнести за счет других релакса-
ционных процессов, так как если их учесть, то теоретическое зна-
чение 7\ будет еще меньше, чем значение, вычисленное с по-
мощью соотношения Корринги, и несоответствие будет еще
больше. С другой стороны, значения Т\, полученные Пайнсом на
основе учета взаимодействия электронов друг с другом, больше,
чем экспериментальные значения. Расхождение между значе-
ниями Пайнса и экспериментальными значениями, возможно,
является мерой вклада других релаксационных процессов, кото-
рые здесь не учитывались.
Спин-решеточная релаксация и сужение линий 175
§ 4. Матрица плотности. Общие соотношения
Как отмечалось выше, понятие спиновой температуры приме-
нимо не всегда. Теперь мы рассмотрим метод исследования,
очень полезный в тех случаях, когда понятие спиновой темпера-
туры не применимо, — метод матрицы плотности. Особенно хоро-
шее обсуждение метода матрицы плотности можно найти в кни-
ге [5].
Этот метод имеет также то преимущество, что он позволяет
рассмотреть процессы как продольной, так и поперечной релак-
сации (релаксации /г и 1Х, 1У). Он особенно пригоден для иссле-
дования в тех случаях, когда резонансная линия сужена за счет
движения ядер. Метод матрицы плотности применим также
к широким спектральным линиям; в этом случае он может быть
использован для альтернативного вывода формулы для Ти при-
веденной в § 3. Как мы увидим ниже, метод матрицы плотности
представляет собой просто вариант обычной нестационарной тео-
рии возмущений в наиболее удобной форме.
Начнем с рассмотрения системы, описываемой волновой фун-
кцией W в некоторый момент времени, и поставим вопрос о том,
каково среднее значение (Мх} некоторого оператора, например
оператора х-составляющей намагниченности Мх. Имеем
(Мх) = (??, MXW). E.60)
Разложим теперь функцию ЧР" по полному набору не зависящих
от времени ортонормированных функций н„:
Ф = Еспи„. E.61)
п
Если ЧР" изменяется во времени, то с„ также изменяются во вре-
мени. Используя функции ип, получаем
(Мх)= Z c*mCn{m\Mx\n). E.62)
п, m
Если изменить волновую функцию, то изменится и <МЖ>, так как
коэффициенты с*тсп станут другими, а матричные элементы
(т\Мх\п} останутся прежними. Соответственно для данной фун-
кции W при вычислении средних значений разных операторов
матричные элементы различны, а коэффициенты с'тсп остаются
теми же. Коэффициенты спс'т удобно представлять в виде ма-
трицы. Заметим, что для вычисления какого-либо наблюдаемого
значения необходимо знать или все с„, или все произведения
спс"т. Однако, поскольку для вычисления наблюдаемых свойств
системы всегда желательно иметь коэффициенты с в виде произ-
ведений, знать произведения более полезно, чем знать отдель-
ные коэффициенты с.
176 / .шва 5
Магрипу спс"т можно считать некоторым оператором Р, опре
деляемым своими матричными элементами:
E.63)
Пользуясь E.63), мы можем записать
(Мх) =Т,{п\Р\т)(т\Мх\п). E.64)
п, т
Результат действия оператора Р на функцию ит можно пред-
ставить в виде
Ptim^YjanU-n, E.65)
ti
поскольку функции ип составляют полный набор. Как обычно,
значения а„ находим, умножая обе стороны слева на и*п и ин-
тегрируя:
^dx = {n\P\m). E.66)
Отсюда
Рит = Т1ип(п\Р\т). E.67)
п
Аналогично получаем
Мхип = ^ит(т1Мх\п). E.68)
т
Следовательно,
РМхип = YJPum(m\Mx\n)='Z Un,{n' \P\m)(m\Mx\n) E.69)
т т, п'
и, таким образом,
(«' | РМХ | п) = ? (п' IР | т) (т\Мх\ п). E.70)
т
Пользуясь E.62), имеем
(Мх)= Е (п\Р\т){т\Мх\п) =
т, п
= I (п IРМХ | я) - Sp (PAf,,) = Sp (AJXP). E.71)
Заметим также, что Р — эрмитов оператор. Докажем это. По
определению, эрмитов оператор Р должен удовлетворять соотно-
шениям
и'пРит dx s ^ (Pun)* um dx = ( J *4/>«« rft)*, E.72)
или
r. E.73)
Спин-решеточная релаксация и сужение линий 177
Но
(п | Р | /л) = спс'т, (т\Р\п) = стс'п, E.74)
и, следовательно, соотношение E.73) выполняется.
Часто приходится иметь дело с задачами, в которых необхо-
димо вычислить среднее значение по ансамблю систем. В этом
случае матричные элементы спс*т меняются от системы к си-
стеме, поскольку они имеют различные волновые функции, но
матричные элементы (m|Mx|n) одинаковы. Обозначая чертой
усреднение по ансамблю, мы можем написать
п, т
E.75)
Величины спс*т образуют матрицу, которую мы назовем «ма-
трицей плотности». Будем рассматривать ее как матрицу опе-
ратора р, определяемого соотношением
спс*т = (п\Р\т). (Б.76)
Поскольку Р — эрмитов оператор, очевидно, что р — также эрми-
тов оператор. Теперь вместо E.64) имеем
Ш = I(n|pM(m|MJn) = Sp(pMx) = Sp(M*p). F.77)
п, т
В дальнейшем для упрощения обозначений мы будем опускать
черту, обозначающую усреднение по ансамблю; при этом, конеч-
но, нужно помнить, что всякий раз, когда используется символ
р, предполагается усреднение по ансамблю.
Волновая функция W, описывающая рассматриваемую си-
стему, конечно, изменяется со временем. Поскольку функции ип
не зависят от времени, зависимость от времени должна содер-
жаться в коэффициентах сп. Легко найти дифференциальное
уравнение для коэффициентов сп, содержащее гамильтониан си-
стемы Ж, поскольку
-J^j—MV, E.78)
откуда, пользуясь E.61), можно получить
Уравнение для определенного коэффициента, например Сн, мо-
жно найти, умножая обе стороны на и% и интегрируя:
178 Глава б
Это уравнение представляет собой хорошо известный исходный
пункт нестационарной теории возмущений. Пользуясь уравне-
нием E.79), находим дифференциальное уравнение для матрич-
ных элементов оператора Р:
ku [n\m\m)-{k\m\n) cnc'm\= jr (k IРЖ-ЖР I m). E.80)
Здесь в последнем равенстве использовано соотношение E.70).
Уравнение E.80) можно записать в операторной форме
-§- = |[Л^]. E.81)
Это уравнение очень похоже на уравнение B.31) для производ-
ной по времени от оператора наблюдаемой величины (за исклю-
чением другого знака в правой части).
Если мы выполним усреднение по ансамблю на различных
этапах вывода E.80), считая гамильтониан Ж одинаковым для
всех членов ансамбля, то найдем уравнение для матрицы плот-
ности р. Поскольку при усреднении Р просто заменяется на р,
уравнение для р имеет вид
l-=f[P. Ж\. E.82)
Матрица плотности представляет собой квантовомеханиче-
ский аналог классической плотности точек в фазовом простран-
стве, а уравнение E.82) является квантовомеханической формой
теоремы Лиувилля, описывающей изменение плотности со вре-
менем в фиксированной точке фазового пространства.
Если Ж не зависит от времени, то можно получить формаль-
ное решение уравнения E.82) в виде
р (/) = e-iim тр @) еда> ж, E>83)
В представлении функций ип, являющихся собственными функ-
циями гамильтониана Ж, найдем, например,
(ft | р (/) |т) = J u*ke~m)m9 @)е<"*> mumdx =
E>84)
Воспользовавшись тем, что Жит = Етит, а также разложением
в степенной ряд экспоненциального оператора для зависящего
ог времени матричного элемента, выраженного через матричный
Спин-решеточная релаксация и сужение линий 179
элемент при t = О, получим
[k | р @ ] m) = e(m <*»-**>' (k | p @) | m). E.85)
До сих пор мы говорили о матрице плотности, не обращаясь
к явному виду оператора р. Для конкретности теперь сделаем
это. Возьмем, например, спиновую систему, находящуюся в со-
стоянии теплового равновесия при температуре Т. Примем так-
же, что наши базисные состояния и„ являются собственными со-
стояниями гамильтониана задачи Жо. Тогда населенности соб-
ственных состояний задаются множителями Больцмана, тем са-
мым определяя диагональные элементы р:
CmCm — g ' E.86)
где, как обычно,
Если написать
то мы имеем
cmcl^\cm || cn\el <e»-e»>. E.87)
Обычно в статистической механике предполагается, что фазы
<Хп статистически независимы от амплитуд |с„| и, кроме того,
что ат или ап принимают все возможные значения с одинаковой
вероятностью. Эта гипотеза, называемая гипотезой случайных
фаз, приводит к тому, что все недиагональные элементы в E.87)
обращаются в нуль. Если, например, вычислять среднюю намаг-
ниченность, перпендикулярную постоянному полю, для групп не-
взаимодействующих спинов, как это делалось при выводе выра-
жения B.19), то обращение в нуль недиагональных элементов р
привело бы к исчезновению поперечных составляющих намагни-
ченности, что и должно быть, конечно, при тепловом равновесии.
Вообще из соотношения E.85) видно, что недиагональные эле-
менты р гармонически осциллируют со временем. Если они не
равны нулю, то должно существовать некоторое наблюдаемое
свойство системы, которое осциллирует со временем в соответ-
ствии с E.85). Но тогда не будет истинного теплового равновесия,
поскольку предполагается, что при тепловом равновесии все
свойства системы не зависят от времени. Следовательно, необхо-
димо принять, что все недиагональные элементы обращаются в
нуль. Однако из соотношения E.85) (которое применимо в слу-
чае, когда базисные функции являются собственными функциями
гамильтониана) видно, что если недиагональные элементы обра-
щаются в нуль в какой-либо момент времени, то они равны
нулю все время,
180 Глава 5
Таким образом, имеем
{n\p\m) = ^p-e-Enlk\ E.88)
Следует заметить, что оператор р занимает особое положе-
ние, отличающееся от большинства других операторов, таких,
как, например, оператор импульса. Последний в отсутствие маг-
нитного поля всегда равен hV/i. В то же время матрица плотно-
сти в данном представлении может быть определена совершенно
произвольно; необходимо лишь, чтобы выполнялись следующие
условия: матрица плотности должна быть эрмитовой, ее диаго-
нальные элементы должны быть больше нуля или равны нулю,
а их сумма должна быть равна единице. Следовательно, опера-
тор р заранее не известен. Однако в некоторых случаях матрич-
ные элементы (n|p|m) могут быть получены очень просто из
определения оператора р. Если это невозможно, то для вычисле-
ния свойств системы можно пользоваться операторным методом.
Поставим теперь вопрос: какой оператор будет давать матрич-
ные элементы E.88) с учетом того, что функции ип являются
собственными функциями Mq. Пользуясь тем, что
т E.89)
(это можно доказать, разлагая экспоненты в ряд), легко заме-
тить, что р имеет следующий явный вид:
p = _Le-%/fer. E.90)
Воспользуемся теперь выражением E.90) для вычисления
среднего значения некоторой физической величины. Например,
предположим, что имеется ансамбль не взаимодействующих друг
с другом спинов со спином /, на которые действует постоянное
внешнее поле. Тогда Жъ имеет вид гамильтониана для одного
спина
Жо=-УпПНоГг. E.91)
Проиллюстрируем применение матрицы плотности на примере
вычисления среднего значения z-компоненты намагниченности
<Afz>. Имеем
<Ж> = Sp (Mzp) = -J Sр Щ*-*-*'). E.92)
В приближении высоких температур можно разложить экс-
поненту, оставляя только первые члены разложения. Пользуясь
тем, что Sp Мг = 0, получаем
Спин-решеточная релаксация и сужение линий 181
В предельном случае высоких температур Z = 2/+ 1. Так как
Sp /| = '/г/ (/ + 1) B/ + 1), среднее Щ будет равно
(Мг)='п 3feV 'И*. E.94)
В этом выражении мы узнаем закон Кюри для намагниченности.
Следовательно, метод матрицы плотности представляет собой
удобный и компактный способ вычисления равновесных свойств
системы.
Очень часто гамильтониан состоит в основном из не завися-
щей от времени части Жо и малой добавки Ж\(г), зависящей от
времени. В этом случае уравнение движения для матрицы плот-
ности имеет вид
Если бы добавка <3#i была равна нулю, то решение уравнения
E.95) имело бы вид
р (t) = е-(*/л> 3Cotp @) eu/h) aca% E.96)
Определим теперь величину р* (звездочка не имеет смысла ком-
плексного сопряжения) с помощью соотношения
р (t) = e-tf/ft> «p* до ey/ft) 3s,tm E 97)
Сравнивая E.96) и E.97), мы видим, что если Ж\ равно нулю,
то величина р* должна быть постоянной. (Заметим, кроме того,
что р* совпадает с р при t = 0.) Тогда в случае малой величины
Ж\ можно ожидать, что р* медленно изменяется со временем.
Подставляя E.97) в левую часть уравнения E.95), получаем
дифференциальное уравнение для р*:
- х [Зво, Р] + е-{|/*> «¦' -^Г *т *' = Т fP> ^о + Жх]. E.98)
Заметим, что коммутатор р с Жо сокращается в обеих частях
уравнения. Тогда, умножая слева на ex\>(i2$ot/ti) и справа на
ехр(—Uffiot/h) и вводя величину Ж\, определяемую соотноше-
нием
Ж = #'х'^,е-'«*(, E.99)
из E.98) получаем
^==т[р*,Ж@]. E.100)
Из E.100) мы видим, что, как уже указывалось, оператор р*
будет не зависящим от времени, если гамильтониан Ш\ равен
нулю.
Преобразование оператора Зв\, определяемое соотношением
E.99), является каноническим, а новое представление, связанное
182 Глава 5
с ним, называется представлением взаимодействия. Рассмотрим
связь между р и р*, используя разложение волновой функции Ч*
в ряд в виде
Ч' = ?апе~т)Е»'ип F.101)
вместо разложения
Ч^Еси,,. E.102)
п
Здесь Utt и Еп — собственные функции и собственные значения
гамильтониана Жо- Если гамильтониан Ж\ равен нулю, то коэф-
фициенты ап постоянны во времени. Покажем теперь, что апа*т
равно просто (п|р*|/п). Вначале заметим, что, заменив р@) иа
р* в выражениях E.83) — E.85), найдем
(и | р* | т) = ет) <-Еп~Ет)' (п | р | /и). E.103)
Поскольку выражения E.101) и E.102) дают одну и ту же
функцию W, имеем
г, = ^г'' F.104)
Отсюда
а^ = «;/й)(?»-У!. E.105)
Сравнивая E.105) с E.103), получаем
п (п\(>*\т), E.106)
что и требовалось доказать. Так же просто связаны между собой
(п\Ж\\т) и (nl^ijm). Аналогично тому как мы получили из
E.83) выражение E.85), найдем
(п| Ж \т) = ^ ы»е<'/А>ж15&,е-<«« »'«„их =
«-««"«(««-^'(ni^im). E.107)
Теперь приступим к решению уравнения движения E.100)
для р*. Интегрируя по t от t = 0, получаем
t
р* (/) = р* @) + -1 J [р« (О, 5К @1 Л'- E.108)
о
Выражение E.108) не является решением, так как величина
p*(t') под интегралом неизвестна. Найдем приближенное реше-
ние, заменяя р*(О его значением при t = 0, т. е. р*@). Тогда
имеем
t
Р* (t) = Р* @) + i J [р* @), Ж @1 <W. (Б. 109)
о
Спин-решеточная релаксация и сужение линий 183
Можно улучшить приближение с помощью итерирования, под-
ставляя вместо р*(/') в уравнение E.108) выражение E.109).
Найдем
Р* @=Р* @)+ тг \ [(р* @) + х \ [р* @), Ж\ (Г)] <U"J. Ж\ (О
тJ \ \ Нр* №)•ж О!» ^!
о и
\ \
о и
Этот процесс можно продолжить. Поскольку каждая итерация
добавляет член, содержащий Ж\ в степени на единицу более вы-
сокой, последовательное итерирование приводит к разложению
по все более высоким степеням взаимодействия Ж\. Для наших
целей не понадобятся члены выше второй степени. В действи-
тельности удобнее вычислить производную от р*. Дифференци-
руя выражение E.110), имеем
t
E.111)
Важно отметить, что выражение E.111) совершенно эквивален-
тно выражениям, получаемым во втором порядке обычной не-
стационарной теории возмущений. Однако, вместо того чтобы
определять о„ и ат, мы находим произведения апат, которые
более непосредственно используются при вычислении средних
значений.
§ 5. Матрица плотности. Пример
Поскольку формальные уравнения для матрицы плотности
очень сложны, полезно рассмотреть пример, который сделает
обсуждение более конкретным. Вычислим вероятность перехода
в единицу времени из состояния k в состояние т. Примем, что
в момент времени / = 0 заполнено только состояние k. Это пред-
положение не является необходимым, однако оно обладает тем
преимуществом, что в этом случае (d/dt) (т \ р | т) сразу дает
вероятность перехода в единицу времени.
Таким образом, вначале все сп равны нулю, за исключением
ел. Отсюда следует, что при t — 0 отличен от нуля только один
матричный элемент матрицы плотности (fe|p|fe), который равен
единице. Пользуясь соотношением E.103), находим, что для
184 Глава б
всех man, для которых не выполняется условие п = т = k,
) = 0, E.112)
Взяв матричный элемент между состояниями т и т в E.111) и
воспользовавшись снова соотношением E.103), получим
e7 Z [(
ОС D
- Ж (t) P* @) Ж if') + Ж (t) Ж (О Р* @)] I от) <Й'. E.113)
' Е~ ' ? '
Рассмотрим сначала члены Л и В. Так как тФ k (переход меж-
ду двумя различными состояниями), то, согласно E.112), А и В
равны нулю. Чтобы рассмотреть члены вида С, заметим, что
(от | р* @) Ж. (?) Ж @1 от) = ? (от | р* @) | отО (от' 15»i (О 5*1 @1 от).
т'
Поскольку
(от|рв@)|от0 = 0 О
члены С и F обращаются в нуль, что приводит в результате
к выражению
t
(т\р\т)
о
Ж. @ I k) (k 15»I (O | m)] di'. E,114)
Матричные элементы под интегралом можно преобразовать с
помощью соотношения E.107) следующим образом:
(т |Жх (t) | п) = е('/Л) <?т-?п)< (т | 5», (/) |„). E.115)
Введем новые сокращенные обозначения. Определим квантовые
числа т, п и т. д. через соответствующие энергии, измеряемые
в радианах в единицу времени:
^f^m, -f-^fc и т. д. E.116)
Спин-решеточная релаксация и сужение линий 185
С учетом E.115) и E.116) получим
t
?(го | р \m) = -^ J [(m | 5», (О | ft) (ft 15», @ | т) в* <«-» «'-<> +
)в* cm-»f«-«'i] Л'. E.117)
До сих пор наши уравнения совершенно не зависели от вида
возмущения Mi(t). Например, возмущение могло бы синусо-
идально изменяться во времени. В нашем примере примем, что
Ж\ (t) — случайная функция времени. При этом рассматривается
набор ансамблей систем с одинаковыми 3№о и р@). Однако
Ж\Ц) меняется от одного ансамбля к другому (свойства этих
изменений рассмотрены ниже). Следовательно, необходимо
усреднять по ансамблям. Обозначим это усреднение чертой
сверху. Тогда
t
E.118)
Предположим, например, что M\{i) представляет собой диполь-
дипольное взаимодействие ядерных моментов в жидкости. Оно
изменяется со временем вследствие теплового движения в
жидкости. Это движение, вообще говоря, различно в разных ча-
стях жидкости, находящихся при одной и той же температуре.
Кроме того, примем, что средние значения по ансамблю, такие,
как
E.119)
не зависят от / и /' в отдельности, а зависят только от разности
f —*' = т. E.120)
Тем самым предполагается, что
I) E.121)
не зависит от t и является функцией т, а также двух уровней
энергии m и ft. Тот факт, что E.121) не зависит от t, означает
стационарный характер возмущения1). Зависимость E.121) от
т, m и k позволяет определить функцию Gmk (т) в виде
Gmk (т) = (т 15», (/ - т) | k) (ft 15», (/) | m). E.122)
') Можно было бы рассмотреть более общий случай, но это сделало
бы все выводы значительно более сложными.
186 Глава 5
Поскольку M\(i) —стационарное возмущение, имеем
B,(/)|ft) = Gftm(-T). E-123)
Функция Gmk(i) называется «функцией корреляции» для
3e\(t), так как она показывает, насколько функция Ж\ в данный
момент времени коррелирована с ее значением в последующий
момент времени. Для типичного возмущения
(ft I 5», (/)|/и) = 0. E.124)
Если бы Ж\ (t) и Ж\ {t -+- т) были независимы, то можно было бы
усреднить оба множителя в произведении по отдельности и по-
лучить
Gmk (т) = (ft|5»,@|m) (m|5»,(/ + f)|ft) = 0. E.125)
Однако при т = 0
@1 т)|2>0. E.126)
Для реальной физической системы возмущение 3f6\{t) ме-
няется во времени вследствие какого-либо физического движе-
ния. Для значений времени, меньших некоторого критического
времени тс, называемого «временем корреляции», можно прене-
бречь движением и считать, что M\{t) « M\{t + т). Однако для
т > тс значения M\(t-\-x) становятся все менее коррелирован-
ными с 5^i @. и ПРИ достаточно больших т функция Gkm стре-
мится к нулю. Таким образом, Gmk(%) имеет максимум при т = 0
и спадает при |т|>тс, как это показано на рис. 5.4. Функция
Ж\{(), которая имеет определенные выше свойства, будет в
дальнейшем называться стационарной случайной функцией ере-
мени.
Пользуясь этим определением функции Gmk(i), представим
уравнение E.118) в виде
? («I PI m) = -jjr \ \Gmk (т) e~' <«-« * + Gmft (- т) в' («-«1 rfT =
^ J. E.127)
Это уравнение дает скорость изменения (m|p|m) в зависимости
от времени t. Однако если t > xc, то пределы интегрирования
можно продолжить до ± оо, п, таким образом, скорость (d/d/)X
X(wi|p|m) не зависит от времени. В области 0 < t < тс веро-
ятность перехода зависит от времени. Кроме того, очевидно, на-
Спин-решеточная релаксация и сужение линий
187
селенность (т|р|га) уровня т должна быть много меньше еди-
ницы, так как в противном случае это означало бы значительное
изменение начальной населенности (&|р|А), что противоречит
условию применимости теории возмущений.
Будем рассматривать теперь только значения времени, боль-
шие тс, считая при этом, что для них населенность (m|p|m) не
принимает слишком больших значений. Тогда получим
-i-
Wkm, E.128)
где W/tm — вероятность перехода в единицу времени из состоя-
ния k в состояние т.
Рис. 5.4. Вид функции 0т*(т) для типичной физической системы.
Выражение E.128) тесно связано с хорошо известным резуль-
татом нестационарной теории возмущений
где (&|V|/n)—матричный элемент взаимодействия между со-
стояниями k и m, a p(Ef) — плотность конечных состояний. Дей-
ствительно, обращаясь к формуле E.122), можно увидеть, что
Wkm включает произведение двух матричных элементов возму-
щения. В нашем случае уровни энергии строго дискретны, а воз-
мущение имеет частотное распределение, тогда как обычно воз-
мущение монохроматично, а энергетический спектр размазан.
Ввиду указанного сходства с обычной нестационарной теорией
возмущений не вызывает удивления обращение в нуль членов А
и В в выражении E.113), которые включают в себя только один
матричный элемент возмущения.
Интеграл E.128) напоминает преобразование Фурье. Поэто-
му определим величину Jmk(®) соотношением
+00
E.129)
188 Глава б
и запишем обратное соотношение
+ 00
^ иИ^Л». E.130)
Величину /m*(w) можно считать спектральной плотностью ма-
трицы взаимодействия Gm*(r). Следовательно, можно ожидать,
ш~1/хс ш
Рнс. 5.5. Характерная кривая спектральной плотности.
что величина /т* распределена в области частот до со да 1/тс,
как показано на рис. 5.5. Пользуясь определением /тй, можно
написать
Wkm=Jmk{mhrk) , E.128а)
В типичном случае матричный элемент (m\2e\(t)\k) с тече-
нием времени принимает ряд значений. При изменении, напри-
мер, температуры скорость изменения (m\M\(t) \k) может увели-
чиваться или уменьшаться (меняется те), однако ряд значений,
которые пробегает этот матричный элемент, остается неизмен-
ным. В качестве физического примера рассмотрим два ядра, свя-
занные диполь-дипольным взаимодействием, величина которого
зависит от их относительного расположения. Если ядра диффун-
дируют одно относительно другого, то их взаимодействие прини-
мает различные значения. Возможные значения этого взаимодей-
ствия не зависят от скорости диффузии; они зависят только от
радиуса-вектора, проведенного от одного ядра к другому, и от
пространственной ориентации их моментов. Однако время, в те-
чение которого имеет место каждое значение взаимодействия, за-
висит от скорости диффузии. Заметим, что величина
Gmk(O) E.131)
не зависит от тс. Но из E.130) имеем
+ 00
/„*(«) d<o, E.131a)
откуда видно, что площадь под кривой спектральной плотности
остается постоянной при изменении %с. Кривые /m*(w) для трех
Спин-решеточная релаксация и сужение линий 189
различных значений хс показаны на рис. 5.6. Простое следствие
из того факта, что площадь под кривой остается постоянной при
изменении хс, усматривается из рис. 5.6. Если разность частот
m — k равна ©i, то спектральная плотность /mft(toi) для кривой
со средним значением хс будет наибольшей из всех трех при ©i.
Следовательно, вероятность перехода Wkm имеет максимум при
Лл/f
JL
-Длинное Тс
I
&
к^
О со, ш
Рис. 5.6. Кривые /т*(ш) для трех значений времени корреляции те.
При изменении ге плошадь под кривыми остается постоянной; 1т/г (о^) имеет наибольшее
изменении хс. Максимум достигается, когда (т — k)xc « 1, так
как при этом значении тс спектр простирается без существенного
изменения до значения (m — k).
Если Хс <С \/{т — k), то спектр /т*((о) простирается далеко
за частоту перехода. В этом случае часто в хорошем приближе-
нии можно принять
/„*(«-ft) «/„*(()). E.132)
Определим величину а следующим образом:
2 (¦?)/„*(())= J /„*(©) da, E.133)
—оо
где 2(а/те)—ширина прямоугольника с высотой /т*@) и с пло-
щадью, равной площади, занимаемой реальным спектром /т*(и).
Из сделанных замечаний следует, что а да 1. Тогда, объединяя
выражения E.131), E.131а) и E.133), имеем
'т* @) = -gr 2n\{m\^{t)\k)?. E.134)
Затем, используя E.128а) и E.132), получаем формулу
1(т|ЯГ,@|*)Г п «
Wkm~ р -*с> (D.I
которая справедлива при хс <€. l/(m — k).
Поскольку часто можно оценить как средний квадрат вза-
имодействия, так и время корреляции, формула E.135) дает
190 Глава 5
простой способ вычисления вероятности перехода в предельном
случае малого времени корреляции (быстрого движения). Доба-
вим, что для достаточно пологого спектра /т*(со) формула
E.135) приближенно справедлива для всех тс ^ l/(tn — k). Мы
можем воспользоваться этим для грубой оценки максимальной
скорости перехода под влиянием Ж\{() в наиболее благоприят-
ных условиях, которые имеют место при хс « \/{m — k). При-
ближенная формула имеет вид
Kc~ ff. a (m _ щ ¦ ^
До сих пор наше обсуждение относилось к более или менее
произвольному виду взаимодействия Ж\{1). Для конкретности
рассмотрим теперь специальный вид взаимодействия 2/6\(t).
Предположим, что ядерный момент находится во флюктуирую-
щем магнитном поле с х-, у- и z-составляющими. В этом случае
взаимодействие 9в\ (t) имеет вид
5»i @=- v»a \нх (о ix + нв @1У + нг (I) /j =
= -У«Й S Hq{t)Iq. E.137)
q-x, у, z
Тогда
^Z (m |lq| ft) (/г| lq.\m)Hq(t) Hq. (t + т), E.138)
причем Я?(/) меняется от одного члена ансамбля к другому.
Предположим для простоты, что х-, у- и г-составляющие поля
флюктуируют независимо1). Таким образом, значение Нх в не-
который момент времени не определяет значения Ну в тот же
момент времени. Следовательно, принимая это предположение,
нужно оставить в E.138) только члены с q~q'. Введем вели-
чину /^ft(co), определяемую выражением
|(|,|)| \ E.139)
— оо
Тогда имеем
E EЛ40)
Для вычисления }^к (со) необходима информация о физиче-
ских свойствах флюктуирующего поля. Более того, даже если
') Это предположение выполняется во всех случаях, когда среду можно
считать изотропной. — Прим. ред.
Спин-решеточная релаксация и сужение линий 191
такая информация имеется, вычисление функции корреляции
может оказаться слишком трудной математической задачей.
В этом случае часто из общих физических соображений можно
сделать заключение о приближенном поведении функции. В не-
которых простых случаях можно вычислить функцию корреля-
ции, например, если поле Hq(r) принимает одно из двух возмож-
ных значений, причем вероятность перехода от одного значения
к другому не зависит от времени, прошедшего с момента преды-
дущего перехода. Пусть поле Hq{%) принимает значения ± hq,
тогда (см. приложение В) имеем
Hq(t)Hq{t + x) = h2qe-]%Ux\ E.141)
где то — время, которое определяется вероятностью W в единицу
времени того, что #<?(т) скачком переходит от значения + hq
к значению — hq:
~^=2W. E.142)
В нашем примере будем считать это время одинаковым для всех
трех компонент поля. Очевидно, то можно рассматривать как
время корреляции '). Подставляя его в E.139), находим
^r^TT^!- EЛ43)
Тогда для вероятности перехода имеем
Интересно применить эту формулу для вычисления Т\ в случае
спина 'Д. В этом случае, как показано в гл. 1, Т{ определяется
соотношением
^- = 2Wi/2,-i/2. E.145)
Если сильное постоянное поле направлено по оси г, то матрич-
ные элементы между данными состояниями равны
') Заметим, что, хотя мы не дали точного определения времени корреля-
ции, однако, если функция корреляции чадаиа, то всегда имеется строго
определенный параметр (в данном случае т0), играющий роль характерного
масштаба времени.
192 Глава 5
Примем hx = hy = hz\ тогда
hl=-~h% F.147)
где hi = h\ + ft* + А*. Следовательно, поскольку ларморовская
частота соо — tn — k, для 7\ получаем
Г, Vn 3 1+
Вид этой функции показан на рис. 5.7. Характер ее поведе-
ния действительно такой, как предсказывалось выше из общих
соображений, основанных на постоянстве площади под кривой
In г,
inrov
Рис. 5.7. Зависимость Ti от времени корреляции То.
/тл(<о). Минимум этой функции соответствует юото=1. Вычис-
лим минимальное значение Гь пользуясь формулой F.148).
В согласии с F.136) получим
1 1
(м)мии ¦
Если То очень велико, то действие поля Нг проявится только в
статическом уширении линии (в данном случае, поскольку поле
имеет только два дискретных значения, спектр состоит иа двух
линий при *fc Аг); А^ просто связано с шириной линии. В обыч-
ных экспериментах ©о, конечно, известно. Следовательно, зная
ширину линии в жесткой решетке и резонансную частоту, с по-
мощью формулы F.149) можно оценить наибольшую скорость
релаксации за счет флюктуационного взаимодействия, расши-
ряющего линию. Вообще говоря, время корреляции меняется при
изменении температуры образца. Хотя формула F.149) дает ми-
нимальное значение Ти нельзя сказать, при какой температуре
достигается этот минимум, пока не известна температурная за-
висимость то. В заключение отметим, что, измеряя Т\ как функ-
цию температуры, можно получить информацию об изменениях
с температурой тех или иных физических процессов, ответствен-
ных за флюктуации.
Спин-решеточная релаксация и сужение линий 193
§ 6. Теория Блоха — Вангснесса — Редфилда
Обратимся теперь к более общему рассмотрению матрицы
плотности, следуя идеям Редфилда [6], тесно связанным с тео-
рией релаксации Вангснесса и Блоха [7, 8]. Все основные физи-
ческие представления были выдвинуты еще раньше в работе
Бломбергена, Пёрселла и Паунда [9]. Вывод основного уравне-
ния теории Редфилда представляет собой обобщение приведен-
ного в предыдущем параграфе расчета вероятности перехода.
Редфилд показал, что элементы матрицы плотности подчиняются
системе линейных дифференциальных уравнений следующего
вида:
ТГ - Е *«'. и»-*1 b-'-WtV»- E-150)
РР'
где величины /?оа\рр' не зависят от времени1). Наличие зави-
сящих от времени экспонент в этом уравнении приводит к тому,
что существенными оказываются только те члены, для которых
выполняется равенство а — а' = р — р'. Следовательно, урав-
нение E.150) можно переписать в виде
dt '
где штрих у знака суммы означает, что суммируются только те
члены, для которых а — а' = р — {$'. Диагональная часть этого
уравнения (т. е. та часть, которая остается, если положить
а = а', р = Р') имеет ту же форму, что и основное кинетическое
уравнение E.13). Условия, при которых справедливы уравнения
E.150) или E.151), зависят от соотношения между коэффициен-
тами Raa'. рр'» временем корреляции те и величиной интервала
времени At, определяющего «крупнозернистость» времени (для
интервалов времени, меньших At, ничего нельзя сказать о дета-
лях поведения р*). Необходимо, чтобы существовал такой интер-
вал времени At, для которого одновременно должны выполняться
условия
E.152)
->Д*. E.153)
Выполнение условия E.152) позволяет распространить пределы
интегрирования до ± «э, как это сделано при выводе формулы
E.128). При выполнении условия E.153) матрица плотности не
') В целях более компактной записи мы пользуемся обозначением раа»
для элемента матрицы (а|р|а').
7 Зак. 727
194 Глава 5
слишком сильно изменяется за время At, что позволяет приме-
нять теорию возмущений. Поскольку коэффициенты Raa', рр' сра-
внимы с величинами, обратными временам релаксации, эти
условия эквивалентны требованию, чтобы времена релаксации
7*1 и Т2 были много больше хс. Эти условия представляют собой
также условия сужения линии благодаря молекулярному движе-
нию. Читатель, возможно, заметит, что эти условия совпадают
с условиями, которые приведены в гл. 2, § 10, и выполняются,
когда вероятности переходов не зависят от времени. Настоящее
рассмотрение представляет собой обобщение обычной нестацио-
нарной теории возмущений, включающее эффекты когерентно-
сти, связанные с фазовыми множителями в волновой функции.
Большое преимущество уравнения E.151) состоит в том, что
оно приводит к системе простых линейных дифференциальных
уравнений для элементов матрицы плотности, а эту систему в
принципе всегда можно решить. Решение приводит к набору
«нормальных колебаний». Заметим, что здесь много сходства с
уравнением движения, описывающим изменение населенностей.
Кроме того, формулы для Raa', pp', которые дает теория Редфил-
да, позволяют выразить времена релаксации через величины,
связанные с атомными свойствами.
Прежде чем перейти к выводу уравнений E.150) и E.151),
заметим, что есть два пути использования этих уравнений. Пер-
вый путь состоит в том, что решается уравнение и находится по-
ведение каждого элемента матрицы плотности, а затем нахо-
дится зависимость от времени интересующей нас физической ве-
личины (например, х-компоненты магнитного момента Мх) с по-
мощью основного уравнения
Щ-Т,Р^^\Мх\а). E.154)
Второй путь заключается в попытке найти дифференциальное
уравнение непосредственно для (Мх}. Для этого выполняются
следующие операции:
E.155)
a, a'
Затем, используя уравнение E.150), находят выражение для
производной dpaa,/dt. Действительно, поскольку
p;a, = e'(a-a'>'paa,, E.156)
то
do* > do
aa " /v * ' "-¦-"' Waa E.157)
Спин-решеточная релаксация и сужение линий 195
Соотношение E.157) позволяет преобразовать уравнение E.150).
Подставляя в него E.157) и пользуясь E.156), получаем
¦%?• = I (а' - а) раа,
Raa'.pP'Ppp- <5Л58>
Р.Р'
Подставляя это выражение в соотношение E.155), находим
^Р—У. {т[Р.»оЬ + ^-«'M-Pea-lKlAfJa). E.159)
Хотя это и не видно непосредственно из E.159), при некоторых
условиях правая часть уравнения E.159) пропорциональна ли-
нейной комбинации величин <Л1Л:(^)>, (My(tI) и (Mz(t)}, что
приводит к системе дифференциальных уравнений, аналогичных
уравнениям Блоха. Если число полученных уравнений меньше,
чем число уравнений для элементов матрицы плотности, то про-
ще рассматривать решение такой системы уравнений, чем ис-
ходной. Этот способ применим в тех случаях, когда релаксаци-
онный механизм и операторы таковы, что в средние значения
операторов входит лишь небольшое число из всех возможных
нормальных колебаний. Такое применение уравнения E.159)
будет проиллюстрировано несколько ниже. Сначала мы рассмо-
трим вывод основного уравнения Редфилда.
Исходным пунктом является выражение E.111) для произ-
водной по времени от р*:
t
-TJr = i IV @), Ж @1 + (тгJ S Ир* @), Жх (/')], Ж @] dt'. E.160)
о
Вычислим матричный элемент между состояниями а и а'. В пра-
вой части оба члена не равны нулю. Рассмотрим первый из них
[*@)Ж@]
(<х| [р'@), ЖШ |аО-^(а| р'@) IPHPI Ж® W) -
-(а|Ж@1Р)(Р1Р*@)|аО. F.161)
Введем теперь понятие ансамбля ансамблей, матрицы плотности
которых совпадают при ? = 0, но возмущения 26\(t) различ-
ны1). Мы примем, что при усреднении по ансамблю Зв\{?) обра-
') Следовательно, наличие внешнего переменного поля не допускается,
т. е. рассматривается релаксация в отсутствие переменного поля. Однако
действие переменного поля легко учесть. Мы обсуднм это в следующем па-
раграфе.
7*
196 Глава б
щается в нуль. Это означает, что 2/в\ (t) в среднем не дает вклада
в сдвиг частоты').
Обсудим это соображение. В общем случае можно ожидать,
что
Ж @ = 1 Hq{t)Kq, E.162)
Q
где К4 — функция спиновых координат, a Hq (t) не зависит от
спина. Например, когда с/в\ (t) представляет собой взаимодей-
ствие флюктуирующего магнитного поля с х-, у- и г-компонен-
тами спина, оно выражается в форме E.162), если х-, у- и г-ком-
понентам сопоставить три значения q. Если Ж\{г) —диполь-ди-
польное взаимодействие двух спинов, то будет шесть значений q,
соответствующих членам А, В, .... F, на которые было разло-
жено это взаимодействие в гл. 3.
Поскольку возмущение стационарно, усреднение Ж\Ц) по
ансамблю эквивалентно усреднению по времени. Вообще, будем
считать, что среднее по времени Hq (t) равно нулю, и поэтому
обращается в нуль и среднее по ансамблю M\(t). Следователь-
но, положим
0, E.163)
где черта сверху означает усреднение по ансамблю. Это значит,
как было замечено выше, что 36\(t) зависит от времени совсем
не так, как внешнее поле при наблюдении резонанса.
На основании E.163) первый член правой части E.160) об-
ращается в нуль при усреднении по ансамблю.
Рассчитаем аналогичным образом матричный элемент меж-
ду состояниями а и а' для второго члена в правой части E.160).
Пользуясь тем, что
(PI Ж(/) IP') = e'»-Mf (PI Xx (t) IP'), F.164)
и полагая
%~*t-t', E.165)
находим
Р.Р'0
(а | Жх @ IP) (P' I 3»i (/
~ Р*ар (Р W - ?) | Р') (Р' I
- (а | Шх (t) |Р) (Р | Я?! 0 - т) | р') ег»'-» гег ««-Ю' р*Р'„'] dr. E.166)
') Если имеется сдвиг частоты, то его можно включить в 2ёо, переопре-
делив Яв\ (<) так, чтобы сдвиг был равен нулю, .
Спин-решеточная релаксация и сужение линий 197
Теперь выполним усреднение по ансамблям с различными 3@i(t),
Мы получим члены вида
t
-}р- $ (а| 30, (/ - *) IP)(P'I 30, (/) |а')е-г(а-р>тег («-Р+В'-»')' dr. E.167)
о
Примем, что среднее
(а | 3», (/ - т) | Р) ф' 13», (/) | а') E.168)
не зависит от t и стремится к нулю, когда х превосходит некото-
рое критическое значение хс. В этом случае, как нетрудно заме-
тить, при временах t, больших хс, верхний предел интегрирова-
ния можно положить равным х = -f- oo.
Теперь определим функцию корреляции Gapa'p' (т) в виде
(т) ^ (а | 30, @ | р) IP' 130, (/ + т) | а')- E.169)
Используя E.162), получаем
G w (т) = 5 (а \К" | Р) (Р' | К"' | а') Я, (/) Hq- (t + x). E.170)
Определим затем спектральную плотность Lqq> (а) взаимодей-
ствия в виде
+ 0О
(t + x)e-™dx. E.171)
Пользуясь тем, что Нq (t) Hq- (t -f-1)— действительная1) и чет-
ная функция х, удобно определить действительную и мнимую
части Lqq'((a):
Re Lqq' (со) = -~ \ Hq(t)Hq'(t-\-x) cos (ax dx^kqq',
EЛ72)
ImL??'(cu) = — \ Я,; (/) Hq- (t"+ x) sin сот dx.
о
Поскольку заметные вклады в выражение E.166) вносят
только те члены, для которых выполняется условие a — а' =
= Р — Р', представим первые два члена в правой части E.166)
') Поскольку Kq — эрмитовы операторы, Нч — действительные величины.
Можно выбрать операторы Kq неэрмитовыми, тогда величины Hq будут ком-
плексными, но Lqq, будут отличны от нуля только в том случае, если q
и q' таковы, что Нq (I) Hq, (I -f т) — действительная функция т.
198 Глава 5
следующим образом:
wZ I {(°1^1р)(р/1^1«/)[^(«
Р.Р' ?.?'
+ kqq. (а' - рО]*1 <«-Р+Р'-а'> <PpV}. F.173)
Последние два члена в выражении F.166) будут иметь вид
i«о к- (р
р.р;
+ р|'а'[(р|Г|рО(а|^|р)^(Р-Р/)]в'(а-е')'}. E.174)
Можно показать, что мнимая часть Lqq- вносит вклад в сдвиг ча-
стоты, соответствующий сдвигу частоты, вычисленному во втором
порядке по статическому взаимодействию. Мы пренебрежем
этим эффектом и оставим только члены, пропорциональные
ReLqq't поскольку они вносят вклад в релаксацию. Таким обра-
зом, МЫ ЗаМеНИМ Lqq' На kqq-.
Аналогично тому как это было сделано выше, определим те-
перь спектральную плотность Jaa'№ (to):
+00
/aa-pp'N= J (aj50i @ I a') (p# I 50i (i +1) |p) e~™ dr. E.176)
Тогда, принимая во внимание E.173) — E.175), получаем
^f e Z Raa>- W'ei (a-a'-p+p/) 'P*PP' @), E.176)
P.P'
где
[' (a' — PO + ^aPa'B' (a — p) —
- fiev Z W (Y - P) - 6aP I V'vP' (Y - P01 • E.177)
v _ v J
Уравнение E.176) связывает dp*/dt в момент времени t> xc
с р* в момент времени / = 0. Это первый член в разложении в
степенной ряд. Чтобы сходимость степенного ряда была хоро-
шей, необходимо предположить, что значение Ррр в момент вре-
мени t мало отличается от значения РвУ в момент времени
t = 0. Это означает, что должен существовать такой отрезок вре-
мени, для которого />тс> но еще можно считать ррр' (t) я» рру @).
Последнее приводит К следующему условию;
J*. E.178)
Спин-решеточная релаксация и сужение линий 199
Важно заметить теперь, что если условие E.178) выполняется,
то в правой части уравнения E.176) ppV(O) можно заменить на
ррр'(/). Тогда уравнение E.176) сведется к дифференциальному
уравнению для р*, из которого можно найти р* с помощью «ин-
тегрирования» по временам настолько более поздним, чем t = О,
что ррр' (/) будет отличаться от своего значения при t = 0. Та-
ким образом, мы приходим к уравнению E.150).
Физический смысл условий применимости состоит в том, что
нельзя получить информацию о развитии системы на отрезке
времени, сравнимом с тс, и что за этот интервал времени матри-
ца плотности не должна заметно изменяться. Практически это
приводит к условию
E.179)
Как мы увидим при более детальном рассмотрении, условие
Тс -С Т2 означает, что каждая резонансная линия «сужается»
благодаря «движению», которое определяет флюктуационный
характер M\{t).
Поскольку
а E.180)
(вероятности переходов изав|3иизрва равны), решение
уравнения Редфилда приводит к одинаковой населенности всех
состояний. Это соответствует бесконечно большой температуре.
Следовательно, уравнение Редфилда не описывает приближения
к равновесию при конечной температуре. Причина этого оче-
видна—ведь в уравнение входят только спиновые переменные
и совершенно не учитывается наличие теплового резервуара (ре-
шетки) . Координаты решетки необходимы для того, чтобы спины
«знали» температуру.
При строгом методе учета решетки в уравнении E.160) ис-
пользуется матрица плотности для общей системы, состоящей
из решетки и спинов. Так как в отсутствие с/в\ спины и решетка
не связаны, можно принять, что матрица плотности равна произ-
ведению спиновой а и решеточной pL матриц плотности. Теперь
основной гамильтониан Жо будет представлять собой сумму, ре-
шеточного и спинового гамильтонианов (которые, конечно, ком-
мутируют друг с другом). Возмущение Ш\ не коммутирует ни с
одним из них, поэтому оно вызывает одновременные переходы в
решетке и в спиновой системе. Таким образом, имеем
р* = оу>. E.181)
Вводя спиновые квантовые числа shs'h решеточные кванто-
вые числа / и /', заменим а на s/ и т. д. Затем примем, что ре-
шетка остается все время в тепловом равновесии, несмотря на
200 Глава 5
спиновую релаксацию. Следовательно,
1 е~ЩШ E.182)
Далее, найдем дифференциальное уравнение для
и просуммируем по /. В результате в предельном случае высоких
температур получим просто модифицированное уравнение Ред-
филда, в котором спиновая матрица плотности а заменена раз-
ностью между а и ее равновесным значением при температуре
решетки а(Т).
Следовательно, можно утверждать, что во взаимодействии
Зв\ решетки со спинами (которое зависит от времени по отноше-
нию к спинам) 1) учет решетки приводит к преобразованию урав-
нения Редфилда к виду
E.184)
где а, а', р, р' — спиновые квантовые числа, а стрр' (Т) — значе-
ние стрр' при тепловом равновесии:
<трц'(Г)=»брр' V-№- E-185)
Р"
Справедливость уравнения E.184) не должна вызывать удивле-
ния, если принять во внимание замечания, сделанные в гл. 1,
относительно достижения теплового равновесия. Заметим здесь,
однако, что данное рассмотрение относится не только к населен-
ностям уровней (диагональным элементам а), но также и к не-
диагональным элементам.
§ 7. Пример применения теории Редфилда
Обратимся теперь к примеру, иллюстрирующему как метод
Редфилда, так и некоторые его простые физические следствия.
Рассмотрим ансамбль не взаимодействующих друг с другом спи-
') 36\ включает как спиновые, так и решеточные координаты. При кван-
товомеханическом описании решетки переменные решетки представляют со-
бой операторы и Эё\ ие включает явно время. При классическом описании
решетки Sei явно включает время. Это очевидно, поскольку взаимодействие
должно зависеть от времени, для того чтобы могли возникнуть переходы
между спиновыми состояниями с различной энергией. Однако взаимодействие
не зависит от времени, если решетка одновременно совершает переходы, при
которых имеет место резонансное поглощение спиновой энергии.
Спин-решеточная релаксация и сужение линий 201
нов, связанных с внешним флюктуирующим полем, различным
для каждого спина. Внешнее поле имеет х-, у- и z-компоненты.
Этот пример обладает многими особенностями системы спинов
с диполь-дипольным взаимодействием. Однако в данном случае
рассмотрение существенно упрощается; более того, оказывается
возможным точно решить задачу о релаксации в пределе очень
малого времени корреляции. В случае диполь-дипольного вза-
имодействия флюктуации дипольного поля возникают благо-
даря реальному движению ядер, например когда имеет место
самодиффузия. Время корреляции соответствует среднему вре-
мени, в течение которого два данных ядра находятся вблизи
друг друга. Эта простая модель дает основные качественные
черты системы с диполь-дипольным взаимодействием, если в ка-
честве времени корреляции взять соответствующее время для
диффузии. В частности, тогда в модели находит отражение важ-
ное явление сужения линии, обусловленного движением, которое
было превосходно объяснено в первоначальной работе Бломбер-
гена, Пёрселла и Паунда [9].
Прежде чем перейти к анализу данного примера, отметим
общие черты, которые проявятся здесь. В конце параграфа эти
простые аргументы будут развиты и будет показано, как исполь-
зовать их для получения количественных результатов.
Следует различать влияние х- и «/-компонент и влияние
z-компоненты поля. Компонента Нг увеличивает или уменьшает
скорость прецессии. Она, так сказать, обусловливает распреде-
ление скорости прецессии. Очевидно, компонента Нг не вносит
вклада в спин-решеточную релаксацию, так как она не изменяет
компоненты намагниченности, параллельной Яо, но Нг вносит
вклад в затухание поперечной компоненты намагниченности,
даже если флюктуации настолько медленны, что эффективно их
можно считать постоянными. В действительности, как мы уви-
дим, именно Нг вносит вклад в ширину линии в твердой решетке.
Явление сужения линии, обусловленного движением, соответст-
вует некоторому типу усреднения результата воздействия Нг,
когда флюктуации достаточно быстры.
Влияние х- и «/-компонент флюктуирующего поля наиболее
удобно рассматривать в системе координат, вращающейся со
скоростью прецессии. Компоненты, флюктуирующие с частотой
прецессии в лабораторной системе координат, можно рассматри-
вать как постоянные в системе координат, вращающейся пер-
пендикулярно постоянному полю. Они могут вызывать изменение
как параллельной, так и перпендикулярной постоянному полю
компонент намагниченности. Первое явление представляет собой
продольную релаксацию с временем релаксации Т\, а второе —
поперечную релаксацию с временем релаксации 7V Очевидно,
эти два процесса тесно связаны между собой, поскольку вектор
202 Глава 5
намагниченности индивидуального спина обладает фиксирован-
ной длиной. Поперечная компонента флюктуирующего магнит-
ного поля будет наиболее эффективна в том случае, если ее
спектр Фурье имеет достаточную плотность на ларморовской ча-
стоте. Как для очень медленных, так и для очень быстрых дви-
жений спектральная плотность на ларморовской частоте будет
мала, однако для движений, времена корреляции т которых по-
рядка 1/соо, спектральная плотность будет максимальна. Следо-
вательно, вклады компонент Нх и Ну в продольную и попереч-
ную скорости релаксации проходят через максимум при изме-
нении т.
Рассмотрим взаимодействие Ж\ (t) вида
Я* @ = ~ УпП I Hg (t) V, E.186)
ч
здесь q = х, у, г и
Я?о = — Ynft#0/2 = ~ *Ы» E.187)
где соо — ларморовская частота. Охарактеризуем собственные
состояния собственными значениями а гамильтониана E.187).
Последние равны частоте со0) умноженной на собственное значе-
ние т оператора /2 (здесь m = I, I— 1 —/). Однако мы
сохраним обозначения а, а', р, р', чтобы получить уравнения,
соответствующие выведенным выше. Матричные элементы
(a\3@i(t) \a') имеют вид
(al^WlaO^-Ynftltf^Hal/Ja'). E.188)
ч
Тогда функции спектральной плотности /ора'р'(со) будут опре-
деляться выражениями
Т) \a!)e-™dx =
+
'|/<rla') \ ЩШ7?Тх)е-^с1х. E.189)
Теперь воспользуемся обозначением fe??'(©), введенным в пре-
дыдущем параграфе:
VH=1 \ HiWHtflt + ^e-t^dT. E.190)
Ясно, что флюктуационные эффекты, время корреляции и т. д. —
рее связано со значениями кц>. Для простоты примем,
Спин-решеточная релаксация и сужение линий 203
флюктуация каждой из трех компонент поля не зависит от дру-
гих, т. е. положим
-т) = 0, если q?=q'. E.191)
Например, это условие выполняется, если при любом значении
Hq компонента Hq- с равной вероятностью принимает значения
\Н„-\ и —\Hq-\. Заметим, что kqq((u) определяет спектральную
плотность на частоте со <7-компоненты флюктуирующего поля.
Итак, предполагая, что условие E.191) выполняется, имеем
W Y
Попытаемся теперь найти релаксацию х-, у- и г-компонент спи-
нов. Чтобы это сделать, воспользуемся вторым способом, опи-
санным в предыдущем параграфе, — способом отыскания диффе-
ренциального уравнения для среднего значения спиновых ком-
понент. Следовательно, будем искать d </r>/d?, где г = х, у, г.
Используя уравнение E.159), находим
т = Е т[р> Жо]™-(а''1г'а)+ZRaa'- вр'рад-(а/'и • а>- ^5-193>
аа' аа'
8В'
Первый член правой части, включающий 5^0, можно преобразо-
вать следующим образом:
? -j [р, Эёо]аа (а'| /г |а) = -jj- Sp \(p3ff0 ~ ^op) /r] =
аа'
={ Sp [p^o/r - Р/Л! = { Sp (p [Жо, IA) = - 1УпНо Sp (p [/„ /r]).
E.194)
Если г — z, то этот член обращается в нуль. Если г = х, то мы
имеем
- 1УпН0 Sp (р [/„ /*]) = - г\„Я0 Sp 0/,р) = + у„Я0 </„>. E.195)
Если г '= у, то мы получим —Yn#o ^*^- Таким образом находим
основной член, входящий в уравнение Блоха и описывающий мо-
мент сил, обусловленный внешним полем:
? f [р, Жо}^ (а' | /г | а) = y» «О X Н0}г. E.196)
аа'
Второй член в правой части уравнения E.193) содержит релак-
сационные члены:
J (а' | /г |«). E.197)
204 Глава 5
Как мы видели, /йш'.вв' состоит из суммы четырех членов [фор-
мула E.177)]. Рассмотрим первый член /ава'В' (а' — Р')- Ис-
пользуя E.192), находим
-^г /_, ^оВо'В' (а' ~~ Р') Рве' (а' I //• I а) =
аа'
аа'
РВ',?
= Y2rt ? Ф' I /, I a') (a' I Uffi IР") *„ («' - П E.198)
а'В'
последнее равенство следует из основных свойств ортогональ-
ности и полноты системы собственных функций |ос) и т. д. Мо-
жно было «опустить» индексы а и Р, просуммировав по ним;
однако нельзя то же сделать с индексами а' и Р', так как они
присутствуют не только в матричных элементах, но и в kqq.
Подобным же образом можно найти выражения для осталь-
ных трех членов в Raa', вр'- В итоге мы получим
2 —Y
2 Rm.. w («' I lr I о) РррY» Е
aa' a» p
ВР' Я
+ У^(Р|
а, р
= \l E (Р1/,1а)(а|Н/„ /,], р]1Р)*„(Р-а); E.199)
а. р
в последнем равенстве использован тот факт, что kQq((a) — чет-
ная функция со. Чтобы продвинуться дальше, нужно теперь кон-
кретизировать г. Сначала рассмотрим г = z. Тогда, поскольку /,.
коммутирует с Iz, последняя строка E.199) при q = z обращается
в нуль. Так как матричные элементы 1Х отличны от нуля только
при Дт = ±1, единственными состояниями (or и Р), связан-
ными оператором Iq при q = x, будут состояния, для которых
| a — р | = соо (ларморовская частота). Поскольку [h, Ix] = Иу
и [1х, 1У] = И г, находим
V? Z (PI/*|a)
SP G,P) - - Vj*« Ы </,>. EЛ99а)
Спин-решеточная релаксация и сужение линий 205
Аналогичным способом получим, что член с q = у равен
-?»^Ы<'г>. E-200)
Окончательно имеем
? Ка'. РИ>мг («' |'. I «)—? [*« Ы + *w Ы] <Л>. E-201)
Р0'
Подставляя в E.193) выражения E.196) и E.201), находим
3/г = V [0> X Н0]г - ?п \kxx (coo) + kyy (coo)] </,). E.202)
Из этого уравнения следует, что </2> релаксирует не к своему
равновесному значению /0, а к значению </2> = 0. Чтобы испра-
вить положение, нужно заменить р на р — р(Т), как это было
показано в предыдущем параграфе. После такой подстановки
</г> релаксирует к своему равновесному значению /о, а уравне-
ние E.202) принимает вид
Чг " У [<!> X НJ, - yl\kxx (О + к„ (соо)][</г) - /0]. E.203)
Очевидно, это — уравнение Блоха с Т\, определяемым выраже-
нием
2[^K) + ^(coo)]. E.204)
Точно так же можно найти релаксацию лг-компоненты. При
этом значение q = х не вносит вклада, а значения q — у и q = z
вносят вклады. При q = у ситуация аналогична той, которая
рассмотрена выше (связываются состояния аир, для которых
I а — р | = ©о) • С другой стороны, при q = z состояния а и 6
совпадают (/2 диагонально), так что а — р = 0. Таким образом,
появляется спектральная плотность Нг на нулевой частоте. В ре-
зультате находим
? *-'• ЭВ'РЭГ КI h I«) - - У1 lkyy Ы + Кг @)] </,), E.205)
РР'
что приводит к уравнению
^— Y.[@ X Щх ~ УЦКу Ы + *гг@)Ш- E-206)
В уравнении E.206) замена р на р — р{Т) не нужна, так как при
тепловом равновесии </*> = 0. Уравнение E.206) и аналогичное
уравнение для </i/>, очевидно, являются уравнениями Блоха и
описывают процесс поперечной релаксации с временем релакса-
ции Т2, которое определяется выражением
Т7 = №><>) +МО)! E-207)
206 Глава 5
Следовательно, рассмотренный механизм релаксации приво-
дит к уравнениям Блоха. Конечно, нельзя ожидать, что в общем
случае для произвольного взаимодействия 36i(f) получатся
уравнения Блоха; в каждом частном случае необходимо специ-
альное исследование для выяснения этого вопроса.
Чтобы продвинуться дальше, необходимо иметь некоторые
сведения о спектральной плотности х-, у- и z-компонент флюк-
туирующего поля. Мы предположим опять, что функция корре-
ляции представляет собой простую экспоненту с одинаковым
временем корреляции т0 для q = х, у, z:
, H,(t)Hq{t + %) =• Я?еч r |/t0. E.208)
Отсюда находим
*«(ffl)e*577kr E-209)
и, используя E.209), получаем
E.210)
Заметим прежде всего, что Т\ как функция т0 проходит через
минимум при cooto^I. Время релаксации Т\ определяется х-
и ^-компонентами флюктуирующих полей на ларморовской ча-
стоте. Если мы пользуемся системой координат, вращающейся с
ларморовской частотой, то этот результат очевиден, так как Т\
соответствует изменению z-компоненты намагниченности. Это
изменение вызывается «постоянными» полями в направлении х
или у во вращающейся системе координат, поскольку во вращаю-
щейся системе координат эффективное поле равно нулю (Ни ко-
нечно, отсутствует). Но «постоянные» поля в направлениях хну
во вращающейся системе координат осциллируют с частотой соо
в лабораторной системе координат.
С другой стороны, затухание х-компоненты намагниченности
должно быть обусловлено «постоянными» полями в направле-
ниях у и z во вращающейся системе координат. Поскольку оси z
в лабораторной и вращающейся системах координат совпадают,
то в лабораторной системе координат этим «постоянным» полям
соответствует действительно постоянная z-компонента и флюк-
туирующая с ларморовской частотой у-компонента. Заметим, что
в предельном случае очень быстрого движения ((оото <С 1) и при
условии, что флюктуирующее поле изотропно, т. е.
г?х=~Н\ = Н\, E.211)
времена релаксации Т\ и Т2 равны. Физически в нашей модели
этот результат означает, что для очень малого времени корреля-
Спин-решеточная релаксация и сужение линий 207
ции спектральная плотность флюктуирующего поля представляет
собой «белый шум» по отношению к ларморовской частоте, и по-
этому по направлениям х, у и г во вращающейся системе коор--
динат флюктуирующие поля будут эквивалентны.
Два члена в выражении для Т2 имеют простой физический
смысл. Один член зависит от Нг. Он представляет собой расфа-
зировку спинов, обусловленную размазыванием скоростей пре-
цессии за счет того, что Нг может усиливать или ослаблять поле
Но- Этот член можно получить из простых соображений, которые
приведены ниже. Второй член, как мы увидим, представляет со-
бой результат уширения уровней энергии, обусловленного конеч-
ным временем жизни спина в данном энергетическом состоянии.
Рассмотрим теперь простой вывод первого члена в выраже-
нии для Т2. Предположим, что поле имеет значение \Нг\ в тече-
ние времени т. Затем оно случайным образом меняет свое зна-
чение на ±|#z|. Такой вид изменения поля вполне реален, по-
скольку движение ядра относительно своих соседей носит диф-
фузионный характер. За время т избыток угла спиновой прецес-
сии бф относительно нормальной прецессии будет равен
бф = ±у„|#2|т. E.212)
После п таких интервалов т средний квадрат расфазировки Дф2
будет определяться выражением
Дф2 = пбф2 = пу^Н^т2. E.213)
Для числа интервалов п за время t имеем просто
п = 4- E.214)
Если определить Т2 как время, за которое группа спинов, нахо-
дящихся в фазе в момент времени t = 0, расходится по фазе
приблизительно на 1 рад, то мы получим
ИЛИ
JL = Y2#2T. E.216)
Мы замечаем, что чем меньше т (чем быстрее движение), тем
уже линия резонанса. Поэтому это явление называется сужением,
обусловленным движением1). Таким образом, движение сужает
резонансную линию, так как в результате движения данный спин
в образце испытывает воздействие многих полей Я2, одни из ко-
') Слово «движение», конечно, относится к перемещению ядра, а не
изменению ориентации спина, • ¦ '
208 Глава 5
торых вызывают опережение по фазе, а другие — отставание.
Следовательно, расфазировка происходит вследствие случайных
малых скачков фазы, каждый из которых много меньше 1 рад.
В противоположном случае, когда движения нет, каждый
данный спин испытывает воздействие постоянного локального
поля. Его прецессия будет или более быстрой,, или более медлен-
ной, чем средняя, и расфазировка группы спинов возникает
вследствие непрерывного накопления положительной или отри-
цательной фазы.
Рассмотренное явление резко отличается от уширения спек-
тральной линии при столкновениях. В этом случае фаза колеба-
ния меняется при каждом столкновении. Так как частота не
меняется между столкновениями, фазовая память сохраняется
все время, за исключением момента столкновения. Поскольку
каждое столкновение ведет к потере фазовой памяти, более ча-
стые столкновения приводят к более короткой фазовой памяти
и линия уширяется. В случае же сужения линии, обусловленного
движением, в момент изменения поля Нг от одного значения к
другому фаза не меняется, так как поле изменяется очень быст-
ро; фазовые изменения происходят в течение времени, когда Нг
постоянно. Следовательно, быстрое движение уменьшает потерю
фазовой памяти в каждый интервал времени.
Мы рассмотрели один член в выражении для Г2. Другой член,
о
включающий Ну, очевидно, имеет точно такую же зависимость
от то, как выражение для спин-решеточной релаксации. Его мо-
жно интерпретировать как уширение линии, обусловленное ко-
нечным временем жизни спина в некотором собственном состоя-
нии вследствие спин-решеточной релаксации. Это время жизни
конечно, так как поле в направлении у вызывает изменение
z-компоненты намагниченности. По порядку величины это уши-
рение, обусловленное конечным временем жизни, составляет
Д? = -?. E.217)
или
Лео = —г- = -^-.
Считая флюктуирующее поле изотропным, в нашем примере
получим
T—F+ТГ- E18)
где \рГг2— уширение, обусловленное размазанностью z-компо-
ненты поля. Величину 1/Гг часто называют секулярным ушире-
нием, а член l/2Ti—несекулярным уширением или уширенцем,
обусловленным конечным временем окцзни. В более общем слу->
Спин-решсточная релаксация и сужение линий
209
чае 1/27") заменяется на 1/71, причем 71 (несекулярное ушире-
ние) связано с 7\.
Как мы уже говорили, можно заметить, рассматривая секу-
лярное уширение, что при уменьшении то время релаксации 7г
возрастает, или, иначе говоря, линия сужается. С другой сто-
роны, при возрастании то (замедлении движения) до значений
то « Т2 условия применимости уравнений Редфилда нарушают-
ся. При еще больших значениях то уравнения Редфилда приме-
Рис. 5.8. Зависимость секулярного (Т{) и иесекулярного G уширения от То.
Для приведенною в тексте примера Т1 ¦=27" .
нять нельзя. Наибольшее значение то, при котором применима
еще теория Редфилда, равно то = Т2, или
т. е.
о» E-219)
E.220)
Как мы видим в нашей простой модели, это как раз то значение
то, при котором типичный спин набирает избыточную фазу, рав-
ную 1 рад, до того как поле изменится. При больших значениях
то расфазировка спинов наступает раньше, чем происходит скач-
кообразное изменение поля. Это означает, что расфазировка не
представляет собой случайного процесса. При этом ширина лиш-
ний не будет зависеть от частоты скачков и, следовательно, от
температуры и будет представлять собой ширину линии в твер-
дой решетке.
Два вклада в ширину линии (секулярный и несекулярный)
представлены на рис. 5.8.
Те же общие черты можно обнаружить при анализе других
механизмов релаксации. В действительности при релаксации
могут возникнуть одновременно несколько переходов. При этом
становится важным значение спектральной плотности при ча-
стоте, отличной ОТ 0 и (Од. Часто может играть роль частота 2щ,
210 Глава 5
Например, если релаксация вызвана диполь-дипольным взаи-
модействием спинов, то члены Е и F (см. гл. 3), включающие
произведение двух операторов, переводящих спин на более вы-
сокий или на более низкий уровень, связывают состояния, отли-
чающиеся по энергии на 2/коо-
Из приведенных формул видно, что, измерив Т\ и Т2, можно
определить т0. При изменении температуры меняется тепловое
движение и, следовательно, характер флюктуации взаимодей-
ствия 9e\{t). Поэтому, пользуясь резонансом, можно изучать
температурную зависимость т0. Часто для теплового движения
существует «барьер» (энергия активации Е), так что
то^т^, E.221)
где Too — значение то при бесконечно высокой температуре. Тем-
пературная зависимость Т\ или Т2 позволяет найти значения Е
и Too. Примером могут служить исследования Эндрю и Идеса,
выполненные на молекулярных кристаллах. Другими примерами
являются изучение Голкомбом и Норбергом [10] самодиффузии
в щелочных металлах и последующее изучение Сеймуром [12] и
Спокасом и др. [11] самодиффузии в алюминии. Интересно, что,
используя резонанс, они смогли измерить скорость самодиффу-
зии как в литии,' так и в алюминии (не имеющем радиоактив-
ного изотопа, который можно было бы использовать в обычном
методе изотопных индикаторов).
§ 8. Влияние внешнего переменного поля
До сих пор в зависящее от времени взаимодействие 36\{Ц
не входило внешнее переменное поле. Теперь мы примем, что
такое поле наложено и в гамильтониан входит соответствующий
член 5#г@- Учет переменного поля можно провести прямым пу-
тем, как сделал Блох. Для этого в выражении E.160) заменим
просто ^1@ на 3%"i(t) + d@2(t). Тогда получим
E.222)
При усреднении по ансамблю вклад от Ж\(()в первый член пра-
вой части обращается в нуль. Поэтому перейдем к рассмотрению
второго члена. Вообще говоря, вклад от Ж> (t) в первый член не
равен нулю, так как 3ffi(t)одинаково для всех членов ансамбля.
Если 3@l(t) не слишком велико, то можно ожидать, что доста-
точно учесть член первого порядка по Ж\, пренебрегая ролью
"*** под интегралом. Физически это приближение сводится к
Спин-решеточная релаксация и сужение линий 211
тому, что мы полагаем
где (dp*/dt)X2 — скорость изменения р*, обусловленная только
3%>2, а (ф*Д#) релакс — скорость изменения р*, когда Эё2 равно
нулю. Следовательно, здесь не учитываются нелинейные эффек-
ты взаимодействия Ж2.
При каких условиях можно считать справедливым это при-
ближение? Ответ состоит в том, что ни одно из возмущений не
должно слишком сильно изменять р* за время t (верхний пре-
дел интегрирования), так как присутствие членов, содержащих
Жг под знаком интеграла, означает, что Ж\ действует на р*,
которое нельзя уже считать равным р*@), поскольку оно ме-
няется за счет взаимодействия Ж\. Так как t должно быть боль-
ше Тс, это требование означает, что
Если Жг настолько велико, что условие E.224) не выполняется,
то нужно попытаться сначала найти результат суммарного дей-
ствия Жо и Жг, пользуясь теорией возмущений для Ж\. Напри-
мер, используя не представление взаимодействия, а переход к
вращающейся системе координат, можно свести Жъ{г) к посто-
янному взаимодействию, после чего уже перейти к представле-
нию взаимодействия для эффективного поля.
Интересно отметить, что имеется большое сходство между
представлением взаимодействия и обычным переходом к вра-
щающейся системе координат, который приводит к постоянному
полю Н\. Оба преобразования представляют собой переход к
вращающейся системе координат. Представление взаимодей-
ствия является переходом к системе координат, вращающейся
с ларморовской частотой, а обычное преобразование приводит
к системе координат, вращающейся с частотой переменного
поля #ь
Для простоты предположим, что условие E.224) выполняет-
ся. Заметим, что оно легко может быть выполнено даже в усло-
виях насыщения, поскольку все наши уравнения применимы,
когда Т\ и Т2 много больше тс.
Имеется еще одно следствие введения члена Жч (t). Мы отме-
тили, что при классическом рассмотрении решетки релаксация
приводит к матрице плотности при бесконечно высокой темпе-
ратуре, а не к равновесной матрице плотности р(Т), имеющей
вид
е-ы'ы E.225)
212 Глава 8
где Z(T) —сумма состояний. Если 3^@ мало меняется за вре-
мя тс, характеризующее «решеточное» движение, то следует ожи-
дать, что Ж2(t) представляет собой «постоянное» взаимодей-
ствие по отношению к решетке, и, следовательно, можно счи-
тать, что система релаксирует в каждый момент времени к
мгновенной матрице плотности
p(T,t)=e z(Tt) . E.226)
Это выражение можно получить при квантовомеханическом рас-
смотрении решетки. Если же хс велико по сравнению с периодом
изменения Жъ, то нужно пользоваться выражением E.225).
В условиях, когда применимы уравнения Блоха, малое время
Тс часто приводит к равенству Т\ = Т2. В этом случае уравнения
Блоха принимают вид
^ ^^., E.227)
Мо = ьН@, E.228)
а Н@ — мгновенное значение внешнего поля. Сравнивая точное
решение уравнения E.227) с решением обычного уравнения
Блоха (для которого Тх = Т2, но Мо = %оНо), можно заметить,
что они значительно различаются только в том случае, когда
ширина линии сравнима с резонансной частотой.
Пользуясь уравнениями E.223) и E.158), можно получить
полное дифференциальное уравнение для матрицы плотности,
включающее внешнее переменное поле. Это уравнение имеет вид
-(a\M2{t)\a")pa»a']+ ? flaa'.pp'fPpp'-Ppp'^L E.229)
P.P'
где в зависимости от условий для ррР'СП используется выраже-
ние E.225) или E.226).
Чтобы представить себе более конкретно уравнение E.229),
рассмотрим систему, состоящую из двух уровней. Другими сло-
вами, рассмотрим частицу со спином 1/2 с уровнями энергии,
расщепленными в постоянном поле, которое направлено по оси г.
Обозначив состояния индексами 1 и 2, получим четыре элемента
матрицы плотности ри, р^, Р12, Psi-
Как мы видели выше, имеют значение только те релаксаци-
онные члены ^aa'.pp'. Для которых выполняется равенство
a — a' = p — р". Поэтому должны учитываться только следую-
Спин-решеточная релаксация и сужение линий 213
щие члены:
п __ d ^ _1_ n __ а ^ \_ /g 930)
И, 22 22. Т) . 12. 12 21, 21 Tj • К • )
Полагая, что для 3@2 отличен от нуля только матричный элемент
между состояниями 1 и 2, и вводя обозначение 3@i2(t), для
' ' ~" находим
dpn rfp22 р22 — Pll — [р22 (Т) — pu (T)]
dt dt ~ т,
+ J [Pi2^2i @ -.5»й М Pail E.231)
= - "^ + ? (?2 - ?l) PIS + J (P,l - P22) 5g.2 @. E-232)
Если ?г больше Е\, а ^12 осциллирует с частотой со, то мы мо-
жем найти стационарное решение уравнений E.231) и E.232),
полагая
E.233)
Ри — ги>
Р22 ^ r22t
где гаа> — комплексные постоянные. Подробное решение мы
предлагаем в качестве задачи, а окончательный ответ совпадает
с решением уравнений Блоха. Если
^2 (t) = V cos at, E.234)
где V — оператор, и если соо — частота, определяемая соотноше-
нием Еч — ?1 н= йшо, то для достаточно малых V (в отсутствие
насыщения) найдем
Заметим, что ги отлично от нуля только вблизи резонанса, а тг
характеризует интервал частот, в котором ri2 не равно нулю.
Если состояния 1 и 2 соответствуют двум зеемановским уровням
ядерного спина 1/2, помещенного в постоянное магнитное поле,
параллельное оси г, то оператор поперечной составляющей на-
магниченности Мх имеет матричные элементы только между со-
стояниями 1 и 2, а диагональные элементы равны нулю. Следо-
214 Глава В
вательно,
(Мх (/)> = r12eto* B1 Мх 11) + r21eto* A1 Мх 12) =
= 2Re[r12e^B|MJl)]. E.236)
Полагая
V = MxHx0 E.237)
и вспоминая, что % определяется соотношением
(МхЦ)) = Яе[%Нхае**% E.238)
находим
Используя тот факт, что / = 1/2, получаем
2
Это выражение согласуется с выражением для %, полученным
в гл. 2 для уравнений Блоха.
Отметим, что оказалось возможным независимо определить
Ti и т2, вычисляя /?ц, 22 и Ri2.12- Можно также рассматривать п
и Тг просто как феноменологические константы, определяемые
экспериментально.
Если система имеет больше двух уровней, то решение можно
получить аналогичным образом, полагая все недиагональные
элементы оаа равными нулю, за исключением тех матричных
элементов, для которых частота, определяемая разностью
Еа — Еа' « йсо, близка к частоте переменного поля.
ЛИТЕРАТУРА
1. Gorter С. J., Paramagnetic Relaxation, Elsevier Publishing Co., New York.
1947, p. 127.
2. Hebel L. C, Stickler С. Р., Phys. Rev., 113, 1504 A959).
3. Korringa J., Physica, 16, 601 A950).
4. Pines D., Solid State Physics, Vol. 1, Academic Press, New York, 1955.
5. Tolman R. C., The Principles of Statistical Mechanics, Oxford University
Press, New York, 1946.
6. Redfield A. G., IBM Journ. Res. Develop., 1, 19 A957).
7. Wangsness R. K., Btoch F., Phys. Rev., 89, 728 A953).
8. Block F., Phys. Rev., 102, 104 A956).
9. Bloembergen N.. Purcell E. M., Pound R. V., Phys. Rev., 73, 679 A948).
10. Holcomb D. F., Norberg R. E., Phys. Rev, 98, 1074 A955).
11. Spokas J J.. Slichter С. Р., Phys Rev., 113, 1462 A959)
12. Seymour E. F. W.t Proc. Phys. Soc. (London), A66, 85 A953).
Глава 6
Спиновая температура в магнетизме
и магнитном резонансе
§ 1. Введение
Мы уже пользовались понятием спиновой температуры в гл. 5
при обсуждении явления релаксации. Это понятие было введено
Казимиром и дю-Пре [1] для термодинамического описания
экспериментов Гортера и сотр. по парамагнитной релаксации.
Ван Флек [2] впервые применил представление о спиновой тем-
пературе в подробном расчете времен релаксации парамагнит-
ных ионов методами статистической механики. В этом расчете,
а также в общем анализе статических свойств парамагнитных
атомов методами статистической механики [3] он отметил и
особо подчеркнул тот факт, что разложение статистической сум-
мы Z по степеням \/Т позволяет найти Z, не прибегая к вычи-
слению собственных значений энергии и собственных функций
гамильтониана. Очевидно, первым это свойство использовал
Валлер [4]. Зная статистическую сумму, можно вычислить все
статические характеристики системы, такие, как теплоемкость,
энтропия, намагниченность и энергия. Например, средняя энер-
гия системы Е при температуре Т определяется формулой
?=ftr-^rlnZ. F.1)
В 1955 г. в одной из наиболее важных работ, когда-либо
опубликованных по магнитному резонансу, Редфилд [5] пока-
зал, что общепринятая теория насыщения не в состоянии объяс-
нить экспериментальные факты по ядерному магнитному резо-
нансу в твердых телах и, по существу, противоречит второму за-
кону термодинамики. Он нашел способ простого описания явле-
ния насыщения в твердых телах, обратившись к представлению
о спиновой температуре в системе координат, вращающейся син-
хронно с переменным полем Н\. Чтобы понять его идеи, следует
разобраться в некоторых явлениях, известных до открытия маг-
нитного резонанса, например таких, как адиабатическое размаг-
ничивание.
Начнем данную главу с описания простого эксперимента,
демонстрирующего несостоятельность доредфилдовской теории
магнитного резонанса. Обсудим применения понятия спиновой
216 Глава б
температуры в нерезонансных случаях, обоснуем возможность
его применения во вращающейся системе координат. Затем рас-
смотрим теорию насыщения Редфилда в твердых телах.
§ 2. Следствия из уравнений Блоха
Рассмотрим с помощью уравнений Блоха простой резонанс-
яый эксперимент во вращающемся с угловой частотой со магнит-
ном поле #i, приложенном перпендикулярно постоянному полю
Но. Частота вращающегося поля настроена точно в резонанс
<o = Y#o. F.2)
Для удобства перейдем в систему координат, которая вращается
с частотой шив которой поле #i направлено вдоль оси х, как
это было сделано в гл. 2, § 8. При точном выполнении условий
резонанса уравнения Блоха имеют вид
_^-—_ yMyHt-\ ^—-, F.3а)
T = -Tf« (б-зб)
(б.Зв)
Предположим, что в начальный момент времени t = 0 вектор
намагниченности М направлен вдоль Нь т. е. Мх = Мо, Му =
= Mz = 0. Из уравнения F.36) видно, что Мх затухает до нуля
с постоянной времени Т%. Стационарным решением уравнений
Блоха при малом значении Я] является функция Лоренца с ха-
рактеристической шириной в единицах частоты
Аш=^-. F.4)
Обычно для твердого тела
Аш « уНЛ0К да -f-« ?¦ VUJTT) л/Z, F.5)
где #Лок — локальное магнитное поле, обусловленное соседними
ядерными-магнитными дипольными моментами, а — расстояние
до Z ближайших соседних моментов. Для типичных твердых тел
величина Аю порядка нескольких десятков килогерц (например,
для металлического алюминия Асо « 2я-10 кГц).
Анализ выражений F.3а) и F.3в) показывает, что Мх в них
не входит, и если в начальный момент Му и Mz были равны
нулю, то они остаются равными нулю в случае отсутствия члена,
содержащего 7V Следовательно, если Т\ » 7, а намагничен-
ность М первоначально ориентирована вдоль Нь то на коротких
Спиновая температура в магнетизме 217
временах, вплоть до времен порядка Т\, мы все еще будем иметь
Му = Mz = 0.
Таким образом, эти уравнения предсказывают затухание на-
магниченности М, предварительно ориентированной вдоль Нь
до нуля с постоянной времени Т2 обычно порядка от 10-4 до
Ю-5 с.
Приведенный вывод (затухание с постоянной времени Гг, ко-
гда намагниченность М ориентирована вдоль Н) эксперимен-
тально подтверждается для жидкостей, но несправедлив для
твердых тел. Оказывается, что в твердых телах в резонансном
достаточно сильном поле Н\ скорость затухания Мх определяет-
ся постоянной времени не Тг, которая характеризует ширину ли-
нии, а скорее Т\. Первым этот факт установил Редфилд из своих
экспериментов по стационарному ЯМР. Он объяснил, почему
уравнения Блоха, хорошо описывающие резонанс в жидкостях,
теряют силу в случае твердых тел. Однако Редфилд не прово-
дил описанный выше эксперимент. Такой эксперимент впервые
осуществил Холтон (см. [6]). Ниже в этой главе мы обсудим
условия справедливости уравнений Блоха после того, как рас-
смотрим некоторые основополагающие сведения о спиновой тем-
пературе в случаях отсутствия переменного магнитного поля Н\.
§ 3. Понятие спиновой температуры
в лабораторной системе координат
в отсутствие переменных магнитных полей
Вернемся теперь к обсуждению применения понятия спиновой
температуры в нерезонансных магнитных экспериментах. Типич-
ной системой, которую следует рассмотреть, является группа из
N спинов / с гиромагнитным отношением у, которые находятся
во внешнем поле Но и между которыми существует магнитное
диполь-дипольное взаимодействие, описываемое дипольным га-
мильтонианом Жа- Обозначим зеемановский гамильтониан через
Жг. Решениями уравнения Шредингера являются волновые
функции фп, соответствующие собственным значениям энергии
Е„ всей системы:
Ж1рп = (Ж2 + Жй) <рп = ?„г1>„. F.6)
К сожалению, уравнение F.6) чрезвычайно трудно решить, так
как в него входят координаты 1022 спинов. Однако, если пред-
положить, что спиновая система находится в тепловом равнове-
сии с термостатом, имеющим температуру 6, то различные со-
стояния п всей системы должны заполняться с парциальной ве-
роятностью рП, определяемой фактором Больцмана,
Pn=jre-E»>k\ F.7)
218 Глава б
где Z — статистическая сумма
Z=Ze-?«/*e. F.8)
п
Тогда средняя энергия Е и средняя намагниченность Mz будут
определяться формулами
E = ZpnEn, F.9а)
п
Mz=Z\h(n\rz\n)pn. F.96)
п
Как было отмечено, Ван Флек показал, что явный вид формул,
подобных F.9), можно найти, не решая уравнения Шредингера,
так как Е и М можно выразить через сумму диагональных эле-
ментов статистического оператора. Например, статистическую
сумму можно представить в виде
Z= ? e-En/k»= Z {п\е-ж1т\п) = Ме-Ж1к*1 F.10)
п л
Для вычисления статистической суммы можно выбрать наиболее
удобное представление, так как сумма диагональных элементов
статистического оператора от выбора представления не зависит.
Например, в качестве базисных функций для вычисления F.10)
удобно использовать собственные функции z-компонент спинов
Izk отдельных ядер. Однако при этом необходимо представить Z
в виде степенного ряда.
Часто для системы ядер и электронов справедливо высоко-
температурное приближение, поэтому в разложении экспоненты
в степенной ряд разумно сохранить лишь главные члены. Тогда
легко провести суммирование
Z = Sp{l —§+l-gr-...}==B/+l)"V+^grSp{^}+ ....
F.11)
где использовано равенство Sp {Ж} = 0, которое легко прове-
рить, вычисляя шпуры Жг и Жа.
Используя такие представления, находим
где
—постоянная Кюри, а Ялок — так называемое локальное поле,
которое по порядку величины (несколько гаусс) равно нолю, оь
здаваемому одним ядром в месте нахождения соседнего
Спиновая температура в магнетизме 219
Поле Ялок следует рассматривать как точно известное, так как
шпур в выражении F.14) можно вычислить. Находим
tfLK = YV/(/+ D ? A/Ы6. FЛ5)
Можно вычислить намагниченность М и убедиться в том, что она
подчиняется закону Кюри
^ F.16)
Заметим, что это — векторное выражение, следовательно, М и
Но параллельны.
Выражение F.16) имеет замечательную особенность. Оно
утверждает, что векторы М и Но параллельны независимо от ве-
личины Но, пока справедливо высокотемпературное приближе-
ние. Если Но мало по сравнению с локальным полем на ядре,
создаваемым его соседями, то можно предположить, что магнит-
ные моменты ядер выстраивеются вдоль направления локаль-
ного поля, а не вдоль Но. Казалось бы, следует думать, что на
единицу приложенного поля достижимая степень поляризации
меньше при Но >с Н„ок, чем при Но ~> Нлок. Формула F.16) по-
казывает несостоятельность этого интуитивного вывода — сте-
пень поляризации на единицу приложенного поля не зависит от
величины Но по сравнению с локальным полем. Это справед-
ливо не только для модуля величины М, но также и для направ-
ления.
Следует заметить еще одно полезное свойство выражения
F.16), а именно М = 0 при Яо = 0. Теперь предположим, что
Но было выключено настолько резко, что намагниченность JW не
успела измениться. Немедленно после выключения поля М =/= О,
Но = 0. Однако, если система имела конечную температуру, то
из выражения F.16) следует, что намагниченность М должна
быть равна нулю. Поэтому на основании F.16) можно сделать
заключение, что в этот момент времени систему нельзя описы-
вать температурой.
Другой важной величиной является энтропия с. Из стати-
стической механики известно, что энтропия является мерой сте-
пени порядка в системе. В обратимых процессах, когда нет пере-
носа тепла в систему или из нее, энтропия сохраняется постоян-
ной и определяется формулой
f. F.17)
Вычислив Z и Е, получим
0 = Nk in B/ + 1) - |(Я°+/*ок), F.18)
220 Глава б
§ 4. Адиабатическое и быстрое изменения
магнитного поля
Значение полученных результатов наиболее полно выясняется
при рассмотрении поведения спиновой системы во внешнем маг-
нитном поле Но, зависящем от времени. Для простоты предпо-
ложим, что спиновая система термически изолирована от внеш-
ней среды, но сама может быть или не быть в состоянии тепло-
вого равновесия. Первое из упомянутых предположений удовле-
творяется, если эксперименты выполняются за интервалы вре-
мени, малые по сравнению с временем спин-решеточной релак-
сации. В этом случае гамильтониан системы зависит только от
ее внутренних переменных, тогда как спин-решеточная релакса-
ция описывается членами гамильтониана, зависящими, как сле-
дует из E.33), от внутренних и внешних переменных системы.
Если система находится во внутреннем тепловом равновесии, то
ее можно описывать спиновой температурой и тогда справед-
ливо выражение F.18). Теперь рассмотрим три возможных
случая.
а. Гамильтониан системы не зависит от времени (приложен-
ное поле является постоянным). В этом случае средняя энергия
постоянна во времени независимо от того, описывается система
спиновой температурой или нет. Если система состоит из многих
сильно взаимодействующих друг с другом подсистем, которые в
начальный момент времени выведены из состояния равновесия,
то следует ожидать, что необратимые процессы приведут систе-
му к внутреннему равновесию, описываемому единой спиновой
температурой 6. В течение этого процесса полная энергия со-
храняется, так как система, на которую не действуют внешние
силы, описывается не зависящим от времени гамильтонианом.
Доказательство последнего утверждения предоставляется чита-
телю (задача 6.5).
б. Гамильтониан медленно изменяется во времени. Крите-
рием медленного изменения является такая высокая скорость
внутреннего переноса энергии в любой момент времени, что си-
стему всегда можно описать единой температурой 6. При этом
условии изменения являются обратимыми и энтропия системы
остается постоянной.
в. Гамильтониан изменяется скачком. Такое изменение мо-
жет быть результатом резкого переключения поля Яо. Термин
«скачок» означает настолько быстрый процесс, что за время его
протекания различные спины системы не изменяют свое направ-
ление.
Исследуем более подробно все перечисленные ситуации,
а. Гамильтониан системы не зависит от времени. Рассмотрим
систему, которая в начальный момент времени не находится в
Спиновая температура в магнетизме 221
тепловом равновесии. Предположим, что составные части систе-
мы взаимодействуют между собой и система достигает внутрен-
него равновесия, описываемого «конечной» температурой 6f. Если
в начальный момент времени t = О энергия системы (обозначим
ее Ео) известна, то температуру Qf можно вычислить, используя
факт сохранения энергии системы, описываемой гамильтониа-
ном, не зависящим от времени. Из выражения F.12), связываю-
щего энергию Е с температурой, учитывая сохранение энергии
Ё = Ео, F.19)
. получаем
?Й2+^1 F.2О)
Закон Кюри позволяет вычислить намагниченность М/, которую
приобретает система после установления внутреннего теплового
равновесия;
Mf=-^-. F.21)
где 6f определяется формулой F.20). В течение процесса уста*
новления внутреннего теплового равновесия энтропия не являет-
ся постоянной, поскольку идут необратимые процессы. Но в ко-
нечном итоге энтропия Of принимает равновесное значение, со-
ответствующее температуре 6f:
af = Nk In B/ + 1) - C^°2^Ok) • F.22)
Если гамильтониан можно разделить на две коммутирующие
части, описывающие две подсистемы, то энергия каждой из них
в отдельности сохраняется. Тепловое равновесие всей системы
в этом случае нельзя описать единой температурой. Следует
считать, что в равновесном состоянии каждая из подсистем
имеет свою характерную температуру. Мы встретимся ниже с
такой ситуацией при рассмотрении спиновой системы во вра-
щающейся системе координат. В некоторых случаях с полной
уверенностью нельзя считать подсистему достаточно замкнутой,
чтобы описывать ее единой температурой, но часто мы будем
пользоваться таким описанием, надеясь, что оно все же воз-
можно.
б. Медленное, или адиабатическое, изменение магнитного
поля. Чтобы изменение поля Но было адиабатическим, оно дол-
жно удовлетворять двум условиям.
Во-первых, должен отсутствовать поток тепла между спино-
вой системой и ее окружением. Для этого необходимо, чтобы
изменение поля Но происходило за интервалы времени, меньшие
времени сшш-решеточной релаксации Т\. Часто Т\ имеет поря-
222
Глава б
док несколько секунд, и путем охлаждения системы можно до-
вести времена Т\ до нескольких часов. Такие большие времена
практически бесконечны.
Во-вторых, необходимо, чтобы после каждого малого изме-
нения поля Но, прежде чем произойдет следующее, в спиновой
—I
HL Hf
Рис. 6.1. Зависимость конечной температуры 6/ от конечного магнитного
поля Hf при адиабатическом уменьшении поля от значения Hi при начальной
температуре 6г. *)
Видно, что 6^ слабо зависит от Hf при Hf < Ядок.
системе установилась новая температура. Это условие обычно
выполняется, если изменение поля Но за период прецессии маг-
нитных моментов ядер в локальном поле \/уНлок ничтожно
мало. Период прецессии ядерного магнитного момента в ло-
кальном поле составляет несколько десятых миллисекунды. Ме-
жду рассмотренными временными интервалами существует об-
ласть интервалов, на которых изменение поля Но является адиа-
батическим. В адиабатическом процессе энтропия постоянна. Из
выражения F.18) следует, что величина (Яо + #лок)/б2 также
остается постоянной. Если адиабатически изменять поле от на-
чального значения Hi до конечного Hf, то конечная температура
8f определится соотношением
е?
F.23)
где Qi — начальная температура. Из F.23) следует известный
результат — возможность охлаждения спиновой системы при
адиабатическом размагничивании. Если начальное сильное маг-
нитное поле Hi » #лок1 в котором находится образец, адиаба»
•) На рис, 6.1, 6,2, 6.5 Hl — локальное поле. — Прим. ред.
Спиновая температура в магнетизме
223
F.24)
тически уменьшить до значения Hf -С Нпок, то
6f _^_ #лок „ ,
Таким образом, конечная температура спинов много меньше пер-
воначальной. Если первоначально спины находились в тепловом
равновесии с термостатом (например, решеткой, охлажденной
до температуры жидкого гелия), то конечная температура будет
много меньше температуры термостата. Заметим, что, чем боль-
ше Hi и чем меньше Нлок, тем охлаждение более эффективно.
Обычно для уменьшения Нлок магнитные атомы разбавляют.
На рис. 6.1 изображена зависимость конечной температуры
8f от значения конечного поля Hf для произвольной начальной
температуры в,- и Hi» Н„ок. Как видно, температура резко
уменьшается до тех пор, пока приложенное магнитное поле па-
дает от начального значения до значения, сравнимого с локаль-
ным полем. Дальнейшее уменьшение внешнего поля не приводит
к заметному снижению температуры.
Закон Кюри позволяет вычислить намагниченность, если тем-
пературу определить из выражения F.23). Если вначале в поле
Рис. 6.2. Зависимость намагниченности Mf от приложенного поля Hf в случае
его адиабатического изменения.
Предполагается, что и\ > #лок. Видно, что Mf ие зависит от Hf для Я| > #лок и изме-
няется до нуля, когда Hf стремится к нулю.
Hi ~Э> Нлок намагниченность системы была Mi, то конечная на-
магниченность Mf определится формулой
М М= • F-25)
224 Глава б
Эта зависимость представлена на рис. 6.2. Поскольку для боль-
ших значений поля Я температура Gf пропорциональна Hf, то
в процессе охлаждения М/ почти не отличается от М,- до тех пор,
пока внешнее поле Hf не станет сравнимым с локальным полем
Зависимость, изображенная на рис. 6.2, показывает, что с по-
нижением внешнего поля до нуля намагниченность Mf также
уменьшается до нуля. Так как изменения поля обратимы (эн-
тропия сохраняется постоянной), то намагниченность может воз-
вратиться к исходному значению Mt при увеличении поля Я/ от
нуля до его первоначального значения Я*. Спин-решеточная ре-
лаксация не влияет на процесс восстановления намагниченности
Mf, потому что, как мы постулировали выше, длительность этого
процесса гораздо меньше Т\. Процесс восстановления намагни-
ченности может показаться удивительным тем, кто впервые
встретился с магнетизмом, изучая магнитный резонанс. В маг-
нитном резонансе учат, что для намагничивания образца из не-
намагниченного состояния необходим интервал времени порядка
Т\. Действительно, одно лишь адиабатическое включение стати-
ческого магнитного поля Яо > Ялок, действующего на спины,
первоначально находящиеся в нулевом поле при термодинамиче-
ском равновесии с решеткой (G = Qi), приведет, согласно закону
Кюри и выражению F.23), к намагниченности
F.26)
где Мо— намагниченность при тепловом равновесии между спи-
нами и решеткой в поле Яо, которая устанавливается в резуль-
тате спии-решеточной релаксации. Если Яо 3> ЯЛОк, намагничен-
ность мала, но тем не менее не равна нулю.
Важным следствием выражения F.25) или рис. 6.2 является
равенство Mf = О при Hf = 0. Как уже отмечалось, оно является
очень общим следствием закона Кюри независимо от темпера-
туры. (Заметим, однако, что при выводе закона Кюри использо-
валось высокотемпературное приближение. При достаточно низ-
ких температурах это приближение нарушается и в нулевом поле
возможно появление спонтанной намагниченности.) Замечатель-
но то, что степень порядка спиновой системы совершенно одина-
кова в случаях, когда М = 0 и М = Mi. Очевидно, что система
с конечной намагниченностью упорядочена, однако какой поря-
док может быть в системе с М = 0? Этот парадокс можно объ-
яснить тем, что даже в отсутствие внешнего поля Яо = 0 на
спины действуют локальные магнитные поля, создаваемые со-
седними спинами. Каждый отдельный спин ориентируется вдоль
или против направления локального поля на нем. В сильно упо-
рядоченной системе имеется значительный избыток спинов, ори-
ентированных вдоль локальных полей, по сравнению со спинами,
Спиновая температура в магнетизме 225
ориентированными против локальных полей. Однако, поскольку
в различных ядерных узлах локальные поля имеют случайные
направления (здесь не рассматриваются высокоупорядоченные
спиновые конфигурации, такие, как в ферромагнетиках), то ре-
зультирующая макроскопическая намагниченность равна нулю,
в. Резкое переключение магнитного поля. Мы рассмотрели
обратимый процесс. Теперь вернемся к процессам, скоротечность
которых приводит к необратимости. Предположим, что система
описывается волновой функцией я|х Зависящее от времени урав-
нение Шредингера запишется в виде
-~^- = M(t)q = -M-H(t)q + 3%A, F-27)
где М — оператор полного магнитного момента, a Md — гамиль-
тониан дипольного взаимодействия. Гамильтониан Ж зависит от
времени вследствие зависимости от времени приложенного поля
Н. В случае резкого переключения полагаем, что напряженность
поля Н скачком изменяется от одного значения к другому в мо-
мент времени t = 0 и в дальнейшем не зависит от времени. Обо-
значая через 0~ и 0+ моменты времени непосредственно до и
после t = 0, имеем
о+
*@+)-ф((Г) = - \ jr2e(t)ty(t)dt = O, F.28)
или
я1>@+) = я1>@-), F.29)
так как гамильтониан 3e(t) не принимает бесконечного значе-
ния, хотя и испытывает разрыв. Таким образом, волновая функ-
ция непосредственно до и после переключения имеет одинаковые
значения.
Используя равенство F.29), можно показать, что скачкооб-
разное изменение поля Н приводит к изменению среднего значе-
ния энергии Е, которое в любой момент времени t равно
?(/) = (*(/), 5»@Ф@>. F.30)
Тогда
(М (О")) • Н (О") + {Жа @-)), F.31)
— средние значения
= 0~, определяемые
(М ((Г)> = <ф ((Г), Мф (О')),
где <М@~)> и <Жг @~) >— средние значения намагниченности
и дипольной энергии при t = 0~, определяемые как
226 Глава 6
Аналогично
? @+) = <М @+)) • Н @+) + {Md @+)>. F.33)
Равенство г|) @~) = г|) @+) означает, однако, что ожидаемые зна-
чения как намагниченности, так и дипольной энергии в моменты
t — 0+ и t = 0~ совпадают. Этот результат отражает физический
факт совпадения ориентации всех спинов в моменты времени
t = 0+ и t = 0-.
Таким образом, можно написать
Ё @+) - <М @-)) • Н @+) + {Жй @-)). F.34)
Если предположить, что непосредственно перед скачком поля
система находилась в состоянии теплового равновесия при тем-
пературе 6,-, то, используя полученное уравнение, можно мето-
дами, рассмотренными в § 3, определить средние значения.
До сих пор мы не использовали матрицу плотности, чтобы
сделать эту главу доступной тем читателям, которые еще не до-
статочно знакомы с формализмом. Полученные результаты мо-
жно записать компактно, учитывая, что уравнение F.29) экви-
валентно следующему равенству для матрицы плотности р:
р@+) = р(<Г). F35)
Тогда
(М @+)) = Sp {р @+) М} = Sp {р (О") М} = <М @-)). F.36)
Предполагая, что в момент времени t = 0~ при температуре 6,-
имеет место тепловое равновесие, получаем
==7(FTe^@)//ee'- F>37)
Поэтому
(о-)) = sP {Р (о") жй} - -ф^ sP U«"w @~Шв{} • F.38)
Используя высокотемпературное приближение и определение
F.14), после преобразований находим
0-)>=--^*. F.39)
откуда имеем
В@*)--сЛ?!??1-??=.. F.40)
Немедленно после переключения поля спиновая система вообще
не находится во внутреннем тепловом равновесии, даже если
Спиновая температура в магнетизме
227
она была в таком состоянии в момент времени t — 0~. Через
достаточно большой промежуток времени tj в системе установит-
ся определенная температура 6f, которую можно вычислить. По-
скольку для t > 0 гамильтониан ие зависит от времени, то энер-
гия сохраняется:
?(/,) = ?@+). F.41) н
Однако
р
'< ' *
а Е@+) определяется выра-
жением F.40). Таким обра-
зом, Е
е,-
==Di—-
F.42)
Смысл выражения F.42)
можно понять из частного
примера. Предположим, что
внешнее магнитное поле
скачком выключается в мо-
мент времени t = 0 от зна-
чения Но до нуля. Тогда
Н @-) = Но, Н @+) = 0, что
дает
6f = ef. F.43)
ь^ неопределенности
! спиновой, температуры
Рис. 6.3. Зависимость от времени маг-
нитного поля Н, волновой функции г|>,
энергии Е, спиновой температуры 6 и
намагниченности М при выключении
магнитного поля скачком.
Эта конечная температура
резко отличается от темпе-
ратуры, достигаемой при адиабатическом выключении поля,
3f!
F.44)
При выключении поля скачком температура остается неизмен-
ной, тогда как медленное выключение приводит к охлаждению
системы.
Временные зависимости различных физических величин при
выключении поля Но скачком при / = 0 приведены на рис. 6.3.
Мы описали эксперимент, который очень близок к известному
эксперименту Паунда и Переела [7] по достижению отрицатель-
ной температуры. За счет резкого переключения направления
магнитного поля на обратное им удалось ориентировать намаг-
228 Глава 6
ниченность антипараллельно постоянному полю. При такой ори-
ентации верхние зеемановские уровни заселены больше нижних,
что соответствует отрицательной зеемановскои температуре. Лю-
бая система с преимущественной заселенностью верхних энерге-
тических уровней в принципе может иметь отрицательную тем-
пературу. В дополнение к оригинальной статье Паунда и Пер-
еела обращаем внимание читателя на лекцию ван Флека [8],
посвященную общим представлениям о температуре в магне-
тизме, в которой превосходно объяснен этот эксперимент и об-
суждено понятие отрицательной температуры. (Профессор ван
Флек предупреждает, что в тексте лекции имеется несколько
неверных цифр.)
§ 5. Магнитный резонанс и насыщение
Следуя Бломбергену и др., можно, используя стандартную
теорию возмущений, провести анализ явления магнитного резо-
нанса в простейшем случае с помощью дифференциального
уравнения A.32) для разности населенностей п двух энергетиче-
ских уровней системы частиц со спином 1/2:
§й)п + ^т^., F.45)
где W((a)—вероятность опрокидывания спина в единицу вре-
мени под действием радиочастотного поля Hi, По — разность на-
селенностей при тепловом равновесии, Т^ — время спин-реше-
точной релаксации. Согласно теории возмущений,
№(co) = fY2tffe(co), F.46)
где g(a)—нормированная функция формы линии поглощения.
Функция g((a) выражает тот факт, что поле Hi индуцирует пе-
реходы лишь тогда, когда частота этого поля близка к резонанс-
ной.
Полагая время Т\ бесконечно большим, получим простейшее
решение F.45):
n=Ae-'2Wt, F.47)
где А — постоянная интегрирования.
Стоит напомнить два условия справедливости F.46):
1. Матричные элементы гамильтониана возмущения, индуци-
рующего переходы, должны быть малы по сравнению с шириной
энергетических уровней конечного состояния. Это означает, что
Hi -С Нлок.
2. Волновые функции не должны сильно изменяться.
Однако, согласно выражению F.47), п->-0 при t-*-oo. По-
этому для выполнения второго условия необходимо рассматри-
Спиновая температура в магнетизме 229
вать интервалы времени, меньшие 1/W. Таким образом, хотя
всегда легко удовлетворить первому условию, выбрав Н\ до-
статочно малым, тем не менее независимо от малости Hi, если
подождать достаточно долго, то можно нарушить второе усло-
вие. (Заметим, что если не справедливо принятое здесь предпо-
ложение 1/W <С Т\, то член с Т\ в уравнении F.45) обеспечит
выполнение второго условия даже для интервалов времени, боль-
ших \/W.)
^ ч . Область, где обычная теория
К возмущения справедлива
\
\
V
ZlW t
Рис. 6.4. Простая теория насыщения предсказывает экспоненциальное умень-
шение до нуля разности населенностей п со временем /.
Предположения, на которых эта теория основана, справедливы только для начальной части
кривой, где n**rii.
Нас теперь интересует задача, как проинтегрировать урав-
нения движения во временной области, где п значительно отли-
чается от п0 при t = 0 (рис. 6.4).
Решение этой задачи было найдено Редфилдом [9] в его за-
мечательной статье, которая была его первой работой по маг-
нитному резонансу. Редфилд показал, что уравнения Блоха в
применении к твердому телу не согласуются со вторым законом
термодинамики. Он справедливо заметил, что зависящее от вре-
мени резонансное возмущение, безотносительно к его слабости,
будет в конечном итоге приводить к большим эффектам. Всякий
раз, когда малое возмущение приводит к большому эффекту,
опасно анализировать его простейшим образом. Редфилд, по
существу, исключил зависимость гамильтониана рассматривае-
мой спиновой системы от времени путем преобразования его
к удобной системе координат, в которой такая зависимость зна-
чительно проще, а энергия сохраняется. Поскольку исследуемая
система состоит из многих взаимодействующих спинов и яв-
ляется в высшей степени сложной, то можно ожидать, что после
достаточно длительного промежутка времени она придет в со-
стояние внутреннего равновесия и будет находиться в одном из
230 Глава б
наиболее вероятных ее состояний. Это означает, что энергети-
ческие состояния будут заселяться в соответствии с распределе-
нием Больцмана при некоторой температуре G.
Запишем гамильтониан системы в виде
Ж = Жг{1)+Жа, F.48)
где dfSz(t) — зеемановское взаимодействие с постоянным полем
Но и вращающимся с угловой частотой to в направлении ядерной
прецессии переменным полем с амплитудой Н\. Вращающееся
поле обусловливает временную зависимость Жг- Считаем Т\
бесконечно большим. Используя методы, рассмотренные в гл. 2,
§ 6, перейдем во вращающуюся систему координат. Преобразо-
ванный гамильтониан имеет вид
Ж' = - yh [(Но - f) /. + Я,/,] + Щ +
+ члены, осциллирующие с частотой ± со и 2со. F.49)
При выводе гамильтониана Ж' были использованы соотношения
- Ix sin ф + 1У cos ф = е~и^1/'^ F.50)
чтобы преобразовать произведения вида
^'V/"A' F.52)
к выражениям, содержащим sin a>zt и cos azt. Член Ж%. пред-
ставляет собой часть гамильтониана дипольного взаимодействия
Жй, коммутирующую с оператором /z. Эта часть гамильтониана
Жй сохраняется при повороте системы координат вокруг оси z.
(Два последних утверждения физически эквивалентны, посколь-
ку оператор /г можно рассматривать как оператор поворота.)
Гамильтониан Ж\ является суммой членов Л и В, определенных
в гл. 2, § 3, и имеет вид
A-3cos2^) I, • 1Л F.53)
где б/* и rjk — координаты ядра/относительно ядра k.
Первый член выражения F.49) можно рассматривать как
оператор взаимодействия спинов с эффективным статическим
полем
= к (Яо - у) - Шь F.64)
Спиновая температура в магнетизме 231
что отмечалось уже в гл. 2. Поле Нэфф и дипольное поле Нлок
расщепляют энергетические уровни, соответствующие гамиль-
тониану Ж. Если не учитывать члены, зависящие от времени, то
типичные расщепления равны
Квадратный корень в этом выражении оправдывается двумя пре-
дельными случаями Яэфф ^> Ялок и Язфф <С #лок«
Члены гамильтониана Ж, зависящие от времени, связывают
состояния, отстоящие по энергии на величину уНН0. Они не вы-
зывают резонансных переходов, и поэтому ими можно прене-
бречь, исключая случай очень слабого резонансного поля, когда
Но «* //Лок + ЯЭфф. Таким образом, получаем гамильтониан Ш:
НЭфф -j- (ffla = cf6z "t" <ffid, F.56)
где для простоты опущен штрих. Операторы Звг и Зв*& в отсут-
ствие поля #i коммутируют, так как по определению Жг спра-
ведливо равенство [/г, 5^] = 0. В этом случае 36z и Ж\ по
отдельности должны быть интегралами движения. Однако, если
#i ф 0, то \Шг, <%>d\ Ф 0 и тогда зеемановская и дипольная си-
стемы могут обмениваться энергией. Поскольку Ж не зависит
от времени, то полная энергия сохраняется. Более того, система
очень сложная, и поэтому Редфилд постулировал, что незави-
симо от начального состояния системы при t = 0 через некото-
рое время она придет в состояние внутреннего равновесия, опи-
сываемое распределением Больцмана. Другими словами, в кон-
це концов установится температура 6, которую можно приписать
спиновой системе. Таким образом, можно ввести матрицу плот-
ности
е-да/%е
р=-Ч-« F-57>
где Z = Sp{e~w/fce}, ^—эффективный гамильтониан F.56).
Конечно, по истечении достаточно большого времени следует
ожидать, что предположения Редфилда будут выполнены (если
не существует скрытых правил отбора, которые мы просмотрели,
таких, как полная изоляция зеемановской и дипольной систем
друг от друга в случае Ht = 0). Однако возникает важный воп-
рос: через какое время спиновая система достигнет равновесного
состояния? Ясно, что ответ на данный вопрос зависит от вели-
чины поля #i, которое связывает дипольную и зеемановскую си-
стемы. Позже мы вернемся к этому вопросу, а сейчас будем счи-
тать, что установление конечной температуры системы происхо-
дит за достаточно короткий интервал времени.
232 Глава 6
§ 6. Теория Редфилда в пренебрежении
спин-решеточным взаимодействием
Смысл выражения F.56) можно оценить, если снова вычис-
лить энергию Е, энтропию о и намагниченность М. Легко найти
Ё=-С 3^J"»°\ F.58
5 F.59)
2SSL,
о = Nk In B/ + 1) -
где С —постоянная Кюри и
Вычисление шпура в этом выражении для системы с одним сор-
том сшшов дает
я:12ок=|<дя2)> F.62)
где <ДЯ2> — второй момент резонансной линии. Ранее мы усло-
вились опускать штрихи. Поэтому локальное поле будем теперь
обозначать Нлок вместо Н'лок, а штрих будем использовать лишь
тогда, когда необходимо провести различие между локальным
полем в лабораторной и вращающейся системах координат.
Важно отметить, что предположение Редфилда приводит к
закону Кюри, векторная природа которого всегда обусловливает
параллельность ядерной намагниченности эффективному полю,
если спиновую систему можно описать температурой во вращаю-
щейся системе координат. Таким образом, точно в резонансе,
когда НЭфф = i#i, намагниченность перпендикулярна постоян-
ному полю.
Поскольку вид выражений F.58) — F.60) идентичен виду со-
ответствующих выражений в лабораторной системе координат,
то большинство формул § 4 можно непосредственно переписать
во вращающейся системе координат с заменой Но на Н3фф и
„2 гг'2
Ллок US П лок.
1. Адиабатическое размагничивание
во вращающейся системе координат (АРВСК)
Как продемонстрировал Холтон (см. [6]), эксперимент по
АРВСК легко выполнить. Предположим, что первоначально
Hi — 0 и образец намагничен до равновесного значения кМ0.
Сдвинем статическое поле Но значительно выше резонансного
Спиновая температура в магнетизме 233
значения а/у и включим РЧ-поле Яь (Предполагаем, что
Яо— а/у значительно больше Нлок и Н\.) В результате этого
эффективное поле фактически оказывается параллельным на-
магниченности М. Затем достаточно медленно, так чтобы удовле-
творить условию обратимого изменения, приблизим Яо к резо-
нансному значению. (Предполагаем здесь Т\ = оо. Практически
это достигается путем проведения всех экспериментов за интер-
валы времени, значительно меньшие по сравнению с Т\.)
Тогда имеем
Ь^=. F.63)
Заметим, что М параллельно НЭфф, как и требует закон
Кюри. Таким образом, по мере приближения к резонансу на-
магниченность М, всегда направленная вдоль эффективного
поля НЭфф, меняет направление. Вообще, исключая случай
ЯэФФ > Ялок. изменяется также величина М. Экспериментально
можно измерить М, если скачком выключить Н\ и наблюдать
свободную прецессию М вокруг поля Яо. Напряжение, индуци-
руемое в катушке с образцом, непосредственно после выключе-
ния Н\ пропорционально Мх. (Применяя фазочувствительный
детектор, можно независимо измерить составляющие Мх и Му,
однако для рассматриваемого случая Му = 0.) Хотя Мх зату-
хает до нуля за время порядка 1/уНлок после выключения Яь
составляющая Mz не изменяется » ее можно измерить. Для этого
необходимо подождать, пока Мх затухнет и затем повернуть Мг
в плоскость ху с помощью импульса я/2. Теоретические значе-
ния Мх и Mz равны
Мх = М н ' = Мо , ' , F.64)
F.65)
где ho — составляющая эффективного поля в направлении оси г:
F.66)
Заметим, что если адиабатическое размагничивание происходит
точно в резонансе, то значение намагниченности
Мх = МоЯ./д/я? + Н\ок F.67)
будет сохраняться бесконечно долго (в действительности, если
учесть спин-решеточиую релаксацию, намагниченность будет за-
тухать со временем на интервале порядка ^i). Этот вывод резко
234
Глава 6
отличается от рассмотренного выше следствия из уравнений
Блоха, согласно которому намагниченность Мх затухает до нуля
на интервале времени порядка Т% fa 1/уНлок. Эффект постоян-
ства намагниченности М, до тех пор пока сохраняется неизмен-
ное поле ЯЭфф и синфазность прецессии М и Н\, часто описы-
вается термином «спин-локинг» (захват спинов). Если величина
Я? сравнима с ЯЛок> то Мх будет меньше Мо. Однако «потерю»
Рис. 6.5. Зависимость поперечной намагниченности Мя в эксперименте по
адиабатическому размагничиванию во вращающейся системе координат от
напряженности переменного поля Ни
Предполагается, что вначале образец имел термодинамически неравновесную намагни-
ченность Ми и поле Н, включается с большой расстройкой от резонанса.
намагниченности можно восстановить. При отходе от резонанса
намагниченность М должна возрастать до Мо, если Яэфф ~> ЯЛОк-
На рис. 6.5 показана зависимость F.67).
«Спин-локинг», т. е. захват спинов полем ЯЭфф, был одним
из самых удивительных результатов теории Редфилда. Конечно,
этот результат является не чем иным, как утверждением, экви-
валентным тому, что намагниченность при адиабатическом раз-
магничивании в обычной лабораторной системе координат одно-
значно соответствует полю Яо, как выражено формулой F.25).
Если статическое магнитное поле Яо изменять от значения
значительно больше резонансного, когда (Но — а/у) » Ни а
Ялок До значения значительно меньше резонансного, т. е.
(Но — га/у) <0, то в результате намагниченность М окажется
повернутой антипараллельно Яо. При этом вблизи резонанса
может случиться, что М < Мо (если Я! < ЯЛОк), однако спустя
некоторое время далеко w резонанса снова будем иметь
Спиновая температура в магнетизме 235
Мй Мо. Эксперимент такого типа дает простой способ опроки-
дывания намагниченности.
Остановка поля Но точно в резонансе при размагничивании
дает Мх = Мо при условии Hi » Нлок (формула 6.64). Резонанс-
ный сигнал получается такой же большой, как после РЧ-импуль-
са я/2. При Н\ ^ Нлок поперечная намагниченность оказывает-
ся меньше Мо- Медленное уменьшение РЧ-поля Hi до нуля
после достижения резонанса приводит к исчезновению намаг-
ниченности М. Весь зеемановский порядок, определявший на-
магниченность Мо до размагничивания, оказывается перенесен-
ным в дипольную систему, когда спины выстраиваются вдоль их
локальных полей. Спустя некоторое время можно снова восста-
новить намагниченность, медленно включив РЧ-поле Н\.
2. Изменение эффективного поля скачком
В эксперименте часто встречается другая интересная ситуа-
ция, противоположная адиабатическому размагничиванию, ко-
гда эффективное поле НЭфф изменяется скачком. Рассмотрим
самый простой случай — включение скачком РЧ-поля Hi в мо-
мент / = 0. Предположим, что до включения РЧ-поля Hi си-
стема имела намагниченность Мо вдоль поля Но и что введена
расстройка величиной (Но — а/у) = ho. Используем представ-
ления о скачкообразном изменении статического поля, развитые
в §4.
Будем полагать, что поле Н\ включается настолько быстро,
что волновые функции или матрица плотности системы до и не-
медленно после включения поля одинаковы. Дипрльная энергия
Ed, зависящая от относительной ориентации спинов, таким об-
разом, одинакова в моменты времени / = 0+ и t = 0~. Более
того, поскольку дипольный гамильтониан Ж& одинаков в лабо-
раторной и вращающейся системах координат, то
Ёа = —^=-Мо-%. F.68)
где 6/ — температура решетки. Зеемановская энергия имеет вид
Ez — - М • Нзфф = - МЛ, F.69)
и, следовательно, полная энергия Е = Ez-\- Ed равна
F.70)
Спустя достаточно продолжительное время установится спино-
вая температура, и намагниченность М будет параллельна ЯЭфф.
Глава 6
Тогда полная энергия определяется формулой
эфф Т лок = - М эфф лок . F.71)
Однако она сохраняется с момента включения поля Ни поэтому,
приравнивая F.70) и F.71), получаем
л А°
°7^—TW
"эфф "г "лок "эфф ~ "лок "эфф "г "лок
F.72а) F.726) F.72в)
Эти формулы показывают, что точно в резонансе намагничен-
ность должна исчезать. Намагниченность исчезает очень резко.
Поперечная намагниченность Мх изменяется линейно с h0, по-
этому, если уменьшить сигнал до нуля, то можно точно зареги-
стрировать момент резонанса.
Интересно сравнить полученные результаты с выводами
обычной теории насыщения. Для системы спинов '/г намагни-
ченность М.г связана с разностью населенностей п уравнением
Мг~=У?-. F.73)
Теория насыщения утверждает, что равновесная разность насе-
ленностей п = 0 в предположении бесконечного Т\ и, следова-
тельно, Mz = 0. С другой стороны, из формулы F.72в) следует,
что Мг = 0, лишь когда насыщение производится точно в резо-
нансе (/zo = O). Обычная теория насыщения приводит к выводу,
что поперечная намагниченность также исчезает. Из формулы
F.726) следует, что вообще намагниченность Мх велика и мо-
жет быть больше Mz.
Если #Эфф 3§> #лсж, то формулы F.72) имеют простой гео-
метрический смысл. После выключения поля Hi намагниченность
М прецессирует вокруг Яэфф. Компонента М, параллельная
Нэфф, не может затухать без энергетического обмена с решет-
кой, хотя перпендикулярная ей компонента может затухать за
счет разброса частот прецессии в локальных полях. Таким об-
разом, через несколько интервалов времени, равных 1/уНЛ0К,
намагниченность М окажется направленной вдоль поля НЭфф и
будет иметь величину, равную проекции первоначальной намаг-
ниченности Мо на ЯЭфф.
Спиновач температура в магнетизме 237
§ 7. Приближение к равновесию
в слабом РЧ-поле Hi
В § 5 мы отметили, что стандартная теория возмущений
предсказывает уменьшение разности населенностей п до нуля
в течение длительного времени после включения слабого поля
Ни хотя, строго говоря, ее нельзя применять для описания со-
бытий спустя интервалы времени, большие \/W. Будем считать
поле Hi слабым, для того чтобы теория возмущений оказалась
справедливой, по крайней мере на коротких интервалах вре-
мени. Поскольку намагниченность Мг пропорциональна п, то и
она должна уменьшаться до нуля. Однако в § 6 мы видели, что
при этих условиях Мг стремится к равновесному значению
гРЯ„„ =- Afo-,
" + "лок
, - F.74)
"О + "лок
Формула F.74) получается, если предположить Н\ <С h\ и
Н\ < Ялок (хотя при выводе выражений для равновесных ве-
личин в § 6 мы не ограничивались случаем слабого поля Н\).
Таким образом, как мы и предполагали, теория возмущений не-
правильно описывает поведение системы на больших интерва-
лах времени. Однако для коротких интервалов времени она
должна быть верна. Учитывая пропорциональность между Мг
и п, можно написать
^l = -2W(«>)Mz. F.75)
Уравнение F.75) справедливо для t <C l/W((a). Возникает важ-
ный вопрос: как описать Мг для больших времен?
Решение этой задачи было дано Провоторовым [10], кото-
рый в своей классической статье использовал мощный обобщен-
ный метод. Прежде чем описать анализ, проведенный Прово-
торовым, рассмотрим альтернативный вывод его результата.
Заметим, что в отсутствие Н\ гамильтониан зеемановского
взаимодействия во вращающейся системе координат имеет вид
Шг = — yhholz. F.76)
Предположим, что зеемановской системе, описываемой этим га-
мильтонианом, можно приписать температуру Qz, а дипольной
системе (гамильтониан д@а) — температуру Qd. Это предположе-
ние нельзя считать строго правильным, но оно п.о крайней мере
является простым и соответствует действительности в момент
включения поля Н\. Непосредственно перед включением поля Нх
дипольная система имеет температуру решетки 6/, так как га-
мильтониан ctid одинаков во вращающейся и лабораторной си-
238 Глава 6
стемах координат. В лабораторной системе координат намагни-
ченность имеет вид
М0 = -^Ч F.77)
а во вращающейся системе координат —
Мо = -^-- F.78)
Поскольку Но >• ho, то 6z <C 6,. Таким образом, во вращающей-
ся системе координат зеемановская температура 6Z значительно
^
Наклон, известный
из теории возмущения
\
\
\
vn» Конечное значение,
***.^ определяемое теорией
^-,. Ред/рилда.
Рис. 6.6. Зависимость намагниченности Мг от времени / в процессе насыще-
ния, согласно описанию, данному в тексте.
Эта зависимость получается непрерывным соединением начальной области, где производ-
ная dMJdt известна нз теории возмущения, с равновесным значением, определяемым из
теории Редфилда. Используется вывод Шумахера о том. что приближение к равновесию
определяется единственной эксноиентой.
меньше температуры 6d. При включении РЧ-поля Н\ возникает
контакт двух резервуаров, т. е. поле И\ возбуждает переходы
между энергетическими уровнями зеемановской и дипольной си-
стем, и они вместе достигают конечной равновесной темпера-
туры 6, определенной в § 6. Мы предполагаем, что населенности
различных состояний подчиняются простым кинетическим урав-
нениям. (Такое предположение аналогично использованному в
гл. 5, § 2. Оно является вполне общим для всех расчетов кросс-
релаксации. Провоторов неявно использовал это предположение
в своей работе при оценке времени релаксации.) Поскольку
имеется много состояний, то число связанных кинетических
уравнений, подобных E.13), велико.
Шумахер [11] показал, что в случае двух систем, характе-
ризуемых своими температурами, большое число уравнений сво-
дится к двум связанным линейным кинетическим уравнениям
Спиновая температура в магнетизме 239
(одно для 1/Oz, другое для l/ва), подобно тому как большое
число уравнений E.13) сводится к одному кинетическому урав-
нению E.27). Кроме того, условие сохранения энергии приво-
дит к связи между Ог и Qa:
^-^ = const. F.79)
Выражение F.79) является первым интегралом системы урав-
нений. Из него следует, что если одна из результирующих по-
стоянных времени бесконечно велика, то процесс описывается
единственной экспонентой. Но поскольку Мг ~ \/Qz, то релак-
сация Мг к ее равновесному значению также идет по одной-
единственной экспоненте. Используя начальное условие
Мг = Мо, для зависимости Мг от времени получаем выражение
Mz - Мг равн = (Мо - Мг равн) е~*К F.80)
Единственной неизвестной величиной в уравнении F.80) яв-
ляется постоянная т. Однако ее легко определить, если прирав-
нять значение производной выражения F.80), вычисленной при
/ = 0, значению производной F.75) (которое должно быть вер-
ным в начальный промежуток времени, когда справедлива тео-
рия возмущений). Находим
М
Используя формулу F.72в) для Мгравн, имеем
1 = 2W (со) Ц^- = щ*Н\ (Ц^) В И. F.82)
Этот результат совпадает с результатом, впервые полученным
Провоторовым, как в действительности и должно быть, по-
скольку мы использовали такие же приближения, как он. Таким
образом, зависимость намагниченности от времени имеет окон-
чательный вид
iJ^^]}. F.83)
Выражение F.83) очень полезно, так как удалось успешно про-
интегрировать уравнения движения на интервале времени, зна-
чительно превышающем величину 1/W, до которой обычно спра-
ведлива теория возмущений (рис. 6.6),
240 Глава б
§ 8. Условия справедливости
гипотезы Редфилда
Как мы уже отмечали, введение понятия спиновой темпера-
туры во вращающейся системе координат возможно при выпол-
нении основного требования —пренебрежения некоторыми зави-
сящими от времени членами в гамильтониане, преобразованном
к вращающейся системе координат. Это требование, в сущности,
означает, что Но > уН1фф + #л<ж • На основании предыдущего
параграфа теперь можно сформулировать другое требование.
Мы видели, что в отсутствие РЧ-поля Hi равенство дипольной и
зеемановской температуры в лабораторной системе координат
означало их неравенство во вращающейся. Спин-решеточная
релаксация стремится привести обе температуры к температуре
решетки в лабораторной системе координат с постоянной вре-
мени Т\. С другой стороны, РЧ-поле Н\, если оно включено,
стремится уравнять эти температуры во вращающейся системе
координат. Эти два процесса противоборствуют. Интенсивность
процесса характеризуется соответствующими временами релак-
сации (малое время релаксации соответствует большой интен-
сивности процесса установления связанного равновесия). Таким
образом, спиновая температура будет устанавливаться во вра-
щающейся системе координат и мы можем использовать метод
Редфплда лишь при условии
или
я^-^к^НГ.»!. F.84)
Выражение F.84) почти точно совпадает с традиционным усло-
вием насыщения. Заметим, что, чем больше Ти тем меньше Ни
при котором будет удовлетворяться условие F.84). Часто усло-
вие F.84) удовлетворяется даже при Hi <C #ЛОк.
§ 9. Влияние спин-решеточной релаксации
До сих пор мы рассматривали магнитный резонанс на ин-
тервалах времени, малых по сравнению с временем спин-реше-
точной релаксации. Во многих случаях нестационарные экспе-
рименты удовлетворяют этому условию. Однако не менее важ-
ны эксперименты, которые выполняются на интервалах времени,
больших Ти как, например, в стационарном случае с примене-
нием аппаратуры непрерывного возбуждения. В этом случае
еще можно удовлетворить условию справедливости теории Ред-
Спиновая температура в магнетизме 241
филда F.84), однако теперь спиновая температура 6 во вра-
щающейся системе координат определяется взаимодействием с
решеткой. Как мы увидим, это утверждение никоим образом не
означает равенства 6 = 6;, а приводит к функциональной зави-
симости 6 от 6/. К счастью, очень просто обобщить наши преды-
дущие вычисления, с тем чтобы учесть взаимодействие с решет-
кой. Вообще говоря, Редфилд в своей известной статье рассмо-
трел именно этот случай, однако мы исключили рассмотрение
спин-решеточной релаксации до настоящего момента, чтобы
упростить предыдущее обсуждение.
Обычно, когда спиновая система обменивается энергией с
решеткой, внутреннее равновесие спиновой системы во вращаю-
щейся системе координат мгновенно нарушается. Наше основ-
ное предположение состоит в том, что кросс-релаксация между
дипольной и зеемановской системами происходит значительно
быстрее, чем спин-решеточная релаксация, поэтому после об-
мена энергией между спинами и решеткой быстро устанавли-
вается новая спиновая температура. Таким образом, по отно-
шению к решетке спиновую систему всегда можно описать спи-
новой температурой во вращающейся системе координат.
Рассмотрим три основных релаксационных уравнения для
классических намагниченностей Mxl), Mz и для ожидаемого
значения дипольной энергии {#)ф- Уравнения запишем фено-
менологически в такой форме, которая гарантирует достижение
спиновой системой теплового равновесия с решеткой в отсут-
ствие РЧ-поля Н\\
дМг Мв — Мг
~Ж~== Та '
дМх Мх
dt
F.87)
Здесь Та, Ть и Тс — времена релаксации, соответствующие об-
мену энергией с решеткой, a \3@d)i — значение E&S), когда спи-
новая температура равна температуре решетки. Уравнения
F.85) — F.87) описывают изменения рассматриваемых величин
лишь за счет взаимодействия с решеткой, что подчеркивается
использованием частных производных. Поэтому время Та яв-
ляется обычным временем Ти однако Ть не равно Т2
(ж \/уНлок), а значительно больше, обычно порядка Т\. Хоро-
шей аналогией этих уравнений следует считать уравнение
') Нас не беспокоит релаксация Mv, так как она не изменяет энергии во
вращающейся системе координат (по существу, мы предполагаем, чтоЛ}^=0).
242 Глава 6
Больцмана в статистической механике, содержащее ряд столк-
новительных членов, каждый из которых изменяет функцию рас-
пределения / и для каждого из которых можно вычислить df/dt.
Таким образом, если зеемановская и дипольная подсистемы,
имеющие энергии соответственно —М-НЭфф и Bёа), не были
в тепловом равновесии друг с другом, то намагниченность будет
возрастать (или убывать) до тех пор, пока не будет достигнуто
равновесие. Ясно, что такой процесс дает вклад в три производ-
ные по времени F.85) — F.87), который мы не включили в урав-
нения. Следует предполагать, что взаимодействие с решеткой,
описываемое членами, содержащими постоянные времени Та, Ть
и Тс, должно выводить спиновую систему из теплового равно-
весия во вращающейся системе координат, однако взаимодей-
ствия внутри спиновой системы, индуцирующие энергетический
обмен между спинами, противодействуют этому. Изменения вну-
три спиновой системы должны происходить с сохранением пол-
ной энергии спинов. Поэтому если мы рассматриваем скорость
изменения среднего значения энергии Е, то можем пренебречь
любыми изменениями, которые просто перераспределяют энер-
гию внутри спиновой системы, и сохранить лишь изменения,
обусловленные взаимодействием с решеткой.
Используя выражение для средней энергии
Ё = - Мг/ю - МХН{ + (Ж°а), F.88)
можно найти скорость ее изменения за счет взаимодействия с
решеткой, взяв производную по времени от выражения F.88):
dE дМг н дМх д
Единственные вклады в производные по времени, которые нам
необходимо рассмотреть, определены выражениями F.85) —
F.87), так как все другие не изменяют полную энергию Е. Ис-
пользуя выражения F.85) — F.87), а также F.58), F.59) и пред-
полагая, что намагниченность М всегда направлена вдоль ЯЭфф,
легко получить уравнения для М:
^ = J-(MpaBn-M) F.90а)
и для спиновой температуры 6:
Спиновая температура в магнетизме 243
где
М
равн ~
^ '
„2 \^~"r ' T /'
lp О1 "лок V/a УЬ Tc '
[Членом Bfe°d)t в F.87) пренебрегаем.]
Заметим, в частности, что точно в резонансе величина
Мравн = 0, при ho > 0 величина МраВн > 0, т. е. намагниченность
М параллельна Нэфф, однако при h0 < 0 величина МраВн < О,
т.е. намагниченность М антипараллельна НЭфф. Последний слу-
чай соответствует отрицательной спиновой температуре во вра-
щающейся системе координат. Из формулы F.91а) видно, что
равновесное значение спиновой температуры 6 сильно отличает-
ся от значения температуры решетки 6/ и даже может иметь
противоположный знак. Поскольку Мо обратно пропорциональ-
но 6/, то утверждение, что 6/ определяет 6, остается справедли-
вым, хотя эти температуры сильно различаются. Иногда счи-
тают, что отрицательная температура является проявлением
стремления Мг всегда быть положительной величиной незави-
симо от того, положительна или отрицательна расстройка ho.
Действительно, можно сказать, что равновесие достигается сле-
дующим образом. Сильное внутреннее взаимодействие спиновой
системы (которое является гарантией справедливости введения
спиновой температуры) удерживает М в направлении НЭфф в
силу векторного характера закона Кюри. Решетка стремится
сделать так, чтобы г-составляющая М равнялась Мо, а х-состав-
ляющая М — нулю. Если бы намагниченность М стала больше
Мо, так чтобы, согласно первой тенденции, ее проекция на ось
2 равнялась Мо, то тогда, согласно второй тенденции, М должна
быть равна нулю. Таким образом, решетка борется сама с со-
бой, поскольку первая и вторая тенденции несовместимы. В ре-
зультате достигается равновесное значение F.91а).
§ 10. Спиновый захват (спин-локинг).
Время спин-решеточной релаксации
во вращающейся системе координат Tip.
Медленное движение
Как обсуждалось выше и как показано на рис. 6.7, спиновая
температура во вращающейся системе координат устанавли-
вается за промежуток времени т от произвольного начального
состояния без обмена энергией с решеткой. Но это только ква-
зиравновесное значение спиновой температуры, так как в тече-
244
Глава 6
нис последующего времени Т\р она изменяется из-за энергети-
ческого обмена спиновой системы с решеткой. При этом М до-
стигает значения Мравн, F.91а) (рис. 6.7). В течение этого про-
цесса намагниченность М направлена вдоль НЭфф. Таким обра-
зом, если в резонансе намагниченность М первоначально ориен-
тирована вдоль Н\, то затухание М будет происходить не с по-
стоянной времени, определяемой обратным значением ширины
м
Величина, определенная
U3\F.7Za)
Т
Величина, определенная
пр
Рис. 6.7. Иерархия времен после включения РЧ-поля Hi скачком.
За время х во вращающейся системе координат устанавливается спиновая температура»
величина которой определяется средним значением энергии Е непосредственно после
включения Н\.
В течение более длительного времени Г, происходит энергетический обмен спиновой си-
стемы с решеткой. Спиновая температура во вращающейся системе координат изменяется,
соответственно изменяя М.
Поскольку мы предположили, что х <? Т{ , то анализ обоих процессов можно Проводить
на основе гипотезы спиновой температуры Редфилда
линии, а с постоянной 1\р, значение которой определяется энер-
гетическим обменом с решеткой. В принципе время 7tp можно
значительно увеличить за счет понижения температуры. В этом
случае после установления спиновой температуры во вращаю-
щейся системе координат спустя интервал времени г намагни-
ченность, параллельная полю НЭфф, будет затухать очень мед-
ленно с большой постоянной времени 7\р. Величина Т\р может
достигать нескольких секунд в металлах и даже часов в изоля-
торах.
Хотя мы и можем в течение времени 71р удерживать намаг-
ниченность в направлении НЭфф при включенном поле Н\, од-
нако, если скачком убрать Ни то намагниченность М будет за-
тухать до нуля за время порядка обратной ширины линии. Ина-
Спиновая температура в магнетизме 245
че говоря, уравнения Блоха с обычным значением Т2 дают гру-
бое количественное описание происходящего процесса.
При рассмотрении теории Редфилда полезно вернуться к си-
туации, возникающей в лабораторной системе координат без
переменных полей. Мы видели, что путем медленного изменения
поля Но до нуля и обратно намагниченность предварительно
намагниченной системы можно вернуть к исходному значению.
Когда Но = 0, то и М = О, но М полностью восстанавливается
при последующем увеличении поля до Но, если эти изменения
происходят без энергетического обмена с решеткой. Порядок
в нулевом поле сохраняется благодаря предпочтительному вы-
страиванию ядерных моментов вдоль направлений локальных
полей.
Существование порядка в локальных полях является осно-
вой методики наблюдения медленных движений [12—14], гораз-
до более медленных, чем те, которые удается обнаружить по ми-
нимуму Т\ или по сужению линии. Рассмотрим ядро 1, ближай-
шим соседом которого является ядро 2. Предположим, что
ядро 2 скачком перемещается как в процессе диффузии. Про-
должительность такого скачка порядка 10~12—10~13 с, т. е. зна-
чительно меньше периода ядерной прецессии. Поэтому локаль-
ное поле на ядре 1, создаваемое ядром 2, резко меняется как
по величине, так и по направлению. Ориентация спина ядра 1
относительно локального поля становится в некоторой степени
случайной величиной. Если среднее время жизни данного ядер-
ного состояния между скачками обозначить через хт, то вы-
страивание ядер в локальных полях соседей, т. е. упорядоченное
состояние, может существовать лишь в течение времени тт. Та-
ким образом, чтобы провести весь цикл размагничивание — на-
магничивание с полным восстановлением первоначальной на-
магниченности, можно оставаться в нулевом поле лишь в тече-
ние интервала времени, меньшего тт. Конечно, если даже скачки
не происходят, любой процесс спин-решеточной релаксации из-
меняет энтропию спиновой системы так, что в любом случае
следует полностью завершить цикл за время, меньшее Тх. От-
сюда следуют выводы:
1) Цикл размагничивание — намагничивание можно исполь-
зовать для контроля Т\ в нулевом поле.
2) Скачки ядер можно обнаружить при условии тт < Тх.
Аналогичные представления применимы для описания экспери-
ментов по АРВСК- Анализ воспроизводится непосредственно
(Сликтёр и Эйлион [12, 13]). Поскольку скачки ядер вызывают
внезапные изменения дипольной энергии, то они дают вклад в
\/Тс, равный
_L_==J_A_p)> F-92)
1 с, ск тт
246 Глава 6
где р — величина, учитывающая тот факт, что значение локаль-
ного поля после скачка не является совершенно случайным по
отношению к его значению до скачка. Эту величину можно вы-
числить. Ее значение зависит от природы скачков (по вакан-
сиям, междоузлиям и т. д.). Коэффициент 2 в F.92) возникает
потому, что локальное поле определяется взаимодействием ме-
жду парой ядер, каждое из которых может перемещаться.
Таким образом, простые измерения Г1р дают возможность
анализировать атомное движение или молекулярную переори-
ентацию, когда время %т сравнимо с временем 7lfi) обусловлен-
ным другими причинами.
ЛИТЕРАТУРА
1. Casimir И. В. С, duPre F. К., Physica, о, 507 A938).
2. Van Vleck J. H., Phys. Rev., 57, 426 A940).
3. Van Vleck J. H., Journ. Phys., 5, 320 A937).
4. Waller /., Zs. Phys., 79, 370 A932).
5. Redfield A. G., Phys. Rev., 98, 1787 A955).
6. Slichter C. P., Holton W. C, Phys. Rev., 122, 1701 A961).
7. Pound R. V., Purcell E. M., Phys. Rev., 81, 279 A951).
8. Van Vleck J. H., Nuovo Cim. Suppl., 6, Ser. X, 1081 A957).
9. Redfield A. G., Phys. Rev., 98, 787 A955).
10. Провоторов Б. Н., ЖЭТФ, 14, 1126 A962).
11. Schumacher R. Г., Phys. Rev., 112, 837 A958).
12. Slichter С P., Ailion D., Phys. Rev., 135, A1099 A964).
13. Ailion D., Slichter C. P., Phys. Rev., 137, A235 A965).
14. Look D. C, Lowe I. J., Journ. Chern. Phys., 44, 29 A966).
Глава 7
Двойной резонанс
§ 1. Для чего выполняются эксперименты
по двойному резонансу?
Одной из наиболее важных разработок, вышедшей за пре-
делы первоначальных представлений о магнитном резонансе, яв-
ляется двойной резонанс. В экспериментах по двойному резонан-
су, как следует из названия, в системе одновременно возбуж-
дается один резонансный переход и наблюдается другой. В этой
области науки был сделан ряд ярких открытий, вдохновляющих
на новые размышления. Для проведения экспериментов по двой-
ному резонансу имеется много причин. Мы попытаемся на-
глядно представить эти причины, описывая некоторые пионер-
ские эксперименты по двойному резонансу. Довольно произ-
вольно разделим описание на три части. В первой части рассмо-
трим эксперименты по двойному резонансу типа Оверхаузера —
Паунда, которые включают динамическую поляризацию ядер,
двойной электронно-ядерный резонанс (ДЭЯР), твердотельные
квантовые генераторы (мазеры) и все разнообразие лазеров. Во
второй части опишем сочетание специальных методов, таких, как
импульсный двойной резонанс. В третьей части познакомимся
с методом, открытым Ханом, в котором сильный резонанс рас-
пространенных ядер используется для обнаружения слабого ре-
зонанса редких ядер за счет значительного увеличения эффек-
тивности обычного взаимодействия между двумя спиновыми си-
стемами.
§ 2. Особенности двойного резонанса
типа Оверхаузера — Паунда
Первый эксперимент по двойному резонансу выполнил Паунд
[1] на ядрах Na23 в NaNO3. Он хотел доказать, что механизмом
спин-решеточной релаксации является квадрупольное взаимо-
действие с флюктуирующим во времени градиентом электриче-
ского поля. Исходя из этого, Паунд вычислил вероятности тер-
мически индуцированных переходов между различными спино-
выми состояниями. Резонансная линия Na23 в кристалле NaNO3
расщепляется аксиально симметричным градиентом электриче-
ского поля на три отдельные линии поглощения, соответствую?
218 Глава 7
щне переходам между уровнями с различными значениями т:
3Л ¦*-* 'Л. h *""* — h п —'Л ч~> —3А- Он предсказал и экспе-
риментально подтвердил, что насыщение одного любого пере-
хода (например, 3/2—^'Л) должно приводить к изменению рав-
новесных населенностей уровней всех состояний. Поэтому при на-
сыщении перехода 3/2 ¦*-> '/а интенсивность перехода 'Д-*-*- —'Д
увеличивалась в 5/3 раза но сравнению с ее нормальным значе-
нием. Ниже в связи с эффектом Оверхаузера мы обсудим, по-
чему возникают такие изменения интенсивности. Серией экспе-
риментов, в которых насыщались различные переходы и одно-
временно наблюдались другие, Паунд подтвердил, что механиз-
мом спин-решеточной релаксации является квадрупольное вза-
имодействие.
Второй эксперимент по двойному резонансу выполнил Кар-
вер [2]. Эксперимент был основан на предсказании [3], кото-
рое сделал Оверхаузер, еще будучи студентом университета в
Беркли. Оверхаузер теоретически показал, что если насыщать
спиновый резонанс электронов проводимости в металле, то по-
ляризация ядерных спинов может возрасти в 1000 раз по сра-
внению с ее значением при тепловом равновесии в отсутствие
электронного насыщения. (См. хороший обзор [4] методов ди-
намической поляризации ядер, написанный одним из ее пионе-
ров.) Грубо говоря, Оверхаузер предсказал поляризацию ядер,
которую они имели бы, если бы вместо больцмаиовского фак-
тора ядерного спина использовался больцмановский фактор
электронного спина. Может быть, современному читателю труд-
но понять глубокий скептицизм, с которым было встречено пред-
ложение Оверхаузера со стороны специалистов по резонансу,
ибо в настоящее время существует много схем динамической
поляризации и многие другие важные методики основываются
на этом предложении. Однако в 1953 г. было широко распро-
странено мнение (хотя и короткоживущее), что схема ядерной
поляризации Оверхаузера нарушает второй закон термодина-
мики. Эксперимент Карвера явился не только первой демонстра-
цией динамической поляризации ядер, но, что, по-видимому, бо-
лее важно, подтвердил правильность революционной идеи Овер-
хаузера, которая изменила ход научной мысли о резонансе. Эта
идея стимулировала последующее открытие других схем дина-
мической поляризации. По-видимому, еще важнее было то, что
идея Оверхаузера привела к исследованию других эффектов,
связанных с накачкой переходов и двойным резонансом.
На рис. 7.1 показан первый эффект динамической поляри-
зации ядер Li в металлическом литии. Для насыщения спино-
вого резонанса электронов проводимости в этом эксперименте
поле Их должно иметь величину от 5 до 10 Гс. Кроме того,
чтобы все ядра поляризовались при электронном насыщении,
Двойной резонанс
249
необходимо также иметь частицы металла размером меньше
глубины скин-слоя на частоте спинового резонанса электронов.
Карвер использовал соленоид, создающнй постоянное поле около
30 Гс. В этом поле частота спинового резонанса электронов
была 84 МГц, а частота ядерного резонанса лития 50 кГц. При
Рис. 7.1. Осциллограммы, полученные в эксперименте Карвера по динамиче-
ской поляризации ядер Li7 в металлическом литии, подтверждающие эффект
Оверхаузера.
Осциллограммы представляют сигналы ядерного поглощения в зависимости от напряжен-
ности магнитного ноля. Ширина развертки поли около 0,2 Гс. а—нормальный ядерный
резонанс L17 на частоте 50 кГц (сигнал теряется в шумах аппаратуры), б—сигнал ЯМР L17,
увеличенный благодаря насыщению электронного спинового резонанса, в — сигнал протон-
ного резонанса при тех же экспериментальных условиях от образца глицерина, содержа-
щего в 8 раз больше протоцов, чем образец ядер Li'. Сравнение сигналов позволило за-
ключить, что поляризация ядер L17 увеличилась примерно в 100 раз.
такой низкой частоте сигнал ядерного резонанса был слишком
слаб н непосредственно не наблюдался (рис. 7.1, а), однако при
включении генератора, насыщающего спиновый резонанс элект-
ронов, сразу становился выше уровня шумов. Степень поляри-
зации Карвер прокалибровал по сигналу протонного резонанса
от образца глицерина (осциллограмма на рис. 7.1, в). Карвер
показал также, что динамическая поляризация возможна не
только в металле, повторив эксперимент на растворе натрия в
жидком аммиаке. Атомы натрия в таких растворах ионизи-
руются, выделяя свободные электроны, резонанс которых легко
насыщается.
250 Глава 7
Принципы, лежащие в основе эффекта Оверхаузера, факти-
чески идентичны тем, на которых базируется эксперимент Паун-
да. Этот эффект в значительной мере стимулировал развитие
методов двойного резонанса, в частности, потому, что Оверхау-
зер сделал остроумное и смелое предсказание, которое многие
талантливые физики посчитали неправильным, а также потому,
что это предсказание представляло интерес для значительно
большего круга ученых, а не только для специалистов по маг-
нитному резонансу. Однако не следует сомневаться, что даже
без идей Оверхаузера изобретение двойного резонанса Паундом
привело бы к развитию методов двойного резонанса, хотя Паунд
и не распознал вначале возможность получения большой поля-
ризации ядер по своей схеме, если ее применить к другим си-
стемам. В связи с этим для обсуждаемого ниже класса экспе-
риментов, включая эксперименты других ученых, выбрано назва-
ние «эффект Оверхаузера — Паунда» без всякой попытки прини-
зить роль последующих новых идей. Новые идеи привели к
дальнейшим успехам и свидетельствуют об удивительной интуи-
ции и поразительной самобытности их авторов. С педагогической
точки зрения важно показать их взаимосвязь.
§ 3. Энергетические уровни и переходы
между ними в модельной системе
Для понимания основ многих приложений двойного резонан-
са рассмотрим простейшую систему взаимодействующих между
собой ядра и электрона с соответствующими спинами / = 1/2 и
S = '/г, находящуюся во внешнем постоянном магнитном поле
Hq. Гамильтониан этой системы имеет вид
Ж = \eHHoSz +AI-S- ynhH0Iz, G.1)
где индексы е и п использованы для обозначения электронов и
ядер, а электронно-ядерное взаимодействие выбрано в форме,
соответствующей s-состоянию.
Предположим yeb,HG ^> А (приближение сильного поля) и,
конечно, уе^> \Уп\- Эти предположения означают, что Sz комму-
тирует с Ж; следовательно, ms — собственное значение Sz — яв-
ляется хорошим квантовым числом. У гамильтониана электрон-
но-ядерного взаимодействия диагональные элементы имеет толь-
ко член AIzSz, поэтому гамильтониан можно записать в виде
Ж =• yehH0Sz + А^г - \пПН012. G.2)
В качестве другого хорошего квантового числа можно взять
пц — собственное значение /2. Тогда собственные значения энер-
Двойной резонанс
251
гии равны
E — yehHoms ¦
1
\nhHomh
m5 = =tT, m7=±-5-
G.3)
2 *
Состояния системы и волновые функции удобно представить
в виде
G.4)
где е = 2ms, \х = 2т7. Состояние ms — +'/2. mi = —ХЫ обозна-
чим как |-) ). Запишем правила отбора для переходов, инду-
A.
' гь
а
Рис. 7.2. Диаграммы Э11сргетических уровней и разрешенных переходов в си-
стеме взаимодействующих электронного E = Vs) и ядерного (/ = '/*) спинов,
на которую действует ввешнее постоянное магнитное поле Но.
а—переходы ядерного резонанса; б—переходы электронного спинового резонанса.
цированных переменным полем: Ams — ±1, hm, — 0 или &ms =
= 0, Л/я/ = ±1. Первое соответствует электронному спиновому
резонансу, второе — ядерному резонансу (подробное обсужде-
ние см. в гл. 10, § 3).
Резонансные частоты а»е и со„ определяются формулами
G.56)
Таким образом, имеются четыре разрешенных перехода. Они по-
казаны на рис. 7.2. Отношение величин \А\ и (уЛИ) несколько
влияет на положение энергетических уровней, как это показано
на рис. 7.3. Если рассматриваемые ядро и электрон далеки друг
от друга, то \А \ ¦< |-упЙЯо| (рис. 7.3,а). Если ядро и электрон
расположены близко друг к другу, то \А \ > \yJiH0\ (рис. 7.3, б).
Первый случай характерен для ядер в твердых телах с малой
концентрацией парамагнитных центров. Последний — для ядер
252 Глава 7
парамагнитных атомов или для ядер, расположенных очень
близко к парамагнитным центрам.
Для облегчения обсуждения будем пользоваться диаграм-
мами, подобными изображенной на рис. 7.2, а, не обращая вни-
мания на отношение величин \А\ и \упЛН0\.
Мы предположили особенно простую форму гамильтониана
взаимодействия спинов электронов и ядра, которая справедлива
для фермиевского контактного сверхтонкого взаимодействия. Бо-
лее общая форма спин-спинового взаимодействия должна также
¦ +-
-+ ¦
а о
Рис. 7.3. Диаграммы энергетических уровней в заннсимоста от соотношения
величины постоянной электронно-ядерного взаимодействия Ajh и частоты
ядерного резонанса шя.
а—удаленное ядро, б — соседнее ядро. Обычно для ядер, далеких от электрона,
IA I < | \nhHe |. Часто для ядер, близких к электрону, |Л |> \ЧпкН0\. Диаграммы изо-
бражены для отрицательного значения уп. Как они будут выглядеть при положитель-
ном значении уп?
включать гамильтониан диполь-дипольного взаимодействия спи-
нов электрона и ядра (см. гл. 3, § 2). В этом случае, как по-
казано в гл. 10, гамильтониан будет иметь вид
9$ = \ehHoSz + AX-X'SX'IX' + AyylySy +
+ AZ-Z'1Z>SZ> - ynHHolz, G.6)
где х', у', z' — система главных осей.
До тех пор пока \еНН0 » | А*х> |, | Ау>у |, | Az-Z> |, более об-
щей форме гамильтониана G.6) соответствует диаграмма энер-
гетических уровней, которая выглядит подобно рис. 7.2, о или б.
В этом приближении собственные значения nis оператора Sz яв-
ляются еще хорошими квантовыми числами, однако собственные
значения mi оператора /2 не обязательно будут таковыми. Таким
образом, волновые функции гр* наинизшего порядка (где t — ин-
декс любого из четырех состояний) могут и не иметь простого
вида
G.7
Двойной резонанс
253
а быть линейными комбинациями таких состояний
¦Ф<= Z CimmAntstni).
mS. ml
G.8)
Если более точно решать задачу для случая гамильтониана G.2),
то окажется, что состояния описываются волновыми функциями
вида G.8), а не G.7).
Поскольку существует у( = |++) -
только четыре энергети-
ческих уровня, обозначе* ——
ние |ep.) [т.е. Ц-+),
I-+), I+-), I )]
еще справедливо и доста-
точно, чтобы различать
четыре уровня. Уг~1~+) ——
Однако, хотя
обычно
Рис. 7.4. Обозначения четырех состояний
1, 2, 3, 4, используемые вместо прежних
обозначений
G.9)
Описание состояний системы волновыми функциями общего
вида G.8) независимо от того, является ли это результатом бо-
лее точного решения задачи в случае простого гамильтониана
G.1) или результатом решения задачи в случае более общего
гамильтониана G.6), приводит к тому, что между энергетиче-
скими уровнями, изображенными на рис. 7.2, оказываются воз-
wzl
тт
=1+-)
I
I
I
I i
I I
I I
Рис. 7.5. Релаксационные пере-
ходы, при которых изменяются
состояния электронного спина.
Стрелками показаны напрзвлеиия
переходов, скорости которых соот-
ветственно равны Wa, Wa н т. д.
-1-1- V*-!—)
можными другие переходы, кроме показанных. Они возбуждают-
ся внешним переменным магнитным полем. Условимся называть
такие переходы «запрещенными».
Населенности энергетических уровней объединенной спиновой
системы при тепловом равновесии и отсутствии внешних пере-
менных полей определяются факторами Больцмана. Как обсуж-
далось в гл. 1, можно считать, что тепловое равновесие дости-
гается в результате переходов, индуцированных взаимодействием
254
Глава 7
с тепловым резервуаром. Вероятность термически индуцирован-
ного перехода Weix.^ из состояния \ец) в состояние |е'ц)
связана с вероятностью обратного перехода W^u'. ev,соотношением
W it P''
G.11)
где рЕц —вероятность того, что при тепловом равновесии состоя-
ние |ец) занято. Или, используя соотношение Больцмана, имеем
е'ц'-'
G.12)
Перейдем к более компактным обозначениям. Так как суще-
ствуют четыре состояния, то обозначим их 1, 2, 3 и 4, как пока-
зано на рис. 7.4. Тогда обозначение Wij соответствует скорости
УН-+)
!
Рис. 7.6. Эффект Оверхаузера.
Релаксационные переходы W^. поддерживают тепловое равновесие. Приложенное пере-
менное ноле индуцирует электронные спиновые переходы между состояниями 1 и 2 со ско-
росхыо Wg.
теплового перехода из состояния t в состояние /. Переходы, в
которых опрокидывается спин электрона, а состояние ядерного
спина не меняется, показаны на рис. 7.5.
Напомним, что переходы между состояниями 1 и 2 или 3 и 4
являются электронными, а переходы между состояниями 1 и 3
или 2 и 4 —ядерными. Кроме того, на рис. 7.4 уровень 2 распо-
ложен ниже уровня 1, а уровень 4 — ниже уровня 3.
§ 4. Эффект Оверхаузера
Хотя первоначальное предложение Оверхаузера касалось по-
ляризации ядер в металлах, его принцип можно проиллюстриро-
вать, рассматривая модельную систему, обсужденную в преды-
дущем параграфе. Возьмем простейший гамильтониан G.1) с
собственными значениями энергии G.3).
Предположим, что главные механизму релаксации в системе
показаны на рис. 7.6 и включают электронную спиновую релак-
Двойной резонанс 265
сацию (W\2, W21, WM, W43) и релаксацию, индуцирующую пере-
ходы со взаимным опрокидыванием электронных и ядерных спи-
нов {W23, Ws2). Механизмом последней может быть контактное
взаимодействие Ферми в металлах, как объяснялось в гл. 5, § 3.
Внешнее переменное поле индуцирует электронные переходы ме-
жду уровнями 1(| + +)) и 2(| [-)) с вероятностью We. Это
электронный спиновый резонанс. Тогда вероятности pt заселения
уровней i подчиняются следующей системе дифференциальных
уравнений, аналогичных E.13):
?L = p2w2l _ piWl2 + (P2 - Pl) We, G.13а)
*?2. = PlWl2-p2W21 + Рз^-рЛ + (р, - p2)We, G.136)
^ G.13в)
G.13г)
Вероятности заселения уровней удовлетворяют соотношению
р, + р2 + р3 + Р4==1- G.14)
Нас интересует стационарное решение, поэтому левые части
уравнений G.13а) — G.13г) приравняем нулю. Предположим
также, что вероятность We может быть достаточно большой, что-
бы полностью насытить электронный переход (в пределе устре-
мим We к бесконечности). Тогда
Pi = ft. G.15)
Из уравнения G.13г) следует, что отношение населенностей со-
стояний 3(| + —)) и 4(| ))
XV7
Рз = Р4-^- G.16)
соответствует тепловому равновесию.
Подставляя G.13г) в G.13в), получаем
Рз = Р2|^. G.17)
т. е. отношение населенностей состояний 2 и 3 тоже соответствует
тепловому равновесию.
Таким образом, хотя насыщение будет изменять все населен-
ности в системе указанных уровней и переходов, оно непосред-
ственно влияет лишь на отношение заселенностей пары состоя-
ний, связанных сильным переходом с вероятностью We- Этот ре-
зультат обусловлен предположением, что нет переходов, связы-
вающих состояние 1 с состояниями 3 или 4.
256 Глава 7
Поскольку отношения ръ/Pi и Рг/Рз соответствуют тепловому
равновесию, то отношение р4/рг также является равновесным.
Для пары уровней i и / в тепловом равновесии имеем
G.18)
Это выражение определяет величину Вц — отношение Больцмана
(отсюда и символ В). Обращаем внимание на порядок символов
Ei и Е,- и индексов /, / в В,,-. Тогда для нашей четырехуровневой
системы имеем
Pi = Р2.
Рз = Р2В2з, G.19)
Pi — P2B24.
или
— — 1
Pi — Pi — 2 + Bi3 + Bit •
Pi-
23
Д24
G.20)
2 + B23 +
Мы установили, что эффект Оверхаузера приводит к ядерной
поляризации. Вычислим эту поляризацию.
В состоянии |ец) ожидаемое значение ядерного спина равно
ц/2(ц=+1 или —1). Поэтому среднее ожидаемое значение
г-составляющей ядерного спина </г> можно записать в виде
ЛШг10 = ^(Р1 + р2-Рз-Р4) = ^|~^-§ft- G.21)
Чтобы понять смысл этого выражения, используем его для оцен-
ки </г> в высокотемпературном приближении, когда
kT '
MTbj=:^L- G-22a)
Поскольку
Е3 — Е2 = уеЬН0 + YпйЯo
и
?4 - Ей = 4 + УпАЯо, G.226)
" G.23а)
то
Двойной резонанс 257
Учитывая, что уе/Ш0 значительно больше других слагаемых в
числителе G.23а), получаем
4^- G-236)
Легко показать, что при тепловом равновесии, когда электрон-
ный спиновый резонанс не насыщается, ядерная поляризация
определяется выражением
L Д21 + 1 — Дгз — Ви ,- пл\
L
2 Вп + 1 + В23
В высокотемпературном приближении оно принимает вид
// \ — l (E,-El) + (Ei-Et) + (Et-Et) . „«
Vz/терм — ~2 4fcT " * '
Так как Е2 — Е{ — — yehH0 — А/2, то
//\ *
Vz/терм— 2
Выражение G.26) совпадает с тем, которое получается для
ядра, если на него действует одно лишь внешнее постоянное
поле1).
Сравнивая выражения G.236) и G.26), видим, что насыще-
ние спинового резонанса увеличивает </г>:
__ G ?\
</г)теРМ "" 2Yn * ('-Z/)
Отношение G.27) означает, что ядро поляризуется так, как если
бы его магнитный момент стал сравнимым по величине со значи-
тельно большим моментом электрона! Если одновременно насы-
щаются оба электронных перехода, то
тгг1-^- G-28)
Формула G.28) — результат, первоначально предсказанный
Оверхаузером для металла. В металле один электрон взаимо-
') На первый взгляд может вызвать удивление, что взаимодействие
электрона с ядром не влияет на величину (/*) терм поскольку, казалось бы,
энергетические уровни определяются эффективным магнитным полем на ядре
Л/п„
ГГ I S
Однако, поскольку фактически ms с равной вероятностью принимает значе-
ния + 1/2 и —1/2 и в высокотемпературном приближении намагниченность
пропорциональна эффективному полю, член Ainslyntl усредняется до нуля по
ансамблю электронно-ядерных систем.
258
Глава 7
действует сразу со многими ядрами, поэтому электронный спи-
новый резонанс имеет одиночную линию, а не разрешенный дуб-
лет, как в нашем примере.
§ 5. Поляризация ядер при насыщении
запрещенных переходов
Эффект Оверхаузера возможен лишь тогда, когда процессы
ядерной релаксации (индуцирующие переходы с вероятностями
W13, W24) не могут подавить релаксацию, в процессе которой
одновременно опрокидываются электронный и ядерный спины,
т. е. индуцируются переходы с вероятностями №23 или Wn. Эти
условия не всегда выполняются.
Вообще говоря, можно вполне уверенно считать, что условие,
согласно которому процессы чисто электронной релаксации с оп-
рокидыванием одного лишь электронного спина (WI2 или W34)
значительно быстрее любых других процессов (Wu), справед-
ливо, так как электроны сильнее взаимодействуют с решеткой,
чем ядра. Джеффрис [5] и независимо от него Абрагам с сотр.
[6] установили, что так называемые запрещенные переходы не
являются строго запрещенными во многих случаях и их можно
с успехом использовать для получения поляризации. Действи-
тельно, Эрб и другие исследователи [7] независимо открыли эф-
фект экспериментально. Используя этот метод, Джеффрис с кол-
легами в Беркли и экспериментаторы в Сакле под руководством
Рнс. 7.7. Насыщение запрещенного перехода (вероятность перехода Wen),
при котором одновременно опрокидываются электронный и ядерный спины,
приводит к ядерной поляризации.
Предполагается, что единственными имеющими значение релаксационными процессами
являются переходы с опрокидыванием одних лишь электронных спинов.
Абрагама получили поляризацию протонов свыше 70% и нашли
ей много полезных применений. Изобретение этого нового ме-
тода ядерной поляризации было значительным шагом вперед.
Возможны два типа запрещенных переходов. Они показаны
на рис. 7.7 и 7.8. Переход, изображенный на рис. 7.7, можно
Двойной резонанс
259
индуцировать переменным полем, параллельным постоянному
полю. В этом случае следует рассмотреть гамильтониан простого
изотропного электронно-ядерного взаимодействия G.3) во вто-
ром порядке теории возмущений, чтобы учесть влияние члена
A(ISx + IySy), смешивающего состояния | + —) и | |-).
у, =1++)
Рис 7.8. Запрещенный переход, приводящий к ядерной поляризации противо-
положного знака.
Переходы, показанные на рис. 7.7 и 7.8, можно индуцировать
переменными полями, перпендикулярными полю Яо. Тогда за-
дача решается с адекватной точностью для гамильтониана более
общего вида G.6). Например, в случае диполь-дипольного взаи-
модействия ядра с электроном на расстоянии г вычисления при-
водят к отношению матричных элементов переходов со взаим-
ным опрокидыванием электронного и ядерного спинов (рис. 7.7
и 7.8) к матричному элементу перехода с опрокидыванием од-
ного лишь электронного спина (рис. 7.6) порядка yeh/r^Ho. От-
ношение зависит от угла между направлением постоянного поля
и вектором, соединяющим ядро и электрон. (Влияние диполь-
дипольного взаимодействия можно учесть точнее, если исполь-
зовать составляющие постоянной взаимодействия АХ'Х>, АУ'У', AZ'Z.)
Даже если вероятность запрещенного перехода Wen мала,
часто можно с помощью достаточно сильного переменного маг-
нитного поля добиться того, чтобы она была больше скорости
релаксационных переходов W;,-, при которых опрокидываются
ядерные спины. В этом случае достигается эффективное вырав-
нивание населенностей уровней, связанных переходом Wen.
Проанализируем ситуацию, изображенную на рис. 7.8, когда
насыщается переход между состояниями l[ih = |++)] и
4[я|L= | )]. Полагая, что имеют значение лишь те тепловые
переходы, которые показаны на рис. 7.8, немедленно получаем
Р\ = Рл
р2 —
Рз =
G.29а)
G.296)
G.29в)
260 Глава 7
поэтому
G.30a)
<7'30б>
Используя G.216), находим
Чтобы оценить значение этого выражения, рассмотрим его в вы-
сокотемпературном пределе (оценку выражения для любой тем-
пературы предоставляем читателю). Имеем
G-32)
и увеличение поляризации относительно нормальной соответ-
ствует полному эффекту Оверхаузера:
Цг) Ye
ТГ\ = 7Г"€
vz/терм Yn
§ 6. Двойной электронно-ядерный резонанс
(ДЭЯР)
Эксперимент по двойному резонансу большой исторической
важности был выполнен Фехером [8]. Он ставил цель добиться
разрешения резонансных линий, не разрешаемых в обычном
электронном спиновом резонансе. Новый метод Фехер назвал
двойным электронно-ядерным резонансом (ДЭЯР). Идея метода
заключается в том, что в сущности, наблюдается ядерный ре-
зонанс через его влияние на электронный спиновый резонанс.
Фехер изучал электронный спиновый резонанс электронов, свя-
занных с донорными атомами в кремнии. Природный кремний
содержит 5% изотопа Si29, ядра которого имеют спин 1/2 и маг-
нитный момент. Вследствие большого радиуса орбиты электрон*
ный спин магнитно связан со многими ядрами Si29. Поскольку
сверхтонкие поля ядер Si29 на электроне зависят от того, через
какие ядерные позиции проходит донорная орбита, а ядро Si29
может иметь две спиновые ориентации, то на электрон действует
много различных локальных полей.
Сущность ситуации можно понять, рассматривая гамильто-
ниан одного электрона, который взаимодействует с N спинами
ядер Si29. (Для простоты, чтобы избежать необходимости обсуж-
дать статистический эффект, связанный с природной распро-
Двойной резонанс 261
страненностью изотопов, предположим, что все атомные узлы
кремния заняты изотопом Si29.) Возьмем гамильтониан в виде
Ж = yehHoSz + S • ? Atlt - Ynft#o/Z, G.34)
где Ai — постоянная сверхтонкого взаимодействия i-ro ядра (для
простоты предполагаем, что сверхтонкое взаимодействие имеет
форму контактного взаимодействия Ферми, а не более общую
тензорную форму). Постоянная Л,- определяется кристаллогра-
фическим положением i-ro ядра относительно донорного атома.
Используя N квантовых чисел пи, являющихся собственными
значениями операторов hi, обобщим результаты § 3 на наш слу-
чай. Энергия системы определится выражением
Е = yehHums + ? А(т,т3 - ? упПНот(. G.35)
Электронному резонансу соответствуют переходы с правилами
отбора Ams = ±1, Am,- = 0 для всех и Частоты резонанса юв
определяются формулой
!4-m'- G-36)
i
Имеется много возможных значений постоянных Л,-, каждое
число пи может иметь два значения +V2 или —'/г, поэтому фор-
мула G.36) описывает много частот, фактически непрерывный
континуум, а не ряд частот, соответствующих разрешенным ли-
ниям, как, например, в случае взаимодействия электрона только
с одним ядром.' Для образца, содержащего много доноров, су-
ществует 2Ы различных способов задать значения чисел nil.
Проблема разрешения линий сверхтонкой структуры похожа
на ситуацию, в которой находится человек, имеющий несколько
телефонов на своем рабочем столе, когда все они звонят одно'
временно. Если он пытается отвечать всем сразу, то услышит не-
разбериху сообщений, так как абоненты говорят с ним одновре-
менно. Конечно, у его собеседников не возникает никаких проб-
лем — они слышат только один голос, в то время как он слышит
несколько.
Фехер понял, что каждое ядро Si29 находится в сверхтонком
поле только одного электрона. Поэтому сигналы ядерного резо-
нанса хорошо разрешены. Спин ядра Si29 в любом узле дает
вклад в два резонансных перехода, соответствующих тому,
складывается или вычитается сверхтонкое поле электрона с
внешним магнитным полем. Частоты ядерных переходов ядер
«>n« = 4nhHu + Aims G.37)
Si29, расположенных в различных кристаллографических поло-
жениях относительно донорного атома, приводят к отдельным
262 ' Глава 7
парам линий. Для многих узлов постоянные Ai являются доста-
точно большими, так что эти линии хорошо разрешены относи-
тельно линий, соответствующих другим узлам.
иь! J
lii-
I Viz
¦О
/А
11
¦Рг
¦Рг
Рис. 7.9. Схема Фехера наблюдения ядерного резонанса по его влиянию на
электронный спиновый резонанс.
а—состояния G.35) системы электрон и /-е ядро. Показаны электронный переход между
состояниями 1 и 2 и те же релаксационные переходы, что и при эффекте Оверхаузера.
б—относительные населенности уровней, возникающие в результате насыщения электрон-
ного перехода, в—изменение относительных иаселенностей уровней при быстром адиаба-
тическом прохождении через ядерный резонанс, соответствующий переходу между со-
стояниями 1 и 3, после выключения переменного поля, индуцирующего электронный пере-
ходе результате населенности уровней, сталн следующими (сверху вниз): p2B2s. Рг, Рг, РгВ-н.
Последующее включение этого поля позволяет наблюдать всплеск сигнала спинового
резонанса, как прн отсутствии насыщения.
Понимание того, что ядерный резонанс будет иметь хорошо
разрешенные линии, хотя разрешение невозможно в электрон-
ном спиновом резонансе, было большой заслугой Фехера. Од-
нако сигнал ядерного резонанса должен быть очень слабым, так
как концентрация доноров обычно мала (~1017 см). Фехер
придумал остроумный метод детектирования ядерного резонанса
по его влиянию на электронный спиновый резонанс.
Рассмотрим ситуацию, представленную на рис. 7.9. На диаг-
рамме показано только 4 уровня, энергии которых получим, за-
фиксировав все mi, кроме /-го ядра:
2] <4,тЛ tns + А,т,т8 — ynhHotn,. G.38)
2]
Очевидно, в этом случае можно определить эффективное по-
стоянное поле, действующее на электрон:
т,. G.39)
Для определенности допустим, что процессы тепловой релак-
сации те же, что при эффекте Оверхаузера (§ 4), и что насы-
Двойной резонанс 263
щается тот же переход. Результирующие населенности показаны
на рис. 7.9, б. Предположим, что мы мгновенно выключили на-
сыщающее поле {We), включили ядерный генератор (Wn), час-
тота которого близка к частоте перехода со„ между состояниями
1 и 3, и осуществили адиабатическое быстрое прохождение через
линию ядерного резонанса. Прохождение переменит населенно-
сти состояний 1 и 3. Если затем снова включить переменное поле,
индуцирующее электронный переход (с вероятностью We), то в
первый момент амплитуда сигнала электронного резонанса будет
велика как при отсутствии насыщения, а затем" она будет умень-
шаться по мере насыщения. Таким образом, ядерный резонанс
влияет на электронный спиновый резонанс.
Мы описали один из методов ДЭЯР. Существует много дру-
гих его модификаций. Этот метод чрезвычайно важен для на-
хождения волновых функций различных парамагнитных центров
и поэтому является одним из основных способов изучения струк-
туры многих важных точечных дефектов в твердых телах (см.
хороший обзор [9] использования ЭСР и ДЭЯР для изучения
структуры точечных дефектов). Он также представляет большой
интерес для изучения структуры молекул в биологии. За свое
открытие и применение двойного резонанса Фехер был удостоен
премии Бекли по физике твердого тела Американским физиче-
ским обществом.
§ 7. Трехуровневый мазер Бломбергена
Принцип работы мазера заключается в следующем. Рабочее
вещество облучается на частоте, равной частоте линии погло-
щения, соответствующей переходу между двумя энергетическими
уровнями. Это приводит к излучению энергии на другой частоте,
если в результате поглощения верхний уровень оказывается бо-
лее заселенным, чем нижний. Таунс (см. [10, 11]) и независимо
Прохоров и Басов [12] показали, что такую систему можно ис-
пользовать в качестве основы для генератора электромагнитного
излучения нового типа. Таунс осуществил инверсию населенно-
стей в газообразном аммиаке физическим разделением молекул,
находящихся на верхнем и нижнем энергетических уровнях, с по-
мощью электрических полей соответствующей формы. Была ис-
пользована аппаратура для работы с молекулярными пучками.
Частота генерации попадает в диапазон СВЧ.
Вскоре после этого Бломберген обнаружил, что инверсию
энергетических уровней можно осуществить, используя эффект
Оверхаузера — Паунда, в котором перезаселение уровней произ-
водится путем насыщения перехода. Для осуществления идеи
264 Глава 7
Бломбергена требуется система с тремя или более энергетиче-
скими уровнями (рис. 7.10).
Пренебрежем для, простоты тепловой релаксацией между со-
стояниями 2 и 3, тогда
р1 = Рз, G.40а)
Р% = Р\Ва, G.406)
поэтому
Pi = p» = TTbT- G>41а)
й-ттвт- G-41б)
Таким образом, рг/рз = Bi2 и поскольку
В12 = е(?.-?2У*Г>1, G.42)
то
{J->1, G.43)
т. е. верхний уровень заселен больше нижнего, а это как раз и
есть условие для работы мазера на частоте (Е\ — Е2)/Л.
Pi Рис. 7.10. Трехуровневый мазер Блом-
бергена.
Переходы, обусловленные тепловой релак-
сацией, показаны пунктирными линиями.
Индуцированный переход обозначен сплош-
ной линией с двумя стрелками. Прн вырав-
нивании населенностей pi u рз в результате
п насыщения населенность ра оказывается
г2 инвертированной относительно населен-
ностей р\ или рз в зависимости от относи-
тельных величин вероятностей релакса-
ционных переходов между состояниями 1 и
2 или 2 и 3.
Рз
Бломберген показал [13], что ситуацию, которую он описал
теоретически, можно осуществить экспериментально в парамаг-
нитных ионах.
Идея Бломбергена имела громадное значение. Инверсия за-
селенностей уровней под действием накачки другого перехода
является основой работы всех лазеров. Накачку можно сделать
оптически (когда используется источник света), или осуществить
эквивалент накачки в химических реакциях (когда создаются
неравновесные населенности двух уровней системы и, следова-
тельно, условия для работы химического лазера), или с по-
мощью электрического разряда (лазер с электрическим разря-
дом). Прохоров и Басов [12] независимо развили многие из
этих принципов.
Двойной резонанс 265
§ 8. Беглый обзор других интересных
методов двойного резонанса
Хан предложил остроумный метод двойного резонанса для
двух типов ядер, названный им двойным резонансом спинового
эха (ДРСЭ). Важность этого метода состоит в том, что сигнал
ДРСЭ позволяет определить, насколько близко друг к другу
расположены два интересующие нас ядра. Рассмотрим обычное
спиновое эхо, которое формируется в моменты времени 2т им-
пульсом л/2 и следующим за ним спустя время т импульсом л.
В течение первого интервала времени т до импульса л спины
расфазируются, а в течение второго интервала времени после
импульса л они вновь сфазируются. Хан показал, что если ря-
дом с ядром, имеющим спин /, находится ядро другого сорта со
спином 5, то это соседнее ядро создает локальное поле, которое
может увеличивать или уменьшать внешнее магнитное поле,
уширяя резонансную линию подобно неоднородности поля маг-
нита. Конечно, неоднородность поля магнита не влияет на ам-
плитуду эха, так как эффект расфазировки из-за неоднородно-
сти в течение первого интервала времени т точно компенсирует-
ся фазировкой спинов с течение второго интервала времени т.
Однако, как показал Хан, если с помощью другого генератора
опрокинуть спины 5 импульсом л в тот же момент времени т,
когда опрокидываются спины / своим импульсом я, то направ-
ление локальных полей, создаваемых спинами S на спинах /,
будут противоположны в течение двух интервалов времени т до
и после импульса л, действующего на спины /. Таким образом,
спины / будут продолжать расфазироваться в течение второго
интервала времени т точно так же, как они расфазировались в
течение первого интервала времени т. В результате сигнал эхо
в момент времени 2т будет меньше. Эту идею экспериментально
подтвердили Каплан и Хан [14]. Пример резонанса, наблюден-
ного таким способом, показан на рис. 7.11.
Бойс [15] изучал разбавленный сплав Со в Си. Он хотел
обнаружить ядерный резонанс на ядрах Си, расположенных
рядом с ядрами Со. Сигнал резонанса таких ядер очень слаб
в разбавленных сплавах и часто закрывается краем сигнала
резонанса на ядрах Си, удаленных от примесей, т. е. краем так
называемой «главной линии меди». Бойс сумел обнаружить
«скрытый» резонанс ближайших соседей методом ДРСЭ. Он
наблюдал зависимость амплитуды сигнала эха ядер Со от ча-
стоты заполнения импульса л, близкой к частоте «главной ли-
нии» Си. Так как удаленные ядра Си не создают заметных
полей на ядрах Со, то импульс с частотой «главной линии»
имеет пренебрежимо малое влияние на амплитуду сигнала эха
Со. Другое дело — импульс п с частотой, равной частоте резо-
266
Глава 7
нанса ближайших соседей. В таком случае влияние велико. Из
этого примера, можно видеть, что ДРСЭ позволяет обнаружить
и выделить пары ядер, близко расположенные в пространстве.
Хотя в данной книге рассматриваются главным образом маг-
нитный резонанс в твердых телах, мы тем не менее обратимся
теперь к важному методу двойного резонанса, позволяющему
Частота Ш0-градусного импульса, действующего на ядра Си,
измеренная относительно основной линии ЯМР Си , кГц
[Положение
основной
\линииЯМР Си.63
Рис. 7.11. Сигнал ДРСЭ, наблюдавшийся Бойсом в порошке сплава Со в Си,
содержащего 0,54 ат.% Со.
Сигнал представляет собой сателлнтную резонансную линию от ядер Сии—ближайших
соседей ядер Со. Линия обусловлена переходом '/« ¦*—*¦ —'/» в системе уровней ядер Си.
Частота этого перехода близка к частоте резонанса Си6* в чистой меди в магнитном
поле 9907 Гс при температуре 1,5 К. Параметры импульса л, возбуждающего переход
'/2 -t—>- —'Д: г=250 мкс, Н\?*°*5Гс Каждая точка получена в результате усреднения по
100 сигналам эха. Размеры точек больше величины экспериментальной ошибки. Главная
резонансная линия от очень большого числа ядер Си63, удаленных от ядер Со, на сиг-
нале ДРСЭ Со не проявляется.
упростить сложные спектры в жидкостях. Этот метод разрабо-
тали Блох [16], Ройден [17], Блум и Шулери [18]. Если между
двумя сортами ядер со спинами I и S в образце существует ска-
лярное взаимодействие Л1-8, то резонанс спинов / расщепляется
на 2S + 1 линий равной интенсивности. Эти 25 + 1 линии сли-
ваются в одиночную линию, когда включается достаточно силь-
ное переменное магнитное поле на частоте резонанса спинов S.
Таким способом можно идентифицировать резонансную частоту
спинов S, которые расщепляют резонанс других спинов /. Наи-
более часто этот метод используется для измерения химического
сдвига спинов S, когда спины / и S принадлежат ядрам одного
сорта, различающимся лишь химическим сдвигом.
Рассмотрим два ядра с различающимися резонансными ча-
стотами, гамильтониан спин-спинового взаимодействия которых
Двойной резонанс 267
можно определить членом AIZSZ. Сфокусировав внимание на
спинах 5, запишем часть гамильтониана, включающую лишь
спины 5, в системе координат, вращающейся с резонансной ча-
стотой этих спинов:
Ж = Л/А - yshHls + Sx. G.44)
Если предположить, что поле His очень велико, то второй член
преобладает. На языке классической физики это означает, что
спины S прецессируют вокруг поля His и Sz гармонически изме-
няется во времени с угловой частотой \sHis. При достаточно
большой частоте эта прецессия будет усреднять взаимодействие
AlzSz до нуля. В результате спины / «не чувствуют» взаимодей-
ствия со спинами S. Это явление аналогично эффекту, вызван-
ному быстрыми перескоками спина S между состояниями, ха-
рактеризуемыми собственными значениями оператора Sz, кото-
рый обсуждается в приложении Е.
Формальную теорию можно разработать по схеме, изложен-
ной в § 11, на основе гамильтониана в дважды вращающейся
системе координат:
т=- yjhhoh + л/а - yshHiSsx, G.45)
где ho — Ho — <b//y/ — расстройка для спинов / в единицах на-
пряженности поля. Найдя BS + 1) B/+1) собственных значе-
ний энергии, можно определить частоты переходов, индуциро-
ванных поперечным переменным полем, приложенным к спи-
нам /.
В 1948 г. Танер и др. [19] выполнили эксперимент, который,
вообще говоря, можно отнести к эксперименту по двойному ре-
зонансу и который явился стимулом для других исследователей.
Сеш и Танер изучали спин-решеточную релаксацию протонов
в изоляторах. Времена релаксации Т\ в некоторых случаях
были порядка нескольких минут. Для наблюдения зависимости
Ti от напряженности постоянного поля они использовали цикли-
рование этого поля от высокого значения, при котором наблю-
дали резонанс, до низких значений, при которых в промежутках
между измерениями шла релаксация. Если рассматривать ре-
лаксационный процесс как резонансные переходы, индуцирован-
ные полем решетки, то их эксперимент можно считать одной из
форм двойного резонанса.
Хебел [20] и Редфилд [33] применили этот способ (размагни-
чивание до нулевого поля) для изучения ядерной релаксации в
сверхпроводниках. Проблема в данном случае состоит в том, что
сверхпроводник вытесняет магнитное поле, поэтому наблюдать
магнитный резонанс трудно. Циклирование магнитного поля
производилось начиная от значения напряженности, достаточной,
чтобы подавить сверхпроводимость. Уменьшая поле до нуля, они
268 Глава 7
достигали двух эффектов: 1) охлаждали ядерные спины и 2) пе-
реводили образец в сверхпроводящее состояние. В нулевом поле
температура ядерных спинов релаксировала к температуре ре-
шетки. Поэтому, когда напряженность поля магнита снова воз-
вращалась к исходному высокому значению через регулируемый
интервал времени т и образец переходил в нормальное состоя-
ние, спины нагревались до более высокой температуры по сравне-
нию с той, которую они имели в начале цикла. Хебел и Редфилд
измеряли увеличение температуры по изменению сигнала при
быстром прохождении через резонанс. Меняя т, они могли опре-
делить время спин-решеточной релаксации в нулевом поле.
Андерсон [21] совместно с Редфилдом объединили циклиро-
вание поля с возбуждением образца переменным магнитным
полем звуковой частоты, действующим в то время, когда по-
стоянное поле было равно нулю. Переменное поле нагревало
спины и позволяло найти характеристики поглощения спиновой
системы в нулевом поле. Циклирование поля позволило им реги-
стрировать эффекты, проявляющиеся в нулевом поле, с чув-
ствительностью резонансного метода, соответствующей силь-
ному полю.
Редфилд [22], Фернелиус [23], Слашер и Хан [24], Мини
[25] и другие применили циклирование поля для наблюдения
квадрупольных расщеплений ядер, находящихся вблизи атомов
другого сорта. Наблюдение очень больших квадрупольных рас-
щеплений связано с проблемой переноса энергии, поглощенной
при квадрупольном переходе в остальную часть спиновой си-
стемы. В этом случае необходимо отрегулировать амплитуду пе-
ременного магнитного поля со «звуковой» частотой в соответ-
ствии с условиями Хана и Хартмана. Эти условия обсуждаются
ниже в данной главе.
Были развиты другие многочисленные методы двойного резо-
нанса, включая некоторые приемы акустического и электриче-
ского возбуждения. Один из наиболее интересных и важных ме-
тодов был изобретен Ханом и экспериментально проверен им и
его студентом Хартманом [26]. Цель метода состояла в увели-
чении чувствительности детектирования. Обсудим это более по-
дробно.
§ 9. Проблема чувствительности
Рано или поздно все исследователи в области магнитного ре-
зонанса приходят к необходимости регистрировать такие слабые
сигналы, которые непосредственно не наблюдаются. Сигналы
резонанса могут быть слабыми при малом числе спинов, напри-
мер если исследуется редкий изотоп или если ядра занимают
особые положения, как в случае атомов на поверхности кпи-
Двойной резонанс 269
сталла или вблизи дефектов. Сигнал резонанса может быть сла-
бым и вследствие малого значения гиромагнитного отношения у.
Разработка сверхпроводящих соленоидов, генерирующих
магнитные поля высокой напряженности, способствовала значи-
тельному повышению чувствительности аппаратуры ЯМР, по-
скольку при этом возросла величина поглощаемых при резонан-
се квантов. Снижению шума способствует сужение частотной
полосы регистрирующей аппаратуры. Практически сужение ши-
рины полосы достигается за счет выбора больших постоянных
времени интегрирующих цепей, что в свою очередь требует уве-
личения времени прохождения через резонансную линию. При
большом времени прохождения дрейф базовой линии аппара-
туры приводит к искажению формы линии и появлению ложных
сигналов. Разработка многоканальных цифровых усреднителей
сигналов резко изменила ситуацию, поскольку появилась воз-
можность многократного сложения (накопления) большого чи-
сла сигналов, полученных при быстром прохождении. Если ап-
паратура начинает дрейфовать, то накопление можно прервать,
произвести регулировку спектрометра и продолжать накопление.
Кроме того, накопление производят лишь до тех пор, пока не
будет достигнуто необходимое отношение сигнал — шум. Нако-
пленный сигнал пропорционален числу прохождений N. По-
скольку шум имеет случайный характер и принимает положи-
тельные и отрицательные значения, то его амплитуда увеличи-
вается пропорционально V^. В результате после N прохожде-
ний через резонанс и накопления сигнала с шумом получают
увеличение отношения сигнал — шум в N/^/W = -\/1Т раз.
Практически это означает, что для повышения отношения
сигнал — шум в 2 раза необходимо увеличить время накопления
в 4 раза. Это увеличение не вносит проблем при переходе от
1 к 4 мин. Однако, если накопление, проводившееся уже в тече-
ние 1 часа хотят удлинить до 4 часов, то это уже тяжелый путь
улучшения отношения сигнал — шум! Отсюда непосредственно
следует, что при использовании усреднения большое значение
имеет оптимальная установка параметров, таких, как Ни ам-
плитуда модуляции, амплитуда развертки и т. д. Следовательно,
когда производится поиск неизвестного резонанса, желательно
установить параметры оборудования так, чтобы получить макси-
мальный сигнал даже ценой возможного искажения резонанс-
ной линии (например, из-за использования слишком большой
амплитуды модуляции или из-за частичного насыщения). После
того как резонанс найден, можно обратить внимание на регули-
ровку параметров аппаратуры, чтобы избежать искажения.
Независимо от того, что делается для улучшения аппаратуры,
в конце концов достигается предел, обусловленный современным
270 Глава 7
состоянием экспериментального искусства. Что же делать в том
случае, если сигнал остается слишком слабым и не «вытяги-
вается» из шума. Следует применить двойной резонанс, предпо-
лагая, что в образце одновременно можно возбудить два резо-
нанса. Один резонанс «слабый», и его очень трудно или невоз-
можно наблюдать непосредственно, а другой — «сильный» —на-
блюдается стандартными методами. Например, слабый и силь-
ный резонансы могут давать ядра соответственно с низкой (спи-
ны S) и высокой (спины /) естественной распространенностью.
-X-
- Ms = +1/Z
Редкие спины S Распространенные спины I
Рис. 7.12. Взаимное опрокидывание спинов из начальных состояний X в ко-
нечные состояния О, прн котором происходит обмен энергией между редкими
и распространенными спинами.
Стрелками показаны разрешенные переходы. В этом примере предполагается, что расщеп-
ление уровней одинаково для двух сортов спниов, которые равны '/»•
(Для простоты мы используем термин «редкие ядра», подразу-
мевая тот сорт, резонанс которого слабый. Слабый резонанс
дают также ядра с малым значением у, поэтому в большинстве
случаев такие ядра можно тоже называть «редкими».)
Если переменным магнитным полем Hi возбуждается резо-
нанс редких ядер, то они поглощают энергию и их спиновая
температура растет. Обмен энергией между редкими и распро-
страненными спинами приведет к нагреву распространенных
спинов и уменьшению амплитуды их резонансного сигнала. Если
распространенные ядра термически изолированы от окружаю-
щей среды ( т.е.имеют большое Т\), их спиновую температуру
можно значительно увеличить просто путем достаточно длитель-
ного насыщения слабого резонанса. Большое увеличение спи-
новой температуры распространенных ядер легко наблюдать.
Время релаксации Ti многих систем можно сделать чрезвы-
чайно большим, переходя к низким температурам. Решающим
становится вопрос: каким образом обеспечить хороший обмен
энергией между двумя сортами ядерных спинов?
Предположим, что спины редких и распространенных ядер
равны 1/2 и расщепления их энергетических уровней одинаковы
(см. рис. 7.12). Тогда начальное состояние двух спинов, обозна-
ченное крестиками, имеет энергию, равную энергии конечного
Двойной резонанс 271
состояния этих спинов, обозначенного двумя кружками. Пере-
ходы между уровнями, при которых происходит обмен энергией,
могут описываться членом S+I~ гамильтониана диполь-диполь-
ного взаимодействия. Время обмена определяется величиной Т$.
Зеемановские расщепления двух различных сортов спинов
могут оказаться близкими лишь случайно. Конечно, если энер-
гетические уровни уширены (дипольным взаимодействием с
другими спинами), то возможна некоторая согласованная ре-
лаксация. Однако это мало поможет в случае, когда постоянное
поле Но порядка тысяч гаусс, а дипольные поля всего несколько
гаусс.
Если расщепление уровней спинов / в 2 раза превышает рас-
щепление уровней спинов S, то энергетический обмен между
ними возможен путем одновременного опрокидывания вниз'двух
спинов S и вверх одного спина /. Такие процессы описываются
матричными элементами, вычисленными в более высоком по-
рядке, а не простым дипольным матричным элементом (который
включает координаты лишь двух спинов). Такие матричные эле-
менты значительно меньше, поэтому энергетический обмен го-
раздо слабее.
Таким образом, мы видим, что наблюдать слабый резонанс
путем резонансной накачки энергии в спиновую систему с силь-
ным резонансом вообще не представляется возможным, потому
что затруднен обмен энергией между двумя различными сор-
тами спинов.
§ 10. Метод Хана
Задачу согласования зеемановских расщеплений двух раз-
личных сортов спинов можно было бы решить, если бы каким-то
магическим способом подействовать на спины / одним магнит-
ным полем, а на спины S —другим магнитным полем. Как это
можно сделать, если ядерные спины расположены рядом на
атомном расстоянии?
Магическое решение этого вопроса было найдено чародеем
резонанса Ханом, который вместе с Хартманом — подмастерьем
чародея, — экспериментально подтвердил его [26]. Хан пони-
мал, что переменное магнитное поле влияет на ядра только то-
гда, когда его частота близка к частоте прецессии. Во всех дру-
гих случаях его влияние пренебрежимо мало. Поэтому, если он
приложит к системе два переменных ноля Ни и HiS с частотами
и/ и as, которые удовлетворяют соответствующим резонансным
условиям
Ю;==^ G.46)
272
Глава 7
то влияние поля Ни будет пренебрежимо мало на спины 5, а
поля H\S — на спины Л Тогда каждый сорт спинов можно рас-
сматривать в его собственной вращающейся системе координат.
На рис. 7.13 показаны две такие вращающиеся системы коор-
динат. Оси z этих систем совпадают. Это фактически направле-
ние магнитного поля Ио в лаборатории. На рис. 7.13 показаны
также векторы намагниченности М/ и Ms. В общем случае на-
правления этих векторов не обязательно совпадают с осью z или
с направлением соответствующего поля Н\, хотя такое совпаде-
ние может быть, если использовать специальные приемы приго-
товления системы. Если намагниченность М не параллельна
Рис. 7.13. Две вращающиеся системы координат, в которых оси Xi и xs на-
правлены вдоль соответствующих РЧ-полей Ни и His.
Ось г общая.
своему полю Н\, то она будет прецессировать вокруг Н\ во вра-
щающейся системе координат с частотой Q/ или Q,s:
«s-rs»is. G'47)
Из формул G.47) немедленно следует, что согласовать частоты
прецессии можно с помощью простой регулировки амплитуд
переменных полей, так чтобы их отношение удовлетворяло усло-
вию
Н
и
И,
G.48)
которое известно как условие Хана. Оно соответствует равенству
зеемановских расщеплений спинов / в поле Нц и спинов S в
поле His, причем каждый сорт спинов рассматривается в своей
собственной вращающейся системе координат.
Условие Хана согласует зеемановские расщепления, но в си-
стемах отсчета, которые в лучшем случае являются экзотиче-
скими. Реальная цель согласования состоит в том, чтобы обе-
Двойной резонанс 273
спечить возможность взаимодействия двух спиновых систем. Ка-
ким образом возникает это взаимодействие систем при рассмо-
тренном экзотическом согласовании? Известно, что между спи-
новыми системами существует диполь-дипольное взаимодей-
ствие. Уширение линии в случае двух спинов разного сорта опре-
деляется членом А гамильтониана диполь-дипольного взаимо-
действия:
Жлл = —^ h4zSz A-3 cos2 6/s). G.49)
ris
Поскольку оси г вращающейся и лабораторной систем коорди-
нат совпадают, то этот гамильтониан не изменяется при преоб-
разовании спиновых переменных во вращающуюся систему.
(Замечание. Иногда возникает путаница относительно того, ка-
кие переменные преобразуются. В квантовой механике фор-
мально можно ввести операторы, которые преобразуют I, S, г
в отдельности или любую их комбинацию. Поскольку rts и 8/s
не изменяются при вращении пространственных координат во-
круг оси г, гамильтониан G.49) не изменяется независимо от
того, преобразуется или нет радиус-вектор г. Как будет пока-
зано ниже, обычно преобразуют лишь операторы I и S, чтобы
исключить временную зависимость поля Н\, взаимодействую-
щего с соответствующими спинами.)
С точки зрения классической физики прецессия намагничен-
ности Ms вокруг поля His во вращающейся системе координат S
приводит к синусоидальной осцилляции составляющей MzS с ча-
стотой Qs = VsHis- Через диполь-дипольное взаимодействие Звал
[см. G.49)] появится зависящее от времени влияние на Мг1,
составляющую намагниченности М/, перпендикулярную полю
Ну. Следовательно, взаимодействие в этом случае дает такой же
эффект, как и переменное магнитное поле вдоль оси z с частотой
Qs. Если частота возбуждения Qs согласована с резонансной ча-
стотой Qi спинов /, то спины / поглощают энергию из системы
спинов S. Намагниченность М/ отклоняется от направления Ни.
Мы рассмотрели две связанные спиновые системы. Известно,
что если собственные частоты связанных систем совпадают, то
происходит резонансный перенос энергии и следует учитывать
обратную реакцию. Так, системе двух связанных маятников,
один из которых вначале покоится, а другой находится в движе-
нии, через некоторое время произойдет отклонение первого ма-
ятника на максимальную амплитуду, а второй будет в это время
покоиться. Тогда обмен энергией обращается, маятник, который
возбуждался, теперь сам возбуждает, а тот, который возбуж-
дал, теперь сам возбуждается.
Если имеется лишь пара спинов, то ситуация подобна рас-
смотренной. Однако обычно имеется много спинов / и много спи-
274 ' Глава 7
нов 5, которые могут быть связаны со спинами / и могут не
быть связаны, но всегда имеется много различных окружений.
Для такого случая становится полезным приписать спинам /
температуру 6/ в их вращающейся системе координат и темпе-
ратуру 6s спинам 5 в их вращающейся системе координат. При
этих обстоятельствах намагниченности Л\у и Ms направлены
вдоль соответствующих переменных полей Нц и His, но изме-
няются по величине вследствие обмена энергией. При равнове-
сии 6; = 6S. Увеличение 6s приводит к росту 6/.
Таким образом, мы видим, что существует возможность
связи двух различных спиновых систем, когда они могут обме-
ниваться энергией. Теперь необходимо выполнить следующее:
1) подвести под качественные аргументы твердую квантово-
механическую базу;
2) описать экспериментальные приемы, позволяющие осу-
ществить идею Хана;
3) проанализировать экспериментальные результаты.
§ 11. Квантовомеханическое описание
Запишем гамильтониан системы в лабораторной системе ко-
ординат
, G.50)
где &6zi(t)—зеемановский гамильтониан спинов /. Он описы-
вает взаимодействие спинов / как с постоянным полем к#0, так
и с двумя переменными полями. Удобнее рассматривать случай,
когда приложены вращающиеся поля, а не линейно-поляризован-
ные переменные поля. Тогда
Mzl (/) = - у,М • [кЯ0 -f itfucos (oj -f
+ jtf 17 sin azlt + itf iS cos azSt + j#is sin azSt], G.51)
где частоты сог/ и cozs могут быть положительными или отрица-
тельными в зависимости от направления вращения поля и
— полный спиновый вектор спинов /. Члены с индексом d пред-
ставляют собой гамильтонианы магнитного диполь-дипольиого
взаимодействия, например, {2^a)is — гамильтониан диполь-ди-
польного взаимодействия спинов / со спинами 5 и т. д.
Преобразуем теперь гамильтониан системы во вращающуюся
систему координат. При этом будем следовать методу Редфилда,
обсужденному в гл. 6. Рассматриваемая здесь задача, однако,
несколько отличается от задачи Редфилда, поскольку мы имеем
Двойной резонанс 275
два вращающихся поля. Поэтому преобразование будем делать
так, чтобы описывать движение спинов / и 5 в их соответствую-
щих системах координат. Такое преобразование легко выпол-
нить, вводя унитарный оператор Т следующего вида:
Т = exp {iazlfzt) exp (iazSSzt), G.52)
где
/, = Е/,|, Sz = ZS2k G.53)
/ к
— полные z-составляющие угловых моментов двух сортов спинов.
Новую волновую функцию системы определим уравнением
•ф' = Г1]з. G.54а)
Заменяя волновую функцию г]з на Г-'г]/, получаем уравнение
Шредингера
где Ж— преобразованный гамильтониан системы. Используя
приемы гл. 2, вычислим Ж в явном виде. В результате имеем
о -f co2//Y/) /z + HUIX] -
- Ys* [(# о + (WYs) Sz + HlsSx] +
^d// "T JGdlS "T <^dSS "Г (/.00)
-f- члены, зависящие от времени, которыми мы пренебрегаем.
Члены вида cfedii представляют собой те части гамильтонианов
диполь-дипольного взаимодействия Жст и других, которые ком-
мутируют с гамильтонианом зеемановского взаимодействия спи-
нов с постоянным лабораторным полем Но. Такие члены обычно
называют «секулярными частями» гамильтонианов диполь-ди-
польного взаимодействия. Мы их выпишем ниже в явном виде.
Гамильтониан Ж содержит зависящие от времени члены
двух видов. Один вид^—это несекулярные части гамильтонианов
диполь-дипольного взаимодействия. Они осциллируют с часто-
тами coz/, (>izs и (сог; ± cozs). Второй вид — это гамильтонианы
взаимодействия спинов / с полем His и спинов 5 с полем Нц,
которые осциллируют с частотой (ю2/ — azs) ¦ Поскольку частоты
©z/, azs и (сог/ ± cozs) значительно больше расстояния между
уровнями во вращающейся системе координат в единицах ча-
стоты, то всеми зависящими от времени членами можно прене-
бречь. Однако следует помнить, что может оказаться необходи-
мым учесть квадрупольное взаимодействие или тот факт, что
два ядра имеют близкие значения у (как, например, в случае
Си63 и Си65. Тогда частота (юг/ — azs) фактически может быть
близка к частоте возможного перехода.
276 Глава 7
Выберем частоты, точно соответствующие резонансным для
обоих сортов ядер,
«г/ = — Y/#oo. a*s = — Ys#oo, G.56)
где #оо — значение статического магнитного поля Яо. Позже мы
будем варьировать постоянное магнитное поле Яо около значе-
ния #оо. Заметим, что обе частоты отрицательны, если оба гиро-
магнитных отношения у положительны. Это означает, что спин
ядра с положительным значением у прецессирует в «отрицатель-
ном» направлении вокруг #0. Пренебрегая зависящими от вре-
мени членами гамильтониана 36'', учитывая G.56) и вводя обо-
значение #о — #оо = ho, получаем
+ Hulx] - ysh [hoSz + H1SSX] +
+ 3&is + As- G.57)
Выпишем зеемановские члены этого гамильтониана
Mzl = -Y/A Wг + HUIX] G.58)
и аналогично для 36Zs- Дипольные гамильтонианы имеют вид
U k r1k
и аналогичное выражение для 3e%ss- К этим членам может
оказаться необходимым добавить гамильтонианы псевдодиполь-
ного и псевдообменного взаимодействий, если ими нельзя прене-
бречь.
Именно гамильтониан !№dis описывает эффекты, которые
наблюдали Бломберген и Сорокин [27] при изучении CsBr. Они
нашли, что быстрая спин-решеточная релаксация ядер брома
способствует ускорению релаксации ядер Cs, когда они кван-
туются вдоль направления их резонансного поля #ь
Мы можем рассматривать различные взаимодействия, опи-
сываемые соответствующими членами гамильтониана G.57),
как зеемановские или дипольные энергетические резервуары.
Поскольку различные члены гамильтониана не коммутируют, то
между резервуарами возможен обмен энергией. Процессы об-
мена энергией можно назвать процессами кросс-релаксации в
дважды вращающейся системе координат. Скорость кросс-ре-
лаксации зависит от выравнивания расщеплений энергетических
уровней, соответствующих различным членам, от теплоемкостей
резервуаров и от интенсивности взаимодействия, определяемой
Двойной резонанс 277
величиной коммутатора этих членов. Мы видим, что зееманов-
ский гамильтониан c/Gzi спинов / коммутирует с зеемановским га-
мильтонианом <№zs спинов 5. Однако, если Ни Ф О, то 26zi не
коммутирует ни с cflfdu, ни с <№uis и, следовательно, между
зеемановским резервуаром спинов / и резервуарами дипольных
взаимодействий спинов / между собой и со спинами 5 возмо-
жен перенос энергии. Кроме того, член 3$dis определяет меха-
низм переноса энергии между зеемановскими резервуарами спи-
нов / и 5 (при условии, что His Ф 0).
Все эти замечания, следуя Редфилду, приводят к предполо-
жению, что спустя достаточно долгое время различные энерге-
тические резервуары придут в равновесие, при котором систему
можно описать общей температурой 6. Возможно также и удо-
бно для некоторых целей предположить, что различные резер-
вуары могут приходить к внутреннему равновесию, описывае-
мому своей температурой, быстрее, чем вся система достигнет
единой температуры. Эта точка зрения Лурье [28] принимается
при вычислении некоторых времен кросс-релаксации.
Таким образом, мы сделаем предположение, что система по-
сле достижения общей единой температуры описывается матри-
цей плотности
Р "~
Sp{exp (- Ж/kQ)} ' t'-bU)
где Ж — гамильтониан G.57). Используя р, можно вычислить
среднюю энергию Е и вектор средней намагниченности <М/>
в высокотемпературном приближении
G.616)
где Ci и Cs — постоянные Кюри, определяемые числом спинов /
или 5 в единице объема, т. е. Ni или Ns, и постоянной Больц-
мана k, например,
С, = ш '- и т. д., G.62)
и где Ядок получается из уравнения
^4
После вычисления следа находим
Я2ЛОК = У,<ДЯ,2,> + (AHh) + }1^Tj? <АЯ**>. G.64)
278 Глава 7
где <Д#ар) — вклад (в гауссах) спинов сорта |3 во второй мо-
мент резонансной линии спинов а. Ялок имеет размерность на-
пряженности магнитного поля. Хотя мы называем Нлок «локаль-
ным полем», его не следует путать с локальным полем Лорен-
ца. Действительно, Ялок вводится просто для того, чтобы полу-
чить возможность найти постоянную С/ из различных уравне-
ний. Дипольная энергия определяется выражением С/ЯЛок/0-
На первый взгляд такая запись, казалось бы, учитывает только
вклад спинов /. Однако это не так. В выражениях G.63) и
G.64) явно виден дипольный вклад спинов 5 в локальное поле
ЯЛок. Величина CiHjiOK определяет полный дипольный вклад
в спиновую теплоемкость. Заметим, что, хотя термин «локаль-
ное поле» звучит довольно неопределенно, величина Ялок по-
всюду может рассматриваться как вполне определенная пред-
сказуемая величина, которую можно вычислить точно. Един-
ственное исключение из этого утверждения находят, когда вклад
псевдодипольного взаимодействия становится заметным, как, на-
пример, в случае элементов с большими атомными номерами.
Тогда необходимо знать величину псевдодипольного взаимодей-
ствия, чтобы сделать количественные предсказания.
Величину <М/> можно определить по фотографии с экрана
осциллографа, измеряя начальную амплитуду затухающего сиг-
нала свободной индукции, который следует за выключением
поля Ни.
Необходимо еще одно выражение, а именно для намагни-
ченности M.I, которая получается после размагничивания спи-
нов /. Предположим, что HIS = Ни = 0 и 1№/ = кМ/0, где
MI0 = C,Ho/Qi G.65)
— термически равновесная намагниченность спинов / при тем-
пературе решетки 0г. При ho~> Ялок включаем Ни и медленно
уменьшаем h0 до нуля. В конце этого процесса в соответствии
с G.61) получаем
г "" -..,, • G.66)
1/4/ + ".tokJ
Если бы мы медленно изменяли Нц, то намагниченность <М/>
следовала бы за Ни в соответствии с G.66).
§ 12. Цикл смешивания и его уравнения
Существует два способа выполнения эксперимента по двой-
ному резонансу. Первый предложил Хартман и Хан [26]. Вто-
рой, являющийся разновидностью первого, продемонстрировал
Лурье [28].
Двойной резонанс 279
Как станет очевидным, два разных метода имеют простые
термодинамические аналоги. Рассмотрим два тела, связанные
стержнем, обеспечивающим тепловой контакт. Одно тело с ма-
лой теплоемкостью — аналог спинов 5 с малой распространен-
ностью, другое тело с большой теплоемкостью — аналог спинов
/. Аналогией экспериментов Хартмана и Хана может служить
нагревание большого тела при поддержке постоянной повышен-
ной температуры малого тела. Скорость нагревания зависит от
теплопроводности стержня и от теплоемкости большого тела
(системы спинов /), но не зависит от теплоемкости малого тела
(системы спинов 5), поскольку его температура не изменяется.
Для теоретического предсказания скорости нагревания боль-
шого тела необходимо знать его теплоемкость и теплопровод-
ность стержня. На языке резонанса это означает, что необхо-
димо вычислить время' кросс-релаксации. Это нельзя сделать
точно.
Аналогией эксперимента Лурье может служить разрыв теп-
лового контакта между стержнем и малым телом, нагревание
малого тела до известной температуры, отсоединение нагрева-
теля и подсоединение стержня. Через достаточно большой ин-
тервал времени вся система в целом, включающая большое и
малое тела, а также стержень, достигнет общей температуры.
Так как система спинов S имеет сравнительно малую теплоем-
кость, конечная температура всей системы будет мало отли-
чаться от начальной температуры большого тела. Однако можно
повторить цикл. Фактически, если проделать тепловое смешива-
ние N раз, то нагрев системы спинов / будет таким же большим,
как если бы было проделано единственное смешивание с систе-
мой спинов 5, теплоемкость которой в TV раз больше, чем в дей-
ствительности. Число TV может быть очень велико, и поэтому
можно достичь значительного эффекта, даже если спины 5
имеют очень малую относительную теплоемкость.
Чтобы вычислить рост температуры, необходимо знать лишь
теплоемкости всех частей системы. Нет необходимости даже тре-
бовать, чтобы теплоемкость стержня была малой, так как ее
влияние легко учесть. Теплоемкости спиновых систем вычислить
просто, и это можно сделать точно. Следовательно, мы имеем
точную теорию, которую можно сравнить с экспериментом.
Анализ Хана и Хартмана показал, что эффективная тепло-
проводность стержня зависит от величины двух вращающихся
полей. Условие Хана обеспечивает самое быстрое смешивание
или максимальную теплопроводность. Теплоемкость спиновой
системы определяется в значительной мере амплитудой поля Н\.
Поэтому можно изменять теплоемкости экспериментально, хотя
следует помнить, что если отношение полей #i не удовлетворяет
условию Хана, то для достижения однородной температуры мо-
280 Глава 7
жет потребоваться больший интервал времени. Дипольное вза-
имодействие между двумя различными сортами спинов является
тем самым «стержнем», который обеспечивает тепловой контакт
между системами. Как отмечалось, можно легко вычислить его
теплоемкость. Аналогично существует вклад в теплоемкость от
дипольного взаимодействия внутри спинов / и внутри спинов 5.
Все эти эффекты можно просто и строго учесть. Лурье показал,
что поля #i не обязательно должны быть велики по сравнению
с локальными полями, и далее продемонстрировал возможность
контакта между спиновыми системами в случаях, когда Н1Г
уменьшается до нуля.
Проанализируем теперь эксперимент Лурье. Всюду будем
предполагать, что спин-решеточной релаксацией можно прене-
бречь на тех интервалах времени, в пределах которых выпол-
няется эксперимент. Процессы спин-решеточной релаксации мож-
но легко учесть, однако необходимо соблюдать осторожность при
учете поперечных эффектов Оверхаузера, описанных Бломберге-
ном и Сорокиным [27].
Начнем с процесса размагничивания. Он приводит к ориен-
тации <М/> вдоль оси xi. Величина <М/> определяется форму-
лой G.66). Обозначим намагниченность через <М,>/. В течение
этого процесса, поскольку поле H1S равно нулю, 2@Zs точно ком-
мутирует с остальной частью гамильтониана. Поэтому коммути-
рует и с yshSz. Таким образом, намагниченность <MS> остается
неизменной и направленной вдоль постоянного лабораторного
поля Но. Резервуары (кроме зеемановского) спинов 5 имеют
общую температуру 6;, которую можно вычислить, используя
выражения G.61) и G.66):
6t = CiHd{Mt)t. G.67)
Эта температура, конечно, значительно ниже температуры ре-
шетки 6/.
Теперь внезапно включим переменное поле HIS. Такой бы-
стрый процесс не изменит состояния системы. Дипольная и зее-
мановская энергии спинов / не изменятся. Зеемановская энергия
спинов 5 станет равной нулю:
= 0, G.68)
поскольку векторы <MS> и (НЭфф)$ оказываются перпендику-
лярными. Поэтому полная энергия системы Ei определяется
формулой
Ei = /L \ •°°kJ . G.69)
После достаточно большого интервала времени зеемановский
резервуар спинов 5 приходит в тепловое равновесие с остальной
Двойной резонанс 281
частью системы, причем конечная температура всей системы бу-
дет равна 0f. Конечная энергия Ef в этом случае выражается в
виде
Поскольку, однако, вся система в целом изолирована и ее га-
мильтониан не зависит от времени, ее энергия не может изме-
ниться. Следовательно,
Et = Ef, G.71)
откуда следует, что
ef
C(H2+H2 ) + C H2 — 1 + 8 ' \'-'z)
где
8SE cf (//», + //» )' GJ3)
В этом процессе величина намагниченности <М/> падает от
начального значения Мц до конечного значения Мц, которое, со-
гласно закону Кюри, равно
Мп/Мн = 1/A + е). G.74)
Далее также внезапно выключим поле HlS- Снова немедленно
после выключения волновая функция системы не будет отличать-
ся от волновой функции до выключения. Зеемановская энергия
спинов / и дипольная энергия не изменяются, однако зееманов-
ская энергия спинов 5 становится равной нулю, так как
(Я9фф) s = 0. Поэтому полная энергия Ef определяется форму-
лой
^--С/(Я1/е^Ял°к)- G-75)
Немедленно после выключения His намагниченность <1WS> не
равна нулю, т. е. теплового равновесия нет. Через достаточно
долгое время система в целом придет в равновесие с общей тем-
пературой вц. Намагниченность <Ms) при этом затухает до
нуля. Это — необратимое затухание. Ниже мы фактически будем
вычислять увеличение энтропии.
Когда система достигнет конечной температуры 0f/, ее энер-
гия Eff, согласно G.61а), будет выражаться в виде
Eff = - Cj (H2U + ЯЛОК)/6Г G.76)
Однако Eff = Ef, так как спиновая система изолирована от вне-
шнего мира и описывается не зависящим от времени гаыильто-
282
Глава 7
нианом. Поэтому, используя G.75) и G.76), получаем
G.77)
Из закона Кюри следует, что после выключения поля His на-
магниченность <М/> не изменяется. Таким образом, можно no-
40 SO 1Z0
Число импульсов
160
гоо
Рис. 7.14. Экспериментальные данные Лурье.
Зависимость 1пЛ17 от числа импульсов при 1,5 К. Значения РЧ-полей Я17=2,14 Гс,
Я|в=5,4 Гс почти удовлетворяют условию Хаиа t.
вкл выкл
-\ мс Сплошная линия
рассчитана по формулам G.78) и G.79).
казать, что за один полный цикл включение — выключение поля
His уменьшение намагниченности <М/> определяется множите-
лем 1/A -f e).
Рассуждение можно повторить для другого цикла включе-
ние— выключение //is. После TV циклов отношение намагничен-
ности Mi(N) к ее начальному значению перед первым циклом
Mi @) будет равно
be)]". G.78)
Двойной резонанс
283
Если е ^С 1, как в рассматриваемых экспериментах, то можно
написать
где 8 определяется формулой G.73).
Двойной резонанс возможен даже при условии Нц •< Н„ок.
В этом случае намагниченность Mi сначала ориентируется вдоль
60
1,2
О Z 3 U 5 6 7 8 9 W
Амплитуда РЧ-поля, действующего
на. ядра Ы6, Гс
Рис. 7.15. Зависимость 1пМ7 от Н\6 при 1,5 К для N-+22, <„кл =
и 10 мс, Нп = 2,30 Гс.
Услоиие Хана для Hi7=2,30rc выполняется при Hie=6.1 Гс. Сплошная линия рассчитана
по G.73) и G.78).
поля Нц во вращающейся системе координат, которое затем
адиабатически уменьшается. Согласно закону Кюри, УИ/ « 0
при Нц fa 0, однако в спиновой системе / порядок остается, но
теперь он устанавливается относительно локального поля [29].
Поле His циклически включается и выключается N раз. После
iV-ro цикла Ни адиабатически возвращается к его первона-
чальному значению. И наконец, наблюдается результирующая
намагниченность Mi по затухающему сигналу свободной индук-
ции после быстрого выключения поля Ни-
Анализ двойного резонанса при условии Ни •< НДОК, по су-
ществу, не отличается от приведенного выше. Однако теперь
в формулах G.69) и G.70) не появляется член CjH2u/Q, и вели-
284 Глава 7
чина е определяется выражением
G.79)
Лурье изучал металлический литий, который имеет два изо-
топа Li7 и Li6 с распространенностями 93 и 7%. Изотоп Lir
дает сильный сигнал резонанса и в эксперименте по двойному
резонансу является сильной спиновой системой /. Изотоп Li6
является слабой спиновой системой S. Лурье измерял амплитуду
затухающего сигнала свободной индукции Lir после N циклов
смешивания.
На рис. 7.14 приведены данные Лурье, показывающие влия-
ние N на уменьшение сигнала Li7. Сплошная линия не имеет под-
гоночных параметров, кроме точки пересечения с прямой N = 0.
Рис. 7.15 показывает, что описание двойного резонанса на
языке спиновой температуры справедливо, даже когда условие
Хана выполняется неточно. Отметим, что сплошная линия не
имеет подгоночных параметров. Отклонения для больших зна-
чений резонансного поля Я16, действующего на ядра Li6, и ма-
лых /вкл и /выкл появляются потому, что за эти интервалы вре-
мени не успевает установиться общая спиновая температура.
В эксперименте Лурье наблюдается очень большое уменьше-
ние амплитуды сигнала Li7. Другими словами, можно сказать,
что значительно меньшее число ядер Li6 могло бы дать наблю-
даемое уменьшение сигнала. В таком случае пришлось бы бес-
покоиться о том, что энергия должна переноситься спиновой
диффузией на большое расстояние от горячих спинов Li6 к уда-
ленным спинам Li7. Эта задача исследована экспериментально
несколькими авторами [30—32].
§ 13. Энергия и энтропия
Интересно проследить за изменениями энергии и энтропии
спинов, которые участвуют в двойном резонансе. Сущностью
эксперимента является нагревание спинов / через контакт с го-
рячими спинами S. Существует макроскопический поток энергии
в систему как результат проделанной над спинами S работы.
Разрушение намагниченности спинов / соответствует необрати-
мой потере порядка, т. е. увеличению энтропии. Конечно, энер-
гия системы является средним значением гамильтониана G.57).
Основные теоремы квантовой (и классической) механики утвер-
ждают, что полная энергия остается постоянной до тех пор, пока
Ш не зависит явно от времени. Перераспределение энергии вну-
три полной системы даже тогда, когда Ж не зависит от времени,
мы идентифицируем как тепловой поток внутри системы. Изме-
Двойной резонанс 285
нения полной энергии системы, обусловленные вариациями внеш-
них параметров, мы называем работой над спиновой системой.
Можно проследить за циклом, рассматривая работу и пере-
нос тепла во вращающейся системе координат. Обсудим один
полный цикл включения и выключения поля HxS. Начнем с бы-
строго включения His. Вспомним, что зеемановская энергия спи-
нов S равна
H1S. G.80)
Включение поля происходит настолько быстро, что дипольная
энергия не успевает измениться. В период включения поля His
работа не затрачивается, так как намагниченность <Ms> вна-
чале равна нулю. Установление намагниченности у спинов S
приводит к изменению (ffizs) от нуля к отрицательному значе-
нию. Таким образом, возникает тепловой поток из зеемановского
резервуара спинов S к остальным частям спиновой системы. Это
направление теплового потока вполне разумно, поскольку сразу
после включения HIS намагниченность <Ms> = 0, и мы можем
считать, что зеемановский резервуар спинов S имеет бесконеч-
ную температуру. С этим тепловым потоком между системами,
находящимися при различных температурах, должно быть свя-
зано увеличение энтропии.
После установления намагниченности <Ms> поле H\s выклю-
чается. Из формулы G.80) видно, что необходимо совершить по-
ложительную работу над зеемановским резервуаром. [Заметим,
что тепловой поток в течение включения и выключения поля His
равен нулю, так как эти процессы происходят скачком, поэтому
мы можем вычислить работу исключительно из изменения вели-
чины (JMzs), определенной формулой G.80).] В период после
выключения Hxs намагниченность <Ms> затухает до нуля. Снова
должно быть увеличение энтропии, связанное с необратимостью.
Мы теперь готовы повторить цикл снова. За период цикла было
произведено определенное.количество работы над спиновой си-
стемой и были необратимые потери порядка.
Если бы мы включили His в следующем цикле до того, как
намагниченность <Ms> смогла затухнуть, то спины совершили
бы положительную работу обратно над полем HiS. Фактически,
если бы намагниченность <Ms> не затухала совсем, мы бы полу-
чили обратно такое же количество работы, какое мы совершили
над спиновой системой S при выключении поля His. Мы бы то-
гда не совершили какого-либо определенного количества ра*
боты в цикле. Более того, кроме эффектов при первоначальном
включении, не было бы необратимых потерь намагниченности в
обоих спиновых системах. Для протекания необратимого про-
цесса необходим достаточно большой интервал времени.
286 Глава 7
Энтропию системы а можно вычислить, исходя из основного
выражения
Е + fee In Z
п
0==
_
где Z — статистическая сумма. Мы можем оценить G.81) в вы-
сокотемпературном приближении
0» k[in (Sp/) - 2^e2 S| f ], G.82)
где Sp / означает полное число состояний, равное
Sp / = B/ -Ь if1 BS + 1L G.83)
Оценка Spa%!2, подобная проделанной при получении формул
G.61а), дает (при Но = 0)
а = k [Nt In B1 + 1) -f Ns In BS + 1)] -
— ^ ^-^ • G.84)
[Заметим, что формула G.66), описывающая адиабатиче-
ское размагничивание, следует из закона Кюри G.616) и требо-
вания, чтобы энтропия, определяемая G.84), оставалась посто-
янной.] Так как мы рассматривали температуру в каждой части
цикла, мы можем использовать формулу G.84) и приближение
о малости е для нахождения полного увеличения энтропии
Of — о, за один полный цикл, начиная с температуры 0,
of-at = ^^-. G.85)
Половина этого увеличения происходит после включения, дру-
гая половина следует за выключением поля His. Чем больше
поле His, тем больше изменение энтропии за цикл. Существова-
ние намагниченности М/ означает наличие порядка, поэтому
большое поле His ведет к большому разрушению М;, что факти-
чески уже следовало из формулы G.79).
ЛИТЕРАТУРА
1. Pound R. V., Phys. Rev., 79, 685 A950).
2. Carver T. R., Slichter С. P., Phys. Rev., 92, 212 A953); Phys. Rev., 102,
975 A956).
3. Overhauser A. W., Phys. Rev., 91, 476 A953); 92, 411 A953).
4. Dynamic Nuclear Orientation, ed. by C. D. Jeffries, Interscience Publ., New
York, 1963. (Имеется перевод: Джеффрис К- Динамическая ориентация
ядер. — М.: Мир, 1965.)
5. Jeffries С. D., Phys. Rev-, 106, 164 A957); 117, 1056 A960).
6. Abragam A., Combrisson У., Solomon /., Compt. Rend., 247, 2237 A958).
Двойной резонанс 287
7. trb ?., Montchane J. L., Uebersjeld L, Compt. Rend., 246, 2237 A958).
8. Feher C, Phys. Rev., 105, 1122 A957).
9. Seidel H., Wolf H. С, в книге: Physics of Color Centers, Academic Press,
New York, 1968.
10. Gordon J. P., Zeiger H. Л, Townes С. H., Phys. Rev., 95, 2821 A954).
11. Nobel Lectures-Physics 1963—1970, Elsevier Publishing Co., Amsterdam,
1972.
12. Басов H. Г., Прохоров А. Л1, ЖЭТФ, 27, 431 A954).
13. Bloembergen N.. Phys. Rev., 104, 324 A956).
14. Kaplan D. E., Hahn E. L., Journ. Phys. Rad., 19, 821 A958).
15. Boyce J. В., Thesis, Univ. of Illinois," 1972.
16. Block F., Phys. Rev., 93, 944 A954).
17. Royden V., Phys. Rev., 96, 543 A954).
18. Bloom A. L, Schoolery J. N.. Phys. Rev., 97, 1261 A955).
19. Turner E. H., Sachs A. M., Pur cell E. M., Phys. Rev., 76, 465 (A) A949).
20. Hebel L. C, Slichter С. Р., Phys. Rev., 113, 1504 A959).
21. Anderson Л. С, Phys. Rev., 115, 863 A959).
22. Redfleld A. C, Phys. Rev., 130, 589 A963).
23. Fernelius N. C, Proc. of the XIV Colloque Ampere, 1966, p. 497.
24. Slusher R. E., Hahn E. L, Phys. Rev., 166, 332 A968).
25. Minier M., Phys. Rev., 182, 437 A969).
26. Hartmann S. R., Hahn E. L., Phys. Rev., 128, 2042 A962).
27. Bloembergen N.. Sorokin P., Phys. Rev., 100, 865 A958).
28. Lurie F. M., Slichter С P., Phys. Rev., 133, A1108 A964).
29. Slichter С P., Holton W. C, Phys. Rev., 122, 1701 A961).
30. Slusher R. E., Hahn E. L., Phys. Rev., 166, 332 A968).
31. Spencer P. R., Schmid N. D'., Slichter С P., Phys. Rev., Bl, 2989 A970).
32. Lang D. V., Moran P. R., Phys. Rev.. Bl, 53 A970).
33. Redfleld A. G., Phys. Rev. Lett., 3, 85 A959).
Глава 8
Новые идеи в импульсном
магнитном резонансе
§ 1. Введение
Открытие спинового эха, сделанное Ханом [1], показало, что
можно устранить уширение линий магнитного резонанса, возни-
кающее из-за неоднородности магнитного поля. Амплитуда сиг-
нала эха МBх) уменьшается по экспоненциальному закону
МBт) = ехр(—2%/Т2), где т — интервал времени между двумя
импульсами, а 1/Т2— истинная полуширина линии. Однако, если
неоднородность магнитного поля очень велика и скорость диф-
фузии ядер достаточно большая, то
1
_хЮ(у
М Bт) = М @) е-2х^е 3 \ дг ', (8.1)
где D — постоянная диффузии и дН/dz — градиент постоянного
поля. С одной стороны, в некоторых случаях второй экспонен-
циальный множитель может исказить измеряемые значения Т2.
С другой стороны, если градиент поля дН/dz известен, то этот
множитель позволяет найти D. Вывод диффузионного члена при-
веден в приложении Ж.
Карр и Пёрселл [2] изобрели остроумный метод исключения
диффузионного затухания сигнала эха. Их предложение поло-
жило начало целому классу экспериментов, в которых исполь-
зуются многоимпульсные последовательности. В данной главе
мы сначала обсудим метод Карра — Пёрселла, затем его про-
стую модификацию, предложенную Мейбумом [3], и наконец
рассмотрим наиболее сложные импульсные методы, которые
имеют замечательное свойство: они дают возможность устранить
дипольиое уширение резонансных линий в твердых телах. Эти
методы продолжают изобретать. Начало им положили идеи Уо
[4] и Менсфилда [5]. Многое для их развития сделали Воэн
[6] и большая группа талантливых учеников этих исследовате-
лей.
§ 2. Последовательность Карра — Пёрселла
Предположим, что можно пренебречь диффузионным членом.
Чтобы измерить Т2 обычным методом спинового эха, необходимо
проделать серию экспериментов при различных интервалах ме-
Новые идеи в импульсном магнитном резонанс*
289
жду импульсами т. Огибающая амплитуд сигналов эха в зависи-
мости от 2т даст значение Т2. Карр и Пёрселл указали, что оги-
бающую в целом можно получить гораздо быстрее, если приме-
нить правильную последовательность импульсов.
Предположим, в момент времени t = 0 действует РЧ-импульс
я/2, поле Hi которого направлено вдоль оси -\-х вращающейся
системы координат, а РЧ-частота ш точно равна частоте Лар-
мора ©о- Такой импульс поворачивает намагниченность Мо вок-
руг оси х и ориентирует ее вдоль оси —у. Если теперь прило-
жить импульс я в момент времени t = т, РЧ-поле #i которого
3-е
5г
6г
7г
6г
п
Огибающая
сигналов эха
Огибающая
сигналов эха
Рнс. 8.1. Импульсная последовательность Карра — Пёрселла и возбуждаемые
ею сигналы эха.
В тексте показано, что положительные сигналы эха формируются вдоль оси +у вращаю-
щейся системы координат, а отрицательные сигналы —вдоль оси —у.
также направлено вдоль оси -\-х, то в момент времени 2т по-
явится эхо, а намагниченность будет ориентирована вдоль оси
-\-у. Прикладывая далее импульсы я в моменты времени Зт,
5т, ..., {2п-\-\)% (n = 0,l,2, ...), будем наблюдать сигналы
эха в моменты времени 4т (намагниченность вдоль оси —у),
6т Bп + 2)т. Эха формируются, когда намагниченность
ориентируется вдоль оси —у для нечетных п или вдоль оси -\-у
для четных п. Так как все составляющие намагниченности в пло-
скости ху затухают экспоненциально с постоянной времени Т2,
то аналогичным образом затухает последовательность эха.
Последовательность таких импульсов и эха показаны на
рис. 8.1. Положительный знак эха соответствует формированию
его вдоль оси -\-у, отрицательный — вдоль оси —у.
Очевидно удобство рассмотренного метода. Он позволяет по-
лучить полную огибающую сигналов эха с помощью только од-
ной импульсной последовательности. Если сигнал слабый и важ-
ное значение приобретает отношение сигнал — шум, то последо-
вательность Карра — Пёрселла имеет огромное преимущество.
290 Глава 8
Шум зависит от ширины полосы пропускания аппаратуры. Эту
ширину выбирают из условия пропускания сигнала эха без чрез-
мерного ослабления. Очевидно, что можно использовать одну и
ту же ширину полосы для приема последовательности сигналов
эха Карра — Пёрселла и обычного двухимпульсного эха. Однако
прием только одного сигнала эха занимает такой же интервал
времени, какой необходим для приема всей последовательности
сигналов эха Карра — Пёрселла. Если для определения затуха-
ния огибающей обычного эха необходимо взять N сигналов, то
за это время мы можем получить N последовательностей Кар-
ра — Пёрселла. Поэтому каждый сигнал эха в этой последова-
тельности записывается N раз. Таким образом, при одинаковой
затрате времени мы получаем выигрыш в отношении сигнал —
шум в -yfW раз.
Как уже отмечалось, импульсная последовательность Кар-
ра — Пёрселла уменьшает влияние диффузии на затухание сиг-
налов эха. Рассмотрим, почему это происходит. Если диффузии
нет, спины расфазируются в течение интервала времени т после
каждого эха и вновь сфазируются в течение интервала т после
импульса п. Диффузия нарушает процесс фазирования спинов,
что приводит к уменьшению последующего эха. В приложении Ж
выведена формула
М Bт) = Мф-*1т"е 3 Vv в» / ¦¦ Mod, (8.2)
описывающая уменьшение сигнала эха вследствие диффузии.
Рассматривается случай, когда в момент времени t = 0 импульс
л/2 поворачивает намагниченность Мо в плоскость ху и затем,
спустя время т, импульс л создает эхо в момент времени 2т,
амплитуда которого пропорциональна МBт). В момент времени
2т в процессе формирования эха повторяется ситуация, которая
существует в момент времени t = О, за исключением того, что
намагниченность в плоскости ху уменьшена в а раз и направ-
лена вдоль оси -\-у, а не —у. Поэтому значение и направление
намагниченности в момент времени 2т можно рассматривать как
начальное условие при решении задачи (приложение Ж) о пове-
дении намагниченности в период времени между моментами 2т
и 4т; фазирующий импульс я действует в момент Зт. В резуль-
тате получаем
(8.3)
Следовательно, для п интервалов 2т находим
М(/12т) = М0а", (8.4)
.поэтому
М (п2т) = Мф-'а*-т'е a V д* >. (8.5)
Новые идеи в импульсном магнитном резонансе 291
Таким образом, если мы будем уменьшать т, но выдерживать
постоянным значение п2% так, чтобы можно было сравнить ам-
плитуды эха последовательностей Карра — Пёрселла в один и
тот же фиксированный момент времени п2%, то мы будем умень-
шать диффузионный множитель и не менять релаксационный
множитель. Увеличивая п и уменьшая т, мы можем уменьшить
влияние диффузии до пренебрежимо малой величины. Очевидно,
здесь играют роль два факта:
1) в течение каждого интервала времени 2т между двумя
эхами в последовательности Карра — Пёрселла намагниченность
уменьшается в \/а раз;
2) относительный вклад диффузионного члена по сравнению
с релаксационным зависит от т.
§ 3. Чередование фазы
и метод Мейбума — Гилла
Импульсная последовательность Карра — Пёрселла может
содержать много импульсов. Если поворот намагниченности
каждым импульсом слегка отличается от я, то может накопиться
большая ошибка. Это показано на рис. 8.2. Для простоты на-
чальный импульс я/2, поворачивающий намагниченность вокруг
оси -\-х, мы взяли совершенным и пренебрегали диффузией. К мо-
менту времени t = т~ спины в плоскости ху расходятся в веер.
Пусть некоторый спин направлен под углом 0 к оси —у. В мо-
мент времени t = т действует импульс я -f- бф вдоль оси -{-х. Угол
бф — неточность установки импульса я. Этот импульс в момент
времени / = тне влияет на спин, для которого 8 = я/2, т. е. на
спин, направленный вдоль оси —х. Спин, направленный вдоль
оси —у, для которого 8 = 0, будет поворачиваться импульсом,
как показано на рис. 8.2, в. Он будет направлен под углом бф
выше оси -{-у в плоскости уг. Такая ориентация будет сохра-
няться в течение интервала 2т до следующего импульса я -j- бф.
Результат действия следующего импульса показан на рис. 8.2, г.
Спин после импульса направлен под углом 2бф к оси —у. Каж-
дый последующий несовершенный импульс я увеличивает на
бф отклонение спина от направления оси у.
Практически этот накапливающийся эффект становится чрез-
вычайно серьезным потому, что поле Н\ никогда не бывает од-
нородным по объему образца. Следовательно, если даже на
часть образца будет действовать точный импульс п, на другие
части образца будет действовать неточный импульс я.
Такие затруднения являются основными для всех многоим-
пульсиых последовательностей, подобных тем, какие описаны
ниже в этой главе. Простой способ устранить влияние несовер-
292
Глава 8
шенства импульсов я заключается в попеременном изменении
направления поля Hi этих импульсов вдоль оси х. В этом случае
направление вращения спина вокруг оси х обращается от им*
пульса к импульсу. Результат показан на рис. 8.2, д. Вместо на-
капливающейся ошибки вращения 2бф (рис. 8.2, г) получается
нулевая ошибка.
¦Мв -*-
Jr-y
0<t<t
d
?6y ~
я + Stp
Рис. 8.2. Результат действия несовершенного импульса п.
Начальный импульс я/2, предполагаемый совершенным, поворачивает Afo к оси —у в мо-
мент времени t=0*. К моменту времени (=т~ непосредственно перед вторым импульсом
некоторый спии в результате прецессии в плоскости ху образует угол 6 с направлением
оси—у вследствие неоднородности постоянного поля. Несовершенный импульс л + 6ф в мо-
мент времени х поворачивает спины вокруг осн +jt на угол я + 6<р. Если в момент времени
t=x~ спнн был ориентирован по оси — у F=0), то после поворота он окажется в пло-
скости yz, как показано иа рис. 8.2, в. Спнн уже не находится в плоскости ху Сразу
после второго импульса л + 6ф в момент времени <=Cт)"^" тот же спнн направлен под
углом 26ф к плоскости ху (рис. 8.2, г). Если поле Hi второго РЧ-импульса направлено
вдоль осн —х, то направление поворота обращается, поэтому поворот на угол —(я + 6д>)
возвращает спин к его исходной ориентации в момент (=0+ (рис. 8.2, д).
Мейбум и Гилл [3] впервые нашли решение этой задачи.
Они, конечно, использовали фазово-когерентиый метод и ввели
90-градусный фазовый сдвиг между РЧ-полями начального им-
пульса я/2 и последующих импульсов п. Таким образом, если
поле Н\ импульса я/2 направлено вдоль оси -\-у, то поля Hi им-
пульсов л должны быть направлены вдоль оси -\-х. В результате
такого фазового соотношения все эхи формируются вдоль оси -\-х.
Мы предоставляем читателю показать, что если вместо импульса
п действует импульс л — б, то ошибка не будет накапливаться.
Новые идеи в импульсном магнитном резонансе 293
§ 4. Связь импульсного сужения линии 1)
магнитного резонанса с сужением линии,
обусловленным молекулярным движением
Характерное для твердых тел сильное спин-спиновое взаи*
модействие существенно для достижения высокой чувствитель-
ности в методе двойного резонанса. Однако оно приводит к уши-
рению линии и поэтому маскирует детали резонансной линии,
связанные, например, с анизотропными взаимодействиями (хи-
мический и найтовский сдвиги или квадрупольные взаимодей-
ствия). В этом его вред. В течение последних нескольких лет
были предложены разнообразные остроумные методы, в которых
сильные РЧ-импульсы используются для значительного умень-
шения дипольного уширения. Обратимся теперь к принципам, на
которых основаны эти методы. Они обязаны своим развитием
нескольким группам физиков. Пионерские эксперименты были
выполнены двумя группами исследователей: одна возглавлялась
Джоном Уо [4], а другая — Петером Менсфилдом [5]. Позже
Воэн [6] и его коллеги, а также другие ученые [7, 8], работав-
шие с Уо, Менсфилдом и Воэном, много сделали для развития
методов импульсного сужения линии ЯМР.
Сущность этих методов состоит в том, что образец возбуж-
дается повторяющейся серией РЧ-импульсов [9—14], которые
поворачивают спины в разных направлениях на большие углы,
и этот процесс, подобно сужению линии за счет молекулярного
движения, усредняет дипольное взаимодействие до нуля. Каж-
дый цикл состоит из небольшого числа импульсов (было ис-
пользовано до 8 импульсов в цикле). Чтобы достигнуть эффекта
сужения линии, необходимо повторить много циклов в течение
интервала времени расфазировки, соответствующего ширине ли-
нии жесткой решетки. Так как РЧ-импульсы должны поворачи-
вать спины на большие углы (обычно используются импульсы
я/2), а повороты должны занимать малую часть времени цикла
импульсов, то необходимо, чтобы поле #i в импульсе было боль-
шим по сравнению с шириной линии жесткой решетки.
Рассмотрим аналогию между сужением линии в твердом теле
в многоимпульсных экспериментах, которое будем называть
«импульсным сужением», и сужением линии вследствие молеку-
лярного движения.
Рассмотрим два спина / и S. Пусть г is — вектор, соединяю-
щий спины / и S. Магнитное поле Н/, создаваемое спином /
') В советской литературе по магнитному резонансу используется термин
«импульсное сужение линии» вместо «сужение линии, обусловленное сшшовым
опрокидыванием», — Прим. ред.
294
Глава 8
в точке нахождения спина S, равно
3 (ГЛ.-г.-
H/(r/s) = -
5
rIS
(8.6)
'is
Пусть вектор М/ направлен вдоль к. Рассмотрим три случая,
когда спин S находится на расстоянии а и направлен соответ-
а
Рис. 8.3 Три возможных положения (а — в) спина S, находящегося на рас-
стоянии а от спина /.
Спин / создает в точке нахождения спина S магнитное поле, силовые линии которого
показаны штриховыми линиями.
ственно вдоль осей х, у и z (см. рис. 8.3). Если спин S находит-
ся на оси z, на него, согласно формуле (8.6), действует поле
2М,
Н;(о, о, а) = —г-.
На осях х и у спин S «чувствует» поле
м,
Н;(а, о, о) = Н;(о, а, о) == — —f.
(8.7)
(8.8)
Новые идеи в импульсном магнитном резонансе 295
Если по какой-либо причине спин S будет быстро перескакивать
между этими тремя положениями, находясь в среднем в каждом
из них одинаковое время, он будет «чувствовать» среднее во
времени поле <#/>, равное нулю:
<Н/> = ~Ш,(а, о, о) + Н,(о, а, о) + ?1,(о, о, а)] =
= |-^BМ/-М,~М/) = 0. (8.9)
В этом заключена сущность сужения за счет движения. В рас-
смотренном случае мы выбрали дискретные точки нахождения
спина S. Такой же результат получается для непрерывного на-
бора положений, описываемых углом ориентации Qis вектора r/s
относительно оси г. Интенсивность взаимодействия зависит от
угла Bis как 3cos29/s — 1- Среднее значение этой величины по
сфере равно нулю.
Теперь мы видоизменим рассмотренную выше картину. Пред-
положим, что спин находится в точке (о, о, а), т. е. на оси г, и
будем рассматривать ориентацию обоих спинов М/ и Ms
(рис. 8.4).
Введем названия некоторых характерных ориентации вектора
r;s относительно М,. Обратимся к рис. 8.3. Конфигурацию, изо-
браженную на рис. 8.3, в, назовем осевой для спина S. Конфи-
гурации на рис. 8.3, а и б — боковыми. В случае осевой конфи-
гурации поле His параллельно М/, тогда как при боковых кон-
фигурациях H/s антипараллельно М/ и вдвое меньше по вели-
чине.
Возвращаясь к рис. 8.4, мы видим, что конфигурации а и б —
боковые, а конфигурация в — осевая. Поскольку мы выбрали па-
раллельную ориентацию М/ и Ms во всех случаях, то магнитная
энергия /?Магн = —Ms • His в случае конфигурации а и б равна
6 = -Ms.H/s = -^, (8.10)
а в случае конфигурации в
1JS'
(8.11)
Предположим, мы начинаем с осевой конфигурации на
рис. 8.4, в, когда М/ и Ms параллельны. Через интервал времени
т быстро поворачиваем М/ и Ms на угол я/2 вокруг оси у, чтобы
получить боковую конфигурацию на рис. 8.4, а. Затем, спустя
время т, быстро поворачиваем оба спина, чтобы получить боко-
вую конфигурацию на рис. 8.4,6, и снова ждем в течение вре-
мени х.
SQ6
Глава 8
Чему будет равна средняя по интервалу времени Зт магнит-
ная энергия <?Магн>? Используя (8.10) и (8.11), получаем
1 / — 2MJW-T М-М-т М,М,,Т\
<?магн> = 7 ^ Н5 ' Е^~~ "Т ^ J — О- (8-12)
Следовательно, циклом, в котором в установленные моменты
времени производятся повороты обоих спинов на выбранные
Рис. 8.4. Три параллельные ориентации (а — в) магнитных моментов М, и Ms
спинов / и S по осям координат х, у, г.
углы л/2, мы можем усреднить магнитную энергию до нуля. Та-
кие опрокидывания спинов устраняют дипольное взаимодействие
точно так же, как прыжки спинов по различным пространствен-
ным положениям (рис. 8.3). В этом заключается принцип им-
пульсного сужения линии. Дипольная энергия усредняется до
нуля благодаря поворотам спинов от одной выбранной конфигу-
рации— осевой — к другим — боковым, когда боковые конфигу-
рации существуют во времени в 2 роза дольше осевой.
Все более сложные импульсные циклы основаны на этом
принципе.
Новые идеи в импульсном магнитном резонансе . 297
§ 5. Формальное описание
импульсного сужения линии
В предыдущем параграфе мы рассмотрели возможность ус-
реднения до нуля диполь-дипольного взаимодействия благодаря
опрокидыванию спинов между осевыми и боковыми конфигура-
циями. В традиционном сужении линии за счет движения суже-
ние происходит, когда время корреляции тс и ширина линии в
жесткой решетке (в единицах частоты) бюЖр удовлетворяют со-
отношению
<1. (8.13)
Если перескоков спинов по положениям нет, то группа спинов,
прецессирующих сначала в фазе, расфазируется за интервал
времени порядка A/бсоЖр). Условие (8.13) выражает тот факт,
что сужение за счет движения получается тогда, когда перескоки
спинов происходят до их расфазировки. В нашем примере суже-
ния линии за счет движения время корреляции должно быть по-
рядка среднего времени, в течение которого спин находится в
одном из трех положений, изображенных на рис. 8.3. Если т —
время жизни спина в любой из трех конфигураций, то грубо
можно считать
тс«3т. (8.14)
Совершенно аналогично следует ожидать, что опрокидывания
спинов будут сужать линию только тогда, когда эти опрокиды-
вания между необходимыми конфигурациями случаются до того,
как произойдет расфазировка спинов. Таким образом, мы полу-
чаем условие для т
Зтбожр<1. (8.15)
Чем лучше удовлетворяется неравенство, тем более длительное
время спины будут прецессировать в фазе.
Поэтому необходимо все время опрокидывать спины по кон-
фигурациям на рис. 8.4. Этого можно достичь повторением цик-
ла импульсов. Основной цикл будет возвращать спины обратно
к их исходным состояниям в конце каждого цикла.
Формальное описание того, что происходит при импульсном
сужении линии, начинаем с определения гамильтониана. Мы ис-
пользуем его, чтобы вычислить развитие волновой функции во
времени. Запишем гамильтониан в виде
Ж (t) = Mv4 (Q + 3®B3. (8.16)
Будем работать во вращающейся системе координат, ось z ко-
торой направлена вдоль постоянного поля. Гамильтониан 26>рч (t)
описывает поворот спинов РЧ-импульсным полем. Он зависит от
298 Глава 8
времени, потому что импульсы включены в течение очень корот-
ких интервалов tw. В принципе поле РЧ-импульса Н! можно
ориентировать вдоль осей х, у и г. Направление вдоль х или
у — это вопрос фазы РЧ-импульса. Вообще говоря, РЧ-импульсы
вдоль оси z можно применять, однако практически они не ис-
пользуются, так как для их создания необходима другая катуш-
ка в экспериментальной установке. Поворот вокруг оси г можно
осуществить двумя последовательными поворотами вокруг осей
х и у.
Гамильтониан 5^вз включает два члена:
$, (8.17)
где
Жй = — П (©о - со) 1г — Пщ Ц агг11г! (8.18)
= ZBlt (г„) (I,. I, - 3/г,/г/). (8.19)
Член 5^о включает химический и найтовский сдвиги Ozzi. Член
ffifd — секулярная часть гамильтониана диполь-дипольного вза-
имодействия; коэффициенты Вц(гц) зависят от расстояний и уг-
лов.
Цель заключается в том, чтобы опрокидыванием спинов вы-
звать исчезновение 3@а и оставить отличным от нуля Жо-
Для иллюстрации принципов импульсного сужения линии по-
лезно идеализировать ситуацию. Поправки к идеализации
важны с практической точки зрения, и мы вернемся к ним в § 7.
Идеализация состоит в том, что <3$рч принимается равным
нулю все время, за исключением коротких интервалов времени,
в течение которых З^рч ^> Ж« и Шъъ можно пренебречь. Это при-
ближение позволяет нам описывать повороты спинов во время
действия РЧ-импульсов только гамильтонианом Ж?ч и вычис-
лять развитие волновой функции ty(t) в промежутках между им-
пульсами только с учетом не зависящего от времени гамильто-
ниана 3@ВЗ-
Таким образом, между импульсами волновую функцию в мо-
мент I можно связать с ее значением в более ранний момент t\
с помощью выражения
ф@ = е * ВЗ< 1Ч(/.) = ?/вз(' -/,)*(/,), (8.20)
которое определяет оператор L^. Действие РЧ-импульса дли-
тельностью tw и амплитудой Н\, приложенного вдоль оси а (а =
= х, у, z) в момент времени U, описывается унитарным опера-
тором Pi, преобразующим волновую функцию в соответствии
Новые идеи в импульсном магнитном резонансе
299
с выражением
ty(tt) = et'vHltw'aty(t7)' (8.21)
Если yHitw выбрать равным л/2, то РЧ-импульс поворачивает
спин на л/2 вокруг оси а (а = х, у, г) и, следовательно,
(8.22)
Для конкретности и простоты рассмотрим трехимпульсный
цикл. Мы всегда начинаем эксперимент, имея образец, который
достиг теплового равновесия в магните. В момент t = 0 импульс
поворачивает намагниченность в плоскость ху. Такой импульс
мы назовем приготавливающим. Через интервал времени то
включаем повторяющийся импульсный цикл. Интервал т0 и фаза
приготавливающего импульса выбираются так, чтобы получить
сигнал в некоторый удобный для наблюдения момент времени
в течение импульсного цикла (в момент времени, который в ли-
тературе по импульсному сужению линии называют «окном»).
Пусть ф(*п)—волновая функция системы после п циклов
(т.е. как раз перед импульсом Р\П-\- 1-го цикла). Тогда мы мо-
жем проследить за изменением волновой функции во времени по
таблице
Время
tn (непосредственно перед Pj)
<+ (сразу после Р,)
tn + xj" (непосредственно перед Р%)
tn + xj1" (сразу после Р2)
'п + Т1 + Х2 (непосредственно перед
Рз)
'л + Т1 + Т2 + TJT (непосредственно
перед п + 1-м циклом)
-в * B5lPiWn) =
¦ Ubs Ы) Pity {tn)
= Un (т2)Р2?/вз (тО Р,ф (/„) (8.23)
(tn+i) -* UB3(rs) P3 UB3 (т2) Р2 X
Последняя формула в таблице определяет оператор Ut- Можно
написать
. (8-24)
где оператор Ut не зависит от п. Оператор UT равен произведе-
нию унитарных операторов, поэтому сам является унитарным.
После N импульсных циклов имеем
(8.25)
300 Глава 8
Поэтому задачу можно считать решенной, если определить ре-
зультаты действия оператора UT-
Исследуем один цикл. Введем унитарные операторы PJ , об-
ратные по действию операторам Р,-, Для унитарного оператора
справедливо равенство
Р7' = Р\, (8.26)
где «звездочка» означает комплексное сопряжение. Теперь запи-
шем 1)т в виде
Vt = ^вз Ы PzU** Ы Р2^вз (тО Pi =
= РгР*Р\ \jPTxPiWVv (тз) Р3Р2Р1] X
X Of lPa lUm (т2) Р2Р)] [РГlUm (ti) Pi]. (8.27)
На примере, рассмотренном в § 4, мы показали, что полный
цикл спиновых поворотов должен все вернуть к исходному со-
стоянию, после чего можно снова повторять цикл поворотов спи-
нов между «осевой» и «боковыми» конфигурациями. Поэтому
импульсный цикл из трех импульсов Р\, Р%, Ръ должен все вер-
нуть к исходному состоянию. Следовательно,
Р3Р2Р, = 1 (8.28)
UT = [P^PzWu^ (тз) РзРгРЛОг'Рг-'^вз Ы P2Pi] X
X[Pf!C/»s(Ti)Pi], (8.29a)
VT = U» (тз) [РГ'Рг'^вз Ы PzPi] [PxXUm (т,) Pi]. (8.296)
Смысл отдельных членов произведения становится очевид-
ным после нескольких преобразований. Рассмотрим сначала опе-
раторное выражение
ffC(t-U)
P~lU(t-h)P=P~xe * Р, (8.30)
где Р и U — унитарные операторы, а Ж — гамильтониан. Разла-
гая экспоненту в ряд, вставляя между сомножителями единицу
Р~1Р(=: 1) и производя перегруппировку членов, находим
(р
* . (8.31)
Оператор P~lUP преобразует во времени волновую функцию,
которая является решением уравнения Шредингера с преобра-
зоваипым гамильтонианом Р-^ЖР.
Чтобы оценить выражение в экспоненте, определяющей пре-
образованный оператор U^{x2)
11 (8.32)
Новые идеи в импульсном магнитном резонансе 301
мы можем сначала проделать преобразование Рг^взРя, а затем
полученный результат зажать между операторами PTi и Р\.
При вычислениях используются соответствующие выражения
для экспоненциальных операторов. Порядок применения опера-
торов обратен порядку действия во времени операторов спино-
вых поворотов. Почему это так?
Рассмотрим уравнение Шредингера
Мы можем преобразовать это уравнение с помощью унитарного
оператора R, который не зависит от времени и оставляет задачу
неизменной:
^ - mR'X <*+> (8-34)
Если R является оператором поворота спина на угол +я/2
вокруг некоторой оси, то выражение R3@R~l должно означать
преобразование координат гамильтониана, соответствующего
этому повороту.
Если Ж = —уННо1г и спин находится в верхнем состоянии,
то преобразование, которое поворачивает спиновую функцию в
верхнее спиновое состояние, соответствующее направлению +г/,
требует такого же поворота координат гамильтониана Ж, кото-
рый осуществляется заменой lz на 1У в Ж.
Поэтому выражение
р-}ЖР=(Р~1)ж(Р~1)~1 (8.35)
можно интерпретировать как гамильтониан 5$, соответствующий
повороту Р 1. Рассмотрим следующие два описания действия
гамильтониана два после поворота на я/2:
1) используется непреобразованный гамильтониан !Md, дей-
ствующий на спин, который поворачивается на угол л/2;
2) спин оставляется нетронутым, но поворачиваются спино-
вые координаты в гамильтониане Ж\ на угол —л/2. Этот пово-
рот обратен повороту спина, согласно п. 1.
Если поворот состоит из нескольких последовательных по-
воротов, то обратный ему состоит из обратных поворотов, вы-
полненных в противоположном порядке.
Так, при опрокидывании спина, характеризуемом произведе-
нием операторов Р2Р\, обратное преобразование Q = (Рг^О-
Поэтому преобразование гамильтониана Ж записывается так:
— Р\ ^21ЖР*Р\. (8.36)
302 Глава 8
Для получения преобразованного гамильтониана Ж, соответ-
ствующего ?-му интервалу т, п-й импульсной последовательности,
следует взять операторы поворотов спина Pi, P2, .... Р<, кото-
рые предшествуют интервалу, и преобразовать координаты в га-
мильтониане путем применения операторов обратных поворотов
в обратной последовательности (например, первый Р?\ затем
РГ-1,..., наконец Рг1).
Определим теперь три преобразованных гамильтониана ЗвА,
= Pi lP2lZeB3P2Pu (8.37)
Разлагая экспоненты в ряд, получаем
-±де х ~i-3C т —1-
UT — е * cze h B 2e h
_ 1 _ L
~ h
i \2
• - • • (8.38)
Если интервалы времени т малы, то
где \(\2$а,в,с/Ь.\У\ — средняя величина типичных матричных
элементов преобразованных гамильтонианов. Если выполняются
условия (8.39), то хорошим приближением для оператора UT
является выражение, в котором сохраняются лишь основные два
члена в правой части (8.38). Условие, налагаемое на xi, анало-
гично условию, налагаемому на время корреляции х в режиме
сужения линии благодаря движению.
Введем период цикла tc = ti + тг + тз, тогда получим
Ут~ * —*~I о$с~*—г <™в ~i—г »д ~2— I'с» (o.4Ua)
п \ гс тс 'су
UT = 1 — •?¦ 5^с, (8.406)
(8.40в)
здесь выражение (8.406) определяет средний гамильтониан 5#вз,
а (8.40в) напоминает нам, что в пределах цикла развитие си-
Новые идеи е импульсном магнитном резонансе 303
стемы в хорошем приближении идет в соответствии со средним
гамильтонианом <2$Вз.
Выпишем <2$вз в явном виде
Wzi -f 5#S — 38о + Я#. (8.41)
Трюк заключается теперь в том, чтобы выбрать такой импульс-
ный цикл (РиР2,Рз и т. д.), который позволит устранить ди-
польное взаимодействие, но сохранить информацию о химиче-
ском и найтовском сдвигах:
5$ = 0, (8.42а)
— h (mo - ©) /а - Йюо ? стгг4/г* # 0. (8.426)
Таким образом,если
А = Z
== Z fij/ (Ii ¦ I/ - 3/„/я/). (8.43)
/1
и т, = т2 = т3, то
5 = 0. (8.44)
Эти результаты получаются, когда оператор РГ эквивален-
тен повороту на угол я/2 вокруг оси х, т. е. преобразует /г,- в
Iyi, а оператор РТ^Рг1 эквивалентен повороту на угол я/2 вок-
руг оси у, т. е. преобразует hi в /*,-. Операторы этих поворотов
преобразуют также гамильтониан Ж§:
= — Й (ш0 — ш) /^ —
= - Й (соо - со) /^ ~ ficoo E (T22i/xJ, (8.45)
i
Полагая для простоты ш = шо, находим
^ Z " (8'46)
где
/,', = ^(/,1+ /„, + /,!> (8.47)
304 Глава 8
Из формулы (8.47) следует, что химический и найтовский сдвиги
уменьшаются в л/Ъ раз по сравнению с их значениями до ус-
реднения. Нам удалось устранить дипольное взаимодействие,
сохранив химический сдвиг. Что касается члена, включающего
(со 0—со) (он представляет собой расстройку частоты или неод-
нородность постоянного поля), то он также уменьшается в такой
же пропорции.
В соответствии с уравнениями (8.24) и (8.40в) волновая функ-
ция т])(<) связана с -ф (^о) преобразованием
Ч> @ = UH (to) = е"Т Хвз ('~'°Ч (to) (8.48)
при условии
t = to + Ntc. (8.49)
А что можно сказать о значении ty(t) в другие моменты вре-
мени? Рассмотрим момент времени
*«=/о + Ме + 'ь 0</,</е. (8.50)
Момент времени t\ может попасть в любой из интервалов вре-
мени Ть Т2, ..., т,-, которые образуют основной цикл tc. В пре-
делах любого одного полного цикла не происходит большого из-
менения волновой функции 1]з, если справедливы выражения
(8.37). Однако каждый импульс цикла вызывает большое резкое
(скачком) изменение спина — обычно производит поворот на
угол л/2. Эти импульсы могут, например, попеременно в преде-
лах цикла ориентировать спины вдоль осей х, у и z вращающей-
ся системы координат. Если наблюдение всегда вести в течение
t-ro интервала, то большие импульсы в последующих циклах бу-
дут всегда возвращать ядерную намагниченность к одному и
тому же направлению во вращающейся системе координат.
Таким образом, можно записать
Ч)(/) = в"^Жвз('"'оЧ(/о), (8.51)
где оба момента времени t и to находятся в пределах одного и
того же субинтервала т«, т. е. части длительности цикла tc. Если
же моменты времени t и t0 относятся к различным интервалам
т,- и т/, так что
Ntc<t-t0<(N+l)tc, (8.52)
to следует соответственно вернуться к выражениям типа'(8.20)
и (8.21). Если отдельные интервалы т настолько малы, что не-
равенство (8.39) справедливо, то гамильтониан Жъ% не харак-
теризует больших изменений в течение времени tc, однако им-
пульсы t + 1, t'rh2, *г|-_3, .... / — 1, / вносят такие изменения.
Новые идеи в импульсном магнитном резонансе 305
Определим оператор
P^P,P,.i...Pt+sPt+l. (8.53)
Имеется два почти равных выражения
Ре-т *W
Поскольку Ntc <t — t0 <(N + \)tc, то можно записать
ф @ « Ре~ "*"^вз ('"'°Ч (/о); (8.55)
это выражение связывает значение волновой функции т])(/о) в
t-м интервале с ее значением в /-м интервале импульсной после-
довательности.
Уравнение (8.55), по существу, позволяет вычислить эволю-
цию волновой функции в период между моментами времени t и
to, когда весь этот период взаимодействия характеризуется га-
мильтонианом Ж>з и затем следует быстрая последовательность
поворотов Р.-+1,.... Р/_ь Р/.
§ 6. Наблюдение импульсного сужения линии
Каким образом можно экспериментально наблюдать эффект
сужения линии благодаря опрокидыванию спинов? Обычно су-
жение линии за счет движения можно видеть с помощью стацио-
нарной или импульсной аппаратуры. В первом случае наблю-
даются очень узкие линии, а во втором — медленные блоховские
затухания или медленно затухающие сигналы эха.
Для импульсного сужения линии образец должен возбуж-
даться импульсами большой амплитуды. Предположим, имеется
оборудование для генерации таких импульсов и возбуждения
ими образца, тогда можно в принципе добавить стационарный
или импульсный спектрометр для наблюдения получающегося
при таком воздействии резонанса. Практически усилители ста-
ционарной аппаратуры будут блокироваться на входе мощными
РЧ-импульсами. Время восстановления после блокирования
может быть значительно больше времени т между импульсами,
опрокидывающими спины. Следовательно, для наблюдения им-
пульсного сужения линии следует применить импульсное обору-
дование, которое позволяет управлять мощными РЧ-импульсами
и детектировать ЯМР.
Когерентная импульсная аппаратура позволяет различать
отдельные составляющие намагниченности (Мх или Му) во вра-
щающейся системе координат. Если ее отрегулировать для де-
тектирования Мх, то обычно оказывается, что эта составляющая
максимальна в отдельные интервалы т,- цикла и может быть рав-
на нулю в другие. Вначале на систему, находящуюся в тепловом
306
Глава 8
равновесии, действует импульс я/2, который поворачивает на-
магниченность вокруг оси х в плоскость ху, а затем действуют
импульсы цикла. Для простоты обсуждения будем считать, что
мы можем поворачивать намагниченность на угол я/2 вокруг
осей х, у и z в импульсном цикле, хотя практически поворот во-
круг оси г не используется. Возможная группа импульсов, осу-
м
X
а
Ось
Рис. 8.5. Повороты намагниченности во вращающейся системе координат
различными импульсами.
а — начальная ориентация намагниченности М вдоль оси г (вдоль постоянного поля), кото-
рая существует при тепловом равновесии; б—поворот М к оси у приготавливающим им-
пульсом Рс; в —первый импульс Pi цикла импульсного сужения поворачивает М к оси +х;
г — второй импульс Рз поворачивает М к оси г; д — третий импульс Рз по действию должен
быть инверсией действия первых двух PsPi. Это —поворот на угол 2я/3 вокруг осн (—I + 1+к)
(Заметим, что его не то же самое, что поворот на угол —я/2 вокруг оси +х.)
ществляющая импульсное сужение линии, показана на рис. 8.5.
На рис. 8.5, а изображена намагниченность М вдоль направле-
ния постоянного магнитного поля (г — направление). В момент
времени t = 0 импульс Ро ориентирует М вдоль направления
+ у. Импульс Ро называют приготавливающим. В момент вре-
мени то включаются импульсы Pi, P2, Рз, которые последова-
тельно поворачивают М на угод —я/2 вокруг оси г, на угол
+ я/2 вокруг оси у и наконец на угол + 2я/3 вокруг оси
•— i -|- j -f- k. Поворот Р3 фактически является инверсией поворо-
тов Р2Р1 и может быть также представлен математически про-
сто как Р\ Рг~ или физически как последовательные повороты
Новые идеи в импульсном магнитном резонансе
307
сначала на угол —я/2 вокруг оси у, а затем на угол + л/2 во-
круг оси 2. Хотя поворот Р3 выглядит на первый взгляд как по-
ворот на угол — я/2 вокруг оси х, это не так, что можно прове-
рить, если рассмотреть повороты трехмерного предмета, харак-
теризуемые операторами Рь Р2, Р3, а не повороты вектора М,
направленного вначале вдоль оси у. Это различие является важ-
ным, потому что Жа — тензор второго ранга и, следовательно,
1
"I
¦3
Р,
I „
Рис. 8.6. Временная диаграмма резонансного сигнала в процессе действия
импульсной последовательности.
Рассматриваются следующие условия: а—аппаратура настроена точно в резонанс, б—хи-
мический сдвиг приводит к появлению со временем в интервале между импульсами Р3 и
Pi сигнала, пропорционального Мх, по мере уменьшения сигнала в окне между импуль-
сами Pi и Pi.
характеризуемая им величина должна рассматриваться как эл-
липсоид, а не вектор.
Если аппаратура отрегулирована для измерения Мх и если
она настроена точно в резонанс с учетом любых возможных хи-
мических и найтовских сдвигов, то должен быть сигнал ядер-
ного резонанса лишь между импульсами Р\ и Р2. В случае рас-
стройки резонанса (имеются два сорта ядер с химическим сдви-
гом относительно друг друга) Мх будет постепенно изменяться
в интервале между импульсами Р\ и Р2 для последующих цик-
лов, испытывая осцилляции (см. рис. 8.6), как показано ниже.
Составляющая Мх будет также появляться в промежутке" между
импульсами Р3 и Pi в ходе повторения циклов.
Вернемся к математическому описанию и вычислению на-
блюдаемого сигнала ЯМР. Для конкретности вычислим зависи-
мость Мх от времени во вращающейся системе координат
308 Глава 8
(Mx(t)y. Зная волновую функцию -ф(^), найдем
(Мх (/)> = <* @, Мхф @) - у* <Ф @, *Л @>. (8.56)
Предположим, что действует импульсная последователь-
ность, подобная изображенным на рис. 8.5 и 8.6. Пусть в момент
времени t = 0~ волновая функция гИО-). Приготавливающий
импульс изменяет волновую функцию
(8.57)
Затем она развивается под влиянием среднего гамильтониана
Жъз- Нас интересует значение волновой функции в интеграле
времени между импульсами Рз и Pi после целого числа циклов,
состоящих из трех последовательных импульсов Рх, Р3 и Р$-
Пользуясь уравнением (8.51), получаем
~ ^ю Чф @~). (8.58)
Если нас интересует значение волновой функции ¦§(*) на цикл
позже, то с помощью (8.55) находим
гК/) = Ре~~^вз'р0гК0-), (8-59)
где Р = Pi или Р = Р1Р2, в зависимости от того, попадает ли t
в интервал между импульсами Pi и Рг или в интервал между
импульсами Р2 и Рз.
Теперь необходимо учесть факт, что начальная волновая фун-
кция ф(О-) соответствует начальному тепловому равновесию об-
разца. Для этого выразим ip(O-) через волновую функцию в ла-
бораторной системе координат ф(О^). Эти две волновые функ-
ции связаны преобразованием
(8.60а)
поэтому в момент времени t — 0~ имеем
Ф@~) = ф@~). (8.606)
Пусть \п) собственные состояния секулярного гамильтониана с/в
в лабораторной системе. Тогда имеем
= ?с„@-)|п), (8.61)
п
и, следовательно,
п. m
спст (т |Ро Хе* ^в>'р"'/х • Яе"^"*ю'р0|я). (8.62)
Новые идеи в импульсном магнитном резонансе 309
Теперь найдем статистическое среднее коэффициентов спс*т
используя больцмановское распределение населенностей состоя-
ний с гамильтонианом Ж, который описывает систему до начала
действия импульсов:
( '
Подставляя (8.63) в (8.62), получаем
(М (t)\ = -^- Sn (Рп 1р~ь ю P~1f Рр~~ь вз Р^рКНктЛ (9,9,А\
В высокотемпературном приближении можно написать
где No — число спинов /. Основной член исчезает, неисчезающий
член пропорционален 1/kT. Теперь запишем
efts — — Y/j/iQ/z) ^O.DDj
под знаком шпура перенесем оператор Ро слева направо в
соответствии с выражением
Sp (ABC) = Sp (ВСА) (8.67)
и выберем Ро таким,чтобы
О'г —*Х> (O.DOj
т. е. приготавливающий импульс поворачивает спин от направ-
ления вдоль оси z к направлению оси х. В результате находим
(8.69)
Для простоты возьмем Р = 1 (т. е. между моментом времени
t = 0 и моментом времени измерения проходит целое число им-
пульсных циклов Р\, Pz, Рг)- Теперь
t Za v+7"+7*)== - тг ?а^^ (8-70)
где [гЧ — (l/д/З ) (/j.( + /^i + Izi). Предположим, что все спины
имеют одинаковые сдвиги azz. Тогда получаем
310 Глава 8
Теперь в штрихованных координатах, используя очевидные обо-
значения
1Х = Ix COS (*, *') + V COS (X, у') + /*- COS (x, z')>
/*' = Ix cos (х, х') + Iy cos (у, х') + 1г cos (г, *')>
имеем
cos M[/, cos
+ cos (*, y') [- /x- sin (-^-) + /«,• cos(i^L)] + cos (x, z') Is.
(8.73)
Учитывая, что Sp(/^, Iy) — 0 и Sp (/|/) = Sp(/^), после вы-
числения шпуров находим
(8-74)
где Мо — намагниченность при тепловом равновесии.
Таким образом, мы видим, что химический или найтовский
сдвиги Gzz дают осциллирующий вклад в (Mx(t)y в единицах
частоты, уменьшенный в -\/3 раз по сравнению с нормальным
сдвигом шсАгг, который наблюдается, если его можно разрешить
в стационарном резонансном эксперименте.
Если имеется несколько групп ядер с разными химическими
или найтовскими сдвигами, то добавляются соответствующие
вклады в (Mx(t)y с интенсивностями, пропорциональными числу
ядер в группе.
Выражение (8.74) имеет постоянный и осциллирующий чле-
ны. Осуществив преобразование Фурье, можно получить спектр
и найти величину уменьшенного химического сдвига (<»ooz2/V3~)'
Используя приставку для преобразования Фурье к спектрометру
ЯМР, можно переходный сигнал, содержащий несколько хими-
ческих или найтовских сдвигов, разложить в спектр с дискрет-
ными частотами.
§ 7. Практические импульсные последовательности
До сих пор наше обсуждение касалось объяснения принципов
импульсного сужения линии. Практическая реализация этих прин-
ципов встречает определенные трудности. Обсудим их кратко и
Новые идеи в импульсном магнитом резонансе 311
затем перечислим несколько импульсных последовательностей,
которые были придуманы для преодоления этих трудностей. Пре-
красное обсуждение всех проблем дано Хеберленом в его лекции
в Летней школе НАТО1). Воэн с сотр. [13, 14] дали полное тео-
ретическое описание, включая формулы, готовые для примене-
ния. В краткой библиографии приведено еще несколько ссылок.
1. Как избежать поворота вокруг оси z
В импульсных установках РЧ-поле Н\ возбуждается в плоско-
сти ху. Выбирая фазу РЧ-поля импульса, можно осуществить по-
вороты вокруг любой произвольной оси, расположенной в пло-
скости ху, но не вокруг оси г. Чтобы осуществить поворот во-
круг оси z одним импульсом, требуется добавочная катушка, ось
которой параллельна оси г, а также необходима соответствую-
щая электроника для возбуждения в катушке тока. Избежать
этого усложнения аппаратуры можно, если перейти к четырех-
импульсному циклу. Тогда один поворот вокруг оси z заменяется
эквивалентными ему двумя последовательными поворотами во-
круг оси х и оси у. Однако обычно такие два импульса разде-
лены во времени так, что основные временные интервалы можно
формировать более просто.
Чтобы записать последовательность импульсов, удобно вве-
сти обозначения, исходя из того, что обычно используют им-
пульсы я/2. Например, рассмотрим следующее выражение, ко-
торое определяет четырехимпульсный цикл:
х (т, — х, т, у, 2т, — у, х, х, т). (8.75)
Первый символ «х» означает приготавливающий импульс л/2,
действующий вдоль оси -\-х. В скобках заключены импульсы
л/2, образующие один цикл. Цикл начинается временным интер-
валом т после приготавливающего импульса, затем подается им-
пульс л/2 вдоль оси —х (или импульс —я/2 вдоль оси +х).
Последовательность импульсов можно также записать в виде
х, т (— х, х, у, 2т, — у, х, х, 2т);
она означает, что цикл начинается с импульса я/2 вдоль оси —х.
Это обозначение показывает в явном виде наличие двух интер-
валов времени длительностью 2т и двух — длительностью т.
Первое обозначение полезно для доказательства определенных
теорем, в которых используется симметрия времени одного им-
пульсного цикла.
') Институт перспективных исследований НАТО опубликовал ряд пре-
восходных лекций по ЯМР в твердых телах, которые состоялись в 1974 г.
в Лёвене (Бельгия). Хеберлен и ван Хек, в частности, рассмотрели импульсное
сужение линии (Nuclear Magnetic Resonance in Solids, ed. L. Van Gerven,
Plenum Press, New York, 1977),
312 Глава 8
2. Неидеальность импульсов
Длительность импульса. До сих пор мы рассматривали мгно-
венные повороты, для осуществления которых требуются им-
пульсы бесконечной амплитуды #i нулевой длительности. Реаль-
ные импульсы имеют конечную длительность. Можно было бы
предположить, что основные проблемы будут связаны с конеч-
ной длительностью импульсов. Однако теоретическое исследо-
вание этого вопроса показало, что он не так важен [9, 10, 13,
14]. Действительно, медленные повороты сохраняют способность
полностью усреднять дипольное взаимодействие. В этом смысле
их действие эквивалентно сужению за счет движения, при кото-
ром происходит усреднение величины Ccos20—1) до нуля при
непрерывном изменении угла 0, в противоположность дискрет-
ным изменениям ориентации спинов при мгновенных поворотах
(рис. 8.1). Важным следствием для эксперимента является воз-
можность обойтись гораздо меньшей РЧ-мощностыо, чем каза-
лось из первых предположений.
Неоднородность РЧ-поля Hi. В § 3 уже обсуждалось, что все-
гда трудно сделать РЧ-поле Н\ однородным по объему образца,
особенно в случае малых размеров РЧ-катушки (катушка дол-
жна иметь малые размеры для уменьшения необходимой мощ-
ности, так как при данных добротности Q и Н\ последняя про-
порциональна объему катушки). Неоднородность поля Hi при-
водит к нежелательному эффекту, она вызывает распределение
углов поворота по объему образца. Этот эффект можно устра-
нить в первом порядке, если использовать прием Мейбума и
Гилла или парные положительные и отрицательные повороты
вокруг любой данной оси и тем самым осуществлять рефокуси-
ровку.
Модуляция фазы. Легко говорить о возможной настройке
фазы РЧ-поля Hi для получения его необходимой ориентации во
вращающейся системе координат. Однако практически сделать
это очень трудно. Обычно фаза поля Н\ колеблется в течение на-
растания и спада импульса. Такие колебания могут рассматри-
ваться как модуляция фазового угла <р РЧ-поля. Она эквива-
лентна введению расстройки Ato = dq>/dt в интервалах времени,
когда dcp/ШфО [15]. Влияние этой модуляции можно исклю-
чить в первом порядке, если отрегулировать значения dq>/dt в
течение включения и выключения РЧ-импульса так, чтобы они
были равны и противоположны. Сделать значение dy/dt равным
нулю практически невозможно, однако указанную выше балан-
сировку можно осуществить.
Из различных импульсных последовательностей, которые ис-
пользовались или предлагались, мы рассмотрим только три. Они
известны под названиями WAHUHA, HW-8 и REV-8. Символы
Новые идеи в импульсном магнитном резонансе 313
последовательностей составлены из первых букв фамилий их
изобретателей, а цифры означают число импульсов в цикле.
Последовательность WAHUHA предложена Уо, Хубером и
Хеберленом (WAugh, HUber, HAeberlen) [9, 10]. Она имеет вид
х, т(т, —х, х, у, 2т, — у, т, х, т).
Сигнал, пропорциональный составляющей Mv, регистрируется в
интервалах времени т, указанных перед скобками. Приготавли-
вающий импульс можно выбрать так, чтобы иметь удобные вы-
борки времени. Последовательность характерна тем, что приго-
тавливающий импульс х и следующий за ним интервал времени т
в начале цикла фактически совпадают с последним импульсом
и интервалом в конце цикла. Следовательно, нет нужды в спе-
циальных интервалах выборки в начале цикла. Приготавливаю-
щий импульс в этом случае является частью цикла.
Приготавливающий импульс, приложенный вдоль оси х, ори-
ентирует намагниченность вдоль оси —у. Сигнал, пропорцио-
нальный составляющей Ми, детектируется в интервале между
импульсами х и — х.
Последовательность HW-8 [9, 10] можно изобразить следую-
щим образом:
(т, — х, 2т, х, х, — у, 2т, у, х, у, 2т, у, х, х, 2т, — х, т).
Существует ряд эквивалентных разновидностей этого цикла.
Последовательность REV-8 [13, 14] имеет вид
х, т(т, х, т, у, 2т, — у, х, —х, 2т, — х, т, у, 2т, — у, т, х, т).
Видно, что пара импульсов х, у, разделенных интервалом т, сле-
дует через интервал 2т после пары инверсных импульсов —у,
— х.
Рим, Эллеман и Воэн достигли наивысшего разрешения с их
импульсной последовательностью REV-8.
ЛИТЕРАТУРА
1. Hahn E. L, Phys. Rev., 80, 580 A950).
2. Сап Н. У., Purcell Е. M., Phys. Rev., 94, 630 A954).
3. Meiboom S., Gill D., Rev. Sci. Instr., 29, 6881 A958).
4. Ostroff E. D., Waugh J. S., Phys. Rev., Lett., 16, 1097 A966).
Б. Mansfield P., Ware D., Phys. Rev. Lett., 22, 133 A966).
6 Stacey L. M., Vaughan R. W., Elleman D. D., Phys. Rev. Lett., 26, 1163
A971).
7. Mehring M., High Resolution NMR Spectroscopy in Solids, в серии Basic
Principles and Progress, Vol. 11, ed P. Dlehl, E. Fluck, R. Kosfeld, Berlin,
Heidelberg, New York, 1976. (Имеется перевод в книге: Хеберлен У. и Ме-
ринг М. ЯМР высокого разрешения в твердых телах. — М.: Мир, 1980.)
314 Глава 8
8. Haeberlen U., High Resolution NMR in Solids: Selective Averaging: Suppl. 1,
в серии Advances in Magnetic Resonance, Academic Press, New York, 1976.
(Имеется перевод в книге Хеберлен У., Меринг М. ЯМР высокого разре-
шения в твердых телах. — М.: Мир, 1980.)
9. Waugh J. S., Huber L. М., Haeberlen U., Phys. Rev. Lett., 20, 180 A968).
10. Haeberlen V., Waugh I. S., Phys. Rev., «75, 453 A968).
11. Mansfield P., Journ. Phys., C4, 1444 A971).
12. Mansfield P., Orchard M. J., Stalker D. C., Richards К. И. В., Phys. Rev.,
B7, 90 A973).
13. Rhim W. K., Elleman D. D., Vaughan R. W., Journ. Chem. Phys., 59, 3740
A973).
14. Rhlm W. K., Elleman D. D., Schreiber L. В., Vaughan R. W., Journ. Chem.,
Phys., 60, 4595 A974).
15. Moron P. R., Journ. Phys. Chem. Solids, 30, 297 A969).
Глава 9
Электрические квадрупольные
эффекты
§ 1. Введение
До сих пор рассматривались только магнитные взаимодей-
ствия ядра с его окружением. При этом, конечно, косвенно учи-
тывалось влияние заряда ядра, поскольку он определяет элек-
тронные орбиты и расположение ядер в молекуле. Однако влия-
ние электрических полей на ориентацию ядра не рассматрива-
лось. В том, что такое влияние существует, можно убедиться на
-ч
+ч
а
,-q
Рис. 9.1. Сигарообразное ядро в поле четырех зарядов: +9 на оси х и — q
на оси у.
Конфигурация 6 энергетически более выгодна, чем конфигурация а, так как в положе-
вии 6 положительно заряженные концы сигары расположены ближе к отрицательным
зарядам -д.
примере несферического ядра. Предположим, что несколько вы-
тянутое ядро находится в окружении зарядов, как это видно из
рис. 9.1. Ясно, что в положении, показанном на рис. 9.1,6, ядро
обладает более низкой энергией, так как в этом положении вы-
тянутые положительно заряженные концы ядра находятся ближе
к отрицательным внешним зарядам. Таким образом, существует
электростатическая энергия, которая зависит от ориентации
ядра. Если ядро повернется так, что его вытянутые концы поме-
няются местами, электростатическая энергия, конечно, не изме-
нится1). Отсюда следует, что для ядер со спином у2 электриче-
ское поле не снимает вырождение по проекции момента mi.
') См. в библиографии, помещенной в конце книги, раздел «Квадруполь-
иые эффекты» и статьи Коэна и Рейфа, а также Даса и Хаиа в разделе
«Учебники, монографии и обзорные статьи».
316 Глава 9
§ 2. Гамильтониан квадрупольного
взаимодействия (часть 1)
Чтобы получить количественную теорию квадрупольных эф-
фектов, начнем с классического описания явления, используя
плотность ядерного заряда р. Мы можем перейти к квантовоме-
ханическому описанию, заменив классическую плотность р ее
оператором. Классическую энергию Е взаимодействия заряда,
распределенного с плотностью р, с внешним полем, потенциал
которого равен V, можно представить в виде
(r)V(r)dx. (9.1)
Разложим V(r) в ряд Тейлора относительно начала координат:
F(r) = F@) + ?*.(^)^ + i ?*^G?y,»+ -• <9'2)
где переменные ха (а = 1, 2, 3) соответствуют х, у или г. Опре-
деляя
получаем
Если начало координат выбрано в центре масс ядра, то первый
член отвечает электростатической энергии ядра, рассматривае-
мого как точечный заряд. Второй член включает электрический
дипольный момент ядра, который обращается в нуль, поскольку
центр масс совпадает с центром заряда ядра. Последнее можно
доказать, если состояния ядра обладают определенной чет-
ностью, а наличие определенной четности подтверждается всеми
экспериментальными данными. Более того, в положении равно-
весия ядро находится в нулевом среднем электрическом поле
Va- Интересно отметить, что, даже если бы дипольный момент
не был равен нулю, стремление ядра занять положение в точке,
где электрическое поле равно нулю, все равно приводило бы к
тому, что дипольный член не оказывал бы заметного влияния.
Именно по этой причине Смит, Пёрселл, Рэмси [1] решили опре-
делять ядерные электрические дипольные моменты у нейтронов,
а не у заряженных ядер.
Электрические квадрупольные эффекты 817
Третий член разложения представляет собой так называемый
электрический квадрупольный член. Заметим здесь, что для по-
тенциала V всегда можно найти главные оси, такие, что
Vap = 0. если аф$. (9.5)
Кроме того, потенциал V должен удовлетворять уравнению
Лапласа
V2V = 0. (9.6)
В начале координат это уравнение приводит к условию
Z Vaa-0. (9.7)
а
(Иногда вместо (9.7) применяют уравнение Пуассона. Тогда
необходимо соблюдать некоторую осторожность, так как нас
должна интересовать только часть потенциала, зависящая от
ориентации, а сферически симметричная часть должна быть от-
брошена.) Если положение ядра имеет кубическую симметрию,
то
Vxx = Vtty = Vzz, (9.8)
а учитывая (9.7), найдем, что все три производные равны нулю.'
В этом случае квадрупольное взаимодействие равно нулю. Та-
кая ситуация возникает, например, для Na23 в металлическом
натрии. В объемноцентрированной кубической решетке положе-
ние каждого ядра имеет кубическую симметрию.
Удобно использовать величины Qa&, определяемые выраже-
нием
Qap = 5 C*a*p - 6a/) Р &*\ (9.9)
при этом
\ Хохр dx = j (Qap + \ барг2Рс/т) . (9.10)
Как увидим, введение величин Qap позволяет выделить в левой
части (9.10) член, не зависящий от ориентации ядра. Для ква-
друпольной энергии ?B) тогда получим
W dx -1 ? (l/afjQap+ Vap6ap 5 r*p dx). (9
0
a.
Поскольку V удовлетворяет уравнению Лапласа, второй член
в правой части выражения (9.11) обращается в нуль. В резуль-
тате имеем
318 Глава 9
Даже если бы второй член в (9.11) не был равен нулю, он не
зависел бы от ориентации ядра *)•
Чтобы найти квантовомеханическое выражение для квадру-
польного взаимодействия, нужно просто вместо классической
плотности р подставить соответствующий оператор плотности
р(°р) в виде
Хг*). (9.13)
где суммирование ведется по индексам ядерных частиц
1, 2, ..., k N с зарядом Щк. Поскольку для нейтронов за-
ряд равен нулю, а для протонов е, в сумме можно учитывать
только протоны. Тогда
р(ор)(г) = е ? 6(г-г*). (9.14)
протоны
Подставляя (9.14) в классическое выражение для Qap, полу-
чаем квадрупольный оператор
$ C*л - Vs) р(ор) (f>d%
протоны
?
протоны
Тогда для квадрупольного члена гамильтониана <5^<j будем иметь
(9-16)
') Если у ядра есть электронный заряд, то необходимо воспользоваться
виеиием Пуассона
р
уравнением Пуассона
где |^@) |2 — электронная плотность вероятности на ядре. Не зависящий от
ориентации член Д? в выражении (9.11) будет равен
^dx" ~ "f
Величина ДЕ будет различна для двух ядер с одинаковым зарядом, если
распределение зарядов у них различно (изотопы) нли если при одинаковых
массах и зарядах они находятся в разных ядерных состояниях (изомеры).
При электронных переходах между s- и р-состояниями Д? будет, вообще го-
воря, вносить вклад, различный для разных изотопов или изомеров [2].
Электрические квадрупольные эффекты 319
Выражения (9.15) и (9.16) очень неудобны для применения,
поскольку они содержат сумму по всем ядерным частицам. Это
приводит к необходимости рассматривать ядро как многочастич-
ную систему, чего удалось избежать при рассмотрении магнит-
ных взаимодействий. На самом деле подобная трудность возни-
кает и в случае магнитного диполя, однако мы ее просто обошли.
Выражение (9.15) для квадрупольного взаимодействия по-
зволяет рассматривать значительно более сложные задачи, чем
те, которые возникают при изучении резонансных явлений. В по-
следнем случае, вообще говоря, имеют дело только с основным
состоянием ядра или с достаточно долгоживущим возбужденным
состоянием. Собственные состояния ядра характеризуются пол-
ным моментом количества движения / каждого состояния,
2/ -f 1 значением компоненты момента количества движения и
набором других квантовых чисел ц, которые мы не будем кон-
кретизировать. Поскольку нас будет интересовать только про-
странственная переориентация ядра в данном энергетическом
состоянии, нужно рассмотреть только диагональные по / и ц
матричные элементы. Таким образом, необходимы лишь следую-
щие матричные элементы квадрупольного взаимодействия:
Можно показать, что для них выполняется равенство
(Imi\ | <$р I /т'ч) = С (/т 14 (/в/р + ВД - 6ар/211тг), (9.17)
где С — коэффициент, зависящий от квантовых чисел / и ц. Что-
бы доказать равенство (9.17), нужно рассмотреть коэффициенты
Клебша — Гордана, так называемые неприводимые тензорные
операторы Tlm и теорему Вигнера — Эккарта.
§ 3. Коэффициенты Клебша — Гордана,
неприводимые тензорные операторы
и теорема Вигнера — Эккарта
Теорема Вигнера — Эккарта является одной из наиболее по-
лезных теорем в квантовой механике. Чтобы ее сформулировать,
нужно ввести коэффициенты Клебша — Гордана C{LJ'J;
MMj'Mj) и неприводимые тензорные операторы TLM. Мы сна-
чала сформулируем теорему Вигнера — Эккарта и определим
коэффициенты Клебша — Гордана. После этого мы рассмотрим
неприводимые тензорные операторы, а затем укажем вывод тео-
ремы Вигнера — Эккарта.
Рассмотрим ряд волновых функций, характеризуемых кванто-
выми числами полното момента количества движения / или /'
820 Глава 9
и z-компоненты момента количества движения Mj или Mj>. Со-
вокупность всех остальных квантовых чисел, определяющих со-
стояние системы, обозначим т) или т)'. Нам нужно вычислить ма-
тричные элементы операторов TLm, используя эти волновые фун-
кции как базисные. Теорема Вигнера — Эккарта состоит в том,
что все эти матричные элементы выражаются с помощью соот-
ветствующих коэффициентов Клебша — Гордана через величины
(Jr\\\ TL || 7'т)'), которые зависят от /, /', т), т)' и L, но не зависят
от М}, М}> и М. Математически теорема Вигнера — Эккарта
формулируется следующим образом:
Определим теперь коэффициенты Клебша — Гордана. Их по-
явление связано с проблемой сложения двух моментов количе-
ства движения. Поэтому рассмотрим систему, состоящую из
двух частей. Пусть одна из них характеризуется квантовыми
числами момента количества движения L и его а-компоненты М,
а другая соответственно квантовыми числами /' и Му. Введем
также квантовые числа / и My, относящиеся к системе в целом.
Тогда волновые функции $ш и ц>гмг описывают каждую часть
системы в отдельности, а волновая функция^/м — всю систему.
Поскольку все возможные произведения волновых функций двух
подсистем составляют полный набор, функцию Ч?/м можно
представить в виде линейной комбинации таких произведений:
Т/д>= Е С (Г LI; М
' УМу
LM
Коэффициенты С(ГЫ; MyMMi) называются коэффициентами
Клебша — Гордана. Некоторые их свойства хорошо известны.
Например, они отличны от нуля только в том случае, если
Mj = M + Мг. Другое свойство, которое часто называют прави-
лом треугольника, широко используется в атомной физике. Оно
состоит в том, что коэффициенты C(J'LJ; Mj-MMj) обращаются
в нуль, если / не равно ни одному из значений /' + L,
J' + L-l, ..., |/'-L|.
Определим теперь неприводимые тензорные операторы TLM-
Пусть 1х, 1у и /г — операторы компонент момента количества
движения некоторой системы. Введем, как обычно, операторы /+
и /-, определяемые выражениями
J+^Jx + iJy, r^Jx-Uy. (9.20)
Конструируя из операторов системы различные операторные
функции G, можно найти затем коммутаторы вида [/+, G],
[/-, G] и |7г, G]. Часто можно определить семейство 1L + 1 one-
Электрические квадрупольные эффекты 821
раторов Tlm {L — целое число), которые характеризуются ин-
дексом М (М = L, L — 1, ..., — L) и для которых выполняются
следующие правила коммутации:
[Л TLM\=^L(L+l)-M{M±l)TLM±u n
[4, tlm] = mt
Такие операторы TLM называются неприводимыми тензорными
операторами. В качестве примера приведем набор операторов
для L = 1:
^ ^ (9.22)
Другой набор операторов Т1М можно составить, пользуясь опе-
раторами спинового, орбитального и полного моментов s, 1 и J.
Вводя операторы
l+ = lx + ily, r^lx-ilv, (9.23)
можно показать, что операторы
T Tl0=l*' 7-^Ж (9-24)
удовлетворяют соотношениям (9.21). [Действительно, операто-
ры (9.24) представляют собой компоненты неприводимого тен-
зорного оператора Т1М относительно операторов /+, /- и 4, а так-
же J+, J- и Уг.] Операторы Т1М, определенные соотношениями
(9.22), можно обозначить ГШ(Л), так как они являются функ-
циями компонент Jx, Jy и /г оператора J. Соответственно опера-
торы Tim, определенные соотношениями (9.24), можно обозна-
чить ТшО).
Полезно представить себе более наглядно определение опе-
раторов Tlm с помощью правил коммутации (9.21). Для этого
вспомним (см. гл. 2), что операторы момента количества движе-
ния являются операторами поворота. Поэтому неудивительно,
что при повороте системы координат, как это следует из (9.21),
Tlm переходит в линейную комбинацию TLM' точно так же, как
сферические функции Ylm переходят в линейные комбинации
функции YLM'. Доказательство этой теоремы дано в книге Роуза
[3].
Перейдем теперь к вычислению матричных элементов Tlm-
Хорошо известно, что матричные элементы момента количества
движения можно получить непосредственно из правил коммута-
ции для его компонент. Покажем, что подобным же образом
можно вычислить матричные элементы TLM с помощью (9.21).
Пусть имеется набор коммутирующих друг с другом опера-
торов J2, /г и других, определяющих состояние системы, которым
322 Глава 9
соответствуют собственные значения /(/+ 1). Щ и *!• Здесь г)
означает все остальные квантовые числа. Вычислим матричный
элемент вида
'гг\% (9.25)
Пользуясь правилом коммутации
Uг, ТШ) = МТШ, . (9.26)
получим
(Ш/ц | [4, Тш) I ГМггП = М (Шл | Тш | ГМгц'). (9.27а)
Но, с другой стороны,
Тш1г
Г 2
= (Mj - Mr)(JMjn | TLM
Последнее равенство следует из эрмитовости оператора ]г, дей-
ствующего в члене 1 на функцию, стоящую слева от него, а в
члене 2 — на функцию, стоящую справа от него.
Таким образом,
(Mj - Mr) (JMjri | Тш | J'Mrr\) = M (IMjt) | TLM | I'Mrt)). (9.276)
Из (9.276) следует
ЦМл\Тш\1'Мгг\')=*0, если Mj — МгфМ. (9.28)
Аналогичным образом можно найти соотношения для матричных
элементов остальных коммутаторов (9.21). Имеем
-lm ± 11 J'Mrf). (9.29)
Но
J =F lr, I Тш |
=F lr] 17tM | /'M^'). (9.30)
Из (9.29) и (9.30) следуют рекуррентные соотношения
ш | ГМ^ dh ltiQ УГ (Г + 1) - Mr {Mr ± 1) =
^^ I^lm±11/'Afj.ii'). (9-31)
Соотношение (9-276) имеет смысл только для неисчезающих чле-
нов. При этом, если какой-либо один из матричных элементов
Электрические квадрупольные эффекты 323
в (9.31) удовлетворяет этому соотношению, то оно выполняется
и для всех остальных. Рекуррентные соотношения (9.276) и
(9.31) позволяют связать матричные элементы одного оператора
Tlm с матричными элементами другого оператора TLM-. Это дает
возможность выразить все матричные элементы с данными зна-
чениями /, /', г), г)' через какой-либо один матричный элемент.
Дальнейший анализ рекуррентных соотношений требует при-
влечения коэффициентов Клебша — Гордана. Попутно будет
приведен в основных чертах вывод теоремы Вигнера — Эккарта.
Как показал Роуз, для коэффициентов Клебша — Гордана
справедливы такие же рекуррентные соотношения, как и для
матричных элементов TLm- Выведем одно из правил отбора для
М, Mj и Му. Для этого рассмотрим оператор
Iz^Lz + 1'z, (9.32)
причем
I4 MjV
Jz.
(9.33)
Рассмотрим также следующий матричный элемент оператора
(9.34)
Здесь оператор Jz действует на функцию, стоящую справа. Пред-
ставив оператор /2 в виде Ьг + Уг и подействовав им на функ-
ции, стоящие слева, получим
(М + Мг) С (I'LJ; MfMMj). (9.35)
Приравнивая (9.34) и (9.35), находим
(М + Mf - Mj) С {J'U; Mj-MMj) = 0. (9.36)
Это соотношение полностью совпадает с соотношением (9.276),
если заменить в нем
на
С (J'U; M
Вычисляя таким же способом матричные элементы операторов
/+ и /~, получаем соотношения, аналогичные (9.31). Действи-
тельно, для коэффициентов C{J'LJ; MfMMj) выполняются та-
кие же рекуррентные соотношения, как и для(/М/г) \ТШ \1'Муг\').
Таким образом, между коэффициентами Клебша — Гордана и
324
Глава 9
матричными элементами оператора TLM существует связь, кото-
рая и составляет содержание теоремы Вигнера — Эккарта
| Т
ш
) = С (J'U;
) (/tj || Tl || Гц'). (9.37)
Здесь величина (/tj || Tl || /'tj') одинакова при заданных /, L, /',
tj, tj' для всех значений MJt M/ и М.
Как можно видеть из примеров (9.22) и (9.24), тензоры TLM
для данных L и М могут быть построены из различных операто-
ров. При этом, конечно, коэффициенты Клебша — Гордана будут
одинаковыми для любых TLM с данными L и М, однако значение
(/т; II Tl II /'tj') будет зависеть от того, из каких переменных
строится оператор Tlm.
Рассмотрим этот вопрос несколько подробнее на примере ча-
стицы со спином s и орбитальным моментом количества движе-
ния 1. Полный момент количества движения
J = s + I, (9.38)
где
dz Z dy
У~~ i lZdx X dz\'
/ \X dy y дх\'
(9.39)
I
a x, у к z — координаты частицы. Построим теперь два набора
компонент Т2М, один из которых будет функцией полного мо-
мента J, а другой — координат г. Можно убедиться, что функции,
представленные в табл. 9.1, которые обозначены Т2МC) и Т2м(г),
действительно удовлетворяют правилам коммутации (9.21) с
/+, /- И Jz.
Таблица 9.1
7*22
7*20
Г*-,
Т3-3
Т2М (J>
J+2
— (Izl+ + I* I г)
VFw-'*)
1гГ + Пг
Г3
T2M (г)
(х + iyJ
-2z{x + Iy)
l~2~
a/v Cz2-r2)
V d
1z (x — iu)
(x - iyJ
Здесь обозначение Т2м(г) использовано для функций Т2м,
составленных из компонент х, у и z вектора г. Легко установить
соответствие между Т2м{3) и Т2м(г). Действительно, при за-
Электрические квадрупольные эффекты 325
мене 1+ на (х + iy), /~ на (х — iy) и 1г на z оператор Т2мC) пе-
реходит в Т2м(г). Это соответствие следует из подобия соотно-
шений коммутации для J и г с Ix, 1У и 1г:
Ux, y] = lz, (9.40a)
Ux, Iy\ = U, и т. д. (9.406)
Здесь (9.40а) можно проверить, пользуясь выражениями (9.38)
и (9.39). Следовательно, любая функция G(x, у, г) переменных
х, у и 2 будет подчиняться точно таким же правилам коммута-
ции с Jx, Iy, Iz, что и функция G(IX, Iy, Iг), в которой вместо х
подставлено Jx и т. д. Таким образом, если известно, что неко-
торая функция операторов 1Х, 1У, 1г представляет собой Тш, то,
заменяя 1Х, 1У, 1г на л;, у, z соответственно, получаем компоненты
такого же тензора. При подобных заменах нужно соблюдать не-
которую осторожность, так как операторы, из которых строятся
неприводимые тензоры, могут не коммутировать друг с другом.
Так, например, оператор T2i(J) имеет вид симметризованного
произведения I+Iz + hl+, а не 2/+/г. Такой способ построения
неприводимых тензорных операторов путем прямой замены воз-
можен для любых других переменных, для которых выполняют-
ся правила коммутации (9.40) ')•
Принимая во внимание сделанные выше замечания и соотно-
шение (9.37), можно установить связь между матричными эле-
ментами двух операторов Тш, зависящих от разных переменных
q и р. Получаем
Поскольку множитель (/tj || TL(q) || I'v()/(Ir\ || TL{p) || I'v() постоя-
нен (т. е. не зависит от М, Mj и Mr), можно найти все мат-
ричные элементы для TLM{q) фиксированных /, /', т] и ц',
зная соответствующую постоянную и матричные элементы
AМЛ\Тш(р)\1'МХ).
Здесь нужно отметить одно обстоятельство. Может случиться
так, что (9.41) не имеет смысла, поскольку для некоторых опе-
раторов р матричный элемент (IMjr\ \ TLM (p) \ I'M/ц ) обра-
щается в нуль, хотя матричный элемент (IMjif\\TLM(q) \I'Myr{)
отличен от нуля. Например, если Тш (р) составлен из компонент
оператора J, все матричные элементы с I ф Г исчезают. При
этом, конечно, обращается в нуль также (/||T2(J)||/') и соотно-
шение (9.41) содержит неопределенность.
') См, обзорную статью [4], включающую таблицы Tim для различных
L и М.
326 Глава 9
§ 4. Гамильтониан квадрупольного
взаимодействия (часть 2)
Применим теперь теорему Вигнера — Эккарта для вычисле-
ния матричных элементов Q15j'. Имеем
р
=e ? Кл,-бЛ 0.42)
Операторы полного момента количества движения ядра /*, 1У и
h представляются в виде
1х = Z '** + «*ft и т. д. для 10 и /z, (9.43)
где Ixk и s^ft — ^-компоненты орбитального и спинового моментов
&-го нуклона. Так как
[Ixk, Ук1 = 1гк, [sXk, Ук\ = 0 и т. д., (9.44)
мы видим, что
Ux, Ук\ == izb и т. д. (9.45)
Выражение Зхакх^к — барг| можно представить в виде линей-
ной комбинации компонент Twirk), подобных приведенным в
правом столбце табл. 9.1.
Соотношение (9.41) применимо в несколько более общей
форме не только к Tlm, но и к линейным комбинациям компонент
тензора Тш с данным значением L. Таким образом, если мы
рассмотрим функцию операторов р
F(p)=*Y.aMTLM(p) (9.46)
м
и функцию операторов q
С(«?)вЕаЛм(?) (9.47)
м
с теми же коэффициентами ам, то легко убедиться в том, что из
(9.41), (9.46) и (9.47) следует
(IMn \G(q)\ J'Mrf) =
Применяя эту теорему, получаем
I протоны
'Tj) C. (9.49)
Электрические квадрупольные эффекты 827
Здесь коэффициент С1) один и тот же для всех га, га', аир.
Можно выразить С через матричный элемент с m = m' — I и
а = р = 2 следующим образом:
протоны
= С (//tj 13/1 - /21 //tj) = С/ B/ - 1). (9.50)
Так как квантовые числа т] связаны с операторами, которые ком-
мутируют с /2 и /г, можно не принимать их во внимание при вы-
числении правой части равенства (9.50). Введем величину eQ,
определяемую выражением
(протоны . \
//г, е Z C2*-г*) 11ц); (9.51)
величину Q называют квадрупольным моментом ядра. Пользуясь
(9.50) и (9.51), находим
Поскольку нас интересуют матричные элементы, соответ-
ствующие одному определенному набору квантовых чисел /, tj,
оператор Q^\ входящий в гамильтониан, можно заменить, ис-
пользуя выражения (9.49) и (9.52). Вводя в гамильтониан эф'
фективный квадрупольный член Жа вида
(% % [4 вд+V-) -
мы получим все матричные элементы, диагональные по / и tj.
Интересно, что для определения Qa$ вместо девяти компо-
нент нужно знать только одну величину eQ. Причина состоит
•в следующем. Согласно классическим представлениям, у ядра,
обладающего определенным моментом количества движения,
распределение заряда имеет осевую симметрию. Тогда, выбирая
ось 2 в направлении оси симметрии, можно заметить, что зави-
симость энергии от ориентации ядра связана только с различием
в распределении заряда вдоль оси г и в перпендикулярном к ней
направлении. Именно разность между
\ д;2р dx
*) Коэффициент С не имеет отношения к коэффициентам Клебша — Гор-
дана.
328 Глава 9
определяет характерную величину
Очевидно, последний интеграл представляет собой классический
аналог величины eQ.
Выражение (9.53) для эффективного квадрупольного взаимо-
действия справедливо в случае произвольной ориентации прямо-
угольной системы координат (а, C = х, у, z). Поскольку тензор
Уар симметричен по х, у, г, можно выбрать систему координат,
связанную с главными осями тензора Vap, в которой Vap = О
при а ф |3. В этой системе координат
(9.55)
Используя уравнение Лапласа X Vaa—®> эт0 выражение
a
можно переписать в виде
Из (9.56) видно, что для определения 2Sq необходимо только два
параметра, связанных с производными от потенциала, а именно
Vzz и Vxx — Vyy. Обычно используют параметры ц к q, которые
называются параметром асимметрии и градиентом поля и опре-
деляются в виде
eq=Vzz, ^aV»y~V (9.57)
Для случая аксиальной симметрии, являющегося часто хорошей
аппроксимацией, ц = 0, если ось z совпадает с осью симметрии.
Как уже отмечалось, удобно пользоваться операторами /
и 1-> так как для них существуют простые правила отбора. По-
этому полезно выразить Ж<г, определяемое выражением (9.53),
через операторы/4", /~ и 1г в произвольной (не связанной с глав-
ными осями) системе координат. Вводя величины
V±l = VztJ±iVzx, (9.53)
V±2 = ±(Vxx-Vys)±iVxy,
с помощью простых алгебраических операций найдем
жч = тт$=Т){уо(з;2 -;2) + v+l (Г1г + /в/~)+
+ V_,(/f/2 + hl+) + V+S(rJ+ V-2{l+)% (9.59)
Электрические квадрупольные эффекты
329
Гамильтониан квадрупольного взаимодействия в форме (9.59)
обычно используют при рассмотрении процесса релаксации, ко-
гда положение главных осей нельзя считать фиксированным в
пространстве, поскольку оно зависит от времени. В этом случае
использование системы координат, связанной с главными осями,
приводит к трудностям. Здесь мы не будем рассматривать ядер-
ную релаксацию за счет квадрупольного взаимодействия, хотя
этот механизм играет важную роль в кристаллических диэлек-
триках и часто является доминирующим при комнатных темпе-
ратурах.
§ 5. Случаи сильного и слабого
магнитных полей
Предположим для простоты, что электрическое поле имеет
аксиальную симметрию (или любую другую, при которой в си-
стеме координат, связанной с главными осями, Vxx = Vvv).
Пусть магнитное поле приложено
вдоль оси г', не совпадающей в У
общем случае с главной осью 2.
Тогда гамильтониан имеет вид
рис 9.2. Оси *', г' и х, г.
Рассмотрим сначала случай ква-
друпольного взаимодействия, ела-
бого по сравнению с магнитным
взаимодействием. В этом случае можно считать, что спин кван-
туется по оси г". Применим к квадрупольной части гамильто-
ниана теорию возмущений. Проводя ось х* в плоскости осей г'
и z (рис. 9.2), имеем
/2 = /г- cos 6 + /*' sin 6. (9.61)
Подставляя в (9.60), получаем
4/B?l)
+ 3 (IZ>IX- + /*-/«-) sin 6 cos 6 - /*]. (9.62)
В этом выражении члены с 1гЛх- не вносят вклада в первый
порядок теории возмущений, так как 1Х- не имеет диагональных
матричных элементов в представлении, когда // диагонально.
С другой стороны, член с 1% имеет диагональные элементы, по-
скольку он состоит из произведений недиагональных элементов.
Соотношения I* = A/2) (/' * + /~) и 1У- = A/20 (/'+ - /'") поз-
330
Глава 9
воляют легко увидеть, что диагональные элементы Гх- и 1у рав-
ны между собой. Поэтому диагональные матричные элементы
можно найти следующим образом:
В результате получим
(9.63)
[8m» - / (/ + 1)].
На рис. 9.3 показано влияние квадрупольного взаимодействия
на уровни энергии спина / = 3/г в магнитном поле Но. По-
скольку
Z [Зт2 - / (/ + 1)] = S р (З/2 - /2) = 0, (9.64)
т
квадрупольное взаимодействие не дает сдвига центра резонанс-
ной линии в первом порядке теории возмущений. Более того,
сдвиги для +т и —т одинаковы. Поэтому уровни энергии
имеют вид, показанный на рис. 9.3.
Представляет интерес то обстоятельство, что для полуцелого
спина уровни энергии с т= ±1/2 сдвигаются на одну и ту же
величину, а частота перехода между ними не меняется в первом
-'/*
т = 7л
d
Рис. 9.3. Влияние квадрупольного взаимодействия в первом порядке тео-
рии возмущений.
а—уровни энергии. Сдвиги всех уровней для / = 8/! имеют одинаковую величину;
б — спектр поглощения, соответствующий такому расположению уровней энергии. Квадру-
польное взаимодействие в первом порядке не оказывает влияния на центральную линию.
порядке теории возмущений. Переходы между уровнями +'/2
и —'/г совсем не чувствительны к деформациям в кристалле,
тогда как для других переходов они могут привести к сдвигу
частоты. Поэтому для ядер с очень сильной квадрупольной
связью весьма вероятно, что даже в случае хороню отожженных
кристаллов будет наблюдаться только переход между уровнями
Н- 7s и - 72.
Электрические квадрупольные аффекты 381
В следующих порядках теории возмущений появляется сдвиг
частоты и для перехода между уровнями + x/z и — XJ% равный
по порядку величины (е*дОJ/упМ10.
Другая экспериментальная ситуация возникает, когда ква-
друпольное взаимодействие намного больше магнитного взаимо-
действия. В этом случае в качестве первого приближения рас-
+ !¦
Рис 9.4. Уровни энергии, обусловленные квад- j
рупольным взаимодействием, в отсутствие зеема* 4-
невского расщепления. ~г
сматривается квадрупольное взаимодействие. В отсутствие вне-
шнего поля гамильтониан имеет вид
гC/_-/") (9.65)
(снова предполагаем аксиальную симметрию). Очевидно, /2 и /z
коммутируют с 36, давая квантовые числа I к т. Поэтому для
энергии получаем
Расположение уровней для спина / = 5/2 показано на
рис. 9.4. Мы замечаем, что уровни с __ т двукратно вырождены.
Это соответствует тому, что поворот ядра на 180° не меняет
электростатическую энергию. Если наложить переменное маг-
нитное поле с не равной нулю компонентой, перпендикулярной
оси г, то это вызовет резонансные переходы между уровнями
с |А/п|== 1, поскольку между этими состояниями имеются ма-
тричные элементы. В этом случае обычно говорят о «чисто ква-
друпольном резонансе», хотя переходы индуцированы магнитной
дипольной связью с переменным полем.
В связи с формулой (9.66) важно отметить следующее. Для
спина / = V2. 3h и т. д. (вообще для спина / = п-\- '/г, где п —
целое число) все уровни энергии дважды вырождены в отсут-
ствие магнитного поля, в то время как для целого спина вырож-
дение может быть полностью снято, например в состоянии с
т == 0. Этот результат является частным случаем теоремы Кра-
мерса, играющей важную роль при рассмотрении как электрон-
ного, так и ядерного магнитного резонанса. Теорема Крамерса
формулируется следующим образом:
Для системы с моментом количества движения I == п-\- '/2i
где п = 0 1, 2, .... в любом состоянии нельзя полностью снять
вырождение электрическими полями.
332
Глава 9
Из этой теоремы следует, что если система состоит из не-
четного числа частиц со спином 1/2, то электрические поля не
могут полностью снять вырождения.
Это вырождение обычно называют крамеровским вырожде-
нием. Доказательство его существования связано со свойствами
системы при инверсии времени.
§ 6. Вычисление градиентов поля
Мы видели, что квадрупольное взаимодействие зависит от
вторых производных Уар (а, Р = х, у, z) потенциала, а в случае
системы координат, совпадающей с главными осями, — от Vzz
и Vx.x — Vyy. Потенциал V обусловлен окружающими данное
ядро заряженными частицами (другими ядрами или электро-
нами). Вычислим производ-
ные в начале координат от
потенциала, который со-
здает заряд е, находящийся
в точке х, у, г. Для Vzz по-
лучим
V« = e^-. (9.67)
где г2 = х2 + у2 + г2. В сфе-
рической системе координат
(рис. 9.5) имеем
Рис. 9.5. Сферические координаты г, 6, <р
заряда е.
V —
" ZZ
з cos2 e — 1
(9.68)
Из выражений (9.67) и (9.68) видно, что градиенты убывают
как 1/г3, поэтому наиболее сильное влияние оказывают заряды,
расположенные в непосредственной близости от ядра. Таким об-
разом, главный вклад в Vzz вносят электроны, принадлежащие
атому с данным ядром,. Однако, если атом имеет заполненную
электронную оболочку, то электронная плотность обладает сфе-
рической симметрией и, следовательно, не вносит вклада в ква-
друпольные эффекты (ниже будут сделаны некоторые дополни-
тельные замечания о заполненных оболочках). Случай незапол-
ненной оболочки мы рассмотрим на примере одного р-электрона
с орбитой zf(r).
Найдем для этого случая квадрупольный оператор. По-
скольку электрон движется очень быстро, выражение (9.68)
нужно усреднить по электронной орбите. Это усреднение эквива-
лентно вычислению матричных элементов полного гамильто-
ниана, описывающего движение электрона и ядерный спин,
когда учитываются только матричные элементы, диагональные
относительно орбитальных квантовых чисел, и пренебрегается
Электрические квадрупольные эффекты
333
возмущением электронного движения,
спиновым моментом. Итак, имеем
3cos2G-l . .
вызываемым ядерным
= — е \
cos2
,.3 Те
3 cos2 G — 1
sin
(9.69)
Здесь —е — заряд электрона, a A/V3)— среднее значение от
1/г3 для р-орбиты. Заметим, что для атомов с большим Z значе-
ние (V3) велико и, следовательно, велики градиенты поля.
Эту тенденцию отражает табл. 9.2, в которой приведены типич-
ные значения e2qQ для ядер галогенов в кристаллах с ковалент-
ной связью.
Таблица 9.2
Типичные значения e2qQ для ядер галогенов в кристаллах
с ковалентной связью
Ядро
С136
Вг79
J127
e*qQ, МГц
80
500
2000
Q,10~24 см2
-7,97 • 10~2
0,30
—0.59
Интересно отметить, что, как следует из приведенных в
табл. 9.2 значений e2qQ, частоты чисто квадрупольных переходов
для ковалентно связанных галогенов намного превышают часто-
ты зеемановских переходов упН0 для типичных лабораторных
магнитных полей.
Если электронная волновая функция содержит смесь s- и
р-состояний («гибридная связь»), то s-состояние не вносит
вклада в квадрупольное взаимодействие. Аналогичное положе-
ние возникает, когда атом галогена обладает промежуточным
типом связи между чисто ковалентной связью (соответствующей
р-состоянию) и ионной связью (заполненная оболочка). Ионная
связь не вносит вклада в квадрупольное взаимодействие. Следо-
вательно, квадрупольные эффекты можно использовать для изу-
чения гибридизации связи, степени ковалентности, двойных свя-
зей и т. д.
Поскольку электроны заполненной оболочки расположены
очень близко к ядру, очень важно учитывать нарушение их сфе-
рически симметричного распределения. Например, заряд е будет
вызывать возмущение электронов заполненной оболочки, Этот
эффект исследовался многими авторами. Он приводит к по-
правке к значению градиента Viz, обусловленному зарядом е.
334
Глава 9
Теоретические
1
Ион
сг
Си*
Rb+
Cs+
Таблица 9 3
значения разности
— Yoo
1-Yoo
48
10
51
99
Истинное значение градиента Vzz определяется выражением
V«,= V»[l-Y(r)]. (9.70)
Величину у (г) называют коэффициентом антиэкранирования
Штернхаймера [5] по имени автора, который внес наибольший
вклад в объяснение этого явления. Коэффициент антиэкраниро-
вания зависит от расстояния г заряда е до ядра, что подчерки-
вается формой записи величины у{г). Вообще т(/")-С 1, если за-
ряд находится внутри заполненной оболочки. Если же расстоя-
ние г достаточно велико, то у перестает зависеть от г. Это значе-
ние у мы обозначим у°°- Не-
сколько теоретических значе-
ний разности 1—у™ приведено
в табл. 9.3. Как видно из этих
данных, поправка очень вели-
ка: прямой эффект, связанный
с Vzz, увеличивается на один
или два порядка.
Существование эффекта
Штернхаймера значительно
усложняет определение ядер-
ных квадрупольных моментов.
Трудность состоит в точном
теоретическом определении величины у. Однако, рассматривая
(9.68), можно заметить сходство этого выражения с выраже-
нием для магнитного взаимодействия между ядерным и элек-
тронным спинами. Действительно, радиальная и угловая зависи-
мости точно такие же, как у членов Л и В диполь-дипольного
взаимодействия. А так как ядерный и электронный магнитные
моменты известны, можно определить среднее значение вели-
чины C cos2 0 — 1 )/г3, измеряя сверхтонкое взаимодействие. По-
скольку при этом заполненные оболочки не используются (для
заполненной оболочки сверхтонкое взаимодействие исчезает, так
как электронный спин равен пулю), коэффициент Штернхай-
мера вносит лишь малую поправку. Этот метод применялся в
экспериментах с атомными пучками галогенов и явился основой
для наиболее надежных экспериментальных определений ядер-
ных квадрупольных моментов.
ЛИТЕРАТУРА
1. Smith ]. Н„ Pur cell Е. M., Ramsey N. /\, Phys. Rev.. 108, 120 A957).
2. Walker I. R., VCertheim G. K.., Jaccario V., Phys. Rev. Lett., 6, 98 A961).
3. Rose M. E., Elementary Theory of Angular Momentum, John Wiley and Sons,
New York, 1957.
4. Ambler E., Eisenslcin I. C, Schooleij I. F., Journ Math. Phys, 3. 118 A962);
3, 760 A962).
5. Sternhetmer R. M., Phys. Rev., 84, 244 A951); 86, 316 A952); 95, 736
A954),
Глава 10
Электронный спиновый резонанс
§ 1. Введение
До сих пор наше внимание было сосредоточено на ядерном
магнитном резонансе, хотя многие основные положения приме-
нимы и к электронному спиновому резонансу. Мы рассмотрели
также некоторые вопросы, относящиеся к электронам, такие, как
замораживание орбитального момента количества движения и
магнитное взаимодействие ядерного спина с электронным спи-
ном. В этой главе рассматриваются некоторые проблемы, специ-
фичные для электронного спинового резонанса1)» которые не
возникают в случае ядерного резонанса.
Вероятно, основное различие между электронным и ядерным
магнитным резонансом состоит в том, что такие ядерные свой-
ства, как спин, магнитный момент и квадрупольный момент, с
высокой степенью точности можно считать не зависящими от
окружения, в то время как для электронных систем ввиду отно-
сительно большого их размера и очень малой энергии возбуж-
дения свойства сильно зависят от окружения. Один и тот же
атом в кристалле и в свободном состоянии может иметь совер-
шенно различные значения момента количества движения, маг-
нитного момента и квадрупольного момента. В ядерном резо-
нансе это приводило бы к тому, что величины уп, I и Q приходи-
лось бы заново вычислять для каждого вещества, в котором на-
ходится исследуемое ядро.
Поскольку состояние атома в твердом теле или в жидкости
сильно отличается от свободного состояния, невозможно пред-
сказать характер или даже существование резонанса на основа-
нии данных об электронном моменте количества движения и
магнитном моменте атома в свободном состоянии.
Например, атом натрия не обладает орбитальным магнитным
моментом и моментом количества движения, но имеет спин 1/2
и соответствующий спиновый магнитный момент. Его магнитные
свойства можно изучить методом атомных пучков. В металличе-
ском натрии валентные электроны находятся в зоне проводимо-
') См. в библиографии, помещенной в конце книги, раздел «Электронный
спиновый резонанс в парамагнитных системах»,
336 Глава 10
сти со спаренными спинами. Однако существует слабая элек-
тронная спиновая намагниченность, что позволяет наблюдать
спиновый резонанс. В хлористом натрии атом натрия отдает свой
внешний электрон, который заполняет р-оболочку хлора. В ре-
зультате спиновая намагниченность равна нулю и электронного
спинового резонанса нет. Даже у атомов с ковалентной связью,
например у молекулярного водорода, обычно нет чисто спиновой
намагниченности, так как электронные пары образуют спиновый
синглет. Конечно, есть такие исключения, как молекула кисло-
рода. Как уже отмечалось в связи с химическим сдвигом, обычно
орбитальный момент количества движения электронов заморо-
жен и в первом порядке орбитального вклада в резонанс нет.
Таким образом, для большинства диэлектриков резонанс
можно наблюдать лишь после какого-либо воздействия, в ре-
зультате которого спаренность спинов нарушается. Некоторые
атомы, такие, как атомы элементов группы железа или редкозе-
мельных элементов, имеют незаполненные внутренние оболочки.
Эти атомы даже в ионизованном состоянии обладают электрон-
ным спиновым моментом. Так, например, атом меди имеет кон-
фигурацию CdI04s. Ион Си++ обладает конфигурацией Cd)9,
и он парамагнитен. В таком ионном соединении, как
CuSO4-5H2O (сульфат меди), атомы меди парамагнитны, и, сле-
довательно, может наблюдаться резонанс.
Приведем список различных классов веществ и условий, в
которых должен наблюдаться резонанс (конечно, в отдельных
случаях могут быть исключения из правил):
1. Вещества, содержащие атомы переходных элементов с не-
заполненными внутренними оболочками, например атомы груп-
пы железа или редкоземельных элементов.
2. Обычные металлы, электроны проводимости.
3. Ферромагнетики и ферримагнетики.
4. Дефекты в диэлектриках, которые могут быть электрон-
ными ловушками или дырками, например F-центр (электрон на
месте отсутствующего иона галоида в щелочио-галоидном со-
единении) или доноры и акцепторы в полупроводниках.
Рассмотрение всех этих случаев с единой точки зрения при-
обретает настолько общий характер, что не может описать ка-
кнх-либо важных деталей явления. Приближение, имеющее
смысл в одном случае, совершенно неприменимо в других. На-
пример, если исследуется резонанс на Си++, то электронная вол-
новая функция в значительной мере известна, так как она мало
отличается от соответствующей функции для свободного иона
Си++. Следовательно, можно начать обсуждения, рассматривая
состояния свободного иона меди. С другой стороны, в случае
/¦'-центра эквивалента свободному нону нет. Поэтому нельзя
определить состояния «свободного иона».
Электронный спиновый резонанс 337
Мы приведем список наиболее важных типов взаимодействия,
а затем рассмотрим несколько примеров, соответствующих раз-
личным физическим ситуациям, но включающих основные яв-
ления.
Электронный гамильтониан состоит из следующих основных
частей:
1. Кинетическая энергия электрона.
2. Потенциальная энергия электрона. Часто ее удобно пред-
ставлять в виде двух частей — потенциальной энергии «свобод-
ного иона» и потенциальной энергии, возникающей за счет кри-
сталлического окружения (так называемого кристаллического
потенциала). Такое разделение, конечно, не имеет смысла для
/•¦-центра, поскольку в этом случае отсутствует понятие «свобод-
ного иона».
3. Спин-орбитальное взаимодействие. Для электрона, движу-
щегося в электрическом поле Е, возникает взаимодействие меж-
ду спином и орбитальным движением; этому взаимодействию
соответствует гамильтониан
A0.1)
Часто электрическое поле в атоме имеет радиальное направле-
ние и зависит только от г, так что
E(r) = f?(r).
Тогда ЕХр выражается в виде (\/г)Е{г)ту^$=Aг/г)Е(г)Ъ.
Это приводит к хорошо известной форме спин-орбитального вза-
имодействия %:
A0.2)
Для свободных атомов с рассел-саундерсовской связью спин-
орбитальное взаимодействие приводит к расщеплению состоя-
ний с данными значениями L и S, классифицируя их в соответ-
ствии с полным моментом количества движения / = L + S,
I + S-1, ..., \L-S\.
4. Взаимодействие электронного спинового и орбитального
магнитных моментов с внешним магнитным полем.
5. Магнитное взаимодействие ядерного.спина с электронным
спиновым и орбитальным моментами.
6. Взаимодействие ядерного электрического квадрупольиого
момента с электронным зарядом.
Перейдем теперь к примерам, иллюстрирующим роль некото-
рых наиболее важных типов взаимодействия. В следующем па-
раграфе рассматриваются кристаллические поля и спин-орби-
тальное взаимодействие. В § 3 обсуждается взаимодействие с
ядерным магнитным моментом.
338 Глава 10
§ 2. Пример спин-орбитального
взаимодействия и кристаллических полей
Рассмотрим атом, помещенный в начале координат, обла-
дающий одним р-электроном, на который действуют четыре оди-
наковых заряда (два положительных и два отрицательных), рас-
положенных на одинаковом расстоянии от начала координат.
Расположение зарядов (рис. 10.1) совпадает с тем, которое ис-
пользовалось при рассмотрении химических сдвигов.
Рис. 10.1. Схематическое изображе-
ние двух положительных и двух от-
/ рицательных зарядов, расположенных
* на одинаковых расстояниях от нача-
ла координат.
Пренебрегая взаимодействием с ядром, получаем следующий
гамильтониан для электрона с зарядом q (заряд q отрицатель-
ный) :
^(%J A0.3)
где А — векторный потенциал, соответствующий внешнему по-
стоянному магнитному полю Н, Vo—потенциал «свободного
атома», Vi — потенциал, создаваемый четырьмя зарядами, и
2PH-S — взаимодействие электронного спинового момента с вне-
шним полем. В выражении для электронного магнитного момен-
та используется магнетон Бора |3. Гиромагнитное отношение уе
и спиновый магнитный момент це связаны с f5 следующим об-
разом:
|i» = -YeftS--2pS, A0.4)
или
\еЙ = 2р.
Знак минус в A0.4) соответствует тому, что спин и магнитный
момент направлены в противоположные стороны.
В первом члене выражения A0.3)
векторный потенциал представим в конкретной форме
А = ~-НХг, A0.6)
Электронный спиновый резонанс 339
что дает
Здесь, как обычно, L = (l/t)fXV, а оси xf я tf перпендикулярны
направлению поля г1 (направление поля г' не совпадает с кри-
сталлической осью г). Член, пропорциональный Н2, ответствен
за обычный диамагнетизм. В случае электронного спинового ре-
зонанса им можно пренебречь по сравнению с членом H-L.
Следовательно, используя тот факт, что |3 = eh/2mc, получаем
гамильтониан в виде
3»=^ + PH-L + V0 + V, + XL-S + 2pH.S. A0.8)
Мы полагаем, что основной вклад в гамильтониан вносят кине-
тическая энергия и потенциал «свободного атома» Vo', остальные
члены учтем методом теории возмущений. В нашем примере при-
мем во внимание три вырожденных р-состояния xf(r), yf(r) и
zf(r), представляющие собой решения для потенциала Vo- Мы
предположим, что влияние других состояний свободного атома
относительно невелико, так что остальные члены гамильтониана
можно учесть, рассматривая часть матрицы гамильтониана,
включающую только эти три орбитальных состояния.
В лабораторных условиях поля Н таковы, что члены HL и
H-S имеют величину порядка 1 см-1, тогда как V\ может состав-
лять значительную долю электрон-вольта (т. е. от 100 до
10000 см-1). Константа
спин-орбитального взаимо- Таблица 10.1
действия может принимать Константа спии-орбитального
значения в широких преде- взаимодействия иа одни электрон
.. ' у для некоторых атомов
лах. Некоторые типичные ;
значения константы спин-
орбитального взаимодей-
ствия на один электрон при-
ведены в табл. 10.1.
Можно заметить, что в
некоторых случаях домини-
рующим будет Vi, а в дру-
гих — спин-орбитальное вза-
имодействие. Первая ситуа-
ция типична для элементов группы железа, вторая — для редко-
земельных элементов.
Рассмотрим сначала случай, когда V\ намного больше, чем X.
Вначале учтем влияние только Vi. Потенциал V\ поля зарядов,
Атом
В
с
F
С1
Вг
Константа, см—1
10
28
271
440
1842
340 Глава 10
изображенных на рис. 10.1, снимает орбитальное вырождение.
В результате получатся уровни энергии, показанные на рис. 10.2.
Все они дважды вырождены по спину электрона. Волновые
функции обозначим xf(r)um и т. д., где ит — спиновая функция.
Если бы спин-орбитальное взаимодействие отсутствовало, то спин
квантовался бы независимо от орбитального состояния и ит
были бы обычными собственными функциями Sz>, где г' — на-
правление магнитного поля.
Рассмотрим теперь влияние двух остальных членов
РН • L + XL • S. A0.9)
Исследуем матричные элементы этих членов. Они могут быть
двух типов: одни относятся к одному и тому же орбитальному
yf(r)um
Рис. 10.2. Уровни энергии трех р-состоя-
zf(r)um ний в поле зарядов, показанных на
рис. 10.1.
xf(r)um
состоянию, а другие —к разным. Первые, конечно, наиболее
важны, если они не равны нулю, так как орбитальное расще-
пление достаточно велико. Таким образом, представляют инте-
рес матричные элементы вида
. xf (r) u^HzLzxf (г) um- dx dxs A0.10)
или
\ xf (r) umXLzSzxf (r) unt dx dxs, A0.11)
где dx относится к интегрированию по пространственным коорди-
натам и dxs — по спиновым. Оба выражения A0.10) и A0.11)
включают интеграл вида
\xf(r)Lzxf(r)dx. A0.12)
Вспоминая проведенное выше рассмотрение замораживания ор-
битального движения, заметим, что интеграл A0.12) обращается
в нуль. Следовательно, единственными неисчезающими матрич-
ными элементами членов XL-S и pH-L являются матричные эле-
менты, относящиеся к орбитальным состояниям с разной энер-
гией. Поэтому в первом порядке такие члены не вносят вклада
в энергию.
Электронный спиновый резонанс 341
Мы рассмотрели эту же самую задачу без учета спина и за-
метили, что, так как в состояниях xf(r) и т. д. нет результирую-
щего вращения электрона, член f5H-L в первом порядке обра-
щается в нуль. То же замечание можно сделать и для случая
спин-орбитального взаимодействия. Спин связан с состояниями,
в которых электрон не имеет преимущественного направления
вращения. Поэтому действующее на спин среднее магнитное
поле, обусловленное орбитальным движением электрона, обра-
щается в нуль.
При рассмотрении химических сдвигов мы заметили, что член
PH-L связан с некоторым орбитальным движением. Следова-
тельно, на спин действует отличное от нуля поле, обусловленное
орбитальным движением электрона.
Можно найти точное решение для волновых функций при на-
личии внешнего поля и вычислить матричные элементы XL-S,
пользуясь такими точными волновыми функциями. Практически
для вычисления волновых функций с учетом pH-L мы приме-
няем теорию возмущений и оставляем только первый неисчезаю-
щий член1). С учетом этой поправки волновая функция tyxm
имеет вид
ЦЩ и*. (юла)
m' w*y, z
Поскольку pH-L не зависит от спина, m = m'. Записывая вза-
имодействие pH-L в компонентной форме, находим
^]Ыт. A0.14)
Воспользуемся теперь этой функцией для вычисления матрич-
ных элементов XL-S, которые относятся к основному орбиталь-
ному состоянию. В действительности имеются матричные эле-
менты, включающие возбужденные состояния; эти состояния во
втором порядке теории возмущений примешиваются к основному
') Оба члена гамильтониана PH-L н XL-S ие дают вклада в первом по-
рядке теории возмущений. Во втором и более высоких порядках эти члены
вносят изменения в волновую функцию. Пользуясь аналогией с вычислением
химического сдвига, мы рассматриваем сначала влияние на волновую функ-
цию члена PH-L. Может показаться более естественным рассматривать сна-
чала влияние члена XL-S, который больше. Однако, как мы увидим, вычис-
ленный приближенно конечный результат пропорционалев произведению
PH-L и XL-S (что получается в результата комбинации двух эффектов).
С этой точки зрения безразлично, какое взаимодействие ответственно за изме-
нение волновой функции.
342 Глава 10
состоянию. Однако такие матричные элементы не содержат
внешнего поля //. Пренебрегая ими, находим энергию взаимо-
действия, зависящую от поля (члены второго порядка по спин-
орбитальной связи не дают расщепления для спина '/г)'-
zoi—y, г <7, !?'—х, у% г
1М*) + (*1М»)(*1УИ1у A0Л5)
~ Ex-Ew
При вычислении матричных элементов, относящихся к основ-
ному орбитальному состоянию, выражение A0.15) эквивалентно
замене взаимодействий |3H-L и AL-S эффективным членом га-
мильтониана:
=Ys н <Ар у К* IV ИО» IV !*) + (* IV!»)(»1М*I =
= р У Sqaqq'Htf. A0.16)
Величина fl^?' представляет собой тензор второго ранга, так как
матричные элементы, составляющие а^, при повороте системы
координат преобразуются как произведение Lq и Lq>. Из выра-
жения A0.16) следует, что этот тензор симметричный (aqq — a4'Q).
В рассматриваемом примере мы можем вычислить матрич-
ные элементы с помощью операторов
1 / д д \
l\y~di~ 2ду)'
Используя эти операторы, находим
Lxxf{r)=O,
Lyxf(r) = jzf(r), A0.18)
Таким образом, матричные элементы оператора Lx обращаются
в нуль, а матричные элементы операторов Lu и Lz относятся
Электронный спиновый резонанс 343
только к состояниям zf (r) и yf(r) соответственно. Следователь-
но, сумма содержит вклады только от членов с q = cf. Таким
образом, оси х, у и г являются главными осями тензора aqq'.
Используя A0.16) и A0.18), получаем
^ )A0.19)
Объединяя этот результат с зеемановским членом 2f5H-S, нахо-
дим спиновый гамильтониан для основного орбитального со-
стояния
Э& = ШххНх?х + gyyHiSy + gJHJj, A0.20)
где
Воспользуемся диадным обозначением, которое определяется
следующим образом:
k. A0.22)
Тогда взаимодействие можно записать в виде
^ = pH-g-S A0.23)
вместо
^ = 2pH-S. A0.24)
Сравнивая A0.23) и A0.24), замечаем, что совместный эффект
спин-орбитальной связи и зеемановской энергии эквивалентен
замене реального поля Н эффективным полем:
Нэфф—~==1Нх^ + \Ну^ + кНг-^. A0.25)
При этом резонанс определяется гамильтонианом
)-S. A0.26)
Эффективное поле отличается от приложенного поля как по
величине, так и по направлению, поскольку gxx, gyy и gzz, вообще
говоря, различны. Если ось г" новой системы координат выбрать
в направлении эффективного поля, то, очевидно, при переходе
к этой системе координат выражение A0.26) принимает вид
Ф ¦ S2», A0.27)
344 Глава 10
где #Эфф — абсолютная величина НЭфф. Следовательно, резонанс-
ная частота «о определяется соотношением
где ai, a2 и a3 — косинусы углов между Н и осями х, у и г. Ча-
сто A0.28) записывают в виде
Цщ = ц$Н, A0.29)
где g-фактор определяется выражением
* = *!&& +(&& + &А- A0.30)
Из соотношений A0.29) и A0.30) видно, что при данной ори-
ентации поля Н расщепление спиновых состояний прямо пропор-
ционально величине поля. Часто употребляют термин «сдвиг
g-фактора», который относится к разнице между значением g
в данном случае и значением g = 2 для свободного спина. По-
скольку величины Ег— Ех и Еу— Ех положительны, из A0.21)
и A0.30) мы видим, что при положительных значениях К g-фак-
тор меньше или равен 2, а при отрицательных значениях X
g-фактор больше или равен 2. Положительные значения К обыч-
но относятся к атомным оболочкам, заполненным меньше чем
наполовину, а отрицательные значения К — к оболочкам, запол-
ненным больше чем наполовину. Иногда говорят, что при элек-
тронном резонансе величина К положительна, а при дырочном —
отрицательна. В § 4 мы вернемся к данному вопросу и увидим,
что эту простую интерпретацию нужно применять с большой
осторожностью.
Величина сдвига g-фактора, очевидно, возрастает с зарядом
ядра, как это видно из данных табл. 10.1. Она зависит также от
величины расщепления в кристаллическом поле. Принимая энер-
гию расщепления равной 1,3 эВ A0 000 см-1) и К порядка
100 см~!, находим 2 — g« 0,02, что представляет собой вполне
наблюдаемый эффект.
Как было показано, сдвиг g-фактора происходит благодаря
интерференции спин-орбитального и орбитального зеемановского
взаимодействий. Это аналогично химическому сдвигу, возни-
кающему в результате интерференции взаимодействия ядерного
спина с орбитальным движением электронов и орбитального эф-
фекта Зеемана. В обоих случаях можно говорить, что спин
(электронный или ядерный) испытывает воздействие двух маг-
нитных полей — внешнего поля и некоторого дополнительного
индуцированного поля. Все подобные явления, включающие ин-
терференцию двух взаимодействий, можно рассматривать также
Электронный спиновый резонанс 845
с применением обобщенной формы теории возмущений во втором
порядке. Действительно, в этом и состоит метод Рэмси вывода
формулы химического сдвига. Мы проиллюстрируем этот метод
при расчете сдвига g-фактора.
С общей точки зрения проблема рассматривается в прило-
жении Г, где показано, что вместо возмущения к гамильтониану
можно добавить эффективно член <Э^Нов, обладающий матричны-
ми элементами между состояниями |0) и |0')- В данном при-
мере эти элементы имеют одинаковую орбитальную часть xf(r)]
' и могут иметь разные спиновые функции.
Выбирая возмущение в виде
L, A0.31)
находим матричные элементы @1ЖИОВ | 0') между состояниями
|0) и |0'), следуя приложению Г:
.,уч V @ 1 ^возм I К) (К | Жвош 1 0')
В 10 ) = 2
п
Пользуясь A0.31), получаем
— 2Л ео-еп
. @\$H-L\n)(n\XL-S\0') . @|ftH-L|n)(/tlftH-L10')
"+¦ Е0-Еп "Г Ев-Еп
Первые два члена в правой части, которые дают сдвиг g-фак-
тора, мы уже вычислили. Последние два члена сдвигают оба
спиновых состояния на одну и ту же величину. Следовательно,
они не вызывают расщепления дважды вырожденного основного
состояния и не дают вклада в сдвиг g-фактора. (Однако если
спин больше 1/2, то эти члены могут привести к расщеплению
основного спинового состояния даже при Н = 0.) Присутствие
только двух последних членов означало бы, что каждое возму-
щение действует само по себе и не интерферирует с другим. Эти
члены не появились выше при вычислении g-сдвига, так как мы
рассматривали влияние одного члена возмущения (pH-L) на
другой (XL-S). Этот подход можно распространить для нахож-
дения всех членов в A0.33), однако прямое применение формулы
A0.32) дает систематический метод вычисления. С другой сто-
роны, физические основы первого подхода более очевидны.
В примере, который мы до сих пор рассматривали, предпо-
лагалось, что потенциал кристаллического поля V\ намного
больше константы Я, спин-орбитального взаимодействия. В ре-
вультате орбитальное движение оказалось в значительной мере
346 Глава 10
замороженным и значение g-фактора было близким к 2, т. е.
к значению для свободного спина. Такая ситуация осуществля-
ется в атомах группы железа, а также для многих электронных
и дырочных центров. Теперь обратимся к противоположному
случаю сильной спин-орбитальной связи и относительно слабых
кристаллических полей, который характерен для редкоземельных
атомов.
Если преобладает спин-орбиталыюе взаимодействие, то атом
в первом приближении можно рассматривать как свободный.
В самом деле, гамильтониан
X - {- Н- Vo + KL • S + РН • L + 2РН • S + Vu A0.34)
за исключением члена Vit совпадает с гамильтонианом свобод-
ного атома. В качестве первого приближения рассмотрим влия-
ние одного члена XL-S. При этом будем учитывать только со-
стояния, образованные из спиновых функций и трех р-орбит
xf(r), yf(r) и z/(r)- Полный момент количества движения J ра-
вен сумме орбитального L и спинового S моментов:
J = L + S. A0.35)
Возводя J в квадрат, находим
XL-S = -|(j2""L2-sa)' A0-36)
причем собственные значения
± 1)- L{L+ 1)-S{S + 1)]. A0.37)
Так как здесь фигурируют состояния, характеризуемые орби-
тальным квантовым числом L и спиновым квантовым числом S,
возможными значениями / будут L + -S, L + 5 — 1, ..., \L — S\.
В данном случае L=\, S = 1/2, так что J ==3/2 или !/2. Оче-
видно, состояния с / = 3/г и / = 'Д отделены друг от друга энер-
гетическим интервалом
А? = |л. A0.38)
(В общем случае состояние / лежит выше состояния / — 1 на
Я/.) Для положительных значений К уровни энергии показаны
на рис. 10.3.
Рассмотрим теперь влияние члена V\. Здесь удобно записать
этот член в специальной форме. Считая, что потенциал возни-
кает благодаря внешним по отношению к атому зарядам, потен-
циал Vi в области атома можно представить в виде
Ki=IC(mr'y,ra, A0.39)
l.tn
Электронный спиновый резонанс 347
где Yim — сферические функции, a Ctm — постоянные коэффи-
циенты. Если потенциал образован зарядами, показанными на
рис. 10.1, он обращается в нуль на оси г и меняет знак при за-
мене к на у, а у на—х (вращение системы координат). При
фиксированном расстоянии от начала координат он максимален
на оси к и имеет минимум на оси у. Отсюда видно, что наимень-
шее значение / в разложении A0.39) равно 2. Из пяти функций
Рис. 10.3. Уровни энергии для L •= 1, S = Vs. обусловленные спин-орбнталь*
ным взаимодейстнием XL-S.
с / — 2, ху, xz, yz, 3z2 — г2, х2 — у2 существенна только послед-
няя. Следовательно, пренебрегая членами с / > 2, приближенно
имеем
Vy = A(x2-y2), A0.40)
где А — константа. (Ниже мы увидим, что высшие члены не ну-
жны при точном рассмотрении.) Обсудим теперь влияние потен-
циала Vi на состояния, представленные на рис. 10.3. Нужно учи-
тывать два типа матричных элементов: матричные элементы
с одним и тем же J, такие, как (JAlj \Vi\JMj), и матричные эле-
менты, относящиеся к состояниям с разными /. Первые имеют
более важное значение, так как они связывают вырожденные
состояния. Вычислим матричные элементы, относящиеся к со-
стояниям с данным J, с помощью теоремы Вигнера — Эккарта,
поскольку по отношению к операторам Lx, Ly и Lz (и, следова-
тельно, по отношению к операторам /*, 1У и 1г) потенциал Vi
представляет собой линейную комбинацию операторов Т2м. Это
означает, что коммутационные соотношения для V\ с /г, /* ± ily
такие же, как для линейной комбинации Т2м. (В действительно-
сти потенциал 1Л пропорционален Г22 + ?Y_2.) Таким образом,
имеем
(JMj | Vi | JM'j) = A (JMj | x - y21 JM'j) = Cj (JMj |4-4| JMj).
A0.41)
Это эквивалентно замене V\ оператором
^i = СУ (Л-/?;), A0.42)
если вычисляются только диагональные по / матричные эле-
менты.
348 Глава 10
В качестве альтернативы возможен потенциал Vi вида
В (Зг2 — г2); эквивалентный оператор для него можно записать
следующим образом:
^1=с;(з/1-/2). (Ю.43'
Это есть так называемый случай «аксиального поля»; он встре-
чается довольно часто. Ниже описано вычисление С/ и C'j.
Учтем теперь влияние членов с магнитным полем. Рассмот-
рим опять только диагональные по / матричные элементы. Они
имеют вид
(JMj |рн • L + 2РН • S | JMj) — РН • (JMj IL + 2S | IMS). A0.44)
Поскольку эти операторы представляют собой линейные комби-
нации операторов Tim, можно применить теорему Вигнера — Эк-
карта для вычисления матричных элементов. Следовательно,
можно написать
(IMi | L + 2S | JM'j) = gj {JMj IJ 11 Mi), A0.45)
где gj — величина, постоянная для данного / независимо от
Mj и Mj. Эти матричные элементы уже встречались нам при
рассмотрении эффекта Зеемана для свободных атомов. Таким
образом, величина gj представляет собой известный g-фактор
Ланде:
Из соотношения A0.45) видно, что два члена с магнитным полем
можно заменить (если матричные элементы диагоняльны по /)
членом 2@z вида
^z = gyPH.J. A0.47)
Объединяя выражения A0.42) и A0.47) с A0.36), получаем
эффективный спин-гамильтониан Ж,фф, описывающий данную
задачу для состояний с фиксированным /:
5?8фф = С/(/?-4) + ?/РН-,1; A0.48)
в случае аксиального поля
^эФф = G C/1 - f) + g/PH • J. A0.49)
Два члена взаимодействия в правой части A0.48) п A0.49) сни-
мают B/+ 1)-кратное вырождение уровня с данным /. Даль-
нейший расчет формально эквивалентен решению задачи для
ядра, которое обладает квадрупольным моментом и на которое
действуют неоднородное электрическое поле и постоянное маг-
нитное поле. Мы не будем здесь приводить деталей этого рас-
чета.
Пока не определены еще коэффициенты С/ н C'j; проиллю-
стрируем вычисление их на примере C'j.
Электронный спиновый резонанс 349
Согласно A0.43), имеем
В (JMj | Зг2 - г21 JM'j) = C'j (JMj 13/1 - f I JM'j). A0.50)
Выбирая Mj = M'j = J, получаем
В (// IЗг2 - r21 //) = C'j [ЗЯ — / (/ + 1)], A0.50a)
При / = '/2 все матричные элементы 3/z — / обращаются в
нуль (аналогия с тем фактом, что квадрупольное взаимодей-
ствие не может снять вырождение уровня со спином '/г)- При
/ = 3/г имеем
?+^ A0.52)
где ш/2—спиновая функция с Sz = + '/г- Отсюда находим
^t^ /2(О(Зг2-г2)^т. (Ю.53)
Пользуясь сферическими координатами, можно вычислить угло-
вую часть интеграла. В результате получим
~
(Ю.53а)
где г2 — среднее значение г2 в р-состоянии.
Спин-гамильтонианы A0.48) и A0.49) не включают матрич-
ные элементы, связывающие состояния с / = 3/г и с / = 2/г-
Чтобы учесть такие эффекты, нужно по-другому использовать
теорему Вигнера — Эккарта. Рассмотрим все матричные эле-
менты Vi между состояниями с данным L = 1, т. е. только такие,
как (LMl I Vi I LM'l). Из коммутационных соотношений Lx, Ly и
Lz с Vi следует опять, что V\ представляет собой линейную ком-
бинацию компонент Т2м- Следовательно, все матричные элемен-
ты имеют вид
A (LML | х- - у21 LM'L) = CL (LML \L2X-L2y\ LM'L),
В (LMLIЗ22 — r21 LM'l) = CL (LMLI 3l| - L21 LM?)
Другими словами, Vi можно заменить гамильтонианом <2?ч вида
Ж\ = Cl (Z-X — Z-y),
или
5g, = С? CL| - L2). A0.55)
Таким образом, эффективный гамильтониан <Э^эфф, у которого
все матричные элементы относится к трем /j-состояниям xf(r),
350 Глава 10
yf(r) и zf (r), имеет следующий вид:
2e3bb = KL-S + CL(L2x — Ly)+PH -BS + L),
или
= AL • S + С? C/J - L2) + РН • BS + L). A0.56)
Для диагональных по / матричных элементов выражения A0.56)
сводятся к A0.48) или A0.49).
В отсутствие магнитного поля уровни энергии гамильтониана
A0.56) будут по крайней мере дважды вырождены в соответ-
ствии с упомянутой в гл. 9, § 5, теоремой Крамерса, так как в
данном случае L = 1, S = '/г.
Интересно отметить, что соотношение A0.45)
(JAb | L + 2S | /Mi) = gj {JMj | J | /Mi),
полученное с помощью теоремы Вигнера — Эккарта, совершен-
но аналогично соотношению между ядерным магнитным момен-
том ц и спином I
*I A0.57)
которое в более точной формулировке имеет вид
(IM | ц | IM') = yh {IM 111Ш'). A0.58)
В выражении для потенциала, соответствующего расположе-
нию зарядов, показанному на рис. 10.1, был оставлен только
один член разложения с 1 = 2. Можно предполагать, что необхо-
димо также учесть члены с / = 4, 6 и т. д. (Нечетные / в данном
случае не дают вклада, так как при инверсии расположение за-
рядов не меняется.) Если бы был учтен, например, член с / = 4,
то необходимо было бы вычислить матричный элемент вида
(LML\rlYlm\LMi), A0.59)
где / = 4. Однако по отношению к Lx, Ly и Lz функции r'Yim
являются компонентами Тш. Следовательно, для их определения
можно воспользоваться теоремой Вигнера — Эккарта. Интеграл,
соответствующий такому матричному элементу, существенно за-
висит от момента количества движения (посредством коэффи-
циентов Клебша — Гордана) и обращается в нуль, когда L и I
не связаны с моментом количества движения L по правилу тре-
угольника. В случае когда L = 1, / = 4, величины L и / связаны
с моментом количества движения, равным 5, 4 или 3. Поэтому
интеграл A0.59) равен нулю. В самом деле, при L = 1 только
компоненты с 1 = 2 дают непсчсзающие матричные элементы.
Следовательно, члены с I = 4, 6 и т, д. в разложении потенциала
можно отбросить.
Электронный спиновый резонанс 351
§ 3. Сверхтонкая структура
До сих пор мы не учитывали магнитное взаимодействие элек-
трона с ближайшими ядрами. Основная форма взаимодействия,
которая рассматривается в гл. 4, имеет один вид в s-состоянии
электрона и другой во всех остальных состояниях. В s-состоянии
^ISr = 4р УеУпПЧ . S6 (Г). A0.60)
Во всех остальных состояниях
^] A0.61)
Влияние сверхтонкого взаимодействия можно проиллюстри-
ровать на примере предыдущего параграфа, когда орбитальное
движение было заморожено (что соответствует случаю, когда
потенциал кристаллического поля Vi много больше константы
спин-орбитального взаимодействия К). В этом случае гамиль-
тониан содержит матричные элементы сверхтонкого взаимодей-
ствия относительно состояний, соответствующих одной и той же
орбитальной энергии электрона, и матричные элементы между
состояниями с различной энергией, такими, как xf(r) и yf(r).
Последними матричными элементами в дальнейшем мы будем
пренебрегать. Таким образом, рассмотрим только матричные
элементы вида
(xmsmi | Жisr I xm'smi) =»
;«У (О MISrVm>um>.xf М dx dxs dxp A0.62)
где ins и mi — собственные значения S2 и /z, q>m. и ums— ядер-
ные и электронные спиновые функции, a dx к dxs означают ин-
тегрирование по электронным пространственным и суммирова-
ние по спиновым переменным соответственно, a dxi — суммиро-
вание по ядерной спиновой переменной. Как обычно, вопрос о
квантовании ядерного и электронного спинов решим несколько
ниже, поскольку квантовые состояния зависят и от других частей
гамильтониана. Поэтому опустим ядерные и электронные спи-
новые функции и суммирование по спиновым состояниям и вы-
числим пока интеграл \ xf (r) Ж18г xf (r) dx. При этом ядерные
и электронные спиновые координаты остаются операторами.
Введем обозначение
З&к = \ xf (r) MlSrx\ (r) dx. A 0.63)
352 Глава 10
Подставляя сюда A0.61), получаем
*/s = ЧеЧп& \ тг [3 (-т^) (S • г) -1 • S] x2P (r) dr. A0.64)
Такие члены, как IxxSyy, не вносят вклада, поскольку в этом
случае подынтегральная функция нечетна по х и у. Остальные
члены представим в виде произведения угловых и радиального
интегралов. В результате получим
Ш1& = \eVnh2 (~) ~ CIXSX - I • S), A0.65)
где, как обычно, A/г3)— среднее значение 1/г3 в состоянии xf(r).
Если вместо р-состояния имеется s-состояние или в более
общем случае волновая функция г]з содержит некоторую примесь
s-состояния, то нужно вычислять Mis, возникающее за счет кон-
тактного взаимодействия A0.60). В этом случае имеем
MIS = J ^* (г) ЖкЯ (г) dx = Щ- yeynh* | г]) @) РI • S. A0.66)
В наиболее общем случае, конечно, взаимодействие представ-
ляет собой сумму взаимодействий A0.60) и A0.61):
Ж18 - J | it (r) f { f- УеУпЬЧ ¦ S6 (г
Это выражение линейно по спиновым переменным 1Х, 1У, /г,
Sx, Su, Sz и имеет общий вид
^/s= Z ^aa'Sa/a'. A0.68)
о, а'—х, у, г
Коэффициенты Л симметричны (т.е. Ааа' — Аа'а)- Следователь-
но, всегда можно найти систему координат, совпадающую с
главными осями тензора Ааа', в которой он диагоналей. Обозна-
чая эти диагональные коэффициенты Аа, получаем для сверх-
тонкого взаимодействия выражение
^is = AXIXSX + AyIySy + AJzS^ I • A • S, A0.69)
где тензор А определяется следующим образом:
А = \АХ\ + }АУ] + кАгк. A0.70)
Если бы орбитальное движение не было заморожено, то необ-
ходимо было бы включить взаимодействие ядерного момента с
магнитным полем, возникающим благодаря орбитальному дви-
жению электрона. Нужно было бы также выбрать другой набор
базисных электронных состояний, чтобы получить «спиновый» га-
Электронный спиновый резонанс 353
мильтониан, например состояний, являющихся собственными
функциями Р.
Для случая, когда орбитальное движение заморожено, общий
для ядра и электрона спин-гамильтониан мы получим, объеди-
няя A0.69) и A0.23):
(Если ядро обладает квадрупольным взаимодействием, то необ*
ходимо добавить член 2@q.)
Посмотрим на простом примере, какие эффекты описываются
спин-гамильтонианом A0.71). Заметим, что нет никаких основа-
ний для того, чтобы главные оси тензоров g и А совпадали, хотя
в некоторых простых случаях это имеет место. (В ряде прове-
денных экспериментов они не совпадали.) Предположим, что в
данном случае они совпадают. Кроме того, будем считать, что
поле Н направлено вдоль одной из главных осей, например
вдоль оси г. Тогда
36 = $HgJSz - ynhHIz + AXIXSX + AyIySu + AZIZSZ. A0.72)
He делая приближений, нельзя найти решение задачи с этим га-
мильтонианом в замкнутой форме. Предположим, что электрон-
ная зеемановская энергия спина f>Hgzz много больше энергии
сверхтонкой связи Ах, Ау и Аг. Это предположение хорошо вы-
полняется, когда магнитное поле достаточно велико B|3# =
= 1010 Гц при Н ¦= 3300 Гс, тогда как А имеет величину поряд-
ка 109 Гц или меньше). Если электронное зеемановское взаимо-
действие достаточно велико, то с достаточной степенью точности
можно считать, что Ж коммутирует с Sz. В качестве собственных
функций задачи выберем собственные функции оператора Sz
с собственным значением ms. Члены AXIXSK и AyIySu не имеют
матричных элементов, диагональных по ms. В первом прибли-
жении их можно опустить. С другой стороны, член AJZSZ диа-
гонален по ms и, следовательно, его нужно оставить. В этом при-
ближении гамильтониан имеет вид
+ AJZSZ. A0.73)
Мы видим, что /г коммутирует с гамильтонианом A0.73). По-
этому в качестве базисных функций возьмем собственные функ-
ции оператора 1г с собственными значениями ти Тогда в первом
порядке энергия определяется выражением
Е = §gzzHms - ynhHmi + Azmsm,. A0.74)
Поскольку операторы /2, S2, 1г и Sz коммутируют с гамильтониа-
ном A0.73), в качестве собственных функций можно взять про-
изведение ядерной и электронной спиновых функций
^mjms = <PlmjUSms- A0.75)
19 Зак. 727
364 Глава 10
Вынужденные переходы под действием переменного поля можно
найти, вычисляя матричные элементы оператора
Жт (/) = (yehSx — УпМх) Нх cos at A0.76)
между состояниями, определенными посредством A0.75). Таким
образом, найдем, что часть оператора 2em(t), включающая Sx,
дает переходы между состояниями с Ams = ± 1, A/m=sO, a
часть, включающая /*, — переходы, для которых Ams = 0,
Дт/=±1. Можно считать их относящимися соответственно к
электронному и к ядерному резонансам. Переходы разрешены
только в том случае, если со удовлетворяет закону сохранения
to
Рис. 10.4. Расположение линии электронного резонансного поглощения в слу-
чае ядра со спнном 31г.
В первом приближении линии расположены эквидистантно.
энергии. Поэтому, используя A0.74) и правила отбора, получаем
для электронного резонанса
и для ядерного резонанса
, Az"lS
A0.78)
Как мы видим, влияние сверхтонкого взаимодействия на элек-
тронный резонанс эквивалентно добавлению внешнего поля, про-
порционального z-компоненте ядерного спина. Так как ориента-
ция ядра квантуется, линия электронного резонанса расщепляет-
ся на 21 + 1 (эквидистантных) линий. Если ядро не имеет пре-
имущественной ориентации, то линии, соответствующие перехо-
дам при разных значениях mi, равновероятны и картина резо-
нанса имеет вид, показанный на рис. 10.4.
В ядерном резонансе должны наблюдаться линии на часто-
тах, которые даются выражением A0.78). Чтобы интерпретиро-
вать это выражение, необходимо знать, больше или меньше зее-
мановская энергия ядра упЬН0 по сравнению с энергией сверх-
тонкого взаимодействия Azms, так как выражение A0.78) для
частоты может иметь как положительный, так и отрицательный
знак. Если зеемановская энергия больше Azms (рис. 10.5), то ре-
зонансная линия расщепляется на 25 + 1 линий, отстоящих друг
от друга на расстоянии Az/h с центром на частоте упН0.
Электронный спиновый резонанс
355
Если зеемановская энергия меньше Azms, то, поскольку
имеются два значения tns (tns и — ms), возникают две линии на
частотах
А I у-и I
A0.79)
В случае электронного спина 1/2 результат показан на рис. 10.6.
Из рис. 10.4—10.6 видно, что с помощью электронного резо-
нанса можно определить тензор сверхтонкого взаимодействия и
спин ядра, но нельзя измерить магнитный момент ядра. Однако,
используя совместно электронный резонанс и ядерный резонанс,
г-тгН
ш
Рис. 10.5. Спектр ядерного резонанса
для случая, когда ядерная зееманов-
ская энергия больше A,ms в предпо-
ложении, что спин электрона ра-
вен '/2.
Аг ш
гь
Рис. 10.6. Спектр ядерного резонан-
са для случая, когда сверхтонкое
взаимодействие больше ядерной зее-
мановской энергии в предположении,
что спин электрона равен '/а-
можно найти также магнитный момент ядра. Последнее особен-
но важно при изучении центров окраски, так как этим способом
можно определить сорт ядра, приводящего к сверхтонкому
расщеплению, поскольку ядерные гиромагнитные отношения у
известны из других экспериментов. С другой стороны, с по-
мощью ядерного резонанса можно измерить спин электронной
системы.
До сих пор наше рассмотрение было ограничено случаем, ко-
гда постоянное поле направлено вдоль одной из главных осей
g-тензора и тензора сверхтонкого взаимодействия. Новые эффек-
ты возникают, если поле имеет другое направление. В этом слу-
чае ось квантования ядерного спина не совпадает с осью кванто-
вания электронного спина и зависит от того, как направлен элек-
тронный спин — параллельно или антипараллельно полю. Для
простоты примем, что g-фактор электрона изотропен. Примем
также, что поле направлено вдоль оси г', лежащей в плоскости
xz, где х, у, z—главные оси сверхтонкого взаимодействия. На-
правление осей показано на рис. 10.7.
В этом случае гамильтониан имеет вид
. A0.80)
356 Глава 10
Будем считать по-прежнему, что 2р#0 » Ах, Ау, Аг, так что в
хорошем приближении гамильтониан коммутирует с Sx\ Попро-
буем теперь определить часть гамильтониана, которая диаго-
нальна в представлении, диагонализирующемЗг'. Для этого най-
дем выражения для спиновых компонент 1Х, 1У, 1г и Sx, Sy, Sz в
системе координат, связанной с главными осями. (На самом
деле достаточно выразить Sx, Sy и Sz через SX', Sy' и Sz>, од-
нако преобразование ядерных компо-
/z' нент позволяет более наглядно пока-
/ зать, что направление квантования
спина ядра не параллельно направле-
нию квантования электронного спина.)
Замечая, что у = у', имеем
Sx — Sx> cos 0 + SZ' sin 0,
*•"- s, = s^ cos e-s,. sine,
Phc. 10.7. Ориентация глав- ж , /РП<го i / , sin fi
ных осей x, z тензора сверх- '* ~ Jx'cos B + '«' Sln 0'
тонкого взаимодействия А /« = Iu'
относительно направления у '
постоянного поля z'. lz = /г' cos 0 — /jt' sin 0.
Подставляя эти выражения в A0.80), находим
Ж = 2рЯо5у - VnhHoh' + Ix>Sx> (Ax cos2 6 + Аг sin2 6) +
+ IySy'Ay + h'Sz' {A» sin2 0 + Az cos2 0) +
+ {IX'SZ> + IZ'SX){Ax — A,) sin 0 cos 0. A0.82)
В первом порядке члены сверхтонкого взаимодействия, вклю-
чающие Sx- или S,/, не имеют диагональных элементов в пред-
ставлении, диагонализирующем Sz', и, следовательно, их можно
опустить. Во втором порядке они дают вклад в сдвиги энергии
порядка Л2/2рЯ0, где Л2 —средний квадрат величины матричных
элементов Ах, Аи или Az, а 2|ЗЯо — расстояние между электрон-
ными уровнями энергии, отвечающими разным ориентациям
электронного спина в постоянном поле. Отбрасывая все члены
с Sx' и Sy-, получаем сокращенный гамильтониан
^сокр = 2рЯ05г- - yntiH0Iz> + [1г> (Ах sin2 0 + Аг cos2 0) +
+ IX' (Ax — Az) sin 0 cos 0] Sz'. A0.83)
Очевидно, Sz' коммутирует с Жокр, a lz> не коммутирует. По от-
ношению к ядру Жокр соответствует взаимодействию ядерного
спина с магнитным полем, компоненты которого Нх-, Ну' и Нг'
Электронный спиновый резонанс 367
имеют вид
НХ' = -^ (Аг — Ах) sin G cos eSj.-,
Ну=0, A0.84)
Ах sin2 6 + Аг cos2 6
Поскольку эти выражения включают 5г', эффективное поле за-
висит от электронного спинового состояния. Обозначая собствен-
ные значения оператора S2- через ms, получаем
И х- (ms) — утГ ^г ~ ^ sin 6 cos ®ms'
A0.85)
\ms.
Следовательно, ядерный спин квантуется в направлении эффек-
тивного поля A0.85), а не в направлении постоянного поля. Это
направление меняется в зависимости от значения ms. Таким об-
разом, величина ядерного расщепления А?Ядерн равна
), (Ю.86)
где ЯЭфф {ms) — поле A0.85), которое зависит от ms. Следова-
тельно, полная энергия электрона и ядра равна
Е = 2p//0ms - ynhHm (ms) m,. A0.87)
Изменение направления оси квантования ядерного спина при
изменении nis можно рассматривать с другой точки зрения. Бла-
годаря различному направлению оси квантования ядерные фун-
кции Um, различны для разных ms. Подчеркнем это, введя обо-
значение um[{ms). Можно установить связь между 2/+ 1 функ-
циями um[{ms + 1) и 2/ + 1 функциями um] (tns):
щ
где а > — постоянные коэффициенты. Это означает, что
возможны переходы из состояния ms, mi в состояние ms + 1,
mi, где m] Ф m, (так как, вообще говоря, amsmim't не равны
нулю), т. е. одновременные переходы ядерного и электронного
спинов.
В действительности соотношение A0.88) не отражает изме-
нения ядерной ориентации. Оно престо выражает тот факт, что
ядро с данным mi в поле #s<i><j>('«s) при изменении электронной
358 Глава 10
ориентации переходит в смешанное состояние с различными т'/
(так как его пространственная ориентация фиксирована в мо-
мент электронного перехода), причем т\ относятся уже к дру-
гому направлению квантования.
§ 4. Kft-центры
Особенно интересный пример применения идей предыдущих
параграфов представляет собой открытие и идентификация так
называемых Ул-центров Кастнером и Кенцигом [I]. Детальный
анализ соответствующих спектров позволит нам более полно
рассмотреть сдвиг g-фактора, включая влияние наличия не-
скольких электронов и более чем одного силового центра.
За первой работой по электронному спиновому резонансу
Кастнера и Кенцига последовал ряд красивых экспериментов
Делбека, Смоллера и Юстера [2], которые сочетали оптические
методы с электронным резонансом, чтобы найти I) оптическое
поглощение, соответствующее У*-центру, и 2) энергетический
спектр возбужденных состояний. Полный обзор всех работ по
Vft-центрам увел бы нас слишком далеко от цели этой книги.
Остановимся лишь на методе отождествления центров и на
некоторых особенностях сдвига g-фактора, которые не наблю-
даются для «одноатомных» одноэлектронных центров.
Удобнее начать рассмотрение этих вопросов, заранее зная
физическую природу явления. ^-центры образуются при рентге-
новском облучении кристаллов щелочно-галоидных соединений
при температуре жидкого азота. При этом из отрицательного
иона галогена выбивается электрон и его электронная конфигу-
рация с замкнутой оболочкой превращается в конфигурацию, в
которой в р-оболочке не хватает одного электрона. Выбитые
электроны могут иметь самую различную судьбу. Мы примем
лишь, что не все они рекомбинируют с нейтральными атомами
галогена.
Рассмотрим в качестве примера хлор. Нейтральный атом
хлора неустойчив, и он образует с соседним ионом С1~ комплекс,
который удобно назвать молекулой С1г. Ось С1 — С1 занимает
положение [ПО] или эквивалентное для данного кристалла, как
показано на рис. 10.8.
Электронная структура оказывается очень сходной со струк-
турой, рассмотренной в § 2, где имелся р-электрон с заморожен-
ным орбитальным моментом. Электрон с неспаренным спином
находится на орбите, ось которой параллельна направлению
связи в молекуле С1г. Влияние возбужденных состояний приво-
дит к сдвигу g-фактора, который меняется при изменении ори-
ентации магнитого поля относительно кристаллографических
Электронный спиновый резонанс
осей, а взаимодействие неспаренного спина с ядерными момен-
тами двух атомов хлора дает сверхтонкое расщепление.
+ -
Рис. 10.8. Молекула С12 . или Vk -центр, в КС1.
Центр можно представить себе как дырку Л. захваченную
двумя ионами С1~.
Как было замечено выше, эти центры были обнаружены впер-
вые с помощью электронного спинового резонанса. Наблюдае-
мая картина для случая, когда постоянное магнитное поле при-
ложено в направлении [lOO] кристалла, показана на рис. 10.9.
Рис. 10.9. Спектр резонанса Vs-центрон в КС1 для случая постоянного поля,
направленного вдоль кристаллографической оси [100].
Спектр любезно предоставлен Кастнером и Кенцигом.
На первый взгляд спектр кажется слишком сложным, чтобы
его можно было объяснить, но, к счастью, в качестве отправного
пункта могут служить семь линий особенно большой интенсив-
ности. Они разделены одинаковыми промежутками, и их интен-
сивности относятся как 1:2:3:4:3:2:1. Эти линии можно
объяснить взаимодействием неспаренного электронного спина
с магнитными моментами двух ядер хлора.
860
Глава 10
Рассмотрим подробнее это предположение. Существуют два
изотопа хлора С135 и С137. В природном хлоре содержится 75%
C13S и 25% С1ЗГ. Оба имеют спин 3/2, но их магнитные моменты
несколько отличаются друг от друга (узг/уз5 = 0,83). Как мы
покажем ниже, семь выделенных линий возникают от пар ядер
С136. Примем, что поле Яо приложено вдоль главной оси моле-
кулы Cli, которую назовем осью z. Легко обобщить рассмотрев
ние предыдущего параграфа на случай двух ядер и получить
условие электронного резонанса в виде
+ Аг (т, + т2)].
A0.89)
где т,\ пт.2 — значения квантового числа m для двух ядер хлора.
Таким образом, частота зависит только от суммы т\ + tn%. Наи-
большее значение гп\ + tn% равно 3/2 + 3/а = 3. Следующее по
величине значение равно '/а + 3Л = 2. То же значение тп\ -+- т%
получается для т\ = 3Д т'л = /а- Поскольку мы предполагаем,
что каждое ядро с одинаковой вероятностью может находиться
в состоянии с любым т, интенсивность линии с т\ -J- ггц — 2
должна быть вдвое больше интенсивности линии с т\ -\- тц = ?>.
В табл. 10.2 указаны возможные комбинации квантовых чисел
Ш\ и та.
Таблица 10.2
Комбинация квантовых чисел т, и т2, приводящая к данному
значению суммы т, + ">2, С00ТветсТВУюШие частоты и статистические веса
/3 3\
42' 2)
42' 2) \2'
\~2' ~J\2
/3 3W1
V2' 2^42
(-44) (-
V ~2' ~~2)
(-1 -i^
V 2 ' 2)
2)
' ~2)
> —
~~2'
—-
(mi, тг)
1 W 1 1 W 3 34
2j\ 2' 2J \ 2~' 2)
2) \2' 2)
о * о у
A {mi + m2)
ЗА
2A
\A
OA
-\A
-2A
-ЗА
Статистиче-
ский вес
1
2
3
4
3
2
I
Электронный спиновый резонанс 361
То обстоятельство, что семь основных линий можно объяс-
нить в рамках приведенной схемы, явилось ключом Для понима-
ния данного спектра. Принимая эту схему, т. е. считая, что элек-
трон проводит одинаковое время около каждого из двух атомов
хлора, необходимо учесть следующее замечание, относящееся
к молекулам СЦ. Ядра этой молекулы могут быть оба С137 или
одно из них может быть С137, а другое С1зБ. Вероятность встре-
тить атом с ядром С135 равна 3/4, а та же вероятность для С187
равна 1/4. Следовательно, вероятности появления пар ядер
равны
Г135 pi35 j*. ч/ JL 9^
Г135— П37 — У— —}
ы *-1 4 А 4 — 16 I 6
а»-а» |хт—л)
J_J_
4Л4 16
Для двух неодинаковых ядер вместо выражения A0.89) полу*
чаем
» = Т Cff«P"o + (A>m + *fm*)l A0'9°)
Обозначения здесь очевидны. Как известно, сверхтонкое вза-
имодействие пропорционально гиромагнитному отношению ядра
у; поэтому
4зг = —• A0.91)
Л37 уз? v '
Таким образом, присутствие неодинаковых ядер приводит к
тому, что такие комбинации, как (8/2, 'А) и С/2, sh), не дают
одинаковой частоты. Если принять интенсивность линии с ком-
бинацией C/а, 3А) за «единицу», то линии, интенсивность кото-
рых в случае одинаковых ядер равна 2, в случае разных ядер
расщепляются на две линии с единичной интенсивностью. Точно
так же линия с интенсивностью 3 расщепляется на три линии
с единичной интенсивностью и т. д. Используя измеренные зна«
чения Af и соотношение A0.91), можно предсказать положение
всех линий. Интенсивность линий в случае пары С138 и С137 со-
ставляет 6/9 интенсивности наиболее удаленных линий спектра
для пары ядер С136. Кроме того, имеется еще семь линий от пар
ядер С137, положение которых можно указать и интенсивности
которых составляют 1/9 интенсивностей линий для пар ядер
С136. Все эти линии были найдены в соответствующих положе-
ниях и с соответствующими интенсивностями. Таким путем уда-,
лось объяснить много спектров.
362 Глава 10
Заметим еще одно обстоятельство, важное для идентифика-
ции спектров. Сдвиг g-фактора определяет положение центра
картины сверхтонкой структуры спектра. Главные оси g-тензора
молекулы показаны на рис. 10.10. Как видно из рис. ШЛО, маг-
нитное поле будет параллельно оси у, если оно перпендикулярно
плоскости рисунка (приложено в направлении [001]). Если бы
поле было приложено вдоль направления [100] или [010], то
оно составляло бы угол 45° с осью г молекулы на рис. 10.10. При
любой заданной ориентации магнитного поля по отношению к
кристаллографическим осям имеется, вообще говоря, несколько
Рис. 10.10. Главные оси х, у, z g-тензора для У*-центра.
Ось у направлена вверх от плоскости рисунка.
классов l/fe-центров, различающихся углами, которые состав-
ляет поле Но с главными осями центра. Если Но параллельно на-
правлению [111], то существует два класса молекул. Если поле
Но параллельно направлению [100], у 1/3 центров линия связи
перпендикулярна Но, а у 2/3 связь составляет угол 45° с Яо.
В общем случае существует несколько картин сверхтонкой
структуры, центры тяжести которых смещены относительно друг
друга благодаря анизотропии g-фактора. Более того, сверхтон-
кое расщепление само по себе обладает сильной анизотропией,
поскольку Аг много больше, чем Ах или Ау (если ось z выбрана
в направлении связи). Эта анизотропия возникает вследствие
того, что индивидуальная функция связи каждого атома пред-
ставляет собой линейную комбинацию s-функции g(r) и р-функ-
ции zf (r) ').
Тогда, пользуясь A0.65) и A0.66) для сверхтонкого взаимо-
действия, получаем выражение
S, A0.92)
[A -а2
') Электронные волновые функции рассматриваются ниже. Заметим
только, что функция связи, упоминаемая здесь, является функцией z, -}- z$,
которая обсуждается ниже,
Электронный спиновый резонанс 363
где а2 — доля р-функции в волновой функции электрона, а
A/г3)—среднее значение 1/г3 в состоянии zf(r). Здесь в отли-
чие от A0.67) введен множитель '/2, так как волновая функция
относится к двум атомам. (Перенормировкой, связанной с пере-
крытием атомных функций, мы пренебрегаем.) Два члена в ква-
дратной скобке в A0.92) почти взаимно уничтожаются, что при-
водит к сильной анизотропии.
То обстоятельство, что электрон не принадлежит уже одному
атому, создает новые трудности при вычислении сдвига g-фак-
тора. В приведенном примере спин-орбитальное взаимодействие
представляется в виде ЯЬ-S, пригодном для свободного атома.
Орбитальный момент определяется по отношению к началу ко-
ординат, где находится ядро, так как движение электронного
спина относительно заряда ядра приводит к спин-орбитальному
взаимодействию. Если же имеется несколько ядер, то неясно,
какое ядро выбирать в качестве начала координат. Чтобы раз-
решить эту трудность, вернемся к исходной форме спин-орби-
тального взаимодействия
^ A0.93)
В этом выражении Е—электрическое поле, в котором движется
электрон, а р — оператор импульса электрона {h/i)S/. Так как
для изолированного атома Е направлено вдоль радиуса-вектора
из начала координат, оператор ЕХР пропорционален оператору
момента количества движения г X р. Таким образом, обычное
выражение KL-S следует из A0.93). Поскольку электрическое
поле Е имеет наибольшее значение вблизи ядра, главный вклад
в Шво вносят ближайшие к ядру электроны.
Кроме наличия двух силовых центров, дополнительная труд-
ность связана с необходимостью учета нескольких электронов.
В самом деле, в l/ft-центре не хватает только одного электрона,
чтобы заполнить валентные оболочки двух атомов хлора. Для
дальнейшего изложения необходимо рассмотреть электронные
состояния. Опишем их в схеме молекулярных орбит, которые
будем строить из линейных комбинаций р-состояний свободных
атомов. Введем обозначение х\ для атомной р-функции xf(r) с
центром в первом атоме. В подобных обозначениях х\, у\, Z\, хг,
</2 и z2 — волновые функции соответствующих атомных орбит;
при этом ось г направлена вдоль связи.
Функции Z\ + z2 и z\ — z2 схематически показаны на
рис. 10.11. Как видно на рис. 10.11, орбите Z\ — z2 соответствует
более низкая энергия, чем орбите z\ + z2, так как у нее меньше
узлов и повышенная электронная плотность между атомами, где
она вносит вклад в потенциал притяжения. Действительно, со-
стояния Zi — z2 относятся к связывающим орбитам, а состояния
364 Глава 10
z\ + Z2 — к разрыхляющим. Аналогично х\ -\- х2 и у\ + Уг— свя-
зывающие орбиты, а Х\ — х2 и у\—у2 — разрыхляющие (z-co-
стояния представляют собой так называемые а-состояния, а х-
и {/-состояния — л-состояния). Уровни энергии этих состояний схе-
матически представлены на рис. 10.12. В действительности со-
стояния xi + Хч и у\ + У2, вырожденные в свободной молекуле,
у-\ у\ ^ч
\7V \У
XS-*.
a
Рис. 10.11. Функции 2i + 22 (a) HZt — z2 (б).
Функции Zi + гг соответствует более высокая энергия, так как 1) оиа имеет больше узлов
и 2) узел лежит в области электронного потенциала притяжения.
не вырождены в кристалле, однако мы пренебрегаем этим рас-
щеплением.
Имеется 6 орбитальных состояний, и, следовательно, имеется
12 мест для р-электронов. Поскольку У*-центр имеет только
i ! xt — x{\ Рис. 10.12. Молекулярные орбиты иоиа молекулы
~ '"" ' галогена, образованные из р-состояний.
Пунктиром показаны разрешенные оптические переходы
| в незаполненное состояние <тц.
' ' г I/_ \ <Переходы»| дающие вклад в сдвиг г-фактора, покаааны
:;:)
I
рд дщ д д гф
Vt "*" V I сплошной стрелкой.
в, - гг {од)
11 электронов, одно место в состоянии z\ + Z2 остается пустым,
т. е. в этом состоянии имеется неспаренный электрон. На
рис. 10.12 состояния имеют индексы и или g, соответствующие
нечетности или четности данного орбитального состояния.
Можно наблюдать оптическое поглощение ^-центров. Так
как дипольные переходы разрешены, только между состояниями
с различной четностью, оптическое поглощение будет наблю-
даться при переходах электрона из состояния z\ — z2, xi — х^
или у\ — г/г в незаполненное состояние z\ + 22. Наиболее интен-
сивным будет оптический переход из состояния z\ + 22 в состоя-
ние «1 — г2, так как для этого перехода электронный дипольный
Электронный спиновый резонанс 365
матричный элемент наибольший (он соответствует длине плеча
дипольного момента молекулы).
Таким образом, мы видим, что необходимо обобщить преды-
дущее рассмотрение в двух направлениях. Во-первых, нужно
рассмотреть случай более одного силового центра и, во-вторых,
учесть наличие нескольких электронов.
Чтобы проиллюстрировать подход в первом направлении
(случай более одного силового центра), не усложняя вторым
(наличие нескольких электронов), примем, что на орбитах Vk-
центра имеется только один электрон. Тогда, без учета перекры-
тия, волновая функция Wo основного орбитального состояния
имеет вид
I-z2). A0.94)
40 = ,Blz2).
В этом состоянии орбитальное движение заморожено.
Выше, при рассмотрении сдвига ^-фактора для случая одного
силового центра, мы видели, что этот сдвиг возникает благодаря
интерференции спин-орбитального взаимодействия и незначи-
тельного размораживания орбитального момента, вызываемого
внешним магнитным полем. Если имеется более одного силового
центра, то не существует единственной точки, относительно кото-
рой должен определяться орбитальный момент. Поэтому есте-
ственно обратиться к исходной форме спин-орбитального вза-
имодействия
S(EXp) A0.95)
Это выражение справедливо в отсутствие внешнего магнитного
поля. При наличии магнитного поля, описываемого векторным
потенциалом А, это выражение нужно модифицировать так, что-
бы выполнялась калибровочная инвариантность, а именно
где —е — заряд электрона. Выражение A0.96) следует непо-
средственно из уравнения Дирака; кроме того, его форма инту-
итивно очевидна, поскольку, как уже указывалось выше, в при-
сутствии магнитного поля оператор р всегда нужно заменять на
р — (q/c) А (в данном случае q = — е).
Орбитальная зеемановская энергия Жог имеет вид
?A (Ю.97)
Мы можем рассматривать сумму Жа и 3@so как возмуще-
ние;
^возм== <7®S0 I <y&QZ'
366 Глава 10
При вычислении матричных элементов п означает орбитальные
квантовые числа, а о — спиновые квантовые числа. Согласно
приложению Г, возмущение Жвози эквивалентно добавлению
взаимодействия <3^Нов, матричные элементы которого, диагональ-
ные по основному орбитальному состоянию |0), имеют вид
(Оа | Жаов | Оа') = (Оа | Жвош | Оа') +
/ (Оа | ЗЕГвозм | па") (по* | ЖЪОЗ№ \ Ос')
I у/
(Ю 99)
П.О"
где 2' означает суммирование по всем значениям, кроме п = О,
а в знаменателе пренебрегается вкладом спина в энергию. Сдвиг
^-фактора получается только за счет тех членов в A0.99), кото-
рые пропорциональны векторному потенциалу и спину элек-
трона. Таким образом, получаем
(Оа \Ж^\ ОаО = -^-@a|s • Е Xj A | Ос/) +
+Z' (?о ~ ?"Г' [(°а IS • Е X Р I«О № I р • А+А • р | 0@+
+ (Оа |р • А + А • р \по")(оа" |S • Е X Р |0<О]. A0.100)
Так как р-А + А-р не зависит от спина, имеем
(оа"|р • А + А • р|0а0 = (п |р • A+ А • р 10N^. A0.101)
Следовательно,
, 1 Г;ГС IЕ X РI п) (w | р • А + А • р 10) + компл. conp.
+ ~2trLl ~ Ев-Еп
п
Выражение A0.102) является основой для рассмотрения про-
блемы нескольких силовых центров. Однако, прежде чем при-
ступить к этой задаче, необходимо выяснить некоторые не затро-
нутые нами вопросы, возникающие в задаче для одного сило-
вого центра. В частности, нужно решить, какая калибровка век-
торного потенциала наиболее удобна и что происходит при из-
менении калибровки.
Предположим, что интересующий нас атом находится в на-
чале координат. Тогда волновая функция \п) в общем случае
либо классифицируется по моменту количества движения отно-
сительно начала координат, либо представляет собой линейные
комбинации таких атомных орбиталей. Если векторный потен-
циал A(R) определить в виде
^-R), A0.103)
Электронный спиновый резонанс 367
где R — произвольный постоянный вектор, то, учитывая, что
divA(R) = 0, для матричного элемента (я|р-А -f- А - р j 0) по-
лучим
= ЛН0 • J u'nL (R) u0 dx, A0.104)
где
L(R)s-j-(r-R)XV A0.105)
— безразмерный оператор момента количества движения отно-
сительно произвольной точки R. Пользуясь соотношениями
A0.17) и A0.18), легко вычислить интегралы, подобные послед-
нему интегралу в A0.104), при условии что R равно нулю, т. е.
орбитальный момент определяется относительно начала системы
координант, естественной для атомных орбит \п). Такую кали-
бровку мы назовем «естественной».
Еще более важно рассмотреть член первого порядка в выра-
жении A0.102)
A0.106)
Используя тот факт, что электрическое поле Е велико лишь
вблизи ядра, где оно в хорошем приближении радиально, полу-
чаем
E(r) = f?(r). A0.107)
Тогда, выбирая ось г в направлении постоянного поля, находим
\Хг-\Yz]\ о)}, A0.108)
где X и Y— компоненты R.
Если волновая функция 10) имеет определенную четность, то
второй член в правой части обращается в нуль. Если она не об-
ладает определенной четностью (например, в случае s — р-гиб-
ридизации), то второй член не равен нулю. Так как этот член за-
висит от выбора R, в последнем случае он может принимать лю-
бые значения. Поскольку сдвиг ^-фактора не может зависеть от
868 Глава 10
калибровки, этот член должен компенсироваться за счет измене-
ния в A0.100) членов, имеющих в знаменателе энергию. Так и
происходит на самом деле.
Если принять «естественную» калибровку, при которой R = 0,
то правая часть A0.108) по порядку величины будет равна при-
близительно рЯ0Гс/ая, где го — классический радиус электрона
е2/тс2(& Ю-13 см), а ан — боровский радиус @,5• 10~8 см). Сле-
довательно, матричный элемент приближенно равен 1О~5рЯо, и
им можно пренебречь. Именно по этой причине член первого по-
рядка обычно опускают.
Итак, «естественная» качибровка упрощает вычисление ма-
тричных элементов типа A0.104). Когда имеется несколько си-
ловых центров, ни одну из калибровок нельзя считать естествен-
ной; удобно было бы воспользоваться смесью калибровок — од-
ной калибровкой вблизи одного ядра и другой — вблизи другого
ядра. Такой прием оказывается действительно возможным, если
можно пренебречь некоторыми интегралами перекрытия. Мы
сформулируем теорему, затем приведем ее доказательство, после
чего покажем, как использовать эту теорему при решении про-
блемы многих силовых центров способом нескольких «естествен-
ных» калибровок.
Рассмотрим систему, состоящую из двух атомов. Основное
состояние представляет собой линейную комбинацию вида
|O) = «o+fo, A0.109)
где «о — линейная комбинация атомных орбит первого атома, а
1>о — линейная комбинация орбит второго атома. Возбужденные
состояния \п) также представляют собой линейные комбинации
вида
\n) = un + vn. A0.109а)
Пренебрежем всеми вкладами в матричные элементы, содержа-
щими произведения и и v. Такое приближение часто оказывается
достаточно хорошим, но в некоторых случаях может привести
к ошибкам.
Тогда мы можем сформулировать нашу теорему следующим
образом: сдвиг g-фактора, обусловленный совместным влиянием
спин-орбитального взаимодействия и орбиталнього эффекта Зее-
мана, определяется выражением
(а |S| а') • {(«о IE X А'| «о) + (fol Е X А"|
(О|ЕХр|и)((««1А'-р + Р-А'|ио)+ v
_\ V' + (Рп I А" • р + р • А" | р0)] + компл. сопр. I
" (ЮЛЮ)
Электронный спиновый резонанс 369
где А' и А"— любые векторные потенциалы, которые дают поле
Но (они отличаются друг от друга, самое большее, калибровоч-
ным преобразованием) и где
(и„| А' • р + р • А' |ыо)— \ ип(А' • р + р • АО ею Л. (ЮЛИ)
Преимущество выражения A0.110) состоит в том, что век-
торный потенциал А', используемый для вычисления интегралов
с и, можно выбирать независимо от векторного потенциала А",
используемого в интегралах с v. [Матричные элементы типа
@|ЕХр|") рассматриваются ниже.]
В частности, как мы увидим, если Ri и R2—координаты двух
ядер, то легко вычислить матричные элементы, выбирая
A0.112)
Доказательство теоремы A0.110) начнем с выражения
A0.102). Запишем матричные элементы, включающие А, с по-
мощью и и v и пренебрежем членами перекрытия. Например,
@ |Е X А| 0) = («ol Е X А| ыо) + (fo IE X А | v0). A0.113)
Введем теперь два векторных потенциала А' и А", отличающихся
преобразованием калибровки
А' = А" + Щ, A0.114)
которое определяется функцией q>. [Тот факт, что A0.114) есть
просто преобразование калибровки, следует, конечно, из равен-
ства V X А' = V X А".] Подставим А' вместо А в интегралы, со-
держащие и, и А" + Уф вместо А в интегралы, содержащие о.
Тогда получим
+ р|о) +
+ (оп I Р • А" + А" • р 1 ор)] + компл. сопр. ,
_1_
2/и
' @1Е X РI я) (Рп I Р • Уф + Уф • РI До) + компл. сощЛ /до
Для доказательства теоремы A0.110) нужно показать, что
члены, содержащие q>, в сумме равны нулю. Поскольку мы пре-
небрегаем перекрытием, теорема будет доказана, если удастся
Показать, что величина @а]<3^дйAр) |foa'), определенная ниже,
370 Глава 10
обращается в нуль:
сопр.
"^ 2т Lt Ео-Е„
A0.116)
Интеграл /, определяемый выражением
можно преобразовать к виду
7 = Т $ (WV8*» - *tfV4) Л, A0.118)
интегрируя по частям и учитывая, что волновые функции дей-
ствительны. Для преобразования первого члена в правой части
можно использовать уравнение
(VEJ1b, A0.119)
где V—потенциал, действующий на электрон. Для второго чле-
на, пренебрегая перекрытием, можно написать
т. A0.120)
Используя A0.119) и A0.120) и снова пренебрегая перекры-
тием, найдем
(л |р • Vq> + Уф- p|fo) = 7'lF (?°-?«) \ ^VodT. A0.121)
Подставляя это выражение в A0.116), получаем
(Оог I ^дв (ф) I»ооО = -^г (а IS I °0 [@ IE X УФ | оо) -
] A0.122)
Штрих у знака суммы можно опустить, так как диагональные
матричные элементы спин-орбитального взаимодействия обра-
щаются в нуль. Тогда имеем
@а |^Д8(фI foa0 = -^|r(a| S| оО ¦ [@ |ЕХУФ-2
T, (Ю.123)
где (EX У) означает, что ЕХ У действует на все функции спра-.
ва, в данном случае — на <р и v$.
Электронный спиновый резонанс 371
Пользуясь уравнением V X Е == 0 и заменяя интеграл
\ V X (Еф1^) dr интегралом по поверхности, можно показать,
что A0.123) обращается в нуль. Мы не приводим детали вычис-
лений, так как они совершенно стандартны. Таким образом,
наша теорема доказана.
Еще ничего не было сказано о спин-орбитальных матричных
элементах для возбужденных состояний. Пользуясь тем, что
электрическое поле Е велико только вблизи ядер, перекрытием
всегда можно пренебречь при вычислении спин-орбитальных ма-
тричных элементов. Таким образом,
Xp|fn). A0.124)
Чтобы показать всю важность соотношения A0.124) и про-
иллюстрировать теорему A0.110) на конкретном примере, вер-
немся к частной задаче молекулярного комплекса, у которого
заполнена только одна орбита У^-центра. В этом случае основ-
ное состояние определяется выражением A0.94), т. е. Фо —
= (l/V2) Bi — 2г). Рассмотрим возбужденные состояния вида
(/V) ± х2). Используя A0.124), имеем
(Ю.125)
Поскольку атомы идентичны, а поле Е велико только вблизи
ядра, находим
(z,!EXp!*i) = (z2|EXpl*2). A0.126)
Следовательно, если выбрать верхний знак в A0.125), то члены
в квадратной скобке сокращаются и @|ЕХр|я) обращается
в нуль. С другой стороны, при нижнем знаке члены в квадратной
скобке складываются, давая удвоенное значение. Таким обра-
зом, состояние (xi -\- х^1л/2 ъ& вносит вклада в сдвиг ^-фактора,
а состояние (xi—xj/'ffi вносит. То_же самое относится к со-
стояниям (#i + №>)/л/2~ и (#i — #2)/V2. Состояния, дающие вклад
в сдвиг g-фактора, показаны на рис. 10.13 стрелкой.
Для свободного атома спин-орбитальные матричные элемен-
ты можно было бы выразить через константу спин-орбитального
взаимодействия свободного атома К согласно соотношению
A0.127)
где k и I означают состояния свободного атома; при этом каж-
дому состоянию соответствует свое значение К. В данном случае
372 Глава 10
л'ь у\ и г представляют собой р-состояния свободного атома.
Следовательно, мы можем написать
^ , A0.128)
где ftLi — момент количества движения относительно ядра пер-
вого атома, а к — константа спин-орбитального взаимодействия
в случае (пр) -конфигурации внешних электронов. Вычисление
матричного элемента (jzti J Li J Jtx) выполняется так же, как в § 2
с помощью A0.17) и A0.18),
———— г{ + г2 ((Гц)
"" У\ — У») Рис. 10.13. Стрелкой показаны состояния, кото-
рые примешиваются к основному состоянию
¦ » 2t — 22 благодаря наличию спин-орбитальиого
_ «1 т л2 i , . взаимодействия.
/л + г/2 J
— г, — г2 (ag)
Перейдем теперь к вычислению матричного элемента
(ы„|А'-р + р-А'|у0) в выражении A0.110). Имеем un=^xJ^\/2
или WV2, а «о = Z\lV2- Используя выражение A0.104) и учи-
тывая тот факт, что и — действительные функции, находим
(««I А, • р + Р • Ai I«o) == йН0 ^
*z,) или ^a-.^IL.Iz,). A0.129)
Но благодаря симметрии атомов
(«« IA, • Р + р • A, l«o) = (fJ А2 • р + р ¦ А2|и0); A0.130)
поэтому, пренебрегая членами первого порядка в выражении
A0.110), получаем
A0.131)
Это выражение эквивалентно тому, что к гамильтониану добав-
ляется член вида
A0.132)
Электронный спиновый резонанс
373
Вычисляя матричные элементы, получаем aqq> = 0, если q ф q',vi
Я
пуу .
A0.133)
Интересно остановиться на вопросе о том, почему состояния
(*i + *2)/V2 и (</i + №)/V2 не вносят вклада в сдвиг g-фак-
тора. Мы замечаем, что не только спин-орбитальные матричные
элементы этих состояний равны нулю, но, кроме того, сокра-
щаются и орбитальные зеемановские члены. Примесь этих воз-
бужденных состояний соответствует появлению тока в основном
состоянии, как это показано на рис. 10.14.
Рис. 10.14. Ток, возникающий благода-
ря некоторой примеси состояния
(xi + *2)/V2 к основному состоянию
(г, - г2)/У2Г
Согласно выражению A0.96), калибровочно-инвариантное
спин-орбитальное взаимодействие представляет собой взаимо-
действие между спином и калибровочно-инвариантной плот-
ностью тока j(r). Если токи в двух атомах текут в противопо-
ложных направлениях, как показано на рис. 10.14, то спин-ор-
битальное взаимодействие обращается в нуль. Это и означает,
что спин-орбитальные матричные элементы равны нулю. Обра-
щение в нуль орбитальных зеемановских членов следует из того,
что внешнее поле не может индуцировать в двух атомах токи, те-
кущие в противоположных направлениях. Поле индуцирует токи,
направленные так, как это показано на рис. 10.15.
Таким образом, метод решения задачи для нескольких сило-
вых центров состоит в разбиении интегралов, соответствующих
матричным элементам, на члены, которые имеют заметную вели-
чину только вблизи отдельных ядер. Тем самым задача для не-
скольких силовых центров сводится к нескольким задачам дня
одного силового центра.
Вторая проблема, возникающая при анализе У*-центров, за-
ключается в том, как вычислять сдвиг ^-фактора, если в данной
системе имеется несколько электронов. В отсутствие спин-орби-
тального взаимодействия спин и орбитальное движение элек-
тронов не связаны друг с другом, поэтому многоэлектронное со-
стояние можно охарактеризовать квантовым числом 5 полного
374
Глава 10
спина и собственными значениями М какой-либо его компонен-
ты. Кроме того, энергия будет зависеть также от других кванто-
вых чисел, для которых введем общее обозначение п. Таким об-
разом, основное состояние мы обозначим \oSM), а возбужден-
ные состояния \nS'M'). Как и выше, в данном случае имеется
спин-орбитальное взаимодействие Ж&о и орбитальная зееманов-
екая энергия Жог, для которых применимы те же выражения,
Рис. 10.15. Ток в молекулярном комплексе, индуцированный внешним маг-
нитным полем Но-
а—без учета перекрытия (ток через границу между атомами отсутствует), б—с учетом
перекрытия.
что и в случае одного электрона, но для переменных нужно вве-
сти индекс / и просуммировать по нему, поскольку имеется N
электронов. Следовательно, получаем
A0.134)
==Z 2j <™OZt
1
где
A0.135)
Здесь пренебрегается квадратичной по векторному потенциалу
частью орбитальной зеемановской энергии, поскольку интерес
представляют члены, линейные по Но.
Спин-орбитальное взаимодействие удобно разделить на две
части, одна из которых включает векторный потенциал А, а дру-
гая — нет, а именно
A0.136)
Электронный спиновый резонанс 375
Таким образом, cfesoo представляет собой спин-орбитальное вза-
имодействие в нулевом внешнем поле. Следовательно, считая
орбитальное движение замороженным, имеем
0,
ЛП 1471
(oSM | Ж800 \qSAV) = 0. К '
Тогда совместный эффект спин-орбитального взаимодействия и
орбитальной зеемановской энергии эквивалентен добавлению
к гамильтониану члена «З^дг, матричные элементы которого
имеют вид
{oSM | Жав | oSM') = {oSM | Ж&0А | oSMr) +
1 nS'M") inS'M" I »ог I °SM')
nS'M"
, («^| ™oz \nS'M") {nS'M» | ^SOQ ]OSM')
-\ Er — E ' U
Здесь оставлены только те члены, которые вносят вклад в сдвиг
g-фактора, а в знаменателе пренебрегается энергией спина по
сравнению с орбитальной энергией.
В случае Vft-центра волновую функцию |п5М) можно взять
в виде антисимметризованного произведения одноэлектронных
молекулярных орбит. Последующие вычисления аналогичны тем,
которые проведены при рассмотрении косвенного спин-спинового
взаимодействия ядер в гл. 4, § 8. Обозначим состояние
(zj — z2)/V2, заполненное электроном с индексом 1 и спином,
направленным вверх (т = +1/2), через
иг1-г„ + A). A0.139)
Поскольку полный спин Vft-центра равен 1/2, состояние \oSM) =
= |о'/2 xh) можно представить в виде
X и,.-*, - B) иХ1+Хл + C) ... uZl+Zu + A1). A0.140)
Таким образом, все орбиты, за исключением uZl+Zu -, запол-
нены электронами.
Удобно ввести обозначения / для орбитального состояния, на-
пример fa — z2)/V 2, и а для спинового квантового числа (так
как m уже использовано для обозначения массы электрона).
В этих обозначениях индивидуальные электронные орбиты за-
писываются в виде |/о). Как это следует из гл. 4, § 8, все ма-
тричные элементы в A0.138) образуются одноэлектронными опе-
раторами, поэтому матричный элемент (oSM\Жso\\oSM') мо-
376 Глава 10
жно выразить с помощью одноэлектронного оператора З^Иоа сле-
дующим образом:
(oSM\ZeSOA\oSM')= Z (M^soAlto'). A0.141)
la. la1
где la пробегает все значения, соответствующие заполнению со-
стояния \oSM), a la'— все значения, соответствующие заполне-
нию \oSM'). Мы не включаем матричные элементы вида
(Ia\2f6soh\l'or), где V ф I, так как эти состояния отвечают дру-
гому заполнению молекулярных орбит. Таким образом, мы не
принимаем во внимание орбитальное вырождение основного со-
стояния.
Аналогичным образом можно выразить члены второго по-
рядка. Суммирование по электронам можно свести к суммиро-
ванию по орбитам, заполненным в основном состоянии, а сумми-
рование по п — к суммированию по орбитам, не заполненным в
основном состоянии. Таким образом, получаем
{oSM \Ж^\oSM') = ? (la 1 Я$оа\la') +
¦+¦
/о в \oSM)
lo' в \oSM')
L е.-е..
ограничение А
ограничение В
Здесь под ограничением А понимается следующее:
орбита
орбита
орбита
la) заполнена в состоянии \oSM),
la') заполнена в состоянии \oSM'
1'а) не заполнена ни в состоянии \oSM),
ни в состоянии | oSM');
а под ограничением В:
орбита |/<г) заполнена в состоянии \oSM),
орбита
орбита
la') заполнена в состоянии \oSM'),
1'а') не заполнена ни в состоянии \oSM),
ни в состоянии \oSM').
Член второго порядка можно выразить с помощью A0.142)
для любой системы, волновую функцию которой можно пред-
ставить в виде произведения волновых функций отдельных элек-
тронов.
Удобно было бы, конечно, применить теорему A0.110), чтобы
использовать «естественную» калибровку. Это легко сделать,
если учесть следующие два обстоятельства. Во-первых, так как
Электронный спиновый резонанс 377
»z не зависит от спина, то
\fa). (Ю.143)
Используя это, можно заметить второе обстоятельство, заклю-
чающееся в следующем. Если в ограничении А отбросить усло-
вие, что орбита \1'а) не заполнена ни в состоянии \oSM), ни в
состоянии \oSM'), а в ограничении В — условие, что орбита
1'а') не заполнена ни в состоянии \oSM), ни в состоянии
oSM'), то получаемые при этом дополнительные члены попарно
сократятся. Следовательно, можно написать
(oSM | Жь& | oSM') = ? (to | Ж%к | la) +
ii
la l l
f A0.144)
Здесь требуется только, чтобы орбита |/<г) была заполнена в
состоянии |oSM), а орбита \1а') —в состоянии \oSM').
Рассмотрим теперь все члены с фиксированными la и /</:
la
la'
v(la\ П%_ | I'a) (fa \ 3^00 \ la') + (to \ Л%0 \ fa') (fa' | 3»ffz \ lor
V ' ' A0.145)
Это выражение совпадает по форме с выражением A0.102). По-
этому его можно свести к выражению, включающему смешан-
ную калибровку. Имея это в виду, определим
(to | VW | lo') = -ggr (а | S, | af) • [(m | E, X К I aj) + (oj IE, X Af | vi)]
и
(la \№\ /V) = -?^(a |S, a'). [(tt/1 A{ • pi + Pl • A{ \ur) +
АГ.р, + р,.АГ|0г)]. (Ю.146)
С помощью этих определений мы можем переписать выражение
A0.145) в виде
(to | UlX) | fa) (fa 13V%0 j to') + (la 13$g00 \ fa') (fa' | t/m | la )
l/ ' '' A0.147)
378 Глава 10
Таким образом, найдем
(oSM | M^ | oSM') =l^{lo\ F<:> | la') +
la
la'
(la| UA) |i'a)(I'a\M%0 \ la') + (la\96%O | /V) (fa 11/A) | la')
A0.148)
la ' '
Здесь /а включает все значения, отвечающие заполненным орби-
там в состоянии \oSM), а 1а' — все значения, отвечающие запол-
ненным орбитам в состоянии \oSM'). Как отмечалось выше, до-
пущение для 1'о и 1'а' значений, соответствующих заполненным
состояниям |о5М) или \oSM'), приводит к тому, что появляются
дополнительные члены, которые попарно сокращаются. Поэтому
на практике проще восстановить ограничения А и В, чтобы в
суммах не возникали лишние члены.
С помощью теоремы Вигнера — Эккарта можно показать, что
все матричные элементы (oSM\3@&g\oSM'), определяемые вы-
ражением A0.148), можно получить из гамильтониана, который
имеет вид
ОЮ ig = *ьр 2-i tiqdqq'Ciq'. (Ш.14У)
q, q'-x. у. z
Здесь все компоненты Sqr означают величины
Sx=}ZSx. и т. д. A0.150)
г-i '
Однако в случае 1/&-центра проще вычислить выражение
A0.148), чем использовать теорему Вигнера — Эккарта. Из со-
ображений симметрии следует, что главными осями g-тензора
являются оси х, у, z молекулы, причем ось г направлена вдоль
связи. Предположим теперь, что постоянное поле направлено
вдоль оси х; тогда М будет собственным значением Sx. Посколь-
ку это главная ось, отличны от нуля только те матричные эле-
менты, для которых М — М'. Это нетрудно проверить путем не-
посредственного вычисления A0.148). Конечно, S равно '/2. Вы-
числим выражение A0.148) при М = М = 1/2. Проще всего
рассматривать эти матричные элементы с помощью диаграммы
состояний. Так как вычисляется диагональный член
(oSM\3%Ag\oSMf), состояния \1а) и \1&) в A0.148) совпадают
(электрон должен вернуться в исходное состояние, виртуально
побывав в возбужденном состоянии). Полагая о' = а и прене-
Электронный спиновый резонанс
379
брегая членами, содержащими (la \ Vw \ la), имеем
(to\uil)\l'o)(l'o\M{!P001 la) + компл. сопр.
I la) заполнено
I I'o) не заполнено
A0.151)
Здесь суммирование ведется по заполненным орбитам \1а) и
незаполненным орбитам \1'о) в основном состоянии. В случае
¦н
¦н-
-к-
¦н-
¦н
¦н-
Vt-Уг
Vi + Уг
Рис 10.16. Основное состояние
Мы предполагаем, что кристаллическое
поле расщепляет состояния xt ± х3 и р, ± г/;.
Сплошными стрелками указаны заполнен-
ные орбиты, пунктирной стрелкой—неза-
полненная.
X, -X,
Рнс. 10.17. Образование возбужден-
ного состояния.
Двойная стрелка соединяет состояния, свя-
занны* матричными элементами A0.120) для
поля, направленного вдоль оси х. Стрелки
указывают направление квантования спнна:
стрелка ^ обозначает спин, параллельный
постоянному полю, а стрелка ¦if —спнн,
аитипараллельиый полю. Пунктирная стрел-
ка указывает незаполненную в основном
состоянии орбиту.
S = Уг, М = '/2 суммирование по состояниям | I'o) и 11о) мож-
но провести с помощью диаграммы, на которой сплошными
стрелками указаны состояния, заполненные электронами, при-
чем стрелка, направленная вверх, соответствует а = + А,
стрелка, направленная вниз, о = —1/2, а пунктирными стрел-
ками указаны незаполненные состояния. Диаграмма основного
состояния показана на рис. 10.16.
Возбужденные состояния возникают при переходе электрона
с заполненной орбиты на вакантную. В случае когда поле на-
правлено по оси х, орбитальный зеемановский член связывает
только состояния у\ + Уг и Z\ + z2, в чем можно убедиться, рас-
суждая так же, как при выводе формул A0.133). Состояния, даю-
щие вклад в сдвиг g-фактора, показаны на рис. 10.17.
Следуя рассуждениям, относящимся к соотношениям
A0.124) и A0.129), можно вычислить матричные элементы. Мы
380
Глава 10
получим
A0.152)
где Msoox — одноэлектронное спин-орбитальное взаимодействие,
относящееся к лс-компоненте спина, которое определяется выра-
жением
Z\ —^
A0.153)
где dx означает интегрирование по электронным пространствен-
ным координатам.
Выражение A0.153) включает только одноатомные функции
и поэтому соответствует аналогичному матричному элементу
для свободного атома. В свободном атоме, пренебрегая взаимо-
действием спина одного электрона с орбитой другого, спин-орби-
тальную связь N электронов можно представить в виде
S&so-IJSiL'-S1. A0.154)
Для эквивалентных электронов все коэффициенты & равны.
Если в свободном атоме имеется рассел-саундерсовская связь, то
квантовые числа полного момента количества движения L и пол-
ного спина S являются хорошими квантовыми числами, а ма-
тричные элементы при фиксированных L и S выражаются с по-
мощью эффективного взаимодействия вида
^SO = XL-S. A0.155)
Если Л' = 1, то, очевидно, К = ?. Если N соответствует атомной
оболочке, в которой не хватает только одного электрона, то
X = — ?. Отсюда следует, что для дырки значение К отрицатель-
ное, поскольку ? всегда положительная величина.
Значения ? для свободного атома удобно использовать при
вычислении A0.153), так как это сразу дает
—г)- A0л56)
Используя этот способ, находим
<10Л57>
Электронный спиновый резонанс
381
Поскольку спиновая зеемановская энергия [о-^-^ fe °тт)
равна
У 1 1 114 /Л ,и I 1 Ч
A0.158)
что совпадает с выражением для одного неспаренного спина, по-
лучаем
A0.159)
где % — константа спин-орбитального взаимодействия для сво-
бодного атома хлора. Заметим, что gxx > 2.
Поступая точно так же, находим
If
41-
z. + zz
x, -хг
Уг + ta
A0.160)
Интересно отметить, что вычисленный нами сдвиг g-фактора
положителен, а не отрицателен (как это имеет место для од-
ного электрона) вследствие появления в A0.157) матричного
элемента (— 7г | S*' I — 7г)- Его по-
явление объясняется тем, что один
из спаренных спинов переходит в
состояние, в котором вначале нахо-
дится неспаренный спин. При этом,
очевидно, возбужденный спин на-
правлен противоположно М.
В отличие от рассмотренного при-
мера в случае, показанном на
рис. 10.18, имеется только пять элек-
тронов, заполняющих те же состоя-
ния. Примем, что для состояний
f/i+f/2 и jci+jc2, а также для Состоя-
ний у\—{/2 и х\ — Xi снято вырож-
дение, как показано на рис. 10.18.
Поле в направлении х свяжет со-
стояния |i/i4-«/2, 'А) и \zi+z2, '/2).
что приведет к^<2 («электронный» сдвиг). С другой стороны,
поле в направлении г свяжет почти-вырожденные состояния
\у\+Уг, -~1/г) и |jci + *2, — У2); в этом случае g>2 («ды-
рочный» сдвиг). Благодаря тому что эти состояния расположены
очень близко друг к другу, | Д#гг|»| Agxx\, a gyy, конечно, равно
2, так как соответствующие матричные элементы обращаются
в нуль.
В данном случае 12 состояний заполнены менее чем напо-
ловину, однако преобладает «дырочный» сдвиг g-фактора. Сле-
довательно, необходимо соблюдать крайнюю осторожность, на->
Рис. 10.18. Заполнение орбит
Vt-центра, когда на них раз-
мещено только пять электрс
нов.
382 Глава 10
зывая центры «электронными» или «дырочными» на основании
одних только данных по сдвигу ^-фактора.
Необходимо отметить, что для вычисления матричных эле-
ментов мы выбрали очень простые функции без перекрытия ме-
жду атомами. В общем случае нужно учитывать поправки, об-
условленные перекрытием, а также тем, что функции х\, у\, z\
и т. д. могут быть линейными комбинациями атомных орбит, как
это было при рассмотрении сверхтонкого взаимодействия. Од-
нако эти поправки не меняют основных выводов, хотя их учет
чрезвычайно усложняет вычисления.
ЛИТЕРАТУРА
1. Castner Т. G., Kanzig W., Journ. Phys. Chem. Solids, 3, 178 A957).
2. Delbecq С I., Smaller В., Yuster P. H., Phys. Rev., Ill, 1235 A958).
Глава 11
Заключение
Мы рассмотрели целый ряд специфических эффектов, таких,
как уширение линий, химический сдвиг, найтовский сдвиг и
сверхтонкое расщепление. Некоторые из них можно было рас-
сматривать в первом порядке теории возмущений, для других по-
требовалось провести вычисления до более высоких порядков.
Поскольку эти явления рассматривались по отдельности, полезно
теперь написать единый гамильтониан, включающий все рас-
смотренные эффекты. Такой гамильтониан поможет более ясно
представить себе значение каждого члена взаимодействия.
Написанный ниже гамильтониан описывает взаимодействие
ядра с электроном в присутствии внешнего магнитного поля Но.
Векторный потенциал Ао соответствует полю Но, а векторный
потенциал А„ связан с действующим на электрон полем, кото-
рое создает ядерный момент (обычно Ап = ц X г/г3). Величина
л определяется выражением
В этих обозначениях гамильтониан имеет вид
Кинетическая Потенциальная Потенциальная
энергия энергия электрона энергия электрона,
электрона в поле ядра и обусловленная внеш.
других электронов ними по отношению
к атому зарядами
Спни-орбнтальное взаимодействие Зеемановская
электрона энергия элек-
тронного спина
Связь орбитального движения Взаимодействие ядерного
электрона с Нц момента с орбитальным
движением электрона
384 Глава 11
Взаимодействие ядерного момента Взаимодействие ядерного
со спиновым моментом электрона магнитного момента со
в состоиниях, отличных от спиновым моментом элек-
s-состояння трона в s-состояиии
Связь ядерного квадру- Зеемановская
польиого момента с гра- энергия ядра
диеитом поля, обусло-
вленного зарядом
электрона н внешними
зарядами
Сюда можно добавить взаимодействие ядер между собой и маг-
нитное взаимодействие электронов друг с другом.
Задачи
К главе 2
1. Рассмотрите зависящий от времени эрмитов оператор F
(например, оператор F =— yhIxHxcos(ot, характеризующий
энергию взаимодействия спина с переменным магнитным полем,
направленным вдоль оси х). Докажите, что
dF / г^, Г1 ! dF
где dF/dt — обычная производная от F(t) по времени.
2. Выражение B.22а) определяет величину <ц*(<)> для час-
тиц со спином '/г- Обобщите это выражение на случай частиц
со спином /.
3. Магнит создает неоднородное постоянное магнитное поле.
Доля спинов df, на которые действует магнитное поле в интер-
вале от Н до Н 4- AН, равна
df = p(H)dH,
где
\p(H)dH=l.
Неоднородность магнитного поля мала и проявляется только в
изменении его величины, а не направления в различных точках
образца.
Вычислите зависимость от времени компоненты намагничен-
ности вдоль оси х, перпендикулярной направлению постоянного
поля, для случая, когда полная намагниченность Мо при t = О
направлена вдоль оси х, а функция р{Н) имеет следующий вид:
а) постоянна в области Я0-о<//<йо+ои равна нулю
вне этой области,
б) p{H)~e-w-H°>''a\
в)
4. Ядро имеет спин '/г. квантованный в направлении посто-
янного поля Но, параллельного оси г. При ? = 0 оно находится
13 За к. 727
386 Задачи
в состоянии т = + 'Л- В этот момент времени включается вра-
щающееся магнитное поле амплитуды #i на время tw, в течение
которого намагниченность поворачивается на 90° (90-градусиый
импульс).
а) Вычислите зависимость от времени волновой функции
спина во вращающейся системе координат в течение времени
действия импульса и после него.
б) Вычислите волновую функцию спина в лабораторной си-
стеме координат в течение времени действия импульса и после
него.
в) Вычислите <ц*@> в течение времени действия импульса
и после него.
5. Соленоид единичной длины с поперечным сечением А, со-
стоящий из п витков, расположен так, что его ось направлена
вдоль оси х. Постоянное поле Но направлено вдоль оси г.
а) Считая, что ядерные магнитные моменты находятся в со-
стоянии теплового равновесия, выразите магнитный момент еди-
ницы объема Мо через Но и статическую магнитную восприимчи-
ность %0-
б) Найдите численное значение %0 для протонов воды при
комнатной температуре по формуле
__ N-fhH (I + 1)
Я° ~ ЪкТ
где N — полное число спинов в единице объема. (Величину у
для протонов можно найти, зная, что резонансная частота про-
тонов в поле #о = Ю* Гс равна 42 МГц.)
в) Выведите формулы для амплитуды Vo переменного напря-
жения, возникающего в соленоиде из-за прецессии вектора Мо
после 90-градусного импульса.
г) Вычислите Vo для протонов, полагая, что длина соленоида,
состоящего из 10 витков, равна 2 см, диаметр равен 1 см, а поле
Яо равно 6000 Гс.
6. Считая, что индуктивность и сопротивление катушки в
предыдущей задаче равны Lo и Ro соответственно и эта катушка
соединена последовательно с конденсатором С,
а) выведите выражение, определяющее напряжение на кон-
денсаторе через напряжение Vo предыдущей задачи, 10, Ro, С
Q(L/)
(/)
б) используя численные данные задачи 5, г и полагая
Q— 100, вычислите напряжение на конденсаторе С.
7. Из равенства B.124) имеем
Xo =
Задачи 387
Покажите, что максимальное значение эСмакс Аля линии погло-
щения равно
у" = il?n_f!!°.
Амакс 2 м До '
где Дсо— надлежащим образом определенная ширина линии.
Полагая, что ширина резонансной линии протонов воды рав-
на 0,1 Гс (эта ширина обусловлена неоднородностью поля магни-
та), а поле Но = 104 Гс, вычислите ЭСмакс для воды и максималь-
ное относительное изменение сопротивления катушки с Q — 100.
8. Реакция образца из некоторого вещества на действие
включающегося в момент времени / = 0 скачкообразно изменяю-
щегося магнитного поля единичной высоты характеризуется
функцией
М(О
а) Вычислите у/ (со) их"(й).
б) Покажите, что %' и %" удовлетворяют соотношениям Кра-
мерса — Кронига.
9. В приложении Е получено выражение для комплексной на-
магниченности Мх + iMy:
а) Покажите, что в пределе очень медленных перескоков
(тбсо ^> 1) спектр поглощения состоит из двух отдельных резо-
нансных линий на частотах
тт , &0
со = у И о ± — •
б) Покажите, что в пределе очень быстрых перескоков
(тбсо <^С 1) наблюдается одиночная линия поглощения на ча-
стоте
со = у#о.
10. В приложении Е уравнения Блоха применялись для ана-
лиза ситуации, когда группа ядер в среднем одинаковое время
находится в каждом пз двух положений, в которых резонансные
частоты различны.
Это равенство временных интервалов проявляется в утверж-
дении, что две величины С\ и Сг, входящие в уравнения (Е.13),
равны, а последний член, включающий Ни содержит М0/2. На-
пишите уравнения для случая, когда ядро может перескакивать
между двумя положениями, заселенными в среднем неодина-
ково. Например, энергия ядра в положении «а» выше энергии
в положении «й», поэтому термически равновесные населенности
различны,
388 Задачи
а) Какое должно быть соотношение между постоянными С\
и С2, если Ма и Мь термически равновесные статические намаг-
ниченности?
б) Установите соответствующую этому случаю форму урав-
нений (Е. 13) и выведите выражение для результирующей на-
магниченности Мх -f- iMy.
11. Постоянное магнитное поле Н(г) можно записать в виде
где ф — магнитный потенциал, который в свободном пространстве
удовлетворяет уравнению
Пусть магнитное поле лабораторного магнита имеет аксиальную
симметрию вокруг оси z. Покажите, что наинизший порядок не-
однородности поля можно выразить формулой
И И —,дН
где Но — напряженность поля Н в начале координат и производ-
ная (дН/дг) определяется в начале координат.
12. Используя условие задачи 11, покажите, что наиболее об-
щей формой записи поля Н{х, у, г), основанной на включении
в магнитный потенциал сферических гармоник порядка не выше
1 = 2, является формула
13. Используя выражение для Н(х, у, г), полученное в пре-
дыдущей задаче, и методы, развитые в приложении Ж, выведите
более общее выражение по сравнению с B.98), описывающее
влияние диффузии на затухание сигнала эха.
14. В приложении Е уравнения Блоха применяются для опи-
сания движения спина, который может прецессировать с каждой
из двух естественных частот в зависимости от того, в каком по-
ложении он находится: в «а» или «й».
а) Пусть Т2 = оо, Н\ = О (свободная прецессия) Сх~ С2 =
= 0, намагниченности Ма и Мь при / = 0 направлены вдоль
оси х системы координат, вращающейся с частотой уН0. Нари-
суйте Ма и Mb в плоскости ху в момент времени, когда Ма обра-
зует с осью х угол 6.
б) Нарисуйте векторы ЬМа — С\МЬЫ и ЬМЬ — —С\МЬЫ, ко-
торые появляются, если теперь константа С\ не равна нулю.
в) Нарисуйте новые векторы М'а и М'ь с учетом добавок
М'а = М* + ЪМа и М'ь^Мь
Задачи 389
К главе 3
1. Два одинаковых спина 1\ = /г ='Д связаны магнитным
диполь-дипольным взаимодействием. Внешнее постоянное маг-
нитное поле равно нулю. Покажите, что собственные волновые
функции этой системы являются синглетными и триплетными
волновыми функциями, и найдите уровни энергии различных со-
стояний.
2. Рассмотрите два спина задачи 1 в постоянном магнитном
поле #о, параллельном вектору, соединяющему спины.
а) Найдите волновые функции и уровни энергии в зависимо-
сти от поля Но.
б) Рассмотрите задачу в присутствии переменного магнит-
ного поля, направленного перпендикулярно вектору, соединяю-
щему ядра. Найдите частоты и относительные интенсивности
разрешенных переходов в случаях, когда магнитное поле #о
много больше или много меньше поля, создаваемого одним из
магнитных моментов в точке, где находится другой.
3. В равенство C.43) входит величина Sp ([^,ц~] ц+). По-
кажите, что она равна нулю.
4. Рассмотрите два одинаковых ядра, спины которых равны
'/г- Вычислите двумя различными способами Sp/«, где lz —
полная г-компонента момента количества движения h ^
e hz -\- !&'¦
а) определяя диагональные матричные элементы в представ-
лении, в котором диагональны операторы 1\г и hz\
б) определяя диагональные матричные элементы в представ-
лении, в котором диагональны операторы /2 и 1г.
Покажите, что вычисления в обоих случаях приводят к оди-
наковому результату.
5. Рассмотрите ядро со спином /. Вычислите Sp(/z/x) и
sP (/?*).
6. Рассмотрите систему TV невзаимодействующих спинов /,
гиромагнитное отношение каждого из которых равно у. Полную
волновую функцию такой системы можно выбрать в виде произ-
ведения волновых функций отдельных спинов, а полную энергию
системы — в виде суммы собственных энергий отдельных спинов.
При помощи равенства B.144) вычислите величину эс"(со), опре-
деляющую поглощение. Для упрощения вычислений примите
Z=B/+l)w и e~B<JkT =\, что соответствует высокотемпера-
турному приближению.
7. Электростатическое обменное взаимодействие между дву-
мя электронами можно учесть, добавляя в гамильтониан член
ASrS2.
390 Задачи
а) Докажите, что этот член коммутирует с зеемановской
энергией.
б) Покажите, что при добавлении такого члена к диполь-ди-
польному взаимодействию величина второго момента не изме-
няется.
8. Покажите, что для трех операторов А, В и С
Sp (ABC) = Sp (CAB) = Sp (ВС А).
9. Рассмотрите ядро со спином ъ/%, гамильтониан которого
Ж 2@ + 2@
имеет вид Ж = 2@z + 2@q, где
Гамильтониан ^6q подобен гамильтониану, характеризующему
ядра, обладающие электрическим квадрупольным моментом.
К ядру приложено переменное магнитное поле, приводящее к
появлению поглощения.
а) Докажите, что Звг и ?Sq коммутируют.
б) Считая, что 36q аналогично взаимодействию Md в гл. 3,
§ 3, покажите, что при А «С уп%Н0
<)
Найдите <Дю2>.
10. Выведите равенство C.61) в случае равномерного враще-
ния пары ядер.
К главе 4
1. В гл. 4, § 4, рассматриваются калибровочные преобразо-
вания.
а) Пользуясь выражением D.18), докажите справедливость
равенства D.19).
б) Докажите, что оператор момента количества движения
rX(iv_iA)
является инвариантным относительно калибровочного преобра-
зования.
в) Рассмотрите ^-состояние "ф(г) == и(/) в отсутствие магнит-
ного поля. Выведите выражение для среднего значения орби-
тального момента количества движения в присутствии магнит-
ного поля, задаваемого векторным потенциалом Ао — 'ДНоХг!
и получите численный ответ в единицах % для основного состоя-
ния водорода в поле Но — 10 000 Гс.
2. Вычислите магнитное поле на ядре атома водорода, обус-
ловленное орбитальным движением электрона в состоянии п=2,
/==1, т = +1 (действием спина электрона пренебрегите).
Задачи 891
3. Рассмотрите расщепление состояний xf(r), yf{r) и zf(r)
кристаллическим полем, потенциал которого равен А(х2 — у2).
Пусть начальное состояние системы в момент t = О характери-
зуется волновой функцией
)=^-±Д/(г).
Вычислите среднее значение г-составляющей момента коли»
чества движения. Убедитесь, что оно осциллирует во времени
между значениями +1 и —1 и с угловой частотой A/ft.
Обратите внимание на то, что полученный результат соответ-
ствует классической картине движения круговой орбиты в кри-
сталлическом поле, которое приводит к периодическому обра-
щению направления кругового движения по этой орбите.
4. Сверхтонкое взаимодействие в s-состоянии легко вычис-
лить в приближении, в котором ядро заменяется равномерно
намагниченной сферой.
Равномерно намагниченную сферу, намагниченность которой
на единицу объема равна М, можно заменить распределением
токов, текущих по поверхности сферы, причем плотность токов
нужно выбрать пропорциональной величине М-п, где п — внеш-
няя нормаль сферы. Заменим ядро такой сферой радиуса R и
рассмотрим токи, текущие по окружностям вокруг оси z. Тогда
плотность поверхностных токов будет равна /@) = /osin8.
Join чертежа.
J за чертезю
Сфера с распределением поверхностных токов
/(G)=/osinG, обладающая равномерной на-
магниченностью М.
а) Покажите, что магнитное поле Н внутри сферы постоянно,
а вне сферы эквивалентно полю диполя.
б) Покажите, что поле внутри сферы равно
392 Задачи
в) Покажите, что магнитный момент jj, сферы равен
Dл/3) R40.
г) Покажите, что
где сферически симметричная функция и (г) достаточно мало
изменяется в пределах расстояния R от центра сферы, а Нг —
г-компонента создаваемого сферой поля.
5. В атоме имеется один валентный электрон в s-состоянии;
спин ядра атома равен /. Время спин-решеточной релаксации
электрона настолько мало, что на ядро действует только усред-
ненное по времени магнитное поле электрона. Выразите резо-
нансную частоту ядра в присутствии постоянного магнитного
поля Но через %е. Рассмотрите зависимость резонансной частоты
от температуры и поля:
а) в случае высоких температур (где kT ^> yehH0)t
б) в случае низких температур (где yehH0 ~ kT).
6. В тексте книги найтовский сдвиг вычисляется в первом по-
рядке теории возмущений при учете изменений населенностей
электронных спиновых состояний под влиянием поля Но.
Можно получить выражение для найтовского сдвига и во вто-
ром порядке теории возмущений, если предположить, что маг-
нитное поле изменяется в пространстве таким образом, что под
его влиянием не происходит изменения населенностей электрон-
ных спиновых состояний.
Предположим, что внешнее магнитное поле направлено вдоль
оси z и изменяется в зависимости от х по закону
Hz =* Но cos qx.
Пусть ядро находится в точке х = 0. Используя второй порядок
теории возмущений, покажите, что возмущение электронных
волновых функций приводит к появлению найтовского сдвига,
величина которого при q «s 0 совпадает с результатом, приве-
денным в тексте.
7. Электронную структуру молекулы водорода можно опи-
сать с помощью модели молекулярных орбит, которые представ-
ляют собой линейные комбинации атомных орбит. Молекуляр-
ная орбита основного состояния молекулы водорода представ-
ляет собой связывающую орбиту, образованную линейной ком-
бинацией ls-орбнт свободного атома водорода. Получите выра-
жение, определяющее косвенное взаимодействие между спинами
протонов, учитывая только возбужденное состояние, соответ-
ствующее разрыхляющей орбите, образованной линейной ком-
бпнацней ls-орбнт свободного атома водорода.
Задачи
К главе 5
1. Пользуясь выражениями E.39) и E.40) убедитесь, что
Wmn = Wnmexp[(Ет — En)$L], где Pz. = l/kTL, a TL— темпера-
тура решетки.
2. Дана система N спинов, связанных друг с другом диполь-
дипольным взаимодействием; на эту систему действует магнит-
ное поле Н в направлении г. Принимая для матрицы плотности
р выражение
е-Э€1кТ
р== z •
соответствующее тепловому равновесию (Z — статистическая
сумма), покажите, что среднее равновесное значение полной на-
магниченности в высокотемпературном приближении равно
Mv2h2I (I A- W
Y<tV "
(Мх) = (Му)^0, (Мг)=
Интересно заметить, что эти выражения имеют форму за-
кона Кюри М = СН/Т, причем константа С не зависит от того,
велико или мало поле Н по сравнению с локальным полем, со-
здаваемым соседними диполями.
3. В металле имеется система ядерных спинов, связанных
между собой только диполь-дипольным взаимодействием. Поль-
зуясь выражением E.49), докажите, что время спин-решеточной
релаксации такой системы в 2 раза меньше времени релаксации
в сильном постоянном поле (Т\ = 1/аоо).
4. Для ядра со спином 3/2 статическая часть гамильтониана
имеет вид Фв§ = —упННо1г. Связь со средой описывается зави-
сящим от времени гамильтонианом
3<М/) = Л @ (/*-/*),
где A (t)— случайная функция времени. Для A(t) принимается
следующая функция корреляции:
а) Запишите Ж\{() с помощью операторов /+ и /-.
б) Вычислите вероятность перехода в единицу времени под
действием Зв\ (t) из состояния m = 3/г в остальные три т-со-
стояния.
5. Даны условия задачи 4. Предполагая, что в любой момент
времени относительные населенности m-состояний можно опи-
сать с помощью спиновой температуры, вычислите время спин-
решеточной релаксации, обусловленное взаимодействием 9e\{t).
394 Задачи
6. В гл. 5, § 8, влияние переменного поля рассматривается
в рамках формализма матрицы плотности.
а) Покажите, что решения E.235) верны при малых V.
б) Найдите решение для <M*(f)> при больших V, описываю-
щее эффект насыщения.
7. Система имеет три уровня энергии: 1, 2 и 3. К системе при-
ложено переменное поле, создающее взаимодействие V{t) —
= V cos at с частотой, близкой к резонансной для перехода меж-
ду уровнями 1 и 2.
а) Напишите дифференциальные уравнения для матрицы
плотности, аналогичные уравнениям E.231) и E.232).
б) Вычислите <Л1*(/)> в случае, далеком от насыщения, и
покажите, что ширина резонансной линии зависит от релакса-
ции на уровень 3. (Это — эффект уширения линии за счет конеч-
ного времени жизни, связанного с переходами на уровень, кото-
рый непосредственно не относится к данной спектральной ли-
нии.)
К главе 6
1. Пользуясь уравнениями F.3) с начальными условиями
Мх = Мо, Му = Мг = 0 при t = 0, покажите, что на интервалах
времени, меньших Ти составляющие намагниченности Му и Мг
будут оставаться малыми, намагниченность М будет направлена
вдоль поля Н\ и будет экспоненциально затухать с постоянной
времени Т2.
2. Покажите, что выражение для средней энергии, приведен-
ное в гл. 6, § 3, т. е.
?¦== 2-1
можно найти как производную статистической суммы Z по
р[р = \/(kT)\, подтверждая, таким образом, выражение F.1),
3. Покажите, что средняя энергия Е системы /V ядер, на ко-
торые действует внешнее поле Но и дипольное взаимодействие
которых описывается гамильтонианом Жг, равна
? = —С
где
г. „2
и С
4. Энтропия а системы определяется выражением
? + *е in z
Задачи 395
Пользуясь этим выражением, покажите, что в высокотемпера-
турном приближении для системы N ядер
б. Пусть гамильтониан системы Ж не зависит от времени.
В этом случае наиболее общим решением уравнения Шредин-
гера является волновая функция
где коэффициенты с„ не зависят от времени, а ип являются соб-
ственными функциями, соответствующими собственным значе-
ниям энергии Е„.
Докажите, что среднее значение энергии такой системы не
зависит от времени, т. е. энергия системы сохраняется.
6. Выведите формулу F.46),
из формул, приведенных в гл. 2, § 11, пользуясь высокотемпера-
турным приближением.
7. В гл. 6, § 4, получены формулы, из которых следуют соот-
ношения
Щ Hi
-оГ = -вГ и Mf = Mt'
справедливые в случае медленного изменения внешнего магнит-
ного поля Hit если оно всегда остается значительно больше ло-
кального.
Покажите, что такой результат можно также получить, рас-
сматривая населенности 2/ -f- 1 зеемановских уровней отдельных
спинов ансамбля из N невзаимодействующих спинов. (Исклю-
чение спин-спинового взаимодействия соответствует предполо-
жению, ЧТО Ядок = 0.)
8. Рассмотрите эксперимент по адиабатическому размагни-
чиванию, подобный описанному в гл. 6, § 6. Покажите, что знак
спиновой температуры во вращающейся системе координат зави-
сит от того, выше или ниже резонансного значение постоянного
поля Но в момент включения РЧ-поля Hi. Нарисуйте расположе-
ние векторов М и НЭфф в плоскости ху для нескольких значений
Нэфф по мере приближения к резонансу в случае отрицательной
спиновой температуры.
396 Задачи
9. Пусть //лок = 3 Гс. Нарисуйте зависимость М/Мо от Ло для
трех случаев:
а) Я, = 1 Гс,
б) Я, = 3 Гс,
в) Я, = 9 Гс.
Считайте, что в каждом случае Hi включается при Ао ^ Но,
К главе 7
1. Покажите, что точное выражение G.31), определяющее
</г> при насыщении запрещенного перехода, эквивалентно сле-
дующему:
2 2 +
2. Покажите, что ядерная поляризация </г>, получаемая по
схеме на рис. 7.7, противоположна по знаку поляризации, полу-
чаемой но схеме на рис. 7.8, если |Л/2|^; yeTiH0.
3. Рассмотрите систему, которую можно использовать в трех-
уровневом мазере. Энергии уровней — Е\, Е2 и Е% (Ех — наивыс-
шая энергия, а Ег — наинизшая энергия, см. рис. 7.10). Пусть
насыщается переход между уровнями 1 н 3.
а) Напишите уравнения, аналогичные G.13), для случая ста-
ционарного решения.
б) Решите уравнения, определив населенности р2 и р$.
в) Какие необходимы соотношения между вероятностями пе-
реходов W12, W23 и расстояниями между энергетическими уров-
нями, чтобы получить инверсию населенностей уровней 2 и 3?
Каковы соответствующие соотношения для получения инверсии
населенностей состояний 1 и 2?
4. Рассмотрите эксперимент по двойному резонансу, в кото-
ром регистрируется сигнал эха спинов /. Спины S{S = x/z) со-
здают в месте нахождения спинов / магнитные поля dzhis. Пусть
сигнал эха спинов / наблюдается с помощью импульсной после-
довательности л/2 — л, а спины S опрокидываются импульсом п.
а) Покажите, что сигнал эха спинов /, М/Bт), изменяется в
зависимости от т как
М, Bт) = Мо cos Byth,sx).
б. В гл. 7, § 11, обсуждался метод двойного резонанса, пред-
ложенный Ханом. Покажите, что оператор Т, определяемый вы-
ражением G.52), преобразует гамильтониан G.51), записанный
в лабораторной системе координат, в гамильтониан G.55), запи-
санный в дважды вращающейся системе координат.
Задачи 897
6. Блох, Ройден, Блум и Шулери предложили метод исклю-
чения мультиплетных структур в ЯМР- Этот метод можно опи-
сать, пользуясь упрощенным гамильтонианом G.45):
Ш = - \,hholz + Л/А — \shHlsSx.
Положите 7=5 = '/г-
а) Найдите энергии уровней при условии А ^ ysfiHis и по-
кажите, что переменное поле с частотой, близкой к резонансной
частоте спинов /, будет индуцировать переходы, соответствую-
щие двум резонансным линиям, отстоящим по частоте друг от
друга на величину A/h.
б) Сделайте то же самое для случая А <С ystiHis и пока-
жите, что две линии сливаются в одну.
7. Рассмотрите диаграмму энергетических уровней на рис. 7.4.
Предположите, что, используя быстрое адиабатическое прохож-
дение на частоте электронного резонанса (Е\ — E^)j% мы обра-
тили населенности уровней 1 и 2 и затем быстро наблюдаем
ядерный резонанс.
а) Покажите, что скорость поглощения энергии на частоте
ядерного резонансного перехода (Ец— Ei)/h увеличится, и вы-
числите отношение этой скорости к ее нормальному значению.
б) Покажите, что на частоте ядерного резонансного перехода
(Е\ — Е3)/Тг будет наблюдаться стимулированная эмиссия, и
вычислите отношение скорости эмиссии энергии к нормальной
скорости поглощения на частоте этого перехода.
К главе 8
1. Предположите, что спиновое эхо возбуждается двумя им-
пульсами. Первый импульс я/2 в момент времени t = 0, РЧ-поле
Н\ которого направлено вдоль оси -\-х вращающейся системы
координат, поворачивает намагниченность к оси —у. РЧ-поле
Нх второго импульса п в момент времени t = т направлено вдоль
оси -\-у.
а) Покажите, что эхо формируется в момент времени 2т
вдоль оси —у.
б) Пусть РЧ-поле импульсов создается катушкой образца,
ось которой совпадает с осью х лабораторной системы коорди-
нат, и является линейно-поляризованным. Покажите, что в этом
случае можно удовлетворить условию задачи, если РЧ-поле пер-
вого и второго импульсов соответственно будет иметь вид
при t<x и Hx(i) = 2H
при / > т.
398 Задачи
2. Нарисуйте векторные диаграммы во вращающейся системе
координат и докажите, что рис. 8.1 правильно изображает сиг-
налы эха в импульсной последовательности Карра — Пёрселла.
3. Чтобы понять смысл импульсного сужения линии с по-
мощью различных импульсных последовательностей, можно на-
чать с предположения, что дипольное уширение линии и уши-
рение из-за неоднородности внешнего магнитного поля прене-
брежимо малы, и проследить за движением намагниченностп.
Проверьте этим способом результаты, представленные рис. 8.6
для трехнмпульсного цикла, описанного в гл. 8, § 6.
4. Опишите движение вектора намагниченности во вращаю-
щейся системе координат в результате действия одного цикла че-
тырехимпульсной последовательности (т, —х, т, у, 2т, —у, т, х, т),
используя условие задачи 3.
К главе 9
1. В гл. 9, § 3, установлено, что соотношения (9.276) и (9.31)
представляют собой рекуррентные соотношения между матрич-
ными элементами (JM}r\\ T LM\J' Mytf) для любых возможных зна-
чений Mj, М и Му при фиксированных значениях /, L, Г, r\, rf.
Покажите для случая / = /', что действительно с помощью этих
рекуррентных соотношений все матричные элементы можно вы-
разить через какой-либо один (например, через матричный эле-
мент, ДЛЯ КОТОРОГО М] = Mj' = /).
2. Проверьте, что функции Г2м(.1), приведенные в табл. 9.1,
удовлетворяют коммутационным соотношениям для 'компонент
тензорного оператора Т2м с J.
3. Спин находится в поле аксиально-симметричного потен-
циала. Кроме того, на пего действует слабое магнитное поле.
В этом случае гамильтониан имеет вид
Если Н = О, то спин квантуется в соответствии с квадрупольным
взаимодействием так, как показано на рис. 9.4. Состояния с
m = ± '/г вырождены. Покажите, что в слабом поле Н эти со-
стояния расщепляются, а энергия расщепления меняется от зна-
чения упЬН, когда г' совпадает с г, до значения (/+ '/2)v«^^>
когда г' перпендикулярно г.
4. Имеются гамильтониан и энергетический спектр, опреде-
ляемые формулами (9.65) и (9.66). К системе приложено пер-
пендикулярно оси 2 переменное поле HxcoS(at. Найдите разре-
шенные переходы, их частоты и относительные интенсивности.
Получите численные результаты для случаев / = 3/г и / = 5/г-
Задачи 399
5. Покажите, что заряд е, расположенный в точке хо, Уо, г-
создает градиент поля
равный
ч~2 2
6. Имеется ядерный спин Б/2, связанный электрическим ква-
друпольным взаимодействием
а) Покажите, что собственные значения энергии равны
О, ±2д/7А
б) Покажите, что собственные функции имеют вид
9 \1/2Г /5 У/2
!
!
где ф5/а — собственная функция /* с m *= 5/2 и т. д.
в) Покажите, что слабое постоянное поле Яо в направлении
г' приводит к расщеплению вырожденного уровня Е = 0; расще-
пление не зависит от ориентации z7 по отношению к осям х, у, г
и равно yntiH0(l5/7).
7. Докажите, что собственные значения Ей Еъ и т. д. гамиль-
тониана Ж<= A(l2x — fy) составляют пары ± Еи ±Е2 или рав-
ны нулю. {Указание: рассмотрите операцию R, которая перево-
дит ось х в у, а ось у в —х.)
К главе 10
1. Вычислите коэффициент С/, входящий в соотношение
A0.41), и получите ответ, аналогичный (Ю.БЗа).
2. Пользуясь определениями гл. 10, § 2, покажите, что по от-
ношению к Lx, Ly u Lz функция х2 — у2 представляет собой ли-
нейную комбинацию компонент Т%».
400 Задачи
3. Покажите, что выражение A0.65)
2®IS = УеУпЬ* (-рг) 4 (SIXSX - I • S)
следует из выражения A0.64)
MIS = уеУпН* ] jr [3 A'Г)/'Г) - I • S] xT (r) dr.
4. В гл. 10, § 3, получено выражение для сверхтонкого рас-
щепления в случае изотропного g-фактора электрона. Обобщите
этот результат на случай гамильтониана для внешнего поля,
имеющего только компоненты х и г:
ж=$ (gxxHxsx + g.yH^Sy+g^tfA) +
+ AJXSX + AyIuSu + AJ^ - ynh (HXIX + HVIU).
5. Рассмотрите матричные элементы {a.\La'\x}, где a, a' —
= x, у, z\ они часто встречаются в задачах, в которых |х> —
основное электронное состояние.
Покажите, что имеются только два матричных элемента, ко-
торые не равны нулю (а = у, а' = г и а = г, а' = у), в опре-
делите их. Решение этой задачи полезно для следующих.
6. Имеется атом, содержащий один р-электрон, на который
действует кристаллическое поле с потенциалом А(х2 — у2). Уров-
ни энергии электрона (без учета спина) показаны на рисунке.
Полагая Д ^> kT, вычислите главные значения не зависящего
от температуры тензора магнитной восприимчивости.
¦Упг)
¦zf(r)
¦ xf(r)
7. Имеется атом, как в задаче 6, однако теперь следует
учесть спин электрона и добавить к гамильтониану член, описы-
вающий спин-орбитальное взаимодействие ^.(r)L-S. В качестве
основных состояний следует взять состояния | ams), где a =
= х, у, г и ms = ± '/г — спиновое квантовое число.
а) Покажите, что матричные элементы (xs Щг) L• S |xs7),
описывающие примешивание подсостояний внутри основного ор-
битального состояния, равны нулю.
б) Пользуясь теорией возмущений, покажите, что спин-ор-
битальное взаимодействие примешивает волновые функции воз-.
Задачи 401
бужденных состояний к исходной волновой функции основного
состояния \xs), и найдите уточненные волновые функции
l^sjucnp, исправленные до членов, линейных по К.
в) Предполагая, что направление внешнего магнитного поля
совпадает с осью г, и пользуясь волновыми функциями сначала
\xs), а затем исправленными (см. п. «б» этой задачи), вычислите
полную энергию состояний (орбитальную плюс зеемановскую),
г) Покажите, что зеемановское расщепление в условиях
п. «в» равно А? = 2$Н, если используются функции \xs), и рав-
но Д? = g$H, если используются исправленные волновые функ-
ции. Найдите выражение для g, исправленное до членов, линей-
ных по Я,.
8. На атом с одним р-электроном, находящийся в начале ко-
ординат, действуют 6 одинаковых зарядов q. По осям х и у за-
ряды симметрично размещены на расстоянии а от начала ко-
ординат, а по оси z — на расстоянии Ь. Предположите, что b <.a,
и пренебрегите спином.
а) Покажите, что наинизший не равный нулю член гамиль-
тониана, описывающий расщепление р-состояний, равен Ж =
= А (Зг2 — г2) и определяется знаком А.
б) Найдите правильные собственные состояния и энергии,
выраженные через А и <г2>, где <г2> — средний квадрат радиуса
орбиты р-состояния.
в) Полагая, что магнитное поле направлено вдоль оси г, вы-
числите матрицу 3X3 гамильтониана.
г) Найдите собственные состояния, которые допускают вы-
рождение.
д) Для каких состояний гасится угловой момент?
9. Имеется система, как в задаче 8. Предположите, что рас-
щепление р-состояний производится кристаллическим полем,
большим по сравнению с kT, но рЯ <с kT.
а) Покажите, что при Ъ> а расщепление р-состояний в кри-
сталлическом поле обратно по знаку расщеплению при b <. а.
б) Закон Кюри утверждает, что тензор магнитной восприим-
чивости иа атом ХосДо, a/==x, у, г) обратно пропорционален
температуре
Покажите, что для одного знака кристаллического поля приме-
ним закон Кюри. Покажите, что в этом случае оси х, у и г яв-
ляются главными, и оцените соответствующие коэффициенты
Lxx, i-'yy И Czz-
10. Имеется атом с одним р-электроном, орбитальное движе-
ние которого заморожено благодаря воздействию кристалличе-"
402 Задачи
ского поля, подобного полю, создаваемому зарядами, располо-
женными, как показано на рис. 10.1.
Пользуясь теорией возмущений во втором порядке, пока-
жите, что интерференция спин-орбитального взаимодействия
XL-S и взаимодействия (е/2тс) (р'Ап-\-А„-р) между ядерным
моментом и орбитальным движением электрона приводит к эф-
фективному спин-спиновому взаимодействию между ядром и
электроном.
11. Имеется один р-электрон с сильной спин-орбитальной
связью. В этом случае хорошими квантовыми числами являются
/ и Mi. Гамильтониан взаимодействия ядерного момента с орби-
тальным движением электрона имеет вид
р-ь» + К'Р), A)
где Л,,-— yjil ХГА3 — векторный потенциал, создаваемый ядром.
а) Пользуясь теоремой Вигнера — Эккарта, покажите, что
для матричных элементов, диагональных по электронным кван-
товым числам /, этот гамильтониан совпадает с эффективным
гамильтонианом
^эфФ^Л/J'I. B)
где А] — постоянный при фиксированном / коэффициент, не за-
висящий от Mi.
б) Найдите А, для состояния с / = 3/г-
Приложения
А, Теорема об экспоненциальных операторах
Рассмотрим экспоненциальные функции операторов Л и Б и
обозначим коммутатор этих операторов через С:
С**[А, В]. (АЛ)
Теорему можно сформулировать следующим образом: если опе-
раторы А и В коммутируют с С, то
e*+*=eVe-c/2 (A.2)
или
еА+в^евеАес^ (А.З)
Докажем равенство (А. 2).
Для доказательства удобно ввести функцию е^(А+в). Будем
искать такую функцию О (К), для которой справедливо соотно-
шение
(A.4)
Составим дифференциальное уравнение, которому удовлетворяет
функция С(Х). Это дифференциальное уравнение, очевидно, бу-
дет определять изменение величины е^л+в) при малых измене-
ниях I. Величину е^Л+в'> можно найти, интегрируя дифференци-
альное уравнение по 7. в пределах от К = 0 до К — 1.
Дифференцируя обе части равенства (А. 4) по К, получаем
(А + В) е%и+в) = еЫ(А + В) e™G (X) + е'-ле'-в -^ . (А.5)
Используя (А.4) и умножая слева на е~%ве-%А, мы можем перепи-
сать (А. 5) в виде
Вычислим величину
е-мВеМ&ЩХ). (А.7)
Для этого продифференцируем обе части (А. 7) по К; получаем
е-ХА (ВА _ щ еы = _g e _ с, (А.8)
поскольку оператор АВ — ВА =з С коммутирует с А.
404 Приложения
Интегрируя (А.8), находим
# (Я) = - СК + const. (A.9)
Постоянная интегрирования легко определяется из равенства
(А. 7), которое при Я = 0 дает R@)= В. Следовательно,
Подставляя (АЛО) в (А. 6) и учитывая коммутативность опе-
раторов С и В, получаем
отсюда следует
G = e-<w/2+const). (Ал 2)
Константа в этом выражении равна нулю, поскольку из равен-
ства (А. 4) находим G@)= 1. Следовательно,
-/2, (A. 13)
что и требовалось доказать.
Б. Некоторые новые выражения
для восприимчивости')
Величина %" определяется выражением B.144). В литературе
часто встречается другое выражение для %", позволяющее иначе
вычислять моменты линии поглощения. Это выражение можно
получить из B.144)
fc/Д'ТГ V "^ р 1141 1 / f I \|П
Г=§^ e~E"lkT | (а | ц я | Ь) f 6 (Еа -Еь- Лео). (Б. 1)
о, ь
если воспользоваться интегральным представлением б-функции
+ ОО
—то
Подставляя в (Б. 1), находим
-со Еа.
(Б.З)
') Перед чтением этого приложения необходимо познакомиться с содержа-
пнем гл. 2, 3 и 5.
Приложения 405
Введя вместо т новую переменную интегрирования t, имеющую
• азмерность времени
Т = т, <Б-4)
получим
— оо О, 6
(Б.5)
-Это выражение можно записать в более компактном виде, если
учесть, что состояния |о) и \Ь) являются собственными функ-
, циями гамильтониана Ж. Тогда
+ов
— оо а, Ь
(Б.6)
Сумма по а и Ь, очевидно, представляет собой след. Поэтому
-1°°
]е-^Л. (Б.7)
В высокотемпературном приближении величину ехр(—3^/kT)
заменим единицей. Вводя в рассмотрение оператор ц*@» опре-
деляемый выражением
Цх (t) = ei w\r! <^№», • (Б.8)
мы можем записать (Б.7) в виде
S (Б.9)
Величина Sp[n* (/)(!*] представляет собой функцию корреляции.
Поэтому из выражения (Б.9) следует, что величина % (о) яв-
ляется трансформантой Фурье этой функции.
Используя выражение для %"(&), легко показать, что если
отбросить дипольные члены С, D, Е и F (см. гл. 3), то получим
выражение, определяющее поглощение только на ларморовской
частоте, а если учесть эти члены, то придем к появлению погло-
щения на частотах 0 и 2соо-
Выражение (Б.9) позволяет также в очень компактном виде
записать выражение для функции f(co), описывающей форму ли-
нии поглощения:
406 Приложения
Докажем теперь другую интересную теорему. Для этого при-
меним преобразование Фурье к обеим частям равенства (Б. 10);
получим
+ОО
Полагая здесь t = 0, находим
Дифференцируя равенство (Б.11) п раз по < и полагая затем
t = 0, получаем
+ ОО
Это равенство позволяет найти компактное выражение, опреде-
ляющее и-й момент функции f(a>):
Для иллюстрации выведем выражение для второго момента
<оJ>. После выполнения дифференцирования iix(t) получаем
откуда находим
Этот метод позволяет очень просто получать выражения для мо-
ментов более высоких порядков. Отметим, что все нечетные мо-
менты оказываются равными нулю в соответствии с тем, что
/"(со) является четной функцией со.
До сих пор, за исключением предположения о применимости
высокотемпературного приближения, мы не налагали никаких
ограничений на свойства гамильтониана. Предположим теперь,
Приложения 407
что гамильтониан состоит из зеемановского члена Шг и комму-
тирующего с Шг члена 9вР, который часто представляет собой
возмущение. В качестве Жр, например, можно рассматривать
члены А и В дипольного взаимодействия. Тогда, поскольку 36Р
И Звг КОММУТИРУЮТ,
= e(i/ft) *V (цх cos «о/ + |i, sin своО е""/й) ^', (Б. 17)
где мы воспользовались равенством B.55). Отсшда следует
Sp [|i, @ Ц*1 = cos coo/ Sp[e<'№)^V^-^W^VJ +
+ sin coo/ Sp^^Vg»-™4*^.! (Б.18)
Если величина Жр инвариантна относительно поворота во-
круг оси х или у на 180° (что обычно имеет место), то второй
член в правой части (Б. 18) равен нулю. В этом можно убе-
диться, если вычислить след в системе координат х1 = х, у' =
= —у, г' = — г, которая получается после поворота на 180°
вокруг оси х. Поскольку, согласно нашему предположению,
<Уёр — Жр, находим
am)ас t -кцщэе t -i Г umac't
e РЦв pHJSpLe *(
Wh)9C't -№)8CJl
(Б.19)
Последний след, очевидно, совпадает с исходным и в то же
время отличается от него знаком. Следовательно, он равен
нулю. В соответствии с этим функцию корреляции можно за-
писать в виде
Sp [ця (/) ця1= cos coo/ Spfe'"*»^W-'""» VnJ. (Б.20)
Поскольку эта величина равна трансформанте Фурье функции
/(со), отсюда следует, что переходное поведение определяется
функцией coscoof, умноженной на функцию, представляющую
собой огибающую.
Если определить величину ц* (/) равенством
то огибающая будет иметь вид Sp[n*
408 Приложения
Представим теперь функцию cosco0? в виде суммы двух экс-
понент соответствующих частотам + и0 и — соо:
cos Off = у (eto< + e~**0, (Б.22)
и обозначим вклад в функцию f(co) от частоты + соо через /+(«).
Тогда
-too
и<&*=-Ш1 \ Sp[|*;@l»Je+to''e-'-'A; (Б.23)
после применения преобразования Фурье к обеим частям равен-
ства (Б. 23) получаем
JOO
^JL J f+(co)e+^da., (Б.24)
или
+ О0
1 * 1 f
_____ Сг\ Гц l/l и 1 —= \ r (n\\ (>l («о—ио) t /li,-\ (K 9K\
— CO
Дифференцируя обе части этого равенства, находим
(со — со0)" f + (со) da
V"
= in «со — ©о)п>. (Б.26)
Выражение (Б. 26) определяет и-й момент относительно часто-
ты ио- В этом выводе мы исключили экспоненциальный член,
соответствующий частоте —©0; включение этого члена привело
бы к появлению слишком большого вклада в величину
<(со-соо)я>.
Точно так же, как при выводе равенства (Б. 15), теперь по-
лучаем
Последняя величина равна нулю, если оператор Жр состоит из
членов А и В, приведенных в гл. 3,
Приложения 409
I. Вывод функции корреляции для поля,
случайным образом принимающего
значения ± Ао
Предположим, что поле случайным образом принимает толь*
|со два значения ± h0, которые обозначим индексами 1 и 2. Сле-
довательно,
+ Ао-=Я„ -Ао=-Я8.
ЗНам нужно найти функцию корреляции
т), (В.2)
»ерта здесь означает усреднение по ансамблю.
Если в момент времени t = О поле имеет значение Hlt то для
юдного из членов ансамбля можно написать
Я @) Я (т) = Н{ [Р, (т) Я, + Р2 (т) Я2], (В.З)
где P^(r) и Р2(т) могут быть равными нулю или единице в за-
висимости от того, какое значение (Hi или Я2) принимает поле
в момент времени т. Теперь усредним выражение (В.З) по ан-
самблю для различных путей изменения поля. При этом вели-
чины Pi(t) и Pi{x) заменяются их средними по ансамблю зна-
чениями pi(x) и Рг(т). представляющими собой вероятности того,
что в ансамбле, в котором при т = 0 поле имело значение Н\,
в момент времени т оно примет значение Н\ или Я2.
Таким образом, имеем
Я@)Я(т) = Я, [HlPl (т) + Н2р2 (т)]. (В.4)
Здесь конечно, предполагается, что при т = 0 Я(т)= Ни так что
при т -> 0 pi (т)-> 1, а Р2(т)->- 0.
Если в начальный момент т = 0 поле имеет значение Яг (что
одинаково вероятно), то выражение для функции корреляции
будет отличаться от приведенного только перестановкой индек-
сов 1 и 2.
Предположим, что изменение во времени вероятностей pi и
р2 определяется уравнениями вида
-p2). (B.5)
Это задача о «нормальных колебаниях», решение которой мож-
но найти, пользуясь подстановкой
р, (т) + р2 (т) = const (— 1 по условию нормировки),
р,(т)-Ыт) = Се-2^, (В<6)
где С = pi@)—p2@) = pi@). Поскольку р2@) обращается в
нуль, a Pi@)= 1, имеем С = I. Используя выражение (B.1),
410 Приложения
(В. 4) и (В.6), находим
ЩЩЩ= Я, [Я,р, (т) + р2 (т) Я2] = Щр~™\ (В.7)
Такой же результат для #@)#(т) получается, если в мо-
мент т = 0 поле имеет значение Н2. Чтобы получить окончатель-
ное среднее по ансамблю, нужно учесть эти два случая с оди-
наковым весом (т. е. усреднить результат по начальным значе-
ниям поля). Это среднее значение мы обозначим двойной чертой
сверху, так как усреднение производится как по ансамблю на-
чальных условий, так и по ансамблю различных путей изменения
поля при данных начальных условиях. Тогда
Н @) Н (т) = /&-*" = G(t).
Это и есть та самая функция корреляции с временем корреля-
ции то, определяемым соотношением 2W « 1/то, которая фигу-
рирует в гл. 5.
Г. Теорема, следующая из теории возмущений
В этом приложении мы выведем из теории возмущений тео-
рему, имеющую широкое применение в магнитном резонансе.
Эта теорема тесно связана с применением второго порядка тео-
рии возмущений, причем она особенно полезна в тех случаях,
когда имеется вырождение. Типичная ситуация, в которой при-
меняется эта теорема, возникает при вычислении сдвига g-фак-
тора в гл. 10, § 2. В этом случае гамильтониан состоит из трех
частей
где
= 2рН • S, (Г.2)
Поскольку гамильтониан Жй не содержит спиновых переменных,
его собственные состояния можно представить в виде произве-
дений орбитальной и спиновой функций. Введем обозначения I
для орбитальных квантовых чисел и а для спиновых квантовых
чисел. Тогда
(Г.З)
Состояния с данным / вырождены по спиновым квантовым чи-
слам. Гамильтониан Ж\ снимает спиновое вырождение. Так как
Ж\ зависит только от спиновых переменных, он не имеет матрич-
ных элементов, связывающих различные орбитальные состояния.
Приложения
411
Поэтому
(la
'a)
(/a
a').
(Г.4)
В общем случае матричные элементы 3#i между состояниями
|/а) и |ta') при а фа' не равны нулю. Следовательно, взаимо-
действие Ж\ дает группу субматриц {1а\Ж\\1а'), которые мо-
жно диагонализировать. В данном случае это матрицы второго
ранга, так как спин равен 1/2 и диагонализация проводится
легко.
, отлично от нуля
?г тгтичт от нуля
Рис. ГЛ. Матрица гамильтониана.
Области, где матричные элементы гамильтониана ЭС\ отличны от нуля, заштрихо-
ваны. Квантовые числа li h, h относятся к различным собственным значениям «??¦»
Затруднения вызывает гамильтониан Ж%, так как он имеет
недиагональные по / матричные элементы. С другой стороны,
благодаря тому что орбитальное движение заморожено, диаго-
нальные по / матричные элементы Жч. обращаются в нуль:
\Ш | <7©2 | »Ct ) = U. \l ,0)
Схематически матрицу гамильтониана можно представить себе
так, как показано на рис. Г. 1, где отмечены области, в которых
одна из частей гамильтониана имеет не равные нулю матричные
элементы.
Описанный ниже метод, в сущности, состоит в преобразова-
нии, которое уменьшает величину недиагональных по I матрич-
ных элементов 3@2 и приводит к появлению добавочных диаго-
нальных по / матричных элементов. При этом состояния с раз-
ными / оказываются как бы несвязанными, что позволяет опять
иметь дело только с субматрицами, диагональными по /.
Формально основные черты этого метода можно представить
себе следующим образом. Имеется полный набор базисных фун-
кций ф/а, при котором, однако, у Жъ возникают нежелательные
матричные элементы между состояниями с различными /. Нуж-
но найти другой набор функций <р*е, связанный с исходным
412 Приложения
набором преобразованием
<P*a = e's«/a. (Г.6)
где S — эрмитов оператор, для которого недиагональные по /
матричные элементы 3@2 будут значительно меньше. С новым
набором базисных функций <р матричные элементы гамильто-
ниана выражаются следующим образом:
¦Va.dxdxs, (Г.7)
где dx соответствует интегрированию по пространственным пе-
ременным, а dxs — суммированию по спиновым переменным. Ис-
пользуя преобразование (Г.6) и эрмитовость оператора S, полу-
чаем
, dx dxs = (la |е-«5»е« |/V).
(Г.8)
Здесь для матричных элементов, вычисляемых с помощью функ-
ций г]), применено обозначение |/а). Из соотношения (Г.8) вид-
но, что вместо преобразования функций можно говорить о пре-
образовании гамильтониана в следующей форме:
(Г.9,
Теперь нужно так определить эрмитов оператор S, чтобы га-
мильтониан Ж не имел недиагональных по / матричных эле-
ментов.
По-видимому оператор S должен быть малым, так как у ис-
ходного гамильтониана Ж недиагональные по I матричные эле-
менты невелики. Поэтому экспоненты в выражении (Г. 9) можно
разложить в ряды и оставить только первые члены. Тогда
[\ + iS-~ + .
?3®
- т +1 [ж, S] - у [ [ж, s], s]. (г.ю)
Подставив в это выражение Ж = 3@о + Яв\ -|- %, постараемся
выбрать S так, чтобы Жч уничтожалось.
Выпишем (Г. 10) подробнее:
3»' —3&0 + 3», + 3fra + /[3»0 + 3fri, S] + /[3»8,S]— y[S[S, 3fg\].
(Г. И)
Третий член в правой части можно исключить, положив
^з + i №о + ЭЮи S] = 0. (Г. 12)
Приложения 413
Тогда имеем
^ + Ж1г S], S] +
Если 5^2 равно нулю, то S также обращается в нуль. Следо-
вательно, можно ожидать, что 5 будет порядка Жъ, а последний
член —порядка (З^K- Пренебрегая им и используя (Г. 12), по-
лучаем
Ж =. Жо + Жх + -|- [Жъ S]. (Г. 14)
Чтобы найти явный вид оператора S, выпишем условие (Г. 12)
в матричной форме. Вспоминая, что Ж\ не имеет матричных эле-
ментов между состояниями с различными /, а Ж2 имеет только
недиагональные по / матричные элементы, находим
(la | Ж* | /V) + i Е [(/«I ^о + ^ I /'V') (Га" | S | /'аО -
/". а"
- (/а | S | /"а") (Га" | Жо + Жх \ /'а')] = 0. (Г. 15)
Таким образом,
(/а | Ж21 /V) + i (Е, - ?г) (/а | S | I'a') +
+ i T [(la | Ж11 /а") (/а'71S | /'а') -
а"
-/ (/а |S| Га") (/V| д», |Га')] = 0. (Г.16)
Если / ф /', то можно пренебречь членами, содержащими М\, по
сравнению с матричным элементом, который умножается на
Ег — Ef. В этом случае
Если I = V, то соотношение (Г. 16) принимает вид
(la | Жх | la") (la" | S | /a') => Е (/«IS | /а") (/а'' | Ж11 /аО- (Г. 18а)
а"
Это соотношение легко удовлетворить, полагая
(la\S\la") = 0. (Г. 186)
Следовательно, S не имеет диагональных по / матричных эле-
ментов. [Из (Г.17) и (Г.186) видно, что (/a|S|/'a')=- (/'a'|S|/a)*,
где звездочка означает комплексное сопряжение. Поэтому при
таком определении S — эрмитов оператор.] Используя (Г.17) и
(Г. 14), находим матричные элементы Ж между состояниями
414 Приложения
[ la) и 11'a'). Сначала заметим, что если / ф /', то
поскольку Ж> и Эё\ диагональны по /. Таким образом,
{1а\Ж\1'а') = ± ? №\Эё2\1"а"){1"а" \S\IW) -
L". о"
- (/а | S | /"а") (/"а" | Ж21 Га.1)}«
= 1 ? {1а\Ж2\Го."){Го."\Ж2\1'о.')\ Е Х__Ея +.g-L_-]. (Г.20)
/", о" ' ' ' '
Следовательно, недиагональные матричные элементы выра-
жаются через отношение <9$2 к разности между собственными
значениями 3@ъ\ в этом смысле состояния с разными / можно
считать «несвязанными». Диагональные по / матричные эле-
менты также изменяются. Пользуясь соотношениями (Г. 14) и
(Г. 17), получаем для них следующее выражение:
(/а |3»' |/а') = (/а |Жй + Пх + -| [Ж2, S] | /а') =
[(/а 13%21 Га") (/"а" | S | la') -
(/а 15 | /"а") (/"а" 15g21 /а')] = ?/баа- + (/а 15»! | /а') +
E, — Е,„
I", a" ' l
Когда а = а', члены в (Г. 21), включающие Жч., совпадают с
поправкой к энергии, вычисленной во втором порядке теории
возмущений. Однако данное выражение справедливо также при
а Фа'. В связи с этим подчеркнем, что обычно в теории возму-
щений при наличии вырождения находят в нулевом порядке
собственные функции, не содержащие недиагональных матрич-
ных элементов, относящихся к данному вырожденному уровню.
В описанном методе не налагается таких ограничений па базис-
ные функции \1а). Если квантовые числа а выбраны так, что
возникают матричные элементы Aа\9ё'\1аг) между состояниями
с различными а, то нужно просто дпагоналнзироватъ матрицу
{1а\Ж'\1а'), определенную выражением (Г.21). В заключение
заметим, что часть, включающая Ж% в хорошем приближении
эквивалентна добавлению к гамильтониану а6о-\-Ж\ диагональ-
ных по / матричных элементов вида
(la 1 Жъ | Га") A"а" | Жг | la')
Et - Е.„
и пренебрежению связью между состояниями с разными /.
Приложения 415
Д. Высокотемпературное приближение
В различных местах в тексте используется высокотемпера-
турное приближение. Например, в формуле C.16) экспоненты в
выражении для х"(со) заменяются единицей:
a,b
где
— статистическая сумма. Поскольку fa —энергия системы из N
частиц, ее значение меняется в пределах от —NytiH0I до
+ NytiHoI, если учитывать только зеемановскую энергию. Ко-
нечно, энергия равна —NytiH0I только в том случае, когда все
спины находятся в состоянии с т = I, что чрезвычайно мало-
вероятно в статистическом смысле. Однако можно ожидать, что
наиболее вероятное значение Еа составляет \Еа\^ ^/NyflHoI,
если N спинов имеют случайные значения т. Поскольку для
типичного образца N « 1023, приближение Ea/kT <С 1 вызывает
недоумение.
Вместе с тем очевидно, что ни один из спинов не взаимо-
действует со многими другими спинами, поэтому при вычисле-
нии х" Нет необходимости рассматривать 1023 спинов. Таким
образом, утверждение о том, что нужно учитывать 1023 спинов,
является просто фикцией. В конце концов, при достаточно силь-
ном внешнем поле можно описать поглощение, рассматривая
только один спин.
Следовательно, можно положить, что высокотемпературное
приближение применимо, если энергия одного спина меньше КГ.
Посмотрим теперь, как показать это более строго. Рассмотрим
простой случай N одинаковых невзаимодействующих спинов и
будем считать, что те же аргументы применимы в случае взаимо-
действующих спинов при условии, что эффективное взаимодей-
ствие пары спинов меньше kT, т. е. в образце нет сильных внут-
ренних магнитных полей, таких, как в ферромагнетиках.
В случае невзаимодействующих спинов в качестве точных
квантовых чисел можно выбрать индивидуальные спиновые
квантовые числа ти т2, ..., mN. Тогда для энергии Еа получим
/V
Еп = - ytiH, Z т, = - ПщМ, (Д.2)
416
Приложения
где coo — ларморовская частота, а М — Е rnt. Волновые функ-
ции \а) и операторы ц* определяются выражениями
| а) == | ти т2, ...,
И*
= Е И*/-
Тогда
El**/
Е
/. ft
(Д.З)
(Д-4)
). (Д.5)
Поскольку ц*/ содержат переменные только одного ядра, из
определения (Д.З) мы видим, что в (Д.5) остаются только
члены с / = k. Поэтому
(Д.6)
откуда получаем
'U't> •••)\2 X
Если определить /л как т = М — пц, то
Теперь, пользуясь тем, что (/Л), т2 т;., ... [ц^тр
т2, ..., /л^, .. •)==(m/|fix/lm/)' BMeCT0 (Д-7) получаем
J.1 tTtnt •••! ^t—1» 11» I
-^)-н- (д.»)
x z /"
/. m . m
Здесь использовано то обстоятельство, что сумма по N — 1 пере-
менным, исключая nij, не зависит от /, так как все спины одина-
ковы. Но
"V Ш2 "'/-I' '"
(д
V Ш2 "'/-I' '"/+!¦ ¦¦¦
Приложения 417
Если теперь /too "С kT, то экспоненту с /и/ можно заменить еди-
ницей, что дает
Хет/*в«/ет = B/+1). (Д. 11)
Следовательно,
где Z(N—1) — статистическая сумма N—1 частиц. Теперь
сумма
в числителе и знаменателе (Д. 9) сокращается, и для %" мы по-
лучаем выражение
N
1"^ m , m
(Д.12)
Перепишем это выражение в другой форме, содержащей со-
стояния \а) и \Ь). Для этого заметим, что
mrm'i
поэтому
Но это как раз тот результат, который получается при замене
в (Д. 1) всех экспонент единицами.
В данном рассмотрении нигде не предполагалось, что
|?a|<t; kT. Более того, в этом отношении не делалось никаких
приближений. Единственное приближение состояло в том, что
статистическую сумму для N спинов мы представили в виде
произведения статистической суммы для N— 1 спинов и
B/ + 1).
Аналогичное положение возникает в целом ряде других слу-
чаев, когда используется высокотемпературное приближение.
Суть дела состоит в том, что, хотя формально энергия соответ-
ствует большому числу N спинов, фактически всегда играет роль
только малое число спинов. Поэтому ограничения на темпера-
418 Приложения
туру, появляющиеся в связи с тем, что N я» 1023, никаких за-
труднений не вызывают, за исключением тех случаев, когда
энергия небольшого числа спинов сравнима с kT.
Е. Эффекты изменения частоты прецессии.
Применение ЯМР для изучения
молекулярных движений
Затухание спинового эха вследствие объемной диффузии
ядер в неоднородном постоянном поле, впервые наблюдавшееся
Ханом, является одним из многих эффектов, которые позволили
в
Рис. ЕЛ. Молекула N.N-диметиламида, где R означает либо Н, либо СНз.
На структуре (слева) показана одинарная N—С связь, однако за счет смешивания со-
стояний возникает двойная связь; в результате конфигурация моле улы становится пло-
ской и возникает барьер, препятствующий вращению вокруг N—С оси. Две группы СНа
обладают немного различающимися химическими сдвигами. Однако, если фрагмент RCO
преодолевает потенциальный барьер и переходит в конфигурацию в, группы СНз обмени-
ваются химическими сдвигами.
магнитному резонансу найти полезные применения в физике,
химии и биологии. В процессе диффузии ядра перемещаются в
пространстве между различными положениями, в которых зна-
чения напряженности магнитного поля отличаются и, следова-
тельно, отличаются частоты прецессии. Вследствие такого дви-
жения возникает частотная модуляция.
Подобные эффекты легко рассмотреть, пользуясь уравне-
ниями Блоха. Для упрощения задачи мы проанализируем эле-
ментарный процесс частотной модуляции, который возникает
при скачках ядра между двумя положениями с разными часто-
тами прецессии. Рассмотрим, например, молекулу N.N-диме-
тиламида, изображенную на рис. ЕЛ. Две метнльные группы
СНз имеют различные электронные окружения и, следовательно,
различные резонансные частоты в одном и том же постоянном
Приложения
419
—8,5 °С
гз°с
29,5 "С
46,5 °С
магнитном поле. Этот эффект (называемый химическим сдви-
гом) рассмотрен в гл. 4. Молекула может находиться в одной из
двух планарных конфигураций (рис. ЕЛ, а или е), между ко-
торыми при достаточном тепловом возбуждении, способном пре-
одолеть потенциальный барьер, происходят скачки. При низких
температурах молекула жесткая, скачков нет я поэтому наблю-
даются две резонансные линии (для каждой из СН3 групп), раз-
деленные по частоте на величину разности химических сдвигов
бсо. При высоких температу-
рах происходят частые скач-
ки между двумя планарны-
ми конфигурациями. Когда
это движение достаточно
быстрое, протоны в каждой
группе чувствуют лишь их
среднее по времени окруже-
ние. Различие между двумя
положениями в молекуле
теряется, и наблюдается
только одна резонансная
линия.
Для молекулы, в кото-
рой молекулярным фраг-
ментом R является СС13, на-
блюдались сигналы, пока-
занные на рис. Е.2. Данные
взяты из работы Гутовского
и Холма [1]. При темпера-
туре — 8,5 °С наблюдаются
две линии равной интенсив-
ности. Повышение темпера-
туры приводит к постепен-
ному уширению линий и их слиянию в одиночную линию, кото-
рая при дальнейшем увеличении температуры сужается.
Пользуясь уравнениями Блоха, эту задачу впервые решили
Гутовский и др. [2] и независимо Хан и Максвелл [3]. Метод
Хана и Максвелла, который будет рассмотрен ниже, был неза-
висимо развит ван Флеком [4] и Мак Коиеллом [5]. Используя
несколько другой подход, Арчер [6] и Андерсон [7] получили тот
же результат. Ван Флек написал: «Довольно удивительно, что
формула..., основанная на простейшем примере частотного пре-
рывания, не была представлена в явном виде до 1953 г., хотя
задача имеет значительный физический интерес и вычисления
формы линии, основанные на фазовом прерывании, начались
очень давно и проводились главным образом с ранней работы
Лоренца, опубликованной полвека назад».
Ю Гц
Рис. Е.2. Температурная зависимость
протонного спектра магнитного резо-
наса N.N-даметилтрихлороацетатамида
(ДМТСА), измеренная Гутовским и
Холмом при 60 МГц.
Шкала частот, но не интенсивности, одинаковая
для всех температур.
420 Приложения
Будем считать приложенное вращающееся поле #i слабым,
чтобы можно было пренебречь насыщением. Уравнение Блоха
--Л. = -М+а + 1чМ<Ри (ЕЛ)
где
M+ = Mx + iMy, (E.2)
a=-^ + iyh0, (E.3)
Ло = Я0 — ю/y, (Е.4)
описывает одиночную резонансную линию.
Нам необходимо учесть, что ядра могут находиться в двух
положениях а и Ь. Обозначим полную поперечную намагничен-
ность Мх + Шу ядер в положении а через Ма, а в положении
Ь — через Мь. Ма и Мь — комплексные величины. Введем от-
клонение частоты от резонансного значения в поле Но
Асо == ю — Ytf0 (E.5)
и боа — разность резонансных частот в положениях а и Ъ.
Если скачки между положениями а и Ь не происходят, то
поперечные намагниченности ядер в этих положениях подчи-
няются следующим дифференциальным уравнениям:
' О + Чг
=+' (Аю ^)Мб + /Y т"Яь (Е-6б)
где Мо — термически равновесная намагниченность ядер в обоих
положениях.
Стационарные решения уравнений (Е.6) получаются, если
положить dMa/dt = dMb/dt = 0. Они совпадают с решением,
данным в гл. 2, § 8, и описывают две лоренцевы линии равной
амплитуды на частотах
о == y^o ^' Аа = Г (Е.7а)
и
o==Y^o + —, Асо = —. (Е.76)
Теперь включим молекулярное движение. Предположим, что мо-
лекула переориентируется, т. е. ее спины попадают из положе-
ния а в положение Ь и наоборот. Переориентация молекулы
происходит настолько быстро, что спины протонов не изменяют
своей ориентации. Тогда за достаточно большой интервал вре-
мени Ы из положений b в положение а перескочит много спинов,
Приложения 421
что приведет к приращению намагниченности
6Ма = С1МьЫ. (Е.8)
Это выражение является фактически векторным потому, что ве-
личины Ма и Мь — комплексные вида Mx-\-iMy. Добавочная
намагниченность бМа имеет ориентацию, совпадающую с Мь, и
пропорциональна интервалу времени 6Л Вещественная констан-
та Сх зависит от частоты скачков.
В процессе переориентационного скачка молекулы спины про-
тонов одной группы СНз покидают положение Ь и переходят в
положение а. Намагниченность протонов сорта а увеличивается,
а сорта Ъ — уменьшается. В целом по образцу уменьшение равно
Шь=-СгМьЫ. (Е.9)
Одновременно в том же процессе спины другой группы СНз
молекулы, рассматриваемой в нашем примере, перескакивают
из положений а в положения Ъ. Эти скачки увеличивают Мь на
величину
бМь = С2МаЫ (ЕЛО)
и уменьшают Ма на величину
В более общем случае скачки из а в Ъ не зависят от скачков из
Ъ в а (например, если бы одна метильная группа молекулы
была дейтерирована и рассматривался бы лишь протонный ре-
зонанс).
Таким образом, мы можем написать скорости изменений на-
магниченностей Ма и Мь, вызванных молекулярным движением,
^ (Е.12а)
(Е.126)
и добавить их к уравнениям (Е. 6а) и (Е. 66)
(Е.13а)
^Г = —77 +' (Лю -1?) Мь + СгМ« - CiM» + ^Я' 1Г •
(ЕЛ 36)
В нашем примере при каждом акте переориентации молекулы
спины сорта а превращаются в спины сорта Ь, а спины сорта
Ъ — в спины сорта а, поэтому С\ = С2 = С.
422 Приложения
Легко найти стационарные решения этих уравнений, так как
они превращаются в систему линейных алгебраических уравне-
ний для комплексных величин Ма и Мь. В результате решения
для полной комплексной намагниченности Мх + iMy получаем
где
^ (^) (Е.15а)
f = C. (E.16)
Сигнал поглощения пропорционален составляющей Му, которая
определяется мнимой частью выражения (Е.14). Результирую-
щие сигналы, вычисленные Гутовским и Сэйка [8], показаны на
рис. Е.З. Кривые, пронумерованные цифрами 1, 2, 3 и 4, соот-
ветствуют различным значениям тбсо. Теоретически вычисленные
кривые имеют форму, совпадающую с экспериментальными сиг-
налами (рис. Е.2). #з кривых рис. Е.З видно, что переход от
случая медленных скачков к случаю быстрых скачков происхо-
дит при условии тбсо та 1. Это соотношение часто встречается и
имеет большое значение для многочисленных применений маг-
нитного резонанса. Оно описывает сужение резонансной линии
вследствие движения.
Условие тбсо « 1 определяет границу резкого изменения об-
щей картины сигналов. Однако изменения начинаются уже при
условиях тбсо >1 и тбсо <С 1. Так, на рис. Е.2 видно, что низко-
температурные узкие линии начинают уширяться задолго до
их слияния в одиночную линию, которая в свою очередь дли-
тельное время продолжает сужаться при постепенном увеличе-
нии температуры.
В общем случае изменение спектра определяется величиной
расщепления бсо в пределе отсутствия движения (длинное т) и
физическим процессом, который приводит к изменению резо-
нансной частоты ядер с характерным временем т, определяю-
щим, как часто в среднем происходят эти изменения.
Например, в твердом теле на отдельное ядро действует ло-
кальное поле АН порядка ±li/R3, где ц — ядерный магнитный
момент ближайшего соседнего ядра и R — расстояние до него.
Знак локального поля зависит от ориентации соседнего момен-
та. Следовательно, частота резонанса исследуемых ядер будет
распределена выше и ниже значения со = уН0. В твердом теле
данное ядро имеет много соседних ядер, одни из которых увели-
Приложений.
423
чивают, а другие уменьшают внешнее поле. Поэтому вместо
двух узких резонансных линий, как в рассмотренном выше слу-
чае, получим размытую широкую линию с шириной, несколько
превышающей распределение только от одного ближайшего со-
седа. Определим приблизительно полуширину этой линии как
R3
(Е.17)
где Z — небольшой числовой множитель, учитывающий наличие
нескольких соседей. Процесс самодиффузии приводит к замене
ZtBw
/ 10
Z I
3 10
« юг
-бш/г
о
Лео
6w/Z
Рис. Е.З. Усреднение химического сдвига в результате молекулярной пере-
ориентации в спектре ЯМР высокого разрешения.
Предполагается, что взаимная переориентация происходит между двумя положениями
а и Ь), которые имеют одинаковую населенность и резонансные частоты которых в отсут-
ствие обмена отличаются на 6ш рад/с
одного соседнего атома на другой. Резонансная частота иссле-
дуемого ядра может изменяться в зависимости от того, заме-
няется ли ближайшее соседнее ядро другим ядром с моментом,
ориентированным в том же направлении или в противополож-
ном относительно момента заменяемого ядра. Если хт — среднее
время, в течение которого соседнее ядро находится около иссле-
дуемого до его перемещения, то можно предположить
При низких температурах полуширина линии ядерного резонан-
са, согласно (Е.17), должна быть порядка бсо/2. При увеличе-
нии температуры время хт должно уменьшаться. При выпол-
нении условия
бю
(Е.19)
следует ожидать начала сужения линии ядерного резонанса. Та-
кие эффекты обсуждались в гл. 5.
424 Приложения
Химический обмен можно изучать по его влиянию на линии
ядерного резонансного поглощения. Например, в жидкости спин-
спиновое взаимодействие в молекуле приводит к структуре спек-
тра, показанного на рис. 4.11. В жидком этаноле СН3СН2ОН
протон группы ОН расщепляет протонный спектр группы СН2,
если протон группы ОН остается все время в молекуле. Однако
быстрый химический обмен протона группы ОН с другими про-
тонами в жидкости может размыть наблюдаемую структуру
спектра [9].
ЛИТЕРАТУРА
1. Gutowsky H. S., Holm С, Journ. Chem. Phys., 25, 1228 A956).
2. Gutowsky H. S., McCall D. W., Slichter С P., Journ. Chem. Phys., 21, 279
3. Hahn E. L., Maxwell D. E., Phys. Rev., 88, 1070 A952).
4. Van Vleck I. H., Ned. Tijdschr. Naturrk, 27, 1 A961).
5. McConnell H. M., Journ. Chem. Phys., 28, 430 A958).
6. Archer D. H., Thesis, Harvard Univ., 1953.
7. Anderson P. W., Journ. Phys. Soc. Jap., 9, 316 A954).
8. Gutowsky H. S., Saika A., Journ. Chem. Phys., 21, 1688 A953).
9. Arnold I. T., Phys. Rev., 102, 136 A956).
Ж. Диффузия в неоднородных магнитных полях
В гл. 2, § 9, мы объяснили, как диффузия в неоднородном
постоянном магнитном поле вызывает уменьшение сигнала спи-
нового эха по мере увеличения интервала времени между им-
пульсами. Причина уменьшения сигнала эха заключается в том,
что частота прецессии ядер изменяется. В процессе диффузии
ядра перемещаются от точки к точке, значения внешнего маг-
нитного поля в которых различны из-за его неоднородности. Си-
туация близка к той, которую мы рассмотрели в приложении Е.
Там предполагалось, что ядро имеет два возможных, естествен-
ных значения частоты прецессии. В случае диффузии в неодно-
родном магнитном поле имеется континуум значений напряжен-
ности магнитного поля. Для простоты предполагаем аксиаль-
ную симметрию неоднородного поля
Н(х, y,z) = H0 + z^§-. (ЖЛ)
В приложении Е мы описали с помощью кинетических урав-
нений (Е. 12а) и (Е. 126) процесс перескока спинов между двумя
положениями с различными частотами прецессии. В случае
диффузии возможные частоты прецессии образуют континуум,
как следует из формулы (Ж. 1).
Диффузию обычно описывают диффузионным уравнением.
Торри [1] рассмотрел диффузионное уравнение совместно с
Приложения
425
уравнением Блоха. Мы последуем его вычислениям с неболь-
шими упрощениями.
Предположим, что каким-либо способом в постоянном одно-
родном магнитном поле вдоль оси z при отсутствии переменного
поля создали неоднородную намагничен-
ность Мг, распределение которой пока-
зано на рис. Ж.1, а. Предположим так-
же, что величина Т\ бесконечно велика.
Тогда полная 2-составляющая намагни-
ченности измениться не может, но в ре- А
зультате диффузии намагниченность Мг
будет перераспределяться по объему об-
разца, как показано на рис. Ж-1,б, и в
конечном счете мы получим ее однород-
ное распределение (рис. Ж.1,в). (Напо-
мним, что символ Мг означает здесь плот-
ность намагниченности.) Процесс, изо-
браженный на рис. Ж1), описывается
уравнением
дМг
dt
(Ж-2)
где D — постоянная диффузии.
Если в начальный момент времени
имеются также составляющие плотности
а
Рис Ж.1. Образец в постоянном поле, приложен-
ном вдоль осн z, намагничивается в направле-
нии г.
Плотность намагниченности Mz считается вначале не
однородной. На рис. Ж.1, а дана зависимость намагни-
ченности Mz в начальный момент времени от коорди-
наты х (образец имеет протяженность от х—0 до x=L).
В результате диффузии плотность намагниченности в по-
следующие моменты времени (рис. Ж-1, б) распреде-
ляется по всему образцу и высота пика понижается. На-
конец намагниченность Mz становится однородной
(рнс. Ж.1. в). Заметим, что если величина Г] бесконечно
велика, полная z-составляющая намагниченности, кото-
рая характеризуется площадью под кривой Mz (х)> имеет
одинаковую величину во всех трех случаях.
М,
намагниченности Мх и Му, то в постоянном однородном магнит-
ном поле диффузия будет их изменять. Постоянное магнитное
поле вызывает прецессию Мх и Му. Поэтому изменения Мх и Ми
возникают из-за диффузии и из-за прецессии. Путем преобразо-
вания к системе координат, вращающейся с частотой прецессии,
426 Приложения
можно исключить прецессию, и в этой системе записать
^ (Ж.За)
(Ж-Зб)
или, воспользовавшись соотношением М+ == Мх -\- iMy,
~- = DV2M+. (Ж.4)
Уравнение (Ж.4) описывает векторный эффект, так как вели-
чина М+ двумерная. Это аналогично уравнению (Е. 12), если
принять во внимание, что М+— функция положения.
Теперь поступим так же, как в приложении Е, чтобы рассмо-
треть случай, когда постоянное поле неоднородно. Мы должны
включить влияние распределения частоты прецессии.
Учитывая прецессионный и релаксационный члены, получаем
- м+<****> + Ш*М+ (х, у, г, О, (Ж.5)
где
h (x, y,z) = H (х, у, z) - Но, (Ж.6)
Яо — среднее поле по объему образца. Подставляя в (Ж. 5) вы-
ражение для h(x, у, z) из (Ж. 1), получаем уравнение, описы-
вающее свободную прецессию в постоянном неоднородном маг-
нитном поле, которое имеет аксиальную симметрию
*-4 + W^. (Ж.7)
Уравнение (Ж. 7) включает естественные эффекты спин-спино-
вой и спин-решеточной релаксации. [То, что эффект спин-реше-
точной релаксации включается, можно проверить, исследуя
уравнение B.77) при Ht = 0.] Градиент поля dH/dz опреде-
ляется в начале координат (x = y = z = Q) и постоянен. Един-
ственная зависимость от координат в пределах образца в урав-
нении (Ж. 7) содержится в первом члене правой части.
Если диффузии нет (D = 0), уравнение (Ж-7) решить про-
сто, так как для каждого слоя образца при фиксированном зна-
чении z оно описывает прецессию во вращающейся системе ко-
ординат в постоянном поле h с учетом затухания с постоянной
времени Т2. Решение имеет вид
М у (г, /) = М (г, 0) е ~"VV3 ("^', (Ж.8)
Приложения 427
где М{г, 0)—комплексная плотность намагниченности при ?=0.
Предположим, что намагниченность M(r,t) однородна. Однород-
ную намагниченность М(г, 0) можно получить с помощью приго-
тавливающего импульса л/2, который действует на образец, на-
магниченный до теплового равновесия вдоль постоянного поля.
(Здесь мы пренебрегаем небольшими вариациями статической
намагниченности при тепловом равновесии, связанными с не-
однородностью постоянного магнитного поля.) Рассмотрим плот-
ность намагниченности в слоях образца с координатами г — Az,
z и z-\-Az, где Az— малая часть размера образца вдоль оси z.
Эти три плоскости находятся на одинаковом расстоянии друг от
друга, поэтому частоты прецессии ядер в этих плоскостях отли-
чаются на одну и ту же величину. В момент времени t — 0 фазы
прецессии ядер в этих трех слоях совпадают, затем намагничен-
ность слоя 2 + Az опережает намагниченность слоя z, а намагни-
ченность слоя z — Az отстает. Углы опережения и отставания по-
степенно растут во времени, но всегда остаются равными. Если
спины из слоев z + Az и z — Az диффундируют в слой z, то их
количество будет одинаково. Поэтому они будут приносить в на-
магниченность слоя z одинаковые по величине добавки как с
опережением, так и с отставанием по фазе. В результате фаза
полной намагниченности слоя z не будет изменяться. Следова-
тельно, можно ожидать, что диффузия не влияет на фазу изме-.
няющейся намагниченности слоя z, но влияет на величину этой
намагниченности. До тех пор пока значение z не попадает на
границу образца, каждый слой г имеет два симметрично распо-
ложенных с разных сторон слоя на расстоянии Az. Из этих двух
слоев намагниченность диффундирует в слой z с опережением
или отставанием по фазе в зависимости от Az и независимо от z.
Поэтому мы попытаемся искать решение уравнения (Ж.7) в сле-
дующем виде:
дН
М+(г, О = Мое~'/Гге v дг J A(t). (Ж.9)
После подстановки этого решения в уравнение (Ж. 7) получим
уравнение для величины A {t):
1 dA Df дН \2 2
или
-D ( dfiY Р
. Л = Л@)е~ ^у вг) зш
Постоянную Л @) внесем в Мо. Тогда находим
М+(г, t) =
428 Приложения
Эта формула описывает изменение во времени намагниченности
от ее начального значения Мо в момент t = О после импульса
я/2.
Теперь необходимо рассмотреть, что случится, если мы при-
меним импульс я в момент времени т, который поворачивает
намагниченность вокруг оси у. Плотность намагниченности не-
посредственно перед импульсом равна
М+{т, т") = Мф-^е V ez) йе ** вг хш (Ж. 13)
Импульс я не меняет Му, но превращает Мх в —Мх. Это
. дН
эквивалентно изменению фазового угла от значения —Уг~я~~т Д°
значения n + yz-^-x. Таким образом, при t = x+
_ ( дН V 2т3
М+ (г, 2т) = - Мф-^^е V dz> 3
М+{т, т+) =
Далее намагниченность М+ будет изменяться во времени в со-
ответствии с формулой (Ж.12)
М+(т, t-x) = M+(T, %)e-it-WH! VV вг) з е iyzez (t ^
(Ж. 14)
Подставляя в выражение (Ж-14) в качестве начального условия
значение (Ж-13), получаем в момент t — т = т (или t — 2x)
(Ж. 15)
Комплексные фазовые множители в (Ж. 15) сокращаются, и мы
получаем известный результат Хана.
Важно отметить, что диффузионный член после двух интерва-
лов времени т равен экспоненте с показателем (удН/dz) Ю Bт3/3),
а не с показателем (ydH/dzJD[BxK/3]. Это означает, что по-
теря фазы происходит независимо в каждый интервал времени т.
Метод Карра и Пёрселла [2], обсужденный в гл. 8, основан имен-
но на этом факте. Они заметили, что если применить последова-
тельность импульсов л, разделенных интервалами 2т, то можно
получить последовательность эха и, выбрав т достаточно малым,
можно значительно уменьшить диффузионное затухание намаг-
ниченности и сделать его меньше релаксационного.
ЛИТЕРАТУРА
1. Тоггеу И. С, Phys. Rev., 104, 563 A956).
2. Can И. У., Purcell E. M., Phys. Rev., 94, 630 A954).
3. Соотношение между единицами гауссовой системы и СИ
Основная величина
Намагниченность
Магнитная проницаемость в вакууме
(магнитная постоянная)
Константа анизотропии
Постоянная обменного взаимодействия
Гиромагнитное отношение
Параметр Гильберта
Гауссова система единиц
Обозначение
4яМ
—
К
А
Y
а
Единица
Гс
—
' эрг/см3
эрг/см
(с-Э)-1
си
Обозначение
м
цо = 4я-1О-7
К
А
V
а
Единица
А/м
Вб/(А • м)
Дж/м3
Дж/м
(с-А/м)-1
~~"
Отношение *
СИ/Гауссова
система
103/4я
4я-10~7
ю-1
10
4я/103
1
Параметр
Напряженность маг-
нитного поля
Магнитная индукция
Магнитный поток
Магнитная энергия
Н
В
Ф
Определяющая формула
{ Hdl = 4nNI/lO
В = Н + 4 яМ
<р= [ BdA
В Н/8л -> М Н/2
Единица
э
Гс
Мкс
эрг/см3
Определяющая формула
\ tidl=-NI
В = цо(Н + М)
ф=^ BdA
ВЯ->ц0МЯ/2
Единица
А/м
Вб/м2
Вб
Дж/м3
Отношение
103/4я
ю-4
10~8
ю-1
Продолжение
Параметр
Размагничивающий
фактор
Объемная магнитная
восприимчивость
Магнитная проница-
емость
Поле анизотропии
Фактор стабильности
Плотность энергия
доменной стенкн
Характеристическая
длина
Подвижность домен-
ной стенки
N
"к
Q
а
1
Л
Определяющая формула
я.--»-
ц = d Bid H = 1 + 4яХ
Нк = 2 KIM
Q = HR/4nM
1 = а/4л Af2
Единица
—
—
—
э
—
эрг/см2
см
см/(с • Э)
Определяющая формула
Hd=-N M
х s™ A JyifU, п
jj, = d $1 и, Нsssa jxq A ~т" ^)
if -~~ 2/С/IX i"
a = 4V^
/ = а/,0М2
Единица
—
—
—
А/м
—
Дж/м2
м
м2/(с • А)
Отношение
1/4Я
An
4я.10- = (г0
103/4я
1
ю-3
ю-2
4я-КГ5
м — метр
см — сантиметр
с — секунда
N — число витков
А — ампер
Дж — джоуль
Э — эрстед
Вб — вебер
Гс — гаусс
Мкс — максвелл
* Чтобы получить значение в системе СИ. нужно умножить значение в гауссовой системе на величину соответствующего отношения.
Краткая библиография^
Безнадежна попытка составить полную библиографию по маг-
нитному резонансу: слишком много статей опубликовано по это-
му вопросу. Да и вряд ли такая библиография может принести
пользу читателю, впервые приступающему к изучению новой для
него области науки, так как он не смог бы понять, с чего начать
изучение. Поэтому был выбран краткий список работ, в кото-
рых рассматриваются наиболее важные положения магнитного
резонанса. В ряде случаев отобраны основополагающие статьи,
а в других — обзорные статьи. Приводятся также статьи, до-
полняющие содержание книги. Важным способом поиска не-
обходимой литературы является использование Индекса цити-
руемости. Индекс содержит списки всех статей в любом данном
году, к которому отсылает читателя отдельная статья или книга
(статья в Индексе помещена по фамилии первого автора, напри-
мер Bloembergen в случае статьи Bloembergen, Purcell, Pound).
Таким образом, чтобы найти более новую из работ в данной
области, можно посмотреть основную раннюю работу в этой об-
ласти, на которую вероятнее всего, ссылаются авторы более
поздней работы. Использование Индекса цитируемости в соче-
тании с данной библиографией является наилучшим способом
получения представления о научной деятельности в самое по-
следнее время в перечисленных областях.
Основные статьи
Purcell Е. М., Тоггеу И. С, Pound R. V., Resonance Absorption by Nuclear
Magnetic Moments in a Solid, Phys. Rev., 69, 37 A946).
Bloch t., Hanzen W. W., Packard M., Nuclear Induction, Phys. Rev., 69, 127
A946).
Bloch F., Hansen W. W., Packard M., The Nuclear Induction Experiment, Phys.
Rev., 70, 474 A946).
Bloch F., Nuclear Induction, Phys. Rev., 70, 460 A946).
Bloembergen N., Purcell E. M., Pound R. V., Relaxation Effects in Nuclear Mag-
netic Resonance Absorption, Phys. Rev., 73, 679 A948). (Имеется сокращен-
ный перевод в научно-реферативном сб. Парамагнетизм и [3-распад, сер. 2,
вып. 8. —М.: ИЛ, 1958).
') Звездочкой (*) отмечена литература, добавленная редактором перево-
да. — Прим. ред. ...
432 Краткая библиография
Учебники, монографии и обзорные статьи
Pake G. Е., Nuclear Magnetic Resonance, в кн. Solid State Physics, Vol. 2, ed.
by Seitz and Turnbull, Academic Press, New York, 1956, pp. 1—91. Collected
articles, Nuovo Cimento, Suppl., Vol. VI, Ser. X, 808 A957).
* Pake G. E., Paramagnetic Resonance, New York, 1962. (Имеется перевод:
Пейк Дж. Парамагнитный резонанс. — М.: Мир, 1965.)
Andrew E. R., Nuclear Magnetic Resonance, Cambridge University Press, Cam-
bridge, 1955. (Имеется перевод: Эндрю Э. Ядерный магнитный резонанс. —
М.: ИЛ, 1957.)
Pople J. A., Schneider W. G., Bernstein H. J., High-Resolution Nuclear Magne-
tic Resonance, McGraw-Hill Book Co., New York, 1959. (Имеется перевод:
Попа Дж., Шнейдер В., Бернстейн Г. Спектры ядерного магнитного резо-
нанса высокого разрешения. — М.: ИЛ, 1962.)
Gorter С. /., Paramagnetic Relaxation, Elsevier Publishers, New York, 1947.
(Имеется перевод: Гортер ft. Парамагнитная релаксация. — М.: ИЛ,
1949.)
Ingram D. I. ?., Sprectroscopy at Radio and Microwave Frequencies, But-
terworth's Scientific Publications, London, 1955. (Имеется перевод: Ин-
грам Д. Спектроскопия на высоких и сверхвысоких частотах. — М.: ИЛ,
1959.)
Saha A. K-, Das T. P., Theory and Applications of Nuclear Induction, Saha In-
stitute of Nuclear Physics, Calcutta, 1957.
Cohen M. H., Reif F., Quadrupole Effects in Nuclear Magnetic Resonance Stu-
dies of Solids, в кн. Solid State Physics, Vol. 5, ed. by Seitz and Turnbull,
Academic Press, New York, 1957, pp. 321—438.
Das T. P., Hahn E. L., Nuclear Quadrupole Resonance Spectroscopy, в кн. So-
lid State Physics, Suppl. 1, ed. by Seitz and Turnbull, Academic Press, New
York, 1958.
Rowland T. J., Nuclear Magnetic Resonance in Metals, Progr. Mater. Sci.,
9, 1 A961). (Имеется перевод: Роуланд Т. Дж. Ядерный магнитный резо-
нанс в металлах. — М.: Металлургия, 1964.)
Pound R. V., Progr. Nuclear Phys., 2, 21 A952).
Low W., Paramagnetic Resonance in Solids, в кн. Solid State Physics, Suppl.
2, ed. by Seitz and Turnbull, Academic Press, New York, 1960. (Имеется
перевод: Лоу В. Парамагнитный резонанс в твердых телах. — М: ИЛ,
1961.)
Griffith J. S., The Theory of Transition-Metal Ions, Cambridge University Press,
Cambridge, 1961.
Ramsey N. F., Nuclear Moments, John Wiley and Sons, New York, 1953. (Имеет-
ся перевод в кн. Экспериментальная ядерная физика, под ред. Э. Сегре,
т. I. — М.: ИЛ, 1955.)
Ramsey N. F., Molecular Beams, Clarendon Press, Oxford, 1956. (Имеется пе-
ревод: Рамзей Н. Молекулярные пучки. — М.: ИЛ, 1960.)
Abragam A., The Principles of Nuclear Magnetism, Clarendon Press, Oxford,
1961. (Имеется перевод: Абрагам А. Ядерный магнетизм. — М.: ИЛ,
1963.)
Bloembergen N., Nuclear Magnetic Relaxation, W. A. Benjamin, New York,
1961.
Roberts I. ?>., Nuclear Magnetic Resonance, McGraw-Hill Book, New York, 1959.
(Имеется перевод: Роберте Дж. Ядерный магнитный резонанс. — М.: ИЛ,
1961.)
Schumacher R. Т., Introduction to Magnetic Resonance, W. A. Benjamin, New
York, 1970.
McLattchlan K. A., Magnetic Resonance, Clarendon Press, Oxford, 1972. (Имеет-
ся перевод: Маклечлан /<. А. Магнитный резонанс. — М.: Химия, 1976.)
Краткая библиография 433
Pake G. Е., Estle Т. L, The Physical Principles of Electron Paramagnetic Reso-
nance, W. A. Benjamin Advanced Book Program, Reading, Mass., 1973.
Abragam A., Bleaney В., Electron Paramagnetic Resonance of Transition Ions,
Clarendon Press, Oxford, 1970. (Имеется перевод: Абрагам А., Блини б'.
Электронный парамагнитный резонанс переходных ионов. — М.: Мнр, т. I,
1972, т. II, 1973.)
Goldman M., Spin Temperature and Nuclear Magnetic Resonance in Solids,
Clarendon Press, Oxford, 1970. (Имеется перевод: Гольдман М. Спиновая
температура и ЯМР в твердых телах. — М.: Мир, 1972.)
КШе1 С., Introduction to Solid State Physics, 5th ed., Wiley and Sons, New
York, 1976. (Имеется перевод: Киттель Ч. Введение в физику твердого те-
ла. — М.: Наука, 1978.)
Poole Ch. P., Jr., Farach H. A., The Theory of Magnetic Resonance, Wiley-ln-
terscience, New York, 1972.
*Таунс Ч., Шаолов А. Радиоспектроскопия. Пер. с англ. — М.: ИЛ, 1959.
*Ингрэм Д. Электронный парамагнитный резонанс в свободных радикалах.
Пер. саигл. —М.: ИЛ, 1961.
*Блюменфельд Л. А., Воеводский В. В., Семенов А. Г. Применение электрон-
ного парамагнитного резонанса в химии. — Новосибирск: Наука, 1962.
*Леше А. Ядерная индукция. Пер. с немец. — М.: ИЛ, 1963.
*Робертс Дж. Введение в анализ спектров ЯМР высокого разрешения. Пер.
с англ. — М.: ИЛ, 1963.
*ЯМР- и ЭПР-спектроскопия. Сб. статей. Пер. с англ. — М.: ИЛ, 1964.
*Слоним И. Я-, Любимов А. Н. Ядерный магнитный резонанс в полимерах. —
М.: Химия, 1966.
*Туров Е. А., Петров М. П. Ядерный магнитный резонанс в ферро- и антифер-
ромагнетиках.— М.: Наука, 1969.
*Робертс Док. Ядерный магнитный резонанс. Пер. с англ. — М.: ИЛ, 1961.
*Людвиг Дж., Вудбери Т. Электронный спиновый резонанс в полупроводни-
ках. Пер. с англ. — М.: Мир, 1964.
*Александров И. В. Теория магнитной релаксации. — М.: Наука, 1975.
*Альтшулер С. А., Козырев Б. М. Электронный парамагнитный резонанс со-
единений промежуточных групп. — 2-е изд. — М.: Наука, 1972.
*Джеффрис К- Динамическая ориентация ядер. Пер. с англ. — М.: Мир, 1965.
*Герсон Ф. Спектроскопия ЭПР высокого разрешения. Пер. с англ. — М.: Мир,
1973.
*Ингрэм Д. Электронный парамагнитный резонанс в биологии. Пер. с англ. —
М.: Мир, 1972.
*Эткинс П., Саймоне М. Спектры ЭПР и строение неорганических радикалов.
Пер. с англ. — М- Мир, 1970.
*Пул Ч. Техника ЭПР-спектроскопии. Пер. с англ. — М.: Мир, 1970.
*Керрингтон А., Мак-Лечлан Э. Магнитный резонанс и его применение в хи-
мии. Пер. с англ. — М.: Мир, 1970.
*1Аейльман, Самойлович М. И. Введение в спектроскопию ЭПР активирован-
ных монокристаллов.—М.: Атомиздат, 1977.
*Винтер Ж- Магнитный резонанс в металлах. — М.: Мир, 1977.
*Метод спиновых меток. Теория и практические приложения метода ЭПР: Сб.
статей. Пер. с англ. — М.: Мир, 1975.
*Вертц Дж., Болтон Дж. Теория и практические приложения метода ЭПР.
Пер. с англ. — М.: Мир, 1975.
*Проблемы магнитного резонанса: Сб. статей, посвященный памяти Е. К. За«
войского. — М.: Наука, 1978.
*Макомбер Дж. Динамика спектроскопических переходов. Пер. с англ. — М.:
Мир, 1979.
*Уо Дж. Новые методы ЯМ.Р в твердых телах. Пер. с англ. — М.: Мир, 1978.
*Салихов К- М., Семенов А. Г., Цветков Ю. Д. Электронное спиновое эхо и
его применение. — М.: Наука, 1976,
434 Краткая библиография
Общая теория магнитного резонанса
Pines D., Slichter С. P., Relaxation Times in Magnetic Resonance, Phys. Rev.,
100, 1014 A955).
Torrey H. C, Bloch Equations with Diffusion Terms, Phys. Rev., 104, 563
A956).
Kubo R., Tomita K, A General Theory of Magnetic Resonance Absorption, Journ.
Phys. Soc. Jap., 9, 888 A954).
Anderson P. W., Weiss P. R., Exchange Narrowing in Paramagnetic Resonance,
Rev. Mod. Phys., 25, 269 A953).
Anderson P. W., A Mathematical Model for the Narrowing of Spectral Lines by
Exchange or Motion, Journ. Phys. Soc. Jap., 9, 316 A9541.
Wangness R. K., Bloch F., The Dynamical Theory of Nuclear Induction, Phys.
Rev., 89, 728 A953).
Bloch F., Dynamical Theory of Nuclear Induction II, Phys. Rev., 102, 104
Redfiela A. C, On the Theory of Relaxation Processes, IBM Journ., 1, 19
A957).
Torrey H. C, Nuclear Spin Relaxation by Translational Diffusion, Phys. Rev.,
92,962 A953).
*Redfield A. C, The Theory Relaxation Processes, в кн. Advances in Magnetic
Resonance, Academic Press, New York, Vol. 1, 1966.
Ядерный магнитный резонанс в металлах
Townes С. Н., Herring С, Knight W. ?>., The Effect of Electronic Paramagne-
tism on Nuclear Magnetic Resonance Frequencies in Metals, Phys. Rev., 77,
852 A950).
Knight W. ?>., Electron Pararnagnetism and Nuclear Magnetic Resonance in Me-
tals, в кн. Solid State Physics, Vol. 2, ed. by Seitz and Turnbull, Academic
Press, New York, 1956, pp. 93—136.
Korringa J., Nuclear Magnetic Relaxation and Resonance Line Shift in Metals,
Physica, 16, 601 A950).
Holcomb D. /¦'., Norberg R. ?., Nuclear Spin Relaxation in Alkali Metals, Phys.
Rev., 98, 1074 A955).
Benedek G., Kushida Т., The Pressure Dependence of the Knight Shift in the
Alkali Metals and Copper, Journ. Phys. Chem. Solids, 5, 241 A958).
*Щеголев И. Ф., Изучение электронной структуры металлов с помощью
ЯМР. —УФН, 1962, т. 78, с. 267.
*Bennett L. H., Watson R. ?., Carter G. С, Relevance of Knight Shift Measure-
ments to the Electronic Density of States, Journ. Res. NBS, 74A, 569 A970).
"Drain L. E., Nuclear Magnetic Resonance in Metals, Metallurgical Reviews,
119, 195 A967).
*Нарат А. Ядерный магнитный резонанс в магнетиках и металлах, в сб. Сверх-
тонкое взаимодействие в твердых телах —М.: Мир, 1970, с. 163—236.
"Weisman 1. D., Swartzendruber L. L, Bennett L. H., Nuclear Resonances in
Metals, в кн. Techniques of Metals Research, Vol. VI, John Wiley, 1973,
part 2, pp. 165—504.
"Carter G. C, Bennett L H., Kahan D. J., Metallic Shifts in NMR, в кн. Prog-
ress in Materials Science, Vol. 20, Pergamon Press, 1977.
Ii-12-связь
Ramsey N. F., Purcell E. M., Interactions between Nuclear Spins in Molecules,
Phys. Rev., 85, 143 A952).
Hahn E. L., Maxwell D. ?., Spin Exho Measurements of Nuclear ,Sp'n Coupling
in Molecules, Phys. Rev., 88, 1070 A952),
Краткая библиография . 435
Gutowsky И. S., McCall D. W., Slichter С. P.. Nuclear Magnetic Resonance
Multiplets in Liquids, Journ. Chem. Phys., 21, 279 A953).
Ramsey N. F., Electron Coupled Interactions Between Nuclear Spins in Mole-
cules, Phys. Rev., 91, 303 A953).
Bloembergen N., Rowland T. J., Nuclear Spin Exchange in Solids: Tl203 and Tl205
Magnetic Resonance in Thallium and Thallic Oxide, Phys. Rev., 97, 1679
A955).
Ruderman M. A., KUtel C, Inderect Exchange Coupling of Nuclear Magnetic
Moments by Conduction Electrons, Phys. Rev., 96, 99 A954).
Yosida K., Magnetic Properties of Cu—Mn Alloys, Phys. Rev., 106, 893 A957).
McConnell H. M., McLean A. D., Reilly C. A., Analysis of Spin-Spin Multiplets
in Nuclear Magnetic Resonance Spectra, Journ. Chern. Phys., 23, 1152 A955).
McConnell H. Л1, Molecular Orbital Approximation to Electron Coupled Inte-
raction between Nuclear Spins, Journ. Chem. Phys., 24, 460 A956).
Anderson W. A., Nuclear Magnetic Resonance Spectra of Some Hydrocarbons
Phys. Rev., 102, 151 A956).
"Barfield M., Grant D. M., Theory of Nuclear Spin — Spin Coupling, в кн. Ad-
vances in Magnetic Resonance, Vol. 1, Academic Press, New York, 1966.
Импульсные методы
Hahn E. L, Spin Echoes, Phys. Rev., 80, 580 A950).
Can H. У., Purcell E. M., Effects of Diffusion on Free Precession in Nuclear
Magnetic Resonance Experiments, Phys. Rev., 94, 630 A954).
'Померанцев Н. М. Явление спиновых эхо н его применение. — УФН, 1958,
т. 65, с. 87.
Второй момент
Broer L J. F., On the Theory of Paramagnetic relaxation, Physica, 10, 801
A943).
Van Vleck J. H., The Dipolar Broadening of Magnetic Resonance Lines in Crys-
tals, Phys. Rev., 74, 1168 A948).
Pake G. E., Nuclear Resonance Absorption in Hydrated Crystals: Fine Struc-
ture of the Proton Line, Journ. Chem. Phys., 16, 327 A948).
Gutowsky H. S., Pake G. E., Nuclear Magnetism in Studies of Molecular Struc-
ture and Rotation in Solids: ammonium Salts, Journ. Chem. Phys., 16, 1164
A948).
Andrew E. R., Eades R. G., A Nuclear Magnetic Resonance Investigation of
Three Solid Benzenes, Proc. Roy. Soc, A218, 537 A953).
Gutowsky H. S., Pake G. E., Structural Investigations by means of Nuclear Mag-
netism II —Hindered Rotation in Solids, Journ. Chem. Phys., 18, 162 A950).
Ядерная поляризация
Overhauser A. W., Polarization of Nuclei in Metals, Phys. Rev., 92, 411 A953).
Carver T. R., Slichter C. P., Experimental Verification of the Overhauser Nuc-
lear Polarization Effect, Phys. Rev., 102, 975 A956).
Abragam A., Overhauser Effect in Nonmetals, Phys. Rev., 98, 1729 A955).
Jeffries С D., Polarization of Nuclei by Resonance Saturation in Paramagnetic
Crystals, Phys. Rev., 106, 164 A957).
Uebersfeld /., Motchane J. L, Erb E., Augementation de la Polarisation Nucleai-
re dans les Liquides et Gaz Adsorbes Sur un Charbon. Extension aux Solides
Contenant des impuretes paramagnetiques, Journ. Phys. Rad., 19, 843 A958).
Abragam A., Proctor W. C, Une nouvelle methode de polarisation dynamique
dcs noyaux atomique dans les solides, Compt. Rend., 246, 2253 A958).
436 Краткая библиография
Jeffries С. ?>., Dynamic Nuclear Polarization, Progress in Cryogenics, Heywood
and Company, London, 1961.
Хуцишвили Г. Р., Спиновая диффузия. — УФН, 1965, т. 87, с. 189.
Webb R. H., Steady-state Nuclear Polarizations via Electronic Transitions, Amer.
Journ. Phys., 29, 428 A961).
*Polenza J., Measurements and Applications of Dynamic Nuclear Polarization,
Advan. Mol. Relaxation Processes, 4, 229 A972).
*Hausser K. H., Stehlik D., Dynamic Nuclear Polarization in Liquids, в кн. Ad-
vances in Magnetic Resonance, Vol. 3, 79 A969).
Квадрупольные эффекты
Pound R. V., Nuclear Electric Quadrupole Interactions in Crystals, Phys. Rev.,
79, 685 A950).
Bloembergen N., Report of the Conference on Defects in Crystalline Solids,
Phys. Soc, 7, 1 A955).
Rowland T. J., Nuclear Magnetic Resonance in Copper Alloys. Electron Distribu-
tion around Solute Atoms, Phys. Rev., 119, 900 A960).
Kohn W., Vosko S. H., Theory of Nuclear Resonance Intensity in Dilute Al-
loys, Phys. Rev., 119, 912 A960).
Das T. P., Pomerantz M., Nuclear Quadrupole Interaction in Pure Metals, Phys.
Rev., 123,2070 A961).
Kushida Т., Benedek C, Bloembergen N., Dependence of Pure Quadrupole Re-
sonance Frequence on Pressure and Temperature, Phys. Rev., 104, 1364 A956).
*Гречишкин В. С. Ядерные квадрупольные взаимодействия в твердых телах. —
М.: Наука, 1973.
Химические сдвиги
Proctor W. G., Yu F. С, The Dependence of a Nuclear Magnetic Resonance Fre-
quency upon Chemical Compound, Phys. Rev., 77, 717 A950).
Diskinson W. C, Dependence of the F1' Nuclear Resonance Position on Chemi-
cal Compound, Phys. Rev., 77, 736 A950).
Gutowsky H. S., Hoffman C. J., Chemical Shifts in the Magnetic Resonance of
P9, Phys. Rev., 80, 110 A950).
Ramsey E. F., Magnetic Shielding of Nuclei in Molecules, Phys. Rev., 78, 699
A950).
Ramsey N. F., Chemical Effects in Nuclear Magnetic Resonance and in Diamag-
netic Susceptibility, Phys. Rev., 86, 243 A952).
Saika A., Slichter С P., A Note on the Fluorine Resonance Shifts, Journ. Chem.
Phys., 22, 26 A954).
Pople J. A., The Theory of Chemical Shifts in Nuclear Magnetic Resonance. I —
Induced Current Densities, Proc. Roy. Soc, A239, 541 A957).
Pople J. A., The Theory of Chemical Shifts in Nuclear Magnetic Resonance. II —
Interpretation of Proton Shifts, Proc. Roy. Soc, A239, 550 A957).
McConnell H. M., Theory of Nuclear Magnetic Shielding in Molecules. I —
Long Range Dipolar Shielding of Protons, Journ. Chem. Phys., 27, 226 A957).
Freeman R., Murray C, Richards R., Cobalt Nuclear Resonance Spectra, Proc.
Roy. Soc, A242, 455 A957).
*Musher J. I., Theory of the Chemical Shift, в кн. Advances Magnetic Resonan-
ce, Vol. 2, Academic Press, New York, 1967.
Спиновая температура
Bloembergen N.. On the Interaction of Nuclear Spins in a Crystalline Lattice,
Physica, 15.386 A949).
Purcell E., Pound R. V., A Nuclear Spin System at Negative Temperature,
Phys. Rev., SI, 279 A951).
Краткая библиография 437
Abragam A., Proctor W. I., Experiments on Spin Temperature, Phys. Rev.,
106, 160 A957).
Abragam A., Proctor W. G., Spin Temperature, Phys. Rev., 109, 1441 A958).
Redfield A. C, Nuclear Magnetic Resonance Saturation and Rotary Saturation
in Solids, Phys. Rev., 98, 1787 A955).
Redfield A. C, Nuclear Spin-Lattice Relaxation Time in Copper and Aluminum,
Phys. Rev., 101, 67 A956).
Van Vleck J. H., The Physical Meaning of Adiabatic Magnetic Susceptibilities,
Zs. Phys. Chem. Neue Folge, 16, 358 A958).
Van Vleck J. H., The Concept of Temperature in Magnetism. II Nouvo Cimento,
Suppl. 6, Ser. X, 1081 A957).
Slichter C. P., Honlton W. C, Adiabatic Demagnetization in a Rotating Refe-
rence System, Phys. Rev., 122, 1701 A961).
Anderson A. G., Redfield A. G., Nuclear Spin-Lattice Relaxation in Metals, Phys.
Rev., 116, 583 A959).
Hebel L. C, Slichter C. P., Nuclear Spin Relaxation in Normal and Supercon-
ducting Aluminum, Phys. Rev., 113, 1504 A959).
Anderson A., Nonresonant Nuclear Spin Absorption in Li, Na and Al, Phys.
Rev-, 115, 863 A959).
Hebel L. C, Jr., Spin Temperature and Nuclear Relaxation in Solids, Vol. 15,
в кн. Solid State Physics, Academic Press, New York, 1963.
*Ацаркин В. А., Родак М. И., Температура спин-спиновых взаимодействий в
электронном парамагнитном резонансе, УФН, 107, 3 A972).
*Jeener J., Thermodinamics of Spin Systems in Solids, в кн. Advances in
Magnetic Resonance, Vol. 3, pp. 205—310, 1968.
*Redfield A. C, Nuclear Spin Thermodinamics in the Rotating Frame, Science,
164, 1015 A969).
Химический обмен
Gutowsky H. S., Saika A., Dissociation, Chemical Exchange and the Proton
Magnetic Resonance in Some Aqueous Electrolytes, Journ. Chem. Phys., 21,
1688 A953).
Arnold J. Т., Magnetic Resonances of Protons in Ethyl Alcohol, Phys. Rev., 102,
136 A956).
Kubo R., Note on the Stochastic Theory of Resonance Absorption, Journ. Phys.
Soc. Jap., 9, 935 A954).
McConnell H. M., Reaction Rates by Nuclear Magnetic Resonances, Journ. Chem.
Phys., 28, 430 A958).
Meiboom S., Luz Z., Gill D., Proton Relaxation in Water, Journ. Chem. Phys.,
27, 1411 A957).
*Johuson Ch. J., Jr., Chemical Rate Processes and Magnetic Resonance, в кн.
Advances in Magnetic Resonance, Vol. 1, 1966.
*3амараев К. И., Молин Ю. Н., Салихов К. М. Спиновый обмен. — Новоси-
бирск: Наука, 1977.
Кросс-релаксация
Bloembergen N., Shapiro S., Pershan P. S., Artman J. O., Cross-Relaxation in
Spin Systems, Phys. Rev., 114, 445 A959).
Pershan P. S., Cross Relaxation in LiF, Phys. Rev., 117, 109 A960).
Электронный спиновый резонанс
в парамагнитных системах
Bleaney В., Stevens К- W. H., Paramagnetic Resonance, Rep. Progr. Phys.,
16, 108 A953).
Castner T. G., Kanzig W., The Electronic Structure of V-Centers, Journ. Phys.
Chem. Solids, 3, 178 A957).
438 Краткая библиография
Watkins G. D., Electron Spin Resonance of Mn++ in Alkali Chlorides: Asso-
ciation with Vacancies and Impurities, Phys. Rev., 113, 79 A959).
Watkins G. ?>., Motion of Mn++-Cation Vacancy Paris in NaCl: Study by Elec-
tron Spin Resonance and Dielectric Loss, Phys. Rev., 113, 91 A959).
Feher G., Observation of Nuclear Magnetic Resonances via the Electron Spin
Resonance Line, Phys. Rev., 103, 834 A956).
Feher G., Electronic Structure of F Centers in KC1 by the Electron Spin Double
Resonance Technique, Phys. Rev., 105, 1122 A957).
Feher G., Electron Spin Resonance Experiments on Donors in Silicon. I —
Electronic Structure of Donors by the Electron Nuclear Double Resonance
Technique, Phys. Rev., 114, 1219 A959).
Woodbury H. H., Ludwig G. W., Spin Resonance of Transition Metals in Sili-
con, Phys. Rev., 117, 102 A960)
Kip A. F., Kittel C, Levy R. A., Partis A. M., Electronic Structure of F Cen-
ters: Hyperfine Interactions in Electron Spin Resonance, Phys. Rev., 91, 1066
A953).
Delbecq C. J., Smaller В., Yuster P. H., Optical Absorption of Clif Molecule-
Ions in Irradiated Potassium Chloride, Phys. Rev., Ill, 1235 A958).
Weger M., Passage Effects in Paramagnetic Resonance Experiments, Bell. Syst.
Techn. Journ., 39, 1013 (I960) (Monograph 3663).
Feher G., Kip A. F., Electron Spin Resonance Absorption in Metals. I. — Expe-
rimental, Phys. Rev., 98, 337 A955).
*Schultz Sh., Microwave Resonances in Metals, в кн. Techniques of Metal Re-
search, Vol. VI, part 1, pp. 337—408, 1972.
*Сорин Л. А., Власова М. В., Левандовский В. Д. Введение в радиоспектро-
скопию парамагнитных монокристаллов. — Киев: Наукова Думка, 1969.
*Электроннын спиновый резонанс в полупроводниках. Сб. статей. Пер. с
англ. — М.: ИЛ, 1962.
Ядерный резонанс в ферромагнетиках
Portis A. M., Gossard А. С, Nuclear Resonance in Ferromagnetic Cobalt, Journ
Appl. Phys., 31, 205S A960).
Marshall W., Orientation of Nuclei in Ferromagnetics, Phys.. Rev., 110, 1280
A958).
Watson R. E., Freeman A. I., Origin of Effective Fields in Magnetic Materials,
Phys., Rev., 123,2027 A961).
Benedek G., Armstrong J., The Pressure and Temperature Dependence of the
Fe57 Nuclear Magnetic Resonance Frequency in Ferromagnetic Iron, Journ.
Al Ph 32 1965 A961)
g
Appl. Phys., 32, 1965 A961).
eller P., Bdk G Nl
pp y, , ()
Heller P., Benedek G., Nuclear Magnetic Resonance in MnF2 near the Critical
Point, Phys. Rev. Lett 8, 428 A962).
*Сверхтонкне взаимодействия в твердых телах: Сб. статей. Пер. с англ. — М.:
1970.
Ядерный резонанс в парамагнитных
и антиферромагнитных веществах
Bloembergen N., Fine Structure of the Magnetic Resonance Line of Protons in
CuSO4-5H2O, Physica, 16, 95 A950).
Poulis N. J., Handeman G. E. G., The Temperature Dependence of the Sponta-
neous Magnetization in an Antiferromagnetic Single Crystal, Physica, 19, 391
A953).
Shulman R. G., laccarino V., Nuclear Magnetic Resonance in Paramagnetic
MnF2, Phys. Rev., 108, 1219 A957).
Краткая библиография 439
Jaccarino N., Shulman R. С, Observation of Nuclear Magnetic Resonance in
Antiferromagnetic MnF2, Phys. Rev., 107, 1196 A957).
Benedek C, Kushida Т., Phys. Rev., 118, 46 A960).
Marshall №.. Stuart R. JV, Theory of Transition Ion Complexes, Phys. Rev., 123,
2048 A961).
*Антиферромагнетизм: Сб. статей. Пер. с англ. — М.: ИЛ, 1956.
Ферромагнитный резонанс
Lax В., Button К-, Microwave Ferrites and Ferrimagnetics, McGraw-Hill Book,
New York, 1962. (Имеется перевод: Лаке Б., Баттон К. Сверхвысокочастот-
ные ферриты и феррнмагнетики.—М.: Мнр, 1965.)
*Ферромагнитный резонанс: Сб. статей. Пер. с англ. — М.: ИЛ, 1952.
*Ферромагннтный резонанс: Сб. статей. — М.: Физматгнз, 1961.
*Гуревич А. Г. Магнитный резонанс в ферритах и антнферромагнетнках. — М.:
Наука, 1973.
*Саланский Н. М., Ерухимов М. Щ. Физические свойства и применение маг-
нитных пленок. — Новосибирск: Наука.
Методы фурье-спектроскопии ЯМР
Ernst R. R., Anderson W. A., Application of Fourier Transform Spectroscopy to
Magnetic Resonance, Rev. Sci. Instr., 37, 93 A966).
Farrar T. C, Becker E. ?>., Pulse and Fourier Trasform NMR, Academic Press,
New York, 1971. (Имеется перевод: Фаррар Т., Беккер Э. Импульсная и
фурье-спектроскопия ЯМР. — М.. Мир, 1973.)
*Мпйеп К., Pregosin P S., Fourier Transform NMR Techniques: A Practical Ap-
proach, Academic Press, London, 1976.
*Show D., Fourier Transform NMR Spectroscopy, Elsevier Amsterdam, 1976.
Двойкой резонанс в твердых телах
Hartmann S. R., Hahn E. L., Nuclear Double Resonance in the Rotating Frame,
Phys. Rev., 128, 2042 A962).
Lurie F. M., Slichter C. P., Spin Temperature in Nuclear Double Resonance,
Phys. Rev., 133, АП08 A964)
Slusher R. E., Hahn E. L., Sensitive Detection of Nuclear Quadrupole Interac-
tions in Solids, Phys. Rev., 166, 332 A968).
Redfield A. G., Pure Nuclear Electric Quadrupole Resonance in Impure Copper,
Phys. Rev., 130, 589 A963).
Kaplan D. ?., Hahn E. L., Experience de Double Irradiation en Resonance Mag-
netique par la Methode d'lmpulsions, Journ. Phys. Rad., 19, 821 A958).
*Schmid ?>., Nuclear Magnetic Double Resonance—Principles and Applications
in Solid-State Physics, в кн. Springer Tracts in Modern Physics, Vol. 68, Ber-
lin, 1973, pp. 1—75.
Двойкой резонанс в жидкостях
Bloch F., Recent Developments in Nuclear Induction, Phys. Rev., 93, 944 П954).
Royden V., Measurement of the Spin and Gyromagnetic Ratio of C13 by the Col-
lapse of Spin-Spin Splitting, Phys. Rev., 96, 543 A954).
Bloom A. L., Schoolery J. N., Effects of Perturbing Radiofrequency Fields on
Nuclear Spin Coupling, Phys. Rev., 97, 1261 A955).
440 Краткая библиография
Аие W. P., Bartholdi ?., Ernst R. R., Two-Dimensional Spectroscopy: Applica-
tion to Nuclear Magnetic Resonance, Journ. Chem. Phys., 64, 2299 A976).
*Липмаа Э. Т. Ядерный магнитный двойной резонанс. — Ж. структ. хим., 1967,
8, с. 717.
Мазеры и лазеры
Gordon J. P., Zeiger H. J., Townes С. И., Molecular Microwave Oscillator and
New Hyperfine Structure in the Microwave Spectrum of NH3, Phys. Rev., 95,
282 A954); 99, 1264 A955).
Bloembergen N., Proposal for a New Type Solid State Maser, Phys. Rev., 104,
324 A956).
*Басов Н. Г., Прохоров А. М. Предложения о квантовом усилителе и генера-
торе, трехуровневый пучковый газовый квантовый генератор. — ЖЭТФ,
1954, 27, с. 431; 1955, 28, с. 249; УФН, 1955, 57, с. 485.
*3ингер Дж. Мазеры. Квантовые усилители и генераторы. — М.: ИЛ, 1961.
*Троуп Г. Квантовые усилители и генераторы. — М.: ИЛ, 1961.
*Ораевский А. Н. Молекулярные генераторы. — М.: Наука, 1964.
*Беннет В. Газовые лазеры. — М.: Мир, 1964.
*Хивенс О. Лазеры на твердых веществах. — М.: Мир, 1964.
*Климонтович ГО. Л. Квантовые генераторы света и нелинейная оптика. — М.:
Наука, 1966.
*Мэйтлэнд А., Данн М. Введение в физику лазеров. — М.: Наука, 1978.
*3велто О. Физика лазеров. — М.: Мир, 1979.
Медленное молекулярное движение
Slichter С. P., Ailion D. С, Low-Field Relaxation and the Study of Ultraslow
Atomic Motions by Magnetic Resonance, Phys. Rev., 135, A1099 A964).
Ailion D. C, Slichter С. P., Observation of Ultra-Slow Translational Diffusion
in Metallic Lithium by Magnetic Resonance, Phys. Rev., 137, A235 A965).
Look D. C, Lowe I. J., Nuclear Magnetic Dipole-Dipole Relaxation along the
Static and Rotating Magnetic Fields: Application to Gypsum, Journ. Chem.
Phys., 44,2995 A966).
*Ailion D. C, NMR and Ultraslow Motions, в кн. Advances in Magnetic Reso-
nance, Vol. 5, Academic Press, New York, 1971, pp. 177—227.
Двойной электронно-ядерный резонанс
Feher С, Electronic Structure of F Centers in KC1 by the Electron Spin Double
Resonance Technique, Phys. Rev., 105, 1122 A957).
Seidell H., Wolf H. С, в кн. Physics of Color Centers, ed. by W. Beall Fow-
ler, Academic Press, New York, 1968.
Импульсное сужение линий ЯМР
Waugh J. S., Huber L M., Haeberlen U., Approach to High-Resoiuiion NMR in
Solids, Phys. Rev., 20, 180 A968).
Haeberlen U., Waugh J. S., Coherent Averaging Effects in Magnetic Resonance,
Phys. Rev., 175, 453 A968).
Mansfield P., Symmetrized Pulse Sequences in High Resolution NMR in Solids,
Journ. Phys., C4, 1444 A971).
Mansfield P., Orchard M. J., Stalker D. C, Richards К. И. В., Symmetrized
Multipulse Nuclear-Magnetic-Resonance Experiments in SoJids: Measurement
of the Chemical Shift Shielding Tensor in Some Compounds, Phys. Rev., B7,
90 A973).
Краткая библиография 441
Rhim W. К., Elleman D. D., Vaughan R. W., Analysis of Multiple Pulse NMR
in Solids, Journ Chem. Phys, 59, 3740 A973).
Rhim W. K., Elleman D. D., Schrelber L В., Vaughan R. W., Analysis of Mul-
tiple Pulse NMR in Solids, II. Journ. Chem. Phys., 60, 4595 A974).
Mehrlng M., High Resolution NMR Spectroscopy in Solids в кн. NMR: Basic
Principles and Progress, Vol. 11, ed. P. Diehl, E. Fluck, R. Kosfeld, Berlin,
Heidelberg, New York, 1976. (Имеется перевод в книге: Хеберлен У., Ме-
ринг М. ЯМР высокого разрешения в твердых телах. — М.: Мир, 1980.)
Haeberlen V., High Resolution NMR in Solids: Selective Averaging; Suppl. 1
to Advances in Magnetic Resonance, Academic Press, New York, 1976.
(Имеется перевод в книге: Хеберлен У., Меринг М. ЯМР высокого разре-
шения в твердых телах. — М.: Мир, 1980.)
Именной указатель
Абрагам (Abragam) 258
Андерсон A. (Anderson A.) 268
Андерсон П. (Anderson P.) 419
Арчер (Archer) 419
Басов Н. Г. 263. 264
Бломберген (Bloembergen) 145, 131, IS3,
264, 276, 280
Блох (Bloch) 19. 193, 266
Влум (Bloom) 266
Бойс (Воусе) 265
Бом (Bohm) 126
Валер (Waller) 215
Вангснесс (Wangsness) 193
Ван Флек (Van Vleck) 24, 228. 419
Ван Хек (Van Hecke} 311
Воэн (Vaguhan) 281, 293, 311
Гнлл (GUI) 292
Гобсон (Hobson) 60
Гортер (Gorter) 167
Госсард (Gossard) 141
Гутовский (Gutowsky) 68, 142, 154. 419, 422
Делбек (Delbecq) 358
Джеффрис (Jeffries) 258
Дю-Пре (Du Ргё) 215
Идее (Eades) 87
Иоснда (Yoslda) 145
Пагшс (Pines) 126. 138
Пакард (Packard) 19
Паунд (Pound) 18, 193. 227
Пейк (Pake) 68
Пёрселл (Purcell) 18, 144, 193. 227, 281. 316,
428
Попл (Pople) 114
Портис (PortlS) 141
Провоторов Б. Н. 237
Прохоров А. М. 263, 264
Райтер (Ryter) 136
Редфнлд (Redfield) 193, 215, 229, 268
Ройден (Royden) 266
Роуз (Rose) 321
Роуланд (Rowland) 154
Рэмсн (Ramsey) 99, 117, 144, 316
Сеймур (Seymour) 210
Сеш (Sachs) 267
Слашер (Slusher) 268
Слнктер (Slichter) 52, 136, 137, 245
Смит (Smith) 316
Смоллер (Smaller) 358
Сорокин (Sorokin) 276, 280
Спокас (Spokas) 52
Сэйка (Salka) 422
Танер (Turner) 267
Таунс (Townes) 263
Томнта (Tomlta) 58
Торрн (Тоггеу) 18, 424
Казимнр (Caslmlr) 215
Каплан (Kaplan) 265
Карвер (Carver) 248
Карр (Сагг) 281. 428
Кастнер (Castner) 358
Кенциг (Kanzlg) 358
Кнттель (КШе1) 145
Кон (Kohn) 136
Коррннга (Korringa) 174
Кьелдас (KJeldaas) 136
Лурье (Lurie) 277, 278
Лэмб (Lamb) 112
Мак-Колл (McCall) 142
Мак Конелл (McConnell) 419
Максвелл (Maxwell) 142
Маршалл (Marshall) 141
Мейбум (Melboom) 281
Менсфилд (Mansfield) 288. 293
Мнни (Mlnler) 268
Уо (Waugh) 281, 293, 313
Фернелиус (Fernelius) 268
Фехер (Feher) 260
Фрелнх (Frdhlich) 145
Хан (Hahn) 49, 142, 265, 268. 278, 419
Хансен (Hausen) 19
Хартман (Hartman) 268, 278
Хебел (Hebel) 267
Хеберлен (Haeberlen) 313
Холкомб (Holcomb) 52
Холм (Holm) 419
Холтон (Holton) 217, 232
Хубер (Huber) 313
Штернхаймер (Sternheimer) 334
Шулери (Schoolery) 266
Шумахер (Schumacher) 136, 137, 238
Набарро (Nabarro) 145
Норберг (Norbere) 52
Оверхаузер (Overhauser) 247, 248, 2Б4—258.
263
Эйлиои (Aillon) 245
Эндрю (Andrew) 87
Эрб (Erb) 258
Юстер (Yuster) 358
Предметный указатель
Векторный потенциал A(R) 366
Вероятность заселения уровней 255
— термически индуцированного перехода
Взаимодействие дипольное 75, 155
— квадрупольное 330, 349
— спии-орбитальное 337—350, 363, 365, 371,
374. 383
одноэлектронное 380
пример 338—350
— Ферми 261
— электронно-ядерное 252
— электронных спинов 118—124
— ядерного момента с орбитальным мо-
ментом электрона 383
— со спиновым моментом электрона
В СОСТОЯНИЯХ, ОТЛИЧНЫХ ОТ S-СОСТОЯНИя
384
в s-состоянии 284
Взаимодействия магнитные ядер с элек-
тронами 93—159
Внешнее переменное поле, влияние 210—214
Восприимчивость 404—408
— действительная часть 54—63
•— значения 138
— магнитная 113
— мнимая часть 54—63
Время жизни спина 297
— корреляции 189, 192
V-центры 358—384
Уй-центры в КС1 359
Гамильтониан II, 127, 157, 177, 250, 261,
274, 303, 329, 339, 342, 343, 353, 355, 356,
382
— диполь-дипольного взаимодействия 70,
252, 273
— для Двух магнитных диполей 118
— зеемаиовский 71, 93
— квадрупольного взаимодействия 325—329
— спиновый 343
— электронный 337
— эффективный 349
Гамильтонианы дипольные 276
Гиромагнитное отношение 338
Градиентное поле, вычисление 332—334
g-фактор 344
— Ланде 348
— расчет сдвига 345
Движение магнитного момента 40
— невзаимодействующих спинов 20—68
Диамагнитный вклад в магнитный ыо-
меит 113
— ток 109
Дисперсия 63—68
б-функция Дирака 121
Диффузия 288. 290
— в неоднородных магнитных полях 424—
428
Закон Больцмана 64
— Кюрн 181. 286
— сохранения энергии 354
Замораживание орбитального движения
95-99
Запрещенные переходы 258—260
Зеемановскне уровни 71
— члены гамильтониана 276
Импульса длительность 312
Импульсное сужение линий 293—296
наблюдение 305—310
— формальное описание 297—305
Импульсные последовательности 310—313
Инверсия адиабатическая 36
Калибровочное преобразование 100
Квантовые числа 360
Константа спин-орбитального взаимодей-
ствия 339
Коэффициент антиэкранирования Штерн-
хаймера 334
Коэффициенты Клебша — Гордана 319—
3^5, 350
Кристаллические поля 338—350
Критические поля 338—350
Лореицевы линии 48
Магнетон Бора 333
Магнитное дипольное уширеиие линий
69—92
Магнитные поля сильные 329—334
слабые 339—334
Мазер трехуровневый Бломбергена 263, 264
Мазеры 15
Матрица гамильтониана 411
— Паули 122
— плотности 175—193, 199, 211, 277
Метод Бома — Пайнса 138
— Карра — Пёрселла 288
— Лондона 114
— матрицы плотности 175
— Мейбума — Гилла 291. 292
— моментов 76—87. 92
— Хана 271—274
Методы двойного резонанса 265—268
— приближенные 115
Множители Больцмана 179
Модуляция фазы 312
Молекулы ClJ 359
Молекулярные движения 160—214, 293—296,
418-424
орбиты иона молекулы галогена 364
Момент квадрупольный ядра 327, 384
— магнитный 338
— — спиновый 338
электронов 103
--ядра 119,, 121
— парамагнитный 115
Найювский сдвиг 124—141
Насыщение запрещенного иерехода
444
Предметный указатель
Обменное сужение линии 155
Операторы унитарные 300
— экспоненциальные 36—40
— эрмитовы 176, 197
Отклик -системы переходный 54—63
стационарный 54—63
Отношение Больцмана 256
Парамагнитный вклад в магнитный момент
ИЗ
— момент 115
Плотность тока 101
вычисление 104—118
Поверхность Фермн 146, 153, 170
Поглощение, зависимость от частоты 75
— электронное резонансное 354
— энергии 13—19
Поляризация остова 141
— ядер 258—260
Li7 динамическая 249
Последовательность Карра — Пёрселла
288—291
— HW-8 312, 313
— REV-8 312, 313
— WAHUHA 312. 313
Постоянная Больцмана 277
— диффузии 425
— электронно-ядерного взаимодействия 252
Преобразование Фурье 187, 310, 406
Приближение высокотемпературное 415—418
Принцип Паулн 147, 160
Проблема чувствительности 268—271
Резонанс двойной 247—296
спинового эха (ДРСЭ) 265, 266
типа Оверхаузера — Паунда 247—250
электронио-ядерный 260—263
— магнитный 293—296
импульсный 289—313
понятие 9—19
— электронный спиновый 335—382
Резонансная кривая 155
Резонансные частоты 251
Релаксационные переходы 253—254
Релаксация системы 161
— ядерная в металле 167—174
РЧ-нмпульсы 293
— мощность 312
— поле 311. 312
Ряд Тейлора 316
Связь косвенная ядерная 142—159
— орбитального момента электрона с Но
383
— ядерного квадрупольного момента с
градиентом поля 384
Сдвиг g-фактора 344, 362, 363. 368, 373, 379,
410
Сигнал ЯМР, наблюдение 307
Соотношение Коррннгн 173
— Крамерса — Кроннга 61, 137
Состояние возбужденное, образование 375
— молекулы сннглетное 158
трнплетное 158
— Vfo -центра 379
Спектр протонного магнитного резонанса
319
— резонанса V/; центров в КС1 359
— ядерного резонанса 355
— F» 142
— PJI 142
Спнн, квантовомеханнческое описание в
постоянном поле 22—27
Спиновая температура 161—167, 215—246
Спиновое эхо 49—54, 265
Спин-решеточная релаксация 13—19.
160—214
Статистика Бозе — Эйнштейна 162
— Максвелла — Больцмана 162
— Ферми — Дирака 1S2
Структура сверхтонкая 351—358
Сужение линии ЯМР 293
— линий 160—214
Схема Фехера наблюдения ядерного
зонанса 262
53.
ре-
Тензорные операторы 319—325
Теорема Внгнера — Эккарта 10, 319—326.
347, 349, 350, 378
— Кошн 61
— Крамерса 331, 350
— Крамерса — Кронига 59
— Лнувилля 178
— об экспоненциальных операторах 403,
— следующая из теории возмущений 410—
414
Теория Блоха — Вангснесса — Редфнлда
193—200
— возмущений 410
— поглощения микроскопическая 63—68
— Редфнлда, применение 200—210
— резонанса 11—13
Ток в молекулярном комплексе 374
Уравнение движения для средних значе-
ннй (»х), (»„), (»г) 27-29
— Дирака 122, 365
— диффузное 424
— Лапласа 317
— основное теории Редфнлда 193
вывод 195
— Пуассона 318
— Шредннгера 22, 28. 40, 41, 101, 102, 275,
300. 301
Уравнения Блоха 42—44, 195, 203. 205, 206.
212-214, 418. 420. 425
— — решение 45—48
— Редфнлда 209
Уровни энергетические 250—254
диаграмма 252
— эпергнн двух одинаковых спннов 72
р-состояннй 340
Условие Коши 59
— Хана 272, 284
Условия Хана и Хартмана 268
Уширеиие несекулярное 208, 209
— секулярное 208
Фазы чередования 2911, 292
Ферми-газ 173
Флюктуирующее поле 208, 209
Формула Внгнера 138
— Ланжевена — Дебая 81
Функции Блоха 129, 160
— спиновые электронные 353
ядерные 353
— Фермн 151. 170
Функция волновая электрона 129
— корреляции 409
— Лагранжа 100
— Ферми 131
Предметный указатель
445
Химические сдвиги 99, 112, 341, 423
— — формальная теория 99—104
— — экспериментальные данные 94, 95
Химический обмен 424, 437
Частота ларморовская 22, 202, 416
— ядерного резонанса 252
Элементарная ячейка кристалла бензола
88
Энергия 284—286
— возмущения 102
— дипольная 296
— зеемановская 71, 343, 355
орбитальная 365
спинов 280, 285
• электронного спина 383
ядерная 355, 384
— магнитная 296
— Ферми 134, 152
Энергия электрона кинетическая 383
— — потенциальная в поле ядра и других
электронов 383
_ _ _ создаваемая внешними по отно-
шению к атому зарядами 383
Энтропия 284—286
Эффект динамической поляризации 248
— Зеемана 344, 348
— Оверхаузера 136, 249, 254—258, 288
— Оверхаузера ~- Паунда 250, 263
— спин-орбитальной связи 343
— Фрелиха — Набарро 145, 157
— Штернхаймера 334
Эффекты второго порядка 142—159
— изменения частоты прецессии 418—424
— электрические квадрупольные 315—332
— ядерные 354, 355
Ядерный магнитный резонанс, применение
418-424
•— спнн 258
Оглавление
Предисловие редактора перевода g
Предисловие автора ко второму исправленному изданию 7
Предисловие автора ко второму изданию g
Глава 1. Понятие о магнитном резонансе g
§ 1. Введение 9
§ 2. Элементарная теория резонанса И
§ 3. Поглощение энергии и спии-решеточная релаксация ... 13
Литература 19
Глава 2. Основы теории . . 20
§ 1. Движение невзаимодействующих сшшов. Классическое
рассмотрение 20
§ 2. Квантовомеханическое описание спина в постоянном поле 22
§ 3. Уравнения движения для средних значений . . ... . .27
§ 4. Эффекты, связанные с переменными магнитными полями 30
§ 5. Экспоненциальные операторы 36
§ 6. Квантовомеханическое рассмотрение движения магнитного
момента во вращающемся магшпномполе 40
§ 7. Уравнения Блоха 42
§ 8. Решение уравнений Блоха в случае малых Hi .... 46
§ 9. Спиновое эхо 49
§ Ю.Соотношения между переходным и стационарным откли-
ками системы и между действительной и мнимой частями
восприимчивости 54
§ 11. Микроскопическая теория поглощения и дисперсии ... 63
Литература 68
Глава 3. Магнитное дипольиое уширеиие резонансных линий в жесткой
решетке 69
§ 1. Введение 69
§ 2. Основное взаимодействие ™
§ 3. Метод моментов '6
§ 4. Пример применения вторых моментов °?
Литература °*
Глава 4. Магнитные взаимодействия ядер с электронами 93
§ 1. Введение •**
§ 2. Экспериментальные данные по химическим едзигам . . • ¦**
§ 3. Замораживание орбитального движения jj~
§ 4. Формальная теория химических сдвигов •*¦*
§ 5. Вычисление плотности тока |~*
§ 6. Взаимодействие электронных спинов |~
§ 7. Наитовскнй сдвиг {^*
| 8. Эффекты второго порядка. Косвенная ядерная связь . . • ™
Литература 1ав
Оглавление 447
Глава 5. Спин-решеточная релаксация и сужение линий, обусловленное
молекулярным движением 160
§ 1. Введение 160
§ 2. Релаксация системы, описываемой спиновой температурой 161
§ 3. Ядерная релаксация в металле 167
§ 4. Матрица плотности. Общие соотношения 175
§ 5. Матрица плотности. Пример 183
§ 6. Теория Блоха — Вангснесса — Редфилда 193
§ 7. Пример применения теории Редфплда 200
§ 8. Влияние внешнего переменного поля 210
Литература 214
Глава 6. Спиновая температура в магнетизме и магнитном резонансе . .215
§ 1. Введение 215
§ 2. Следствия из уравнений Блоха 216
§ 3. Понятие спиновой температуры в лабораторной системе
координат в отсутствие переменных магнитных полей . 217
§ 4. Адиабатическое и быстрое изменения магнитного поля 220
§ 5. Магнитный резонанс и насыщение 228
§ 6. Теория Редфнлда в пренебрежении спин-решеточным
взаимодействием 232
§ 7. Приближение к равновесию в слабом РЧ-поле Hi . . . 237
§ 8. Условия справедливости гипотезы Редфилда 240
§ 9. Влияние спин-решеточной релаксации 240
§ 10. Спиновый захват (спин-локинг). Время спин-регаеточной
релаксации во вращающейся системе координат Т]р. Мед-
ленное движение 243
Литература 246
Глава 7. Двойной резонанс 247
§ 1. Для чего выполняются эксперименты по двойному резо-
нансу? 247
§ 2. Особенности двойного резонанса типа Оверхаузера —
Паунда 247
§ 3. Энергетические уровни и переходы между ними в модель-
ной системе 250
§ 4. Эффект Оверхаузера 254
§ 5. Поляризация ядер при насыщении запрещенных переходов 258
§ 6. Двойной электронно-ядерный резонанс (ДЭЯР) .... 260
§ 7. Трехуровневый мазер Бломбергена 263
§ 8. Беглый обзор других интересных методов двойного ре-
зонанса 265
§ 9. Проблема чувствительности 268
§ 10. Метод Хана 271
§ 11. Квантовомеханическое описание 274
§ 12. Цикл смешивания и его уравнения 278
§ 13. Энергия и энтропия 284
Литература 286
Глава 8. Новые идеи в импульсном магнитном резонансе 288
§ 1. Введение 288
§ 2. Последовательность Карра — Пёрселла 288
§ 3. Чередование фазы и метод Мейбума — Гнлла 291
448 Оглавление
§ 4. Связь импульсного сужения линии магнитного резонанса
с сужением линии, обусловленным молекулярным движе-
нием 293
§ 5. Формальное описание импульсного сужения линии . . . 297
§ 6. Наблюдение импульсного сужения линии 305
§ 7. Практические импульсные последовательности ..... 310
Литература 313
Глава 9. Электрические квадрупольные эффекты 315
§ 1. Введение 315
§ 2. Гамильтониан квадрупольного взаимодействия (часть 1) 316
§ 3. Коэффициенты Клебша — Гордана, неприводимые тензорные
операторы и теорема Внгнера — Эккарта 319
§ 4. Гамильтониан квадрупольного взаимодействия (часть 2) . 326
§ 5. Случаи сильного и слабого магнитных полей 329
§ 6. Вычисление градиентов поля 332
Литература 334
Глава 10. Электронный спиновый резонанс 335
§ 1. Введение 335
§ 2. Пример спин-орбитального взаимодействия и кристалли-
ческих полей 338
§ 3. Сверхтонкая структура 351
§ 4. V/t-центры 358
Литература 382
Глава 11. Заключение 383
Задачи 385
Приложения 403
A. Теорема об экспоненциальных операторах 403
Б. Некоторые новые выражения для восприимчивости . . . 404
B. Вывод функции корреляции для поля, случайным образом
принимающего значения ±hB 409
Г. Теорема, следующая из теории возмущений 410
Д. Высокотемпературное приближение 415
Е. Эффекты изменения частоты прецессии. Применение ЯМР
для изучения молекулярных движений 418
Ж. Диффузия в неоднородных магнитных полях 424
3. Соотношение между единицами гауссовой системы н СИ .
Краткая библиография 429
Именной указатель 441
Предметный указатель , 442