,	С. А. ГОРБАТЕНКО
МЕХАНИКА	8. М. МАКАШОВ
Р	т	л	Ю.Ф. ПОЛУШКИН
ООП	Е	Т	А	Л. В, ШЕФТЕЛь

с. А. ГОРБАТЕНКО, Э. М. МАКАШОВ,
Ю. Ф. ПОЛУШКИН, Л. В. ШЕФТЕЛЬ
МЕХАНИКА ПОЛЕТА
(ОБЩИЕ СВЕДЕНИЯ. УРАВНЕНИЯ ДВИЖЕНИЯ)
ИНЖЕНЕРНЫЙ СПРАВОЧНИК
ИЗДАТЕЛЬСТВО
МАШИНОСТРОЕНИЕ*
Москва 1969

УДК 629.7.015(031)
В книге, представляющей собой инженерный справочник,
в систематизированной и сжатой форме приведены сведения,
необходимые для описания и решения разнообразных задач
механики полета на начальной стадии исследования. В спра¬
вочник вошли важнейшие физические постоянные, орбиты п
характеристики планет, элементы небесной механики, харак¬
теристики атмосферы Земли, системы координат механики по¬
лета, полные сводки уравнений движения летательных аппара¬
тов как твердых тел постоянной или переменной массы, описа¬
ние действующих на летательные аппараты сил и моментов, а
также сводки замкнутых решений уравнений прямолинейного,
плоского и пространственного движения в частных случаях н
ряд других справочных сведений. Большая часть материала
представлена в таблицах, графиках и сводках формул.
Справочник предназначен для научных работников п инже¬
неров, занимающихся механикой полета и смежными дисцип¬
линами; он может быть полезен также учащимся высших
учебных заведений.
К книге прилагается бандероль вклеек (рис. 2. 14, табл. 3. 4а
и 5. 15)
Рецензент докт. техн. наук И. В. Стражева
Научный редактор канд. физ.-мат. наук В. Г. Демиь
2-4-3
43-68

ПРЕДИСЛОВИЕ
С развитием летательных аппаратов (ЛА) и, следовательно,
с развитием современной механики полета все более ощутимым
является отсутствие инженерного справочника, в котором в удоб¬
ном для читателя виде были бы приведены необходимые сведе¬
ния по механике полета, изложенные сжато, без доказательств
и выводов формул.
В настоящее время из-за отсутствия такого рода справочника
подбор и обработка необходимой для инженера информации
представляет собой весьма трудоемкий процесс. Кроме того,
использование материала, разнородного по содержанию, глубине
разработки, принятым ограничениям и допущениям, а также раз¬
нородного по обозначениям величин, часто вызывает серьезные
затруднения. Следует также заметить, что многие важные резуль¬
таты исследований содержатся в журналах и сборниках, часто
мало доступных широкому кругу читателей.
В предлагаемой книге авторы на основе опыта своей работы
в промышленности и высших учебных заведениях сделали по¬
пытку заполнить пробел между учебниками с их подробным
методологическим изложением материала и периодическими из¬
даниями с их фрагментарными результатами.
Справочник содержит совокупность таких сведений, которые
в большинстве случаев необходимы в начальной стадии решения
любых задач механики полета.
В гл. 1 даны важнейшие физические постоянные и таблицы-
матрицы для перевода англо-американских единиц измерения
величин в метрические единицы и метрических единиц в англо-
американские, а также перевод всех названных единиц в между¬
народную систему единиц СИ.
1669	3

В гл. 2 приведены краткие сведения по орбитам планет сол¬
нечной системы и даны модели атмосферы Земли (СА—64 и
CIRA 1965).
Системы координат, используемые в механике полета, и фор¬
мулы преобразований между ними изложены в гл. 3. В механике
полета всегда придавалось большое значение четкому описанию
и удобным обозначениям для применяемых систем координат
вплоть до регламентации их с помощью общесоюзных стандар¬
тов. Однако в последнее время в связи с возникновением новых
научно-технических направлений в механике полета (кроме тра¬
диционной механики околоземного полета и небесной механики,
появились ракетодинамика, астродинамика, задачи наведения,
навигации, автоматического управления и т. д.) количество упо¬
требляемых систем координат существенно увеличилось. Вместе
с тем последний общесоюзный стандарт на системы координат,
относящийся к 1941 г., уже не может удовлетворить новым зада¬
чам механики полета. Авторы предлагают свою систему класси¬
фикации и описания систем координат, в которой по возмож¬
ности учтены сложившиеся традиции и действующий ГОСТ. Для
всей совокупности систем координат используется десятичная
классификация, что позволяет ввести для них простые шифро¬
ванные обозначения. Это дает возможность компактно записы¬
вать обозначения формул преобразования из одной системы
в другую и ускоряет поиск самих преобразований в таблицах.
Новая классификация потребовала введения новых названий.
Так, например, по аналогии с геоцентрическими и гелиоцентри¬
ческими системами координат, начала которых находятся
в центрах Земли и Солнца, системы координат, начала которых
находятся в центре масс летательного аппарата, названы
ЛА-центрическими.
В гл. 4 в соответствии с изложенной в предыдущей главе
классификацией систем координат приведены записи замкнутых
систем уравнений движения летательного аппарата, состоящих
из уравнений движения центра масс, уравнений движения отно¬
сительно центра масс, уравнений изменения массы, а также
кинематических, позиционных и угловых соотношений. При этом
всюду указывается, в какой системе координат записаны уравне¬
ния движения, относительно какой системы координат рассмат¬
ривается движение и какая система координат принята за инер-
циальную систему отсчета.
4

Гл. 5 содержит выражения для действующих на летательный
аппарат сил и моментов, их представления через аэродинамиче¬
ские коэффициенты, записанные в различных системах коорди¬
нат, а также выражения для составляющих перегрузок в различ¬
ных системах координат.
В гл. 6 дана сводка аналитических и номографированных
решений некоторых частных случаев уравнений движения
центра масс JIA, причем они классифицированы для прямоли¬
нейного, плоского и пространственного движения по обращению
в нуль или постоянству того или иного параметра. Это облегчает
отыскание нужного результата.
В конце книги в виде приложений I и II приведены таблицы
стандартной атмосферы СА—64 (ГОСТ 4401—64) и междуна¬
родной справочной атмосферы CIRA 1965. В приложении III
приводятся две программы вычисления параметров стандартной
атмосферы СА—64 на электронной вычислительной машине
БЭСМ-2М.
Каждая глава справочника снабжена списком литературы,
к которой следует обращаться в том случае, когда необходимо
восстановить доказательства или промежуточные выкладки.
Размерности использованных в данной книге величин приве¬
дены преимущественно в Международной системе единиц СИ
ГОСТ 9867—61.
Для отыскания в справочнике нужных сведений следует
пользоваться не только оглавлением, но (чаще всего) и предмет¬
ным указателем. При этом надо помнить, что в предметном ука¬
зателе одно и то же понятие может встретиться в различных
местах, в зависимости от того, с какого из ключевых слов оно
начинается. Объяснения обозначений тех величин, которые встре¬
чаются в нескольких разделах в пределах одной главы, приво¬
дятся в списке основных обозначений перед началом каждой
главы. Более подробные сведения содержатся обычно в табли¬
цах, найти которые можно с помощью предметного указателя.
Объяснения обозначений величин, которые встречаются лишь
в одном месте главы, даются непосредственно вслед за обозна¬
чением.
Авторы старались сохранить общепринятые обозначения по
всей книге, однако даже в пределах одной главы это часто не
представлялось возможным. Поэтому читателю следует быть

внимательным к обозначениям при переходе от одной главы
к другой.
При отборе и изложении материала, вошедшего в эту книгу,
авторы стремились всюду к лаконичности и ясности изложения
в сочетании с удобствами пользования. Насколько удачно ре¬
шена эта задача — судить читателю.
Авторы с благодарностью примут все замечания читателей
как по содержанию, так и по построению книги; их следует на¬
правлять по адресу: Москва К-51, Петровка, 24, изд-во «Машино¬
строение».
В заключение авторы считают своим приятным долгом выра¬
зить искреннюю благодарность за ценные замечания, сделанные
при просмотре рукописи, нашему учителю доц. Н. Н. Завидоно-
ву, д-ру техн. наук, проф. И. В. Стражевой и д-ру техн. наук
Л. Б. Горощенко.

Глава 1. ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
И ЕДИНИЦЫ ИЗМЕРЕНИЯ
1.1.	НЕКОТОРЫЕ ФИЗИЧЕСКИЕ ПОСТОЯННЫЕ
Абсолютный нуль температур	 0° К=—273,15°	С
Скорость света в вакууме	 2,997925 -108 м/сек±
±5-102 м/сек
Гравитационная постоянная £2 	 (6,670zh0,007)• 10—и н-м211кг<2
Нормальное (стандартное) ускорение
силы тяжести (на уровне моря и географи¬
ческой широте 45°32'40") go	 9,80665 м/сек"2
Газовая постоянная сухого воздуха:
— универсальная	 (8,31431 ±0,31) дж/моль -град
— удельная	 287,039 дж/град-кг
Скорость звука а\
— в сухом воздухе (£=0° С)	 331,36 м/сек
— в воде (£=13° С)	 1440 м/сек
Динамический коэффициент вязкости
воздуха при температуре 283,15° К	....	17,1616• 10 G н-сек/м2
Отношение теплоемкости воздуха при
постоянном давлении к его теплоемкости
при постоянном объеме (при ^=0-М00° С) 1,405
Световой год	 9,4605-1012 км
Астрономическая единица (а. е.)	.	.	.	.	(149 599 300±2000) км
1.2.	МЕЖДУНАРОДНАЯ СИСТЕМА ЕДИНИЦ ИЗМЕРЕНИЯ (СИ)
Таблица 1. 1
Международная система единиц СИ [1J, (2J, [3]
Наименование величины
Единица измерения
¥
Сокращеннее
обозначение
единиц
Некоторые основные единицы
Длина
метр
М
Масса
килограмм
кг
7

Продолжение
Наименование величины
Единица измерения
Сокращенное
обозначение
единиц
Время
секунда
сек
Термодинамическая темпе¬
ратура
градус Кельвина
°К
Некоторые дополнительные единицы
Плоский угол
радиан
рад
Телесный угол
стерадиан
стер
Некоторые производные единицы
Сила
ньютон = (1 кг)-( 1 м/сек2)
н
Площадь
квадратный метр
м2
Объем
кубический метр
Плотность (объемная масса)
килограмм на кубический
метр
кг,'м$
Секундный расход
килограмм в секунду
кг/сек
Удельный вес
ньютон в метре кубическом
н\мъ
Давление
ньютон на квадратный метр
н/м2
Динамическая вязкость
ньютон-секунда на квад¬
ратный метр
н-сек/м2
Кинематическая вязкость
квадратный метр-секунда
м2-сек
Работа и энергия
джоуль
дж
Мощность
ватт
вт
Примечание. При переходе на систему единиц СИ в форму¬
лах исключается постоянный коэффициент g (ускорение силы тяже¬
сти), а массовый расход вещества и плотность в системе СИ численно
совпадают соответственно с весовым расходом вещества и удельным
весом в системе МКГСС. Кроме того, в формулах исключается коэф¬
фициент, равный термическому эквиваленту работы.
8

1.3. СООТНОШЕНИЯ МЕЖДУ МЕТРИЧЕСКИМИ И АНГЛО-АМЕРИКАНСКИМИ МЕРАМИ
9

Единицы объема
10

Единицы давления
11
Фунт на квадрат- lbf/ft2 4,726* 10 4 4,788-10 4 4,88-10 4 4,78803-10 35,9-10 3 6,943-10
ный фут

Единицы массы
12
Фунт Ibf 4,53718-10-1 4,4482-105 4,44822

мильем 0,44704 1,6093 1,4666

Единицы температур
Таблица L II
Г радус
Цельсия
Г радус
Кельвина
Г радус
Фаренгейта
градус
Ренкина
*С
7К
*F
^R
Г радус
Цельсия
1,0
Гк—273,15
у7к-273,15
Градус
Кельвина
Тк
/с+273,15
1,0
^p-f 255,37
"э"7*
Г радус
Фаренгейта
т/с+32
9
-Гк-459,7
о
1,0
Tr—459.7
Г радус
Ренкпна
Tr
9
— ^с+491,7
0
JLr
5 Гк
/р-^-459,7
1,0
ЛИТЕРАТУРА
1. Б у р д у н Г. Д., Калашников Н. В., Стойкий Л. Р., Между-
народная система единиц, изд-во «Высшая школа», 1964.
2. Известия ВУЗ, сер. «Авиационная техника», № 2, 1963.
3. Международная система единиц. ГОСТ 9867—64.

Глава 2. ОРБИТЫ НЕБЕСНЫХ ТЕЛ
И АТМОСФЕРА ЗЕМЛИ
Основные обозначения
а — скорость звука (в разд. 2. 2),
а—большая (действительная) полуось орбиты (в разд. 2.1),
<тм—градиент молекулярной температуры,
b — малая (мнимая) полуось орбиты,
2с—расстояние между фокусами,
С—постоянная закона площадей,
е— эксцентриситет орбиты,
Е—эксцентрическая аномалия,
g—ускорение силы тяжести,
go—ускорение силы тяжести на уровне моря и широте 45° Земли,
h — геометрическая высота,
i — угол наклона плоскости орбиты к эклиптике,
/ — постоянная интеграла энергии,
К — гравитационный параметр,
/ — длина свободного пробега молекул,
¥—масса притягивающего центра,
Af0, Mh— молекулярный вес воздуха на уровне моря и рассматриваемой
высоте,
р — давление (в разд. 2.2),
р — фокальный параметр конического сечшия (в разд. 2.1),
q—скоростной напор,
гА— расстояние от центра притяжения до апоцентра,
гп—расстояние от центра притяжения до перицентра,
г— радиус-вектор,
R — газовая постоянная,
/?з — средний радиус Земли,
Rq — средний радиус планеты,
t — время,
Т — кинетическая температура,
Tq—кинетическая температура па геометрической высоте, равной нулю,
Тм—молекулярная температура,
v— скорость,
vi—индикаторная скорость,
vK[)—круговая скорость,
^пар—параболическая скорость,
— скорость в апоцентре,
t'n — скорость в перицентре,
3—величина, обратная высоте однородной атмосферы (показатель
экспоненты),
А — отношение плотности воздуха на данной высоте к плотности воз¬
духа на геометрической высоте, равной нулю,
г — угол наклона плоскости орбиты к плоскости экватора,
5

О—истинная аномалии,
8ср — средняя аномалия,
и.—динамическая вязкость,
и-о—динамическая вязкость на геометрической высоте, равной нулю,
v—кинематическая вязкость,
Q—плотность среды,
Qo— плотность среды на геометрической высоте, равной нулю,
Ф — геопотенциальная высота,
w — долгота перицентра.
Для расчета околопланетных и космических полетов требуется
знание как физических характеристик пространства, так и зако¬
нов движения самих планет.
В данной главе приводятся основные сведения из небесной
механики, а также характеристики планет солнечной системы
и межпланетного пространства.
2 1. ОРБИТЫ НЕБЕСНЫХ ТЕЛ
2. 1.1. Задача двух тел. Законы Кеплера
Небесные тела солнечной системы (искусственные и естест¬
венные) движутся вокруг Солнца и других небесных тел. Обыч¬
но при изучении движения тел солнечной системы исходят из
следующих упрощающих предположений.
1. Размеры небесных тел пренебрежимо малы по сравнению
с расстояниями между ними.
2. Масса одного из притягивающих тел больше массы дру¬
гого тела. В этих предположениях можно полагать, что небесные
тела притягивают друг друга как материальные точки по закону
Ньютона и рассматривать движение одного небесного тела
в поле тяготения другого. Это составляет содержание задачи
двух тел.
Движение планеты солнечной системы в поле тяготения
Солнца определяется тремя законами Кеплера:
1. Орбита (траектория) каждой планеты есть эллипс, в од¬
ном из фокусов которого находится Солнце.
2. Радиус-вектор, соединяющий центры планет и Солнца, при
движении планеты в равные промежутки времени описывает рав¬
ные площади.
3. Квадраты времени обращения планет вокруг Солнца, умно¬
женные на сумму масс Солнца и планеты, пропорциональны ку¬
бам их средних расстояний от Солнца.
Движение по орбите любого небесного тела в поле тяготения
любой планеты в условиях задачи двух тел также определяется
законами Кеплера.
2. 1. 2. Типы орбит
Орбиты в задаче двух тел являются коническими сечениями.
Определения элементов и параметров орбит приведены в табл. 2. 2.
Различают следующие типы орбит (рис. 2.1): эллиптическая,
16

параболическая, гиперболическая. Частным случаем эллиптиче¬
ских орбит является круговая орбита. Тип орбиты определяется
величиной эксцентриситета е (табл. 2. 1).
Таблица 2.1
Типы орбит
Тип орбиты
Эксцентриси¬
тет е
Скорость v движе¬
ния в поле тяготе¬
ния небесного тела
Эллиптическая
0 < е < 1
к 9 2/С
— < v2< —
г г
Круговая
е = 0
г
Параболичес¬
кая
е — 1
„2=2А
г
Г иперболичес-
кая
е>1
2/С
1/2 >
Г
Рис. 2. 1. Типы орбит
Уравнение конического сечения
г =	-	 (2.1)
Н- е cos &	v 7
Гравитационный параметр /С, характеризующий силу притя¬
жения небесного тела, отнесенную к единице его массы, связан
с гауссовой постоянной k2 и массой М притягивающего тела со¬
отношением
K = k2M,	(2.2)
Таблица 2.2
Элементы орбит и некоторые понятия, используемые в небесной механике
Название
Обо¬
значе¬
ние
Определение
Фокус конического
сечения
F
Одна из точек, сумма (разность) рас¬
стояний от которых до любой точки ко¬
нического сечения постоянна
Апоцентр (апогей,
афелий, апоселений и
т. д.)
А
Точка орбиты, наиболее удаленная от
фокуса, в котором находится притягиваю¬
щее тело
Перицентр (перигей,
перигелий, периселений
и т. д.)
77 1
, Точка орбиты, ближайшая к фокусу,
в котором находится притягивающее тело
17

Продолжение
Название
Обо¬
значе¬
ние
Определение
Фокусное расстояние
2 С
Расстояние между фокусами кониче¬
ского сечения
Линия апсид
АП
Линия, проходящая через апоцентр и
перицентр
Центр орбиты
О
Точка на линии апсид, лежащая на оди¬
наковых расстояниях от фокусов
Эксцентриситет орби¬
ты
е
Отношение фокусного расстояния к
большой полуоси
Большая полуось
а
Половина расстояния между апоцентром
и перицентром
Малая полуось
Ь
Половина расстояния между точками
орбиты, лежащими на прямой, проходя¬
щей через центр орбиты перпендикуляр¬
но к линии апсид (для гиперболической
орбиты, см. рис. 2.3)
Истинная аномалия
$
Угол между прямыми, проведенными
из притягивающего центра в перицентр
и в точку нахождения небесного тела
(см. рис.. 2. 3)
Эксцентрическая ано¬
малия для эллиптиче¬
ской орбиты
Е
I
Угол между прямыми, проведенными
из центра орбиты в точку на вспомога¬
тельной окружности радиуса, равного
большой полуоси а, и в перицентр (по¬
строение угла Е см. рис. 2. 3)
Эксцентрическая ано¬
малия для гиперболи¬
ческой орбиты
Ег
Угол между прямой, проходящей через
фокусы гиперболы, и перпендикуляром к
касательной к вспомогательной окружно¬
сти радиуса а (см. рис. 2.3)
Средняя аномалия
^Ср
Угол между прямыми, проведенными
из центра орбиты в перицентр и вообра¬
жаемую точку, движущуюся по вспомо¬
гательной окружности радиуса, равного
большой полуоси а, с постоянной угловой
скоростью 360°/7\ где Т — период обра¬
щения тела по орбите (см. рис. 2.3)
Плоскость эклиптики
Плоскость орбиты Земли
18

Продолжение
Название
Обо¬
значе¬
ние
Определение
Небесная сфера
Вспомогательная сфера произвольного
радиуса
Точка весеннего рав¬
ноденствия
т
Точка, в которой Солнце пересекает
небесный экватор, переходя из южного
полушария в северное
Восходящий узел
а
Точка, в которой планета переходит из
южного полушария в северное
Линия узлов
°£1
Прямая, по которой плоскость орбиты
планеты пересекается с плоскостью эк¬
липтики (см. рис. 2.2)
Долгота восходящего
узла
я
Угол между направлениями на точку
весеннего равноденствия и на восходя¬
щий узел, вершина которого находится в
Солнце
Наклон орбиты
1, е
Угол между плоскостью орбиты и ос¬
новной плоскостью (эклиптика, экватор
планеты)
Сфера действия пла¬
неты
Пространство, в котором планета рас¬
сматривается как центральное притяги¬
вающее тело, а Солнце как возмущающее
тело
Отвесная (вертикаль¬
ная) линия
Прямая, проходящая через центр не¬
бесной сферы и совпадающая с направ¬
лением отвеса в месте наблюдения
Ось мира
Ось собственного вращения небесной
сферы
Северный и южный
полюс мира
Точки пересечения оси мира с небес¬
ной сферой (северный полюс—по положи¬
тельному направлению вектора собствен¬
ного вращения для правой системы
координат)
Северный и южный
полюсы Земли
Точки пересечения оси собственного
вращения Земли с ее поверхностью (се¬
верный полюс — по положительному на¬
правлению вектора собственного враще¬
ния для правых систем координат)
19

Продолжение
Название
Обо¬
значе¬
ние
Определение
Истинный горизонт
(математический)
Большой круг небесной сферы, перпен¬
дикулярный отвесной линии
Небесный экватор
Большой круг, образованный пересече¬
нием небесной сферы плоскостью, прохо¬
дящей перпендикулярно оси мира через
точку наблюдения
Земной экватор
Большой круг, образованный пересече¬
нием поверхности Земли плоскостью, про¬
ходящей перпендикулярно ее оси враще¬
ния
Небесный меридиан
Большой круг, образованный пересече¬
нием небесной сферы плоскостью, прохо¬
дящей через ось мира
Земной меридиан
Большой круг, образованный пересече¬
нием поверхности Земли плоскостью,
проходящей через ось вращения Земли
Постоянная площадей
С
Площадь, описываемая радиусом-век¬
тором за единицу времени в поле цен¬
тральной силы
Постоянная интеграла
энергии
I
Полная механическая энергия
Сидерический (звезд¬
ный) период
Период обращения в инерциальной си¬
стеме координат (например, в системе
отсчета, связанной с неподвижными звез¬
дами)
Тропический год
Промежуток времени между двумя
последовательными прохождениями цент¬
ра Солнца через точку весенне1о равно¬
денствия
20

Продолжение
Название
Обо¬
зна¬
чение
Onj еделение
Световой год
Расстояние, которое проходит в один
тропический год луч света
Астрономическая еди¬
а, е.
Среднее расстояние от Земли до Солнца
ница
2.1.3.	Элементы и параметры орбит
Орбиту характеризуют различные геометрические параметры:
большая и малая полуоси, эксцентриситет, расстояния до апо¬
центра и перицентра и т. д. Знание двух из этих параметров до¬
статочно для описания орбиты (но не ее положения в простран-
Рис. 2.2. Элементы орбит
стве). Кроме того, орбита может быть определена с помощью
кинематических и динамических параметров: скорости в апо¬
центре и перицентре, момента количества движения, полной энер¬
гии и т. д.
Орбита небесного тела и ее параметры показаны на рис. 2. 2,.
2.	3. Определения элементов и параметров орбит даны в табл. 2. 2.
Соотношения между геометрическими, кинематическими и
динамическими параметрами орбит приведены в табл. 2.3,
21

Эллиптическая орбита
Тело на орбите
Вспомогательная окружность
Точка, движущаяся по
вспомогат. окружности
с постоянной угловой
/скоростью отно¬
сительно ц ентра О
Линия апсид
Фокус
Притягивающий центр
(сроку с F)
Т-период обращения тела по эллиптической орбите
At = t-t0
Рис. 2.3. Элементы эллиптической и гиперболической орбит
22

Таблица 2. 3
Соотношения между параметрами эллиптической, параболической
и гиперболической орбит
Наименование
Значение параметра орбиты
параметра
параболической
орбиты
эллиптической
гиперболической
Большая
полуось а
г 4-г
А П
гп + с
К
2 К ,
п
|*-1|
Р
I «2 — 1 |
С?
К I £?2 — 1 |
К
2 К
'и*
(е~\)
Р
|*2-1|
С*
К К2- 1|
Малая
полуось b
/Vn
V ар
а /1 е2 _ 1
2/С
С
/гл
/ZE
Р 1Л
V ар
W-l|
К
2 К
°п~гт
С
у\п
Л/гж
V m
Расстоя¬
ние от цент¬
ра притя¬
жения до
апоцентра
г.
а (1	&)
2а~гп
1 + е
п 1 — е
Р
\ — е
23

Продолжение
Наименование
параметра
орбиты
Значение параметра орбиты
эллиптической
параболической
гиперболической
Расстояние
от центра
притяжения
до апоцент-
ра гк
К(\-е)
<
vu
v Гп
А
о/' 2 2
2Krnvu
2/С — гиу~и
оо
оо
Расстояние
от центра
притяжения
до пери¬
центра гп
1 а(е— 1)|
Р
\а{е-\)\
Р
\+е
ка+е)
4
р
1 + е
1 — е
г д
А 1 + е
К
—Г"(1 + е)
vh
^гА
vn А
2Kr\v\
Ж ~ rAv\
1 + е
К
2 О + е)
Расстояние
от центра
притяжения
до тела на
орбите г
Р
Р
P
1 + е cos &
1 4- е
1 4- cos $
14-е
1 4- е cos $
1 + е
п 1 + е cos $
С
Гп 1 4- cos %
п 14-е cos $
С
К ГК1
-+COS»j/ /+-
а\е* — \\
а | е2 — 1 |
1 + е cos &
а — (а — /*п) cos Е
1 4~ е cos $
•24

Продолжение
Наименование
параметра
орбиты
Значение параметра орбшы
эллиптической
параболической
гиперболической
Расстояние
от центра
притяжения
до тела на
орбите г
а( 1 — е cos Е)
Kv 2П
1 + е cos $
гА( 1-е)
1 + В cos ф
а( * -Л
\cos Ег /
ael—1 tg£rcosec&
Фокусное
расстояние
"~2~ (ГА “ гп)
со
с
ае
ае
Эксцентри¬
ситет орби¬
ты е
Параметр
орбиты р
V1 + e>
25

Продолжение
Значение параметра орбиты
Наименование
параме rpa
орбиты
эллиптической
параболической
гиперболической
Параметр
орбиты р
г (1 + е COS ft)
2 2
/п*'п
г (1 + cos ft)
rWn
г (1 + е cos 9)
2 2
rYlVU
К
к
К
С2
С2_
С]_
К
к
К
Истинная
аномалия $
arc cos
cos Е — е
1 — е cos Е
4f-
2 arc t
1 (/£■'*
2 arc tg
в -Ь 1
e — 1
X
ET
arc sin |	■/"в-— 1 ><
X tg ET
arc cos
X (e — sec £r)
Эксцент¬
рическая
аномалия E
sin ( — sin ft ]
I b )
yrr sin -
2 arc sin
■/ a( 1+ e)
a — r
arc cos
n
a — r
arc cos
ae
2 arc tg
/■
<«T
}/ r cos ■
2 arc cos
у Л(1 — e)
2 arc cos
У cos Er
26

Продолжение
Наименование
параметра
орбиты
Значение парамеи'а орбты
эллиптической
параболической
гиперболической
Эксцент¬
рическая
аномалия Е
г cos %■ + ае
arc cos
а
Постоян¬
т
ная закона
площадей С
Укр
Укр
Ук~р
rYlVYl
rnvn
rY\VYl
ГАУА
r\VA
У 2Кгп
1 AV А
Постоян¬
2 К
1/2 —
0
о 2/^
г/2 —
ная интег¬
/'
г
рала энер¬
гии /
К2
— (<?2— 1)
С2
К2
. / 1 \
К2
	(е2— 1)
С2 V )
К2
(л 1 \
2 2 (£“ — И
rnvn
2 2 С'“ '
'п^'п
КЬ2
КЬ2
ра2
ра2
а
а
Средняя
аномалия $сР
n(t — t0)+ &сро
Е—е sin Е
Скорость
движения v
/т(’-т)
Vkp
^КР |//2 + “
С
Укр
г cos $
г cos ft
27

Продолжение
Наименование
параметра
орбиты
Значение параметра орбиты
эллиптической
параболической
гиперболической
Скорость
в апоцентре
1/4
/
-(
ГА 1
2-^)
a )
2 К
rn
Fa
ГА + ГП
/ A
0-e)
r_K_
V
r„
A
П
Скорость
в перицент-'
ре
Гп * А^~ГП
Р
/'f
V 2vKp
гж
VV
V-
Производ¬
ные
dr
dt
■ — г — е s
ей
г2 — sin 1
Р
(1-Г
dt°-
■■ к Л К (Р- Г)
-r=—e cos& = —	=
С/Ь
db
dt '
пГ2й __
dr
b^c sin й
( a+ с cos й)2
V Kp
r2
2/C
_C_
r2
^i/n
. .	2	VKp •
e sin й =—	  r
г3	r3
г2	/	2a62
= 1/ 	— б2——
62 |/ г	r2
dr
db
b^c sinЙ-
(a-f с cos й)2
r2 /" 2a62	/И
=A2[/ r +*2-^

Соотношения между геометрическими параметрами Эллиптической орбиты
Геометрический параметр
29

Геометрический параметр
О»
*
о
ч
о
м ГГ
ч.
о
CM
ч.
4-
(М <
ч.
+
+
■.й
: о,
CN
а <
о
•&«
£ £
о л
+
+
см
+
см
V
I ч.
ч
+
4-
V
С
ч.
+
<
л о.
х 2 н
а: а, 4»
30

н-
+
+
+
I I
I +
CM
I
c<i -<
v*
V
H- I
+
+
+
31

Соотношения между геометрическими и динамическими параметрами эллиптической орбиты
ю
см'
<3
а
+
со
I к
се х
н <и
* %
«3
СМ
с
<3
СМ
со <
<3
V
а
1
СО
<3
<3
СМ
<3
см
+
<3
+
см
<3
V
I
<3
'<3
<3
<3
см
V*
^ I
(3
и «
-ь
с
V. _
V	С	и	се
~	и.	—	са	О
5	-	к	с	О.
“	Й	^	•“
2	Н	X	4)
™ са = ;
Ю х s х
*3
32

р
v.
+
мС
V
«а
I
см
ч Р
+ I
с
V*
5*
CM i
+
+
N Р
V*
«а
I
V
V
см
+
V
+
(М
‘С)
V
V.
+
<
V.
+
<
<^>
+
о
-\~
см
с
см
р
V.
см
~т~
см
V
<
V.
+
Р
+
Р
СМ
+
р
V*
СМ
+
р
*4.
+
С
Р
v.
см
+
р
+
+
*1 .с
р
см
+
р
+
<^> I о»
«а
1
+
£'
1 u
2	1669
33

Таблица 2. 6
Круговая и параболическая скорости в поле одного притягивающего
центра
Скорость
Обозна¬
чение
Формула
Определение
Круговая (пер¬
вая космическая)
скорость
^кр
М ^
а.
-
£
Скорость тела, дви¬
жущегося по круго¬
вой орбите радиуса г
Параболическая
(вторая космичес¬
кая или скорость
освобождения)
скорость
^пар
f 2К I/O
^пар — 1 / ^ ~~ У 2^кр
Скорость тела, дви¬
жущегося по пара¬
болической ^траекто¬
рии
Таблица 2. 7
Значения круговой и параболической скоростей
для некоторых высот над поверхностью Земли
Высота
км
Круговая скорость
км/сек
Параболическая
скорость
км/сек
0
7,909
11,186
50
7,879
11,142
100
7,848
11,099
200
7,788
11,014
300
7,730
10,931
400
7,672
10,850
500
7,616
10,771
1 000
7,353
10,399
5 000
5,920
8,373
10 000
4,934
6,978
50 000
2,659
3,760
100 000
1,935
2,738
923 900
(на границе сферы
действия)
0,655
0,926
34

Элементы орбит планет солнечной системы [3|, [4|, [5J, [20|
CD
C\j
«
S'
а
Vo
s
hi
< 35

Продолжение
Сред¬
няя
ско-
г О «О V
л с (- *
s s V-
О в Я
13,05
9,64
6,80
5,43
4,73
Средняя
угловая
скорость
движения
по орбите
"/сутки
299,1283
120,4547
42,231
21,534
14,29
2
S
к эква¬
тору
О
о
ос
ib
о
со
см
05
IQ
О
С^
05
о
05
СМ
1
о.
о
см
О
о
X
о
>=:
X
X
| эклип¬
тике*
см
оо
о
2°29' 26"
см
см
сЪ
о
о
00
см
сЬ
о
см
оо
О
о
Г-'
*
<я
н
о
перигелия
СС
СО
со
о
СС
05
СО
О
о
СМ
05
tO
о
05
СО
о
о
О
СС
о
СС
СМ
СМ
4
о
ч
восходя¬
щего
узла
Ю
1-0
О
Ю
о
05
05
113°13'37"
к
СС
о
СС
Г-
1
131°13'51"|
04
О
ОО
СС
о
05
О
Афелийпое
расстояние
а. е.
5,454777
10,070082
1
20,087385
30,315374
1
49,343581
Периге-
лииное
расстоя¬
ние
а. е.
4,950829
9,007604
18,276561
о
■чт*
О
О
о
ОО
оГ
см
29,691899
Эксцент1 и-
ситет
г-
оо
О
o'
0,055720
0,0471
Г-
ОО
О
о
o'
0,247
Большая
полуось
а. е.
5,2027
9,546
19,20
30,09
39,5
Число
СПУТНИ-
ков
(есте¬
ствен¬
ных)
см
05
ю
см
1
Обозна-
чение
rt
«•>
ЭЧ +
а*
Планета
Ю тер
Сатурн
Е
со
Си
>5
Нептун
Плутон
36
На эпоху 1950,0.

Физические характеристики планет солнечной системы [4J, [5], [20]
О)
см’
а
S'
а
'о
а
Ь*
« £ a?
о О *
>>’*
К <Ц
S Л? у
Я «еГ S
сз Q-л; <о
£ с II "Г
Q. 2
U я
S S S
<и ^ ч
Л Iе 5
O'g S
о со
СХ
>Я i;
*<
О)
а
О
о «
О
CN
СО
o'
СО
Ю
о
СО
СО
-Ь
о
со
со
см
'ф
см
о
1-0
о-
05
LO
оо
+1
ю
см
00
о
-н
см
о
со
о
оо
со
со
г
а;
ГО
о<Ьсо
см .
СО^
СО ж
н
о
о
-н
ю
а
a
о
со
со
оо
to
U
lO
ОО
ю
Zr
см
-Н
о
о-
ОО
О
ю
-fi
о
о
ю
LO
см
о.
>3
ч
с
37
По данным XII Генеральной ассамблеи (1964 г.) Международного астрономического союза (MAC) [9].

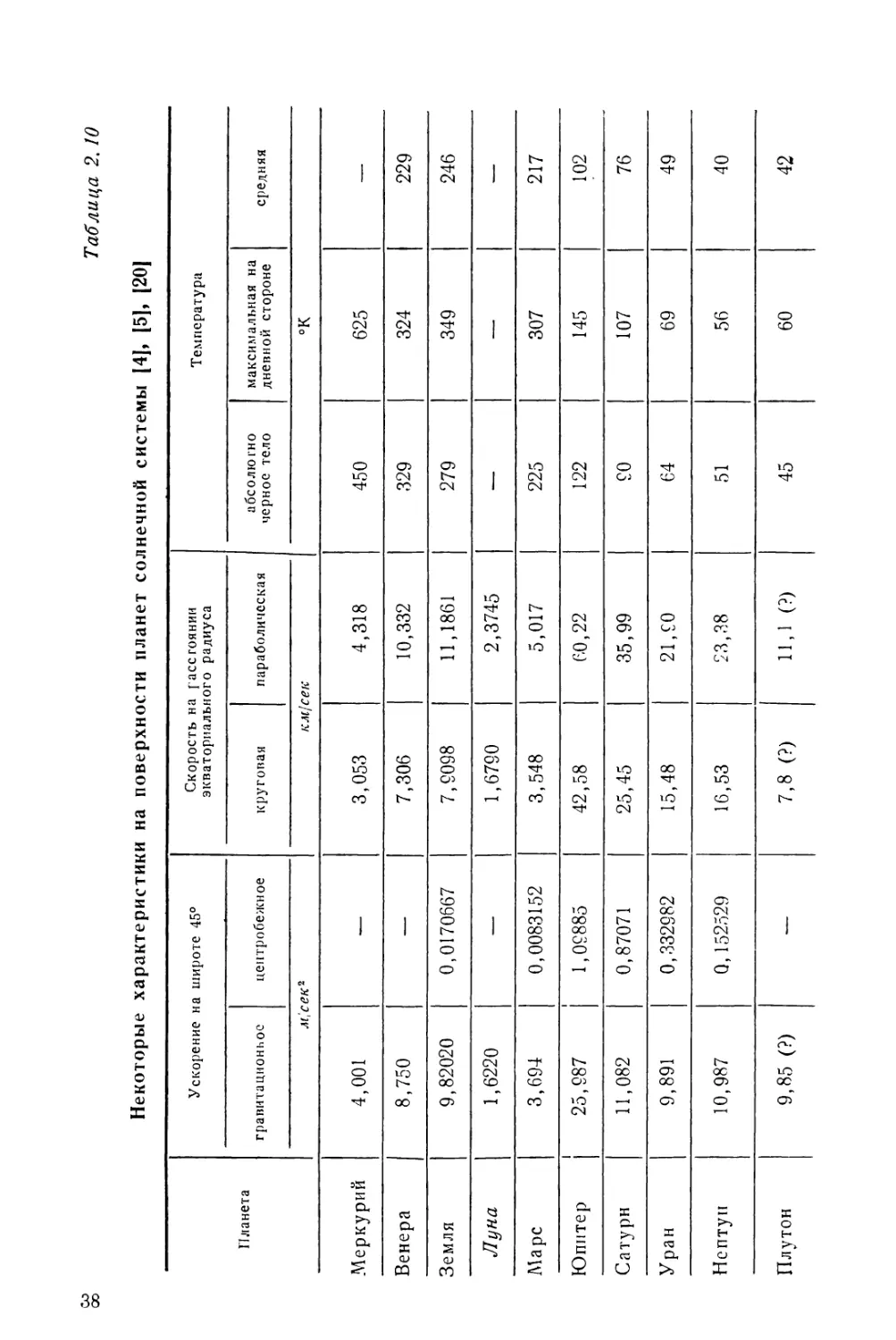
Некоторые характеристики на поверхности планет солнечной системы [4J, [5], [20|
38

Таблица 2.11
Некоторые астрономические постоянные, принятые в 1964 г.
на XII Генеральной ассамблее Международного астрономического
союза (MAC) [9]
Величина
Размерность
Значение
Число секунд в тропиче¬
ском году (1900,0)
сек
31556925,9747
Скорость света
м]сек
299792,5‘103
Астрономическая единица
(а. е.)
м
149600*1О6
Гравитационная постоянная
Г аусса
(а. е.)3//г (масса Солн-
ца)1^2 (сутки)-1
0,01720206895
Геоцентрический гравитаци¬
онный параметр K=^k2M
.и3/сек2'
398603-109
Экваториальный радиус
Земли
м
6378160±80
Коэффициент сжатия Земли
—
1/(298,25±g;g|)
Наклонение эклиптики
(1900,0)
23°27'08",26
2.2.	АТМОСФЕРА ЗЕМЛИ
Физические свойства атмосферы изменяются в зависимости
от географических координат места, времени года и суток, вы¬
соты. В механике полета применяется стандартная атмосфера
(СА), представляющая собой условную атмосферу, предназна¬
ченную для приведения результатов расчетов и измерений лет¬
ных характеристик к одинаковым условиям. В стандартной атмо¬
сфере исключено влияние географических координат и суток на
свойства атмосферы *.
В приложениях I и II даются значения характеристик приня¬
той в СССР стандартной атмосферы СА—64 (ГОСТ 4401—64)
и Международной справочной атмосферы CIRA 1965 [21].
2.2.1. Стандартная атмосфера СА—64 [17]
Модель стандартной атмосферы разбивается по высоте на
И вертикальных слоев. Каждый слой до высоты /*<95 000 м
характеризуется законом изменения температуры атмосферы:
* Вариации параметров атмосферы Земли см. Международную атмосфе¬
ру CIRA 1965 (приложение II).
39

— температура в слое постоянная (изотермический слой);
— температура в слое изменяется по линейному закону в за¬
висимости от геопотенциальной высоты (табл. 2. 12).
На высотах, больших 95 000 м, каждый слой характеризуется
еще и молекулярным весом (табл. 2. 12).
Таблица 2. 12
Распределение молекулярного веса и температуры по высоте
Высота h в м
Молекулярный
нес
Температура в °К
Градиент „моле¬
кулярной*
температуры
ах, в °К!гп. м
м
о
И ООО
25 ООО
46 ООО
54 000
80 000
95 000
110 000
120 000
150 000
16 0 000
170 000
180 000
190 000
200 000
28.966
28.966
28.966
28.966
28.966
28.966
28,966
28,934
28,727
28,107
27,900
27,700
27,476
27,245
27,000
288,15
216,66
216,66
274.00
274.00
185.00
185.00
257,64
335.00
1010,00
1199,40
1228,71
1257,93
1287,06
1316,10
288,15
216,66
216,66
274.00
274.00
185.00
185.00
257,36
332,24
980,05
1155,26
1175,00
1193,20
1210,60
1226,80
-0,00651122
0
0,00276098
0
-0,00349544
0
0,00500000
0,00801741
0,02346357
0,01987408
0,00308461
0,00308461
0,00308461
0,00308461
0,00308461
Характеристики стандартной атмосферы на уровне моря и
географической широте 45°32/45" приведены в табл. 2. 13, а соот¬
ношения между параметрами стандартной атмосферы —
в табл. 2. 14.
40

Таблица 2.13
Физические характеристики стандартной атмосферы
на уровне моря и географической широте 45°32/45"
Наименование характеристик
Значение величины
в системе СИ
Значение величины
по ГОСТ 4401—64
Барометрическое дав¬
ление
101359,86 н/м1
1013,25 мбар—
= 10332,3 кГ/м^
=760 мм рт. ст.
Температура
288,15° К
15° С
Скорость звука
340,28 м/сек
1225 км/нас
Плотность воздуха
1,2250 кг/м*
1,2492*10-1 кГ -сек1/
.Молекулярный вес
28,966
28,966
Динамическая вяз¬
кость
1,7895*10-5 н-сек/м*
1,8242*10-6 кГ-секЦж*
Кинематическая вяз¬
кость
1,4607*10-5 мЦсек
1,4607*10-5 м1/сек
41

Рис. 2.5. Зависимость плотности q и давления р
от высоты h
42

' м г/сек
Рис. 2 .6. Зависимость кинема¬
тической вязкости v от вы¬
соты h
Рис. 2.7. Зависимость средней
длины свободного пробега мо¬
лекул / от высоты h
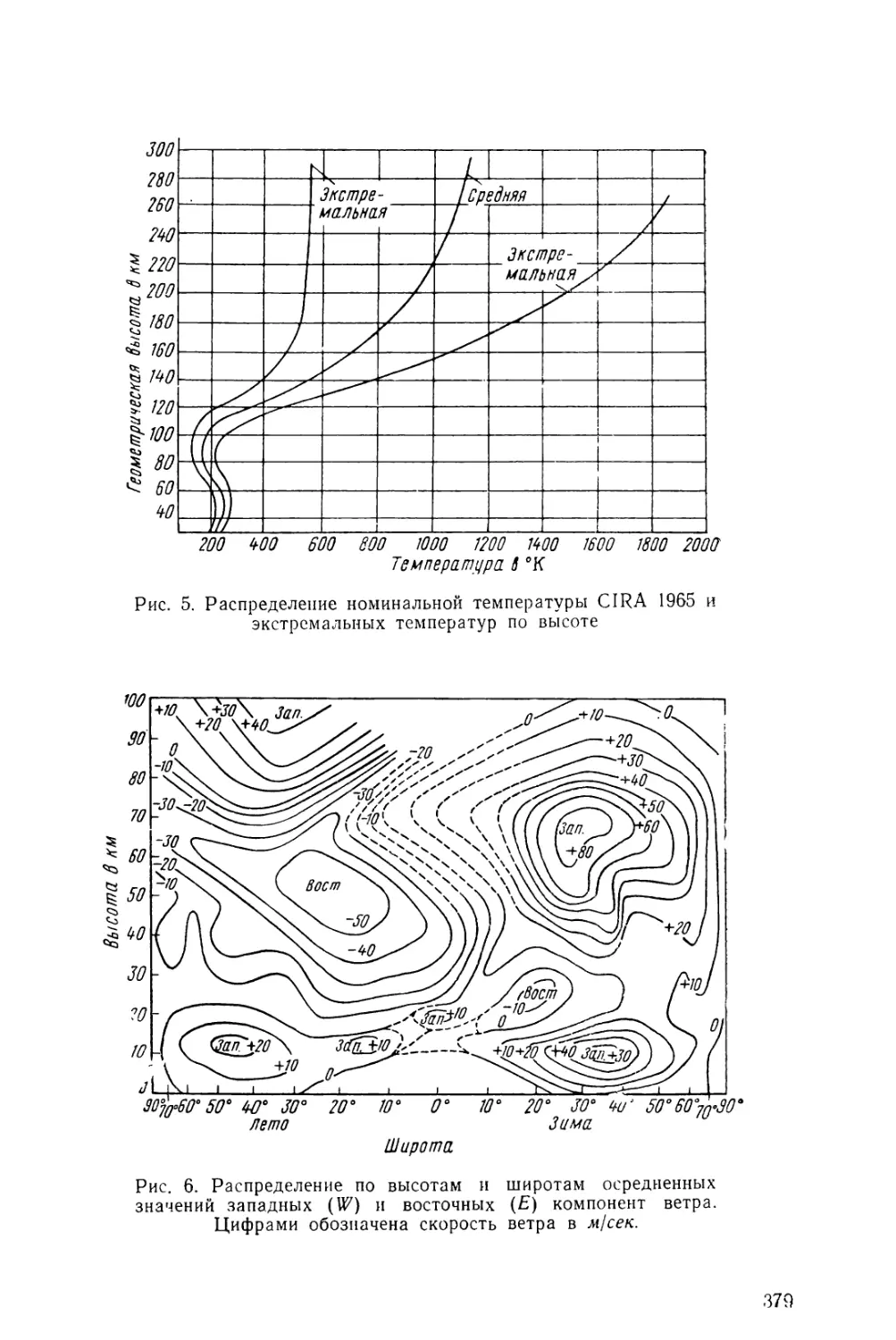
2.	2. 2. Ветры в атмосфере
Ветер — пространственное движение масс воздуха. Обычно
вертикальные движения атмосферы значительно меньше горизон¬
тальных. Поэтому под ветром обычно понимают горизонтальные
воздушные течения, величины скоростей и направления которых
осреднены за некоторый промежуток времени.
Ветровое поле в любом географическом районе определяют
следующие основные характеристики.
1.	Вертикальный профиль (разрез) скоростей ветра. На
рис 2 9 представлен вертикальный разрез средних зональных
ветров для высот 90—120 км. График показывает характерный
переход восточного ветра летом в западный ветер зимой для вы¬
сот в диапазоне 30—90 км и изменение ветра на западный летом
и восточный зимой для высот больше 90 км.
На рис. 2.10 показано среднее распределение скорости ветра
по сезонам (лето, осень, весна, зима) над Москвой на высотах
О—16 км.
43

Соотношения между параметрами стандартной атмосферы
<М
3
Чр
о . s
s ^ г=
Рн OVO
СО
S 5
Ю -у
о
X
X
О)
U
S
к.
о
о
о
ю
05
О
О
о
о
о
о
о
о
V
V
5й
О
о
о
£<м
о
о
о
о
со
V
о
о
о
о
СО
СО
05
оо
<М
V
О
СО
О
со
о
°!
ю
Ю~
+
•«
S
и
CJ Ю
£<м
о
о I ^
05
(М
со
С5,
ьд
ho
о
ho
С5,
ho
1-н
*
*
о
и
о E^i
о|ос
05
см
Tj-
со
гг1
о
С)
со
OJ
ьо
1-н
*
г
о
+
О/
ho
о/
ho
*
so
X
X
оч
ЮЗ
X
X
1=4
ЮЗ
X
Cf
X
05
н
о
с
о
05
юз
U
н
о
CJ
X
о.
си
*=4
ЙЙ
О 03
^ о,
< jr
со
* о
X s
Я о;
Он 03
« ю
>-> Он
* н
О со
юз <и
Он н
§ 2
X CU
=S н
05
X с?
X о
ег 3S
-рХ
о
Эо
2 Он
X ^
X н
О) юз
2 ^
СО о
X с
Он
. . CD
X Н
н ®
CJ 2
о ~
CD
С О
S X
CD ЭХ
Н 05
CJ 5
о' «=:
о
5 э~~
о
X Он
44

няющейсяпо геопо-
тенциальной высоте
4^
500 WOO Т °К высоты

Характерным явлением на высотах 7—18 км являются струй¬
ные течения, распространяющиеся на большие расстояния
в длину (до тысяч километров), в ширину (до сотен километ¬
ров), в высоту (до нескольких километров)'. Скорость струйных
течений может достигать 360—540 км/час. Над СССР струйные
течения наблюдаются в основном на высотах 7—12 км зимой
Рис. 2 .9. Средние зональные компоненты скорости ветра в узлах
(1 узел= 1,852 км/час)
(летом они наблюдаются реже). Скорость ветра в них обычно
100—200 км/час, но может достигать 300 км/час.
На рис. 2. 11 представлен вертикальный разрез фронтального
струйного течения, где нанесены линии равных скоростей.
Примечание. Некоторые данные о ветрах приведены в Междуна¬
родной справочной атмосфере CIRA 1965 (см. приложение II).
2. Ветровой сдвиг (градиент скорости ветра по высоте). Мак¬
симальные сдвиги ветра по высоте обычно имеют место между
двумя максимумами средней скорости ветра. Для высот 25—
80 км ветровые сдвиги обычно не превосходят 20 м/сек на 1 км
высоты. На высотах 80—110 км сдвиги достигают 30 м/сек на
1 км высоты. Знак ветровых сдвигов чередуется по высоте.
3. Турбулентность. При описании атмосферной турбулент¬
ности обычно используется теория случайных функций. Турбу¬
лентные пульсации скорости ветра рассматриваются как квази-
46

стационарный процесс по временной или пространственной коор¬
динате.
Интенсивность пульсации скорости ветра характеризуется
спектральной плотностью этого случайного процесса. Спектраль¬
ное представление атмосферной турбулентности позволяет полу¬
чить простое соотношение между ветровым возмущением и реак¬
цией JIA. По данным измерения турбулентности в нижних слоях
атмосферы спектральная плотность в большей части диапазона
частот изменяется как некоторая степень т частоты (т=5/3-^-2).
Условные
. обозначения
	лето
. 	 осень
весна
			 зама
/
/
/
./■/
\ (
- X1
V
у®
Щ '• W
-
-
\ \
\ ■
\
\
^
У
у' /
-
/
/
У'
	^
/ У
г
Уу
!
16
15
14
13
12
11
х 10
9
а 8
5 7
2 6
«2 5
4
3
2
1
5	10	15
Скорость ветра 6 м/сек
20
Рис. 2. 10. Среднее распределение скорости ветра по сезонам над Москвой [2]
В инженерной практике для аналитических расчетов исполь¬
зуются соотношения, аппроксимирующие экспериментальные
значения продольной и поперечной спектральной плотности:
L 2
snp(s)-^ я 1 + (2Л)2 -
5п(2) = о^ — -1-+--(-Z'-)2-,
nV '	jt	[1	+(S2£)2]2
где	L	—масштаб турбулентности, характеризующий ли¬
нейные размеры области, в которой составляю¬
щие скорости коррелированы;
—волновое число (приведенная частота пульса-
х
ций атмосферы);
X — длина волны спектральных составляющих тур¬
булентного движения атмосферы;
47

а^, — дисперсия компоненты скорости ветра:
>Пр(2), 5П(2) — продольная и поперечная спектральные плот¬
ности соответственно.
Циклоническая часть
Йнти циклон и чес кая часть
Рис. 2.11. Вертикальный разрез фронтального струйного
течения
Этим спектральным плотностям соответствуют автокорреля-
ционные функции ^пр(г) и ^п(г):
Rn;(r) = ^e-^;
/?п(г)=<^(1-г/21)е-'№,
где г — величина радиуса-вектора произвольной точки поля
скоростей.
Чаще всего масштаб турбулентности принимается равным
305 м. При этом в однородной изотропной турбулентной атмо¬
сфере продольный масштаб в два раза больше поперечного мас¬
штаба турбулентности.
На рис. 2. 12 показаны графики нормированной спектральной
плотности ^ - для различных значений масштаба турбулент-
Qw
ности L = 200, 600, 1000, 2000 м. Эти кривые различаются по ча-
48

стотам, на которых функция Sn(Q) начинает отклоняться от ква¬
дратичного закона.
Рис. 2. 12. Аналитическое представление спектра атмосферной
турбулентности
Порывы определенной интенсивности, характеризуемой вели¬
чиной дисперсии о^г, встречаются на разных высотах полета
с той или иной вероятностью. В табл. 2. 15 приведены значения
вероятности /?(сф) встречи вертикального порыва, равного вели¬
чине или превосходящего ее, для высот ~300 м.
Таблица 2.15
Вероятность встречи вертикального порыва
Значение дисперсии
0,305
0,61
1,22
1,83
2,44
3,05
3,66
Вероятность встречи поры-
-ва ветра /?(<%)
0,8
0,58
0,31
0,13
0,05
0,02
0,003
2.3.	НЕКОТОРЫЕ ВСПОМОГАТЕЛЬНЫЕ ГРАФИКИ ДЛЯ РАСЧЕТА
ПАРАМЕТРОВ ПОЛЕТА В АТМОСФЕРЕ ЗЕМЛИ
При проведении аэродинамических расчетов и обработке
летного эксперимента нашли применение некоторые вспомога¬
тельные графики характерных аэродинамических величин, вы¬
численные по параметрам стандартной атмосферы СА—64. На
рис. 2. 13—2. 16 приведены графики следующих зависимостей:
49

— скоростного напора от высоты и скорости полета
(рис. 2. 13);
— индикаторной скорости (табл. 2. 16) от высоты и скорости
полета (рис. 2. 14, см. вклейку);
Рис. 2.13. Зависимость скоростного напора q от скорости v и вы¬
соты полета h
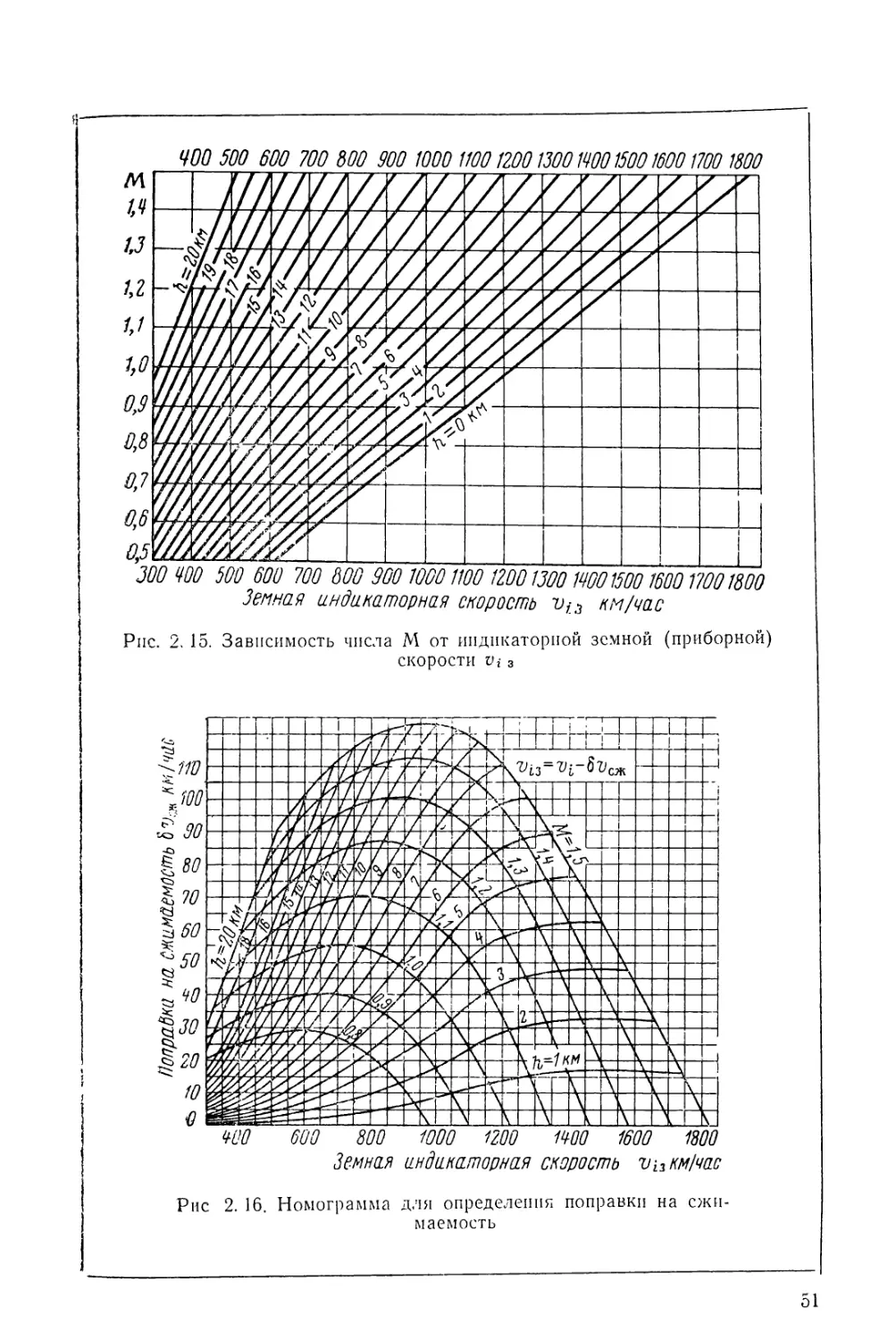
— индикаторной земной (приборной) скорости (табл. 2. 16) от
высоты и числа М (рис. 2. 15);
— поправки на сжимаемость воздуха от высоты и земной
индикаторной скорости.
Таблица 2.16
Название
Обозна¬
чение
Определение
Индикаторная ско¬
рость
Vi
Скорость полета на какой-либо
высоте, соответствующая скорости
полета на уровне поверхности Зем¬
ли при одинаковых скоростных на¬
порах
Индикаторная земная
(приборная) скорость
vi3
Индикаторная скорость с учетом
поправки на сжимаемость воздуха
50

400 500 600 700 800 900 1000 110012001300 WO0150016001700 1800
300 400 500 600 700 800 900 10001100 1200130014001500160017001800
Земная индикаторная скорость vi3 км/час
Piic. 2. 15. Зависимость числа М от индикаторной земной (приборной)
скорости Vi з
%11д
%юо
й 90
I 80
/и
ч
%60
У о
(Н ои
%20
1
Щ
>fci-
j ■
—1—i—|-
4i
А
f
,Vl3
1 1 !
~У[~8Угж
—H
J	1
п
т
'-tt
J ‘7“и
4-4>
-A
<CT
4—
Л-
и
т
ги
'T-t
yf-b
4 v
Л. ...
fe
JP Vc
7Vi
п
Ш
Ltz
(I
S'
т
^ V_\
=5Г7
m
Z*
Ж
4=^
v
x
\ш
тт
у/
ж
A
-Л-
T ^
-Л-
—s
№
ft
&
4 3
\
Л-
v-
i4
\
-v-
'MuUV
Ж
*
fl
V
A
\
A
;==
- \
\
Л
'-X-
K
A
\
i -
A
V ■ “
-M-
-1m
rV
—a
-V
- \
\
- \
s'
5-
1
\
\
- \
\
\ -
-V-
л “
A:
-v
т боо 800 юоо 1200 то то то
Земная индикаторная скорость ъь км/час
Рис 2. 16. Номограмма дли определении поправки на сжи¬
маемость

ЛИТЕРАТУРА
1. Бэтти н Р., Наведение в космосе, пер. с англ., изд-во «Машинострое¬
ние», 1966.
2. Авиационный справочник (для летчика и штурмана), под ред. В. М. Лав-
ского, Воениздат, 1964.
3. Астрономический календарь. Постоянная часть, Физматгиз, 1962.
4. Б а л к М. Б., Элементы динамики космического полета, изд-во «Наука»,
1967.
5. Б а к у л и н П. И., К о н о и о в и ч Э. В., М о р о з В. И., Курс общей'
астрономии, изд-во «Наука», 1966.
6. Бессерер К. У., Инженерный справочник по управляемым снарядам,
Воениздат, 1962.
7. Добро ленский Ю. П., Турбулентность атмосферы как источник,
возмущения для систем автоматического управления самолетом, Изв. АН
СССР, сер. «Энергетика и автоматика», № 5, 1961.
8. Космические траектории, ИЛ, 1963.
9. Куликов К. А., Система астрономических постоянных, «Астрономи¬
ческий журнал», 42, № 3, 1965.
10. Лахтин Л. М., Свободное движение в поле земного сфероида, Физ¬
матгиз, 1963.
11. Митра С. К., Верхняя атмосфера, ИЛ, 1955.
12. Научные проблемы искусственных спутников, сб. статей под ред.
А. А. Орлова и Э. Э. Шпильрайна, ИЛ, 1959.
13. Околоземное космическое пространство, Справочные данные, под ред..
Ф. С. Джонсона, изд-во «Мир», 1966.
14. По гор ело в Д. А., Теория кеплеровых движений летательного аппа¬
рата, Физматгиз, 1961.
15. Ре пн ев А. И., Свойства верхней атмосферы и искусственные спут¬
ники Земли, Труды Центральной аэрологической обсерватории, вып. 25, 1959.
16. Р е й с о у л, Строение атмосфер планет, журн. «Ракетная техника w
космонавтика» (русский перев.), 1963, № 1.
17. Таблицы стандартной атмосферы. ГОСТ 4401—64.
18. Хансен, Некоторые характеристики верхних слоев атмосферы, свя¬
занные с проблемой скорости полета. Вопросы ракетной техники, ИЛ, 1958г
№ 5, стр. 26—33.
19. Хвостиков И. А., Высокие слои атмосферы, Гидрометеоиздат^
1964.
20. Э р и к е К., Космический полет, том I. Окружающие условия и небес¬
ная механика, Физматгиз, 1963.
21. CIRA 1965. COSPAR International Reference Atmosphere, Amsterdam.
1965.
22. E g g 1 e s t о n I. М., Evans D. E., Harris I. W., Lunar and
planetary environments. Towards Deeper Space Penetration. No. 4, Americ.,
Astronaut. Soc. 1964.
23. ICAO Standard atmosphere extension. Jet propulsion, v. 26. No. 2„
1956.
24. S ton I. Atmosphere Data to Alter Vovager Design. Aviation Week
and Space Technology, v. 83, No. 21, 1965.

Глава 3. СИСТЕМЫ КООРДИНАТ
Основные обозначения
А - угол азимута,
а— гелиоцентрическое прямое восхождение,
В—вектор конечного поворота,
Ь[— проекция вектора конечного поворота на ось Oi,
D— положение полюса неизменяемой части тела,
— положение полюса подвижной части тела,
d— гелиоцентрическое склонение,
h— высота,
L—матрица направляющих косинусов,
//—матрица координат в i-й системе,
1ц—направляющие косинусы,
М—матрица поворота прямоугольного трехгранника,
пх, Ну, nz—направляющие косинусы оси вращения прямоугольной
системы координат,
qi — криволинейная координата,
(<7,) — координатная поверхность,
[qi\ — координатная линия,
R, г — радиус,
^грЕ — гринвичское звездное время,
х, у, z— прямоугольные координаты,
а— угол атаки,
а*— геоцентрическое прямое восхождение,
аи—угол наклона оси инерции,
р—угол скольжения,
Э*— астрономическая широта,
у—угол крена,
ус—угол скоростного крена,
5* — геоцентрическое склонение,
£ — наклон эклиптики к экватору,
е1» Ес> £п—высота над горизонтом в соответствующей геотопической
системе координат,
б—угол наклона траектории,
0С—угол наклона плоскости ортодромии,
X — географическая долгота,
Xj, Х2, Х3 — эллипсоидальные координаты,
Xрг, Qpr, vpr, fxpr—параметры Родрига—Гамильтона,
Хс— долгота узла ортодромии,
X*— астрономическая долгота,
р.— гелиоцентрическая широта,
уе—угол наклона соприкасающейся плоскости,
гр С—прямоугольные координаты,
<р— географическая широта,
ф' — геоцентрическая широта,
53

<рт—угол поворота системы координат относительно осп
вращения,
<Ркр—угол поворота крыла,
X— гелиоцентрическая долгота,
4 с— угол скоростного курса,
4 — угол курса,
о) — угловая скорость,
Vi» V2> V3—углы, определяющие положение подвижного элемента
ЛА относительно его неизменяемой части,
(Q — долгота восходящего узла орбиты,
X — точка весеннего равноденствия.
3.1.	ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛЫ
ПРЕОБРАЗОВАНИЯ КООРДИНАТ (общие сведения)
3.	1. 1. Основные определения
Основные понятия систем координат, приводимые с геометри¬
ческой точки зрения, сведены в табл. 3. 1.
3.	1. 2. Виды систем координат
и формулы преобразования между ними
В механике полета наиболее распространены правые прямо¬
угольные, цилиндрические и сферические системы координат,
реже употребляются эллипсоидальные, географические, гипер¬
болические и косоугольные системы координат. Описание первых
пяти систем координат приведено в табл. 3. 2; частные случаи
гиперболической и косоугольной систем координат имеются
в разд. 3.2. Формулы перехода между наиболее распространен¬
ными системами координат приведены в табл. 3.3. Связи между
прямоугольными и эллипсоидальными координатами приведены
в конце разд. 3,1.2, а связи между системами координат других
видов на примерах указаны в разд. 3.2.
Формулы перехода от прямоугольных
к эллипсоидальным координатам
Прямоугольные координаты х, у, л связаны с эллипсоидаль¬
ными координатами Хи ta, (при	условии а>Х\>Ь>‘к2>с>Хг)
соотношениями:
х^= I f	—
у	(Ь — а)	(с — а)
/ (b-li)(b-l2)(b-h)
У	(с — Ь)	(а — Ь)
z 1 /~(с —	(с — ^2) (с — ^з)
\	(а — с)	(Ь — с)
54

Эллипсоидальные координаты	определяются	через
прямоугольные координаты х, у, 2 из уравнения третьей степени
относительно %
*2
22
а — X
■X 1 с — X
: 1 .
Это уравнение имеет всегда три действительных корня
> Х,2> Аз-
В плоском случае (z = X3 = c = 0) формулы приобретают вид:
У =
(a — \х).(а — Х2)
b — а
— X,) ^ — Х2)
а — b
В этом случае координаты
называются эллиптическими.
3.1.3.	Преобразование
прямоугольных систем
координат. Способы задания
их взаимного углового
положения
Переход от одной прямо¬
угольной системы координат
к другой прямоугольной си¬
стеме координат можно осуществить при помощи параллельного
переноса (до совмещения начал координат) и поворота системы
относительно начала (до совмещения осей).
Поворот прямоугольной системы координат можно задать
с помощью направляющих косинусов, углов Эйлера, вектора ко¬
нечного поворота, параметров Родрига—Гамильтона, парамет¬
ров Кэли—Клейна и др.
Параллельный перенос системы координат
Новые координаты х', у\ zf связаны со старыми х, у, z соот¬
ношениями (рис. 3. 1):
или
xf = x — x0l; у'---=у — г/о,; £' = z-z0l
х =х-
где x0l, у о,, z0l — координаты нового начала координат Ох в
системе Oxyz;
x'0i yQi zQ — координаты начала О в системе Oxxryrz\
55

Определения основных Элементов различных систем координат
5Г
а
<о
N
Е- га -Z <D
С о О =Г
К >-> ас i>
S X U
И С( CJ <и
к яз t( С-
СУ (D Q
„ ш с;
5 о
^ s а-
^ к сО
“ Sj! •
К С ='
« О) сз *
4 о Он “Г
X °"° та
дЕ с Н н
»J id
« <и со
У Ш S
к с
о
с
„	id
ГО х! О
“ 2 ©
х 1 с
* о*
►а К X
х та Е-
~	СТ)
та id
CL, X 2
40 2*
2 r.js
ю С 9.
Он о
<U о
С id
со	го	i	<d	i=;
о	и	о	„
^ “
со^^О	i^«c
^	О	О	и
та ►
Он:
•ь Mrt
£х х s
М м
1 та:
С-
<и
та х
та
о
X i
•=* !
о
; X
I 2
та си
X	s	S
о	ш	„
X	н	X	-
X"	а	х	> v
N
?s
V»*
н
ч
v_^
СО
см
о
II
1!
li
<м
С>
II
то
N
>ч?
Ч^
X 3 о S
° К л 358
-° х 2 2
^ х s 38
«о<=5
X >-,
та id
Он X
\о та:
з =
§:
QJ
5*=
Он (D
<1) н
X Он-
та Ч х 'о н g. <
, эХ
о- a g
>5 CJ Е- W
с а
х
о, 2
та id 2 та х та
Он
- о
с =
g ST1 (D (L)
эХ 2 ^ Ё
О О о н
?!§ =
X to та
та о-
° к '“
та - к с.-
то го- “
г*|£
S £5 «
sts -
1^5 2
^ Он о
2 ^ о та
с о о
>э «■> <и
X о х
та х х
о - то о
та >ii о
^ о - о-
а> id
о х н
ю х а
= та о
Он Qh Ои
SjS о х
об

>■,
о
я
X
о
о
н
~
о
Е
- О
СО
*
<=:
VO
я
О
эЕ
ф
О
Он
ф
со
:г
со
£ ^
— о
5 ф =
я
с ^
с.° 2
Я - ф
о s 2
«Ни
'Я “
s 2 Он
к о s
:=< Я О
N
N
7Г
=5>
=£>
- -t—1
- 4—1
- 4-i
V* СО
^ СП
^ СО
ч—' С
ч'-" С
4—-' Е
— О
сч О
со О
^ а
^ о
^ CJ
1! II
ii i.
1! 1!
-н
ГО
о
О
п,
п
2^
О)
со
о
'
'
w
2 0 § |S
£§§§£
« vo ***
£ о s
o-
E
^DS
n о
я =
Он и
ф
Я
сс
*"*"* со
UL, И ^
^ S|2i S
со О Я л
П х
5> ii
co
ГС Ф
П ф
03 Ф X
= ^ о
S Ф 2
С и
Он со
О S ^
О и S эГ
^ = 5 с
Е со 5
ч—' со
- о
s>, ,
•—' со
-
О О
- ^ •“
О- О
О £
я о ~ * я
X со и о Ф
Он ° з Ф -
<d Н я „ ~
и О «	«-
5 Я эЕ О со
° . ф
ПИ х о о ф
X
СО
я
две
Я
н
сО
1
СО
СО
V
Я
О
я
ф
Е-
о
сэС
о
VO
Он
я
X
Е
О
я
ф
«=;
О
Сч
ф
я
ф
я
я
ф
о
ь
ф
о
я
СО
Б.
о
я
я
Я
я
эЕ
~ я *
s »:
s	О	г?	я
К	СХ,	О	СО	<3J
к	о	и	о,	я
1=3	н	s	х	я
О Он О ф
 	 	Я	Я	ф	я
о о.
О О)
а
Он
о к
57

Координатные Касательные к коорди-: Х[, Хо, т3 В каждой точке обла-
оси натным линиям в некоторой! сти можно построить
X л
о* х
«Э CJ
Ь о,
ё *
Ч. CJ
, О) о
, О* Ч
с С
оз
Ч
Он
о
о
sc
X
Он
о К
о. ^
§!
О)
а.
51. ..
а О) OQ (D
X О) О о?
О X С е; ч
X эХ
Ь О
CJ VO
2 °
к а
X
си
О)
1 ЬИ I
Ъ ~ Си
= X о
,-ss
Р°5
s?t?«
5 Р-5 5
I— М-1 Г_
° -
Си г, со О
к ^ • н
!iv§?
” Он£ х
Q
о
и о
о
ч> и
03
X Ч -*
х s Ч
<D К Он
(=1 R5 О
<и о
И а х
о Ч
о,
г- ГО Он»
^ о
> а
<L>
, 2
w	2
«>■>>">
X и
о Ь
Он а
X си
Он Он
ч> ч>
к К J
5 ч X
Г О fcC
X rv
= Й °
X Он о
чс *
5* - °
2 ^ 4
О (_ 03
й (J ^
О се
X X
X
X
X
о
О Он о
ь 5 2
£ нй
1,-1
^ О Ч
и и а
о
5 в °
о о “
Он О)
S 2 2
^	*Т"
о ° ,Е
<и и«
X (
оз X X с
« ч _
х „ох
о н X X
с-н X х X
^ Он 03
х ix: Он
ч
Он
х: Е-
X >,
X 5Й
X
ЭХ О
X н
X m
S н
Ч се
2 к
X к
2 <
^ Он
с о
о
СО v
2 ОХ
2 °
X *г
> *
Is
Ч ГО
03 s ^
^ 2
Он X
с *
58

о
1=5 О,
« о
ЕГ Н
О О
О Й -
!Г Я £
U ~
(-. 03 *»
О л
о те:
о
^ 33
2 °
R го
° да Го
' Н О уо
; к ж
«
2*2
Ли Л *'Я
59

Продолжение
i s
s.*
с 2
О ж
О в
Н зк
СХ а>
о ж
«I
03
« S Ж
у йч
£ О) та
5-e-g
§ ®
Н <ц g
о s Е
5 1
о СП
Н ЕГ
со Ж
ка.
S О)
1=( В Ж
Л К * Л1
о ч О ^
О ж О) Л
* К ЕГ х
N Х^Р
^ р-
V» *.!>
ОО
= 2
К Л <и
а с
&S о.
2og
г> а.
ic°
о «*- _
э* s Г,
СО О та
2 Н S 2
V ЭК *°
н О К =
^§ао.
- v Н К
US ч
со со >■>
Ж 03 Ж
О
ж К
Ж Ь
р=(
Z, Од
о со X
о к 3
— о о
X X
£ 2
а «т-
•-5 :
Ж а ;
* 2 х с
гг1 О с
а^а;
S 2 i
с к
S
1«
= g
£5S х
<v о 7
в
ж
>=£
а
U
Ж эК
03 о
g 5 J-х о
1«яё
О О И ^
S- £ ^СЧ ~
К Ж о Ж
а
о
ЕГ о -
О о <33
о Ж ж
О) X
а а£-Г
О (1)
ж 03
В О эЖ
ЕГ Ж 1)
ООО
н о о
2 а
2 °
ч °
та *
ж
о
U со
н 2
О О н
« ж
со *=ч
ж а
Ж о
S °
о в
>1 "-• *
§2
С о (
60

Виды сиСгем координат
8
8
8
“Г
+
+
V
V
V
V»
N
V
V
V
8
8
8
а а.
s с
U о
03 с-
к
= ч
с. >>
н *
t=c
о, о
61

о
»=t
о
Q-
Е
Е CQ (-N
а; о ^
a а ^
а о ~
<1) ° н
а О
к» го °
^ I «
О а. о
« 2
л ч ч
<J >i с
°£*§
К X
+
V
v.
о
о
О
О
оо
со
СО
V/
V
a
V
о
V/
О
00
о
О
7
+
CQ
^	О
=	X
I	О
М
1° 1
w 2 и5
с л с
о и о
и о и
a
к
со,
О ,д I
О- cj 1
с о
О-эН
ТО о
а х
т Щ
О 0J
Л «
»=* 2
62

ос
w
о
« V/
V ж^
^ § V
9-
V/
о
о
С75
CJ ЕГ
«3
го X
Он
си
&»
со С
2 Ж .
О ж I
Он •=( ч-
! Ь Он сл
' X О С
> <и о о
' ХГ и о
го -
- ^ £
I Он?
I d) *
) ? к
)	R
:	Он
I о- о
> £ §
о?
Й °
О е;
X со
О -г
Он СО
С X
° 5? £
§.§ga
ж а - о,
Ч О £>-, cl>
^5 о. ж
а С v
Н • эх
СО Ж Q
X «=С X
X X со
« <и о
О- Ж X
о Он О
^ 0J о
и х
t<2S
is:
% a~ «
5 ° c ^
Он X о х
о си
-’К ,
2 £ '
<и о (J
Ж о ,,
ь
- х х а
о п 5 О
ЕГ 2 Он X
со о к и
X ° ч о
Ш X
и с
- 9-
ос
со
Он ^
ш *
•©«
и
1
к и
и
Он Е-
<и
2
И
к ж 2
О
с
ч s ж
03 « н
о? х а
Он
х о
а ж
н
х
<и
к « О-
а
н о <и
CQ
О »0< CQ
° О 2
X о с
+
+
+
о
л
л
2
со
CJ
Л
Л
CS
Л
л
<0
<0
Л
Л
Он
л
2
со
О) 2
1=( О)
О) S
Он X
X <и
О X
О со
а ж
X X
X ч
С-! со
Ф X
63

Продолжение
! <D
О) о-
я
Я зЯ
■' *
: 03 g J^cd
, « н
СО V
о _ ^
са л ~
Н O.S
S £?* 5 6 ^ н
га 5L я" °	!?	°
S^C g О |о
Я	s	R	cj
0Q ч	к	«	*	о
<и	s	Я	S	о)	ГО
р=С	■=;	(Г)	я	я	я	Q.
а> 5
я R
? о
О» ь;
Л
Л
Л
+
V
>ci
V/
о
о
О
о
03
О
V/
СО
$ъ
V
V/
о
О
V/
О»
1
о
о
+
+
+
н *
Я
о 2
G.
§ о ^
2 vo 5Я
^ D-.
и а
3
*< §
о
я
1
«=?
1
сл
аи
аз
Z
2
С 0S
S 2
О,
я
аЗ
Я
о
я
Л е? С?
Н CD
CJ
о
Я Cs
X га
G. Ж
<и н
CQ Я
О ГО
+
я	5"
%2
я	га
го о ^
О* >-> го
и я с
1 .2 и
-	о
»	t=C I о
Я I
[О^о*
о сл 2
I я с Л
sou
. е; О о
я
Cl О
я
О
я
аи
Я
&
о
го
сЕ>
а.
ю
га
я
я эЯ
2
о
2
я
о
CJ
я
я
о
CJ
я
ч
я
СП
hQ
га
S
3~
О !
я ^
X сл
С- Я
о о
Я CJ
*3 £
о сг
X ~
я о
£ Я
64

з 1669
65

«о
*0
а
s
«5
Н
«5
X
5
<
О.
о
о
X
О Z
О сл
Ctr Ctr II
■&
о
N
,<
сл)
с
N
о
СЛ)
V.
!*»
н
1;
||
tv*
5t>
Б
£
СХ
<
Б
S
с;
s
£
2
х
J3
ч
о
(-
>>
о
£
Б
О.
С
>»
ef
*
J3
м
Б
X
CJ
* N
Н =а> N
N
Ч'
СХ
С
*
I!
v.
v-t
ЬЛ
N
о
li
£
N
li
/<:
ОС
I;
ос
Л5®
о ° о
§ « б
с °
С и с
« Я °
* 5
• • щ 0) О
£ o^s
к Б О «
So D-.
® °^С
а •-с?
Я Н „ О
>>Я Н „
С свч II
О с( 9-у
_ С
^ 03
. о
*
с
я
Я s
.	^	CL)
et н
<1) о
N | ц.
Ы)
о о С
5 *эЯ
Си S о
с И я
О Б
3 0D О
CQ tr Б
Я к О
4 СХ °
с* о»
<и ^
Б г,
ei
£ 5
о °
о
я О
CJ
о
г; с 2
Я . Б
о о, ч
r> 'w Г'.
оГЗ О ^
■Я Б
CM
5*1 * N
■f
!M
1
'CJD
^ I
V
P 1
го ЬЛ
I. с
J
,< ir
i
II
Cl's S
‘ 0,9
о н
о
Н Б -_
О) О с
40 - Б
К® о
Ю о и
« S s
о £ <и
о н
s*§
Си о
*=с 2
сэ ^
с Л
£ = Б
Я б го
CL к
К О
g К
!С t? у Й' и
Я Я
2 но*
- \о
-	0S	0J	О	^
Б о я в- о,^
Я,- Б С S
р * s 1 ^ у’
юб£^«£
U	ч	±	Н
2	5	£	S	°
£	Р я	О, Б	£	О
Я	-
О)
§ £ Б <*
О 5-6- Б -
сх
с<
S s КОЙ S ~Э- Я
Б ^	у—ч 2 К v «
ас
I—н	®	I	5	£	,5	и
С	о	11	о	л	со	Р
** х	^	^	ч	.	0
л	w	>■>	а>	=
°	нО	fJ
—•Яр;
Б 0 с*
Б ■=[ и Н
X CL>~>U
О О я
= S S Н
^|°
-. £ я я
я
4 Б
S й
Б ^ s эЯ
О, О м о
ЕО *
о
с
1 *“> Ё
<D а>
, ST ч
Я пз
* 5
р, Б
О <->
О
^о4
Я 1,1
СЗ v
Б э-
О
а
+
см
*
V
а,
: б
со Б ^
II ^ w О 0,5 |
^22
►Д <1) О)
Н Н 5-
о и и
О Я Б
« о и
= см’
•&
U
66

Определение углового положения систем координат
с помощью направляющих косинусов
Направляющими косинусами /г?- осей системы Охуг относи¬
тельно осей системы координат Ox\yxZ\ называются косинусы
Рис. 3.2. Направляющие косинусы осей си*
стем координат
углов между осями Oi (i = x, у, г) системы Oxyz и осями
Oj (j = xь Уи z\) системы Ox\y\Z{ (рис. 3.2). Например,
/\
/и = COS(x, Хг);
/ч
^23 = COS (^/, Z}).
Матрица направляющих косинусов
1\\
/12
Лз
L = \\lij\\ =
I'll
/ 22
^23
h\
(32
^33 1
однозначно определяет угловое положение системы координат
Oxyz относительно системы координат Ox{yiZ\. Координаты
точки в прямоугольной системе Oxyz при переходе к системе
ОХ\у\Z\ преобразуются с помощью матрицы L (см. [14])
*1
X
У\
= L
У
*1
Z
3*
67

В координатной форме это преобразование записывается
в виде:
xl=lnx -j- luy -7-/132:;
Уl — h\X 4~ ^22У 4~
z\ ~ h\x 4- ^32//1- hzz-
Орты i, j, k системы Oxyz и орты ib jb k\ системы Ox\y\Z\
связаны соотношениями:
*1 = /ц1 ~r/l2j 4“ ^13
jl ~ 44 4“ ^22 j 4“ ^23^1
^1 ~ 44 "Г ^32j ~\~ 4з^
ИЛИ
i“/l4l4“ ^ljl+^зЛь
j — Л2Ч “h^ji ~f
k = /1311 "i~ /23J1 ~r /33 ^1 •
В силу ортогональности преобразования на направляющие
косинусы накладываются 6 условий (см. [14])
U= 1,^,3),
1^214“/12/22 "4 /13/23 — 0;
/21/314- /22/32 4~ 4з'сз ~
/31/11 ~г /32/12 + /33/13= 0*
Определение углового положения системы координат
с полющью направляющих косинусов в случае
конечного поворота относительно заданной оси
Задана неподвижная система координат Oxyz. Через точку О
проходит ось вращения п твердого тела, с которым свя¬
зана система координат Ox\y\Z\. Угол поворота тела относитель¬
но оси вращения равен срт.
1.	Ось вращения п задана направляющими косинусами пХу пуу
nz относительно неподвижной системы координат (рис. 3.3).
Матрица направляющих косинусов имеет вид
L =
68.
nl + (1-
• П2) COS'fT
(1
-cos?M +
(1
-cos <?т)лхл,—
“Г ^2 sin ®T
— riy sin cpt
пупх(\ -
■ COScpT) —
n2
у
+ (1 —/l*)COS<pT
(1
-cos? T)nynz +
~*г
sin срт
ЛгПх sill C?T;
пхпг{ 1-
■ COScpT) -f
(1
— cos»T) nvtiz —
<
+ (1 -n\) COS®T
+ /7г/
sin cpT
— nx sin cpT

или в другом виде
L = (M\)~'Mk,
где
1
Mg
y.
2
— nytg
Tt
9
1
nxtg
Tt
2
Mg-^r
— Mg
<Pt
2
1
-И* =
М\ — транспонированная матрица Мк.
Способ получения обратной матрицы (MTky~l см. в [14].
\у, h
Заданная ось
вращения
Рис. 3.3. Поворот системы коор¬
динат вокруг заданной осп вра¬
щения
2.	Ось вращения п задана направляющими косинусами пХг,
пУг, nZl в системе координат Oxlylzl. В этом случае L — MUx
п2 +(1 — п\ )cos®.
Мп,=
(1 — cosyT)nXtnyi +	(1 — cos 4r)nXln2l —
-f Пгх sin (рт	—	nUx	sin ®T
nblnXl{\— COSCPt)- «£, + (1—rt*,)cos<pT (i_cos®>i/l«Zl +
"	+	/г*.	sinc?.T
Лг.+(1—«z.)C0S®7
nZl sintpT
nZtnjc,(\ — cos®T)-
+ nVl Sin <PT
(l-cos®^,^,-
— nx. sin cpT
69

Определение углового положения системы координат
с помощью углов Эйлера
Системой углов Эйлера называются три угла, через тригоно¬
метрические функции которых можно определить все 9 направ¬
ляющих косинусов матрицы поворота прямоугольного трехгран¬
ника.
0XYZ-исходная
система координат
Первый поворот на угол <[>
вокруг оси 0Y
Второй поворот на угол 0
вокруг оси 0z1
Оху1 г j - вторая промежуточная
система координат
N
Третий поворот на угол у
вокруг оси Ох
Oxyz-конечная
система координат
Рис. 3. 4. Последовательность поворотов осей координат в пер¬
вой системе углов Эйлера
Имеется 6 систем углов Эйлера, соответствующих преобра¬
зованию одноименных координат путем трех последовательных
поворотов. Первый поворот происходит относительно одной из
осей преобразуемой системы координат, второй — относительно
одной из двух не совпадающих с исходной системой осей, обра-
70

зовавшейся в результате первого поворота промежуточной си¬
стемы координат; третий поворот производится относительно
той оси второй промежуточной системы, которая совпадает
с осью конечной системы координат.
Последовательность поворотов на примере первой системы
углов Эйлера показана на рис. 3.4.
Три наиболее распространенные системы углов Эйлера опи¬
саны в табл. 3.4а (см. вклейку).
Три остальные системы углов Эйлера являются модифика¬
циями предыдущих. При расчетах траекторий углы Эйлера рас¬
сматриваются в пределах, указанных в табл. 3.4а.
Связь углов Эйлера с направляющими косинусами
Элементы 1ц матрицы L преобразования системы координат
OxgijgZg в систему Ox\y\Z\ являются направляющими косинусами
осей системы Ox\ij\Z\ относительно осей системы Oxgygzg. Срав¬
нивая элементы матрицы L с элементами матрицы LT Lb- Ц
(табл. 3.46, первая система углов Эйлера), можно получить
g
Уё
•*1
hi
^12
^13
У\
-
^21
^22
^23
z\
4l
^32
4з
где
/\
COS (JC^, Xj)
/\
cos(xg, г/х)
/\
COS(Xff,
•*1
/\
COS(i/ Xj)
/\
cos г,’х)
/\
cos {yg, уi)
z/l
CO
/\
cos (zg, yx)
/\
cos (zg, zj
«1
\
lu = cos (xg, x1) = cos<l>cos &; U\ = cos (xg, уг)= — cos 6 sin 8 cos у —
-(- sin ф sin у ;
I x = cos zY) — cos 6 sin b sin y + sin 6 cos у ; Z12 = cos {y„, xx) = sin b;
/\
/22 = cos (у yx) = cos 0 cos v ;	^32 = cos (yg, zx) = — cos 8 sin у ;
Лз ~ cos (z хг)= — cos 8 sin^ ; l2s = cos (zg, y1) = cos ф sin у —
-)- sin 8 sin ф cos у ;
/33 = cos (z z:) = cos ф cos у — sin 8 sin ф sin у .
71

Матрица общего поворота
3
'о
св ч
S >s
5 СО
=:
с
ел
ел
>•
ел
О
С
сл
а
сл
О
О
-Э-
-D-
-Э-
с
С
сл
сл
ел
+
1
|
>•
?-
С
сл
О
СЛ
СJ
-Э*
-Э-
сл
ел
О
О
а
о
dp
СЛ
О
О
>•
СЛ
О
о
О
с
С
ел
сл
>•
сл
С
dp
о
о
сл
ел
О
ч>-
-э-
О
-э-
сл
О
CJ
сл
О
CJ
сл
О
]
+
а
р-
с:
сл
О
ел
О
-Э~
-э-
С
с
сл
сл
*-0
сЬ
*-0
*-0
;(
?-
сл
О
-Э-
с
-Э-
сл ел
О О
ел
О
>- ?-
ел с
О —
0 СЛ
-э-
ел т
2 S
1 +
о и
С ^
•- О
-э-
с
<=>
*-0
— _э" с
СЛ с —
— сл
^ СЛ ,
-э- + t
ел о
О	ej
cj	_
С
■Э- ~
.5 -£
~ СЛ
^ +
*-0
-э-
*-0
-=/-
СЛ
О
+
с
S-
CJ
сл
с
_
сл
<хг
С
ел
О
а
с£Г
С
С
сл
+
с
ел
сл
—t
сл
Г"?
_
aS*
?-
с£»
сл
сл
С
сл
с
-Э--
О
О
сл
О
а
СЛ
1
сл
О
CJ
CJ
X
X
X
сл
с
CJ
ел
£
СЛ
сл
+
О
CJ
сл
О
О
+
О
а
с£*
С
eS*
С
с
сл
сл
ел
О
сл
ел
\ ■"
/\
CJ
X
-Э-
с
сл
сл
О
CJ
ел
Г' О
О? {j
СЛ
О
^Е>-
*-0
72

Определение углового положения системы координат
с помощью вектора конечного поворота
и параметров Родрига—Гамильтона
Вектором конечного поворота называется вектор В(6Ь&2, &з)>
коллинеарный оси поворота, модуль которого равен
I В | = 2tg	,
где фт — угол поворота.
При двух последовательных конечных поворотах системы
координат	вокруг	двух произвольных	осей вращения	на	углы	фт,
и ф12,	задаваемых	векторами	и В2	соответственно,	вектор	ре¬
зультирующего конечного поворота В определяется соотноше¬
нием
в =	р	( Bi + B2	+ e-B2XB,).
1	— — IBxl |В2|	4
Если повороты выполняются в обратном порядке, то резуль¬
тирующий вектор конечного поворота В'
В'= р fo + Bj + ^XB^B .
1- —IBiIIBjI
При задании направляющих косинусов пх, пу, п: оси враще¬
ния п относительно неподвижной системы координат (см. рис.
3.	3) вектор В выражается через них и угол фт по формуле
Ъ\
пх
ь2
ЬЛ
II
Пу
=
2tg пу
h
Пг
2tg -^nz
Для определения углового положения системы координат
можно использовать параметры Родрига—Гамильтона дрг, лрг.
|ыРг, vpr, определяемые через компоненты вектора конечного по¬
ворота соотношениями:
V=-^-QPrN;
i*pr=YePrN:
73

V = vQp^3|;
epr^^-COS ?T •
Матрицу направляющих косинусов L можно выразить с по¬
мощью параметров Родрига—Гамильтона
Q2pr "Г ^рг ~ Р*рг ~ vpr 2 (OprV + ^ргР'рг) 2 ( ~ QprP'pr + Aprvpr)
2( QprVpr Н” ^ргР*рг) Qpr^^pr Vpr %г 2 (^рг^рг “Г ^ ргН'рг)
2 (бргРрг + VV) 2 ( “ ^pгXpг -Г Vpr[Xpr) Qpp + V9-r - д2)г - [х2рг
Параметры Родрига—Гамильтона связаны с первой системой
углов Эйлера соотношениями:
$ V .	6	.	&	. г
q —QOS — COS COS Sin — Sin Sill — ;
Anr = sm —sin — cos
pr 2 2 2
e;	Y
txnr— Sin — cos COS —
rpr	222
2
fb	ъ	.	у
cos — cos — sin ;
2	2	2
b . b	.	Y
-COS— sin — sin— ;
2	2	2
6 . & у ь & • y
V = cos — sin COS Sill — cos — sin — ,
pr 2 2 2 2 2 2
а углы Эйлера выражаются через параметры Родрига — Гамиль¬
тона следующим образом:
sin» = 2(eprvpr + V!V);
2(QprApr ^ргррг)
tgv =
tg ф =
Spr + Р*рг — V — Хрг
2 (QprPpr Xprvpr)
о + A — u/ —vz
Ург “ pr ^рГ	pr
Связь параметров Родрига — Гамильтона Qpr, Арг, [ipr, vpr ре¬
зультирующего поворота с параметрами первого дрГ1, лрГ1, p,pri>
vPrt и второго рРг2, ХРг2, рьРг2, vpr2 поворотов выражаются форму¬
лами:
Qpr = Qpr^prj,	Арг^рг2 Р-рг^рГа	Vpr, vpr2 J
Арг = ^РгiQprа	Qpr,^pr2	+ Vpr,Ppr2	P,pr1vpr2^
P'pr==P'Pr1Qpra	"Ь QpraPpra	“Г ХРП VPra ~~ Vpr,^pr2;
Vpr “ VPriQpr2	Qpr!Vpr2	“Ь Р'рг1^рг2	Арг1Р'рг2-
74

3.2. СИСТЕМЫ КООРДИНАТ МЕХАНИКИ ПОЛЕТА
И ФОРМУЛЫ ПЕРЕХОДА МЕЖДУ НИМИ
3.2.1. Классификация систем координат
По расположению начала системы координат условно разби¬
ваются на четыре класса, каждому из которых присваи¬
вается наименование и шифр, состоящий из буквы и трехзнач¬
ного числа:
1. Класс планетоцентрических систем координат с началом
в центре небесного тела (шифр П000).
2. Класс планетотопических систем координат с началом на
поверхности небесного тела (шифр Т000).
3. Класс космоцентрических систем координат, начало кото¬
рых расположено вне небесных тел или ЛА (шифр К000).
4. Класс связанных с ЛА систем координат с началом в ка¬
кой-либо точке ЛА (шифр С000).
Каждый класс систем координат в зависимости от конкрет¬
ного небесного тела, характерной точки в космическом простран¬
стве или на ЛА делится на следующие типы (подклассы):
1. Класс планетоцентрических систем координат:
— гелиоцентрические (шифр П100),
— геоцентрические (шифр П200),
— селеноцентрические (шифр П300) и т. д. по названию
небесного тела.
2. Класс планетотопических систем координат:
— геотопические * (шифр Т100),
— гелиотопические (шифр Т200) и т. д.
3. Класс космоцентрических систем координат:
— орбитоцентрические (шифр К100),
— барицентрические (шифр К200) и т. д.
4. Класс связанных с ЛА систем координат:
— ЛА-центрические (шифр С100),
— нецентральные, связанные с неизменяемой частью ЛА
(шифр С200),
— нецентральные, связанные с подвижной частью ЛА (шифр
С300).
Для каждого типа системы координат используются следую¬
щие виды систем координат:
— прямоугольные (к шифру типа прибавляется 010);
— сферические (к шифру прибавляется 020);
— цилиндрические (к шифру прибавляется 030);
— географические (к шифру прибавляется 040) и т. д.
* Системы координат этого класса обычно называют топоцентрпческими.

Дальнейшая классификация производится по положению
основной плоскости, ориентации осей координат или отсчету
углов. Конкретный признак этого класса индексируется прибав¬
лением чисел 001, 002 и т. д. к шифру системы координат. Бук¬
венный индекс в шифре иногда опускается.
Полное название системы координат складывается из на¬
званий ее типа, вида и характеристики ориентации осей коор¬
динат.
Пример. Гелиоцентрическая прямоугольная эклиптическая-Ш
система координат имеет шифр ПИЗ (см. рис. 3.5).
3.	2. 2. Планетоцентрические системы координат
Системы координат, начало которых совпадает с центром пла¬
неты (Земля, Венера, Марс и т. д.), а также с центрами Солнца,
Луны или других небесных тел, относятся к классу планетоцент¬
рических систем координат. К планетоцентрическим системам ко¬
ординат условно относится географическая система координат.
Определения и характеристики наиболее употребительных си¬
стем координат даны в табл. 3.5. Классификация планетоцентри¬
ческих систем координат приведена на рис. 3. 5.
Формулы преобразования между геоцентрическими
и гелиоцентрическими системами координат
Для того чтобы получить формулу перехода от одной системы
координат к другой, необходимо знать положение начала первой
системы координат относительно второй и их взаимное угловое
положение.
Координаты начал гелиоцентрических систем в геоцентриче¬
ских и геоцентрических систем в гелиоцентрических системах
координат приведены в табл. 3. 6, а некоторые величины, опре¬
деляющие взаимное угловое положение систем координат, даны
в табл. 3.7. Формулы, связывающие координаты в различных
планетоцентрических системах, приведены в табл. 3.8а.
Для удобства отыскания необходимого преобразования
в табл. 3.8а приводится вспомогательная табл. 3.86, в которой
на пересечении столбца и строки, соответствующих шифрам пре¬
образованной и исходной систем координат, дается число, соот¬
ветствующее номеру строки в табл. 3.8а. При отсутствии числа
в табл. 3.86 («пустая клетка») преобразование координат можно
выполнить по формулам табл. 3.8а с помощью промежуточных
систем координат. Пример применения табл. 3. 8а и 3. 86 приве¬
ден на стр. 96.
76

Класс систем ПООО Планетоцентрические
координат  1 1
*§■
§ э 5
§§§
§5
<§^
77
Рис. 3.5. Классификация планетоцентрических систем координат

Определения и характеристики некоторых планетоцентрических систем координат
78

s н S'S £ <
2 2 И о Е [
Ь?о°5'
■I
8
8
8
V
V
V
><
X
N
V
V
V
8
8
8
5 ± ж н
Ч ~	«
Р ■* 5S о
С 4> Ч Ж
«Ю ►, о
О ^ ^
S&5
О V к
5«|’§
О э О. X
* <U ас
* с о
°
I S I
01 о „(
><:	n
о	о
Г" ' JC
а о О
<U s «
Ж н
о
о S
_ о. ч
5 * «
^ «со
«,я л
^ ° я 2
= !§!
= 5 « 6
>,aU
о ч
=: ^
С л
л к
‘ ч са
« о ж
J и и
- U «и
cIPn
0 = 40
79

Продолжение
О,	£	С.	О	~
н	rt	О	X	=
а	5-	е	е	г:
-	S	о	О	и
О	<=1	С	X
8
8
8
V
V
V
><
N
V
V
V
8
8
8
I J I
“S К
ф о
и <=1
и «и <
|™с
~ « ;
л * н
£ §•*
КЗ
е Е
со «
«J о
£7 о S
£||.
о = pN
ч сг»
О) S -
u S
5 г О
г1фиутт
•doii ou ojvf
80

81

Продолжение
г 2 2». сс '
;2 1 С" “ g
с-!“=§1
= сч о. К - и
;	-	я	и	—- —
) — С 0“ —■
2 я
^ X
<0 <и
в
V
8
V
8
V
8
V
ч
=г>
N
!-
V
V
V
V
8
8
8
8
I I I
е х
о э*
X о
о = ?
X я С
Q.H с
к О {
X Ч О -
X >- X $
х id а с
н х о
и [< с; с
а. ''■
ос;
х со
X х с
I f- с
I и с
О
: £ «*
1 S* § ?
: ч о я 2
iSo^o
; ач 30
I I I
I I о
о со U
х >. о
и х
о >> а
ч S <и
“ <и VU
Я (U
3 х
о с
° =
а. х
О -Q.
|§1 2\
5gS g
“ S' “1
« О 1)
*	с
.X Ч С
Н>>«) I (
1 (j ч н I :
N
! °i
; О ixi со
- X CJ
: Ч -S
5 ^ S £ 1
?2.чЗо
О
о н
X с
U X
О с-
Ч X
са f=j f—
х a, =
я с х
£ 2
Зсо
I—f v
Псо
S.* я
*- 5 х
12н^
с_ к с
asv
с ч О
*£ *
* 2 о -
S S ^ =2?
U К С V;
с1фит
*dou оц о\г
82

V V
2 х ^
5 ftS9-
а..
5 с»
,s ^ °
° Ь « -
= S °
К X § о
° 4 и 5
X о = С
о о 2
0 Н«
а ?*о
к J; I
1 S с в
.- I О
а I х
> uu
VO
>» о о
а. г
о я
С Н _
* и S
4» о Ч
* Q.S
о 2 "
а
л а " е
«в О ч,Ч
ачЭи
2 s
о н
ь* с
« s
о ч
►5 *
С л
Е s
« £
Ilf со
= £S с
S^J N
5 2х ^
v S j- 7?
U, к = w
§5о
83

Продолжение
5*115 «я s
5°1?52§5
<м ч « —< cj a
s я S	н
as -tj* cj
84

Продолжение
вб

5	<-> u S’s
* b q_ 2 2 о
*	—	a-	_	— rv
~	л r- ^	I	S	X
О	CJ	О	^	О)	Э
-	о	ь-	«	«(
<->	a	>>	2
О	x
87

Таблица 3.6
Координаты, определяющие положение начал гелиоцентрических
и геоцентрических систем координат относительно друг друга
№
no
nop.
Наймемование
Обозначс! не
1
Геоцентрические прямоугольные эклиптичес¬
кие координаты центра Солнца
■*©» г/©.
г®
2
Геоцентрические прямоугольные экваториаль¬
ные координаты центра Солнца
х©’ У®
• 4
3
Геоцентрические сферические эклиптические
координаты центра Солнца
Г®, А©,
Р®
4
Геоцентрические сферические экваториальные
координаты центра Солнца
г®, а®.
6©
5
Гелиоцеитрические прямоугольные эклиптичес¬
кие координаты центра Земли
Z©, У©, Z©
6
Гелиоцентрические прямоугольные экватори¬
альные координаты центра Земли
Ч’ у©•
Z©
7
Гелиоцентрические сферические эклиптичес¬
кие координаты центра Земли
А?©, X®.
8
Гелиоцентрические сферические экваториаль¬
ные координаты центра Земли
Я®, a®, d©
Примечание. Величины названных координат приводятся в Аст¬
рономическом ежегоднике СССР.
Пример. Координаты, заданные в гелиоцентрической прямо¬
угольной эклиптической-П системе координат П112, преобразо¬
вать в координаты гелиоцентрической сферической эклиптиче¬
ской системы П121.
Для определения преобразования берем 18-ю строку
габл. 3.8а (формулы преобразования для систем 121 и 111)
X — R cos у;cos р.;
Y = /?sin/cosp.;
Z = #sin p.
и подставляем в формулу из 1-й строки табл. 3.8а (формулы
преобразования систем 111 и 112)
Хг = X cos ь1 -f Y sin Q ;
-= — X sin SI -f Y cos Я ;
z1 = z.
«8

Искомые формулы преобразования имеют вид
Xi = R (cos х cos p. cos Я -f- sin X cos Iх sin ;
Уi =	(— cos x cos [x sin Я -f- sin x cos |x cos Я) ;
ZX = R sinjx.
Количество подстановок может быть произвольным, а вид
формул преобразования — не единственный.
Таблица 3.7
Параметры, определяющие ориентацию осей гелиоцентрических
и геоцентрических систем координат друг относительно друга
(при совмещенном начале координат)
№
по
пор.
Параметр
Обозначение
Определение
1
Наклон эквато¬
ра к эклиптике
£-23°27,8''26
(эпоха
1900,0)
Угол поворота геоцентрической
(гелиоцентрической) прямоугольной
эклиптической системы координат
Oxyz (ОXYZ) относительно оси
Ох (ОХ) до совмещения с геоцент¬
рической (гелиоцентрической) пря¬
моугольной экваториальной систе¬
мой координат Ох’у'z' (OX'Y'Z')
2
Долгота восхо¬
дящего узла ор¬
биты Земли
(Солнца)
я
Угол поворота геоцентрической
(гелиоцентрической) прямоугольной
эклиптической-I системы координат
Oxyz (OXYZ) относительно осп
Oz (OZ) до совмещения с геоцент¬
рической (гелиоцентрической) пря¬
моугольной эклиптической-11 систе¬
мой координат Oxiy}z-i (OX{Y\Z{)
3
Г ринвичское
звездное время
<Г|)Е
Угол между направлением на
точку весеннего равноденствия и
плоскостью Гринвичского меридиа¬
на
4
Угол наклона
ортодромии
ес
Угол между плоскостью ортодро¬
мии и плоскостью экватора
5
Долгота узла
ортодромии
Л с
Угол по меридиану от Гринвича
в восточном направлении до восхо¬
дящего узла ортодромии
Примечание. Время, протекшее от верхней кульминации точки
весеннего равноденствия в данном месте Земли до любого другого поло¬
жения, выраженное в долях звездных суток, называется звездным време¬
нем.
89

Таблица 3.8а
Формулы преобразования некоторых планетоцентрических
систем координат
№
по
пор.
Шифр пре¬
образован¬
ной сис¬
темы ко¬
ординат
Шифр ис¬
ходной
системы
координат
Формулы перехода от исходной к преобразованной
системе координат
1
112
11 1
X i = X с О s <Q “г У s i п £2
У т =— X sin Q + У cos й
ZX^Z
2
113
111 '
Z2 X cos х® 4- у Sin Хф
У2 —X sin х® + У cos х®
z2-=z
3
114
111
X1 - *
У' = Y cos е + Z sin £
Z' =— У sin £ + Z COS £
4
121
111
R /*2 H- Г2 + Z2
К
x== arc tg —
Z
fx - arc tg
|/ Z2+ Г2
5
122
111
У X2 --i- K2 -i- Z2
/ K 2 \
<3 = arc tg 	 COS £ 4- 	 Sin £
5 \ X X )
Z COS £ — У sin £
d — arc sin r _
у X? + Г2 + Z2
6
211
111
г = Z —z@
7
214
111
=*-*e
у’ = Z cos £ + Z sin £ — Z® cos £ — Z0 sin £
z' ~ Z cos £ — Z sin £ — Z® cos £ 4- Z® sin £
SO

Продолжение
№
по
пор.
Шифр пре¬
образован¬
ной систе¬
мы коор¬
динат
Шифр ис¬
ходной
системы
координат
Формулы перехода от исходной к преобразованной
системе координат
8
221
111
Г=\(Х — /?® cos u® cos X®)2 +
i
+ {Y—R® cos (AgSin Х,э)2+ (Z—R® sin f1^)2]2"
У — R® cos fig, sin x®
X* __ arc tg
x— /?@cosfi@ cos x®
. z-*esinj*e
3* - arc sin
r
9
111
112
X -- Xi cos Q_ — Yi sin <Q
Z = *1sin£ + V\COs£l
Z-- Zx
10
111
113
X—- X2 cos Хф — Z2 sin ^0
Y — X2 sin *^0 -j- Z2 cosy-@ .
Z= Z2
11
213
113
x2 —— X2-|-^0
i/2 =— Y 2
г2 = Z2
12
111
114
Л"
Z — Z' cose — Z' sins
Z = Z' sin e -j- Z' cos £
13
122
114
R=-V X'2+ Z'2 + Z'2
Z'
a =- arc tg
Z'
<1 ~ arc sin
R
14
211
114
x-X'-Xq
у = (У — K®) cos г— (Z'—Zq) sin £
z — (Z'—Z®) cos г + (Y' — У®) sins
91

Продолжение
»
по
пор.
Цифр пре¬
образован¬
ной систе¬
мы коор¬
динат
Шифр
исходной
системы
координат
Формулы перехода от исходной к преобразованной
системе координат
15
214
114
х’=Х'-Х'@
У'=У -У®
z' =-- Z' — z0
16
221
114
г— \(Х' — /?0 cos Д0СОях0)2-ь(К' cos е—Z' sin e —
“fl©cosfi0siny.@)2+
l
+ (Z' cose + Y' sin £ — #0sinfi0)2]2
Y' cose—Z' sine—cos s in */
'/r- — arc tg
X’ —R& cos (хф cos Хф
Z' COS e 1 1" sin e — sin u-0
3:-— arc sin
r
17
222
1 14
r- [(X’ ~Re cos (i@ cos x@)2+
+ (^'—cos (J-ф sin хФ)2 + (Z’-Rq sin ^ф)2]Г
У'—R^cos (Лф sin Хф
a!- — arc tg
X’—Rq C0SUQ cosX@
Z /?ф sin(xffi
o* — arc sin
r
18
111
121
X = R cos i cos p.
Y = R sin у cos u.
Z == /? s i n p.
19
122
121
R = R
f sine \
д-агс tg tg X cos e + tgfx
V COS xl
'1 =- arc sin (sin и cos e — cos jj. sin у sin e)
20
211
121
X =- R cos ft cos X — /?ф COS (Хф cos x@
у = R cos (i sin x — Rq cos fx@ sin x@
z = R sin (x — /?ф sin (Хф
92

Продолжение
№
по
пор.
Цифр пре¬
образован¬
ий систе¬
мы коор¬
динат
Шифр ис¬
ходной сне¬
ге мы коор¬
динат
Формулы перехода от исходной к nj еобразованной
системе координат
21
214
121
х' = R cos p. cos х — /?@ COS р@ cos х^
у' — R cos u sin х cos е — R^ cos p.^ sin x@ cos £ +-
+ (R sin }x — R@ sin p.@) sin e
г' = (/? sin p. — Rq sin p@) cos e —
— cos p. sin x — R@ cos sin x@) sin £
22
221
121
r= [(Я COS fl COS x — R@ COS u.@ COS X©)2 +
+ (Я cos (X sin x — /?@ COS (Л@ sin x@)2 +
1
+ (# sin p. — sin p-@)2]2
/? cos p, sin r — R@ COS p0 sin x@
X* — arc tg
# COS p. COS X — COS pe cos x@
# sin p — sin P0
p* - arc sin
r
23
111
122
X = cos a cos d
Y — R cos d sin <2 cos e — R sin d sin £
Z = R cos d sin a sin £ R sin d cos e
24
114
122
X' — R cos a cos d
Y' — R sin a cos d
Z' — R sin d
25
121
122
R
( sin £ \
у - arc tg ( tg a cos £ — tg d
\ cos aj
p. arc sin (cos d sin a siri £ + sin d cos e)
26
211
122
x — R cos a cos d — Rq cos a@ cos d^
у ~— R sin d sin e + R cos d sin a cos £ +
+ Rq sin d^ sin £ — /?0 cos d^ sin <20 cos £
г — R sin d cos e -f R cos d sin <2 sin £ —
— Rq sin ^0 cos £ —/?0 sin <20 cos d^ sin £
РЗ

Продолжение
№
по
пор.
Шифр пре¬
образован¬
ной сис;е-
мы коор¬
динат
Шифр ис¬
ходной сис¬
темы
координат
Формулы перехода от исходной к преобразованной
системе координат
27
222
122
г= |/?2+/?2@+2/?#@[ cos d cos dф cos (й]-йэ) —
, l
— sin d sin 12
R cos d sin cl — /?0 cos d^ sin
a* - arc
Rcos d cos a
R sin d — /?ф sin dq
b* arc sin -■ .
r
28
111
211
X ^x — x0
у у —у®
Z^z-z^
29
114
211
X' ----x — Xq
Y' — у COS E -j- 2 sin £ — ^0 COS £ — ^0 sin £
Z’ ——у sin £ -f 2 COS £	^0 COS £ 4- I © sin E
30
121
211
R - У(х-х<эу+ (у—Уф)2+ (z- Z(sy.
. у-l'®
x - arc tg
-*-*©
. g — *®
у - arc sin
R
31
122
211
/? = У (X— *0)2+ (У — </©)2+ (*~ ■г©)2
a— arc tg cose+ " sine
• L x~x® x~x®
— (У — .V©) sine + (z —Zq) cos4
d — arc sin
32
212
211
X\ ~ x cos Й 4■ у sin <Q
y\—— x sin <Q 4- у cos <Q
zx^z
94

Продолжение
№
по
пор.
Шифр пре-
образоиан-
ной
системы
координат
Шифр
исходной
системы
координат
Формулы перехода о г исходной к преобразованной
системе координат
33
213
211
х2 = -Г cos Aq + у sin Xq
у2 х sin Xq+ у cos Aq
г2= г
34
214
211
х' = X
у' — у COS е + г sin е
z' г cos е — у sin е
35
211
212
х -- х1 cos Q — ух sin
у — Хх siii S} + ух cos Q
Z^=Zx
36
113
213
Х2 =/•©— х2
Y 2 ~— У 2
Z2 Z2
37
211
213
х = х2 cos А0 — */2sin А'0
у = хо sin А0 +у2 cos Aq
* ^ г2
38
111
214
X = х' — Х0
Y--у' -х'@
Z=z' -г'е
39
114
214
X' --х' — х0
Y' — У' — %
Z' =- г' - г0
40
121
214
R- 1 (х'~
х — arc tg
f
p. -- arc sin
■Jf©)2+ (y' ~ %)2+ [z~г©)2
у'—у® z' — Zq
, с 0 s £ — , sine
-r'—x©
//' —//©) sin e + (*' — г'®) cos £
R

Продолжение
М
по
пор.
Шифр пре¬
образован¬
ной систе¬
мы коор-
линат
Шифр
исходной
системы
координат
Формулы перехода о г исходной к преобразованной
системе координат
41
122
214
R - ]/(*' — х@)2+(у — V@Y+(z— z®)2
a - arctg^®
• Z'~Z®
d — arc sin
R
42
211
214
x ~x'
у — у' cos e — г' sin e
Z = z' cos e + yf sin e
43
222
214
г—- У x">+ y'2+ z' 2
a* = arc tg——
x'
z'
й* = arc sin —■
r
44
111
221
X = r cos 3* cos X* -f- Rq cos cos y
Y - r cos 3* sin X* + R^ cos sin
Z = /-sin p* + R@ sini*@
45
114
221
X' r cos 3* cos X* — /*0 cos cos Xq
Y' — r cos e cos 3* sin X* 4- r sin 3* sin £ —
—Г0 cos 3q sin Xq cos s — ^*@sin 3q sine
Z' =— r COS 3* sin X* sin e + r sin 3* COS e +
+ /*0 cos З0 sin Xq sin e— /*0 sin 3q cos e
46
121
221
R — {/*2+ #0+ 2r#@[cos3* cos fx@ cos (X*—^0)4-
+ sinp* sin(x@])r
r cos 3* sin X* — cos p.0 sin Xq
X - - arc tg
r COS 3* COS X*—#0COS {X0COS X0
г sin p* — Rq sin [X@
и arc sin
R
96

Продолжение
№
по
пор.
Шифр пре¬
образован¬
ной сис1е-
мы
координат
Шифр
ИСХОДНОЙ
системы
координат
Формулы перехода от исходной к преобразованной
системе координат
47
222
221
Г -= Г
[ sill £ \
cr = arc tg tg k'- cos s + tg g*
\ cos Л*/
8* = arc sin (sin 3* cos £ — cos j3* sin /.* sin e)
48
122
222
R — r®~2rr© cos b* cos 5® X
X (cos ai: cos «0 -f sin a* sin а©)]2Г
r cos o* cos a* — г^ cos cos aX
a =- arc tg			^^
r cos S* sin a* — Гг-, cos sin
(y (•) ©
rsin 5* —r0 sin о"
d = arc sin 			—
R
49
214
222
x' — r cos o:;: cos a*
y' = r cos o* sin a*
z' ~ r sin 8*
50
221
222
r = r
cos o* sin a* cos £ — sin o:;: sin e
a* -= arc tg
cos 5* cos a*
3* — arc sin (sin o* cos £ -f- cos o* sin a* sin £)
51
223
222
r — r
A • “"—Op,,
cp' = 5*
52
222
223
r = r
a — 7 -f- ^rPg.
8* = cp'
4	1669
97

Продолжение
№
по
пор.
Шифр пре¬
образован¬
ной
системы
координат
Шифр
ИСХОДНОЙ
системы
координат
Формулы перехота от исходной к преобразованной
системе координат
53
224
223
срорт = arc sin {sin [ср' — arc tg [sin (X—Xc) tg 0C]] X
X sin arc cos [cos (X — Xc) sin 0cj}
_ tg (X — \c) t
оPt — ЯГС tg -f-
cos 0C
4- arc tg {tg [<?' — arc tg [sin (X — Xc) tg 6CJ X
X cos (X — Xc) sin 0C}
r = r (h = h)
54
241
223
X = X
. tgcp'
^аГС‘Ч-Д2:
A — эксцентриситет эллипсоида
h^h
55
223
224
<p' = arc sin (sin Xopx sin 0C) + arc tg (tg cpoPT cos 6C)
X = Xc + arc tg (tg XopT cos 0C) —
— arc sin (sin cpoPT sin 0C)
r = r3 + h
56
223
241
X = X
hmh
9' ^ arc tg[(l — A2) tgcp'];
A — эксцентриситет эллипсоида
98

Таблица 3. 86
Вспомогательный указатель для отыскания формул
преобразования, приведенных в табл. 3.8а
о Я
х s .
о а) н
s н 2
о *
^5 *
•в* Оч
S« О
Э О о
Я ^
Шифр преобразованной системы координат
111
112
113
114
121
122 211
212
213	214
221
222	223
224	241
111
112
113
114
121
122
211
212
213
10
12
18
23
28
24
29
36
13
19
11
25
30	31
14
20
26
35
37
15
16
21 22
27
32
I
33	34
214
38
39
40
41
42
43
221
44
45
46
47
222
48
49
50
51
223
224
241
52
53
54
55
56
Примеча н и е. Пример пользования таблицей приведен на стр. 84.
4*
99

3. 2. 3. Планетотопические системы координат
Системы координат с началом на поверхности планеты
(Земли, Венеры, Марса, Солнца, Луны и т.д.) относятся к классу
планетотопических систем. При расчете стартов или посадок на
подвижную платформу, не находящуюся на поверхности Земли
(корабль, подвижные направляющие и т. д.), системы коорди¬
нат, связанные с платформой, отнесены также к планетотопиче¬
ским системам координат.
Классификация рассматриваемых планетотопических систем
координат приведена на рис. 3. 6.
Ниже рассматриваются только системы, связанные с Зем¬
лей— геотопические системы координат. Определения и харак¬
теристики наиболее употребительных геотопических систем при¬
ведены в табл. 3. 9.
Формулы преобразования геотопических систем координат
Для получения соответствующих формул преобразования не¬
обходимо знание положения начала первой системы координат
относительно второй и их взаимное угловое положение. Необхо¬
димые величины приведены в табл. 3. 10.
В табл. 3.11а приводятся формулы преобразования коорди¬
нат JIA из одной геотопической системы координат в другую.
Для удобства отыскания нужного преобразования в табл
3.11а приводится таблица 3.116, в которой на пересечении
столбца и строки, соответствующим шифрам преобразованной
и исходной систем координат, дается число, соответствующее
номеру строки в табл. 3.11а. При отсутствии числа в клетке
табл. 3. 116 преобразование координат можно выполнить по при¬
веденным в табл. 3.11а формулам с помощью промежуточных
систем координат (см. пример в разд. 3.2.2).
При пользовании формулами табл. 3.11а необходимо иметь
в виду следующее:
1. Поверхность Земли апроксимируется либо поверхностью
шара, либо плоскостью, касательной к поверхности шара в на¬
чале неподвижной системы координат, либо эллипсоидом
вращения.
2. Все подвижные (при сферической модели фигуры Земли)
системы координат имеют общее начало.
3. Все неподвижные системы координат имеют общее начало.
4. Основные плоскости произвольных прямоугольной и сфери¬
ческой систем координат совпадают. Ось Ох является линией
отсчета произвольной сферической системы координат.
5. Проекция оси Ох (0\х) на плоскость местного горизонта
совпадает с осью 0£n(Oi£n).
100

J—I
1
Б
1
I
1
P
<o
<b
5S
8fc%
§
s
1
ll
1?
Л*
$ '
If
£ь
43.
ir
!a*
S3
p
at
II
§3
p
2f
Qq V:
I I * Д
P
P
^1
P
3 g
<5 3-
1
IS
SI
$ §J
<P
CX; »-h
P
§1
II
^1
P
i|
P
^ cv
|.§
<5s-
f*
£• <<s
£ ^
55 §
ea
$\i
§ j
^1
it
$ ^
ii
и
i^
Is
p
51
§;3J
I
§3»
jl
p
£s
ь
8*?
* 4
p
^ S
**>
ll
Is* 5s
^ <b
S§l
^x
J
o>
I
t
I
23
I
a
з
<§
<§
I
I_E
I ^
p
3 s g
P4
H*§
ftn
<§33^
101

Определения и характеристики геотопических систем координат
102

103

Продолжение

105

Продолжение
106

О Я
° 2
Ч О
с о
к
■ ,s«
о 5
i 2 *
К са
Л о а
'5*5.
°о ^ 1
М о *
О й)
* с
° ш а
о х :
X Ч
о о
О С=.
а. - в
« s
Ч н
>*2,
=5)
и ‘г "
о 5
" Л о >1 Q,
! Н И й(ч
>ЙР =<s
S« S 3
1?Й"
о o£-m
с ~ * S
й) К О н
£ Я с О
~*Е
Ч 5— N
о О—i с
2 О
s а о
£ 1=
с
107

родолжение
108
Плоскость горизонт 5 точке О

V
CJ
с « f;
i°-x
I x a
I s °
* £
„ О О
I
u
.	та	ДЙ
S О О
<У >1 О
9й£Ч
-вис
то
0-22
^ я 2
>> х л
И D* Н
¥ О и
4
- 2 So
i о о
5 _. О.Ч
0 °с
■г ьс «
>> а» о
1 в с
«0*1-4
'6*1%Ъ
С « ■“ х СО
<и са —
Xх*
°	S	1ч	*	С
-	*	I	я	S	f
° £ £о!
и» О 5 П о О
V	о-	к
О	о	Р	У	о.	II
I „ То >4 <
I CQ С сп ;
“	°	И	О
. ® S Й
2 а о. л
?1|И
5 So 0.0 1
^§с:1
-О * *
I 4
¥ то И
2 * cl
*5£?4
?н goS
«|-Вп
— s с
<и н <и *
с. то с *
Й £ - °ск
ufS-^
> 5 *
О о
;н!
• £ о
В X
юэ

Продолжение

Ill
Угловая ориентация прямоугольных произ- Vi> V2* V3 Первая система углов Эйлера (см. табл. 3.4а),
вольной и ориентированной систем координат определяющих положение прямоугольной произволь-
отпосительно друг друга н°й системы координат относительно прямоугольной
ориентированной системы

Таблица 3.11а
Формулы преобразования геотопических систем координат*
№
IIO
1 ор.
Шифо про¬
образован¬
ной
СИС 1С.МЫ
коортинат
Шифр
исходной ! Форм\'лы перехода от исходной к преобразованной
системы j спсiеме координат
координат
1
112
111
£с— £п cos (Аи—Ас) — Tin sin (Ап—Ас)
Па—- £п sin (Лп—Ас) + % cos (Ап—Ас)
1--Т
^С • ^п
2
113
111
£=£ncos Аи— г|п sin Ап
. п=;п sin An+ rincos Ап
с = сп
3
111
112
I„=*c cos (Лп—1с) 4- Tie sin (~АП—АС)
Ип=— ес sin (Лп— Лс) + T]c cos (лп— Ас)
4
113
112
£ — £с cos ^4С— т|с sin Ас
г| = 1с sin Ас+ Лс cos Ас
С=Сс
5
111
113
£п=--5 cos 4п+ т| sin Ап
I г|п-= — £ sin Лп+ т] cos Лп
сп=с
6
112
113
cos Лс4- т] sin Ас
т|с—— z sin Ас-\- Л cos Ас
Сс=С
7
117
113
-Yn-=£ cos у~2 COS V3+ Т] sin Уз— с Sin V2 cos Уз
7i~r— С, (sin у2 sin Vi— cos у2 COS yj sin Уз) 4-
-\-v\ cos yj cos y24-
4- I (cos y2 sin Vi— sin y2 cos yj sin y3)
Fn-r I (sin у2 COS V! 4- COS y2 sin yj sin y3) —
— T] sin уг cos y2 4-
4- С (cos y2 cos yj — sin y2 sin yj sin y3)
* Преобразования даны для левых прямоугольных систем координат.

Продолжение
№
по
пор.
Шифр
преобразо-
ван 'он
сис: емы
коорчинат
Шифр
исходной
системы
координат
Формулы перехода от исходной к преобразованной
системе координат
8
115
114
Сс — ?п COS (^п ^с) Лп sin (-^п ^с)
11с = £п sin (Ап — Ас) + 11 п cos (Ап — Ас)
Сс = Сп
9
116
114
£ = £п cos Ап — У)п sin Ап
Л ~ in sin Ап + iin cos Ап
С = Сп
10
118
114
^n = ^ncosv3 + ^nSin V3
Уп=— £п cos Vi Sin v3 + Лп cos Vi + Cn sin vi
= gn sin Vi sin v3 — Лп sin Vi -f Cn cos vi
11
119
114
x=in cos An — £n sin Au — Д£
У = Лп
z = ZU sin An + Cn COS Ап — Д£
12
'121
114
Лп
ДA„ = arc tg-^-
£n
. Cn
en= arc sin —
13
114
115
Sn = tc cos (A„ — Лс) + T)c sin (A„ — Л)
Hn=— tc sin (An — Ac) + % cos (Лп — Лс)
C„=CC
14
116
I
115
£ = £c cos Дс — r)c sin Ac
Г] = £c sin Дс + T|c cos Дс
C=C с
15
119
115
x = Sc cos Лс — £c sin Ac — Д;
У = 11c
z — Sc sin Дс + Cc cos Дс — Д£
113

Продолжение
№
по
пор.
Шифр
преобразо¬
ванной
системы
координат
Шифр
исходной
системы
координат
Формулы перехода от исходной к преобразованной
системе координат
16
122
115
Лс
АЛ = arc tg —
£с
. Сс
ес — arc sin —
R
17
111
116
Sn=6 cos Acp' cos An -f С [cos (AX cos cp^j sin Acp' X
X cos An — sin (AX cos sin Лп] 4-
4-т) [sin (AX cos cp^j sin A<p' cos Au-\-
cos (AX cos cp^) sin An] + R3 {— sin Ao' x
X cos Лп [2 cos Acp' + cos cpQ—
— cos <pо cos (AX cos To)-1]
— cos сPq sin An sin (AX cos <Pq) } .
1^=— £ cos Acp' sin An—£ [cos(AX cos <p0) sin Acp' X
X sin An 4- sin (AX cos <p0) cos Лп] —
—г] [sin (AX cos cpQ^ sin Acp' sin An—
— cos (AX cos cp0) cos An\ + R3 {sin Acp' x
X sin Лп [2 cos Acp' 4- cos <Pq — cos ?o X
X cos (AX cos <Ро)~“*] —
—	cos cpQ cos Au sin (AX cos <p0)}.
Cn=— 5 sin Acp' -f £ cos Acp' cos (AX cos v’q) 4-
4- T] cos Acp' sin (AX cos cpQ) 4-
4- R3 {sin2 Acp' 4- cos Acp' (1 — COS Acp' ) —
—	cos cpQ [l—cos (AX cos ?o)]}
114

Продолжение
№
по
пор.
Шифр пре¬
образован¬
ной
системы
координат
Шифр
исходной
системы
координат
Формулы перехода от исходной к преобразованной
системе координат
18
113
116
£ = £ cos Дер' + г] cos (ДХ cos <рq) sin Д<р' +
-г С sin (ДХ cos <Pq) sin Дер' — R3 sin Дер' X
X [2 COS Дер' + COS ср^ — cos cpQ cos (ДХ COS ep^—lj
T) =— £ sin Дер' + r\ COS Дер' COS (ДХ COS <Pq) H-
+ С COS Дер' sin (ДХ COS <Pq) 4- #3 [sin2 Дер' +
+ COS Дер' (1 — COS Дер' ) —
—	COS ep^l — COS (AX COS <Pqjj
— T) sin (дХ COS ep^j -J- С COS (дХ COS ep^ —
—	#3 COS «Pq sin (дХ COS <Pq)
19
114
116
£n = £ cos Лп + r\ sin Лп
Tin =— £ sin Лп + Г] cos An
Cn=C
20
115
116
Sc = £ cos Ac + Y] sin Ac
T]c =— £ sin Ac -f* “П cos Ac
Cc = C
21
118
116
xn = £ cos V2 cos V3 + Л sin V3 — С sin V2 cos 73
£/n = £ (sin V! sin V2— cos Vl cos V2 s^n V3) +
+ i”| cos Vi cos V3 + С (cos V2 sin Vi —
— cos Vl Sin V2 sin V3)
zn = £ (sin V2 cos Vi + cos V2 sin Vi sin V3) —
— r\ sin Vi cos V3 —
— С (cos V2 cos Vi — sin V2 sin Vi sin V3)
22
119
116
x ~ i — Д£
У = 4
.г = С — ДС
115

Продолжение
№
по
пор.
Шифр пре¬
образован¬
ной
системы
координат
Шифр
исходной
системы
координат
Формулы перехода от исходной к преобразованной
системе координат
23
123
116
R = У г- -ь л2 + £2
л
Л = arc tg —
. С
ei = arc sin—
R
24
131
116
r = /£2+ T|2
л
-4 = arc tg —
h = *
25
113
117
6 — xn cos y2 cos уз -r yn (sin Vi sin V2
— cos vi cos V2 sin V3) +
+ zn (sin V2 cos vi -r sin vj cos V2 sin Vs)
T} = xn sin y3 -j- £/n cos vi cos y2 — Zn sin vi cos y2
.vnsinV2cos v3 +
+ yu (sin vi cos v2— cos vj sin 72 sin V3) —
— zn (cos Vi cos 72 — sin vj sin y2 sin y3)
26
114
118
£n = xn cos v3 — Уп cos Vi Sin y3 + ^n sin Vi sin 73
rin = xn sin гз + Уп cos vi — sin vi
Cn^ г/nSinvi — zn cos Vi
27
116
118
£ = x„ cos 72 COS V3 + Уп X
X (sin vi sin — cos 7! cos 72 sin 73) +
+ zn (sin 72 cos 7j -j- sin yx cos 72 sin 7.3)
Tl = -^n Sin 73 -f yn cos 71 cos 72 — zn sin cos 72
£ =— xn sin 72 cos 73 + yn X
X (sin 7: cos 72 — cos 71 sin 72 sin 73) —
— zn (cos 7i cos 70 — sin 7! sin y2 sin 73)
116

Продолжение
№
по
пор.
Шифр пре¬
образован¬
ной
системы
координат
Шифр
исходной
системы
координат
Формулы перехода от исходной к прео'бгазованной
системе координат
28
123
118
R = Vxl+yl+xt
А — arc tg {(хи sin Ъг+Уп cos vi cos V2—
— 2n sin Vl COS 72) [*n COS V? COS V3 -r
-f- yn (sin vi sin V2 — cos vi cos V2 sin V.?)+
+ 2n (sin V2 cos vi + sin vi cos V2 sin V.-)] 1}
— x„ sin v^ cos v?
£j — arc sin +
R
yv (sin vi cos V2 — cos Vi sin V2 sin V?)
+ R
2n (COS Vl COS V2 — ?in Vl sin V2 sin V3)
R
29
114
119
Sn = x cos An + z sin An 4- AS
Cn =— x sin Au-V z cos An + ДЛ
Лп = IJ
30
115
119
Sc — x cos Ac + 2 sin Ac + AS
Cc =— x sin Ас -f* 2 cos Aq -f* AC
Лс = У
31
116
119
s = x + AS
С-=2+ AC
Л =- у
32
114
121
Zn—R COS A An COS £n
Cn — R sin ДЛП cos £n
Tin = R sin £n
33
122
121
R = R
£c = £n
A Aq = An — Aq -f* АЛл
117

Продолжение
№
по
пор.
Шифр пре¬
образован¬
ной
системы
коорлинаг
Шифр
исходной
системы
координат
Формулы перехода от исходной к преобразованной
системе координат
34
123
121
R=R
е1 = £п
А = Лп -р ААп
35
115
122
£с = R cos ДЛС cos ес
r\c= R sin АЛс cos ес
Сс = R sin ес
36
121
122
R=R
£п=- ес
АЛП — Aq Ап -}- ААс
37
123
122
R = R
£1 =£с
А = Aq -j- A Aq
38
116
123
£ —■ R cos A cos ej
T] = R sin A cos £ j
£ = R sin £2
39
118
123
= R (cos £j cos A cos v2 cos Vs + ei V3 —
— cos ej sin A sin cos Vs)
Уп = R [cos £2 COS A (sin Vl sin V2 —
— COS V2 COS V2 s'm V3) + sin £1 COS Vl COS V2 +
+ cos £2 sin A (sin vi cos V2— cos Vi sin V2 sin v3)]
zn = R [cos £2 cos A (cos vi sin 72 +
+ sin vi cos V2 s^n V3) — s^n £i sin Vi cos V2 —
—cos £2 sin A (cos Vi cos V2 — sin Vi sin V2 s*n V3)]
40
121
123
R = R
en = £1
A An = A An
118

Продолжение
№
по
пор.
Шифр
преобра¬
зованной
системы
координат
Шифр
исходной
системы
координат
Формулы перехода от исходной к преобразованной
системе координат
41
122
123
R = R
£с= е1
ДЛС = А — Ас
42
124
123
Д = Я
в! = arc sin [cos <рп sin (vi + ^п)]
A = V2 — arc tg [tg <pn cos (vi + X„)]
43
131
123
Г = R COS
A = A
h = R sin
44
123
124
R=R
Xn —arctgf ] — VI
Lcos (v2 — A) J
Г sin£i 1
?n — arc cos - -
L sin (Vi + Xn)J
45
116
131
2 = r cos A
T] = r sin A
46
123
131
f> = yr2+ ffi
A = A
h
£i = arc tg —
r
119

Таблица 3.116
Вспомогательный указатель для отыскания формул преобразования,
приведенных в табл. 3.11а
Шифр
ИСХОДНО!
системы
коорди¬
нат
Шифр преобразованной системы кг ординат
111
112
11Я
114
115
116
117
118
119
121
122
123
124
131
151
111
112
113
114
10
11
12
115
13
14
15
16
116
17
18	19	20
21
22
23
24
117
25
118
26
27
28
119
29
30	31
121
32
33
34
122
35
36
37
123
38
39
40
41
42	43
124
44
131
45
46
Пр и м е ч а н и е. Пример пользования таблицей дан на стр. 108.
3. 2. 4. Космоцентрические системы координат
Системы координат, начала которых находятся в точке, лежа¬
щей вне небесного тела или летательного аппарата, называются
космоцентрическими. К ним, в частности, относятся системы
координат с началом в какой-либо точке орбиты (орбитоцентри¬
ческие системы координат) или в центре масс системы небесных
тел (барицентрические системы координат). Классификация
этих систем координат приведена на рис. 3.7. Определения
некоторых космоцентрических систем координат приведены
в табл. 3. 12.
120

Формулы преобразования космоцентрических систем координат
Связи между орбитоцентрической прямоугольной апсидной
системой координат	(Kill)	и	орбитоцентрической	сфери¬
ческой апсидной системой координат Orvcpq/ (К121) даются
формулами:
;r-_=r cos vc“ cos cp' ;
i*l = r sin vcpcos«';
L = r sin cp' ;
vCp = arctg
o'= arctg-
V С2 -Г Д2
Связи между барицентрической прямоугольной орбитальной
системой координат 0Qxyz (К211) и орбитоцентрической прямо-
Класс систем
координат
Тип систем
координат
Вид систем
координат
Положение основ
ной плоскости и
линии отсчета
\K000 Космоцентрические |
- t
1100 Орбитой, ентрические |
1200 барицентрические [
1
110 Прямоугольные |	|	1ZQ	Сферические	[	]	210	Прямоугольные
1111 Япсидные |
! 121 Апсидные |
1211 Орбитальные
Рис. 3.7. Классификация космоцентрических систем координат
угольной апсидной системой координат	(Kill)	даются
формулами:
■ • - П1г>
* = $cosvc; + T,sin Vcp-—г;
у= —; sin vCp -f- r\ cos vcp;
z = t,
где тът2 — массы двух тел (т^ > т2);
г — расстояние между центрами масс этих тел;
vcp—средняя аномалия тела.
121

Определения и характеристики некоторых
о.
о
с
о
с
я
Шифр
Название
и обозначение
Начало
координат
Основная
плоскость
Направление осей
и отсчета углов
1
Kill
Орбитоцентрическая
прямоугольная апсид-
нтя
01 т(С
Центр
орбиты
Плоскость
орбиты
ОС — в основной плоскости вдоль
линии апсид к перицентру
ОС — вдоль вектора угловой ско¬
рости тела в орбитальном дви¬
жении
2
К121
Орбитоцентрическая
сферическая апсидная
0nV'
Центр
орбиты
Плоскость
орбиты
vcp — Угол в основной плоскости,
отсчитываемый от направления
на перицентр по движению
тела
<рг — угол между радиусом-векто¬
ром точки М и его проекцией
на основную плоскость. Поло¬
жительный отсчет (от 0 до 90°)
в полусфере, содержащей век¬
тор угловой скорости тела в
орбитальном движении
3
К211
Барицентрическая
прямоугольная орби¬
тальная
06xyz
Центр масс
системы
двух тел
Плоскость
орбиты
О^х — в основной плоскости, по
линии, соединяющей центры
масс двух тел, в сторону при¬
тягиваемого тела
О^г — перпендикулярно основной
плоскости по вектору угловой
скорости тела в орбитальном
движении
122

космоцентрических систем координат
Таблица 3.12
Плоскость
орбиты
Тело ка орбите
'и направление
движения
Кроме эллиптической воз¬
можны другие типы орбит(ги¬
перболическая и др.)
0<vcp<36C°
—90°<9'<90°
Барицентрическая система
может рассматриваться как
для задачи двух тел, так и для
задачи п тел
123

3.2. 5. Системы координат, связанные с летательным аппаратом
Системы координат, начала которых совпадают с некоторой
точкой конструкции JIA или точкой, заключенной внутри кон¬
тура JIA, или его поверхности, называются системами координат,
связанными с летательным аппаратом.
К этим системам, в частности, относятся:
— системы координат с началом в центре масс ЛА (JIA-
центрические);
— системы координат, связанные с неизменяемой частью
ЛА, но не с его центром масс (нецентральные-1);
— системы координат, связанные с какой-либо подвижной
частью ЛА (нецентральные-II).
В качестве неизменяемой части ЛА рассматривается его кор¬
пус с элементами силового набора. В качестве подвижных частей
ЛА могут рассматриваться подвижные элементы органов управ¬
ления, гироплатформы, подвижные антенны, отдельные ступени
ракет и т. д.
Классификация систем координат, связанных с ЛА, приве¬
дена на рис. 3.8, а определения и характеристики некоторых из
них даны в табл. 3. 13.
Формулы преобразования систем координат,
связанных с летательным аппаратом
Для получения формул перехода от одной системы коорди¬
нат, связанной с ЛА, к другой должны быть известны положение
начала и угловая ориентация первой системы относительно вто¬
рой. Параметры, определяющие взаимное положение различных
систем координат, приведены в табл. 3.14.
Для облегчения нахождения формул преобразования, приве¬
денных в табл. 3.16—3.29, составлен вспомогательный указа¬
тель — табл. 3. 15.
В этой таблице трехзначные числа, стоящие на пересечении
строки и столбца с номерами, соответствующими шифрам исход¬
ной и преобразованной систем координат, обозначают номер
таблицы, где указано исходное преобразование (табл. 3. 17—
3.29), а одно- и двухзначные числа — порядковый номер строки
в табл. 3. 16.
При отсутствии числа в клетке («пустая клетка») необходимые
формулы перехода можно получить с помощью промежуточных
систем координат (см. пример в разд. 3.2.2).
Примечание. Формулы преобразования, приведенные
в табл. 3. 16—3.29, справедливы при совмещении начал исходной
и преобразованной систем координат. Если начала координат
исходной и преобразованной систем не совмещены, следует при¬
менить операцию параллельного переноса начала координат
(см. разд. 3. 1. 3).
.124

1
?
I
Г
!
,1
и
18
1
^ s
<o
«41
il
r
II.
^ Ct;'
C3 ^
‘ ^ *
ill
ZL
§ !
t3 ^
* ^s
I s
3S §J
C4j *:
Z, ^
zn
Ct; ^
5 $
<Ъ ^
> 5
^ i
^ ^ ^
ill
^ < <4
^ £ c>
gp
♦
i ^
«5» ^
^ ^
Pi
1§<§
§ ^ Zj
^ §?
^o C5:
П
ь
t!
Co ^
I <*;
§
III
ft I
sga^
♦
03
S S
f< O
Oh H
О <Я
О Он
« «Л
4 $
£ I
It
t!
£ £
S> ^
zzi
| g
& <
§1
I ^
ii
ZJ
is
i*
s§
3i
■= t
СЭ *;
p
II
•£!
Kc
s§
1§
l!
'S: %
125

Таблица 3.13
Определения и характеристики некоторых систем координат, связанных с летательным аппаратом (J1A)
126

So!
о 2 \
S S о “ I S*
' 5 — ^ н JJ tL «
: 2 ^
:s«ggs& J
!^2й>Ьй9*~ОД
:°§<5	5	=	£
! hsJS!*^
CQ 04 ~
ГГ 4 w 0«
о о = cx o
f- 2 Ш a
*5S“«!
« ° § « s ‘
* 06 « E s
5 о ex “< «
айсашя
fo5^s
) к о о
: “	о	e;
: £ се s	С
^ P" J ы	Ж UL,
оэ a	s	s cc a>
2о„£ьоа
« о * « *3 «
о о ex О
'авевL
о S СХ“ 3"
^чо«
с ё X о.«
II и
§в!" *
° ч 0 я ^
° Н в 5
cj Cl, *q !
,5	О	О	— S f-	®	О
i	Ьй	Ж	а X и	I	а
Ч
О
*ё
л ° ^
н ^ я
и л*
S3|
8S§
4f-5
С ex ^
CJ s
s«
e-^
sc
s	S	e	5	в	к	(a
a	к	7	и	«	^
H	CX	«	о	CJ	X	T*
=	i=	«	X	“	a	=S)
<U	Ж	.a	S	re	e<
а К Д c; an /
I	еа	ч	я	н	к
Ьй	о	Ьй	CJ	ОС	О
р	tJ	U	s	S	tJ
^	>1	H
j°cs«7
s S m cj ж сч *
ex к	' <-> «
f-	ex к	о	a>	E	<
я	С я	Я	J	g	н
О)	I	ifl	я	_	^
?	я в	я	н«о
>	V О	V	0	К
х	о u	S	2	у
*=*	>,	Н
127

Продолжение
128

ю
1669
129

13 0

131

Продолжение
132

J о О X
S «
сх - к
> 2 £
л:53 ®
сх £
я о © -
н н ° н
е	и	^	в	и
I	О	0>	I	о
I	*	ю	I	^
Q
Q
л о L
es§-ss
Л A £ С. С
н ч ° «У а
С к «
2£?
: £ ^
I «О
v
.	О	W	Ж
С	1й	те	К
'	(-	К	О)
г	о	К	2
э	а»	«	п	-
-	*	S	g	»=
ю	S	<
5	*	:
<
**=:
Ч S2*? о =
2 к й £ 5 о. N_
S’eSS&gtSs,"
8-5й538чв
3g£.||S Q
X * сс ° о
133

Продолжение
134

135

В табл. 3.17—3.29 представлены формулы перехода в ма¬
тричной форме, допускающей как прямое, так и обратное пре¬
образование.
Пример пользования табл. 3. 19.
Прямое преобразование (сумма строк):
хс — х cos 2: sin 3 ;
ус — х sin 3 sin yc~f У cos Ус~г cos ? sin Yc;
zc = — x sin p cos Yc + У sin Yc + г cos P cos Yc •
Обратное преобразование (сумма столбцов):
X = хс COS р + Ус sin Р sin Yc гс sin р C0S Yc ;
и=ус cos Yc + ^c sinYc;
z == xc sin 3 — yz cos 3 sin yc + cos P cos Yc •
Дополнительные соотношения между углами,
характеризующими взаимную ориентацию различных
JIA-центрических систем координат
Взаимное расположение ЛА-центрических систем координат
можно задать с помощью нескольких систем углов (ф, *&, у)?
(фс, 0, Yc), (а, Р) (см. табл. 3.14). Это позволяет найти допол¬
нительные соотношения между указанными углами. Так, исполь¬
зуя связи между земной 118, связанной 112, скоростной 115 и
поточной 116 системами координат (см. матрицы табл. 3. 17, 3.20,
3.22, 3.23) и приравнивая соответствующие элементы произве¬
дения транспонированной матрицы табл. 3. 17 на матрицу
табл. 3.22 элементам матрицы, найденной в результате пере¬
множения матриц табл. 3. 20 и 3. 23, получим соотношения между
углами 0, Yc, фс и углами ф, у, 'O', а, (3. Этим соотношениям можно
придать различную форму. Ниже приводятся наиболее распро¬
страненные формы их представления.
а)	Выражение углов 6, ус, бс через углы ft, у, ф, а, р:
sin 0 = sin ft cos а cos 3 — cos ft cos у sin a cos£—cos ft sin у sin p;
cos yc = (cos ft cos a cos у + sin ft sin a) sec 6;
sin 0C = (sin ф cos ft cos a cos-f- cos ф sin у si n a cos 3 -f	[(3.1)
-\- sin ф sin ft cos у sin a cos 3 — cos ф cos у sin 3 -)-
-f sin ф sin ft sin у sin p) sec 6.
137

Углы, определяющие взаимное положение систем координат, связанных
<
о О
Р-Е
ЭЕ <и
<и
~ ° ЭЕ
= о> аз
V В- ъ
'	~	О	J
« O.S:
о
О*о
е е
р о
<L»
>=;
QJ
и;
о
CJ	о	о
о“эт
5	“	s
О	*=1	^
(3J о
и Е
0,Ь
S о	О
1	Н	О	та
:	е	н	£
Д и	о	о	с;
О	Ч	п	о»
^?Я	С	У	с?
^ О) Он Е
* =	2	о	^
о У
н а а ге
си си	с
>>о	К	о	_
по Си
Л с
:§г?
£ к
ООО
О Е Е
СьН h
О о о
О О) QJ
Н йа
я д н
д си о
s о s
< «
Си О Си
о - f
о a 1
*
~ cf и
~ а н
о
- fc(
2
S
Н ЭЕ
та о
ОС
си
си
та
н
<и
н
Е
Он та
та
О
53
О
о
Е
о
S
Си «
2
Е
о
2
аЗ
Он
О
со
S
н
о
<и
Е
Е
.
VO
<и
н
и
С J
О
2
та
S
Е
CJ
н
s
н
ЭЕ
о
си
н
о
CD
СО
о
о
«
О
S
О
’—1
и
S
о
та
н
ОСИ
О
со
S
Он
эЕ
о
О)
У
о
Е
CD
о
О
Он ь
Е
и
CD
*
О
!§•
CL)
1 О)
У о Г-
е и <и о
О О е; О
Он н
С и
<1) ^ ..
Г- *
У та
V-.	*0
с: ^
^ О ^ °0
^ е л
и Си 2
5 о о 2
о с; ь *
У- С о -
^>5 га ■—
аз <и Си
е е е
Ч та
О g
^ о
2 m
>-> о
к* -
*§
>э 2
ё<
S-*
и К
*=* »
* £
<и -а
S а
эУ Ч
go
s иа «
Он «Ч о
та о
Е
a £ 33
з§1
о я
си
f- о V
О Е Е
Он
>->
Е
is-
Е ■"
и ~
>5 =
о со £> ~ t: ^
Э ^ о
>Л§ о
I " *
*л>
о
н г Ь
иди
к О s
О СО и ОС
Он
та Е
С- О
24 й
Е Он О
У О Е
Он
я о
с -
о °
2 9
си Е
Е ^
CJ
S?
— CJ
>* §
си Я
О “
<1> о О
: а =
г Ои
<D Н
° 9
Си $
У ^
'-н о
о
^Е
г=* с
о о е
О, О
>> О п
>5
> о.
138

>-> та
£
t 2.5
if 9=
о-к 2
•О е ь
g
. 2 ~ я
О QJ О •=*
Зро
S 5 ё g
2~ 2
^2 S
р 03
о
О) со
5: CU
Он
CU
о
*
2
Я о
о
X
< s
*СО
3
S s
О <и
Я о
Ч Он
со о
« «
К и
о Он Он
S <и о
CJ СО (-
с
D3 О ^"
эЯ я сг
CU Я
ЙГ та s
Си Он
С CU s
оо SCO
г?^ =
Й а JT^
(D ^
S Я^Н
h V и
Ч О Я
р о л и
>5 о О
S So
2 =
Он с
о
£ °
2 °
Он Я
си С
сс
эЯ
з я
О	<D
5«п
U Й 5
-
Он 00
»s <
“ я ^
л 2 § к
^ к л ь
О	Ч
СО <и со
Я Н от
О ^
.о О
о
ч.
* .. _
СО V>
s Я
4 f-
о (О,1—а
>■» Ч
£ о*
о
С <и
^я
КС В
* я
<U сд
>s =я Я
си о
я с
эЯ
1
Я
си
си
о
X
>г,
2
а
о
Он
2
со
си
с
си
СО
я
я
со
Он
2
Ч
0) ЭЯ
о
я
я
Я
си
я
1—1 ■"»
3 ^
5 §
§е
с ё
5 о
си Я
£э§ “
Он® %
£*2
К э£
С эЯ
у	Ш	^	9
к,	S	Я	°	S
>3	^	с	О)
СО	R	о	Он
CU	с-	с	Я
| К
Я о
со Я _
Н н ^
К ° и
0) £
2< в-
° ^ эЯ
О)
Я со
3 Ё
2 <D
w 2
4 О)
CU е-
Ч СП
О)
а *
ч К .-
и 0Q 2
>> Э ^
О <и
С Ч
О СО
с;С>
о
*
о
*
О
я
а>
*
О
о
о
£
<
о.
с
О О с
>> S
я
>» 2
1Я0

140
Припер пользоиания таблицей прим еден на стр. 132,

Таблица 3.16
Формулы преобразования систем координат, связанных с J1A
№ по
пор.
Шифр
преобразо¬
ванной сис¬
темы коор-
дина г
Шифр
исходной
системы
координат
Формулы преобразования
1
112
111
*12 ~ *11 cos <ри уц sin сри
.«/12 = *12 sin <Ри + У\\ COS сри
*12 “ *11
2
111
112
хи = х12 cos сри + у12 sin сри
У\\ "= *12 sin У и + «/12 C0S <Ри
*11 = *1?
3
113
112
*1 = ‘ *12 cos ?кр + «/12 sin <РкР
i/1 = “*12 Sin сркр + Vlo COS сркр
*1 =- *12
4
114
112
л: — xl2 cos а — yV2 sin а
у — х12 sin а + у\з cos а
* = *12
5
112
ИЗ
*12 ““ *1 COS сркР Ух sin <ркр
Ух2 — *1 Sin <ркР + Ух COS сркР
*1? = *1
б
112
114
Хх2 — х cos а + у sin а
г/12 —* sin а + г/ cos а
*12=- *
7
116
114
хп — х cos р — г sin р
«/п = «/
гп =- .v sin р + г cos р
8
117
115
Jfe — хс
уе -= г/с cos Ye + *с sin Ye
*е = Ус sin Ye + *с COS Ye
141

Продолжение
№ no
nop.
Шифр пре¬
образован¬
ной систе¬
мы коорди¬
нат
Шифо ис¬
ходной си¬
стемы
координат
Формулы преобразования
9
121
115
0.= V Х1 + у\ + г\
хс
срл -= arc cos
Гл
10
114
116
х = Хп COS Р + sin Э
и = У п
-г — —хп sin р -f zn cos р
11
115
117
хс = хе
у с — r/e cos Ve — 'S'e Уе
zc = ye sin Ve 4- COS \e
12
115
121
xc = гл cos срл
y\ + z\ = r\ sin2 cp,,
221
211
r=V
X2 + y\ + z\
cpB == arc cos
cpr ■= arc cos
V x\ +A
У\
V y\ + z\
14
211
221
*\ =
У\ =
=
r COS cpB COS cpr
Y 1 — sin2 cpB sin2 cpr
r cos cpB sin cpB
Y1 — sin2 cpB sin2 cpr
r cos cpr sin cpr
Y 1 — sin2 cpB sin2 cpr
142

Таблица 3. 17
Матрица преобразований между JlA-центрической прямоугольной
горизонтальной ориентированной (земной) Oxgygzg (Cl 18) и JlA-центрической
прямоугольной вертикально-скоростной Oxcyczc (Cl 15) системами координат
Покрашенное название
Земная система координат С118
сис темы
Xg
lJg
Скорост¬
ная система
■*с
COS 0 COS d>c
sin 0
—cos 0 sin^c
координат
С115
Ус.
—sin 0 cos <bc
cos 0
sin 0 sin фс
sin фс
0
cos 4 c
Таблица 3. 18
Матрица преобразований между JlA-центрической прямоугольной
вертикально-симметрической связанной-1 Ох\2Ум^\2 (С112) и ЛА-центрической
прямоугольной вертикально-скоростной Oxcyczc (Cl 15) системами координат
Сокращенное название
Связанная система координат С112
сис 1 емы
х, 2
| //12
| 2 I 2
Скорост¬
ная система
хс
cos a cos р
sin a cos (3
sin p
коордипат
С 115
Ус
j sin а cos ус
+ cos a sin 3 sin Yc
cos a cos У с —
— sin a sin (3 sin Yc
—cos (3 sin 7c
sin a sin Yc —
— cos a sin (3 cos Yc
sin a sin (3 cos Yc -f
+ cos a sin Yc
cos 3 cos Yc
Примечание. Данная таблица справедлива для центральных-!
систем координат С211 и С212.
Таблица 3. 19
Матрица преобразований между JlA-центрической прямоугольной вертикально¬
симметрической полусвязанной Oxyz (Cl 14) и JlA-центрической
прямоугольной вертикально-скоростной Oxcyczc (Cl 15) системами координат
Сокращенное название
смет емы
Полусвизаиная сис1ема координат С114
X
// | ^
Скорост¬
ная система
координат
С По
хс
cos (3
0
sin (3
Ус
sin р sin Yc
cos Yc
—cos p sin Yc
?с
—sin (3 cos Yc
sin Yc
cos p cos Yc
143

Таблица 3.2G
Матрица преобразований между JIA-центрической прямоугольной
вертикально-симметрической связанной-1 OxX2yA2zx2 (Cl 12) и JIA-центрической
прямоугольной горизонтальной ориентированной (земной) Oxgygzg (Cl 18)
системами координат
Сокращенное название
Связанная система координат С112
сис I емы
Хм |
Ум
ZM
Земная си¬
стема коор¬
динат С118
xg
COS ф COS ft
sin ф sin Y —
— cos ф sin 6 cos Y
sin ф cos Y +
-f cos ф sin 6 sin Y
yg
sin ft
cos 6- cos Y
—cos 6 sin Y
2g
—sin 6 cos ft
cos ф sin Y +
-f sin ф sin 6 cos Y
cos ф cos V —
— sin 6 s i n ft s i n Y
Таблица 3. 21
Матрица преобразований между JIA-центрической прямоугольной
вертикально-симметрической полусвязанной Oxyz (Cl 14) и JIA-центрической
прямоугольной горизонтальной ориентированной (земной) Oxgygzg (Cl 18)
системами координат
Сокращенное название
сист емы
Полусвязаеная система координат С114
X
V
z
Земная си¬
стема коор¬
динат С118
Xg
cos a cos $ cos ф —
—sin a(cosф sinY—
— sin $ cos ф cos Y)
sin a cos 6- cos ф -f
+ cosа(втф sinY —
— sin ft cos ф cos Y)
sin 6 cos ф sin Y +
+ sin ф cos Y
У g
cos a sin $ —
— sin a cos ft cos Y
sin a sin & +
-f cos a cos 6 cos Y
— cos $ sin Y
Zg
— cosa cos ftsin ф—
—sin а (совф siny+
-f sin $ sin ф cos Y)
—sin a sin ф cosft+
+ соза(со8ф sinY+
4- sin 6- sin ф cos Y)
cos щ cos Y —
— sin ft sin ф sin V
Таблица 3.22
Матрица преобразований между JIA-центрической прямоугольной
вертикально-симметрической скоростной (поточной) Oxnynzn (Cl 16)
и JIA-центрической прямоугольной вертикально-скоростной Oxcyczc (Cl 15)
системами координат
Сокращенное название
системы
Поточная система координат Cl 16
X \ \Г I z
n I 'ii 1 ri
Скорост¬
ная система
координат
115
Xq
1
0
0
Ус
0
cos Yc
— sin Yc
zc | 0 | sinYc j cos Yc
Примечание. Данная матрица справедлива для нецентральных-1
систем координат С213 и С212.
144

Таблица 3.23
Матрица преобразований между JlA-центрической прямоугольной
вертикально-симметрической скоростной (поточной) Oxnynzn (Cl16)
и ЛА-центрической прямоугольной вертикально-симметрической связанной-1
ОхЛ2У\2*\2 (С112) системами координат
Сокращенное название
системы
Поточная система координат (С116)
«и \ гп
Связанная
спсте ма
координат
С112
Xi2
cos a cos р
sin а
—cos а sin р
Уп
—sin а cos р
cos а
sin а sin р
г\2
sin р
0 | cos р
Таблица 3. 24
Матрица преобразований между ЛА-центрической прямоугольной
вертикально-симметрической скоростной (поточной) Oxnyuzn (С116)
и JIA-центрической прямоугольной горизонтальной ориентированной
{земной) Oxgygzg (Cl 18) системами координат
Сокращенное название
Поточная система координат (С116)
системы
Ум
Zw
Земная си¬
стема коор¬
динат СПЯ
xg
COS фс cos 0
sin фс sin Yc —
— cos фс sin 0 cos yc
sin фс cos Yc 4-
+ cos фс sin 0 sin Yc
yg
sin 0
cos 0 cos Yc
—cos 0 sin Yc
zg
—зтфс cos 0
cos фс sin Yc +
+ sin фс sin 0 cos Yc
cos фс cos Yc —
—sin фс sin 0 sin Yc
Таблица 3.25
Матрица преобразований между нецентральной-!! прямоугольной
вертикально-симметрической связанной DAx{yxz{ (С311) и нецентральной-II
прямоугольной произвольной DAx2y2^2 (С312) системами координат
Сокращенное название
системы
Произвольная система координат С312
х2
У2
Z2
Нецепт-
ральная-II
связанная
система ко¬
ординат
С311
COS V2 COS V3
sin v3
sin y2cos V3
У\
sin у2 cos vi —
— cos vi cos у2 sin V.3
cos Vi cos у о
cos у2 sin Vi +
+ sin y2 cos vi sin уз
2\
sin У2 cos Vi +
-f sin vi cos у2 sin Va
—sin Vicos уз
COS у2 cos Vl —
— sin vi sin V2 sin уз
145

Таблица 3. 26
Матрица преобразований между ЛА-центрической прямоугольной
вертикально-симметрической полу связанной Oxyz (Cl 14) и ЛА-центрической
прямоугольной вертикально-симметрической связанной-/ ОхЛ2у\2Z\2 (Cl 12)
системами координат
Сокращенное название
Полусвязанная система координа! С114
сис! емы
X
1 lJ 1
Z
Связанная
х12
соя а
Sin а
0
система ко-
ординат
С112
У12
—я i п а
| соя а
1
0
гп
0
1 °
1
Таблица 3. 27
Матрица преобразований между ЛА-центрической прямоугольной
вертикально-симметрической полусвязанной Oxyz (Cl 14) и ЛА-центрической
прямоугольной вертикально-симметрической скоростной (поточной) OxnynzVj
(Cl 16) системами координат
Сокращенное название
системы
Полусвязанная система координат С114
X
У
Z
Поточная
система ко¬
ординат
С116
хи
COS р
0
—sin р
У п
0
1
0
2„ J Sin Э
0 | соя р
Таблица 3. 28
Матрица преобразований между ЛА-центрической прямоугольной
сопроводительной естественной OxeyGze (Cl 17) и ЛА-центрической
прямоугольной вертикально-симметрической скоростной (поточной) Охпупгп
(G116) системами координат
Сокращенное название
системы
Поточная система координат СПб
*11 Уи | ги
Естествен¬
ная система
координат
С117
хе
1
0
0
Уе
0
соя (Ye — Yc)
sin (Ye — Yc)
0
—sin(Ye —Yc) | cos(Yc —Yc)
146

Таблица 3. 29
Матрица преобразований между ЛА-центрической прямоугольной
сопроводительной естественной Oxcycze (Cl 17) и ЛА-центрической
прямоугольной вертикально-скоростной Oxcyczc (Cl 15) системами координат
Сокращенное название
системы
Скоростная система координат С115
^с | *'с гс
Естествен¬
ная система
координат
€117
*е
1
0
0
Уе
0
соя уе
sin Ye
^е
0
—sin Ye
cos Ye
При полете с нулевым углом скольжения ((3 = 0) соотношения
{3. 1) принимают вид:
sin 0 = sin ft cos а — cos ft cos у sin a;
ч cos yc ~ (cos ft cos a cos у + sin ft sin a) sec 0;
sin <bc = (sin ф cos ft cos a -f- cos ф sin у sin a + sin ф sin ft cos y sin a) sec 0.
При полете с нулевым углом крена (y = 0) соотношения (3. 1)
имеют вид:
sin 0 —- cos $ sin (ft — a);
cos yc = cos (ft — a) sec 0;
sin d»c = (sin ф cos 3 cos (ft — a) — cos ф sin 3) sec 0.
б)	Выражение углов Ф, ф, у через углы 0, фс, Yc, a, (3.
Перемножая матрицы преобразований, помещенные в табл.
3.17, 3.22 и 3.23 (предварительно транспонировав матрицы из
табл. 3, 17 и 3.23), и приравнивая элементы матрицы произведе¬
ния соответствующим элементам матрицы из табл. 3.20, полу¬
чаем соотношения:
sin ft — sin 0 cos a cos 3-j- cos 0 (sin a cos cos a sin $ sin ус);]
cos у = [cos a cos 0 cos yc — (s*n P cos 0 sin yc +
-fcos 3 sin 0) sin a] sec ft;
i- (O. A)
sin ф = [sin фс cos 0 cos a cos 3-f cos a sin jii (cos фс cos yc —
— sin фс sin 0 sin yc) — sin a (cos фс sin yc -f
-f- sin фс sin 0 cos Yc)] sec ft.
147

При полете с нулевым углом скольжения ((3 = 0) соотношения
(3.2) принимают вид:
sin ft ==. sin 0 cos а -j- cos 0 sin а cos ус;
cos у —(cos a cos 0 cos yc — sin 0 sin a) sec ft;
sin ф = [sin фс cos 0 cos a — sin a (cos фс sin yc + sin фс sin 0 cos yc)] sec ^ *
При полете с нулевым углом скоростного крена соотношения
(3.2) принимают вид:
sin ft = sin 0 cos a cos p -f cos ® s*n a;
cos y = (cos a cos 0 — cos p sin 0 sin a) sec ft;
sin ф = (sin фс cos 0 cos a cos p -f cos a sin p cos фс —
— sin a sin фс sin 0) sec ft.
При полете с нулевыми углами скоростного крена и скольже¬
ния (yc = 0, (3 = 0) соотношения (3.2) имеют вид:
sin ft -= sin (0 — ct);
cos y = 1;
sin d> = sin фс
или
ft — 0 — a;
Y = 0;
При полете с нулевыми углами атаки и скольжения (а = 0,
(3 = 0) соотношения (3.2) принимают вид:
ft = 0;
Y —yc;
ф = фс.
в)	Выражения углов а, р через углы ft, ф, у, 0,	фс:
^ ^	 cos 0 sin ф sin Y — cos Y (sin 9 cos 0 cos ф — sin 0	cos ft) ^	.g ^
cos ft cos 0 cos ф + sin 9- sin 0	’
sin p — cos 0 sin ф cos y-f- sin у (sin ft cos 0 cos ф — sin 0 cos ft).
При полете с нулевым углом крена (у = ус=-0) соотноше¬
ния (3.3) принимают вид:
л! 1 /	V
1
sin ft cos 0 cos <L» — sin 0 cos ft	W	*Tu	■-■
tg a ==	!	; ^
cos ft cos 0 cos ф + sin ft sin 0
sin p = cos 0 sin ф. цл'Д.-. v-\® V' ;nJ:-
148

3.	2. 6. Формулы преобразования между системами координат
различных классов
В табл. 3. 30 приведен вспомогательный указатель для нахож¬
дения формул преобразований между различными классами
(планетоцентрическими, планетотопическими, космоцентриче¬
скими и связанными с JIA) систем координат.
Сведений, на которые даны ссылки в табл. 3.30 (совместно
с формулами из табл. 3.31, 3.8а, 3. 11а, 3. 16—3.29), обычно до¬
статочно для построения формул перехода между любыми част¬
ными видами, типами и ориентациями систем координат.
Таблица 3. 30
Вспомогательный указатель для отыскания формул преобразования
между различными классами систем координат
Шифр исходной
системы координат
Шифр преобразованной системы координат
П214
П223
Т113
Т116
Kill
СИЯ
П214
Табл.
3.31
П223
(3.5)
Т113
(3. 7)
Т116
(3. 4)
Kill
Cl 18
Табл.
3.	31
(3. 6)
Алгоритм построения недостающих в табл. 3.30 преобразова¬
ний ясен из следующего примера.
Пример. Найти преобразование, связывающее координаты
£, т), £ орбитоцентрической прямоугольной апсидной (КШ) си¬
стемы с координатами £, т], £ геотопической прямоугольной гори¬
зонтальной ориентированной-I (Т113) системы.
Искомое преобразование в табл. 3.30 отсутствует, но в ней
имеется связь между координатами £, т], £ системы (КШ)
и координатами х\ уz' системы П214. Кроме того, в табл. 3.30
указано, что преобразование между координатами систем
(П223) и (Т116) дано формулами (3.4). Таким образом, имеют¬
ся связи между системами координат:
КШ —П214; П223—>Т116.
149

Таблица 3. 31
Матрица преобразований между геоцентрической прямоугольной
экваториальной Ox'y'z' (П214) и орбитоцентрической прямоугольной апсидной
(Kill) системами координат
Геоцентрическая	Орбитоцентрическая	прямоугольная	апсидная	система	координат
прямоугольная	O-r?	(Kill)
экваториальная система	^	^
координат Ox’t/'z’
(Г1214)
Z — с
-n
\ с
.V'
COS со COS £1 —
— sin со sin ££ cos i
sin 03 COS SI —
— cos со sin cos i
sin/ sin Д
у'
cos со sin SI +
+ sin (o cos Si cos i
—sin со sin SI +
+ COS CO COS Si COS i
—sin i cos О
Z'
I ...
1 Sin со sin I
i
cos 03 sin I
cos i
Примечания. 1. Здесь 2 • с — фокусное расстояние.
2. Определения для углов <Я>. 6 со даны в табл. 2. 2.
Далее необходимо установить, имеются ли в табл. 3.8а, 3. 11а
преобразования Т116 —>Т113 для геотопических систем и
П214^П223 для геоцентрических систем. Наличие этих преобра¬
зований можно установить по вспомогательным указателям пре¬
образований— табл. 3.116 и 3.86. Табл. 3.116 показывает, что
в табл. 3.11а в строке 18 имеется преобразование Т116 —*Т113.
Табл. 3.86 показывает, что в табл. 3.8а преобразование
П214—+П223 отсутствует и поэтому в соответствии с примером,
приведенным в п. 3.2.2, следует использовать промежуточные
преобразования. В качестве таких промежуточных преобразова¬
ний можно использовать следующую цепочку, имеющуюся
в табл. 3. 8а, в строках 43 и 51:
П214-+П222; П222-+П223.
Окончательный алгоритм искомого преобразования
Kill—Т113 получится следующим образом.
Преобразование
Номер таблицы, содержащей
преобразование
Kill - П214
Табл. 3. 31
П214 П222
Табл. 3.8а, строка 43
П222 П223
Табл. 3.8а, строка 51
П223 — T116
Формула (3.4)
T116 — T113
Табл. 3. 11, строка 18

Произведя вычисления в указанной этой таблицей последова¬
тельности, получим искомые формулы преобразования.
Формулы связи между геотопической прямоугольной левой
горизонтальной ориентированной-II От£т]£ (Т116) и геоцентриче¬
ской сферической экваториальной-П Or, А,, ср' (П223) системами
координат:
arctg
arctg
Г 0 + с
Л
(3.4)
— — Гп
/'о н- -
r = V(r0+Q М-^+п2-
i = (r0-rQtg(c?' — ср0);
Л = (Л) + С) COS Ю0 tg (X — Х0);
Г
1 + tg2 (w' — cpQ) -1- COS2 cpQ Ig2 (X -
(3.5)
■Ли)
I
Формулы связи между ЛА-центрической прямоугольной гори¬
зонтальной ориентированной Oxgygzg (Cl 18) и геотопической
прямоугольной левой горизонтальной ориентированной-I От1,т],£
(Т113) системами координат:
yg=^—h,\
zg=\
^ — xg\
4\ = zg + h\
^ = У g •
(3.6)
(3.7)
Предполагается, что начала координат систем Т113 и СПЗ
лежат на одном геоцентрическом радиусе-векторе.
В аэродинамических расчетах наиболее употребительны сле¬
дующие связанные с ЛА системы координат:
1. Связанная (С111, С112, СПЗ).
2. Полусвязанная (С 114).
3. Скоростная (С115).
4. Поточная (С116).
5. Земная (С 118).

03
Q
5Г
*2
<5
К
<
x
2
z
X
АО
>»
SS-
Is
о S
§•■*
о =X
X О
s
cu
H
o
X
о
- <1)
X H
Q, О
2»
О
as
<u 2
X £
К к
5 8-
о
X
M -
VO ^
X
cd
X
«
eg
X
£ к
К
U
*
О
£,
<и
U
X ^
ж
£ ^
2 ^
о
с
е С)
о
и
ж
VO <D
0 ж
S Ж
-T
5 1
CO ^
с о
VC f-H
:be
«0
се О
к =
ж
Ж ’Ж
sSg
I"*
0 ^’S
- CX Ж
ж
Ж i=r ea
ж 5 <
«J э
о
X
с
X
*
О
£ N
S	^
£	(М
02 ц
£> °
о
X
CQ О
и
с	м
£	6
£	*
сс О
а X
? °
О
X
I «
Us ^
* *
£> О
>=?
О
X
Он
о
с:
сз
be
X
к
N
5-
=з->
СЗ
_fc>e
о
о
С-
*
О
0J
'be
о
irS
со
О
а
(Ж ^
СЗ Cs
X сз
Н ~
is
о- н
о о
х с
О ^
и
*
О
СЗ Os
t- N
о ^
2 4
О °
X
О
о JT
2 °
о- н
о о
X с
*
О
с
*
о
30
о
X
О
О
N
а*
о
*
О
о -
*
о
В-
Ьс
N
сЗ
be
—
=л
ь«
(D
СО
О
о
со
be
Ьо
be
ч
о
со
be
**
be
=51
Ьс
н
о
00
X
Ьл
CJ
N
be
сз
=5i
сз
be
X
*
S
<L>
СО
О
152

Однако в отечественной литературе наблюдается большое
разнообразие в обозначениях и названиях приведенных систем
координат. В табл. 3.32 представлены названия и обозначения
этих систем координат, употребляемые в основной учебной и
научной литературе по аэродинамике самолета и ракет и по ди¬
намике полета.
ЛИТЕРАТУРА
1. ГОСТ 1075—41. Оси координат и основные обозначения, применяемые
в аэродинамических и гидродинамических расчетах в самолетостроении, Стан-
дартгиз, 1941.
2. Бакулин П. И., Кононович Э. В., Мороз В. И., Курс общей
астрономии, изд-во «Наука», 1966.
3. Д у б о ш и н Н. Г., Небесная механика. Основные задачи и методы,
Физматгиз, 1963.
4. Иродов Р. Д., Расчет перегрузок и углов крена самолета при двпже-
нии по пространственной кривой, Труды ЦАГИ, вып. 702, Оборонгнз, 1957.
5 К и л ь ч е в с к и й Н. А., Элементы тензорного анализа и его приложе¬
ния к механике, Гостехиздат, 1954.
6. Лебедев А. А., Чернобровкин Л. С., Динамика полета беспи¬
лотных летательных аппаратов, Оборонгиз, 1962.
7. Литвин-Седой М. 3., Введение в механику управляемого полета,
изд-во «Высшая школа», 1962.
8. М а р т ы н о в А. К-, Экспериментальная аэродинамика, Оборонгнз, 1958.
9. Лурье А. И., Аналитическая механика, Физматгиз, 1961.
10. Ми еле А., Механика полета, т. I, изд-во «Мир», 1965.
11. О сто ела веки й И. В., Аэродинамика самолета, Оборонгиз, 1957.
12. Остославский И. В., Страж ев а И. В., Динамика полета. Тра¬
ектории летательных аппаратов, Оборонгиз, 1963.
13. О с т о с л а в с к и й И. В., Страж ев а И. В., Динамика полета.
Устойчивость и управляемость летательных аппаратов, изд-во «Машинострое¬
ние», 1965.
14. Фрезер Р., Дункан В., Коллар А., Теория матриц и ее прило¬
жение к дифференциальным уравнениям и динамике, ИЛ, 1950.
15. Чеботарев Г. А., Аналитические и численные методы небесной
механики, изд-во «Наука», 1965.
16. Эрике К., Космический полет, т. I, Физматгиз, 1963.
17. Baker R., Макет son М. An Introduction to Astrod vnam ics.
N-Y, 1960.
18. Knox E., Comment on Transformation of Coordinate Axis Systems
of Aircraft, J. Aero/Space Sci. 29. No. 5, 1962.
19. Ко lk W., Mod erne Flight Dynamics, N-Y, 1961.
20. Rothman H. L., Pittel М., Transformation of Coordinate
Axis Systems of Aircraft, J. Aero/Space, Sci. 28, No. 7, 1961.
21. Pio P. L., Euler Angle Transformations. IEEE Trans. Automat
Control. AC-11. No. 4, 1966.
22. Schulz W., Ludwig R., Die Koordinatensvsteme der Flugme-
chanik. Zeitschrift fur Flugwissensch. 2. Nr. 3—4, 1954; 3, Nr. 5, 1955.

Глава 4. УРАВНЕНИЯ ДВИЖЕНИЯ
ЛЕТАТЕЛЬНОГО АППАРАТА
Основные обозначения
Л—угол азимута,
а— вектор,
b—единичный вектор бинормали к траектории,
Bk— проекция главного вектора внешних сил, дей¬
ствующих на Л А, на ось к системы координат
(* = *, у, г, £, г), £),
Ьд—характерный размер ЛА (например, средняя
аэродинамическая хорда),
сх— коэффициент силы лобового сопротивления,
су—коэффициент подъемной силы,
cz— коэффициент боковой силы,
О— вес,
g— гравитационное ускорение,
h— высота,
//, Iij—момент инерции относительно оси i и центро¬
бежный момент инерции соответственно,
i, j, k — орты осей прямоугольной системы координат,
I—характерный размер ЛА (например, размах
крыла),
М — число Маха,
Мх. Му, мг п ЛК? Mr, М. —проекции главного момента внешних сил на оси
Ох, Оу, Oz, 01, Or], 0£ соответственно,
т — масса ЛА,
тх, ту, mz— коэффициенты аэродинамического момента от¬
носительно осей Ох, Оу, Oz соответственно,
п — единичный вектор главной нормали к траекто¬
рии,
ял—режим работы двигателя,
Р— сила тяги,
Q—сила лобового сопротивления,
Р,	?— сферические координаты,
г. X, z—цилиндрические координаты,
г — радиус-вектор,
г/ — радиус-вектор i-й точки,
v— скорость,
W — ускорение,
A', Y, Z—проекции аэродинамических сил па оси Ох, Оу,
Oz соответственно,
х, у, z—прямоугольные координаты,
а— угол атаки,
ап—угол атаки относительно путевой скорости и.
Р—угол скольжения,
Рп—угол скольжения относительно путевой ско¬
рости V,
1о 4

Y—угол крена,
Yc — угол скоростного' крена,
Ьэ, он— утлы отклонения руля высоты, элеронов, руля
направления соответственно,
А —угол наклона траектории,
&—угол тангажа,
а—долгота (географическая пли геоцентрическая),
М-сек — секундный расход массы,
г|» £—прямоугольные координаты,
Q—плотность атмосферы,
QK—радиус кривизны,
Qpr» арг> Ург» vpr—параметры Родрига—Гамильтона,
т— единичный вектор касательной к траектории,
<Р— географическая широта,
<р' — геоцентрическая широта,
ерр— угол установки двигателя,
ф—угол курса,
фс— угол скоростного курса,
o>i—вектор угловой скорости вращения связанной
системы координат СИЗ относительно земной
системы координат С118,
(оп—вектор угловой скорости вращения поточной
системы координат С116 относительно земной
системы координат С118,
(ое — вектор угловой скорости вращения естественной
системы координат С117 относительно земной
системы координат С118,
(ос—вектор угловой скорости вращения скоростной
системы координат СПЗ относительно зем¬
ной С118.
4.1.	ЭЛЕМЕНТЫ КИНЕМАТИКИ ЛЕТАТЕЛЬНОГО АППАРАТА
Летательный аппарат рассматривается или как материаль¬
ная точка, или как твердое тело. Выражения для абсолютных
скоростей и ускорений JIA, как материальной точки, в проекциях
на оси некоторых систем координат приведены в табл. 4. 1.
Угловое положение твердого тела относительно неподвижных
или подвижных систем координат задается либо эйлеровыми
углами, либо параметрами Родрига—Гамильтона, либо направ¬
ляющими косинусами (см. гл. 3).
4.1.	1. Связь проекций вектора угловой скорости
некоторых ЛА-центрических прямоугольных систем координат
с производными от углов Эйлера
Углы Эйлера я|з, О, у, определяющие положение связанной
системы координат Ox\y\Zx (СИЗ) относительно земной системы
координат OxgygZg (Cl 18), являются функциями времени:
lb=lb(^);	frr=0(/);	y	=	Y(0-
Если известны производные от углов Эйлера ф, О, у (рис. 4. 1),
то соотношения между проекциями вектора (Oj угловой скорости
135

Скорость и ускорение ЛА как материальной точки в прямоугольных, сферических, цилиндрических системах координат
и в осях сопровождающего трехгранника
:Н :	:	N
N
+
,<N
+
*
• 9-
Oy
1
+
9-
C
9-
cn
<N
С
<У
cn
(M
+
СУ
1
9-
С
СП
:Cy
II
•п<
•оу
см
ii
,4
6*
9-
СП
О
CJ
ОУ
* 9-
СМ
+
+
^ +
<м
. 9-	9-
о; с
1 -Л
c-f а:
•Н +
Z 9-
-S
^ сп
I '*<
т +
9-
«
+:
9-
• 9-
.QC
3 о
+
9- сл
СП (М
О •<<.
о og
^ I
: 9-
1
CN
+
су • -
^ СУ -
су
• 9-
I'
+ -|е
ОУ
+
<м
•оу
су
+
+
+
(N
'г<
• ч
см
+
:*<
+ :
+
ч
I
• ч
■ ^
+
(N
.лЧ
СМ
ч
+
+
•
О
I!
о,
о
оо
К
Си
Си
с
•&
и 9-
^ к
р=с N
5 ч
3 «
*
о .
га Л -о
§.*S
§ “о
и о «
U id
<L> S
5 3 =
о ? £
ct u
156

вращения связанной системы координат СПЗ относительно зем¬
ной С118 и производными ф, ft, у имеют вид:
(0U'! = ф sin 0 -j- у;
щУг =-- ф cos В cos у -f ft sill у;
со1г1= — фcos ilsiny-}-^ cosy.
(4.1)
Рис. 4. 1.
Формулы перехода от ф, В, у к щХх, oj1Vi, to1Zi:
ф = ((о1г/1 cosy —sin у) sec ft;
® — sin у + (01г, cosy;
у = ^1хг — («>1^ cos у — (,)i2j sin y) tg &.
(4.2)
Проекции вектора о>п угловой скорости вращения поточной
системы координат С116 на оси той же системы определяются
через скорости изменения углов Эйлера фс, 0, Yc и значения углов
Эйлера 6, ус формулами:
tcSin0 + Yc;
% У„ = i cos 9 cos Yc + 9 sin Yc;
= — фс cos 0 sin yc -j- 0 cos yc-
n ZU
(4.3)
157

Формулы перехода от «>ПХп, «>«„ к фс, 0, ус
i = («>„ и., cos Yc - <“п*п sin Vc)sec 6;
0 = wn.vn sinYc + <“n*„cosYc;
Yc = % ,n - (u)n »n C0S Yc - «П Zn Siu Yc) tg 0-
(4.4)
Проекции вектора o>e угловой скорости вращения естественной
ситемы координат С117 на оси той же системы координат выра¬
жаются через скорости изменения углов Эйлера *фс, 0, ус и значе¬
ния углов Эйлера 0, уе формулами:
Связи между проекциями соСхс, сос vc, o)czc вектора сос угловой
скорости вращения скоростной системы координат (СПб) на оси
Кроме соотношений (4.7) и (4.8), существуют соотношения
между проекциями указанных угловых скоростей на оси земной
системы С118 и производными от углов Эйлера. Так, проекции
®ixg, wiVg, ulZg вектора (Oj угловой скорости вращения связанной
158
''We^cSinO + Yel
ше = C0S 0 C0S Ye + 0 Sill Ус;
<»e Ze= — 4С COS 0 sin Ye + 0 COS Ye-
(4.5)
Формулы перехода от о>ед.е, шсУе, ше2е к <ьс, 6, уе
Фс = (0|е 4-е C0S Ye ~ “е ze sin Ye) seC
б = ше i/eSinYe + we ze C0S Ye!
Ye = "’e Xe ~ (wc *e C0S Ye ~ ‘°e *e sln Yc) tg 6.
(4.6)
той же системы и производными ipc, 0 углов Эйлера (для системы
С115 ус = 0) имеют вид:
(ос^с=^сС059;
u,czc = 0-
(4.7)
Формулы для обратного перехода:
(4.8)

системы координат СПЗ на оси земной системы С118 с произ¬
водными ф, О, у углов Эйлера связаны соотношениями:
Н)1х = -Й- sin ф -|- Y COS ф cos ft;
(01^ = ФЧ“ У s*n
p = ft cos ф — у sin ф cos В.
Иг,
(4.9)
Обратные соотношения:
ф = — tg ft cos ф +	+	mltg	tg	&	sin	ф;
ft = Sin ф	COS	6;
Y =- (»>ljc cos ф — wlzg sin ф) sec ft.
(4.10)
Аналогичные соотношения для поточной системы координат
С116:
°п xg = 0 sin Фс -р Yc C0S Фс C0S 0;
<’>л!/г = Фс + 7с5‘пб;
(,)л 2<г = 'е C0S Фс_ Yc sin Фс C0S 0
(4.11)
Фс = - (,,п xg tg 0 COS фс + соп ч + о,п Zg tg 0 sin фс;
f’=‘un^sin«l»c + <«n^C0Silic;
Yc = (% xg cos Фс - wn zg sin фс) sec 0.
(4.12)
Соотношения для естественной системы координат Cl 17:
(»е	=	0	sin	фс	-j-Ye COS фс COS 0;
“еу^Фс+Ye sin 6;
r = 6 cos фс — ye sin фс cos 0	,
(4.13)
Фс ~~~ — l4e xg tg 0 COS Ф,
"e eg'Ь(,)е z^tg 0 sin фс;
0 = we.,gSinic-l--«)e Zg COS фс;
Yc = {mexg COS фс - we Zg Sin Фс) sec 0.
(4.14)
159

.Ус Ус
Ч Zz
Рис. 4.2.
Рис. 4.3.
1(50

Соотношения для скоростной системы координат С115 имеют
вид (рис. 4. 2):
(4.15)
Для системы углов Эйлера тЭц, фц, уп (см. гл. 3, табл. 3.4а)
связи между проекциями , coiy , wJz вектора сох угловой ско¬
рости вращения связанной системы координат СПЗ и производ-
4. 1.2. Связи проекций вектора Oj угловой скорости
связанной системы координат СИЗ с производными
направляющих косинусов между осями этой системы
и осями земной системы координат С118
Если ЛА-центрическая прямоугольная вертикально-симмет¬
рическая связанная-II система координат Ox\y\Z\ (СПЗ) вра¬
щается с угловой скоростью (0[ относительно ЛА-центриче¬
ской прямоугольной горизонтальной ориентированной (зем¬
ной) системой координат С118, то проекции coi*,. coiZl век¬
тора o)j на оси системы координат Ox\y\Z\ выражаются через
направляющие косинусы 1ц между указанными двумя система¬
ми и их производными 1ц формулами:
Wljf, = ^13^12 "Т ^2^22 "Г I3J32 =	(^12^13	^22^23	~Ь	^32^3з);
ными Оц, фц, уц (рис. 4.3)' даются формулами:
MlXi= — В li sin Фц Ч-у„;
о)1/л = 8п cos би sin уи + фп cos уп;
w\zx = &ц COS 'Ьи COS уп — 'bu sill уп.
(4.16)
Обратные соотношения:
^ii^Kvi sinyn + o^ cos у„ )sec 4П;
cosyn —co1Zi sin уп;
Уп =--щХ1 — sin уи + coUi cos уп) tg би.
(4.17)
6	1669
161

Обратные соотношения:
lu=WlzJi2	colf//l3’	^21 ~0)lzj22	(0l//i^23>
/l2 = (0U.,/i3	/22	— Wljr/23	colZi^2b
^13 =	o:)lA-/l2^	4з = Ш1г/1^21	0)l^i^22»
/31 =o)iZi/32	0)1///зЗ»
1ъ2 = Щхх1ы	(01г/зГ,
^33 = 0Jl//i^3l	С01^/з2*
(4.19)
В силу условий ортогональности для /г-7- имеется шесть гео¬
метрических интегралов:
з	'l
4. 1.3. Связи проекций вектора o)j угловой скорости
связанной системы координат СИЗ с производными параметров
Родрига—Гамильтона
Проекции со 1 х,» ooiy,, сои, вектора угловой скорости враще¬
ния ЛА-центрической прямоугольной вертикально-симметриче¬
ской связанной системы координат OxiyiZx (СПЗ) на оси этой
системы координат, вращающейся относительно ЛА-центриче¬
ской прямоугольной ориентированной связанной-I (земной С118),
связаны с параметрами Родрига—Гамильтона и их производ¬
ными соотношениями
2^ = 1	/=1,2,3;
з
(4.20)
£/,/,* = 0 k,j = 1,2,3, ]фк.
2 (рр,Лрр	^'prQ^r “Ь '/г	^prl^pr),
ш1(/,=2 (бргРрг—1Ар,ерГ"г vpr','pr‘_^prv|,r);
Ш1г, 2 (QpjApp	^p;Qpr	^'ргР'рг ' Р'р/'рг) •
(4.21)
Соотношения для обратного перехода:
(4.22)
162

Проекции (x)\Xg, coiyg, coiz вектораcoj угловой скорости врагце*
ния ЛА-центрической прямоугольной вертикально-симметриче¬
ской связанной системы координат Ox\ij\Zx (СПЗ) на оси
0%, Oyg, Ozg ЛА-цснтрической прямоугольной горизонтальной
ориентированной связанной-I (земной) системы координат СПЗ
связаны с параметрами Родрига—Гамильтона и их производ¬
ными соотношениями
^ (брУ'рг ^pi брг ~Т~ Р'рг^рг ^ргР'рг) 1
С°1 t/g == 2 (буг^рг рI брг "Ь ^ рДрг ^рг^рг)?
г ~ 2 (брр^'рг VpiQpr ~\~ ^рг^рг Р'рГ^рГ*
(4.23)
Обратные соотношения:
l.r^' pr - wii/^pr I “u^’pr);
»v=t(-
•0>Uo.VP'- + (,>'PgQpr-ru'lzI,'-p
о)’у-Рг);
(4.24)
V = T	“ M«/p''+“4epr)-
Удобство использования параметров Родрига—Гамильтона
состоит в том, что соотношения (4. 22) и (4. 24) симметричны и
линейны относительно параметров при заданных проекциях
озтл; (t), со1г/ (t),.. . Кроме того, при применении параметров Род¬
рига— Гамильтона правые части дифференциальных уравнений
(4.22)	и (4.24) всегда определены [в отличие от соотношений
(4. 10) и (4. 14)] для производных углов Эйлера, которые стано¬
вятся неопределенными при некоторых значениях углов •& и 0.
4.2.	УРАВНЕНИЯ ДВИЖЕНИЯ МЕХАНИКИ ПОЛЕТА
Уравнения движения механики полета основываются на
общих законах механики точки и тела постоянной и переменной
массы. Они описывают как движение ЛА в целом, так и отдель¬
ных его частей.
Полная система уравнений движения ЛА обычно состоит из:
— динамических уравнений движения центра масс (соотно¬
шений, связывающих компоненты ускорения центра масс ЛА
с действующими на него силами);
— динамических уравнений движения относительно центрш
масс (соотношений, связывающих компоненты углового ускоре¬
6*
16S

ния JIA относительно центра масс с приложенными к нему мо¬
ментами) ;
—■ уравнений, описывающих изменение массы * и моментов
инерции JIA;
—■ кинематических уравнений (соотношений, связывающих
линейные и (или) угловые скорости с линейными и (или) угло¬
выми координатами);
— геометрических и вспомогательных соотношений (уравне¬
ний связи между различными системами координат, соотноше¬
ний между углами, явных выражений для проекций сил, момен¬
тов и т. п.).
В этом же порядке уравнения движения приводятся в тексте
главы.
Фо рма уравнений движения. Динамические уравне¬
ния движения (как центра масс, так и относительно центра масс)
представляют систему обыкновенных дифференциальных урав¬
нений не выше второго порядка, линейных относительно старших
производных тех или иных координат, выбранных для описания
движения JIA. Роль аргумента в дифференциальных уравнениях
движения обычно играет время t, хотя могут использоваться и
другие аргументы (например, длина дуги s или любой другой
монотонно меняющийся в процессе движения параметр).
Кинематические уравнения могут быть как дифференциаль¬
ными, так и конечными (не дифференциальными)'. В последнем
случае их иногда называют кинематическими соотношениями.
В кинематические уравнения не входят выражения для сил
и моментов.
Конечными уравнениями поступательного движения центра
масс являются законы движения, т. е. выражения, определяющие
координаты центра масс (точки) в виде известных функций вре¬
мени. Например, в декартовых координатах закон движения
имеет вид
x=h(t)-,	У=Ш)\	z = fs(t).
Закон движения может рассматриваться как параметрическая
форма (с параметром t) траектории Л А. Траектория JIA есть
кривая, которую описывает движущийся в пространстве центр
масс JIA.
Конечными уравнениями вращательного движения JIA вокруг
центра масс называются соотношения, определяющие изменение
параметров углового положения JIA в виде известных функций
времени. Например, при определении ориентации JIA с помощью
* Так как ЛА в большинстве случаев рассматривается как твердое тело
переменной массы, т. е. моменты инерции не изменяются и центр масс ЛА
относительно неизменяемой его части не движется, то приводится только
уравнение, описывающее изменение массы ЛА.
164

углов Эйлера конечные уравнения вращательного движения
имеют вид
Ф=Л(0; *=/»(*); У=Л(0-
Классификация уравнений движения. Вид урав¬
нений движения зависит как от выбора системы координат, при¬
нимаемой в качестве инерциальной системы отсчета, так и от вы¬
бора системы координат, в проекциях на оси которой записы¬
ваются динамические уравнения движения. В разд. 4.3—4.6
уравнения движения расположены по названию той системы ко¬
ординат, на оси которой проектируются действующие на JIA
активные силы в уравнениях движения центра масс. Уравнения
движения относительно центра масс приводятся в соответствии
с установившейся в механике полета традицией в записи, при
которой действующие на JIA активные моменты проектируются
на оси одной из связанных с ЛА систем координат (С111, С112,
СПЗ). Внутри раздела, соответствующего выбранной системе
координат для проектирования сил, приводятся записи уравне¬
ний движения для различных инерциальных систем отсчета, кото¬
рые определяют различный вид выражений для сил инерции.
В приведенных сводках уравнений движения выражения для сил
и моментов в некоторых случаях не выписываются явно, а обо¬
значаются символами Вк и Мк (k — индекс соответствующей оси,
например, k = x, у, z). Для вычисления Вк и Мк следует обра¬
титься к табл. 5. 17 (для Вк), табл. 5.6 (для Мк), табл. 3. 17—
3.29 (для пересчета Вк и Мк на другие оси).
Таблица 4.2
Наиболее употребительные системы координат
в задачах механики полета
За чача механики полета
Шифр систем координат
Межпланетный полет
П100, П200, К100, К200, Т100, СПб
Полет в околоземном космическом
пространстве
П200, К100, ТЮЗ, С200, СПб,
С116, С118
Полет в плотных слоях атмосфе¬
ры Земли
П200, Т100, С112, СПб, С116, С118
Расчеты устойчивости и управ¬
ляемости
С111, С112, С114, СПб, С116, С200
Навигационные задачи
П200, Т100, С114, СПб, С116,
С118, СЗОО
Расчеты старта
Т100, С111, С112, С114, С115,
С116, С118, С200
165

4.3.	УРАВНЕНИЯ ДВИЖЕНИЯ В ПЛАНЕТОЦЕНТРИЧЕСКИХ
СИСТЕМАХ КООРДИНАТ
4.3.1.	Уравнения движения в гелиоцентрической прямоугольной
эклиптической-I системе координат OXYZ (П111)
ЛА рассматривается как точка переменной массы. В качестве
инерциальной системы отсчета принимается гелиоцентрическая
прямоугольная эклиптическая-I система координат OXYZ (П111).
Уравнения движения JIA имеют вид
тХ =
rtiY =
mZ =
k-m^mX
(Х2 + Y2 + Z2)J ^
W-m^mY
(X2 +Y 2 +
Ю-m^mZ
(X2 + Y2 + Z 2)3/*
rn= —j
Rx~\~Px~t Ax',
- Ry ~t Py ~r Ay\
+ ^z~rPz~t Az\
(4.25)
(4.26)
где
m® — масса Солнца;
k2— гравитационная постоянная (см. гл. 2);
Ayx,RY,Rz — проекции сил тяготения других планет;
PX,PY,PZ — проекции силы тяги;
Ах, Ay,Az — проекции аэродинамических и других сил.
4. 3. 2. Уравнения движения в гелиоцентрической сферической
эклиптической системе координат R, %*, р*(П121)
ЛА рассматривается как точка переменной массы. В качестве
инерциальной системы отсчета принимается гелиоцентрическая
сферическая эклиптическая система координат R, х*> Ц* (П121).
Уравнения движения ЛА имеют вид
m(R — Ry*2 sin2(j.* — R\P2) = BR\
m | (A*/* + 2Ri*) sin f -j- 2/?xV cos a*] = Вгк
m (2R\x* -}-	— A*-/*2 sin p.* cos (a*) = B^*
= —Реею
(4.27)
(4.28)
где BR,By*,Bp.*— проекции вектора равнодействующей внешних
и реактивных сил на направление радиуса-век¬
тора и перпендикуляров к нему, один из ко¬
торых параллелен эклиптике, а другой пер¬
пендикулярен к ней.
166

4. 3. 3. Уравнения движения в геоцентрической прямоугольной
экваториальной системе координат Ox'y'z' (П214)
JIA рассматривается как точка переменной массы. В качестве
инерциальной системы отсчета принимается геоцентрическая
прямоугольная экваториальная система координат Ox'y'z'
(П214).
Уравнения движения JIA в центральном поле тяготения
Земли имеют вид
тх
ту'
mz ■==
k-m q/я х'
/ ,2	,2	2	V
\х + у + г' )
2\3/2
/г2 т q ту'
U'2
Т
(л-'Ч
т :
-Rx' + P Х'~\~Ах'\
Ау ;
-Rz' + Pz' + Az-;
(4.29)
(4.30)
где
/7г@ — масса Земли;
&2— гравитационная постоянная (гл. 2);
Rx',Ry',Rz—проекции на оси Ох', Оу', Oz’ сил тяготения
иных небесных тел;
Рх , Ру', Pz—проекции силы тяги на оси Ох’, Оу’, Oz'\
АХ', Ay’, Az> — проекции сил от взаимодействия с окружающей
средой.
4.	3. 4. Уравнения движения в геоцентрической сферической
ортодромической системе координат г, Хорт, форт(П224)
JIA рассматривается как точка переменной массы. В каче¬
стве инерциальной системы отсчета принимается геоцентриче¬
ская прямоугольная экваториальная система координат Ox’y’z'
(П214).
Предполагается, что движение происходит в плоскости орто¬
дромии (форт = 0). На JIA действует сила тяги, направленная
под углом фPl по отношению к тангенциальной скорости vs,
и аэродинамические силы: Q, направленная по скорости полета,
и У, направленная перпендикулярно скорости полета.
Уравнения движения JIA имеют вид
m(vr — ^A,pT) = jDsiru?P, — mgo ( —) +V COS0— QsinO;
m\v
-vl,
г орт
) = P cos tpp, — Y sin 0 — Q cos 6.
m=—p. ceK.
(4.31)
(4.32)
167

Кинематические соотношения выражаются формулами
r = vr
A0'J
рт
6 = arctg-
,=yv*r-
- 7JA.
(4.33)
4.	3. 5. Уравнения движения в геоцентрической сферической
экваториальной-И системе координат г, ср', к (П223)
ЛА рассматривается как точка переменной массы. В каче¬
стве инерциальной системы отсчета принимается геоцентриче¬
ская прямоугольная экваториальная система координат Ox'y'z'
(П214).
На ЛА действуют: сила тяжести, сила лобового сопротивле¬
ния Q, подъемная сила Y и сила тяги Р, направленная по связан¬
ной оси Ох\ системы С112.
Уравнения движения центра масс:
mvr = — (ti2, -j- г»2) -f mrco2 cos2 o' -|- 2/жо3гц cos o' 4-
+ Gr + P sin ft Y (sin a sin ft -f cos a cos ft cos y) -[-
-fQ (sin a cos ft cos у — cos a sin ft) — Z cos ft sin у ;
mvc> =
III / n .	,
r’= -(^tgcp
-vrv^\-mno~smo coscp —
— 2mo)3vx sin o' -|- Gcr -p P cos ft cos 6 —
— Q[sina (sin ft cos 6 cos у— sin 6 sin y)+cos 6 cos a cos 6]-f-
-|- Y [sin a cos ft cos 6 — cos a (sin ft cos 6 cos у —
— sin 6 sin y)] + Z (cos 6 sin у sin ft -|- sin 6 cos y);
mv\ = — (■zv'flx tg ср' — ,у/.'Ух) -p 2mco3 (?v sin ©' —
r
— vT cos cp')-)~G\ — P sin 6 cos ft-f Y [ — sin a cos ft sin Ф-[~
-j- cos a (cos ф sin у —sin ft sin ф cos y)] -|-
Q[sin a (cos ф sin у -\~ sin ft sin ф cos y) + cos a cos ft sin ф] -j-
-j- Z (cos ф cos у — sin ft sin ф sin y).
(4.34)
168
m= Р'сек*
(4.35)

Кинематические соотношения:
г
(4.36)
I
Г COS <р'
л	• Vr
0 = arc sin—— ;
V
v2r + v-.,-\-vl ;
(4.37)
sin a= I [sin 0 cos у cos (фс — ф)Д- sin у sin (фс — ф)] cos 0 —
— cos г} cos y sin 0} sec 3;
sin 3= [sin 0 sin y cos (фс — ф) — cos y sin (фс — ф)] cos 0 —
— cos 8 sin y sin 0.	!
Проекции ускорения силы тяготения в нецентральном поле
Земли (с точностью до полиномов Лежандра второго порядка)
выражаются формулами:
где ;i3 = (l,637± 0,004). 10“8;
£^2 = 3,9862.1014 м3/сек2;
/?е = 6 378 245 я.
(Данные величины приводятся по состоянию на 1962 г.)
Совокупность уравнений (4.34) — (4.37)' образует замкнутую
систему, если известны законы изменения углов ф(£), ^(t), y(t),
модуль силы тяги P(t) или режим работы двигателя пд.
Gr=—тДД-J 1+рз(-^-)2 (1—3 sin2 <?')]; |
}	(4-38)
Gx = 0,
169

Примечание. Пересчет в географические координаты X, cp, h произ¬
водится с помощью геоцентрических координат X, ср', h по формулам:
h = r — R (ср');
tg <р"	.
? = arctg •
А = Х;
*(?') = '
1 е\
У 1 — е\ cos 2ср'
где ^ = 0,0066934;
/?, = 6356863 ж
(4.39)
4.4.	УРАВНЕНИЯ ДВИЖЕНИЯ В ГЕОТОПИЧЕСКИХ
СИСТЕМАХ КООРДИНАТ *
4.4.	1. Уравнения движения в геотопической прямоугольной^
горизонтальной произвольной-!! системе координат 0Tlcr\ctc
(Т112)
ЛА рассматривается как точка переменной массы. В каче¬
стве инерциальной системы отсчета принимается геотопическая
прямоугольная горизонтальная ориентированная-II система
координат 0£г]£ (Т116) .
Уравнения движения имеют вид:
тТс = 5£- ;
тг\=В-
ml=B-
(4.40)
Ш— — и
(4.41)
4.4.	2. Уравнения движения
в геотопической прямоугольной горизонтальной стартовой-!!
системе координат От£сг)с?с(Т115)
ЛА рассматривается как твердое тело переменной массы.
Инерциальная система отсчета — геоцентрическая прямоуголь¬
ная экваториальная система координат Ox'y'z' (П214).
В баллистике управляемых ракет дальнего действия [1] полу¬
чила распространение система уравнений движения, учитываю¬
щая специфику этих объектов. Основные особенности объектов
баллистики ракет следующие.
* Рассматриваются правые прямоугольные системы координат.
170

1. Баллистические ракеты дальнего действия обычно стартуют
вертикально (0 = 90°). Это обстоятельство делает более целесо¬
образным применение второй (II) системы углов Эйлера: тан¬
гажа Ац, рысканья г|?ц, крена уп (см. табл. 3.4а, 3.46), так как
первая система углов Эйлера приводит к неопределенности в ки¬
нематических соотношениях [см. например, (4. 10)] при '0 = 90°.
2. Баллистические ракеты дальнего действия являются осе¬
симметричными в аэродинамическом и инерционно-массовом *
смысле, т. е. центробежные моменты Iххух = Ixizx = IyxZl= 0, связан¬
ные оси Ox\2y\2Z\2 (Cl 12) и главные связанные оси Охиу\\^и
(С111) совпадают друг с другом. Кроме того, в силу осесиммет-
ричности тела эллипсоид инерции является эллипсоидом враще-
НИЯ (/у. =/*,).
3. Для управляемых баллистических ракет характерны режи¬
мы, при которых малы углы атаки а, рысканья г|?ц (отсчитываемо¬
го в системе Т115 от заданного начального азимута ЛСо, по кото¬
рому эта система	ориентирована в начальный	момент),	крена
уп = у, скольжения (3 и разности углов (flu—0ц), (4>ц—фсн).
Здесь углы 0ц, г[)сп являются аналогами углов 0, \j>c в первой си¬
стеме углов Эйлера для поточной системы координат СПб.
При этих предположениях система уравнений движения
центра масс имеет вид:
mvzc=--(P — Х1?) cos 0П — cxqS cos 0И — ^^S(^n — 0u)sin 6П —1
- 2Н'Ь2 sin »п  т  mwelc - mWKzc;
У ?с + (*3 + 4с)2 + t2
тг'ъ = (Р~Хlp) sin 8n - cxqS sin в„ + c'flS (&„ -
— 6n) cos 6n-j-2/?'&,cos &n — mg —-	+ ^		 1(4.42)
Г 5ё + (*3 + 4c)2 + C2
-mWeTtC-rnW^c-
mvCc ~ (P ^4p) i'll —	—	'r’cll) —	"Г
-f 82' cos 8, [ — mg	^	—— mWe-c — mWK^\
1 -c + (R3 + Пс)2 + ?c
т=-!"се,о	(4.43)
где Zip — осевая сила от 1азовых рулей;
Uye:c, V^etjc> U^e:c,	WKic, WKnc, Wk:c — проекции	переносного и
кориолисова ускорения соответственно.
* В литературе вместо термина «инерционно-массовая симметрия» упо¬
требляется также термин «динамическая симметрия».
171

Последние величины вычисляются по следующим формулам:
Wе^с = («I (Гсо COS ср' cos ф — £с);
We
3
^есс= — w3 (г* COS ср' sin Ф+ Сс);
WKzc = 2о)3 (г)с cos ф' sin 6 -]- Сс sin ср');	•	(4.44)
WKTtc = — 2о)з (?с cos ср' sin ф — Сс cos ср' cos ф);
м^ьсс=2(о3 (— =с sin ?' + л сcos ?'cos ф);
Гш = =с COS ср' COS ф -j- (/?3 + Лс) sin “ 4 cos sin Ф »
где со3 —угловая скорость вращения Земли;
R3 — радиус Земли.
Уравнения движения относительно центра масс в проекциях
на оси JIA-центрической прямоугольной (главной связанной)
системы координат Охпупги (С 111) имеют вид:
(Гсо sincp' — /?3 — Т]с);
/х СО.	М х *
Л ! 1 Д ! I	* Л]П
■^i/ii(0i/ii “-\-(Iy,,	,)0Jjra 1(,,г,,;
Мх„ = Н'Ьх„ (8з — 8l) - m"*"SPQVwXll;
= - ^y^S (хЛ-хт)('Ьп-’ЬсП)4Г (lhii-x,)(b^r
+ h)-	■	-5/2ewoyi, -
. = - <$, (хд - *T) (V- 0„) - 2У?' (4,, - xr) S2 -
— m“*> ■ ОДм»*, t — m“Zi uoZi i,
(4.45)
(4.46)
)
где
/?'— коэффициент пропорциональности
между подъемной силой руля и уг¬
лом его отклонения;
hXll—плечо приложения силы руля отно¬
сительно оси Ох\\\
= ^м—расстояние от вершины ракеты до
точки приложения управляющей
силы на газовом руле;
хл—расстояние от вершины ракеты до
центра давления;
хт—расстояние от вершины ракеты до
центра масс;
172

°ь °з—углы отклонения пары рулей крена
(положительное направление — вле¬
во, смотря с кормы ракеты по по¬
лету) ;
2Ь2 — угол отклонения пары «рулей вы¬
соты» (положительное направле¬
ние— вниз, смотря с кормы по по¬
лету) ;
тяУ11> т*ягг—коэффициент реактивного момента;
тГмМ’ — коэффициенты демпфирующего мо¬
мента;
2/-=л:д>ст — хг (здесь хк>ст—расстояние от вершины ракеты до
центра давления стабилизатора).
Кинематические соотношения:
?с='и£с;	^0=^;	^0=^-
= (“</,. sinYn + Wz,, cos Yii)sec^n;
^11 = ®!/,, cos Yu — «/„sinvn.
(4.47)
v = V‘0i + ‘°b + ''
tg вц =
Пс
Фс11 =
V vl+vi+
(4.48)
Уравнения (4.42) — (4.48) образуют замкнутую систему при
известных законах управления	бг(0> МО и изменения
силы тяги P(t).
4.4.	3. Уравнения движения
в геотопической прямоугольной горизонтальной
ориентированной-II системе координат Ogr}t (Т116)
JIA рассматривается как точка переменной массы. Инерциаль-
ная система отсчета — геотопическая прямоугольная горизон¬
тальная ориентированная-II система координат	(Т116).
Предполагается, что полет происходит над плоской Землей
в однородном поле тяготения (£?з = оо, сокр = 0). На JIA действуют:
сила тяги Р, направленная по оси Ох{ системы С112, и аэродина¬
мические силы.
173

Уравнения движения центра масс:
mi = P cos 9 cos ф-д^ [sin a cos 9 cos 6 —
—cos a(sin 9 cos ф cos у—sin ф sin y)]—Q[sin a (sin 9 cos ф cos у—
— sin ф sin y) -f cos a cos 9 cos Ф] + Z (cos ф sin у sin 9 -f
-f-sin ф cos y);
mr\ = — mg -j- P sin 9 -j- Y (sin a sin 9 cos a cos 9 cos y) -f
-f- Q (sin a cos 9 cos y — cos a sin 9) — Z cos 9 sin y ;
mt = — P cos 9 sin ф-j-K [ — sin a cos 9 sin ф-J-
-f- cos a (cos ф sin y -f sin ^ s*n Ф cos y)] +
-|-Q[sina(cos ф sin Y + sin 9 sin ф cos y)4" cos a cos 9 sin ф] -f-
-\- Z (cos ф cos y — sin 9 sin ф sin y).
-Р'сек-
Кинематические соотношения:
sina= {[sin 9 cos у соб(Фс — ф)sin Y sin (фс — ф] cos 0 —
— cos 9 cos y sin 9} sec ^ ;
sin p = [sin 9 sin у cos (фс — ф) — cos y sin (фс — ф)] cos 0 —
— cos 9 sin y sin 0;
0 = arc sin ■-ri— ;
(4.49)
(4.50)
—arctg
:/52.
(4.51)
Совокупность уравнений (4.49) — (4.51) образует замкнутую
систему, если известны законы изменения углов 4>(/),	y{t),
модуль вектора тяги Р или режим работы двигателя /?д.
4.4.	4. Уравнения движения
в геотопической сферической горизонтальной ориентированной
системе координат г, А, г\ (Т123)
JIA рассматривается как точка переменной массы. В качестве
инерциальной системы отсчета принимается геоцентрическая
прямоугольная экваториальная система координат Ox'y'z'
(П214).
На Л А действуют: сила тяги Р и аэродинамическая сила А,
заданные проекциями Рг+Лг, Ра-\-Аа, PEi+A£j на направление
радиуса-вектора и перпендикуляров к нему, один из которых
174

лежит в плоскости меридиана, а другой — в плоскости, парал¬
лельной экватору.
Уравнения движения центра масс:
т(г — гА2 sin2 ej — rs2) = Pr -f Ar;
m \{r A -f 2rA) sin ^ -jr2rAe1 cos ej =ЯЛ -j- Aa
m (2rsj 4-^£i — sin Ej cos sx )= P4 -f- A4 .
tTl = Pcqk*
(4.52)
(4.53)
4.4.	5. Уравнения движения в геотопической
цилиндрической горизонтальной ориентированной
системе координат г, A, z (Т131)
ЛА рассматривается как точка переменной массы. Инер-
циальная система — геотопическая цилиндрическая горизон¬
тальная ориентированная система координат г, .4, z (Т131).
Уравнения движения центра масс:
т [г — гА1\ = Вг;
т [гА-}-2гЛ\ = ВА;
mz = B9
(4.54)
где Вп Вл, В2
т=— р-сек»	(4.55)
■ проекции равнодействующей всех внешних
сил на направление радиуса, перпендикуля¬
ра к нему и на вертикаль соответственно.
4 5. УРАВНЕНИЯ ДВИЖЕНИЯ В СИСТЕМАХ КООРДИНАТ,
СВЯЗАННЫХ С ЛА
4.5.1.	Уравнения движения в JIA-центрической прямоугольной
главной связанной системе координат Ox\y\Z\ (С111)
ЛА рассматривается как твердое тело переменной массы,
имеющее плоскость инерционно-массовой симметрии, условно
именуемой плоскостью вертикальной симметрии. Ниже приводят¬
ся уравнения движения ЛА для конкретных инерциальных систем
отсчета.
а)	Инерциальная система отсчета — геоцентрическая прямо¬
угольная экваториальная система координат Ox'y'z' (П214).
Движение центра масс рассматривается относительно гео¬
центрической сферической экваториальной-П системы координат
г, X, ф7 (П223), угловое положение ЛА в пространстве опреде¬
ляется углами Эйлера ф, О, у между связанной системой Ох^у^п
(С 112) и земной системой Oxgygzg (Cl 18).
175

Уравнения движения центра масс и относительно центра масс
в главной связанной системе координат С111:
т Ьх,, + VZl, («V,, + UJKpJ/l Л — Vyi, («>*,, -j- 0)Kp-Zj,) +
+ 2 (v2l 0)3y,, — Vy, ,ад3г1,) — <»! (#3 + h) cos ®' (cos cp' sin 9 —
— sin cp' cos & cos ф)] =	;
m I®//.. 4“‘z,x11 (“г,, 4“ “крг,,) — VZli (wjTh + Wkp JT,,) +
+ 2(vXi^zZll —	— u>| (R3-\-
-|- /z) cos cp' [ — cos ®' cos 9 cos y + sin cp' (sin <]j sin у —
— sin & cos <l> cos v)]} = By,,;
m {^., + ^1, (tojr,, 4-wkPx,,) — vXll к„ 4-(«крг/,,)4-
4- 2 (Vg, W3x,, - vXl, o»3ff.,) - «4 (Я з 4-
4-Л) cos cp' [ — cos cp' cos Ь sin y + sin cp' (sin ф cos'y —
— cos ф sin 0 sin ф sin ¥)]} = £*„.
(4.56)
Ix„ (‘^и + ^кр-г,, +t,)3x11)-h(-'rz1, ~ I2/ll) (°Vll +t0Kpc/i. +
+ 0)3//,t)((')z,14~ wKpzM 4~ w3z,,) — Mx,,;
I c/ll ((UJ/li + 0)Kpi/ll"f (°3^,,) + (/x„—12M) («х,, 4~шкрх11 +
+ <вЗХ! Л (<uz,, 4“ 0)крг,, + w3z, Л = МVl 1;
IZj, (“z,, 4" “кр'гц 4~(0Згм)4"Цy„ — Ix„) («x., + “крХц Г
4'(йЗл-,Л(мс/,1 4_WKPc/n 4~w3p1,) = -44zJ1 .
1
кр •* 1 1
Rz + h
(vVll sin Y4-^гц COS y)COS 8;
■(vXll COS 8 sinY + 'Z’z,, sin 8);
r (4.57)
(4.58)
(4.59)
(vUt 1 sin 9 — vXl t cos 8 cos y) .
w3x,, = °>3 (sin cp' sin 8 4“ COS cp' cos 9 cos <]/);
w3;/n -- (03 [sin cp' cos 8 cos y — cos cp' (sin 6 sin y —
— sin 8 cos *4» cos y)] ;
co3Zl, = — co3 [sin cp' cos 9 sin y — cos cp' (sin 6 cos y 4~
4- sin 9 cos cb sin y)[.
(4.60)
176

Кинематические соотношения между производными от коор¬
динат в системе П223 и углами Эйлера ф, О, у и проекциями ско¬
ростей полета vXll,vy„, vZll:
[vXll cos В cos ф-'ь vtJll (sin ф siny-
R3 4- h
— sin В cos ф cos y)-\- vzll (sin ф cos уsin 0 cos ф siny)];
h = vXlx sin В-j-u^ cos 8 cos y — vZll cos В sin у ;
X =
— cos В sin Ф + (cos ф sin у-
(4.61)
R3 + h
-f sin & sin ф cos y)-f ^zlx (cos ф cos у — sin В sin^ siny)] sec 9'.
Производные углов Эйлера ф, у выражаются через проек¬
ции угловой скорости вращения ЛА на оси связанной системы
координат С111 следующим образом:
Y=0)Jfi, — К,! cos у — coZi х sin у) tg В ;
sin y + wZll cosy;
^=((0^ cosy — wZii siny) sec B-
tg?'
R3 ~r h
[vXll sin ф cos B-|-
Л~гиуи (cos ф siny — sinфcosy sin B)-j-xiZii (cos ф cos y-(-
-f-sinфsin В siny)] .
(4.С2)
Проекции BXll, Byil, BZil главного вектора сил, действую¬
щих на ЛА:
BXl t = (Р cos 9Р ^ sin ot — Q cos a — G sin 8) cos сри -\~
-j-(P sincpp-f"^ cosa-j-Q sina —G cos В cosy)sincpH;
BtJii— —(P cos 9P + K sin a — Q cos a — G sin B) sin сри-|- (4.63)
-J- (P sin cpp -f- Y cos a -f- Q sin a — G cos 8 cos y) cos ои;
Z?*M=Z-fG cos 8 siny ,
где фи — угол между главной осью инерции Охц и строительной
осью ЛА Oxi2 (рис. 4.4).
Углы атаки а и скольжения (3 определяются следующими соот¬
ношениями:
tg a =
*J1
(4.64)
sin i = -
У v'i,
v~ -r vi
lh 1	1	г
177

Совокупность уравнений (4.56) — (4.64) образует замкнутую
систему, если известны законы изменения положения органов
управления бв(0»	бн(0>	модуль вектора тяги Р(/), режим
работы двигателя яд, а также угол фр.
б)	Инерциальная система отсчета — геоцентрическая сфери¬
ческая экваториальная-Н система координат г, i, ф' (П223).
Движение центра масс рассматривается относительно этой же
системы координат и соответствует полету над невращающейся
сферической Землей; угловое положение ф, О, у JIA определяется
Рис. 4. 4. Взаимное расположение вертикально-симметрических
систем координат С111, С112, СПЗ и направление вектора
тяги Р
относительно JIA-центрической прямоугольной горизонтальной
ориентированной (земной) системы координат Oxgygzg (С 118).
Уравнения движения центра масс и относительно центра масс
в проекциях на оси связанной системы координат С111 могут
быть получены из уравнений (4.56) — (4.64). При со3 =0 они
имеют вид:
Строительная ось Лй /
Проекция вектора скорости на плоскость
вертикальной симметрии
/.г,, ('".г, , - Г р X,(/г,, —	,	)	(«V,	,	-Г	l'Yp	//,	,	)	К,, +
—	)	— У- г ■
I р - ы '	^11 I
I сок •
(4.67)
178

икр Vii '
R3 + h
(vu,, sill у -Ь г'г,, COS у) COS &;
(d.Vii cos 9-sin ^ + tiz,, sin 9);
Kp *ii '
я* + л
(^м sili 9 — vXll cos 9 cosy) .
(4.68)
Кинематические уравнения, связывающие производные от
координат в системе П223 с углами Эйлера 4>, Ф, у и проекциями
скорости полета vXll ,ъУ11,	:
1
R3 -f- h
\vXll cos9 cos<b —(sinOsiny —
— sin 9 cos ф cos y) ~b Vzl, (sin 6 cos у J- sin & cos ф sin у)];
h = vXll sin 9-f-vtJt, cos 9 cos у — vZl, cos & sin у ;
sec cp
[vXll cos 9 sin ф^^(cos'-bsin у -f-
(4.69)
-j- sin 9 sin ф cos y)-\-rvZll (cos ф cos у — sin 9 sin ф sin y)|.
Производные углов Эйлера ф, О, у выражаются через проек¬
ции угловой скорости вращения ЛА на оси связанной системы
координат С111 следующим образом:
Y = «X.. - к,, COS у — <вг,, sill у) tg Ь ;
Й = <*),,,, sinY+ «>*,,COSY ;
tg' cp'
R'd -t- h
[vXll sinф cos 9-f-	(4.70)
(cos ф sin y— sin Ф cos у sin 9)-f vZil (cos ф cos у-f-
-}- sin ф sin 9 sin y)] .
Проекции BXll, Byil, Bzм главного вектора действующих на
ЛА сил:
ВXil = (Р cos срр -\-Y sin а — Q cos а — G sin 9) cos <?H-f
-f (P sin vP-\-Y cos a -j- Q sin а — G cos 9 cos y) sin <pn;
Byil = — (P cos	sin а — Q cos а — G sin 9) sin <ри -J-	(4.71)
-f (P sin cpp -j- Y cos a -f- Q sin a — G cos 9 cos y) cos <ри;
BZll = Z-\-G cos 9 sin y,
гДе фи — угол между главной осью инерции Охц и строительной
осью Ох 12 ЛА (см. рис. 4.4).
179

Углы атаки а и скольжения [3 определяются формулами:
v,
tga= -
v
(4.72)
sin 3
Совокупность уравнений (4.65) — (4.72) образует замкнутую
систему, если известны законы изменения положения органов
управления 6В(/), 6Э(/), 6П(/), модуль вектора тяги P(t) или ре¬
жим работы двигателя а также угол фР.
в)	Инерциальная система отсчета — геотопическая прямо¬
угольная горизонтальная ориентированная-II система координат
Движение центра масс рассматривается относительно этой
же системы и соответствует полету над плоской невращающейся
Землей. Положение JIA, заданное углами ф, О, у, определяется
относительно JIA-центрической прямоугольной горизонтальной
ориентированной (земной) системы Oxgygzg (Cl 18).
Уравнения движения центра масс и относительно центра масс
в проекциях на оси связанной системы координат С111 могут
быть получены из уравнений (4.56) — (4.64) при со3 =0, R3 =оо;
они имеют вид:
* 3 отличие от определения системы Т116 (см. гл. 3, табл. 3.9) началу
координат О этой системы дай индекс «т» (Ог), чтобы отличить начало си¬
стемы Т116 от начала системы Oxgygzg (Cl 18), которые принадлежат разным
точкам пространства.
Ох|Л£ (T116)*.
(4.73)
(4.74)
(4.75)
180

Кинематические уравнения, связывающие производные от
координат в правой системе Т116, углы Эйлера ф, ft, у и проекции
скорости vXli, vy„, vZll полета:
i = vXl x cos ф cos ft -{- Vy l x (— cos ф sin 8 cos у 4- sin ф sin у) -f
+ vZl, (cos ф sin 8 sin у + sin ф cos y) ;
ц = vXi x sin ft -f vUl x cos ft cos y — vZll cos ft sin у ;
t — —vXll cos 8 sin ф-j-, (cos ф sin у-[-sin ft sin ф cos y)-f~
-f , (cos ф cos y — sin ft sin ф sin y) .
(4.76)
Производные углов Эйлера 4», ft, у выражаются через проек¬
ции угловой скорости вращения JIA на оси связанной системы,
координат С111 следующим образом:
Y =	, — К., cos Y — wz,, sin y) tg 9 ;
8 = o)tJi x sin y-f coZj i cos у ;
iz=(o)^ii cos y — W*M sin у) sec 8 .
(4.77)
Проекции BXllJ Byil, BZll главного вектора действующих
на ЛА сил:
BXi Х = (Р cos Op -|- Ksin a — Q cos a — G sin ft) cos ovl -f-
-\- (P sin op -f Y cos a-|- Q sin a — G cos 8 cos y) sin ои ;
BlJx x = — (P cos op-j-Y sin a — Q cos a — G sin 8) sin ou -}-
-f (P sin op -[- Y cos a -j- Q sin a — G cos 8 cos y) cos сри;
BZli = Z G cos 8 sin у ,
(4.78)
где фи — угол между главной осью инерции Охп и строительной
осью Ох 12 ЛА (см. рис. 4.4).
Углы атаки а и скольжения (3 определяются формулами:
V,.
iga =
У11
(4.79)
У«*м + <.чЧ.	!
Совокупность уравнений (4.73) — (4.79) образует замкнутую
систему, если известны законы изменения положения органов
управления 6В(/), бэ(0» бн(0 и модуль вектора тяги Р (t) или
режим работы двигателя гад(/), а также угол фР.
г)	Линеаризированные уравнения продольного возмущенного
движения.
Инерциальная система отсчета — геоцентрическая сфериче¬
ская экваториальная-II система координат /г, Я, ф' (П223). Пол¬
181

ная система уравнений движения (4.65) — (4.72) разделяется
на две независимые системы (продольного и бокового движе¬
ния) и линеаризируется при следующих допущениях:
1. Параметры vXll,	возмущенного движения отличают¬
ся от параметров vXiyo, г^]]0, . . . невозмущенного движения на
такие малые величины LvXll, Дг^,, . . . , что их степенями вы¬
ше первой можно пренебречь,
2. Проекции сил и моментов, действующих на JIA в плоскости
вертикальной симметрии хОу, не зависят от параметров бокового
движения Р, Y.'Ф. «ж,,, «</„, vZll и Yo = 0. Ро = 0-
3. Масса ЛА постоянна.
4. Полет происходит в плоскости экватора (q/ = 0).
После разложения в ряд Тейлора с учетом перечисленных
допущений уравнения продольного возмущенного движения ЛА,
записанные относительно отклонений AvXllt AvVlli. .. в системе
координат С111, а также кинематические соотношения между
отклонениями имеют вид:
~Г Д(0крг,,)] — Д^-r.i
(4.80)
+ Д®кр*„)] = Д5»„ •
(4.81)
Да =
4v„sinao + %,,
-f vu
д i ] о	У11	о
(4.82)
? (4.83)
— \vXl, cos »0 4- Дг'у,, sin 90] — (vXl, 0 cos 90 +
182

дBXl, = Bvx*i .e ixijr,, +	.Д vffl , + £*,, 0да + £*» _ oдЗ„ + j
Д^гл, =	Д^,.	+	5"fr0^V,.	+	5*,.	„Д«	+	5I",	„Дйв	+
} (4.84)
4-B* д» + Вл ДА
1 У mo	'	w,, n
У11 о
со	о	„	г,
Д УИг =М 2" Дсо7 -f-44 в д& X./W* да|/Мй	дЛ4-	(4.85)
11	Z\\ О	1,1	Z\ \ Q И ‘	^110	Z	\ \	О	1	V
-f УИ/‘ ■ дг-'д-, -+- УИ/< ■ Д-г-’у,, -f АГ Да ,
*11 0	111	2^110	J	*110
где индекс «О» относится к параметрам невозмущенного движе¬
ния, а Д обозначает отклонение параметров возмущенного дви¬
жения от невозмущенного движения.
Частный случай. В случае плоской Земли (сокр = О,
/?3 =оо) уравнения (4.80) — (4.85) принимают вид:
т
т
dAv „
dt
d Avt
■ 'Wv ov — vЛ to*
■-* У 11 z 11 о	У11 о —* z 11
а/
х + дг>,04-vXlt „Д^г,,
— Д^х,,;
= Д£</,, •
(4.86)
Л (ДА)
dt
,, sin ?>0 + Дг1,,., cos г% -f Д« (г’.г,, 0 cos «0 ■
г’г/.. ,sin»0);
dL
dt
— Д^;/]1 sin i^0 ,
( —	,	a	sin	f>0	-	,	0	cos	fl0)	д	ь	X	Лг,Xi _ COS &0
(4.87)
1
где L — продольная дальность.
Остальные уравнения из (4.81), (4.82), (4.84), (4.85)
остаются без изменения.
д)	Линеаризированные уравнения бокового возмущенного
движения.
Инерциальная система отсчета — геоцентрическая сфериче¬
ская экваториальная-П система координат г, q/, X (П223). Пол¬
ная система уравнений движения (4.65) — (4.72) разделяется на
две независимые системы продольного и бокового движения
и линеаризируется при допущениях, указанных в разд. 4.5. 1, «г».
Дополнительно предполагается, что проекции сил и моментов,
действующих на ЛА в плоскости Х\0у\ и у\Оги не зависят от па¬
раметров v, а, 0, О, coZll продольного движения и высоты h.
183

При этих условиях уравнения бокового возмущенного движе¬
ния ЛА в проекциях на оси связанной с ним системы координат
OxnynZu (Cl 11), а также необходимые кинематические соотно¬
шения имеют вид:
т
dAv,
dt
+ Vy,, о (х,, + ДМк'х,.) — VXl, 0 (Д«о„,, + Д <ок,,)
d Да)
11 |
dt
d До
/У 1
dt
d Ay
dt
= Д5гп.
г(7гм — /у,,„Дм,/,, = Д/И^ ;
i Ь(У-r,,	/г,,) шг,, „Дм.г,, == ДД,М .
-=>Д(«лгм — tg ftoOv,, — w*„ оД^);
^Дсоу,,—WZ11 оду) sec 90.
Д“крх,, = тгА (Дг’г.. + vur ■ o^v);
A(0Kpt/i i
/?3 + /г
1
/?3 -4- /£
(sin 0оДг1г,, + г>,,, „ cos &0Ду).
Д?:
дщ
(4.92)
v0=V г£„в + г£11в;
^Bz —В Zii^vz	-\-B^	Д 3-1-5	н А8Н ;
11	2,,0	1	1	1	2, ,	о	2 1 1	О н
со	со	о
ДУИЛ.,, = Мх*<-оAcoXi, + M/t‘-оД<»1/,, + mXi_ одз +
+ мх* Д8Э + Ж>	Д8Н +	/И*« Д8	;
1	Xj 1 о	d 1	Д11	О	Н	-*110	11
00	СО	р
ДМ,,— /И Л'11 Дсог	4-М	Дсо„ДЗ —[_
//11 о	Л,!	1	//но	1/11	1	//11	о 1	1
+ Af; Д8э + /И‘н	д8н +	/И*" Д8	.
1	У mo	э‘	//11 о	Н1	У11 о	н
Частный случай. В случае плоской Земли (со1ф = 0,
R3 =оо) уравнения (4. 88) —(4. 92) принимают вид:
(4.88)
(4.89)
(4.90)
(4.91)
т
I rl\vz	\
I—„Дм*., — г>Л11 „Дм,., 1 = ДВг„ .
(4.93)
184

Д,
/у„
//Дсо
(//
//До
///
(/AY
(it
dA'b
dt
1" (^п	IZix)'"zix 0А(,'л-,1
А(,)ц tg 9-q (t wZll 0AV);
= (д«»4,11—w*I10AY) sec »0.
д?=-
At;,
=V4.
(4.94)
(4.95)
(4.96)
Выражения для ЛBZll, AMXxi,	см. формулу (4.92).
4. 5. 2. Уравнения движения в JTA-центрической прямоугольной
вертикально-симметрической связанной системе
координат Ох\2У\2%\2 (С112)
Уравнения движения центра масс в	системе координат	С112
в предположениях, изложенных в разд.	4.5. 1,«в», имеют вид	со¬
отношений (4.73) — (4.79), если в них нижние индексы «11» за¬
менить индексами «12». Кроме того, выражения для проекций
сил (4.78) следует заменить выражениями
BXi2 — P cos yP-\-Y sin a — Q cos а — G sin S ;	1
В tJi2 = P sin vp-{-Y cosa-fQ sin a — G cos ft cos у ;	\	(4.97)
i?Zl2 = Z+G cos 8 siny ,	j
а уравнения (4.74) вращательного движения относительно
центра масс при IXz = Iyz = 0 примут вид:
/х12°Ц'12 + (/z12 — Iг/12) 03г/,20)^12 — А*12У12 (С0//12 ~С0^,2с0-г:12) = ^л'12;
А/.Л.атСх,,— /*J«w>zia —	(‘^„ + «^,,«7,0 = ^,,; I (4.98)
/~	0)7 -{-(/„ — /г )(')и СО,,   /г ,, (соТ —) = 714 z .
I V //1 2	-*12/	■* 1 2	С/12	Aj	2С/]2 \	Л]2	//12/	*12
4. 5. 3. Уравнения движения в ЛА-центрической
прямоугольной вертикально-симметрической связанной
системе координат Ox\t)\Zx (СИЗ)
Уравнения движения в системе координат СПЗ при предпо¬
ложениях, изложенных в разд. 4.5. 1,«в», получаются из (4.73) —
185

(4.79) посредством замены нижних индексов «11» на индекс «1».
Кроме того, в выражениях для проекций сил (4.78) следует за¬
менить уГОЛ фи УГЛОМ фКр.
4. 5. 4. Уравнения движения в ЛА-центрической
прямоугольной вертикально-симметрической полусвязанной
системе координат Oxyz{Cl 14)
ЛА рассматривается как твердое тело переменной массы,
имеющее плоскость инерционно-массовой симметрии (плоскость
Х\Оу\ вертикальной симметрии ЛА).
Инерциальная система отсчета — геотопическая прямоуголь¬
ная горизонтальная ориентированная-II система координат Т116.
Движение центра масс рассматривается относительно системы
Г116; угловое положение ЛА определяется углами Эйлера тр, Ф,
у, связывающими систему координат СПЗ с земной системой
Уравнения движения центра масс и относительно центра масс
ЛА в системе С114 имеют вид
Кинематические соотношения между производными углов
Эйлера гр, Ф, у и проекциями	coZj	угловой	скорости	вра¬
щения ЛА:
С118.
mv K = mvz(«)X) sin а — ыУх cos а) -f Р cos (а — ?р) —
— Q — mg (cos а sin Ь — cos D cos у sin а);
mvb = — mvxcoZj -f- mvz ((»*, cos a -j- wyi sin a) -j-	|	(4.	99)
-}- P sin (a — vP) -j- Y—mg (sin a sin ft -j- cos a cos & cos y)»
mvz = mvx( — MXl sina-f-^Vi cosa)-{- Z — mg cos & sin y.
™ = ~ IW
(4. 101)
{,Vi siny-f co2j cosy;
У = ^—tg&(w^ cosy — coZl sin y);
Ф = О°01 cosy — siny) sec ft.
(4. 102)
186

Кинематические соотношения между производными коорди¬
нат £, г|, £ правой системы Т116 и параметрами О, 9, г|)с:
c = v cos 0 cos 'К;
11 = ^ sin 6;
£= — г* cos 0 sin 'К.
(4. 103)
tga =
г'г/ = 0;
tgP=-^;
VX
cos 0 sin о sin Y — cos Y ('sin ft cos 0 cos b — sin 0 cos ft)
(4. 104)
cos ft cos 0 cos ф + sin ft sin 0
sin фс = [cos a cos p sin ф cos 9- -\- sin a cos p (cos ф sin у -!-
-j-sin ф sin 8- cos y) — sin p (cos 6 cos у—sin ф sin 9- sin y] sec 0.
Частный случай. Если углы a, (3 малы, фр = 0, I х,у, =0, то
уравнения (4. 99)—(4. 104) принимают вид
mvx= mvz (coXia — мУ1)4-Я —Q — mg (sin 0 — a cos 9 cos y);
mvb= — mvxtoZi -f- шг'г (wjri -f-	-[- Pa -\- Y —
— (a sin ft -[- cos 9 cos y);
: mvx( — ao)JCi -j- o^J-j-Z -j- mg cos 9 sin у
™ = I^ceK*
/лг^лг, + (/*, — 1у1)®у1®г1 = Мх1;
mv9
(4. 105)
*/i Tn i
(4. 106)
(4. 107)
J г/м
IZi(0z, T (^*/i ^l) t0* Ai ~ ^<гп
sin dicz=[sin tbcos ft —}— ot (cos ф sin у -j- sin ф sin 9 cos y) —
— p (cos ф cos у — sin ф sin ft sin y)] sec 6.	(4. 108)
Уравнения (4. 102) — (4. 104) остаются без изменения.
4. 5. 5. Уравнения движения в JTA-центрической
прямоугольной вертикальной скоростной системе
координат ОясуС(гс(С115)
ЛА рассматривается как твердое тело переменной массы,
имеющее плоскость инерционно-массовой симметрии (плоскость
х\Оух вертикальной симметрии ЛА при его горизонтальном, пря¬
молинейном полете относительно Земли).
187

Ниже приводятся уравнения движения JIA для ряда инер-
циальных систем отсчета.
а)	Инерциальная система отсчета — геоцентрическая прямо¬
угольная экваториальная система координат Ox'y'z' (П214).
Движение центра масс JIA рассматривается относительно
геоцентрической сферической экваториальной-П системы коор¬
динат г, ср', X (П223); угловое положение в пространстве опреде¬
ляется углами Эйлера ф, О, у, связывающими систему С111 с си¬
стемой С118. Уравнения движения центра масс и относительно
центра масс JIA в системах С115 и С111 соответственно имеют
вид:
mv = Р cos (а -у ур) cos $ — Q cos 3 -4- Z sin 3 — mg sin 0 —
— mu>| _l_ /у) cos (sjn ^ cos Q cos oc _ COs cp' sin 6);
mvQ = P [sin (a -j- op) cos yc -f cos (a — cpp) sin 3 sin yc] —
—Q sin rp sin yc -I-K cos yc — Z cos 3 sin yc — mg cos 0 -]-
i ZI1Z— cos 0 — 2mv«u cos со' sin -I-
Лз+А	3‘ ,c 1
—	(/?3	/2) cos cp' (sin cp' sin 0 cos фс -j- cos cp' cos 0);
— mv cos 0фс = P [sin (a 4- ?p) sin yc — cos (a — cpp) x
X s'n p cos yc] + Q sin 3 cos уc -f У sin yc + 2Г cos 3 cos yc —
— 2mvu)3 (cos cp' sin d cos фс — sin cp' cos 0) — mwl (/?3 -|- /2) X
'i
X cos cp' sin cp' sin 6C
cos2 0 tg cp' sin фс
■ (4. 109)
m-— — u„
(4. 110)
4„ {^Х1х -f ^кр-ГцТ" 0)3*11) +
+ (^11—411)	X
X (^ц+^крz„ + w3 zll) = A4JCll;
4n (шг/| 1 +c°KP2/ii T"C03 г/м)4~
+ (4,, — 4ц)	+	^крхц	-Ьо:)з	jcm)X
X К.+^кр^п +^3 zxl) = Myii\
4i (0J^11 "Ь wKpz,j +«3.n) +
“b (4n	4ц)	(%ц	~Ь(0крг/ц	'"Ь	с°3	r/ц)	X
X К ! , + CPKp ^ ! + 0J3 J == MZl 1 .
(4.111)
188

oKpJCll=— cos 0 (sin a sin yc — cos a sin $ cos yc);
r
oKpyiiz=— cos 0 (sin a sin 8 cos vc + cosa sin yc);
"кр 2,, •
cos 0 cos p cos yc.
<o3 Xi t =. o>3 (sin cp' sin 8 -f- cos o' cos 8 cos ф);
oj3 yii = o)3 [sin cp' cos 8 cos у — cos 9' (sin ф sin у -
— sin 8 cos ф cos y)];
co3Zii= — co3 [sin cp7 cos 8siny —coscp' X
X (sin ф cos у + sin 8 cos ф sin y)].
Кинематические соотношения:
r = ^sin0;	л
o' — cos 0 cos фс
r
I
Г
X = cos 0 sin фс sec cp'.
Ф = (0)//м cosy —coZii silly) sec 8;
8= w^i, siny-|-ojZii cosy;
Y = ^ , - tg 8 (oVi i cos у - wZl , sin y).
sin 8 = [sin 8sinусо8(фс —ф) — cosy sin (фс — ф)] X
X cos 0 — cos 8 sin у sin 0;
•sin a = {[sin 8 cos у cos (фс—ф) -f- sin у sin (фс — ф)] X
X cos 0 —cos 8 cos у sin 0} sec
sin yc = cos a cos (фс — ф) sin y + (s*11 a cos 8 —
— cos a sin 8 cos y)sin(6c —6) = [cos a sin p sin ft —
— (sin a sin ° cos у — cos [3 sin y) cos 8] sec 0.
h = r — R 3 (cp');
R3WY-
Rl
COS2 cp'
1—e\ cos2 cp'
Значения Rp, Re, e\ приведены в разд. 4. 3. 5.
(4. 112)
(4.113)
(4. 114)
(4. 115)
(4. 116)
(4.117)

Совокупность уравнений (4.109) — (4.117) образует замкну¬
тую систему, если известны законы изменения положения орга¬
нов управления 6В(/), бн(0»	М°ДУЛЬ вектора тяги P(t) или
режим работы двигателя яд, а также угол фР.
б)	Инерциальная система отсчета — геоцентрическая сфери¬
ческая экваториальная-П система координат г, q/, X (П223).
Движение центра масс рассматривается относительно этой
же системы координат и соответствует полету над невращающей-
ся сферической Землей; положение JIA определяется углами
Эйлера ф, Ф, у, связывающими систему Ox\2y\2Z\2 (С 112) с зем¬
ной системой OxgtjgZg (Cl 18).
Уравнения движения в скоростной системе координат СПЗ
можно получить из уравнения (4. 109) — (4. 117), полагая со3 =0:
mv = Р cos (a -f- срр) cos р — Q cos р -{- Z sin р — mg sin б;
mvb = Р [sin (а-|- срр) cos ус -j- cos (а — срр) sin р sin ус] —
— Q sin р sin ус + К cos ус — Z cos р sin ус —
— mg cos 0 +
cos (
#з+ л
— mv'jc cos 6 = P[sin(a-f ?P)sinyc—cos(a—cpp)sin 3 cos yc]-f
-f Q sin p cos yc -j- Y sin yc + Z cos p cos yc —
mi/2
#3+ h
cos2 0 tg»' sin 6C.
(4. 118)
m - - — i*Cl
(4. 119)
X,,	+	‘“kp j:, ,) + ( / г,, — / .(/11)(<,)//,I + °’кр I/,,) X
X (wz,, + “'кр z„) = Mx,,;
^i/n (“Vn H" (I)KP </n) "i" Ux, i Д,) О'Ъг,, X (,)кр jrn) X
X , ”Г ‘’Vpz,,) = N у
I г,, (loz,i + (,)кр г,,— / *,,) (wjc, , + 0)кр *u) X
I Wk-n
(4.120)
икр -Г,
, = — cos б (sin a sin ус — cos a sin р cos ус);
nvp улг
10 к р Z • •
— cos б (sin a sin 8 cos ус -f cos a sin ус);
— cos б cos р cos ус.
г
(4. 121}
190

Кинематические соотношения:
r = v sin 0;
Cf/ = — cos 0 cos '1>C;
r
k= —— cos 0 sin фг sec o'.
Ф = К.. cosy —o)*M sin y)sec &;
9 =- c.)£^i l sin Y + 0^,, cos y;
Y = ^, — tg& К,, cos y (,)zjj sin y).
sin 3 = [siii 0 sin у cos (фс — ф) — cos у sin(6c — ф)] cos 0 —
— cos	9 sin у sin 0;
sin a =	sec	3	{[sin	9 cosy	cos (фс — ф) -}- sin у sin (фс — ф)] X
X cos	0 —cos0 cosy sin 0};
sin yc =	cos	a	cos (фс —Ф)	sin у 4- (sin a cos 0 —
— cos a sin 9 cos y) sin (фс — ф) = [cos a sin 3 sin 9 —
— (sin a sin 3 cos у — cos £ sin y) cos 9-] sec 0.
h = r-R з(ср');
(4. 122)
(4. 123)
(4.124)
Re
V\-e\
COS-2 Сo'
(4.125)
Значения Rp, Re, e\ приведены в разд. 4.3.5.
Совокупность уравнений (4.118) — (4.125) образует замкну¬
тую систему, если известны законы изменения положения орга¬
нов управления бв(/), бэ(0» 6П(£), модуль вектора тяги P(t) или
режим работы двигателя яд, а также угол фР.
Частные случаи.
1.	Если углы а, р, фР малы (sin a —a, cos a— 1, sin p~p и т. д.),
то уравнения (4. 118) — (4. 119) принимают вид:
mv = P-Q-\-Zb — mg sin 0;
mvb = P[(a -f Op) cos yc-[-c sin yc] —Q 3sinyc-}-
-f-Kcosyc — Z s?nyc — mo-cos 0-4-
mv 2
R3+h
COS 0;
— mv cos бфс = P [(a -j- <op) sin yc — cos vc] + Q P cos vc
-f-K sin\’c-)-ZcosYc
R3+h
cos2 6 tg <p/ sin <|)c.
(4. 126)
m — ~V-c
(4. 127)
191

2.	Если углы а, срР малы, (3 ^0, Ус^-0 и Р(а—срР) = 0, то урав¬
нения (4.118) — (4.119) описывают продольное движение JIA
в плоскости большого круга Земли и имеют вид:
mv = Р — Q — mg sin 0;
mv2
COS 0;
mvh = Y — mg cos 0-
1 Я3+А
■ mvir cos 0 = Z — ~тг~~г cos2 0tg cp' sin фг.
(4.128)
(4. 129)
Соотношения (4. 120) — (4. 125) сохраняются.
в)	Инерциальная система отсчета — геотопическая прямо¬
угольная горизонтальная ориентированная система координат
01ч]1 (Т116).
Движение центра масс рассматривается относительно си¬
стемы Т116 и соответствует полету над плоской невращающейся
Землей.
Уравнения движения центра масс в скоростной системе коор¬
динат Ох\2у 12^12 (С 112):
mv = Р cos (a -f- с?р) cos $ — Q cos В -j- Z sin 3 — mg sin 0;
mv® = P [sin (a ?p) cos yc cos (a — cpp) sin £ sin yc] —
— Q sin 3 sin yc-\-Y cos yc — Z cos sin yc — mg cos 0;	(4.	130)
— mvbc cos d = P [sin (a f cpp) sin yc — cos (ct-j-op) X
X sin cosy c] -j- Q sin 3 cos yc -\- Y sin yc -j- Z cos 3 cos yc.
1W	(4.131)
Уравнения движения вокруг центра масс в системе координат
OxwtjwZu (С111):
(4.132)
Кинематические соотношения для правой системы Т116:
£ — V COS 0 COS бс;
Л = ту sin 0;	(4.133)
С=—v cos 0 sin фс.
I X,xwxtl
+ (/г„
,=лц,
1у 11 (lVii
+ (/*„
Уп
192

ф = к„ cos y — ioZii sin у) sec ft;
0 = 0^, sin y -j- (oZm cos y;	(4. 134)
V = (°л-,, - tg ft К, cos Y ““«m sin Y)- .
sin a--=sec 3 ([sinft cos YCOs(<l>c — (b)-f-sin y sin (фс — ф)] X
X cos 0 —cos ft cosy sin б};
sin 3 = [sin ft sin y cos (фс — ф) — cos y sin (фс — ф)] cos 0 —
— cos ft sin y sin 0;	(4.135)
sin yc = cos a cos (фс — ф) sin y + (sin a cos ft —
— cos a sin ft cos y) sin (фс — ф) = sec 0 [cos a sin p 9in ft —
— (sin a sin 8 cos y — cos 8 sin y) cos ft].
Система уравнений (4.130) — (4.135) является замкнутой,
если известны законы изменения углов 6В(0,	^н(0 и за¬
коны изменения модуля силы тяги P{t)>
г)	Линеаризированные уравнения продольного возмущенного
движения. ’
Инерциальная система отсчета — геотопическая прямоуголь¬
ная горизонтальная система координат 0£т|£ (Т116). Полная си¬
стема уравнений движения (4.118) — (4.125) также разделяется
на две независимые системы и линеаризируется при условиях,
изложенных в разд. 4.5.1, «г». Линеаризированные уравнения
имеют вид:
dAv
т0	= ДР cos (a0 -f срр) — ДаР0 sin (а0 + '?/>) —
dt
— Щ — Д0то£о cos I
dAf)
rn0v0 —= Др Sin (а0 4- срр) -j- ДссР0 cos (a0-f<рр)+
dt
“Ь -4- ДбШо^о sin
(4.136)
dt
dM__
dt "
= Д MZi
: Д(02
(4.137)
dt
= (Av cos 60 — a6v0 sin 0O) cos ф(
c0>
1^3=(дг» sin 0O -j- Д0^о cos 0O\
dt
(4. 138)
1669
193

Да = Д& — Д0;
Л = п. I
(4. 139)
аР = P0Av-\- Р0 дй -{- РолАпд;
AQ = Q0Av -)-(20ДЛ-(-(30Дсс-[-С()овД8в;
AV=Yv0Av +^д/г + к“да + КовД8в;
&MZll — M*tl Q&V	0Аа	-j-	MhZil0Mi-\-
Mzzll0AMZil + MZll0Aa -f ^zfieASB4- MzTl0AbB.
(4. 140)
Частный случай. Если угол ao—фр мал [sin(ao—фр) ~
~ao—фр], то уравнения движения (4. 136) — (4. 137) и кинемати¬
ческие соотношения (4.138) — (4.140) для правой системы Т116
запишутся в виде:
тп
d Av
dt
--АР — AaP0(a0-\-wp) — aQ — AQm0g0cos I
movo ~7.г = Д/3(ао + ?р) + Д«^’о + ДК-f A0mO(eosin0o;
dt
d Aar
dt
^- = дА?
zM.
(4.141)
(4. 142)
db,b
dA%
dt
dAt\
dt
--(Av COS 60—A6v0 sin e0)cos *c0;
= Av sin 0O -f- Дбг’о cos 0O.
да= Д& — Д0;
/z = n.
(4. 143)
(4. 144)
AP = P0Av -j- P0Ah	РолАпл;
AQ == QqAv -(- Q0Ah -f- Q0Aa -f-Qo"A^B',
AY=YqAv-j- YqAh-\-Y0Aa -(-КоВД^В;
*V	OL	00
AMz,, = -442u 0Д-r»-j— MZllQДа-)- Mz*\\До^п o-
+	0Да-(-Л1г®од8в-(- MZtl0Afi.
\ (4. 145)
194

Линеаризированные уравнения продольного возмущенного
движения (4. 141) — (4. 144) можно записать также в виде:
d Av
dt
d ДВ
:	Ат;	a13Ад -j- #14Да	#i5A&b+	clIQ)Xq\
—- — a3lAv + #з3Дб -f #34Да -f- #35A&B -|- #36K B.
dt
(4.146)
 ALL — #21ДТ/ -j- Ct22^^z1 x “j-	-f“	0>24Д^	“j-	^2бД^в	~\~
dt
-j- #25A^B"f a26^z в!
dA$
dt
- = До)*
(4. 147)
или
да = д8 — Дб
^ — auLv — а13Д0 - а14Да = а15Д§в + а16Х0;
dt
dAd
dt
и31 Дт; #33Д0	#34Да—#3яД^п b #3fil R.
^зз1
34
35а в I “36'
(4. 148)
(4. 149)
d 2Д0-	//ДО-	,	//Да	4	А*	I
• #22 Д #24Да —^24 ~~Z	.^21	Ат;	—	#25Д°в“Г
dt 2
dt	dt
+ #25ASb-{-#26^zb*
да = дй — Д0.
(4. 150)
(4. 151)
Здесь величины Хв, Ув, MZB— приращения возмущающих сил
и момента соответственно.
Нумерация i и j и значения коэффициентов приведены
в табл. 4. 11а и 4. 116.
Частный случай. Продольное короткопериодическое воз¬
мущенное движение.
Если До = 0, то вместо системы (4.149) — (4.151) получается
следующая система:
CLi _ йззАе - а34 Да = й35д8в -f а36Кв.
dt
(4.152)
d 2Д&
flf/2
— а
22 ‘
dAb
dt
-024Да ~ан~- =aAJra,5^Aa26MZB.
Да— дй-f Д0 = О.
(4. 153)
(4. 154)
195

Нумерация линеаризированных уравнений возмущенного продольного
движения и параметров движения J1A
196

197

д)' Линеаризированные уравнения бокового возмущенного
движения. Инерциальная система отсчета — геотопическая пря¬
моугольная горизонтальная ориентированная система коорди-
Полная система уравнения движения (4.130) — (4.135) раз*
деляется на две независимые системы и линеаризируется при
следующих допущениях:
1. Параметры фс, о)*п,	возмущенного	движения отли¬
чаются от параметров фс0, ю*мо, о)^110... невозмущенного дви¬
жения на такие малые величины дфс, Дю*,,, До.^,,..., что их
значениями при степенях выше первой можно пренебречь.
2. Боковые параметры невозмущенного движения ф0, 'фсо, Ро>
Yco, уо, бэо, (Ох0, о)^0, бно и производные по времени продольных па¬
раметров невозмущенного движения ао, бво, 0о, (0гю==®о малы и
их степенями выше первой можно пренебречь.
3. Проекции сил и моментов, действующих на ЛА в плоскостях
X\Oz\ и y\Ozu не зависят от параметров а, О, 0, coz продольного
движения.
4. Масса ЛА постоянна.
После разложения в ряд Тейлора с учетом перечисленных до¬
пущений уравнения бокового возмущенного движения ЛА, запи¬
санные относительно отклонений Дфс, АсоХм, АсоУ11 ... в системах
координат С115 и С111, а также кинематические соотношения
между отклонениями для правой системы Т116 имеют вид:
нат 0£т]£ (Т116).
— m0v0 cos 0О —-A = (Q0 — Р0) Дй + Y0Дус + ДZ -f Я sin (а + срр) дус.
at
(4. 155)
(4. 156)
— = Дюгм —A«VMtg &0;	[
— = — Дфс®0 cos 60.
at	I
(4. 157)
198
Д? = Дф cos 0О — ДФС cos 0О -j- Ay sin а0;
ДУС = A? tg 0О -f- Ay cos 0О sec 0о.
(4. 158)

A Z— ZoAp-)-ZoHA&H;
Д MXl, = MXl, 0 Д p + .Л1 jrf,' о Д^дг,, +
+ Л^Дш*,, "Ь-М*"„Д&н + M/tl 0Д8Э;
Д^ц — ^^иоДРЧ'^г/моД^и + ^^.'оД^и +^Г.0Д^н J
„ ,	/	а	Л)(“о+<?р)+	Э'о
или в другой форме при cos0o=— 	—
\	Go
(4.159)
d Дфс
dt
dAa
- (^34 4“ ^34) A? -|- &37Д&Н 4“ ^35^V 4“ ^39^B*	(4.	160)
dt
d Aw
: ftu Ao)Jfi t -f- ft12A(Oyt t -f- ^hA? + ^17^+
+ ^18Д5э + ^19^дгв;
1/1 ~	^21	At*>jrM	-j"	^22A^31+ ^24^4“
^27A-(- b^it
^Уи sec &0;
dt
-j- &24A^ 4“ ^27A4“ ^27A“j- b^Mу
dA'b
(4.161)
AY
rf*
dAC
dt
= A(*)Jr11 — A<tyM tg&0;
= — A<lv^ocos eo-
(4.162)
(4.163)
A? = Аф cos 0O — Афс cos 0O 4- AY sin a0.
Величины ZB, iWXB, MyB — приращения возмущающих сил и мо¬
ментов соответственно.
Значения коэффициентов bij приведены в табл. 4. 12а и 4.126.
Частные случаи.
1.	Изолированное движение рысканья. Если дополнительно
предположить, что Фо=0, coXll= 0, у =0, то уравнения (4. 161) —
(4. 163) бокового движения можно записать в виде:
dДфс
dt
- Ьид8 4- ЬЪ1 Д&н 4“ b39ZB
(4. 164)
d Aa
УII
dt
~==b22^yli 4“^24^? 4-^24A^4_^27^^h4_^27A5h4- Ь2дМу B. (4. 165)
rfA'l»
: Д(0,
dt
А? = Аф — Афс.
(4. 166)
(4. 167)
199

Нумерация линеаризированных уравнений бокового возмущенного
и параметров движения ЛА
3
vo
а
Ь-
3
<1
3
<3
<1
<1
N
к
S
X
а>
*
х
3 ч>
е 2
о л
* а п.
о а.
К %
3	«
g|p
с.* « я
О CL СВ
С
+
“Ь
я
ео
<
>^г
+
сп.
<1
ТГ
'СГ
+
3
<
+
3
<
+
+
Я
60
<1
+
.сп.
*с>
+
СП.
<1
■rt<
a?
<м
+
CM
*C>
-
+
3^
=d
OJ
И
• 60
<Ц
*с>
*■ см
*C>
+
+
3
CI
II
о
а
<1
•S
**3
CN
N
+
+
?>-
<
+
СЕЪ
<1
+
-Э
<1
200

2.	Изолированное движение крена. Если дополнительно пред¬
положить, что (3 = 0, АыУ11=0, $н=0, то уравнения (4.161) —
(4.163)	бокового движения примут вид:
±и- — bnA<»x-\- ^i8A^9 + &19Л1^в.	168)
(4.169)
4. 5. 6. Уравнения движения в JIA-центрической
прямоугольной вертикально-симметрической скоростной
(поточной) системе координат Охпу^ги (С116)
ЛА рассматривается как твердое тело переменной массы,
имеющее плоскость инерционно-массовой симметрии (плоскость
хпОуп вертикальной симметрии летательного аппарата при его
нормальном положении относительно Земли), т. е. Ixl2zl2 =
Инерциальная система отсчета — геотопическая прямоуголь¬
ная горизонтальная ориентированная-II система координат
Относительно этой системы координат рассматривается дви¬
жение центра масс ЛА. Угловое положение ЛА определяется
углами Эйлера ф, б1, у между системой С112 и земной системой
координат С118.
Уравнения движения центра масс и относительно центра масс
в системах координат С116 и С112 соответственно имеют вид:
mv = Р cos р cos (а -\- сря) — mg sin 0 — Q cos p -f- Z sin P;
/ттоп = -{- Я sin (a -f- сpp) — mg (sin a sin 0 4-
 IyuZ12 — 0.
оы (T116).
-f cos a cos & cos y) -f- Y;
— mvu>nyn =-P sin p cos (a + сря) -f
mg (sin 3 cos a sin & — sin a cos & cos у sin p -f-
-f cos p cos & sin y) -f- Z cos p -f- Q sin p.
(4.179)
201

Обозначения и выражения для динамических коэффициентов
движ
Рорядковый
номер уравне¬
ния движения
/
Порядковый номер
1
2
3
4
1
со ^
М /’1
, Л 11
Л1>>
/ -*11
^13 ~ 0
м*
Ь,л
*11- -
-*11
1 jceic
*’2- 7
-* 1 1
1 С£/<
"14 — г
-*и
Х/сек*
2
0) ~
Af/”
L У11
it У XX
h
^23 = 0
К
f Ун
024 — г
Уп
\/сек2
м1
г У11
24 г
Уп
\/сек
21 — j
У11
\\сек
ЬТ1 “ 7
Ун
1/сек
3
*31 = 0
о
1!
(N
СО
*£3 = 0
, Po~Qo~ zo
34 щщ cos е0
1 /сек
*34 = ~ *ё <>о
vo
1 /сек
202
/2 —/	/	4-/2
 	//12	Уп *19 ~ -*i2//i2
•a	J	j  j2	1	2 i/1 2
•*12 У 1 2	-*1 2 У12
-* 1 2 //1 2 ( ^1 2	-*12	УI 2 )
	о	 03 Г О)-г
Г Г 	 Г 2	12 *1 2
-*12 //l 2	-*1 2//l 2
2	Л/Г	I	-*1	2//1 2
+
	£1*	 Л/f	I	-*12//
4 4 ~4 и Х' К I. -
-*12 У12	-*i2//i2
/2	^Уп\
■*12 //12	-*1	2//1	2
—4 +4 4 —4
.4		 -*1 ft	-*12	2,2	-*12//l2
/ / _/2
•*12 У Л 2	-*	1	2*/l	2
1	-*	1	2// Т ° ( -*12, ^//l	^	9)
’’ / / _/2
-*12 //12	-*ic//l2
г4"
[	(4.180)

Таблица 4.126
bij в линеаризированных уравнениях бокового возмущенного
ения J1A
параметра движения j
Ь 15 = 0
1 /сек*
^18 =
Mv
х 1
\/сек2
^19 =
*11
1/кг*м2
Ь26 — 0
^27 = ‘
м«
У11
\JceK2
К”
27 '
1/11
\\сек
Ь2& = 0
^29 = ‘
1/и
1//С2-Л£2
go tosh
Vqcos Gq
1 /сек
&36 — 0
p37 :
<•
fflQVQ cos 0O
1 /сек
b-R = 0
^39 =
1
+
/
714,
Ми
I I ~—I2	"*»И>
*1 2 У 12	*	1	2// 1 2
где
*12 У12	Х\чУ \l
К „
■jr.A,. — -£Li£li<’u>2 —с»2 )4- —
"tl2 i'12	f	V	Я	i	о *12/ *	/	’
*12
т=-!Асек (®, h, Яд),
0;	ш	№	_{Д1£»П/Ш2	2
*12	/	•Г’2	^‘2	/	1-	0,2	Jrla
г,2	2г,,
%ХП=%„ cos a cos ? — U)yi2 sin a cos ?-{-(и.г12 sin? — a’sin?;
^пу,, —Чг,, sina	cos a —?;
= — «o^.cosasin^ + M^, sin a sin? -f-
+ ^12c°s? — a cos ?:
171 qV 0cos6o
сек/кг*м
(4.180)
(4.181)
(4. 182)
203

Кинематические соотношения для правой системы Т116:
\ = v [cos ф cos ft cos a cos р — sin а cos 3 (sin ф sin у —
— cos ф sin ft cos y) -\- sinp (sin ф cos y + cos ф sin ft sin y)1;
Ц = v (sin ft cos a cos p — cos ft cos y sin a cos p —
— cos ft sin y sin p);
t = v [ — sin ф cos ft cos a cos p — sin a cos p (cos ф sin y-{-
-|- sin ф sin ft cos y) -г s^n P (cos Ф cos Y “ s^n s^n ^ s*n Y')]«
Ф = (^n cos Y — 0)*I2 sin y) sec ft;
^ = 0Vi2 sin Y + “^12 cosy;
Y =	, - К,, cos у — «>*., sin у) tg 0.
11 = h;
sin 0=(cos a sin & — sin a cos & cos y) cos £—cos & sin у sin?.
(4.183)
(4. 184)
(4. 185)
Совокупность уравнений (4.179)—(4.185) образует замкну¬
тую систему, если известны законы изменения положения орга¬
нов управления 6в(0> М0> бн(0> модуль вектора тяги P(t) или
режим работы двигателя пл, а также угол фр.
Уравнения движения центра масс (4. 179) можно записать
в другой форме:
mv = Р cos р cos (а 4- ур) — Q cos р -(- Z sinp — mg sin 0;
mva=mv( — «>,„ cosatgP + Шу,, sin a tg ? + №.*,,) —
— P sin (a -)- cpp) sec ? -j-
-j- mg (sin a sin & -f cos a cos & cosy) sec? — Y sec?;	} (4.186)
mv$=mv (co*i2 sin a -f- <oPl 2 cos a) — P sin p cos (a -f- yp) -(-
-f- mg (sin p cos a sin & — sin a cos & cos у sin p -|-
-)-cos pcos & siny)-)-Z cos p-j-Q sin p.
Частные случаи.
1.	Если углы (a + фр), р, у, •& малы (sin а^а, cos 1, sin р = р,
cos р~1 и т. д.) и Iх12У11= 0, то уравнения (4. 179) — (4. 185) прини¬
мают вид:
mv = P—Q— mg(b — a);
mva = mv (— 2p + coZi,) — P (a -j- yp) + mg — Y;
m-yp = mv (о)д-, ,a +	—	Яр	-f	mgy -f Z -f Qp.
(4. 187)
204

^ U\4	^	zi	*>
СО r =	   0).,	CO,
ЛГ 1 О	•	I/	10^1
M
■X 1 2
*x '
л 1 о
>z ~>x
шУч=—7	  0).v,	“z12
Ум,
M
У12 .
/
Ун
М9
I *Г12Г,.
о), =— 	—	(юг	со,.	-А
Z i 2	г	“'12	У	\	2	I	г
™ = Р'сек*
ri = /z = TJ(fr — a);
P = ^ (cos^ + S sin^);
C = tj (— sin ф + З cos ф).
^“(0!/i2V “гсо212;
У 1 2
(4.188)
(4.189)
(4. 190)
(4.191)
2.	Если углы a, |3 малы (sin a —a, cosa~l и т. д.), ^х,2угл—0,
фР = 0, скорость полета v = const, коэффициенты сил су, сг и мо¬
ментов тх, ту, mz разложены в ряды Тейлора с точностью до
членов второго порядка (см. гл. 5), то уравнения движения
(4. 179) — (4. 185) принимают вид:
a — я34а — соZi2 — — (cos у cos & -f « sin &)-f faXlt = 0;
f* — ^34 Pcos eo — °V,2 “ — (sin у cos » -f 3 sin &) — aco^ = 0.
n ^ll0^] »	^19(0M, „	'^17^И	=r	0*
(4. 192)
/12wyi
14'J	^17	H	”l8	э	:
*>ti
У 12
— ^22°Vii — ^24^ — ^2l“jr,2	^27^h	—	Ф
wz12 й22сог12 #24® a2a\
qSbA = 0.
(4. 193)
^=(“//1,cos У~tozls siny)sec &;
0 = wi/,jsin'Y + ^12cosY;
Y — 0)-f,2 — (№|/,г cos \ — («Zl2 sin Y)tg
(4. 194)
Значения коэффициентов a,j, 6ij приведены в табл. 4.116
и 4. 126.
205

3. Если углы а, (3, у малы (sin a —a, cos а— 1 и т. д.), произве¬
дения (За)х12 и уа)У12 также малы ((3a)Xl2 —0, усоУ12 — 0), то из систе¬
мы уравнений (4.179) — (4. 185) выделяются уравнения продоль¬
ного движения:
а — а34а — uZi2 — (cos 0-(-а sin fr) = 0.	(4. 195)
т7
— «22«z,2 —а24а— а258в	-+±°-qSbA = 0.	(4. 196)
Z12
«=<»*,.	(4.197)
4. Если углы а, р, у, 0 малы (sina^a, cosa^l и т. д.),
произведения аш*1а, рю*,,, уо)^12 и #(о^1а также малы (acoXjo«0,
SVr12~0 и т- Д-)> то из системы уравнений (4. 179) —(4. 185) вы¬
деляются уравнения бокового движения:
р — ^34Pcos0o—«V.. — — Y=0.	(4.198)
^0
ш^12	*12^1,	^14?	^17^н	^18^э~0;	|	^
0J^, 3 — ^22сог/12	^24^ — ^21^12 — ^27^'н = ^*	^
0 = а) • 1
^’2	(4.200)
Y= <*>*„. J
Значения коэффициентов Ьц приведены в табл. 4.116
и 4. 126.
4. 5.7. Уравнения движения в ЛА-центрической
прямоугольной горизонтальной ориентированной (земной)
системе координат Oxgygzg (Cl 18)
ЛА рассматривается как твердое тело переменной массы,
а)	Инерциальная система отсчета — геоцентрическая прямо¬
угольная экваториальная система координат Ox'y'z' (П214).
Движение центра масс рассматривается относительно гео¬
центрической сферической экваториальной-II системы координат
ОгХф' (П223); угловое положение JIA определяется углами Эй¬
лера ф, Ф, у между связанной системой С111 и земной системой
С118 (см. гл. 3, табл. 3. 13).
206

Уравнения движения центра масс записываются в земной си¬
стеме координат OxgijgZg (Cl 18), а уравнения движения относи¬
тельно центра масс (фр = 0) —в связанной системе координат
OxnynZn (С111):
т v
WygCOs 0 sin фс
*3+*
= Р COS &COS:6-[-
4- Y [sin a cos & cos ф — cos a (sin & cos ф cos у —
— sin ф sin y] — Q [sin a (sin b cos ф cos у — sin ф sin y)+
-f cos a cos & cos ф\ + Z (cos ф sin у sin ft+sin ф cos \)—
— 2trn»3vz sin cp'—m (P3 -f- h) to2 sin cp' cos cp';
/72
, V CCS 0 /	,	,	•	, \1
J ( % cos Лс + vXg sin Фс) I =
,„,=psind-mAr+
-[-У (sina sin i>-]-cosacos cos y)-f Q(sinacos cos y —
— cos a sin b) — Z cos b sin у 4- 2mu)3vz cos cp' -}-
~Tm (/?3 + A) шз COS2 cp';
772
Я
cos 0 cos 4
*3+‘
— ЯзтфсозО-!"
4- Y [ — sin a cos b sin ф -J- cos a (cos ф4т у -j-
-f sin b sin ф cos y)] -f Q [sin a (cos ф sin у -f
-f sin b sin ф cos y) -f cos a cos b sin ф] + Z (cos ф cos у —
\ (4.201)
— sin 0 sin ф sin y)4.2ma>3 sin cp' — vy cos cp').
(4402)
Xr,1 (t0 -^11 + ^KP ) + (/г,, — I у,,)	,	4- U)Kp^i 1) X
^ (°4, 4" (MKP -?i i) =	15
I У11 (°Vm "T" ^Kpf/u) 4" (^11	7 *it) О0*,, "“Ь^крлг,,) X
X (0)-гм H“a)KpzM)=
I zlxQ*)Zll -j- 0JKpz,,) 4" (^11 Ix11)(pxll 4"wKpjfM) X
^ (°4.i +a)KPy11) = MZll9
(4. 203)
207

где
KPjr,,=]фн К.. sin Y + ®*..cos Y) cos ft 4-
4- (1)3 (sin cp' sin b + cos ?7 cos ^ cos Ф);
= — -R^fh (Vx" cos & sin Y + vsin a) +
Kp?/
4- co3 [sin cp' cos & cos y -f-
4- cos cp' (sin ф sin y — sin & cos ф cos y)];
"ip*., =	sln & - ®xMcos & cos y)—a3 [sin cp'
X cos & sin у — cos cp'(s’n Ф cos y — sin & cos ф cos y)].
(4.204)
,vXll = 'nrfi.cos&cos&-f_'rVfi-sin^ — vg sin tb cos &;
<Vyll = vx (sin d> siny — cos^sin&cosYH-T'p cos&cosy +
g	g
4~ vzg (cos Ф sln Y + sin Ф sin ^ cos y);
*vZxx = vXg (sin ф cos y + cos ф sin s’n y) — vVg cos & sin y +
4~ vzg (cos Ф cos Y ~ s^n Ф s^n ^ sm y)-
(4. 205)
v
= VVx +vl +vl •
v g yg g
(4.206)
Кинематические соотношения можно записать в следующей
форме:
Ф = К,. cos Y — «X. sin у) sec &;
siny+<o*„ cosy;
Y=“x7 — Km cos Y — ®z,. Sin y) tg b.
(4.207)
r=V;
У«•»
r
V7.
*g
r COS ©'
(4. 208)
208

Л = г-/?3;
V
cos 6 sin 6 sin V — cos у (sin ft cos fl cos Ф — sin 6 cos &)
cos & cos 0 cos 6 + sin & sin 6
(4. 209)
tga =
sin$ = cos 6 sin^ cos y + sin Y (sin O'cos 0 cos ф — sin 0 cos &). j
Совокупность уравнений (4.201) — (4.209) образует замкну¬
тую систему, если известны законы изменения положений орга¬
нов управления бв(/), М0> бп(0» модуль вектора тяги P(t)
(режим работы двигателя пд).
б)	Инерциальная система отсчета—геоцентрическая сфери¬
ческая экваториальная-II система координат г, X, q/ (П223).
Движение центра масс JIA рассматривается относительно
этой же системы координат и соответствует полету над невра-
щающейся сферической Землей.
Уравнения движения центра масс и относительно центра
масс ЛА в системах С118 и С111 можно получить из уравнений
(4.201) — (4.206), полагая со3 =0:
(VVy	\
	—	cos	б	sin	фг|	=	Я	cos	8	cos	ф	4-
х* Лз + Л	7
-|-Y [sin a cos 8 cos 6 — cos a (sin 8 cos ф cos у —
— sin ф sin у)] — Q [sin a (sin 8 cos ф cos у — sin ф sin y) -f-
-f- cos a cos 8 cos ф] -f Z(cos ф sin у sin 8 sin ф cos y)\
-tng-\-Y [sin a sin 8-[-cos a cos 8 cos y] -f"
-)- Q [sin a cos 8 cos у — cos a sin 8] — Zcos 8 sin y;
(VVyg	\
v7	cos	0	cos	I	=	— P sin ф cos 8 -j-
z* Rs + h	J
-f- Y [ — sin a cos 8 sin ф -f cos a (cos ф sin у -f-
-J- sin&sh^cos y)] + Q [sin a (cos ф sin у -f- sin 8 sin ф cos y) -f
-{- cos a cos 8 sin ф] Z(cos ф cos у — sin 8 sin ф sin y)9 j
(4.210)
™ = — tW
(4.211)
209

Агм («>*,, +W|([) jr„)+ (fz,,	/(/,,)	(<»!/,,	+ №|<p (/,,) (“z,, +
+ <«кр г,,) = -/И jr,,;
Л/ll (“l/.l + №Wr/,,) + (-^,1 _О»»*,, +№кр.г,,) («7,, -j-
+шкр 2,,) = ^,,;
^ zl\ (U)Zll “h^Kpz,,)-)- (/(/,, Лг„) ((0Jr,, -Ь^кр-Г,,) (UVll 4“
+ шкр «/,,) = MZll,
(4.212)
где
икр X1
R3 + h
1
UKp у и ■
^кр 2:- - —■
1
(vyil sin	cos Y) sin 8;
(^„ cos &sin y + ^zm sin 8);
R3 + h
{vyi x sin 8 — vXl, cos 8 sin y).
(4.213)
^Xg cos ф cos 8 -(- sin 8 — sin 6 cos 8;
vy* i — vxg (sin Ф sln Y — cos Ф sin ^ cos Y) + vyg cos ^ cos Y'
+ vzg (cos Ф sin у + sin 6 sin 8 cos y);
= ^^(sin ^cos y + cos 6 sin 8 sin y) — ^ cos 8 sin y
-\-vz (cos 6cosy —sin^sin siny).
(4.214)
_L
V=V Vfg + vlg + V2*
(4.215)
Уравнения (4.207) — (4.209) сохраняются,
в)	Инерциальная система отсчета — геотопическая прямо¬
угольная горизонтальная ориентированная система координат
O&lE (Т116).
Движение центра масс JIA рассматривается относительно
этой же системы координат и соответствует полету над плоской
невращающейсй Землей.
Уравнения движения центра масс и относительно центра
масс JIA в системах координат С118 и С111 могут быть получены
210

из уравнений (4. 201) —(4, 206) при со3 =0, i?3 — оо; они имеют
вид:
mv^ — P cos ft cos ^-\-Y [sina cos ft cos ф -j-
-f cos a (sin ф sin у — sin 0 cos ф cos y)] —
— Q[sina(sinftcos ^cos у — sin ф sin у) + cos a cos & cos ф] -f-
-j- Z(cos ф sin у sin ft -f sin ф cos y);
mvy<r = P sin ft — mg -[- Y [sin a sin ftcos a cos ^ cos Y] ~r
-j- Q [sin a cos ft cos у — cos a sin ft] — Zcos ft sin y;
mvz^ — — Я sin ф cos ft -f- К [ — sin a, cos ft sin ф-f-
-rcos a (cos ф sin у -j- sin ft sin ф cos y)] + Q [sina(cos6siny»|-
-f sin ft sin ф cos y) -j- cos a cos ft sin ф\-j-Z(cos ф cos у —
— sinftsin^siny).
“Реек-
■ (4.216)
(4.217)
+ V *,i — A/h)C01/iiW2ii =MXll\
fyii0)yii	f zlx)	= Myil; ’	(4.218)
Кинематические соотношения для правой системы Т116:
Ф = (со!/11 cos У~ °^и sin у) sec ft;
^ = coi/.i sin Y + ^^n cos Y;	(4.219)
Y = <»*,, — («>yi, cos y — (o2ix sin y) tg ft.
K = Vr
V~-
(4.220)
g ' Jg ' g
sin 3 = cos 0 sin 6 cos у -f sin у (sin & cos 0 cos 6 — sin ti cos &);
tga:
ros 0 sin ф sin у — cos V (sin ft cos 0 cos J/ — sin В cos ft)
cos ft cos 0 cos 6 -j- sin ft sin 0
[ (4.221)
• C VyK
sin 0= 	—
211

Частные случаи.
1.	Движение JIA в вертикальной плоскости. Уравнения дви¬
жения (4.216) — (4.221) инвариантны относительно вращении
системы координат вокруг оси От], поэтому движение в лю¬
бой вертикальной плоскости, заданной в системе	можно
считать эквивалентным движению в плоскости 10г\, что соответ¬
ствует допущению vz = 0, ^ = 0, у = 0.
В этих предположениях уравнения движения центра масс
и кинематические соотношения (фр = 0) имеют вид:
(л ооо\
2.	Движение JIA в вертикальной плоскости при отсутствии
аэродинамических сил.
Если Q = y=Z = 0, то, вводя угол фр^О, уравнения движения
центра масс и кинематические соотношения (4.222) — (4.226)
можно привести к виду
4.6. УРАВНЕНИЯ ДВИЖЕНИЯ ЛА ПРИ НАЛИЧИИ ВЕТРА
При составлении уравнений движения JIA, совершающего
полет при наличии ветра, следует учитывать, что
1)	силы инерции определяются путевой скоростью v (скорость
полета относительно планеты), а аэродинамические силы и мо-
(4.222)
(4.223)
(4.224)
(4.225)
(4.226)
m£ — Pcos(& + ?p);
тЦ = Р sin (ft-f сря) — mg.
(4.227)
“Реек
(4.228)
212

менты зависят от величины воздушной скорости иВОзд (равной
векторной сумме путевой скорости v и скорости ветра и);
2) имеются две поточные системы координат Oxnynzu (Cl 16),
оси Охп которых совпадают с направлением вектора либо путе¬
вой v, либо воздушной скорости ^возд. В первом случае угловая
ориентация этой системы координат относительно связанной си¬
стемы координат С112 определяется углами атаки ап и скольже¬
ния рп. Во втором случае угловая ориентация относительно си¬
стемы координат С112 определяется углами атаки а и скольже¬
ния Р;
3) матрицей преобразования между поточной С116 и связан¬
ной С112 системами координат, приведенной в табл. 3.23, можно
пользоваться для обеих приведенных в п. 2 поточных систем
координат, подставляя в нее либо углы а, р, либо углы
(Хш Рп-
4. 6.1. Уравнения движения в ЛА-центрической
прямоугольной вертикально-симметрической связанной
системе координат Ох\2У\2^\2
(С112)
JIA рассматривается как твердое тело переменной массы, пло¬
скость Х\20у\2—плоскость инерционно-массовой симметрии. На
ЛА действуют аэродинамические силы и сила тяги, вектор кото¬
рой находится в плоскости симметрии и проходит через центр
масс. В качестве инерциальной системы отсчета принята геото-
пическая прямоугольная горизонтальная ориентированная-II си¬
стема координат 0£г]£ (Т116). Скорость ветра и задана проек-
ЦИЯМИ Uxg = UXg (xg, yg, Zg, t), Uyg=Uyg (Xg, yg, Zg, t), uZg =
= иг (xg, yg, Zg, t) на оси ЛА-центрической прямоугольной гори¬
зонтальной ориентированной (земной) Oxgygzg (Cl 18) системы
координат.
Уравнения движения
cx„sQv\
■*12	^	возя
+	=	^	coscpp-
— G sin &;
+	—	vx,tvg„)	=	p	sincpp-|-	_	[	(4.229)
— G COSy COS &;
I
J = —^	+	G	sin	Y	COS	0.
213

■IУ11°Уи ~Ь Ix, »12 (C0.*u	Ш01аЮ2,г)	"Ь	(Л*,.	^Z15)C
= ffl«
^ппз4
-Ka^Z. ,+ /*,.jr„ ("^]2 — "*,„) +K,a — K) “ХЛ,-
= m.
Sqv hA
(4.230)
m=—^сек(р. ^возд,1!).	(4.231)
Кинематические соотношения для правой системы Т116:
ф = sec ft (о^12 cos у — со*i2 sin y);
& = coj,12 sin y + co2i2 cos y;	(4.232)
Y = <»*, 2 — tg & (o)yi 2 cos y — соZi2 s in y).
5 = vx =vXl2 cos cj>cos$+^12 (sin^siny—cos фзш ft cosy) 4“
-\-vZj2 (sin ф cos y + cos ф sin & sin y);
r\ = 'Vp =vXli sin ft 4"^,a cos ftcos y —^z12cos 8 sinY;	\	(4.233)
i = evZg— ~^i2 sin ф cos b-\~Vy12(cos ^sinY+	|
-\- sin ф sin ft cos y) + Vz12 (cos ф cos y — sin ф sin ft sin y);	j
uXi2 = #	cos ф cos ft 4- sin ft — uZg sin ф cos ft;
uyi* — uxg (sin Ф sin Y — cos ф sin ft cos y) t uyg cos ft cos Y4~
4-и* (cos ф8ту4-8*пФ8*п®С08 Y);	•	(4.234)
uZl2 = ux (sin ф cos y 4“cos Ф sin ft sin y) — Uyg cos ft sin y +
4- uZg (cos ф cos y — sin ф sin ft sin y);
*.«. . = К1 + ^1. + <. + И*„ + <. + «
“2 («*„«*,,+г^мИ*11 + ®г1,Иг1,)]Г;
1еа=-^-~ац”.:	}	(4.235)
sin й :
^возд

Частные случаи:
1.	Уравнения продольного движения. Если
■Vzl^=^x„ = ^ul,=y = Z= 0,	4-=%	= const, KzI2 = 0
(вектор скорости ветра не имеет боковых составляющих относи¬
тельно плоскости #120*12), то уравнения движения имеют вид
т
т
ех,
■ G sin i
■G cos 9;
[ (4.236)
I Z. „9	 I	Z, S'^2
mz,Mvlo3KbA
W	^сек	(^*>	*^возд)-
Кинематические уравнения для правой системы Т116:
(4.237)
(4.238)
i — 'Vxg—^,, cos 'I'oCos 9 — vUtl cos 60 sin 9;
i\ = Vy	sin	& + %12cos 9;
C=Vz = — vXt 2 sin % cos 9 4	,	sin	%	sin	9;
(4.239)
«*,,, = и ^ cos % cos &-|-H^sin9 —«..^sindioCOS 9;
uVl„ = — cos ф0 sin 9 4- cos 9 4- uZg sin 60 sin 9;
(4.240)
tga = ■
(4.241)
2.	Уравнения движения при постоянной скорости ветра. При
постоянной скорости ветра w = const полная система уравнений
движения несколько упрощается за счет упрощения конечных
кинематических соотношений, если уравнения движения запи*
215*

сать не относительно путевой скорости v, а относительно воз¬
душной скорости vB03JX:
т
(^-02 ВОЗД “Ь ШУ\В03Д Си212'У(/д2 возд) Р COS ^р
„2
Ч ScwJo»,
■ Gsin&;
2
m (“Off, . „озя +	возд	-	«X,	,®*I2	возд)	=	^	sin	tpp	-j-
2В03Д
с,, ^
■ G COS Y COS 9;
2
с „ Soi/L
(--> i	*	•	\	Z,	о^^^НОЗ	1
^12 ВОЗД + 0j-^12^12 ВОЗД 0412^12ВОЗД)	~
-|-G sin Y COS 0.
^1A1! — IXl,y„ («Ч/12 — “x, ,«>*„) +(/г>,-1у„)
-m SQV™*1 ■
-Юх,,	2
7 </, Л. 2 + Ar, ^ 2 fax, 2 — «Vl “ 3, .) + ( At, 2 — I 3, 2) «>3,2wx, 2
Se»So3^
= ffl,
■in,,	Y
Iz, 2OJ*i2 + ^ X12y12 (“Lj — 4) + ( A/i2 — /xj МХ12Ш(/12 —
_ _ 5е^0зд*д
— mz,t »	•
Ш	Р'сек	(P>	^i>	^возд)-
Кинематические уравнения:
•yB03.= 1f v2	+т)2	-4-г/
^возд у Х\2 возд I г/12 возд I
,2
zl2 возд »
tga =
slnp= Vz'^-°±±-
(4.242)
(4.243)
(4.244)
(4.245)
'Соотношения (4.232) — (4.234) сохраняются.
216

4.	6. 2. Уравнения движения в JIA-центрической прямоугольной
вертикально-симметрической скоростной (поточной)
системе координат Oxuynzu(С116) в случае, когда ось Охи
совпадает с вектором путевой скорости
ЛА рассматривается как твердое тело переменной массы,
Х\Оу\ — плоскость его симметрии. На ЛА действует аэродина¬
мическая сила и сила тяги, вектор которой находится в плоско¬
сти симметрии и проходит через центр масс. В качестве инер-
циальной системы отсчета принята геотопическая прямоугольная
горизонтальная ориентированная-II система координат Oxuyuzu
(Т116). Уравнения моментов рассматриваются относительно свя¬
занной системы координат Ох^Уп^п (С 112).
Скорость ветра и задана проекциями их = их (xg,ug,zgyt\
иу =иу {xg,yg,zgJ)iaz =az (xg^yg'zgJ) на оси ЛА-центрической
прямоугольной горизонтальной ориентированной (земной)
Oxgygzg (Cl 18) системы координат.
Уравнения движения
mv = — [сх cos Рп cos (ап — a) -j- су cos Рп sin (ап — а) —
- Сг Sin р„] X   ь Р COS Рп cos (ал + ?р) -
— G (sin ft cos ап cos рп — cos у cos ft sin ап cos рп —
— sin у cos ft sin p„);
®п =	— К.* cos ап - <оУ1, sin ап)tg 6П + [сх sin (ап - а)
+ (sin ft sinап-[-cosy cos &cosan)——
V COS pn ’
К = sin an -f (O„ cos an -|	—	\\cz cos 3n -f
тч) 1L
(4.246)
Sqv2
+ sin pn cos (a„ - a) + cy sin 3n sin (an - a)]	1
— P sin (3n cos (an -f ?P) + G (sin у cos 0 cos Pn -f-
-f sin & cos an sin pn — cos у cos & sin an sin Sn)J .
217

СцУлг |,г/|.	ЫХ|,Ы;/,.	(О,.	^XtJ	у,„	4~	Ar,-У,»)
/	/	—/2	~	I I —I2	’	'
-*12 ffn	-*12</ll	-*12	i/l	2	-*12</l2
1
C.2
2
“-*12U)I/l2 (^</12	4r,.)]-
™z,	/2	2	\
*-*i2j/i2 Kn ш-*12;—
m=— 1*сек(Л т1. ®в>зд)-
Кинематические уравнения для правой системы Т116:
ф = sec & (ojy, s cos Y — <*>г,a Sin y);
^ = тг/,2 sinY + “z,2 cosy;
y = ^ls — K,2 cosy — u)Zi2 siny).tg&. j
vXll = v cos an cos £in;
г>„,,= — x»sinan cos 3n;
^„^•usinfJ,,.
Ux,2 — Ux COS COS & -j- sin & — Uz^ sin tp cos &;	}
fii/i„ = Mjr^(sin(isiny — cos^sin&cosy)-|-M^cos frcos y-f- j
-f-uz (cos фsiny-(-sintbsin & cosy);	}
^	I
W2J2 = w* (sin tbcos y-)-cos <b sin 0- sin y) — tf^cos ^ sin y +
-(-uz (cos ^ cos y — sin 6 sin ft sin y).
®возд= iVl1, + Vll a + ®L + a*.. + “y..^
1_
— 2(VXl „«.*, , + Vy, ,UUl 4®:,.»,,,]!;
tga =
(4.247)
(4.248)
(4.249)
(4.250)
(4.251)
(4.252)

£ =г»^ ==‘W^12cos<jicos& + ‘WI/lI(siniJ»sinY — cos4»sin^cosv) +
(sinJjcosY + cos^sin&sinY);
r\ = vy =vXlt sin ft-j-'Uj/,, cosftcos y — vz,. cos ^siny; f (4.253)
&	t
i=.-vZg— — Vx„ sinФ cos &-{- ‘iV,!(cos<|>sinY +
-)- sin ф sin & cos y) -j- vZit (cos <b cos y — sin di sin & sin y).
Частиыйслучай. Уравнения продольного движения. При
рп=0, y = °. о)х,2 = Юу,.=0, тр = ф0=const уравнения (4.246) —
(4.253) можно записать в виде
Ч
mv ■= Р cos (с?р-f ап) — [сх cos (а — ап) — су sin (а - ап)] X
’А.031 — G sin 0;
X-
Sq<
2
mvQ = Р sin (<рР4- ап) -\-[сх sin (а -aB) + cv cos 'а -ап)]Х I (42544
■ — G cos б.
X
I г1а^—I zlswZi. —mz,1
Se«Bo злЬА
% = V COS 6 sin ф0;
*] = v sin 6;
C= — v cos 6 cos <!>0.
(4.255)
а =» —6.
®возд = ]/"V2 + uxg+ Uyg+UZg - 2v (uXg[COS б X Uyg sin 6); I
^g(a-«n) =
iiu cos 0 — a v- sin 0
Jg	2£
v —(uXg cos 0 + uug sin 0)
\ (4.256)
4.	6.3. Уравнения движения в JIA-центрической прямоугольной
вертикально-симметрической скоростной (поточной)
системе координат Oxuynzп (СПб) в случае, когда ось Охи
совпадает с вектором воздушной скорости
JIA рассматривается как твердое тело переменной массы. На
JIA действует аэродинамическая сила и сила тяги, вектор кото¬
рой находится в плоскости симметрии х^Оу^ и проходит через
центр масс. В качестве инерциальной системы отсчета принята
геотопическая прямоугольная горизонтальная ориентирован¬
ная-II система координат Ogrjt (Т116). Уравнения вращатель-
219

ного движения рассматриваются относительно связанной си¬
стемы координат С112.
Скорость ветра и задана проекциями uXg = uXg (xg, yg% zgy t);
liyg=uVg(xS’ yg> ZS’ 0; uzg = uZg(xg, yg, Zg, t) на оси JIA-дентриче-
ской прямоугольной горизонтальной ориентированной (земной)
С118 системы координат Oxgygzg.
Уравнения движения:
SQV*
-Pcospcos(a-[-
^возд + (Cjc cos Р - sill p)
+ ¥p) ~b G (sln ^ cos a cos P — cos У cos & s*n a cos P “
— sinу cos ft sin p) = r-m[ux^(cos<bcos ft cos a cos S —
— sin ф sin у sin a cos 8 -j- cos ф sin ft cos у sin a cos p -|-
-f- sin ф cos у sin p -f- cos ф sin ft sin у sin p) -j-
-f uy (sin ft cos a cos p — cos ft cos у sin a cos 3 —
— cos ft sin у sin p) — uz (sin ф sin ft cos у sin a cos 43 —
— cos ф cos у sin p -|- sin ф cos ft cos a cos p -f-
-4-cos ф sin у sin a cos p -{-sin ф sin ft sin у sin p)];
— mvBo3A [acosp —a)Zlscos? + (coXllcosa —^„sin a) X
•Psin(a-|-'pP)4-G(sm&sina-
X sin?]-
-f- cos у cos 8 cos a)= — m [K^(sinacos<l)Cos8-{-
-(- cos a sin ф sin у — cos a cos ф sin & cos y) -f-
-j- iiyg(sin a sin 8 -|- cos acos8cosy)-f-
-{-кг (cos a cos ф sin у-{-cos a sin 4 cos 8 cos у —
— sin a sin ф cos 8)];
mvвозд [P — Km sin a+“0M cos a)] — (cz cos 3 4- cx sin ft) X
X
Sq<
■ P sin (3 cos (a-f- Tp) — G (sin у cos 8- cos ? -J-
—J- sin 0 cos a sin ? — cos у cos 8 sin a sin ?) =
= — m [и (sin i|> cos у sec ? -{- cos ф sin 8 sin у sec 3 —
— cos 4 cos 8 cos a sin ?-{- sin ф sin у sin a sin ? —
— sinЛ cos у sin ptg ? — cos ф sin 8 cosy sin a sin ? —
— cos ф sin 8 sin у sin ? tg ?) — иу^ (cos 8 sin у sec ? -j-
-{- sin $ cos a sin ? — cos a cos у sin a sin 3 —
(4.257)
220

— cos 9 sin у sin rp tg p)-f ^(cos ^cos у sec p —
— sin ф sin & sin y sec В-(-sin ф cos 9 cos a sin p-j-
-\- cos ф sin y sin a sin p-(- sin ф sin & cos у sin a sin p —
— cos ф cos у sin p tgp -j- sin ф sin 9 sin у sin p tg P)].
II —I2
X\4 У12	-^1	2l/l 2
X	+»»„»«„	-	/>.л„+д ) -
^ Z i o^JT j 2 (/* j 2	|	^ У I 2	^^12)	^-^12^/12]^
1
II —I2
■^12 i/ 1 2	■%!	.У	\4
X
"&'l2W212
^ X1 2 ~l~ ^ У\2	^12,
i/l 2
5с^п„йл
m
2^12
/jr. 11. foj2 	(02	)
Al ^12 V у 14	X)2)
/
"* = -^сек(Я, Л, ®вэзд)-
Кинематические уравнения для правой системы Т116:
<i = sec cos у —сог1а siny);
^ = w</12siny + «j2iacosY;
y = 0Jjr12 - к., COS у - 0J2,2 siny) tg &.
: возд == ®возд cos a cos jt;
■^i/l 2 В03Д
Zi2 возд
= — ^возд sina COS p;
= DB.^sinff.
UXl, — llXg cos il) cos t> -j- llyg sin & — uZg sin 6 cos &;
u{/i' = ux^ (sin ф sin у — cos ф sin 9 cos y) -f-
-f cos 9 cos Y + ^(cos Ф sin y +sin ф sin 9 cos y);
иZl 2 === uXg(sin ф cos y + cos ф sin 9 sin y) —
— iiy cos 9 sin y -f uz (cos ф cos y — sin ф sin 9 sin y).
(4.257)
(4.258)
(4.259)
(4.260)
(4.261)
(4.262)

®J(ll — '°Xl, 0-ЗЛ+ Wjr,,;
'Vv^ — VU^B зд + %.г;
" ® *1 2 возд ~)“ ^ Zls.
£=	5	cos	ф	cos	&-f-	sin <]> sin у —
— cos л sin & cos y) + ®г„ (sin tb cos у -{- cos 6 sin & sin y);
i\ = Vy =vXli sin & + cos & cosy — vZl2 cos ftsiny;
C — vz^= —vx,s sin <j) cos	(cos	(J»	sin	y-j-
-{- sin tj» sin & cos y) vz, 2 (cos Ф cos у •
_ C> 1 T1 fll pin
(4.263)
(4.264)
ЛИТЕРАТУРА
1. Аппазов P. Ф., и др., Баллистика управляемых ракет дальнего дей¬
ствия, изд-во «Наука», 1966.
2. Валеев К. Г., Уравнения движения спутника Земли с учетом сопро¬
тивления атмосферы, ПММ, 29, 1965, № 6.
3. Вед ров В. С., Динамическая устойчивость самолета, Оборонгиз, 1938-
4. Г а н т м а х е р Ф. Р., Л е в и и Л. М., Теория полета неуправляемых ра¬
кет, Физматгиз, 1959.
5. Иродов Р. Д., Расчет перегрузок и углов крена самолета при движе¬
нии его по пространственной траектории, Оборонгиз, 1957.
6. Кал и н и н В. М., Уравнения движения искусственного спутника Земли,
сб. «Искусственные спутники Земли», вып. 16, АН СССР, 1963.
7. Карагсдин В. М., Теоретические основы механики тела переменного-
состава, Оборонгиз, 1963.
8. Космодемьянский А. А., Курс теоретической механики, изд-во
«Просвещение», 1966.
9. Крючков Н. В., Об уравнениях движения и измерении углов пово¬
рота летательного аппарата, движущегося вблизи вертикальной плоскости,
Инженерный журнал, 5, 1965, № 2.
10. Кузнецов А. А., Определение начальных условий при старте лета¬
тельного аппарата с подвижной платформы, сб. статей под ред. И. В. Осто-
славского «Исследования по динамике полета», изд-во «Машиностроение», 1965.
11. Лебедев А. А., Ч е р и о б р о в к и н Л. С., Динамика полета беспи¬
лотных летательных аппаратов, Оборонгиз, 1962.
12. Лебедев А. А., О применении метода замороженных коэффициентов
для исследования неустаиовпвшегося движения, Известия ВУЗ, сер. «Авиаци¬
онная техника», № 1, 1958.
13. Литвин-Седой М. 3., Введение в механику управляемого полета,
изд-во «Высшая школа», 1962.
14. Лич Р. Ф., Нематрнчная формулировка преобразования вектора с по¬
мощью углов Эйлера, журн. «Ракетная техника» (русский перев.), 1961, № 6.
15. Лойцянский Л. Г., Лурье А. И., Курс теоретической механики,
ГИТТЛ, 1955.
16. Лурье А. И., Аналитическая механика, Физматгиз, 1961.
17. М а к - К л v р К. Л., Теория инерциальной навигации, изд-во «Наука»,
1964.
18. Ми еле А., Механика полета, т. 1, изд-во «Наука», 1965.
19. Остосл а вский И. В., Аэродинамика самолета, Оборонгиз, 1957.
222

20. О с т о с л а в с к и й И. В., С т р а ж е в а И. В., Динамика полета. Тра¬
ектории летательных аппаратов, Оборонгиз, 1963.
21. О с т о с л а в с к и й И. В., Страж ева И. В., Динамика полета.
Устойчивость и управляемость летательных аппаратов, изд-во «Машинострое¬
ние», 1965.
22. О с т о с л а в с к и й И. В., Страж ев а И. В., О формировании кон¬
тура управления самолетом, Оборонгиз, I960.
23. Свлтодух В. И., Уравнения движения осесимметричной ракеты
в	цилиндрических координатах, Инженерный журнал,	4, 1964,	№	2.
24. Трахтенберг	Г. М., Уравнения движения	самолета с	реактивным
двигателем, Известия ВУЗ, сер. «Авиационная техника», № 4, 1962.
25. Эткин Б., Динамика полета, изд-во «Машиностроение», 1964.
'26. Gibson W. J.,	Convenient equations for projectile	motion	„Amer.
J.	Phys“, 1961, 29, No. 9,	623—626.

Глава 5. СИЛЫ И МОМЕНТЫ,
ДЕЙСТВУЮЩИЕ НА ЛЕТАТЕЛЬНЫЙ АППАРАТ
Основные обозначения
а— скорость звука,
Ьд—характерный размер J1A в продольном движе¬
нии (например, аэродинамическая хорда
крыла),
с к—коэффициент полной аэродинамической силы,
сх—коэффициент силы лобового сопротивления,
Су—коэффициент подъемной силы,
cz—коэффициент боковой силы,
схо—коэффициент силы лобового сопротивления при
нулевых подъемной и боковой силах,
с г/о—коэффициент подъемной силы при нулевом угле
атаки,
Czo— коэффициент боковой силы при нулевом угле
скольжения,
c.vTp—коэффициент сопротивления трения,
схи> cxi§—коэффициенты индуктивного сопротивления,
с*у' суу си’ су’ суу су — частные производные коэффициента подъемной
силы су по параметру, указанному в верхнем
индексе,
в ^
cz, czH —частные производные коэффициента боковой
силы cz по углу скольжения Р и углу отклоне¬
ния руля направления бн соответственно,
сУтах—максимальное значение коэффициента подъем¬
ной силы,
се— удельный расход топлива,
D—диаметр фюзеляжа,
D— отношение удлинения крыла к диаметру фюзе¬
ляжа,
Fтр— сила трения,
Fr— число Фруда,
О—	вес Л А,
g — гравитационное ускорение,
g'—ускорение силы тяжести,
h— высота,
/уд—удельный импульс,
/^,/^,/2—главные моменты инерции относительно осей
Ь системы Oxhykzh (£=1, II, 12	),
Су
К = — — аэродинамическое качество ЛА,
сх
L — длина ЛА или его частей,
224

8	1669
I—характерный размер ЛА в боковом движении
(например, размах крыла),
Д\—число Маха,
^шр—шарнирный момент руля,
Mjk—проекции момента аэродинамических сил на
осп Охи, Оуи, Ozk\ j = x, у, z,
mx— коэффициент момента крена,
ту—коэффициент момента рысканья,
rr.z—коэффициент момента тангажа,
(,) Г и	3 М Т S
т/, ту, тхэ, пгхн, т\, тх , т \ , тх —
частные производные коэффициента момента
крена тх по параметру, указанному в верхнем
индексе,
„О	7.'».	70	J3(0	3 О
т х , тх у, т х н, /77 г 2, тх в —
вторые частные производные коэффициента мо¬
мента крена тх по	параметрам,	указанным
в верхнем индексе,
со..	<» о о 3 М з“ о
тиу, тгх, и/, т», ту, ту, т£ ,	—
частные производные коэффициента момента
рысканья ту по параметру, указанному в верх¬
нем индексе,
т% ml, /«2М, «;*,	«>, т*-
частные производные	коэффициента	момента
тангажа mz по параметру, указанному в верх¬
нем индексе,
пь—эффективность руля высоты,
пя— число оборотов двигателя,
Р—сила тяги,
Q— сила лобового сопротивления,
Qt/2
q —	—	скоростной	напор,
Рз—радиус Земли,
Re—число Рейнольдса,
Ра—полная аэродинамическая сила,
S—характерная площадь ЛА (например, площадь
крыльев),
St—число Струхаля,
V— скорость полета относительно набегающего по¬
тока ^ воздушная скорость),
X— проекция аэродинамической силы па ось Ох,
Y — подъемная сила,
Z— боковая сила,
хр—абсцисса фокуса в системе координат С112,
хл— абсцисса центра давления аэродинамических
сил в системе координат С112,
-*ц.м— абсцисса центра масс ЛА в системе координат
С112,
а—угол атаки,
аба л» ^в.бал — балансировочные значения углов атаки и руля
высоты,
225

3—угол скольжения,
у — угол крена,
е— скос потока,
е7, е° — производные от скоса потока е по углу атаки
а и углу отклонения руля 6 соответственно,
Л— сужение,
0 — угол наклона траектории,
9 — угол тангажа,
&н—угол отклонения органа управления (руля на¬
правления) в боковом движении,
Ьэ—угол отклонения органа управления креном
(элерона),
sb(Уст)—угол отклонения органа управления (руля вы¬
соты, стабилизатора) в продольном движении,
Р-— динамическая вязкость,
v—кинематическая вязкость,
Q— плотность атмосферы,
9— географическая широта,
9' — геоцентрическая широта,
¥кр—угол установки крыла,
<рр—угол наклона вектора тяги к строительной оси,
у,— стреловидность оси вращения,
4х*— угол между консолями крыла,
ф—угол курса.
Тст. 9лест— углы отклонения стабилизатора и дестабилиза¬
тора соответственно,
*%' (%Г 0)Л«»	г)—проекции	вскюра	угловой	скорости со на оси
Одд, Oyh. Oz* {k=\, 11, 12) систем СПЗ,
С111, С112,
а)*п>	0)Уп> °Угп	—	проекции	вектора	угловой	скорости
Охи, Оуп,	Ozn системы С116,
со у	—проекции	вектора	угловой	скорости
Ох с, Оу с, Oz с системы С115,
tojj- соу^,	— проекции вектора угловой скорости
Oxg, Oyg, Ozg системы Cl 18.
со3— угловая скорость вращения Земли.
Индексы:	«ф»	— фюзеляж,
«из.кр» — изолированное крыло,
«г.о» — горизонтальное оперение,
«в.о» — вертикальное оперение,
«нос» — носовая часть,
«кр» — крыло,
«кр+ф» — комбинация «крыло+фюзеляж»,
«кор» — корма,
«дест» •- дестабилизатор,
«заб» — заборник.
«X», « + »— схемы летательного аппарата «крест» и «плюс».
5.1. КЛАССИФИКАЦИЯ СИЛ И МОМЕНТОВ
Силы и моменты, действующие на Л А, подразделяются на
внешние и внутренние, на управляющие и возмущающие.
К внешним силам и моментам относятся:
1.	Гравитационные силы и моменты Земли или другого основ¬
ного притягивающего тела.
со на оси
со на оси
со на оси
226

2. Аэродинамические силы и моменты.
3. Силы и моменты от двигательной установки.
4. Кориолисовы силы и моменты, возникающие при относи¬
тельном движении JIA относительно других, не находящихся в со¬
стоянии равномерного прямолинейного движения объектов.
5. Силы и моменты, возникающие в результате взаимодейст¬
вия с поверхностью Земли или иным объектом при старте и по¬
садке (реакции связей).
6. Прочие силы и моменты (аэростатическая сила и момент,
сила и момент солнечного давления, силы и моменты притяже¬
ния других планет солнечной системы и т. д.).
К внутренним силам и моментам относятся:
1. Гироскопические силы и моменты.
2. Кориолисовы силы и моменты, возникающие при относи¬
тельном движении частей ЛА, а также при движении газа или
жидкости по трубопроводам ЛА.
3. Силы и моменты, возникающие вследствие изменения гео¬
метрии масс ЛА.
4. Силы и моменты, обусловленные упругостью конструк¬
ции ЛА.
Внешние и внутренние силы и моменты с точки зрения управ¬
ления полетом можно разделить на управляющие силы и мо¬
менты и возмущающие силы и моменты.
Управляющими силами и моментами называются силы и мо¬
менты, величина и направление которых могут целенаправленно
изменяться при действиях летчика или автоматических устройств.
Управляющая сила, предназначенная для управления или
регулирования модуля скорости полета, называется тангенциаль¬
ной управляющей силой и равна сумме проекций всех управляю¬
щих сил на направление скорости полета.
Управляющая сила, предназначенная для управления или ре¬
гулирования направления движения, называется нормальной
управляющей силой и равна сумме проекций всех управляющих
сил на плоскость, перпендикулярную скорости полета.
Управляющий момент ЛА предназначен для управления или
регулирования его углового положения и равен главному мо¬
менту всех управляющих моментов. Проекции управляющего мо¬
мента на оси ЛА-центрической вертикально-симметрической свя¬
занной системы координат С112 относительно осей Ozi2, OyV2,
Ox 12 называются продольным управляющим моментом, боковым
управляющим моментом, управляющим моментом крена соот¬
ветственно. Управляющие силы и моменты могут быть созданы
с помощью аэродинамических сил, сил от двигательной уста¬
новки, сил реакций связей, гироскопических сил и т. п.
Возмущающими силами и моментами называются силы и мо¬
менты, возникающие независимо от действий летчика или авто¬
матического устройства, управляющего ЛА. К ним относятся
8*
227

силы и моменты, возникающие при порывах ветра, турбулент¬
ности атмосферы, отклонении параметров J1A от расчетных зна¬
чений и т. д.
5 2. СИЛА ТЯЖЕСТИ
5.2.	1. Модели гравитационного поля Земли.
Гравитационное ускорение
Гравитационное ускорение определяется гравитационным по¬
лем Земли. Гравитационное поле Земли является: 1) нецентраль¬
ным п неоднородным из-за несферичности и неравномерного рас¬
пределения масс; 2) нестационарным из-за непрерывного движе-
жения масс Земли, нестабильности атмосферы и т. п.
Гравитационное поле определяется формой Земли и распре¬
делением ее массы.
Используемые термины и определения приведены в табл. 5. 1.
Таблица 5.1
Некоторые определения
Название
Определение
Сила притяжения
Сила, с которой тело притягивается к Земле
или иному притягивающему телу согласно за¬
кону всемирного тяготения
Вес тела G 1
Сила, с которой неподвижное относительно
Земли тело давит на опору вследствие притя¬
жения его к Земле (векторная сумма силы при¬
тяжения и центробежной силы инерции)
Гравитационное уско¬
рение g
Ускорение тела под действием силы притя¬
жения
Ускорение силы тя¬
жести gf
Геометрическая сумма гравитационного уско¬
рения и центробежного ускорения от вращения
притягивающего тела
Географическая вер¬
тикаль
Лищ1я по нормали к поверхности геоида (ре-
ференц-эллипсоида)
Геоцентрическая вер¬
тикаль
Направление вектора гравитационного уско¬
рения (совпадает с направлением к центру
Земли)
228

Продолжение
Название
Определение
Местная вертикаль	Направление по равновесному положению
математического маятника с неподвижной отно¬
сительно притягивающего тела точкой подвеса
П р и м е ч а и и я. 1. Для Земли вектор ускорения силы тяжести
связан с вектором гравитационного ускорения соотношением
g' - g-fw3 X (ю3Хг)#
ггде соз — угловая скорость вращения Земли;
г — геоцентрический радиус-вектор точки.
2. Угол Дер между географической и геоцентрической вертикалями
та поверхности Земли равен
Дер = cp — р' ^ 11' ,5 sin 2ср.
3. Разность между географической и местной вертикалями обычно
■пе^превосходит 2'—3'.
В механике полета используются обычно следующие модели
гравитационного поля Земли.
1.	Эллипсоидальная модель.
Форма Земли — эллипсоид вращения. Гравитационное поле —
нецентральное, однородное, стационарное. Проекции вектора
гравитационного ускорения на оси геоцентрической прямоуголь¬
ной экваториальной системы координат Ox'y'z' (П214) имеют
вид
  _ Vo х'
~	/*3
1+
Yi
_1 ) + Ж (63^--
1 1 г* \	/-4
-42-
3 + -
Sw
Sx ’У
(5.1)
гз
1+	5-^	3	И
,-2	1,-2	/	Г‘\
Ъ ^63 —
Г4
-70-V+15
где
г — ]/^х1 -f-г/' -\-z' ,
Yo = —3,986329 • 104 ж3/сегс2;
Yl =—6,66425- 1010 ж2;
Y2 = 2,5023 • 1021 ж4.
229

Проекции вектора гравитационного ускорения на оси геото-
пической прямоугольной правой горизонтальной ориентирован¬
ной-! I системы координат 0£г|£ (Т116)
где г — расстояние от центра Земли;
а0 = 3,9861564 • 1014ж3/с#/с2;
#2 = 8,7758500- 1024 м5/сек2;
#4= 1,9325000- 1035 м7/сек2.
Модуль ускорения силы тяжести для небольших высот над
поверхностью Земли определяется формулой
g' = 9,78049 • (1 + 0,005288 sin2 cp—0,0000059 sin2 2cp) —
2.	Сферическая модель. Форма Земли — шар. Грави¬
тационное поле — центральное, однородное, стационарное.
Проекции вектора гравитационного ускорения на оси гео¬
центрической сферической экваториальной-П системы коорди¬
нат Or'kср' (П223) имеют вид
где h = r—Rз — высота над поверхностью Земли;
go = 9,80665 м!сек2.
3.	Плоскопараллельная модель. Форма Земли —
плоская. Гравитационное поле — параллельное, однородное, ста¬
ционарное.
Проекции вектора гравитационного ускорения на оси геото-
пической прямоугольной правой горизонтальной произвольной-П
системы координат 0^пг)пСп (Т114) имеют вид
— f-^-sin2<?' — — -^-(2sin2?>' —7sln4?')+. . -1 ;
[ /-4	2	rs	у	‘	.
g,--[^+^(l-3Siny)+5^(3-30S№c' +	(	(52)
-j-35 sin4 o')-f-. . .];
£e = 0,
—0,0003086 h (где h в м).
(5. 3)
(5.4)

Величина £о = 9,80665 м/сек2 называется стандартным (нор¬
мальным) ускорением силы тяжести. Оно применяется для баро¬
метрических расчетов, в таблице стандартной атмосфере СА—64
(см. гл. 2) и т. д.
5.	2. 2. Момент гравитационных сил
Проекции момента гравитационных сил Мгр на оси ЛА-цент-
рической прямоугольной главной системы координат Oxuynzn
(Cl 11) имеют вид
ЛЛ,, гр = 3g —	(/*,,	—/„Jcosa^cosa,;
Г6
r}
, гР = 3£ ~ (Л., - /,) cos ах cos az; j
м г,, гр = 3^ —р и иг, - U,,) COS ax cos a„,
(5.6)
где	—	местный радиус Земли;
г — расстояние от центра Земли;
g — гравитационное ускорение в точке, совпадающей
с центром масс ЛА;
ах,ау,аг — углы между осями Ох1Ъ Оу1Ъ Ozn и вертикалью
соответственно;
— главные центральные моменты инерции ЛА по
осям Ох1Ъ Оуп, Ozn соответственно.
5.3. АЭРОДИНАМИЧЕСКИЕ СИЛЫ И МОМЕНТЫ
5.3.	1. Некоторые определения
Полной аэродинамической силой RA называется равнодейст¬
вующая сил давления и трения, возникающих при движении ЛА
относительно воздушной среды.
Главным вектором аэродинамических сил называется вектор,
-приложенный в центре масс ЛА, коллинеарный вектору полной
.аэродинамической силы и равный ему по модулю.
Центром давления называется точка приложения полной
•аэродинамической силы.
Фокусом называется точка, относительно которой аэродина¬
мический момент не зависит от коэффициента аэродинамической
силы.
Главным моментом аэродинамических сил называется вектор,
•равный равнодействующему моменту аэродинамических сил от¬
носительно центра масс ЛА.

Аэродинамическая сила и момент в установившемся полете
зависят от формы, размеров и компоновки JIA (см. рис. 5.1), егс
ориентации относительно вектора воздушной скорости, величины
воздушной скорости полета, плотности среды, ее вязкости, от
скорости звука, скорости вращения JIA вокруг центра масс,
отклонения органов управления и т. д.
Аэродинамическую силу и момент можно разложить на осп
различных JIA-центрических прямоугольных систем координат.
Примеры наиболее употребляемых проекций приведены
в табл. 5. 2.
Функциональная зависимость для полной аэродинамической
силы в неустановившемся полете имеет вид
Ra = / (форма Л A, v, S, /, Q, u, a, or, о^, wz, а, 3, v, а, 3,
(Ч.Г. °V> (,)г> • ■ •),	(5-7)
а на основании теории размерности и подобия эта зависимость
может быть выражена через безразмерные переменные
Ra = c/Scr (форма ЛА,	—^=т,а,	v,
Iх а у gl
а, шх, «>г, • • • ),	(5.7')
где cR — коэффициент полной аэродинамической силы.
Величины выражения (5.1') образуют систему критериев
подобия (табл. 5.3) и безразмерных параметров (табл. 5.4).
Зависимости для аэродинамических коэффициентов сх, су, cZr
mv, /77ту, mz имеют функциональный вид, аналогичный виду коэф¬
фициента cR в формуле (5.7х). В практике аэродинамического-
расчета Л А для коэффициента используется обычно зависи¬
мость лишь от части указанных в (5.7х) параметров, а именно:
= Re, u, '?) = cx0-\-cXh + cXi9.	(5.8)
Более подробно составляющие коэффициента сх рассмотрены
в разд. 5. 3. 2.
Для коэффициентов су, сг, тх, ту, тг можно ограничиться
(с достаточной для практики точностью) линейными членами
разложения в ряд Тейлора
су — суо	-f-	су	а-f	суЪ-\-	су	о	.	.	.	;
^ = ^o(M) + f^ + cz5"8H + . . . .
(5.9)
232

тх = т/'оv-f т'/«iy + т/оэ -f тх'\ + тЦ? + .
ти
ту
У
: Шу Ц)у
: mz0 4” т*а 4“ тг а 4" -f mzZ0)z 4-.. .
(5.10)
Величины с^-.
■,...— частные про-
^у_ с% =дсу_	C?J= dcz
с>Д\ ’ *	г?сх ’	2	д?
изводные коэффициентов аэродинамических сил cy,cz,... по па¬
раметру, указанному в верхнем индексе; величины т"хх,
т'ух,... — частные производные коэффициентов аэродинамичес¬
ких моментов тх, ту, mz по параметру, указанному в верхнем
индексе (табл. 5.5).
Более подробно о составляющих коэффициентов су, cZi тх,
.тущ тг см. разд. 5. 3. 3, 5. 3. 4, 5. 3. 6—5. 3. 8.
Коэффициенты аэродинамических сил и моментов и их вра¬
щательные производные определяются обычно с помощью экс¬
перимента в аэродинамических трубах и даются, как правило,
в полусвязанной системе координат Oxyz (Cl 14).
Пересчет коэффициентов в другие системы координат можно
произвести с помощью соотношений, приведенных в табл. 5. 6а,
5.	66.
5.	3. 2. Коэффициент лобового сопротивления сх
летательного аппарата
Коэффициент лобового сопротивления сх JIA в полусвязанной
системе координат Oxyz (Cl 14) является безразмерной положи¬
тельной величиной, зависящей от формы JIA, его ориентации
относительно вектора воздушной скорости (углов атаки а и
скольжения (3), чисел М и Re, углов отклонения органов аэро¬
динамического управления, степени шероховатости поверхности,
режима обтекания и т. д. Коэффициент сх определяется обычно
экспериментально для каждого ЛА или аэродинамически подоб¬
ной ему модели и является в общем случае периодической функ¬
цией угла атаки а с периодом 2л.
При траекторных расчетах и при обработке результатов
аэродинамического эксперимента коэффициент сх обычно пред¬
ставляется в виде
(М, Re) + ^(M, а) + ^.з(М, ?),	(5.	11)
где сх0, сХ' , сХшо носят названия коэффициента лобового со¬
противления при нулевой подъемной силе, коэффициентов
индуктивного сопротивления по углу атаки а и углу скольжения
|3 соответственно.
233

234

235
Примечание. Проекции аэродинамических сил (за исключением силы сопротивления) считаются положи¬
тельными, если они направлены вдоль положительных полуосей соответствующих систем координат. Сила сопротив¬
ления Q(QbQn) считается положительной, если она направлена вдоль отрицательной полуоси соответствующей си¬
стемы координат. Все аэродинамические моменты считаются положительными, если их векторы направлены вдоль по¬
ложительных полуосей соответствующих систем координат.

Критерии подобия
в
vo
а
E-i
Я q a
X „
—f 1-и
03 с -
>< О- g
У л -
<
о с
QJ CU
чЗ 5
зО т\
■§ = 3
| 3 §
,a ^ Н
О 2 °
л о
о
°н£
U1 со о о
<2 к
н s
а 5
о у
1 5*
9 S
2 S.
О
Он»К
с 2 ?
х ч
Сч5 О
CU С
О^-Ч
о о
оа
л «
Cl, о
К
§ §
о 2
'S'
° аз cj
о
2 ~г й
3 я 2
сг 2 2
2 о
G ° —
:г 3 3
о сз
G со
О о
^ 2и х
: Ь 3
■ 2 о
s S*§
2 =< ~
3 3* „
за -Э с£
— ГО О Q
,Г - S a
С С го а
2, a
I йо
S.
о a '
— — <и
= ^
5 ?s a
га 2 §
G о
"If
| § |
G К 5-
й 2
К — “
ч 3 о
X 2 “
^ 2 ^
Н - О
U d i?
н 2
о —
° О о"
^ 2 н
о ~ Щ
G a
х :
<
со
сз
си ^
о
О t=
о ю
а с]
О С—.
э ^
2 о
t о
Он
U
о
236

Размерный и. безразмерный вид некоторых параметров движения и производных коэффициентов
аэродинамических моментов
10
сз
3
vd
сз
СМ
*
13 *
•см
см
3 ^
I 3 as
iC
г: <- л
-9-^*3
<т> а о, d
° Q d
~ Q 5-
g S d
0 S к И
30^2
5- ^ ° °
'ч О CXO,
o S о с
CQ Я
2 и u 0
о P S J
J—1 я 2 3
С cu cq с;
= О О
с; н
*л <м
.'в
II
•I г>
'*> г
• а
ll
•I а
. а
' с2 ®
:	ь
) К я
U
>&
U
237

Pno\ о m 11 m Размерный ..
Название nai averpa ‘Mu Без'азмерпын впд Название производной м,,л Безразмерным вид
см
• ос. Н
£
I
. *-<	N
£
I
. I О	N
^	^	С	S
С	С	w	а
^ к - с
СЭ = К С-
н о —
с:	I	-	о
2	о	о	^	ш
В	S	a	j	2
^	О	fo	q	-
О	5	—	г?	та
са	*=	^	~
g.	£	I	=	к
сйоМ
~ о н о
О ^
Г! Е
о
U
ja
н = к
О о =
с с; as
О)
С н ^
^ о й
U S
см
I г
г>
см
о к
ч л
32
>5 я
к
к
к
о
VO
о
238
Vo — начальная скорость полета,
Ьа>Ьао* &Аю Ьаэ — средняя хорда крыла, руля высоты, руля направления, элеронов соответст¬
венно.

Таблица 5.5
Основные частные производные коэффициентов аэродинамических моментов
Название
Аргумент, го которому
выполнится диффереш и-
рование коэффициент
Дифференинр' емая компогента
аэродинамического мо\енга
мо.vein а
тх
111У
111Z
Меры статической ус¬
тойчивости
Угол атаки а
Г£
т z
Угол скольжения р
ml
т1
Чгсло Maxa М
м •
тх
<
м
mz
Коэффициент подъ¬
емной СИЛЫ Су
тСгу
Вращательные произ¬
водные (демпфирующие
Угловая скорость
крена wr
т/
“V
ту
коэффициенты)
Угловая скорость
рысканья о* у
т7
<•
Угловая скорость]
тангажа с.г |
т /
Производные по углам
отклонения органов уп¬
Угол отклонения
элеронов оэ
т X
т1э
равления (эффективность
органов управления)
Угол отклонения
руля направления оч
О
т н
П'Х
т1н
Угол отклонения
руля высоты (стаби¬
лизатора) ом
0
тгв
Производные по скоро¬
стям изменения углов
атаки, скольжения, углов
Скорость измене¬
ния угла атаки а
т\
отклонения органов уп¬
равления
Скорость измене¬
ния угла скольжения
Р
т*
X
т1
Скорость измене¬
ния угла отклонения
элеронов 6Э
ГП°гЭ
Скорость изменения
угла отклонения руля
направления 5Н
Скорость измене¬
ния угла отклонения
руля высоты Ьп
ь
т z в
239

Продолжение
Название
Аргумент, по которому
выпо тняется дифференци¬
рование коэффициента
момента
Дифференцируемая компоненia
аэродинамического момента
тх
Шу
mz
Производные второго
порядка
Угол атаки а и
угол скольжения р
mf
Угол атаки а и
углов з я скорость
РЫСКГНЬЯ сОу
т;«
Угол атаки а и
угол отклонения ру¬
ля направления он
т'*«
Угол скольжения р
и угловая скорость
тангажа со2
[5 со
т v 2
Угол скольжения р
и угол отклонения ру¬
ля высоты (стабили¬
затора) ов
[3 6
тх"
При м ечан п е. Некоторые производные имеют следующие назва¬
ния:
mz^ (т1) ~~ степснь (мера) продольной статической устойчивости;
тJ — степень (мера) поперечной статической устойчивости;
1V\ —стспспь (мера) боковой статической устойчивости.
2-10

241

Преобразованная система Формулы преобразования коэффициентов Формулы преобразования коэффициентов
Исходная система координат координат аэродинамических сил аэродинамических моментов
+
+
+
+
+ СО-
СО- сд
+
к «
5 н
о О.
О)
в* И
I *
50
* К О)
Q
з»
О
Я Ьч
Он о
^ =:
S КГ1
к со О
к о а;
ад а
С Л СО
Ч Ч ^
са со со
К * ^ ~
я *	Г-;
* £ р
а)
£ ” « N
Я О Оч
ак о й)
и 2 я *
О)
<
Л ^
§!=
+
с: о д?
о- Я С
^ Ч Ч ^
Я CD СО
гг Д
Я О
0. к о
11 Iе5
< = s-
^ 5 S ч
Ч
та TJ4
к я 2 ^
2 н
(У О ^
7 и Д ч
= б ?
hS £о
JoSo
242
П р и м е ч а н и с. Для связанных систем координат С111 и С112 пересчет осуществляется по формхлам для
системы СПЗ, но ппжнип индекс «1» заменяется индексом «11» или «12»,

Таблица 5. 66
Формулы преобразования производных коэффициентов аэродинамических
моментов, выраженных в JIA-центрической прямоугольной вертикально¬
симметрической (полусвязанной) Oxyz (Cl 14) системе координат,
в ЛА-центрическую прямоугольную вертикально-симметрическую (связанную)
Oxlylz{ (СИЗ) систему координат
Название производной
козффмцпена аэродинамичес¬
кого моме на
Формула преобразования
Производная по углу
•скольжения р
п о о
/77‘ = га‘ cos а + га , sin а
л, л У
гаf = mt cos а — т\ sin а
у 1 У х
Производная по углу
отклонения руля направ¬
ления 6Н
5 о Ъ
т ” = га ” cos а + га” sin а
л ! л у
со 5
т ” = га ” cos а — га ” sin а
и i у х
Производная по угл\
отклонения элерона 6Э
6 о Ь
га .. = га„э cos а 4- га„э sin а
л 1 л у
6 о 5
т „э = га„э cos а — га „э sin а
У1 У х
Вращательная произ¬
водная по угловой скоро¬
сти крена coJCi
пг 1 -= т/ cos2 а + -i- sin 2а (тху -f -f
+ 1ПуУ sin2a
ray*1 = ra^ cos2 a —тУ sin2 a +
У i У x
i / CO.. CO \
+ — sin 2a \myy — m/)
О)	со	со	.
Вращательная пропз- пг ХУ1 ~ тху cos2 а — т х sin2 а +
водная по угловой скоро-
ст.. рысканья	+	_L	sin	2а	(т«у	_

Для ЛА типа самолета нормальной схемы (рис. 5. 1) коэффи¬
циентом схп обычно пренебрегают. Для ЛА с несколькими пло¬
скостями симметрии (например, для ракеты, выполненной по
схеме « + » или «X») зависимость коэффициента сХ[3 от угла
скольжения аналогична зависимости коэффициента cXiy от угла
атаки. Примерный характер поведения коэффициентов сх0 и ciL
показан на рис. 5. 2 и 5.3.
Коэффициенты cXjrj и схп для малых углов атаки а и сколь¬
жения р можно представить (в зависимости от диапазона чи¬
сел М) в виде функций от коэффициента подъемной силы cv
и коэффициента боковой силы сг (см. разд. 5.3.3 и 5.3.4) вместо
функций от углов атаки а и скольжения 6:
где коэффициенты пропорциональности Ва, ЬХ, В'а, В\ опреде-
[15], [18]). Характер поведения коэффициента Вприведен
на рис. 5.4. Формулы для определения коэффициента сХ(7 для
ЛА различных аэродинамических схем приведены в табл. 5. 7.
При определении сопротивления ЛА расчетным путем пред¬
полагается, что коэффициент лобового сопротивления всего ЛА
при нулевой подъемной силе сх0 складывается из коэффициентов
лобового сопротивления при нулевой подъемной силе отдельных
его частей с учетом интерференции между ними и определяется
по формуле:
где kv 'l и kB о — коэффициенты торможения потока;
/а— число пар крыльев;
£и~1,1 — коэффициент, учитывающий аэродинамическую
интерференцию между частями ЛА;
дс^о — дополнительное сопротивление от прочих час¬
тей ЛА (щитки, антенны и прЛ
для М<о-г-10
для М5>5-ь-10
(5.12')
(5. 12)
ляются из эксперимента или расчетным путем (см. [10], [12], [13],
1 S1
Л'О из.кр из.кр
(5.13)
244

<
S n-l
s Я ~
й« = ~
245

с*0
1,50
7,25
7,00
0,75
0,50
0,25
/
Со

J
/ si
V
а
V
	1
<н
' 1
10
1?
/4
ы
Рис. 5. 2. Коэффициент сх0 некоторых летательных аппара¬
тов больших скоростей [11]:
/— капсула типа «Меркурий»; 2— головка баллистической
ракеты; 3—ракетоплан типа «Дайна-Сор». Коэффициент с*о
для 1 и 2 отнесен к площади миделя, для 3—к площади
крыла
Рис. 5. 3. Характер зависимости коэффициента ин¬
дуктивного сопротивления cxia от угла атаки а
(при малых а)
1246

Выражение коэффициента cXia JIA через коэффициенты ин¬
дуктивного сопротивления отдельных его частей существенно
зависит от аэродинамической компоновки (см. табл. 5.7).
Рис. 5. 4. Характер зависимости коэффициента Ва от числа
М (на примере ракетоплана типа «Дайна-Сор»).
Пересчет коэффициента лобового сопротивления сх из полу¬
связанной системы координат в другие системы координат дав
в табл. 5. 6а.
Таблица 5Т
Формулы для определения индуктивного лобового сопротивления
для летательных аппаратов различных аэродинамических схем
Схема ЛА
Формула для определения коэффициента с „
/а
Нормальная
С y — С г 	С х
1* * 1ф £ 1 кр
„Утка“
Ч. Ч, s -s + *'[“(’ ’♦ 4 J]
,Бесхвостка“
(с дестабили¬
затором)
Примечание. Выражения сх. для схем «утка» и «бесхвостка»’
1а.
(см. рис. 5. 1) справедливы при малых значениях углов атаки а и числах
М<5-г-10.
247"

5. 3. 3. Коэффициент подъемной силы су летательного аппарата
Коэффициент подъемной силы су Л А в полусвязанной системе
координат Oxyz (Cl 14) зависит от формы JIA, угла атаки а,
углов отклонения руля высоты 6В (стабилизатора фст), элеронов
бэ, от числа М, числа Re, характера обтекания и т. д. Знак коэф¬
фициента су, как правило, совпадает со знаком угла атаки а.
Коэффициент су является в общем случае периодической функ¬
цией угла атаки а с периодом 2я. Обычно коэффициент су опре¬
деляется экспериментально для каждого конкретного ЛА или
аэродинамической подобной ему модели.
Рис. 5. 5. Характер зависимости
коэффициента подъемной силы
су ЛА от угла атаки а при
различных углах отклонения
руля высоты 6В
Су1
су max
/ *
/ I
/ 1
/ •
0
/ 1
/ 1
/ 1
/ 1
/ 1
/ 1
/
акрит
а
Рис. 5 .6. Характер зависимости коэф¬
фициента подъемной силы ЛА с.,
от угла атаки а
Для расчета траекторий зависимостью коэффициента су от
некоторых из перечисленных выше параметров можно пренебречь
и представить су в форме:
Су(М, а, Ъв) = Су0(Щ + суа(М, а) + г„5в(М,8в),	(5.14)
где сУо~ коэффициент подъемной силы при нулевых значениях
угла атаки а и угла отклонения руля высоты
(а = ов = 0);
сУа — часть коэффициента подъемной силы, зависящая от
угла атаки а;
■суьв— часть коэффициента подъемной силы, зависящая от
угла отклонения руля высоты Ьв (стабилизатора срст).
В механике полета обычно пользуются приближенной зави¬
симостью
гу = с<м (M)-f-c’ (М)а -j- cfy (М) 8Я.	(5.	15)
248

К такому виду коэффициента су приводятся результаты аэроди¬
намического эксперимента.
Представление коэффициента су в форме (5. 15) справедливо
при | а | 10°—12°; —20°<6В<20° и используется как в граек-
торных расчетах, так и при расчете возмущенного движения (при
фиксированном значении М).
Вид различных функциональных зависимостей су =
— су (а, 6) указан на рис. 5.5 и 5.6.
С другой сторону, для определения коэффициента су суще¬
ствуют различные полуэмпирические методы расчета [10], [12],
[15]. В этом случае коэффициент подъемной силы си ЛА счи¬
тается суммой коэффициента подъемной силы отдельных его
частей (крыльев, фюзеляжа, стабилизатора и т. п.), скорректи¬
рованной некоторыми коэффициентами, учитывающими интер¬
ференцию между частями JIA.
Некоторые определения и формулы расчета коэффициента
подъемной силы ЛА в целом и отдельных его частей для различ¬
ных аэродинамических схем компоновки (см. рис. 5. 1) приве¬
дены в табл. 5.8, 5.9, 5. 10. См. также специальные руководства
[10], [12], [13], [15].
Пересчет коэффициента су, заданного в полусвязанной си¬
стеме координат Oxyz (Cl 14), в другие системы координат, свя¬
занные с ЛА, дан в табл. 5. 6а.
5. 3. 4. Коэффициент боковой силы сг летательного аппарата
Коэффициент боковой силы сг ЛА, определенный в полусвя¬
занной системе координат Oxyz (Cl 14), зависит от формы,Л А,
утла скольжения (3, утла отклонения руля направления бк (пово¬
ротного вертикального оперения фв.0), от числа М, характера-
обтекания и т. д.
Коэффициент сг является в общем случае периодической
функцией угла скольжения (3 с периодом 2л. Знак коэффициента
сг, как правило, совпадает со знаком угла скольжения (3. Боко¬
вая сила Z и ее коэффициент сг создаются в основном вертикаль¬
ным оперением и фюзеляжем ЛА. Коэффициент сг обычно опре¬
деляется экспериментально.
Для расчета траекторий зависимостью коэффициента сг от
некоторых из указанных параметров можно пренебречь и, учи¬
тывая симметрию ЛА относительно вертикальной плоскости и ма¬
лость углов (3 и бп, представить сг в форме
с, = с*(М)Р + сК,	(5.16)
где величины с\, с" всегда отрицательны.
Пересчет коэффициента сг, заданного в полусвязанной си¬
стеме координат Oxyz (Cl 14), в другие системы, связанные
с ЛА, дан в табл. 5. 6а.
249

ОсйоНныё составляющие В выражениях для коэффициента Подъемной силы d
ОО
Q
а*
а
-К
I О
о
: 2 z га
о g о _
Г О со s
al * u f-
^ о <и
о ^
< _ VO ^
со <
° tT о
а. S'
< 5 С ^
^ <и О ^
к 5 Е
§ к 2: га
<521
^ С? VO
К О
с э'х
м <U
Ч
u о
о Си
Stf
а
сз VO
а, о
s си
— с
<VO
*Q	СО
*=3	°
о	s	и
ь;	*
со	с->	m	а)
Os
со	о	S	“	s
^	2	«
3	о	s	ь	s
'Т	СО	>-> G2 ^
~	-н
COJS - с->
J3	0	5
3 ^
а< 5
С S
*в-v
о о
Ч to
u К
>> о
н н н н 3
ОООО 2
СЧ СО Я1 &
>>
= я
£ =
Я <=:
о .о
-S га
-t- 'w
В ^ СО
-3 з 5
р, О-i *q
X* ^
tQ-1 s
ГГ>
О S о
to u
к .о
о x
со о
9 =
т& 3
о
со ~
gg
сJ о
СО рз
3 5
о о
2
^ О ^
° £
>—1 со ^
с СЗ
л га
s § «
о
aU q
О S U
’в- я >>
h* Н Н
ООО
*©< 2
♦в-*©*
■8*
а>
О-
С
IQ
Си
Я Я со
! с- S g
; s з*
2 «
> о ет
1 у 2 2
! * =-0-
о
а..
^ о
2 >>
а,
к « i<2	*
н 3
- з о
Л
c-IQ
- ^ S
: vo ^
: с С
а>
•«г
сэ os
о
а,
о
-*в«
3 га
■9* 00 3
. CJ ts й
(L) 5 *0«
ЕГ “
S <и
P-S
•&
-в*
ю
о~
■I-
со :
о“ !
V i
iq ;
Stf
с
3
о
а,
я
S
-в*
*6-
^ га Си
~ ^ *
еГ § [J
— aj Я
= О *
Ж 0J
*8-3
5 « и
Л = р
^ - 5
В S
5 1 2
s Ьс: ~г
<и <
g W я
а г °
«н=^
ЙО ^ «
В . <ь» 5
3 СО Н* <
S Сь
И а «
Я ^
*9-я
»©* ^
ГО
О 5
'250

Коэффициент подъемной су г>0 1. От схемы Л А
силы горизонтального one- .	2. От углов атаки а, отклонения	стабилпзато-
ренпя ра <рст пли руля высоты ов
• 3. От коэффициента торможения	потока в зо¬
не горизонтального оперения kr,0 и	производных
о —
га га £
t %
= ЯЯ
м V а
и ц С-
-
с Ех2
3 ьг; ~
“ « =
0-5
s-ё
о- -
=
гК
— тО- X
X X е;
па
о
О ■
X
5
о
о
X
•<
ja>
X
D-
X
га
ц_
га
_
И
3
Ч
X
сх
о
г-
a
О
О
X
сх
о
о
о
X
хг
о
га
X
к
X!
3
га
~—г
га
X
’~'v
га
о
2
2
га
о
о
fH
о
о
СХ
о
X
о
о
о
X
<
о
о
X
X
X
га
X
н
о
га
о
га.
СХ
эх
о
О
сх
о
X
X
о
о
: v х
g*S:
а, и гг с
о ;
Ь £
— о
V я б
ю
ООП
X “ “
S	О *
2*	О т~
^	5	^
с? 13 — о
g
*.« §■£ -I-
5 *« Е-
1Д»Л
о в
F—' ' -
X
о
X
<^)
X
га
„—s
X
X
о
X
Н
X vo
о
о
сх
' ч
S
X
о
га
X
га
X
VO
3
О
сх
X
о
X
X
о
о
X
га
с
га
о
н
ъ,
ЭХ
га
X
X
га
СХ
О
X
га
га
_ в *
tr «3	•
го н
О *
СХ ~ X
(Т) га
га га О
. 2 5
а. сх ^
о ^ сх
S
= « га
а- н ~
с
л а- х
х х х
х
га
О
о
« £
га О-
- VO
s s.
Ч С
х о
•=3 га
CQ s-
оо_
Н
Н ь-
ОО
га га
^ £
*=* га
5 ^
га х
д. - — р- s
S g-g о a
£•	<0	ч
н га h* q
О SOvo
га
О	СХ
С X С
2 *=3
х га
га о
■< н X
га о
о п га
’ о га га
О, с
о ;
*&■ X >->
Н Н Н Н
осоо
Sg
ГС 3
= 1<
-t-
ч— •& уО
-0-
а. +
^х
5 g
X
с £?
f'is
о о *3
О X
S
о
*6-
+
о
а-
х
<
га
га
3
а,
X
251

Величина Обозначение От каких факторов зависит Примечание
£
с
о
VO
о
о
S
о
с
2
о,
о S
а ^
Z* га
р, я
х 5
£ 2
га
н
о
ГО
о Ь5
= с
Е о
гс
0Q С
О -
Си О
си «
о =
о га
сх к
U
:	2	га	о	^
:	SH	о	о	с
>	Ь	н	С	Е
■	£	°	°
;	я	с	и	с
5 О h ^
2 ~ О Р
ja о о. 2
к = с S
Л Э £
Д - га _
о ^ о_ л
f- г-f ас га
о g
«0-9“ А
ш
5*^
со н
К о
о
О- >,
с ^
U
Н га
о
С >>Ю
ьз м
га Ь 5
с-> ^ р
о -р
Ш О CU
о с 5
2^5
с; л о
и га ж
>> е( О
О 1=3
Й &й
2
о
•=3
К
£=Г
\о
S
о
«
I I
2-52

253

254

5. 3. 5. Поляра летательного аппарата
Кривая cy = f(cx), лежащая в плоскости коэффициентов сх, су,
определяемых в полусвязанной системе координат Oxyz (С 114),
и описываемая концом вектора коэффициента полной аэродина¬
мической силы с л = Ус'\-тС<2у (при (3 = 0), называется полярой
первого рода (рис. 5.9).
Кривая cyi = j(cXl), описываемая в плоскости коэффициентов
сХУ, cVl, определенных в связанной системе координат Oxxy\Z\
(СПЗ), концом вектора коэффициента полной аэродинамической
силы cR= Yс<1х Л~с2и (при (3 = 0), называется полярой второго
рода (полярой Лилиенталя, рис. 5. 10).
Аэродинамическим качеством К летательного аппарата на¬
зывается отношение коэффициента подъемно!* си’лы су к коэффи¬
циенту лобового сопротивления сх.
Поляра летательного аппарата в основном зависит от формы
ЛА и числа М полета.
В динамике полета для расчета траекторий используются:
1. Семейство поляр для различных чисел М и графики (фор¬
мулы) поправок к величине лобового сопротивления в зависи¬
мости от:
— высотной поправки Acxh (изменения числа Re полета),
— режима работы двигателя Асх дв,
— наличия подвесок (баков, ракет и т. д.) или выпуска раз¬
личных устройств (шасси, створки люков и т. д.) Асх0.
2. Семейство посадочных поляр, учитывающее влияние бли¬
зости Земли и применение средств повышения коэффициента
подъемной силы (выпуск закрылков, щитков, предкрылков,
поворот крыла, применение управления пограничным слоем
И т. д.).
Характерными точками на поляре являются:
1. Точка максимального аэродинамического качества Кшах =
= (—)	,	обычно соответствующая режиму максимальной
\ Сх / max
дальности в прямолинейном установившемся полете. Графически
эта точка определяется касательной, проведенной к поляре из
начала координат (см. рис. 5.9).
2. Точка минимального аэродинамического сопротивления
Cvmm, обычно соответствующая режиму максимальной скорости
в горизонтальном прямолинейном установившемся полете (см.
рис. 5. 9).
3. Точка максимального коэффициента подъемной силы сушах,
соответствующая посадочным режимам.
Различные виды поляр и диапазон определяющих их пара¬
метров приведены в табл. 5. 11 и на рис. 5.9—5. 12.
255

256

9	1669
257

Рис. 5. 9. Поляра первого рода для летательного аппа¬
рата
Рис. 5. 10. Поляра
второго рода для
летательного аппа¬
рата
258

Ряс. 5.11. Модифицированная поляра Ньютона:
р = 0; с*0= 0,042;
^0=1-82; Схтах- 1.505;
Cyr шах = 0,702; Ктах = 2;	<**^	=	20,5°;
%шах-54,7°; М > 12 — 15
I
9* "
2,51

260
рическое представление)

Модифицированная по- сх = сх0 (М) + Ва (М) с j2	M>5-f-7 ±12 ~-2о Полусвязанная С114
ляра Ныотона для малых
углов атаки
261

5.3.6. Коэффициент момента крена тх летательного аппарата
Коэффициент момента крена тх в полусвязанной системе
координат Oxyz (С114) зависит от формы ЛА, числа М, углов
атаки а и скольжения (3, углов отклонения органов управления
6В, 6э, fi„, угловых скоростей сох, соу, coz и др. факторов, т. е.
тх--=тх(М., а, 8в, 8Э, 8H,w_r,	т2, ...).	(5. 17)
При рассмотрении возмущенного движения ЛА относительно
центра масс и при решении задач устойчивости в выражении
(5. 17) обычно ограничиваются членами ряда Тейлора до второго
порядка включительно
тх = тм +	+	'п°х%	+
со —	со..—	со —	а,3	ао
+ т/со r -f- m/wy	т/o>z -f-	тх аЗ	тх	паон -ф
-}- тх в;-ов 4- тхауао)у -ф тх -ф ...,	(5. 18)
где пгхо — момент от производственной несимметрии ЛА;
т*х, тп\л т*/, т*х\	тф,
статические и вращательные производные,	а	также
производные второго порядка соответственно (см.
табл. 5. 5).
Для	ЛА нормальной самолетной	схемы	(см.	рис. 5.1)	влия¬
ние параметров продольного	движения, а также	момента тх0 на
движение крена слабое и поэтому выражение (5. 18) принимает
вид
тх = тхэЪэ -ф гп/^х-ф т?Ъ + т°/'Ън ~ф .	(5.18')
Для ЛА, имеющих малые углы скольжения (3 и малые угло¬
вые скорости рысканья соу, выражение (5. 18') принимает вид
wx = гп*\ -!г тхх о)х.	(5.18 "у
Степенью (мерой) поперечной статической устойчивости
называется величина
з дтх
пгх
аз
При т£<О ЛА обладает поперечной статической устойчи¬
востью.
Для ЛА с крылом малого удлинения, особенно для ЛА схемы
«утка», на коэффициент момента крена тх оказывает большое
262

влияние несимметричность обтекания при углах (3^0, поэтому
часто следует учитывать члены со вторыми производными.
Описание основных производных коэффициента момента
крена тх сведены в табл. 5. 12. Пересчет коэффициента тх из
полусвязанной в другие ЛА-центрические системы координат
дается в табл. 5. 6а и 5. 66.
5. 3. 7. Коэффициент момента рысканья ту летательного аппарата
Коэффициент момента рысканья ту в полусвязанной системе
координат Oxyz (Cl 14) зависит от формы ЛА, числа М полета,
утла скольжения, угла отклонения руля направления, угловых
скоростей (ох, со у и т. п.:
ту = т„(М, ?, 8Н, тх, шу, 8Н...).	(5.19)
Вместо (5. 19) обычно используют приближенную формулу
ту=т'у? + т°ун\-j- rnux<»x -f -f ml 3 -f m^'S.	(5.20)
Величина mj* называется степенью (мерой) боковой статиче¬
ской устойчивости. При mf,<0 летательный аппарат статически
устойчив в боковом движении.
Для ЛА, имеющих плоскость симметрии, проходящую через
ось Ох! связанной системы СПЗ под углом 45° к основной пло¬
скости Х\Оуи коэффициент момента рысканья ту равен коэффи¬
циенту момента тангажа mz (см. разд. 5.3.8).
Описание основных производных коэффициента момента
рысканья ту дано в табл. 5. 13. Пересчет коэффициента ту из
полусвязанной в другие системы координат дается в табл. 5. 6а
и 5. 66.
5. 3. 8. Коэффициент момента тангажа тг летательного аппарата
Коэффициент момента тангажа тг в полусвязанной системе
координат Oxyz (С] 14) зависит от конфигурации ЛА, чисел М
и Re полета, угла атаки а, угла отклонения руля высоты бв (ста¬
билизатора фст), угловой скорости тангажа coz, скорости измене¬
ния утла атаки а, скорости отклонения руля высоты 6В и т. д.:
mz=mz{ М, Re, а, а, 8в, 8В, шг,...).	(5.21)
Выражение для коэффициента момента тангажа (5.21) при
рассмотрении возмущенного движения относительно центра масс
и задач устойчивости приближенно представляют в виде
mz = m2o + m^a+m^BSB + m^toz+^a+	..	.	(5.22)
263

Основные производные коэффициенты момента крена тх летательного аппарата
lo
С
Я
'О
к
<
*5
о
VO
к
*5
CL?
н
я _
н
я
я
»=(
Я О
CU ~
£ я
я S
Р а»
оо
д 5 •
я со £_,
о х -
S3 н
я 3
а»
н ^ р
я >-.«о
о? я
1=^
•е-с"в
'В* х
СП с^з Я
о Я s
^ О? я
Он а»
я ^
я
н" К
я ~
си я
Я CU
си
я
а»
СП- К(
5 °
5 о
5 °
а, к
о Я
О t-
Я го
И си
^ СО
Я Я
5 я
S н
я я
я «=3
О О)
Н со
О Q
*я -
О 5
я ~
я
си
■) •§*
- СП
я я
Ё§
3 &
я к я
я
: Я
о
я *
я °
з я
я
К^шо
Ё,е>
' ГО
VO
о
*[5*3
си я
«=3 си
Р си
2.5 g
“ 1 S
я «=3 я
я я я
о сз Я
г~>	я
2 й а
Р ^ я
Я я я
г,	Я
я
Я К
я
X
Е-1
о
я о н
S Е
&{
у \
. ’я Я С
^ ts t
О Я С
-	s	я	Я
!	и	£*	Ч
я я го
я я я
н я н
1^000
: 'g4	.	.	.
I	S	^	СО ^
>»
fc[ я
о я
я я
со Я
С о
С- оо_ Ч
* S
A S
.£,8 4
si £:
и я
< S
^ Я
в Ч
и
о
Си $
С 3
го ^ я
я	ч
2 s . р
я SS-, g
О О
§°s§
§ 5 я §
сь о я
*> ,Я л Я
^ оо^
СП со CU'B-
о ^
2 5 S °>
О Р ^
я я S
я я 5
о сз ^ S
у “ Я Л
£ = 2 ^
? г s й
53
„ я
Я я
си
н
о
1 н
го
я
Л м
я
>1 2
я 5
я я
я си
я ts
Си Я
*9- ю
S
я о
ЯО
О А
н и О
о о %
я я
Я я я
я (Л
в Я 0~
3 со г—*
СО 3
ГО п*1 ГО
я я
ГО
Я	го	СО	.
О	я	°	О	С=^
я	я	к	си	о
о	си	о	о	Я
си Я	Си	я
X
го
(-,
X
я
го
s
Оч
с
я
я
е
Я
я
ГО
го
Я
С-1
го
Я
Я
го
я
я
и
я
о
н
я
о
о
я
я со
го
го а?
5 *
о
X S
го
я я
^5
X
го
•&
*&•
я я
VO го с
S Е
5 о-?
~<0
с^'
я с
эЯ ^ с
< о :
Я ГО С
гЯ со С
<ч д ?
я
я - я си
о я
S я
>>
с л
5 «о
>»
С я
264

Ён<
■ ^
•&
F-
O
ls\
°| O ^
eg « О CU
*S
О
ffl
К
к
Oh g
н о
Он
к «
S>S
<v
<v
3 о
>» о
Он га
03 о
о 2
13 ч
СП
о
о 'S- с
*8-	(—I
С « о ^
‘ о
о «
И —' га
5 в
3 03
^ га
о
2 3
С Он
ч
Я {
Он
Ев
I N
I з ч
s
л
SI 3 4
с S
<
t=z
к
ч
п
ч
U
о
ч
с
PQ
С »я
Он о
О 03
га си
с
к га
га ч
CD
Н Он
VO
° я
К
£ Р
3 „
£2
2 g
-- иа
Е- 4 К
Jr га о
О я га
к а;
н ч
сГ га
о га
5^ Он
с
03
к
£ 5.
5 о,
Ч к
о S3
га — -
2 аз <о
° о к
з- ч га
С * га
^ о 6 5
И а3
к Н о
* н s s
га д ^ о
Н о Ч "
VO S о<о
О ^ Ц-4
^ о S
^ о,
s >, гО
Н га с
g Ч га ’£
ё ^ ‘О
2 5 м
о га о к
-г га сх,
Р- н о С5
н О tZ,
3 *га 5 —
PC
§gg«
5 я § я
1*25
* 35 2 “
a S.^56
CQ O' S
о О й Й
га к « ^
ffi Ч 2
о м %
о я g и «
Он ►—г о
га 3 га н
ч
СП.
5
45
CN
а
45
45
445
S
45	(
4>
OCL
45
=5»
3
а
45
« Ч
2 ч
С о.
265

Основные производные коэффициента момента рысканья ту летательного аппарата
У
VO
Q
К
га га
х н
CQ X
га OJ
Он S
о
' Он а
£ к
2 к
S
CD hQh
CQ m
о
я
л
<
к
а
jэ
Ч
о
VO
сЗ w Я к II
я «о ^ II
О S О
CL CQ Ю С
:о
VO
о
a *
! О
*& X
-О* 3
<Т> CQ
CD Он es
rQn	CQ.	jS
'В*	и-	°
К CQ
Q	s	О
S	Я	Я
1—1	о	о
* §
>* а
£	=я
я CEL	S
О ^ Я
Н
О *я
о
<Я
fc( -*
^ S
CD о
S Он
1=1
о
PQ
8	?	2
я	£	~
1	_	S
ТГ	К	0J
'Q*	а	!?
>*
о
Он
о §
я н
8 У
!	* 8
: а Он 2
: fo м S
<о ~
,	О к Д
jr	S	<D
О =s в
с <о
« 5
2 сз
~ CQ
§ а
О ВТ
я «
о я
J£ Я
я:
о
с
о
X
PQ
к к
2 ^
Н <D
<D со
га о
а^н
<
Он О)
2 с
•&• о
о §
О *
со о
с г
а
к
§13
о (Л
О. S£j
С 2
1=3
о
со к
00 J 3
| га
с I
266

Я <i>
cf Cl,
О, ^
О С
о °
* о
S о
si-
Я
о Я
н
с °-
с»
о и
о s
о я
CD
О Ч
с S
с^З
cd Ч
н
cd cd
Я Он
О S
О Я
3 S
Я о
е- ч
°« 3
£ Он
PQ t?
— о
&S
1	°
2	а
о
со
CD Е-
Ч cd
о Я
<
Я
3 а
Я £f CD
a	s
я	я
я
CQ
Я
Е_
>>
я t
о LO
я ^
я о
>5
я -I-
О LO
с —Г
я
Я
я
>>
3 s
£ ^
Он ^
CD
ю 3
, S
о ф
° X
о
я
(2t?
gк
ч
я ^
о о
а я
0	а
CD
h- Ю
1	3
S3
а
3 к
го я
Я о
я я*
я £
п §
о 2
о
я
с,
с 5
.|*о	С5>
S
CD CD
Я Ч
CD Я
£ Я
СО Он
Я с
о я
о ч
о >»
о о
я
о я
Я
я
3 °
в н
4 О
о
а сз
2 Ч
С 5
267

При получении коэффициента момента тангажа mz расчет¬
ным путем целесообразно представить его в виде суммы коэффи¬
циентов моментов тангажа отдельных частей Л А:
mz = mz ф + mz кр 4- mz r 0 + mz,	(5.	23)
где Дтг — коэффициент момента тангажа от щитков и прочих
частей Л А, а также дополнительный момент от скоса
потока для ЛА схемы «утка».
с mz
Величина кпу = —	называется степенью (мерой) продоль-
су
ной статической устойчивости. ЛА является статически устойчи¬
вым в продольном движении при пгс/<О, статически нейтраль¬
ным при пгСу = 0 и статически неустойчивым при тСу >0.
Описание основных производных коэффициента момента
тангажа пг2 дано в табл. 5. 14. Пересчет коэффициента тг из*
полусвязанной в другие системы координат приведен в табл.
5. 6а.
Значение угла атаки или угла отклонения руля высоты, при
котором в установившемся режиме полета (а = бв = 0) коэффи¬
циент момента тангажа mz обращается в нуль, называется балан¬
сировочным углом атаки абал (балансировочным значением угла
руля ВЫСОТЫ бвбал):
«бал= Г \tnzo + tnz%4- mzzMz);
ь _	1	(
в бал	§	V
(5.24)
где а* и 6*—некоторые фиксированные значения угла атаки
и руля высоты.
5. 3. 9. Шарнирные моменты органов управления
Шарнирными моментами называются аэродинамические мо¬
менты, возникающие от действия аэродинамических сил на ор¬
ганы аэродинамического управления. Шарнирные моменты вы¬
числяются относительно осей вращения органов управления. Ве¬
личина шарнирного момента определяет размер усилий лет¬
чика или привода, прилагаемых на рычаги (тяги) управления,
необходимых для отклонения управляющих поверхностей.
268

Шарнирный момент МШтр любого органа аэродинамического
управления (руля направления, элерона, руля высоты, подвиж¬
ного стабилизатора, подвижного киля, поворотного крыла
и т. д.) представляется обычно в виде
А1ш.р = Tnm,vqSvbv,
где тш.р — безразмерный коэффициент шарнирного момента
соответствующего руля (элерона, руля высоты, руля
направления и т. д.);
5Р — площадь руля;
bv — средняя хорда руля.
Функциональная зависимость для коэффициентов шш.Р неко¬
торых конкретных рулей имеет вид:
— для элерона
тш.э = тш.э («. Р, (,).п <«». К)
(в первом приближении шш э = Шш.эа+ти®э^э);
— руля направления
Н	Н	°Н’	со*/)
(приближенно тшл = /г^нР + тшн„он);
— руля высоты (подвижного стабилизатора)
™ш.ъ = тшъ{а, р, 8В> 8В> о>2)
(в упрощенной форме тш	0 -|-
Для коэффициента шарнирного момента руля, находящегося
под воздействием аэродинамических сил, справедливо соотно¬
шение
где су р — коэффициент аэродинамической силы, действующей
на руль;
хл, хт — координаты центра давления и оси вращения руля
относительно передней кромки в долях средней хор¬
ды руля соответственно.
Наиболее надежный способ определения коэффициента тш.р
состоит в проведении аэродинамического эксперимента. Прибли¬
женные расчетные зависимости для тшр приводятся в работах
[12], [18].
26Э

Основные производные коэффициента момента тангажа тг и координаты центра давления частей J1A
5 ^
а ^ ^
hCO S
VO —' О
or; a
S°s
а ь
п ей О
ь К *
а> a £
I
5 § э
« * £
Я 3 О
С у со
4—" н о
о a
Я
<
sq
^ *
н о н ■
о §о
CJ
*
си
CU
15
a
a
си
a a
a
§ S
Is
^ о
и s
a a
си 2
х ~
1°
§<
а^
а *►*« .
о Е<
« ос;
Со
° а аЗ
£
О н «
о си
а a
I—L, "Г
с £•
О CvJ
ё +
Ef “Я
CU
о А
а ^
S s
о S
<и сз
“ Ч
о
•I a N
£
a
со
«1*
I 3 м
£
ft,
*
S
a
со 2
'V
.1 a N
К
о о-
о V
о о
R
4 х a
3 н
—1 о
3
I
£
•1 a м
o>
X
о
A
|!
sa
a
о
a
i ю
H
• |«Э M
3
>г
5
r
a
a
?5
a
cu
о
i-*
a
<
<
t=:
*~S
к
R
T“
t=s
|«э N
К
1 ®
• 1сО N
5
а х -I ;
£ 3 1
*— a
3 a, S
’Э* СчЗ
-e< a
£ a
£ *
a
u-. u-.
4 H
a a
о
о 1?
“■e-„
-8* ^
К сто ^
a § 5
° ^ о
Ss§
i^5 fi
u, a ^
н о
°[3 °
^ a -Э*
S a^
§ -I*
§
cu u ^ a
i—< ~ ^ a
U =s с ±
о a
си н
о a
a
a
о 5
С j>^
a s
Й- я
R. CL)
£ *
a cu
2 £
° a I
cu
C
о 3
Си PQ
о
ttj к
° §
° &
К «
a я
DP ®
§ £
о 5
270

2
VO
О
cu
ч 2
н cd
53 5
К £
СГ
*9* cd
f «
* I
cd
•6*
О л
К cd
3 И
3 Ь
VO о*
о ^
*2 ъ
S £
<D <5
X 2
° S
>3
о
3<
cd ^
к *
На О О
KVA
о о
•&
•&
S S
>а
+
со
И
cvj cd
&■
О о
^ -
4 Ё
Cs 5
■3S
н ч
к о»
си со
5 2
Э-е-
*&• cd
^ £
О £
^ я
СЗ
С с;
-е- cd 5
*& £ к
со cd <и
О и, си
^ S £
cd о
II *
сг о 2
0 — 0
■&я"
о
CD
^ Н ^
s°
ЕС
4 LO
н- I
Он^ /\-^
<D o' . н
*<5 Й
00 ,
со
о
4 X
« а о
2 о. с
■с ■■
VS ■ 2.
ь* з
о- а
| о <и
* £
I	CQ
cd cd
l ьс: t(
•&
о
3 <
го
S- *
?°
I § g
I С 3
5"а &
2 с
a g
CD ^
Н
К —
V
+
+
+
+
О
Л
271

Продолжение
Л з К О
* S * 2
^2 5 s sS
■e^g-S 2
о ~ vo tc о
У X X О V
х	2	ч	-&R
о	-	m	о,
о	0	й	s	о
^	ti	н	о
2
•&
is
К о
CL) д
-- с
о
х н
>, к
*Д си
СО к
2 Я
о.
п
к •
ь*
X
о, с^ % -0*
X t( Д1 СГ)
Он О со р
5 _• с с
Ч Л -
X г- О
S’ t °
д ^ з
CD Р-
со ^
2 \о
5 . . ^ " CD
х сч £*,s S
я ° н
&и Sg у
«Й
п 2 й n m
о = и ОнШ
х Я и tt
* 3 5 £
1-г Он я о
X с;
3 з'и
“ •©■> я
S § о S
ГО X X -С
CN !
- г; ;
ч и
о л
ь* >=*
-	% 5
з я
:	о	о
«gg
1 х
VO О
X о
о *
X S
>?0 X
^ й
СО чо ^
О О к
га и с*
*
<1
СО
СО
со
со
=5»
<1
+
4-
4-
<1
•в*
со
•е*
о
°	о	2
f-c я
X	CL)	о
X	сеЗ
CCJ	н	о
5 5
Н
QJ о
К Н
Ч <->
CD х
О
(1) on
о Я
Я 3
X X
2 сх
X .-н
н Я О
о
СЗ
0J
X
•сг ^
сх —
2	я
. 5	^	-
—	ей	<и
L	^	“
X
о е?
<? о S
ц а?
X
4 5
о я
о я
CD
11
и §.«
*8* х
СХ ° Я
р:	си
5 < а
*	я
§ 5
51
Он
\о <j->
- X
S1
X -в"
172
[тру

5.3.	10. Влияние изменения положения центра масс
летательного аппарата на аэродинамические коэффициенты
Пусть аэродинамические моменты известны относительно
начала D нецентральной-I прямоугольной вертикально-симмет¬
рической связанной системы координат Dx\y\Z{ (С211). Коорди¬
наты центра масс при продувке (момент t0) в системе Dx\y{Z\
будут xx(t0), у{ (to), Zi(to).
Если в момент t\ координаты центра масс в системе Dx\yxZ\
будут xi{ti), y\(t\), Z\ (t{) (обычно zi(t0) =z\(ti)\To коэффици¬
енты аэродинамических моментов относительно центра масс
в момент t\\
mZl (^) = тг, (t0) — cffl j£Llill_z£LWL .
A
tnZomZo(/0)-cyo fXl f^~Xl ^o)1 ;
A
ml: Vi)=ml: (t0)- 4:[Xl (t])px' ^o)] ;
A
< Ы=< (W + 4	;
mf, (I,)=т!?М + с1: I*'«'>-*';
"h1!' Vi) = m2'(t0)
mz['{t^) = tnz^1 (/o)
1 +
xx (tl) — XX (t0)
^•r.o
ml: (ti)=ml:(t0)- 4:[yi w~yi (ад]
5.4. СИЛЫ И МОМЕНТЫ, СОЗДАВАЕМЫЕ ДВИГАТЕЛЬНЫМИ
УСТАНОВКАМИ
5.4.	1. Типы двигательных установок
Двигательные (силовые) установки создают управляющую
силу — силу тяги, приложенную к JIA.
Сила тяги может быть получена одним из следующих спосо¬
бов или в результате их комбинации:
— от реакции струи рабочего тела, образованного при сгора¬
нии или ускорении вещества, находящегося на борту JIA (реак¬
тивная сила);
— от изменения количества движения части атмосферного
воздуха, проходящего через JIA при впрыскивании в него топ¬
лива и последующего сгорания (воздушно-реактивная сила);
273

— за счет отбрасывания с относительной скоростью некото¬
рой массы воздуха с помощью воздушного винта (сила тяги
винта)'.
Все двигательные установки (условно) разбиваются на че¬
тыре группы:
1. Основные, наиболее часто употребляемые (ракетные, газо¬
турбинные, прямоточные, поршневые двигатели и т. д.).
2. Экзотические (перспективные схемы и типы двигателей, ос¬
новные двигатели на перспективном топливе и т. д.).
3. Комбинированные (турбовинтовые, ракетно-прямоточные
и т. д.).
4. Редкоупотребляемые.
5. 4. 2. Основные характеристики двигательной установки
Основными характеристиками двигательной установки яв¬
ляются:
1. Тяга Р, зависящая в общем случае от скорости полета v
(числа М), характеристик атмосферы и режима работы двига¬
теля яд. Функциональная зависимость для тяги Р имеет вид:
P = P(v, /г, /гд)	(5. 25)
и называется при фиксированном яд = яд высотно-скоростной ха¬
рактеристикой. Для воздушно-реактивных двигателей она за¬
дается обычно графически в виде семейства кривых на плоскости
(Р, v) или (Р, М) с параметром h и фиксированным режимом
я* (рис. 5. 13 и 5. 14), рассчитанных для стандартной атмосферы.
Реактивная и воздушно-реактивная силы задаются в связанной
системе координат OxuynZn (Cl 12), лежат часто в плоскости
вертикальной симметрии ЛА (или в какой-либо ей параллельной
плоскости).	Сила	тяги	Р может быть направлена	под	углом ср^
установки вектора	тяги	к оси Ох\2 (угол срр>0	при	повороте век¬
тора Р против часовой стрелки).
2. Удельный импульс (удельная тяга) /уд, зависящий в общем
случае от скорости полета v (числа М), параметров атмосферы
и режима работы двигателя яд:
/уд = /уд(г'’ k' Яд)‘	(5’26)
Удельный импульс /уд характеризует расход массы (веса)
топлива в единицу времени на единицу тяги:
/ =-Р(Р| Н’ п,,)	(5.27)
У' GceK(v, h, пЛ)
где GceK(v, k, Яд) —секундный расход топлива.
274

Рис. 5. 13. Примерные высотно-скоростные ха¬
рактеристики ТРД с форсажной камерой на
режиме полного форсажа:
Р0— сила тяги на уровне моря при нулевой
скорости
Рис. 5. 14. Примерные высотно-скоростные ха¬
рактеристики ТРД на режиме работы 85%
номинала
275

Рис. 5. 15. Примерная зависимость удель¬
ного импульса /Уд от числа М для пер¬
спективного ПВРД [21]
Рис. 5. 16. Примерная зависимость удельного
расхода топлива Се ТРД от числа М на фор¬
сажном режиме [21]
Рис. 5. 17. Примерная зависимость удельного расхода топлива
Се/Сео ТВД от скорости v при /г = const:
Сео—удельный расход топлива на уровне моря при нулевой ско¬
рости
276

Примерный вид зависимости удельного импульса от скорости
полета показан на рис. 5. 15. Величина, обратная удельному им¬
пульсу, называется удельным расходом топлива Се. Примеры
зависимости СГ(М) и Ce(v) приведены на рис. 5. 16 и 5. 17.
Дополнительными характеристиками двигательной установки
являются:
1. Удельный объемный импульс, определяющий расход объ¬
ема топлива за единицу времени на единицу тяги.
2. Тяга (мощность, расход топлива) в зависимости от режима
работы двигательной установки, числа оборотов двигателя, поло¬
жения рычага управления, поло¬
жения сопла или воздухозаборни¬
ка и т. д. Эти зависимости назы¬
ваются дроссельными характери-
Рис. 5. 18. Примерная зависи¬
мость Р/Ро и nlrio от хода ры¬
чага управления х
Рис. 5. 19. Примерная зависимость мощ¬
ности на валу двигателя Nn, тяги Р н
удельного расхода Сс от числа оборо¬
тов п ТВД
стиками двигательной установки. Примерный характер некоторых
из них приведен на рис. 5.18 и 5.19.
3. Удельный вес двигателя (двигательной установки) харак¬
теризует конструктивное совершенство двигателя по весу. Он ра¬
вен отношению веса двигателя к создаваемой им тяге на стенде.
4. Чувствительность основных характеристик Р, /уд двига¬
тельной установки к отклонению параметров атмосферы от стан¬
дартных значений.
5. Приемистость двигателя — время выхода двигателя на
установившийся режим работы.
Характеристики некоторых конкретных видов двигателей при¬
ведены в табл. 5. 15 (см. вклейку) и 5. 16 (по зарубежным данным).
277

Характеристики экзотических двигателей |7j, [20], [21]
278
Турбореактивный двига-	0—(4—6)	0—35	Водород и атмосфер- Дает возможность полета в
тель (ТРД) на водородном ный воздух атмосфере с большими скоро-
топливе стямп

Проекции вектора перегрузки на оси различных JIA-центрических прямоугольных систем координат
280

?-
сл
О
CJ
+
о,
9-
+
+
+
а
О
О
1
+
?-
9-
9-
ел
X
+
+
2
а
о
-г
ел
II
>-
CJ
ел
С
ел
С
9-
~|о
"Г
II
II
=>
с
+
.г:	сп¬
ел ел
о- 8
I N
£ 1
о.
9-
+
а
с
+
?-
ел о
О ?-
w ел
со. О
С °
'Ч °°-
ел
о °
CJ
+ N
3 +
СО-
с
Q,
9-
О
ИЗ
281

*
о
«=(
О
0-0
и II
«N
+
-Э-
++
о-
+
о
С -Э--
сл м
ср u
С 1—'
сл N
+ +
в а s
с .5 §
+ О +
+
О
I
9-
+
в
+
9-
+
в
2i -
-ь +
+
9-
+
в
■|о
+
+
а
О
CD-
s;
(Л
О
!l
CJ
=
9-
П
+
II
в
CDL
c
СЛ
cn
CJ
N
+
-|o
+
9-
+
е
О
+
CD-
О,
9-
+
в
ч
с
к;
о,
9-
+ Т
- о
и _г ^
- э 2
ее ВС
« о- 2
03
К К
Л н
я о
л Си
«=: я
£ а
я
О Л
t—I с-
Я
я
«=:
на
1 «2 1
я ^ s °
0J щК U
£
о V°c «
Urs^I
b^fs Л
U _ t-
DJ ' о
свП '-
о к
О. Го
282
+ [Z cos 13 + Q sin 3 — Р cos (а + + К] sin (Yc — Ve>
+ <рР) sin (3] cos (Ve — Yc) }

5.5. ПЕРЕГРУЗКА
Векторная мера, характеризующая способность к маневрен¬
ности ЛА в различных направлениях полета называется пере¬
грузкой п. Вектор перегрузки направлен по равнодействующей
всех активных сил^Р* (т. е. всех внешних сил, кроме силы веса,
i
сил от переносного движения, кориодисовых и инерционных сил,
сил, возникающих от учета кривизны и вращения Земли и т. д.),
а его модуль равен отношению модуля указанной равнодейст¬
вующей к весу G:
/
Перегрузкой по заданному направлению называется проек¬
ция вектора перегрузки на это направление.
Обычно вектор перегрузки п проектируется на оси какой-либо
ЛА-центрической прямоугольной системы координат. Выражение
для перегрузок вдоль осей различных систем координат через
аэродинамические силы, заданные в полусвязанной системе коор¬
динат, и силу тяги, заданную в связанной системе координат,
даны в табл. 5. 17. Пересчет проекций перегрузок из одних си¬
стем координат в другие производится по формулам для коэф¬
фициентов аэродинамических сил (см. табл. 5.6а), в которых
коэффициенты аэродинамических сил следует заменить соответ¬
ствующими компонентами перегрузок. При отсутствии соответ¬
ствующего преобразования в табл. 5.6а можно использовать
матрицы табл. 3. 17—3.29.
ЛИТЕРАТУРА
1. Аржа ников Н. С., С а д е к о в а Г. С., Аэродинамика больших ско¬
ростей, изд-во «Высшая школа», 1965.
2. Беспилотные летательные аппараты, изд-во «Машиностроение», 1967.
3. Аэродинамика частей самолета при больших скоростях, под ред.
А Ф. Доновена, Г. Р. Лоуренса, ИЛ, 1959.
4. Бони Э. А., Ц у к р о у М. Д., Б е с с е р е р К. У., Аэродинамика. Тео¬
рия реактивных двигателей. Конструкция и практика проектирования, Воеи-
издат, 1959.
5. Гудков А. И., Лешаков П. С., Райков Л. Г., Внешние нагрузки
и прочность летательных аппаратов, Оборонгиз, 1963.
6. Д о у Р. Б., Основы теории современных снарядов, изд-во «Наука», 1964.
7. Ионные, плазменные и дуговые ракетные двигатели, Госатомиздат, 1961.
8. Краснов Н. Ф., Аэродинамика тел вращения, изд-во «Машинострое¬
ние», 1964.
9. Лебедев А. А., Ч е р н о б р о в к и и Л. С., Динамика полета беспи¬
лотных летательных аппаратов, Оборонгиз, 1962.
10. М а р т ы н о в А. К-> Экспериментальная аэродинамика, Оборонгиз, 1958.
11. Ми еле А., Механика полета, т. I, изд-во «Наука», 1965.
12. Нильсен Дж., Аэродинамика управляемых снарядов, Оборонгиз, 1962.
13. Остославский И. В., Аэродинамика самолета, Оборонгиз, 1957.
283

14. Остосл авский И. В., Стражева И. В., Динамика полета, Тра¬
ектории летательных аппаратов, Оборонгиз, 1963.
15. О сто ела век ий И. В., Стражева И. В., Динамика полета
Устойчивость и управляемость летательных аппаратов, изд-во «Машино¬
строение», 1965.
16. Реактивные двигатели, под ред. О. Е. Ланкастера, Воениздат, 1962
17. Принципы инерциальной навигации, изд-во «Мир», 1965.
18. Чернобров кин Л. С., Аэродинамика самолета, изд-во МАИ, 1950.
19. Э т к и и Б., Динамика полета, изд-во «Машиностроение», 1964.
20. Propulsion and Accesory Equipment. Space/Aeronautics, v. 37,
No. 5, .1962.
21. Research and Development handbook. Space/Aeronautics, No. 4,
1964—1965.
22. Uberschall Verkehrsf lugzeuge. Verlag Techmsche Rundschau, Bern
1961.

Глава 6. НЕКОТОРЫЕ ЧАСТНЫЕ СЛУЧАИ
ДВИЖЕНИЯ ЛЕТАТЕЛЬНЫХ АППАРАТОВ
Основные обозначения
а— ускорение летательного аппарата,
Ci (ut)y Si (ut)—интегральный косинус и синус соответственно,
су—коэффициент подъемной силы,
Ei (и)—интегральная показательная функция,
F (?, р.), Е (<р, р.)—эллиптические интегралы 1 и 2-го рода соответственно,
О—вес летательного аппарата,
(7*— вес пустого летательного аппарата,
AG—вес истекшей массы,
g— гравитационное ускорение,
Я*—характеристическая высота в законе изменения плот¬
ности,
К—аэродинамическое качество,
тп—масса летательного аппарата,
—сек—секундный расход массы,
P—Q
пх— ——— — продольная перегрузка,
и
Пу— поперечная перегрузка,
п1 пУ — cos ®— избыточная перегрузка,
  Р—сила тяги,
Р — Р/G о—тяговооруженность,
Q—сила сопротивления,
Яз—средний радиус Земли,
г— радиус разворота летательного аппарата,
5—площадь летательного аппарата,
6— путь,
t— время,
ц, w—безразмерные проекции вектора скорости на оси прямо¬
угольной системы координат,
Иист— скорость истечения массы,
v— скорость полета,
х, у, z—прямоугольные координаты,
у—угол крена,
г|, £—безразмерные прямоугольные координаты,
0 — угол наклона траектории,
9— угол тангажа,
Q— плотность среды,
Q*— значение плотности среды на высоте, равной нулю,
т— безразмерное время,
Ф— интеграл вероятности,
Ур—угол наклона вектора тяги к строительной оси ЛА,
ф— угол курса.
Индексы:
«О» — обозначает величины в момент / = 0,
«к»—обозначает величины в конечный момент времени.
285

Движение летательного аппарата описывается системой нели¬
нейных дифференциальных уравнений. Однако при некоторых
дополнительных допущениях эти уравнения можно привести
к квадратурам.
В главе приведены решения некоторых частных случаев дви¬
жения ЛА. При этом ЛА рассматривается как точка переменной
или постоянной массы. Глава делится на два раздела: в одном
описывается движение ЛА постоянной массы, в другом — дви¬
жение ЛА переменной массы. В каждом из разделов рассматри¬
ваются прямолинейные (одномерные), плоские (двумерные) и
пространственные (трехмерные) траектории, систематизирован¬
ные по формальному признаку — заданию закона изменения
одного из параметров движения. Все решения получены для ну¬
левого значения угла скольжения (3.
Приведенные в главе решения даны в конечном виде или
в квадратурах, или сведены к функциям, которые затабулиро-
ваны и в основном приведены в тексте или графиках. Если реше¬
ния выражаются через специальные функции, то значения пос¬
ледних можно найти в специальных математических справочни¬
ках [4], [21]. Некоторые решения выражены в квадратурах, кото¬
рые в общем случае в конечном виде проинтегрированы быть не
могут. Их вычисление может быть произведено с помощью из¬
вестных методов численного интегрирования [8], [12].
6.1. ДВИЖЕНИЕ ЛЕТАТЕЛЬНОГО АППАРАТА ПОСТОЯННОЙ МАССЫ
(т=т0)
6.1.1.	Прямолинейное горизонтальное движение (0=0)
Уравнения движения ЛА (см. гл. 4) имеют вид
В табл. 6. 1—6.3 приводится решение системы (6. 1) для ряда
законов изменения силы тяги и силы сопротивления.
6.1.2. Прямолинейное вертикальное движение (0=90°)
Уравнения движения (см. гл. 4) имеют вид
Решение уравнения (6.2) для ряда частных законов измене¬
ния силы тяги, силы сопротивления и т. д. приведены в табл..
m^v = Р Q;
(6.1)
Х= V.
6.4—6.8.
286

6.1.	3. Плоское движение с нулевым углом наклона
траектории (6=0)
Этот случай движения соответствует горизонтальному полету
JIA. Его уравнения движения (см. гл. 4):
m0v = P — O;	^
fn0wb= ~Y sin у;
Kcosy —G0 = 0;	[	(6.3)
x = v COS 6;
z = — v sin 6
или
v = gon'x,
^ —- — — /ZySiny;
v
ny = secy;
x = v cos 6;
z= — v sin ф.
(6.4)
Решение системы (6.4) для постоянных углов крена, угловой
скорости крена, при постоянной силе тяги и квадратичном законе
сопротивления представлены в табл. 6.9, 6. 10.
6.1.4.	Плоское движение с постоянным углом наклона траектории
и при нулевом угле крена (0 = 0о, у = 0)
Уравнения движения (см. гл. 4):
mQv -- Р — Q — G0 sin 90; j
m0v(J = Y — G0 cos 60 = 0; j
X — V cos
y = v sin 0O
(6.5)
или
sin eo);}
Lyo-
^cos 6n
x = v cos 60;
y = v sin 0O.
(6.6)
)
Решение системы (6. 6) при различных законах силы сопро¬
тивления, при квадратичном по скорости законе ускорения даны
в табл. 6. 11, 6. 12.
287

Решение уравнений прямолинейного горизонтального движения JIA при постоянной силе тяги (0 =0, Р=Р0)
288

10	1669
289

Решение уравнений прямолинейного горизонтального движения JIA
при постоянной силе сопротивления (0=0, Q = Qo)
VO
«3
vo
<3
к
о
о
S3
+
< СМ
+
+
+
Ь/З
S3
о
Ь<3
X
I
X
+
+
о
Ъ
Ь/3
+
Ь/.
+
+
Я W
<и н
S -
+
£
+
о
11
О.
£
+
290

о
V
+
+
+
о
£
р
8
о
с/.
I
+
+
с
+
X
X
о
О
ч
SC
о
о
JJ;
С
-/
'-/
S
1
н
-4
+
22
X
10*
291

сО
а,
е=С
сО
3
2
к
X
05
я
о
а.
oj о
Ч*!
s 4-
<-> Т
я СУ
§■ I!
СУ
< .
11
s ^
х w
<u _
* 2
Я 4)
са с;
е* о
X
а,
о
х
я
*5
О
S
Я
а.
со
о.
;>>
О)
я
X
О)
3
Зз
S 4
Ь/3
X
£
CN
+
X
* I СМ
I
£
+
+
Ь/з
+
I
X
X
+
*
с
Ь/)
см
>сс
+
X
X
ья
^Х
■-13
х
+
-Is
+
X
+
£
?<
+
292

*2 gOnxOmO
А
о
К
293

Решение уравнений движения
о
Л
|=С
о
Он
с
I
X
X
I
+
!
I
+
Ь/)
о
Si
s
о
*o
i
*05
1
o/:
X
с
0
"s'
1
•ьг
X
I
*ог
fc/j
a
+
"T
0
bo <=>
1
•ce
x
+
4
S2
о
b/j
X
x
*o
+
4
S2
0
1
*ee
294

V
s
д
's4
I
+
X
X
H
I
о
о
о
д
о
*
с
о
£
S'
с
о
Ъд
о
1
Д
S
I
5
S
1
1
1
г*
+
X
X
с
о
д
S'
+
txo
X
295

296

X
ч
с
X
о
ч
с
X
с'
I
J^
о
1
1
С/
<5
*«£
1
о
ч
с 1
*5
bJD
X
X
+
•ое
297

298

29Э

Решение уравнений движения
300

301

Решение уравнении движения
302

(k— у.)г/0
•ее
I
I
=s>
+
+
о
Ью
7
|
1
о
s
о
о
Н
С
о
0/
)
*<5е
1
»*«
о
1
К
1
>££
X,
4
+
X
+
7
о
Ьо
S
о
S-*
7
|
s;
о
о
Ь/3
ч
о
Ч
1
&
+
T
X
4
ci
I
о
I
WJ>
V
4
s;
<5
+
о
Ь С
с
X
Ь/;
7
0
с
1
ч ? ч
I	1
7
0
*
1
•£*
7
0
н
с
^7
1
303

Решение уравнении движения
304

+
о
O'
O'
li
303

Решение уравнений движения
+
о| о
О к
I
ч«»
О
£
II
0
1
о
и
+
3
Vn>
о] о
0| £
я
си
к
о
о
+
о
CU
С
*
-н ^
Iv
jo —
O'
w
40»
я
s
яГ
ы
я
«
s
я
CU
Я
CT3
CO
О
+
о
O'
l(N
V
+
O'
II
O'
«
я
я
си
С
Н«	«
и	к
<
о
я
о
О
О
О
+
о
о
l(N
V
Ii
306
Рис. 6. 1. Интегральная показательная
функция Ei(*)

307

Закон изменения Решение уравнений движения
О
О
Л
0Q
S
о t
С
х
см СО
0^
о
Ьд
СМ
+
см о
0
1
см
oq
V
I
CQ
О
I
oq
+
cq
s
о
t=t
о
к
о
hQ
\o
о
=;
о
V
oq
s
cu
с
J ^
oq cm
v
i
oq
cm CO
0:Г
о
h/)
04
О
<N CO
0^
О
bo
CM
I
о
a>
I as
с
о со
Б «
СО
о
Tf
I
СМ
oq
+
oq
cq
см
II
— СМ	см	см
5	^	^
3
5 к
К
си
а
VO
о
O'
II
308

Таблица 6.9
Решение уравнений плоского движения Л А при нулевом угле наклона траектории и при постоянной скорости полета
309
Примечание. На рис. 6.2, 6.3 приведены графики для определения радиуса установившегося виража (разво¬
рота) по заданной скорости полета и углу крепа.

Рис. 6.3. График для определения радиуса г установившегося
виража при ^>300 м/сек
310

Решение уравнений движения при показательном законе из¬
менений плотности среды и при нулевом значении продольной
перегрузки, различных законах изменения коэффициента подъем¬
ной силы, а также при постоянном отношении продольной пере¬
грузки к радиусу разворота даны в табл. 6. 13.
6. 1.5. Плоское движение при нулевом угле крена
и при постоянном значении продольной перегрузки
или нулевой поперечной перегрузке (у = 0, пх = пх0 или пу = 0)
Уравнения движения (см. гл. 4):
Решения системы (6.7) при постоянных значениях скорости
изменения угла наклона траектории 0, или поперечной перегрузки
пу, или избыточной перегрузки пу—cos 0, или при различных за¬
конах изменения продольной перегрузки пх0 даны в табл. 6. 15
и 6. 16.
6.1.6. Пространственное движение с постоянной скоростью
(у = у0)
Уравнения движения (см. гл. 4):
Решение при постоянных значениях угла крена, угла наклона
траектории, поперечной перегрузки и тяговооруженности
v = go('ho —sin0);
0 = — (пи — cos 6);
(б. 7)
m0v0 = Р — Q — G sin 9 = 0;
m0v0Q = У cos у — G cos 0;
то'^оФ= — У sin y sec 9;
(6.8)
x=vQcos 0 cos ф;
t/ = z;osin0;
z— —v0 cos 0 sin tp.
В этом случае выполняются соотношения:
(6.9)
ny^cos 0О sec Yo-
311

vc
S3
к
s
—
4
c* II
| £
2 II
?-
ч о;
>i н
л
5 £5
<
О
4
с
*s
5
CQ
ctf
Q.
>>
O'
•S3
-Э“
+
о
•S3
-Э-
c
ЬО
I о
CM
?-
tO
«I»
I
о
-Э-
II
-Э-
+
^ C4
^ cr.
+ о
0%
os
о
A
•S3
-Э-
•S3
-Э-
+
+
bo
<£
bjQ
*
bo
bo
+
b0
a
*«e
*
с
о
bo
*
e
о
bo
•ae
X
I1
s>
312

313

Таблица 6.11
Решение уравнений плоского движения J1A при постоянных значениях угла наклона траектории и силы тяги (0 =0 0* Р-=Ро)
314

Решение, приведенное на номограмме (рис. 6.6), позволяет
найти любую из следующих величин:
— перегрузку пу0;
— аэродинамическое качество К;
— угол наклона траектории 0О;
— угол крена у0;
— величину /Ccosyo, если заданы некоторые параметры из*,
приведенных в табл. 6. 17—6.21.
Определяемые параметры находятся по номограмме на
рис. 6.6 по схеме, представленной в табл. 6.20.
Пример. Дано: /С = 6, — =1, 0о = 5О°. Найти значение попереч¬
но
ной перегрузки пу0.
Решение. По известным величинам Pq/G0 и 0О в соответствии
с табл. 6.20 находится на рис. 6.6 величина К cosy0. Затем по
известному значению К и найденному значению К сosyo опре¬
деляется угол крена у0 = 62°. Далее по известной величине угла
наклона траектории 00 и найденному значению угла крена у0 по
рис. 6.6 определяется величина поперечной перегрузки пу0= 1,4.
Величины в четвертой группе определяются по следующей
схеме. Пусть заданы величины К, Pq/Gq, 0О. Тогда искомая вели¬
чина угла крена у0 определяется по номограмме рис. 6. 6 следую¬
щим образом. Сначала находится точка пересечения кривых
0 = 0о и P/G = Po/G0. Затем через эту точку проводится верти¬
кальная прямая до пересечения с прямой К = Ко. Полученная
точка определяет угол крена уо, необходимый для движения по
заданной траектории.
р
Пример. Дано: К= 6, —0 =1, 0о = 2О°. Найти угол крена у0-
Со
Решение. Находится по рис. 6.6 величина /(cos уо= М2. За¬
тем по известным значениям величин К = 6 и /(cosyo=M2 опре¬
деляется по номограмме величина угла крена у0 = 74°.
Решение при постоянных значениях угла крена
и поперечной перегрузки (у = уо, Пу = Пуо)
Угол курса:
Р о
— тяговооруженность — ;
Со
при n?Q COS2Yo> 1
X arctg
y^ocos2Yo— 1
tiyQ cos Yq Ч- 1
315

Решение уравнений плоского движения J1A при нулевых значениях силы тяги и подъемной силы (Р=О, У=0)
316

VO
сз
о
\о
о
X
.—.
S
со
г?
1
1
V
|
+
г>
*^Г
г>
СМ
1
<м
X
I
V
X
о
V
V
\Q
О
«ч
X
СО
н
I
V
+
+
S
со
*
I
V
+
о
£
гг
X
о,
С
<
ва
си
С
о
S
X
2
а>
си
с
317

Решение уравнений движения
318

319

Решение уравнений движения
320
приведены в табл. 6. 14.

!. Функция УУ(0, пуо) определяется по формуле
о
=5>
s:
+
н
о
=5>
С
ехГ
СО
11	1669
+
м
V
+
СО | СМ
Й3
о
=s>
с
+
V
СМ
с
5 | СМ
biO
о
ал
с
+
V
с
е
|е
Я
X
X
ас
>>
■&
ас
со
=3>
с
X о
03 со
СЛ
О
«“с
g!>
а> -к
ас 1
Э °
ГО й
а,
?*-> л
ас
v as
Я ЕГ
Я Я
а ф
ф и
а. _
го
»я с
и”
а о
Н -5!
О «
О V
a s
а
_ <v
СО д,
го
а а
а го
си
О 0:1
н
а
Ф X
го
о. S
ф
lO
со
со
о
а
о,
го
а
го
СО
а в
оО
5 го
го а
а а
а
^ £
о ^
U <1>
^ го
a g
с ^
5 <-*
w -
h-
Ю со
321

0	JO	60	30	120	150	180	6°
Рис. 6.4. График функции
2
®i(Mw) = —,	—- агс tg
Vя'*-
(/
пУ0 + 1
пУ0— *	2
Рис. 6.5. График функции
$1 (М*ю) = 1п
/1 + %0 tg + V1 — пУ0
1Л + Пуо tg ~Y— V"1 — %о
322

Таблица 6.14
6
Г dx
Значения интеграла /(0, пу0) = \
J (%о-COS Х)Ь
о
Пере-
грузка
Угол наклона траектории 0е
пУ0
10
50
30
40
50
Си
70
80
90
1,5
2,6836
4,8227
^,2343
7,0563
7,5054
7,7460
7,8774
7,9517
7,9938
2,0
0,1725
0,3232
0,3801
0,5351
0,5978
0,6402
0,6686
0,6877
0,7009
2,5
0,0341
0,0-54
0,0925
0,1114
0,1313
0,1440
0,1534
0,1603
0.1655
3,0
0,0108
0,0210
0,0300
0,0378
0,0441
0,0491
0,0531
0,0562
0,0586
3,5
0,0071
0,0087
0,0125
0,0159
0,0188
0,0211
0,0231
0,0247
0,0260
4,0
0,0021
0,0042
0,0061
0,0078
0,0093
0,0105
0,0116
0,0125
0,0133
4,5
0,0012
0,0023
0,0033
0,0043
0,0051
0,0058
Q,0065
0,0070
0,0075
5,0
0,0007
0,0013
0,0020
0,0025
0,0030
0,0035
0,0039
0,0042
0,0045
5,0
0,0003
0,0005
0,0009
0,0011
0,0013
0,0015
0,0017
0,0019
0,0020
7,0
0,0001
0,0003
0,0004
0,0005
0,0006
0,0007
0,0008
0,0008
0,0009
8,0
0,0001
0,0001
0,0002
0,0003
0,0003
0,0003
0,0004
0,0004
0,0005
9,0
0,0000
0,0001
0,0001
0,0002
0,0002
0,0003
0,0003
0,0004
0,0004
10,0
0,0000
0,0000
0,0000
0,0001
0,0001
0,0002
0,0002
0,0003
0,0003
Продолжение
Пере¬
грузка
Угол наклона траектории 0е
Чо
90
100
110
120
130
150
160
170
180
1,5
7,9938
8,0244
7,8606
8,0550
8,0649
8,0779
8,0829
8,0876
8,0922
2,0
0,7009
0,7102
0,7269
0,7219
0,7259
0,7321
0,7344
0,7366
0,7388
2,5
0,1655
0,1694
0,1725
0,1748
0,1768
0,1799
0,1812
0,1824
0,1835
3,0
0,586
0,0605
0,0621
0,0634
0,0644
0,0662
0,0669
0,0676
0,0683
3,5
0,0260
0,0270
0,0279
0,0271
0,0291
0,0303
0,0308
0,0312
0,0317
4,0
0,0133
0,0139
0,0144
0,0149
0,0153
0,0160
0,0163
0,0165
0,0168
4,5
0,0075
0,0079
0,0082
0,0085
0,0088
0,0092
0,0094
0,0096
0,0098
5,0
0,0045
0,0048
0,0050
0,0052
0,0054
0,0057
0,0059
0,0060
0,0062
6,0
0,0020
0,0021
0,0022
0,0023
0,0025
0,0026
0,0027
0,0027
0,0028
7,0
0,0008
0,0009
0,0011
0,0011
0,0012
0,0012
0,0013
0,0013
0,0015
8,0
0,0005
0,0005
0,0006
0,0006
0,0007
0,0008
0,0008
0,0009
0,0010
9,0
0,0004
0,0004
0,0004
0,0004
0,0004
0,0005
0,0005
0,0005
0,0005
10,0
0,0003
0,0003
0,0003
0,0003
0,0003
0,0003
0,0003
0,0003
0,0003
11*
323

+
X
X
сГ
&
'Ил
см
+
X
-(
X
CD <х> .
Г с - '
^ 'от с 1К о?
ЭД * кД
СЧ	 <л
51 g '1
CJ 1""ц
Hi |[:
+ OI
<м Ч j ЛГ
+
- , dl К
Si X
X X
+
X
к:	сл
II	s
в	I
325

326

+
о
Ч
С
*ъв|4?
+
X
X
4~
о
II
. С
1§
V
о
Ч
С
X
+
. с
е
I
£-|<n
+
X
327

Решение уравнений движения
О) <и
и
с'
X
г*
С
+
5?
1
+
/—ч
О
<D
CD
О
О
ч
X
С!
С!
СМ
СМ
✓
со
СО
о
О
=3>
С
с
1
/—V
CD
Ш
О
©
Ч
о
С
ч
СМ
✓
1
С
X
С
СМ
X
*5?
Ью
+
С!
СМ
С!
со
+
X
с
см
с
+
с;
см
с;
см
(N ^
С!
X
с»
С
С
СМ
с;
со
X
с;
к:
+
X
+
X
X
I X
с;
55»
с
* •&
X
с
& Ьс
ct
с;
328

329

Решение уравнений движения!
X
X
ч
с
(N
=5>
=5>
с
+
С
СМ
с
см
+
^ о
С
см
:з>
с
:з>
с
1*0
с
см
I ‘i
®- ,S
00
+
•—	=п
X	II
X
+
X
:з>
с
ч
с
*0
X
ьо
•е*
ьо
+
§
с
■V
<N ^
I с
ч
с
ч
с
о
\о
о
X
X
\о
03
0Q
о
ч
с
:з>
с
г*>
С
+
+
о
s?
С
+
о
CS ч
С
X
к
X
X
ч
с
=з>
С
X
а.
с
* * s ¥
са«55
m s g *
330

331
/=3(0. 0)= 2(п2„0-1) L(%o-cos0)2

Решение уравнений плоского движения J1A при нулевом значении поперечной перегрузки (пуо = 0)
332

333

Решение уравнений движения
«я
н
«
ч
о
С
А
н
и
о
О.
О
ж
U
X «с Ж
«I о *
г*£
5
п
S
X "
ч р.
о ь
§о.
CQ
334

Примечания. 1. Интегралы, определяющие величины х, у, t, вычисляются приближенно.
2. В формулах использованы интегралы 1\ и h при некотором среднем значении угла наклона траектории 0Ср-
Обозначения:
335

^ COS Y0
Рис. 6 .6. Номограмма для определения параметров движе-
ния летательного аппарата при развороте с постоянной
скоростью
336

Таблица 6.17
Первая группа задаваемых и определяемых параметров
Заданный параметр
Параметр, определяемый по номограмме
рис. 6. 6
УголАнаклона траектории 0О
Угол*'крсна уо
Поперечная перегрузка пуо
Угол наклона траектории 0О
Поперечная перегрузка пу0
Угол крена у0
У юл крена уо
Поперечная перегрузка пуо
Пример. Дано: 0О = 50°; у0 ~ 20°,
днтся поперечная перегрузка пуо — 0
Вторая группа задаваемых i
Угол наклона траектории 0О
. По номограмме на рис. 6.6 нахо-
>,69.
Таблица 6.18
w определяемых параметров
Заданный параметр
1
Параметр, определяемый по номог| амме
рис. 6. 6
1
Угол наклона траектории 0О
Велич! на К cos у0
Тяговооруженность Pq/Gq
ТяГОВООруЖеНИОСТЬ Pq/Gq
Угол наклона траектории 0q
Велич! на К cos у0
Тяговооруженность Pq/Gq
Величина К cos уо
Пример. Дано: 0О — 30°, К cos у0
определяется тя1 овооруженность Р0Ц
Третья группа задаваемых
У юл наклона траектории 0О
= 10. По номограмме на рис. 6.6
JQ = 0,59.
Таблица 6. 19
и определяемых параметров
Заданный параметр
Параметр, определяемый по номограмме
рис. 6. 6
Тя1 овооруженность Pq/Gq
Угол наклона траектории 0О
Аэрод! намическое качество К
Поперечная перегрузка nyQ
Тяговооруженность Pq/Gq
Угол наклона траектории 0О
Поперечная перегрузка пуо
Аэродинамическое качество К
337

Продолжение
Заданный параметр
Параметр, определяемый по номограмме
рис. 6.6
Угол наклона траектории 0О
Поперечная перегрузка пуо
Аэродинамическое качество К
Тяговооруженность Pq/Gq
Тяговооруженность Pq/Gq
Поперечная перегрузка пуо
Аэродинамическое качество К
Угол наклона траектории
Таблица 6. 20
Схема определения искомых параметров
Этап оп¬
ределения
Заданный параметр
Параметр,
определяемый
по номограмме
рис. 6. 6
Этап оп¬
ределения
Заданный параметр
Параметр,
определяемый
по номограмме
рис. 6. 6
1
Pq/Gq, бо
К cos у0
1
Пуо. «0
То
2
К cos у0, К
То
2
Yo. К
К COS Yo
3
То, G0
пУ0
3
К cos Vo. во
Po/Gq
1
Ро Gq, 0Q
К cos Yo
1
Пуо, 00
То
2
Go. %0
То
2
V0. К
К cos Yo
3
Y0, К cos То
К
3
К cos Yo. Pq/Gq
Go
Таблица 6.21
Четвертая группа задаваемых и определяемых параметров
Заданный параметр
Параметр, определяемый по номограмме
рис. 6. 6
Тяговооруженность Pq/Gq
Угол наклона траектории 0О
Аэродинамическое качество К
Угол крена уо
Тяговооруженность Pq/Gq
Угол наклона траектории 0О
Угол крена Yo
Аэродинамическое качество К
Угол наклона траектории 0О
Угол крена у0
Аэродинамическое качество К
Тяговооруженность Pq/Gq
Тяговооруженность Pq/Gq
Угол крена у0
Аэродинамическое качество К
Угол наклона траектории 0О
338

при /z20cos2y0<1
Ф=% —tgYo1п
tg
(М)
tg Yo
tg + А')	Vt	п1о cos2Yo
X
X In
(1 + пуо cos Yo) tg — — V1— л20 cos2 Yo
X
(1 + nyo cos Yo) tg — + V1—■«20 cos2 Yo
X
|\l + ny0 cos Yo) tg -у + V1—«40cos2 Yo
[o + nyo cos Y0) tg -у — V 1—n20cos2 Y0
при nyQ COS Yo = 1
/ n e \
tg — + —I
Ф=% - tg Yoln —Ц  	+ tg Yo (ctg -y - ctg^-j .
tg
(JL,1L
V 4	2
Время полета:
при «20COS2Yo> 1
2t>n
V"4ocos2 Yo—1
arc tg
(%0 cos Y0 — 1) tg —
V n20cos2 Yo—1
(%0COS Yo — 1) tg •
— arc tg
при ti2y0 cos2 Yo < 1
t = -
»o
ln
V«20cos2Yo— 1
jo + ni/0 cos Yo) tg -у — V1—n20cos2 Yo
So У 1 »yocos2 Yo j |^(1 + riyo cos Yo) tg -у + V1—n20cos2 yoJ
r	0	 •
1(1 + nyo cos Yo) tg + V1—n20cos2Y0
X
X
|o + ny0 cos Yo) tg -у — V1—n20cos2Y0j
339

при пу0 CQSYo^l
Координаты
t
x=x0-}-v0 j* cos 6 cos 0 dt;
0
t
У = Уо+г'о f sin 0dt\
0
t
z = zQ-{-vQ j* sinф cos 0 rf/.
0
Приведенные интегралы вычисляются приближенным спосо¬
бом [8], [12].
6.2. ДВИЖЕНИЕ ЛЕТАТЕЛЬНОГО АППАРАТА ПЕРЕМЕННОЙ МАССЫ
ПРИ ПОСТОЯННОЙ СКОРОСТИ ИСТЕЧЕНИЯ МАССЫ
(m = var; «ncT = const)
6.2.1. Прямолинейное горизонтальное движение (0=0)
Уравнения движения (см. гл. 4):
mv= —tiHCTm — Q\
x=v.
Решение уравнений движения (6. 10) при различных законах
изменения силы сопротивления приведены в табл. 6. 22.
В табл. 6.23 приведены значения функции — In (1 —
\ то /
облегчающие вычисление решения при отсутствии силы сопро¬
тивления.
6.2.2. Прямолинейное вертикальное движение (6=90°)
Уравнения движения (см. гл. 4):
mv= — иИС1.т — Q — G;
y = v.
Решение уравнений движения (6. 11) при постоянной плотно¬
сти среды и различных законах изменения силы сопротивления
приведены в табл. 6.24—6. 26.
340
(6.11)
(6.10)

Решение уравнений прямолинейного горизонтального движения ЛА (0=0°)
Решение уравнении движения
341

Решение уравнений движения
342

Таблица 6.23
(	жсек	\
Значения функции — In 1 — t
\	т о	/
тсек
in 11 Шсек Л
т0
‘т щ Ч
0,1
0,1054
0,2
0,2231
0,3
0,3567
0,4
0,5108
0,5
0,6931
0.6
0,9163
0,7
1,2040
0,8
1,6095
Примечание.
Функцию — ln^l — t
можно аппроксимировать зависимостью
^^сек	/?2сек
	с	точностью	1%	для	t <
niQ — 0,omceKt	/72	о
тсек
< 0,3 и с точностью 2% для 	^	<	0,4.
т0
Таблица 6. 24
Решение уравнений прямолинейного вертикального движения J1A
при постоянном ускорении (0=90°, u = a=const)
Закон изме¬
нения силы
сопротивления
Решение уравнений движения
Масса
Скорость
полета
Пройденный путь
о
II
O'
a+go f
т = т$е ^ист
v=v0~\- at
1
У — у 0= V0t + — а/2
q = q0+№
(k = const)
/ ([ 1
/72= в ИСТ { /720—	X
1 а-\~ So
a + go i
}<е "ист [Оо + *(*'о+^ —
<г“ЯСТ')2+
а + go/ \a+^o/JJ
v=Vq Л-at
у—yo=Vot+ at2
343

344

\*t \ 5
со
I!
;>
x
к
s
a
»
к
>»
+
cs
II
7*
o£i
a
0 to
1 5
co Oi
VO 2
о V
CO
s*
S >—'
4
vo «
CO 1=3
н о
о
CQ g
^ s
s
s в
к >->
СО *©н
5 I
s ^
Oh -
i—i *
+
•oe I
о
£ I
+
7<\ 7*
a*
с
N
С
о
<->
I&I f
а
*
о
о,
3
и
к
4
'к
N
к
N
>»
*&
;>
S
си
С
Ю
К
К
а
а
в
>»
*&
-Н
к
си
С
си
с
345

Таблица 6. 26
Решение уравнений прямолинейного вертикального движения J1A при переменном гравитационном ускорении
о
а>
0?1
5S1
Ъо
II
Ь*)
+
a
с
СМ
+
jS§§
§
CS ГО
or
см
+
5	*	.
55	ГЗ	<_ 1—1
О	5	X!	Ч	f
м	<=>	я	СО	°СМ
II	m	a	o.w —
Оуо
О О
S' h s,
s я. ^
h Slbuj
i^l ^
cn\
Г0
Qc
fc?
CM
csfo
or
b*)
X
о
346

6. 2. 3. Плоское движение в вертикальной плоскости
Уравнения движения (см. гл. 4):
mv= — иистт + Р — Q — mg0 sin 0;
mvd = Y — mgQ cos 0;
x = vqos 0;
(6.12)
^==^sin0.	)
Решения системы (6.12) при различных законах изменения
продольной перегрузки и угловой скорости, силы сопротивления
даны в табл. 6.27.
6. 2. 4. Плоское движение при линейном изменении
тангенса угла наклона силы тяги по времени
и при постоянном значении силы тяги
Закон изменения тангенса угла наклона ф силы тяги к оси
абсцисс
tgcp = (Ti-TK)
tg <Ро
1 хк
tg?K
1 — Тк ’
(6.13)
где tj —отношение мгновенной массы к начальной,
тк —отношение конечной массы к начальной,
а —отношение скорости горения к начальной массе,
= — =	=	(p.2	+ tgc?)-
т0
Уравнения движения (см. гл. 4):
Л)
Х=— COS ср;
т
У = — sincp-go
т
(6.14)
или
Т=Шо±и..
_m0goa
р О
_mog0a
•W
Ро
cos <р;
sincp —
/mo£oaj2
где
gox
\ Ро
go‘J
(6.15)
-Т
Р о V2
т0а)
W-
/720а
т0а
(6.16)
— безразмерные величины.
347

Решение уравнений плоского движения J1A переменной массы
Решение уравнений движения
348

349

350

+
о
£
О
vo
о
CQ
ti cm
2,
(n
CU
с
3ol

352
Для облегчения вычислений Xq и Yq на рис. 6.8 приведен график функции w—

:s
■в-
(?•»
* I a
I ’
С
a
1669
35o
1 + v

Значения функции Yq (i/j)
op
См
<©*
a
a
a
К
0-1
о
го

N
гг
го
оо
	,
Ю
ю
02
со
го
к
.
04
гС
оо
ОС
rf
O'!
ОС
о
D-
о
CD
CM
о
—г
о
t--
04
иС
ю
oo
С—•
1C
оо
со
—1
rT
Г»
о
ГГ
02
ГГ
—1
а:
ОС
02
Ol
t--
LC
гс
о
оо
о
^_7
_7
__7
04
О)
О)
ГО
г-"
тг
to
гс"
ОО
02
_7
со"
гс
оо
Ol
■
’ 1
’ 1
1
О!
OD
го
оо
Е--
iC
ГО
го
,
04
,Г
го
ю
ГГ
iO
05
оо
ОС
со
04
LO
Г"-
02
rT
02
о
СО
1C
ОС
LO
CD
C4
о
-о
CO
о
'Г-
ГО
оо
гГ
1-С
оо
1-С
04
гГ
•—1
ГГ
V-
о
ГГ
CD
гГ
—<
CD
00
02
О!
ОО
гс
D-
04
о
1—t
1—-
—1
04
04
04
СО
ТГ
ТГ
ьо
го
ОС
02
—1
СО
гс
02
О)
11
1
- '
0-1
о
о
to
04
о
00
bQ
00
гс
О
О
_
гс
о
CD
ГО
ГГ
02
о
ос
LO
гс
ГГ
СО
00
СО
о
05
ГО
о
-т
гг
о
ю
ГГ
-Г
о
гГ
о
04
Г—
•d4
Г-~
о
ГГ
02
гГ
CD
ос
О
СО
CD
Г—
02
гГ
СО
с^
°
—7
_Г
_7
04
04
оГ
СО
гг
гГ
ьО
г-7
00
02
—7
СО
гс
02
04
- 1
1
’ 1
0-1
T_1
to
_М
го
04
го
ю
Ю
lO
О!
о
С4
го
о
о
ГГ
ГО
оо
ю
02
СО
ГГ
——4
D—
С—•
>с
О)
Ю
CD
CO
ОО
Ю
:Р
00
гс
СО
04
о
04
ГО
•d4
о
гГ
02
гг
02
02
о
СО
02
00
О
гс
гс
—
о
,_7
_7
1—г
О)
04
04
СО~
’Г
ю
00
02
—Г
гГ
гс
02
Г^
1
1—1
04
CO
CD
04
о
го
гГ
О
СО
02
о
	,
О
С-)
гс
о
го
iO>
04
00
ю
гс
02
*^г
г-
ГГ
©
CD
ГО
ГГ
гГ
04
CD
го
Г-
СО
04
04
LC
оо
оо
ГГ
t—
о
гГ
02
гГ
02
02
О
гГ
О
02
D-
оо
L-C
°
^_7
_7
—Г
04
оГ
04
СО
•'Г
гГ
LC
Г-
ОО
о"
—Г
гГ
гс
02"
ГО
1—1
*
0-1
iC
CO
,
iC
,
04
О
ГГ
СО
гс
04
04
LC
rvO
04
г-
00
го
Г—
г-
ОО
СО
04
D-
о
оо
04
гс
VC
02
ГО
ГГ
ГГ
04
02
t--
оо
1C
О
гс
00
о
00
D-
ГТ
1—1
rr
г77
о
ГГ
02
гГ
—1
02
02
-г
О
о
04
02
оо
о
		1
—1
1—1
OJ
04
04
го
гГ
-г4
LO
Г—
00
о
04
гГ
гс
о
СО
‘
’ 1
1—1
1
04
0-1
го
00
г-
02
CO
О
го
04
оо
02
	,
Ю
ГО
SP
04
00
о
О
04
—<
Г'"'
04
О
о
02
СО
02
гс
гс
о
02
CO
'ГГ
lO)
ГО
О
со
о
о~
ьс
02
1<С
—ч
Г-
СЧ
ГГ
г-
о
ГГ
02
Ю
—
О
02
—1
LC
О
гГ
гГ
О!
о
_7
_7
^_7
О!
04
04
СО
rjT
L-C
LO
Г—
ОО
о
04
гГ
г-7
о"
-ц"
’ 1
11
04
ol
!>•
04
го
ГО
с-
00
ю
о
СО
гс
гГ

го
04
ГО
о
04
ГО
ОО
L-O
со
СО
ГО
О
гГ
02
02
о
VO
CD
ro
ю
iC
ГО
О
CD
'О
1C
02
гГ
гГ
ОО
г-
■’■"I.
ГТ
Г—
о
ГГ
02
ю
i—i
о
О-
—•
1C
04
—1
LC
СО
гс
гс
©
,—1
,—1
.—,
04
04
04
СО
гГ
Ю
1-0
D—
оо
О
О)
гГ
г-
О
гг
1
1
1
04
04
CD
Ю
Ю
ОС
04
го
Ю
ГО
гГ
оо
02
02
го
CN
гГ
1C
г-
гГ
ОО
О
гс
<-Г!
02
04
ОС
со
о
02
ro
iC
ю
ГО
О
0-1
С2
02
Г—
об
Г—
—С
’"С
rr
г-7
о
ГГ
02
ю
04
о
о
LO
04
04
гс
ю
02
о
о
_7
_7
_Г
О!
04
оГ
СО
гГ
1C
гс
00
о"
04
ГГ
г-
О
ю
- 1
1—1
1
04
0-1
CD
ГО
04
ГГ
гГ
iC

о
О-
О
00
ОО
'
D-
04
ю
ГО
с-
О
04
со
О
О
D-
гс
о
Ю
ОС
£
CD
CO
1.0)
гг
04
СО
О!
-Г
Г—
гГ
1C
ОС
ГГ
с-
о
гГ
02
iC
04
о
о
04
гс
СО
СО
00
D-
0-1
ГГ
[
to
	,
^.7
_Г
04
04
CN
СО
U0
гс
г-~
00
О
04"
гг
—Г
ю
“4
■ '
О)
0-1
04
CO
о
го
оо
ГО
иО
гс
1C
Г—
02
04
|
CO
гГ
ю
04
LC
о
О
гс
—н
СО
—-1
О)
о
CD
ГО
V5
lO
гГ
04
04
1C
>-С
L- Г
ОО
о
D-
LC
—1
о
Г-
-г
02
ю
CN
о
о
04
гс
02
1-С
02
о
_7
__7
_7
О)
оГ
04
со"
-г
Ю
гс
ю
00
с"
04
—Г
t-7
_7
1C
1
’ 1
^1
^1
04
04
1 -Г'
г-~
04
Г-
1
00
00
Г-
гс
-Г
04
О
г-
ГО
1 D
GO
го
~Т
о
о
-г
LO¬
о
• о
-Г
ьС
гс
ГО
ГО
CD
Ю
-Г
г-
гГ
го
ю
£
Г^1
оо
04
02
04
оо
0-1
ГО
f-
02
ГО
го
02
СО
GO
о
оо
02
0-1
02
ОО
04
О
" *4
о
о
04
04
ГО
iC
оо
02
D-
о
о
о
о
о
О
О
О
о
CD
О)
CD
О
о
О
—_
—
02
о
—'
о
CD
CD
О
Cd"
о
о"
cd"
CD
02
о"
о
о"
О
354

ГО
	,
to
СО
Тр
со
05
го
3
СО
—
~м
05
Г-
оо
^М
50
3
> с
3
о
СО
О
05
.04
О!
О
50
tO
Г"
о
тг
со
оо
ОО
О
СО
Г--
ГО
О
см
‘О
—’
05
о
3
—1
iO
05
тр
гм
см
о
СО
tO
Г-"
о"
СМ
-Р
о
ГС
з"
05
го
50
—г
Т-Г
Р^
з"
-Р
ОС
го
о
го
оо
СМ
см
СМ
СО
го
го
ГО
-гг
-ГГ
-Р
-Р
to
tO
50
50
50
Ю-
р-~
р^
оо
ОС
05
05
ГО
тр
см
—
50
—,
со
р»
со
—г
50
—,
тг
о
05
»о
05
г-
05
05
50
оо
р-
тр
з
50
-ГГ
р-
ос
тр
тр
О
3
см
см
со
50
о
50
ТР
-гг
to
• о
-гг
р»
СО
з
со
см
50
lO
-гг
О
о
тр
50
оо
О
со
to
сс
—7
тр
Р^
_г
to
оГ
-гг
t>
_г
ю
05
р
ОО
ГО
о
см
СМ
о»
го
го
го
со
-тг
тт
-гг
LO
to
LO
50
о
р-
р-
ОС
О5
о
—1
—1
Р-
о
00
о
05
-о*
г-
го
ос
ГС
ос

О
50
50
-гг
оо
см
to
о
см
о»
см
CM
50
—(
ОС
СМ
!>•
О
05
ГО
00
50
ю
р^
о
о
р-~
05
р-
ОС
тр
50
1:0
ОС
ГС
30
з
тр
50
оо
—Г
го
50
05
см
50
з"
со
ОС
см"
«с
_г
»о
о
>с
—Г
ОС
ОС
-тГ
тр
0-1
СМ
см
СО
СО
го
СО;
-О1
тр
тр
t-O
t-O
со
о
о
ОС
ОС
05
05
О
см
см
ю
тр
05
р-
СО
05
г—
СМ
оо
о
о
СО
ю
г—
05
ОО
со
50
50
тр
—ч
о
см
СО
со
05
о
-гг
г-
см
3
тр
оо
05
ОС
05
см
ю
О
Р^
50
Г"
о
з
о
Г--
О:
х>
05
см
ГО
Ю
-гг
50
СМ
о
to
05
oi~
ТР
о
тр"
Р—
_г
50
о
to
_г
50
о"
50
СМ
05"
ОС'
50
оГ
см
см
см
см
го
ГО
СО
-ГГ
-гГ
тр
ьо
ю
50
о
о
оо
оо
05
05
О
0-1
тр
0
00
CO
00
CO
CM
50
р-
CM
00
05
00
50
CO
to
ГО
50
00
00
CO
тр
го
to
-tP
to
50
05
05
iO
50
CM
p-
oc
CM
to
P-
uo
50
05
to
тр
p-
-P
50
ТГ
0
0
to
00
0
оо
-r
30
0
to
r-
0"
CM
to
oc
—г
to
05
P"'
00
CO
05
50
3"
CM
0
OC
oT
tO
50
t-O
01
CM
CO
CO
CO
CO
ТГ
тр
-Гр
io
to
50
50
0
30
00
05
0
О
CO
2
CM
CM
05
to
50
о
05
to
05
,	.
50
to
50
CO
CO
CM
00
0
CM
to
p-
50
CM
CM
00
Ю
CO
05
Ю
0
CO
00
to
тр
f-
01
0
CM
05
0
00
CO
0
-ГГ
00
-p
30
CO
CO
Г-
0
50
00
0
CO
50
05
со
_7
to
—Г
50
CO
0
50
CM
0"
oc
05
со
~-T
30
-rp
CM
01
CO
CO
CO'
CO
-гг
тр
50
Ю
50
50
p-
30
30
05
0
0
Ю
50
05
0
50
CM
О
30
CM
CM
—1
CO
CM
Tp
50
LO
ro
p-
CO
50
5 M
CM
Ю
50
0
тр
p-
CO
05
CO
Г0
тр
О
ГМ
-Tp
00
Tp
CO
тр
00
uo
50
-4
CM
30
Ы
Tp
05
-P
OO
тр
oc
г-
05
ГО
—1
О)
CO
00
__T
тр
Г-
0"
Tp
00
CO
00
CO
0"
p-
lO
CM
05
OC
oc
_г
ОС
Ю
•О
см"
CM
01
CO
CO
CO
тр
Tp
тр
1/Г
L
50
p-
p-
30
05
05
О
—1
гО
тр
сл
го
—<
—1
—•
—1
Pi
01
-Tp
CO
05
05
0
_,
05
50
0
-Tp
CM
TP
CM
05
OO
lO
LO
0
CO
00
OC
—1
50
50
05
Tp
CO
05
05
ГО
CM
p^
30
05
0
0
00
Г0

05
Ю
го
0
50
05
cm"
tO
30
__7
0
0
LO
0
50
ro
CM
—Г
05
p-~
О
50
Г—
ОМ
_?
го"
CM
CM
CO
CO
CO
TP
Tp
LO
LO
50
50
p^
00
05
05
0
—1
го
тр
о
о
го
30
—1
—1
—1
—*
—'
.м
О.1
см
CO
CO
CM
CO
CO
tO
00
00
50
CM
0
тр
CO
CO
—1
CO
CO
0
Tp
0
05
0
05
О
50
CO
—-<
50
50
-Tp
0
OO
05
тр
Cm
ТГ
—'
ТГ
CO
—'
OC
0
OO
Ю
Ю
o>
50
—1
ОС
30
05
о
v^T
0
CM
tO
Oi"
CO
r^-
CM
p^.
со"
0
Г-
0
Г-
5o"
50
00
ГО
гр
о"
50
50
-Р
CM
CO
CO
CO
CO
•^p
rr
to
to
50
p-
1^-
30
05
О
—
CM
-р
505
ГО
1 о
—
—1
—•
—1
—1
О!
ом
СО
-Tp
со
50
CO
lO
pr
t.O
01
30
to
CM
01
-p
CM
0
CO
CO
tO
30
05
Ю
00
L(0
OC
50
—-
50
ОО
05
50
to
OO
-P
-P
05
0
50
1 г
CM
-p
OO
to
05
О
со
00
50
lO)
о.
1^-.
0
CO
50
Tp
30
-P
505
50
го"
CM
CM
-m"
50
О
оГ
~о
30
50
тр
01
CO
CO
ГО
-P
-p
LO
tO
p-
30
05
0
—H
CM
тр
tO
оо
ОО
го
LO
—>
—I
—1
—4
—<
—•
гм
см
го
-р
Г—
-Tp
Ol
tO
t--
30
LO
01
50
CO
CM
CO
to
CM
1—1
—I
OC
—<
tc
t-
-p
CM
CO
P"
to
OO
Ю
05
T-
ro
05
тр
LO
0
05
О
—1
тр
тр
ТГ
50
3)
CO
—г
TP
r^-
__7
tO
0"
to
CM
05
p-
50
30
CM
-p"
P-
Ю
р-
р->
го"
гС
05"
—Г
CM
CO
CO
CO
Tp
-P
to
tO
50
oc
05
.—1
Ol
ro
LO
р-
О
ьЬ
го
г—1
о
—'
—1
—1
—1
—1
СМ
05
ГО
-Р
'О
-р
50
о
го
to
го
05
00
го
СМ
50
05
3
00
р-~
-г
3
Тр
30
—.
to
3
Р-.
см
го
-р
ГО
50)
го
to
0
р-
3
см
см
Г--
оо
3
3
3
го
05
см
30
05
оо
05
тр
to
ОО
-Р
3
3
?0
ю
р-~
3
р-
-р
50
го
Тр
р-
см
2
05
00
30
30
3
р-
г-~
оо
го
3
3
ГО
3
со
о
05
со
0
тр
3
Гр
3
3
тр
—1
см
ы
05
05
05
ГО
го
го
тр
тр
L С
to
3
со
ОО
3
3
3
о
о
о
о
о
о"
о
50
50
о"
О
3
3"
3
з"
з"
з"
3
3
3
з"
з"
з"
355

Решение уравнений движения в безразмерной форме (6. 15)
представляется в виде:
— безразмерные скорости
tg
~Ь
а —ил — cos 6n In -
tg
?0“b
W = Wn
tr — i
1 , /l-fsin? 1 — sin<p0\	/	ч
vln 1	7~I —J*s(«-«o);
2	\ \ — sin cp	1 ~f- sin C30/
(6.17)
— безразмерные координаты
где
-=г + ир-т ш,__ецп
(г
4- sin 9 cos fo \ .
*1=V
4-sin'fQ cos <
fJ-t
)=
tv
!j-2= t§'1
2p2 f}
TK—1
tg Tk — tg ?0 ’
. tg Тк — Tk tg To
-t- (sec cp — sec ft),
’0"
tk — 1
(6.18)
m0 a
Частный случай. Вертикальная скорость в конце раз¬
ворота Л А равна нулю ^док = -у- =oj.
Если о/к=0, то после разворота Л А переходит в горизонталь¬
ный полет, В этом случае решение дается с помощью кривых
Вводятся функции
tg
-t- Bn
4t = — cos 60 In
tg
1 ,	/1	— sincn 1-f- sin	,	.	л
^-2 = — In '°	+	'K	stu	80;
2 \l + sinTo t — sinTKC
, (tk — l)(secTi< — sec?o)
(6.19)
tg To - tg T,c
356

Эти функции выражаются через начальные и конечные зна*
чения основных параметров
03=тк?кдл
Vl	^0’
1 .
где
2ткРк
лп^=ок-л0;
(6.20)
Графики функций фь фг, фз строятся для заданных значений
Фк, тк в зависимости от величины начального угла наклона век-
V/
Рис. 6.9. График функции г|ч
тора тяги ф0. На рис. 6.9—6. 11 приведены графики функций фь
ф2, Фз для фк = 0 и нескольких значений тк в диапазоне от 0,05
до 0,9. Вычисление параметров конечной точки траектории для
заданного значения фк производится следующим образом.
1.	Заданы Ац, рк, тк. По формуле (6.20) определяется функ¬
ция ф3. Далее по графикам кривых на рис. 6.9—6. 11 находится
угол ф0, а затем по известным величинам тк и ф0 вычисляются
функции фг и фз. Далее из (6. 20) определяются скорости ик и Uq.
12	1669
357

Рис. 6. 10. График функции ф2
Рис. 6. П. График функции ф3
358

2. Заданы величины ик, а0, фо. По первому уравнению (6.20)
находится функция фь Затем по известным фо и фч определяется
величина тк. Далее находятся функции ф3 и ф2 по известным ве¬
личинам тк и ф0. Теперь по уравнениям (6.20)’ вычисляются
величины рн и Дг|.
3. Заданы величины м0, фо, Р = ткРк- Совместное решение соот¬
ношения фг(тк) при фиксированном значении ф0 (по кривой) и
одного из уравнений (6. 19) определяет значения тк. Затем по из¬
вестным величинам тк и ф0 находятся остальные параметры
ик, Аг|.	__
При этом безразмерная координата £к определяется из соот¬
ношения:
Пример. Задано: Дт] = 0,5; тк = 0,3; рк = 5,0.
Из (6.20) для величины тк = 0,3 определяется величина
фз = —0,0833. Из рис. 6.11 находится величина ф0 = 0,57 —33°.
Далее определяются значения
Из уравнений (6.20) находятся значения а0 и и{: ш0 = 0,186;
w0 = 0,286; ик= 1,610.
6. 2. 5. Плоское движение при линейном изменении
синуса угла наклона силы тяги по времени
и при постоянном значении силы тяги
Закон изменения синуса угла наклона силы тяги
I и о хкик
| о(1-1У)кН2-ф, tgOp)
tg <Рк — tg/Po
if2 = —0,280; if, = 1,33.
(6.21)
где
sin To — si*1 Tk
tk sin To — sin ¥к*
Уравнения движения (см. гл. 4):
Ро
х— — coslt;
т
(/ = — sill С5 — fr
т
(6.22)

или
— m0g0a • mQg0a
с _ ua-u_ ц — usu ■ cos ®;
Po Po
^ = ?oggg	moasinu_(mQgoa)2
Po
Po
I Po I '
(6.23)
Решение представляется в виде:
— безразмерные скорости полета
« = «о + ^4(?о — ?) + coscp0 — cos ср + /?*(сР. (*ч) — F*(%, ^4);
I Ti — 1 1 1 — тг ,	«
w=wq -|	-—|	--\-ра
(6. 24)
— безразмерные координаты
; — +
Uq — ti и
■t*s
f — fo
2р
+ ^з -77 (sin 2<р0 — sin 2ср);
01 й 1	232
• 1^3—(cos2<р — cos 2cp0),
(6. 25)
где
V1 — i4in
Д4 tg — + 1 + V 1—H-4
N tg— +1— VI—I
r	 1^4	tg	—	+	1
2 9u,4—larctg-
V&-\
при I 1*4 I < 1
ПРИ | Р-4 I > 1
Графики функции F*{ ф, p4) для диапазонов значений
0<р,4<1 и 1<р4<2 и для 0<ф<1 представлены на рис. 6.12
и 6. 13.
Частный случай. Конечный угол разворота вектора тяги
равен 0° (фк=0, ф0 = 90°)
В этом случае
IV
1 - Т„.
360

О	0}	ко	1,5	2,0	2,5	3,0 ГЧ<р,/;ij
Рис. ъ. i2. График функции Т7*(ф, щ) для 0<р>4<1
Рис. 6. 13. График функции F*(cp, |я4) для 1<^4<2

Решение уравнений (6.23) при и0 = Ео=0 имеет вид:
— безразмерные скорости полета
лтк , . У 1 — 2тк . (1—-/l—2тк) (1—тк+уг1—2тк) .
(1+ /1=2^) (1-тк-/Т=2^)' '
(6. 26)
2(1 — тк)
1 хк
(при тк<-1
лт,.
2 У 2тк—1
2(1-тк)
1 тк
arc tg
\ 2
1
/2тк - 1
arctg
У 2тк—1
(6. 27)
Ww=Wn
хк 1
(при Тк > у
■Тк In.—^	и 1;
1 тк
(6. 28)
— безразмерные координаты
Г   ТКИК I /1	^	\.
р + 4l
,Т_гГ I w0 + t,<wk . т1~1 , 1—тк
'•к— ‘О Л	о	~	~	~~
Р2
2?
(6. 29)
ЛИТЕРАТУРА
1. Барр ер М. и др. Движение ракет, ИЛ, 1959.
2. Белецкий В. В., О вертикальном подъеме точки переменной массы
в среде постоянной плотности, ПММ, т. 20, № 4, 1956.
3. Управляемые снаряды, ИЛ, 1960.
4. Бронштейн И. Н., Семендяев К. А., Справочник по математике
для инженеров и учащихся ВТУЗов, изд-во «Наука», 1965.
5. Ветчин кин	В.	П.,	Динамика полета, Госмашметиздат, 1933.
6. Гантмахер	Ф.	Р.,	Левин Л. М.,	Теория полета неуправляемых
ракет, Фпзматгиз, 1959.
7. Горощенко	Б.	Т.,	Динамика полета	самолета, Оборонгиз, 1954.
8. Демидович	Б.	П.,	Марон И. А.,	Основы вычислительной мате¬
матики. Физматгиз, 1960.
9. Дэвис Л., Фоллин Д., Блитцер Л., Внешняя баллистика ракет,
Воениздат, 1961.
10. Ко ой И., Ютенбогарт И., Динамика ракет, Оборонгиз, 1950.
11. Космодемьянский А. А., Лекции по механике переменной массы,
Ученые записки МГУ, 154, Механика, 4, 1952.
12. Ланцош К., Практические методы прикладного анализа, Фпзматгиз,
1961.
13. Л е б е д е в А. А., Ч е р н о б р о в к и н Л. С., Динамика полета, Оборон¬
гиз, 1962.
14. Ми еле А., Механика полета, изд-во «Наука», 1965.
15. О с т о с л а в с к и й И. В., Стражева И. В., Динамика полета.
Траектории летательных аппаратов, Оборонгиз, 1963.
16. Реактивное движение, Сб. статей, ОНТИ, 1935—1938.
362

17. Фокин А. В., Восходящее движение ракеты в поле силы тяготения,
Бюлл. ин. теор. астр. АН СССР, 8, № 5 (98), 1962.
18. Чун-Хун-Ци, Активные участки траектории ракет при тяге, по¬
стоянной по величине и направлению, журн. «Ракетная техника и космонав¬
тика» (русский перев.), 1963, № 3.
19. Ч о н г - X а н г - Ц и, Спиральные траектории с малой постоянной тан¬
генциальной тягой, журн. «Ракетная техника и космонавтика» (русский перев.),
1963, № 7.
20. Э л е р с, Траектории снарядов с линейным изменением по времени или
угла тяги, журн. «Ракетная техника» (русский перев.), 1961, № 5.
21. Япке Е., Эмде Ф., Таблицы функций с формулами и кривыми, Физ-
матгиз, 1959.
22. Casci С. SuIIe possibility del Missile in volo verticale, Aerotec-
nica, 36, No. 1, 1956.
23. Cobb E. R. Constant velocity Gravity Turns, Climb Trajectory
ARS Journ. 32, No. 2, 1962.
24. Cones A. D., Generalized trajectory charts. Planet, and Space
Science, 7, 1961.
25. Fried B. D., Culler C. J. Universal Gravity Turns, Journ.
Appl. Phys. 28, No. 6, 1957.
26. Mackay J. S., Approximate solution for rocket flight with linea-
.tangent thrust attitude control. ARS Journ., 30, No. 11, 1960.
27. M i с k e 1 w a 11, Trajectory analysis. Сборник „Ballistic Missile
and Space Vehicle Systems" N. J., London, 1961.
28. Nadean G.^ Projectile Motion with Damping proportional to ve¬
locity. Amer. Journ. Phys. 30, No. 9, 1962.
29. Punga V., Campbell R. G., Solution in Quadratures for the
Trajectory of a Rocket in a Gravity Turn. Journ. Aerospace Sciences, 29,
No. 9, 1962.
30. S ponder E., A chart for Steady Circling Flight. Journ. Roy
Aeronaut. Soc. 59, No. 536, 1965.	,
31. Sguire W., Some Comments on Generalized Trajectories for Free-
'Falling Bodies of High drag. Jet. Propulsion, 28, No. 12, 1958.
32. Sung K. S., Park C., Two Analytical Results of Fin-stabilized
Rocket Trajectory under Quadratic Drag Law. Journ. Aero/Space Sci., 27,
No. 5, 1960.
33. S t r u b 1 e, Stewart С h., G г a n t о n J., The Trajectory of a
Rocket with Thrust. Jet Propulsion, 28, No. 7, 1958.
34. Turnacliff R. D., Hartnett J. P., Generalized Trajectories
for Free-Falling Bodies of High drag, Jet Propulsion, 28, No. 4, 1958.

Таблица стандартной атмосферы СА—64 (ГОСТ 4401—64)
ьц
К
о
с:
5Г
- J 5 о ч 1
йг о с,о
О 1ю с В
&SIIS8
|я§^~
>» г > Г- ”
^ « 44
й 5<а
S
о»
£ « ^
® э*
Ъй
<и ^
S « 5й
SSi
J о ^
«< ii
I Д Л ^
о Н « *
* ~ ^
м ° в V
' О, <П 3;
ч Cj
CN
V
•« в
«5. ^
_ •«!
о
з ш
о я
а. ч
5
о.
*1
1Н м Ol N
N П CS Ю
Ч СО СО 03
СО Ю 00 О
^ СО О) N
_ О СО
CD N СО
М н СО I
Ч N- Ч 03
СО Ю О) СО Ю О гг ОО (N N
ю ю ю со со со со
со оо со а о ч
« N СО О)
ОО О) N н
« н О) ОС
ч ч О О
СО 00 со со
СО 05 СО СМ ОО Ю '
Ю О Ч 03 ч ОО
СО N О — -
ООО
ОО со ОО
со ее
Ч см
03 03
ON'}' О
_	см	со	.
н	03	со	со	ю
03	00	<30	00	ОО
N	N	N	N	N
СО О Ш О Ч
03 03 03 03	03	03	03	03	03	03	03	03	03	03	03	03	03	03	О)	03	С)	03	03	О)
N	СО	(N	г-i	СО
О	О)	Н	СО	'f
со	ГН	ОО	^	гн
тг	Ю	Ю	СО	N-
(N N СО О О Ю
ю о со
-I	Н	н	О)	тг	N	О	^	а	Ю
с_з	ч	СМ	СО	Ч	Ю	СО	N-	03	О	ч	СО
см"	см-	см"	см"	см*	см	см*	см"	см'	СО	со"	со*
СМ Й* СО N со ю со о
ОО IN	(О	О	ч	со	см	со	о
ОЭ N	Ю	ТГ	М	О	О)	N	(О
00 00	СО	ОО	СО	ОО	N	N	N
CO N О К N
М1 О Н oi N
N- NN со со
«—I	С4)	1—I	03	N~
О	СО	СО	СО	м
СО	Ч	СМ	О	03
СО	СО	СО	СО	Ю
со	ас	го	со	со
Ч	со	03	т—	СО
N-	Ю	ОО	СМ	О
Ю	Ю	Ю	LO	ю
03 О Н О
ч ч со см
N~	СО	Ч	СМ	О	СО	О	Й*	СМ	О	ОО	СО	Ч	СМ	О	ОО	СО	М1	СМ	О ОО 1Q СО 1—I
Ч	Ч	Ч	Ч	Tf	СО	CO	СО	СО	СО	CM	CM	CM	CM	CM	t-н	I—I	ч	ч	—I О О О О
со	со	со	со	со	со	со	со	со	со	со	со	СО	СО	со	СО	СО	СО	СО	СОСОСОСОСО
см со
T-н СО
со см
СО со
Ч Ч
СТЗ со
О О О О О N Ю in О
О)	со	ю	со	^
СО	н	сз	N	(О
СО	СО	СО	н	03
N Ю СО I—I 03	LO
СО	СМ	СМ	н	г-
Ч	СМ	СМ	ю	ч
Ю	О	N	О
1-н «—I «—if—I г-1 Оз 03 03 03 00 00 ОО СО N
СО СО СО LQ
О Ю	03	^	О	CM	I"-	СО	ч	ч	<
СМ ч	О	О	О	Ю	О	СО	СМ	00	'
ч ч"	—Г	ч	1—<	оз"	03	СО	ОС	N.	I
' О СО СО О
LO ю ю см
М ^ 03 N
-	00	03
СО О 00 Ю СМ О
см о
со о
Г-н СТЗ
ОО ю
со со СО Ю Ю LO ч
CM	CM	LO	СО	N	И	(О	н	ю	СО	Й’	00	ОО	о
N	03	М	О	03	о	со	О)	СО	оз	со	ч	ю	ч
-ч.	—	^	^	м	ю	N	О	Ю	IN
N СМ СО СО 03
|	ч	03	СТЗ	00	00	N-
133 со со
СО	Ч	Ч	СМ	Ч	Ч	ОО	ГО	СО	Ч
О	СО	СМ	N	N	см	см	со	со	ч
« Н со со н ООСОЮСООО
LO	1—I	N-	СО	О	СО	СО	О	N*	Ч
N	N	СО	СО	СО	Ю	Ю	Ю	Ч	Ч
О О О О СО Ю ч
О ОО со оо ч о ч
СМ 4—1 ч О	О	Ч ОО СО ОО
ч i ,—Г ч гн Ст)" OQ xi* N
_	Ю	03
СМ	03	ОО	03
СО	03	Ч	О	со
00	Ч	Ю	СО	О
СО	N	О)	03	(О
СО	ОО	ю	ч	ю
СО	03	со	СО	О
СО СО СО Ю LO ч
СО СО СО СО I
I	1—I
СО О I-н СО
О СО СО 03
СО CM f-H О
М	Ю	ОО	СО	Ю	се	СО	Н	(N	СО	<—I	1—I	Ч	00	ОО
см’	СО*	Ч	СО	со	(О	О	N	N	ОО	ч"	СО*	Ч*	СО	о"	Ч	Ю*	о"	Оз"	Ч
СО	СО	СО	СМ	О	н	Ю	О	ОО	ОО	IH	Ю	03	03	О	со	СО	СО	-I
СО	N-	I-н	СО	ч	СО	н	N	см	ОО	LO	<-н	СО	Ч	'	03	СО	СО	н	03
О 03 03 СО 00 N N 0 СО Ю ЮЮЧЧЧ СОСОСОСОСМ
I ^ со см
О	О	СМ	г-н	о	СО	СМ	О	ОО
Ю	СО	Ю	СМ	О	О)	Н	(О	С-1
ОО LO ч со оюччео" о" Ю СО см’
Ю	О	Ю	О	0	Н	N	СО	03	СО	СМ	03	со
ОЗОЗОООО	N	N	СО	СО	Ю	Ю	Ю	Ч	Ч
Ю	03	Ч	О	ОО
О	N-	Ю	СО	О
Ч	СО	СО	СО	СО
N-	Ч	ч	ОО	Ч	ч	СО	Ю
'	03	03	03	ОО	ОС	СИ	N	N
I	см	см	см	см	см	см	см	см
ч	ОО	Ю	СМ	ОО
N	СО	СО	to	L1
см	см	см	см	см
LO СМ 03 ю см
ЮЮЧЧЧ
см см см см см
со	г—	со	СО	ч
03	СО	СМ	Оз	со
СО	ПО	ГО	£м	СМ
CM	CM	CM	СМ	СМ
СМ Ю N- О СМ Ю t— О СМ Ю
со	ч	1—I	оо	ю	1—I	оо ю -
СМ	СМ	СМ	ч	ч	1-н
О	СМ	Ю	N-
ч"	Ч	ч	ч"	N-C34N-0	И	N	О	го"	со
I	I	I	т-н	I-н	ч СМ СМ СМ СО	СО	00	Ч	Ч	Ч
1 1 1 1 1 I 1 1 I I Mill
о о о о
О О о о
О Ю о LO
СМ 1—1 1—1 I
I I I
о о о о о
о	о	о	о	о
о	о	о	о	о
Ю	О	Ю	О	ю
о о о о о
о о о о о
О иг о ю о
СМ СМ со со
00 00 03 03
364

i-i СО О СО 05 CC d СО
Ю О)
N П
CO Cl О
1-1 <-■ d d СО СО
a oc n со
Cl с ю со
N (О со (О
■ Р- Г~ рн 1-н
00 со
id со
СО С1
тр 'С
00
<о Ю Ю Ю
г— г— г— г— t—
VO	00	СО	^0	О!
О	1C	Н	03	ю
ю	!-<	о	оо	о
О	^	н	CJ	LJ
СС	О	1—1	1—1	1—Г
1^-	Cl	N	СО	00
СО	СО	d	d	г-н
Ю	Cl	05	со	СО
t	rr	п	со	m
I d Cl d со
О СО СО О тр
rf Ю N н и
тр 00 d СО 1-1
о рн тр рн
С J d d d 1—1
рн рн
О	d	Cl	ID
О	СО	О	05
05	1—1	CO	N-
OO	CO	CO	CO
i-н	d	со	•
CO	d	05	CO	'
(O	to	ID	n
ip	00	d	CO	'
05 05 C5 05 05 05	05	05	05	05	05	05	05	05	05	05
h- NN CO «3
05 05 05 05 05	0505050505
05	00	05	C5
05	ID	^	CO
Ю	i-н	T—	1—
ID	N	05	i-T
d	l—	О
ID	ID	ID
if	oo	ci
ID	^	■tf
CD	CO	CO
05 05 05 05 05	05	05	C)
(O CO CO to CO
d	о	CO	ID	l-н	О
СО	тр	CD	05	LO	d
d	О	05	LO	CO	TP
Ю	N	CC	ID	CO	d
O)	N	Cl	CS	(O
d	CC	ID	05	N
О	rf	05	CO	CO
СО	Ю	О	i—i	CO
рн*	oo	05"	i-T	1—
N-	O	CO	CO	05
05	г-н	OO	05	Ci
05	N	00	ID	05
ID	00	i-t	ID	05
00 d
05 Tp •—
05 00 05 CO
05 05 О CO
Ю CD 1-1 г-н
LD	05	CD	1—(	Q	'f	«
05	О	CO	00	LO	О)	1-
O	ID	CO	рн	Cl	Ю	О	CD
r—< C5 d Cl И rf	ID	N
I 1—■	1-1	d	CO	тр	IQ	рн	q>
рн рн рн r-^ рн о
Ю	N	Q	Ol	D	О	0505050505	0505050505
00	О	^	if	if	if	sf if Tf if -	—	—	—	—	—
тр	тр	тр	тр	тр	-p	тр p тр Tp
05 ID О Ю
тр	r-t	rP	ID	CO
ID	Ю	TP	CO	d
05	Ю	OO	i-н	’tP
ю	LO	Ю	CO	CO
N	OO	N	Cl	d	ddd
О	00	СО	тр	тр	тр	тр	тр
рн	05	d	Ю	Ю	Ю	ID	1-0
to	CO	NN	N	рн	рн	P-
■ pH P-
Ph	N* N* N	N*	N*	рн	N.	рн	Рн	Г~н	Рн
dOOOO	00000	00
------	-	ID	IО	ID	ID	Ю	LO	LO	LO	LO	ID
05	05	O)	O)	05	05	05	05	05	05
d	d	d	d	d
05	P-	LD	Ю	Ю	LD	LD	ID	ID	ID	Ю
05	05	05	05	05	05	~	—	—-	—
d	Cl	ci	ci	d	d
d d d d d
О о
сл	со	00	o'	d”
05	05	05	о	О
d	d	d	со	со
“J	"	^	it	„
Cl	00	CO	00	со
H	N	H	sf	00	г-н	LO	OO	т—	г-н
О	О	тН	г-н	г-н	d	Cl	d	СО	СО
СО	со	со	со	со	СО	со	со	со	со
d
тр d тг
О d рн
fH СО ID
00 СО тр
LD тр cN
тр СО г-н
О СО СО
СО	to	ID	ID	О
СО	ID	N	о	СО
СО	СО	О	ID	Н
О!	СО	tP	iH	05
ОС СО LD Г* СО
ID LD LQ UP тр
CO CO CO CO d Cl d d d i—1	i-i ,-1 ,-1 ,-t
00	d	i—I	05	00	LD	i—l
00	CO	CO	CO	d	тр	00
О	со	CO	CO	05	1-1	CO
(N	©	ОС	CO	ID	1^-05
2" OO* N-* CO* ID* тр*
ID О i-t
г-н OO О
СО СЮ ID
CO N CO
d О CC
CO d r-
05 CO CO
с-Г d ci
CO 1—t 05 LD —1 OO
CO CO d d d i—1
•-H	тр	1—t	N-	P~	N N CO N CO
05	00	1—1	Ю	ID	rPdcOrPl^
00	Ю	CO	d	00	IDOOCONh
LD	CO	1—t	05	Tp	d d CO ID OO
О	О	СО	тр	05
СО	СО	гР	СО	ГР
Г-н	©	рн	Г-н
СО	00	СО	О	рн
coddosco	оо	те	тр
ID	00	со	^	d	ao	оо	тг
(D	Ю	N	П	d	Рн	СО	Рн
d	tf	СО	-tP	н	t^OOCO
1—I 1—I 1—t 05 СО
CO LD Tp CO COdddi-н г-н г-н	LO	тр	CQdi-i.—	i-H	00	CO	LQ
<M	ID	Tp	ID	CO	LO
pH	d	О	05	Р»	d
r-	CO	d	N-	i-l	d
d	05	Ph	i-l	рн	CO
г-н	00	ТГ	05	о	CO	H	N	ID	00
LD	СО	О	05	o	d	СО	TP	rp	ГО
OO	05	LO	CO	CD	Ю	sf	d	(О	^
05	CO	rp	d	О	О	P~	CD	CD	OO
d	CO	05	00	1H
d	г-н	LO	OO	d
rf	О	Ш	н	if
i—1	ID	05	ID	i-l
■ЧР	CO	тр	СО	Tp
Ю	CO	05	05	05
d	CO	i-н	рн	d
00	OO	00	d	Tp
CO LO Tp
 	  CO	05	CO
pH 00 ГР 05 О 05 рн г—г
OOCOt^TP О LD рн
d СЧ N	05
~ CO CO d r;H
тр CO CO CC <M d нн гн 1-H ri I—1 05 pH CO ID TP TP CO d d d i-т i—I 05 f- LD TpCOd'
1 i-н f-t 00 CO
TP	рн	CO	N	ID	Cl
TP	О	05	CO	LD	P-
1—I	Cl	CO	i-н	CO	05
CO	Tp	d	05	CO	CO
05	CO	Cl	О	d	(О	СО	Ю	Ю	ID
Tp	i-н	О	cO	О	тр	СО	рн	05	ID
Cl	d	П	CO	00	Ю	CO	00	О	1-H
i-н	©	N	Tj<	CQ	TP	CO	05	Tp	05
d	i-t	Cl	CO	CO	1—<	о	о	I
со	^	О	cc	ч1	со	рн	d	1
05	CO	CO	pH	ID
Tp	,-1	00	ID	CO
05	CO	CD	тр	d	ID	O)	CC
05	CO	00	TP	рн	Рн	о	О
1—I	Ю	Tp	CO	CO	Tp	СО	1—
05	d	N	СО	О	СП	Ю	н
1— ^н г-н 00 Рн СО ID
СО d рн СО 05 СО СО d О
Г—	СО	pH	05	Тр
’ О	1—I	t "	О0	тр
LfJ	СО	05	СО	тр
d	d	г-1	г-н
Тр	LD	d	Г—I	05
СО	LD	О	Рн	Ю
d	О	05	р-	СО
СО СО d d d г-i
00 со тр со d d
«-г сю со ю
тр рн ОО со
О) N О Ю О
СО d О LD СО
__	05	05	-н
05	LD	рн	00	СО	ср	N	О
СО	ОО	СО	05	d	dTpOO
i-н	d	О	О	О	СО	рн	d
СО	^Н	d	d	1-н
СО	СЮ	г-н	ID	О
СО	тр	со	СО
О	05	d	05
ID	d	00	СО	СО
d	d	г-1	Г-н	«-Н
05 Q
О со O 05
05
ID
CO
ID d
00
00
05
О
05
LO
pH
pH
0
CO
d
Tp
d
d
05
00
d
0
05
0
I"-
О
2
ID
CO
00
CO
2 05
г-н тр CO d
00 to CO N
TP
TP
тр
CO 05
2
05
d
05
05
d
00
CO
0
pH
00
d
pH
CO
О
те
05
DO
00* со
05 00
О ID TP CO
N. тр d О
О рн со со
05 pH CO ID
00
тр
ID
CO
О ID
CO d
d*
d
OO*
CO
CO
3
О
00*
CO
10
CO
d
d“
00"
CO
тр
CO
ID О
i-H 05
CO CO CO CO
CO CO CO CO
to rO to to
CO CO CO CO
CO
CO
CO
CO
CO
CO
CO CO
со со
со
CO
CO
CO
0
тр
TP
pH
°o
co
10
CO
d
00
00
d
Tp
0
d
co
CO
Д
CO
10
О
О
0
0
0
0
О
О
0
0
СО 05
CO CO CO to
CO CO to CO
CO
CO
CO
CO CO*
CO
CO
05
d
Tp
p-T
0
10
Г-Н*
co
d
pH
CO
00
Tp
Tp
TP
Tp
TP
d d
d d d d
d d d d
d
d
d
d d
d
d
d
d
d
d
d
d
d
d
d
d
d
d
d
d
d
d
d
О CD
О d
05 05 05 05
тр тр тр тр
05 05 05 05
Tp Tp rp TP
05
тр
05
05
TP
05 05
тр Tp
05
Tp
05
тр
LO
0
CO
d
s
0
00
CO
CO
pH
00
T?
10
05
05
Tp
Tp
0
05
LD
LD
00
ID
00
ID
00
ID
ao
ID
00
0 СО
LD ID
1 1
CO CO CO CO
LD LD LD LD
1 1 1 1
CO CD CD CO
ID ID ID LD
1 1 II
CO
ID
1
s
1
CO
ID
1
со со
ID ID
1 1
CO
LO
1
CO*
LO
1
CO
LO
1
10
1
00*
TP
1
10
тр
1
d
T
pH
CO
1
CO
1
CO
d
1
0
d
1
10
7
0
7
тр
1
О
О
О
0
О
8 8 :
OOOO
OOOO
О
0
О
0 0
0
0
g
0
О
О
0
0
0
0
g
0
0
0
О
О
О
0
О
O ID 1
OOOO
§000
О
0
О
0 0
0
0
О
0
О
О
0
0
0
0
0
0
0
0
О
О
О
0
О
2 2
2 2 2 2
2 2 2 2
2
0
d
d
d со
d d
d
d
CO
d
pH
d
00
d
05
d
0
CO
d
CO
Tp
CO
CO
CO
00
CO
0
Tp
d
Tp
тр
Tp
CO
тр
00
О
LD
ID
LD
365

Продолжение
КвОЯЧ
ж	0	и	U	>,
X	О	О)	* .
<	а	х^	<и *
4>	К	Ч	О	с; 1
Е О о. о
и “40 с 2
© О UD I—<
1—1-1 (N О
05	Tf	©	©	05
Ю	Ю	Ю	Ю	©
rf	00	О!	СО	о
05	1—■	1—|	О	О
со	со	со	со	со
©	©	©	©	©
if	ОО	05	©	О
О)	03	ОО	N	N
LO	Ю	Ю	Ю	LO
05	05	05	05	05
О) rf м Ю
•1 if 05
Ю 05 Ю СО
05 1—1	1—	1—I	СЧ СО
©	©	LO	LO	LO
СО 05 ОО
co Ю 00 СО
•—<	г-(	.—.	О	©
СО ОС	со	со	со
© © © Tf if
Г- О СО LO ©
© © ОО СО	Г-
СЯ 05 05 05	05
Ю ОО ОО 1Г
D1 Ю СО Я
г- ю ю ю
Ю LO со сю
05	©
1-1 ©
OS	Tf	©	СО	©
т-	05	05	СЮ	05
СО 11 СО
©	©	©	ОО	©
СО © О © 05
СО 05 05 и	и
ii	©	СУ)	(У)
I'-	LO	СО	05
©	Ю	©	©	©
О	О	и	О	LO
ОО	05	ОО	ч-	N
СО	00	СО	О	О-
да со ©
и да 05
СО 05 и и
Ю 05 СУ)
ю да 05
05 н и
да и о со
да да
и	05	©
СО 05 —Г
и 03	00
СО 05 КПП
к да да ©
о	if	да	со	©
тг	ю	со	да	©
СО	©	©	05	ю
LO	та*	со	со	05
05	05	05	05	05
ю 1— да ю 05
и	со	f	©	да
05	05	05	и	ч
LO	и	I'-	05	©
I"-	©	if	СО	и
©	©	СО	©	t"~
1	05	СО	if	"3*
1111
© © ©
1111 1 1 1
8 8
© © о ©
366

Таблица стандартной атмосферы СА—64^(ГОСТ 4401—64)
S3
*©
<и о
I о К *
О О (U <
-'О £ н~
и о 2	:
U (С с
—• г-« о 05 —I
Ю 05 СМ 'О 05
О Ю —< СО —■ t"-
CNOO>NCC-^
LO u J ^ ^ ^ ^
OOOiOXN
OOCCOi^ О
CM OO CO 05 1-0
CO '—1 О CO h
^ ^ ^ CO CO
05 l"~ to —« о
cncOON't
OCDCNtTW
CO ^ CO i—< О
CO CO CO CO CO
—I О СО О О) о
CNOOOhiOiC
OO ^ О- Ю -I N
OO l"~ Ю ^ CO
CM CN CN (M CN O)
СJ5 05 05 05 05 05 05 05 05 05 05 05 05 05 05 05 05 05 05 05 05 05
CO CM (M ^	1	N
CO CC UO CO CO CM
05 05 05 03 OO t"-
о r- о
CN CN —< —< ,—i
CIO^COCM
Is* СО о о о
о о о — о
—. О 05 ОО 1>.
GO СО t"- 1>-~ оТ
СМ СМ СМ СМ СМ
ОО СО —• Ю Ю О
OO ^ С£5 СМ О
to СО см — о
tC tC rC tC оГ оГ
04 CM CM CM CM СМ
£
I I
о о
ю 051>. см 05 см смо^оо^
Ю ОО СО 05 СО СО —■ t"-
CM —< СО OO СО ^ ь -I Ю N о
Oi CO 'Ф Oi ОЮ^^ЮО
N CO CN CO CO N	CO CM Ю	t"- OO	05 CL' С О O)	CM Ю О 'С CO
О Cl- CO O') О ^	О OO CM	-—i СО	ЬСООЫО	Tt CM rH O) OO	N
<NCOiO^ CO CO CO CM CM CM CM CM ’
UD t^~	CO
I I	I
о о о
I
о
I
о
' t"-СО со—«00005
CO l"~ 05 05 СО О CO CO OO CO
lOOOCOCON CCCMONCM
—I TF OO CL —• —< О —< О) CO 05
—< ^ —■ OO ^ CM
'tObOC’-i
CO —• Ю О 00
M'COM' ^ LO
^-"OOON
Ю СО ^ СО О N
OO OO N О N
ICJ OO CM Ю b M'
OO О ^ OO CO OJ
CO CO CM ’—1
H 05 t"- CO lOiOTt' CO CO CM
I I
о о
I
о
J
о
О OO CM CM со о
ЮЮЮСЬн
'tCCCNCD'H
^u:cOOrHN
CM IQ N CM О
OO CM —< —I t—
CMiQOO^tO
СО СО СО' СО
—< 00 О 05 O)
CO CM О CO —•
О —I со Ю
OO	-—<
MQCM-HiQCM —'	^t1	CO	cm
< Ooo l"~ сс Ю^^со
00
05
О
1
О
О
—1
—•
—< l"~ t"- 05 05 1"-
05 со 05 г- о
СО ОО 00 05 05
СМ 00 СО 05 —< —1
—1 —. LO ОО —<
си СО СМ 00 05
СМ 05
—1 — ю см
Ю 05 СМ ОО о
1-0 СО СО ОО t'—
—.
lONCMiO
СО —. —1 СМ о
о со Ь СМ ОО
со
—' С"- 'ф СМ
—Г — <оГ оГ сс
Ю 'Ф со со см
со
[
м*
1
LO
1
о
1
о
1
о
Ь005ЮСМЮ
00 to со со со ю
со о СО 05 о
со СО Ю 05 со со
ОО 05 —1 05
со О 05 О О
О со СМ со о
^ CM ^ LCD СМ
^ со
—1 г- ^ см
—1 —« 05 СО
ю
со
CO 00 05 CM Ю	CM	N o> О OO	(M
t"~ t"- 00 CD	О	CO 00 О —<	О
CM 00 05 t"-	—I	02 —I OO t"-	CD
CMM'OOCOCJ)	О	CM О Ь Ю	CO
Ю ^ CO CO CN	CM	CM CM — —>	—1
CS.
4
OO О rH Tt ю
О —< О —■ CO
'Ф СО Ю CO CO —'
CO ^ —i OO CM О
1-0 CM —I Ю CO r
00	00	CO
CM CO 05 05 00
'tOiOOoO
OO CM OO •
— 05 СО Ю ^ CO CO cm" cm" cm
ЮОЬ^СО
Ю ^ lO О О
Ю Ю со со со
см о о ю ю
О СМ О со СМ со
о N О) СО СМ
СМ ОО 00 О lO см
05 со ^ со —' О
О СМ со со 'Ф
О СМ со СО О) см
10 05 СО см"
00 О со 1-0 05 со
—' СМ СМ СМ СМ СО
Tf ^ —1 О ОО
со о ю о ^
СМ СМ сГ 00*"
Tf Ю СО СО Г-
'Ф Ю СО t"~ 00
< со со О СМ СМ О со 05 ОО
оооююю
ОО СО lO СО t'—
05 о —• —• —<
^ со см О ОО СО
00 05 О —< —I СМ
—I —I см см см см
1-0	05	05 СМ 05	05 О) со	Ю со	00501010	"Ф	"Ф	"Ф О 1-
—<^CO t"- 1"~ ОО О	^ ОО СО	ОО СО	05 ОО —<	ОО	оооо^ьс
00 СО 05 О гн О)	oToOt^''~
ОО со СО СМ Ю	со г^. 00	05 о
<ооомосо
L, Я) я
о « н s
^ о о ^
~ <D U
SSSSSS	ооооо	о о о о о	оооооо
SSSSSS	ооооо	ооооо	оооооо
оооооо	ооооо	ооооо	оооооо
VQSbQ0100	iPoiooio	оюоюо	юоюоюо
0500—.—.CM CMcOCO^fTf 1-0 lO CD СО t'— ОО ОО С75 05 О
367

Рекомендуемые физические характеристики для высот от 200 000 до 300 000 м (ГОСТ 4401—64)
Ускорение
свободного
падения
тела
м1 сек2
О N О ОО О (М
^СОС7)ЮгнГч
—' О 00 t-- CD Tf
С4) CN '—i >—i '—i '—i
С7э ОЗ 03 ОЗ 03 03
О 03 о 00 о о
ОО —' СЧ ТГ 0 ОО
со аз со сч оо ^
согноаз^со
—< —1 О О О
аз аз аз аз аз аз
о^о-ноаз
—1 ^ оо сч со о
—' СО О СО со
то со сч >—| аз оо
О О О О 03 03
аз аз аз аз оо оо
ООО
о —< ^
аз со сч
СО lO
аз аз оз
ОО ОО 00
Моле¬
куляр¬
ный
вес
М
ОЮООЬОО
О Г*- го СЧ 00
О ОО СО СО
со" СО со" СО СО
счсчсчсчсчсч
ТО то 03 03 г^. СЧ
о то аз со аз
СЧ О ОО то со
со СО то то то то
счсчсчсчсчсч
СО СО ^ СЧ ОО Оз
—1 со то оо аз
СЧ ООО СО^СЧ
ТО то rf
сч сч сч сч сч сч
24,110
23,920
23,731
ю
1
1
о
1
о
1
OiWOiOrHpH
CD СО оз сч *—•
HOOOCN^
t- CD Ю Tf СО СЧ
^ ^ ^ —' 03
СО СО —« ТО СО Г*»
со аз со •—«то сч
-НООГ-РНСО
—• СЧ СО аз ОО
NOONCOO
СО ОО ТО ТО 00
—• СО СЧ ОО ^
аз со о
^ —'
^^со
ОО то СЧ
—- •—■ ’—• •—. ^ ,—.
’—(г—« —1 аз аз оо
ОО Г^4 ьГ СО СО со
ТО 10 то
О
1
1
•с
о
1-
1
О
1
о
II
<3
Ь- 00 05 CD ОЗ
Г- 05—1 со о
^ h- CD 00 Tf
0)10 CN аз Ю
СЧ Сч" СЧ —Г —Г
Ь- 1—1 Tf то Ю •—'
аэсч ^ аз со ^
то О со со оо ^
СО СЧ О со
—Г аГ оо ьГ
СОТО^^ОО
—1 00 СЧ СЧ 00
счазеоооь
со ОО сч сч
СО то то СО
3,3848
3,0410
2,7464
А *
и i
§
5 й
ii
т
о
| CD i-О CD СЧ
СМ СЧ Ю —1 со ^
00 СЧ СЧ ОО 00 СЧ
СО СМ ОО Tf •—| Оз
см
т
о
то со со —• сч аз
оо ^ аз аз со
C730C4N^03
СО то СО — О СЧ
—• со — со
—< ОО со со о
СО то —1
СЧ СО Ю ОО СЧ
—• сч
00 GO ОО
сч аз 1—1
сч ^
СО СО СЧ СЧ СЧ —1
г—<Г ^-Г ^-ГГ аз
GO t*- со то то
со со
01-
6-
1 1
о о
ЮОСОСОЮ'Ф
ТО 1—| S Оз СО 00
ОЭ то Оз со то
СО —• о со со ^
СЧ О со о
00 СО О 00 о со
' ТО то СО оз то
со 03 СО h- СЧ 00
Tf то СО оо
СЧ О СО то СО со
со сч то —« аз
rf —. оо то СО О
со сч —1
СО аз со
о сч г-
оз Г- то
—> —« аГ ао г-Г
CO то то Tf "'f со
со со сч сч сч сч
—Г —Г —Г
О)
S
5
ю со
1 1
о о
и
cd
*=с
1)
*м
ii
СЧ ТО 00 CO то (М
О —' СМ —< СО
03 со 03 —1 Tf О
со СЧ О h- со h-
03 г—1 г—1 Tf СО оо
Оэ —' h- СЧ
ТО о со со оо
ОО г-н ю аз Tf аз
00 ОО Tf СО ^ ТО
Ь^ОООО
00 со СЧ аз со
ТО СЧ 03 СО СО 1
со со
СО со то
СО ОО СЧ
аз г- со
§ •«
г: &
-Н^н r-tDOOt^
СО СО ТО со
со" со" сч" сч сч сч
—Г —Г —Г
О *4,
<и
=Г
S
Л
н
о
о
а.
са
Ш
g
Б
i
СО f-
1 1
о о
СО СО 03 то ю
(М ОО Г"» СО 00 00
СЧ Ю со Tf то со
О О О —' СО со
СО то ОО 1"- ^ —'
О^О’-'Он
со СЧ тгэ СО СО со
о то о со сч аз
О ^ ’—1 гН г-( со
03 03 оо сч 00 со
со г- ^ ^ то аз
СО СО ’—| ОЗ Г”-- то
1
о
то СМ со
со Ю
—, 03
СО —'
аз 00 СО то
то*4 со со сч"
СЧ СЧ СЧ ’—|
—Г —Г -7
ООО ОЬ ОО
Tf rf аз о оо то
сч со оо со о аз
то 03 О
•si
Ьм
cd
сх,
>>
н
itj
о
со со то со сч аз
СЧ СО Tf ТО со со
сч сч сч сч сч сч
ь^о^счаз
оо аз аз о о
СЧ СЧ СЧ СЧ со со
СО СЧ 00 о ^
—' СЧ СЧ со ^ ^
со со со со СО со
03 СО оо
Ю то
со СО со
cd
сх,
а»
с
-нСЧСО^н^^
СО 00 ОО ТО 00 Is'*
сч сч оо со со
О со ^ ОО
СО г- СО
а>
Ь
О
о
со СЧ о ОО со
ю со ^ оо оо аз
аз аз аз оэ аз аз
^ t^eo аз со
О — — СЧ СМ со
о о о о о о
СО 03 то ^ СО —'
Tf ТО со СО
о о о о о о
со" о ^
оо оо
ООО
а. к
v 2
cd
о *5
о о о о о о
о о о о о о
о о о о о о
о о о о о о
О О О О О' о
о о о о о о
о о о о о о
о о о о о о
о о о о о о
ООО
ООО
ООО
5 ^
о ®
« г
и
и
3
с
О то О то О то
ОО-—1 —счсч
сч сч сч сч сч сч
О то О то О то
СО СО то то
счсчсчсчсч сч
О Ю О ТО О то
СО СО N t4» ОО 00
сч сч сч сч сч сч
О то О
аз аз о
сч сч со
368

ПРИЛОЖЕНИЕ II
МЕЖДУНАРОДНАЯ СПРАВОЧНАЯ АТМОСФЕРА CIRA 1965
МЕЖДУНАРОДНОГО КОМИТЕТА ПО ИССЛЕДОВАНИЮ
КОСМИЧЕСКОГО ПРОСТРАНСТВА (КОСПАР)*
Атмосфера CIRA 1965 составлена по данным различных из¬
мерений характеристик атмосферы Земли, проведенных стра¬
нами: США, СССР, Англией, Францией, ФРГ, Японией с по¬
мощью ракет и искусственных спутников Земли. Охватывает
экспериментальные данные до 1964 г.
Ниже приведены основные фрагменты из CIRA 1965.
Часть 1. Номинальная модель атмосферы
в диапазоне высот от 30 до 300 км
Таблица 1
Максимальные отклонения плотности и температуры
относительно номинальных значений
Г еометри-
ческая
высота
км
Отклонение
плотности
%
Отклонение
температуры
°К
Г еометри-
ческая
высота
км
Отклонение
плотности
%
Отклонение
температуры
°К
—
+
—
+
-
+
+
30
20
19
29
15
170
50
56
260
400
40
33
28
30
23
180
50
64
307
439
50
46
35
34
19
190
50
72
350
490
60
54
42
25
43
200
0,50**
1,80**
386
536
70
59
52
27
50
210
0,46
1,89
419
576
80
45
42
36
52
220
0,42
1,98
448
611
90
30
30
40
40
230
0,37
2,20
473
642
100
40
35
50
50
240
0,32
2,43
494
669
110
60
60
75
75
250
0,28
2,61
512
694
120
40
40
100
100
260
0,25
2,79
527
716
130
45
45
150
125
270
0,23
3,01
540
736
140
45
45
170
200
280
0,20
3,25
551
754
150
; 50
50
200
300
290
0,18
3,49
561
770
160
50
50
230
360
300
0,15
3,74
569
784
* CIRA 1965. COSPAR International Reference Atmosphere Amsterdam
1965.
** Эти и последующие числа являются множителями к номинальным
значениям.
369

h
км
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
температуры, плотности, давления и высоты
атмосферы для модели стандартной атмосфе
в диапазоне высот от 30 до 80 км
Плотность
IgQ
г/см*
Давление
Высота
однород¬
ной атмо¬
сферы
Р
1 gp
дин см-
км
1,200-104
4,079
6,808
1,037
4,016
6,870
8,969-103
3,953
6,934
7,769
3,890
6,995
6,739
3,829
7,050
5,852
3,767
7,121
5,089
3,707
7,183
4,430
3,646
7,247
3,861
3,587
7,309
3,369
3,528
7,373
2,944
3,469
7,436
2,575
3,411
7,500
2,254
3,353
7,562
1,976
3,296
7,627
1,734
3,239
7,688
1,524
3,183
7,753
1,340
3,127
7,815
1,180
3,072
7,880
1,039
3,017
7,942
9,169-102
2,962
8,007
8,096
2,90S
8,059
7,148
2,854
7,988
6,303
2,800
7,910
5,551
2,744
7,829
4,882
2,689
7,748
4,288
2,632
7,670
3,761
2,575
7,589
3,294
2,518
7,508
2,881
2,460
7,427
2,517
2,401
7,348
2,195
2,341
7,267
1,911
2,281
7,188
1,662
2,221
7,113
1,443
2,159
7,034
1,250
2,097
6,956
1,082
2,034
6,880
9,349-10
1,971
6,802
8,053
1,907
6,723
6,943
1,842
6,644
5,968
1,776
6,569
5,120
1,709
6,490
4,384
i
1,642
6,399
1,817*10-5
1,556
1.334
1,146
9,853*10-6
8,484
7.315
6.315
5,458
4,724
4,094
3.551
3,085
2,682
2.335
2.036
1,776
1.551
1,357
1,189
1,041
9,284-10-7
8,271
7.36 Г
6,543
5,809
5.151
4,561
4,034
3,563
3,142
2,767
2.433
2,136
1,873
1,639
1.433
1,251
1,090
9,48Ы0-8
8,234
7.152
5,259
5,192
5,125
5,059
6,994
6,929
6,864
6,800
6,737
6,674
6,612
6,540
6,489
6,428
6,368
6,309
6,249
6,191
6,133
6,075
6,017
7,968
7,918
7,867
7,816
7,764
7,712
7,659
7,606
7,552
7,497
7,442
7,386
7,330
7,273
7,215
7,156
7,097
7,037
8,977
8,916
8,854

Продолжение
Геометри¬
ческая
высота
h
Темпера¬
тура
Т
Плотность
Давление
Высота
однород¬
ной атмо¬
сферы
Ускорение
силы
тяжести
S
Q
lg Q
Р
I ер
км
°К
г/см*
дин/см2
км
с м/сек2
72
210,5
6,199
8,792
3,746
1,574
6,311
957,48
73
207,4
5,362
8,729
3,193
1,504
6,220
957,18
74
204,4
4,629
8,665
2,715
1,434
6,132
956,88
75
201,3
3,987
8,601
2,304
1,362
6,041
956,58
76
198,2
3,427
8,535
1,950
1,290
5,949
956,29
77
195,2
2,938
8,468
1,646
1,216
5,861
955,99
78
192,1
2,513
8,400
1,386
1,142
5,770
955,69
79
189,1
2,144
8,331
1,164
1,066
5,682
955,39
80
186,0
1,825
8,261
9,745-10°
0,989
5,590
955,10
* Ускорение силы тяжести соответствует широте 30° и вычисляется
по формуле ^-- 979,3244 — 3,086597- 10~4/г— 7,259-10_u/г2, где g в см/сек2,
h в м.
Таблица 3
Значения молекулярной температуры, плотности, давления
и высоты однородной атмосферы для номинальной модели
в диапазоне высот от 80 до 120 км
Геомет¬
риче¬
ская
высота
Молеку¬
лярная
темпера¬
тура
Плотность
Давление
Высота
однород¬
ной атмо¬
сферы
Ускорение
силы
тяжести
О
ig е
Р
lgp
км
°1<
г /см*
дин/см
км
cMjceK2
80
186,0
1,825-10-8
8,261
9,745
0,989
5,590
955,10
81
186,0
1,526
8,184
8,149
0,911
5,592
954,80
82
186,0
1,276
8,105
6,814
0,833
5,593
954,50
83
186,0
1,057
8,028
5,699
0,756
5,595
954,21
84
186,0
8,926-10-9
9,951
4,766
0,678
5,597
953,91
85
186,0
7,466
9,873
3,986
0,600
5,599
953,61
86
186,0
6,245
9,796
3,334
0,523
5,600
953,32
87
186,0
5,223
9,718
2,789
0,445
5,602
953,02
88
186,0
4,369
9,640
2,333
0,368
5,604
952,72
89
186,0
3,655
9,563
1,952
0,290
5,606
952,43
90
186,0
3,058
9,485
1,633
0,213
5,608
952,13
91
188,7
2,525
9,402
1,368
0,136
5,690
951,84
92
191,4
2,091
9,320
1,149
0,060
5,774
951,54
93
194,1
1,736
9,240
9,673-10-1
1,986
5,857
951,25
94
196,8
1,445
9,160
8,164
1,912
5,940
950,95
95
199,5
1,205
9,071
6,907
1,839
6,024
950,66
371

Продолжение
Геомет¬
риче¬
ская
высота
Молеку¬
лярная
темпера¬
тура
Плотность
Давление
Высота
однород¬
ной атмо¬
сферы
Ускорение
силы
тяжести
Q
18 6
Р
1 gp
км
°К
г1см3
дин/см2
км
см/сека
93
202,2
1,009
9,004
5,857
1,768
6,107
950,36
97
204,9
8,463.10-ю
10,928
4,978
1,697
6,191
950,07
98
207,6
7,114
10,852
4,240
1,627
6,274
949,77
99
210,3
5,995
10,778
3,619
1,558
6,358
949,48
100
213,0
5,052
10,704
3,095
1,491
6,441
949,18
101
218,0
4,243
10,628
2,655
1,424
6,587
948,89
102
223,0
3,570
10,553
2,285
1,359
6,748
948,60
103
228,0
3,016
10,479
1,974
1,295
6,902
948,30
104
233,0
2,557
10,408
1,710
1,233
7,055
948,01
105
238,0
2,176
10,338
1,486
1,172
7,208
947,72
105
243,0
1,858
10,269
1,296
1,113
7,362
947,42
107
248,0
1,591
10,202
1,133
1,054
7,516
947,13
103
253,0
1,357
10,136
9,930*10-2
2,997
7,670
946,84
109
258,0
1,178
10,051
8,727
2,941
7,824
946,54
110
263,0
1,019
10,008
7,690
2,886
7,978
946,25
111
274,8
8,624.10-п
11,936
6,802
2,832
8,339
945,96
112
285,5
7,354
11,867
6,049
2,782
8,696
945,67
113
298,3
6,311
11,800
5,404
2,733
9,057
945,37
114
310,1
5,449
11,736
4,850
2,686
9,419
945,08
115
321,9
4,730
11,675
4,370
2,640
9,780
944,79
116
333,6
4,127
11,615
3,952
2.597
10,139
944,50
117
345,4
3,618
11,558
3,587
2,555
10,501
944,20
118
357,2
3,186
11,503
3,267
2,514
10,863
943,91
119
368,9
2,817
11,450
2,984
2,475
11,222
943,62
120
380,7
2,501
11,398
2,733
2,437
11,584
943,33
Таблица 4
Значения плотности, молекулярной температуры, давления
и высоты однородной атмосферы для номинальной модели
в диапазоне высот от 120 до 300 км
Геоме¬
триче¬
ская
высота
Моле ку-
лярная
темпера -
тура
Плотность
Давление
Высота
однород¬
ной атмо¬
сферы
Ускорение
силы
тяжести
Q
lgQ
Р
1 gp
км
°К
г/сж3
dunjcM
2
км
см1сек2
120
380,7
2,501.10-п
11,398
2,733*10-2
2,437
11,584
943,33
121
395,1
2,214
11,345
2,511
2,400
12,026
943,04
122
409,4
1,969
11,294
2,314
2,364
12,465
942,75
123
423,8
1,758
11,245
2,139
2,330
12,907
942,40
124
438,1
1,576
11,198
1,982
2,297
13,347
942,17
125
452,5
1,417
11,141
1,841
2,265
13,790
941,88
372

Продолжение
'Г еоме-
гриче-
ская
высота
Молеку¬
лярная
темпера-
тура
Плотность
Давление
Высота
однород¬
ной атмо¬
сферы
Ускоре¬
ние силы
тяжести
Q
lg Q
Р
lg р
км
°К
г!см3
дин/см2
км
см/сек2
126
466,9
1,279
11,107
1,714
2,234
14,233
941,59
127
481,2
1,158
11,064
1,600
2,204
14,674
941,30
128
495,6
1,052
11,022
1,496
2,175
15,118
941,01
129
509,9
9,574-10-12
12,981
1,401
2,146
15,559
940,72
130
524,3
8,740
12,941
1,315
2,119
16,003
940,43
131
536,4
8,032
12,905
1,237
2,092
16,377
940,14
132
548,4
7,395
12,869
1,164
2,066
16,749
939,85
133
560,5
6,821
12,834
1,097
2,040
17,124
939,56
134
572,5
6,303
12,800
1,036
2,015
17,496
939,27
135
584,6
5,833
12,766
9,788-Ю-з
3,990
17,871
938,98
136
596,6
5,408
12,733
9,261
3,967
18,243
938,69
137
608,7
5,021
12,701
8,772
3,943
18,619
938,40
138
620,7
4,668
12,669
8,318
3,920
18,992
938,11
139
632,8
4,347
12,638
7,895
3,897
19,368
937,82
140
644,8
4,053
12,608
7,501
3,875
19,742
937,53
141
655,4
3,792
12,579
7,134
3,853
20,072
937,25
142
666,0
3,552
12,550
6,790
3,832
20,403
936,96
143
676,5
3,330
12,522
6,468
3,811
20,731
936,67
144
687,1
3,126
12,495
6,166
3,790
21,063
936,38
145
697,7
2,937
12,468
5,882
3,770
21,394
936,09
146
708,3
2,762
12,441
5,615
3,749
21,726
935,81
147
718,9
2,600
12,415
5,365
3,730
22,058
935,52
148
729,4
2,449
12,389
5,129
3,709
22,387
935,23
149
740,0
2,310
12,364
4,906
3,691
22,719
934,95
150
750,6
2,180
12,338
4,696
3,672
23,052
934,66
151
760,4
2,061
12,314
4,498
3,653
23,360
934,37
152
770,3
1,950
12,290
4,311
3,635
23,671
934,09
153
780,1
1,846
12,266
1,134
3,616
23,980
933,80
154
789,9
1,749
12,243
3,966
3,598
24,289
933,51
155
799,8
1,658
12,219
3,807
3,581
24,600
933,23
156
809,6
1,573
12,197
3,656
3,563
24,910
932,94
157
819,4
1,494
12,174
3,513
3,546
25,219
932,65
158
829,2
1,419
12,142
3,378
3,529
25,529
932,37
159
839,1
1,349
12,130
3,249
3,512
25,841
932,08
160
848,9
1,283
12,108
3,126
3,495
26,151
931,80
161
858,3
1,222
12,090
3,009
3,478
26,448
931,51
162
867,6
1,164
12,066
2,898
3,462
26,744
931,23
163
877,0
1,109
12,045
2,793
3,446
27,042
930,94
164
886,4
1,058
12,025
2,692
3,430
27,339
930,66
165
895,8
1,009
12,004
2,596
3,414
27,634
930,37
166
905,1
9,637-10-13
13,984
2,504
3,399
27,934
930,09
167
914,5
9,204
13,964
2,416
3,383
28,232
929,80
168
923,9
8,795
13,944
2,333
3,368
28,531
929,52
169
933,2
8,409
13,925
2,253
3,353
28,830
929,23
170
942,6
8,043-10-13
13,905
2,176*10-3
3,338
29,127
928,95
171
951,6
7,699
13,886
2,103
3,323
29,413
928j.67
172
960,5
7,374
13,868
2,033
3,308
29,698
928,38
373

'еоме-
гриче-
ская
шсота
км
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
4
Продолжение
Плотность
IgQ
ZjCMz
Давление
Р
IgP
дин/см
2
7,065
6,771
6,493
6,228
5,977
5.737
5,510
5,293
5,089
4,894
4,708
4,531
4,362
4,200
4,046
3,898
3,757
3,623
3,495
3,373
3,256
3,143
3,036
2,932
2,833
2.738
2,647
2,560
2,477
2,398
2,322
2,248
2,177
2,109
2,044
1,981
1,920
1,861
1,805
1,751
1,699
1,649
1,600
1,553
1,508
1,465
1,422
13,849
13,831
13,812
13,794
13,776
13,759
13,741
13,724
13,707
13,690
13,673
13,656
13,640
13,623
13,607
13,591
13,575
13,559
13,543
13,528
13,513
13,497
13,482
13,467
13,452
13,437
13.243
13,408
13,396
13,380
13,366
13,352
13,338
13,324
13,310
13,297
13,283
13,270
13,256
13.243
13,230
13,217
13,204
13,191
13,178
13,166
13,153
1,966
1,902
1,840
1,782
1,725
1,671
1,619
1,569
1,520
1,474
1,430
1,387
1,346
1,306
1,268
1,232
1,-196
1,162
1,129
1,098
1,067
1,038
1,009
9,816-10-4
9,550
9,293
9,046
8,806
8,574
8,350
8,133
7,923
7,719
7,522
7,332
7,147
6,968
6,794
6,626
6,463
6,305
6,152
6,003
5,858
5,718
5,582
5,450
3,294
3,279
3,265
3,251
3,237
3,223
3,209
3,196
3,182
3,169
3,155
3,142
3,129
3,116
3,103
3,090
3,078
3,065
3,053
3,040
3,028
3,016
3,004
4,992
4,980
4,968
4,956
4,945
4,933
4,922
4,910
4,899
4,888
4,876
4,865
4,854
4,843
4,832
4,821
4,810
4,800
4,789
4,778
4,768
4,757
4,747
4,736
Высота
однород¬
ной атмо¬
сферы
км
29,985
30,273
30,560
30,846
31,134
31,422
31,707
31,996
32.269
32,546
32,821
33,093
33,367
33,645
33,919
34,193
34,470
34,745
35,008
35.270
35,530
35,793
36.056
36,319
36,583
36,843
37,107
37,371
37,610
37,852
38,092
38,334
38,574
38,814
39.057
39,297
39,540
39,780
40,012
40,243
40,474
40,705
40,937
41,169
41,401
41,633
41,865
Ускорение
силы
тяжести
см'сек2
928.10
927.82
927.53
927.25
926,97
926,68
926,40
926,12
925,84
925,56
925,27
924.99
924.71
924.42
924.14
923.86
923,58
923,30
923,02
922,74
922,46
922,18
921,90
921,62
921,34
921,06
920,78
920,50
920.21
919,94
919,66
919,38
919.10
918.82
918.54
918.26
917.99
917.71
917.43
917.15
916.87
916,60
916,32
916,04
915,76
915,49
915.21

еоме-
риче-
:кая
ысота
км
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
Продолжение
Плотность
Давление
Высота
однород¬
ной атмо¬
сферы
У скорение
силы
тяжести
Q
lg Q
Р
1 gp
г 1см3
дин! см2
км
см/сек2
1,382
13,140
5,322
4,726
42,097
914,93 1
1,343
13,128
5,197
4,716
42,317
914,66
1,305-10-13
13,116
5,076.10-4
4,705
42,537
914,38
1,269
13,103
4,958
4,695
42,761
914,10
1,233
13,090
4,844
4,685
42,980
913,83
1,199
13,079
4,733
4,675
43,201
913,55
1,166
13,067
4,625
4,665
43,421
913,27
1,134
13,054
4,520
4,655
43,642
913,00
1,103
13,043
4,418
4,645
43,864
912,72
1,074
13,031
4,318
4,435
44,087
912,45
1,045
13,019
4,222
4,625
44,308
912,17
1,017
13,007
4,128
4,616
44,510
911,90
9,901-10-14
14,996
4,036
4,606
44,716
911,62
9,642
14,984
3,947
4,596
44,918
911,35
9,390
14,973
3,861
4,587
45,124
911,07
9,146
14,961
3,776
4,577
45,327
910,80
8,910
14,950
3,6.94
4,568
45,530
910,52
8,681
14,939
3,614
4,558
45,736
910,25
8,458
14,927
3,536
4,549
45,938
909,98
8,242
14,916
3,460
4,539
46,145
909,70
8,033
14,905
3,386
4,530
46,348
909,43
7,831
14,894
3,314
4,520
46,539
909,15
7,636
14,883
3,243
4,511
46,733
908,88
7,446
14,872
3,175
4,502
46,924
908,61
7,262
14,861
3,108
4,492
47,115
908,33
7,083
14,850
3,043
4,483
47,306
908,06
6,909
14,839
2,979
4,474
47,501
907,79
6,741
14,829
2,918
4,465
47,692
907,51
6,576
14,818
2,857
4,456
47,884
907,24
6,417
14,807
2,798
4,447
48,078
906,97
6,262
14,797
2,741
4,438
48,270
905,70
6,112
14,786
2,685
4,429
48,453
906,42
5,967
14,776
2,630
4,420
48,638
906,15
5,826
14,765
2,576
4,411
48,821
905,88
5,688
14,755
2,524
4,402
49,003
905.61
5,554
14,745
2,473
4,393
49,186
905,34
5,424
14,734
2,424
4,385
49,372
905,03
5,297
14,724
2,375
4,376
49,555
904,79
5,174
14,714
2,328
4,367
49,738
904,52
5,054
14,704
2,282
4,358
49,925
904,25
4,937
14,693
2,236
4,349
50,108
903,98
4,825
14,684
2,192
4,341
50,278
903,71
4,715
14,673
2,149
4,332
50,449
903,44
4,609
14,664
2,107
4,324
50,623
903,17
4,505
14,654
2,066
4,315
50,794
902,90
4,403
14,644
2,026
4,307
50,965
902,63
4,305
14,634
1,987
4,298
51,136
902,36
4,209
14,624
1,948
4,290
51,309
902,09
375

Геоме¬
триче¬
ская
высота
км
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
220
291
292
293
294
295
296'
297
298
299
300
376
Плотность
Давление
Высота
однород¬
ной атмо¬
сферы
е
IgQ
Р
1 gp
г/см*
дин/см2
км
4,115
14,614
1,911
4,281
51,482
4,024
14,605
1,874
4,273
1 51,653
3,935
14,595
1,838
4,264
51,825
3,849
14,585
1,803
4,256
51,987
3,765
14,576
1,769
4,248
52,149
3,683
14,566
1,735
4,240
52,315
3,603
14,557
1,702
4,231
52,477
3,526
14,547
1,670
4,223
52,639
3,450
14,538
1,639
4,215
52,802
3,376
14,528
1,608
4,206
52,964
3,303
14,519
1,578
4,198
53,130
3,233
14,510
1,549
4,190
53,293
3,164
14,500
1,520
4,182
53,456
3,098
14,491
1,492
4,174
53,609
3,033
14,482
1,464
4,166
53,763
2,969
14,473
1,437
4,152
53,916
2,908
14,464
1,411
4,150
54,071
2,847
14,454
1,385
4,141
54,223
2,788
14,445
1,360
4,134
54,374
2,730
14,436
1,335
4,125
54,528
2,674
14,427
1.311
4,118
54,682
2,619
14,418
1,287
4,110
54,840
2,566
14,409
1,264
4,102
54,990
2,514
14,400
1,241
4,094
55,131
2,463
14,391
1,219
4,086
55,276
2,413
14,382
1,197
4,078
55,417
2,365
14,374
1,176
4,070
55,562
2,317
14,365
1,155
4,063
55,704
2,271
14,356
1,134
4,055
55,846
2,226
14,348
1,114
4,047
55,990
2,181
14,339
1,094
4,039
56,132
2,138
14,330
1,075
4,031
56,278
2,096
14,321
1.056
4,024
56,420

Геометрическая высота h км
Часть 2. Структура атмосферы и ее вариации в диапазоне
высот от 30 до 100 км
Границы доверительных интервалов
Рис. 1. Среднегодовая температура для северного
полушария и распределение температуры различ¬
ных вероятностей
377

нм 15°сш
80
-70
годовал
■JO-j
20
;г
С
2-
-то 20%
Л
№
"ян$
=L
июль
\
* ~ Л
\
-■
-+-L
1
Л\
* rjc.
лУ
о . г
1 п
7%
-Щ-20% Ws 20%. *0%
/1®
ки
Т>
if
\
250.
Л
След,
ьс
" \
rtrU/tD
-h
7Ц0
голос
’ V
r-v
V v
Тепл.
\
f-
\ V
-Л
1
ISO¬
\
i
-V
1
M/O'
50-
20%	10%	Ш	6Ь%
Рис. 2. Сезонные вариации плотности в процентах относительно
стандартной атмосферы США 1962 для четырех широт 15°, 30°,
45°, 60° северной широты по высоте
Геометрическая высота 6 км
Рис. 3. Распределение среднегодовой и
экстремальной плотности по высоте для
северного полушария
378
Рис. 4. Распределение средне¬
годового и экстремального дав¬
лений по высоте для северного
полушария

Температура 5 °К
Рис. 5. Распределение номинальной температуры CIRA 1965 и
экстремальных температур по высоте
Широта
Рис. 6. Распределение по высотам и широтам осредненных
значений западных (U?) и восточных (Е) компонент ветра.
Цифрами обозначена скорость ветра в м]сек.
379

Таблица 5
Вариации температуры по высотам, широтам и месяцам
Широта северная в град.
те
н
о
а
Месяц
0
10
20
30
40
50
60
70
| 80
| 90
52
АТ
о
ж
АТ
т °к |
т °с
АТ
30
Янв.
+2
4-1
4-1
228
—45
—3
+ 7
213
—60
—7
—12
— 13
Февр.
— 1
0
0
227
—46
—2
4-8
212
—61
—9
-12
— 13
Март
+2
4-2
4-1
228
—45
—3
4-7
214
-59
—8
-12
— 13
Апр.
+з
+з
4-2
234
—39
—6
4-5
218
-55
—5
—7
—8
Май
+6
4-5
+з
234
—39
—4
+4
223
—50
— 1
-2
_2
Июнь
+2
4-2
-Ы
234
—39
—1
0
232
—41
0
+ 1
+ 1
Июль
—2
_2
—1
232
—41
4-2
—3
240
—33
+ 2
+3
+4
А в г.
—3
—2
—2
229
—44
+4
—1
236
—37
+ 1
+1
+ 1
Сент.
— 1
0
0
231
—42
0
-Ы
230
—43
_2
—3
—4
Окт.
+4
+4
+3
233
—40
—3
+3
224
—49
—3
—5
—7
Ноя.
+ 7
+6
+4
233
—40
—5
+4
219
—54
—4
—8
—9
Дек.
+4
4-4
+3
232
—41
—5
4-5
216
—57
—6
— 11
— 13
40
Янв.
0
+2
4-2
256
— 17
—6
4-11
227
—46
—4
—5
—5
Февр.
—1
0
0
255
—18
—6
+ 11
227
—46
—4
—5
—5
Март
+ 1
4-1
4-1
254
— 19
—4
+ 10
232
—41
—4
—5
—5
Апр.
+4
+4
+2
254
— 19
—3
+3
246
—27
—2
—4
—5
Май
+2
+2
+ 1
257
— 16
0
—3
260
—13
+3
+ 5
+ 5
Июнь
0
0
0
259
— 14
4-3
—3
268
—5
+3
+5
+6
Июль
— 1
— 1
—1
257
-16
+ 3
—4
268
—5
+3
+5
+6
Авг.
— 1
—2
—1
255
—18
+2
—3
262
—11
+2
+3
+4.
Сен.
0
0
0
255
—18
0
+ 1
254
—19
0
— 1
—1
Окт.
+2
4-3
+2
256
— 17
—3
+ 4
246
—27
—3
—4
—4
Ноя.
+з
4-4
+3
256
— 17
—5
+7
238
—35
—5
—7
—8
Дек.
+ 3
4-4
+4
256
—17
—6
+ю
231
—42
—5
—6
—7
30
Янв.
0
4-1
4-1
271
—2
—7
+5
250
—23
0
+4
+6
Фев.
+2
4-2
+2
269
—4
—7
+4
250
—23
0
+4
+6
Март
+5
4-4
+3
267
—6
—4
+3
255
—18
+ 1
+4
+8
Апр.
+5
+3
+ 1
268
—5
—1
—3
269
—4
+6
+ 12
+ 16
Май
+4
4-2
+ 1
271
—2
+2
—6
284
+ П
+8
+ 15
+ 19
Июнь
— 1
—2
—2
275
+2
4-4
—6
290
+ 17
+7
+ 11
+ 14
Июль
—3
—3
—2
274
+ 1
+4
—4
287
+ 14
+4
+6
+6
Авг.
0
0
0
271
—2
4-2
—2
276
+3
+2
+5
+7
Сен.
0
0
— 1
272
—1
0
— 1
273
0
+ 1
+2
+3
Окт.
—1
4-1
+2
274
+ 1
—3
0
269
—4
+ 1
+3
+4
Ноя.
0
4-1
+2
275
+2
—6
+3
260
—13
+ 1
+5
+6
Дек.
+1
4-1
+ 1
273
0
—7
+6
253
—20
+ 1
+5
+7
60
Янв.
+3
+з
+2
237
—36
—3
+3
228
—45
-2
—4
—5
Фев.
+3
+з
+2
236
—37
—1
0
233
—40
0
0
0
Март
+4
4-3
+2
238
—35
—2
—3
240
—33
+3
+5
'+5
Апр.
+4
4-4
+2
249
—24
—3
—3
248
—25
+5
+ 10
+ 13
Май
+2
+2
+ 1
252
—21
—1
—4
255
—18
+8
+ 16
+21
Июнь
— 1
— 1
—1
247
—26
+3
—7
262
—11
+8
+ 17
+22
Июль
-2
— 1
—1
242
—31
4-5
—9
264
—9
+ 10
+ 18
+22
Авг.
—2
—2
—1
241
-32
+3
—8
261
—12
+ю
+ 16
+ 19
Сен.
—2
—2
—1
244
—29
4-1
—5
253
—20
+6
+ 10
+ П
Окт.
+3
4-3
+2
250
—23
—4
0
242
—31
+ 1
+4
-и
Ноя.
+9
4-9
+5
245
-28
—6
+4
231
—42
—2
—5
—5
Дек.
4-6
4-о
+4
240
—33
—5
+3
227
—46
—3
—6
—7
380

Продолжение
Широта северная
в град.
со
Месяц
0
10
20
30
40
50
60
70
80
90
д т
т °к
Т °С
ДГ
т °к
| т° с
д т
70
Янв.
-15
—13
—8
226
—47
4-7
—5
244
—29
+3
+5
+6
Февр.
—11
—11
—6
224
—49
4-5
—4
239
—34
+2
+3
+4
Март
—2
—3
—3
217
—56
4-6
—4
232
—41
+2
+4
+4
А пр.
0
0
0
218
—55
4-2
—2
224
—49
+3
+4
+5
Май
-3
—2
0
223
—50
—3
—1
220
—53
+ 1
+3
+3
Июнь
4-1
0
0
214
—59
0
— 1
216
-57
+ 1
+2
+2
Июль
—2
—1
—1
213
—60
0
0
214
-59
+ 1
+ 1
+ 1
Авг.
—1
4-1
4-1
214
—59
0
+ 1
213
-60
0
0
0
Сен.
—2
0
4-1
217
—56
—1
0
215
—58
—1
— 1
— 1
Окт.
0
0
0
218
—55
Q
0
219
—54
0
+ 1
+ 1
Ноя.
4-2
— 1
—2
218
—55
4-4
—4
229
—44
+2
+3
+3
Лек.
—6
—5
—3
221
-52
4-5
—8
242
-31
+3
+5
+6
80
Янв.
—18
—14
—10
225
—48
4-13
—10
260
— 13
+7
+ 11
+ 12
Фев.
—20
—15
-9
223
—50
4-11
—6
250
—23
+4
4-6
+7
Март
—11
—8
—5
212
—61
4-4
—4
229
—44
0
+ 1
+ 1
А пр.
4-1
4-1
4-1
200
—73
0
— 1
202
—71
+ 1
0
—2
Май
4-13
4-Ю
4-6
192
—81
—6
-1
182
—91
— 1
—2
—3
Июнь
4-18
4-15
4-8
190
—83
—8
+5
171
—102
—4
—7
—9
Июль
4-16
4-12
+7
191
—82
—8
+7
169
— 104
-8
— 16
—20
Авг.
4-8
4-5
4-3
195
—78
—7
+ 10
170
— 103
—12
—22
—26
Сен.
+2
4-1
—1
199
—74
—5
+ 10
177
—96
—13
—21
—21
Окт.
-2
—2
— 1
203
—70
0
+ 1
199
—74
+ 1
+5
+7
Ноя.
—4
—3
—2
209
—64
4-4
—16
236
—37
+ 10
+ 16
+ 17
Дек.
-8
-5
—4
216
—57
+ 12
— 11
253
—20
+8
+ 14
+ 16
Таблица 6
Вариации давления по высотам, широтам и месяцам (10л дин/см2)
Высо¬
та
км
Меся ц
Широта северная
п
0°
10°
20°
30°
40°
50°
60°
70°
80°
90°
30
Янв.
+03
+02
+01
1,18
—03
+07
1,05
—09
—18
—23
4
Фев.
+04
+02
+01
1,17
—03
+06
1,05
—10
—24
—33
4
Март
+03
+02
+01
1,18
—02
+05
1,07
-06
—21
—36
4
Апр.
+02
+01
+01
1,21
—01
+04
1,13
—03
—13
—26
4
Май
00
00
00
1,24
—01
+01
1,21
—02
—04
—07
4
Июнь
—03
—02
—01
1,26
+01
—01
1,29
+01
+03
+04
4
Июль
—07
—06
—04
1,28
+03
—02
1,36
+02
+ 03
+05
4
Авг.
—08
—06
—03
1,29
+03
—02
1,36
+01
+02
+03
4
Сен.
—07
—04
—02
1,28
+01
00
1,29
—01
—02
-02
4
Окт.
—02
—01
—01
1,25
00
+03
1,20
—03
—04
—05
4
Ноя.
+02
+01
+01
1,22
—01
+05
1,13
—05
—08
—10
4
Дек.
+03
+02
+01
1,20
—02
+06
1,08
—07
— 12
—16
4
381

Продолжение
Высо¬
та
км
Месяц
Широта северная
0°
10°
20°
30°
40°
50°
60°
70°
80°
90°
40
Янв.
4-10
+06
4-05
2,91
—13
+30
2,26
—28
—51
—62
3
Фев.
4-08
+05
4-04
2,87
—14
+29
2,24
—31
—62
—81
3
Март
4-Ю
+07
+03
2,90
—11
+25
2,34
—22
—58
—89
3
Апр.
ч-13
4-Ю
+07
3,03
—10
+ 17
2,62
—13
—40
—70
3
Май
+05
+05
+03
3,14
—06
+04
2,97
—05
—10
—18
3
Июнь
—06
—04
—03
3,21
+03
—06
3,35
+04
+ 11
+ 17
3
Июль
—21
— 18
-12
3,21
+ 12
—12
3,58
+ 10
+ 18
+25
3
Авг.
—24
—20
-11
3,19
+ 12
—08
3,50
+06
+ 11
+ 14
3
Сен.
—18
— 10
—04
3,18
+03
00
3,20
—05
—09
—11
3
Окт.
+04
+04
+02
3,12
—05
+ 12
2,84
—12
—18
—22
3
Ноя.
4-13
4-11
4-08
3,03
—12
+21
2,56
—19
—30
—36
3
Дек.
+ 15
+ 13
+ 07
3,00
—14
+28
2,36
—23
—39
—51
3
50
Янв.
+03
+02
+02
0,82
—03
+ 11
0,55
—07
—13
—15
3
Фев.
+01
4-01
+01
0,81
—07
+ 10
0,55
—08
—16
—20
3
Март
+04
+03
+01
0,81
-05
+09
0,59
—06
—15
—22
3
Апр.
Май
+06
+05
+03
0,83
—03
4-05
0,71
—03
—09
—17
3
+03
+02
+02
0,88
—01
—01
0,88
00
+01
00
3
Июнь
—02
—02
—02
0,92
+02
—04
1,02
+03
+06
+08
3
Июль
—06
—04
—04
0,91
+05
—06
1,08
+04
+07
+09
3
Авг.
—08
—07
—01
0,90
+04
—03
1,01
+03
+04
+05
3
Сен.
—05
—03
—01
0,90
00
00
0,90
—02
—03
—04
3
Окт.
00
4-01
4-01
0,89
—03
+05
0,78
-04
—05
—05
3
Ноя.
+04
-1-04
+03
0,87
—05
+08
0,67
—06
—08
— 10
3
Дек.
+05
+ 04
+03
0,85
—07
+ 10
0,59
—05
—09
—12
3
60
Янв.
+20
4-16
4-11
2,15
-22
+29
1,34
—19
—32
—37
2
Фев.
4-13
4-11
+09
2,13
—23
+27
1,36
—20
-38
—49
2
Март
4-16
4-14
+07
2,14
—16
+21
1,53
—15
—35
-55
2
Апр.
+22
+ 16
4-Ю
2,32
—12
+ 11
1,96
—03
—16
—37
2
Май
4-14
+ 10
+05
2,47
—04
—09
2,54
+ 12
+23
+23
2
Июнь
—06
—04
—04
2,58
+ 10
—21
3,06
+ 19
+38
+51
2
Июль
—15
—13
—10
2,50
+20
—30
3,27
+21
+35
+46
2
Авг.
—18
— 17
—12
2,44
+ 16
—17
2,95
+ 12
+25
+32
2
Сен.
-15
-08
-03
2,45
+03
—05
2,54
—01
—01
—02
2
Окт.
+06
+09
+07
2,48
—11
+ 14
2,08
—07
—07
—10
2
Ноя.
+20
+20
4-16
2,41
—22
+23
1,72
— 17
—23
—26
2
Дек.
+ 19
+ 18
+ 13
2,33
—26
+30
1,47
—18
—26
—34
2
70
Янв.
+02
+02
4-02
0,50
—04
+07
0,32
—04
-08
—09
2
Фев.
4-01
4-01
+01
0,49
—04
+05
0,33
—05
—09
—12
2
Март
+04
+03
+01
0,49
—08
+04
0,37
—03
—08
— 13
2
Апр.
+06
+04
+02
0,55
—03
+01
0,48
00
—03
—08
2
Май
+03
+03
+02
0,60
—01
—03
0,62
+04
+08
+ 10
2
Июнь
-03
-03
—02
0,60
+03
—06
0,75
+07
+ 14
+ 19
2
Июль
—05
—05
-03
0,57
+05
—09
0,80
+08
+ 15
+ 19
2
Авг.
—06
—04
—03
0,56
+04
—05
0,71
+06
+ 11
+ 13
2
Сен.
-04
—02
—01
0,57
+01
—03
0,61
+01
+03
+03
2
Окт.
+03
+07
+03
+02
0,58
-03
+03
0,49
—02
—02
—02
2
Ноя.
п-05
+04
0,56
—05
+05
0,40
—04
—05
—07
2
Дек.
-{-03
-т-03
+03
0,53
—05
+05
0,35
-04
—06
-08
2
382

Продолжение
Высо¬
та
км
Месяц
Широта северная
п
0°
10°
20°
30°
40°
50°
60°
70°
80°
90°
80
Янв.
—09
-07
—04
1,14
—03
+ 14
0,86
— 11
— 17
—21
1
Фев.
— 10
—09
-03
1,10
—05
-1-11
0,84
— И
—22
—28
1
Март
+03
+02
00
1,02
—02
+08
0,86
—06
—17
—28
1
Апр.
+ 12
+09
+05
1,11
—05
+02
0,99
+02
—04
— 14
1
Май
+09
+09
+06
1,20
—07
—05
1,16
+ 10
+ 18
+ 19
1
Июнь
+03
+03
+01
1,13
+02
-12
1,35
+08
+ 16
4-20
1
Июль
—03
—04
-03
1,08
+08
—10
1,36
+07
+ 10
+ 14
1
Авг.
-08
-06
-04
1,08
+06
—04
1,24
—01
—03
—01
1
Сен.
-09
—04
-02
1,14
-01
+01
1,09
—04
—07
—08
1
Окт.
+04
+04
+03
1,19
—06
+07
0,98
—03
—01
—01
1
Ноя.
+ 13
+ 10
+06
1,16
—06
+07
0,94
—07
—09
— 10
1
Дек.
00
+02
+02
1,16
—06
+ 12
0,91
—08
— 12
— 17
1
Таблица 7
Вариации плотности по высотам, широтам и месяцам (10 zJcmД
Высо¬
та
км
30
40
Месяц
Янв.
Фев.
Март
Апр.
Май
Июнь
Июль
А вг.
Сен.
Окт.
Ноя.
Дек.
о°
10°
20°
+03
+07
+ 03
+01
—05
—05
-09
—09
-Ю
-06
-02
+02
+03
+ 03
+02
—01
—04
-05
—07
—07
—06
—05
-03
00
Янв.
+01
+ 01
Фев.
+01
+01
Март
+01
+01
Апр.
+01
+01
Май
00
00
Июнь
—01
-01
Июль
—03
—02
Авг.
—03
—02
Сен.
—03
—01
Окт.
00
00
Ноя.
+01
+01
Дек.
+02
+01
+01
+ 01
+ 01
00
-03
—04
—05
-03
-03
—04
—01
—01
00
+01
00
+01
00
00
—01
-01
—01
00
+ 01
00
Широта северная
£0°
1,80
[,80
[,80
[,80
[,85
[,88
[,92
[,96
1,93
1,87
1,82
1,80
0,40
0,39
0,40
0,42
0,43
0,43
0,44
0,44
0,44
0,43
0,42
0,41
40°
-02
—03
00
+ 03
—01
+ 02
+ 03
+01
-1-02
+02
+03
+01
—01
—01
—01
—01
-01
00
+01
+01
00
00
—01
—01
50°
+05
-4-03
+03
+02
-02
-02
00
— 02
00
+ 02
+04
+03
60°
1.72
1.73
1.74
1,81
1,89
1.94
1,97
2,01
1.95
1,87
1,80
1.74
+03
+03
4-02
+02
+01
00
—01
—01
00
+01
+02
+03
0,35
0,34
0,35
0,37
0,40
0,44
0,47
0,47
0,44
0,40
0,37
0,36
70°
90°
— 10
— 10
—03
-01
-02
+ 01
+ 02
СО
+ 01
—03
—05
-06
-04
-04
-03
-02
-01
00
-01
00
-01
-01
-02
-03
—21
-32
-26
— 16
-05
+03
+02
+ 02
00
—02
—07
— 11
-07
—09
-08
—05
—02
+01
+ 01
-401
—01
—02
—03
—05
—29
—47
—51
—37
-09
05
+ 04
03
01
02
-09
— 16
-09
— 12
— 13
—09
—03
т-01
-02
+01
—01
—03
—04
-07
—о
— 5
—5
—5
—5
383
<+ + Си Сл О1 О1 Oi Oi <+ Oi Си (pi 6» 6i Cn Qi

Продолжение
Высо¬
та
км
Месяц
Широта северная
п
0°
10°
20°
30°
40°
50°
60°
70°
80°
90°
50
Янв.
+03
+02
+02
1,06
—06
+13
0,77
—10
— 19
—23
—6
Фев.
+01
00
+01
1,05
—07
+ 13
0,77
— 11
—23
—30
—6
Март
+02
+02
00
1,06
—05
+ 11
0,81
—09
—21
—32
—6
Апр.
+06
+05
+04
1,08
—03
+07
0,93
—06
— 16
—27
—6
Май
+01
+02
+01
1,14
—03
+01
1,08
—03
—04
—07
—6
Июнь
—02
—01
—01
1,16
+02
-02
1,22
+01
+03
+04
—6
Июль
—07
—06
—04
1,16
+05
—05
1,31
+03
+06
+09
—6
Авг.
— 10
—09
-05
1,16
+04
—03
1,28
+02
+03
+04
—6
Сен.
—07
—03
—01
1,15
+01
+01
1,14
—02
—04
—05
—6
Окт.
+01
+02
+01
1,13
—02
+05
1,01
-05
—07
-09
—6
Ноя.
+05
+04
+03
1,10
—04
+09
0,90
—08
—13
— 15
—6
Дек.
+05
+05
+03
1,09
—06
+ 11
0,82
—09
—14
—19
—6
60
Янв.
+25
+ 19
+ 14
3,16
—29
+41
2,05
—27
—46
—54
—7
Фев.
+ 15
+ 13
+ 10
3,14
-32
+40
2,03
-29
—56
—72
—7
Март
+ 17
+ 14
+07
3,14
—21
+34
2,22
—24
—55
—83
—7
Апр.
+26
+ 18
+ 12
3,24
—12
+ 18
2,76
—10
—34
—64
—7
Май
+ 16
+ П
+05
3,42
—04
—07
3,47
+05
+09
+03
—7
Июнь
—07
—04
—04
3,63
+ю
-18
4,07
+ 12
+23
+31
— 7
Июль
—18
— 17
-12
3,59
+21
—25
4,31
+ 11
+ 16
+23
—7
Авг.
—23
-20
—16
3,52
+ 19
—11
3,94
+01
+08
+ 13
—7
Сен.
—19
—09
—04
3,50
+03
+ 01
3,49
—08
—14
—16
—7
Окт.
+04
+08
+07
3,46
—10
+20
2,99
—11
—15
—18
—7
Ноя.
+ 15
+ 15
+ 16
3,43
—24
+30
2,59
—23
—29
-34
—7
Дек.
+ 18
+ 19
+ 13
3,38
-31
+44
2,25
—25
—34
—45
—7
70
Янв.
+08
+07
+05
0,78
—10
+ 11
0,46
-07
—12
— 14
—7
Фев.
+06
+05
+04
0,76
-08
+09
0,48
—07
—14
— 17
—7
Март
+07
+06
+04
0,78
—06
+08
0,55
—04
—12
— 19
—7
Апр.
+09
+07
+04
0,88
—05
+03
0,74
—01
—05
— 13
—7
Май
+05
+05
+02
0,94
—01
—04
0,98
+0э
+ 14
+ 15
—7
Июнь
—05
—04
—03
0,97
-t-06
—11
1,22
+ 10
+21
+28
—7
Июль
—07
—07
—05
0,93
+ 10
—15
1,30
+13
+23
+30
—7
Авг.
—08
—06
—05
0,90
+08
—10
1,17
+08
+ 16
+20
—7
Сен.
—06
—03
—01
0,91
+02
—03
0,98
+03
+05
+06
—7
Окт.
+04
+04
+03
0,93
—04
+05
0,77
-02
—02
—03
—7
Ноя.
+09
+08
+06
0,90
—10
+ 10
0,60
—06
—09
—10
—7
Дек.
+08
+07
+06
0,84
— 10
+ 12
0,50
—06
—09
—12
—7
80
Янв.
—01
—01
+01
1,77
—15
+24
1,15
— 17
—27
-32
—8
Фев.
00
—03
+02
1,72
—16
+ 19
1,17
— 17
-32
—41
-8
Март
+ 14
+ю
+04
1,68
—06
+ 15
1,31
—09
—26
—43
—8
Апр.
+ 19
+ 14
+08
1,93
—09
+ 04
1,71
+02
—07
—23
—8
Май
+02
4-04
+03
2,18
—06
—09
2,22
+20
-4-37
+40
—8
Июнь
—12
— 10
—07
2,07
+ 13
—31
2,75
+23
+45
+58
—8
Июль
—21
—19
—12
1,97
+24
—32
2,81
+29
+52
+69
—8
Авг.
—22
—16
+ П
1,94
+ 17
—20
2,53
+ 18
+32
+44
—8
Сен.
—17
—07
—02
1,99
+04
—10
2,15
+08
+ 12
+ 10
—8
Окт.
+08
+09
+07
2,04
-10
+ 10
1,72
—06
—06
—08
—8
Ноя.
+26
+ 19
+ 12
1,94
—15
+20
1,94
—15
—21
—23
—8
Дек.
+08
+ 07
+07
1,87
-19
+23
1,25
-14
—21
—29
—8
384

На рис. 7—12 показаны изменения скорости ветра по широ¬
там на первое число месяца. Положительным цифрам соответ¬
ствуют скорости ветра в м!сек в направлении «запад—восток».
ю
60
so
00
JO
30° с ш 1июля
1 июля 30° ю.ш
Рис. 7.
385

высота в км Высота в км
Рис. 9.
386

Высота В км Высота В км
Рис. И.
30°с ш 1июни	1июня90°	w	ии
Рис. 12.
3^7

Часть 3. Структура атмосферы и ее вариации в диапазоне
высот от 120 до 800 км
Атмосфера CIRA 1965 имеет 10 моделей для десяти различ¬
ных уровней солнечной активности. Каждая из моделей разде¬
лена на 12 частей через каждые 2 часа времени суток.
В табл. 8—11 приводятся данные по пятой модели атмосферы
CIRA 1965, соответствующей среднему уровню солнечной актив¬
ности (максимальная температура экзосферы в 14 час местного
времени Т(14) = 1460° К, минимальная температура в 4 час мест¬
ного времени Г(4)=979°К).
Таблицы приведены для четырех значений местного времени:
0, 6, 12, 18 час и справедливы для экватора и умеренных широт.
Таблица 8
Местное время 0 час
Максимальная и минимальная температура экзосферы
в течение дня Т (14) = 1460° К, Т(4) = 979° К
Высота
км
Темпера¬
тура
°К
Плотность
г/см3
Давление
дин/см2
Высота
однородной
атмосферы
км
Средний
молекулярный
вес
120
355
2,490.10-п
2,722-10-2
11,6
27,01
130
497
8,507*10-12
1,332
16,6
26,36
140
605
4,002
7,805*10-3
20,8
25,79
150
687
2,211
5,004
24,2
25,25
160
750
1,343
3,388
27,1
24,72
170
799
8,672*10-13
2,379
29,5
24,20
180
836
5,845
1,716
31,7
23,69
190
866
4,066
1,263
33,6
23,18
200
890
2,898
9,457-10-4
35,4
22,68
210
909
2,107
7,178
37,1
22,19
220
925
1,557
5,513
38,7
21,72
230
938
1,166
4,278
40,2
21,26
240
948
8,843*10-14
3,351
41,6
20,81
250
957
6,778
2,646
43,0
20,39
260
964
5,245
2,104
44,4
19,98
270
971
4,094
1,685
45,6
19,60
280
976
3,221
1,357
46,9
19,25
290
980
2,553
1,100
48,1
18,91
300
983
2,036
8,952.10-5
49,2
18,60
320
989
1,319
6,013
51,3
18,04
340
993
8,724*10-15
4,102
53,2
17,56
360
996
5,870
2,835
55,0
i 17,15
380
998
4,008
1,981
56,6
16,79
400
1000
2,771
1,398
58,2
16,47
420
1001
1,932
9,934-10-6
59,6
16,18
440
1002
1,361
7,132
61,1
15,90
460
1002
9,671.10-16
5,162
62,6
15,61
480
1003
6,917
3,766
64,2
■
15,32
388

Продолжение
Высота
км
Темпера¬
тура
°К
Плотность
г/см3
Дапление
дин/см2
Высота
одноролнй
атмосферы
км
Средний
молекулярный
вес
г 00
1003
4,979
2,770
66,0
14,99
520
1004
3,605
2,056
68,1
14,64
540
1004
2,625
1,540
70,4
14,24
560
1005
1,923
1,165
73,2
13,78
580
1005
1,417
8,918-
10-7
76,4
13,28
600
1005
1,051
6,908
80,3
12,71
62.0
1005
7,847-10-17
5,421-
10-7
84,9
12,10
640
1005
5,604
4,314
90,3
11,44
660
1006
4,479
3,482
96,6
10,76
680
1006
3,340
2,851
103,9
10,06
700
1006
2,653
2,369
112,3
9,36
720
1006
2,075
1,996
121,7
8,69
740
1006
1,642
1,705
132,0
8,06
760
1006
1,316
1,474
143,2
7,47
780
1006
1,069
1,289
155,0
6,94
800
1006
8,768-10-18
1,139
167,3
| 6,47
Таблица 9
Местное время 6 нас
Максимальная и минимальная температура экзосферы
в течение дня Г (14) =1460° К, Т (4) = 979° К
Высота
км
Темпера¬
тура
°К
Плотность
г/см3
Давление
дин,j см*
Высота
однородной
атмосферы
км
Средний
молекулярный
вес
120
355
2,490-10-п
2,722-10-2
11,6
27,01
130
479
8,694-10-12
1,314
16,1
26,35
140
573
4,059
7,510-Ю-з
19,7
25,74
150
645
2,201
4,691
22,8
25,16
160
703
1,305
3,100
25,5
24,59
170
750
8,213-10-13
2,132
27,9
24,03
180
790
5,402
1,511
30,2
23,48
160
823
3,676
1,067
32,3
22,94
200
852
2,570
8,124-10-4
34,3
22,41
210
877
1,839
6,118
36,2
21,91
220
898
1,341
4,674
38,1
21,42
230
916
9,949-10-14
3,615
39,8
20,95
240
931
7,488
2,827
41,5
20,51
250
944
5,709
2,232
43,1
20,09
260
956
4,403
1,776
44,6
19,69
270
965
3,430
1,425
46,1
19,32
280
974
2,697
1,150
47,4
18,98
290
981
2,139
9,344-10-5
48,7
18,66
13—1669
389

Продолжение
Высота
км
Темпера¬
тура
°К
Плотность
г/см5
Давление
дан} см1
Высота
одноротной
а[мосферы
км
Средни!';
мо leivV 'ярнын
нес
300
987
1,708
7,631
50,0
18,37
320
996
1,111
5,161
52,3
17,84
340
1003
7,393*10-15
3,546
54,3
17,39
360
1008
5,008
2,469
56,2
17,01
380
1012
3,444
1,738
57,8
16,67
400
1015
2,397
1,236
59,4
16,36
420
1016
1,682
8,840*10-6
60,9
16,07
440
1018
1,193
6,393
62,5
15,80
460
1019
8,535*10-16
4,660
64,1
15,51
480
1020
6,145
3,424
65,8
15,21
500
1020
4,452
2,537
67,6
14,89
520
1021
3,244
1,896
69,8
14,52
540
1021
2,377
1,431
72,3
14,11
560
1022
1,752
1,091
75,2
13,65
580
1022
1,299
8,406*10-7
78,6
13,13
600
1022
9,696*10-17
6,558
82,6
12,57
620
1022
7,285*10-17
5,182*10-7
87,4
11,95
640
1023
5,516
4,151
93,0
11,30
660
1023
4,210
3,372
99,5
10,62
680
1023
3,243
2,777
107,1
о f 03
700
1023
2,523
2,320
115,6
9,25
720
1023
1,985
1,965
125,2
8,59
740
1023
1,579
1,685
135,7
7,67
760
1023
1,272
1,463
147,0
7,40
780
1023
1,038
1,283
158,9
6,89
800
1023
8,585*10-18
1,137
171,2
6,43
Таблица 10
Местное время 12 час
Максимальная и минимальная температура экзосферы
в течение дня Т (14) = 1460° К, Т (4) — 979° К
Высота
км
Темпера¬
тура
°К
Плотность
г}см5
Давление
duajcM2
Высота
однородной
атмосферы
км
Средний
молекуляриый
вес
120
355
2/90.10-п
2,722*10-2
11 ,6
27,01
130
491
8,566* 10—12
1,326
16,4
26,36
140
609
3,945
7,748*10-3
20,9
25,78
150
719
2,122
5,021
25,3
25,25
160
818
1,268
3,483
29,5
24,76
170
906
8,170*10-13
2,533
33,3
24,29
180
987
5,567
1,906
36,9
23,85
190
1048
3,956
1,471
40,2
23,43
200
1104
2,904
1,157
43,3
23,03
210
1152
2,188
9,252*10-4
46, 1
22,64
390

Продолжение
Вы с'от а
км
Темпера -
Tvpa
°К
Плотность
г/см3
Давление
дин/см-
Высота
однородной
атмосферы
км
Средний
молекулярный
вес
220
1192
1,082
7,491
48,6
22,27
230
1227
1,316
6,129
51,0
21,90
240
1250
1,044
5,059
53,2
21,56
250
1281
8,382.10-н
4,208
55,3
21,22
2Г0
1303
6,799
3,524
57,3
20,90
270
1321
5,564
2,908
59,1
20,59
280
1336
4,589
2,512
60,9
20,29
290
1349
3,810
2,136
62,5
20,00
300
1303
3,183
1,824
64,1
19,73
320
1377
2,257
1,345
67,1
19,22
340
1390
1,030
1,004
69,8
18,75
300
1399
1,194
7,578-10-5
72,3
18,34
380
1406
8,808-10-15
5,771
74,6
17,96
400
1411
6,056
4,431
76,7
17,62
420
1414
5,037
3,420
78,7
17,32
440
1417
3,840
2,661
80,6
17,04
400
1419
2,903
2,082
82,4
16,79
480
1421
2,296
1,038
84,2
16,56
500
1422
1,789
1,295
85,9
16,34
520
1423
1,401
1,028
87,6
16,13
540
1424
1,103
8,198-10-5
89,3
15,92
55 0
1424
8,717-10—16
6,566
91,0
15,72
580
1425
6,917
5,282
92,8
15,51
(00
1425
5,508
4,266
94,6
15,30
020
1426
4,401-10-15
3,401-10-5
96,6
15,07
040
1426
3,528
2,821
98,8
14,83
000
1426
2,837
2,309
101,1
14,57
180
1425
2,289
1,899
103,7
14,29
700
1427
1,852
1,570
106,6
13,99
720
1427
1,504
1,305
109,7
13,67
740
1427
1,224
1,091
113,3
13,32
7(0
1427
1,001
9,109-10-7
117,2
12,94
780
1427
8,206-10-17
7,755
121,6
12,55
800
1427
6,740
6,599
126,5
12,13
Таблица 11
Местное время 18 час
Максимальная и минимальная температура экзосферы
в течение дня Т (14) = 1460° К, Т (4) = 979° К
Высо-1 а
км
Темпера-
ту а
°К
Пло гность
г/см3
Давление
дин, см2
Высота
однородной
атмосферы
км
Средний
молекулярный
вес
120
355
2,490-10-п
2,722-10-2
11,6
27,01
130
508
8,377-10-12
1,343
17,0
26,37
140
637
3,910
8,015-Ю-з
21,8
25,82
391

Продолжение
Высота
км
Темпера¬
тура
°К
Плотность
г/см3
Давление
дин/см2
Высота
однородной
атмосферы
км
Средний
молекулярный
нес
150
744
2,160
5,280
26,1
25,31
160
834
1,324
3,696
29,9
24,84
170
908
8,700-10-13
2,694
33,3
24,39
180
970
6,004
2,021
36,3
23,95
190
1021
4,297
1,550
39,0
23,52
200
1063
3,162
1,210
41,5
23,10
210
1098
2,379
9,568-10-4
43,8
22,70
220
1128
1,822
7,656
45,9
22,31
230
1152
1,415
6,186
47,9
21,92
240
1173
1,114
5,040
49,7
21,55
250
1191
8,853-10-14
4,136
31,5
21,19
260
1206
7,105
3,417
53,2
20,84
270
1218
5,748
2,839
54,8
20,51
280
1229
4,684
2,371
56,3
20,19
290
1238
3,842
1,990
57,8
19,88
300
1246
3,170
1,677
59,2
19,59
320
1259
2,193
1,205
61,9
19,04
340
1268
1,545
8,780.10-5
64,3
18,56
360
1275
1,106
6,470
66,7
18,12
380
1281
8,020.10-15
4,816
68,8
17,74
400
1285
5,887
3,616
70,8
17,39
420
1287
4,354
2,729
72,7
17,08
440
1290
3,257
2,079
74,4
16,80
460
1292
2,456
1,594
76,2
16,55
480
1294
1,865
1,230
77,8
16,31
500
1295
1,424
9,535-10-6
79,5
16,08
520
1296
1,094
7,432
81,1
15,86
540
1297
8,444.10-16
5,823
82,8
15,64
560
1298
6,547
4,585
84,6
15,41
580
1299
5,098
3,629
86,5
15,17
600
1299
3,965
2,887
88,5
14,91
620
1300
3,127*10-16
2,310.10-6
90,8
14,63
640
1300
2,463
1,859
93,2
14,33
660
1301
1,947
1,504
96,0
14,00
680
1301
1,545
1,226
99,1
13,64
700
1301
1,231
1,005
102,7
13,25
720
1301
9,842.10-17
8,302.10-7
106,6
12,83
740
1302
7,902
6,908
111,1
12,38
760
1302
6,373
5,793
116,2
11,91
780
1302
5,163
4,897
121,9
11,41
800
1302
4,204
4,174
128,4
10,91
392

ПРИЛОЖЕНИЕ III
СТАНДАРТНАЯ ПРОГРАММА ВЫЧИСЛЕНИЯ НА ЭЛЕКТРОННОЙ
ВЫЧИСЛИТЕЛЬНОЙ МАШИНЕ БЭСМ-2М ПАРАМЕТРОВ
СТАНДАРТНОЙ АТМОСФЕРЫ СА-64 *
1.	Стандартная программа вычисления параметров атмосферы
для высот от —2000 до 200 000 м
Данная программа (СП-0200)** служит для вычисления зна¬
чений термодинамических и физических параметров атмосферы
в соответствии с ГОСТ 4401—64.
Программа производит расчеты в основном по формулам,
приведенным в таблицах стандартной атмосферы СА—64. Глав¬
ные отличия вычисления параметров атмосферы по данной про¬
грамме состоят в следующем:
— скорость звука а и кинематическая вязкость v вычис¬
ляются и для высот h>95 000 м (в ГОСТ только до высот
й<95 000 ж);
— по данной программе можно вычислять значения парамет¬
ров и вне диапазона высот — 2000 ж</г<200 000 м. Получаю¬
щаяся при этом погрешность по сравнению с рекомендациями
Координационной комиссии АН СССР по составлению ГОСТ на
стандартную атмосферу приведена в табл. 1. Производить вы¬
числения по СП-0200 для высот выше 300 000 м не рекомен¬
дуется. При /г>340 000 м наступает АВОСТ;
— изменение молекулярного веса по высоте в диапазоне
ft>160 000 м заменено приближенным, удобным для расчета на
ЭВМ, способом. Погрешность аппроксимации дана в табл. 1;
— длина свободного пробега молекул Т не вычисляется. При
необходимости ее можно вычислить вне программы по формуле
По заданной высоте h программа вычисляет величины:
— геопотенциальную высоту Ф в гп м;
— ускорение силы тяжести g в м/сек2;
— молекулярный вес воздуха М;
— молекулярную температуру Тм в °К;
* Составлена И. С. Крикун.
** Нумерация стандартных программ дана по выпускам № 4—6 «Стан¬
дартные и типовые программы БЭСМ-2», издание Вычислительного центра
АН СССР, 1963.
393

— кинетическую температуру Т в °К;
— давление воздуха р в кГ/м2\
— 1 ОООX плотность воздуха, IOOOq в кГ • сек2/мА*\
— скорость звука а в м/сек;
— кинематическую вязкость воздуха v в м2/сек.
Программа предназначена для использования с компилирую¬
щей программой и вводится с перфокарт.
Объем оперативной памяти, занимаемой программой, состав¬
ляет 217 ячеек (в восьмеричной системе). Среднее время одно¬
кратного вычисления параметров стандартной атмосферы с по¬
мощью СП-0200 составляет 17 мсек.
Перед обращением к программе нормализованный аргумент
находится в ячейке 0001.
Обращение к программе осуществляется с помощью псевдо¬
команды:
I
77
—
0200
3777
Результаты вычислений (в нормализованном виде) полу¬
чаются в ячейках.
Величина
Ф
£
м
7м
Т
р
103. Q
а
V
1
№ ячейки ре¬
зультата
1
0012
0011
0010
0007
0006
0005
0004
0003
0002
Исходное значение h после выхода из программы находится
в ячейке 0017.
Внутри программы имеются обращения к стандартным про¬
граммам СП-0012 (ех), СП-0013 (1пх), СП-0011 {Vх), записан¬
ным на магнитном барабане. Программа работает на ЦУК и
самовосстанавливается.
Рабочие ячейки 0001-0017. В программе нет ОСТАНОВов при
значениях аргумента в диапазоне высот — 2000 ж</г<300 000 м.
При А>340 000 м возникает АВОСТ из-за переполнения при вы¬
числении V.
В программе использованы следующие исходные данные и
физические константы:
— давление воздуха на уровне моря и на географической
широте 45°32/40//	10332,3	кГ/м2;
* Увеличение величины q в 1000 раз связано с выходом ее из разрядной
сетки машины БЭСМ-2М при /г> 135 км, где Qi35~10-8 (диапазон чисел в
БЭСМ-2М: 0,233 • 10-9<\х\<0,215 • 1010). Сдвиг на три десятичных разряда
обеспечивает достаточную точность вплоть до высот —^300 км.
394

— кинетическая температура Т0 = Гм0 = 288,15° К;
— молекулярный вес М = 28,966;
— ускорение силы тяжести go = 9,80665 м/сек2',
— радиус сферы, равновеликой Земле, R3 =6371 210 м;
с р
— отношение удельных теплоемкостей воздуха —=1,4000;
С т.
постоянная сухого воздуха R =
Т = 273,15° К	цо = 1,75 X
при
— удельная газовая
287,039 м2/град • сек2;
— динамическая вязкость
X 10~6 кГ • сек/м2.
В программе использованы следующие соотношения между
параметрами атмосферы.
Геопотенциальная высота
Ф =
hR3
Ускорение силы тяжести
h + R3
Rs
+ А?з
Молекулярная температура
288,15 —0,00651122 Ф
216,66
216,66 + 0,00276098 (Ф - Ф25)
274.00
274.00 - 0,00349544 (Ф - Фи)
г \ 185,00
м
185.00 + 0,005 (Ф — Ф9Б)
257,64 + 0,00801741 (Ф - Фпо)
335.00 + 0,02346357 (Ф—Ф120)
1010,00	+0,01987408 (Ф-Ф150)
VI 199,4- +0,00308461 (Ф-Ф160)
Молекулярный вес
128,966
5.Р66
М =
h < 11 000 м
11 ООО м < h < 25 000 м
25 000 м + h + 46 000 м
46000 ж</г< 54000 м
54 000 м + h + 80 000 м
80 000 м + h + 95 000 м
95 000 м + /г + 110 000 м
110 000 м < h < 120 000 м
120 000 м < А < 150 000 м
150 000 л<А< 160 000 м
160 000 ж < // < 200 000 м
h + 95000 м
23,000	+
145 000
V145ООО2-(/г-95 ООО)2
28,933 —0,00002066 (А — 110 000)
95 000 ж<А< 110000 м
110000 м <А< 160000 м
395

В диапазоне высот 160 ООО м</г<200 ООО м изменение в ГОСТ
задается таблично. Для упрощения вычислений в данной про¬
грамме принято, что в указанном диапазоне молекулярный вес
вычисляется по формуле
М = 27,90—0,0000225 (Л—160 000)	 160	000	ж	<А	<200	000	м.
Для вычисления плотности воздуха и давления используется
уравнение состояния идеального газа
р = RqT м
и уравнение статики атмосферы
Яз
dp _ G0p I
dh RTm\7
\Рз + Л
где G0—9,80665 л/сак2.
Интегрирование последнего уравнения приводит к формуле
In р = In	(Ф	—	Ф	J
м
— для изотермических слоев (/?*, Ф* — значения величин на
нижней границе рассматриваемого слоя)
и
In р = In р — In
и* auR Гм*
— для слоев с линейно изменяющейся температурой.
Здесь
а =*±
м дФ
— градиент молекулярной температуры по геопотенциальной
высоте.
Скорость звука рассчитывается по формуле
а = 20,0463 УТи.
Динамическая вязкость определяется выражением
/ Т \з/2 Го+110,4
Т +110,4*
которое упрощается к виду:
103-р—7,41673-Л0-6 —-—.
г	т	+110,4
Расчеты по этой формуле совпадают с данными ГОСТ до вы¬
сот h = 95 000 м (выше h = 95 000 м величина р в ГОСТ не ука¬
зана) .
396

Кинематическая вязкость вычисляется по формуле
103.fi
~~ 103.Q ’
Для больших высот (/г >>95 ООО м) воздух уже не может рас¬
сматриваться как непрерывная среда, так как в силу большого
разрежения длина свободного пробега молекул соизмерима
с характерными размерами обтекаемого тела.
В этих условиях параметр а = Л/ —— RTM нельзя рассматри-
У cv
вать как скорость распространения слабых возмущений (скорость
звука). В аэродинамике разреженных (молекулярных) течений
определяющей является скорость теплового возбуждения
молекул
v =	2 — а,
которая пропорциональна величине а. В силу этого и в области
молекулярных течений в качестве параметра подобия может
употребляться число М= — , а аэродинамические коэффициенты
а
сохраняют функциональный вид
сх=--сх(а> М), СУ = Су(а, М),
где а — угол атаки, принятый в аэродинамике сплошных течений.
Сказанное показывает целесообразность вычисления скорости
звука для высот h>95 000 м, что и сделано в данной программе.
Кинематическая вязкость v для высот ЯД>95 000 м вычис¬
ляется для справки.
Точность вычислений
Принимая данные, опубликованные в ГОСТ, за точные, полу¬
чаем следующие характеристики относительной погрешности гу
вычислений различных параметров СА—64 (см. табл. 1):
У СП-0200 ~' У С А
у,
СА
100%
где
y = (g, М, Т, р, q, a, v).
Схема программы
(^)l‘32^3^4^5^6^7^)8^9^10^11v3l2^:>13^l45	^15^16^17^18^19^20
it	j	;	tt
10	8	15	16	13 14
Ф1 (2001)	—переход на центральное управление и
формирование команды выхода;
397

32 (2002)	—засылка h в	рабочую ячейку 0017;
/13 (2003—2005)	— вычисление	Ф;
/14 (2006—2007)	— вычисление	g\
/15 (2010—2033)	—вычисление	М;
36 (2034)	—засылка нулей в рабочие ячейки 0015
(номер слоя) и 0016 (Ф*);
А7 (2035—2041)	—определение номера слоя Лг;
Р8 (2042)'	—сравнение N с нулем; если N = 0, то управ¬
ление передается в Лю(Ф* = 0);
/19 (2043—2047)	— вычисление Ф*;
A j о (2050—2054)	—вычисление Гм;
/4ц (2055—2056)	—вычисление Г*;
312 (2057—2060)	—засылка In р* в рабочую ячейку 0013;
Pi3 (2061)	—сравнение (Ф—Ф*) с нулем; если
ам(Ф—Ф*) = 0, то управление передается
в А1Ъ\
Аи\	—вычисление In р по формуле для слоев
1 /опп 1	9П7Д\ с изменяющейся температурой, обход Л]5;
A is I (^ut)l 20/4)	—вычисление In р по формуле для изотер-
J	мических слоев;
>416 (2075—2076)	—обращение к СП-0012 для вычисления р\
Ап (2077—2101)	—вычисление (1000-q);
A is (2102—2104)	— вычисление а\
А19 (2105—2111)	—вычисление v;
#2о (2112)	—выход из программы.
Таблица 1
Относительная погрешность гу вычисления параметров атмосферы
с помощью СП-0200 (в %)
Диапазон высот, км
g
м
т
р
Q
а
—2< /г< 1С0
0,001
0,005
1
0,01
0,06
0,06
0,002
0,05
160 < Л< 200
0,013
0,1
0,1
0
0,1
200 < h <250
0,02
1,2
0,25
0,5
0,4
—
—
о
о
со
11
0,02
3,5
I 0,6
2
0,6
1 -
При м е ч а н и я. 1. Величина g при /г> 160 000 м в ГОСТ 4401—64
вычислена недостаточно точно. Данная программа производит вычис¬
ление этой величины на порядок точнее.
2. При h > 250 000 м ошибки во всех параметрах, за исключением g,
возрастают монотонно.
398

ПРОГРАММА СП-0200 В КОДАХ МАШИНЫ БЭСМ-2М
СП-0200. Вычисление параметров стандартной атмосферы
30
0100
0220
Карта ввода
0200
2
3
4
5
0
7
8
9
10
11
12
02
1511
0174
3102
Дополнение
9
3
4
5
()
7
8
9
10
11
12
399

Продолжение
СП-0200. Вычисление параметров стандартной атмосферы
2000
0121
1
1
34
2112
2002
2
2
0001
0017
3
3
01
2127
0017
0016
4
4
04
2127
0016
0016
5
5
03
0016
0017
0012
6
6
03
0016
0016
0016
7
7
03
2202
0016
0011
8
2010
36
0017
2150
2015
9
1
02
0017
2150
0016
10
2
03
0016
2136
0016
11
3
02
2135
0016
0010
12
2014
34
2034
2
5
36
0017
2145
2022
2
6
02
0017
2145
0016
3
7
03
0016
2134
0016
4
2020
02
2125
0016
0010
5
1
34
2034
6
2
36
0017
2144
2033
7
3
02
0017
2144
0016
8
4
04
0016
2131
0016
9
5
03
0016
0016
0016
10
6
02
2126
0016
0001
11
7
77
0011
3777
12
400

Продолжение
СП-0200. Вычисление параметров стандартной атмосферы
2030
03
0002
2132
0016
3
1
01
0016
2133
0010
2
2
34
2034
3
3

2130
0010
4
4
14
0015
0016
5
5
2113
2036
6
6
33
0001
7
7
22
0016
2122
0016
8
2040
22
2036
2123
2036
9
1
34
2036
10
2
35
0016
2050
11
3
22
2114
0016
2044
12
4
33
0002
4
5
01
0014
2127
0015
2
6
04
2127
0015
0015
3
7
03
0015
0014
0015
4
2050
02
0012
0015
0015
5
1
22
2115
0016
2053
6
2
22
2116
0016
2054
7
3
33
0003
8
4
33
0004
9
5
03
0007
0010
0013
10
6
04
0013
2130
0006
11
7
22
2117
0016
2060
12
401

Продолжение
СП-0200. Вычисление параметров стандартной атмосферы
2060
33
0005
5
1
35
0014
2166
2071
2
2
22
2120
0016
2063
3
3
33
0006
4
4
77
0013
3777
5
5
22
2121
0016
2066
6
6
33
0007
7
7
04
0002
0014
0014
8
2070
34
2072
9
1
04
0015
0006
0014
10
2
03
0014
2202
0014
11
3
04
0014
2201
0014
12
4

02
0013
0014
0001
6
5
77
0012
3777
2
6
0002
0005
3
7
04
0005
0007
0014
4
2100
03
0014
2124
0014
5
1
04
0014
2201
0004
6
2
0007
0001
7
3
77
0011
3777
8
4
03
0002
2200
0003
9
5
01
0007
2203
0016
10
6
04
0003
0016
0016
11
7
03
0016
0007
0016
12
402

Продолжение
СП-0200. Вычисление параметров стандартной атмосферы
2110
03
0016
2217
0016
7
1
04
0016
0004
0002
2
2
33
0010
3
3
30
0017
2137
2042
4
4
2136
0014
5
03
2165
0015
0014
6
0
02
2152
0014
0007
7
7
2204
0013
8
2120
04
2152
0007
0001
9
1
2165
0014
10
2
0001
11
3
0001
12
2124
12
1750
8
о
05
1635
3331
0265
2
6
01
1000
3
7
27
1411
2742
2000
4
2130
05
1636
3513
3066
5
1
22
1066
1500
6
2
03
1373
2457
0325
7
3
05
1340
8
4
61
1265
0740
1436
9
5
05
1574
3146
1463
10
6
61
1362
3714
0717
11
7
16
1257
2000
12
403

Продолжение
СП-0200. Вычисление параметров стандартной атмосферы
2140
17
1415
1000
9
1
20
1316
3000
2
2
20
1513
3000
3
3
21
1161
4
4
21
1346
0600
5
5
21
1533
1400
6
6
21
1651
2000
7
7
22
1111
3600
8
2150
22
1161
9
1
23
1415
1000
10
2
11
1100
1146
1463
11
3
10
1542
2436
2703
12
4
10
1542
2436
2703
10
5
11
1044
2
6
11
1044
3
7
10
1344
4
2160
10
1344
5
1
11
1003
1075
1605
6
2
11
1236
7
3
12
1762
8
4
13
1127
2631
2315
9
5
71
1525
1602
1172
10
6
40
11
7
70
3323
3061
3317
12
404

Продолжение
СП-0200. Вычисление параметров стандартной атмосферы
2] 70
40
11
1
70
1624
1170
0173
2
2
40
3
3
71
3217
1341
1076
4
4
72
3015
1556
2157
5
5
73
3400
3325
2073
6
6
73
3213
0736
3565
7
7
70
3450
2345
1422
8
2200
05
1201
1732
1211
9
1
11
1076
0237
2764
10
2
04
1163
2401
0725
11
3
07
1563
0631
2315
12
4
04
1117
2156
1640
12
о
03
1737
2205
2202
2
(3
03
1306
2244
1141
3
7
02
1245
1423
1220
4
2210
01
1523
3604
3246
5
1
02
3054
3135
3411
6
2
03
3157
1600
2652
7
3
03
3621
0415
2062
8
4
04
3020
0543
3663
9
о
04
3167
0036
0316
10
6
04
3211
3543
2121
11
7
57
1743
1647
0675
12
405

2.	Укороченная программа вычисления параметров стандартной
атмосферы для высот от —2 км до 46 км (по ГОСТ 4401—64)
Стандартная программа СП-0201 служит для вычисления
значений термодинамических и физических параметров стан¬
дартной атмосферы (СА) в диапазоне высот от —2000 м до
46 000 м в соответствии с общесоюзным стандартом ГОСТ
4401—64.
Метод вычисления параметров стандартной атмосферы, осно¬
ванный па указанном ГОСТ, приведен в СП-0200. Данная про¬
грамма отличается от СП-0200 меньшим диапазоном высот /г,
в котором производится вычисление параметров, и меньшим на¬
бором вычисляемых параметров. В силу этого программа на¬
звана «укороченной» (по сравнению с СП-0200).
1. По заданной высоте (аргументу) h программа вычисляет
величины:
— геопотенциальную высоту Ф;
— ускорение силы тяжести g\
— температуру атмосферы Т (для /г<Д95 км кинетическая и
молекулярная температуры совпадают);
— давление воздуха р\
— плотность воздуха q;
- скорость звука а\
—■ кинематическую вязкость v.
Формулы вычисления указанных величин приведены
в СП-0200. Там же указана погрешность вычислений.
Программа предназначена для использования с компили¬
рующей программой и вводится с перфокарт.
Перед обращением к программе нормализованный аргумент
находится в ячейке 0001.
Обращение к программе осуществляется с помощью псевдо¬
команды
77
0201
3777
Результаты вычислений в нормализованном виде получаются
в ячейках.
Величина
1 Ф
1
О'
Т
Р
! е
а
V
№ ячейки результата
о
о
го
0011
0010
0007
0006
0005
0004
Исходное значение высоты h после выхода из прсграммы на¬
ходится в ячейке 0017. Внутри программы имеются обращения
к стандартным программам СП-0011 (вычисление У х), СП-0012
(вычисление ех), СП-0013 (вычисление In я), записанным на
магнитном барабане. Программа работает на ЦУК и самовос-
станавливается. Рабочие ячейки 0001-0017. Программа занимает
103 (в восьмеричной системе)' ячейки оперативной памяти. Сред¬
нее время однократного обращения и вычисления параметров
406

стандартной атмосферы составляет 11 мсек. В программе каж¬
дый раз возникает «ОСТАНОВ» в том случае, когда аргумент км
становится больше или равен 46 000 м. При нажатии кнопки
«Пуск» счет может быть продолжен. При этом вычисления будут
производиться по формулам, соответствующим слою
25 000 лг''/ь<46 000 м (т. е. с определенной погрешностью).
В случае к<—2000 м «ОСТАНОВ» не происходит, а вычис¬
ления производятся по формулам, соответствующим слою
—2000<А<11 000 м.
Схема программы
8 10	13
c^i^2P3r~f 4A5A6P4AS; Рп А10; AnPl2Al3\ A14A15A1GA17A18//19
I	t	I I	t I 4	t	4	4	t
5	3	9	12	7 11 12	9	14	15	12
ФI (2001)	—переход на центральное управление и за¬
сылка выхода,
32 (2002)	—засылка к в рабочую ячейку 0017;
Р3 (2003)	— сравнение к с 4-6 000 м\ если А <46 000 м,
то управление передается в А5;
Я4 (2004)	— останов, если /г>46 000 м\
А5 (2005—2007)	—вычисление Ф;
А6 (2010—2011)	—вычисление g;
Р7 (2012)	—сравнение к с 25 000 м\ если Л <25 000 ж,
то управление передается в
А8 (2013—2021)	—вычисление	Т	по	формуле	для
25 000 <Л<46 000	м, засылка в рабочие
ячейки 71*, ам, In р*, передача управления
в Р\2;
Р9 (2022)'	— сравнение Л с 11 000 м\ если к< 11 000 ж,
то управление передается в Ац‘,
А ю (2023—2025)	—засылка Г* и In р* в рабочие ячейки (для
11 С00<Л<25 000 ж); передача управле¬
ния в Рi2;
Ап (2026—2032)	—вычисление	Т	по	формуле	для
—2000<Л<11 000 ж, засылка в рабочие
ячейки Г0, аУ1, In р0;
Р\2 (2033)	—сравнение Г с 216,66; если 7" = 216,66, то
управление передается в А14;
А13 \	— вычисление In р по формуле для слоев
I /опод 9плл\ с изменяющейся температурой; обход А14;
Аи М	'	—вычисление In р по формуле для изотер-
J	мического слоя;
A is (2045—2046)	—вычисление	р\
А16 (2047—2050)	— вычисление q;
А17 (2051—2053)	— вычисление а\
А18 (2054—2060)	— вычисление v;
Н 19 (2061)	— выход из программы.
407

ПРОГРАММА СП-0201 В КОДАХ МАШИНЫ БЭСМ-2М
СП-9201. Вычисление параметров СА для — 2 км < h < 46 км

30
0100
0104
Карта ввода
0201
2
3
4
о
6
7
8
9
10
11
12
44
1612
0404
1305
Дополнение ^
2
3
4
5
6
7
8
9
10
11
12
408

Продолжение
СП-0201. Вычисление параметров СА для —2 км < h < 46 км
2000
0057
1
1
34
2061
2002
2
2
0001
0017
3
3
36
0017
2071
2005
4
4
33
0201
5
5
01
0017
2072
0016
6
6
04
2072
0016
0016
7
7
03
0016
0017
0012
8
2010
03
2066
0016
ООП
9
1
03
ООП
0016
ООП
10
2
36
0017
2070
2022
11
3
02
0012
2065
0016
12
2014
03
0016
2064
0014
2
5
01
20ГЗ
0014
0010
2
6
2063
0015
3
7
2064
0014
4
2020
2101
0013
5
1
34
2033
6
2
36
0017
2067
2026
7
3
2063
0010
8
4
2100
0013
9
5
34
2033
10
6
03
0012
2062
0016
11
7
01
2102
0016
0010
12
409

Продолжение
СП-0201. Вычисление параметров СА для—2 км < к < 46 км
2030
2102
0015
3
1
2032
0014
2
2
2077
0013
3
3
35
0010
2063
2040
4
4
04
0010
0015
0001
5
5
77
0013
3777
6
6
04
0002
0014
0014
7
7
34
2042
8
20-10
02
0012
2103
0016
9
1
04
0016
0010
0014
10
о
03
0014
2066
0014
11
3
04
0014
2076
0014
12
4
02
0013
0014
0001
4
5
77
0012
3777
2
6
0002
0007
3
7
04
0007
2076
0006
4
2050
04
С006
0010
0006
5
1
0010
0001
6
2
77
0011
3777
7
3

03
0002
2075
0005
8
4
01
0010
2074
0016
9
5
04
0005
0016
0016
10
6
03
0016
0010
0016
11
7
03
0016
2073
0004
12
410

1 Ino.i(мженпе
СП-0201.
Вычисление параметров
С Л длл -
— 2 км < /; : 46 км
2000
04
0004
0000
000-1
5
1
33
0001
2
2
71
3525
1002
1172
3
3
10 '
1542
2430
2703
4
4
70
1323
3001
3317
5
5
17
1412
0022
1150
0
0
04
1103
2401
0725
7
7
10
1257
2000
8
2070
17
1415
1000
9
1
20
1310
3000
10
2
27
1411
2742
2000
11
3
45
1773
1307
3470
12
4
07
1503
0631
2315
6
5
05
1201
1732
1211
2
0
И
1076
0237
2704
3
7
04
1117
2150
1040
4
2100
03
1737
2205
2202
5
1
03
1300
2244
1141
0
2
11
1100
1140
1403
7
3
10
1250
1205
0354
8
9
10
11
12
411

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Азимут 111
Аномалия истинная 16, 18, 26
— средняя 16, 18, 27, 121
— эксцентрическая 18, 26, 27
Астрономическая единица 7, 21, 39
Астрономические постоянные 39
Атмосфера Земли 39
— международная	справочная
CIRA—65 39, 47, 369
— стандартная СА—64 39, 50, 364,
393
Аэродинамическое качество 255
Вектор
— главный аэродинамических сил
231
— конечного поворота 73
Венеры физические характеристики 37
— характеристики поверхности 38
— элементы орбит 35
Вертикаль географическая 228
— геоцентрическая 228
— местная 102, 105, 229
Вес тела 228
Ветры в атмосфере Земли 46, 385
Время гринвичское звездное 89
Вязкость динамическая 8, 16, 41, 45,
364—366, 394
— кинематическая 8, 16, 41, 43, 45,
236, 364—366, 393, 406
Год световой 21
— тропический 20
Горизонт истинный 20
Гравитационный параметр 15, 37
Гравитационная постоянная 7, 17, 39
Движение
— ЛА переменной массы 286, 340
— плоское 286, 287, 309, 311, 314,
316, 324, 332, 347, 348, 359
— ЛА постоянной массы 286
—пространственное 286, 311
— прямолинейное горизонтальное
286, 288, 290, 292, 340, 341
— прямолинейное вертикальное 286,
295, 298, 300, 304, 307, 340, 343,
344, 346
Долгота астрономическая 53, 87
— восходящего узла 89
— геоцентрическая 86
— гелиоцентрическая 80
— географическая 87
— ортодромическая 87
— узла ортодромии 89
Единицы измерения 9
Задача двух тел 16
Законы движения 164
—Кеплера 16
Земной меридиан 20
— экватор 20
Земли атмосфера 39, 369
— физические характеристики 37
— характеристики поверхности 38
— элементы орбиты 35
Импульс удельный 274, 276
Интеграла энергии постоянная 20, 27
Качество аэродинамическое 255
— максимальное 255
Кинематические соотношения (уравне¬
ния) 164
Коническое сечение 17
Координат декартовы 56
— криволинейные 56
— прямоугольные 56
— эллипсоидальные 54, 63
— эллиптические 55
Косинусы направляющие 55, 67—71,
74, 155, 161, 162
Коэффициент
— боковой силы 224, 249
— взаимовлияния консолей 257
— демпфирования 239
— индуктивного сопротивления 224,
233, 246, 247
— интерференции 244
— лобового сопротивления 233, 244,
247
— лобового сопротивления при ну¬
левой подъемной силе 233, 244
— момента крена 225, 262, 264
— момента крена от производствен¬
ной песимметрии 262
— момента рысканья 225, 263, 266
412

— момента тангажа комбинации
«крыло-рфюзеляж» 271
— момента тангажа при нулевой
подъемной силе 263, 270
— момента шарнирного руля высо-
ты (стабилизатора) 269
— момента шарнирного руля на¬
правления 269
— момента шарнирного элеронов
269
— полной аэродинамической силы
224, 232
— подъемной силы частей ЛА 248,
249—252
— сжатия Земли 39
— торможения потока 244, 254
Критерии подобия 232, 236
Линия апсид 18, 22, 122
— базовая 59
— координатная 57
-- отсчета 59
— узлов табл. 3. 4а
Луны физические характеристики 37
— характеристики поверхности 38
— элементы орбиты 35
Маха число 236
Марса физические характеристики 37
— характеристики поверхности 38
— элементы орбиты 35
Международная справочная атмосфе¬
ра CIRA—65, 39, 47, 369
Международная система единиц СИ 7
Мера статической устойчивости 239
— боковой 240
— поперечной 240, 262
— продольной 240, 268
Момент
— внешний 226
— внутренний 227
— возмущенный 227
— главный аэродинамических сил
231, 234, 235,
— гравитационный 226, 231
— кориолисовых сил 227
— управляющий 227
— шарнирный 268, 269
Наклон орбиты 19, 35
Небесная сфера 18
Небесный меридиан 20
— экватор 20
Ось координатная 58
—мира 19
Параметры Родрига—Гамильтона 73,
74, 162, 163
Перегрузка 280—283, 285
Период сидерический 20
Перенос параллельный систем коор¬
динат 55
Планеты Солнечной системы 35, 37,
38
Плоскость основная 58, 75 77, 78, 80,
82, 84, 86, 102, 104,	106,	108,	110,	121,
122, 125, 126, 128,	130,	132,	134,	136
Плотность 41, 42,	44,	226,	285,	295
296, 300, 304, 314,	317,	340,	344,	364,
366—376, 394, 396, 406
Поляра 255, 256—261
Постоянная
— газовая удельная 7
— газовая универсальная 7
— геоцентрическая гравитационная
39
— гравитационная 7, 17, 166, 167
— гравитационная Гаусса 39
— интеграла энергии 20, 27
— площадей 20
Постоянные астрономические 39
Производная вращательная 239, 243
Прямое восхождение гелиоцентриче¬
ское 81
— геоцентрическое 85
Решение уравнений прямолинейного
горизонтального движения ЛА 341
— при постоянной силе сопротив¬
ления 291
— при силе сопротивления, изме¬
няющейся по квадрату скорости
полета 292
— при постоянной силе тяги 288
Решение уравнений прямолинейного
вертикального движения ЛА
— в среде постоянной плотности
344
— при постоянной плотности среды
полета и при постоянной силе
тяги 385
— при постоянной плотности среды
полета и при постоянной силе
сопротивления 298
— при постоянной плотности среды
полета и при силе сопротивле¬
ния, изменяющейся по квадрату
скорости полета 300
— при показательном законе изме¬
нения плотности среды полета
и при силе тяги, равной нулю
304
— при переменном гравитационном
ускорении 346
— при заданном законе изменения
гравитационного ускорения 307
—■ при постоянном ускорении 343
Решение уравнений плоского движе¬
ния ЛА
— ЛА переменной массы 348
— при нулевом значении попереч¬
ной перегрузки 332
— при нулевом угле наклона тра¬
ектории и при постоянной ско¬
рости полета 309
413

— при нулевом угле наклона тра-
ектории и постоянных значениях
угла крена и силы тяги 312
— при постоянных значениях угла
наклона траектории и силы тяги
314, 316
— при показательном законе изме¬
нения плотности среды полета
317
— при постоянной продольной пе¬
регрузке 324
Радиус средний 37
— экваториальный 37
Расход топлива секундный 274
Реакции связей 227
Сила
— аэродинамическая 226
— внешняя 226
— внутренняя 227
— возмущающая 199, 227
— гравитационная 226
— гироскопическая 227
—двигательной установки 227, 273
— лобового сопротивления 225, 234
— нормальная 234
— полутангенциальная 235
— поперечная 234, 235
— по скорости полета 234
— сопротивления 235
— реактивная 272
— тангенциальная 235
— тяги 274, 285—288, 290, 292, 294,
295, 298, 300, 302, 304, 307, 312,
314, 316, 347, 359
— тяжести 228
— управляющая 227
Система координат
— барицентрическая К200 75, 120—
122
  прямоугольная орбитальная
К211 120—122
— гелиоцентрическая П100 75, 77
 прямоугольная П110 77
	эклпптпческая-1, -II, -III
П111, П112, П113 77—79,
88, 166
	экваториальная П114 77, 80
 сферическая Г1120 77
	эклиптическая-I, П121 77,
88, 166
	экваториальная П122 77, 81
— геотоппческая Т100 75, 101
 прямоугольная Т110 101
	горизонтальная 101 —107
	произвольная-I, -II, Till,
Т114 101, 102, 104
	стартовая-1,-П Т112, Т115
101, 103, 105, 170
	орпентироваиная-I, -II
Т113, Т116 101, 103, 105,
151, 170, 173, 180, 186, 192,
193, 198, 210, 213, 217, 220
	произвольная I, II Т117,
Т118 101, 106, 107
	сопроводительная Т119
101, 108
 сферическая Т120 101, 108—111
	горизонтальная	101,	108—
110
	произвольная Т121	101,
108
	стартовая	Т122 101, 109
	ориентпрованиая-I Т123
101, 109, 174
   — произвольная Т124 101, 110
	цилиндрическая	горизон¬
тальная ориентированная
Т131 101, 110, 175
	гиперболическая на рефе-
ренц-эллипсоиде Т151	101,
111
— геоцентрическая П200 75, 77
 географическая П240 77
 прямоугольная П210 77
	эклиптическая-1,-П,-1П
П211, П212, П213 77, 82, 83
	экваториальная	П214 77, 84,
150, 167, 174, 175, 188, 208
 сферическая П220 77
	ортодромическая П224 77,
87, 167
	экваториальная	П222, П223
77, 85, 86, 151, 168, 175, 178,
181, 183, 190, 208, 209
		эклиптическая П221 77, 85
— земная С118 131, 143—145, 151,
152, 157—159, 161 — 163, 175, 178,
186, 190, 201, 202, 208, 217, 220
— космоцентрическая КО00	75,
120—122
— ЛА-цептрическая С100	75,	124,
125
 прямоугольная С110 125
	вертикально-симметриче¬
ская 125, 127, 128
		полусвязанная С114 125,
126, 143, 144, 146, 186, 235,
241, 242, 243
	связанная-I, -II С112 125,
127,	143—146, 171,	175,
185, 213
	связанная-II СПЗ 125,
127, 157,	161—163,	185,
234, 242, 243
	скоростная С116 125, 130,
144—146, 201, 217, 219,
234, 241
	 вертикально-скоростная
С115 125, 129, 143, 144, 147,
187
414

	главная связанная Cl 11 125,
126, 171, 172, 175, 176
		горизонтальная ориентиро¬
ванная С118 125, 131, 143—
145, 151, 163, 178, 208, 217,
220
	сопроводительная естествен*
ная С117 125, 131, 146, 147
  полярная лучевая скоростная
С121 125, \3\
— нецентральная С20'0, СЗОО 124,
125
  косоугольная гироскопическая
С261 125, 136
 прямоугольная С210, С310 125
	вертикально-симметриче¬
ская 125
	связанная С211, С311	125,
132, 145
	скоростная С213 125, 133
	 вертикально-скоростная
С212 125, 132
	произвольная С312 125, 138,
145
 сферическая лучевая С221 125,
134
— орбитоцентрическая КЮО 75, 120,
121
 прямоугольная апсидная КШ
121, 122, 149, 150
 сферическая апсидная К121
121, 122
— ортогональная 60
— планетоцентрическая П200 75—78
— планетотопическая ТО'ОО 75, 100,
101
— полусвязанная С114 128, 143, 144,
146," 151, 152, 235, 241—243
— полярная 65, 66
— поточная С116 130, 144—146, 151,
152, 157, 201, 217, 219, 234, 241
— прямоугольная 60, 61, 66
— связанная с ЛА 75, 126, 127, 152
— скоростная С115 129, 143, 144, 147,
151, 152, 161, 192
— сферическая 63, 66
— цилиндрическая 62, 66
— эллипсоидальная 54, 55
— эллиптическая 55
Система отсчета инерциальная 165
Склонение гелиоцентрическое 81
— геоцентрическое 85
Скоростной напор 50
Скорость в апоцентре орбиты 28, 32,
33
— в перицентре орбиты 28, 32, 33
— вторая космическая 34
— звука 7, 41, 45, 364—368
— индикаторная 50
— круговая 34
— освобождения 34
— параболическая 34
— первая космическая 34
— приборная 50
— света в вакууме 7
— средняя угловая движения по
орбите 35, 36
Скос потока 252
Соотношения кинематические 164
Стандартная атмосфера	СА—64
39—41, 44, 45, 364
Точка весеннего равноденствия 19
Тяга 273, 274
— удельная 274
Угловая скорость 155, 157—161
— безразмерная 238
Угол
— азимута 109, 111
— атаки 139
— гироскопический 139
— крена 138
 скоростного 139
— курса 138
 скоростного 138
— наклона соприкасательной плос¬
кости 139
 оси инерции 139
 ортодромии 89
 траектории 138
 хорды крыла 139
  экватора к эклиптике 89
— отклонения крыла 253
  руля высоты (стабилизатора)
253
— подвижных элементов Л А 139
— процессии табл. 3.4а
—рысканья 138
— скольжения 139
— стреловидности 253
— установки двигателя 274
Уравнения динамические
— движения центра масс 163
— движения относительно центра
масс 163
— кинематические 164
—траектории полета 164
Ускорение
— гравитационное 38, 228—230
—материальной точки 156
— силы тяжести 45, 228, 230, 231,
369
— свободного падения 364
Установка двигательная 273—274
— основная 274
— комбинированная 274
— экзотическая 274, 278
Фокус конического сечения 17
— ЛА или его частей 231
Формулы
— преобразования
415

— коэффициентов аэродинамиче¬
ских сил и моментов 241—243
— между космоцентрическими
системами координат 121
— между планетоцентрическими
системами координат 76, 88—
98
— между планетотопическими си¬
стемами координат 100, 112—
119
— между связанными с JIA си¬
стемами координат 124,	137,
147
— между системами координат
различных классов 149—151
связи
— между скоростями изменения
углов Эйлера и проекциями
вектора угловой скорости 155,
157—159, 161
— между производными направ¬
ляющих косинусов и проек¬
циями вектора угловой скоро¬
сти 161, 162
 между производными парамет¬
ров Родрига—Гамильтона и
проекциями вектора угловой
скорости 162, 163
Центр давления 231
Число Маха 236
— Рейнольдса 236
Широта астрономическая 85
— гелиоцентрическая 81
— географическая 87
— геодезическая 87
— геоцентрическая 86
— ортодромическая 87
Эклиптики наклонение 89
—плоскость 18
Элементы орбиты 17—22, 35, 36
Эффективность органов управления
253

СОДЕРЖАНИЕ
Стр.
Глава 1. Физические величины	и	единицы	измерения	 7
1.1. Некоторые физические постоянные	 7
1.2. Международная система единиц измерения (СИ)	 7
1.3. Соотношения между метрическими и англо-американскими
мерами 	 9
Литература	 14
Глава 2. Орбиты небесных тел	и	атмосфера	Земли	 15
2. 1. Орбиты небесных тел	 16
2. 1. 1. Задача двух тел. Закон Кеплера	 16
2. 1. 2. Типы орбит	 16
2.1.3. Элементы и параметры орбит	 21
2. 2. Атмосфера Земли	 39
2.2.1. Стандартная атмосфера СА—64	 39
2.2. 2. Ветры в атмосфере	 43
2.3. Некоторые вспомогательные графики для расчета параметров
полета в атмосфере Земли	 49
Литература	 52
Глава 3. Системы координат	 53
3. 1. Основные определения и формулы преобразования координат
(общие сведения)	 54
3. 1. 1. Основные определения	 54
3.	1.2. Виды систем координат и формулы преобразования между
ними	 54
3.	1.3. Преобразование прямоугольных систем координат. Способы
задания их взаимного углового положения	 55
3.2.	Системы координат механики полета и формулы перехода
между ними	 75
3.2.1. Классификация систем координат	 75
3.2. 2. Планетоцентрические системы координат	 76
3.2.3. Планетотопические системы	координат	 100
3.2.4. Космоцентрические системы	координат	 120
3.	2. 5. Системы координат,	связанные	с	летательным аппаратом 124
3.2.6.	Формулы преобразования	между системами	координат
различных классов	 149
Литература	   153
Глава 4. Уравнения движения летательного аппарата	 154
4. 1. Элементы кинематики летательного аппарата	 155
4.1.4. Связь проекций вектора	угловой скорости	некоторых
ЛА-центрических прямоугольных систем координат с про¬
изводными от углов Эйлера	 155
417

Стр.
4.1.2. Связи проекций вектора (щ угловой скорости связанной
системы координат СПЗ с производными направляющих
косинусов между осями этой системы и осями земной си¬
стемы координат С118	 161
4.1.3. Связи проекций вектора соi угловой скорости связанной
системы координат СПЗ с производными параметров
Родрига—Гамильтона	 162
4.2. Уравнения движения механики полета	 163
4.3. Уравнения движения в планетоцентрических системах коор¬
динат 	 166
4.3.1. Уравнения	движения	в	гелиоцентрической	прямоугольной
эклиптической-I системе координат OXYZ (П111)	....	166
4.3.2. Уравнения	движения	в	гелиоцентрической сферической
эклиптической системе координат R, %*, ,и* (П121)	.	.	.	166
4.3.3. Уравнения	движения	в	геоцентрической прямоугольной
экваториальной системе координат Ox'y'z' (П214)	.	.	.	167
4.	3. 4. Уравнения движения в геоцентрической сферической орто-
дромпчсской системе координат г, А,0рТ, ср0рТ (П224)	...	167
4.	3. 5. Уравнения движения в геоцентрической сферической эква-
ториальной-II системе координат г, ср', X (П223)	....	168
4.4. Уравнения движения в геотоппческих системах координат	.	.	170
4.4.1. Уравнения движения в гсотопической прямоугольной гори¬
зонтальной произвольной-II системе координат 0T£(-v|ctc
(Т112)	170
4.4.2. Уравнения движения в геотоппческой прямоугольной гори¬
зонтальной	стартовой-Н	системе координат Ог£сг],.£с
(Т115)	 170
4.4.3. Уравнения	движения	в	геотоппческой прямоугольной
горизонтальной орнентпроваиной-Н системе координат
ОШ (Т116)	 173
4.	4. 4. Уравнения движения в геотоппческой сферической горизон¬
тальной ориентированной системе координат г, A, gj	(Т123)	174
4.	4. 5. Уравнения движения в геотоппческой цилиндрической го¬
ризонтальной ориентированной системе координат г, A, z
(Т131)	 175
4.5. Уравнения движения в системах координат, связанных	с	ЛА	175
4.5.	1. Уравнения	движения	в	ЛА-центрической	прямоугольно!!
главной связанной системе координат Ox\ij\Z\ Cl 11)	.	.	.	175
4.5.2. Уравнения	движения	в	ЛА-центрической	прямоугольной
вертикально-симметрической связанной системе коорди¬
нат Ox\2y\2Z\2 (С 112)	 185
4.5.3. Уравнения движения в ЛА-центрической прямоугольной
вертикально-симметрической связанной системе координат
0xiyiz{ (СПЗ)	 185
4.5.4. Уравнения	движения	в	ЛА-центрической	прямоугольной
вертикально-симметрической полусвязанной системе коор¬
динат Oxyz (Cl 14)	 186
4.5.5. Уравнения	движения	в	ЛА-центрической	прямоугольной
вертикальной скоростной системе координат Oxcyczc
(Cl 15)	 187
4.5.6. Уравнения	движения	в	ЛА-центрической	прямоугольной
вертикально-симметрической скоростной (поточной) системе
координат Oxnynzn (Cl 16)	 201
4.5.7. Уравнения движения в ЛА-центрической прямоугольной
горизонтальной ориентированной (земной) системе коор¬
динат OxgygZg (Cl 18)	 206
418

Стр.
4.6.	Уравнения движения ЛА при наличии	ветра	 212
4.6.1. Уравнения	движения	в	ЛА-центрической	прямоугольной
вертикально-симметрической связанной системе координат
0X12^12^12 (С112)	 213
4.6.2. Уравнения	движения	в	ЛА-цептрнческой	прямоугольной
вертикально-симметрической скоростной (поточной) системе
координат Oxnynzn (Cl 16) в случае, когда ось Ох„ совпа¬
дает с вектором путевой скорости 	 217
4.6. 3. Уравнения	движения	в	ЛА-центрической	прямоугольной
вертикально-симметрической скоростной (поточной) системе
координат Oxnynzn (Cl 16) в случае, когда ось Охи совпа¬
дает с вектором воздушной скорости 	 219
Литература	 222
Глава 5. Силы и моменты, действующие	на летательный аппарат. 224
5. 1. Классификация сил п моментов	 226
5.2. Ста тяжести	 228
5.2.1. Модели гравитационного поля Земли. Гравитационное ус¬
корение 	 228
5.2.2. Момент гравитационных сил 	 231
5.3. Аэродинамические силы и моменты	 231
5.3.1. Некоторые определения	 231
5.3.2. Коэффициент лобового	сопротивления сх летательного
аппарата	 233
5.3.3. Коэффициент подъемной силы су летательного	аппарата	248
5.3.4. Коэффициент боковой силы cz летательного аппарата . .	249
5.	3. 5. Поляра летательного аппарата	 255
5.3.6. Коэффициент момента крена тх летательного	аппарата	262
5 .3. 7. Коэффициент мемента рысканья ту летательного	аппарата	263
5.	3. 8. Коэффициент момента тангажа тг летательного	аппарата	263
5.3.9. Шарнирные моменты органов управления	 268
5.	3. 10. Влияние изменения положения центра масс летательного
аппарата на аэродинамические коэффициенты	 273
5.4. Силы и моменты, создаваемые двигательными установками 273
5.4.1. Типы двигательных установок	 273
5. 4. 2. Основные характеристики двигательной установки ....	274
5. 5. Перегрузка	 283
Литература ....	.	  283
Г лава 6. Некоторые частные случаи движения летательных аппаратов	285
6. 1. Движение летательного аппарата постоянной массы (ш = ш0)	286
6.1.1. Прямолинейное горизонтальное движение (0=0)	....	286
6.1.2. Прямолинейное вертикальное движение (0=90°)	....	286
6.1.3. Плоское движение с пулевым углом наклона траектории
(0=0)	;	 287
6. 1.4. Плоское движение с постоянным углом наклона траектории
и при нулевом угле крена (0 =()0, у = 0)	 287
6. 1.5. Плоское движение при нулевом угле крена п при постоян¬
ном значении продольной перегрузки или пулевой попе¬
речной перегрузке (у = 0, пх = пх0"пли п,,= 0)	 311
6.1.6. Пространственное движение с постоянной скоростью
(v = vQ)	 311
6.2.	Движение летательного аппарата переменной массы при по¬
стоянной скорости истечения массы (ш = \таг; илст = const)	340
6.2.1. Прямолинейное горизонтальное движение (0 =0)	310
6.2.2. Прямолинейное вертикальное движение (0=90°)	340
6. 2. 3. Плоское движение в вертикальной плоскости .	.	347
419

Стр.
6.2.4.	Плоское движение при линейном изменении тангенса угла
наклона силы тяги по времени и при постоянном значении
силы тяги	 347
6 2. 5. Плоское движение при линейном изменении синуса угла
наклона силы тяги по времени и при постоянном значении
силы тяги	 359
Литература	   362
IIриложение I.	Таблица стандартной атмосферы	СА—64	(ГОСТ
4401—64)	 364
Приложение II. Международная	справочная атмосфера CIRA 1965 . .	369
Приложение	III. Стандартная программа вычисления на электронной
вычислительной машине БЭСМ-2М параметров стан¬
дартной атмосферы	СА—64	  393
Предметный указатель	 412
Станислав Алексеевич Горбатенко, Эрнст Михайлович Макашов,
Юрий Федорович Полушкин, Леонид Вольфович Шефтель
МЕХАНИКА ПОЛЕТА
(Общие сведения. Уравнения движения)
Редактор Г. Ф. Лосева	Художник	И.	Т.	Дворников
Техн. редактор Т. С. Старых	Корректор	Е.	П.	Карнаух
'Г—08572	Сдано	в набор 22/VII 1968 г.	Подписано в печать ЭЛИ—>1969 г.
Формат бОХЭО’Ае	Печ.	л.	27,	25,	в	т. ч. 3 вкл.	Уч.-изд. л. 24,30
Бум. л. 13,63	Бумага JV« 1	Тираж 13 500 экз.	Изд.	зак.	1924
Цена 1 р. 48 к.	Тем.	план	1968	г.	№	43
Издательство «Машиностроение», Москва, К-51, Петровка, 24.
Московская типография № 8 Главполиграфпрома
Комитета по печати при Совете Министров СССР,
Хохловский пер., 7. Зак. 1669

•
а,
н
U
71
76
99
140
172
175
186
190
190
192
216
217
218
218
221
Замеченные опечатки
Напечатано
Должно быть
X
s
У\
*1
па стр. 96.
на стр. 84.
па стр. 132.
Сс cos ср' cos ф);
+ Z — mg cos Ь sin у.
+ cos (а — срр) s
COS (а — срр) s
+ CQS (а — срр) S
П Р sin Yc]
n р cos Yc] +
n p sin Yc] —
X12У\i
0) CO
У12 *12 V
(lz Iv +l\. u )
12 \ *1* У 1 2	Л	1 2У I 2/
II —12
Xi 2 У12 X i ol/1?
I/ I 2	~12	^12
“x M« (/2v -;r lи +/2r V )
Л12	//1 - \	д12	-4*2	i/1 '	^12)12/
coc/
л I 2 У
(/’
1 2 \ л I
•^12 У 1 2
/2 ^
1 2*/l 2/
S’
11 a стр. 88.
na стр. 76.
na стр. 124.
+ £c cos cp' cos ф);
• •
+ Гг j
+ Z + mg cos 9 sin Y-
-f cos (a+ ?p) sin P sin Yc]
cos (а-j-cpp) sin p cos Yc] +
+ COS (a+cpp) sin P sin Yc] —
щ
IX	V (wr "h00
Л 1 2 ) 1 о '	1	о
У1
03
1 2
) +
»	'-'К (/,	/„	—.. )
j/12	^12	^12 У 12	X 1*1/12
I I	—/2
3Ti о У1 2	1	2	У	1	2
0)// coz	1,
У 12 ^12	л 1 2	л 1 21/1	2
со X
Л | 2
х (ii — л. 1, +il .. )
\ ^ I 2	^	1	2	^1	2	1	2	i/	1	*2/
х('1„
0)r (07 X
Л 1 2	*12

4Г

Таблица 5.15
Характеристики основных двигателей [16]» [20) — (22J
Вид двигателя
Диапазон применения
Диапазон тяг
Р
Диапазон удельных
импульсов
'уд
Удельный пес
двигателя
кГ веса двиг.
Влияние на характеристики двигателя
Характеристика
работы сопла
и воздухозаборника
Возможность
регулирования
тяги
Рабочее тело
Ограничения в работе
Время работы
Эксплуатационные
характеристики
Основные
характеристики
Примечание
ПО ЧИСЛУ
М
по высоте
h, км
числа
М
высоты
h
отклонения пара¬
метров атмосферы
от стандартной
кГ тяги
Ракетные двигатели
Жидкостный ракет¬
ный двигатель (ЖРД)
Не 01 раннчи-
вается
102—Ю6 к Г
200—290 сек
0,01
Незначительно
Очень важно со¬
гласование с соп¬
лом
Практически от¬
сутствует
Окислитель: ки¬
слород, азотная
кислота
Топливо: керо¬
син, спирт и т. д.
По температуре и
давлению в камере
сгорания, по произ¬
водительности систе¬
мы подачи
10—500 сек
Наиболее пригодны
для полетов с большой
тягой в безвоздушном
пространстве. Взрыво¬
опасны, одноразового
действия, трудности при
длительном хранении
Тяга, удельный рас¬
ход, разгонная характе¬
ристика, прибавка к тя¬
ге от высоты полета
Регулирование тяги
производится выключе¬
нием ряда двигателей
или камер сгорания. Су¬
ществуют двигатели ма¬
лой тяги с длительным
временем работы
Ракетный двига¬
тель твердого топ¬
лива (РЛТТ)
10—7.106 кГ
170-220 сек
Незначительно
Тяга очень силь¬
но зависит от на¬
чальной темпера¬
туры топлива
Только по про¬
грамме, в зависи¬
мости от формы
заряда
Порох
По прочности ка¬
меры сгорания
10 сек
Высокая степень на¬
дежности, возможность
длительного хранения,
отсутствие подготови¬
тельного времени, про¬
стота обслуживания
Тяга, как функция
времени, при различных
начальных температу¬
рах
(
Так как топливо нахо¬
дится в самом двигате¬
ле, то вес последнего
зависит от суммарного
импульса и конструкции
двигателя
1 Газотурбинные двигатели
Турбореактивный
двигатель (ТРД)

о
*1* !
со
0—30
70—2,5*104 кГ
3000—4000 сек
0,2
Рост тяги при
увеличении числа
М
Падение
тяги с ро¬
стом высо¬
ты
Падение тяги с
ростом темпера¬
туры воздуха
Требуется со¬
гласование расхо¬
да воздуха с се¬
чением воздухо¬
заборника
В широких пре¬
делах
Углеводородное
топливо (типа ке-
росша) и атмо¬
сферный воздух
По температуре
газа за турбиной, чи¬
слу М, скоростному
напору, производи¬
тельности системы
подачи топлива
До 5—10 час
непрерывно,
до 6000 час в
cvm ме
V*
Возможность длитель¬
ной работы и хранения,
безопасность. Требует
времени на прогрев и
запуск (около 1—2 мин)
Высотно-скоростные
по тяге и расходу топ¬
лива на различных ре¬
жимах, относительная
тяга по положению ры¬
чага управления и по
числу оборотов турбм-
н ы
Двукоитурный
турбореактивный
двигатель (ДТРД)
До 1
До 11-5-13
До 2.105 кГ
4000—6С00 сек
0,25
Вытесняет ТРД для
околозвуковых Л А в ви¬
ду большей экономич¬
ности
Турбореактивный
двигатель с форсаж¬
ной камерой (ТРД с
ФК)
0—«3.5
о
со
1
о
До 20*103 кГ
1300—2000 сек
0,2—0,25
Большинство
двигателей имеет
ступенчатую ре¬
гулировку фор¬
сажной камеры
Как у ТРД и до¬
полнительно по вре¬
мени работы фор¬
сажной камеры
В сумме
2000 час
Без включения фор¬
сажной камеры работа¬
ет, как ТРД
Турбовинтовой
двигатель (ТВД)
0—0,9
До 11—13
300—15000 л. с.
0,21—0,25 кг/а. с •час
Слабое до
^^0,7, далее изме¬
няется из-за ха¬
рактеристик вин¬
та
Сильное
падение с
ростом h
В широких пре¬
делах
Как у ТРД и до¬
полнительные огра¬
ничения по винту
Непрерывно
до 20 час, в
сумме до
4000 час
Как у ТРД
Мощность и расход в
зависимости от высоты
и скорости полета, ре¬
жима работы, оборотов
Широко применяется
для дозвуковых самоле¬
тов.
Характерно задание
мощности в л. с. вместо
тяги, удельного расхода
(кг/л. с,-час) — вместо
удельного импульса и
размерности удельного
веса {кг/л. с.)
Прямоточный воздуш¬
но-реактивный двига¬
тель с нерегулируемой
геометрией (ПВРД)
*
|—|
1
*
о
До 11—15
1000—2000 сек
0,02
Рост тяги при
увеличении числа
М
Очень важно со¬
гласование с за-
борником и соп¬
лом
В узких преде¬
лах
По минимальному
и максимальному
скоростным напорам,
числу М, высоте по¬
лета, производитель¬
ности системы пода¬
чи топлива
Требует разгона до
определенного скорост¬
ного напора, взрыво¬
безопасен, очень дешев
и прост
Высотно-скоростная
характеристика
Прямоточный воздуш¬
но-реактивный двига¬
тель с регулируемой
геометрией
2—4
До 30
1800-2200 сек
0,02
Поршневой двигатель
(ПД)
0—0,7
До 14
25—4000 л. с.
0,22—0,25 кг/л. с •час
0,4—0,8
кГ/л,. с.
Слабое
Сильное
Слабое падение
тяги при росте
температуры
В широких пре¬
делах
Углеводородное
тотиво (типа бен¬
зин!) иатмосфер-
нън воздух
По предельным
оборотам, темпера¬
туре блока цилинд¬
ров, подаче топлива
Непрерывно
до 100 час в
сумме до
2000 час
Надежен в работе,
экономичен, безопасен,
требует времени на про¬
грев
Дроссельная, высот¬
ная
Падение тяги при
увеличении высоты мо¬
жет быть частично ком¬
пенсировано применени¬
ем нагнетателей
За к. 1669

«о
£
Эс
У
£
Ц
С:
■и
Со
ГА.
СО
*С
<о
11000
15000
14000
13000
2000	3000	4000	5000	6000	7000	8000	3000	10000
Индикаторная скорость полета vi км!час
Рис. 2. 14. Зависимость скорости почета v от индикаторной скорости vt is высоты h
Зак. 1669.

Системы углов Эйлера
Система
углов Эйлера
Первая
Вторая
Третья
Углы в порядке выполнения поворотов систем координат
Первый
Второй
Третий
Матрицы последонателиных поворотов
Первый
1. Угол рысканья
(азимута, прецессии)
— угол между ли¬
нией узлов ON и не¬
подвижной осью ОХ
Угол тангажа (ну¬
тации) 0— угол меж¬
ду линией узлов ON
и осью Ох
Угол крена (соб¬
ственного вращения)
У— угол между ося¬
ми Оу и Оу 1
cos
0 -
-sin
0
1
0
sin
0
cos
2. У гол скоростно¬
го курса <рс — угол
между линией узлов
ON и осью ОХ
Угол наклона тра¬
ектории 0—угол меж¬
ду линией узлов ON
и осью Ох
Угол скоростного
крена \'с — угол меж¬
ду осями Оу и Оу\
COS ус
О
sin о
ГС
0
1
О
sin ev
i v.
О
COS фс
3. Угол 0ц —угол
между линией узлов
ON и осью ОХ
Угол	—угол
между линией узлов
QN и осью Ох
Угол
между
Оу\
Ун — угол
осями О у и
cos О
II
sin О
О
II
L, =
ип
sin О
cos О
II
I!
О
Второй
Третий
Матрица общего
поворота
Пределы изменения углов
Эскиз
L
&
cos 0 sin 0
sin 0 cos 0
О О
0
I
1
1
i
1
=
0
0
0
i
i
,
i

0
COS у
sin У
1 1
;
0
1
— sin у
cos У
/ — / О I
О < ф < 2я
О < 0 < я
. О < у < 2я
или
— я < ф < я
я
— < 0 <
2
— я < у < я
я
О
cos 0 sin б
sin 0 cos В
О О
О !
О
1
’с
1
О
о
о
о
cos ус sin ус
-sin Yc cos Yc j
б ^
•С	*	С
О < 0 < я
О < фс < 2я
О < Ус < 2я
или
— я < c < я
— гг < У’с < я
я	я
— < 0 < —
2	2
11
°!i
0	is
1
i.
и-
|:cos ^ л
о
ji sin .,
l!	*11
0 —
1
ь
(\
sin О., ,
: 1 1 I
L,
II
о
i:
СО:- с., !,
‘ II 1!
II
1
О
О
о
cos уп
— s i п Y.
it
О
sin Уп
cos \, [ |
г
L
’II 'II
о
II
0
< 0И
n
\ Г
^ • II
0
< V
^ ‘II
2я
я
2я
4. Угол Уш —угол
между линией узлов
ON и осью ОУ
Угол
между
Оу
0Ц1 — угол
осями ON и
Угол фш—угол
между осями Oxi и
Ох
Ly =~-
UlI
и =
411
1
0 0
cos 0jj j sin0
0
cos Уш sin УП1
—
— sin0ni cos 0
0 -
sinYjjj cos Yjjj
О
О
III
Ш
°1
О
]
C-Os Vjji
О	1
!sin<|/	О
U - :
III
О	—sin 'Ь.
III
О
cos 6
ill
L	L^ Z.Q.	L„
III ill ill
О < 0Ц1 < л
О < <ЬШ < 2я
О < .Уш < 2я
Примечания. 1. 'Линия узлов ON есть линия пересечения двух плоскостей, в которых происходит поворот на первый и втгорой углы Эйлера.
2. Матрицы общего поворота L даны в табл. 3.46.
Y