Text
Б. ГОЛДСУОРТ
ПРОЕКТИРОВАНИЕ
цифровых
логических
устройств
Digital Logic Design
B. Holdsworth, BSc(Eng), MSc, FIEE
Senior Lecturer in Electronics,
Chelsea College, University of London
Butterworths
London Boston Durban Singapore Sydney Toronto Wellington
Б.ГОЛДСУОРТ
ПРОЕКТИРОВАНИЕ
цифровых
логических
устройств
Перевод с английского
канд. техн, наук М. В. Сергиевского
Под редакцией
д-ра техн, наук проф. Ю. И. Толчеева
МОСКВА
• МАШИНОСТРОЕНИЕ»
1965
ББК 32.973.2
Г60
УДК 681.325.5.001.2 = 03.20= 82
Голдсуорт Б.
Г60 Проектирование цифровых логических устройств/Пер.
с англ. М. В. Сергиевского; Под ред. Ю. И. Топчеева. — М.:
Машиностроение, 1985. — 288 с., ил.
В пер,: 1 р. 60 к.
Книга английского специалиста представляет собой введение в теорию и прак-
тику проектирования комбинационных логических схем, дискретных устройств с па-
мятью и микропроцессоров на базе микросхем со средним уровнем интеграции.
Для инженеров, проектирующих устройства дискретной автоматики и цифровых
вычислительных машин.
2404000000-017 8 ББК 32.973.2
038 (01)-85 0 6Ф7.3
© Butterworth & Со (Publishers),
Ltd, 1982
© Перевод на русский язык,
«Машиностроение», 1985 г,
ОГЛАВЛЕНИЕ
Предисловие ......................................................
1. Булева алгебра ................................................
1.1. Введение ..............................................
1.2. Логика переключателя...................................
1.3. Функция И..............................................
1.4. Функция ИЛИ............................................
1.5. Функция НЕ.............................................
1.6. Реализация булевых функций с помощью переключательных
и электронных схем..........................................
1.7. Теорема идемпотентности................................
1.8. Теоремы объединения и пересечения .....................
1.9. Теорема избыточности или поглощения....................
1.10. Определение дополнения функции........................
1.11. Теоремы перестановки, сочетания и распределения.......
1.12. Теорема согласования .................................
Упражнения .................................................
2. Карты Карно и упрощение функций...............................
2.1. Введение ..............................................
2.2. Конъюнкции и дизъюнкции................................
2.3. Канонические формы.....................................
2.4. Булевы функции двух переменных ........................
2.5. Карты Карно ...........................................
2.6. Представление булевых функций с помощью карт Карно. . ,
2.7. Упрощение булевых функций..............................
2.8. Отрицание функции......................................
2.9. Термы, «не доставляющие беспокойства»..................
2.10. Представление и упрощение конъюнктивных нормальных форм
Упражнения .................................................
3. Элементы И—НЕ и ИЛИ—НЕ ........................................
3.1. Введение ..............................................
3.2. Функция И—НЕ...........................................
3.3. Реализация функций И или ИЛИ с помощью элементов И—НЕ
3.4. Реализация дизъюнктивных нормальных форм с помощью эле-
ментов И—НЕ.................................................
3.5. Функция ИЛИ—НЕ.........................................
3.6. Реализация функций ИЛИ и И на основе элементов ИЛИ—НЕ
3.7. Реализация конъюнктивных нормальных форм с помощью эле-
ментов ИЛИ—НЕ...............................................
3.8. Реализация дизъюнктивных нормальных форм с помощью эле-
ментов ИЛИ—НЕ...............................................
3.9. Расширение элементов.................................. •
3.10. Смешанные схемы ......................................
3.11. Элементы с тремя состояниями..........................
3.12. Элемент ИСКЛЮЧАЮЩЕЕ ИЛИ ............................;
Упражнения .......................
4. Проектирование комбинационных логических схем..................
4.1. Введение ...............................................
4.2. Полусумматор............................................
4.3. Полный сумматор.........................................
4.4. Четырехразрядный сумматор параллельного действия....
4.5. Сумматор с ускоренным переносом ........................
4.6. Полное вычитающее устройство............................
4.7. Дополнительный код......................................
4.8. Обратный код............................................
4.9. Двоичное представление чисел............................
4.10. Использования дополнительного кода для сложения и вычита-
ния чисел ...................................................
4.11. Двоичное умножение.....................................
4.12. Преобразования кодов ..................................
4.13. Преобразователь из двоичного кода в код Грея...........
4.14. Классификаторы прерываний..............................
4.15. Метод формирования цепочки.............................
Упражнения ..................................................
5. Однобитовые элементы памяти ...................................
5.1. Введение................................................
5.2. Т-триггер...............................................
5.3. 57?-триггер.............................................
5.4. УК-триггер..............................................
5.5. D-триггер ..............................................
5.6. Запирание триггера......................................
Упражнения ..................................................
6. Счетчики ......................................................
6.1. Введение ...............................................
6.2. Двоичный счетчик........................................
6.3. Счетчик по модулю 4 ..................................
6.4. Счетчик по модулю 8 ..................................
6.5. СчеТчнк по модулю 2N................................
6.6. Одновременная и последовательная подача сигналов на входы
элементов счетчика ..........................................
6.7. Синхронные счетчики обратного счета.....................
6.8. Счетчик по модулю 5 ....................................
6.9. Двоично-десятичный счетчик..............................
6.10. Двоично-десятичный счетчик обратного счета ............
6.11. Десятичный счетчнк, использующий код Грея..............
6.12. Реверсивные счетчики по модулю 16 .....................
6.13. Асинхронные двоичные счетчики..........................
6.14. Асинхронный десятичный счетчик.........................
6.15. Асинхронные счетчики с автоматическим сбросом..........
6.16. Счетчики на интегральных схемах .......................
6.17. Каскадирование счетчиков на интегральных схемах........
Упражнения ..................................................
7. Сдвиговые регистры и генераторы................................
7.1. Введение ...............................................
7.2. Четырехразрядный сдвиговый регистр с параллельной загрузкой
7.3. Четырехразрядный регистр для сдвига влево и вправо....
7.4. Использование сдвиговых регистров в качестве счетчиков . . .
7-5. Универсальная диаграмма состояний сдвиговых регистров . .
7.6. Проектирование десятичного счетчика.................
7.7. Генераторы последовательностей на сдвиговом регистре....
7.8. Кольцевой счетчик.......................................
7.9. Счетчик Дж.онсрна . , ; ............. . < ,
7.10. Сдвиговые регистры с обратной связью типа ИСКЛЮЧАЮЩЕЕ
ИЛИ...................................................... 134
Упражнения .................................................. 139
8. Синхронные последовательные схемы............................. 140
8.1. Введение................................................. 140
8.2. Анализ синхронной последовательной схемы................. 140
8.3. Процедура проектирования синхронных последовательных схем 144
8.4. Проектирование устройства обнаружения последовательности цифр 151
8.5. Автоматы Мура и Мили..................................... 153
8.6. Импульсные синхронные схемы ................................. 156
8.7. Сокращение состояний ........................................ 157
8.8. Кодирование состояний.................................... 163
Упражнения .................................................. 168
9. Асинхронные схемы............................................. 171
9.1. Введение.................................................... 171
9.2. Задача определения числа посетителей музея ................. 171
9.3. Гонки и циклы............................................... 175
9.4. Противогоночное кодирование для автомата с тремя состояниями 177
9.5. Задача о подаче воды в водонапорную башню................... 178
9.6. Противогоночное кодирование для автомата с четырьмя состоя-
ниями ........................................................ 180
9.7. Устройство обнаружения последовательности................... 183
Упражнения ...................•................................... 188
10. Логическое проектирование на основе ИМС со средним уровнем интег-
рации .............................................................. 191
10.1. Введение............................................... 191
10.2. Устройство выбора линии передачи информации или мульти-
плексор ....................................................... 191
10.3. Мультиплексор как генератор логических функций........... 194
10.4. Дешифраторы и демультиплексоры........................... 200
10.5. Применение дешифраторов.................................. 201
10.6. Постоянные запоминающие устройства (ПЗУ)................. 205
10.7. Методы адресации для ПЗУ................................. 206
10.8. Проектирование последовательных схем с помощью ПЗУ . . . 209
10.9. Программируемые логические матрицы (ПЛМ)............. 211
10.10. Проектирование последовательных схем на ПЛМ............. 216
10.11. Арифметические устройства на ИМС со средним уровнем инте-
грации ........................................................ 217
10.12. Десятичное сложение с помощью сумматоров иа ИМС со сред-
ним уровнем интеграции ........................................ 221
Упражнения .................................................... 223
11. Ситуации риска в логических схемах................................ 226
11.1. Введение ................................................ 226
11.2. Явления временной задержки в логических элементах........ 226
11.3. Условия возникновения выбросов........................... 226
11.4. Возникновение ситуаций статического риска в комбинационных
схемах ........................................................ 228
11.5. Устранение статического риска............................ 230
11.6. Построение гарантированных от риска комбинационных схем 233
11.7. Анализ схем для обнаружения ситуаций риска............... 235
11.8. Ситуации динамического риска............................. 237
11.9. Ситуации существенного риска............................. 239
Упражнения .................................................... 240
12. Введение в микропроцессоры........................................ 242
12.1. Введение............................................. 242
12.2. Двоичное умножение................................... 243
12.3. Аппаратура, необходимая для реализации устройства двоичного
умножения ..................................................... 243
12.4. Двоичное устройство умножения........................ 245
12.5. Схемы алгоритмов ......................................... 246
12.6. Устройство двоичного умножения, управляемое программой 248
12.7. Длина слова.......................................... 249
12.8. Счетчик программы.................................... 250
12.9. Команды н счетчик команд............................. 251
12.10. Шестнадцатеричная система представления чисел..... 253
12.11. Сравнение упрощенного микропроцессора с реальным. . . . 254
12.12. Обобщенная структурная схема микропроцессорной системы 255
12.13. Программирование для микропроцессоров ............. 258
Ответы к упражнениям.................................................. 259
Список литературы.................................................... 283
Предметный указатель.................................................. 285
ПРЕДИСЛОВИЕ
Книга создана на основе курса лекций, читаемых студентам факультета элек-
троники в колледже Челси, и материалов недельных курсов по цифровому проекти-
рованию, регулярно проводимых в том же институте для инженеров и научных ра-
ботников. По существу книга является учебным пособием, но она также будет по-
лезна всем инженерам, которые, не имея специального образования в области про-
ектирования цифровых устройств, в своей деятельности постоянно сталкиваются
с ним. Содержание книги найдут полезным будущие абитуриенты, которые зани-
маются электроникой перед поступлением в университет, и студенты, добивающиеся
степени магистра по методам проектирования цифровых устройств, ранее не изучав-
шие этот предмет.
В течение последних десяти лет методам проектирования цифровых устройств
уделялось возрастающее внимание, и в настоящее время они входят в учебные про-
граммы большинства университетов и политехнических институтов. Сначала при
проектировании использовались дискретные компоненты, но в последние десять лет
стали широко применяться схемы с малым и средним уровнями интеграции. Это
позволило упростить процесс проектирования и свести его к задаче сборки устройств
из интегральных схем. Совсем недавно появились большие интегральные схемы,
что дало возможность разрабатывать микропроцессоры. В связи с этим уже сейчас
можно выделить два альтернативных метода проектирования цифровых устройств,
основанных на использовании схем с «жесткой» логикой и на применении микро-
процессоров. Первый подход требует знания методов проектирования, которые из-
ложены в данной книге, в то время как второй подход является программным способом
решения той же проблемы. На завершающей стадии анализа проектного задания
необходимо выбрать один из этих двух подходов, используя экономический крите-
рий.
Однако на практике при решении многих задач обычно сочетают оба подхода.
Поэтому следует добиваться, чтобы проектировщики обладали хорошими знаниями
по булевой алгебре и умели применять ее методы для решения задач проектирования
Цифровых устройств. Кроме того, проектировщик должен обладать глубокими зна-
ниями методов программирования. По мнению автора, студент, владеющий фунда-
ментальными знаниями по проектированию устройств с «жесткой» логикой как ком-
бинационного, так и последовательного типов, легче перейдет к проектированию
на базе микропроцессоров.
Книга состоит из 12 глав. Первые три главы составляют вводную часть,
в которой изложены основы, знание которых необходимо для решения задач, харак-
терных для комбинационной логики. В первой главе описываются основные поло-
жения булевой алгебры. Гл. 2 посвящена использованию карт Карно и методам
минимизации булевых функций. Хотя методы минимизации теряют свое значение
из-за появления схем со средним уровнем интеграции, автору кажется, что для
читателя будет более чем полезным развить собственные навыки работы со схемами.
Гл. 3 посвящена использованию элементов ИЛИ — НЕ и И — НЕ. В настоящее
время большинство интегральных схем с малым уровнем интеграции проектируется
с помощью элементов И — НЕ и ИЛИ — НЕ, а не на элементах И, ИЛИ и НЕ.
Поэтому в гл. 3 описана реализация булевых функций на основе именно этих эле-
ментов. В гл. 4 ставится и решается ряд проблем, обычно возникающих при проек-
тировании комбинационных схем.
Главы, начиная с пятой, связаны с проектированием последовательных схем.
В гл. 5 описываются свойства и приводятся характеристические уравнения триг-
геров различных типов. Материал этой главы в тесной связи с материалом предыду-
щих глав используется для разработки методов проектирования в гл. 6—9. Гл. 6
и 7 посвящены проектированию синхронных и асинхронных счетчиков на основе
дискретных триггеров и сдвиговых регистров. В гл. 8 анализируются синхронные
последовательные схемы и предлагается универсальная процедура их проектирова-
ния. Гл. 9 посвящена проектированию асинхронных логических схем и реализации
их с помощью схем последовательного действия, построенных на элементах И — НЕ.
В гл. 10 исследуются свойства ряда схем со средним уровнем интеграции и по-
казывается, как они могут быть использованы при проектировании комбинационных
и последовательных устройств. В гл. И описываются условия возникновения си-
туаций статического и динамического риска в комбинационных схемах и ситуаций
риска в последовательных схемах. В гл. 12 показано, что микропроцессор является
ничем иным, как довольно сложным синхронным устройством последовательного
действия.
В заключение хочу поблагодарить всех, кто помогал мне при подготовке этой
книги. Прежде всего выражаю признательность проф. Д. Зиссосу из университета
Калгари, привившему мне интерес к проектированию цифровых логических уст-
ройств. Затем хочу поблагодарить студентов, с чьей помощью мне удалось подгото-
вить материал, который лег в основу этой книги. Наконец, благодарю жену за
перепечатку рукописи и остальных членов семьи за доброжелательное отношение
к моей работе.
1. БУЛЕВА АЛГЕБРА
1.1. Введение
Как правило, в цифровых системах используются два уровня
напряжения электрических сигналов, например, 5 и О В. Электри-
ческие устройства, применяемые в таких системах, обычно рассчи-
таны только на эти два уровня напряжения. Нужное напряжение
обеспечивается источниками питания. Так, биполярный транзи-
стор, не проводящий ток в системе, обеспечивающей напряжение 5 В,
поддерживает между коллектором и эмиттером напряжение около
5 В. Однако, когда транзистор открывается и начинает проводить
ток, при подходящем выборе нагрузки можно считать, что напря-
жение между коллектором и эмиттером приблизительно равно 0.
Следовательно, цифровая система может быть описана как двоич-
>ная, и двум используемым уровням напряжения можно поставить
в соответствие двоичные значения 0 и 1. Два состояния, определен-
ные таким способом, можно интерпретировать логически как наличие
и отсутствие определенного условия.
В прошлом столетии английский священник Дж. Буль разрабо-
тал специальную алгебру, которая оказалась очень удобной для
представления ситуации, описанной выше. Впоследствии эта ветвь
математики получила название булевой алгебры — дискретной ал-
гебры, которая оперирует с переменными, принимающими только
два значения: 0 или 1. В ней существует множество правил и ряд
теорем, которые дают возможность оперировать булевыми выраже-
ниями.
Знание булевой алгебры необходимо для выполнения любой
работы, связанной с проектированием цифровых систем. В этой
главе будут рассмотрены правила и даны формулировки теорем бу-
левой алгебры. Ясное понимание принципов, лежащих в ее основе,
позволит применять алгебраический подход для решения задач про-
ектирования, и поэтому исключительно важно для каждого, кто
предполагает заниматься проектированием цифровых систем.
1.2. Логика переключателя
Рассмотрим переключатель, показанный на рис. 1.1, а. Этот
переключатель связывает между собой две точки: Р и Q. Состояние
переключателя может быть выражено с помощью булевой перемен-
ной А, которая может принимать два значения 0 и 1. Если переклю-
чатель разомкнут, то Л = 0, а если замкнут, то А = 1. Состояние
соединения PQ может быть выражено с помощью булевой перемен-
р ___ /1 о
о ........-о л о---------°
а)
Переключатель
разомкнут
Переключатель
замкнут
б)
Рис. 1.1. Переключатель:
а — простейшая переключательная контактная схема; б — таблица истинности
ной Д которая принимает одно из двух значений: 0 или 1. Если связи
между точками Р и Q нет, то f = 0, если есть — f = 1. Эти резуль-
таты сведены в таблицу (рис. 1.1, б). Такого рода таблицы называются
таблицами истинности. При просмотре таблицы, изображенной на
рис. 1.1, б, ясно, что
f = A.
Уравнения такого типа называются булевыми, а переменные f и А —
булевыми или двоичными переменными, так как они могут принимать
только два значения: 0 или 1.
1.3. Функция И
Два переключателя х и у соединены последовательно и связы-
вают точки Р и Q (рис. 1.2, а). Пусть состояния переключателей вы-
ражаются с помощью двух булевых переменных А и В. Если переклю-
чатель х разомкнут, то А = 0, если замкнут, то Л = 1. Аналогично,
В = 0 или В = 1 в зависимости от того, разомкнут или замкнут
переключатель у. Как и в случае одного переключателя, состояние
соединения PQ выражается с помощью булевой переменной f, зна-
чение которой зависит от наличия связи между точками Р и Q.
Существует четыре возможные комбинации значений перемен-
ных А и В. Они сведены в таблицу истинности, приведенную на
рис. 1.2, б. Например, если переключатели х и у разомкнуты, то
А = О, В = 0, и связи между точками Р и Q нет. Следовательно,
f == 0. С другой стороны, если х и у замкнуты, то Л = 1, В = 1
и, следовательно, f == 1.
Рис. 1.2. Функция И:
а — переключательная контактная схема, реализующая функцию И; б — таблица истин-
ности функции И; в — правила двоичного и булевого умножения (прав.: Ы =1)
Рис. 1.3. Условное обозначение элемента И
f= Ав
Таблица истинности, изображенная на рис. 1.2, б, является таб-
лицей истинности функции И. Ее иногда называют функцией буле-
вого умножения и алгебраически записывают в виде
f = А-В,
где «точка», интерпретируется как И. Обычно точку опускают, и
уравнение записывают в виде
f = АВ.
Правила булевого умножения тождественны правилам двоичного
умножения. Они приведены на рис. 1.2, в.
В цифровых системах функция И реализуется с помощью элек-
тронной схемы, называемой элементом И. На рис. 1.3 показано ус-
ловное обозначение элемента И. На выходе этого элемента получаем
логическую «1» только в том случае, если значениями его двух вхо-
дов являются логические «1». Для всех других комбинаций входов
значением функции f является логический «О».
1.4. Функция ИЛИ
На рис. 1.4, а два переключателя х и у соединены параллельно
и связывают точки Р и Q. Состояния переключателей и соедине-
ния PQ выражаются с помощью булевых переменных А, В и f соот-
ветственно. На рис. 1.4, б показана таблица истинности этой схемы.
Если оба переключателя х и у разомкнуты, то А — О, В = 0 и ясно,
что связи между точками Р и Q нет; следовательно, f = 0. С другой
стороны, если переключатель х замкнут, а у разомкнут, то Л = 1,
В = 0, и связь между точками Р и Q осуществляется с помощью
переключателя х; следовательно, f — 1.
Таблица, изображенная на рис. 1.4, б, является таблицей истин-
ности функции ИЛИ. Функцию ИЛИ иногда называют функцией
булевого сложения. Анализ таблицы истинности показывает, что
между точками Р и Q существует связь, если переключатель х замк-
нут или переключатель у замкнут или оба переключателя замкнуты.
0+0=0 0+0=0
0 + 1 = 1 0 + 1=1
1 +0 = 1 1+0 = 1
1+1=1 1 + 1 =0 Перенос 1
булево Двоичное
сложение сложение
Рис. 1,4. Функция ИЛИ:
И)
а — переключательная контактная схема, реализующая функцию ИЛИ; б — таблица истин-
ности функции ИЛИ; в правила двоичного и булевого сложения
4
Рис. 1.6. Условное обозначение элемента ИЛИ
В
f-A+B
Строго говоря, эту функцию следует трактовать как ВКЛЮЧАЮ-
ЩЕЕ ИЛИ. Это название можно объяснить так: f = 1 в случае,
когда А = 1 и В = 1; другими словами, условие А = 1, В = 1
включается. Ниже, когда будет определена функция ИСКЛЮЧАЮ-
ЩЕЕ ИЛИ, читатель увидит, что условие А = 1, В — 1 исклю-
чается, т. е. когда А = 1 и В = 1, значение функции ИСКЛЮЧАЮ-
ЩЕЕ ИЛИ будет ра^но 0.
Алгебраически функцию ИЛИ записывают в виде
f = А + В,
где знак «+» интерпретируется как ИЛИ. Правила логического сло-
жения сведены в таблицу, показанную на рис. 1.4, в; рядом раз-
мещены правила двоичного сложения. Их сравнение позволяет
установить единственное отличие. При двоичном сложении 1 +
+ 1 — 10, где 0 — результат сложения, а 1 — единица переноса,
которая должна быть добавлена на следующей стадии операции сло-
жения; при булевом сложении 1 + 1 = 1.
В цифровых системах функция ИЛИ реализуется с помощью
электронной схемы, называемой элементом ИЛИ. На рис. 1.5 пока-
зано условное обозначение элемента ИЛИ. На выходе схемы будет
логическая «1», если на входе А или В, или на обоих входах А и В
одновременно появятся логические «1». Для любых других комби-
наций входных сигналов на выходе получаем логический «0».
1.5. Функция НЕ
В булевой алгебре есть операции сложения и умножения, но нет
операций деления и вычитания. Однако в булевой алгебре суще-
ствует еще одна фундаментальная операция —это операция инвер-
сии или дополнения. Рассмотрим переключательную схему, изобра-
женную на рис. 1.6, а. Она состоит из двух связанных переключа-
телей: если один из них замкнут, то другой обязательно разомкнут.
На рис. 1.6, а разомкнутый переключатель представляется булевой
переменной А, замкнутый—-булевой переменной А. Для верхнего
переключателя А = 0, когда этот переключатель разомкнут, а для
нижнего переключателя, который замкнут, когда верхний разомкнут,
А = 1. Говорят, что А есть инверсия А или НЕ А. Следовательно,
А А
0 1 / 0 1 1
Рис. 1.6. Функция1=А+А:
а — переключательная схе-
ма функции f » Л4-Л; б —
таблица истинности функ-
ции f — Л+Д
Рис. 1-7. Функция f =
= А-А:
а — переключательная схе-
ма функции f = А А; б —
таблица истиииости функ-
ции f = А • А
черта над булевой переменной А означает инверсию (или отрица-
ние) переменной. _
Таблица истинности функции f = А + А приведена на
рис. 1.6, б. Когда А ~ 0 и А = 1, то f = 1; аналогично, когда А = 1
и А = 0, то f = 1. Это означает, что связь между точками сущест-
вует всегда и не имеет значения, какой переключатель — верхний или
нижний замкнут. Следовательно, уравнение для этой схемы выгля-
дит
А + А = 1;
это уравнение — алгебраическая запись теоремы дополнительности.
Уравнение, двойственное по отношению к любому булевому
уравнению, получается заменой каждого знака «+» на «» и заменой
всех 1 на 0 и наоборот. По отношению к вышеприведенному уравне-
нию эта процедура приводит к
А-А = 0.
Переключательная контактная схема, соответствующая этому урав-
нению, показана на рис. 1.7, а, а таблица истинности этой схемы —
на рис. 1.7, б.
Инвертор может быть реализован с помощью электронной схемы,
условное обозначание которой приведено на рис. 1.8. Если на входе
схемы логический «0», то на выходе логическая «1» и наоборот. Если
два инвертора связаны последовательно, как показано на рис. 1.9,
то вход второго инвертора А, а его выход — инверсия от А, которая
может быть записана как А. Однако очевидно, что двойная инвер-
сия приводит к тому, что на выходе второго инвертора тот же сигнал,
что и на входе первого, поэтому
А = А.
Рис. 1.8. Условное обозначение инвертора
Рис. 1.9. Схема, иллюстрирующая теорему двойного отрицания
1.6. Реализация булевых функций с помощью переключательных
и электронных схем
Теперь появилась возможность представлять булевы функ-
ции, используя переключательные и электронные схемы. При реа-
лизации булевых функций переключательными контактными схе-
мами знаку «+» соответствует пара параллельных ветвей, знаку
«•» — последовательное соединение переключателей, а знаку «—» —
замкнутый переключатель. Например, функция
f = АВ + ВС
может быть реализована на основе переключательных контактных
схем (рис. 1.10, а) и на основе электронных схем (рис. 1.10, б).
Более сложная булева функция, например,
f = А (В + С) + BD
может быть реализована так, как показано на рис. 1.11, а и 1.11, б.
1.7. Теорема идемпотентности
В теореме утверждается, что
А + А = А.
Ясно, что если А — 1, то уравнение приводят к виду
1 + 1 = 1.
Рис. 1.10. Функция, f ~ АВАгВС:
а — реализация функции f = ABA-ВС с помощью переключателей; б — реализация функ-
ции f = АВ—ВС с помощью логических элементов
Рис. 1.11. Реализация функции f = А (В + С) 4- BD:
а — с помощью переключательных схем; б — с помощью логических элементов
т
I
Рис. 1.12. Иллюстрация теоремы идемпотентности с помощью переключательных
схем:
а — реализация f — АЦ-А; б — реализация f = А-А
Если же А = 0, то
0 + 0 = 0.
Оба эти результата согласуются с правилами булевого сложения,
приведенными на рис. 1.4, в.
Существует двойственная форма теоремы идемпотентности. Она
может быть получена посредством применения правил, сформулиро-
ванных выше. Ее вид А-А = А.
Если А = 1, то выражение будет иметь вид
1-1 = 1.
Если же А = 0, то
0-0 = 0.
Два последних результата согласуются с правилами булевого ум-
ножения, приведенными на рис. 1.2, в.
Для иллюстрации теоремы на рис. 1.12 приведены две переключа-
тельные контактные схемы.
1.8. Теоремы объединения и пересечения
В этих теоремах утверждается, что
. А + 0 = А, ) .. А + 1 = 1, ]
а) ’ I и б) I
Л-1 = A j А-0 = 0. |
Представим читателю возможность самому доказать справедливость
этих теорем.
1.9. Теорема избыточности или поглощения
В этой теореме утверждается, что
А + АВ = А.
Ниже приведено одно из доказательств этого утверждения:
А + АВ = А-1 + АВ
= А (В + В) + АВ
= AB + AB + AB
= AB + ЛВ
= А (В + B)
= A.
Говорят, что функция f = Л-1 + AB выражена в виде суммы про-
изведений (конъюнкций) или в дизъюнктивной нормальной форме.
Например, терм АВ является конъюнкцией двух переменных А
и В и, следовательно, называется конъюнктивным термом.
Таким образом, в теореме утверждается, что в любой булевой
функции, которая выражена в дизъюнктивной нормальной форме,
конъюнкция, содержащая все переменные другой конъюнкции,
является лишней. Это позволяет удалять лишние конъюнкции.
Например, из функции
f = AD 4- ABD + ACD
могут быть удалены термы ABD и ACD, поскольку они содержат
обе переменные, присутствующие в AD. Тогда функция примет вид
f = AD.
На рис. 1.13 приведена иллюстрация теоремы с помощью пере-
ключательных контактных схем. Очевидно, что наличие связи
между точками Р и Q не зависит от того, замкнут или разомкнут
переключатель В: следовательно, переключатель В лишний. Уравне-
ние, двойственное по отношению к уравнению А = А + АВ,
имеет вид
А = А (Л + В).
Переключательная контактная схема, иллюстрирующая это соот-
ношение, приведена на рис. 1.14.
р ““ О
0—0
Рис. 1.13. Переключательные контактные схемы, иллюстрирующие теорему по-
глощения А = А +ЛВ
Рис. 1.14. Иллюстрация двойственной формы теоремы поглощена : с помощью
переключательных схем
1.10. Определение дополнения функции
Дополнение булева выражения может быть Получено заменой
переменной ее дополнением в соответствующем двойственном выра-
жении. Например, для f = А + ВС двойственная форма имеет вид
fd = А (В + С),
а дополнение или инверсия функции
7= А (В + С).
Что это действительно дополнение функции f, может быть подтвер-
ждено с помощью таблицы истинности, изображенной на рис. 1.15.
Просмотр столбцов 9 и 10 этой таблицы показывает, что А (В + С)
является дополнением А + ВС. Две переключательные контактные
схемы, соответствующие дополняющим друг друга функциям, изобра-
жены на рис. 1.16.
Теперь рассмотрим базисные функции И или ИЛИ. Функция,
двойственная по отношению к функции f = АВ,
fd = A + В.
Дополнение функции получают заменой переменных их дополне-
ниями в двойственной форме
f = А + В.
Рис±1.15. Таблица истинности, подтверждающая, что f~
= А (В -|- С) является инверсией f = А + ВС
Рис. 1.16. Дополняющие друг друга схемы
f=A(B+C)
Рис. 1.17. Дополнения функций И и ИЛИ:
а — дополнение функции И; б — дополнение функции ИЛИ
Аналогично, функцию, двойственную по отношению к f = А + В,
определяют как
fd = АВ,
и дополнение функции f имеет вид
f = АВ.
Таким образом дополнение функции И — это функция ИЛИ, опе-
рандами которой являются дополнения переменных, присутствую-
щих в И; и наоборот, дополнение функции ИЛИ — это функция И,
операндами которой являются дополнения переменных, присутствую-
щих в ИЛИ. Процедура дополнения функций И и ИЛИ иллюстри-
руется с помощью электронных схем (рис. 1.17).
Так как дополнением функции f = АВ является функция f =
= А + В и f'= АВ, то, следовательно,
АВ = А + В.
Аналогично, поскольку дополнение f = А + В задается в виде
f = АВ и f = А + В, то, следовательно,
А + В = АВ.
Эти два выражения являются двумя формами теоремы де Моргана.
В более общем виде теорема де Моргана записывается
АВ ... N = А + В^--------1- N;
А + В ++ N = Л-В ... N.
1.11. Теоремы перестановки, сочетания и распределения
Кроме теорем, которые уже были рассмотрены ранее, существуют
также теоремы перестановки, сочетания и распределения. Алгебраи-
ческая запись этих теорем приводится ниже:
А + В = В + А,
АВ = ВА
(перестановка);
А + (В + С) = (Л + В) + С,
А (ВС) = (ЛВ) С
Л + ВС = (Л + В) (Л + С),
Л (В + С) = АВ + АС
(сочетание);
(распределение).
Наиболее полезной из всех этих теорем является первая форма
теоремы распределения. В частности, она необходима в процессе
минимизации булевых функций.
1.12. Теорема согласования
Если функция, например, / = АС + ВС содержит переменную С
в одном терме и ее дополнение в другом, то необязательную конъюнк-
цию или терм согласования формируют следующим образом: берут
булево произведение оставшихся переменных, в данном случае это
переменные А и В. Далее терм согласования может быть добавлен
к первоначальной функции f, что дает новую функцию
f = АС + ВС + АВ.
Значения /' равны соответствующим значениям f для всех воз-
можных комбинаций значений переменных А, В и С. Таблицы истин-
ности для f и f приведены на рис. 1.18. Просмотр столбцов таблицы
для f и показывает, что значения этих функций идентичны для
всех возможных значений переменных А, В и С.
Равенство f — f может быть доказано и алгебраически:
f — АС + ВС + АВ = АС + ВС + АВ (С + С) =
= АС + ВС + АВС + АВС =
= ДС(1 + В) + ВС(1 + Д),
однако 1 + А = 1 + В = 1 и, следовательно,
АС + ВС = f.
В связи с этим терм согласования может быть определен как
терм, присутствие которого в булевой функции не изменяет ее зна-
чения. Поэтому терм АВ в булевой функции [' = АС Д- ВС Д- АВ
является лишним. Однако термы согласования все-таки полезны,
так как введение их в булеву функцию может привести к исключе-
ние. 1.13. Доказательство теоремы согласования
с помощью таблицы истинности
Например, для
f = С + АВС
терм согласования имеет вид АВ. Добавляя его к /, получаем
f = С + АВС + АВ.
Применяя теорему поглощения, устанавливаем, что терм АВС
лишний и что его можно исключить. Тогда
f=C + AB.
Важно отметить, что длина терма АВ меньше длины удаленного
терма АВС.
Метод, заключающийся в определении термов согласования и
добавления их к функции без изменения ее значения, очень полезен
для проектировщиков цифровых систем. В последующих главах
будет показано, как этот метод может быть использован для устра-
нения ситуаций динамического риска в комбинационных схемах.
Упражнения*
У 1.1. Найти отрицание для каждого из следующих выражений:
a) А = А + ВС;
б) f2 = А (В + Q + BD (А + Q;
в) /3 = [АВ + С (А + DE)] [В + АС (Ё+ ВО)].
Результаты не упрощать.
У1 .2. Упростить выражения, используя метод, основанный на применении
термов согласования:
a) АС + BCD + АВС + ACD;
б) f2 = В х АВ + ACD + АС;
в) А = BCD + ABD + ABC + ABD + ACD.
У1.3. Составить таблицы истинности для следующих функций и из таблиц
истинности получить выражения для инверсных функций:
а) А = А + ВС;
б) А = Ас вс 4- АВ;
в) А = BD + АС + BD;
г) А = BD + А С + BD.
У1.4. Преобразовать следующие выражения, используя теорему де Моргана:
а) А = А + В + АВС-АС;
б) А = (АВ 4-ВС) + (ВС + АВ);
в) А = (АВ + ВС) (АС + АС).
* См. ответы в конце книги — Прим. ред.
У 1.5. Для следующих булевых функций нарисовать переключательные кон-
тактные схемы и реализовать их с помощью элементов И/ИЛИ:
а) Д= 4 + B(C+D);
б) h = И + В) (В + С) + (АВ + С);
в) /з = (Л + В + С) (А + D) + ВС + А (В + D) (С + D).
У1.6. Доказать следующие утверждения:
а) АВ + АВ = (Г+ В) (Л + В);
б) (АВ + С) В = АВС + АВС + АВС;
в) ВС + AD = (В + Л) (В + D) (Л + Q (С + £>);
г) АВ + ЛВС+ АВ = А.
2. КАРТЫ КАРНО И УПРОЩЕНИЕ ФУНКЦИЙ
2.1. Введение
Одна из задач проектировщика цифровых устройств, собираемых
из дискретных элементов, состоит в минимизации их числа, необхо-
димого для реализации булевой функции. Чем меньше количество
используемых логических элементов, тем ниже стоимость устрой-
ства. Упрощение может быть проведено и чисто алгебраическим пу-
тем, но это достаточно трудоемкий процесс, и к тому же проектиров-
щик не всегда может быть уверен, что простейшее решение действи-
тельно получено. Гораздо легче использовать способ упрощения,
основанный на составлении для булевых функций карт Карно, и
применения ряда простых правил для получения минимальной
формы. Этот метод очень удобен для функций, зависящих не более
чем от шести переменных. Для более сложных функций лучшие ре-
зультаты дают метод Квайна—Мак-Класки и итерационный метод
упрощения, основанный на использовании термов согласования.
Сейчас, когда существуют схемы со средним и большим уровнем
интеграции, задача минимизации функций не так важна, как прежде,
когда для реализации булевых функций использовались дискретные
элементы. Поскольку знание приемов минимизации позволит глубже
понять методы, используемые для преобразования булевых выра-
жений, они и предлагаются вниманию читателей.
2.2. Конъюнкции и дизъюнкции
Конъюнкцией (Р-термом) п переменных называется логическое
произведение всех п переменных, в котором любая переменная
может быть представлена также своим пополнением. В случае двух
переменных А и В существуют четыре возможные комбинации пере-
менных (рис. 2.1). К-аждой такой комбинации соответствует свой
Р-терм, который может быть получен следующим образом. Рассмо-
трим первую строку таблицы, представленной на рисунке. Для
нее А = О, В = 0 и, следовательно, АВ 1. Искомый Р-терм
формируем из таких значений переменных, которые делают зна-
чение Р-терма равным 1, следовательно, Ро = АВ. Оставшиеся три
Р-терма получаем тем же самым путем.
Дизъюнкцией (S-термом) п переменных называется логическая
сумма всех п переменных, в которой любая переменная может быть
представлена также своим дополнением. S-терм формируем на ос-
нове таких значений переменных, которые делают значение S-терма
равным нулю.
Так как Ро = АВ = 1 и Ро = АВ = 0 для А = 0 и В = О,
то Рп = Sn = А + В = 0 для А = 0 и В = 0. Таким образом мо-
гут быть получены еще три S-терма. Для трех переменных А, В
и С существует восемь возможных комбинаций переменных и, следо-
вательно, существует восемь Р-термов и восемь S-термов. В случае п
переменных существует 2п воз-
можных комбинаций значений
этих переменных и, следовательно,
существует 2'! Р-термов и 2" S-тер-
мов. Ясно, что число Р- и S-тер-
мов быстро растет с ростом п.
Сформулируем одно важное
свойство Р-термов: сумма всех Р-
термов равна единице, т. е.
2«-1
S Pi = 1.
i=0
А В Р-термы S-термы
0 0 Р = АВ So = А + В
0 1 Ру = АВ Sx = А + В
1 0 Рг = АВ S2 = А + В
1 1 Р3= АВ S3 ~ А + В
Рис. 2.1. Р- и S-термы двух перемен-
ных
Здесь используется операция булевого сложения. Уравнение, двой-
ственное по отношению к вышеприведенному, имеет вид
2«-1
Пй = о,
«=о
где операция умножения является булевым умножением.
В случае двух переменных логическую сумму всех Р-термов оп-
ределяем так:
S = АВ + АВ + АВ + АВ = А (В + В) + А (В + В) =
= А + А = 1.
Выражение, двойственное для суммы, имеет вид
(Я + В) (Д + В) (Д + В) (А + В) = 0
и представляет собой произведение всех возможных сумм термов
для двух переменных.
2.3. Канонические формы
Если булева функция записывается в виде суммы Р-термов или
произведения S-термов, то говорят, что она представлена в канони-
ческой форме. Так, функция
А = ДВС + АВС + АВС
представлена в канонической S—Р форме *, а функция
А = (А + В + С) (Я + В + С) (Я + В + Q
в канонической Р—S форме *.
* В советской научной литературе приняты термины: совершенная дизъюнк-
тивная нормальная форма и совершенная конъюнктивная нормальная форма. —
Роим- пер.
2.4. Булевы функции двух переменных
Количество булевых функций двух переменных ограничено.
Каждая булева функция состоит из определенного числа Р-термов,
например,
f = АВ + АВ
является булевой функцией двух переменных, содержащей два
из четырех возможных Р-термов. Все булевы функции двух перемен-
ных могут быть получены следующим образом. Обозначим присут-
ствие Р-терма в функции 1, а отсутствие 0. Например, если Р-терм
АВ присутствует в функции, то в соответствующей строке записы-
ваем 1, а если отсутствует — то 0. В случае, когда все четыре Р-
терма отсутствуют, столбец состоит из 0000 (рис. 2.2), и, следова-
тельно, булева функция будет иметь вид fn = 0.
В первую позицию каждого столбца можно записать либо 0,
либо 1. Во вторую позицию, соответствующую второй строке, то же.
Таким образом, существует четыре разных способа заполнения сим-
волами 0 и 1 первых двух строк. Для четырех строк число, способов
возрастает до 2' = 16. Все эти способы заполнения таблицы пока-
заны на рис. 2.2 и все 16 булевых функций двух переменных могут
быть немедленно получены. Они приведены на рис. 2.3.
Р-термы fo в В А В /в А А А А /10 /11 /12 /13 /14 /15
Ро= ЛВ 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
Рх= АВ 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
Р2= АВ 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
Р3= АВ 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
Рис. 2.2. Таблица, служащая для определения всех булевых функций двух
переменных
/о= о /1= АВ /а = АВ fa = А В=АВ Ноль И И (НЕ В) Тож- дество И (НЕ Л) О’** II II II II II 1 II Й 1 col । -4~ Со 11 f “ + 4^ II to tol Тождество ИСКЛЮ- ЧАЮЩЕЕ ИЛИ ИЛИ ИЛИ—НЕ Совпадение £ W w** w** Li' Ч1 °i II м £ tol tel HE ИЛИ (HE B) HE ИЛИ (HEA) И-НЕ Единица
Рис. 2.3. Шестнадцать булевых функций двух переменных
С увеличением числа переменных быстро растет и число булевых
функций. Для трех булевых переменных число возможных булевых
функций равно 28 = 256, для четырех 216 = 65536, для' п — 22п.
2.5. Карты Карно
Как показано выше, для двух булевых переменных существуют
четыре Р-терма. Эти термы могут быть удобно размещены на карте
(рис. 2.4). Карта представляет собой квадрат, разделенный на че-
тыре ячейки, по одной на каждый Р-терм. Строки карты связаны
с переменной А, столбцы — с переменной В. Следовательно, распо-
ложенная слева вверху ячейка соответствует Р-терму, являюще-
муся конъюнкцией А и В, т. е. АВ, а расположенная справа внизу
ячейка — терму АВ, помеченному Р3. Такого рода карта называется
картой Карно.
Карты Карно размечают различными способами. Во-первых,
каждая ячейка может содержать индекс Р-терма, которому она
ответствует (рис. 2.5, а). Например, в ячейку, расположенную
слева вверху, записывают 0, являющийся индексом Р-терма, соот-
ветствующего этой ячейке. Во-вторых, в ячейку карты можно запи-
сать двоичное представление индекса (рис. 2.5, б).
В случае трех переменных карта содержит восемь ячеек, по од-
ной для каждого Р-терма (рис. 2.6, а). Переменная А связывается
с двумя строками карты, а переменные В и С — с четырьмя столб-
цами. Существуют четыре комбинации возможных значений пере-
менных В и С и каждой комбинации соответствует отдельный стол-
бец карты. Карты заполняют таким образом, что два соседних столбца
всегда связаны либо с самой переменной, либо с ее отрицанием.
Анализируя рис. 2.6, а, можно заметить, что первые два столбца
связаны с В, второй и третий — с С, а третий и четвертый — с В.
По какой причине карта Карно заполняется именно таким образом,
будет видно в дальнейшем при изложении метода минимизации бу-
левых функций. Карта Карно для четырех переменных изображена
на рис. 2.6, б. Поскольку для четырех переменных существует 16
Р-термов, карта разделена на 16 ячеек. Каждая ячейка содержит
индекс того Р-терма, которому она соответствует.
£ $ 'Л
Рис. 2.4. Карта Карно для двух переменных
Рцс. 2.5. Разлучные способы заполнения карты Карно
\gc \C27 01
A \ 0 0 0 1 11 10 AB \ 00 01 1 1 10
Чо' к
ч»
a)
0 1 3 г
ч 5 7 6
12 13 15 14
8 3 11 10
£F(10)
EF(11)
Рас. 2.6. Карты Карно для:
a — трех переменных; б — четырех переменных: в — пяти переменных; г — шести перемен*
ных
В случае пяти переменных целесообразно использовать две 16-
ячеечные карты (рис. 2.6, в), а не одну 32-ячеечную. Карты, распо-
ложенные на рисунке, справа, соответствуют истинному значению
переменной Е, а карты, расположенные слева, — дополнению Е,
т. е. Е. В случае шести переменных для размещения 64 термов по-
требуется уже четыре 16-ячеечные карты. Эти четыре карты изобра-
жены на рис. 2.6, г. Каждая карта связана с одной из четырех воз-
можных комбинаций значений переменных Е и F.
2.6. Представление булевых функций с помощью карт Карно
Для функции двух переменных карта Карно содержит четыре
ячейки, по одной для каждого Р-терма. Изображение функции
f = АВ с помощью карты Карно показано на рис. 2.7, а. В первую
верхнюю ячейку карты записывают «1».
Рассмотрим теперь функцию двух переменных А и В, f = А.
Применяя теорему дополнительности, получаем
f = А (В + В) = АВ + АВ.
Эта функция изображена на рис. 2.7, б. Заполнены только нижние
ячейки карты. Следовательно, при представлении с помощью карты
Карно функции двух переменных, зависящей только от одной из них,
заполняют две соседние ячейки.
Так как для трех переменных существуют восемь Р-термов, для
функции трех переменных f (А, В, С) потребуется восьмиячеечная
карта Карно (рис. 2.8, а). На этой карте изображена функция f =
= АВС + АВС. Поскольку помеченные «1» ячейки карты не яв-
ляются соседними, два составляющих функцию Р-терма не могут
быть объединены и, следовательно, функция f не может быть упро-
щена.
На рис. 2.8, б изображена карта Карно, представляющая состоя-
щий из двух переменных терм ВС; на этой карте заполнены только
две ячейки. Анализ карты показывает, что терм ВС является логи-
ческой суммой Р-термов АВС и АВС, т. е.
f —~АВС + АВС = (А + А) ВС;
f = ВС.
Состоящий из одной переменной терм занимает четыре соседние
ячейки на карте, предназначенной для представления функций,
зависящих от трех переменных. Например, карта Карно для терма
f = С изображена на рис. 2.8, в. Кажется, что четыре ячейки, по-
меченные «1», не являются соседними. Однако, если свернуть карту
Рис. 2.7. Представление с по-
мощью карты Карно функции:
а - f = АВ; 6-/ = ЛВ+Ла' =
а)
6)
Рис. 2.8. Представление с по-
мощью карты Карно функции:
a — f = АВС+~АВС; б - f =
= ВС; в — f = С
Рис. 2.9. Представление с пол
a — f — TECD; б - f ~ ACD; в
в вертикальный цилиндр, то будет видно, что первый и последний
столбцы расположены рядом.
На карте Карно, рассчитанной на представление функций, за-
висящих от четырех переменных, Р-терм также занимает одну
ячейку (рис. 2.9, а). В связи с этим термы, состоящие из трех, двух
и одной переменной, при размещении на карте Карно займут две,
четыре и восемь ячеек, соответственно, как показано на рис. 2.9, б,
в, г. Анализ рис. 2.9, г показывает, что, во-первых, верхняя и ниж-
няя строки карты Карно могут считаться соседними и, во-вторых,
как и в случае с картой Карно для трех переменных, первый и пос-
ледний столбцы также могут считаться соседними.
2.7. Упрощение булевых функций
Процесс упрощения булевых функций с помощью карт Карно
основан на поиске соседних заполненных ячеек. Поясним это на
примере функции
f = 20, 1, 2, 3, 4, 6, 7, 8, 12, 13.
Здесь функция f представлена в виде логической суммы Р-термов,
каждый из которых заменен стоящим под знаком суммы индексом.
Изображение функции с помощью карты Карно показано на рис. 2.10.
На карте можно выделить четыре группы соседних ячеек: три группы
содержат по четыре ячейки и одна группа — две ячейки. Четыре
ячейки в верхней строке карты соответствуют терму АВ, четыре
ячейки первого столбца — терму CD, четыре ячейки справа вверху —
терму АС и, наконец, две соседние ячейки — терму АВС. Следова-
тельно, после упрощения функция примет вид
f = АВ + CD + АС + АВС.
Термы, входящие в состав упрощенной функции, обычно называют
главными импликантами.
Теперь стало ясным, почему переменные С и D, а также А и В
связаны со строками и столбцами именно таким способом, как опи-
сано выше. Используемый способ
гарантирует, что ячейки, связанные
с переменными С, С, D и D, всегда
принадлежат двум соседним столб-
цам, в то время как ячейки, свя-
занные с переменными А,А,ВнВ,
всегда принадлежат соседним стро-
кам. Если бы переменные были свя-
заны с ячейками карты в строгом
соответствии с числовым порядком,
определяемым двоичными кода-
ми 00, 01, 10 и 11, тогда ячейки,
связанные, например, с D, не
принадлежали бы соседним столб-
цам, и процесс упрощения не мог
функции f — АВ + CD + ДС-Ь
+ АВС
Puc_2.ll, Карта Карно_для функции f = BDE Ц- BDE + CDE + ВСЕ + ДВС+
+ ДСР + ACDE + ABDE
бы быть сведен к обнаружению соседних заполненных ячеек карты
Карно.
Упрощение функций, зависящих от пяти переменных, — не-
сколько более сложный процесс. Рассмотрим функцию
f = £0, 1, 2, 3, 4, 5, 10, 11, 13, 14, 15, 16, 20, 21, 24, 25,
26, 29, 30, 31.
Представляющая ее карта Карно изображена на рис. 2.11. Ниже
приведена процедура упрощения этой функции.
1. Сначала описанным ранее способом находим упрощенные
формы представления для двух функций fp и fE, соответствующих
левой и правой частям карты Карно на рис. 2.11:
f-g =~BDE + BDE + ACDE + АВСЁ-,
fE = CDE + BCE + ABDE + ABCE.
2. Второй шаг заключается в поиске таких главных импликант
двух функций и fE, которые можно объединить. В результате по-
лучим упрощенную форму логической суммы двух функций
?Ё + ?Е-
Например, АВСЕ — главная импликанта и АВСЕ — главная
импликанта fE. Эти две импликанты можно объединить, получив
в результате терм, состоящий из трех переменных АВС. Также
возможно дополнить функцию f-£ несущественной главной импли-
кантой ACDE. Объединив ее с главной импликантой ACDE функ-
ции fE, получим терм ACD. Этот процесс можно изобразить так:
fe = BDE + BDE + ACDE +
ABC
A CD
= CDE + BCE + ABDE +
Таким образом, упрощенная форма функции имеет вид
f = BDE + BDE + CDE + ВСЕ + ABC + ACD +
+ ACDE + ABDE.
2.8. Отрицание функции
В некоторых случаях выгоднее реализовывать не саму функ-
цию, а ее отрицание, или инверсную функцию. Например, предпо-
ложим, что задана функция
f (Л, В, С, D) = 2 2, 6, 7, 8, 12, 13.
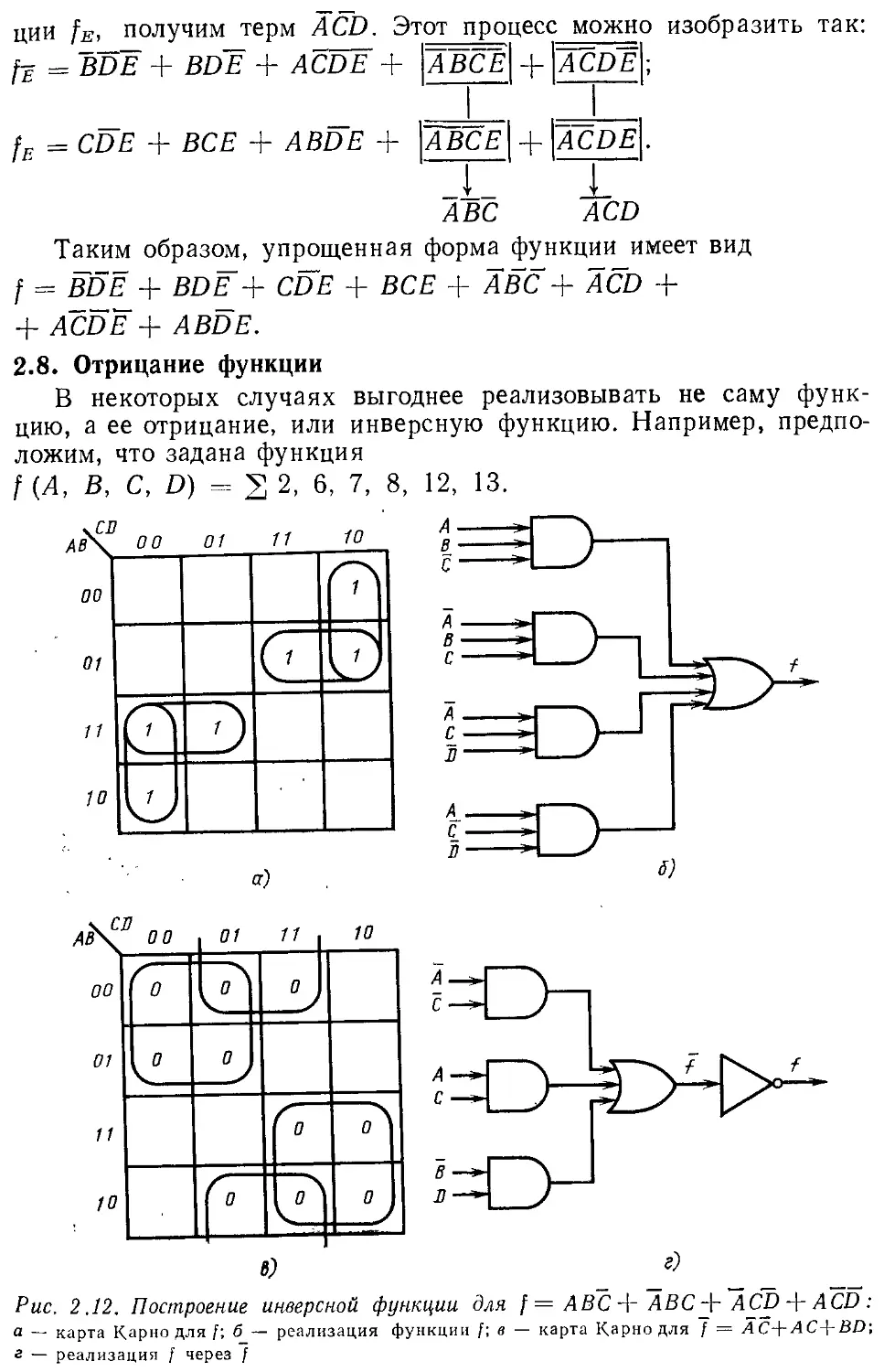
Рис. 2.12. Построение инверсной функции для f = АВС + АВС + ACD + ACD :
а — карта Карно для f; б_— реализация функции f; в — карта Карно для 7 = A C+AC-\-BD;
з — реализация f через f
Эта функция изображена на рис. 2.12, а. Ее упрощенная форма
имеет вид
f = АВС + АВС + ACD + ACD.
Для реализации этой функции потребуются четыре схемы И с тремя
входами и одна схема ИЛИ с четырьмя входами (рис. 2.12, б). Кроме
того, требуется 17 соединительных проводников.
Отрицание функции f может быть представлено так: незаполнен-
ные ячейки карты, показанной на рис. 2.12, а, заполняют 0. Резуль-
тат показан на рис. 2.12, в. Упрощенную форму функции f получаем
в результате анализа карты Карно, изображенной на рис. 2.12, в:
7 =АС + АС + BD.
Реализация f показана на рис. 2.12, г. Для того чтобы получить
первоначальную функцию, необходимо инвертировать сигнал на
выходе. Это делают с помощью инвертора. Таким образом, аппарат-
ное обеспечение включает три схемы И с двумя входами, одну
схему ИЛИ с тремя входами и один инвертор; кроме того, требуется
еще 11 соединительных проводников.
2.9. Термы, «не доставляющие беспокойства»
Следует отметить, что при решении некоторых логических задач
определенные комбинации переменных могут никогда не использо-
ваться. Например, для представления десятичных цифр часто ис-
пользуют код NBCD (рис. 2.13, а). Это четырехбитовый код с 16
возможными комбинациями, но только десять из них применяют на
практике. Оставшиеся шесть комбинаций, а именно 1010, 1011,
1100, 1101, 1110 и 1111, появиться не могут и, следовательно, могут
быть использованы для целей упрощения представления функций.
Такие термы называют «.термами, не доставляющими беспокойства».
Для распознавания цифр, представленных в NBCD-коде, исполь-
зуют декодирующее логическое устройство (рис. 2.13, б). Очевидно,
что для его реализации потребуется десять независимых схем, по
одной для каждой цифры.
Для определения функций, реализуемых каждой схемой, исполь-
зуют карту Карно, изображенную на рис. 2.13, в. На этой карте
термы, «не доставляющие беспокойства», помечают символами «d»,
а оставшиеся десять ячеек — десятичными цифрами, соответствую-
щими кодам ячеек. Например, ячейка, определяемая термом ~ABCD-
0000, помечается десятичной цифрой «0». Найти комбинации этой
ячейки с ячейками, помеченными «d», не удается. Следовательно,
0 = A BCD.
Аналогично, ячейка, помеченная десятичной цифрой 1, не может
быть объединена с хотя бы одной ячейкой, помеченной «d». Поэтому
1 = ABCD.
Рис. 2.13. Дешифратор для кода NBCD:
а — код NBCD-, б — структурная схема дешифратора; в — карта Карно, служащая для
определения логических функций, реализуемых дешифратором; г — реализация дешифратора
Однако ячейка, помеченная десятичной цифрой «2», может быть
объединена с ячейкой, помеченной «d», как это показано на рис. 2.13, в.
Следовательно,
2 = BCD.
Функции, соответствующие оставшимся десятичным цифрам, могут
быть найдены тем же самым путем. Приведем их:
3 = BCD; 5 = BCD- 7 = BCD; 9 = AD;
4 = BCD; 6 = BCD; 8 = AD.
Реализация всех найденных десяти функций показана на
рис. 2.13, г.
Это декодирующее логическое устройство является примером
комбинационной логической схемы. Любая комбинационная логи-
ческая схема характеризуется тем, что ее выход полностью опреде-
ляется сигналами на входах.
2.10. Представление и упрощение конъюнктивных нормальных
форм
Известно, что конъюнктивную нормальную форму непосредст-
венно представить на карте Карно нельзя, если найдено ее отрица-
ние, которое будет уже дизъюнктивной нормальной формой, то его
непосредственно представить на карте Карно все-таки можно. За-
полняя непомеченные ячейки этой карты, мы тем самым получим
отрицание инверсной функции, т. е. искомую функцию.
Например,
f = А + В
Функция, двойственная к /, имеет вид
Ь = А-В.
И, наконец, отрицание функции f есть
f = АВ.
Функция f может быть представлена с помощью карты Карно
обычным способом; только ячейку, соответствующую терму АВ,
помечают «0», поскольку строят карту Карно для инверсной функ-
ции. Эта функция изображена на рис. 2.14, а. Непомеченные ячейки
карты Карно соответствуют дополнению инверсной функции, т. е.
функции f = А + В. Карта! Карно'” функции f изображена на
рис. 2.14, б. Ячейки карты заполняют «1», поскольку речь идет
об искомой функции, которую необходимо представить с помощью
карты Карно.
Рассмотрим процесс заполнения карты Карно для дизъюнктив-
ных нормальных форм, зависящих от трех переменных. Пусть за-
Рис. 2.15. Карты Карно для функции:
a-f= АВС + ВС; б - f = (А + В + С) (В + С)
Функция, двойственная к f, имеет вид
fd = АВС + ВС,
а инверсная функция
J = АВС + ВС.
Эта функция изображена на рис. 2.15, а, а ее отрицание (т. е. иско-
мая функция) — на рис. 2.15, б.
Инверсная функция может быть упроще_на при использовании
методов, изложенных выше. Поскольку для f существуют две глав-
ные импликанты, она может быть представлена в виде
Т= ~АВ А-~ВС.
Проведя инвертирование этого выражения, перейдем снова к конъ-
юнктивной нормальной форме. Эта новая форма будет минимальной.
В данном случае двойственная форма инверсной функции будет
иметь вид
Id = (Л + В) (В + С),
а отрицание инверсной функции
f = (Л + В) (В + С).
Это и есть минимальная конъюнктивная нормальная форма выраже-
ния, задаваемого функцией
f = (Л + В + С) (В + С).
Упражнения
У2.1. Представить следующие булевы функции в канонической форме:
a) fi = АВ + С;
б) f2 = АВ+АС+ АВС;
в) f3 = В + CD + ABD + ABCD.
У2.2. Упростить следующие булевы функции, зависящие от трех переменных:
a) fi = Pi + Р2 + Pi, + Ре;
6) fi = Ро + Pi + Pi + Ps + Pi',
B) f»~ + P„ + e + Pt
У2.3. а. Выразить функцию трех переменных f = Ро + Pt в совершенной конъ-
юнктивной нормальной форме.
б. Представить функцию трех переменных f = SoSiS2SeSeS7 в совершенной дизъ-
юнктивной нормальной форме.
в. Определить отрицание функции / = Р3 + Ps + Ра + Р7 и выразить его в со-
вершенной дизъюнктивной нормальной форме.
У2.4. Минимизировать выражение, заданные в совершенной дизъюнктивной
нормальной форме:
a) ft (Д, В, С) = £0, 1, 3, 4, 6, 7;
б) h (Л, В, С, D) = 2°, 1, 2, 3, 7, 8, 9, 11, 12, 15;
в) h (Л, В, С, D) = ПО, 4, 5, 6, 7, 8, 9, 10;
г) ft (А, В, С, D, Е) = £°, 1, 3, 5, 6, 7, 8, 9, 10, 15, 16, 20, 21, 22, 23,
24, 25, 28, 29, 30, 31.
У2.5. Минимизировать следующие функции, используя, где это возможно,
термы, «не доставляющие беспокойства» ТНБ:
a) f (Д, В, С) = J 3, 5 + ТНБ (0, 7);
б) f (Д, В, Q = 2 1, 2, 3, 5, 6, 7, 10, И + ТНБ (9, 12, 15);
в) f (Д, В, С, О) = П 0, 4, 7, 11, 14 + ТНБ (6, 8, 9, 13);
г) f (Д, В, С, D) = 2 4. 5, 6, 7, 12, 14, 16, 20, 21, 24, 26, 27, 31 +
+ ТНБ (0, 11, 19, 22, 30).
У2.6. Определить минимальную дизъюнктивную нормальную форму следующих
функций:
a) f (Д, В, С) = 2 °- *> 2- 5, 7<
б) f (д, в, с, D) = 2°- 9> 10> и;
в) f (Д, В, С, D, Е)= 2 1- 2, 5, 6, 10, II, 14, 15, 16, 17, 20, 21;
г) f (Д, В, С, D) = 25, 7, 9, 10, 11 + ТНБ (2, 13, 15).
У2.7. Найти минимальную дизъюнктивную нормальную форму логического
произведения F=Ff F2 следующих пар функций:
a) Ft (Д, В, С, D) = 2 1, 3, 5, 7; F2 (А, В, С, D) = 2 2, 3, 6, 7;
б) Ft (Д, В, С, О) = 2 1. 3, 5, 6, 8, 10, 11, 12, 13;
F2(A, В, С, D) = 2 0, 3, 5, 8, 9, 11, 13, 15;
в) Ft (Д, В, С) = П 0, 3, 6, 7; F2 (Д, В, Q = П 1, 3, 7.
У2.8. Код XS3 (см. таблицу на стр. 36) используется для представления деся-
тичных цифр. Разработать для него декодирующее логическое устройство.
3. ЭЛЕМЕНТЫ И — НЕ И ИЛИ — НЕ
3.1. Введение
В предыдущих двух главах рассматривались только элементы И,
ИЛИ и НЕ. На практике многие логические схемы реализуются на
основе элементов И—НЕ и ИЛИ—НЕ, поскольку именно эти эле-
менты являются базисными для большинства серий ТТЛ-и КМОП-
логик. Правда, в этих сериях существуют элементы И и ИЛИ, но
их выбор существенно ограничен и они стоят дороже. Более того,
элементы И и ИЛИ имеют большее время задержки, поскольку со-
стоят из большего числа каскадов, чем элементы И—НЕ и ИЛИ—НЕ.
К тому же, элементы И и ИЛИ имеют более высокую мощность рас-
сеяния.
В связи с этим в данной главе речь пойдет об использовании эле-
ментов И—НЕ и ИЛИ—НЕ для реализации булевых функций.
В процессе проектирования логических устройств будут использо-
ваться именно эти элементы, пока не возникнут веские причины для
их замены.
3.2. Функция И — НЕ
Функция И—НЕ определяется
f = АВ.
Таблица истинности этой функции показана на рис. 3.1, а, а услов-
ное обозначение функции И—НЕ с двумя входами дано на
рис. 3.1, б. Анализ таблицы истинности показывает, что если на
одном или обоих входах элемента И—НЕ логический «О», то на его
выходе будет логическая «1». Сформулируем общее правило, харак-
теризующее работу элемента И—НЕ, имеющего произвольное число
входов: если хотя бы на одном входе элемента — логический «О»,
то на выходе — логическая «1».
Представление функции И—НЕ, зависящей от двух переменных,
с помощью карты Карно показано на рис. 3.1, в. Все ячейки карты,
исключая одну, соответствующую терму АВ, помечаются «1». Из
материала второй главы ясно, что эти три ячейки представляют до-
полнение терма АВ, т. е. АВ.
Анализ таблицы истинности показывает, что функция И—НЕ
может быть также представлена как
f = АВ + АВ + АВ = А + АВ = А + В.
Следовательно,
АВ = А + В.
Это равенство является одной из форм теоремы де Моргана.
Две строки таблицы истинности, обведенные штриховой линией,
характеризуют состояние элемента И—НЕ, когда на входе А
a)
Рис. 3.1. Функция И—НЕ:
а — таблица истинности функции И—НЕ; б — условное обозначение элемента И—НЕ;
в — карта Карно функции И — НЕ; г — использование элемента И—НЕ в качестве инвертора
постоянно присутствует логическая «1». Просмотр этих строк пока-
зывает, что если В = 0, то f = 1 и если В = 1, то f = 0. Другими
словами, сигнал на выходе является инверсией сигнала на входе.
Следовательно, элемент И—НЕ можно рассматривать как инвертор
в том случае, когда на всех входах, кроме одного, имеются логиче-
ские «1» (рис. 3.1, г).
3.3. Реализация функций И и ИЛИ с помощью элементов И—НЕ
Реализация функции И осуществляется достаточно просто с по-
мощью двух последовательно соединенных элементов И—НЕ; пер-
вый выполняет операцию И—НЕ, а второй используется как инвер-
тор (рис. 3.2).
На рис. 3.3, а изображена карта Карно для функции ИЛИ.
Просмотр карты показывает, что отрицанию функции ИЛИ соответ-
ствует одна ячейка, помеченная «0». Следовательно,
f = АВ,
откуда
f = ТЁ.
Анализ этого уравнения показывает, что функция ИЛИ может
быть выражена с помощью операции И—НЕ, выполняемой над
А ' , - ___
8 J у, Рис. 3.2. Реализация функции И с по-
»I у | у мощью элементов И—НЕ
f-A+B
V)
Рис. 3.3. Реализация функции ИЛИ с помощью элементов И—НЕ:
а — карта Карио для функции ИЛИ; б — схема реализации
отрицаниями переменных. На рис. 3.3, б представлена реали-
зация функции ИЛИ на основе элементов И—НЕ.
3.4. Реализация дизъюнктивных нормальных форм
с помощью элементов И — НЕ
Функция f = АВ + CD считается выраженной в дизъюнктив-
ной нормальной форме. На рис. 3.4, а показана реализация этой
функции с помощью элементов И/ИЛИ. На этом же рисунке выде-
лены два уровня расположения элементов в схеме: на первом уровне
размещен элемент ИЛИ, па втором — два элемента И. Данную схему
можно преобразовать в схему, построенную на элементах И—НЕ,
используя правила, изложенные в п. 3.3. Процедура преобразова-
ния показана на рис. 3.4, б. Первый блок, обведенный штриховыми
линиями, представляет собой два элемента И, а второй — элемент
ИЛИ. Можно заметить, что в обеих ветвях схемы присутствуют по
два одновходовых элемента И—НЕ, которые будут производить двой-
ную инверсию сигналов АВ и CD. Поэтому четыре элемента И—НЕ
являются лишними (на рис. 3.4, б они перечеркнуты). После удале-
ния этих элементов схема принимает вид, приведенный на рис. 3.4, в.
Из рассмотренного примера ясно, что схемы, построенные на эле-
ментах И/ИЛИ, очень просто (практически «один к одному») преобра-
зовать в схемы, реализуемые на элементах И—НЕ.
Даже функция более сложного вида, такая, как
f = (Л + BD) С + (С 4- D) (А 4- С) В,
может быть представлена в дизъюнктивной нормальной форме
f = PQ 4- SRT,
где Р = А 4- BD-, S = С + D; Q = С; R = А 4- С‘ Т = В.
ИроВень 2 Уровень 1
HAB+CD
Рис. 3.4. Реализация f = ABA-CD
с помощью элементов И—НЕ:
а — реализация f на элементах И/ИЛИ;
б — преобразование схемы на элемен-
тах И/ИЛИ в схему на элементах
И — НЕ; в — результирующая схема
Рис. 3.5. Реализация f = (А + BD) С + (С + D) (Д + С) В на элементах И—НЕ:
а — план реализации f; б — реализация С + D на элементах И—НЕ; в — реализация f
Реализация f — PQ + SRT показана на рис. 3.5, а. Для того чтобы
реализовать терм С + D на элементах И—НЕ, требуется одна схема
И—НЕ с входами, представляющими отрицания переменных, ко-
торые необходимо получить на выходе (рис. 3.5, б). На рис. 3.5, в
представлена полная схема, используемая для реализации искомой
функции.
Описанные методы представления булевых функций с помощью
элементов И—НЕ не обязательно приводят к минимальной реали-
зации. Однако иногда, используя процесс факторизации *, доста-
точно просто получить реализацию на элементах И—НЕ, состоя-
щую из меньшего числа элементов.
В качестве примера возьмем функцию
/ = АС + АВ + CD.
Непосредственная реализация этой функции приводит к схеме, изоб-
раженной на рис. 3.6, а, которая требует следующих элементов
И—НЕ: одного с тремя входами, трех с двумя входами и двух с од-
ним входом (на практике элементы И—НЕ, значения всех входов
которых равны логической «1», используются в качестве инверторов).
Однако эта же функция может быть представлена в виде
f = А (В + С) + CD
* Под факторизацией автор понимает процесс изменения записи булевой функ-
ции, основанный на выделении общих сомножителей. — Прим. пер.
Рис. 3.6. Три способа (а, б, в) реализации функции f= ДС+ВДЦ-CD на элемен-
тах И—НЕ
и реализована на элементах И—НЕ так, как показано на рис. 3.6, б.
Кроме того, функцию f можно представить и так:
f = С (Л + D) + ЛВ.
Тогда для реализации потребуется восемь элементов И—НЕ
(рис. 3.6, в).
Очевидно, что для реализации схемы, показанной на рис. 3.6, б,
потребуется меньше элементов И—НЕ, чем для схем, представлен-
ных на рис. 3.6, а и 3.6, в. Зиссос предложил формальный метод
определения минимальной по числу элементов И—НЕ реализации
при условии соблюдения ограничений, накладываемых на число
входов. Этот метод основан на использовании принципа слияния,
дающего возможность преобразовать выражения в скобках, напри-
мер (Л + В) (Л + С), к виду Л + ВС. В одних случаях слияние
позволяет уменьшить число элементов в схеме, в других же, наобо-
рот, приводит к их увеличению. Метод Зиссоса позволяет определить
влияние процесса слияния на количество элементов И—НЕ, необ-
ходимых для реализации схемы логической функции.
3.5. Функция ИЛИ — НЕ
Функция ИЛИ—НЕ определяется так:
f “ Л + В.
Таблица истинности этой функции показана на рис. 3.7, а, а услов-
ное обозначение элемента ИЛИ—НЕ с двумя входами — на
Рис. 3.7. Функция ИЛИ—НЕ:
а — таблица истинности функции ИЛИ —НЕ; б — условное обозначение элемента ИЛИ —НЕ;
в — карта Карно для функции^ИЛИ —НЕ; г —'использование^элемеита ИЛИ —НЕ в ка-
честве инвертора
рис. 3.7, б. Анализ таблицы истинности показывает, что если на од-
ном или на обоих входах логическая «1», то на выходе элемента будет
логический «О». На основании этого можно сформировать общее пра-
вило для элементов ИЛИ--НЕ, имеющих произвольное число вхо-
дов: если хотя бы на одном входе имеется логическая «1», то на вы-
ходе — логический «О». На рис. 3.7, в изображена карта Карно для
функции ИЛИ—НЕ, зависящей от двух переменных. Ее анализ позво-
ляет определить еще один способ представления функции ИЛИ—НЕ:
f = АВ - А + В.
Две обведенные штриховой линией строки таблицы истинности
характеризуют состояние элемента ИЛИ—НЕ с двумя входами,
когда на входе А присутствует логический «О». Анализ двух этих
строк показывает, что если В = 0, то f = 1 и если В — 1, то f = 0.
Следовательно, элемент ИЛИ—НЕ с одним активным входом дей-
ствует как инвертор (рис. 3.7, г).
Следует отметить, что для любых элементов надо стремиться не
оставлять свободными неиспользуемые входы. Неиспользуемые
входы элементов И—НЕ можно связать с логической «1», а элемен-
тов ИЛИ—НЕ — с логическим «0». Кроме того, неиспользуемые
входы элементов И—НЕ и ИЛИ—НЕ могут быть соединены с одним
из используемых входов. Эти два способа иллюстрируются на
рис. 3.8.
3.6. Реализация функций ИЛИ и И на основе элементов ИЛИ—НЕ
Реализация функции ИЛИ осуществляется путем последователь-
ного соединения двух элементов ИЛИ—НЕ, как это показано на
рис. 3.9, а. В этой схеме первый элемент выполняет операцию
Рис. 3.8. Способы нагружения неиспользуемых входов элементов:
а — И —НЕ; б - ИЛИ —НЕ
A
7
f*AtB-A8
Рис. 3.9. Реализация с помощью элементов ИЛИ—HE функции:
a — ИЛИ; б — И
ИЛИ—НЕ над двумя входными переменными Л и В, в то время как
второй элемент действует как инвертор.
Схема, реализующая функцию И, строится следующим образом.
Так как для ее реализации могут использоваться только элементы
ИЛИ—НЕ, на выходе последнего элемента ИЛИ—НЕ должно быть
значение функции / = АВ (рис. 3.9, б). Для того чтобы получить
такой выходной сигнал, входами элемента ИЛИ—НЕ должны быть А
и В, поскольку А + В — АВ. Завершая формирование схемы, перед
элементом ИЛИ—НЕ вводим два таких же элемента, выполняющих
операцию отрицания над переменными Л и В, соответственно.
Не встретится принципиальных трудностей при обобщении этого
правила на случай п переменных, т. е. на тот случай, когда на выходе
надо получить произведение п булевых переменных. Тогда у послед-
него элемента ИЛИ—НЕ должно быть и входов, по одному для каж-
дой переменной, содержащейся в произведении. Сигнал, подавае-
мый на каждый вход, будет отрицанием соответствующей перемен-
ной, т. е. если на выходе нужен сигнал С, то на входе должен быть
сигнал С.
3.7. Реализация конъюнктивных нормальных форм
с помощью элементов ИЛИ — НЕ
Функции, имеющие вид f = (Л -f- В) (С -f- D), называются двух-
уровневыми конъюнктивными нормальными формами. Реализация
функции f с помощью элементов И/ИЛИ приведена на рис. 3.10, а.
Применяя г равила, изложенные в предыдущем параграфе, преобра-
зуем эту схему в схему на элементах ИЛИ—НЕ (рис. 3.10, б). Ее
анализ показывает, что по два элемента ИЛИ—НЕ в каждой ветви
являются лишними, так как они производят двойную инверсию
сигнала. Эти элементы перечеркнуты на рис. 3.10, б. На рис. 3.10, в
изображена простейшая форма схемы на элементах ИЛИ—НЕ.
Таким образом, можно сделать вывод, что схемы на элементах И/ИЛИ
«один к одному» преобразовываются в схемы на элементах ИЛИ—НЕ.
3.8. Реализация дизъюнктивных нормальных форм
с помощью элементов ИЛИ — НЕ
Чтобы реализовать функцию, выраженную в дизъюнктивной
нормальной форме, на элементах ИЛИ—НЕ, ее сначала следует пре-
образовать в конъюнктивную нормальную форму. Например, пред-
6).
Рис. 3.10. Реализация функции f = (ЛЦ-В) (C+-D) с помощью элемен-
тов ИЛИ—НЕ:
а — реализация функции f на элементах И/ИЛИ; б — преобразование схемы на элемен-
тах И/ИЛИ в схему из элементов ИЛИ—НЕ; в — результирующая схема
Рис. 3.11. Реализация f— Y,0, 1, 3, 4, 5, 8, 12, 13, 15_на^элементах ИЛИ—НЕ:
а — карта Карно функции f; б — упрощение функции f" — CD -j- ABC + ABC; в — реали-
зация f (С + D) (Я J- В + С) (Д 4- В 4- D)
положим, что на элементах ИЛИ—НЕ требуется реализовать функ-
цию
f SO, 1, 3, 4, 5, 8, 12, 13, 15.
Первым шагом будет построение для этой функции карты Карно
(рис. 3.11, а). Как обычно, ячейки карты помечаем «1». Отрицание
функции можно получить, заполняя свободные ячейки карты Карно
«О», как показано на рис. 3.11, б.
Минимальная форма отрицания функции, получаемая в резуль-
тате анализа карты Карно (см. рис. 3.11, б), имеет вид
/ = CD + АВС + ABD.
Следовательно,
L = (С + D) (Д + В + С) (Л + В + D)
и _ _ _
/ = (С + D) (Л + В + С) (Л + В + D).
Это и есть минимальная конъюнктивная нормальная форма ис-
комой булевой функции. Ее схема, построенная на элементах ИЛИ—
НЕ, приведена на рис. 3.11, в.
3.9. Расширение элементов
Число входов элемента И—НЕ можно увеличить двумя спосо-
бами: с помощью схем И, реализуемых на элементах И—НЕ
(рис. 3.12, а), и за счет использования непосредственно самих эле-
ментов И (рис. 3.12, б). Для увеличения числа входов элемента
ИЛИ—НЕ применяют аналогичные методы (рис. 3.12, в).
Рис. 3.12. Методы увеличения числа входов элементов И—НЕ и ИЛИ—НЕ:
а — расширение входов элемента И — НЕ с помощью схем И, реализованных иа элементах
И — НЕ; б — расширение входов элемента И —НЕ с помощью элементов И; в — расширение
входов элемента ИЛИ —НЕ с помощью схем ИЛИ, реализованных иа элементах ИЛИ —НЕ
Возможность расширения числа входов зависит от типа элемента
и от принятых в данной серии ограничений. Например, в некоторых
сериях ТТЛ-логики допускается не более восьми входов для эле-
мента И—НЕ. Следовательно, применение первого метода позволит
расширить число входов элемента И—НЕ до 64. Но, с другой сто-
роны, элементы И этой же серии могут иметь не более четырех вхо-
дов, и это означает, что применение второго метода позволит про-
вести расширение только до 32 входов.
3.10. Смешанные схемы
На рис. 3.13, а показана схема, выполняющая операцию
И—ИЛИ—НЕ. Эту схему легко реализовать в ряде серий ТТЛ-ло-
1ики. Схема И—ИЛИ—НЕ двухуровневая: на первом уровне рас-
положен элемент ИЛИ—НЕ, который выполняет функцию опера-
ции логического умножения и отрицания; на втором уровне — два
элемента И. В случае необходимости схема И—ИЛИ—НЕ может ис-
полнять функции элемента ИЛИ—НЕ. Для этого надо просто умень-
шить число входов обоих элементов И до одного, как это показано
на рис. 3.13, б. С другой стороны, если на входы элементов И подать
отрицания переменных, то схема И—ИЛИ—НЕ будет работать как
элемент И.
Схему И—ИЛИ можно построить на элементах многих серий
ТТЛ-логики Причем целесообразно использовать высокоскорост-
ные серии. Соответствующая двухуровневая схема изображена на
рис. 3.14, а. На первом уровне находится элемент ИЛИ, на вто-
ром — два элемента И.
Если сделать по одному входу для каждого элемента И, как
показано на рис. 3.14, б, то схема будет работать как элемент ИЛИ.
С другой стороны, если на входы элементов И подавать отрицания
переменных, используемых на рис. 3.14, б, то схема будет действо-
вать как элемент И—НЕ (рис. 3.14, в).
Еще одним из наиболее распространенных типов элементов яв-
ляется элемент с открытым коллектором. Его используют совместно
с внешним нагрузочным резистором, что позволяет объединить не-
сколько выходов элементов с открытым коллектором.
Рис. 3.13. Использование схемы И—ИЛИ—НЕ:
а — схема И —ИЛИ —НЕ; б — использование схемы И —ИЛИ —НЕ в качестве элемента
ИЛИ; в — использование схемы И —ИЛИ—НЕ в качестве элемента И
Рис. 3.14. Использование схемы И—ИЛИ:
а — схема И—ИЛИ; б — использование схемы И—ИЛИ в качестве элемента ИЛИ; в — ис-
пользование схемы И—ИЛИ в качестве элемента И—НЕ
На рис. 3.15, а выходы двух элементов И—НЕ связаны с помощью
внешнего нагрузочного резистора RL. Эта схема выполняет логи-
ческую операцию, получившую название операции объединения
по коллектору, которая аналогична операции И. Точку соединения
коллекторов можно рассматривать как часть элемента И, которого
в действительности не существует. Поэтому ее называют мнимым
элементом И.
На рис. 3.15, б приведена таблица истинности для схемы, изобра-
женной на рис. 3 15, а. Анализ этой таблицы показывает, что на
выходе Z схемы присутствует логическая «1», только если на выхо-
дах Р и Q — логические «1».
Следовательно,
Рис. 3.15. Элемент с открытым коллектором:
а — соединение элементов с открытым коллектором; б — таблица истинности для операции
объединения по коллектору
Взяв отрицание Z, получаем
Z = АВ + CD.
С другой стороны, если операцию инверсии применить к входным
переменным элементов И—НЕ, то на выходе получим
Z = ЖйВ' = (Л + В) (С + D)
и отрицание этого выражения
Z = Л В + CD.
3.11. Элементы с тремя состояниями
На рис. 3.16, а изображен элемент с тремя состояниями, который
широко применяется в микропроцессорных системах. Он является
инвертором с тремя состояниями. Его таблица истинности изобра-
жена на рис. 3.16, б. Из таблицы видно, что элемент выполняет
операцию инверсии входного сигнала при условии, что на входе Е
логическая «1». Кроме обычных двух состояний этого элемента су-
ществует и третье состояние, которое возникает, если на входе Е
логический «О». Это состояние с высоким значением полного сопро-
тивления.
Инвертор с тремя состояниями можно использовать для передачи
данных к одной из линий шины данных, когда он открыт. Когда ин-
Е (разрешающий сигнал)
А Е (разрешаю- щий сигнал) Выход
0 0 Высокое 7.
7 0 Высокое 7.
0 1 1
1 1 0
S)
Рис. 3.16. Элемент стре-
мя стабильными состоя-
ниями:
а — условное обозначение
элемента; б — таблица ис-
тинности элемента
вертор закрыт, он не нагружает шину, что делает последнюю доступ-
ной для других устройств, которые передают данные в микропро-
цессорную систему.
3.12. Элемент ИСКЛЮЧАЮЩЕЕ ИЛИ
Ниже приведено булево выражение, определяющее функцию
ИСКЛЮЧАЮЩЕЕ ИЛИ:
f = АВ + АВ
или
f = А ф В,
где символ @ обозначает операцию ИСКЛЮЧАЮЩЕЕ ИЛИ.
Таблица истинности функции ИСКЛЮЧАЮЩЕЕ ИЛИ приве-
дена на рис. 3.17, а, а условное обозначение на рис. 3.17, б. На
О ф о - о
о ф 1 = 1
1 Ф о = 1
1 Ф 1 = О
в)
Рис. 3.17. Функция ИСКЛЮЧАЮЩЕЕ ИЛИ:
а — таблица истинности; б — условное обозначение элемента ИСКЛЮЧАЮЩЕЕ ИЛИ;
в — сумма по модулю 2 двух двончиых цифр
рис. 3.17, в показана таблица, представляющая результаты опера-
ции ИСКЛЮЧАЮЩЕЕ ИЛИ, проводимой с двоичными перемен-
ными. Анализ этой таблицы позволяет считать эту операцию суммой
по модулю 2 двух двоичных цифр (сумма по модулю 2 определяется
как сумма двух цифр без переноса). Например, обычная сумма 1 +
+ 1 = 10, но сумма по модулю 2 равна 0. На рис. 3.18, а изображена
карта Карно этой функции, а на рис. 3.18, б — карта Карно допол-
нения этой функции. Просмотр карты на рис. 3.18, б показывает,
что дополнение функции ИСКЛЮЧАЮЩЕЕ ИЛИ имеет вид
J — АВ + АВ.
Принята следующая условная запись этого выражения:
/ = А О В,
где символ о используется для обозначения операции совпадения
или ИСКЛЮЧАЮЩЕЕ ИЛИ—НЕ. Условное представление эле-
мента ИСКЛЮЧАЮЩЕЕ ИЛИ—НЕ приведено на рис. 3.18, в,
а таблица истинности этого элемента изображена на рис. 3.18, г.
Анализ таблицы позволяет установить, что дополнение функции f
принимает значение, равное логической «1», когда числа А и В,
представленные двоичными цифрами, равны.
Из вышесказанного ясно, что функция ИСКЛЮЧАЮЩЕЕ
ИЛИ имеет непосредственное отношение к операции двоичного сло-
жения, в то время как функция ИСКЛЮЧАЮЩЕЕ ИЛИ—НЕ
может использоваться для сравнения значений двух двоичных чисел.
Рис. 3.18. Функция ИСКЛЮЧАЮЩЕЕ ИЛИ—НЕ:
о — карта Карно функции ИСКЛЮЧАЮЩЕЕ ИЛИ; б — карта Карио функции ИСКЛЮ-
ЧАЮЩЕЕ ИЛИ —НЕ; в — условное обозначение функции ИСКЛЮЧАЮЩЕЕ ИЛИ —НЕ;
а — таблица истинности функции ИСКЛЮЧАЮЩЕЕ ИЛИ—НЕ
Рис. 3.19. Реализация функции ИСКЛЮЧАЮЩЕЕ ИЛИ с помощью:
а — элементов И/ИЛИ; б — элементов И —НЕ; в — минимального числа элементов И—НЕ;
г — элементов ИЛИ — НЕ
Можно предложить несколько способов реализации функции
ИСКЛЮЧАЮЩЕЕ ИЛИ. Например, она может быть построена
на элементах И, ИЛИ и НЕ, как показано на рис. 3.19, а. С другой
стороны схему ИСКЛЮЧАЮЩЕЕ ИЛИ можно собрать из элемен-
тов И—НЕ (рис. 3.19, б). Однако функция ИСКЛЮЧАЮЩЕЕ
ИЛИ f = АВ + АВ может быть преобразована к виду, допускаю-
щему более простую реализацию.
Добавляя термы АА и ВВ к первой части приведенного выше
уравнения, получаем
f = АВ + ВВ + АВ + АА = В (Л + В) + А (Л + В).
Выражение в правой части является двухуровневой дизъюнктивной
нормальной формой. На рис. 3.19, в изображена его реализация на
элементах И—НЕ. Схема, показанная на рис. 3.19, в, состоит из
четырех элементов, в то время как схемы на рис. 3.19, а и 3.19, б —
из пяти.
Выразим ИСКЛЮЧАЮЩЕЕ ИЛИ в конъюнктивной нормальной
форме, преобразовав для этого последнее выражение к виду
f = (Л + В) (Л + В).
Это выражение удобно для реализации на элементах ИЛИ—НЕ.
Соответствующая схема приведена на рис. 3.19, г. Простейший
f-AQB
Рис. 3.20. Реализация функции ИСКЛЮ-
ЧАЮЩЕЕ ИЛИ—НЕ
Рис. 3.21. Два способа (а, б) соединения элементов ИСКЛЮЧАЮЩЕЕ ИЛИ
способ реализации функции ИСКЛЮЧАЮЩЕЕ ИЛИ—НЕ состоит
в последовательном соединении элемента ИСКЛЮЧАЮЩЕЕ ИЛИ
и инвертора (рис. 3.201.
Существует два способа соединения элементов ИСКЛЮЧАЮ-
ЩЕЕ ИЛИ, имеющих по два входа. Они показаны на рис. 3.21, а, б.
Схема на рис. 3.21, а, реализующая операцию ИСКЛЮЧАЮЩЕЕ
ИЛИ для четырех переменных, располагается на трех уровнях.
В то же время схема на рис. 3.21, б, реализующая ту же функцию
и состоящая из стольких же элементов, располагается на двух уров-
нях. Поэтому вторая схема позволит получить выходной сигнал
быстрее, чем первая. На рис. 3.22 показано, как элемент ИСКЛЮ-
ЧАЮЩЕЕ ИЛИ можно использовать в качестве управляемого ин-
вертора. Двоичные данные передаются по двум линиям Do и Dlt
а на другие входы элементов подается управляющий сигнал М, ко-
торый может быть либо 0, либо 1.
Если М = 0, то на выходах элементов появляются 1 и 0, соответ-
ственно (рис. 3.22, а). С другой стороны, если управляющий сиг-
нал М == 1, то на выходах элементов появляются 0 и 1 (рис. 3.22, б).
Следовательно, если М — 0, то информация с линий Db и Di
без изменения передается на выходы элементов ИСКЛЮЧАЮЩЕЕ
ИЛИ. В случае же, когда М = 1, сигналы на выходах элементов
являются отрицаниями сигналов на входах. Данная схема часто ис-
пользуется совместно со схемой сумматора, поскольку она позволяет
выполнить операцию арифметического дополнения.
На карте Карно функция ИСКЛЮЧАЮЩЕЕ ИЛИ имеет харак-
терный вид. Для трех переменных А, В л С эта функция может
быть представлена следующим образом:
f = А ф В @ С = (АВ + АВ) ф С =
= (АВ + АВ) С + (АВ + АВ) С =
= АВС + АВС + АВС + АВС.
Карта Карно с заполненными ячейками (рис. 3.23) напоминает
доску для игры в шашки.
Для помеченных ячеек выполняется одно общее правило: сумма
по модулю 2 двоичных кодов соответствующих им переменных равна
единице. Например, АВС = 001 и сумма по модулю 2 этих трех дво-
ичных цифр равна единице.
Рис. 3.22. Использование элемента ИСКЛЮЧАЮЩЕЕ ИЛИ в качестве управляе-
мого инвертора:
а — для передачи сигнала без преобразований; б — для передачи инвертированного сигнала
Рис. 3.23. Карта Карно для функции ИСКЛЮЧАЮЩЕЕ ИЛИ, зависящей от
трех переменных
Существует несколько правил, связанных с использованием опе-
рации ИСКЛЮЧАЮЩЕЕ ИЛИ. Их алгебраическая запись приве-
дена ниже:
А ф А = АА + АА = 0; '
А ф А = АА + АА = 1;
А ф 0 = Л-0 + Л-1 = А:
Л ф 1 = Л-1 + Л-0 = Л.
Может быть также показано, что
Л ф В ф АВ = Л + В;
Л ф В ф 1 = Л ф В = Л о В.
Упражнения
У3.1. Используя элементы И—НЕ, реализовать следующие функции:
а) В = АВ + (В + С) А;
б) В = (АВ + С) (В + D) + А (В + С) (D + £).
УЗ.2. Минимизировать следующие функции и реализовать их, используя эле-
менты И—НЕ:
a) f(A, В, С) = SO, 1, 2, 3, 4, 5, 6;
б) f (А, В, С, D) = 22, 8, 9, 10, 12, 13, 14;
в) f(A, В, С, D, Е) — £8, 9, 10, И, 15, 16, 17, 18, 19, 20, 20, 21, 22,
23, 24, 25, 26, 27, 31.
УЗ.З. Используя элементы ИЛИ’—НЕ, реализовать следующие булевы функции:
а) В = А (Л + В) (В + CD);
б) В = А (В + С + DE) (B + CD + АЕ).
УЗ.4. Найти минимальную конъюнктивную нормальную форму для каждой из
следующих функций и реализовать на элементах ИЛИ—НЕ:
a) f(A, В, С) *= SO, 2, 4, 6, 7;
б) f (А, В, С, D) = 2 0, 1, 2, 3, 4, 9, 10, 13, 14;
в) f (А, В, С, D, Е) = SO, 1, 2, 3, 4, 6, 10, 11, 12, 13, 14, 15, 16, 29, 31.
УЗ.5. Реализовать максимально возможным числом способов следующие функции
на элементах И—НЕ (для преобразования использовать только метод факторизации):
а) /1 = BCD + BCD + Л;
б) /2 = АС + ВС + AD;
в) /8 = ABD + АВС + CD.
УЗ.6. Реализовать следующие функции на элементах И—НЕ, имеющих не более
трех входов:
а) Д = АВС + AD + BCD + ACD;
б) Д = АВ + AD + BD + CD + АС;
в) Д = ABCD + ABCD + ABD + CD.
УЗ.7. Реализовать на элементах ИЛИ—НЕ, имеющих не более трех входов, следу-
ющие функции:
а) Д = (Л + В)(С + 7))(В + С) (Л+Р)(Л + С);
б) Д=(ЛС + ВС) (Л + С);
в) f3 = АВ + BCD + ABD.
УЗ.8. Представить в минимальной дизъюнктивной нормальной форме следу-
ющие функции:
a) fi = Л (Л ф В ф С);
б) Д = Л (Л © S О Q;
в) Д = Л + (Л ф В ф С);
г) = А + (Л © В © Q.
УЗ.9. Доказать следующие утверждения:
а) Л ф В ф С = Л ф В © С;
б) A Q в QC = Л 0 В ф С;
В) (Л ф В ф ЛВ) (Л ф С ф ЛС) = Л + ВС.
4. ПРОЕКТИРОВАНИЕ КОМБИНАЦИОННЫХ
ЛОГИЧЕСКИХ СХЕМ
4.1. Введение
На рис. 4.1 представлено условное обозначение комбинационной
логической схемы. Она состоит из прямоугольного блока, содержа-
щего только логические элементы, в который входят стрелки, являю-
щиеся входными сигналами 7Ь 72, ..., 1п, и из которого выходят
стрелки, являющиеся выходными сигналами Оь О2, ..., От. Входные
и выходные сигналы могут быть логическими «О» и «1». Каждый вы-
ход является функцией нескольких или всех входных переменных.
Следовательно,
Oi = Л (71, 72, 7П);
О2 = /2(7!, 72, ..., 7П);
От — fm (71, 72, .... 1п).
Если допустить, что все логические элементы в комбинационной
логической схеме действуют без задержек, то сигналы (Оь О2, ...
.... От) будут появляться на выходах схемы точно в тот же самый
момент, когда подаются сигналы на входы. Более того, сигналы на
выходах будут сохраняться до тех пор, пока есть сигналы на вхо-
дах. Конечно, на практике каждый элемент комбинационной логи-
ческой схемы имеет конечную задержку, и, следовательно, сигналы
на выходах будут появляться через какой-то (свой для каждого вы-
хода) интервал после подачи входных сигналов. Для каждого вы-
хода задержка будет определяться задержками элементов в схеме
и количеством уровней, связанных с этим выходом.
4.2. Полусумматор
Полусумматор является одной из простейших комбинационных
логических схем. Полусумматор используется для сложения двух
наименьших значащих цифр при двоичном суммировании, как по-
казано на рис. 4.2, а. При сложении двух двоичных цифр А и В
существуют четыре различные комбинации, которые показаны на
рис. 4.2, б. В каждом из четырех случаев ищут сумму двух цифр,
А Комбинационная логическая схема 0,
• •
In От
Рис. 4.1. Условное обозначение комби-
национной схемы
но следует заметить, что в по-
следнем случае, когда А = 1
и В = 1, появляется еще и еди-
ница переноса, которая долж-
на быть учтена на следующей
стадии выполнения операции
сложения, где ее прибавляют
к сумме.
3 О О 1 fl]
+ I
9 1 О О [11
12 110 0
Я)
Рис. 4.2. Полусумматор:
а — двоичное сложение; полусумматор используется для сложения двух наименьших зна-
чащих цифр (обведены штриховой линией); б — четыре различных случая, возникающих
при сложении двух двоичных цифр Л и В (с переносом, который учитывается на следующей
стадии сложения); в — таблица истинности полусумматора; г — реализация полусумма-
тора иа элементах И —НЕ
Все случаи суммирования двух двоичных цифр, отраженные
на рис. 4.2, б, сведены в таблицу (рис. 4.2, в). В ее столбцах А и В
расположены значения переменных, которые необходимо сложить.
В третьем и четвертом столбцах таблицы хранятся сумма S и пере-
нос С, соответственно. Анализ таблицы позволяет определить булевы
функции для S и С
S = АВ + АВ,
т. е. значения S = 1 дают две комбинации переменных. Таким об-
разом получаем, что S соответствует функция ИСКЛЮЧАЮЩЕЕ
ИЛИ с двумя входами
S = А ф В.
Для С устанавливаем
С = АВ.
На рис. 4.2, г показана реализация функций суммы и переноса
на элементах И—НЕ.
4.3. Полный сумматор
Для сложения наименьших значащих цифр требуется полусум-
матор, а для сложения всех остальных цифр — полный сумматор.
Как показано на рис. 4.3, а, схема полного сумматора содержит
три входа: два соответствуют двоичным цифрам А и В, а третий —
Рис, 4.3. Полный сумматор:
а — структурная схема; б — таблица истинности; в — карта Карно для Свых; г — реали«
зация
переносу из предыдущего разряда Свх. Кроме того, схема имеет
два выхода: сумму S и перенос в следующий разряд Свых.
На рис. 4.3, б изображена таблица истинности полного сумма-
тора. Анализируя эту таблицу, получаем булевы выражения для
суммы S и переноса в следующий разряд Свых:
S = АВСвх + АВСвх + АВСвх + АВСвх;
СВых = АВС»* + АВСвх + АВСвх + АВСвх.
Выражение для суммы может быть приведено к виду
S = А (ВСвх + ВСвх) + А (ВСвх + ВСвх) =
= Л (В ф Свх) + Л (В ф Свх) = А ф В ф Свх.
На рис. 4.3, в представлена карта Карно для Свых. Проведя уп-
рощения; получаем, что
Свых = АСВХ + ВСвх + АВ.
Схема полного сумматора дана на рис. 4.3, г. .
4.4. Четырехразрядный сумматор параллельного действия
Теперь уже не составит труда построить, например, четырех-
разрядный сумматор параллельного действия из четырех однораз-
рядных полных сумматоров. На рис. 4.4 показана структурная схема
Рис. 4.4. Четырехразрядный сумматор параллельного действия
многоразрядного сумматора. Заметим, что для полного сумматора,
производящего сложение младших разрядов чисел, линия пере-
носа С_! заземлена, т. е. значением С_г всегда является логиче-
ский «О».
Иногда схемы такого типа называют сумматорами со сквозным
переносом, поскольку перенос, полученный на какой-нибудь стадии
суммирования, может распространиться и на последующие стадии.
В худшем случае перенос, сформированный сумматором FA0, мо-
жет пройти по всем четырем линиям переноса и только после этого
появится на выходе последнего сумматора FA3. Например, пусть
требуется сложить следующие два числа:
А 1111 1.5
Т~
В 1 0 0 1 9
1 1 0 0 0 24
В этом случае перенос возникает при суммировании самых млад-
ших разрядов и распространяется на все старшие разряды. В конце
концов он появляется на выходе С3 сумматора старших разрядов,
где становится первой значащей цифрой результата. Следовательно,
сигнал переноса проходит последовательно четыре двухуровневые
логические схемы, и сумма не может быть полностью сформирована
до тех пор, пока не пройдет время, равное сумме задержек восьми
элементов. Таким образом для сумматоров этого типа максималь-
ная задержка прямо пропорциональна числу разрядов (или стадий
суммирования) п.
4.5. Сумматор с ускоренным переносом
Так как время задержки сумматора со сквозным переносом ра-
стет с ростом разрядности суммируемых чисел, было разработано
несколько методов, позволяющих уменьшить время выполнения
операции сложения. Один из таких методов — метод ускоренного
переноса — описан ниже.
Функция переноса для полного сумматора имеет следующий вид:
Свых = ЛВСвх + ЛВСвх + АВСвх + АВСвх.
Преобразуем ее к виду
Свых =(Л ф В) Свх + АВ
или
Свых = РСКУ. + G,
где Р = А ф В — терм распространения, a G — АВ — терм по-
рождения. Если G = 1, то 4 = 1, аВ = 1 и именно на этой стадии
суммирования формируется сигнал переноса. С другой стороны,
если Свх = 1 и А = 1 или В = 1, то сигнал переноса, поданный на
вход, проходит дальше. Для четырехразрядного сумматора термы
порождения и распространения имеют вид
Go — Л0В0; = Ао ф В0‘,
Gj = AiBi‘, Р1 = Аг ф Bi,
G2 — А2В2, Р2 = А2 ф В2,
G3 — Л3В3; Р3 — Аз ф В3.
Функции переноса, в свою очередь, определяются как
Со = Р0С_г + Go;
G = ЛС0 ф Gi;
С2 = Р 2С1 + G2;
G3 = Р 3С2 + G3.
Подстановка значений Со, С1 и С2 приводит уравнения для Clt С2
и С3 к виду
Gi = Р iP 0C_i + PiG0 + Gi,
Сг = РгРуР.С^ + PJA + PJ\ + G2;
С3 = Р^РгРхР.С^ + РзРгРА + PJA + P3G2 ф G3.
Определим значение наименьшего значащего разряда сумматора
So = Ао ф Ва ф C_i = Ра ф С_1
и остальных разрядов
<$i = Рi ф Со;
S2 = Р2 ф Ci,
S3 = Р3 ф с2.
На рис. 4.5, а изображена структурная схема четырехразрядного
сумматора с ускоренным переносом. Она состоит из трех блоков:
один служит для формирования термов порождения и распростране-
ния, другой — термов переноса и третий — термов суммы. Реализа-
ция сумматора показана на рис. 4.5, б.
Если стоит задача реализовать схему сумматора только на эле-
ментах И—НЕ, то надо все элементы ИСКЛЮЧАЮЩЕЕ ИЛИ
на рис. 4.5, б заменить схемами, состоящими из четырех элементов
И—НЕ. Блок порождения и распространения состоит из четырех
полусумматоров, для реализации каждого из которых требуется пять
элементов И—НЕ (рис. 4.2, г). Следовательно, для реализации блока
потребуется двадцать элементов И—НЕ.
В блоке переноса элементы И и ИЛИ можно заменить элемен-
тами И—НЕ. Причем, как показано в гл. 3, одному элементу
И/ИЛИ соответствует один элемент И—НЕ. Кроме того, потре-
буются дополнительные элементы И—НЕ для инверсии термов G
в уравнениях переноса. Следовательно, для реализации блока пере-
носа потребуется восемнадцать элементов И—НЕ.
Наконец, блок суммирования состоит из четырех элементов
ИСКЛЮЧАЮЩЕЕ ИЛИ, для
с3
Блок распространения
и порождения
___ yL-f L „1
Блок переноса
С, Сд
Блок суммирования
представления каждого из кото-
рых необходимы четыре элемен-
та И—НЕ. Поэтому для реали-
зации этого блока потребуется
шестнадцать элементов И—НЕ.
Таким образом, для реализации
сумматора потребуется пятьдесят
четыре элемента И—НЕ. Каждый
каскад четырехразрядного сумма-
тора со сквозным переносом
состоит из двух элементов
ИСКЛЮЧАЮЩЕЕ ИЛИ и четы-
рехэлементов И—НЕ (см. рис. 4.3).
Следовательно, для реализации
каждого каскада необходимо иметь
двенадцать элементов И—НЕ, а для
Sj Sj So CL J
Рис. 4.5. Сумматор с ускоренным переносом:
а — структурная схема четырехразрядного сумматора с ускоренным переносом; б— ап-
®*ратная реализация сумматора
реализации схемы четырехразрядного сумматора со сквозным пере-
носом потребуется сорок восемь элементов И—НЕ.
Схема, реализующая сумматор с ускоренным переносом на
элементах Й—НЕ, располагается на восьми уровнях. Три уровня
соответствуют блоку распространения и порождения, два — блоку
переноса и три — блоку суммирования. Важно, что количество
уровней не зависит от разрядности суммируемых чисел. Хотя схема
четырехразрядного сумматора со сквозным переносом располагается
также на восьми уровнях, для каждой пары дополнительных раз-
рядов потребуется -еще два добавочных уровня.
В связи с этим можно сделать вывод, что сумматор с ускоренным
переносом быстрее производит операцию сложения, если разряд-
ность суммируемых чисел больше четырех.
4.6. Полное вычитающее устройство
Ниже приведены все возможные варианты, возникающие при
вычитании двух двоичных цифр А и В:
Л 0 0 1 1
В 0 1 0 1
D 0 1 1 О
Объяснений требует только один вариант, возникающий при вычи-
тании 0—1. В этом случае для того чтобы выполнить вычитание,
необходимо занять цифру у следующего более высокого разряда
и провести операцию 10— 1 = 1.
Вычитание двух четырехразрядных двоичных чисел Л3Л2^Ио
и В3В2В1В0 показано ниже:
Л3Л2Л1Ло 1010 Уменьшаемое
В3В2ВхВо 0111 Вычитаемое
ООН Разность
BbJ 111
Число Л3Л2Л1Л0 называется уменьшаемым, а ВдВ^В^Вц — вычи-
таемым. Для того чтобы провести операцию для младших разрядов,
необходимо занять 1 у следующего более высокого разряда. Раз-
ностью является 1, и она является результатом операции вычитания
для младшего разряда. Однако то, что была занята 1, необходимо
учитывать. Это делается с помощью специальной строки Ввх.
Для следующего разряда результат получаем после выполнения
вычитания Л1 — (Вх + Ввх), т. е. 1—10. Для того чтобы провести
вычитание, опять необходимо занять цифру в следующем разряде.
Тогда разность будет равна 11 — 10 = 1.
Теперь, используя изложенные выше правила, можно построить
таблицу истинности полного вычитающего устройства. Анализируя
£>ЗГ>
%
Рис. 4.6. Полное вычитающее устройство:
а — таблица истинности полного вычитающего устройства; б — карта Карно функции Ввых;
в — реализация полного вычитающего устройства
таблицу истинности, изображенную на рис. 4.6, а, можно получить
следующие выражения для разности D:
D = АВВВТ + ~АВВ^ + АВВвх + АВВБТ
и, упрощая,
D = А (ВВв* + ВВвх) + А (ВВвх + ВВвх) =
= А (В ф Ввх) + А (В®ВВ1) = А ф В ф Ввх.
На рис. 4.6, б изображена карта Карно для функции Ввых. Проведя
упрощения, получаем
^вых = АВБк + АВ + ВВвх.
На рис. 4.6, в показаны две логические схемы, реализующие функ-
ции, описывающие D и Ввых.
Бессмысленно искать полное вычитающее устройство в реальной
ЭВМ. Его там нет. Очевидно, удобнее использовать одну и ту же
аппаратуру для выполнения операций сложения и вычитания.
Применение дополнительного кода позволит использовать схему
сумматора как для сложения, так и для вычитания. Это ведет к эко-
номии аппаратурных средств и является обычной практикой при
выполнении арифметических операций на ЭВМ.
4.7. Дополнительный код
Для «-разрядного двоичного числа дополнительный код опреде-
ляем следующим образом:
М* = 2" — N,
где N* — дополнительный код N; N — число, дополнительный код
которого ищем; п — число цифр в N. Если М = 1011, то
М* = 24 — 1011 = 10 000 —1011= 00101.
С другой стороны, дополнительный код числа может быть найден
так: берем отрицания всех двоичных цифр числа и к минимальному
значащему разряду добавляем 1.
Для двоичного числа 1011 эта процедура дает
0100 — инверсия всех цифр
1 — добавление 1 к минимальному значащему разряду
оТоТ
Допустим также любой другой метод для нахождения дополни-
тельного кода числа. Например, можно предложить такой метод.
Ищем первую справа 1 в числе. Все цифры, стоящие слева от этой 1,
преобразовываем, а цифры справа, включая 1, не меняем.
Дополнительный код иногда называют дополнением по основа-
нию 2, так как 2 — это основание двоичной системы счисления.
4.8. Обратный код
Обратный код, или уменьшенное дополнение по основанию,
определяем так:
+** = (2п — 1) — N,
где N** —обратный код числа N. Для двоичного числа 1011
N** = (10 000 — 1) — 1011 = 0100.
Простейший метод определения кода заключается в инвертирован ии
всех двоичных цифр данного числа.
4.9. Двоичное представление чисел
В ЭВМ двоичное число может быть представлено одним из сле-
дующих трех способов:
а) в прямом коде;
б) в дополнительном коде;
в) в обратном коде.
В каждом из этих трех случаев для представления знака числа
используют двоичный сигнал: 0 — для положительных чисел, 1 —
для отрицательных. Знаковый бит размещают на левом конце числа
и отделяют от числовой части запятой.
Характеризуя первый способ представления двоичных чисел
в ЭВМ, следует сказать, что в самом левом разряде хранится знак,
а остальные биты представляют модуль числа в двоичной форме.
Например,
+ 13 = 0,1101
и
— 13 = 1,1101.
Проектирование логических, схем, выполняющих арифметические
операции с двоичными числами, представленными в прямом коде,
достаточно трудоемко. Поэтому чаще используют представления
в дополнительном или обратном коде.
В дополнительном коде положительные числа представляют так:
слева — знаковый бит, значение которого равно 0, справа — мо-
дуль числа в двоичной форме. Что касается отрицательных чисел,
то для них действует следующее правило: слева — знаковый бит,
значение которого равно 1, справа — модуль числа в дополнитель-
ном коде. Следовательно,
+ 13 = 0,1101
и
— 13 = 1,0011.
Аналогично, в обратном коде положительные числа представляют
так же, как и в дополнительном, а отрицательные — в виде обрат-
ного кода модуля числа, слева от которого расположен знаковый
бит. Например,
+ 13 = 0,1101
и
— 13 = 1,0010.
4.10. Использование дополнительного кода для сложения
и вычитания чисел
Сложение производится всегда одинаково, независимо от того,
какие числа, положительные или отрицательные, участвуют в опе-
рации. Знаковые биты принимают участие в операции, а перенос
из знакового разряда игнорируется. Если результат сложения поло-
жительный, то в знаковом бите 0, а модуль числа выражается в пря-
мом коде. Если же результат сложения отрицательный, в знаковом
разряде 1, а абсолютная величина числа выражается в дополни-
тельном коде. Это проиллюстрировано на примерах, приведенных на
рис. 4.7, а. В качестве слагаемых использованы положительные
и отрицательные числа, абсолютные величины которых равны, соот-
ветственно, 5 и 7.
На рис. 4.7, б изображено устройство, предназначенное как для
сложения, так и для вычитания чисел, представленных в дополни-
тельном коде. Число А3А2А1А0 будет первым слагаемым при выпол-
нении операции сложения, и уменьшаемым при вычитании, в то
время как число В3В2В1В0 будет вторым слагаемым и вычитаемым,
соответственно, для сложения и вычитания. Для реализации схемы
необходимо иметь пять полных сумматоров, причем сумматор FA4
используется для сложения знаковых разрядов А4 и В4. Управляе-
мые инверторы, реализованные на схемах ИСКЛЮЧАЮЩЕЕ ИЛИ,
используются для инвертирования цифр В3,В2, Blt Во в том случае,
когда М = 1, т. е. тогда, когда необходимо осуществить вычитание.
+ 7 + 5 0,0111 0,0101
+ 12 0,1100
+7 0,0111 —7 1,1001
—5 1,1011 +5 0,0101
+2 0,0010 —2 1,1110
Рис. 4.7. Сложение и вычитание
двоичных чисел:
а — использование дополнительного кода
для сложения и вычитания; б — устрой-
ство для сложения н вычитания, рабо-
тающее в дополнительном коде
—7 1,1001
—5 1,1011
Сигнал М также подается на вход, формирующий функцию переноса
сумматора для наименьших значащих разрядов чисел. Когда М = О,
то С_! = 0 и FA0 работает как полусумматор; однако, когда Л-1 = 1,
C_i = 1 и единица добавляется к наименьшему значащему разряду
обратного кода числа, формируя тем самым дополнительный код.
4.11. Двоичное умножение
Один из самых простых и наиболее быстрых методов умножения
основан на использовании комбинационной логической схемы,
состоящей из элементов И, сумматоров и полусумматоров. В его
основу положено то, что правила булевого и двоичного умножения
одинаковы, и поэтому группы элементов И могут использоваться
для формирования частичных произведений, которые возникают
в процессе двоичного умножения.
Если, например, требуется найти произведение двух трехразряд-
ных двоичных чисел Л2Л1Л0 и В^В^Во, то обычно используют хорошо
известный метод, который проиллюстрирован на рис. 4.8, а. Сначала
наименьший значащий разряд множителя по очереди умножают на
каждый разряд множимого, формируя три конъюнктивных терма
первой строки Л2В0, и ЛоВо- Следующую строку конъюнкций
получают так: осуществляют сдвиг влево, и затем каждый разряд
множимого умножают на следующий за наименьшим разряд множи-
теля. Остальные строки формируют аналогично. Процесс закончится,
когда будут исчерпаны все разряды множителя. После этого содер-
Множимое 1 А, . Ao
Множитель вг в, ! Bo
) 1 1
1 1 1 Аг В 0 I AfBo I A0B0
1 1 1 Ai в. । AaBf I
1 | ^2^2 । Аовг ! I
1 1 Сз 1 с; I
1 Сц | 1 # | Ci г I
Произведение 1 Р5 1 Рь 1 Рз Рг I Pl I Po
Рис. 4.8. Схема, реализующая операцию умножения двух чисел:
а — двоичное умножение; б -» параллельное двоичное устройство умножения
жимое столбцов складывают по очереди справа налево. В результате
получают все цифры (от Ро Д° Рь) произведения.
При формировании разрядов от до РБ необходимо учитывать
возможность образования переноса. Во втором столбце справа от-
кладывают ЛХВО и XqBj, образуя Выполняя эту операцию, надо
учитывать возможность образования единицы переноса Сх, которая
должна быть добавлена в следующий столбец для суммирования.
Для третьего столбца должны быть выполнены две операции сложе-
ния, так как складываются четыре слагаемых. Это приводит к воз-
можности образования двух единиц переноса Cj и С?, которые поме-
щают в следующий столбец и т, Д.
Деся- тичная цифра NBCD 2 из 5
А в с D Р Q R S т
0 0 0 0 0 0 0 0 0 0
1 0 0 0 1 0 0 0 1 1
2 0 0 1 0 0 0 1 0 1
3 0 0 1 1 0 0 1 1 0
4 0 1 0 0 0 1 0 0 1
5 0 1 0 1 0 1 0 1 0
6 0 1 1 0 0 1 1 0 0
7 0 1 1 1 1 0 0 0 1
8 1 0 0 0 1 0 0 1 0
9 1 0 0 1 1 0 1 0 0
a)
Рис. 4.9. Преобразование из ко-
да NBCD в код ч.2 из 5»;
а — коды NBCD н «2 из 5»; б —
структурная схема преобразователя
из кода NBCD в код «2 из 5»; в —
карты Карно преобразователя; г —
реализация преобразователя
Логическая схема устройства умножения показана на рис. 4.8, б.
Следует отметить, что число элементов, необходимых для реализации
устройства умножения параллельного действия, быстро растет с ро-
стом числа разрядов множителя и множимого. До появления БИС
большое количество элементов комбинационной логики, требуемых
для реализации схемы, было препятствием для использования этого
метода. Но сейчас, когда БИС получили широкое распространие,
появились реализующие этот метод устройства, размещенные на одном
кристалле.
4.12. Преобразования кодов
Возможность осуществлять преобразования из одного кода
в другой — наиболее общее требование, предъявляемое к цифровым
системам.
Десятичная информация часто выражается в двоичной форме,
поэтому очень широкое распространение получил двоично-десятич-
ный код NBCD (рис. 4.9, а). В этом коде для представления одной
десятичной цифры используют четыре двоичных. Вообще сущест-
вует 24 возможных комбинаций четырех двоичных цифр, но в коде
NBCD используется только десять. Следовательно, существует
шесть запрещенных комбинаций. Поэтому говорят, что код в неко-
торой степени избыточен.
Другой код, используемый в цифровых системах, — это код
«2 из 5». В нем каждая допустимая комбинация содержит две 1,
и поскольку в пятиразрядном коде таких комбинаций всего десять,
каждая соответствует десятичной цифре. Этот код на рис. 4.9, а
расположен рядом с кодом NBCD. Благодаря тому, что точно две
1 должны присутствовать в кодовой комбинации, код «2 из 5» обла-
дает средствами защиты от ошибок, возникающих при передаче по
цифровым каналам связи. Поэтому перед передачей данные, пред-
ставленные в коде NBCD, должны быть преобразованы в код «2
из 5». В конце приема данных проверяют, содержит ли каждая ко-
довая комбинация ровно две 1. Схема, обеспечивающая выполнение
преобразования, будет чисто комбинационной. Ее изображение
в виде «черного ящика» приведено на рис. 4.9, б.
Таблица на рис. 4.9, а может служить таблицей истинности
устройства преобразования кодов. Карты Карно для выходных
сигналов Р, Q, R, S и Т могут быть получены прямо из таблицы
(рис. 4.9, в). Каждая ячейка, помеченная символами d, представляет
комбинацию четырех двоичных цифр, не используемую в коде NBCD.
Следовательно, появление такой комбинации исключено. Термы,
соответствующие таким ячейкам, являются «термами, не достав-
ляющими беспокойства». Поэтому их можно использовать в процессе
упрощения.
Анализируя карты Карно, изображенные на рис. 4.9, в, получим
выражения для выходных сигналов;
Р = А + BCD + BCD;
Q = ВС + BD + ACD]
R -= AD + CD + BC;
5 = AD + ~ACD + ABD;
T «= BCD + BCD + BCD + ABCD.
На рис. 4.9, г показана реализация этих функций с помощью
элементов И—НЕ.
4.13. Преобразователь из двоичного кода в код Грея
Другой широко используемый код — это одношаговый код,
обычно называемый кодом Грея. Отметим характерную особенность
этого кода: при переходе к следующей кодовой комбинации меняется
только одна цифра.
Существует несколько кодов Грея. В частности, один можно
получить, беря по модулю 2 сумму соседних цифр четырехбитового
двоичного кода. Например, десятичная цифра 3 в четырехразрядном
двоичном коде имеет вид ООН. Ниже показано, как эта комбинация
преобразуется в соответствующую комбинацию в коде Грея. При
проведении этого преобразования следует считать, что второй бит,
который участвует в формировании В3, равен 0.
Вг В, Во
Четырехразрядный 0 о 1 j
двоичный код S
© 0 © ©
о 0 7 о —3
Код Грея Bs ег Gt Go
Анализ приведенного выше преобразования показывает, что
цифры G3, G2, Gi и Go кода Грея связаны с двоичными цифрами Ва,
Ва, Bi и Во следующими соотношениями:
G3 Bq Ф BiJ Gg в Ва ф B3J
G1 Bl @ Bq', Gq = Bq.
Логическая схема, реализующая эти соотношения, приведена на
рис. 4.10, а, а на рис. 4.10, б изображены соответствующие друг
другу комбинации в двоично-десятичном коде и коде Грея. Для
реализации схемы преобразования требуются только элементы
ИСКЛЮЧАЮЩЕЕ ИЛИ, которые имеются во многих сериях
ТТЛ-логики.
Данная форма кода Грея называется отраженной двоичной.
Если провести горизонтальную линию ниже кодовой комбинации
0100 (см. рис. 4.10, б), то будет видно, что последние три цифры
кодовых комбинаций, расположенных ниже этой линии, совпадают
с соответствующими цифрами кодовых комбинаций, расположенных
симметрично по отношению к этой линии.
Чтобы получить логические уравнения для обратного преобра-
зования, строят карты Карно для всех двоцчных цифр Bq, В?, Вг
и Во. Переменными, связанными со строками и столбцами карт,
являются отдельные разряды кода Грея G3, G2, Щ и Go. На рис. 4.10, в
в0 приведена карта Карно обратного пре-
Ж---------' образования.
Карта Карно для Во похожа на шах-
_43D матную доску и соответствует функ- ции ИСКЛЮЧАЮЩЕЕ ИЛИ. Следова-
бг тельно, Во = G3 + G.2 + G, + Go.
о)
в3 to to Bl to О G3 G2 G1 Go to w B2 Bl to О G3 G2 Gx Go
0 0 0 0 0 0 0 0 1 0 0 0 1 1 0 0
0 0 0 1 0 0 0 1 1 0 0 1 1 1 0 1
0 0 1 0 0 0 1 1 1 0 1 0 1 1 1 1
0 0 1 1 0 0 1 0 1 0 1 1 1 1 1 0
0 1 0 0 0 1 1 0 1 1 0 0 1 0 1 0
0 1 0 1 0 1 1 1 1 1 0 1 1 0 1 1
0 1 1 0 0 1 0 1 1 1 1 0 1 0 0 1
0 1 1 1 0 1 0 0 1 1 1 1 1 0 0 0
б)
Рис. 4.10. Преобразование из четырехразрядного двоичного кода в отраженный
двоичный (код Грея):
а — реализация преобразователя; б четырехразрядный двоичный и отраженный двоич-
ный коды; в — карты Карно для преобразования из отраженного двоичного кода в четырех-
разрядный двоичный; г — схема для преобразования отраженного кода в четырехраарядный
двоичный
Функции Blt В2 и В3 имеют следующий вид:
Вг = G3 (GA + GA) + G3 (GA + GA) -
— G3 (G3 ф Gi) + G3 (G2 ф Gx) = G3 ф Gj ф Gi,
B2 = G3G2 + G3G2 = G3 ф G2;
B3 = G3.
Логические схемы, реализующие эти функции, приведены на
рис. 4.10, г. Ясно, что и в данном случае для реализации преобра-
зователя кодов потребуются только элементы ИСКЛЮЧАЮЩЕЕ
ИЛИ.
4.14. Классификаторы прерываний
Часто при проектировании цифровых систем возникает ситуация,
когда сразу несколько периферийных устройств необходимо соеди-
нить с одним центральным. Примером таких систем являются микро-
процессорные системы с развитой периферией. Каждое периферий-
ное устройство может генерировать сигнал прерывания в тот момент,
когда оно хочет связаться с микропроцессором. В этом случае гово-
рят, что периферийное устройство вырабатывает сигнал прерывания.
Прерывания от всех периферийных устройств подаются на схему
ИЛИ, на выходе которой возникает сигнал главного прерывания.
Если центральным устройством является микропроцессор, то глав-
ное прерывание обычно называют сигналом запроса на прерывание.
Этот сигнал «просит» микропроцессор прервать текущую деятель-
ность и перейти на программу обслуживания периферийного
устройства.
Запрос на прерывание сообщает микропроцессору, что одному
из периферийных устройств необходимо установить с ним связь.
Тогда определение того, что именно хочет установить с ним связь,
становится главной задачей микропроцессора. На рис. 4.11 показан
Рис. 4.11. Схема работы классификатора
прерываний
метод, использующий схему
сортировки прерываний.
Каждое периферийное устрой-
ство имеет свой собственный
канал прерывания. Сигна-
лы /0, /х, /2 и 13, переда-
ющиеся по этим каналам,
поступают на классификатор
прерываний. Он вырабаты-
вает сигнал главного преры-
вания
I — 1о + Л 4 Л + Ц
и определяет периферийное
устройство, которое послало
сигнал прерывания. В дан-
ном случае имеются четыре периферийных устройства и, следо-
вательно, двух адресных линий достаточно для того, чтобы вы-
делить одно из них.
Ясно, что на практике могут возникнуть ситуации, когда один
сигнал прерывания должен обладать приоритетом по отношению
к другим. В комбинационной схеме проектируемого здесь класси-
фикатора прерываний принято, что чем больше номер устройства,
тем выше его приоритет.
На .рис. 4.12, а приведена структурная схема классификатора
прерываний. Во-первых, для того чтобы сообщить о наличии одного
или более сигналов прерывания, надо уметь вырабатывать сигнал
главного прерывания 1 и, во-вторых, для определения, какое из че-
тырех периферийных устройств подало сигнал прерывания, нужны
два адресных сигнала А и В.
На рис. 4.12, б изображена таблица истинности классификатора
прерываний. Символ «d», появляющийся в таблице, используется
для обозначения как 0, так 1. Например, присутствие этого символа
во второй строке таблицы показывает, что 1=1, Л'= 1, В = 1
в том случае, если 13 равно 1 независимо от значений 10, Ц и /2-
Из таблицы истинности можно получить следующие формулы:
I = /0 + /1 + /2 + /3; А = h + ш = 13 + 7.1с,
В ='/я’Ч-:7з72’= /з+Л-
На рис. 4.12, в показана реализация классификатора прерыва-
ний на элементах И—НЕ логики.
Рис. 4.12. Четырехка-
нальный классификатор
прерываний:
а — структурная схема; б —
таблица истинности; в —
реализация
4.15. Метод формирования цепочки
Наиболее общий аппаратный метод определения номера перифе-
рийного устройства, которое хочет установить связь с центральным
устройством, называется методом формирования цепочки. В сущ-
ности это метод аппаратного опроса. Схема, иллюстрирующая
этот метод, приведена на рис. 4.13, а. Центральное устройство, при-
нимающее запросы на прерывание, узнает о них с помощью сигнала
опроса 1А, который сначала проходит через устройство с наивысшим
приоритетом (в данном случае устройство <3). Если устройство 3
нуждается в обслуживании, оно сообщает об этом, инициируя сиг-
нал I, и не пропускает сигнал опроса 1Л дальше. Если же, с другой
стороны, устройство 3 не вырабатывает сигнала прерывания, то оно
а)
6)
Рис. 4.13. Метод формирования цепочки:
а — схема; б — таблица истинности; в — логика формирования цепочки для устройства 3
передает сигнал опроса дальше к устройству со следующим По стар-
шинству приоритетом, в данном случае — устройству 2. Эта про-
цедура продолжается, и все устройства опрашиваются по очереди
до тех пор, пока не обнаружится запрос на прерывание.
В такой системе с каждым периферийным устройством связаны
три выходных сигнала. Во-первых, это сигнал прерывания, который
вместе с сигналами прерываний, идущими от остальных устройств,
подается на схему ИЛИ, формируя сигнал запроса прерывания.
Во-вторых, существует сигнал DE. инициирующий передачу данных.
Этот сигнал, позволяющий связать шину данных с периферийным
устройством, требующим обслуживания, обычно играет роль разре-
шающего сигнала по отношению к буферу, связывающему периферий-
ное устройство с шиной данных Буфер, в свою очередь, является
устройством с тремя стабильными состояниями и открыт для выборки
только в состоянии высокой нагрузки. И, в-третьих, имеются еще
сигналы Р, Q и R, которые передают сигнал опроса к следующим пе-
риферийным устройствам только в том случае, если уже опрошенные
устройства не потребовали обслуживания.
.На рис. 4.13, б показана таблица истинности для сигналов, ис-
пользуемых в методе формирования цепочки. Анализируя эту таб-
лицу, можно получить следующие уравнения:
I — + К + А + 1з’>
р = Г3/а;
Q — 1з^Ч^А Р
R — /3/2ЛЛ4 = QJi\
Вез 1з^а\
ВЕч = IsR^a = Р1ч\
Dei — РРР^а = QI1,
DEo — I3I lilial а —' Rio-
Логические схемы, реализующие эти соотношения для перифе-
рийного устройства <3, приведен >i на рис. 4.13, в.
Упражнения
У4.1. Спроектировать комбинационные логические схемы, на вход которых
подаются данные в NBCD-коце и которые позволяют обнаружить:
1) цифры, кратные 3;
2) числа, большие или равные 7;
3) числа, меньшие 4.
Реализовать все эти схемы на элементах И —НЕ.
У4.2. Разработать комбинационные логические схемы, которые могут быть
использованы для сравнения величин двух двоичных цифр А и В. Эти схемы должны
показывать, является ли: 1) А > В\ 2) А = В; 3) А < В. Расширить схемы так,
чтобы можно было сравнить четырехразрядные числа Д3Д2Д1Д0 и В^В^д.
У4.3. Разработать комбинационную логическую схему, которая позволит
проводить преобразование четырехразрядных двоичных чисел в дополнительный код.
d
a) d)
Рис. У4.4 Изображение десятичных цифр:
a — изображение отрезков; б — представление десятичных цифр с помощью отрезков
У 4.4. Разработать декодировщик кода NBCD. Этот декодировщик принимает
на входе десятичные числа в коде NBCD и вырабатывает на выходе номера отрезков
прямой, составляющих изображение десятичной цифры. Все отрезки показаны на
индикаторе (рис. У4.4, а). Из этих отрезков могут быть построены десятичные
цифры, как показано иа рис. У4.4, б.
У 4.5. Спроектировать комбинационную логическую схему, которая позволит
получать квадраты всех возможных комбинаций трехразрядного двоичного числа
Д2Д1Д0.
У 4.6. Спроектировать комбинационную логическую схему, с помощью которой
можно получить дополнение до 9 для каждой десятичной цифры. Десятичные цифры
представляются в коде NBCD.
У 4.7. Блок квартир размещается на четырех этажах. Необходимо сделать так,
чтобы свет, освещающий межэтажную лестницу, мог быть включен или выключен на
любом этаже. Спроектировать логическую схему, удовлетворяющую этим требо-
ваниям.
У 4.8. Используя линии связи, необходимо передать сообщение в трехразряд-
ном двоичном коде. Необходимо также организовать защиту его от ошибок. Для этого
следует ввести в код дополнительный бит, называемый битом соответствия, который
добавляется к каждой комбинации с таким расчетом, чтобы в ней было нечетное ко-
личество 1. Разработать логическую схему, которая будет образовывать бит соответ-
ствия тогда, когда это необходимо, на передающем конце линии. Кроме того, разрабо-
тать вторую логическую схему, которая располагается на принимающем конце
линии и которая может быть использована для контроля каждой кодовой ком-
бинации.
У 4.9. Разработать логическую схему, которая будет показывать, когда боль-
шинство цифр пятиразрядного двоичного числа равно 1. Реализовать ее на базе
элементов И — НЕ.
У 4.10. Разработать коды Грея, соответствующие:
а) коду 2-4-2-1;
б) коду XS3.
Код XS3 получается из кода NBCD добавлением к каждой кодовой комбинации
ООН.
У4.11. Разработать логическую схему для преобразования кода XS3 в соот-
ветствующий код Грея.
У4.12. Получить десятичные эквиваленты чисел: а) 0,1011; б) 1,0110101,
если считается, что они выражены в коде:
1) прямом;
2) дополнительном;
3) обратном.
У4.13. Спроектировать устройство двоичного умножения, которое умножает
четырехразрядное число В = В3В2В1В0 на трехразрядное А = Реализо-
вать схему не базе элементов И и полных сумматоров.
У4.14. Положительные и отрицательные числа представляются в ЭВМ в форме
восьмибитовых слов. Для арифметических операций используется дополнительный
код. Как будут выглядеть числа -(-21 и —29 в регистрах ЭВМ?
5. ОДНОБИТОВЫЕ ЭЛЕМЕНТЫ ПАМЯТИ
5.1. Введение
Схемы цифровых логических устройств обычно состоят из ком-
бинационных элементов, таких, как И—НЕ и ИЛИ—НЕ, и элемен-
тов памяти. В качестве элементов памяти могут выступать, с одной
стороны, однобитовые элементы памяти, такие, как дискретные триг-
геры, а с другой — цепочки триггеров. Цепочки триггеров исполь-
зуются, например, в сдвиговых регистрах.
Появление нового компонента цифровых систем — памяти при-
водит к необходимости введения дополнительной переменной,
а именно, времени. Эта переменная должна учитываться при решении
многих задач, связанных с проектированием цифровых систем.
С появлением памяти стало возможно логические операции выполнять
последовательно, так как информация может храниться в памяти
и в нужные моменты выбираться оттуда для управления операциями
комбинационной логики. Схемы, работающие таким образом, назы-
ваются последовательными. Для управления некоторыми схемами
такого типа используются периодические временные сигналы. В этом
случае схемы называются синхронными, или схемами, управляемыми
временем. Для управления последовательными схемами также ис-
пользуются случайные события. Такие схемы носят название асин-
хронных или схем, управляемых событиями.
Основным свойством любого триггера является то, что он имеет
два устойчивых состояния, которые могут быть представлены логи-
ческим «О» и логической «1», соответственно. В цифровых системах
используется несколько типов триггеров. Они называются Т -,
ST?-, J К- и D-триггерами. В этой главе описаны все эти типы триг-
геров.
5.2. Т-триггер
Условное обозначение Т-триггера дано на рис. 5.1, а. Это уст-
ройство имеет один вход Т и взаимно дополняющие друг друга
выходы Q л Q. Продемонстрировать работу триггера можно с по-
мощью диаграммы состояний * (рис. 5.1, б). На диаграмме состоя-
ний триггеры представлены двумя квадратами, т. е. имеются два
возможных состояния триггера, Q = 0 и Q = 1, которые связаны
с внешним миром. Переходы из одного состояния в другое показаны
сплошными линиями, а стрелки указывают направления переходов.
Сигнал, вызывающий переход, размещается под стрелкой. Анализ
рис. 5.1, б показывает, что если триггер находится в состоянии
Q = 0 и на его вход поступает сигнал Т, то он переходит в альтер-
нативное состояние Q = 1. С другой стороны, если в состоянии
Q = 1 на вход триггера проходит сигнал Т, он переходит в состоя-
* Наряду с этим термином в советской научной литературе часто используется
граф переходов — Прим. пер.
ние Q = 0. Иначе говоря, триггер меняет свое состояние каждый раз,
когда приходит сигнал на вход Т.
Понятие диаграммы состояний является фундаментальным для
проектировщиков цифровых систем. Если удается описать задачу
с помощью диаграммы состояний или последовательности диаграмм
состояний, то обычно нетрудно перейти от такого рода диаграмм
непосредственно к аппаратной реализации.
Существует два типа диаграмм состояний. На рис. 5.1, б дан
пример диаграммы внешних состояний. В этом случае поведение
триггера описывается с помощью двух состояний, которые связаны
с внешним миром. В то же время нет ссылок на внутренние состоя-
ния, в которых схема может находиться при переходе из состояния
Q — 0 в состояние Q — 1 и наоборот. В действительности можно
описать поведение Т-триггера с помощью внутренних состояний.
Такое описание получило название диаграммы внутренних состоя-
ний. Применение диаграмм внутренних состояний может оказаться
полезным проектировщику цифровых логических устройств.
Вторым важным методом, используемым для описания функцио-
нирования Т-триггера, является метод таблиц состояний *. На
рис. 5.1, в изображена таблица состояний Т-триггера. Она разделена
на две части: левую и правую. Левая часть отражает текущее состоя-
ние входа Tf и текущее состояние триггера Qf, правая — следующее
состояние триггера QZ+6Z. Следующее состояние триггера зависит
от текущих состояний триггера и входа. Состояние триггера может
измениться только через время б/ после подачи входного сигнала.
* В советской научной литературе также используется термин таблица пе-
реходов. — Прим. пер.
Таблицу состояний строят точно таким же путем, как таблицу
истинности. Первые два столбца таблицы содержат все возможные
комбинации значений текущих состояний Т и Q, а первую строку
таблицы интерпретируют следующим образом:
если значение Т не меняется в момент времени t и,остается рав-
ным 0, то не будет меняться и состояние триггера, т. е. Qt+6t = 0.
Аналогично интерпретируется и третья строка: если значение Т
меняется с 0 на 1 в момент времени t, то состояние триггера, которое
соответствовало значению Q = 0, изменится на Q — 1 в момент вре-
мени t + б/.
Из таблицы состояний может быть получено уравнение, описы-
вающее поведение триггера. Это уравнение носит название харак-
теристического уравнения триггера. Оно показывает, как меняется
состояние триггера в зависимости от текущих значений состояния
и входа, и имеет вид
_ (7Q + Tqy = {т ф оу.
Выражение, стоящее справа от знака равенства, является дизъюнк-
тивной нормальной формой. На рис. 5.1, а показано, как оно может
быть реализовано с помощью элементов И—НЕ.
Имеются два важных момента, которые следует отметить. Так,
уравнения, полученные из таблицы состояний, являются булевыми
уравнениями. Они отличаются от обычных комбинационных уравне-
ний, рассмотренных выше: в них явно учитывается время, и значе-
ние Q в правой части уравнения может отличаться от значения Q
в его левой части, так как эти два значения относятся к разным мо-
ментам времени. Вторым важным моментом является то, что схема,
показанная на рис. 5.1, г, только условно может считаться комбина-
ционной. Анализ этой схемы показывает, что ее выход связан с вхо-
дом и, следовательно, существует обратная связь.
К сожалению, схема, изображенная на рис. 5.1, а, будет рабо-
тать неудовлетворительно по следующей причине: если Qz =-• 0 и
Т* = 1, то QZ+6Z = 00 + 11 = 1. Следовательно, имеет место
переход из одного состояния в другое в момент времени t + 6t
Если допустить, что сигнал Т еще не успел стать равным 0 в момент
времени Qt+6t, то имеем Qt+6t = 1 и Tt+6t = 1. Тогда
Qz+26z = 01 + 10 = 0,
т. е. осуществляется переход 1 -> 0 в момент времени t + 26Л
Значение выходного сигнала Q будет становиться равным то 0,
то 1 до тех пор, пока Т не станет равным 0. Этот процесс показан на
рис. 5.1, д. Более того, окончательное значение будет зависеть от
длительности промежутка времени, в течение которого подавался
сигнал Т, и от времени задержки б/ схемы. Поэтому говорят, что
выходное состояние Q неопределенно.
Когда осуществляется переход 1 -> 0 для Т, то никакого изме-
нения выходного сигнала триггера Q не происходит. Что это дей-
ствительно так, позволяет понять характеристическое уравнение.
7 ------------
Q.
О-------------
к)
Рис. 5.2. SR-триггер:
а — условное обозначение; б — таблица состояний; в — диаграмма внешних состояний;
е — условное представление S^-триггера; ж — реализация характеристического уравне
цня (Си) SJ^-трнггера; к — временная диаграмма; .? — управляющие входы очистки и пре
и предустановки; н — диаграмма внешних состояний, учитывающая входы очистки и предуста
Если Q' = 0 и Т меняется с 1 на О в момент времени t, то
Qt+(,t = 1-1 + 0.0 - 1.
С другой стороны, если Qz = 1 и осуществляется переход 1 -»0
для Т в момент времени I, то
Qt+6t = м + о.О = 1.
Причиной нестабильности схемы Т-триггера, изображенной на
рис. 5.1, г, является возникновение гонок. Если новое значение Q,
сформировавшееся в момент времени t, подать на входы элементов go
и ёз до того, как будет прекращена подача сигнала Т, произойдет
новое изменение состояния Q. Эта ситуация хорошо иллюстрируется
временной диаграммой, изображенной на рис. 5.1, д. Разбор диа-
граммы показывает, что если At $t, то налицо нестабильность.
Ниже в этой главе будет описан более удовлетворительный способ
построения схемы Т-триггера.
5.3. 57?-триггер
Условное обозначение S/?-триггера дано на рис. 5.2, а. Входы
установки и сброса обозначены S и /?, соответственно, а взаимно
дополняющие друг друга выходы — Q и Q.
Ц Таблица состояния триггера показана на рис. 5.2, б. В ее первых
трех столбцах расположены все возможные комбинации текущих
состояний S, R и Q, т. е. значения сигналов, характеризующих эти
состояния в момент времени t. Четвертый столбец отражает состоя-
ние триггера в момент времени t
Анализ таблицы показывает, что только в ситуациях, описывае-
мых строками 4 и 5, происходит изменение состояния триггера.
Рассмотрим строку 4. После того, как подается сигнал на вход R,
триггер запирается, т. е. переходит из состояния 1 в состояние 0.
Рассмотрим строку 5. Триггер отпирается, т. е. переходит из состоя-
ния 0 в состояние 1, в результате подачи сигнала на вход S.
Для строк 1и25 = 0и/?==0и, следовательно, никаких изме-
нений в состоянии триггера не происходит (отражающие это записи
в последнем столбце остаются равными 0 и 1, соответственно). Для
Разре-
шение
Очистка
Предус-
тановка
п) н)
г — карта Карно: д — реализация характеристического уравнения на элементах И —НЕ;
ния на элементах ИЛИ—НЕ; з — управляющая таблица S/^-триггера; и — сннхрониза-
дустановки; м — таблица, описывающая работу триггера, снабженного входами очистки
Новей
строки 3 R = 1, и этот сигнал в нормальных условиях должен за-
переть триггер, но так как триггер уже заперт и Q/ = 0, то сигнал
R = 1 не изменяет его состояния.
Аналогично для строки 6S = 1, и этот сигнал будет в обычных
условиях отпирать триггер, но = 1, и, следовательно, состояние
триггера останется без изменения. Наконец, для этого типа тригге-
ров запрещено, чтобы на входах S и R одновременно присутствовали
логические «1». Это условие может быть выражено алгебраически
SR = 0.
Итак, условие отпирания триггера имеет вид
отпирание = SRQ,
а условие запирания задается как
запирание = SRQ.
С учетом этих двух условий диаграмма внешних состояний при-
мет вид, показанный на рис. 5.2, в. Анализ диаграммы показывает,
что переход из состояния Q = 0 в состояние Q = 1 происходит,
если SR = 1, а обратный переход осуществляется, если SR = 1.
Характеристическое уравнение триггера получается в результате
выполнения операции логического сложения конъюнкций перемен-
ных, для которых Qt+6t = 1, и терма SR. Добавление терма SR
не оказывает влияния на значение Qi+6t, но ведет к упрощению
выражения. Следовательно,
Qt+ы = ($RQ + SRQ + SRQ + SR)*.
На рис. 5.2, г приведено изображение этой функции с помощью
карты Карно. Терм SR является «термом, не доставляющим беспо-
койства», и ему на карте Карно соответствуют ячейки, помеченные
символом «Л>. Упрощая это выражение, получаем характеристиче-
ское уравнение в виде
Q/+M = (S _|_
где S и R —отпирающий и запирающий входы, соответственно.
На рис. 5.2, д показано, как это уравнение можно реализовать
на элементах И—НЕ. Условно эта схема может быть изображена
так, как показано на рис. 5.2, е. Уравнение для выхода Q имеет вид
Q/+M = (S + Ццу =(S(R + Q)}C
Тогда для выхода элемента 4 получаем
ft+6t = Qt+Ы Rt,
а подстановка значения для Qt+6t дает
f‘+6t = (SQ + SR + RY = (SQ + R)f.
Анализ карты Карно (рис. 5.2, г) показывает, что функция, ко-
торой соответствуют ячейки, помеченные «0», и к которой
могут быть присоединены ячейки, помеченные «с/», имеют вид
Q/+6/ = (SQ + R)t.
Следовательно,
ft+6t _ Qt+M,
и выход элемента 4 является дополнительным выходом триггера.
Вторую форму характеристического уравнения получаем путем
исключения терма SR из уравнения для Q/+6/.
Тогда
= (SRQ + SRQ + SRQY.
Эти три терма соответствуют трем «1», присутствующим на карте
Карно (рис. 5.2, г).
Упрощая выражение, стоящее справа, получаем
= (SR + QRY = {(5 + Q)
Это двухуровневая конъюнктивная нормальная форма. На рис. 5.2, ж
дана ее реализация на элементах ИЛИ—НЕ.
Работа 5/?-триггера может быть описана с помощью управляющей
таблицы (рис. 5.2, з). Эта таблица немного отличается от таблицы
состояний. Два ее первых столбца характеризуют все возможные
переходы триггера, в то время как два последних показывают, при
каких значениях 5 и R эти переходы происходят. Например, первая
строка показывает, что переход 0 -> О будет происходить только,
если 5 = 0, a R = 0 или R = 1. Так как значение R может быть
равно как 0, так и 1, то на пересечении первой строки и четвертого
столбца записывается символ 0. Для второй строки, описывающей
переход 0-> 1, находим, что 5=1. Так как S и R одновременно
не могут равняться 1, то, следовательно, значение входа R равно 0.
Значения 5 и R для оставшихся двух строк могут быть определены
аналогично.
С помощью незначительной модификации 5А?-триггер может быть
синхронизирован (рис. 5.2, и). Анализ диаграммы показывает, что
если сигнал синхронизации Си = 0, то на выходах элементов gx
и g2 всегда логические «1» независимо от текущих значений 5 и R
и от любых изменений, связанных с сигналами на этих входах. Сле-
дует отметить, что триггер может изменить' свое состояние только
во время изменений значений сигнала синхронизации. Считая за-
держку элементов схемы равной нулю, получим, что значение Q
будет изменяться во время формирования положительного фронта
импульса синхронизации, когда сигнал Си изменяется от 0 до 1
(рис. 5.2, к).
Кроме входов 5, R и Си 5/?-триггер может иметь один или два
дополнительных управляющих входа. Эти входы дают возможность
триггеру менять свое состояние независимо от того, Си — 1 или
Си — 0. Управляющие входы обычно называют входами очистки и
предустановки. Большинство используемых на практике триггеров
снабжаются входами очистки, ё то время как вход предустановки
не является обязательным. Действие этих управляющих входов
описывается с помощью таблицы на рис. 5.2, м. Следует отметить,
что в схеме, изображенной на рис. 5.2, л, управляющие сигналы
проходят на выходы элементов И—НЕ только тогда, когда их зна-
чение равно 0.
Если на обоих управляющих входах логические «1», то триггер
работает как обычно. Если г = .0 и р = 1, то выход Q элемента gt
на рис. 5.2, л принимает значение 1. Следовательно, Q = 0, и триг-
гер запирается. Если г = 1 и р = 0, выход Q элемента g3 прини-
мает значение 1, и триггер .отпирается. Если на линии риг по-
дать логический «0», то это приведет к подавлению сигналов на вхо-
дах S и R. Появление двух управляющих входов, естественно,
изменит диаграмму внеших состояний. Новая диаграмма показана
на рис. 5.2, и. Читатель, должно быть, заметил, что в том случае,
когда изготовителем не предусмотрен вход р, нужна предварительная
установка триггера. Иначе можно перепутать выхода Q и Q и входы
S и R. Для предварительной установки можно использовать вход
очистки.
5.4. .//(-триггер
На рис. 5.3, а приведено условное обозначение //(-триггера.
Логика его работы описывается с помощью таблицы состояний,
изображенной на рис. 5.3, б.
Поведение триггеров этого типа отличается в одном отношении
от поведения S/J-триггеров: допускаются одновременно две логиче-
ские «1» на входах J и К. Если J = К = 1, то триггер перебрасы-
вается, т. е. меняет свое состояние на противоположное. Например,
строка 7 таблицы состояний показывает, что триггер меняет свое
состояние с 0 на 1, а строка 8 показывает, что происходит обратный
процесс. Строки 4 и 5 соответствуют обычным операциям сброса и
установки, описанным для 5/?-триггера, описанного в п. 5.3.
Просмотр таблицы состояний позволяет определить, что триггер
отпирается в строках 5 и 7, а запирается в строках 4 и 8.
Отпирание: S = JKQ + J КО. = JQ',
Запирание: R = JKQ + J KQ = KQ-
Эти два уравнения показывают, что //(-триггер можно рассматривать
как S2?-триггер, снабженный двумя элементами И, которые выпол-
няют функции отпирания и запирания, как показано на рис. 5.3, в.
Диаграмма состояний, описывающая поведение триггера, дана на
рис. 5.3, г.
Рассмотрим работу триггера в режиме синхронизации. Если
триггер находится в состоянии Q = 0 и / = 1, то изменение сиг-
нала синхронизации Си от 0 к 1 приводит к перебросу триггера
в состояние Q = 1. Аналогично, если триггер находится в состоя-
з)
Рис. 5.3. J К-триггер:
а — условное обозначение JX-триггера; б — таблица состояний; в — представление JK-
триггера с помощью S/^-триггера и двух элементов И; г — диаграмма внешних состояний;
д — управляющая таблица; е — реализация JK-триггера с помощью элементов И —НЕ;
ж — минимальная схема JK-триггера; з — возникновение гонок в /Х-триггере
нии Q = 1 и К = 1, то изменение См от 0 и 1 приводит триггер в со-
стояние <2 = 0.
На рис. 5.3, д показана управляющая таблица //^-триггера.
Сравнение управляющих таблиц 5/?-триггера (см. рис. 5.2, з) и
J/(-триггера (см. рис. 5.3, д) позволяет установить, что у //(-триг-
гера больше входных условий, помеченных символом «0», и, следо-
вательно, этот тип триггеров в синхронных схемах может быть проще
реализован.
Как уже отмечалось, //(-триггер может быть реализован путем
присоединения выходов двух элементов И к S и R входам 5/?-триг-
гера, схема которых приведена на рис. 5.2, и. Выходы Q и Q этого
триггера и его линия синхронизации соединяются с входами двух
элементов И, к которым, в свою очередь, уже присоединены линии J
и К (рис. 5.3, е). Заметим, что элементы И формируют с помощью
двух пар элементов И—НЕ, соединенных последовательно, а именно
g5 и ёт, ge и gs. Ясно, что элементы g7 и g1; gs и g2 выполняют операции
двойного отрицания, поэтому эти элементы являются лишними и их
можно удалить из схемы. Таким образом, //(-триггер состоит только
из четырех элементов. Схема //(-триггера приведена на рис. 5.3, ж.
Сравнение схем на рис. 5.1, г и 5.3, ж показывает, что //(-триггер
проявляет так же, как и Т-триггер, свойство неустойчивости. Это
объясняется тем, что в обеих схемах линии обратной связи соединяют
выходы Q и Q со входами. Неустойчивость в работе //(-триггера по-
является тогда, когда на входах / и /( одновременно присутствуют
1
к
о
7 г
Ст |
О—I
О
fi)
Рис. 5.4. JК-триггер типа «хозяин—слуга»:
а — схема триггера; б — временная диаграмма
Рис. 5.5. Т-триггер:
а — условное обозначение; б — временная диаграмма работы Г-триггера
логические «1», а на входе синхронизации высокое напряжение.
Анализ таблицы состояний показывает, что в этом случае //(-триггер
ведет себя так же, как Т-триггер.
Если сигнал на выходе Q изменяется до окончания действия им-
пульса синхронизации, то входы элементов & и g6 также изме-
няются, и это приведет к очередному изменению сигнала на вы-
ходе Q. Следовательно, значение Q не может быть точно определено
к моменту завершения действия импульса синхронизации. Эта си-
туация иллюстрируется на рис. 5.3, з. Условие возникновения
гонок имеет вид Ai < Тс. Так как на практике это условие удовле-
творяется, то ясно, что схема, приведенная на рис. 5.3, ж, будет
работать неустойчиво. Поэтому была разработана схема, состоящая
из двух //(-триггеров: «хозяина» и «слуги» * (рис. 5.4, а).
Для триггера-хозяина используется обычная синхронизация,
в то время как для триггера-слуги импульс синхронизации инверти-
руется. Изменение выхода триггера-хозяина будет происходить
в момент появления положительного фронта импульса синхрониза-
ции, и эти изменения будут переданы на вход триггера-слуги. Однако
никаких изменений не будет происходить на выходе триггера-слуги
до тех пор, пока не появится положительный фронт инвертированного
импульса синхронизации, т. е. отрицательный фронт импульса син-
хронизации. Следовательно, изменений на выходах Q и Q, которые
линиями обратной связи соединены со входом, не будет до тех пор,
пока не появится отрицательный фронт импульса синхронизации.
Таким образом, условие возникновения гонок выполняться не будет.
На рисЛ 5.4, б показана временная диаграмма работы триггера.
С помощью //(-триггера типа «хозяин—слуга» достаточно просто
сконструировать схему Т-триггера. Для этого требуется соединить
входы / и /( с логической «1», а роль входного сигнала Та будет
играть сигнал синхронизации Си (рис. 5.5, а).
В момент появления отрицательного фронта каждого импульса
Т-триггер будет изменять свое состояние, т. е. триггер ведет себя
так, что на выходе Q периодически будет то 0, то 1. Такая схема
является основой всех счетчиковых схем. Она, в действительности,
Имеется в виду триггер типа master—slave — Прим. пер.
является двоичным счетчиком, поскольку анализ поведения сиг-
нала Q показывает, что его частота в 2 раза меньше частоты сигнала Т.
Поэтому эту схему иногда называют схемой деления на 2,
5.5. £)-триггер
На рис. 5.6, а дано условное обозначение триггера типа D. D-триг-
гер имеет один вход, обычно обозначенный буквой D, и выход Q.
Значение сигнала на выходе Q в момент времени t + 6^ всегда равно
значению сигнала на входе D в момент времени t. Такое поведение
описывается таблицей состояний, показанной на рис. 5.6, б.
Характеристическое уравнение триггера может быть получено
из таблицы истинности. Для этого необходимо определить логиче-
скую сумму тех комбинаций сигналов/)z и Qz, которые соответствуют
значению Q в момент времени t + 6^, равному логической «1». Итак,
= (DQ _|_ DQ)t = Dt.
Схема D-триггера может быть построена с помощью 7/С-триггера.
Для этого нужно только поставить инвертор между линиями J и Д,
как показано на рис. 5.6, в. Тогда получим, что 7 = Д, и таблица со-
стояний D-триггера будет соответствовать части таблицы состоя-
ний //(-триггера, в которую войдут строки с 3 по 6. Заметим, что
таблица состояний D-триггера получена из таблицы состояний JR-
триггера (см. рис. 5.3, б) при условии, что J = D = Д.
Аналогично, таблица состояний D-триггера —это часть таблицы
состояний ДД-триггера при условии, что Д = D = R. Таким обра-
зом, схема D-триггера может быть получена в результате появления
инвертора между входами Д и R ДД-триггера (рис. 5.6, г).
5.6. Запирание триггера
ДД-триггер, показанный на рис. 5.2, и, иногда называют запи-
рающим: до тех пор, пока есть сигнал на входе синхронизации, на
выходе Q будут отслеживаться любые изменения входных сигна-
лов R и Д при условии, что ДД = 0. Если состояние синхронизиру-
ющего’входа'равно 0, то триггер запирается и не может изменить
Рис. 5.6. D-триггер:
а — условное обозначение; б — таблица состоянии; в — D-триггер, построенный на основе
JK-триггера; г — D-триггер, построенный на основе 5/?-триггера
Рис. 5.7 Запирающий триггер:
а — временная диаграмма, иллюстрирующая процесс за-
пирания S^-триггера; б — временная диаграмма запи-
рающего D-триггера; в — запирающий D-трнггер, реа-
лизованный с помощью ЗЯ-триггера
свое состояние до тех пор, пока не появится сигнал на входе син-
хронизации. Такое поведение триггера хорошо иллюстрируется
с помощью временной диаграммы, изображенной на рис. 5.7, а.
Запирающий SK-триггер может быть преобразован в запира-
ющий D-триггер так, как показано на рис. 5.7, в. Когда есть сигнал
на входе синхронизации, выход триггера отслеживает его вход;
в противном случае триггер запирается, и значение выхода остается
равным логическому значению входа в момент запирания. Этот
процесс наглядно показан на временной диаграмме (рис. 5.7, б).
Объединив два запирающих 77-триггера, можно получить триггер,
который приводится в действие положительным фронтом импульса
синхронизации. Схема, показанная на рис. 5.8, а, состоит из двух
запирающих 77-триггеров, «хозяина» и «слуги», причем выход «хо-
зяина» Qm соединен с входом «слуги» Ds- В том случае, когда нет
Рис. 5.8. D-триггер, реагирующий на положительный фронт импульса синхронизации:
а — реализация; б — временная диаграмма
б)
сигнала на входе синхронизации, выход триггера-хозяина отслежи-
вает вход триггера-слуги. Однако при возникновении положитель-
ного фронта импульса синхронизации триггер-хозяин запирается
со значением на выходе, равным значению на входе, и это значение
передается на выход триггера-слуги.
Упражнения
У5.1. На рис. У5.1, а показан S-R-триггер, построенный на элементах И—НЕ.
Определить уровни напряжений в точках а, b и с схемы в следующих трех слу-
чаях:
1) S = О, Р = О, Q = 0;
2) то же, что в п. 1, но S изменяется от 0 к 1;
3)S=0, Р = 0, Q = 1 и Р изменяется от 0 к 1.
Сигналы 5 н Р приведены на рис. У5.1, б. Нарисовать диаграмму сигнала Q
при условии, что начальное значение Q равно 0.
У5.2. На рнс. У5.2 показан D-триггер, реагирующий на положительный фронт
импульса синхронизации. Этот триггер состоит из двух запирающих D-триггеров.
Необходимо с помощью временной диаграммы показать, как триггер реагирует на
присутствие входных данных в момент появления положительного фронта импульса
синхронизации Си.
У5.3. J/f-триггер типа «хозяин—слуга» показан на рис. У5.3. Заданы началь-
ные значения входов и выходов триггера: J = К = Q.m = Qs = 0. С помощью вре-
менной диаграммы определить уровни напряжений в следующих случаях:
1) J, 0-*- 1, К, 0 -> 0 подается первый импульс синхронизации;
2) J, 1 -> 1, К, 0 —>• 1 подается второй импульс синхронизации;
3) J, 1 0, К, 1 -> 1 подается третий импульс синхронизации;
4) J, 0 —> 0, К, 0 -> 0 подается четвертый импульс синхронизации.
<-Рис. У5.1
t
Рис. У5.2
Рис. У5.5
Изменения сигналов J и К. происходят в интервалы времени между подачей
импульсов синхронизации. Нарисовать временные диаграммы, показывающие вид
сигналов J, К, Qm и Qs в период времени, в течение которого было подано четыре
импульса синхронизации Си.
Считая, что начальные условия остаются прежними, определить конечное зна-
чение сигнала Qs при условии, что входные сигналы изменяются в следующем по-
рядке:
5) Си, 0-*- 1, J, 0 1, Си, 1 ->• 0;
6) J, 0 1, Си, 0 1, К, 0 1, Л 1 0, Си, 1 0.
У5.4. С помощью дополнительных логических элементов преобразовать D-
триггер в J/f-триггер.
Построить временную диаграмму J/f-триггера и показать, что выход триггера
зависит только от присутствия входных данных в момент появления положитель-
ного фронта импульса синхронизации.
У5.5. На рис. У5.5 изображен 7'/С-триггер, представляющий собой модифика-
цию J/f-триггера. Нарисовать таблицу состояний и вывести характеристическое
уравнение этого триггера.
J' и К входы ./'/^-триггера объединяются вместе. В результате получается
другой триггер. Нарисовать таблицу состояний и определить характеристическое
уравнение этого нового триггера.
У5.6. Нарисовать диаграммы внешних состояний триггеров, характеристиче-
ские уравнения которых имеют вид
a) QMt = (X ® У ® Q)';
б) Q*+6* = (X QY ©(?/.
6. СЧЕТЧИКИ
6.1. Введение
Счетчиковые схемы являются простейшей формой последова-
тельных схем. На практике счетчиковые схемы, так же как и другие
последовательные схемы, формируют из элементов памяти, таких,
как триггеры, и элементов комбинационной логики.
Все последовательные схемы подразделяются на два класса:
синхронные (управляемые временем) и асинхронные (управляемые
событиями). В синхронных схемах все изменения согласуются по
времени с подачей синхронизирующих импульсов, а в схемах, упра-
вляемых событиями, все изменения состояния схемы регулируются
определенными событиями, такими, как появление неисправностей.
Каждая счетчиковая схема относится к одному из описанных
выше классов. Схемы, управляемые временем, называются син-
хронными счетчиками, а схемы, управляемые событиями, асинхрон-
ными счетчиками или счетчиками со сквозным переносом. Схему син-
хронного счетчика используют для подсчета импульсов синхрони-
зации (тактовых импульсов); это число хранится в нескольких эле-
ментах памяти. Асинхронные счетчики применяют для определения
количества нерегулярных событий, например, для определения числа
людей, входящих в банк. Как и в случае синхронного счетчика,
это число хранится в нескольких элементах памяти.
Счетчики являются основными компонентами цифровых систем
и могут использоваться для целей управления и синхронизации.
Они появляются в вычислительных системах и системах связи; они
могут использоваться для деления частот. В одних случаях они
могут быть чисто двоичными, в других ведут счет в коде Грея или
в десятичном BCD-коде.
6.2. Двоичный счетчик
Самым простым счетчиком является двоичный. Он может нахо-
диться в одном из двух состояний. Так как триггер также может
находиться в одном из двух состояний, ясно, что двоичный счетчик
можно реализовать с помощью единственного триггера'.
Один из методов проектирования счетчиков заключается в по-
строении таблицы состояний, в первом столбце которой будут отра-
жены текущие состояния счетчика, а во втором следующие за ними
состояния. Такая таблица показана на рис. 6.1, а. Анализ таблицы
позволяет установить соответствие между поведением счетчика и
триггера. Если реализовать счетчик с помощью триггера, то пере-
ходы триггера должны осуществляться при переходе счетчика от
текущего к следующему состоянию. Предположим, что для реали-
зации счетчика выбран //(-триггер. Тогда состояния его входов J
и К, требуемые для реализации переходов счетчика, можно взять
из управляющей таблицы JK.-триггера, приведенной на рис. 6.1, б.
Поскольку значения входов J и К. для второй и третьей строки
равны либо 0, либо 1, то можно считать, что /Л = /(4 = 1,
Рис. 6.1. Двоичный
счетчик:
а — таблица состоя-
ний; \б — управля-
ющая таблица JК-
триггера; в — реали-
зация двоичного счет-
чика; г — диаграмма
состояний
Схема счетчика приведена на рис. 6.1, в, а диаграмма состояний
на рис. 6.1, г. В рассматриваемом случае диаграмма состояний яв-
ляется диаграммой как внешних, так и внутренних состояний счет-
чика, поскольку, с одной стороны, Л = 0 и Л = 1 являются внутрен-
ними состояниями счетчика, а с другой стороны, значение А всегда
присутствует на входе счетчика.
6.3. Счетчик по модулю 4
Счетчик по модулю 4 имеет четыре состояния и поэтому для его
реализации достаточно двух триггеров. На рис. 6.2, а показана
таблица состояний счетчика. Для того чтобы заполнить столбцы JA,
В* А* О At+tt 3ц Aj За Ка
0 0 1 1 0 1 0 1 0 г г 0 1 0 1 0 05 0 Й 0 1 1 0 1 0 0 1 Й 1
3/-А К/гА
S') г) ———1—-------------—I ’
Рис. 6.2. Счетчик по модулю 4:
а — таблица состояний; б — карты К,арно; в — диаграмма состояний; ? — реализация
счетчика
JB, Ка и Kb, сначала определяем те переходы, которые должны
быть сделаны, а затем с помощью управляющей таблицы JK-триггера
находим позволяющие осуществить эти переходы значения входов
триггеров.
Анализ JA и Ка столбцов таблицы состояний показывает, что
все их значения равны либо Ф, либо 1. Следовательно, JА = Ка — 1-
Для определения значений Ка и Кв используем карту Карно, изоб-
раженную на рис. 6.2, б. После упрощений находим, что JB = Кв =
= А. На рис. 6.2, в дана реализация счетчика, а на рис. 6.2, г по-
казана его диаграмма состояний.
6.4. Счетчик по модулю 8
Проектирование двух первых разрядов счетчика по модулю 8
производим так же, как и проектирование разрядов А и В счетчика
по модулю 4. Добавление последнего разряда счетчика осуществ-
ляем так, чтобы не менялись схемы двух первых разрядов. Напом-
ним, что JA = К а = 1 и = Кв = А.
На рис. 6.3, а изображена таблица состояний счетчика, а на
рис. 6.3, б — карты Карно для входов J и К триггера С. После упро-
С4 в± А* 8i±St Ai+” Pc Лс
0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 0 a ==> ==> sa, | 0 0 0 0 0 0 0 1
а)
С''\ 00 01 11 ю
0 0 '7' ’Si
1
КС«АВ
S)
Рис. 6.3. Счетчик по модулю 8:
а — таблица состояний; б — карты Карн»; в — Диаграмма состояний; г — реализация
счетчика
щения находим, что Jc = Кс = АВ. Схема реализации счетчика
приведена на рис. 6.3, в, а диаграмма состояний — на рис. 6.3, г.
6.5. Счетчик по модулю 2N
Напомним результаты проектирования счетчиков по модулю 2,
4, 8:
JA ~ 1; Jb = A; Jc = АВ — JвВ;
Ка = 1; Кв=а-, Кс -=ав=кбв.
Проанализировав эти уравнения, делаем вывод, что уравнения для
разрядов D, Е, ..., N счетчика по модулю 2N имеют, вид
JD = АВС = JcC; JE = ABCD = JdD~
JN = ABC ... (A — 1) = JN_X (A — 1); KD = ABC = K<£\
KE = ABCD = KdD; Kn = ABC ... (2V — 1) = KN_i (N — 1).
6.6. Одновременная и последовательная подача сигналов
на входы элементов счетчика
Существует два способа формирования входных сигналов триг-
геров, составляющих счетчик. Они показаны на рис. 6.4, а и
рис. 6.4, б. В первом способе сигналы на элементы, обеспечивающие
формирование входов триггеров счетчика, подаются одновременно.
Когда число разрядов счетчика увеличивается, коэффициент объеди-
нения по входу первого элемента И—НЕ также увеличивается.
Однако задержки для входных сигналов всех триггеров равны 2tg,
где tg — время задержки одного элемента И—НЕ.
Во втором способе коэффициент объединения по входу первого
элемента И—НЕ всегда равен 2, но задержки входных сигналов
триггеров увеличиваются с ростом числа разрядов счетчика. Анализ
рис. 6.4, б показывает, что задержка для входа Jc равна 2tg, для
входа JD — 4tg и т. д. Так как в этом случае время задержки больше,
Рис. 6.4. входные элементы триггеров:
а — одновременная подача сигналов на вход; б — последовательная подача сигналов на вход
ясно, что верхний предел частоты следования импульсов для счетчика,
использующего этот способ формирования входных сигналов, ниже.
Предположим, что ' время переключения триггеров равно tf.
Тогда в первом случае верхний предел частоты счетчика
f — ____!__
,и itg + tj ’
а во втором случае
2(N-2)tg + tf ’
где tf — число разрядов счетчика.
Следует также отметить, что в первом случае сигнал с триггера,
формирующего первый разряд счетчика, подается на (tf—1) эле-
ментов И—НЕ, сигнал с триггера, формирующего второй разряд
счетчика, — на (tf — 2) элементов и т. д., в то время как во втором
случае все триггеры кроме последнего используются для управления
только одним элементом И—НЕ.
6.7. Синхронные счетчики обратного счета
Для проектирования счетчиков обратного счета используем те же
методы, что и для проектирования обычных счетчиков. В резуль-
тате получим
Ja = Кл = 1;
= Кв = Л;
Jc = Кс = А В = JBB-
jd = Kd = Авс = jcc-
Jn = Kn = ABC ... (tf - 1) = JN_{ (tf - 1).
Используя дополнительные выходы триггеров, можно применять
обычные счетчики для обратного счета. Но это справедливо только
d С в А с в А
0 0 0 0 1 1 1
1 0 0 1 1 1 0
2 0 1 0 1 0 1
3 0 1 1 1 0 0
4 1 0 0 0 1 1
5 1 0 1 0 1 0
6 1 1 0 0 0 1
7 1 1 1 0 0 0
Рис. 6.5. Использование допол-
нительных выходов триггеров для
счетчиков обратного счета
для двоичных счетчиков. На рис. 6.5
показано, как это можно сделать для
счетчика по модулю 8.
6.8. Счетчик по модулю 5
Счетчик по модулю 5 имеет пять
состояний. Для его реализации необхо-
димы три триггера. На рис. 6.6, а
изображена диаграмма состояния счет-
чика, причем выделены три неисполь-
зуемых состояния. Карта Карно
для неиспользуемых состояний по-
казана на рис. 6.6, б. Ниже приве-
Рис. 6.6. Счетчик по модулю 5:
а — диаграмма состояний счетчика по модулю 5; б — карта Карно неиспользуемых состоя-
ний; в — реализация счетчика по модулю 5; г — схема формирования блокирующего сигнала
синхронизации н сигнала аварийной тревоги
дено булево уравнение, описывающее три неиспользуемых со-
стояния
fu = АС + ВС.
Иногда удобнее определять уравнения для входных сигналов
триггеров на основе алгебраических, а не табличных методов. Про-
цедура определения приводится ниже:
1. Для каждого триггера определить выражения для S и 7?.
2. Используя термы согласования, определяемые:
а) неиспользуемыми состояниями;
б) переходами 1 -> 1, когда триггер открыт;
в) переходами 0 -> 0, когда триггер заперт, упростить выраже-
ния для S и 7?.
3. Получить выражения для J и К, используя уравнения
Sq — JqQ и Rq — KqQ-
Триггер А отпирается, когда осуществляется переход от So к Si
и от S2 к S3. Следовательно,
SA = 50П + S2II.
Обычно импульсы синхронизации опускают в уравнениях, опи-
сывающих процессы запирания и отпирания триггеров. Поэтому
уравнения для SA запишем в виде
SA = ЛВС + ЛВС = АС.
Поскольку триггер Л не совершает переходов типа 1 -> 1, уравне-
ние, описывающее отпирание триггера, примет вид
SA = АС + (ЛС) + (ВС),
где в скобках расположены термы согласования, определяемые не-
используемыми состояниями. Введение термов согласования не
приводит к дальнейшему упрощению выражения, поэтому
J А = С.
Уравнение, описывающее запирание триггера Л, приведено ниже:
s3 = ЛВС + ЛВС = ЛС.
Добавив термы согласования, получаем
Ra = AC + (Л С) + (ВС) + (ЛВС).
Последний терм определяется переходом 0 -> 0.
Комбинируя два первых терма, получаем
Ra = Л + (ВС) + (ЛВС).
Дальнейшие упрощения невозможны и
Ка = 1.
Для триггера В имеем
5^ = 5, + (52) + (ВС) + (Л С) =
= ЛВС + (ЛВС) + (Л С) + (ВС).
Первый и третий термы могут быть использованы для формирования,
терма согласования АВ. После этого первоначальный терм ЛВС
может быть устранен. Тогда
= АВ + (ЛВС) + (ЛС) + (ВС);
Уд = Л;
RB = 53 + (S4) + (So) + (Л С) + (ВС) =
= ЛВС + (ЛВС) + (ЛВС) + (ЛС) + (ВС).
Первый и четвертый термы могут быть использованы для формиро-
вания дополнительного терма согласования АВ, присутствие кото-
рого позволит устранить терм ЛВС. Следовательно,
RB = АВ + (АВС) + (АВС) + (ЛС) + (ВС)
и
Кв = Л.
Аналогично для триггера С
Sc = S3 + (AC) + (ВС) = ABC + (AC) + (ВС)
и
Jc = АВ;
Rc-S.A- (So) + (Si) + (S2) + (AC) + (BC) =
= ABC + (ABC) + (ABC) + (ABC) + (AC) + (BC).
И после упрощения
Rc = С + (ABC) + (ABC) + (ABC) + (AC) + (BC).
Отсюда
Kc = I-
На рис. 6.6, в показана реализация счетчика по модулю 5.
Если счетчик из-за неисправности окажется в одном из запре-
щенных состояний, то его работа может быть прервана специальным
синхросигналом и также может быть подан сигнал тревоги. Обна-
ружить то, что счетчик находится в запрещенном состоянии, позво-
ляет схема, реализующая выражение, описывающее функцию не-
используемых состояний, fu = АС + ВС. На рис. 6.6, г показано,
как эта схема используется для формирования цепи аварийной сиг-
нализации и генерации блокирующего сигнала синхронизации.
Выражение, описывающее новый сигнал синхронизации, имеет вид
Си' = fu-Cu.
Следовательно, когда fu — 1, то Си — 0, и синхроимпульсы будут
отсутствовать до тех пор, пока счетчик не выйдет из запрещенного
состояния.
6.9. Двоично-десятичный счетчик
На рис. 6.7, а показана диаграмма состояний десятичного счет-
чика, а на рис. 6.7, б — таблица состояний. В правой части таблицы
приведены значения входных сигналов четырех триггеров. Для
поиска этих значений были проанализированы те переходы, которые
должны быть сделаны, а затем с помощью управляющей таблицы
(см. рис. 6.1, б) определены соответствующие значения J и К вхо-
дов триггеров.
На рис. 6.7, в приведены карты Карно для триггеров В, С и D.
После упрощения для входов J и К были получены следующие вы-
ражения:
Jd ~ АВС; Kd — А;
Jc = АВ; Кс = АВ;
JB = AD; Кв = А,
Просмотр столбцов JA и К а на рис. 6.7, б показывает, что все
значения равны либо 0, либо 1. И так как неиспользуемые состоя-
ния могут также участвовать в процессе упрощения, то все ячейки
карт Карно для JA и Ка оказываются заполненными символами «0»,
«1» и «И». Следовательно,
Ja = Ка = 1.
Предположим, что из-за неисправности счетчик оказывается
в одном из запрещенных состояний. Тогда необходимо предусмотреть
специальные действия, блокирующие сигнал синхронизации и по-
дающие сигнал тревоги. Для этого, как и раньше, может быть ис-
пользована функция, описывающая неиспользуемые состояния fu —
= BD + CD. На рис. 6.7, г показана схема счетчика. В этой схеме
предусмотрена специальная цепь, подавляющая в случае необходи-
мее. 6.7, а
D* с* в* А‘ •о + Q «о X) 3 + ч •о Jd Kd Jc кс Кв Ja Кл
0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0
0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 1
0 0 1 0 0 0 1 1 0 0 0 0 0 0 1 0
0 0 1 1 0 1 0 0 0 0 1 0 0 1 0 1
0 1 0 0 0 1 0 1 0 0 0 0 0 0 1 0
0 1 0 1 0 1 1 0 0 0 0 0 1 0 0 1
0 1 1 0 0 1 1 1 0 0 0 0 0 0 1 0
0 1 1 1 1 0 0 0 1 0 0 1 0 1 0 1
1 0 0 0 1 0 0 1 0 0 0 0 0 0 1 0
1 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1
рие. 6.7, б
Рис. 6.7. Двоично-десятичный счетчик:
а — диаграмма состояний; б — таблица состояний; в — карты Карно; а — схема реализации
мости импульсы синхронизации. Выражение, описывающее новый
сигнал синхронизации, имеет вид
Си' = Си + BD + CD.
Если BD « 1 или CD » 1, то Си' » 0 и синхроимпульсы подав-
ляются.
вЛО. Двоично-десятичный счетчик обратного счета
Используя описанный выше метод, можно спроектировать
двоично-десятичный счетчик обратного счета. Выражения для вход-
2° k21 k2z izs
Си
Рис. 6Д. Схема двоично-десятичного счетчика обратноео счета
ных сигналов триггеров счетчика имеют вид
JD = ABC; KD = АВС;
Jc = AD; Кс = АВ;
JB^AC + AD; Кв = А;
Ja = 1; КА = 1.
Схема счетчика приведена на рис. 6.8.
6.11. Десятичный счетчик, использующий код Грея
Рассмотрим переход из состояния 0001 в состояние 0010 для
двоично-десятичного счетчика. Предположим, что триггер В изме-
няет свое состояние быстрее, чем триггер А. Последовательность, ха-
рактеризующая изменения состояния триггеров, будет тогда иметь
вид
D С В А
0 0 0 1
0 0 11 (промежуточное состояние).
0 0 10
Если дешифратор, служащий для преобразования кода сигнала,
передаваемого по четырем линиям, в один из десяти выходов (рис. 6.9)
используется для формирования десятичного представления сигна-
лов, которые поступают с выхода двоичного счетчика, то на выход-
ной линии 3 будет появляться незапланированный выброс. Он
может появиться в любой момент в такой двоичной счетчиковой схеме,
где два и более триггеров используются для изменения состояния
счетчика во время одного перехода. Эта трудность может быть пре-
одолена, если применять для счета код Грея. Тогда во время каждого
перехода только один триггер будет изменять свое состояние. Ха-
рактерной особенностью кода Грея является то, что при переходе от
любой кодовой комбинации к следующей за ней по порядку изме-
няется только одна цифра. При построении счетчика будем исполь-
зовать код Грея, соответствующий ко-
Рис. 6.9. Декодировщик,
преобразующий сигналы, по-
ступающие с четырехразряд-
ного двоичного счетчика, в
десятичную форму
ду 2-4-2-1.
Сначала покажем, как из кода 2-4-2-1
может быть получен код Грея. На рис. 6.10
код 2-4-2-1 размещен в столбцах, поме-
ченных буквами W, X, У и Z. Для пре-
образования кода 2-4-2-1 в соответству-
ющий ему код Грея можно использовать
уравнения, полученные для преобразова-
ния двоичных чисел в код Грея (см, гл. 4).
А = Y@Z;
В = X © Г;
W @ X;
Р = Г,
Применяя эти уравнения, получим конкретные значения для всех
разрядов кода Грея. На рис. 6.10 код Грея расположен в столб-
цах D, С, В и А.
Существует много различных четырехразрядных кодов Грея.
На рис. 6.11, а показано, как изменяются позиции кодовых ком-
бинаций на карте Карно при переходе от одной кодовой комбинации
к другой для кода Грея с весовыми характеристиками разрядов
2-4-2-1. Следует заметить, что соседние кодовые комбинации зани-
мают соседние ячейки карты Карно. Следовательно, для создания
кода Грея, включающего десять комбинаций, достаточно на карте
Карно начертить замкнутую кривую, которая проходит десять со-
седних ячеек. Одна из таких кривых показана на рис. 6.11, б.
Соответствующий этой кривой код Грея приведен на рис. 6.11, в.
Рис. 6.11. Коды Грея:
а — кривая на карте Карно, соответствующая коду Грея с весовыми характеристиками раз-
рядов 2-4-2-1; б — задание кода Грея с помощью кривой, проведенной на карте Карно; « —
кодовые комбинации для кода Грея, определенного в п. б.
Вернемся к проектированию счетчика. На рис. 6.12, а показана
диаграмма его состояний, а на рис. 6.12, б — таблица состояний.
Эта таблица позволяет определить поведение каждого триггера в те
моменты, когда счетчик изменяет свое состояние. Далее с помощью
управляющей таблицы (см. рис. 6.1, б) можно получить значения
входных сигналов триггеров. Они приведены в правой части таблицы
состояний счетчика.
На рис. 6.12, в изображены восемь карт Карно, по одной для
каждого входного сигнала. Как обычно, ячейки, соответствующие
неиспользуемым состояниям, помечены символом «d», а осталь-
ные ячейки заполнены в строгом соответствии с таблицей (см.
рис. 6.12, б).
о)
Текущее состояние Следующее состояние Входные сигналы триггеров
D С в А D С в А J& Ля Jc Лс Jb Кв Ja Ка
0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0
0 0 0 1 0 0 1 1 0 0 0 0 1 0 0 0
0 0 1 1 0 0 1 0 0 0 0 0 0 0 0 1
0 0 1 0 0 1 1 0 0 0 1 0 0 0 0 0
0 1 1 0 1 1 1 0 1 0 0 0 0 0 0 0
1 1 1 0 1 0 1 0 0 0 0 1 0 0 0 0
1 0 1 0 1 0 1 1 0 0 0 0 0 0 1 0
1 0 1 1 I 0 0 1 0 I 1 0 0 1 0 0
1 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0
б)
Рис. 6.12. Счетчик, работающий в коде Грея с весовыми характеристиками раз-
рядов 2-4-2-1:
а — диаграмма состояний; б — таблица состояний; в — карты Карно\ г — реа-
лизация счетчика
Проведем упрощение описанным выше методом и в результате
получим следующие выражения для входных сигналов триггеров:
JA = BD + BCD-, Ка = BD + BD;
JB = AD; Kb = AD;
Jc = ABD; Kc = D;
JD = C; KD = ~AB.
На рис. 6.12, г приведена схема, реализующая этот счетчик.
6)
г)
Продолжение рис. 6.12
6.12. Реверсивные счетчики по модулю 16
В некоторых случаях необходимо, чтобы счетчик мог работать
как в прямом, так и в обратном направлениях.
Уравнения счетчика по модулю 16, предназначенного для пря-
мого счета, имеют вид
Jли ж Kau == 1; Jви = Кви — A; Jси Кси АВ
и JDu = Kdu — АВС,
а уравнения соответствующего счетчика, предназначенного для об-
ратного счета, — вид
JAd — К Ad = 1; JBd = &Bd = A', J Cd ~ &Cd ~ АВ
и JDd = АВС.
Для выбора направления счета обычно используется управляющий
сигнал Z. Допустим, что когда Z = 1, то счет ведется в прямом на-
правлении, а когда Z = 0 — в обратном. Тогда для счетчика по
модулю 16 имеем
Ja — К.А ~ U
«Тд = ZJ Ви + ZJBd = ZA + ZA;
Кв = ZKbu + ZKBd =ZA+ ZA.
Аналогично
J с = Kc = ZAB + ZAB;
JD =KD = ZABC + Z~ABC.
На рис. 6.13 приведена реализация реверсивного счетчика по
модулю 16.
Рис. 6.13. Реализация счетчика по модулю 16 прямого и обратного расчета
6.13. Асинхронные двоичные счетчики
Для проектирования наиболее удобны асинхронные, или, как
их еще называют, двоичные счетчики со сквозным переносом. Ап-
паратура, предназначенная для реализации счетчиков по модулю
2, 4, 8 и т. д., состоит из Т-триггеров (или, что равноценно, из JK-
триггеров, входы которых постоянно соединены с логической «1»),
соединенных последовательно, как показано на рис. 6.14, а. Причем
в качестве тактового сигнала для всех триггеров, кроме первого,
выступает выходной сигнал предыдущего триггера. Входной сигнал
X является тактовым для первого триггера. На рис. 6.14, б изобра-
жены временные диаграммы, характеризующие работу счетчика по
модулю 8. Считается, что все изменения состояний триггеров проис-
ходят во время формирования отрицательных фронтов тактовых
импульсов, подаваемых на входы триггеров. Анализ временной
диаграммы показывает, что триггер А изменяет свое состояние вся-
кий раз, когда появляется отрицательный фронт очередного такто-
вого импульса сигнала X. Выход триггера А используется в качестве
генератора тактовых импульсов для триггера В, причем триггер В
всегда меняет свое состояние в момент появления отрицательного
фронта импульса, приходящего с выхода триггера А. Аналогично
для триггера С в роли генератора тактовых импульсов выступает
триггер В, и триггер С перебрасывается в другое состояние, как
только появляется отрицательный фронт импульса, приходящего
с выхода триггера В.
в)
Рис. 6.14. Трехразрядный счетчик со сквозным переносом:
а — реализация счетчика; б — временные диаграммы; в — распространение сигнала пере-
носа в счетчике
Рис. 6.15. Счетчик со сквозньиГпереносом по модулю 8, предназначенный для счета
в обратном направлении:
а — реализация счетчика; б — временные диаграммы
На временных диаграммах входов А, В и С присутствуют дво-
ичные цифры, характеризующие текущее состояние счетчика.
Счетчик по модулю 8 иногда называют схемой деления на 8.
Анализ временной диаграммы показывает, что в ответ на каждые
восемь тактовых импульсов, подаваемых на вход триггера А, на
выходе триггера С образуется один импульс. Следовательно, если
частота импульсов на входе схемы f, то частота на выходе //8, т. е.
входная частота делится на 8. В ответ на каждые восемь входных
импульсов на выходе триггера В появляются два импульса, т. е.
частота равна /74; аналогично, частота на выходе триггера А равна
f/2. Таким образом, после прохождения очередного разряда счет-
чика входная частота делится на 2.
На рис. 6.14, б показано идеализированное поведение схемы.
Например,считается, что в момент появления отрицательного фрон-
та восьмого импульса на выходах всех трех триггеров появится О,
т. е. они одновременно осуществят переход 1 0. В действитель-
йости, изменение состояния триггеров йе происходит мгновенно,
а распространяется по схеме. Так, триггер А перебрасывается в со-
стояние А = 0 только спустя время, равное tj, после того как будет
сформирован отрицательный фронт восьмого импульса X. Анало-
гично состояние триггеров В и С изменяется не сразу, а спустя ин-
тервалы времени 2tf и 3tf, после того как появится отрицательный
фронт восьмого импульса X. Эти ситуации иллюстрируются на рис.
6.14, в. Если асинхронный счетчик имеет п разрядов, то максималь-
ная задержка равна ntf. Следовательно, если Т-период появления
тактовых импульсов, то
Т > nij,
и верхний предел частоты счетчика определим как
f
lu Т ntf ’
Модифицируем схему, на рис. 6.14, а следующим образом: в ка-
честве тактовых для триггеров В и С будем использовать сигналы А
и В, соответственно. Тогда схема будет действовать как счетчик
обратного счета. На рис. 6.15, а изображена схема счетчика обрат-
ного счета, а на рис. 6.15, б — его временные диаграммы. Для иллю-
страции работы счетчика временные диаграммы сигналов, соответ-
ствующих выходам А, В и С, размечены двоичными цифрами. В дан-
ном случае тактовым сигналом для триггера является А. Поэтому
триггер В изменяет свое состояние в момент появления отрицатель-
ного фронта сигнала А. Аналогично, тактовым сигналом для тригге-
ра С является В, и триггер С реагирует на отрицательный фронт
сигнала В.
6.14. Асинхронный десятичный счетчик
Так как десятичный счетчик имеет десять состояний, то для его
реализации необходимо четыре триггера. На рис. 6.16, а показана
схема счетчика, а на рис. 6.16, б — его временные диаграммы.
Первоначально все триггеры установлены в состояние 0. Счет осу-
ществляется в соответствии с нормальной двоичной последователь-
ностью чисел, включая число 8. В момент появления отрицательного
фронта десятого тактового импульса триггер А перебрасывается
из состояния 1 в состояние 0. Поскольку сигнал с выхода триггера А
является тактовым для триггера В, то его изменение должно привести
к переходу триггера В в состояние 1. Однако этого не происходит
по следующей причине. В этот момент входной сигнал JB триггера В
равен D = 0 и, следовательно, триггер В остается в состоянии сброса.
В этот же момент в состояние сброса необходимо установить и триг-
гер D. Так как JD = ВС = 0 и KD — 1, то, когда в момент оконча-
ния импульса S9 триггер А осуществляет переход 1 0, триггер D
устанавливается в состояние D = 0. Теперь все триггеры установ-
лены в нулевое состояние и готовы для приема первого импульса и
S)
Рис. 6.16. Асинхронный десятичный счетчик:
а — реализация счетчика; б — временные диаграммы
начала следующего цикла. Десятичный счетчик является так же
схемой, производящей деление на 10, поскольку в ответ на каждые
десять импульсов, подаваемых на вход триггера А, на выходе триг-
гера D появляется один импульс.
6.15. Асинхронные счетчики с автоматическим сбросом
В счетчике с автоматическим сборосом используются несколько
иные методы счета. Счетчик по модулю N производит счет от 0 до 7V,
причем логический сигнал, представляющий число N, используется
для очистки всех триггеров счетчика. На рис. 6.17, а показана диа-
грамма состояний Счетчика с автоматическим сбросом по модулю 5.
Счетчик остается в каждом из первых пяти состояний в течение интер-
вала времени, равного периоду тактового сигнала. Но при записи
шестого состояния (101) элемент И—НЕ вырабатывает сигнал сброса
г = АВС. Как это делается, показано на рис. 6.17, б. На рис. 6.17, в
изображены временные диаграммы, характеризующие работу схемы
счетчика.
Время сброса для разных триггеров, образующих счетчик, бы-
вает разным. Например, в только что рассмотренной схеме триггер А
может сбрасываться быстрее, чем триггер С. Тогда возникает сле-
дующая ситуация. Как только состояние триггера А изменится на
Рис. 6.17. Счетчик по модулю 5 с автоматическим сбросом:
а — диаграмма состояний; б — реализация счетчика; в — временные диаграммы; г — диа-
грамма состояний для схемы запирания; д — реализация схемы запирания
А = 0, низкий уровень сигнала сброса перейдет в высокий, и дли-
тельности этого сигнала окажется недостаточно для сброса триггера С.
Эта проблема может быть решена, если сигнал сброса будет за-
фиксирован (заперт) до начала шестого тактового импульса. На
рис. 6.17, в этот процесс проиллюстрирован штриховой линией.
Диаграмма состояний схемы запирания приведена на рис. 6.17, г.
Уравнение отпирания имеет вид Q = АВС, а запирания Q = X.
Использование полученного в гл. 5 характеристического уравнения
для элемента И—НЕ дает
Q = АВС + XQ.
Выражение в правой части является двухуровневой дизъюнктивной
нормальной формой. Ее реализация приведена на рис. 6.17, д.
На самом деле, эта схема является /^-триггером, а выход элемента
4 — инверсным выходом триггера.
В этой схеме на выходе элемента 3 появляется логическая «1»,
когда счетчик переходит в состояние S5. Это означает,_что на выходе Q
появляется логический «О». Следовательно, сигнал Q = г использу-
ется для очистки триггеров счетчика. Схема запирания остается в со-
стоянии Q = 1 до тех пор, пока не появится шестой тактовый импульс.
Этот импульс сбрасывает триггер, и значение Q — г становится рав-
ным логической «1». Цикл работы схемы запирания завершается,
когда значение АВС становится равным логической «1».
6.16. Счетчики на интегральных схемах
На практике синхронные и асинхронные счетчики могут быть
построены на основе обычных //(-триггеров, которые входят в со-
став многих серий ТТЛ-логики. Для проектирования как синхрон-
ных счетчиков, так и счетчиков со сквозным переносом могут быть
использованы описанные выше методы. В ряде серий ТТЛ-логики
счетчики реализованы в виде интегральных схем (микросхем). Так,
например, реализованы десятичный счетчик (микросхема 7490),
счетчик по модулю 12 (микросхема 7492), счетчик по модулю 16 (ми-
кросхема 7493).
Десятичный счетчик (микросхема 7490) состоит из двух частей:
триггера, действующего как двоичный счетчик, и трех триггеров,
работающих как счетчик по модулю 5. Если выход двоичного счет-
чика связать со входом счетчика по модулю 5, то получим десятичный
счетчик.
Для того чтобы пользоваться таким счетчиком, не обязательно
обладать детальными знаниями схем и не обязательно знать ее ло-
гическую диаграмму. Однако инженер должен хорошо знать все
Сдрасывамщие входы выходы
RO(1) ^о(г) ^911) ^9(г1 Л с в А
1 1 4 в 0 0 А 1 1 4 0 А А 0 0 А 1 4 0 4 0 4 0 1 0 4 0 4 0 0 1 0 0 0 Сч Сч Сч СЧ 0 0 0 ет °т ет ет 0 0 1
Рис. 6.18. Интегральная микросхема деся-
тичного счетчика (ИМС 7490):
а — выводы ИМС; б — таблица истинности для
входов сброса; в — использование ИМС как счет-
чика по модулю 6; а — временные диаграммы счет-
чика по модулю 6; д — устранение вубросов с по-
мощью разрешающего сигнала Е
С В А
8)
выводы микросхемы и, чтобы пра-
вильно ее использовать, должен по-
нимать основные принципы счета.
На рис. 6.18, а показаны все вы-
воды микросхемы:
1) четыре выхода, обозначае-
мые D, С, В и А, причем D — наи-
больший значащий разряд;
2) вход Лвх, на который подает-
ся входной сигнал;
3) вход Ввх, который соединяет-
ся с выходом А, когда нужен де-
сятичный счетчик; если же нужен
счетчик по модулю 5, входной сигнал
Выходы
Рис. 6.19. Использование ИМС
счетчика по модулю 16 в качестве
счетчика по модулю 13
подается на вход Впх;
4) 7?о(1ь 7?о <2) — входы очистки (для очистки всех триггеров
необходимо, чтобы на этих входах была логическая «1»);
5):входы 7?э(1), 7?э<2> (если на этих входах логические «1», то
в счетчик заносится число 9).
Укажем еще одно правило, которое необходимо для работы с ми-
кросхемой. Для того чтобы счетчик находился в режиме счета, нужно,
чтобы по крайней мере на одном из входов Ro и на одном из входов
Т?9 были логические «1». На рис. 6.18, б приведена таблица истин-
ности, описывающая действие входов Ro и Т?8.
После знакомства с выводами микросхемы и их функциями,
а также с основными принципами счета, инженер-проектировщик
может использовать микросхему. - Предположим, что ему нужен
счетчик по модулю 6. Тогда надо соединить входы и выходы микро-
схемы так, как показано на рис. 6.18, в. В этом случае микросхема
будет представлять собой счетчик со сквозным переносом. Когда
на выходе будем иметь В — 1, С = 1 и А = 0, на входах /?01 и Д02
появятся логические «1», и произойдет очистка всех триггеров.
На рис. 6.18, г изображены временные диаграммы счетчика. Необ-
ходимо заметить, что после того как в счетчик будет записано числоЧэ,
триггер В на короткое время перейдет в состояние В = 1 и на линии В
появится выброс. Если показание счетчика нужно декодировать,
то желательно, чтобы это было сделано в такие промежутки времени,
когда влияние выбросов может быть устранено. Это делается
с помощью разрешающего сигнала Е, который позволяет снимать
значения с выходов элементов только в определенные моменты
времени. Схема, иллюстрирующая этот метод, приведена на
рис. 6.18, д.
Подобным образом и другие микросхемы могут быть использо-
ваны для проектирования различных счетчиков. Рассмотрим микро-
схему 7493, реализующую счетчик по модулю 16. Она состоит
из двоичного счетчика, за которым следует счетчик по мо-
дулю 8. На рис. 6.19 показано, как с помощью этой микросхемы
может быть построен счетчик по модулю 13 со сквозным пере-
носом,
6.17. Каскадирование счетчиков на интегральных схемах
Соединим последовательно две микросхемы 7490 и 7493, реали-
зующие десятичный счетчик и счетчик по модулю 16, соответственно
(рис. 6.20). Частота входного сигнала первой микросхемы равна
320 кГц. Тогда частота сигнала, появляющегося на выходе шестнад-
цатеричного счетчика, будет равна 2 кГц. Единственный использу-
емый на практике способ деления частоты на большое число заклю-
чается в каскадировании счетчиковых схем.
Аналогично, для того чтобы построить счетчик по модулю N,
необходимо соединить микросхемы так, как показано на рис. 6.20.
Например, если требуется счетчик по модулю 92, то его можно по-
строить, соединив последовательно две микросхемы 7490 так, как
показано на рис. 6.21. Сигнал, соответствующий наибольшему зна-
чащему разряду первой микросхемы, подается на вторую микросхему
и является для нее тактовым. В ответ на каждые десять импульсов
на входе X появляется один импульс на выходе Do и в момент появ-
ления десятого импульса X микросхема 10° совершает переход из
состояния 1С01 в состояние 0000, а микросхема 1С1 переходит из
состояния 0000 в состояние 0001. Как только код числа 92
устанавливается на выходах счетчика, специальный сигнал по
цепи запирания поступает на входы очистки обеих микросхем.
Схема запирания сигнала позволяет преодолеть трудности, воз-
никающие в том случае, если триггеры имеют разное время
сброса.
Соединим последовательно три микросхемы десятичных счетчи-
ков (рис. 6.22). Результирующую схему можно использовать как
трехдекадный счетчик, работающий в коде NBCD. Предположим,
что необходимо периодически получать изображения результатов
Рис. 6.20. Использование
ИМС десятичных счетчи-
ков для деления частоты
на 160
Рис. 6.21. Соединение двух ИМС для получения счетчика по модулю 92
Рис. 6.22. Трехдекадный
счетчик с отображением
результатов счета
работы счетчика. Тогда информация, снимаемая с выходов каждой
микросхемы, сначала декодируется, а затем ^подается на вход си-
стемы отображения, как показано на рис. 6.22.
Упражнения
У6.1. Спроектировать синхронный счетчик по модулю 12 на основе логических
элементов И—НЕ и следующих элементов: а) Т-триггеров; б) 5/?-триггеров;
в) УК-триггеров; г) О-триггеров.
Разработать логическую схему декодирования результатов счета.
Уб.2. Используя УК-триггеры и элементы И—НЕ, спроектировать цикличе-
ский генератор для последовательности из таблицы, внизу, справа.
Проследить за поведением схемы в неиспользуемых состояниях и показать,
что одно из неиспользуемых состояний является запирающим. Предложить способ
устранения запирающего состояния.
У6.3. Преобразовать двоичный код (см. таблицу па стр. 116) в соответству-
ющий код Грея и разработать схему счетчика, работающего в этом коде, используя
УК-триггеры и элементы И—НЕ.
Уб.4. Ниже приведены правила, характеризующие работу PQ-триггера:
PQ-00 следующее состояние триггера 1 независимо от его текущего состояния;
PQ=01 следующее состояние триггера является инверсией его текущего со-
стояния;
PQ=10 следующее состояние триггера такое же, как и текущее;
PQ= 11 следующее состояние триггера 1 независимо от текущего состояния.
Используя приведенную выше информацию, построить управляющую таблицу
PQ-триггера, а для двоичного счетчика по модулю восемь, построенного на PQ-
триггерах, получить выражение для входных сигналов.
Уб.5. Схему, показанную на рис. Уб.5, необходимо использовать для генера-
ции импульса Q, длительность которого равна сумме 14 периодов тактового сигнала.
Номер импульса синхрони- зации С В А
1 0 0 1
2 1 0 0
3 0 1 0
4 1 0 1
5 1 1 0
6 0 1 1
Рис. Уб.5
Нарисовать временные диаграммы, отражающие Пове-
дение наиболее важных сигналов схемы. Спроекти-
ровать счетчик и управляющую логику на основе
JK-триггеров типа «хозяина — слуга» и элемен-
тов И—НЕ.
Уб.6. В пятиразрядном счетчике со сквозным
переносом использованы триггеры, имеющие время
задержки 30 нс и время декодирования 50 нс.
Определить максимально допустимую частоту работы
счетчика. Для случая, когда счетчик работает на мак-
симальной частоте, начертить временные диаграммы
работы триггеров при переходе из состояния 01111
в состояние 10000.
Предположим, что счетчик действует на часто-
те 8,33 МГц. Начертить временные диаграммы, хара-
ктеризующие поведение счетчика в интервале
времени между пятнадцатым и шестнадцатым тактовыми импульсами.
Уб.7. Начертить временные диаграммы для следующих асинхронных счетчиков:
а) четырехразрядного двоичного счетчика обратного счета;
б) четырехразрядного двоичного счетчика, считая, что используемые для счета
триггеры срабатывают в момент появления положительного фронта импульса, по-
даваемого на тактовый вход.
Уб.8. Спроектировать счетчик по модулю 822, используя микросхемы деся-
тичных счетчиков. Предусмотреть схему запирания, которая необходима для устра-
нения трудностей, связанных с разным временем сброса триггеров.
?. СДВИГОВЫЕ РЕГИСТРЫ И ГЕНЕРАТОРЫ
7.1. Введение
Сдвиговый регистр представляет собой схему, состоящую из
связанных между собой однобитовых элементов памяти, располо-
женных в едином корпусе интегральной схемы (ИС). Элементами
памяти являются триггеры, соединенные друг с другом таким об-
разом, что выход одного служит входом другого.
Обычный четырехразрядный сдвиговый регистр показан на
рис. 7.1. Информация, поступающая в этот регистр бит за битом, син-
хронизируется тактовыми импульсами. При поступлении бита в пер-
вый триггер другие биты, ранее записанные в регистр, перемещаются
на новые места таким образом, чтобы бит, хранящийся в триггере А,
переместился бы в триггер В и т. д. до тех пор, пока бит, первона-
чально хранящийся в триггере D, не будет потерян.
Сдвиговые регистры могут быть разделены на четыре группы:
а) с последовательным входом/последовательным выходом; при
этом данные как на вход регистра, так и с его выхода поступают
последовательно, бит за битом;
б) с последовательным входом/параллельным выходом; при этом
регистр загружается последовательно, бит за битом, и когда требу-
ется получить результат, хранящиеся во всех триггерах данные мо-
гут быть считаны одновременно;
в) с параллельным входом/последовательным выходом; при этом
все триггеры в регистре загружаются одновременно, и когда требу-
ется получить результат, то хранящиеся в регистре данные извле-
каются последовательно, бит за битом, под управлением тактовых
импульсов;
г) с параллельным входом/параллельным выходом; при этом все
триггеры в регистре загружаются одновременно, и когда требуется
результат, все хранящиеся в триггерах данные считываются одновре-
менно.
Возможна также другая классификация сдвиговых регистров,
зависящая от их входов:
а) с двумя входами (регистр такого типа имеет два входа — им-
пульсы подаются либо на входы J—В, либо на входы S—R);
б) с одним входом, как показано на рис. 7.1 (здесь первый триг-
гер в каскаде преобразован в D-триггер путем размещения инвертора
между входами J и А).
Аналогичным образом можно выделить регистры с двумя выхо-
дами, в которых основной и дополнительный выходы последнего
триггера в цепи выведены на ножки панели, и регистры с одним вы-
ходом, когда на ножку панели выведен только основной выход по-
следнего триггера.
Сдвиговые регистры имеют широкий диапазон применений. Их
можно использовать для временного хранения данных, преобразо-
вания из последовательной формы хранения в параллельную и
наоборот. Как будет показано ниже, они также могут быть исполь-
Рис. 7.1. Четырехразрядный сдвиговой регистр на JК-триггерах
зованы в качестве счетчиков и генераторов последовательностей, и,
конечно, сдвиговые регистры применяются в центральном процессоре
(ЦП) микропроцессорных систем, где они выполняют разнообразные
функции.
7.2. Четырехразрядный сдвиговый регистр с параллельной
загрузкой
Типичная схема четырехразрядного сдвигового регистра показана
на рис. 7.2. В ней имеется возможность как параллельной, так и
последовательной загрузки, однако результат извлекается после-
довательно с последнего триггера каскада. Параллельная загрузка
достигается подачей сигнала предустановки от одного из двух источ-
ников. Важно, чтобы перед параллельной загрузкой все триггеры
были очищены, так как в результате предустановки триггер может
принять значение, равное только логической «1». Данные в этом ре-
гистре могут быть сдвинуты только вправо.
7.3. Четырехразрядный регистр для сдвига влево и вправо
Типичным примером универсального сдвигового регистра явля-
ется регистр, реализованный в форме ИМС 7495. Логическая схема
этого регистра показана на рис. 7.3, а. Регистр имеет средства для
Рис. 7.2. Четырехразрядный сдвиговый регистр для параллельной и последователь-
ной загрузок
Выходы
А кВ
п
Последова - “
тельный Вход . _
для сдвигах --------------*“
ВпраВо
________„ четырехбитоВый
сдвиговый регистр
Си
Последовательный
вход для сдвига влево
ABCD
Параллельные входы в)
Рис. 7.3. Универсальный сдвиговый регистр (ИМС 7495):
а — реализация на £Д-триггерах; б — схема соединений ИМС для выполнения операций
реверсивного сдвига
параллельной загрузки и параллельного вывода, последовательной
загрузки и последовательного вывода и, кроме того, средства для
сдвига влево и вправо. Таким образом, это сдвиговый регистр, кото-
рый может работать в любом из четырех режимов, описанных в
п. 7.1, и, кроме того, он имеет возможность осуществлять операции
сдвига влево и вправо.
Вход «Управление режимами» (УР) задает последовательный или
параллельный ввод данных. При УР = 0 работают элементы И, поме-
ченные по схеме цифрой 1, и синхронизация происходит по цепи Си\.
В этом режиме данные поступают последовательно. Если же УР = 1,
то работают элементы И, помеченные цифрой 2, и синхронизация
происходит по цепи Си2. В этом случае данные вводятся параллельно.
Операция по управлению режимами является асинхронной в том
смысле, что никаких изменений на входе УР не должно происходить,
если на одном из двух синхронизирующих входов высокое напря-
жение.
Если данные на входы сдвигового регистра поступают параллель-
но, то с помощью сдвига вправо они могут считываться последова-
тельно. И, наоборот, при последовательном поступлении данных
в сдвиговый регистр они могут считываться параллельно по выход-
ным линиям. Следует отметить, что ИМС 7495 может быть приспо-
соблена для реверсивного сдвига. Для этого необходимо осуществить
соединения выводов ИМС так, как показано на рис. 7.3, б.
7.4. Использование сдвиговых регистров в качестве счетчиков
Один из способов проектирования цифровых счетчиков или гене-
раторов последовательностей заключается в применении ИМС,
реализующей сдвиговый регистр. Стандартная схема счетчика на
сдвиговом регистре приведена на^рис. 7.4. Отдельные триггеры N-
каскадного сдвигового регистра и соединения между ними поме-
щаются внутри ИМС. Основной и^дополнительный выходы каждого
триггера выведены'на’контактные штыри’панели и могут быть исполь-
зованы для’управления комбинационной логической схемой, присут-
ствующей 'в’цепи обратной связи. Именно эта схема формирует си-
гналы, подаваемые’на входы J и Д’ наименьшего значащего разряда
сдвигового регистра. Такая'схема, например, может использоваться
для генерации двоичных последовательностей или работать как
счетчик по модулю М.
Взаимосвязи вход-выход каждого разряда счетчика, приведенного
на рис. 7.4, определяются следующей системой уравнений:
=/ (ЛВ ... М)С
В*+в* = Л;
= (М — 1)/.
Цепь обратной связи вырабатывает сигнал либо 0, либо 1, кото-
рый подается на вход триггера А, определяя тем самым при поступ-
лении’^очередного тактового'’импульса следующее состояние этого
триггера. Например, если^М-разрядный сдвиговый регистр находится
Рис. 7.4. Общая схема
сдвигового' регистра с об-
ратной связью
В состоянии N ... СВ А = 0 ... 001, то его следующим состоянием
будет либо 0 ... 010, либо 0 ...ОН в зависимости от того, какое зна-
чение 0 или 1 вырабатывается схемой, стоящей в обратной связи,
и подается на 7-вход триггера А.
7.5. Универсальная диаграмма состояний сдвиговых регистров
Таблица переходов двухразрядного сдвигового регистра показана
на рис. 7.5, а. Если сдвиговый регистр первоначально находится
в состоянии 00, то возможны два последующих состояния: 00, если
на /-входе первого триггера 0, или 01, когда на /-входе первого триг-
гера 1. Аналогично, если сдвиговый регистр первоначально находится
в состоянии 01, его последующими состояниями могут быть либо 10,
либо 11.
Таблица переходов, приведенная на рис. 7.5, а, может быть пре-
образована в универсальную диаграмму состояний, показанную
на рис. 7.5, б. Из диаграммы видно, что сдвиговый регистр посто-
янно блокирован в состоянии 00, если сигнал обратной связи равен 0,
Рис. 7.5. Двухразрядный
сдвиговый регистр:
а — таблица переходов; б —
универсальная диаграмма
состояний
Рис. 7.6. Трехразряд-
ный сдвиговый ре-
гистр:
а — таблица переходов;
б — универсальная диа-
грамма состояний
и точно также блокирован в состоянии 11, если сигнал обратной связи
равен 1.
Аналогичная таблица переходов может быть построена для трех-
разрядного сдвигового регистра (рис. 7.6, а). Затем ее можно преоб-
разовать в универсальную диаграмму состояний (рис. 7.6, б). Уни-
версальная диаграмма состояний четырехразрядного сдвигового
регистра, полученная таким образом, показана на рис. 7.7. Оче-
видно, что с увеличением числа разрядов сдвигового регистра диа-
грамма сильно усложняется.
Как следует из предыдущей главы, посвященной счетчикам,
универсальная диаграмма состояний является исходной для диаг-
рамм состояний, которые задают определенную последовательность
счета. На универсальной диаграмме состояний показаны все возмож-
ные внутренние состояния сдвигового регистра и все возможные пе-
реходы из одного состояния в другое. Пользуясь такой диаграммой,
проектировщик логических устройств может выбрать подходящую
последовательность состояний и разработать логическую схему в цепи
обратной связи таким образом, чтобы сдвиговый регистр мог возвра-
щаться к заранее выбранной последовательности состояний.
7.6. Проектирование десятичного счетчика
Первым шагом при проектировании десятичного счетчика явля-
ется выбор последовательности десяти состояний из универсальной
диаграммы состояний четырехразрядного сдвигового регистра. Как
следует из рис. 7.7, тремя такими последовательностями являются:
a) So St S2 S5 Six S7 §15 S14 §12 58 §0>
6) So Si—S3—S7 S15—Six—§13 S10 S4 S8 So;
в) So Si—S2—S5 S11 -So S13 S10 S4 S8 So.
Кроме этих существуют, безусловно, и другие возможные после-
довательности десяти состояний регистра. На рис. 7.8, а показана
диаграмма состояний для третьей из вышеприведенных последо-
вательностей.
So Sr Sz Sf S„
Sff Si/ Зю $r3 Sg
a)
Ю
ДЦ S D C в A f= J A
0 1 2 3 4 5 6 7 8 9 So Si sa S6 Sii se Sis $10 s4 Sg 0 0 0 0 1 0 1 1 0 1 0 0 0 1 0 1 1 0 1 0 0 0 1 0 1 1 0 1 0 0 0 1 0 1 1 0 1 0 0 0 1 0 1 1 0 1 0 0 0 0
6)
s D C в A
s9 1 0 0 1 0
s2 0 0 1 0 1
S3 0 0 1 1 1
s, 0 1 1 1 1
$15 1 1 1 1 0
<$14 1 1 1 0 0
$12 1 1 0 0 0
Se 1 0 0 0 0
г)
Sit g) Ss
e)
Puc. 7.8. Десятичный счетчик:
о — диаграмма состояний; б — таблица состояний, где ДЦ — десятичная цифра; в — карта
Карио для функции обратной связи f = J д, г — поведение счетчика после перехода в неис-
пользуемое состояние; д — полная диаграмма состояний; е — реализация десятичного счет-
Чика иа основе сдвигового регистра
Вторым шагом является составление таблицы состояний, изобра-
женной на рис. 7.8, б, и определение логического значения функции
обратной связи для каждого перехода. Например, при переходе
из So в Sx триггер должен перейти из состояния 0 в 1 и поэтому не-
обходимо, чтобы на входе этого триггера была 1, т. е. JA — 1. Это
значение является логическим значением функции обратной связи,
требуемой для такого перехода; оно приводится в последнем столбце
таблицы состояний.
Функция обратной связи и неиспользуемые состояния представ-
ляются с "помощью’карты Карно, изображенной на рис. 7.8, в. В
ячейках карты эти значения обозначены соответственно «1» и «Л.
Заметим, что состояние Заявляется неиспользуемым для данного
счетчика, и, казалось бы, что ?в соответствующей этому состоянию
ячейке таблицы должен стоять символ «Л. Однако существует об-
щее правило, которое необходимо учитывать при проектировании
счетчиков такого типа, заключающееся в том, что содержимое ячеек
S15 и So карты Карно должно быть всегда равно 0 и 1 соответственно
независимо от того, используются ли эти состояния в счетной после-
довательности. Таким образом, гарантируется то, что счетчик
никогда не будет'блокирован в состояниях 0000 или 1111.
Применяя обычные методы минимизации, можно найти значение
функции обратной связи
f = jA = BD + ACD + ACD.
Если схема содержит неиспользуемые состояния, то их логика
может быть описана с помощью следующей функции:
fu = ABD + ~ACD + ABCD + ABCD.
Ее можно применять для остановки счетчика, выработки сигнала
тревоги и сброса всех триггерров в нуль.
Если счетчик из-за неправильного срабатывания схемы или в мо-
мент включения перейдет в неиспользуемое состояние, а соответствую-
щая реакция в нем не предусмотрена, то возврат к правильной по-
следовательности произойдет не позже, чем через пять тактовых им-
пульсов. Поведение схемы в неиспользуемых состояниях описано
в помощью таблиц на рис. 7.8, г, а полная диаграмма, включающая
неиспользуемые состояния, изображена на рис. 7.8, д.
На рис. 7.8, е показана реализация десятичного счетчика. Если тре-
буется получить десятичный результат, то на выходе счетчика_можно
использовать дешифратор типа из 4 в 16. Например, при ABCD =
= 1 на выходе дешифратора должна быть десятичная цифра 3. Кроме
того, если требуется изображение цифр, то счетчик вместе с подхо-
дящей комбинационной логической схемой может быть использован
для управления семисегментным индикатором (см. гл. 4).
7.7. Генераторы последовательностей на сдвиговом регистре
Счетчик на сдвиговом регистре, снабженный логической схемой
в цепи обратной связи, может быть использован для генерации лю-
бой требуемой двоичной последовательности. Для этого необходимо
Выходная логика
Рис. 7.9. Общая схема генератора двоичной последовательности
добавить логическую схему, преобразующую сигналы с выходов
триггеров. Длина сгенерированной двоичной последовательности I
будет зависеть от разрядности счетчика, из которого она получена.
Для Л/^-разрядного сдвигового регистра длина двоичной последова-
тельности I < 2N. Функциональная схема такого генератора последо-
вательности приведена на рис. 7.9.
В качестве примера рассмотрим процесс проектирования схемы,
генерирующей двоичную последовательность 1 — 0 — 1 — 1 — 0 —
— 1 — 1 — 0. Дак как в этой последовательности содержится восемь
бит, необходим трехразрядный сдвиговый регистр. Для генерации
данной последовательности требуется восемь трехбитовых комби-
наций, указанных в таблице на рис. 7.10, а. Здесь двоичные цифры
в столбце qa представляют требуемую последовательность, в то время
как в столбцах qb и q~ содержится та же последовательность, но с за-
держкой по отношению к qa на один и два тактовых импульса, со-
ответственно.
Заметим, что состояния 101 и ПО встречаются в таблице неодно-
кратно. Причем для состояния 101 имеет место неоднозначность,
заключающаяся в том, что в одном случае следующим состоянием
является 010, а в других-—011. Следовательно, эти восемь комби-
наций не могут быть построены только с помощью логики обратной
связи, как в случае проектирования десятичного счетчика, и для ге
нерации требуемой последовательности необходима логическая схема
на выходе.
Таким образом, предлагаемый метод основан на генерации после-
довательности из восьми состояний с помощью логики обратной связи,
после чего требуемая двоичная последовательность может быть
. получена из последовательности из восьми состояний с помощью
выходной логики.
На рис. 7.5, б приведена последовательность из восьми состояний
для трехразрядного сдвигового регистра, полученная из универ-
сальной диаграммы состояний. Эта последовательность имеет сле-
дующий вид:
$0 — S, -— S?; — Sg S3 S7 Sg Sg S0,
а на рис. 7.10, б приведена диаграмма состояний для этой последо-
вательности.
Из этой диаграммы получаем таблицу состояний (рис. 7.10, в),
в которой значение функции обратной связи, равное 0 или 1, опре-
деляем для каждого перехода, как описано выше.
После этого функцию обратной связи изображаем с помощью
карты Карно (рис. 7.10, г). Применяя обычные методы минимизации,
находим, что функция обратной связи имеет вид
f = ВС + АС + АВС.
Требуемую выходную двоичную последовательность qa совместно
е)
Рис. 7.10. Генератор
двоичной последователь-
ности 1-0-1-1-0-1-1-0:
а — восемь трехбитовых
комбинаций, необходимых
для генерации двоичной по-
следовательности; б — диа-
грамма состояний для по-
следовательности из восьми
состояний; в — таблица со-
стояний для функции обрат-
ной связи; г — представле-
ние функции обратной свя-
зи с помощью карты Карио;
д — таблица состояний для
функции выхода; е — пред-
ставление функции выхода
с помощью карты Карно;
wc — реализация генератора
сим в таблицу (рис. 7.10, д). Минимальная форма выходной функ-
ции, полученная с помощью карты Карно (рис. 7.10, е), имеет вид
(]а ~ АС -|- АВ -|- АС.
Существуют другие выходные последовательности, а именно
$ь и qc, приведенные на рис. 7.10, а, которые лишь смещены по вре-
мени относительно qa. Могут быть определены логические схемы,
необходимые для их реализации, и тогда появится возможность
выбрать вариант (qa, qb или qc), требующий минимального количества
оборудования. Схема генератора последовательности приведена
на рис. 7.10, ж.
7.8. Кольцевой счетчик
Простейшим видом счетчика на сдвиговом регистре является
кольцевой. В нем сигнал обратной связи подается с выходом послед-
него триггера на входы первого, как показано на рис. 7.11, а. Эта
схема, состоящая из десяти каскадов, может быть использована
в качестве десятичного кольцевого счетчика, поскольку число каска-
дов равно числу состояний схемы. Первоначально первый триггер
устанавливается в 1, в то время как остальные сбрасываются в 0.
Затем, при поступлении тактового импульса, информация, содержа-
щаяся в каждом разряде, сдвигается в соседний и, таким образом,
в счетчике циркулирует 1. Счетная последовательность такого ре-
гистра приведена в таблице состояний на рис. 7.11, б.'
Схему, представленную на рис. 7.11, а, можно преобразовать
в схему с самозапуском (рис. 7.11, е). Вход в этой схеме, описываемый
в виде
= ABCDEFGHT,
можег принимать значение 1 только при условии, что А = В =
= C = D= £ = F= G = // = / = 0.
а)
^Тактовый 1 импульс L I н G F Е D с в А
0 0 0 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 1 0
2 0 0 0 0 0 0 0 1 0 0
3 0 0 0 0 0 0 1 0 0 0
4 0 0 0 0 0 1 0 0 0 0
5 0 0 0 0 1 0 0 0 0 0
6 0 0 0 1 0 0 0 0 0 0
7 0 0 1 0 0 0 0 0 0 0
8 0 1 0 0 0 0 0 0 0 0
9 1 0 0 0 0 0 0 0 0 0
б)
Рис. 7.11. Десятиразрядный кольцевой счетчик:
а — схема счетчика; б —таблица состояний; в — схема кольцевого счетчика со средст-
вами самозапуска
Очевидно, что если какой-либо разряд счетчика, за исключением
последнего, содержит 1, то JА = 0, и счетчик будет содержать тре-
буемую последовательность не позднее, чем через десять тактовых
импульсов.
Десять выходов данного счетчика можно непосредственно исполь-
зовать в качестве десятичных без применения декодирующих схем
и, кроме того, циркулирующая в счетчике цифра 1 может, в част-
ности, последовательно отпирать целую группу схем. Очевидно,
что в последнем случае число разрядов счетчика будет равно числу
схем, которые необходимо отпереть.
Очевидным преимуществом десятичного кольцевого счетчика
является его простота, и поскольку для работы этого счетчика не
требуется логических схем обратной связи или декодирующих це-
пей, для его реализации необходимо меньше компонентов, чем для
других счетчиков. Однако данный счетчик имеет недостаток, заклю-
чающийся в невозможности осуществления вывода информации
в двоичной форме. Кроме того, его счетная последовательность зна-
чительно изменяется, если из-за ложного срабатывания схемы он
перейдет в одно из многих неиспользуемых состояний.
Как известно, двоичный десятиразрядный счетчик может нахо-
диться в 210 = 1024 различных состояниях, т. е. он может факти-
чески вести счет до 10231о, в то время как десятичный кольцевой
счетчик имеет только десять состояний. Тогда очевидно, что деся-
тичный кольцевой счетчик имеет 210 — 10 = 1014 неиспользуемых или
запрещенных состояний, и это ведет к неэкономическому использо-
ванию триггеров. Если по какой-либо причине счетчик окажется
в одном из неиспользованных состояний, которых достаточно много,
т. е. будет иметь место запрещенная счетная последовательность,
то счетчик не сможет перейти к правильной последовательности без
постороннего вмешательства.
При работе данного счетчика возможны две основные ошибочные
ситуации: первая состоит в том, что в результате ложного срабаты-
вания схемы цифра 1 появляется не только в разряде, который дол-
жен содержать циркулирующую 1; вторая представляет собой сброс
в состояние 0 разряда, который должен содержать циркулирующую 1.
Однако нетрудно дополнить счетчик довольно простыми логическими
схемами, которые помогут обнаружить присутствие дополнитель-
ных 1. На рис. 7.12, а изображен трехразрядный кольцевой счетчик,
снабженный средствами обнаружения дополнительных 1. Также
нетрудно ввести логическую схему, которая реагирует на ситуацию,
когда все разряды сдвигового регистра содержат 0. Такая схема
изображена на рис. 7.12, б.
Функция, которую можно использовать для обнаружения допол-
нительных единиц в трехразрядном сдвиговом регистре, имеет вид
fl = И + В) с.
Использование этой функции не позволяет мгновенно проинформи-
ровать об ошибочной ситуации, поскольку ее значение зависит от
того, в каких триггерах в результате сбоя содержится 1. Если 1
содержится в триггерах А и В, то функция Д примет значение, рав-
ное 1, не сразу, а с задержкой на один тактовый импульс. Мгновенная
реакция на ошибку достигается с помощью функции
fiM = АВ + АС + ВС.
К сожалению, при возрастании числа разрядов счетчика реали-
зация функции, мгновенно реагирующей на ошибку, требует зна-
S)
Рис. 7.12. Трехразрядный кольцевой счетчик:
а — схема, позволяющая обнаружить дополнительные 1; б — схема, позволяющая обна-
ружить 1, когда значения всех разрядов счетчика равны О
чительного усложнения схемы. Например, в случае четырех разря-
дов счетчика эта функция будет иметь вид
/1М = АВ + АС + AD + ВС + BD + CD
и, следовательно, рациональнее использовать функцию вида
fl = И + В) (С + D),
которая реагирует на сбой не позднее, чем через один тактовый им-
пульс.
Для того чтобы обнаружить, все ли разряды счетчика содержат О,
может быть использована функция
/о = Л + В + С = АВС.
Если требуется кольцевой счетчик с циркулирующим 0, а не 1,
то необходимо сначала установить (АГ — 1)-й триггер в Л/-разряд-
ном сдвиговом регистре в состояние 1 (это можно сделать, подавая
сигналы на предустановочные входы триггеров) и очистить остав-
шийся триггер. Счетчик с циркулирующим 0 может быть получен
и другим способом, который заключается в использовании дополни-
тельных выходов триггеров стандартного кольцевого счетчика.
7.9. Счетчик Джонсона
Счетчик Джонсона отличается от обычного кольцевого счетчика
наличием в нем такой обратной связи, которая обеспечивает соеди-
нение инверсного выхода последнего триггера с входом J первого
и подачу инвертированного сигнала с инверсного выхода послед-
него триггера на вход К первого. Если все триггеры предварительно
установлены в одинаковое состояние (либо в 0, либо в 1), то число
различных состояний, входящих в требуемую счетную последова-
тельность, равно удвоенному числу разрядов сдвигового регистра.
Следовательно, десятичный счетчик может быть получен из пятираз-
рядного сдвигового регистра (рис. 7.13, а). Предполагая, что все триг-
геры первоначально установлены в 0, получаем счетную последо-
вательность схемы, которая приведена на рис. 7.13, б.
Эта последовательность содержит десять состояний. Ее можно
выбрать из универсальной диаграммы состояний пятиразрядного
сдвигового регистра. Логическая схема в цепи обратной связи может
быть получена следующим образом: в столбец f таблицы (см. рис.
7.13, б) заносятся требуемые значения функции обратной связи,
и затем эта функция и неиспользуемые состояния изображаются
на карте Карно, как показано на рис. 7.13, в. Упрощение, проведен-
ное с помощью обычных методов, дает
f = Ja = Ё.
Для организации десятичного счета данную схему необходимо до-
полнить декодирующим логическим устройством. Выражения для
логических функций могут быть получены с помощью карты Карно
для пяти переменных (рис. 7.13, г).
На этой карте десятичными цифрами помечены все состояния
в цикле счета, причем каждая десятичная цифра соответствует но-
меру тактового импульса на рис. 7.13, б. На рисунке также показаны
ячейки, которые можно использовать для упрощения выражений,
описывающих десятичные 0 и 1. Если читатель продолжит этот про-
цесс, то обнаружит, что каждая ячейка, помеченная десятичной
цифрой, всегда может быть объединена с семью ячейками, соответ-
ствующими неиспользуемым состояниям.
После упрощений декодирующие функции примут вид
О = А~Ё; 5 = АЕ;
1 = АВ; 6 = АВ;
2 = ВС; 7 = ВС;
3 = CD; 8 = CD;
4 = Д£; 9 = РЕ.
На рис. 7.13, д приведена схема, реализующая декодирующую функ-
цию для десятичной цифры 0.
CL
Очистка
a)
Тактовый импульс Е п с в л Е
0 0 0 0 0 0 1
1 0 0 0 0 1 1
2 0 0 0 1 1 1
3 0 0 1 1 7 1
Ч 0 1 1 1 1 1
5 1 1 1 1 1 0
6 1 1 1 1 0 0
7 1 1 1 0 0 0
8 1 1 0 0 0 0
9 1 0 0 0 0 0
ксв
ed\ oo 01 11 10
с 1 d d d'
Id d d j
d
d d d
в)
Рис. 7.13. Десятичный счетчик Джонсона:
а _ логическая схема; б — счетная последовательность; в — определение
функции обратной связи счетчика с помощью карты Карно; г — карта Карно,
служащая для определения декодирующей логики; д — декодирующая логи-
ческая схема для десятичной цифры 0; г — карта Карно, служащая для опре-
деления функции, корректирующей в случае ошибки счетную последователь-
ность
Для счетчика Джонсона существуют также следующие три неже-
лательные последовательности счета:
1) S2 —> S6 —> Sn —> S23 —> S14 —> S29 —> S2s —*• S2o Ss —>
—>Sj7 —> S2;
2) S4
>$18
->S4;
3)
io ~* S21 —> 5’io.
Если из-за неисправности схемы или в результате ее включения
счетчик будет функционировать, переходя из состояния в состояние,
в соответствии с этими последовательностями, то без применения
дополнительных средств он не сможет перейти к правильной после-
довательности счета.
Нежелательные последовательности счета могут быть представле-
ны с помощью карты Карно, которая изображена на рис. 7.13, е. Ячей-
ки карты помечены 1, 2 или 3 в зависимости от того, к какой из трех
последовательностей принадлежит соответствующее ячейке состо-
яние. Следует отметить, что четыре смежные ячейки S2, Se, Slo,
S14 охватывают состояния, принадлежащие всем трем нежелатель-
ным последовательностям. Булева функция, описывающая эти четыре
состояния, имеет вид
f = АВЁ.
Если использовать эту функцию для очистки всех пяти триггеров
счетчика, то не позже, чем через интервал времени, в течение кото-
рого будут поданы десять тактовых импульсов, счетчик перейдет
к правильной последовательности счета.
Счетчик Джонсона имеет четную длину цикла счета, равную 2 Д'’,
где W — число разрядов сдвигового регистра. Однако немного из-
менив обратную связь, можно сделать длину цикла счета нечетной,
равной (2W— 1). Например, если опустить состояние 00000, то
счетная последовательность станет такой, как показано в таблице
на рис. 7.14, а. В последнем столбце таблицы приведены значения
а)
Рис. 7.14. Счетчик Джонсона с нечетной дли-
ной цикла счета, равной (2/V—/):
а — счетная последовательность; б — определение
функции обратной связи счетчика
функции обратной связи, которая позволяет сделать цикл счетчика
нечетным. Эта функция вместе с неиспользуемыми состояниями пред-
ставлена с помощью карты Карно (рис. 7.14, б). Приведя упрощения,
получим выражение для новой функции обратной связи в виде
f = D + Ё.
Можно из последовательности счета исключить не состояние 00000,
а состояние 11111. Тогда функция обратной связи будет иметь вид
f = DE.
7.10. Сдвиговые регистры с обратной связью типа
ИСКЛЮЧАЮЩЕЕ ИЛИ
На рис. 7.15, а показан четырехразрядный регистр. В цепи об-
ратной связи регистра стоит элемент ИСКЛЮЧАЮЩЕЕ ИЛИ,
который подает на основной вход первого триггера сигнал J А =
= C@D. Для того чтобы определить последовательность состоя-
ний регистра, допустим сначала, что сдвиговый регистр находится
в состоянии D = 0, С = 0, В = 0, Л = 1. В этом случае JA = 0 @
@0 и при получении следующего тактового импульса регистр пе-
рейдет в состояние D = 0, С = 0, В = 1, Л = 0. В таблице на рис.
7.15, б показана последовательность состояний регистра. В послед-
нем столбце этой таблицы находятся значения функций обратной
связи.
Всего существует пятнадцать различных состояний регистра.
Это максимальное число состояний для четырехразрядного регистра
с элементом ИСКЛЮЧАЮЩЕЕ ИЛИ в обратной связи. Поэтому
данная последовательность состояний называется последователь-
ностью максимальной длины
(ПМД). Состояние So не входит
в ПМД, так как попадание в него
приводит к блокировке реги-
стра. Предположим, что регистр
попал в состояние So. Тогда Jл =
= 0 @ 0 = 0 и регистр не сможет
покинуть это состояние, посколь-
ку на вход JA всегда будет
подаваться 0. Таким образом,
Рис. 7.15. Генератор ПМД на основе четырехразрядного сдвигового регистра:
а — реализация генератора на //(-триггерах; б — ПМД
S D c в A f
S1 s3 s4 S9 S3 Se S13 S10 s5 Sil S7 Si 5 S14 Si 2 S8 0 0 0 1 0 0 1 1 0 1 0 1 1 1 1 0 0 1 0 0 1 1 0 1 1 1 1 1 1 0 0 1 0 0 1 1 0 1 0 1 1 1 1 0 0 1 0 0 1 1 0 1 0 1 1 1 1 0 0 0 0 0 1 1 0 1 0 1 1 1 1 0 0 0 1
6)
Число разрядов N Уравнения обратной связи Число разрядов N Уравнения обратной связи
1 А 10 G ф J
2 А ф’В 11 I Ф К
3 В ф’С 12 F ф Н ® К ф L
4 С ф D 13 I Ф J Ф L ф М
5 С ф Е 14 D ф Н ф М ф .V
6 Е ф F 15 N Ф 0
7 F ф G 16 D ф М ф 0 ф Р
8 D ф Е ф F ф Н 17 N Ф Q
9 Е ф 18 к ф и
Рис. 7.16. Функции обратной связи, позволяющие сформировать ПМД
с помощью п-разрядных регистров сдвига
максимальная длина последовательности состояний определяется
следующим образом: I = 2N — 1,
где А — число разрядов сдвигового регистра. Только
определенным образом связав элемент ИСКЛЮЧАЮЩЕЕ ИЛИ
с выходами триггеров, можно построить регистр с ПМД. В таблице
на рис. 7.16 приведены выражения для функций обратной связи,
использование которых позволяет сформировать ПМД. Число раз-
рядов регистра изменяется в таблице от 1 до 18. Можно также сфор-
мировать другие ПМД. Например, если в цепи обратной связи четы-
рехразрядного регистра стоит инверсия функции С © D, то генери-
руется другая ПМД. Как это происходит, показано на рис. 7.17, а.
Анализ выражений для функций обратной связи, приведенных
на рис. 7.16, показывает, что один из операндов, входящих в выра-
жение, всегда является переменной, принятой для обозначения
А-го разряда регистра. Все остальные операнды получаются путем
просмотра регистра в обратном направлении. Например, для М=4 пере-
менной, принятой для обозначения четвертого разряда регистра, явля-
ется D; другой операнде является переменной, связанной с третьим
разрядом регистра. Две другие ПМД для четырехразрядного регистра
могут быть получены путем просмотра кольцевого регистра
в прямом направлении, начиная с четвертого разряда. Тогда (А +
+ 1), т. е. пятому разряду, в данном случае будет соответство-
вать переменная А. Следовательно, две другие ПМД могут быть полу-
чены, если функциями обратной связи являются A @D и A QD.
Соответствующие последовательности состояний приведены на рис.
7.17, б.
Очевидно, что схема на рис. 7.15, а может быть использована для
генерации двоичных последовательностей. Причем элементы после-
довательности могут формироваться непосредственно на выходе
одного из триггеров. Тогда двоичная последовательность, появляю-
щаяся на выходе триггера D, имеет вид 0 — 0 — 0 — 1 — 0 — 0 —
— О — 0 — 1 — 0 —1 — 1 — 1 — 1. Такого рода генераторы иногда
называют генераторами псевдослучайных двоичных последователь-
Рис. 7.17. ПМД, полученные с помощью четырехразрядного сдвигового регистра
с обратной связью вида:
a—CQD; 6 — A&D-, e-AQD
ностей, поскольку порядок появления цифр только кажется слу-
чайным. Однако цифры последовательности начинают повторяться
через 2N — 1 тактовых импульса. При заданной тактовой частоте
период последовательности быстро растет с ростом числа разрядов
регистра.
Если
N = 10, 2N — 1 = 1023
и если тактовая частота равна 1 МГц, то период равен 1,02 мс. Если
N = 20, 2N — 1 = 1 048 575,
то период равен 1,05 с. И, наконец, если
N = 30, 2N — 1 = 1 073 730 624,
то период равен 1073,73 с.
При использовании других типов обратной связи, основанных
на элементе ИСКЛЮЧАЮЩЕЕ ИЛИ, с помощью четырехразрядного
регистра могут генерироваться последовательности немаксимальной
длины. Например, если функция обратной связи имеет вид В @ D,
то любая из четырех последовательностей, представленных на рис.
7.18, может быть получена. Вид последовательностей будет зависеть
от начального состояния регистра.
Основной генератор ПМД показан на рис. 7.15, а. Он не всегда
сам может начать работу, так как при включении начальным состо-
S D C в A f s D C В A s D c В A
S1 0 0 0 1 0 S3 0 0 1 1 1 A 1 1 A
s2 0 0 1 0 1 s7 0 1 1 1 1 Se U 1 1 U 1
s5 0 1 0 1 0 S15 1 1 1 1 0 i 1 A 1
^10 1 0 1 0 0 Si 4 1 1 1 0 0 ^13 1 1 U 1 1
s4 0 1 0 0 0 S12 1 1 0 0 1 c i A 1 1
1 0 0 0 1 Sg 1 0 0 1 1 Sji 1 U 1 1 и
Рис. 7.18. Последовательности немаксимальной длины, полученные с помощью че-
тырехразрядного сдвигового регистра с обратной связью В ф D
янием генератора может быть 0000. У схемы, представленной на
рис. 7.15, а, нет средств для того, чтобы выйти из состояния 0000.
Однако, проведя небольшие изменения цепи обратной связи, можно
снабдить генератор средствами самозапуска. Для этого необходимо
добавить терм ABCD и функции обратной связи. Сделав это, получим
f = С ф D + ABCD.
На рис. 7.19, а эта функция представлена с помощью карты Карно.
После упрощений имеем
f = С ф D + ABD.
На рис. 7.19, б приведена схема проектируемого генератора.
Метод скачка также может быть использован для генерации по-
следовательностей немаксимальной длины. Этот метод основан на
применении генератора ПМД с элементом ИСКЛЮЧАЮЩЕЕ ИЛИ
в цепи обратной связи. Длина последовательности может быть умень-
шена в результате введения дополнительной обратной связи. Метод
скачка рассмотрим на примере генератора, построенного на четы-
рехразрядном сдвиговом регистре (см. рис. 7.15, а).
Предположим, что первоначально генератор находится в состо-
янии DCBA =0011 (S3). Если в этом случае значение сигнала об-
ратной связи равно 0, то следующим состоянием генераторajбудет
Рис. 7.19. Генератор ПМД со средствами самозапуска:
а — представление функции обратной связи с помощью карты Карно; б — реализация ге-
нератора ПМД
•Чг Sff 5>s S7 S„ Ss Sto
a)
S П c в A -f
S, s2 5* 5s 5j 57 % 5» 5jz 5g 0 0 0 1 0 0 z z z 1 0 0 1 0 0 1 1 1 1 0 0 1 0 0 1 1 1 1 0 0 1 0 0 1 1 1 1 0 0 0 0 0 1 1 1 7 0 0 0 1
г)
Рис. 7.20. Четырехразрядный генератор ПМД, с модифицированной обратной
связью, позволяющей совершить скачок:
а — диаграмма состояний генератора; б — модифицированная ПМД; в — представление
функции обратной связи f с помощью карты Карно; г — реализация генератора
DCBA =0110 (Ss). С другой стороны, если значение сигнала об-
ратной связи равно 1, то следующим состоянием генератора будет
DCBA=0111 (S7).
Анализ таблицы состояний четырехразрядного генератора ПМД,
изображенной на рис. 7.15, б, показывает, что С © D =0, когда
генератор находится в состоянии S3, и, следовательно, следующим
состоянием генератора будет S6. Если же цепь обратной связи моди-
фицирована так, что значение сигнала в ней равно 1, то следующим
состоянием генератора будет S7.
На рис. 7.20, а показана диаграмма состояний четырехразряд-
ного генератора ПМД. Изменив обратную связь, можно добиться,
чтобы состояния S6, S13, Хю, S6, Sn не попадали в рабочую после-
довательность генератора. В результате, в последовательность будут
входить только десять состояний из 15.
На рис. 7.20, б показана модифицированная последовательность
состояний генератора, причем выделено новое значение функции
обратной связи для состояния S3. Функция обратной связи вместе
с неиспользуемыми состояниями S6, S13, Slo, S6, Su и состоянием
блокировки So представлена с помощью карты Карно на рис. 7.20, в.
Используя обычные методы упрощения, получим модифицирован-
ную функцию обратной связи в виде
/м = С ф D + ABD + ABD.
На рис. 7.20, г показана реализация генератора последователь-
ности немаксимальной длины, обладающего средствами для самоза-
пуска.
Упражнения
У 7.1. Содержимым сдвигового регистра с последовательным входом/последо-
вательным выходом является DCBA = 0101, где А — наименьший значащий разряд
регистра. Последовательность 10011 вводится в регистр слева направо, причем наи-
больший значащий бит вводится первым. Ввод регулируется пятью тактовыми
импульсами. Начертить временные диаграммы, показывающие, как изменяются
выходы четырех триггеров во время ввода данных в регистр.
У 7.2. Разработать счетчик по модулю 12, используя сдвиговый-регистр и логи-
ческие схемы в цепи обратной связи.
У 7.3. Используя сдвиговый регистр и комбинационную логику, спроектиро-
вать генератор последовательности 0-1-0-0-1-0-1-1-1-0-1.
У 7.4. Разработать диаграммы состояний для генераторов на сдвиговых реги-
страх с элементом ИСКЛЮЧАЮЩЕЕ ИЛИ в цепи обратной связи. Ниже ука-
зана разрядность регистра и вид функции обратной связи:
а) четырехразрядный f= В ф С;
б) пятиразрядный f=D ф Е.
У7.5. Для генерации двух последовательностей, длиной 7 и 5, соответственно,
используется трехразрядный сдвиговый регистр. Когда сигнал управления т= 1,
производится генерация первой последовательности, а когда т = 0, генерируется
вторая последовательность. Построить удовлетворяющий этим требованиям генератор
на сдвиговом регистре с элементом ИСКЛЮЧАЮЩЕЕ ИЛИ в цепи обратной связи.
У7.6. Трехразрядный сдвиговый регистр АВС, где А — наименьший значащий
разряд, снабжен цепью обратной связи, реализующей функцию В ф С с помощью
элемента ИСКЛЮЧАЮЩЕЕ ИЛИ. Этот регистр должен использоваться для пе-
риодической генерации последовательности, представляющей число е (2.718282)
в двоично-десятичном коде, на выходах Р, Q, Я и S. Определить последовательность
счета для генератора и разработать комбинационную логическую схему, необходимую
для получения последовательности цифр, составляющих е.
У7.7. Начертить временные диаграммы, характеризующие работу четырех-
разрядного счетчика Джонсона в течение восьми тактовых импульсов. Изобразить
на временных диаграммах значения выходов всех триггеров, входящих в состав
счетчика. Определить, как надо изменить логическую схему в цепи обратной связи
счетчика, чтобы исключить состояние 1111 из счетной последовательности.
8. СИНХРОННЫЕ ПОСЛЕДОВАТЕЛЬНЫЕ СХЕМЫ
8.1. Введение
В этой главе описывается процедура, лежащая в основе проекти-
рования и реализации синхронных последовательных схем. Такие
схемы широко применяются в цифровых устройствах и состоят как
из элементов комбинационной логики, так и из однобитовых элемен-
тов памяти. В действительности, комбинационными элементами
будут являться компоненты широко используемых логик, а двоич-
ными запоминающими элементами будут //(-триггеры. Использо-
вание //(-триггеров в синхронных схемах является обычным явле-
нием, так как эти триггеры позволяют наиболее просто реализовать
схемы.
Как показал опыт, накопленный в других областях электроники,
анализ схем гораздо проще, чем их синтез, и первым шагом при раз-
работке процедуры проектирования является анализ тех схем, ре-
жимы работы которых хорошо известны. Этот анализ позволит оп-
ределить шаги, которые необходимы для синтеза схем.
8.2. Анализ синхронной последовательной схемы
На рис. 8.1, а приведена синхронная последовательная схема.
Анализ этой схемы показывает, что она имеет два входа: вход X и
вход синхронизации и один выход Z. В качестве элементов па-
мяти схемы используются два //(-триггера типа «хозяин—слуга»,
которые определяют четыре возможных внутренних состояния схемы:
АВ = 00, 01, 10 или 11. Ее также можно изобразить в виде струк-
турной схемы, приведенной на рис. 8.1, б. Структурная схема пред-
ставляет собой логический блок, в котором содержатся как элементы
комбинационной логики, так и два триггера А и В, состояния ко-
торых определяют четыре внутренних состояния схемы. Входами
блока являются сигналы X и синхронизации Си, а выходом — сигнал
Z. Непосредственно из рис. 8.1, а можно получить уравнения для
выходных сигналов триггеров А и В:
JА ~ В', J- Л\
Ка = 1; Хв = X + А.
В п. 5.4 для //(- триггера была приведена таблица состояний,
которая для удобства воспроизведена на рис. 8.1, в. Из таблицы можно
получить карту Карно для функции Qi+6i (рис. 8.1, г). После пре-
образований эту функцию можно записать в виде
Q‘+6i = (/Q + KQ)<
Подставляя в это уравнение выражения для /А, /(А, /в, Кв, по-
лучим
Л/+6/ = (ЛВ)/;
B‘+6t (АВХ + А ву.
Рис. 8.1. Изучение поведения синхронной последовательной схемы:
а — реализация синхронной последовательной схемы; б — структурная схема, где Л Б —
логический блок; в — таблица состояний УК-триггера; г — карта Карио для УК-триггера;
д — таблица состояний схемы, где ТС — текущее состояние и СС — следующее состояние;
е — диаграмма состояний схемы; ж — генерация выходного сигнала; з — временная диа-
грамма работы схемы
Теперь с помощью этих уравнений можно для заданных текущих
значений Л и В и заданного значения входного сигнала определить
значения А и В для следующего состояния. Например, если А — О,
В = О, X = 0, то Л/+б/ = 0. Аналогично, если А = 0, В = 0,
X = 0, то Bt+&t = 1.
Тем же самым путем, которым были получены значения для сле-
дующих состояний триггеров Л и В, можно определить выход Z
схемы для всех возможных сочетаний X, Л иВ. Для этого требуется
знание уравнения выхода, которое получаем непосредственно из
рис. 8.1, а:
Z = АВИ.
Это уравнение показывает, что выходной сигнал равен единице
(Z = 1) тогда, когда текущее внутреннее состояние схемы есть
А = 1, В = 1 и на вход подается сигнал синхронизации. При всех
других комбинациях Л и В выход равен нулю (Z = 0) независимо
от значения X или наличия сигнала синхронизации. Далее заметим,
что интервал времени, когда на выходе Z = 1, никогда не может быть
больше длительности синхронизирующего импульса.
Теперь можно разработать таблицу, отражающую текущее со-
стояние схемы, ее следующее состояние и выход. Эту таблицу, при-
веденную на рис. 8.1, д, можно рассматривать как таблицу состоя-
ний схемы. Читатель может заметить, что в этой таблице внутренние
состояния обозначены So, Si и т. д.
Имея таблицу состояний, можно построить диаграмму внутрен-
них состояний (рис. 8.1, е). Диаграмма-состоит из четырех блоков,
каждый из которых отражает внутреннее состояние схемы. Переход
из одного состояния в другое обозначен прямой линией между этими
двумя состояниями, причем стрелкой указано направление перехода.
Рядом со стрелкой помещен сигнал, инициирующий переход. На-
пример, для того чтобы перейти из Sx в S3, необходимо на вход схемы
подать сигнал X и сигнал синхронизации (ХП).
Необходимо отметить, что если в качестве триггеров использу-
ются //(-триггеры типа «хозяин—слуга», то переход всегда будет
иметь место в момент появления отрицательного фронта синхро-
низирующего импульса. Например, переход из в S2 происходит
в момент появления отрицательного фронта синхронизирующего
импульса, формирующего часть сигнала перехода ХП.
Выходной сигнал Z = 1 соответствует вершине, обозначенной
S3. Это нужно понимать следующим образом: Z 1 тогда, когда
схема находится в состоянии S3, т. е. АВ = 11, и получен синхрони-
зирующий импульс. Следовательно, Z =- АВП, как и указано выше.
На рис. 8.1, ж показано, как происходит генерация выходного
сигнала Z. Схема переходит из состояния Si в S3 во время формиро-
вания отрицательного фронта синхронизирующего импульса, от-
меченного цифрой 1. Для того чтобы этот переход осуществлялся,
сигнал X должен быть таким, как показано на диаграмме. Схема
будет оставаться в состоянии S3 до момента появления отрицатель-
ного фронта синхронизирующего импульса, обозначенного на диаг-
рамме цифрой 2, после чего начнется переход схемы из состояния S3
в состояние So. Выходной сигнал Z = ЛВП формируется с помощью
операции логического умножения (И) сигнала АВ с синхронизи-
рующим импульсом, отмеченным цифрой 2. Оба эти сигнала имеют
значение логической «1» в заштрихованной зоне, поэтому в этой зоне
выходной сигнал равен единице (Z = 1). Необходимо отметить, что
выходной сигнал в данном случае не зависит от значения X, т. е.
в течение интервала времени, показанного на диаграмме штрихов-
кой, Z всегда равно 1.
Что можно сказать о работе этой схемы, исходя из диаграммы со-
стояний? Сразу можно заметить, что из состояния So имеется два
пути: первый приводит к возвращению в 80 через S3, а второй к воз-
вращению в 80 через S2. Очевидно также, что независимо от выбора
пути, начинающегося в So, всегда необходимо осуществить три пе-
рехода для возврата в состояние So. Это означает, что последова-
тельности, состоящие из трех двоичных цифр и поступающие на
линию X, будут проверяться схемой.
Выход Z = 1 будет появляться во время третьего импульса
синхронизации как реакция на определенные комбинации трех цифр
на входе. Это будет иметь место, если на графе состояний выбран
путь, проходящий через состояние S3. Другие комбинации трех
цифр приводят к выбору пути, проходящего через состояние S2.
В этом случае в течение третьего синхронизирующего импульса
на выходе Z не будет сигнала.
Первый в трехшаговой последовательности переход из 80 в St
инициируется синхронизирующим импульсом и происходит неза-
висимо от того, имеет ли первая цифра, подаваемая на вход, значе-
ние 1 или 0. Если выбирается путь, проходящий через состояние S3,
то переход из Si в S3 может произойти только в том случае, если
вторая цифра на линии X равна 1. Третий переход из S3 в So также
инициируется синхронизирующим импульсом и происходит неза-
висимо от того, X = 0 или X = 1.
Приведенная ниже диаграмма показывает, что, для того чтобы
значение выхода Z равнялось 1, необходимо на вход X подать одну
из следующих четырех последовательностей цифр: 010, 011, ПО и
111.
о 1
. I I
? /
/ \ / \
0 1 0 1
Очевидно, что оставшиеся четыре комбинации трех цифр будут со-
ответствовать альтернативному пути на графе состояний, и для этого
пути вырабатывается значение Z = 0 в момент появления третьей
цифры последовательности.
Временная диаграмма работы схемы для трех различных после-
довательностей цифр 011, 001 и ПО приведена на рис. 8.1, з. Сигнал
X синхронизирован и предполагается, что все изменения этого сиг-
нала происходят в промежутки времени между синхронизирующими
импульсами. В случае комбинации 011 и ПО во время действия
синхронизрующего импульса, отмеченного цифрой 3, на выходе Z
имеется сигнал, в то время как в случае комбинации 001 выходной
сигнал Z = 0.
По диаграмме также может быть установлена длительность си-
гнала для Z = АВ, т. е. в случае удаления из уравнения выхода
сигнала синхронизации выходной сигнал возникает в момент появ-
ления отрицательного фронта синхронизирующего импульса 2
и исчезает в момент появления отрицательного фронта синхронизи-
рующего импульса 3. Интересно отметить, что в случае Z = АВ
напряжение на выходе становится высоким до появления третьей
цифры. В этом случае достаточно знать, что значение второй цифры
последовательности приводит в состояние S3, и безразлично, явля-
ется ли третья цифра 0 или 1, т. е. третья цифра может не распоз-
наваться. В случае же, когда Z = ЛВП, сигнал на выходе не появ-
ляется до тех пор, пока не начнется формирование положительного
фронта синхронизирующего импульса, обозначенного цифрой 3.
Схема должна распознать этот синхронизирующий импульс до того,
как появится сигнал на выходе.
8.3. Процедура проектирования синхронных
последовательных схем
Анализ синхронной последовательной схемы, проведенной в
п. 8.2, позволил установить все необходимые для проектирования схем
действия, за исключением сокращения состояний, о котором речь
пойдет ниже. Функциональная схема процесса проектирования
приведена на рис. 8.2.
Шаг 1. Постановка задачи. Весьма важно, чтобы проектиров-
щик детально знал внешние характеристики проектируемой схемы.
Сначала устно формулируется задача и, в частности, детализируются
имеющиеся в распоряжении входы и требуемые выходы. Эту инфор-
рацию легче всего изобразить в виде структурной схемы, как по-
казано на рис. 8.1, б, и при необходимости привести временные диаг-
раммы входных и выходных сигналов. Обычным примером инфор-
мации о форме сигналов может служить временная диаграмма, при-
веденная на рис. 8.1, з.
Точно сформулировать условия задачи очень трудно, и для этого
может потребоваться несколько консультаций проектировщика с за-
казчиком. Если на этой стадии не будут полностью устранены неяс-
ности, процесс проектирования, тем не менее, следует продолжить
несмотря на то, что полученная аппаратная реализация схемы, воз-
можно, не будет удовлетворять требованиям заказчика. Если это
так, то необходимо будет возвратиться после шага 5 процедуры к
шагу 1. В действительности, для того чтобы полностью удовлетво-
рить требования заказчика, возможно придется несколько раз повто-
рить процесс проектирования.
Что касается студентов, то неясно-
сти в устной формулировке задачи очень
часто будят в них излишние сомнения.
В стадии изучения предмета такие со-
мнения не должны быть слишком серьез-
ными. Студент должен настроиться на
решение задачи и дать лишенную неточ-
ностей версию ответа. Предложенный
вариант ответа должен быть реализован.
В дальнейшем, при изучении поведения
созданной схемы можно установить, под-
тверждает ли оно правильность решения.
Шаг 2. Диаграмма внутренних состоя-
ний. На этом шаге словесно сформулиро-
ванная задача выражается в терминах
внутренних состояний схемы. Для раз-
работки диаграмм внутренних состояний
не существует общих правил и умение
изображать их приобретается только на
практике. Для схемы, анализируемой
в п. 8.2, диаграмма внутренних состоя-
ний, изображенная неопытным проекти-
ровщиком, будет иметь вид, показанный
на рис. 8.1, е. Для проектирования диа-
граммы внутренних состояний проекти-
ровщиком может быть дана следующая
словесная формулировка условий задачи.
Рис. 8.2. Функциональная
схема процесса проектирова-
ния синхронных последова-
тельных устройств
Логическая схема получает двоичную
информацию, подаваемую последователь-
но на линию X, работа которой син-
хронизирована с внешним сигналом син-
хронизации. Последовательность, состоя-
щая из трех двоичных цифр, которые не перекрывают друг друга,
проверяется логической схемой и при обнаружении комбинаций 010,
011, 110 и 111 на линии Z появляется 1. Сигнал на выходе должен
появиться при подаче третьей цифры последовательности и должен
иметь длительность, равную длительности синхронизирующего им-
пульса. При всех других комбинациях трех двоичных цифр сигнал
на линии Z должен быть равен 0.
Неопытный проектировщик может разработать древовидную
диаграмму состояний, показанную на рис. 8.3. Движение по этой
диаграмме всегда будет начинаться из состояния So. Из него можно
попасть в состояние если подается сигнал ХП, или в состояние S2,
если подается сигнал ХП. Из состояний Sr и S2 ведут два пути:
один путь связан с сигналом перехода ХП, а другой — с сигналом
перехода^ХП. Таким образом, всего имеется четыре пути, которые
приводят к состояниям S3, S4, S5, Sis. Для каждого из этих четырех
состояний существуют два выходных пути, но так как следующий
Рис. 8.3. Диаграмма внутренних состояний устройства обнаружения последова-
тельностей цифр
переход является третьим по счету, то все восемь выходных путей
должны вести в начальное состояние So. -
Путь So—-Si—S3 — So связан с комбинациями 111 и ПО,
поэтому в состоянии S3 выходной сигнал Z = 1. Точно также путь
So — S2 — S5 — So связан с комбинациями ОН и 010 и, следова-
тельно, в состоянии S5 Z = 1. Другие два пути на диаграмме состо-
яний связаны с теми последовательностями, рассматривать которые
нет необходимости.
При разработке этой диаграммы никаких сокращений не про-
изводилось. Каждая комбинация из трех двоичных цифр отобра-
жена на диаграмме. Однако эта диаграмма внутренних состояний
имеет восемь состояний, а диаграмма на рис. 8.1, е — всего четыре
состояния. Это означает, что для реализации схемы, представлен-
ной на рис. 8.3, требуется три //(-триггера и некоторое дополни-
тельное количество схем комбинационной логики.
Шаг 3. Сокращение состояний. Чем больше состояний на диаграмме
внутренних состояний, тем больше аппаратуры требуется для реа-
лизации схемы. По этой причине в интересах проектировщика
уменьшить число состояний настолько, насколько возможно. Про-
цесс уменьшения числа состояний называется сокращением состоя-
ний и соответствует процессу минимизации, проводимому при про-
ектировании комбинационных схем.
Сокращение состояний может осуществляться по строго опреде-
ленным правилам с помощью таблицы состояний и процедуры слия-
ния Колдуэлла. Например, на рис. 8.4, а приведена таблица состо-
яний, соответствующая диаграмме состояний, изображенной на
рис. 8.3. В этой таблице для каждого состояния схемы отведена строка,
а для каждой комбинации входных сигналов — столбец. В дан-
ном случае имеется только один входной сигнал и поэтому в таблице
всего два столбца. В каждой ячейке таблицы присутствуют две за-
писи: первая запись показывает следующее состояние схемы при
условии, что в текущий момент схема находится в состоянии,
указанном в начале данной строки, и получает входной сигнал,
значение которого указано в верхней части данного столбца; вто-
рая запись содержит выход схемы.
В соответствии с правилами слияния Колдуэлла две строки в таб-
лице состояний можно объединить, если значения следующих со-
стояний и выходов, указанные в соответствующих ячейках каждой
строки, совпадают. В таблице на рис. 8.4, а строки, озаглавленные
S4 и S6, удовлетворяют этим двум условиям точно так же, как и
строки, озаглавленные S3 и S6. После объединения состояний S4 и
Se получается новое состояние, обозначаемое S4e, и если в таблице
где-либо присутствуют состояния S4 или S6, то их надо заменить на
S46. Точно также состояния S3 и S6 после объединения образуют
новое состояние S3d.
Используя процедуру слияния Колдуэлла, таблицу состояний,
приведенную на рис. 8.4, а, можно преобразовать в таблицу состо-
яний, изображенную на рис. 8.4, б. Во вновь полученной таблице
присутствуют две строки, обозначенные S4 и S2, которые могут быть
объединены, в результате чего будет образовано новое состояние S12.
Следовательно, таблица на рис. 8.4, б может быть преобразована
в таблицу, п риведенную на рис. 8.4, в. Таблица на рис. 8.4, в дальней-
шему упрощению не поддается. Сокращенная диаграмма состояний,
которую можно получить из этой таблицы, тождественна диаграмме
состояний, приведенной на рис. 8.1, е, и воспроизведена на рис. 8.5.
На этом рисунке использованы обозначения состояний, взятые из
рис. 8.4, в.
Наилучшей на практике является такая ситуация, когда число
состояний схемы равно некоторой степени числа 2, т. е. 2п. Существу-
ет небольшая неприятность, заключающаяся в том, что при умень-
шении числа состояний от 2" до числа, большего, чем 2"-1, образу-
ются неиспользуемые состояния. Например, если АГ есть число со-
\Х 0 1 \X 0 7 \ 0 7
s2 s, $г S, Stz
z=o z=o So Z=0 Z=0 So z=o Z=0
s. S1 c Sos S35 c Sos S35
S? z=o z=o Z=0 z=o S/2 z=o z=o
С Se S5 Sos Sos So Sq
z=o z=o z=o z=o Z=1 Z=1
S3 Sq Z=1 Sq Z=7 S35 5o Z'1 Sq Z=1 Sos Sq Z=0 So z=o
So z=o So z=o Sq z=o So Z=Q 9
% So 2=1 So Z=7 f)
se So So Puc. 8.4. Устройство обнаружения последа
Z=Q z=o вательностей цифр:
а — полная таблица состояний; б — сокращенная
таблица состояний; в — минимальная таблица
состояний
So
10 11
Рис. 8.5. Диаграмма состояний уст-
ройства обнаружения последователь-
ностей цифр
стояний и 2'!-1 < Af < 2П, то
число неиспользуемых состояний
равно 2'1 — АС
Неиспользуемые состояния
приводят к дополнительным труд-
ностям, встающим перед проекти-
ровщиком. Они могут появляться
в результате ложного срабатыва-
ния схемы. В обязанности проек-
тировщика логических устройств
входит точное определение пове-
дения ’схемы при попадании ее
в одно из неиспользуемых состоя-
ний; игнорирование же этого
может привести к блокировке схе-
мы. Это означает, что если не
предусмотрен выход из неиспользуемого состояния, то схема будет
оставаться в нем неопределенное время. Необходимо отметить, что
неиспользуемые состояния не являются «состояниями, не доста-
вляющими беспокойства», и по этой причине они не должны ис-
пользоваться для упрощения уравнений, описывающих работу
логических устройств.
Шаг 4. Разработка уравнений схемы. После получения миними-
зированной диаграммы состояний проектировщик должен связать
вторичные переменные с различными состояниями. Число вторичных
переменных, необходимых для однозначного определения состояний,
определяется общим числом состояний. Например, на рис. 8.5
можно выделить четыре состояния. Поэтому для однозначного
определения каждого состояния потребуется две вторичные пере-
менные.
На рис. 8.5 показан один из вариантов назначения вторичных
переменных. Очевидно, что возможны другие варианты и, следова-
тельно, существует несколько различных схемных реализаций,
причем одни из них могут быть выгоднее других. Однако не следует
акцентировать большое внимание на рассмотрении этих вариантов,
поскольку для поиска минимального решения требуется слишком
много времени.
Число вторичных переменных, необходимых для определения
состояния, связано с числом триггеров, используемых при реали-
зации устройства. На диаграмме состояний, приведенной на рис. 8.5,
имеются две вторичные переменные А и В, следовательно, для реа-
лизации схемы потребуется два триггера.
Существует не менее двух методов для определения логических
уравнений схемы. Первый метод состоит в определении J- и /(-вхо-
дов триггеров для каждого перехода с помощью управляющей таб-
лицы //(-триггера, разработанной в гл. 5. Затем эта информация
наносится на карту Карно и производится упрощение. Второй метод
использует процедуру алгебраического упрощения, описанную
в гл. 6.
Состояния Входы триггеров
о ф S' след} /ющее X-- = 0 X = 1 X = 0 X = 1
X = 0 X = 1 — о О
АВ АВ J A KA Ja KA Jb Kb J в Кв
0 0 0 0
00 01 01 0 0 0 0 1 0 1 0
01 Z = 0 10 Z= 0 11 1 0 1 0 0 1 0 0 0 1 1 0
Z = 0 Z= 0
и 00 00 0 1 0 1 0 1 0 1 1 0 0 1
Z= 1 Z= 1
10 00 Z = 0 00 Z= 0 0 1 0 1 0 0 0 0 1 1 0 0
a)
Рис. 8.6. Определение функций J- и
К-входов триггеров, необходимых
для реализации устройства обна-
ружения последовательностей цифр:
а — таблица состояний, используемая
для определения входов J- и Х-тригге-
ров; б — управляющая таблица JК,-
триггера; в — карты Карно для вхо-
дов J- и К-триггеров
Рассмотрим первый метод. Таблица состояний, приведенная
на рис. 8.4, в, преобразуется в таблицу, показанную на рис. 8.6, а,
которая составлена уже для вторичных переменных. К таблице
состояний примыкает восемь столбцов, в которых содержатся данные
о входных сигналах JA, КА, Jв, Кв триггеров. Значения входных
сигналов получены из управляющей таблицы /К-триггера, которая
для удобства приведена на рис. 8.6, б. В действительности, эта
таблица дает значения сигналов, необходимые для осуществления всех
возможных переходов из Q1 в Qt+6t. В этой таблице значениями си-
гналов па входах /К-триггеров могут быть 0, 1 или 0 («не достав-
ляющие беспокойства»).
Значения входных сигналов триггеров, которые приведены в таб-
лице состояний, определяются следующим образом. Если текущее
состояние АВ = 00 и X = 0, то следующим состоянием будет АВ =
= 01. Значит А1 = 0 и Л/+6< = 0. Таким образом, из управляющей
таблицы получаем JA = 0 и КА = 0. Точно также В1 = 0 и Bt+6t =
= 1, поэтому из управляющей таблицы получаем JB = 1 и Кв =
= 0. Подобным образом могут быть определены все остальные зна-
чения входных сигналов в восьми столбцах этой таблицы.
Теперь заполним карты Карно для входных сигналов всех тригге-
ров. Карты Карно изображены на рис. 8.6, в. После упро-
щений получаем уравнения для входных сигналов триггеров:
JA = В- JB = A;
КА = 1; Кв = X + А.
Как и следовало ожидать, эти уравнения и уравнения входов триг-
геров для схемы, приведенной на рис. 8.1, а, совпадают.
Непосредственно из таблицы состояний, приведенной на рис.
8.6, а, можно получить уравнение, описывающее выходной сигнал
схемы:
Z = АВИ.
Во втором методе уравнения отпирания и запирания для каждого
триггера получаем непосредственно из диаграммы состояний (см.
рис. 8.5). Для упрощения этих уравнений используем термы согласо-
вания. После этого с помощью уравнений SQ = JqQ и Rq = KqQ,
полученных в пятой главе, определяем выражения для входов J и
К каждого триггера:
SA = S12XII + s12xn = sun = ДВП.
Следовательно,
JA = ВП.
Так как в синхронных схемах всегда присутствует синхронизация,
то обычно сигнал синхронизации опускают, и уравнения прини-
мают вид
Ja - В;
К а В3-а + S4e + (So),
где So — терм согласования, который, если возможно, будет исполь-
зоваться для минимизации. При переходе из So в S42 триггер А не
меняет свое состояние (оно остается равным 0), и в этом случае не-
важно RA равно 0 или 1. Следовательно,
Т?А = АВ + АВ + (ЛВ) = А + (АВ)
и
Ка = 1.
В этом случае нет необходимости использовать АВ для упрощения
RA, так как, применяя соотношение RA = ХАД, получаем, что зна-
чение КА равно 1:
Sb = So + (S12X) = АВ + (ЛВХ).
Это выражение не поддается упрощению с помощью введения терма
согласования, следовательно,
J в = А.
В этом случае термом согласования является S12X, так как возможен
переход 1 1 для вторичной переменной В при переходе из S12
к S36. Тогда не важно J в = 1 или JB = 0:
RB ~ Н- (*^4в) =
= АВХ + АВ + (АВ) = ВХ + АВ.
Следовательно, уравнение
Кв - X + А,
полученное с помощью этого метода, совпадает с уравнением, полу-
ченным альтернативным методом, который был описан выше.
Шаг 5. Реализация схемы. Используя уравнения, полученные на
шаге 4, можно очень просто реализовать схему устройства. Очевидно,
что схема будет идентична той, которая приведена на рис. 8.1, а.
8.4. Проектирование устройства обнаружения
последовательности цифр
Шаг 1. Постановка задачи. Двоичные данные в последовательной
форме поступают на вход X логической схемы, причем время появ-
ления каждого бита входных данных совпадает с подачей синхро-
низирующего импульса. Каждый раз, когда схема обнаруживает
последовательность 101, на линии Z генерируется выходной сигнал.
Структурная схема устройства приведена на рис. 8.7, а. На этом
рисунке также показан поток входных данных, поступающий на
линию X, и соответствующий выходной поток, появляющийся на
линии Z.
Шаг 2. Диаграмма внутренних состояний. Диаграмма состояний
для решаемой задачи приведена на рис. 8.7, б. Чтобы обнаружить
последовательность вида 101, требуются только три состояния So,
S2. Для определения трех состояний необходимы две вторичные
переменные А и В. Так как существуют четыре комбинации этих пе-
ременных, то появляется одно неиспользуемое состояние S3. Если
схема окажется в этом состоянии в результате ложного срабатыва-
ния, то желательно быстро осуществить возврат к основной последо-
вательности состояний. Возврат из состояния S3 в So осуществляется
с помощью перехода, инициируемого первым синхронизирующим
импульсом, поданным после того, как схема окажется в состоянии S3.
Шаг 3. Сокращение состояний. Анализ таблицы состояний, при-
веденной на рис. 8.7, в, показывает, что уменьшить количество со-
стояний невозможно.
Шаг 4. Разработка уравнений схемы:
Sa=S1X-ABX Ja -= ВХ;
Ra = S2 + S3 + (S0X) + (SiA) =
= AB + A~B + (АВХ) + (ABX) -
= A + (АВХ) + (ABX) .'.Ka = 1;
Sb = S0X + (S2X) + Sx =
= ABX -I- (ABX) + (AB)
RB = S2X + (S3) +2s_o*) =
= ABX + (AB) + (ABX)
Из диаграммы состояний
получаем,
в
.-.Кв
что Z = ЛВЛТ1.
x
Sj
г
1011011100010101
1
Логическая
схепа
= AX;
= AX-
г
АВ
00
АВ
10
X
S,
АВ —
01 _
Z=X_TL
s2
АВ
fl
Лв В
В
Ja А
К а А
А.
X
А-
х-
В —
Z
Гс(Си)
г)
Кв В
X
о
г
о
о
АВ
1
о
о
Z=ABX
О
0)
Рис. 8.7. Устройство обнаружения последовательности
ci — структурная схема; б — диаграмма внутренних состояний;
г — реализация устройства; д — временные диаграммы
101:
в — таблица состояний;
Шаг 5. Реализация схемы. Схема устройства обнаружения при-
ведена на рис. 8.7, г, а временные диаграммы работы схемы при
подаче на ее вход последовательности цифр вида 101 показаны на
рис. 8.7, д. Будем считать, что в схеме используются //(-триггеры
типа «хозяин — слуга». Тогда схема переходит в состояние АВ
в момент появления отрицательного фронта второго синхронизирую-
щего импульса и выходит из состояния АВ во время появления отри-
цательного фронта третьего синхронизирующего импульса, обозна-
ченного цифрой 3. Если выход схемы определяется как Z = АВХ,
то сигнал на выходе появляется тогда, когда схема распознает по-
ложительный фронт сигнала X, который соответствует по времени
третьему синхронизирующему импульсу. С другой стороны, если
выход определяется уравнением Z = ДВХП, то сигнал на выходе
не появляется до тех пор, пока не будет сформирован положитель-
ный фронт третьего импульса синхронизации.
8.5. Автоматы Мура и Мили
Существует два типа синхронных последовательных устройств.
Выходы устройств первого типа зависят только от состояний триг-
геров. Такие устройства называются автоматами Мура. Выходы
устройств второго типа зависят как от состояний триггеров, так и от
логических значений входов. Такие устройства называются автома-
тами Мили.
Схема, представленная на рис. 8.7, г, является автоматом Мили,
так как выход Z = АВАЛ зависит как от состояния триггеров, так
и от значений двух входов X и П. Для того чтобы преобразовать ло-
гическую схему, изображенную на рис. 8.7,^г, в схему, удовлетво-
ряющую определению автомата Мура, необходимо провести неболь-
шую модификацию диаграммы состояний автомата Мили (см. рис.
8.7, б). Результатом этой модификации является диаграмма состо-
яний, приведенная на рис. 8.8, а. Как видно из рисунка, введено
дополнительное состояние Z = АВ, являющееся выходным состо-
янием схемы, т. е. именно в этом состоянии формируется выходной
сигнал, поэтому Z = АВ. Временные диаграммы, соответствующие
диаграмме состояний, представлены на рис. 8.8, б.
Уравнения для входных сигналов //(-триггеров, определяющих
состояние автомата Мура, получены обычным путем:
/А = ВХ; JB = А + X; Z = АВ;
КА = ВХ + ВХ; Кв = А.
На рис. 8.8, в изображена логическая схема автомата Мура,
выполняющего функции устройства обнаружения последователь-
ности цифр.
Ниже приведен пример, который дает возможность еще раз
остановиться на работе автоматов Мили и Мура.
Логическая схема получает двоичную информацию в последова-
тельной форме по линии X, причем работа схемы синхронизируется
Рис. 8.8. П редставление устройства обнаружения последовательности 101 в виде
автомата Мура:
а — диаграмма состояний автомата Мура; б — временные диаграммы, ^характеризующие
работу автомата Мура; в — реализация автомата Мура
внешним сигналом. Схема анализирует поступающие на ее вход
не перекрывающие друг друга строки символов, состоящие из трех
цифр. Если последняя цифра строки 1, на выходной линии Z по-
является 1.
Структурная схема для э*гой задачи представлена на рис. 8.9, а,
а древовидная диаграмма состояний, изображенная на рис. 8.3,
с небольшими модификациями может рассматриваться как диаграмма
внутренних состояний схемы. Диаграмма внутренних состояний для
нашей задачи приведена на рис. 8.9, б. После попадания схемы
в состояния S3, S4, S6, S6 выходной сигнал Z = ХП. Это озна-
чает, что сигнал на выходе появляется лишь тогда, когда последняя
цифра трехбитовой строки равна 1. Из таблицы состояний, приве-
денной на рис. 8.9, в, видно, что состояния S3, S4, S6 и S6 можно
объединить в одно состояние S3466. После слияния таблица состоя-
ний будет выглядеть так, как показано на рис. 8.9, г.
На рис. 8.9, д изображена сокращенная диаграмма внутренних
состояний устройства. Она получена на основе информации, находя-
щейся в сокращенной таблице состояний. Диаграмма состояний
показывает, что проектируемое устройство является автоматом Мили,
так как выход Z = ДВХП зависит не только от текущего состоя-
ния, но и от значений входных сигналов. Преобразуем эту диа-
грамму состояний таким образом, чтобы получить автомат Мура.
Для этого необходимо состояние So разделить на два состояний S0A
и S0B. Теперь выход Z будет формироваться, когда устройство
Рис. 8.9. Устройство, проверяющее, равна ли 1 последняя цифра в трехбитовой
последовательности:
а — структурная схема; б— основная диаграмма состояний; в — таблица состояний; г —
сокращенная таблица состояний; д — диаграмма состояний для устройства типа автомата
Милн; е — диаграмма состояний для автомата Мура
находится в состоянии S0A и будет зависеть только от текущего со-
стояния, поэтому Z = АВС. Необходимо отметить, что в данном
случае преобразование приводит к увеличению числа состояний от
четырех до пяти и, следовательно, для реализации автомата Мура
потребуется дополнительный триггер.
8.6. Импульсные синхронные схемы
В задачах, которые решались выше, считалось, что входным
сигналом является синхронный сигнал заданного уровня (не путать
с сигналом синхронизации), как показано на рис. 8.10. Все измене-
ния сигналов такого типа происходят в интервалах между тактовыми
импульсами, а входная последовательность определяется значени-
ями входного сигнала в течение тех интервалов времени, когда зна-
чение сигнала синхронизации равно 1.
Существуют входные сигналы другого типа. Их можно применять
в последовательных схемах. Эти сигналы называют синхронными
импульсными сигналами. Пример такого сигнала дан на рис. 8.10.
Необходимо заметить, что длительности входного и тактового сиг-
налов совпадают, а входная последовательность точно так же оп-
ределяется значением входного сигнала в те интервалы времени,
когда значение сигнала синхронизации равно 1.
Рассмотрим задачу, для решения которой необходимо разрабо-
тать импульсную синхронную схему. Пусть двоичные данные по-
ступают на линию X в импульсной форме, причем каждый бит вход-
ных данных синхронизирован с поступающими извне тактовыми
импульсами. Схема должна распознавать входные строки вида X =
= 111, включая и перекрывающие друг друга строки, как показано
на рис. 8.11, а.
На рис. 8.11, б приведена диаграмма внутренних состояний.
Состояние So можно считать начальным состоянием схемы. Схема
меняет свои состояния при получении сигнала X = 1 до тех пор,
пока не окажется в состоянии S2. При появлении входного сигнала
X = 0 всегда происходит возврат в So, и если схема по какой-либо
причине попадает в неиспользуемое состояние S3, то она остается
там до тех пор, пока не поступит сигнал X = 1.
На рис. 8.11, в изображены таблица состояний схемы и при-
мыкающие к ней столбцы, в которых расположены значения входных
сигналов J и К для двух триггеров А и В. На рис. 8.11, г по-
казаны четыре карты Карно для входных сигналов триггеров. Ана-
лиз этих карт позволяет получить следующие выражения для вхо-
дов:
JA = ВХ; КА = ВХ + ВХ;
JB = X; КВ = Х.
с” :лл______________________п________
Синхронный 1 ।--------- -----------------------------
сигнал задан- / 0 g /
ног о уродня 0—' ------------------- I------------
Синхронный 1 _
импульсный Л 0 0 ГЛ
сигнал 0----------1 I-------------------------1 I-------
Рис. 8.10. Входные сигналы синхронных схем
Выражение для выходного сигнала имеет вид
Z = АВХ.
Логическая схема устройства обнаружения показана на
рис. 8.11, д. Как видно нз рисунка, сигнал синхронизации пода-
ется на элемент И вместе с входными сигналами обоих триггеров,
чтобы гарантировать синхронность выполнения операций. На
рис. 8.11, е изображено типичное множество временных диаграмм
для этой схемы.
8.7. Сокращение состояний
Метод сокращения состояний, основанный на анализе таблицы
состояний, уже был рассмотрен в п. 8.3. В действительности все
методы сокращения состояний зависят от принципа эквивалентно-
сти, ранее определенного в правилах слияния Колдуэлла. Однако
заметим, что два состояния Sp и SQ синхронной последовательной
схемы могут считаться эквивалентными тогда и только тогда, когда
в ответ на входную последовательность вырабатывается та же самая
выходная последовательность, независимо от того, является Sp
или S? начальным состоянием схемы. Поэтому любой метод опреде-
ления эквивалентности состояний должен перебрать все возможные
входные последовательности и определить соответствующие выход-
ные последовательности, рассматривая в качестве начального все
состояния схемы по очереди. Ясно, что этот процесс достаточно дли-
телен для схем, имеющих многочисленные входные сигналы и мно-
гочисленные внутренние состояния. К счастью, кроме метода, ос-
нованного на просмотре таблицы состояний, существуют два простых
и дающих быстрые результаты метода, которые вкратце будут
описаны в этом параграфе. Этими методами являются: а) метод
разбиения; б) метод, использующий таблицу импликаций.
Предположим, что таблица состояний, приведенная на рис. 8.12, а,
получена из диаграммы внутренних состояний для задачи, стру-
ктурная схема которой содержит один выходной сигнал X и один
выходной сигнал Z.
В результате первого разбиения в одну и ту же секцию поме-
щаются все те состояния, для которых значения выходных сигналов
совпадают при всех возможных значениях входов. Например, если
текущее состояние схемы So, то существуют два возможных входа
(X = 0 и X = 1), для которых значения сигнала на выходе равны
О и 1 соответственно. Точно так же, если текущим состоянием яв-
ляется Ss, то для X = 0 и X = 1 на выходе будет Z = 0 и Z = 1.
Следовательно, эти два состояния появятся в одной и той же сек-
ции разбиения. Повторяя этот процесс для оставшихся состояний,
получим первое разбиение в виде
Pi = (So, S3, S6) (Si, S4) (S2, Se).
В действительности, это разбиение получено путем анализа поведе-
ния схемы при подаче на ее вход последовательности единичной
Длины.
Л 111011110010101111 — ----------*"
Z 100011000000001100 —- Л.
Логическая
схема
Z
а)
КА=ВХ+ВХ
г)
Второе разбиение Р2 получается с помощью следующей проце-
дуры. Для текущих состояний So, S3, S6 и X = 0 следующие со-
стояния находятся в той же самой секции разбиения Рг. Однако
при X = 1 следующими состояниями для So, S3, S5 являются со-
ответственно S4, S6 и S5. Следующее состояние для S3 при X = 1
е)
Рис. 8.11. Устройство обнаружения последовательности 111:
а — структурная схема; б — диаграмма внутренних состояний; в — таб-
лица состояний; г — карты Карно, служащие для определения входных
сигналов JK-триггеров; д — реализация устройства; е — временные диа-
граммы, иллюстрирующие работу устройства
Состояния
текущее следующее
x = 0 X = 1
So Si s2 S3 s4 S5 Se N N N N N tsa tsj II li II <?> II £> II II 1! — 0 0 0 — — 0 0 0 — co" 11 03 II co" II co45 II co” II 0? II co” II tsj N N N N N N
Состояния
текущее следующее
X = 0 X = 1
Sq5 su S«fi S3 N tsj tsj tsj II & II & II E3 II s’ 0 ь— ь— О <O -4 — cz? II cl II 0? II tf II N N N N
а) б)
Рис. 8.12. Пример использования метода разбиения:
а — таблица состояний; б — сокращенная таблица состояний после разбиения
Состояния
текущее следующее
Х = 0 X=1
$о So Z = 0 S2 z=o
5, S3, z= 1 So z=o
Sz S3 z=o S5 z=o
S3 ^z-t S, z=o
Sy Ss Z= 1 Ss z=o
S3 Sz Z=0 Sz z=o
56 S, z= 1 s? z=o
S? s? z=o Sz z=o
д)
Состояния
текущее следующее
x=o X=1
$0257 Sq257 2-0 $0257 2 = 0
Sr S3 Z=1 $0257 2=0
s3 Sy Z=1 It ** Cb
Sy Ss Z=1 Ss z=o
Ss Г\4 II "* $0257 Z=0
*)
рис. 8.13. Пример использования метода импликаций:
а — таблица состояний, которую необходимо минимизировать с помощью метода имплика-
ций; б — таблица импликаций; в — исключение ячеек, соответствующих состояниям, имею-
щим неодинаковые выходы; г — дополнение таблицы парами импликаций; д — таблица
импликаций после анализа; е — список секций разбиения; ж — сокращаемая таблица со-
стояний
не лежит в той же секции Ръ следовательно, первая секция Ръ
в свою очередь, разделяется на две подсекции: в первой подсекции
остаются состояния So и S5, а вторая подсекция содержит только
состояние S3. Эта процедура повторяется для второй секции разбие-
ния, но так как следующие состояния для Si и S4 будут оставаться
в той же секции Р2 независимо от значения X, то нет необходи-
мости проводить разбиение этой секции. Анализируя третью секцию
разбиения, видим, что эту секцию также невозможно разделить.
Следовательно,
Р2 = (S0S5) (S3) (SA) (SA).
Это разбиение получено с помощью применения входной последо-
вательности, длина которой равна 2.
Описанная процедура используется для определения Р3, но
в данном случае Р3 = Р2. Следовательно, все секции Р2 содержат
эквивалентные состояния схемы, и дальнейшее разбиение невоз-
можно. На рис. 8.12, б приведена таблица состояний схемы после
использования метода разбиения.
Второй метод сокращения состояний, которым может пользо-
ваться проектировщик, основан на применении таблицы имплика-
ций. На рис. 8.13, а изображена таблица состояний синхронной
последовательности схемы. Анализ этой таблицы показывает, что
не существует состояний, которые можно объединить.
Покажем, как составляется таблица импликаций (рис. 8.13, б).
Строкам таблицы соответствуют состояния, причем первой строке —
состояние Si, второй — S2 и т. д. Столбцам также соответствуют
состояния: первому — So, второму — Si и т. д. В таблице импли-
каций содержатся всевозможные комбинации пар состояний и каж-
дая ячейка таблицы используется для проверки эквивалентности
данной пары состояний. Например, верхняя левая ячейка таблицы
определяет два состояния (So и Si), которые проверяются на экви-
валентность.
Одно из условий эквивалентности состояний гласит: два состоя-
ния являются эквивалентными в том случае, когда выходы, порожда-
емые следующими для них состояниями, идентичны. В таблице имп-
ликаций перечеркнуты все ячейки, которым соответствуют неэкви-
валентные, с этой точки зрения, пары состояний.
Например, состояния So и Si не могут быть эквивалентными, так
как выходные сигналы следующих состояний равны 0, 0 и 1, О
соответственно. Поэтому ячейка таблицы, находящаяся на пересе-
чении So и St, будет перечеркнута. Точно также перечеркнуты
ячейки, содержащие другие неэквивалентные пары состояний
(рис. 8.13, в).
Следующим шагом является заполнение импликациями непере-
черкнутых ячеек таблицы (см. рис. 8.13, в). Импликация позволяет
установить, при каких условиях данная пара состояний будет
эквивалентна, например, ячейка на пересечении So и S2 содержит
импликацию, указывающую на следующее: для того чтобы состоя-
ния So и S2 были эквивалентными, необходимо, чтобы So было
эквивалентно S5 и S2 было эквивалентно S5. Таблица импликаций
с заполненными ячейками приведена на рис. 8.13, г.
Если импликация, относящаяся к какой-либо ячейке, включает
два состояния, совпадающие с двумя состояниями, определяющими
эту ячейку, и если состояния, следующие за двумя состояними,
определяющими ячейку таблицы, являются одинаковыми для дан-
ного входа, то два состояния, определяющие ячейку, эквивалентны.
Соответствующая ячейка помечается галочкой. Первая часть этого
правила может быть применена к двум ячейкам таблицы, приве-
денной на рис. 8.13, г; это ячейки, определяемые состояниями So
и S7, а также состояниями S2 и S6. На рис. 8.13, г эти две ячейки
помечены галочками.
Анализ таблицы показывает, что состояния S2 и S5 образуют
пару, которая «блокирует» все остальные состояния. При подаче
синхронизирующего импульса можно перейти из S2 в S5 и наоборот,
но переход к другим состояниям невозможен. Следовательно, эти
два состояния можно объединить, сформировав новое состояние,
и тогда при постуглении синхронизирующего импульса схема будет
оставаться в этом новом состоянии. Ясно, что для выхода из этого
состояния необходим сигнал сброса. То же самое можно сказать
по отношению к состояниям So и S7.
После этого необходимо проанализировать всю таблицу имплика-
ций, строка за строкой, начиная с правой нижней ячейки. Перечер-
кивать нужно ячейки, содержащие хотя бы одну из пар, которая
ранее была уже перечеркнута. Сначала можно перечеркнуть ячейку,
находящуюся на пересечении S4 и Se, поскольку указанная в ней
пара состояний 86—S7 ранее уже была перечеркнута. Эта процедура
повторяется до тех пор, пока в таблице еще есть неперечеркнутые
ячейки. Окончательная форма таблицы импликаций изображена
на рис. 8.13, д.
Теперь составим список состояний так, как показано на
рис. 8.13, е. Проанализируем таблицу импликаций (см. рис. 8.13, д)
столбец за столбцом справа налево для того, чтобы установить, не
осталось ли неперечеркнутых ячеек, так как именно такие ячейки
определяют пары эквивалентных состояний. В первом столбце пере-
черкнута единственная ячейка, поэтому против состояния Stt
в списке разбиения ничего нет. Просматривая второй столбец,
обнаруживаем, что состояния S2 и S7 эквивалентны . и поэтому
они присутствуют рядом с состоянием 86. В третьем и четвертом
столбцах все ячейки перечеркнуты, поэтому запись (S2S7) повторя-
ется рядом с S4 и 83. В пятом столбце существуют две перечерк-
нутые ячейки, которые определяют две пары эквивалентных состоя-
ний (S2S5) и (S5S7).
Правило транзитивности устанавливает, что
(SPS9) (S9Sr) ->(SpS?Sr).
Используя это правило, вносит в список рядом с S2 запись (S2S5S7).
Для оставшихся столбцов все делается точно также. В результате
окончательное разбиение будет иметь следующий вид:
Р = (S0S2S5S7) (Si) (S3) (S4) (Se).
Таблица состояний для этого разбиения представлена на
рис. 8.13, ж.
8.8. Кодирование состояний
Во всех рассмотренных выше задачах состояния кодировались
совершенно произвольно. Например, для устройства обнаружения
последовательности 111, описанного в п. 8.6, кодирование состоя-
ний было проведено так: So = 00, Si = 01, Sa = 11, S3 = 10.
Совершенно очевидно, что можно выбрать другой способ кодирова-
ния, который приведет к другой схемной реализации. Критерием
качества кодирования состояний является простота схемной реа-
лизации.
Проблема кодирования состояний заключается в выборе связи
вторичных переменных с состояниями таким образом, чтобы схемное
решение получалось если не самым простым, то было бы значительно
проще большинства решений, полученных при случайном коди-
ровании. К сожалению, пока не существует метода кодирования
состояний, приводящего к простейшей реализации. Однако в этом
параграфе будут рассмотрены некоторые правила, позволяющие
получить сравнительно простые схемные решения.
Термин «более простые схемы» означает, что для их реализации
требуется меньше логических элементов, а значит и меньше инте-
гральных схем. Если проектируемая схема должна производиться
в больших количествах, то можно ожидать значительного умень-
шения средств, затраченных на ее производство. Более простая схем-
ная реализация предполагает также уменьшение количества входов
составляющих ее элементов и, как следствие, сокращение количества
внутрисхемных соединений, а также значительную экономию за-
нимаемого схемой места.
Следующий пример демонстрирует целесообразность «хорошего»
кодирования.
На рис. 8.14, а приведена структурная схема устройства. По
входной линии X устройства поступают числа в четырехразрядном
коде NBCD. Информация передается последовательно (первым идет
наибольший значащий бит), причем каждая цифра синхронизирована
тактовым импульсом.
Соответствующая этой задаче диаграмма внутренних состояний
показана на рис. 8.14, б. Путь So -> S4 -> S2 -> S3 связан с первыми
восемью комбинациями кода NBCD с 0000 по 0111 включительно.
Второй путь So -> S4 -> S7 -> S3 связан с двумя другими кодовыми
Со- стоя- ние Варианты кодирования CBA
1 2 3
So ООО ООО ООО
Si 001 001 001
S.. ОН 010 он
S3 010 ОН 010
s4 110 100 100
s6 111 101 101
S6 101 но 111
s7 100 111 но
8)
Элементы И—НЕ Варианты кодирования
1 2 3
22 18 16
ИМС: 2 с 4 входами 3 с 3 входами 4 с 2 входами 1 2 4 1 1 4 1 1 4
Всего ИМС 7 6 6
Всего входов 49 39 33
г)
Состояния
теку- щее следу- ющее
о II II
So Si s2 S3 s4 S5 So s7 s4 s2 s3 So S7 S6 So S3 S4 So s; So S5 So So So /X oo oi и io
0 1 S3 S6 Sz 5?
S, 5» So %
Состояния Входные сигналы триггеров
текущее следующее X=0 X = 1 X = 0 X = 1 X= 0 X = 1
СВА x=o CBA x=i CBA Jc Kc Jc Kc Jb Kb J в Кв Ja Ka Ja Ka
So 111 100 101 0 0 0 0 0 1 0 1 0 1 0 0
S4 100 Oil Oil 0 1 0 1 1 0 1 0 1 0 1 0
So 011 000 000 0 0 0 0 0 1 0 1 0 1 0 1
Sg 000 111 111 1 0 1 0 1 0 1 0 1 0 1 0
S4 101 010 110 0 1 0 0 1 0 1 0 0 1 0 1
s5 110 001 001 0 1 0 1 0 1 0 1 1 0 1 0
So 001 111 111 1 0 1 0 1 0 1 0 0 0 0 0
S, 010 000 001 0 0 0 0 0 1 0 1 0 0 1 0
ж)
Рис. 8.14. Устройство обнаружения неправильных кодовых комбинаций:
а — структурная схема устройства; б — диаграмма внутренних состояний; в — три варианта
кодирования состояний; г — сравнение количества элементов н микросхем, требуемых для
реализации устройства при трех случайно выбранных вариантах кодирования; д — таблица
состояний устройства; е — таблица кодирования внутренних состояний; ж — таблица со-
стояний, в которой коды состояний получены на основе использования правил 1 и 2; з —
карты Карно для входных сигналов триггеров; и — реализация устройства
комбинациями — 1000 и 1001. Неиспользуемые кодовые комбина-
ции связаны со следующими путями: So -> St -> S5 -> Se с кодо-
выми комбинациями с 1100 по 1111 включительно и So->S4—>-
-► Se -> S7 с кодовыми комбинациями 1010 и 1011. Выходной сиг-
нал Z = 1 формируется в состоянии Se. Он появляется только в слу-
чае обнаружения неиспользуемых кодовых комбинаций.
Три случайно выбранных варианта кодирования для этой схемы
показаны на рис. 8.14, в. Уравнения входов для триггеров А, В и С,
требующихся для реализации схемы, и уравнение выхода приведены
отдельно для каждого варианта кодирования.
Вариант кодирования 1
JА — СХ -X ВСХ; JB = СХ + АС + АСХ; Jc = АВХ;
КА=~ВС + ВС; Кв = СХ + АС + АВС; Кс = ВХ + АВ;
Z = лвсп.
Вариант кодирования 2
JA = А + ВС +ВС + ВХ; JB = А + СХ; Jc = АВХ;
КА = В + С + X; Кв = АС + АС; Кс = АВ + ВХ;
Z = АВСП.
Вариант кодирования 3
JA = СХ + ВСХ; JB = А + СХ; Jc = АВХ;
КА = В; Кв = АС + ЛС; Кс = АВ + ВХ; Z = ЛВСП.
На рис. 8.14, г приведены результаты сравнения числа элемен-
тов, требуемых для реализации схемы, для трех вариантов коди-
рования состояний. Анализ этой таблицы показывает, что для реа-
лизации варианта 3 потребуется наименьшее количество аппара-
туры. Однако гораздо быстрее и надежнее, чем при использовании
случайного выбора, можно прийти к простой схемной реализации,
используя два простых правила кодирования.
Таблица состояний устройства обнаружения неиспользуемых
кодовых комбинаций приведена на рис. 8.14, д, а правила, позво-
ляющие провести успешное кодирование внутренних состояний,
даны ниже.
Правило 1. Те состояния, из которых^ возможны переходы
только в одни и те же состояния хотя бы для одного значения вход-
ного сигнала, необходимо кодировать так, чтобы их кодовые комби-
нации отличались только одной цифрой, т. е. эти состояния должны
быть логически смежными. Например, анализ таблицы состояний,
приведенной на рис. 8.14, д, показывает, что при X = 0 следующим
для состояний S3 и Se является состояние So. Значит, коды этих
состояний должны отличаться не более чем одной цифрой. По тем же
причинам состояния S2 и 57(атакже56 и S7) являются логически
смежными.
Правило 2. Если состояния являются следующими для одного
и того же состояния, то им необходимо назначать логически смежные
кодовые комбинации. Применение этого правила, например, для
устройства, таблица состояний которого изображена на рис. 8.14, д,
позволяет сделать вывод, что состоянием Si и S4 следует назначить
логически смежные значения, так как эти состояния являются сле-
дующими для состояния SB. По этой же причине состояниям S7
и S5, а также S3 и Se следует назначить логически смежные зна-
чения.
Таким образом, в результате применения правил 1 и 2 получим
следующие наборы смежных состояний:
Правило 1: (S3, S6) (S2, S7) (S6, S7).
Правило 2: (S4, S4) (S6, S7) (S3, Se).
На рис. 8.14, e показано, как следует закодировать состояния,
чтобы удовлетворить полученным выше условиям смежности. Если
при использовании этих правил невозможно удовлетворить всем
условиям смежности, то приоритетом должно пользоваться пра-
вило 1.
На рис. 8.14, ж приведена таблица состояний. Состояния в ней
закодированы так, как показано на рис. 8.14, е. К таблице до-
бавлены значения входов триггеров, полученные обычным путем.
Карты Карно для упрощения входных сигналов J и К изображены
на рис. 8.14, з. Заметим, что нет необходимости составлять карты
Карно для сигналов JB и Кв, так как все значения JB и Кв
равны 1 или 0. Следовательно, JB = Кв — 1-
Формулы для входных сигналов триггеров приведены ниже:
]с = В; JB = L- JA = В + С + X;
Кс=^ + ВХ; Кв = L; КА = ВС + ВХ + ВС; Z = ЛВСП.
На рис. 8.14, и показана действующая схема устройства об-
наружения неиспользуемых кодовых комбинаций. Для ее реализа-
ции необходимы десять элементов И—НЕ или четыре следующие
микросхемы: одна микросхема, содержащая два четырехвходовых
элемента И—НЕ; одна микросхема, содержащая три трехвходовых
элемента И—НЕ, две микросхемы, содержащие четыре двухвходо-
вых элемента И—НЕ. Таким образом, общее число входов будет
равно 23.
Очевидно, что в результате такого кодирования для реализации
схемы потребуется меньше аппаратуры, чем при любом из трех слу-
чайных вариантов кодирования, приведенных на рис. 8.14, в.
У пражнения
У8.1. Для последовательной схемы, показанной на рис. У8.1, найти:
а) таблицу состояний;
б) диаграмму внутренних состояний;
в) функцию схемы.
У 8.2. Двоичные данные в последовательной форме, синхронизируемые такто-
выми импульсами, поступают по линии X в логическую схему, изображенную на
рис. У8.2. На выходе Z сигнал появляется только тогда, когда на вход подается
строка 1101 (отметим, что если две строки перекрывают друг друга, то должно фор-
мироваться два выходных сигнала). Разработать синхронную последовательную
схему устройства обнаружения строк 1101.
У 8.3. Данные в коде XS3 в последовательной форме, синхронизируемые так-
товыми импульсами, поступают на вход логической схемы (рис. У8.3). Схема пред-
назначена для генерации выходного сигнала в случае подачи на ее вход неиспользу-
емой в данном коде комбинации цифр. Разработать синхронную последовательную
логическую схему, используя //(-триггеры и элементы И—НЕ.
У 8.4. Синхронизирующий сигнал X стробируется сигналом т. Стробирую-
щий сигнал должен поступать в схему так, чтобы на ее выходе вырабатывались
только полные синхронизирующие импульсы. Временная диаграмма работы схемы
приведена на рис. У8.4. Спроектировать синхронную последовательную схему,
удовлетворяющую этим требованиям.
У 8.5. Спроектировать схему, в которой с помощью сигнала кнопочного уп-
равления S выбирается один синхронизирующий импульс Z. Интервалы времени
между моментами нажатия кнопки носят случайный характер, и длительность сиг-
нала зависит от продолжительности нажатия на кнопку и значительно больше дли-
тельности синхронизирующих импульсов. На рис. У8.5 показана временная диа-
грамма работы схемы.
У 8.6. На вход полного сумматора последовательного действия поступают две
двоичные цифры А и В. Работа сумматора управляется сигналом синхронизации, и,
кроме того, подача цифр А и В согласована по времени с приемом единицы переноса
из предыдущего разряда. На выходе сумматора формируются сигналы суммы и пе-
реноса. Сигнал переноса хранится в блоке памяти (рис. У8.6) до тех пор, пока
вместе с синхронизирующим импульсом не поступит следующая пара двоичных цифр.
Разработать логическую схему для блока памяти, используя триггеры и элементы
И—НЕ. Нарисовать временное диаграммы характеризующие поведение устройства
во время выполнения операции.
У 8.7. Последовательная схема имеет вход X, вход синхронизации и выход Z-
Считается, что поступающие на линию X данные делятся на группы, содержащие по
четыре цифры. Значение выходного сигнала Z равно 1, когда обнаруживается любая
из следующих трех последовательностей: 1010, ОНО, 0010. Построить диаграмму
состояний и реализовать схему устройства, используя JX-триггеры и элементы
ИЛИ—НЕ.
У 8.8. Последовательная логическая схема должна использоваться для под-
счета количества 1 в строке двоичных цифр. Если в строке содержится четное число
единиц, то на выходе схемы должен появиться сигнал Z— 1, но только при ус-
ловии, что в строке не было подряд двух 0. Если встречаются подряд два 0, то схема
должна возвратиться в свое первоначальное состояние и начать счет с нуля.
Разработать схему, выполняющую эти функции.
У 8.9. На вход изображенного на рис. У8.9 устройства сравнения последо-
вательного действия поступают четырехбитовые двоичные числа: А3А2А1Ао и
B^B2BiB0, причем наибольшим значащим битом является первый. Разработать
синхронную последовательностную схему, на выходе которой должны быть следу-
ющие сигналы при следующих условиях: Zi = 1 при А > В, Z2 = 1, при А — В,
Zs = 1 при А < В.
У 8.10. Для управления схемой синхронного счетчика используются два сигнала
А и В. Если А = 0, В — 0, то схема должна находиться в нерабочем состоянии;
если А = 0, В = 1, то схема должна работать как счетчик по модулю 4; если
А= 1, В = 0, то схема должна работать как счетчик по модулю 8. Спроектиро-
вать такую схему.
Рис. У8.2 Рис. У8.3
—I I--------------
< п п п п_______________________________
Рис. У8.4
Рис. У8.5
Рис. У8.9
Рис. У8.6
У8. 11. Используя:
а) правила слияния Колдуэлла;
б) метод разбиения;
в) метод таблиц импликаций,
найти минимальные таблицы состояний для синхронных последовательных авто-
матов, таблица состояний которых приведена ниже:
Текущее состояние Следующее состояние Текущее состояни Следующее состояние Текущее 1 состояние Следующее состояние
X 0 X=1 x~o X=1 X-° X=1
•$0 Si z=o N Il Co II ts О So Si z=o N II °0 11 00 0 S8 IN 0” Si 2 z=o
Sr о z"ll NJ S4 z=o Si s. z=o N 11^ 0 So S10 Z-0 S11 z=o
s2 № 11^' о о c^ll N S2 He?1 0 0 o?ll N S10 So z=o 0 0? II N
S3 N 11=^ N II ¥ о S3 So z=o So z=o Su 0 co II NJ О 0? II N
S4 So Z=0 So z=o s4 II & 0 II & S12 S13 Z=0 S14 z=o
s5 So Z=0 So z=o S5 0 z”ll NJ 0 N S13 So z=o So z=o
«о So z=o N 11=^ S6 s, II & II & 0 0 So z=o So z=\ S14 So z=o NJ 11=^
У8.12. Синхронный последовательный автомат имеет следующую таблицу
состояний:
Для всех возможных входных последовательностей длиной 1, 2, 3, .... п оп-
ределить соответствующие выходные последовательности. Кроме того, провести раз-
Текущее состояние Следующее состояние Текущее состояние Следующее состояние Текущее состояние Следующее состояние
x--=o x- 1 X=--0 X=1 X с х=н
So 0 zT II NJ 1 0 ^IL N S2 0 z II N S5 Z=1 s4 N II О S2 z=o
Si tN 0 z" II NJ S3 0 z II NJ tN S6 S6 о о Z° II z"* И NJ NJ °° z" II II NJ NJ
биение состояний.
У8.13. Используя правила, приведенные в настоящей главе, провести коди-
рование состояний для тех таблиц состояний, которые были получены при решении
задач У8.2 и У8.3.
У8.14. Используя JK-триггеры, разработать синхронную последователь-
ную схему, характеристические уравнения которой имеют вид
At+&t = (АВХ+ ВХ)1', Bt+&t = (AX)‘,
где X — входной сигнал, а уравнение выхода определяется как Z — АВ. Построить
для этой схемы таблицу состояний и диаграмму состояний.
9, АСИНХРОННЫЕ СХЕМЫ
9.1. Введение
Существует очень много последовательных схем, для управления
которыми используются не сигналы синхронизации, а определенные
события. Так, например, цифровая система может приводиться в дей-
ствие только в момент появления неисправности. В этом случае по-
явление неисправности как раз и является тем событием, которое
управляет работой схемы. Поскольку события такого рода возни-
кают нерегулярно, схемы получили название асинхронных последо-
вательных схем или, более точно отражая сущность происходящего,
схем, управляемых событиями.
В этой главе будет рассматриваться процедура проектирования,
применяемая для создания асинхронных схем, причем она будет
основана на использовании характеристического уравнения QMt =
= (S + RQ)1, полученного в гл. 5 для SR-триггера.
9.2. Задача определения числа посетителей музея
В качестве примера асинхронной схемы рассмотрим проектиро-
вание последовательной схемы, предназначенной для определения
числа посетителей музея. На рис. 9.1, а показано, что в качестве
входных сенсорных устройств используются два световых луча,
разнесенных на расстояние 152 мм. Считается, что в любой момент
времени войти в музей может только один человек. Кроме того,
предполагается, что человек вошел в музей, если он сначала пересек
линию луча Xi, а затем линию луча Х2- Если кто-то выходит из му-
зея, то прерывается сначала луч Х2, а затем Хх. В том случае, если
прерывается только один луч, подсчет не ведется. Будем считать,что
прерыванию луча соответствует сигнал, равный логической «1».
На рис. 9.1, б приведена структурная схема задачи. Сигналы на
входах Xi и Х2 возникают, когда прерываются лучи сенсорных
устройств. Будем называть эти два сигнала главными переменными.
Схема имеет только один выход/, который должен на короткое время,
когда человек входит в музей, приобрести значение, равное логи-
ческой «1». Именно этот сигнал может быть использован в качестве
асинхронного тактового входа для многокаскадного счетчика.
На рис. 9.1, в приведена диаграмма внутренних состояний для
решаемой задачи. Состояние So может считаться состоянием покоя
в том смысле, что человек либо окончательно вошел в музей, либо
окончательно вышел из него. Путь на диаграмме состояний, соот-
ветствующий процессу входа человека в музей, имеет вид So -> Si ->
-» S2 -> S3 -» So; аналогично, путь, соответствующий процессу вы-
хода, имеет вид So -> S3 -> S4 —> Si -> So. На диаграмме состояний
учтен также тот случай, когда человек колеблется, входя в музей
или покидая его. Например, для человека, который пересекает
только линию луча Xj, а затем поворачивает обратно, последователь-
ность состояний имеет вид So-^Sj-^Sg.
Теперь, когда проанализирована диаграмма внутренних состоя-
ний, можно построить таблицу состояний. Таблица имеет пять строк,
по одной для каждого текущего состояния, и четыре столбца, по
одному для каждой комбинации входных сигналов. Таблица состоя-
ний показана на рис. 9.1, г. Каждая из двадцати ячеек таблицы на-
ходится на пересечении столбца, соответствующего определенному
текущему состоянию системы, и строки, соответствующей опреде-
ленной комбинации входных сигналов. В каждую ячейку помещена
1
I
I
--------к
Вход |
I
Z
.1
I
Луч 1
X,
Выход
I
Текущее состо - яние Следующее состояние и Выход
X, Хг О О *1 %2 0 1 XtXz 11 Х,Хг 10
So z=o S, z = o S, z = o
St So z=o Sz Z=1 ^z=o
Sz S3 z=o z = 1 St z=o
s3 So z=o ^z=o s4 z=o
Sj z=o ® Z=0 St z = o
Рис. 9.1. Задача определения числа посетителей музея:
а — схема входа людей в музей (и выхода из музея); б — структурная схема; в — диаграмма
сокращенная диаграмма внутренних состояний; ж — реализация устройства контроля
информация о следующем состоянии и выходном сигнале, которая
однозначно определяется текущим состоянием и значениями входных
сигналов. Для примера возьмем первую строку таблицы. Ей соот-
ветствует текущее состояние So. Если входные сигналы и Х2
равны соответственно 0 и 1, следующим состоянием системы будет S3,
а выходом Z = 0.
Заметим, что, пытаясь совершить переход, можно остаться в том
же самом состоянии. Такие состояния называются стабильными.
Рассмотрим первую строку таблицы. Для нее текущее состояние —
So. Возьмем значения входных сигналов XjX2 = 00. Тогда следую-
щим состоянием будет также So, т. е., по существу, перехода
делать не надо, и <S0 — стабильное состояние. Если, однако, те-
кущее состояние системы So и XjX2 = 10, то следующим состоя-
нием будет Si, и переход, на совершение которого требуется время,
будет иметь место. Очевидно, что во время перехода система не на-
ходится в стабильном состоянии.
Условие стабильности имеет вид
S* = $<+«,
где — текущее состояние системы и S/+6i — следующее состоя-
ние. Опираясь на вышеизложенное, можно сказать, что условие
нестабильности имеет вид
S* =£ St+bt.
Дальнейший анализ таблицы показывает, что ее некоторые
ячейки не заполнены. Например, в первой строке, которая связана
с состоянием So, нет данных в ячейке, соответствующей входной
комбинации Х1Х2 = 11. Из диаграммы состояний видно, что в со-
стояние So можно попасть либо из состояния Sj, либо из состояния S3
Текущее состо- яние Следующее состояние и выход
х,хг 0 0 х,хг 0 1 Х,Хг 1 1 XrXz 10
$012 ($oiz\ ^-^=0 $34 z=o (p) ^z=o
$34 $012 Z=0 z=o z= 0 $012 Z=0
s)
вНутреииих состояний; г — таблица состояний; д — сокращенная таблица состояний; е
с входным сигналом XjX2 = 00. Если теперь потребовать, чтобы
сразу после переходов в состояние 30 входной сигнал стал XiX2 =11,
то должно произойти одновременное изменение двух главных пере-
менных Xj и Х2.
В этой главе будет разрабатываться схема, которая будет допу-
скать изменение только одной главной переменной в один момент
времени. Это ограничение справедливо в данном случае, поскольку
световые лучи разнесены на расстояние 152 мм и не могут быть
прерваны одновременно. Говорят, что схема, созданная с учетом
этого ограничения, работает в основном режиме.
Таблицы состояний, которые содержат незаполненные ячейки,
называются не полностью определенными таблицами. В таблице
состояний, изображенной на рис. 9.1, а, незаполненные ячейки
соответствуют запрещенным входным комбинациям. Эти незапол-
ненные ячейки сродни «термам, не доставляющим беспокойства»
(см. гл. 1), и они могут быть использованы для упрощения таблицы
состояний, которую, на первый взгляд, упростить нельзя. Поскольку
условия, которым соответствуют незаполненные ячейки, не могут
возникнуть, то у проектировщика «не вызывает беспокойства» по-
ведение схемы в этих условиях.
В процессе упрощения таблицы состояний можно присваивать
значения состояниям и выходам незаполненных ячеек так, чтобы
строки таблицы полностью совпадали. Две идентичные строки
можно слить, используя правила слияния Колдуэлла, описанные
в гл. 7.
Анализ таблицы состояний, изображенной на рис. 9.1, г, пока-
зывает, что строки So, и 32 идентичны и могут быть слиты;
также могут быть слиты и строки З3 и 34. После слияния состоя-
ния So, Sj и S2 образуют новое состояние S012, а состояния З3
и 34 образуют новое состояние S3i. Упрощенная таблица состояний
приведена на рис. 9.1, д; упрощенная диаграмма состояний, полу-
ченная из таблицы состояний, показана на рис. 9.1, е.
Так как в новой сформированной диаграмме всего два состоя-
ьяи, то вполне достаточно одной вторичной переменной А для их
идентификации. Будем считать, что А = 0 для состояния S0j2 и
А = 1 для состояния S3i. Тогда значением выходного сигнала Z
будет логическая «1», если схема находится в состоянии S012 и на
вход подается сигнал Х4Х2 =11.
Попробуем настроить логическую схему для нашей задачи с по-
мощью характеристического уравнения ЯЗ-триггера:
Qt+6t =(S + RQY,
выведенного в гл. 5. В этом уравнении S и R — отпирающий и за-
пирающий входы триггера. Если считать А переменной, отражающей
состояние триггера, то условия запирания и отпирания триггера
могут быть получены непосредственно из упрощенной диаграммы
состояний.
Отпирание: А = Х4Х2.
Запирание: А = Х2.
Следовательно, А = XjX2 + Х2Л, а для выхода Z получаем
Z = ЛХЛ.
На рис. 9.1, ж приведена реализация логической схемы.
9.3. Гонки и циклы
Когда вторичные переменные связываются с внутренними со-
стояниями синхронного автомата (т. е. производится кодирование
внутренних состояний), то основным критерием, лежащим в основе
этой связи, является минимизации аппаратуры, необходимой для
реализации автомата. Было отмечено, что пока неизвестен такой ме-
тод кодирования, который позволял бы минимизировать количество
аппаратуры, хотя были предложены способы, приводящие к про-
стой, а возможно и простейшей реализации. В асинхронных схемах
критерий, лежащий в основе кодирования внутренних состояний,
несколько иной. В этом параграфе будут рассмотрены те факторы,
которые влияют на кодирование переменных.
На рис. 9.2, а изображена диаграмма внутренних состояний
автомата. Вторичные переменные связаны с внутренними состояни-
Рис. 9.2. Циклические переходы и некритические гонки:
а — диаграмма состояний автомата, позволяющая продемонстрировать условия возникно-
вения циклических переходов и некритических гонок; б — таблица состояний, иллюстри-
рующая циклические переходы; в — таблица состояний, иллюстрирующая некритические
гонки
ями автомата произвольным образом. На рис. 9.2, б изображена
таблица состояний автомата, которая была получена с помощью
диаграммы состояний.
Предположим, что первоначально автомат находится в стабиль-
ном состоянии, которое определяется так: АВ = 10 (S3), X = 0.
Затем X изменяется от 0 к 1. Тогда автомат совершит переход
в нестабильное состояние So (АВ = 00). Так как значение X про-
должает оставаться равным 1, когда автомат перешел в состояние X,
то следующий переход будет сделан в состояние Предполагая,
что в дальнейшем входной сигнал не изменится, получаем, что авто-
мат, пройдя через состояние S2, возвратится в S3. Таким образом
совершен обход всей диаграммы состояний. Этот процесс будет про-
должаться, пока X = 1.
Анализ таблицы состояний показывает, что автомат, покинув
состояние S3, перейдет в состояние So (см. правую нижнюю ячейку
таблицы). После этого автомат по очереди попадает во все нестабиль-
ные состояния, которые располагаются в столбце, соответствующем
X = 1. Это будет продолжаться до тех пор, пока X не станет рав-
ным 0. Такое поведение автомата называется зацикливанием.
Если X изменяется от 1 до 0, когда автомат находится в состоя-
нии АВ = 00, то автомат должен перейти в состояние АВ =11.
После этого автомат перейдет в стабильное состояние, которое ха-
рактеризуется следующими значениями переменных состояния и
входного сигнала: X = 0 и АВ = 10. Автомат может попасть в это
заключительное состояние несколькими путями, поскольку АВ
может изменяться от 00 к 11 различными способами. Например,
А и В могут изменяться одновременно, и тогда цепочка переходов
будет такой, как описано выше. Однако В может изменяться раньше,
чем А. В этом случае сначала произойдет переход в состояние
Si ( АВ = 01), затем в S2 (11), и, наконец, автомат окажется в ста-
бильном состоянии S3 (10). С другой стороны, А может измениться
быстрее В. Тогда автомат перейдет в стабильное состояние непо-
средственно из So. Если автомат попал в стабильное состояние, то
он будет оставаться там до тех пор, пока не изменится хотя бы одна
из главных переменных. Следовательно, если А изменится раньше,
чем В, автомат перейдет в состояние S3 по пути, не показанному на
рис. 9.2, а, и будет оставаться там до тех пор, пока значение X
не станет равным 1. На рис. 9.2, в показаны три варианта перехо-
дов, соответствующие трем различным ситуациям, описанным выше.
Из материала, который был изложен в предыдущих главах, мо-
жно сделать следующий вывод: если изменение главной переменной
ведет к изменению двух вторичных переменных, то могут возник-
нуть гонки. Причиной возникновения гонок являются задержки эле-
ментов при генерировании сигналов А и В. В случае, описанном
выше, гонки называются некритическими, поскольку, независимо
от совершаемых переходов, автомат всегда окажется в одном и том
же стабильном состоянии.
Кроме того, существуют гонки, появляющиеся в асинхронных
схемах, характерной особенностью которых является то, что дости-
f)
Рис, 9.3. Критические гонки:
а — диаграмма состояний автомата, позволяющая продемонстрировать условия возникно-
вения критических гонок; б таблица состояний, иллюстрирующая критические гонки
жение стабильного состояния в них зависит от порядка изменения
вторичных переменных. Такие гонки называются критическими.
Рассмотрим пример. На рис. 9.3, а изображена диаграмма внутрен-
них состояний автомата, а на рис. 9.3, б—таблица состояний ав-
томата. Будем считать, что первоначально автомат находится в со-
стоянии, которое определяется следующим образом: АВ = 00,
X = 0. Если значение X становится равным 1, то автомат будет
осуществлять переход сразу в стабильное состояние (АВ = И,
X = 1), но только в том случае, если А и В изменяются одновременно.
Если же А изменяется быстрее В, то автомат перейдет в состояние
АВ = 10, X = 1.Это стабильное состояние, и автомат будет оста-
ваться в нем неопределенное время, так как выход из этого состоя-
ния отсутствует. Такой же вывод позволяет сделать и беглый взгляд
на рис. 9.3, а.'
Рассмотрим случай, когда В изменяется быстрее А. Тогда сна-
чала автомат делает переход в состояние АВ = 01, X = 1. По-
скольку это состояние не является стабильным, автомат совершает
следующий переход в состояние АВ = 11, X = 1. Описанные пе-
реходы могут привести к неправильному функционированию авто-
мата. Критические гонки появляются в автомате, так как его ра-
бота может завершиться в одном из двух стабильных состояний.
Причем, в каком именно из этих двух состояний окажется автомат,
зависит от порядка изменения вторичных переменных.
На рис. 9.3, б изображена таблица состояний автомата. На ней
стрелками указаны возможные переходы.
9.4. Противогоночное кодирование для автомата
с тремя состояниями
Ясно, что ситуаций, когда могут возникнуть критические гонки,
следует избегать. Добиться этого позволяет противогоночное коди-
рование внутренних состояний автомата. При противогоночном
Рис. 9.4. Противогоночное кодирование:
а — диаграмма состояний автомата, для которого
надо провести противогоиочиое кодирование; б —
включение дополнительного состояния для прове-
дения противогоиочиого кодирования
кодировании в момент пере-
хода из одного внутреннего
состояния в другое должна
изменяться только одна вто-
ричная переменная.
На рис. 9.4, а показана
диаграмма, состоящая из
трех состояний. Для иденти-
фикации этих состояний до-
статочно двух вторичных
переменных. Кодирование
внутренних состояний про-
изведено произвольно. Ана-
лиз всех возможных пере-
ходов показывает, что при
переходе из состояния S2 в So должны изменяться значения обеих
вторичных переменных. Вообще говоря, невозможно провести поз-
воляющее избежать гонок кодирование внутренних состояний ав-
томата, содержащего три состояния, если допустим переходы между
любыми двумя состояниями.
Далее, с помощью двух вторичных переменных можно закоди-
ровать четыре состояния. Поэтому для автомата, диаграмма состоя-
ний которого изображена на рис. 9.4, а, остается одно неиспользу-
емое состояние, которого нет на рисунке. Отметим, что наличие этого
состояния также создает определенные трудности проектировщику.
Так в п. 9.3 было показано, что если выход из состояния не пре-
дусмотрен, то возможна блокировка автомата.
Эти две проблемы можно решить введением в диаграмму состоя-
ний неиспользуемого состояния АВ = 10 (So), из которого автомат
всегда будет переходить в состояние So. Таким образом, еще одно
дополнительное состояние потребуется теперь для реализации
схемы.
9.5. Задача о подаче воды в водонапорную башню
Шаг 1. Постановка задачи. Два насоса и р2 используются
для подачи воды в водонапорную башню. Оба насоса начинают ра-
боту, когда вода опускается ниже уровня 1, и продолжают ее до
тех пор, пока вода не достигнет уровня 2. В этом случае насос рг
прекращает работу и ждет, пока уровень воды не станет ниже от-
метки 1. Насос р2 продолжает работу до тех пор, пока вода не до-
стигнет уровня 3. После этого он останавливается и ждет, пока вода
не опустится ниже уровня 1.
Датчики уровней вырабатывают следующие сигналы:
а — 1, когда уровень воды достигнет или поднимется выше отметки 1, в
противном случае а = 0;
b= 1, когда уровень воды достигнет или поднимется выше отметки 2, в про-
тивном случае b = 0;
с= 1, когда уровень воды достигнет или поднимется выше отметки 3, в про-
тивном случае с = 0.
Рис. 9.5. Задача о подаче воды в водонапорную башню:
а — схема работы водонапорной башни; б — структурная схема устройства управления на-
сосами; в — основная диаграмма внутренних состояний; г — таблица состояний; |д — мо-
дифицированная диаграмма состояний; в — реализация устройства управления насосами
Задача заключается в разработке асинхронной схемы, служа-
щей для управления насосами рх и р2.
Схематическое изображение водонапорной башни приведено на
рис. 9.5, а, а структурная схема проектируемого автомата управле-
ния насосами — на рис. 9.5, б.
Шаг 2. Диаграмма внутренних состояний. На рис. 9.5, в пред-
ставлена диаграмма внутренних состояний автомата. Состоянию So
соответствует ситуация, когда вода поднялась выше уровня 3,
и оба насоса отключены. Когда резервуар пустеет и уровень воды
падает ниже отметки 1, осуществляется переход в состояние Sx,
так как а = 1. В состоянии Зх оба насоса работают. Если вода, про-
должая прибывать, достигает уровня 2, осуществляется переход
в S2, и насос рх отключается. Из состояния S2 возможны два перехода:
если уровень воды упадет ниже отметки 1, произойдет возврат в Sx
в ответ на сигнал а = 1; если уровень воды будет подолжать расти
и достигнет отметки 3, будет осуществлен переход в So, и оба насоса
прекратят работу.
Шаг 3. Таблица состояний. На рис. 9.5, г показана таблица
состояний для этой задачи. Следует отметить, что комбинации вход-
ных сигналов abc = 001, 010, 011 и 101 не присутствуют в таблице,
поскольку они могут возникнуть только в результате сбоя в работе
датчиков.
Для определения трех состояний потребуются две вторичные
переменные А и В. Так как переходы возможны между любыми
двумя состояниями, то свободное от гонок кодирование провести
нельзя. Следовательно, необходимо ввести в диаграмму состоя-
ний дополнительное состояние Sd. На рис. 9.5, д приведена мо-
дифицированная диаграмма состояний.
Шаг 4. Разработка уравнений схемы:
Условие отпирания для А: ЬВ.
Условие запирания для А: В + Ва = В + а.
Условие отпирания для В: аА.
Условие запирания для В: сА.
Следовательно,
А = ЬВ 4- (В 4- а) А = ЬВ ф- аАВ
и
В = аА 4- (сЛ) В = аА 4~ (с 4- Л) В.
Также
Pi = АВ
и
р2 = АВ 4- АВ = В.
Шаг 5. Реализация. На рис. 9.5, е показана реализация уст-
ройства управления насосами.
9.6. Противогоночное кодирование для автомата
с четырьмя состояниями
На рис. 9.6 показана диаграмма внутренних состояний автомата
с четырьмя состояниями. Переходы осуществляются только между
соседними состояниями. Например, возможны переходы из So в Sx,
из Sx в S2 и т. д. Кодирование внутренних состояний может быть
проведено с помощью двух вторичных переменных А и В. Причем
кодирование проводится таким путем, что
когда осуществляется переход из одного
состояния в другое, только одна вторичная
переменная изменяет свое значение.
На рис. 9.7, а изображена диаграмма
состояний автомата, который допускает пере-
ход в несоседнее состояние. Примером
такого перехода является переход из S3 в Sj.
В этом случае при использовании двух вто-
ричных переменных не удается провести
свободное от гонок кодирование. Если коди-
рование провести так, как показано на
рис. 9.6, то при переходе из состояния S3
в состояние Sj сразу две вторичные пере-
менные изменят свое значение. При любом
способе связи вторичных переменных с вну-
тренними состояниями будет существовать
хотя бы один переход, выполнение которого
значений сразу у двух вторичных переменных. Этот факт позволяет
So
So Si
Sj s2
Рис. 9.6. Диаграмма со-
стояний автомата с
четырьмя состояниями
(переходыразрешены толь-
ко между соседними со-
стояниями)
приведет к изменению
а)
Рис. 9.7. Противо-
гоночное кодирова-
ние автомата с че-
тырьмя состояния-
ми и одним диаго-
нальным переходом:
а — диаграмма со-
стояний; б — карта
Карно для проведе-
ния потивогоночного
кодирования; в — но-
вая диаграмма со-
стояний, позволя-
ющая избежать гонок
Рис. 9.8. Противогоночное кодирование автомата с четырьмя состояниями и двумя
диагональными переходами:
а — диаграмма состояний; б — карта Карно для противогоночного кодирования; в — новая
диаграмма состояний, позволяющая избежать гонок
сделать вывод о том, что противогоночное кодирование может быть
осуществлено только с использованием трех вторичных переменных.
На рис. 9.7, б изображена карта Карно для трех вторичных
переменных. Противогоночное кодирование может быть легко про-
ведено с помощью этой карты. Напомним важное свойство карт
Карно: коды соседних ячеек отличаются только одной позицией,
поэтому состояния, соответствующие соседним ячейкам, будут иметь
коды, отличающиеся только одной позицией.
Четыре внутренних состояния автомата должны быть связаны
с ячейками карты Карно таким образом, чтобы были смежными
ячейки, соответствующие So и St, ST и S2 и т. д. Однако, чтобы
обеспечить противогоночное кодирование, необходимо, чтобы были
смежными ячейки, соответствующие состояниям S2 и S3, а также
S2 и So. Просмотр карты Карно показывает, что добиться этого не-
возможно. Следовательно, переходы из S2 в S3 и из S3 в So
должны осуществляться через промежуточные состояния Sdl и Sd2
соответственно. На рис. 9.7, в изображена модифицированная ди-
аграмма состояний. Она содержит пять состояний, два из которых
дополнительные. Каждый переход в этой диаграмме связан с изме-
нением только одной вторичной переменной; следовательно, гонок
возникнуть не может.
Единственным изменением, которое проведено с диаграммой
состояний, изображенной на рис. 9.7, в, является введение второго
диагонального перехода из состояния S2 в состояние So, как по-
казано на рис. 9.8, а. На карте Карно (рис. 9.8, б) четыре перво-
начальных состояния So, S1; S2 и S3 размещены так же, как и
в предыдущем случае. Но поскольку требуется предусмотреть пере-
ход из S2 в So, вводится дополнительное состояние Sd3. На
рис. 9.8, в показана модифицированная диаграмма состояний. Она
может быть использована для реализации автомата с помощью
элементов И—НЕ.
9.7. Устройство обнаружения последовательности
В заключение рассмотрим еще один пример асинхронной схемы-
Он поможет снова обратить внимание на те проблемы, которые стоят
перед проектировщиком асинхронных схем.
Этот пример касается проектирования устройства обнаружения
последовательности. Устройство имеет два входа Х± и Х2 и один
выход Z. Структурная схема устройства обнаружения последо-
вательности приведена на рис. 9.9, а. На выходе устройства будет
логическая «1», если на входе появляется следующая последова-
тельность входных сигналов Х±Х2 : 00, 10, 11.
Как обычно, сначала проектировщик должен разработать диа-
грамму внутренних состояний. Для этого требуется выделить основ-
ные элементы в диаграмме состояний. В данном случае потребуется
четыре состояния, которые связаны между собой тремя переходами,
отмеченными сигналами Х1Х2, Х}Х2 и Х}Х2 соответственно.
Для того чтобы завершить построение диаграммы состояний,
необходимо только предусмотреть дополнительные переходы. Причем
эти дополнительные переходы могут затронуть любое состояние.
Например, автомат переходит из состояния So в состояние Si при
появлении входного сигнала Х±Х2. Поскольку автомат проектиру-
ется для работы в основном режиме, то главные переменные Х±
и Х2 одновременно измениться не могут. Следовательно, автомат
может покинуть состояние St только при следующих значениях
входных сигналов: XtX2 или Х±Х2. Сигнал перехода представляет
собой вторую нужную комбинацию искомой последовательности и
используется как сигнал, инициирующий переход из Si в S2.
С другой стороны, изменение Х2 от О-> 1 даст в результате
сигнал перехода Х±Х2. В этом случае автомат должен предусматри-
вать возврат в состояние So, где он будет ожидать появления пер-
вого сигнала последовательности Х±Х2. На рис. 9.9, в изображена
полная диаграмма состояний автомата. На этой диаграмме сигнал
Z = 1 появляется в состоянии S3, когда завершено формирование
искомой входной последовательности. Если на вход автомата, нахо-
дящегося в состоянии S3, приходит сигнал Х±Х2 или Х^ц автомат
будет возвращаться в состояние So, где он будет ожидать появления
сигнала перехода ХгХ2. Напомним, что ХГХ2 — первый сигнал ис-
комой последовательности.
Многие проектировщики имеют привычку дополнять диаграмму
состояний петлями. Например, если автомат переходит в состояние
по сигналу Х1Х2 и продолжает оставаться там до тех пор, пока
сигнал существует на входных линиях, это может быть пока-
зано путем изображения на диаграмме состояний петли, начинаю-
щейся в и оканчивающейся там же. Рис. 9.9, г иллюстрирует
Л,
х2
Устройство
оЗнаружения
последователь'
ности цифр
а)
эту ситуацию. На этой диаграмме состояний изображены все воз-
можные петли. Например, когда автомат находится в состоянии So,
переходу So -> So соответствует сигнал ХГХ2 + ХгХ2 + XtX2. Это
означает, что автомат, перешедший в состояние So в ответ на один
из сигналов ХГХ2 или XiX2, будет оставаться в этом состоянии, даже
если сигнал на входе изменится с XtX2 на ХАХ2 в первом случае
и с Х^Х2 на Л1Х2 во втором случае. Предположим, что сигнал на
входе стал XtX2. Тогда автомат сможет покинуть состояние So,
если сигналы и Х2 будут изменяться в соответствии со следую-
щими двумя последовательностями:
а) 11 01 00;
б) 11 10-> 00.
На рис. 9.9, д изображена таблица состояний, которая построена
на основе информации, содержащейся в диаграмме состояний.
Рис. 9.9. Устройство обнаружения последовательности цифр (реализация на эле-
ментах И—НЕ):
а структурная схема устройства; б — основные элементы диаграммы внутренних состоя-
ний; в — диаграмма внутренних состояний; г — диаграмма внутренних состояний с пет-
лями; д — таблица состояний; е — упрощенная таблица состояний; ж — упрощенная диа-
грамма состояний; з — диаграмма состояний, включающая дополнительное состояние (на
рисунке присутствуют также коды сдстояний); и — реализация
Анализ таблицы состояний показывает, что строки St и 52 могут
быть слиты. Следовательно, таблица состояний может быть упрощена.
Но, с одной стороны, это упрощение приведет к нежелательным по-
следствиям по следующим двум причинам: во-первых, появится
неиспользуемое состояние, и, во-вторых, кодирование, позволяю-
щее избежать гонок, не может быть проведено, поскольку в диаграмме
состояний остается теперь только три состояния. Однако, с другой
стороны, неиспользуемое состояние может рассматриваться как
дополнительное состояние, из которого предусмотрен безусловный
переход в следующее состояние. Наличие безусловного перехода
на диаграмме состояний приведет к упрощению условий за-
пирания и отпирания триггеров и, следовательно, к более простой
логической реализации.
На рис. 9.9, е показана новая упрощенная таблица состояний.
Следует заметить, что в таблице существует одна незаполненная
ячейка (она расположена в строке 53). Этой ячейке соответствуют
условия (53X5X2 = 00), «не вызывающие беспокойства», т. е. если
текущее состояние автомата 53, то сигнал перехода ХГХ2 запрещен.
Так как этот сигнал не может появиться, когда автомат находится
в состоянии S3, он может быть использован как терм согласования.
Этот терм может быть добавлен к булевому выражению для функции
перехода 53 -> 50, как показано на диаграмме состояний, изобра-
женной на рис. 9.9, ж. Добавление терма согласования приводит
к упрощению выражения, описывающего сигнал перехода.
На рис. 9.9, з изображен окончательный вариант диаграммы со-
стояний. Она образована из диаграммы состояний, представленной
на рис. 9.9, ж, добавлением одной дополнительной переменной.
Каждому состоянию присвоен код.
Условия отпирания и запирания могут быть получены непосред-
ственно из диаграммы состояний.
Условие отпирания для А: ВХ±Х2 -f- В (Х± -f- Х2).
Условие запирания для А: ВХгХ2;
А = ВХЛ + В (Xi + Х2) + (ВХА) А = BXjX2 + В (%! + Х2) +
+ (В -f- Х1 + Х2) А.
Условие отпирания для В: АХхХг.
Условие запирания для В: А;
В='АХ1Ха + АВ.
Уравнение для выхода Z имеет вид Z = 53 = АВ. На рис. 9.9, и
показана схема реализации автомата.
Другой метод проектирования устройства обнаружения последо-
вательности основан на использовании 57?-триггеров. На рис. 9.10, а
изображена таблица состояний, полученная из диаграммы состоя-
ний, представленной на рис. 9.9, з. Также на рис. 9.10, а, рядом
с текущими состояниями, расположены их коды. Однако удобнее
поменять местами строки таблицы состояний так, чтобы вторичные
00 01 11 10
S/2 Z = 0 N _ z = o Z = 0
г= о So Z = 0 N II @ Z = 0
Sd z = o Sd z = o Z = 1 Sd z = o
So z=o N Il So z=o So z = o
а)
00 10 01 00
11 11 01 11
10 10 10 10
00 10 10 10
S)
Qt ^st s R
0 0 1 1 0 1 0 1 0 1 0 0 0 0 1 0
S)
С
г)
5^ -XfXz+SXz
Рис. 9.10. Устройство обнаружения последовательности цифр (реализация на SR-
триггерах):
а — таблица состояний, используемая для реализации устройства на основе 5/?-триггеров;
б — таблица возбуждения триггеров; в — управляющая таблица для S/^-триггера; г — карты
Карио для входных сигналов £/?-триггеров; д — реализация устройства
переменные располагались в порядке, принятом для карт Карно.
В то же время состояния внутри ячеек таблицы целесообразно за-
менить теми значениями вторичных переменных, которые их опре-
деляют, как это показано на рис. 9.10, б.
Полученную таблицу можно рассматривать как таблицу воз-
буждения триггеров. Она вместе с управляющей таблицей S7?-
триггера, изображенной на рис. 9.10, в, даст возможность проекти-
ровщику получить карты Карно для S- и 7?-входов двух триггеров.
Например, когда текущее состояние автомата АВ = 00 и входной
сигнал Х±Х2 = 01, то следующее состояние АВ = 10. Ясно, что
в этом случае триггер А осуществляет переход 0-> 1, а состояние
триггера В не меняется.
На рис. 9.10, г изображены карты Карно для входных сигналов
триггеров. После упрощений можно получить следующие выражения
для сигналов сброса:
SA = + ВХ2, SB = АХхХ2;
Ra = BXtX2, RB = А.
Выход определяется как Z = S3 = АВ. На рис. 9.10, д пред-
ставлена реализация автомата с помощью 57?-триггеров и элементов
И—НЕ.
Упражнения
У9.1. Устройство обнаружения последовательности имеет два входа Xi и Х2
и один выход Z. Выходной сигнал Z становится равным 1 только при входной по-
следовательности 00, 01, 11. Выходной сигнал Z становится равным 0 после по-
явления на входах последовательности сигналов 11, 10, 00. На рис. У9.1 изоб-
ражена временная диаграмма работы устройства обнаружения;
Разработать для проектируемого устройства диаграмму состояний и получить
таблицу состояний. Упростить, если возможно, таблицу состояний и реализовать
устройство, используя:
а) элементы И—НЕ;
б) SP-триггеры и элементы И—НЕ.
У9.2. Ниже определены характеристики JK-триггера:
а) если Q = 0, когда J = 1, К = 0 и Си = 1, триггер изменяет свое состоя-
ние с 0 на 1 в момент появления отрицательного фронта импульса синхронизации;
б) если Q = 0, когда J = 0, К = 1 и Си = 1, триггер изменяет свое состоя-
ние с 1 на 0 в момент появления отрицательного фронта импульса синхронизации;
в) если J = 1, К — 1 и Си = 1, триггер запирается.
Разработать асинхронную схему для реализации такого триггера и начертить
временную диаграмму, характеризующую его работу.
У9.3. Xi и Х2 — два входа, a и Z2 — два выхода асинхронной схемы. Ко-
гда Х±Х2 = 00, тогда Z\Z2 = 00. Если изменение сигнала Xi с 0 на 1 предшест-
вует изменению сигнала Х2 с 0 на 1, то на выходе схемы появляется Z^Z2 = 01.
Рис. У9.1
Рис. У9.5
Рис. У9.4
С другой стороны, если изменение Х2 с 0 на 1 предшествует изменению Xi с О
на 1, то на выходе схемы появляется ZiZ2 = 10. В обоих случаях значение выхода
остается равным 01 и 10, соответственно, пока значение XiX2 не станет равным 00.
У 9.4. Разработать асинхронную схему, которая будет пропускать на выход
импульс синхронизации после того, как на входе X появляются два импульса.
Импульсы на входе появляются совершенно случайно и предполагается, что ин-
тервалы времени между появлением этих импульсов больше периода сигнала син-
хронизации. Временнйе диаграммы, поясняющие условие задачи, показаны на
рис. У9.4.
У 9.5. Логическая схема (рис. У9.5) имеет два асинхронных входных сигнала и
входной сигнал синхронизации. Схема должна быть построена так, чтобы тактовый
импульс пропускался на ее выход Z только, когда сначала на входе Xlt а затем на
входе Х2 появляются 1. После того, как тактовый импульс появится на выходе
схемы, она должна возвратиться в состояние покоя, когда Х±Х2 = 00.
Разработать схему, выполняющую описанные выше функции, и реализовать ее
на элементах И—НЕ.
У 9.6. Проанализировать основной режим работы схемы, показанной на
рис. У9.6. Для этого необходимо выполнить следующее:
а) построить таблицу состояний;
б) построить диаграмму состояний;
в) используя таблицу состояний, определить реакцию системы на входную
последовательность XiX2 = 00, 01, 11, 10, 11, 01, 00, 10, 00, 01. Начальные
условия определяются как Х2 = 0, Х2 ~ 0, А = 0.
У9.7. Изучить схему, показанную на рис. У9.7:
а) построить таблицу состояний;
б) построить диаграмму состояний;
в) используя таблицу состояний, определить реакцию системы на входную
последовательность XiX2 = 00, 01, И, 10, 00, 01, 11, 01, 11, 10, 00. Считать, что
начальные условия определяются как Xi = 0, Х2 = 0, А = 0, В = 0.
Рис. У9.6
Рис. У9.7
Рис. У9.8
Рис. У 9.10
У9.8. На рис. У9.8 показана диаграмма состояний цифрового автомата с че-
тырьмя состояниями. Построить для этого автомата таблицу состояний. Определить
все возможные условия возникновения гонок в том случае, если автомат будет ре-
ализован в соответствии с диаграммой состояний, показанной на рис. У9.8. Опреде-
лить, какие гонки являются критическими, а какие нет. Для каждой гонки указать
те нежелательные переходы, которые могут возникнуть. Модифицировать диаграмму
состояний таким образом, чтобы гонок между вторичными переменными не возни-
кало. Найти условия запирания и отпирания для вторичных переменных.
У9.9. Управление трехламповой электрической цепью осуществляется с по-
мощью трех переключателей. Если переключатели замыкаются последовательно —
сначала X, затем Y и, наконец, Z (XYZ) — загорается лампа £х. Если переключа-
тели замыкаются в порядке YZX, загорается лампа £2. И если переключатели за-
мыкаются в порядке ZXY, загорается лампа L3. Если переключатели замыкаются
в каком-либо другом порядке, красная лампа загорается для оповещения оператора,
который должен привести все переключатели в первоначальное разомкнутое состоя-
ние. Реализовать схему, выполняющую эти функции, на элементах И—НЕ.
У9.10. На рис. У9.10 дана таблица состояний автомата. Провести противого-
ночное кодирование и реализовать автомат иа основе SP-триггеров и элементов
И-НЕ.
10. ЛОГИЧЕСКОЕ ПРОЕКТИРОВАНИЕ НА ОСНОВЕ ИМС
СО СРЕДНИМ УРОВНЕМ ИНТЕГРАЦИИ
10.1. Введение
В течение последних лет разработано большое число интеграль-
ных микросхем (ИМС) со средним и большим уровнями интеграции,
которыми могут пользоваться разработчики логических систем.
Интегральные микросхемы делятся на три следующие группы:
а) ИМС с малым уровнем интеграции, содержащие отдельные
дискретные логические элементы, триггеры и т. д.;
б) ИМС со средним уровнем интеграции, представляющие собой
функциональные части логических систем, например, сумматоры,
мультиплексоры, устройства для выполнения операций сравнения,
умножения и т. д.;
в) БИС, или интегральные микросхемы с большим уровнем ин-
теграции, которые по праву можно считать логическими системами,
например, восьмибитовые микропроцессоры, контроллеры устройств
прямого доступа, калькуляторы и т. д. ,п
Внедрение ИМС со средним уровнем интеграции приводит к из-
менению старых методов логического проектирования. Обычно
разработчик получает логическую функцию как решение частной
задачи. Эта функция минимизируется с использованием методов,
описанных в предыдущих главах, а затем реализуется при помощи
ИМС с малым уровнем интеграции. Однако когда логическая функ-
ция реализуется при помощи ИМС со средним уровнем интеграции,
таких, как мультиплексор, она выражается в каноническом виде
(т. е. в любой терм булевой функции входит каждая из переменных
или ее отрицание) и реализуется непосредственно без минимизации.
Стоимость логической системы приблизительно пропорциональна
числу интегральных схем, содержащихся в ней. Таким образом, для
того чтобы сделать систему более дешевой, необходимо минимизи-
ровать число ее физических блоков. Поэтому разработчику логиче-
ских схем следует искать возможность замены большого числа ИМС
с малым уровнем интеграции на одну или более ИМС со средним уров-
нем интеграции. Часто предпочтительнее использовать стандартную
ИМС со средним уровнем интеграции, чем проектировать схему на
ИМС с малым уровнем интеграции, несмотря на то, что в результате
появятся избыточные или неиспользуемые логические элементы.
10.2. Устройство выбора линии передачи информации
или мультиплексор
Мультиплексор выбирает одну из п линий, где п обычно равно 4,
8 или 16. На рис. 10.1, а показана структурная схема мульти-
плексора, имеющего четыре входные линии Do, Dlt D2 и Ds и две
выходные линии f и f. У устройства есть также две управляющие
линии А и В и может быть линия сигналов разрешения Е. При
выборе информационной линии мультиплексор можно считать одно-
H3
Hz
a) fl
Puc. 10.1. Мультиплексор'
a — структурная схема
мультиплексора с четырьмя
входами; б — выбор одной
из четырех линий при помо-
щи однополюсного переклю-
чателя; в — реализация
мультиплексора с четырьмя
входами
полюсным переключателем, выбирающим, например, одну из че-
тырех линий, как показано на рис. 10.1, б. Реализация мультиплек-
сора с помощью логических элементов показана на рис. 10.1, в.
В сущности схема представляет собой элемент И—ИЛИ—НЕ,
имеющий два инвертированных по отношению друг к другу выхода.
Булева функция, описывающая выход f этой схемы, имеет следующий
вид:
f = ABD0 + ABDr + АВЪ2 + ABD3.
Выбор информационной линии может осуществляться подачей соот-
ветствующих двоичных сигналов по линиям А и В. Когда управля-
ющий сигнал АВ = 1, на выходе схемы появляется сигнал Do и т. д.
Некоторые мультиплексоры снабжены входной линией разре-
шающих сигналов, как это изображено на рис. 10.1, в. Когда на вход
этой линии подается логический «0», разрешается доступ к четырем
элементам И. Если разрешающий сигнал равен логической «1»,
работа мультиплексора запрещена.
Число информационных линий, из которых производится выбор,
может быть увеличено или с помощью одного мультиплексора, рас-
считанного на большое число информационных линий, или посред-
ством комбинации мультиплексоров. Комбинация двух четырех-
входовых устройств выбора, обеспечивающая выбор одной из восьми
линий, показана на рис. 10.2, а. Разрешающий сигнал в этом слу-
чае используется как дополнительный управляющий сигнал. Инфор-
мационные линии последовательно выбираются с помощью двоич-
ного счетчика. Двоичные значения управляющих сигналов Е, А
и В изменяются от ООО до 111 вместе с поступающим через равные
интервалы времени сигналами синхронизации. Таким образом, ин-
формационные линии Do, Dr, ..., D7 становятся поочередно дос-
тупны. Таблица истинности для схемы показана на рис. 10.2, б.
Пользуясь этим принципом, можно осуществлять выбор из большого
числа информационных линий. Например, изображенная на рис. 10.3
схема мультиплексирования, состоящая из девяти восьмивходовых
мультиплексоров и имеющая двухуровневую организацию, позво-
ляет осуществлять выбор одной из 64 линий.
Может быть предложен другой способ проектирования мульти-
плексора, если его рассматривать как преобразователь параллель-
ной информации в последовательную. Например, входные сигналы
на восьми линиях устройства, изображенного на рис. 10.2, а, со-
стоящего из двух мультиплексоров АД и М,,, могут быть пред-
ставлены как восьмибитовый код в параллельной форме, который при
использовании метода последовательного доступа может быть выдан
в последовательной форме.
Мультиплексор можно также использовать для генерации пов-
торяющихся двоичных последовательностей. На рис. 10.4 на ин-
61
Рис. 10.2. Восьмивходовая
мультиплексорная систе-
ма:
а — комбинация из двух
мультиплексоров, обеспе-
чивающая выбор одной нз
восьми информационных ли-
ний; б — таблица истинно-
сти для устройства выбора
одной нз восьми информа-
ционных линий
Но
л
Иг
и,
Ич
и.
По
И,
По
Ия
Лг
Hfz
Hi,
О14
П1}
Т>50
Поя
Doo
По,
Йог
По,
формационные линии восьмивходового мультиплексора подается
напряжение +5 или О В, т. е. логическая «1» или логический «О».
На управляющие линии А, В и С подаются сигналы с двоичного
счетчика. Повторяющаяся выходная последовательность при ис-
пользовании изображенного на рисунке способа соединений равна
10010011.
0.3. Мультиплексор как генератор логических функций
Уравнение для мультиплексора с четырехвходовыми линиями
имеет вид
/ = ABD0 + ABD, + ABD2 + ABD3,
где булевы переменные А и В представляют собой сигналы на ли-
ниях управления. А и В могут быть выделены как множители
из любой функции от п переменных, после чего остаточные функции *
от п — 2 переменных могут быть поданы на информационные линии.
* Функции г/;, у2, y<2k, зависящие от п—k переменных Xk+i, Xk+2, ..., Хп,
представляют собой остаточные функции разложения f (X,, Х2, ..., Хп) ~
= Х,Х2..... Xhyi+ XiX2, .... Xhy2+, ..., + Х,Х2, .... Xhy2h. —Прим. nep.
тырехвходового мультиплексора с управляющими переменными:
а — А нВ; б — А н С; в — В н С
Например, если п = 3, на каждую из информационных линий могут
поступить четыре функции от одной переменной. Допустим, что
третья переменная есть С. Тогда на информационные линии могут
поступить сигналы С, С, 0 и 1. В общей сложности существует
44 = 256 возможных комбинаций четырех входных сигналов, и
мультиплексор с четырьмя входными линиями может сгенерировать
любую из 256 возможных булевых функций от трех переменных.
Для мультиплексора с четырьмя входами возможны три сочета-
ния управляющих переменных (ЛВ, АС и ВС) и эти комбинации
можно поставить в соответствие отдельным информационным линиям,
как показано на рис. 10.5. Например, когда переменные А и В
являются управляющими, входной линии Do соответствуют ячейки
карты Карно, для которых А ~ 0 и В = 0, т. е. две верхние левые
ячейки карты Карно (см. рис. 10.5, а). Фактически карта Карно
для трех переменных теперь разбита на четыре двухячеечные карты
Карно для одной переменной, и каждой из этих двухячеечных карт
ставится в соответствие информационная линия.
Для примера рассмотрим реализацию функции трех переменных
f = АВС + АВС + АВС + АВС
при помощи мультиплексора с четырьмя входами. Сначала функцию
изображаем на карте Карно, как показано на рис. 10.6, а, и про-
извольно выбираем управляющие переменные, например, А и В.
Затем минимизируем набор из четырех функций от одной переменной,
соответствующих каждой из информационных линий. Например,
обе ячейки, соответствующие Dr, помечаем единицей и, следовательно,
на вход информационной линии Dr подается С + С = 1. Оставши-
еся входные функции, полученные при помощи карты Карно, на
рис. 10.6, а имеют следующий вид:
Do = С, D2 = 0, D3 = С.
Реализация функции изображена на рис. 10.6, б. Если бы в ка-
честве управляющих переменных были выбраны А и С, то на входы
мультиплексора подавались бы сигналы
Do = В, Di= 1, D2 = 0, D3 = В
и аналогично этому, если бы управляющими переменными были
выбраны В и С, входные сигналы имели бы следующий вид:
Do = 0, = A, D2 = A, D3 = 1.
Рис. 10.6. Получение
функции от трех пере-
менных с помощью четы-
рехвходового мультиплек-
сора:
а — функция f = АВС 4*
4- АВС -}- АВС 4- АВС; б,
в н г — генерация функ-
ции с использованием четы-
рехвходового мультиплексо-
ра прн помощи управляю-
щих сигналов А и В, А и С,
В н С соответственно
Соответствующие схемы подключения мультиплексора показаны
на рис. 10.6, в, г.
Рассмотрим теперь реализацию функции четырех переменных
f = £0, 1, 5, 6, 7, 9, 10, 14, 15
при помощи мультиплексора с четырьмя входами. Поскольку ис-
пользуется мультиплексор с четырьмя входами, то при передаче
двух переменных по управляющим линиям на информационные ли-
нии подаются остаточные функции от двух переменных. При выборе
управляющих переменных возможны шесть их сочетаний: АВ, АС,
AD, ВС, BD или CD. Эти комбинации можно поставить в соот-
ветствие информационным линиям, показанным на рис. 10.5. В этом
примере управляющими переменными выбраны Л и В, и карта
Карно, устанавливающая соответствие между ними и информаци-
онными линиями, показана на рис. 10.7, а. Карту Карно для четы-
рех переменных разделяем теперь на четыре четырехячеечные карты
для двух переменных и выполняем минимизацию для каждой из
этих карт отдельно.
Карта Карно для этой функции показана на рис. 10.7, б, и вход-
ные сигналы для информационных линий, полученные из четырех
строк этой карты, имеют вид
Do = С, Dr = С + D, D2 = CD + CD, D3 = С.
Реализация функции показана на рис. 10.7, в.
Следует отметить, что полезно сопоставлять различные варианты
выбора управляющих переменных, чтобы проверить минимальность
полученного решения. В рассматриваемом случае для реализации
решения, получаемого, когда переменные С и D являются управля-
ющими, требуется меньшее число элементов.
Соответствие между информационными линиями и управляю-
щими переменными показано на рис. 10.7, г. Входные функции для
с и
Рис. 10.7. Получение функции от четырех переменных с помощью четырехвходового
мультиплексора:
а — соответствие между информационными линиями и переменными А и В; б — карта Карно
для функции f = £ 0, 1, 5, 6, 7, 9, 10, 14, 15; в — реализация функции с использова-
нием четырехвходового мультиплексора; г — соответствие между информационными ли-
ниями н управляющими переменными С и D\ д — другая реализация функции прн исполь-
зовании переменных С и D как управляющих
информационных линий получают при помощи карт Карно, изоб-
раженных на рис. 10.7, б. Они имеют вид
Do = АВ; D, = А + В; D2 = А + В; D3 = В.
Реализация функции показана на рис. 10.7, д. При этом выборе
управляющих переменных, как можно видеть, требуется на одну
логическую ячейку И—НЕ меньше.
Данную функцию также можно непосредственно реализовать
с помощью мультиплексора с восемью входами. Для управления
таким устройством необходимы три сигнала. В рассматриваемом
примере можно считать, что булевы переменные А, В и С являются
управляющими.
Карта Карно, устанавливающая соответствие информационных
линий управляющим переменным Л, В и С, изображена на
рис. 10.8, а. Из рисунка видно, что она разделена на восемь карт
для одной переменной. По рис. 10.8, б задаем функцию и ее мини-
мизацию выполняем с помощью карт для одной переменной. Сопо-
ставление заданной таким образом функции с рис. 10.8, а показы-
вает, что входные функции для информационных линий мульти-
плексора имеют вид
Do = 1; D2 = D; Dt = D; De = 0;
= 0; D3 == 1; £>3 = P; B>7 = 1.
a) 5)
Рис. 10.8. Получение функции от четырех переменных с помощью восьмивходового
мультиплексора:
а — соответствие информационных линий управляющим переменным АВС; б — упрощение
функции f = Е 0» 1. 5, 6, 7, 9, 10, 14, 15; в — реализация функции
Функция DE НЕ НЕ НЕ
Е - АВЕНЕ (0) АВЕНЕ (1) ABCDE_ (3) АВЕНЕ (6) АВСН_Е_ (7) А_ВЁНЁ_ (8) АВЕНЕ (14) А8_ЕП_Е (15) АВ_С_НЕ_ (17) АВ_СПЕ_ (18) АВЕНЕ .(20) АВЕНЕ (21) АВЕНЕ (22) АВЕНЕ (24) АВСНЕ_ (27) АВЕНЕ (28) АВЕНЕ (31) АВЁ АВЁ АВС АВЁ АВС АВЁ АВЁ АВС АВЕ АВЕ АВС АВС АВС АВЕ АВС АВЁ АВС
о
7
а)
Л
В)
Рис. 10.9. Двухуровневая схема получения функции, зависящей от пяти пере
а — определение входных функций для мультиплексора первого уровня; {б — соответствие
деления входных информационных сигналов на втором уровне мультиплексирования; г —
Реализация функции с помощью восьмивходового мультиплексора
изображена на рис. 10.8, в.
Если число переменных реализуемой булевой функции увеличи-
вается, необходимо использовать более одного уровня мультипле-
ксирования. Этот метод продемонстрируем на следующем примере,
в котором функция от пяти переменных, имеющая вид
f = 2°, 1, 3, 6, 7, 8, 14, 15, 17, 18, 20, 21, 22, 24, 27, 28, 31,
реализуется при помощи мультиплексоров с четырьмя входами.
Для первого уровня мультиплексирования управляющими выб-
раны переменные D и Е. Значения функции f приведены в левой
части таблицы, изображенной на рис. J0.9, а._Эта таблица содержит
четыре столбца, озаглавленных DE, DE, DE и DE. В столбце DE
перечислены все термы, состоящие из трех переменных (Д, В и С),
соответствующие DE. Терм ABCDE помечен в столбце DE термом
АВС, называемым входным. Эту процедуру повторяем для каждого
г)
менных:
информационных лнннй управляющим переменным В н С; в —карты Карно для опре-
два уровня мультиплекснровання, используемые для генерации функции /
терма функции от пяти переменных, и входной терм каждый раз
помещаем в соответствующем столбце таблицы.
Теперь очевидно, что для мультиплексора с пятью входами вход-
ные функции имеют вид
£>и = АВС + АВС + АВС + АВС + АВС;
Dn = АВС + АВС + АВС;
£>21 = АВС + АВС + АВС + АВС;
D31 = АВС + ~АВС + АВС + АВС + АВС.
Эти функции от трех переменных могут быть сгенерированы на
втором уровне мультиплексирования при помощи мультиплексора
с четырьмя входами описанным выше способом.
На втором уровне мультиплексирования, как показано на карте
Карно на рис. 10.9, б, управляющими переменными выбираются
В и С. На рис. 10.9, в изображены карты Карно для определения
входных функций для информационных линий на втором уровне
мультиплексирования. При помощи этих карт можно определить,
что входные функции имеют вид
£^02 = А, D12 = А; В22 ~ К ^32 ~ А,
D33 = 1, D13 = А; £>2з = 0, D33 = 0,
£\|4 ~ A, Z?14 “ 1, £^24 “ 0, £) 34 — А,
~ A, D13 = А, £>25 = A, D-i71 = 1.
Реализация функции f показана на рис. 10.9, г.
10.4. Дешифраторы и демультиплексоры
Демультиплексор выполняет функцию, противоположную функ-
ции мультиплексора. Его структурная схема показана на
рис. 10.10, а. Единственную входную информационную линию можно
подключить к одной из нескольких выходных линий с помощью соот-
ветствующего выбора сигнала на линиях управления.
Используя две входные линии, можно сформировать четыре
адреса и, следовательно, как показано на рис. 10.10, б, максималь-
ное число выходных линий, среди которых может быть осуществлен
выбор, равно четырем.
Разрешающая и информационная линии, обозначенные соот-
ветственно Еп и Da, соединяются с выходными логическими элемен-
тами при помощи элемента ИЛИ—НЕ. Такая организация входных
сигналов обеспечивает два режима работы устройства.
В первом режиме К = 1 при Ен = 0 и Da = 0, поэтому все
выходные логические элементы открыты. Для любых других значе-
ний Еп и Da в этом режиме К = 0, поэтому все выходные логиче-
ские элементы закрыты, а выходные линии постоянно установлены
в состояние логической «1». В рассматриваемом режиме демульти-
плексор с одним входом и четырьмя выходами будет работать как
дешифратор, обеспечивая на каждой отдельной входной линии лю-
бую из четырех возможных комбинаций входных сигналов А и В.
Например, выходом на линии 0 будет АВ и т. д. Кроме того,
эту схему можно использовать как генератор четырех канонических
термов от двух булевых переменных. Если на вход управляющих
линий А и В подан сигнал = АВ, то выходом на линии 1 бу-
дет Рх.
Рассмотрим второй режим. К = 1, если = 0 и Da = 0, и
тогда при управляющем сигнале = АВ выходной сигнал на линии
2 равен 0, т. е. Da. Напротив, если Еп = 0, a Da = 1, то К = 0,
и для управляющего сигнала f3 = АВ выходной сигнал на линии 3
равен 1 = Du. В этом режиме данные передаются через выход-
ной логический элемент, выбираемый при помощи адреса, заданного
на линиях управления.
10.5. Применение дешифраторов
В реальных системах часто используется дешифратор, имеющий,
как показано на рис. 10.11, четыре входных и десять выходных ли-
ний. Если входные сигналы имеют значения А = 0, В = 0, С = 0
и D = 0, то выходная линия, обозначен-
ная 0, будет установлена в логический «0».
Этот дешифратор можно использовать как
преобразователь двоично-десятичного ко-
да в десятичный. В сочетании с устрой-
ствами комбинационной логики его можно
применять для преобразования кодов.
Примером использования дешифра-
тора с четырьмя входными и десятью
выходными линиями может служить при-
менение его для преобразования двоично-
десятичного кода в пятиразрядный код
с тремя единичными разрядами или
Рис. 10.11. Структурная
схема дешифратора на четы-
ре входа и десять выходов
Р-термы Двоично-десятичный код Код «3 из 5»
А В с D V’ W X У 2
Ри 0 0 0 0 1 0 0 1 1
Pi 0 0 0 1 1 0 1 0 1
Р„ 0 0 1 0 1 1 0 0 1
Ps 0 0 1 1 0 0 1 1 1
Pi 0 1 0 0 0 1 0 1 1
Рь 0 1 0 1 0 1 1 0 1
Ре 0 1 1 0 0 1 1 1 0
Р- 0 1 1 1 1 0 1 1 0
Р* 1 0 0 0 1 1 0 1 0
Рь 1 0 0 1 1 1 1 0 0
a)
АВСП
Рис. 10.12. Использова-
ние дешифратора для пре-
образования кодов:
а — таблица соответствия
двоично-десятичных кодов
кодам «3 из 5»; б — преобра-
зователь двоично-десятич-
ного кода в код «3 из 5»
д)
код «3 из 5». Таблица соответствия этих кодов изображена на
рис. 10.12, а. С помощью этой таблицы можно сразу записать вы-
ражения выходных величин для кода «3 из 5» через Р-термы:
V == Ро + Р, + Р.2 + Р7 + Ps + Pv-,
W = Р2 + Р4 + Ръ + Р» + Ps + Р^
X = Р, + Р3 + Р5 + Ре + Р7 + Р9;
Y = Ро + Р3 + Р4 + Ре + Р7 + Р8;
Z = Ро + Р4 + Р2 + Р3 + Р4 + Р5.
Теперь имеем
v р3 + р4 ; рь р6,
следовательно,
V = Ра + Р< + Р6 + Рв
V = Р3Р4Р6РЪ.
Аналогично получаем
W ^~рор1рар7-,
X = Р0Р2Р4Р8;
Z Р еР -jP gP g.
Дешифратор с четырьмя входными и десятью выходными лини-
ями выдает инвертированные значения требуемых десяти Р-термов,
как показано на рис. 10.12, б. Для полной реализации преобразова-
теля кода соответствующие выходы дешифратора присоединяют
к пяти комбинационным схемам, используемым для генерации сиг-
налов V, W, X, Y и Z.
Метод, рассмотренный в этом примере, следует применять, если
реализуется много функций от одного и того же числа переменных.
По сравнению с этим для реализации схемы на мультиплексорах
потребовалось бы меньше дополнительных элементов, но необхо-
дим по крайней мере один мультиплексор для реализации каждой
функции.
Если для реализации булевых функций этим методом требуются
все Р-термы, необходимо использовать дешифратор с 4 входными
и 16 выходными линиями, который будет генерировать все 16 Р-
термов от четырех булевых переменных.
Дешифраторы также широко используются в микропроцессорных
системах. Очень часто в этих системах встречается задача выбора
центральным процессором одного из нескольких элементов памяти.
Для этой цели можно, например, использовать дешифратор «Интел
8205» (Intel), имеющий три входных и восемь выходных линий.
Структурная схема этого устройства показана на рис. 10.13, а,
а его таблица истинности изображена на рис. 10.13, б.
Так как используемый дешифратор имеет восемь независимых
выходных линий, может быть осуществлен выбор одного из восьми
элементов памяти. Процессор «Интел 8085» имеет 16 адресных
линий, и на две из них, А15 и А14, можно постоянно подавать нуле-
вой потенциал и использовать как разрешающие сигналы £4 и Р2,
тогда как на оставшуюся линию может быть подано напряжение
+5 В. Три адресные линии Ai3, Л12 и Аи можно присоединить
к трем входным линиям /0, /4 и /2 соответственно.
Путем изменения сигналов на линиях А13, А12 и Ап микропро-
цессор осуществляет выбор различных выходных линий, а значит
и различных элементов памяти. Все остальные адресные линии
(Ао — А10) подведены к элементам памяти, как показано на
рис. 10.14.
Рис. 10.13. Использование дешифратора для адресации в микропроцессорных си-
стемах:
а — дешифратор «Интел 8205» на трн входа и восемь выходов; б — таблица истинности
Минимальный адрес памяти, к которому может быть организован
доступ с помощью дешифратора, имеет вид
Л15Л14Л13Л12 Л11Л10Л8Л8 Л7Л6Л6Л4 Л3Л2Л1Л0 адресный бит
0000 0000 0000 0000 двоичное пред-
ставление
0000 шестнадцатерич-
ное представление
Рис. 10.14. Система выбора блока памяти для процессора «Интел 8085»:
МС ~ элемент памяти; СЕ — разрешение выбора элемента
При изменении Л13Л12Лп от ООО до 001 адрес принимает следующее
значение:
216214213 21а 2П21О2828 27262624 2322212°
0000 0111 1111 1111 двоичное представление
0 7 F F шестнадцатеричное пред-
ставление
Число, представляющее второй адрес, выражается в виде 211 = 2048.
Следовательно, первая выходная линия Оо может быть использована
для доступа к элементу памяти, имеющему максимальную емкость
2К байт. Аналогично, каждая выходная линия может быть исполь-
зована как разрешающая для следующих 2К байт памяти. Следо-
вательно, максимальная общая емкость памяти для системы, изоб-
раженной на рис. 10.14, равна 16К байт.
В терминологии, принятой в микропроцессорной технике, вы-
ходные линии дешифратора называют линиями выбора кристалла.
Элемент памяти, соответствующий отдельной линии выбора кри-
сталла, будет открыт, когда на нее подан нулевой потенциал.
10.6. Постоянные запоминающие устройства (ПЗУ)
Схема, изображенная на рис. 10.15, представляет собой ПЗУ
емкостью в 64 бит, организованное в виде восьми восьмиразрядных
слов. Оно состоит из трехразрядного дешифратора адреса, матрицы
памяти объемом 64 бит и восьми неинвертирующих буферных эле-
ментов. Разрешающий вход Е, если он находится в состоянии логи-
ческого «0», обеспечивает доступ ко всем элементам дешифратора
адреса. Вертикальные линии в матрице памяти называют линиями
слов, горизонтальные — линиями битов.
Слова записываются в ПЗУ по каждому адресу, а выход на линии
битов зависит от коммутации ее с адресуемой линией слов. Комму-
тация выполняется при помощи МОП- или биполярных транзисторов
в зависимости от применяемой технологии изготовления. Если
линия битов коммутируется через транзистор с линией слов, то ли-
ния битов переходит в состояние логической «1», когда выполняется
адресация к этой линии слов. Если коммутации нет, она остается
в состоянии логического «0». Таким образом, слово, записанное по
выбранному адресу, передается на выход. Схематическое предста-
вление запрограммированного ПЗУ объемом 64 бит показано на
рис. 10.16, а. Пересечения линий битов и слов, отмеченные точками,
означают вход ИЛИ для выходной функции. Например, выход Z8
задается формулой
= Ро + Ръ + Pi-
Следовательно ПЗУ, изображенное на рис. 10.16, а, используется
для генерации восьми функций от трех переменных, каждая из
которых выражается в каноническом виде. Если проектировщик
хочет реализовать функции, изображенные на рис. 10.16, а, он
Линии слов
Рис. 10.15. ПЗУ емкостью 64 бит. с дешифратором адреса и разрешающим входом
должен предоставить изготовителю ПЗУ коммутационную матрицу,
аналогичную изображенной на рисунке, или таблицу (истинности,
подобную таблице на рис. 10.16, б. В том же случае, если проекти-
ровщик хочет иметь возможность для самостоятельного программи-
рования памяти, ему следует воспользоваться программируемым по-
стоянным запоминающим устройством (ППЗУ).
10.7, Методы адресации для ПЗУ
Коммутационная матрица, показанная на рис. 10.17, а, состав-
лена для ПЗУ емкостью 2 х8 бит, адресуемого только в одном из-
мерении. Общая емкость этого ПЗУ равна 16 бит, и булевы функции,
генерируемые с его помощью, имеют следующий вид:
Zi = Р? + Ръ + Ру!
Z2 = Ро + Р4 + Р-о + Р7.
Линии слов
•1 И 1» И И II и И С» со со| 00 со Сж>| Го г>| Г-э Г1| п Г-э Г5| Линии битов А Г
0 f 1 '3 р f /> р 6 р
а)
Za=P<,+ Ps+P7
z7=p3+p5
Zi=PS
^Po+Pi+Pi+Pt+P-,
Z4=PO + P,+P5+P7
Z3=P7+P3+Plf+Ps+P7
Z2=PO+P7
^l~Po + Pz+P3+ Рц
Адрес Выходные функции
А в с А z2 z4 26 Z-, Z6
0 0 0 1 1 0 1 1 0 0 1
0 0 1 0 0 0 1 0 0 0 0
0 1 0 1 0 1 0 1 0 1 0
0 1 1 1 0 1 0 1 0 0 0
1 0 0 1 0 1 0 1 0 0 0
1 0 1 0 0 0 1 0 1 1 1
1 1 0 0 0 1 0 0 0 0 0
1 1 1 0 1 1 1 1 0 0 1
б)
Рис. 10.16. Использование
ПЗУ:
а — коммуникационная
матрица для ПЗУ с объ-
емом памяти 64 бит;
б — таблица истинности
Для этого метода адресации общее число соединений на входе и
выходе матрицы ПЗУ равно десяти.
Другой, двумерный, метод адресации для ПЗУ объемом 2 х8 бит
показан на рис. 10.17, б. Коммутационная матрица здесь обеспечи-
вает генерацию тех же самых булевых функций, что и в пре-
дыдущем примере. Каждая линия битов разделена на две сек-
ции, и выбор соответствующей секции выполняется при по-
мощи схем на элементах И/ИЛИ, управляемых булевой пере-
менной С.
При использовании метода двумерной адресации уменьшается
число соединений матрицы ПЗУ. Общее число соединений на входе
и выходе матрицы равно восьми, т. е. на два соединения меньше
по сравнению с одномерными методами адресации. Чем больше число
входных переменных, тем существеннее эта разница в числе соеди-
нений.
Рис. 10.17. Методы адресации ПЗУ:
8)
а — ПЗУ емкостью 2X8 бит, адресуемое в одном измерении; б — ПЗУ емкостью 2X8 бит,
адресуемое в двух измерениях; в — генерация одной булевой функции от четырех перемен-
ных с помощью двумерной схемы адресации
Та же самая матрица ПЗУ в сочетании с одним мультиплексором
на четыре входа может генерировать одну функцию от четырех пе-
ременных, имеющую вид
Z = Ра + Ръ + Р13 + Р15,
как показано на рис. 10.17, в. Для подключения этой матрицы тре-
буется восемь внешних контактов. Однако для генерации той же са-
мой функции при помощи адресуемого в одном измерении ПЗУ
потребовалось бы 17 внешних соединений матрицы.
Очевидно, что ПЗУ большой емкости также могут адресоваться
в двух измерениях. Например, при реализации ПЗУ объемом 1024
восьмиразрядных слов при использовании одномерного способа
адресации требуются: адресный дешифратор на десять входов и
1024 выхода и восемь выход-
ных линий. Общее число
соединений равнялось бы в
этом случае 1032. Рассмо-
трим использование схемы
двумерной адресации, изо-
браженной на рис. 10.18.
Шесть переменных А, В, С,
D, Е и F из общего числа
используются для управле-
ния дешифратором адреса на
шесть входов и 64 выхода,
а остальные четыре перемен-
ные (G, Н, I и J) приме-
няются как управляющие
сигналы для восьми 16-вхо-
довых мультиплексоров. Об-
щее число соединений для
Рис. 10.18. Уменьшение числа входных и вы-
ходных линий ПЗУ с помощью двумерной адре-
сации
матрицы ПЗУ этой схемы составляет 192, т. е. значительно
меньше, чем при одномерном способе адресации.
10.8. Проектирование последовательных схем с помощью ПЗУ
Для реализации последовательных схем, работа которых зависит
от времени, удобно использовать ПЗУ. Например, рассмотрим реа-
лизацию с помощью ПЗУ устройства обнаружения неверных дво-
ично-десятичных кодов, схема которого, построенная на JК. -триг-
герах и элементах И — НЕ, была описана в гл. 8.
В этой задаче последовательный двоично-десятичный код пода-
ется на линию X, причем первым идет старший разряд. Каждый
бит данных приходит вместе с синхроимпульсом. Требуется постро-
ить при помощи ПЗУ схему, которая генерирует сигнал ошибки
Z = 1 всякий раз, когда появляется неверный код.
Структурная схема устройства и диаграмма внутренних состояний
показаны на рис. 10.19, а, б. Таблица состояний, изображенная
на рис. 10.19, в, имеет форму, удобную для программирования
ПЗУ. Например, первая строка таблицы указывает на то, что при
входных для ПЗУ сигналах А = 0, В = 0, С =0 и X = 0, вы-
ходным словом ПЗУ будет А = 1, В = 0, С = 0 и Z = 0.
В соответствии с этой таблицей состояний строят коммутационную
матрицу для ПЗУ, как показано на рис. 10.19, г. Слуцуеч отметить,
что для ее реализации требуется ПЗУ емкостью 64 бит.
Кроме ПЗУ необходима дополнительная логическая схема для
выполнения выходной функции Z АВС, а также три триггера D-
типа, по одному на каждую из линий обратной связи для синхрони-
зации работы схемы с генератором синхроимпульсов. Соединение
этих дополнительных устройств с ПЗУ изображено на рис. 10.19, д.
Выходные сигналы будут передаваться из ПЗУ по линиям А, В и С
обратно ко входу ПЗУ при появлении отрицательных фронтов син-
хроимпульсов.
ПЗУ можно также использовать для построения асинхронных
последовательностных схем. Для примера такого их применения
рассмотрим устройство схемы управления уличным светофором.
Структурная схема устройства управления светофором изображена
на рис. 10.20. Временной сигнал и сигнал синхронизации Р являются
входными для устройства управления. Выходные же сигналы ис-
пользуются для переключения зеленой, красной и желтой ламп.
На рис. 10.20, б изображена диаграмма временных и синхрони-
зирующих импульсов и последовательность световых сигналов. Соот-
ветствующая диаграмма внутренних состояний показана на
рис. 10.20, в. При первоначальном включении устройства управле-
ния оно может оказаться в любом из восьми внутренних состояний,
но переход из S2 в S3 возможен только, если поданы сигналы Р и X.
Из временной диаграммы следует, что эта комбинация сигналов
появляется только во втором двухминутном интервале и, следова-
тельно, состояние S3 соответствует этому периоду времени. Синхро-
низация временных сигналов с последовательностью состояний
ABC
ООО
в)
Рис. 10.19. Устройство обнаружения неправильных кодов:
а — структурная схема устройства: б — диаграмма внутренних состояний: в — таблица
состояний; г — коммуникационная матрица; д — функциональная схема реализации
устройства с помощью ПЗУ
будет осуществляться тогда, когда схема переходит из состояния S2
в состояние S3.
Состояния Se и S7 избыточны. Если схема принудительно или
под воздействием каких-либо неисправностей попадает в одно из
этих состояний, обе красные лампы будут гореть одновременно.
Переход из Se в S7 безусловен, и схема будет оставаться в S7 до тех
пор, пока не придет сигнал РХ = 1, который осуществит переход
в состояние S3, и в результате будет обеспечена согласованная ра-
бота.
Синхронизация может быть также достигнута при помощи пере-
хода из S4 в S3, если следующая принимаемая схемой комбинация
сигналов РХ. Однако синхронизация посредством прямого перехода
в состояние S3 из состояний So, SL и S5 невозможна, так как для этого
потребовалось бы изменение более одной вторичной переменной, что
послужило бы причиной возникновения ситуации риска.
Таблица состояний, которая может быть использована для про-
граммирования ПЗУ, изображена на рис. 10.20, г, а соответствующая
двумерная матрица ПЗУ показана на рис. 10.20, д. Для реализации
схемы требуется ПЗУ объемом 288 бит. Схема соединений ПЗУ ука-
зана на рис. 10.20, е.
10.9. Программируемые логические матрицы (ПЛМ)
У ПЗУ на десять входов имеется 2О10 = 1024 адресных линий.
Если у ПЗУ восемь выходных линий, его общий объем памяти равен
8Х 1024 = 8192 бит, т. е. 8К бит. При увеличении числа входных
линий от 10 до 12 число адресных линий возрастает до 4096, а емкость
памяти становится равной 8 X 4096 = 32768 = 32К бит.
Один из способов реализации памяти для 12 входных линий за-
ключается в использовании четырех ПЗУ по 8К бит, соединенных
параллельно. Выбор каждого ПЗУ осуществляется одним из выходов
дешифратора на два входа и четыре выхода, как это показано на
рис. 10.21. Первые 1024 восьмиразрядных слова хранятся в верхнем
модуле памяти. Этот модуль доступен при К = 0 и L = 0. Второй
модуль доступен при К = 0 и L = 1 и т. д. Выходы четырех модулей
памяти соединены при помощи схемы монтажного * ИЛИ. Поскольку
адресация четырех модулей произвольна, для управления адрес-
ными линиями с А по J требуются буферные устройства.
Каждый из модулей ПЗУ на рис. 10.21 может выдавать любой
из 1024 возможных канонических конъюнктивных термов И от десяти
переменных. В действительности разработчику может потребоваться
лишь небольшая часть от всех 1024 термов И, что может привести
к неэкономичному использованию модулей ПЗУ. Например, холле-
ритовские коды ** имеют 12 переменных, но используются только 96
комбинаций этих переменных. Следовательно, если четыре модуля
* Схема, получаемая при непосредственном соединении нескольких входных
линий — Прим. пер.
* * 12-разрядные коды, используемые при вертикальной пробивке перфокарты. —
Прим. пер.
^o—l 2 пин
] 70с I Юс I
2 пин
10 С
2 пин
1
Р
о—
Светофор 1
» 1 ।
Светофор
2 I
So
АвС
ООО
Зг
зеленый
красный
\жел-\крас.\
тый \крас)
\крас-\жет.
Iный I I
красный
зеленый
, t
\крас-\крас.\ зеленый |
I ный \желт\ |
\жел-\крас.\ красный |
\тый | I I
S)
10 С 10 с 2 пин
в)
t
Текущее состояние Выходное слово
А В с X р А в с 81 01 1 82 а2 7*2
0 0 0 0 0 0 1 0 0 1 0 0 0 1
0 0 0 0 1 0 1 0 0 1 0 0 0 1
0 0 0 1 0 0 0 0 1 0 0 0 0 1
0 1 0 0 0 0 1 0 0 1 0 0 0 1
0 1 0 0 1 0 1 0 0 1 0 0 0 1
0 1 0 1 0 1 1 0 0 0 1 0 1 1
1 1 0 0 0 1 1 0 0 0 1 0 1 1
1 1 0 0 1 1 1 1 0 0 1 1 0 0
1 1 0 1 0 1 1 0 0 0 1 0 1 1
1 1 1 0 0 1 1 1 0 0 1 1 0 0
1 1 1 0 1 1 1 1 0 0 1 1 0 0
1 1 1 1 0 0 1 1 0 0 1 0 1 0
0 1 1 0 0 0 0 1 0 1 1 0 0 1
0 1 1 0 1 1 1 1 0 0 1 1 0 0
0 1 1 1 0 0 1 1 0 0 1 0 1 0
0 0 1 0 0 0 0 1 0 1 1 0 0 1
0 0 1 0 1 0 0 1 0 1 1 0 0 1
0 0 1 1 0 0 0 0 1 0 0 0 0 1
1 0 0 0 0 1 0 1 0 0 1 0 0 1
1 0 0 0 1 1 0 1 0 0 1 0 0 1
1 0 0 1 0 1 0 1 0 0 1 0 0 1
1 0 1 0 0 1 0 1 0 0 1 0 0 1
1 0 1 0 1 1 1 1 0 0 1 1 0 0
1 0 1 1 0 1 0 1 0 0 1 0 0 1
г}
АВСХ
оооо
0001
0010
0011
0100
0101
0110
от
юоо
1001
. 1010
1011
1100
1101
1110
1111
ю
Рис. 10.20. Устройство управления
светофором:
а — структурная схема для устройства
управления светофором; б — временные
диаграммы ' импульсов синхронизации и
сигналов времени; в — диаграмма внутрен-
них состояний; г — таблица состояний;
д — матрица ПЗУ; е — функциональная
схема, изображающая соединения ПЗУ
ПЗУ на 10 входах используются для преобразования холлеритов-
ского кода в код ASCII *, то 4000 линий слов не будут использованы
вообще. По этой причине для указанного преобразования кодов
использование ИМС со средним уровнем интеграции, реализующего
ПЛМ, было бы предпочтительнее использование ИМС типа ПЗУ.
В сущности, может потребоваться, чтобы ПЛМ была выпол-
нена в виде двух независимых ПЗУ: одно называется И-ПЗУ (или
схема получения термов И), а другое, называемое ИЛИ-ПЗУ (или
схема логического сложения). Структурная схема простой ПЛМ
изображена на рис. 10.22, а.
* ASCII (American Standard Code for Informational Interchange) — приня-
тый в США восьмибитовый код для передачи информации между внешними устрой-
ствами. — Прим. пер.
Рис. 10.21. Реализация ПЗУ емкостью 4096 восьмиразрядных слов
Рис. 10.22. Построение ПЛМ с помощью двух ПЗУ:
а — структурная схема простой ПЛМ; б — матрица соединений ПЛМ
На этой схеме показаны два входа И-ПЗУ А и В. На двух выход-
ных линиях этого ПЗУ генерируются два Р-терма: Ро = АВ и Р3 =
= АВ. Эти два Р-терма поступают на вход ИЛИ-ПЗУ, где выпол-
няется их логическое сложение, таким образом выходная функция
имеет вид
f - Ро + Р3 = АВ + АВ ---= AQB.
Структурная схема на рис. 10.22, а может быть представлена при
помощи коммутационной матрицы, изображенной на рис. 10.22, б.
Номера вертикальных линий в матрице И соответствуют номерам
генерируемых термов И. В рассматриваемом примере матрица И
имеет только две вертикальные линии и, следовательно, только два
из четырех возможных Р-термов могут быть сгенерированы. Номера
горизонтальных линий матрицы ИЛИ определяют номера выход-
ных функций. В рассматриваемом примере имеет место одна
функция.
Выходные функции всегда генерируются в двухуровневой форме,
в виде суммы термов. Элементарные термы, так же как и канониче-
ские, могут быть получены при помощи программируемой логиче-
ской матрицы.
ПЛМ, так же как и ПЗУ, может использоваться в качестве гене-
ратора булевых функций. Продемонстрируем реализацию булевых
Рис. 10.23. Реализация булевой функции с помощью ПЛМ
функций при помощи ПЛМ на примере следующих четырех функций
от шести переменных:
1 2 3 4
Л = ABCDEF + AEF + ACD + BD:
5 6 4 7
Л = ABEF + ACD + BD + EF-,
8 9 10 11
/3 = ACDEF + ABCD +ACD + ABD;
12 13 4 14 7
Л = ABCDE + AEF + BD + CD + EF.
Рассмотрев приведенные выше равенства, заметим, что они со-
стоят из 14 независимых термов И, отмеченных номерами. Одни из
этих термов имеют каноническую форму, другие — упрощенный вид.
Для генерации 14 термов И от шести переменных требуется матрица
И размером 12 X 14, как показано на рис. 10.23. Термы И подаются
на вход матрицы ИЛИ размером 4Х 14, с помощью которой осуще-
ствляется логическое сложение, и таким образом генерируются че-
тыре требуемые булевы функции. В общей сложности для реализа-
ции этих четырех функций с помощью ПЛМ требуется матрица
объемом 224 бит, в то время как при использовании ПЗУ необходи-
мый объем памяти равен 256 бит, т. е. применение ПЛМ приводит
к экономии объема памяти, приблизительно равной 12,5 %.
10.10. Проектирование последовательных схем на ПЛМ
Выше было показано, что ПЗУ может быть использовано для
реализации последовательных схем, поэтому точно также можно
использовать и ПЛМ. Например, можно создать универсальный
элемент ПЛМ, состоящий из матрицы И для получения произведений,
матрицы ИЛИ для выполнения сложения и триггеров для синхрони-
зации операций схемы. Каждая конкретная функция, которая долж-
на быть выполнена на ПЛМ, может быть запрограммирована в этом
универсальном элементе, выполненном на БИС, при помощи простого
изменения маски. Существуют целые серии практически доступных
для разработчиков универсальных элементов ПЛМ, каждый из кото-
рых имеет свои размеры матриц произведений и матриц сложений,
а также свои наборы триггеров определенного типа. Проектировщик
выбирает для своей схемы универсальный элемент ПЛМ нужной
конфигурации и выполняет необходимые действия для программи-
рования, чтобы получить требуемую схему. Рассмотрим построение
шестнадцатеричного счетчика при помощи £>-триггеров для исполь-
зования ПЛМ при разработке последовательных схем. Выход счет-
чика должен декодироваться для получения визуального изображе-
ния с помощью семисегментного индикатора.
Таблица состояний шестнадцатеричного счетчика показана на
рис. 10.24, а. В правой части таблицы показаны входные сигналы,
необходимые для соответствующих смен состояний четырех тригге-
ров. Управляющая таблица для одного D-триггера изображена на
рис. 10.24, б. На рис. 10.24, в при помощи карт Карно определены
и упрощены входные функции для всех триггеров. Минимальные
формы, соответствующие исходным уравнениям, имеют следующий
вид:
Dd = CD + BD + AD + ABCD-, DB =AB + AB;
Dc = ABC + AC + BC-, Da = A.
На рис. 10.24, г показано расположение семи сегментов индика-
тора, а также представлены изображения всех шестнадцатеричных
цифр, получаемые при помощи этих сегментов. Таблица истинности
для дешифратора, управляющего семью сегментами, показана на
рис. 10.24, д, а рис. 10.24, е представляет реализацию счетчика и
логической схемы дешифратора изображений.
Для дешифрирования шестнадцатеричных цифр требуется 16
линий термов. Например, для получения изображения шестнадцате-
ричной цифры А, соответствующей двоичному коду 1010, необходимо,
чтобы были высвечены сегменты Р, Q, R, Т, V и V. Следовательно,
при этой бинарной комбинации управляющие сигналы для указан-
ных сегментов должны быть установлены в логическую «1». С по-
мощью таблицы истинности предварительно получены функции для
каждого из сегментов. Например, для сегмента Р функция имеет
вид
p=0+2+3+5+6+7+8+9+4+C+D+F
И т. д.
10.11. Арифметические устройства на ИМС
со средним уровнем интеграции
В гл. 4 было показано, как можно построить четырехразрядный
сумматор из четырех полных сумматоров (см. рис. 4.4) и каким об-
разом при помощи четырех элементов ИСКЛЮЧАЮЩЕЕ ИЛИ его
можно преобразовать в устройство для сложения/вычитания чисел,
представленных в четырехразрядном дополнительном коде (см.
рис. 4.7). С появлением ИМС со средним уровнем интеграции четырех-
разрядные сумматоры выпускаются на одном кристалле. Типичным
примером такого сумматора является элемент SN 7483. Это устрой-
ство принимает два четырехразрядных числа и выполняет их сло-
жение с формированием сигнала переноса, как показано на
рис. 10.25, а.
Для сложения двух восьмиразрядных чисел можно соединить
два элемента SN 7483 в каскад, как показано на рис. 10.25, б. Выход-
ная линия переноса СвЫХ элемента с меньшими значащими разрядами
соединяется с входной линией переноса Свх второго элемента. Оче-
Состояния Входы триггеров
текущее следующее
D С в А D с в А Dd De DB Da
0 0 0 0 0 0 0 1 0 0 0 1
0 0 0 1 0 0 1 0 0 0 1 0
0 0 1 0 0 0 1 1 0 0 1 1
0 0 1 1 0 1 0 0 0 1 0 0
0 1 0 0 0 1 0 1 0 1 0 1
0 1 0 1 0 1 1 0 0 1 1 0
0 1 1 0 0 1 1 1 0 1 1 1
0 1 1 1 1 0 0 0 1 0 0 0
1 0 0 0 1 0 0 1 1 0 0 1
1 0 0 1 1 0 1 0 1 0 1 0
1 0 1 0 1 0 1 1 1 0 1 1
1 0 1 1 1 1 0 0 1 1 0 0
1 1 0 0 ,1 1 0 1 1 1 0 1
1 1 0 1 1 1 1 0 1 1 1 0
1 1 1 0 1 1 1 1 1 1 1 1
1 1 1 1 0 0 0 0 0 0 0 0
Q‘ Q!‘+6z D*
0 0 1 1 0 1 0 1 0 1 0 1
a)
б)
Dd-CD+BU+AU+ABCU
uj^o
rl_l*
s
г)
Состояние счетчика Входы сегментов семи- сегментного дешифратора
D С в А Р Q R S Т и V
0 0 0 0 1 1 1 1 1 1 0
0 0 0 1 0 1 1 0 0 0 0
0 0 1 0 1 1 0 1 1 0 1
0 0 1 1 1 1 1 1 0 0 1
0 1 0 0 0 1 1 0 0 1 1
0 1 0 1 1 0 1 1 0 1 1
0 1 1 0 1 0 1 1 1 1 1
0 1 1 1 1 1 1 0 0 0 0
1 0 0 0 1 1 1 1 1 1 1
1 0 0 1 1 1 1 0 0 1 1
1 0 1 0 1 1 1 0 1 1 1
1 0 1 1 0 0 1 1 1 1 1
1 1 0 0 1 0 0 1 1 1 0
1 1 0 1 0 1 1 1 1 0 1
1 1 1 0 1 0 0 1 1 1 1
1 1 1 1 1 0 0 0 1 1 1
д)
Рис. 10.24. Устройство получения изображения шестнадцатеричных цифр:
а — таблица состояний для шестнадцатеричного счетчика; б — таблица переходов D-триг-
гера; в — карты Карио для шестнадцатеричного счетчика; г — изображение шестнадцати-
ричных цифр при помощи семи сегментов; д — таблица истинности дешифратора для семи
сегментов; е — реализация шестнадцатеричного счетчика при помощи ПЛМ
Cgta SjSzSrSn С1ЫХ S7SeS5S, Зз5г8,80
a) i)
Y3YZY,YO
*з*г*Л
Illi Генератор
Illi прямого/дополнительного
ПП кодов 74Н87
Y3Y2Y,Yo
ШХ,
7483
_М
Выбор режима
М=0 Вычитание
М-1 сложение
74Н87
Свих 7483 Свх
М=0
вычитание
М=1
сложение
Свих или I I I
Ввых till
S3 s2 5, So
или или или или
Из ^г А Ио
8)
53 S2 5, 5„
или или или или
Из Пг Df Pt
i)
Рис. 10.25. Устройства для выполнения сложения!вычитания:
а — четырехразрядный сумматор (ИМС 7483); б — суммирование двух восьмиразрядных
чисел; в — устройство сложення/вычнтания, использующее дополнительный код; г — устрой-
ство сложення/вычнтання, использующее обратный код
видно, что порядок сложения может быть повышен увеличением числа
четырехразрядных сумматоров в каскаде.
Сумматоры на ИМС со средним уровнем интеграции (такие, как
элемент 7483) могут быть использованы в сочетании с ИМС, форми-
рующей прямой или обратный четырехразрядный код (например,
элементом 74Н87), для выполнения действий в дополнительном или
обратном кодах. Примеры устройств сложения/вычитания в обрат-
ном и дополнительном кодах приведены на рис. 10.25, в, г.
Элемент 74Н87 формирует обратный код входного двоичного
числа если управляющий сигнал М равен 0. Однако при
44 = 1 на выходе элемента прямого/обратного кода появляется пря-
мой код числа У3У2У1У0- В случае схемы, реализующей действия над
дополнительными кодами (рис. 10.25, в), при 44 = 0 значение сиг-
нала переноса Свх = 1; таким образом, прибавляется единица в са-
мый младший разряд, и, следовательно, формируется дополнитель-
ный код числа YgY^YjYQ. Для реализации арифметики обратных ко-
дов выходная линия сигнала переноса Свых соединяется с входом
сумматора Свх, обеспечивая таким образом сигнал переноса, необхо-
димый для данного типа арифметики. Устройство сложения/вычита-
ния в обратном коде показано на рис. 10.25, г.
Для сложения чисел, представленных в дополнительном и обрат-
ном кодах и имеющих большую разрядность, сумматоры могут быть
соединены последовательно, как показано на рис. 10.25, б.
10.12. Десятичное сложение с помощью сумматоров на ИМС
со средним уровнем интеграции
Иногда желательно выполнить арифметические операции над
десятичными числами. Это требование часто возникает тогда, когда
результат арифметических операций должен быть представлен в де-
сятичной форме.
Десятичные числа обычно представляются при помощи четырех-
разрядного двоично-десятичного кода, приведенного в таблице на
рис. 10.26. Если должны быть сложены два десятичных числа, а их
сумма S < 9, то результат сложения двоично-десятичных кодов
этих чисел представляет собой правильный двоично-десятичный
код. Например,
3 ООП
+
4 0100
7 0111
С другой стороны, если сумма двух чисел S > 9, то суммиро-
вание двух двоично-десятичных кодов, соответствующих этим чис-
лам, приведет к неправильному ответу. Это иллюстрируется на сле-
дующем примере:
7 0111
+
7 0111
14 1110
Четырехразрядная комбинация, полученная при сложении двух
двоично-десятичных кодов в этом случае, отсутствует в таблице и,
следовательно, является запрещенной. Для
правильного представления числа (14)10
в двоично-десятичном виде требуется два
четырехразрядных кода
(14)10 = 0001, 0100.
Следовательно, если сумма S > 9, не-
обходимо выполнить корректировку непра-
вильного результата. Эта корректировка
может быть проведена вычитанием (Ю)10 =
= (1010)2 из неправильной комбинации или
прибавлением к ней дополнительного ко- _______________________
да (1010)2. Дополнительным кодом для Рис. 10.26. Двоично-деся-
(1010)2 является (0110)2, следовательно, пгичный код
при суммировании необходимо прибавить (6)10, как показано в следу-
ющем примере:
7 0 111
+
7 0 111
1 ПО
О 110
14 10 100
При S > 9 необходим перенос в старший разряд. Следовательно,
для обнаружения запрещенных комбинаций 1010, 1011, 1100, 1101,
1110 и 1111 должна быть разработана логическая функция. Эти за-
прещенные комбинации изображаются при помощи карты Карно
(рис. 10.27, а) и упрощаются обычным способом.
Таким образом, функция переноса, представляющая указанные
комбинации, имеет вид
/с = АВ + АС.
В случае сложения двух десятичных чисел, дающих в сумме
S > 15, четырехразрядный сумматор сгенерирует сигнал переноса
Свых. Например,
9 1001
+
9 1001
1,0010
ОНО
1,1000
Следовательно, для' десятичного сумматора уравнение переноса
в следующий десятичный разряд задается как
Свх = Со + АВ + АС.
Реализация одного разряда двоично-десятичного сумматора по-
казана на рис. 10.27, б. Для него требуются два четырехбитовых
сумматора (ИМС 7483), три элемента И—НЕ и инвертор. Сумматор
Р используется для сложения двух четырехбитовых двоично-деся-
тичных кодов K8K4KaKi и XsX4XaXv Выходы этого сумматора соеди-
нены с цепью элементов И—НЕ, генерирующей часть функции Свх
для следующего разряда. Кроме того, они соединяются с сумматором
Q, единственное назначение которого заключается в прибавлении
кода (0110)2, когда сумма двух десятичных чисел S > 9. При выпол-
нении этого условия генерируется входной для следующего разряда
сигнал переноса Свх. Этот сигнал также поступает на входы R и S
сумматора Q, генерируя, таким образом, число (0110)2 на его
четырех правых входах.
Если соединить последовательно п таких одноразрядных деся-
тичных сумматоров, то в результате получится n-разрядный деся-
тичный сумматор.
Упражнения
У10.1. Реализовать с помощью четырехвходовых мультиплексоров следующие
булевы функции от трех переменных:
a) f = 2 0, 2, 3, 5, 7 управляющие переменные А и В;
б) f = J 1, 3, 4, 6, 7 управляющие переменные В и С;
в) f = J 0, 2, 4, 5, 6, 7 управляющие переменные А и С.
У10.2. Реализовать с помощью четырехвходовых мультиплексоров и логи-
ческих элементов И—НЕ следующие булевы функции от четырех переменных:
a) f = J 0, 1, 3, 5, 6, 8, 9, 11, 12, 13 управляющие переменные А и В;
б) f = 2 0, 7, 8, 9, 10, 11, 13, 14, 15 управляющие переменные В и С;
в) / = 2 0, 1, 3, 5, 9, 10, 11, 13, 14, 15 управляющие переменные С и О;
г) f= J 1, 8, 9, 10, 12, 13, 14, 15 управляющие переменные А и D.
У10.3. Реализовать с помощью четырехвходового мультиплексора следующие
булевы функции от четырех переменных:
a) f= JO, 1, 2, 3, 4, 8, 9, 11, 12, 13, 14, 18, 19, 20, 21, 25, 26, 39, 30 и 31;
б) 25, 6, 7, 8, 9, 10, 14, 15, 16, 17, 18, 19, 22, 23, 24, 25, 26, 29, 30
и 31.
У10.4. Реализовать с помощью:
а) мультиплексоров с четырьмя входами и логических элементов И—НЕ;
б) мультиплексоров с восемью и четырьмя входами следующую булеву функ-
цию от шести переменных:
f = SO, 1, 3, 5, 7, 12, 14, 16, 18, 20, 22, 26, 28, 30, 32, 34, 37, 39, 41, 45,
50, 51, 53, 60, 61, 62 и 63.
У10.5. С помощью мультиплексора реализовать полный четырехразрядный
сумматор.
У10.6. Разработать преобразователь двоично-десятичного кода в десятичный:
а) со структурой, обеспечивающей отбраковку всех неправильных данных;
б) с простейшей структурой, используя логические элементы И—НЕ и ин-
верторы.
У10.7. Комбинационная схема определена с помощью следующих уравнений;
Л = АВ 4- АВС;
f2 = А + В + С;
/3= АВ+ АВ.
Разработать схему, реализующую эти три уравнения с помощью дешифратора
и внешних по отношению к нему логических элементов И—НЕ.
У10.8. С помощью нижеприведенной таблицы задаются четыре часто исполь-
зуемых иа практике кода: 8-4-2-1, 2-4-2-1, XS3 и код Грея XS3. Разработать
три преобразователя кода 8-4-2-1 в остальные указанные коды с помощью дешифра-
тора с четырьмя входами и десятью
выходами, а также внешних по отно-
шению к нему логических элементов.
У10.9. Комбинационная схема опре-
деляется с помощью уравнений:
Л = АВС 4- АВС;
f2= А 4" В + С 4- D;
fa= А 4- В 4- СВ 4- AD;
fi = ACD 4- ACD 4- BCD 4- BCD.
Построить схему, реализующую эти
четыре уравнения с помощью дешифра-
тора и внешних для него логических
элементов И—НЕ.
У10.10. Разработать дешифратор на
три входа и восемь выходов, используя
только логические элементы ИЛИ—НЕ,
и изобразить его логическую струк-
туру.
У10.11. Разработать структурную
схему для дешифратора на шесть входов
и 64 выхода при помощи девяти дешиф-
раторов на три входа и восемь выходов.
У10.12. ПЗУ принято использовать для преобразования обычных двоичных
чисел в двоичио-десятичные. Определить объем ПЗУ, необходимый для преобразо-
ваний восьмиразрядного двоичного числа в двоично-десятичное, а также изобразить
матрицу ПЗУ, отмечая единицы в ней точками.
У10.13. Определить емкость ПЗУ, необходимую для реализации:
а) преобразователя двоично-десятичного кода в код «2 из 5»;
б) устройства сравнения четырехразрядных величин;
в) устройства двоичного умножения, перемножающего два трехразрядных
числа.
У10.14. реализовать с помощью ПЗУ следующие четыре булевы функции:
а) /1 = ABCD + ACD + BCD;
б)/2= А + В+_С;
в) f3 = АВ + АВ + С£>_+ CD;
г) Л = (А + В + CD) (А + В + CD) + АВС.
У10.15. Разработать счетчик по модулю 7, имеющий вывод на семисегментный
индикатор и использующий триггеры £>-типа, схемно объединенные с ПЛМ. Выпол-
нить подробный чертеж матриц памяти ПЛМ и внутренних связей в схеме.
У10.16. Реализовать каждую из следующих переключательных функций с по-
мощью двух ПЗУ:
a) f (А, В, С) 0, 1, 2, 6, 7;
б) f (А, В, С, £>) = £0, 1, 8, 9, 10, 11, 12, 14, 15;
в) / (А, В, С, D, Е)= У 0, 1, 16, 17, 18, 19, 20, 21, 22, 23, 24, 26, 28,
29, 30, 31;
г) / (А, В, С, D, Е, F) = 2 0, 1, 2, 3, 4, 5, 10, 11, 12, 13, 14, 15, '19,
20, 21, 22, 23, 24, 27, 28, 29, 30, 31, 47, 48, 60, 61, 62, 63.
У10.17. Реализовать следующие преобразователи кодов с помощью ПЗУ:
а) двоично-десятичный в XS3.
б) двоично-десятичный в код Грея XS3;
в) двоично-десятичный в 6, 3, 1, —1.
У10.18. Разработать четырехразрядный сумматор, предусматривающий сигнал
переноса с помощью ПЛМ.
У10.19. Разработать логическую схему устройства для сложения/вычитания
трехзначных десятичных чисел в коде XS3, используя сумматор (ИМС 7483) и лю-
бые логические элементы, которые могут при этом потребоваться. Для процесса
вычитания следует использовать код дополнения до 9.
11. СИТУАЦИИ РИСКА В ЛОГИЧЕСКИХ СХЕМАХ
11.1. Введение
Во многих случаях неправильная работа реальных логических
схем может объясняться наличием в них ситуаций риска, поэтому
для разработчика логических схем необходимо иметь ясное предста-
вление о причинах появления таких ситуаций и знать об их влиянии
на работу схем.
Существует три типа риска в логических схемах:
а) статический риск;
б) динамический риск;
в) существенный риск.
Статический и динамический риск может возникнуть в комбина-
ционных, а также в асинхронных схемах, реализованных на логиче-
ских элементах. Существенный риск может возникать только в асин-
хронных схемах.
В этой главе описываются случаи появления ситуаций риска
в логических схемах, а также излагаются методы их обнаружения.
Кроме этого, приводятся методы проектирования, позволяющие из-
бавляться от ситуаций риска.
11.2. Явления временной задержки в логических элементах
Если в комбинационной схеме в качестве инвертора исполь-
зуется двухвходовый логический элемент И—НЕ, как показано
на рис. 11.1, то между требуемым изменением на выходе и вызываю-
щим его изменением на входе существует конечная временная за-
держка tg. Это показано на временных диаграммах^из которых видно,
что в результате изменения А от 0 до 1 изменение А от 1 до 0 происхо-
дит на tg секунд позднее. Аналогично этому, при изменении А от 1
до 0 соответствующее изменение А от 0 до 1 осуществится также на
tg позднее.
11.3. Условия возникновения выбросов
Если, как показано на рис. 11.2, на входы элемента И подаются
одновременно сигнал А и его отрицание А, полученное при помощи
логического элемента И—НЕ, изображенного на рис. 11.1, то по
Рис. 11.1. Воздействие
временной задержки в ло-
гическом элементе при ин-
вертировании сигнала А
правилам алгебры логики сигнал на его выходе должен быть равен
А-А =0. Однако, как можно видеть на временных диаграммах,
в течение интервалов времени, отмеченных штриховкой, А и А одно-
временно равны 1, так что в это время выходной сигнал А-А = 1.
Выходная функция этого элемента, равная А-А, состоит из серии
положительных выбросов, возникающих при изменении А от 0 до 1
и имеющих длительность в tg с. Это явление, безусловно, объясняется
временной задержкой логического инвертора, показанного на
рис. 11.1. _
Схему, в которой возможна генерация сигнала А А, называют схе-
мой со статическим нулевым риском (0-риском), поскольку
выходной сигнал, который должен быть все время равен логическому
«0», в короткие временные интервалы устанавливается в «1».
В другом случае, если сигналы А и А поступают на входы двух-
входового элемента ИЛИ, как показано на рис. 11.3, то на выходе
элемента появится функция / = А + А, которая в соответствии
с алгеброй логики должна быть равна логической «1». Расположение
импульсов А и А на рис. 11.3 показывает, что в течение временных
периодов, соответствующих заштрихованным частям рисунка, оба
они одновременно равны «0». В течение этих заштрихованных интер-
валов, имеющих небольшую продолжительность, выходной сигнал
равен логическому «0». В таком случае говорят, что схема имеет ста-
тический единичный риск (1-риск), так как сигнал на ее выходе, рав-
Рис. 11.3. Генерация выбросов элементом ИЛИ
Рис. 11.4. Генерация выбросов элементами И—НЕ и ИЛИ—НЕ
ный в нормальном состоянии «1», на короткие периоды времени пере-
ходит в логический «О». Следует отметить, что для элемента ИЛИ от-
рицательные выбросы появляются в моменты, когда А изменяется
от 1 до 0.
Возникновение выбросов на выходах элементов И — НЕ
ИЛИ—НЕ показано на рис. 11.4. Отрицательные выбросы генери-
руются элементом И—НЕ в момент перехода Л из 0 в 1. Схема имеет
статический 1-риск. В схеме ИЛИ—НЕ генерируются положитель-
ные выбросы во время переходов Л из 1 в 0. Эта схема имеет статиче-
ский 0-риск.
11.4. Возникновение ситуаций статического риска
в комбинационных схемах
При изменении входных сигналов комбинационной схемы на ее
выходе могут возникнуть выбросы. Они появляются из-за того, что
на различных путях прохождения сигналов через схему от входа к ее
выходу могут возникать различные временные задержки. Например,
булева функция вида
f = АВ + АС
может быть реализована с помощью изображенной на рис. 11.5
схемы из элементов И—НЕ. Сигналы через эту схему проходят по
двум путям: первый — через элементы glt g2 и g3 и второй — через
gt. и g3. Если считать, что все элементы имеют одинаковую времен-
Рис. 11.5. Появление статического 1-риска в комбинационной схеме
ную задержку, равную tg с, то очевидно, что задержка, возникаю-
щая на первом пути, больше задержки на втором.
На рис. 11.5 показаны изменения, происходящие в схеме при
условии, что В = 1 и С = 1, а А изменяется от 1 до 0. В случае ука-
занного изменения сигнала А выход элемента gx изменяется от 0 до 1
и вызывает изменение выхода элемента g3 от 1 до 0. На другом пути
через схему сначала происходит изменение на выходе элемента gx от 0
до 1, вследствие которого изменяется выходной сигнал у элемента
g2 от 1 до 0, что приводит к изменению сигнала на выходе элемента
gs от 0 до 1. Поскольку путь через g± и g3 имеет меньшее время за-
держки, очевидно, что сигнал, проходящий поэтому пути, попадет на
выход схемы раньше сигнала, распространяющегося по пути^х, g2, gs.
Поскольку было принято, что В = 1 и С = 1, уравнение схемы
упрощается до выражения / = А + А и при этом появляется ве-
роятность возникновения статического 1-риска. Временная диа-
грамма, изображенная на рис. 11.5, показывает, что в выбранном
примере в течение короткого периода времени, следующего за мо-
ментом изменения А из 1 в 0, сигналы А и А равны одновременно 0
и, следовательно, А + А = 0. Поэтому в начале этого интервала
времени сигнал А + А изменяется из 1 в 0, возвращаясь назад,
когда А изменяется из 0 в 1. Схема генерирует статический 1-риск.
На рис. 11.5 показано возникновение отрицательных выбросов.
Наличие их подтверждает полученный в результате изучения струк-
туры схемы вывод, заключающийся в том, что последовательность
переходов выходного сигнала имеет вид 1 —>-0 —1. Функция, двой-
ственная к функции / = АВ + АС, имеет вид
fd = (А + В) (А + С).
На рис. 11.6 показано, как можно реализовать это равенство
с помощью элементов ИЛИ—НЕ. При условии, что В = 0 и С = 0,
уравнение этой схемы упрощается до вида f = А А. Если можно вы-
полнить такое упрощение, появляется вероятность статического
0-риска для схемы, реализующей уравнение = (А + В) (А + С).
Сразу после изменения А из 0 в 1 сигналы А и А одновременно равны
1 и, следовательно, А А = 1. Это значение остается до тех пор, пока
сигнал А не станет равным 0 и вновь не восстановится значение А А,
равное 0.
Рис. 11.6. Появление статического 0-риска в комбинационной схеме
Изменения сигналов в схеме также показаны на рис. 11.6 при ус-
ловии, что В = С = 0, а сигнал А изменяется из 0 в 1. Если все
элементы схемы имеют одинаковую временную задержку, равную
tg, то путь g4, g3 имеет минимальное время задержки, и изменение А
от 0 до 1 достигнет выхода по этому пути быстрее, чем по пути glf
g2, й'з, что приведет к изменению на выходе от 0 до 1. Когда то же са-
мое изменение сигнала А попадет на выход схемы по другому пути,
то выходной сигнал станет равен 0.
11.5. Устранение статического риска
На рис. 11.5 показана схема на элементах И—НЕ, реализующая
функцию
f = АВ + АС.
Термом согласования для этого уравнения является ВС, который
может быть прибавлен к исходному уравнению без изменения его
значения. Такое преобразование приведет к следующему выражению:
f = АВ + АС + ВС.
При условии, что В = С = 1, уравнение упрощается до вида
f = А + А + 1 _
и даже, если сигналы А и А на короткое время становятся равны 0,
значение / остается равным 1.
Результат дополнения уравнения термом согласования можно
проверить, если сопоставить изображение функции на карте Карно
до включения терма согласования и после включения. Исходная функ-
ция показана на рис. 11.7, а, а на рис. 11.7, б показана функция
после включения терма согласования. Из сравнения двух рисунков
видно, что перед дополнением функции термом согласования две
смежные ячейки с единицами не покрыты одной и той же первичной
импликантой. Ситуация риска устраняется из схемы включением
терма согласования, как показано на рис. 11.7, б.
Таким образом, путем выявления"единиц в смежных ячейках
карты Карно с изображением функции, не покрытых одной и той же
первичной импликантой, можно обнаружить ситуации статического
1-риска. Они могут быть устранены на стадии проектирования схемы
включением дополнительных первичных импликант, покрывающих
смежные пары ячеек с единицей, не покрытых одной и той же первич-
ной импликантой.
Гарантированная от риска схема, реализующая булеву функцию
/ = АВ + АС, изображена на рис. 11.7, в. Для получения инверсии
терма согласования ВС, как видно из рисунка, требуется дополни-
тельный логический элемент.
Функция, реализуемая схемой на элементах ИЛИ—НЕ, кото-
рая изображена на рис. 11.6, имеет вид
fd = (А + В) (А + С).
A
Рис. 11.7. Устранение
статического 1-риска:
а — изображение функции;
f = АВ т АС; б — изобра-
жение функции f = АВ 4-
+ АС + ВС', в — реали-
зация гарантированной от
риска функции f = АВ -|-
+ АС + ВС
Терм согласования для дополнения этого уравнения имеет вид В + С
и может быть добавлен к нему без изменения его значения. Таким
образом, эта функция принимает вид
fd = (А + В) (А + С) (В + С).
Если В = С = 0, то
fd = А-А-0 = 0.
При включении терма согласования значение функции всегда равно
О независимо от того, что А и А могут одновременно быть равны 1.
Статический 0-риск устраняется из схемы включением терма со-
гласования В + С в уравнение, описывающее работу схемы. При
устранении риска требуется дополнительный элемент для получения
терма согласования В + С.
Карта Карно обычно изображается так, что ячейки с единицами
соответствуют тем комбинациям переменных, где значение опреде-
ляемой функции равно. 1. Статический 1-риск возникает в схеме,
построенной на элементах И—НЕ и изображенной на рис. 11.8, при
условии, что А = 1, В = 1, С = 1 и А изменяется до 0. На карте
Карно, показанной на рис. 11.7, а,
появление риска обусловливается
переходом от клетки 111 к клет-
ке ОН, что можно установить по
наличию единиц в смежных ячей-
ках, не покрытых одной и той же
первичной импликантой.
При поиске статического 0-рис-
ка на карте Карно необходимо
отметить нулевые значения функ-
ции. Для получения изображения
0-термов должна быть определена
ванной от риска функции fd =
= (А+В) (А+С) (В+С)
a)
Рис. 11.9. Устранение
статического 0-риска:
а — изображение функции
fd = АВ 4- АС7, б — из-
ображение функции —
- ДВ + АС -}- ВС~
инверсия функции fd. Функция, соответствующая рассматриваемой
схеме, имеет вид
fd = И + В) (А + С).
Найдем двойственную к fd функцию
f = АВ + АС
и ее инверсию
fd -АВ + АС.
На рис. 11.9, а показана инверсия функции fd. Можно 'заметить,
что два нуля в смежных ячейках ООО и 100 не покрыты одной и той же
первичной импликантой. Включение дополнительной первичной им-
пликанты ВС на рис. 11.9, б обеспечивает теперь покрытие смежных
нулей одной и той же импликантой.
Функция, включающая дополнительную первичную импликанту,
принимает вид
fd = АВ + АС + ВС.
Получим двойственную к ней функцию
f = (А + В) (А + С) (В + С)
и ее инверсию
fd = (А + В) (А + С) (В + С),
которая представляет собой гарантированную от риска функцию,
полученную введением терма согласования, как это было показано
ранее.
Итак, статический 0-риск может быть выявлен при помощи сле-
дующей процедуры:
1) изобразить на карте Карно инверсную функцию;
2) найти смежные ячейки с нулевыми значениями функции,
не покрытые одной и той же первичной импликантой;
3) включить дополнительные первичные импликанты для покры-
тия всех смежных нулевых ячеек, не покрытых одной и той же пер-
вичной импликантой;
4) преобразовать функцию путем повторного ее инвертирования
в гарантированную от риска форму.
11.6. Построение гарантированных от риска комбинационных схем
В этом разделе рассматривается реализация функции
/ - >2 2, 5, б, 7, 10, 13, 15
в двух вариантах: а) при помощи элементов И—НЕ и б) при помощи
элементов ИЛИ—НЕ. Предположим, что схемы строятся из элемен-
тов с максимальным числом входов, равным 3.
Поскольку в первом варианте реализации схемы используются
элементы И—НЕ, необходимо получить функцию, гарантированную
от статического 1-риска. Сначала следует отразить на карте Карно
все те комбинации переменных, при которых функция равна логиче-
ской «1», как показано на рис. 11.10, а, и упростить их обычным спо-
собом. Далее необходимо проверить, нет ли единиц в смежных ячей-
ках, не покрытых одной и той же первичной импликантой. В рас-
сматриваемом случае такими ячейками являются 0111 и ОНО и для
устранения непокрытых смежных ячеек добавлена дополнительная
первичная импликанта. Единицы, соответствующие дополнительной
первичной импликанте, обведены на карте Карно штриховой линией.
Полученная на карте гарантированная от риска функция может
быть записана в виде
/ = BD + ACD + BCD + АВС.
Чтобы удовлетворить условию ограниченности числа входов, это
выражение может быть факторизовано, после чего оно примет сле-
дующий вид:
f = CD (А + В) + BD + АВС.
В результате такой факторизации ситуации риска повторно не возни-
кают. В рассматриваемой задаче риск должен был бы появляться при
А = 0, В = 1 и С = 1, а также при изменении D от 1 до 0. При этих
условиях факторизованное выражение примет вид
f = D (1 + 0) + D + 1 = D + D + 1,
т. е. функция удовлетворяет условию устранения риска.
Рис. 11.10. Построение гарантированной от 1-риска схемы:
а — изображение функции / = S 2, 5, 6, 7, 10, 13, 15; б — реализация гарантирован-
ной от риска схемы с помощью элементов И —НЕ
Рис. 11.11. Построение гарантированной от 0-риска схемы-
а — изображение нулевых значений функции f = S 2, 5, 6, 7, 10, 13, 15; б — реализа-
ция гарантированной от риска схемы на элементах ИЛИ — НЕ
Реализация гарантированной от риска функции с помощью эле-
ментов И—НЕ показана на рис. 11.10, б.
Для того чтобы получить гарантированную от риска реализацию
данной функции на элементах ИЛИ—НЕ, сначала необходимо изоб-
разить на карте Карно все те комбинации переменных, при которых
значение функции равно логическому «0», а затем упростить ее обыч-
ным способом. Определенная на нулевых значениях функция пред-
ставляет собой инверсию рассматриваемой функции, и карта Карно
с ее изображением получается из карты на рис. 11.10, а при помощи
заполнения ее свободных ячеек нулями, как показано на рис. 11.11,а.
Наличие нулей в смежных ячейках, не покрытых одной и той же
первичной импликантой, показывает, что упрощенная функция
имеет статический 0-риск, обусловливаемый некоторыми опреде-
ленными ранее условиями. В этом примере такими смежными ячей-
ками являются: а) 0000 и 0001; б) 1000 и 1001. Присоединение до-
полнительной первичной импликанты ВС позволяет покрыть эти
смежные ячейки и удалить 0-риск. Нули, соответствующие дополни-
тельной первичной импликанты, обведены штриховыми линиями на
рис. 11.11, а. Полученная на карте инверсная функция имеет вид
f = CD + BD + ВС + ABID
В результате факторизации, выполняемой для удовлетворения огра-
ничения на число входов у одного элемента, получаем следующую
функцию:
/ = CD + В (С + D) + ABD.
Найдем двойственную к ней функцию
fd = (С + D) (В + CD) (А + В + D)
и затем ее инверсию
fd = (C + D)(B + CD) (А +В + D).
Реализация этой гарантированной от риска функции с помощью
элементов ИЛИ—НЕ показана на рис. 11.11, б.
11.7. Анализ схем для обнаружения ситуаций риска
На рис. 11.12, а изображена схема на элементах ИЛИ/И, которую
следует проверять на наличие какого-либо риска. Так как схема со-
стоит из элементов ИЛИ и И одновременно, в ней может возникать
ситуация статического риска как в нуле, так и в единице. Функция
для этой схемы имеет вид
f = АВС + (А + В) (A+D),
и она может быть развернута следующим образом:
f = АВС + А~А + AD + ~АВ + BD.
Это выражение содержит терм АА, который при обычных обстоя-
тельствах был бы устранен, так как по законам алгебры логики он
равен логическому 0. Однако, поскольку А и А в комбинационных
схемах могут быть одновременно равны логической «1», они считаются
независимыми переменными в приведенном выражении, полная
форма которого необходима для демонстрации переходных процес-
сов.
Рис. 11.12. Выявление
ситуаций риска в логиче-
ской схеме:
а — схема на элемен-
тах И/ИЛИ, реализующая
функцию f = АВС +
+ (Л + В) (Л + 5); б —
изображение функции на
карте Карно; в — изображе-
ние инверсной функции; г —
повторное упрощение функ-
ции; д — изображение ин-
версии повторно упрощен-
ной функции
Для того чтобы обнаружить ситуации риска, необходимо при
определенных входных условиях рассмотреть, к какой форме сво-
дится развернутое выражение (к XX или X + X). Например, если
В = О, С = 0 и D = 1, то выражение приводится к f = А А. Следо-
вательно, для этих входных условий при изменении А из 0 в 1 появ-
ляется статический 0-риск.
При определении временного уравнения схемы некоторыми тео-
ремами алгебры логики нельзя пользоваться. Для преобразования
временного уравнения схемы не могут быть применены те правила,
в которых используются тождества А А = 0 и А + А = 1. Напри-
мер, нельзя пользоваться теоремой алгебры логики, согласно кото-
рой А + АВ = (А + А) (А + В) = А + В, поскольку в ней с по-
мощью тождества А + А = 1 выражение А + АВ приводится
к форме А + В. Выше в этой главе было показано, что А и А могут
быть одновременно равны нулю, и в этом случае А + А =# 1. Тогда
приведенная выше теорема не является справедливой для всех мо-
ментов времени.
Если В = 1, С = 0 и D = 1, выражение преобразуется к виду
f = А + ДА + А. В этом случае при изменении А от 1 до 0 появ-
ляется ситуация статического 1-риска. Следует отметить, что при из-
менении А от 1 до 0 значение терма АА = 0 и оно может стать рав-
ным 1, только когда А изменяется из 0 в 1.
Если В = 1, С = 0, и D =0, равенство преобразуется к виду
f = Д 4- А А + А + А + 1. В этом случае f = 1 независимо от
значений А и А, следовательно, ситуация статического риска не воз-
никает.
Другим способом статический 1-риск может быть обнаружен
определением на картах Карно тех комбинаций переменных, при
которых значение функции / = 1, как показано на рис. 11.12, б. Ана-
лизируя эту карту, можно заметить, что две смежные ячейки 1101
и 0101, отмеченные «1», не покрыты одной и той же первичной им-
пликантой. Включение дополнительной первичной импликанты ВС
обеспечит покрытие этих двух ячеек одной и той же первичной им-
пликантой и устранит статический 1-риск.
Для обнаружения статического 0-риска функция должна быть сна-
чала инвертирована и изображена на карте Карно. Рассматриваемая
здесь функция имеет вид
f = АВС + (А + B)(A+D).
Определим двойственную к ней функцию
fd = АВ + AAD + АВр + АВС + ACD,
затем функцию, инверсную к ней:
f = АВ + ~AAD -F ABD + ABC + ACD
и, наконец, используя теорему поглощения, приведем ее к следую-
щему виду:
f = АВ + ABD + ACD + AAD.
Первые три терма инверсной функции изображены на карте Карно,
показанной на рис. 11.12, в. Четвертый (временной) терм не может
быть представлен на этой же карте.
На карте Карно для инверсной функции можно видеть, что нули
в ячейках 1001 и 1011 являются смежными для нулей в ячейках 0001
и ООН, соответственно, и не покрываются одной и той же первичной
импликантой. Статический 0-риск устраняется включением дополни-
тельной первичной импликанты для покрытия этих четырех ячеек.
Этот терм следует добавить к инверсной функции, которая затем
повторно инвертируется для получения функции в гарантированном
от риска виде.
Анализ схемы, приведенной на рис. 11.12, а, показывает, что в ней
могут возникать ситуации риска обоих видов. На практике целесооб-
разнее было бы провести преобразование схемы при помощи карты
Карно, показанной на рис. 11.12, б, которая для удобства повторена
на рис. 11.12, г. На этой карте функция упрощена таким способом,
что в результате получилась гарантированная от статического
1-риска функция. Она имеет следующий вид:
f = АВ + BD + AD + ВС.
Теперь осталось только проверить изображение на карте Карно ин-
версной функции для выявления 0-риска. Инверсная функция имеет
вид
f = АВ+ BD + ACD
Она изображена на рис. 11.12, д. Поскольку на этой карте Карно нет
смежных нулей, не покрытых одной и той же первичной импликан-
той, то нет и статического 0-риска, и функция является гарантиро-
ванной также и от этого типа риска.
11.8. Ситуации динамического риска
Второй тип ситуаций риска, появляющихся в комбинационных
схемах, называется динамическим риском. Он возникает при изме-
нении выходного сигнала схемы от 0 до 1 или, наоборот, от 1 до 0.
Если при разработке схемы предусмотрено изменение выходного
сигнала от 1 до 0, а в действительности его изменение имеет вид 1 ->
-> 0 -> 1 -> 0, то это свидетельствует о наличии в схеме динамиче-
ского риска. Аналогично
этому вместо требуемого из-
менения выходного сигнала
от 0 в 1 при условии дина- ______ ____ 0 __
мического риска будет иметь
место изменение 0 —> 1 —Рис. 11.13. Ситуации динамического риска
->0-> 1. В каждом из этих случаев выходной сигнал изменяется
минимум 3 раза, как показано на рис. 11.13.
Ситуации динамического риска могут появиться в тех схемах,
где сигнал от одной переменной проходит по трем или более путям
и каждый из них имеет свое время задержки. Например, функция
f = (АС + ВС) (А + С)
может быть реализована с помощью схемы на элементах И и ИЛИ,
как показано на рис. 11.14, а. Проверка этой схемы показывает, что
сигнал от переменной С может проходить по трем различным путям,
и, следовательно, в этой схеме есть вероятность существования дина-
мического риска. Перечислим эти пути:
а) через элементы gx и g2;
б) через элементы g3, g5 и g2;
в) через элементы g4, g5 и g2.
Восемь возможных комбинаций переменных А, В и С сведены
в таблицу (рис. 11.14, б). Для каждой из этих комбинаций считается,
что следующее изменение в ней произойдет с переменной С, как по-
казано в четвертом столбце таблицы. Наличие динамического риска
отмечается в последнем столбце.
Для первых четырех комбинаций, указанных в таблице, А = 1,
и этот сигнал является одним из входных для элемента^, реализую-
щего функцию ИЛИ. Тем не менее, на выходе этого элемента будет
оставаться единичный сигнал независимо от любых изменений,
происходящих с С, и, следовательно, выходной сигнал элемента g2
a) в)
А В С Изменение С Динамический риск
0 0 0 0 — 1 Нет
0 0 1 7 — 0 Нет
0 1 0 0 — 1 Нет
0 1 7 1 —0 Нет
. 1 0 0 0 — 1 Нет
1 0 7 1 —0 Нет
1 1 0 0 —1 Да,если tglt<tg$
7 7 1 1 —0 Нет
б)
Л
Рас. 11.14, Выявление динами-
ческого риска в схеме:
а — схема с динамическим риском;
б — возникновение динамического
риска в схеме; в — представление
функции иа карте Карно, показы-
вающее отсутствие ситуации 1-рис-
ка; г — представление функции на
карте Карно, показывающее отсут-
ствие ситуации 0-риска
будет также оставаться неизменным. Поскольку для всех четырех
комбинаций изменение сигнала С на входе элемента gr не вызывает
изменения выходного сигнала для элемента g2, динамический риск
не возникает.
Однако в том случае, если Д ~= 1, В — 1 и С = 0 и при этом С
изменяется от 0 в 1, верхний вход элемента g изменяется от 0 до 1.
Другой вход Ц2 описывается выражением АС + ВС = 1, и, следова-
тельно, выход элемента также изменяется из 0 в 1. При условии
^4 < следует обратить внимание на результат изменения вход-
ного для gi сигнала С от 1 до 0. Это изменение вызовет изменение на
выходе элемента от 1 до 0, вследствие чего выход элемента g5 изме-
нится из 1 в 0, а на выходе элемента g2 произойдет второе изменение
сигнала от 1 до 0. Теперь, рассматривая изменение сигнала С от 0
до 8 на входе g3, можно видеть, что оно приводит к третьему изме-
нению на выходе g2 от 0 до 1. Эти изменения показаны на функцио-
нальной схеме, изображенной на рис. 11.14, а. Очевидно, что при
указанных входных условиях, когда С изменяется от 0 до 1, на вы-
ходе схемы возникает ситуация динамического риска.
Проанализировав аналогичным образом все остальные комбина-
ции таблицы, изображенной на рис. 11.14, б, можно установить,
что для них ситуация динамического риска не возникает.
Если изобразить функцию, реализуемую этой схемой на карте
Карно, как показано на рис. 11.14, в, то можно отметить, что в ней
отсутствует статический 1-риск. Изображение инверсной функции
на карте Карно (рис. 11.14, г) показывает, что в ней также нет и ста-
тического 0-риска.
So
Si
sz
Рис. 11.15.
состояний для
торая может
щественный риск
Диаграмма
схемы, на-
ймете су-
11.9. Ситуации существенного риска
Этот тип риска характерен для асинхронных схем и возникает
в результате возникновения гонок между входным и вторичным сиг-
налами. Диаграмма состояний для асинхронной дискретной схемы,
имеющей избыточные элементы, гарантирующие от гонок, изобра-
жена на рис. 11.15. Допустим, что схема находится в состоянии 50.
Тогда при изменении величины X от 0 до 1
произойдет переход схемы из состояния So
в состояние и, оказавшись в схема
останется в этом состоянии. Однако опе-
рация коррекции этой схемы, как было
указано выше, будет выполняться в за-
висимости от соотношения величин вре-
мени инверсии tt входного сигнала X
и времени отпирания вторичного сиг-
нала В. Если схема попадает в состоя-
ние перед тем, как значение сигнала X
изменится от 1 до 0, произойдет следую-
щий переход в состояние S3. Так какХ=1,
когда схема не переходит в состояние S2, то,
следовательно, очередной переход будет
осуществлен в состояние^, в котором схема теперь останется в резуль-
тате того, что изменение сигнала X уже произошло. Следовательно,
при ti > tt схема будет функционировать неправильно из-за возник-
новения гонок между инверсией первичного сигнала X и отпиранием
вторичного сигнала В.
Анализ уравнения для вторичного сигнала А показывает с еще
большей очевидностью сущность явления риска. Сигнал отпирания
для А задается термом ВХ, а сигнал для его запирания —термом
ВХ. Тогда
А = ВХ + (ВД А = ВХ + (В + X) А.
Первый терм полученного выражения представляет собой сигнал
отпирания для А при условии, что схема находится в состоянии Sv
Если В изменяется до 1 до того, как X перейдет в 0, то ВХ = 1, и
произойдет отпирание вторичной переменной А.
Для того чтобы устранить этот тип риска, следует включить за-
держку в выходную линию схемы, генерирующей сигнал В. В ре-
зультате этого изменение сигнала не достигнет входа схемы, генери-
рующей вторичную переменную А, до тех пор, пока не изменится
значение X.
Упражнения
У11.1. Составить карты Карно для функций:
a) f(A, В, С, D) — 20, 2, 4, 5, 6, 8, 9, 11, 12, 14, 15;
б) f (А, В, С, D)= S3, 4, 5, 6, 11, 12, 13, 14, 15
и построить для них гарантированные от риска схемы, используя для реализации:
1) элементы И—НЕ, 2) элементы ИЛИ—НЕ. Можно считать, что элементы имеют
максимум по три входа.
У 11.2. Найти все виды статического риска в двух схемах, показанных на
рис. 11.2, а, б. Определить, при каких входных условиях появляется риск, и изоб-
разить усовершенствованную логическую схему, гарантированную от риска.
Рис. У11.2
У 11.3. При помощи карты Карно объяснить, почему функция f = (А + В) X
X (В + С) имеет статический 0-риск при изменении входных сигналов АВС от 100
до ПО, а при изменении тех же сигналов от 100 до ООО этого риска нет.
У 11.4. Проверить, есть ли в схемах, изображенных на рис. УН.4а и б дина-
мический риск? Какие значения принимают входные переменные до возникновения
явлений риска и после них? Определить последовательности переключений в схемах,
вызывающих явления риска.
12. ВВЕДЕНИЕ В МИКРОПРОЦЕССОРЫ
12.1. Введение
В предыдущих главах обсуждались методы, используемые при
проектировании логических схем. Для применения этих методов
необходимо знать алгебру логики и уметь ее использовать при
решении задач построения комбинационных и последовательных
схем.
На ранних этапах логического проектирования для построения
схем использовались отдельные логические элементы и триггеры.
Однако с появлением интегральных микросхем для этих целей стали
применять ИМС с малым уровнем интеграции. Каждая такая микро-
схема, как правило, содержит более одного логического элемента.
Связывая между собой отдельные ИМС, можно создавать устройства,
выполняющие арифметические операции, например, сложение и вы-
читание, а также логические операции.
Развитие технологии производства полупроводниковых элемен-
тов привело к появлению ИМС со средним уровнем интеграции,
которые предназначены для выполнения отдельных операций, таких
как сложение, вычитание и умножение. Типичным примером ИМС
со средним уровнем интеграции служит рассмотренный в гл. 10 че-
тырехразрядный двоичный сумматор SN7483. С помощью внешних
управляющих сигналов эта схема может выполнять операции сложе-
ния и вычитания четырехразрядных двоичных чисел или двоично-
десятичных кодов. Кроме того, можно увеличивать разрядность сло-
жения или вычитания с помощью последовательного соединения
элементов.
Дальнейшее развитие технологии производства ИМС привело
к появлению БИС. Некоторые из них под воздействием внешних
управляющих сигналов могут выполнять требуемый набор арифме-
тических и логических операций. Каждая такая микросхема содер-
жит арифметико-логическое устройство (АЛУ), реализующее нужную
в данный момент функцию. Управление АЛУ осуществляется про-
граммой, хранящейся в памяти и определяющей необходимую после-
довательность арифметических и логических операций. БЙС такого
типа называются микропроцессорами и обычно используются как
центральные процессоры (ЦП) в микро-ЭВМ.
В этой главе рассмотрен процесс создания логической схемы
устройства умножения при помощи ранее описанных методов. Из
этой синхронной схемы, после того как к ней будет присоединена
память и дополнительные регистры, получается упрощенная схема
микропроцессора. Наконец, дополнив эту упрощенную схему
еще рядом элементов, получаем схему реального микропроцес-
сора.
12.2. Двоичное умножение
Ниже показано, как можно вручную перемножить два двоичных
числа:
Множимое ................................. 1110 14
Множитель................................. 1010 10
Частичное произведение 1 0000
Частичное произведение 2 1110
Частичное произведение 3 0000
Частичное произведение 4 1110
Произведение .......................... 10001100 140
Процесс вычислений строится по следующим трем правилам:
1) Если бит множителя равен 1, тогда частичное произведение
равно множимому. Если бит множителя равен 0, то частичное произ-
ведение тоже равно 0.
2) Для каждого из четырех битов множителя формируется от-
дельное частичное произведение. Затем при помощи суммирования
всех частичных произведений получается конечный результат.
3) Во время выполнения умножения, начиная с младшего разряда
и кончая старшим разрядом множителя, каждое промежуточное ча-
стичное произведение сдвигается на один бит влево.
Для реализации двоичного умножения с помощью логического
устройства необходимо использовать операции сложения и сдвига,
описанные в предыдущих главах. Сложение можно выполнить, ис-
пользуя схему сумматора, в то время как сдвиг осуществляется с по-
мощью регистра сдвига. Устройство умножения, работающее на ос-
нове этих двух операций, называется устройством типа сдвига и.сло-
жения.
Для реализации такого устройства”следует внести еще одно изме-
нение в ранее описанный метод. Приведенный выше пример показы-
вает, что все частичные произведения вычисляются прежде, чем
произойдет их суммирование с образованием конечного результата-
Для этого потребовалось бы четыре регистра, по одному для каж-
дого частичного произведения, и ясно, что число регистров стало бы
возрастать при увеличении разрядности множителя. С точки зрения
аппаратуры это было бы очень невыгодно, и на практике сложение
выполняется каждый раз, когда частичное произведение не равно
нулю, т. е. когда бит множителя равен 1.
12.3. Аппаратура, необходимая для реализации устройства
двоичного умножения
Анализ описанного в п. 12.2 процесса умножения двух четырех-
разрядных чисел позволяет определить следующий предварительный
список элементов:
1) четырехразрядный регистр для множимого;
2) четырехразрядный регистр для множителя;
3) восьмиразрядный регистр для произведения;
4) логическое устройство для управления операциями сдвига
и сложения.
На практике этих элементов обычно бывает достаточно. Читатель
обнаружит, что первоначально регистр удвоенной длины для хра-
нения результата пуст и, следовательно, целесообразно использовать
часть этого регистра для временного хранения множителя. В про-
цессе умножения биты множителя, равные 1, последовательно вы-
Регистр произведения
Множитель
Аккумулятор
0J
Z5
а)
Рис. 12.1. Устройство двоичного умножения'.
а — функциональная схема устройства умножения; б — диаграмма внутренних состоянии;
бираются из регистра произведения, освобождая, таким образом,
место для накопления частичных произведений. Часть регистра
удвоенной длины, используемая для накопления частичных произ-
ведений, называется аккумулятором.
12.4. Двоичное устройство умножения
Основная схема устройства показана на рис. 12.1, а. В нее входят
четырехразрядный сумматор, девятиразрядный регистр результата
и блок логического управления. В регистре результата предусма-
тривается дополнительный разряд для хранения единицы переноса,
появляющейся при сложении двух четырехбитовых чисел в четырех-
разрядном сумматоре.
Блок логического управления выполняет следующие две функ-
ции: 1) проверку бита множителя на равенство нулю или единице;
2) генерацию сигналов сдвига и сложения. Нужно также отметить,
что на устройство логического управления поступают синхронизи-
рующие импульсы и стартовые сигналы для синхронизации работы
устройства умножения и его пуска.
Если бит множителя равен 1, устройство логического управления
вырабатывает сигнал сложения А, затем содержимое регистра мно-
жимого и последние четыре значащие разряда аккумулятора посту-
пают на четырехразрядный сумматор, где производится их сложе-
ние. После этого результат возвращается в аккумулятор. Далее
подается импульс сдвига S и данное, хранящееся в регистре произ-
ведения, сдвигается на один разряд вправо, убирая, таким образом,
наименьший значащий разряд множителя и заменяя его на следую-
щий значащий разряд. Если бит множителя равен 0, генерируется
импульс сдвига, а сложение не производится.
Сравнивая машинную операцию с описанным в п. 12.2 методом
умножения, нужно отметить, что в нем множимое сдвигается влево,
а множитель остается на месте. В схемной же реализации множитель
и накапливающееся произведение сдвигается вправо относительно
множимого, которое остается на месте.
9 — схема реализации устройства умножения
Соответствующая диаграмма внутренних состояний устройства
показана на рис. 12.1, б. Когда получен стартовый сигнал X, в со-
стоянии So вырабатывается импульс сложения или сдвига в зависи-
мости от значения бита множителя М. При Л1 = 1 вырабатывается
импульс сложения и в момент появления отрицательного фронта
следующего тактового импульса происходит переход в Sv Наоборот,
если М = 0, генерируется импульс сдвига и в момент появления
отрицательного фронта следующего тактового импульса осущест-
вляется переход в состояние S2. Внешний контур диаграммы состоя-
ний задает последовательность операции сдвига и сложения. Если
все четыре разряда множителя равны 1, движение осуществляется
только по этому контуру. Наоборот, если все четыре разряда множи-
теля равны 0, тогда движение происходит по внутреннему контуру
диаграммы состояний.
Поскольку устройство имеет восемь внутренних состояний, то
для его построения требуется три триггера (Р, Q и R). Применяя
способ, описанный в гл. 8, можно получить уравнения для входов
JK-триггеров:
Jp = QR + QM; Кр = QR + QM;
JQ = R + MX + MP- KQ = RM М;
JR = M (X + P + Q); Kr — 1
и уравнения для выходов схемы:
S = М (X + Р + Q) + R;
А = MR (X + Р + Q).
Реализация устройства показана на рис. 12.1, в.
Двоичное устройство умножения, построение которого рассма-
тривается в этом параграфе, состоит из следующих трех основных
элементов:
1) регистров общего назначения;
2) арифметического устройства;
3) устройства управления.
В микропроцессорах перечисленные выше элементы являются
тремя основными компонентами. Чтобы создать микропроцессор на
базе устройства двоичного умножения, необходимо организовать
передачу данных в регистры произведения и множителя и обеспе-
чить команды сдвига и сложения. При этом используется метод,
заключающийся в хранении команд в следующих друг за другом
ячейках памяти в необходимом порядке и обеспечении последова-
тельного доступа к памяти с помощью устройства, называемого счет-
чиком программы.
12.5. Схемы алгоритмов
Основным средством для проектирования логических схем слу-
жит диаграмма состояний. По устной или письменной постановке
задачи инженер строит диаграмму состояний, которую можно ис-
пользовать для разработки схемы с по-
мощью определенных правил. В проти-
воположность этому, если инженер ре-
шает задачу на микропроцессоре, основ-
ным средством проектирования стано-
вится схема алгоритма. Она строится
по устной или письменной постановке
задачи, а затем преобразуется в про-
грамму, состоящую из набора команд
используемого микропроцессора.
Схема алгоритма является удобным
способом определения заданной после-
довательности операций. Она состоит
из блоков, связанных прямыми лини-
ями. Внутри блоков указаны выпол-
няемые операции, а прямые линии
между блоками определяют путь от
одной операции к следующей. Суще-
ствуют следующие два типа блоков на
диаграмме:
1) прямоугольный блок, в котором
указаны выполняемые операции;
2) ромбовидные блоки, по которым
принимаются решения о переходах на
основании условий, определенных вну-
три блоков.
Фактически схема алгоритма ана-
логична диаграмме состояний, где каж-
дое состояние подобно прямоугольному
блоку схемы алгоритма, в которых
представлена одна из заданных опера-
ций. Например, изучение диаграммы
состояний на рис. 12.1, б показывает,
как операции сдвига и сложения свя-
заны с состояниями. В состоянии Sx
создается сигнал сдвига, в то время
как в S2 создается либо сигнал сложе-
ния, либо сигнал сдвига в зависимости
от значения М. Логические сигналы,
относящиеся к путям переходов на диа-
грамме состояний, аналогичны содержи-
мому блоков условных переходов схемы
алгоритма. Например, в состоянии S2
Рис. 12.2. Алгоритм умножения
выбранный путь перехода
зависит от значения М, т. е. от нулевого или единичного значения
разряда множителя. Для Л1 = 1 переход осуществляется к S3, а для
М = 0 происходит переход к S4.
Типичный пример схемы алгоритма приведен на рис. 12.2. Эта
схема описывает процесс умножения с помощью операций сдвигам
сложения. Первый прямоугольный блок А устанавливает начальные
состояния перед выполнением программы. В этом блоке содержимое
регистра произведения устанавливается в 0, а на другом регистре
устанавливается показание счетчика, равное 4, т. е. числу необхо-
димых сдвигов. Кроме того, множимое и множитель запоминаются
в ячейках памяти 50 и 51 соответственно.
Блок В на рис. 12.2 является блоком условного перехода, кото-
рый имеет два выхода. Если разряд множителя равен 1, выполняется
переход по условию «да» к следующей операции блока С, где произ-
водится сложение множимого с содержимым регистра произведения
для формирования очередного частичного произведения. Наоборот,
если разряд множителя равен 0, то производится переход по условию
«нет» в обход блока сложения С. Здесь два пути соединяются и вхо-
дят в блок операции D, в котором осуществляется сдвиг.
Число, полученное в регистре произведения в результате выпол-
нения сдвига и сложения или только сдвига, нужно уменьшить. Эта
операция производится в блоке Е. После уменьшения счетчика осу-
ществляется вход в блок условного перехода F. Если счетчик не ра-
вен нулю, производится переход к повторению цикла BCDEF. На-
оборот, если значение счетчика равно 0, то выполняется вход в блок
G и произведение помещается в ячейки памяти 50 и 51.
12.6. Устройство двоичного умножения, управляемое программой
На рис. 12.3, а изображена модификация устройства двоичного
умножения (см. рис. 12.1, а), функционирующего под управлением
программы. Модификация заключается в добавлении счетчика про-
грамм PC, регистра команд 1R, регистра счетчика CR, а также до-
полнительных устройств памяти. Последние два регистра, связанные
дополнительной логикой и управляемые программой, образуют уст-
ройство управления.
Память разделена на две отдельные области. Первая область дан-
ных в этом случае содержит множитель и множимое в ячейках па-
мяти 50 и 51 соответственно. Этот тип информации хранится в опера-
тивном запоминающем устройстве (ОЗУ), которое используется в ми-
кропроцессорных системах для накопления данных, изменяемых во
время выполнения программы. В рассматриваемом случае, например,
множитель и множимое замещаются в ячейках 50 и 51 на конечное
произведение в конце работы программы. Вторая область памяти
содержит команды программы и константы. В общем случае этот
тип информации хранится в ПЗУ. На практике ПЗУ используется
для хранения данных, не подлежащих изменению.
Программа, записанная в памяти, в точности соответствует схеме
алгоритма на рис. 12.2. Команды в ячейках памяти 00—08 пред-
ставляют начальный блок А, Команды анализа условия и условного
перехода находятся в ячейках памяти 08—О А, что соответствует
блоку условного перехода в схеме алгоритма. Команды, соответ-
ствующие первому блоку условного перехода В из схемы алгоритма,
расположены в ячейках 08—ОА. Следующие три команды —сложить
(ОВ), сдвинуть (ОС) и уменьшить на единицу содержимое счетчика
I
6)
Рис. 12.3. Устройство двоичного умножения с программным управлением-
а — функциональная схема устройства умножения; б — команда «загрузить»
(0D) —соответствуют блокам схемы алгоритма. Ячейки памяти ОЕ —
—10 представляют блок условного перехода F, операция записи
произведения, указанная в блоке G, соответствует команде записи
в память в ячейках 11—13. Устройство заканчивает работу по
команде, расположенной в ячейке 14.
12.7. Длина слова
Число двоичных разрядов, которые одновременно используются
для операций как с командами, так и данными, называется длиной
слова машины. Длина слова устройства умножения равна 4 бит (см.
рис. 12.2), так как оно предназначено для перемножения двух четы-
рехразрядных слов. Следовательно, каждая ячейка памяти, указан-
ная на рис. 12.3, хранит четырехразрядное слово. Например в ячейке
50 хранится множитель (1010), а в ячейке 51 - множимое (1110).
Поскольку конечное произведение содержит максимум 8 бит,
то для его запоминания нужно две ячейки памяти 50
и 51.
От выбора длины слова также зависит число доступных команд.
Если машинные команды содержат только 4 бит, то общее число
доступных команд равно 24 = 16, и это накладывает очень жесткие
ограничения на набор команд машины. Тем не менее надо признать,
что набор команд можно расширить с помощью формирования каж-
дой команды, состоящей из двух последовательных слов в памяти.
Используя эту модификацию, машина может иметь максимальное
число команд, равное 256. Реально существующие микропроцессоры
имеют длину слова, равную 4, 8 и 12 разрядам, а в последнее время
появились микропроцессоры, оперирующие с шестнадцатиразряд-
ными словами.
12.8. Счетчик программы
Счетчик программы—это четырехразрядный регистр, располо-
женный в блоке управления устройства. Его функция заключается
в обеспечении последовательного доступа к ячейкам памяти про-
граммы, если только не выполняется команда перехода.
Регистр содержит восемь разрядов, следовательно, все адреса
памяти также состоят из восьми разрядов. На практике обычно адреса
памяти представлены в шестнадцатеричной системе кодирования, а не
в двоичной. По этой причине все адреса на рис. 12.3 обозначены двумя
шестнадцатеричными цифрами. В начале выполнения необходимо
задать содержимое счетчика программы, равное начальному адресу
программы (т. е. 00//, где Н показывает, что адрес представлен
в шестнадцатеричном виде). Когда команда уже выбрана из памяти
и введена в управляющую область машины, содержимое счетчика
программы увеличивается на 1.
Некоторые из команд, такие, как «очистить регистр произведе-
ния», представлены в памяти одним четырехразрядным словом. Тем
не менее можно заметить, что следующая команда «загрузить мно-
жимое» состоит из трех последовательных четырехразрядных слов.
В таких случаях за один шаг обрабатывается одно слово команды,
а содержимое счетчика программы увеличивается на единицу по мере
обработки каждого последующего слова. Чтобы начать выполнение
программы, необходимо установить в счетчике программы начальный
адрес ООН и подать сигнал выполнения.
При определенных условиях счетчик программы вместо того,
чтобы быть увеличенным на 1, указывает на очередную команду,
расположенную не в следующей ячейке памяти. Например, если при
обращении к ячейке памяти 08Н (см. рис. 12.3) бит множителя не ра-
вен нулю, то будет выполнен переход к ячейке ОСН, где содержится
команда «сдвиг». В этом случае команда «переход» будет содержать
адрес ОСН, который не является следующим за этой командой, но
будет загружен в счетчик программы при выполнении данной ко-
манды.
12.9. Команды и счетчик команд
Регистр команд для упрощенного микропроцессора, представлен-
ного на рис. 12.3, расположен в блоке управления и имеет длину,
равную четырем разрядам. Первое четырехразрядное слово каждой
команды в памяти программы выбирается в регистр команд, где оно
хранится до тех пор, пока команда не будет выполнена, а затем в де-
шифратор, где оно декодируется. Команда «загрузить», например,
может быть представлена четырехразрядным словом (0011В) (3/7).
Это слово поступает в блок управления и после декодировки опреде-
ляет команду «загрузить».
Согласно рис. 12.3 каждая команда выбирается из памяти про-
граммы и затем передается в регистр команд. Типичный пример
команды показан на рис. 12.3, б.
Команда «загрузить множитель»” состоит из трех четырехразряд-
ных слов. Первое слово является собственно командой, которая
передается из памяти в регистр команд, в то время как вторые два
слова определяют адрес в памяти данных, по которому нужно осуще-
ствить выборку множителя.
Команды в памяти машины можно разделить на три отдельные
категории:
1) пересылки;
2) управления;
3) выполнения.
Для данной машины существует четыре команды, связанные
с пересылкой данных:
1) загрузить множитель;
2) загрузить множимое;
3) запомнить произведение;
4) загрузить регистр счетчика.
Первые три из этих команд состоят из трех слов, а длина четвер-
той из них равна двум словам.
При выполнении команды «загрузить множимое» первое из трех
слов, расположенное в ячейке памяти 01Н, содержит код команды
загрузки. Это слово выбирается из памяти в регистр команд, разме-
щенный в блоке управления микропроцессора, где оно декодируется
для выполнения команды. Другие два слова, хранящиеся в ячейках
памяти 02Н и ОЗН, задают адрес в памяти данных, по которому
ищется множимое. Описать словами эту команду можно так: «загру-
зить данные, хранящиеся в ячейке памяти 51Н, в регистр множи-
мого».
Команда «загрузить множитель» может быть описана подобным же
образом, как и команда «загрузить множимое»: каждая из них свя-
зана с пересылкой данных из памяти в регистр.
Аналогично, команда «запомнить» связана с пересылкой данных
в память устройства. В рассматриваемом случае команда исполь-
зуется для запоминания содержимого регистра произведения в ячей-
ках 50Н и 51Н. Когда команда выбирается из ячейки ПН, второе и
третье слова задают адрес ячейки памяти 50Н, в которой запоми-
наются четыре последних значащих разряда произведения. Четыре
первых значащих разряда затем автоматически записываются в сле-
дующую по счету ячейку памяти с адресом 51Н.
Последняя команда, касающаяся передачи данных, является
командой «загрузить счетчик». Эта команда состоит из двух слов.
Первое из них является кодом команды, который декодируется
в блоке управления устройства, а второе слово содержит значение
числа циклов, загружаемого в регистр счетчика циклов.
В данном примере это значение равно четырем (0100В).
Две команды можно отнести к командам управления. Это
команды:
1) перейти;
2) остановиться.
Для команды «перейти» требуется три четырехразрядных слова,
первое из которых содержит код команды, передаваемой в блок
управления, где она затем декодируется (08Н). Второе и третье слова
команды (09Н и ОАН) определяют адрес в памяти программы, по
которому необходимо выполнить переход (ОСН). Эти два слова также
поступают в блок управления, где они загружаются в счетчик про-
граммы, чтобы затем быть использованными для выполнения пере-
хода по указанному адресу.
Команда «остановиться» занимает одно слово. Она используется
в данном случае для того, чтобы остановить устройство после выпол-
нения программы. Чтобы теперь вновь запустить устройство, необ-
ходимо воздействие внешних сигналов.
Четыре оставшиеся команды выполняют следующие операции:
1) уменьшить;
2) очистить;
3) сдвинуть;
4) сложить.
В случае первых трех команд все действия выполняются на спе-
циальном регистре и не связаны с передачей данных. Например,
команда «очистить» делает содержимое регистра произведения рав-
ным нулю, команда «уменьшить» просто уменьшает содержимое счет-
чика циклов на 1, а команда «сдвинуть» сдвигает содержимое реги-
стра произведения на один разряд вправо. Последняя среди них
команда «сложить» предназначена для выполнения одной из арифме-
тических и логических операций над данными.. Подобные операции
выполняются арифметико-логическим устройством микропроцес-
сора. Для микропроцессора, показанного на рис. 12.3, арифметико-
логическое устройство может обеспечить только операцию сложения.
Более сложные микропроцессоры имеют АЛУ, обеспечивающие более
сложные операции, т. е. вычитание, сравнение, И, ИЛИ, ИСКЛЮ-
ЧАЮЩЕЕ ИЛИ и т. д.
Следует отметить, что команды сложения и сдвига представляют
собой ядро процесса умножения. Каждая из этих двух команд зани-
мает по одной ячейки памяти программы. Тем не менее, анализ
рис. 12,3 показывает, что вся программа занимает 22 ячейки памяти.
Следовательно, 20 ячеек памяти программы нужны для того, чтобы
организовать в устройстве выполнение двух основных команд:
«сдвиг» и «сложение».
12.10. Шестнадцатеричная система представления чисел
Адреса ячеек памяти на рис. 12.3 были представлены в виде шест-
надцатеричных цифр. Подобное представление также обычно исполь-
зуется для обозначения слов, хранящихся в ячейках памяти. Хотя
микропроцессор во время работы принимает коды команд в двоичном
виде и обрабатывает данные также в двоичном виде, оказывается, что
шестнадцатеричная система счисления является очень удобным ком-
пактным способом представления двоичных чисел.
Шестнадцатеричная числовая система имеет 16 цифр. Это, ко-
нечно, вызывает осложнения, поскольку существует только десять
цифровых символов и, следовательно, приходится вводить шесть
дополнительных цифр для представления десятичных чисел от 10
до 15. Обычно используются шесть первых букв латинского алфа-
вита А, В, С, D, Е и F. Таблица соответствия шестнадцатеричных
цифр десятичным числам показана на рис. 12,4. Числовая система,
использующая как цифры, так и буквы для представления чисел,
называется алфавитно-цифровой системой.
Основанием для шестнадцатеричной системы является число 16.
Такое шестнадцатеричное число, как, например, 8АС2, преобра-
зуется в десятичное с помощью приведенной ниже формулы:
(А)10 = апЬп 4- а,^-1 + • • • aft1 ф- а0Ь°,
где b — основание числовой системы; а — шестнадцатеричная
цифра; п + 1 — число членов ряда.
Таким образом,
(2V)10 = 8-16® + Л-162 + С-161 + 2-16° =
= 8-163 + 10-162 + 12-161 + 2-16°;
(А)10 = 35 522.
Существует 16 комбинаций четырех двоичных цифр и эти комби-
нации можно использовать для представления 16 шестнадцатерич-
ных цифр. В таблице на рис. 12.5 каждая из этих четырехбитовых
шк ДК шк ДК Рис. 12.4. Таблица соответствия шестнадцатеричных десятичных (ШК) и (ДК) кодов
0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 8 9 А В С D Е F 8 9 10 11 12 13 14 15 ДК шк ДК шк ДК шк ДК шк
0000 0001 0010 ООН 0 1 2 3 0100 0101 оно 0111 4 5 6 7 1000 1001 1010 1011 8 9 А В 1100 1101 1110 1111 с D Е F
Рис. 12.5. Таблица соответствия двоичных (ДК) и шест- надцатеричных (ШК) кодов
комбинаций расположена рядом с шестнадцатеричной цифрой.
С помощью этой таблицы шестнадцатеричное число можно легко
представить его двоичным эквивалентом, как показано ниже:
2 А С 8 Шестнадцатеричное
становится
0010 1010 1100 1000 Двоичное
Очевидно, что шестнадцатеричное число, состоящее из четырех
цифр, преобразуется в шестнадцатибитовое двоичное число.
В простейшем микропроцессоре, изображенном на рис. 12.3,
адреса ячеек памяти представлены двумя шестнадцатеричными циф-
рами, которые после преобразования превращаются в восемь двоич-
ных цифр. Например, множимое хранится в ячейке памяти с адресом
51Н = 01010001В. Данное двоичное представление можно считать
машинным кодом адреса. Из этого также следует, что четырехраз-
рядное слово, хранящееся в отдельной ячейке памяти, можно пред-
ставить одной шестнадцатеричной цифрой.
Обратное преобразование также легко выполняется. Например,
1011 0010 1001 1010 Двоичное
преобразуется в
В 2 9 Л Шестнадцатеричное
12.11. Сравнение упрощенного микропроцессора с реальным
На практике микропроцессор намного сложнее, чем программно-
управляемое устройство умножения, рассмотренное в п. 12.6. Пере-
числим их основные отличия, и
1) реальный микропроцессор имеет большее число рабочих реги-
стров. Например, у микропроцессора «Интел 8085» пять шестна-
дцати- и два восьмиразрядных регистра.
2) Вместо сумматора в реальном микропроцессоре размещается
арифметико-логическое устройство, которое позволяет выполнять
большое число арифметических и логических операций. К их числу
относятся логические операции: И, ИЛИ, ИСКЛЮЧАЮЩЕЕ ИЛИ,
а также арифметические операции: получение дополнительного
кода, вычитание, увеличение на единицу содержимого регистра,
десятичное сложение. Во многих микропроцессорах также обе-
спечивается возможность перевода двоичных чисел в двоично-
десятичные.
3) Длина слова в наиболее известных и широко используемых
сейчас микропроцессорах составляет восемь или 16 разрядов.
4) В таких микропроцессорах, как «Интел 8085», регистры, АЛУ,
устройства управления и синхронизации, дешифратор команд и ге-
нератор тактовых импульсов расположены в одной БИС с 40 выво-
дами.
5) Для памяти могут использоваться или отдельные устройства
ОЗУ и ПЗУ или их сочетания. В последнее время применяются неза-
висимые элементы для ОЗУ и ПЗУ.
6) Для организации обмена данными с микропроцессором обычно
используются порты ввода/вывода. Например, в микропроцессорной
системе SDK85 порты ввода/вывода являются частью элементов па-
мяти.
7) Взаимодействие элементов микропроцессорной системы обычно
осуществляется через общую шину.
12.12. Обобщенная структурная схема микропроцессорной
системы
На рис. 12.6 показана структура типичной микропроцессорной
системы, изображенная в виде четырех блоков А, В, С и D.
1) Блок А представляет собой ЦП. Он состоит из АЛУ, регистров
общего назначения, дешифратора команд, устройства управления и
средств синхронизации.
2) Блок В обозначает ОЗУ, которое содержит изменяемые данные
и результаты.
3) Блок С обозначает ПЗУ, которое хранит команды программы и
константы.
4) Блок D представляет собой секцию ввода-вывода. Это или про-
стой порт ввода/вывода или в более сложном случае контроллер
внешнего устройства. С помощью этого блока, осуществляющего
взаимосвязь между процессором и внешней средой, осуществляется
взаимодействие с микропроцессорной системой таких периферийных
устройств, как преобразователи аналог—код и код—аналог, теле-
тайпы, печатающие устройства, контроллеры памяти на гибких
дисках, а также контроллеры прямого доступа к памяти (ПДП).
Эта взаимосвязь заключается
в координации периферийных
устройств и микропроцессора
и осуществляется с помощью
сигналов управления состоя-
ниями и посредством генера-
ции необходимых последова-
тельностей сигналов команд.
Линии, связывающие от-
дельные блоки, представляют
систему шин, которую можно
разделить на три отдельные
части:
1) однонаправленная адрес-
ная шина F, обычно состоящая
из шестнадцати линий;
2) двунаправленная шина
данных G, обычно состоящая
из восьми линий (в некоторых
Рис. 12.6. Структурная схема микропро-
цессора
INTA RST6.5 TRAP SIB SOU
Puc. 12.7. Функциональная схема микропро eccopa «.ИНТЕЛ 8085т>
микропроцессорах, таких, как «Интел 8085», восемь линий данных
мультиплексно связаны по времени * с восемью младшими адресными
линиями).
3) шина управления Н, по которой передаются сигналы управле-
ния, создаваемые процессором и распространяемые по всей системе.
Однако в определенных случаях сигналы управления могут созда-
ваться периферийными устройствами, например сигнал «готов»,
генерируемый ОЗУ 8385 в системе «Интел 8085».
В заключение рассмотрим изображенную на рис. 12.7 функцио-
нальную схему ЦП 8085. Она содержит все элементы, перечисленные
выше, такие, как АЛУ, счетчик программы и т. д. Следует отметить,
что существует регистр, называемый аккумулятором. Это наиболее
важный из всех регистров общего назначения. В него записываются
результаты арифметических и логических операций, получаемых
в АЛУ. Он также служит одним из входов в АЛУ.
Управление всей системой осуществляется в основном при по-
мощи блока синхронизации и управления. Однако в двух особых
случаях управляющие сигналы поступают в это устройство из внеш-
них источников. Примером первого из них служит сигнал «запрос
на ПДП». Он создается контроллером ПДП и сообщает ЦП, что
внешнее устройство, такое, как накопитель на гибких магнитных
дисках, готово передать блок данных в память или, наоборот, полу-
чить блок данных из памяти. Упомянутый выше сигнал «готов» пред-
ставляет второй тип сигналов, принимаемых устройством управле-
ния извне.
Один из регистров общего назначения называется указателем
стека. Этот регистр предназначен для работы со стеком, который
представляет собой либо набор регистров, либо отдельную область
памяти, выделенную программистом, и используется для чтения и
записи данных или адресов в вершину стека в режиме обслуживания
в порядке, обратном поступлению (первым пришел — последним
ушел). Операции со стеком в модели 8085 осуществляются с помощью
двух команд «поместить» и «взять». Команда «поместить» записывает
данные или адреса в вершину стека, а команда «взять» выполняет
обратный процесс. Указатель стека — это регистр, содержащий
адрес элемента вершины стека. Обычно в микропроцессорных систе-
мах стек используется для записи состояний машины во время выпол-
нения подпрограмм и прерываний.
Изображенный на функциональной схеме ЦП 8085 регистр флаж-
ков представляет собой другой важный элемент микропроцессора.
На самом деле это пятиразрядный регистр, хранящий данные о со-
держимом аккумулятора. Эти пять флажков перечислены ниже:
* Мультиплексная связь во времени означает, что линии в разное время имеют
различное функциональное назначение, что позволяет осуществлять дополнительные
функции, используя то же самое число выводов корпуса микропроцессора. Приме-
нение этого метода в микропроцессоре «Интел 8085» позволяет в момент передачи
адреса устанавливать младшие восемь разрядов адреса на шине данных, а по адрес-
ной шине передавать только восемь старших разрядов адреса. — Прим. пер.
1. Перенос. Когда установлен этот флажок, он показывает, что
произведен перенос старшего бита аккумулятора после выполнения
арифметической операции.
2. Нуль. Флажок устанавливается в 1, когда все восемь разрядов
аккумулятора равны 0.
3. Четность. Если аккумулятор содержит четное число единиц,
флажок устанавливается в 1. Иначе он равен 0.
4. Знак. Этот флажок устанавливается по значению самого стар-
шего бита аккумулятора. Если бит равен 1, то флажок устанавли-
вается также в 1, и это означает, что аккумулятор содержит отри-
цательное число.
5. Дополнительный перенос. Флажок устанавливается в 1, если
производится перенос из третьего разряда в четвертый. Обычно ис-
пользуется в операциях над двоично-десятичными числами.
12.13. Программирование для микропроцессоров
Микропроцессор — это устройство, которое обрабатывает двоич-
ные данные с помощью набора команд, поступающих в устройство
в двоичном виде. Для восьмиразрядного микропроцессора каждая
команда представлена строкой из восьми двоичных цифр, а макси-
мально доступное число команд 28 = 256. Например, такая команда,
как «взять дополнительный код содержимого аккумулятора», может
быть записана в виде 00101111.
Для устройства двоичного умножения (см. рис. 12.3) все команды,
записанные в памяти программы, могли бы быть представлены двоич-
ными четырехразрядными словами. Поскольку программа содержит
только 22 строки, нетрудно написать ее в двоичном виде, т. е. на
языке машинных кодов. Тем не менее , составление программы любой
длины в машинных кодах требует больших затрат времени и, кроме
того, является утомительным занятием. К тому же такой способ про-
граммирования приводит к ошибкам, которые трудно устранить.
Другой способ подготовки программы заключается в использовании
шестнадцатеричной системы кодирования команд. Например,
команда «взять дополнение к содержимому аккумулятора» в шест-
надцатеричной форме обозначается как 2F. Очевидно, что написать
программу таким способом намного легче, к тому же упрощается и
проверка написанной программы, так как вместо двух цифр исполь-
зуется 16.
Практически вполне возможно составить программу в машинных
кодах вручную. Программист записывает объектную программу
в шестнадцатеричных кодах, используя при этом таблицу команд,
входящую в описание модели микропроцессора. В этой таблице
обычно содержатся шестнадцатеричные и двоичные представления
кодов команд, а также указывается, сколько восьмиразрядных слов
(байтов) занимает каждая команда. Например, в набор команд для
микропроцессора «Интел 8085» команда «взять дополнение к акку-
мулятору», обозначенная в мнемонической форме как С МА, имеет
шестнадцатеричный код 2F и занимает одно слово (или байт) памяти.
Другая команда «загрузить аккумулятор из памяти», представляемая
в мнемоническом виде как LDA, соответствует шестнадцатеричному
коду 3/4 и занимает три байта памяти. Когда программа написана,
ее можно загрузить в память, используя, например, шестнадцате-
ричную клавиатуру или телетайп, с помощью средств, обеспечиваю-
щих связь микропроцессора с внешними устройствами.
Другой способ программирования заключается в преобразовании
(компиляции) программы из мнемонической формы. Программа, на-
писанная в таком виде, называется программой на языке АССЕМБ-
ЛЕР. Очевидно, что процесс перевода такой программы в машинные
коды можно выполнить вручную, используя мнемонические коды
из таблицы команд. При этом необходимо преобразовать мнемони-
ческие коды в соответствующие шестнадцатеричные, вычислить
адреса с помощью расчета числа слов и подставить на соответствую-
щие места в записи команд данные и адреса. АССЕМБЛЕР (про-
грамма перевода мнемонических кодов в машинные) преобразует
исходный текст, т. е. программу на языке АССЕМБЛЕР, в программу
в машинных кодах.
Ответы к упражнениям
1
У1.1: а) 7 = А (В + С); б) f2 = (А + ВС) (В + D + АС);
в) f3= (Д’-b В) [С+А(р+Ё)] + В [A + C+E(B + D)1.
У1.2: а) А = АС + АВ + BD + BCD; б) f2 = А + В + С + D;
в) f3 = ABD + ABC + ABD.
У1.3: a) А = А (В + C); 6) f2 = (A + С) (В + С) (A + B);
в) 7з = AB + ABC; r) 74 = (B + D) (A + С) (B + D).
У 1.4: a) fi = ABC; 6) f2 = ВС; в) fs = A + C.
У 1.5; см. рис. У1.5 на стр. 260.
2
У 2.1: a) fi = ABC + ABC + ABC + ABC + ABC;
6) f2 = ABC + ABC + ABC + ABC + ABC-,
в) f3 = ABCD + ABCD + ABCD + ABCD + ABCD + ABCD +
+ ABCD + ABCD + ABCD + ABCD + ABCD.
У 2.2: a) fi = ВС + BC; 6) f2 = A + ВС; в) f3= AB + AC + BC.
У 2.3: a) f = SaSgSaSgSgS,; 6) f = P3A~Pi> в) f = SgS6SeS7.
У 2.4: a) f = AB + AC + BC; 6) f = AB + BC 4- CD + ACD;
в) f = AB + ABC + ~ABD + ACD;
r) f = AC + ABE + BCD + BCD + CDE + CDE + ~ABCE.
У2.5: a) /= AC + BC; 6) f =~AC AD BC;
в) f = AC + CD + ABC + ABD + ABD;
r) f = ABD 4- ACB + BCD + ABC Д АВСЁ + ABDE.
Рис. У1.5
У2.6: a) f = (А + С) (4 + В + Q; б) f = В (4 + С) (4 + С + D);
в) f = (4 + В) (4 + D) (4 + О D) (4 + D + Е) (В + D + £);
г) f = (4 + В)_ (4 + В) (С + D) (В + D).
У2.7: a) F = ACD; б) F = BCD + BCD + ABCD;
в) F= АВ + ABC.
У2.8: 0 = АВ, 1 = ACD, 2 = ACD, 3 = ACD или BCD, 4 = BCD,
5 = BCD, 6 = BCD, 7 = BCD или ACD, 8 = ACD, 9 = AB.
Рис. УЗ.2
A
У3.7:
Рис. У3.7
У3.8: а) АВС + АВС; б) АВС + АВС;
в) А + ВС + ВС; г) А + ВС + ВС.
4
У4.1. Четырьмя цифрами кода NBCD являются А, В, С и D, где А — на-
ибольшая значащая цифра:
1) f = AD + BCD + BCD; 2) f=A + BCD; 3) f = AB.
У4.2. Для чисел, состоящих из одной цифры:
1) А > В, h = АВ; 2) А < В, = АВ; 3) А = В, fa = АВ + АВ.
Для чисел, состоящих из четырех цифр:
О = Wai^32^33’ где Азо= Лово +Лов0' ^31= V1 + V1 и т- Д'>
2) ^>В = ^1з + W12 + W32^n + WaaWlO’ где ^10= Л0В0 И Т- Д-’
3) f А<В = ^23 “Ь W22 "Ь ^33^32^21 “Ь ^33^32^31^20’ ГДе ^20 = ^0^0 И Т> Д’
У4.3. Двоичное число имеет вид ABCD, дополнительный код — PQRS. Тогда
Р = А ф (В + С + D); Q = В ® (С + D); R = С ф D; S = D.
У4.4. Буквы А, В, С, D служат для обозначения четырех цифр кода NBCD,
буква А соответствует наибольшему значащему разряду. Уравнения сегментов имеют
следующий вид:
а = А + С + B~®D; b=B+ С ® D; с = BCD; d = е + BCD + ВС;
е = D (В + С); f= А +CD + BD + ВС; g = А +CD + (В & С).
У4.5. Число PQRSTU является квадратом числа A2AiA0, где Р=Л2Л1;
Q — A2Ai + А2А0; R — Ло Ф — ++', Т — О, U — ^о-
У 4.6. Число в коде NBCD имеет вид ABCD, где А — наибольшая значащая
цифра. Дополнением до девяти ABCD является PQRS, где Р — наибольшая зна-
чащая цифра. Тогда Р = ABC; Q = ВС + ВС; R = С; S = С.
У 4.7. Четыре переключателя обозначаются буквами А, В, С и D, а перемен-
ная, показывающая, горит свет или нет, буквой L. Тогда Ь=АфВфСфО,
У 4.8. Будем считать, что Л, В и С—это отдельные биты двоичного кода,
ар — бит четности. Тогда р = A (S В Q С; F=AqBqCqp, где F = 1,
когда появляется недопустимая кодовая комбинация.
У 4.9. Если считать, что пятибитовое число обозначается ABCDE, где А —
наибольший значащий разряд, то М = А (В + Е) (С + D) + BE (Л + С + D) +
+ CD (Л + В + Е). Здесь М — логическая функция, принимающая значение,
равное 1, когда большинство цифр числа ABCDE являются 1.
У4.10.
У 4.11. Если кодовые комбинации для кода Грея представляются в виде ABCD,
где А — наибольший значащий разряд, а кодовые комбинации для кода Грея, соот-
ветствующего коду XS3, имеют вид PQRS, где Р — наибольший значащий
разряд, то
Р = A; Q = А ® В; R = В ® С; S = С ® D.
У 4.12. Десятичные эквиваленты имеют вид: 1) +11, —53; 2) +11, —75;
3) +11, —74.
У4.13.
У4.14. 0,0010101; 1,1100011.
5
У5.1: 1) a = 1, b = 0, c = 1; 2) a = 0, b = 1, c = 1; 3) a = 1, b = 0, c = 0.
Рис. У5.1
У5.2.
Рис. У5.2
1
Qs
О
У5.3: 1) В момент формирования положительного фронта первого тактового
импульса происходят следующие изменения:
а) 1 —0; б) 0 -* 1; в) 1 ->1; г) 0 -> 0; д) 1 -> 1; е) 1 0; ж) 0->-1; з) 1->1.
В момент формирования отрицательного фронта первого тактового импульса
происходят следующие изменения:
а) 0^ 1; б) 1 1; в) 1 0; г) 0 -> 1; д) 1 -> 1; е) 0-> 0; ж) 1 -> 1; з) 1 ->0;
5) Qs= 1; 6) Qs= 1.
Рис. У5.3
У5.4.
1
as
о
V5.5.Qt+st +Q'Q + KQ)t
У5.6. Для обоих случаев диаграмма внешних состояний будет иметь вид:
(XY+XY)Sl
У6.1. Считается, что D — наибольший значащий бит счетчика.
Td = ABC + ABD-, Tc = ABD; ТВ = А; Та=1;
Sd = ABC\ Rd = ABD или ABC; Bp = ABCD',
Rc=~-ABC; Sb = AB; Rb=AB; Sa=~A; Ra = A;
Jd = ABC; Kd = AB; JC-=ABD; Kc^AB;
JB = A; KB = A; JA=1; KA=1; Dd =~BD+~AD + ABC;
Dc = BC + AC+ABCD; Db = AB + AB; Da = A.
У6.2. Считается, что С — наибольший значащий бит генератора
JC=A + B; Кс—~А’> JB = C; КВ = С; JA = B; КА = В.
Блокировка в состоянии СВ А =111.
Ув.З. Считается, что Р — наибольший значащий бит счетчика
Jp^RS-, Kp = Q-, Jq-P; Kq = PRS-,
JR — PS; KR = PS- Js=~PQR + PR',
Ks= PR+~PR-
Ув.4. Управляющая таблица PQ -триггера имеет вид
Z* р Q
0 0 1 0
0 1 0 0
1 0 0 1
1 1 0 0
Считается, что С — наибольший значащий бит счетчика. Тогда Рс = А + В;
Qc = АВ- Рв= A; QB= А- РА= О', Qa = L
Ув 5 1 2 3 4 5 6 7 В 9 10 11 12 13 14
Запуск Ч I I _______________
e г о !
Остановка ®________________________________I I—
с/ ? ПППППЛПППП П- л_л_п__
г=cSpoc счетчика
Ув. 6: a) fu = 5 мГц
Си
Рис. Уб.5
К счетчику
Рис. У 6.6
I_____I----1 I--------L___I------1_____Г
______________________1_____________________I__1_Г
--------------------------------------------L__-Г
Рис. У6.7
Уб.8.
Рис. Уб.8
7
У7.1.
У7.2. Выбранная последовательность счета: So = Si = S2 = S6 = Sn = S, =
= Si6 = Si4 = Si3 = Si0 = S4 = S8 = So. Считая, что A — наименьший знача-
щий разряд регистра, получаем выражения для функций обратной связи и декоди-
рующей логики в виде f = BD + ACD + ABC + ACD + ACD;
0 = ABCD; 1 = ACD; 2 = BCD; 3 = ABCD; 4 = ACD; 5 = ABD; 6 = ABCD;
7 = ABC; 8 = BCD; 9 = ABCD; 10 = ABC; 11 = ABD.
У7.3. Поскольку нельзя однозначно поставить в соответствие заданной двоич-
ной последовательности последовательность состояний сдвигового регистра, то сна-
чала необходимо разработать счетчик иа S/^-триггерах, имеющий 11 состояний.
Одна из возможных последовательностей состояний, полученная из универсальной
диаграммы состояний (рис. 7.7), имеет вид So = Si = S2 = S5 = Sn = S7 =
= SJ4= Si3= Si0 = S4 = S8 = So. Считая, что A — наименьший значащий раз-
ряд регистра, получаем, что функции обратной связи и выхода имеют вид f =
= ACD + BCD -j- ACD + ABCD; g = D+ AC.
a)
У7.5. f = В © С 4- АВ 4- тВ,
где f — функция обратной связи, А—наименьший значащий разряд сдвигового
регистра. _ _ ____ ______ __________ _
У7.6. Р = АВС 4- ABC; Q = AC; R = АВ + ВС + АС + ABC; S = АВС 4-
4- АС.
У7.7.
7 --------------------
Рис. У7.7
6)f=~cb.
8
У8.1.
Рис. У8.1
в) схема предназначена для просмотра трехбитовых последовательностей. На
выходе Z появляется сигнал, если последние два бита равны 1.
У8.2.
Рис. У8.2
У8.3. Схемное решение зависит от того, как закодированы состояния.
У8.4. Зд = АтХ\ J д = тХ; Кд = АтХ; Кд = тХ; Z = АХ.
Рис. У8.4
У8.5. JA = B; JB = AS; KA = S + B; KB = AS; Z = АВП
Рис. У8.5
Рис. У8.6
У8.8.
Рис. У8.8
У8.9.
Рис. У8.9
У8.10.
Рис. У8.10
У8.11.
а) Pf — (S4SB) (So) (Sj) (S3) (S3) (S6);
6) Pf — (SsSsSiqSuSiz) (S3SbS12) (S4S7S14) (So) (S() (S8) (S9).
У8.12. Pf= (S0Si) (S4SB) (S2S3) (S6).
У8.13.
S)
So S3
Si 5z
a)
Рис. У8.13
У8.14.
' Г-s., -
z
9 Рис. У 8.14
У9.1. Главная диаграмма состояний задачи
Рис. У9.1
У9.2.
Рис. У9.2
У9.3.
So St Sz
Ss X,Xz+X,r2 Sj 5, X,X2+X,X2 Sj
Рис. У9.3
Рис. У9.4
Рис. У9.6
У9.7.
Рис. У9.7
У9.8. Гонки, возникающие при переходах So S3, Si S2 и подаче на вход
сигнала XiX2, являются критическими.
Противогоночное
кодирование
Рис. У9.8
У9.10. Коды состояний: So = АВ = 0; Si =01; S2= 11; S3 = 10.
Рис. У 9.10
10
У10.1: a) Do= C, Di = 1, Da = C, Da = C;
6) Do = A, Di = A, Da = Д, Da = 1;
в) Do = 1, Di = 0, D2 = 1, Da = 1.
У10.2: a) Do = C + D, Di = CD + CD, Da = C + D, Da = C;
6) Do = A + D, Di = Д, O2 = 0, Da = D;
в) Do = AB, Di = 1, D2 = A, Da = A + B;
r) Do = 0, Di = BC, Da = I, Da = В + C.
Рис. У10.3
Рис. У10.6
б) входы в MUXr. Do = A, Di = 0,
D2 = 1, Da = 0; в MUX2: Do = A, Di = A,
Da = 1, £>3 = А; в MUX3: Do = A, Di = 1,
D2= 1, D8= 1; в MUX4: Do= A, Di= 1,
Da — 0, Da — 1.
У10.4: а) входы в MUX1; Do = A + B, Di = AB, Da= 0, О8=Л'+В;
в MUX2-. Do = AB, Di = A + B, Da = AB, Da = Aj_B MUX3: Do =_A + B,
Di=_AB, Da= AB, О8=Д + В; в MUX4: Do= AB + AB, Di= B, Da =
= AB, Da = AB;
б) для MUX5 управляющие сигналы Е и F; для MUX1—4 управляющие сиг-
налы В, С и О; входы в MUX1: Do =1, Di = О, О2 = О, D3 = A, = А,
D3 = A, Dej- О, О7 = Д; в MUX2: D0=A, D± = 1, О2 = A, D3 = Д, О4 = О,
DB = A, De = О, D, = Д; в MUX3: Do= A, Dt =1, D2 = A, D3 = А, Dt = 1,
Ов = Д, D^A, О7=1; ъ MUX4: D0=A, Dt = 1, D2 = А, D3 = О, О4 = Д,
Ов =0, D9 = О, О7 = Д.
У10.5. 4 и В — цифры суммы; С,,х— входной сигнал переноса; входы в
мультиплексор, формирующий сумму: управляющие сигналы В и Свх, а также
DB= AiDi = Д1О3 = AiD3 = Д; входы в мультиплексор переноса: управляющие
сигналы В и СВХ) а также £>0 = 0, Di = Д, D2 — A, D3-- 1.
10.6: а) см. рис. У10.6,а на стр. 278;
б) 0 = 'ABCD, Т = ABCD, 2 — BCD, 3~— BCD, 4 — BCD, 5 — BCD, 6 — BCD,
7 = BCD, 8 = AD, 9 = AD.
У10.7.
Рис. У10.7
У10.8. Требуется один дешифратор из 4 в 16, генерирующий дополнения для
каждого из Р-термов. Например, Ро, Pj_ и т. д. Тогда
a) W =~Р3-Рв-Р,Р8.Ра , X = Р4-Р6-Р7-Р8-Р9, Г = Р2-Р3-Рв-Р8Р9 ,
2 = Pi• Р3 -Р6 * Р? Ря г
где 1Г — старший разряд кода 2-4-2-1;
б) W = Рв-Р6-Р7-Р8-Р9, X = Р1-Р2-Р3-РеРа, У = Ро-Рз-РгРтЛ.
1= P0-P2-PfP3-Ps, где W — старший разряд кода;
в) W = Рв-Р6-Р7-Р8-Р0, X = Ро Ря, Y = Р3-Р4-Рв Рв.
Z= Р2-Р3-Р3-Р7, где Д7 — старший разряд кода Грея на основе XS3.
У10.9. Требуется один дешифратор из 4 в 16. Тогда /4= P2-P3-Pi4-PiB
fi = P12> fi~ РЯ'Pg'Pii'Р12'P13'Pli'Plb-
Рис. У 10.10
Рис. У 10,11
В £ F
У10.12. Емкость ПЗУ равна 3072 бит.
У10.13: а) 80 бит; б) 768 бит; в) 384 бит.
У10.14.
У10.15.
У10.16 (и У10.18). Типичное решение для таких задач показано в ответе на
задачу У10.17.
У10.17.
Рис. У10.17
У10.18. См. У10.16.
У10.19. Один десятичный разряд трехразрядиого устройства вычитаиия/сло-
жения для чисел в коде XS3.
Рис. У 10.19
11
У11.1: а: 1) f = CD + AD + BD + ABC + ABC + ACD + ABD + ABC;
2) f = (A + В + £>) (A + C + D) (A + B"+ C + D) (A + В + C + £>);
6: l)f=AB + BC + BD + ACD + BCD-,
2) f = (В + С) (B + D) (A + В + C + D). Читателю предоставляется право
самостоятельно выполнить факторизацию, чтобы удовлетворить требованиям ограни-
чения на число выводов.
У11.2: а) Ситуации статического 1-риска возникают при А = В= С= 1
и А = 1, В = 1, С = 0; ситуации статического 0-риска при В = С = 0, D = 1.
б) Ситуация статического 1-риска при С=В=1иА = 0и при В = D = 0;
ситуация статического 0-риска при А = В = С = 0.
У11.4: а) Ситуация динамического риска при А = 1, В = С = 0 при изме-
нении С из 0 в 1.
б) Ситуация динамического риска при А = 0, В = 0, С = 1 и при изменяю-
щемся из 1 в 0.
СПИСОК ЛИТЕРАТУРЫ
Bannister В. R.( Whitehead D. G. Fundamentals of digital systems. McGraw-Hill,
1973.
Blakeslee T. R. Digital design wish standard MSI and LSI, Wiley, 1975.
Boyce J. C. Digital logic and switching circuits: operation and analysis, Prentice-
Hall, 1975.
Caldwell S. H. Switching circuits and logical design, Wiley, 1967.
Clare C. R., Designing logic systems using state machines, McGraw-Hill, 1973.
Dietmeyer D. L. Logic design of digital systems, Boston, Allyn & Bacon, 1978.
Doktor F., Steinhauer J. Digital Electronics, Macmillan, 1973.
Fletcher W. 1. An engineering approach to digital design, Prentice-Hall, 1980.
Friedman A. D. Logical design of digital systems, Woodland Hills, Computer
Science Press, 1975.
Friedman A D., Menon P. R. Theory and design of switching circuits Woodlad Hills,
Computer Science Press, 1975.
Givonie D. D. Introduction to switching circuit theory, McGraw-Hill, 1976.
Gothmann W. H. Digital Electronics: an introduction to theory and practice,
Prentice-Hall, 1977.
Greenfield J. D. Practical digital design using ICs, Wiley, 1977.
Hill F. J., Petersen G. R. Introduction to switching theory and logical design,
Wiley, 1974.
Humphrey W. H. Switching circuits with computer applications, McGraw-Hill,
1958.
Hurley R. B. Transistor Logic Circuits, Wiley, 1963.
Hurst S. L. The logical processing of digital signals, Crane, 1978.
Johnson D. E. Digisal circuits and microcomputers, Prentice-Hall, 1979.
Kohavi Z. Switching theory and finite automatic theory, McGraw-Hill, 1978.
Kostopoulos G. K. Digital engineering, Wiley, 1975.
Lee S. C. Digital circuits and logic design, Prentice-Hall, 1976.
Lee S. C. Modern switching theory and digital design, Prentice-Hall, 1978.
Lenk J. D. Handbook of Logic Circuits, Resten, 1972.
Lenk J. D. Logic designer’s manual, Resten, 1977.
Levine M. E. Digital theory and practice using integrated circuits, Prentice-Hall,
1978.
Lewin D. Logical design of switching circuits, Neben, 1976.
Lind L. F.( Nelson J. С. C. Analysis and design of sequential digital systems,
MacMillan, 1977.
McCluskey E. J. Introduction to the theory of switching circuits, McGraw-Hill,
1965.
Maley G. A., Earle J. Logic design of transistor digital computers, Prentice-Hall,
1963.
Malvino A. P., Leach D. P. Digital principles and applications, McGraw-Hill,
1975.
Мало M. Digital logic and computer design, Prentice-Hall, 1979.
Marcus M. P. Switching circuits for engineers, Prentice-Hall, 1967.
Morris N. M. Digital electronic circuits and systems, Macmillan, 1974.
Morris N. M., Logic circuits, McGraw-Hill, 1976.
Nagle H. T., Carroll B. D., Irwin J. D. An introduction to computer Icgic, Pren-
tice-Hall, 1975.
Oberman R. M. M. Digital circuits for binary arithmetic, Macmillan, 1979.
Oberman R. M. M. Disciplines in combinational and sequential circuit design,
McGraw-Hill, 1970.
Poratt D. J., Barna A. Introduction to digital techniques, Wiley, 1979.
Rhyne V. T. Fundamentals of digital systems design, Prent ice-Hall, 1973.
Roth С. H. Fundamentals of logic design, West, 1975.
Triebel W. A. Integrated digital electronics, Prentice-Hall, 1979.
Unger S. H. Asynchronous sequential switching circuits, Wiley, 1969.
Wickes W. E. Logic design with integrated circuits, Wiley, 1968.
Wood P. E. Switching theory, McGraw-Hill, 1968.
Zissos D. Logic design algorithms, OUP, 1972.
Zissos D. Problems and solutions in logic design, OUP, 1976.
ПРЕДМЕТНЫЙ УКАЗАТЕБЬ
А
Автомат Милли 153
— Мура 153
— с тремя состояниями 177
— с четырьмя состояниями 180
Аккумулятор 257
Алгебра булева 11
Б
БИС 69, 242
В
Вход неиспользуемый 44
— предустановки 83
— Уравнения 97
Выбросы 227, 228
Г
Генератор последовательности 124
----Диаграмма состояний 126
----максимальной длины 136, 137
----Проектирование 125
---- псевдослучайной двоичной 135
Гонки 81, 87, 176, 177
— критические 177
— Условия возникновения 81, 87
Д
Демультиплексор 200
Дешифратор 201
Диаграмма состояний 77
— временная 80, 86, 87, 108, 111
Диск гибкий 257
3
Запирание триггера 88
И
ИМС со средним уровнем интеграции
191
---------мультиплексоров 191—200
---------ПЗУ 205—209
- ПЛМ 211—217
— сумматоров 217, 220, 221
К
Карта Карно 24—37
--- входных сигналов триггеров
104, 105
--- канонических форм 25
--- мультиплексора 196, 197
---полного вычитающего устрой-
ства 63
---Противогоночное кодирование
182
---Статические риски 238—239
---счетчиков 93, 94, 101, 219
--- сумматора 58
---функции ИЛИ—НЕ 44
-------И-НЕ 40
-------ИСКЛЮЧАЮЩЕЕ ИЛИ 51
-------ИСКЛЮЧАЮЩЕЕ ИЛИ-
НЕ 52, 53
Классификатор прерываний 72
---Реализация 73
---Таблица истинности 73
Код Грея 70
---Преобразователь 70—71
— дополнительный 62, 63
— обратный 64
— отраженный двоичный 70
— NBCD 69
Команда выполнения 151
— пересылки 251
— управления 251
Л
Логика комбинационная 56—75
— переключателя 11
М
Матрица коммутационная для ПЗУ
206, 207
---ПЛМ 214, 215
Метод адресации для ПЗУ 206, 209
— Зиссоса 43
— Квайна—Мак-Класки 24
— формирования цепочки 74, 75
Микропроцессор 242—259
— Аккумулятор 257
— Память 248
— Программирование 258
— Регистр команд 251
— Структурная схема 255
— Счетчик программ 250
— Устройство умножения 245, 246
— ЦП 256
Мультиплексор 191—201
— восьмивходовый 192
— как генератор логических функ-
ций 194—200
— четырехвходовый 191
О
ОЗУ 248, 257
П
Переключатель 11
Переменные вторичные 175—177, 181
Петля 184
ПЗУ 205—211
— Методы адресации 206
— Проектирование 209
— Секционирование 248
ПЛМ 211—217
Полусумматор 56, 57
Порт ввода—вывода 255
Последовательность максимальной
длины 134
Процедура слияния Колдуэлла 147,
157, 174
Р
Расширение элементов 47, 48
Регистр микропроцессора 250, 251, 257
— сдвиговый 116—139
---Применение 117, 118
---с обратной связью типа ИСКЛЮ-
ЧАЮЩЕЕ ИЛИ 134—139
---Универсальная диаграмма со-
стояний 121, 122
---четырехразрядный 122
Резистор нагрузочный 49
Риски 226—241
— динамические 237—239
— Обнаружение 235—237
— статические 228—237
— существенные 239—240
С
Связь обратная 79
--- сдвигового регистра 120
---типа ИСКЛЮЧАЮЩЕЕ ИЛИ
134
---Функции 124, 126, 134—136
Сигнал выходной 140, 143
— прерывания 72
— синхронизации 142
Система управления шиной 255
Слово 249
Состояние внешнее 78
— внутреннее 145, 146
— Диаграмма 78, 80
— Кодирование 163, 177, 180
— Сокращение 157
Сумматор 56—62
— на ИМС 217
— полный 57
— работающий в коде NBCD 223
— с ускоренным переносом 59
— четырехразрядный параллельный 58
Схема алгоритмов 246
— асинхронная 171—190
---Диаграмма внутренних состоя-
ний 171, 172, 175
---Петли 184
---Проектирование с помощью ПЗУ
209
---Ситуации существенного риска
239
--- Условия возникновения гонок
176
— гарантированная от риска 233
— запирания 111, 124
— импульсная 156
— синхронная последовательная
140—170
-------Временная диаграмма 141, 152
-------Диаграмма внутренних со-
стояний 145—146
-------Проектирование 144—151
---------на основе ПЗУ 209
------------ПЛМ 216
-------Уравнение выхода 142
Счетчик 92—116
— асинхронный двоичный 107
---десятичный 109
--- обратного счета 101
---с автоматическим сбросом ПО
— двоично-десятичный 99
— двоичный 92, 93
— Джонсона 131
— использующий код Грея 102
— Каскадирование 114
— кольцевой 127—130
— иа интегральных схемах 112
— программы 250
— по модулю «4» 93
-------«5» 96
------- «8» 94
------- «16» 106
Т
Таблица импликаций 157
— истинности 12
— состояний 78
— управляющая 83, 85
Теорема де Моргана 20
— идемпотентности 16
— избыточности 17
— объединения 17
— пересечения 17
— перестановки 20
— поглощения 17
— распределения 20
— согласования 21
— сочетания 20
Термы, «не доставляющие беспокой-
ства» 34
Триггер 77—91
—• Диаграмма внешних состояний 78
— Гонки 81
— Запирание 88
— Таблица возбуждений 187
—• — состояний 78, 80, 85, 88
— типа «хозяин—слуга» 87
— Характеристическое уравнение 79,
82, 88
— D88
— JK 84
— S/? 81
— Т 77
У
Указатель стека 257
Уменьшаемое 62
Упрощение функции 24—38
Уравнение характеристическое 79
Устройство вычитающее полное 62
— умножения двоичное 245
----программно-управляемое 248
— обнаружение последовательности
184—188
Ф
Флажок 257
Форма каноническая 25
— мнемоническая 258
Функция И 12, 13
----Реализация на элементах ИЛИ—
НЕ 44
--------И—НЕ 41
----Таблица истинности 12
— ИЛИ 13, 14
----Реализация на элементах ИЛИ—
НЕ 45
--------И—НЕ 42
----Таблица истинности 13
— ИЛИ—НЕ 43
----Карта Карно 44
----Таблица истинности 44
— И—НЕ 39
----Карта Карно 40
----Таблица истинности 40
— ИСКЛЮЧАЮЩЕЕ ИЛИ 50
------Карта Карно 51
------ Каскадирование 53
------Реализация 52
------Таблица истинности 51
— ИСКЛЮЧАЮЩЕЕ ИЛИ—НЕ 51
— НЕ 14
----Карта Карно 14
Ц
Цикл 175
Ш
Шина двунаправленная 255
—• однонаправленная 255
Э
Элемент задержки 226
— И 13
— ИЛИ 14
— ИЛИ—НЕ 44
— И—НЕ 40
— ИСКЛЮЧАЮЩЕЕ ИЛИ 51
— Расширение входов 47
— смешанный 48
— с открытым коллектором 49
— с тремя состояниями 50
Я
Язык АССЕМБЛЕР 259
Брайен Голдсуорт
ПРОЕКТИРОВАНИЕ ЦИФРОВЫХ ЛОГИЧЕСКИХ УСТРОЙСТВ
Редактор Д. П. Бут
Художественный редактор С. Н. Голубев
Переплет художника О. В. Камаева
Технический редактор Ф. П. Мельниченко
Корректор Л. Е, Санюшкина
ИБ № 4330
Сдано в набор 11.07.84. Подписано в печать 22.10.84.
Формат 60X90 ,/1в. Бумага типографская № 2. Гарнитура литературная.
Печать высокая. Усл. печ. л. 18,0. Усл. кр.-отт 18,0. Уч.^изд. л. 19,03.
Тираж 8000 экз. Заказ № 189. Цена 1 р. 60 к.
Ордена Трудового Красного Знамени издательство «Машиностроение»,
107076, Москва, Стромынский пер., 4.
Ленинградская типография № 6 ордена Трудового Красного Знамени
Ленинградского объединения «Техническая книга» нм. Евгении Соколовой
Союзполиграфпрома при Государственном комитете СССР
по делам издательств, полиграфии и книжной тоговли.
193144, г. Ленинград, ул. Моисеенко, 10.