С. П. ФИНИКОВ
ТЕОРИЯ ПОВЕРХНОСТЕЙ
ОНТИ
ГОСУДАРСТВЕННОЕ
ТЕХНИКО-ТЕОРЕТИЧЕСКОЕ ИЗДАТЕЛЬСТВО
МОСКВА — 1934 — ЛЕНИНГРАД

Т-24-5-2
Гостехтеоретиздат. Выход в свет март 1934 г.
3-я тип. ОНТИ им. Бухарина. Ленинград, ул. Моисеенко, 10.

ОГЛАВЛЕНИЕ.
Стр.
Предисловие 7
Глава первая. Кривые в пространстве.
I. Элементы первого поря ока.
1. Определение кривой • 11
2. Касательная 11
3. Длина дуги 12
II. Элементы второго порядка.
4. Главная нормаль 14
5. Сопровождающий трехгранник Френе 15
6. Соприкасающаяся плоскость 15
III. Элементы третьего порядка.
7. Движение трехгранника Френе 16
8. Характеристика движения трехгранника Френе 18
9. Кривизна и кручение 18
10. Кривые Бертрана 19
11. Натуральные уравнения кривой 22
12. Винтовые линии 23
IV. Развертывающиеся поверхности, связанные с кривой.
13. Огибающая семейства поверхностей 24
14. Развертывающаяся поверхность 26
15. Полярная поверхность 26
16. Эволюты кривой • . . . 27
17. Спрямляющая поверхность 28
V. Соприкасающиеся поверхности.
18. Соприкасающаяся плоскость . . • . • 29
19. Соприкасающаяся сфера 30
20. Формула для вычисления кручения кривой 32
Упражнения • 33
Глава вторая. Линейный элемент поверхности.
I. Элементы первого порядка на поверхности.
1. Криволинейные координаты на поверхности 37
2. Касательная плоскость . • 38
3. Линейный элемент поверхности . . . . • 39
4. Угол двух кривых на поверхности 40
5. Площадь поверхности 41
II. Примеры поверхностей.
6. Плоскость и сфера • 42
7. Поверхность вращения • 43

4 ОГЛАВЛЕНИЕ
Стр.
8. Катеноид *.«..* 44
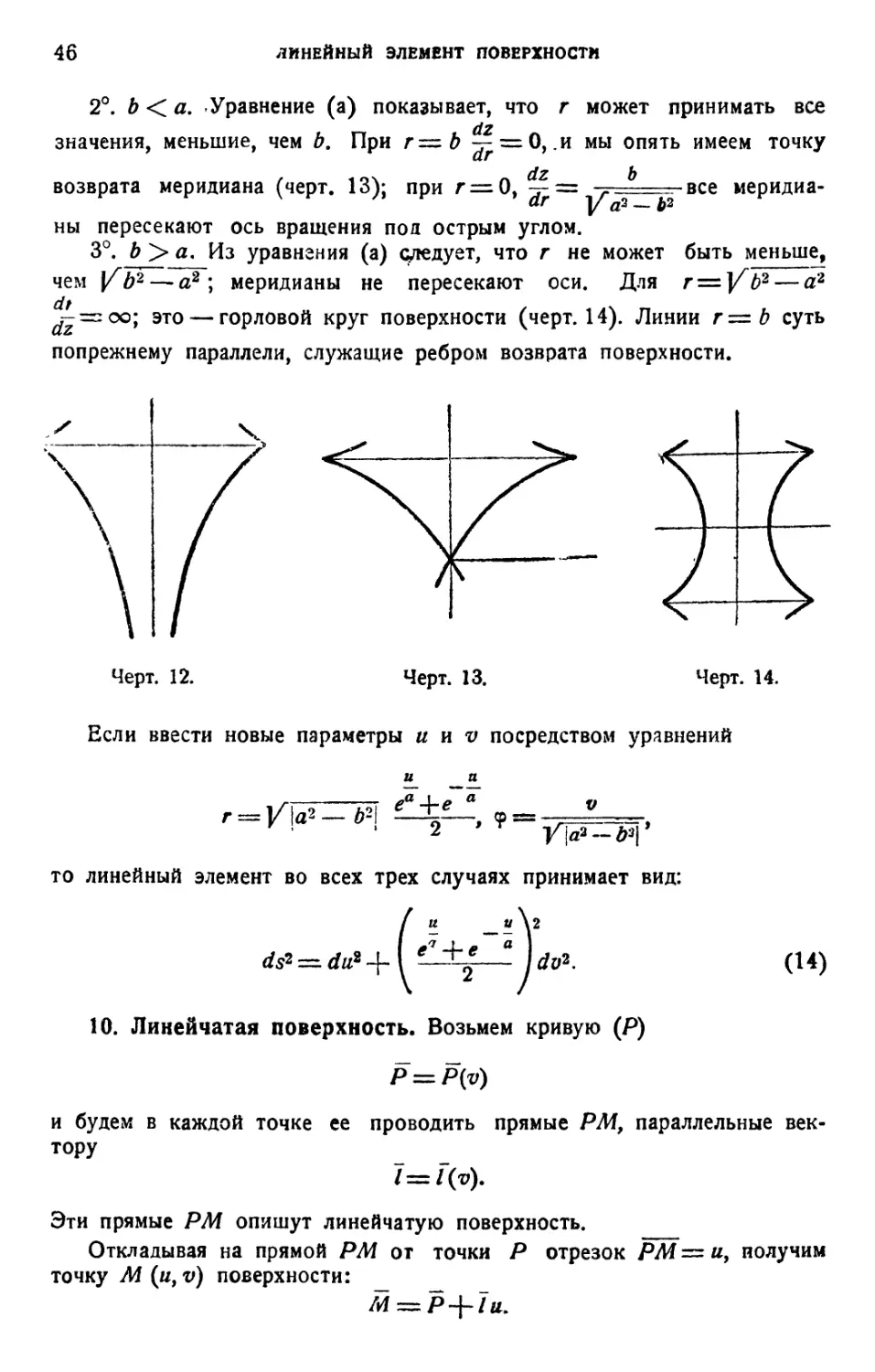
9. Псевдосфера • 45
10. Линейчатая поверхность 46
II» Налагающиеся поверхности.
11. Изгибание поверхностей 49
12. Развертывающаяся поверхность 49
13. Изгибание поверхностей вращения 50
14. Изгибание шара • . . . 51
IV. Конформное отображение.
15. Конформное отображение 52
16. Конформное отображение поверхности вращения на плоскость... 53
17. Изотермическая система 54
18. Линии нулевой длины 55
Упражнения . . . . • 57
Глава третья. Вторая квадратичная форма.
I. Нормальная кривизна кривой на поверхности.
1. Кривизна кривой на поверхности 60
2. Нормальная кривизна кривой • 61
3. Индикатриса Дюпена 62
4. Формула Эйлера 64
5. Главные радиусы кривизны 65
II. Трехгранник Дарбу.
6. Трехгранник Дарбу 66
7. Кинематическое значение квадратичных форм Гаусса 68
8. Сферическое изображение поверхности 69
9. Кривизна поверхности 70
III. Линии кривизны.
10. Линии кривизны 71
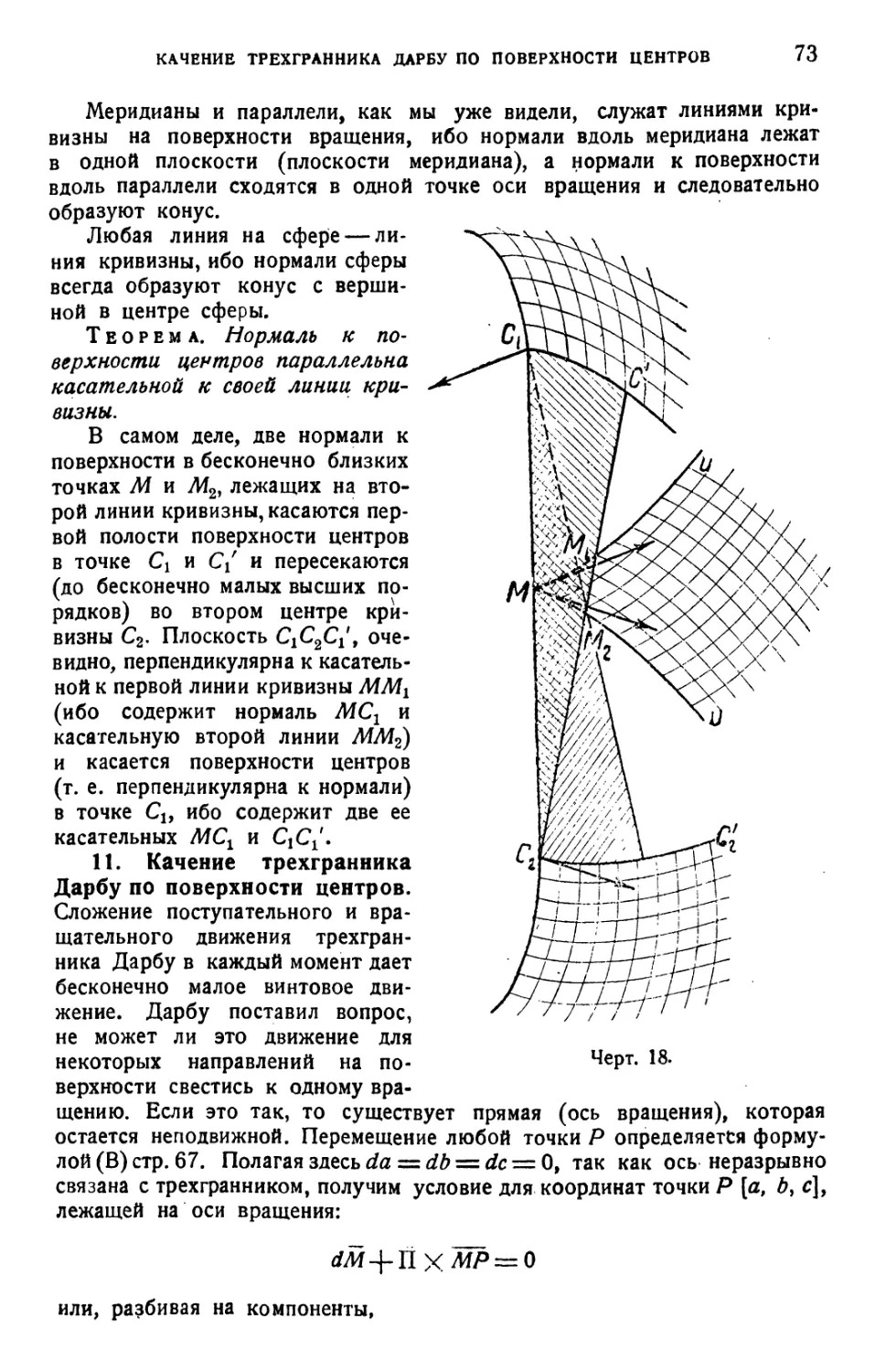
11. Качение трехгранника Дарбу по поверхности центров 73
IV. Сопряженные линии.
12. Сопряженные направления 74
13. Поверхность, отнесенная к сопряженной системе 76
V. Асимптотические линии.
14. Асимптотические линии 77
15. Асимптотические касательные к поверхности 78
16. Поверхность, отнесенная к асимптотическим линиям 80
17. Формулы Лельёвра • • . . 81
18. Теорема Епперег'а 83
VI. Добавление.
19. Проективное преобразование пространства 83
20. Квадратичные формы поверхности 84
Упражнения 85
Глава четвертая. Основные уравнения теории поверхности.
I. Уравнения Гаусса-Кодацци.
1. Основные уравнения в форме Дарбу 89
2. Единственность поверхности с заданными инвариантами 90

ОГЛАВЛЕНИЕ 5
Стр.
3. Определение конечных уравнений поверхности 91
4. Определение трехгранника Дарбу по коэфициентам двух
квадратичных форм 92
5. Уравнения Кодацци . . > 93
II. Проблема изгибания поверхности.
6. Две задачи изгибания 95
7. Теорема Гаусса • 96
8. Первая задача изгибания 97
9. Поверхности постоянной кривизны 98
10. Изгибание с одной твердой линией 101
11. Изгибание с сохранением асимптотических линий одного семейства 102
12. Изгибание с сохранением сопряженной системы 103
III. Сферическое изображение поверхности.
13. Сферическое изображение и его линейный элемент 105
14. Третья квадратичная форма Гаусса 106
15. Поверхность с заданным сферическим изображением сопряженной
системы 107
16. Сферическое изображение асимптотических линий 109
17. Примеры ' . 110
Упражнения 112
Глава пятая. Геодезические линии. Геометрия на поверхности.
1. Геодезические — как линии постоянного направления на поверхности 115
2. Уравнение геодезической линии 116
3. Геодезическая линия как кратчайшее расстояние 117
4. Теорема Дарбу • 118
5. Геодезические на поверхности вращения . . . . • 120
6. Развертывание линии на плоскость 121
7. Геодезическое кручение 124
8. Кривизна геодезического треугольника 125
9. Геодезические круги Дарбу 127
10. Геодезические эллипсы и гиперболы 128
11. Теорема Якоби • 129
12. Поверхности Лиувилля 131
13. Геометрия на псевдосфере 134
Упражнения 138
Глава шестая. Минимальные поверхности.
1. Поверхности с наименьшей площадью • 141
2. Основные свойства минимальной поверхности 142
3. Формулы Монжа • 143
4. Формулы Вейерштрасса 144
5. Односторонние минимальные поверхности 146
6. Изгибание минимальных поверхностей 149
7. Формулы Шварца 150
8. Следствие из формул Шварца 152
9. Частные случаи 153
Упражнения , 156
Глава седьмая. Теория конгруэнции.
1. Линейчатая геометрия 158
2. Конгруэнция кривых 158
3. Конгруэнция прямых t ,..,... , 161

6 ОГЛАВЛЕНИЕ
Стр.
4. Фокусы луча 162
5. Граничные точки луча 164
6. Изотропная конгруэнция 166
7. Нормальная конгруэнция 169
8. Конгруэнция W 172
9. Поверхности Вейнгартена 173
10. Псевдосферическая конгруэнция 176
11. Основные формы Санниа 177
Упражнения . • . . 179
Глава восьмая. Триортогональная система поверхностей.
1. Криволинейные координаты в пространстве 183
2. Теорема Дюпена 185
3. Уравнение Ляме . ч 186
4. Теорема Лиувилля о конформном отображении пространства .... 187
5. Теорема Дарбу • 189
6. Уравнения для семейства поверхностей Ляме 191
7. Софокусные поверхности второго порядка 192
8. Изотермическая система 194
Упражнения . . . . , 195
Таблица основных формул 196

ПРЕДИСЛОВИЕ.
Диференциальная геометрия родилась в работах Монжа и его
учеников как приложение анализа к геометрии. Гаусс значительно раздвинул
эти рамки. Введение криволинейных координат, основных квадратичных
форм, сферического изображения поверхности создало тот фундамент, на
котором могла свободно развиваться теория, изложенная в четырех томах
курса Бианки. Изящный метод Дарбу много помог ее пышному развитию.
Она значительно переросла замыслы Гаусса. Не только теория
поверхности в тесном смысле слова, но и теория конгруэнции прямых,
циклических систем или трижды ортогональных семейств поверхностей стала
предметом исследования. Работами Вильчинского, Блашке, Фубини были
созданы новые отрасли нашей науки — афинная, проективная,
конформная, диференци,альные геометрии. Идеи Римана и Картана еще
раздвинули ее рамки вводя в круг исследования наиболее общее пространство,
а гениальная мысль Эйнштейна по существу сделала всю физику одной
из глав диференциальной геометрии.
В этом блестящем развитии самый метод нашей науки не мог
оставаться неизменным. От элементарных приемов Монжа, которые по
существу были простым приложением аналитической геометрии, к теории
квадратичных форм Гаусса, к исключительной по своей общности и силе
символике тензорного анализа и абсолютному диференцированию Риччи;
от опирающегося на простейшие кинематические представления метода
Дарбу и Рибокура к методу внешних форм и подвижной системы
отнесения Картана, — таков путь развития диференциальной геометрии за сто
с небольшим лет.
Это необычайное развитие метода, который в своих последних
обобщениях представляет изумительно стройную и совершенную систему и сам
по себе достоин изучения, эти поражающие успехи нашей науки таят
в себе и некоторую опасность, по крайней мере для начинающих:
аппарат исследования может в их глазах заслонить самый предмет изучения.
Читая многие работы по диференциальной геометрии и даже учебники,
не сразу можно уловить, что дело идет об исследовании вещественных
свойств окружающего мира, хотя бы и в идеальном представлении его.
Между тем диференциальная геометрия есть все же геометрия; ее
должно интересовать и интересует исследование простых или более
глубоких свойств линий, поверхностей или более сложных образований
вплоть до пространств Картана с кривизной и кручением.
Мне казалось поэтому полезным написать такую книгу по
диференциальной геометрии, где геометрическая сторона дела стояла бы на
первом месте, а самый метод вводился бы постепенно, по мере надобности.
Из поставленной задачи вытекали и содержание, и выбранный метод,

8
ПРЕДИСЛОВИЕ
и самое расположение материала. Почти вся книжка посвящена теории
поверхности, как наиболее простому и осязаемому объекту диференци-
альной геометрии. Только первая глава отводится теории кривых, и в
двух последних намечена теория конгруэнции и триортогональных систем.
Основным методом избран кинематический метод Дарбу. Тут формулы
более просты, и геометрическая сущность выступает с большей
ясностью,— только здесь, например, можно вывести основные условия
совместности (уравнения Гаусса-Кодацци), не переходя на другой лист
бумаги.
Я все же не решился совершенно исключить теорию квадратичных
форм Гаусса и почти во всех основных вопросах провел параллельное
изложение с помощью основных форм поверхности. Это было тем более
необходимо, что только в свете гауссовой теории компоненты переноса
и вращения Дарбу получают свое полное значение с точки зрения
теории поверхности.
Чтобы сделать его еще более наглядным, метод Дарбу дан в
векторных обозначениях. Векторная символика стала теперь обычным языком
геометрии на Западе. Элементарные сведения основных операций над
векторами и у нас достаточно распространены, но даже и отсутствие
знакомства с векторами вряд ли явится препятствием к пониманию этой
книги, — настолько незначителен объем необходимых обозначений,
которые, кстати, все объяснены в сносках.
Первая глава закончена сама в себе и может читаться отдельно. Со
второй главы начинается теория поверхности. Здесь с самыми
элементарными сведениями разбирается целый ряд наиболее известных
поверхностей и ставятся основные задачи изгибания поверхности и конформного
отображения. Не следует забывать, что большинство этих результатов
было получено до того, как была построена общая теория, и что знание
конкретных поверхностей и отдельных случаев изгибания составляет в
такой же мере содержание диференциальной геометрии, как и общие
методы исследования.
В третьей главе вводятся вторая квадратичная форма Гаусса,
компоненты движения трехгранника Дарбу и все те линии на поверхности,
которые непосредственно с ней связаны, и только гл. IV — основные
уравнения теории поверхности и их приложение к двум основным
задачам: задаче изгибания поверхности и задаче определения поверхности по
ее сферическому изображению — содержит изложение основной теории.
Для читателя, который хотел бы в немногих словах ознакомиться
с теорией поверхности без всяких приложений, можно указать гл. II,
отд. I; гл. III, отд. I и II, и гл. IV, отд. I.
Чтобы сделать еще более близкими те поверхности, которые мы
изучаем, в конце книги приложена таблица фотографий.
Рисунки 2 и 10—14 заимствованы из книги Hilbert & Cohn Vossen
„Anschauliche Geometrie", все остальные сняты с моделей кабинета
математики Московского университета. Пользуюсь случаем выразить свою
глубокую благодарность всем лицам, которые оказывали мне в этом
содействие.
Несмотря на элементарность этой книжки, я думаю, что она может
служить введением для чтения оригинальных мемуаров и даже для соб-

ПРЕДИСЛОВИЕ
9
ственных исследований. Чтобы облегчить ее использование в этом
направлении, в конце приведена таблица формул, а в конце каждой главы даны
задачи и упражнения. Большинство из них отличается от оригинального
исследования только тем, что ответ заранее известен. К ним можно было
бы присоединить все те теоремы, приведенные в тексте, доказательство
которых намечено более или менее сжато и требует от читателя
самостоятельного проведения выкладок.
К сожалению, я здесь совершенно не мог коснуться вопросов
бесконечно малого изгибания, преобразования поверхностей и всех тех
вопросов связи между элементами поверхностей, конгруэнции и т. д.,
которые Рибокур назвал геометрией около поверхности и которые особенно
хорошо разрабатывались за последние полвека. Эти вопросы могли бы
составить отдельную тему, к когорой я вернусь, если позволят
обстоятельства.

ГЛАВА ПЕРВАЯ.
Кривые в пространстве.
I. Элементы первого порядка.
1. Определение кривой. Линия в пространстве определяется двумя
уравнениями между текущими координатами произвольной точки ее
М{х, у, z)
/Ч*, Л *) = 0, Ф(*,Л г) = 0. (1)
Гораздо удобнее ввести вспомогательный параметр t и определить
линию тремя уравнениями, задавая текущие координаты как функции
одного переменного L Чтобы не вводить лишних знаков, мы будем
обозначать функции теми же буквами, которыми обозначены сами
переменные координаты
* = *(0. У = У(*)> z = z{{). (2)
Очевидно, одну из этих функций можно дать произвольно, и тогда
две другие определятся из уравнений (1). Если / есть время, то
уравнения (2) определяют закон движения по кривой.
Три уравнения (2) можно записать одним
Ж = Ж(0, (2Г)
которое определяет вектор М = ОМ, соединяющий начало координат О
сточкой М кривой (текущий радиус-вектор). Координаты вектора ОМ —
проекции отрезка ОМ на оси координат — совпадают с координатами
точки М.
Записывая в фигурных скобках координаты вектора, имеем:
М = {х, у, г}.
Дать вектор — значит дать его координаты; следовательно три
уравнения (2) и уравнение (2') представляют две записи одного и того же
факта.
Мы будем предполагать, что функции (2) однозначны, конечны и
непрерывны так же, как и все те производные их, которыми мы будем
пользоваться. При изменении t в той области, которую мы будем
рассматривать, точка М должна пробегать кривую (или часть ее) только
один раз.
То направление на кривой, которое соответствует возрастанию /,
будем называть положительным.
2. Касательная. Возьмем на кривой (2) около точки М (х, у, г)
вторую точку Мх (xv уи zx).

12
КРИВЫЕ В ПРОСТРАНСТВЕ
Пусть точкам М и Мt соответствуют значения параметра t и tv
Хорда, соединяющая эти точки, дает вектор
ММХ = Мх — М = М (tx)—М (/) 1),
как это непосредственно видно из черт. 1.
Разделим эту разность на разность параметров tx— t. Вектор
Л/№)-Л7(0
имеет направление хорды MMv В пределе при tt = t точка Мх совпадет
с точкой М% секущая ММХ обратится в касательную; следовательно
производная
dM_mmt1)-M(f)
dt /lSB/ tx — /
есть вектор, расположенный на касательной 2).
Если точка Р (£, г\, С) лежит на
касательной, то вектор MP — Р — М = {£—х,
г\—у, С—z) параллелен вектору -gr = {*', У, с'}
следовательно их координаты
пропорциональны. Отсюда уравнение касательной
6-*_Ч-,У_С —г П\
х' ~ у' ~ г1 ' ^ '
3» Длина дуги. Параметр t имеет для
Черт. 1.
кривой случайное значение.
х) Здесь и далее мы обозначаем одной буквой М радиус-вектор точки Mt
т. е. вектор, соединяющий начало координат с этой точкой,
Al=OM = M(t)z={x,y, z}t
Af1== OMt= M(tt)= [х19уигг}.
3) Нетрудно выяснить значение и скаляра производной
Ш
dt '
Припишем параметру t значение времени, протекшего от некоторого
начального момента. Тогда уравнение (2') определяет движение точки М по нашей
кривой. Скаляр производной, очевидно, есть предел отношения хорды ЛШХ к
промежутку времени t\ — U в течение которого точка М проходит дугу ММХ.
dM
dt
= МтММг
tl=t tt-t'
Если воспользоваться определением длины дуги кривой (см. далее § 3) и в
частности применить постулат: предел отношения дуги к хорде равен единице,
то это отношение преобразуется
v ММХ v (ММуММЛ и ммх п%
hm ^=hm(7 ~ =lim7 t = v>
t^t h - * t?=t \h-t MMJ tv-t h - t
где v — скорость движения точки_Л1 по кривой.
dM ._ „
Итак, скаляр производной -~тг— скорость движения точки М по кривой
определяемого законом движения (2'),

ДЛИНА ДУГИ
13
Вместо t можно ввести новое независимое переменное $. Производная —
получается по правилу диференцирования сложной функции
dM_dMdt_
ds ~ dt ds*
Этот вектор тоже расположен на касательной, но он другой длины. Мы
dM ds п
видим, что скаляр вектора —тт- делится на производную -г. Следова-
тельно, если скаляр производной —гг не равен нулю (см. далее
замечание), то Есегда можно выбрать так s =/(0> чтобы скаляр вектора —-г-
равнялся единице
I dM
dM
ds
=
dM
dt
ds - ds
di~ l>Tt~
dt
Так как длина вектора М = { at, у, z) с координатами ху у, г
равна
|ж | = ]/" х2 4-У + *1»
то наше требование запишется уравнением
Этот особенный параметр 5 есть длина дуги кривой, отсчитываемая от
некоторой произвольной точки на кривой, которая соответствует
значению s = 0.
Действительно, длина дуги кривой, очевидно, есть некоторая функция
5 =/(0i удовлетворяющая аксиомам:
1°. Если А, В, С — три точки на кривой, то
АС==АВ + ВС.
2°. Предел отношения дуги ММХ к хорде ММи когда дуга
стягивается в точку, равен единице.
В силу первой аксиомы дуга ММг равна разности значений sx п s
ММг = sx — s;
в силу второй
lira ШЬ=:\.
s^s Si—S _
Это в точности совпадает с требованием, что скаляр производной
-отравен единице.
В курсах интегрального исчисления доказывается, что вписанная в дугу
АВ ломаная линия при неограниченном увеличении числа сторон и
неограниченном уменьшении каждой стороны имеет пределом интеграл
ют ds.

14
КРИВЫЕ В ПРОСТРАНСТВЕ
внение
НАЛ
Единичный (длина равна единице) вектор касательной —у- мы будем
обозначать буквой х
Ж = *' (5)
Замечание. Уравнение (4) предполагает, что скаляр вектора
-jr- не равен нулю. Это выполняется для всех действительных кривых. Ура-
(~5F/ ==*'2-ЬУ2-Ьг'2=10 определяет мнимые линии, которые
называются линиями нулевой длины. Выбор особого параметра на линии
нулевой длины гораздо сложнее (зависит от вторых производных), см.
зад. № 26, стр. 36.
И. Элементы второго порядка.
4. Главная нормаль. Длина дуги 5 инвариантно 1) связана с кривой,
поэтому и производные по длине дуги внутренне (инвариантно) связаны
с кривой и имеют для нее особое значение.
Первая производная
dM -
дает единичный вектор касательной. Обозначим скаляр (длину) второй
йЧЛ 1
производной -jt чеРез —» а единичный вектор, совпадающий по своему
направлению с ней, буквой v, тогда, очевидно,
IF-J- (6)
Скаляр — называется кривизной кривой (см. далее, стр. 19),
очевидно 2), _
Т = {™У=*'*+У* + *"- (7)
Вектор v называется вектором главной нормали кривой.
Главная нормаль (как всякая другая нормаль) перпендикулярна к
касательной.
Действительно, т = -з единичный вектор, а производная единич*
ного вектора всегда перпендикулярна к самому вектору 8).
*) Инвариантность понимается в смысле независимости от выбора системы
координат.
з) В дальнейшем штрихом всегда обозначается производная по длине дуги.
8) Диференцируя очевидное тождество
Т> = 1,
получим: .—
Здесь _ da
T£ = x,x» + yy + z,z'.

СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ
IS
5. Сопровождающий трехгранник Френе. Касательная т и главная
нормаль v определяют третий вектор — бинормаль f, который дополняет
их до прямого трехгранника так же, как ось г прямоугольной
декартовой системы координат дополняет две оси: х и у.
Векторным произведением двух векторов
х — {х\ У, /} и 7=р{^, /, z"}
называется вектор
тХ v=[xv] = p{/z' — *Y, *V — *'*', xY—y'x?}.
Он перпендикуляоен к обоим векторам
х и v, расположен относительно них,
как ось z относительно осей х и yt а
длина его равна произведению скаляров
множителей х и v, умноженному на
синус угла между ними.
Так как х и v — оба единичные
векторы, а угол между ними прямой, то
скаляр произведения xXv равен
единице, и следовательно мы имеем
непосредственно
p = xXv=p{/*" — z'y\ z'x'—x'z*
х'У—у'х?}.
Бинормаль перпендикулярна и к
касательной и к главной нормали.
Три плоскости трехгранника называются:
(vp) — нормальная, (рх)— спрямляющая (черт.
6. Соприкасающаяся плоскость. В трехмерном пространстве можно
рассматривать два линейных образа: одномерное многообразие точек —
прямая и двумерное многообразие — плоскость.
Прямая, наиболее близко идущая к кривой, инвариантно связанная
с ней, и есть касательная. Она содержит две бесконечно близких точки
кривой: М и M-\-dM. Всякая плоскость, проходящая через касательную,
есть касательная плоскость, но среди них можно выбрать одну, которая
особенно тесно связана с кривой; эта плоскость — соприкасающаяся
плоскость кривой.
Теорема. Соприкасающаяся плоскость содержит две бесконечно
близкие касательные кривой. Действительно, плоскость, проходящая
через касательную х в точке M(s) и параллельная касательной х-|-Ах
в соседней точке М (s -f- As), содержит два вектора: х и Дх или х и -^-.
есть скалярное произведение векторов. Оно равно произведению их скаляров
(длины того и другого вектора), умноженному на косинус угла между ними.
Равенство нулю скалярного произведения покажет перпендикулярность
векторов ХИ~.
U9
Черт. 2.
(x~Y).
2).
- соприкасающаяся,

16
КРИВЫЕ В ПРОСТРАНСТВЕ
. dM dz сРМ
В пределе, когда обе точки совпадут, получим т = — и — = -^.
Плоскость, содержащая эти два вектора,— соприкасающаяся
плоскость. С другой стороны, плоскость, проходящая через касательную т
в точке М (s) и через точку кривой Мх = М (s -f- As), содержит два вектора
*М ттт; п / \ к \ м( \ к* dM I (As)2 <РМ ,
Т="5Г и MMl = M(s-]rb&) — M(s) = As _-{--— _+...;
она содержит, очевидно, и вектор
(Д5)2 fl^ » __ _
В пределе, когда точки М и Л^ совпадут, она будет содержать —г- и -т-^-.
Это — опять соприкасающаяся плоскость.
III. Элементы третьего порядка.
7. Движение трехгранника Френе. Три вектора т, v, р образуют
трехгранник Френе Г, стороны которого особенно удобно принимать за
координатные оси при исследовании геометрических образов, связанных
с кривой в данной ее точке М.
При движении точки М по кривой трехгранник Т переносится и
поворачивается, как твердое тело. Будем называть скоростью
поступательного движения трехгранника скорость его вершины М. Если за
параметр на кривой выбрана длина дуги s, то эта скорость — единичный
вектор
dM
_ ds
Обозначим буквой1) П
П = рх + ^ + гр=[/>, q, г] (8)
угловую скорость вращения трехгранника Т около точки М\ это —
вектор, отложенный на оси вращения. Тогда скорость движения любой
точки Р, координаты которой относительно трехгранника Г (местные
координаты) суть а, Ь% с, можно представить как сумму:
1°. Скорости относительного движения точки Р по отношению к
трехграннику Т
~ da 1 - db 1 q dc r # ., n
она равна нулю, если а, Ь% с — постоянные.
2°. Скорости поступательного движения трехгранника Т
d~M _~
ds
*) Мы будем заключать в квадратные скобки координаты вектора по осям
трехгранника Френе т, v, р.

ДВИЖЕНИЕ ТРЕХГРАННИКА ФРЕНЕ 17
3°. Скорости точки Р, вызванной вращением трехгранника около оси П.
Эта скорость перпендикулярна к оси вращения П и равна произведению
скорости вращения на расстояние точки Р от оси вращения, т. е.
ГЬMP sin (П.MP).
Так как направление вектора П на оси вращения согласовано с
направлением вращения как положительное направление оси z с поворотом
от оси х к оси j/, то рассматриваемая слагающая скорости точки Р будет
непосредственно равна векторному произведению
Соединяя все три компонента, получим элементарную формулу
кинематики твердого тела:
£ = [<»', e'l + t+nxHiP. (9)
Развернем ее. По правилу векторного произведения (см. стр. 15)
П X МР= [р9 q, г] X [a, bt с] = [qc — rb, га — />с, pb — qa].
Собирая вместе компоненты по каждому направлению т, v или р,
мы получим:
+ р(с' + pb — qa).
Эта формула у нас будет постоянно встречаться, она позволит нам
вывести все остальные свойства кривых.
Если отбросить скорость т поступательного движения трехгранника,
то получим движение трехгранника с неподвижной вершиной, например
трехгранника Т с вершиной в начале координат О и осями,
параллельными векторам т, v, р.
Скорость точки Р с координатами [а, Ь, с] по осям этого
трехгранника будет определяться формулой
яли _ f = K^HnXFA (10)
—£- = * (a' + qc-rb)+v(b' + ra-pc)+Hc'+pb-qa).(lO')
Если сюда вместо координат а, Ь, с вектора MP подставить по очереди
числа 1, 0, 0 или 0, 1, 0 или 0, 0, 1, то мы получим формулы, которые
показывают, как поворачиваются основные единичные векторы т, v, (3, когда
точка М двигается по кривой
■ га-рс)+ (9')

18
КРИВЫЕ В ПРОСТРАНСТВЕ
8. Характеристика движения трехгранника Френе. Движение
трехгранника Френе характеризуется условием: вектор скорости
вращения П всегда лежит в спрямляющей плоскости ф т), иначе: компонент
вращения по главной нормали q равен нулю.
Действительно, так как плоскость (т v) — соприкасающаяся
плоски
кость, то она содержит вектор -г-. Но по формуле (11)
если — лежит в плоскости (ту), то, очевидно,
q = 0.
Обратно, пусть мы имеем такое движение трехгранника Г, что
скорость вершины М направлена по его первой оси т и ось вращения
лежит в плоскости (т р).
Подбирая параметр s, получим:
dM п
= т, q=0.
ds
Тогда из первого условия следует, что т есть касательная к линии (М),
а второе показывает, что -£- по формуле (11) лежит в плоскости (т v),
т. е. что эта плоскость — соприкасающаяся плоскость кривой (Ж).
Следовательно, если скорость поступательного движения трехгранника
7ЧТ> v> ?) направлена по его осиi и скорость вращения лежите
плоскости (рх)П= /п-|- гр, то он описывает своей вершиной кривую, для
которой служит трехгранником Френе.
9. Кривизна и кручение. Компоненты вращения /? иг, очевидно,—
инварианты кривой, ибо ни в какой мере не зависят от выбора осей
неподвижной системы координат. Мы увидим, что это — единственные
инварианты кривой, ибо и сама кривая пщ определена (вплоть до
расположения в пространстве).
Выясним геометрическое значение их.
Возьмем точку Р на касательной к кривой, так что ЖР = т.
Формула (И) дает теперь
£-«• on
Следовательно, если из начала координат провести вектор т= От,
то конец его т за время ds пройдет элемент дуги mmi = rds
некоторой кривой. Эта кривая называется сферической индикатрисой
касательных. Так как длина вектора х равна единице, то дуга тт±
непосредственно измеряет1) угол тОт19 т. е. угол между двумя бесконечно близ-
*) Точка т описывает дугу сферической индикатрисы, а угол mbmv
измеряется дугой окружности (дугой большого круга); но обе дуги имеют одну и
ту же хорду ттпъ а так как отношение дуги к хорде в пределе равно единице,

КРИВЫЕ БЕРТРАНА
19
кими касательными (угол смежности). Предел отношения угла смежности
к дуге есть кривизна кривой. Следовательно,
т?-Н- о»)
есть кривизна кривой; р— радиус кривизны.
Мы его уже ввели при помощи формулы (6), которая вполне
совпадает с формулой (11).
На плоскости направление кривой вполне определяется касательной.
Мы видели, что в пространстве есть два линейных образа, связанных с
кривой: касательная прямая и соприкасающаяся плоскость. Каждая из
них характеризует направление кривой.
Плоская кривая сохраняет одну и ту же соприкасающуюся плоскость:
ту плоскость, в которой она лежит; пространственная кривая меняет
ее. Скорость поворота соприкасающейся плоскости есть кручение кривой
так же, как скорость поворота касательной — кривизна.
Угол двух соприкасающихся плоскостей есть угол прямых,
перпендикулярных к ним, т. е. угол двух бинормалей. Поэтому для определения
кручения надо искать скорость поворота бинормали.
Возьмем опять в начале координат трехгранник Т и отложим на
третьей оси его ф) отрезок От\ равный единице.
Формула (11) дает нам
§=пх!=-Я (И")
Когда точка М пройдет по кривой дугу ММХ = ds, точка т!
опишет дугу т!т^'==.—pds. Эта дуга измеряет1) угол rn'Ortii —угол
смежности двух бинормалей, или угол двух соприкасающихся плоскостей.
Предел отношения угла смежности двух бинормалей к дуге кривой
называется кручением кривой. Обозначая кручение через —, имеем:
i—G—' " <1з>
(pi — радиус кручения).
Итак, кривизна есть компонент вращения трехгранника Френе в
соприкасающейся плоскости (около бинормали); кручение — компонент
вращения в нормальной плоскости (около касательной).
10. Кривые Бертрана. Чтобы дать сейчас же хотя одно
приложение формул (9), решим задачу Бертрана: найти две кривые с общими
главными нормалями.
Если первая кривая описывается точкой М, а вторая точкой Р
(черт. 3) то, очевидно, точка Р лежит на главной нормали v кривой (М\
то и отношение обеих дуг —тоже в пределе единица. Следовательно, отношение
угла смежности к дуге кривой или отношение дуги большого круга к дуге
кривой можно заменить отношением дуги индикатрисы, как это принято в тексте.
*) См. примечание на предыдущей странице по поводу индикатрисы
касательных.

20
КРИВЫЕ В ПРОСТРАНСТВЕ
:;(1__r*)+vg+p^.
(а)
на расстоянии МР=*Ь от точки М так, что координаты точки Р по
осям трехгранника Т равны
MP = [0, b, 0]
и скорость точки Р по формуле (9') равна
dP
ds *ч* ' v/ l ' ds
Так как прямая v служит нормалью и для кривой (Р), то компонент
скорости по оси v равен нулю, т. е.
^ = °> * = const,
Ъ — постоянно, что, впрочем,
можно было предвидеть.
Если скорость точки Р
(обозначим ее буквой v) образует с
осью х угол ш так, что
1—rb=v cos (»> pb=v sin <s>, (b)
то трехгранник Френе V для
второй кривой (Р) повернут
относительно трехгранника Т на угол ш
около оси v, ибо главные
нормали их совпадают1).
Следовательно скорость вращения П
трехгранника Т получится
добавлением к скорости вращения П
трехгранника Г относительной ско-
du>
рости вращения — —, осью
которого служит, очевидно, вектор v.
n'-n-v£-v-v£ + pr. (с)
Черт. 3.
7Zi f=7 "day
ds M ds
Если v — главная нормаль для кривой (Р), то компонент вращения
по оси v равен нулю
-^ = 0, ш = const.
ds '
Соприкасающиеся плоскости кривых Бертрана пересекаются под
постоянным углом.
Исключая v из уравнений (Ь), получим:
г sin ш -f- р COS О):
Sin о)
или
Sin со
~7~
COS (О
Sin со
Pi
(14)
*) Для определенности мы предположим, что они одинаково направлены.

КРИВЫЕ БЕРТРАНА
21
Кривизна и кручение кривой Бертрана связаны линейным соотношением
с постоянными коэфициентами.
Очевидно, кривые Бертрана составляют особый класс кривых.
Уравнение (14) их вполне характеризует.
Если существует линейное соотношение между кривизной и
кручением кривой (М)
7+1=с' <и'>
то, сравнивая его с уравнением (14), имеем:
и А * В
ь=с> с^ш=-л
и формулы (а) и (Ь) покажут, что точка Р [О, Ьу 0] описывает кривую
с теми же главными нормалями.
Если С=0 и Л не равно нулю, то &=оо, вторая кривая (Р)
уходит в бесконечность. Соотношение (14') показывает, что отношение
кривизны и кручения постоянно. Это — общие винтовые линии (см.
далее § 12).
Есл и А = 0 и С не нуль, то кривая имеет постоянное кручение
(не равное нулю); в этом случае 4 = 0 и обе кривые (/И) и (Р)
совпадают.
Если В = О, то кривизна кривой постоянна; р = Ь. Теперь ш = -^-, т. е.
соприкасающиеся плоскости перпендикулярны. Точка Р лежит в центре
кривизны кривой (М) (на расстоянии радиуса кривизны от точки М).
Так как касательная кривой (Р) параллельна бинормали кривой (М), то
компоненты вращения трехгранника Г, р\ / по формуле (с) равны:
Р' = Г = Т> г'=-р-
Подсчитывая еще по формуле (Ь) скорость точки Р, получим: v = pb,
кривизна -у и кручение ~ кривой (Р) равны
г Pi
, V , / V_ .2 Ь»
Следовательно обе кривые (М) и (Р) имеют одну и ту же постоянную
кривизну, а кручения их противоположны по знаку и их произведение
равно квадрату кривизны.
Кривая (Р) неопределенна: Г если значение Ъ неопределенно, т. е.
если А = О, С = 0 и кривая плоская; в этом случае, очевидно, все семейство
параллельных кривых (с общей эволютой) удовлетворяет условиям задачи;
2° если между кривизной и кручением кривой (М) существует несколько
соотношений вида (14')>т- е. если р и рх постоянны; тогда Ь —
произвольно и уравнение (14) определяет ш. Все ортогональные траектории
главных нормалей имеют их своими главными нормалями. Все кривые —
обыкновенные винтовые линии (см, § 12).

22
КРИВЫЕ В ПРОСТРАНСТВЕ
dz v
ds ~ р '
dv т Э
^ _ Р Pi'
dp v
<& — Pi
П. Натуральные уравнения кривой. Если в уравнения (11) внести
то они принимают вид:
(15)
Эти формулы носят название формул Серре-Френе. Вся теория кривых
покоится на применении этих формул.
Как и следовало ожидать, формулы Серре-Френе содержат кроме
векторов т, v, (Зтолькодва коэфициента: кривизну — и кручение—. Можно
ли их задать произвольно? Эго равносильно вопросу: можно ли задать
произвольно вращение трехгранника Г?
Как бы ни задавать р и рх функциями от длины дуги s, они
определяют кривую и только одну, если не принимать во внимание ее
расположения в пространстве.
Уравнения
7 ='<•>• 7вЛ(в)
называются натуральными уравнениями кривой, ибо не зависят ни от
какой системы координат.
Следовательно натуральные уравнения определяют кривую вплоть
до ее перемещения в пространстве.
Уравнения между векторами распадаются на 3 уравнения между их
координатами. Очевидно, координаты векторов т, v, ^ суть три решения
av аъ а3, bv Ьъ ft3> cv с2> сг системы
da Ъ_ db а с_ dc b^ (\Ъ'\
ds р ' ds р pt9 ds р! * ^ '
Общий интеграл системы (15') содержит три произвольных постоянных.
Следовательно мы всегда можем выбрать три решения (ai9 bu ct)9
(а2, Ьъ с2)у {аъ ЬЬу с3), так, чтобы для начального момента s = s0 они
принимали произвольно выбранные значения. Примем их за координаты
наших векторов
т = [аи аъ я3}, v = [bu Ъъ Ъъ\, р = [cv сг, с3].
Будут ли эти векторы единичными и будут ли они взаимно
перпендикулярны?
Обозначим
Л=.т2, Д=72, С = р, Л' = и|, Я' = тр, C' = xv;
диференцируя и пользуясь уравнениями (15), получим для этих величин
систему уравнений:
dA 2С dB 2С 2А' dC 2А'

ВИНТОВЫЕ линии
23
Выберем теперь какое-нибудь произвольное положение трехгранника Т
для начального момента s = s0
т0 = \ah а% аз}, v0 = {ft?, Ь% b\)y % = {с?, с* c°s} (b)
и возьмем три решения системы (15) так, чтобы для s = s0 они
сводились к выбранной системе значения (b).f Тогда для начального момента
s = s0) очевидно,
А=В = С=1, А'=В' = С' = 0. (с)
Эти значения удовлетворяют систему (а), а так как при заданных
начальных значениях (с) система (а) имеет только одно решение, то
равенства (с) будут справедливы для всякого значения s.
Следовательно выбранная система решений определяет три
единичных ортогональных вектора, т, v, (J. Мы знаем в любой точке s
направления осей трехгранника Т. _
Уравнение (5) определяет теперь в квадратурах вектор М
S
M = pds+M0, (d)
где М0 — любой постоянный вектор.
Нетрудно проверить, что кривая (d) имеет трехгранник Т своим
сопровождающим трехгранником Френе.
Интересно отметить, что произвольным остался только начальный
вектор М0 и начальное положение осей трехгранника т0, v0, р0.
Очевидно, тот или иной выбор этих произвольных постоянных определит
положение кривой в пространстве, но не ее форму или размеры.
12. Винтовые линии. 1°. Рассмотрим в виде примера
интегрирование натурального уравнения
р: рх = k = const.
Полагая для удобства k = — ctg <р и внося pt = — р tg <р в уравнения
Серре-Френе, получим:
*L = ± ^ = jcmz:4sinV J#=_Ictg<p. (а)
ds р* ds р sin ср » ds Р т
Исключая — из двух крайних уравнений, имеем:
г
d'z , d& Л
cos ?-S- +sin ф-£ = 0,
ds l r ds
т cos cp + P sin 9 = A> (b)
где A— произвольный постоянный вектор, очевидно, длиною равный
единице. _ __
формулы (Ь) показывают, что три вектора т, р и А всегда лежат
в одной плоскости, причем касательная образует с вектором А
постоянный угол <р, а бинормаль — |- — <р (А т = cos <р, А р ==р sin <р). Главная
нормаль v? следовательно, перпендикулярна к А*

24
КРИВЫЕ В ПРОСТРАНСТВЕ
Примем направление вектора А за ось z. Тогда
x={ab&1,coscp}, P={a3,ft3,sin<p}, v={a2,ft2,0}.
Спроектируем нашу кривую на плоскость (х, у) и пусть
х = х{и)> У = у(и) (с)
— уравнения проекции, где и — длина дуги проекции. Так как
касательная всегда проектируется в касательную, а главная нормаль у нас
параллельна плоскости (х, у) и, следовательно, проектируется в нормаль
кривой (с), то
ах = х1 sin 9 = ^ sin 9, bx =yf sin 9, а% = — у', Ь2 = х\
р = т X v = (— *' cos 9,—У cos <р, sin <р).
Эти значения удовлетворят системе (а), если положить
w= s- sin 9.
Итак, кривая расположена на цилиндре, у которого направляющей
служит произвольная кривая (с), а образующая пардллельна оси z. Она
пересекает все образующие цилиндра под постоянным углом <р- Такая
кривая называется общей винтовой линией. Так как главная
нормаль ее совпадает с нормалью к цилиндру, то (см. гл. V) она служит
геодезической линией на цилиндре и при
развертывании цилиндра на плоскость
обращается в прямую.
Уравнение общей винтовой линии
х = х(и), у=у(и), z = actg<p.
2°. Если оба радиуса кривизны р и рх
постоянны, то винтовая линия — обыкновенная
(Puiseux).
Первое уравнение (а) дает тогда
х sin* 9
*„>-_>:
р'
у' sin2 9 = —,
откуда
(*'*+/») sin* 9:
шх'*+у*
Черт. 4.
J_ sin2y
7_ R '
где R — радиус крив- зны проекции (с). Если р постоянно, то и /?
постоянно; следовательно,.проекция (с) — окружность, и цилиндр — круглый.
Обыкновенная винтовая линия— винтовая линия круглого цилиндра (черт. 4).
IV. Развертывающиеся поверхности, связанные с кривой.
13. Огибающая семейства поверхностей. Уравнение
F(x,ytz,a)=*09 (а)
содержащее переменный параметр а, определяет для разных значений
а со 1 поверхностей, составляющих семейство поверхностей.

ОГИБАЮЩАЯ СЕМЕЙСТВА ПОВЕРХНОСТЕЙ 25
Два уравнения
F(xty)z9a) = Oi F(*,jsz,a-f-Aa) = 0
определяют линию пересечения, которую можно также определить
системой уравнений
В пределе при Да = 0 эта линия пересечения обращается в
характеристику *)
F(*,.y,*,a) = 0, F.(x,y,z,*) = 0. (b)
Геометрическое место характеристик называется огибающей семейства.
Огибающая определяется уравнениями (Ь), если считать а переменным.
Уравнение касательной плоскости к огибающей
{'-+'--=)(«-*)+('/+''-^(,'-')+(,,'+л=)(с-*)-0
в силу второго уравнения (b) Fa = 0 непосредственно переходит в
уравнение касательной плоскости поверхности семейства (а):
Следовательно огибающая касается всех поверхностей семейства вдоль
общей характеристики.
Две характеристики
F (*, у, z, а) = 0, Fa (х,у, г9 а) = О (с)
и
^ (*,>>,*,« + Да) = 0, Fa{x,y,z,*-\-^) = 0 (с')
несомненно пересекаются, ибо обе лежат на одной и той же
поверхности: исключение а из уравнений (с) и из уравнений (с') приводит
к одному и тому же уравнению—уравнению огибающей;
следовательно в системе 4 уравнений (с) и (с') одно есть следствие
остальных.
Точку пересечения можно определить любыми тремя из 4 уравнений
(с) и (с'), например системой
F(x,y,zta) = Q> Fa(x,y9z,a) = Ot Е =0.
Предельное положение ее при Да = 0 определится системой
F(x>y >***) = 0* Fa{x>yyzia) = 09 FM(x,y9:,a) = 0. (d)
При переменном а она описывает огибающую характеристик — ребро
возврата огибающей семейства поверхностей (а).
^ - idx dv dz\
Вектор касательной к характеристике т = I —, ^, ^ \ определяется
3F
да *

26
КРИВЫЕ В ПРОСТРАНСТВЕ
тремя диференциалами dx, dy, dz, которые получаются диференцирова-
нием уравнений (с) при постоянном а
Fxdx+Fydy + F2dz = 0,
^dx + Faydy + Fazdz = 0.
Диференцируя два первых уравнения (d) при переменном а, получим:
Fxdx + Fydy + F2dz + Fad* = Ot
Faxdx + F*ydy + Fa2dz + Faada = 0.
Так как в силу уравнений (d) последние члены F* da и Faa da пропадают,
то касательная к ребру возврата совпадает с касательной к
характеристике, т. е. ребро возврата касается всех характеристик.
14. Развертывающаяся поверхность. Если все поверхности
семейства (а) — плоскости, то характеристики (Ь) — прямые линии.
Огибающая семейства плоскостей — особая линейчатая поверхность, так
называемая развертывающаяся поверхность. Так как все характеристики
касаются ребра возврата, то можно сказать, что развертывающаяся
поверхность есть геометрическое место касательных пространственной
кривой линии L.
Самая плоскость семейства (а) — соприкасающаяся плоскость
кривой L. В этом легко убедиться непосредственно, отыскивая огибающую
соприкасающихся плоскостей кривой (2) по формулам (Ь). Мы быстрее
найдем огибающую из следующих С09бражений:
Развертывающаяся поверхность касается каждой плоскости семейства
вдоль характеристики. Всякая точка характеристики описывает на
огибающей кривую, касательная к которой лежит в плоскости (а).
Следовательно в каждой плоскости семейства (а) должна существовать линия,
точки которой при изменении а двигаются в самой плоскости.
Скорость любой точки Р соприкасающейся плоскости мы получим
по формуле (9'), если туда подставить с = 0 и ^=0:
S = ^(e/+*-'*) + v(*' + 'a) + M.
Так как компонент по бинормали должен быть равен нулю, то
pb = 0.
Следовательно все такие точки (£ = 0) лежат на касательной. Итак,
характеристика соприкасающейся плоскости — касательная, а ребро
возврата развертывающейся поверхности — сама кривая (Ж).
15. Полярная поверхность. Трехгранник Френе содержит три
плоскости. Каждая из них огибает при движении трехгранника
развертывающуюся поверхность, которая занимает свое место в теории кривой.
Первая из этих поверхностей — огибающая соприкасающихся
плоскостей; она образована касательными, а ребром возврата служит сама
кривая (М).
Рассмотрим теперь полярную поверхность — огибающую нормальных
плоскостей. Уравнение нормальной плоскости в координатах
относительно трехгранника Т
а = о,

ЭВОЛЮТЫ КРИВОЙ
27
Внося это в формулу (9), получим скорость некоторой точки Р
нормальной плоскости в виде вектора
g = ;(l_rft) + ;(ft'-pC)4-?(c' + pA). (а)
Если точка Р лежит на характеристике нормальной плоскости, то ее
скорость лежит в этой плоскости, т. е. компонент по касательной т
равен нулю.
Следовательно
1—^ = 0, ft = l = p. (b)
Наша прямая идет параллельно бинормали и отсекает на главной
нормали радиус кривизны. Эта прямая называется осью кривизны. Ось
кривизны служит образующей полярной поверхности.
Если кроме того
Ь'—рс = 0, *==--, (с)
то скорость точки Р направлена по бинормали, т. е. кривая С,
описываемая точкой Р, касается оси кривизны и служит ребром возврата
полярной поверхности. Координаты этой точки по осям трехгранника
а = 0, b = p9c = — Pl^. (16)
Кривая (С) касается оси кривизны; следовательно ее касательная
параллельна бинормали кривой (Af), а так как соприкасающейся
плоскостью кривой (С) служит нормальная плоскость кривой (УИ), то
бинормаль (С) параллельна касательной (М) и обе главные нормали
параллельны между собой.
16. Эволюты кривой. Эволютой кривой (М) называется кривая (N),
касательная к которой служит нормалью кривой (/И). Следовательно
вектор скорости точки N лежит в нормальной плоскости (Ж) и
проходит через точку М.
Так как точка N, очевидно, лежит в нормальной плоскости кривой (Ж),
то ее координаты по отношению к трехграннику Т суть [0, ft, с] и
скорость точки N определяется по формуле (9'):
M^xil-rq + fy'-pcy + W+pb). (а)
С другой стороны, по условию задачи она пропорциональна вектору
Следовательно ее координаты [0, Ь, с] относительно трехгранника Т
связаны уравнениями
1_r*=0,-*l=^=-£-±£L. (b)
Первое
показывает, что точка N лежит на оси кривизны; следовательно все
эволюты кривой расположены на полярной поверхности.

28
КРИВЫЕ В ПРОСТРАНСТВЕ
Второе уравнение можно переписать в виде:
cdb — bdc ,
или
Поворот касательной к эволюте в нормальной плоскости по
отношению к главной нормали кривой пропорционален кручению кривой, а так
как сама главная нормаль поворачивается вместе с трехгранником
Френе на этот же угол, то касательные ко всем эволютам кривой
сохраняют свое направление в нормальной плоскости..
При развертывании полярной поверхности на плоскость все
нормальные плоскости совместятся *), так что точки, где они пересекают
кривую (/W), совпадут, и все эволюты обратятся 2) в пучок прямых с
центром в этой точке.
Обозначая через X множитель пропорциональности, имеем:
Диференцируя еще раз, получим с помощью уравнений (Ь)
d*N ,и- , Z\ \ Ь*
— = !x(*v-f ср)-Хт,
где {г — некоторый новый множитель пропорциональности. Отсюда
следует, чго главная нормаль каждой эволюты параллельна касательной
к кривой Ж, а значит, нормальная плоскость служит им всем
спрямляющей плоскостью, а полярная поверхность — спрямляющей s) поверхностью.
17. Спрямляющая поверхность есть огибающая спрямляющих
плоскостей. Если точка Р лежит в спрямляющей плоскости, то ее вторая
координата & = 0, и формула (9) принимает вид:
£ = х (J + 1) +v(ar-cp) + $c>.
Скорость этой точки лежит в спрямляющей плоскости, если
аг—ср — 0, (17)
и тогда точка Р лежит на характеристике этой плоскости. Следовательно
уравнение (17) есть уравнение характеристики в местных координатах;
характеристика проходит через точку М и параллельна вектору скорости
вращения трехгранника Т
П=/>т+гр.
Спрямляющая поверхность содержит нашу кривую М9 и при движении
по кривой ее трехгранник Френе вращается около образующей этой
поверхности. Следовательно в касательной плоскости ее он не повора-
*) Ибо точка М в нормальной плоскости не двигается.
*) Ибо каждая эволюта и после развертывания будет сохранять постоянное
направление касательной.
8) Поэтому при развертывании ее они и обратились в прямые (см» дадее).

соприкасающаяся плоскость
2d
чиьается. После развертывания спрямляющей поверхности на плоскость
касательная к кривой М будет сохранять и в плоскости одно и то же
направление, т. е. кривая М развернется в прямую (см. гл. V). Отсюда
название спрямляющей поверхности (Лянкре).
Точка касания характеристики с ребром возврата определяется из
условия, что скорость ее направлена по характеристике. Следовательно
(в'4-1) г-с/> = 0,
но, диференцируя уравнение (17), имеем:
а! г—с'р = ср' — ar*
и, исключая производные а' и с\
ср' — аг,4-г=0,
откуда
а= ,рг , ; Ь = 0; с= /' ,. (18)
рг' — гр' * pr' — r/r v '
Спрямляющая поверхность обратится в цилиндр, если
гр'—рг, = 0,
т. е. если
— — — — — cons,
и в этом случае касательная образует постоянный угол с образующей
цилиндра.
Кривые, пересекающие все образующие произвольного цилиндра под
постоянным углом, называются общими винтовыми линиями.
Следовательно мы снова получаем, что постоянное отношение радиусов
кривизны и кручения характеризует общие винтовые линии.
Если кроме того скорость вращения трехгранника постоянна,
/?2 4- q2 = const,
то трехгранник передвигается винтовым движением; каждая точка его
и в частности вершина М описывает винтовую линию.
В этом случае и радиус кривизны и радиус кручения
JL— JL__
Р Г И Pi Р
постоянны.
Постоянные радиусы кривизны и кручения характеризуют
обыкновенные винтовые линии, т. е. винтовые линии круглого цилиндра.
V. Соприкасающиеся поверхности.
18. Соприкасающаяся плоскость. Проведем через точку М какую-
нибудь плоскость р (черт, б) и рассмотрим расстояние d какой-нибудь
точки Мx(s 4- As) от плоскости /7. Пусть п — единичный вектор нор-

30
КРИВЫЕ В ПРОСТРАНСТВЕ
мали к этой плоскости. Расстояние d, очевидно, равно проекции ММХ
на вектор я, т. е. скалярному произведению:
d = nAml = n- {М (s-|-As) — М (s)}
или, разлагая в ряд по степеням As,
- dM , (As)2 - d*M
ds ' 1
2 п ds*
+ ...
(а)
Мы видим, что расстояние d того же порядка малости, как и As —
расстояние по кривой между точками М и Мг\ но, если
- dM л
то d — бесконечно малое 2-го порядка. Тогда плоскость проходит
через касательную (ибо нормаль п перпендикулярна к касательной
dM
ds
и называется касательной плоскостью. Так как член низшего порядка
содержит теперь (As)2, то расстояние d не
меняет знака при изменении знака As, т. е.
кривая и справа и слева от точки М лежит по
одну сторону касательной плоскости.
Примером касательной плоскости служит
спрямляющая плоскость (рт). Кривая лежит с
положительной стороны спрямляющей плоскости.
Если
- dM п - dm л
П —г— = О И П —г-5" = О,
ds ds2 '
Черт. 5.
dM d2M
го п перпендикулярно и к-т— и к -g^-;
плоскость содержит оба вектора ^М dM и
ds ds^
является соприкасающейся плоскостью. Расстояние точки Mi от
соприкасающейся плоскости — бесконечно малое 3-го порядка.
Соприкасающаяся плоскость теснее всех других плоскостей подходит к кривой.
Говорят, что соприкасающаяся плоскость имеет с кривой касание 2-го
порядка. Кривая располагается по обе стороны соприкасающейся
плоскости: член низшего порядка в разложении (а) содержит (As)3 и
следовательно меняет знак вместе с As.
19. Соприкасающаяся сфера. Среди всех сфер, проходящих через
данную точку кривой М, можно выделить одну, которая особенно тесно
касается кривой. Если С — центр нашей сферы (черт. 6), R — ее радиус
и М1 = М (s -|- As) — какая-нибудь точка кривой, то расстояние точки Мх
от сферы, очевидно, равно
где
\=CMX — R =
CM{ — R* F(xuyt, zt)
CMX + R — CMt + R '
F(x¥ y, z) = 0
есть уравнение сферы и (хи уи zj — координаты точки Мх.

СОПРИКАСАЮЩАЯСЯ СФЕРА
31
Если в разложении F(xv уи zx) по степеням As сохранятся только
члены п -|- 1-го порядка, то 8 будет того же порядка малости
относительно As и сфера будет и"меть касание л-го порядка с кривой.
Пусть
F& -П, С) = ($-а)Ч-(*1-*)2 + (С-')2-Я2 = ()
уравнение нашей сферы по отношению к координатному трехграннику
Г(т, v, р).
Подставим сюда вместо текущих координат £, tj, С компоненты от
вектора _
MMx = M(s + Ls) — M(s) = As- _+^ —+.. —
= As.x + (As)2
по осям трехгранника T
1 (As)3
2p
+TH+'(-f)4]+--
S = As-
p2 6
1 /A 42 ! /1\Г(А5)3
1 (Ад)»
ppl 6
и приравняем нулю коэфициенты при
последовательных степенях As; мы получим
ряд уравнений
(Д5)°
(Д5)1
О*)2
а2 + 62 + с2 — #2 = 0,
— 2а = 0,
i-^-.
(Д,)з 4-*(—У+—=0. Черт'6-
4 ' Р2 V р / ' PPi
Первые два уравнения определяют сферы, имеющие касание 1-го
порядка с кривой. Это всякая сфера с центром в нормальной плоскости
(а — 0), если она проходит через точку М.
Если добавить третье уравнение
Ь = 9,
то получим сферу, имеющую касание 2-го порядка. Центр сферы
(а = 0, £ = р) лежит на оси кривизны. Все эти сферы пересекаются
по одному кругу, который лежит в соприкасающейся плоскости, с
центром на главной нормали в центре кривизны, т: е. на расстоянии радиуса
кривизны от кривой. Этот круг есть круг кривизны кривой.
Добавим четвертое уравнение и мы получим соприкасающуюся сферу.
Ее центр имеет координаты
а = 0, ft = p, c = -p,-g-. (19)
Следовательно центр соприкасающейся сферы лежит на ребре
возврата С полярной поверхности.

32 КРИВЫЕ В ПРОСТРАНСТВЕ
Радиус соприкасающейся сферы
* = РЧ-Р?(5-)*. (20)
20. Формула для вычисления кручения кривой. При выводе
понятий кривизны и кручения мы воспользовались кинематическим образом
движения трехгранника Френе. Это придает больше наглядности всем
рассуждениям, но несколько затемняет связь этих элементов с первоначальными
уравнениями кривой. Мы могли бы притти к этим понятиям путем
последовательного диференцирования радиуса вектора М по особому
инвариантному параметру—по длине дуги s.
Первая производная
устанавливает направление касательной (и позволяет выбрать параметр s).
Вторая производная
^г-7 (6)
вводит понятие главной нормали v и своим скаляром определяет
кривизну кривой -.
Разлагая третью производную на компоненты по осям х, v, р
— = ат-f ftv-f-#f
легко заметить 1), что
Третий компонент с дает новый инвариант кривой. Если продифе-
ренцировать (6), принимая во внимание формулу Серре-Френе (15), то
прямо получим:
ds* р
Уравнение (6) определяет кривизну кривой
^+vf-L)'-i. (21)
7- = (W=^+y2+^ <7>
*) Диференцируя очевидные тождества
Ш<РМ Л*Ш\2___ 1
4sl№~~ • \dJj~~~p
получим;
dM
Us
ШсРМ __ ЛЯМУ d*Md*M __1 /IV
is dss ~~"" \d&) * ~d& ds* ~~ p \ p/ '
Отсюда сейчас же получаются уравнения текста, ибо

УПРАЖН1НИЯ
33
Уравнение (21) даст кручение —. Умножим для этого обе части на
мы получим:
ГдМ dm] сРМ_ 1_
}L ds ds* j ds* ~ p?t >
откуда
— _ 2 ( dM (PM d*M\ — _
— p V ds ds* ds* j ~ i
x
X*
x"
У -'
У z"
Эта формула не содержит извлечения корня, следовательно
определяет р! не только по величине, но и по знаку. В противоположность
всегда положительной кривизне кривой кручение может быть и
положительно и отрицательно.
Связь кручения с вращением трехгранника Френе
-JT = -P <")
показывает геометрический смысл знака кручения: при положительном
кручении трехгранник Френе вращается около касательной в
направлении от бинормали к главной нормали, т. е. он ввинчивается, как
обыкновенный Оуравчик.
Замечание. Приведенный метод исследования пространственной
кривой легко распространяется на пространство любого числа измерений.
Первая производная дает направление касательной к кривой. Тот
параметр, который приводит первую производную к единичному вектору,
есть длина дуги. Диференцируя по длине дуги, мы вводим нормаль
кривой, а компонентом при единичном векторе нормали—первую кривизну
кривой. Диференцируя единичный вектор нормали, мы вводим вторую
нормаль и т. д., пока не исчерпаем всех взаимно перпендикулярных
нормалей и следовательно не получим всех независимых инвариантов
кривой.
Упражнения.
1. Показать, что для всякой кривой х' Р' = — .
PPi
2. Если (М" М" Л|",г)=0| то кривая — общая винтовая линия.
3. Показать, что, выбирая оси координат по осям трехгранника Френе
в данной точке, можно привести уравнения кривой к виду:
Л*
х = s-
. kk'
sz _ — s*+.
б 8 ^
z^ — kbf-ji (2k'kl+kk'l)s* + ...

34
КРИВЫЕ В ПРОСТРАНСТВЕ
Вывести отсюда расположение' кривой относительно плоскостей"
трехгранника Френе.
4. Показать, что проекция кривой на спрямляющую плоскость имеет
вершину тр >гранника точкой перегиба, а проекция на нормальную плоскость —
точкой возврата.
5. Показать, что в той точке кривой, где — = 0, кривая имеет касание
Р
2-го порядка с касательной, 3-го порЛдка с соприк дающейся плоскостью и
располагается по обе стороны всякой касательной плоскости и по одну сторону
от соприкасающейся (стационарная касательная), а в точке, где— = 0, она
Pi
имеет касание 1-го порядка с касательной и 3-го порядка с соприкасающейся
плоскостью, располагаясь по одну сторону и той и другой плоскости
(стационарная соприкасающа. ся плоскость); если— = 0 и — =0 одновременно, то
соотгетствующие порядки будут 2 и 4.
6 Если соприкасающаяся плоскость проходит всегда через одну точку,
то кривая плоская.
Р d
7. Если 1- —г (р' pi) =г 0, то кривая расположена на сфере.
Pi as
8. Эвольвентой кривой (М) называется такая кривая (Р), что нормаль (Я)
совпадает с касательной к (М). Показать, что касательные к эвольвенте
параллельны гланной нормали крив >й {М). Существует о©1 эвольвент данной
кривой (М), каса.ельные к кот( рым все параллельны между собой.
9. Показать, что эвольвенты обыкновенной винтовой линии — плоские кривые,
плоскости которых перпендикулярны к оси цилиндра: они все — эвольвенты
окружности основания цаиндра.
10. Показать, что место центров кривизны есть эволюта кривой только, если
кривая плоская.
11. Показ 1тьг что из всех эволют плоской кривой только одна — плоская
кривая, а все остальные винтовые линии.
12. /еорема Маннгейма. Если (М) и (Л/*) —две сопряженные кривые
Бертрана, С и С* —их центры кривизны, то сложное отношение (ММ*СС*)
постоянно и рапно sec2?, где <р — Угол касательных {М) и (Л**).
13. Показать, что для сферической кривой центр кривизны есть основание
перпендикуляра, опущенного из центра сферы на соприкасающуюся плоскость
кривой.
14. Если главные нормали кривой (Л/) служат бинормалями кривой (М1),
то первая »ривая удовлетворяет уравнению
- + ---1
где Ъ — постоянное расстояние между соответствующими точками обеих кривых
(кри?ая Манжейма)
15. Если две кривые взаимно служат друг для друга местом центров
сгприкасающихся сфер, то обе обладают одной и той же постоянной кривизной,
соприкасающиеся тоскости их взаимно перпендикулярны и произведение
их кручений в соответствующих то ках равно квадрату кривизны.
16. Е ли касательные первой кривей параллельны бинормалям второй,
то и обратно, бинормаля первой кривой пар1ллельны касательным второй,
и главные нормали обеих кривых параллельны. Кривизна и кручение обеих
кривых обратно пропорциональны. В местных координатах \at Ь, с) относительно
трехгранника Френе вторая кривая определяется уравнениями
da Ь db __ л с
ds р ds~~ р рг
€ произвольной функцией.

УПРАЖНЕНИЯ
35
17. Преобразование Комбескюра. Если кривые (М) и (М*) однозначно
соответствуют своими точками так,что касательные их гараллельны.то параллельный
трехгранники Френе; оба радиуса кривизны и кручения пропорциональны
J = h = ds
Р* р* "" ds* '
Обратно, если соприкасающиеся плоскости двух кривых (М) и (Af*)
параллельны, то (Л4*) есть преобразование Комбесьюра от (М). Отсюда следует такое
построение {М*)\ ко всякой соприкасающейся плоскости П кривой (М) строим
параллельную ей плоскость П* на произвольном расстоянии; ребро возврата
огибающей плоскостей ГР есть преобразование Комбескюра от (М).
* = /"т/(*)Л,
м-
где f(s)—произвольная функция.
Кривая (ЛЯ*) определяется в местных координатах [а, Ь, с] относительно
трехгранника Френе уравнениями:
'=~р[(*Ъ)'+^]. * = «'pi,
где c—f(s) — произвольная функция.
18. Если кривая (М) служит местом центров соприкасающихся сфер
кривой (М*), то эга последняя (ЛГ*) определяется в координатах [а, Ь, с]
относительно трехгранника Френе кривей (М) уравнениями
da __ b db __ а
ds р ds р
/И* — - [$tds;
J Pl
существует oo2 кривых (ЛР) для цанной кривой (М).
Если кривая (М) изгибается, сохраняя кривизну— (и меняя кручение --),
то а9 Ь, с не меняются, т. е. все кривые (Л/*) уносятся вместе с трехгранниками
Т кривой (М). Если (М) станет плоской ( — = о), то каждая из кривых (М*)
обратится в точку. Обратно, каждая точка плоскости П опишет кривую (М*), если
эту плоскость катить по кривой (М) так, чтобы она в каждом положении была ее
соприкасающейся плоскостью.
19. Показать, что характеристикой семейства соприкасающихся сфер данной
кривой (М) служит круг кривизны ее, а ребром возврата — сама кривая (М).
20. Показать, что все кривые постоянного кручения — = а могут быть полу-
чены по формуле
где fz=f{f)--любой единичный вектор.
21. Если m = m(Q) есть кривая на сфере радиуса единицы и о —длина дуги
ее, т. е. если существуют равенства

36
КРИВЫЕ В ПРОСТРАНСТВА
есть кривая постоянной или даже переменной заданной кривизны _,длякото-
р
рой кривая (/я) служит сферической индикатрисой касательных. Если р задано
1 d9
функцией от длины дуги sj то надо положить - = —.
Р ds
22. Показать, что натуральные уравнения
р = as, рх = bs; a,b-=z const
определяют винтовую линию, лежащую на круглом конусе и пересекающую
его образующие под постоянным углом. Проекция на плоскость основания
конуса — логарифмическая спираль (цилиндро-коническая винтовая линия).
23 Показать, что кривые Берфана, заданные натуральным уравнением
а Ь
1 = 1, atb = const,
определяются формулой
М = а Cm d<s-\-b С [т dm],
где т = /71 (в) — произвольная кривая на сфере ив — ее дуга, так что
21. Теорема Бельтпами. Развертывающаяся поверхность касательных к
кривой L пересекается соприкасающейся плоскостью по линии /.*, кривизна которой
составляет 3/4 кривизны кривой L.
25. Если на бинормалях кривой постоянного кручения pt = l отложить
отрезки i= уг=П\ то полученные точки образуют изотропную линию (линию
нулевой длины МГ2 = 0>.
26. Изотропные линии (линии нулевой длины) определяются условием
(§)'=»• - т, *»•
ный параметр а так, что
Показать, что в этом случае [ ) не нуль, и можно ввести инвариант-
и тогда, полагая
=(0)'—•
М' = ev Мп = е* М'ХМ*= ег,
причем
^?=^з=0' *! = —If ^7?2=^2^s = 0, *t *а= — 1,
получим формулы Френе:
dux de2 dez
~da = e» ~di=z~ket-e* ~dz~ke*
k — псевдокривизна, a — псевдодуга изотропной линии. Изотропные прямые
(М* = 0) исключаются.

ГЛАВА ВТОРАЯ.
Линейный элемент поверхности.
I. Элементы первого порядка на поверхности.
1. Криволинейные координаты на поверхности. Поверхность
определяется одним уравнением между тремя текущими координатами точки
М (х, у, г)
F(x,y, z) = 0; (1)
гораздо удобнее задать поверхность тремя уравнениями
х — х(и9 v), у — у(и9 v), z — z(u, v) (2)
с помощью двух параметров и и v. Исключая их, мы вернемся к
уравнению (1).
Три уравнения (2) можно соединить в одно, задавая рад ус-вектор
М=(х, у, z) точки М{х, у у z) как функцию от двух параметров
и и v
M=zM(u, v). (2')
Разбивая векторное равенство (2') на три уравнения межау тремя
координатами векторов, мы снова вернемся к системе уравнений (2).
Параметры (и, v) определяют точку на поверхности подобно тому,
как два числа — абсцисса и ордината — определяют точку на плоскости,
а потому называются координатами точки на поверхности, точнее
криволинейными координатами.
Положим, что v равно постоянному числу, например
v = vt = const;
тогда уравнение (2') будет содержать только один переменный
параметр и
М = М(и, Vi)
и будет определять кривую линию — линию v = vt.
Давая v новое значение: v = v2, получим новую кривую
М=М(и, v2)
и т. д. Меняя значение v = vu v = v2, v = vt и т. д., мы получим
семейство кривых v = const или линий и.
Все они лежат на поверхности. Можно сказать иначе: при
изменении постоянного v кривая v = const, деформируясь, движется в
пространстве и описывает нашу поверхно.ть. Поверхности есть гер^стриче»
£ко$ иерто линий v:=cop§t или линий и.

38
ЛИНЕЙНЫЙ ЭЛЕМЕНТ ПОВЕРХНОСТИ
Точно так же можно сказать, что поверхность есть геометрическое
место линий и = const. Полагая в уравнениях (2) [или (2')] постоянным
параметр и, например u = uXi получим:
М — М{ии v)
— кривую a — uv Меняя этот постоянный параметр и~иХу u = u2t
и — ил и т. д., получим второе семейство линий на поверхности — линий
и = const или линий v. Эти дв.а семейства линий называются
координатными линиями.
Мы будем рассматривать только ту часть поверхности, где
координатные линии представляют правильную сеть: каждая линия и
пересекает каждую линию v один раз, две линии и или две линии v не имеют
общих точек. Образец правильной сети — система линий х = const,
у =z const на тоскости (ху).
Аналитически это значит допустить, что в рассматриваемой области
три якобиана *)
д(х,у) д(у, z) д (г. х)
д (и, г)' д(и, V)' д{и, v)
нигде одновременно не обращаются в нуль.
Действительно, при этом условии можно выделить одно решение
(и> v) уравнений (2), т. е. в этом случае каждой точке (*, у, z) на
поверхности (в рассматриваемой области) соответствует только одна
пара значений (и, v).
Мы будем кроме того предполагать, что функции (2) конечны и
непрерывны, так же как и все те производные их, которыми мы будем
пользоваться (до ?-го порядка включительно).
2. Касательная плоскость. Зададим параметры и, v функциями
вспомогательной переменной t
u — u(t), v — v(t). (3)
Тогда формулы (2) дадут три координаты х, у, z в виде функций
одного переменного /. С изменением / точка М опишет линию;
следовательно уравнения (3) определяют на поверхности линию.
Касательная к кривой (3) определяется вектором -т--. Нам удобнее
б^дет вместо производной рассмотреть диференциал от Мг)
dM = Madu-\-Mvdv, (4)
где du и dv вычисляются из уравнений (3).
Вектор dM отличается только скалярным множителем от
производной — и следовательно также определяет касательную нашей кривой.
n д (ху) __ дх ду дх ду
д (uv) ~~ дади dv ди '
ч - дМ — дМ
3) *в=__, м .

ЛИНЕЙНЫЙ 8ЛБМЕНТ ПОВЕРХНОСТИ
39
В выражении (4) производные Ми и Mv можно вычислить, не зная
еще кривой (3). Сюда входят только координаты точки и и v и,
конечно, функции (2).
Касательные к различным кривым, проходящим на поверхности чер:з
данную точку М, отличаются следовательно только скалярами du, dv.
По правилу сложения векторов, dM есть диагональ параллелограма,
построенного на сторонах Mudu и Mvdvy и во всяком случае лежит
в их плоскости. Все касательное ко всем кри шм, проходящим на
поверхности через точку М, лежат следовательно в одной пло.кости. Эга
плоскость называем касательной плоскостью поверхности, а прямая,
перпендикулярная к касательной плоскости в точке М,— нормалью
поверхности.
Касательная плоскость определяется двумя векторами, которые она
содержит: Ми и Mv. Нетрудно видеть, что это—касательные к
координатным линиям и и v. Их векторное произведение
N = MUXMV= {yuzv —yvZUy zuxv — zvxa, xayv — xvyu)
есть вектор, перпендикулярный к обеим касательным; эго вектор
нормали к поверхности (черт. 7).
Мы булем считать направление
вектора N положительным
направлением нормали. Очевидно,
положительное направление нормали
зависит от выбора координатных линий;
оно так же расположено относительно
касательных к линиям и и v, как
ось z относительно осей х а у.
Заметим еще, что для
определения направления касательной dM
к кривой (3) достаточно знать
отношение дифергнциалов du:dv.
Поэтому нередко кривую в данной
точке поверхности задают просто отношением диференциалов du:dv.
3. Линейный элемент поверхности. Длина дуги 5 кривой (3)
определяется из уравнения
Черт. 7.
'ds\* (dM\* /dx\2 /dy\* , /dz\*
jt) =Ы =U) +U) +Ы
Нам удобнее будет искать диференциал дуги ds:
ds* = dAPss (M„du + Mv dv)\
Возвышал в квадрат, получаем:
ds' = Жа2 rf«84- 2M„MV dudv -f- AT.» d и».
(S)

40 ЛИНЕЙНЫЙ ЭЛЕМЕНТ ПОВЕРХНОСТИ
В этом выражении коэфициенты
F=MaMv = xuxv + yuyv + *и zVi (6)
G = Mv2 = xv* +yv* + z*
могут быть вычислены из урабнений поверхности (2), независимо от
того, какая кривая (3) задана, и только диференциалы du и dv
вычисляется из уравнений кривой (3). Поэтому выражение
ds* = Edu* + 2F dudv-\-G dv* (5')
определяет диференциал дуги любой кривой на поверхности и
называется линейным элементом поверхности.
Линейный элемент имеет существенное значение в целом ряде
вопросов теории поверхности. Мы увидим, что для решения всех задач из
области геометрии на поверхности нет надобности иметь конечные
уравнения поверхности (2), а достаточно знания одного линейного
элемента ее.
4. Угол двух кривых на поверхности. Углом двух кривых
называется угол их касательных. Вектор касательной (4) вполне определен
отношением диференциалов du:dv. Аусть нам задано отношение ди-
ференциалов duidv для одной кривой и 8и:8х/ — для другой. Если
известны конечные уравнения кривой (3), то указанные диференциалы
легко найдутся диференцированием этих уравнений.
Угол в между касательными определяется скалярным произведением
единичных векторов касательных
dM Mudu-\-Mvd'J ЬМ Mubu+Mvw
_ ___ ^ _ _
Здесь ds и bs — элементы дуг той и другой кривой — находятся по
формуле (5), если туда подставить диференциалы duidv и Ьи:8г*.
Так как скалярное произведение двух векторов равно произведению
их скаляров (теперь единица) на косинус угла между векторами, то
dM ЬМ (Ми du + М„ dv) (Ми Ьи + М„ bv)
cos в = -т- — = — / > —.
ds os ds bs
Развертывая произведение и пользуясь формулами (6), мы приведем
эту формулу к виду
а Edubu + F(dubv-\-dvhu)-\-Gdvbv .-ч
costf = ^-^ . (7)
Следовательно две линии на поверхности ортогональны, если
Edubu^F{dubv-\-dvbu)-^Gdvbv = 0. (8)
Эти формулы кроме днференциало» dw.dv и 8«:?v содержат только
коэфициенты линейного элемента.

ПЛОЩАДЬ ПОВЕРХНОСТИ
41
В частности, подставляя в формулу (7)
dv = 0, Ьи = 0, ds* — Е du*, os* = G Ъь2,
мы получим угол о) между координатными линиями:
cos ш = —=- (9)
Координатные линии образуют ортогональную сеть, если
F=0.
5. Площадь поверхности. Разобьем поверхность координатными
линиями и = const, v = const на криволинейные четырехугольники. При
достаточно большом числе линий деления каждый четырехугольник
с вершинами (и, v)y (u-\-du, v), (u-^-du, v-\-dv), (и, v-\-dv) можно
заменить параллелограмом, построенным на касательных к линиям и и v
в точке М(и, v)9 если на них отложить элемент дуги каждой из этих
кривых, т. е. параллелограмом, построенным на векторах
Ми du, Mv dv.
Площадь параллелограма равна скаляру векторного произведения
Ма du XMvdv = (Ми X Mv) du dv,
т. е. скаляру нормали N, умноженному на произведение диференциалов
du dv:
dS = Y (М* X Mv)* du dv.
В курсах интегрального исчисления доказывается, что предел, суммы,
таких параллелограмов не зависит от способа перехода к пределу и
равен двойному интегралу от элемента dS:
S = ffY(MaXMv)2dudvf
распространенному на всю площадь поверхности. Этот предел называется
площадью поверхности S.
Следовательно dS — элемент площади поверхности. Развертывая по
правилам умножения векторных произведений (тождество Лагранжа) *)>
получим:
dS = Ymu*MJ — (MuMvf du dv = |/"£G —Я du dv. (10)
Мы видим, что и площадь какой-либо части поверхности может
быть вычислена только на основании знания линейного элемента ее.
*) Для всяких четырех векторов А, В, С и D справедливо тождество
[л5]-[с5]=(лс)(а5)^(А5)(вс),
это тождество есть не что иное, как теорема о перемножении матриц
я, а2аг N *! СъСгъ\а2аг\ \с2 съ , \ах аг 1 \et cz
С- I «J C\ + *2*2 + Wz b\ C\ + V* + Ъ%Сг
I a\d\ + Q%d* + o-^i% bx dx -f- b2d2 + Ь%йг
где a-, bj, е(, d( суть координаты векторов A,IF9CtD-
Q\a* .\ci c2L-.
bxb%\ I dt d21

42
ЛИНЕЙНЫЙ ЭЛЕМЕНТ ПОВЕРХНОСТИ
II. Примеры поверхностей.
6. Плоскость и сфера. 1) Плоскость в декартовых косоугольных
координатах:
ds2 = dx2 -f- 2 cos <o dx dy -{- dy2f dS = sin a> dx dy,
dx bx + cosv{dx by -f. д?у o.v) 4- dy by
Условие перпендикулярности
l-fcosa>(ft-f Л')4-Л*' = 0, где *==!£, *'=^.
Координатная сеть состоит из прямых, параллельных оси х (линии х) и
оси у (линии у).
2) Плоскость в полярных координатах:
* = rcos9, j/ = rsin<p,
tfs* = dr* -f r2 d<p2, rfS — rdrdv,
cos в = tfrSr + ffltfy8?
Условие перпендикулярности
0.
Координатная сеть состоит из концентрических кругов (линии г •= const
или линии ср) и пучков прямых с центром в полюсе (линии <? = const
или линии г) (черт. 8).
r^ const
Черт. 8.
Черт. 9.
Сеть правильна везде кроме полюса.
3) Сфера радиуса R отнесена к широте f и долготе &:
x = /?cos<pcos<}/, ^riiflcoscpsin^, z = /?sin<p,
^ = d<p2 + cos2^^2, rf5 = sin ? rf(p </ф.
Условие ортогональности
d<f by -f- cos* 9 rf^ 8ф ас: в.

ПОВЕРХНОСТЬ ВРАЩЕНИЯ
43
Координатные линии: <р = const (параллели), ф -= const (меридианы) —
ортогональны (черт. 9). Сеть правильна везде кроме полюсов.
7. Поверхность вращения. Пусть осью вращения служит ось z
(черт. 10) и уравнение профиля 2=/(r). Выберем за параметру
полярные координаты ги <рв плоскости х% у. Тогда уравнение поверхности
имеет вид: . х, ч
* = rcos<p, у = г sin 9, *=fvh
ds* = [ 1 +/'2 (г)) dr> -f г2 rf?«, flf5 = г l/l-t-Z'HO ^ <*?•
Координатные линии: 9 = cons* (меридианы) и г = const (параллели)
образуют ортогональную сеть.
Введем новый параметр и
посредством уравнения
da = Vl+r(r)dr,
тогда линейный элемент примет
вид
ds* = du* +1* dfp9
Очевидно, и есть дуга меридиана,
отсчитываемого от какой-нибудь
параллели. Линейный элемент
сферы получится, если положить
г = cos и, ср = v. Нормаль Пиверх-
нопи вращения
A^={cos9, sin9./(r)}X{— г sin 9,
г cos 9, 0} = г {—f'(r) cos 9,
-f(r) sin ?, 1},
очевидно, лежит в плоскости
меридиана, а потому пересекает ось
вращения.
Следовательно нормали к
поверхности вращения вдоль одной
параллели образуют конус с вершиной на оси вращения; нормали вдоль
одного меридиана огибают в плоскости меридиана его эволюту.
Центром кривизны плоской кривой называется точка пересечения
двух бесконечно близких нормалей кривой. Подобно этому точка
пересечения нормали к поверхности с своей бесконечно близкой называется
центром кривизны поверхности. Мы видим, что нормаль к поверхности
вращения встречается с бесконечно близкими в двух точках Сх и С2,
когда мы продвигаемся по меридиану и когда мы идем по параллели.
Эти две точки называются центрами кривизны поверхности; отрезки
МСХ — /?t и МС2 = R2 - главными радиусами кривизны, а те линии, вдоль
которых нормали к поверхности встречаются (образуя развертываю-
щиеся поверхности), — линиями кривизны. Почти очевидно, что через
каждую точку поверхности проходят только две таких линии — меридиан
и параллель. В следующей главе мы докажем, что так же дело обстоит
и для всякой поверхности.
Черт. 10.

44 ЛИНЕЙНЫЙ ЭЛЕМЕНТ ПОВЕРХНОСТИ
Главные радиусы кривизны поверхности вращения: Rt — радиус
кривизны меридиана, R2 — отрезок нормали до оси вращения.
Следовательно главные кривизны поверхности
1 _ f"(r) 1 _ f(r) (и)
их произведение К и сумма Н называются полной и средней
кривизнами поверхности. Имеем:
A-r[l+/"MK К }
Кривизна К положительна, если оба центра кривизны лежат по одну
сторону поверхности; тогда поверхность выпуклая. Кривизна шара
1
равна £-3.
8. Катеноид — поверхность вращения
целой линии (черт. 11) вокруг своего основания
как оси.
Уравнение профиля
г
г=~\еа -\-е а j, а = const.
Черт. 11.
2
Следовательно
*41/-е")й = ^^,
и так как
ТО
откуда
dU = ^l+r(r)dr=yr\ + 7^^dr:
rdr
Уг> — а*'
и линейный элемент
ds2 = du* + («а + a2) dv\
Главные радиусы кривизны
#1 = — -, #2=-
равны по абсолютной величине и противоположны по знаку, тяк что
средняя кривизна равна нулю. Такая поверхность называется мини-*
мальиой.
Так как цепная линия — единственная кривая, радиус кривизны
которой равен отрезку нормали, то катеноид — единственная минимальная

ПСЕВДОСФЕРА 45
поверхность вращения, в чем впрочем нетрудно убедиться,
непосредственно проинтегрировав уравнение
9. Псевдосфера. Если кривизна поверхности К равна нулю, то
f(r) = 0,
меридиан имеет уравнение
z=zar-\-b9
т. е. представляет тобой прямую, а поверхность — конус или цилиндр.
Кривизна шара постоянна и притом положительна. Это не
единственная поверхность вращения постоянной положительной кривизны. В § 14
мы найдем целый ряд дру«их, а сейчас будем искать поверхности
вращения постоянной отрицательной кривизны.
Если положить постоянную кривизну поверхности К= — ^, то
Г (г) fir) _ 1
rll+fW? а*>
или
fifsftfi _ г 1 _ г* , t
и, обозначая постоянную интеграцию через ?—1—f
/i(r)= Ь*~г* Л
следовательно меридиан поверхности определяется уравнением:
а линейный элемент
<-±SV ■&=**. w
<*=?££*+*<v- <13>
Могут представиться три случая:
1°. b = а. Поверхность принимает наиболее простую форму. Уравнение
меридиана интегрируется:
г = a sin t
Это — уравнение трактрисы !), и ось z — ее асимптота (черт. 12): для
/=0 имеем г==0 и z=co. Для t = ~получаем r=ay z = 0, ^ = 0;
кривая имеет точку возврата, а поверхность — ребро возврата.
Эта поверхность — простейшая поверхность постоянной отрицательной
кривизны. Она называется псевдосферой.
1) Геометрически определяется свойством: отрезок касательной между
кривой и ее асимптотой имеет постоянную длину.

46
ЛИНЕЙНЫЙ ЭЛЕМЕНТ ПОВЕРХНОСТИ
2°. Ь < а. Уравнение (а) показывает, что г может принимать все
dz
значения, меньшие, чем Ь. При r—b — = 0, .и мы опять имеем точку
возврата меридиана (черт. 13); при г = 0, ^- =
-все меридиа-
dr у & _ Ь2
ны пересекают ось вращения под острым углом.
3°. Ь > а. Из уравнения (а) следует, что г не может быть меньше,
чем [/б2— а2; меридианы не пересекают оси. Для r = j/^2 — а1
-=оо; это — горловой круг поверхности (черт. 14). Линии r—b суть
попрежнему параллели, служащие ребром возврата поверхности.
/
Черт. 12. Черт. 13. Черт. 14.
Если ввести новые параметры и и v посредством уравнений
то линейный элемент во всех трех случаях принимает вид:
."V
ds* — du*+\ '-^— )dv*.
(Н)
10. Линейчатая поверхность. Возьмем кривую (Я)
Р = P(v)
и будем в каждой точке ее проводить прямые РМ, параллельные
вектору
7=/».
Эти прямые РМ опишут линейчатую поверхность.
Откладывая на прямой РМ от точки Р отрезок РМ = и, получим
точку М {и, v) поверхности:
М = Р + 1и.

ЛИНЕЙЧАТАЯ ПОВЕРХНОСТЬ
47
Диференцируя, имеем *):
dM = Idu -f- (Р + /и) Л,
<fca = {7Л* + (Р' + /'«) л }2.
Если Г— единичный вектор и г> — длина дуги кривой (Р), то
?=1Э IV = 0, Р' = т, Р'* = тя = 1, /P' = cos9, (а)
где т — вектор касательной к кривой (Р), 6 — угол между
образующей I и кривой (Р), и
rfs2 = du2 -f 2 cos 8 du dv -f (1 -j- 2te -f cV) da2, (15)
где
b = Pl', c*~J'K (b)
Линии ^ = const — прямолинейные образующие. Если cos 9 = 0, то
направляющая (Р) пересекает образующие^ под прямым углом и все
линии и = const — ортогональные траектории образующих.
Линейный элемент (15) дает квадрат расстояния между двумя
точками (utv) и (u-\-du, v-\-dv) на поверхности. Задаваясь постоянными
значениями v и v-\-dv и меняя и и u-\-du9 мы будем получать
расстояния между различными точками двух образующих.
Преобразуя линейный элемент в виде
ds* = (du -J- cos G dv)2 -j- (sin2 9 -{- 2bu -f сV) dv*,
видим, что это расстояние будет наименьшим, если
Лг-f cos 6 А? = 0, Ь-{-с2и = 0.
Первое условие определяется, т.е. точку на втором луче, второе — и,
т. е. точку на первом, так, что расстояние между ними — кратчайшее
расстояние между двумя образующими v и v-\-dv. Эта точка с
параметром
Ь
называется центром луча, а геометрическое место центров — линия
сжатия. Если
6 = 0, (с)
то направляющая и = 0 есть линия сжатия.
Вектор нормали
N^^x^==/X(P4^") = ('X?,)+(^X/r)«-
По смыслу векторного произведения первое слагаемое (/ X Р') есть
перпендикуляр к образующей / и к касательной Р' к линии (Р), т. е.
нормаль к поверхности в точке и = 0; длина его равна sin 8, ибо оба
— dP _ dl
dv dv

48
ЛИНЕЙНЫЙ ЭЛЕМЕНТ ПОВЕРХНОСТИ
множителя — единичные векторы, а угол между ними есть 6. Второе
произведение (7 X П перпендикулярно к первому, ибо по условию
Ь—Р1' = О,
следовательно Р перпендикулярен к 7', и общий перпендикуляр к
образующей 1 и к Г повернут на прямой угол против перпендикуляра к 7
и к Р'. Оба множителя 7 и 7' теперь взаимно перпендикулярны (ибо 7—
единичный вектор, а /'—его производная), первый длиною единица,
второй имеет с единиц длины; следовательно длина(7x7) равна с.
Обозначая буквами /Zp и rii взаимно перпендикулярные единичные векторы
первого и второго произведений, имеем:
7x^ = /z0sin9, iyj=zcnu
_ - (16)
N = /t0sin9-}-/z1£W.
Эта формула показывает, что лри движении точки М от центра луча
и X 0 до и Х °° нормаль N поворачивается от п0 до пг на прямой
угол. Обозначая через Q угол двух нормалей N и л0, имеем:
о N^o sin8 , ~ , си ,-«4
cos Q = —~ = -г=: , tg2 = :±: —«-. (17)
^ Vsin'O + ^ii» ' б sine v '
о sin 6
Величина называется параметром распределения касательных
плоскостей вдоль луча.
Если в = 0, то образующая касается линии сжатия (Р) и поверх-
ность становится развертывающейся; параметр распределения равен нулю,
т. е. нормали N вдоль образующей параллельны.
Пример. Прямой (минимальный) геликоид. Если направляющая —
прямая линия (например ось z), а образующая перпендикулярна к ней
и, оставаясь перпендикулярной, равномерно вращается около нее,
поднимаясь винтовым движением, то линейчатая поверхность, которую она
описывает, называется прямым геликоидом.
Так как теперь
Я== {О, 0, av), 7={cosx>, sinv, о},
то уравнение геликоида
х = и cos v, у = и sin vt z = av,
откуда
ds* = du*-}-(u2-\-a*)dv.
Нетрудно видеть, что все линии и = const — обыкновенные винтовые
линии, линии v = const — прямые, которые служат общими главными
нормалями винтовых линий. Прямая я = 0—линия сжатия и параметр
распределения равен единице. (См. табл. I в конце книги.)

РАЗВВРТЫВЛЮЩЛЯСЯ ПОВЕРХНОСТЬ
4»
III. Налагающиеся поверхности.
11. Изгибание поверхностей. Мы видим, что линейный элемент
катеноида тот же, что и геликоида Следовательно длина любой линии
на одной поверхности равна длине соответавуюшей линии на другой,
если считать соответствующими те точки обоих поверхностей, которые
имеют одни и те же криволинейные координаты (и, v).
Сходственные линии пересекаю 1ся под равными углами, площади
сходственных фигур равны — словом, 'вся геометрия поверхности,
поскольку она зависит о г линейного элемента, одна и та же на обеих
поверхиоаях.
Если осуществить поверхность из гибкой нерастяжимой пленки и
изгибать ее без складок и разрывов, то длины всех линий, углы и
площади будут сохраняться. Поэтому преобразование поверхности с
сохранением линейною элемента называется изгибанием поверхности, а две
поверхнэсти с общим линейным элементом — налагающимися, независимо
от того, мо.кно ли осуществить непрерывное преобр кование одной
поверхности в другую с сохранением линейного элемента.
Мы можем следовательно сказ»ть, чго прямой геликоид налагается
на кагеиоид. Мы увидим впрочем, чго здесь существует оо1
налагающихся поверхностей с произвольным параметром, меняя который можно
непрерывно преобразовать катеноид в геликоид.
При н«лО/кеняи координатные линии совпадут; следовательно
образующие прямые z> = const геликоита перей iyr в меритианы катеноида, а
винтовые линии «=con$t наюжатся на параллели. Оч.'витно, геликоид
при наложении на катеноид навернетса на него бесчисленное множество
раз.
12. Развертывающаяся поверхность. Развертывающуюся
поверхность можно рассматривать как геометрическое место касательных к про*
странственпой кривой.
Возьмем какую-нибудь кривую
P = ?(v);
пусть здесь v—элемент дуги кривэй; распространим на нее обычные
обозначения всех элементов для кривой. Если РМ = и — отрезок
касательной от точки касания Р до какой-либо точки ее М, то, очевидно,
M = P + TU.
Здесь вектор Ри вектор касательной т —функции одного v.
Диференцируя и помня, что dp—xdv$ d?=-^dv, получим:
dM^xdu -|- f х -j- ~ и J dv%
откуда
ds2= Izdu-^lx-^-- ujdv\ =

50
ЛИНЕЙНЫЙ ЭЛЕМЕНТ ПОВЕРХНОСТИ
ИЛИ ds> = <fa» + 2<*ii «to + (l + т) Л». (18)
Очевидно, эту форму линейного элемента можно было прямо получить
из формулы (15) § 10, полагая 6 = 0, £ = 0, так как теперь
образующая касается направляющей, которая является линией сжатия
поверхности.
Нормаль к поверхности
N=.MuXMv = -xx(r + l) = lu,
как и следовало ожидать, совпадает с бинормалью кривой (Р).
Полученный линейный элемент (18) содержит только радиус
кривизны р кривой (Р) и не содержит кручения ее. Будем уменьшать
кручение кривой, сохраняя ее кривизну. Кривая станет деформироваться,
поверхность ее касательных тоже будет меняться, но линейный элемент
ее (18) сохранится без изменения. Таким образом мы непрерывно
преобразуем нашу кривую в плоскую кривую (кручение равно нулю), не
изменив линейного элемента развертывающейся поверхности; но
касательные плоской кривой, очевидно, лежат в ее плоскости; значит, наша
поверхность обратится в плоскость, откуда и следует, что всякую
развертывающуюся поверхность можно непрерывным движением развернуть на
плоскость.
13. Изгибание поверхностей вращения. Мы вычислили для
поверхности вращения 5
x = rcosv, y = rsinv, z=f(r)
линейный элемент
ds2 = [1 -f/2 (г)] dr2 + г2 dv2.
Пусть теперь две поверхности вращения S и St налагаются друг на
друга так, что меридианы переходят в меридианы и параллели в
параллели. Снабжая значком 1 все величины, относящиеся ко второй
поверхности, мы скажем, что точка (г, v) первой поверхности переходит
в точку (ru v^) второй так, что линия r= const переходит в линию
rt = const и v = const переходит в ^ = const.
Следовательно
ri = ¥ (г)> «1 = ф (*0
[1 +Р W1 ** f г* d* = [1 +//»(rt)] dr\ + r\ dv\. (a)
Так как
drt = <p' (r) dr, dvx =<J/ (v) dv
и независимые диференциалы dr и dv не могут быть связаны никаким
уравнением, то равенство (а) распадется на два:
1+/«С) = [1+/*('.)]?'« (г),
r = r^'(v). (Ь)
Из второго следует, что
£ = «}/'(©) = -£-= const,

ИЗГИБАНИЕ ШАРА
51
ибо функция от независимого переменного г не может равняться
функции от другого независимого переменного v.
Подбирая постоянные интеграции, мы можем положить,
ri=<?(r)=kr.
Внося эти значения в первое уравнение (Ь) и полагая
получим:
откуда
«ie/l_tf+/i(r).
Следовательно поверхность вращения Su налагающаяся на поверхность S,
определяется уравнениями
x=2krcos?,y = krsiti£$ z = JV1 +/2(г) — k* dr.
Полному обороту первой поверхности, т. е. изменению v от 0 до 2 тс
будет соответствовать изменение vx от 0 до -р при этом точки на
расстоянии г от оси вращения перейдут в точки на расстоянии гг = kr от
нее. Следовательно, если k < 1, то поверхность «S, налагаясь на Su
завертывается, покрывая ее несколько раз, и сжимается.
Если k > 1, то поверхность 5, наоборот, развертывается, покрывая
только часть поверхности Sv и становится шире; ее точки отходят от
оси. При этом только та часть поверхности остается действительной,
для которой
f2(r)>&—\.
14. Изгибание шара. Рассмотрим в качестве примера изгибание
шара радиуса единицы. Уравнение меридиана здесь
Следовательно меридиан изогнутой поверхности
Если £<1, то zx действительно, если г находится в пределах 0 <г2< 1.
При этом
Idz1_ \dh— V"^1^
drt~ °° для г — 0\(!п~ k
rx = k lr, = 0
Меридиан пересекает ось вращения под острым углом.

52
ЛИНЕЙНЫЙ ЭЛЕМЕНТ ПОВЕРХНОСТИ
Поверхность имеет вид веретена (черт. 15, а). На нее налагается часть
сферы, лежащая между меридианами zi = 0 и v — 2i:k.
Если к> 1, то zx действительно, если г лежит в пределах—-— <г2< 1.
При этом
для r=l[|;— для r=J^i[£=0
Меридиан не пересекает оси вран ения (черт. 15, Ь)\ в точке гх = ]/к* — I
он имеет точку возврата с касательной, параллельной оси ги и
периодически повторяется с возрастанием zim
На эту поверхность налагается часть шара между двумя параллелями
г = —g—.
Заметим, что полный шар (черт. 15, г), как и всякую выпуклую
поверхность, без особой точки изгибать нельзя.
IV. Конформное отображение.
15. Конформное отображение. Линейные элементы двух нала аю-
щихся поверхностей совпадают. Поэтому вся геометрия на поверхности
у них общая: одни и те же длины линий, углы и площади.
Если линейные элементы двух поверхностей S и Sx не равны, но
пропорциональны
ds2 = Edu*-\-2Fdudv-\-Qdv\
dst* = X2 (Е du* Jr2FdudvJrQ dv%
то сходственные линии и площади уже неравны, а углы попрежнему
будут равны, ибо формула
a Edubu + F(dubv + dolu)4-Gdvbv
COS о =
"У Edw + 2Fdudv-f Оdu* V Eoti* + 2Fouop + Оbv*

КОНФОРМНО! ОТОБРАЖЕНИЕ ПОВЕРХНОСТИ ВРАЩЕНИЯ НА ПЛОСКОСТЬ 53
и в числителе и в знаменателе содержит однородные функции первого
измерения от коэфициентов линейного элемента и зависит только от
отношения их. Такое соответствие между поверхностями называется
конформным отображением одной поверхности на другую. Можно сказать,
что поверхности подобны в малом с отношением подобия X, ибо при
малом изменении переменных и, v можно считать X постоянным и
отношения сходственных линий равными X.
Есть существенная разница между изометрическим соответствием
(налагающиеся поверхности) и конформным отображением. Наложимость
двух поверхностей требует равенства линейных элементов, т. е.
равенства трех коэфчциентов
E=Eit Fz=zFlt G = GV (а)
Между тем для конформности достаточно равенства их отношений
ti-Fi-Qi9 (b)
т, е. только двух уравнений. Поэтому, каковы бы ни были две
поверхности 5 и 5Ь всегда можно подобрать такую зависимость между их
криволинейными координатами
чтобы удовлетворить уравнениям (Ь), так что соответствие между точками
поверхностей 5и 5j
(и,г>)—► (ии vx)
установит конформное отображение 5 на Su но вообще нельзя
удовлетворить трем уравнениям (а), так что поверхности, налагающиеся на
данную поверхность S, составляют особый класс поверхностей.
По терминологии Петерсона конформное отображение есть
отношение, а наложимость — сродстно поверхности.
16. Конформное отображение поверхности вращения на
плоскость. В § 10 мы получили линейный элемент поверхности вращения
x = rco$v, j> = rsinv, z=/(r)
в форме
ds* = du* + r*dv\ и= f\fl-\-f2(r)dr.
Слелаем еще преобразование: вынесем г2 за скобку и введем новый па*
раметр
. da
du% = -y;
мы получим:
J ds*=ir*(dul + dv*).
Сравнивая его с линейным элементом плоскости
замечаем их подобие. Следовательно, полагая

54
ЛИНЕЙНЫЙ ЭЛЕМЕНТ ПОВЕРХНОСТИ
мы получим конформное отображение поверхности вращения на
плоскость. При этом параллели Ui = const и меридианы v = const перейдут
в прямые, параллельные оси т) и оси L
В силу конформности отображения кривая, пересекающая все
меридианы под постоянным углом (локсодромия), перейдет в прямую,
пересекающую все прямые t) = const под тем же самым углом. Отсюда,
например, сумма углов треугольника, образованного тремя локсодромиями
на поверхности вращения, равна двум прямым углам.
Если сравнить линейный элемент (а) с линейным элементом
плоскости, отнесенной к полярным координатам
ds2 = dp2 + Р2 df = р2 {d In р2 4- dp2),
то получим другое конформное отображение поверхности вращения на
плоскость:
]ap = fV±±pldr,9 = v.
Применяя это отображение для шара, получим стереографическую
проекцию шара на плоскость, которая иногда применяется при
построении географических карт. Геометрически ее можно получить, проектируя
шар из полюса на плоскость экватора.
17. Изотермическая система. Та система линий на поверхности,
которая конформно отображается на прямоугольную сеть координатных
линий х = const, у = const на плоскости, носит название
изотермической. Название это связано с тем, что уравнение Лапласа, которое
пишется на плоскости в декартовых координатах (xt у) в виде
д*У , д*У_п
дх* *ду* ~v>
сохраняет тот же самый вид и на любой поверхности, отнесенной к
изотермическим координатам (и, v):
д*У , д*У_п
ди* "+" dv* '
а так как температура V любой точки поверхности при установившейся
передаче тепла определяется уравнением Лапласа, то на любой
поверхности с постоянной теплопроводностью и без отдачи тепла в
пространство все линии и = const одного семейства изотермической системы
будут изотермами (одна и та же температура вдоль линии), если только
две из них сохраняют постоянную температуру.
Линейный элемент поверхности, отнесенный к изотермической системе
(и, v)y очевидно, имеет вид:
ds* = \*(du*-\-dv*). (19)
Координатные линии делят поверхность на бесконечно малые квадраты.
Меридианы и параллели на поверхности вращения образуют
изотермическую систему. Полярная система координат — изотермическая система
на плоскости.
Таким образом, чтобы конформно отобразить поверхность на
плоскость, надо найти на ней изотермическую систему, а отобразив две

линии НУЛЕВОЙ длины
55
поверхности Sx и 52 конформно на плоскость, мы тем самым получим
конформное отображение Si на S2.
18. Линии нулевой длины. Разлонаш сумму квадратов du2-\-dv2 в
формуле (19) на мнимые множители
ds2 = X2 (du -f i dv) (du — i dv).
Если теперь ввести новые переменные
а = и -|- lvf Р = и — iv, (20)
то линейный элемент примет вид:
ds2 = l*dad?>. (21)
Эти координаты Darboux называют симметричными. Координатные линии
а = const, р = const, очевидно, обращают линейный элемент в нуль,
а потому длина любой дуги этих мнимых линий равна нулю и они носят
название линий нулевой длины.
Линейный элемент (21) заслуживает внимания потому, что он
содержит наименьшее число коэфициентов, а именно — один; благодаря этому
им пользуются иногда, чтобы упростить выкладки. Мы видим, что эта
система мнимых координат тесно связана с изотермической. Зная одну,
можно найти по формулам (20) другую.
Чтобы привести какой-нибудь линейный элемент к виду (21),
достаточно разложить его на мнимые множители
d*=(yWdu+^dv} (yEdu + ^fih),
Приравнивая нулю каждый множитель, проинтегрируем получаемые дифе-
ренциарьные уравнения; пусть а = const и р = const — их интегралы.
Обозначая тогда через р. и [х; интегрирующие множители, имеем;
и следовательно
ds*=— ,d<xd%

Неоткуда нетрудно перейти к изотермической системе.
Пусть мы нашли одну систему линий нулевой длины; как найти
все другие?
Уравнение ds* = 0 имеет, очевидно, только два семейства
интегральных кривых. На всякой поверхности существуют только два семейства
линий нулевой длины. Линейный элемент в форме (21) получается
отнесением поверхности к этим двум семействам линий, и различные формы
его могут зависеть только от выбора тех или других параметров.
Вводя новые параметры
а1 = /7(а), pi=^(P), 00

5g ЛИНЕЙНЫЙ ЭЛЕМЕНТ ПОВЕРХНОСТИ
мы преобразуем линейный элемент, но не изменим его вида. Отсюда
следует, что если известна одна изотермическая система на поверхности
(л, v)f то всякая другая {ии т/,) получится как действительная и
мнимая части любой аналитической функции комплексного переменного
их + «Ч = F(u + to).
Действительно, так как
ai^=LUxArivu Pi = Hi — ivu a = e-f-to, р = и — to,
то формулы (а) принимают вид:
их -j- toj = Z7 (и -}- to), i*! — toi = Ft(u — to).
Функции F n Fu очевидно, должны быть сопряженными, чтобы ut и vt
были действительными.
Нетрудно заметить, например, что полярная система на плоскости:
ds2 = dr2 + r d^ = г2 (du* -f tf?2),
II =г 1П Г,
получится из декартовой, если взять F(x-\-iy) = In (а:-(-/у):
. . _v
a-f to = ln(A: + /y) = ln{l/"^-tev2^ агс2*}.
Переменное a-f"to называется комплексным переменным поверхности.
Например на сфере
х = sin и cos v, у = sin и sin v, г = cos и,
где т> = ф — долгота и «= ,-т —ф — дополнение широты (угловое
расстояние точки от полюса и = 0), линейный элемент
ds2 = du2 -|~ sin2 и dv*
принимает изотермический вид, если псложить
* = f-£L «In ig«
1 J sinn &2
Следовательно за комплексное переменное на сфере можно принять
их -}- to и любую его функцию, например
w = <rB'+"=ctg^"\
Если за комплексное переменное в плоскости его экватора принять
где р и ф — полярные координаты на плоскости, то
т. е.
Р —ctg2, ? = t,
определят конформное отображение сферы на плоскость«— стереогра*
фическую проекцию шара, которую мы получили в § 16.

УПРАЖНЕНИЯ
«7
Упражнения.
1. Найти линейный элемент плоскости, отнесенной к софокусным эллипсам
и гиперболам
где г — постоянное, a ut v — криволинейнье ксординаты Показать, что система
линий <ы, Vi ортогональна и образует изотермическую сеть.
2 Если кривая z — <р (р движется около оси z винтовым движением, то она
описывает винюв^ю поверхность, уравнение ко оро i монно записать в виде:
х = р cos v, у = р sin v, z :г 9 (р) + mv; (1)
pt v — криволинейные координаты, т — постоянный шаг винтт. Составить
линейный элемент винтозой поверхности, привести его к ортогональному виду,
введя новый параметр vx посредством равенства
: const
п+**<<)'='+^
и показать, что винтовая поверхность (1) налагается на поверхность вращения
x = rcosvlt y = r%lnvuz=z^(r), (2)
если положить
гв = Л»(р« + «а).
та
Обратно, заданную поверхность вращения (2) можно изгибать в винтовую
поверхность с днумя произвол! ными постоянными т и k (Вош).
3. Показать, ч о катеноид можно непрерывно изогнуть в минимтльный
геликоид.
4. Найти винтовое поверхности, налагающиеся на шар. на псевдосферу.
5. Показать, чго винтовая повер.нисть, описанная прямой, пересекающей
ось вращения под углом а:
z = pctga,
налагается на однополостный гиперболоид вращения
j4^L. — !i = 1
mactg3ct m*
6. Ес^и кривая х ~я, z-=.b пер носится в пространстве так, что каждая
точка ее описывает кривую х = а9 у = р (или ра-н^ю ей), то получается
поверхность переноса
x=za + at .у = 0, * = &, (1)
где а и Ь — функции од того переменного и, а и р — одного переменного v.
Составить линейный э if мент по ерхносги (1), показать, что она может
изгибаться, острая.ь поверхностью переноса, если положить
4 з= at, а1=: у, *,'» _ у* + (1 - Я) а", (V2 = Р" + (l - £) «'».
где аи Ъи ши ft — соответствующие функции новой поверхности, / — параметр
изгибания,
.# dbt , da л, d? , dot
Ъл = -з-ь, а9 = -г-. Р« = -т> «' = тит.д.
Так как линии к, v сопряжены на всех поверхностях (см. гл. III), то повзрх*
ность переноса изгибается на главном основании (Пётерсон).
7. Найти линейный элемент поверхности
х =r аа, y=za?$ гт=Ь, (1)

58 ЛИНВЙНЫЙ ЭЛЕМЕНТ ПОВЕРХНОСТИ
где а и & — функции одного щ а и 0— одного переменного v. Показать, что
поверхность (1) может изгибаться, не теряя своего характера, если положить
<x = YCOS<p, g==TSin<p> ? — Л;
в^Ут^Гсов*, Pi = V^=Tsin?1> K^fyW-W-W'^
где *—параметр изгибания; yj, у и <р —функции одного v; a1 = — tyl = ~ и т.д.
Линии и = const — линии уровня (ибо z=z const), т. е. сечения поверхности
плоскостями, параллельными плоскости ху; линии v = const — меридианы, т. е.
сечения поверхности пучком плоскостей, проходящих через ось z (—= const].
Это — конические линии (линии прикосновения описанного конуса) и
цилиндрические линии (линии прикосновения описанного цилиндра). Поверхность может быть
получена из поверхности вращения, если абсциссы меридианов изменить в
отношении у — постоянном на одном и том же меридиане, но переменном от одного
меридиана к другому. Они называются производными от поверхности вращения
(Петерсон).
8. Показать, что при
Y2 = i42cos3t> + £2sin2ff, *}2гз = А2В*, а = cos и, b=zCslnu
поверхность (1) предыдущего яримера есть поверхность 2-го порядка
А* ^ Д2 ^ С2 "~
Исследовать пределы действительности изгибания эллипсоида (Петерсон).
9. Распространить формулы задачи 7 на поверхности
x=zaa + fvda, у = а$+ fvd$, z — b,
где V — любая функция от v, линии (и, v) — попрежнему сопряженные (см. гл. III) —
система конических и цилиндрических линий, поверхность Петерсона).
10. Показать, что при т=1 поверхности задачи 9 — поверхности каналов.
Они образованы движением линии
у1 =za, z'=z Ь,
когда плоскость (У, z') навивается на цилиндр с осью z (оси z и z' параллельны)
и с направляющей
x=zjvda9y=fvd$
(surface raoulure de Monge).
11. Показать, что поверхности (surface tetraedrale de Darboux)
x=Ax (a - s$ (v - sj, y=A2 (u - s$ (v - s2)\
z = Az(u~s$(v — s3)*,
где Ai> Si —• постоянные, изгибаются в поверхности того же типа, если старые
(Ait Si и новые Ai\ s{ связаны соотношением
2^? J*c2^ *?- где * = 0' 1» 2» 3-
Линии (и, v) сопряжены (гл. III) на всех поверхностях, так что поверхности
изгибаются на главном основании (гл. IV) (Егоров)!

УПРАЖНЕНИЯ
59
12. Если две поверхности S и S1 заданы уравнениями
М = М (u, v), М' = Л?' («', v')
и между криволинейными координатами (ы, v) и («', v') дано два уравнения,
однозначно разрешимых (в рассматриваемой области) относительно (и, и) и
относительно (u', v'), например
и' = и, V1 = V,
то каждой точке М поверхности S соответствует точка М' поверхности S'.
Говорят, что поверхность S отображена на поверхность S'.
Показать, что существует одна и только одна система линий, ортогональная
и на поверхности 5 и на поверхности S', определяемая уравнением (теорема
Тиссо).
\Edu + Fdv9 Fdu + Gdv\_n
\E'du + F'dvf F'du + G'dvl-"'
Отношение линейных элементов ds и ds' называется модулем линейного
растяжения
ds'
Показать, что в данной точке модуль меняется для разных направлений du:dv,
как обратная величина полудиаметра эллипса. Если поверхности отнести к общей
ортогональной системе, то уравнение этого эллипса можно написать в виде:
И = ]/ g-.ft = y о
суть главные модули.
Если S отображается на S' с сохранением площадей, то произведение главных
модулей |*! и [д.2 равно единице.
Если оба главных модуля постоянны» изображение называется униформным.
Главные модули в произвольной системе координат определяются как корни
уравнения
(EG - F*) |л* + (2/7* - EG' - GE') ц* + E'G' - 5'*=0.
Написать линейный элемент поверхности, униформно отображающейся на
плоскость.
13. Сеть Чебышева и проблема одевания поверхности. Если допустить,
что материя соткана из двух семейств нерастяжимых нитей, но может
деформироваться так, что угол между пересекающимися нитями принимает произвольную
величину, то линейный элемент той поверхности, форму которой имеет материя,
отличается от линейного элемента плоскости
ds* = du* + dv*
только средним членом, который может иметь произвольную величину
ds2 = du2 + 2 cos ш du dv + dv*. (a)
Поэтому, чтобы одеть поверхность, надо привести ее линейный элемент
к виду (а). Система линий (и, v) называется в таком случае системой Чебышева.
Показать, что отыскание системы Чебышева (а) равносильно изысканию
системы (а, р), которая приводит линейный элемент к виду:
ds2 = cos* ~ ДО + sin' ~ rfpa.
Показать, что плоскость, отнесенная к системе Чебышева, принимает вид
поверхности переноса
х =л (и) + <pi (t>), у =/8 («) + ъ («0. *=о.
14. Показать, что нормали к линейчатой поверхности вдоль прямолинейной
образующей составляют равносторонний гиперболический параболоид с
вершиной в центре образующей.

ГЛАВА ТРЕТЬЯ.
Вторая квадратичная форма.
I. Нормальная кривизна кривой на поверхности.
1. Кривизна крив эй на поверхности. Дяференцируя по длине дуги s
вектор касательной к кривой [(4) гл. II]:
~ dM М
ds а ds
du i Тя dv
получим по формулам Френе -^- = -
dW
ds*
Тм (da\* I oZt dudv i Тл fdv\*\TA &и 1 л1 d*v
=iM"Ury +2M"*ds-ds-+M™ *)+м»ш+м-
ds**
(a)
Здесь v — вектор главной нормали и р — радиус кривизны кривой.
Чтобы найти из уравнения (а) кривизну криьой, умножим обе части
на единичный вектор нормали к поверхности
п =
Af-XAf.
Ми X Mv
V№.xMv)* V~EG-F%
В левой части мы получим скалярное произведение v я = cos9 (косинус уг«
ла между главной нормалью к кривой и нормалью к поверхности), а в пра-»
вой часги пропадут члены с первыми производными /Ии и Mv9 ибо это
касательные к координатным линиям и следовательно перпендикулярны к л-
Мы получим
C0S9 — <РМ --rs fdu\2 , 0- т. du dv , - rz (dv\l
— я М иа dip + 2я $уу dudv + n М^ dv*
~ ds*
Введем обозначения:
(Ь)
1
ym-F>
хи Yvxua
УаУуУиа
Zu Zv Ziut
Xa Xv Xuv
Vuyvy*o
tu Zv Zgp
Хц Xp Хфр
УиУюУт
Za Zff Zqh
(1>

НОРМАЛЬНАЯ КРИВИЗНА КРИВОЙ
61
Очевидно, что эти величины имеют в данной точке поверхности вполне
определенную величину и не зависят от выбора кривой.
Формула (Ь) для кривизны кривой примет вид:
cosy _ Ddu* + Wdudv + ITdv* (<2\
P ~ Edu'-t-2Fdudv + Gdv* ' * '
Квадратичная форма
ndM = Ddu*4-2D'dudv-\-D'dv* (Г)
называется второй квадратичной формой поверхности. Она введена
Гауссом *).
Формула (I') определяет кривизну кривой -; кроме криволинейных
координ!т (utv) дачной точчи поверхности, она содержит отношение
диференциалов du:dv% которое о феделяет касательную к нашей кривой,
и <р — yroi между главной нормалью к кривой и нормалью к
поверхности. Очевидно, досгагочно дагк соприкасающукЛя плоскость кри ой,
ибо ее пересечепие с касательной плоскостью определит касательную
к кривой и следовательно отношение диференциалов du.dv, а ее угол
с нормалью п есть угол у.
Следовательно все кривые на поверхности с обшей соприкасающейся
плоскостью имеют одну и ту же кривизну. Ту же кривизну имеет
и плоская кривая, получаемая от сечения поверхности плоскостью через
касательную под углом о к нормали.
Кривизна любой кривой на поверхности равна кривизне плоского
сечения поверхности ее соприкасающейся плоскостью.
2. Нормальная кривизна кривой. Будем поворачивать секущую
плоскость около одной и той же касательной du:dv; наклон ее к
нормали п — угол (р — будет меняться, а вместе с ним будет изменяться
и кривизна.
Когда секущая плоскость пройдет через нормаль п {нормальное
сечение), угол <р будет равен л^бо 0 либо я в зависимости от того, совпадет
ли главная нормаль кривой v с положительным направлением ьормали к
поверхности или будет ему прямо противоположна.
Кривизна -Q нормального сечения через касательную du:dv
определяется формулой
^_ \_ _ Ddu'+Wdu dv + D* dv* т
— R ~ Edu* + 2Fdu du +Gdv** * '
где верхний знак соответствует ^ = 0 и нижний у = к.
Сравнивая эту формулу с формулой (2), имеем:
cosy н _1__
Р R '
или
p = :±:#cos<p; (4)
*) Гаусс ввел форму Nd*M9 которая отличается от приведенной в тексте
множителем YbG — F*.

62
ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА
так как р и R положительны, то двойной знак соответствует двум
возможным знакам cos ср. Если выбирать для ср острый угол между двумя
нормалями или между двумя секущими плоскостями, то можно
остановиться на верхнем знаке.
Если радиус кривизны каждого сечения откладывать по его главной
нормали, то, очевидно, радиус кривизны наклонного сечения будет равен
проекции радиуса кривизны нормального сечения' на плоскость косого
сечения.
Иначе говоря (теорема Менье), центр кривизны наклонного
сечения есть проекция на плоскость этого сечения центра кривизны
нормального сечения.
Отсюда следует, что, поворачивая секущую плоскость около
касательной du: dv, мы заставим центр кривизны сечения описать
окружность, построенную на радиусе кривизны нормального сечения как на
диаметре.
Кривизна нормального сечения через касательную к кривой duidv
носит название нормальной кривизны кривой.
Зная нормальную кривизну кривой и угол соприкасающейся
плоскости с нормалью к поверхности, легко найдем кривизну кривой. Таким
образом исследование кривизны любой кривой на поверхности сводится
к исследованию кривизн нормальных сечений поверхности.
3. Индикатриса Дюпена. Условимся приписывать радиусу
кривизны нормального сечения R положительный или отрицательный знак
в зависимости от того, каково направление главной нормали сечения,
именно, мы будем считать R положительным, когда центр кривизны будет
лежать внзпгри поверхности, т. е. на отрицательном направлении нормали
к поверхности п. Иными словами, R положителен, когда ср = ic, и R
отрицателен, когда <р=0. В таком случае в формуле (3) надо всегда
брать отрицательный знак:
-bD(l)"+2°'SS+0'(s)- <3')
Для наглядного изображения изменения кривизны нормального сечения
с поворотом касательной duidv Дюпен построил в касательной
плоскости кривую (индикатриса Дюпена), а именно: от точки М по
касательной du: dv он откладывает отрезок МРУ равный корню квадратному
из абсолютной величины соответственного радиуса кривизны/?:
mp=VW\-
Обозначим единичные векторы касательных к линиям и и v через xt и та
так, что __ _ _
Тогда единичный вектор касательной к кривой du: dv будет равен
dM jrz du х п dv - yr^du , - 1r-p;dv
вектор MP больше его в j/l/?| раз:

ИНДИКАТРИСА ДЮПЕНА
63
Значит, если через (х\ у') обозначим координаты точки Р (т. е.
координаты вектора MP) относительно косоугольной системы координат, оси
* которой совпадают с касательными к координатным линиям, то
Определяя отсюда -^ и у и подставляя в уравнение (3'), мы получим
уравнение для координат (х\ у') точки Р, т. е. уравнение индикатрисы
Дюпена
Верхний знак соответствует положительному знаку радиуса кривизны
нормального сечения /?, нижний — отрицательному.
Индикатриса Дюпена — центральная кривая 2-го порядка с центром
в точке М. Она хорошо связана со второй квадратичной формой
поверхности и отражает наиболее глубокие свойства поверхности в данной
ее точке.
ЕСЛИ D' = 0,
то индикатриса отнесена к сопряженным диаметрам (х\ у').
Направления сопряженных диаметров индикатрисы называются сопряженными
направлениями на поверхности.
Два семейства кривых, касательные к которым сопряжены, образуют
сопряженную сеть кривых на поверхности. Всякому семейству кривых
можно найти второе ему сопряженное.
Если
D' = 0 и F = 0,
то сопряженные направления ортогональны; система координат (х\ у')
прямоугольна, и ее оси служат осями индикатрисы. Главные
направления (направления осей) индикатрисы называются главными
направлениями поверхности в точке Ж. Таких направлений два; они всегда
действительны и соответствуют наибольшей и наименьшей величине
радиуса-вектора MP индикатрисы, т. е. наименьшей и наибольшей
кривизне нормального сечения поверхности. Два семейства кривых,
касательные к которым везде совпадают с главными направлениями,
называются линиями кривизны. Радиусы кривизны нормального сечения
поверхности по главным направлениям называются главными радиусами
кривизны поверхности.
Наконец, направления асимптот индикатрисы (если они
действительны) называются асимптотическими направлениями на поверхности,
а кривые, касательные к которым имеют асимптотическое направление
называются асимптотическими линиями. Такие линии существуют
(действительны) только там, где индикатриса — гипербола, в
параболических точках (где индикатриса — парабола)1) два семейства асимпто-
1) Так как точка М всегда центр индикатрисы, то последняя может
быть параболой, только распадаясь на пару параллельных прямых.

64
ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА
тических линий совпадают, а в точках, где индикатриса — эллипс, они
мнимы. Если поверхность отнесена к асимптотическим линиям (а
следовательно индикатриса к асимптотам), то
/5 = 0, £Г = 0.
4. Формула Эйлера. Отнесем поверхность к линиям кривизны. Тогда
D' = 0, F = 0
формула (3') примет вид:
-^-"(S)'+'(S)'
С другой стороны, векторы zt и т2 будут ортогональны и компоненты
единичного вектора -т- будут просто косинусами углов касательной
с осями координат {х\ у'), т. е. с координатными линиями. Если
нормальное сечение образует угол 0 с лини й и, то
Косове. Кс? g=«те,
du dv
и, исключая —, -J-, получим:
-l = §cos'e-fi£sin'0. (а)
Для 0 = 0 и 0 = ~ касательная к сечению совпадает с главными
направлениями, полудиаметр индикатрисы MP, а также радиус кривизны
нормального сечения /? принимают наибольшее и наименьшее значение /?х и /?2.
Очевидно,
JL — _£. _L — _^ (й\
Rt— £ ' R2 ~ W w
Вводя это в уравнение (а), получим формулу Эйлера
1 _cos*8 , sin3 6 ,-v
R—~RT~r-Rrm K)
Если индикатриса Дюпена — эллипс, то R{ и R2 одного и того же
знака, пусть, например, положительного. Тогда все радиусы кривизны R
будут положи«ельны и будут изменяться между значениями Rx и /?2;
вся поверхность расположится по одну сторону от касательной
плоскости. Такая точка поверхности называется эллиптической.
В частности Rt и /?2 могут быть равны между собой; тогда
индикатриса— окружность. Такая точка назывзется точкой округления
(ombilique). Все нормальные сечения поверхности через точку
округления имеют в ней одну и ту же кривизну.
Если /?i и /?2 разных знаков, то индикатриса Дюпена состоит из
двух сопряженных гипербол, одна из которых соответствует
положительному, другая отрицательному знаку в правой части уравнения (5).
По мере увеличения Ь от нуля до в', где tg6'=ex|/ —jr f радиус
кривизны растет, пока для асимптотического направления 0 = 6' не сдеда-

ГЛАВНЫЕ РАДИУСЫ КРИВИЗНЫ
65
ется бесконечно большим, а кривизна не обратится в нуль. Затем
кривизна -5 становится отрицательной, главная нормаль сечения переходит
по другую сторону касательной плоскости, и радиус кривизны R,
уменьшаясь по абсолютной величине, доходит до значения R2 для 6 = -^-.
Поверхность располагается по обе стороны касательной плоскости;
асимптотические направления — направления касательных к линии пересечения
поверхности с касательной плоскостью. Нормальное сечение
поверхности по этому направлению имеет в точке М точку перегиба. Такая
точка поверхности называется гиперболической.
Наконец, один из главных радиусов может обратиться в
бесконечность. Тогда индикатриса обращается в пару параллельных прямых.
Все радиусы кривизны R одного знака, поверхность расположена по
одну сторону касательной плоскости, но есть одно (асимптотическое)
направление, совпадающее с одним из главных направлений, когда
кривизна р- обращается в нуль. Такая точка поверхности называется
параболической.
5. Главные радиусы кривизны. Формулы (6) определяют главные
радиусы кривизны, если за координатные линии выбраны линии кривизны
поверхности. Чтобы найти величины главных радиусов кривизны в
произвольных координатах (и, v), надо, очевидно, искать максимум и
минимум радиуса кривизны нормального сечения R из формулы (3) или (3').
Независимой переменной при этом будет направление касательной или
отношение диференциалов du : dv.
Мы несколько облегчим, выкладки, если предварительно освободимся
от знаменателя
Edu2 + 2Fdudv-frGdv* + R(Ddu2-{-2D'dudv + D''dv2)=zO (а)
и будем искать максимум R как функции двух переменных a = du
и р = dv. В силу однородности формулы (а) два уравнения, получаемые
диференцированием уравнения (а) по а и по р, будут равносильны
основному уравнению (а) и его производной по —.
Итак, диференцируем уравнение (а) по переменным а = Лг и (3 = dv
и сразу же полагаем производную от R равной нулю. Мы получим
два уравнения
Е du-{-Fdv+R(Ddu-\-D'dv)=:0,
Fdu-\-Gdv-{-R(D,du-\-D"dv)=:0, ^
которые определят и отношение диференциалов du: dv, соответствующее
тому и другому главному направлению, и самые главные радиусы
кривизны Rt и /?2.
Исключая /?, получим:
(D du -f D'dv) (Fdu-\-G dv) — (D'du -f- D'dv) {Edu+F dv) = 0. (9)
Это—диференциальное уравнение линий кривизны. Это уравнение —
второй степени относительно отношения du: dv, следовательно через ка-

66
ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА
ждую точку проходят две линии кривизны. Они всегда действительны,
подобно тому как всегда действительны главные направления кривой 2-го
порядка.
Исключая диференциалы du и dv, получим:
(E+RD) (G + RD") — (F+ /?D')2 = О,
или
R\DD" — D'2) + R(ED"-j- GD — 2FD') -f EG — F2 = 0. (10)
Это уравнение определяет главные радиусы кривизны Rt и /?2. По
свойству коэфициентов квадратного уравнения отсюда следует:
K = Rfi2~ EG — F ' (П)
^ 1,1 2FD' - ED" - GD .
RX^R2~ EG-F* * l1^
К—называется полной кривизной поверхности (иногда гауссовой
кривизной или просто кривизной поверхности), Н—средней кривизной ее
(ср. гл. II, § 7, стр. 43).
II. Трехгранник Дарбу.
6. Трехгранник Дарбу. Оси координат тх и т2 вообще не
ортогональны. Это значительно осложняет выкладки. Поэтому для
построения своего трехгранника Дарбу взял в касательной плоскости две
произвольно расположенные взаимно перпендикулярные оси.
Обозначим единичные векторы по этим осям буквами ех и е2 и
допустим, что координатные линии и и v образуют с первой осью ех углы
аир.
Очевидно,
ji — а= аз
есть угол между координатными линиями.
Произвольное движение любого прямого трехгранника T(ev е2, ez)
с единичными векторами осей ег, е2 и еъ разлагается на поступательное
движение (перемещение его вершины М) и вращение.
Бесконечно малое перемещение вершины вектора dM удобно задать
компонентами по осям трехгранника
dM = (£du-{- lidv) eY -J- (tj du -f- -i\xdv) e2 -j- (Zdu -\~ r^dv) e3. (A)
Обозначим бесконечно малый поворот трехгранника при этом
перемещении вершины буквой П. Это есть вектор, который откладывается
на оси вращения. Мы его задаем тоже его компонентами по осям ех,
[l = (pdu-\~p1dv)ei -\-(q du-{-qldv)e2-\-(rdu-\-r1dv)ez. (13)
С помощью этих формул можно вычислить перемещение любой точки Р,
связанной с трехгранником. Если обозначить буквами [ау Ь, с]
координаты точки Р относительно трехгранника Г, то перемещение точки Р
будет складываться: 1) из перемещения, точки Р относительно трех-

ТРЕХГРАННИК ДАРБУ 67
гранника; это — вектор с компонентами [da, db, dc], 2) перемещения,
вызываемого поступательным движением трехгранника; это — вектор dM
и 3) перемещения в силу вращения трёхгранника. Это перемещение
перпендикулярно к оси вращения П и по величине равно произведению
угловой скорости вращения на расстояние точки Р от оси вращения.
Его можно дать как векторное произведение скорости вращения П и
вектора МР=[а, Ь, с]. _
Соединяя все три слагающие dP, получим:
dP=[da, db, *с] + ЛИ + ПХ[я> b, с)
или в развернутой форме:
dP = e\da -j-i£du-\- £iflto + (q du -\-q\dv) с — (rdu -\- rxdv) b] -f-
-\- e2[db -f- t\du -f- ^dv + (r du -\- rxdv) a —(p du JfPidv) c] -j-
-j- ez[dc -f- С du -J- Zidv -f- (p du-\-pxdv) b — (q du -\- q^dv) a].
Трехгранник {eu e2t n) мы будем называть трехгранником Дарбу.
Движение трехгранника Дарбу, когда его вершина М описывает
поверхность, можно разложить на поступательное движение вершины
трехгранника и вращение его.
Разложим перемещение вершины dM, которое, конечно, лежит в
касательной плоскости, по осям трехгранника ех и е2:
dM— (idu-f-\xdv) ех -f (r\du-f i\xdv) e2. (A')
Соответствующее бесконечно малое вращение мы обозначим вектором
U = (pdu-{~p1dv)e1 -\-(qdu-\-qxdv)e2 -\-(rdu-\- r^vjn, (13)
так что перемещение какой-нибудь точки Р с координатами [я, Ь, с]
по осям трехгранника Дарбу равно вектору1)
dP = [da, db, dc] + dM -f fi X [a. b, с] (B)
или, развертывая:
dP = et[da -j- 6 du -f- \xdv -(- (q du-j- qxdv) c — {rdu~\- rxdv) b] -f-
-f- e2[db-\-t\du-{-t\xdv-J-(rdu-f-гх^)a — (pdu-\-pxdv)c] -f-
-f- л [dc -}-(/* dw-f- /^flfo) ft — (qdu-\-qxdv) a).
Если построить в начале координат трехгранник, параллельный
трехграннику Дарбу, то перемещение его вершины, конечно, будет равно нулю,
а вращение останется то же самое. Следовательно перемещение точки Р,
связанной с этим трехгранником, будет определяться формулой
dP = [da% db, Ж?] + П X [л, *, с]. (В')
!) Квадратными скобками, мы обозначаем компоненты вектора по осям
еъ е2 и п:
[ia, db, dc] = etda -\~ e2 db + n dc.

68
ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА
В частности, если точку Р брать на осях ev е2, п на расстоянии
единицы от вершины, то получим:
^ = ПХ^ = (г du -f- rxdv) е2 — (qdu-\- q\dv) я,
Л2 = ПХ^ = (Р du -f-/?i dv) n — (rdu-\-rldv)eu (C)
dn=UXn=:(qdu-\-q\dv) e{ — (pdu-f-pxdv)e2.
7. Кинематическое значение квадратичных форм Гаусса. Четыре
компонента скорости поступательного движения [два при изменении
параметра и (£, т]) и два при изменении v'(tu r\i)] и шесть компонентов
скорости вращения [три для изменения и (р, q, г) и три для изменения
v (Ри qu ri)] определяют все элементы поверхности. Таким образом
линейный элемент поверхности немедленно получается, как скаляр
бесконечно малого перемещения вершины dMy возведением в квадрат
формулы (А):
ds* = d№ = (£</« + \xdv)* -f (r\ du+'nidv)*, (14)
откуда
E = 5* + ^. ^ = & + Ч%. 0 = l\+-n\, EG-F2 = a-ni-^rly.(l4')
Обратно, компоненты скорости поступательного движения £, тг), очевидно,
являются проекциями на оси ег и е2 вектора скорости вершины М при
изменении одного и. Помня, что касательная к линии и образует
с осью ех угол а, а касательная к линии v образует, угол fi, мы из
уравнений
Ми — 1ех -j- 'f\e2, Mv = \хех + Ъ^2
сейчас же получим:
£ = yTrcosa, 4 = Vr£sine> 5i=KrOcospl тц = /G sin p. (14")
Вторая квадратичная форма Гаусса
n(PM=Ddu* + 2D'dudv-\--iydv* (12)
есть проекция на нормаль п перемещения конца бесконечно малого зек-
тора касательной сРМ.
Так как нормаль п перпендикулярна к касательной dM, то
п dM = О,
и, диференцируя, мы получим:
hd*M = — dhdM.
Следовательно, перемножая по формулам (А) и (С),
п d2M=(pdu -\~Pidv) (у\ du -\-f\idv) — (qdu -f- qxdv) (£ du -f-\xdv). (15)
Совершенно таким же образом, если мы будем диференцировать
очевидные тождества
п Ми = 0, п Mv = О,
получим:

СФЕРИЧЕСКОЕ ИЗОБРАЖЕНИЕ ПОВЕРХНОСТИ
69
п Мац = — ПиМц, п Muv = — nuMv = — nvМи, п Mvv = — nvMv,
а так как из формулы (С) следует
пи = Че\ —Ре2> п*> — Ч\е\ —Piez>
то в формулах (1)
0=РП — Я%9 & =Р-Ц\ — Я1\~Р\Ч\ — Я\1> iy=Prti — q&i- О5')
Конечно, отсюда сейчас же следует уравнение (15).
Обратно, уравнения (15') позволяют найти компоненты вращения
Л Ч) Ри 4i по заданным D, D', D\
8. Сферическое изображение поверхности. Если направление
кривой в данной точке определяется ее касательной, то за направление
поверхности можно принять направление касательной плоскости, или,
что то же самое, нормали к поверхности. Откладывая единичный вектор
касательной к кривой т от начала координат, мы получаем индикатрису
касательных, и сравнение ее дуги с дугой кривой приводит нас к понятию
кривизны кривой. Естественно, что для того, чтобы получить представление
об искривленности поверхности, надо строить из начала координат
единичный вектор нормали к поверхности я. Конец этого вектора точка- п
заполнит часть поверхности сферы радиуса единицы, ибо всякая точка п
находится на расстоянии единицы от начала координат 0. Каждой
точке М поверхности соответствует точка п сферы, каждой линии на
поверхности — линия на сфере и т. д. Таким образом Гаусс приходит
к понятию сферического изображения поверхности, которое играет
большую роль в его теории поверхности.
Линейный элемент сферы
ds'2 z=zedu*-\- 2fdu dv + g dv2 (16)
есть третья квадратичная форма Гаусса.
Перемещение точки п дано третьей из формул (С)
dn = {q du-\- qxdv) ex — (p du-{- p1du)e2. (C3)
Следовательно, возводя в квадрат, мы немедленно получим:
ds'2 — dn2 — (р du +ptdv)2 -f (q du + qxdv)2,
e=P2 + q\ f=ppi + qqu g = P*i+4\, *g-f2 = (Wi — Pi<l)2- (16')
Нетрудно заметить, что первая форма Гаусса ds2 зависит только от
компонентов поступательного движения £, тг], £1? т^, третья ds'2 — от
компонентов вращения р, q, ри qv Наконец, вторая квадратичная форма
Гаусса—dndM есть (с обратным знаком) скалярное произведение
векторов перемещений точки М на поверхности и точки п на сфере, т. е.
произведение перемещений на косинус угла между ними. Поэтому она
содержит и компоненты поступательного движения и компоненты
вращения.
Компоненты вращения около нормали к поверхности г и гх
(вращение в касательной плоскости) совсем не входят в эти формулы; мы

70
ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА
увидим, что они целиком выражаются через коэфициенты линейного
элемента поверхности.
9. Кривизна поверхности» Сферическое изображение поверхности
позволяет совершенно естественно притти к понятию кривизны
поверхности, о которой мы уже говорили в § 5.
Направление плоскости везде одно и то же, все перпендикуляры
плоскости параллельны. Кривая поверхность меняет свое направление,
ее нормаль поворачивается. Естественно принять угол поворота
нормали за меру искривления поверхности. Угол поворота касательной
к кривой — плоский угол и измеряется дугой окружности радиуса
единицы с центром в вершине угла (дуга окружности и соответствующий ей
центральный угол). Вектор я, проведенный из начала координат
параллельно нормалям к поверхности в точках какой-нибудь ее области Q,
заполнит телесный угол — конус с вершиной в начале. За меру его
можно принять площадь той части Q' сферы радиуса единицы с
центром в начале, которая высечена на ней этим конусом. Очевидно,
область Q' на сфере ест£ сферическое изображение области Q на
поверхности.
Следовательно площадь сферического*7 изображения области Q можно
принять за меру кривизны ее (полная кривизна области Q на
поверхности).
Отношение площади сферического изображения области к площади
самой поверхности Q есть средняя кривизна, а предел этого отношения,
когда область Q сжимается в точку, — кривизна поверхности в данной
точке (гауссова или полная кривизна поверхности).
Так как элемент площади поверхности dS^^EG— F'dudv и
соответствующий ему элемент площади сферического изображения dS' =
■=i'\/reg—t2 dudv, то, очевидно, гауссова кривизна поверхности
К= Ж = Уъ^Р_
Формулы (14) и (16) позволяют привести ее, к виду
К=+Р*1^™. (17)
Двойной знак выбирают таким образом, чтобы кривизна была
положительна, когда положительная сторона поверхности отображается на
положительную сторону сферы, т. е. когда нормали к поверхности п и
к сфере
N' = {q eY —ре2) X (?i*i — A^)=(Wi — Р\Я) п .
будут не только параллельны, но и одинаково направлены. Очевидно,
при Зтом условии надо выбрать знак плюс.
Можно еще иначе определить знак кривизны. Если мы будем
обходить элемент площади поверхности dS по контуру на положительной
стороне поверхности так, чтобы эта площадь оставалась влево
(положительное направление обхода), то в сферическом изображении мы
получим по южительный обход, если кривизна положительна (черт. 16), и

ЛИНИИ КРИВИЗНЫ 71
противоположный ему, отрицательный, если кривизна отрицательна
(черт. 17).
Так как по формулам (15')
DD9 — D^ = (pgl — plq) (fri —Si*]),
то, очевидно, формула (17) вполне совпадает с формулой (11).
Черт. 16. Положительная кривизна.
Черт. 17. Отрицательная кривизна.
III. Линии кривизны.
10. Линии кривизны. Монж в мемуаре „Application de Г Analyse
a la Geomelrie", который можно рассматривать как первый опыт теории
поверхности, приходит к линиям кривизны, поставив задачу: найти на
поверхности линию, вдоль которой нормали к поверхности образуют
развертывающуюся поверхность.
Пустьлиния, определяемая отношением диференциалов du: dv, обла-
дает этим свойством: нормали п вдоль этой линии касаются некоторой
кривой (Я)—ребра возврата развертывающейся поверхности, и пусть
точка С есть точка касания нормали в точке Мк ребру возврата, так что,
если отрезок нормали МС обозначить буквой — R х), то
MC = — nR
и
C—M — nR.
*) Мы выбираем знак минус, чтобы согласовать определение этого отрезка
с определением радиуса кривизны нормального сечения: положительный радиус
кривизны откладывается в направлении, противоположном п.

72 ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА
При движении точки М по кривой du:dv бесконечно малое
перемещение точки С направлено по нормали п. Следовательно
dC= dM—ndR — Rdn
не имеет компонентов в касательной плоскости, а так как перемещения
dM и dn точки М и точки п (конца вектора п) лежат в касательной
плоскости, то, очевидно, при движении по нашей кривой
dM — Rdn, (18)
или
Mudu-\- Mvdv — R (nadu -f- nvdv) = 0.
Умножая скалярно на. Mu и Mv и помня, что
Mu* = Et,MttMv=zF% MJ — G,
Мипи = — Д Munv = Mvna = — D', Mvnv = — £>",
мы сейчас же придем к уравнению (8) стр. 65, откуда и следует результат,
полученный Монжем: нормаль п образует развертывающуюся поверхность
вдоль линии кривизны. Отрезок нормали от поверхности (М) до точки С
касания ее с ребром возврата (С) есть главный радиус кривизны,
соответствующий этому главному направлению.
Две точки Сх и С2, где нормаль п касается ребра возврата той и
другой развертывающейся поверхности, называются центрами кривизны
поверхности. Центры кривизны С\ и С2 описывают две полости
поверхности центров, которые несут на себе ребра возврата
развертывающихся поверхностей нормалей. Следовательно все нормали к поверхности
(М) касаютад в точках Сх и С2 двух полостей поверхности центров. Если
кривизна К= -н~5-положительна, то точка М — эллиптическая, Rx и R2
одного знака и обе полости поверхности центров лежат по одну
сторону поверхности (М); если Л' отрицательна (точка гиперболическая),
то — по разную. При /С = 0 точка М — параболическая, /?1==оо, и
один из центров Сг лежит в бесконечности.
Формула (18) есть формула Olinde Rodrigues'a (Родрига). Она
показывает, что касательная к линии кривизны dM параллельна
касательной к ее сферическому изображению dn.
Подставляя сюда dM и dn из формул (А') и (С) стр. 67, мы получим:
£ du -f- ^dv — R (q du -\- qxdu) = О,
t\du-\-r\ldv + R(pdu-\-pldv) = Qy 00
откуда диференциальнбе уравнение линий кривизны в компонентах
поступательного и вращательного движения трехгранника Дарбу будет
(рdu + pxdv) (£ du -f l\dv) -\-{qdu + qtdv) (yj du + Ъ^) = °> (9)
уравнение для главных радиусов кривизны — *
WiPlx-P^ + HPil-ply+qSl-q^ + ^-^r^b 0°)
а полная и средняя кривизны поверхности —

КАЧЕНИЕ ТРЕХГРАННИКА ДАРБУ ПО ПОВЕРХНОСТИ ЦЕНТРОВ 73
Меридианы и параллели, как мы уже видели, служат линиями
кривизны на поверхности вращения, ибо нормали вдоль меридиана лежат
в одной плоскости (плоскости меридиана), а нормали к поверхности
вдоль параллели сходятся в одной точке оси вращения и следовательно
образуют конус.
Любая линия на сфере —
линия кривизны, ибо нормали сферы
всегда образуют конус с
вершиной в центре сферы.
Теорема. Нормаль к
поверхности центров параллельна
касательной к своей линии
кривизны.
В самом деле, две нормали к
поверхности в бесконечно близких
точках М и М2, лежащих на
второй линии кривизны, касаются
первой полости поверхности центров
в точке Q и С\ и пересекаются
(до бесконечно малых высших
порядков) во втором центре
кривизны С2. Плоскость CiC2Ci,
очевидно, перпендикулярна к
касательной к первой линии кривизны ММХ
(ибо содержит нормаль МСХ и
касательную второй линии ММ2)
и касается поверхности центров
(т. е. перпендикулярна к нормали)
в точке Си ибо содержит две ее
касательных МСХ и QC/.
11. Качение трехгранника
Дарбу по поверхности центров.
Сложение поступательного и
вращательного движения
трехгранника Дарбу в каждый момент дает
бесконечно малое винтовое
движение. Дарбу поставил вопрос,
не может ли это движение для
некоторых направлений на
поверхности свестись к одному
вращению. Если это так, то существует прямая (ось вращения), которая
остается неподвижной. Перемещение любой точки Р определяется
формулой (В) стр. 67. Полагая здесь da = db-=dc-=. О, так как ось неразрывно
связана с трехгранником, получим условие для координат точки Р [а, Ь, с],
лежащей на оси вращения:
Черт. 18.
АИ-f ЙХМ° = 0
или, разбивая на компоненты,

74
ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА
Zdu-\- Zidv -\-(qdu \- qxdv) c — {rdu-\- rxdv) b = 0, ]
ridu-\-f\xdv-\-(rdu-\-rldv)a— (p du-\-pxdv)c = 0, > (b)
(pdu-^-pi dv)b — (q du \-qidv)a = Q. j
Если эти уравнения умножить соответственно на
(pdu-{-pxdv)t (qdu-\-qrfv), (rdu-\-rxdv)
и сложить, то я, b, с исключатся, и мы подучим уравнение (9) для
отношения du: dv, которое следовательно определяет направление
движения по поверхности. Отсюда: при движении точки М по линии
кривизны — и только в этом случае — движение трехгранника Дарбу в
каждый момент сводится к одному вращению.
Для каждого из этих направлений duidv одно из уравнений (Ь)
есть следствие остальных двух, и система (Ь) определяет в текущих
координатах [а, Ь, с] относительно трехгранника Дарбу неподвижную
прямую— ось вращения.
Полагая а = Ь — 0, найдем ее пересечение с нормалью. Ввиду
полного совпадения с системой (а) имеем:
с — — R.
Значит, мгновенная ось вращения пересекает нормаль в центре кривизны.
Последнее из уравнений (Ь) показывает, что ось вращения лежит в
плоскости, перпендикулярной к касательной dM к соответствующей линии
кривизны (что, впрочем, очевидно, так как траектории всех точек
твердого тела перпендикулярны к оси вращения, а нормаль к поверхности
центров параллельна к этой касательной).
Таким образом мгновенная ось вращения перпендикулярна к нормали
поверхности центров и лежит в касательной плоскости ее: следовательно
неподвижная аксоида (геометрическое место осей в пространстве) есть
линейчатая поверхность, описанная около первой полости поверхности центров
вдоль линии, которая соответствует первой линии кривизны. Подвижная
аксоида (геометрическое место мгновенных осей вращения в движущемся
теле), очевидно, — плоскость, нормальная к первой линии кривизны, ибо
все оси пересекают нормаль к поверхности и „ перпендикулярны
к касательной. При движении точки М по линии кривизны трехгранник
Дарбу вращается таким образом, что нормальная к линии кривизны
плоскость катится по неподвижной аксоиде.
IV. Сопряженные линии.
12. Сопряженные направления. Если около поверхности (Ж) описана
развертывающаяся поверхность D, то касательная \х к линии прикосновения
L и образующая развертывающейся поверхности t2 сопряжены на
поверхности.
Пусть отношение диференциалов du: dv определяет касательную tt
к кривой L на поверхности. Семейство плоскостей, касающихся
поверхности в точках линии L, имеет огибающей развертывающуюся
поверхность D. Характеристика касательной плоскости лежит на поверхности D,

СОПРЯЖЕННЫЕ НАПРАВЛЕНИЯ
75
а следовательно всякая точка этой характеристики описывает при
движении плоскости кривую, касательная которой лежит в этой плоскости.
Иными словами, мы найдем характеристику как место точек, бесконечно
малое перемещение которых лежит в касательной плоскости.
Пусть *) Р[а, Ь, 0] какая-нибудь точка характеристики. Ее
перемещение по формуле (В) стр. 67
dP = dM + II X (ае{ + be2).
Выписывая компонент по нормали, который должен быть равен нулю,
получим:
(р du -)- Pidv) b — (qdu-\- qxdv) a = 0. (a)
Это — уравнение характеристики в координатах относительно
трехгранника Дарбу.
Если мы обозначим через Ьи: bv отношение диференциалов, которое
соответствует направлению прямой (а), то компоненты бесконечно малого
перемещения точки (М) вдоль этой линии, очевидно, пропорциональны
координатам а: Ь, т. е.
а: b = {I Ьи -f £xbv) : (t| Ьи + г\№).
Подставляя это отношение в формулу (а), получим уравнение,
связывающее два сопряженных направления:
(pdu + p^v) (ulu + nity — iqdu + qidv) ^bu + ^bv) = 0 « (19)
или
(РЪ — <?0 du Ьи -f (р^у — q&) dv bv -f (ру\х — q%x) du bv -f
+ (Prt-4il)*"dv = 0 (19')
или в силу (15') стр. 69
Dduiu-\-D,(dubv + dvbu)-\-D'dvbv = 0. (19")
Так как это уравнение симметрично относительно диференциалов du: dv
и Ьи: bv, то сопряженные направления взаимны: если итти по
поверхности в направлении bu:bvt то характеристикой касательных плоскостей
будет касательная du: dv.
Если координатные линии сопряжены, то уравнение (19)
удовлетворяется диференциалами du=?0, 8z/ = 0. Внося туда эти значения, полу*
чим условие сопряженности
D' = 0. (20)
Мы видим, что оно совпадает с условием сопряженности двух
направлений относительно индикатрисы Дюпена (см. § 3).
Так как
д' = q du -f- qxdv, b' = — (p du -f- ptdv)
компоненты перемещения в сферическом изображении первой линии
du: dv, то условие (а) можно записать в форме
aa'-\-bb'—0y
г) В квадратных скобках Р \а, bt 0] — координаты точки Я относительно,
трехгранника Дарбу.

76
ВТОРАЯ КЭАДРАТИЧНАЯ ФОРМА
откуда следует, что каждое направление перпендикулярно к
сферическому изображению своего сопряженного.
Линии кривизны можно определить как линии, везде
перпендикулярные к своим сопряженным. Сферическое изображение линии кривизны
параллельно ей, так как оно перпендикулярно ко второй линии кривизны.
Поэтому, например, параллели и меридианы сопряжены на поверхности
вращения; и действительно, касательные к меридианам вдоль одной
параллели образуют конус с вершиной на оси вращения, а касательные
к параллелям вдоль одного меридиана — цилиндр, описанный около
поверхности вдоль этого меридиана: то и другое — развертывающиеся
поверхности.
Это построение можно обобщить (теорема Кенигса):
Сечения любой поверхности S пучком плоскостей с осью I
сопряжены линиям прикосновения конусов с вершинами на прямой /.
Действительно, образующие конуса, очевидно, служат касательными
этих плоских сечений; следовательно касательные к плоским сечениям
пучка / вдоль какой-нибудь линии прикосновения образуют
развертывающуюся поверхность (конус).
13. Поверхность, отнесенная к сопряженной системе.
Условие (20), показывающее, что поверхность отнесена к сопряженной
системе, очень просто пишется в декартовых координатах (х, у, z) точки М
поверхности.
Действительно, по определению коэфициента D' (см. формулу (1)]
оно равносильно уравнению
(MnMvMuv)^0t (20')
т. е. оно требует, чтобы три вектора Ми, Mv и Muv лежали в одной
плоскости. В таком случае один из векторов линейно выражается через
два остальных. Значит,
Muv — AMu-\-BMv, (21)
где А и В — скаляры, но вообще — функции от и и v.
Разбивая уравнение (21) на три уравнения для трех координат
вектора М = {ху у, z}, видим, что все три декартовы координаты
точки М поверхности, отнесенной к сопряженной системе, являются
решением одного и того же диференциального уравнения в частных
производных 2-го порядка
dudv du*dv' ^ '
Это уравнение носит название уравнения Лапласа.
Обратно, любые три решения уравнения вида (21') определяют по-
верхностЬ) откесенную к сопряженной системе линий (и, v), ибо
составляют вектор М, который удовлетворяет условию (21), а отсюда прямо
вытекает (20).
Пример. Общее решение уравнения
ди dv

АСИМПТОТИЧЕСКИЕ ЛИНИИ
if
есть сумма двух произвольных функций одного переменного и и одного
переменного vt Следовательно, каковы бы ни были функции фДи) и фДи),
поверхность
отнесена к сопряженной системе линий (и, v).
Эту поверхность, очевидно, можно получить, если линию
х = ?i («)i У = Ъ (")» z = ?з (и) (а)
переносить, не поворачивая, так, чтобы каждая точка описывала кривую,
равную кривой
* = <К (v), У = Ь (*)> z = ф3 (v). (Ь)
Отсюда название — поверхность переноса.
V. Асимптотические линии.
14. Асимптотические линии. Асимптотической линией на
поверхности называется линия, нормальная кривизна которой равна нулю.
По формуле (3) стр. 61 мы немедленно получаем для асимптотических
линий диференциальное уравнение
D du* -f 2D' da dv -f D" dv* = 0. (22)
По смыслу построения индикатриссы Дюпена (полудиаметр, т. е.
расстояние точки индикатрисы от ее центра, равен корню квадратному
из кривизны нормального сечения поверхности, проходящего через этот
диаметр) очевидно, что направления асимптотических линий
совпадают с направлениями бесконечно больших полудиаметров
индикатрисы, т. е. с асимптотическими направлениями индикатрисы.
Из определения асимптотической линии следует, что всякий раз,
как прямая лежит на поверхности, она является
асимптотической линией на поверхности, ибо ее кривизна равна нулю, а
следовательно и кривизна нормального сечения тоже нуль.
Если асимптотическая линия на поверхности не прямая, то ее сопри*
касающаяся плоскость совпадает с касательной плоскостью поверхности.
Это непосредственно следует из теоремы Meusnier (4) стр. 61: кривизна
нормального сечения -^ равна:
1 . cosy
R~± р ;
если кривизна кривой— не. нуль, то равен нулю cos<p, т. е. ср (угол
соприкасающейся плоскости и нормали к поверхности) равен у.
Так как характеристикой соприкасающейся плоскости является
касательная к кривой, то следовательно семейство плоскостей, касающихся
поверхности вдоль асимтотической линии, имеет огибающей
развертывающуюся поверхность, образованную касательными к этой
асимптотической линии.

78
ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА
Отсюда вытекает, что асимптотические линии сами себе сопряжены,
что, впрочем, вполне согласуется со свойством асимптотических
направлений кривой 2-го порядка. Полагая в условии (19') или (19") стр. 75
сопряженности двух направлений du:dv и buiov на поверхности 8w:Sz/ =
= du: dv, мы немедленно получим уравнение (22) для асимптотических
линий или в компонентах вращения равносильное ему уравнение:
(РЧ — ql) du2 + (РЪ — Ri+Prt — <j£) du dv -f
Можно и непосредственно доказать, что характеристиками касательных
плоскостей на поверхности вдоль асимптотических линий служат ее
касательные. Требуя, чтобы перемещение какой-нибудь точки Р
касательной плоскости лежало в плоскости (условие на характеристику), мы
немедленно придем по формуле (В) стр. 67 к уравнению
(р du +ptdv) b—{qdu-\- q{dv) a —0, (23)
где (a, by 0) — координаты точки P относительно трехгранника Дарбу
и duidv — направление асимптотической линии. Так как теперь точка Р
лежит на касательной к той же самой кривой и ее координаты (а, Ь)
пропорциональны компонентам перемещения точки М
a:b — (£du-\-lxdv) : (т)du-f ^dv),
то уравнение (23) совпадает с уравнением асимптотических (22).
Если вспомнить, что отношение
(q du -f- q\dv) : — (p du -{-pidv) — a' \b'
определяет касательную к сферическому изображению линию du: dv, то
из уравнения (23)
ЪЬ% + аа' = О
немедленно вытекает: асимптотическая линия всюду ортогональна
к своем)! сферическому изображению.
Это предложение, конечно, является предельным случаем общей
теоремы о сферическом изображении сопряженных направлений: каждое
направление на поверхности перпендикулярно к сферическому
изображению своего сопряженного — асимптотическое направление совпадает
со своим сопряженным, поэтому его сферическое изображение
перпендикулярно к нему самому.
15. Асимптотические касательные к поверхности.
Асимптотические линии наиболее глубоко и тесно связаны с поверхностью, ибо
определение их вытекает из наиболее простых и вместе с тем глубоких
свойств поверхности.
Рассмотрим линию пересечения поверхности с ее касательной
плоскостью. Такая линия, очевидно, действительна только в таких точках
поверхности, где поверхность лежит по разные стороны своей
касательной плоскости, т. е. в гиперболических точках ее.
Спроектируем вектор ММи соединяющий какую-нибудь точку
Mx=.M(u-\-du, v-\-dv) поверхности с ее точкой М(и,v), на нормаль
п в точке М. Если точка Мг лежит на линии пересечения поверхности

АСИМПТОТИЧЕСКИЕ КАСАТЕЛЬНЫЕ к ПОВЕРХНОСТИ 79
с ее касательной плоскостью в точке М, то проекция ММХ п равна
нулю. Следовательно уравнение линии пересечения
\ ММг = 0 или л (Л?! — М) = 0.
Разложив разность Мх—М в ряд по степеням dutdvf получим:
ndM + ^-nd2M-\- ~ nd*M+.. . = 0
или, так как ndM=Qt a nd2M по определению — вторая квадратичная
форма поверхности,
у (Ddu*^2D' dudv + D"dv2)+ ± (nMauudu* + ...) + ... = 0. (a)
Величины da, dv можно рассматривать как абсциссу и ординату
в той особой косоугольной *) системе координат в касательной
плоскости, осями которой служат касательные к координатным линиям с
единичными векторами
М„
М„
ч
Ve9 2~Vg
и различными масштабами 2) YE и Yo.
Мы видим, что линия (а) имеет в точке М (du = Q,dv = 0) особую
точку — двойную, и направление двух касательных в этой точке
определяется уравнением
D du1 + 2D' da dv-}-D"dv2 = 0. (22)
Если точка поверхности — эллиптическая (DD" — D'2 > 0), то
касательные мнимы; точка М — изолированная точка кривой (а). Если —
гиперболическая (DD" — D'2 < 0), то
касательные действительны и совпадают с
асимптотическими направлениями на поверхности в
точке М. Если точка М на поверхности —
параболическая точка {DD,f —D'2 = 0), то
для кривой (а) это — точка возврата,
касательные совпадают с единственным
асимптотическим направлением в этой точке, или точка
самоприкосновения (черт. 19).
Итак, асимптотическое направление —
направление двух касательных в двойной то<ке
линии пересечения поверхности с ее
касательной плоскостью.
Можно, накЪнец, определить
асимптотические касательные как прямые, имеющие
с поверхностью касание 2-го порядка. Это прямо следует из того,
Черт. 19.
*) Если угодно сохранить прямоугольную систему координат, то надо только
допустить, что система координат на поверхности (и, v) изотермическая.
2) Перемещение в касательной плоскости
dM = Mudu + Mvdv — ^ YEdu + i2YO dv
имеет компонентами Y&du и YOdv.

80
ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА
что нормальное сечение поверхности по асимптотическому
направлению имеет кривизну, равную нулю, следовательно рассматриваемая точка
поверхности является для него точкой возврата, а касательная в точке
возврата имеет с кривой касание 2-го порядка. Это же вытекает
из формулы (а) этого параграфа: расстояние точки поверхности
Мх=.М{и-\-(1и, v-\-dv) от ее касательной плоскости в точке М есть
проекция на нормаль п хорды ММи т. е. скалярное произведение пММх,
и левая часть уравнения (а) дает разложение этого скалярного
произведения по степеням du, dv. Мы видим, что это расстояние вообще
бесконечно малое 2-го порядка по отношению к du, dv (а следовательно
и к ds)y но для асимптотических направлений (22) оно становится
бесконечно малым 3-го порядка.
Таким образом асимптотические касательные занимают такое же
положение по отношению к поверхности, как соприкасающаяся плоскость
по отношению к кривой.
16. Поверхность, отнесенная к асимптотическим линиям. В точках
с отрицательной кривизной {DD" — D'2 < 0) асимптотические линии
можно принять за координатные линии («, v). Диференциальное
уравнение асимптртических линий (22) удовлетворится тогда решениями
и —. const, v = const, т. е. du =0, dv = 0, откуда следует:
D = 0, D" = 0,
Если воспользоваться формулами (1) стр. 60, то эти условия примут вид
(MuMvMuu)==:0, (MuMvMvv) = 0. (а)
Векторы Мт и Mvv лежат в плоскости векторов Мт Mv (в касательной
плоскости поверхности), а потому линейно выражаются через эти векторы
Мии= АМа-{- BMV,
Mvv = AxMa-\rBlMv. (24)
Следовательно координаты точки М (х, у, z) поверхности (координаты
вектора М) суть три решения системы уравнений
еяв=дев+яо„, е^ = л1еи + ^19^ (24')
Величины А, В, Aiy Вх — скалярные функции от и и v. Они не могут
быть взяты произвольными: чтобы система (24') имела три линейно
независимых решения х, у, z> необходимо выполнение условий
интегрируете
мости системы (значения ^ ад а» вычисленные из первого и из второго
уравнения системы, должны совпадать), что наложат на функции А, В>
Ai9 Вх известное ограничение.
Пример. Если А = В = АХ = Вх = 0, то система (24')
Vuu == 0, 4vv == О
имеет общее решение
6 = auv -f- (to -f- yv -|- 8, a, 48, 7,8 = const.
Давая постоянным a, p, 7, 8 произвольные значения, получим три решения

ФОРМУЛЫ ЛЕЛЬёВРА
81
лг, у у г, причем при подходящем выборе начала координат все 8t. = 0.
Следовательно текущий радиус-вектор М равен
М = auv -f- ри -f- 7 z/,
где а= {elf а2, а3}, ^ = {pi, Р2э Рз}, Y = {Yi> Т2» Гз}~ тРи произвольных
вектора. Принимая их за оси координат, получим:
где a, р, 7 теперь скаляры одноименных векторов, и следовательно
Это — уравнение гиперболического параболоида в косоугольной системе
координат.
17. Формулы Лельёвра. Гораздо удобнее определять поверхность,
отнесенную к асимптотическим линиям, формулами, которые предложил
Лельёвр.
Так как касательные к асимптотическим линиям перпендикулярны
к своим сферическим изображениям и, конечно, перпендикулярны к
нормали поверхности, то, пользуясь свойствами векторного произведения
быть перпендикулярным к обоим множителям, мы представим их в виде
Ми=\(пХпи), Mv = \>>(hX*v), (а)
где X и |х — множители пропорциональности.
Подсчитывая из обоих равенств (а) вторую производную Muv и
сравнивая результаты, получим:
\v(nXnu) + ^(nv Хпи)+1 (пXnUv) — Ри(п X л») +
+ КлйХ^) + КлХ /*«*)- (Ь)
Умножая скалярно на нормаль я, мы заметим, что пропадут в силу
перпендикулярности все те члены, которые содержат векторные
произведения с одним из множителей п и останется
\tl (nv Хпа)=^П (Пи X П„) .
Откуда ввиду изменения знака у векторного произведения от
перестановки множителей
jx = — X.
.Следовательно
Ма = \(пХп„)$ Лр = -МйХ4 '(26)
Так как для всякой функции р
(рп)ц — рап-\-рпи
и следовательно
рпХ(?п)и =р2 (пХ"и)>
то, полагая
Й^пУГ, (26)

82
ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА
мы напишем ^ ^
MU = (NXNU), Mv = -(NXUv)- (25')
Условия совместности мы получим в виде уравнения (Ь), если там
заменим п на N и одновременно положим X = — jx == 1
(NXUuv) = 0.
Так как векторное произведение равно нулю только при параллельности
векторов, то вектор Nuv параллелен вектору N и следовательно
отличается от него только скалярным множителем
NttV = QNy
где Q — произвольная скалярная функция переменных и и #.
Итак, три координаты вектора N удовлетворяют одному и тому же
уравнению Лапласа
ew = Q0. (27)
Обратно, выбирая три решения 6Ь б2, 63 произвольного уравнения
вида (27), мы получим по формулам (25'), полагая N = {bu б2, 63},
поверхность М> отнесенную к асимптотическим линиям.
Пример. Полагая Q=0, имеем:
6^ = 0, 0 = <р(в) + <К<0.
где l) U есть произвольная функция одного и и V есть произвольная
функция одного V,
MU = (U+V)XU, mv = -(u+v)xv'-
Интегрируя, получим:
M=VXU+Ut+V1%
где _____ _ _
и^ихи*, Vi' = —VXV\
Возвращаясь к общему случаю, вносим в формулы (25) значения
пи = qex — ре2 nv = q1e1 — р е^
мы получим, разбивая векторные равенства на равенства компонентов,
I — Ьр> Ч = Ц, £i = — iPu Щ = — ty_. (28)
Следовательно кривизна поверхности равна
K-PfrzjM^-i (29)
Srii —5,1) Хз v >

ПРОЕКТИВНОЕ ПРЕОБРАЗОВАНИЕ ПРОСТРАНСТВА
83
Таким образом в формулах Лельёвра кривизна поверхности (М) равна
обратной величине четвертой степени скаляра вектора N, взятой
с обратным знаком.
18. Теорема Эннепера. Из формул (28) следует простая
зависимость между линейным элементом поверхности, отнесенной к
асимптотическим линиям, ds2 и линейным элементом ее сферического изображения ds'2
ds'2 = edu2-\- 2fdudv + gdv*> ds* = I*(edu* — 2fdudv + g dv*). (30)
Совместим первую ось трехгранника Дарбу с касательной к первой
асимптотической линии и. Так как бинормаль асимптотической линии
совпадает с нормалью к поверхности (или прямо противоположна ей),
то трехгранник Дарбу будет служить для асимптотической линии, и
трехгранником Френе (или будет повернут на 180° около первой оси).
Так как кручение кривой равно с обратным знаком отношению
компонента вращения около касательной Р к скорости* поступательного
движения^, то кручение первой асимптотической будет:
!—_£—_!
Pi — 6 - * '
Так же найдем кручение второй асимптотической
J__J_
Pl' - х •
Отсюда теорема Эннепера: кручения двух асимптотических линий в
любой точке поверхности равны и противоположны по знаку, и их
произведение равно кривизне поверхности.
VI. Добавление.
19. Проективное преобразование пространства переводит каждую
точку его М в другую точку М' так, что бесконечно близкие точки
остаются бесконечно близкими, и точки, лежащие в одной плоскости
переходят в точки, лежащие в какой-нибудь другой плоскости.
Следовательно плоскости переходят в плоскости, прямые — в прямые,
и точки пересечения их — в точки пересечения. Очевидно, поверхность
F переходит в поверхность F'} семейство касательных плоскостей вдоль
ее линци l перейдет тоже в семейство касательных плоскостей вдоль
некоторой линии Z/, и характеристики первого семейства будут
соответствовать характеристикам второго семейства.
Отсюда следует, что сопряженные направления на поверхности
переходят в сопряженные и асимптотические—в асимптотические.
Сопряженная система линий и асимптотические линии сохраняв
ются в проективном преобразовании пространства.
Если точкам пространства соответствуют в преобразованном
пространстве плоскости так, что бесконечно близкие точки соответствуют бесконечно
близким плоскостям и точкам одной плоскости соответствуют плоскости,
проходящие через одну точку, то преобразование называется корреляцией.
Поверхность F как место точек переходит в поверхность F' как
огибающую касательных плоскостей. Линия L на поверхности F и се-

84
ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА
мейство D касательных к поверхности плоскостей вдоль нее перейдут
в семейство оо1 касательных плоскостей D' к поверхности F1 и линию
их точек прикосновения V; касательная к L и характеристика семейства
D перейдут в характеристику П и касательную к V. Следовательно
сопряженные направления останутся сопряженными и асимптотические—
асимптотическими.
Коррелятивное преобразование сохраняет сопряженную систему
линий и асимптотические линии.
То и другое преобразование переводит линии кривизны в сопряженную
систему линий, но не ортогональную. Зато линии кривизны сохраняются
в преобразовании обратных радиусов-векторов. Этот результат мы
получ .м как простое следствие теоремы Лиувиля в последней главе.
Он является основой конформной геометрии поверхности (геометрии
инвариантной относительно группы инверсий), как аналогичная теорема
об асимптотических линиях — проективно-диференциальной геометрии.
20. Квадратичные формы поверхности. При выводе второй
квадратичной формы поверхности мы исходили из вопросов исследования кривой
на поверхности. Это несколько затемняет зависимость диференциальных
форм от основного уравнения поверхности, и самое введение их может
казаться случайным. Между тем это введение можно провести вполне
последовательно, подобно тому как это было сделано для кривой.
Первый диференциал от текущего радиуса-вектора
dM = Madu -J- Mvdv
определяет касательную плоскость поверхности, и линейный элемент
поверхности — первую квадратичную форму
ds2=dM2 = (Madu + Mvdv)2 = Edu2 + 2Fdudv-\-Gdv2.
Второй диференциал
d*M = Мии du2 -\-2Muv du dv -f Mvv dv2 -j- Mu d2u+Mv d2v
уже не укладывается в касательной плоскости. Его компонент в
касательной плоскости уже известен. Умножая d?M скалярно на dM, получим:
dM dm = i- d(dM2) = \d(E du2 -f 2F dudv + G dv2),
dMd2M = (Mudu-\-Mv dv) (Muadu2-\- 2MUV du dv+Mvv dv* +
+Mud*u+Mvd*v).
Откуда, сравнивая члены при одинаковых диференциалах, получим:
МиМии = -i- Еи, 2МиМии + MvMuu = -J Ev +^">
М Mvv -}- 2MvMav = у Gu -f- Fv , MVMVV = -j GVt
а так как
MuMav = у (м1 )v = -у Ev, MVMUV = у Gu,

УПРАЖНЕНИЯ
85
то проекция сРМ на любое направление в касательной плоскости ЬМ
ЬМ d2M = (М£и + Mvbv) (Мии du-\-2Mav du dv-\-Mvv dv2 -f
-\~Mad2u + MvcPv)
выражается через коэфициенты линейного элемента и их производные.
Слагаемая d2M, не лежащая в касательной плоскости, определяет
нормаль л (если бы она не была известна ранее N=MB*Mv)y а ее
скаляр — вторую квадратичную форму
hd*M = D du* -f 2D'du dv -f- D"dv\
Этим построение основных диференциальных форм закончено. Зная
проекции сРМ на три направления, мы разложим на компоненты все три
вторые производные
Миц = аМи -J- bMv -f- Dn,
Muv = ахМа -f bJVIv + Drn, (31)
Mvv = a2Ma -{-- b2Mv + D"n.
Умножая эти уравнения по очереди на Ми и на MVi получим:
aE + bF=±Eu, a^ + bf^^Ev, a2E + b2F = Fv-±Gu,
aF + bG = Fa-±Ev> alF + b1G=±Gu, a2F+b2G = ±Gv,
откуда все ap b( немедленно вычисляются.
Таким образом все; следующие производные от М будут выражены
только через Е, F, О, Dy D\ D\ Ими исчерпаны все независимые
инварианты поверхности.
Если бы мы имели дело с поверхностью в пространстве Е большого
числа измерений, то нам пришлось бы совершенно также выделять из
третьего диференциала d*M ту слагаемую, которая выходит из пространства,
определяемого векторами dM и (РМ и т. д., пока не исчерпаем всех
наравлений пространства Е.
Мы вернемся к формулам {31) в следующей главе.
Упражнения.
1. Показать, что все коэфициенты второй квадратичной формы плоскости
равны нулю и что это свойство характеризует плоскость.
2. Показать, что только у сферы коэфициенты второй квадратичной формы
пропорциональны коэфициентам линейного элемента. Геометрически это следует
из того, что в таком случае линии кривизны неопределенны, нормали к
поверхности вдоль любой линии образуют развертывающуюся поверхность и
следовательно все нормали попарно пересекаются. Для аналитического доказательства
надо воспользоваться уравнениями Кодацци (см. гл. IV).
3. Вычислить вторую квадратичную форму для поверхности вращения (стр. 43).
Исследовать, как ведут себя асимптотические линии в параболической точке.
4. Показать, что из поверхностей вращения только у катеноида
асимптотические линии взаимно перпендикулярны.
5. Подсчитать вторую квадратичную форму линейчатой поверхности (стр. 46)

86
ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА
Показать, что одно семейство асимптотических линий совпадает с
прямолинейными образующими, а определение другого зависит от интегрирования
уравнения Рикатти.
Теорема Серре. Четыре асимптотические линии пересекают всякую
прямолинейную образующую в точках, составляющих одно и то же ангармоническое
отношение.
6. Исследовать изменение кривизны линейчатой поверхности вдоль одной
прямолинейной образующей.
7. Показать, что при наложении катеноида на геликоид асимптотические
линии переходят в.линии кривизны.
8. Показать, что в точках округления коэфициенты двух квадратичных форм
пропорциональны.
9. Показать, что точки округления эллипсоида
имеют координаты
д2(д2_^) g2(62_c2)
Х = Л2_С2 > У"*' *—#—ёГ-
у* Z*
10. Показать, что линии кривизны параболоида 1 = 4* лежат на софо-
а с
кусных параболоидах с произвольным параметром X:
У2 , **
а — X ' с—X
= 4(*-Х),
и исследовать их течение на поверхности.
11. Показать, что каждая полость поверхности центров псевдосферы
налагается на катеноид.
12. Теорема Бонне. Поверхность, параллельная поверхности постоянной
гауссовой кривизны — на расстоянии а от нее обладает постоянной средней кривизной.
13. Показать, что для поверхности
z = f{x,y)
линейный элемент
<fc2 = (1 -f/>2) dx* + Ipq dx dy + (1 -f q*) dy*
вторая квадратичная форма
rdx*+2sdxdy+tdy*
Vl+P + 4*
Средняя и полная кривизна
2pqs-(\+p*)t-(\ + q2)r rt-s>
(l+p2 + q2fl* > A (l+p2+(22)2
и уравнение линий кривизны
lV+P*)s-pqr]dx* + [(\+p*)t-(l + q*)r] dx dy + lpqt-(\+q*)$] dy* = 0,
где
df df _ d*f _ аз/ аз/
"""а*' *~~ay г~ а**' 5~алгаз>' '~ ау
14. Показать, что поверхность
лг = Л(и — а)т (v—a)n, у = В(и-Ь)т (v — b)nt z = C(u-c)m (v — c)n,
где Л, J5, С, л, 6, £, /ид л — постоянные, отнесена к сопряженной системе лицьй
(uf v). В частности для т = п
111

УПРАЖНЕНИЯ
87
тетраэдральные поверхности Дарбу, для т = п = 2 — поверхности Штейнера,для
т = п = — 1 —известная кубическая поверхность.
15. Показать, что в начале координат на поверхности
z = ах2 + 2Ьху + су2 + члены степени выше второй относительно х и у,
асимптотические направления суть:
ах7 + 1Ьху + су2 = 0.
16. Найти асимптотические линии на тетраэдральной поверхности.
17. Показать, что радиус кривизны асимптотической линии равен 2/П радиуса
кривиз «ы той ветви кривой пересечения поверхности ее касательной плоскостью,
которая имеет с асимптотической линией общую касательную.
18. Найти асимптотические линии на поверхности, полученной вращением
круга около своей касательной.
19. Если мы имеем одну эвольвенту Г и две ее эволюты Lx и L29 то
касательные к L\ и 12> исходящие из одной и той же точки Г (где они ее
пересекают нормально), образуют между собой постоянный угол, в какой бы точке
кривой Г их ни проводили. Иначе говоря: если все образующие
развертывающейся поверхности D в точках, где они пересекают свою ортогональную
траекторию Г, повернуть на постоянный угол в плоскостях, нормальных к Г, то
они образуют новую развертывающуюся поверхность D'.
Вывести отсюда теоремы:
Если две поверхности S и S' пересекаются вдоль линии /*, которая на обеих
поверхностях является л нией кривизны, то S и S' пересекаются под
постоянным углом во всех точках Г.
Обратно, если S и S' пересекаются под постоянным углом вдоль кривой Г
и она является линией кривизны на поверхности 5, то Г есть линия кривизны
и на поверхности Sf.
Если плоскость или сфера пересекают поверхность S вдоль линии Г под
постоянным углом, то Г есть линия кривизны на поверхности S.
Обратно, если Г есть плоская или сферическая линия кривизны поверхности5,
то плоскость или сфера, на которой л.жит Г, пересекают «S под постоянным
углом
Вывести отсюда линии кривизны,поверхности вращения.
20. Единственная поверхность, каждая точка которой есть точка округления,
есть сфера.
21. Если поверхность S пересечь плоскостью, параллельной касательной
плоскости и на бесконечно малом расстоянии от нее, то линия пересечения до
бесконечно малых 2-го порядка включительно совпадает с индикатрисой Дюпена
в этой точке.
22. Поверхность, все точки которой параболические (гауссова кривизна равна
нулю), есть развертывающаяся поверхность.
Отнести к линиям кри изны и показать, что вдоль той линии кривизны,
которая совпадает с асимптотической линией, поверхность имеет одну и ту же
касательную плоскость.
23. Прямая, делящая в постоянном отношении угол между нормалью к
поверхности и касательной к линии кривизны, описывает развертывающуюся
поверхность. Это свойство характеризует линии кривизны.
24. Показать, что четыре однородных координаты хь х2, х3, х4
произвольной точки М поверхности, отнесенной к сопряженной системе линий и, v
удовлетворяют одному уравнению Лапласа:
dudv du ' dv
и обратно, любые четыре решения такого уравнения могут служить однородными
координатами точки поверхности, отнесенной к сопр>женной системе.
25. Сопряженная система линий и, v, в параметрах которых два крайние
коэфициента второй квадратичной формы равны между собой (исключая, может
быть, знаки).
называется изотермически сопряженной.

88
ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА
мически
Координаты х, у, г произвольной точки поверхности, отнесенной к изотер-
гски сопряженной системе линий и, v, удовлетворяют системе уравнений
ди* ± dv2 ~~ а ди + * dv'
ди dv du*dv
и обратно, три линейно независимых решения (если они есть) такой системы
определяют поверхность, отнесенную к изотермически сопряженной системе.
26. Два пучка плоскостей, оси которых полярно сопряжены относительно
сферы, секут ее по двум семействам взаимно ортогональных кругов. Эти два
семейства образуют на сфере (наиболее общую) изотермически сопряженную
систему. Применяя проективное преобразование, показать, что на всякой
поверхности 2-го порядка два пучка плоскостей с осями, сопряженными относительно
этой поверхности, определяют изотермически сопряженную систему.
27. Система уравнений
би2 dv*~~ ' dudv~~
Определяет эллиптический параболоид, как поверхность переноса; линии
щ v образуют изотермически сопряженную систему.
28. Поверхности переноса и только они одни обладают сопряженной сетью
Чебышева (зад. 13, стр. 59).
29. Уравнение Лапласа
ди dv~~ ди ' dv *
определяющее поверхность, отнесенную к линиям кривизны, имеет решениями
не только координаты х, у, z произвольной точки поверхности, но и сумму их
квадратов х2-\-у2-\-z2. Это свойство характеризует линии кривизны.
Вывести отсюда, что линии кривизны сохраняются в преобразовании обрат*
ных радиусов-векторов.
30. Формулы Лельёвра обобщаются на изотермически сопряженную систему,
причем уравнение Мутара принимает вид
31. Единственная винтовая поверхность, у которой меридианы служат
линиями кривизны, есть псевдосферическая винтовая поверхность Дини. Она
образована винтовым движением трактрисы около своей асимптоты и налагается на
псевдосферу радиуса
где t — длина постоянной касательной трактрисы и /и — шаг винта. Одно
семейство линий кривизны состоит из этих трактрис, другое образовано
сферическими локсодромиями, расположенными на сферах радиуса t с центрами на оси.
32. Если одно семейство линий кривизны плоское и плоскости их образуют
пучок с осью dt то второе семейство линий кривизны сферическое; сферы их
с центрами на прямой d секут поверхность ортогонально. Все эти поверхности
(поверхности Иоахимсталя) могут быть получены, если взять произвольное
семейство оо1 сфер с центрами на прямой и провести оо1 траекторий
ортогональных к сферам. Геометрическое место этих траекторий есть искомая поверхность;
о лно семейство линий кривизны (плоское) образовано построенными траекториями,
другое (сферическое) состоит из линий пересечения поверхности со сферами.
33. Показать, что решением уравнения buv = О можно получить наиболее
общий прямой коноид—поверхность, образованную движением прямой, которая
все время пересекает направляющую (например, ось z) под прямым углом,

ГЛАВА ЧЕТВЕРТАЯ.
Основные уравнения теории поверхности.
I. Уравнения Гаусса-Кодацци.
1. Основные уравнения в форме Дарбу. Мы видели в первой
главе, что компоненты вращения трехгранника Френе риг могут быть
взяты произвольно. Каковы бы ни были функции
P=fi(s), r=f%(s)9
существует движение трехгранника Френе, определенное вплоть до
начального положения, в котором компонентами вращения являются
p-=zfx(s)t q — 0, r=/2(s); тем самым определена вплоть до перемещения
в пространстве кривая, описываемая его вершиной.
Не так дело обстоит в случае поверхности, когда трехгранник
движется с 2 степенями свободы. Компоненты поступательного и
вращательного движений трехгранника £, т), С, £ь V)b d, р, q, г, pu qu r±
попрежнему вполне определяют его движение (вплоть до «начального
положения), но уже их нельзя задать произвольными функциями от
параметров щ v. Они связаны 6 уравнениями, которые, естественно,
лежат в основе всей теории поверхности.
Вернемся к формулам § 6, гл. Шгстр. 66:
Ш = (£ du+lidv) ei+ (tj du + 4l<fo) ~e2 -f (C du -f Ci dv)eb% (A)
dei = (rdu-\- rxdv)e% — (q du -f- q\dv)ez,
dej — — (rdu-\- rxdv)ex + (p du -\-p{dv)ez, ™
dez = (qdu-{-q1dv)el—(pdu-\-p1dv)e29
которые можно сравнить с формулами Френе в теории пространственных
кривых. Каждое из них теперь — уравнение в полных диференциалах
и распадается на два уравнения в частных производных
Ми = lex -f т\е2 + Се3 Mv = \хех + 4i*2 + ^\еъ
дГл - дех
ЪЦ = ге*~qe*> dU = Г*е* ~ W*>
§ = -re1 + Pezt | = _Г1,1+^з,
.jg = ?*i — РЪ, fv = Ч\е\ —Р\Ч*
(А')
(С)
Сравним вторые смешанные производные Muv, ^вычисленные из левого
«из правого столбца. Диференцируя левое уравнение по V, правое

90
ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПОВЕРХНОСТИ
по а и заменяя производные от единичных векторов еи еъ еъ их
значениями из той же таблицы, мы получим уравнение между независимыми
векторами еъ е2> ег
(tv — Ъхи + гцх — W 4- ?1С — qQ ~ех -f (Чг— Ъи+^—Ьг+^р— (.рг)е2+
+\Zv — Z1u — Ziq + liq—py\i+Pi'n)e3 = 0t
которое, очевидно, не может существовать (ибо еи е2 и е3 не лежат в
одной плоскости). Следовательно все коэфициенты при *ь е2, ег равны
нулю.
Это дает нам первые три уравнения основной системы
К—Ьм = Vi — V+trf—^i>
Ч„ —4ie = ^i —^+ЛС — pClf (I)
С — С1И = /?% — /yt) + <7i5 — ^^i-
Три остальные нижние уравнения (С) дадут нам таким же образом еще
три уравнения
pv—Piu = qrt — qtrf
qv — qiu = rpi — r1p, (И)
r0 — rlB = pq1—p1q.
Связанный с поверхностью трехгранник Дарбу двигается так, что его
вершина М не покидает поверхности, а плоскость (еи е2) все время
служит касательной плоскостью ее. Таким образом перемещение
вершины dM всегда лежит в касательной плоскости, и компоненты по третьей
оси равны нулю
С = 0, d=0.
Система (И) при этом не изменится, а уравнения (I) примут вид:
$*—Si«=Vi —чл
%—Ъи = г£1—г& (У)
pt\i—Pi4\ = qli—qit
Уравнение (А) напишется теперь
dM = (£du 4- Zidv) е{ -f- (r^du -\- i\\dv) e2. (A")
2. Единственность поверхности с заданными инвариантами. При
выполнении условий (Г), (11)10 величин £, тг], %l9 -гц, р, q, г, ри qv гх
определяют движение трехгранника Дарбу и притом единственное, .если
задать начальное положение трехгранника для и = и0, v = vQ.
Действительно, диференцируя последовательно уравнения (С), мы
выразим производные любого порядка от еи еъ п линейно через эти
векторы и через производные от компонентов вращения р% q, г, ри qu гх\
при выполнении условий (II) мы здесь не встретим противоречий, т.е. будем
получать единственные значения для каждой производной. Зададимся
какой-нибудь начальной системой векторов
ег = ей е* = £з, п = п° Для и = и09 v — vQ*

ОПРЕДЕЛЕНИЕ КОНЕЧНЫХ УРАВНЕНИЙ ПОВЕРХНОСТИ 91
Мы будем знать тогда все производные от векторов еи е2у п и сможем
разложить их в рядТэйлора:
^=-+(i)0(«-"o)+(i)0(---o)+®U(«-«o)2+...
"="° + (1)0("-"о)+-
и эти разложения будут сходиться при достаточно малых \и— и0\,
\v — т/0|, как это доказывается в курсах интегрирования диференци-
альных уравнений.
В силу линейности основных уравнений (С) все производные -р
и т. д. будут тоже линейны и однородны относительно произвольных
—о -о -о
постоянных ей #2, п •
Следовательно решение (а) можно написать в виде:
~ ~о г . ^о , -о
е1 = ate\ ~f- о^е2 +- схп ,
е2 = a2e°i + Ь2е\ -f с2й°, (b)
п = azet -{- Ьъе2 + съп ,
где а., Ър с.— определенные функции от и, v.
Если начальные векторы е°и е°2, п° единичны и ортогональны, то и
функции (Ь) будут определять такую же систему векторов. Это
доказывается совершенно так же, как в случае трехгранника с одной
степенью свободы (см. гл.1, стр.22).
Подставим значения (Ь) в уравнение (А) и, интегрируя, получим
М = М0 + x?i+yel + zn\ (с)
где М0 — произвольный постоянный вектор и х> у, z — определенные
функции от и9 V.
Эти уравнения определяют поверхность, описываемую вершиной
трехгранника.
Мы видим, что произвольные векторы М0, еи е2, п°, которые входят
в формулу (с), зависят только от выбора начального положения вершин
трехгранника и направления его осей, т. е. по существу от выбора
системы координат.
Итак, 10 компонентов движения трехгранника Дарбу,
удовлетворяющие условиям (Г) и (II) определяют поверхность вплоть до ее по-
ложения в пространстве.
3. Определение конечных уравнений поверхности. Уравнения (Cf)
можно привести к двум уравнениям Рикатти. Рассмотрим, например,
уравнения левого столбца; каждая из трех координат наших единичных
векторов удовлетворяет системе

92
ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПОВЕРХНОСТИ
б1э 82, 63, очевидно, являются косинусами углов одной какой-нибудь
оси координат с нашими векторами ev е.2, п, т. е. координатами по осям
трехгранника Дарбу единичного вектора, отложенного на выбранной
неподвижной оси; следовательно
и мы можем рассматривать б1э 62, 03 как точку на единичной сфере.
Отнесем сферу к прямолинейным образующим (линиям нулевой
длины) a, (J
мы получим для аир одно и то же уравнение Рикатти:
Таким образом, чтобы найти конечное уравнение поверхности по
заданным компонентам движения трехгранника £, т] и т. д., надо помимо
квадратур проинтегрировать уравнение Рикатти. Хотя это уравнение
обладает многими замечательными свойствами, все же оно в квадратурах не
интегрируется, так что задачу определения поверхности по заданным
компонентам движения трехгранника Дарбу нельзя считать элементарной.
Тем более замечательно, что поверхность вполне ими определена, если
не говорить о ее расположении относительно выбранной системы
координат. Мы можем определить любые свойства поверхности, решить для
нее всякую задачу, не связанную с системой координат, и не отыскивая
конечных уравнений поверхности. Поэтому задачу определения
поверхности можно считать разрешенной, если удалось найти компоненты
движения трехгранника Дарбу (или, что то же, коэфициенты двух
квадратичных форм).
4. Определение трехгранника Дарбу по коэфициентам двух
квадратичных форм. Трехгранник Дарбу обладает значительным
произволом в выборе осей, и в этом он существенно разнится от
трехгранника Френе, который инвариантно связан с кривой. В сущности он
подчинен только одному условию, что его третья ось совпадает с
нормалью к поверхности1). Поэтому компоненты £, т), /?, q9 г и т. д.
определяют не только поверхность и выбранную на ней систему
координат и9 v, но и выбор того или другого трехгранника.
В этом отношении большим преимуществом по сравнению с ними
обладают 6 коэфициентов двух первых квадратичных форм
Е, F, G, D, D', D".
*) В качестве инвариантного трехгранника, связанного с поверхностью,
можно было бы дать название трехгранника Дарбу трехграннику, образованному
нормалью и касательными к линиям кривизны; но пользоваться ими удобно
только в том случае, если поверхность отнесена к линиям кривизны, а это нд«.
лагает большое стеснение в выборе параметров и> v.

УРАВНЕНИЯ КОДАЦЦИ
93
В § 7 гл. Ill мы уже вывели соотношения, связывающие эти гауссовы
коэфициенты с компонентами движения трехгранника, введенного Дарбу:
* = F + 4'f F=Ki + 44b о = Й+ ч?, (i)
D=pri — qZ, D' = pril—q^i=plri — qlEi D" =/Mi — ?i$i>
и обратно
5 = V^Bcosa, Yj = V^Esinaf ^ = KGcosp, ^ = |/o sin p,
SD^JiD -чР'-^Р _^~e^ _^-^Р' ,
P — д > ?— д » -Pi— д > ?i — J > I*)
p_a = a>> д_ fa_gl4 = ±-j/^o — Я = j/i&Osina>.
Три первые уравнения (1) разрешаются относительно 4 компонентов
поступательного движения £, -rj, £ь тг^ с помощью двух углов а и р,
которые образуют с первой осью касательные к линиям и и г/ и из
которых только один является произвольным параметром, определяющим
положение трехгранника, так как разность их, очевидно, равна углу
между координатными линиями со.
Три уравнения (1) второй строчки разрешаются относительно 4
компонентов вращения р, q, ри qx добавлением сюда еще третьего уравнения
из основной системы (Г) — единственного уравнения, содержащего все
компоненты в конечном виде (без производных).
Остаются два компонента вращения около третьей оси (нормали) г и ги
но они определяются первыми двумя уравнениями системы (I). Если
туда внести значения £, ц, £1э % из таблицы (2), то получим:
ар 1 / дУШ dVG \
ди j/Gsincol dv ди cosa)/»
да
Гх =
dv~yEsiTU
■№-^«-). да-
f . А
COS СО = ■■>—J. SinC0 = —===.
Таким образом задание 6 коэфициентов двух первых форм Гаусса
(и угла а между первой осью и линией и) равносильно заданию 10
компонентов движения трехгранника Дарбу. Поэтому две первые
квадратичные формы, так же как и. компоненты движения, определяют
поверхность вплоть до ее перемещения в пространстве.
б. Уравнения Кодацци. Внося величины (2), (3) в уравнения (Г),
мы естественно придем к тождеству, ибо они отсюда именно и были
получены.
Следовательно три уравнения системы (II) — единственные, которые
связывают коэфициенты двух квадратичных форм Гаусса.
Умножая первые из них на ?), вторые на \ или первые из них на y\i9
вторые на $г и вычитая, мы получим, пользуясь формулами (1), два ди-
ференциальных уравнения для D, D\ D", которые были получены
впервые Кодацци *).
*) С о d а г г i, Memoire relatif A Implication des surfaces les unes sur les autres
envoyё au concours ouvert sur cette question en 1859 par TAcademie des Sciences,

94
ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПОВЕРХНОСТИ
Было бы слишком сложно записывать их в коэфициентах двух
квадратичных форм, не внося никаких сокращений. Поэтому если
отказаться от пользования компонентами движения трехгранника, то надо
ввести другие обозначения. Эти обозначения были введены Кристоффелем
в задаче гораздо более общей: исследования пространства многих
измерений, где они получают свое полное значение;
Вернемся к формулам конца предыдущей главы (стр. 85). Разлагая вторые
производные радиуса-вектора М по трем направлениям МаУ Mv и я, мы
пришли к формулам (31). Обозначим координаты в этих разложениях
символами1) {w, где два верхних указателя / и у относятся ко второй
производной Muv, которая разлагается на компоненты; при этом дифе-
ренцированию по и приписывается значок 1, по v — значок 2.
Очевидно, два верхних указателя можно переставить, не меняя величины
символа Кристоффеля. Нижний значок относится к той производной Ми
или Mvy при которой в виде коэфициента стоит скобка Кристоффеля:
Muv={l?}Ma + {tyMv + D% (4)
Mvv = {»j Ми + {222} Mv + Drn.
Скобки Кристоффеля зависят от первых производных коэфициентов
линейного элемента и имеют вид:
дЕ , дЕ dF dG , да nr^dF
ди dv ди ioo\ dv ди dv
fill О* w °u {221
\lJ-~ 2(EG-F*) ' 12J-
2(EG-F*) ' l Л 2(EG-F*)
d£ JG dG JE
G- F— E—-F
/121 _ 0v vu r i2\ du ov
l1/~~Т{Ё(Г—П) ' l2J"~ 2(EG-F*) ' W
JE , ndF JE dG , dF ^dG
-.F—+2E — -E— -F —+ 2C — -0 —
(]\\__ du ди dv J22\__ ^v "v °u
\2J~~ 2 (EG — Z72) ' IW"" 2(EG — F>) "
Диференцируя вектор n
n =
Mn X Mv
Veg-f*
и пользуясь формулами (4), получим:
- _FD' -GD Гл j^FD-Eiy J/f
n"— EG — F*~ u ' EG — F* v%
- _FD'— GD' jj. л FD'-ED' ^
nv~ EG-F* ">" EG-F* mv ,
(6)
*) Скобки Кристоффеля второго рода.

Д£Е ЗАДАЧИ ИЗГИБАНИЯ
95
Уравнения (4) и (6), очевидно, заменяют собой таблицу диференциалов
(А"), (С). Естественно, что условие совместности систем (4) и (6)
приведет нас снова к уравнениям (II). Два уравнения Кодацци получат вид:
f4£+{>+(l?H1.V-r22)°'=<>-
Третье уравнение из этой системы основных уравнений было получено
еще Гауссом и составляет содержание его theorema egregium. Мы
немедленно получим его из третьего уравнения (II), воспользовавшись
выражением гауссовой кривизны (11), (17) гл. III и формулами (3)
/ dYG дУ"Е
РГУ-р'* 1
COS <t>
д3ш \ д I ди ди
[ди dv* дй у У В sin ш
~*\7Л" cos<"/(- w
\ YG sin а)
Шесть коэфициентов двух квадратичных форм Гаусса,
удовлетворяющие уравнениям (7) и (8), определяют поверхность и притом
единственную, если не обращать внимания на ее положение в пространстве.
И. Проблема изгибания поверхности.
6. Две задачи изгибания. Уравнения Кодацци были получены
в связи с проблемой изгибания поверхности, поставленной на конкурсе,
опубликованном Парижской академией наук в 1859 г.; и действительно,
уравнения (7), (8) получают новое значение в свете этой проблемы.
Две поверхности налагаются, если при подходящем выборе
криволинейных координат (и, v) линейные элементы их совпадают. В связи
с этим возникают два основных вопроса?
1. Даны две поверхности S и S'\ как узнать, налагаются они или
нет?
2. Дана поверхность S; найти все поверхности, на нее
налагающиеся.
Системы уравнений (7), (8) дают решение второй из этих проблем.
Мы даже формулируем ее несколько шире: найти все поверхности с
данным линейным элементом.
Мы видим, что эта задача устанавливает различие между 6 коэфициен-
тами Е, F, О, D, D', D\ Первые три считаются заданными — они
устанавливают линейный элемент, общий всем налагающимся поверхностям.
Коэфициенты второй квадратичной формы D, D\ D" определяют
индивидуально каждую из налагающихся поверхностей.
Итак, можно ли задать произвольно три функции Е, F, О и как
определить три другие D, D', D\ чтобы получить поверхность с
линейным элементом (а)
ds* = Edu* + 2Fdudv + Gdv2? (а)

96
ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПОВЕРХНОСТИ
Прежде всего заметим, что дискриминант формы
EG — F* = {MuXMvf
должен быть положителен и не обращаться в нуль (форма дефинитная)
но этим и ограничиваются все условия, накладываемые на задаваемый
линейный элемент. Для определения поверхности по заданному
линейному элементу, надо найти вторую квадратичную форму, т. е. три функции
D, D\ D", так, чтобы уравнения (7) и (8) были удовлетворены.
Так как три названные функции связаны тремя уравнениями, из
которых одно (Гаусса) — конечное, а два Кодацци диференциальные
в частных производных 1-го порядка, то в силу теоремы Коши задача
всегда возможна и общее решение зависит от двух произвольных функций
одного аргумента.
7. Теорема Гаусса. В Свете проблемы изгибания поверхности особое
значение получает последнее уравнение (8), конечное относительно
D, D\ D\
Мы видим, что в сущности шести функций для определения
поверхности слишком много: можно было бы оставить только пять, а шестую
определить из уравнения (8), подобно тому как мы при переходе от
компонентов Дарбу к коэфициентам Гаусса исключили компоненты
вращения гиг! формулами (3). Другими словами, хотя все три коэфи-
циента второй квадратичной формы и меняются (вообще говоря) при
изгибании поверхности, но их дискриминант остается неизменным. Этох
дискриминант и входит в формулу гауссовой кривизны поверхности.
Отсюда theorema egregium Гаусса:
Полная кривизна поверхности остается неизменной при изгибании
поверхности.
Этим самым гауссовой кривизне поверхности придано во всей теории
изгибания особо важное значение. Это — внутренняя кривизна
поверхности, характеризующая геометрию на поверхности; это — кривизна
линейного элемента поверхности. Интересно посмотреть с той же точки
зрения изгибания поверхности на 10 компонентов движения
трехгранника Дарбу.
Формулы (1), (2) показывают нам, что компоненты поступательного
движения £, т), 5ь Ъ и два компонента вращения г и гг зависят только
от коэфициентов линейного элемента и углов а и р, определяющих
положение трехгранника относительно координатных линий. Таким образом
скорость поступательного движения вершины М трехгранника (лежащая
в касательной плоскости, т. е. в данном двумерном многообразии) и
вращения трехгранника около нормали (т. е. опять в касательной
плоскости) при изгибании поверхности не меняется. Все эти элементы
определяют поверхность, так сказать, саму в себе вне ее отношения к
окружающему пространству.
Четыре компонента р, q, ри qif определяющие вращение трехгранника
около осей, лежащих в касательной плоскости, существенно зависят от
коэфициентов второй квадратичной формы и следовательно меняются
при изгибании.
Мы вернемся к проблеме геометрии на поверхности в следующей
главе.

ПЕРВАЯ ЗАДАЧА ИЗГИБАНИЯ
97
8. Первая задача изгибания. Тзорбма Гаусса о полной кривизне
поверхности открывает путь к решению первой задачи в теории
изгибания поверхности.
Даны две поверхности 5 (и, v) и Si (uif v{)\ определить, налагаются ли
они? Это значит — существует ли такое соответствие между параметрами
обеих поверхностей, т. е. такие две функции
чтобы длины соответствующих линий были равны, т. е. чтобы эти функции
обращали в тождество уравнения
ds2=ds\?
Вся трудность проблемы заключается в том, что обе поверхности могут
быть отнесены к совершенно различным системам координатных линий,
и вот здесь теорема Гаусса оказывает существенную помощь. Так как
при изгибании кривизна остается неизменной, то поверхности 5 и Sx
могут налагаться только теми точками, в которых кривизна обеих
поверхностей одна и та же.
Отнесем каждую из наших поверхностей к линиям, вдоль которых
кривизна,поверхности постоянна, и к их ортогональным траекториям
ds2 = Edu*-\-G dv*f ds\ — E^du\ -f G de\,
и пусть первые координаты и и щ — гауссовы кривизны той и другой
поверхности. Тогда соответствующие в наложении обеих поверхностей
точки определятся, очевидно, уравнениями
уравнение
Edu2-\-G dv* = Exdu2 -f Gi <p'* (v) dv2
в силу независимости диференциалов du и dv распадется на два
Е = Еи G=Gi9'2(v). (а)
1°. Если коэфициент Е содержит v, то и коэфициент £х должен
содержать vu и первое уравнение должно определять щ как функцию
одного v
*>1 = ¥ (*)•
Если эта функция удовлетворяет второму уравнению (при всяком и),
то поверхности налагаются, ибо линейные элементы совпадают.
2°. Если Е и Ег зависят только от и и тождественно равны (иначе
поверхности не наложимы), то обращаемся ко второму уравнению и берем
от обеих частей логарифмическую производную по и
d\nG_d\nGl
ди ди
Если это уравнение содержит vy стало быть и ^i, то оно так же, как
раньше первое уравнение (а), должно определить i>i как функцию одного v,
и если эта функция удовлетворяет второму уравнению (а), то поверхности
налагаются.

91
ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПОВЕРХНОСТИ
3°. Если
содержат только одно переменное #, то обе поверхности налагаются на
одну и ту же поверхность вращения (а стало быть, и между собой)
бесчисленным числом способов.
Действительно, интегрируя второе уравнение (Ь), получим:
\nG = \nG1+\nV, G=Grl/,
где V—произвольная функция одного переменного v.
Подставляя в уравнение (а), имеем:
отсюда
где С—произвольное постоянное. Поверхности S и 5j налагаются и
притом бесчисленным числом способов, ибо, изменив С, мы заставим
совпасть при наложении уже другие точки поверхностей. Очевидно, при
изменении С меняется параметр vu и одна поверхность скользит по
другой так, что линии и = const, т. е. линии одинаковой кривизны обеих
поверхностей скользят одна по другой.
Остается показать, что они обе налагаются на поверхность вращения.
Так как теперь
Е = Е(и), *|=Г = + («>.
то, интегрируя, имеем:
lnO = lnt/-f In V, \nU=fty(u)du9 G—U-V,
и линейный элемент равен
ds* = E (u)du* + UVd<o\
Вводя новые параметры и обозначая
fi=U, y^f^Vdv, E(u)(£f=l+f'2(r),
мы приведем линейный элемент к виду:
Л» = [ 1 +/'2(г)1 drl + r*df ;
это — линейный элемент поверхности вращения. См. гл. II, § 7, стр. 43.
Теория диференциальных параметров, которой мы здесь совершенно
не касаемся, позволяет провести все выкладки, необходимые для решения
вопроса о наложимости поверхностей в произвольных координатах (и, v),
(#i, ^i)» не выполняя в действительности перехода к линиям постоянной
гауссовой кривизны поверхности.
9. Поверхности постоянной кривизны. Рассуждения предыдущего
параграфа теряют силу, если во всех точках поверхности кривизна одна
и та же. Очевидно, обе налагающиеся поверхности должны быть одной
и той же постоянной кривизны. Покажем, что поверхности постоянной
гауссовой кривизны всегда налагаются, притом бесчисленным числом

ПОВЕРХНОСТИ постоянной КРИВИЗНЫ
99
способов, именно: можно выбрать на каждой поверхности произвольную
точку М0 и M0f и произвольное направление / и /', выходящее из этой
точки, и наложить обе поверхности так, чтобы точка М0 совпала с точкой
М0( и направление / попало на направление /'.
Пусть начальное положение трехгранника Дарбу # = 0, v = 0
соответствует точке М0 и вторая ось трехгранника совпадает с направлением I.
За линию и = 0 примем ту линию, которую огибает вторая ось, когда
трехгранник движется в направлении ее, не вращаясь в касательной
плоскости 2), и за параметр v — длину дуги этой линии; за линии v = const —
линии, огибаемые первой осью, когда трехгранник движется, не вращаясь
около нормали, в направлении первой оси, отправляясь от любой точки
линии и — 0. Наконец, за остальные линии и = const возьмем
ортогональные траектории линий ф = const.
Очевидно, при этом выборе координатных линий первая ось всегда
совпадает с касательной к линии и, а вторая — с касательной к линии v;
следовательно
и таблица (2) стр. 93 даст
£ = /£, ч = о, 5i = o, 4i =/а
Далее так как с изменением и при всяком v компонент вращения
около нормали г равен нулю, то внося эти значения в первые два
уравнения (Г), стр. 90, получим:
*, = °> 4i. = fo; (а)
откуда
ds*=[<i>(u)}*du?-{--i\\dv*,
но так как для v = 0 параметр и = s есть дуга кривой, то
</иа = [<р («)]*<*«*, t — y^ — x
Подставляя эти значения г и \ в третье уравнение (II), получим для
постоянной гауссовой кривизны К выражение:
PJt-
*h-
-РхЧ
-5i1
V
frh-
~r\u
-«л
1
ra
*4i
a«»
(b)
Кроме уравнения (b) мы имеем для определения ч\х еще два условия:
на^линии и = 0 параметр v есть дуга, т. е. щ = 19 и на той же линии
и 0 компонент вращения около нормали п равен нулю, т. е. в силу
равенства (а) для
« = 0, 4l=l, ч]ж = 0. (с)
10- Кривизна К равна нулю
*3i = 0
ди* v*
Геодезическая линия — см. следующую главу.

100
ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПОВЕРХНОСТИ
Интегрируя это уравнение при начальных данных (с), получим :
Линейный элемент
ds* — du2 + dv*
принадлежит плоскости х = и, y — v, z = 0; все поверхности постоянной
нулевой кривизны налагаются на плоскость (развертывающиеся
поверхности); при этом произвольная точка М0 налагается на начало координат
и направление / на ось х.
2°. Кривизна положительна К——^. Диференциальное уравнение (Ь):
имеет общий интеграл
A U t г> . U
щ = A cos h В sin — ,
11 a l а '
где А и В— произвольные функции от v. Начальные данные (с)
приводят к значениям
4=1, В = 0.
Линейный элемент
ds2 = du2 + cos* — dv*
1 a
принадлежит сфере радиуса а, отнесенной к меридианам и параллелям
(и — длина дуги меридиана, отсчитываемая от экватора, v — длина дуги
экватора)
и V и . V .и
х = a cos — cos — , v = a cos — sin —, z = a sin—.
a a * ^ a a * a
Все поверхности постоянной положительной кривизны К = -^
налагаются на сферу радиуса а; при этом любая тонка поверхности
М0 ляжет в заданную точку экватора и=0, i> = 0, так что
направление I совпадает с направлением экватора.
3°. Кривизна отрицательна К = ^. Диференциальное уравнение (Ь)
д*ц 1 _п
имеет общий интеграл
и и
ъ=Ае*+Ве~а,
где А и В — опять произвольные функции от v. Начальные данные (с)
дадут
А + В=1, Л-В = 0, % = L+J— .
Линейный элемент

ИЗГИБАНИЕ С ОДНОЙ ТВЕРДОЙ ЛИНИЕЙ
101
Следовательно обе поверхности налагаются так, что совпадают две
произвольно выбранные точки М0 и М0( и два направления / и /', из них
исходящие.
10. Изгибание с одной твердой линией. Только для очень
небольшого числа поверхностей вторая задача изгибания полностью решена,
т. е. известны все изгибания их, и мы имеем мало надежды, что круг
их значительно расширится; зато довольно много сделано в области
решения отдельных вопросов изгибания, особенно по исследованию
изгибания, связанного дополнительным условием. Чтобы дать понятие о
характере' этих задач, рассмотрим несколько примеров.
Прежде всего рассмотрим, возможно ли изгибание поверхности, на
которой некоторая линия, например линия v = 0, остается неподвижной.
В таком случае, очевидно, и кривизна и кручение ее не меняются.
Отнесем нашу поверхность к ортогональной системе линий и, v
и возьмем оси трехгранника Дарбу по касательным к координатным
линиям
т) = о, 5, = о.
Тогда для кривой v = 0 будем иметь в обычных обозначениях 1)
. * . Sz v~ dex re«—qn 1 /^+я2 , ч
1 7(dMd'Md*M\ pfrz Гл Гл \
= — $[er(re2—qn) • (rue2— qun + prn-\-pqe2))..
— — %\ rrtt + pq-qqu + pr\=— i[P^ + 42) — rqu + ruqj. (b)
Здесь при вычислении ^ = у|Ду Ми ) = уДш + у^(у) Ми
опущен второй член, ибо он все равно пропадает в тройном произве-
(dM d'2M dzM\
~d~ IT* ~J^r где пеРвый множитель параллелен ему. То же
сделано при вычислении -^ и далее Миии.
ds*
J) Следует иметь в виду формулы:
dM 1 _
dm 1 д (1 _\ 1 й , 1 д (1\_
^=T^UNePA,-"+T*iWAf|lf
dm idri-,id/i\_i
В тройном^ скалярном произведении сохраняются только векторы разного
направления Мш Миш Мшш (ибо произведение с двумя равными множителями

102
ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПОВЕРХНОСТИ
Так как £, у]и г, гх останутся при изгибании неизменными, то при
сохранении р и рх на линии i>=0 останутся неизменными р и q.
Третье уравнение (Г) стр. 90 даст теперь в силу т) = ^ = 0,
следовательно мы будем знать во все время изгибания на этой линии ди
и уравнение Гаусса (II) определит нам pit если только q не равно нулю;
но при заданных значениях р, q, ри qx для v = 0 решение диферен-
циальных уравнений первого порядка (II) вполне определено (теорема
Коши). Следовательно^ при данной форме кривой -р = 0 форма
поверхности вполне определена. Одна твердая кривая линия на поверхности
сохраняет всю поверхность от изгибания.
Исключением является случай, когда для г> = 0
<7 = 0.
Тогда начальное значение рх остается неопределенным, и следовательно
возможны различные формы поверхности с неподвижной кривой ^ = 0.
Уравнение (1) стр. 93 показывает, что в этом случае кривая v = 0 есть
асимптотическая линия на поверхности.
Итак, при неподвижной кривой поверхность может изгибаться в том
и только в том случае, если эта кривая является на ней
асимптотической линией.
Из этих же рассуждений вытекает, что всегда можно так изогнуть
поверхность, чтобы заданная линия v = 0 приобрела любую кривизну,
(но не меньше-н и любое кручение; в частности всякую линию можно
сделать плоской.
11. Изгибание с сохранением асимптотических линий одного
семейства. Отнесем поверхность к асимптотическим линиям и и их
ортогональным траекториям v и возьмем оси трехгранника по касательным
к координатным линиям. В этом случае формулы (2) дадут
Si = 0, т) = 0, ,7 = 0.
Внося эти значения в систему (V) (II) стр. 90, получим:
' = — JVi=!y, />4i = — 4i*> pq\-=rv — rlu% (а)
Pv — Piu = — qir, qia^prx—Pir. (b)
Уравнения первой строчки определяю р и ql9 а второе уравнение
последней строчки, если г не нуль, дает ри т. е. поверхность будет
определена до положения в пространстве.
Если г = 0, то /?х определяется из первого уравнения (Ь) с
произвольной функп?ией, меняя которую мы будем изгибать поверхность.
Формула (а) предыдущего параграфа показывает нам, что в этом случае
кривизна любой линии и
1 _/*+<?*
J* — —р~
равна нулю, т. е. что все эти линии — прямые.

ИЗГИБАНИЕ С СОХРАНЕНИЕМ СОПРЯЖЕННОЙ СИСТЕМЫ
103
Итак, если поверхность изгибается с сохранением семейства
асимптотических линий, то поверхность — линейчатая и изгибается с сохранением
своих прямолинейных образующих.
Так как кривизна и кручение линии и = О, очевидно, равны
то всегда можно так изогнуть линейчатую поверхность с сохранением
ее прямолинейных образующих, что любая ортогональная траектория
получит любую кривизну ( но не меньше — ) или любое кручение.
В частности всякую ортогональную траекторию можно сделать плоской.
Эти предположения, впрочем, справедливы для всякой директрисы1)
линейчатой поверхности.
12. Изгибание с сохранением сопряженной системы. Каковы бы
ни были две налагающиеся, поверхности, вторые квадратичные формы
которых суть
D du2 + 2 D'du dv -f £>'W,
Dxdu* -f 2D/ du dv+ D^'dv^
всегда существует одна и только одна действительная или мнимая общая
система сопряженных линий (теорема Петерсона), которая определяется
двумя уравнениями
D dubu + Df (duU -f dvU) -f D'dvbv = 0,
Dx du bu -f D/ {du bv -f dv §tf) + D/ dv bv = 0.
В частности две системы линий du:dv и Ьи: bv могут совпасть
и тогда общая сопряженная система выродится в одно общее семейство
асимптотических линий (и следовательно прямолинейных образующих).
Общую сопряженную систему Петерсон называет простым
основанием изгибания, если она принадлежит только двум налагающимся
поверхностям, — главным основанием, если она принадлежит трем
поверхностям; в последнем случае существует оо1 поверхностей с общим
основанием изгибания.
Действительно, пусть 5 и S*— две налагающиеся поверхности с абщей
сопряженной системой (и, v). Если £, т), £ь r\t—общие компоненты
поступательного движения, /?, #, Ри Я\ и Р*> <7*> Р\*у Я* — компоненты
вращения той и другой поверхности, то- условие сопряженности (20)
гл. III, стр. 75 и формулы (1) стр. 93 дадут
Отсюда следует, что м#жно подобрать ). и ja так, чтобы
Р* = >•/>» 4* = *Я, Pi* = №> <1* = Mi- (*У
г) Директрисой называется кривая, пересекающая все образующие
линейчатой поверхности.

204 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПОВЕРХНОСТИ
Внося эти значения в уравнения (II), получим:
~te q ~ Ж^ = ^ —Х) (Pir + ^i«)-
Выберем теперь трехгранник Дарбу так, чтобы первая QCb была
параллельна касательной к линии и в сферическом изображении
поверхности1); тогда
Р=0,
и первое уравнение (Ь) примет вид:
Повторяя для сферического изображения рассуждение § 4 стр. 93, мы получим
да1 , 1 (d]/g д]/~е
_^ — COS О)
** ■/«sin»'* dn ди
Здесь а' — угол первой оси с касательной к линии и на сфере —
равен нулю; а/ — угол координатных линий на сфере. Средняя из
формул (5) стр. 94 дает
„ _Vg sin со' f!2V
Г1-~7Г~Ь>;-
штрихом обозначены скобки Кристоффеля, вычисленные для сферы.
Внося это в уравнение (г/) и помня, что по формулам (16') гл. III стр. 69
теперь
? = УЧ Р\Я = — l/Vsina/,
получим
Й=*-»{?}• w
Величины 1 и р., очевидно, не зависят от положения трехгранника;
следовательно уравнение (с) сохранится при всяком расположении осей.
Аналогично получим
£=<>-*> {\2)' с)
Так как гауссова кривизна при изгибании не меняется, то
P*qi*—P*<l*=P<Ii—Pi9
и
Х{Х = 1.
Мы можем следовательно положить
v ' г v + 1
1) См. § 9 гл III, а также следующий-параграф этой главы.

СФЕРИЧЕСКОЕ ИЗОБРАЖЕНИЕ И ЕГО ЛИНЕЙНЫЙ ЭЛЕМЕНТ 105
Система уравнений (с), (с') примет вид:
£=*+!>(?}'. £-*1'.а}'- <о
Диференцируя и исключая производные, получим
Если это значение v удовлетворяет системе (d), то существует
поверхность S* и при этом только одна, налагающаяся на поверхность 5
с сохранением сопряженной системы (и, v). Система («, v) — простое
основание изгибания.
Если существуют две поверхности Sx* и 52*, налагающиеся на 5 так,
что линии (и, v) остаются сопряженными, то существуют два решения vx
и v2 системы (d). Уравнение (е) тогда исчезает тождественно; v
определяется из вполне интегрируемой системы (d) с произвольным
постоянным. Поверхность S изгибается непрерывно с сохранением
сопряженной системы (и, v). Система (и, v) — главное основание изгибания.
Обращая в нуль коэфициент при v и свободный член в уравнении (е),
придем к условию Коссера (Cosserat):
Если система линий (и, v) на сфере удовлетворяет этому условию,
то всякая поверхность, которая имеет их изображением своей
сопряженной системы, может изгибаться с сохранением этой сопряженной
системы.
III. Сферическое изображение поверхности.
13. Сферическое изображение и его линейный элемент. Основная
система уравнений (Г), (II) стр. 90 допускает еще другое истолкование.
В проблеме изгибания поверхности мы считаем заданными компоненты
поступательного движения трехгранника £, % %v r\v ибо они непосредственно
вычисляются из линейного элемента по формулам (2) стр. 93. По заданным
компонентам £, т), %и щ мы вычисляем с помощью первых двух уравнений (1')
компоненты вращения около нормали г и ги которые являются
следовательно просто комбинациями из производных от заданных коэфициентов
линейного элемента. Последнее уравнение (Г) и три уравнения (II)
служат для определения р, q, ри qu которые уже дают форму поверхности
с данным линейным элементом.
Мы можем посмотреть еще иначе на эти уравнения (Г) и (II). Будем
считать заданными компоненты вращения р, qy pv qx. Они тоже связаны
с одной из квадратичных форм поверхности, именно с третьей формой
Гаусса, с линейным элементом сферического изображения поверхности.
Третья формула из таблицы (С):
пи = qex — ре2, nv=q1e1—рге29
дает проекции перемещения той точки п на сфере, которая служит
образом точки At. Если обозначим через а' и р' углы, которые обра-

106
ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПОВЕРХНОСТИ
зуют координатные линии и и v на сфере с первой осью, то мы
получим, как в § 4 стр. 92,
q — *\/е cos а', /? = — ]/е sin а', qx — V g cos £', p1 — — \/g sin £',
£' —а' = а>', cos со' = -£=-, (9)
где V eg
els'* = edu* + 2fdudv-\-gdv* = (qdu + q^v)2 + (pdu+p^v)2 (10).
линейный элемент сферы и а>'—угол, образованный координатными
линиями на сфере.
Следовательно, если дано сферическое изображение (10) и
расположение трехгранника Дарбу относительно сферы (углы а' и £'), то
компоненты вращения р, q, pv qx известны. Тогда первые два уравнения (II)
Ру — Р\и — Ягг—Я1Г>
9v — 9iu=rPi — riP
определят г и rv которые можно рассматривать как комбинации из
производных от коэфициентов линейного элемента (10), Они должны
тождественно удовлетворять последнему уравнению (II)
гу — г1и = РЯ1—Р1Я, (Н3)
которое является следовательно условием того, что линейный элемент
(10) принадлежит сфере. Записывая, что кривизна сферы единичного
радиуса равна единице, и вычисляя ее через коэфициенты линейного
элемента (10), мы придем как раз к уравнению (И3).
Наконец, три уравнения (Г):
\ — \и — Г^—Г^
РПх — яЬ =р%п —q&,
представляют собой все те уравнения, которые определяют
компоненты поступательного движения £, т), £ь тц, т. е. линейный элемент
и вторую квадратичную форму поверхности.
14. Третья квадратичная форма Гаусса Если отбросить
уравнение Гаусса, которому в системе (Г) нет аналога, то эта задача
определения поверхности по ее сферическому изображению представляет
полное подобие задачи определения поверхности по ее линейному элементу.
Если еще заметить, что величины £, т), £ь тг)х входят в формулы,
определяющие D, D\ D" совершенно так же, как q, qu — /?,—А, то станет
понятным, что, переходя к коэфициентам второй и третьей
квадратичных форм, мы придем к тем же самым уравнениям
f -ти---{\гУ°+({Ч}'-{х!}')°'+ С.1}' D°=°> <n>
т—w-+{?}'D+({?},-{,.T)D'-{V}' d'=°-
как и в первой эадаче, но где гее скобки Кристоффеля {/}', {г/
и т. д. вычислены по формулам (5) стр. 94 от коэфициентов линейного
элемента сферического изображения (10).

ПОВЕРХНОСТЬ С ЗАДАННЫМ СФЕРИЧЕСКИМ ИЗОБРАЖЕНИЕМ 107
Зная вторую и третью квадратичные формы поверхности, мы найдем,
задаваясь углами a', fi' = ш' -(- а', по формулам (2), (9) компоненты
движения трехгранника и все элементы поверхности. В частности, гауссова
и средняя кривизны поверхности получат выражение:
-/3 ^__ 2fD' — eD'' — gQ
DD" — Z)'* '
К-
// =
(12)
DD" — D'2'
и коэфициенты линейного элемента будут связаны уравнениями
K£ + HD + e = 0, KF + HD'+f=0, KG+ HD"-\-g = 0. (13)
Проще всего получить последние формулы, заметив (Бляшке), что
всякое перемещение на поверхности dM и на сфере dn можно разложить
на компоненты по главным направлениям dxM и d2M. Пользуясь
формулами Родрига, где /?! и R2—главные радиусы кривизны, мы имеем:
Ш = dxM + d7M, dh = din+d2n = -^ + $fi%
откуда получим три квадратичные формы, которые просто обозначим
римскими цифрами I, II, III,
l=dM* = d1AP+d2M*
diJWi d$P_
Rx i_" *> '
-11= dMdn —
\\\=dn
:z_djM*i d2M
Исключая dxM и d2My получим определитель
11,1
— П -,
ш L —
«1 *2
#3
1
:0,
(130
или, развертывая и помня, что К =——,// = н- + ^- ,
/П + # н + ш = о,
откуда непосредственно вытекают формулы (13).
15. Поверхность с заданным сферическим изображением
сопряженной системы. Так как на четыре функции £, i), £t, Y]t мы имеем в
системе (Г) стр. 90 только три уравнения, то одна из них осталась
произвольной, и мы можем наложить на них еще одно условие, не стесняя выбора
линейного элемента (10). Отсюда следует, что любую систему линий
(и, v) на сфере можно рассматривать как сферическое изображение
сопряженной системы на поверхности, в то время как нельзя
произвольно задать линейный элемент поверхности, отнесенной к
сопряженной системе.
Поверхность с заданным изображением сопряженной системы
определяется из уравнения (I), если сюда добавить
РЪ — ЧЪ\ —Р)У\—Ч\1 — о.

108
ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПОВЕРХНОСТИ
В частности, если система линий (и, v) на сфере ортогональна,
то сопряженная система на поверхности, ей соответствующая, будет
тоже ортогональна и следовательно будет системой линий кривизны.
Все поверхности с общим сферическим изображением сопряженной
системы имеют в соответствующих точках параллельные касательные ку
линиям этой системы. Это непосредственно следует из того, что каждое
направление на поверхности перпендикулярно к сферическому изображению
своего сопряженного, а так как сферические изображения обеих
поверхностей совпадают, то и направления на поверхности будут параллельны.
Но и обратно, если две поверхности обладают системой линий с
соответственно параллельными касательными, то эта система сопряжена
и на первой и на второй пдверхности. Исключение составляют только
подобные и подобно расположенные поверхности, где все
соответствующие направления параллельны.
Действительно, если координатные линии поверхностей (М) и (Л4*)
параллельны, то
ж:=Ши, M*v=?MVy (14)
где X и jx — множители пропорциональности. Исключая отсюда М*9
получим:
lvMa + bMuv = paMv-\-\i.MUVy (а)
и, умножая на нормаль л,
Хл Muv= \>>nMuv,
откуда или
nMuv = 0
и линии сопряжены или Х = ц, и тогда, умножая уравнение (а) на Ми
и на Mv, получим:
и
Хц = 0, >^ = 0, Х = const,
т. е. поверхности подобны.
Преобразование (14) дано Петерсоном и носит его имя.
Оно позволяет по одной поверхности, отнесенной к сопряженной
системе координатных линий, найти бесконечность других. Коэфициенты
X и [а находятся из диференциальных уравнений
^ р г р. — X dG
которые получатся умножением уравнения (а) на Ми и Mv. Так как X
и |i зависят только от коэфициентов линейного элемента, то они не
меняются при изгибании поверхности. Следовательно, если поверхность (Ж)
станет изгибаться с сохранением сопряженной системы (и, v), то и (ЛР)
будет тоже изгибаться, сохраняя эту систему сопряженной.

СФЕРИЧЕСКОЕ ИЗОБРАЖЕНИЕ АСИМПТОТИЧЕСКИХ ЛИНИЙ 109
Поверхность с заданными сферическими изображениями линий
кривизны можно получить преобразованием Петерсона из сферы.
16. Сферическое изображение асимптотических линий. Если линии
(и, v) на сфере служат изображением асимптотических линий на
поверхности (Af), то [см. § 17, гл. III, формулы (25) и (28) стр. 81]
Ма = XпXпи, Mv = — UX^o, (а)
£ = Х/?, y] = X?, Ъх = — \ри 4l = —Xft. (15)
Внося эти значения в уравнение (Г) стр. 90, мы получим для X два
уравнения 1-го порядка. Мы быстрее получим их непосредственно, вычисляя
условие интегрируемости для М.
Диференцируя Ми по v, a Mv по и к сравнивая результаты, м'Ь
получим
К П X па + *а п X nv + 2 X П X Л/,*, = 0
или, умножая на ли и на лФ:
d In X /~ ~ " \ а/~ ~ ~~ \
—fa~ • 1л «и я«г)= —Z(n пи nuv),
д 1пХ ,- - ~ ч о/" " ~ \
Если сюда внести вторую производную nuv из уравнений (4) стр. 94,
написанных для сферы 1)
где скобки Кристоффеля {?'}, j?}' вычислены по формулам (5) стр.94,
для коэфициентов линейного элемента сферы
12\/ * dv J ди (\2\i ди J ду
(12\i ° ov ' ou (Щ, __
2(eg-P) > {Z} ~ 2(eg-P)
то сейчас же прлуним
-sr=-2i2b~^r=-2bf •
(16)
Следовательно система линий на сфере может служить изображением
асимптотических линий некоторой поверхности (Af), если линейный
элемент удовлетворяет условию
* Pi2}' *{?}'
Это условие получено Дини и носит его имя.
Если условие Дини выполнено, то уравнения (16) определяют X
в квадратурах, а уравнения (а) тоже только помощью квадратур дадут
*) _Так как для сферы нормаль п совпадает^ радиусом-вектором
поверхности л, то вторая квадратичная формула — dn dM = — dn* равна первой с
обратным знаком.

по
ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПОВЕРХНОСТИ
конечное уравнение поверхности (М). Произвольное постоянное, которое
войдет при интегрировании уравнений (а), зависит от выбора начала
и определяет положение поверхности в пространстве; произвольное
постоянное из уравнений (16) войдет множителем и в Ж и определит
размеры поверхности, но не ее форму.
Итак, при выполнении условий Дини (17) линии (и, v) на сфере
служат изображением асимптотических линий поверхности (Ж), которая
определяется с помощью квадратур вплоть до положения в пространстве
и размера единственным образом.
Из формул (28) главы III, стр. 82, где ^- = К есть кривизна
поверхности, следует для трех квадратичных форм поверхности
ds* = 12е dvP — 2\2fdu dv + \2g dv\
— dn dM = — 21 \/eg—f* dudv,
ds'2 = edu* + 2fdudv-lrgdv2.
17. Примеры. I. Минимальная поверхность. Минимальная поверхность
определяется как поверхность, средняя кривизна которой равна нулю.
Так как главные радиусы кривизны ее равны по абсолютной величине
и противоположны по знаку, то индикатриса
Дюпена—равносторонняя гипербола (вместе со своей сопряженной) и асимптотические
направления перпендикулярны, а так как в сферическом изображении они
поворачиваются на прямой угол, то и на сфере асимптотические линии
изображаются ортогональной сетью.
Это сейчас же получим и из наших формул. Относя минимальную
поверхность к асимптотическим линиям, т. е. полагая D = О, D" = О,
получим для средней кривизны
2FD' _ 2/.
если она равна нулю, то
/=0, F = 0,
т. е. и на поверхности и на сфере координатные линии ортогональны.
Так как теперь на поверхности и на сфере имеются уже две общие
ортогональные системы линий (асимптотические линии и линии кривизны),
то следовательно *) линейные элементы их пропорциональны и
сферическое изображение конформно, что, впрочем, сейчас же следует из
формул (13) стр. 107.
Так как теперь
(12U 1 д \пе (1211 1 ding
t1 J ~2 dv ' *2' —2 ди '
*) Общие ортогональные системы du: dv, Ьи: bv определяются из равенств
Edu Ьи + F(du bv + dv Ьи) + Gdvbv~0,
edubu+f(dubv-\-dvbu) + gdvbv — 0.
Эта система уравнений определяет только одну пару решений, если коэфици-
енты Е, F, G и е, /, g непропорциональны.

ПРИМЯРЫ 111
то уравнения (16)
<МпХ д In g д lnX <Ип е
да дш ' #9 ~~ dv
дают
,._№(*)]' ^_1у(«)Р
* — X ' ^ — ~Т~-
Вводя новые параметры ии vx посредством равенств
dux = <р (и) afo, rftfx = <|/ (t/) </*;,
мы приведем линейный элемент сферы (и поверхности) к
изотермическому виду:
л'1 = J [? ИР л1 + х № WP ^2 = J (rf*i + *>') > I (18)
rfs2 = X(rf«?-|-<foi), —dndM— — 2duidvl. j
Асимптотические линии на минимальной поверхности и их
сферические изображения образуют изотермические системы.
2. Поверхность постоянной отрицательной кривизны. Так как
теперь X постоянно 1), то j1!2}' и {г2}' равны нулю,
* do J ди ~ u' 7 ди e ди — u'
Откуда
-fe=°> -1=°- «=?(«).*= + <«).
Замена переменных, как в предыдущем примере, приведет к виду (мы
пишем вместо их и vt просто и и v):
Л'2 tzz du2 — 2 cos со du dv -f- cfo2,
<fc« = X2 (du2 -f 2 cos o> ife rfw -f dv*).
Здесь a) — угол между асимптотическими (координатными) ^линиями
на поверхности.
Так как условие Дини выполнено, то остается единственное
требование, чтобы кривизна линейного элемента ds'2 (кривизна сферы) была
равна единице.
Формула (8) стр. 95 немедленно дает нам
ИГ = 5Ш<и- О9)
Каждое решение этого уравнения определяет одну поверхность
постоянной отрицательной кривизны вплоть до ее положения в пространстве
и размеров.
Например, полагая
а) = о) (/г), k = и -J- v,
!) По формуле (29) гл. III, стр. 82 имеем:

112
ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПОВЕРХНОСТИ
имеем
^2 ' I у д3 _ 2 cos а)
■Й- = sin о), Г ^ "~_ = = * + const> * = con$t-
Полученная поверхность есть поверхность вращения. Уравнение (19)
в общем виде не интегрируется. Поэтому особую ценность
приобретает указанный Бианки и обобщенный Бэклундом (Baclund) прием
преобразования поверхности постоянной отрицательной кривизны,
позволяющий по одному решению уравнения (19) находить другие (см. стр. 177).
Упражнения.
1. Теорема Бонне. Если одна линейчатая поверхность налагается на другую,
то прямолинейные образующие переходят в прямолинейные образующие или
они обе налагаются на поверхность 2-го порядка так, что их прямолинейные
образующие совпадают с двумя семействами прямолинейных образующих поверхности
2-го порядка.
2. Единственные линейчатые поверхности, налагающиеся на поверхности
вращения, суть изгибания минимального геликоида или однополостного
гиперболоида вращения.
3. Теорема Лагерра. Если однополостный гиперболоид вращения изгибается
с сохранением прямолинейных образующих, то горловой круг переходит
в кривую Бертрана.
Если взять две сопряженные (с общими главными нормалями) кривые
Бертрана Г и Л и через точки Г провести прямые параллельно бинормалям
в соответствующих точках Ги то получаемая таким образом линейчатая
поверхность налагается на однополостный гиперболоид вращения и кривая Г
переходит в горловой круг.
4. Если три коэфициента линейного элемента поверхности — функции одного
аргумента [например, функция о = а (и, v)]\ то поверхность налагается на
поверхность вращения и линии о = const переходят в параллели поверхности вращения.
Если все шесть козфициентов двух квадратичных форм Гаусса — функции одного а,
то поверхность — винтовая и а = const — винтовые линии ее.
5. Показать, что поверхность всегда можно изогнуть так, чтобы любая
заданная кривая стала асимптотической линией или линией кривизны.
6. Показать, что единственные поверхности, изгибающиеся с сохранением
линий кривизны, суть поверхности каналов задачи 10, гл. II.
7. Найти поверхности, способные изгибаться с сохранением сопряженной
системы, состоящей из плоских линий.
8. Найти поверхности, где асимптотические линии пересекаются под
постоянным углом.
9. В сферическом изображении поверхности главные направления (см.
задачу 12, гл. II)— линии кривизны, а главные модули растяжения равны
абсолютным величинам главных кривизн.
10. Уго£ двух сопряженных направлений в сферическом изображении
сохраняется или переходит в дополнительный до 180° в зависимости о г знака
гауссовой кривизны поверхности.
И. Если (Afj) и (Af2) — две поверхности с одними тем же сферическим
изображением сопряженной системы, то всякая точка М, которая делит расстояние
между соответствующими точками Мх и М2 в постоянном отношении,
описывает поверхность (Л/), обладающую тем же свойством.
12. Декартовы координаты *, у, z произвольной точки поверхности с
линейным элементом
ds* =zEdu* + 2Fdu dv + G dtp
удовлетворяют одному и тому же уравнению в частных производных
2-го порядка.

УПРАЖНЕНИЯ
113
Из очевидного равенства
Edtf + 2Fdu dv + Gdv* = dx* + dy* + dz*
следует, что линейный элемент
Edu* + 2Fdudv + Gdv>-dz* =[f -^yjiw + 2 [^-JJ]^* +
+[°-(§)']-
dudv
принадлежит плоскости, а следовательно гауссова кривизна его равна нулю.
13. Виртуальными асимптотическими называются такие линии, которые
становятся асимптотическими на одном из изгибаний поверхности. Линии <р(и,1>) =
= const, ф (и, v) = const обладают этим свойством, если функции «риф
удовлетворяют уравнениям Дарбу
«11\ ainp\ djdjp /Ф2\ _! dlnp\ /'дудф Ар £Ф\ ,
1/"" ди ) du'dv^Kyif 2 dv )\dudv'i"Sv du)^
+ \ 1 J dudv ^
дид*+12/ а« &> + Ц2/ 2 а« / \ди dv ~^dv du}^
/J22V d In р\ *[»*[» _
"М\ 2 J dv ) du dv~~V'
где /( = j- есть гауссова кривизна поверхности.
Отсюда следует:
Какова бы ни была поверхность S отрицательной кривизны и две линии на ней
Lx и Z,2> которые пересекаются (но не касаются), существует единственное
изгибание поверхности, которое обе линии делает асимптотическими.
Это предложение позволило Леви доказать, что поверхность £', обладающая
тем же линейным элементом, как и поверхность £, если кривизна его
отрицательна, всегда может быть непрерывно изогнута до совпадения с 5.
14. Линейчатая поверхность, у которой линией сжатия служит
асимптотическая линия постоянного кручения, и ее изгибания обладают тем свойством, что
параболоид, образованный нормалями к поверхности вдоль одной образующей,
один и тот же для каждой образующей.
15. Теорема Киефи (Chieffi). Если вточках произвольной асимптотической какой-
нибудь (не линейчатой) поверхности S, налагающейся на линейчатую поверхность R,
провести касательные к геодезическим g, которые после изгибания перейдут
в прямолинейные образующие R> то получится новая линейчатая поверхность Ru
которая налагается на 5 так, что асимптотическая L остается неизменной.
16. Кроме surface monlure ДОонжа, только поверхности, имеющие общее с
поверхностями 2-го порядка или циклидами Дюпена изображение линий кривизны,
могут соединяться в семейства оо3 поверхностей так, что все поверхности
семейства соответствуют линиями кривизны и в соответствующих точках имеют одни
и те же главные радиусы кривизны.'
17 Теорема Кристоффеля. Если соответствие параллельными нормалями
(в соответствующих точках той и другой поверхности их нормали параллельны)
конформно отображает поверхность 5 на поверхность £', то имеет место один
из трех случаев: a) S' есть подобное преобразование S} Ъ) S и S' — две
произвольных минимальных поверхности, с) 5 и S' - изотермические поверхности (линии
кривизны образуют изотермическую систему), при этом асимптотические линии
кажаой поверхности соответствуют сопряженной системе и линии кривизны
соответствуют между собой.
18. Какова бы ни была поверхность 5, можно найти (и бесчисленным числом
способов) поверхность S' так, чтобы обе поверхности соответствовали линиями
кривизны и в соответствующих точках нормали к каждой поверхности и
касательные к линиям кривизны S и S' соответственно пересекались.
Такие поверхности являются двумя полостями огибающей семейства оо* сфер
(конгруэнция сфер Рибокура).

114 ОСНОВНЫЕ УРАВНЕНИЯ ТЕОРИИ ПОВЕРХНОСТИ
На поверхности центров сфер линиям кривизны S и S' соответствует
сопряженная система.
Различные поверхности S' можно соединить в семейство оо* поверхностей
так, что соответствующие точки их образуют окружности, нормальные к S и
к S' (циклическая система Рибокура). Соответственные касательные плоскости
образуют пучок, осью которого является ось круга.
Фокусы (см. гл. VII) оси лежат в точках ее пересечения с касательными к
линиям кривизны, и развертывающиеся поверхности соответствуют линиям кривизны.
Если все круги —- одного радиуса, то поверхности S и S' — поверхности
постоянной кривизны.
19. Если* существует одна поверхность S't которая соответствует данной
поверхности S линиями кривизны, так что касательные к линиям кривизны
в соответствующих точках той и другой поверхности попарно пересекаются, а
нормали не пересекаются, то существует еще оо2 таких поверхностей S', так
что соответствующие точки их образуют сферу, проходящую через
соответствующую точку L поверхности S, а соответствующие касательные плоскости—
пучок, осью которого служит диаметр сферы.
Все многообразие оо3 поверхностей S' можно разложить на оо1 семейств С
по оо1 поверхностей S' так, что соответствующие точки поверхностей S' одного
семейства образуют окружность ортогональную ко всем поверхностям семейства.
Все окружности, соответствующие одной точке S, лежат на одной сфере и
имеют одну ось.
Сферическое изображение конгруэнции осей (см. гл. VII) удовлетворяет
условиям Коссера.
20. Семейство оо3 сфер называется конгруэнцией Рибокура, если на обеих
полостях Si и S2 огибающей соответствуют линии кривизны. Если поверхность
центров сфер S0 можно изогнуть так, что все сферы, увлекаемые вместе с
точками поверхности S0, пройдут через одну и ту же точку (причем конгруэнция
оо3 сфер потеряет свойство быть конгруэнцией Рибокура), то обе поверхности
Si и S2 изотермические (см. задачу 17) и соответствие точек прикосновения одной
и той же сферы есть конформное отображение St на 52.
Вели одна изотермическая поверхность St дана, то существует оо4
поверхностей 52, которые ей соответствуют в этом преобразовании (преобразование Дарбу).
21. Если поверхность S, налагающуюся на поверхность £0, перемещать
(катить) так, чтобы во всякий момент соответствующие (в изгибании) точки 5 и
S0 совпадали, поверхности касались, и в точке касания соответствующие
направления совпадали, то направление перемещения точки касания и мгновенная ось
вращения составляют два кинематически сопряженных направления. Они взаимны
(их можно поменять местами) и они удовлетворяют условию кинематической
сопряженности.
(D ~ DQ) du Ъи + (D'-D0') (du Zv + dv lu) + (D"-ZV) dv Iv = 0,
где Д/>Д D" и D0, Д/,D0" — коэфициенты второй квадратичной формы
поверхности S и S0.
На трех налагающихся поверхностях существует одна и только одна общая
кинематически сопряженная система. Если существует оо1 налагающихся
поверхностей «S так, что три коэфициента D, £>', D" удовлетворяют одному и тому
же линейному уравнению
aD + pZ)r + чГУ + Ь = 0,
то на всех поверхностях 5 есть одна общая кинематически сопряженная система
(изгибание на кинематическом основании); если 8 = 0, то общая кинематически
сопряженная система сопряжена в смысле Дюпена (изгибания на главном
основании).
Если все кинематически сопряженные системы S и S0 ортогональны, то S
и S0 — поверхности постоянной средней кривизны, которые налагаются с
сохранением главных радиусов кривизны (изгибание Бонне).
Кинематически самосопряженная линия имеет одну и ту же нормальную
кривизну на той и на другой налагающейся поверхности. Если обе поверхности
отнести к системе самосопряженных линий, то обе вторые квадратичные формы
отличаются только знаком среднего члена
D = D0, Z)' = -A/, £)" = ДЛ

ГЛАВА ПЯТАЯ.
Геодезические линии. Геометрия на поверхности.
1. Геодезические линии как линии постоянного направления на
поверхности. Прямые линии на плоскости (и в пространстве) обладают
двумя основными свойствами, каждое из которых может служить
определением их. Прежде всего это — прямые линии, т. е. линии, которые
не имеют кривизны, сохраняют на плоскости одно и то же направление;
затем отрезок прямой линии — кратчайшее расстояние между двумя
точками, следовательно они служат экстремалями в простейшей задаче
вариационного исчисления.
Всем этим условиям в геометрии на поверхности отвечают
геодезические линии.
Рассмотрим прежде всего постоянство направления. Поскольку речь
идет о геометрии на поверхности, все доступные направления лежат в
касательной плоскости. Следовательно мы должны потребовать, чтобы
касательная к кривой при движении по кривой не поворачивалась в
касательной плоскости к поверхности.
Мы знаем, что трехгранник Френе, связанный с кривой, движется
так, что его компонент вращения около главной нормали равен нулю.
Следовательно, если главная нормаль кривой совпадает с нормалью к
поверхности, то компонент вращения касательной к кривой около нормали
к поверхности равен нулю, касательная к кривой при движении по кривой
не поворачивается в касательной плоскости к поверхности и кривая является
геодезической линией на поверхности.
Таким образом мы получаем основное геометрическое свойство
геодезической линии в данной точке поверхности: соприкасающаяся
плоскость геодезической линии проходит через нормаль к поверхности.
В этом отношении геодезическая линия составляет прямую
противоположность асимптотической линии, соприкасающаяся плоскость которой
совпадает с касательной плоскостью к поверхности.
Только прямые линии могут быть одновременно и геодезическими
и асимптотическими, ибо их соприкасающаяся плоскость неопределенна.
С другой стороны, мы видели, что прямая линия на поверхности всегда
служит асимптотической и, очевидно, ома является геодезической, ибо
сохраняет всегда свое направление.
Геометрическое определение геодезической линии (главная нормаль
совпадает с нормалью к поверхности) объясняет механическое значение
геодезической линии.
Соединим две точки абсолютно гладкой поверхности, натянутой упругой
нитью. Равнодействующая упругих сил в каждой точке нити может

116
ГЕОДЕЗИЧЕСКИЕ ЛИНИИ. ГЕОМЕТРИЙ НА ПОВЕРХНОСТИ
лежать только в соприкасающейся плоскости кривой, а сопротивление
поверхности направлено по нормали к поверхности. В случае равновесия
эти две силы взаимно уничтожаются и соприкасающаяся плоскость
содержит нормаль к поверхности. Нить имеет форму геодезической линии.
Таким образом можно притти к мысли, что только геодезическая линия
осуществляет кратчайшее расстояние между двумя точками на
поверхности. Мы вернемся к этому основному свойству геодезической в § 3.
Совершенно так же можно показать, что при отсутствии внешних
сил точка двигается по поверхности по геодезической линии.
Действительно, единственная сила, действующая на точку, —
сопротивление поверхности, и оно направлено по нормали к поверхности. Оно
должно совпадать с ускорением, которое лежит всегда в
соприкасающейся плоскости. Следовательно соприкасающаяся-плоскость содержит
нормаль к поверхности, и траектория движения является геодезической
линией.
2. Уравнение геодезической линии. Трехгранник Френе Т для
геодезической линии, как мы видели, имеет первой и второй осью
касательную к кривой и нормаль к поверхности; он получается из
трехгранника Дарбу Т поворотом около нормали на угол б, если касательная
к нашей кривой образует с первой осью трехгранника Т угол 6.
Следовательно скорость вращения трехгранника Т получится из скорости
вращения 11 трехгранника Т добавлением относительной скорости вращения
~-г-, которая, очевидно, имеет осью вращения нормаль к поверхности п
1 ds
Если наша линия — геодезическая, то трехгранник V в касательной
плоскости не вращается, т. е. компонент вектора П' по нормали п равен
нулю. Умножая все члены на nds, чтобы не связывать себя с элементом
дуги кривой, мы получаем таким образом уравнение геодезических линий
на поверхности в форме
db-\-rdu-\-r1dv = 0. (1)
Здесь 6 — угол геодезической линии с первой осью; следовательно
tg8 равен отношению компонентов перемещения точки М на оси
трехгранника
Ig0 tdu + bdv9 у '
Система уравнений (1) и (2) относительно переменных 6, и, v имеет
определенное решение, если дано начальное значение
•о, ^о> ео5
следовательно через всякую точку поверхности M0(uQi щ) п0 всякому
направлению 60 проходит одна и только одна геодезическая линия.
Вс величины, входящее в эти уравнения: 0, г, ги зависят только от
коэфициентов линейного элемента поверхности. Поэтому на всех
налагающихся поверхностях геодезические линии одни и те же.

ГЕОДЕЗИЧЕСКАЯ ЛИНИЯ КАК КРАТЧАЙШЕЕ РАССТОЯНИЕ 117
Если в уравнение
v d*M d /^"Vi ол! du du , 7z (dvV , т~л d2u , т> d*v
подставим
и вместо вторых производных вектора М их значения из таблицы (4)
гл. Ш, стр. 94, то^оно распадается тогда на три уравнения по трем
направлениям Ma,Mv,n. Одно из них определит радиус кривизны р, а
два другие дадут уравнения геодезической линии
S+m (*)+*«> *г+га (£)'-».
S+t¥>ft)'+»{?iS2+ffl (£)"=•• (3)
3. Геодезическая линия как кратчайшее расстояние. Покажем
теперь, что кривая, определяемая на поверхности уравнением (1), служит
кратчайшим расстоянием на поверхности между двумя ее точками, если
они достаточно близко друг от друга расположены.
Пусть нам дана геодезическая линия, которую мы примем за линию
0 = 0. Проведем к ней ортогональную линию L и во всех точках ее
перпендикулярные к ней геодезические линии. Примем их за
координатные линии и, а ортогональные траектории (в том числе и линию L) за
линии V.
Это предполагает, очевидно, что геодезические линии нигде в
рассматриваемой области друг друга не пересекают.
Если оси трехгранника Дарбу совместим с касательными к линиям
и и v, то компоненты £i и т\ будут равны нулю и линейный элемент
примет вид:
ds2 = ¥du2-\-rildv\
Два первые уравнения (Г) примут теперь вид:
Так как линии и — геодезические, то они по условию удовлетворят
уравнению (1). Подставляя туда 0 = 0, dv = 0, мы получим:
г = 0,
и первое уравнение (а) дает нам
gi = 0, $ = ?(«)•
Мы можем следовательно ввести новый параметр ut посредством
уравнения
du i ~%du

118 ГЕОДЕЗИЧЕСКИЕ ЛИНИИ.—ГЕОМЕТРИЯ НА ПОВЕРХНОСТИ
и линейный элемент примет вид:
Мы видим, что параметр щ имеет простое геометрическое значение;
полагая v = const, имеем:
ds = duif
т. е. их—длина дуги геодезической линии и.
Ортогональные траектории семейства геодезических линий называются
геодезически параллельными линиями. * Следовательно геодезически па*
раллельные линии везде одинаково отстоят друг от друга, если
расстояние между ними измерять дугами ортогональных к ним
геодезических линий.
Нетрудно теперь показать, что дуга их — и0 геодезической линии
г> = 0 есть действительно кратчайшее расстояние между двумя ее точками
Mq (и0, 0) и Мх (ии 0), т. е. короче дуги любой другой линии,
проходящей на поверхности между этими двумя точками.
Действительно, дуга М0МХ определяется интегралом
щ
куда вместо v надо подставить
найденное из уравнения той кривой, на которой лежит дуга M0MV Но
очевидно, что интеграл (Ь) примет наименьшее значение, когда под-
интегральное выражение будет наименьшим, а это будет иметь место,
когда второе слагаемое под корнем обратится в нуль. Тогда
-^ = 0, v = const, т. е. 1> = 0.
4. Теорема Дарбу. Нам остается показать, что геодезические линии
действительно на некотором расстоянии от А/0 друг друга не
пересекают. Для этого заметим вместе с Дарбу, что уравнения (3), очевидно,
не изменятся, если вместо дуги 5 ввести ms, где т любая постоянная.
Решение и, v этих уравнений — функции от s и от начальных данных м0,
v°> [~Я~) 9 ("/Г/ ' ^ни> очевидно> не изменятся, если мы заменим
idu\ (dv\ 1 ldu\ 1 idv\
s> "с "о, Ы0, (Ts)0 на ms, и0, щ, - (-Д, - (-Д,
это показывает, что щ v зависят только от u0j v0 и
Разлагая функции
«=/i («о, vQ, и', «'), •о=/2(и0, «о» «'. «')

ТЕОРЕМА ДАРБУ
119
по степеням uf, v' [что возможно, если точка (u0f vQ) на поверхности
регулярная], получим, очевидно,
v — Vo-v9+bn u'2 + b12u' v' + b2$]**+... (a)
где а.р bik зависят от u0t vQ> и ряды сходятся для достаточно малых
Для и' = 0, v' — О якобиан
d(uv) _ -
Следовательно уравнение (а) можно разрешить относительно и', v\ и
мы получим ряды по степеням и— uQ, v — vot сходящиеся для
достаточно малых значений этих разностей.
и' = и — «о-fa* (« — «о)2 + <2 О — tto)0 — *о) + «£ (^ —^о)2 + ---
*' = tf — Vo + Ai(« — «о)2 +*!*2(И — "о) (V — V0) + b;2 (V — V0)2 + ...
Зто показывает, что две достаточно близкие точки М0 (и0, v0) и
М(и, v) определяют вполне и', v\ достаточно малые по абсолютной
величине, т. е. определяют только одну геодезическую линию, длина которой 5
не превосходит определенной величины. Иными словами, можно
выделить около точки М0 на поверхности область так, что любая точка
М этой области соединена с точкой М0 только одной геодезической,
лежащей вполне внутри области.
Если принять эти геодезические линии за линии и, а их ортогональные
траектории за линии V, то мы получим опять систему координат прошлого
параграфа и линейный элемент (4). При этом, очевидно, одна из линий v
сжимается в точку (и0, щ), а каждая из других линий представляет
геометрическое место точек, равно удаленных от нее, если измерять
расстояние по геодезической ЛШ0 (геодезические круги Гаусса-Бианки).
Вся система координат имеет много общего с полярной системой координат
на плоскости.
Эти рассуждения показывают, что на всякой геодезической L можно
выделить дугу около любой точки М0 так, что отрезок геодезической
между М0 и всякой другой точкой дуги М будет кратчайшим
расстоянием между ними. Дуга, очевидно, оканчивается на границе той области,
где координаты и> v однозначно определяют точку, т. е. где две линии
и не имеют общих точек (кроме М0). Таким образом конец дуги, где
геодезическая линия L осуществляет кратчайшее расстояние, есть первая
точка М\ общая с другой геодезической, выходящей из М0. Точки М0 и
М* называются сопряженными точками геодезической.
Итак, в достаточно малой области две точки определяют одну
геодезическую линию, не выходящую из области, подобно тому как
две точки на плоскости определяют прямую.
Оба условия существенны: две точки должны лежать достаточно
близко, и длина геодезическая должна быть ограничена. Как бы близко
ни были точки, можно провести между ними бесчисленное множество
геодезических, если не ограничивать их длины. Например, геодезические

120 ГЕОДЕЗИЧЕСКИЕ ЛИНИИ.—ГЕОМЕТРИЯ НА ПОВЕРХНОСТИ
линии на цилиндре—винтовые линии, и между двумя сколь угодно
близкими точками цилиндра можно провести любое число винтовых линий,
совершающих несколько оборотов около цилиндра, прежде чем дойти от
одной из них до другой. С другой стороны, если точки лежат
достаточно далеко, то может случиться, что их соединяет оо1 геодезических
одной и той же длины; например, через два полюса сферы проходит
бесконечное множество геодезических линий — все меридианы. Такие
точки называются сопряженными точками на поверхности.
5. Геодезические линии на поверхности вращения. Чтобы показать,
как ведут себя геодезические линии на поверхности, рассмотрим
поверхность вращения, на которой уравнение геодезических интегрируется.
Отнесем поверхность вращения к меридианам и параллелям (см. стр. 43)
ds* = [1 +/2 (г)] df* -f г2 dv2.
Совместим оси трехгранника с касательными к координатным линиям и
будем обозначать компоненты вращения т и rt жирным шрифтом в
отличие от радиуса параллели г поверхности. Тогда
5,=0, 7) = 0, 5=1/1 -\-f'4r), 41 = г,
dt dy\t *
г = 0, г, = . -,
и уравнения (1) и (2) принимают вид:
*° = 0, tg6:- rdV
Vl+ГЧг) l/l+f>(r)dr
Исключая отсюда dv, имеем:
de+tge-£=o,
откуда
г sin 6 = А, Л = const. (5)
В каждой точке геодезической линии произведение радиуса параллель-
ного круга на синус угла наклона геодезической линии к меридиану
постоянно (теорема Клеро).
Исключая 6, получим:
h rdv
V7*^Hp y~T+7*(rj dr
(6)
}rY+^±drM const.
Мы видим, что г всегда больше, чем А, и, чем ближе к А, тем ближе
угол в к у.
Пусть радиус параллели поверхности вращения имеет г=а своим
максимумом, r—b своим минимумом. Тогда, очевидно, не может быть
геодезической, у которой параметр А был бы больше, чем а.

РАЗВЕРТЫВАНИЕ ЛИНИИ НА ПЛОСКОСТЬ
121
1°. й = я. Единственное возможное значение г=л. Параллель
наибольшего рациуса — геодезическая линия (например экватор на сфере).
2°. b < h < а. Геодезическая пересекает наибольшую параллель r = а
под острым углом 6а
smea=^<i.
По мере уменьшения радиуса параллели г, угол б геодезической с
меридианом h
sin 6 = —
г
увеличивается и для г=А сделается равным -у. Геодезическая
касается параллели г = А, поворачивается назад, снова пересекает
наибольшую параллель г=а под тем же углом, но с противоположным знаком,
доходит до параллели r=h по другую сторону ее, снова возвращается
назад и т. д.
Колебанию геодезической от одной до другой параллели г = А
соответствует поворот поверхности на конечный угол
b = 2hf^^dr, (а)
J rVr*-h? ч '
h
если он соизмерим с тс, то геодезическая линия — замкнутая линия.
3°. h = b. Геодезическая также подходит к параллели г = 6, но
теперь под знаком интеграла в формуле (а) для r = b знаменатель
обращается в нуль, а числитель обращается в бесконечность, ибо для
наименьшей параллели
fir)= со
(касательная к меридиану параллельна оси z). Нетрудно заметить, что 8
обращается ,ъ бесконечность. Следовательно геодезическая подходит
асимптотически к наименьшей параллели r = b, совершая
бесчисленное множество оборотов по поверхности.
Сама параллель тоже геодезическая линия.
4°. г<й. Геодезическая пересекает наименьшую параллель г=&под
острым углом бь
. л h
sin Vb = -j
так же, как и наибольшую. Конечно б6 > 0а.
5°. /* = 0. Геодезическая совпадает с меридианом.
Нетрудно заметить, что в случае 2° сопряженной точкой всегда
служит точка касания к параллели г=Л.
6. Развертывание линии на плоскость. Из основного
геометрического определения геодезических линий (главная нормаль совпадает
с нормалью к поверхности) непосредственно следует: если две
поверхности касаются вдоль линии и линия касания служит геодезической
для одной поверхности, то она геодезическая и на второй.
Это дало возможность Леви Чивита дать наглядное истолкование
геодезических линий. Рассмотрим семейство со1 касательных плоскостей к по.

122 ГЕОДЕЗИЧЕСКИЕ ЛИНИИ.—ГЕОМЕТРИЯ НА ПОВЕРХНОСТИ
верхности 5 в точках некоторой линии L. Огибающая этого
семейства— развертывающаяся поверхность Z), которая, очевидно, касается
поверхности S в каждой точке i, ибо касательными плоскостями ее
служат плоскости семейства. Развернем поверхность D на плоскость —
линия L обратится в плоскую кривую /. Так как при изгибании все
углы в касательной плоскости сохраняются, а касательные плоскости
поверхности 5 и описанной около нее вдоль L развертывающейся
поверхности D общие, то полоска плоскости вдоль линии / дает представление
о геометрии на поверхности вдоль линии L. Если линия L служит
геодезической на поверхности S, то она геодезическая и на
развертывающейся поверхности D и останется геодезической после развертывания
ее, т. е. обратится в прямую /. Таким образом основное свойство
геодезической не менять направления в касательной плоскости поверхности
получает наглядное представление. Касательные, пересекающие
геодезическую L под одинаковыми углами, перейдут в параллельные прямые,
пересекающие прямую / под тем же углом.
Если линия L не геодезическая, то после развертывания на
плоскости она обратится в плоскую кривую /, кривизна которой не равна
нулю. Эта кривизна называется геодезической или тангенциальной
кривизной. Она зависит от того, что линия L не сохраняет своего
направления в касательной плоскости, так как поворот касательной благодаря
искривленности поверхности исправляется при развертывании D на
плоскость. Это интуитивно ясное положение нетрудно обосновать вполне
строго.
Повернем трехгранник Френе Т около касательной на угол <р так,
чтобы главная нормаль совпала с нормалью к поверхности.
Скорость вращения П' трехгранника V получится добавлением к
скорости вращения П" нового трехгранника V скорости относительного
вращения -з?, осью которого, очевидно, служит касательная т
n' = fl'+gt. (7)
Проектируя этот вектор на нормаль к поверхности я, получим искомое
вращение касательной в касательной плоскости поверхности. Так как
касательная т перпендикулярна к нормали л, а компонент вращения
трехгранника Френе около главной нормали равен нулю, то искомая
проекция вектора П на нормаль п будет равна проекции компонента
вращения Т' около бинормали, т. е. г". Угол бинормали р с нормалью
поверхности л, очевидно, равен у — ?•
Следовательно искомый компонент вращения равен
- / ъ \ sin ф
r-cos^- ?) = -^,
где — = г" — кривизна кривой. Итак, геодезическая кривизна
кривой ъ-^- есть проекция кривизны кривой^ отложенной на главной нор-
мали, на касательную плоскость поверхности*

РАЗВЕРТЫВАНИЕ ЛИНИИ НА ПЛОСКОСТЬ
123
С другой стороны, в § 2 мы видели, что поворот касательной около
нормали к поверхности, или компонент вращения трехгранника V около
нормали, равен
d§-\-rdu-\-ridv.
Следовательно геодезическая кривизна
(8)
плоскости, то и проекция кривизны — на касательную
т. е.
^ sin? d8 + г du + rx dv
Vg ~ ~ ~ ds
не меняется при изгибании.
Теперь нетрудно обосновать то предложение, которое мы высказали
в начале этого параграфа. Так как поверхность 5 и описанная около
нее вдоль L развертывающаяся поверхность D имеют общие касательные
1
"" плоскость,
геодезическая кривизна кривой L
на той и другой поверхности,
одна и та же. С другой стороны,
выражение (8) содержит только
величины, зависящие от линейного
элемента поверхности,
следовательно при изгибании не меняется, а
для кривой на плоскости
геодезическая кривизна, очевидно,
совпадает с кривизной кривой (ибо
главная нормаль лежит в
плоскости).
Если кривую L спроектировать
на касательную плоскость, то ее
проекцию V можно рассматривать
как нормальное сечение
проектирующего цилиндра, а кривизна
самой кривой L равна кривизне
его наклонного сечения
соприкасающеюся плоскостью кривой.
Применяя теорему Менье 1) к этим двум сечениям, получим для
кривизны проекции выражение (8). Следовательно геодезическая кривизна
кривой есть кривизна ее проекции на касательную плоскость.
Геодезическая кривизна есть предел отношения угла смежности двух
касательных к поверхности, нормальных к кривой, к ее длине, ибо этот
угол измеряется тем же компонентом вращения трехгранника Т" около
нормали п.
Бельтрами предложил интересное построение радиуса геодезической
кривизны: центр кривизны кривой L лежит на касательных к семейству
геодезических линий g, ортогональных к кривой L, в точках пересечения
их с бесконечно близкими касательными линий семейства. Так как
касательные к геодезическим g вдоль линии L (черт. 20) не образуют раз-
х) Радиус кривизны косого сечения поверхности равен проекции на
плоскость сечения радиуса кривизны нормального сечения.
Черт. 20

124 ГЕОДЕЗИЧЕСКИЕ ЛИНИИ. — ГЕОМЕТРИЯ НА ПОВЕРХНОСТИ
вертываюшейся поверхности (если линии L и g не сопряжены), то эти
касательные не пересекаются, но касательные к геодезическим g вдоль
линии hy сопряженной с g, огибают ребро возврата развертывающейся
поверхности, и отрезок касательных к g от точки М на линии L до
точки т, где прямая Mm касается ребра возврата, равен радиусу
геодезической кривизны I.
Действительно, принимая геодезические g за линии v, а
ортогональные траектории за линии и и совмещая оси трехгранника Дарбу с
касательными к ним, имеем:
^1 = 0, $1 = 0, п = 0,
последнее потому, что линии v— геодезические.
Точка т имеет координаты по осям трехгранника [0, /, 0], и ее
перемещение по формуле (В) [гл. III, § 6, стр. 67]:
dm ~ех[Ыи — г du] -}- е2 [dl -)- t\idv] + л (р tfc -f-/?i dv) I
должно быть направлено по касательной е2; отсюда
(pdu-\-pxdv)l=0, I — /7=0,
между тем по формуле (8) геодезическая кривизна линии и
1 rdu г_
?и~ ds — V
откуда непосредственно следует
7. Геодезическое кручение. Компонент вращения трехгранника V
около касательной по формуле (7) равен
Н р * ds9
Здесь мы уже положили р' = согласно формуле (13) гл. I. С
другой стороны, проектируя на касательную х вектор 1Г = П-{-л-7-,
получим:
р" z=.(pdu -\-р\ dv) cos О -j- (q du -f- Я\ dv) sin 6.
Следовательно
Правая часть зависит только от направления касательной к кривой
в касательной плоскости. В этом отношении это выражение вполне
аналогично нормальной кривизне кривой. Бонне предложил называть ее
геодезическим кручением, ибо оно в точности совпадает с кручением
геодезической линии, проведенной в направлении du: dv, как это сейчас же
видно, если вспомнить, что для геодезической линии ср = 0.

КРИВИЗНА ГЕОДЕЗИЧЕСКОГО ТРЕУГОЛЬНИКА
125
Если поверхность отнести к линиям кривизны и оси трехгранника
совместить с касательными к координатным линиям, то
du cos 6 dv sin 6
ds T~' ds y)!
-i-i=Gu-k) ",m*- (8'>
где /?i и /?2— главные радиусы кривизны и 6 — угол касательной с
первой линией кривизны.
Следовательно геодезическое кручение двух ортогональных линий
равно по величине и противоположно по знаку.
Формула (9') показывает, что геодезическое кручение обращается
в нуль в точке округления (Rt=:R2).
Кроме того оно равно нулю только для главных направлений
б=о, е = ?.
Итак, линии кривизны — линии с геодезическим кручением, равным
нулю.
Если две поиерхности пересекаются под постоянным углом, то
геодезическое крученое их общей линии одно и то же на обеих
поверхностях, ибо, очевидно, углы <pi и ?2 отличаются на постоянную
величину, а производные их совпадают.
Отсюда, если две поверхности пересекаются под постоянным углом
и линия пересечения служит линией кривизны для одной поверхности*
то она является ею и для другой поверхности; и обратно: если две
поверхности имеют общую линию кривизны, то они пересекаются под
постоянным углом.
Так как на плоскости и на сфере всякая линия есть линия кривизны,
то плоскость или сфера, пересекающие поверхность под постоянным
углоМу секут ее по линиям кривизны; и обратно: если линия кривизны
плоская или сферическая, то плоскость или сфера, которым
принадлежат эти линии секут поверхность под постоянным углом (теорема
Иоахимсталя).
Отсюда следует также, что сферическое изображение плоской линии
кривизны есть круг, плоскость которого параллельна плоскости самой
линии, ибо нормаль к поверхности вдоль линии кривизны образует
с этой плоскостью постоянный угол.
Геодезическое кручение асимптотических линий так же, как и
геодезических линий, совпадает с кручением самой линии, ибо ср —
постоянно ( ср = |).
8. Кривизна геодезического треугольника. Вернемся к геометрии
на поверхности.
При выводе в § 9, гл. III, стр. 70 гауссовой кривизны поверхности, как
предела отношения площади сферического изображения к площади самой
бесконечно малой части поверхности, мы ввели понятие полной
кривизны некоторой области на поверхности (curvatura integra) как пло-

126 ГЕОДЕЗИЧЕСКИЕ ЛИНИИ.—ГЕОМЕТРИЯ НА ПОВЕРХНОСТИ
щади ее сферического изображения. Нетрудно видеть, что curvatura
Integra равна
ffKdS,
где К есть кривизна поверхности и dS — элемент площади ее. Внося
и пользуясь третьим уравнением (II) стр. 90, мы получим:
IIKdS= ff(P9i-Pi9) *»*>=//(£-Й) *>*>•
К этому интегралу можно применить формулу Грина, именно, разбивая
его на два слагаемых, выполнить в каждом одно интегрирование
ffKdS = fdufd£dv-fdvfd£du=fdu\r-fdv'\r1 =
= — ф (rdu -j- rxdv).
Здесь последний интеграл уже взят по контуру нашей области. Нетрудно
заметить, что на положительной стороне нашей поверхности два
интеграла
ъ ь а
j{f)Vl du и —j {г)щ du = f (r)Va dv
a a b
дают обход в отрицательную сторону контура, так же как интегралы
d с d
— f (г\)щ dv = f (ri)«i dv nf (rx)Ul dv.
с d с
Геодезическая кривизна контура — определяется формулой (8),
откуда
— (rdu + r1dv)= — --{-db.
?g
Следовательно
ffKdS+ffg=№>
О — есть угол касательной к контуру с первой осью трехгранника.
После обхода касательная вернется в прежнее положение,
повернувшись на 360°. Следовательно полный интеграл равен 2гс, и мы получим
формулу Бонне
£+ffKdS = 2*. (10)

ГЕОДЕЗИЧЕСКИЕ КРУГИ ДАРБУ
127
Если контур образован геодезической линией (замкнутой), то ^" = 0 и
полная кривизна
л " KdS = 2«,
я<
т. е. сферическое изображение односвязной области, ограниченной
замкнутой геодезической линией без особых точек, равно половине
площади сферы. При этом надо иметь в виду, что области с кривизной
разного знака дают и сферическое изображение разных знаков, и
теорема говорит об алгебраической сумме их.
Для полной поверхности связности 1) шара сферическое изображение,
очевидно, будет 4тс; при этом нет надобности предполагать
существования замкнутой геодезической линии, ибо, разбивая поверхность
произвольной линией, на две части и складывая полную
кривизну нашей части по формуле (10), мы
уничтожим интеграл по контуру как пройденный в
противоположных направлениях.
Если контур имеет углы, то формулу (10) нельзя
применять непосредственно, ибо в угловых точках
формула (8) потеряет силу. Так как эта
последняя получена из подсчета вращения трехгранника
в касательной плоскости, то, очевидно, мы должны
будем теперь добавить в правой части формулы
(10) все те углы, которые описывает касательная
к контуру при поворотах в угловых точках. рт*
Рассмотрим треугольник ABC, образованный тремя геодезическими
линиями (черт. 21). Если ДВи С—внутренние углы треугольника, то,
очевидно, касательные к контуру поворачиваются в угловых точках на
углы я—Л, я — £, 1С —С.
Следовательно
ffKdS + ъ — Л + 1С — В + 1С — С=2я,
и
KdS = A-{-B+C—*.
Полная кривизна геодезического треугольника равна избытку суммы
его углов сверх двух прямых.
Только на развертывающихся поверхностях сумма углов
геодезического треугольника всегда равна 180°.
9. Геодезические круги Дарбу. Пользуясь понятием геодезической
линии, геодезической кривизны линий, можно найти в геометрии на про-
*) Такие поверхности можно характеризовать свойством: всякая замкнутая
линия, проведенная на поверхности, делит ее на две части. Нетрудно видеть,
что .не всякая поверхность обладает этим свойством, например поверхность,
полученная вращением круга около прямой, лежащей в его плоскости и не
пересекающей его (тор), очевидно, этим свойством не обладает: меридиан есть
замкнутая кривая (круг) и не делит поверхность на части.

128 ГЕОДЕЗИЧЕСКИЕ ЛИНИИ.—ГЕОМЕТРИЯ НА ПОВЕРХНОСТИ
извольной поверхности много понятий и теорем, представляющих
обобщение теорем планиметрии.
Мы уже видели, что, откладывая от произвольной кривой по
ортогональным геодезическим одну и ту же произвольную дугу, мы получаем
геодезически параллельную линию. Все геодезические параллели
пересекают семейство геодезических под прямым углом.
На плоскости этому соответствует семейство параллельных кривых —
эвольвент одной и той же кривой, нормально пересекающих ее
касательные.
Если эти геодезические исходят из одной точки, то параллельные
линии называются геодезическими окружностями (Гаусс).
К другому понятию геодезических окружностей (окружности Дарбу)
придем, требуя, чтобы геодезическая кривизна их оставалась постоянной.
Оба определения не совпадают, как видно хотя бы из того, что
геодезическая кривизна геодезически параллельной линии v
ds2 = du2-\-Gdv2,
5=1, Y) = 0, $! = 0, 4l = O,r=0
равна по формуле (8) стр. 123
1 d§-\-rdu-\-rxdv гх
Если pg на кривой постоянно, например - = а (и), то
rl = a{u)y\l
и средняя формула (Г) стр. 90 дает
где U—функция одного и и V—одного v\ кривизна поверхности
в силу формулы (II) стр. 90
РЯ\—РЧ\ _ rv-rUl _ (дЦ),У_ (aU)'
&4i-6in >Qi — M uv — U
есть функция одного и. Поверхность налагается на поверхность
вращения так, что геодезические и ортогональные к ним линии постоянной
геодезической кривизны налагаются на меридианы и параллели. Если же
все круги Гаусса — постоянной кривизны, то и кривизна поверхности
постоянна.
Только на поверхности постоянной кривизны геодезические круги
Гаусса суть круги в смысле Дарбу.
Заметим, что и на поверхности постоянной кривизны есть круги
Дарбу, которые не являются кругами Гаусса. Если, например, на
касательных к винтовой линии отложить равные отрезки, то получим новую
винтовую линию, которая обратится в окружность при развертывании,
следовательно обладает постоянной геодезической кривизной и не будет
замкнута, т. е. не будет окружностью в смысле Гаусса.
10. Геодезические эллипсы и гиперболы. Возьмем на поверхности
две произвольные кривые С и С; геометрическое место точек, сумма

ТЕОРЕМА ЯКОБИ
129
или разность расстояний которых от этих точек постоянны, называется
соответственно геодезическим эллипсом или гиперболой (Вейнгартен).
Пусть параметры и и v означают расстояние точки М от той или
другой линии и
ds2 = Е du 2 + 2 F dи dv + G dv2
— линейный элемент поверхности.
Если поверхность отнести к линиям, параллельным кривой С, и к
ортогональным геодезическим, то линейный элемент будет
ds* — du2 -f о2 du\
Причем и имеет то же самое значение» как и раньше (дуга
геодезической). Следовательно, исключая ds2, имеем:
<з2du'*=(E— 1)du*-\-2Fdu dv + Gdv*%
и так как правая часть есть полный квадрат, то
(£—1) G = F*.
Так же получим
откуда
и, заменяя
(0—1) E = F\
E=G, F* = E(E—\)
Е = ~±-
Sin2 ш>
получим линейный элемент
, 2 du1 -f- 2 cos (о du dv + йФ
US ~ sli2^ •
Очевидно, а) имеет значение угла между геодезически параллельными
линиям С и С.
Введем теперь новые параметры
и -|~ v = 2а, и — v = 2(3,
так что линии а и (S будут геодезическими эллипсами и гиперболами.
Линейный элемент примет вид:
*•=-*!.+ _«!_. (И)
sin2 -^ cos2 -х-
Геодезические эллипсы и гиперболы всегда образуют ортогональную
сеть.
Отсюда прямо следует теорема Лиувилля.
Только на развертывающейся поверхности два семейства
геодезических могут пересекаться под постоянным углом.
Если два семейства геодезических g и g' пересекаются под
постоянным углом, то и ортогональные траектории их С и С тоже образуют
постоянный угол; ш — постоянно и линейный элемент (11), очевидно,
принадлежит плоскости.
И. Теорема Якоби. Мы теперь коснемся бегло вопросов
интегрирования уравнения геодезических линий. Начнем с отыскания геодези-

130 ГЕОДЕЗИЧЕСКИЕ ЛИНИИ.— ГЕОМЕТРИЯ НА ПОВЕРХНОСТИ
чески параллельных линий. Чтобы найти семейство геодезически
параллельных линий, надо привести линейный элемент к виду
Е du* -f 2F du dv -f G dv* = db* + o» rfO^,
но, очевидно,
Edu* + 2Fdudv+Gdv2 — d62 =
=M5),]«+»('-£S)**+[°-(S)>--««!
есть полный квадрат. Следовательно
[*-(£)!["-(£)■]-["-£5]".
откуда
,,_/(g)'+o(g)'-<g ,
*r— EG — F* ~U
Это выражение Бельтрами назвал диференциальным параметром 1-го
порядка.
Итак, чтобы найти геодезически параллельные линии, надо
проинтегрировать уравнение
д1е= 1.
Пусть теперь мы имеем решение 6 этого уравнения, содержащее
существенным образом произвольно постоянное а. Чтобы найти систему
линий 6, 91э надо еще найти 6Х так, чтобы
ds2 = d№-\-o*dQl
Будем рассматривать в этом уравнении и, v> du, dvy а как независимы
переменные (ибо оно тождественно относительно всех пяти величин
и продиференцируем по а.
Переменное а содержат только 0, о, 01в
При этом
^- dv =^- ^~du + з- dv = . . du -+■ л . dv = d .—.
ад ал \dw ' (^t/ / дм да ' dz> да да
Следовательно после диференцирования получим:
Так как уравнение (а) тождественно относительно du, dv и каждый издифе-
ренциалов db и dbi — линейная функция от du и dz/, то, очевидно, d6x делит
либо dO, но тогда б есть функция от Ь1у что невозможно, либо d^-, и
тогда -j- есть функция от 61#

ПОВЕРХНОСТИ лиувилля
131
Так как бх всегда можно заменить любой функцией от него, то мы
можем просто положить
1 да
Следовательно геодезические линии, ортогональные к геодезически
параллельным 6 = const, имеют уравнением
g^ = ft, Ь = COnst, (Ь)
и длина дуги их есть функция 6.
Но уравнение (Ь) содержит два произвольных постоянных а и Ь\
следовательно это общее решение. Нетрудно видеть, что выбирая а и Ь,
можно провести геодезическую линию через любую точку и по любому
направлению.
Действительно, уравнение
б («, v9 а) = 6 (и0) v0)a) = const
определяет семейство кривых б, проходящих через точку (w0, vQ). На
правление этих линий зависит от отношения
ди' dv'
но это отношение существенно содержит а, иначе с помощью уравне-
ния Дхб = 1 мы найдем ^-, ^-, не содержащие а, что невозможно, ибо а
входит в б существенно (не в виде слагаемого). Итак, выбирая а,
проведем линию б по любому направлению, а следовательно по любому
направлению проведем и геодезическую, которая к ней ортогональна.
12. Поверхности Лиувилля. Поверхность, обладающая
изотермической системой геодезических эллипсов и гипербол, называется
поверхностью Лиувилля.
Пусть линейный элемент
. 9 ш ' п О)
slnT C0S 2"
приводится к изотермическому виду заменой
и1 = <p(w), v' =ty(v).
9'Чи) _ V4v)
Тогда
откуда
sin2 — cos2 -у
<^(г>; » we 2 — ср'^О
ф'2(^
sin*-»- cos*-
2

132 ГЕОДЕЗИЧЕСКИЕ ЛИНИИ. — ГЕОМЕТРИЯ НА ПОВЕРХНОСТИ
Итак, линейный элемент Лиувилля имеет вид:
ds* = {а (и) + $ (v)} (du* + dv*).
Тогда уравнение Аб = 1 принимает вид:
(S)'+(Sr=.w+p«.
Его можно удовлетворить решением
U = U+V9
1/= £/(«),
V= V(<v).
Подставляя, получим:
£/'2 _ а (и) = р («) -*- К2 = а = const,
ибо функция независимого переменного и не может быть равна функции
другого независимого переменного v.
Отсюда
b = jYa{u)-\-adu±:fyv(v) — a dv (13)
и уравнение геодезических линий в конечном виде:
2^9 Г du г dv , ....
да ~JV«(u) + a~+~JvY(vr^a~ ' (
Заметим еще, что угол 9 с геодезической линией и теперь опреде-
, fi dv
ляется уравнением щЬ = —у следовательно
Р {v) cos2 б — a (a) sin* 6 = а. (15)
Частный случай поверхности Лиувилля — поверхность вращения,
геодезические на которой мы уже рассматривали.
Другим примером могут служить поверхности 2-го порядка.
Рассмотрим поверхность 2-го порядка
а ' b ' с v '
и систему софокусных поверхностей
я + Х^& + Х ' с+Х"
или, освобождаясь от знаменателя,
(а + ЩЬ+Х)(с + Х)-хЧЬ + \)(с + \)-?(а + Щс + У)-
— *»(<* +X) (& + *) = О-
Если иметь в виду, чго один корень этого уравнения относительно "к
есть 0 [он соответствует самому данному уравнению (а)], а два другие
обозначить через — и и — v, то можно положить
X(X-f-M)(* + tO=(a + X)(& + X)(c-f*)— х*(Ь + Х)(с + \) —
-У2 (а + X) (с + X) - ^ (в +Х) (6 + X).

ПОВЕРХНОСТИ ЛИУВИЛЛЯ
133
Полагая в этом тождестве Х = —а, или Х = —- £, или 1 = — с, получим:
„ _ aj^a-j^ja-^ 2 _ Ъ(Ъ - и) (Ь - у) л_с(с — и){с — у) ,м
л ~ (а~Ь){а-с) > у — {b-a)(b-cf> Z ~ ~V=a) (с=Ц* W
ds2 z=z(u_y\ I Ц^2 vdv* l
1 ' \4 {a — u) (b — и) (с — и) 4(a — v){b — v){c — v)j>
Следовательно на поверхности 2-го порядка линии кривизны образуют
систему Лиувклля.
Первый интеграл геодезических линий
и sin2 G -\- v cos2 9 = ft = const
или
(и - ft) sin* б -f (v — ft) cos2 9 = 0, tg 9 = |/^^£-f.
Мы видим, что 9=0 при v = k и 9= со при u = k. Так как 9 есть
угол с линией и, то геодезическая ft касается линии кривизны v = k
и u = k.
Через каждую точку (и, v) проходят
две геодезические с этим значением ft,
равно наклоненные к линиям кривизны.
Рассмотрим для определенности эллипсоид
и пусть я > Ь> с. Тогда а > и > Ь,
Ь > v > с как это видно из формул (Ь).
Так как, очевидно, величина ft должна
заключаться между и и v, то всегда
а > ft > с.
1°. Если ft = a, то геодезическая
совпадает с линией кривизны я = а, т. е. д: = 0.
2°. я < ft < £, все геодезические
огибаются линией кривизны u = k.
Эта линия кривизны состоит из двух замкнутых частей, между
которыми протекают все эти геодезические линии. В этой области нет точек
округления, которые, очевидно, соэтветсгвуют значению u = v = b.
3°. b > ft > с; то же с заменой линии « = ft на линию v = k.
4°. k-=.b\ все геодезические проходят через точки округления « =
= v = b.
Следовательно точки округления соединены со геодезических линий.
Так как через всякую точку М (черт. 22) проходят две геодезические
с этим значением ft, равно наклоненные к линиям кривизны, а линии
кривизны — геодезические эллипс и гипербола, то следовательно точки
округления А и В — фокусы этих геодезических эллипса и гиперболы.
Возьмем одну какую-нибудь линию кривизны и пусть она будет
геодезическим эллипсом для фокусов А и В\ тогда она будет наверно
геодезической гиперболой относительно фокусов А1 и В' (ибо разделяет их) *)
*) Д В, А' и В' — четыре точки округления эллипсоида,

134 ГЕОДЕЗИЧЕСКИЕ ЛИНИИ.— ГЕОМЕТРИЯ НА ПОВЕРХНОСТИ
Следовательно для любой точки ее
MA -\-МВ — const
MA1 — MB = const
MA -\-MA' — const
Мы получили, что сумма двух отрезкбв одной и той же геодезической
линии, соединяющей две точки округления А и А' и проходящей чергз
точку М, постоянна, т. е. не зависит от того, где мы возьмем точку М
на выбранной линии кривизны.
Отсюда длины геодезических, соединяющих две точки округления, все
равны ме/кду собой, и, очевидно, каждая такая геодезическая делится
точками округления пополам.
Такие две точки называются сопряженными точками на поверхности.
Точки округления — сопряженные точки эллипсоида.
13. Геометрия на псевдосфере. Мы видели, что только
поверхность постоянной кривизны может налагаться сама на* себя любой
точкой и направлением на любую точку и направление. Поэтому только
на поверхности постоянной кривизны возможна теория конгруэнтных
фигур.
В основу исследования геометрии на псевдосфере *) кладется (Клейн)
конформное отображение псевдосферы на плоскость.
Если линейный элемент2) псевдосферы
ds*~du2 + eRdv2, (а)
а плоскости
ds* = dx*Jr dy2,
то, очевидно, изображение будет конформным, если положить
и
dx = dv, dy = e Rdu,
т. е.
U
y = Re~*} v = t/. (b)
Очевидно, у всегда положительно, т. е. псевдосфера отображается на
положительную полуплоскость. Ось у = 0 мы будем называть
предельной прямой; ей соответствуют бесконечно удаленные точки
псевдосферы (и = со).
Геодезические линии на псевдосфере как на поверхности вращения
определяются уравнением (6), если в нем положить
и
\/l-\-f'2(r)dr = du и г=еП:
J) На черт. 12, стр. 46 даны три поверхности вращения постоянной
отрицательной кривизны, из которых средняя есть псевдосфера. См. также табл.
в конде книги.
2) Этот линейный элемент получится из линейного элемента (13) гл. II,
стр. 45, если положить
и
г = е*у
R=za~b —радиус псевдосферы.

ГЕОМЕТРИЯ НА ПСЕВДОСФЕРЕ
135
а в изображении
или
Следовательно геодезические линии изображаются окружностями
ортогональными к предельной прямой. Отсюда через всякие две точки,
псевдосферы проходит одна и только одна геодезическая линия.
Пучок геодезических линий изображается пучком окружностей с
центром на оси абсцисс; ортогональные к ним траектории — второе
семейство кругов. Обратно: ко всякому кругу на плоскости можно провести оо1
ортогональных кругов с центрами на оси абсцисс. Следовательно круги
Дарбу изображаются кругами на тоскости; и обратно: всякий круг
на плоскости изображает линию постоянной геодезической кривизны.
Геодезическая кривизна круга
определяется для линейного элемента
rf5' = f (rfx' + tfy*)
в виде1)
-L — 1*
9,-R'e'
Отсюда все геодезические круги делятся на три категории.
1°. — > •#> & > с- Круг не пересекается с осью абсцисс (черт. 23).
Строим пучок ортогональных к нему окружностей с центрами на оси
абсцисс. Так как ось абсцисс пересекает все круги пучка под прямым
углом, то она вместе с заданным кругом входит в состав второго пучка.
Они не пересекаются, следовательно второй пучок эллиптический (без
общих точек), а первый гиперболический (с общими точками). Два
центра его (общие точки окружностей) лежат по разные стороны оси
абсцисс. Центр на положительной полуплоскости изображает точку
пересечения геодезических, изображаемых кругами первого пучка, т. е. центр
геодезической окружности, изображаемой первым кругом.
*) Н* трудно подсчитать, если принять х и у за криволинейные координаты
на псевдосфере, связанные с прежними параметрами и и v уравнениями (Ь).
Искомая геодезическая кривизна нашего круга определяется по формуле (8),
dy dx Л 1
?<уда вд?о подставить 0 = arctg -—, dv = -, г = 0, гг = —.
dx y — b у

136 ГЕОДЕЗИЧЕСКИЕ ЛИНИИ. — ГЕОМЕТРИЯ НА ПОВЕРХНОСТИ
2°. — =~о, Ь = с. Круг касается оси абсцисс (черт. 24). Все круги,
ортогональные к нему и к оси абсцисс, проходят через их точку
касания. Эта точка касания изображает центр геодезического круга;
следовательно центр геодезического круга с. кривизной -^ лежит в
бесконечности {предельный круг геометрии Лобачевского).
R
Черт. 23.
Черт. 24.
3°. — < ^, b < с. Круг пересекает ось абсцисс (черт. 25). Второй
пучок гиперболический, а следовательно первый — эллиптический.
Геодезические, ортогональные к геодезическому кругу, не имеют общей точки
(круги с мнимым центром).
Около всякого треугольника можно описать круг, ибо тремя точками
определяется на плоскости окружность, но описанный геодезический круг
может оказаться предельным или иметь мнимый центр.
Геодезические линии, проходящие через< данную точку и
пересекающие данную геодезическую линию, изображаются кругами, с центром на
оси абсцисс,
проходящими через данную
точку.
Пусть даны точка С
(черт. 26) и
геодезическая линия PQ, которая
изображается кругом,,
пересекающим ось
абсцисс в двух точках А
и В. Через каждую из
этих точек и через
точку С проходит по
окружности, ортогональной к
Черт. 25.
оси абсцисс. Эти окружности изображают те две геодезические линии,
которые пересекают геодезическую АВ в бесконечно удаленных
точках А и В (черт. 26). Геодезические СА и СВ называются
параллельными линии Pg. Круги, проходящие внутри угла АСВ, пересекают
окружность А В, круги, проходящие в смежном углу, не пересекают.

ГЕОМЕТРИЯ НА ПСЕВДОСФЕРЕ
137
То же можно сказать о геодезических, проходящих через точку С
Угол геодезических
АСВ
= а называется углом параллельности.
Чтобы определить его, отобразим плоскость (ху) переобразованием
обратных радиусов-векторов (инверсия) на плоскости (xf, у) (черт. 27).
Центр инверсии поместим во втором центре пучка окружностей САУ СВ.
Тогда весь этот пучок окружностей изобразится пучком прямых с
центром в точке с — изображением точки С;
ортогональный к нему пучок окружностей и
ось абсцисс перейдут в семейство
концентрических кругов с центром в g. Круг АБ
изображается кругом abt пересекающим
предельный круг в точках а и Ъ.
но
Черт. 27.
В силу конформности изображения
£_АСВ — l_acb = 2а. Из чертежа видно
ac* + ag*=gd*t
ac=l, ag = tg<x, gc = gp-\-pc = tga+pc.
Следовательно
1 + tg2« = (tg « + /*)*. (a)
Это отображение можно получить, непосредственно отображая полярную
геодезическую систему координат на псевдосфере
ds* = du* + R*
на полярную систему на плоскости
eR —е
U \ 2
"W
dv2
Полагая
dr
ds2 = dr2 + r2df
2du
(и и \'
Следовательно
Внося это в уравнения (а), получим:
l+tg*a=(tga+th£)
ctg a = sh -^ .
eR — e R .< и
eR _i_ e R

138 ГЕОДЕЗИЧЕСКИЕ ЛИНИИ. ГЕОМЕТРИЯ НА ПОВЕРХНОСТИ
Здесь и — расстояние по геодезической линии от точки С до
геодезической АВ.
Упражнения.
1. Центр геодезической кривизны кривой L на поверхности (М) есть точка
пересечения оси кривизны кривой L с касательной плоскостью к поверхности
(М) в рассматриваемой точке.
2. Формула Лиувилля:
к= _J Нэ« | * /^Л д (¥К)\.
YEG-F2\dudv~r ди \ ри )~*~dv \ pv ))
К—гауссова кривизна поверхности, ри и pv— радиусы геодезической кривизны
параметрических линий и и v и <о — угол между ними.
Если —=z а, —=6 постоянны, то эта формула принимает вид:
Pa Pv
К = — -Дг- (я2 + &8 + 2д& cos <о).
Отсюда только на поверхности постоянной отрицательной кривизны существует
два семейства кругов Дарбу, пересекающихся под постоянным углом.
3. Если к линии L на поверхности (М) в какой-нибудь точке ее М0
провести касательную геодезическую g и от точки М0 отложить по линии L дугу
М0М! = h и по геодезической g дугу — М0М2 = Л той же длины, то геодезическая
кривизна — кривой L в точке М0 есть предел отношения
Р* 1 г 2d
Pg Л-*0 Л2
где d—MxMt есть расстояние (на поверхности) между концами отложенных
дуг Мг и Af2.
4. Радиус геодезической кривизны параллели поверхности вращения равен
отрезку касательной к меридиану между Точкой касания и осью поверхности
(развернуть на плоскость, касающую вдоль параллели развертывающуюся
поверхность).
5. Равенство нулю скобки Кристоффеля
{УН
— необходимое и достаточное условие для того, чтобы координатные линии и были
геодезические.
6. Поверхность (М1) отображена геодезически на поверхность (М), если
установлено взаимнооднозначное соответствие их точек М' и М так, что
геодезические (ЛГ) соответствуют геодезическим поверхности (М).
Теорема Бельтрами. Только поверхности постоянной кривизны
геодезически отображаются на плоскость.
Геодезическое отображение плоскости на плоскость есть подобие.
Теорема Дини. Если поверхность {М') геодезически отображается на
поверхность (М), то обе принадлежат к классу поверхностей Лиувилля. Главные линии
(см задачу 12, гл. II) в этом отображении на той и другой поверхности—
система геодезических эллипсов и гипеобол.
Всякая поверхность Лиувилля отображается геодезически на оо1 других
поверхностей Лиувилля.
7. Поверхность, обладающая семейством геодезически параллельных кругов
Дарбу, налагается на поверхность вращения, причей геодезические окружности
переходят в параллели.
8. Если линия L, пересекающая все образующие линейчатой поверхности,
обладает двумя из следующих трех свойств: Г быть геодезической, 2е быть
линией сжатия и 3е пересекать образующие под посеянным углом, то она
обладает и третьим.
9. Линия сжатия линейчатой поверхности есть геометрическое место точек
где равна нулю геодезическая кривизна ортогональной траектории образующих

УПРАЖНЕНИЯ
139
10. Если на развертывающейся поверхности, образованной касательным»
к кривой Г, провести произвольную геодезическую g и в каждой точке Г
посроить прямую / параллельно касательной g в тичке, лежащей на одной с ней
образующей, то прямая / опишет линейчатую поверхность, на которой Г служит
одновременно и линией сжатия и асимптошческой
11. Ьсли одно семейство линии кривизны состоит из геодезических линий,
то все они конгруэнтны, и поверхность (surface moulure) образована движением
неизменной линии, лежащей в плоскости, когда эта плоскость катится без
скольжения по разве тывающейся поверхности.
12. Поверхность Фосса (Voss) обладает сопряженней системой, состоящей
из геодезических линий Ома может непрерывно изгибаться с сохранением этой
сопряженной системы <главн е основание Фосса).
Поверхности вращения Фосса определяются в квадратурах.
Единст енная минимальная поверхн сть Фосса с действительным основанием
Фосса — минимальный геликоид. Он обладает оо1 оснований Фосса.
13. В геометрии на псевдосфере радиуса R (кривизна—~-) площадь геоде-
Н
зического треугольника ABC равна
АЛЛ
А = /ез (п-А — В-С),
Л Л Л
где Ау В, С —углы треугольника. Наибольшей площадью kR2 обладает
треугольник, все углы которого равны нулю. Все такие треугольники конгруэнтны.
Формулы псевдосферической тригонометрии радиуса R получаются из
формул сферической тригонометрии того же радиуса заменой R на Ri (где / =
г— а Ь
= У — 1); при этом тригонометрические функции сторон треугольника^-, —
с
-5- переходят в гиперболические (замечание Ламберта).
Если А, В, С— углы геодезического треугольника, а а, Ь, с — его стороны, то
sh_ sh_ sh_
sin A sin В sin С
cos A = sin В sin С ch — — cos В cos C.
К
14. Если (и, v) — геодезическая полярная система координат на псевдосфере
радиуса единицы с линейным элементом
ds* = du? + sh2 и dv^y
то величины
х0 = ch и, хх = sh и cos v, х0 = sh и sin v
суть координаты Вейерштрасса. Они удовлетворяют соотношению
лг02- jtf —лг3з=:1.
Расстояние Ь между двумя точками (х0, хи *2) и (х0'9 хх\ дга') равчо
chB = х0х0' — *i*i' — x2xj.
Линейный элемент
ds2 = dxf + dxf — dx<?.
Уравнение прямой (геодезической)
— &о*о + ?Л + &2*з = 0.
Постоянные вдоль прямой
t dxx t dx2 t __dx0
суть координаты Вейерштрасса прямой; они удовлетворяют соотношению

140 ГЕОДЕЗИЧЕСКИЕ ЛИНИИ. ГЕОМЕТРИЯ НА ПОВЕРХНОСТИ
Угол б двух прямых (£0, 6i, ?2) и ft/, 6/, 1з') равен
COS 6=^' + ^' -Wo'-
Прямые параллельны (в неэвклидовом смысле), если
еА' + еа5а'-е0ео' = ±1.
15. Поверхность вращения [Цолль (Zoll)] с меридианом, заданным в
параметрической форме,
Л/ з
* = cosyj, z=z I у (1 +ycos4 YjSinv])* — sin 2-/) Л),
о
есть замкнутая поверхность, обладающая зоной с отрицательной кривизной, и
имеет все геодезические замкнутыми.
16. Поверхность вращения Таннера (груша) имеет меридиан
* = cosy], z = 4^1-cos y + sln^-j, —y<ri<y.
Геодезические пересекают каждую параллель в двух точках и совершают два
обхода около поверхности прежде чем замкнуться.
17. Поверхность с линейным элементом
ds* = (2 — Ф — V2) (du* + dv*)
изображается на плоскости (и, v) так, что геодезические переходят в эллипсы
с центрами в начале координат.
На какой из поверхностей вращения с этим линейным элементом
геодезические замкнуты?
18. Формула Лягерра. Для всех кривых на поверхности, с общей
касательной в датой точке выражение
, /Q <*р . 2 \ sin «pi d I 1 \
где ср — угол между главной нормалью и нормалью к поверхности, имеет одно и
то же значение.
19. Если из данной точки М0 провести пучок геодезических линий и
отложить на них от точки М0 постоянные дуги MqM = г, то геометрическое место
точек Л1— геодезический круг (Гаусса-Бианки). Если L — длина этой окружности,
a F— его площадь, то
3 2тгг — /
Ко = Ит =■ з— (Бертран и Пюизе, 1848),
Ko=\im=z~ -L—L (Диге, 1848),
r«o * r
где j(0 — гауссова кривизна поверхности в точке М0.

ГЛАВА ШЕСТАЯ.
Минимальные поверхности.
1. Поверхности с наименьшей площадью. К минимальным
поверхностям естественно приводит задача: дан контур £, найти поверхность,
проходящую через линию L так, чтобы ее площадь была наименьшей.
Пусть поверхность (М) есть решение задачи. Отложим на нормали
бесконечно малый отрезок
где е — бесконечно малая величина и ср — произвольная функция,
подчиненная единственному условию (кроме непрерывности, диференци-
руемости и т. д.), что на контуре L она обращается в нуль.
Мы получим, таким образом, новую поверхность (М')
M' = M + qn,
где я, как всегда, единичный вектор нормали поверхности (М).
Линейный элемент поверхности (Ж')
dM'2 = {dM + qdn-\-~ndq)2 =
= dM2 + 2q dM dn+ q2 dn2 -\- dq2,
члены п dM, ndn пропали как произведения перпендикулярных
векторов и п2= 1.
Заменяя еще
dM2 = ds* =zEdu2-\-2Fdudv-f- Gdv2,
— dMdn = D du2 + 2D'du dv + D"dv2
и ограничиваясь первой степенью бесконечно малого q} имеем:
dM'2 = {Е— 2qD) du* -f- 2 (F — 2qD') du dv+(G — 2qD")dv*.
Откуда, пренебрегая членами, содержащими q2, получим^
Е' G — F'2 = EG — F2 — 2q (DG -f D"E — 2FD') =
1

142
МИНИМАЛЬНЫЕ ПОВЕРХНОСТИ
где, разлагая [\-\-2qH\ по биному Ньютона, мы попрежнему
ограничиваемся первой степенью qt и
н_ 2FD' - ED" - GD
EG — F*
— средняя кривизна поверхности.
Площадь поверхности (М% если еще заменить q = t<f, равна
ffVE'O' — F'2 du dv =j jVEQ — F*du dv + e j f cptf VEG—F2du dv.
Отброшенные члены содержат по крайней мере е2. Меняя знак е, мы
увеличим или уменьшим площадь, следовательно, для того чтобы
поверхность (М) давала минимум площади, необходимо
£>G-f D"E — 2FD' = 0. (1)
Средняя кривизна во всякой точке поверхности должна равняться нулю.
Поверхности с средней кривизной, равной нулю, называются
минимальными поверхностями.
Конечно, условие (1) не является достаточным. Подобно тому как
геодезическая линия не всегда дает минимум расстояния между двумя
точками на поверхности (несколько геодезических через две точки), так
и минимальная поверхность может не осуществить минимум площади
для данного контура. Исследование достаточных условий здесь труднее,
так как мы имеем дело не с простым, а с двойным интегралом.
Задаче, которую мы сейчас разбирали, можно дать физическое
решение, основанное на свойствах поверхностного натяжения жидких
пленок. Если изготовить контур Z,, состоящий из одной или нескольких
кривых в виде проволочного каркаса и обмакнуть его в мыльный
раствор, то на проволоке образуется мыльная пленка. В силу
поверхностного натяжения пленка стремится сжаться, а потому принимает форму
минимальной поверхности (опыт Плато).
На табл. в конце книги дана фотография пленки, имеющей
контуром две окружности. Она принимает форму катеноида — минимальной
поверхности вращения.
2. Основные свойства минимальной поверхности. Условие (1)
сейчас же позволяет получить целый ряд свойств, характеризующих
минимальную поверхность; часть из них мы имели уже ранее.
1°. Главные радиусы кривизны равны по абсолютной величине и
обратны по знаку. Отсюда следует, что индикатриса Дюпена —
равносторонняя гипербола.
2°. Следовательно асимптотические линии перпендикулярны. Это
вытекает и из уравнения (1), ибо при D = 0 и D" = 0 оно дает F = 0.
Оба свойства характерны для минимальной поверхности.
3°. Асимптотические линии на минимальной поверхности и в ее
сферическом изображении образуют изотермическую систему [см. (18),
§ 17, гл. IV, стр. 111]:
ds^_=\(du^ dv*\
— dndM — — 2du dvf (2)
ds'* = Y(du2 + dv2y

формулы монжд 148
4°. Сферическое изображение конформно. Непосредственно вытекает
из формулы (2). Это свойство кроме минимальных поверхностей
принадлежит сфере.
5е. Линии кривизны образуют изотермическую систему.
Заменим в формулах (2) и, v на новые переменные а и р
а+Р а—3
И=-т=- V = -
V~2 Y~2 '
мы получим
ds2 = 'k(da*-{-d¥)y —dndM= — (do? — d^\ ds'2 = ±(da* + dp), (2')
где/С=^ — кривизна поверхности. Мы видим, что координатные линии
а = const, Р = const сопряжены (нет члена с произведением dec d$ во второй
квадратичной форме) и ортогональны (нет члена с произведением d<xd$
в линейном элементе), следовательно это — линии кривизны; они
образуют изотермическую систему и на поверхности и в сферическом
изображении.
Обратное предложение неверно. Существует целый класс
изотермических поверхностей, на которых линии кривизны образуют
изотермическую систему; среди них можно отметить поверхность вращения,
центральные поверхности 2-го порядка, поверхности с постоянной средней
кривизной (не равной нулю).
6°. Линии нулевой длины сопряжены. Действительно, если отнести
поверхность к линиям нулевой длины, то
£ = 0, 0 = 0 (а)
и тогда уравнение (1) дает
D' = 0.
Это свойство характерно для минимальных поверхностей.
7°. Сферическим изображением линий нулевой длины служат линии
нулевой длины на сфере (мнимые асимптотические линии сферы), ибо из
условий (а) сейчас же следует [см. (13), § 14, гл. IV, стр. 107]
* = 0, ^ = 0.
3. Формулы Монжа. Отнесем поверхность к линиям нулевой длины.
Имеем:
£=0, 0 = 0, D' = 0,
т. е.
ЛЙ = 0, ЛИ-0, Muvn = 0. (b)
Диференцируя первое уравнение по v, второе по и, получим:
MaMuv = о, MVMUV = 0.
Проекции вектора Muv на три направления равны нулю; и сам
вектор Muv равен нулю
Muv=0. М = Р (и) -f Q(v), (3)

144 МИНИМАЛЬНЫЕ ПОВЕРХНОСТИ
при этом первые два уравнения (Ь) дадут
Р1 = 0, Ql=0. (3)
Уравнение (3) показывает [Ли (S. Lie)], что минимальная поверхность
есть поверхность переноса. Согласно уравнениям (4) две образующие
кривые— мнимые линии нулевой длины (минимальные линии в
пространстве).
Следовательно минимальную поверхность можно получить, как
геометрическое место сргдин хорд, соединяющих точки двух минимальных
кривых (Р) и (Q).
Уравнению (4) можно удовлетворить, если положить
Р = { и, Г(и)9 if ]/l+f2{u) du),
и аналогично для Q. Получаем, таким образом, формулы Монжа
X = и -|- V,
3>=/(и)+ ?(*>),
г = / J |/l-}-/'2(«) du + / /l/l+>'2W dv\ (5)
каковы бы ни были произвольные функции /(«) и <р(^)> они определяют
минимальную поверхность.
4. Формулы Вейерштрасса. Мы видели, что линии кривизны на
минимальной поверхности и в сферическом изображении образуют
изотермическую систему, а любую изотермическую систему на сфере можно
получить, если взять аналитическую функцию от комплексного переменного
на сфере и рассмотреть отдельно действительную и отдельно мнимую
часть ее.
Итак, берем сферу, отнесенную к меридианам и параллелям:
х = sin <р cos ф, у = sin <р sin ф, z = cos <р; (а)
ее комплексное переменное (см. гл. II, § 18, стр. 56)
t = ctg-|-A
Следовательно
определяет сферическое изображение линий кривизны а, (3 минимальной
поверхности. Линейный элемент 1) сферы, отнесенной к этим линиям,
1) w0 = a — /р, т0 = ctg —- е *"" '* — сопряженные комплексные величины
для w и т. Очевидно dw dw0 = (da + / d$) (dz — id$) =z(da*-{- d^).

ФОРМУЛЫ ВЕЙЕРШТРАССА
145
должен быть равен линейному элементу, вычисленному да уравнения (а) *)
Следовательно
dw dw0 . dzdi0 . dw dwp (xtq + 1)2
* — 0*6 + I)2' ~dz dz0 4 '
Здесь /C = —-p —кривизна поверхности, следовательно X и —X —
два главных радиуса кривизны и по формулам Родрира:
Это позволяет определить поверхность (М) в квадратурах.
Действительно, очевидно
дп дп , дп дп . / дп дп \
да dw^dw0 * д$ \dw dwj'
Следовательно
или, внося сюда значения X по формуле (Ь),
,АЛ dw dw0 (хх0 + I)3 Г &п j > &п ^ 1
dM = -г- -rr ^—^—- -г- dw0 + jr—dw 1 =
dz dz0 4 L &w д™о J
_ (ttq+1)2 Гдп{4щ>\* .дп (dwy.l
~ 4 [^fe/^+^^/^J-
Вносим сюда по формулам (а)
я = {sin? cosф, sin? sin ф, coscp}={^±^) -i~£j. ^\].
Обозначая
получим
здесь/^ (t^—сопряженная функция для Z7^).
dz Ф </ф
£a = -JL-**fc ** = **.£.
to sin <p 2

*4£ МИНИМАЛЬНЫЕ ПОВЕРХНОСТИ
Формулы (6) дожно получить быстрее, полагая в формулах Монжа (3)
р.={4<1-т«)/чт)*, ^o+^wi. ^wS}. w
Q„={-^ (i - V) f (V J, -1 (i + V) ^oW £, ^o(*o) £}
что, очевидно, удовлетворяет уравнению (4).
Линейный элемент поверхности (6) и главные радиусы кривизны ее
равны
ds* = («о + 1У F(x) F0 (х0) tfx dx0,
x_(2a±lZ.//r(t)/?e(toj. (7)
Линии кривизны получатся, если приравнять постоянному отдельно
действительную и мнимую части функции
Формулы (6) можно написать без знака интеграла, если заменить
/Чт)=/"(т)
и проинтегрировать по частям. Обозначая буквой R действительную
часть функции комплексного переменного, получим:
х = Я{(1 - х2)/" (х) + 2х/ (х) - 2/(т) } f
j=/?{ /(1+х2)/'(х)-2«/(т) + 2*У(х) ) } («')
z = tf{2x/"(x)-2/'(x)}.
( х), очевидно, тоже произвольная аналитическая функция от т.
5. Односторонние минимальные поверхности. Мы видим, что
каждая функция комплексного переменного F(t) определяет минимальную
поверхность и ее расположение вплоть до переноса в пространстве. Не
может ли случиться, что две разные функции определят одну и ту же
поверхность?
Пусть F(z) и Рх(?) —две такие функции, hxhxi соответствующие
значения переменных. Так как нормали по условию должны быть
параллельны *), то и комплексные переменные в изображении на сфере должны
быть или равны
или обратны по величине и знаку, если нормали противоположно
направлены 2)
1^
*) Мы рассматриваем здесь одну и ту же минимальную поверхность,
различным образом повернутую, как две различные поверхности.
2) т0 - ctg ?- е **, v= = — tg — е ~ '+ — ctg (^ + — ) е "'' , точки ф,
0 s 2 ' * хо ь 2 Б \ 2 ^2 /
ф и *+<р, ^ противоположны на сфере.

ОДНОСТОРОННИЕ МИНИМАЛЬНЫЕ ПОВЕРХНОСТИ
147
В первом случае формулы (6) дают полное тождество
Л (т) = />(*)
во втором
В самом деле,
(»)
и следовательно, например, третья формула (6) даст
т, F (т,) rftj = т0 F0 (х0) <*т0,
т. е.
^w-;;^oW=-^o(g.
1
Заменяя здесь т, = через т и следовательно т0 через — -,
прямо получим формулу (а).
Нетрудно проверить, что все три формулы (6) совпадают для двух
функций
F(t)HF,(T) = -If0(-I).
Если обе эти функции равны между собой
(8)
1
то, очевидно, область поверхности окрло точки тх = или прямо
совпадает с областью около точки т или совпадает после переноса.
В последнем случае поверхность совпадает сама с собой вся после этого
переноса, следовательно она периодична и
необходимо трансцендентна. Если поверхность
алгебраическая, то такая периодичность исключена; еле- j
довательно имеет место первый случай: две точки
1
их совпадают, а нормали к поверхности прямо
противоположны.
Опишем на сфере непрерывный дуть от точки т к
диаметрально противоположной ей точке xt = ;
точка М на поверхности опишет тоже непрерывный
путь по поверхности и вернется в ту же точку, из Черт. 29.
которой вышла, но уже с другим направлением
нормали. Следовательно непрерывным движением можно перейти с одной
стороны нашей поверхности на другую. Поверхность имеет только одну

148 МИНИМАЛЬНЫЕ ПОВЕРХНОСТИ
сторону *). С. Ли называет такие поверхности двойными минимальными
поверхностями.
Обозначим
т«/Чс) = ?(т);
тогда уравнение (8) примет вид:
?W = -?o(-t)- (8'>
Всякое решение этого уравнения дает минимальную поверхность или
периодическую или одностороннюю. При этом <р0, как
всегда—сопряженная функция для <р.
1) Геликоид. Простейшее решение уравнения (8') 2)
ср(х) = /,
откуда
^)=4„/(т)=/[-1пт+1]т.
Следовательно по формулам (6')
x=.r{— (1^-т2)-1 — 2тПпт — 2т/(1 — 1пт)1,
_у=/?|(1_|_т2)1— 2Tint — 2т (1 — 1пт)(,
z=R{ — 2t\ + 2ilm:},
или, полагая т = г е'9,
x=(r — 7)sin<p, y = (r—j)cos<?,z = — 2<f,
X , z
—=-<вт-
Поверхность (геликоид) — трансцендентная, периодическая (допускающая
движение в себе).
2) Поверхность Геннеберга 3)—простейшая минимальная
односторонняя поверхность. Она соответствует решению уравнения (8'):
<р(т) = 6 ( т* - ±), F(r) = 6(1-1), тЦ!±^»,
*) Простейшая односторонняя (не минимальная) поверхность — лист Мебиуса.
Один конец пряыоугольной плоскости бумаги поворачиваем на 180° и
соединяем со вторым. Очевидно, совершив один обход, мы придем в ту же точку
с другой стороны поверхности (см. черт. 29).
Поверхность третьего порядка
лг»(1 — z) = zy*
представляет ту же особенность (Смит). Если в плоскости (ху) перейти к
полярным координатам x = rcos <р, y = rsincp, то уравнение поверхности примет вид
z = cos2 <р.
Это прямой коноид: прямая пересекающая ось z ортогонально поворачивается
около нее, подымаясь и опускаясь от z = 0 до z=l. Обход, переводящий на
другую сторону, должен пересекать ее двойную линию дг = 0, у = 0.
2) Очевидно <ро (т) = —i-
3) Sehiling, Die Minimalflachen funfter Klasse mit dem Stereosc*p-Bil4
eines Modelles derselben, 1880.

ИЗГИБАНИЕ МИНИМАЛЬНЫХ ПОВЕРХНОСТЕЙ
149
откуда
*=3(«+ii)+a(v+^,)
поверхность алгебраическая 15-го порядка.
Линии кривизны и асимптотические линии — алгебраические линии.
в. Изгибание минимальных поверхностей. Если минимальная
поверхность S изгибается, оставаясь минимальной поверхностью, то в
соответствующих точках ее главные радиусы кривизны сохраняют свои
величины, ибо не меняется гауссова кривизна, т. е. их произведение, а
их сумма всегда равна нулю.
Следовательно совпадают не только линейные элементы двух
поверхностей, но и линейные элементы их изображений на сфере. Поэтому
сферические изображения их конгруэнтны или симметричны. Случай
симметричности можно исключить: он приводится к первому, если у одной
из поверхностей изменить направление нормали.
Следовательно налагающиеся минимальные поверхности можно
привести в такое положение в пространстве, что нормали в соответствую-
щих точках будут параллельны.
Так как линейные элементы равны и переменные тит0 одной
поверхности совпадают с переменными другой, то
F(x)F0(x0) = F*(t)F0«(x0\,
а так как F и F0 сопряжены и следовательно модули их равны, то и
модули F и F* не могут быть различны, и мы можем положить
F*(x)=e"F(x), (9)
где а — действительное, постоянное число.
С другой стороны, какое бы постоянное значение не давать а, две
поверхности, вейерштрассовские функции которых связаны равенством (9),
имеют равные линейные элементы, следовательно налагаются. Меняя а
непрерывно, получим непрерывное семейство налагающихся минимальных
поверхностей.
Минимальные поверхности (8) называются ассоциированными
минимальными поверхностями Бонне.
Мы видели, что линии кривизны минимальной поверхности получатся,
если приравнять постоянному отдельно действительную и отдельно
мнимую части функции
w = и -J- iv = J l/2/7(x) dx.
После изгибания мы получим новую функцию
V2eiaF(x)dx=:eJ j V2F(x)dx = e^ w,
* о .о,./.о, о\
w*= и cos у — vsin у + l [usm~£-\~vcos-2 I.

150
МИНИМАЛЬНЫЕ ПОВЕРХНОСТИ
Следовательно линии кривизны на поверхностях определятся уравнениями;
на первой
и = const, v = const,
на второй
и cos у — v sin у = const, и sin -у -J- v cos у = const.
Так как на линиях кривизны и и v — изотермические параметры, то,
очевидно, линии кривизны при изгибании поворачиваются на угол ~.
Если а = -=-, то линии кривизны повернутся на 45е и совпадут
с асимптотическими линиями, которые на минимальной поверхности
всегда делят пополам углы между линиями кривизны.
Такая поверхность называется присоединенной поверхностью Бонне.
Так как
то присоединенная поверхность определяется уравнениями
x0 = Rfl(l~^F(T)dx,y0=-Rf(l+^F(x)<k9
*0 = */2/т/Чт)Ж, (10)
а так как при любом значении а
F*(x)=£^F(x) = F{x)cosa^iF(x)sinat
то координаты точки любой ассоциированной поверхности получаются
по формулам
М* = М cos a -f- Mq sin a , (11)
где M, M0 и Ma — радиусы-векторы соответственных точек заданной
минимальной поверхности ее, присоединенной и ассоциированной.
Мы видим, что с изменением а при изгибании поверхности всякая
точка ее М* описывает эллипс.
7. Формулы Шварца. Из уравнения (11) следует
dMa = dM cos a -{- АИ0 sin a,
dM* = dM2 cos2 a -f- 2 rfAf <Ш0 sin a cos a -f- rfAf02 sin2 a,
а так как этот линейный элемент, очевидно, не зависит от а и равен
линейному элементу dM2, то
dM*=zdM02HdMdMo = 0. (12)
Эти формулы, конечно, непосредственно вытекают из уравнения (10); они
показывают, что соответствующие линейные элементы минимальной
поверхности и ее присоединенной ортогональны.
Добавим теперь еще очевидное равенство
ndM0 = 09 (12')

ФОРМУЛЫ ШВАРЦА 151
которое показывает, что нормали обеих поверхностей параллельны, и
мы получим формулу
dM0 — dMXn. (13)
В самом деле, вектор dM0 перпендикулярен к обоим векторам dM
и л, как это показывают формулы (12) и (12'), а отсюда вытекает
равенство (13) вплоть до скалярного множителя, но в силу
перпендикулярности dM и п скаляр векторного произведения их равен
произведению скаляров dM и п, и так как п есть единичный вектор, а скаляр
dM равен скаляру dM0 в силу первого уравнения (12), то равенство (13)
устанавливается вплоть до знака.
Итак,
*о = f(Z4y — У dz)9 у0 = f(X dz-Z dx),
z0 = f(Ydx-Xdy), (130
где принято М={х, у, z}, л= {х, Y, Z) .
Заметим, что из формул (10) сейчас же вытекает, что y*f и М0 —
действительная и мнимая части той функции комплексного переменного
2Р(и), которая входила в формулу Монжа (3).
Действительно, очевидно,
x + i*0=/(1-t*)/*(t)A, J> + 0*> = '/0+t»)F(T)*,
z-\-izQ=f2%F(x)dx.
Если это сравнить с формулой (3'), то немедленно получим:
М -f Ш0 = 2Р (и), М — Ш0 = 2Q (v),
где можно положить н = т, *> = т0 и рассматривать их как независимые
переменные.
Отсюда сейчас же вытекает данное Шварцем решение задачи:
провести минимальную поверхность через заданную линию L с заданными
вдоль L касательными плоскостями.
Если вдоль кривой L заданы векторы Жил, т. е. даны 6
функций х9 у, z, X, Y, Z от параметра t, то формулы (13') определят
вдоль L функции х0, у0, z0; мы получим две кривые (Р) и (Q) —
формулы
и поверхность (М) по формулам Монжа. При этом мы предполагаем,
что заданные функции М и п — аналитические функции от t, так что
они получат определенное значение и в том случае, если вместо
действительного переменного t подставить комплексное переменное т.
Уравнение поверхности можно записать, как действительную часть функции

152
МИНИМАЛЬНЫЕ ПОВЕРХНОСТИ
комплексного переменного M-\-iM0, т. е. координаты любой точки
поверхности х\ у', zf получатся:
y = fl(x-+-ij (Zdy— Ydz)}t У =/? {y-j-i f (Xdz ^-Zdx)\,
T
zz=zR {z + i j (Ydx — Xdy). (13")
Следовательно минимальная поверхность вполне определена, если
задана линия L и касательная плоскость вдоль этой линии.
8. Следствие из формул Шварца. Из формул Шварца можно
вывести несколько простых следствий.
1°. Пусть линия L — прямая. Повернем поверхность около
прямой L на 180°. Касательные плоскости останутся те же самые, и
следовательно новая поверхность совпадет со своим первоначальным
положением (ибо линия L и касательные плоскости вдоль L определяют
поверхность единственным образом).
Итак, всякая действительная прямая на минимальной поверхности
служит для нее осью симметрии.
2°. Если плоскость пересекает минимальную поверхность ортогонально,
то она служит для нее плоскостью симметрии, ибо можно принять за
ушнию L плоское сечение поверхности, и нормали вдоль L будут лежать
в плоскости. По этим данным поверхность определяется совершенно
симметрично по одну и другую сторону плоскости.
Так как в этом случае главные нормали линии L, очевидно,
совпадают с нормалями к поверхности, то Z — геодезическая линия. Обратно:
плоскость плоской геодезической линии служит плоскостью
симметрии для поверхности.
3°. Если линия L — геодезическая, то нормали к поверхности вдоль L
совпадают с главными нормалями v кривой L. Следовательно, поверхность
определяется по формулам (13"), полагая Lz=z.{ х, у, z} и v= {х, Y,Z\
M=R{l-if(^XdL)} = R{L + if^dx\i
где P = f vX -j-J—.бинормаль кривой Z,, и вместо длины дуги s в
уравнение кривой L подставлено комплексное переменное т. Присоединенная
поверхность (М0) определяется уравнением
На линии (L) вектор L — действительный, и следовательно линия (1+),
оответствующая на присоединенной поверхности линии (L), определяется
уравнением
L0 = f$ds.
Откуда касательная к линии L0 параллельна бинормали L
4^ — 8 ^о_Я
<* ~ р' ds*~ ds

ЧАСТНЫЕ СЛУЧАИ
153
и по формулам Френе для той и другой кривой
Ро Pi'
где ро — радиус кривизны линии (10) и рх — радиус кручения (L).
Итак, у двух соответствующих геодезических линий минимальной
поверхности и ее присоединенной кривизна одной равна кручению
другой.
Отсюда плоской геодезической соответствует прямая линия на
присоединенной поверхности. Например горловой круг катеноида
переходит в директрису (ось z) геликоида.
9. Частные случаи. 1°. Поверхность, налагающаяся на поверхность
вращения. Такая поверхность допускает непрерывное изгибание в себя,,
которое соответствует повороту поверхности вращения около своей оси.
При этом она, конечно, остается минимальной поверхностью.
Следовательно или она совпадает со своими ассоциированными, которые
отличаются от нее только положением в пррстранстве, или при изгибании
она только двигается, оставаясь неизменной (винтовые поверхности),
В первом случае функция Вейерштрасса после изгибания принимает
вид
F%x) = eiaF(x); (а)
но поверхность S* получилась из поверхности 5 поворотом, допустим,
около оси z на угол $; при этом точка (т, т0) перешла в точку
(те ,т0е~ ), ибо в комплексном переменном на сфере x = ctg -|-е долгота
точки на сфере ф увеличилась благодаря повороту поверхности на р.
С другой стороны, при повороте около оси z координата z не изменилась;
следовательно
х^*(т)Л = те*^(«'|,>*Л, F*{x) = J*F{xf). (b>
Исключая F*(x) из уравнений (а) и (Ь), получим:
или, взяв логарифм и диференцируя (и умножая на т),
F(%e#) F(t) '
Следовательно, функция т -~^ не меняется, если аргумент ее т умно-
жить на е .
Прибавляя последовательно р к аргументу х, мы получим (если (S
несоизмеримо с я, что всегда можно выбрать) на каждом круге с центром в
начале, в плоскости комплексного переменного т счетное множество
точек, где функция х -^ сохраняет постоянное значение; в силу
непрерывности она вообще с изменением аргумента не будет меняться и, как
аналитическая функция, будет постоянна на всей плоскости
т F$ = k> F{?> = Сх*> k> С== const-

154
МИНИМАЛЬНЫЕ ПОВЕРХНОСТИ
Все ассоциированные поверхности получаются вращением поверхности 5
около оси z. Формула (с) дает
в = (* + 2)р.
Следовательно при £ = — 2 имеем:
а = 0, F^c) = F(x)9
и поверхность S с изменением (J не изгибается, а скользит по себе.
Формуле (6'), стр. 146, дают тогда
* = /?[с(±+т)], jf = /?[/c(i-t)]t z = — R[2Clnx]
или, полагая
Г—™ Jf - — *-* + **
х = т (cos у ch и cos z/-|- sin у sh и sin v),
у = /я (cos у ch a sin t> -f- sin у sh acos i>),
2 = m (u cos у 4"v sin y)>
все это — винтовые поверхности. При изменении v (аргумент т)
поверхность скользит сама по себе винтовым движением. При изменении у мы
получаем семейство ассоциированных поверхностей, причем у = 0
соответствует катеноиду (поверхность вращения); f = * дает
присоединенный к нему минимальный геликоид.
2°. Единственная минимальная линейная поверхность —
минимальный геликоид (теорема Каталана). Если поверхность S содержит две
прямых с1х и d2, то она симметрична относительно каждой из них.
Следовательно на ней лежит прямая dSi симметричная для d{ относительно d2,
прямая </4, симметричная для d2
относительно dS9 и т. д. Все они
получаются винтовым движением и лежат на
геликоиде^, который имеет следовательно оо*
общих образующих с поверхностью S.
Чем ближе брать образующие d1 и d2
на поверхности S, тем гуще сеть общих
образующих dt\ в пределе они заполнят
всю поверхность, и обе поверхности
совпадут.
3°. Поверхности с плоскими линиями
кривизны. Если линия кривизны —
плоская, то ее плоскость пересекает
поверхность под постоянным углом (теорема
Иоахимсталя); следовательно нормали к поверхности образуют
постоянный угол с перпендикуляром к плоскости и дают в
сферическом изображении круг. Круг, ортогональный к данному кругу на
сфере, очевидно, образован плоскостью, проходящей через полюс 1)
Черт. 30.
*) Полюс плоскости есть вершина конуса, касающегося сферы вдоль линии
пересечения сферы этой плоскостью.

ЧАСТНЫЕ СЛУЧАИ
155
плоскости первого круга. Полюсы плоскостей одного семейства кругов
лежат в каждой плоскости другого семейства. Следовательно каждое
семейство кругов образует пучок плоскостей, проходящих через прямую g%
геометрическое место полюсов другого семейства. Две оси пучков
g и g* (черт. 30)—сопряженные поляры сферы х).
Так как сопряженные поляры сферы перпендикулярны, то мы всегда
можем принять прямые g и g' параллельными осям х и у, а тогда, как
легко видеть, ось z пересекает их в точках (0, 0, ), (О, 0, cos «).
\ COS tX/
Плоскости пучков
X = S^(z — cosa), V=ctgatht/ (z L)
sin a \ /' ь \ COS a/
пересекают сферу в точках
У sin а sin и у sin a sh v ~ cos и -\- cos a ch v
ch v -f- cos a cos и ' ch v + cos a cos и ' ch v + cos a cos и'
Линейный элемент сферы
(ch v -f- cos a cos и)2 '
и уравнения поверхности —
х = и cos a -f- sin и ch v, y = v-\- cos a cos и ch i>, z = sin a cos и ch v.
Сечение плоскостью z = Q содержит бесчисленное множество
конгруэнтных цепных линий, основания которых параллельны оси у. Это линии
кривизны поверхности. При a = -s получаем катеноид.
При а = 0 формулы не годятся. Прямые g и g' касаются сферы,
например в точке (0, 0, 1). Плоскости пучка
X+u(Z— 1) = 0, К + v(Z—l) = 0
пересекаются плоскостями XY в точке (ищ v). Следовательно,
т = и -j- IV,
значит, ш = т и функция Вейерштрасса равна постоянному.
Полагая
получим поверхность Эннепера
х = Зи -f Зи-и2 — и3, j; = 3^ + Зи2 гг — v», г = 3(и* — v2).
Это — алгебраическая поверхность 9-го порядка. Координатные линии —
плоские линии кривизны; их плоскости:
x-\-uz — Su — 2u*=0 и v — vz — 3v — 2vs-—0
параллельны осям у и z\
uJf-v=z const, и — v = const
— асимптотические линии; u — tv пара прямых в плоскости ху.
1) Если и второе семейство линий кривизны — плоское, то оно изображается
на сфере тоже семейством кругов, конечно, ортогональных к кругам первого
семейства. Сферическое изображение линий кривизны минимальной поверхности
образует изотермическую систему, поэтому, если одно семейство состоит из
кругов, то можно доказать, что и другое тоже состоит из кругов. Если
минимальная поверхность обладает одним семейством плоских линий кривизны, то и
второе семейство линий кривизны тоже плоское.

J56 МИНИМАЛЬНЫЕ ПОВЕРХНОСТИ
Плоскости х = О и ^у = О пересекают поверхность по линиям кривизны
и = О, v = 0 и по двойным линиям поверхности
И* = 3(1+^) И !/2=:3(i-f «2).
4°. Поверхности с плоской геодезической линией. Примем плоскость
линии за плоскость ху и пусть уравнение линии
x = x(t), y=y(t)-;
тогда нормаль к поверхности, совпадающая с главной нормалью кривой,
будет
j dy dx п\
n=\-ds> Л'°Г
Формулы Шварца дают
х(*) + хЫ хг_у(*) + уЫ „_П*(*)-*Ы]
л— 2 - , у— 2 , ^— 2
Например, если взять параболу у2 = 2рх в параметрической форме
х = — 2/7 sin2 /, ,у = 2/?/ sin t9
то уравнение поверхности будет
*=/?(—2/> sin* т), jf = /?(2/w'sinx), г = /?^(2т+28,1п^] .
Для действительного значения т получим кривую сечения
поверхности плоскостью xz\ это, очевидно, — циклоида. Она лежит в
плоскости симметрии поверхности, следовательно — тоже геодезическая линия
ее. Поверхность дана Каталаном и носит его имя.
Упражнения.
1. В параметрах линий нулевой длины минимальные поверхности внутренно
•пределены двумя квадратичными формами
d* = -UxVx{%+Vf dado.
— dMdn = Ux du* + К, dv2,
где
2. Если в формулах Вейерштрасса произвольная функция /(-^ —
алгебраическая функция своего аргумента, то и поверхность —• алгебраическая.
3. Показать, что функция
, <„-! + !
определяет периодическую минимальную поверхность.
4. Минимальную поверхность можно рассматривать (С. Ли) как
геометрическое место средин отрезка, концы которого произвольно двигаются по двум
минимальным кривым. Если эти две кривые совпадают, то геометрическое место
средин всех ее хорд есть односторонняя минимальная поверхность.
5. Если две налагающиеся поверхности имеют одно и то же сферическое
иаображение, то одна из них минимальная поверхность, а другая ее
ассоциированная.
Если соответствие изометрии (равенство линейных элементов) есть ц то же
время соответствие ортогональностью линейных элементов, то обе поверхности
минимальные и одна из них есть присоединенная другой.

УПРАЖНЕНИЯ
167
6. Минимальная поверхность, имеющая плоскую линию
■* = ?(*), У=Ш, 2 = 0
своей линией кривизны, определяется уравнениями:
_ <р(и) + ?0) L ,Ф(ц) — Щу)
— 2 ' * о cos ai
ф(ц) + ф(р) ср(ц) - ?(g)
^ _- _ i cos а
г = i —jr— sin а,
где а —постоянный угол, под которым плоскость линии кривизны (плоскость
ху) сечет поверхность.
7. Поверхность
пт cos ах
cosay
— единственная минимальная поверхность, которая имеет два семейства
конгруэнтных плоских кривых в плоскостях х = const и у == const. Присоединенная
поверхность- sin « = Л в* * «у.
8. Функция
F (т) = ат*,
где а — комплексное постоянное число и k — действительное, определяет минн-
М1льную поверхность, налагающуюся на поверхность вращения.
9. Поверхность Каталана
х = sina и + sin2 v, у = 2/ (sin ы — sin t>), 2z = 2и + sin 2u + 2v + sin 2tr.
10. Если между точками двух минимальных поверхностей (Мх) и (MJ
установить соответствие так, чтобы касательные плоскости в соответствующих
точках Мх и М2 были параллельны, то геометрическое место точек М, которые
делят отрезок Мt и М2 в постоянном отношении, есть новая минимальная
поверхность (М) и касательная плоскость к ней в точке М параллельна двум первым
плоскостям.
И. Минимальная поверхность Эннепера есть огибающая плоскостей, которые
перпендикулярны к прямым МХМ%, соединяющим точки двух фокальных парабол
(AfJ и (М2), и делят отрезки М1М2 пополам.
Иначе: Поверхность Эннепера есть средняя огибающая циклиды Дюпена 3-го
порядка (огибающая плоскостей, которые параллельны касательным плоскостям
поверхности и делят расстояние между главными центрами кривизны пополам).
12. Поверхность с линейным элементом *
ds2 = Edu2 + 2Fdudv + Gdv2
налагается на минимальную поверхность, если квадратичная форма
У^1((Е du2 + 2Fdudv + G dv*),
где К — гауссова кривизна повгрхности имеет кривизну равную нулю.
Единственные линейчатые поверхности, налагающиеся на минимальную
поверхность, — изгибание катеноида; они образованы бинормалями кривой
постоянного кручения.
13. Теорема Штейнера. Среди всех поверхностей параллельных Данному
куску минимальной поверхности последняя имеет наибольшую площадь.
14. Теоремы Шварца. Минимальная поверхность 5 осуществляет минимум
площади, по сравнению с бесконечно близкими поверхностями, проходящими
через заданный контур, если существует кусок минимальной поверхности М,
соответствующий S параллельносгью нормалей, так, что ни одна касательная
плоскость в точках М не проходит через заданную неподвижную точку пространства.
Рассматриваемая об засть S минимальной поверхности осуществляет
минимум, если ее сферическое изображение находится все на одной половине сферы.
15. Сечение любой минимальной поверхности параллельными плоскостями
дает семейство изотермических кривых.

ГЛАВА СЕДЬМАЯ.
Теория конгруэнции.
1. Линейчатая геометрия. Плюкеру принадлежит идея принять за
основной элемент пространства прямую линию. Так как положение
произвольной прямой в пространстве определяется 4 параметрами, то
эвклидово пространство, если принять образующим элементом прямую,
есть пространство 4 измерений. Поэтому в линейчатой геометрии
возможны образы трех ступеней: оо1 прямых образуют линейчатую
поверхность, оо2 прямых образуют конгруэнцию, оо3 прямых—комплекс. Через
всякую точку пространства проходит одна или несколько, вообще я,
прямых конгруэнции (п — порядок конгруэнции) и оо1 прямых комплекса,
образующих конус.
Во всякой плоскости лежит одна или несколько, вообще /я, прямых
конгруэнции (т — класс конгруэнции) и оо1 прямых комплекса, которые
огибают в этой плоскости некоторую линию. Например, все касательные
к поверхности образуют комплекс, все нормали к поверхности образуют
конгруэнцию.
Теория конгруэнции особенно тесно связана с теорией поверхностей,
может быть, потому, что и поверхность и конгруэнция являются
многообразиями 2 измерений. Мы начнем с более общего образа —
конгруэнции кривых.
2. Конгруэнция кривых *). Два уравнения между тремя
координатами х, у, z и двумя параметрами и, v
/(*, У, г, и, х>)=0, g(x, у} z, и, г>) = 0 (1)
при постоянных значениях и и v определяют кривую в пространстве;
при переменных и и v они определяют семейство оо2 кривых, которые
мы будем называть конгруэнцией кривых.
Мы будем предполагать, что конгруэнция не вырождается и
параметры входят существенно; следовательно якобиан
d(uv) ди dv dv ди y }
не равен нулю для тех кривых (1), которые мы будем рассматривать.
Связывая параметры (и, v) произвольным уравнением
?(«, w) = 0, (3)
мы получим простую бесконечность кривых (1);х>ни образуют теперь по»
верхность, которую мы будем называть поверхностью конгруэнции.
*) Darboux, Theorie des surfaces, т. II, гл. I.

КОНГРУЭНЦИЯ КРИВЫХ
159
Уравнение этой поверхности получается исключением параметров и
и v из уравнения (1) и (3); но, и не проводя этого исключения,
нетрудно получить уравнение касательной плоскости к поверхности (2).
Вектор нормали N к поверхности (М) перпендикулярен ко всякой
касательной к ней dM—{dx, dy, dz). Следовательно, как только нам
удастся найти соотношение
Adx-\~Bdy-j-Cdz = Ot (4>
которое удовлетворяется всеми системами диференциалов dx:dy: dz,
которые соответствуют перемещениям в касательной плоскости
поверхности, так мы можем считать Л, В, С пропорциональным координатам
вектора N и даже, пользуясь произволом в выборе длины вектора,
JV, положить
N = {A, В, с}.
Диференцируя уравнения (1) и (3), имеем:
а < tv
Исключая отсюда, du dvy получим уравнение вида (5):
£<*+&у+£* £*+Й*
(5>
дх ~ ду У* dz ди ' dv
где отношение диференциалов *du:dv в правой части надо заменить
по формуле
du : dv — <?v : — <pu .
Уравнение (5) следовательно и определяет вектор нормали к
поверхности конгруэнции (3).
Уравнение (5) не содержит отношения 9U'-4V> если якобиан (2)
равен нулю:
д1 дЛ^д1 * = 0 (6)
ди dv dv ди v '
По условию он не может обращаться в нуль вдоль целой кривой
(1); уравнение (6) определяет следовательно на каждой кривой (и, v)
одну или несколько точек, которые мы будем называть фокусами.
В фокусе уравнение (5) не зависит от выбора поверхности (3).
Следовательно все поверхности, проходящие через данную кривую (и, ф), имеют
в этой точке одни и те же нормаль N и касательную плоскость.
В фокусах все поверхности конгруэнции касаются друг друга.
Число фокусов зависит от природы кривых.
Например, в конгруэнции кругов одно уравнение (1) — первой
степени, другое — второй, уравнение (6) — второй степени (ибо при дифе-

160
ТЕОРИЯ КОНГРУЭНЦИИ
ренцировании в уравнении сферы ^=0 квадраты координат пропадут);
следбвательно на каждом круге вообще лежат 4 фокуса.
Геометрическое место фокусов образует фокальную поверхность,
которая имеет столько отдельных полостей, сколько было фокусов на
каждой кривой; впрочем, одна полость может непосредственно переходить
в другую, так что вся поверхность может представлять одно целое.
Уравнение фокальной поверхности получается исключением и и v из4
уравнений (1) и (6).
Вектор нормали N к фокальной поверхности можно получить тем же
приемом, которым мы пользовались выше, только уравнение (3) надо
заменить уравнением (6), которое содержит теперь, кроме параметров и
и v, координаты х> у, z. Тем не менее, составляя отношение (5), мы
заметим, что в силу равенства нулю якобиана (6) диференциалы duidv
сократятся, и мы придем к тому же самому уравнению вида (4), т. е.
получим ту же самую нормаль, которую имеют в фокусе поверхности
конгруэнции.
Итак, все поверхности конгруэнции касаются в фокусах фокальной
поверхности. Следовательно все кривые конгруэнции тоже касаются
фокальной поверхности в каждом из фокусов.
Общие касательные плоскости всех поверхностей конгруэнции в
фокусах называются фокальными плоскостями.
Семейство оо1 кривых в пространстве вообще не имеет огибающей,
ибо две кривые в пространстве вообще не пересекаются, но можно
искать такое семейство (3) из кривых конгруэнции, которое имело бы
огибающую.
Характеристическая точка на кривой есть предел точки пересечения
двух бесконечно близких кривых (1)
А*, У у z, и, ^) = 0, g {х, у, z, и, v) = 0, /(*, у, z, и -j- Дн, v + Д*0 = О,
g (лг, у, zy и -f Д«, v +Av) = О,
или
/(«, •) = (>, g(u, v) = 0
f(u-\-ku, tf-f-Aif)—f(u> v) = 0
^(tt-f-Ды, v + Av) — g(u, <v) = 0
или в пределе
/=0, ^ = 0, gAH-g*r=0, d£du+d£dv = 0, (7)
где отношение диференциалов du:dv определяется уравнением (3).
Исключая х, у, z из уравнений (7), получим диференциальное
уравнение 1-го порядка
Ф (и, v, dut dv) = 0 (8)
для определения искомого семейства кривых (3), имеющего огибающую;
во всяком случае видно, что, исключая диференциалы du:dv из двух
последних уравнений (7), мы придем снова к уравнению (6).
Следовательно характеристические точки всегда совпадают с фокусами, а
огибающие образуют фокальную поверхность.
Мы видели, что все кривые конгруэнции касаются фокальной поверх-

КОНГРУЭНЦИЯ ПРЯМЫХ
161
ности в фокусах; теперь мы можем добавить, что они касаются своих
огибающих на фокальной поверхности. Каждому фокусу соответствует
своя огибающая, следовательно конгруэнцию можно разложить на столько
семейств кривых, имеющих огибающую, сколько имеется фокусов на
каждой кривой.
Если все кривые конгруэнции пересекают одну линию (L), то каждую
точку ее L, в которой сходится оо1 кривых, можно рассматривать как
выродившуюся огибающую их, а всю линию (L) — как одну из полостей
фокальной поверхности.
3. Конгруэнция прямых. Если конгруэнция состоит из прямых, то
оба уравнения (1) — первой степени, уравнение (6) — второй степени;
следовательно на каждом луче (и, v) лежат два фокуса —
действительных, мнимых или совпадающихся. Поэтому фокальная поверхность
состоит из двух полостей, и лучи конгруэнции можно рассматривать как
общие касательные обеих полостей фокальной поверхности (действительной
или мнимой).
Каждая поверхность конгруэнции теперь — линейчатая поверхность,
вообще косая линейчатая поверхность. Если семейство прямых (3) имеет
огибающую, то линейчатая поверхность конгруэнции становится
развертывающейся, и огибающая является ребром возврата ее. Следовательно
конгруэнцию прямых мджно разложить двумя способами на
развертывающиеся поверхности (действительные или мнимые). Ребра возврата
их образуют две полости фокальной поверхности.
Следует заметить, что все линейчатые поверхности конгруэнции
касаются обеих фокальных полостей за исключением развертывающихся:
развертывающаяся поверхность касается только той полости фокальной
поверхности, на которой она не имеет ребра возврата (ибо у
развертывающейся поверхности вдоль всего луча одна и та же касательная
плоскость).
Если одна из полостей фокальной поверхности вырождается в кривую
(L), то одно семейство развертывающихся поверхностей соссоит из
конусов с вершинами на кривой (L).
Если фокальная поверхность не вырождается, то на каждой полости
ее два семейства развертывающихся поверхностей определят два семейства
линий. Одно семейство линий, например линии и, состоит из ребер
возврата развертывающихся поверхностей первого семейства. Второе
семейство линий, например линии v, содержит линии, вдоль которых к
фокальной поверхности прикасаются развертывающиеся поверхности
второго семейства. Следовательно касательные к линиям и (лучи
конгруэнции) вдоль каждой линии v образуют развертывающуюся поверхность.
Такие линии называются сопряженными.
Развертывающиеся поверхности определяют на каждой полости
фокальной поверхности два семейства сопряженных линий.
Если на той же полости фокальной поверхности мы будем проводить
касательные к линиям v, то получим новую конгруэнцию; ее
развертывающиеся поверхности будут иметь ребром возврата линии v (одно
семейство) и будут касаться ее вдоль линий и (второе семейство), ибо
линии и и v сопряжены и касательные к линиям v вдфль линии и
тоже образуют развертывающиеся поверхности. Следовательно разверты-

152 ТЕОРИЯ КОНГРУЭНЦИИ
вающиеся поверхности второй конгруэнции соответствуют
развертывающимся поверхностям первой. Такое преобразование конгруэнции носит
название преобразование Лапласа. Оно, очевидно, может продолжаться
также и далее, если взять у второй конгруэнции другую полость
фокальной поверхности и провести касательные к линиям, сопряженным с
лежащими на ней ребрами возврата развертывающихся поверхностей
конгруэнции.
Таким образом получается цепь кошруэнций, которая называется
последовательностью Лапласа. Вопросы о замкнутых
последовательностях Лапласа, о последовательностях обрывающихся (если одна из
фокальных полостей выродится в линию) и т. д. представляют собою
одну из хорошо разработанных и изящных глав диференциальной
геометрии.
Примером конгруэнции прямых может служить конгруэнция нормалей
к поверхности. Ее развертывающиеся поверхности образованы
нормалями вдоль линий кривизны; ее фокальные полости—две полости
поверхностей центров. Поэтому линиям кривизны соответствует на каждой
полости поверхности центров сопряженная система. Преобразование
Лапласа приводит к конгруэнции, образованной осями вращения
трехгранника Дарбу, когда его вершина описывает ту или другую линию
кривизны.
4. Фокусы луча. Перейдем к более подробному исследованию
прямолинейных конгруэнции.
Пусть М— какая-нибудь точка на луче и е — единичный вектор,
отложенный на луче из точки М. Очевидно, две функции
М=М(и> v)\ е = е{иу v)
вполне определяют конгруэнцию.
Построим в каждой точке М трехгранник 7, вершина которого лежит
в точке М, а первая ось совпадает с лучом конгруэнции. Единичные
векторы по осям трехгранника обозначим
Наконец, сохраним обычное обозначение для компонентов
поступательного и вращательного движения трехгранника
dM — е^ du + ^du)-f e2(rt du -f ^dv)-f e3(C du + \dv)\
П — ex{p du-^p^v) -f- e2(q du - j- q^dv) -|- e3(rdu -f- rtdv). (9)
Здесь dM — перемещение вершины трехгранника; оно теперь не связано
условием опасаться в плоскости первых двух осей, ибо поверхность (М)
пересекает лучи конгруэнции под произвольным углом; поэтому нам
пришлось ввести третий компонент этого перемещения £du-\- ^dv. Вектор
П есть бесконечно малый поворот трехгранника, отложенный на мгно-
венной оси вращения.
Перемещение любой точки Р с координатами [а, Ь, с] по осям трех.

ФОКУСЫ ЛУЧА 163
гранника Т определится формулами {В) гл. III, стр. 90 [и даже (9) гл. I],
куда надо только ввести еще компоненты С, Сь
dP— [da, db, rfc] +AW-J-II X [а, by c] =
= ex {da -f- Idu ~ lxdv -f (q du -f ^rfv) с — (/• dtt -f rxdv) b) -f-
-f <?2 {db -\-v\du-\- r\idv-^ (r du -f rxdv) a — (pdu -\-ptdv)c] -f-
-|-<?з {& + ^и + ^1^ ~{-(pdu-\-pxdv)b—(qdu-\-gidv)a}. (10)
Возьмем точку jp на луче конгруэнции; тогда
£ = 0, с—О.
Вектор dP определяет расстояние этой точки отточки Pl[a-\-da9 О, О]
на соседнем луче (u-\-du, v-\-dv),
dP — ex(da -j- £ du -j-^rftf) -f- £2 fa ^w ~b ^i^~b (r ^w ~b ri^) <*) ■+-
-4- e3 [C da -j- Ci^ — (? du -j- <7!<ft0 a]. (11)
Два луча пересекаются (до бесконечно малых высших порядков), если
вектор dP лежит на луче конгруэнции еи т. е. при условии, что два
остальных компонента (по осям е2 и ег) равны нулю:
r\du-\- ij,A> + (rdu + rtdv)a = 09
С du -}- Сх^ — (</ du -f- ^fifo) a = 0. ' '
В таком случае линейчатые поверхности dw.dv имеют огибающую,
следовательно линейчатая поверхность — развертывающаяся, а точка Р — фокус.
Исключая из двух последних уравнений а или du: dv, получим ди-
ференциальное уравнение развертывающихся поверхностей и уравнение
для абсцисс фокуса
(ч?+Сг) du* + (mi + w + Сг, -Кг) du dv -f (4lft + C^j) A* = 0, (13a)
*\ягх — ?ir) r a{^\ — r& + <ГПх — 9rt) +ИЪ — 4iC = 0. (13b)
Выберем точку M в фокусе луча (действительном или мнимом) и пусть
*> = const — соответствующая развертывающаяся поверхность. Подставляя
в уравнения (12)
а — 0, v = const,
получим
4 = 0, С = 0. (а)
Следовательно касательная к линии и на фокальной поверхности (М)
Ми = ех1
совпадает с первой осью. Как и следовало ожидать, лучи конгруэнции
огибают на ней линии и.
Поворачивая оси трехгранника, мы совместим ось £3 с нормалью к
фокальной поверхности (М) и тогда
С,=0. (Ь)
Когда конгруэнция имеет только одну фокальную поверхность ?

154 ТЕОРИЯ КОНГРУЭНЦИИ
Если оба фокуса совпадают, то уравнение (13Ъ) имеет два корня,
равных нулю, следовательно
qrii^O, т. е. q = 0; (с)
значит линии и на поверхности (М) — асимптотические.
Конгруэнции с совпадающими фокальными поверхностями
образованы касательными к одному семейству асимптотических линий своей
единственной фокальной поверхности.
Если фокусы не совпадают, то и развертывающиеся поверхности
различны, и мы можем принять второе семейство развертывающихся
поверхностей за координатные поверхности и = const. Внося это
предположение в уравнение (12), получим:
?i = 0. (d)
Следовательно координатные линии на поверхности (М) сопряжены, как
и надо было ожидать. Абсцисса второго фокуса
5. Граничные точки луча. Вернемся к общим формулам (11). Выбирав
точку Pi возможно ближе к Р *), мы должны положить в формуле (11)
da + Zdu+lidvz^O,
и тогда расстояние точки Р от соседнего луча будет
dP = е2[у\du -j-y\\dv-\-a(rdu~\-rxdv)] -\-
-f- *з[С du 4 Zndv — a(qdu-\- qxd*9)\9
dP2 = [t] du + t\xdv + a(rdu + r^dv)]* -f
4- [Cdu -j- ddv — a(qdu + qidv)]*. (II1)
Отыскивая минимум этого расстояния в зависимости от переменной а,
найдем ту точку Я, которая ближе всего лежит к соседнему лучу du:dw;
диференцируем (11) по а и приравниваем if нулю
\Л (dP*) = (rdu + rxdv) hdu -f ihtfv + a(r^ + rxdm)\ -
— (qdu-\-qxdv) [Cdu 4Cififo — a{qdu + qtdv)} = 0. (14)
Левую часть уравнения (14) можно рассматривать как скалярное
произведение вектора dp и вектора
de{ = е2 (г du 4- rxdv) — ег (qdu 4 q l dv). (15)
Следовательно вектор dP перпендикулярен к лучу е{ и к бесконечно
близкому ех -\-dex.
Уравнение (14) дает абсциссу той точки Р, которая ближе всего
расположена к соседнему лучу (u-\-du, v-\-dv):
а — (?du + gxdv) (Сdu + Ztdv) — (rdu + rtdv) (t)du -f ^dv) ,..,.
{q du + q.dvy + (r du 4 rxdvf ' v >
*) He забудем, что точка Рг имеет координаты [а -\- day 0,0J; следовательно
выбор da определяет положение точки PY на луче.

ГРАНИЧНЫЕ ТОЧКИ ЛУЧА
165
Если из центра сферы радиуса единицы проводить векторы et
параллельно лучам конгруэнции, то каждый луч изобразится точкой на сфере.
Нетрудно заметить, что в знаменателе формулы (14') стоит de{*—
квадрат линейного элемента этого сферического изображения.
Две формы
do2=_dei2 — (qdu-\-qldv)2-\-(rdu-{-ridv)2 = Е du* -f- 2Fdu dv -\- Odv2
dexdM = —(qdu-{- qtdv) (C du -f Ci dv) + (r du + r, dv) (tj du -f ^dv) =
= e du2 -f (/+/') du dv+gdv2,
где
/= + f 1«Д> = + гт)! — q(.u
f = + ^iz//Wu = + rxy\ — ^jC,
приняты Куммером за основные формы конгруэнции. Вторая форма,
очевидно, зависит от положения точки М на луче и потому не будет
внутренней формой конгруэнции.
Формула (14) для абсциссы точки Р — основания общего
перпендикуляра двух бесконечно близких лучей, вполне аналогична*) формуле (3)
гл. III, определяющей радиус кривизны нормального сечения поверхности,
т. е. центр кривизны его — точку, где наиболее близко сходятся
бесконечно близкие нормали вдоль сечения; эта аналогия и дала повод Кум-
меру ввести его формы.
Так же как в теории поверхности, мы можем построить
индикатрису для изучения движения точки Р по лучу.
В касательной плоскости сферы откладываем на каждой касательной
йв 1
-jr отрезки, равные Геометрическое место таких точек
образует кривую 2-го порядка с центром в точке касания. Выберем
переменные и, v так, чтобы касательные к координатным линиям совпадали
с главными направлениями индикатрисы. Тогда в выражении (14') и в
числителе и в знаменателе пропадут члены е произведением дифереы-
циалов dudv. Простой подсчет приводит нас к уравнениям
ЧЧ\ + т = 0, ?Ci + <7iC — ль — /уч = 0. (а)
Система координатных линий на сфере будет ортогональна, и мы можем
касательные к ним выбрать за оси трехгранника е2 и ег, откуда по
формуле (15)
qi=0, r = 0. (Ь)
Помещая еще точку М на луче посредине между фокусами, мы приведем
к нулю в формуле (13Ь) коэфициент при первой степени а
'п — г£ + 94i — Я\П — °> (с)
J) С той только разницей, что теперь
ше равны между собой.

166
ТЕОРИЯ КОНГРУЭНЦИИ
и формула (14') примет вид:
а— d& w
Если ввести угол 6, образованный вектором de{ с осью е8, то
det dv - du . Л , Л
-fi = e2ri ~d*~e*q~ds~~^sinO + ^cose,
dv 1 . л du 1 ft
-j- = sin 6, -r- = COS 6.
Внося эти значения в формулу (d), получим:
a = ^cos2e— ^sin2e. (е)
Для 6 = 0 и б=~, т. е. для главных направлений мы получим в силу
формулы (е) равные с обратным знаком абсциссы точек Р
а\=\> a2 = —r±ri al = — a2 — d. (15')
Следовательно (формула Гамильтона)
а — d (cos* 6 — sin2 0) = d cos2 е. (16)
Так как общий перпендикуляр двух лучей dp образует прямой угол
с касательной deu то угол 8 можно рассматривать как угол
касательной de\ с осью еъ или угол перпендикуляра dP с осью е2.
Мы видим, что точка Р может удаляться на расстояние d в обе
стороны от средней точки М так, что точка Р пробегает на луче всего
отрезок AB=z2d. Крайние точки А и В (a — dzd) называются грани-
цамц луча, а поверхности (А) и (В), описываемые этими точками,—
граничными поверхностями. Точка М—средина расстояния между
фокусами и между границами луча — называется срединой луна, а
поверхность, описанная ею, — средней поверхностью конгруэнции. При
переходе от центра к границам направление кратчайшего расстояния dP
поворачивается на 45°. Плоскости, перпендикулярные к этим направлениям
в границах А и В, называются главными плоскостями, а линейчатые
поверхности, линии сжатия которых описываются точками А и В,—
главными поверхностями. Очевидно, главные плоскости взаимно
перпендикулярны.
Фокальные плоскости равно наклонены к главным плоскостям, ибо
фокусы расположены симметрично по отношению к границам.
Главные поверхности всегда действительны (в отличие от
развертывающихся поверхностей, которые могут быть и мнимы).
6. Изотропная конгруэнция. Главные поверхности конгруэнции
всегда действительны, но они могут быть неопределенны. В этом случае
индикатриса будет кругом. Выбирая линейный элемент на сфере
ортогональным и направляя оси трехгранника по касательным к координатным
линиям, т. е. при условии (Ь), мы попрежнему приведем формулу (14')
к виду (d, е), но это можно теперь сделать бесчисленным множеством
способов. Следовательно, поворачивая оси на любой угол, т. е. за-

ИЗОТРОПНАЯ КОНГРУЭНЦИЯ
167
меняя 6 на б -f- а, мы не изменим вида формулы (е). Это возможна
только, если коэфициенты при cos2 в и sin2 8 равны1)
а так как уравнение (15') дает
то, очевидно,
C = 0f Ч|=0, (17)
и абсцисса точки Р всегда равна нулю, т. е. границы луча совпадают
с его серединой. Такая конгруэнция называется изотропной (Рибокур).
В изотропной конгруэнции главные поверхности неопределенны;
границы луча совпадают, и следовательно одна и та же точка — середина
луча — находится на кратчайшем расстоянии от всех соседних лучей.
Центральная поверхность содержит линии сжатия всех линейчатых
поверхностей изотропной конгруэнции.
Так как в формуле (14') абсцисса а точки Р имеет только одно
значение для всех отношений du\dt)y то следовательно коэфициенты
двух форм Куммера, стоящих в числителе и в знаменателе ее,
пропорциональны.
Уравнение (13Ь) дает в силу уравнений (Ь) и (17) для абсцисс
фокусов мнимые значения
«V,+*1==о, «-=--^—?=-"Т-
Уравнения (Ь) и (17) приводят к таким элементам сферы и средней
поверхности конгруэнции [см. формулы (9) и (15)]
dex = e2ridv — e3q du,
dM == el (£ du -f- \\dv) -f~ e2r\ du -f- e^dv.
Откуда в силу уравнения (а)
dexdM—(?\rx — ?Ci) du dv = 0. (18)
Соответствующие касательные de^ на сфере и dM на средней
поверхности конгруэнции ортогональны. Средняя поверхность соответствует
сфере ортогональностью линейного элемента. Очевидно, это
необходимое и достаточное условие, чтобы конгруэнция была изотропной.
Этому условию можно придать более наглядный вид.
Отложим от средней поверхности (Ж) по обе стороны ее по лучам
х) Это еще яснее будет, если воспользоваться формулой (16). Если
d cos (20{ -f а) = (/[cos20' cos1 а — sin 20' sin a] ~ dx cos 20'
для всякого a и всякого 0', то
d sin 20' sinо = 0,
что при произвольном 0' и а дает rf = 0, т. е. границы совпадают.

16£
ТЕОРИЯ КОНГРУЭНЦИИ
конгруэнции e± равные постоянные отрезки /. Мы получим две новые
поверхности (Af,) и (М2)
М1=М + 1еи М2 = М — 1е1.
Линейные элементы их
dMJ — (dM -f / de,f = dM* -f- 2/ det dM-\-P dex\
dM2* = (dM— Ide,y = dM* — 2/ dex dM + /2 dex*
в силу уравнения (18) равны между собой
dM* = dM* — dM*-\-P dex.
Следовательно поверхности (Mt) и (М£) налагаются.
Обратно, если две поверхности налагаются и соответствующие
тонки их находятся на постоянном расстоянии друг х>т друга, то
хорды, соединяющие их, образуют изотропную конгруэнцию.
Знание изотропной конгруэнции позволяет построить сколько угодно
пар таких поверхностей.
Наконец, изотропная конгруэнция получает особое значение
благодаря своей связи с минимальными поверхностями.
ТеоремаРибокура. Средняя огибающая поверхность изотропной
конгруэнции — минимальная поверхность.
Под средней огибающей мы подразумеваем огибающую плоскостей,
перпендикулярных к лучам конгруэнции и проходящих через их^ середины.
Пусть (М) — средняя огибающая поверхность, и координатные линии
и, v — линии кривизны ее, так что, выбирая касательные к линиям и, ъ
за оси трехгранника, имеем:
Ci=Of *n=0, р=0, <7i = 0.
По условию луч конгруэнции перпендикулярен к касательной плоскости,
т. е. параллелен оси ег. Пусть он пересекает ее в точке А, координаты
которой относительно осей трехгранника суть [а, Ь, 0].
Расстояние между двумя бесконечно близкими лучами конгруэнции
определяется по формуле (В)
(dPy — (da + ldu + cqdu — rbdu — ribd<v)*+
-\~ (db -f- Tjjdfo -{" ar du -f- arxdv — pxc dv)2,
где точка P = [a, by с] есть та точка на луче, где общий
перпендикуляр dP (кратчайшее расстояние) пересекает луч [а, Ь] [третье
слагаемое (компонент по оси ез) опущено, так как dP перпендикулярно к ег).
Если конгруэнция [а, Ь] изотропная, то для всяких направлений
du:dv точка Р совпадает с точкой А. Это значит, что каковы бы ни
были du: dvt (dP)2 имеет минимум для с = 0.
Диференцируя по с и подставляя с=0, получим:
qdu [da-^^du— rb du — rtb d ] —pxdv [db-\-j\xdv-\- ar du -j- arxdv\ =0.
Это уравнение справедливо для любых направлений du: dv, следовательно

НОРМАЛЬНАЯ конгруэнция 169
все коэфициенты при du2, dudv, dv2 равны нулю. Так как q и ри ко-
нечио, не нули [иначе поверхность (Af) развертывающаяся], то
а„-И — rft = 0, Ь9 + ъ + гга = 0, (а)
?(«*— r,b) —Pi(ba + га) ^= 0.
Вводим вспомогательное переменное л и переписываем эти уравнения
в виде системы
au—rb — £, <z9 = ri6-f-A/>n
*я = —Л1+А?, ^ = — ^ — 4,. (Ь)
Диференцируя левый столбец по v, правый по и и сравнивая вторые
производные, получаем условие интегрируемости системы (Ь). Если
воспользоваться основными уравнениями (I), (II) [см. IV, § 1, стр. 90]:
Р\и = — ЧГи 4v — rPu £* = — ^iu\u — r\l9
rv — riu= — 4Pl
то условие совместности системы (Ь):
к
откуда следует
или в силу уравнений (Ь)
= — bq, К = —
(*?), = («л)«
ЧЪ—Pt^
»
«SPj.
Так как главные радиусы кривизны поверхности (Af) суть
Ri — — ~j-, /?2 —
ft'
(c>,
(d>
то условие (d) непосредственно показывает, что поверхность (Af) —
минимальная, что и доказывает теорему Рибокура. Вместе с тем мы видим,
что определение изотропной конгруэнции по Заданной минимальной
поверхности зависит от интегрирования вполне интегрируемой системы
(Ь), (с); следовательно общее решение содержит 3 произвольных
постоянных.
7. Нормальная конгруэнция. Можно ли рассматривать
произвольную конгруэнцию как конгруэнцию нормалей к некоторой
поверхности (Я)?
Если такая поверхность (Я) существует, то все перемещения точки R
перпендикулярны к лучу и компонент по оси ех в формуле (11), стр. 163,
равен нулю для (всякого выбора диференциалов du: dv
da+Zdu + Zld* = 0\ (IT1)
отсюда
dm — <" dv ч v '

170
ТЕОРИЯ КОНГРУЭНЦИИ
и1)
Если искомую точку М поместить в фокусе луча, а за координатные
поверхности принять развертывающиеся поверхности и выбрать оси так.
чтобы ег совпадала с нормалью к поверхности (Ж), как это было
сделано в § 4, то
С = 0, d=0, т] = 0, ^ = 0
и компоненты движения трехгранника удовлетворяют уравнениям (I)
и (II) гл. IV, § 1, стр. 90.
Первое из этих уравнений в силу формулы (18) дает
/41!= О,
откуда, если tj1 не нуль2),
г^О. (18*)
Мы видим, что уравнения (а) и (Ь) § 5 удовлетворены;
следовательно конгруэнция в то же время отнесена к главным поверхностям
т. е. главные поверхности совпадают с развертывающимися. Впрочем,
и непосредственно ясно, что нормали к поверхности вдоль линии
кривизны образуют развертывающиеся поверхности. Следовательно
развертывающиеся поверхности взаимно перпендикулярны, а потому фокусы
луча совпадают с его границами. Таким образом конгруэнция,
образованная нормалями к поверхности, есть частный вид конгруэнции; она
называется нормальной.
Б нормальной конгруэнции фокальные плоскости перпендикулярны.
Обратно, если фокусы совпадают с границами луча, то уравнения (а)
и (Ь) § 5 стр. 165 и уравнения (а), (Ь) и (d) § 4 стр. 163 имеют место
одновременно, откуда в силу первого уравнения (1) следует
уравнение (18), и из вполне интегрируемого уравнения в полных диференциа-
лах (17') найдем а с произвольной постоянной
а — — f (£ du -\- Eidv)-j~ const.
Если существует одна поверхность, ортогональная к лучам
конгруэнции, то их существует целое семейство. Все поверхности параллельны
и отсекают на лучах конгруэнции равные отрезки.
Условие (18) показывает, что луч конгруэнции ех не вращается в
касательной плоскости фокальной поверхности (Af), следовательно,
огибает на ней геодезическую линию; обратно, касательные к семейству
геодезических линий образуют нормальную конгруэнцию, ибо из условий
1) Если воспользоваться основными уравнениями (I), стр. 90, то из
условий (18) сейчас же получим
nJl — qt — гя— q£,
т. е. в коэфициентах второй формулы Куммера
это необходимое и достаточное условие, чтобы конгруэнция была нормальной
а) В таком случае Ш == ^ $du-\-\vdv\ т.е. фокальная поверхность
вырождается в линию.

НОРМАЛЬНАЯ КОНГРУЭНЦИЯ
171
(18') вытекает, что условие (18) выполнено, и следовательно уравнение
{17') вполне интегрируется.
Впрочем, и геометрически очевидно, что семейство эвольвент (С)
геодезических линий g пересекает касательные к линиям g под
прямым углом. Если теперь выбрать С так, чтобы они
исходили из точек какой-нибудь ортогональной траектории t кривых g,
то всякая другая ортогональная траектория tt отсечет на
геодезических равные отрезки; отрезки касательных к линиям g между tx и
эвольвентой С будут той же самой длины и следовательно все между
собой равны, а так как эти касательные, конечно, служат геодезическими
линиями на той линейчатой поверхности Z), которую они образуют, то
линия tx и линия L пересечения D с поверхностью (С), служат
ортогональными траекториями этих касательных *). Поверхность (С),
геометрическое место эвольвент, содержит две линии, перпендикулярные к
касательным (g), следовательно сечет их ортогонально.
Как бы ни брать исходную поверхность (Af), компоненты £, £t
связаны только с линейным элементом ее и получаются проектированием
на луч конгруэнции ех бесконечно малых перемещений точки М по
линии и и по линии is этой поверхности. Отсюда следует, что, изгибая
произвольную поверхность (М) и сохраняя луч конгруэнции ех
неразрывно связанным с касательной плоскостью поверхности, мы не
нарушим условия (18) и не изменим диференциального уравнения (17').
Следовательно, если до изгибания концы векторов аег образуют
поверхность, нормальную к конгруэнции еи то и после изгибания конгруэнция
останется нормальной, и концы векторов аех, перенесенных вместе с
касательными плоскостями поверхности (М), образуют поверхность,
нормальную к новой конгруэнции et. Пусть координатные линии (и, v) на
поверхности (М) ортогональны, а линии и нормальны к лучу ег(, который
образует с нормалью к поверхности угол <р, а следовательно с линиями v
2 <р. Тогда
£ = 0, ^J/Gsincf,
где ds2 = Edu2~\-G dv2— линейный элемент поверхности (М).
Условие (18) примет вин:
д Уд sin <р _ 0 .
ди '
оно будет выполнено и для той новой конгруэнции, которая получится
после отражения или преломления лучей конгруэнции в поверхности (Л1),
когда угол ^р надо будет заменить новым углом о1 по формуле
©' = — <р (отражение)
или sin ср' = п sin <р (преломление с показателем п = const).
Нормальная конгруэнция останется нормальной после любо:*
числа отражений или преломлений.
г) Если от точек ортогональной траектории, семейства геодезических
отложить на них равные дуги, то получится новая ортогональная траектория нх.

172 ТЕОРИЯ КОНГРУЭНЦИИ
8. Конгруэнция W. Вернемся к общим формулам § 4 и будем
искать конгруэнции, которым на фокальных поверхностях соответствуют
асимптотические линии. Допустим, что поверхность (М) — фокальная
поверхность и ось ег ее нормаль, а координатные линии и, v на ней — ее
асимптотические линии. Тогда (см. стр. 82)
С = 0, d = 0, р = \Ъ, q ='b), рх = — \£и Ч\— — М\ (а)
где /( = — X2 — гауссова кривизна поверхности (Л1).
Уравнение (13Ь) дает абсциссу второго фокуса
л _ 2 ч %
Построим для второй полости фокальной поверхности трехгранник
Дарбу, принимая за его первую ось t{ луч конгруэнции ег. Тогда
tx = еи /2 = е2 cos со — ez sin со, п = е2 sin со -|- е3 c°s <»,
где со — угол между нормалями двух полостей фокальной поверхности,
т. е. угол между фокальными плоскостями конгруэнции. Его нетрудно
получить из условия ndM' — O.
Пользуясь для dM' формулой (11), получим, например, для линии и
(т) -f- ar) sin со — ад cos со == 0;
следовательно в силу формул (а) и (Ь)
tg о) = -S- = J^Wl- = «*_. (с)
Вращение трехгранника Т1'^, 1Ъ п) складывается из вращения
трехгранника Т(еи е2, ez) и поворота Т' относительно Т на угол dm около
луча конгруэнции ех = tv Следовательно компоненты вращения
трехгранника V получатся простым проектированием на новые оси вектора
вращения трехгранника Т и добавлением e1dm. Отмечая их штрихом
наверху, имеем:
p'du -f- pi dv = p uu -f- P\ dv + da)9 |
<7' = grcosa> — rsina>, qi ±=:qlcosis> — TiSina), J (d)
r' = q sin <o -{- r cos со, rx' = qx sin a>-j~ rt cos со J
и компоненты поступательного движения точки М* по формуле (11),
проектируя dM на новые оси,
7)' = (t) -j- ar) cos <л -{- ^a sin со = т)/ = (ir)! -}- arj)cos co-j-^д sin со = J {$}
Sin a> ' Sin a>
Последние две формулы получатся, если исключить v\-\-ar или •»j1-f-fl/'1
с помощью уравнения (с).
Если асимптотическим линиям поверхности (Ж) соответ ствуют асимп.

ПОВЕРХНОСТИ ВЕЙНГАРТЕНА
173
тотические линии на поверхности (ЛГ), то уравнения (а) будут иметь
место и для поверхности (М')9 т. е.
a cos ш — г sin а> =. а' -^— , a* cos со — л sin о> = — X' -^L
* sin о» ' J1 * sin о1
(е)
а'2 = —/Г.
Если в двух последних уравнениях заменить г и гх по формуле (с),
то получим:
:?ctga>— J = ?ctga> — i f
/ tfSina»\ .,
0COS 0) — I^COSO)— -—=— J = У
sin •
^'=^. (19)
Так как a — расстояние между фокусами, а a) = 20 — угол фокальншх
плоскостей, то по формуле Гамильтона (16)
Sine» '
где d — расстояние между границами луча.
Итак, в конгруэнции W произведение гауссовых кривизн в
соответствующих точках двух фокальных полостей равно обратной
величине четвертой степени расстояния между границами луча
КК' = ±. (19')
При этом условии два последних уравнения (е) удовлетворены тожде-
ственно, а два первых определяют отрезок а и положение трехгранника
относительно асимптотических линий (угол а между ег и линией и), т. е.
направление луча е{ в касательной плоскости. Значит, какова бы ни была
поверхность {М)у существует бесконечное множество конгруэнции W,
для которых она служит одной полостью фокальной поверхности.
Если фокусы совпадают, то асимптотические линии на двух
(совпавших) полостях фокальной поверхности, конечно, соответствуют друг
другу; следовательно такую конгруэнцию можно рассматривать как
конгруэнцию W. Поэтому расстояние между границами d конгруэнции,
касательных к асимптотическим линиям поверхности, равно
Pi
где pj—радиус кручения асимптотической линии.
9. Поверхности Вейнгартена. Если конгруэнция нормальная и
фокусы совпадают с границами, то о> = ^ и уравнения (е) принимают вид:
, = V(« + S, „=-!•({,+£).
r——Vaq, r1==Vaqu
Если P—поверхность нормальная к лучам, а Ri и Rt ее два главных
радиуса кривизны, то, очевидно, PM = RU PM' = Rt и следовательно

174
ТЕОРИЯ КОНГРУЭНЦИИ
Р = М— /?!<?!, a = R2 — Rt.
Заменяя в формулах (17') а на —Ru получим:
Вносим теперь эти значения £, £ь а в первые два уравнения (е') и
воспользуемся для р и р1 формулами (а); мы получим:
ди ди * dv dv '
откуда
dRLdRL_dR1 Ml_0 nQ.v
<Эы dv dv ди ~ ' ^ '
т. е. /?2 есть функция только одного Rt.
Поверхности, главные радиусы кривизны которых связаны
уравнением
/?2 = Ф№).
не содержащим других переменных, носят название поверхностей Вейн-
гартена, или поверхностей W.
Следовательно на двух поверхностях центров кривизны
поверхности W соответствуют асимптотические линии.
Отнесем фокальную поверхность (Ж) к геодезическим линиям,
которые огибаются лучами конгруэнции, и к их ортогональным траекториям.
Тогда
С^О, С, = 0, Ч = 0, $1 = 0.
Уравнение (17) дает для расстояния точки М от нормальной
поверхности, т. е. для первого радиуса кривизны ее а = — /?,,
дЖ — ? д*1 -о
ди — *' dv ~~ *
Следовательно Rt есть функция только одного и, и мы можем принять
/?, = u, g=l;
основные уравнения [(I), стр. 90] дадут тогда
Между тем по формуле (13) второй фокус определится абсциссой
a = R2 — Ri = —^-m
Следовательно если /?2, а значит и a — R2 — /?j — функции от /?,, то
где V— произвольная функция одного переменного v, которую выбором
параметра v мы приведем к нулю *), и линейный элемент
поверхности (М) примет вид:

ПОВЕРХНОСТИ ВЕЙНГАРТЕНЛ
17&
-2 Г '*'
ds* — dRx* -\-e *■-*• dv*. (20)
Это — линейный элемент поверхности вращения, отнесенный к
меридианам /?! и параллелям v. Очевидно, к такому же виду можно
привести и линейный элемент второй полости фокальной поверхности.
Следовательно обе полости поверхности центров поверхности
Вейнгартена налагаются на поверхность вращения; при этом
геодезические линии, огибаемые нормалями, налагаются на меридианы.
Эта теорема Вейнгартена открыла новую страницу в теории
изгибания поверхностей, ибо дала возможность получить сколько угодна
поверхностей, налагающихся на поверхности вращения, отыскивая
поверхность центров для поверхности W.
В самом деле, пусть нам дана поверхность вращения, т, е. задан
линейный элемент ее вида
ds* = du2 -f ф2 (и) d<f. (20 )
Сравнивая его с формулой (20), имеем:
и = /?! -f const, v = <р + const, е /?3~/?' = ф (и),
откуда
1 _ <У (и)
/?*-*! _ + («) *
Эта формула определяет связь между главными радиусами кривизны
поверхности Вейнгартена.
Чтобы найти самую поверхность, заметим, что линейный элемент
сферического изображения конгруэнции (т. е. линейный элемент
сферического изображения по Гауссу поверхности Вейнгартена) имеет вид:
ds'* = def = (q dR, + q^dvf -f- rx*dv\
Нетрудно заметить, что
"ЧАчМх + Чх**)
есть полный диференциал, ибо в силу третьего уравнения (I) и второго
уравнения (II) (см. стр. 90)
, Л да дал
и мы получаем
dW__„ д1 — ъ ( dgi—m\ — r> (dgi Uqi d4\\ — dMi
J a i/
*) Так как ^xz=e e v и линейный элемент
ds* = dR\ + e *J a e2v dv~,
-2 Г** ,
e J a e"
то, очевидно, достаточно для этого ввести новый параметр посредством уравнения
dvx = evdv.
В тексте мы предполагаем, что это преобразование уже выполнено.

176
ТЕОРИЯ КОНГРУЭНЦИИ
Полагая
мы приведем ds'* к виду
Это, очевидно, линейный элемент сферического изображения линий
кривизны поверхности Вейнгартена. Требуя, чтобы кривизна его равнялась
единице, мы найдем уравнение для, определения Rt как функции от ult
и после этого поверхность Вейнгартена будет определена.
Полагая
мы напишем
aS a* ^0'2(a)' ^l '
Всякий раз как линейный элемент сферы приведен к такому виду, мы
имеем сферическое изображение линий кривизны поверхности
Вейнгартена с главными радиусами
/?1==»(a), /?2 = ft(a) —ад'(а).
10. Псевдосферическая конгруэнция. Рассмотрим другой частный
вид конгруэнции W, когда
ш = const, а = const. (М)
-Формулы (е) § 8 дают нам тогда
Сравнение их с формулами (а) того же параграфа дает
а
Обе полости фокальной поверхности — поверхности постоянной
отрицательной кривизны *). Такая конгруэнция называется псевдосферической.
Формулы (а) и (сГ) § 8 дадут нам теперь, так как в силу (а) § 8
a sin о»
aq = 2-т— = т] sin a»,
aqv = — irjj sin го
м из формул (с) § 8
'i = ?i(ctg«+^), что
■£' = £• 5t'=Si. V=*n> V =—4t.
/>'=/>, p\=pu q'~q> q\= — qu
l) Нетрудно показать, что условия (22) достаточны, чтобы конгруэнция
была псевдосферической, т. е. если расстояние между фокусами и расстояние
между границами луча постоянно, то обе полости фокальной поверхности —
псевдосферы, асимптотические линии которых соответствуют друг другу.

ОСНОВНЫЕ ФОРМЫ САННИА
177
откуда прямо следует, что линии кривизны
(р du-^-pidv) ($ du -}- lx dv) -\-(qdu-\-q dv) (vj du -f- ^dv) = 0
на обеих поверхностях соответствуют друг другу 1).
Если поверхность постоянной кривизны (Ж) нам дана и
tfs* = Edu* -f 2Fdu dv + Gdv* (a)
линейный элемент ее, то
? = j/zfcos a, 7j = j/Fsin а, Ex = j/O cos p, ^ = j/g sin p,
l/fcosa . Vfsina . „ l/Gcosf .
p = -± sin cd, <7 = - sina>, px = —z—-—-sin со,
■/GsinP .
r = -
dp 1
du VG
sin *
.(i££_i££«.,).
\ dv du /
da 1 IdVG d\/E A
n= -==r-i— cos6 ,
1 du ' ]/Tsin8 \ du dv )
где а и p — углы касательных к асимптотическим.линиям с первой осью,
р — a = 6 — угол между асимптотическими линиями и К = ъ
постоянная кривизна поверхности (Ж). Тогда первые два уравнения (е)
со ^ г sin <о
§ 8 удовлетворены тождественно л = , а вторые два
q cos со — г sin со = q, q{ cos со — rx sin со = — qx (23)
дают для а (или для р =8-{-<*) два диференциальных уравнения первого
порядка, образующих вполне интегрируемую систему, если кривизна
линейного элемента (а) К = j-. Таким образом, какова бы ни была
поверхность постоянной отрицательной кривизны (а), отнесенная к своим
асимптотическим линиям, мы можем задаться произвольной
постоянной со, и уравнения (23) определят нам а, содержащее еще одно
произвольное постоянное. Этим будет определяться псевдосферическая
конгруэнция, а следовательно будет известна и вторая полость ее
фокальной поверхности, т. е. новая поверхность постоянной отрицательной
кривизны (М), отнесенная тоже к асимптотическим линиям.
Преобразование, позволяющее по одной поверхности постоянной
отрицательной кривизны найти другую с помощью псевдосферической
конгруэнции, называется преобразованием Бэкланду.
11. Основные формы Санниа. Конгруэнция определяется единичным
вектором ех направления луча и какой-нибудь точкой М, взятой на луче.
Диференциалы вектора М и ег даны формулами (9) и (15). Если мы
заменим точку М какой-нибудь другой точкой Р натомжелуче/^МЦ-а^ь
то те же диференциалы примут вид:
*) Единственная конгруэнция W с соответствующими линиями кривизны
на обеих полостях фокальной поверхности — псевдосферическая.

178
ТЕОРИЯ КОНГРУЭНЦИИ
dei = е2 {г du + rYdv) — ez (q du-fqtdv). (15)
dP = ex (da -f- 5 du H" й^) + *2 fa rf« + *h<fo 4" (r du + M*>) fl] +
+ ez[1idu + i:1dv — (qdu + ql(Iv)a]. (11)
Первая форма Куммера
de^ = (г Ai + r^)2 -|- (^ rf« -f- ^!^)2 = Edu* + 2F dudv+G dv*
несомненно внутренно связана с конгруэнцией; но этого нельзя сказать
о второй
dexdP= (v\ du -f- r\{dv) (rdu -f- rxdv) — (£ du-{- r^dv) (q du -f- qidv)-{-adei2.
ибо она меняется с изменением абсциссы а, т. е. зависит от выбора точки Р
на луче. Куммер проектирует перемещение dP на направление dex,
перпендикулярное к лучу ei9 и этим уничтожает компонент по первой оси, содер
жащей da, но не освобождает своей формы от зависимости от самого а
Чтобы получить форму, не содержащую ни da, ни а надо, очевидно
проектировать на направление, перпендикулярное и к ех и к deu т. е.
умножить dP скалярно на векторное произведение (^iX^i)-
Форма
dP (ех X dex) —{ех det dP) = (qdu-f- q{dv) (y) du -f- r[{dv)-f-
+ (r rf« + г4Л) (С rf« + d<fo) = 8 rftf2 + 28' du dv-\-i"d& (24)
не зависит от положения точки Р на луче и внутренне связана
с конгруэнцией. Ее ввел Санниа как вторую основную форму
конгруэнции. Так как foX^i) имеет направление общего перпендикуляра
двух лучей, а скаляр его равен бесконечно малому углу между ними,
то форма (24) равна произведению кратчайшего расстояния между
бесконечно близкими лучами на синус угла между ними, т. е. моменту обоих лучей.
Если обозначим буквами а и р углы касательных к координатным
линиям на сфере с первой осью, то
г = |/zf cos a, q = — j/Z? sin a, rt = j/G cos p, qx — — |/0 sin p.. (25)
Введем еще произвольную функцию 9, которая зависит от положения
точки М на луче, и мы можем положить
£Y)-fK = 8, qxi\\-\-r&\=v\ Wi + rZ^b' + biqn— qxr),
tf! к) + rx С = 8' - » fon - ^r), (26)
откуда можно найти компоненты Y), тц, С, Ci. Выписывая условие, что det
и rfAf полные диференциалы, мы опять придем к уравнениям, (I), (II) стр. 90.
Если подставить туда из уравнений (26) т], т)ь С, С, то последние
два уравнения (Н) определят р и рг, а последние два (I) — £, £,.
Первые уравнения (II) и (I) не содержат & и дают одно единственное
условие на коэфициенты двух форм, чтобы они определяли конгруэнцию.
Это условие можно записать в виде
ду' ду ЕЬ> + ОЪ-2М' = () (25)
ди dv Veg~f*

УПРАЖНЕНИЯ
179
и скобки Кристоффеля вычислены для линейного элемента сферического
изображения конгруэнции
ds2 = Edu2-\- 2Fdu dv-\-G dv2.
Зная компоненты движения трехгранника, найдем координаты векторов
М и ех интегрированием уравнений Рикатти, следовательно две формы
Санниа определят конгруэнцию до перемещения в пространстве.
Уравнения развертывающихся поверхностей
8 du2 + 28' du dv + &" dv2 = О,
координаты фокусов определяются уравнением
(Д + &)2+ £0_/*=°»
уравнение главных поверхностей —
К -|(08 cos 26+ £8*— 2/78')tfw2 + 2(£,8''cos6+G8cose — 2^)**+
+ V% {EV cos 26 + G8 — 2FV) dv2 = 0,
границы луча определяются из уравнения
(л 1 (№ 1 88'-*'»_ (£8*+ 08-2/3')»
V" Т и; "Г EG — Z72 — 4(£G — Z72)2
Конгруэнция изотропная, если
8 _ V _ Ъ"
Е ~ F ~~G'
нормальная, если
£8'+ 08 — 2П' = 0.
Упражнения.
1. Если на поверхности S и одной полости ее поверхности центров St
соответствуют асимптотические, то линии постоянной гауссовой кривизны поверхности
о служат линиями кривизны.
2. Только у поверхности постоянной кривизны асимтотические линии
соответствуют асмиптотическим на обоих поверхностях центров.
3. Если на обоих полостях поверх» ости центров 5d и S2 соответствуют
линии кривизны, то St и52- поверхности постоянной отрицательной кривизны, а
их эвольвента, поверхность S, имеет постоянной разность главных радиусов
4. Приложить теорему Вейнгартена к отысканию поверхностей с линейным
элементом
d& = du* + u dv*
*- изгибания катеноида, сферическое изображение эвольвенты в теореме
Вейнгартена из термично. ^ *- к к
о. Если одна полость поверхности центров есть линейчатая поверхность R,
олученная изгибанием гиперболоида, то и вторая полость ей дополнительная яв-

180
ТЕОРИЯ КОНГРУЭНЦИИ
ляется линейчатой поверхностью, которая может быть образована осью
гиперболоида, когда он катится по поверхности R.
6. Дне линейчатые поверхности, налагающиеся на гиперболоид вращения,
образованные парой сопряженных (с общими равными нормалями) кривых
Бертрана, если через точки одн< й провод ть прямые параллельные бинормалям
другой,—составляют две полости одной и той же поверхности центров.
7. Геометрическое место центров геодезической кривизны системы
параллельных орициклов поверхности постоянной орицательной кривизны есть
некоторая новая поверхность такой же отрицательной кривизны.
8. Если одна полость поверхности центров — поверхность постоянной
отрицательной кривизны, то вторая полость налагается на поверхность вращения
1) трактрисы (псевдосфера) или 2) укороченной трактрисы ( = проекция
трактрисы на плоскость, проходящую через асимптоту) или 3) логарифмики.
9. Если
ds* = Edu* + 2Fdudv + б dv* (а)
линейный элемент сферического изображения конгруэнции, отнесенной к
развертывающимся Поверхностям, 2р— расстояние между фокусами, (М) — средняя
поверхность, (Мг) и (М2) — фокальные поверхности ие- единичный вектор
направления луча, так что
Мг = М + ре, М2~М — реу
то р удовлетворяет уравнению
А+-2+» £+(*+£+О»-* <ь>
«=(¥}•»-©■
где скобки Кристоффеля вычислены дтя линейного элемента (а).
Каждому решению уравнения (Ь) соответствует конгруэнц я, причем средняя
поверхность (М) определяется из вполне интегрируемой системы
Основные величины первой фокальной полости (MJ
ds? = 4 Ш + bp Jdifl— Sap (|j! + bp \du dv + 4f(a*+G)dtfl,
2VE№ + bp}s\nudu*-2VGp(^+ b у ^sino) }dv\
где аз — угол между фокальными плоскостями (или между координатными
линиями на сфере).
10. Конгруэнциями Гишара называются те конгруэнции, фокальные поверх
ногти которого секутся развертывающимися поверхностями пэ линиям кривизны
Они характеризуй тся сферическим изображением своих развертывающихся
поверхностей: оно совпатает с изображением асимптотических линий поверхности
постоянной отрицнтельной кривизны.
Обе полости фокальной поверхности ее суть поверхности Гишара. Обе
поверхности центров для поверхности Гишара — поверхности Фосса.
11. Если две поверхности соответствуют линиям кривизны и касательные к
линиям кривизны одной поверхности проходят через центры другой, то обе
поверхности — постоянной отрицательной кривизны и служат двумя полостями
одной и той же поверхности центров (дополнительное преобразование Бианки).
12. Если порерхно1ТИ (М) и (М1) соответствуют ортогональностью линейных
элементов, то прямая, проходящая через точку М параллельно нормали (М'),
описывает конгруэнцию Рибокура. Поверхность Щ') называется производящей
поверхностью конгруэнции. Только в конгруэнции Рибокура развертывающиеся
поверхности секут среднюю поверхность по сопряженной системе.

УПРАЖНЕНИЯ
181
Если производящая поверхность —сфера, то конгруэнция Рибокура есть
наиболее общая изотропная конгруэнция.
Конгруэнции Гишара суть конгруэнции Рибокура с производящей
поверхностью постоянной отрицательной кривизны.
Поверхности с изотермическими сферическими изображениями линий
кривизны и только они одни имеют конгруэнцию нормалей кони уэнцией Рибокура.
Всякая конгруэнция со средней поверхностью плоской есть конгруэнция*
Рибокура.
13. Если главные поверхности конгруэнции секут ее фокальные поверхности
по сопряженной системе, то конгруэнция есть конгруэнция W с равной
гауссовой кривизной фокальных полостей в соответствующих точках (конгруэнция
Бианки). ,В параметрах асимптотических линий и, v кривизна той и другой
полости фокальной поверхности имеет вид
^~ [?(«) + <М*)]2 в
Сферическое изображение асимптотических линий поверхности Бианки
удовлетворяет условию Коссера.
14. Найти конгруэнции, фокальные поверхности которых налагаются
соответствующими точками.
15. Если обе полости фокальной поверхности конгруэнции W-— минимальные
поверхности, то они конформно отображаются лучами конгруэнции (конгруэнция
Тибо). Присоединенные минимальные поверхности служат двумя полостями
огибающей оо3 сфер Рибокура.
16. Если одна полость поверхности центров для поверхности 5 вырождается
в линию Г, то одно семейство линий кривизны 5 состоит из кругов С.
Поверхность 5 можно рассматривать, как огибающую оо1 сфер с центрами на Г.
Циклиды Дюпена суть поверхности, у которых обе полости поверхности
центров вырождаются в линии Гг и Г2. Линии Гх и Г7 образуют пару взаимно
фокальных конических сечений. Если Г, есть эллипс, то Г2 — гипербола с общим
центром и общей осью, расположенной в плоскости нормальной к плоскости
эллипса так, что фокусы одной кривой служат вершинами другой. В таком случае
циклида — поверхность 4-го порядка. Когда ГА обращается в круг, Г2 становится
осью круга, а циклида становится тором (поверхность, образованная вращением
окружности с центром на Г± вокруг оси Л>).
Если /\ — парабола, то и Г3 — парабола; они расположены во взаимно
перпендикулярных плоскостях так, что фокус одной служит вершиной для другой. В
этом случае циклида есть поверхность 3-го порядка.
Исследовать форму этих поверхностей (см. табл. в конце книги).
17. Если прямая
x = pz + a, y=qz + b
и шар
(Х-а)* + (у-№ + (*-*()*=*&
поставлены в соответствие посредством равенств
то пересекающимся прямым
(*i — *а) (<!i — fr) = & — Ь2) (Pi ~р2)
соответствуют касающиеся сферы. Все прямые, касающиеся поверхности S,
переходят в сферы, касающиеся поверхности S'. При этом асимптотические линии
переходят в линии кривизны (С. Ли).

ГЛАВА ВОСЬМАЯ.
Триортогональная система поверхностей.
1. Криволинейные координаты в пространстве. Если текущий
радиус-вектор точки М является функцией переменных параметров и, ,vt w
М — М (и, v, w)} (1)
то точка может занимать, вообще говоря, любое положение в
пространстве, ибо из трех уравнений
х = х (и, vf w), y=y(u,'v,w), z = z(u,v,w) (Г)
при условии, что якобиан
*J£H> ф 0 (2)
можно по данным декартовым координатам (л:, у, z) точки М найти
значение параметров и, v, w, которые мы будем называть криволинейными
координатами точки в пространстве.
Мы будем рассматривать ту область изменения переменных и, v, w,
где ни один из якобианов второго порядка -тт^\ и т. д. не равняется
нулю и где следовательно три значения иу v, w определяют одну точку
М и каждой тачке соответствует только одна тройка чисел и, v, w.
Одно уравнение между криволинейными координатами
F(uy vtw) = 0 (а)
определяет поверхность. Декартово уравнение ее получим, исключая
и, v, w из уравнений (а) и (1').
Два уравнения определяют линию, которую удобнее представить
в параметрическом виде тремя уравнениями
u = u(t), v = v(t), w = w(t). (3)
Три уравнения определяют одну или несколько отдельных точек.
Поверхности
и = const, v = const, w = const
называются координатными поверхностями, их пересечения —
координатные линии. Поверхности и = const, v = const пересекаются по
координатной линии w9 ибо на этой линии, очевидно, только w — переменное.
Через каждую точку пространства (в рассматриваемой области)
проходят три координатные поверхности и следовательно три координатные
линии.

КРИВОЛИНЕЙНЫе координаты в пространстве 183
Так, в цилиндрической системе координат в пространстве
* = rcos<p, ey = /*sin<p, z = z
поверхности /• = const— цилиндры с общей осью z, ср = const — пучок
плоскостей, проходящих через ось г, 2 = const — пучок параллельных
плоскостей.
В полярной системе координат
х= rcoscp cos<J;, у = г cos <р sin ф, z = rsin<p
поверхности г = const — концентрические сферы, <р = const — круглые
конусы с общей вершиной в начале и общей осью z, ф = const — пучок
плоскостей, проходящих через ось z.
Направление касательной к линии (3) определяется бесконечно малым
вектором __ __ __
dM = M„du + Mvdv-{-Mwdw, (4)
где диференциалы du, dv, dw вычисляются из уравнений (3). Линейный
элемент ее
dM* =*= [Mudu + Mvdv-\-Mwdwf = М2 du* +MV2 dv2 -f Mw2 dw2-\-
-f- 2 Л/й/И„ fifo dv -f- 2MVMW dv dw -f- 2MwMudu dw. (5)
Здесь все коэфициенты
At2 = Л?„2, hf=Mv\ кг2 =Mw2,h12= MUMV9 h23=MvMw, h31 — MwM
могут быть вычислены из уравнений (Iх) сразу для всех кривых
пространства (3) и только диференциалы du, dv9 dw определяются из
уравнений кривой (3). Поэтому выражение
ds2 = 2 hi2 du? + 2S hik dui duk
называется линейным элементом пространства.
Суммирование идет по трем указателям 1, 2, 3; причем Ui = uf
и2 = V, «з = w-
пример. Цилиндрическая система координат
ds*=.di* + !*dfp-\-dz*.
Полярная система координат в пространстве
ds2 = rfr2 + Г* £ff2 -J- '2 cos*? d№.
В обоих случаях линейный элемент не содержит членов с произведениями
Диференциалов.
Если
hi2—0, Й2з = 0, Aai = 0,
то все три поверхности взаимно ортогональны во всякой^точке
пространства. Действительно, в этом случае векторы Ми, Mv, Mw взаимно
перпендикулярны, ибо скалярные произведения их равны нулю.
Три семейства взаимно ортогональных поверхностей образуют три-
°Р>погональную систему поверхностей.

184 ТРИОРТОГОНАЛЬНАЯ СИСТЕМА ПОВЕРХНОСТЕЙ
Линейный элемент пространства, если система координатных
поверхностей триортогональна, принимает вид:
ds* = hf da* + V d& -f h* dwK (6)
2. Теорема Дюпена. Рассмотрим прямой трехгранник Г,
образованный касательными к координатным линиям триортогональной системы
(w, v, w), и пусть еи е29 ег — единичные векторы осей;
dM = eihi du -f- e2h2 dv -\- e3h3 dw,
n = ^j £ pi duL-\- e22 qi dut -J- e3E rt йщ (7)
— бесконечно малое перемещение вершины и бесконечно малое вращение
трехгранника Т.
По общему правилу перемещение любой точки Р, координаты которой
по осям трехгранника Т суть [а, Ь, с], равно 1)
dP = [da, db9 <fc] -f *fe + ff X К *» с] • (8)
Подставляя сюда по очереди MP =[1,0,0], [0,1,0], [0,0,1] и вычитая
de9 получим:
dex = e2%ridui — еъЕqidm ,
tf £2 = ^з 2 /7/ fifo/ — £х S Г/ rftt/ , (9)
dez = ^ S <7/tf#/— £2 ^Pidui.
Выражения ЛИ и de, в формулах (7) и (9) должны быть полными
диференциалами, т. е.
t*>.-<*.)..£(2)-|(g).
и то же самое для любой пары переменных и, v, w. Это снова приведет
нас к уравнениям (Г) и (II) стр. 90, написанным для каждой пары
переменных и9 v, w. Уравнения системы (Г) теперь будут иметь вид:
^я=/^1|^ = А1г„^ = А,Л. (Ю)
Ve + нъЧ% = 0, *зЛ + Vs = 0, hxq2 + h2p{ = 0.
Умножая три последние уравнения на /*ь А2, h3 и складывая, получим:
hi h2rs 4- Мз?2 ~Ь МзА = 0,
откуда, вычитая по очереди каждое из слагаемых уравнений,
Л = 0, <7, = 0, г8 = 0. (11)
*) Мы будем заключать координатные векторы по осям трехгранника Т в
квадратные скобки
Ш>=[*, *, г).

УРАВНЕНИЕ ЛЯМЕ
185
Эти условия получают очень простое геометрическое истолкование.
Выписывая, например, для вектора еъ производные по и и по v9 имеем:
део дег
~fc=ei<li> ^ = —*2/V (а)
Заметим, что ег служит нормалью для поверхности w = const.
Следовательно уравнения (а) показывают, что касательные к линиям и на
поверхности и в сферическом изображении параллельны (то же самое
для линии v). Отсюда теорема:
Поверхности триортогональной системы взаимно пересекаются
по линиям кривизны.
Следовательно нельзя взять произвольно семейство поверхностей,
входящих в триортогональную систему: семейство линий, которые
пересекают данное семейство поверхностей ортогонально, устанавливают
между точками их соответствие так, что линии кривизны переходят
в линии кривизны.
Семейство поверхностей, которое входит в какую-нибудь
триортогональную систему, называется семейством Ляме, по имени геометра,
который первый дал теорию таких систем.
3. Уравнение Ляме.
Обозначим о ! ^hi по\
?ki — Tkdirk> W
где независимым переменным их = и, и2 = v, u3 = w приписаны значки.
Тогда л о о
Pi = 0, Р2 = — Рз2> А» = Р2з.
?1 = Рзь ?2 = °. ?а=—Pis (13)
Г\— — ?21» Г2 z=Pl2> ^3 = 0,
и уравнения таблицы (II)
dpi dpk _
дщ ди,~Г,Рк
разобьются на два типа
тЙ=ЫЫ.
^ + ^ + МЬ=0.
-ЯкГп
-rkp ,
-Pk4i*
(Hi)
(14,)
Первый тип содержит 6 уравнений, второй — три.
Если $ik найдены, то ht определяются из вполне интегрируемой
системы (12) с тремя произвольными функциями, каждая от одной
независимой переменной.
Зная /г/, мы знаем все компоненты движения трехгранника. Найдем 1)
*) Определение векторов е, сводится к интегрированию уравнений Рикатти,
Вектор М определяется квадратурами.

186
ТРИОРТОГОНАЛЬНАЯ СИСТЕМА ПОВЕРХНОСТЕЙ
обычным путем из уравнений (7) и (9) векторы М и £/. Движение
трехгранника вполне определено, если задано начальное положение его;
следовательно три функции Ы определяют триортогональную систему
вплоть до ее положения в пространстве.
Этого нельзя сказать относительно функций р#. Мы попрежнему
найдем по заданному начальному положению трехгранника единственным
образом векторы е;- из уравнений (9), но уже определение М требует
значений hit а они определяются, как мы видели, с 3 произвольными
функциями одного аргумента.
Следовательно существует бесконечное множество !) триортогональных
систем, у которых в соответствующих точках касательные плоскости
параллельны плоскостям данной системы.
Такое преобразование триортогональной системы носит название
преобразования Комбескюра.
Преобразование Комбескюра, очевидно, сохраняет сферическое
изображение линий кривизны каждой поверхности.
Если выражение %i по формулам (12) подставить в уравнения (14),
то получим толькЬ 6 независимых уравнений
^2Л/ 1 dhk dht 1 dht dht
diik dui hk дщ duk ' hi ди^ дщ'
dut \ht duj ^ duk\hkduk> ""*" hf dut dUl~u' V°'
которые называются уравнениями Ляме.
4. Теорема Лиувилля о конформном отображении пространства.
Если пространство отображается само на себя конформно, причем точка
(х, у, z) переходит в точку (£, т], С), то, очевидно, линейные элементы
пропорциональны
d\l + drf +d С2 = Г"2 (dx2 + dy* + dz% (a)
В пространстве (£, v\, £) поверхности л: = const, у — const, z = const
изображаются триортогональной системой поверхностей, и формула (а)
дает соответствующий линейный элемент. Следовательно
1
л "
ut = xt и2=у, uz — zy hi = h2—hz=-\
Внося это в уравнения Ляме (15), получим:
ду dz — ' дхду ~ ' dxdz ~ ' к и
~дх*+ ду* - ду*+ д& ~~ dz* Tl д*з ~~ I [\дх! + \ду) + \дг) У К V
Из уравнений (Ъг) следует
где X— функция одного х, Y—одного у и Z — одного переменного z.
х) Зависящее от трех произвольных функций одного аргумента.

ТЕОРЕМА ЛИУВИЛЛЯ О КОНФОРМНОМ ОТОБРАЖЕНИИ ПРОСТРАНСТВА 187
Внося это в уравнения (Ь2), получим *):
У 2 _L V 2 Л. 7' 2
л _r -Z _______ (с)
Так как между независимыми переменными л:, ^у, z не может
существовать никакого соотношения, то, очевидно, каждая из частей
сложного равенства (с) равна постоянному, например к.
Если k = 0, то
откуда Аг/= K'.= Z' ~0, все три функции — постоянные
X ~ const.
Отношение подобия линейных элементов (а) постоянно. Это показывает,
что точки (£, т], С) получаются из точек (х, у, z) подобным
преобразованием.
Если k не нуль, то полагая k = —, получим из первых трех
уравнений (с)
9 9 9
у/г _f_ -yii _~_ yi/ _~
С ' С ' С 9
X=±-[(x-al)2 + b1], Y = ±-[(y-a2)* + b2},
и последнее
Z = T[z — я3)2 + ^з], аи bh a — const,
^2^r2 + Z'2 = l(^+^+2)
с
дает
(х - ар + (у - а2у + (^ - «з)2 = (* - «,)2 + (У - а2)2 + (г - а3)2 +
Следовательно сумма ^ -j- b2 -\- bs равна нулю, и, перенося начало
координат в системе (х, у, z) в точку (а1( а2, а3), получим:
Л- ^ '
dn + *,* + av = (л8+^ + гу (**2+<у2 + **'). (d)
Это уравнение удовлетворяется значениями
р сх су «, CZ , ч
^~" X2+y2 + Z*> 71" x2 + y + ^> ^— л:2-)-д,2^_22' W
а так как линейный элемент определяет триортогональную систему вплоть
до положения в пространстве, ю следовательно общее решение
уравнений (d) отличается от (е) только на произвольное перемещение в
пространстве. Уравнения (е) определяют преобразование обратных радиусов-
векторов с центром в начале и степенью с.

188
ТРИОРТОГОНАЛЬНАЯ СИСТЕМА ПОВЕРХНОСТЕЙ
Имеем теорему:
Всякое конформное преобразование пространства может быть
получено подобным преобразованием пространства или
последовательным выполнением перемещения и преобразования обратных радиусов-
векторов.
Эта теорема лежит в основе конформной геометрии. Она легко
распространяется на пространство любого числа п измерений, но для п = 2
неверна: мы видели, что на поверхности конформное преобразование
получится, если комплексные переменные обеих поверхностей связать
произвольной аналитической функцией.
Из теоремы Лиувилля следует, что инверсия преобразует триорто-
гональную систему в другую триортогональную систему, а отсюда
вытекает, что линии кривизны сохраняются при преобразовании обратных
радиусов-векторов.
5. Теорема Дарбу. Система уравнений Ляме в форме (15) и
в форме (14) содержит больше независимых уравнений, чем неизвестных
функций; поэтому она не позволяет сделать никаких заключений о
существовании .решения и о степени общности его. Чтобы притги к уравнен
нию с одним неизвестным, начнем с обращения теоремы Ляме.
Теорема Дарбу. Если два семейства взаимно ортогональных
поверхностей пересекаются по линиям кривизны, то их можно
дополнить третьим семейством поверхностей так, что они образуют три-
ортргональную систему.
Пусть
/i (х> У> z) — const, /2 (*, у, z) = const
два заданные семейства поверхностей. Примем касательные к их линиям
кривизны за оси трехгранника; выберем за первые два параметры щ и
и2 функции
и пусть бесконечно малое перемещение вершины М и соответствующее
вращение трехгранника определяются формулами
<Ш = ехщ + е2 ш2 -f ег о>3, щ = Еа# duk)
k
П = ei £ pi dui -f- e2^qt dut -{- e3 S n duL.
Так как et и e2 служат нормалями для поверхности их = const и
и2 = const, то
et MUi = О, ё{ Мщ = О, ё2MUx = О, е2Мщ =0,
т. е.
ai2 = °> «1з = 0, «21 = 0, а23 = 0. (*)
Кроме того оси трехгранника касаются линий кривизны обеих
поверхностей. На поверхности их ■■= const это линии
<x22duz = 0(e3) и а38 du% -f a33 du9 =— 0 (ez). (b)

ТЕОРЕМА ДАРБУ 189
По теореме Родриг* касательные к линии кривизны и к ее
Сферическому изображению параллельны, а между тем по формулам (9)
касательными к сферическим изображениям линий (а) служат векторы
— *г ?з + Ч г8> — ез («зз Чч — «32 ?з) + е2 («зз г2 — а32 гь\
Следовательно
/"3 = 0, «33 02 — <*32?3 = 0, (с)
и аналогично для поверхности и2 = const
г3 = 0, «зз/?i — «з1Рз = 0. (d)
Возможно ли выбрать третье семейство поверхностей, которое
пересекало бы ортогонально две первых?
В таком случае, очевидно, существует оо поверхностей, для которых
перемещение dM ортогонально к вектору eZt т, е. которые определяются
уравнением
«31 dut -f- а32 du2 -j- «зз ^"з = 0- (е)
Следовательно такое семейство существует, если уравнения в полных
диференциалах (е) вполне интегрируемы. Условие интегрируемости
пишется в виде:
но система уравнений (I) стр. 90, где £/=«i/, ?]*=0С2/ С/~«з/, дает в силу (а)
Ъи3~ди;—~амрз>
^«33 <^31 _ „ п
di3i _<Ьч2_„ л 4- a п
5^ ~^T-aU02 + «22A.
Внося это в уравнение (/), мы получим:
«11 («33 ?2 — «32 Яг) + «22 («33^1 —«31 Ръ) = <>, (0
и это уравнение удовлетворено в силу условий (с) и (d). Теорема
доказана.
Из теоремы Дарбу сейчас же следует, что произвольное семейство
плоскостей или сфер (Si) может служить для образования триортого-
нальной системы (семейство Ляме). В самом деле на плоскости (и на
сфере) линии кривизны неопределенны и всякое семейство
поверхностей (S,), ортогональное к* семейству поверхностей (Si), пересекает их
по линиям кривизны (теорема Иоахимсталя).
Чтобы построить эту триортогональную систему, надо взять на
исходной поверхности (Si) произвольную ортогональную сеть линий (С),
найти ортогональные траектории семейства (St) и образовать
поверхности (52) и (53) из тех линий нормальной конгруэнции, которые
пересекают исходную плоскость (или сферу) вдоль линий того или другого
семейства системы (С). Очевидно, триортогональная система с одним

190
ТРЙОРТОГОНАЛЬНАЯ СИСТЕМА ПОВЕРХНОСТЕЙ
семейством плоскостей переходит в систему с одним семейством сфер
преобразованием обратных радиусов-векторов. Оба семейства представляют
единственные семейства Ляме, входящие в бесчисленное множество три-
ортогональных систем.
Если взять пучок плоскостей, то ортогональные траектории — круги
с одной осью; следовательно два другие семейства состоят из
поверхностей вращения — около оси пучка — и могут быть выбраны
произвольно, лишь бы меридианы их образовали на одной из плоскостей
ортогональную сеть.
Всякое семейство параллельных плоскостей (ортогональные
поверхности к нормальной конгруэнции прямых) является семейством Ляме.
Два другие семейства — развертывающиеся поверхности нормалей вдоль
линий кривизны.
6. Уравнения для семейства поверхностей Ляме. Пусть теперь
«=/(*» У> z) = const
семейство поверхностей Ляме. В таком случае существует второе семей
ство поверхностей (и третье), которые пересекают поверхности #=cons
по линиям кривизны одного семейства и следовательно служат
нормальными поверхностями к линиям кривизны второго семейства. Обратно,
если линии кривизны какого-нибудь семейства на поверхностях # = const
имеют семейство нормальных поверхностей,то каждая такая поверхность,
ортогональная к одной линии кривизны, содержит в своей касательной
плоскости нормаль к поверхности // = const и касательную к другой
линии кривизны и следовательно пересекает все поверхности и = const
ортогонально по линиям кривизны. В силу теоремы Дарбу семейство
и = const будет семейством Ляме.
Если
* = {а, р, Т}
вектор касательной к линии кривизны поверхности и = const, то
поверхность, нормальная к конгруэнции этих линий кривизны, определяется
уравнением в полных диференциалах
a dx -f- р dy -f- y dz: = 0.
Это уравнение вполне интегрируемо, и такие поверхности
существуют, если удовлетворено условие интегрируемости
•М+ИЙ-в)+1 (£-£)-* о
Это и есть уравнение для неизвестной функции и, если вместо а, р, у
подставить их выражение через функции и.
При движении по линии кривизны диференциалы dx, dy, dz
пропорциональны величинам а, р, ?. Диференцируя вектор нормали к
поверхности п
S=&M} А"-/,'+/,'+»
вдоль линии кривизны, мы получим по теореме Родрига вектор

УРАВНЕНИЯ ДЛЯ СЕМЕЙСТВА ПОВЕРХНОСТЕЙ ЛЯМЕ 191
параллельный вектору е. Два уравнения, которые, таким образом,
получаются, равносильны системе
Й)/Р + (т)/ + ЙЬ-(й«2-(й-Р-(й«т=о. (Ь)
Исключая а, р, у из уравнений (а) и (Ь), получим искомое
уравнение для функции и. Оно, очевидно, содержит производные третьего
порядка от неизвестной функции и. Следовательно общее решение
содержит три произвольные функции от двух аргументов. Например,
м<?жно задать для z = 0 значение /, fz и fzz,
7. Софокусные поверхности второго порядка. Простейший
нетривиальный пример триортогональной системы представляют софокусные
поверхности второго порядка. Уравнение
х2 у2 г* _« , v
а + К "Г ь + l + с + 1 ' W
где а>£>с>0 определяет эллипс для Х>— с, однополостный гиперболоид
для — с > X > — Ь и двуполостный гиперболоид для — b > X > — а.
Через каждую точку пространства проходят три поверхности
системы (а), определяемые уравнением
/(1) = (а + Ъ)(Ь + 1)(с + 1)-х*(Ь + 1)(с + Ъ)-уЦа + 1)(с + 1)-~
-г*(а + \) (ft + X) = 0, (с)
которое мы уже однажды писали (стр. 132), и где х, у, z надо считать
заданными. Так как
/(оо) > 0, /(-с) < 0, /(-*) > 0, /(-<*)< О,
то уравнение (с) всегда имеет три действительных корня в интервалах
oo>\1> — c>l2>—b> U > — а.
Первый корень Xt соответствует эллипсоиду, Х2—однополостному
гиперболоиду, Х3—двуполостному гиперболоиду.
Обратно, если задать Хх, Х2, Х3, то этим определятся три
поверхности (а) и точка их пересечения (х, у, z) — единственная в
нормальном координатном углу. Следовательно можно рассматривать \v Х2, Х3
как криволинейные координаты точки. Они называются эллиптическими
координатами.
Если в тождестве (с), где
/(Х) = (Х-Х1) (Х-Х2) (Х-Х3),
щ Х= — а, Х = — Ъ и Х = —
„ (*+х2) Sa + Ч V2_(» + X1) (&4 «■ ,-
(а — Ъ) (а— с) ' у (й — с)(Ь — а)
положить по очереди Х= — а, X = — Ь и Х = — с, то немедленно
найдем
у2-__(« + >ч) (а 4*2) >4^) V2_(» + X1) (6 4^ (^4Х3)
Г/2 — М Г/7— /Л > -^ Г Л — r\ ih — п\ '
(16)

192 ТРЙОРТОГОНАЛЬНАЯ СИСТЕМА ПОВЕРХНОСТЕЙ
Откуда логарифмическим диференцированием найдем
дх х ду у dz z («ч
д\,жв2(а + 1!У dlt*-2{Ь + 1()' д\^ 2(с + Цш W
Если в уравнение (а) подставить по очереди X = Xi, Х = ХА и
вычесть из одного уравнения другое, то по сокращении на Х^ — lk найдем
или в силу формул (d)
дх дх^ , ду^ ду_ , $z_ dz_ ~
~Ж\Жъ ' d\fWk"Г ах^^ц '
Следовательно три семейства поверхностей (а) образуют триортого-
нальную систему.
Чтобы подсчитать линейный элемент пространства в эллиптических
координатах, разделим тождество (с) на произведение (a-]-X)(£-f-X)(c-|-X).
(Х-Х,) (Х-Х2) а-Х3)__ х* ■ у» . z*_
(а + Х) (b + l) (c + ty ~а + 1 ' b + \*c+l
и, продиференцировав по X, подставим Х = Х,; мы получим:
(а + X,)* "Г (Ь + Х.)2 "Г {с + л/)2 {а ± х,) ф + Ц (с + X,) •
Следовательно линейный элемент имеет вид:
,/С2 LГ (Xi—х3^(Xj—х3) « 2J (х2 — х3)(х2 — хд) „ 2 ,
4 [(а + XJ(* + Х0(с + Хх)а^ Т- (e + h){b + хз)(с + х2)а^ "Г
■ (Хз-^ХХз-Х,) 1 I1''
4e + Xa)(* + *i)(' + As) * J'
Теорема Шаля. Конгруэнция общих касательных двух софокус-
ных поверхност й 2-го порядка — нормальная.
Пусть Mv (xv Уи Z\) и ЛГ2 (дг2, у2, z2) — координаты точки
прикосновения луча конгруэнции к поверхности X! и Х2. Так как они
удовлетворяют уравнениям (а) при соответствующем выборе X = Хх или X = Х2,
то направление фокальных плоскостей конгруэнции (касательные
плоскости к поверхности Х==Х1 и Х = Х2 в этих точках) определяются
векторами
л — ( *i У1 *i \ t—\ о
ni-\a + V b + h> c + xJ' 1—х> z'
Следовательно
п^Мг = 0, n2MxM2 = О,
а так как МХМ2 = {хг — xv уг—уи гг — zx}, то
*1*а х У\У* х *i** _ *ia . 3^ia , *? _,
a + Xt"1" ^ + Х1"1" c + Xt a + Xi"1" а + Х^ г-f-X,"" le
а + Х2"г"б + Х2"г г + Ха— *»

ИЗОТЕРМИЧЕСКАЯ СИСТЕМА
193
откуда, вычитая и сокращая на \i — Х2,
*1*2 , У1У2 , *1*3
(а + л1)(а + Х3)^(^ + ^) (^ + л2)^(с + а1) (с + а2) и>
т. е.
ях л2 = 0.
фокальные плоскости перпендикулярны, следовательно конгруэнция
нормальная.
8. Изотермическая система. Линейный элемент пространства в
эллиптических координатах имеет ту особенность, что на каждой из
поверхностей Х^ —const он принимает изотермический вид. Например, если
Х3 = const, то
"5 - 4 [(в + У (Н >,) (с + >.,) вл1 + (я + Х2) (ft + л2) (с + л2) СЛ2 J '
Такая триортогональная система называется изотермической.
Температура во всякой точке пространства при установившейся
передаче тепла (температура не зависит от времени) определяется
уравнением Лапласа
Если вместо декартовых координат (х, у, г) ввести криволинейные
ортогональные координаты иТ v, w, то оно примет вид:
ди\ ht duJ^dvW dvJ^dwK h, ~dw)~~ K '
Если каждое из трех семейств поверхностей и = const, v = const
w = const может служить семейством изотермических поверхностей
(поверхности постоянной температуры), то уравнение (18) должно допускать
интегралы
9 = и, б = v, 6 = w,
и тогда
откуда
ди h± — ' dv h2 ~~~и' dw А3 — и' w
dw (to /^ ди dv h2 ' дн flto /*i
Следовательно линии (и, v) образуют на поверхности w = const
изотермическую систему и также для двух других поверхностей и = const,
v = const.
Дарбу 1) показал, что наиболее общая изотермическая система
образована тремя семействами поверхностей х = const с общим уравнением
(д* + у2 + 22f + ах2+ by2 + CZ2 + d*± ij^i Х2 +
, 4^2 — ^2 4</2— с2 , п
a, ft, с, d = const.
*) .Ann. de l'Ecole Norm. Sup.*, I860, серия I, т. 3, стр. 133.

194
ТРИОРТОГОНАЛЬНАЯ СИСТЕМА ПОВЕРХНОСТЕЙ
Упражнения.
1. Триортогональные системы с одним семейством поверхностей вращения.
Пусть в триортогональной системе с линейным элементом
ds* = h? du? + hf dv* + hj dw*
поверхности v = const — поверхности вращения и кривые w — их меридианы,
следовательно геодезические линии. В таком случае вращение трехгранника около
оси е2 вдоль линии w равно нулю
018 = ?з = 0.
Уравнение (14) дает тогда
Мзз = 0.
Если р2з = 0> то Рз — 0> а так как всегда г3 = 0, то при движении вдоль линии до-
трехгранник Т совсем не вращается; следовательно меридианы w — прямые линии
и поверхности вращения — цилиндры или конусы. Оставляя это в стороне, имеем
г2 = 0.
Следовательно по формулам (9)
дег л де< л - - . ч
^=°>^=0' '> = '!(»)
и поверхности и = const — плоскости, содержащие меридианы w поверхности
вращения.
Искомая система состоит из семейства поверхностей вращения с общей осью
(v = const), из пучка их меридиональных плоскостей (и = const) и второго
семейства поверхностей вращения. Систему можно получить вращением произвольной
ортогональной сети линий на плоскости около оси, лежащей в этой плоскости.
Линейный элемент
пространства характеризуется тем,
что все коэфициенты —
функции только двух переменных
и и v, как это можно сейчас же
видеть из уравнений Ляме.
2. Семейство плоскостей
х = и
и два семейства цилиндров
v = ср (у, г\ w = ф О, г)
образуют триортогональную
систему при условии на
функции ср и ф.
3. Семейство сфер
x*=y* + z* = u
и два семейства конусов
образуют триортогональную
систему при условии на
функции ср и 4>-
Например
yi + г* = и, у = vx, х% + у* = wzK

ТАБЛИЦА ОСНОВНЫХ ФОРМУЛ
195
4. Семейство сфер
x2+y* + z* __
и
X
и поверхности
,_,(^±г±г, i). .-t(i±ut£,±)
образуют триортогональную систему при условии на функции ср, ф.
5. Гиперболические параболоиды
yz
X
и два семейства поверхностей а = const
(у _ 22)2^2а(>5 + 22 + 2*2) + а2 = О
открытых и замкнутых образуют триортогональную систему.
6. При произвольной функции X = ср (jc) и с = const три семейства
поверхностей
* + £(У2 + *2) = И,
y = vz,
. г dx
Цу* + г*)е CJ *' = w
образуют триортогональную систему.
7. Семейство оо * поверхностей, ортогональные траектории которых суть круги,
есть семейство Ляме.
8. Если винтовую поверхность постоянной кривизны вращать около оси, то
образуется семейство Ляме.
9. Если поверхность Энн^пера постоянной кривизны вращать около оси, то
образуется семейство Ляме.
Таблица основных формул
1. Движение с двумя степенями свободы трехгранника с вершиной М
и осями е19 е2) еъ определяется 6 компонентами поступательного
движения точки М — £, £ь y), Yji С, Ci и 6 компонентами вращения—р, ри
<7» Я\ч rf ri- Они удовлетворяют уравнениям
d£ d$i уху <*Р dpi
Перемещение точки Я [а, 6, с] равно
<*Р = [аГа, Л, Л] + dM + П X [л, *, *]
или
dP = ei{da + i du + ^ du + (q du + q± dv) c — (rdu-\-rx dv) Ь }
+ e2\db + t\du + r\t dv + (r da + ^ flfo) a — (p du + /?x ato) г
+ *3{rfc + С du + CJflto'+ (pdu+pt dv) b — (qdu + q1dv)a }.
В частности
dSf = ^ (6 du + 6t flfo) + jj3 (tj du + *ц dfo) + ^ (C ate + Ci dv)9
dex = £3 (r сГы + rx rft/) — ez(qdu + ^ flft>),
tf?3 = :re1(rdu + rt dv) + ez{pdu+px dv\
dez = ^i (?rfa + ft rf») — e2(pdu + p1 dv).

196
ТРИОРТОГОНАЛЬНАЯ СИСТЕМА ПОВЕРХНОСТЕЙ
II. Поверхность (М) определяется компонентами ?, %и i\y т\и С = Ci = О,
A Piy Я* Я\у г> г\
д~ dq др дрх
dv Stt-^r -ri dv ~d^~rPl riPt
РЛ\ —Prt = ЯЪ — ?i? dv~"du= РЯл ~~pig'
Линейный элемент
ds* = (Ыи + 6j tft/)2 + (yj flf« + y)! Л)2 = £Ai* + 2F du dv + Gdv*,
E=? + ift F= 66i + Th, О = ?!2 + 4l».
Если ot и p — углы координатных линий и и v с первой осью el9 то
5 *= jAE cos a, Y) = ]/*£ sin а, ;х = |/"0 cos (3, щ = |/"G sin p.
Сферическое изображение
<*еъ = ^(д-яГи + q1dv)—e2 (р du + рх dv),
ds'2 = (pdu+p1 dv)2 + (qdu + qt dv? = eafa2 + 2fdudv + y dv*,
e = p* + q*,f=pp1 + qq1, g = Pi2 + q^
Если а' и $*—углы координатных линий на сфере с первой осью е^то
р = — ]/ е sin a', # = J/A£ c6s a', р1 = — *\fg sin g', ^ = "|/g cos g'.
Уравнение асимптотических линий
(/? tfw + /?! fifo) (у) </ы + гц flfv) ~(qdu-\- qx dv) ($du + ^ tft>) = 0
или
(/77] — ??) оГи2 _j_ (рЪ + pft-q^—qfi) du dv + (^Th— ft?,) afo2 = 0.
Условия сопряженности
(pdu + pL dv) (rpu + rn Щ — (qdu-\- qx dv) (? hi + ^ &z>) = 0.
Линии кривизны
? afa + ?j dv + /? (# ato -|- qt dv) = 0,
y] eta + r\1dv — R(pdu + /7j dfo) = 0,
откуда
(/?£ + qrft dv? + (/??! + p£ + qra + q^) du dv + (pfo + q^) dv* = 0,
#з (pqi—prf) + R(qra- q<i\ -\- pli- р£) + ^, - *& = 0.
Вторая квадратичная форма Гаусса
dMdez = Ddu2 + QDl du dv + D" dv*,
D=:prt — ql D,=/?-/i1—^1=/?1r,-^15, D'f=plrll — qLlv
^ д , Я д , A - д , Яг д ,
A = ;та -• SjYj = + 'YEG—F2 = \/ EG sin Ш ,
w = p — a — угол между координатными линиями.
Мив = {111}м„ + {У}^ + Dez,
Muv = {l?}Mu + ^l)'Mv + D'es,
Mvv - {f | Mu + f22} Mv •+ Dfi»
FD'-GD .. ^ FD—ED* -
e*u = EG — F2 ll ^~ EG — F2 v>
FD"—GU n . FD'—ED" n

ТАБЛИЦА ОСНОВНЫХ ФОРМУЛ
197
Уравнения Кодацци
Уравнение Гаусса
D£>"—D'2 1 (д Г F дЕ
К =
EG-
+
F*
[
2 YEG — F* W IF YEG - F* dv Y^G
1 д(П
J^F* du\
+
иначе
д_ Г 2 dF 1 a£ F dE\\
dv lYEG — Л ди "l/£G^?2 <^ EY~FG=7* du] J'
ATi4Csin.a) = -
^2a
Л2:
Скобки Кристоффеля
V Л sin ш / dt/ \
:£», (? = G, AC cos о> = F.
dA
dv'
дС
да
COS <о
(?И
С sin <
п-
ан ' at; аи
{'Я-
in-
2(£G
-/*)
* 12/
_ Г<?1л-2Е — ~- Е —
2(EG — F*)
}дЕ „ dG
\dv
_du (12)
E™-F^
du dv
2 (EG
F™ + 2Gd-f-
dv ' (7t/
2 (£G - Z72)
du
2(EG — F*)
m д In V EG— F*
du
dA dC
я- COS 0)
dv du
A sin2 a)
С sin a) L da
• {?K2}
- {"}
fa
I du
EdG+pdG dF
dv~r da а#
du
2 (EG — Z72)
ainl/~£G—/?2
ал
5— cos a>
dv
dA
dv
С sin2 a)
ас
а«
cos
Л sin с
С sine
dC dA
do> . du du
— tv- COS 0)
аэ
dv
dA
dv
A sinu
ас
=r- COS to
аы
r,=-
ам Csin<
aa . du dv
cos a>
dv
Asinu)
\2f~Csin<o ( Г +du)> \l}-
Л51П<
('■+!)•

198
ПОЯСНЕНИЯ К РИСУНКАМ
Р — точка кривой, 5—соприкасающаяся плоскость,
N — нормальная плоскость, R — спрямляющая
плоскость, t — касательная, А—главная нормаль, Ь —
бинормаль, k — круг кривизны, г—радиус кривизны,
К А — ось кривизны, КМ—центр кривизны, SM—центр
соприкасающейся сферы.
Пояснения к рисункам.
Рис. 1 и 13. К а т е н о и д — поверхность, образованная вращением цепной
линии около своего основания. Единственная минимальная поверхность вращения
х = a cos и ch v, у = a sin ы ch t\ z = av.
На рис. 1 дан отрезок поверхности между двумя параллельными кругами; на
поверхности нанесены геодезические линии: а) подымающиеся до некоторой
параллели и снова опускающиеся, Ь) асимптотически приближающиеся к
горловому кругу, с) пересекающие этот круг.
На рис. 13 показано образование этой поверхности с помощью мыльной
пленки, натянутой на два металлических круга (опыт Плато).
Рис. 2. Прямой (минимальный) геликоид. Винтовая поверхность образована
движением прямой, которая, пересекая ось z под прямым углом, поднимается
и вращается вокруг нее.
х — и cos v, у = и sin t/, z = av.
На поверхности нанесены: 1) прямолинейные образующие и 2) ортогональные
к ним винтовые линии (среди них одна прямая — директриса — ось z); те и flpyj ие
составляют асимптотические линии; 3) два семейства кривых, пересекающих
прямолинейные образующие под углом 45°—линии криэизны.. Поверхность
налагается на катеноид рис. 1, так что прямые образующие налагаются на
меридианы, а винтовые линии на параллели.
Рис. 3. Поверхность эллиптического типа.
и и
х = X sh —- cos v, у = к sh —- sin vt

ПОЯСНЕНИЯ К РИСУНКАМ
199
Поверхность имеет ребро возврата — круг радиуса г = R cos а, коническую
точку, где меридианы, пересекаясь, образуют угол а -— = sin а .
Нанесены геодезические линии и одна асимптотическая (уходит в коническую
точку поверхности). Поверхность периодически повторяется.
Три поверхности вращения постоянной отрицательной кривизны.
Рис. 4— псевдосфера, простейшая поверхность постоянной отрицательной
кривизны, сбразована вращением трактрисы около своей асимптоты
х = R sin и cos vt у = R sin и sin v>
• = R (in tg—- + cos и J.
Имеет ребро возврата и = -—- (круг радиуса /?), асимптотически приближается
к оси z. Нанесены геодезические линии: а) подымающиеся до некоторой
параллели и опускающиеся, Ь) уходящие в бесконечность, завиваясь около оси z% с)
меридиан.
Рис. 5. Линейчатая винтовая поверхность — развертывающаяся. Образована
касательными к винтовой линии. Эта винтовая линия на модели образована
(посредине) сгущением натянутых нитей — образующих поверхности. Как одна из
опор для нитей через всю модель проходит винтовая линия (из металла). На
поверхности она является двойной линией — линией пересечения двух полостей
поверхности. При развертывании на плоскость винтовая линия (ребро возврата)
переходит в окружность, и поверхность налагается дважды на внешнюю часть
плоскости.
Рис. б. Линейчатая поверхность, не развертывающаяся (косая). Прсредине
сгущение нитей {линия сжатия), но нет пересечения их.
Рис. 7. Поверхность гиперболического типа.
и и
х = X сп —- cos v, у-= X ch — sin v,
J У #2 R
Дана часть поверхности между двумя ребрами возврата. Нанесены: а) пучок
параллельных геодезических линий; из них одна асимптотически навивается на
горловой круг, Ь) геодезические круги — замкнутые линии, одна из них замыкается
на передней части поверхности.
Рис. 8—10. Поверхности 4-го порядка
№+У2 + г* + Р — $з)8 = 4|д2 /* + — )*+ Ъ*уА ; с = Y~at—b*.
Поверхности центров: эллипс z = О, 1- — = 1 и гипербола у = 0, 1 = 1;
а2 № с1 Ь2
каждая проходит через фокусы другой. Одно семейство — линии кривизны (малые
круги на чертеже), лежит в вертикальных плоскостях, проходящих через прямую
г— кс
9 У = 0, другое семейство — в плоскостях, проходящих через конические
Т^чки поверхности. В каждой плоскости два круга. В горизонтальных плоскостях
J5 — и) круги CjC2 с центрами в фокусах эллипса (вершины гиперболы) и ра-
Рис. 8. Hornzyclide, к < с < а. Круги СХС<^ пересекаются; 2 конические точки.
с Рис- 9. c = k<^a. Круги касаются изнутри. Точка касания — кониче-
Рис. 10. Ringzyclide, с<£<д. Один круг внутри другого.
Рис 11, 12. Поверхности 3-го порядка — параболические

200
ПОЯСНЕНИЯ К РИСУНКАМ
Поверхности центров: парабола х = 0, у2 = 2pz; парабола у = 0,
х2 = — 2/7 fz — -— ). Каждая проходит через фокус другой. Линии кривизны —
окружности, их плоскости образуют два пучка; в каждой плоскости по 2 круга.
В плоскости у — 0: круг х2 + 22 = № и прямая z = р — k; в плоскости л: = 0:
круг y* + (z — --)=(& — --J и прямая z = — &.
Рис. 11. /><2&. Прямая пересекает круг. Две конические точки.
Рис. 12. p^>2k. Прямая не пересекает круга.
Обе поверхности уходят в бесконечность.'
Рис. 14. Эллипсоид, повернутый боком. Даны два главных сечения (эллипсы)
и геодезические линии, проходящие через точку округления; они все проходят
через противоположную точку округления.
Рис. 15. Триортогональная система, образованная тремя семействами софо-
кусных поверхностей 2-го порядка. Даны: 1) эллипсоид (посредине) с
нанесенными линиями кривизны, 2) однополостный гиперболоид; сверху и снизу — часть
скрыта эллипсоидом; нанесены прямолинейные образующие; 3) двуполостный
гиперболоид без нанесенных линий кроме главного сечения.
Циклиды Дюпена. Обе поверхности центров выродились в линии —
конические сечения в двух перпендикулярных плоскостях. Все линии кривизны —
окружности (нанесены на чертеже.)
Редакция: А. В. Зазкохов. Оформление Р. /7. Основат. Корректура А. X, Артюхава.
Выпускающий А. М. Волкович.
ГТТИ № 33. Тираж 5 000. Сдано в набор 13/111-33 г. Подл, в печ. 8/1-34 г. Формат бумаги 62 X 94-
Авт^орск. лист. 187а- Бум. лист. 672. Печ. зн.»в бум. листе 111488. Заказ № 358. Ленгорлит № 25120»

ТАБЛИЦЫ
Рис. 1.
Рис. 2.

Рис. 3.
Рис. 4.

Рис. 5.
Рис. 6.
Рис. 7.

Рис. 8.
Рис 9.
Рис. 10
Рис. 11.
Рис. 12.
Рис. 13.
Рис. 14.
Рис. 15.

С.П. ФИНИКОВ
ТЕОРИЯ ПОВЕРХНОСТЕЙ
ГТТИ —1934