В.И.Арнольд
МАТЕМАТИЧЕСКИЕ МЕТОДЫ КЛАССИЧЕСКОЙ МЕХАНИКИ

Книга отличается от имеющихся учебников механики большей, чем это
обычно принято, связью с современной математикой. Особенное внимание
обращено на взаимно обогащающее взаимодействие идей механики и геометрии
многообразии.
В соответствии с таким подходом центральное место в книге занимают не
вычисления, а геометрические понятия (фазовые пространства и потоки,
векторные поля, группы Ли) и их приложения в конкретных механических
ситуациях (теория колебаний, механика твердого тела, гамильтонов
формализм). Много внимания уделено качественным методам изучения
движения в целом, в том числе асимптотическим (теория возмущений, методы
осреднения, адиабатические инварианты).
Для студентов университетов и вузов с расширенной программой по
математике, а также преподавателей и научных работников.

ОГЛАВЛЕНИЕ
Предисловие к третьему изданию 6
Ив предисловия к первому изданию 9
ЧАСТЬ I
НЬЮТОНОВА МЕХАНИКА
Глава 1. Экспериментальные факты И
§ 1. Принципы относительности и детерминированности 11
§ 2. Галилеева группа и уравнения Ньютона 12
§ 3. Примеры механических систем 18
Глава 2. Исследование уравнений движения 21
§ 4. Системы с одной степенью свободы 21
§ 5. Системы с двумя степенями свободы 26
§ 6. Потенциальное силовое поле 30
§ 7. Кинетический момент 32
§ 8. Исследование движения в центральном поле 34
§ 9. Движение точки в трехмерном пространстве 42
§ 10. Движение системы п точек 44
§ 11. Соображения подобия 50
ЧАСТЬ II
ЛАГРАНЖЕВА МЕХАНИКА
Глава 3. Вариационный принцип 52
§ 12. Вариационное исчисление 53
§ 13. Уравнения Лагранжа 56
§ 14. Преобразование Лежандра 59
§ 15. Уравнения Гамильтона 61
§ 16. Теорема Лиувилля 64
Глава 4. Лагранжева механика на многообразиях 70
§ 17. Голономные связи 70
§ 18. Дифференцируемые многообразия 72
§ 19. Лагранжева динамическая система 77
§ 20. Теорема Нётер 81
§ 21. Принцип Даламбера 84
Глава 5. Колебания 90
§ 22. Линеаризация 90
§ 23. Малые колебания 94
§ 24. О поведении собственных частот 99
§ 25. Параметрический езонанс 102

4 ОГЛАВЛЕНИЕ
Глава 6. Твердое тело Ш
§ 26. Движение в подвижной системе координат 111
§ 27. Силы инерции. Сила Кориолиса 115
§ 28. Твердое тело 119
§ 29. Уравнения Эйлера. Описание движения по Пуансо 127
§ 30. Волчок Лагранжа 131
§ 31. Спящий волчок и быстрый волчок 136
ЧАСТЬ III
ГАМИЛЬТОНОВА МЕХАНИКА
Глава 7. Дифференциальные формы 142
§ 32. Внешние формы 143
§ 33. Внешнее умножение 148
§ 34. Дифференциальные формы 152
§ 35. Интегрирование дифференциальных форм 158
§ 36. Внешнее дифференцирование 164
Глава 8. Симпл оптические многообразия 175
§ 37. Симплектическая структура на многообразии 175
§ 38. Гамильтоновы фазовые потоки и их интегральные инвари-
инварианты 177
§ 39. Алгебра Ли векторных полей 181
§ 40. Алгебра Ли функций Гамильтона 187
§ 41. Симплектическая геометрия 191
§ 42. Параметрический резонанс в системах со многими степеня-
степенями свободы 197
§ 43. Симплектический атлас 201
Глава 9. Канонический формализм 205
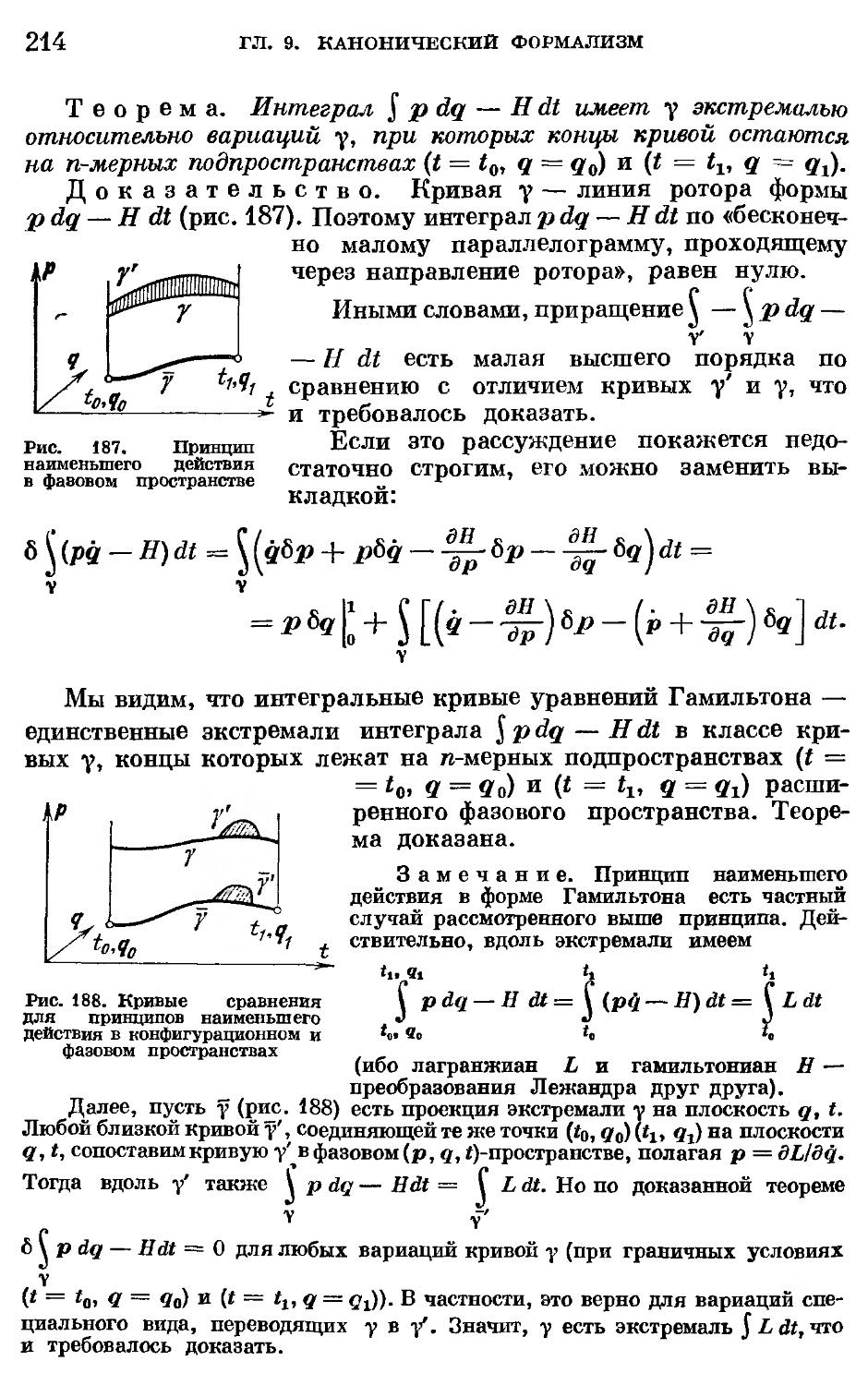
§ 44. Интегральный инвариант Пуанкаре — Картана 205
§ 45. Следствия из теоремы об интегральном инварианте Пуанка-
Пуанкаре — Картана 211
§ 46. Принцип Гюйгенса 218
§ 47. Метод Якоби — Гамильтона интегрирования канонических
уравнений Гамильтона 226
§ 48. Производящие функции 234
Глава 10. Введение в теорию возмущений 238
§ 49. Интегрируемые системы 238"
§ 50. Переменные действие — угол 245
§ 51. Усреднение 250
§ 52. Усреднение вовмущений 256
ДОБАВЛЕНИЯ
Добавление 1. Риманова кривизна 266
Добавление 2. Геодезические левоинвариантных метрик на группах
Ли и гидродинамика идеальной жидкости 283
Добавление 3. Симплектическая структура на алгебраических мно-
многообразиях 308
Добавление 4. Контактные структуры 314
Добавление 5. Динамические системы с симметрией 337
Добавление 6. Нормальные формы квадратичных гамильтонианов 347
Добавление 7. Нормальные формы гамильтоновых систем вблизи
неподвижных точек и замкнутых траекторий 351

ОГЛАВЛЕНИЕ 5
Добавление 8. Теория возмущений условно-периодических движе-
движений и теорема Колмогорова 365
Добавление 9. Геометрическая теорема Пуанкаре, ее обобщения
и приложения 384
Добавление 10. Кратности собственных частот и эллипсоиды, завися-
зависящие от параметров 393
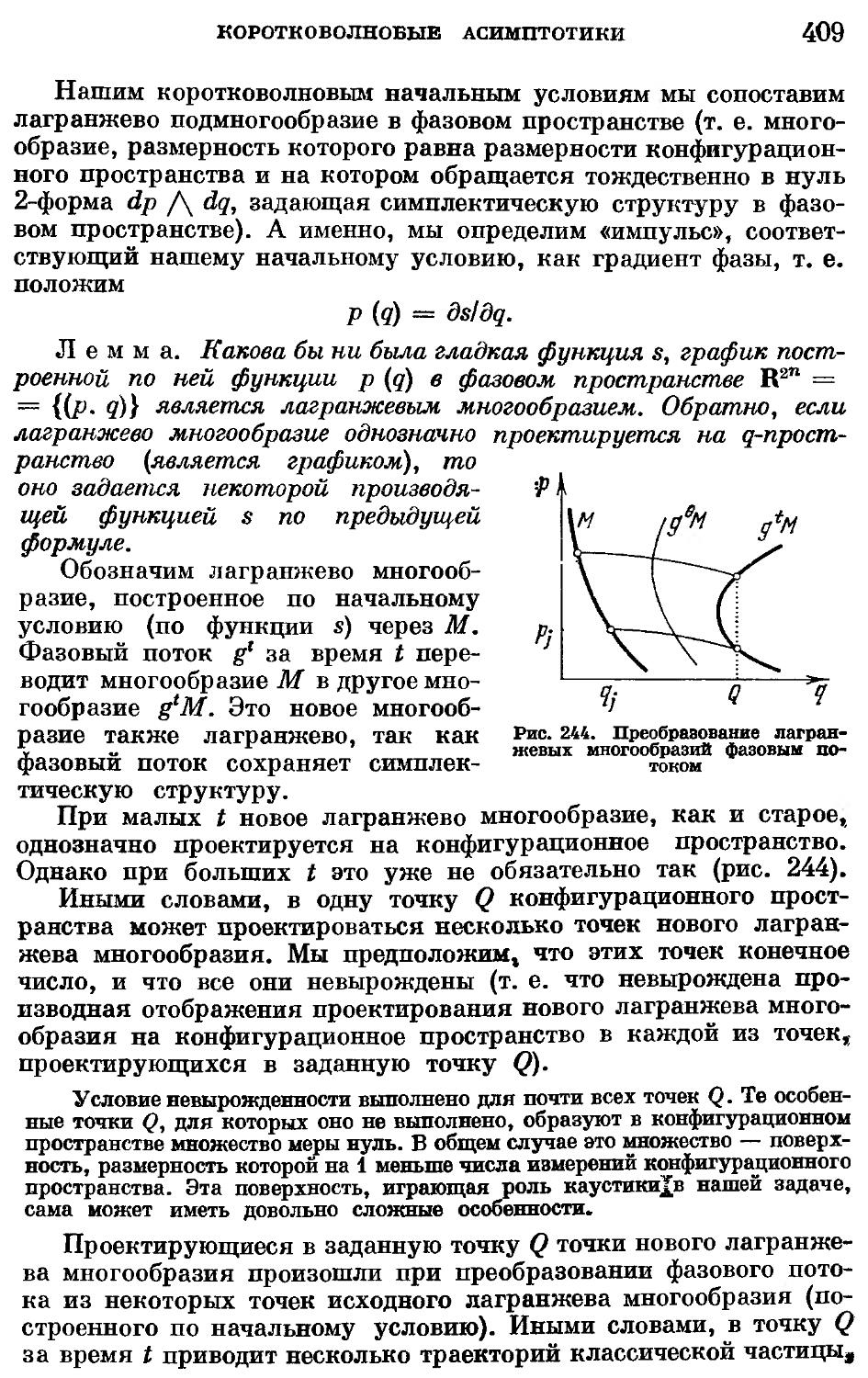
Добавление 11. Коротковолновые асимптотики 406
Добавление 12. Лагранжевы особенности 415
Добавление 13. Пуассоновы структуры 422
Добавление 14. Об эллиптических координатах 435
Добавление 15. Особенности систем лучей 445
Добавление 16. Уравнение Кортевега—де Фриза 465
Предметный указатель 469

ПРЕДИСЛОВИЕ К ТРЕТЬЕМУ ИЗДАНИЮ
Основная часть этой книги написана двадцать лет назад. За это
время идеи и методы симплектической геометрии, на которых ос-
основана книга, нашли многочисленные применения как в матема-
математической физике и других областях приложений, так и в самой
математике. В особенности следует отметить бурное развитие тео-
теории коротковолновых асимптотик, с их приложениями в оптике,
теории волн, акустике, спектроскопии и даже химии, и одновре-
одновременное развитие теории лагранжевых и лежавдровых особенностей
и многообразий, т. е. теорий особенностей каустик и волновых
фронтов, их топологии и их перестроек.
Необыкновенно далеко продвинулось исследование интегри-
интегрируемых задач гамильтоновой динамики. Было открыто неожиданно
большое число интегрируемых динамических систем, изучение
которых привело к неожиданным и взаимообогащающим связям
этих вопросов с трудными проблемами алгебраической геометрии
и математической физики.
Большие успехи достигнуты за последние годы в симплекти-
симплектической топологии. Здесь прежде всего выделяется доказательство
теоремы о неподвижных точках симплектических диффеоморфиз-
диффеоморфизмов, обобщающей «геометрическую теорему» Пуанкаре (добав-
(добавление 9), полученное в 1983 г. Ш. Конли и Э. Цендером. За этим
доказательством последовали работы М. Шаперона, А. Вейн-
стейна, Ж.-К. Сикорава, М. Громова, Ю. Чеканова, Флоера,
Витербо, Хофера и др. Я надеюсь, что в этой интенсивно разви-
развивающейся сейчас области вскоре будет достигнут еще больший
прогресс, который приведет к доказательству сформулированных
и открытию новых теорем симплектической и контактной топо-
топологии — новой области математики, вызванной к жизни вопро-
вопросами механики и оптики.
В настоящее издание включено три новых добавления. Они
отражают новое развитие геометрии систем лучей (теории особен-
особенностей и перестроек каустик и волновых фронтов, связанной с тео-
теорией групп, порожденных отражениями), теории интегрируемых
систем (геометрической теории эллиптических координат, приспо-
приспособленной для бесконечномерных обобщений) и теории пуассоновых
структур (часто встречающихся в математической физике обобще-
обобщений симплектических структур, отличающихся тем, что скобки
Пуассона вырождаются).

ПРЕДИСЛОВИЕ К ТРЕТЬЕМУ ИЗДАНИЮ 7
Более подробное изложение теории возмущений читатель найдет
в книге «Математические аспекты классической и небесной меха-
механики» В. И. Арнольда, А. И. Нейштадта и В. В. Козлова, со-
составляющий третий том энциклопедической серии «Современная
математика. Фундаментальные направления» (М.: ВИНИТИ, 1985).
Четвертый том этой же серии содержит обзор современного со-
состояния симплектической геометрии (В. И. Арнольд, А. Б. Ги-
венталь), статью А. А. Кириллова о геометрическом квантовании
и обзор С. П. Новикова с соавторами о развитии теории интегри-
интегрируемых систем, лишь затронутом в настоящей книге.
Вопросы геометрии систем лучей подробно обсуждаются в двух-
двухтомнике В. И. Арнольда, А. Н. Варченко и С. М. Гусейн-Заде
«Особенности дифференцируемых отображений» (т. I.—М.: Наука,
1982; т. II.—М.: Наука, 1984), и в книге В. И. Арнольда «Теория
катастроф» C-е издание.—М.: Наука, 1990, с обширной библио-
библиографией).
Обзоры по симплектической и контактной геометрии и их при-
приложениям опубликованы в трудах семинара Н. Бурбаки (доклад
Д. Беннекена «Мистические каустики» в феврале 1986 г.) и в ряде
статей (Арнольд В. И. Первые шаги симплектической то-
топологии // УМН.—1986.—Т. 41, вып. 6.— С. 3—18; Особенности
систем лучей // УМН.—1983.— Т. 38, вып. 2.— С. 77—147; Осо-
Особенности в вариационном исчислении // Современные проблемы
математики.— ВИНИТИ.— 1983.— Т. 22.— С. 3-55; Щер-
Щербак О. П. Волновые фронты и группы отражений // УМН.—
1988.— Т. 43, вып. 3.— С. 125—160).
Выпуски 22 и 33 серии «Итоги науки. Современные проблемы
математики» (М.: ВИНИТИ, 1983 и 1988) содержат обширный
дополнительный материал по приложениям симплектической и
контактной геометрии к исследованию вариационных задач,
а тем самым — к механике, оптике, теории оптимального управ-
управления и т. д.
Теория бифуркаций и теория возмущений (не только гамиль-
тоновых, но и общих динамических систем) рассмотрены в
учебнике: Арнольд В. И. Дополнительные главы теории обык-
обыкновенных дифференциальных уравнений.— М.: Наука, 1978
(английское издание: Arnold V. I. Geometrical Methods in
tbe Theory of Ordinary Differential Equations.— Springer, 1988.—
325 p.— значительно полнее). Новую информацию содержат также
доклад «Теория бифуркаций и ее приложения в математике и ме-
механике» на XVII Международном конгрессе по "теоретической и
прикладной механике, Гренобль, 1988 г. и обзор В. И. Арнольда,
В. С. Афраймовича, Ю. С. Ильяшенко и Л. П. Шильникова и так-
также весь выпуск «Динамические системы-5» энциклопедической
серии «Современные проблемы математики. Фундаментальные
направления» (М.: ВИНИТИ, 1986). Второй выпуск этой серии,
написанный Д. В. Аносовым, Я. Г. Синаем и др., посвящен зр-

8 ПРЕДИСЛОВИЕ К ТРЕТЬЕМУ ИЗДАНИЮ
годическим проблемам теории динамических систем, в том числе
механических.
Обнаруженные во всех этих теориях факты потенциально имеют
широчайший круг приложений, но, поскольку они были открыты
лишь недавно, и изложены лишь в специальной литературе, их
применение сдерживается пока относительной труднодоступно-
стью математических текстов для прикладников. Я надеюсь, что
настоящая книга позволит овладеть зтими достижениями не только
математикам, но и механикам, физикам и всем другим потребите-
потребителям теории динамических систем, симплектической геометрии и
вариационного исчисления.
В. И. Арнольд
Ноябрь 1988 г.

ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
В классической механике используются весьма разнообразные
математические методы и понятия: дифференциальные уравнения
и фазовые потоки, гладкие отображения и многообразия, группы
и алгебры Ли, симплектическая геометрия и эргодическая теория.
Многие современные математические теории возникли из проблем
механики и лишь впоследствии приняли тот аксиоматически-
абстрактный вид, который так затрудняет их изучение.
Математический аппарат классической механики строится в
настоящей книге с самого начала, так что у читателя не пред-
предполагается предварительных знаний, выходящих за рамки стан-
стандартных курсов анализа (производная, интеграл, дифференциаль-
дифференциальные уравнения), геометрии (линейное пространство, векторы) и
линейной алгебры (линейные операторы, квадратичные формы).
С помощью этого аппарата разбираются все основные вопросы
динамики системы, включая теорию колебаний, теорию движения
твердого тела и гамильтонов формализм. Автор стремился всюду
выявить геометрическую, качественную сторону явлений. В этом
отношении книга ближе к курсам теоретической механики для
физиков-теоретиков, чем к традиционным курсам теоретической
механики, читаемым математикам.
Значительная часть книги посвящена вариационным прин-
принципам и аналитической динамике. Характеризуя аналитическую
динамику в своих «Лекциях о развитии математики в XIX столетии»,
Ф. Клейн писал, что «физик для своих задач может извлечь из
этих теорий лишь очень немного, а инженер — ничего». Развитие
науки в последующие годы решительно опровергло зто замечание.
Гамильтонов формализм лег в основу квантовой механики и яв-
является в настоящее время одним из наиболее часто употребляемых
орудий в математическом арсенале физики. После того как было
осознано значение симплектической структуры и принципа Гюй-
Гюйгенса для всевозможных задач оптимизации, уравнения Гамильтона
стали постоянно использоваться в инженерных расчетах в этой
области. С другой стороны, современное развитие небесной механи-
механики, связанное с потребностями космических исследований, привело
к новому возрождению интереса к методам и задачам аналити-
аналитической динамики.
Связи классической механики с другими отделами математики
и физики многочисленны и разнообразны. «Добавления» в конце

10 ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
книги посвящены некоторым из этих связей. В качестве прило-
приложений аппарата классической механики здесь рассматриваются
основы римановой геометрии, динамика идеальной жидкости, кол-
могоровская теория возмущений условно-периодических движе-
движений, коротковолновые асимптотики для уравнений математичес-
математической физики и классификация каустик в геометрической оптике.
Эти добавления рассчитаны на любознательного читателя и не
входят в программу обязательного общего курса. Некоторые из них
могут составить основу специальных курсов (например, по асимпто-
асимптотическим методам теории нелинейных колебаний или по квазиклас-
квазиклассическим асимптотикам). В добавления внесен также ряд сведе-
сведений справочного характера (например, список нормальных форм
квадратичных гамильтонианов). В то время как в основных гла-
главах книги автор старался проводить все доказательства как можно
подробнее, избегая ссылок на другие источники, добавления со-
состоят в основном из сводок результатов, доказательства же за-
заменены ссылками на литературу.
Основу книги составил пол утор агодовой обязательный курс
классической механики, читавшийся автором студентам-математи-
студентам-математикам 3-го и 4-го года обучения на механико-математическом факуль-
факультете МГУ в 1966—1968 гг.
В. Арнольд

ЧАСТЬ I
НЬЮТОНОВА МЕХАНИКА
Ньютонова механика изучает движение системы материальных
точек в трехмерном евклидовом пространстве. В евклидовом про-
пространстве действует шестимерная группа движений пространства.
Основные понятия и теоремы ньютоновой механики (даже если
они и формулируются в терминах декартовых координат) инва-
инвариантны относительно этой группы *).
Ньютонова потенциальная механическая система задается мас-
массами точек и потенциальной энергией. Движениям пространства,
оставляющим потенциальную энергию неизменной, соответству-
соответствуют законы сохранения.
Уравнения Ньютона позволяют исследовать до конца ряд важ-
важных задач механики, например задачу о движении в центральном
воле.
ГЛАВА 1
ЭКСПЕРИМЕНТАЛЬНЫЕ ФАКТЫ
В этой главе описаны основные экспериментальные факты, ле-
лежащие в основе механики: принцип относительности Галилея и
дифференциальное уравнение Ньютона. Здесь рассмотрены огра-
ограничения на уравнения движения, накладываемые принципом
относительности, и приведены простейшие примеры.
§ 1. Принципы относительности и детерминированности
В этом параграфе вводится и обсуждается понятие инерциальной системы
координат. Математически точная формулировка утверждений этого парагра-
параграфа приведена в следующем параграфе.
В основе классической механики лежит ряд эксперименталь-
экспериментальных фактов **). Перечислим некоторые из них.
А. Пространство и время. Наше пространство трехмерно
и евклидово, а время — одномерно.
*) и даже относительно более широкой группы галилеевых преобразова-
преобразований пространства — времени.
**) Все эти «экспериментальные факты» верны лишь приближенно и бо-
более точными экспериментами опровергаются. Чтобы избежать громоздких
выражений, мы не будем в дальнейшем этого оговаривать и будем говорить
о наших математических моделях так, как если бы они точно описывали фп-
вические явления.

12 ГЛ. 1. ЭКСПЕРИМЕНТАЛЬНЫЕ ФАКТЫ
Б. Принцип относительности Галилея. Существуют системы
координат (называемые инерциальными), обладающие следующи-
следующими двумя свойствами:
1) Все законы природы во все моменты времени одинаковы
во всех инерциальных системах координат.
2) Все системы координат, движущиеся относительно инер-
циальной равномерно и прямолинейно, инерциальны.
Иначе говоря, если система координат, связанная с Землей,
инерциальна, то экспериментатор, находящийся в равномерно
и прямолинейно движущемся относительно Земли поезде, не мо-
может обнаружить движение поезда по опытам, проводящимся це-
целиком внутри вагона.
В действительности система координат, связанная с Землей,
инерциальна лишь приближенно. С большей точностью инер-
инерциальны системы координат, связанные с Солнцем, со звездами
и т. д.
В. Принцип детерминированности Ньютона. Начальное со-
состояние механической системы (совокупность положений и скорос-
скоростей точек системы в какой-нибудь момент времени) однозначно оп-
определяет все ее движение.
Мы не успеваем удивиться этому факту, так как узнаем его
очень рано. Можно представить себе мир, в котором для определе-
определения будущего системы нужно в начальный момент знать также
и ускорения. Опыт показывает, что наш мир не таков.
§ 2. Галилеева группа и уравнения Ньютона
В этом параграфе определяется и исследуется группа галилеевых преоб-
преобразований пространства — времени. Далее рассматриваются уравнение
Ньютона и простейшие ограничения, накладываемые на его правую часть
свойствами инвариантности относительно преобразований Галилея *).
А. Обозначения. R означает множество всех вещественных
чисел. Через Rn обозначается n-мерное вещественное линейное
пространство.
Аффинное п-мерное пространство Ап отличается от R" тем,
что в нем «не фиксировано начало координат». Группа Rn дей-
« ствует в Ап как группа параллельных пере-
переносов (рис. 1):
а» а + Ъ (а(=Ап, 6ER", а + Ь <= Ап).
рис. 1. параллельный [Таким образом, сумма двух точек Ап
перенос не определена, а разность определена и
есть вектор из Rn.]
Евклидова структура в линейном пространстве Rn — это поло-
положительно-определенная билинейная симметрическая форма, на-
*) Читатель, не испытывающий потребности в математических формули-
формулировках утверждений § 1, может пропустить этот параграф.

§ 2. ГАЛИЛЕЕВА ГРУППА И УРАВНЕНИЯ НЬЮТОНА 13
зываемая скалярным произведением. Скалярное произведение поз-
позволяет определить расстояние
Р (ж, У) = II ж — у || = Y(* — У,х — У)
между точками соответствующего аффинного пространства Ап.
Аффинное пространство с введенным таким образом расстоя-
расстоянием называется евклидовым пространством и обозначается Еп.
Б. Галилеева структура. Галилеева пространственно-времен-
пространственно-временная структура включает следующие три элемента:
1) Мир — четырехмерное аффинное *) пространство А4. Точ-
Точки А* называются мировыми точками или событиями. Параллель-
Параллельные переносы мира А* образуют линейное про-
пространство R4.
2) Время — линейное отображение f. R4 ->-R
линейного пространства параллельных перено-
переносов мира на вещественную «ось времени». Про-
Промежутком времени от события я Е Л4 до собы-
события iei4 называется число t (b — а) (рис. 2).
Если t (b — а) — 0, то события а и Ъ называ-
ются одновременными.
Множество событий, одновременных друг с Рис- 2-
другом, образует трехмерное аффинное подпро-
подпространство в А*. Оно называется пространством одновременных
событий А3.
Ядро отображения t составляют параллельные переносы А*,
переводящие какое-нибудь (и тогда любое) событие в одновремен-
одновременное с ним. Это ядро является трехмерным линейным подпростран-
подпространством R3 линейного пространства R4.
Галилеева структура включает в себя еще один элемент.
3) Расстояние между одновременными событиями
р (а, Ъ) = || а - Ъ || = /(а _ Ъ, а - Ь), а, Ь е= А\
заданное скалярным произведением в пространстве R3. Это рас-
расстояние превращает каждое пространство одновременных событий
в трехмерное евклидово пространство Е3.
Пространство Л4, снабженное галилеевой пространственно-
временной структурой, называется галилеевым пространством.
Можно говорить о двух событиях, происходящих одновременно в разных
местах, однако утверждение «два разновременных события а, Ъ е Л4 проис-
происходили в одном и том же месте трехмерного пространства» не имеет смысла,
пока мы не выбрали систему координат.
Галилеевой группой называется группа всех преобразований
галилеева пространства, сохраняющих его структуру. Элементы
*) В древности мир снабжали не аффинной, а линейной структурой (гео-
(геоцентрическая система + сотворение мира).

14 ГЛ. 1. ЭКСПЕРИМЕНТАЛЬНЫЕ ФАКТЫ
этой группы называются галилеееыми преобразованиями. Таким
образом, галилеевы преобразования являются аффинными пре-
преобразованиями А*, сохраняющими интервалы времени и расстоя-
расстояния между одновременными событиями.
Пример. Рассмотрим прямое произведение *) R X R3 оси
t на трехмерное линейное пространство R8 с фиксированной ев-
евклидовой структурой. Такое пространство имеет естественную га-
лилееву структуру. Это пространство мы будем называть коорди-
координатным галилеевым пространством.
Приведем три примера галилеевых преобразований этого про-
пространства. Во-первых, равномерное движение со скоростью v
gx (t, х) = (t, ос + vt), Vt G R, x e R3.
Далее, сдвиг начала отсчета
g2 (t, x) = {t + s, x + s), VtGR.acG R3-
Наконец, поворот осей координат
g3 {t, x) = (t, Gx), VteR,ice R8,
где G: R8 -*¦ R3 — ортогональное преобразование.
Задача. Докажите, что каждое галилеево преобразование
пространства R X R3 можно представить в виде произведения
поворота, сдвига и равномерного движения (g = g^'gu'Ssi u при-
притом единственным образом (так что размерность галилеевой груп-
группы равна 3 + 4 + 3 = 10).
Задача. Докажите, что все галилеевы пространства изо-
изоморфны друг другу **) и, в частности, изоморфны координатному
пространству R X R3.
Пусть М — множество. Взаимно однозначное отображение
Фх: М -*¦ R X R3 называется галилеевой системой координат в
множестве М. Система координат <р2 равномерно движется отно-
относительно системы координат ф2, если q^-cft1: RxRs->Rx
X R8 — галилеево преобразование. Галилеевы системы коорди-
координат фх и ф2 задают в М одинаковую галилееву структуру.
В. Движение, скорость, ускорение. Движением в W называ-
называется дифференцируемое отображение х: 1 —*- RN интервала /
вещественной оси в R^.
Вектором скорости в точке t0 S / называется производная
t=t, /i-o
*) Напомню, что прямое произведение двух множеств А, В есть множе
ство упорядоченных пар (а, Ъ), где а е А, Ъ е В. Прямое произведение двух
пространств (линейных, аффинных, евклидовых) имеет структуру простран-
пространства того же типа.
**) То есть существует взаимно однозначное отображение одного на дру-
другое, сохраняющее галилееву структуру.

§ 2. ГАЛИЛЕЕВА ГРУППА И УРАВНЕНИЯ НЬЮТОНА 15
Вектором ускорения в точке t0 называется вторая производная
Мы будем считать, что встречающиеся нам функции непрерыв-
непрерывно дифференцируемы нужное число раз. В дальнейшем, если не
оговорено противное, под отображениями, функциями и т. п. по-
понимаются дифференцируемые отображения, функции и т. д. Об-
Образ отображения х: I -*- RlY называется траекторией или кривой
в RN.
Задача. Может ли траектория дифференцируемого движения на
плоскости иметь нарисованный на рис. 3 вид? Может ли вектор ускорения
иметь указанное значение?
Ответ. Да. Нет.
Определим теперь, что такое механическая система из п точек,
движущихся в трехмерном евклидовом пространстве.
Рис. 3. Траектория
движения точки
Рве. 4. Мировые линии
Пусть ж: R -*¦ R3 — движение в R8. График *) этого отобра-
отображения является кривой в R X R3.
Кривая в галилеевом пространстве, являющаяся в какой-ни-
какой-нибудь (и тогда любой) галилеевой системе координат графиком дви-
движения, называется мировой линией (рис. 4).
Движение системы из п точек задается в галилеевом простран-
пространстве п мировыми линиями. В галилеевой системе координат они
описываются п отображениями xt: R —> R3, г = 1, . . ., п.
Прямое произведение п экземпляров R3 называется конфигу-
конфигурационным пространством системы п точек. Наши п отображений
хх: R -у R3 определяют одно отображение
sc: R -*- W, N = Зга,
оси времени в конфигурационное пространство. Такое отображение
и называется движением системы п точек в галилеевой системе
координат R X R8.
Г. Уравнение Ньютона. Согласно принципу детерминирован-
детерминированности Ньютона (§ 1, В) все движение системы однозначно опре-
*) Графиком отображения /: А —»В называется подмножество прямого
произведения А х В, составленное из всех нар вида (в, / (а)), а & А.

16 ГЛ. 1. ЭКСПЕРИМЕНТАЛЬНЫЕ ФАКТЫ
деляется ее начальным положением (ж (t0) €= Rw) и начальными
скоростями (Jc (t0) €5 R^).
В частности, начальное положение и скорости определяют уско-
ускорение. Иными словами, существует функция F: Rw X Rw X R ->¦
->¦ Rw такая, что
ж = F (ж, ас, t). A)
Уравнение A) положено Ньютоном в основу механики. Оно
называется уравнением Ньютона.
По теореме существования и единственности теории обыкно-
обыкновенных дифференциальных уравнений функция F и начальные ус-
условия х (t0), ж (t0) однозначно определяют движение *).
Вид функции F для каждой конкретной механической системы
определяется экспериментально. С математической точки зрения
вид F для каждой системы составляет определение этой системы.
Д. Ограничения, налагаемые принципом относительности.
Принцип относительности Галилея утверждает, что в физическом
пространстве — времени имеется избранная галилеева структура
(«класс инерциальных систем координат»),
обладающая следующим свойством.
Если подвергнуть мировые линии всех
точек любой механической системы **)
t одному и тому же галилееву преобразова-
" нию, то получатся мировые линии той же
рис. 5. принцип относи- системы (с новыми начальными условиями)
телыюсти Галилея (рис. 5). Это налагает на вид правой ча-
части уравнения Ньютона, записанного в
инерциальной системе координат, ряд условий: уравнение A)
должно быть инвариантно относительно группы галилеевых
преобразований.
*) При некоторых условиях гладкости, которые здесь, конечно, предпо-
предполагаются выполненными. Движение определяется уравнением A), вообще го-
говоря, лишь на некотором интервале оси времени. Для упрощения мы будем
считать, что этот интервал есть вся ось времени, что выполняется в большин-
большинстве задач механики.
**) При формулировке принципа относительности следует иметь в виду,
что он относится лишь к замкнутым физическим (в частности, механическим)
системам, т. е. что мы должны включать в систему все тела, взаимодействие
которых играет роль при изучении данного явления. Строго говоря, следова-
следовало бы включать в систему все вообще тела Вселенной. Но опыт показывает,
что часто можно пренебречь влиянием многих из них: например, при изуче-
пии движения планет вокруг Солнца можно пренебречь притяжением других
звезд и т. п.
С другой стороны, при изучении движения тел в окрестности Земли си-
система не замкнута, если в нее не включена Земля, при изучении движения
самолета система не замкнута, пока в ней не включен окружающий самолет
воздух, и т. д. В дальнейшем под термином «механическая система» понима-
понимается в большинстве случаев замкнутая система, когда же будет идти речь
о незамкнутых системах, это будет специально оговариваться (см., напри-
например, § 3).

2. ГАЛИЛЕЕВА ГРУППА И УРАВНЕНИЯ НЬЮТОНА 17
Пример 1. Среди галилеевых преобразований имеется
сдвиг по времени. Инвариантность относительно сдвигов по вре-
времени означает, что «законы природы остаются постоянными», т. е.
если х = <jp (t) — решение уравнения A), то для всякого sER
решением будет также х = <р (t + s).
Отсюда вытекает, что правая часть уравнения A) в инерциалъ-
ной системе координат не может зависеть от времени:
зс = Ф(зс, ас).
Замечание. Дифференциальные уравнения, правые час-
части которых зависят от времени, встречаются в следующей си-
ситуации.
Предположим, что мы изучаем часть I механической системы
I + II. Тогда влияние части II на часть I можно иногда заменить
изменением со временем параметров системы уравнений, описы-
описывающих движение части I.
Например, влиянием Луны на Землю можно пренебречь при
исследовании большинства явлений на Земле. Однако при иссле-
исследовании приливов это влияние нужно учитывать, заменяя притя-
притяжение Луны периодическим изменением силы тяжести на Земле.
Уравнения с переменными коэффициентами могут появиться
также в результате формальных операций при решении задач.
Пример 2. Среди галилеевых преобразований имеются
сдвиги в трехмерном пространстве. Инвариантность относительно
таких сдвигов означает, что пространство однородно или «имеет
одинаковые свойства во всех своих точках». То есть, если зсг =
= <jpi(f) {i = 1, • - -, п) — движение системы п точек, удовлетво-
удовлетворяющее A), то для всякого г ЕЕ R3 движение <рг (t) + r (i = 1, . . .
. . ., п) также удовлетворяет уравнению A).
Отсюда вытекает, что правая часть уравнения A) в инерциалъ-
ной системе координат может зависеть лишь от «относительных
координат» Xj — х^.
Из инвариантности относительно перехода к равномерно дви-
движущейся системе координат (что не меняет х% и ас, — зск, но при-
прибавляет ко всем Xj постоянный вектор v) вытекает, что правая
часть уравнения A) в инерциальной системе координат может
зависеть лишь от относительных скоростей
*» = /i {{Щ — Щ, &з — *fc»> U h А: = 1,..., п.
Пример 3. Среди галилеевых преобразований имеются по-
повороты в трехмерном пространстве. Инвариантность относительно
таких поворотов означает, что пространство изотропно, так что
в нем нет предпочтительных направлений.
То есть, если <рг: R ->- R3 (г = 1, . . ., п) — движение системы
точек, удовлетворяющее A), и G:RS->R! — ортогональное пре-
преобразование, то движение Скрг: R-> R3 (? = 1, . . ., п) также

18 ГЛ. 1. ЭКСПЕРИМЕНТАЛЬНЫЕ ФАКТЫ
удовлетворяет A). Иначе roBopHs
F{Gx, Gx) = GF(x, x),
где Gx означает (Gxlt . . ., Gxn), xt e= R3.
Задача. Докажите, что если механическая система состоит всего из
¦одной точки, то ее ускорение в инерциальной системе координат равно нулю
(«первый закон Ньютона»).
Указание. Согласно примерам 1, 2 вектор ускорения не зависит
¦от ж, ж, t, а согласно примеру 3 вектор F инвариантен относительно враще-
вращений.
Задача. Механическая система состоит из двух точек. В начальный
момент их скорости (в некоторой инерциальной системе координат) равны
нулю. Докажите, что точки будут двигаться по соединяющей их прямой.
Задача. Механическая система состоит из трех точек. В начальный
момент их скорости (в некоторой инерциальной системе координат) равны
нулю. Докажите, что точки всегда останутся в той же плоскости, в которой
«ни лежат в начальный момент.
Задача. Механическая система состоит из двух точек. Докажите, что
при любых начальных условиях существует такая инерциальная система
координат, что в ней эти две точки постоянно остаются в неподвижной плос-
плоскости.
Задача. Докажите, что механика в Зазеркалье тождественна с на-
нашей.
Указание. В галилеевой группе есть преобразования отражения,
меняющие ориентацию R3.
Задача. Единствен ли класс инерциальных систем?
Ответ. Другие классы получатся, если изменять масштабы длины и вре-
времени, а также направление времени.
§ 3. Примеры механических систем
Мы уже отметили, что вид функции F в уравнении Ньютона A) для каж
дой механической системы определяется экспериментально. Приведем не-
несколько примеров.
При рассмотрении конкретных систем разумно не включать в систему
все объекты Вселенной. Например, при исследовании большинства происхо-
происходящих на Земле явлений можно не учитывать влияние Луны. Далее, обычно
можно пренебречь влиянием изучаемых процессов на движение самой Земли
и даже считать систему координат, связанную с Землей, «неподвижной».
Разумеется, принцип относительности уже не накладывает на уравнения
движения, записанные в такой системе координат,
прежних ограничений. Например, вблизи Земли име-
имеется избранное направление: вертикальное.
А. Пример 1. Падение камня на Землю.
Опыт показывает, что
Г777777 х = — g, g zz 9,8 м/с2 (Галилей), B)
Рис"ня та^Хк>кам~ где х ~ высота камня над поверхностью Зем-
Земли (рис. 6).
Если ввести «потенциальную энергию» U = gx, то уравнение
B) можно записать в виде
dx ш

§ 3. ПРИМЕРЫ МЕХАНИЧЕСКИХ СИСТЕМ 19
Если U: EN -*¦ R — дифференцируемая функция в евклидовом
пространстве, то мы будем обозначать через дЩдх градиент функ-
функции U. Если EN — ?"» X ... X Е"к — прямое произведение
евклидовых пространств, то мы будем обозначать точку х €= EN
через (зсц . . ., хн), а вектор dU/dx через (dUldjc^ . . ., dU/dxH).
В частности, если хг, . . ., xN — декартовы координаты в EN, то
компоненты вектора д VIдх равны частным производным dV/dxlt ...
. . ., dUldxn.
Опыт показывает, что радиус-вектор камня относительно ка-
какой-нибудь точки Земли О, удовлетворяет уравнению
х = д— , где U = — дх. (о)
Вектор в правой части направлен к Земле. Он называется векто-
вектором ускорения силы тяжести д.
Б. Пример 2. Падение с большой высоты. Подобно всем экс-
экспериментальным фактам, закон движения B) имеет ограниченную
область применения.
Согласно более точному экспериментальному закону падения,
открытому Ньютоном, ускорение обратно
пропорционально квадрату расстояния от _ г ,
центра Земли: ©->—-—
Рис. 7. Поле тяготения
, < г7\ Земли
где г = г0 + х (рис. 7).
Это уравнение также можно записать в виде C), введя потен-
потенциальную энергию
сбратно пропорциональную расстоянию до центра Земли.
Задача. Определить, с какой скоростью сле-
следует бросить камень, чтобы он улетел с поверхно-
поверхности Земли на бесконечное расстояние *).
Ответ. J» 11,2 км/с.
В. Пример 3. Движение грузика по пря-
прямой под действием пружины. Эксперимент рис. 8. грузик на пру-
показывает, что при небольших отклонени- ншне
ях пружины от ее нейтрального положения
Уравнение движения грузика будет иметь вид (рис.8)
х = —а2х.
уравнение также можно записать в виде C), если ввести
*) Это так называемая вторая космическая скорость v2. Наше уравнение
не учитывает притяжения Солнца. Притяжение Солнца не выпустит камень
™ Солнечной системы, если скорость камня относительно Земли мень-
*» 16,6 км/с.

20 ГЛ. 1. ЭКСПЕРИМЕНТАЛЬНЫЕ ФАКТЫ
потенциальную энергию
Если поместить на место одного грузика два таких же, то окажет-
окажется, что при том же растяжении пружины ускорение в два раза
меньше.
Экспериментально установлено, что для любых двух тел отно-
отношение ускорений xjx2 при одинаковом растяжении пружины пос-
постоянно (не зависит от степени растяжения пружины и от ее свойств,
но лишь от самих тел). Величина, обратная этому отношению, на-
называется отношением масс:
х2 mi
За единицу массы принимается масса какого-нибудь фиксирован-
лого тела, например 1 л воды. Опыт показывает, что массы всех
тел положительны.
Произведение массы тела на ускорение шх не зависит от тела,
а является характеристикой растяжения пружины. Эта величина
называется силой, действующей на тело со стороны пружины.
За единицу силы принимается «ньютон». Например, на 1 л
воды, подвешенный на пружине на поверхности Земли, пружина
действует с силой в 9,8 Н (= 1 кгс).
Г. Пример 4. Потенциальная система. Пусть Езп = Е3 X
X ... X Е3 — конфигурационное пространство системы п то-
точек в евклидовом трехмерном пространстве Е3. Пусть U: Е371 -*•
-> R — дифференцируемая функция, и пусть щ, . . ., тпп — по-
положительные числа.
Определение. Движение п точек масс т1, . . ., тп
•в потенциальном поле с потенциальной энергией U задается си-
системой дифференциальных уравнений
— j?-, i = 1,..., п. D)
Уравнения движения в примерах 1—3 имеют как раз такой
вид. В таком же виде записываются уравнения движения большо-
большого числа многих других механических систем.
Например, небесно-механической задачей трех тел называет-
называется задача D), в которой
U = —,7
К виду D) могут быть приведены некоторые дифференциальные
уравнения совсем другого происхождения, например уравнения
-электрических колебаний.
В следующей главе мы будем главным образом заниматься
.исследованием системы дифференциальных уравнений D).

ГЛАВА 2
ИССЛЕДОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ
В большинстве случаев (например, в задаче трех тел) не удает-
удается ни решить систему дифференциальных уравнений движения,
ни достаточно полно исследовать поведение решений. В этой гла-
главе рассматривается несколько простых, но важных задач, в ко-
которых уравнения Ньютона решаются.
§ 4. Системы с одной степенью свободы
В этом параграфе изучается фазовая плоскость дифференциального урав-
уравнения A). Для качественного исследования такого уравнения достаточно од-
одного взгляда на график потенциальной энергии. Кроме того, уравнение A)
интегрируется в квадратурах.
А. Определения. Системой с одной степенью свободы мы бу-
будем называть систему, описываемую одним дифференциальным
уравнением
* = /(*), IGR. A)
Кинетической энергией называется квадратичная форма
Потенциальной энергией называется функция
Знак в этой формуле выбран так, чтобы потенциальная энер-
энергия камня была тем больше, чем выше он находится.
Заметим, что потенциальная энергия U определяет /. Поэтому
Для задания системы A) достаточно указать потенциальную энер-
энергию. Прибавление постоянной к потенциальной энергии не меняет
Уравнения движения A).
Полной энергией называется сумма
Е = Т + U.
Таким образом, полная энергия — это функция Е (ж, ±).
Б. Теорема (закон сохранения энергии). Полная энергия дви-
движущейся точки при движении A) сохраняется: Е (х (t), х (t)) не
зависит от t.

22 ГЛ. 2. ИССЛЕДОВАНИЕ УРАВНЕНИИ ДВИЖЕНИЯ
Доказательство.
±.(Т + U) = хх + -g- х = х(х- f{x)) = 0, ч. т. д.
В. Фазовая плоскость. Уравнение A) эквивалентно системе
двух уравнений
х = у, у = / (х). B)
Рассмотрим плоскость с координатами х, у. Эта плоскость назы-
называется фазовой плоскостью уравнения A). Точки фазовой плос-
плоскости называются фазовыми точками. Правая часть системы B)
определяет на фазовой плоскости векторное поле. Это поле назы-
называется векторным полем фазовой скорости.
Решение системы B) — это движение фазовой точки по фазо-
фазовой плоскости <jp: R -> R2, при котором скорость движущейся
точки в каждый момент времени равна вектору фазовой скорости
в том месте, где фазовая точка в данный момент времени находит-
находится *).
Образ отображения <р называется фазовой кривой. Таким обра-
образом, фаговая кривая задается параметрическими уравнениями
х = ф (t), у = ф (t).
Задача. Докажите, что через каждую фазовую точку проходит одна
и только одна фазовая кривая.
Указание. См. учебники по обыкновенным дифференциальным урав-
уравнениям.
Заметим, что фазовая кривая может состоять всего из одной
точки. Такая точка называется положением равновесия. Вектор
фазовой скорости в положении равновесия
равен нулю.
Закон сохранения энергии позволяет
легко находить фазовые кривые. Действи-
Действительно, на каждой фазовой кривой значе-
значение полной энергии постоянно. Поэтому
х каждая фазовая кривая целиком принад-
принадлежит одному множеству уровня энергии
Е (х, у) = h.
Г. Примеры.
Рис.9. Фазовая плоскость Пример 1. Основное уравнение теории
уравнения х = —х колебаний
S = —х.
В этом случае (рис. 9) имеем:
$2, 2<2 ?2 2<2
Т =-, U = ~2~, Е =
*) Здесь для простоты предполагается, что решение <р определено на всей
оси времени R.

§ 4. СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
23
и
Е3
Множества уровня энергии — концентрические окружности и начало коор-
пинат Вектор фазовой скорости в фазовой точке (х, у) имеет компоненты
(«Г-—х) Он перпендикулярен радиусу-вектору и равен ему по величине. По-
Поэтому движение фазовой точки по фазовой плоскости есть равномерное вра-
вращение вокруг 0: х = r0 cos (ф0 - 0, У = го sin (Фо - *)• Итак, каждое мно-
даество уровня энергии является фазовой кривой.
Пример 2. Пусть потенциальная энергия задана своим графи-
графиком (рис. 10). Нарисуем множества уровня энергии -^- + U (х) = Е.
При этом полезно иметь в виду следующие обстоятельства.
1 Положения равновесия системы B) лежат на оси х фазовой
плоскости. Точка х = ?, у = 0 является положением равновесия,
если | — критическая точка потен-
потенциальной энергии, т. е. если
dUI dx | *=! = 0.
2. Каждое множество уровня —
гладкая кривая в окрестности каж-
каждой своей точки, не являющейся по-
положением равновесия (это следует из
теоремы о неявной функции). В част-
частности, если число Е — не критиче-
критическое значение потенциальной энер-
энергии (т.е. не равно значению потен-
потенциальной энергии в одной из крити-
критических точек), то множество уровня,
где энергия равна Е,— гладкая кри-
кривая.
При исследовании линий уровня
энергии следует обращать внимание
на критические значениями и значе-
значения Е, близкие к критическим. При
атом удобно представлять себе шарик, катающийся в потенци"
альной яме U.
Например, рассуждение «кинетическая энергия неотрицатель-
неотрицательна. Значит, потенциальная не больше полной. Чем потенциаль-
потенциальная энергия меньше, тем скорость больше» принимает на этом язы-
языке вид: «шарик не может выскочить из потенциальной ямы, под-
поднявшись выше уровня, определяемого его начальной энергией.
Скатываясь в яму, шарик набирает скорость». Далее, мы сразу
замечаем, что точки локального максимума потенциальной энер-
энергии — неустойчивые, а точки минимума — устойчивые положе-
положения равновесия.
Задача. Докажите это.
Задача. Из скольких фазовых кривых состоит сепаратриса (восьмер-
(восьмерка) —- кривая, соответствующая уровню Е2?
Ответ. Из трех.
Задача. Определить время движения по сепаратрисе.
Ответ. Иэ теорема единственности вытекает, что это время бесконечно.
Рис. 10. Потенциальная анергия
в фазовые кривые

24
ГЛ. 2. ИССЛЕДОВАНИЕ УРАВНЕНИИ ДВИЖЕНИЯ
Задача. Докажите, что время движения от а^ до х2 (в одну сторону
X,
равно *_*_
Задача. Нарисовать фазовые кривые, зная график потенциальной
энергии (рис. 11).
Ответ — рис. 12-
a) * 6)
Рис. 11. Потенциальная энергия
б)
Рис. 12. Фазовые кривые
и
Задача. Нарисовать фазовые кривые для «уравнения плоского ма-
математического маятника»: х = —sin x.
Задача. Нарисовать фазовые кривые для «уравнения маятника, ось
которого вращается»: х = —sin х + М.
Замечание. В этих двух задачах х означает угол
отклонения маятника. Фазовые точки, координаты кото-
которых отличаются на 2л, соответствуют одинаковому поло-
положению маятника. Поэтому кроме фазовой плоскости есте-
естественно рассматривать фазовый цилиндр {х (mod 2п), у}.
3 а д а ч а. Найти касательные к ветвям линии кри-
критического уровня, соответствующего максимуму потенци-
потенциальной энергии, Е = U (g) (рис. 13).
Ответ, у = ± Y-U" &) (х - I).
Задача. Пусть S (Е) — площадь, заключенная
внутри замкнутой фазовой кривой, соответствующей уров-
уровню энергии Е. Докажите, что период движения по этой
кривой равен
dS
х
Рис. 13. Линия
критического
уровня^ энергии
Т =
dE
Задача. Пусть Ео — потенциальная энергия в
Найти период малых колебаний в окрестности точки
Ответ.
точке
минимума | -
= Иш Т(Е)

§ 4. СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
25
Задач а. Рассмотрим периодическое движение по замкнутой фазовой
кривой, соответствующей уровню энергии Е. Устойчиво ли оно по Ляпу-
Ляпунову?
Ответ. Нет *).
Д. Фазовый поток. Пусть М — точка фазовой плоскости. Рас-
Рассмотрим решение системы B), начальные условия которого при
t — 0 изображаются точкой М. Предположим,
что любое решение системы продолжается
на всю ось времени. Значение нашего ре-
решения при некотором значении t зависит от
М. Мы обозначим полученную фазовую точ-
точку (рис. 14) через
М (t) = ?М.
Рис. 14. Фазовый поток
Таким образом, мы определили отображение фазовой плоскос-
плоскости на себя g*: Ra -*- Ra. По известным теоремам теории обыкновен-
обыкновенных дифференциальных уравнений отображение g1 является диф-
диффеоморфизмом (взаимно однозначным и взаимно дифференцируе-
дифференцируемым отображением). Диффеоморфизмы g*, feR, образуют груп-
группу: gt+s = g' о gs. Далее, отображение g° тождественное (g°M —
= М), а отображение g~* обратно g*. Отображение g: R X R2 ->
-¦¦ R2» S (U M) = g*M, дифференцируемо. Все эти свойства вместе
выражают короче, говоря, что преобразования gl образуют одно-
параметрическую группу диффеоморфизмов фазовой плоскости.
Эту группу называют так-
же фазовым потоком, за- ^'
данным системой B) (или
уравнением A)).
Пример. Фазовый
поток, заданный уравне-
уравнением х = —х, есть груп-
группа gl поворотов фазовой
плоскости на угол t вок-
вокруг начала координат.
Задача. Покажите, что система с потенциальной энергией U = —г4
никакого фазового потока не определяет.
Задача. Докажите, что если потенциальная энергия положительна,
то фазовый поток существует.
Указание. Воспользуйтесь законом сохранения энергии для дока-
доказательства неограниченной продолжаемости решений.
Задача. Нарисовать образ круга х2 + (у — IJ < 1/4 под действием
преобразования gf фазового потока уравнения: а) «перевернутый маятник»
* = х, Ь) «нелинейный маятник» х = —sin x.
Ответ — рис. 15.
Рис. 15. Действие фазового потока на круг
*) Единственное исключение составляет случай, когда период не зави-
зависит от энергии.

26 ГЛ. 2. ИССЛЕДОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ
§ 5. Системы с двумя степенями свободы
Анализ общей потенциальной системы с двумя степенями свободы выхо-
выходит за рамки возможностей современной науки. В этом параграфе рассмат-
рассматриваются простейшие примеры.
А. Определения. Под системой с двумя степенями свободы мы
будем понимать систему, описываемую дифференциальным урав-
уравнением
где / — векторное поле на плоскости.
Система называется потенциальной, если существует функция
U: Е2 —*¦ R такая, что/= —dlf/дк. Уравнение движения потен-
потенциальной системы имеет, таким образом, вид *)
Ж~ дх ' W
Б. Закон сохранения энергии.
Теорема. Полная энергия потенциальной системы
Е = ^- ж2 + С/ (ж), & = (?, х),
сохраняется.
Доказательство:
аи .\ /.. , аи .
в силу уравнения движения.
Следствие. Если в начальный момент суммарная энер-
энергия равна Е, то вся траектория лежит в области, где U (х) <1 Е,
т. е. точка находится все время внутри потенциальной ямы
U (хг, х2) < Е.
Замечание. В системе с одной степенью свободы можно
всегда ввести потенциальную энергию
Для систем с двумя степенями свободы это не так.
3 а д а ч а. Привести пример системы вида ж = f (х), х е 2?2, которая
не является потенциальной.
*) В декартовых координатах на плоскости Е2
аи .. аи_
Xl = ~ дц ' Х2 = ~~Ы?

5. СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ 27
В. Фазовое пространство. Уравнение движения A) можно
записать в виде системы:
*i = Vi, ?2 = У»
»1 дхг ' »2 ~ дх2 *
Фазовым пространством системы с двумя степенями свободы
называется четырехмерное пространство с координатами хх, х2,
Ух, Уг-
Система B) определяет векторное поле фазовой скорости в че-
четырехмерном пространстве, и тем самым *) фазовый поток нашей
системы (однопараметрическую группу диффеоморфизмов четы-
четырехмерного фазового пространства). Фазовые кривые системы
B) являются подмножествами четырехмерного фазового простран-
пространства. Все фазовое пространство разбивается на фазовые кривые.
Проекции фазовых кривых из четырехмерного пространства на
плоскость хх, х% дают траектории нашей движущейся точки на
плоскости хх, х2. Эти траектории называют также орбитами. Ор-
Орбиты могут иметь точки пересечения, тогда как фазовые кривые
друг друга не пересекают. Уравнение за-
закона сохранения энергии
2
- U (xXJ х2)
определяет трехмерную гиперповерхность
в четырехмерном пространстве: Е (хх, xf/ jx
хй, у,, уЛ = Еп; эта поверхность Пе„ оста- _ ,„ „
27 S/1J а2/ °' „ г ,а> Рис. 16. Поверхность уровня
вТСЯ ИНВариаНТНОИ ОТНОСИТеЛЬНО фаЗОВОГО энергии и фазовые кривые
потока: g'UE, = ПЕо. Можно сказать, что
фазовый поток течет по поверхности уровня энергии. Векторное
поле фазовой скорости касается в каждой точке поверхности ЛЕ.
Следовательно, вся она составлена из фазовых кривых (рис. 16).
Г. Пример i («малые колебания сферического маятника»). Пусть
4+4
U = 5j . Множества уровня потенциальной энергии на плоскости
^lt #2 будут концентрическими окружностями (рис. 17).
Уравнения движения х\ = —х±, х2 = —х2 эквивалентны системе
Эта система распадается на две независимых; иначе говоря, каждая из
Координат xlt x2 меняется со временем так же, как в системе с одной степенью
свободы.
*) При обычных ограничениях.

28
ГЛ. 2. ИССЛЕДОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ
Решения имеют вид
xi — ci cos t + с2 sin t, ж2 = с8 cos t + с4 sin t,
У1 = —ci sin t + c2 cos t, y2 = —c3 sin t + c4 cos t.
Из закона сохранения энергии следует:
Е = ~2-(у1 + у1) + -Т (*? + 4) = const'
т. е. поверхностью уровня ПЕ является сфера в четырехмерном пространстве-
Задача. Доказать, что фазовые кривые являются большими кругами
этой сферы. (Большим кругом называется пересечение сферы и проходящей
через ее центр двумерной плоскости.)
Задача. Доказать, что множество фазовых кривых на поверхности ЛЕ
составляет двумерную сферу. Точнее, формула w = —* , . ¦ задает «отобра-
жение Хопфа» трехмерной сферы ЛЕ на двумерную сферу (плоскость комп-
комплексного переменного w, пополненную бесконечно удаленной точкой). Наши
фазовые кривые — это прообразы точек при отображении Хопфа.
Рис. 17. Линии уров-
уровня потенциальной
энергии сферическо-
сферического маятника
Рис. 18. Области U =S E,
I/, =ё Е и U, ^ Е
Задача. Найти проекции фазовых кривых на плоскость хг, х% (т. е-
нарисовать орбиты движения точки).
Д. Пример 2 («фигуры Лиссажу»). Рассмотрим еще один пример плос-
кого движения («малые колебания с двумя степенями свободы»):
Потенциальная энергия
Из закона сохранения энергии следует, что если в начальный момент времени
полная энергия
то все движение будет происходить внутри эллипса U (хг, #2) ^ Е.
Кроме того, наша система состоит из двух не связанных одномерных
систем. Поэтому закон сохранения энергии выполняется отдельно для каж-
каждой из них: сохраняются величины
1 „ 1 „ 1 „ 1
(Е =
Е2).

§ 5. СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ
29
Следовательно, изменение хг ограничено полосой | хх | <J Alt Лх =
= tf2Et @), и xz тоже колеблется в пределах полосы | хг | < А2. Пересече-
Пересечение этих двух полос определяет прямоугольник, в котором заключена орбита
(рис. 18).
Задача. Доказать, что этот прямоугольник вписан в эллипс U <^ Е.
Общее решение наших уравнений есть х± = Ах sin (t + «pi), #2 =
= А2 sin (ш + ф2): движущаяся точка независимо совершает колебание с час-
лютой 1 и амплитудой Лх по горизонтали и колебание с частотой <в и амплиту-
амплитудой Л2 по вертикали.
Чтобы нарисовать орбиту на плоскости хХ1 х2, поступим следующим об-
образом. Рассмотрим цилиндр с основанием 2Аг и ленту ширины 2Л2. Нари-
Нарисуем на ленте синусоиду с периодом 2пАг/(й и амплитудой Л2 и намотаем лен-
ленту на цилиндр (рис. 19). Ортогональная проекция намотанной на цилиндр
Рис. 19. Построение фигуры Лиссажу
IX,
Рис. 20. Серия фигур Лис-
сашу с ш_=. 1
Рис. 21. Фигура Лиссажу с co^l
Рис. 22. Фигура Лиссажу с а=2 Рис. 23. Серия фигур Лиссажу с а=2
синусоиды на плоскость хи х2 и даст искомую орбиту, называемую фигурой
Лиссажу.
Фигуры Лиссажу удобно наблюдать на осциллографе, подавая два неза-
независимых гармонических колебания на горизонтальную и вертикальную раз-
вертки.
Вид фигуры Лиссажу очень сильно зависит от частоты <в. Если ю = 1
(сферический маятник примера 1), то на цилиндре кривая — эллипс. Проек-
Проекция этого эллипса на плоскость xlt x2 зависит от разности фаз ф2 — фх. При

30
ГЛ. 2. ИССЛЕДОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ
<рх = <р2 получается отрезок диагонали прямоугольника, при малых ф2 —
— ф1 — сжатый к диагонали эллипс, вписанный в прямоугольник. При
<Р2 — (pi = я/2 получается эллипс с главными осями хи а;2; при увеличении
Фг — Ф1 от я/2 до я эллипс сжимается ко второй диагонали, при дальнейшем
увеличении ф2 — <рх весь процесс повторяется сначала (рис. 20).
Пусть теперь частоты равны лишь приближенно: «в -х. 1. Отрезок кри-
кривой, соответствующий 0 ^ t <^ 2я, очень похож на эллипс. Следующий ви-
виток тоже напоминает эллипс, но у него сдвиг фаз ф2 —• фх на 2я («в — 1) боль-
больше, чем у исходного. Поэтому кривая Лиссажу сий1 — деформирующийся
эллипс, медленно проходящий все фазы от сжатия в одну диагональ до сжа-
сжатия в другую (рис. 21).
Если одна из частот вдвое больше другой (со = 2), то при некотором сдви-
сдвиге фаз фигура Лиссажу превращается в дважды пройденную кривую (рис. 22).
Задача. Доказать, что эта кривая — парабола.
Прп увеличении сдвига фаз ф2 — фх последовательно получаем кривые
рис. 23.
Вообще, если одна из частот в п раз больше другой (со = п), то среди со-
соответствующих фигур Лиссажу есть график многочлена степени п (рис. 24);
этот многочлен называется многочленом Чебышева.
1
1/1
[у
л
Рис. 24. Многочлены Чебышева
Задача. Докавать, что если со = т/п, то фигура Лиссажу — замк-
замкнутая алгебраическая кривая, а если со иррационально, то фигура Лиссажу
заполняет прямоугольник всюду плотно. Что заполняет соответствующая
фазовая траектория?
§ 6. Потенциальное силовое поле
В этом параграфе исследуется связь работы и потенциальной энергии.
А. Работа силового поля на пути. Напомню определение рабо-
работы силы F на пути 8. Работа постоянной силы F (например, силы,
с которой мы тянем вверх груз) на пути 8 = МгМг есть, по опре-
определению, скалярное произведение (рис. 25)
A=(F,8)=\F\\8 |-cosq>.
Пусть дано векторное поле jPh кривая Iконечной длины. Прибли-
Приблизим кривую I ломаной со звеньями ASt и обозначим через Рг зна-
значение силы в какой-нибудь точке A8t; тогда работа поля F на пу-
пути I есть по определению (рис. 26)
А = lim
|дв,-|-о

§ в. ПОТЕНЦИАЛЬНОЕ СИЛОВОЕ ПОЛЕ 31
В курсе анализа доказывается, что если поле непрерывно, a nyib
спрямляем, то предел существует. Он обозначается \ (F, d8).
Мг
Рис. 25. Работа постоян- Рис. 26. Работа силового
ной силы V на прямом поля Р на пути I
пути S
Б. Условия потенциальности поля.
Теорема. Векторное полеР потенциально тогда и только
тогда, когда его работа по любому пути МгМ2 зависит только
от концов пути и не зависит от формы пути.
Действительно, пусть работа поля F не зависит от пути. Тог-
Тогда корректно определена функция точки М:
м
U(M) = — J (F,dS).
Af.
Легко проверить, что
F-2L
дх '
т. е. поле потенциально, a U — его потенциальная энергия. Ко-
Конечно, потенциальная энергия определяется только с точностью
до аддитивной постоянной U (Мо), которую
можно выбрать произвольно. ур
Обратно, пусть поле F потенциально и i «г а
V — потенциальная энергия. Тогда легко про- Т *Ч
вернется, что v 1
м V
l(F
м.
Рис. 27. Непотен-
Т. в. работа не ЗавИСИТ ОТ формы ПУТИ. циалыюе поле
Задача. Доказать, что векторное поле Ft = z2, F2 = —хг не потен-
потенциально (рпс. 27).
Задача. Потенциально ли поле, заданное на плоскости с исключен-
яви точкой, Fx = —j 2~ , F% = —^ -j- ? Доказать, что поле потенциально-
t *i + *2 Хх + Ч
*°гда и только тогда, когда его работа по любому замкнутому контуру равна
*Улю.

32 ГЛ. 2. ИССЛЕДОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИИ
В. Центральное поле.
Определение. Векторное поле на плоскости Е2 называ-
называется центральным с центром в О, если оно инвариантно относитель-
относительно группы движений *) плоскости, оставляющих точку О на
месте.
Задача. Доказать, что все векторы центрального поля лежат на лу-
лучах, проходящих через О, а величина вектора поля в точке зависит только от
расстояния точки до центра поля.
Полезно рассматривать также центральные поля, не определен-
определенные в точке О.
Пример. Ньютоновское поле F = — к -,—щ- центрально, а
поля задач пункта Б — нет.
Теорема. Всякое центральное поле F потенциально, а его
потенциальная энергия зависит только от расстояния до центра
поля, U = U (г).
Доказательство. Согласно предыдущей задаче,
F (г) = Ф (г) еТ, где г — радиус-вектор относительно О, г — его
длина, ег — его орт. Тогда
(F-dS)- J O(r)dr,
Mt r (Mt)
а этот интеграл, очевидно, не зависит от пути.
Задача. Вычислить потенциальную энергию ньютоновского поля.
Замечание. Определения и теоремы этого параграфа не-
непосредственно переносятся на евклидово пространство Е™ любо-
любого числа измерений.
§ 7. Кинетический момент
В дальнейшем мы увидим, что инвариантность уравнений механической
задачи относительно какой-либо группы преобразований всегда влечет за
собой закон сохранения. Центральное поле инвариантно относительно груп-
группы вращений. Соответствующий первый интеграл носит название кинетиче-
кинетического момента.
А. Определение. Движение материальной точки (массы 1)
е центральном поле на плоскости определяется уравнением
г = Ф (г) ег,
где v — радиус-вектор с началом в центре поля О, г — его длина,
еТ—его орт. Будем считать нашу плоскость вложенной в трехмер-
трехмерное ориентированное евклидово пространство.
Определение. Моментом количества движения (или
кинетическим моментом) материальной точки единичной массы
*) В том числе и отражений.

§ 7. КИНЕТИЧЕСКИЙ МОМЕНТ
33
относительно точки О называется векторное произведение
М = [г, г].
Вектор М перпендикулярен нашей плоскости и задается одним
числом: М = Мп, где п — [е1? еа] — вектор нормали, ех и еа —
ориентирующий плоскость репер (рис. 28).
Замечание. Вообще, моментом век-
вектора», «приложенного в точке »•» относи-
относительно точки О называют [г, а], например,
в школьном курсе статики рассматривался
момент силы.
Б. Закон сохранения кинетического мо-
момента.
Лемма. Пусть а иЬ — два меняющих-
меняющихся со временем вектора в евклидовом ориентированном R3. Тогда
± [а, Ь] = [а, Ь] + [а, Ь].
Доказательство. Это следует из определения произ-
производной.
Теорема (закон сохранения кинетического момента). При
движении в центральном поле кинетический момент М относи-
относительно центра поля О не меняется со временем.
Доказательство. По определению
М = [г, г].
По лемме
Рис. 28. Кинетический
момент
Из уравнения движения ввиду центральности поля видно, что век-
векторы v и г коллинеарны. Итак, М = 0, ч. т. д.
В. Закон Кеплера. Впервые закон сохранения кинетического
момента был найден Кеплером из наблюдений за движением Мар-
Марса. Кеплер формулировал этот закон в
несколько ином виде.
Введем на нашей плоскости поляр-
полярные координаты г, <р с полюсом в цент-
центре поля О. Рассмотрим в точке г с
координатами | г \ = г; <р два орта:
ег, направленный по радиусу-вектору,
так что
r — rer,
Рис. 29. Разложение векто-
вектора г по базису ег, еф
и еф — ему перпендикулярный, направленный в сторону увеличе-
увеличения ф. Разложим вектор скорости г по базису ег, еф (рис. 29).
Лемма. Справедливо соотношение

34 ГЛ. 2. ИССЛЕДОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ
Доказательство. Очевидно, векторы ег, еф вращаются
с угловой скоростью ф, т. е.
ёг =
ёФ = — фег.
Дифференцируя равенство г = гег, получаем
г = fer + гёт = гег + гфеф, ч. т. д.
Следовательно, кинетический момент есть
М = [г, г] = [г, гег] + [г, гфеф] = гф \г, еф] = г2ф [ег, еф].
Таким образом, сохраняется величина
М = г2ф.
Эта величина имеет простой геометрический смысл.
Кеплер назвал векториальной скоростью С скорость изменения
площади S (t), заметенной радиусом-вектором
(рис. 30):
r dS
Найденный Кеплером из наблюдений движе-
движения планет закон гласит:
В равные времена радиус-вектор заме-
заметает равные площади, так что секториаль-
Рис. зо. секториальная ная скорость постоянна: —тг- = const.
скорость ох
Это — одна из формулировок закона сох-
сохранения кинетического момента. Ибо
AS = S (t + At) — S (t) = ~ r2q>At + о (At),
и, значит, секториальная скорость
n dS 1 .. 1 ,,
с г^ м
вдвое меньше кинетического момента нашей точки массы 1 и,
следовательно, постоянна.
Пример. Спутники связи «Молния» имеют сильно вытяну-
вытянутые орбиты. По закону Кеплера большую часть времени такой
спутник проводит в дальней части орбиты, где величина ф мала.
§ 8. Исследование движения в центральном поле
Закон сохранения кинетического момента позволяет свести задачу о дви-
движении в центральном поле к задаче с одной степенью свободы. Благодаря
этому движение в центральном поле можно исследовать полностью.

§ 8. ИССЛЕДОВАНИЕ ДВИЖЕНИЯ В ЦЕНТРАЛЬНОМ ПОЛЕ 35
А. Сведение к одномерной задаче. Рассмотрим движение точ-
точки (массы 1) в центральном поле на плоскости:
«• = - — , U = V(r).
Естественно перейти к полярным координатам г, ф.
По закону сохранения кинетического момента величина М =
== ф (t) г2 (t) постоянна (не зависит от t).
Теорема. При движении материальной точки единичной
массы в центральном поле ее расстояние от центра поля меняет-
меняется так, как г в одномерной задаче с потенциальной энергией
Доказательство. Дифференцируя доказанное в § 7
соотношение г = гет + гфеф, находим
г = (г — гф2) ет -f- Bгф + ГФ) *"(р-
Ввиду центральности поля
аи аи
дг дг т
Поэтому уравнение движения в полярных координатах принима-
принимает вид
Но по закону сохранения кинетического момента
¦ ?
где М — не зависящая от t постоянная, определяемая начальны-
начальными условиями. Поэтому
аи
аи , м
г = — -1гг + г—j-или г= —
2г2 '
Величина F (г) называется эффективной потенциальной энер-
энергией.
Замечание. Полная энергия в полученной одномерной
задаче
? + F(r)
совпадает с полной энергией в исходной задаче

36 ГЛ. 2. ИССЛЕДОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ
ибо
2~2~} ~ 2 "•" 2i* '
Б. Интегрирование уравнений движения. Полная энергия
в полученной одномерной задаче сохраняется. Следовательно,
зависимость г от t определяется квадратурой
г =
г
|/2(? —F(r))
Поскольку ф = Mir3, то-^2- = — ' —, и уравнение орбиты
dr ]/2(E—V(r)) *
в полярных координатах находится квадратурой:
М\гЧг
-К (г))
В. Исследование орбит. Зафиксируем значение постоянной
момента М. Изменение г со временем легко исследовать, нарисо-
нарисовав график эффективной потенциальной
** энергии V (г) (рис. 31).
Пусть Е — значение полной энергии.
Вся орбита, соответствующая данным Е и
М, лежит в области V (г) <^ Е. На границе
этой области V = Е, т. е. f = 0. При этом
скорость движущейся точки, вообще говоря,
¦ не равна нулю, так как ф ф 0 при М Ф 0.
Неравенство*. V (г) <; Е задает на плоско-
Рис. 31. график вффек- сти °ДНУ или несколько кольцевых областей:
тивной потенциальной
энеРгии 0 < ГШ|П < Г < Гщах < оо .
Если 0 ¦< rmjn ¦< гтах <. оо, то движение ограничено и проис-
происходит внутри кольца между окружностями с радиусами rmin и rmax.
Вид орбиты показан на рис. 32. Угол ф меняется монотонно,
а г колеблется между rmin и rmax периодически. Точки, где г =
= тЫп называются перицентрами, а где г = гшах — апоцентрами
(если центр Земля — перигей и апогей, если Солнце — периге-
перигелий и афелий, если Луна — периселений и апоселений).
Каждый из лучей, ведущих иэ центра в апоцентр или в пери~
центр, является осью симметрии орбиты.
В общем случае орбита не замкнута: угол между последова-
последовательными перицентром и апоцентром дается интегралом
гтах
rmln
Угол между двумя последовательными перицентрами вдвое
больше.

§ 8. ИССЛЕДОВАНИЕ ДВИЖЕНИЯ В ЦЕНТРАЛЬНОМ ПОЛЕ
37
Орбита замкнута, если угол Ф соизмерим с 2зт, т. е. если
ф = In — , где тип целые.
Можно показать, что если угол Ф несоизмерим с 2л, то орбита
заполняет кольцо всюду плотно (рис. 33).
Если rjnin = rmax, т. е. Е — значение V в точке минимума,
то кольцо вырождается в окружность, которая и будет орбитой.
Рис. 32. Орбита точки в цент-
центральном попе
Рис. 33. Всюду плотная в коль-
кольце орбита
Задача. При каких а движение по круговой орбите в поле
с потенциальной энергией U = г", — 2 <^ а <С оо, устойчиво по
Ляпунову?
Ответ. Только при а = 2.
При несколько больших минимума V значениях Е кольцо
rmin <C r *C rmax будет очень узким, а орбита будет близка к ок-
окружности. В соответствующей одномерной задаче г будет совер-
совершать малые колебания вблизи точки минимума V.
Задача. Найти угол Ф для орбиты, близкой к круговой
радиуса г.
Указание. См. пункт Г ниже.
Рассмотрим теперь случай rmax = оо. Если lim U (г) =
г-»оо
= lim V (г) = ?/„ <С оо, то возможен уход в бесконечность. Если
начальная энергия Е больше ?/„, то точка уходит на бесконеч-
бесконечность с конечной скоростью fa, = 1^2 (Е — С/»). Заметим, что
если U (г) стремится к своему пределу медленнее, чем г, то
эффективный потенциал V на бесконечности будет притягиваю-
притягивающим (здесь предполагается, что потенциал U на бесконечности
притягивающий).
Если | U (г) | при г -> 0 не растет быстрее М2/Bга), то rmin ]> О
и орбита не подходит к центру. Если же U (г) + М2/Bг2) -> —оо
при г -> 0, то возможно «падение в центр поля». Попасть в центр
поля можно даже за конечное время (например, в поле U (г)=
1/2)

38 ГЛ. 2. ИССЛЕДОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ
Задача. Исследовать вид орбиты в случае, когда полная энергия рав-
равна значению эффективной энергии V в точке локального максимума.
Г. Центральные поля, в которых все ограниченные орбиты
замкнуты. Из следующей цепочки задач вытекает, что все огра-
ограниченные орбиты в центральном поле замкнуты только в двух
случаях:
U = аг\ а>0и[/ = -к/r, к > 0.
Задача 1. Докажите, что угол Ф между перицентром и апоцентром
равен полупериоду колебаний в одномерной системе с потенциальной энер-
I М \ , г2
гией W(x) — V I — ) + ~2~ •
Указание. Подстановка х = Mir дает
а'шах
Ф= \
— W) '
xvaia
Задача 2. Найти угол Ф для орбиты, близкой к круговой радиуса г«
Ответ. Ф и Фкр = л
кр = л ~?у^Щ = п V W +
Задача 3. При каких U величина Ф не зависит от радиуса г?
Ответ. U (г) = ага (а > —2, а ф 0) и U (г) = Ъ log г.
При этом Фкр = л / У a -j- 2 (логарифмический случай соответствует
а = 0). Например, при а = 2 имеем Ф = л/2, а при а = —1 имеем Фкр =
= п.
Задача 4. Пусть U (г) —» оо при г —» оо. Найти lim Ф (Е, М).
Е-»оо
Ответ, л/2.
Указание. Подстановка х = г/агтах приводит Ф к виду
При ?¦ -* оо пмеем хтах —* оо, j/mIn -* 0, и второе слагаемое в W* можно
откинуть.
Задача 5. Пусть U (г) = —кг~ , 0 < Р < 2. Найти Фо = lim Ф.
Е-»—0
1
Sdx _ я
—7== л 5~.
о VxR — x* * — v
Sdx _ я
—7== л 5~. Заметим, что Фо не зависит
о VR * * — v
от М.
Задача 6. Найти все центральные поля, в которых ограниченные
орбиты существуют и все замкнуты.
Ответ. V = ar2 или U = —к/г.
Решение. Если все ограниченные орбиты замкнуты, то, в частности,
Фкр = 2n~jj~ = const. Согласно задаче 3, U = ara (a > —2), либо V =
= Ь 1ц г (а = 0). В обоих случаях Фкр = nl]fa + 2. Если а > 0, то сог-
согласно задаче 4, lim Ф (Е, М) = я/2. Итак, Ф = л/2, а = 2. Если а < 0,
Е—хзо

§ 8. ИССЛЕДОВАНИЕ ДВИЖЕНИЯ В ЦЕНТРАЛЬНОМ ПОЛЕ
39
К», согласно задаче 5, lim Ф (Е, М) = п/B + а). Итак, я/B + а) =
в—о
= я/|А2 + а, а = —1. В случае а = О находим Фкр = n/]/Y, что несоиз-
несоизмеримо с 2я. Итак, все ограниченные орбиты могут быть замкнуты только
в полях U = аг2 или V = —к/г. В поле U = аг2, а > О, все орбиты замкнуты
(это эллипсы с центром в О: см. пример 1 § 5). В поле V = —ft/r все ограни-
ограниченные орбиты также замкнуты и также эллиптичны, как мы сейчас докажем.
Д. Кеплерова задача. Речь идет о движении в центральном
к
поле с потенциалом U =—к/г, и, следовательно, V (г) = — +
(Рис. 34).
По общей формуле
'-$¦
йг
Интегрируя, получаем
ср = arccos
К этому выражению следовало бы прибавить произвольную кон-
константу. Мы считаем ее равной нулю, что эквивалентно выбору
Рис. 34. Эффективный потен-
потенциал кеплеровой задачи
1+е
Рис. 35. Кеплеров эллипс
начала отсчета угла ф от перицентра. Введем следующие обоз-
обозначения
-г--* V1
2ЕМ%
Теперь получаем ф = arccos ——
•, т. е.
г =
е COS <p
Это так называемое фокальное уравнение конического сечения.
Движение ограничено (рис.35) при Е <; 0. Тогда е<1, т.е.

40 ГЛ. 2. ИССЛЕДОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ
коническое сечение — эллипс. Величина р называется параметром
эллипса, а е — эксцентриситетом. Первый закон Кеплера, от-
открытый им экспериментально из наблюдений за движением Марса,
состоит в том, что планеты описывают эллипсы, в фокусах кото-
которых — Солнце.
Если принять, что планеты движутся в центральном поле тя-
тяготения, то из первого закона Кеплера вытекает закон тяготения
Ньютона: U = —klr (см. пункт Г выше).
Параметр и эксцентриситет связаны с полуосями соотноше-
соотношениями
Р _ 2Р m „ - Р
е = — = -^-^ —, где с = ае — расстояние от центра до фокуса
(см. рис. 35).
Замечание. Эллипс с малым эксцентриситетом очень по-
похож на окружность *). Если расстояние фокуса от центра —
первого порядка малости, то различие полуосей — второго:
Ь — а ~\[\ — е2 zzz a 11 %г-1. Например, в эллипсе с большой полу-
полуосью 10 см и эксцентриситетом 0,1 разность полуосей составляет
0,5 мм, а расстояние между фокусом и центром — 1 см.
Эксцентриситеты орбит планет очень малы. Поэтому Кеплер
сначала сформулировал свой I закон так: планеты движутся
вокруг Солнца по окружностям, но Солнце находится не в центре.
II закон Кеплера: секториальная скорость постоянна — спра-
справедлив в любом центральном поле.
III закон Кеплера: время обращения по эллиптической орбите
зависит только от величины большой оси.
Квадраты периодов обращения двух планет по разным эллип-
эллиптическим орбитам относятся как кубы их больших полуосей **).
Доказательство. Обозначим через Т период обращения,
через S — площадь, заметенную радиусом-вектором за время Т.
2S = MT, так как М/2 — секториальная скорость. Но площадь
с. г. гр 2nab „ МЩ
эллипса S = nab, откуда Т = —^—. И так как а = ^j- _
I р \ , М* 1 М
ИЗ а = —. 5- 1,0= —;— - jj- = —. , ТО
Т =2п. * .-; но 2|?| = — , итак Г =
•) Капните каплю чая недалеко от центра стакана. Волны соберутся
в симметричной точке. Причина в том, что, согласно фокальному определе-
определению эллипса, волны, вышедшие из одного фокуса эллипса, собираются
в другом.
••) Под планетами понимаются здесь точки, находящиеся в централь-
центральном поле.

§ 8. ИССЛЕДОВАНИЕ ДВИЖЕНИЯ В ЦЕНТРАЛЬНОМ ПОЛЕ 41
Заметим, что полная энергия Е зависит, таким образом, только
от большой полуоси орбиты а, и одинакова для всего семейства
эллиптических орбит, от окружности радиуса а до отрезка дли-
длины 2а.
Задача. При запуске спутника на круговую орбиту на расстоянии
300 км от Земли направление скорости отклонилось от расчетного на 1°
в сторону к Земле. Как изменится перигей?
Ответ. Высота перигея уменьшится примерно на
110 км.
Указание. Отличие орбиты от окружности —
второго порядка малости, и им можно пренебречь. Радиус
имеет расчетное значение, так как начальная энергия
имеет расчетное значение. Следовательно, орбита получа-
получается из расчетной поворотом на угол Iе (рис. 36). Рис. 36. Орбита,
Задача. Как изменится высота перигея, если 6лизк^)Ик круго"
набранная скорость будет на 1 м/с меньше расчетной?
Задача. Первой космической скоростью называется скорость движе-
движения на круговой орбите, радиус которой близок к радиусу Земли. Найдите
величину первой космической скорости vx и докажите, что v2 = i/ТГv, (ср.
§ 3, Б).
Ответ. 8,1 км/с.
Задача *). Во время выхода в открытый космос космонавт А. Лео-
Леонов бросил в сторону Земли заглушку от киноаппарата. Исследовать движе-
движение заглушки относительно космического корабля, считая скорость броска
равной 10 м/с.
Ответ. Заглушка будет двигаться относительно космонавта приблизи-
приблизительно по эллипсу с большой осью около 32 км и малой осью около 16 км.
Центр эллипса расположен в 16 км впереди космонавта по орбите, а период
обращения по эллипсу равен периоду движения по орбите.
Указание. Примем за единицу длины радиус круговой орбиты кос-
космического корабля, а единицу времени выберем так, чтобы период обращения
по этой орбите был 2л. Мы должны изучить решения уравнения Ньютона
г = —г/г3,
близкие к круговому решению г0 = 1, <р0 = t. Ищем эти решения в виде
Г = Г0 + Гц ф = ф0 + ф1, /1 <g 1,
По теореме о дифференцируемости решения по начальным условиям,
функции гг (t) и <рх (t) с точностью до малых выше первого порядка по на-
начальному отклонению удовлетворяют системе линейных дифференциальных
уравнений (уравнений в вариациях).
Подставляя выражения для г и <р в уравнение Ньютона, получаем после
несложных вычислений уравнения в вариациях в виде
г1 = Згг + 2ф!, ф! = — 2?!-
Решая эти уравнения при заданных начальных условиях (гг @) = фх @) =
= qij @) = 0, гг @) = —1/800), получаем приведенный выше ответ.
Отброшенные малые второго порядка дают эффект порядка 1/800 от полу-
полученного (т. е. порядка десятков метров за один виток). Таким образом, через
виток заглушка, описав тридцатикилометровый эллипс за полтора часа,
возвращается к космическому кораблю со стороны, противоположной Земле,
и проходит мимо на расстоянии нескольких десятков метров.
•) Эта задача взята из увлекательной книги В» В. Белецкого «Очерки
движении космических тел» (М.: Наука, 1972).

42 ГЛ. 2. ИССЛЕДОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ
Разумеется, мы пренебрегли в этом расчете отличием орбиты от круго-
круговой, влиянием сил, отличных от силы тяготения, и т. п.
Следующие задачи дают другой вывод эллиптичности орбит в поле тя-
тяготения — он основан на своеобразной двойственности между законами Гу-
Гуна и Ньютона и на функции Жуковского z + 1/z.
Задача 1. Докажите, что эллипс Гука с центром в точке 0 плоскос-
га комплексного переменного при возведении комплексных чисел в квадрат
переходит в эллипс Ньютона (с фокусом в точке 0).
Решение. Если | г | = Я > 1, то z + 1/z пробегает эллипс Гука
с фокусами ^2. Поэтому w2 = z2 -\- 1/z2 -f- 2 пробегает эллипс Ньютона.
Задача 2. Докажите, что орбита движения точки в поле степени о
переходит при возведении z в подходящую степень а в орбиту движения точ-
точки и> = za в поле степени А, где (а -f- 3) (А + 3) = 4, а = (а -+- 3)/2.
В частности, при а = 1 (закон Гука) получаем А = —2 (закон тяготе-
тяготения Ньютона), а = 2. Вместе с задачей 1 это доказывает эллиптичность
орбит. Гиперболические и параболические орбиты можно получить так же.
Задача 3. Докажите, что среди орбит движения в поле притяжения,
пропорционального любой степени А расстояния до центра, имеются орби-
орбиты, получающиеся из (не проходящих через 0) прямых на плоскости комплекс-
комплексного переменного при возведении комплексных чисел в степень а.
Решение. Нулевое поле имеет степень а при любом а, поэтому дос-
достаточно воспользоваться задачей 2.
При А = —2 получаются параболические орбиты w = A + 1у)г. В об-
общем случае получаются орбиты г = sec0" (ф/а), соответствующие параболам—
«нейтральные» орбиты поля степени А = 21а — 3.
При а=—5 получается А =—5 и а = —1. Нейтральные орбиты —
окружности, проходящие через нуль, и мы получаем теорему Ньютона: при
движении в центральном поле, сила которого обратно пропорциональна пя-
пятой степени расстояния до центра, среди орбит имеются окружности, про-
проходящие черев центр.
Конформное преобразование w (z) переводит орбиты движения в поле
с потенциалом V (г) = | dw/dz |a в орбиты движения в поле с потенциалом
V(w) = — \ dz/dw | 2 (см. § 45, Г).
§ 9. Движение точки в трехмерном пространстве
В этом параграфе определяется кинетический момент относительно оси
и доказывается, что при движении в осесимметричном поле он сохраняется.
А. Потенциальное поле. Рассмотрим движение в потенциаль-
потенциальном поле
г = ~, где U = U(r),r€EE*.
Имеет место закон сохранения энергии:
Б. Центральное поле. Закон сохранения момента количества
движения М = [г, г]. При движении в центральном поле вектор
JH не меняется:

§ В. ДВИЖЕНИЕ ТОЧКИ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ 43
Всякое центральное поле потенциально (доказывается, как в дву-
двумерном случае), и
-ЗГ=[*% r] + [r,r] = О,
так как г = —dU/dr, а вектор dU/dr коллинеарен г ввиду цент-
центральности поля.
Следствие. При движении в центральном поле всякая
орбита плоская.
Доказательство. (М, г) = ([г,г], г) = 0, следова-
следовательно, >• (t) _[_ М, а так как М = const, то вся орбита лежит
в плоскости, перпендикулярной к М *). Итак, исследование орбит
в центральном поле в пространстве сводится к плоской задаче,
разобранной в предыдущем параграфе.
Задача. Исследовать движение в центральном поле в п-мерноьГевк-
лидовом пространстве.
В. Осесимметричное поле.
Определение. Векторное поле в Е3 имеет осевую сим-
симметрию, если оно инвариантно относительно группы вращений
пространства, оставляющих на месте каждую точку некоторой оси.
Задача. Докажите, что если поле осесимметрично и потенциально,
то его потенциальная энергия имеет вид U — U (г, г), где г, <р, z — цилинд-
цилиндрические координаты.
В частности, отсюда вытекает, что вектор поля лежит в плоскости, про-
проходящей через ось г.
Примером такого поля может служить поле тяготения, создан-
созданное телом вращения.
Пусть z — ориентированная ортом ег ось в трехмерном ориен-
ориентированном евклидовом пространстве Е9, F — вектор евклидова
линейного пространства R3, О — точка на оси z,
г = х — OgR3 — радиус-вектор точки х GE Е3 *
относительно О (рис. 37).
Определение. Моментом Мг вектора
F, приложенного в точке г, относительно оси z
называется проекция на эту ось момента век-
вектора F относительно какой-нибудь точки оси z:
Mz = (ez, [r, F\). Рис. 37. Момент
v l " вектора F отно-
Число Mz не зависит от выбора точки О на оси z. сительно оси
Действительно, рассмотрим точку О' на оси, тогда по свойству
сметанного произведения:
Мг = (ег, [г', F]) = Aег, г'], F) = (lez, r], F) = Мг.
Замечание. Мг зависит от выбора направления оси z:
если изменить ег на —ez, то Мж изменит знак.
•) Случай М = 0 оставляется читателю.

44 ГЛ. 2. ИССЛЕДОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ
Теорема. При движении в потенциальном поле с осевой
симметрией вокруг оси z момент количества движения относи-
относительно оси z сохраняется.
Доказательство. Мг = (ez, [r, г]),
&z = (ez, [г, г]) + (е„ [г, г]) = О,
так как г = F, следовательно, г и г лежат в плоскости, прохо-
проходящей через ось z, следовательно [г, г] перпендикулярно ez.
Замечание. Доказательство сохраняет силу для всякого
силового поля, у которого вектор силы F лежит в плоскости
г и ez.
§ 10. Движение системы п точек
В этом параграфе доказываются законы сохранения энергии, импульса
и кинетического момента для системы материальных точек в Е3.
А. Внутренние и внешние силы. Уравнениями Ньютона для
движения системы п материальных точек с массами mt и радиу-
радиусами-векторами rjE^3 называются уравнения
m{rt = Ft, i = 1, 2, . . ., п.
Вектор Ft называется силой, действующей на i-ю точку.
Силы Ft определяются экспериментально. Наблюдения пока-
показывают, что часто в системе из двух точек эти силы равны по
величине, действуют вдоль прямой, соединяю-
/у/ Ffl щей точки, и противоположно направлены
/ •—*- < >/ (рис. 38).
Такие силы называются силами взаимо-
Рис. 38. силы взаимо- действия. (Пример: силы всемирного тяготе-
действия )
Если все силы, действующие на точки системы, являются
силами взаимодействия, то система называется замкнутой. По
определению, в замкнутой системе сила, действующая на i-ю точ-
точку, есть
п
Вектор Ftj называется силой, с которой /-я точка действует на
i-ю.
Так как силы Ftj и FJt противоположны (Ftj = —Fjt), то можно
записать их в виде FtJ = fijetj, где/г7- = fjt определяет величину
силы, a etj — орт направления от i-й точки на j-ю.
Если система не замкнута, то часто можно представить дейст-
действующие на нее силы в виде

10. ДВИЖЕНИЕ СИСТЕМЫ п ТОЧЕК
45
где Fa — силы взаимодействия, a Fi (?*г) — так называемая внеш-
внешняя сила.
Пример (рис. 39). Разобьем замкнутую систему на две
части / и //. Сила Ft, приложенная к i-й точке системы /, опре-
определяется силами взаимодействия
внутри системы / и силами,
действующими на i-ю точку со f' >^i \ F/
стороны точек системы //, т. е.
i^j Рис. 39. Внутренние и внешние силы
Fi — внешняя сила по отношению к рассматриваемой системе I,
Б. Закон сохранения импульса.
Определение. Импульсом (или количеством движения)
системы называется вектор
п
Теорема. Скорость изменения количества движения сис-
системы равна сумме всех внешних сил, действующих на точки системы»
Доказательство.
dP
dt
Действительно, 51 ^a = 0, так как для сил взаимодействия FtJ =
—ш„. V^
Следствие 1. Количество движения замкнутой системы
сохраняется.
Следствия 2. Если сумма внешних сил, действующих на
систему, перпендикулярна оси х, то проекция Рх количества
движения на ось х сохраняется: Рх = const.
Определение. Центром инерции системы называется
точка
Г =
Задача. Доказать, что центр инерции определен корректно, т. е.
не зависит от выбора начала отсчета радиусов-векторов.
Количество движения системы равно количеству движения
точки, лежащей в центре инерции системы и имеющей массу,
равную 2то

46 ГЛ. 2. ИССЛЕДОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ
В самом деле, (Ет{)г = ^(пг^), откуда Bт{)г =
Мы можем теперь сформулировать теорему о количестве дви-
движения как теорему о движении центра инерции.
Теорема. Центр инерции системы движется так, как
если бы все массы были сосредоточены в нем и все силы были при-
приложены к нему.
Доказательство. Bmi) ** = •'*• поэтому
dt
г
Следствие. Если система замкнута, то центр инерции
ее движется равномерно и прямолинейно.
В. Закон сохранения кинетического момента.
Определение. Кинетический момент материальной точ-
точки относительно точки О есть момент вектора импульса отно-
относительно точки О:
М = [г, тг].
Кинетическим моментом системы относительно точки О на-
зычается сумма кинетических моментов точек системы:
п
Л? = />* Г»*- т-гЛ
Теорема. Скорость изменения кинетического момента сис-
системы равна сумме моментов внешних сил, действующих на точки
системы.
Доказательство.
п п
ам
dt
Первое слагаемое равно нулю, а второе, согласно уравнениям
Ньютона, равно
Действительно, сумма моментов двух сил взаимодействия равна
нулю, ибо
Fa = - FH, [rit Fi3] + [rit FH] = [(r, - r}), Fi3) = 0.
Поэтому равна нулю сумма моментов всех сил взаимодействия:
Итак,

§ 10. ДВИЖЕНИЕ СИСТЕМЫ п ТОЧЕК 47
Следствие!. (Закон сохранения кинетического момента.)
Если система замкнута, то М = const.
п
Обозначим сумму моментов внешних сил через If = 2 \гг, Ft].
Тогда по доказанной теореме —^— = Ж, откуда вытекает
Следствие 2. Если момент внешних сил относительно
оси z равен нулю, то Mz сохраняется.
Г. Закон сохранения энергии.
Определение. Кинетической энергией точки массы т
называется
Определение. Кинетической энергией системы мате-
материальных точек называется сумма кинетических энергий точек:
где mt — массы точек, rt — их скорости.
Теорема. Приращение кинетической энергии системы равно
сумме работ всех сил, действующих на точки системы.
Доказательство.
п п
= ^ (Л, тг?г) = ? (rlf Fx).
г=1 г=1 г=1
Поэтому
t п t п
F)dt]?Al, ч.т.д.
г=1 «о г=1
Конфигурационное пространство системы ге материальных то-
точек в Е3 есть прямое произведение п евклидовых пространств:
Езп = Е3 X . . . X Е3. Оно имеет само структуру евклидова про-
пространства. Обозначим через г = (г1? . . ., гп) радиус-вектор точки
конфигурационного пространства, а через F = {Fx, . . ., Fn) —
вектор силы. Предыдущую теорему можно записать в виде
пи) «1
Т (*i) ~ т (Q = S (F, dr) = J (r, F) dt.
r(U) U
Иными словами:
Приращение кинетической энергии равно работе Зп-мерной
«силы» F на «пути» г (t) в конфигурационном пространстве.
Определение. Система называется потенциальной (или
консервативной), если силы зависят только от положения точек

48 ГЛ. 2. ИССЛЕДОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ
системы: F — F (г), и работа F на любом пути зависит только
от начальной и конечной точек пути:
Теорема. Для потенциальности системы необходимо и до-
достаточно, чтобы существовала потенциальная энергия, т. е. такая
функция U (г), что
-
дг
Доказательство. См. § 6, Б.
Теорема. Полная энергия потенциальной системы Е =
= Т + U при движении сохраняется: Е (tj = Е (t0).
Доказательство. По доказанному выше
Т (h) - Т (t0) = I (F,dr) = U (r (tB)) -U (r (*,)), ч. т. д.
»•«„)
Пусть все силы, действующие на точки системы, делятся на
силы взаимодействия и внешние силы:
где Ft] = — Fn = Ufiu-
Утверждение. Если силы взаимодействия зависят толь-
только от расстояний, ft] = fi} (\rt — r} \ ), то они потенциальны.
Доказательство. Если система состоит всего из двух
точек i, j, то, как легко проверить, потенциальная энергия взаимо-
взаимодействия дается формулой
Действительно, тогда
Поэтому потенциальная энергия взаимодействия всех точек буде<с
Если и внешние силы потенциальны, т. е. Fi = —dU\ldvu
то система потенциальна, и ее полная потенциальная энергия

§ 10. ДВИЖЕНИЕ СИСТЕМЫ п ТОЧЕК 49>
Для такой системы сохраняется полная механическая энергия
Е = Т + U =
Если же система не потенциальна, то полная механическая
энергия, вообще говоря, не сохраняется.
Определение. Уменьшение механической энергии^
Е {t0) — Е (tx), называется приращением немеханической энергии
Е' (ij - Е' {to) = Е {t0) - Е {tt).
Теорема (закон сохранения энергии). Полная энергия
Н = Е + Е' сохраняется.
Разумеется, эта теорема — очевидное следствие предыдущего
определения. Ее значение состоит в том, что в конкретных физи-
физических системах для величины немеханической энергии Е' най-
найдены выражения через другие физические величины (температу-
(температуру и т. п.).
Д. Пример. Задача двух тел. Пусть две точки с массами тг, тг
взаимодействуют с потенциалом U так, что уравнения движения
имеют вид
аи .. аи ,, ,,,, 1Ч
тЛгЛ = -—, m*rz = 5—, U — U ( r,—rJ).
Теорема. Изменение г = гх — г2 в задаче двух тел такое
же, как при движении точки массы т = —^^— в поле с потен-
потенциалом U (| г |).
Обозначим через г0 радиус-вектор центра инерции
тггг -f- тцг2
Согласно теореме о сохранении количества движения точка »•„,
движется равномерно и прямолинейно.
Рассмотрим теперь вектор г = гх — г2. Умножая первое иа
Уравнений движения на т2, второе на т1 и вычитая, находим
гг = — (mx + m2) —gj-, где U =
'! — rt\) = U(\r |).
В частности, в случае ньютоновского
притяжения точки описывают вокруг их
общего центра инерции конические сече-
сечения с фокусами в центре инерции (рис. 40).
Задача. Определить большую полуось Рис 40. Задача двух тел
эллипса, который описывает центр Земли вокруг
общего центра инерции Земли и Луны. Где расположен этот центр инер-
Ции: внутри Земли или вне? (Масса Луны в 81 раз меньше массы Земли.)

•50 ГЛ. 2. ИССЛЕДОВАНИЕ УРАВНЕНИЙ ДВИЖЕНИЯ
§ 11. Соображения подобия
В некоторых случаях важную информацию можно получить, не решая
уравнений движения, из одного их вида, используя так называемые сообра-
соображения подобия и размерности. Сущность этих соображений состоит в таком
подборе изменения масштабов (времени, длины, массы и т. д.), при котором
уравнения движения сохраняют свой вид.
А. Пример. Пусть /• (t) удовлетворяет уравнению
dU
га
dr
Положим tt = at, m, = а2т. Тогда г (tj) удовлетворяет уравне-
d2r dU „
шло т1 ¦ ,.. = -—. Иными словами:
Если уменьшить массу точки в четыре раза, то она сможет
пройти ту же орбиту в том же силовом поле вдвое быстрее *).
Б. Задача. Пусть потенциальная энергия центрального поля —
однородная функция степени v:
U (ar) = avU (г) для любого а ^> 0.
Доказать, что если кривая у есть орбита движения, то гомо-
гомотетичная кривая ау также есть орбита (при соответствующих
начальных условиях). Определить отношение времен обращения
по этим орбитам. Вывести отсюда изохронность колебаний маят-
маятника (v = 2) и III закон Кеплера (v = —1).
Задача. Считая, что радиус планеты в а раз меньше радиуса Земли,
а масса в Р раз меньше, найти, во сколько раз ускорение силы тяжести, а так-
также первая и вторая космические скорости на ней меньше, чем на Земле.
Ответ, у = $аг*, 6 = fAp/a.
Например, для Луны а ж 3,7, Р ~ 81. Следовательно, ускорение сипы
тяжести составляет примерно 1/6 земного (у х- 6), а космические скорости —
примерно 1/5 земных F «4, 7).
Задач а**). Животным пустыни приходится преодолевать большие
расстояния между источниками воды. Как зависит максимальное время, ко-
которое может бежать животное, от размеров животного L1
Ответ. Прямо пропорционально L.
Решение. Запас воды пропорционален объему тела, т. е. L3, испа-
испарение же — площади поверхности, т. е. ZA Поэтому максимальное время
пробега от одного источника до другого прямо пропорционально L.
Заметим, что максимальное расстояние, которое может пробежать жи-
животное, также растет пропорционально L (см. следующую задачу).
3 а д а ч а**). Как зависит скорость бега животного по ровному месту
и в гору от размеров животного L?
Ответ. По ровному месту —L0, в гору *~L~l.
Решение. Мощность, развиваемая животным, пропорциональна L?
¦(к. п. д. мышц примерно постоянен—• около 25%, остальные 75% химиче-
*) Здесь предполагается, что U от т не зависит. В поле тяготения потен-
потенциальная энергия U пропорциональна то, и поэтому период не зависит от мас-
•сы движущейся точки т.
**) Смит Дж. Математические идеи в биологии.— М.: Мир, 1970.

§ 11. СООБРАЖЕНИЯ ПОДОБИЯ 51
ской энергии переходят в тепло; теплоотдача же пропорциональна поверх-
поверхности тепа, т. е. L2, значит, и полезная мощность пропорциональна I?).
Сила сопротивления воздуха прямо пропорциональна квадрату скорости
и площади поперечного сечения; затрачиваемая на ее преодоление мощность
пропорциональна поэтому \?I?v. Итак, iPL2 ~ L2, следовательно, v — L°.
И действительно, скорость бега по ровному месту у животных не мельче
зайца и не крупнее лошади практически не зависит от размер особи.
Для бега в гору необходима мощность mgv ~ L3v\ поскольау развивае-
развиваемая мощность ~1?, находим v — L~l. И действительно, собак легко взбе-
взбегает на холм, а лошадь замедляет шаг.
Задача.*). Как зависит от размеров животного высота прыжка?"
Ответ. ~L°.
Решешение. Нужная для прыжка на высоту h энергия пропорциональ-
пропорциональна Lsh, а совершаемая силой мышц F работа пропорциональна FL. Сила F
пропорциональна L? (так как прочность костей пропорциональна площади
их сечения). Итак, Lsh ~ L%L, т. е. высота прыжка не зависит от размеров
животного. И действительно, тушканчик и кенгуру прыгают примерно на
одинаковую высоту.
*) См. сноску ** на с. 50.

ЧАСТЬ II
ЛАГРАНЖЕВА МЕХАНИКА
Лагранжева механика описывает движение механической сис-
системы при помощи конфигурационного пространства. Конфигу-
Конфигурационное пространство механической системы имеет структуру
дифференцируемого многообразия. На дифференцируемом много-
многообразии действует группа диффеоморфизмов. Основные понятия
и теоремы лагранжевой механики (даже если они и формулиру-
формулируются в терминах локальных координат) инвариантны относитель-
относительно этой группы *).
Лагранжева механическая система задается многообразием
(«конфигурационным пространством») и функцией на его каса-
касательном расслоении («функцией Лагранжа»).
Каждая однопараметрическая группа диффеоморфизмов кон-
конфигурационного пространства, оставляющая неизменной функ-
функцию Лагранжа, определяет закон сохранения (т. е. первый интег-
интеграл уравнений движения).
Ньютонова потенциальная система — частный случай лагран-
лагранжевой (конфигурационное пространство в этом случае евклидово,
а функция Лагранжа равна разности кинетической и потенциаль-
вой энергий).
Лагранжева точка зрения позволяет исследовать до конца
ряд важных задач механики, например, в теории малых колеба-
колебаний и в динамике твердого тела.
ГЛАВА 3
ВАРИАЦИОННЫЙ ПРИНЦИП
В этой главе показано, что движения ньютоновой потенциаль-
-ной системы являются экстремалями вариационного принципа,
так называемого «принципа наименьшего действия Гамильтона».
Из этого факта вытекает много важных следствий, например
способ быстро писать уравнения движения в криволинейных
системах координат, а также ряд качественных выводов, напри-
например теорема о возвращении в окрестность начальной точки.
В этой главе используется координатное тг-мерное простран-
пространство. Вектор такого пространства х есть набор чисел (хи . . ., хп).
¦Соответственно dfldx означает {df/dxlt..., df/dxn), (a, b) = аф^ ...
*) И даже относительно более широкой группы преобразований, затра-
затрагивающих также и время.

§ 12. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
53
§ 12. Вариационное исчисление
Для дальнейшего нам потребуются некоторые сведения из вариацион-
вариационного исчисления. Более подробное изложение см., например, в учебниках
М- А. Лаврентьева и Л. А. Люстерника «Курс вариационного исчисления»
(М.: ГОНТИ, 1938) или Г. Е. Шилова «Математический анализ. Специаль-
Специальный курс» (М.: Физматгиз, 1961).
Вариационное исчисление занимается отысканием экстремумов
функций, область определения которых — бесконечномерное про-
пространство: пространство кривых. Такие
функции называются функционалами.
Примером функционала является, нап-
например, длина кривой на евклидовой пло-
плоскости
у = {*, х: х (t) = х; t0 < t < tj,
t,
Рис. 41. Вариации кривой
Вообще функционалом называется всякое отображение про-
пространства кривых в числовую ось.
Рассмотрим «близкую» к у кривую у' = {t, х: х — х {t) +
+ h (t)}. Будем обозначать ее у' — у + h. Рассмотрим приращение
функционала Ф, Ф (у -\- К) — Ф (у) (рис. 41).
А. Вариации.
Определение. Функционал Ф называется дифферент
цируемым *), если Ф (у + h) — Ф {у) — F + R, где F зависит
от h линейно (т. е. при фиксированном у F (кг + hs) = F (кг) +
+ F (h2), F [ch) = cF (h)), a R {h, у) = О {№) в том смысле, что
из | h | <Z е, | dhldt \ < е вытекает | R \ < Се2. Линейная часть
приращения, F (h), называется дифференциалом.
Можно доказать, что если функционал Ф дифференцируем,
то его дифференциал определен однозначно. Дифференциал функ-
функционала называют также его вариацией, a h называют вариацией
кривой.
Пример. Пусть у = {t, х: х = х (t), ?0 <^ t <^ tj) — кривая
на плоскости t, х\±= -?-; L = L (а, Ь, с) — дифференцируемая
функция трех переменных. Составим функционал:
= 1 L{x(t),x(t),t)dt.
*) Следовало бы указать, на каком классе кривых определен функцио-
функционал Ф и какое линейное пространство пробегает h. Можно считать, напри-
*юр, что в обоих случаях речь идет о бесконечно-дифференцируемых функ-
функциях.

54 ГЛ. 3. ВАРИАЦИОННЫЙ ПРИНЦИП
Например, в частном случае L = \fi + Ъ2 получаем длину
кривой у.
Г г
Теорема. Функционал Ф (у) = ^ Z, (z, a1, ?) dt дифференциру-
дифференцируемый, и его дифференциал дается формулой
Доказательство.
A)-
I,
H
где /"(A) = jj (-§?-* + -It" л) df' Д = ° №2)' Интегрируя по час-
и
тям, находим
Б. Экстремали.
Определение. Экстремалью дифференцируемого функ-
функционала Ф (у) называется такая кривая у, что F (п, у) = 0 при
любом п.
(Точно так же, как у — стационарная точка функции, если
в этой точке дифференциал равен нулю.)
Теорема. Чтобы кривая у: х = х (t) была экстремалью
функционала Ф (у) = \ L (х,.?, t) dt на пространстве кривых, про-
проходящих через точки х (t0) = х0, х (гг) = хг, необходимо и до-
достаточно, чтобы вдоль кривой х (t)
d I dL\ dL __ q
dt \ дг j дх ~~ '
Лемма. Если непрерывная функция j (t), t0 <^ t <^ t,, такова,
что\ f(t)h(t)dt = 0для любой непрерывной *) функции h (t), для
to
которой h (t0) = h (tx) = 0, mo f (t) = 0.
*) Или хотя бы для любой бесконечно дифференцируемой функции h.

§ 12. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ 55
Доказательстволеммы. Пусть / (t*) ^> 0, t0 < t* <;
< tv В силу непрерывности / (t) >¦ с в некоторой окрестности
Д точки «*: t0 < t* — d < t < t* + d < V, пусть Л (t) = 0 вне Д,
Д @>Ов ДиЬ(*) = 1в -*L(** —-!|-<«<** + -!-). Тогда.оче-
видно, ^ f(t)h(t)dt >dc>0(pnc. 42). Полученное противоречие
доказывает, что /(?*) = 0 для всех t0 <
< f* < tx, ч. т. д.
Доказательствотеоремы.
По предыдущей теореме
Рис-42- п^:ргние фуик-
Внеинтегральный член равен нулю, так как h (t0) = h (?x) = 0.
Если у — экстремаль, то F (h) = 0 при всех к, для которых
h
h (t0) — h (fj) = 0. Поэтому при всех таких h(t)\^ f(t)h(t)dt = 0,
П№/(*) =-5-(-!?-)--|г- По лемме /W = 0. Обратно, если
-5()
/ (t) = 0, то, очевидно, F (h) = 0, ч. т. д.
Пример. Проверим, что экстремали длины — прямые. Имеем:
дЬ дЬ
В. Уравнение Эйлера — Лагранжа.
г\ ,, d I dL \ dL n
Определение. Уравнение -тг (-дт-) g— = « называ-
называется уравнением Эйлера — Лагранжа для функционала
Ф = ) L(x,x,t)dt.
и
Пусть теперь х — вектор «-мерного координатного пространства
Rn, у= {t, х: х = х (t), t0 ^ t <; tj} — кривая п+ 1-мерного
пространства R X Rn, L: RnxRn X R -> R — функция 2n + 1
аргумента. Аналогично предыдущей доказывается
Теорема. Чтобы кривая у была экстремалью функционала
= \L(ac, a;, t)dt на пространстве кривых ж (t), соединяющих

56 ГЛ. 3. ВАРИАЦИОННЫЙ ПРИНЦИП
две данные точки (t0, x0), (tu acj, необходимо и достаточно выпол-
выполнение вдоль нее уравнения Эйлера — Лагранжа
~St дх дх ~
Это — система п уравнений второго порядка, и решение за-
зависит от 2га произвольных постоянных. Для нахождения их
служат 2га условий ас (t0) = эе„, х (tj) = xv
Задача. Приведите примеры, когда экстремалей, соединяющих две
данные точки, много и когда их нет совсем.
Г. Важное замечание. Свойство кривой у быть экстремалью
функционала не зависит от выбора системы координат.
Например, один и тот же функционал — длина кривой — в декартовых
и полярных координатах дается разными формулами
фд
А 'о
Экстремали одни и те же — прямые линии на плоскости. Уравнения прямых
в декартовых и полярных координатах задаются различными функциями:
xi = *i (t), х2 = x2(t); г ~ г (t), ф = ф (*). Однако и те и другие функции
удовлетворяют уравнению Эйлера—Лагранжа
dt \di )~ дх ~0'
только в первом случае ждек = я^, х2; LneK = V if + *|, а во втором —
Таким образом, мы легко можем написать дифференциальное уравнение
семейства всех прямых в любых координатах.
Задача. Напишите дифференциальное уравнение семейства всех
прямых в полярных координатах на плоскости.
§ 13. Уравнения Лагранжа
иационный принцип, экстрема
их уравнений движения поте
Сравним уравнения динамики Ньютона
Здесь указан вариационный принцип, экстремалями которого являются
решения ньютоновских уравнений движения потенциальной системы.
4 ЙГ=° A)
п- тт d dL dL г.
с уравнением Эйлера—Лагранжа —=г- -р ~-- = и.
А. Принцип наименьшего действия Гамильтона.
Теорема. Движения механической системы A) совпадают
«1
с экстремалями функционала Ф (у) = \ L dt, где L = Т — U —
и
разность кинетической и потенциальной энергий.

§ 13. УРАВНЕНИЯ ЛАГРАНЖА 57
Доказательство, Так как U — U(г), Т = 2,mi~i~> т0
dL ат . аь аи
имеем—:— = —т— = тлГь -%— = —
0г{ дгг г <>ri dr.
Следствие. Пусть (qt, . . ., q3n) — любые координаты
в конфигурационном пространстве системы п материальных то-
точек. Тогда изменение q со временем подчиняется уравнениям Эйле-
Эйлера — Лагранжа
—тт- (-ЗТ-) з— = и> где L= 1 —
Т7
и.
Доказательство. По предыдущей теореме движение —
экстремаль функционала V L dt. Следовательно, в любой системе
координат удовлетворяется записанное в этой системе координат
уравнение Эйлера — Лагранжа, ч. т. д.
Определение. В механике приняты следующие наимено-
наименования: L (q, Cj,t) = T — U — функция Лагранжа, лагранжиан, qt —
обобщенные координаты, cdi — обобщенные скорости, -р— = рг —
обобщенные импульсы, ~^~ — обобщенные силы, } L(q,Cj,t)dt —
действие, -^- 1-р—] ^— = 0 — уравнения Лагранжа.
Последняя теорема называется «принципом наименьшего дейст-
действия в форме Гамильтона» потому, что в некоторых случаях дви-
движение q (t) является не только экстремалью, но и доставляет
наименьшее значение функционалу действия \ Ldt.
и
Б. Простейшие примеры.
Пример 1. Для свободной материальной точки в Е3
L-1_ 2 ,
в декартовых координатах gi = гг находим ?= -тр G*+ q\-\- q|).
Здесь обобщенные скорости — компоненты вектора скорости, обобщен-
обобщенные импульсы pi — mqi — компоненты вектор а количества движения; урав-
dp
нения Лагранжа совпадают с уравнениями Ньютона -jg- = 0. Экстремали
являются прямыми линиями. Из принципа Гамильтона следует, что пря-
прямые являются не только кратчайшими (т. е. экстремалями длины
У <j2_l- «2 Л. а\ dt\ , но и экстремалями действия
«.

58 ГЛ. 3. ВАРИАЦИОННЫЙ ПРИНЦИП
Задача. Докажите, чго этот экстремум есть минимум.
Пример 2. Рассмотрим движение в плоском центральном
поле в полярных координатах qx = г, q2 = ф. Из соотношения
, • /п тг2
г = ver + фгрф находим кинетическую энергию 1 = —к— =
= тг (г2+г2ф2) и лагранжиан L (g, д) = Г (д, q)—U (q), U =
dL
Обобщенные импульсы будут р = "Т1" • т- е*
рх = тг, р2 = тг2<р.
Первое уравнение Лагранжа р1 = -^— принимает вид
dU
тг =,
Это уравнение мы уже получили в § 8.
Так как q2 = ф не входит в L, имеем -^— = 0. Поэтому второе
уравнение Лагранжа будет р2 = 0, р2 = const. Это — закон со-
сохранения кинетического момента.
В общем случае, когда поле не центральное, U = U (г, ф),
dU
находим р2 = — — .
Это уравнение можно переписать в виде -jt- (M, ez) = N,
fill
где N = ([г, F], ez), F = -х— . (Скорость изменения кинетиче-
кинетического момента относительно оси z равна моменту силы F отно-
относительно оси z.)
Действительно, имеем
UU = -^r-dr + -f^-Лр = - (F,dr) = - (F, er)dr-r(F, ev) dq>,
поэтому ~~ = r (F, еф) = r ([er, F], ez) = ([r, F], ez).
Разобранный пример подсказывает следующее обобщение за-
закона сохранения кинетического момента.
Определение. Координата qi называется циклической,
если она не входит в функцию Лагранжа: —— = 0.
Теорема. Обобщенный импульс, соответствующий цикли-
циклической координате, сохраняется: pt = const.
Доказательство. Согласно уравнению Лагранжа,
°чтд

S 14. ПРЕОБРАЗОВАНИЕ ЛЕЖАНДРА
59
§ 14. Преобразование Лежандра
Преобразование Лежандра — вспомогательный математический прием,
состоящий в переходе от функций на линейном пространстве к функциям на
сопряженном пространстве. Преобразование Лежандра сродни проективной
двойственности и тангенциальным координатам в алгебраической геометрии
яли построению сопряженного банахова пространства в анализе. Оно часто
встречается в физике (например, при определении термодинамических ве-
величин).
А. Определение. Пусть у = f (x) — выпуклая функция^
Г (*) > о.
Преобразованием Лежандра функции / называется новая функ-
функция g нового переменного р, которая строится следующим обра-
образом (рис. 43). Нарисуем на плоскости х, у
график функции /. Пусть дано число р.
Рассмотрим прямую у = рх. Возьмем точку
х = х (р), в которой кривая всего дальше
от прямой по вертикали: функция
рх — f (х) = F (р, х) в точке х (р) имеет мак-
максимум по х при фиксированном р; тогда
g(p) = F iP, х 0»)).
Точка х (р) определяется из условия
экстремума: dFldx = 0, т. е. /' (х) — р.
Ввиду выпуклости функции / (х) такая точка х (р) единственна *).
Б. Примеры.
Пример 1. Пусть / (х) = х2. Тогда F (р, х) = рх — х2, х (р) =¦ р/2,
S (р) = V4p2.
mac* n2
Пример 2. Пусть / (х) = —тт— . Тогда
Рис. 43. Преобразование
Лежандра
х р
Пример 3. Пусть / {х) = -^— . Тогда в (р) =
•1,
Р
где
а
Пример 4. Пусть / {х) — выпуклая ломаная. Тогда g (p) — тоже
выпуклая ломаная, причем вершинам / (х) соответствуют отрезки g (p),
а отрезкам / (х) — вершины g (p). На-
Например, угол, изображенный на рис. 44,
при преобразовании Лежаидра перехо-
переходит в отрезок.
Ал
гг в,
В. Инволютивность. Будем счи-
считать функцию / нужное число раз
Дифференцируемой, а /" (х) > 0.
Легко проверить, что преобразо-
преобразование Лежандра переводит выпук-
выпуклые функции в выпуклые. Поэтому его можно применить дважды.
Рис. 44. Преобразование Лежандра пе-
переводит угол в отрезок
*) Если существует.
Задача. Покажите, что областью определения g может оказаться
одна точка, отрезок или луч, если функция / определена на всей оси х. До-
Докажите, что если функция / определена на отрезке, то функция g определена
ва всей оси р.

60 ГЛ. 3. ВАРИАЦИОННЫЙ ПРИНЦИП
Теорема. Преобразование Лежандра инволютивно, т. е.
его квадрат равен тождественному преобразованию: если f при
преобразовании Лежандра переходит в g, то преобразование
Лежандра от g будет снова /.
Доказательство. Чтобы сделать преобразование Ле-
Лежандра функции g переменного р, мы должны, по определению,
рассмотреть новое независимое переменное (обозначим его через
х), составить функцию
G (х, р) = хр — g (p),
найти точку р (х), в которой G имеет максимум:
-|^- = 0, т. е. g' (р) = х,
и тогда преобразованием Лежандра g (p) будет функция от х,
равная G (х, р (х)).
Докажем, что G (х, р (х)) = / (х). С этой целью заметим, что
G (х, р) — хр — g (p) имеет простой геометрический смысл: это
ордината касательной к графику f(x), имею-
имеющей наклон р, при абсциссе х (рис. 45).
Действительно, при фиксированном р функ-
функция G (х, р) есть линейная функция от х,
причем dG/dx = р, и при х = х (р) имеем
G (х, р) = хр — g (р) = / (х) по определе-
определению g (p).
Зафиксируем теперь х = х0 и будем ме-
менять р. Тогда значения G (х, р) будут орди-
ординатами точек пересечения прямой х = х0
рИс45. инволюшв- с касательными к графику / (х), имеющи-
ность преобразования ми разный наклон р. Из выпуклости гра-
лежандра фика следует, что все эти касательные лежат
ниже кривой, а потому максимум G (х, р) при фиксированном
х (ро) равен / (ж) (и достигается при р = р (х0) = /' (х0)), ч. т. д.
Следствие*). Пусть дано семейство прямых у = рх —
— g (р). Тогда огибающая имеет уравнение у = / (х), где / —
преобразование Лежандра функции g.
Г. Неравенство Юнга.
Определение. Две функции /, g, являющиеся преобра-
преобразованиями Лежандра друг друга, называются двойственными по
Юнгу.
По определению преобразования Лежандра, F (х, р) — рх —
— / (х) ^ ё (р) ПРИ любых х, р. Отсюда вытекает неравенство
Юнга
px^f(x) + g (р).
*) Легко усмотреть, что это — теория «уравнения Клеро».

§ 15. УРАВНЕНИЯ ГАМИЛЬТОНА 6J
Я* р2
Пример 1. Если / (я) = -у , то g (р) = -g- , и мы получаем извест-
известят2 ра
ное неравенство ря <^-q--г-?~ для всех х, р.
ха /11
Пример 2. Если /(а:) = —, то g (р) =-р~ , — + -р- = 1, и мы
получаем неравенство Юнга
1 1
для всех а;>0, р > О, а>1, р ]> 1, -^- + -g- =1.
Д. Случай многих переменных. Пусть теперь / (ас) — выпуклая
функция векторного переменного ас = (xlf . . ., хп) (т. е. квадра-
квадратичная форма (-~dx, dx\ положительно определена). Тогда
преобразованием Лежандра называется функция g (p) векторного
переменного р = {рг, . . ., рп), определенная аналогичными пре-
предыдущим равенствами
g(p) = F (р, х (р)) = max F (р, ас), F {р, х) = {р, х) — / (ас),
X
df
р = ——
Все предыдущие рассуждения, в том числе неравенство Юнга,,
без изменений переносятся на этот случай.
Задача. Пусть /: Ru -*¦ R —выпуклая
функция в линейном пространстве R".
Обозначим через R"* сопряженное линей-
линейное пространство. Покажите, что предыду-
предыдущие формулы задают вполне определенное
отображение g: Rn* —*¦ R (при условии, что
линейная форма df I» пробегает все прост-
пространство R"*, когда ас пробегает R").
Задача. Пусть / — квадратичная фор-
, . . ^ , т-т Z. Рис. 46. Преобразова-
ма: f{x) = 2jfijxixj' Показать, что ее преоб- ние лежандра квад-
разование Лежандра есть снова квадратич- ратичной формы
ная форма g (p) =^2?i)PiPh причем значения обеих форм в соответ-
соответствующих точках совпадают (рис. 46):
f{x(p)) = g{p), g(p(x))=f(x).
§ 15. Уравнения Гамильтона
После преобразования Лежандра лагранжева система дифференциаль-
дифференциальных уравнений второго порядка переходит в замечательно симметричную
систему 2п уравнений первого порядка — систему уравнений Гамильтона
(или канонических уравнений).

€2 ГЛ. 3. ВАРИАЦИОННЫЙ ПРИНЦИП
А. Эквивалентность уравнений Лагранжа и Гамильтона. Рас-
Рассмотрим систему уравнений Лагранжа р = dLldq, где р = dLldq,
заданную функцией Лагранжа L: R" xR" X R->-R, которую
мы предположим выпуклой *) относительно второго аргумента q.
Теорема. Система уравнений Лагранжа эквивалентна си-
системе In уравнений первого порядка — уравнений Гамильтона:
• — дН ¦ _ дН
^ dq ' " dp '
где И (р, q, t) = pq — L (q, q, t) есть преобразование Лежандра
функции Лагранжа, рассматриваемой как функция от q.
Доказательство. По определению, преобразование
Лежандра L (q, q, t) по g-есть функция//(р) = pq — L (q), в ко-
которой q выражено через р по формуле р ~ dLldq, и которая за-
зависит еще от параметров q, t. Эта функция Н называется
функцией Гамильтона.
Полный дифференциал функции Гамильтона
,„_ dH j dH , dH
равен полному дифференциалу pq — L при р = —— :
Оба выражения для dH должны совпадать. Поэтому
. _ dH dH dL_ dH_ dL_
У ~ dp ' dq ~ dq ' dt ~ dt '
Принимая во внимание уравнение Лагранжа р = dLldq, полу-
получаем уравнения Гамильтона.
Итак, если q (t) удовлетворяет уравнениям Лагранжа, то
(Р @> 9 (*)) удовлетворяет уравнениям Гамильтона. Обратное до-
доказывается аналогичным образом. Итак, системы Лагранжа и
Гамильтона эквивалентны, ч. т. д.
Замечание. Доказанная теорема относится ко всем ва-
вариационным задачам, а не только к лагранжевым уравнениям
механики.
Б. Функция Гамильтона и энергия.
Пример. Пусть уравнения все-таки механические, и функ-
функция Лагранжа имеет обычный вид L — Т — U, где кинетическая
энергия Т — квадратичная форма относительно q:
Т = -у ^ ацЫь aU = ан («. fy U = U (q).
*) В приложениях эта выпуклая функция будет обьгано положительно
определенной квадратичной формой.

§ 15. УРАВНЕНИЯ ГАМИЛЬТОНА 63
Теорема. При сделанных предположениях функция Гамиль-
Гамильтона Н есть полная энергия Н = Т + U.
Доказательство основано на лемме о преобразовании Лежанд-
ра квадратичной формы.
Лемма. Значения квадратичной формы f (x) и ее преобра-
преобразования Лежандра g(p) в соответствующих точках совпадают:
f(x) = g {р).
Пример. Для формы / (х) = а-2 это известное свойство касательной
тх2 р2 тх2
к параболе. Для форны / (х) = —п— имеем р = тх и g (р) = -п— = ~2~=
= /(*)•
Доказательство леммы. По теореме Эйлера об одно -
родных функциях
df x = 2f.
дх
Следовательно, g (р (х)) = рх — / (ас) = -J— х — f = 2/ (ас) — /(ас) —
= / (х), ч. т. д.
Доказательство теоремы. Рассуждая, как в лем-
лемме, находим Н = pq — L = IT — (Т — U) = Т + U, ч. т. д.
Пример. Для одновременного движения
" __ аи
9 -~~ЬТ"
В этом случае Т = -j- if, U = U (q), p = q, H = -y- + U (q), и урав-
уравнения Гамильтона принимают вид
дЯ
Этот пример позволяет быстро вспомнить, в каком из двух
уравнений Гамильтона стоит знак минус.
Из теоремы об эквивалентности уравнений движения гамиль-
тоновой системе вытекает ряд важных следствий. Например,
закон сохранения энергии принимает простой вид:
Следствие 1. Справедливо равенство dHldt = dHldt и,
в частности, для систем, функция Гамильтона которых явно
не зависит от времени (dHldt = 0), выполняется закон сохранения
функции Гамильтона: Н (р (t), q (t)) = const.
Доказательство. Рассмотрим изменение Н вдоль траек-
траектории Н (р (t), q (t), t). Тогда в силу уравнений Гамильтона
dH _ дН I дИ \ дН дН дН __ дИ
dt ~~ dp \ dq j^ dq dp *~ dt ~~ dt ' Чт Т' Д'
В. Циклические координаты. Рассматривая центральное поле,
Мы заметили, что введением полярных координат задача сводится
к одномерной. Оказывается, всякая симметрия задачи, позволяю-

64 ГЛ. 3. ВАРИАЦИОННЫЙ ПРИНЦИП
щая выбрать систему координат q так, чтобы от некоторых коор-
координат функция Гамильтона не зависела, позволяет найти неко-
некоторые первые интегралы и свести такую задачу к задаче с мень-
меньшим числом координат.
Определение. Если координата qx не входит в функцию
Гамильтона Н (рх, р2, . . ., рп; qlt . . ., qn; t), так что дН/ддг = О,
то такая координата называется циклической (термин происходит
¦от частного случая — угловая координата ф в центральном поле).
Очевидно, координата qx циклическая тогда и только тогда, когда
она не входит в функцию Лагранжа (dL/dq1 = 0). Из гамильто-
нова вида уравнений движения вытекает
Следствие 2. Пусть qx — циклическая координата. Тогда
рх — первый интеграл. При атом изменение остальных координат
<:о временем такое же, как в системе с п — 1 независимой коорди-
координатой <72, • • ., qn и с функцией Гамильтона
Н (pz, . . ., рп, qz, . . ., qn, t, с),
¦зависящей от параметра с = рг.
Доказательство. Положим р' = {рг, . . ., pn)s q' =
= (q2, . . ¦, qn). Тогда система Гамильтона примет вид
_d_ ,_ дН _d_ _ дН
dt У ~~ dp' ' at 1Х~ дрх '
Последнее уравнение показывает, что рх = const. Поэтому в си-
систему уравнений для р', q' величина рх входит лишь как пара-
параметр в функции Гамильтона. После того как эта система 2га — 2
уравнений решена, уравнение для qx принимает вид
—-?! = / (*). где f(t)=-±-H (pvp' (t), q' (t), t),
и легко интегрируется.
Почти все решенные в механике задачи решаются с помощью
следствия 2.
Следствие 3. Автономная система с двумя степенями сво-
свободы (ге=2), имеющая циклическую координату, интегрируема. Ибо
в этом случае система для р', q' одномерная и немедленно интег-
интегрируется с помощью интеграла Я (р', q') =с.
16. Теорема Лиувилля
Фазовый поток гамильтоновых уравнений сохраняет фазовый объем.
Отсюда вытекает, например, что устойчивость в гамильтоновой системе не
может _быть асимптотической.
Рассмотрим для простоты случай, когда функция Гамильтона
времени явно не содержит: Н = Н (р, q).

§ 16. ТЕОРЕМА ЛИУВИЛЛЯ 65
А. Фазовый поток.
Определение. 2п-мерное пространство с координатами
рг, . . ., рп; qt, . . ., qn называется фазовым пространством.
Пример. В случае п = 1 это — фазовая плоскость систе-
системы х = ^—, рассмотренной в § 4.
Так же, как в этом простейшем примере, правые части урав-
уравнений Гамильтона задают векторное поле: в каждой точке (р, q)
фазового пространства приложен 2га-мерный вектор (—дН/dq,
дН/др). Предположим, что каждое решение уравнений Гамиль-
Гамильтона можно продолжить на всю ось времени *).
Определение. Фазовым потоком называется однопа-
раметрическая группа преобразований фазового пространства
gl : (р @), q @)) -* (р (t), q (t)),
где р (t), q (t)— решение системы уравнений Гамильтона (рис. 47).
Задача. Доказать, что {g'} — группа.
р(ЩШ
pm,q(O)
Рис. 47. Фазовый поток Рис. 48. Сохранение объема
Б. Теорема Лиувилля. 1) Фазовый поток сохраняет объем:
для любой области D имеем (рис. 48)
объем g'D = объем D.
Мы докажем несколько более общее предложение 2), также
принадлежащее Лиувиллю.
Пусть дана система обыкновенных дифференциальных уравне-
уравнений х = / (ас), х = (#j, . . ., хп), решения которой продолжа-
продолжаются на всю ось времени. Пусть g' — соответствующая группа
преобр азов аний:
? {х) = х + f (x) t + О (f2) (t -> 0). A>
Пусть D @) — область в пространстве {ас} и v @) — ее объем;
v (t) = объем D (t), D (t) = g'D @).
2) Если, div / = 0, то g* сохраняет объем: v (t) = v @).
*) Например, для этого достаточно, чтобы множества уровня функции
Н были компактны.

66 ГЛ. 3. ВАРИАЦИОННЫЙ ПРИНЦИП
В. Доказательство.
Лемма 1. Справедливо соотношение
dv
= \ div fdx (dx = dx± ... dxn).
dt
Доказательство. При любом t по определению яко-
якобиана
Вычисляя dg'x/dx по формуле A), находим при
Воспользуемся теперь известным алгебраическим фактом.
Лемма 2. Для любой матрицы А = \\ ац || справедливо со-
соотношение
det | Е + At | = 1 + t tr A + О (t2), t -+ О,
n
где tr A = 5j о,ц — след матрицы А {сумма диагональных элемен-
тов).
(Доказательство леммы 2 получается непосредственным рас-
раскрытием определителя: получается 1, п. слагаемых с t, остальные
с fa, t3 и т.д.).
Итак,
что и доказывает лемму 1.
Доказательство теоремы 2). Так как t = t0 ни-
ничем не хуже t = 0, лемму 1 можно записать в виде
dv U) I [' ,.
^М = \ di
И если div / = 0, то и -^- ^ 0, ч. т. д.
В частности, для системы Гамильтона имеем
д

S 16. ТЕОРЕМА ЛИУВИЛЛЯ 67
Теорема Лиувилля 1) доказана.
Задача. Распростравить теорему Лиувилля на случай неавтономных
систем (Я = Я (р, д, t) или / = / (ов, <))•
Задача. Докажите формулу Лиувилля W = Woe'tTAdt для определи-
определителя Вронского линейной системы а> = A (t) ж.
Теорема Лиувилля имеет многочисленные приложения.
Задача. Доказать, что в гамильтоновой системе невозможны асимп-
асимптотически устойчивое положение равновесия и асимптотически устойчивый
предельный цикл в фазовом пространстве.
Особенно важные приложения теорема Лиувилля имеет в ста
тистической механике.
Теорема Лиувилля позволяет применять к исследованию ме-
механических систем методы так называемой эргодической теории *).
Приведу лишь простейший пример.
Г. Теорема Пуанкаре о возвращении. Пусть g — сохраняющее
объем непрерывное взаимно однозначное отображение, переводя-
переводящее ограниченную область D евклидова прос-
пространства в себя: gD = D.
Тогда в любой окрестности U любой точ-
точки области D найдется точка х €Е U, кото-
которая возвращается в область U, т. е. gnx ?E U
при некотором п ]> 0.
Эта теорема применима, например, к фазо-
вому потоку gl двумерной системы с расту-
растущим на бесконечности потенциалом U (хг, х2);
в этом случае инвариантная ограниченная рИс. 49. как будет
область в фазовом пространстве дается уело- ^У'
( 49)
ф р Км^ичнУча
вием (рис. 49) ке, неизвестно; одна-
г ' ко теорема Пуанкаре
D = in О- Т 4- /7 ^Г Е\ предсказывает воз-
i/ — Х-**» У' -* т У Ч fi/' вращение в окрест-
окрестность исходного по-
Теорему Пуанкаре можно усилить, доказав, ложения
что почти всякая движущаяся точка много-
многократно возвращается к своему исходному положению. Это—один
из немногих общих выводов о характере движения. Детали дви-
движения никому не известны уже в случае
X ^-, X — (Хг, Х2)-
Несколько парадоксальным выводом из теорем Пуанкаре и
Лиувилля является следующее предсказание: если открыть пере-
перегородку, разделяющую камеру с газом и камеру с вакуумом, то
через некоторое время молекулы газа почти наверное снова со-
соберутся в первой камере (рис. 50).
*) См., например, книгу: X а л м о ш П. Лекции по эргодической тео-
теории.— М.: ИЛ, 1959.

68
ГЛ. 3. ВАРИАЦИОННЫЙ ПРИНЦИП
Разгадка парадокса в том, что «некоторое время» больше вре
мени существования Солнечной системы.
Доказательство теоремы Пуанкаре. Рас-
Рассмотрим образы окрестности V (рис. 51):
U, gU, g*U, . . ., gnU, . . .
Все они имеют одинаковый положительный объем. Если бы они
В
Рис. 50. Молекулы вер-
вернулись в первую камеру
Рис. 51. Теорема о возв-
возвращении
не пересекались, объем D был бы бесконечен. Поэтому при некото-
некоторых к > 0, I > 0, к > I
g*u n iv Ф о.
Следовательно, gk lU (~) U ф 0. Пусть gk lx = y, x^U, у GU.
Тогда x E= V, gnx E= U (n = к — Г), что и требовалось доказать.
Д. Приложения теоремы Пуанкаре.
Пример 1. Пусть D — окружность, g—поворот на угол а. Если
ес=2п-^-,то gn — тождественное преобразование, и теорема очевидна.
Если же а несоизмеримо с 2я, то теорема Пуанкаре
дает
V6 > 0, Зп: ( gnx — х |< б (рис. 52).
Отсюда легко вытекает
Теорема. Если аф2я , то множе-
множество точек вида g*x всюду плотно *) на окруж-
Рис. 52. всюду плот- ности (к = 1, 2, . . .).
вое множество на ок-
окружности Задача. Докажите, что всякая орбита движе-
движения в центральном поле с U = г4 либо замкнута, либо
всюду плотно заполняет кольцо между двумя окружностями.
Пример 2. Пусть D — двумерный тор, <j)j и <р2 — угловые координа-
координаты на нем (широта и долгота) (рис. 53).
Рассмотрим систему обыкновенных дифференциальных уравнений на
торе
<Pi = <*!, Ф2 = а2.
•) Множество А всюду плотно в В, если в каждой окрестности каждой
точки В есть точка А.

§ 16. ТЕОРЕМА ЛИУВИЛЛЯ 69
Очевидно, div / = 0, и соответствующее движение
gU- («Pi. «Pa) •"•¦ («Pi + «A «Pa + M
сохраняет объем dq>jdq>2. Из теоремы Пуанкаре легко выводится
Теорема. Если aja^ иррационально, то «обмотка» тора
g' (фх, ф2) всюду плотна на торе.
3 а д а ч а. Докажите, что если ш иррационально, то
фигура Лиссажу (х = cos i, у = cos Ш) всюду плотна в
квадрате | х \ < 1,J у | < 1.
ПримерЗ. Пусть D — n-мерный тор Г", т. е. пря-
прямое произведение *) п окружностей: ^~
D = ffl х Si х ... X ffl = Гп. р,,,.. 53. Тор
п
Точка n-мерного тора задается п угловыми координатами ф = (фх, . . ., фп)'
Пусть а = (аи . . ., ап), gl — преобразование, сохраняющее объем
Задача. При каких условиях на а всюду плотны: а) траектория #'ф,
б) траектория #6ф (ieR принадлежит группе вещественных чисел R, k e
eZ — группе целых чисел).
Преобразования примеров 1—3 тесно связаны с механикой.
Но так как теорема Пуанкаре абстрактная, она имеет и не свя-
связанные с механикой приложения.
Пример 4. Рассмотрим первые цифры чисел 2П: 1, 2, 4, 8, 1, 3, 6,
1, 2, 5, 1, 2, 4...
Задача. Есть ли в этой последовательности цифра 7? и какая цифра
встречается чаще: 7 или 8? И во сколько раз?
*) Прямое произведение множеств А, В, . . . есть множество наборов
точек (а, Ь, . . .), а е А, Ь е В, ....

ГЛАВА 4
ЛАГРАНЖЕВА МЕХАНИКА НА МНОГООБРАЗИЯХ
В этой главе вводятся понятия дифференцируемого многооб-
многообразия и касательного расслоения. Функция Лагранжа, заданная
на касательном расслоении, определяет на многообразии лагран-
жеву «голономную систему». Частными случаями являются си-
системы материальных точек, стесненных голономными связямив
например маятник или твердое тело.
§ 17. Голономные связи
В этом параграфе дано определение системы материальных точек, стео-
ненной голономными связями.
А. Пример. Пусть у — гладкая кривая на плоскости. Если
в окрестности у имеется очень сильное силовое поле, направлен-
направленное к кривой, то движущаяся точка будет все время находиться
вблизи у- В предельном случае бесконечно сильного поля точка
Рис. 54. Связь как
бесконечно сильное
поле
Рис. 55. Потенциальная
энергия Upf
вынуждена оставаться на кривой у. В этом случае говорят, что
на систему наложена связь (рис. 54).
Чтобы дать точную формулировку, введем в окрестности кри-
кривой у криволинейные координаты qlt q2: qx — вдоль кривой yt
Qz — расстояние от кривой.
Рассмотрим систему с потенциальной энергией
UN = Nql + Uо (qlf q2),
зависящей от параметра N (который будет затем стремиться
к бесконечности) (рис. 55).
Рассмотрим начальные условия на у:
«1 @) = q°u 9i @) = 41, дг @) = о, B @) =.о.

§ 17. ГОЛОНОМНЫЕ СВЯЗИ 71
Обозначим через qt — <р (t, N) изменение координаты qx при дви-
движении с такими начальными условиями в поле C/jv-
Теорема. При N ->- оо существует предел
Предельная функция qt = -ф (f) удовлетворяет уравнению Лагранжа
d
где L^ (gu t\) = T\ _• _ — Uo |в2=о(^ — кинетическая энергия
движения вдоль у).
Таким образом, при N —*- оо система уравнений Лагранжа
для qx, q2 порождает уравнение Лагранжа для qx = я)з (t).
Точно такой же результат получится, если рассмотреть вместо
плоскости Зп-мерное пространство конфигураций п точек, состав-
п
ляющих механическую систему, с метрикой ds2 = 51 пцЛг* (т4 —
массы), вместо кривой у — подмногообразие Зп-мерного прост-
пространства, вместо qx — какие-нибудь координаты qx на у, вместо
q2 — координаты q2 в направлении, перпендикулярном у. Если по-
потенциальная энергия имеет вид
U = U0 {qr) + Nql,
то при N ->- оо движение на у определяется уравнениями Лаг-
Лагранжа с функцией Лагранжа
Б. Определение системы со связями. Мы не будем доказывать
сформулированную теорему *) и не будем ею пользоваться. Она
нужна нам лишь для того, чтобы оправдать следующее
Определение. Пусть у — m-мерная поверхность в Зп-
мерном конфигурационном пространстве точек гг, . . ., гп масс
ГОц . . ., тп. Пусть q = (gu . . ., qm) — какие-нибудь коорди-
координаты на у: ri = rt (q)- Система, описываемая уравнениями
d dL _ dL j _J_
dt gg ~ 6q f Ь ~ 2
называется системой п точек, стесненной Зп — m идеальными
голономными связями. Поверхность у называется конфигурацион-
конфигурационным пространством системы со связями.
*) Доказательство основывается на том, что вследствие сохранения
энергии движущаяся точка не может удаляться от у на расстояние, большее
чем cN~1^, что стремится к нулю при N -* оо. Определение связей при по-
помощи такого предельного перехода предложено Р. Курантом. См.: Rubin H.,
Ungar P. Motion under a strong constraining force // Comm. on the Pure and
Applied Math.— 1957.— V. 10, No. 1.— P. 65—87.

72 ГЛ. 4. ЛАГРАНЖЕВА МЕХАНИКА НА МНОГООБРАЗИЯХ
Если поверхность у задается к — Зп — т функционально не-
независимыми уравнениями fx (г) = 0, . . ., /fc (г) = 0, то говорят,
что система стеснена связями fl = 0, . . ., /s = 0.
Голономную связь можно было бы определить и как предель-
предельный случай системы с большой потенциальной энергией. Значе-
Значение этих связей для механики в том, что, как показывает экспе-
эксперимент, многие механические системы с той или иной точностью
относятся к этому классу.
Идеальные голономные связи в дальнейшем для краткости
будем называть просто связями. Другие связи в этой книге рас-
рассматриваться не будут.
§ 18. Дифференцируемые многообразия
Конфигурационное пространство системы со связями является диффе-
дифференцируемым многообразием. В этом параграфе приведены простейшие све-
сведения о дифференцируемых многообразиях.
А. Определение дифференцируемого многообразия. На мно-
множестве М задана структура дифференцируемого многообразия,
если М снабжено конечным или счетным набором карт, так что
каждая точка изображена хотя бы на одной карте.
Картой называется открытая область U в евклидовом коор-
координатном пространстве q = (дг, . . ., дп) вместе со своим взаим-
взаимно однозначным отображением ф
на некоторое подмножество М,
ф p
Если какая-нибудь точка М
имеет изображения на двух кар-
картах U, U' сразу, то то же должно
быть справедливо для некоторых
окрестностей V, V этой точки на
Рис.156. Совместные карты КЭЖДОЙ ИЗ Карт (рИС. 56). ТаКИМ
образом, возникает отображение
ф'-1ф: V -*¦ V части одной карты V d U на часть другой кар-
карты V С V.
Это — отображение области V координатного евклидова про-
пространства q на область V координатного евклидова пространст-
пространства д', и оно задается п функциями п переменных q' = q' (q),
(п = Q (<?'))• Карты U, U' называются совместными, если эти
функции дифференцируемы *).
Атласом называется совокупность совместных друг с другом
карт. Два атласа эквивалентны, если их объединение есть снова
атлас.
*Ч Под дифференцируемостью здесь понимается г~кратная непрерывная
дифференцируемость; точное значение г A ^ г ^ оо) несущественно (можно
считать, например, что г — оо).

§ 18. ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ
73
Дифференцируемое многообразие есть класс эквивалентности
атласов. Мы будем рассматривать только связные многообра-
многообразия *). Тогда число п для всех карт одно и то же — оно назы-
называется размерностью многообразия.
Окрестностью точки многообразия называется образ при ото-
отображении <р: U —>¦ М окрестности изображения этой точки на
карте U. Мы будем предполагать, что у каждых двух разных то-
точек многообразия есть непересекающиеся окрестности.
Б. Примеры.
Пример 1. Евклидово пространство Rn есть многообразие, атлас
которого состоит из единственной карты.
Пример 2. Сфера S2 = {(х, у, z): х2 + у2 + z2 = 1} имеет структуру
многообразия, атлас которого состоит, например, из двух карт (Ui, ф(, i =
= 1, 2) в стереографической проекции (рис. 57). Аналогичная конструкция
годится и для n-мерной сферы
S» = {(*„ .. ., Хк+1): Ъх\ = 1}.
Пример 3. Рассмотрим плоский маятник. Конфигурационное прост-
пространство — окружность S1 — есть многообразие. Обычный атлас доставля-
доставляется угловой координатой <р: R1 —¦ S1, Vl = (—я, я), U2 = @, 2я) (рис. 58).
Рис. 57. Атлас сферы
Рис. 58. Плоский, сферический и двойной
плоский маятники
Пример 4. Конфигурационное пространство «сферического» математи-
тического маятника есть двумерная сфера ?2 (рис. 58).
Пример 5. Конфигурационное пространство «плоского двойного маят-
маятника» есть прямое произведение двух окружностеп, т. е. двумерный тор Т2 =
= S1 X S1 (рис 58).
Пример 6. Конфигурационное пространство сферического двойного
маятника есть прямое произведение двух сфер S2 X S2.
9,
Рис. 59. Конфигурационное про-
пространство отрезка на плоскости
/о- *-
Рис. 60. Конфигурационное про-
пространство треугольника
Пример 7. Жесткий отрезок на плоскости gt, g2 имеет конфигура-
конфигурационным пространством многообразие R'x S1 с координатами gt, q2, q3
(рис. 59).
Оно покрывается двумя картами.
•) Многообразие связно, если его нельзя разбить на два непересекаю-
непересекающиеся открытые подмногообразия.

74 ГЛ. 4. ЛАГРАНЖЕВА МЕХАНИКА НА МНОГООБРАЗИЯХ
Пример 8. Жесткий прямоугольный треугольник ОАВ, вращающийся
вокруг вершины О. Положение треугольника задается тремя числами. Дейст-
Действительно, направление ОА е S2 задается двумя числами, а если ОА задано,
можно еще вращать OB <= S1 вокруг оси О А (рис. 60).
С положением треугольника ОАВ можно связать ортонормированный
ОА ОБ
правый репер e% = . п . ¦ •, е2 = . пв . , е« = [ег, е2]. Соответствие взаимно
I иА / I иг> (
однозначно, поэтому положение треугольника задается ортогональной мат-
матрицей третьего порядка с определителем 1.
Множество всех матриц третьего порядка есть девятимерное пространство
R9. Шесть условий ортогональности выделяют два трехмерных связных много-
многообразия матриц с определителем +1 и —1. Вращения трехмерного простран-
пространства (определитель +1) образуют группу, которая обозначается SOC).
Таким образом, конфигурационное пространство треугольника ОАВ
есть группа SOC).
Задача. Показать, что многообразие SOC) гомеоморфно трехмерному
вещественному проективному пространству.
Определение. Размерность конфигурационного прост-
пространства называется числом степеней свободы.
П р и м е р 9. Рассмотрим систему из к шарнирио соединенных в замк-
замкнутую цепь стержней.
Задача. Сколько степеней свободы имеет эта система?
Пример 10. Вложенное многообразие. Говорят, что М есть
вложенное в евклидово пространство Еп подмногообразие размер-
размерности к (рис. 61), если в окрестности U каж-
каждой точки xGMсуществуют п — к функций fx:
?/->R, . . ., /„_к: U -у R таких, что пересече-
пересечение окрестности U с М задается уравнениями
fx = 0, . . ., /„.с = 0, и векторы grad flt ...
. . ., grad /„_& в х линейно независимы.
Рис. 61. вложенное Легко ввести на М структуру многообразия^
подмногообразие т е координаты в окрестности ас (как?).
Можно доказать, что всякое многообразие можно вложить
в евклидово пространство.
В примере 8 SOC) есть подмножество R9.
Задача. Доказать, что SOC) вложено в R9 и тем самым проверить,
что SOC) — многообразие.
В. Касательное пространство. Если М — вложенное в Еп
^-мерное многообразие, то в каждой точке х оно имеет /с-мерное
касательное пространство ТМЖ. А именно, ТМЖ есть ортогональ-
ортогональное дополнение к {grad flt . . ., grad fn-м) (рис. 62). Векторы
касательного пространства ТМХ с началом в ас называются ка-
касательными векторами кМ вас. Эти векторы можно определить
и непосредственно, как векторы скорости кривых на М:
t-ю
Определение касательного вектора можно дать и во внутрен-
внутренних терминах, не обращаясь к вложению М в Еп.

§ 18. ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ 75
Назовем две кривые х = ср (?), ас = чр (J) на многообразии
эквивалентными, если ср @) = чЬ @) = х и lim ^(' ^ = 0
<-*> г
на какой-нибудь карте. Тогда это же соотношение касания верно
на любой карте (докажите!).
Определение. Касательным вектором к многообразию
М в точке х называется класс эквивалентности кривых ср (t),
ср @) = х.
Легко определить операции умножения касательного вектора
на число и сложения касательных векторов. Множество каса-
касательных векторов к М в х образует линейное
пространство ТМЖ. Это пространство и на-
называется касательным пространством к М
в х.
Для вложенных многообразий введенное
определение совпадает с предыдущим. Но его
преимущество в том, что оно годится и для У Еп
абстрактных, никуда не вложенных много-
многообразий М. Рис. 62. Касательное про-
Определение. Пусть U — карта странство
атласа М с координатами qY, . . ., дп.
Тогда компонентами касательного ьектора к кривой д = ср (t)
dcp.
называются числа ii, . . ., !„, где|г = —^-
м
Г. Касательное расслоение. Объединение касательных прост-
пространств к многообразию М в разных точках (J ТМЖ имеет естест-
м
венную структуру дифференцируемого многообразия, размерность
которого вдвое больше размерности М.
Это многообразие называется касательным расслоением мно-
многообразия М и обозначается ТМ. Точка ТМ — это вектор s,
касающийся М в какой-нибудь точке х. Локальные координаты
на ТМ строятся следующим образом. Пусть дг, . . ., дп — ло-
локальные координаты на многообразии М, |lt . . ., 1„ — компо-
компоненты касательного вектора в этой системе координат. Тогда 2/г
чисел (д^, . . ., дп, ?lf . . ., |п) задают на ТМ локальную систему
координат.
Отображение р: ТМ-*-М, сопоставляющее каждому касатель-
касательному вектору | ту точку х Е= U, в которой вектор касается М
(| ?Е ТМа,), называется естественной проекцией. Прообраз точки
ж GE М при естественной проекции, р~х (х), есть касательное про-
пространство ТМХ. Это пространство называется слоем расслоения
над точкой х. Ш
Д. Риманово многообразие. Если М — вложенное в евклидово
пространство многообразие, то метрика евклидова пространства
позволяет измерять на М длины кривых, углы между векторами,
объемы и т. п.

76
ГЛ. 4. ЛАГРАННСЕВА МЕХАНИКА НА МНОГООБРАЗИЯХ
Все эти величины выражаются через длину касательных век-
векторов, т. е. через положительно определенную квадратичную фор-
форму, заданную на каждом касательном пространстве ТМХ (рис. 63):
как
Например, длина кривой у на многообразии выражается через эту форму
J(y)= \ tf<dsc, da>>, или, если кривая задана параметрически:
У- [*о. hi — м. ' ^ ж О s Mi
то г (y) =
Определение. Дифференцируемое многообразие М
с фиксированной положительно определенной квадратичной фор-
формой <?, ?> в каждом касательном пространстве ТМХ называется
римановым многообразием. Эта квадратич-
квадратичная форма называется римановой метри-
метрикой.
Замечание. Пусть U — карта ат-
атласа М с координатами qlt . . ., дп. Тогда
риманова метрика задается формулой
Рис. 63. Риманова метрика
где
тора.
ds2= 2 aij(g)dqidgj,aij=:aji,
i,J=l
?д. — координаты касательного век-
Функции ai} (q), разумеется, предполагаются дифференцируе-
дифференцируемыми нужное число раз.
Е. Производная отображения. Пусть /: М -*¦ N — отображе-
отображение многообразия М в многообразие N. Отображение / называ-
называется дифференцируемым, если в локальных координатах на М
и на N оно задается дифференци-
дифференцируемыми функциями.
Определение. Производ-
Производной дифференцируемого отобра-
отображения /: М -*¦ N в точке жеМ
называется линейное отображе-
отображение касательных пространств
Рис. 64. Производная отображения
которое задается следующим образом (рис. 64).
Пусть v е ТМХ. Рассмотрим кривую <р: R -*¦ М, <р @) = х,
с вектором скорости —?-\ = v. Тогда fg.xv есть вектор
at \t^=n

§ 19. ЛАГРАНЖЕВА ДИНАМИЧЕСКАЯ СИСТЕМА 77
скорости кривой /о(р: R ->¦ N,
3 а д а ч а. Докажите, что вектор / xv зависит не от кривой «р, но лишь
от вектора v.
Задача. Докажите, что отображение f^x: ТМХ —> TNj^ линейное.
Задача. Пусть ж = (xlt . . ., xm) — координаты в окрестности точки
х е М, а у — (yt, . . ., уп) — координаты в окрестности точки у е N. Пусть
| — набор компонент вектора л, aij- набор компонент вектора f^xv. По-
Покажите, что
9
Объединяя отображения j^x при всех х, получаем единое ото-
отображение всего касательного расслоения
/*: TM->TN, f^v^f^v для
Задача. Докажите, что /„ — дифференцируемое отображение.
Задача. Пусть /: М —» N, g: N —> К, h = g о /: М -* К. Докажите,
что h* = g* о /„.
§ 19. Лагранжева динамическая система
В этом параграфе определяется лагранжева динамическая система на
многообразии. Система с голономньши связями является частным случаем.
А. Определение лагранжевой системы. Пусть М — дифферен-
дифференцируемое многообразие, ТМ — его касательное расслоение,
L: ТМ -v R — дифференцируемая функция. Отображение у: R -*¦
-*¦ М называется движением в лагранжевой системе с конфигура-
конфигурационным многообразием М и функцией Лагранжа L, если у есть
экстремаль функционала
где у — вектор скорости, yty^
Пример. Пусть М — область в координатном пространстве с коор-
координатами q = (qx, . . ., qn). Функция Лагранжа L: ТМ —» R записывается
в виде функции 2п координат L (g, q). Как доказано в § 12, изменение коор-
координат движущейся точки со временем удовлетворяет уравнениям Лагранжа.
Следствие. Изменение локальных координат q =
= (ди . . ., qn) точки у (t) при движении в лагранжевой системе
на многообразии М удовлетворяет уравнениям Лагранжа
d dL _ dL
dt dq ~ dq '
где L (q, q) — выражение функции L: ТМ -> R через координа-
координаты q и q на ТМ.

78 ГЛ. 4. ЛАГРАНЖЕВА МЕХ НИКА НА МНОГООБРАЗИЯХ
Особенно часто встречается следующий частный случай.
Б. Натуральная система. Пусть М — риманово многообра-
многообразие. Кинетической энергией называется квадратичная форма на
каждом касательном пространстве
Потенциальной энергией называется дифференцируемая функция
Определение. Лагранжева система на римановом мно-
многообразии называется натуральной, если функция Лагранжа рав-
равна разности кинетической и потенциальной энер-
1,У гий, L = Т — U.
Пример. Рассмотрим две точки масс тпх, т2, со-
соединенные отрезком длины I на плоскости х, у. Тогда
конфигурационное многообразие трех измерений
М = R2 х S1 С Ra X R2
Р1на е5поскости°К определяется в четырехмерном конфигурационном про-
пространстве Ra X Ra двух свободных точек (xlt yj, {x2, у2)
условием ']f(xl — х2J + (уг — у2J = I (рис. 65).
В касательном пространстве к четырехмерному пространству (хг, хг,
Уи Уг) есть квадратичная форма
Наше трехмерное многообразие, как вложенное в четырехмерное, снабжа-
снабжается римановой метрикой. Полученная голономная система и называется
в механике отрезком постоянной длины на плоскости х, у. Кинетическая
энергия дается формулой
В. Система с голономными связями. В § 17 мы определили
систему материальных точек, стесненных голономными связями.
Покажем, что эта система является натуральной.
Действительно, рассмотрим конфигурационное многообразие
М системы со связями как вложенное в Зп-мерное конфигурацион-
конфигурационное пространство системы свободных точек. Метрику в Зп-мерном
?г
пространстве зададим квадратичной формой 2j трЬ
Тогда соответствующая вложенному риманову многообразию
М и потенциальной энергии U натуральная система совпадает
с системой, определенной в § 17 или с предельным случаем си-
системы с потенциалом U-{- Nq\, N -*¦ <х>, быстро растущим вне М.
Г. Рецепт решения задач со связями. 1. Найти конфигурацион-
конфигурационное многообразие и ввести в нем координаты qlt . . ., q^ (в ок-
окрестности каждой точки, вообще говоря, свои).

§ 19. ЛАГРАНЖЕВА ДИНАМИЧЕСКАЯ СИСТЕМА 79
2. Выразить кинетическую энергию?' = \ -^-т^ в виде
квадратичной формы относительно обобщенных скоростей
3. Составить функцию Лагранжа L = Т — U (q) и решать
уравнение Лагранжа.
Пример. Рассмотрим движение материальной точки массы 1 по по-
поверхности вращения в трехмерном пространстве. Можно показать, что ор-
орбиты суть геодезические на поверхности. В цилиндрических координатах
г, ф, z поверхность задается (локально) в виде г = г (z) или z = z (r). Соот-
Соответственно кинетическая энергия и..1еет вид (рис. 66)
Т = -у (*2 + у2 + г*) = ~y [A + rj) z2 + т* (z) ф2] в координатах q>, z;
1
= -тг [A + 42) ^2 + г2Ф2] в координатах г, q>.
Использовано соотношение i2 -\- у2 = г2 -{- г2ф2.)
Функция Лагранжа L = Т. В обеих системах координат ф — цикличе-
циклическая координата. Соответствующий импульс сохраняется; р„ = г2ф — не
что иное, как z-компонента момента количества движения. Так как система
имеет две степени свободы, знания циклической координаты ф достаточно,
чтобы проинтегрировать задачу до конца (см. следствие 3 § 15, стр. 64).
r=rBsinaB
Рис. 66. Поверхность вра- Рис. 67. Геодезические на
щения поверхности вращения
Ясное представление о виде орбит проще получить, рассуждая немного
по-другому. Обозначим через а угол орбиты с меридианом. Имеем: гф =
= j v | sin а, где | v | — величина вектора скорости (рис. 66).
Но по закону сохранения энергии Н = L = Т сохраняется. Следова-
Следовательно, | v | = const. Поэтому закон сохранения р„ принимает вид
г sin a = const
(«теорема Клеро»).
Это соотношение показывает, что движение происходит в области | sin a \ <
<С 1, т. е. г ^ r0 sin a0. Кроме того, наклон орбиты к меридиану увеличи-
увеличивается при уменьшении радиуса г. Достигнув наименьшего возможного
г = r0 sin а0, орбита отражается и возвращается в область с большим г
(рис. 67).
Задача. Доказать, что все геодезические на нарисованной поверх-
поверхности вращения делятся на три класса: меридианы, замкнутые кривые, и
геодезические, всюду плотные в кольце г ^ с.
Задача. Исследовать поведение геодезических на поверхности тора

80 ГЛ. 4. ЛАГРАНЖЕВА МЕХАНИКА НА МНОГООБРАЗИЯХ
Д. Неавтономные системы. Лагранжева неавтономная система
отличается от автономной, которую мы рассматривали до сих пор,
дополнительной зависимостью функции Лагранжа от времени:
L:WxR-)-R, L = L (q, q, t).
В частности, в неавтономной натуральной системе от времени
может зависеть как кинетическая, так и потенциальная энергия:
r:rixR->R, U: М X R -* R, Т = Т (q, q, t),
U=U{q, t).
Система п материальных точек, стесненных голономными свя-
связями, зависящими от времени, определяется при помощи меняю-
меняющегося со временем подмногообразия конфигурационного прост-
пространства свободной системы. Такое многообразие задается ото-
отображением
i: М х R -> Esn, i (q, t) = x,
которое при каждом фиксированном tGR определяет вложение
М -+¦ Езп. Рецепт п. Г остается в силе для неавтономных систем.
Пример. Движение бусинки по вертикальной окруншости радиуса г
(рис. 68), вращающейся с угловой скоростью to вокруг вертикальной оси,
проходящей через центр О окружности. Многообразие М — окружность.
Обозначим через q угловую координату на окруж-
окружности, отсчитываемую от верхней точки.
Пусть х, у, z — декартовы координаты в Е3 с нача-
началом О и вертикальной осью z. Пусть ф — угол плоско-
плоскости окружности с плоскостью xOz. По условию ф = to*.
Отображение i: M x R —> -Б3 задается формулой
i (q, t) = (г sin q cos (at, r sin q sin at, r cos q).
Из этой формулы (а проще — из «прямоугольного
бесконечно малого треугольника») находим
Рис. 68. Бусинка на
вращающейся окруж- т
ности1 Т = -у (to2/-2 sin* q + г2 у2), U = mgr, os g.
На наше счастье функция Лагранжа L = Т — U оказалась не зависящей
от *, хотя связь и зависит от времени. Кроме того, функция Лагранжа
оказалась такой же, как в одномерной системе с кинетической энергией
Уо = -2-9а, M = mr\
и с потенциальной энергией
V = A cos q — В sin* q, A = mgr, В = -«г- to2ra.
Вид фазового портрета зависит от соотношения между А и В. При 2В < А
(т. е. при таком медленном вращении окружности, что toar < g) нижнее по-
положение бусинки (q = я) устойчиво и характер движения в общем такой же,
как в случае математического маятника (о = 0).

5 20. ТЕОРЕМА НЁТЕР
81
При 2В ^> А, т. е. при достаточно быстром вращении окружности, нижнее
положение бусинки становится неустойчивым, зато появляются два устой-
Ряс. 69. Эффективная потенциальная энергия и фазовая плоскость бусинки
A g
чивых положения бусинки на окружности, cos q = — -gg = — j^ • По-
Поведение бусинки при всевозможных начальных условиях ясно из вида фазо-
фазовых кривых на плоскости q, q (рис. 69).
§ 20. Теорема Нётер
Различные законы сохранения (импульса, момента и т. д.) являются
частными случаями одной общей теоремы: всякой однопараметрической
группе диффеоморфизмов конфигурационного многообразия лагранжевой
системы, сохраняющих функцию Лагранжа, соответствует первый интеграл
уравнений движения.
А. Формулировка теоремы. Пусть М — гладкое многообразие,
L: ТМ -*¦ R — гладкая числовая функция на его касательном
расслоении ТМ. Пусть h: М -+¦ М — гладкое отображение.
Определение. Лагранжева система (М, L) допускает
отображение h, если для любого касательного вектора v Ez ТМ
L (h*v) = L (v).
Пример. Пусть М = {(Xl, x2, x3)}, L = -j
— U (х2, х3). Система допускает сдвиг h: (xt, x2, z3) —» (х1 + s, x2, xs) вдоль
оси хг и не допускает, вообще говоря, сдвигов вдоль оси х2.
Теорема Нётер. Если система (М, L) допускает одно-
параметрическую группу диффеоморфизмов hs: М-*¦ М, sGR,
h° = Е, то соответствующая L система уравнений Лагранжа
имеет первый интеграл I: ТМ -*- R.
В локальных координатах q на М интеграл I записывается
в виде
-. dL dhs(q) I
Б. Доказательство. Пусть сначала М = Rn — координатное
пространство. Пусть <р: R -*- М, q = ф (t) — решение уравнений
Лагранжа. Так как h* сохраняет L, то сдвиг решения^ h8oq>: R -*¦

82 ГЛ. 4. ЛАГРАНЖЕВА МЕХАНИКА НА МНОГООБРАЗИЯХ
—г- М при любом s также удовлетворяет уравнениям Лагран-
жа *). Рассмотрим отображение Ф: R X R -*• R", q = Ф (s, t) =
= hs (Ф (t)) (рис. 70).
Будем обозначать производные по t точками, а по s штрихами.
По условию
где частные производные L взяты в
точке q = Ф (s, t), q = Ф (s, t).
Рис. 70. к теореме нётер Как мы подчеркнули выше, при лю-
любом фиксированном значении s отобра-
отображение Ф |s = const: R -»- R" удовлетворяет уравнению Лагранжа
4- [~ (Ф (*, 0. * (*,«))] = -|f (Ф (в, t), Ф {s, t)).
Введем обозначение .F7 (s, t) = -тт— (Ф (s, t), Ф (s, t)) и подставим
dFJdt в A) вместо dL/dq.
Записывая q' в виде —тт—ff', находим
d dL\ , . dL I d ,\ d I dL
оамечание. Первый интеграл 1 = -^-q определен вы-
выше с помощью локальных координат д. Оказывается, величина
I (v) не зависит от выбора координатной системы q.
Действительно, / есть скорость изменения L (v), когда вектор
v ЕЕ ТМХ меняется внутри ТМХ со скоростью —=— hsx. Итак,
as [s=o
/ (v) есть корректно определенная в целом функция касательного
вектора v ЕЕ: ТМХ. Тем самым теорема Нётер доказана и в случае,
когда М — многообразие.
В. Примеры.
Пример 1. Рассмотрим систему материальных точек с мас-
массами mt:
= у
стесненную связями fj (ас) = 0. Предположим, что система до-
допускает сдвиги вдоль оси е2:
hs: xt ь*- Xi + se-i при всех i.
*) Авторы некоторых учебников ошибочно утверждают, что верно и об-
обратное, т. е. если hs переводит решения в решения, то h% сохраняет L.

§ 20. ТЕОРЕМА НЁТЕР 83
Иными словами, связи допускают движение системы как цело-
целого вдоль оси elt и потенциальная энергия при этом не меняется.
Из теоремы Нётер заключаем:
Если система допускает сдвиги вдоль оси ег, то проекция ее
центра инерции на ось ех движется прямолинейно и равномерно.
Действительно, —5— hsXi = ег. Согласно замечанию в кон-
конце пункта Б, сохраняется величина
1 ^!
т. е. первая компонента Рх вектора импульса. Для систем без
связей мы это уже доказывали раньше.
Пример 2. Если система допускает вращения вокруг оси et,
то сохраняется кинетический момент относительно этой оси
Действительно, легко проверить, что если hs—поворот вокруг оси ег
на угол s, то ~^- |8=0йвэс* = [ех, xt], откуда I = ^Г-Ц^ [е17 хг] =
ь [elt хг\) =
Задача 1. Пусть частица движется в поле однородной винтовой линии
х = cos ф, у = sin Ф, z = сф. Найти соответствующий этой винтовой симмет-
симметрии закон сохранения.
Ответ. В любой системе, допускающей винтовые движения, оставляю-
оставляющие на месте нашу винтовую линию, сохраняется величина / = сР3 + М3.
Задача 2. Пусть твердое тело движется по инерции. Доказать, что
firo центр инерции движется прямолинейно и равномерно. Если центр инер-
инерции покоится, то кинетический момент относительно него сохраняется.
Задача 3. Какие величины сохраняются при движении тяжелого
твердого тела, закрепленного в некоторой точке О? В частности, если тело
симметрично относительно проходящей через О оси?
Задача 4. Распространить теорему Нётер на неавтономные лагран-
жены системы.|
Указание. Пусть Мг = М х R — расширенное конфигурацион-
конфигурационное многообразие (прямое произведение конфигурационного многообразия
М на ось времени R).
Определим функцию Lt: TMl —» R как L dtfdx, т. е. в локальных коор-
координатах q, t на Мг зададим ее формулой
*' dx ' dx ) = L\9> dx I dx
Применим теорему Нётер к лагранжевой системе (Ми Lj).
Если Lt допускает преобразования hs: Ml —* Мг, то мы найдем первый
интеграл It: ТМ1 -¦ R. Поскольку \ Ldt = \ Ltdx, это приводит к первому
интегралу /: ТМ х R —-> R исходной системы. Если в локальных коорди-
/ dq dt \
ватах (g, t) на; М, имеем Д = h \q, t,-jj~ , -^ J , iol{q,q,t) = /x (q, t, q, 1).

84 ГЛ. 4. ЛАГРАНЖЕВА МЕХАНИКА НА МНОГООБРАЗИЯХ
В частности, если L не зависит явно от времени, то Lx допускает сдвиги
по времени hs (q, t) = (q, t -\- s). Соответствующий первый интеграл / есть
интеграл энергии.
§ 21. Принцип Даламбера
Здесь дается новое определение системы материальных точек, стеснен-
стесненной голономными связями, и доказывается его эквивалентность определе-
определению, данному в § 17.
А. Пример. Рассмотрим голономную систему (М, L), где М —
поверхность в трехмерном пространстве {х}:
В механических терминах: «материальная точка х массы т вы-
вынуждена оставаться на гладкой поверхности М».
Рассмотрим движение точки х (t). Если бы выполнялось урав-
уравнение Ньютона т'х -(- -g— =0, то в отсутствие внешних^ сил
(U = 0) траектория была бы прямой и не
R | могла бы лежать на поверхности М.
С точки зрения Ньютона это указывает
на присутствие новой силы, «вынуждающей
точку оставаться на поверхности».
Определение. Величина
_ .. аи
Рис. 71. Реакция связи ах
называется силой реакции связи (рис. 71).
С учетом силы реакции It (t) уравнения Ньютона, очевидно,
справедливы:
Физический смысл силы реакции R становится ясным, если мы рас-
рассмотрим нашу систему со связью как предел систем с потенциальной энер-
энергией U + NUt, N —> оо, Ut (as) = р2 (ж, М). При больших ЛГ потенциал
дО\
связи NUt обусловливает быстропеременную силу2^ = — ^' qx ? ПРИ
дельном переходе (N -* оо) остается среднее значение В силы F по коле-
колебаниям ж около М. Сила F перпендикулярна к поверхности М. Поэтому сила
реакции В перпендикулярна М: (В, %) = 0 для всякого касательного век-
вектора %.
Б. Формулировка принципа Даламбера—Лагранжа. В меха-
механике касательные векторы к конфигурационному многообразию
называются виртуальными перемещениями. Принцип Даламбе-
Даламбера — Лагранжа гласит:

§ 21. ПРИНЦИП ДАЛАМБЕРА 85
для всякого виртуального перемещения %., или еще иначе: работа
силы реакции на любом виртуальном перемещении равна нулю.
Для системы из материальных точек ас» с массами mt силы
реакции Ht определяются как Лг = тп^ + ~т—, а принцип Да-
ламбера имеет вид 2 (Hi, h) = 0, или JT ( (тгхг + -|^-1, ?. J = О,
т. е.:
сумма работ сил реакций на любом виртуальном перемеще-
перемещении {ij} e= ГЛ/я равна нулю.
Указанное выше свойство связей называют идеальностью.
Если определять систему с голономной связью как предел при N —» оо,
то принцип Даламбера — Лагранжа становится теоремой; ее доказательство
намечено выше для простейшего случая.
Можно, однако, определять идеальную голономную связь при помощи
принципа Даламбера — Лагранжа.
Таким образом, имеется три определения голономной системы со свя-
связями:
1) Предел систем с потенциальной энергией U + NU^ N —• оо.
2) Голономная система (М, L) где М — гладкое подмногообразие кон-
конфигурационного пространства системы без связей, L — лагранжиан.
3) Система, удовлетворяющая принципу Даламбера — Лагранжа.
Все три определения математически эквивалентны.
Доказательство утверждений 1) =ф- 2) и 1) =ф 3) намечено выше и в де-
деталях проводиться не будет. Мы докажем, что 2) фф 3).
В. Эквивалентность принципа Даламбера—Лагранжа и вариа-
вариационного принципа. Пусть М — подмногообразие евклидова
пространства М С R^i и ж: R ->¦ М — кривая; х (t0) = х0,
X (tj) = Хх.
Определение. Кривая ж называется условной экстре-
экстремалью функционала действия
и
если дифференциал 6Ф = 0 при условии, что для сравнения бе-
берутся близкие кривые *), соединяющие х0 с х1 на М.
Мы будем писать
бмФ = 0. A)
Очевидно, уравнение A) эквивалентно уравнениям Лагранжа
d dL dL Т ж2 тт/ \ i \
-dT-W = ~W> L = — -Ufr), * = ж to),
¦ каждой локальной системе координат g на М.
*) Строго говоря, чтобы определить вариацию 6Ф, нужно определить
структуру области линейного пространства в множестве близких к х кривых
8а М. Это можно сделать при помощи координат на М; причем свойство быть
Условной экстремалью от выбора системы координат не зависит.

86
ГЛ. 4. ЛАГРАНЖЕВА МЕХАНИКА НА МНОГООБРАЗИЯХ
Теорема. Чтобы кривая ж: R-»-j?c Rw была условной
экстремалью действия (т. е. удовлетворяла уравнению A)), необ-
необходимо и достаточно, чтобы она удовлетворяла уравнению Да-
Даламбера
B)
Лемма. Пусть f: {t: t0 <^ t <I tj -*- RN — непрерывное век-
векторное поле. Если для каждого непрерывного касательного к М
векторного поля ? вдоль ж (Е; (t) (=
€Е TMx(t), I (t) обращается в 0 при
Рис. 72. Лемма о нормаль-
нормальном поле
mo поле / (t) e каждой точке ж (t) перпен
дикулярно поверхности М (т. е.
(/ (t), h) = 0 для каждого вектора h (=
е ГЛГ.от) (рис. 72).
Доказательство леммы повторяет рассуждения, с помощью ко-
которых выводились уравнения Эйлера — Лагранжа в § 12.
Доказательство теоремы. Сравним значения Ф
на двух кривых зс (/) и ж (/) +1 (/), | (t0) = | (h) = 0. Получим,
интегрируя по частям:
U
Из этой формулы видно *), что уравнение A) 6М Ф = 0 эквива-
эквивалентно совокупности уравнений
для всех касательных векторных полей ? B) €= ТМЖф, 1 (?0) =
= I (*i) = 0- По лемме (где надо положить / = ж + -^—) сово-
совокупность уравнений C) эквивалентна уравнению Даламбера —
Лагранжа B), ч. т. д.
Г. Замечания.
Замечание 1. Выведем из доказанной теоремы принцип
Даламбера — Лагранжа для системы из п точек жь ЕЕ Rs, i =
= i. . . ., п, с массами mt, с голономными связями.
*) Расстояние точки ж (() + % (() до М второго порядка малости по срав-
сравнению с | (t).

§ 21. ПРИНЦИП ДАЛАМБЕРА 87
В координатах ас = {jc,- = ymfxt} кинетическая энергия при-
принимает вид Т = -g- У тгх\ = *2~ jc2-
По доказанной теореме экстремали принципа наименьшего
действия удовлетворяют условию
/- , аи
(принцип Даламбера — Лагранжа) для точки в R3n: Зп-мерная
сила реакции ортогональна многообразию М в метрике Т). Воз-
Возвращаясь к координатам xt, получаем
о =
т. е. принцип Даламбера — Лагранжа в указанной раньше фор-
форме: сумма работ сил реакции на виртуальном перемещении равна
нулю.
Замечание 2. Принципу Даламбера — Лагранжа мож-
можно придать несколько иную форму, если обратиться к статике.
Положением равновесия называется такая точка ж0, которая яв-
является орбитой движения: ж (t) = а?0.
Пусть материальная точка движется по гладкой поверхности
М под действием силы / = —dU/dx.
Теорема. Чтобы точка ж0 поверхности М была положе-
положением равновесия, необходимо и достаточно, чтобы сила была ор-
ортогональна поверхности: (/ (осо), |) == 0 для всех § (= ТМХс.
Это следует из уравнения Даламбера — Лагранжа ввиду х = 0.
Определение. — тх называется силой инерции. Те-
Теперь принцип Даламбера — Лагранжа принимает такой вид:
Теорема. Если к действующим в данный момент времени
силам добавить силы инерции, то занимаемое движущейся точкой
в данный момент времени положение ж станет положением рав-
равновесия.
Действительно, уравнение Даламбера
(-тх + ft |) = 0
выражает, согласно предыдущей теореме, тот факт, что ас есть
положение равновесия системы с силами —тх + /.
Совершенно аналогичные предложения справедливы и для си-
системы точек:
Если зс = {Xi} — положение равновесия, то сумма работ дей-
действующих сил на виртуальном перемещении равна нулю.
Если к действующим в данный момент времени силам добавить
силы инерции — mtxi (t), то конфигурация х (t), в которой си-
система- находится в этот момент, станет положением равновесия.
Итак, задача о движении приводится к задаче о равновесии
под действием других сил.

88 ГЛ. 4 ЛАГРАНЖЕВА МЕХАНИКА НА МНОГООБРАЗИЯХ
Замечание 3. До сих пор мы не рассматривали случаи,
когда связи зависят от времени. Все сказанное выше переносится
на такие связи без изменений.
Пример. Рассмотрим бусинку, скользящую по стержню,
наклоненному под углом а к вертикальной оси и вращающемуся
равномерно, с угловой скоростью со, вокруг этой оси (весом пре-
пренебрежем). За координату q примем расстояние
от точки О (рис. 73). Кинетическая энергия и
лагранжиан:
I —Т — — -2 — — пB -1- — 2г2
?i ?t ?t
г = qsina.
рис. 73. вусияка. Уравнение Лагранжа: mq = m^q sin2 a.
скользящая по вра- Сила реакции в каждый момент времени
вдающемуся стержню ОрТОгональна виртуальным перемещениям(т. е.
направлению стержня), но вовсе не ортогональна действитель-
действительной траектории.
Замечание 4. Из уравнения Даламбера — Лагранжа
легко выводятся законы сохранения. Например, если среди вир-
виртуальных перемещений есть сдвиг вдоль оси х1
?.• = elf
то сумма работ сил реакции на этом перемещении равна нулю:
Будем теперь рассматривать силы реакции как внешние силы.
Тогда замечаем, что сумма первых компонент внешних сил равна
нулю. Значит, сохраняется первая компонента, Рх, вектора коли-
количества движения.
Этот же результат мы получили выше из теоремы Нётер.
Замечание 5. Подчеркнем еще раз, что голономность
той или иной физической связи (с той или иной степенью точно-
точности) есть вопрос эксперимента. С математической точки зрения
голономность связей есть постулат физического происхождения;
его можно вводить в разных эквивалентных формах, например
в виде принципа наименьшего действия A) или принципа Далам-
Даламбера — Лагранжа B) — но при определении связей речь всегда
идет о новых, по сравнению с уравнениями Ньютона, эксперимен-
экспериментальных фактах.
Замечание 6. Наша терминология несколько отличается
от принятой в учебниках механики, где принцип Даламбера —
Лагранжа распространяется на более широкий класс систем («не-
голономные системы с идеальными связями»). В этой книге мы
не будем рассматривать неголономные системы. Замечу только,
что примером неголономной системы является катящийся по плос-

§ 21. ПРИНЦИП ДАЛЛМБЕРА 89
кости без скольжения шар. В касательном пространстве к конфи-
конфигурационному многообразию неголономнои системы в каждой точ-
точке фиксировано подпространство, которого должен касаться век-
вектор скорости.
Замечан'ие 7. Если система состоит из материальных то-
точек, соединенных стержнями, шарнирами и т. п., то может воз-
возникнуть соблазн говорить о силе реакции той или иной отдельной
связи.
Мы определили суммарную «силу реакции всех связей» Bj
для каждой материальной точки mi. Понятие силы реакции от-
отдельной связи определить нельзя, как видно уже из простого
примера балки, опирающейся на три колонны. Если попытаться
определять силы реакции колонн Rlt 2?2, Ss предельным перехо-
переходом (считая колонны очень жесткими пружина-
пружинами), то мы убедимся, что результат зависит от
распределения жесткости.
Задачи в задачниках подобраны |так, чтобы ^^/JLp
это затруднение не встречалось.
Задача. Стержень веса Р, наклоненный к по-
поверхности стола под углом 60°, начинает падать без на- ?™«г74" «!??•
р д у , д Samm стола
чальной скорости (рис. 74). Найти силу реакции стола
в начальный момент, считая стол: а) абсолютно гладким, б) абсолютно ше-
шероховатым. (В первом случае голономная связь удерживает конец стержня
на плоскости стола, а во втором — в данной точке.)

ГЛАВА 5
КОЛЕБАНИЯ
Поскольку линейные уравнения легко решать и исследовать,
теория линейных колебаний является самым разработанным от-
отделом механики. Во многих нелинейных задачах линеаризация
приводит к удовлетворительному приближенному решению. Да-
Даже когда это не так, исследование линеаризованной задачи часто
является первым шагом при изучении соответствия движений не-
нелинейной системы и ее линейной модели.
§ 22. Линеаризация
Здесь дано определение малых колебаний.
А. Положения равновесия.
Определение. Точка эс0 называется положением равно-
равновесия системы
= /(*), ^R",f A)
если х (t) = зс0 есть решение этой системы. Иными словами т
/ (хо)= 0, т. е. в точке х0 векторное поле / (ж) обращается в нуль.
Пример. Рассмотрим натуральную динамическую систему
с функцией ЛагранжаХ(q, q) = Т — U,T = — \ ai5 (q) с1гсх5 > О,
U = U (q)
ff fa &) B)
Уравнение Лагранжа можно записать в виде системы 2п урав-
уравнений первого порядка вида A). Постараемся найти положения
равновесия.
Теорема. Точка q = q0, q = q0 тогда и только тогда
будет положением равновесия системы B), когда q0 = 0, а точ-
J — критическая точка потенциальной энергии, т. е.
= 0. C)
Доказательство. Запишем уравнения Лагранжа
d дТ _ дТ 6U
dt di/ dq dq '

§ 22. ЛИНЕАРИЗАЦИЯ 91
/57* fffl
Из B) видно, что при q = 0 будет -^— = 0, —- = 0. Поэтому
q = Qo е°ть решение в случае C) и только в этом случае, ч. т. д.
Б. Устойчивость положений равновесия. Займемся теперь ис-
исследованием движений при начальных условиях, близких к по-
положению равновесия.
Теорема. Если точка q0 есть строгий локальный минимум
потенциальной энергии U, то положение равновесия q = q0 устой-
устойчиво по Ляпунову.
Доказательство. Пусть U (q0) = h. При достаточно
малом е ^> 0 содержащая q0 связная компонента множества
{q: U (q) <^ h -f- e} будет сколь угодно малой окрестностью точки
q0 (рис. 75). При этом связная ком-
компонента соответствующей области
{р, q: Е (р, ?)< h + е} [р = -Ц- — ^?
импульс, Е = Т -\- U — полная энер-
энергия) в фазовом пространстве р, q будет
сколь угодно малой окрестностью точки ^
Р = 0, q = q0-
Но область {р, q: E^.h + e} инва-
инвариантна относительно фазового потока
по закону сохранения энергии. Значит, Рис- 75- равновесия
при достаточно близких к @, q0) началь-
начальных условиях р @), q @) вся фазовая траектория р (t), q(t)
близка к @, q0), ч. т. д.
Задача. Может ли положение равновесия q = q0, p = 0 быть асимп-
асимптотически устойчивым?
Задача. Докажите, что в аналитической системе с одной степенью
свободы положение равновесия ^о, не являющееся точкой строгого локаль-
локального минимума потенциальной энергии, неустойчиво по Ляпунову. Приве-
Приведите пример бесконечно дифференцируемой системы, где это не так.
Замечание. Кажется правдоподобным, что в аналитиче-
кой системе с п степенями свободы положение равновесия, не яв-
являющееся точкой минимума, неустойчиво, но это не доказано.
В. Линеаризация дифференциального уравнения. Вернемся
теперь к общей системе A). При исследовании решений системы A),
близких к положению равновесия х0, часто пользуются лине-
линеаризацией. Предположим, что х0 — 0 (общий случай приводится
к этому сдвигом системы координат). Тогда первый член ряда Тей-
Тейлора / линейный:
где линейный оператор А в координатах хх, . . ., хп задается мат-
матрицей ац:

92 ГЛ. 5. КОЛЕБАНИЯ
Определение. Переход от системы A) к системе
D>
называется линеаризацией системы A).
Задача. Докажите, что линеаризация — корректно опре-
определенная операция: оператор А не зависит от системы координат.
Преимущество линеаризованной системы состоит в том, что
она линейна и потому немедленно решается:
где ем = Е + At ¦+
Зная решения линеаризованной системы D), можно сказать кое-
что о решениях исходной системы A). При достаточно малых ж
разница между линеаризованной и исходной системами В2 (ж)
мала по сравнению с ас. Поэтому в течение долгого времени реше-
решения у (t), ж (t) обеих систем с начальным условием у @) = ж @) =
= ж0 остаются близкими. Точнее, легко доказывается следующая
Теорема. Для любого Т ^> 0 и для любого е ^> 0 найдется
б ^> 0 такое, что если \ ж- @) | < б, то | ж (t) — у (t) | < еб для всех
t из интервала 0 < / < Т.
Г. Линеаризация лагранжевой системы. Обратимся снова к
лагранжевой системе B) и постараемся ее линеаризовать в окрест-
окрестности положения равновесия q = q0. Для упрощения формул вы-
выберем координаты так, чтобы qb = 0.
Теорема. Чтобы линеаризовать лагранжееу систему B)
в окрестности положения равновесия q = 0, достаточно заменить
кинетическую энергию Т = -^- У o.it{q) d(jee значением при q =
= 0,
а потенциальную энергию U (q) — ее квадратичной частью
ею
_ 1 Г1
в=0
Доказательство. Приведем систему Лагранжа к виду
A), используя канонические переменные р, q:
¦ — _ IE. • — IE- hi \ — г л-TJ
Так как р = q — 0 есть положение равновесия, то разложения
праъых частей в ряд Тейлора в нуле начинаются с линейных по
р, q членов. Так как правые части — частные производные, то
эти линейные члены определяются квадратичными членами Н2
разложения Н (р, q). Но Н2 есть в точности функция Гамильтона
системы с лагранжианом L2 = ТЛ — U2, так как, очевидно, Н2 —

§ 22. ЛИНЕАРИЗАЦИЯ
93
= ^2 (р) + U2 (q). Итак, линеаризованные уравнения движения
суть уравнения движения для описанной в теореме системы с
L2 = Т2 — Uz, ч. т. д.
Прим ер. Рассмотрим систему с одной степенью свободы:
T = ±a(q)i\ U=U(q).
Пусть q — q0 — устойчивое положение равновесия:
дЧТ
аи
= 0,
>0 (рис. 76).
Как мы знаем из фазового портрета, при близких к q = q0J
р = 0 начальных условиях решение периодично, с периодом т,
зависящим, вообще говоря, от начальных условий.
Из предыдущих двух теорем вытекает
Следствие. Период т колебаний вблизи
0,1
положения равновесия q0 стремится при умень-
уменьшении амплитуды колебаний к пределу т0 = —-— ,
а '
1 84J I
-U
а = а (<70). Рис. 76. Линеари-
" "ч~ |«=«о зация
1
Действительно, для линеаризованной системы Т2 — -^-ас^,
U2 = -у Ь<72 (считаем q0 = 0). Решения уравнения Лагранжа
2я
q = —{oog имеют период т0 =
q = cl cos соо? + с2 sin
при любой начальной амплитуде.
Д. Малые колебания.
Определение. Движения в линеаризованной системе
(L2 = Т2 — U2) называются малыми колебаниями *) вблизи по-
положения равновесия q = q0. В одномерной задаче числа т0, соо
называются периодом малых колебаний и
частотой малых колебаний.
Пример. Найти период малых колебаний
бусинки массы 1 на проволоке у = V (х) в поле тя-
тяжести с g = 1 вблизи положения равновесия х = х0
(рис. 77).
Решение. Имеем
Рис. 77. Бусинка .3 нэ
проволоке
*) В случае, коща положение равновесия неустойчиво, мы будем гово-
говорить о «неустойчивых малых колебаниях», хотя движение при этом и не имеет
колебательного характера.

94 ГЛ. 5. КОЛЕБАНИЯ
аи | а*и |
Пусть a;0 — устойчивое положение равновесия: ~д?\ = Ф -g^[ >0.
Тогда частота малых колебаний со определяется формулой
1 1
ибо для линеаризованной системы Г2 = ~2~921 U*— "^^ФкЯ — х — *о)«
Задача. Показать, что не только малые колебания, но и все движе-
движение бусинки в точности эквивалентно движению в некоторой одномерной
системе с функцией Лагранжа
Указание. Принять за q длину вдоль проволоки.
§ 23. Малые колебания
Здесь показано, что лагранжева система, совершающая малые колеба-
колебания, распадается в прямое произведение систем с одной степенью свободы.
А. Задача о паре форм. Рассмотрим подробнее задачу о малых
колебаниях. Иными словами, рассмотрим систему, у которой ки-
кинетическая и потенциальная энергия — квадратичные формы
T = ±(Aq,q), U = ~(Bq,q), q<=TC, ffER". A)
Кинетическая энергия — положительно определенная форма.
Чтобы проинтегрировать уравнения Лагранжа, выберем разум-
разумным образом координаты.
Как известно из линейной алгебры, пару квадратичных форм
(Aq, q), (Bq, q), первая из которых положительно определена,
можно привести к главным осям единой линейной заменой коорди-
координат *):
Q = Cq, Q - (Qx , Qn).
При этом координаты Q можно выбрать так, что форма (Aq, q)
приведется к сумме квадратов (Q, Q). Пусть Q — такие координа-
координаты; тогда, как так Q = Cq, имеем
Числа Яг называются собственными числами формы В относитель-
относительно А.
*) Если угодно, можно ввести евклидову структуру, приняв первую
форму за скалярный квадрат, и затем ортогональным в смысле этой евкли-
евклидовой структуры преобразованием привести вторую форму к главным осям.

§ 23. МАЛЫЕ КОЛЕБАНИЯ 95
Задача. Докажите, что собственные числа В относитель-
относительно А удовлетворяют характеристическому уравнению
det | В — Ы | = 0, C)
все корни которого, таким образом, вещественны (матрицы А и В
симметричны, А ^> 0).
Б. Собственные колебания. В координатах Q система Лагран-
жа распадается на п независимых уравнений
Qi = —hQt- D)
Итак, доказана
Теорема. Система, совершающая малые колебания, есть
прямое произведение п одномерных систем, совершающих малые
колебания.
Для каждой одномерной системы могут представиться три слу-
случая:
Случай 1. Я = со2 ^> 0; решение Q = С1 cos a>t -J- C2 sin Ш
(колебания).
С л у ч а й 2. Я= 0; решение Q = Сг + C2t (безразличное рав-
равновесие).
Случай. 3. X = —F < 0; решение Q = Сх ch kt + C2 sh kt
(неустойчивость).
Следствие. Пусть одно из собственных чисел C) поло-
положительно: X = о2 ^> 0. Тогда система A) _
может совершать периодическое колебание вида *
q (t) = (Сх cos at + С2 sin at) g, E)
где | — соответствующий Х собственный век-
вектор (рис. 78):
Это колебание — произведение одномерно- Рис-
го движения Q^ = Сг cos tuff -f- C2 sin tOjf и
тривиальных движений Q} = 0 (j Ф i).
Определение. Периодическое движение E) называется
собственным колебанием системы A), а число со называется собст-
собственной частотой.
Замечание. Собственные колебания и частоты называют
также главными или нормальными. Неположительным Я также
соответствуют собственные векторы; соответствующие движения
Для краткости мы тоже будем называть «собственными колебания-
колебаниями», хотя они и не периодичны; соответствующие «собственные
частоты» мнимые.
Задача. Доказать, что число линейно независимых настоя-
Щих собственных колебаний равно положительному индексу инер-
потенциальной энергии -^-{Bq, q).
Теперь результат можно сформулировать так:

96 ГЛ. 5. КОЛЕБАНИЯ
Теорема. Система A) имеет п собственных колебаний,
направления которых попарно ортогональны в смысле скалярного
произведения, заданного кинетической энергией Т.
Действительно, система координат Q в силу B) ортогональна
в смысле скалярного квадрата (Ад, д).
В. Разложение по собственным колебаниям. Из доказанной
теоремы вытекает
Следствие. Всякое малое колебание есть сумма собствен-
собственных колебаний.
Сумма собственных колебаний, вообще говоря, не периодична
(вспомним фигуры Лиссажу).
Для разложения движения в сумму собственных колебаний
достаточно спроектировать начальные условия д, д на собственные
направления |г- и решить соответствующие одномерные задачи D).
Итак, уравнения Лагранжа для системы A) можно решать сле-
следующим образом. Вначале ищем собственные колебания в виде
д = еш%. Подставляя это в уравнения Лагранжа
находим
Из характеристического уравнения C) 'находим п собственных
чисел Я^= g>V Им соответствуют п попарно ортогональных собст-
собственных векторов |jf. Общее решение в случае Я ^ О имеет вид
Jr=l
Замечание. Этот результат справедлив и тогда, когда сре-
среди собственных чисел К есть кратные.
Таким образом, в лагранжевой системе, в отличие от общей
системы линейных дифференциальных уравнений, резонансные
'//////////////////, члены вида t sin mt и т. п. не возникают
к к" г даже в случае кратных собственных чисел.
*' ¦ 7\ г- Примеры.
Пример 1. Рассмотрим систему из двух оди-
одинаковых математических маятников длин 1х = 1г = \,
масс т1 = т2 = 1 в поле тяготения с g = 1.
Пусть маятники соединены невесомой пружиной,
Рис. 79. Связанные оди- длина которой равна расстоянию между точками
наковые маятники подвеса (рис. 79). Обозначим через qlt q2 углы откло-
отклонения маятников. Тогда для малых колебаний Т = -тг- Gj+ 9^' U ^
= -g- (9J + 92 + о Ci — ЗаJ), где -g~ (gi— даJ — потенциальная энергия упру-
упругости пружины. Положим
п gi+ дг п gi — ga
VI = г= V =

§ 23. МАЛЫЕ КОЛЕБАНИЯ
Тогда
9i =
92 =
и обе формы приведены к главным осям:
где а^ = 1, о>2 = jAl
дующие (рис. 81):
1) Q2 = 0, i.e.
Яг
+ 2а (рис. 80). Итак, два собственных колебания сле-
слеg1 = g2: оба маятника движутся игефазно с прежней
частотой 1, пружина не работает,
2) Qx = 0, т. е. 9i = —9г: маятники дви-
/Q1 жутся в протпвофазе с увеличившейся бла-
благодаря действию пружины частотой со2 > 1.
'////////////////////А '///////////////////Л
\ffTZa.
Рис. 80. Конфигурацион-
Конфигурационное пространство связан-
связанных маятников
Рис. 81. Собственные колебания связанных
маятников
Пусть теперь пружина очень слаба: а <^ 1. Тогда появляется интересный
эффект перекачки энергии.
Пример 2. Пусть в начальный момент маятники покоятся, и одному
из них сообщена скорость ii^ = v. Показать, что через некоторое время Т
первый маятник будет почти неподвижен, а вся энергия перейдет второму.
Из начальных условий следует Q± @) = Q2 @) = 0. Поэтому Q± =
— ct sin t, Q2 = c2 sin Ш, со = |Al + 2a я1+а (й<^1). Ho Oi @) =
V V V
I = ~f~. Поэтому cx = —7=-, c2 = j=-, и наше решение имеет вид
g2
1 \
п ( + — sin cot I,
со /
= -|-(sin(- —sinarf),
, пренебрегая слагаемым v l\ — — j sin tot,
или
льда вместе с a
v
Qi ж -«j" (sin t -f- sin let) = v cos et sin cu'i,
v
q2 ~ -«r- (sin I — sin cot) = — v cos co't sin e(,
со — 1 a o)+1
Л.
Рис. 82. Биения: траек-
траектория в конфигурацион-
конфигурационном пространстве
a
Величина е ~ -тг мала вместе с а, поэтому дх испытывает колебания частоты
со' ~ 1 с медленно меняющейся амплитудой i;cos et (рис. 82).

98
ГЛ. 5. КОЛЕБАНИЯ
Через время Т = — ж — будет колебаться практически один второй
маятник, через 2Г — опять один первый и т. д. («биения») (рис. 83).
ч,
Рис. 83. Биения
г™
Рис. 84. Связанные
маятники
2.
Рис. 85. Потенциальная
внсргия сильно связан-
связанных маятников
Рис. 86. Зависимость
собственных частот от
жесткости пружины
Рис. 87. Предельный слу-
случай маятников, связан-
связанных бесконечно жесткой
пружиной
Пример 3. Исследовать собственные колебания двух разных
ков (тг ф щ, h Фк,1?= »). соединенных пружиной с энергией ^а (ft
(рис. 84). Как ведут себя собственные частоты при а -. О и при а
Имеем
маятни-
маятниU = mih -j- + m2l2 ~y + ~2 («i ~ '¦
Поэтому (рис. 85)
пЛ °
О шЛ
и характеристическое уравнение имеет вид
#-а— 1
det IJ5 — X-4[ = i
— а
— а
= 0,
или
— (Ьо + bi«)^ + (со

§ 24. О ПОВЕДЕНИИ СОБСТВЕННЫХ ЧАСТОТ 99
где
Ьо =
с0 = m1m2l1h^ ci =
Это — уравнение гиперболы на плоскости а. Я, (рис. 86). При а —> О
слабая пружина) частоты стремятся К частотам свободных маятников (со^ 2 =
= 1712I ПРИ а ~* °° (очень сильная пружина) одна из частот стремится к оо,
а вторая — к собственной частоте со^ маятника из двух масс на одном стерж-
стержне (рис. 87):
Задача. Исследовать собственные колебания плоского двойного маят-
маятника (рис. 88).
Задача. Найти вид траектории малых колебаний материальной точки
на плоскости, находящейся в центре правильного треугольника и соединен-
соединенной одинаковыми пружинами с вершинами (рис. 89).
'////////////////Л
Рис. 88. Двойной ма- Рис. 89. Сиситема с бесконечным множе-
ятник ством собственных колебаний
Решение. При повороте па 120° система переходит в себя. Следо-
Следовательно, все направления собственные, а обе собственные частоты одинако-
одинаковы: U = -tj-со2(я2 + у2). Значит, траектории—эллипсы (см. рис.20).
§ 24. О поведении собственных частот
Здесь доказаны теоремы Редея — Куранта — Фишера о поведении соб-
собственных частот системы при увеличении жесткости и при наложении связи.
А. Поведение собственных частот при изменении жесткости.
Рассмотрим совершающую малые колебания систему с кинети-
кинетической и потенциальной энергиями
Т =^-(Aq,q)>0, U = -\- (Bq, q) > 0 для всех q, q ф 0.
О п р е д е-'л е н и е. Система с такой же кинетической энер-
энергией и потенциальной энергией U' называется более жесткой,
если
1 1
V = -у (B'q, q) > -у (Bq, q) = U для всех q.

100 ГЛ. 5. КОЛЕБАНИЯ
Мы хотим выяснить, как изменятся собственные частоты при уве-
увеличении жесткости системы.
Задача. Рассмотрите одномерный случай.
Теорема 1. При увеличении жесткости все собственные
частоты увеличиваются, т. е. если щ <; со2 ^ . . . <С соп — соб-
собственные частоты менее жесткой системы, a coi <^ щ ^ . . . ^
<С а>п — более жесткой, то со, <; щ; . . .; соп <; con-
Эта теорема имеет простой геометрический смысл. Не нарушая
общности, можно считать, что А = Е, т. е. что мы рассматри-
рассматриваем евклидову структуру, заданную кинетической энергией
Т = -у (</, q). Каждой системе сопоставим эллипсоид: Э: {Вд, д)
¦-= 1, Э': (В'д, д) = 1. Очевидна
Лемма 1. Если система U' жестче системы U, то соответ-
соответствующий ей эллипсоид Э' лежит внутри Э.
Столь же очевидна
Лемма 2. Главные полуоси эллипсоида обратпы собственным
частотам сог:
1
Поэтому теорема 1 эквивалентна сле-
следующему геометрическому утверждению
Рис. 90. Полуоси внутрен- (рИС. 90).
него эллипсоида меньше Теорема 2. Если эллипсоид Э с
полуосями аг ;> с2 > . . . ^ ап содержит
эллипсоид Э' с полуосями а[ ^ а^ ^ . . . ^> а'п с тем же цент-
центром, то полуоси внутреннего эллипсоида меньше:
°1 > <h.i «2 > «2. • • -1 ап > <С-
Пример. При увеличении жесткости а. пружины, соединяющей
маятники примера 3 § 23 потенциальная энергия растет, и по теореме 1 соб-
dco.
ственные частоты растут: — -> о
Рассмотрим теперь случай, когда жесткость пружины стремится к бес-
бесконечности: а —* оо. Тогда в пределе маятники жестко связаны и получается
система с одной степенью свободы; предельная собственная частота — <s>x <
Б. Поведение собственных частот при наложении связи. Вер-
Вернемся к общей системе с п степенями свободы, и пусть
1 1
Т = ~y {Q, q), U = ~y (Bg, g), q €E Rn — кинетическая и потен-
потенциальная энергия системы, совершающей малые колебания.
Пусть R11 CI Rn — п — 1-мерное подпространство в R"
(рис. 91). Рассмотрим систему с п — 1 степенями свободы (g e
€= R71), у которой кинетическая и потенциальная энергии равны

§ 24. О ПОВЕДЕНИИ СОБСТВЕННЫХ ЧАСТОТ
101
ограничениям Т и U на Rnl. Говорят, что эта система получена
из исходной наложением линейной связи.
Пусть исходная система имела п собственных частот щ <^
<; (о2 <^ - • • ^ wn, а система со связью— п—1
собственную частоту
0};^ ^^ Ш2 ^^ ... ^^ @ji_j«
Т е о р е м а 3. Собственные частоты си
стемы со связью разделяют собственные час-
частоты исходной системы (рнс. 92):
G>i <; G>i ^ С02 <5 @2 ^ • • • <й Рис. 91. Линейная
В соответствии с леммой 2 эта теорема эквивалентна следующему
геометрическому утверждению.
Теорема 4. Рассмотрим сечение п-мерного эллипсоида
Э = {q- (Bq, Я) = 1} с полуосями
ai ^ аг ^ • • • J3» ап гиперплоскостью
R". Тогда полуоси п — 1-мерного
9 Ф
Ф '" ф
а„
Рис. 92. Разделение частот
Рис. 93. Полуоси сечения раз-
разделяют полуоси эллипсоида
эллипсоида—сечения Э' разделяют полуоси эллипсоида Э (рис. 93):
«1 > «2
G2
«п-1
fln-
В. Экстремальные свойства собственных чисел.
Теорема 5. У любого сечения эллипсоида Э с полуосями
> я2 > . - . > а„ k-мерным подпространством R^ малая полу-
полуmin
а\
ось меньше или равна
(верхняя грань достигается на подпространстве, натянутом ни
полуоси ах ^ а2 ^ . . . 1> а^).
Дока зательство*). Рассмотрим подпространство
R"""*, натянутое на оси ak ^ a%+1 ^ . . . ^ д„. Его размерность
равна п — к + 1. Поэтому оно пересекается с RK. Пусть х — точ-
точка пересечения, лежащая на эллипсоиде Э. Тогда |[ х \\ <; ак, по-
•) Полезно представлять себе случай п = 3, к = 2.

102 ГЛ. 5. КОЛЕБАНИЯ
скольку х 6Е Rn~R+1. Так как || х || не меньше длины малой полу-
полуоси эллипсоида Э (~) К*, последняя не больше аь, ч. т. д.
Доказательство теоремы 2. Меньшая полуось
каждого fc-мерного сечения внутреннего эллипсоида Rk f] Э' не
больше меньшей полуоси Rfc f] Э. По теореме 5
ак = max min ||ac||<^max min ||эс|| = ак, ч. т.д.
Доказательство теоремы 4. Неравенство а\ <^
<I afc следует из теоремы 5, так как при вычислении ак максимум
берется по более широкому множеству. Чтобы доказать неравенст-
неравенство ак ^ ак+1, пересечем R" с любым к + 1 -мерным подпро-
подпространством Rfc+1. Пересечение имеет размерность не меньше к.
Малая полуось эллипсоида Э' (~) RK+1 не меньше малой полуоси
Э П R*+1- По теореме 5
aJc = max min \\х\\^ max min ||эс||>
{r^+Ich"'" «sRIf+1n3'
> max min ||эс|| = ак+1, ч. т. д.
Теоремы 1 и 3 непосредственно вытекают из доказанных.
Задача. Докажите, что если, не меняя потенциальной энер-
энергии системы, увеличить кинетическую (например, сохранив пру-
пружины, увеличить массы), то каждая собственная частота умень-
уменьшится.
Задача. Докажите, что при ортогональном проектировании эллип-
эллипсоида, лежащего в одном подпространстве евклидова пространства, на дру-
другое подпространство все его полуоси уменьшаются.
Задача. Пусть квадратичная форма А (е) на евклидовом пространстве
Rn непрерывно дифференцируемо зависит от параметра е. Покажите, что
каждое собственное число дифференцируемо зависит от е, и найдите произ-
производные.
Ответ. Пусть Я.х, . . ., Я*—собственные числа А @). Каждому собствен-
собственному числу Xi кратности Vj отвечает подпространство R *. Производные
собственных чисел А (е) в 0 равны собственным числам сужений формы
08 |е=о
В частности, если все собственные числа А @) простые, то их производ-
производные равны диагональным элементам матрицы В в собственном базисе А @).
Из утверждения этой задачи следует, что при увеличении формы ее соб-
собственные числа растут. Мы получаем, таким образом, новое доказательство
теорем 1 и 2.
Задача. Как меняется высота звучания колокола при появлении
трещины?
§ 25. Параметрический резонанс
Если параметры системы периодически меняются со временем, то поло-
положение равновесия может сделаться неустойчивым, даже если оно и устой-
устойчиво при каждом фиксированном значении параметра. Благодаря такой неус-
неустойчивости можно раскачиваться на качелях.

5 25. ПАРАМЕТРИЧЕСКИЙ РЕЗОНАНС
103
А. Динамические системы, параметры которых меняются со
временем периодически.
Пример 1. Качели, у которых длина эквивалентного мате-
математического маятника I (t) меняется со временем периодически:
I (t + Т) = I (t) (рис. 94).
Пример 2. Маятник в поле с периодически меняющейся си-
силой тяжести (например Луна) описывается
уравнением Хилла
q = — со2 (t) q, со (t + T) = <а (t). A)
Пример 3. Маятник с периодически вер-
вертикально колеблющейся точкой подвеса также У
описывается уравнением вида A).
Для систем с периодически меняющимися
параметрами правые части уравнений движения —
периодические функции t. Уравнения движения
можно записать в виде системы обыкновенных дифференциаль-
дифференциальных уравнений первого порядка
x = f{x,t), f (x, t + Т) = / (х, t), x^Rn, B)
с периодическими правыми частями. Например, уравнение A)
можно записать в виде системы
Рис. 94. Качели
L2 — ш Х11 1
C)
Б. Отображение за период. Напомню общие свойства систем B).
Обозначим через gf: Rn -*¦ Rn отображение, переводящее х GE
€= Rn в значение в момент t g*x = <p (t) редпения <р системы B) с
начальным условием <р @) = ж (рис. 95).
Отображения gf не образуют группы:
вообще говоря,
Задача. Докажите, что {g1} груп-
группа тогда и только тогда, когда правые п - ~.
части f не зависят от t.
Задача. Докажите, что если Т — Рис. 95. отображение на
период f, mo gT+s = gs-gT и, в частно- псриод
emu, gnT = (gT)n, так что отображения gnT образуют группу
(п — целые).
Отображение gT: Rn -> Rn играет важную роль в дальнейшем;
мы назовем его отображением за период и обозначим через
А : Rn-* Rn, Ax @) = ж (Т).

104
ГЛ. 5. КОЛЕБАНИЯ.
Приме р. Для систем
Г ±х = Х2, f*l = XU
1*4 = Х\, \ #2 = — Х2,
которые можно считать периодическими с любым периодом Т, отображение А
есть поворот и гиперболический поворот (рис. 96).
Рис. 96. Поворот и гиперболический поворот
Теорема. 1) Точка х0 есть неподвижная точка отображе-
отображения А (Ах0 = х0) тогда и только тогда, когда решение с началь-
начальным условием х @) = ж0 периодическое с периодом Т.
2) Периодическое решение х (t) устойчиво по Ляпунову (асимп-
(асимптотически устойчиво) тогда и только тогда, когда неподвижная
точка х0 отображения А устойчива по Ляпунову (асимптотиче-
(асимптотически устойчива) *).
3) Если система B) линейна, т. е. f (x, t) = / (t) x — линейная
функция х, то отображение А линейно.
4) Если система B) гамилътонова, то отображение А сохра-
сохраняет объем: det А = 1.
Доказательство. Утверждения 1) и 2) вытекают из
соотношения gT+s = g*A. Утверждение 3) вытекает из того, что
сумма решений линейной системы есть снова решение. Утвержде-
Утверждение D) вытекает из теоремы Лиувилля.
Применим доказанную теорему к отображению А фазовой
плоскости {(#!, #г)}> на себя, соответствующему уравнению A) и
системе C). Так как система C) линейна и гамильтонова
( Н =
X2
со2
получаем
Следствие. Отображение А линейно и сохраняет площа-
площади (det A =1). Для устойчивости нулевого решения уравнения A)
необходима и достаточна устойчивость отображения А.
Задача. Доказать, что поворот плоскости — устойчивое отображе-
отображение, а гиперболический поворот — неустойчивое.
*) Неподвижная точка ж0 отображения А устойчива по Ляпунову (соот-
(соответственно асимптотически устойчива), если Ve ~^> 0, 36 ~^> 0, так что из
\зс —• ж0 | < 6 вытекает( | Апх — Апж0 | •< е для всех 0 < п < со сразу
(соответственно Апх — Апя>0 —» 0 при п —* со).

§ 25. ПАРАМЕТРИЧЕСКИЙ РЕЗОНАНС 105
В. Линейные отображения плоскости на себя, сохраняющие
площадь.
Теорема. Пусть А — матрица сохраняющего площадь ли-
линейного отображения плоскости на себя (det A = 1). Тогда отоб-
отображение А устойчиво, если | tr A | < 2, и неустойчиво, если
| tr А | > 2 (tr А = ап + С22).
Доказательство. Пусть А17 Аг — собственные числа А.
Они удовлетворяют характеристическому уравнению Я2 — tr ЛЯ -f*
-{- 1 = 0 с вещественными коэффициентами Ах + А2 = tr Af
^i-^2 = det A = 1.
Корни А2, Я2 этого вещественного квадратного уравнения ве-
вещественны при | tr А | ^> 2 и комплексно-сопряжены при
| tr А |< 2.
В первом случае одно из собственных чисел больше, а другое
меньше единицы по модулю; отображение А есть гиперболический
поворот и неустойчиво (рис. 97).
Во втором случае собственные
числа лежат на единичной окружно-
окружности (рис. 97):
j = Aj" А2 == Aj • Aj == [ Aj I .
Отображение А эквивалентно поворо- Рис- 97- Со6 ж|НияЫлчисла отобра"
ту на угол а (где Аь2 = е±га), т. е.
приводится к повороту соответствующим выбором координат
на плоскости. Поэтому оно устойчиво, ч. т. д.
Таким образом, весь вопрос об устойчивости нулевого реше-
решения уравнения вида A) свелся к вычислению следа матрицы А*
К сожалению, вычислить этот след явно удается лишь в специаль-
специальных случаях. Его всегда можно найти приближенно, численно ин-
интегрируя на отрезке 0 <; t <I T. В важном случае, когда со (?)
близка к постоянной, помогают простые общие соображения.
Г. Сильная устойчивость.
Определение. Нулевое решение гамильтоновой ли-
линейной системы сильно устойчиво, если оно устойчиво, и у всякой
достаточно близкой линейной гамильтоновой системы нулевое ре-
решение тоже устойчиво *).
Из предыдущих двух теорем вытекает
Следствие. Если | tr A | < 2, то нулевое решение силь-
сильно устойчиво.
Ибо если | tr А | < 2, то для отображения А', соответствую-
соответствующего достаточно близкой системе, тоже выполнено условие
I tr А' |< 2, ч. т. д.
•) Расстояние между линейными системами с периодическими коэф-
коэффициентами * = B-l (t) х, & =В2 (t) х определяется как максимум расстояния
между операторами Вх (t) и В2 (t) по (.

106
ГЛ. 5. КОЛЕБАНИЯ
Применим это к системе с почти постоянными (мало меняю-
меняющимися) коэффициентами. Рассмотрим, например, уравнение
х = -о2 A + га (t)) х, г < 1,
D)
где a (t + 2л) = a (t), например, a (t) = cos t (рис. 98). (Маятник,
частота которого колеблется около со с малой амплитудой и с перио-
периодом 2л.) *)
Каждую систему D) будем изображать точкой на плоскости
параметров е, а ]> 0. Очевидно, устойчивые системы с | tr A | < 2
Рис. 98. Мгновенная частота
как функция времени
Рис. 99. Зоны параметрического резо-
резонанса
образуют на плоскости (а, г) открытое множество, так же как и
неустойчивые системы с | tr A | ^> 2 (рис. 99).
Граница устойчивости дается уравнением | tr A \ = 2.
Теорема. Все точки оси а, исключая целые и полуцелые
точки а = к/2, к = 0, 1, 2, . . ., соответствуют сильно устой-
устойчивым системам D).
Таким образом, множество неустойчивых систем может подхо-
подходить к оси а только в точках а = к/2. Иными словами, раскачать
качели малым периодическим изменением длины можно лишь в
том случае, когда один период изменения длины близок к целому
числу полупериодов собственных колебаний,— результат, всем из-
известный из эксперимента.
Доказательство сформулированной теоремы основано на том,
что при г = 0 уравнение D) имеет постоянные коэффициенты и
явно решается
Задача. Вычислить для системы D) с е = 0 матрицу преоб-
преобразования А за период Т ~ 2п в базисе х, х.
Решение. Общее решение: х = сг cos at + c2 sin at.
Частное решение с начальным условием ж = 1, ж = 0: ж = cos cot,
х = — a sin at. Частное решение с начальным условием х = О,
х = 1: х = — sin at, t = cos (at.
Ответ. А =
cos 2яа> —— sin 2л<о
— a sin 2л<о
*) В случае a (t) = cos t уравнение D) называется уравнением Матье.

§ 25. ПАРАМЕТРИЧЕСКИЙ РЕЗОНАНС 107
Поэтому
| tr А | = | 2 cos 2сол | < 2,
если со Ф к/2, к = 0, 1, . . ., и теорема вытекает из предыдущего
следствия.
Более внимательный анализ *) показывает, что вообще говоря,
(и при a (t) = cos t) вблизи точек со = к/2, к = 1, 2, . . ., область
неустойчивости (заштрихованная на рис. 99) действительно под-
подходит к оси со.
Таким образом, при со;^ к/2, к =1,2, . . ., нижнее положение
равновесия идеализированных качелей D) неустойчиво и они рас-
раскачиваются при сколь угодно малом периодическом изменении
длины. Это явление называется параметрическим резонансом.
Характерной особенностью параметрического резонанса являет-
является то, что он сильнее всего проявляется в случае, когда частота
изменения параметров v (в уравнении D) v = 1) вдвое больше
собственной частоты со.
Замечание. Теоретически параметрический резонанс
наблюдается при бесконечном наборе соотношений ш/v ^t /c/2,
к = 1, 2, ... Практически наблюдаемы обычно лишь случаи,
когда к невелико (к = 1, 2, реже 3). Дело в том, что
а) При больших к область неустойчивости подходит к оси со
узким языком и для резонансной частоты « получаются очень
жесткие пределы (—ек для a (t) = cos t; если а — тригонометри-
тригонометрический полином степени d, то •—ет, где т = —[—k/d] — наи-
наименьшее целое число, не меньшее kid; если а в D) — аналитичес-
аналитическая функция общего положения, то ширина к-й резонансной об-
области порядка ев*, где | в | < 1. См., например: Арнольд В. И.
Замечания о теории возмущений для задач
типа Матье // УМН.— 1983.— Т. 38, № 4.
~ С. 89—203).
б) Сама неустойчивость слабо выражена
при больших к, так как | tr A \ — 2 неве-
невелик и собственные числа близки к единице
при больших к.
в) Сколь угодно малое трение приводит
к тому, что для возникновения параметри- Рнс 100 Влшшве тре_
ческого резонанса имеется минимальное ния на параметрический
значение амплитуды ек (при меньших е резонанс
колебания затухают). С ростом к ек быстро растет (рис. 100).
Заметим также, что для уравнений D) в неустойчивом случае
величина х растет неограниченно.
В реальных системах колебания достигают лишь конечной амп-
амплитуды, так как при больших х само линеаризованное уравнение
D) теряет силу и нужно учитывать нелинейные эффекты.
*) См., например, разобранную ниже задачу.

108
ГЛ. 5. КОЛЕБАНИЯ
Задача. Найти вид областей устойчивости на плоскости е, to для
системы, описываемой уравнением
где
=/A).
Решение. Из решения предыдущей задачи следует, что Л
. = cos ящк.,
Поэтому граница зоны устойчивости имеет уравнение
E)
Так как е <^ 1, имеем -^- =
(О — 8
^- Введем обозначение
2е2
Тогда, как легко сосчитать, Д = ~^г~+ ® (е*) «^ *• Пользуясь соотношениями
2схсг = cos 2яе -}- cos 2я<», 2sts2 = cos 2яе—
— cos 2ясо, перепишем уравнение E) в
виде
— Д cos 2яе + B 4- A) cos 2яю = ±2,
идя
cos 2лю
cos 2лсо =
Рис. 101. Зоны параметрическо-
параметрического резонанса для / = <а ± е
2 + А
- 2 -f- Д cos 2ле
2 + А
В первом случае cos 2яа> ss 1. Поэтому положим
<а — к -\- а, | а | <^ 1; cos 2жо = cos 2яв = 1 — 2п2а2 + О (а4).
Д
Перепишем уравнение FХ) в виде cos 2гвд = 1 — 2 4- А ^ — cos 2пе)
или 2я2а2 -f О (а4) = Дя%2 + О (е4).
2s2
Подставляя значение Д = -^г + О (е4), находим
а = ^Ь ~zz~ ~Ь ° (е2)» т- е- t° = '':i:~fc2" + ° (е2))-
Аналогично решается уравнение F2); в результате получаем
, 1 е
<o-ft+ 2 ±-
Итак, ответ имеет вид, изображенный на ряс. 101.

§ 25. ПАРАМЕТРИЧЕСКИЙ РЕЗОНАНС
109
Д. Устойчивость перевернутого маятника с вертикально колеб-
колеблющейся точкой подвеса.
Задача. Может ли верхнее, обычно неустойчивое, положение
равновесия маятника стать устойчивым, если точка подвеса колеб-
колеблется в вертикальном направлении (рис. 102)?
Пусть длина маятника I, амплитуда колебаний точки подвеса
а<^ I, период колебаний точки подвеса
2т, причем в течение каждого полуперио-
полупериода ускорение точки подвеса постоянно
и равно ±с (тогда с = 8а/т2). Оказы-
вается, при достаточно быстрых коле-
баниях подвеса (т <^ 1) верхнее поло-
положение равновесия становится устойчи-
вым.
Решение. Уравнение движения мож-
можно записать в виде х = (со2 + d?) х (знак ме-
няется через время т), где со2 = gll, & = с/1. рис перевернутый ма-
Если колебания подвеса достаточно быстры, ятник с колеблющейся точ-
парабола
X It A
щ
кой подвеса
C
)
Аналогично предыдущей задаче, А = A2At, где
ch kx -^- sh kx
k sh kx ch kx
cos Qr -Q- sin Qt
— Q sin Qt cos Qt
fc2 = d? + <o2, Q2 = d2 — со2.
Условие устойчивости | tr A | <С 2 имеет поэтому вид
2 ch kx cos сот -f- I-p -^
sh kx sin сот
G)
Покажем, что условие это выполнено при достаточно быстрых колеба-
колебаниях точки подвеса, т. е. когда с ^> g. Введем безразмерные переменные
Тогда
kx = 2
+ u2, Qt = 2
1 —
Поэтому при малых е, ц справедливы разложения с ошибкой о (е 4 + [г4)
2 8
4+..., cosQt= I 4гA 2)+
ft~)sh kz sin Gt; =

110 ГЛ. 5. КОЛЕБАНИЯ
Итак, условие устойчивости G) принимает вид
4
2 A — 16 е4 + 4ре* + 8eV + • • •) + 16е2ца < 2,
2 е
т. е. пренебрегая малыми высшего порядка, -n- 16e4 ^ 32ц.2еа или и.<-т=
или еще — ¦< -gf. Это условие можно переписать в виде
N > Vi а -г ~ °'3w 4" (Кж ~ °-
где iV = -я— — число колебаний точки подвеса в единицу времени. Напри-
Например, если длина маятника I = 20 см, а амплитуда колебаний точки подвеса
о=1 см, то
¦ 2Q " •
/9Ш
¦ 2Q " • 20 ;=: 43 (колебаний в секунду).
Например, верхнее положение устойчиво, если число колебаний подвеса
в секунду больше 50.

ГЛАВА 6
ТВЕРДОЕ ТЕЛО
В этой главе подробно исследуется несколько весьма частных
механических задач. Эти задачи включаются в курсы классичес-
классической механики по традиции, основанной на том, что они решены
Эйлером и Лагранжем, а также на том обстоятельстве, что мы
живем в трехмерном евклидовом пространстве и большинство ме-
механических систем с конечным числом степеней свободы, с которы-
которыми приходится встречаться, состоит из твердых тел.
§ 26. Движение в подвижной системе координат
В этом параграфе определяется угловая скорость.
А. Подвижные системы координат. Рассмотрим лагранжеву
систему, которая в координатах q, t описывается функцией Лаг-
ранжа L (q, q, t). Часто бывает полезно перейти к подвижной сис-
системе координат Q = Q (q, t).
Чтобы записать уравнения движения в подвижной системе,
достаточно выразить через новые координаты функцию Лагранжа.
Теорема. Если траектория у: q = ср (t) уравнений Лагран-
Лагранжа —г— —^r- ~ -z— записывается в локальных координатах Q, t (Q =
= Q (Q, t)), в виде у: Q = Ф (t), то функция Ф (t) удовлетворяет
уравнениям Лагранжа -гг—— = -^тг» г^е L' (Q, Q,t) = L (q, q, t):
Доказательство. Траектория у является экстремалью:
6§ Z, (q, q, t) dt = 0. Следовательно, 6§L' (О, Q, t) dt = 0 и Ф (t)
у у
удовлетворяет уравнениям Лагранжа, ч. т. д.
Б. Движения, вращения, поступательные движения. Рассмот-
Рассмотрим, в частности, важный случай, когда q — декартов радиус-век-
радиус-вектор точки относительно инерциальной системы координат к (кото-
(которую мы будем называть неподвижной), a Q — декартов радиус-
вектор той же точки относительно подвижной системы координат К.
Определение. Пусть к, К — ориентированные линей-
линейные евклидовы пространства.
Движением К относительно к называется гладко зависящее
от t отображение
Dt : К -> к,
сохраняющее метрику и ориентацию (рис. 103).

112 ГЛ. 6. ТВЕРДОЕ ТЕЛО
Определение. Движение Dt называется вращением'
если оно переводит начало координат К в начало координат А-,
т. е. если Dt — линейный оператор.
Теорема. Всякое движение Dt однозначно разлагается в про-
произведение вращения Bt: К —> к и сдвига С{. к —> к:
Dt — CtBt,
где Ctq = q + г (t) (q, r ЕЕ к).
Доказательство. Положим г (t) = DtO, Bt = CtXDt.
Тогда BtO = О, ч. т. д.
О п р е'д е л е н и е. Движение Dt называется поступатель-
поступательным, если соответствующее ему отображение Bt: К —> к от t не
зависит: В, = Во = В, DtQ = BQ + г (t).
Рис. 103. Движение D. разлага- Рис. 104. Радиус-вектор точки от-
ется в произведение вращения носительно неподвижной (в) и под-
В и сдвига С вижной (Q) системы координат
Мы будем называть к неподвижной системой координат, К —
подвижной, q (t) ?E k — радиусом-вектором движущейся точки от-
относительно неподвижной системы; Q (t) называется радиусом-век-
радиусом-вектором точки относительно подвижной системы, если (рис. 104)
q (t) = DtQ (t) = BtQ (t) + r (t). A)
Предостережение. Вектор BtQ (t) e k не следует
путать с Q (t) ЕЕ К — они лежат в разных пространствах!
В. Сложение скоростей. Выразим теперь «абсолютную скорость»
q через относительное движение Q (t) и движение системы коор-
координат Dt. Из формулы A) находим, дифференцируя по t, формулу
сложения скоростей
q^BQ + BQ + r. B)
Чтобы выяснить смысл входящих в B) трех слагаемых, рассмот-
рассмотрим вначале частные случаи.
Случай поступательного движения (В = 0). В этом случае
уравнение B) дает q = BQ + >'¦ Иначе говоря, доказана
Теорема. Если подвижная система К движется относи-
относительно к поступательно, то абсолютная скорость равна сумме
относительной скорости и скорости движения системы К:
v = v' + v0, C)

6 26. ДВИЖЕНИЕ В ПОДВИЖНОЙ СИСТЕМЕ КООРДИНАТ ИЗ"'
где
v = q ЕЕ к — абсолютная скорость,
v' = BQ ЕЕ к — относительная скорость (не путать с Q ЕЕ К\),
и, = г Е /t — скорость движения подвижной системы коорди-
координат.
Г. Угловая скорость. В случае вращения системы К связь
между относительной и абсолютной скоростями не столь проста.
Рассмотрим сначала случай, когда наша точка покоится относи-
относительно К (т. е. Q = 0), а система координат К вращается (т. е.
г = 0). В этом случае движение точки q (t) называет-
называется переносным вращением. 'ы
Пример. Вращение с постоянной угловой /" \
скоростью ю ЕЕ к. Пусть U (t): к-+к— поворот про- V_^_ _^?-*r-
странства к вокруг оси <й на угол | ю | t. Тогда ~f^
В (t) = U (t) В @) называется равномерным врахцени- \Ц
ем К с угловой скоростью ю. _ I
Очевидно, в этом случае скорость переносного
движения точки q дается формулой (рис. 105) Угчовая0с'ко-
ff = l©,ff]. "рость
Вернемся теперь к общему случаю вращения К (г = 0, Q = Э .
Теорема. В каждый момент времени t существует вектор
ft) (t) ЕЕ к, через который переносная скорость выражается по фор-
формуле
Я = К Q], Vff ЕЕ к. D)
Вектор <й называется мгновенной угловой скоростью; очевидно, ов
определен равенством D) однозначно.
Следствие. Пусть твердое тело К вращается вокруг непо-
неподвижной точки О пространства к. Тогда в каждый момент времени
существует мгновенная ось вращения — такая прямая в теле,
проходящая через О, что скорости ее точек в данный момент
раены 0. Скорости остальных точек перпендикулярны этой прямой
и пропорциональны расстоянию до нее.
Мгновенная ось вращения в пространстве к задается своим век-
вектором ю; в К соответствующий вектор обозначается через й =
= В~1еь ЕЕ К; Q называется вектором угловой скорости в теле.
Пример. Угловая скорость Земли направлена от центра к Северно-
2л.
ну полюсу и равна 'зб00-24 rl~'^^" c-1-
Доказательство теоремы. Согласно B) имеем
Поэтому, если мы выразим Q через q, получим q = BB~xq = Aqr
где А = ВВ~1 : к—>- к — линейный оператор из к в к.
Лемма 1. Оператор А — кососимметрический: A' -f А = 0_

114 ГЛ. 6. ТВЕРДОЕ ТЕЛО
Доказательство. Поскольку В : К —>- к — ортого-
ортогональный оператор из одного евклидова пространства в другое,
его сопряженный совпадает с обратным, В' = В'1 : к-*- К. Диф-
Дифференцируя по t соотношение ВВ' = Е, получаем
ВВ' + ВВ' = О, ВВ1 + (ВВ'1)' = 0, ч. т. д.
Лемма 2. Всякий кососимметрический оператор А в трех-
трехмерном ориентированном евклидовом пространстве есть оператор
векторного умножения на фиксированный вектор:
Aq = [<й, q] для всех q ?E R3-
Доказательство. Все кососимметрические операторы
R3 -*- R3 образуют линейное пространство. Размерность его равна 3,
так как кососимметрическая 3x3 матрица определяется тремя
своими наддиагональными элементами.
Оператор векторного умножения на ю линеен и кососиммет-
ричен. Операторы векторного умножения на всевозможные век-
векторы трехмерного пространства ю образуют линейное подпро-
подпространство пространства всех кососимметрических операторов.
Размерность этого подпространства равна 3. Поэтому подпро-
подпространство, образованное векторными умножениями, совпадает с про-
пространством всех кососимметрических операторов, ч. т. д.
Окончание доказательства теоремы. Со-
Согласно леммам 1, 2
q = Aq = Ы, q], ч. т. д.
В декартовых координатах оператор А задается кососиммет-
рической матрицей; обозначим ее элементы через ±<0i,2,3:
10 — й>з fc^ |
Юз 0 — (О! .
— @2 fc>i 0 ||
При таком обозначении элементов вектор о> = ы^ + со2е2 ~^~
+ сй303 будет собственным с собственным значением 0. Применяя
А к вектору q = q^ + §2^2 ~Ь 9зез> получаем непосредственной
выкладкой
Aq = [<й, q].
Д. Переносная скорость. Случай чисто вращательного движе-
движения. Пусть теперь система К вращается (г = 0), а точка в систе-
системе К движется (О Ф 0). Из B) находим (рис. 106).
Иначе говоря, доказана
Теорема. Если подвижная система К вращается относи-
относительно О ЕЕ к, то абсолютная скорость равна сумме относительной

I 27. СИЛЫ ИНЕРЦИИ. СИЛА КОРИОЛИСА 115»
и переносной скоростей вращения:
v = v'+vn,
где
v = qGk — абсолютная скорость, \ E)>
v' == BQ ЕЕ к — относительная скорость,
vn = BQ = [at, q] ЕЕ k — переносная скорость вращения,
Наконец, общий случай можно свести к двум предыдущим,
рассматривая вспомогательную подвижную систему Кг, движу-
движущуюся поступательно относительно к и относительно которой К
движется, вращаясь вокруг О ЕЕ Кг. Можно
также и из формулы B) усмотреть, что
V = V' + Vn + Vo,
где
v = q ЕЕ к — абсолютная скорость,
v' = BQ ?r k — относительная скорость,
vn = BQ == [<й, q — г] ЕЕ к — переносная
скорость вращения, ^ 106 Сложение ск0_„
v0 = г ЕЕ к — скорость движения подвиж- ростей
ной системы координат.
Задача. Покажите, что угловая скорость твердого тела не
зависит от выбора начала координат подвижной системы К в
теле.
Задача. Покажите, что самое общее перемещение твердого
тела есть винтовое перемещение, т. е. произведение поворота на<
угол ф вокруг некоторой оси и сдвига на h вдоль нее.
Задача. На столе лежат часы. Найти угловую скорость часовой
стрелки а) относительно Земли, б) относительно инерциальной системы ко-
координат.
Указание. Если даны три системы координат k, Kx, Kt, то угло-
угловая скорость К$ относительно к равна сумме угловых скоростей Кг относи-
относительно к и Kt относительно Kt. Ибо
§ 27. Силы инерции. Сила Кориолиса
Уравнения движения в неинерциальной системе координат отличаются-
от уравнений движения в инерциальной системе дополнительными слагае-
слагаемыми, называемыми силами инерции. Это позволяет экспериментально обна-
обнаруживать неинерциальность (например, вращение Земли вокруг ее оси).
А. Поступательно движущаяся система координат.
Теорема. В системе координат К, движущейся поступа-
поступательно относительно инерциальной к, движение механических сис-
систем происходит так, как если бы система координат была инер—
Циальной, но на каждую точку массы т действовала дополнитель-
дополнительная «сила инерции» F = —т'г, где г — ускорение системы К.

116
ГЛ. 6. ТВЕРДОЕ ТЕЛО
//|\\
7/////J/1//M//7
Рис. 107. Пере-
грузка
Доказательство. Если Q = д — г (?), то mQ = тд —
— тг. Влияние поступательного движения системы координат
«водится, таким образом, к появлению дополнительного однород-
^_^ ного силового поля — mW, где W — ускорение
начала координат, ч. т. д.
Пример 1. Ракета при старте имеет направлен-
направленное вверх ускорение г (рис. 107). В соответствии с этим
система координат К, связанная с ракетой, не пнерциаль-
на, и наблюдатель, находящийся внутри, может обна-
обнаружить появление силового поля — mW, и измерить си-
лы инерции, например, пружинными весами. В этом
случае сила инерции называется перегрузкой.
Пример 2. При прыжке с вышки прыгун имеет
ускорение д, направленное вниз. В соответствии с этим
сумма сил инерции п веса равна нулю; пружинные весы
показывают, что вес любого предмета равен нулю, поэтому
такое состояние называется невесомостью. Точно так же при свободном бал-
баллистическом полете спутника наблюдается невесомость, так как сила пнер-
ции противоположна силе притяжения Землей.
Пример 3. Если точка подвеса маятника движется с ускорением
W (t), то маятник движется так, как если бы ускорение силы тяжести д
было переменным и равным д — W (t).
Б. Вращающаяся система координат. Пусть Bt: К ->- к — вра-
вращение системы координат А" относительно неподвижной системы
координат к. Будем обозначать через Q (t) e= К радиус-вектор
движущейся точки в подвижной системе координат, а через д (t) =
== BtQ (t) G/t — в неподвижной. Вектор угловой скорости вра-
вращения в подвижной системе координат обозначим, как в § 26. че-
через п.
Предположим, что в системе координат к движение точки д
подчиняется уравнению Ньютона тд = f {g, д).
Теорема. Во вращающейся системе координат движение
происходит так, как если бы на каждую движущуюся точку Q мас-
массы т действовали три дополнительные «силы инерции»:
сила инерции вращения — т [Q, Q],
сила Кориолиса — 2т [Q, Q],
центробежная сила — т [Q, [Q, Q11.
Итак,
= F-m[Q, Q] - 2т[Q, Q]-m[G, [Q, <?]].
Q) = f(BQ,(BQ)).
где
Первая из трех сил инерции наблюдается лишь в случае не-
неравномерного вращения; вторая и третья присутствуют и при рав-
равномерном вращении.
Центробежная сила (рис. 108) направлена всегда от мгновенной
оси вращения Q, и равна по величине | Q |2г, где г — расстояние

§ 27. СИЛЫ ИНЕРЦИИ- СИЛА КОРИОЛИСА 117
до этой оси. Эта сила не зависит от скорости относительного дви-
движения и действует даже на покоящиеся в системе координат К
тела.
Сила Кориолиса зависит от скорости Q- В северном полушарии
Земли она отклоняет всякое движущееся по Зе-
Земле тело вправо, и падающее — на восток.
Доказательство теоремы. За-
Заметим, что для любого вектора X ее К имеем
ВХ = В [Q, X]. Действительно, согласно
§ 2G, ВХ = [о>, ж] = [BQ, ВХ\. Это рав-
равно В [Р., X], так как оператор В сохраняет PJ.'108. Центробеж.
метрику И Ориентацию, а ПОТОМУ И векторное ная сила инерция
произведение.
Из q = BQ заключаем, что q = BQ + BQ = В (Q + [Й, Q\).
Дифференцируя еще раз, находим
4 = B(Q + [Q, Q\) Л- 5@ + |Й, О] + [Q- <?!) =
= В ([Q, (Q + [fi, Q])] + Q + [Q, Q] + [Q. Q]) =
= B(Q+2[Sl,Q] + [fi, [fi, Q]] + [fi, Q\), ч. т. д.
^Мы еще раз воспользовались соотношением ВХ = В Ш, X]; на
этот раз X = Q + [fi, ©].)
Рассмотрим подробнее влияние вращения Земли на лабораторные экспе-
эксперименты. Так как Земля вращается практически равномерно, можно счи-
считать d = 0. Центробежная сила наибольшее значение имеет на экваторе.
Q2P G,3-10-5J.6,4-106 з
где она достигает -¦х g-g ~ "lOOO" веса* Однако в
пределах лаборатории она меняется мало, и потому для ее наблюдения
приходится путешествовать.
В соответствии со сказанным, в пределах лаборатории вращение Земли
проявляется лишь в виде силы Кориолиса: в системе координат Q, связан-
связанной с Землей, с большой точностью
Q +2[Q, Щ
(центробежная сила учтена в д).
Пример 1. Камень брошен (без начальной скорости) в шахту глу-
глубиной 250 м на широте Ленинграда (л = 60^. Насколько он отклонится от
?
вертикали?
Р
Решаем уравнение
Q = 0 + 2 [Q. Q]
последовательными приближениями, учитывая, что fi<ggl. Положим
(рис. 109)
где ?2@) = Q2@) = 0, a Qi =
Для Q2 получим тогда

118
ГЛ. 6. ТВЕРДОЕ ТЕЛО
Отсюда видно, что камень отклоняется на Восток примерно на
2 7
-о- мж4 см.
Задача. Насколько сила Кориолиса отклонит от падения обратно
в жерло пущенный вертикально вверх в Ленинграде снаряд, если он под-
поднялся на 1 км?
Пример 2. Маятник Фуко.
Рассмотрим малые колебания математического маятника с учетом силы
Кориолиса. Пусть оси ех, еу, ez системы координат, связанной с Землей,
направлены: ez — вверх, ех, еу — в гори-
Qi@) oj зонтальной плоскости (рис. 110). В приб-
1 лижении малых колебаний z = 0 (по срав-
Рис. 109. Отклонение
падающего камня си-
силой Кориолиса
Рис. 110. Система координат
для исследования движения
маятника Фуко
нению с ±, у), поэтому горизонтальная составляющая силы Кориолиса
будет 2tnyQzex — 2miilzey. Отсюда получаем уравнения движения
(?= — иРх + 2упг, ._.„..,
1 у' = _ Ы2у _ 2*Q (®z ~\ui Sln *«• гДе *o — широта).
Если положить х -{- iy = w, то ie = i -{- iy, w = ж -f- iy, и два урав-
уравнения сводятся к одному комплексному
Решаем его: w = еи, А,* +
+ со2. Но
о2. Поэтому Р' Q\ + со2 = со + О (Qz), откуда, пре-
пренебрегая й^,
А л; —Шг ± ш,
или, с той же точностью,
Рис. Ш^ ^Раек- При Qz = О получаются обычные гармонические
Т°Р Я Фуко колебания сферического маятника. Мы видим, что влия-
влияние силы Кориолиса приводит к вращению всей карти-
картины с угловой скоростью—Qz, где | Qz \ = | Q | sin Яо.
В частности, если начальные условия соответствуют плоскому движе-
движению (у @) = у @) = 0), то плоскость качаний будет поворачиваться с угло-
угловой скоростью-—ilz относительно земной системы координат (рис. 111).
На полюсе плоскость качаний за сутки совершает один оборот (и не-
неподвижна относительно не вращающейся с Землей системы координат). На
широте Москвы E6°) за сутки плоскость качаний повернется на 0,83 оборо-
оборота, т. е. за час — на 12,5°.

§ 28. ТВЕРДОЕ ТЕЛО 119
Задача. Река течет со скоростью 3 км/ч. При каком радиусе кри-
кривизны излучины сила Кориолиса, происходящая от вращения Земли, боль-
больше центробежной силы, определяемой поворотом реки?
Ответ. Радиус кривизны должен быть не меньше величины порядка
10 км для рек средних широт.
Решение этой задачи «объясняет», почему большие реки Северного полу-
полушария (например, Волга в среднем течении) подмывают в основном правый
берег, в то время как на реках типа Москвы-реки с их крутыми излучинами
малого радиуса кривизны подмывается попеременно то левый, то правый
(внешний по излучине) берег.
§ 28. Твердое тело
В этом параграфе определяются твердое тело и его тензор инерции,
эллипсоид инерции, моменты инерции и оси инерции.
А. Конфигурационное многообразие твердого тела.
Определение. Твердым телом называется система ма-
материальных точек, стесненных голономной связью, выражающейся
в том, что расстояния между точками постоянны:
| щ — Xj | = ru — const. A)
Теорема. Конфигурационное многообразие твердого тела
есть шестимерное многообразие, а именно R3 X SOC) (прямое
произведение трехмерного пространства R3 и е к
группы SOC) его вращений), если только в те-
теле есть три точки не на одной прямой.
Доказательство. Пусть жх, х2 и
жв — три точки тела, не лежащие на прямой. >?""""""""?
Рассмотрим правый ортонормированный репер, /?
у которого первый вектор направлен как х2 — 3
Й
— SCi, а ВТОРОЙ — В СТОРОНУ Х3 В ПЛОСКОСТИ Хх, ^| ^бр
Ж2, &з (РИС. 112). Из УСЛОВИЙ \хг — Xj | = rtj зие твердого тела
(i = 1, 2, 3) следует, что положение всех то-
точек тела однозначно определено положением жх, ас2, х3, последнее
зке задано положением репера. Наконец, пространство реперов
в R3 есть R3 х SOC), так как каждый репер получается из фик-
фиксированного вращением и сдвигом *).
Задача. Найти конфигурационное пространство твердого тела, все
точки которого лежат на прямой.
Ответ: R3 X S2.
Определение. Твердое тело с неподвижной точкой О
есть система материальных точек, стесненных, кроме связей A),
связью хг = 0.
Очевидно, его конфигурационное многообразие — трехмерная
группа вращений SOC).
*) Строго говоря, конфигурационное пространство твердого тела есть
И3 X 0C), a R3 х SOC) — лишь одна из двух связных компонент этого
многообразия, соответствующая определенной ориентации тела.

120 ГЛ. 6. ТВЕРДОЕ ТЕЛО
Б. Законы сохранения. Рассмотрим задачу о движении сво-
свободного твердого тела по инерции, вне силовых полей. Примером
(приближенно) может служить кувыркание космического аппа-
аппарата.
Система допускает все поступательные перемещения: они не
меняют функции Лагранжа. По теореме Нётер существуют три
первых интеграла: три компоненты вектора количества движения.
Или, иначе, доказана
Теорема. При свободном движении твердого тела его
центр инерции движется равномерно и прямолинейно.
Но тогда мы можем рассмотреть инерциальную систему коор-
координат, в которой центр инерции неподвижен. Итак, получено
Следствие. Свободное твердое тело вращается около
центра инерции так, как если бы центр инерции был закреплен
в неподвижной точке О.
Тем самым задача сведена к задаче с тремя степенями свободы
о движении твердого тела вокруг неподвижной точки О. Исследуем
подробнее эту задачу (не обязательно предполагая, что О есть
центр инерции тела).
Функция Лагранжа выдерживает все вращения вокруг точки О.
По теореме Нётер существуют три соответствующих первых
интеграла: три компоненты вектора кинетического момента. Со-
Сохраняется также полная энергия системы Е = Т (она сводится
здесь к кинетической). Итак, доказана
Теорема. В задаче о движении твердого тела вокруг не-
неподвижной точки О при отсутствии внешних сил имеется четыре
первых интеграла: Мх, Му, Mz, E.
Из этой теоремы можно без всяких вычислений получить ка-
качественные выводы о движении.
Положение и скорость тела определяются точкой шестимерного
многообразия Т SO C) — касательного расслоения конфигура-
конфигурационного многообразия SOC). Первые интегралы Мх, Mv, Mz,
Е суть четыре функции на многообразии Т SOC) размерности 6.
Можно проверить, что в общем случае (если тело не обладает
особой симметрией) эти четыре функции независимы. Поэтому
четыре уравнения
Мх = Clt Mv = С2, М2 = С3, Е = С4 > 0
определяют двумерное подмногообразие Fc в шестимерном много-
многообразии 7 50C).
Это многообразие инвариантно: если начальные условия дви-
движения задают точку на многообразии Vc, то во все время движе-
движения точка Т SOC), соответствующая положению и скорости тела,
остается на Vc.
Поэтому многообразие Vc допускает касательное векторное
поле (а именно, поле скоростей движения на Т SOC)); при С4 ^> О
это поле не может иметь особых точек. Далее, легко проверить,

§ 28. ТВЕРДОЕ ТЕЛО
121
что Vc компактно (использовать Е) и ориентируемо (так как
Т SOC) ориентируемо) *).
В топологии доказывается, что все связные ориентируемые
компактные двумерные многообразия суть сферы с п ручками,
п>0 (рис. 113).
Рис. 113. Двумерные контактные связные ориентируемые
многообразия
Из них только тор (п = 1) допускает касательное векторное
поле без особых точек.
Итак, инвариантное многообразие Vc есть двумерный тор
(или несколько торов).
Мы увидим в дальнейшем, что на этом торе можно так выбрать
угловые координаты ц>г, ф2 (mod 2я), что движение изображаю-
изображающей точки по Vc будет задаваться уравнениями
«Pi = Ш1 (с)> Ф2 = G>2 (c)- й>1
Иными словами, вращение твердого тела пред- ^- ~-s.
ставляет собой наложение двух периодических ( *Х**и
движений с разными, вообще говоря, периодами: ~Jq
если частоты щ и а>2 несоизмеримы, то тело никог- л»Ч /
да не возвращается к пройденному состоянию \/
и ш2 зависят от
Рис. 114. Радиус-
вектор, вектор
скорости, угло-
угловая скорость
и кинетический
момент точки те-
тела в пространстве
движения. Величины частот
начальных условий с.
В. Оператор инерции. Перейдем теперь к ко-
количественной теории и введем следующие обоз-
обозначения. Пусть к — неподвижная, К — вращаю-
вращающаяся вместе с телом вокруг точки О система ко-
координат: в ней тело покоится. Каждый вектор в
пространстве К переводится в пространство к оператором В. Соот-
Соответствующие векторы пространств К и к мы будем обозначать
одинаковыми буквами: прописными для К, строчными для к.
Так, например (рис. 114):
*) Легко доказываются, следующие утверждения.
1. Пусть Д. . . .,/t-: M —» R — функции на ориентированном много-
многообразии М. Рассмотрим множество V, заданное уравнениями f1 = c1,...
. . ., //с = c/f. Предположим, что градиенты ft, . . ., fk в каждой точке V
линейно независимы. Тогда У ориентируемо.
2. Прямое произведение ориентируемых многообразий ориентируемо.
3. Касательное расслоение Т SOC) есть прямое произведение R3 X
X SOC).
Многообразие, касательное расслоение которого является прямым про-
произведением, называется параллелизуемым. Группа SOC) (как и всякая груп-
группа Ли) параллелизуема.
4. Параллелизуемое многообразие ориентируемо.
Из 1—4 вытекает ориентируемость SOC), rSOC) и Vc.

122 ГЛ. 6. ТВЕРДОЕ ТЕЛО
д Ez к — радиус-вектор точки в пространстве,
Q Ez К — ее же радиус-вектор в теле, д — BQ.
v = q Ez к — вектор скорости точки в пространстве,
V Ez К — тот же вектор в теле, v = BV,
& Ez к — угловая скорость в пространстве,
Q Ez К — угловая скорость в теле, © = BQ,
т Ez к — кинетический момент в пространстве,
Ш Ez К — кинетический момент в теле, т = ВАГ.
Так как оператор В: К —* к сохраняет метрику и ориентацию,
он сохраняет скалярные и векторные произведения.
По определению угловой скорости (§ 26)
По определению кинетического момента точки массы т отно-
относительно О,
т = [д, mv] = m [q, [ю, д]].
Итак,
ЛГ = то[О,[О, ОН-
Возникает линейный оператор, переводящий Q в Ы:
А: К-> К, AQ = М.
Этот оператор зависит еще от точки тела (Q) и ее массы (т).
Лемма. Оператор А симметрический.
Доказательство. При любых X Ez К, Y Ez К ввиду
соотношения (la, b], с) = ([с, а], Ь) имеем
(АХ, Y) = m([Q, [X, 01], Г) = ш([Г, Q], [X, Q]),
а последнее выражение симметрично относительно X и Y, ч. т. д.
Подставляя вместо 1иГ вектор угловой скорости О и заме-
замечая, что [О, Q]2 = F2 = v2, получаем
Следствие. Кинетическая энергия точки тела есть ква-
квадратичная форма относительно вектора угловой скорости Q, а
именно:
Т
Симметрический оператор А называется оператором (или тен-
тензором) инерции точки Q.
Если тело состоит из многих точек Qt с массами mt, то, сум-
суммируя, получаем:
Теорема. Кинетический момент Ж твердого тела относи-
относительно неподвижной точки О линейно зависит от угловой скорости
Q, т. е. существует линейный оператор А : К —* К, AQ = М.
Оператор А симметричен.

S 28. ТВЕРДОЕ ТЕЛО 123
Кинетическая энергия тела есть квадратичная форма относи-
относительно угловой скорости Q,
Доказательство. По определению, кинетический мо-
момент тела равен сумме моментов его точек:
= AQ, где А =
г i i
Так как оператор инерции каждой точки At по лемме симметри-
симметрический, оператор А также симметрический. Для кинетической
энергии, по определению, получаем
Q) ±(AQQ), ч. т. д.
Г. Оси инерции. Как всякий симметрический оператор, А
имеет три взаимно ортогональных собственных направления.
Пусть elT е2, es?? — их орты, 1Х, /2, /3 — собственные числа.
В базисе et оператор инерции и кинетическая энергия имеют
особенно простой вид:
Мг = hUu
Т =\{ISl\ + I?% + IfL%).
Оси et называются осями инерции тела в точке О.
Конечно, если не все числа /1? /2, /3 различны, то оси инерции
«; определены неоднозначно. Выясним подробнее смысл собствен-
собственных чисел /lt /2, /3.
Теорема. При вращении твердого тела, закрепленного
в точке О, с угловой скоростью Q = Qe (Q = | О |) вокруг оси е
кинетическая энергия равна
Т=~1еп\ где /е=2 mrf,
г i
и Vi означает расстояние i-й точки до оси е (рис. 115).
Доказательство. По определению, Т = -«г 2,m*^'
i
но | Vi | = йгг, поэтому Т = -g- ^ V тр1\ Q2, ч. т. д.
Число /е зависит от направления е оси вращения О в теле.
Определение. 1е называется моментом инерции тела
относительно оси е:
Сравнивая два полученных выражения для Т, получаем

124
ГЛ. 6. ТВЁРДОЕ ТЕЛО
Следствие. Собственные числа 1% оператора инерции А
суть моменты инерции тела относительно осей инерции et.
Д. Эллипсоид инерции. Чтобы изучить зависимость момента
инерции 1е от направления оси е в теле, рассмотрим векторы
е/]А/е, где орт е пробегает единичную сферу.
Рис. 115. Кинетическая энергия
тела, вращающегося вокруг оси
Эллипсоид
инерции
Рис. 116. Эллипсоид
инерции
Теорема. Векторы е!\!Ie образуют эллипсоид в К.
Доказательство. Если Q = el\fIe, то квадратичная
форма Т =-w-(Aii, Q) равна 1/2. Поэтому {Q} есть множество
уровня положительно определенной квадратичной формы, т. е.
эллипсоид, ч. т. д. Можно сказать, что эллипсоид этот составлен
из векторов угловой скорости Q, для которых кинетическая энер-
энергия равна 1/2.
Определение. Эллипсоид {О: (AQ, Q) = 1} называется
эллипсоидом инерции тела в точке О (рис. 116).
В осях инерции е% его уравнение имеет вид
Итак, главные оси эллипсоида инерции направлены по осям инерции,
а их длины обратно пропорциональны \l It.
Замечание. Если тело вытянуто вдоль какой-нибудь
оси, то момент инерции относительно этой оси мал, следовательно,
эллипсоид инерции тоже вытянут вдоль этой оси,
так что эллипсоид инерции повторяет некоторые
черты тела.
Если тело имеет проходящую через О ось сим-
симметрии порядка к (так что оно совмещается с
собой при повороте вокруг нее на 2л/к), то и
эллипсоид инерции имеет такую же симметрию
относительно этой оси. Но у трехосных эллипсои-
эллипсоидов не бывает осей симметрии порядка к ^> 2.
Поэтому всякая ось симметрии тела порядка
к ^> 2 есть ось вращения эллипсоида инерции и, следовательно,
его главная ось.
Пример. Эллипсоид инерции трех точек массы т в вершинах рав -
ностороннего треугольника относительно центра О есть эллипсоид вращения
вокруг нормали к плоскости треугольника (рис. 117).
Рис. 117. Эллип-
Эллипсоид инерции рав-
равностороннего треу-
треугольника

§ 28. ТВЕРДОЕ ТЕЛО
125-
Если же имеется несколько таких осей, то эллипсоид инерции —
шар, и любая ось — главная.
Задача. Провести через центр куба прямую так, чтобы сумма квад-
квадратов ее расстояний от вершин куба была: а) наибольшей, б) наименьшей.
Заметим теперь, что эллипсоид инерции (или оператор инерции,
или моменты инерции /17 12, /3) полностью определяет вращатель-
вращательные свойства нашего тела: если мы рассмотрим два тела с одина-
одинаковыми эллипсоидами инерции, то при оди-
одинаковых начальных условиях они будут двига-
двигаться одинаково (так как у них одинаковые фун-
функции Лагранжа L = Т).
Итак, пространство всех твердых тел с точки
зрения динамики вращения вокруг О трехмерно,
из скольких бы точек тела ни состояли.
Мы можем даже рассматривать «сплошное
твердое тело плотности р@)», имея в виду
предел при AQ —> 0 последовательности тел из
конечного числа точек Qt с массами p(Qi)&Qi (рис. 118) или-
что сводится к тому же, любое тело с моментами инерции
Рис. 118. Сплошное
твердое тело
где г — расстояние от Q до оси е.
Пример. Найти оси и моменты инерции однородной плоской плас-
тинки | z | ^ a, |j/|^b, z = 0 относительно О.
Решение. Так как пластинка имеет три плоскости симметрии,
эллипсоид инерции имеет те же плоскости симметрии и, значит, оси инерции:
х, у, z. Далее,
ь
•-W
х*р ах а у =
-а-Ь
точно так же
mb2
очевидно, Iz = Ix + 1у.
Задача. Доказать, что моменты инерции любого тела удовлетворяют
иераьенствам треугольника
причем равенство может иметь место только для плоского тела.
Задача. Найти оси и моменты инерции однородного эллипсоида-
массы т с полуосями а, Ъ, с относительно центра О.
Указание. Рассмотрите сначала шар.
Задача. Доказать теорему Штейнера:
Моменты инерции любого твердого тела относительно двух
Параллельных осей, одна из которых проходит через центр инерции^
связаны соотношением
= /„
тг2,

126
ГЛ. 6. ТВЕРДОЕ ТЕЛО
где т. — масса тела, г — расстояние между осями, /0 — момент
инерции относительно оси, проходящей через Центр инерции.
Таким образом, момент инерции относительно оси, проходящей
через центр инерции, меньше момента инерции относительно любой
параллельной оси.
Задача. Найти оси и момент инерции однородного тетраэдра отно-
относительно его вершины.
Задача. Нарисовать вектор кинетического момента М для тела с за-
заданным эллипсоидом инерции, вращающегося с данной угловой скоростью Q.
Ответ. М имеет направление нормали к эллипсоиду инерции в точке
.на оси Q (рис. 119).
Рис. 119. Угловая
скорость, элли-
псоид инерции
и кинетической
момент
",.-.'
Рис. 120. Поведе-
ние моментов инер-
ции при уменыпе-
нии тела
Задача. От твердого тела, закрепленного в неподвижной точке О,
отрезали кусок (рис. 120). Как изменятся главные моменты инерции?
Ответ. Все три главных момента уменьшатся.
Указание. Ср. § 24.
Задача. К твердому телу с моментами инерции It > /2 > /3 доба-
добавили малую массу е в точке Q = х1е1 + х2е2 + х3е3. Найти изменение /х
и ej с погрешностью О (е2).
Решение. Центр инерции сместится на расстояние порядка е.
Следовательно, моменты инерции старого тела относительно параллельных
осей, проходящих через старый и новый центры инерции, различаются на
величину порядка е2. В то же время добавление массы меняет момент инер-
инерции относительно любой фиксированной оси на величину порядка е. Поэто-
Поэтому при вычислениях с погрешностью О (е2) мы можем пренебрегать смеще-
смещением центра инерции.
Итак, кинетическая энергия после добавления малой массы принимает
вид
где Го =-g-(/xQj +/2Q| +/Зй|) —кинетическая энергия исходного тела.
Ищем собственное число /х (е) и собственный вектор et (e) оператора инер-
инерции в виде рядов Тейлора по е. Приравнивая коэффициенты при е в соотно-
соотношении А (е) et (е) = /t (е) et (е), находим с погрешностью О (е2):
Из формулы для /t (e) видно, что изменение главных моментов инерции
(в первом приближении по е) такое же, как если бы ни центр, ни оси инерции
не менялись. Формула для ех (е) показывает, как меняется направление

§ 29. УРАВНЕНИЯ ЭЙЛЕРА 127
главных осей: ближайшая большая полуось эллипсоида инерции прибли-
приближается к добавляемой точке, а малая — удаляется от нее. Далее, добавле-
добавление малой массы на одной из главных плоскостей эллипсоида инерции по-
поворачивает две оси, лежащие в этой плоскости, и не меняет направление-
третьей оси. Появление разностей моментов инерции в знаменателе связано
с тем, что у эллипсоида вращения главные оси не определены. Если эллипсо-
эллипсоид инерции близок к эллипсоиду вращения (скажем, /t ж /2), то добавление-
малой массы может сильно повернуть главные оси et и в2 в натянутой на них
плоскости.
§ 29. Уравнения Эйлера. Описание движения по Пуансо
Здесь исследуется движение твердого тела вокруг неподвижной точки
в отсутствие внешних сил и тем самым движение свободного твердого тела.
Движение оказывается двухчастотным.
А. Уравнение Эйлера. Рассмотрим движение твердого тел»
вокруг неподвижной точки О. Пусть М — вектор кинетического
момента тела относительно О в теле, Q — вектор угловой скоро-
скорости в теле, А — оператор инерции (AQ = Ж); векторы Q, М
принадлежат подвижной системе координат К (§ 26). Вектор ки-
кинетического момента тела относительно О в пространстве т =
— ВМ сохраняется при движении (§ 28, Б).
Значит, вектор М в теле (М ее К) должен двигаться так,
чтобы вектор т = BtM(t) при изменении t не менялся.
Теорема. Имеет место соотношение
=№, Q]. A>
Доказательство. Применим формулу E) § 26 для
скорости движения относительно неподвижного пространства к
«точки» М (t) ЕЕ К. Получаем
т=ВМ + [&,т] = В(М+ [Q, М]).
Но так как момент относительно пространства т сохраняется
(т = 0), то М + [fi, M] = 0, ч. т. д.
Соотношение A) называется уравнением Эйлера. Так как М =
= Ли, A) можно рассматривать как дифференциальное уравнение
относительно М (или относительно Q). Если
й = п1в1 + Q2e2 + fi3e3, M = Мхе^ + М2е2 + М3е3,
разложения Q и М по осям инерции ъО, то Mt = /,Q,- и A) при-
принимает вид системы трех уравнений
-Sf- = a1M2M3, -sf- = a2MstM1, -jf-^a^M^^, B)
где аЛ = 2 ~ 3 , аа= 3~ 1, ач = -Ц-т-2, или же вид системы трех
У2'3 'З'! *V2

128
ГЛ. 6. ТВЕРДОЕ ТЕЛО
уравнений для трех компонент угловой скорости
т ^ it ПО О
Замечание. Если на тело действуют внешние силы, сум-
сумма моментов которых относительно О равна п в неподвижной си-
системе координат и Л" в подвижной (н = BN), то
т—п,
да уравнение Эйлера принимает вид
dM
dt ~
Б. Исследование решений уравнения Эйлера.
Лемма. Уравнение Эйлера B) имеет два квадратичных
первых интеграла
М2 Л/Т^ АТ^
Доказательство.
¦энергии, а ЛР — по закону
2
сохраняется по закону сохранения
сохранения момента т, так как
р, у р
т2 = Мг = АР. Лемма доказана.
Итак, М лежит на пересечении эллипсоида со сферой. Чтобы
разобраться в строении кривых пересечения, зафиксируем эл-
эллипсоид ?>0и будем менять радиус
сферы М (рис. 121).
Предположим для определенности,
что /г > /2 > /3- Полуоси эллипсоида
будут У2Щ > У2ЁТг > У2Е7;. Если
радиус сферы М меньше меньшей по-
полуоси или больше большей (M<^jY2EI3
или М ^> \f2EIx), то пересечение пу-
пусто, и таким значениям Е и М ника-
никакое действительное движение не отве-
отвечает. Если радиус сферы равен малой
полуоси, то пересечение состоит из двух
точек. При увеличении радиуса (У2Е13 < М < /2?72) получаются
две кривые вокруг концов малой полуоси. Точно также, если радиус
сферы равен большой полуоси, получаются ее концы, а если не-
немного меньше,— то две близкие к концам большой полуоси
замкнутые кривые. Наконец, если М = rf2EIv пересечение со-
состоит из двух окружностей.
Рис. 121. Траектории уравнений
Эйлера на поверхности уровня
энергии

§ 29. УРАВНЕНИЯ ЭЙЛЕРА 129
Каждый из шести концов полуосей эллипсоида есть отдельная
траектория уравнений Эйлера B) — стационарное положение
вектора М. Ему соответствует постоянное значение вектора уг-
угловой скорости, направленного вдоль одной из осей инерции е*;
при этом Й остается все время коллинеарным М. Поэтому вектор
угловой скорости сохраняет свое положение © в пространстве
коллинеарным т: тело просто вращается с постоянной угловой
скоростью вокруг неподвижной в пространстве оси инерции е,-.
Определение. Движение тела, при котором его угловая
скорость остается постоянной (<а = const, й = const), называ-
называется стационарным вращением.
Доказана
Теорема. Твердое тело, закрепленное в точке О, допускает
стационарное вращение вокруг любой из трех своих осей инерции
"ц ®2» Из-
Извели, как мы предполагали, /х > /2 > Is, то правая часть
уравнения Эйлера больше нигде в 0 ве обращается, т. е. других
стационарных вращений нет.
Исследуем теперь устойчивость стационарных решений урав-
уравнения Эйлера (по Ляпунову).
Теорема. Стационарные решения М — Мгег и М = МЗе3
уравнений Эйлера, соответствующие большей и меньшей осям
инерции, устойчивы, а решение, соответствующее средней оси
(М = М2е2), неустойчиво.
Действительно, при малом отклонении начального условия
от Мгег или Мъеъ траектория будет малой замкнутой кривой,
а при малом отклонении от М2е2 — большой.
Задача. Устойчивы ли по Ляпунову стационарные вращения тела
вокруг большой и малой осей инерции?
Ответ. Нет.
В. Описание движения по Пуансо. Мы хорошо представляем
себе движение векторов момента и угловой скорости в теле (ЗХ
и й) — оно периодично, если М Ф \f2Elf
Чтобы увидеть, как вращается тело в пространстве, рассмот-
рассмотрим его эллипсоид инерции
Э = {Q : (AQ, Q) = 1} d К,
где А : й —> М — симметрический оператор инерции тела, за-
закрепленного в О.
В каждый момент времени эллипсоид Э занимает в неподвиж-
неподвижном пространстве к положение Bt3.
Теорема (Пуансо). Эллипсоид инерции катится без сколь-
скольжения по неподвижной плоскости, перпендикулярной вектору
момента т (рис. 122).
Доказательство. Рассмотрим плоскость л, перпен-
перпендикулярную вектору момента т и касательную к эллипсоиду

130
ГЛ. 6. ТВЕРДОЕ ТЕЛО
т
инерции Bt3. Таких плоскостей всего две, и в точке касания нор-
нормаль к эллипсоиду параллельна т.
Но эллипсоид Э имеет в точке й нормаль grad (AQ, Q) =
= 2ЛЙ = 2М. Поэтому в точках + § = ¦ пересечения
оси с» с Bt3 нормаль к ВгЭ как раз коллинеарна т.
Итак, плоскость л касается Btd в точках на мгновенной оси
вращения, +§. Но скалярное произведение | с неподвижным
вектором т равно ^г~г=г{т, <•>)==: ^Ь |/г277 и потому постоянно.
Итак, расстояние плоскости л от О не
меняется, т. е. плоскость зх неподвижна.
Так как точка касания лежит на
мгновенной оси вращения, ее скорость
равна нулю. Значит, эллипсоид BtB
катится по л без скольжения, ч. т. д.
Следствие. При близких к
стационарному вращению вокруг боль-
большой (или малой) оси инерции началь-
начальных условиях угловая скорость остает-
остается всегда близкой к своему начальному
положению не только в теле (Q), но и
в пространстве (©).
Рассмотрим теперь траекторию точки
касания на неподвижной плоскости зх.
Когда на эллипсоиде точка касания сде-
сделает полный оборот, начальные условия повторятся, с той лишь
разницей, что тело повернется на некоторый угол а вокруг оси т.
Второй оборот будет в точности подобен первому; если а = 2зх —,
движение в целом периодично, если же угол несоизмерим с 2зх,
то тело никогда не вернется в исходное состояние.
Точка касания заметает при этом на плоскости л всюду плотно
кольцо с центром О' (рис. 123).
Задача. Докажите, что связные компоненты инвариантных
двумерных многообразий Vc (§ 28, Б) в шестимерном пространстве
rSOC) — торы и на них можно выбрать координаты фг, <p2mod2n
так, чтобы фг = о)г (с), ф2 = со2 (с)-
Указание. За ^ принять фазу периодического измене-
изменения М.
Рассмотрим важный частный случай, когда эллипсоид инер-
инерции есть эллипсоид вращения:
Рис. 122. Качение эллипсоида
инерции по неподвижной пло-
плоскости
В этом случае ось эллипсоида, Btelt мгновенная ось вращения
© и вектор т всегда лежат в одной плоскости. Углы между ними

30. ВОЛЧОК ЛАГРАНЖА
131
и величина вектора © сохраняются, точка касания описывает
и на эллипсоиде, и на плоскости окружности; оси вращения (©)
и симметрии {Btei) c одинаковой угловой скоростью описывают
конусы вокруг вектора мо-
момента т (рис. 124).
Это движение вокруг т
называется прецессией.
Задача. Найти
скорость прецессии.
угловую
Рис. 123. Траектория точки ка-
касания на неподвижной плоскости
Рис. 124. Качение эллипсоида
вращения по неподвижной пло-
плоскости
Ответ. Разложим вектор угловой скорости со по направлениям векто-
векторов момента т и оси тела Bte1. Первая компонента и даст угловую скорость
прецессии сопр = М/12.
Указание. Представить движение тепа в виде произведения пово-
поворота вокруг оси момента и последующего поворота вокруг оси тела. Угло-
Угловая скорость произведения обоих движений равна сумме векторов их угло-
угловых скоростей.
Замечание. Твердое тело, закрепленное в точке О, в отсутствие
внешних сил, представляет собой лагранжеву систему, конфигурационным
пространством которой является группа, а именно SOC), причем функция
Лагранжа инвариантна относительно левых сдвигов.
Можно показать, что значительная часть эйлеровой теории твердого
тела использует только это обстоятельство, а потому сохраняет силу для
произвольной певоинвариантной лагранжевой системы на произвольной
группе Ли.
В частности, применяя эту теорию к группе диффеоморфизмов римано-
вой области D, сохраняющих элемент объема, можно получить основные
теоремы гидродинамики идеальной жидкости.
§ 30. Волчок Лагранжа
Здесь рассмотрено днижение осесимметричного твердого тела, закреплен-
закрепленного в неподвижной точке, в однородном силовом поле. Движение это со-
составляется из трех периодических процессов: вращения, прецессии и ну-
нутации.
А. Углы Эйлера. Рассмотрим твердое тело, закрепленное в
неподвижной точке О и подверженное действию силы веса тд.
Задача о движении такого «тяжелого твердого тела» в общем случае
До сих пор не решена и в некотором смысле неразрешима.
В этой задаче с тремя степенями свободы известны лишь два

132
ГЛ. 6. ТВЕРДОЕ ТЕЛО
777777777777777////////////
Рис. 125. Волчок
ранжа
лаг-
первых интеграла: интеграл энергии Е = Т + U и проекция ки-
кинетического момента на вертикаль М2.
Есть важный частный случай, когда задачу можно полностью
решить — случай симметричного волчка. Симметричным или ла-
гранжевым волчком называют закрепленное в
неподвижной точке О твердое тело, у которо-
которого эллипсоид инерции в О есть эллипсоид
вращения и центр тяжести лежит на оси вра-
вращения е3 (рис. 125).
В этом случае поворот вокруг оси е3 не
меняет функции Лагранжа, и по теореме Нё-
тер должен существовать дополнительный к
Е и Mz первый интеграл (как мы увидим, им
оказывается проекция М3 вектора момента
на ось е3).
Если удастся ввести три координаты так, чтобы среди них были
углы вращения вокруг оси z и вокруг оси волчка, то эти координа-
координаты будут циклическими, и задача с тремя степенями свободы све-
сведется к задаче с одной степенью свободы (для третьей координаты).
Такой выбор координат в конфигурационном пространстве
SOC). возможен; эти координаты <р, ч|5, в называются углами Эй-
Эйлера и образуют в SOC) локаль-
локальную систему координат, подобную
географическим координатам на
сфере: с особенностями у полю-
полюсов и многозначностью на одном
меридиане.
Введем следующие обозначе-
обозначения (рис. 126):
ех, ev, ег — орты правой де-
декартовой неподвижной системы
координат в неподвижной точке О.
вц е2, е3 — орты связанной с
телом правой подвижной системы
координат, направленные по осям
инерции тела в О.
1\ — 1% Ф 1з — моменты инерции тела в точке О.
ву — орт оси [е2, е3], называемой «линия узлов>>. (Все векторы —
в «неподвижном пространстве» А:.)
Чтобы перевести неподвижный репер (ех, еу, ех) в подвижный
(е1? е2, е3), нужно выполнить три поворота:
1) на угол ф вокруг оси ez. При этом ег остается на месте,
а ех переходит в е^.
2) на угол в вокруг оси е^. При этом ех переходит в е3, a eN
остается на месте.
3) на угол ч|з вокруг оси е3. При этом еу переходит в elt а е3
остается на месте.
Ось
Волчка
Горизонтальная
плоскость
7е"
Линияузлод
Рис. 126. Углы Эйлера

§ 30. ВОЛЧОК ЛАГРАНЖА 133
В результате всех трех вращений ех переходит в е1т а е2 в e3f
поэтому еу переходит в е2.
Углы ф, чр, в называются углами Эйлера. Легко доказывается
Теорема. Каждой тройке чисел <р, в, ip предыдущая кон-
конструкция сопоставляет вращение трехмерного пространства
В (ф, в, чр) ЕЕ SOC), переводящее репер (ех, еу, ег) в репер (elf
е2, е3). При этом отображение (ф, Э, чр) ь* В (ф, в, гр) задает ло-
локальные координаты
О < ф < 2л, 0 < ч|з < 2л, 0 < 6 < л
в конфигурационном пространстве волчка SOC).
Подобно географической долготе, ф и гр можно считать углами
mod 2зх; при Э = 0 или в = л отображение (ф, в, гр) —> В имеет
особенность типа полюса.
Б. Вычисление функции Лагранжа. Выразим функцию Лаг-
ранжа через координаты ф, в, гр и их производные.
Потенциальная энергия, очевидно, равна
U = \\ \ zg dm = mgz0 = mgl cos в,
где z0 — высота центра тяжести над О (рис. 125).
Сосчитаем кинетическую энергию. Здесь полезна маленькая
хитрость: рассмотрим частный случай, когда ф = ч|? = 0.
Лемма. Угловая скорость волчка выражается через произ-
производные углов Эйлера по формуле
<й = 6er -f- (ф sin в) е2 + (я]) + ф cos 6) е3,
если ф = i|) = 0.
Доказательство. Рассмотрим скорость точки волчка,
занимающей в момент времени t положение г. Через время dt эта
точка займет положение (с точностью до (dtJ)
В (Ф + Ар, в + dQ, у + d^B-^y, В, у) г,
где ^ф = ф dt, dQ = 6 dt, dty = ф dt.
Следовательно, с той же точностью вектор перемещения есть
сумма трех слагаемых
В (ф + Ар, в, \р)В-г (ф, в, ч|з)г — г = 1щ, r]dt,
В (ф, в + dQ, ip)?-r (ф, Э, чр)г — г = [<»е, НЛ,
Б (ф, в, ip + dtpJjB (ф, в, ip)r — г =
(угловые скорости соф, юе и ©^ определены этими формулами).
Поэтому скорость точки г есть г> = [щ + сое + щ,, г]
угловая скорость тела есть
со = ©<р + ©
где слагаемые определены предыдущими формулами.

134 ГЛ. 6. ТВЕРДОЕ ТЕЛО
Остается разложить по ег, е2, е3 векторы <я<р, ©е и щ. До сих
пор мы не пользовались тем, что <р = гр = 0. Если ф = ч|з = 0, то
в (ф + dp, e, ч^в-Чф. е, ю
есть просто вращение вокруг оси ех на угол йф, так что
юф = фе,.
Далее, В (ф, в + йв, -ф)^ (ф, в, if) есть в случае ф = г|э = 0
просто вращение вокруг оси ец = ех = ег на угол d6, так что
©е = 0ег.
Наконец, В (ф, в, if + d^B'1 (ф, Э, ч|з) есть вращение на угол
dty вокруг оси е3, поэтому
©Ф = фе3.
Окончательно, при ф = г|э = 0 получаем
© = фе2 + 6ег + ¦фвд.
Но очевидно при ф = ч|5 = 0
ez = e3cos в + е2 sin Э.
Итак, компоненты угловой скорости по осям иьэрции ег, е2, е3
суть
©! = 6» ©г = ф sin в, со3 = ф + ф cos в, ч. т. д.
Поскольку Т = -7г- (/х©? + /2ci>2 + ^з6^)» кинетическая энергия
-7г
при ф = ijj = 0 дается формулой
Т = -§- Fа + <p«sin«e) + А(ф + ф cosBJ.
Но кинетическая энергия от ф и ч|5 зависеть не может: это цикличе-
циклические координаты, и не меняющим Т выбором начала отсчета ф
и if мы всегда можем сделать ф = 0, ч|5 = 0.
Итак, полученная формула для кинетической энергии спра-
справедлива при всех ф, i|).
Мы получаем, таким образом, функцию Лагранжа
Ь = Ц- (б2 4- Ф2 sina6) 4- 4г(Ф + фсовЭJ — mgl cos 6.
Г. Исследование движения. Циклическим координатам ф,
соответствуюг первые интегралы
^Ь- = Mz = ф (/r sin2 в 4- h cos20) + ф
dtp
л т
—r-=Mz=ф/3 cos e 4- ?з-

S 30. ВОЛЧОК ЛАГРАНЖА 135
Теорема. Наклон в оси волчка к вертикали меняется со
временем так же, как в одномерной системе с энергией
где эдЗфектиеная потенциальная энергия дается формулой
(Mz — A/3cos6J , 7 „
2/lSi^e + mgl cos e*
Доказательство. В соответствии с общей теорией
выразим фиф через М3 и Мг. Получим полную энергию системы
в виде
и
Mz — М3 cos В
т /i sin2 6
Постоянный по в член -^т~ =Е — Е' на уравнение для Э не влияет.
Теорема доказана.
Чтобы изучить полученную одномерную систему, удобно сде-
сделать замену cos в = и (—1 <^ и < 1).
Обозначая, кроме того,
Мг Мъ '?Е'
мы можем переписать закон сохранения энергии Е' в виде
н2 = / (и), где / (и) = (о - р«)A - w2) - (а - Ъи)\
и закон изменения азимута ф в виде
а — Ъи
Ф =•
1—
Заметим, что / (и) — полином третьей степени, / (+ оо) = + оо
а / (± 1) = — (а + ЪJ < 0, если только аф ±Ъ. С другой
стороны, действительному движению отвечают лишь такие по-
постоянные а, Ъ, а, р, при которых / (и) ^ 0 при некоторых —1 ^
<«<1.
Итак, / (и) имеет ровно два вещественных корня иг, и2 на отрез-
отрезке —1 ^ и <J 1 (и один при и > 1, рис. 127).
Следовательно, наклон оси волчка в меняется периодически
между двумя предельными значениями 61? в2 (рис. 128).
Это периодическое изменение наклона называется нутацией.
Рассмотрим теперь движение оси волчка по азимуту. Точка
пересечения оси с единичной сферой движется в кольце между
параллелями Э] и в2. При этом изменение азимута оси определяется

136
ГЛ. 6. ТВЕРДОЕ ТЕЛО
уравнением
^
1-й2
Если корень и' уравнения а = Ьи лежит вне (ы1? ы2), то угол
¦у меняется монотонно и ось чертит на единичной сфере кривую
¦типа синусоиды (рис. 128, о).
Если корень и' уравнения а — Ьи лежит внутри (ых, uz), то
¦скорости изменения ф на параллелях 6j. и 62 противоположны, и
ось чертит на сфере кривую с петлями (рис. 128, б).
Если же корень и' уравнения а = Ьи лежит на краю (скажем,
и' = и2), то ось чертит кривую с остриями (рис. 128, е).
-1
Г\ \
fui
Фис. 127. График! функции f (и) Рис. 128. След оси волчка на единичной сфере
Последний случай, хотя и исключительный, наблюдается вся-
всякий раз, когда мы отпускаем ось запущенного с наклоном 62 волч-
волчка без начальной скорости: волчок сперва падает, но потом вновь
поднимается.
Азимутальное движение оси волчка называется прецессией. Окон-
Окончательное движение волчка состоит из вращения вокруг собствен-
собственной оси, нутации и прецессии. Каждое из трех движений имеет
¦свою частоту. Если частоты несоизмеримы, то волчок никогда не
возвращается в начальное состояние, хотя и подходит к нему сколь
угодно близко.
§ 31. Спящий волчок и быстрый волчок
Полученные в § 30 формулы сводят решение уравнений движения волчка
к эллиптическим квадратурам. Однако качественные выводы о движении
обычно проще получать, не обращаясь к квадратурам.
В этом параграфе исследуется устойчивость вертикально стоящего
волчка и даны приближенные формулы для движения быстро запущенного
волчка.
А. Спящий волчок. Рассмотрим сперва частное решение урав-
уравнений движения, при котором ось волчка все время вертикальна
F = 0) и угловая скорость постоянна («спящий» волчок). В зтом
случае, очевидно, Mz = М3 = /Зю3 (рис. 129).
Задача. Показать, что стационарное вращение вокруг вертикали
всегда неустойчиво по Ляпунову.

§ 31. СПЯЩИЙ ВОЛЧОК И БЫСТРЫЙ ВОЛЧОК 137
Мы рассмотрим движение оси волчка, а не самого волчка. Будет
ли ось волчка устойчиво оставаться вблизи вертикали, т. е. будет
ли 6 оставаться малым? Разложим эффективную
потенциальную энергию системы
mgl cos 6
в ряд по степеням 6. Находим
,2 2 е4
'ЛТ , 7 ег
z
О
Рис. 129. Спящи»
Если А > 0, положение равновесия 6 = 0 одномерной системы
устойчиво, а если А <[ 0,— неустойчиво. Итак, условие устойчиво-
устойчивости имеет вид
Когда трение уменьшает скорость спящего волчка ниже этого
предела, он просыпается.
Задача. Докажите, что при ш|^> —— ось спящего волчка ус-
'з
тойчива и относительно таких возмущений, которые меняют значения Mz,
М3, а не только 6.
Б. Быстрый волчок. Волчок называется быстрым, если кине-
кинетическая энергия его вращения велика по сравнению с потенци-
потенциальной:
Из соображений подобия ясно, что увеличение угловой скоро-
скорости в TV раз в точности эквивалентно уменьшению веса в JV2 раз.
Теорема. Если, сохраняя начальное положение волчка,
увеличить в N раз угловую скорость, то траектория волчка будет,
в точности такой же, как если бы угловая скорость осталась преж-
прежней, а ускорение силы тяжести g уменьшилось в iV2 раз. При
этом в случае большей угловой скорости траектория, разумеется,
проходится в N раз быстрее *).
*) Обозначим через qrg (t, |) положение волчка в момент времени t
при начальном условии | е ГБО(З) п ускорении силы тяжести g. Тогда
теорема утверждает, что
<Pg (t, Щ) = <Pjv-*g (M. 6).

138 ГЛ. 6. ТВЕРДОЕ ТЕЛО
Таким образом, мы можем исследовать случай g —> 0, и при-
применять полученные результаты для изучения случая ю —> оо.
Рассмотрим сперва случай g = 0, т. е. движение симметрич-
симметричного волчка в отсутствие силы тяжести. Сравним два описания этого
движения: по Лагранжу (§ 30, Г) и по Пуансо (§ 29, В).
Рассмотрим вначале уравнение Лагранжа для изменения угла
наклона оси волчка 6.
Л е м м а. В отсутствие силы тяжести угол 60, для которого
Мг = Мз cos 60, является устойчивым положением равновесия
уравнения движения оси волчка.
зфФ Частота малых колебаний 6 около этого поло-
положения равновесия равна
\ / „ 'зсоз
\~7 Юн*т - ~7
Во в- Доказательство. В отсутствие силы тяже-
тяжести эффективная потенциальная энергия сводится к
Рис. 130. Эффек- ,м _л/,со«6>2
тиввая потен- тт K™z '»з^уъу)
тт
v э
тиввая потен тт __
циальная энергия v эфф 21 \ sin2 6
волчка
Эта неотрицательная функция имеет нулевой минимум при угле 6 = 60,
определенном условием Mz = М3 cos 60 (рис. 130).
Итак, угол наклона 60 оси волчка к вертикали — устойчивый стацио-
стационарный: при малом отклонении начального наклона 6 от 60 будут происхо-
происходить периодические колебания в около 60 (нутация). Частоту этих колеба-
колебаний легко определить по общей формуле: частота малых колебаний в одно-
одномерной системе с энергией
о*2
E=~2-+U(x), U(xo)=minU{x)
определяется формулой (§ 22, Г)
Энергия одномерной системы, описывающей колебания наклона оси волчка,
есть
При 6 = 60 + х находим Мг — Мг cos в = Мг (cos 60 — cos F0 +
= М& sin в0 + О (ж2)
um= 2/lSin'e0 +o(*2) =-277"
откуда получаем для частоты нутации выражение
„ _ М — Af3cosG
Из формулы ф = — / sin20 видно, что при 6 = 60 азимут
оси также не меняется со временем: ось неподвижна. Азимутальное

§ 31. СПЯЩИЙ ВОЛЧОК И БЫСТРЫЙ ВОЛЧОК
139
т
/77
Рис. 131. Сравнение описаний движения
волчка по Лагранжу и по Пуансо
движение оси при малом отклонении 6 от 60 можно было бы также
изучить с помощью этой формулы, но мы поступим иначе.
Движение волчка в отсутствие силы тяжести можно рассматри-
рассматривать как движение по Пуансо. Следовательно, ось волчка равно-
равномерно вращается вокруг вектора
кинетического момента, сохраняю-
сохраняющего свое положение в простран-
пространстве.
Итак, ось волчка описывает на
сфере окружность, центр которой
соответствует вектору кинетичес-
кинетического момента (рис. 131).
Замечание. Таким образом,
то движение оси волчка, которое по
Лагранжу называется нутацией, в опи-
описании движения Пуансо называется
прецессией.
Разумеется, полученная выше формула для частоты малой ну-
нутации юНут == ^зюз/Д согласуется с формулой частоты прецессии
ю = М11г в движении по Пуансо: когда амплитуда нутации стре-
стремится в нулю, /Зю3 —> М.
В. Волчок в слабом поле. Перейдем теперь к случаю, когда
сила веса не отсутствует, но очень мала (при этом значения?Л/2,
М3 фиксированы). В этом случае к эффективной потенциальной
энергии добавляется слагаемое mgl cos 6, малое вместе с произ-
производными. Покажем, что это слагаемое
мало меняет частоту нутации.
Лемма. Пусть функция ] (х) имеет
минимум при х = 0 и тейлоровское разложе-
х*
ние f (х) = А ~2~ -\- ..., А > 0. Пусть функция
h (x) имеет в 0 тейлоровское разложение
h (х) = В + Сх + ... Тогда при достато-
достаточно малом е функция /е (х) = f (х) + eh (x)
имеет минимум в близкой к 0 точке (рис. 132)
_ Рис. 132. Перемещение миниму-
kc иа при малом изменении функ-
•*"? == — "д ~т~ ^ (^ )• ции
При атом /е (хе) = А + О (е).
Действительно, имеем /е (х) = Ах + С е + О(ех) + О (хг), и резуль-
результат получается применением к /е (х) теоремы о неявной функции.
Согласно лемме эффективная потенциальная энергия при ма-
малых g имеет близкую к 60 точку минимума 6g, причем в этой точке
V" мало отличается от U" F0). Следовательно, частота малой ну-
нутации около 60 близка к полученному при g = 0 значению:
lim
?-•0
= -7-ю3.

140 ГЛ. 6. ТВЕРДОЕ ТЕЛО
Г. Быстро запущенный волчок. Рассмотрим теперь специаль-
специальные начальные условия, когда мы отпускаем ось волчка без на-
начального толчка из положения с наклоном 60 к вертикали.
Теорема. Если в начальный момент ось волчка неподвижна
(ф = 6 = 0) и волчок быстро вращается вокруг своей оси (ю3 —*¦
—* оо), наклоненной к вертикали под углом 60 (Mz = M3 cos 60),
то асимптотически при ю3 —> оо:
1) частота нутации пропорциональна угловой скорости;
2) амплитуда нутации обратно пропорциональна квадрату уг-
угловой скорости;
3) частота прецессии обратно пропорциональна угловой ско-
скорости;
4) справедливы асимптотические формулы (при ю3 —> оо)
/3 hmgl . Q mgl
©нут J— <й3, Онут ~ 2 2 Sin О0, СОпРец
3 3
(здесь /(ш3)— g(bi3)' если lira — = 1J.
V СО»—>оо о '
Для доказательства перейдем к случаю, когда начальная угло-
угловая скорость фиксирована, но g —> 0.
Истолковывая затем полученные формулы с помощью подобия
(см. пункт Б), получим сформулированную теорему.
У
ЖГ
Рис. 133. Определение Рис. 134. Движение оси
амплитуды нутации волчка
Мы уже знаем из § 30,Г, что при наших начальных условиях ось волч-
волчка чертит на сфере кривую с остриями.
Применим лемму к нахождению точки минимума Qg эффективной потен-
потенциальной энергии. Положим (рпс. 133)
е = е0 + х, cos е = cos g0 — х sin 60 + ...
Тогда получим, как выше, тейлоровские разложения по х
^эфф |g=o = 77" х* + -"' mgl cos в = mgl cos до — xmgl sin Qo+ ¦..
Применяя лемму к / = U^ |g=0, g — 8, h — ml cos F0 + x), находим,
что минимум эффективной потенциальной энергии U^^ достигается при угле
наклона
Ijml sin 6n
g, Xg= ' °
'зшз

§ 31. СПЯЩИЙ ВОЛЧОК И БЫСТРЫЙ ВОЛЧОК 141
Итак, наклон оси волчка 6 будет колебаться около dg (рис. 134). Но
в начальный момент 6 = 60, а 6 = 0. Значит, 60 соответствует наивысшему
положению оси волчка. Итак, при малых g амплитуда нутации асимптоти-
асимптотически равна
hml sin 60
(g0)
Теперь найдем прецессионное движение оси. Из общей формулы
М2 — М3 cos 6
*= h sin2 6
при Мг = М3 cos 60. 0 = 60 + х, находим
Mz — М3 cos 0 = Мз х sin 0О + . . .,
поэтому
Но х колеблется от 0 до 2rg гармонцческп (с точностью до О (if2)). Поэтому
среднее за период нутации значение скорости прецессии асимптотически
равно
- Щ mgl
<р~ /lSine0 х— {g^0)
Задача. Доказать, что
hmlim

ЧАСТЬ III
ГАМИЛЬТОНОВА МЕХАНИКА
Гамильтонова механика — это геометрия в фазовом простран-
пространстве. Фазовое пространство имеет структуру симплектического
многообразия. На симплектическом многообразии действует груп-
группа симплектических диффеоморфизмов. Основные понятия и тео-
теоремы гамильтоновой механики (даже если они и формулируются
в терминах локальных симплектических координат) инвариантны
относительно этой группы (и относительно более широкой группы
преобразований, затрагивающих также и время).
Гамильтонова механическая система задается четномерным
многообразием («фазовым пространством»), симплектической струк-
структурой на нем («интегральным инвариантом Пуанкаре») и функ-
функцией на нем («функцией Гамильтона»). Каждая однопараметри-
ческая группа симплектических диффеоморфизмов фазового про-
пространства, сохраняющих функцию Гамильтона, связана с первым
интегралом уравнений движения.
Лагранжева механика включается в гамильтонову как частный
случай (фазовое пространство в зтом случае есть кокасательное
расслоение конфигурационного, а функция Гамильтона — пре-
преобразование Лежандра функции Лагранжа).
Гамильтонова точка зрения позволяет исследовать до конца
ряд задач механики, не поддающихся решению иными средствами
(например, задачу о притяжении двумя неподвижными центрами
и задачу о геодезических на трехосном эллипсоиде). Еще большее
значение гамильтонова точка зрения имеет для приближенных
методов теории возмущений (небесная механика), для понимания
общего характера движения в сложных механических системах
(эргодическая теория, статистическая механика) и в связи с дру-
другими разделами математической физики (оптика, квантовая
механика и т. п.).
ГЛАВА 7
ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
Дифференциальные внешние формы возникают при обобщении
на многомерный случай таких понятий, как работа поля на пути
и поток жидкости через поверхность.
Гамильтонову механику нельзя понять без дифференциальных
форм. Нужные нам сведения о дифференциальных формах — это
внешнее умножение, внешнее дифференцирование, интегрирова-
интегрирование и формула Стокса.

§ 32. ВНЕШНИЕ ФОРМЫ 143
§ 32. Внешние формы
Здесь определены внешние алгебраические формы.
А. 1-формы. Пусть R" — n-мерное вещественное линейное
пространство *). Векторы этого пространства будем обозначать
через 1, т), . . .
Определение. Формой степени 1 (или, короче, 1-фор-
мой) называется линейная функция от вектора, ю: Rn -> R,
+ Kh) = V (li) + № (I2), V^i» К е R, Si, 12 <= R"-
Напомню основные факты об 1-формах, известные из линейной
алгебры. Множество всех 1-форм превращается в вещественное
линейное пространство, если определить сумму
форм формулой }
(щ + ю2) (|) = щ (|) + ю2 (|), | tUftfFA)
а умножение на число — формулой [^(перемещение)
(Щ (|) - Лю (|). рис 135 работа
_ _„ силы—1-форма от
Пространство 1-форм На R Само П-мерНО И На- перемещения
зывается также сопряженным пространством, (Rn) *.
Пусть в R" выбрана линейная система координат, хг, . . ., хп.
Каждая координата, например xt, сама является 1-формой. Эти
гг 1-форм линейно независимы. Поэтому каждая 1-форма ю имеет
вид
ю = ад + . . . + anxn, at S R.
Значение ю на векторе | равно
ю(|) = ajx^il) + . . . + anxn(l),
где a^d), . . ., xn(%) — компоненты вектора | в выбранной систе-
системе координат.
Пример. Если в евклидовом R3 дано однородное силовое поле F,
*о его работа А на перемещении | есть 1-форма от | (рис. 135).
Б. 2-формы.
Определение. Внешней формой степени 2 (или, короче,
2-формой) называется функция от пары векторов, ю2: Rn X
X Rn -> R, которая билинейна и кососимметрична:
<»2 (^|x + Ь212, |3) = К<»2 (Si, Ы
¦) Существенно отметить, что мы не фиксируем в Rn никакой специаль-
специальной евклидовой структуры. В некоторых примерах такая структура исполь-
используется; тогда это специально оговорено — («евклидово Rn»).

144 ГЛ. 7. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
Пример 1. Пусть S (Si,12) — ориентированная площадь паралле-
параллелограмма, построенного на векторах Ъ,и |2 ориентированной евклидовой
плоскости R2, т. е.
- _ I In I121 Si = Inex + |i2e2,
2) = |bi |22|, где h =
где ej, e2 — базис, задающий ориентацию R2.
Легко видеть, что S (|l7 g2) есть 2-форма (рис. 136).
Пример 2. Пусть «; — однородное поле скоростей жидкости в трех-
трехмерном ориентированном евклидовом пространстве (рис. 137). Тогда поток
Рис. 136. Ориентирован- Рис. 137. Поток жидкости через
ная площадь — 2-форма площадку — 2-форма
жидкости через площадь параллелограмма Su g2 есть билинейная кососим-
метрическая функция от |j, g2, т. е. 2-форма
©2 (Si, h) = (*>. Si. S*)-
Пример 3. Ориентированная площадь проекции параллелограмма
со сторонами fi, I2 в евклидовом R3 на плоскость х1У х2 есть 2-форма.
Задача 1. Докажите, что для всякой 2-формы ©2 в R" имеем
Решение. Ввиду кососимметричности ©2(|, ?) = —©2 (|, ?)-
Множество всех 2-форм в R" превращается в вещественное
линейное пространство, если определить сложение форм формулой
(юх + ю2) (ij, |2) = ©! (|1? |2) + ю2 (|х, |2),
а умножение на число — формулой
Задача 2. Докажите, что это пространство конечномерно, и най
дите его размерность.
п(п—1)
Ответ. « i базис указан ниже.
В. А'-формы.
Определение. Внешней формой степени к, или к-фор-
мой, называется функция от к векторов, которая к линейна и

§ 32. ВНЕШНИЕ ФОРМЫ
145-
О)
где v =
кососимметрична:
'О, если перестанов-
перестановка iv ..., ik чет-
четная
1, если перестанов-
перестановка ?•!,..., ik не-*
четная.
Пример 1. Ориентированный объем параллелепипеда с ребрам»
%!, . . ., ?п в ориентированном евклидовом пространстве Rn есть тг-форма
(рис. 138)
ц """ Ьпп
где I; = %цех + . . . + ljnen и е1? . . ., е„ — базис R*1.
Пример 2. Пусть R" — fc-мерная ориентированная плоскость
в и-мерном евклидовом пространстве Rn. Тогда ^-мерный ориентированный
объем проекцип параллелепипеда с ребрами |lt 12, . . ., ^eR" на R*
есть fc-форма на Rn.
Множество всех /с-форм в R" становится вещественным ли-
линейным пространством, если ввести в нем опера-
операции сложения
Rn,
и умножения на число
Рис. 138. Ориен-
Ориентированный объ-
объем — 3-форма
Задача 3. Доказать, что это линейное пространство конечномерно,
и найти его размерность.
Ответ. С*; базис указан ниже.
Г. Внешнее произведение двух 1-форм. Введем теперь еще
одну операцию: внешнее умножение форм. Если ©*—А-форма и
(л1 — i-форма в Rn, то их внешнее произведение &)к Д юг будет
к -\- /-формой. Вначале определим внешнее произведение 1-форм,
сопоставляя каждой паре 1-форм ю1? ©2 в R" некоторую 2-форму
юх Д ю2 в Rn.
Пусть | — вектор R". 14мея две 1-формы а>± и ю2, можно опре-
определить отображение Rn на плоскость R X R, сопоставляя
IgR" вектор & (;) с компонентами ©х (|), со2 (|) на плоскости
с координатами ю15 ю2 (рис. 139).
Определение. Значение внешнего произведения щ Д <о2
на паре векторов сх, |2 ^ R" есть ориентированная площадь об-

146 ГЛ. 7. ДИФФЕРЕНЦИАЬНЫЕ ФОРМЫ
раза параллелограмма со сторонами |15|2 на плоскости coj, co2:
Задача 4. Доказать, что ©j Д ю2 действительно есть 2-форма.
Задача 5. Доказать, что отображение
Л
билинейно и кососимметрично:
u>i Л % = —Щ Л
(X'ol + Van) Д ю2 = Ji/coi Л
Л
Рис. 139. определе-
веденияШдауГх
Указание. Определитель билинеен и косо-
симметричен не только по строкам, но и по столбцам.
Пусть теперь в Rn выбрана система линей-
ных координат, т. е. заданы п независимых 1-
Ф<>РМ Хг, . . ., Хп. ЭТИ формы МЫ будем наЗЫ-
вать базисными.
Внешние произведения базисных форм суть 2-формы xt Д xj.
Ввиду кососимметричности, xt /\ хг = 0, xt Д xt = —xj Д xt.
Геометрический смысл формы xt Д xt очень прост: ее значение
на паре векторов |lt g2 равно ориентированной площади проек-
проекции параллелограмма %lt la на координатную плоскость xt, xt
параллельно остальным координатным направлениям.
п(п — 1)
2 форм х» Д xj (i < /) ли-
Задача 6. Докажите, что С2 =
аейно независимы.
В частности, в трехмерном пространстве (хи х^, х3) площадь
проекции на плоскость (х1, хг) есть хг Д х2, на плоскость (х2, х3) —
—х2 Д #3, на плоскость (xa, xt) — х3 Д а^.
Задача 7. Докажите, что все 2-формы в трехмерном пространстве
(xt, x2, х3) исчерпываются формами
Д х3 + Qxa Д
Д
Задача 8. Докажите, что каждая 2-форма в n-мерном пространстве
с координатами хи . . ., хп однозначно представляется в виде
Указание. Пусть е% — i-й базисный вектор, т. е. х$ (cj) = 1,
(ei) = 0, j Ф i. Рассмотрим значения формы ю2 на паре Cj, ey. Тогда
oij = ю3 (€i, ej).
Д. Внешние одночлены. Пусть теперь даны к 1-форм щ, . . .
. ., сок. Определим их внешнее произведение сох Д . . . Д щ.

I 32. ВНЕШНИЕ ФОРМЫ 147
Определение. Положим
КЛ-Л^ХЬ 60= «^F.)..
Иными словами, значение произведения 1-форм на параллеле-
параллелепипеде ?х, . . ., ?к равно ориентированному объему образа парал-
параллелепипеда в ориентированном евклидовом координатном простран-
пространстве RK при отображении | >-*¦ (щ (|), . . ., щ (|)).
Задача 9. Докажите, что ь>1 Д ... Д% есть ft-форма.
Задача 10. Докажите, что операция внешнего умножения 1-форм
задает полилинейное кососимметрическое отображение
@)lt . . ., Oft) — ©! Д . . . Д COfc.
Иными словами,
(ЛЦ + *¦"«?) Д «г Д • • • Д wfc = ^Ц Д ©г Д ... Д а>н + 1"а[ Д а2 Д... Д шк>
»цЛ-Л% = (— !)v«1Д • • • Д «V
где
(О, если перестановка i.,...,i. четная,
\ 1, если перестановка ii,..., i^ нечетная.
Рассмотрим теперь в Rn систему координат, заданную базис-
базисными формами хг, . . ., хп. Внешнее произведение к базисных
форм
Х1г Л • • • Л xv 4 < *m < ",
есть ориентированный объем проекции /с-параллелепипедов на
fc-плоскость (xti, . . ., xik) параллельно остальным координатным
направлениям.
Задача 11. Докажите, что если среди индексов %, . . ., % есть два
одинаковых, то форма х,- Д . . . Д х^ равна нулю.
Задача 12. Докажите, что формы
хи Д . . . Д ziH, где 1 < «1 < . . . < to < и,
линейно независимы.
Число таких форм, очевидно, С^. Мы будем называть их базисными
к-формами.
Задача 13. Докажите, что каждая ft-форма в R" однозначно пред-
представляется в виде линейной комбинации базисных:
ш!с= S \..лл-л\
l^ii<...<ifc<n fc R
Указание, а^ _^ = а" (ек, . . ., ei)f).
Из результата этой задачи следует, что размерность линейного
пространства /с-форм в R™ равна С?. В частности, при к = п,
С\ = 1, откуда вытекает

48 ГЛ. 7. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
Следствие. Всякая п-форма в Rn есть либо ориентиро-
ориентированный объем параллелепипеда при некотором выборе единицы
-объема, либо нуль:
со" = а-хг Д . . . Д хп.
Задача 14. Доказать, что всякая fc-форма в R" при k > n равна
нулю.
Переходим теперь к умножению /с-формы coft на /-форму со'.
Пусть вначале даны два одночлена
ШК = COj Д . . . Д С0к, СО' = C0fc+1 Д . . . Д С0М,
где coj, . . ., cofc+7 — 1-формы. Их произведение со* Д со' мы
определим как одночлен
Д • • • Л »к) Л Kai Л - • • Л Щщ) =
= К»! Д . . . Д С0к Д С0(?т1 /\ . . . /\ COftjj.
Задача 15. Докажите, что умножение одночленов ассоциативно:
(а* Д со') Д шт = ш* Д (а1 Д «»т)
я косокоммутатявно:,1
toR.
Указание. Чтобы переставить каждый из I множителей о/ вперед,
иужно к инверсий с к множителями иЛ".
Замечание. Полезно запомнить, что косокоммутатпвность озна-
означает коммутативность, если хотя бы одна из степеней к, I четная, и анти-
антикоммутативность, если обе степени к, I нечетные.
§ 33. Внешнее умножение
Здесь определяется операция внешнего умножения форм и доказыва-
доказывается, что она косокоммутативна, дистрибутивна и ассоциативна.
А. Определение внешнего произведения. Мы определим теперь
внешнее умножение произвольной /с-формы со* на произвольную
Z-форму со'. Результат сок Д со' будет к + ^-формой. Операция
умножения окажется:
1) косокоммутативной: сок Д со' = (—1)и со' Д cofc,
2) дистрибутивной: (^со* + h^l) Л »' = \<&Л »' + ^гюг Д «Л
3) ассоциативной: (сок Д со') Д со = со* Д (со' Д со).
Определение. Внешним произведением со* Д со1 к-формы
<о* в R" ка l-форму со' в R" называется /с -f- /-форма в Rn, значе-
значение которой на к + I векторах ?lt . . ., |fc, |)f+l, - . •, ?к+? S Rn
равно
(«о* Д ©')(?!, •.., ?t+l) = S (- l)v«ft (S^, • • ¦, ?гк) со' (|4 Ц),
A)

§ 33. ВНЕШНЕЕ УМНОЖЕНИЕ 149
где ij < . . . < ц, Л < . . . < /г; (il5 . . ., ц, jlt . . ., /,) — пере-
перестановка номеров A, 2, . . ., к + Z), а
A, если эта перестановка нечетна,
О, если эта перестановка четна.
Иными словами, каждое разбиение к + I векторов ?lt . . .
. . ., P,k+M на #ве группы (из к и из I векторов) дает одно слагаемое
е нашей сумме A). Это слагаемое равно произведению значения
k-формы со на к векторах первой группы на значение l-формы со'
на I векторах второй группы, со знаком -\- или — в зависимости
от того, как упорядочены векторы в группах. Если они упорядо-
упорядочены так, что написанные подряд к векторов первой группы и
I векторов второй образуют четную перестановку векторов
in la» • • -1 ?jrTti то берется знак +, а если нечетную — знак —.
Пример. Если к = 2, то разбиений всего два: ?lt ?2 и
?2i li- Поэтому
К Л «г) (?it h) = «1 (?i) со2 (е2) — со2 (У сох A2),
в согласии с определением умножения 1-форм из § 32.
Задача 1. Доказать, что приведенное выше определение действи-
действительно определяет некоторую к + Z-форму (т. е. что значение (ш* Д и')
A1 . . ., ?к+г) зависит от векторов 1 полилинейно и кососимыетрично).
Б. Свойства внешнего произведения.
Теорема. Определенное выше внешнее умножение форм косо-
коммутативно, дистрибутивно и ассоциативно. Для одночленов
оно совпадает с умножением, определенным в % 32.
Доказательство косокоммутативности основано на простейших
свойствах четных и нечетных перестановок (см. задачу в конце
§ 32) и предоставляется читателю.
Дистрибутивность следует из того, что каждое слагаемое в A)
линейно относительно сок и со'.
Доказательство ассоциативности требует несколько больше
комбинаторики; так как соответствующие рассуждения уже про-
проводились в курсе алгебры при доказательстве теоремы Лапласа
о разложении определителя по минорам столбцов, можно восполь-
воспользоваться этой теоремой *).
*) Прямое доказательство ассоциативности (содержащее также доказа-
доказательство теоремы Лапласа) состоите проверке согласованности знаков в тож-
тождестве
<(ш* д и') д ©"кь....,
Где ix < . . . < ifc, h< ¦ ¦ ¦ <ji, К < • - • < V; (»i> • ¦ ¦> Am) — переста-
вовка чисел A, . . ., k + I -(- m).

150 ГЛ. 7. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
Начнем со следующего замечания: Если ассоциативность
доказана для слагаемых, то она верна и для суммы, т. е.
. . влечет (A% + «i) Д »г) Л «з =
(«х Л е»2) Л »з = «1Л («2 Л »з))
(со2 А ю3).
Ибо в силу дистрибутивности, которая уже доказана, имеем
((о>1 + »i) Л ю2) Л »з = ((«1 Л »г) Л »з) + ((«i Л »г) Л »з).
(»i + »i) Л («г Л »з) = («i Л («г Л »з)) + («1 Л («г Л ®з))-
Но мы уже знаем из § 32 (задача 12), что всякая форма в Rn
есть сумма одночленов. Поэтому достаточно доказать ассоциатив-
ассоциативность умножения одночленов.
Так как пока не доказана эквивалентность определения умно-
умножения к 1-форм из § 32 с общим определением A), мы будем вре-
временно обозначать умножение к 1-форм символом Д, так что наши
одночлены имеют вид
со
= щ Д ... Д cofc, «' = сок+1Д...
где щ, . . ., щ+1 — 1-формы.1
Лемма. Внешнее произведение двух одночленов есть одночлен:
_ _ _ _ _
= toj Д ... Д щ Д coft^ Д ... Д ыц+i-
Доказательство. Вычислим значения левой и правой
частей на к + I векторах |15 . . ., |ft+I. Значение правой части
равно определителю det [ со? (|7) [ порядка к -\- I. Значение левой
части по формуле A) равно сумме произведений
det K&JI- det \щ{%1т)\
миноров первых /с столбцов определителя порядка к + I на до-
дополнительные миноры. Теорема Лапласа о разложении по мино-
минорам первых к столбцов как раз и утверждает, что эта сумма с тем
же правилом выбора знаков, что в определении A), равна опре-
определителю det | (Hi (i.j) | . Лемма доказана.
Из леммы вытекает, что операции Д и Д совпадают. Дей-
Действительно, мы получаем последовательно
Щ Д «2 = Ю1 Д И2'
»] Д «а Д »з = («1А »г) А «з = (Ю1 Д соа) Л ю3,
«! Л Ю2 Д • • • Д «fc = (• • • ((«! Д С02) Д С03) А • • • А

§ 33. ВНЕШНЕЕ УМНОЖЕНИЕ 151
Из очевидной ассоциативности Д-умножения к 1-форм сле-
следует поэтому ассоциативность Д-умножения одночленов. Тем
самым, в силу сделанного выше замечания, ассоциативность до-
доказана и в общем случае.
Задача 2. Докажите, что внешний квадрат 1-формы или вообще
формы нечетного порядка равен нулю: ш^ Д шЛ = 0, если к нечетно.
Пример 1. Рассмотрим в R2TV систему координат р1? . . ., рп, qlt ...
п
. . ., дп и 2-форму шг = 2 Рг Л Яг-
[Геометрически эта форма ш2 означает сумму площадей ориентирован-
ориентированных проекций параллелограмма на п координатных двумерных плоскостей
<Ри 9i)? ¦ ¦ ¦! (Рл. 9п)- В дальнейшем мы увидим, что 2-форма ш2 имеет ос-
основное значение для гамильтоновой механики. Можно показать, что всякая
невырожденная *) 2-форма в R2n имеет вид ш2 в некоторой системе коорди-
координат (Pl, . . ., дп).]
Задача 3. Найти внешний квадрат 2-формы ш2.
Ответ, ш2 Д ш2 _ _2 ^ р. Д р. Д д. Д д..
i>l
Задача 4. Найти внешнюю к-ю степень ю2.
Ответ, to2 Д to2 Д . ¦ ¦ Д и2 = ±к\ 2 Рч А" -Л Р. Л9ц Л- --Л%-
S 4<...<ifc
В частности,
to2 Д ¦¦¦ Д со2 = ± в! и Д ... Д рп Д ?1 Д ... Д gn
п
есть, с точностью до множителя, объем 2п-мерного параллелепипеда в R2n.
Пример 2. Рассмотрим теперь ориентированное евклидово прост-
пространство R3. Каждому вектору ieR3 сопоставим 1-форму а^А, полагая
<а^ (|) = (А, |) (скалярное произведение),
и 2-форму а>2А, полагая
шл (Si. 1г) = (-4. Si. Is) (смеша ное произведение).
Задача 5. Доказать, что отображения At-*- &А и -4 ь+ а>л устанав-
устанавливают изоморфизмы линейного пространств^ R3 векторов А с линейными
пространствами 1-форм в R3 и 2-форм в R3. Если в R3 выбрана ортонорми-
рованная, ориентированная система координат (xt, x2, х3), то
> = Агхх + Azxz + А3х3, аА = Ахх% Д х3 + А2х3 Д хх + А^ Д х2.
Замечание. Итак, выписанные изоморфизмы не зависят от выбора
ортонормированной и ориентированной системы координат (xt, х%, xs). Но
они зависят от выбора евклидовой структуры R3, а изоморфизм А *->¦ <а>л
также и от ориентации (входящей неявно в определение смешанного произ-
произведения) .
Задача 6. Доказать, что в силу установленных изоморфизмов внеш-
внешнее умножение 1-форм превращается в векторное умножение векторов R3,
т. е. что
юл Д шв = ш[д, в] Для любых А, В е R3.
•) Билинейная форма ю2 невырождена, если Vg ф 0, 3tj: со2 (|, ц) ф 0.

152 ГЛ. 7. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
Таким образом, внешнее умножение форм можно рассматривать как
перенос на многомерный случай векторного умножения в R3. Только в много-
многомерном случае произведение не есть вектор того же пространства: прост-
пространство 2-форм в R™ изоморфно R™ только при п = 3.
Задача 7. Доказать, что в силу установленных изоморфизмов внеш-
внешнее умножение 1-формы на 2-форму превращается в скалярное умножение
векторов R3:
">а A <4j = (Л,В) Xl Д х2 Д х3.
В. Поведение при отображениях. Пусть /: R -*¦ R" — ли-
линейное отображение, й со* — внешняя fc-форма на Rn. Тогда на
Rm возникает /с-форма /*coft, значение которой на к векторах
Ej, . . ., Sj G R" равно значению cofc на их образах:
Задача 8. Проверить, что /*си* — внешняя форма.
Задача 9. Проверить, что /* — линейный оператор из пространства
/г-форм на Rn в пространство fc-форм на Rm (звездочка сверху указывает,
что /* действует в сторону, противоположную i).
Задача 10. Пусть /: Rm — R", g: R™ — Rp. Проверить, что
(g о /)* = /* о g*.
Задача 11. Проверить, что /* сохраняет внешнее умножение:
/* (<о* Д <»г) = (/*ш*) Д (/*ш').
§ 34. Дифференциальные формы
Здесь дано определение дифференциальной формы иа дифференцируе-
дифференцируемом многообразии.
А. Дифференциальные 1-формы. Простейшим примером диф-
дифференциальной формы является дифференциал функции.
Пример. Рассмотрим функцию у = / (х) = х2. Ее дифференциал
dj = 2х их зависит от точки х и от «приращения аргумента», т. е. от каса-
касательного вектора \ к оси х. За-
, .у фиксируем точку х. Тогда диффе-
дифференциал функции в точке .г, dj \x,
зависит ст | линейно. Так, если
х = 1 и координата касательного
вектора | равна 1, то dt = 2, а
,, если координата | равна 10, то
х
df = 20 (рис. 140).
Рис. 140. Дифферен- Рис. 141. К задаче 1 ПуСТЬ /." М—»-R — ДшЬфе-
циал функции v
ренцируемая функция, задан-
заданная на многообразии М (можно представлять себе «функцию многих
переменных» /: Rn -*- R). Дифференциал df \x функции / в точ-
точке х есть линейное отображение
dfx: TMX-+R
касательного пространства к М в точке х в вещественную пря-
прямую. Напомню определение этого отображения.

§ 34. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ 153
Пусть | S ТМХ — вектор скорости кривой х (t): R-r M,
ж @) = х,х @) = §. Тогда, по определению,
Задача 1. Пусть § — вектор скорости плоской кривой х (t) =
= cos t, у (t) = sin t при < = 0. Вычислить значения дифференциалов dx,
•dy функций х, у на векторе \ (рис. 141).
Ответ, dx |1>0 (i) = 0. dj/ |1>0 (?) = 1.
Заметим, что дифференциал функции / в точке х Е= М есть
1-форма d/^ на касательном пространстве ГМ».
Дифференциал df функции / на многообразии М есть гладкое
отображение касательного расслоения ТМ в прямую
df: ТМ -* R (ТМ = U ГМ,.).
Это отображение линейно на каждом касательном пространстве
ТМХ CZ ТМ и дифференцируемо.
Определение. Дифференциальной формой степени 1
{или 1-формой) на многообразии М называется гладкое отобра-
отображение
со: ТМ ^R
касательного расслоения многообразия М в прямую, линейное
на каждом касательном пространстве ТМХ.
Можно сказать, что дифференциальная l-форма на М есть
алгебраическая 1-форма на ТМХ, «дифференцируемая по у».
Задача 2. Докажите, что всякая дифференциальная 1-форма на
прямой является дифференциалом некоторой функции.
Задача 3. На окружности и на плоскости найти дифференциальные
1-формы, не являющиеся дифференциалами никаких функций.
Б. Общий вид дифференциальных 1-форм в R". Рассмотрим
в качестве многообразия М линейное пространство с координата-
координатами ж15 . . ., хп. Напомню, что компонентами |х, . .., |п касательного
вектора % Е= TR'^ называются значения дифференциалов коорди-
координат dxt, . . ., dxn на векторе %. Эти п 1-форм на TR'x линейно
независимы. Итак, 1-формы dxt, . . ., dxn образуют базис в п-мер-
ном пространстве 1-форм на ZTC-
Следовательно, всякая 1-форма в ЛС однозначно записы-
записывается в виде atdxt + . . . -f- andxn, где at — вещественные коэф-
коэффициенты. Пусть теперь со — произвольная дифференциальная
1-форма в R". В каждой точке х она однозначно разлагается по
базису dxl7 . . ., dxn. Отсюда вытекает
Теорема. Всякая дифференциальная i-форма в простран-
пространстве Rn с выбранной системой координат хг,..., хп однозначно

154
ГЛ. 7. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
записывается в виде
со = аг (х) йхг + . . . + ап (х) dxn,
где коэффициенты at (x) — гладкие функции.
Задача 4. Вычислить значения форм о^ = dxu со2 = xtdx2, со3
= dr2 (г2 =
на векторах |г, §2, §3 (рис. 142).
Ответ.
COs
ооо
12
—1
—2
—8
Is
1
2
0
0 1 Z 3 xf
Рис. 142. К задаче 4
Задача 5. Пусть xt, . . ., хп — функции на многообразии М,
образующие локальную координатную систему в некоторой области. Дока-
Докажите, что каждая 1-форма в этой области однозначно записывается в виде
со = at (x) dxx + . . . + an (x) dxn.
В. Дифференциальные /•'-формы.
Определение. Дифференциальной fe-формой со* \ж в пин-
пинке х многообразия М называется внешняя k-форма на касательном
пространстве ТМЖ к М х, т. е. k-линейная кососимметричная
функция от к векторов |15 . . ., 1к, касательных к М в х.
Если такая форма cos \x задана в каждой точке х многообра-
многообразия М и если она дифференцируема, то говорят, что дана к-форма
со* на многообразии М.
Задача 6. Ввести естественную структуру дифференцируемого мно-
многообразия в множество, элемент которого — набор к векторов, касающихся
М в какой-нибудь точке х.
Дифференциальная /с-форма есть гладкое отображение полу-
полученного многообразия в прямую.
Можно сказать, что к-форма на М есть внешняя к-форма на
ТМХ, «зависящая дифференцируемым образом от ас».
Сложение, умножение на число и внешнее умножение форм
на М определяются поточечно: в каждой точке х GE М надо сло-
сложить, умножить на число или внешне перемножить соответствую-
соответствующие алгебраические внешние формы на касательном пространстве
ТМХ.
Задача 7. Докажите, что все fc-формы на М образуют линейное
пространство (бесконечной размерности, если к не превосходит размерно-
размерности М).
Дифференциальные формы можно умножать не только на
числа, но и на функции. Множество С^-дифференциальных

§ 34. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
155
Л-форм имеет, таким образом, естественную структуру модуля
над кольцом бесконечно дифференцируемых вещественных функ-
функций на М.
Д. Общий вид дифференциальных Л1-форм в R". Рассмотрим
в качестве многообразия М линейное пространство Rn с фиксиро-
фиксированными координатными функциями хг, . . ., хп: R"-»-R. Зафик-
Зафиксируем точку х. Мы видели выше, что п 1-форм dxu . . ., dxn
образуют базис в пространстве 1-форм на касательном простран-
пространстве JR2.
Рассмотрим внешние произведения базисных форм
dxZl/\.../\dx4, i1<...<ilt.
В § 32 мы видели, что эти С* /с-форм образуют базис в простран-
пространстве внешних й-форм на ГК?. Следовательно, каждая внешняя
Ж-форма на TRJJ однозначно записывается в виде
S аи . г dxH/\ ... f\'dxir
ч< <\
Пусть теперь cofr — произвольная дифференциальная /с-форма
в пространстве R". В каждой точке х она однозначно разлагается
но выписанному выше базису. Отсюда вытекает
Теорема. Всякая дифференциальная к-фор-
ма в пространстве W с выбранной системой ко- s
ординат х1У . . ., хп однозначно записывается в ^
виде
со
= S
ч<
(x)dxx,/\ .
t,
где a1%... lft (ас) — гладкие функции на R". *г
Задача 8. Вычислить значения фор« ах = dxx Д Рис. 143. К задаче 8
Д dx3, «2 = Щйху Д dx2 — x2dx2 Д dxu to3 = г dr Д dtp
<где Xi = г cos ф, х2 = г sm ф) на парах векторов (g^ %), (|2, ij2), A3, ij3)
<рис. 143).
Ответ.
«01
G>2
СО3
(Si. 4i)
1
2
1
(Si. Ч2)
1
1
1
(?з, Щ)
—1
—3
—1
Задача 9. Вычислить значения форм «! = dx2 Д dx3, ш2 =
Д
Д dx2, ш3 = dx3 Д dr3, г2 = х\ + х\ + х\, на паре векторов | = A, 1, 1),
Ч = A, 2, 3), приложенных в точке а: = B, 0, 0).
Ответ, щ = 1, ш2 = —2, ю3 = —8.
Задача 10. Пусть хг, . . ., хп: М —» R — функции на многообра-
многообразии, образующие локальную координатную систему в некоторой области.

158
ГЛ. 7. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
Докажите, что каждая дифференциальная форма в этой области однозначно
записывается в виде
it
Пример. Замена переменных в форме. Пусть в R3 имеются
две системы координат: хг, х2, хъ и ух, уг, у3. Пусть со — 2-форма
в R3. Тогда по последней теореме в системе ж-координат со запи-
записывается в виде со = Xrdx2 Д dx3 -f X2dxs /\ dxx -f X3dxl Д dx2,
где Xl7 X2, X3 — функции от хх, х2, х3, и в системе у-коорди-
нат — в виде и = Угйу2 Д dy3 + Y2dy3 Д dyx -f Ysdy1 Д dy2,
где Yu У2, У3 — функции от у1л у2, у3.
Задача 11. Зная вид формы в ^-координатах (т. е. Х$) и формулы
аа51ены переменных, ж = ас (у), найти вид формы в г/-коордпнатах, т. е.
найти У.
dxi dx.t d.ct
Решение. Имеем dr. = -щ- dyx-\- -g— dy2-{- -щ- dys. Поэтп.му
щ-
откуда
0x2
D (г/1, г/г)
dr3
D (-1, х2)
D (г/ь г/г)
И Т. Д.
2,
р
Рис. 144. К зада-
задаче 12
Рис. 145. К за-
задаче 13
Б. Добавление. Дифференциальные формы в трехмерном про-
пространстве. Пусть М — трехмерное ориентированное риманово мно-
многообразие (во всех дальнейших
примерах М — евклидово трех-
мерное пространство R3). Пусть
х-у, хг, х3 — локальные координаты,
и пусть квадрат элемента длины
имеет вид
ds2 = Exdx\ + E%dx\ + Esdxl
(т. е. система координат триорто-
гональная).
Задача 12. Найтп Ег, Е2, Е3 для декартовых координчт х, у, г.
цилиндрических координат г, ф, z и сферических координат R, ф, в в евкли-
евклидовом пространстве R3 (рис. 144).
Ответ.
ds2 = dx2 + dif + dz2 = dr2 + r2dq? + dz2 = dR2 + R2 cos2 G d(f + R2dQ2.
Обозначим через ех, е2, е3 орты координатных направлений.
Эти три вектора образуют базис в касательном пространстве.
Задача i3. Найти значения форм йг1? dx2, dx3 на векторах е,, е2, es*
Ответ. dxi(ei)^=—, — , с стальные 0. В частности, в декартовой си-
V Ei
стеме dx (ex) = dy (еу) — dz (ez) = 1; в^ цилиндрической dr (er) = dz (ez) =

§ 34. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ 157
= 1, dq> (e^) = llr (рис. 145); в сферической dR (eR) = 1, Лр (e^) = -д cps e ,.
Метрика и ориентация многообразия М снабжают касательное-
пространство к М в каждой точке структурой евклидова ориенти-
ориентированного трехмерного пространства. В смысле этой структуры
мы будем говорить о скалярных, векторных и смешанных про-
произведениях.
Задача 14. Вычислить \ех, е2], (ед, ce) и (ez, ex, еу).
Ответ. е3, О, 1.
В ориентированном трехмерном евклидовом пространстве каж-
каждому вектору А соответствуют 1-форма иы и 2-форма ы2А, опре-
определяемые условиями
Соответствие между векторными полями и формами не зависит
от системы координат, но лишь от евклидовой структуры и ори-
ориентации. Поэтому каждому векторному полю А на нашем много-
многообразии М соответствуют дифференциальная 1-форма шд на М и
дифференциальная 2-форма ы2а на М.
Формулы перехода от полей к формам и обратно имеют в каж-
каждой системе координат свой специальный вид. Пусть в координа-
координатах a?i, х2, х3, описанных выше, векторное поле имеет вид
А = Ахег + А2е2 + А3е3
(компоненты А{ — гладкие функции на многообразии М). Соот-
Соответствующая 1-форма аул разлагается по базису dxi, а соответ-
соответствующая 2-форма шл — по базису dx{ Д dxj.
Задача 15. Зная компоненты векторного поля А, найти разложе-
разложения 1-формы (оА и 2-формы (оА.
Решение. Имеем (оА (е,) = (А, е,) = А±. В то же время (a1dx1 -f-
+ azdx2 + а^х3) (ех) = aydxx (ex) = ajVЕг- Отсюда находим ex = Ax"\fЕ,*
так что
«л =
Точно так же имеем ш^, (е2, «з) = Mi*e2> ез) — А\- В то же время
1
(axdx2 Д da-s + a2dx3 Д dxx + a3 dxx Д dx2) (е2, е3) =
Отсюда ах = АХУЕ2ЕЬ, т. е.
> = А^ЕЕ^х Д dxs

158 ГЛ. 7. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
Ь частности, в декартовых, цилиндрических и сферических координатах
в R3 векторному полю
А = Ахех + Ауеу + Afz = Атет + ЛЛ + Azez = АПеВ + ^Ф
отвечает 1-форма
ш^ = Axdx + /4ydy -J- Azdz = /4rdr + M^dtp -f- A.zdz =
= 4Rdi? -f R cos G Л^йср + RA^dk)
й 2-форма
<*г + Aydz /\dx + Azdx /\ dy =
= rArd<p /\dz + Aq>dz/\dr+ rAzdr Д d<p =
= i?2 cos e/4Hd<p Д d8 + Л^^^б Д dff + i? cos G/4zdi? Д d(p.
Примером векторного поля на многообразии М является гра-
градиент функции /: М -*¦ R. Напомню, что градиентом функции
называется векторное поле grad /, соответствующее дифферен-
дифференциалу:
4 = d/, т.е.
Задача 16. Найти компоненты градиента функции в базисе ег, е2, еа.
df df df
Решение. Имеем df = -z— dx\ -f- -z— dx2 + -s— dx3. Согласно пре-
предыдущей задаче
i df i df 1 df
grad/=e+w1^e+ ^
В частности, в декартовых, цилиндрических и сферических координатах
A f gf , df , *t df \ df df
df_ 1 df 1 df
= dReR+ R cos 6 d<p % + R 59 V
§ 35. Интегрирование дифференциальных форм
Здесь определены понятия цепи, границы цепи и интеграла формы поце-
пи. Интеграл дифференциальной формы есть многомерное обобщение таких
понятий, как поток жидкости через поверхность
или работа силы на пути.
А. Интеграл 1-формы по пути. Нач-
Начнем с интегрирования 1-формы о1 на
многообразии М. Пусть у: [О <I t <I 1] ->•
—> М — гладкое отображение («путь ин-
интегрирования»). Интеграл формы to1 на
пути у определяется как предел интег-
Рис. 146. интегрирование ральных сумм. Каждая интегральная сум-
1-формы по пути «vi
ма составляется из значении формы шА
на касательных векторах |f (рис. 146):

§ 35. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ 159
Касательные векторы §,- строятся следующим образом. Отрезок
0< t <; 1 точками ^делится на части Дг: ?г <; t <I ti+1. Отрезок Д*
можно рассматривать как касательный вектор Д{ к оси t в точ-
точке tt. Его образ в касательном пространстве к М в точке у ()
и есть
При стремлении наибольшего из отрезков Аг к нулю интег-
интегральные суммы имеют предел. Он и называется интегралом
1-формы со1 по пути у.
Замысел определения интеграла А-формы по fr-мерной поверх-
поверхности аналогичен. Поверхность интегрирования разбивается на
малые криволинейные А-мерные параллелепипеды (рис. 147) ^
Рис. 147. Интегрирование 2-формы Рис. 148. Интегрирование fc-фор-
по поверхности мы в fe-мерном пространстве
эти параллелепипеды заменяются параллелепипедами в касатель-
касательном пространстве, сумма значений формы на параллелепипедах
касательного пространства стремится к интегралу при измель-
измельчении разбиения. Рассмотрим вначале частный случай.
Б. Интеграл А"-формы в fc-мерном ориентированном евклидовом
пространстве Rfc. Пусть хх, . . ., хк — ориентирующая система
координат в Rfc. Тогда всякая А-форма в RK пропорциональна
форме dxx /\ . . . /\ dxb, т. е. имеет вид шк = ф (х) йхг Д . . .
. . . Д dxb, где ф (х) — гладкая функция.
Пусть D — выпуклый ограниченный многогранник в Rs
(рис. 148). По определению, интегралом формы tok no D назы-
называется интеграл функции ф:
^ к = ^ ф (х) dxx . . . йхц,
D D
где интеграл справа понимается как предел обычных римановых
интегральных сумм.
Такое определение является реализацией намеченного выше
замысла, так как в рассматриваемом случае касательное простран-
пространство к многообразию отождествляется с многообразием.
Задача 1. Докажите, что \ ш зависит от ш* линейно.
D
Задача 2. Докажите, что если разбить D на два выпуклых многогран-
многогранника, />, и D2, то { ш* = V шк + С шк.

160
ГЛ. 7. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
В общем случае (А-форма в n-мерном пространстве) отождест-
отождествить элементы разбиения с касательными параллелепипедами не
так просто; ниже мы сведем этот случай к рассмотренному.
В. Поведение дифференциальных форм при отображениях.
Пусть /: М -*¦ N — дифференцируемое отображение гладкого мно-
многообразия М в гладкое многообра-
многообразие N и и — дифференциальная к-
форма на N (рис. 149).
Тогда на М также возникает оп-
определенная fc-форма; она обознача-
ется через /*ш и определяется со-
соРис. 149. Форма на N индуци-
рует форму на М
отношением
(/*ш)
., |ft е= ТМЖ. Здесь
лри любых касательных векторах |
есть дифференциал отображения /.
Иными словами, значение формы /*со на векторах ?х, . . ., §fc
равно значению формы to на образах этих векторов.
Пример. Если у = f {хг, х2) = а^ + я| и ш
то
/*ш =
Задача 3. Докажите, что f*(n есть fc-форма на М.
Задача 4. Докажите, что отображение f* сохраняет операции над
¦формами:
/*
/• («1 Л »2) = (/*%) Л СРш»).
Задача 5. Пусть g : L ~^> М — дифференцируемое отображение. До-
Докажите, что (fg)* = g*/*.
Задача 6. Пусть Dx и D2 — два компактных выпуклых многогранни-
многогранника в ориентированном Л-мерном пространстве R* и f : Dx —» D2 — дифферен-
дифференцируемое отображение, осуществляющее диффеоморфное *), сохраняющее
¦ориентацию отображение внутренности Dx на внутренность D2- Тогда для
.любой дифференциальной А-формы шк в D2
S
S
D.
Указание. Это — теорема о замене переменной в кратном ннте-
трале:
д(у ,у ) I»
а(х,...,х) ч»<"<х»^"• • dxn = )«рto)*i-~*vn.
г п D,
Г. Интегрирование /t-формы на /j-мерном многообразии. Пусть
— дифференциальная fe-форма на n-мерном многообразии М.
D,
*) То есть взаимно-однозначное и взаимно-дифференцируемое.

§ 35. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ
161
Пусть D — ограниченный выпуклый
ник в /с-мерном евклидовом пространстве
Роль «пути интегрирования» будет иг-
играть А-мерный кусок *) а в М, представ-
представляющий собой тройку а = (D, /, Ор), со-
состоящую из
1) выпуклого многогранника D с Rfc,
2) дифференцируемого отображения
/с-мерный многогран-
многогранRk (рис. 150).
Н
Рис. 150. Сингулярный
fe-ыерный полиэдр
3) ориентации Rk, обозначаемой Ор.
Определение. Интегралом /с-формы о по /с-мерному
куску сг называется интеграл соответствующей формы по много-
многограннику
Задача 7. Докажите, что интеграл зависит от формы линейно:
\ ^1<Й1 + 1-2.®Л = Я,1 \ ©! -(- Х2 \ (Й2.
Л-мерный кусок, отличающийся от а лишь выбором ориентации
Ор, называется противоположным о и
обозначается—сг или—1-сг (рис 151).
Задача 8. Докажите, что при изменении
ориентации интеграл меняет знак:
АД
Рис. 151. К задаче 8
Д. Цепи. Множество / (D) не обязательно является гладким
подмногообразием М. Оно может иметь «самопересечения», любые
«складки» и вырождаться даже в точку. Однако уже в одномер-
одномерном случае ясно, что неудобно ограничиваться контурами интег-
интегрирования, состоящими из одного куска: полезны также конту-
контуры, составленные из нескольких кусков, которые могут прохо-
проходиться в ту или иную сторону по нескольку раз. Аналогич-
Аналогичное понятие в многомерном случае называется цепью.
Определение. Цепь размерности к на многообразии М
состоит из конечного набора fe-мерных ориентированных кусков
Oj, . . ., ог в Ми целых чисел пгх, . . ., тг, называемых крат-
ностями (кратности могут быть положительными, отрицательны-
отрицательными или нулями). Цепь обозначается
• • • + тгаг.
*) Кусок о называют обычно сингулярным k-мерным полиэдром.

162
ГЛ. 7. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
При этом вводятся естественные отождествления
TWjO -f- т2о = (пг1 + т2) а,
тп1а1 + т2а2 = тп2о2 + /WiO^, Ост = 0, сч + 0 = cft.
Задача 9. Докажите, что множество всех ^-мерных цепей в многооб-
многообразии М становится коммутативной группой, если определить сложение цепей
формулой
(т^ + 1- mrar) + (mjaj + h "Var') =
= т&г -i + mrcr+ mjaj -f ... + m'r,c'r,.
E. Пример: граница многогранника. Пусть D — ориентиро-
ориентированный, выпуклый /с-мерный многогранник в /с-мерном евклидовом
пространстве Rfc. Границей D называется к — 1-мерная цепь 0D
в Rk, определенная следующим образом (рис. 152).
Кусками с,- цепи 0D являются к — 1-мерные грани Dt много-
многогранника D вместе с отображениями ft: Di-*~ R* вложения гра-
граней в Rft и ориентациями Ор,-, определенными ниже; кратности
же равны 1:
dD = ?о-г, а, = (Dt, ft. Op,)-
Правило ориентации граней. Пусть е1? . . .
. . ., еч — ориентирующий репер Rk. Пусть Dt — одна из граней D.
Выберем внутреннюю точку Dt и построим в ней вектор п
Рис. 152. Ориентация границы
Рис. 153. Граница цепи
внешней нормали к многограннику D. Ориентирующим грань Df
репером будет такой репер flt . . ., /Vx, в Dt, для которого репер
(»*, /i, . . ., fk-i) ориентирован правильно (т. е. как репер ех, . . .
• • -, ек).
Граница цепи определяется аналогичным образом. Пусть а =
= (D, /, Ор) — /с-мерный кусок в многообразии М. Его границей
да называется к — 1-цепь да = 2°*ь составленная из кусков
a,- = (D;, fu Орг), где Di — к — 1 мерные грани D, Орг — ориен-
ориентации, выбранные согласно приведенному выше правилу, f% —
ограничение отображения /: D -*- М на грань Dt.
Границей дсч /с-мерной цепи ск в М называется сумма границ
кусков цепи сй с кратностями (рис. 153):
дсь = д (пцо! + . . . + тгаг) = гщр^ + . . . + тгдаг.

§ 35. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ 163
Очевидно, дсь есть к — 1-цепь на М *).
Задача 10. Доказать, что граница границы любой цепи равна нулю:
ддск = 0.
Указание. Ввиду линейности д достаточно доказать ddD = 0 для
выпуклого многогранника D. Остается проверить, что каждая к — 2-мерная
грань D входит в цепь ddD дважды с разными знаками. Это достаточно про-
проверить для к = 2 (плоские сечения).
Ж. Интеграл формы по цепи. Пусть теперь шк есть А-форма
на многообразии М, а ск — А-цепь на М, сч = 2тгсгг. Интегра-
Интегралом формы toft no цепи ск называется сумма интегралов по кускам
с учетом кратностей
Задача 11. Докажите, что интеграл линейно зависит от формы:
Чг Чс Чг
Задача 12. Докажите, что интегрирование фиксированной формы
ш* по цепям ск определяет гомоморфизм группы цепей
в прямую.
Пример 1. Пусть М есть плоскость {(р, q)},
форма ш1 есть р dq, цепь сг состоит из одного куска ох с
кратностью 1:
[0 ^ t ^ 2п] -^ (р = cos t, q = sin t).
Тогда
Рис. 154. Интеграл
: я. формы р dq по гра-
границе области равен
d площади области
Вообще, если цепь сг представляет границу области G (рис. 154), то \р dq
с,
равен площади G со знаком + или — в зависимости от того, ориентирована
ли пара векторов (внешняя нормаль, ориентирующий вектор границы) так
же, как базисная пара (орт р, орт q), или наоборот.
Пример 2. Пусть М есть ориентированное трехмерное евклидово
пространство R3. Тогда каждая 1-форма в М соответствует некоторому век-
векторному полю А (ш1 = о>1А), где
Интеграл формы аЛ по цепи с1? представляющей ориентированную кри-
кривую I, называется циркуляцией поля А по кривой I:
*) Мы считаем здесь к > 1. Одномерные цепи включаются в общую схему,
если принять следующие определения: нульмерная цепь состоит из набора
точек с кратностями; граница ориентированного отрезка А В есть В — А
(точка В с кратностью 1, А с кратностью —1); граница точки пуста.

164 ГЛ. 7. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
Каждая 2-форма в М также соответствует некоторому полю A (со2 =
= в?л, где «^ (|, ч) =(АЛ, Ч)).
Интеграл формы со^ по цепи с2, представляющей ориентированную по-
поверхность S, называется потоком поля А через поверхность S:
\ = ^(А, dn).
S
Задача 13. Найти поток поля А = -^ eR через поверхность сферы
я* + J/2 + z2 = 1, ориентированную векторами ех, еу в точке z = 1. Найти
поток того же поля через поверхность эллипсоида хг1а2 + y2/b2 + zs = 1,
ориентированную так же.
Указание. См. стр. 171.
Задача 14. Пусть в 2ге-мерном пространстве R2n = {(р±, . . ., рп;
9i, ¦ ¦ ч <7п)} Дана 2-цепь с2, представляющая ориентированную двумерную
поверхность S с краем I. Найти
{ +dpn/\dqn и
с, 1
Ответ. Сумма ориентированных площадей проекций S на координатные
двумерные плоскости р%, gj.
§ 36. Внешнее дифференцирование
Здесь определяется внешнее дифференцирование ft-форм и доказывается
формула Стокса: интеграл производной формы по цепи равен интегралу
самой формы по границе этой цепи.
А. Пример: дивергенция векторного поля. Внешняя произ-
производная А-формы to на многообразии М есть к + 1-форма dco на
том же многообразии. Переход от формы к ее внешней производ-
производной аналогичен образованию дифференциала функции или дивер-
дивергенции векторного поля. Напомню определение
дивергенции.
Пусть А — векторное поле в евклидовом
ориентированном трехмерном пространстве R3
и S — граница параллелепипеда П с ребра-
ребрами |х, |2, ?3 при вершине х: S — дП (рис.
_- ,7 155). Рассмотрим поток поля А через поверх-
? ность S («наружу»):
Рис. 155.' К опреде- „
пению дивергенции р /гтх — \(Л Дп\
векторного поля г \1Ч — J И1» ап)'
S
Если параллелепипед П очень мал, то поток F приблизительно
пропорционален произведению объема параллелепипеда, V =
— (In ?2» 1з)» на «плотность источников» в точке х. Иными сло-
словами, существует предел

§ 36. ВНЕШНЕЕ ДИФФЕРЕНЦИРОВАНИЕ
165
где еП — параллелепипед с ребрами e|lf e|2, е?3. Этот предел
не зависит от выбора параллелепипеда П, но лишь от точки х,
и называется дивергенцией поля А в х, div А.
Чтобы перейти к многомерному случаю, заметим, что «поток А
через элемент поверхности» есть 2-форма, которую мы обозначили
а&. Дивергенция же есть плотность в выражении 3-формы
to3
to3 = div A dx Д dy Д dz,
h) = ^v A- V
12, !3),
характеризующей «источники в элементарном параллелепипеде»»
Внешняя производная d(ok А-формы шк на к-мерном многооб"
разии М определяется как главная полилинейная часть интег-
интеграла ы" по границе к + 1-мерного параллелепипеда.
Б. Определение внешней производной. Определим значение
формы da на А; + 1 векторе |j, . . ., |k+1, касающемся М в х. Рас-
Рассмотрим для этого какую-нибудь систему координат в окрестности
М
Рис. 156. Криволинейный параллелепипед П
точки ж на М, т. е. диффеоморфное отображение / окрестности
точки 0 в евклидовом пространстве R" на окрестность точки ж
в М (рис. 156).
Прообразы векторов \х, . . ., 1к+1 ?: ТМХ при дифференциа-
дифференциале / лежат в касательном пространстве к R" в 0. Это касательное
пространство естественно отождествляется с Rn, поэтому можно
считать прообразы векторами
5
fci: « •
Натянем на эти векторы в R" параллелепипед П* (строго го-
говоря, надо рассмотреть стандартный ориентированный куб в Rfc+1
и его линейное отображение на П*, переводящее ребра elf . . .
. . ., ejr+1 в ?*, . . ., |*+1, как А: + 1-мерный кусок в R").
Отображение / переводит параллелепипед П* в к + 1-мерный
кусок П на М («криволинейный параллелепипед»). Граница кус-
куска П есть /с-мерная цепь, 9ГГ. Рассмотрим интеграл формы ю*
по границе дП параллелепипеда П:
= \ GO".
en

166 ГЛ. 7. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
Пример. Будем называть О-формой на_М гладкую функцию <р: М ¦
' формы ф по О-цепи
точки М) назовем
• R. Интегралом б-формы ф по О-цепи с0 = ЪпцАг (где mi — целые,
Тогда предыдущее определение дает «приращение»
F (|х) = ф (xj) — ф(ж) (рис. 157) функции ф, а главная
линейная часть ^(li) в 0 есть просто дифференциал
функции ф.
Рис. 157. интеграл по 3 а д а ч а 1. Докажите, что F (lt, . . ., %к+1) косо-
рранице одномерного симметрична по |.
пар аллелепипеда— это
приращение Функции Оказывается, главная к + 1-линейная
часть «приращения» F (§1} . . ., %>k+i) есть внеш-
внешняя к + 1-форма на касательном пространстве ТМЖ к М в ас.
Эта форма не зависит от системы координат, с помощью которой
определялся криволинейный параллелепипед П. Она называется
внешней производной формы to* (в точке х) и обозначается dco*.
В. Теорема о внешней производной.
Теорема. На ТМЖ существует и единственна к + 1-форма Q,
которая является главной к + 1-линейной частью в 0 интеграла
по границе криволинейного параллелепипеда F (|1? . . ., |it+i): т. е.
F (eb, . . ., e|fc+1) = e*«Q (glf .... ?K+1) + о (e*«) (e -*» 0). A)
Форма Q «e зависит от выбора системы координат, участвую-
участвующей в определении F.
Если в локальной системе координат х1г . . ., хп на М форма ч>*
записывается в виде
rjP^j to = 2jfK ¦ ¦ • iicdxh Л • • • Л dxik'
If / / то форма Q записывается в виде
п = dtoR = Zjdait . . . ik Л dxu Д - • . Л dxik- B)
%1 Доказательство этой теоремы я приведу
для случая формы to1 = а (хх, х2) dxx на плос-
Рис. 158. к теореме кости xlt x2. В общем случае доказательство
о внешней^производ- совершенно аналогичное, но выкладки несколь-
несколько длиннее.
Сосчитаем значение F, т. е. интеграл to1 по границе паралле-
параллелограмма П со сторонами §, ц и вершиной в 0 (рис. 158). Цепь
дЛ задается отображениями отрезка 0 <[ t <^ 1 на плоскость t >->-
*-*-%t, t ¦-»- | + r\t, ti->- if, t ь-+ц + %t с кратностями 1, 1, —1, —1.
Поэтому
5
on
l
= I [a (It) -а(Ь + Ц)] h - [a (rf) - а

§ 36. ВНЕШНЕЕ ДИФФЕРЕНЦИРОВАНИЕ 167
где 1г = dxx (?), % = dxx (ц), |2 = dx2 (g), tj2 = dx2(\\) — ком-
компоненты векторов §, tj. Ho
(производные берутся при хх = х2 = 0). Точно так же
Подставляя эти выражения в интеграл, находим
F it, п) = \ ю1 = —— (toTi, — tiilo) + о (tz + Ti2).
en
Главная билинейная часть F, как обещано в A), оказалась зна-
значением внешней 2-формы
на паре векторов |, tj. При этом полученная форма дается фор-
формулой B), ибо
da/\dx1 = -^-dx1/\dx1 + -^-dx2/\ dxt = -^-dx2/\ dxt.
Наконец, если систему координат хх, х2 заменить другой (рис. 159),
то параллелограмм П заменится близким криволинейным паралле-
параллелограммом П', так что разница значений интег-
интегралов \ to1 — \ to1 будет малой выше второго
еп еп'
порядка (проверьте!), ч.т.д.
Задача 2. Провести доказательство теоремы в
общем случае.
Задача 3. Доказать формулы дифференцирова-
дифференцирования суммы и произведения: Рис. 159. Независи-
Независимость внешней про-
d (to* Д to') = do* Л й' + (—1)кю* Д d@l, изводной от системы
координат
d ((Oj^ + щ) — dtOj + dtOj.
Задача 4. Доказать, что дифференциал дифференциала равен нулю:
dd = 0.
Задача 5. Пусть /: М -+ N — гладкое отображение, ю — Л-форма
на Л^. Докажите, что /* (dto) = d (/*to).
Г. Формула Стокса. Одним из важнейших следствий теоремы
о внешней производной является формула Ньютона —
Лей б н и ца — Гаусса — Грина — Остроградско-
Остроградского — Стокса — Пуанкаре:
\ to = \ d<D, C)
дс с

168
ГЛ. 7. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
где с — любая к + 1-цепь на многообразии М, а <й — любая
/с-форма на многообразии М.
Доказательство этой формулы достаточно провести
для случая, когда цепь состоит из одного куска а. Предположим
сначала, что этот кусок а задается ориентирован-
ориентированным параллелепипедом П С Rft+1 (рис. 160).
Разобьем П на N**1 малых равных парал-
параллелепипедов Л,, подобных П. Тогда, очевидно,
г
1
~|
1
<о =
ь где Ft =
со.
Рис. 160. Дока-
вательство фор- „ ...
мулы стокса для 11о формуле A) имеем
параллелепипеда
Ft = d<o (И, . .
где И, . . ., Ц+1 — ребра Пг. Но 2j
г=1
тральная сумма для J dco. Легко проверить, что о (N-^+u) —
п
равномерное, поэтому
U, • • •. Ifc+i) есть инте-
lim 2i Fi =
Окончательно находим
П
еп
Отсюда автоматически следует формула C) для любой цепи, мно-
многогранники которой — параллелепипеды.
Чтобы доказать формулу C) для любого вы-
выпуклого многогранника D, достаточно доказать
ее для симплекса *), так как D всегда можно
разбить на симплексы (рис. 161):
Рис. 161. разбиение Докажем формулу C) для симплекса. За-
выпуклого много- ... -
метим, что Аг-мерный ориентированный куб
грэшникэ нэ сим— v v ^ 1
плексы
можно дифференцируемо отобразить на йг-мер-
ный ориентированный симплекс так, что:
*) Двумерный симплекс есть треугольник, трехмерный — тетраэдр,
Л-мерный — выпуклая оболочка к + 1 точки в R71, не лежащей ъ к — 1-мер-
1-мерной плоскости.
к
Пример. {xi=R : ж. >0, >2 ж,<1} .

§ 36. ВНЕШНЕЕ ДИФФЕРЕНЦИРОВАНИЕ 169
1) внутренность куба диффеоморфно и с сохранением ориента-
ориентации переходит во внутренность симплекса;
2) внутренности некоторых к — 1-мерных граней куба диф-
диффеоморфно и с сохранением ориентации переходят во внутренности
граней симплекса; образы остальных к — 1-мерных граней куба
лежат в к — 2-мерных гранях симплекса.
Например, для к — 2 такое отображение куба 0 <^ xv xa <^ 1
на треугольник дается формулами yt = хг, у2 = xtx2 (рис. 162).
Теперь формула C) для симплекса вытекает из доказанной фор-
формулы (З)для куба и теоремы о замене переменной (см. стр. 160).
Пример 1. Рассмотрим в R2n с ко-
координатами pv . . ., рп; ди . . ., дп 1-форму
to1 = pxdqx + . . . + pndqn = p dq.
Тогда dto1 = dpx Д dqx + . . . + dpn Д dqn =
= dp A dq, поэтому
¦^ ' N a' J Рис. 162. Доказатель-
pp n ctbo формулы Стоке»
y^ dp Д dq = J p dq. для симплекса
с, дс,
В частности, если с2 — замкнутая поверхность (дс2 = 0), то
Д. Пример 2. Векторный анализ. В трехмерном ориентирован-
ориентированном римановом пространстве М всякому векторному полю А
соответствует 1-форма ©д и 2-форма (о^. Поэтому внешнее диффе-
дифференцирование можно рассматривать как векторную операцию.
Внешнему дифференцированию 0-форм (функций), 1-форм в
2-форм отвечают операции градиента, ротора и дивергенции,
определенные соотношениями
df = <4rad /. d<o]i = torot л, d<?>2A = div A<o3
(форма to3 — элемент объема на М). Итак, из C) вытекает
f(y) — f (х) = I grad / • d*. если dl = y —
=\ § rot A • dn, если dS = I,
s
divA<o3, если dD — S.
S D
3 а д а ч а 6. Докажите, что
div [A, B] = (rot A, B) — (rot B, A),
rot aA = [grad a, A] + a rot A,
div aA = (grad a, A) -\- a div A.

170 ГЛ. 7. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
Указание. По формуле дифференцирования произведения форм
d (Ш[Л, л]) = d («л Л <4) = &*а Л ч>д - <*л Л dwi,.
Задача 7. Докажите, что rot grad = div rot = 0.
Указание, dd = 0.
E. Добавление 1. Векторные операции в< триортогональной
системе. Пусть хх, х2, х3 — триортогональная система коорди-
координат в М, ds% = Ejdxl + Egdxl + ?3dx| и et — координатные орты
(см. стр. 156).
Задача 8. Зная компоненты векторного поля А = А1е1 + Аге2 -f-
-Ь itae3, найти компоненты его ротора.
Решение. Согласно стр. 157,
«Л =.
Поэтому
По стр. 157 находим
В частности, в декартовых, цилиндрических и сферических координатах в R3:
0Az 6Ау\ (вАх вА\ (дАу в А
1 / дАг drAv \ (^\,_^Л 1 / дгАу дАг \
1 / дАв g^
~ iicosG \ Зф З
1 /Мд ^Д^е 1 ,J_/.^ ^
+ Д \ вв ЗЛ у еФ+ R \ dR cos в Зф У ев
Задача 9. Найти дивергенцию поля А = Ахех + А2е2 + А3е3.
Решение. ш^= A{\fE2E3 dx2 Д dx3 + . . . Следовательно,
iAVE&) dXl/\dx2/\dx3+...
По определению дивергенции,
dwA = div AyfE^E, dxj /\ dx^ /\ dxs.
Значит,

§ 36. ВНЕШНЕЕ ДИФФЕРЕНЦИРОВАНИЕ 17f
В частности, в декартовых, цилиндрических и сферических координатах в R*t
дА,
г V дг т Зш / ' дг
1 (
л^совв V
Г" "
да т а<р ^ ае J
Задача 10. Оператором Лапласа на М называется оператор Д
= div grad. Найти его выражение в координатах xi.
л, * Г 9 (Л[~ЕЖ df
Ответ- Л/= [[V
В частности, в R3
er*j т &f _<pj i df
— 3^ T ду2 "Г g22 Зг2 "Г г Зг
Ж. Добавление 2. Замкнутые формы и циклы. Поток несжи-
несжимаемой жидкости (без источников) через край области D равен
нулю. Сформулируем многомерный аналог этого очевидного пред-
предложения.
Многомерный аналог потока без источников называется замк-
замкнутой формой.
Поле А не имеет источников, если div A = 0.
Определение. Дифференциальная форма to на много-
многообразии М замкнута, если ее внешняя производная равна нулю!
dv> = 0.
В частности, 2-форма <о2А, отвечающая полю без источни-
источников А, замкнута. Из формулы Стокса C) сразу следует
Теорема. Интеграл замкнутой формы to"
по границе любой к + \-мерной цепи ск+1 равен
нулю:
\j tofc = 0, если d<ok = 0.
eek+l
Задача 11. Докажите, что дифференциал фор-
формы всегда замкнут.
С Другой СТОРОНЫ, Существуют замкнутые Рис. 163. Поле Л
формы, не являющиеся дифференциалами.)
Например, рассмотрим в качестве многообразия М трехмерное
евклидово пространство R3 без точки О: М = R3 — О, а в качестве
2-формы — поток поля А = -щ ен (рис. 163). Легко убедиться, что
div А = 0, так что наша 2-форма «& замкнута. В то же время
поток через любую сферу с центром в О равен 4я. Покажем, что
интеграл дифференциала формы по сфере должен равняться нулю.

172 ГЛ. 7. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
Определение. Циклом на многообразии М называется
цепь, граница которой равна нулю.
Ориентированную поверхность нашей сферы можно рассматри-
рассматривать как цикл. Из формулы Стокса C) сразу следует
Теорема. Интеграл дифференциала по любому циклу
равен нулю:
= 0, если дсъ+1 = 0.
Итак, наша 2-форма со^ не есть дифференциал никакой
1-формы.
Существование на мнообразии М замкнутых форм, не явля-
являющихся дифференциалами, связано с топологическими свой-
свойствами М. Можно показать, что в линейном пространстве всякая
замкнутая йг-форма есть дифференциал некоторой к — 1-формы
(«лемма Пуанкаре»).
Задача 12. Докажите лемму Пуанкаре для 1-форм.
—'1
Указание. Рассмотрите \ со1 = ср{х{).
Задача 13. Докажите, что в линейном пространстве интеграл замкну-
замкнутой формы по любому циклу равен нулю.
Указание. Построить к + 1-цепь, границей которой является дан-
данный цикл (рис. 164).
А именно, для любой цепи с рассмотрите «конус
над с с вершиной 0». Если обозначить операцию пост-
построения конуса через р, то
дор -\- род = 1 (тождественное преобразование).
Поэтому, если цепь с замкнута, то д (рс) = с.
Задача 14. Докажите, что в линейном простран-
Рис. 164. Конус над стве всякая замкнутая форма является полным диффе-
циклом ренциалом.
Указание. Воспользоваться конической кон-
конструкцией. Пусть со*—дифференциальная ft-форма в Rn. Определим диффе-
дифференциальную к — 1-форму («коконус над со») рсо* следующим образом: для
любой цепи Cfj^
рсо = ^ со
Легко проверить, что к — 1-форма рсо* существует и единственна; ее значе-
ние^на векторах |х, . .. , ?к_1? касательных к R" в ж, равно
l, • • •. Sfc-i) = J 4>tx (*. *|l. • • •. *lK-l) dt-
Легко проверить, что
d°p + p°d = 1 (тождественное преобразование).
Поэтому, если форма <ок замкнута, то d (/?со^) = «А

§ 36. ВНЕШНЕЕ ДИФФЕРЕНЦИРОВАНИЕ 173
Задача 15. Пусть X — векторное поле на Л/, а со — дифференциаль-
дифференциальная fc-форма. Определим дифференциальную к — 1-форму (так называемое
внутреннее произведение X на со) ix<o соотношением
(ixco) (|1? . . ., |fc_i) = со (X, 1и . . ., gfc_J.
Докажите формулу гомотопии
где Lx — оператор дифференцирования по направлению поля X.
[Действие оператора Lx на формы определяется с помощью фазового
потока {g*} поля X соотношением
xw — dt \t=ow g*
Оператор Lx называют производной Ли или производной рыбака: поток несет
мимо рыбака всевозможные {дифференциально-геометрические объекты, а ры-
рыбак сидит на месте и их дифференцирует.]
Указание. Обозначим через Н «оператор гомотопии», сопоставляю-
сопоставляющий jfe-пепи у: о* —» М к + 1-цепь Ну: (/ х от) —» М по формуле (Ну) (t, х) =
= g*v (*) (где / = [0,1]). Тогда
giy _ т = д (Ну) + Н (ду).
Задача 16. Докажите формулу дифференцирования векторного про-
произведения в трехмерном евклидовом пространстве (или римановом многообра-
многообразии):
rot [а, Ь] = {а, Ь) + a div Ь — Ь div а
(где {а, Ъ) = Lab — скобка Пуассона векторных полей, см. § 39).
Указание. Если т — элемент объема, то
'rot [а, 6] т = diahx, div « = dia*, {«. *>} = Lab;
пользуясь этими соотношениями и не забывая, что dx = 0, легко вывести фор-
формулу для rot [а, Ь] из формулы гомотопии.
3. Добавление 3. Когомологии и гомологии. Все /с-формы
на М образуют линейное пространство, замкнутые Л-формы —
его подпространство, а дифференциалы к — 1-форм — подпро-
подпространство пространства замкнутых форм. Фактор-пространство
(замкнутые формы)/(дифференциалы) = Нк (М, R)
называется к-мерной группой когомологии многообразия М. Эле-
Элементом этой группы является класс замкнутых форм, отличаю-
отличающихся друг от друга лишь на дифференциал.
Задача 17. Доказать, что для окружности S1 имеем Я1 (S1, R) = R.
Размерность пространства Hk (M, R) называется к-мерным
числом, Бетти многообразия М.
Задача 18. Найти одномерное число Бетти тора Т2 = S1 X S1.
Поток жидкости (без источников) через поверхности двух
концентрических сфер одинаков. Вообще, при интегрировании

174
ГЛ. 7. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
замкнутой формы по ^-мерному циклу можно заменять цикл на
другой при условии, что их разность есть граница к + 1-мерной
цепи («пленки», рис. 165):
Рис. 165. Гомологичные циклы
ь
если а — Ъ = дск+1 и do? — 0.
Такие два цикла с, Ъ Пуан-
Пуанкаре назвал гомологичными.
При надлежащем определе-
определении *) группы цепей на много-
многообразии М и лежащих в ней
подгрупп циклов и границ (т. е.циклов, гомологичных нулю),
фактор-группа
(циклы)/(границы) = Нк (М)
называется к-мерной группой гомологии М.
Элементом этой группы является класс гомологичных друг
другу циклов.
Ранг этой группы также равен ^-мерному числу Бетти мно-
многообразия М («теорема Де Рама»).
*) Нашу группу {ejc} следует для этого уменьшить, отождествив между
собой куски, отличающиеся лишь выбором параметризации / и выбором
многогранников D. В частности, можно считать, что D — всегда один и тот
тот же симплекс или куб. Далее, следует считать равным нулю всякий к-
мерный кусок (D, /, Ор), если он вырожден, т. е. / = /2-/х, где /х: D —» D'
и D' имеет меньше чем к измерений.

ГЛАВА 8
СИМПЛЕКТИЧЕСКИЕ МНОГООБРАЗИЯ
Симплектическая структура на многообразии — это замкну-
замкнутая невырожденная дифференциальная 2-форма на нем. Фазовые
пространства механических систем имеют естественные симплек-
тические структуры.
На симплектическом многообразии, как и на римановом,
имеется естественный изоморфизм между векторными полями
и 1-формами. Векторное поле на симплектическом многообразии,
соответствующее дифференциалу функции, называется гамиль-
тоновым векторным полем. Векторное поле на многообразии
задает фазовый поток: однопараметрическую группу диффеомор-
диффеоморфизмов. Фазовый поток гамильтонова векторного поля на симплек-
симплектическом многообразии сохраняет симплектическую структуру
фазового пространства.
Векторные поля на многообразии образуют алгебру Ли. Га-
мильтоновы векторные поля на симплектическом многообразии
также образуют алгебру Ли. Операции в этих алгебрах называ-
называются скобками Пуассона.
§ 37. Симплектическая структура на многообразии
Здесь определены симплектические многообразия, гамильтоновы вектор-
векторные поля на них и стандартная симплектическая структура в кокасательном
расслоении.
А. Определение. Пусть М2?г-четномерное дифференцируемое
многообразие.
Симплектической структурой на М2п называется замкнутая
невырожденная дифференциальная 2-форма со2 на М2п:
Пара (М2П, со2) называется симплектическим многообразием.
Пример. Рассмотрим линейное пространство R2n с координатами
Pi, 5j, и пусть ю2 = SdPi Д dqi.
Задача. Проверить, что (R2™, ю2) — симплектическое многообразие.
При п = 1 пара (R2, ш2) есть пара (плоскость, площадь).
Следующий пример объясняет появление симплектических
многообразий в динамике. Наряду с касательным расслоением
дифференцируемого многообразия часто полезно рассматривать
Двойственное ему кокасательное.

176
ГЛ. 8. СИМПЛЕКТИЧЕСКИЕ МНОГООБРАЗИЯ
P'
*
t
Л
г
Рис. 166. 1-форма р dq
на касательном расслое-
расслоении
Б. Кокасательное расслоение и его симплектическая струк-
структура. Пусть V — дифференцируемое n-мерное многообразие. 1-
форма на касательном пространстве к У в точке ж называется
кокасателъным вектором к V в точке ж. Множество всех кокаса-
тельных к У в точке х векторов образует n-мерное линейное про-
пространство, сопряженное к касательному пространству TVX. Это
линейное пространство кокасательных векторов обозначается
через Т* Vx и называется кокасателъным пространством к много-
многообразию V в точке ж.
Объединение кокасательных пространств к многообразию во
всех его точках называется кокасателъным расслоением V и обо-
обозначается через T*V. Множество T*V име-
имеет естественную структуру дифференцируе-
дифференцируемого многообразия размерности 2п. Точка
из T*V — это 1-форма на касательном
пространстве к У в какой-либо точке из V.
Если q — набор п локальных координат
точки из V, то такая форма задается своими
п компонентами р. Вместе 2п чисел р, q со-
составляют набор локальных координат точки
T*V.
Существует естественная проекция
/ : T*V—*- V (сопоставляющая каждой
1-форме на ТVx точку ас). Проекция / является
дифференцируемым отображением на. Прообраз точки х €Е V
при отображении / есть кокасательное пространство T*VX.
Теорема. Кокасательное расслоение T*V имеет естествен-
естественную симплектическую структуру. В описанных выше локальных
координатах эта структура задается формулой
[со2 = dp /\dq = dPl Д <ki + — + dpn Л dqn.
Доказательство. Вначале мы определим на T*V
замечательную 1-форму. Пусть \EzT (T*V)P — вектор, касатель-
касательный к кокасателъному расслоению в точке р GE T*VX (рис. 166).
Производная Д: Т (T*V) —> TV естественной проекции / : T*V —> V
переводит | в вектор /„,?, касательный к У в точке ж. Определим
1-форму и1 на T*V соотношением ю1 (|) = р (/*?). В описанных
выше локальных координатах эта форма имеет вид ю1 = р dq.
Согласно примеру пункта А замкнутая 2-форма ю2 = daI не
вырождена.
Замечание. Рассмотрим лагранжеву механическую систему с кон-
конфигурационным многообразием V и функцией Лагранжа L. Легко сообразить,
что лагранжева «обобщенная скорость» q — касательный к конфигурацион-
конфигурационному многообразию V вектор, а «обобщенный импульс» р = dLldq — кока-
сательный. Поэтому фазовое «р, 9»-пространство лагранжевой задачи — зто
кокасательное расслоение конфигурационного многообразия. Итак, предыду-
предыдущая теорема показывает, что фазовое пространство механической задачи име-
имеет естественную структуру симплектического многообразия.

§ 38. ГАМИЛЬТОНОВЫ ФАЗОВЫЕ ПОТОКИ 177
3 а д а ч а. Покажите, что преобразование Лежандра не зависят от
системы координат: оно сопоставляет функции L : TV —» R на касательном,
расслоении функцию Н '. Т* V —» R на кокасательном.
В. Гамильтоновы векторные поля. Риманова структура на
многообразии устанавливает изоморфизм между пространствами
касательных векторов и 1-форм. Симплектическая структура также
устанавливает подобный изоморфизм.
Определение. Сопоставим вектору |, касательному
к симплектическому многообразию (Min, ш8) в точке ас, 1-форму
а»| на ТМХ по формуле
Задача. Доказать, 4toJ соответствие | ь-»- ю| есть изоморфизм линей-
линейных 2п-мерных пространств векторов и 1-форм.
Пример. В Rsn = {(р, q)\ будем отождествлять векторы и 1-формы
в соответствии с евклидовой структурой (л, со) = р2 -f- gz. Тогда соответствие
% >-*¦ со* задает преобразование R*ra —> В2П.
Задача. Вычислить матрицу этого преобразования в базисе р, q%
Ответ
Л ° Е\
Мы будем обозначать через / построенный выше изоморфизм
/ : Т*МХ -*- ТМХ.
Пусть теперь Н — функция на симплектическом многообра-
многообразии М2". Тогда dH есть дифференциальная 1-форма на М, и ей»
соответствует в каждой точке некоторый касательный к М вектор.
Мы получаем таким образом на М векторное поле / dH.
Определение. Векторное поле / dH называется гамилъ-
тпоновым векторным полем, Н — функцией Гамильтона.
Пример. Если Min = R2n = {(p, q)), то мы получаем поле фазовой,
скорости канонических уравнений Гамильтона
дН 6Н
§ 38. Гамильтоновы фазовые потоки
и их интегральные инварианты
Теорема Лиувилля утверждает, что фазовый поток сохраняет объемы.
Пуанкаре нашел целый ряд дифференциальных форм, сохраняемых гамиль-
тоновым фазовым потоком.
А. Гамильтоновы фазовые потоки сохраняют симплектическую
структуру. Пусть (М2™, ю2) — симплектическое многообразие»
Н : Л/2" -*- R — функция. Предположим, что соответствующее Н
гамильтоново векторное поле / dH задает однопараметрическую
группу диффеоморфизмов gl : Мгп -*¦ М2П,

178 ГЛ. 8. СИМПЛЕКТИЧЕСКИЕ МНОГООБРАЗИЯ
Группа g1 называется гамилътоновым фазовым потоком с ункцией
Гамильтона Н.
Теорема. Гамильтонов фазовый поток сохраняет симплек-
тическую структуру:
В случае в = 1, М2п = R2 эта теорема означает, что фазовый
лоток g1 сохраняет площади (теорема Лиувилля).
Для доказательства теоремы полезно ввести следующие
обозначения (рис. 167).
Пусть М — произвольное многообразие, с — А-цепь в М,
g1 : М —>- М — однопараметрическое семейство дифференциру-
дифференцируемых отображений. Построим
к + 1-цепь Jc в М, назы-
называемую следом цепи с при
гомотопии g1, О <^ t <^ т.
Пусть (D, /, Ор) — один
из кусков цепи с. В цепи Jc
ему будет соответствовать
Рис. 167. След цепи при гомотопии КУСОК (D', /', Ор'), ГДв
и = 1 X D — прямое произ-
произведение отрезка О <I t ^ т на D, отображение /' : D' —>-
—*• М выражается через / : D -*- М по формуле /' (t, x) =
= glf (x), и ориентация Ор' пространства Rk+1, содержащего D'g
задается репером е0, е1? . . ., ек, где е0 — орт оси f, a e1( ...
. . ., в|с — ориентирующий репер D.
Можно сказать,! что Jc — это цепь, которую с заметает при
гомотопии gl, 0 <; t <^ т. Граница цепи Jc из «торцов», образо-
образованных начальным и конечным положениями с, и «боковой поверх-
поверхности», заметенной границей с.
Легко проверить, что при указанном выборе ориентации
д (Jc^ = gxcb — ск — Jdck. A)
Лемма. Пусть у — i-цепъ в симплектическом многообразии
(М*п, а»2). Пусть g' — фазовый поток на М с функцией
Гамильтона Н. Тогда
d Г ¦¦• - [dH.
dx
Доказательство. Достаточно рассмотреть цепь у из
одного куска / : [0, 1] —*¦ М. Введем обозначения
/' (s, t) = g*f (s), 1 = dflds, tj = dfidt e TMr(?, t).
По определению интеграла
IX
j2 = ^aPfarfidtds.
о о

§ 38. ГАМИЛЬТОНОВЫ ФАЗОВЫЕ ПОТОКИ 179*
Но по определению фазового потока г\ есть вектор гамильтонова
поля с функцией Гамильтона Н (в точке /' (s, t)). По определению*
гамильтонова поля со2 (г\, %) = dH (|). Итак,
JY 0 V V
Лемма доказана.
Следствие. Если цепь у замкнута (ду = 0), mo j ш2 = 0-
Действительно, ^ dH = ^ Н = 0.
¦у ду
Доказательство теоремы. Рассмотрим любую»
2-цепь с. Имеем
A — ввиду замкнутости ю2, 2 — формула Стокса, 3 — формула
A), 4 — предыдущее следствие, у = дс). Итак, интегралы формы'
и2 по любой цепи с и по ее образу g^c одинаковы, что и требовалось
доказать.
Задача. Всякая ли однопараметрическая группа диффеоморфизмов
Ж2", сохраняющих симплектическую структуру, является гамильтоновым-
фазовым потоком?
Указание. См. § 40.
Б. Интегральные инварианты. Пусть g: М ->¦ М — дифферен-
дифференцируемое отображение.
Определение. Дифференциальная й-форма со называет-
называется интегральным инвариантом отображения g, если интегралы о>.
по любой А-мерной цепи с и по ее образу при отображении g оди-
одинаковы:
gc с
Пример. Если М = R2, а юа = dp Д dq — элемент площади, то ю2'
является интегральным инвариантом всякого отображения g с якобианом 1.
Задача. Докажите, что форма ю* является интегральным инвариан-
инвариантом отображения g тогда и только тогда, когда g*wlt = со*.
Задача. Докажите, что если формы юк и со1 — интегральные ин-
инварианты отображения g, то форма со* Д со1 — также интегральный инва-
инвариант g.
Теорему пункта А можно сформулировать так:
Теорема. Задающая симплектическую структуру форма а>а
является интегральным инвариантом гамильтонова фазового*
потока.
Рассмотрим теперь внешние степени формы со2,
(со2J = со2 Д »2. («>2K = со3 Л «8 Л «2, ....

180 ГЛ. 8. СИМПЛЕКТИЧЕСКИЕ МНОГООБРАЗИЯ
Следствие. Каждая из форм (со8)8, (со2K, . .. является
интегральным инвариантом гамилыпонова фазового потока.
3 а д а ч а. Пусть размерность си&шлектического многообразия (Л/2,
ю2) равна 2п. Покажите, что (ю2)к = 0 при к >¦ п, а (<в2)п — невырожденная
2ге-форма на М2п.
Определим элемент объема на ЛРП при помощи (оJ)п. Тогда
гамильтонов фазовый поток сохраняет объемы, и мы получаем из
предыдущего следствия теорему Лиувилля.
Пример. Рассмотрим координатное симплектическое прост-
пространство Mzn = R2n = {{р, q)}, <o* = dp /\dq = %dPl Д dqt.
В этом случае форма (со2)* пропорциональна форме
tf* = 2 dpil/\.../\dpik/\dqil/\.../\dqik.
г1<—<гЛ:
Интеграл формы (oafc равен сумме ориентированных объемов
проекций на координатные плоскости (ри ..., р,к, qh, . .. , qiH),
Отображение g: Ra" -*- R2n называется каноническим, если
оно имеет ю2 интегральным инвариантом. Каждая из форм со4,
to6, . . ., и2™ является интегральным инвариантом всякого канони-
канонического отображения. Следовательно, при каноническом отобра-
отображении сохраняется сумма ориентированных площадей проекций на
координатные плоскости (ph, . .., pif!, q^, . .., qiJt), 1 <Ik <! n.
В частности, канонические отображения сохраняют объемы.
Гамильтонов фазовый поток, заданный уравнениями р =
дН . дН , 1 „ j
= г—, а = —— состоит из канонических отображении g .
dq dp
Рассмотренные выше интегральные инварианты называют
также абсолютными.
Определение. Дифференциальная /с-форма со называет-
называется относительным интегральным инвариантом отображения
g: M -*• М, если
gc
для всякой замкнутой й-цепи с.
Теорема. Пусть со — относительный интегральный инва-
инвариант отображения g, тогда da — абсолютный интегральный
инвариант g.
Доказательство. Пусть с — к + 1-цепь, Тогда
вс gdc Sgс gc
<A и 4 — формула Стокса, 2 — определение относительного инва-
инварианта, 3 — определение границы).

§ 39. АЛГЕБРА ЛИ ВЕКТОРНЫХ ПОЛЕЙ 181
Пример. Каноническое отображение g: R211 -¦ R2n имеет относи-
относительным интегральным инвариантом i-форму
Действительно, всякая замкнутая цепь с в К2™ является границей неко-
некоторой цени а, и мы находим
go g da Of о go а да с
A и 6 — определение a, 2 — определение д, 3 и 5 — формула Стокса, 4 —
каноничность g и выкладка duf = d (p dg) = dp /\ dq = ю2).
Задача. Пусть dto" — абсолютный интегральный инвариант отобра-
отображения g: М —* М. Вытекает ли из этого, что ю* — относительный интеграль-
яый инвариант?
Ответ. Нет, если в М есть fc-мерные замкнутые цепи, не являющиеся
границами.
В. Закон сохранения энергии.
Теорема. Функция Н является первым интегралом гамиль-
тонова фазового потока с функцией Гамильтона Н.
Доказательство. Производная Н по направлению
вектора ц равна значению dH на векторе т). По определению га-
мильтонова поля tj = / dH находим
dH (Ч) = со2 (Ч, / dH) - со2 (Ч, ц) = 0.
Задача. Докажите, что 1-форма dH является интегральным инвариан-
инвариантом фазового потока с функцией Гамильтона Н.
§ 39. Алгебра Ли векторных полей
Каждой паре векторных полей на многообразии сопоставляется новое
векторное поле, называемое их скобкой Пуассона. Скобка Пуассона превра-
превращает линейное пространство бесконечно дифференцируемых векторных по-
полей на многообразии в алгебру Ли.
А. Алгебра Ли. Примером алгебры Ли является трехмерное
ориентированное евклидово линейное пространство, снабженное
операцией векторного умножения. Векторное произведение били-
билинейно, кососимметрично и удовлетворяет тождеству Якоби
UAS В], С] + [IB, C]t А] + [[Сх Alt В] = 0.
Определение. Алгеброй Ли называется линейное прост-
пространство L вместе с билинейной кососимметричной операцией
L X L -*¦ L, удовлетворяющей тождеству Якоби.
Операция обычно обозначается квадратными скобками и назы-
называется коммутатором.
3 а д а ч а. Докажите, что множество п X n-матриц становитс я алгеб-
алгеброй Ли, если определить коммутатор как [А, В] = А В — В А.

182 ГЛ. 8. СИМПЛЕКТИЧЕСКИЕ МНОГООБРАЗИЯ
Б. Векторные поля и дифференциальные операторы. Пусть
М — гладкое многообразие, А — гладкое векторное поле на М:
в каждой точке жеЛ/ задан касательный вектор А (ас) 6= ТМт.
С каждым таким векторным полем связаны сле-
дующие два объекта.
!• Однопараметрическая группа диффеомор-
физмое *), или поток А1 : М -*¦ М, для которо-
го Л есть поле скоростей (рис. 168):
Рис. 168. Группа ~~^
диффеоморфизмов, за-
данная векторным по- „ _ ,
лем 2. Дифференциальный оператор первого
порядка LA. Речь идет о дифференцирова-
дифференцировании функций по направлению поля А: для всякой функции
<р: М -*¦ R производная по направлению А есть новая функ-
функция ?лф, значение которой в точке ж есть
(LA<p) (ас) = тг Ц *
Задача. Докажите, что оператор ЬЛ линейный:
Докажите формулу Лейбница1 ?л (Ф1Ф2) = ф^лФа + ф2^лФ1-
Пример. Пусть (хи . . ., хп) — локальные координаты на М. В этой
системе координат вектор А (ас) задается компонентами (Ах (ас), . . ., Ап (ас));
поток А задается системой дифференциальных уравнений
*\ = А\ (*h ¦¦•i*n = ^n W
и, следовательно, производная ф = ф (хг, . . ., хп) по направлению А есть
Можно сказать, что оператор| LA в координатах (хг, . . ., хп) имеет вид
д д
а это и есть общий вид линейного дифференциального оператора первого по-
порядка в координатном пространстве.
Задача. Докажите, что соответствие между векторными полями А,
потоками А* я дифференцированиями LA взаимно однозначно.
В. Скобка Пуассона векторных полей. Пусть на многообра-
многообразии М даны два векторных поля А и В. Соответствующие по-
*) По теоремам существования, единственности и дифференцируемости
теории обыкновенных дифференциальных уравнений группа А* определена,
если многообразие М компактно. В общем случае отображения Аг опреде-
определены лишь в окрестности ас и лишь для малых t; этого достаточно для даль-
дальнейших конструкций.

§ 39. АЛГЕБРА ЛИ ВЕКТОРНЫХ ПОЛЕЙ
токи А1 и В1, вообще говоря, не коммутируют: AlBs ф В*А*
(рис. 169).
3 адата. Привести пример.
Решение. Поля А = et, В = xte2 на плоскости (xlt x2).
Для измерения степени некоммутативности двух потоков
А1, В" рассмотрим точки A'Bsx и В*А'х. Чтобы оценить различи»
между этими точками, сравним значение в них какой-нибудь
гладкой функции ф, заданной на много-
многообразии М. Разность
Д (t, s; x) = ф {А1В"х) — ф (BsAlx)
есть, очевидно, дифференцируемая функ-
функция, обращающаяся в 0 при s = 0 и при
t = 0. Поэтому первый отличный от 0 член
ряда Тейлора Д по s и t в 0 содержит st, a
другие члены второй степени исчезают. Со- _ ... „
**rJ r - „ Рис. 169. Некоммути-
считаем этот главный билинейный член рующие потоки
Д в 0.
Лемма 1. Смешанная производная Д по s, t в 0 равна комму-
коммутатору дифференцирований по направлениям А и В:
——— I Ф (А ох) — ф (В А х) = (LBLAq> —¦ LALBa>) (x).
OS Ot |s=f =0 lx/ ' т/г/
Доказательство. По определению LA,
Если обозначить функцию LA<p через if, то по определению LB
Итак,
что и требовалось доказать.
Рассмотрим теперь возникший коммутатор дифференцирований
LBLA — LALB. На первый взгляд это — дифференциальный опера-
оператор второго порядка.
Л е м м а 2. Оператор LBLA — LALB есть линейный дифферен-
дифференциальный оператор первого порядка.
Доказательство. Пусть (А17 . . ., Ап); {Вх, . . ., Вп) —
компоненты полей А, В в локальной системе координат (zlt • . ., #„)¦
на М. Тогда

184 ГЛ. 8. СИМПЛЕКТИЧЕСКИЕ МНОГООБРАЗИЯ
Если вычесть LALBff, то слагаемое со вторыми производными <р
пропадет, и мы иолучим
г, 1=1
Итак, лемма доказана.
Но поскольку каждый линейный дифференциальный оператор
первого порядка задается векторным полем, наш оператор LBLA —
— LaLb также соответствует некоторому векторному полю С.
Определение. Скобкой Пуассона или коммутатором
двух векторных полей А, В ъ& многообразии М называется *)
векторное поле С, для которого
Скобка Пуассона двух векторных полей обозначается
С=[АгВ].
Задача. Пусть поля А, В заданы в координатах xj компонентами
, Bi). Найти компоненты их скобки Пуассона.
Решение. При доказательстве леммы 2 уже доказана формула
Задача. Пусть Ау — векторное поле линейных скоростей твердого
тела, вращающегося с угловой скоростью щ, а А%—с угловой скоростью щ
вокруг точки О. Найти скобку Пуассона [Alt А^).
Г. Тождество Якоби.
Теорема. Скобка Пуассона превращает линейное простран-
пространство векторных полей на многообразии М в алгебру Ли.
Доказательство. Линейность и кососимметричность
скобки Пуассона очевидны. Докажем тождество Якоби. Имеем
по определению скобки Пуассона
^[И.в],с] = LcL[A,b] — L[AtB\Lc =
= LqLbLa — LcLaLb -I- LaLbLc — LbLcLa.-
Всего в сумме LllAt Bj, cj + LllB, c], aj + Llic, Aj, n] будет 12
слагаемых. Каждое слагаемое войдет в сумму дважды с противо-
противоположными знаками. Теорема доказана.
Д. Условие коммутативности потоков. Пусть А, В — вектор-
векторные поля на многообразии М.
Теорем а. Два потока А', В* коммутируют тогда и только
тогда, когда скобка Пуассона соответствующих векторных полей
[А, В\ равна нулю.
*) Во многих книгах принимается другой знак. Наш знак согласован
со знаком коммутатора в теории групп Ли (см. п. Е).

§ 39. АЛГЕБРА ЛИ ВЕКТОРНЫХ ПОЛЕЙ
185
Доказательство. Если AlBs == BsAl, то по лемме 1
[А, В] = 0. ЕслиЫ,-В1 = 0, то по лемме 1 для любой функции
<р в любой точке х
Ф (А1Вах) — ф (В3Агх) = o(s" + ?),
Мы покажем, что отсюда вытекает ф (А'В*х) — ф (В*А*х) при
достаточно малых s и t.
Применяя это соотношение к локальным координатам (ф = xlt ...
. . ., ф = хп), получим AlBs = BSA{.
Рассмотрим прямоугольник 0 < t ^ tB, 0 ^ s < sB (рис. 170) на плоско-
плоскости (t, s). Каждому пути, ведущему из @, 0) в (tB, s0) и состоящему из конеч-
конечного числа отрезков координатных направлений, сопоставим произведение
преобразований потоков А1 и Bs. Каждому отрезку tt <sj t ^ t2 сопоставим
** отрезку «1 < s < s2 —
применять преобразо- ^__Лю*о
вания будем в порядке, в ка- ^-^" А Ч. я
ком идут отрезки от @, 0).
о
Рис. 170. К-доказатель-
К-доказательству коммутативности
потоков
Рис. 171. Криволинейный четырех-
четырехугольник б
Так, например, сторонам @ < t ^ t„, s = 0) и (t = tB, 0 ^ s ^ s0) от-
отвечает произведение BS°A<0, а сторонам (t = 0, 0 ^ s ^ sB) и (s = s0, 0 «^ t <
< t0) — произведение AtoBs°.
Кроме того, мы сопоставим каждому такому пути на плоскости (t, s)
путь на многообразии М, выходящий из точки х, составленный из траекторий
потоков А* и Bs (рис. 171). Если пути на плоскости (t, s) соответствует преоб-
t t g
разование А^В*1 . . . А пВп, то на многообразии М соответствующий путь
f t г
заканчивается в точке АЧВ * . . . А пВ пх.
Наша цель — доказать, что все эти пути в действительности заканчива-
заканчиваются в одной точке А1°В8'х — Bs«At°x.
Разобьем отрезки @ < t <sj t0) и @ ^ s ^ s0) на N равных частей так,
что весь прямоугольник разделится на N2 маленьких прямоугольников. Пе-
Переход от сторон @, 0) — @, t0) — (s0, t0) к сторонам @, 0) — (s0, 0) — (s0,
*о) можно совершить в TV* шагов, в каждом из которых пара соседних сторон
маленького прямоугольника заменяется другой парой (рис. 172).
На мяогообразии М этому маленькому прямоугольнику соответствует,
вообще говоря, незамкнутый криволинейный четырехугольник Py^ecc
(рис. 171). Рассмотрим расстояние *) между его вершинами а, Р, соответствую-
*) В какой-нибудь римановой метрике М.

2
3
1
186 ГЛ. 8. СИМПЛЕКТИЧЕСКИЕ МНОГООБРАЗИЯ
«дими наибольшим значениям/ и «. Как мы видели выше (стр. 185), р (а, Р) ^
<; С^'3 (где постоянная Сх > 0 не зависит от TV). Используя теорему диф-
дифференцируемое™ решений дифференциальных уравнений по начальным дан-
данным, отсюда нетрудно вывести оценку расстояния между
концами а', р'путей a;6vPP' и a;6saa' на многообразии Mr
р (а', р') < C2N~S, где постоянная С2 > О снова не зависит
от N. Но весь переход от Bs°A*°x к А{"В'°х мы разбили на
N* таких шагов. Итак, р (AuBs'x, Вэ'А*°х) < N2C2N~3VN.
Следовательно, Аг°В*°х = BS°A* x.
Рис. 172. пере- Е. Добавление. Алгебра Ли группы Ли. Груп-
ход'от одной па- пой Ли называется группа G, являющаяся диф-
ры сторонок дру- ференцдруемым многообразием, причем операции
(умножение и обращение) — дифференцируемые
¦отображения G X G—>- G, G—*-G.
Касательное пространство к группе Ли G в единице TGe имеет
естественную структуру алгебры Ли; она определяется следующим
образом.
Каждому касательному вектору А С TGe отвечает однопара-
метрическая подгруппа A' (ZG с вектором скорости А = -^ А*-
Степень некоммутативности двух подгрупп А', В' измеряется
произведением А1В&А~гВ-*. Оказывается, существует одна-един-
¦ственная подгруппа С, для которой
р {А*В°А-*В-\ С*') = о (s2 + *2) приз, t -> 0.
Соответствующий вектор С = -т— С называется коммутатором
аг |г=о
Ли С = [А, В] векторов А и В.
Можно проверить, что введенная таким образом в касательное
пространство TGe операция коммутирования превращает его
в алгебру Ли (т. е. операция билинейна, кососимметрична и
удовлетворяет тождеству Якоби). Эта алгебра называется алгеб-
алгеброй Ли группы Ли G.
Задача. Вычислить операцию коммутирования в алгебре Ли группы
?0C) вращений трехмерного евклидова пространства.
Лемма 1 показывает, что скобку Пуассона векторных полей
можно определить как коммутатор Ли для «.бесконечномерной
группы Ли» всех диффеоморфизмов многообразия *) М.
С другой стороны, коммутатор Ли можно определять с по-
помощью скобок Пуассона векторных полей на группе Ли G.
Пусть g?G. Правым сдвигом Re называется отображение Rgi
G —у G, Rgh = hg. Дифференциал Rg в точке g отображает TGe
в TGg. Таким образом, каждому вектору А е= TGe соответствует
целое векторное поле на группе: оно составлено из всех правых
•) Знак в определении скобки Пуассона векторных полей выбран исхо-
исходя из этого соображения.

§ 40. АЛГЕБРА ЛИ ФУНКЦИЙ ГАМИЛЬТОНА 187
сдвигов {Rg)%A и называется правоинвариантным полем. Очевид-
Очевидно, правоинвариантное поле на группе однозначно определяется
своим значением в единице.
Задача. Докажите, что скобка Пуассона правоинвариантных вектор-
векторных полей на группе Ли G есть правоинвариантное поле, и значение его в едини-
единице группы равно коммутатору Ли значений исходных полей в единице.
§ 40. Алгебра Ли функции Гамильтона
Гамильтоновы векторные поля на симплектическом многообразии обра-
образуют подалгебру алгебры Ли всех полей. Функции Гамильтона также образу-
образуют алгебру Ли: операция в этой алгебре называется скобкой Пуассона функ-
функций. Первые интегралы гамильтонова фазового потока образуют подалгебру
алгебры Ли функций Гамильтона.
А. Скобка Пуассона двух функций. Пусть {М2П, со2) — сим-
плектическое многообразие. Функции Н : М2п —>- R, заданной
на симплектическом многообразии, соответствует однопарамет-
рическая группа g#: М2П -»- М2П канонических преобразований
Мгп — фазовый поток, функция Гамильтона которого равна Н.
Пусть F: М2п -*- R — другая функция на многообразии Мгп.
Определение. Скобкой Пуассона (F, Н) функций F и Ht
заданных на симплектическом многообразии (М2п, со2), называет-
называется производная функции F по направлению фазового потока с
функцией Гамильтона Н:
Таким образом, скобка Пуассона двух функций на М есть снова
функция на М.
Следствие 1. Функция F тогда и только тогда является
первым интегралом фазового потока с функцией Гамильтона Н,
когда ее скобка Пуассона с Н равна тождественно нулю: (F, Н) н= 0.
Мы можем дать определению скобки Пуассона несколько иную
форму, если воспользуемся изоморфизмом / между J-формами
и векторными полями на симплектическом многообразии (М271, о2).
Этот изоморфизм определен соотношением (см. § 37)
СО2 (Х\, /to1) = ОI (!]).
Вектор скорости фазового потока #я есть / dH. Отсюда вытекает
Следствие 2. Скобка Пуассона функций F и Н равна
значению 1-формы dF на векторе I dH скорости фазового потока
с функцией Гамильтона Н:
(F, H) = dF(I dH).
Пользуясь предыдущей формулой еще раз, получаем
Следствие 3. Скобка Пуассона функций F и Н рав-
равна «кососк алярному произведению» векторов скоростей фазовых

188 ГЛ. 8. СИМПЛЕКТИЧЕСКИЕ МНОГООБРАЗИЯ
потоков с функциями Гамильтона Н и F:
(F, Я) = а>гA dH, I dF).
Теперь становится очевидным
Следствие 4. Скобка Пуассона функций F и Я является
кососимметрической билинейной функцией от F и Н:
(F, Н) = - (Я, F), (Я, ^г + KFJ = К (Я, Fx) + К {Н, FJ)
Сколь ни очевидны предыдущие рассуждения, они приводят
к нетривиальным выводам, в том числе к следующему обобщению
теоремы Э. Нётер.
Теорема. Если функция Гамильтона Я, заданная на симп-
лектическом многообразии (jkf2™, со2), выдерживает однопарамет-
рическую группу канонических преобразований, заданную гамиль-
гамильтонианом F, то F есть первый интеграл системы с функцией
Гамильтона Я.
Действительно, по условию Я есть первый интеграл потока
gF- Значит, (Я, F) = 0 (следствие 1). Поэтому (F, Я) = 0 (след-
(следствие 4) и F — первый интеграл (следствие 1), ч.т.д.
Задача 1. Вычислить скобку Пуассона двух функций F, Н в коор-
координатном каноническом пространстве R2n = Up, q)}, to2 (E, tj) = [|, tj] =
= dl, 4).
Решение. Согласно следствию 3 имеем
п
\П дН dF dH OF
(Р, H) = [IdH /dF] [dtf dFJ^
/О —Е\
(мы пользуемся симплектичностью / и тем, что / имеет вид ( ) в ба-
\Е 0 /
/О —Е\
( )
\Е 0 /
аисе (р, д)).
Задача 2. Вычислить скобки Пуассона базисных функций pj, gj.
Решение. Градиенты базисных функций образуют «симплектический
базис»: их кососкалярные произведения суть
(Pi, Pj) — (PU Qj) = (<1Ь Qj) = 0, (ди pi) = — (Pi, gj) = 1.
Задача 3. Докажите, что отображение A: R2™ —» R2n, (p, q) !->¦
i->- (P(p, g), Q (р, д)) каноническое тогда и только тогда, когда скобки Пуас-
Пуассона любых двух функций по переменным (р, д) и (Р, Q) совпадают:
dH
dp
dF
dg
dH
dq
dF
dp
dH
dP
dF
<>Q
dH
dQ
dF
dP
Решение. Пусть А — каноническое. Тогда симплектические струк-
структуры dp /\dg и dP Д dQ совпадают. Но определение скобки Пуассона (F, И)
инвариантно связано с симплектической структурой, а не с координатами.
Поэтому
(F, H)ptq= (F, Н) = (F,
Обратно, пусть скобки Пуассона (Pi, QilPt g имеют стандартный вид задачи 2.
Тогда, очевидно, dP /\dQ = dp Д dq, т. е. отображение А — каноническое.

§ 40. АЛГЕБРА ЛИ ФУНКЦИЙ ГАМИЛЬТОНА 189*
Задача 4. Докажите, что скобка Пуассона произведения вычисляется
по правилу Лейбница:
(Р^2, H) = F1 (F2, H) + F2 (Flt H).
Указание. Скобка Пуассона (FxF2t H) есть производная произве-
произведения FXF% по направлению поля IdH.
Б. Тождество Якоби.
Теорема. Скобки Пуассона трех функций А, В, С удовлет-
удовлетворяют тождеству Якоби:
((А, В), С) + ((В, С), А) + ((С, А), В) = 0.
Следствие. Теорема Пуассона. Скобка Пуассона
двух первых интегралов (Fu F%) системы с функцией Гамильтона
Н есть снова первый интеграл.
Доказательство следствия. По тождеству Якоби
((Fi, F2), H) = (Fu (Ft, Щ) + (*¦„ (Я, FJ) = 0 + 0,
что и требовалось доказать.
Таким образом, зная два первых интеграла, можно простой
выкладкой получить третий, четвертый и т. д. Конечно, не все
получающиеся интегралы будут существенно новыми, так как
всего независимых функций на М2П не более In. Иногда может
получиться функция от старых интегралов, или константа, напри-
например нуль. Но иногда получается и новый интеграл.
Задача 5. Сосчитать скобки Пуассона компонент plt p2, pg, Мг, М2г
Ма векторов импульса и кинетического момента механической системы.
Ответ. (Мг, М2) = М8, (Мх, Pl) = 0, (Мг, р2) = р8, (Мг, р3) = — р2.
Отсюда вытекает
Теорема. Если в некоторой механической задаче сохраняются две
компоненты кинетического момента, Мх и М2, то сохраняется и третья.
Доказательство тождества Якоби. Рассмот-
Рассмотрим сумму
((А, В), С) + ((Б, С), А) + ((С, А), В).
Эта сумма есть «линейная комбинация вторых частных производ-
производных» функций. Сосчитаем члены, содержащие вторые производ-
производные А:
((А, В), С) + ((С, А), В) = (LCLB - LBLC)A,
где Lg — дифференцирование по направлению |, a F — гамиль-
тоново поле с функцией Гамильтона F.
Но по лемме 2 § 39 коммутатор дифференцирований LcLB —
— LbLc есть дифференциальный оператор первого порядка. Зна-
Значит, никаких вторых производных А наша сумма не содержит.
То же относится ко вторым производным В ж С. Следовательно,
сумма равна нулю, ч.т.д.
Сл едствие 5. Пусть В, С — гамильтоновые поля с функ-
функциями Гамильтона В, С. Рассмотрим скобку Пуассона векторных

90 ГЛ. 8. СИМПЛЕКТИЧЕСКИЕ МНОГООБРАЗИЯ
толей [В, С]. Это векторное поле гамильтоноео, и его функция
Гамильтона равна скобке Пуассона функций Гамильтона (В, С).
Доказательство. Положим (В, С) = D. Тождество
Якоби можно переписать в виде
(A, D) = ((А, В), С) - ((А, С), В),
что и требовалось доказать.
В. Алгебры Ли гамильтоновых полей, функций Гамильтона
и первых интегралов. Линейное подпространство алгебры Ли
¦называется подалгеброй, если коммутатор двух любых элементов
подпространства ему принадлежит. Подалгебра алгебры Ли сама
является алгеброй Ли. Предыдущее следствие содержит, в част-
частности,
Следствие 6. Гамильтоновы векторные поля на симплек-
тическом многообразии образуют подалгебру алгебры Ли всех полей.
Теорема Пуассона о первых интегралах может быть перефор-
переформулирована так:
Следствие 7. Первые интегралы гамильтонова фазового
потока образуют подалгебру алгебры Ли всех функций.
Алгебру Ли функций Гамильтона можно естественно отобразить
на алгебру Ли гамильтоновых векторных полей. Для этого каждой
функции Н сопоставим гамильтоново векторное поле II с функ-
дией Гамильтона Н.
Следствие 8. Отображение алгебры Ли функций на
¦алгебру Ли гамильтоновых полей является гомоморфизмом алгебр.
Его ядро состоит из локально постоянных функций. Если М2п
¦связно, то ядро одномерно и состоит из постоянных.
Наше отображение линейно. Следствие 5 утверждает, что наше
отображение переводит скобку Пуассона функций в скобку
Пуассона векторных полей. Ядро состоит из функций Н, для
которых / dH = 0. Поскольку / — изоморфизм, dH == 0, Н =
= const, ч.т.д.
Следствие 9. Для того чтобы фазовые потоки с функциями
Гамильтона Нг и Н% коммутировали, необходимо и достаточно,
чтобы скобка Пуассона функций Нг и Н2 была (локально) постоянной.
По теореме пункта Д § 39 необходимо и достаточно, чтобы
[II1, II2] = 0, а по следствию 8 последнее условие эквивалентно
d(Hu Я2) = 0.
Мы получили еще одно обобщение теоремы Э. Нётер: зная nomoKt
коммутирующий с исследуемым, можно построить первый интеграл.
Г. Локально гамильтоновы векторные поля. Пусть (М2П, ю2) — симплек-
тическое многообразие, g(: М2п —» М2п — однопараметрическая группа диф-
диффеоморфизмов, сохраняющих симплектическую структуру. Будет ли g* ra-
мильтоновым потоком?
Пример. Пусть Мгп — двумерный тор У2, точка которого задается
парой координат (р, д) modd 1. Пусть ю2 — обычный элемент площади dp Д

§ 41. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ 191
Д dq. Рассмотрим семейство сдвигов g* (р, q) = (р + t, q) (рис. 173). Отоб-
Отображения g* сохраняют симплектическую структуру (т. е. площадь). Можно-
ли задать соответствующее векторное поле (р = 1, q = 0) функцией Гамиль-
Гамильтона? Если бы р = — dHldq, q = дН/др, мы имели бы дН/др = 0, dH/dq =
= — 1, т. е. // = —q -\- С. Но g — вто лишь локаль-
локальная координата на У2; отображения Н: Т2 —» R, для
которого дН/др = 0, dHldq = — 1, не существует.
Итак, g* не есть гамильтонов фазовый поток.
Определение. Локально гамилыпоновым век-
векторным полем на симплектическом многообразии (М2П,
со2) называется векторное поле /со1, где ю1 — замк-
игтяя 1 Аппх.я ня лДп- Рис 173. Локально
HJTaH l-форма на т ¦ гамильтоново поле ва
Локально замкнутая 1-форма является дифферен- торе
циалом функции, ю1 = dH. Однако при попытке про-
продолжить функцию Н на все многообразие М2п, мы можем получить «мно-
«многозначную функцию Гамильтона». Ибо замкнутая 1-форма на неодносвязномг
многообразии может не быть дифференциалом (например, форма dq на Г2).
Фазовый поток, заданный локально гамильтоновым векторным полем,
называется локально гамильтоновым потоком.
Задача 6. Докажите, что однопараметрическая группа диффеоморфиз-
диффеоморфизмов симплектического многообразия тогда и только тогда сохраняет симплек-
симплектическую структуру, когда она является локально гамильтоновым фазовым
потоком.
Указание. См. § 38, А.
Задача 7. Докажите, что в симплектическом пространстве R2n вся-
всякая однопараметрическая группа канонических (сохраняющих dp Д dq) диф-
диффеоморфизмов всегда является гамилыпоноеым потоком.
Указание. Всякая замкнутая 1-форма в R2™ является дифферен-
дифференциалом функции.
Задача 8. Докажите, что локально гамилыпоновы векторные поля,
образуют подалгебру алгебры Ли всех полей. При этом скобка Пуассона двуяг
локально гамилътоновых полей — это настоящее гамильтоново поле, его функ-
функция Гамильтона однозначно *) определена данными полями %, i) no формуле
Н = ш2 (|, ц).
Таким образом, гамильтоновы поля образуют идеал в алгебре Ли локаль-
локально гамильтоновых полей.
§ 41. Симплектическая геометрия
Евклидова структура в линейном пространстве задается симметричес-
симметрической билинейной формой, а симплектическая — кососимметрической. Геомет-
Геометрия симплектического пространства освежающе непохожа на евклидову,,
хотя и имеет много сходных черт.
А. Симплектическое линейное пространство. Пусть R2n — чет-
номерное линейное пространство.
Определение. Симплектической линейной структурой
в R2n называется невырожденная **) билинейная кососимметри-
ческая 2-форма, заданная в R2". Эта форма называется кососка-
лярным произведением и обозначается [|, г\] = — [tj, |J.
Пространство R2n вместе с симплектической структурой I,]
называется симплектическим линейным пространством.
*) А не с точностью до постоянной.
**) 2-форма [ , ] в R2" невырождена, если ([%, tj] = 0 Vtj) -ф (| = 0).

92 ГЛ. 8. СИМПЛЕКТИЧЕСКИЕ МНОГООБРАЗИЯ
Пример. Пусть (рг, . . ., рп; qlt . . ., qn) — координатные
'функции в R2™, и о2 — форма
«>2 = Pi A 4i + • ¦ • + рп Л ?„.
Поскольку эта форма невырождена и кососимметрична, ее
можно принять за кососкалярное произведение: [g, ч\] = о2 (?, ц).
Таким образом, координатное пространство R2™ = {(р, q)} полу-
получает симплектическую структуру. Эта структура называется
стандартной. В стандартной симплектической структуре кососка-
кососкалярное произведение двух векторов |, ц равно сумме ориентиро-
ориентированных площадей проекций параллелограмма (|, ц) на п координат-
координатных плоскостей (pi, qi).
Два вектора %, х\ в симплектическом пространстве называются
косоортогональными (g -t. ц), если их кососкалярное произведение
равно нулю.
Задача. Докажите, что % -*- \: каждый вектор себе косоортогонален.
Множество всех векторов, косоортогональных данному век-
вектору i\, называется косоортогоналъным дополнением к ij.
Задача. Докажите, что косоортогональное дополнение к г\ есть
~2п — 1-мерная гиперплоскость, содержащая т).
Указание. Если бы все векторы были косоортогональны т), то фор-
форма Г,] была бы вырожденной.
Б. Симплектический базис. Евклидова структура при подхо-
подходящем выборе базиса (он должен быть ортонормирован) задается
скалярным произведением специального стандартного вида. Точно
так же и симплектическая структура принимает стандартный вид,
указанный выше, в надлежащем базисе.
Задача. Найти кососкалярные произведения базисных векторов е_ ,
¦*5- ('= ^' •••' п) в приведенном выше примере.
Решение. Из определения Pi/\ gi+ ••• + РпД Чп следуют соотно-
лпения
[ep.,ep.] = [ep.,eg.] = [e?.,eg.l = 0, [eP|, e,f] = 1. A)
Вернемся теперь к общему симплектическому пространству.
Определение. Симплектическим базисом называются 2п
векторов ePi, e4i (i = 1, . . ., п), кососкалярные произведения ко-
которых имеют вид A).
Иными словами, каждый базисный вектор косоортогонален
всем базисным векторам, кроме одного, с ним сопряженного;
а произведение сопряженных векторов равно ±1.
Теорема. В каждом симплектическом пространстве су-
существует симплектический базис. Более того, за первый вектор
базиса можно взять любой ненулевой вектор е.
Эта теорема вполне аналогична соответствующей теореме
евклидовой геометрии и доказывается почти так же.

S 41. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ 193
Поскольку вектор е не нулевой, существует ему не косоорто-
гональный вектор f (форма [,] невырождена). Выбрав длину этого
вектора, можно добиться того, что его кососкалярное произве-
произведение с е станет равным единице. В случае п = 1 теорема доказана.
Если же п ^>1, рассмотрим косоортогональное дополнение D
(рис. 174) к паре векторов в, /. D есть пересечение косоортогональ-
ных дополнений к е и /. Эти два 2га — 1-мерные подпространства
не совпадают, так как е не лежит в косоортого-
нальном дополнении к /\ поэтому их пересечение
D имеет четную размерность 2п — 2.
Покажем, что D есть симплектическое под-
подпространство в R2n, т. е. что кососкалярное про- /ц
изведение [,] на D невырождено. Действительно,
если бы вектор |g?) был косоортогонален всему Рис 174 Косо.
Пространству D, ТО, будучи КОСООрТОГОНалеН ортогональное до-
также к е и к /, этот вектор | был бы косо- полнение
ортогонален R2n, что противоречит невырожденности [,] на R2'\
Итак, D2n~z — симплектическое.
Теперь, если добавить к симплектическому базису в D2n~2
векторы ей/, мы получим симплектический базис в R2n, и дока-
доказательство теоремы завершается индукцией по размерности п.
Следствие. Все симплектические пространства одинако-
одинаковой размерности изоморфны.
Если принять векторы симплектического базиса за координат-
координатные орты, то мы получим систему координат pt, дг, в которой
[,] принимает стандартный вид р± Д qx + . • • + рп /\ Яп- Такая
система координат называется симплектической.
В. Симплектическая группа. С евклидовой структурой связана
ортогональная группа линейных отображений, сохраняющих
евклидову структуру. В симплектическом пространстве аналогич-
аналогичную роль играет симплектическая группа.
Определение. Линейное преобразование S : R2n -»- R2n
симплектического пространства R2tl в себя называется симплекти-
ческим, если оно сохраняет кососкалярное произведение:
Множество всех симплектических преобразований R2n называется
симплектической группой и обозначается SpBn).
Что произведение двух симплектических преобразований сим-
симплектическое — очевидно. Чтобы оправдать термин симплектичес-
симплектическая группа, нужно только доказать, что симплектическое преоб-
преобразование невырождено, тогда ясно, что обратное также симплек-
тично.
Задача. Докажите, что группа SpB) изоморфна группе веществен-
вещественных матриц второго порядка с определителем 1 и гомеоморфна трехмерной
внутренности баранки.

194 ГЛ. 8. СИМПЛЕКТИЧЕСКИЕ МНОГООБРАЗИЯ
Теорема. Преобразование S: R2n -»- R2n стандартного сим-
плектического пространства (р, q) симплектшеское тогда и только
тогда, когда оно линейное и каноническое, т'. е. сохраняет диффе-
дифференциальную 2-форму
«>2 = dpi Л ^i + • • • + Фп Л dQn-
Доказательство. При естественном отождествлении
касательного пространства к R2n и R2n 2-форма (о2 переходит в [,].
Следствие. Определитель любого симплектического пре-
преобразования равен единице.
Доказательство. Мы уже знаем (§ 38, Б), что канони-
канонические преобразования сохраняют внешние степени формы со2.
Но ее п-я внешняя степень есть (с точностью до постоянного мно-
множителя) элемент объема в R2n. Значит, симплектические преобра-
преобразования S стандартного R2™ = {(р, q)} сохраняют элемент объема,
так что det S = 1.
Но поскольку всякая симплектическая линейная структура
записывается в стандартном виде в симплектической системе коор-
координат, определитель симплектического преобразования любого
симплектического пространства равен единице, ч.т.д.
Теорема. Линейное преобразование S: R2'1 -*¦ R271 симплек-
тично тогда и только тогда, когда оно переводит некоторый
(и тогда любой) симплектический базис в симплектический.
Доказательство. Кососкалярное произведение лю-
любых двух линейных комбинаций базисных векторов выражается
через кососкалярные произведения базисных векторов. Если пре-
преобразование не меняет кососкалярные произведения базисных
векторов, то оно не меняет и кососкалярные произведения любых
векторов, ч.т.д.
Г. Плоскости в симплектическом пространстве. В евклидовом
пространстве все плоскости равноправны: каждую из них можно
перевести в любую другую движением.
Рассмотрим с этом точки зрения линейное симплектическое
пространство.
Задача. Докажите, что ненулевой вектор симплектического простран-
пространства можно перевести в любой другой ненулевой вектор симплектическим
преобразованием.
Задача. Докажите, что не всякую двумерную плоскость симплекти-
симплектического пространства R2™, п > 1, можно получить из данной 2-плоскости
симплектическим преобразованием.
Указание. Рассмотрите плоскости (р1? р2) и (plf gj.
Определение, /с-мерная плоскость симплектического про-
пространства называется нулевой *), если она себе косоортогональна,
*) Нулевые плоскости называют также изотропными, а при к = п —
лагранжевыми.

§ 41. СИМПЛЕКТИЧЕСКАЯ ГЕОМЕТРИЯ 195
т. е. кососкалярное произведение любых двух векторов плоскости
равно нулю.
Пример. Координатная плоскость (plt . . ., pt) в симплектической
системе координат р, q нулевая (докажите!)
Задача. Докажите, что любую ненулевую двумерную плоскость мож-
можно перевести в любую другую ненулевую симплектическим преобразованием.
При вычислениях в симплектической геометрии бывает
полезно ввести в симплектическом пространстве еще какую-ни-
какую-нибудь евклидову структуру. Мы зафиксируем симплектическую
систему координат р, q и введем евклидову структуру с помощью
координатного скалярного произведения.
(aCj х) = S Pi + 9?, где х = 2 Pfivi + &Ч-
Симплектический базис ер, eq в этой евклидовой структуре
ортонормирован. Кососкалярное произведение, как всякая били-
билинейная форма, выражается через скалярное в виде
где: /: R2n -»- R2n — некоторый оператор. Из кососимметричности
кососкалярного произведения следует, что оператор / кососим-
метричен.
Задача. Сосчитать матрицу оператора / в симплектическом базисе
V е"
-а -г)-
Ответ. ( I , где Е — единичная матрица порядка п.
Таким образом, при п = 1 (на плоскости р, д) I есть просто
поворот на 90°, а в общем случае / есть поворот на 90° в каждой
из п плоскостей pt, qt.
Задача. Доказать, что оператор I симплектический и что Р = —Еяп.
Хотя евклидова структура и оператор / связаны с симплек-
симплектическим пространством неинвариантно, они часто бывают удобны.
Из B) непосредственно вытекает
Теорема. Плоскость п симплектического пространства
нулевая тогда и только тогда, когда плоскость In ортогональна я.
Заметим, что размерности плоскостей я и 1л совпадают, так
как / невырожден. Отсюда
Следствие. Размерность нулевой плоскости в R2n не
превосходит п.
Действительно, две Анмерные плоскости я и /я в R2n не могут
быть ортогональными, если к~^> п.
Рассмотрим несколько подробнее и-мерные нулевые плоскости
в координатном симплектическом пространстве R2a. Примером
такой плоскости служит координатная /ьшюскость. Всего 71-
мерных координатных плоскостей в R2" = {(р, q)} имеется С?„.

196 ГЛ. 8. СИМПЛЕНТИЧЕСКИЕ МНОГООБРАЗИЯ
Задача. Доказать, что среди С?п n-мерных координатных плоскостей
нулевых ровно 2п. А именно, каждому из 2п разбиений множества A, . . ., п)
на две части (it,.. ., i>) O'it • • •• jn-k) соответствует нулевая координатная
плоскость р^, . . ., pifc, 93j, . . ., q^.
При изучении производящих функций канонических преобра-
преобразований нам потребуется
Теорема. Всякая п-мерная нулевая плоскость п в симплек-
тическом координатном пространстве R2n трансверсальна *) хо-
хотя бы одной из 2" координатных нулевых плос-
плоскостей.
Доказательство. Пусть Р — нулевая
плоскость Рх, . . ., рп (рис. 175). Рассмотрим пе-
пересечение
Рис. 175. По- _ р р
строение коорди- 1 — п I I * •
натной плоско*
с^ьной^даЗ ПУСТЬ размерность т равна к, 0 < к < п. Как
плоскости я всякое /с-мерное подпространство n-мерного про-
пространства Р, плоскость т трансверсальна хотя
бы одной п — /с-мерной координатной плоскости в Р, скажем
плоскости
т) = (ph, . . ., pi^y, т-\-г) = Р, т П г) = 0.
Построим нулевую n-мерную координатную плоскость
о = (Pis • • •» Pin-*' Qh ¦ • • •» ?/fc)> Tl = ст f] -P.
и докажем, что наша плоскость л трансверсальна а:
я П с = 0.
Действительно, имеем
[=Ф(т + т1)^.(л Па)=ФР^.(л По).
Но Р — n-мерная нулевая плоскость. Поэтому всякий вектор,
косоортогональный Р, принадлежит Р (см. следствие выше).
Итак, (л С] о) а Р. Окончательно,
что и требовалось доказать.
Задача. Пусть пи п2 — две ^-мерные плоскости в симплектическом
R271. Всегда ли можно перевести я^ в щ, симплектическим преобразованием?
Сколько существует классов плоскостей, не переводимых друг в друга?
Ответ, -g- I + 1, если А; ^ п; —g + *» если
*) Два подпространства Lt и L2 линейного пространства L трансверсаль-
ны, если Lt + L2 = L,. Две n-мервые плоскости в R2n трансверсальны тогда
и только тогда, когда они пересекаются лишь в точке О.

§ 42. ПАРАМЕТРИЧЕСКИЙ РЕЗОНАНС 197
Д. Симплектическая структура и комплексная структура. По-
Поскольку /2 = —Е, мы можем ввести в наше пространство R2™
наряду с симплектической структурой (,] и евклидовой структу-
структурой (,) еще и комплексную структуру, определяя умножение на i =
= Y—1 как действие 1. Пространство R2n отождествляется при
этом с комплексным пространством С" (если угодно, координат-
координатным пространством с координатами zk = pk + iqb).
Линейные преобразования R2n, сохраняющие евклидову струк-
структуру, образуют ортогональную группу ОBп), сохраняющие комп-
комплексную структуру — комплексную линейную группу GL(n, С).
Задача. Докажите, что ортогональные и одновременно симплектичес-
симплектические преобразования комплексны, комплексные и ортогональные симплектичны,
а симплектические и комплексные ортогональны, так что пересечения двух из
трех групп равны пересечению всех трех:
0Bп) П SpBn) = SpBn) П GL(n, С) = GL(n, С) f] 0Bn).
Это пересечение называется унитарной группой U(n).
Унитарные преобразования сохраняют эрмитово скалярное
произведение (?, rj) + i [|, т)]; скалярное и кососкалярное про-
произведения в R2n — это его вещественная и мнимая части.
§ 42. Параметрический резонанс в системах
со многими степенями свободы
При исследовании колебательных систем с периодически меняющимися
параметрами (см. § 25) мы выяснили, что параметрический резонанс зависит
от поведения собственных чисел некоторого линейного преобразования («ото-
ображения за период»). Зависимость состоит в том, что положения равновесия
системы с периодически меняющимися параметрами устойчиво, если собст-
собственные числа отображения за период по модулю меньше единицы, и не-
неустойчиво, если хотя бы одно из собственных чисел по модулю больше единицы.
Отображение за период, полученное из системы уравнений Гамильтона
с периодическими коэффициентами, является симплектическим. Исследо-
Исследование параметрического резонанса в системах с одной степенью свободы,
проведенное в § 25, опиралось на анализ поведения собственных чисел сим-
лектических преобразований плоскости.
В настоящем параграфе проведен аналогичный анализ поведения соб-
собственных чисел линейных симплектических преобразований фазового про-
пространства любого числа измерений. Результаты этого анализа (принадлежа-
(принадлежащего М. Г. Крейну) применяются при исследовании условий возникновения
параметрического резонанса в механических системах со многими степенями
свободы.
А. Симплектические матрицы. Рассмотрим линейное преобра-
преобразование симплектического пространства S: R2n -*¦ R2n. Пусть
Ри • • •, Pn'i ?i> • • м ?п — симплектическая система координат.
В этой системе координат преобразование задается матрицей S.
Теорема. Чтобы преобразование было симплектическим,
необходимо и достаточно, чтобы его матрица S в симплектиче-

198 ГЛ. 8. СИМПЛЕКТИЧЕСКИЕ МНОГООБРАЗИЯ
ской системе координат (р, q) удовлетворяла соотношению
S'IS = I,
я г /О —Е\ с „
где i = \E о/1 а —матрица, транспонированная к S.
Доказательство. Условие симплектичности ([5|, Sr\] =
— IS, ^l для всех |, ц) с помощью оператора / записывается
через скалярное произведение в виде
(ISl, Si\) = G|, к)) VI, к).
или еще
(<S'/<S?, tj) = (/I» i|) V|, ч»
что и требовалось доказать.
Б. Симметрия спектра симплектического преобразования.
Теорема. Характеристический полином симплектического
преобразования
р (К) = det | S — IE |
возвратный *), от. е. р (X) = Я,2пр A/Я).
Доказательство. Мы будем пользоваться тем, что
det S = det 1 = 1, Р = —Е и det A' = det А. По предыдущей
теореме S = —/S"/. Поэтому
р (X) = det (S — Х?) = det (— IS — Х?) = det (— S- + Х?) =
= det(—? + X^) = X2ndet/^ —-i-
что и требовалось доказать.
Следствие. Если % — собственное число симплектического
преобразования, то 1/К — также собст-
собственное число.
С другой стороны, характеристический
полином веществен; поэтому, если Я — ком-
комплексное собственное число, то Я — соб-
- ственное число, притом не совпадающее
А с Я.
Рис. 176. Расположение Отсюда вытекает, что все корни X ха-
плек^ескогоЧИпреобра- рактеристического полинома лежат сим-
вования метрично относительно вещественной оси
и относительно единичной окружности (рис. 176). Они разбива-
разбиваются на четверки
и пары, лежащие на вещественной оси:
*) Возвратным называется полином аохт -\- а^ -)-..,-|-%с сим-
симметричными коэффициентами: ао= ат, ау= am_v . . .

§ 42. ПАРАМЕТРИЧЕСКИЙ РЕЗОНАНС 199
или на единичной окружности:
Нетрудно сообразить, что кратности всех четырех точек четверки
(или обеих точек пары) одинаковы.
В. Устойчивость.
Определение. Преобразование S называется устойчи-
устойчивым, если
Ve > 0 36 > 0: | х |< б =Ф | S"x |< e, VN > 0.
Задача. Докажите, что если хотя бы одно иа собственных чисел си.ч-
плектического преобразования S лежит не на единичной окружности, то S не-
неустойчиво.
Указание. Ввиду доказанной симметрии, если хоть одно из соб-
собственных чисел лежит не на единичной окружности, существует собственное
число вне единичного круга | k | > 1; в соответствующем инвариантном под-
подпространстве 5 — «растяжение с поворотом».
Задача. Докажите, что если все собственные числа линейного преоб-
преобразования различны и лежат на единичной окружности, то преобразование
устойчиво.
Указание. Перейти к собственному базису.
Определение. Симплектическое преобразование S на-
называется сильно устойчивым, если всякое достаточно близкое
к нему *) симплектическое преобразование 5Х устойчиво.
В § 25 мы установили, что S: R2-»- R2 сильно устойчиво, если
h ±to %Ф%
,2 12
Теорема. Если все 2п собственных числа симплектического
преобразования S различны и лежат на единичной окружности,
то преобразование S сильно устойчиво.
Доказательство. Заключим 2я собственных чисел Я
в Ъг непересекающихся окрестностей, симметричных относитель-
относительно единичной окружности и вещественной оси (рис. 177). 2п кор-
корней характеристического полинома зависят от элементов матрицы
S непрерывно. Следовательно, если матрица S% достаточно близка
к S, то в каждой из 2п окрестностей 2м точек X лежит ровно одно
собственное число kt матрицы S%. Но если бы какая-либо из то-
точек X, не лежала на единичной окружности, а, например, вне,
то по теореме стр. 198 в той же окрестности лежала бы еще одна
точка %2, | Яг | < 1, и общее число корней было бы больше 2и,
что невозможно.
Итак, все корни St лежат на единичной окружности и раз-
различны: значит, S1 устойчиво, что и требовалось доказать.
Можно сказать, что собственное число симплектического пре-
преобразования X может покинуть единичную окружность, лишь
*) S± «достаточно близко» к S, если элементы матрицы 5а в фиксиро-
фиксированном базисе отличаются от элементов матрицы S в том же базисе меньше
чем на достаточно малое число е.

200 ГЛ 8. СИМПЛЕКТИЧЕСКИЕ МНОГООБРАЗИЯ
столкнувшись с другим собственным числом (рис. 178); при этом
одновременно сталкиваются комплексно-сопряженные числа, и из
двух пар корней на окружности получается одна четверка (или
пара вещественных Я).
Из результатов § 25 следует, что условия возникновения пара-
параметрического резонанса в линейной канонической системе с пе-
периодически меняющейся функцией Гамильтона состоят как раз
в том, что соответствующее симплектическое преобразование фа-
фазового пространства перестает быть устойчивым. Из доказанной
Рис. 177. Поведение про- Рис. 178. Поведение крат-
стых собственных чисел ных собственных чисел при
при малом изменении малом изменении симплек-
симплектического пре- тического преобразования
образования
теоремы видно, что это может случиться лишь при столкновении
собственных чисел на единичной окружности. В действительности,
как заметил М. Г. Крейн, не всякое такое столкновение опасно.
Оказывается, собственные числа Я, | % | = 1, делятся на два
класса: положительные и отрицательные. При столкновении двух
корней одинакового знака корни «проходят друг сквозь друга»
и не могут сойти с единичной окружности. Напротив, два корня
разных знаков при столкновении, вообще говоря, покидают еди-
единичную окружность.
Теория М. Г. Крейна выходит за рамки этой книги, но здесь
будут сформулированы основные результаты в виде задач.
Задача. Пусть К, "к — простые (кратности 1) собственные числа сим-
плектического преобразования S и | к | = 1. Докажите, что соответствующая
X, К двумерная инвариантная плоскость я ненулевая.
Указание. Пусть |1? |2 — комплексные собственные векторы S
с собственными значениями \, Х2. Тогда, если h^2 =f= 1, векторы ?t, gg косо-
ортогональны: [|1? |21 = 0.
Пусть | — вещественный вектор из плоскости я^, Im К >¦ О, | К | = 1.
Собственное число Я, называется] положительным, если [S|, §J >¦ 0.
Задача. Докажите, что это определение корректно, т. е. не зависит
от выбора вектора |^0 в плоскости пх.
Указание. Если бы плоскость я^ содержала два косортогональных
неко л линеарных вектора, она была бы нулевой.
Точно так же й-кратное собственное число к, | %. | = 1, знакоопределен-
иое,_если квадратичная форма [Sg, |] знакоопределена на соответствующем
Я, Я инвариантном 2&-мерном подпространстве.

§ 43. СИМПЛЕКТИЧЕСКИЙ АТЛАС 201
Задача. Докажите, что для сильной устойчивости S необходимо в
достаточно, чтобы все собственные числа к лежали на единичной окружности
я были знакоопределенными.
Указание. Квадратичная форма [S|, |) инвариантна относительно S.
§ 43. Симплектический атлас
В этом параграфе доказывается теорема Дарбу, согласно которой каждое
симплектическое многообразие имеет локальные координаты р, q, в которых
симплектическая структура записывается простейшим образом: ш2 =
= dp/\ dq.
А. Симплектические координаты. Напомню, что в определе-
определении многообразия участвует условие совместности карт атласа.
Это условие на отображения фГх<Ру перехода с одной карты на
другую. Отображения фГ*Фу — это отображения областей коор-
координатного пространства.
Определение. Атлас многообразия М2п называется симп-
лектическим, если в координатном пространстве R2n = {(р, q)}
введена стандартная симплектическая структура со2 = dp Д dqt
и переход с одной карты на другую осуществляется каноническим
(т. е. сохраняющим со2) преобразованием *) фТ^/-
Задача. Покажите, что симплектический атлас определяет симплек-
тическую структуру на М2п.
Справедливо также и обратное предложение: каждое симплек-
симплектическое многообразие имеет симплектический атлас. Это выте-
вытекает из следующей теоремы.
Б. Теорема Дарбу.
Теорема. Пусть со2 — невырожденная замкнутая диффе-
дифференциальная 2-форма в окрестности точки ж пространства R2n.
Тогда в некоторой окрестности точки ж можно выбрать токуго-
систему локальных координат (plt . . ., рп; qx, . . ., qn), что форма
прилет стандартный вид
п
со2 = S dPi Л dqi.
Эта теорема позволяет немедленно распространить на все
симплектические многообразия любое утверждение локального
характера, инвариантное относительно канонических преобразо-
преобразований и доказанное для стандартного фазового пространства
(R*\ со2 = dp Л dq).
*) Аналогично определяются, например, комплексно-аналитические мно-
многообразия: в координатном пространстве должна быть комплексная струк-
структура, а переход с одной карты на другую должен быть комплексно-анали-
комплексно-аналитическим.

202
ГЛ. 8. СИМПЛЕКТИЧЕСКИЕ МНОГООБРАЗИЯ
гп-г
Рис. 179. Построе-
Построение симплектических
координат
В. Построение координат рг и дг. В качестве первой коорди-
координаты р1 возьмем линейную непостоянную функцию (можно было
бы взять любую дифференцируемую функцию, дифференциал
которой отличен от нуля в точке ж). Будем для простоты считать,
что рг (х) = 0.
Обозначим через Т>1 = Idpx гамильтоново поле, соответствую-
соответствующее функции рх (рис. 179). Заметим, что Рг (х) Ф 0. Поэтому
через точку х можно провести гиперплоскость
N2'1'1, не содержащую вектор Рг (ж) (вместо
N2n~x можно было бы взять любую поверхно-
поверхность, трансверсальную Рх (ас)).
Рассмотрим гамильтонов поток Рг с функ-
функцией Гамильтона р%. Рассмотрим время t, нуж-
нужное, чтобы дойти от N до точки » = Р\у (у ЕЕ
ЕЕ N) под действием потока Р{, как функцию
точки ». По обычным теоремам теории обык-
обыкновенных дифференциальных уравнений эта
функция определена и дифференцируема в ок-
окрестности точки х ЕЕ R2rl. Обозначим ее через
qx. Заметим, что qt = 0 на N и что производ-
производная функции qx по направлению поля Рх равна 1. Итак, скоб-
скобка Пуассона построенных функций qx и рх равна 1:
(ft. Pi) = 1-
Г. Построение симплектических координат индукцией по п.
Если га = 1, то построение закончено. Пусть п > 1. Мы бу-
будем предполагать, что теорема Дарбу для Rs«-2 уЖе до-
доказана.
Рассмотрим множество М, заданное уравнениями рг = qt = 0.
Дифференциалы dpx и dqx в точке ж линейно независимы, так как
к»2 (/ dpu I dqj = (дг, рг) = 1. Итак, по теореме о неявной функ-
функции в окрестности точки х множество М является многообразием
размерности 2п — 2; мы будем обозначать его М2п~2.
Лемма. Симплектическая структура со8 е R2n задает в не-
некоторой окрестности точки ж на М2п~2 симплектическую струк-
структуру.
Доказательство. Нуждается в доказательстве лишь
невырожденность со2 на ТМХ. Рассмотрим линейное симплекти-
ческое пространство TRlT. Векторы Рг (sc), Q% (ж) гамильтоновых
полей с функциями Гамильтона р1 и qx принадлежат JRi".
Пусть | S ТМХ. Производные р1 и q1 по направлению | равны
нулю. Значит, dPl (I) = со2 (|, Рх) = 0, dqt (?) = со2 (|, QJ = 0.
Итак, ТМЖ есть косоортогональное дополнение к Рг (х), Qx (x).
Согласно § 41, Б форма со2 на ТМХ невырождена. Лемма до-
доказана.

§ 43. СИМПЛЕКТИЧЕСКИЙ АТЛАС 203
По предположению индукции на симплектическом многообра-
многообразии (М2п-2, со2 \м) в окрестности точки ж существуют симплек-
тические координаты. Обозначим их pt, qt (i = 2, . . ., я). Про-
Продолжим функции pz, ¦ ¦ .» qn на окрестность точки ж в R2n следую-
следующим образом. Каждую точку s окрестности точки ж в R2n можно
единственным образом представить в виде » = P[(fyv, где w Er
€Е М2п~2, a s и t — малые числа. Значения координат pz, • • ., qn
в точке » положим равными их значениям в точке w
(рис. 179).
Построенные 2гс функций рг, . . ., рп; qt, . . ., qn образуют
в окрестности точки ж в R2n локальную координатную си-
систему.
Д. Доказательство симплектичности построенных координат.
Обозначим через Р\, Q% (i = 1, . . ., п) гамильтоновы потоки
с функциями Гамильтона pt, qt, а через Ри Qt — соответствую-
соответствующие векторные поля. Сосчитаем скобки Пуассона функций ри . . .
. . ., qn. Мы уже видели в пункте В, что (qu pt) = 1. Следова-
Следовательно, потоки Р[ и Ql коммутируют: Р[(? = Q{P{.
Вспоминая определение функций рг, . . ., qn, видим, что каж-
каждая из них инвариантна относительно потоков Рх и Ql. Итак,
скобки Пуассона р% и qt со всеми In — 2 функциями ph qt (i ^> 1)
равны нулю.
Отображение P\Q\ коммутирует поэтому со всеми In — 2
потоками Р\, Q\ (i ^> 1). Следовательно, оно оставляет на месте
каждое из 2п — 2 векторных полей Pt, Qt (i > 1). Отображение
PxQl сохраняет симплектическую структуру со2, так как потоки
Pi и Ql гамильтоновы. Поэтому значения в точках » = Р$%№ е R2"
ии)Е М 2"~г формы со2 на векторах любых двух из In — 2 полей
-Р«» Qi (г ^> 1) одинаковы. Но эти значения равны значениям
скобок Пуассона соответствующих функций Гамильтона. Итак,
значения скобки Пуассона любых двух из 2п — 2 координат pt, qt
(i ^> 1) в точках » и го одинаковы, если z = P[Qlw.
Функции рг и qt являются первыми интегралами каждого
из 2п — 2 потоков Р\, @| (i ^> 1). Поэтому каждое из Ъг — 2
полей Pi, Qt (i ^> 1) касается многообразия уровня р1 = qt = 0.
Но это многообразие есть М2™~2. Поэтому каждое ив Ъг — 2
полей Pit Qi (i ^> 1) касается М2п~2. Следовательно, эти поля яв-
являются гамильтоновыми полями на симплектическом многооб-
многообразии (М2П~2, со2 |м), и соответствующие функции Гамильтона
равны pt |M, qi \M (i ^> 1). Итак, скобка Пуассона во всем простран-
пространстве (R2n, со2) любых двух из Ъг — 2 координат ри qt (i ^> 1),
рассматриваемая на Ж2", совпадает со скобкой Пуассона этих
координат в симплектическом пространстве (М2п~2, со2 |м)-
Но по предположению индукции координаты на М2П~2 (pt \ы,
Яг \м', i ^> 1) симплектические. Поэтому во всем пространстве R2n

204 ГЛ. 8. СИМПЛЕКТИЧЕСКИЕ МНОГООБРАЗИЯ
скобки Пуассона построенных координат имеют стандартные
значения
(Pt> Pi) = (Pi, ?/) = (ft. 4j) = 0, (gt, pt) = 1.
Такой же вид имеют скобки Пуассона координат р, q в R2", если
<о2 — ^dpt Д dqt. Но билинейная форма со2 определяется своими
значениями на парах базисных векторов. Следовательно, скобки
Пуассона координатных функций определяют вид <а2 однозначно.
И
со2 = dpx Д dqx + . . . + dpn Д dqn.
Теорема Дарбу доказана.

ГЛАВА 9
КАНОНИЧЕСКИЙ ФОРМАЛИЗМ
В этой главе преобладает координатная точка зрения. Раз-
Развитый Гамильтоном и Якоби аппарат производящих функций
канонических преобразований является самым мощным из имею-
имеющихся методов интегрирования дифференциальных уравнений ди-
динамики. Кроме этого аппарата, глава содержит «нечетномерный»
подход к гамильтоновым фазовым потокам.
Эта глава независима от предыдущей. Она содержит новые
доказательства ряда результатов главы 8, а также объяснение
происхождения теории симплектических многообразий.
§ 44. Интегральный инвариант Пуанкаре — Картана
В этом параграфе рассматривается геометрия 1-формы в нечетномерном
пространстве.
А. Гидродинамическая лемма.'Пусты,* — векторное поле в трех-
трехмерном ориентированном евклидовом пространстве R3, г = rot v—
поле его ротора. Интегральные кривые г называются линиями
ротора или вихревыми линиями. Пусть уг — замкнутая кривая
в R3 (рис. 180). Линии ротора, проходящие через
точки Yi» образуют трубку ротора.
Пусть 72 — другая кривая, охватывающая
ту же трубку ротора, так что yt — yz = да,
где о — 2-цепь, представляющая часть трубки
ротора. Справедлива
Лемма Стоке а. Циркуляция поля v no
обеим кривым Yi и yz одинакова:
ф V dl = ф V dl. Рис. 180. Трубка
J .T ротора
Доказательство. По формуле Стокса \ vdl— \ vdl =
Yi Y«
= \ \ rot v dn = 0, так как rot v касается трубки ротора, ч. т. д.
с
Б. Многомерная лемма Стокса. Оказывается, лемма Стокса
допускает обобщение на случай любого нечетномерного много-
многообразия Л/2П+1 (вместо R3). Чтобы сформулировать это обобщение,
перейдем от векторных полей к дифференциальным формам.

206
ГЛ. 9. КАНОНИЧЕСКИЙ ФОРМАЛИЗМ
Циркуляция поля v есть интеграл 1-формы со1 (со1 (|) = (v, ?)).
Ротору поля v соответствует 2-форма со2 = da1 (day1 (?, ц) =
== (**> Ij Ч))- Из этой формулы видно, что в каждой точке сущест-
существует направление (а именно, направление ротора г, рис. 181),
обладающее тем свойством, что циркуляция v по краю всякой
«бесконечно малой площадки», содержащей г,
равна нулю:
da1 (г, г\) = О
Действительно, dm1 (r, г\) = (г, г, и\) = 0.
Замечание. Переход от 2-формы ю2 = da1
к полю ротора г — не инвариантная операция:
Рис. 181. ось, она зависит от евклидовой структуры R3.
инвариантно ев»-' Однако направление *) ротора г инвариантно
в нечетномерном СВЯЗЭНО С 2-форМОЙ ОJ (и, ЗНЭЧИТ, С 1-форМОЙ
пространстве а^ Действительно, легко проверить, что если
гфО, то направление г определяется условием {со2 (г, г\)= 0 Ут]}
однозначно.
Алгебраической основой многомерной леммы Стокса является су-
существование оси у всякого вращения нечетномерного пространства.
Лемма. Пусть to2 — алгебраическая внешняя 2-форма в не-
нечетномерном линейном пространстве R2n+1. Тогда существует
вектор | Ф 0 такой, что
со2 (i,ii) = о ViieR2n+1.
Доказательство. Кососимметрическая форма со2 за-
задается кососимметрической матрицей А
нечетного порядка 2п + 1. Определитель такой матрицы равен
нулю, так как
А' = —A, det A = det A' = det (—А) = (—!)"»¦« det A =
= —det A.
Итак, определитель А равен нулю. Значит А имеет собственный
вектор | Ф 0 с собственным значением 0, что и требовалось дока-
доказать.
Вектор |, для которого ю2 (|, т]) ^ 0 при всех г\, называется
нулевым вектором формы со2. Очевидно, все нулевые векторы со2
образуют линейное подпространство. Форма называется неосо-
неособой, если размерность этого пространства —¦ минимальная возмож-
возможная (т. е. 1 в нечетномерном пространстве R2n+1, 0 в четномерном).
Задача. Рассмотрим в четномерном пространстве R2n с координатами
Ри • • - Рп, 9i, ¦¦ -,9п 2-форму и2 = dpt Д dqt + .. . + dpn Д dqn. Докажите,
что форма со2 неособа.
*) То есть неориентированная прямая с направляющим вектором г
в TR%.

§ 44. ИНТЕГРАЛЬНЫЙ ИНВАРИАНТ ПУАНКАРЕ—КАРТАНА 207
3 а д а ч а. Рассмотрим в нечетномерном пространстве R2n+1 с коорди
ватами р1У . . ., рп; qu . . ., qn; t 2-форму to2 = Sdpj Д dgj — to1 Д dt, где со1—
любая 1-форма в R2"+1. Докажите, что форма со2 неособа.
Если со2 — неособая форма в нечетномерном пространстве R2n+1,
то все нулевые векторы ? формы со2 лежат на одной прямой. Эта
прямая инвариантно связана с формой со2.
Пусть теперь M2n+1 — нечетномерное дифференцируемое мно-
многообразие, со1 — 1-форма на М. По предыдущей лемме в каждой
точке х ?= М имеется направление (т. е. прямая {с|} в касатель-
касательном пространстве ТМХ), обладающее тем свойством, что интег-
интеграл со1 по краю «бесконечно малой площадки, содержащей это на-
направление», равен нулю:
Пусть далее 2-форма da1 неособа. Тогда направление | опреде-
определено однозначно. Мы назовем его «направлением ротора» формы to1.
Интегральные кривые поля направлений ротора называются
линиями ротора (или характеристиками) формы со1.
Пусть уг — замкнутая кривая на М. Линии ротора, выходя-
выходящие из точек Yu образуют «трубку ротора». Справедлива
Многомерная лемма Стоке а:
Интеграл 1-формы со1 no любой из двух кривых, охватывающих
одну и ту же трубку ротора, одинаков: ф со1 = ф со1, если
я/ я/
Yi У*
Yi — Уг = d°i г&е ° — кусок трубки ротора.
Доказательство. По формуле Стокса
(j) и1 — (|) ю1 = (j) со1 = 5 da1.
V, у2 да а
Но значение dco1 на любой паре векторов, касательных к трубке
ротора, равно нулю. (Действительно, эти два вектора лежат в
2-плоскости, проходящей через направление ротора, а на этой
плоскости do1 обращается в 0.)
Итак, \ dco1 = 0, что и доказывает лемму.
а
В. Канонические уравнения Гамильтона. Из леммы Стокса
непосредственно вытекают все основные положения гамильтоно-
вой механики.
Рассмотрим в качестве M2n-1 «расширенное фазовое простран-
пространство R2n+1» с координатами ри . . ., рп; дг, . . ., qn; t. Пусть дана
функция Н — Н (р, q, t). Тогда можно составить *) 1-форму
со1 = pdg — Hdt (pdq = pxdqt + . . . + pndqn).
Применим к со1 лемму Стокса (рис. 182).
*) Форма со1 кажется взятой с потолка. Мы увидим в следующих пара-
параграфах, как идея рассмотреть эту форму возникла из оптики.

208 ГЛ. 9. КАНОНИЧЕСКИЙ ФОРМАЛИЗМ
Теорема. Линии ротора формы со1 = р dq — Н dt в 2п +
¦4- 1-мерном расширенном фазовом пространстве р, q, t однозначно
проектируются на ось t, т. е. задаются функциями р = р (t),
q = q (t). Эти функции удовлетворяют
q у у, системе канонических дифференциалъ-
^^^^^ пых уравнений с функцией Гамильтона
dp _ дН dq _ дН ..
dt dq ' dt djp ' ^
Иными словами, линии ротора фор-
формы pdq— Н dt суть траектории фазо-
ис" линииарттора^°формыЛе и вого потока в расширенном фазовом про-
pdq — mt странстве, т. е. интегральные кривые
канонических уравнений A).
Доказательство. Дифференциал формы р dq — Н dt
равен
Из этого выражения видно, что матрица 2-формы do1 в коор-
координатах р, g, t имеет вид (проверьте!)
1° ~~Е НА II1 II
Е ° яJ гттр р — \'- я —т я дН
_яр -Hqo\' meE-\ '-J1 H>—Sp*H*—W
Ранг этой матрицы равен 2п (левый верхний 2п-угол невырож-
невырожден). Поэтому 2-форма dto1 неособа. Непосредственно проверяется,
что вектор (—Hq, Нр, 1) — собственный вектор матрицы А с соб-
собственным значением 0 (проверьте!). Значит, он задает направление
линий ротора формы pdq — Hdt. Но вектор (—Hq, Hp, 1) есть как
раз вектор скорости фазового потока A). Итак, интегральные кри-
кривые A) суть линии ротора формы р dq — Hdt, что и требовалось
доказать.
Г. Теорема об интегральном инварианте Пуанкаре — Картана.
Применим теперь лемму Стокса. Получается фундаментальная
Теорема. Пусть две замкнутые кривые уг, у2 охватывают
одну и ту же трубку фазовых траекторий A). Тогда интегралы
формы pdq — Н dt no ним одинаковы:
§ = j)pdq — Hdt.
•Vi Уг
Форма pdq — Hdt называется интегральным инвариантом Пу-
Пуанкаре — Картана *).
•) В вариационном исчислении \ р dq — Н dt называется инвариант-
инвариантным интегралом Гильберта.

S 44. ИНТЕГРАЛЬНЫЙ ИНВАРИАНТ ПУАНКАРЕ—КАРТ AHA
2091
Доказательство. Фазовые траектории суть линии
ротора формы pdq — Hdt, а интегралы по охватывающим одну
трубку ротора замкнутым кривым одинаковы по лемме Стокса,
ч. т. д.
Рассмотрим, в частности, кривые, составленные из одновремен-
одновременных состояний, т. е. лежащие в плоскостях t = const (рис. 183).
Вдоль таких кривых dt = 0, и §pdq — Hdt = §pdq. Из преды-
предыдущей теоремы получается важное
Следствие 1. Фазовый поток
сохраняет интеграл формы pdq = ptdqx -f-
+ . . . + pndqn no замкнутым кривым.
Действительно, пусть gfc R2n-vR2Tl —
преобразование фазового пространства
(р, q), осуществляемое фазовым потоком
за время от t0 до ^(т. е. g\, (р0, q0)
есть решение канонических уравнений A)
с начальными условиями р (t0) = р0,
Q (h) = Qo)- Пусть у — любая замкнутая
кривая в пространстве R2n CZ R2n+1 (t = t0).
Тогда glly есть замкнутая кривая в пространстве R2" (t = tx), ох-
охватывающая ту же трубку фазовых траекторий в R2n+2. По пре-
предыдущей теореме, так как dt = 0 на у и на gtly, находим.
ф р dq = ф р dq, что и требовалось доказать.
у и
Форма pdq называется относительным интегральным инва-
инвариантом Пуанкаре. Он имеет простой геометрический смысл.
Пусть а — двумерная ориентированная цепь, у = до. Тогда на-
находим по формуле Стокса
Рис. 183. Интегральный ин"
вариант Пуанкаре
Итак, доказано важное
Следствие 2. Фазовый поток сохраняет сумму ориенти-
ориентированных площадей проекций поверхности на п координатных плос-
плоскостей (pi, qi):
Иными словами, 2-форма to2 = dp Д dq является абсолютным ин-
интегральным инвариантом фазового потока.
Пример. При п = 1со2 есть площадь, и мы получаем тео-
теорему Лиувилля: фазовый поток сохраняет площадь.
Д. Канонические отображения. Пусть g — дифференцируемое
отображение фазового пространства R2n = {(p, q)} в R2".

210 ГЛ. 9. КАНОНИЧЕСКИЙ ФОРМАЛИЗМ
Определение. Отображение g называется канониче-
каноническим, если g сохраняет 2-форму to2 = Edp,- Д dq%.
Из предыдущих рассуждений видно, что это определение мож-
можно записать в любом из трех эквивалентных видов:
1) g*co2 = to2 (g сохраняет 2-форму 2фг Д dqt);
2) U со2 = JJ co2Vo (g сохраняет сумму площадей проекций лю-
бои поверхности);
3) ф р dq — ф р dq (форма pdq — относительный интеграль-
•V вУ
ный инвариант g).
Задача. Покажите, что определения 1), 2) эквивалентны 3), если
речь идет об отображении односвязной области в фазовом пространстве R2n;
в общем случае 3 =» 2 фф 1.
Предыдущие следствия теперь можно сформулировать так:
Теорема. Преобразование фазового пространства, осу-
осуществляемое фазовым потоком, каноническое.
Пусть g: R8n -*¦ R2n — каноническое преобразование: "g со-
сохраняет форму to2. Тогда g сохраняет также и внешний квадрат со2:
g* (<о2 Д <о2) = <оа Д со2, g* (ш2)* = (соа)к.
Внешние степени формы Edjp,- Д dqt пропорциональны формам
to4 = S d/>i Д dp^- Д dffj
Итак, доказана
Теорема. Канонические преобразования сохраняют интег-
интегральные инварианты со4, . . ., со2п.
Геометрически интеграл формы to2R означает сумму ориенти-
ориентированных объемов проекций на координатные плоскости (pit, . . .
В частности, форма со2п пропорциональна элементу объема,
и мы получаем
Следствие. Каноническое преобразование сохраняет эле-
элемент объема в фазовом пространстве:
объем gD = объем D для любой области D.
В частности, в применении к фазовому потоку получаем
Следствие. Фазовый поток A) имеет интегральными
инвариантами формы со2, со4, . . ., со2™.
Последний из инвариантов есть фазовый объем, так что мы
вновь доказали теорему Лиувилля.

§ 45. СЛЕДСТВИЯ ИЗ ТЕОРЕМЫ ОБ ИНТЕГРАЛЬНОМ ИНВАРИАНТЕ 211
§ 45. Следствия из теоремы об интегральном инварианте
Пуанкаре — Картана
В этом параграфе докавано, что канонические преобразования сохраняют
вид уравнений Гамильтона, что один первый интеграл уравнений Гамиль-
Гамильтона позволяет понизить порядок системы сразу на две единицы и что движе-
движение в лаграюкевой натуральной системе происходит по геодезической конфи-
конфигурационного пространства, снабженного некоторой римановой метрикой.
А. Замены переменных в канонических уравнениях. Из инва-
инвариантности связи формы р dq — Hdt с ее линиями ротора вытекает
способ писать уравнения движения в любой системе In + 1 ко-
координат в расширенном фазовом
пространстве {(р, q, t)}.
Пусть (xlt . . ., #2n+1) — коорди-
координатные функции в некоторой карте
расширенного фазового пространст-
пространства (рассматриваемого как многооб-
многообразие Af2n+1, рис. 184). Координаты
(р, q, t) можно рассматривать как
задающие другую карту М. Форму
' Zn*1
со
1 =
р р р
= р dq — Hdt можно рассматри-
рассматрифф 1ф
Рис"
р рр
вать как дифференциальную 1-форму на М. С этой формой ин-
инвариантным (не зависящим от карт) образом связано семейство
линий на М — линий ротора. На карте (р, q, t) эти линии изоб-
изображаются траекториями фазового потока
dp
dt
дН_
dq '
dq
dt
дН
dp
.л.
с функцией Гамильтона Н (р, q, t).
Пусть форма to1 в координатах (xlt ...» х2п+1) записывается
в виде
pdq — Hdt = Х$хг + . . . + Xsm+i&Wi-
Теорема. Ha карте (щ) траектории A) изображаются
линиями ротора формы ЪХга\сг.
Доказательство. Линии ротора форм HXidxt и pdq —
— Н dt суть изображения на двух разных картах линий ротора од-
одной и той же формы на М. Но интегральные кривые A) суть линии
ротора pdq — Нdt. Значит, их образы на карте (х{) суть линии
ротора формы HXidxt, что и требовалось доказать.
Следствие. Пусть (Ри . . ., Рп; Qlt . . ., Qn; T) — ло-
локальная система координат в расширенном фазовом пространстве
(р, q, t) и К (Р, Q, T), S (P, Q, Т) — такие функции, что
pdq — Hdt^TdQ — KdT + dS
(левая и правая части суть формы на расширенном фазовом прост-
пространстве)*.

212 ГЛ. 9. КАНОНИЧЕСКИЙ ФОРМАЛИЗМ
Тогда траектории фазового потока A) изображаются на карте
<(Р, Q, Т) интегральными кривыми канонических уравнений
dP дК dQ дК
dT dQ ' dT ~~ дР
B)
Доказательство. По предыдущей теореме траектории
{1) изображаются линиями ротора формы PdQ — KdT + dS. Но
dS на линии ротора не влияет (так как ddS — 0). Поэтому изоб-
изображения траекторий A) суть линии ротора формы PdQ — KdT.
Согласно § 44, В, линии ротора такой формы суть интегральные
кривые канонических уравнений B), что и требовалось доказать.
В частности, пусть g: R2n ->• R2" — каноническое преобразова-
преобразование фазового пространства, переводящее точку с координатами
{р, q) в точку с координатами (Р, Q).
Функции Р (р, q), Q (p, q) можно рассматривать как новые
координаты в фазовом пространстве.
Теорема. В новых координатах (Р, Q) канонические урав-
уравнения A) имеют канонический вид *)
dP дК dQ дК ,о.
со старой функцией Гамильтона: К (Р, Q, t) = Н (р, q, t).
Доказательство. Рассмотрим 1-
¦¦*' о форму р dq — PdQ в R2n. Для любой замкну-
^^ той кривой у имеем (рис. 185)
— Р dQ = ф р dq —
2i.9t
Рис. 185. замкну- ввиду каноничности g. Поэтому \ р dq —
тость формы p^t Va
pdq — pa — -p^q __ g не зависит от ПуТИ интегрирова-
интегрирования, но зависит лишь от конечной точки (pt, qj
(при фиксированной начальной точке (р0, q0)). Итак, dS =
= pdq — PdQ. Следовательно, в расширенном фазовом простран-
пространстве
pdq — Hdt = PdQ — Hdt + dS,
и применима предыдущая теорема. При этом B) превращается
в C), что и требовалось доказать.
Задача. Пусть g (t): R2n —» R2n — каноническое преобразование
фазового пространства, зависящее от параметра *, g(i)(p, q) — (P(p, q, t),
Q (P» Q, *))• Докажите, что канонические уравнения A) в переменных Р, Q,
•) В некоторых учебниках свойство сохранять канонический вид уравне-
уравнений Гамильтона принято за определение канонических преобразований.
В действительности это определение не эквивалентно общепринятому и при-
приведенному выше. Например, не каноническое в нашем смысле преобразование
Р = 2р, Q — q сохраняет гамильтонов вид уравнений движения.

( 45. СЛЕДСТВИЯ ИЗ ТЕОРЕМЫ ОБ ИНТЕГРАЛЬНОМ ИНВАРИАНТЕ 213
t имеют канонический вид с новой функцией Гамильтона К (Р, Q, t), где
К (Р, dS/дР, t) = dSldt + Н (dSldq, q, t),
p = dSldq, Q = dSldP, S = S (P, q, t).
Б. Понижение порядка с помощью интеграла энергии. Пусть
теперь функция Гамильтона Н (р, q) не зависит от времени. Тог-
Тогда канонические уравнения A) имеют первый интеграл: Н (р (t),
q (t)) = const. Оказывается, с помощью этого интеграла можно по-
понизить размерность пространства B/г + 1) на две единицы, сведя
задачу к интегрированию некоторой системы канонических урав-
уравнений в 2п — 1-мерном пространстве.
Предположим, что (в некоторой области) уравнение h =
= Н (plt . . ., рп; ?j,..., qn) можно разрешить относительно рг:
Рг = К (Р, Q, T; h),
где Р = (р2, . . ., рп); Q = (q2, . . ., qn); T = —qx.
Тогда находим
р dq — Hdt = PdQ — KdT — d (Ht) + t dH.
Пусть теперь у — интегральная кривая канонических уравне-
уравнений A), лежащая на 2п-мерной поверхности Н (р, q) = h в R2n+1.
Тогда у есть линия ротора формы pdq — Hdt (рис. 186). Спроекти-
Спроектируем расширенное фазовое пространство
д2п+1 _ Цр^ д^ ?)} на фазовое пространство
R2n = {(р, q)}. Поверхность Н = h спроек-
тируется в 2п — 1-мерное подмногообразие
M2n-1: H (p, q) = h в R2", а кривая у — в
кривую у, лежащую на этом подмногообра-
подмногообразии. Величины Р, Q, Т образуют локальные
Координаты В Л/2". Рис. 186. Понижение по-
_ рядка гамнльтоновой си-
3 а д а ч а. Докажите, что кривая у является стемы
линией ротора формы р dq = PdQ — К dT на М2".
Указание, d (Ht) не влияет на линии ротора, a dH на М есть нуль.
Но линии ротора формы PdQ — К dT удовлетворяют уравне-
уравнениям Гамильтона B). Итак, доказана
Теорема. Фазовые траектории уравнений A) на поверх-
поверхности М2"", Н = h, удовлетворяют каноническим уравнениям
dPi дК dq, вК ,. ~
где функция К (р2, . . ., рп; q2, . . ., qn; T, h) определяется из урав-
уравнения Н (К, р2, . . ., рп; —Т, q2, . . ., qn) = h.
В. Принцип наименьшего действия в фазовом пространстве.
Рассмотрим в расширенном фазовом пространстве {(р, q, t)} ин-
интегральную кривую у канонических уравнений A), соединяющую
точки {р0, q0, te) и (plt qlt ttf.

214
ГЛ. 9. КАНОНИЧЕСКИЙ ФОРМАЛИЗМ
Теорема. Интеграл J р dq — Н dt имеет у экстремалью
относительно вариаций у, при которых концы кривой остаются
на п-мерных подпространствах (t = 10, q = q0) и (t = tx, q — qt).
Доказательство. Кривая у — линия ротора формы
р dq — Н dt (рис. 187). Поэтому интеграл р dq — Н dt по «бесконеч-
«бесконечно малому параллелограмму, проходящему
через направление ротора», равен нулю.
Иными словами, приращение ^ — \pdq —
У у
— Н dt есть малая высшего порядка по
сравнению с отличием кривых у' и у, что
и требовалось доказать.
Если это рассуждение покажется недо-
недостаточно строгим, его можно заменить вы-
выкладкой:
Рис. 187. Принцип
наименьшего действия
в фавовом пространстве
Мы видим, что интегральные кривые уравнений Гамильтона —
единственные экстремали интеграла \pdq — Н dt в классе кри-
кривых у, концы которых лежат на п-мерных подпространствах (t =
= *о. Q = Qo) и (t = «!, q = qj) расши-
расширенного фазового пространства. Теоре-
Теорема доказана.
Замечание. Принцип наименьшего
действия в форме Гамильтона есть частный
случай рассмотренного выше принципа. Дей-
. ствительно, вдоль экстремали имеем
С pdq — Hdt=\(pq — H)dt= С L dt
*o. 9. <o h
Рис. 188. Кривые сравнения
для принципов наименьшего
действия в конфигурационном и
фазовом пространствах
(ибо лагранжиан L и гамильтониан И —
преобразования Леягандра друг друга).
Далее, пусть у (рир- 188) есть проекция экстремали у на плоскость g, t.
Любой близкой кривой у', соединяющей те же точки (*о, <7о) (*i> 9i) на плоскости
q, t, сопоставим кривую у'^в фазовом (р, q, ^-пространстве, полагая р = dL/dq.
Тогда вдоль у' также \ р dq — Hdt = f L dt. Но по доказанной теореме
v -'
f У
б \ p dq — Hdt = 0 для любых вариаций кривой у (при граничных условиях
у
(* = 'о> Q — 9о) и (* — hi Я — Ci))- В частности, это верно для вариаций спе-
специального вида, переводящих у в у1. Значит, у есть экстремаль J L dt, что
и требовалось доказать.

( 45. СЛЕДСТВИЯ ИЗ ТЕОРЕМЫ ОБ ИНТЕГРАЛЬНОМ ИНВАРИАНТЕ 215
В доказанной теореме к сравнению с у допускается значитель-
0О более широкий класс кривых у', чем в принципе Гамильтона:
0а связь р с д не накладывается никаких ограничений. Может по-
показаться удивительным, что оба принципа, тем не менее, эквива-
эквивалентны: из экстремальности в более узком классе вариаций (р =
= дЫдд) следует экстремальность при любых вариациях. Объяс-
Объяснение состоит в том, что при фиксированном g величина р = дЫдд
экстремизирует рд — Н (см. определение преобразования Лежанд-
ра, § 14, стр. 61).
Г. Принцип наименьшего действия в форме Мопертюи—
Эйлера—Лагранжа—Якоби. Пусть теперь функция Гамильтона
Н (р, д) не зависит от времени. Тогда Н (р, д) есть первый интег-
интеграл уравнений Гамильтона A). Спроектируем поверхность
И (р, д) = h из расширенного фазового пространства {(р, д, t)}
в пространство {{р, д)}. Получится 2п — 1-мерная поверхность
Н (Pi Q) = h в R2n, которую мы уже рассматривали в пункте Б и
которую мы обозначили М271.
Фазовые траектории канонических уравнений A), начинаю-
начинающиеся на поверхности М2™", целиком лежат на поверхности
Мгп~г. Они являются линиями ротора формы pdq = IPdQ — К dT
(в обозначениях пункта Б) на М2п~г. Согласно теореме пункта В,
кривые A) на М271'1 — экстремали вариационного принципа,
соответствующего этой форме. Итак, доказана
Теорема. Если функция Гамильтона Н = Н (р, д) не
зависит от времени, то фазовые траектории канонических урав-
уравнений A), лежащие на поверхности М2": Н (р, д) = h, являются
экстремалями интеграла j p dg в классе кривых, лежащих на М2П~Х
и соединяющих подпространства g = g0 и g = дг.
Рассмотрим теперь проекцию экстремали, лежащей на поверх-
поверхности М2п~1ш. Н (р, д) = h, на g-пространство. Эта кривая соединя-
соединяет точки д0 и дг.
Пусть, далее, у — другая кривая, соединяющая точки д0 и дг
(рис. 189). Эта кривая у является проекцией некоторой кривой у
на поверхности Мт"г. А именно, вы-
выберем на у параметр т, а ^ т <^ Ь,
У (а) = по, Т (Ь) = 9-1- Тогда в каждой
точке д кривой у определен вектор ско-
ростид = —j—у(т), и соответствующий
импульс р = дЫдд. Если параметр т
Подобран так, ЧТО Н (р, д) = Я, ТО МЫ Рис. 189. Принцип Мопертюи
получаем кривую у: q = у (т), р = »
= dLldq на поверхности М2П~1. Применяя предыдущую теорему
к кривым у на М2п-1, получаем
Следствие. Среди всех кривых g = у (т), соединяющих
две точки д0 и дг на плоскости q и параметризованных так,
что функция Гамильтона имеет фиксированное значение
p
7~7м2"-1
A

216 ГЛ. 9. КАНОНИЧЕСКИЙ ФОРМАЛИЗМ
Н (dLldq,q) = h, траекторией уравнений динамики A) является
экстремаль интеграла «укороченного действия»
= J pq dx = jj-||- (г) q (г) dr.
Это и есть принцип наименьшего действия Мопертюи (Эйлера—
Лагранжа — Якоби) *). Важно отметить, что отрезок о <^ г <^ Ь,
параметризующий кривую у, не фиксирован и может быть разным
у сравниваемых кривых. Зато одинаковой должна быть энергия
(функция Гамильтона). Заметим также, что принцип определяет
форму траектории, но не время: для определения времени нужно
воспользоваться постоянной энергии.
Особенно простую форму доказанный принцип принимает
в случае, когда система представляет движение по инерции по
гладкому многообразию.
Теорема. Материальная точка, вынужденная оставаться
на гладком римановом многообразии, движется по геодезической
линии (т. е. по экстремали длины \ ds).
Доказательство. Действительно, в нашем случае
Следовательно, чтобы обеспечить фиксированное значение Н = h,
параметр т надо выбирать пропорциональным длине: dx = _1_ »
у 2h
Интеграл укороченного действия тогда равен
У У
поэтому экстремали суть геодезические нашего многообразия, что
и требовалось доказать.
В случае, когда имеется также потенциальная энергия, траек-
траектории уравнений динамики тоже являются геодезическими неко-
некоторой римановой метрики.
Пусть ds2 — риманова метрика на конфигурационном простран-
пространстве, задающая кинетическую энергию (так что Т = -тр (-зт-) ) •
Пусть h —~ постоянная.
Теорема. Зададим в области конфигурационного простран-
пространства, где V (q) <C h, риманову метрику формулой
dp = Yh — U (q) ds.
*) «Почти во всех учебниках, даже в лучших, этот принцип представлен
так, что его нельзя понять». (Я к о б и К. Лекции по динамике, 1842—1843.—
М.; Л.: ОНТИ, 1936). Не решаюсь нарушать традицию.

S 45. СЛЕДСТВИЯ ИЗ ТЕОРЕМЫ ОБ ИНТЕГРАЛЬНОМ ИНВАРИАНТЕ 217
1 / ds \2
Тогда траектории система с кинетической энергией Т = -к- (—д-) ,
потенциальной энергией U (q) и полной энергией h будут геодези-
геодезическими линиями метрики dp.
Доказательство. Действительно, в нашем случае
L= T-U,H= T + U, -§|-д = 2Г = (-§-J = 2(Л-г7).Следо-
вательно, чтобы обеспечить фиксированное значение Н = h, пара-
параметр г надо выбрать пропорциональным длине: dx — .
у A \h — U)
Интеграл укороченного действия тогда будет равен
По принципу Мопертюи траектории суть геодезические метрики
dp, что и требовалось доказать.
Замечание 1. Метрика dp получается из ds «растяже-
«растяжением», зависящим от точки q, но не зависящим от направления.
Поэтому углы в метрике ф совпадают с углами в метрике ds. На
границе области V ^ h метрика dp имеет особенность: чем ближе
мы подходим к границе, тем меньше становится р — длина. В част-
частности, длина любой кривой, лежащей на самой границе (U = h)t
равна нулю.
Замечание 2. Если начальная и конечная точки геоде-
геодезической у достаточно близки, то экстремум длины есть минимум.
Зто оправдывает название «принцип наименьшего действия». Что
в общем случае экстремум действия не обязательно минимум,
видно из рассмотрения геодезических на единичной сфере
Рис. 190. Немини- Рис. 191. Периодическое дви-
мальная геодсзиче- жение двойного маятника
екая
(рис. 190). Каждая дуга меридиана является геодезической, но
минимальны лишь те из них, которые короче я: дуга NS'M коро-
короче дуги меридиана NSM.
Замечание 3. Если h больше максимума V на конфигу-
конфигурационном пространстве, то метрика ф не имеет особенностей.
Поэтому мы можем применить топологические теоремы о геодези-
геодезических на римановых многообразиях к изучению механических
задач.

218 ГЛ. 9. КАНОНИЧЕСКИЙ ФО РМАЛИЗМ
Так, например, рассмотрим тор Т2 с некоторой римановой
метрикой. Среди всех замкнутых кривых на Т2, делающих пг обо-
оборотов по параллели и п по меридиану, существует кривая крат-
кратчайшей длины (рис. 191). Эта кривая — замкнутая геодезическая
(доказательство см. в книгах по вариационному исчислению в це-
целом или «теории Морса»).
С другой стороны, тор Т2 является конфигурационным про-
пространством плоского двойного маятника. Отсюда вытекает
Теорема. Для любых целых m, n существует периодиче-
периодическое движение двойного маятника, при котором одно звено делает
т оборотов за время, за которое второе звено делает п оборотов.
Более того, такие периодические движения существуют при
любом достаточно большом значении постоянной энергии h (h дол-
должно быть больше потенциальной энергии в верхнем положении).
В качестве еще одного примера рассмотрим твердое тело, за-
закрепленное в неподвижной точке и находящееся в произвольном
потенциальном поле. Конфигурационное пространство (SOC))
не односвязно: на нем существуют нестягиваемые кривые. Из пре-
предыдущих рассуждений вытекает
Теорема. Каково бы ни было потенциальное силовое поле,
существует по крайней мере одно периодическое движение тела.
Более того, существуют такие периодические движения, для ко-
которых постоянная энергии h сколь угодно велика.
§ 46. Принцип Гюйгенса
Основные понятия гамильтоновой механики (импульсы р, функция Га-
Гамильтона Н, форма pdq — Hdt, уравнение Гамильтона — Якоби, о котором
будет идти речь ниже) возникли при перенесении на общие вариационные
принципы (и, в частности, на принцип стационарного действия Гамильтона,
б\L dt ~ 0) некоторых весьма простых и естественных понятий геометриче-
геометрической оптики, управляемой частным вариационным принципом — принципом
Ферма.
А. Волновые фронты. Рассмотрим коротко *) основные поня-
понятия геометрической оптики. Согласно экстремальному принципу
Ферма, свет распространяется из точки q0 в точку q± за кратчай-
кратчайшее время. При этом скорость света может зависеть как от точки q
(«неоднородная среда»), так и от направления луча («неизотропная
среда» — например, кристаллы).
Свойства среды можно описать, задав в касательном про-
пространстве в каждой точке q поверхность («индикатрису»). Для это-
этого отложим по каждому направлению вектор скорости распростра-
распространения света в данной точке по данному направлению (рис. 192).
*) Мы не будем здесь гнаться за строгостью и будем считать, что все оп-
определители отличны от нуля, и т. п. От полуэвристических рассуждений это-
этого пункта доказательства дальнейших теорем не зависят.

§ 46 ПРИНЦИП ГЮЙГЕНСА
219
Рис. 192. Неизотроп-
Неизотропная неоднородная
среда
Пусть теперь t ^> 0. Рассмотрим множество всех точек q, до
которых свет из данной точки q0 может дойти за время, меньшее
или равное t. Граница этого множества, Фдо (t), называется вол-
волновым фронтом точки q0 через время t и состоит из точек, до ко-
которых свет может дойти за время t и не может
дойти быстрее.
Между волновыми фронтами, соответствую-
соответствующими разным значениям t, имеется замечатель-
замечательное соотношение, открытое Гюйгенсом (рис.
193).
Теорема Гюйгенса. Рассмотрим
волновой фронт точки q0 через время t, Фд„ (t).
Построим для каждой точки q этого фронта
волновой фронт через время s, Фд (s). Тогда вол-
волновой фронт точки q0 через время s + t,
ФЧо (s + t), будет огибать построенные фронты Фд (s), q ЕЕ Ф«„ (t)-
В самом деле, пусть qt+s ?= Ф«о (* + *)¦ Тогда существует путь
из q0 в qt+si по которому время распространения света равно t -f- s,
и нет более короткого. Рассмотрим точку qt на этом пути, до кото-
которой свет идет время t. Никакого более короткого пути от q0 до qt
не может быть, иначе путь qoqn-s не был бы кратчайшим. Поэтому
точка qt лежит на фронте Фво (t). Точно так же путь qtqt+s свет
проходит за время s, и из точки qt в qt+s нет более короткого пути.
Поэтому точка qt+s лежит на фронте точки qt за время s, Фв( (s).
Покажем, что фронты Фв4 (s)
и Фво (t + s) в точке qt+s ка-
касаются. Действительно, если
бы они пересекались (рис. 194),
(t+s)
Рис. 193. Огибающая волновых фронтов
Рис. 194. Доказательство теоремы
Гюйгенса
то в некоторые точки Фв0 (t -f- s) можно было бы добраться из qt
за время, меньшее s, а значит, из q0 — за время, меньшее s+t.
Это противоречит определению Фво (t + s); итак, фронты Фв4 (s)
и Ф9о (t + s) касаются в точке qt+s, что и требовалось доказать.
Доказанная теорема называется принципом Гюйгенса. Разу-
Разумеется, точку q0 можно было бы заменить кривой, поверхностью
Или вообще замкнутым множеством, трехмерное пространство

220
ГЛ. 9. КАНОНИЧЕСКИЙ ФОРМАЛИЗМ
{<?} — любым гладким многообразием, а распространение света —
распространением любого возмущения, передающегося «локально».
Принцип Гюйгенса приводит к двум описаниям процесса рас-
распространения. Во-первых, мы можем следить за лучами, т. е. крат-
кратчайшими путями распространения света. В этом случае локаль-
локальный характер распространения задается вектором скорости q. Если
направление луча известно, то величина вектора скорости за-
задается свойствами среды (индикатрисой).
С другой стороны, мы можем следить за волновым фронтом.
Предположим, что в пространстве {q} задана риманова метри-
метрика. Тогда можно говорить о скорости движения волнового фронта.
Рассмотрим, например, распространение света в среде, заполняю-
заполняющей обычное евклидово пространство. Тогда движение волнового
фронта можно характеризовать перпендикулярным фронту век-
вектором р, который строится следующим образом.
Для каждой точки q0 определим функцию Sqc (q) как оптиче-
оптическую длину пути от q0 до q, т. е. наименьшее время распростране-
распространения света от q0 до q.
Множество уровня {q: Sq^ (q) = f) есть не что иное, как вол-
волновой фронт Фво (t) (рис. 195). Градиент функции S (в смысле
а Напрабленив
луча
pq
Направление
движения
фронта
/21
Фронт
Рис. 195. Направление луча и
направление движения фронта
'Сопряжен-
ное
направление
Рис. 196. Сопряженная ги-
гиперплоскость
упомянутой выше метрики) перпендикулярен волновому фронту
и характеризует движение волнового фронта. При этом, чем боль-
больше градиент, тем медленнее движется фронт. Поэтому Гамильтон
назвал вектор
_ 6S
Р~ 6q
вектором нормальной медлительности фронта.
Направление луча q и направление движения фронта р в не-
неизотропной среде не совпадают. Однако они связаны друг с дру-
другом простым соотношением, легко выводящимся из принципа Гюй-
Гюйгенса. Напомню, что свойства среды в каждой точке характери-
характеризуются поверхностью векторов скорости света — индикатрисой.

§ 46. ПРИНЦИП ГЮЙГЕНСА
221
Определение. Направление гиперплоскости, касающей-
касающейся индикатрисы в точке v, называется сопряженным к направле-
направлению v (рис. 196).
Теорема. Направление волнового фронта Фво (t) в точке qt
сопряжено направлению луча, q.
Доказательство. Рассмотрим (рис. 197) точки q%
луча «ZofZf» 0 <^ г <[ i. Пусть 8 очень мало. Тогда фронт ФЯ(_е (в)
отличается от индикатрисы точки qt, умноженной на 8, лишь
малыми порядка О (е2). По
принципу Гюйгенса, этот
фронт Ф9._ (8)
Направление
луча
'Направление
движения
Фронта
Рис. 197. Сопряженность направлений луча и
фронта
) касается
фронта Фд, (t) в точке qt.
Переходя к пределу при
е -»- О, получаем сформули-
сформулированную теорему.
При изменении вспомога-
вспомогательной метрики, с помощью
которой мы определили век-
вектор р, будет меняться поня-
понятие скорости движения фрон-
фронта, а значит, и величина и
направление вектора р.
Однако дифференциальная форма р dq = dS на пространстве-
{q} = R3 определена не зависящим от вспомогательной метрики
образом; ее значение зависит лишь от выбранного фронта (или
луча). На гиперплоскости, сопряженной вектору скорости луча,
эта форма равна 0, а ее значение на векторе скорости равно 1 *).
Б. Оптико-механическая аналогия. Вернемся теперь к меха-
механике. Здесь траектории движения также являются экстремалями
вариационного принципа, и можно строить механику как геомет-
геометрическую оптику многомерного пространства. Именно так и посту-
поступил Гамильтон; мы не будем проводить это построение во всех
деталях, а только перечислим те оптические понятия, которые при-
привели Гамильтона к основным механическим понятиям.
Оптика
Оптическая среда
Принцип Ферма
Лучи
Индикатриса
Нормальная медлительность
фронта р
Выражение р через скорость луча q
1-форма р dq
Механика
Расширенное конфигурационное-
пространство {(qt)),
Принцип Гамильтона 6 J L dt = О
Траектории q (t)
Лагранжиан L
Импульс р
Преобразование Лежандра
1-форма р dq — Hdt
¦) Таким образом, векторы р, соответствующие всевозможным фронтам,
проходящим через данную точку, не произвольны, но подчинены одному ус-
условию: допустимые значения р заполняют в пространстве {р) гиперповерх-
гиперповерхность, двойственную индикатрисе скоростей

222 ГЛ. 9. КАНОНИЧЕСКИЙ ФОРМАЛИЗМ
Неиспользованными остались оптическая длина пути SQo (q)
и принцип Гюйгенса. Их механические аналоги — функция дейст-
действия и уравнение Гамильтона — Якоби, к которым мы теперь и пе-
перейдем.
В. Действие как функция координат и времени.
Определение. Функцией действия S (q, t) называется
интеграл
вдоль экстремали у, соединяющей точки (q0, t0) и (q, t).
Чтобы это определение было корректным, нужно принять не-
некоторые предосторожности: нужно потребовать, чтобы экстрема-
экстремали, выходящие из точки (q0, t0), более не пересекались, а образо-
образовывали так называемое «центральное поле экстремалей» (рис. 198).
Точнее, сопоставим каждой паре (q0, t) точку (g, t) — конец экстре-
экстремали с начальными условиями q @) = q0, q @) = q0. Говорят, что
экстремаль у включена в центральное поле,
если отображение (q0, t) и-»- (q, t) невырождено
(в точке, соответствующей рассматриваемой
экстремали у и, следовательно, в некоторой
ее окрестности).
Можно доказать, что при достаточно малом
\ t — t0 \ экстремаль у включается в централь-
центральное поле *).
зкстршалей Рассмотрим теперь достаточно малую окрест-
окрестность конечной точки (q, t) нашей экстремали.
Каждая точка этой окрестности соединена с (q0, t0) единствен-
единственной экстремалью рассматриваемого центрального поля. Эта
экстремаль дифференцируемо зависит от конечной точки (q, t).
Поэтому в указанной окрестности корректно определена функция
действия
В геометрической оптике мы рассматривали дифференциал оп-
оптической длины пути. Естественно и здесь рассмотреть дифферен-
дифференциал функции действия.
Теорема. Дифференциал функции действия (при фикси-
фиксированной начальной точке) равен
dS = pdq — Hdt,
где р = dL/dq uH = pq — L определяются по конечной скорости q
траектории у.
*) Задача. Покажите, что при больших t — t0 это уже не так.
Указание, q = —q (рис. 199).

§ 46. ПРИНЦИП ГЮЙГЕНСА
223
Доказательство. Поднимем каждую экстремаль и8
(q, ^-пространства в расширенное фазовое пространство {(р, д, t)},
нолагая р = dL/dq, т. е. заменяя экстремаль фазовой траекторией.
Мы получим тогда в расширенном фазовом пространстве
п + 1-мерное многообразие, составленное из фазовых траекторий,
т. е. линий ротора формы р dq — Н dt. Дадим
теперь конечной точке (q, t) приращение (Aq, At)
и рассмотрим семейство экстремалей, соединяю-
соединяющих {q0, t0) с точками отрезка q + QAq,
t + QAt, 0 < Э < 1 (рис. 200). В фазовом про-
пространстве мы получим составленный из линий
ротора формы р dq — Л dt четырехугольник а,
граница которого
t.
да = уг — у2 + р — а
Рис. 199. Экстремаль
с фокальной точкой,
которую нельзя
включить в централь-
центральное поле
состоит из двух фазовых траекторий уг и у2, отрезка кривой а,
лежащей в пространстве (q = q0, t = t0), и отрезка кривой р, про-
проектирующегося в отрезок (Aq, At). Так как а состоит из линий ро-
ротора формы pdq — Нdt, имеем
0=§d{pdq-Hdt)= J pdq-
а да
Yi
Уг
и
Но на отрезке а имеем dq = 0, Рис. 200. Вычисление дифферен-
dt = 0. Ha фазовых траекториях ъ циала *ункции действия'
и yz р dq —Hdt = Ldt(§ 45, В). Итак, разность^ — ^ р dq — Н dt
равна приращению функции действия, и мы находим
J p dq — Н dt = S (q + Aq, t + At) - S (q, t).
Если теперь Aq -*¦ 0, At-*- 0, то
p dq — H dt = pAq — HAt + о (At, Aq),
что и доказывает теорему.
Мы видим, что форма pdq — Н dt, прежде введенная нами ис-
искусственно, сама собой возникает при проведении оптико-механи-
оптико-механической аналогии из рассмотрения функции действия, соответст-
соответствующей оптической длине пути.
Г. Уравнение Гамильтона — Якоби. Вспомним, что «вектор
нормальной медлительности р» не может быть совсем произволь-
произвольным: он подчиняется одному условию pq = i, вытекающему из

224
ГЛ. 9. КАНОНИЧЕСКИЙ ФОРМАЛИЗМ
зпринципа Гюйгенса (стр. 219). Аналогичное условие накладыва-
накладывается и на градиент функции действия iS".
Теорема. Функция действия удовлетворяет уравнению
dS , „l&S \ п
A)
Это нелинейное уравнение первого порядка в частных произ-
производных называется уравнением Гамильтона — Якоби.
Для доказательства теоремы достаточно заметить, что по пре-
предыдущей теореме
dS „, .. 8S
-—=-H(p,q,t), Р = -щ-.
Установленную связь между траекториями механической си-
системы («лучами») и уравнением в частных производных («волновы-
(«волновыми фронтами») можно использовать в двух
направлениях.
Во-первых, некоторые решения урав-
уравнения A) можно использовать для ин-
интегрирования обыкновенных дифферен-
дифференциальных уравнений динамики. В этом
состоит метод Якоби интегрирования ка-
канонических уравнений Гамильтона, из-
изложенный в следующем параграфе.
Во-вторых, связь лучевой и волновой
точек зрения позволяет свести интегри-
интегрирование уравнения в частных производ-
производных A) к интегрированию системы обыкновенных дифферен-
дифференциальных уравнений Гамильтона.
Остановимся на этом несколько подробнее. Поставим для урав-
яения Гамильтона — Якоби A) задачу Коши
= 0. B)
Чтобы построить решение этой задачи, рассмотрим систему кано-
вических уравнений Гамильтона
Рис. 201. Характеристики
для решения задачи Коши
для уравнения Гамильто-
Гамильтона — Якоби
р = —
6Н
dq
ен
дР
Рассмотрим начальные условия (рис. 201):
Соответствующее этим начальным условиям решение изображает-
изображается в (q, ^-пространстве кривой q = q (t) — экстремалью принци-
принципа S ^ L dt = 0 (где лагранжиан L (q, q, t) есть преобразование

§ 46. ПРИНЦИП ГЮЙГЕНСА
225
Лежандра по р от функции Гамильтона Н (р, q, t)). Эта экстремаль
называется характеристикой задачи B), выходящей из точки q0.
Если значение tt достаточно близко к t0, то характеристики,
выходящие из близких точек q, не пересекаются при t0 <[ t <^ tlt
\q — q0 1 < R. Более того, значения qovit можно принять за ко-
координаты точки А в области | q — q0 | < jR, to^t ^ tt (рис. 201).
Построим теперь «функцию действия с начальным услови-
условием So»:
L(q,q,t)dt
C)
(интегрирование вдоль характеристики, ведущей в А).
Теорема. Функция C) есть решение нашей задачи B).
Действительно, начальное условие, очевидно, выполнено. Вы-
Выполнение уравнения Гамильтона — Якоби проверяется, как в тео-
теореме о дифференциале функции
действия (рис. 202).
Рис. 202. Функция действия как решение
уравнения Гамильтона — Якоби
Рис. 203. Типичная особенность ре-
решения уравнения Гамильтона—Якоби
По лемме Стокса \ — \ + \ — \ р dq — И dt = 0. Но на a dt = 0, р =
Yi Y2 P «
= eS0/dq, поэтому \pdq- Н dt={pdq = \ dS0 = So (q0 + &q) — So (g0).
a a a
Далее, у1 2 — фазовые траектории, поэтому
f pdq—Hdt= f Ldt.
Итак,
p dq — H dt =
Vl,2
o (qo +
L dt
] —
(g0) + §L dt] =
P Ys Yi
= S (A + ДЛ) —
При Д* —» 0, получаем dSldt = —H, dS/dq = p, что и доказывает теорему.
Задача. Доказать единственность решения задачи B).
Указание. Продифференцировать S вдоль характеристик.
Задача. Решить задачу Коши B) при Н = р2/2, So = ф12.
Задача. Нарисовать графики многозначных «функций» S (g) и
р (д) при t = i3 (рис. 201).
Ответ. См. рис. 203.

226 ГЛ. 9. КАНОНИЧЕСКИЙ ФОРМАЛИЗМ
Точке самопересечения графика S соответствует на графике р прямая
Максвелла: заштрихованные площади равны. График S (g, t) имеет особен-
особенность, называемую ласточкиным хвостом в точке (q = 0, t2).
§ 47. Метод Якоби — Гамильтона интегрирования
канонических уравнений Гамильтона
В этом параграфе определяется производящая функция свободного ка-
канонического преобразования.
Идея метода Якоби — Гамильтона состоит в следующем. При
канонической замене координат сохраняется канопический вид
уравнений движения, а также функция Гамильтона (§ 45, А).
Следовательно, если нам удастся найти каноническое преобра-
преобразование, приводящее функцию Гамильтона к такому виду, что
канонические уравнения удастся проинтегрировать, то тем самым
мы сумеем проинтегрировать и исходные канонические уравнения.
Оказывается, задача построения такого канонического преобразо-
преобразования сводится к отысканию достаточно большого числа решений
уравнения Гамильтона — Якоби в частных производных. Этому
уравнению должна удовлетворять производящая фупкция искомо-
искомого канонического преобразования.
Переходя к аппарату производящих функций, замечу, что он
Удручающе неинвариантен и существенно использует координат-
координатную структуру в фазовом пространстве {(р, q)}. В соответствии
с этим приходится пользоваться аппаратом частных производных,
а это такой объект, в самом обозначении которого уже кроется
двусмысленность *).
А. Производящая функция. Пусть In функций Р (р, д), Q (р, д)
от In переменных р, д задают каноническое преобразование g:
R2n ->- R2n. Тогда 1-форма pdg — Р dQ есть полный дифферен-
дифференциал (§ 45, А):
PdQ = dS(:p,g). A)
Задача. Докажите, что и обратно, если эта форма ¦— полный диффе-
дифференциал, то преобразование — каноническое.
Предположим теперь, что в окрестности некоторой точки (р0, д0)
за независимые координаты можно принять (Q, д). Иными
словами, предположим, что отличен от нуля якобиан в (р0, д0)
, q)
*) Следует ясно понять, что величина ди/дх на плоскости х, у зависит не
только от того, какая функция принята за х, но и от того, какая функция
принята за у: в новых переменных (х, z) значение duldx будет уже другим.
Следовало бы писать
ди I ди I
дх ly=const' дх lz=const

§ 47. МЕТОД ЯКОБИ—ГАМИЛЬТОНА 227
Такие канонические преобразования называют свободными. Тогда,
в частности, функцию S можно локально выразить через эти коор-
координаты:
S (р, q) = St (Q, q).
Определение. Функция Sx (Q, q) называется произво-
производящей функцией нашего канонического преобразования g.
Подчеркнем, что S^ не есть функция на фазовом пространстве
R2n: эта функция задана в области прямого произведения!^ X
X Rq некоторых двух тг-мерных координатных пространств, точ-
точки которых обозначаются через q и Q.
Из A) следует, что «частные производные» 5Х суть
dSi(Q,Q) aSi (Q, q) p (9,
Оказывается, и обратно, всякая функция Sx задает некоторое ка-
каноническое преобразование g по формулам B).
Теорема. Пусть Sj (Q, q) — функция, заданная в окрест-
окрестности некоторой точки (Qo, q0) прямого произведения двух п-мер-
ных координатных евклидовых пространств. Если
то функция Sx является производящей функцией некоторого сво-
свободного канонического преобразования.
Доказательство. Рассмотрим уравнение относитель-
относительно координат Q
dq —P-
По теореме о неявной функции это уравнение разрешимо и опреде-
определяет в окрестности точки \q0, р0 = —1 ^ \ функцию Q (p, q)
(причем Q (р0, q0) = Qo). Действительно, нужный определи-
определитель здесь как раз det — *5 * , а он по условию отличен
"У "Q lOoi в»
от 0.
Рассмотрим теперь функцию
и положим
P{p,q) = P1(Q(p,q),q).
Тогда локальное отображение g: R2n —*- R2n, переводящее точ-
КУ (Р, п) в точку Р (р, q), Q (p, q), будет каноническим с

228 ГЛ. 9. КАНОНИЧЕСКИЙ ФОРМАЛИЗМ
производящей функцией Slt ибо по построению
pdq-PdQ = dS^q)dq+ **««>
Оно свободно, так как det -—-=det(—Л> g ] ^0. Теорема
доказана.
Преобразование g: R2™ ->- R2n задается вообще 2п функциями
от 2п переменных. Мы видим, что каноническое преобразование
задается всего одной функцией 2п переменных — своей произво-
производящей функцией. Легко сообразить, какую выгоду дает примене-
применение производящих функций во всех вычислениях, связанных
с каноническими преобразованиями. Эта выгода тем больше, чем
больше число переменных 2п.
Б. Уравнение Гамильтона—Якоби для производящей функ-
функции. Заметим, что канонические уравнения, в которых функция
Гамильтона //зависит от одних лишь переменных О, легко интег-
интегрируются. Действительно, если Н = К (О), то канонические урав-
уравнения имеют вид
0 = 0, Р=-^, C)
откуда непосредственно
Будем теперь искать каноническое преобразование, приводящее
функцию Гамильтона Н (р, q) к виду К (О)- С этой целью будем
искать производящую функцию такого преобразования S (О. <?)•
Мы получаем из B) условие
^ D)
где после дифференцирования вместо q следует подставить q (JP, Q).
Заметим, что при фиксированном Q уравнение D) имеет вид урав-
уравнения Гамильтона — Якоби.
Теорема Якоби. Если найдено решение S (Q, q) уравне-
уравнения Гамильтона — Якоби D), зависящее от п параметров Qt *)
и такое, что det Ф 0, то канонические уравнения
дН . дН /с-.
решаются явно в квадратурах. При этом функции Q (p, q), опреде-
определенные уравнениями -
ралами уравнений E).
0S (О, а)
ленные уравнениями ^ ¦ = р, являются п первыми интег-
*) n-параметрическое семейство решений уравнения D) называется пол-
полным интегралом, уравнения.

§ 47. МЕТОД ЯКОБИ—ГАМИЛЬТОНА 229
Доказательство. Рассмотрим каноническое преобра-
преобразование с производящей функцией S (Q, д). Имеем, согласно B),
р = -g-(Q, Q), откуда находимО (р, д). Вычислим функцию Н (р, д)
в новых координатах P,Q. Имеем Н{р, д) = Н (~д— (Q, <?). Я) .
Чтобы найти функцию Гамильтона в новых координатах, надо
было бы подставить в это выражение (после дифференцирова-
дифференцирования) вместо д его выражение через Р и Q. Однако, согласно D), это
выражение от д вовсе не зависит, так что просто
Н (р, д) = К (Q).
Таким образом, в новых переменных уравнения E) имеют вид C),
откуда непосредственно вытекает теорема Якоби.
Теорема Якоби сводит решение системы обыкновенных диффе-
дифференциальных уравнений E) к отысканию полного инте!рала урав-
уравнения в частных производных D). Может показаться удивитель-
удивительным, что такое сведение более простого к более сложному достав-
доставляет эффективный метод решения конкретных
задач. Между тем оказывается, что это — самый
сильный, из существующих методов точного ин-
интегрирования, и многие задачи, решенные
Якоби, вообще не поддаются решению други-
другими методами.
В. Примеры. Рассмотрим задачуопри-
тяжении двумя неподвижными цен-
центрами. Интерес к этой задаче возрос в по- Рис. 204. эллипти-
следнее время в связи с изучением движения ческие координата
искусственных спутников Земли. Достаточно ясно, что два близ-
близких притягивающих центра на оси z аппроксимируют притяжение
слегка вытянутого вдоль оси z эллипсоида. К несчастью, Земля
не вытянута, а сплюснута. Выход состоит в том. чтобы поместить
центры в мнимые точки на расстоянии ± 1г вдоль оси z. Аналитиче-
Аналитические формулы для решения сохраняют, конечно, силу и в комплекс-
комплексной области. Таким образом, получается приближение к полю тя-
тяготения Земли, в котором уравнения движения точно интегриру-
интегрируются и которое ближе к реальности, чем кеплеровское приближе-
приближение (Земля — точка).
Рассмотрим здесь для простоты лишь плоскую задачу о притя-
притяжении двумя неподвижными равными массами. Успех метода Яко-
Якоби основан на применении подходящей системы координат, так
называемых эллиптических координат. Пусть расстояние между
неподвижными точками Ог, О2 равно 2с (рис. 204), а расстояния
Движущейся массы от них равны гг и г2. Эллиптические координаты
?> т] определяются как сумма и разность расстояний до точек Ои
°2- I = Гг + Г2, Т] = Гх — Г2.

230
ГЛ. 9. КАНОНИЧЕСКИЙ ФОРМАЛИЗМ
Задача. Выразить функцию Гамильтона черев эллиптические коор-
координаты.
Решение. Линии | = const суть эллипсы с фокусами в Ог и Ог,
и\ = const — гиперболы с теми же фокусами (рис. 205). Они взаимно ортого-
ортогональны, поэтому ds2 = a2d|2 + 62«ft]2. Найдем коэффициенты а и Ъ. При дви-
движении вдоль эллипса имеем drx = ds cos a, dr2 = — ds cos a, di\ = 2 cos a ds.
При движении вдоль гиперболы имеем drx = ds sin a,
dr2 = ds sin a, d| = 2 sin a ds. Итак, a =B sin a),
b= B cos a)-1.
Далее, из треугольника О1МО2 находим
ri
Г2 + 2rirs cos 2a = 4c2,
откуда
Рис. 205. Конфокаль-
Конфокальные эллипсы и гиперболы
(Г1+Г2J_4С2
Л
Но rx + г2 ^ |, rj — r2 ^ т], 4»1?-2 =
2rxr2 rx r2 *
— т[2. Поэтому окончательно
Теперь будем решать уравнение Гамильтона — Якоби.
Определение. Если в уравнение
Ф,
dS
dS
и)-
о
переменная qx и производная dSldq1 входят лишь в виде комбина-
комбинации ф \-~—, q-Л , то говорят, что переменная q1 отделяется.
В этом случае полезно поискать решения уравнения вида
Полагая в исходном уравнении ф l-g-^ i ?i) = clt получаек
уравнение для iS" с меньшим числом переменных
dS' dS'
Пусть S' = S' (q2, . . ., qn; сг, с) — семейство решений этого
уравнения, зависящее от параметров ct. Функции Sj (дг, сг) + S'

§ 47. МЕТОД ЯКОБИ—ГАМИЛЬТОНА 231
будут удовлетворять исходному уравнению, если 5Х удовлетворя-
удовлетворяет обыкновенному уравнению ф (-г-^ , дО = сг. Это уравнение лег-
dSx dS! , . .
ко решить; выражая -j-=- через q1 и сх, получаем -^— = г]з (qv Cj),
откуда Sj = § гр (qlt сг) dqv
Если в новом уравнении (с Ф2) отделяется одна из переменных^
скажем q2, мы можем повторять эту процедуру и (в благоприятном
случае) найдем зависящее от п постоянных решение исходного
уравнения
Si (qi, cx) + S2 (qz; сг, с2) + . . . + Sn (qn; clt . . ., cn).
В таком случае говорят, что переменные полностью разделяются.
Если переменные полностью разделяются, то зависящее от п
параметров[решение уравнепия Гамильтона — ЯкобиФх f-т— , q) =0
находится квадратурами. Но тогда интегрируется в квадратурах
и соответствующая система канонических уравнений (теорем?
Якоби).
Применим сказанное к задаче о двух неподвижных центрах
Уравнение Гамильтона — Якоби D) имеет вид
Dс* - tf) = К (?2 - rj») + 4*1-
Мы можем разделить переменные, например, полагая
Тогда находим полный интеграл уравнения D) в виде
с if ч
Теорема Якоби дает теперь явное выражение движения в задаче
о двух неподвижных центрах через эллиптические интегралы.
Подробное качественное исследование этого движения можно
найти в книге Шарлье «Небесная механика» (М.: Наука, 1966.—
628 с).
Другое применение задачи о притяжении двумя неподвижными
центрами — это исследование движений с постоянной тягой в поле
одного притягивающего центра.
Речь идет о движении материальной точки под действием нью-
ньютоновского притяжения неподвижного центра и еще одной силы
(«тяги»), постоянной по величине и направлению.

232 РЛ. 9. КАНОНИЧЕСКИЙ ФОРМАЛИЗМ
Эта задача может рассматриваться как предельный случай
задачи о притяжении двумя неподвижными центрами. В процес-
процессе предельного перехода второй центр удаляется на бесконечность
в направлении силы тяги (причем его масса должна расти так,
чтобы обеспечить постоянство тяги, т. е. пропорционально квад-
квадрату удаления).
Получающийся предельный случай задачи о притяжении дву-
двумя неподвижными центрами интегрируется в явном виде (в эллип-
эллиптических функциях). В этом можно убедиться при помощи предель-
предельного перехода или же непосредственно разделяя переменные
в задаче о движении с постоянной тягой в поле одного центра.
Координаты, в которых разделяются переменные в этой задаче,
получаются предельным переходом из эллиптических координат,
когда один из центров удаляется на беско-
бесконечность. Они называются параболическими
координатами и даются формулами
и = г — х, v = г -f- х
(тяга направлена вдоль оси х).
Описание траекторий движения с постоян-
постоянной тягой (многие из которых весьма замыс-
замысловаты) можно найти в книге В. В. Белец-
Рис. 206. геодезическая кого «Очерки о движении космических тел»
на трехосном эллипсоиде (М . Наука^ щщ
В качестве еще одного примера рассмотрим задачу о геодези-
геодезических на трехосном эллипсоиде *). Здесь помогают эллиптиче-
эллиптические координаты Якоби Кх, Я2, Я3, которые суть три корня уравнения
где хх, х2, х3 — декартовы координаты. Я не буду приводить вы-
выкладок, показывающих, что переменные разделяются (их можно
найти, например, в «Лекциях по динамике» Якоби), но приведу
лишь результат: опишу поведение геодезических.
Поверхности Ях = const, Аа = const, Я3 = const суть поверх-
поверхности второго порядка, называемые софокусными. Одна из них
эллипсоид, другая однополостный гиперболоид, третья двуполост-
ный. Эллипсоид может вырождаться во внутренность эллипса, од-
однополостный гиперболоид — во внешность эллипса или в часть
плоскости между ветвями гиперболы, двуполостный — в часть
плоскости вне ветвей гиперболы или в плоскость.
Пусть рассматриваемый эллипсоид — один из эллипсоидов се-
семейства с полуосями а [> Ь^> с. Каждый из трех эллипсов хг =
*) Задача о геодезических на эллипсоиде и близкая задача об эллипсо-
эллипсоидальном бильярде нашли применение в ряде недавних физических работ,
связанных с лазерными устройствами.

§ 47. МЕТОД ЯКОБИ—ГАМИЛЬТОНА
233
¦= 0, х2 = О, х3 = 0 есть замкнутая геодезическая. Геодезическая,
выходящая из точек большого эллипса (с полуосями а, Ь) по на-
направлению, близкому к направлению эллипса (рис. 206), касается
поочередно двух замкнутых линий пересечения эллипсоида с одно-
полостным гиперболоидом нашего семейства Я = const *).
Эта геодезическая либо замкнута, либо заполняет кольцо меж-
между линиями пересечения всюду плотно. По мере увеличения накло-
наклона геодезической, гиперболоиды сжимаются к области «внутри»
гиперболы, пересекающей наш эллипсоид в его четырех «точках
округления». В предельном случае мы получаем геодезические,
проходящие через точки округления (рис. 207).
Интересно отметить, что все геодезические, выходящие из точ-
точки округления, снова собираются вместе в противоположной точ-
точке округления и все они имеют между двумя точками округления
одинаковую длину. Однако только одна из этих геодезических
Рис. 207. Геодезические,
выходящие из точек
округления
Рис. 208. Геодезические вллипсои-
да, касающиеся двухполостного
гиперболоида
замкнута: это средний эллипс с полуосями а, с. Если идти вдоль
любой другой геодезической, проходящей через точку округле-
округления, в любую сторону, то мы будем асимптотически приближаться
к этому эллипсу.
Наконец, еще более «круто» пересекающие большой эллипс
геодезические (рис. 208) касаются поочередно двух линий пересе-
пересечения нашего эллипсоида с двуполостным гиперболоидом **).
Они заполняют, вообще говоря, всюду плотно кольцо между эти-
этими линиями.
Среди таких геодезических выделяется малый эллипс с полуося-
полуосями Ь, с. Об эллиптических координатах см. также добавление 14.
«Главная трудность при интегрировании данных дифферен-
дифференциальных уравнений состоит во введении удобных переменных,
для разыскания которых нет никакого правила. Поэтому мы долж-
должны идти обратным путем и, найдя какую-либо замечательную под-
подстановку, разыскивать задачи, в которых она может быть с успе-
*) Эти линии пересечения софокусных поверхностей являются также
линиями кривизны эллипсоида.
**) Являющихся также линиями кривизны.

234 ГЛ. 9. КАНОНИЧЕСКИЙ ФОРМАЛИЗМ
хом применена» (Я к о б и К. Лекции по динамике.— М.:
ОНТИ, 1936).
Таблица задач, допускающих разделение переменных в сфе-
сферических, эллиптических и параболических координатах, имеется
в § 48 «Механики» Ландау и Лифшица (М.: Физматгиз, 1958).
§ 48. Производящие функции
В этом параграфе строится аппарат производящих функций для несвобод-
несвободных канонических преобразований.
А. Производящая функция S2 (Р, q). Пусть g: R2" -*- R2n —
каноническое преобразование, g (р, д) = (Р, Q). По определению
канонического преобразования, дифференциальная 1-форма наК2™:
pdq~ PdQ = dS
является полным дифференциалом некоторой функции S (р, q).
Каноническое преобразование свободное, если за 2п независимых
координат можно принять q, Q. В зтом случае функция S, выра-
выраженная через координаты q и Q, называется производящей функ-
функцией St (q, Q). Зная эту единственную функцию, можно найти
все 2п функций, задающих преобразование, из соотношений
_ asx (g, Q) р_ aSi (g, Q) ,,
Однако далеко не все канонические преобразования — свобод-
свободные. Например, в случае тождественного преобразования q и Q —
= q зависимы. Поэтому тождественное преобразование нельзя
задать производящей функцией Sx (q, Q).
Однако можно перейти к производящей функции иного вида
посредством преобразования Лежандра. Пусть, например, за не-
независимые локальные координаты в R2" можно принять Р, q
(т. е. отличен от нуля определитель det ' q =¦ det -^—) . Тог-
Тогда имеем
pdq - PdQ = dS, pdq + QdP = d (PQ + S).
Величина PQ + S, выраженная через (Р, q), называется так-
также производящей функцией
S2 (P, q) = PQ+S (p, q).
Для этой функции находим
) п _ dS2(P, q) /оч
Р ~~ dq ' v "~ dP к >
Обратно, если S2 (P, q) — произвольная функция, для которой
отличен от нуля определитель det —* ' , то в окрестно-
OQ О Mr |-Рй, Qe

§ 48. ПРОИЗВОДЯЩИЕ ФУНКЦИИ 235
сти точки
dq
, во
.)
д0) можно разрешить первую
группу уравнений B) относительно Р и получить функции Р (р, д)
(где Р (р0, дв) = Ро). После этого вторая группа уравнений B)
определяет Q (р, д), и отображение (р, q) >->- (Р, Q) — канониче-
каноническое (докажите!).
Задача. Найти производящую функцию Sz для тождественного отоб-
отображения Р = р, Q = q.
Ответ. Pq.
Замечание. Производящая функция St (P, q) удобна еще и потому,
что в формулах B) нет минусов, и их легко вспомнить, если помнить, что
производящая функция тождественного преобразования есть Pq.
Б. 2п производящих функций. К сожалению, переменные Р, q
также не всегда могут быть выбраны за локальные координаты.
Однако всегда можно выбрать некоторый набор п новых коор-
координат
Pt = (Ph, . . ., Pik), Q} = (Qht . . ., QJnJ
так, что вместе со старыми д мы получим 2п независимых коор-
координат.
Здесь (it, . . ., iK) (ju . . ., /„-ь) — любое разбиение множе-
множества A, . . ., п) на две непересекающиеся части, так что всего
имеется 2" случаев.
Теорема. Пусть g: R2" ->- R2n — каноническое преобразо-
преобразование, заданное функциями Р (р, q), Q (р, д). В окрестности каж-
каждой точки (р0, д0) можно принять за независимые координаты
в R271 по меньшей мере один из 2™ наборов функций (Pi, Qj, g):
л , d(PvQ.,q) d(P.,Q.)
det ; =Аеь1-^
В окрестности такой точки можно восстановить каноническое
преобразование g no функции
S3(Pi, Qj, д) - (Pi, Qi) + \pdg-PdQ
из соотношений
P — dq ' Чг - дРг' ^з — dQ. • W
Обратно, если Ss (Pt, Qj, g) — любая функция, для которой
отличен от нуля определитель det 3 (И — Рг, Qj), то со-
otc oq \Rot q0
отношения C) задают каноническое преобразование в окрестности
точки р0, q0-
Доказательство этой теоремы почти такое же, как проведенное
выше в частном случае к = п. Нужно лишь проверить, что для
одного из 2" наборов (Pt, Qj, g) отличен от 0 определитель

236 ГЛ. 9. КАНОНИЧЕСКИЙ ФОРМАЛИЗМ
Рассмотрим дифференциал нашего преобразования g в точке (р0, д0).
Отождествляя касательные пространства к R2n с R2n, мы можем считать dg сим-
плектическим преобразованием S: R2" —> R2n.
Рассмотрим координатную р-плоскость Р в R2n (рис. 209). Это нулевая
n-мерная плоскость, и ее образ SP — тоже нулевая плоскость. Спроектируем
плоскость SP на координатную плоскость о = {(р1у Qj)} параллельно осталь-
остальным координатным осям, т. е. по направлению нулевой n-мерной координат-
координатной плоскости а = {(Pj, д{)}. Обозначим через Т: SP —> о оператор проек-
проектирования.
*<рг Qj)
Условие det^jT г- =/= 0 означает невырожденность TS: Р —» о. Опе-
" vP Pj)
; j
ратор S невырожден. Поэтому для невырожденности TS необходимо и доста-
достаточно, чтобы проектирование Т: SP —* о~ не вырождалось.
Иными словами, нулевая плоскость SP должна быть
трансверсальной нулевой координатной плоскости б. Но
мы доказали в § 41, что хотя бы одна из 2" нулевых коор-
координатных плоскостей трансверсальна SP. Значит, один из
наших 2" определителей отличен от нуля, что и требова-
требовалось доказать.
Задача. Доказать, что приведенная система 2"
видов производящих функций минимальна: существуют ка-
канонические преобразования, для которых отличен он нуля
лишь один из 2" определителей *).
Рис. 200. к про- В. Бесконечно малые канонические преобразо-
верКденноетиРСЖ" вания. Рассмотрим теперь каноническое преобра-
преобразование, близкое к тождественному. Его произ-
производящую функцию можно взять близкой к производящей функции
тождества Pq. Рассмотрим семейство канонических преобразова-
преобразований ge, дифференцируемо зависящих от параметра е, так что
производящая функция имеет вид
Pq+BS(P,q;e); p = P + eJg-, Q = g+e^.. D)
Бесконечно малым каноническим преобразованием называется
класс эквивалентности семейств ge; два семейства ge и he эквива-
эквивалентны, если они отличаются малыми выше первого порядка,
Us - К I = о (е2), e -> о.
Теорема. Бесконечно малое каноническое преобразование
удовлетворяет дифференциальным уравнениям Гамильтона
dP I _ дН_ jlQ_\ _ дН
<2в б=о dq ' de ^=0 dp
с функцией Гамильтона Н (р, q) = S (p, q, 0).
Доказательство получается из формул D): Р->-р при е -> 0.
Следствие. Однопараметрическая группа преобразований
фазового пространства R2" удовлетворяет каноническим уравне-
уравнениям Гамильтона тогда и только тогда, когда преобразования
канонические.
¦) Число видов производящих функций в разных учебниках колеблется
от 4 до 4П.

§ 48. ПРОИЗВОДЯЩИЕ ФУНКЦИИ
237
Функцию Гамильтона Н называют в связи с этой теоремой
«производящей функцией канонического бесконечно малого пре-
преобразования». Заметим, что, в отличие от производящих функций
S, функция Н есть функция точки фазового пространства, инва-
инвариантно связанная с преобразованием.
Функция Н имеет простой геометрический смысл. Пусть х
я у — две точки из R2n (рис. 210), у — соединяющая их кривая,
ду = у — х. Рассмотрим сдвиги кривой у при .
ваших преобразованиях, g%y, 0 <^ т ^ е. Они
образуют полоску а (е). Рассмотрим интеграл
формы to2 = 21Ф« Л dQi п0 2-цепи а, да =
=&7 — Т + g%y — ёхх.
Задача. Докажите, что
о(е)
Рис. 210. Геометри-
Геометрический смысл функ-
функции Гамильтона
существует и не зависит от представителя класса ge.
Из этого результата мы еще раз получаем уже известное
Следствие. При каноническом преобразовании канониче-
канонические уравнения сохраняют свой вид, а также величину функции
Гамильтона.
Действительно, мы вычислили приращение функции Гамиль-
Гамильтона, используя только бесконечно малое каноническое преобра-
преобразование и симплектическую структуру R2" — форму <о2.

Г Л А В А 10
ВВЕДЕНИЕ В ТЕОРИЮ ВОЗМУЩЕНИЙ
Теория возмущений представляет собой весьма полезный набор
приемов» предназначенных для приближенного решения «возму-
«возмущенных» задач, близких к «невозмущенным», решенным точно.
Эти приемы легко оправдать, если речь идет об исследовании дви-
движений на небольшом интервале времени. Вопрос о том, в какой
мере можно доверять выводам теории возмущений при исследова-
исследовании движения на больших и бесконечных интервалах времени,
изучен весьма мало.
Мы увидим, что во многих «невозмущенных» интегрируемых
задачах движение оказывается условно периодическим. При ис-
исследовании движения как в невозмущенной, так и особенно в воз-
возмущенной задаче полезны специальные симплектические коорди-
координаты: переменные «действие — угол». В заключение мы докажем
теорему, обосновывающую теорию возмущений одночастотных си-
систем, и докажем адиабатическую инвариантность переменной дей-
действия в таких системах.
| [§ 49. Интегрируемые системы
Чтобы проинтегрировать систему 2и обыкновенных дифференциальных
уравнений, нужно знать 2и первых интегралов. Оказывается, если дана ка-
каноническая система дифференциальных уравнений, то во многих случаях
достаточно знать лишь п первых интегралов — каждый из них позволяет
понизить системы не на одну, а на две единицы.
А. Теорема Лиувилля об интегрируемых системах. Напомню,
что функция F является первым интегралом системы с функцией
Гамильтона Н тогда и только тогда, когда скобка Пуассона
(Я, F) = 0
тождественно равна нулю.
Определение. Две функции Fu F2 на симплектическом
многообразии находятся в инволюции, если их скобка Пуассона
равна нулю.
Лиувилль доказал, что если в системе с п степенями свободы
(т. е. Ъг-мерным фазовым пространством) известны п независимых
первых интегралов в инволюции, то система интегрируема в квад-
квадратурах.
Вот точная формулировка этой теоремы.

§ 49. ИНТЕГРИРУЕМЫЕ СИСТЕМЫ 239
Предположим, что на симплектическом 2п-мерном многообра-
многообразии даны п функций в инволюции
Fl7 . . ., Fn; (Ft, Fj) = 0, i, / = 1, 2, . . ., п.
Рассмотрим множество уровня функций Ft
Mt = {х: F, (х) = U, i = l,..., л).
Предположим, что на Mf п функций Ft независимы (т. е. п 1-форм
dFt линейно независимы в каждой точке Mf).
Тогда:
1) Mf — гладкое многообразие, инвариантное относительно
фазового потока с функцией Гамильтона Н = Fx.
2) Если многообразие Mj компактно и связно, то оно диффео-
морфно п-мерному тору
Тп = {(ф1, . . ., Фп) modd 2л}.
3) Фазовый поток с функцией Гамильтона Н определяет на Mt
условно-периодическое движение, т. е. в угловых координатах <р =
= (фь • • •, 4>п)
4) Канонические уравнения с функцией Гамильтона Н инте-
интегрируются в квадратурах.
Прежде чем доказывать эту теорему, отметим некоторые из ее
следствий.
Следствие 1. Если в канонической системе с двумя сте-
степенями свободы известен один первый интеграл F, не зависящий
от функции Гамильтона Н, то система интегрируема в квадра-
квадратурах; компактное связное двумерное подмногообразие фазового
пространства Н = h, F = / есть инвариантный тор, а движение
на нем условно-периодично.
Действительно, F и Н находятся в инволюции, так как F —
первый интеграл системы с функцией Гамильтона Н.
В качестве примера с тремя степенями свободы рассмотрим
лагранжев тяжелый симметричный волчок, закрепленный в точке
на оси. Здесь сразу видны три первых интеграла Н, Mz, M3.
Легко проверить, что интегралы М% и М3 находятся в инволю-
инволюции. Далее, многообразие Н = h в фазовом пространстве компакт-
компактно. Поэтому мы без всяких вычислений сразу можем сказать, что
при большинстве начальных условий *) движение волчка условно-
периодично: фазовые траектории заполняют трехмерные торы
Н = Cj,, Mz = с2, Ms = ca. Соответствующие три частоты назы-
называются частотами собственного вращения, прецессии и нутации-
*) Исключение составляют особые множества уровня интегралов, где
нарушается их независимость.

240 ГЛ. 10. ВВЕДЕНИЕ В ТЕОРИЮ ВОЗМУЩЕНИЙ
Другие примеры получаются из следующего замечания: если
каноническая система интегрируется методом Якоби — Гамиль-
Гамильтона, то она имеет п первых интегралов в инволюции.
Действительно, метод состоит в каноническом преобразовании
{Pi О) -*" (^*> О), таком, что Pt — первые интегралы. Но функ-
функции Pt, Pj, очевидно, находятся в инволюции.
В частности, сказанное применимо к задаче о притяжении
двумя неподвижными центрами. Число примеров легко умно-
умножить; фактически сформулированная выше теорема Лиувилля
охватывает все проинтегрированные на сегодняшний день пробле-
проблемы динамики.
Б. Начало доказательства теоремы Лиувилля. Перейдем
теперь к доказательству теоремы. Рассмотрим множество уровня
интегралов
Mt = {х: Ft = fit i = 1, . . ., п}.
По условию п 1-форм dFt линейно независимы в каждой точ-
точке Mf. Следовательно, по теореме о неявной функции, Mf есть
n-мерное подмногообразие 2п-мерного фазового пространства.
Лемма 1. На п-мерном многообразии Mf существуют п ка-
касательных векторных полей, попарно коммутирующих и линейно
независимых в каждой точке.
Доказательство. Симплектическая структура фазо-
фазового пространства определяет оператор /, переводящий 1-формы
в векторные поля. Этот оператор / переводит 1-форму dFt в поле
I dFt фазовой скорости системы с функцией Гамильтона Ft. Пока-
Покажем, что п полей I dFf касаются Mf, коммутируют и независимы.
Действительно, из независимости dFi и невырожденности изо-
изоморфизма / следует независимость / dFt в каждой точке Mf. По-
Поля IdFt попарно коммутируют, так как скобки Пуассона их
функций Гамильтона (Ft, Fj) = 0. По той же причине производ-
производная функции Fi по направлению поля / dFj равна нулю для
любых ?, / = 1, . . ., п. Значит, поля / dFt касаются Mf, и лем-
лемма 1 доказана.
Заметим, что доказано даже больше чем лемма 1:
1') Многообразие Mf инвариантно относительно каждого из п
коммутирующих фазовых потоков gi с функциями Гамильтона F^,
1") Многообразие Mf — нулевое (т. е. 2-форма ю2 обращается
в нуль на TMf\x).
Действительно, п векторов / dFt \x попарно косоортогональны
((Ft, Fj) = 0) и образуют базис в касательной плоскости к мно-
многообразию Mf в точке х.
В. Многообразия, на которых транзитивно действует группа
R". Теперь мы воспользуемся следующим топологическим пред-
предложением (доказательство заканчивается на стр. 244).

49. ИНТЕГРИРУЕМЫЕ СИСТЕМЫ
241
Лемма 2. Пусть М71 — компактное, связное дифференци-
дифференцируемое п-мерное многообразие, на котором задано п векторных
полей, попарно коммутирующих и линейно независимых в каждой
точке М*1. Тогда многообразие М71 диффеоморфно п-мерному тору.
Доказательство. Обозначим через g\, i = 1, . . ., п,
однопараметрические группы диффеоморфизмов М, соответствую-
соответствующие заданным п векторным полям. Поскольку поля коммутируют,
группы gi, gSj коммутируют. Поэтому мы можем определить дей-
действие g коммутативной группы Rn = {t} на многообразии М,
полагая
g*: М^М, gt^gl1--.gan
Очевидно, ?*+* = gtgsVt, 8 Е= Rn-
Тогда возникает отображение
(t = (tv -,УЕВ").
Зафиксируем точку х0
М.
(точку х0 надо сдвинуть на время tt по траектории первого пото-
потока, t2 — второго и т. д.).
Задача 1. Докажите, что построенное отображение g (рис. 211)
достаточно малой окрестности V точки О е Rn задает карту окрестности
точки ас0: у каждой точки хь е М существует такая окрестность U, х0 е
е U С М, что g отображает V на U диффеоморфно.
Указание. Применить теорему о неявной функции и воспользовать-
воспользоваться линейной независимостью полей в точке х0.
Рис. 211. К задаче 1
Рис. 212. К задаче 2
Задача 2. Докажите, что g: Rn —» М есть отображение н а.
Указание. Соедините точку х е М с х0 кривой (рис. 212), покройте
кривую конечным числом окрестностей U предыдущей задачи и определите
t как сумму сдвигов t-%, соответствующих кускам кривой.
Заметим, что отображение g: Rn -v M71 не может быть взаимно
однозначным, так как Мп компактно, a Rn нет. Изучим множест-
множество прообразов точки х0 Е= Мп.
Определение. Стационарной группой точки х0 называ-
называется множество Г точек * Е= Rn, для которых glx0 = х0.
Задача 3. Докажите, что Г есть подгруппа группы Rn, не зависящая
притом от точки х0.
Решение. Если gtx0 = х0, g"x0 = х0, то
g*+tXD =
= g'xo = XD,

242
ГЛ. 10. ВВЕДЕНИЕ В ТЕОРИЮ ВОЗМУЩЕНИИ
Поэтому
V
Г — подгруппа Rn. Если х = grx0, (
Г, то gfx = gt+rx0 =
Таким образом, стационарная группа Г есть вполне опреде-
определенная, не зависящая от точки х0 подгруппа группы Rn. В част-
частности, точка t = 0, очевидно, принадлежит Г.
Задача 4. Докажите, что в достаточно малой окрестности V точки
t — 0 в R" нет других точек стационарной группы Г, кроме точки t = 0.
Указание. Отображение g: V —> U диффеоморфно.
Задача 5. Докажите, что в окрестности t -f- V (рис. 213) любой точки
t е Г CI Rn нет точек стационарной группы Г, отличных от точки t.
Рис. 213. К задаче 5
Рис. 214. Дискретная под-
подгруппа плоскости
Рис. 215. К доказатель-
доказательству леммы о дискрет-
дискретных подгруппах
Таким образом, точки стационарной подгруппы Г лежат в R"
дискретно. Такие подгруппы называются дискретными подгруп-
подгруппами.
Пример. Пусть ег, . . ., ек — к линейно независимых век-
векторов в R", 0 <^ к <С п. Множество всех их целочисленных ли-
линейных комбинаций (рис. 214)
+ + тг <= Z = (. . . —2, —1, 0, 1, . . .).
образует дискретную подгруппу в R". Например, множество всех
целых точек на плоскости есть дискретная подгруппа плоскости.
Г. Дискретные подгруппы в R". Мы воспользуемся теперь
следующим алгебраическим фактом: приведенным примером ис-
исчерпываются все дискретные подгруппы в R". Точнее, будет до-
доказана
Лемма 3. Пусть Г — дискретная подгруппа группы R".
Тогда существуют к @ <^ /с ^ п) линейно независимых векторов
elf . . ., efc (ЕЕ Г, таких, что Г есть в точности множество всех
их целочисленных линейных комбинаций.
Доказательство. Будем рассматривать в R" какую-
нибудь евклидову структуру. Имеем всегда ОеГ. Если Г =
= {О}, лемма доказана. Если нет, существует точка е0 ЕЕ Г,
е0 Ф О (рис. 215). Рассмотрим прямую Re0. Покажем, что на этой
прямой существует точка ех, ближайшая к О. Действительно,
в шаре радиуса | е0 | с центром в О лишь конечное число точек Г

§ 49. ИНТЕГРИРУЕМЫЕ СИСТЕМЫ 243
(у каждой точки Г, как мы видели выше, есть окрестность стан-
стандартной величины V, не содержащая других точек Г).
Ближайшая к О из конечного числа точек этого шара, лежа-
лежащих на прямой Re0, будет ближайшей к О точкой из Г на всей
прямой.
На прямой Re0 группе Г принадлежат целые кратные
ех (тех, т е= Z) и только они. Действительно, точки тех делят
прямую на части длины | ех ]. Если бы внутри одной из этих
частей, (тех, (т + 1) ех), была точка е е= Г, то точка е — тех е= Г
была бы ближе к О, чем ех.
Если у Г нет точек вне прямой Re1; то лемма доказана. Пусть
существует точка е?Г, е 1= Re2. Покажем, что существует точ-
точка е2 ЕЕ Г, ближайшая к прямой Rej (сама не лежащая на пря-
прямой). Спроектируем е ортогонально на прямую Rex. Проекция
лежит ровно в одном отрезке Д == {кех}, т <; Я< т + 1. Рас-
Рассмотрим прямой круговой цилиндр Ц с осью Д и радиусом, рав-
равным расстоянию от Д до е. В этом цилиндре лежит конечное (не-
(ненулевое) число точек группы Г.
Пусть е2 — ближайшая из них к оси Relf но не лежащая на
оси.
Задача 6. Докажите, что расстояние от любой точки группы Г,
не лежащей на оси Rex, до этой оси не меньше, чем расстояние от точки е2 до
оси Rex.
Указание. Сдвигом на те1 можно загнать проекцию на ось в отре-
отрезок Д.
Целочисленные линейные комбинации ех и е2 образуют решет-
решетку в плоскости Rex + Re2.
Задача 7. Докажите, что никаких других точек подгруппы Г, кроме
целочисленных линейных комбинаций ех и е2, на плоскости Rex Ч~ Re2
нет.
Указание. Разделите плоскость на параллелограммы (рис. 216)
Д = {Ягвх + Я2е2}, тг ^ hi < mi + 1. Если бы е е Д, е ф Щ?\ + т2е2,
то точка е — тхех—яг2е2 была бы ближе к Rex,
XJOJl* f>
Если у Г [нет точек вне плоскости
Rex + Re2, то лемма доказана. Пусть су-
существует точка е Е=Т вне этой плоско-
плоскости. Тогда существует ближайшая к плос- _______^^
кости Re] + Re2 точка е3 (= Г; точки ~ef
тхех + т2е2 + т3е3 исчерпывают Г в Рис 216 к 8адаче 7
трехмерном пространстве Нех + Re2 + Ке3.
Если Г этим не исчерпана, берем бли-
ближайшую точку к этому трехмерному пространству, и т. д.
Задача 8. Докажите, что ближайшая точка каждый раз существует.
Указание. Взять ближайшую из конечного числа точек соответст-
соответствующего «цилиндра» Ц.

244 ГЛ. 10. ВВЕДЕНИЕ В ТЕОРИЮ ВОЗМУЩЕНИИ
Заметим, что все получаемые векторы elt е2, е3, . . . линейно
независимы. Поскольку все они принадлежат R", число их к не
больше п.
Задача 9. Покажите, что Г исчерпывается целочисленными линей-
линейными комбинациями ег, . . ., е\-.
Указание. Плоскость Rex + ... -+- Rejc разбить на параллелепипе-
параллелепипеды Д и показать, что ни в одном Д не может быть точек Г. Если есть ех е Г
вне плоскости Rex + ... + Rejc, то построение не окончено.
Итак, лемма 3 доказана.
Теперь нетрудно доказать лемму 2: Mf диффеоморфно тору Тп.
Рассмотрим прямое произведение к окружностей и п — к пря-
прямых:
7* X К71"* = {(ф1, . . ., Ф|с; Уи . . ., Уп_к)}, <р modd 2я,
вм есте с естественным отображением р: R" -*• Тн X R"-*
Р («Р. У) = (<Р modd 2я, у).
Точки /lt . . ., /„gR" (fi имеет координаты фг = 2я, ф^ = 0,
у = 0) переходят при этом отображении в 0.
Пусть еи . . ., ек е= Г CZ R" — образующие стационарной
группы Г (см. лемму 3). Отобразим линейное пространство R" =
= {(<р, у)} на пространство R" = {*} так, чтобы векторы ft пере-
перешли в е,-. Пусть A: R" ->- Rn — такой изоморфизм.
Заметим теперь, что R" = {(<р, у)} задает карты Тк X Rn~K,
a R" = {*} — карты нашего многообразия Mf.
Задача 10. Докажите, что отображение карт A: Rn —¦ Rn задает
диффеоморфизм Ж: Т* X Rn~* -» Mf,
= {(Ф, У))
Г х R"-K —»- Mf
Но так как многообразие Mf по условию компактно, то к = п
и Mf есть n-мерный тор. Лемма 2 доказана.
Ввиду леммы 1 доказаны первые два утверждения теоремы.
Одновременно мы построили на Mf угловые координаты
ф}, . . ., фп modd 2зт.
Задача 11. Показать, что под действием фазового потока с функцией
Гамильтона Н угловые координаты <р меняются равномерно:
Фг = щ; щ = щ (Л; ф @ = ф @) + <о*.
Иными словами, движение на инвариантном торе Mf условно-периоди-
условно-периодическое.
Указание. q> = А~Ч.
Из всех утверждений теоремы осталось доказать лишь послед-
последнее: что система интегрируется в квадратурах.

§ 50. ПЕРЕМЕННЫЕ ДЕЙСТВИЕ—УГОЛ 245
§ 50. Переменные действие — угол
Здесь показано, что в условиях теоремы Лиувилля можно выбрать та-
такие свыплектические координаты (X, <р), что первые интегралы F зависят
от I, а «р — угловые координаты на торе М*.
А. Описание переменных действие—угол. В § 49 мы занима-
занимались исследованием одного-единственного связного, компактного
многообразия уровня интегралов Mf = {х: F (х) = /}; оказалось,
что Mf есть n-мерный тор, ивариантный относительно фазового
потока. Мы выбрали угловые координаты срг на Mf так, что фа-
фазовый поток с функцией Гамильтона Н = Fx принимает на Mf
особенно простой вид:
-2L =©(/)
Рассмотрим теперь окрестность п-мерного многообразия Mf в 2п-
мерном фазовом пространстве.
Задача. Докажите, что многообразие М* имеет окрестность, диф-
феоморфную прямому произведению п-мерного тора Тп на шар Dn п-мерного
евклидова пространства.
Указание. Принять за координаты функции Fi и построенные выше
углы cpj. Ввиду линейной независимости dFi, функции F-% и q>j (i = 1, . . ., n)
задают диффеоморфизм окрестности Mf на прямое произведение Тп X Dn.
Во введенных координатах (F, <р) фазовый поток с функцией
Гамильтона Н = Ft записывается в виде особенно простой систе-
системы 2п обыкновенных дифференциальных уравнений
которая немедленно интегрируется: F (t) = F @), <р (t) = <р@) +
+ © (F @)) t.
Таким образом, чтобы явно проинтегрировать исходную кано-
каноническую систему дифференциальных уравнений, достаточно
в явном виде найти переменные <р. Оказывается, зто можно сде-
сделать, используя лишь квадратуры. Такое построение переменных
<р приведено ниже.
Заметим, что переменные (F, <р) не являются, вообще говоря,
симплектическими координатами. Оказывается, существуют не-
некоторые функции от F, мы обозначим их I — I (F), I = (/2, . . .
• . ., /„), такие, что переменные (J, <р) уже являются симплекти-
симплектическими координатами: исходная симплектическая структура <о8
выражается через них по обычной формуле
о2 = Sd/,- д лр,.
Переменные I называются переменными действия *) и вместе
с угловыми переменными <р они образуют в окрестности мно-
•) Нетрудно сообразить, что J имеет размерность действия.

246 ГЛ. 10. ВВЕДЕНИЕ В ТЕОРИЮ ВОЗМУЩЕНИЙ
гообразия Mf систему канонических координат действие —
угол.
Величины /г являются первыми интегралами системы с функ-
функцией Гамильтона Н = Fx, как функции от первых интегралов F,-.
В свою очередь переменные Ft можно выразить через I, и, в част-
частности, Н = Fx = Н A). В переменных действие — угол диффе-
дифференциальные уравнения нашего потока A) имеют вид
4^=0, -? = »(!¦). B)
3 а д а ч а. Может ли функция со (-F) в B) быть произвольной?
Решение. В переменных (Z, tp) уравнения потока B) имеют канони-
канонический вид, с функцией Гамильтона Л (I). Следовательно, со (J) = dHldl; по-
поэтому, если число степеней свободы п ^ 2, то функции ш (I) не произвольны,
а удовлетворяют условию симметрии duijdlj = du)jfdlt.
Переменные действие — угол особенно важны для теории воз-
возмущений; в § 52 указано их применение в теории адиабатических
инвариантов.
Б. Построение переменных действие—угол в случае одной
степени свободы. Система с одной степенью свободы на фазовой
плоскости (р, q) задается функцией Гамильтона Н (р, q).
Пример 1. Гармонический осциллятор Н ~ у р2 -f уЗ2! или
общее Н = у а2р2 + у b2q2.
Пример 2. Математический маятник И = -к-р2 — cosq.
В обоих случаях имеются компактные замкнутые кривые
Mh {Н = К), и мы находимся в условии теоремы § 49 при п = 1.
Чтобы построить переменные действие — угол, будем искать
каноническое преобразование (р, q) -*- (I, <p), удовлетворяющее
двум условиям:
2) фйФ = 2л. C)
Щ
Задача. Найти переменные действие — угол в случае простейшего
1 1
гармонического осциллятора Н = "^"Р2 + ~2~ 92-
Решение. Если г, ср — полярные координаты, то dp Д dp —
г2 />2 + д2
= rdr/\dq> = d -у Д йф. ПоэтоАгу / = Н = tj .
Чтобы построить каноническое преобразование р, q н*- /, ф
в общем случае, будем искать его производящую функцию S (/, q):
dS (/, q) dS(l,q) . „,^V,4I . , ,, .,
Предположим сперва, что функция h (I) известна и обратима,
так что каждая кривая Mh определяется значением / (Mh =

§ 50. ПЕРЕМЕННЫЕ ДЕЙСТВИЕ — УГОЛ 247
¦= Mh(i))- Тогда при фиксированном значении / имеем из D)
dS |i=const = P dg.
Это соотношение определяет на кривой M/X(i) вполне определен-
определенную дифференциальную 1-форму dS.
Интегрируя вдоль кривой Mh(i) эту 1-форму, мы получим
(в окрестности точки д0) функцию
я
S(I,g) = S^pdg.
Эта функция и будет производящей функцией преобразования
D) в окрестности точки (/, д0). Первое из условий C) выполнено
автоматически: / = I(h). Чтобы удовлетворить второму усло-
условию, рассмотрим поведение S (/, д) «в целом».
При обходе замкнутой кривой Mh(i) интеграл р dg получает
приращение
AS A)= ф р dg,
Mh(I)
равное площади П, ограниченной кривой Мнц)- Поэтому функ-
функция S — «многозначная функция» на кривой Mn^iy она опреде-
определена с точностью до прибавления целого кратного П. На произ-
dS (I, q)
водную 1—— это слагаемое не влияет; но оно приводит к не-
неоднозначности ф = dS/dl. Эта производная оказывается опреде-
определенной лишь с точностью до слагаемого, кратного —rj-AS(I).
Точнее говоря, формулы D) определяют 1-форму dq> на кривой
d
dl
-,, и интеграл этой формы по Mh(i) равен —rj-AS(I).
Чтобы выполнялось второе из наших условий, ф dtp == 2я,
Щ
нужно, чтобы
/=4^= п
2я 2я '
где П = ф р dg — площадь, ограниченная фазовой кривой Н = h.
Определение. Переменной действия в одномерной
задаче с функцией Гамильтона Н (р, д) называется величина
Окончательно мы приходим к следующему выводу. Пусть
dU/dh Ф 0. Тогда определена обратная / (h) функция к (I).

248 ГЛ. 10. ВВЕДЕНИЕ В ТЕОРИЮ ВОЗМУЩЕНИЙ
Q
Теорема. Положим S(I,q)— ^рйд^н^ад- Тогда фор-
формулы D) задают каноническое преобразование р, q *-*¦ I, ф, удов-
удовлетворяющее условиям C).
Итак, переменные действие — угол в одномерном случае по-
построены.
Задача. Найти S и / для гармонического осциллятора.
Ответ. Если Н = -g-a2/>2 -|- -g- fc2g2 (рис. 217), то Mh — эллипс, огра-
ограничивающий площадь
2nh 2nh
аЪ
io
. Итак, для гармонического осцил-
осцилРис 217 Переменная
действия для гармони-
ческого осциллятора
лятора переменная действия есть отношение энер-
энергии к частоте. Угловая переменная ф — это, ко-
конечно, фаза колебаний.
Задача. Доказать, что период Т движения
по закмнутой кривой Н = h на фазовой плоскости р,
q равен производной площади, ограниченной этой кри-
кривой, по h:
1 — dh '
Решение. В переменных действие — угол уравнения движения B)
дН I dl \-i „ / <Ш \-i _ 2л <ffl
дают ф = ~j -
В. Построение переменных действие — угол в R2n. Перейдем
теперь к системе с п степенями свободы, заданной в R2rt = {(p, q)}
функцией Гамильтона Н (р, q) и имеющей п первых интегралов
в инволюции Fx = H, F2, . . ., Fn. He будем повторять рассуж-
рассуждений, которые привели нас к выбору 2л/ = ф р dq в одномерном
случае, и сразу определим п переменных действия I.
Пусть уг, . . ., уп — базисные одномер-
одномерные циклы тора Mf (приращение координаты
фг на цикле yt равно 2я, если i = /, и О,
если i Ф /). Положим
1г (/) = -«5— ф р dq. E)
Рис. 218. Независи- *
мость переменной дей- Задача. Докажите, что этот интеграл не
ствия от выбора кривой зависит от выбора кривой Vi, представляющей базис-
интегрирования нт цикд (рщ,_ 21g)
Указание. В§49 показано, что на многообразии М * 2-форма со2 =
i равна нулю. По формуле Стокса ф — ф р dq = \ \ dp Д dq = 0,
Y Y о
где da — у — у1.
Определение, п величин It (/), заданных формулами
E), называются переменными действия.

50. ПЕРЕМЕННЫЕ ДЕЙСТВИЕ — УГОЛ
249
Предположим теперь, что при заданных значениях ft n интег-
интегралов Ft п величин It независимы: det -д^-\ т^1*. Тогда в окрест-
окрестности тора Mf можно принять переменные I, <р за координаты.
Теорема. Преобразование р, q>->-1, q> — каноническое,т.е-
Sdpt Д dqt = ^idli Л <%•.
Намечу доказательство этой теоремы. Рассмотрим на Mf диф-
дифференциальную 1-форму р dq. Поскольку многообразие Mf —
нулевое (§ 49), эта 1-форма на Mf замкнута: ее внешняя произ-
производная со2 = dp Д dq на многообразии Mf тождественно равна 0.
Поэтому (рис. 219)
S{x)=\pdq\Mf
не меняется при деформации пути ин-
интегрирования (формула Стокса). Итак,
S (х) есть «многозначная функция» на Mf;
ее периоды равны
Рис. 219. Независимость ин-
интеграла р dq на Mf от пути
Пусть теперь х0 — такая точка на Mf, в окрестности которой
п переменных q служат координатами на Mf, так что подмного-
подмногообразие Mf С R2n задается п уравнениями вида р = р (I, q),
q(x0) = q0. В односвязной окрестности точки q0 определена одно-
8начная функция
S(I,q)=
я.
и мы можем принять ее за производящую функцию канонического
преобразования р, q >-*¦ I, <p:
OS
dq
<Р =
dS
81
Нетрудно проверить, что эти формулы в действительности задают
каноническое преобразование не только в окрестности рассматри-
рассматриваемой точки, но и «в целом» в окрестности Mf. При зтом коорди-
координаты <р будут многозначными с периодами
dS
81,
t = 2пЬи,
что и требовалось.

250
ГЛ. 10. ВВЕДЕНИЕ В ТЕОРИЮ ВОЗМУЩЕНИЙ
Заметим теперь, что все наши построения содержат лишь
«алгебраические» операции (обращение функций) и «квадратуру» —
ф Т б
вычисление интеграла
Рис. 220. Переменные действие-
угол на симплектическом мно-
многообразии
^-^-р2 — cosgj естест-
естестру
известной функции. Таким образом,,
задача интегрирования канонической
системы 2п уравнений, у которых из-
известны п первых интегралов в инво-
инволюции, решается в квадратурах, что и
доказывает последнее утверждение те-
теоремы Лиувилля (§ 49).
Замечание 1. Уже в одномер-
одномерном случае переменные действие — угол
/, ф определены не однозначно усло-
условиями C). А именно, за переменную
действия можно было бы принять /' =
= / + const, а за угловую перемен-
переменную ф' = ф + С (/).
Замечание 2. Мы построили переменные действие —
угол для системы с фазовым пространством R2n. Можно было бы
ввести переменные действие — угол и для системы на произволь-
произвольном симплектическом многообразии. Ограничусь здесь одним
простым примером (рис. 220).
Фазовым пространством маятника
венно считать не плоскость {(р, д)}, а поверхность цилиндра
R1 X S1, получающуюся при отождествлении углов q, отличаю-
отличающихся целым кратным 2зх.
Критические линии уровня Н = -4-1 разбивают цилиндр на
три части А, В, С, каждая из которых диффеоморфна прямому
произведению R1 X S1. В каждой части можно ввести перемен-
переменные действие — угол.
В ограниченной части (В) замкнутые траектории изображают
качание маятника, в неограниченных частях — вращения.
Замечание 3. Как и в разобранном примере, в общем
случае уравнения Ft = ft при некоторых значениях /г перестают
быть независимыми, и Mf перестает быть многообразием. Таким
критическим значениям / соответствуют сепаратрисы, разделяю-
разделяющие фазовое пространство интегрируемой задачи на части, подоб-
подобные частям А, В, С выше. В некоторых из этих частей многооб-
многообразия Mf могут быть неограниченными (части А и С на плоско-
плоскости {(р, <?)}); другие же расслаиваются на к-мерные инвариантные
торы Mf\ в окрестности такого тора можно ввести переменные
действие — угол.
§ 51. Усреднение
В этом параграфе доказывается совпадение временных и пространствен-
пространственных средних в системах, совершающих условно-периодическое дви-
движение.

§ 51. УСРЕДНЕНИЕ 251
А. Условно-периодические движения. В предыдущих парагра-
параграфах нам часто встречалось условно-периодическое движение: фи-
фигуры Лиссажу, прецессия, нутация, вращение волчка и т. п.
Определение. Пусть Тп — re-мерный тор, ф = (ф1, . . ., фэт)
modd 2зх — угловые координаты. Тогда условно-периодическим
движением называется однопараметрическая группа диффеомор-
диффеоморфизмов Г" ->¦ У1, заданная дифференциаль-
дифференциальными уравнениями (рис. 221)
ф = ю, ю = (ши . . ., шп) = const.
Эти дифференциальные уравнения немедленно
интегрируются:
<р @ = ф @) + tot.
Таким образом/ на карте {<р} траектории —пря- Рис 221 Условно.
мые линии. Траектория на торе называется об- периодическое дви-
моткой тора.
Пример. Пусть п = 2. Если щ/щ = кг1к2, то траектории замкнуты;
если Wj/cog иррационально, то траектории на торе всюду плотны (см. § 16).
Величины ffllt . . ., ш„ называются частотами условно-пери-
условно-периодического движения. Частоты называются независимыми, когда
они линейно независимы над полем рациональных чисел: если
к е Z" •) и (к, ю) = 0, то к = 0.
Б. Пространственное и временное средние. Пусть / (ф) — ин-
интегрируемая функция на торе Тп.
Определение. Пространственным средним функции /
на торе Тп называется число
2Я 2Я
о
Рассмотрим значение функции / (<р) на траектории <р (t) ==
— <Ро "т" G>t. Это — функция времени / (<р0 + of). Рассмотрим ее
среднее.
Определение. Временным средним функции / на торе
Тп называется функция
т
/* (<р0) = Шп ^Л / (<р0 + ю*) <Й
(определенная там, где предел существует).
Теорема об усреднении. Временное среднее всюду
существует и совпадает с пространственным, если функция f
непрерывна, а частоты юг независимы. Если функции f на торе и
•) к = (А,, . . ., кп) с целыми kt.

252 ГЛ. 10. ВВЕДЕНИЕ В ТЕОРИЮ ВОЗМУЩЕНИЙ
/ (фо + e>t) на оси t итегрируемы по Риману, то временное сред-
среднее также существует и совпадает с пространственным.
3 а д а ч а. Покажите, что если частоты зависимы, то временное среднее
может не всюду совпадать с пространственным.
Следствие 1. Если частоты независимы, то каждая тра-
траектория {<р(*)} всюду плотна на торе Тп.
Доказательство. Предположим противное. Тогда
в окрестности D некоторой точки тора нет точек траектории <р(<).
Легко построить непрерывную функцию /, равную нулю вне D
и с пространственным средним / = 1. Временное среднее /* (<р0)
на траектории <р(?) равно 0 -ф 1. Противоречие с утверждением
теоремы доказывает следствие 1.
Следствие 2. Если частоты независимы, то каждая тра-
траектория равномерно распределена на торе Тп.
Это означает, что доля времени, которое траектория проводит
в области D, пропорциональна мере D.
Точнее, пусть D — измеримая (по Жордану) область на Тп.
Обозначим через xD (T) количество времени, которое отрезок
0 ^ t <I T траектории <р(<) находится внутри D. (Мы предпола-
предполагаем, что множество таких моментов времени, которые движущая
точка проводит в области, измеримо.) Тогда
Доказательство. Применим теорему к характеристи-
характеристической функции / множества D (/ интегрируема по Риману, так
т
как область D измерима по Жордану). Тогда ^ f(y(t))dt = тх> (Т),
о
а / = Bя)"п mes D, и следствие непосредственно вытекает из тео-
теоремы.
Следствие. В последовательности
1, 2, 4, 8, 1, 3, 6, 1, 2, 5, 1, 2,. . .
lg 8 — Ь 7
первых цифр чисел 2п число 7 встречается чаще, чем 8 в . g . ., раз.
Теорема об усреднении неявно встречается уже в работах
Лапласа, Лагранжа и Гаусса по небесной механике; она явля-
является одной из первых «эргодических теорем». Строгое доказатель-
доказательство дали лишь в 1909 г. П. Боль, В. Серпинский и Г. Вейль
в связи с задачей Лагранжа о среднем движении перигелия Зем-
Земли. Ниже воспроизведено доказательство Г. Вейля.
В. Доказательство теоремы об усреднении.
Лемма 1. Теорема верна для экспонент, f = е*<*> »>, k E=Zn.

§ 51. УСРЕДНЕНИЕ
253
Доказательство. Если к = 0, то / = / = /* = 1 и тео-
теорема очевидна. Если fc^=0, то / = 0. С другой стороны,
) ?ZLJL
Поэтому временное среднее
еН*. Фо)
—_—
i (к,
к, и)Т
что и требовалось доказать.
Лемма 2. Теорема верна для тригонометрических поли-
полиномов
Доказательство. И временное и пространственное
среднее зависят от / линейно, поэтому совпадают по лемме 1,
ч. т. д.
Лемма 3. Пусть f — вещественная непрерывная (или хо-
хотя бы интегрируемая по Риману) функция. Тогда для любого г ^> О
существуют два тригонометрических f f f
полинома Ри Р2 таких, что Рг < / < Ps,
Доказательство. Пусть сна-
сначала / непрерывна. По теореме Вейершт-
расса ее можно приблизить тригономет-
тригонометрическим ПОЛИНОМОМ Р, I / — Р I < е/2.
Полиномы Р, = Р- в/2, Р2 = Р + е/2-
искомые.
Если же / разрывна, но интегрируема по Риману, то сущест-
существуют две непрерывные функции Д, /2, так что /i < / < /г>
Bя)~" j (/2 — /х) d<p < е/3 (рис. 222 соответствует характеристи-
характеристической функции отрезка). Аппроксимируя /х и /2 полиномами
Pi<fi<U< Pz, BяГ J (Р2 - /2) d«p < е/3, BяГи $ (Д -
— jPx) d<p < е/3, получим требуемое. Лемма 3 доказана.
Теперь легко окончить доказательство теоремы.
Пусть е ^> 0. Тогда по лемме 3 существуют тригонометрические
полиномы Л < / < Р*, Bя)-эт J (Р2 — Рг) dq, < e.
При любом Т имеем тогда
т
4- J ^i

254 ГЛ. 10. ВВЕДЕНИЕ В ТЕОРИЮ ВОЗМУЩЕНИИ
По лемме 2, при Т ~^> То (е),
(г = 1,2).
2 — Р1 < е. Поэтому Р2 — J < е, /
е; следовательно, при Т ^> То (е)
т
Далее, Рг< f < Р2 и
что и требовалось доказать.
3 а д а ч а. Двумерный осциллятор с кинетической энергией Т =
энергией U = -д" х2 -(- ^2 совершает
колебания с амплитудами ах = 1,
-тгу* и потенциальной
ay = 1. Найти временное среднее ки-
кинетической энергии.
Задача*). Пусть coj; незави-
независимы, щ; > 0. Вычислить
Рис. 223. К задаче о среднем движении
перигелиев
Ответ.
^где об,, а2, а3 — углы треугольника со
сторонами <% (рис. 223). Если же одно из чисел <% больше суммы двух других,
так что треугольника составить нельзя, то искомая средняя угловая скорость
есть <%.
Г. Вырождения. До сих пор мы рассматривали случай, когда
частоты ю независимы. Целочисленный вектор fcGZ11 называет-
называется соотношением между частотами, если (к, о) = 0.
Задача. Докажите, что множество всех соотношений между данными
частотами ы образует подгруппу Г решетки Z™.
Но мы видели в § 49, что такая подгруппа состоит из всех
целочисленных линейных комбинаций г независимых векторов kt,
1 <J r <J п. Мы скажем, что между частотами имеется г (неза-
(независимых) соотношений **).
*) Лагранж показал, что к подобной задаче сводится исследование сред-
среднего движения перигелиев планет. Решение этой задачи можно найти в ра-
работах Г. Вейля. Эксцентриситет орбиты Земли меняется как модуль аналогич-
аналогичной суммы. С изменением эксцентриситета связаны, по-видимому, леднико-
ледниковые периоды.
**) Докажите, что число г не зависит от выбора независимых векто-
векторов Щ.

§ 51. УСРЕДНЕНИЕ 255
Задача. Докажите, что замыкание траектории {<р (t) = <р0 + Ш}
(на Тп) представляет собой тор размерности п — г, если между частотами
щ имеется г независимых соотношений; в этом случае движение на Тп~г —
условно-периодическое, сп — г независимыми частотами.
Вернемся теперь к интегрируемой гамильтоновой системе, за-
заданной в переменных действие — угол J,<p уравнениями
1 =0, ф = и(Г), где Ю(Г) = -Ц-.
Каждый n-мерный тор Г = const в 2к-мерном фазовом простран-
пространстве инвариантен, и движение на нем условно-периодично.
Определение. Система называется невырожденной, если
отличен от 0 определитель
det—= dt
Задача. Докажите, что если система невырождена, то в любой окрест-
окрестности любой точки имеются условно-периодические движения с п частотами,
а также с любым меньшим числом частот.
Указание. Вместо переменных I можно за локальные координаты
принять сами частоты ш. В пространстве наборов частот множества точек
w с любым числом г соотношений @ ^ г < п) всюду плотны.
Следствие. Если система невырождена, то инвариант-
инвариантные торы I = const определены однозначно, независимо от выбора
координат действие — угол I, <р, в построении которых имеется
всегда некоторый произвол *).
Действительно, торы / = const можно определить как замы-
замыкания фазовых траекторий, соответствующих независимым ю.
Замечу кстати, что при большинстве значений I частоты ю
будут независимы.
Задача. Докажите, что лебегова мера множества тех I, для которых
частоты, т (_Г) в невырожденной системе зависимы, равна 0.
Указание. Сначала докажите, что mes {и: 3fe =f= 0, (w, U) = 0} = 0.
Напротив того, в вырожденной системе можно построить та-
такие системы переменных действие — угол, что торы I — const
в одной и в другой системе будут разными. Это объясняется тем,
что замыкания траекторий вырожденной системы — торы размер-
размерности к < п, и их можно по-разному соединять в гг-мерные торы.
Пример 1. Плоский гармонический осциллятор х = —х;
п = 2, к = 1. Разделение переменных в декартовых и в поляр-
полярных координатах приводит к разным переменным действие —
угол и разным торам.
*) Например, всегда допустимы замены I' = I, <р' = (р + St (Г) или
Iz, Фи Ф21-* Ii + ^г. I* ф1> Ф2 — ф1-

256 ГЛ. 10. ВВЕДЕНИЕ В ТЕОРИЮ ВОЗМУЩЕНИЙ
Пример 2. Кеплерово плоское движение (U = ), п =
<= 2, к = 1. Здесь также разделение переменных в полярных и
в эллиптических координатах приводит к разным I.
§ 52. Усреднение возмущений
Здесь доказана адиабатическая инвариантность переменной действия в
системе с одной степенью свободы.
А. Системы, близкие к интегрируемым. Мы рассмотрели выше
довольно много интегрируемых систем (одномерные задачи, за-
задача двух тел, малые колебания, случаи Эйлера и Лагранжа
движения твердого тела с закрепленной точкой и т. д.). Мы изу-
изучили характер фазовых траекторий в этих системах: они оказались
«обмотками торов», заполняющими всюду плотно инвариантные
торы в фазовом пространстве; каждая траектория распределена
на этом торе равномерно.
Не следует думать что такая ситуация типична для задач
общего вида. В действительности свойства траекторий в много-
многомерных системах могут быть весьма разнообразными и совсем не
похожими на свойства условно-периодических движений. В част-
частности, замыкание траектории системы с п степенями свободы
может заполнять в 2п-мерном фазовом пространстве сложные мно-
множества размерности больше п; траектория может даже быть всю-
всюду плотной и равномерно распределенной на всем 2п — 1-мерном
многообразии, заданном уравнением Н — h*). Термин «неинтег-
рируемые» в применении к этим системам оправдан, так как они
не допускают однозначных первых интегралов, не зависящих
от Н.
Исследование таких сложных систем еще далеко от завершения;
оно составляет задачу «эргодической теории».
Один из подходов к неинтегрируемым системам — изучение
систем, близких к интегрируемым. Например, задача о движении
планет вокруг Солнца близка к интегрируемой задаче о движе-
движении невзаимодействующих точек вокруг неподвижного центра;
упомянем еще задачу о движении слегка несимметричного тяже-
тяжелого волчка и задачу о нелинейных колебаниях вблизи положе-
положения равновесия (близкая интегрируемая задача — линейная).
При исследовании этих и подобных задач чрезвычайно плодотво-
плодотворен следующий метод.
Б. Принцип усреднения. Пусть Г, <р — переменные действие —
угол в интегрируемой («невозмущенной») системе с функцией
*) К этому классу относится, например, движение по инерции на много-
многообразиях отрицательной кривизны.

§ 52. УСРЕДНЕНИЕ ВОЗМУЩЕНИЙ 257
Гамильтона Но (Г):
1 = 0, ф =
В качестве близкой «возмущенной» системы рассмотрим систему
р),
1= едA, ф),
где е << 1.
Забудем временно о гамильтоновости системы и рассмотрим
произвольную систему дифференциальных уравнений A), задан-
заданную на прямом произведении Тк X G ^-мерного тора Тк =
= {<р = (ф1) . . ., фк) modd 2л} и области G Z-мерного пространст-
пространства G a R' = {I = (А, . . ., /;)}- При 8 = 0 движение A) услов-
условно-периодическое, <] ^-частотное, с /с-мерными инвариантными
торами.
Принцип усреднения для системы A) состоит в ее замене дру-
другой системой, называемой усредненной системой:
2Л 2Л
j" = e^ (J), g(J) = Bл)-к
в Z-мерной области GCZ R' = {«^ = (/ц . • ., /{)}•
Утверждается, что система B) «хорошо аппроксимирует» си-
систему A).
Заметим, что этот принцип — не теорема, не аксиома и не оп-
определение, а физическое предложение, т. е. расплывчато сформу-
сформулированное и, строго говоря, неверное утверждение.
Такие утверждения часто бывают плодотворными источниками
математических теорем.
Рассматриваемый принцип усреднения явно встречается уже
у Гаусса (при изучении возмущений планет друг другом Гаусс
предложил размазать массу каждой планеты по ее орбите пропор-
пропорционально времени и заменить притяжение планет притяжением
полученных колец). Тем не менее удовлетворительное исследова-
исследование связи между решениями систем A) и B) в общем случае не про-
проведено и посейчас.
При замене системы A) системой B) мы откидываем в правой
части слагаемое eg(I, <p) = 8gr(J, <p) — eg (I). Это слагаемое име-
имеет порядок 8, такой же, как и оставленное слагаемое eg. Чтобы
понять различие роли слагаемых g и g в д, рассмотрим простей-
простейший пример.
Задача. Рассмотрите случай к = I = 1,
ф = © Ф 0, / = eg (ф).

258 ГЛ. 10. ВВЕДЕНИЕ В ТЕОРИЮ ВОЗМУЩЕНИЙ
Покажите, что при 0<^f<^
с
\I(t)-J (t). | < се, где /(*) = / @) + eg«.
Решение.
t t ш
(t) - /@) = J 8^(Фо + wt)dt = J eg dt + ¦?-
-jj-ft
где h(ф) = \g(ф)^ф — периодическая и, следовательно, ограни-
о
ченная функция.
Таким образом, изменение / со временем состоит из двух час-
частей: осцилляции порядка е, зависящих от g, и систематической
«эволюции» со скоростью eg (рис. 224).
Принцип усреднения основан на представлении о том, что и в
общем случае движение системы A) можно разделить на «эволюцию»
B) и малые осцилляции. В общем виде такое
представление не обосновано, а сам принцип
I(t) неверен.
№ Тем не менее применим его к гамильтоно-
вой системе A):
В качестве правой части усредненной системы B) получим тогда
^ = 0.
Иными словами, в гамилыпоновой невырожденной системе эволю-
эволюции нет.
Один из вариантов этого совсем нестрогого вывода приводит
к так называемой теореме Лапласа:
Большие полуоси кеплероеых эллипсов планет не имеют вековых
возмущений. (
Сказанного достаточно, чтобы убедиться в важности принципа
усреднения; сформулируем теперь теорему, обосновывающую этот
принцип в одном весьма частном случае — случае одночастотных
колебаний (к — 1). Эта теорема показывает, что усредненное урав-
уравнение правильно описывает эволюцию на большом отрезке време-
времени @ < t < 1/е).

I 52. УСРЕДНЕНИЕ ВОЗМУЩЕНИЙ 259
В. Усреднение в одночастотной системе. Рассмотрим систему
1 дифференциальных уравнений
ф = о)(Г) + е/(Г, ф), | ф mod2л е S1,
где/ (J, ф + 2л) == / (I, ф), gr (Г, ф + 2л) = д (I, ф), и «усреднен-
«усредненную» систему из I уравнений
2Я
j = eg (J), где д (J) = -^- jj gr («7, ф) %. B)
Обозначим через I (t), ф (t) решение системы A) с начальным ус-
условием I @), ф @), а через J (t) — решение системы B) с тем же
начальным условием J @) = I @) (рис. 225).
Теорема. Пусть 1) функции о, /, д оп-
определены, когда I меняется в ограниченной обла-
области G, и в этой области ограничены со своими
производными до второго порядка включительно:
II ю« h g Hc«(GxS') < СЦ
2) в области G
/¦»-\^.\л. Рис. 225. Теорема
w \J.) ^> с ^> и, об усреднении
3) при 0 ^ t ^ 1/е точка J (t) принадлежит G с окрестностью
радиуса d:
Тогда при достаточно малом г @ < е < е0)
| J (t) — J (f) |< c9e для всея *, 0 < t < 1/е,
где постоянная с9 ^> 0 зависит от clf с, d, ко не от е.
Некоторые приложения этой теоремы будут даны ниже («адиа-
(«адиабатические инварианты»). Заметим, что основная идея доказатель-
доказательства этой теоремы (замена переменных, убивающая возмущение)
важнее самой теоремы; это — одна из основных идей в теории
обыкновенных дифференциальных уравнений; она встречается
уже в элементарном курсе в виде «метода вариации постоянных».
Г. Доказательство теоремы об усреднении. Вместо перемен-
переменных I введем новые переменные J?
Р = I + efc (I, Ф), C)
где 2я — периодические по ф функции fe подберем так, чтобы век-
вектор JP удовлетворял более простому дифференциальному урав-
уравнению.

260 ГЛ. 10. ВВЕДЕНИЕ В ТЕОРИЮ ВОЗМУЩЕНИЙ
Скорость изменения Р (t), согласно A) и C), равна
г9 + *-%/- D)
Предположим, что замену C) можно обратить, так что
I = Р + еЛ (Р, ф, е) E)
(где функции h 2л-периодичны по ф).
Тогда из D), E) следует, что Р (t) подчиняется системе урав-
уравнений
[ ^]1г, F)
где «остаточный член» М — второго по е порядка малости:
| Л |< с2г\ с2 (с15 с„ с4) > 0, G)
если только
||Л|Ь<с4. (8)
Постараемся теперь выбрать замену переменных C) так, чтобы
обратить в 0 член с е в F). Мы получаем для fc уравнение
дк 1_
<9<р ш "'
Вообще говоря, такое уравнение неразрешимо в классе перио-
периодических по ф функций Тс. Действительно, среднее значение (по ф)
левой части равно всегда 0, а среднее значение правой части мо-
может и не равняться 0.
Поэтому мы не можем выбирать к так, чтобы убить целиком
часть с е в F). Однако мы можем убить всю «периодическую» часть д,
полагая
$^^Ф- (9)
Итак, определим функцию Тс формулой (9). Тогда, ввиду усло-
условий 1) и 2) доказываемой теоремы, функция fc удовлетворяет оцен-
оценке || Тс |Ь <С czi гДе сз (CD с) ^> 0- Чтобы установить неравенства
(8), остается оценить h. Для этого прежде всего нужно показать
что замена C) обратима.
Зафиксируем положительное число а.

§ 62, УСРЕДНЕНИЕ ВОЗМУЩЕНИЙ 261
Лемма. Если е достаточно мало, то ограничение отображе-
отображения C)*)
I -> I + efe, где \ к |c»(G) < с3,
на область G — а (состоящую из точек, входящих в G с а-окрест-
ностъю) есть диффеоморфизм. Обратный диффеоморфизм E) в об-
области G — 2а удовлетворяет оценке \ h \& <С с& с некоторой пос-
постоянной с4 (а, с3) ]> 0.
Доказательство. Нужная оценка непосредственно вы-
вытекает из теоремы о неявной функции. Некоторое затруднение вы-
вызывает лишь взаимная однозначность отображе-
отображения I -*¦ I + efe в области G — а.
Заметим, что функция fc удовлетворяет в об-
области G — а условию Липшица (с некоторой по-
постоянной L (а, с3)). Рассмотрим две точки Ilt /2
из G — а. При достаточно малом е (а именно, при
L е < 1) расстояние между ъкA^) и efc(J2) будет
меньше \11 — 12\. Поэтому 11 + гЩ1,) Ф Jg + Рис. 226. доказа-
+ ей(Г2). Итак, отображение C) в G — а взаим- ^бТсредае^
но однозначно, и лемма доказана.
Из леммы вытекает, что при достаточно малом е справедливы
все оценки (8). Значит, справедлива также оценка G).
Сравним теперь системы дифференциальных уравнений для J
B)
и для JP; последняя ввиду (9) принимает вид
Р = гд(Р) + Л. F')
Поскольку разница между правыми частями порядка ^е2
(см. G)), то за время t ^ 1/е решения разойдутся на расстояние
| Р — J | ^ е (рис. 226). С другой стороны, 11 — JP \ =
= е | к | ^ е. Итак, разность 11 — J \ при t ^ 1/е имеет порядок
^ 8, что и требуется.
Переходя к аккуратным оценкам, введем величину
2 («) = Р (t) - J (t). A0)
Тогда из F'), (9) вытекает
где | R' | < с2еа + све | г |, если отрезок (Р, J) лежит в G — а. В этом пред-
предположении мы находим
I* I < «*! | г | + С2Ё2 (Где Сб = СВ + С,), | 2 @) |< С36. A1)
Лемма. Если I * |< я | * | + Ь, | z @) |< d\ а, Ъ, d, t > 0, то
U(*)K(d+ ^)a<
*) При любом фиксированном значении параметра ср.

262 ГЛ. 10. ВВЕДЕНИЕ В ТЕОРИЮ ВОЗМУЩЕНИЙ
Доказательство. | з (t) | не превосходит решения у (t) уравнения
у = ау + Ь, у @) = d. Решая зто уравнение, находим у = Се*1, Ceat = Ь,
С = e~atb, С @) = d, С ^ d + Ы, что и требовалось доказать.
Теперь из A1), в предположении, что отрезок Р, J" лежит в G — а
(рис. 226),
Отсюда следует, что при 0 <J f <J 1/е
\z{t)\<c7e, С7 = (с3 + с2)Л
Мы видим теперь, что если а = d/З и е достаточно мало, то отрезок Р (t),
J if) (t <^ 1/e) весь лежит внутри G — а, и, следовательно,
| Р (t) — J (t) J < с8б при всех 0 < t < 1/е.
С другой стороны, I P (t) — I (Л) I ¦< | ек I ¦< с3е. Итак, при всех t,
0 < t < 1/е,
| X (t) - J (t) |< с„е, с, = с8 + Ч > 0,
и теорема доказана.
Д. Адиабатические инварианты. Рассмотрим гамильтонову
систему с одной степенью свободы, с функцией Гамильтона
Н (р, q; h), зависящей от параметра %.
Примером может служить маятник:
в качестве параметра % можно взять длину I или ускорение силы
тяжести g.
Предположим, что параметр со временем медленно меняется.
Оказывается в пределе, когда скорость изменения параметра стре-
стремится к 0, появляется замечательное асимптотическое явление:
две величины, вообще независимые, становятся функциями одна
другой.
Предположим, например, что длина маятника медленно (по
сравнению с его собственными колебаниями) изменяется. Оказы-
Оказывается, амплитуда его колебаний становится тогда функцией дли-
длины маятника. Например, если очень медленно увеличить вдвое
длину нити маятника, а затем очень медленно ее уменьшить до
прежней величины, то в конце этого процесса амплитуда колеба-
колебаний станет такой же, какой была вначале.
Более того, оказывается, отношение энергии маятника Н
к частоте <о при медленном изменении параметров почти не меняет-
меняется, хотя сами энергия и частота могут измениться сильно. Такие
величины, которые мало меняются при медленном изменении па-
параметров, физики назвали адиабатическими инвариантами.
Легко сообразить, что адиабатическая инвариантность отноше-
отношения энергии маятника к частоте есть утверждение физического
характера, т. е. без дополнительных предположений неверное.
Действительно, изменяя длину маятника сколь угодно медленно,
но выбирая фазу колебаний, при которой длина увеличивается

§ 52. УСРЕДНЕНИЕ ВОЗМУЩЕНИЙ 263
и уменьшается, можно раскачать маятник (параметрический резо-
резонанс). Чувствуя это, физики предложили формулировать опреде-
определение адиабатической инвариантности так: лицо, меняющее пара-
параметры системы, не должно видеть, в каком состоянии находится
система (рис. 227). Дать этому определению строгий математиче-
математический смысл — весьма деликатная, до сих пор не решенная задача.
К счастью, мы можем обойтись суррогатом, заменяя невмешатель-
невмешательство лица, меняющего параметры, во внутренние дела системы
требованием того, чтобы изменение параметров было плавным,
а именно, два раза непрерывно дифференцируемым.
";' X фиксиродано
Рис. 227. Адиабатичес- Рис. 228. Адиабатичес-
Адиабатическое изменение длины кий инварианту од-
маятника номерной системы
Точнее, пусть Н (р, q; К) — фиксированная дважды непрерыв-
непрерывно дифференцируемая функция %. Положим К = et и будем рас-
рассматривать полученную систему с медленно меняющимся пара-
параметром К = et:
Р=—Щ-' 9=-%-* H = H(p,g;et). (.)
Определение. Величина / (р, q; k) называется адиаба-
адиабатическим инвариантом системы (*), если для всякого и ^> 0 су-
существует е0 ^> 0 такое, что если 0<е<е0, 0<?< 1/е, то
I / (Р (*), Я (О; в<) -1(р @), д@); 0) |< х.
Очевидно, всякий первый интеграл является также адиабати-
адиабатическим инвариантом.
Оказывается, всякая одномерная система (•) имеет адиабати-
адиабатический инвариант. А именно, адиабатическим инвариантом явля-
является переменная действия в соответствующей задаче с постоян-
постоянными коэффициентами.
Предположим, что фазовые траектории системы с гамильтониа-
гамильтонианом Н (р, q; К) замкнуты. Определим функцию / (р, q; К) следую-
следующим образом. При фиксированном К функции Гамильтона
Н (р, q; К) соответствует определенный фазовый портрет (рис. 228).
Рассмотрим замкнутую фазовую траекторию, проходящую через
точку (р, q). Она ограничивает на фазовой плоскости некоторую
площадь. Обозначим эту площадь через 2л1 (р, q; К). На каждой
фазовой траектории (при данном К) I = const. Очевидно, / не что
иное, как переменная действия (см. § 50).

264 ГЛ. 10. ВВЕДЕНИЕ В ТЕОРИЮ ВОЗМУЩЕНИЙ
Теорема. Если частота рассматриваемой системы (*)
<о (/, к) не обращается в 0, то I (p, q; К) — адиабатический инва-
инвариант.
Е. Доказательство адиабатической инвариантности действия.
При фиксированном к в системе (*) можно ввести переменные дей-
действие — угол /, ф каноническим преобразованием, зависящим от h.
р,9^7,Ф: ф =©(/,*,),/ = 0, о>(/Д) = -^-, Я0 = Я0(/Д).
Обозначим через S (/, q; К) производящую (многозначную)
функцию этого преобразования:
as as
P=-aT* Ч = -аГ-
Пусть теперь % = et. Поскольку переход от переменных р, q
к переменным /, ф совершается теперь зависящим от времени
каноническим преобразованием, уравнения движения в новых
переменных /, <р имеют гамильтонов вид, но с функцией Гамиль-
Гамильтона (см. § 45, А, стр. 213)
К=:Но+-дТ = но + Е-дТ~-
Задача. Докажите, что — S (I, q; X) — однозначная функция на
ok
фазовой плоскости.
Указание. Неоднозначность S сводится к прибавлению кратных
2п/.
Мы получаем, таким образом, уравнения движения в виде
ф = о) (/, X) + е/ (/, ф; k), f = -d*S/dIdK
1 = е# (/, ф; %), g = d2S/d<p дк,
^ = e.
Поскольку афО, применима теорема об усреднении (стр. 259).
Усредненная система имеет вид
j — eg, Л = е.
^° ^ = "йпГ ~Ш~' а ~Ж однозначная] функция на окружности
I = const. Поэтому f = Bл) § gdq> = 0, и в усредненной си-
системе / не меняется вовсе: / (t) = / @).
По теореме об усреднении
| / (t) — / @) |< се для всех t, 0 < t < 1/е,
что и требовалось доказать.
Пример. Для гармонического осциллятора (см. рис. 217)

S 52. УСРЕДНЕНИЕ ВОЗМУЩЕНИЙ
265
т. е. адиабатическим инвариантом является отношение энергии
к частоте.
Задача. Длина маятника медленно увеличивается вдвое
(j = l0 (I -f et), 0 < t < 1/е). Как изменяется
амплитудный угол отклонения qma%?
Решение. / =-5-Z3/2g1/2gmaX; поэтому
В качестве второго примера рассмотрим р
движение абсолютно упругого твердого шари-
шарика массы 1 между абсолютно упругими стен- „
ками, расстояние между которыми, I, медлен-
медленно меняется (рис. 229).
Можно считать, что точка движется в «пря-
«прямоугольной потенциальной яме бесконечной ~v
глубины», и что фазовые траектории — прямоу- Рис. 229. Адиабати-
ГОЛЬНИКИ ПЛОЩаДИ 2vl, ГДе V — СКОРОСТЬ ша- ческий инвариант аб-
», ' -. г солютно упругого ша-
шарика. Б этом случае адиабатическим инва- рика между мед-
риантом оказывается произведение vl скорости ленно
шарика на расстояние между стенками *).
Таким образом, если вдвое сблизить стенки, скорость шарика
возрастет также вдвое, а если раздвигать стенки, то скорость
уменьшится.
О теории адиабатических инвариантов многочастотных систем
см. в книге: Арнольд В.И. Дополнительные главы теории
обыкновенных дифференциальных уравнений.— М.: Наука, 1978,
гл. «Теория возмущений».
*) Это не следует формально из доказанной теоремы, так как в ней речь
идет о гладких системах, без ударов. Доказательство адиабатической инва-
инвариантности vl в этой системе — поучительная элементарная задача.

ДОБАВЛЕНИЯ
Добавление 1
РИМАНОВА КРИВИЗНА
Из листа бумаги можно свернуть конус или цилиндр, но нель-
нельзя получить никакого куска сферы без складок, растяжений или
разрывов. Причина заключается в различии «внутренней геомет-
геометрии» этих поверхностей: никакую часть сферы нельзя изометриче-
изометрически отобразить на плоскость.
Инвариант, различающий римановы метрики, называется ри-
мановой кривизной. Риманова кривизна плоскости равна нулю,
а кривизна сферы радиуса R равна Вт2. Если одно риманово мно-
многообразие изометрически отображено на другое, то римановы кри-
кривизны в соответствующих местах равны. Например, поскольку
конус или цилиндр локально изометричны плоскости, то римано-
риманова кривизна конуса или цилиндра в любой точке равна 0. Следова-
Следовательно, никакую область на конусе или на цилиндре нельзя ото-
отобразить изометрически на сферу.
Риманова кривизна многообразия оказывает весьма сущест-
существенное влияние на поведение геодезических на нем, т. е. на движе-
движение в соответствующей динамической системе. Если риманова
кривизна многообразия положительна (как на сфере или на эл-
эллипсоиде), то близкие геодезические в большинстве случаев колеб-
колеблются друг около друга, а если кривизна отрицательна (как на по-
поверхности однополостного гиперболоида), то геодезические быст-
быстро расходятся в разные стороны.
В этом добавлении определяется риманова кривизна и кратко
обсуждаются свойства геодезических на многообразиях отрица-
отрицательной кривизны. Дальнейшие сведения о римановой кривизне
можно найти в книге: М и л н о р Дж. Теория Морса.— М.я
Мир, 1965, а о геодезических на многообразиях отрицательной кри-
кривизны — в книге: А н о с о в Д. В. Геодезические потоки на мно-
многообразиях отрицательной кривизны // Труды МИАН им. Стек-
лова.— М., 1967. < •
А. Параллельное перенесение на поверхностях. Определение
римановой кривизны основано на конструкции параллельного
перенесения векторов вдоль кривых на римановом многообразии.
Начнем с примера, когда данное риманово многообразие дву-
двумерное, т. е. поверхность, а данная кривая — геодезическая на
этой поверхности.

РИМАНОВА КРИВИЗНА 267
Параллельное перенесение вектора, касательного к поверхности,
вдоль геодезической на этой поверхности определяется так: точка
приложения вектора движется по геодезической, а сам вектор
непрерывно перемещается так, что его угол с геодезической и его
длина остаются постоянными.
В результате такого перенесения всех векторов, касательных
к поверхности в начальной точке геодезической, в конечную точку
возникает отображение касательной плоско-
плоскости в начальной точке в касательную плос-
плоскость в конечной точке. Это отображение
линейно и изометрично.
Теперь мы определим параллельное пере-
перенесение вектора на поверхности вдоль лома-
ломаной, составленной из нескольких дуг геоде-
геодезических (рис. 230). Чтобы перенести век- S5?
ТОр ВДОЛЬ ЛОМаНОЙ, МЫ переНОСИМ его ИЗ девической ломаной
первой вершины во вторую вдоль первой дуги
геодезической, полученный вектор переносим вдоль второй дуги
в следующую вершину и т. д.
Задача." Перенесите вектор, касательный к сфере в одной из вершин
сферического треугольника с тремя прямыми углами, обратно в эту вершину
вдоль треугольника.
Ответ. В результате такого перенесения касательная плоскость к сфере
в начальной вершине повернется на прямой угол.
Наконец, параллельное перенесение вектора вдоль любой глад-
гладкой кривой на поверхности определяется с помощью предельного
перехода, в котором кривая аппроксимируется ломаными» состав-
составленными из дуг геодезических.
3 а д а ч а. ПереЕесите вектор, направленный к Северному полюсу и
приложенный в Ленинграде (на широте Я = 60°) вдоль параллели 60° с. ш.
обратно в Ленинград, двигаясь на восток.
Ответ. Вектор повернется на угол 2л A — sin К), т. е. примерно на 50°
к западу. Таким образом, величина угла поворота пропорциональна площади,
ограниченной нашей параллелью, а направление вращения совпадает с на-
направлением обхода Северного полюса при перенесении вектора.
Указание. Достаточно перенести вектор вдоль той же окружности
по конусу, образованному касательными северного направления к Земле,
проведенными во всех точках параллели (рис. 231). Конус же этот можно раз-
развернуть на плоскость, после чего параллельное перенесение на его поверхно-
поверхности становится обычным параллельным перенесением на плоскости.
Пример. Рассмотрим верхнюю полуплоскость у > 0 плоскости
комплексного переменного z = х + iy с метрикой
У
Легко сосчитать, что геодезические этого двумерного риманова многообразия—
это окружности и прямые, перпендикулярные оси х. Дробно-линейные пре-
преобразования с вещественными коэффициентами
az+b
cz +d

268
ДОБАВЛЕНИЕ 1
являются изометрическими преобразованиями нашего многообразия, которое
называется плоскостью Лобачевского.
Задача. Перенести вектор направления мнимой оси из точки z = i
в точку z = t + i вдоль горизонтальной прямой {dy = 0) (рис. 232).
Рис. 231. Параллельное перенесение на сфере
Рис. 232. Параллельное пере-
перенесение на плоскости Лобачев-
Лобачевского
Ответ. При сдвиге на t вектор повернется на t радиан в направлении от
орта оси у к орту оси х.
Б. Форма кривизны. Теперь мы можем определить риманову
кривизну двумерного риманова многообразия (т. е. поверхности)
в каждой точке. С этой целью выберем в окрестности рассматривае-
рассматриваемой точки ориентацию нашей поверхности и рассмотрим парал-
параллельное перенесение векторов вдоль границы малой области D на
нашей поверхности. Легко сообразить, что результат такого пе-
перенесения — поворот на малый угол. Обозначим этот угол через
Ф (D) (направление отсчета угла фиксируется выбором ориента-
ориентации поверхности).
Если разбить область D на две части Dt и D2, то результат па-
параллельного перенесения по границе D можно получить, обойдя
сперва одну часть, а потом другую. Следовательно,
Ф (D) = Ф (DJ + Ф (Д,),
т. е. угол ф является аддитивной функцией области. При измене-
изменении направления обхода границы угол ф также меняет знак. Ес-
Естественно поэтому представить ф (D) как интеграл по D от подхо-
подходящей 2-формы. Такая 2-форма действительно существует; она на-
называется формой кривизны, и мы обозначим ее через Q. Таким об-
образом, мы определяем форму кривизны Q соотношением
!. A)
Значение формы кривизны Q на паре касательных векторов |, т)
из ТМа, можно определить следующим образом. Отождествим
окрестность точки 0 касательного пространства к М в точке х
с окрестностью точки х на М (например, с помощью каких-либо
локальных координат). Мы можем тогда построить на М парад-

РИМАНОВА КРИВИЗНА 269
лелограмм Пе, натянутый на векторы е|, ещ, по меньшей мере при
достаточно малых е.
Теперь значение формы кривизны на наших векторах опреде-
определяется формулой
^ B)
Иными словами, значение формы кривизны на паре бесконечно
малых касательных векторов равно углу поворота при переносе
вдоль построенного по этим векторам бесконечно малого паралле-
параллелограмма.
Задача. Найти форму кривизны на плоскости, на сфере радиуса R
и на плоскости Лобачевского.
Ответ. Q = О, Q = R~2dS, Q = •—dS, где 2-форма dS — элемент площа-
площади на нашей ориентированной поверхности.
Задача. Доказать, что определенная формулой B) функция является
действительно дифференциальной 2-формой, не зависящей от участвовавшего
в построении произвола, и что поворот вектора при переносе вдоль границы
ориентированной конечной области D выражается через эту форму по., фор-
формуле A).
Задача. Доказать, что интеграл формы кривизны по любой выпуклой
поверхности в трехмерном евклидовом пространстве равен 4я.
В. Риманова кривизна поверхности. Заметим теперь, что вся-
всякая дифференциальная 2-форма на двумерном ориентированном
римановом многообразии М может быть записана в виде pdS, где
dS — элемент ориентированной площади, ар — числовая функ-
функция, однозначно определенная выбором метрики и ориентации.
В частности, форму кривизны можно записать в виде
Q = KdS%
где К: М -*¦ R — гладкая функция на многообразии М, a dS —
элемент площади.
Значение функции К в точке х называется римановой кривиз-
кривизной поверхности в точке х.
Задача. Вычислить риманову кривизну евклидовой плоскости, сферы
радиуса R и плоскости Лобачевского.
Ответ. К = О, К = В~2, К = —1.
Задача. Доказать, что риманова кривизна зависит не от ориентации
многообразия, но лишь от его метрики.
Указание. При изменении ориентации 2-формы Q и dS меняют знак
одновременно.
Задача. Доказать, что для поверхностей в обычном трехмерном ев-
евклидовом пространстве риманова кривизна в каждой точке равна произведе-
произведению обратных величин главных радиусов кривизны (со знаком минус, если
центры кривизны лежат по разные стороны от поверхности).
Заметим^ что знак кривизны многообразия в точке не зависит
от ориентации многообразия; этот знак можно определить, вовсе
не используя ориентации.

270 ДОБАВЛЕНИЕ 1
А именно, на многообразии положительной кривизны при па-
параллельном переносе вдоль границы малой области вектор повора-
поворачивается вокруг своего начала в ту же сторону, в какую точка
на границе обходит область; на многообразии отрицательной
кривизны направление вращения обратное.
Далее заметим, что значение кривизны в точке определяется
одной лишь метрикой в окрестности этой точки, и поэтому сохра-
сохраняется при изгибании: у изометрических поверхностей в соответ-
соответственных точках кривизны совпадают. Поэтому риманову кривиз-
кривизну называют также внутренней кривизной.
Формулы для вычисления кривизны через компоненты метрики
в какой-либо системе координат включают вторые производные
метрики и достаточно сложны; см.
ниже задачи пункта Ж (стр. 274).
Г. Многомерное параллельное пере-
перенесение. Конструкция параллельного
перенесения на римановых многообрази-
многообразиях размерности выше 2 несколько сло-
сложнее, чем приведенная выше двумер-
двумерная конструкция. Дело в том, что на-
чиная с трехмерного случая условие
неизменности угла с геодезической не
определяет еще направления перенесенного вектора. А именно,
втот вектор можно еще вращать вокруг направления геодези-
геодезической, сохраняя угол с ней.
Усовершенствование, которое следует внести в конструкцию
параллельного переноса вдоль геодезической,— это выбор двумер-
двумерной плоскости, проходящий через касательную к геодезической,
в которой должен лежать переносимый вектор. Выбор этот про-
производится следующим (к сожалению, довольно сложным) об-
образом.
В начальной точке геодезической нужная плоскость есть: это
плоскость, натянутая на переносимый вектор и вектор направле-
направления геодезической. Рассмотрим все геодезические, выходящие
из начальной точки по направлениям, лежащим в этой плоскости.
Все такие геодезические образуют гладкую (вблизи начальной
точки) поверхность, содержащую ту геодезическую, вдоль которой
мы намерены переносить вектор (рис. 233).
Рассмотрим новую точку на этой геодезической на малом рас-
расстоянии А от начальной точки. Касательная плоскость к описан-
описанной только что поверхности в новой точке содержит направление
геодезической в этой новой точке. Примем эту новую точку за
начальную и используем имеющуюся в ней касательную плос-
плоскость для построения новой поверхности (образованной пучком
геодезических, выходящих из новой точки). Эта поверхность со-
содержит исходную геодезическую. Сдвинемся по исходной геодези-
геодезической еще на Д и повторим все построение сначала.

РИМАНОВА КРИВИЗНА 271
За конечное число шагов мы доберемся до любой точки исход-
исходной геодезической. В результате нашей деятельности в каждой
точке этой геодезической возникнет касательная плоскость, содер-
содержащая направление геодезической. Эта плоскость зависит от шага
Д нашей конструкции. При Л ->¦ 0 полученное семейство касатель-
касательных плоскостей стремится (как можно сосчитать) к определенному
пределу.
В результате вдоль нашей геодезической возникает поле каса-
касательных двумерных плоскостей, содержащих направление геоде-
геодевической и определенное внутренним образом самой метрикой
многообразия.
Теперь параллельное перенесение нашего вектора вдоль геоде-
геодевической определяется как в двумерном случае: этот вектор дон-
жен при перенесении оставаться в предписанных плоскостях,
сохранять свою длину и свой угол с направлением геодезической.
Параллельное перенесение вдоль любой кривой определяется
с помощью аппроксимации геодезическими ломаными, как в дву-
двумерном случае.
Задача. Докажите, что параллельное перенесение векторов из одной
точки риманова многообразия в другую вдоль фиксированного пути является
линейным изометрическим оператором из касательного пространства в пер-
первой точке в касательное пространство во второй точке.
Задача. Перенести параллельно вдоль линии
яу = t, z2 = О, у = 1 @ < t < т)
пространства Лобачевского с метрикой
любой вектор.
Ответ. Векторы направлений осей х1 и у поворачиваются в натянутой
на них плоскости на угол т в направлении от оси у к оси х,_, а вектор направ-
направления я2 переносится параллельно себе и в смысле евклидовой метрики.
Д. Тензор кривизны. Рассмотрим теперь, как и в двумерном
случае, параллельное перенесение по маленькому замкнутому
пути, начинающемуся и кончающемуся в одной точке риманова
многообразия.
Параллельное перенесение вдоль такого пути возвращает век
торы в исходное касательное пространство. Полученное отобра-
отображение касательного пространства в себя является малым поворо-
поворотом (ортогональным преобразованием, близким к тождественному).
В двумерном случае мы характеризовали этот поворот одним числом —
углом поворота <р. В многомерном случае роль числа <р играет кососимметри-
ческий оператор.
А именно, каждый ^ортогональный оператор А, близкий к тождественному,
единственным образом записывается в виде
где Ф — малый кососимметрический оператор.

272 ДОБАВЛЕНИЕ 1
Задача. Вычислить Ф, если А — поворот плоскости на малый
угол ф.
Ответ. А^( cos Ф sin(P\, Ф=( ° f ) .
\—sin ф cos ф/ \—ф 0 /
В отличие от двумерного случая, функция пути Ф не является, вообще
говоря, аддитивной (так как ортогональная группа n-мерного простран-
пространства при п > 2 не коммутативна). Тем не менее мы можем построить при по-
помощи ф форму кривизны, описывающую «бесконечно малый поворот при
обносе бесконечно малого параллелограмма» таким же способом, как в дву-
двумерном случае, т. е. при помощи формулы B).
Итак, пусть |, т] из ТМХ — касательные к риманову многооб-
многообразию М в точке х векторы. Построим на М малый криволиней-
криволинейный параллелограмм Пе. (Стороны параллелограмма Пе полу-
получаются из векторов е|, ет) касательного пространства при коорди-
координатном отождествлении окрестности нуля в ТМХ с окрестностью
точки х на М). Рассмотрим параллельное перенесение вдоль сто-
сторон параллелограмма Пе (обход начинаем с |).
Результатом перенесения будет ортогональное преобразование
пространства ТМХ, близкое к тождественному. Оно отличается
от тождественного преобразования на величину порядка е2 и име-
имеет вид
Аг A, ч) = Е + e2Q + о (е2),
где Q — кососимметрический оператор, зависящий от % и от т].
Итак, мы можем определить функцию Q от пары векторов §,
т] касательного пространства в точке х со значениями в простран-
пространстве кососимметрических операторов на ТМХ формулой
е-»о е
Задача. Докажите, что функция Я является дифференциальной
2-формой (со значениями в кососимметрических операторах на ТМХ) и не
зависит от выбора координат, с помощью которых мы отождествляли ТМХ и М.
Форма Q называется тензором кривизны риманова многообра-
многообразия. Таким образом, тензор кривизны описывает инфинитезималь-
ный поворот касательного пространства при параллельном пере-
перенесении вокруг бесконечно малого параллелограмма.
Е. Кривизна по двумерному направлению. Рассмотрим дву-
двумерную плоскость L в касательном пространстве к риманову мно-
многообразию в какой-либо его точке. Выпустим из этой точки гео-
геодезические по всевозможным направлениям из плоскости L. Эти
геодезические образуют вблизи нашей точки гладкую поверх-
поверхность. Построенная поверхность вложена в риманово многообра-
многообразие и получает из него риманову метрику.
Кривизной риманова многообразия М в направлении 2-плоскос-
ти L в касательном пространстве к М в точке х называется ри-
риманова кривизна описанной выше поверхности в точке х.

РИМАНОВА КРИВИЗНА 273
Задача. Найти кривизны трехмерной сферы радиуса R и простран-
пространства Лобачевского по всевозможным двумерным направлениям.
Ответ. Д, —1.
Вообще говоря, кривизны риманова многообразия по разным
двумерным направлениям в одной точке различны. Их зависимость
от направления описывается приведенной ниже формулой C).
Теорема. Кривизна риманова многообразия по двумерному
направлению, определенному парой ортогональных векторов |, ц
длины 1, выражается через тензор кривизны Q по формуле
К = <Q (|, г,) |, 1]>, C)
где угловые скобки означают скалярное произведение, задающее
риманову метрику.
Доказательство получается сравнением определений тензора кривизны
и кривизны по двумерному направлению. Мы не останавливаемся на его
аккуратном проведении. При желании можно принять формулу C) за опре-
определение кривизны К.
Ж. Коварпантное дифференцирование. С параллельным пере-
перенесением вдоль кривых на римановом многообразии связано свое-
своеобразное дифференциальное исчисление — так называемое кова-
риантное дифференцирование, или риманова связность. Опреде-
Определяется это дифференцирование следующим образом.
Пусть | — вектор, касательный к риманову многообразию М
в точке х, a v — векторное поле, заданное на М в окрестности
точки х. Ковариантная производная поля v по направлению век-
вектора | определяется с помощью какой-либо кривой, выходящей
из точки х со скоростью \.
При движении по этой кривой в течение небольшого интервала
времени t мы окажемся в новой точке х (t). Возьмем вектор поля
v в этой точке х (t) и параллельно перенесем его вдоль кривой
назад в исходную точку х. Мы получим зависящий от t вектор
в касательном пространстве к М в исходной точке х. При t = О это
вектор v (х), а при других t он изменяется в соответствии с непа-
непараллельностью векторов поля v вдоль нашей кривой направле-
направления |.
Рассмотрим производную полученного вектора по t при t = 0.
Эта производная является вектором касательного пространства
ТМХ. Она называется коеариантной производной поля v по %
и обозначается через Vgu.
Легко проверить, что вектор Vg« не зависит от выбора кривой,
участвовавшей в определении, но лишь от вектора % и поля v.
Задача 1. Доказать следующие свойства ковариантного дифферен-
дифференцирования:
1) Vgt> есть билинейная функция | и v.
2) Vg/w = (L^f)v + / (я) Vgt>, где' / — гладкая функция, L^f — произ-
производная функции / по направлению вектора 5 из ТМХ.

274 ДОБАВЛЕНИЕ 1
3) L% <v, w> = <V|«, w (x)> + <v (x),
4) v«(*)«> - Vw(*)*' = I*», v) (x) (где Z[tOj r] = /,„?„, - ?„?,).
Задача 2. Доказать, что тензор кривизны выражается через ковари-
антные производные следующим образом:
чо) &, = - Vg
где ?, tj, ? — любые векторные поля, значения которых в рассматриваемой
точке равны ?„, tj0, g0.
Задача 3. Доказать, что тензор кривизны удовлетворяет следующим
тождествам:
0A.
Задача 4. Пусть риманова метрика задается в локальной системе
координат ху, . . ., хп симметричной матрицей gtf.
Обозначим через ех, . . ., еп координатные векторные поля (так что произ-
производная по направлению e$ есть д^ = д/dxj). Тогда ковариантные производные
можно вычислять с помощью формул задачи 1 и следующих формул:
к
где (glK) — матрица, обратная к
Пользуясь приведенным в задаче 2 выражением тензора кривизны через
связность, мы получаем явную формулу и для тензора кривизны. Числа
•Яум = <й (ei, ef) ек, ео называются компонентами тензора кривизны.
3. Уравнение Якоби. Кривизна риманова многообразия тесно
связана с поведением его геодезических. В частности, рассмотрим
геодезическую, выходящую из какой-либо точки по какому-либо
направлению, и немного изменим начальные условия, т. е. началь-
начальную точку и начальную скорость. Новые начальные условия оп-
определят новую геодезическую. Эта геодезическая вначале мало
отличается от исходной. Для исследования отклонения полезно
линеаризовать вблизи исходной геодезической дифференциальное
уравнение геодезических.
Получающееся при этом линейное дифференциальное уравне-
уравнение второго порядка («уравнение в вариациях» для уравнения
геодезических) называется уравнением Якоби, и его удобно запи-
записать через ковариантные производные и тензор кривизны.
Обозначим через х (t) точку, движущуюся по геодезической
многообразия М с постоянной по величине скоростью v (t) S
е TMx(t).
Если начальное условие гладко зависит от параметра а, то
геодезическая тоже гладко зависит от параметра. Рассмотрим
движение, соответствующее значению параметра а. Положение
в момент t точки на соответствующей геодезической обозначим
через х (t, a) G= M. Мы будем считать, что начальная геодезиче-
геодезическая соответствует нулевому значению параметра, так что
х (t, 0) = х (t).

РИМАНОВА КРИВИЗНА 275
Векторным полем вариации геодезической называется произ-
производная функции х (t, а) по параметру а при а = 0; значение этого
поля в точке х (t) равно
Чтобы записать уравнение в вариациях, определим еще кова-
риантную производную по t векторного поля Z, (t), заданного на
геодезической х (t). Определение состоит в том, что мы должны
взять вектор ? (t + Щ, параллельно перенести его из точки x(t + h)
в точку х (t) вдоль геодезической и затем продифференцировать
получившийся вектор в касательном пространстве ТМхц) по h
при h = 0. В результате получается вектор касательного простран-
пространства TMX(t), который называется ковариантной производной
поля ? (t) no t и обозначается через DtJDt.
Теорема. Векторное поле вариации геодезической удовле-
удовлетворяет линейному дифференциальному уравнению второго порядка
^- = -Q(v,l)v, D)
где Q — тензор кривизны, av = v(t) — вектор скорости движения
по исходной геодезической.
Обратно, всякое решение дифференциального уравнения D) яв-
является полем вариации исходной геодезической.
Уравнение D) называется уравнением Якоби.
Задача. Докажите сформулированную теорему.
Задача. Пусть М — поверхность, у (t) — величина составляющей
вектора j (t) по нормали к рассматриваемой геодезической, и пусть длина
вектора v \t) равна 1. Докажите, что у удовлетворяет дифференциальному
уравнению
У = -Ку, E)
где К — К (t) — риманова кривизна поверхности в точке х (t).
Задача. Пользуясь уравнением E), сравните поведение геодезиче-
геодезических, близких к данной, на сфере (К = + R~2) и на плоскости Лобачевского
(К = -1).
И. Исследование уравнения Якоби. При исследовании урав-
уравнений в вариациях полезно исключить тривиальные вариации,
сводящиеся к изменению начала отсчета времени и величины на-
начальной скорости движения. С этой целью разложим вектор ва-
вариации | на параллельную и перпендикулярную вектору скорости
v составляющие. Тогда (ввиду й(«,»)=0и ввиду кососиммет-
кососимметричности оператора Q (v, |)) для нормальной составляющей
мы получим снова уравнение Якоби, а для параллельной — урав-
уравнение D2l/Dt2 = 0.
Заметим теперь, что уравнение Якоби для нормальной состав-
составляющей можно переписать в виде «уравнения Ньютона»

276 ДОБАВЛЕНИЕ 1
где квадратичная форма U от вектора % выражается черев тензор
кривизны и пропорциональна кривизне К в направлении плоско-
плоскости (|, v):
U (I) = 4" 4
Таким образом, поведение нормальной составляющей вектора
вариации геодезической, проходимой со скоростью 1, описывается
уравнением (неавтономного) линейного осциллятора, потенциаль-
потенциальная энергия которого равна
половине произведения кри-
кривизны в направлении плоско-
плоскости векторов скорости и ва-
вариации на квадрат длины
нормальной составляющей
вариации.
В частности, рассмотрим
случай, когда кривизна по
Рис. 234. Близкие геодезические на многооб- всем ДВумерНЫМ направлени-
разиях положительной^ отрицательной кри- ям> содержащим вектор ск0_
рости геодезической, отри-
-цателъна (рис.234). Тогда отклонение близких геодезических
от данной по нормали описывается уравнением осциллятора с от-
отрицательно определенной (и зависящей от времени) потенциальной
энергией. Следовательно, нормальная составляющая отклонения
близких геодезических ведет себя как отклонение от вершины
горы шарика, находящегося вблизи этой вершины. Положение
равновесия шарика на вершине неустойчиво. Это значит, что близ-
близкие к данной геодезические будут экспоненциально уходить от нее.
Если бы потенциальная энергия получающегося уравнения Ньютона не
зависела от времени, наш вывод был бы вполне строгим. Более того, пред-
предположим, что при этом кривизны по разным направлениям, содержащим v,
заключены в пределах
—а2 < К < —Ь2, где 0 < Ь < а.
Тогда решения уравнения Якоби для нормальных отклонений будут линей-
линейными комбинациями экспонент с показателями rt^j, где положительные чис-
числа Aj заключены между а и Ь.
Следовательно, каждое решение уравнения Якоби растет не медленнее
е ' ' либо при t —» -f- оо, либо при t —» — оо; при этом большинство решений
растет еще быстрее, со скоростью е°'*'.
Неустойчивость положения равновесия при отрицательно
определенной потенциальной энергии в неавтономном случае ин-
интуитивно достаточно ясна. Ее можно доказать сравнением с под-
подходящей автономной системой. В результате такого сравнения
мы убеждаемся, что все решения уравнения Якоби для нормальных
отклонений на многообразии отрицательной кривизны растут
при движении вдоль геодезической не медленнее экспоненты прой-

РИМАНОВА КРИВИЗНА 277
денного пути, показатель которой равен корню квадратному из
модуля кривизны по тому двумерному направлению, для которого
этот модуль наименьший.
В действительности большинство решений растет еще быстрее,
но мы не можем теперь утверждать, что показатель роста боль-
большинства решений определяется направлением самой большой по
модулю отрицательной кривизны.
Резюмируя, мы можем сказать, что поведение геодезических
на многообразии отрицательной кривизны характеризуется экспо-
экспоненциальной неустойчивостью. Для количественной оценки этой
неустойчивости полезно ввести характерный путь s как средний
путь, при прохождении которого увеличиваются в е раз малые
ошибки в начальных условиях.
Точнее, характерный путь s можно определить как обратную
величину показателя "К, характеризующего рост решений уравне-
уравнения Якоби для нормальных отклонений от геодезической, про-
проходимой со скоростью 1:
I = Him ~ max max In I ? (t)\, s = 1/%.
T-~x> * \t\<T ||@)|=l
Вообще говоря, показатель "К и путь s зависят от начальной гео-
геодезической.
Если кривизны нашего многообразия по всем двумерным направ-
направлениям отграничены от нуля числом — Ь2, то характерный путь
не превосходит Ъ~г.
Таким образом, чем более отрицательна кривизна многообра-
многообразия, тем меньше характерный путь s, на котором неустойчивость
геодезических приводит к е-кратному нарастанию ошибок. Ввиду
экспоненциального характера нарастания ошибок ход геодези-
геодезической на многообразии отрицательной кривизны практически
невозможно прогнозировать.
Предположим, например, что кривизна отрицательна и отгра-
отграничена от нуля величиной — 4 м~2. Характерный путь не больше
полуметра, т. е. на пятиметровом отрезке геодезической ошибка
возрастет примерно Be"~ 104 раз. Следовательно, ошибка в де-
десятую долю миллиметра в начальном условии скажется в виде
метрового отклонения конца геодезической.
К. Геодезические потоки на компактных многообразиях отри-
отрицательной кривизны. Пусть М — компактное риманово много-
многообразие, кривизна которого в каждой точке по каждому двумер-
двумерному направлению отрицательна (такие многообразия существуют).
Рассмотрим движение материальной точки массы 1 по многообра-
многообразию М по инерции, вне поля действия всевозможных внешних
сил. Функция Лагранжа этой системы равна кинетической энер-
энергии, равна полной энергии и является первым интегралом урав-
уравнений движения.

278 ДОБАВЛЕНИЕ i
Если многообразие М имеет размерность п, то многообразие
уровня энергии 2п — 1-мерно. Это многообразие является под-
подмногообразием касательного расслоения многообразия М. Зафик-
Зафиксируем, например, значение постоянной энергии 1/2 (что соответ-
соответствует начальной скорости 1). Тогда скорость точки всегда оста-
останется единичной, и наше многообразие уровня оказывается про-
пространством расслоения
ТгМ С ТМ,
составленным из единичных сфер в касательных пространствах
к М в каждой точке.
Таким образом, точка из многообразия ТгМ представляет
собой вектор длины 1, приложенный в точке многообразия М.
Согласно принципу Мопертюи — Якоби, движение материальной
точки с фиксированным начальным условием из ТХМ можно опи-
описать следующим образом: точка движется со скоростью 1 по оп-
определенной указанным вектором геодезической.
Согласно закону сохранения энергии многообразие ТгМ явля-
является инвариантным многообразием в фазовом пространстве нашей
системы.
Следовательно, наш фазовый поток определяет однопараметрп-
ческую группу диффеоморфизмов 2п — 1-мерного многообразия
ТгМ.
Эта группа называется геодезическим потоком на М. Гео-
Геодезический поток может быть описан следующим образом: преоб-
преобразование за время t переводит единичный вектор | €Е ТгМ, при-
приложенный в точке х, в единичный вектор скорости геодезической,
выходящей из точки х по^направлению ?, приложенный в точке
на этой геодезической, лежащей на расстоянии t от точки х. За-
Заметим, что в TjM естественно определяется элемент объема и что
геодезический поток его сохраняет по теореме Лиувилля.
Конечно, до сих пор отрицательность кривизны многообразия
М не имела никакого значения. Но если мы займемся исследо-
исследованием траекторий описанного геодезического потока, то окажется,
что отрицательность кривизны многообразия М накладывает на
поведение этих траекторий сильный отпечаток (это связано с экс-
экспоненциальной неустойчивостью геодезических на М).
Вот некоторые из свойств геодезических потоков на много-
многообразиях отрицательной кривизны (подробнее см. цитированную
на стр. 266 книгу Д. В. Аносова).
1. Почти все фазовые траектории всюду плотны на многообра-
многообразии уровня энергии (исключительные, не всюду плотные траек-
траектории образуют множество меры нуль).
2. Равномерное распределение: доля времени, которое почти
каждая траектория проходит в любой области фазового простран-
пространства ТХМ, пропорциональна объему этой области.

РИМАИОВА КРИВИЗНА 279
3. Фазовый поток gl обладает свойством перемешивания: если
А и В — две области, то
lim mes [{g'A) f] В] = mes A mes В
t-*oo
(где mes означает объем, нормированный условием, что мера всего
пространства равна 1).
Из этих свойств траекторий в фазовом пространстве вытекают
аналогичные предложения о геодезических на самом многообразии.
Физики называют эти свойства «стохастичностью»: асимптотически
при больших t траектория ведет себя так, как если бы точка была
случайной. Например, свойство перемешивания означает, что
вероятность после выхода из А оказаться в В через большое время t
пропорциональна объему В и т. п.
Итак, экспоненциальная неустойчивость геодезических на много-
многообразии отрицательной кривизны приводит к стохастичности
соответствующего геодезического потока.
Л. Другие применения экспоненциальной неустойчивости.
Свойство экспоненциальной неустойчивости геодезических на
многообразии отрицательной кривизны, начиная с Адамара (а в слу-
случае постоянной кривизны — еще Лобачевского), изучалось мно-
многими авторами, в особенности Э. Хопфом. Неожиданным откры-
открытием шестидесятых годов в этой области оказались удивительная
устойчивость экспоненциально неустойчивых систем относительно
возмущений самой системы.
Рассмотрим, например, векторное поле, задающее геодезичес-
геодезический поток на компактной поверхности отрицательной кривизны.
Как указано выше, фазовые кривые этого потока устроены весьма
сложно: почти каждая из них всюду плотно заполняет трехмер-
трехмерное многообразие уровня энергии. У этого потока бесконечно
много замкнутых траекторий, и множество точек замкнутых траек-
траекторий также всюду плотно в трехмерном многообразии уровня
энергии.
Рассмотрим теперь близкое векторное поле. Оказывается, не-
несмотря на всю сложность картины фазовых кривых, при переходе
к близкому полю вся эта картина со всюду плотными фазовыми
кривыми и бесконечным числом замкнутых траекторий почти не
изменится. А именно, существует гомеоморфизм, близкий к тож-
тождественному преобразованию и переводящий фазовые кривые не-
невозмущенного потока в фазовые кривые возмущенного.
Таким образом, наш сложно устроенный фазовый поток об-
обладает таким же свойством «грубости» или «структурной устой-
устойчивости», как, скажем, предельный цикл, или устойчивый фокус
на плоскости. Заметим, что ни центр на плоскости, ни обмотка тора
таким свойством грубости не обладают: топологический тип фазо-
фазового портрета в этих случаях меняется при малом изменении век-
векторного, поля.

280 ДОБАВЛЕНИЕ 1
Возможность грубых систем со сложными движениями, каждое
из которых само по себе экспоненциально неустойчиво, является
одним из основных открытий в теории обыкновенных дифферен-
дифференциальных уравнений последнего времени (гипотеза грубости гео-
геодезических потоков на многообразиях отрицательной кривизны
была высказана С. Смейлом в 1961 г., а доказательство дано
Д. В. Аносовым и опубликовано в 1967 г., основные результаты
о стохастичности этих потоков получены Я. Г. Синаем и Д. В. Ано-
Аносовым также в шестидесятых годах).
Ранее предполагалось, что в системе дифференциальных урав-
уравнений «общего вида» возможны лишь простейшие устойчивые пре-
предельные режимы: положения равновесия и циклы. Если же си-
система устроена более сложно (например, является консервативной),
то предполагалось, что при малом изменении ее уравнений (напри-
(например, при учете малых неконсервативных возмущений) сложные
движения «рассыплются» на простые. Теперь мы знаем, что это не
так, и что в функциональном пространстве векторных полей имеют-
имеются целые области, состоящие из полей с более сложным поведением
фазовых кривых.
Выводы, которые отсюда следуют, затрагивают широкий круг
явлений, в которых наблюдается «стохастическое» поведение де-
детерминированных объектов.
Именно, представим себе, что в фазовом пространстве некото-
некоторой (неконсервативной) системы имеется притягивающее инвари-
инвариантное многообразие (или множество), на котором фазовые кривые
обладают свойством экспоненциальной неустойчивости. Мы знаем
теперь, что системы с таким свойством не являются исключитель-
исключительными: при малом изменении системы указанные свойства не нару-
нарушаются. Что увидит экспериментатор, наблюдающий за движе-
движениями такой системы?
Приближение фазовых кривых к притягивающему множеству
будет восприниматься как установление некоторого предельного
режима. Дальнейшее движение фазовой точки около притягиваю-
притягивающего множества будет вызывать хаотические, плохо прогнозируе-
прогнозируемые изменения «фаз» предельного режима, воспринимаемые как
«стохастичность» или «турбулентность».
К сожалению, до сих пор не был проведен убедительный анализ
физических примеров описанного характера с указанной точки
зрения. Пример, напрашивающийся прежде всего — это гидро-
гидродинамическая неустойчивость вязкой жидкости, описываемой
так называемым уравнением Навье — Стокса.
Фазовое пространство этой задачи бесконечномерно (это —
пространство векторных полей дивергенции 0 в области течения),
но бесконечномерность задачи не является, по-видимому, серь-
серьезным препятствием, по той причине, что вязкость гасит высокие
гармоники (мелкие вихри) тем быстрее, чем выше номер гармоники.
В результате фазовые кривые из бесконечномерного пространства,

РИМАНОВА КРИВИЗНА 281
по-видимому, приближаются к некоторому конечномерному много-
многообразию (или множеству), которому и принадлежат предельные
режимы.
При большой вязкости имеется устойчивое притягивающее
положение равновесия в фазовом пространстве («устойчивое стацио-
стационарное течение»). При уменьшении вязкости оно теряет устойчи-
устойчивость; при этом может возникать, например, устойчивый предель-
предельный цикл в фазовом пространстве («периодическое течение») или
устойчивое положение равновесия нового типа («вторичное ста-
стационарное течение»)*). Затем, по мере уменьшения вязкости,
в игру вступает все большее число гармоник и предельные режимы
могут становиться более многомерными.
При малой вязкости кажется весьма правдоподобным выход
на предельные режимы с экспоненциально неустойчивыми траек-
траекториями. К сожалению, до сих пор соответствующие вычисления
не были проведены ввиду ограниченных возможностей имеющихся
машин. Однако следующий общий вывод можно сделать и без
вычислений: для возникновения явлений типа турбулентности нет
необходимости в несуществовании или неединственности решений:
достаточна экспоненциальная неустойчивость, которая встречается
даже в детерминированных системах с конечным числом степеней
свободы.
В качестве еще одного примера применения экспоненциальной
неустойчивости укажем анонсированное Я. Г. Синаем доказа-
доказательство «эргодической гипотезы» Больцмана для системы твер-
твердых шариков. Гипотеза состоит в том, что фазовый поток, соответ-
соответствующий движению одинаковых абсолютно упругих шариков
в ящике с упругими стенками, эргодичен на связных множествах
уровня энергии. (Эргодичность означает, что почти каждая фа-
фазовая кривая проводит в каждой измеримой части множества
уровня время, пропорциональное мере этой части.)
Гипотеза Больцмана позволяет заменять временные средние
пространственными и считалась долгое время необходимой для
обоснования статистической механики. В действительности для
статистического предельного перехода (число частиц стремится
к бесконечности) гипотеза Больцмана (в которой речь идет о пре-
пределе, когда время стремится к бесконечности) не нужна. Однако
гипотеза Больцмана вызвала к жизни весь анализ стохастических
свойств динамических систем (так называемую эргодическую тео-
теорию), и ее доказательство служит мерой зрелости этой теории.
Экспоненциальная неустойчивость траекторий в задаче Больц-
Больцмана возникает вследствие соударений шариков друг с другом и
может быть объяснена следующим образом.
*) Теория бифуркаций и теория возмущений (не только гамильтоновых,
но и общих динамических систем) рассмотрены в учебнике: Арнольд В. И.
Дополнительные главы теории обыкновенных дифференциальных уравнений.—•
М.: Наука, 1978.

282 ДОБАВЛЕНИЕ 1
Рассмотрим для простоты систему всего из двух частиц на
плоскости и заменим квадратный ящик с отражением от стенок
плоским тором {(х, у) modd 1}. Тогда мы можем считать неподвиж-
неподвижной одну из частиц (пользуясь сохранением импульсов); другую
же частицу можно считать точкой.
Мы приходим, таким образом, к модельной задаче о движении
точки по торическому бильярду с круглой стенкой в середине,
от которой точка отражается по закону «угол
падения равен углу отражения» (рис. 235).
Для исследования этой системы рассмотрим
еще аналогичный бильярд, ограниченный сна-
снаружи плойкой выпуклой кривой (скажем, дви-
движение точки внутри эллипса). Движение на
таком бильярде можно рассматривать как пре-
Рис. 235. торичемшй Дельный случай геодезического потока на повер-
бильярд'с рассеива- хности эллипсоида. Предельный переход состоит
ющей кру™ой стен- в уМеньшении малой оси эллипсоида до нуля.
В результате геодезические на эллипсоиде
переходят в бильярдные траектории на эллипсе. Мы обнару-
обнаруживаем при этом, что эллипс разумно считать двусторонним и
считать, что при каждом отражении геодезическая переходит с
одной стороны эллипса на другую.
Вернемся теперь к нашему торическому бильярду. Движения
на нем тоже можно рассматривать как предельный случай гео-
геодезического потока на гладкой поверхности. Эта поверхность
получается, если рассмотреть тор с дырой как двустороннюю
поверхность и придать ей некоторую толщину, слегка сгладив
острое ребро. В результате получается поверхность с топологией
кренделя (сферы с двумя ручками).
Если при раздувании эллипса в эллипсоид получается поверх-
поверхность положительной кривизны, то при раздувании тора с дырой
возникает поверхность отрицательной кривизны (в обоих случаях
кривизна сосредоточена вблизи края, но раздувание можно про-
провести так, чтобы знак кривизны не менялся).
Итак, движение в нашем торическом бильярде можно рас-
рассматривать как предельный случай движения по геодезическим
на поверхности отрицательной кривизны.
Теперь для доказательства гипотезы Больцмана (в рассматри-
рассматриваемом простейшем случае) достаточно проверить, что анализ сто-
стохастических свойств геодезических потоков на поверхностях отри-
отрицательной кривизны сохраняет силу в указанном предельном
случае.
При подробном проведении доказательства оно оказывается
весьма сложным (Синай Я. Г. Динамические системы с упру-
упругими отражениями // УМН.— 1970.— Т. 25, № 2.— С. 141 — 192;
Синай Я. Г., Чернов Н. И. // УМН. — 1987. — Т. 42,
№ 3).

ГЕОДЕЗИЧЕСКИЕ ЛЕВОИНВАРИАНТНЫХ МЕТРИК 283
Добавление 2
ГЕОДЕЗИЧЕСКИЕ ЛЕВОИНВАРИАНТНЫХ МЕТРИК
НА ГРУППАХ ЛИ И ГИДРОДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ
Эйлерово движение твердого тела можно описать как движение
по геодезическим на группе вращений трехмерного евклидова
пространства, снабженной левоинвариантной римановой метрикой.
Значительная часть теории Эйлера связана лишь с этой инвари-
инвариантностью и потому переносится на случай других групп.
Среди примеров, охватываемых такой обобщенной теорией
Эйлера, движение твердого тела в многомерном пространстве и,
что особенно интересно, гидродинамика идеальной (несжимаемой
и невязкой) жидкости. В последнем случае в качестве группы
выступает группа диффеоморфизмов области течения, сохраняющих
элемент объема. Принцип наименьшего действия в этом примере
означает, что движение жидкости описывается геодезической мет-
метрики, заданной кинетической энергией (при желании можно счи-
считать этот принцип математическим определением идеальной жид-
жидкости). Легко проверить, что указанная метрика (право) инвари-
инвариантна.
Конечно, распространять результаты, полученные для конечно-
конечномерных групп Ли, на бесконечномерный случай следует с осто-
осторожностью. Например, в трехмерной гидродинамике до сих пор
нет теорем существования и единственности решений уравнений
движения.
Тем не менее интересно посмотреть, к каким выводам приводит
формальное перенесение свойств геодезических на конечномерных
группах Ли на бесконечномерный случай. Эти выводы носят ха-
характер априорных предложений (тождеств, неравенств и т. п.),
которые должны выполняться при всяком разумном понимании
решений. В некоторых случаях получаемые здесь выводы удается
затем строго обосновать непосредственно, минуя бесконечномерный
анализ. i
Например, уравнения Эйлера движения тверого тела имеют
своим аналогом в гидродинамике уравнения Эйлера движения
идеальной жидкости. Теореме Эйлера об устойчивости вращений
вокруг большой и малой осей эллипсоида инерции отвечает в гидро-
гидродинамике слегка обобщенная теорема Релея об устойчивости те-
течений без точек перегиба профиля скоростей и т. д.
Из формул Эйлера легко извлечь также явное выражение для
римановой кривизны группы с односторонне инвариантной мет-
метрикой. В применении к гидродинамическому случаю мы находим
кривизну группы диффеоморфизмов, сохраняющих элемент объема.
Интересно отметить, что для достаточно хороших двумерных
направлений кривизна оказывается конечной, и во многих слу-
случаях — отрицательной.

284 добавление: 2
Отрицательность кривизны вызывает экспоненциальную не-
неустойчивость геодезических (см. добавление 1). В рассматриваемом
случае геодезические — это течения идеальной жидкости. Поэтому
И8 вычисления кривизны группы диффеоморфизмов можно извле-
извлекать некоторую информацию о неустойчивости течений идеальной
жидкости.
Именно, кривизна определяет характерный путь, на котором
отклонения начальных условий вырастают в е раз. Отрицатель-
Отрицательность кривизны приводит к практической непредсказуемости те-
течения: на пути, большем характерного всего в несколько раз, от-
отклонения начальных условий от расчетных увеличатся в сотни
раз.
В этом добавлении кратко изложены результаты вычислений,
связанных с геодезическими на группах с односторонне инвариант-
инвариантными метриками. Доказательства и дальнейшие подробности мож-
можно найти в следующих работах:
А г п о 1 d V. Sur la geometrie differentielle des groupes de Lie de dimen-
dimension infinie et ses applications a l'hydrodynamique des fluides parfaits //An-
nales de l'lnstitut Fourier.—1966.— T. 16, № 1. — P. 316—361.
Арнольд В. И. Об одной априорной оценке теории гидродинами-
гидродинамической устойчивости // Изв. вузов. Математика.—1966.—№ 5, вып. 54.—
С. 3—5.
Арнольд В. И. Замечания о поведении течений трехмерной идеаль-
идеальной жидкости при малом возмущении начального поля скоростей //ПММ.—
1972.— Т. 36, № 2.— С. 255—262.
Арнольд В.И. Гамильтоновость уравнений Эйлера динамики твер-
твердого тела и идеальной жидкости//УМН.—1969.—Т. 24, № 3 A47).—
С. 225-226.
Дикий Л. А. Замечание о гамильтоновых системах, связанных
с группой вращений // Функц. анализ и его приложения.-—1972.— Т. 6,
№ 4.
Ebin D. G., Marsden J. Groups of diffeomorphisms and the motion
of an incompressible fluid // Annals of Math.—1970.— V. 92, № 1.— P. 102 —
163.
Ладыженская О. А. О разрешимости в малом нестационарных
задач для несжимаемых идеальных и вязких жидкостей и исчезающей вяз-
вязкости // Краевые задачи математической физики. Т. 5 (Записки научных
семинаров ЛОМИ, т. 21).— М.; Л.: Наука, 1971.— С. 65—78.
Мищенко А. С. Интегралы геодезических потоков на группах
Ли // Функц. анализ и его приложения.—1970.— Т. 4, № 3.— С. 73—78.
Обухов A.M. Об интегральных инвариантах в системах гидродина-
гидродинамического типа // ДАН СССР.—1969.— Т. 184, № 2.
Фаддеев Л.Д. К теории устойчивости стационарных плоско-па-
плоско-параллельных течений идеальной жидкости // Краевые задачи математической
физики. Т. 5 (Записки научных семинаров ЛОМИ, т. 21).— М.; Л.: Наука,
1971.— С. 164—172.
А. Обозначения. Присоединенное и коприсоединенное представ-
представления. Пусть G — вещественная группа Ли, д — ее алгебра Ли,
т. е. касательное пространство к группе в единице, снабженное
операцией коммутирования [,].
Группа Ли действует на себе левыми и правыми сдвигами:
для каждого элемента g группы G определены диффеоморфизмы

ГЕОДЕЗИЧЕСКИЕ ЛЕВОИНВАРИАНТНЫХ МЕТРИК 285
группы в себя
Lg.G^-G, Leh = gh; Rg:G-+G, Rgh = hg.
Индуцированные отображения касательных пространств будем
обозначать через
для всякого h из G.
Диффеоморфизм Rg-tLg является внутренним автоморфизмом
группы. Он оставляет единицу группы на месте. Его производная
в единице есть линейное отображение алгебры (т. е. касательного
пространства к группе в единице) в себя. Это отображение обозна-
обозначается через
Ad^: 9 -* 9, Ad^ = (i?g-.Lg)*e
и называется присоединенным (adjoint) представлением группы.
Легко проверить, что Adg является гомоморфизмом алгебры,
т. е. что
Adg [?, ill = [Adgg, AdgT]J, ?, t]Gj.
Ясно также, что Adgh = Ad^Adft.
Далее, рассмотрим Ad как отображение группы в пространство
линейных операторов на алгебре: Ad (g) = Adg.
Отображение Ad дифференцируемо. Рассмотрим его производ-
производную в единице группы. Эта производная есть линейное отображе-
отображение из алгебры в пространство линейных операторов на ней. По-
Построенное отображение обозначается через ad, а его образ при
действии на элемент | из алгебры через ad|. Таким образом, adg
есть эндоморфизм алгебры, мы имеем
ad = Ad*e: 9 -> End 9, adg = -J- [=o Ade,g,
где e*6 — однопараметрическая группа с касательным вектором |.
Из написанной формулы легко вывести выражение для ad в тер-
терминах одной лишь алгебры:
adST] = II, г\].
Рассмотрим! дуальное к алгебре Ли д линейное пространство
9*. Это — пространство вещественных линейных функций на ал-
алгебре Ли. Иными словами, д* есть кокасательное пространство
к группе в единице, 9* = T*Ge.
Значение элемента Ъ, кокасательного пространства к группе
в какой-либо точке g на элементе г\ касательного пространства
в той же точке мы будем обозначать круглыми скобками:
(Е, ч) е R. Е е T*GS, ч €= твЙ.

286 ДОБАВЛЕНИЕ 2
Левый и правый сдвиги индуцируют в кокасательных прост-
пространствах операторы, дуальные к ЬеФ и ЛеФ. Мы обозначим их
через
L*: T*Ggh-+T*Gh, Л*: Т*вы-+T*Gh
для всякого h из G. Эти операторы определяются тождествами
(L% то = (Б, /;лЧ), (д*Б, г]) == (Б, д„Ч).
Оператор, дуальный оператору Ad^, отображает кокасательное
пространство к группе в единице в себя. Он обозначается через
Ad*-: 9* -> 9*
и определяется тождеством
(Ad*?, ц) = (Б, Adgr]).
Операторы Ad*, где g пробегает группу Ли G, образуют пред-
представление этой группы, т. е. выполняется соотношение
Ad*ft = Ad*Ad*.
Это представление называется коприсоединенным представле-
представлением группы и играет важную роль во всех вопросах, связанных
с (лево) инвариантными метриками на группе.
Рассмотрим производную оператора Ad* no g в единице группы.
Эта производная есть линейное отображение из алгебры в прост-
пространство линейных операторов на дуальном к алгебре простран-
пространстве. Указанное линейное отображение обозначается через ad*,
а его образ при действии на элемент ? из алгебры обозначается
через adf. Таким образом, adf есть] линейный оператор на дуаль-
дуальном пространстве к алгебре,
adf: 9*-»-9*.
Легко видеть, что оператор adg сопряжен с adg:
(adft], ?) == {r\t adg?) для всех ijEj*, ? S 9.
Иногда удобно обозначать действие ad* фигурными скобками:
adfr] = {Б, т]}, где ^Gfl, "П е 9*-
Таким образом, фигурная скобка означает билинейную функцию
из g X 9* в 9*. связанную с коммутатором в алгебре тождествен-
тождественным соотношением
«Б, -л}, О = ft, 1Б, С1).
Рассмотрим орбиты коприсоединенного представления группы
в дуальном пространстве алгебры. На каждой такой орбите име-
имеется естественная симплектическая структура (называемая фор-

ГЕОДЕЗИЧЕСКИЕ ЛЕВОИНВАРИАНТНЫХ МЕТРИК 287
мой Кириллова, так как А. А. Кириллов первым использовал ее
в своем исследовании представлений нильпотентных групп Ли).
Таким образом, орбиты коприсоединенного представления всегда
четномерны. Заметим также, что мы получаем серию примеров
симплектических многообразий, рассматривая различные группы
Ли и всевозможные орбиты.
Симплектическая структура на орбитах коприсоединенного
представления определяется следующей конструкцией. Пусть х —
точка из дуального пространства к алгебре, \ — вектор, касатель-
касательный в этой точке к ее орбите. Поскольку д* — линейное простран-
пространство, мы можем считать вектор \, принадлежащий, честно говоря,
касательному пространству к д* в точке х, лежащим в д*.
Вектор ? можно (многими способами) представить в виде век-
вектора скорости движения точки х в коприсоединенном представле-
представлении однопараметрической группы eat с вектором скорости eGj.
Иными словами, каждый касательный к орбите точки х в копри-
коприсоединенном представлении группы вектор | выражается через
подходящий вектор а из алгебры по формуле
? = {а, х}, а е 9, же 9*.
Теперь мы готовы определить значение симплектической 2-фор-
мы Й на паре векторов ?а, |а, касательных к орбите точки х. Имен-
Именно, мы выражаем |2 и ?2 через какие-нибудь элементы алгебры ах
и а2 по предыдущей формуле, а затем составляем из двух элементов
алгебры и одного элемента дуального к ней пространства скаляр
& Ни У = (ж, \аг, а2]), х е 9*. at e $.
Легко проверить, что: 1) билинейная форма Q определена кор-
корректно, т. е. ее значение не зависит от произвола в выборе ;аг;
2) форма Q кососимметрична и, следовательно, задает дифферен-
дифференциальную 2-форму Q на орбите; 3) форма Q невырождена и замкну-
замкнута (доказательства имеются, например, в добавлении 5).
Итак, форма Q является симплектической структурой на ор-
орбите коприсоединенного представления.
Б. Левоинвариантные метрики. Риманова метрика на группе
Ли G называется левоинвариантной, если она сохраняется при
всех левых сдвигах1 Le, т. е. если производная левого сдвига пере-
переводит каждый вектор в вектор такой же длины.
Левоинвариантную риманову метрику достаточно задать в од-
одной точке группы, например в единице: тогда в остальные точки
метрику можно принести левыми сдвигами. Таким образом, лево-
инвариантных римановых метрик на группе столько же, сколько
евклидовых структур на алгебре.
Евклидова структура на алгебре определяется симметричес-
симметрическим положительно определенным оператором, действующим из ал-
алгебры в дуальное к ней пространство. Итак, пусть A: g -*¦ g* —

288 ДОБАВЛЕНИЕ 2
симметрический положительный линейный оператор:
(А1, г\) = (Аг\, I) для всех ?, ц из д.
(Положительность А не очень существенна, но в механических
приложениях квадратичная форма (Л?, ?) положительно опре-
определена.)
Определим симметрический оператор Ag: TGg -*- T*Ge левым
сдвигом:
Мы получаем, таким образом, следующую коммутативную диа-
диаграмму линейных операторов
9
Ad*
Определенное оператором Ag скалярное произведение будем обоз-
обозначать угловыми скобками:
Это скалярное произведение задает на группе G риманову мет-
метрику, инвариантную относительно левых сдвигов.
Скалярное произведение в алгебре будем обозначать просто
(,У. Определим операцию В: g x 9 ~*~ 9 тождеством
<[а, 6], с> == <JB (с, a), by для всех Ъ из д.
Ясно, что операция В билинейна и при фиксированном первом
аргументе кососимметрична по второму:
<Я (с, a), by + <Я (с, Ь), аУ = 0.
В. Пример. Пусть G = SOC) — группа вращений трехмер-
трехмерного евклидова пространства, т. е. конфигурационное простран-
пространство твердого тела, закрепленного в точке. Движение тела опи-
описывается тогда кривой g = g (t) на группе. Алгебра Ли группы G —
это трехмерное пространство угловых скоростей всевозможных
вращений. Коммутатор в этой алгебре — обычное векторное про-
произведение.
Скорость вращения тела g есть касательный вектор к группе
в точке g. Чтобы получить угловую скорость, нужно перенести
этот вектор в касательное пространство к группе в единице, т. е.
в алгебру. Но это можно сделать двумя способами: левым и пра-
правым сдвигом. В результате получаются два разных вектора в

ГЕОДЕЗИЧЕСКИЕ ЛЕВОИНВАРИАНТНЫХ МЕТРИК 289
алгебре:
Эти два вектора не что иное, как «угловая скорость в теле» (corps)
и «угловая скорость в пространстве» (space).
Действительно, элементу g группы G отвечает такое положение тела,
которое получается из некоторого начального состояния (соответствующего
единице группы и выбираемого произвольно) движением g. Пусть о —
элемент алгебры.
Однопараметрическую группу вращений с угловой скоростью ш мы
обозначим через eat: to — это касательная к указанной одноиараметрической
группе в единице. Теперь рассмотрим перемещение
eaxg, где g = g (t) e= G, aej, т <^с 1,
полученное из перемещения g поворотом с угловой скоростью ш за малое
время т. Если вектор g совпадает с вектором
dx т=о
то ш называется угловой скоростью относительно пространства и обознача-
обозначается ш5. Следовательно, as получается из % правым сдвигом. Аналогично
доказывается, что угловая скорость в теле есть левый сдвиг вектора g в
алгебру.
Дуальное к алгебре пространство 9* в нашем примере — это
пространство кинетических моментов.
Кинетическая энергия тела определяется вектором угловой
скорости в теле и не зависит от расположения тела в простран-
пространстве. Следовательно, кинетическая энергия задает левоинвариант-
ную риманову метрику на группе. Задающий эту метрику сим-
симметрический положительно определенный оператор Ag: TGg -*•
-v T*Gg называется оператором (или тензором) инерции; он свя-
связан с кинетической энергией формулой
Т — ~y <g, g>g = ~y <coc, coc> = -g- (A(DC, coc) = ~2-(Agg, g),
где A: 9 -*¦ 9* есть значение Ag при g = e.
Образ вектора g под действием оператора инерции Ag назы-
называется кинетическим моментом и обозначается через М = Agg,
Вектор М лежит в кокасательном пространстве к группе в точ-
точке g, и его можно перенести в кокасательное пространство к груп-
группе в единице как левыми, так и правыми сдвигами. Получаются
два вектора
Ме = L*M е= 9*,
ме = ifgM e 9*.
Эти векторы из дуального к алгебре пространства — не что
иное, как кинетический момент относительного тела (Мс) и кине-
кинетический момент относительно пространства (Ms). Последнее

290 ДОБАВЛЕНИЕ 2
легко вытекает из выражения кинетической энергии через момент
и угловую скорость:
Т =±(Me,o>e) = -±
Согласно принципу наименьшего действия, движение твердого
тела по инерции (в отсутствие внешних сил) есть геодезическая
на группе вращений с указанной выше левоинвариантной мет-
метрикой.
Мы будем теперь рассматривать геодезические произвольной
левоинвариантной римановой метрики на произвольной группе Ли
как движения «обобщенного твердого тела» с конфигурационным
пространством G. Такое «твердое тело с группой G» определяется
своей кинетической энергией, т. е. положительно определенной
квадратичной формой на алгебре Ли. Точнее, мы будем представ-
представлять себе геодезические левоинвариантной метрики на группе G,
заданной квадратичной формой <со, со> на алгебре, как движения
твердого тела с группой G и кинетической энергией <со, со>/2.
Каждому движению t *-*¦ g (t) нашего обобщенного твердого
тела мы можем сопоставить следующие четыре кривые:
t ьч- сос (?) е 9, t м- cos (t) е g,
t» ме (t) eg*, tb* мй (t) e в*,
называемые движениями векторов угловой скорости и момента
в теле и в пространстве.
Дифференциальные уравнения, которым подчиняются эти
кривые, найдены Эйлером для обычного твердого тела. Однако
они справедливы в самом общем случае произвольной группы G,
и мы будем их называть уравнениями Эйлера для обобщенного твер-
твердого тела.
Замечание. В обычной теории твердого тела отождест-
отождествлены шесть различных пространств размерности 3: R3, R3*,
9, д*, TGg, T*Ge. Совпадение размерностей пространства R3,
в котором движется тело, и алгебры Ли g его группы движений —
случайное обстоятельство, связанное с трехмерностью простран-
пространства: в /г-мерном случае g имеет размерность п (п — 1I2.
Отождествление алгебры Ли g с дуальным к ней пространством
9* имеет более глубокое основание. Дело в том, что на группе
вращений существует (и единственна с точностью до множителя)
двусторонне инвариантная риманова метрика. Эта метрика задает
раз и навсегда выделенный изоморфизм линейных пространств
g и д* (а также TGg и T*Gg). Она позволяет, следовательно, счи-
считать векторы угловой скорости и момента лежащими в одном ев-
евклидовом пространстве. В результате отождествления операция
{,} превращается в коммутатор алгебры, взятый со знаком минус.
Двусторонне инвариантная метрика существует на любой
компактной группе Ли, поэтому при изучении движений твердых

ГЕОДЕЗИЧЕСКИЕ ЛЕВОИНВАРИАНТНЫХ МЕТРИК 291
тел с компактными группами можно отождествить пространства
угловых скоростей и моментов. Однако мы не будем делать этого
отождествления, имея в виду главным образом приложения к
некомпактному (и даже бесконечномерному) случаю групп диф-
диффеоморфизмов .
Г. Уравнения Эйлера. Результаты Эйлера (полученные им
в частном случае G = SOC)) можно сформулировать в виде сле-
следующих теорем о движении векторов угловой скорости и момента
обобщенных твердых тел с группой G-
Теорема 1. Вектор момента относительно пространства
сохраняется при движении:
dMs _ о
dt ~
Теорема 2. Вектор момента относительно тела удовлет-
удовлетворяет уравнению Эйлера
dM
^ М
Доказываются эти теоремы для обобщенного твердого тела
так же, как для обычного.
Замечание1. Вектор угловой скорости в теле а»с линейно
выражается через вектор момента в теле Мс с помощью оператора,
обратного оператору инерции: сос = А~ХМС. Следовательно, урав-
уравнение Эйлера можно считать уравнением для одного лишь вектора
момента в теле; его правая часть квадратична относительно Ме.
Мы можем выразить этот результат еще следующим образом.
Рассмотрим фазовый поток нашего твердого тела. (Его фазовое
пространство T*G имеет размерность вдвое большую, чем размер-
размерность п группы G или пространства моментов $*.) Тогда этот
фазовый поток в 2/г-мерном многообразии факторизуется над по-
потоком, заданным уравнением Эйлера в л-мерном линейном про-
пространстве 9*»
Факторизацией фазового потока g' на многообразии X над фазовым
потоком /* на многообразий У называется такое гладкое отображение я
многообразия X на У, при котором движения g' переходят в движения f,
так что коммутативна диаграмма
т- е- ng'=
В нашем случае X — T*G— фазовое пространство тела, У = д* — про-
странство кинетических] моментов. Проекция эт: T*G—* g* определяется
левыми сдвигами (пМ = L*M для М е T*Gg). Далее, g* есть фазовый
поток рассматриваемого тела в 2п-мерном пространстве T*G, а /* — фазовый
поток уравнения Эйлера в n-мерном пространстве моментов д*.

292 ДОБАВЛЕНИЕ 2
Иными словами, движение вектора момента относительно тела
зависит лишь от начального положения вектора момента относи-
относительно тела и не зависит от расположения тела в пространстве.
Замечание 2. Закон сохранения вектора момента относи-
относительно пространства можно выразить, сказав, что каждая компо-
компонента этого вектора в какой-либо системе координат на простран-
пространстве д* сохраняется. Мы получаем, таким образом, множество пер-
первых интегралов уравнений движения твердого тела. В частности,
каждому элементу алгебры Ли g соответствует линейная функция
на пространстве д* и, следовательно, первый интеграл. Скобки
Пуассона первых интегралов, заданных функциями на д*, как
легко сосчитать, сами будут функциями на д*. Мы получаем,
таким образом, (бесконечномерное) расширение алгебры Ли д,
состоящее из всевозможных функций на д*. Сама алгебра Ли g
вложена в это расширение как алгебра Ли линейных функций
на д*. Конечно, функционально независимы из всех этих первых
интегралов фазового потока в 2п-мерном пространстве только
п штук. В качестве п независимых интегралов можно взять, на-
например, п линейных функций на д*, образующих базис в д.
Имея в виду бесконечномерные приложения, мы хотели бы
избавиться от координат и сформулировать утверждение о первых
интегралах инвариантно. Это можно сделать, переформулировав
теорему 1 следующим образом.
Теорема 3. Орбиты коприсоединенного представления
группыв дуалъномк алгебре пространстве являются инвариантными
многообразиями для потока в этом пространстве, заданного урав-
уравнением Эйлера.
Доказательство. Мс (t) получается из Ме (г) дей-
действием коприсоединенного представления, a Ms (t) стоит на месте,
ч.т.д.
Пример. В случае обычного твердого тела орбиты копри-
коприсоединенного представления группы в пространстве моментов —
это сферы М\ + М% + М\ = const. В этом случае теорема 3 пре-
превращается в закон сохранения квадрата момента. Она состоит в
том, что если начальная точка Мс лежит на какой-либо орбите
(т. е. в данном случае на сфере М2 = const), то и все точки ее
траектории под действием уравнения Эйлера лежат на той же
орбите.
Вернемся теперь к общему случаю произвольной группы G
и вспомним, что орбиты коприсоединенного представления имею?
симплектическую структуру (см. пункт А). Далее, кинетическую
энергию тела можно выразить через момент относительно тела.
В результате мы получаем квадратичную форму на пространстве
моментов
Т = 4" №е, А-*Ме).
Зафиксируем какую-нибудь одну^орбиту V коприсоединенного пред-

ГЕОДЕЗИЧЕСКИЕ ЛЕВОИНВАРИАНТНЫХ МЕТРИК 293
ставления. Рассмотрим кинетическую энергию как функцию на
этой орбите:
Н: V -> R, Н (Ме) = -А- (Ме, А'1Ме).
Теорема 4. Уравнение Эйлера на каждой орбите V копри-
соединенного представления является гамилътоновым, с функцией
Гамильтона Н.
Доказательство. Всякий вектор |, касательный к У в точке М,
имеет вид g = {/, М}, где / е д. В частности, векторное поле в правой
части уравнения Эйлера можно записать в виде X = {dT, M) (здесь диффе-
дифференциал функпии Т в точке М линейного пространства 8* рассматривается
как вектор пространства, дуального к 8*, т. е. как элемент алгебры Ли д).
Из определений симплектической структуры Q и операции { , } (см. пункт А)
вытекает, что для всякого вектора |, касательного к V в точке М,
Q (I, X) = (М, I/, dT]) = (dT, {f, M)) = (dH, I),
что и требовалось доказать.
Уравнение Эйлера можно перенести из дуального к алгебре
пространства в саму алгебру с помощью обращения оператора
инерции. В результате получается следующая формулировка урав-
уравнения Эйлера в терминах операции В (стр. 288).
Теорема 5. Движение вектора угловой скорости в теле
определяется начальным положением этого вектора и не зависит
от начального положения тела. Вектор угловой скорости в теле
удовлетворяет уравнению с квадратичной правой частью
юс = В (юс, сос).
Это уравнение мы будем называть уравнением Эйлера для
угловой скорости. Заметим, что орбиты коприсоединенного пред-
представления под действием оператора А'1: $* —*¦ 9 переходят в
инвариантные многообразия уравнения Эйлера для угловой
скорости: эти многообразия имеют симплектическую структуру
и т. д. Однако, в отличие от орбит в д*, зти инвариантные многооб-
многообразия не определяются самой группой Ли G, но зависят также и от
выбора твердого тела (т. е. оператора инерции).
Из закона сохранения энергии вытекает
Теорема 6. Уравнения Эйлера (для моментов и угловых
скоростей) имеют квадратичный первый интеграл, значение кото-
которого равно кинетической энергии
Т - 4" (Ме, А~Ч1е) = \- (Лсос, сос).
Д. Стационарные вращения и их устойчивость. Стационарным
вращением твердого тела называется такое вращение, при котором
угловая скорость тела постоянна (как в теле, так и в пространстве:
легко видеть, что одно влечет другое). Из теории обычного твер-
твердого тела в R3 мы знаем, что стационарными вращениями являют-

294 ДОБАВЛЕНИЕ 2
ся вращения вокруг главных осей эллипсоида инерции. Ниже
формулируется обобщение этой теоремы на случай твердого тела
с любой группой Ли. Заметим, что стационарные вращения —
это геодезические левоинвариантной метрики, являющиеся од-
нопараметрическими подгруппами.
Заметим также, что направления главных осей эллипсоида
инерции можно определять, рассматривая стационарные точки
кинетической энергии на сфере векторов момента фиксированной
длины.
Теорема 7. Кинетический момент (соответственно уг-
угловая скорость) стационарного вращения относительно тела яв-
является критической точкой энергии на орбите коприсоединенного
представления (соответственно на образе орбиты под действием
оператора А'1). Обратно, всякая критическая точка энергии на
орбите определяет стационарное вращение.
Доказательство — непосредственная выкладка пли ссылка
на теорему 4.
Заметим, что разбиение пространства моментов на орбиты
коприсоединенного представления может в случае произвольной
группы быть устроено не так просто, как в простейшем случае
обычного твердого тела, когда это — разбиение трехмерного про-
пространства на сферы с центром О и саму точку О. В частности,
¦орбиты могут иметь разные размерности, и разбиение на орбиты
может не быть в окрестности данной точки расслоением: такая
особенность есть уже в трехмерном случае в точке О.
Мы назовем точку М пространства моментов регулярной точкой,
если разбиение окрестности точки М на орбиты диффеоморфно
разбиению евклидова; пространства на параллельные плоскости
(в частности, все орбиты, близкие к точке М, имеют одинаковые
размерности). Например, для группы вращений трехмерного про-
пространства регулярны все точки пространства моментов, кроме на-
начала координат.
Теорема' 8. Предположим, что регулярная точка М про-
пространства моментов является критической точкой энергии на
орбите коприсоединенного представления, и что второй дифферен-
дифференциал энергии d2H в этой точке — знакоопределенная квадратичная
форма. Тогда М — устойчивое (по Ляпунову) положение равнове-
равновесия уравнения Эйлера.
Доказательство состоит в том, что вследствие регулярности
на соседних орбитах рядом с точкой М есть условный максимум
или минимум энергии.
Теорема 9. Второй дифференциал кинетической энергищ
суженной на образ орбиты коприсоединенного представления в
алгебре, дается в^критической точке ioSj формулой
(g) = <В (со, /), В (со, /)> + <[/, col, В (со, /)>,
где ? — касательный вектор к указанному образу, выражающийся

ГЕОДЕЗИЧЕСКИЕ ЛЕВОИНВАРИАНТНЫХ МЕТРИК 295
через f по формуле
I = В (со, /), / е 9-
Е. Римаыова кривизна группы с левоинвариантной метрикой.
Пусть G — группа Ли, снабженная левоинвариантной метрикой.
Пусть <,> — скалярное произведение в алгебре, задающее эту
метрику. Заметим, что риманова кривизна группы G в любой
точке определяется кривизной в единице (так как левые сдвиги
переводят группу в себя изометрически). Поэтому кривизну доста-
достаточно вычислить для двумерных плоскостей, лежащих в алгебре Ли.
Теорема 10. Кривизна группы в направлении, определен-
определенном ортонормированной парой векторов ?, г\ из алгебры, дается
формулой
*8.ч = <в, б> + 2 <«, Р> - 3<сс, а> - 4 <% ?„>,
где 26 = В (g, п) + В (Ч, g), 2р = В (g, -q) - В (Ч, g), 2a =
= [g, гЦ, 2ЯЕ = В (g, g), 2Бг, = Б (т], т]), и где В — операция,
определенная в пункте Б (стр. 288).
Доказательство — утомительное, но прямое вычисление. Оно
основано на легко проверяемой формуле для ковариантной произ-
производной
= \ ([g, ц] - В (g, rD-B (ц, g))f
где ? и т] слева — левоинвариантные векторные поля, а справа —
их значения в единице.
Замечание 1. В частном случае двусторонне инвариант-
инвариантной метрики формула для кривизны принимает особенно простой
вид
Замечание 2. Формула для кривизны группы с право-
инвариантной римановой метрикой совпадает с формулой для
левоинвариантного случая. Действительно, правоинвариантная
метрика на группе есть левоинвариантная метрика на группе с
перевернутым законом умножения (gi*g2 = g2&i)- Переход к пе-
перевернутой группе меняет знаки коммутатора и операции В
в алгебре одновременно. Но в каждом слагаемом формулы для
кривизны стоит произведение двух меняющих знак операций.
Следовательно, формула для кривизны сохраняет силу в правоин-
вариантном случае.
В уравнении Эйлера при переходе к правоинвариантному слу-
случаю меняется знак правой части.
Ж. Приложения к группе диффеоморфизмов. Пусть D —
ограниченная область в римановом многообразии. Рассмотрим
группу диффеоморфизмов области D, сохраняющих элемент объема.
Мы будем обозначать эту группу через SDiffZ>.

296 ДОБАВЛЕНИЕ 2
Алгебра Ли, соответствующая группе SDiff Z), состоит из всех
векторных полей дивергенции 0 на D, касающихся края (если он
не пуст). Определим скалярное произведение двух элементов этой
алгебры Ли (т. е. двух векторных полей) как
^2> = 5 (vi' v*>dx'
где (•) — скалярное произведение, задающее риманову метрику
на D, a dx — рпманов элемент объема.
Рассмотрим теперь течение однородной идеальной (несжимае-
(несжимаемой, невязкой) жидкости в области D. Такое течение описывается
кривой t *-*¦ gt на группе SDiff D. А именно, диффеоморфизм
gt — зто отображение, которое переводит каждую частицу жидко-
жидкости из того места, где она была в момент времени 0, в то место,
где она окажется в момент U
Оказывается, кинетическая энергия движущейся жидкости—
это правоинвариантная риманова метрика на группе диффеомор-
диффеоморфизмов SDiffZ).
В самом деле, пусть за время t течение жидкости осуществило диффео-
диффеоморфизм gf, а скорость в этот момент времени задается векторным полем v.
Тогда диффеоморфизм, осуществляемый течением за время t -\- т (где т мало)
будет evxgt с точностью до малых по сравнению с т величин (здесь еп — это
однопараметрическая группа с вектором скорости v, т. е. фазовый поток
заданного полем v дифференциального уравнения).
Следовательно, поле скоростей v получается из касательного к группе
в точке g вектора g правым сдвигом. Отсюда и следует правоинвариантность
кинетической энергии, которая, по определению, равна
Т = -I <i>, v>
(плотность жидкости мы считаем равной 1).
Принцип наименьшего действия (который в математическом
отношении есть определение идеальной жидкости) утверждает,
что течения идеальной жидкости являются геодезическими опи-
описанной правосторонне инвариантной метрики на группе диффео-
диффеоморфизмов.
Строго говоря, бесконечномерная группа диффеоморфизмов не является
многообразием. Поэтому точная формулировка предыдущего определения
требует дополнительной работы: нужно выбрать подходящие функциональ-
функциональные пространства, доказать теоремы существования и единственности реше-
решений и т. д. До сих пор это удалось сделать только в случае, когда размер-
размерность области течения D равна 2. Мы, однако, будем действовать так, как
если бы этих трудностей, связанных с бесконечномерностью, не существо-
существовало. Таким образом, дальнейшие рассуждения носят эвристический харак-
характер. Впрочем, многие результаты можно обосновать строго, независимо от
теории бесконечномерных многообразий.
Теперь мы укажем, в каком виде записываются приведенные
выше общие формулы в случае G = SDiff D, где D — связная об-

ГЕОДЕЗИЧЕСКИЕ ЛЕВОИНВАРИАНТНЫХ МЕТРИК 297
ласть конечного объема в трехмерном римановом^многообразии.
Для этого прежде всего нужно записать явно билинейную опера-
операцию В: 8 X 8 ~"* 8i определенную в пункте Б тождеством
<[а, b], c> =s (В (с, а), Ь>.
Легко проверить, что в трехмерном случае векторное поле
JB (с, а) выражается через векторные поля а и с из нашей алгебры
Ли по формуле
.В (с, о) = (rot с) /\а + grad a,
где Д означает векторное произведение, а а — однозначную в
D функцию, которая однозначно (с точностью до слагаемого)
определяется условием Б?9 (т. е. условиями div jB = 0 и jB
касательно к краю D).
Заметим, что операция В не зависит от выбора ориентации,
так как векторное произведение и ротор оба меняют знак при из-
изменении ориентации.
3. Стационарные течения. Уравнение Эйлера для «угловой ско-
скорости» в случае G = SDiff D имеет вид v = —JB (v, v), так как
метрика правоинвариантна. Оно принимает поэтому в случае
группы диффеоморфизмов трехмерного пространства вид «уравне-
«уравнения движения в форме Бернулли»
-^~ ш> v Д rot v + grad a, div v = 0.
Уравнение Эйлера для момента записывается в виде «уравнения
вихря»
= [v, rot v].
dt
В частности, вихрь стационарного течения коммутирует с полем
скоростей.
Это замечание позволяет немедленно топологически классифи-
классифицировать стационарные течения идеальной жидкости в трехмерном
пространстве.
Теорема 11. Предположим, что область D компактна и
ограничена аналитической поверхностью, а поле скоростей аполи-
аполитично и не везде коллинеарно со своим ротором. Тогда область те-
течения разбивается аналитическим подмножеством на конечное
число ячеек, в каждой из которых течение устроено стандартным
образом. А именно, ячейки бывают двух типов: расслоенные на
инвариантные относительно течения торы и расслоенные на ин-
инвариантные относительно течения поверхности, диффеоморфные
кольцу R X S1. При этом на каждом из торов все линии тока
замкнуты, либо все всюду плотны, а на каждом кольце все линии
тока замкнуты.

298 ДОБАВЛЕНИЕ 2
Доказательство этой теоремы основано на рассмотрении «по-
«поверхностей Бернулли», т. е. поверхностей уровня функции а.
Из условия стационарности (v Д rot v = —grad а) следует, что
как линии тока, так и линии ротора лежат на поверхностях Бер-
Бернулли. Поскольку поля скорости и ротора коммутируют, на
замкнутой поверхности Бернулли действует группа R2, и она обя-
обязана быть тором (ср. с доказательством теоремы Лиувилля в
§ 49). Аналогичные соображения, с учетом граничного условия
на краю D, показывают, что незамкнутые поверхности Бернулли
состоят из колец с замкнутыми линиями тока.
Замечание. Аналитичность поля скоростей не очень су-
существенна, но важно, чтобы поля скорости и ротора не были кол-
линеарны ни в какой области. Машинные эксперименты, прове-
проведенные М. Эно, показывают более сложное, чем описано
в теореме, поведение линий тока для стационарного течения на
трехмерном торе, заданного формулами
vx = A sin z-\- С cos y,vy = В sin х + A cos z, vz = С sin yt-{-B cos x.
Формулы подобраны так, что векторы v и rot ^коллинеарны. Судя
по результатам счета, некоторые линии тока плотно заполняют
трехмерные области.
И. Изозавихренные поля. Двумерная гидродинамика резко
отличается от трехмерной. Сущность этого различия заключается
в различии геометрии орбит коприсоединенного представления
в двумерном и трехмерном случае. Именно, в двумерном случае
орбиты в некотором смысле замкнуты и ведут себя, примерно, как
семейство множеств уровня функции (точнее, нескольких функ-
функций: в действительности даже бесконечного числа функций).
В трехмерном же случае орбиты устроены сложнее, в частности,
неограничены (а быть может и плотны). Орбиты коприсоединен-
коприсоединенного представления группы диффеоморфизмов трехмерного рима-
нова многообразия можно описать следующим образом. Пусть
v1 и v2 — два векторных поля скоростей несжимаемой жидкости
в области D. Мы скажем, что поля vt и v2 изозаеихрены, если су-
существует такой сохраняющий элемент объема диффеоморфизм g:
D —> D, который переводит каждый замкнутый контур у в D в
такой новый контур, что циркуляция первого поля по исход-
исходному контуру равна циркуляции второго по сдвинутому контуру:
ф vt = ф v2.
v gv
Легко проверить, что образ орбиты коприсоединенного представ-
представления в алгебре (под действием обратного к оператору инерции
оператора А'1) не что иное, как множество полей, изозавихренных
данному.
В частности, теорема 3 принимает теперь вид следующего за-
закона сохранения циркуляции.

ГЕОДЕЗИЧЕСКИЕ ЛЕВОИНВАРИАНТНЫХ МЕТРИК 299
Теорема 12. Циркуляция поля скоростей идеальной жидко-
жидкости по замкнутому жидкому контуру не меняется, когда контур
переносится жидкостью на новое место.
Заметим, что если два поля скоростей трехмерной идеальной
жидкости в D изозавихрены, то соответствующий диффеоморфизм
переводит ротор первого поля в ротор второго:
t = rot v2.
Более того, изозавихренность двух полей можно определить
как эквивалентность полей роторов, если область течения одно-
связна. Следовательно, задача об орбитах коприсоединенного
представления в трехмерном случае содержит в себе задачу о
классификации векторных полей дивергенции нуль с точностью
до сохраняющих элемент объема диффеоморфизмов. Эта последняя
задача в трехмерном случае безнадежно трудна.
Рассмотрим теперь двумерный случай. Вначале перепишем
основные формулы в удобных для^ рассмотрения двумерного
случая обозначениях.
Предположим, что область течения D двумерна и ориентиро-
ориентирована. Метрика и ориентация задают на D симплектическую струк-
структуру, векторное поле скоростей имеет дивергенцию нуль и потому
гамильтоново. Следовательно, это поле задается функцией Гамиль-
Гамильтона (вообще говоря, многозначной, если область D неодносвязна).
Функция Гамильтона поля скоростей называется в гидродинамике
функцией тока и обозначается через т]5. Таким образом,
v =
где / есть оператор поворота на 90° «вправо».
Функция тока коммутатора двух полей оказывается якобианом
(или, если угодно, скобкой Пуассона гамильтонова формализма)
функций тока исходных полей
Векторное поле jB (с, а) дается в двумерном случае формулой
В = —(А-фе) grad т]5а + grad а,
где ipa и ipe — функции тока полей о и с, Д = div grad — лапла-
лапласиан.
В частном случае евклидовой плоскости с декартовыми коор-
координатами х, у формулы для функции тока, коммутатора и лапла-
лапласиана принимают особенно простой вид
L ,, ? ^
ду ' У ~~ дх ' ^"»"»] ~~ дх ду ду дх

300 ДОБАВЛЕНИЕ 2
Вихрем (или ротором) двумерного поля скоростей называется
скалярная функция, интеграл произведения которой на ориентиро-
ориентированный элемент площади по любой ориентированной области а
в D равен циркуляции поля скоростей по краю области а:
с JC.
\г аЬ =
а
Легко сосчитать выражение ротора через функцию тока:
г = —Дт]5.
В двумерном односвязном случае изозавихренность полей г\
и v2 означает просто, что функции гх и г2 (роторы этих полей)
переходят друг в друга при подходящем сохраняющем площади
диффеоморфизме.
Две функции г1 и г2 с таким свойством во всяком случае рав-
ноизмеримы, т. е. для них
mes {j;GD : гх (х) <^ с} = mes {х €= D : г2 (х) ^ с}%
каково бы ни было число с. Следовательно, принадлежность двух
полей образу одной орбиты коприсоединенного представления
влечет равенство целой серии функционалов, например, интег-
интегралов от всех степеней ротора
В частности, уравнения Эйлера движения двумерной идеаль-
идеальной жидкости
-^- + vVv = — grad p, div v = 0,
имеют бесконечный набор первых интегралов. Например, интег-
интеграл от любой степени ротора поля скоростей
D
является таким первым интегралом.
Именно существование этих первых интегралов (т. е. относи-
относительно простая структура орбит коприсоединенного представ-
представления) позволило доказать теоремы существования, единствен-
единственности и т. д. в двумерной гидродинамике идеальной (а также и
вязкой) жидкости; и именно сложная геометрия, орбит копри-
коприсоединенного представления в трехмерном случае (или, может
быть, недостаток информации об этих орбитах) делает столь труд-
трудной задачу обоснования трехмерной гидродинамики.
К. Устойчивость плоских стационарных течений. Сформули-
Сформулируем теперь общие теоремы о стационарных вращениях (теоремы

ГЕОДЕЗИЧЕСКИЕ ЛЕВОИНВАРИАНТНЫХ МЕТРИК 301
7, 8 п [f выше) для случая группы диффеоморфизмов. Мы получим
тогда следующие утверждения:
1. Стационарное течение идеальной жидкости выделяется из
есех vзэзавихренных с ним течений тем, что оно является точкой
услов'- ого экстремума {или критической точкой) кинетической энер-
энергии.
2. Если 1) указанная критическая точка — действительно
экстремум, т. е. локальный условный максимум или минимум,
2) выполняется некоторое (вообще говоря, выполненное) условие
регулярности и 3) экстремум невырожден (второй дифференциал
знакоопределен), то стационарное течение устойчиво (т. е. яв-
является устойчивым по Ляпунову положением равновесия уравне-
уравнения Эйлера).
3. Формула для второго дифференциала кинетической энергии
на касательном пространстве к многообразию полей, изозаеихрен-
ных с данным, имеет в двумерном случае следующий вид. Пусть
D — область на евклидовой плоскости с декартовыми координатами
х, у. Рассмотрим стационарное течение с функцией тока т]5 =
= я]) (х, у). Тогда
\ J { ^jjL J dx dy,
где б у — вариация поля скоростей (т. е. вектор указанного выше
касательного пространства), а Ьг = rot б г».
Заметим, что для стационарного течения векторы градиента
функции тока и ее лапласиана коллинеарны. Поэтому отношение
Vi|)/VA«J; имеет смысл. Далее, в окрестности каждой точки, где гра-
градиент ротора не равен нулю, функция тока является функцией
от функции ротора.
Приведенные выше утверждения приводят к заключению, что
знакоопределенность квадратичной формы d?H должна быть до-
достаточным условием устойчивости рассматриваемого стационар-
стационарного течения. Это заключение не вытекает формально из теорем
7, 8, 9, так как применение всех наших формул в бесконечномер-
бесконечномерном случае требует обоснования.
К счастью, можно обосновать окончательный вывод об устой-
устойчивости, не обосновывая промежуточных построений. Таким обра-
образом, удается строго доказать следующие априорные оценки
(выражающие устойчивость стационарного течения относительно
малых возмущений начального поля скоростей).
Теорема 13. Предположим, что функция тока стационар-
стационарного течения t]j = tp (x, у) в области D является функцией от функ-
функции ротора (т. е. от функции — &яр) не только локально, но и
в целом. Предположим, что производная функции тока по функ-
функции ротора удовлетворяет неравенству

302 ДОБАВЛЕНИЕ 2
Пусть я]; + ф (х, у, t) — функция тока другого течения, уже не
обязательно стационарного. Предположим, что в начальный мо-
момент циркуляция поля скоростей возмущенного течения (с функ-
функцией тока ¦ф -+- ф) по каждой компоненте границы области D рав-
равна циркуляции исходного течения (с функцией тока ip). Тогда воз-
возмущение ф = ф (х, у, t) в любой момент оценивается через началь-
начальное возмущение ф0 = ф (х, у, 0) по формуле
1§ (%J + с (ДфJ dx dy < ^ (^ФоJ + С (Дф0J dx dy.
*Ь D
Если же стационарное течение удовлетворяет неравенству
то возмущение ф оценивается через ф0 по формуле
§ § с (ДфJ- (Щ* dx dy < I $ С (Дф0J - (^ФоJ dx dy.
D D
Из этой теоремы вытекает устойчивость стационарного течения
в случае положительной определенности квадратичной формы
относительно Vф (где ф — постоянная на каждой компоненте гра-
границы области D функция, у которой равен нулю поток градиента
через каждую компоненту границы), а также в случае отрица-
отрицательной определенности формы
(^фJ + (max
Пример 1. Рассмотрим плоское параллельное течение в
полосе Ух <^ у <^ У2 на плоскости (х, у) с профилем скоростей
v (у) (т. е. с полем скоростей (и (у), 0)). Такое течение стационар-
стационарно при любом профиле скоростей. Чтобы сделать область течения
компактной, наложим на поля скоростей всех рассматриваемых
течений условие периодичности с периодом X по координате х.
Условие теоремы 13 выполняется, если профиль скоростей не
имеет точек перегиба (т. е. если d2v/dy2 Ф 0). Мы приходим к
выводу, что плоские параллельные течения идеальной жидкости
без точек перегиба профиля скоростей устойчивы.
Аналогичное предложение в линеаризованной задаче называ-
называется теоремой Рэлея.
Подчеркнем, что в теореме 13 речь идет не об устойчивости «в линейном
приближении», а о настоящей строгой устойчивости по Ляпунову (т. е. от-
относительно конечных возмущений в нелинейной задаче). Различие между
этими двумя видами устойчивости в рассматриваемом случае существенно,

ГЕОДЕЗИЧЕСКИЕ ЛЕВОИНВАРИАНТНЫХ МЕТРИК 303
потому что наша задача имеет гамильтонов характер (см. теорему 4). А для
гамильтоновых систем асимптотическая устойчивость невозможна, поэтому
устойчивость в линейном приближении всегда нейтральная, недостаточная
для заключения об устойчивости положения равновесия нелинейной задачи.
П р и м е р 2. Рассмотрим плоскопараллельное течение на
торе
{(х, у), х mod X, у mod 2л}
с полем скоростей v — (sin у, 0), параллельным оси х. Это поле
определяется функцией тока т]5 = —cos у и имеет ротор г =
= — cos у. Профиль скоростей имеет две точки перегиба, однако
функция тока выражается через функцию ротора. Отношение
Vtjj/VAtJj равно минус единице. Применяя теорему 13, убеждаемся
в устойчивости нашего стационарного течения в случае, когда
2Я X 2Я X
I 5 (АфJ dxdy^ J ^ <yyfdxdy
0 0 0 0
для всех функций <р периода X по х и 2 л по у. Легко сосчитать,
что последнее неравенство выполнено при X ^ 2л и нарушается
при X > 2л.
Таким образом, из теоремы 13 вытекает устойчивость синусо-
синусоидального стационарного течения в случае короткого тора, когда
период в направлении основного течения (X) меньше ширины
потока Bл). С другой стороны, можно непосредственно проверить,
что на длинном торе (при X > 2л) наше синусоидальное течение
неустойчиво *).
Итак, в рассматриваемом примере достаточное условие устой-
устойчивости из теоремы 13 оказалось и необходимым.
Следует заметить, что вообще из незнакоопределенности квадратичной
формы в,гН не вытекает еще неустойчивость соответствующего течения. Вооб-
Вообще, положение равновесия гамильтоновой системы может быть устойчивым,
несмотря на то, что функция Гамильтона в этом положении равновесия не
является ни максимумом, ни минимумом. Квадратичный гамильтониан
И = р\ + ?j — v\ — ?2 — простейший пример такого рода.
Л. Романова кривизна группы диффеоморфизмов. Выражение
для кривизны группы Ли, снабженной односторонне инвариантной
метрикой, приведенное в пункте Е, имеет смысл и для группы
SDiff D диффеоморфизмов римановой области D. Эта группа яв-
является конфигурационным пространством для идеальной жидкости,
заполняющей область D. Кинетическая энергия жидкости опре-
определяет на группе SDiff D правоинвариантную метрику. Число,
которое получается при формальном применении к этой бесконеч-
*) См., например, статью: МешалкинЛ. Д., С и н а й Я. Г. Иссле-
Исследование устойчивости стационарного течения одной системы уравнений плос-
плоского движения несжимаемой вязкой жидкости // ПММ.— 1961.— № 6.—
С. 1140—1142.

304 ДОБАВЛЕНИЕ 2
номерной группе формулы для кривизны групп Ли, естественно
назвать кривизной группы SDiff D.
До конца вычисление кривизны группы диффеоморфизмов
проведено лишь в случае течений на двумерном торе с евклидовой
метрикой*). Такой тор получается из евклидовой плоскости R2
отождествлением точек, разность которых принадлежит некото-
некоторой решетке Г (дискретной подгруппе плоскости). Примером такой
решетки является множество точек с целыми координатами.
Рассмотрим теперь алгебру Ли, образованную векторными
полями дивергенции нуль на торе с однозначной функцией тока.
Соответствующая группа S0Diffr2 состоит из оставляющих на
месте центр тяжести тора и сохраняющих элемент площади диф-
диффеоморфизмов. Она вложена в группу SDiff Т2 всех сохраняю-
сохраняющих элемент площади диффеоморфизмов как вполне геодезиче-
геодезическое подмногообразие (т. е. такое подмногообразие, что каждая
его геодезическая является геодезической в объемлющем много-
многообразии).
Доказательство заключается в том, что если в начальный момент поле
скоростей идеальной жидкости имеет однозначную функцию тока, то и во
все моменты времени функция тока однозначна; последнее вытекает из зако-
закона сохранения импульса.
Мы исследуем теперь кривизны группы S0Diffr2 по всевоз-
всевозможным двумерным направлениям, проходящим через единицу
группы (кривизна группы SDiff У2 по каждому такому направ-
направлению та же самая, так как подмногообразие SoDiffZ12 вполне
геодезическое).
Выберем на плоскости R2 ориентацию. Тогда элементы алгебры
Ли группы S0DiffJ2 можно считать вещественными функциями
на торе, имеющими среднее значение нуль (поле дивергенции
нуль получается из такой функции, если считать ее функцией
тока). Следовательно, двумерное направление в касательной пло-
плоскости к группе S0Diff Т2 определяется парой функций на торе со
средним значением нуль.
Такую функцию мы будем задавать набором ее коэффициентов
Фурье. Все вычисления с рядами Фурье удобно проводить в
комплексной области. Обозначим через ей (где к — точка нашей
евклидовой плоскости, называемая волновым вектором) функцию,
значение которой в точке х нашей плоскости равно e*(fc> x). Такая
функция определяет функцию на торе, если она Г-периодич-
на, т. е. если прибавление вектора из решетки Г к аргументу х
не меняет значения функции.
Иными словами, скалярное-произведение (к, х) должно быть
кратно 2л для всех жеГ. Все такие векторы к принадлежат не-
*) Случаи тора Тп и сферы S2 рассмотрены А. М. Лукацким (Функц.
анализ.—1979.—Т. 13, № 3; УМН.—1981.—Т. 36, № 2).

ГЕОДЕЗИЧЕСКИЕ ЛЕВОИНВАРИАНТНЫХ МЕТРИК 305
которой решетке Г* на плоскости R2. Функции ей, где й" (= Г**
образуют полную систему в пространстве комплексных функций
на торе.
Теперь мы комплексифицируем нашу алгебру Ли, скалярное
произведение <,>, коммутатор f,J и операцию В в алгебре, а также
риманову связность и тензор кривизны Q, так что все эти функции
станут (поли) линейными в комплексном линейном пространстве
комплексифицированной алгебры Ли. Функции ек (где к (ЕЕ Г*,
к Ф 0) образуют в этом линейном пространстве базис.
Те о р е м а 14. Явные формулы, для скалярного произведенияг
коммутатора, операции В, связности и кривизны правоинвариант-
ной метрики на группе Sniffy2 имеют следующий вид:
<<?*- егу = 0 при к + I ф 0, О*, e_fc> = №S;
[ей, ei] =
ft2
В (ек, ег) = fcfci tek+i, где bkt г — (к Д I)
¦Rfc, i, m, n = 0, если й;4-^ + »»» + и.^0; если же к + I-\- m -\-
-j- n = 0, mo
^fc, i, m, n = (ainakm —
где n - <* A »)»
В этих формулах S — площадь тора, аиД» — площадь парал-
параллелограмма, натянутого на и и v (при выбранной ориентации
плоскости R2). Круглые скобки означают евклидово скалярное
произведение на плоскости, а угловые — в алгебре Ли.
Доказательство этой теоремы имеется в цитированной на
стр. 284 статье в Анналах института Фурье.
Приведенные формулы позволяют вычислить кривизну do
любому двумерному направлению. Вычисления показывают, что
по большинству направлений кривизна отрицательна, но по не-
некоторым — положительна. Рассмотрим, в частности, какое-либо
течение жидкости, т. е. геодезическую нашей группы. Согласно
уравнению Якоби, устойчивость этой геодезической определяется
кривизнами по направлениям всевозможных двумерных плоско-
плоскостей, проходящих через вектор скорости геодезической во всех
ее точках.
Предположим теперь, что рассматриваемое течение стационар-
стационарное. Тогда геодезическая является однопараметрической подгруп-
подгруппой нашей группы. Отсюда следует, что кривизны во всех пло-
плоскостях, проходящих через вектор скорости геодезической во
всех ее точках равны кривизнам в соответствующих плоскостях»
проведенных через вектор скорости указанной геодезической в

306 ДОБАВЛЕНИЕ 2
начальный момент времени. (Доказательство — правый сдвиг
ш единицу группы.) Таким образом, на устойчивость стационар-
стационарного течения влияют лишь кривизны в направлении тех двумер-
двумерных плоскостей в алгебре Ли, которые содержат вектор алгебры
Ли, являющийся полем скоростей стационарного течения.
Рассмотрим, например, простейшее параллельное синусои-
синусоидальное стационарное течение. Такое течение задается функцией
тока
S- 2 *
Рассмотрим любой другой вещественный вектор из алгебры, tj =
=Hxiei (так что x-i = xi). Из теоремы 14 легко выводится
Теорема 15. Кривизна группы S0DiffT2 во всех двумерных
плоскостях, содержащих направление ?, неположительна. А имен-
именно,
№. ч) Е. ч> = —§- ? «1.11 *i
Из этой формулы, в частности, вытекает, что:
1) кривизна равна нулю лишь для тех двумерных плоскостей,
которые состоят из параллельных течений того же направления,
что и |, так что [g, t]] — 0;
2) кривизна в сечении, определенном функциями тока | =
= cos kx, r\ = cos lx, есть
К = — K2 + P sin2 a sin8 p,
¦где S — площадь тора, а — угол между к и I, § — угол между
к -\- I и к — I;
3) в частности, кривизна группы диффеоморфизмов тора
\[х, у) modd 2л} в направлении, определенном полями скоростей
{sin у, 0) и @, sin x), равна
К
М. Обсуждение. Естественно ожидать, что кривизна группы
диффеоморфизмов связана с устойчивостью геодезических линий
на этой группе (т. е. с устойчивостью течений идеальной жидко-
жидкости) таким же образом, как кривизна конечномерной группы
Ли — с устойчивостью геодезических на ней. А именно, отрица-
отрицательность кривизны вызывает экспоненциальную неустойчивость
геодезических. При этом характерный путь (средний путь, на
котором в е раз нарастают ошибки в начальных условиях) имеет
порядок величины \1\Г —К. Таким образом, значение кривизны
группы диффеоморфизмов позволяет оценить время, на которое
можно предсказывать развитие течения идеальной жидкости по

ГЕОДЕЗИЧЕСКИЕ ЛЕВОПНВАРИАНТНЫХ МЕТРИК 307
приближенному начальному полю скоростей без того, чтобы ошиб-
ошибка возрастала на много порядков.
Следует подчеркнуть, что неустойчивость течений идеальной жидкости
понимается эдесь иначе, чем в пункте К: речь идет об экспоненциальной
неустойчивости движения жидкости, а не его поля скоростей. Возможны
случаи, когда стационарное течение является устойчивым по Ляпунову
решением уравнения Эйлера, и тем не менее соответствующее движение
жидкости экспоненциально неустойчиво. Дело в том, что малое изменение
поля скоростей жидкости может вызывать экспоненциально растущее
изменение движения жидкости. В таком случае (устойчивости решения урав-
уравнения Эйлера и отрицательности кривизны группы) можно прогнозировать
поле скоростей, но невозможно прогнозировать без очень большой потери
точности движение масс жидкости.
Приведенные выше формулы для кривизны можно даже исполь-
использовать для грубой оценки времени, на которое невозможен долго-
долгосрочный динамический прогноз погоды, если согласиться на неко-
некоторые упрощающие предположения. Эти упрощающие предполо-
предположения состоят в следующем.
1. Земля имеет форму тора, получающегося факторизацией
плоскости по квадратной решетке.
2. Атмосфера — это двумерная однородная несжимаемая не-
невязкая жидкость.
3. Движение атмосферы близко к «пассатному потоку», парал-
параллельному экватору тора и имеющему синусоидальный профиль
скоростей.
Для вычисления характерного пути мы должны тогда оценить
кривизны группы S0Diffr2 в направлениях, содержащих «пассат-
«пассатный поток» ? из теоремы 15. При этом мы будем считать Т2 =
= {(ж, у) modd 2я}, к = @, 1). Иными словами, мы рассматри-
рассматриваем 2я-периодические течения на плоскости (х, у), близкие
к стационарному течению, параллельному оси х, с синусоидаль-
синусоидальным профилем скоростей
v = (sin у, 0).
Из формул теоремы 15 легко усмотреть, что кривизна группы
S0Diff Т2 в плоскостях, содержащих наш пассатный поток v,
меняется в пределах
2
?- <^ К <^ 0, где S = 4я2 — площадь тора.
Здесь нижний предел получен довольно грубой оценкой. Однако
направление с кривизной К — —1/B5) заведомо существует, и
есть много других направлений с кривизнами примерно такой же
величины. Чтобы ориентировочно оценить характерный путь, мы
примем в качестве ориентировочного значения «усредненной
кривизны» К0 =—1/B3).

308 ДОБАВЛЕНИЕ 3
Если согласиться исходить из такого значения кривизны Kot
то получается характерный путь
Скорость движения по группе, которое соответствует нашему
пассатному течению, равна У S/2 (так как среднее квадратичное
значение синуса равно 1/2). Следовательно, время, за которое наше
течение проходит характерный путь, равно 2. Самые быстрые
частицы жидкости успеют за это время пройти расстояние 2, т. е,
1/л от полного оборота вокруг тора.
Таким образом, если принять наше ориентировочное значение
усредненной кривизны, то ошибки увеличиваются в е" ~ 20 раз
за время одного оборота самой быстрой частицы. Принимая для
максимальной скорости пассатного потока значение 100 км/ч,
получаем для времени оборота 400 ч, т. е. меньше трех недель.
Итак, если в начальный момент времени состояние погоды
было нам известно с малой ошибкой е, то порядок величины
ошибки прогноза через п месяцев будет
10к"е, где ki^—^-nlgloe^2,5.
Например, для вычисления погоды на два месяца вперед нужно
Ихметь в запасе пять знаков точности. Практически это означает,
что вычислять погоду на такой срок невозможно.
Разумеется, приведенная здесь оценка является весьма не-
нестрогой, и принятая нами модель весьма упрощена. Выбор зна-
значения «усредненной кривизны» также нуждается в обосновании.
Добавление 3
СИМПЛЕКТИЧЕСКАЯ СТРУКТУРА
НА АЛГЕБРАИЧЕСКИХ МНОГООБРАЗИЯХ
Симплектические многообразия классической механики — это
чаще всего фазовые пространства лагранжевых механических си-
систем, т. е. кокасательные расслоения конфигурационных про-
пространств.
Совсем другую серию примеров симплектических многообра-
многообразий доставляет алгебраическая геометрия.
Например, любое гладкое комплексное алгебраическое много-
многообразие (заданное системой полиномиальных уравнений в ком-
комплексном проективном пространстве) имеет естественную симплек-
тическую структуру.
Построение симплектической структуры на алгебраическом
многообразии основано на том, что само комплексное проективное
пространство имеет замечательную симплектическую структуру,
д именно мнимую часть его эрмитовой структуры.

СИМПЛЕКТИЧЕСКАЯ СТРУКТУРА 309
А. Эрмитова структура комплексного проективного простран-
пространства. Напомню, что тг-мерное комплексное проективное простран-
пространство СРП — это многообразие всех проходящих через точку О
комплексных прямых в в+ 1-мерном комплексном линейном
пространстве Сп+1. Чтобы построить на комплексном проективном
пространстве СРП симплектическую структуру, мы используем
эрмитову структуру в соответствующем линейном пространстве
C
Напомню, что эрмитовым скалярным произведением (или эрмитовой
структурой) в комплексном линейном пространстве называется комплексная
•функщгя от пары векторов, которая: 1) линейна по первому и антилинейна
по второму аргументу, 2) меняет значение на комплексно-сопряженное при
перестановке аргументов и 3) превращается в положительно определенную
вещественную квадратичную форму, если взять аргументы равными:
при | =t= 0.
Примером эрмитова скалярного произведения является
где |jc и щ — координаты векторов | и ij в некотором базисе.
Базис, в котором эрмитово скалярное произведение имеет вид A), всегда
•существует и называется эрмитово-ортонормированным базисом.
Вещественная и мнимая части эрмитова скалярного произведения яв-
являются вещественными билинейными формами. Первая из них симметрична,
а вторая кососимметрична, и обе невырождены:
Квадратичная форма (|, §) положительно определена.
Таким образом, эрмитова структура <,> в комплексном линейном про-
пространстве задает в нем евклидову структуру (,) и симплектическую структуру
(,]. Эти две структуры связаны с комплексной структурой соотношением
[ё> Ч] = (ё. Щ)'
Определим теперь на комплексном проективном пространстве
ряманову метрику. С этой целью рассмотрим в соответствующем
линейном пространстве Cn+1 единичную сферу
Эта сфера наследует из Cn+1 риманову метрику. Каждая комплекс-
комплексная прямая пересекает нашу сферу по окружности большого круга.
Определение. Расстоянием между двумя точками ком-
комплексного проективного пространства называется расстояние
между соответствующими двумя окружностями на единичной
сфере.
Заметим, что эти две окружности параллельны в том смысле,
что расстояние от любой точки одной из окружностей до другой
окружности одинаково (доказательство: умножение z на ei<p сох-
сохраняет метрику на сфере). Это обстоятельство позволяет сразу на-
написать явную формулу B) для римановой метрики на комплексном

310 ДОБАВЛЕНИЕ 3
проективном пространстве, задающей определенное выше расстоя-
расстояние.
Действительно, обозначим через р отображение
р: Cn+1 \ 0->-СРП,
сопоставляющее точке # =^= 0 линейного пространства Cil+1 ком-
комплексную прямую, проходящую через О и ».
Каждый вектор ?, касательный к СРП в точке pis, можно пред-
представить (многими способами) в виде образа вектора, приложенного
в точке »; при этом отображении
Теорема. Квадрат длины вектора ? в определенной выше
римановой метрике дается формулой
Доказательство. Предположим сначала, что точка z лежит на
единичной сфере S3".
Разложим вектор | на две составляющих: одна в комплексной прямой,
определенной вектором z, а вторая — в эрмитово-ортогональном направле-
направлении. Заметим, что эрмитова ортогональность вектору z означает евклидову
ортогональность векторам z и iz. Вектор г — это вектор евклидовой нормали
к сфере S2"'1 в точке z . Вектор iz — это вектор касательной к окружности,
по которой сфера пересекается с комплексной прямой, проходящей через
точку z. Значит, эрмитово-ортогональная к вектору z компонента г\ вектора §.
касается сферы ?2"~х и евклидово-ортогональна окружности, по которой
сферу пересекает прямая pz. ¦**
Согласно определению метрики на СРП, риманов квадрат длины векто-
вектора ? равен евклидову квадрату длины эрмитово-ортогональной к z компонен-
компоненты ц вектора |.
Вычислим компоненту ц вектора |, эрмитово-ортогональную к z. Запи-
Запишем наше разложение в
I = eg + Ч. где <i), г> = 0.
Умножая эрмитово на *, находим
<ё, «>
следовательно,
Вычисляя эрмитов квадрат вектора г], находим <г], rj> = <tj, §>,
Тем самым формула B) доказана для точек z единичной сферы. Общий слу-
случай сводится к рассмотренному гомотетией z <->¦ zl \ z |. Теорема доказана.
Заметим, что наша конструкция позволяет определить в каса-
касательном пространстве к СР" не только евклидову структуру B),
но и эрмитову структуру.

СИМПЛЕКТИЧЕСКАЯ СТРУКТУРА 311
Действительно, рассмотрим эрмитово-ортогональное дополне-
дополнение Н к направлению вектора » в пространстве ГС'г1+1, где * (=
€= S2". Отображение р^: Н -*• Т (СРп)рг изоморфно (как мы
показали выше) отображает Н на касательное пространство к СРП
и переносит туда эрмитову структуру из Н.
Ясно, что скалярный квадрат, определенный этой эрмитовой
структурой, дается формулой B). Поэтому формулу для эрмитова
скалярного произведения в касательном пространстве к СРП
можно написать без новых вычислений:
для любых векторов |1? |2 из ГСг+1, удовлетворяющих соотно-
соотношению р?ъ = ?tGT (СРп)рг.
Заметим, что в формуле C) точка ш не обязательно лежит на
единичной сфере.
Построенные евклидова и эрмитова структуры B), C) в каса-
касательных пространствах к СРП инвариантны не относительно всех
проективных преобразований многообразия СР", но лишь отно-
относительно тех, которые задаются унитарными (сохраняющими эр-
эрмитову структуру) линейными преобразованиями линейного про-
пространства Cn+1.
Б. Сшшлектическая структура комплексного проективного про-
пространства. Рассмотрим мнимую часть эрмитовой формы C)^
взятую с коэффициентом —1/я (зачем взят такой коэффициент,
объяснено в задаче 1 на стр. 313)
?}(?Х,У ^Im <&,&>. D)
Как и мнимая часть любой эрмитовой формы, вещественная били-
билинейная форма Q на касательном пространстве к комплексному
проективному пространству кососимметрична и невырождена.
Теорема. Дифференциальная 2~форма Q задает на комп-
комплексном проективном пространстве симплектическую структуру.
Доказательство» В доказательстве нуждается только замкну-
замкнутость формы Q.
Рассмотрим внешнюю производную dQ формы Q. Эта дифференциальная
3-форма на многообразии СР" инвариантна относительно отображений, ин-
индуцированных унитарными преобразованиями пространства Си+1. Отсюда
следувт, что она равна нулю.
В самом деле, рассмотрим в касательном пространстве к СРП в какой-
либо точке s эрмитово-ортонормированный С-баэис ег,. . ., еп. Тогда век-
векторы elt . . ., еп, iel7 . . ., ien образуют евклидово-ортонормированный
R-базис. Покажем, что значение формы dQ на любой тройке этих R-базис-
ных векторов равно нулю. (Мы предполагаем, что п>1: при п=1 доказывать
нечего.)
Заметим, что из любой тройки R-базисных векторов, указанных выше,
по меньшей мере один эрмитово-ортогонален двум другим. Обозначим этот
вектор через е. Легко построить унитарное преобразование пространства

312 ДОБАВЛЕНИЕ 3
C"+1, индуцирующее в СР*1 движение, оставляющее на месте рассматривае-
рассматриваемую точку z и эрмитово-ортогональное дополнение к е и меняющее направ-
направление вектора е.
Значение формы dQ на наших трех векторах е, /, д равно ее значению
на тройке —е, /, д ввиду инвариантности формы dQ и, следовательно, равно
нулю. Теорема доказана.
Замечание. Другой способ построения той же симплекти-
ческой структуры на комплексном проективном пространстве со-
состоит в следующем. Рассмотрим малые колебания математического
маятника с п + 1-мерным конфигурационным пространством. Вос-
Воспользуемся интегралом энергии для уменьшения на 1 числа сте-
степеней свободы системы. Фазовое пространство, полученное Босле
этой операции, есть СРП, а симплектическая структура в нем
совпадает с описанной выше формой Q с точностью до множителя.
Еще один способ построения симплектической структуры на СР" со-
состоит в том, что это пространство можно представить как одну из орбит
копрпсоединенного представления группы Ли, а на каждой такой орбите
всегда есть стандартная симплектическая структура (см. добавление 2,
пункт А). В качестве группы Ли можно взять группу унитарных (сохраняю-
(сохраняющих эрмитову метрику) операторов в п -\- 1-мерном комплексном простран-
пространстве. Орбиты коприсоединенного представления в этом случае такие же,
как и у присоединенного. В присоединенном же представлении оператор от-
отражения в гиперплоскости (меняющий знак первой координаты и остав-
оставляющий остальные) имеет своей орбитой СР". Ибо оператор отражения
в гиперплоскости однозначно определяется ортогональной ей комплексной
прямой.
В. Симплектические структуры проективных алгебраических
многообразий. Мы получаем теперь симплектическую структуру
на любом комплексном подмногообразии М комплексного проек-
проективного пространства. А именно, пусть /: М —*¦ СРП — вложение
комплексного многообразия М в комплексное проективное про-
пространство. Риманова, эрмитова и симплектическая структуры на
проективном пространстве индуцируют на М соответствующие
структуры. Например, симплектическая структура на М задается
формулой
пм = /*Q.
Теорема. Дифференциальная форма Qm задает на многооб-
многообразии М симплектическую структуру.
Доказательство. Невырожденность 2-формы QM сле-
следует из того, что М — комплексное подмногообразие. Действи-
Действительно, квадратичная форма на ТМХ
Х
положительно определена (она индуцирована римановой метри-
метрикой СР71). Следовательно, билинейная форма (|, r\) = QM (|, щ)
невырождена. Значит, невырождена и форма QM. Замкнутость
формы QM следует из замкнутости формы Q. Теорема доказана.

СИМПЛЕКТИЧЕСКАЯ СТРУКТУРА 313
Замечание. Как в комплексном проективном простран-
пространстве, так и на его комплексных подмногообразиях мы определили
эрмитову структуру в касательных пространствах, мнимая часть
которой является симплектической структурой.
Комплексное многообразие с эрмитовой метрикой, мнимая
часть которой является замкнутой формой (т. е. симплектической
структурой) называется келеровым многообразием, а его эрмитова
метрика — келеровой метрикой. В геометрии келеровых многооб-
многообразий получено много важных результатов, в частности они
обладают замечательными топологическими свойствами (см.,
например: В е й л ь А. Введение в теорию келеровых многообра-
многообразий.— М.: ИЛ, 1961).
Не все симплектические многообразия допускают келерову
структуру. Однако неясно, какие из топологических свойств келе-
келеровых многообразий зависят лишь от симплектической структуры.
Задача 1. Вычислить симплектическую структуру Q в аффинной
карте w = zx : z0 проективной прямой СР1.
Ответ. Q = .—?Цг—^гз • гДе и> = х + iy. Коэффициент в опре-
эт A -[- ;с"-|- у2)
делении формы Q выбран так, чтобы получить обычную ориентацию комплекс-
комплексной прямой (dx/\dy) и чтобы интеграл формы Q по всей проективной прямой
¦был равен 1.
Задача 2. Докажите, что симплектическая структура Q в аффинной
карте i% = zkz~x (fc = 1, . . ., п) проективного пространства СРП =
= {(z0 : zL : . . . : z,,)} задается формулой
Я =-1
V (w w J
3 амечание. Дифференциальные формы на комплексном простран-
пространстве с комплексными значениями (например, dw^ и dwk) определяются как
комплексные линейные функции от касательных векторов: если w% =
= хи -\- iyx, то
Пространство таких форм в Сп имеет комплексную размерность 2n; C-
базис образуют, например, 2п форм dw^, dw^ (ft = 1, . . ., п), либо 2п форм
Axk, dyk.
Внешнее умножение определяется обычным образом и подчиняется
обычным правилам. Например,
dw /\dw = (dx +idy) /\ (dx — idy) = —2i dx /\ dy.
Пусть / — вещественно-гладкая функция на С" (с комплексными, вооб-
вообще говоря, значениями). Пример такой функции: | w |2 = S^uJfc. Диф-
Дифференциал функции / является комплексной 1- формой. Следовательно, его
можно разложить по базису du%, dwk. Коэффициенты этого разложения на-
называются частными производными «по i/v> и «по и\»:
df = ^Ldw-\-^L dw.
1 dw ^ dw

314 ДОБАВЛЕНИЕ 4
При вычислении внешних производных также удобно разделить диффе-
дифференцирования d' по переменным w и <Г — по переменным w, так что d =
= d -\- а .
Например, для функции /
d'f = IL dw, d"f = HL dw.
dw dw
Для дифференциальной 1-формы
операторы d' и d" определяются аналогично:
d'a, = ? d'a^ Д dwk + d'bK /\d
d"a = 2 d"«k Л ^fc + dfc Д
Задача 3. Докажите, что симплектическая структура Q в аффинной
карте (i% = %-z) проективного пространства СР™ задается формулой
Добавление 4
КОНТАКТНЫЕ СТРУКТУРЫ
На нечетномерном многообразии не может быть симплекти-
ческой структуры. Аналогом симплектической структуры для
нечетномерных многообразий является несколько менее симме-
симметричная, но тоже весьма замечательная структура — контактная.
Источником симплектических структур в механике являются
фазовые пространства (т. е. кокасательные расслоения к конфигу-
конфигурационным многообразиям), на которых всегда есть каноническая
симплектическая структура. Источником контактных структур
являются многообразия контактных элементов конфшурацион-
ных пространств.
Контактным элементом к тг-мерному гладкому многообразию
в некоторой точке называется п — 1-мерная плоскость, касаю-
касающаяся многообразия в зтой точке (т. е. п — 1-мерное линейное
подпространство п-мерного касательного пространства в этой
точке).
Множество всех контактных элементов п-мерного многообразия
имеет естественную структуру гладкого многообразия размерно-
размерности 2п — 1. Оказывается, на этом нечетномерном многообразии
имеется замечательная дополнительная «контактная структура»
(мы опишем, что это такое, ниже).
Многообразие контактных элементов риманова п-мерного мно-
многообразия тесно связано с 2п — 1-мерным многообразием единич-
единичных касательных векторов этого риманова п-мерного многообра-

КОНТАКТНЫЕ СТРУКТУРЫ 315
зия, или с 2п — 1-мерным многообразием уровня энергии мате-
материальной точки, движущейся по риманову многообразию по
инерции. Контактные структуры в этих 2п — 1-мерных многообра-
многообразиях тесно связаны с симплектической структурой в 2тг-мерном
•фазовом пространстве точки (т. е. в кокасательном расслоении
исходного риманова тг-мерного многообразия).
А. Определение контактной структуры.
Определение. Контактная структура на многообра-
многообразии — это гладкое поле касательных гиперплоскостей *), удов-
удовлетворяющее некоторому условию невырожденности, которое
¦будет сформулировано позже. Чтобы сформулировать это условие,
посмотрим, как вообще может быть устроено поле гиперплоско-
¦стей в окрестности точки iV-мерного многообразия.
Пример. Пусть N = 2. Тогда многообразие — это поверх-
поверхность, а поле гиперплоскостей — поле прямых. Такое поле в
•окрестности точки устроено всегда одинаково и весьма просто,
а именно так, как поле касательных к семейству параллельных
прямых на плоскости. Точнее, одним из основных результатов
локальной теории обыкновенных дифференциальных уравнений
является возможность превратить любое гладкое поле касатель-
касательных прямых на многообразии в поле касательных к семейству
параллельных прямых евклидова пространства при помощи диф-
диффеоморфизма в достаточно малой окрестности любой точки мно-
многообразия.
Если iV ^> 2, то гиперплоскость уже не является прямой, и
дело обстоит значительно сложнее. Например, поле двумерных
касательных плоскостей в обычном трехмерном пространстве не
всегда можно диффеоморфно отобразить на поле параллельных
плоскостей. Дело в том, что существуют такие поля касательных
плоскостей, для которых невозможно провести «интегральную
поверхность», т. е. такую поверхность, которая имела бы пред-
предписанную касательную плоскость в каждой своей точке.
Условие невырожденности поля гиперплоскостей, которое
входит в определение контактной структуры, состоит в том, что
поле гиперплоскостей должно быть максимально удалено от поля
касательных к семейству гиперповерхностей. Чтобы измерять эту
удаленность, да и вообще чтобы убедиться в существовании полей
без интегральных гиперповерхностей, нам придется проделать
некоторые построения и вычисления **).
*) Гиперплоскостью в линейном пространстве называется подпространст-
подпространство, размерность которого на 1 ниже размерности пространства (т. е. множест-
множество нулевого уровня линейной функции, не равной нулю тождественно).
Касательная гиперплоскость — это гиперплоскость в касательном про-
пространстве.
**) Начиная с этого места мы опускаем приставку «гипер». При желании
можно считать, что мы находимся в трехмерном пространстве и гиперповерх-
гиперповерхности — это обычные поверхности. Многомерный случай аналогичен трех-
трехмерному.

316 ДОБАВЛЕНИЕ 4
Б. Условие интегрируемости Фробениуса. Рассмотрим какую-
либо точку на JV-мерном многообразии и попытаемся построить
поверхность, проходящую через эту точку и касающуюся данного
поля N — 1-мерных плоскостей в каждой точке (интегральную
поверхность).
С этой целью введем в окрестности рассматриваемой точки
систему координат так, чтобы в самой точке одна координатная
поверхность касалась плоскости поля. Эту плоскость мы будем
называть горизонтальной плоскостью, а не лежащую в ней коор-
координатную ось — вертикальной.
Построение интегральной поверхно-
поверхности. Интегральная поверхность, если она существует, является
вблизи начала координат графиком одной функции от N — 1 пе-
переменных. Чтобы ее построить, мы можем рассмотреть на гори-
горизонтальной плоскости какой-либо гладкий путь. Тогда верти-
вертикальные прямые над этим путем образуют двумерную поверхность
(цилиндр), а наше поле плоскостей высекает на ней поле касатель-
касательных прямых. Искомая интегральная поверхность, если она естьт
пересекает цилиндр по интегральной кривой поля прямых, вы-
выходящей из начала координат. Такая интегральная кривая есть
всегда, независимо от того, существует ли интегральная поверх-
поверхность. Таким образом, мы можем строить интегральную поверх-
поверхность над горизонтальной плоскостью, двигаясь по гладким
кривым в последней.
При этом для того, чтобы из всех интегральных кривых полу-
получилась гладкая интегральная поверхность, нужно, чтобы резуль-
результат нашего построения не зависел от пути, но определялся лишь
его конечной точкой.
В частности, при обходе замкнутого пути в окрестности нача-
начала координат на горизонтальной плоскости интегральная кривая
на цилиндре должна замкнуться.
Легко построить примеры полей плоскостей, для которых
такого замыкания не происходит, п, следовательно, интегральная
поверхность не существует. Такие поля плоскостей называются
неинтегрируемыми.
Пример неинтегрируемого поля пло-
плоскостей. Чтобы задавать поля плоскостей и измерять коли-
количественно отклонение от замыкания, мы введем следующие обоз-
обозначения.
Заметим прежде всего, что поле гиперплоскостей локально
можно задавать дифференциальной 1-формой. Действительно, пло-
плоскость в касательном пространстве задает 1-форму, с точностью
до умножения на отличную от нуля постоянную. Выберем эту
постоянную так, чтобы значение формы на вертикальных коорди-
координатных касательных векторах было равно 1.
Этому условию можно удовлетворить в некоторой окрестности
начала координат, поскольку плоскость поля в нуле не содержит

КОНТАКТНЫЕ СТРУКТУРЫ 317
вертикального направления. Это условие определяет форму одно-
вначно (по полю плоскостей).
Поле плоскостей в обычном трехмерном пространстве, не имею-
имеющее интегральных поверхностей, можно задать, например,
1-формой
со = xdy -f- dz,
где х и у — горизонтальные координаты, a z — вертикальная.
Доказательство того, что это поле плоскостей неинтегрируемо,
приведено ниже.
Построение 2-ф о р м ы, измеряющей н е и н-
тегрируемость. С помощью формы, задающей поле,
можно измерять степень неинтегрируемости. Делается это при
помощи следующей конструкции (рис. 236).
Рассмотрим пару векторов, выходящих пз начала координат
и лежащих в горизонтальной плоскости нашей координатной
системы. Построим на них параллелограмм. Мы получим два
пути из начала координат в противоположную вершину. Над
каждым из зтих двух путей можно построить
интегральную кривую (двузвенную), как опи-
описано выше. В результате над противоположной
началу вершиной параллелограмма возникнут,
вообще говоря, две разные точки. Разность
высот этих точек является функцией от на-
нашей пары векторов. Эта функция кососнмметри-
чна и равна нулю, если равен нулю один из
векторов. Следовательно, линейная часть ряда
гг, „ г „ ¦. г Рис. 236. Интехраль-
1еилора этой функции пары векторов в нуле Ные кривые, постро-
равна нулю, а квадратичная часть ее ряда Руетыполю
Тейлора является билинейной кососимметри- костей
чной формой на горизонтальной плоскости.
Если поле интегрируемо, то получившаяся 2-форма равна
нулю. Поэтому эту 2-форму можно рассматривать как меру неин-
неинтегрируемости поля.
Пользуясь нашей системой координат, мы можем отождествить
горизонтальную координатную плоскость с плоскостью поля,
проходящей через начало координат. Таким образом, в резуль-
результате нашего построения возникает 2-форма в самой плоскости
поля.
Корректность определения 2-формы. Вы-
Выше 2-форма построена при помощи координат. Однако значение
нашей 2-формы на паре касательных векторов не зависит от
системы координат, но лишь от той 1-формы, с помощью которой
задано поле.
Чтобы в этом убедиться, достаточно доказать следующее.
Теорема. Определенная выше 2-форма на нулевом про-
пространстве l-формы w совпадает с внешней производной последней,
й |со=о-

318 ДОБАВЛЕНИЕ 4
Доказательство. Покажем, что разность высот двух точек,
получающихся в результате наших двух движений по сторонам параллело-
параллелограмма, совпадает с интегралом 1-формы со по четырем сторонам паралле-
параллелограмма с точностью до величин третьего порядка малости относительно
сторон параллелограмма.
С этой целью заметим, что высота подъема интегральной кривой на лю-
любом пути длины е, выходящем из начала координат, имеет порядок е2, по-
поскольку в начале координат плоскость поля горизонтальна. Следовательно,
интегралы 2-формы dto по всем четырем вертикальным площадкам над сторо-
сторонами параллелограмма, ограниченным интегральными кривыми и горизон-
горизонтальной плоскостью, имеют порядок 83, если стороны порядка е.
Интегралы формы to по интегральным кривым точно равны нулю. Стало
быть, по формуле Стокса приращение высоты вдоль интегральной кривой,
лежащей над какой-либо из сторон параллелограмма, равно интегралу 1-фор-
1-формы to вдоль этой стороны с точностью до величин третьего порядка малости.
Теперь доказываемая теорема вытекает непосредственно из определения
внешней производной.
Остается еще произвол в выборе 1-формы е>, с помощью кото-
которой построена наша 2-форма. А именно, форма со определена полем
плоскостей лишь с точностью до умножения на нигде не обра-
обращающуюся в нуль функцию /. Иными словами, мы могли бы на-
начинать с формы /к>. Тогда мы пришли бы к 2-форме
dfa) = fda) + df Д w,
которая на нашей плоскости отличается от 2-формы day умноже-
умножением на отличное от нуля число / @).
Таким образом, построенная 2-форма на плоскости поля опре-
определена инвариантно с точностью до умножения на отличную от
нуля постоянную.
Условие интегрируемости поля пло-
плоскостей.
Теорема. Если поле гиперплоскостей интегрируемо, то
построенная выше 2-форма в плоскости поля равня нулю. Обратно,
если построенная в каждой плоскости поля 2-форма равна нулюг
то поле интегрируемо.
Первое утверждение теоремы очевидно по построению 2-формы. Доказа-
Доказательство второго утверждения можно провести в точности теми же рассужде-
рассуждениями, с помощью которых мы доказывали коммутативность фазовых по-
потоков, для которых равна нулю скобка Пуассона полей скоростей. Можно
и просто сослаться на эту коммутативность, применяя ее к интегральным
кривым, возникающим над прямыми координатных направлений в горизон-
горизонтальной плоскости.
Теорема. Условие интегрируемости поля плоскостей
did = 0 при ю = 0
эквивалентно следующему условию Фробениуса:
dft> = 0.
Доказательство. Рассмотрим значение выписанной 3-формы на
каких-нибудь трех разных координатных векторах. Из них вертикальный

КОНТАКТНЫЕ СТРУКТУРЫ 319
может быть лишь один вектор. Поэтому из всех слагаемых, входящих в оп-
определение значения внешнего произведения на трех векторах, отличным от
нуля может быть лишь одно, равное произведению значения формы to на
вертикальном векторе на значение формы da на паре горизонтальных век-
векторов. Если заданное формой поле интегрируемо, то второй сомножитель
равен нулю, н, следовательно, наша 3-форма равна нулю на всех вообще трой-
тройках векторов.
Обратно, если 3-форма равна нулю для любых векторов, то она равна
нулю для любой тройки координатных векторов, один из которых вертика-
вертикален, а два горизонтальны. Значение 3-формы на такой тройке равно произ-
произведению значения а на вертикальном векторе на значение da на паре горизон-
горизонтальных. Первый сомножитель не нуль, значит, второй нуль, и, значит,
форма da на плоскости поля равна нулю, ч. т. д.
В. Невырожденные поля гиперплоскостей.
Определение. Поле гиперплоскостей называется не-
невырожденным в точке, если ранг 2-формы day |и=0 в плоскости
поля, проходящей через эту точку, равен размерности плоскости.
Это значит, что для всякого ненулевого вектора нашей пло-
плоскости должен найтись другой вектор в плоскости так, что значе-
значение 2-формы для этой пары векторов отлично от нуля.
Определение. Поле плоскостей называется невырож-
невырожденным на многообразии, если оно невырождено в каждой точке
многообразия.
Заметим, что на четномерном многообразии не может быть не-
невырожденного поля гиперплоскостей. Действительно, на таком
многообразии гиперплоскость нечетномерна, а ранг всякой косо-
симметричной билинейной формы в нечетномерном пространстве
меньше размерности пространства (см. § 44).
На нечетномерных многообразиях невырожденные поля пло-
плоскостей бывают.
Пример. Рассмотрим евклидово пространство размерности
2т + 1 с координатами х, у, z (где х и у — векторы т-мерных
пространств, а 2 — число). 1-форма
w = xdy + dz
задает поле гиперплоскостей. Плоскость поля, проходящая через
начало координат, имеет уравнение dz = 0. Координатами в этой
гиперплоскости можно считать х и у. Следовательно, наша 2-фор-
ма в плоскости поля записывается в виде
йь>|и=0 = dx /\dy = dxx Д dyx + ... + dxm Д dym.
Ранг этой формы равен 2т, поэтому наше поле невырождена
в начале координат, а значит, и в его окрестности (в действи-
действительности это поле плоскостей невырождено во всех точках про-
пространства).
Теперь мы, наконец, можем дать определение контактной
структуры на многообразии: контактной структурой на много-
многообразии называется невырожденное поле касательных гиперпло-
гиперплоскостей.

¦320 ДОБАВЛЕНИЕ 4
Г. Многообразие контактных элементов. Термин «контактная
структура» объясняется тем, что такая структура всегда есть на
многообразии контактных элементов гладкого многообразия.
Рассмотрим и-мерное гладкое многообразие.
Определение. Гиперплоскость (размерности п — 1), ка-
касающаяся многообразия в какой-либо точке, называется кон-
контактным элементом, а эта точка — точкой контакта.
Множество всех контактных элементов и-мерного многообра-
многообразия само имеет структуру гладкого многообразия размерности
2и — 1.
В самом деле, множество всех контактных элементов с фиксированной
точкой контакта — это множество всех п — 1-мерных подпространств п-мер-
ного линейного пространства, т. е. проективное пространство размерности
п — 1. Чтобы задать контактный элемент, нужно, следовательно, задать п
координат точки контакта и еще п — 1 координату, определяющую точку
п — 1-мерного проективного пространства, итого 2п — 1 координату.
Многообразие всех контактных элементов и-мерного многооб-
многообразия является пространством расслоения, база которого — наше
л-мерное многообразие, а слой — проективное пространство раз-
размерности п — 1.
Теорема. Расслоение контактных элементов является
¦проективизацией кокасателъного расслоения: его можно получить
из кокасателъного расслоения, заменив каждое кокасателъное ли-
линейное п-мерное пространство п — i-мерным проективным про-
пространством (точка которого — прямая, проходящая через начало
координат в кокасателъном пространстве).
В самом деле, контактный элемент задается 1-формой на кокасательном
пространстве, для которой этот элемент является нулевым множеством уров-
уровня. Эта форма не нулевая, и она определена с точностью до умножения на от-
отличное от нуля число.
Но форма на касательном пространстве есть вектор кокасательного
пространства. Поэтому ненулевая форма на касательном пространстве,
определенная с точностью до умножения на не равное нулю число, есть
ненулевой вектор кокасательного пространства, определенный с точностью
до умножения на не равное нулю число, т. е. точка проективизации кокаса-
кокасательного пространства.
Контактная структура на многообра-
многообразии контактных элементов.
В касательном пространстве к многообразию контактных
элементов имеется замечательная гиперплоскость. Она называется
контактной гиперплоскостью и определяется следующим образом.
Зафиксируем точку 2и — 1-мерного многообразия контактных
элементов на n-мерном многообразии. Эту точку мы можем рас-
рассматривать как п — 1-мерную плоскость, касательную к исход-
исходному и-мерному многообразию.
Определение. Касательный вектор к многообразию
контактных элементов в фиксированной точке принадлежит кон-
контактной гиперплоскости, если его проекция на n-мерное много-

КОНТАКТНЫЕ СТРУКТУРЫ 321
образие лежит в той п — 1-мерной плоскости, которая и яв-
является фиксированной выше точкой многообразия контактных
элементов.
Иными словами, перемещение контактного элемента касается
контактной гиперплоскости, если скорость точки касания при-
принадлежит этому контактному элементу; поворачиваться же эле-
элемент может как угодно.
П р и м е р. Возьмем какое-либо подмногообразие в нашем
и-мерном многообразии и рассмотрим все касательные к нему
п — 1-мерные плоскости (т. е. контактные элементы). Все такие
контактные элементы образуют в 2п — 1-мерном многообразии
всех вообще контактных элементов гладкое подмногообразие.
Размерность этого подмногообразия равна п — 1, какова бы ни
была размерность исходного подмногообразия (которое может быть
п — 1-мерным, а может иметь и меньшую размерность вплоть до
случая кривой и даже до точки).
Полученное п — 1-мерное подмногообразие 2га — 1-мерного
многообразия всех контактных элементов в каждой своей точке
касается поля контактных гиперплоскостей (по определению
контактной гиперплоскости). Таким образом, поле контактных
In — 2-мерных гиперплоскостей имеет п — 1-мерные интеграль-
интегральные многообразия.
Задача. Существуют ли у этого поля плоскостей интегральные мно"
гообразия большей размерности?
Ответ. Нет.
Задача. Можно ли задать поле контактных гиперплоскостей диффе-
дифференциальной 1-формой на многообразии всех контактных элементов?
Ответ. Нет, даже если исходное и-мерное многообразие — евклидово
пространство (например, обычная двумерная плоскость).
Ниже мы докажем, что поле контактных гиперплоскостей на
2п — 1-мерном многообразии всех контактных элементов п-мер-
ного многообразия невырождено.
Доказательство проводится с помощью симплектической струк-
структуры кокасательного расслоения.
Дело в том, что многообразие контактных элементов связано
простой конструкцией с пространством кокасательного расслое-
расслоения (проективизацией которого является многообразие контакт-
контактных элементов). Причем невырожденность поля контактных пло-
плоскостей проективизированного расслоения тесно связана с невы-
невырожденностью 2-формы, задающей симплектическую структуру
кокасательного расслоения.
Конструкцию, о которой идет речь, мы проведем ниже в не-
несколько более общей обстановке. Именно, по всякому нечетно-
мерному многообразию с контактной структурой можно постро-
построить его «симплектизацию» — симплектическое многообразие, чис-
число измерений которого на 1 больше. Взаимоотношения между
этими двумя многообразиями — контактным нечетномерным и

322 ДОБАВЛЕНИЕ 4
симплектическим четномерным — такие же, как между многооб-
многообразием контактных элементов с его контактной структурой и ко-
касательным расслоением с его симплектической структурой.
Д. Симплектизация контактного многообразия. Рассмотрим
произвольное контактное многообразие, т. е. многообразие нечет-
нечетной размерности N с невырожденным полем касательных гипер-
гиперплоскостей (четной размерности N — 1). Эти плоскости мы будем
называть контактными плоскостями. Каждая контактная пло-
плоскость касается контактного многообразия в одной точке. Эту
точку мы будем называть точкой контакта.
Определение. Контактной формой мы будем называть
всякую такую линейную форму на касательном пространстве
в точке контактного многообразия, что ее множеством нулей
является контактная плоскость.
Следует подчеркнуть, что контактная форма — не дифферен-
дифференциальная форма, а алгебраическая линейная форма на одном ка-
касательном пространстве.
Определение. Симплектизацией контактного многообра-
многообразия называется множество всех контактных форм на контактном
многообразии, снабженное структурой симплектического многооб-
многообразия, определенной ниже.
Заметим прежде всего, что множество всех контактных форм
на контактном многообразии имеет естественную структуру
гладкого многообразия четной размерности N + 1. А именно,
мы можем рассматривать множество всех контактных форм как
пространство расслоения над исходным контактным многообра-
многообразием. Проекция на базу — это отображение, сопоставляющее
контактной форме точку контакта.
Слоем этого расслоения является множество контактных форм
с общей точкой контакта. Все такие формы получаются друг из
друга умножением на отличное от нуля число (так как они за-
задают одну и ту же контактную плоскость). Таким образом, слой
нашего расслоения одномерен: это прямая без точки.
Заметим также, что на многообразии всех контактных форм
действует группа отличных от нуля вещественных чисел с опера-
операцией умножения. А именно, произведение контактной формы на
ненулевое число есть снова контактная форма. При этом группа
действует на нашем расслоении, оставляя каждый слой на месте
(при умножении формы на число точка контакта не меняется).
Замечание. До сих пор мы нигде не использовали невы-
невырожденность поля плоскостей. Невырожденность нужна лишь
для того, чтобы получающееся при симплектизации многообразие
было симплектическим.
Пример. Рассмотрим многообразие (размерности 2и — 1)
всех контактных элементов и-мерного гладкого многообразия. На
многообразии элементов есть поле гиперплоскостей (которые мы

КОНТАКТНЫЕ СТРУКТУРЫ
323
определили выше и назвали контактными). Следовательно, можно
симплектизовать многообразие контактных элементов.
В результате симплектизации получается 2и-мерное многооб-
многообразие. Это многообразие есть пространство кокасательного рас-
расслоения исходного и-мерного многообразия без нулевых векторов.
При этом действие мультипликативной группы вещественных чи-
чисел на слое сводится к умножению на числа векторов кокасатель-
кокасательного пространства.
На кокасательном расслоении есть замечательная 1-форма
«р dq». Аналогичная 1-форма имеется и на любом многообразии,
полученном симплектизацией из контактного многообразия.
Каноническая 1-ф орма на прострап-
стве-симплектизации.
Определение. Канонической 1-формой на пространстве-
симплектизации контактного многообразия называется диффе-
дифференциальная 1-форма а, значение ко-
которой на каждом векторе |, касатель-
касательном к пространству-симплектизации в
некоторой точке р (рис. 237), равно
значению на проекции вектора ? в ка-
касательную плоскость к контактному
многообразию той 1-формы на этой каса-
касательной плоскости, которой является
точка р:
а (I) = Р (я*!),
Рис. 237. Симплектизация кон-
контактного многообразия
где л — проекция пространства-симп-
пространства-симплектизации на контактное многообразие.
Теорема. Внешняя производная
канонической l-формы на пространст-
ве-симплектизации контактного многообразия является невырож-
невырожденной 2-формой.
Следствие. Лространство-симплектизация контактного
многообразия имеет симплектическую структуру, которая кано-
канонически (т. е. однозначно, без всякого произвола) определена кон-
контактной структурой исходного нечетномерного многообразия.
Доказательство. Ввиду локальности утверждения теоремы его
достаточно доказать в малой окрестности точки многообразия. В малой
окрестности точки на контактном многообразии поле контактных плоскостей
можно задать дифференциальной формой to на контактном многообразии.
Зафиксируем такую 1-форму to.
Тем самым мы представили часть пространства-симплектизации над рас-
рассматриваемой окрестностью точки контактного многообразия в виде прямого
произведения этой окрестности и прямой без точки.
А именно, паре (х, X), где х — точка контактного многообразия, а % —
отличное от нуля число, мы сопоставляем контактную форму, которую за-
задает дифференциальная 1-форма Xto в касательном пространстве в точке х.
Таким образом, в рассматриваемой части симплектизации определена
функция К, значения которой — отличные от нуля числа. Следует подчерк-

324 ДОБАВЛЕНИЕ 4
нуть, что X является лишь локальной координатой на симплектизованном
многообразии и что эта координата определена не канонически; она вависит
от выбора дифференциальной 1-формы со.
Каноническая 1-форма а в наших обозначениях записывается в виде
а = Хл*а
и не зависит от выбора со.
Внешняя производная 1-формы а имеет, следовательно, вид
da = dX Д я* со + Xn*da.
Докажем, что 2-форма da невырождена, т. е. что для любого вектора ?,
касательного к симплектизации, найдется такой вектор т), что da (g, tj) ф 0.
Выделим среди векторов, касательных к симплектизации, векторы сле-
следующих типов. Мы назовем вектор % вертикальным, если он касается слоя,
т. е. если я»| = 0. Мы назовем вектор | горизонтальным, если он касается
поверхности уровня функции X, т. е. если dX (|) = 0. Мы назовем вектор |
контактным, если его проекция на контактное многообразие лежит в кон-
контактной плоскости, т. е. если со (я»|) = 0 (иными словами, если а (|) = 0).
Вычислим значение формы da на паре векторов |, rj:
da (I, ч) = (dX Д я*со) A, ч) + (Xn*da) A, ц).
Предположим, что вектор | не контактный. Возьмем в качестве ц нену-
ненулевой вертикальный вектор, так что я»ч = 0. Тогда второе слагаемое равно
нулю, а первое равно
-dX (rj) со
и отлично от нуля, так как rj — ненулевой вертикальный вектор, а | не
контактный. Итак, если | не контактный вектор^ то мы нашли rj, для которо-
которого da (I, ч) =,ь 0.
Предположим, что вектор | контактный, невертикальный. Тогда возь-
возьмем в качестве ч любой контактный вектор. Теперь первое слагаемое целиком
обращается в 0, а второе' (и значит, вся сумма) сводится к Xda (я»|, я»ч )•
Поскольку вектор | не вертикальный, то вектор я„|, лежащий в кон-
контактной плоскости, отличен от нуля. Но 2-форма dco в контактной плоскости
невырождева (по определению контактной структуры). Значит, существует
такой контактный вектор ч. что da> (я,!, я»ч) Ф 0- Поскольку X ф 0, мы
нашли вектор ч* Для которого da (%, ч) Ф 0.
Наконец, если вектор | — вертикальный ненулевой, то в качестве ч
можно взять любой неконтактный вектор. Теорема доказана.
амечанив. Конструкции 1-формы а и 2-формы da про-
проходят для произвольного многообразия с полем гиперплоскостей
и не зависят от условий невырожденности. Однако 2-форма da
будет определять симплектическую структуру лишь в случае,
когда поле плоскостей было невырожденным.
Доказательство. Предположим, что поле вырождено, т. е. что
существует такой ненулевой вектор %' в плоскости поля, что da (?',ч') = 0
для всех векторов ч' эт°й плоскости. При таком %' величина dco (|',ч') как
функция от ч' является линейной формой, тождественно равной нулю на
плоскости поля. Следовательно, существует такое не зависящее от ч' число ц,
что
dco (Г, Ч') = Цсо W)
для всех векторов ч' касательного пространства.
Возьмем теперь в качестве 1 такой касательный вектор к симплектизо-
ванному многообразию, для которого я»| = %'. Такой вектор % определен
с точностью до прибавления вертикального слагаемого, и мы покажем, что

КОНТАКТНЫЕ СТРУКТУРЫ 325
при надлежащем выборе этого слагаемого будет
da (|, rj) = 0 для всех ц.
Действительно, первое слагаемое формулы для da равно dX (|) со (Jt»rj) (по-
(поскольку со (я»4) = 0). Второе слагаемое равно Ысо (яв|, я»т)) = кцы (п*г\).
Вертикальную составляющую вектора | выберем так, чтобы dk (|) = —Ьц.
Тогда вектор ? будет косоортогонален всем векторам т).
Итак, если da — симплектическая структура, то исходное поле г ипер-
плоскостен — контактная структура, и выделенное выше утверждение
доказано.
Следствие. Лоле контактных гиперплоскостей задает на
многообразии всех контактных элементов любого гладкого много-
многообразия контактную структуру.
Доказательство. Симплектизация 2и — 1-мерного
многообразия всех контактных элементов на и-мерном гладком
многообразии, построенная по полю 2и — 2-мерных контактных
плоскостей, есть по построению пространство кокасательного рас-
расслоения исходного и-мерного многообразия без нулевых кокаса-
тельных векторов. Каноническая 1-форма а на симплектизации
есть, согласно ее определению, та самая 1-форма на кокасатель-
ном расслоении, которую мы назвали «р dq» и которая лежит
в основе гамильтоновой механики (см. § 37). Ее производная da
есть, следовательно, форма «dp /\ dq», задающая обычную сим-
плектическую структуру фазового пространства. Стало быть,
форма da не вырождена. Значит, по предыдущему замечанию,
поле контактных гиперплоскостей не вырождено. Следствие
доказано.
Е. Контактные диффеоморфизмы в векторные поля.
Определение. Диффеоморфизм контактного многообра-
многообразия на себя называется контактным, если он сохраняет контакт-
контактную структуру, т. е. переводит каждую плоскость задающего
структуру поля гиперплоскостей в плоскость того же поля.
Пример. Рассмотрим 2и — 1-мерное многообразие контакт-
контактных элементов и-мерного гладкого многообразия с его обычной
контактной структурой. Каждому контактному элементу можно
приписать «положительную сторону», выбрав одну из половин,
на которые этот элемент делит касательное пространство к и-мер-
ному многообразию.
Контактный элемент с выбранной стороной мы будем называть
(трансверсалъно) ориентированным контактным элементом.
Все ориентированные контактные элементы на нашем и-мер-
ном многообразии образуют 2и — 1-мерное гладкое многообразие
с естественной контактной структурой (оно двулистно накры-
накрывает многообразие обычных неориентированных контактных эле-
элементов).
Предположим теперь, что на исходном n-мерном многообразии
дана риманова метрика. Тогда на многообразии ориентирован-

326 ДОБАВЛЕНИЕ 4
ных контактных элементов возникает «геодезический поток» *).
Преобразование за время t в этом потоке определяется так. Вы-
Выпустим из точки контакта контактного элемента геодезическую,
ортогональную ему и направленную в сторону, ориентирующую
элемент. В течение времени t будем двигать точку контакта вдоль
геодезической, оставляя элемент ортогональным геодезической.
Через время t получим новый ориентированный элемент. Мы опре-
определили геодезический поток ориентированных контактных эл -
ментов.
Теорема. Геодезический поток ориентированных кон-
контактных элементов состоит из контактных диффеоморфизмов.
Доказательство этой теоремы не приводится, так как она есть
не что иное, как сформулированный в новых терминах принцип
Гюйгенса (см. § 46).
Определение. Векторное поле на контактном много-
многообразии называется контактным, если оно является полем ско-
скоростей однопараметрической (локальной) группы контактных
диффеоморфизмов.
Т е о р е м а. Скобка Пуассона контактных векторных полей
является контактным векторным полем. Контактные векторные
поля образуют подалгебру в алгебре Ли всех гладких векторных
полей на контактном многообразии.
Доказательства непосредственно вытекают из определений.
Ж. Симплектизация контактных диффеоморфизмов и полей.
По каждому контактному диффеоморфизму контактного много-
многообразия каноническим образом строится симплектический диф-
диффеоморфизм его симплектизации.
Этот симплектический диффеоморфизм коммутирует с дейст-
действием мультипликативной группы вещественных чисел на симплек-
тизованном многообразии и определяется следующей конструк-
конструкцией.
Напомним, что точкой симплектизованного многообразия яв-
является контактная форма на исходном контактном многообразии.
Определение. Образом контактной формы р с точкой
контакта х под действием контактного диффеоморфизма / кон-
контактного многообразия на себя называется форма
f\P = (//UrV
Попросту говоря, мы переносим форму р из касательного
пространства в точке х в касательное пространство в точке / (х)
при помощи диффеоморфизма / (производная которого в точке х
устанавливает изоморфизм между этими двумя касательными
пространствами).
Форма f\p контактная, ибо диффеоморфизм / контактный.
*) Строго говоря, здесь нужно потребовать, чтобы риманово многообразие
было полным, т. е. геодезические продолжались неограниченно.

КОНТАКТНЫЕ СТРУКТУРЫ 327
Теорема. Определенное выше отображение /j симплектиза-
ции контактного многообразия в себя является симплектическим
диффеоморфизмом, коммутирующим с действием мультиплика-
мультипликативной группы вещественных чисел и сохраняющим каноническую
i-форму на симплектизации.
Доказательство. Утверждение теоремы вытекает из того, что
каноническая 1-форма, симплектическая 2-форма и действие группы вещест-
вещественных чисел определены самой контактной структурой (при их построении
не использовались координаты или иные неинвариантные средства), а диф-
диффеоморфизм / сохраняет контактную структуру. Из этого следует, что /
переводит в себя все то, что инвариантно построено по контактной структуре,
в частности 1-форму а, ее производную da и действие группы, ч. т. д.
Теорема. Всякий симплектический диффеоморфизм симп-
симплектизации контактного многообразия, коммутирующий с дейст-
действием мультипликативной группы: 1) проектируется на исходное
контактное многообразие в виде контактного диффеоморфизма;
2) сохраняет каноническую 1-форму а.
Доказательство. Всякий диффеоморфизм, коммутирующий
с действием мультипликативной группы, проектируется в некоторый диффео-
диффеоморфизм контактного многообразия. Чтобы доказать, что этот диффеомор-
диффеоморфизм контактный, достаточно доказать второе утверждение теоремы (так как
в контактную плоскость проектируются те и только те векторы |, для кото-
которых а (?) = 0).
Для доказательства второго утверждения выразим интеграл формы а
по любому пути у через симплектическую структуру da:
\ а = lim \ \ da,
У
где 2-цепь а (Е) получена из у умножением на всевозможные числа отрезка
[е, 1]. В границу 2-цепи о входят, кроме у, два вертикальных отрезка и
путь — еу. Интегралы формы а по вертикальным отрезкам равны нулю,
а интеграл по еу стремится к нулю вместе с е.
Теперь из инвариантности 2-формы da и коммутирования нашего
феоморфизма F с умножением на числа следует, что для любого пути у
Fy у
и, значит, диффеоморфизм F сохраняет 1-форму а, ч. т. д.
Определение. Симплектизация контактного векторного
поля определяется следующей конструкцией. Рассматриваем поле
как поле скоростей однопараметрической группы контактных
диффеоморфизмов. Симплектизируем диффеоморфизмы. Полу-
Получаем однопараметрическую группу симплектических диффеомор-
диффеоморфизмов. Рассматриваем поле скоростей этой группы. Оно и назы-
называется симплектизацией исходного контактного поля.
Теорема. Симплектизация контактного векторного поля
есть гамильтоново векторное поле. Гамильтониан можно выбрать
однородным первой степени относительно действия мулътипли-

328 ДОБАВЛЕНИЕ 4
катиеной группы вещественных чисел:
Н {he) = %Н (х).
Обратно, всякое гамильтоново поле на симплектизованном кон-
контактном многообразии, имеющее однородный' степени 1 гамиль-
гамильтониан, проектируется на исходное контактное многообразие
е виде контактного векторного поля.
Доказательство. Гамильтоновость симплектизованно-
го контактного поля следует из симплектичности симплектизации
контактных диффеоморфизмов. Однородность приращений гамиль-
гамильтониана следует из однородности симплектизованных диффео-
диффеоморфизмов (из коммутирования с умножением на Я,). Таким об-
образом, первое утверждение теоремы вытекает из теоремы о симп-
симплектизации контактных диффеоморфизмов.
Вторая часть вытекает таким же образом из теоремы об одно-
однородных симплектических диффеоморфизмах, и теорема доказана.
Следствие. Симплектизация векторных полей является
изоморфным отображением алгебры Ли контактных векторных
полей на алгебру Ли всех локально гамильтоновых векторных
полей с однородными гамильтонианами степени 1.
Доказательство очевидно.
3. Теорема Дарбу для контактных структур. Теорема Дарбу —
это теорема локальной единственности контактной структуры.
Ее можно сформулировать в любой из следующих трех форм.
Теорема. Все контактные многообразия одинаковой раз-
размерности локально контактно диффеоморфны (т. е. существует
диффеоморфизм достаточно малой окрестности любой точки одного
контактного многообразия на окрестность любой точки другого,
переводящий отмеченную точку первой окрестности в отмечен-
отмеченную точку второй и поле плоскостей в первой окрестности в поле
плоскостей второй).
Теорема. Всякое контактное многообразие размерности
2т — 1 локально контактно диффеоморфно многообразию кон-
контактных элементов т-мерного пространства.
Теорема. Всякая дифференциальная l-форма, задающая на
многообразии размерности 2п + 1 невырожденное поле гиперплос-
гиперплоскостей, записываете я в некоторой локальной системе координат
в «нормальном виде»
to = х dy + dz,
где х = (агх, . . ., хп), у = (г/15 . . ., уп) и z — локальные коорди-
координаты.
Ясно, что первые две теоремы вытекают из третьей. Ее же
мы выведем из аналогичной теоремы Дарбу о нормальном виде
2-форм, задающих симплектические структуры (см. § 43).
Доказательство теоремы Дарбу. Симплектизуем ваше
многообразие. На полученном 2п -\- 2-мерном симплектическом многообразии

КОНТАКТНЫЕ СТРУКТУРЫ 329
определены каноническая 1-форма а, невырожденная 2-форма da, проекция я
на исходное контактное многообразие и вертикальное направление в каждой
точке.
Заданная на контактном многообразии дифференциальная 1-форма со
определяет в каждой точке контактную форму. Все эти контактные формы
образуют в симплектическом многообразии 2п -f- 1-мерное подмногообразие.
Проекция я диффеоморфно отображает это подмногообразие на исходное
контактное многообразие, а вертикали пересекают это подмногообразие под
ненулевым углом.
Рассмотрим точку на построенной в симплектическом многообразии
поверхности, лежащую над интересующей нас точкой контактного многооб-
многообразия. В симплектическом многообразии можно выбрать вблизи этой точки
локальную систему координат так, чтобы
da = dp0 Д dq0 + . . . + dpn Д dqn
и чтобы при этом координатная поверхность рв = О совпадала с нашим
2п -\- 1-мерным многообразием (см. § 43, где при доказательстве симплекти-
ческой теоремы Дарбу первая координата выбирается произвольно).
Заметим теперь, что 1-форма pBdq0 -(-...+ pndqn имеет производной
da. Значит, локально
а = podqB + . . . + pndqn + dw,
тде w — некоторая функция, которую можно считать равной нулю в начале-
координат. В частности, на поверхности р0 = 0 форма а принимает вид
а |ро=0 = ptdqt + . . . + pndqn + dw.
Проекция я; позволяет перенести координаты plt . , ., рп; qB; q17 . . ., qn.
и функцию w на контактное многообразие. Точнее, мы определим функции
х, у, z формулами
Ч (лА) = рг (A), yi (пА) = qi (A), z (пА) = w (A),
где А — точка на поверхности рв = 0.
Тогда мы получаем
ш = xdy + dz,
и остается лишь проверить, что функции (хг, . . ., #„; уг, . . ., i/n; z) обра-
образуют координатную систему. Для этого достаточно проверить, что отлична
от нуля частная производная функции w no qB. Иными словами, нужно про-
проверить, что 1-форма а на векторе координатного направления дв отлична от
нуля. Последнее эквивалентно отличию от нуля 2-формы da на паре векторов:
координатном направления дв и вертикальном.
Но вектор координатного направления qB косоортогонаяен всем векто-
векторам координатной плоскости р0 = 0. Если бы он был вдобавок косоортого-
нален и вертикальному вектору, то он был бы косоортогонален всем векторам
вообще, вопреки невырожденности формы da. Итак, dw/dqB =f= 0, и теорема
доказана.
И. Контактные гамильтонианы. Предположим, что контактная
структура контактного многообразия задается дифференциальной
1-формой to, и что эта форма фиксирована.
Определение, (л-еложением контактного многообразия
в свою симплектизацию называется отображение, сопоставляю-
сопоставляющее точке контактного многообразия сужение формы со на ка-
касательную плоскость в этой точке.
Определение. Контактной функцией Гамильтона кон-
контактного векторного поля на контактном многообразии с фикси-

330 ДОБАВЛЕНИЕ 4
рованной 1-формой со называется функция К на контактном много-
многообразии, значение которой в каждой точке равно значению одно-
однородного гамильтониана Н симплектизации поля в образе данной
точки при со-вложении:
К (А) = Н (со Ц).
Теорема. Контактная функция Гамильтона К контакт-
контактного векторного поля X на контактном многообразии с выбранной
1-формой со равна значению формы со на этом контактном поле:
К = со (X).
Доказательство. Воспользуемся выражением для приращения
обычной функции Гамильтона вдоль пути через векторное поле и контактную
структуру (§ 48, В).
Для этого проведем через ту точку В в симплектизации, в которой мы
хотим вычислить функцию Гамильтона, вертикальный отрезок {ХВ}, 0 < >. ^ 1.
Сдвиги этого отрезка за малое время т под действием симплектизации потока,
заданного нашим полем X, заполняют некоторую двумерную полоску а (т).
Значение гамильтониана в точке В равно пределу
Н (В) = lira — [ [ da,
Х-Ч) 1 J J
О A)
так как Н (KB) —> 0 при X —> 0. Но интеграл формы da по полоске равен ин-
интегралу 1-формы а по краю, образованному траекторией точки В (остальные
части границы дают нулевые интегралы). Поэтому двойной интеграл равен
просто интегралу 1-формы а по отрезку траектории, а предел — значению
1-формы а на векторе скорости Y симплектизованного поля. Стало быть,
К (пВ) = Н (В) = а (У) = <о (ЛГ), что и требовалось доказать.
К. Вычислительные формулы. Предположим теперь, что мы
пользуемся координатами теоремы Дарбу, в которых форма со
имеет нормальный вид
со = х dy + dz, x = (хи . . ., хп), у = (уг, . . ., уп).
Задача. Найти компоненты контактного поля с данной
контактной функцией Гамильтона К = К (х, у, z).
Ответ. Уравнения контактного потока имеют вид
х = — Kv + xKz,
z = к — хкх:\
Решение. Точку симплектизации можно задать 2л + 2 числами х^
Уг, z, К, где (х, у, z) — координаты точки контактного многообразия, а Я —
число, на которое надо умножить <о, чтобы получить данную точку симплек-
симплектизованного пространства.
В этих координатах a = Kx dy-\-K dz. Поэтому в системе координат р, д,
где
Р = (Р. Ро). Р = Ь;, рв = X,
9 = (?. ?о). ? = У. ?о = z.

КОНТАКТНЫЕ СТРУКТУРЫ 331
форма а принимает стандартный вид:
а = р dq, da = dp Д dq.
Действие Т^ мультипликативной группы свелось теперь к умножению р на
число:
Гц (Р, д) = (ЦР, д).
Контактный гамильтониан К выражается через обычный гамильтониан
Я = Я (р, д, р0, 50) по формуле
К(х, у, *) = Н(х, у, 1, «).
Функция /Г однородна первой степени по р. Поэтому частные производные К
в точке (я, у, z) связаны с производными Я в точке (р = х, р0 = 1, g = у,
50 = z) соотношениями
Hq ~ Ку, Hq^ = Kz,
Уравнения Гамильтона с функцией Гамильтона Н имеют поэтому в рассмат-
рассматриваемой точке вид
а + А = — Ку, к = — кг,
у = Кх, z = К~хКх,
откуда и получается приведенный выше ответ.
Задача. Найти контактный гамильтониан скобки Пуассона
контактных полей с контактными гамильтонианами К и К'.
Ответ. (К, К') + КгЭК' — К'гЭК, где скобкой обозначена
скобка Пуассона до переменным хну, а Э — оператор Эйлера,
9F = F — xFx.
Решение. В обозначениях решения предыдущей задачи требуется
выразить обычную скобку Пуассона однородных гамильтонианов Н, Н' в точке
(р = х, рв = 1, д — у, дв = z) через контактные гамильтонианы К, К'. Имеем
(Я, в') = HqH-p-HpH'q = HqH'p -нрн'д +ндон'ро-нрондо.
Подставляя значения производных из решения предыдущей задачи, находим
в рассматриваемой точке
(Я, Я') = КуК'х - КхК!у + Kz {К' - хК'х) - K'z (К - хКх).
Л. Лежандровы многообразия. Лагранжевым подмногообра-
подмногообразиям симплектического фазового пространства в контактном слу-
случае соответствует интересный класс многообразий, которые можно
назвать лежандроеыми, так как они тесно связаны с преобразо-
преобразованием Лежандра.
Определение. Лежандроеым подмногообразием контакт-
контактного 2п + 1-мерного многообразия называется n-мерное интег-
интегральное многообразие поля контактных плоскостей.
Иными словами, это интегральные многообразия наивысшей
размерности, которая возможна для интегральных многообразий
невырожденного поля плоскостей.

332 ДОБАВЛЕНИЕ 4
Пример 1. Множество всех контактных элементов, касаю-
касающихся подмногообразия любой размерности в m-мерном много-
многообразии, является лежандровым т — 1-мерным подмногообра-
подмногообразием 2т — 1-мерного контактного многообразия всех вообще
контактных элементов.
П р и м е р 2. Множество всех касательных плоскостей к гра-
графику функции / = ф (х) в п + 1-мерном евклидовом пространстве
с координатами (xlt . . ., хп; /) является лежандровым подмного-
подмногообразием в 2л + 1-мерном пространстве всех невертикальных
гиперплоскостей в пространстве графика (контактная структура
задается 1-формой
to = pxdxx + . . . + pndxn — df,
плоскость с координатами (р, х, f) проходит через точку с коор-
координатами (х, f) параллельно плоскости / = ргхг + . . . + рпхп).
Преобразование Лежандра описывается в этих терминах сле-
следующим образом.
Рассмотрим еще второе 2и + 1-мерное контактное простран-
пространство с координатами (Р, X, F) и контактной структурой, заданной
формой
Q = Р dX - dF.
Инволюцией Лежандра называется отображение, переводящее
точку первого пространства с координатами (р, х, f) в точку
второго с координатами
Р = х, X = р, F = px — f.
Инволюция Лежандра, как легко сосчитать, переводит первую
контактную структуру во вторую. Очевидна
Теорема. Диффеоморфизм одного контактного многообра-
многообразия на другое, переводящий контактные плоскости в контактные,
переводит каждое лежандрово многообразие в лежандрово.
В частности, под действием инволюции Лежандра лежандрово
подмногообразие касательных к графику функции плоскостей
переходит в новое лежандрово многообразие. Это новое много-
многообразие называется преобразованием Лежандра исходного.
Проекция нового многообразия на пространство с координа-
координатами X, F (параллельно Р-направлению), вообще говоря, не
является гладким многообразием, но имеет особенности. Эта
проекция называется преобразованием Лежандра графика функ-
функции ф.
Если функция ф выпукла, то проекция сама является графи-
графиком функции F = Ф (X). В этом случае функция Ф называется
преобразованием Лежандра функции ф.
В качестве другого примера рассмотрим движение ориенти-
ориентированных контактных элементов под действием геодезического
потока на римановом многообразии. Возьмем в качестве «началь-

КОНТАКТНЫЕ СТРУКТУРЫ 333
ного волнового фронта» какое-нибудь гладкое подмногообразие
нашего риманова многообразия (размерность подмногообразия
может быть любой). Все ориентированные контактные элементы,
касающиеся этого подмногообразия, образуют лежандрово много-
многообразие в пространстве вообще всех контактных элементов. Мы
получаем из предыдущей теоремы
Следствие. Семейство всех касательных к волновому фрон-
фронту элементов преобразуется под действием геодезического потока
за время t снова в лежандрово многообразие пространства всех
контактных элементов.
Следует заметить, что это новое лежандрово многообразие
может не быть семейством всех элементов, касательных к какому-
либо гладкому многообразию, так как на волновом фронте могут
возникать особенности.
Возникающие таким образом лежандровы особенности можно
описать аналогично лагранжевым (см. добавление 12). Лежанд-
Лежандрово расслоение в 2п + 1-мерном контактном многообразии —
это расслоение, все слои которого — лежандровы гс-мерные много-
многообразия. Лежандровы особенности — это особенности проекти-
проектирования /г-мерных лежандровых подмногообразий 2п + 1-мерного
контактного многообразия на п + 1-мерную базу лежандрова
расслоения.
Рассмотрим пространство R2n+i с контактной структурой, за-
заданной формой а = х dy + dz, где х — (х1, . . ., хп), у = {уг, . . .
. . ., уп). Проекция (х, у, z) •-*¦ (у, z) задает лежандрово расслое-
расслоение.
Эквивалентностью лежандровых расслоений называется диф-
диффеоморфизм пространств расслоений, переводящий контактную
структуру и слои первого расслоения в контактную структуру
и слои второго. Можно доказать, что всякое лежандрово расслое-
расслоение эквивалентно только что описанному специальному в окрест-
окрестности каждой точки пространства расслоения.
Контактная структура пространства расслоения задает на
слоях локальную структуру проективного пространства. Лежанд-
Лежандровы эквивалентности сохраняют эту структуру, т. е. задают
локально проективные преобразования слоев.
Следующая теорема позволяет локально описывать лежандро-
лежандровы подмногообразия и отображения при помощи производящих
функций.
Теорема. Для любого разбиения I + / множества индексов
A, . . ., п) на два непересекающихся подмножества и для любой
функции S (xi, yj) от п переменных xt, i {= / и yj, j ЕЕ /, формулы
as as c as
у ^ zsX
задают лежандрово подмногообразие в R2rv+1. Обратно, каждое
лежандрово подмногообразие в R2n+i в окрестности каждой своей

334 ДОБАВЛЕНИЕ 4
точки задается указанными формулами хотя бы при одном из 2п
возможных выборов подмножества I.
Доказательство основано на том, что на лежандровом много-
многообразии dz + х dy = 0, поэтому d (z + xiyi) = yidxi — xjdyj.
Подставим в формулы предыдущей теоремы в качестве S функ-
функции из списка простейших лагранжевых особенностей, приведен-
приведенного в добавлении 12. Получатся лежандровы особенности, сохра-
сохраняющиеся при малых деформациях лежандрова отображения
(х, у, z) *-*¦ (у, z) (т. е. переходящие в эквивалентные при малой
деформации функции S). Всякое лежандрово отображение при
п < 6 малым шевелением превращается в такое, у которого все
особенности локально эквивалентны особенностям полученного
списка Лк A < к < 6), Як D < к < 6), Е6.
В частности, мы получаем список особенностей волновых
фронтов общего положения в пространствах менее 7 измерений.
В обычном трехмерном пространстве этот список таков:
Ах: S = ±х\, А2: S = ±х\; А3 : S = ±х\ + х\у2,
где / = {1}, / = {2}, п = 2.
Проекции указанных здесь лежандровых многообразий на
базу лежандрова расслоения (т. е. на пространство с координа-
координатами уи у2, z) имеют соответственно простую точку в случае Alf
ребро возврата в случае А2 и ласточкин хвост (см. рис. 246) в слу-
случае А3.
Таким образом, волновой фронт общего положения в трехмер-
трехмерном пространстве имеет только ребра возврата и точки типа «лас-
«ласточкин хвост». При движении фронта в отдельные моменты вре-
времени наблюдаются еще перестройки трех типов Л4, Dx, ZL (см.
добавление 12, где нарисованы соответствующие каустики, за-
заметаемые особенностями фронта при его движении).
Задача 1. Отложим на каждой внутренней нормали к эллипсу на
плоскости отрезок длины t. Нарисовать полученную кривую и исследовать
ее особенности и их перестройки при изменении t.
Задача 2. Проделать то же для трехосного эллипсоида в трехмерном
пространстве.
М. Контактизация. Наряду с симплектизацией контактных
многообразий существует контактизация симплектических, имею-
имеющих гомологичную нулю симплектическую структуру.
Контактизация U2Tl+1 симплектического многообразия (М2п, со2)
строится как пространство расслоения со слоем R над М2п.
Пусть U — достаточно малая окрестность точки х из М,
в которой существует система канонических координат р, q,
так что со = dp Д dq. Рассмотрим прямое произведение U X R
с координатами р, q, z.
Пусть V X R — такое же произведение, построенное по дру-
другой (или по той же) окрестности F, с координатами/*, Q,Z; dP /\
/\ dQ = со. Если окрестности U и V на М пересекаются, то мы

КОНТАКТНЫЕ СТРУКТУРЫ 335
отождествим слои над точками пересечения в обоих произведениях
так, чтобы форма dz + p dq = dZ + P dQ = а была определена
в целом (это возможно, так как Р dQ — р dq — полный диффе-
дифференциал на U П V).
Легко проверить, что в результате склеивания возникает рас-
расслоение Е2п+1 над М2п, и что форма а задает на Е контактную
структуру. Многообразие Е называется контактизацией симплек-
тического многообразия М. Если класс гомологии формы со2
целочисленный, то можно определить контактизацию со слоем S1.
Н. Интегрирование уравнений в частных производных пер-
первого порядка. Пусть М2п+1 — контактное многообразие, Ein —
гиперповерхность в М2п+1. Контактная структура М определяет
на Е некоторую геометрическую структуру, в частности — поле
так называемых характеристических направлений. Анализ этой
геометрической структуры позволяет свести интегрирование общих
нелинейных уравнений с частными производными первого порядка
к интегрированию системы обыкновенных дифференциальных
уравнений.
Мы предположим, что многообразие Е2п трансверсально кон-
контактным плоскостям во всех своих точках. В таком случае пересече-
пересечение касательной плоскости к Е2п в каждой точке с контактной плос-
плоскостью имеет размерность 2/г — 1, так что на Е2П возникает поле
гиперплоскостей. Более того, контактная структура М2п+1 опре-
определяет на Е2п поле прямых, лежащих в указанных 2и — 1 -мерных
плоскостях.
Действительно, пусть а — 1-форма на М2п+1, локально задаю-
задающая контактную структуру, пусть со = da, и пусть R2n — кон-
контактная плоскость в точке х из Е2п. Пусть Ф = 0 — локальное
уравнение Е2п (так что d<$> в х не 0).
Сужение d<?> на R2n задает ненулевую линейную форму в R2n.
2-форма со задает в R2™ структуру линейного симплектического
пространства, и стало быть, изоморфизм этого пространства с со-
сопряженным к нему. Ненулевой 1-форме йФ | R2n соответствует
поэтому ненулевой вектор | из R2n, так что йФ (•) = со (|, •).
Вектор Ь, называется характеристическим вектором многообразия
Е2п в точке х. Характеристический вектор 5 лежит в пересечении
R2n с касательной к Е2п плоскостью, так как йФ ( ) = 0.
Вектор | определен многообразием Е2п и контактной структурой
на М не однозначно, а с точностью до умножения на отличное
от 0 число. Действительно, как 2-форма со на R2", так и 1-форма
d<?> на R2n определены с точностью до умножения на отличное
от 0 число.
Направления характеристических векторов (т. е. содержащие
их прямые) определены контактной структурой в каждой точке
многообразия Е однозначно.
Таким образом, на гиперповерхности Е в контактном много-
многообразии М возникает поле характеристических направлений.

336 ДОБАВЛЕНИЕ 4
Интегральные кривые этого воля направлений называются
характеристиками.
Пусть теперь дано п — 1-мерное подмногообразие / нашей
гиперповерхности Е2п, которое является интегральным для кон-
контактного поля (так что касательная плоскость к/в каждой точке
принадлежит контактной плоскости).
Теорема. Если в точке х из I характеристика на EZn не
касается I, то в окрестности точки х характеристики на Е2п,
проходящие через точки I, образуют лежандрово подмногообразие
Ьп в М2п+1.
Доказательство. Пусть | — векторное поле на Ezn,
образованное характеристическими векторами. По формуле гомо-
топии (см. стр. 173), на ?2п имеем L^tx = di^a -j- i^da.
Ho i|<x = 0, так как характеристический вектор принадлежит
контактной плоскости. Следовательно, на Е2п имеем L|a = i|co.
Но 1-форма i|to равна нулю на пересечении касательной плоскости
к Е2п с контактной плоскостью (ибо на контактной плоскости
i|to = <1Ф, а на касательной ёФ = 0). Поэтому на касательной
к ?2п плоскости гцо = ca. Итак, на гиперповерхности Е
L^a = ca
(где с — гладкая в окрестности точки х функция).
Пусть теперь {g1} — фазовый (локальный)-поток поля | и ц —
вектор, касательный к Eitl. Положим tj (t) = g^Tj и у (t) =
= a (r\ (t)). Тогда функция у удовлетворяет линейному диффе-
дифференциальному уравнению
dyldt = c(t)y (t).
Если tj @) касается /, то у @) = a (tj @)) = 0. Значит, у (t)=
= a (t] (t)) = 0, т. е. tj (t) при всех t лежит в контактной плоскос-
плоскости. Следовательно, g*I — интегральное многообразие контактного
поля. Поэтому образованное всеми {#'/} при малых t многообра-
многообразие лежандрово. Теорема доказана.
Пример. Рассмотрим R2n+i с координатами хг, . . ., Хп\
рг, . . ., рп; и и с контактной структурой, заданной 1-формой
a = du — р dx. Функция Ф (х, р, и) задает дифференциальное
уравнение Ф (х, ди/дх, и) = 0 и подмногообразие Е = Ф @)
в пространстве R2n+i (называемом пространством 1-струй функ-
функций в Rn).
Начальным условием для уравнения Ф = 0 называется задание
значений / функции и на гиперповерхности Г размерности п — 1
в n-мерном пространстве с координатами хг, . . ., хп.
Начальное условие определяет производные и по п — 1 неза-
независимому направлению в каждой точке Г. Производную по на-
направлению, трансверсальному к Г, можно, вообще говоря, найти
из уравнения; если при этом выполняются условия теоремы о не-

ДИНАМИЧЕСКИЕ СИСТЕМЫ С СИММЕТРИЕЙ 337
явной функции, то начальное условие называется нехарактерис-
нехарактеристическим.
Нехарактеристическое начальное условие задает интегральное
п — 1-мерное подмногообразие / формы а (являющееся графиком
отображения и = f (х), р = р (х), х ?Е Г). Характеристики на ЕТ
пересекающие /, образуют лежандрово подмногообразие в R2ri+1,
являющееся графиком отображения и = и (х), р = ди/дх. Полу-
Полученная функция и (х) — решение уравнения Ф (х, ди/дх, и) = О
с начальным условием и |г = /.
Заметим, что для нахождения функции и нужно лишь решить
систему 2п обыкновенных дифференциальных уравнений первого
порядка для характеристик на ? и проделать ряд «алгебраиче-
«алгебраических» операций.
Добавление 5
ДИНАМИЧЕСКИЕ СИСТЕМЫ С СИММЕТРИЕЙ
По теореме Э. Нётер однопараметрические группы симметрии
динамической системы определяют первые интегралы. Если сис-
система выдерживает более широкую группу симметрии, то возникает
несколько интегралов.
Совместные многообразия уровня этих первых интегралов
в фазовом пространстве являются инвариантными многообразия-
многообразиями фазового потока. Подгруппа группы симметрии, оставляющая
такое инвариантное многообразие на месте, действует на нем.
Во многих случаях можно рассматривать фактор-многообразие
инвариантного многообразия по зтой подгруппе. Это фактор-
многообразие называется приведенным фазовым пространством.
Приведенное фазовое пространство имеет естественную симплек-
тическую структуру. Исходная гамильтонова динамическая сис-
система задает на нем снова гамильтонову систему.
Разбиение фазового пространства на совместные многообразия
уровня первых интегралов имеет, вообще говоря, особенности.
Примером является разбиение фазовой плоскости на линии уров-
уровня энергии.
В настоящем добавлении кратко обсуждаются динамические
системы в приведенных фазовых пространствах и их связь с ин-
инвариантными многообразиями в исходном фазовом пространстве.
Все эти вопросы исследовались еще Якоби и Пуанкаре («исклю-
(«исключение узла» в задаче многих тел, «понижение порядка» в системах
с симметрией, «перманентные вращения» твердого тела и т. п.).
Подробное изложение в современной терминологии имеется в ста-
статьях: С м е й л С. Топология и механика // УМН.— 1972.— Т. 27,
№ 2.— С. 78—133 (Inventiones Mathematicae.— 1970.— V. 10,
№ 4.— P. 305—331; 1970.— V. 11, № 1.— P. 45—64); Марс-
дев Дж., Вейнстейн А. Редукция симплектических много-

338 ДОБАВЛЕНИЕ 5
образий с симметриями (Rep. Math. Ehys.— 1974.— V. 5.—
P. 121—130).
А. Пуассоновские действия групп Ли. Рассмотрим симплекти-
симплектическое многообразие (М2п, to2), и пусть группа Ли G действует
на нем как группа симплектических диффеоморфизмов. Каждая
однопараметрическая подгруппа группы G действует тогда как
локально-гамильтонов фазовый поток на М. Во многих важных
случаях эти потоки имеют однозначные функции Гамильтона.
Пример. Пусть V — гладкое многообразие, G — какая-либо группа
Ли его диффеоморфизмов. Каждый диффеоморфизм переводит 1-формы на V
в 1-формы. Поэтому группа G действует на кокасательном расслоении М =
= T*V.
Напомню, что на кокасательном расслоении всегда имеется каноническая
1-форма а («форма pdq»), и естественная симплектическая структура а> = da.
Действие группы G на М симплектическое, так как оно сохраняет 1-форму а,
а значит, и 2-форму da.
Однопараметрическая подгруппа {g1} группы G задает на М фазовый
поток. Легко проверить, что этот фазовый поток имеет однозначную функцию
Гамильтона. А именно, функция Гамильтона Н дается формулой теоремы
Нётер
/7 (г) = а (II е'А, где хе=М.
\ at |t==0 /
Теперь мы предположим, что задано такое симплектическое
действие группы Ли G на связном симплектическом многообра-
многообразии М, что каждому элементу а алгебры Ли группы G соответ-
соответствует однопараметрическая группа симплектических диффеомор-
диффеоморфизмов с однозначным гамильтонианом На. Эти гамильтонианы
определены с точностью до постоянных слагаемых, которые можно
выбрать так, чтобы зависимость На от а была линейной. Для
этого достаточно как угодно выбрать константы в функциях
Гамильтона для каких-нибудь базисных векторов алгебры Ли
группы G и затем определить функцию Гамильтона для любого
элемента алгебры как линейную комбинацию базисных.
Итак, по симплектическому действию труппы Ли G с одно-
однозначными на М гамильтонианами можно построить линейное
отображение алгебры Ли группы G в алгебру Ли функций Гамиль-
Гамильтона на М. При этом коммутатору двух элементов алгебры Ли
сопоставляется функция Н[Л, щ, равная скобке Пуассона (На, Нъ)
или же отличающаяся от этой скобки Пуассона на постоянную:
Замечание. Появление константы С в этой формуле является след-
следствием интересного явления: существования двумерного класса когомологий
алгебры Ли (глобально) гамильтоновых полей.
Величина С (а, Ь) является билинейной кососимметрической функцией
на алгебре Ли. Из тождества Якоби вытекает, что
С ([а, Ь], с)+С ([Ь, с], а) + С ([с, а], Ъ) = 0.
Билинейная кососимметрическая функция на алгебре Ли с таким свойством
называется двумерным коциклом алгебры Ли.

ДИНАМИЧЕСКИЕ СИСТЕМЫ С СИММЕТРИЕЙ 339
Если выбрать константы в функциях Гамильтона по-другому, то коцикл С
заменится на С, где
С {а, Ь) = С (а, Ь) + р ([а, Ь])
и где р — линейная функция на алгебре Ли.
Такой коцикл С называется когомологичным коциклу С.
Класс когомологичных друг другу коциклов называется классом кого-
мологий алгебры Ли.
Итак, симплектическое действие группы G, при котором существуют од-
однозначные гамильтонианы, задает двумерный класс когомологий алгебры Ли
группы G. Этот класс когомологий измеряет отклонение действия от такого,
при котором функцию Гамильтона коммутатора можно выбрать равной скобке
Пуассона функций Гамильтона.
Определение. Действие связной группы Ли на симплек-
тическом многообразии называется пуассоновским, если функции
Гамильтона для однопараметрических групп однозначны и выбраны
так, что функция Гамильтона линейно зависит от элемента
алгебры Ли и функция Гамильтона коммутатора равна скобке
Пуассона функций Гамильтона:
Н[а, Ь] = (На, Нь).
Иными сливами, пусссоновское действие группы задает гомомор-
гомоморфизм алгебры Ли этой группы в алгебру Ли функций Гамильтона.
Пример. Пусть V — гладкое многообразие, G — некоторая группа Ли,
действующая на V как группа диффеоморфизмов. Пусть М — T*V — кока-
сательное расслоение многообразия V с обычной симплектической структу-
структурой ш = da. Функции Гамильтона однопараметрических групп определим
как указано выше:
(
\dt
g*x\, ieW. A)
Теорема. Построенное действие пуассоновское.
Доказательство. По определению 1-формы а функции Гамиль-
Гамильтона На линейные однородные «по импульсам» (т. е. на каждом кокасательном
пространстве). Следовательно, и их скобки Пуассона линейны и однородны.
Итак, функция
Н1а, 6] ~~ (Яа> Нь)
линейна и однородна по импульсам. Будучи константой, она рьяна нулю,
что и требовалось доказать.
Аналогично проверяется, что симплектизация всякого контактного дей-
действия является пуассоновским действием.
Пример. Пусть V — трехмерное евклидово пространство, а G — шести-
шестимерная группа его движений. Базис алгебры Ли образуют шесть однопара-
однопараметрических групп: сдвиги со скоростью 1 вдоль координатных осей qu g2, q3
и вращения с угловой скоростью 1 вокруг этих осей. Соответствующие функ-
функции Гамильтона, согласно формуле A), равны (в обычных обозначениях)
Pi, P2. Pa, Mt, М2, М9, где Мх = q2p3 — q3p2 и т. д. Доказанная теорема оз-
означает, что попарные, скобки Пуассона этих шести функций равны функциям
Гамильтона коммутаторов соответствующих однопараметрических групп.
Пуассоновское действие группы G на симплектическом много-
многообразии М определяет отображение многообразия М в дуальное

340 ДОБАВЛЕНИЕ 5
пространство алгебры Ли группы
Р :М-+д*.
А именно, зафиксируем точку а; из Ми рассмотрим функцию
на алгебре Ли, сопоставляющую каждому элементу а алгебры Ли
значение гамильтониана На в фиксированной точке х:
Рх (я) = На (х).
Эта линейная функция рх на алгебре Ли и является тем элементом
дуального к алгебре пространства, который сопоставляется точ-
точке х:
Р (х) = рх.
Мы будем называть отображение Р моментом, следуя предло-
предложению Сурио. Заметим, что значение момента — всегда вектор
линейного пространства q*.
Пример. Пусть V — гладкое многообразие, G — группа Ли, дейст-
действующая на V как группа диффеоморфизмов, М = T*V — кокасательное рас-
расслоение, На — функция Гамильтона пуассоновского действия G на М, по-
построенная выше (см. A)).
Тогда отображение «момент» Р: М —* д* может быть описано следующим
образом. Рассмотрим отображение Ф: G —» М, заданное действием всех эле-
элементов группы G на фиксированную точку х из М (так что Ф (g) = gx). Ка-
Каноническая 1-форма а на М индуцирует на G 1-форму Ф*а. Ее сужение на
касательное пространство к G в единице есть линейная форма на алгебре Ли.
Итак, каждой точке х из М мы сопоставили линейную форму на алгебре
Ли. Легко проверить, что полученное отображение в есть момент рассматри-
рассматриваемого пуассоновского действия.
В частности, если V — евклидово трехмерное пространство, a G — группа
его вращений вокруг точки О, то значения момента — это обычные векторы
кинетического момента; если G — группа вращений вокруг оси, то значения
момента суть кинетические моменты относительно этой оси; если G — группа
параллельных переносов, то значения момента — это векторы импульсов.
Теорема. Пуассоновское действие связной группы Ли G при
отображении момента Р переходит в коприсоединенное действие
группы G на дуальном к ее алгебре Ли g пространстве g* (см. до-
добавление 2), т. е. коммутативна диаграмма
М -JL+M
Айд-1
8* —-+S*
Следствие. Пусть функция Гамильтона Н : М —»- R ин-
инвариантна относительно пуассоновского действия группы G на М.
Тогда момент является первым интегралом системы с функцией
Гамильтона Н.
Доказательство теоремы. Теорема утверждает, что функция
Гамильтона На однопараметрической группы hf при диффеоморфизме g пере-
переходит в функцию Гамильтона НАА а оцнопараметрической группы ghfg~l.

ДИНАМИЧЕСКИЕ СИСТЕМЫ С СИММЕТРИЕЙ
341
Пусть gs — однопараметрическая группа с функцией Гамильтона Нъ- До-
Достаточно доказать совпадение производных по s (при s = 0) функций Ha(gsx)
и ffA(J s (х). Первая из производных равна значению скобки Пуассона функ-
функций (Ва, Нъ) в точке х. Вторая же есть #[а>ь] (ж). Поскольку действие пуас-
•соновское, теорема доказана.
Доказательство следствия. Производная каждой ком-
компоненты момента по направлению фазового потока с функцией Гамильтона Н
равна нулю, так как она равна производной функции Н по направлению
разового потока соответствующей однопараметрической группы g, ч. т. д.
Б. Приведенное фазовое пространство. Пусть дано пуассонов-
¦ское действие группы G на симплектическом многообразии М.
Рассмотрим множество] уровня момента, т. е. прообраз какой-
либо точки pEg* при отображении Р. Это множество мы обоз-
обозначим через Мр, так что (рис. 238)
Мр = Р-1 (р).
Во многих важных случаях множество Мр является много-
многообразием. Например, это будет так, если р — регулярное значе-
значение момента, т. е. если дифференциал отображения Р в каждой
точке множества Мр отображает ка-
касательное пространство к М на все
касательное пространство к д*.
Группа Ли G, действовавшая на
М, вообще говоря, переставляет
множества Мр друг с другом. Од-
Однако стационарная подгруппа точки
р в коприсоединенном представлении
(т. е. подгруппа, состоящая из тех 9*
элементов g группы G, для которых
Adgp = р) оставляет Мр на месте.
Обозначим эту стационарную под-
подгруппу через Gp. Группа Gp явля-
является группой Ли, и она действует на множестве уровня момен-
момента Мр.
Приведенное фазовое пространство получается из Мр факто-
факторизацией по действию группы Gp. Для того чтобы такая факто-
факторизация имела смысл, нужно сделать некоторые предположения.
Например, достаточно предположить, что
1) Р — регулярное значение, так что Мр — многообразие.
2) Стационарная подгруппа Gv компактна.
3) Элементы группы Gp действуют на Mv без неподвижных
точек.
Замечание. Эти условия можно ослабить. Например, вместо ком-
компактности группы Gp можно потребовать, чтобы действие было собственным
(т. е. чтобы прообразы компактных множеств при отображении (?, х) >->¦ (е(х), х)
были компактными). Например, действие группы на себе левыми или правыми
сдвигами всегда собственное.
Рис. 238. Приведенное фазовое
пространство

342 ДОБАВЛЕНИЕ 5
Если условия 1), 2), 3) выполнены, то легко определить на
множестве орбит действия Gp на Мр структуру гладкого много-
многообразия. А именно, карту в окрестности точки х Е= Мр доставляет
любая трансверсальная к орбите Gpx площадка, размерность
которой равна коразмерности орбиты.
Получающееся многообразие орбит и называется приведенным
фазовым пространством системы с симметрией.
Мы будем обозначать приведенное фазовое пространство, соот-
соответствующее значению момента р, через Fp. Многообразие Fp
является базой расслоения п: Мр -*- Fp со слоем, диффеоморфным
группе Gv.
На приведенном фазовом пространстве Fp имеется естественная
симплектическая структура. А именно, рассмотрим какие-либо
два вектора |, ц, касательных к Fp в точке /. Точка / является
одной из орбит группы Gp на многообразии Мр. Пусть х — одна
из точек этой орбиты. Векторы Ь, и г), касательные к Fp, полу-
получаются из некоторых векторов |', ц', касательных к Мр в точке
х, при проекции п: Мр —*- Fp.
Определение. Кососкалярным произведением векторов |,
х\, касательных к приведенному фазовому пространству в одной
точке, называется кососкалярное произведение соответствующих
им векторов |', tj', касательных к исходному симплектическому
многообразию М:
В1 [Г']
Теорема*). Кососкалярное произведение векторов |, г) не
зависит от выбора точки х и представителей |', ц' и задает
на приведенном фазовом пространстве симплектическую струк-
структуру.
Следствие. Приведенное фазовое пространство четномерно.
Доказательство теоремы. Рассмотрим в касатель-
касательном к М в х пространстве следующие два подпространства:
Т (№р) — касательное пространство к многообразию уровня
момента Мр;
Т (Gx) — касательное пространство к орбите группы G.
Лемма. Эти два пространства являются косоортогоналъ-
ными дополнениями друг друга в ТМ.
Доказательство.1 Вектор С] лежит в косоортогональном допол-
дополнении к касательной плоскости орбиты группы G тогда и только тогда, когда
кососкалярные произведения вектора ? с векторами скоростей гамильтоновых
потоков группы G равны нулю (по определению). Но эти кососкалярные про-
произведения равны производным соответствующих функций Гамильтона по
направлению ?. Следовательно, вектор ? лежит в косоортогональном допол-
*) В таком виде! эта теорема впервые сформулирована Марсденом и
Вейнстейном. Многочисленные частные случаи рассматривались со времен
Якоби и использовались Пуанкаре и его последователями в механике, Кирил-
Кирилловым и Костантом в теории групп, а Фаддеевым — в общей теории относи-
относительности.

ДИНАМИЧЕСКИЕ СИСТЕМЫ С СИММЕТРИЕЙ 343
нении к орбите группы G, если и только если производная момента по направ-
направлению ? равна нулю, т. е. если ? лежит в Т (Мр). Первое утверждение леммы
доказано; второе очевидно.
Представители g' и tj' определены с точностью до прибавления вектора
из касательной плоскости к орбите группы Gp. Но эта касательная плоскость
есть пересечение касательных плоскостей к орбите Ga: и к многообразию Мр
(по последней теореме пункта А). Следовательно добавление к §' вектора
из Т (Gpx) не меняет кососкалярных произведений со всеми векторами tj' из
Т (Мр) (так как по лемме Т (Gpx) косоортогонально Т (Мр)). Итак, незави-
независимость от выбора представителей |', tj' доказана.
Независимость величины | §, tj |p от выбора точки х на орбите / вытекает
из симплектичности действия группы G на М и инвариантности Мр. Итак,
на Fp определена дифференциальная 2-форма:
Она не,вырождена. Ибо, если [§, г\]р = 0 для всех т], то соответствующий
представитель §' косоортогонален всем векторам из Т (Мр). Следовательно,
§' принадлежит косоортогональному дополнению к Т (Мр) в ТМ. Тогда по
лемме |'ef (Gx), т. е. % = 0.
Форма йр замкнута. Чтобы в этом убедиться, рассмотрим какую-либо
карту, т. е. площадку в Мр, трансверсально пересекающую орбиту группы Gp
в одной точке.
Форма йр изображается на этой карте 2-формой, индуцированной из
2-формы со, задающей симплектическую структуру во всем пространстве М,
при вложении площадки. Поскольку форма со замкнута, индуцированная
форма также замкнута. Теорема доказана.
Пример 1. Пусть М = R2™ — евклидово пространство раз-
размерности Ъг с координатами рк, qk и 2-формой 5jdpk Д dq^. Пусть
G = S1 — окружность, а действие G на М задается гамильтониа-
гамильтонианом линейного осциллятора
\
Тогда отображение момента есть просто Н: R2n ->- R, много-
многообразие нулевого уровня момента есть сфера S2", а фактор-
пространство — комплексное проективное пространство СР".
Следовательно, предыдущая теорема определяет симплекти-
симплектическую структуру на комплексном проективном пространстве.
Нетрудно проверить, что эта структура совпадает (с точностью
до множителя) с той, которую мы построили в добавлении 3.
Пример 2. Пусть М—группа Ли, G — эта же группа,
а действие определяется левыми сдвигами. Тогда Mv — это под-
подмногообразие касательного расслоения группы, образованное теми
векторами, которые при правом сдвиге в единицу группы дают
один и тот же элемент в дуальном пространстве к алгебре Ли.
Следовательно, многообразие Мр диффеоморфно самой группе
и является правоинвариантным сечением кокасательного рас-
расслоения. Все значения р регулярны.
Стационарная подгруппа Gn точки р состоит из тех элементов
группы, для которых левый и правый сдвиги элемента р дают
одинаковый результат. Действия отличных от единицы элементов

344 ДОБАВЛЕНИЕ 5
группы Gp на Мр не имеют неподвижных точек (так как их нет
у правых сдвигов группы по себе).
Группа Gp действует собственно (см. замечание на стр. 341).
Следовательно пространство орбит группы Gp на Мр является
симплектическим многообразием.
Но это пространство орбит легко отождествляется с орбитой
точки р в коприсоединенном представлении. Действительно, ото-
отобразим правоинвариантное сечение Мр кокасательного расслое-
расслоения в кокасательное пространство к группе в единице левами
сдвигами. Получаем отображение
л: Мр -+¦ з*.
Образ этого отображения есть орбита точки р в коприсоеди-
коприсоединенном представлении, а слои — орбиты действия группы Gp.
Симплектическая структура приведенного фазового пространства
определяет, таким образом, симплектическую структуру на ор-
орбитах коприсоединенного представления.
Нетрудно проверить непосредственным подсчетом, что это —
та самая структура, которую мы обсуждали в добавлении 3.
Пример 3. Пусть группа G = S1 — окружность, и пусть
она действует без неподвижных точек на многообразии V. Тогда
возникает пуассоновское действие окружности на кокасательном
расслоении М = T*V. Мы можем определить многообразия уров-
уровня момента Мр (коразмерности 1 в М) и фактор-многообразия Fp
(размерность которых на 2 меньше размерности М).
Кроме того, мы можем построить фактор-многообразие кон-
конфигурационного пространства V, отождествив друг с другом все
точки каждой орбиты группы на V. Обозначим это профакторизо-
ванное пространство через W.
Теорема. Приведенное фазовое пространство Fo симплек-
тически диффеоморфно кокасателъному расслоению профакторизо-
ванного конфигурационного пространства W; Fp диффеоморфно Fo.
Доказательство. Пусть п: V —» W — факторизация, и
— 1-форма на W в точке w = nv. Форма л* со на V в точке v принад-
принадлежит Мо и после факторизации задает точку в Fe. Обратно, элементы Fe—
это инвариантные 1-формы на V, равные нулю на орбитах; они задают 1-формы
на W. Итак, мы построили отображение Т* W —¦ F„; легко видеть, что это —
симплектический диффеоморфизм.
Случай р ф 0 сводится к случаю р = 0 следующим приемом. Рассмотрим
на V риманову метрику, инвариантную относительно G. Пересечение Mv
с кокасательной плоскостью кКв точке v является гиперплоскостью. Квад-
Квадратичная форма, задающая метрику, имеет в этой гиперплоскости единствен-
единственную точку минимума s (v). Вычитание вектора s (i>) переводит гиперплоскость
Мр П T*VK в Мо Г) T*VV, и мы получаем диффеоморфизм Fp —» Fo. Теорема
доказана.
В. Применения к исследованию стационарных вращений и би-
бифуркаций инвариантных многообразий. Пусть дано пуассонов-
пуассоновское действие группы G на симплектическом многообразии М,

ДИНАМИЧЕСКИЕ СИСТЕМЫ С СИММЕТРИЕЙ 345
и пусть Н — функция на М, инвариантная относительно G.
Пусть Fp — приведенное фазовое пространство (мы предполагаем,
что условия, при которых его можно определить, выполнены).
Гамильтоново поле с функцией Гамильтона Н касается каж-
каждого многообразия уровня момента Мр (так как момент — первый
интеграл). Возникающее полена Мр инвариантно относительно Gp.
и задает поле на приведенном фазовом пространстве Fp. Это век-
векторное поле на Fp мы будем называть приведенным полем.
Теорема. Приведенное поле на приведенном фазовом про-
пространстве гамильтоново. Значение функции Гамильтона приведен-
приведенного поля в какой-либо точке приведенного фазового пространства
равно значению исходной функции Гамильтона в соответствующей
точке исходного фазового пространства.
Доказательство. Соотношение, определяющее гамильтоново
поле _ЗГд с гамильтонианом Н на многообразии М с формой а>
dH (I) = ш (Хю |) для всех |
влечет аналогичное соотношение для приведенного поля ввиду определения
симплектической структуры на Fр, ч. т. д.
Пример. Рассмотрим асимметричное твердое тело, закреп-
закрепленное в неподвижной точке и находящееся под действием силы
веса (или иной потенциальной силы, симметричной относительно
вертикальной оси).
На конфигурационном пространстве S0C) действует группа
S1 вращений относительно вертикали. Функция Гамильтона инва-
инвариантна относительно вращений, поэтому возникает приведенная
система на приведенном фазовом пространстве.
Приведенное фазовое пространство является в данном случае
кокасательным расслоением профакторизованного конфигурацион-
конфигурационного пространства (см. пример 3, стр. 344). Факторизация кон-
конфигурационного пространства по действию вращений вокруг вер-
вертикальной оси была проведена Пуассоном следующим образом.
Будем задавать положение тела ортонормированным репером
(ех, е2, еа). Три вертикальные компоненты векторов репера задают
вектор в трехмерном координатном евклидовом пространстве.
Длина этого вектора 1 (почему?). Этот вектор Пуассона *) у опре-
определяет исходный репер с точностью до поворотов относительно вер-
вертикали (почему?).
Таким образом, профакторизованное конфигурационное прост-
пространство представляет собой двумерную сферу S2, а приведенное
•) Пуассон показал, что уравнения движения тяжелого твердого тела
записываются через вектор у в замечательно простом виде «уравнений Эй-
Эйлера — Пуассона»
dM dv
-w- - [ДГ, а] = pg [у, I], -%- = [у, са].

346 ДОБАВЛЕНИЕ 5
фазовое пространство — это кокасательное расслоение двумерной
сферы T*S2.
Приведенная функция Гамильтона на кокасательном расслое-
расслоении сферы представляет собой сумму квадратичной относительно
кокасательных векторов «кинетической энергии приведенного дви-
движения» и «эффективного потенциала» (включающего потенциальную
энергию и кинетическую энергию вращения относительно вер-
вертикали).
Переход к приведенному фазовому пространству в данном случае почти
сводится к «исключению циклической координаты <р>. Разница состоит лишь
в том, что обычная процедура исключения требует, чтобы конфигурационное
или фазовое пространство было прямым произведением на окружность, тогда
как в нашем случае имеется лишь расслоение. Это расслоение можно превра-
превратить в прямое произведение ценой уменьшения конфигурационного простран-
пространства (т. е. введением координат с особенностями у полюсов); преимущество
изложенного выше подхода состоит в том, что выясняется, что никакой ре-
реальной особенности (кроме особенности системы координат) вблизи полю-
полюсов нет.
Определение. Фазовые кривые в М, проектирующиеся
в положения равновесия приведенной системы на приведенном
фазовом пространстве Fp, называются относительными равновесия-
равновесиями исходной системы.
Пример. Стационарные вращения твердого тела, закреплен-
закрепленного в центре инерции, являются относительными равновесиями.
Точно так же относительными равновесиями являются движе-
движения тяжелого твердого тела, сводящиеся к вращению с постоян-
постоянной скоростью вокруг вертикальной оси.
Теорема. Фазовая кривая системы с G-инвариантной функ-
функцией Гамильтона является относительным равновесием тогда и
только тогда, когда она является орбитой однопараметрической
подгруппы группы G в исходном, фазовом пространстве.
Доказательство. Что фазовая кривая, являющаяся орбитой,
проектируется в точку, очевидно. Если фазовая кривая х (t) проектируется
в точку, то ее можно однозначно представить в виде х (t) = g (t) x@), и тогда
легко видеть, что {g (t)} — подгруппа, ч. т. д.
Следствие 1. Асимметричное твердое тело в любом осе-
симметричном потенциальном поле, закрепленное в точке на оси
поля, имеет не менее двух стационарных вращений (при каждом
значении кинетического момента относительно оси симметрии).
Следствие 2. Осесимметричное твердое тело в любом по-
потенциальном силовом поле, закрепленное в точке на оси симметрии,
имеет не менее двух стационарных вращений (при каждом значе-
значении кинетического момента относительно оси симметрии).
Оба следствия вытекают из того, что функция на сфере имеет
не менее двух критических точек.
Другое приложение относительных равновесий состоит в том,
что с их помощью удобно исследовать перестройки топологии
инвариантных многообразий энергии и момента.

НОРМАЛЬНЫЕ ФОРМЫ КВАДРАТИЧНЫХ ГАМИЛЬТОНИАНОВ 347
Теорема. Критические точки отображения момента и
энергии
Р X Н : M-+g* X R
на регулярном множестве уровня момента — это в точности отно-
относительные равновесия.
Доказательство. Критические точки отображения Р х Н —
это условные экстремумы функции Н на многообразии уровня момента Мр
(так как рассматриваемое многообразие уровня регулярно, т. е. для всех х
из Мр имеем РЛТМХ = Тф.
Условные экстремумы функции Н на Мр при факторизации по Gp дают
критические точки приведенной функции Гамильтона (так как Н инвариантна
относительно Gp). Теорема доказана.
Фактическое исследование относительных равновесий и особен-
особенностей отображения энергии — момента не просто и не проведено
полностью даже в такой классической задаче, как задача о дви-
движении асимметричного твердого тела в поле тяготения. Случай,
когда центр тяжести лежит на одной из осей инерции, разобран
в написанном С. Б. Каток приложении к переводу цитированной
на стр. 337 статьи С. Смейла.
В этой задаче размерность фазового пространства 6, а группа
окружность; приведенное фазовое пространство T*S2 четырех-
четырехмерно.
Многообразия неособого уровня энергии в приведенном фазо-
фазовом пространстве бывают (в зависимости от значений момента и энер-
энергии) следующих четырех видов: S3, S2 X S1, RP3 и «крендель»,
получающийся из трехмерной сферы S3 приклеиванием двух «ру-
«ручек» вида
S1 X Я2 (ZJ - круг, {(х, у) : *2 + у2 < 1».
Добавление 6
НОРМА Л Ы1ЫЕ ФОРМЫ КВАДРАТИЧНЫХ ГАМИЛЬТОНИАНОВ
В настоящем добавлении приведена таблица нормальных форм,
к которым можно привести квадратичную функцию Гамильтона
вещественным симплектическим преобразованием. Эта таблица
составлена Д. М. Галиным на основании работы: William-
s о n J. On an algebraic problem, concerning the normal forms of
linear dynamical systems//Amer. J. of Math.—1936.— V. 58,
№ 1.— P. 141—163.
В работе Вильямсона указаны нормальные формы, к которым
можно привести квадратичную форму в симплектическом простран-
пространстве над любым полем.
А. Обозначения. Мы будем записывать гамильтониан в виде
Я = -у- (Ах, ас),

348 ДОБАВЛЕНИЕ 6
где х = (ри . . ., рп; уц..., qn) — вектор, записанный в симп-
лектическом базисе, А — симметрический линейный оператор.
Канонические уравнения имеют тогда вид
х = 1Ах,
где
1-(° -Е)
1 -\Б О)'
Собственными числами гамильтониана мы будем называть соб-
собственные числа линейного инфинитезимально-симплектического
оператора IA. Точно также под жордановой клеткой мы будем
понимать жорданову клетку оператора IA.
Собственные числа гамильтониана бывают четырех типов:
вещественные пары (а, —а), чисто мнимые пары (ib, —ib), чет-
четверки (zkazkib) и нулевые собственные числа.
Жордановы клетки, соответствующие двум членам пары или
четырем членам четверки, всегда имеют одинаковую структуру.
В случаях, когда вещественная часть собственного числа равна
нулю, приходится различать жордановы клетки четного и нечет-
нечетного порядка. При этом клеток нечетного порядка с нулевым
собственным числом четное количество и они естественно разби-
разбиваются на пары.
Окончательный список нормальных форм следующий.
Б. Гамильтонианы. Паре жордановых клеток порядка к с ве-
вещественными собственными числами ±а отвечает гамильтониан
Jc Jc-l
В = — а V, pj?j + J,
3=1 3=1
Четверке жордановых клеток порядка к с собственными числа-
числами +a+fei отвечает гамильтониан
В= —a S pflj + Ъ S (Pzj-iQij — РгзЯа-д + S Ptfj+r
3=1 3=1 3—1
Паре жордановых клеток нечетного порядка к с собственным
числом нуль отвечает гамильтониан
И = S Р№+1 (пРи к = 1,Н= 0).
3=1
Жордановой клетке четного порядка 2к с собственным числом
нуль соответствует гамильтониан ровно одного из следующих
двух видов:
К-1 К К-1
Я = ± Т
± Т (
3=1 3=1 3=1

НОРМАЛЬНЫЕ ФОРМЫ КВАДРАТИЧНЫХ ГАМИЛЬТОНИАНОВ 349
(при к = 1 вида Н = гЬ1/^??)- Гамильтонианы с верхним и ниж-
нижним знаком не переводятся в друга.
Паре жордановых клеток нечетного порядка 2к + 1 с чисто
мнимыми собственными числами ±Ы отвечает гамильтониан ровно
одного из следующих двух видов:
и
Н = ± "у
3=1
к+1 27с
J ~
3=1
л
При к = 0 Н = +~9~ (IPpi + От)- Гамильтонианы с верхним и ниж-
ним знаками не переводятся друг в друга.
Паре жордановых клеток четного порядка 2к с чисто мнимыми
собственными числами ±Ы отвечает гамильтониан ровно одного
из двух следующих видов:
1 i г \П / 1
Jc-l
^2_, i^Pii+iPnt-zi+i +P2J+2P2K-2J+2) ] — 2_i ^
3=1 J=l 3=1
(при fc = lF = ±-g-(^-d)
Здесь также гамильтонианы с верхним и нижним знаками не
переводятся друг в друга вещественным симплектическим преоб-
преобразованием.
Теорема Вильямсона. Линейное вещественное симп-
лектическое пространство, на котором задана квадратичная форма
Н, распадается в прямую сумму попарно косоортогоналъных ве-
вещественных симплектических подпространств так, что форма Н
представляется в виде суммы форм указанных выше видов на этих
подпространствах.
В. Неустранимые жордановы клетки. Индивидуальный га-
гамильтониан «общего положения» не имеет кратных собственных
чисел и приводится к простому виду (все жордановы клетки пер-
первого порядка). Однако если рассматривается не индивидуальный
гамильтониан, а целое семейство систем, зависящих от параметров^
то при некоторых исключительных значениях параметров могут
появиться более сложные жордановы структуры. От некоторых из
них можно избавиться малым шевелением семейства, другие же
неустранимы и при малом шевелении семейства лишь немного де-
деформируются. Если число параметров семейства I конечно, то та-

350 ДОБАВЛЕНИЕ 6
ких неустранимых в Z-параметрическом семействе случаев конеч-
конечное число. Формулируемая ниже теорема Галина позволяет пере-
перечислить все эти случаи при любом фиксированном I.
Обозначим через пх (z) ^ n2 (z) !> . . . ^ ns (z) размеры жорда-
новых клеток с собственным числом z.
Теорема. Многообразие гамильтонианов с указанными раз-
размерами жорданоеых клеток имеет в пространстве всех гамильтониа-
гамильтонианов коразмерность
где k — количество отличных от нуля различных собственных чи-
чисел, т — число жорданоеых клеток нечетного порядка с собственным
числом нуль. (См. К о с a k H. Normal forms and versal deforma-
deformations of linear Hamiltonian systems // J. Diff. Equat.—1984.—V. 51,
№ 3.— P. 359—407; Quadratic integrals of linear Hamiltonian
systems. Monatsherfte Math. — 1984. — V. 98, № 1. — P. 53 —
- 63.)
Следствие. В семействах линейных гамилътоновых систем,
зависящих общим образом от I параметров, встречаются системы
только с такими жордановыми клетками, что вычисленное по пре-
предыдущей формуле число с не превосходит I: все случаи с большим с
устранимы малым шевелением семейства.
Следствие. В одно- и двупараметрических семействах
встречаются как неустранимые только жордановы клетки сле-
следующих 12 типов:
1 = 1: (±а)а, Ша)\ О2
(здесь жордановы клетки обозначаются их определителями, на-
например (±аJ означает пару жорданоеых клеток порядка 2 с соб-
собственными числами аи —а соответственно);
= 2: (±аK, (±aVK, (+а±ЫJ, 0\ (±аJ
(±aiJ (±feO2, (±«J (±Ь02, (±«J О2, (±<иJ О2
(остальные собственные числа простые).
Галин вычислил также нормальные формы, к которым можно
привести любое семейство гладко зависящих от параметров линей-
линейных гамильтоновых систем при помощи гладко зависящей от па-
параметров симплектической линейной замены координат. Напри-
Например, для простейшей жордановой клетки (±аJ такой нормальной
формой гамильтониана будет
Я (К) = —a (pfa + p2q2)
и Я2 — параметры)»

НОРМАЛЬНЫЕ ФОРМЫ ГАМИЛЬТОНОВЫХ СИСТЕМ 351
Добавление 7
НОРМАЛЬНЫЕ ФОРМЫ ГАМИЛЬТОНОВЫХ СИСТЕМ
ВБЛИЗИ НЕПОДВИЖНЫХ ТОЧЕК И ЗАМКНУТЫХ ТРАЕКТОРИЙ
При исследовании поведения решений уравнения Гамильтона
вблизи положения равновесия часто недостаточно ограничиваться
линеаризованным уравнением. Действительно, асимптотически
устойчивые положения равновесия для гамильтоновых систем
невозможны по теореме Лиувилля о сохранении объема. Поэтому
устойчивость линеаризованной системы всегда нейтральная: соб-
собственные числа линейной части гамильтонова векторного поля
в устойчивом положении равновесия все лежат на мнимой оси.
Для систем дифференциальных уравнений общего вида такая
нейтральная устойчивость может быть разрушена сколь угодно
малыми нелинейными добавками. Для систем Гамильтона дело
обстоит сложнее. Предположим, например, что квадратичная часть
функции Гамильтона в положении равновесия (которая и опреде~
ляет линейную часть векторного поля) знакоопределена. Тогда
функция Гамильтона имеет максимум или минимум в положении
равновесия. Следовательно, это положение равновесия устойчиво
(по Ляпунову, но не асимптотически) не только для линеаризо-
линеаризованной системы, но и для полной нелинейной системы.
Однако квадратичная часть функции Гамильтона в устойчивом
положении равновесия может и не быть знакоопределенной.
Простейший пример доставляет функция // = pi + q\ — pi — q\-
Исследование устойчивости систем с такой квадратичной частью
должно учитывать члены ряда Тейлора следующих степеней, преж-
прежде всего кубические члены функции Гамильтона (т. е. квадратич-
квадратичные члены векторов поля фазовой скорости). Исследование это
удобно производить, приводя функцию Гамильтона (и следова-
следовательно, гамильтоново векторное поле) к возможно более простому
виду подходящей канонической заменой переменных. Иными сло-
словами, для изучения решений полезно подобрать систему канони-
канонических координат вблизи положения равновесия так, чтобы по воз-
возможности упростить вид функции Гамильтона и уравнений дви-
движения.
Аналогичный вопрос для общих (негамильтоновых) векторных
полей решается просто: там общим случаем является такой, когда
векторное поле в окрестности положения равновесия линейно
в подходящей системе координат (соответствующие теоремы Пуан-
Пуанкаре и Зигеля имеются, например, в книге: 3 и г е л ь К. Л. Лек-
Лекции по небесной механике.— М.: ИЛ, 1959).
В гамильтоновом случае картина сложнее. Первая трудность:
привести гамильтоново поле к линейной нормальной форме кано-
канонической заменой переменных, вообще говоря, невозможно.
А именно, обычно можно убить кубическую часть функции Га-

352 ДОБАВЛЕНИЕ 7
мильтона, но нельзя убить все члены четвертой степени (это свя-
связано с тем, что в линейной системе частота колебаний не зависит
от амплитуды, а в нелинейной, вообще говоря, зависит). Указан-
Указанное затруднение преодолевается выбором нелинейной нормальной
формы, учитывающей изменение частот (так называемая вариация
частоты). В результате можно (в так называемом нерезонансном
•случае) ввести переменные действие — угол вблизи положения рав-
равновесия так, что система станет интегрируемой с точностью до чле-
членов сколь угодно большой степени в ряду Тейлора.
Это позволяет изучать поведение системы в течение больших
интервалов времени для близких к равновесию начальных усло-
условий. Однако этого недостаточно, чтобы определить, будет ли по-
положение равновесия устойчивым по Ляпунову (из-за того, что
на бесконечном отрезке времени влияние отброшенного остаточ-
остаточного члена ряда Тейлора может разрушить устойчивость). Такая
устойчивость вытекала бы из точного приведения к аналогичной
нормальной форме, без пренебрежения остаточными членами.
•Однако можно доказать, что это точное приведение, вообще говоря,
невозможно, а формальные ряды для канонических преобразова-
преобразований, приводящих систему к нормальной форме, в действитель-
действительности в общем случае расходятся.
Расходимость этих рядов связана с тем, что приводимость к
нормальной форме повлекла бы за собой более простое поведе-
поведение фазовых кривых (они должны были бы быть условно-перио-
условно-периодическими обмотками торов), чем то, которое имеет место на самом
деле. Поведение фазовых кривых вблизи положения равновесия
гамильтоновой системы обсуждается в добавлении 8. В настоя-
настоящем же добавлении приведены формальные результаты о норма-
нормализации с точностью до членов высокой степени.
Идея приведения гамильтоновых систем к нормальным формам
восходит к Линдштедту и Пуанкаре *); нормальные формы в окрест-
окрестности положения равновесия подробно изучал Дж. Д. Биркгоф
(Б и р к г о ф Дж. Д. Динамические системы.— М.: Гостехиздат,
1941).
Нормальные формы для вырожденных случаев приведены в
работе: Б р ю н о А. Д. Аналитическая форма дифференциальных
уравнений // Труды Московского математического общества.—
1971.— Т. 25; 1972.— Т. 26.
А. Нормальная форма консервативной системы вблизи положе-
положения равновесия. Предположим, что в линейном приближении
положение равновесия гамильтоновой системы с п степенями сво-
свободы устойчиво, и что все п собственных частот щ, . . ., юп раз-
различны. Тогда квадратичная часть гамильтониана приводится
•труды
') См.: Пуанкаре А. Новые методы небесной механикя // Избранные
I. Т. 1.—М.: Наука, 1971.

НОРМАЛЬНЫЕ ФОРМЫ ГАМИЛЬТОНОВЫХ СИСТЕМ 353
линейным каноническим преобразованием к виду
Я = 4" <">i(Pi + Qi) + • • • + 4
(Среди чисел tofc могут быть отрицательные.)
Определение. Собственные частоты щ, . . ., ton удов-
удовлетворяют резонансному соотношению порядка К, если существу-
существуют целые не все равные нулю числа к, для которых
кгщ + . . . + кпьзп = 0, | ^ | + . . . + | кп | = К.
Определение. Нормальной формой Биркгофа степени s
для гамильтониана назовем многочлен степени s от канонических
координат (Pt, Qi), являющийся в действительности многочленом
(степени [s/2J) от переменных тг = (Pj + (?f)/2.
Например, для систем с одной степенью свободы нормальная форма сте-
степени 2т (или 2т + 1) имеет вид
а для систем с двумя степенями свободы нормальной формой Биркгофа сте-
степени 4 будет
^ + 2а12т1х2 \
Коэффициенты Oj и а2 — это собственные частоты, а коэффициенты ау опи-
описывают зависимость частот от амплитуд.
Теорема. Предположим, что собственные частоты щ не
удовлетворяют ни одному резонансному соотношению порядка s и
меньше. Тогда существует такая каноническая система координат
в окрестности положения равновесия, что в ней функция Гамиль-
Гамильтона приводится к нормальной форме Биркгофа степени s с точ-
точностью до членов степени s + 1:
Н {р,\ q) = Hs (P,Q) + R, R=O(\P\+\Q |)e+1.
Доказательство этой теоремы легко проводится в системе комплексных
координат,
(при переходе к которым надлежит умножить гамильтониан на —2j). Если
не входящие в нормальную форму члены степени меньше N уже убиты, то
вамена с производящей функцией Pq -\- SN (P, q) (где SN — однородный мно-
многочлен степени N) изменит в разложении Тейлора функции Гамильтона лишь
члены степени N и выше.
При этой замене коэффициент при одночлене степени N в функции Га-
Гамильтона, имеющем вид
4 $ ? («1+• • -+«n + Pi+.. .
изменится, как легко сосчитать, на величш у
•оц I*» (Ь - ai) + • • • + *ь (Рп -«„И.

354 ДОБАВЛЕНИЕ 7
где Я,/ = itoj и где sa^ — коэффициент при zaw в разложении функции
SN (p, q) по переменным z, w.
При сделанных предположениях об отсутствии резонанса коаффициент
в квадратных скобках при sa» отличен от нуля, кроме лишь случая, когда
наш одночлен выражается через произведения гцсц — 2xt (т. е. когда все оц
равны Pi). Таким образом, мы можем убить все члены степени N, кроме вы-
выражающихся через переменные тг. Полагая Л' = 3, 4, . . ., s, получаем до-
доказываемое.
При пользовании теоремой Биркгофа полезно заметить, что
система, гамильтониан которой является нормальной формой,
интегрируется. Именно, рассмотрим «канонические полярные
координаты» т,, фь через которые Р1 и Qt выражаются по фор-
формулам
Р, = ]/2т; cos фг, Qi = У 2т; sin %.
Поскольку гамильтониан выражается через одни лишь переменные
действия %i, система интегрируема и описывает условно-перио-
условно-периодические движения по торам % = const с частотами со = дН/дх.
В частности, положение равновесия Р = Q ~ 0 для нормальной
формы устойчиво.
Б. Нормальная форма канонического преобразования вблизи
неподвижной точки. Рассмотрим каноническое (т. е. просто сохра-
сохраняющее площади) отображение двумерной плоскости на себя.
Предположим, что это преобразование оставляет на месте начало
координат, а его линейная часть имеет собственные числа Я =
= e±ia (т. е. является поворотом на угол а в подходящем симп-
лектическом базисе с координатами р, q). Такое преобразование
будем называть эллиптическим.
Определение. Нормальной формой Биркгофа степени s
для преобразования назовем каноническое преобразование пло-
плоскости в себя, являющееся поворотом на переменный угол, ко-
который является полиномом степени не выше т = [s/2J—1 от пере-
переменной действия т канонической полярной системы координат:
(т, ф) .->- (т, ф + а0 + ахт + . . . + аттт),
где _
р = \f~2x cos ф, q = У 2т sin ф.
Теорема 2. Если собственное число К эллиптического кано-
нонического преобразования не является корнем из единицы степени s
и меньше, то это преобразование приводится канонической заме-
заменой переменных к нормальной форме Биркгофа степени s с по-
погрешностью в членах степени s -\- \ и выше.
Многомерное обобщение эллиптического преобразования —
это прямое произведение п эллиптических поворотов плоскостей
{Ри Qi) с собственными числами Яг = e±iaK Нормальная форма
Биркгофа степени s задается формулой
(т, Ф) -> (т, ф + dSldx)t

НОРМАЛЬНЫЕ ФОРМЫ ГАМИЛЬТОНОВЫХ СИСТЕМ 355
где S — многочлен степени не выше [s/2] от переменных действия
тх, . . ., т„.
Теорема 3. Если собственные числа %t многомерного эллип-
эллиптического канонического преобразования не допускают резонансов
то это преобразование приводится к нормальной форме Биркгофа
степени s (с ошибкой в членах степени s в разложении отображе-
отображения в ряд Тейлора в точке р = q = 0).
В. Нормальные формы уравнения с периодическими коэффи-
коэффициентами вблизи положений равновесия. Пусть р = q = 0 — по-
положение равновесия системы с функцией Гамильтона, зависящей
2я-периодически от времени. Предположим, что линеаризованное
уравнение приведено линейным симплектическим периодическим
по времени преобразованием к автономной нормальной форме с
собственными частотами а>х, . . ., а>п.
Мы скажем, что система резонансная порядка К~^>0, если су-
существует соотношение
&!% + . . . + knWn + К —0
с целыми k0, klt . . ., кп, для которого | кх | + . . . + | кп | = К.
Теорема. Если система не резонансная порядка s и меньше,
то существует 2л-периодически зависящее от времени канониче-
каноническое преобразование, приводящее систему в окрестности положения
равновесия к такой же нормальной форме Биркгофа степени s,
как если бы система была автономной, с той лишь разницей, что
остаточные члены R степени s + 1 и выше будут периодически
зависеть от времени.
Наконец, пусть дана замкнутая траектория автономной системы
уравнений Гамильтона. Тогда мы можем приводить систему
в окрестности этой траектории к нормальной форме, пользуясь
любым из следующих двух приемов:
1) Изоэнергетическая редукция: фиксируем
постоянную энергии и рассматриваем окрестность замкнутой траек-
траектории на 2п — 1-мерном многообразии уровня энергии как рас-
расширенное фазовое пространство системы с п — 1 степенью свободы,
периодически зависящей от времени.
2) Поверхность сечения: фиксируем постоянную
энергии и значение одной из координат (так, чтобы замкнутая
траектория пересекала получившуюся In — 2-мерную площадку
трансверсально). Тогда фазовые кривые, близкие к данной, оп-
определяет отображение этой 2п — 2-мерной площадки на себя,
с неподвижной точкой на замкнутой траектории. Это отображение
сохраняет естественную симплектическую структуру на нашей
2п — 2-мерной площадке, и мы можем изучать его при помощи
нормальной формы пункта Б.

356 ДОБАВЛЕНИЕ 7
При исследовании замкнутых траекторий автономных гамиль-
тоновых систем возникает одно новое обстоятельство по сравне-
сравнению с исследованием положений равновесия систем с периодиче-
периодическими коэффициентами. Дело в том, что замкнутые траектории
автономных систем не лежат изолированно, а образуют (как пра-
правило) однопараметрические семейства.
Параметром семейства является значение постоянной э ергии.
Действительно, предположим, что при некотором выборе згачения
постоянной энергии замкнутая траектория трансверсально пересе-
пересекает описанную выше 2п — 2-мерную площадку в 2п — 1-мерном
многообразии уровня энергии. Тогда и при близких значениях
постоянной энергии будет существовать подобная же замкнутая
траектория. По теореме о неявной функции мы можем даже ут-
утверждать, что эта замкнутая траектория гладко зависит от зна-
значения постоянной энергии.
Если мы захотим теперь воспользоваться нормальной формой
Биркгофа для исследования однопараметрического семейства
замкнутых траекторий, то мы встретимся со следующим затруд-
затруднением. При изменении параметра семейства собственные числа
линеаризованной задачи будут, вообще говоря, меняться. Следо-
Следовательно, при некоторых значениях параметра мы неизбежно
встретимся с резонансами, препятствующими приведению к нор-
нормальной форме.
Особенно опасны резонансы низких порядков, так как они
влияют на первые члены ряда Тейлора. Если нас интересует замк-
замкнутая траектория, для которой собственные числа близки к ре-
резонансному соотношению низкого порядка, то нормальную форму
Биркгофа следует несколько видоизменить. А именно, при ре-
резонансе порядка N обращаются в нуль некоторые из выра-
выражений
&о - К (Р, - а,) + . . . + (оп ((Зп - а»I, | а | + | C | = N,
на которые приходится делить при уничтожении членов степени N
в функции Гамильтона. При близких к резонансу нерезонансных
значениях параметра указанная комбинация собственных частот,
вообще говоря, не равна нулю, но весьма мала (эта комбинация
называется поэтому «малым знаменателем»).
Деление на малый знаменатель приводит к тому, что:
1) приводящее к нормальной форме преобразование разрывно
зависит от параметра (оно имеет полюс при резонансном значении
параметра);
2) область, в которой нормальная форма Биркгофа хорошо
описывает систему, стягивается до нуля при резонансе.
Чтобы избавиться от этих недостатков, надо отказаться от
уничтожения некоторых членов в гамильтониане (именно тех,
которые становятся резонансными при резонасном значении пара-

НОРМАЛЬНЫЕ ФОР Ы ГАМИЛЬТОНОВЫХ СИСТЕМ 357
метра). Причем их следует сохранить не только при резонансном,
но и при всех близких значениях параметра *).
Получающаяся в результате нормальная форма несколько
сложнее, чем обычная, но во многих случаях из нее можно
извлечь полезную информацию о поведении решений вблизи ре-
резонанса.
Г. Пример: исследование резонанса порядка 3. 15 качестве
простого примера исследуем, что происходит с замкнутой траек-
траекторией автономной гамильтоновой системы с двумя степенями
свободы вблизи такого значения постоянной энергии, при котором
период колебаний соседних траекторий около замкнутой траекто-
траектории в три раза больше периода обращения по замкнутой траек-
траектории.
В соответствии со сказанным выше эта задача сводится к ис-
исследованию однопараметрического семейства неавтономных га-
мильтоновых систем с одной степенью свободы, 2л-периодически
зависящих от времени, в окрестности положения равновесия. Это
положение равновесия можно считать бшчэлом координат при всех
значениях параметра (чтобы этого добиться, нужно сделать зави-
зависящую от параметров замену переменных).
Далее, линеаризованную в положении равновесия систему
можпо превратить в линейную систему с постоянными коэффи-
коэффициентами при помощи 2л-периодически зависящей от времени
линейной канонической замены координат. В полученных коорди-
координатах фазовый поток линеаризованной системы представляет со-
Гой равномерное вращение вокруг положения равновесия. Угло-
Угловая скорость ш этого вращения зависит от параметра.
При резонансном значении параметра ш = 1/3 (т. е. за время
2л совершается треть оборота вокруг начала координат). Произ-
Производная угловой скорости ш по параметру в общем случае отлична
от нуля. Поэтому мы можем принять за параметр саму эту угло-
пую скорость или, еще лучше, ее отклонение от 1/3. Это откло-
отклонение мы обозначим через е. Величина е называется расстройкой
частоты. Резонансное значение параметра — это 8 = 0. Нас инте-
интересует поведение системы при малых е.
Если пренебречь нелинейными членами в уравнениях Гамиль-
Гамильтона и пренебречь расстройкой частоты 8, то все траектории нашей
системы замыкаются, сделав три оборота (т. е. имеют период 6л).
Мы хотим теперь исследовать влияние нелинейных членов и рас-
расстройки частоты на поведение траекторий. Ясно, что все траекто-
траектории в общем случае замыкаться не будут. Чтобы исследовать, как
они себя ведут, полезно рассмотреть нормальную форму.
*) Указанный ядесь прием полезен не только при исследовании гамлль-
тоновых систем, но и в общей теории дифференциальных уравнений. См.,
например: АрнольдВ.И. Лекции о бифуркациях и версальных семей-
семействах // УМН.— 1972. — Т. 27, № 5.— С. 120—184.

358 ДОБАВЛЕНИЕ 7
В выбранной системе координат z=p-\-iq, z=p — iq функ-
функция Гамильтона имеет вид
-2iH = -имя. + 2 2
а+р=з К=
где точками обозначены члены степени выше третьей и где со =
= A/3) + 8.
При приведении к нормальной форме мы сможем убить все
члены третьей степени, кроме тех членов, для которых малый
энаменатель
© (а — Р) + к
становится равным нулю при резонансе. Эти члены можно опи-
описать также как такие, которые постоянны вдоль траектории
периодического движения, получающегося при пренебрежении
расстройкой частоты и нелинейностью. Они называются резонаис-
нымичленами. Итак, для резонанса © = 1/3 резонансные члены —
это такие, для которых
а — Р + 3/с = 0.
Стало быть, из членов третьей степени резонансными оказываются
только zbe^* и z3eu. Следовательно, мы можем привести функцию
Гамильтона к виду
—2iH = —tozz + hz3e-u — hz3eu + . . .
(сопряженность h и Ъ соответствует вещественности Я).
Заметим, что при приведении функции Гамильтона к этой
нормальной форме мы сделали 2л-периодически зависящее от вре-
времени гладкое каноническое преобразование, гладко зависящее от
параметра даже в случае резонанса. Это преобразование отлича-
отличается от тождественного лишь членами второго порядка малости
относительно отклонения от замкнутой траектории (а его произ-
производящая функция отличается от производящей функции тожде-
тождественного преобразования лишь кубическими членами).
Дальнейшее исследование поведения решений уравнений Га-
Гамильтона проводится следующим образом. Сначала мы отбросим
в функции Гамильтона все члены выше третьей степени и иссле-
исследуем решения получившейся укороченной системы. Затем нужно
посмотреть, как могут повлиять на поведение траекторий отбро-
отброшенные члены.
Исследование укороченной системы упрощается введением на
плоскости комплексной переменной z равномерно вращающейся
с угловой скоростью 1/3 системы координат, т. е. подстановкой
z = ?е7*^3. Для переменной ? получается] тогда автономная гамиль-
тонова система с функцией Гамильтона
—2»#0 = -юЙ + h%> - ЙР, где е = © - A/3).

НОРМАЛЬНЫЕ ФОРМЫ ГАМИЛЬТОНОВЫХ СИСТЕМ
359
Тот факт, что во вращающейся системе координат укороченная система
автономна, является большой удачей. Полная система уравнений Гамиль-
Гамильтона (с учетом членов степени выше третьей в гамильтониане) во вращающейся
системе координат не только не автономна, но даже и не 2я-периодична (а лишь
бп-периодична) по времени. Автономная система с гамильтонианом Но яв-
является в сущности результатом усреднения исходной системы по замкнутым
траекториям линейной системы с е = 0 (причем мы пренебрегаем членами
выше третьей степени).
Коэффициент h можно сделать вещественным (этого можно
добиться поворотом системы координат). Итак, функция Гамиль-
Гамильтона в вещественных координатах (х, у) приводится к виду
Но = 4" № + У*) + а Or3 - Зху*).
Коэффициент а зависит от расстройки частоты е как от параметра.
При 8 = 0 этот коэффициент в общем случае отличен от нуля.
Поэтому мы можем сделать этот коэффициент равным 1 гладко
зависящей от параметра заменой координат. Итак, нужно иссле-
исследовать зависимость фазового портрета системы с функцией Гамиль-
Гамильтона
на плоскости (х, у) от малого параметра е.
Легко видеть, что эта перестройка состоит в следующем
(рис. 239). При 8 = 0 линия нулевого уровня функции Но состоит
?<0
€=0
Рис. 239. Прохождение резонанса 3 : 1
из трех прямых, пересекающихся в нуле под углами 60°. При
изменении е все время существует линия уровня из трех прямых,
причем эти три прямые перемещаются при изменении е поступа-
поступательно, всегда образуя равносторонний треугольник с центром
в начале координат. Вершины этого треугольника — седловые кри-
критические точки функции Гамильтона. Критическая точка в начале
координат при прохождении е через нуль (т. е. при переходе
через резонанс) превращается из минимума в максимум.
Таким образом, для системы с функцией Гамильтона Но начало
координат является устойчивым положением равновесия при всех
значениях параметра, кроме резонансного, а при резонансном

360 добавленир: 7
значении — неустойчивым. При близких к резонансу значениях
параметра треугольник вблизи начала координат, заполненный
замкнутыми фазовыми кривыми, мал (порядка е), так что «радиус
устойчивости» начала координат при е —*¦ 0 приближается к нулю:
достаточно небольшого возмущения начального условия (поряд-
(порядка е), чтобы фазовая точка оказалась вне треугольника и начала
уходить от положения равновесия.
Возвращаясь к исходной задаче о периодической траектории,
мы приходим к следующим выводам (которые конечно не дока-
доказаны, поскольку мы отбросили члены выше третьей степени, но
могут быть обоснованы):
1. В момент прохождения рассматриваемого резонанса 3 : 1
периодическая траектория в общем случае теряет устойчивость.
2. При близких к резонансному значениях параметра вблизи
рассматриваемой периодической траектории на том же много-
многообразии уровня энергии имеется неустойчивая периодическая траек-
траектория. Она замыкается, обойдя три раза вдоль исходной траек-
траектории и сделав один оборот вокруг нее. При резонансном значении
параметра эта неустойчивая траектория сливается с исходной.
3. Расстояние указанной неустойчивой периодической траекто-
траектории от исходной убывает при подходе к резонансу как первая сте-
степень расстройки частоты (т. е. как первая степень отклонения
параметра от резонансного значения).
4. Через указанную неустойчивую траекторию на все том же
трехмерном многообразии уровня энергии проходят две двумерные
инвариантные поверхности, заполненные траекториями, при-
приближающимися к этой неустойчивой периодической траекто-
траектории при t—*--\-oo на одной поверхности и при t—*- — оо на
другой.
5. Расположение сепаратрис таково, что в пересечении с пло-
площадкой, трансверсалъной исходной траектории, получается фи-
фигура, близкая к трем сторонам равностороннего треугольника
и их продолжениям. Вершины треугольника — это точки пере-
пересечения неустойчивой периодической траектории с трансверсалъной
площадкой.
6. При начальных условиях внутри образованного сепаратри-
сепаратрисами треугольника фазовая точка в течение длительного времени
(порядка не менее 1/е) остается вблизи от исходной периодической
траектории (на расстоянии порядка е), а при начальных условиях
вне его — довольно быстро уходит на большое по сравнению с е
расстояние.
Д. Расщепление сепаратрис. В действительности сеператрисы,
о которых идет речь в предложениях 4, 5 и 6, устроены весьма
сложно (из-за влияния неучтенных в нашем приближении членов
выше третьей степени). Чтобы ясно представить себе картину,
удобно рассмотреть двумерную площадку, трансверсально пере-
пересекающую исходную замкнутую траекторию в какой-либо из ее

нормальные формы гамильтоновых систр: м 361
точек ( и лежащую целиком в одном многообразии уровня энер-
энергии) *).
Траектории, начинающиеся на этой площадке, снова пересе-
пересекают ее через время, близкое к периоду обращения по исходной
замкнутой траектории. Таким образом, возникает отображение
окрестности точки пересечения замкнутой траектории с площадкой
на площадке в площадку. Это отображение имеет неподвижную
точку (в месте пересечения площадки с замкнутой траекторией)
и близко к повороту на угол 120° вокруг этой точки, которую
мы примем за начало координат, на плоскости нашей площадки.
Рассмотрим теперь третью степень указанного выше отобра-
отображения. Это — снова отображение некоторой окрестности нуля
на плоскости площадки, оставляющее начало координат на месте.
Но теперь уже это отображение близко к повороту на 360°, т. е.
к тождественному отображению: оно осуществляется траектория-
траекториями нашей системы за время, близкое к трем периодам рассматри-
рассматриваемой замкнутой траектории.
Приведенные выше вычисления дают нетривиальную информа-
информацию о строении этого «отображения за три периода». В самом
деле, отбрасывая члены степени четыре и выше в функции Га-
Гамильтона, мы меняем члены степени три и выше у отображения.
Стало быть, отображение за три периода, которое соответствует
укороченной функции Гамильтона, аппроксимирует (с кубичес-
кубической ошибкой) настоящее отображение за три периода.
Но свойства отображения за три периода, отвечающего
укороченной функции Гамильтона, нам известны, так как это
есть отображение фазового потока системы с функцией Гамиль-
Гамильтона Но (х, у) за время 6л (доказательство основано на том,
что через время 6л наша вращающаяся система координат возвра-
возвращается к исходному положению). Посмотрим теперь, какие из
этих свойств сохраняются при возмущении третьего порядка
малости относительно расстояния от неподвижной точки, а какие
нет. Щ
Обозначим отображение за три периода для укороченной
системы через Ао, а настоящее отображение за три периода
через А.
1. Отображение Ао включается в поток: оно является преобра-
преобразованием за время 6л в фазовом потоке с гамильтонианом Но.
Нет никаких оснований думать, что отображение А включа-
включается в поток.
2. Отображение Ао выдерживает поворот на 120°: существует
нетривиальный диффеоморфизм g, для которого ^ = ?и который
коммутирует с Ао.
*) Здесь проявляется следующее общее явление: думать удобнее об отоб-
отображениях за период, а считать легче с потоками.

362 ДОБАВЛЕНИЕ 7
Нет никаких оснований думать, что отображение А коммути-
коммутирует с каким-либо нетривиальным диффеоморфизмом g, для
.которого g3 = Е.
3. Отображение Ао имеет три неустойчивых неподвижных
точки на расстоянии порядка е от начала координат, близкие
к вершинам правильного треугольника. При достаточно малых
отклонениях от резонанса (т. е. при достаточно малых е) отобра-
отображение А также имеет три неустойчивые неподвижные точки
вблизи вершин равностороннего треугольника. Это вытекает
из теоремы о неявной функции,
4. Сепаратрисы неподвижных точек отображения Ао образуют
(при близких к резонансу нерезонансных значениях параметра)
фигуру, близкую к сторонам и продолжениям сторон равносто-
равностороннего треугольника. Если начать с точки на одной из сторон
треугольника, то при повторении отображения Ао из этой точки
получится последовательность точек на той же стороне треуголь-
треугольника, стремящаяся к одной из ограничивающих сторону вершин,
скажем к Мо. При применении Л о1 получится последовательность,
сходящаяся к другой вершине, которую мы обозначим через No.
Каждая из трех неустойчивых непод-
неподвижных точек отображения А также имеет
сепаратрисы, близкие к сторонам треуголь-
треугольника (рис. 240). А именно, те точки плос-
плоскости, которые стремятся к неподвижной
точке М при применении к ним отображе-
отображений Ап, п -*¦ +- оо , образуют гладкую кри-
кривую Г+, инвариантную относительно А, про-
проходящую через точку М и вблизи точки М
Рис. 240. Расщепление близкую К Стороне M0N0 треугольника
сепаратрис сеператрис преобразования Ао. Те же точ-
точки, которые стремятся к N при применении Ап, где п —»— оо,
образуют другую гладкую инвариантную кривую Г", проходящую
через точку N и также близкую к M0N0 вблизи точки No.
Однако две кривые Г+ и Г", обе близкие к прямой M0N0, от-
отнюдь не обязаны совпадать. В этом и состоит явление расщепле-
расщепления сепаратрис, коренным образом отличающее поведение траек-
траекторий укороченной и полной систем.
Величина расщепления сепаратрис при малых е экспоненциально мала,
поэтому явление расщепления легко пропустить при вычислениях по той или
иной схеме «теории возмущений». Однако это явление весьма важно в прин-
принципиальном отношении. Например, из его существования сразу следует рас-
кодимостъ рядов многочисленных вариантов теории возмущений (так как
если бы ряды сходились, расщепления бы не было).
Вообще расходимость рядов теории возмущений (при хорошем прибли-
приближении, даваемом несколькими первыми членами) обычно связана с тем, что
ищется несуществующий объект. Если мы пытаемся подогнать изучаемое
явление под схему, которая в действительности не ухватывает существенных
черт явления, то неудивительно, что наши ряды расходятся.

НОРМАЛЬНЫЕ ФОРМЫ ГАМИЛЬТОНОВЫХ СИСТЕМ 363
Ряды Биркгофа (которые получатся если не ограничиваться нормализа-
нормализацией нескольких первых членов ряда Тейлора функции Гамильтона, а идти
до бесконечности) — один из примеров формально состоятельной, но на самом
деле расходящейся схемы теории возмущений. Если бы эти ряды сходились,
то общая колебательная система с одной степенью свободы с периодическими
коэффициентами приводилась бы вблизи положения равновесия к автономной
нормальной форме и в ней не было бы расщепления сепаратрис (а на самом
деле оно есть).
Возвращаясь к исходной замкнутой траектории, мы увидим,;
что трем неустойчивым неподвижным точкам преобразования А
соответствует неустойчивая замкнутая траектория, близкая к
утроенной исходной. Существует семейство траекторий, стремя-
стремящихся к этой неустойчивой траектории при t—*~ + оо, и другое
семейство траекторий, стремящихся к неустойчивой при t —> — оо.
Точки траекторий каждого из этих семейств образуют гладкую
поверхность, содержащую нашу неустойчивую траекторию.
Эти две поверхности и есть сепаратрисы, о которых шла речь
выше в утверждениях 4, 5, 6, стр. 360. При их пересечении с на-
нашей трансверсальной площадкой получаются инвариантные кри-
кривые Г+ и Г" отображения А. Эти две кривые при своем пересечении
образуют запутанную сеть, о которой А. Пункаре, впервые обна-
обнаруживший явление расщепления сепаратрис, писал: «Пересече-
«Пересечения образуют нечто вроде решетки, или ткани, или сетки с бес-
бесконечно тесными петлями; ни одна из двух кривых никогда не
должна сама себя пересекать, но она должна изгибаться столь
сложным образом, чтобы пересечь бесконечное число раз все петли
сети.
Приходится поражаться сложности этой фигуры, которую
даже не пытаюсь начертить. Ничто не может дать нам лучшее
представление о сложности проблемы трех тел и всех проблем
динамики, где нет голоморфного интеграла и ряды Болина рас-
расходятся» (Пуанкаре А. Новые методы небесной механики //
Избранные труды. Т. 2.— М.: Наука, 1972, гл. 33).
Следует заметить, что в картине пересекающихся сепаратрис
до сих пор многое неясно.
Е. Резонансы высших порядков. Резонансы следующих по-
порядков также можно исследовать с помощью нормальной формы.
Заметим при этом, что резонансы порядка выше 4 обычно не вы-
вызывают неустойчивости, так как в нормальной форме появляются
члены четвертой степени, гарантирующие минимум или максимум
функции Но даже в момент резонанса.
В случае резонанса порядка п ^> 4 типичная перестройка фазо-
фазового портрета системы с функцией Гамильтона Но дается формулой
Но =гх + т2а (т) + от"/2 sin nq>,
2т =p2 + q\ а@) = ±1,
и состоит в следующем (рис. 241).

364 ДОБАВЛЕНИЕ 7
При малом (порядка е) отклонении частоты от резонанса на
малом расстоянии (порядка у | е|) от положения равновесия
в начале координат функция Но имеет 2п критических точек
вблизи вершин правильного 2гс-угольника с центром в начале
координат. Половина этих критических то-
точек — седла, а вторая половина -— максиму-
максимумы, если в начале координат минимум,
и минимумы, если в начале координат ма-
максимум. Седла и устойчивые точки переме-
перемежаются. Все п седел лежат на одном уров-
уровне функции Но, и их сепаратрисы, соеди-
соединяя последовательные седла, образуют
п «островов», каждый из которых запол-
заполнен замкнутыми фазовыми кривыми, окру-
Рис. 241. Усредненный ЖЭЮЩИМИ УСТОЙЧИВУЮ ТОЧКУ. Ширина ОСТ-
гамильтониан фазовых ^ J J •> р
колебаний вблизи резо- ровов порядка е<п'4ь1/'!. «Замкнутые фазо-
нанса а: i вые Кривые ВПутри каждого острова назы-
вают фазовыми колебаниями (так как меняется в основном фаза
колебания вокруг начала координат). Период фазовых колеба-
колебаний растет при уменьшении расстройки частоты е как е~"/4.
Внутри узкого кольца, образованного островами, ближе к на-
началу координат, лежат замкнутые фазовые кривые, обходящие
начало координат; вне кольца фазовые кривые также замкну-
замкнуты, но движение по ним происходит в другую сторону, чем внут-
внутри кольца. Заметим, что радиус кольца имеет порядок Y |е I неза-
независимо от порядка резонанса, лишь бы этот порядок был боль-
больше 4. При этом кольцо островов существует только при одном
из двух знаков е.
При переходе от укороченной системы с гамильтонианом Но
к полной сепаратрисы расщепляются подобно тому, как описано
выше для резонанса порядка 3. Величина расщепления сепарат-
сепаратрис экспоненциально мала (порядка е~1/е"/4), однако расщепление
имеет принципиальное значение для исследования устойчивости,
особенно в многомерном случае.
Возвращаясь к нашей исходной замкнутой траектории, мы
приходим к следующей картине. При приближении к резонансу
по оси е с одной определенной стороны *) от периодической тра-
траектории ответвляются две другие: устойчивая и неустойчивая.
Эти новые траектории замыкаются после п оборотов вдоль исход-
исходной траектории и удалены от исходной на расстояние порядка
У|е|. Вблизи устойчивой траектории имеется зона медленных
фазовых колебаний с периодом порядка ?~n/i и амплитудой по-
порядка п/п в азимутальном направлении и порядка E<n/4)~J/2
в радиальном. Потери устойчивости исходной периодической тра-
*) В отличие от резонанса порядка 3, для которого ответвляющаяся
неустойчивая периодическая траектория есть по обе стороны от резонанса.

ТЕОРИЯ ВОЗМУЩЕНИЙ УСЛОВНО-ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ 365
ектории в момент прохождения резонанса не происходит, по
меньшей мере в том приближении, которое мы рассматриваем.
Случай резонанса четвертого порядка стоит несколько особняком. Дело
в том, что в этом случае в нормальной форме имеются как резонансные, так
и нерезонансные члены четвертой степени. Вид фазовых кривых укороченной
системы зависит от того, какой из этих членов нормальной формы перетянет:
резонансный плп нерезонансный. В первом случае перестройка такая же,
как для резонанса третьего порядка, только вместо треугольника — квадрат.
Во втором случае перестройка такая же, как при п > 4.
Заметим в заключение, что даваемое нормальной формой
приближение тем лучше, чем ближе мы находимся к резонансу
(е <^ 1) и чем меньше отклонение начальной точки от периоди-
периодической траектории. А именно, при приближении к точной соиз-
соизмеримости периода замкнутой траектории с периодом колебаний
соседних траекторий около нее и при приближении начального
условия к замкнутой траектории возрастает промежуток времени,
на котором наше приближение правильно описывает поведение
фазовых кривых.
Никакого вывода о поведении незамкнутых фазовых кривых
на бесконечном интервале времени (например, об устойчивости
исходной периодической траектории по Ляпунову) из наших
рассуждений не вытекает, так как отброшенные при приведении
к нормальной форме члены высокой степени могут за бесконеч-
бесконечное время совершенно изменить характер движения. В действи-
действительности в рассматриваемых условиях исходная периодическая
траектория' устойчива по Ляпунову, но доказательство требует
существенно новых соображений по сравнению с нормальной фор-
формой Биркгофа (см. добавление 8).
Добавление 8
ТЕОРИЯ ВОЗМУЩЕНИЙ УСЛОВНО-ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ
И ТЕОРЕМА КОЛМОГОРОВА
Имеющийся в нашем распоряжении набор точно решаемых
«интегрируемых» задач невелик (одномерные задачи, движение
точки в центральном поле, эйлерово и лагранжево движения
твердого тела, задача двух неподвижных центров, движение по
геодезическим на эллипсоиде). Однако, с помощью этих «инте-
«интегрируемых случаев» можно получить довольно значительную
информацию о движении многих важных систем, рассматривая
интегрируемую задачу как первое приближение.
Примером такой ситуации является задача о движении пла-
планет вокруг Солнца по закону всемирного тяготения. Масса планет
составляет примерно 0,001 массы Солнца, поэтому в первом при-
приближении можно пренебречь взаимодействием планет друг с дру-
другом и учитывать только их притяжение Солнцем. В результате

366 ДОБАВЛЕНИЕ 8
получается точно интегрируемая задача о движении невзаимодей-
невзаимодействующих планет вокруг Солнца; каждая планета независимо
от остальных будет описывать свой кеплеров эллипс, и движение
системы в целом будет условно-периодично. Если теперь учесть
взаимодействие планет друг с другом, то кеплерово движение
каждой планеты несколько изменится.
Небесно-механическая теория возмущений призвана учиты-
учитывать это взаимодействие.
При этом ясно, что расчет на времена порядка 1000 лет не
должен вызывать принципиальных трудностей. Однако если мы
захотим исследовать большие промежутки времени, а особенно
если мы заинтересуемся качественными вопросами о поведении
точных решений уравнений движения на бесконечном интервале
времени, то такие трудности возникают.
Дело в том, что накопление возмущений в течение большого
по сравнению с 1000 лет промежутка времени может привести к
полному изменению характера движения: например, планеты
могут падать на Солнце, уходить от него и сталкиваться друг с
другом.
Заметим, что к задаче о движении реальных планет вопрос о поведении
решений уравнений движения на бесконечных промежутках времени имеет
лишь косвенное отношение. Дело в том, что на интервалах времени порядка
миллиардов лет сильно сказываются малые неконсервативные эффекты, не-
неучтенные в уравнениях Ньютона. Таким образом, эффекты гравитационного
взаимодействия планет реально существенны лишь в том случае, если они
серьезно изменяют картину движения за конечное время, малое по сравнению
с временем проявления неконсервативных эффектов.
При расчете движения на такое конечное время существенную пользу
дают вычислительные машины, быстро определяющие движение планет на
много тысяч лет вперед или назад.
Однако следует заметить, что даже применение современных вычисли-
вычислительных средств может оказаться неспособным предсказать влияние возму-
возмущений, если фазовая точка попадает в зону экспоненциальной неустойчивости.
Еще большее значение асимптотические и качественные методы имеют
при исследовании движения заряженных частиц в магнитных полях, так как
при этом частица обгоняет вычислительную машину и успевает сделать столь
много оборотов, что машинное вычисление ее траектории невозможно даже
в отсутствие экспоненциальной неустойчивости.
Для учета возмущений в небесной механике был разработан
целый ряд методов. (Подробный разбор их имеется в книге: Пуан-
Пуанкаре А. Новые методы небесной механики // Избранные труды.
Т. 1, Т. 2.—М.: Наука, 1971, 1972.) Особенностью всех этих
методов является то* что они приводят к расходящимся рядам и
потому не дают никакой информации о поведении движения в це-
целом на бесконечных интервалах времени.
Причиной расходимости рядов теории возмущений являются
«малые знаменатели»: целочисленные линейные комбинации час-
частот невозмущенных движений, на которые приходится делить
при вычислении влияния возмущений. При точном резонансе

ТЕОРИЯ ВОЗМУЩЕНИЙ УСЛОВНО-ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ 367
(т. е. при соизмеримости частот) эти знаменатели обращаются в
нуль, а соответствующий член ряда теории возмущений становится
бесконечно большим. Вблизи резонанса этот член ряда очень велик.
Так, например, Юпитер и Сатурн в своем движении вокруг Солнца про-
проходят за сутки примерно 299 и 120,5 секунды дуги соответственно. Следова-
Следовательно, знаменатель 2сою — 5сос весьма мал по сравнению с каждой из частот.
Это приводит к большому долгопериодическому возмущению планет друг
другом (его период около 800 лет); изучение Лапласом этого эффекта было
одним из первых успехов теории возмущений.
Заметим, что трудность, вызванная малыми знаменателями,
весьма существенна. Действительно, рациональные числа образу-
образуют всюду плотное множество. Поэтому в фазовом пространстве
невозмущенной задачи всюду плотное множество образуют такие
начальные условия, при которых имеются резонансы и малые
знаменатели обращаются в нуль. Таким образом, функции, к
которым приводят ряды теории возмущений, имеют всюду
плотное множество особых точек.
Указанная здесь трудность характерна не только для задач
небесной механики, но для всех задач, близких к интегрируемым
(например, для задачи о движении асимметричного тяжелого
волчка, приведенного в очень быстрое вращение). Пуанкаре даже
называл основной задачей динамики задачу об исследовании воз-
возмущений условно-периодических движений в системе, заданной
гамильтонианом
Н = #0 (/) + гНх (/, Ф), е < 1,
в переменных действие / — угол ф.
Здесь Но — гамильтониан невозмущенной задачи, а е/^ —
возмущение, являющееся 2я-периодической функцией угловых
переменных ф1? . . ., ф„. В невозмущенной задаче (е = 0) углы
Ф меняются равномерно, с постоянными частотами
а все переменные действия являются первыми интегралами.
Требуется исследовать фазовые кривые уравнений Гамильтона
/ = — дН/дср, ф = dHldl
в фазовом пространстве, которое является прямым произведением
области в n-мерном пространстве с кооординатами / и и-мерного
тора с угловыми координатами ф.
Существенное продвижение в исследовании возмущенных фазо-
фазовых кривых этой задачи было начато в 1954 г. работой А. Н. К о л-
могорова «О сохранении условно-периодических движений
при малом изменении функции Гамильтона» (ДАН СССР.— 1954.—
Т. 98, №4.— С. 527—530). В настоящем добавлении излагаются
основные результаты, полученные с тех пор в этой области.
Доказательства можно найти в следующих работах:

368 ДОБАВЛЕНИЕ 8
Арнольд В. И. Малые знаменатели I: Об отображениях окружности
на себя // Изв. АН СССР.— 1961.— Т. 25, № 1.— С. 21—86.
Арнольд В.И. Малые знаменатели II: Доказательство теоремы
А. Н. Колмогорова о сохранении условно-периодических движений при
малом изменении функции Гамильтона // УМН.— 1963.— Т. 18, вып. 5.—
С, 13—40.
Арнольд В. И. Малые знаменатели III: Малые знаменатели и проб-
проблемы устойчивости в классической и небесной механике // УМН.— 1963.—
Т. 18, вып. 6.—С. 81—192.
Arnold V. I., Avez A. Problemes ergodiques de la mecanique clas-
sique.— Paris: G. V., 1967.
M о з е р Ю. Об инвариантных кривых сохраняющего площадь отобра-
отображения кольца в себя // Математика.— 1963.— Т. 6, № 5.— С. 51—67 (Nachr.
Acad. Wiss. Gottingen//Math. Phys.—1962.—Bd. Ha, № 1.— S. 1— 20).
M о з е р Ю. Быстро сходящийся метод итераций и нелинейные диффе-
дифференциальные уравнения // УМН.— 1968.— Т. 23, вып. 4.— С. 179—238
(Annali della Scoula Norm. Sup. de Pisa, Ser III.— 1966.— T. 20, N 2.—
P. 265—315; 1966.— № 3.— P. 499—535).
M о з е р Ю. О разложении условно-периодических движений в сходя-
сходящиеся степенные ряды // УМН.— 1969.— Т. 24, вып. 2.— С. 165—211
(Math. Ann.— 1967.— Т. 169— Р. 136—176).
Siegel С. L., Moser J. К. Lectures on Celestial Mechanics.— Sprin-
Springer, 1971.
Sternberg S. Celestial Mechanics I, II.—N. V.: Benjamin, 1969.
Прежде чем формулировать результаты, мы коротко обсудим
поведение фазовых кривых невозмущенной задачи, уже изученное
в гл. 10.
А. Невозмущенное движение. Система с гамильтонианом
Но (/) имеет п первых интегралов в инволюции (п переменных
действия). Каждое множество уровня всех этих интегралов пред-
представляет собой «.-мерный тор в 2п-мерном фазовом пространстве.
Этот тор инвариантен относительно фазового потока невозмущен-
невозмущенной системы: каждая фазовая кривая, начавшаяся в точке такого
тора, на нем и останется.
Движение фазовой точки по инвариантному тору / = const
является условно-периодическим. Частоты этого движения суть
производные невозмущенного гамильтониана по переменным дей-
действия:
<Рк = Щ (!), где cofc = дН0/д1н.
Следовательно, фазовая кривая всюду плотно заполняет тор
такого числа измерений, сколько среди частот щ арифметически
независимых.
Заметим, что частоты зависят от того, какой именно из торов
мы рассматриваем, т. е. какие именно значения первых интегра-
интегралов мы зафиксировали. Система п функций со от и переменных /,
вообще говоря, функционально независима; в таком случае мы
можем просто нумеровать торы частотами, выбрав переменные со
за координаты в окрестности рассматриваемой точки в простран-
пространстве переменных действия /.

ТЕОРИЯ ВОЗМУЩЕНИЙ УСЛОВНО-ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ 369
Случай, когда частоты функционально назависимы, мы будем
называть невырожденным случаем. Таким образом, условие невы-
невырожденности имеет вид
det
dl
Итак, в невырожденном случае на различных инвариантных
торах в фазовом пространстве невозмущенной задачи реализуются
условно-периодические движения с разным числом частот.
В частности, всюду плотное множество в фазовом пространстве
образуют инвариантные торы, на которых число частот максималь-
максимально возможное (т. е. п); такие торы называются нерезонансными.
Можно показать, что нерезонансные торы образуют в фазовом
пространстве множество полной меры, так что мера Лебега объеди-
объединения всех резонансных инвариантных торов невозмущенной
невырожденной системы равна нулю. Тем не менее резонансные
инвариантные торы существуют и перемежаются с нерезонансными
таким образом, что они также образуют всюду плотное множество.
Более того, всюду плотно множество резонансных торов с любым
числом независимых частот от 1 до п — 1. В частности, всюду
плотное множество образуют такие инвариантные торы, на кото-
которых все фазовые кривые замкнуты (число независимых частот 1).
Заметим все же, что вероятность попасть на резонансный тор
при случайном выборе начальной точки в фазовом пространстве
невозмущенной системыравна нулю (так же как вероятность попасть
на рациональное число при случайном выборе вещественного
числа). Таким образом, пренебрегая множествами меры нуль
можно сказать, что почти все инвариантные торы в невырожденной
невозмущенной системе нерезонансные и имеют полный набор
из п арифметически независимых частот.
На нерезонансном торе траектория условно-периодического
движения всюду плотна. Таким образом, для почти всех начальных
условий фазовая кривая невозмущенной
невырожденной системы всюду плотно за-
заполняет инвариантный тор, размерность
которого равна числу степеней свободы
(т. е. половине размерности фазового про-
пространства).
Чтобы лучше представить себе всю кар-
картину, рассмотрим случай двух степеней
свободы (п =B). В этом случае фазовое про-
странство четырехмерно. Следовательно,
Рис 242 Инвариантные то-
множества уровня энергии трехмерны. ры '„ трехмерном многооб-
Зафиксируем одно из таких множеств Разии ур°вня энергии
уровня. Это трехмерное многообразие,
расслоенное на двумерные инвариантные торы, можно предста-
представить себе в обычном трехмерном пространстве как семейство кон-
концентрических торов, вложенных друг в друга (рис. 242).

370 ДОБАВЛЕНИЕ 8
Фазовые кривые являются обмотками этих торов, причем обе
частоты обращения меняются от тора к тору. В общем случае
от тора к тору будут меняться не только обе частоты, но и их отно-
отношение. Если производная отношения частот по переменной дей-
действия, нумерующей торы на заданном множестве уровня функции
Но, отлична от нуля, то мы скажем, что наша система изоэнерге-
тически невырождена. Условие изоэнергетической невырожден-
невырожденности имеет (как нетрудно сосчитать) вид
'Н0 дН0
dl
dl
Условия невырожденности и изоэнергетической невырожденности
независимы одно от другого, т. е. невырожденная система может быть изо-
изоэнергетически вырожденной, а изоэнергетически невырожденная — вырож-
вырожденной. В многомерном (п > 2) случае изоэнергетическая невырожденность
означает невырожденность следующего отображения п — 1 -мерного много-
многообразия уровня функции Но от п переменных действия в проективное прос-
пространство размерности п — 1:
I (-»¦ (сох (/) : со2(/):... :со„ (/)).
Итак, рассмотрим изоэнергетически невырожденную систему
с двумя степенями свободы. Легко построить двумерную площадку f
трансверсально пересекающую двумерные торы нашего семейства
(по семейству концентрических окружностей в модели в трех-
трехмерном евклидовом пространстве).
Фазовая кривая, начинающаяся на такой площадке, снова на
нее возвращается, сделав оборот вокруг тора. В результате мы
получаем новую точку на той же окружности, по которой тор
пересекает площадку. Тем самым возникает отображение площадки
на себя.
Это отображение плоскости на себя оставляет на месте кон-
концентрические меридианные окружности, по которым плоскость
пересекают инвариантные торы. При этом каждая окружность
поворачивается на некоторый угол, а именно на такую долю пол-
полного оборота, какую частота вдоль меридиана тора составляет
от частоты вдоль экватора. Следовательно, если система изоэнер-
изоэнергетически не вырождена, то угол поворота инвариантных окруж-
окружностей на плоскости сечения будет меняться от одной окружности
к другой.
Стало быть, на одних окружностях этот угол будет соизмерим
с полным оборотом, на других же несоизмерим. Те и другие
окружности будут образовывать всюду плотные множества, но
на почти всех окружностях (в смысле меры Лебега) угол поворота
несоизмерим с полным оборотом.
Соизмеримость или несоизмеримость следующим образом ска-
сказываются на поведении точек окружности при отображении пло-

ТЕОРИЯ ВОЗМУЩЕНИЙ УСЛОВНО-ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ 371
щадки на себя. Если угол поворота соизмерим с полным оборотом,
то после нескольких итераций отображения точка возвращается
на прежнее место (число итераций тем больше, чем больше знаме-
знаменатель дроби, выражающей угол поворота). Если же угол поворота
несоизмерим с полным оборотом, то последовательные образы
точки при повторении преобразования всюду плотно заполняют
меридианную окружность.
Заметим еще, что соизмеримость соответствует резонансным
торам, а несоизмеримость — нерезонансным. Заметим также,
что из существования резонансных торов вытекает следующее
обстоятельство. Рассмотрим некоторую степень отображения на-
нашей площадки на себя, осуществляемого фазовыми кривыми.
Пусть показатель степени является знаменателем дроби, выражаю-
выражающей отношение частот на одном из резонансных торов. Тогда воз-
возведенное в указанную степень отображение имеет целую окруж-
окружность, сплошь состоящую из неподвижных точек (а именно, мери-
меридиан рассматриваемого резонансного тора).
Такое поведение неподвижных точек является противоестест-
противоестественным для отображений сколько-нибудь общего вида, даже
канонических (обычно неподвижные точки изолированы). В дан-
данном случае целая окружность неподвижных точек появилась
из-за того, что мы рассматривали невозмущенную, интегрируемую
систему. При сколь угодно малом возмущении общего вида
указанное свойство отображения (иметь целую окружность
неподвижных точек) должно пропасть. Окружность из неподвиж-
неподвижных точек должна рассыпаться, так что их останется только ко-
конечное число.
Иными словами, при малом возмущении нашей интегрируемой
системы следует ожидать изменения качественной картины фазо-
фазовых кривых хотя бы в том отношении, что целые инвариантные
торы, заполненные замкнутыми фазовыми кривыми, должны
распасться, причем останется конечное число замкнутых кривых,
близких к невозмущенным, а остальные фазовые кривые будут
вести себя сложнее. Мы уже встречались с таким случаем в добав-
добавлении 7 при исследовании фазовых колебаний вблизи резонанса.
Посмотрим теперь, что происходит при малом возмущении
функции Гамильтона с нерезонансными инвариантными торами.
Формальное применение принципа усреднения (т. е. первое при-
приближение классической теории возмущений, см. § 52) приводит
к выводу, что никакой эволюции нерезонансный тор не претерпе-
претерпевает.
Заметим, что здесь весьма существенна гамильтоновость возмущений,
так как при неконсервативном возмущении переменные действия, очевидно,
могут эволюционировать. В небесно-механической ситуации их эволюция
означает вековое изменение больших полуосей кеплеровых эллипсов,
т. е. падение планет на Солнце или их столкновение, или уход на большое
расстояние за время, обратно пропорциональное величине возмущения.

372 ДОБАВЛЕНИЕ 8
Если бы консервативные возмущения приводили к эволюции в первом при-
приближении, это сказалось бы на судьбе планет через время порядка 1000 лет.
К счастью, порядок величины неконсервативных возмущений много меньше.
Формулируемая ниже теорема Колмогорова доставляет одно
из оправданий приведенного вывода нестрогой теории возмущений
об отсутствии эволюции переменных действия.
Б. Инвариантные торы возмущенной системы.
Теорема. Если невозмущенная гамилътоноеа система не
вырождена, то при достаточно малом консервативном гамилыпо-
новом возмущении большинство нерезонансных инвариантных то-
торов не исчезнет, а лишь немного деформируется, так что в фазовом
пространстве возмущенной системы также имеются инвариант-
инвариантные торы, заполненные всюду плотно фазовыми кривыми, обматы-
обматывающими их условно-периодически, с числом частот, равным
числу степеней свободы.
Указанные инвариантные торы образуют большинство в том
смысле, что мера дополнения к их объединению мала вместе с воз-
возмущением.
Доказательство этой теоремы А. Н. Колмогорова основано
на следующих его двух замечаниях.
1. Зафиксируем нерезонансный набор частот невозмущенной
системы так, чтобы частоты не только были независимы, но и не
удовлетворяли приближенно никаким резонансным соотношениям
малого порядка.
Точнее говоря, фиксируется набор частот со, для которого существуют
такие С и v, что | (со, к) | > С \ к \~v при всех целых векторах к -t= 0.
Можно показать, что если v достаточно велико (скажем, v = п + 1),
то мера множества таких векторов со (лежащих в фиксированной ограничен-
ограниченной области), для которых указанное условие нерезонансности нарушается,
мала вместе с С.
Далее, будем искать вблизи нерезонансного инвариантного
тора невозмущенной системы, соответствующего фиксированным
значениям частот, такой инвариантный тор возмущенной системы,
на котором происходит условно-периодическое движение в точ-
точности с теми самыми частотами, которые мы фиксировали и кото-
которые, стало быть, удовлетворяют выписанному выше условию
нерезонансности.
Таким образом, вместо обычной для многих схем теории воз-
возмущений вариации частоты (состоящей во введении частот, зави-
зависящих от возмущения), следует сохранять частоты нерезонансными
и постоянными, но зато подбирать начальные условия по данному
возмущению так, чтобы обеспечить движение с фиксированными
частотами. Добиться этого малым вместе с возмущением изменением
начальных условий можно потому, что частоты меняются с пере-
переменными действия согласно условию невырожденности.
2. Второе замечание состоит в том, что для отыскания инва-
инвариантного тора вместо обычных для многих схем теории возму-

ТЕОРИЯ ВОЗМУЩЕНИЙ УСЛОВНО-ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ 373
щений разложений в ряды по степеням возмущения можно исполь-
использовать быстросходящийся метод типа ньютоновского метода каса-
касательных.
Метод касательных Ньютона для отыскания корней алгебраи-
алгебраических уравнений при начальной погрешности е дает после
п приближений ошибку порядка е2". Такая сверхсходимость поз-
позволяет парализовать влияние малых знаменателей, появляющих-
появляющихся в каждом приближении, и в результате удается не только про-
провести бесконечное число приближений, но и доказать сходимость
всей процедуры.
Предположения, в которых все это удается сделать, состоят
в том, что невозмущенная функция Гамильтона Но (/) аналитична
и невырождена, а возмущающая функция Гамильтона еНг (/, (р)
аналитична и 2я-периодична по угловым переменным (р. При-
Присутствие малого параметра е несущественно: важно лишь, чтобы
возмущение было достаточно мало в какой-нибудь комплексной
окрестности радиуса р вещественной плоскости переменных ф
{меньше некоторой положительной функции М (р, Но)).
Как показал Ю. Мозер, требование аналитичности можно
заменить дифференцируемостью достаточно высокого порядка,
если комбинировать метод Ньютона с предложенным Дж. Нэшем
сглаживанием функций в каждом приближении.
Получающиеся в результате условно-периодические движения
возмущенной системы с фиксированными частотами со оказываются
даже гладкими (в аналитическом случае — аналитическими)
функциями параметра возмущения е. Следовательно, их можно
было бы искать и без метода Ньютона в виде ряда по степеням е.
Коэффициенты этого ряда, называемого рядом Линдштедта,
действительно можно найти; однако доказать его сходимость
удается только косвенно, с помощью ньютоновских прибли-
приближений.
В. Зоны неустойчивости. Присутствие инвариантных торов
в фазовом пространстве возмущенной задачи означает, что при
большинстве начальных условий в системе, близкой к интегриру-
интегрируемой, движение остается условно-периодическим с максимальным
набором частот.
Возникает, естественно, вопрос, что же происходит с осталь-
остальными фазовыми кривыми, начальные условия которых попадают
в щели между инвариантными торами, образовавшиеся на месте
резонансных инвариантных торов невозмущенной задачи.
Распад резонансного тора, на котором число частот на 1 мень-
меньше полного, легко исследовать в первом приближении теории воз-
возмущений. Для этого нужно усреднить возмущение по тем п — 1-мер-
1-мерным инвариантным торам, на которые распадается резонан-
резонансный инвариантный тор и которые всюду плотно заполняются фазо-
фазовыми кривыми невозмущенной системы. В результате усреднения
получим консервативную систему с одной степенью свободы (см.

374 ДОБАВЛЕНИЕ 8
исследование фазовых колебаний вблизи резонанса в добавлении 7),
которую легко изучить.
В рассматриваемом приближении мы получаем вблизи рас-
распавшегося n-мерного резонансного тора перемежающийся набор
неустойчивых и устойчивых п — 1-мерных торов, причем вокруг
устойчивых происходят фазовые колебания. Соответствующие им
условно-периодические движения имеют полный набор из п
частот, в том числе п — 1 быструю частоту исходных колебаний и
одну медленную (порядка |Ле) частоту фазовых колебаний.
Однако не следует думать, что все отличие движений в невоз-
невозмущенной и возмущенной системе сводится к возникновению
«островов» фазовых колебаний. В действительности явление го-
гораздо сложнее, чем описанное выше первое приближение. Одним
из проявлений этого сложного поведения фазовых кривых возму-
возмущенной задачи является расщепление сепаратрис, обсуждавшееся
в добавлении 7.
При исследовании движений возмущенной системы вне инва-
инвариантных торов следует различать случаи двух и большего числа
степеней свободы. В случае двух степеней свободы размерность
фазового пространства равна четырем и многообразие уровня
энергии трехмерно. Поэтому инвариантные двумерные торы делят
множество уровня энергии.
При этом начавшаяся в щели между двумя инвариантными
торами возмущенной системы фазовая кривая вечно остается
запертой между этими торами. Стало быть, как бы сложно ни ви-
вилась эта кривая, она не выходит из своей щели, и соответствующие
переменные действия вечно остаются вблизи своих начальных
условий.
Если же число степеней свободы п больше двух, то и-мерные
инвариантные торы не делят 2п — 1-мерное многообразие уровня
энергии, но расположены в нем подобно точкам на плоскости или
линиям в пространстве. В этом случае «щели», отвечающие раз-
разным резонансам, соединяются друг с другом, поэтому инвариант-
инвариантные торы не препятствуют начавшейся вблизи резонанса фазовой
кривой уйти далеко. Стало быть, нет оснований ожидать, что
переменные действия вдоль такой фазовой кривой будут оставать-
оставаться близкими к своим начальным значениям во все моменты вре-
времени.
Иными словами, в системах с двумя степенями свободы (удов-
(удовлетворяющих условию изоэнергетической невырожденности, вооб-
вообще говоря, выполненному) при достаточно малых возмущениях
переменные действия вдоль фазовой траектории не только не имеют
векового возмущения ни в каком приближении теории возмуще-
возмущений (т. е. мало меняются в течение времени порядка (l/e)N при
любом N, где е — величина возмущений), но и вечно остаются
вблизи своих начальных значений как для нерезонансных фазовых
кривых, условно-периодически заполняющих двумерные торы

ТЕОРИЯ ВОЗМУЩЕНИЙ УСЛОВНО-ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ 375
(и составляющих большую часть фазового пространства), так
и при остальных начальных условиях.
В то же время существуют удовлетворяющие всем условиям
невырожденности системы с большим двух числом степеней сво-
свободы, в которых, несмотря на то, что при большинстве начальных
условий движение условно-периодично, при некоторых начальных
условиях возможен медленный уход переменных действия от их
начальных значений. Средняя скорость этого ухода в имеющихся
примерах *) оказывается порядка е~11^е, т. е. эта скорость убывает
при уменьшении возмущения быстрее любой его степени. Поэто-
Поэтому неудивительно, что указанный уход не обнаруживается ни
в каком приближении теории возмущений (здесь под средней
скоростью понимается отношение приращения переменных дейст-
действия к времени, так что фактически речь идет о приращении поряд-
порядка 1 за большое время порядка е1^8).
Оценка сверху средней скорости ухода переменных действия
от начальных условий в общих системах канонических уравнений
Гамильтона с п степенями свободы, близких к интегрируемым,
содержится в работе Н. Н. Нехорошева **).
Эта оценка, как и приведенная выше оценка снизу, имеет вид
e-i/ed- таким образом, приращение переменных действия мало, пока
время мало по сравнению с e1/ed, если е < е0. Здесь е — величина
возмущения, ad — заключенное между 0 и 1 число, определяемое,
как и е0, свойствами невозмущенного гамильтониана Но. При
этом на невозмущенный гамильтониан накладывается некоторое
условие невырожденности (конечнократность критических точек
ограничений Но на подпространства; достаточна квадратичная
выпуклость невозмущенного гамильтониана, т. е. знакоопреде-
знакоопределенность второго дифференциала функции Но).
Из указанной оценки сверху видно, что вековые изменения
переменных действия не улавливаются ни в каком приближении
теории возмущений, так как средняя скорость этих изменений
экспонециально мала. Заметим также, что вековые изменения
переменных действия, по-видимому, не имеют направленного
характера, а представляют собой более или менее случайное
блуждание по резонансам вокруг инвариантных торов. Подробное
обсуждение возникающих здесь вопросов можно найти в статье:
Заславский Г. М., Чириков Б. В. Стохастическая неус-
неустойчивость нелинейных колебаний // УФН.—1971.—Т. 105, № 1.—
С. 3—39.
*) См. АрнольдВ. И. Неустойчивость динамических систем с0
многими степенями свободы//ДАН СССР.—1964.—Т. 156, № 1.—С. 9—12-
**) Нехорошее Н. Н. О поведении гамильтоновых систем, близких
к интегрируемым. Функциональный анализ и его приложения // 1971.—
Т. 5, вып. 4.— С. 82—83.

376 ДОБАВЛЕНИЕ 8
Г. Разные варианты теоремы об инвариантных торах. Анало-
Аналогичные теореме о сохранении инвариантных торов в автономной
системе утверждения доказаны для неавтономных уравнений
с периодическими коэффициентами и для симплектическпх ото-
отображений.
Другие случаи, где имеют место аналогичные утверждения,
связаны с теорией малых колебаний в окрестности положения
равновесия автономной системы или системы с периодическими
коэффициентами, а также в окрестности замкнутой фазовой кри-
кривой фазового потока или в окрестности неподвижной точки сим-
плектического отображения.
Условия невырожденности, нужные в разных случаях, различ-
различны. Поэтому здесь для справок приведены эти условия невырож-
невырожденности. Мы ограничиваемся простейшими требованиями невы-
невырожденности, которые все выполнены в системах «общего положе-
положения». Во многих случаях требования невырожденности можно
ослабить, но достигаемый при этом выигрыш не окупает усложне-
усложнения формулировки.
1. Автономная система. Функция Гамильтона
Н = Но (/) + еНх (/, ф), /EGCR", ф mod 2я е Г*.
Условие невырожденности
гарантирует сохранение *) большинства инвариантных торов при
малом возмущении (е «^ 1).
Условие изоэнергетической невырожденности
дН0
dl
det
0H0
dl
гарантирует существование на каждом многообразии уровня
энергии множества инвариантных торов, дополнение к которому
имеет малую меру. Частоты на этих торах, вообще говоря, зависят
от величины возмущения, но отношения частот сохраняются при
изменении е.
Если п = 2, то условие изоэнергетической невырожденности
гарантирует также устойчивость переменных действия в том смы-
смысле, что они остаются вечно вблизи своих начальных значений при
достаточно малом возмущении.
2. Периодическая система. Функция Гамиль-
Гамильтона:
Н = Но (/) + e#i (/, Ф, t), /EGC R", ф mod 2я е Тп;
*) Разумеется, при возмущении торы несколько деформируются.

ТЕОРИЯ ВОЗМУЩЕНИЙ УСЛОВНО-ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ 377
возмущение 2я-периодично не только по ф, но и по t. Невозмущен-
Невозмущенную систему естественно рассматривать в 2п -\- 1-мерном про-
пространстве {(/, ф, ?)} = R" X Тп+1. Инвариантные торы имеют
размерность п -f- 1. Условие невырожденности
гарантирует сохранение большинства п -\- 1-мерных инвариант-
инвариантных торов при малом возмущении (е <^ 1).
Если п = 1, то это условие невырожденности гарантирует
также устойчивость переменной действия в том смысле, что она
вечно остается вблизи своего начального значения при достаточно
малом возмущении.
3. О т о б р а ж е н и е (/, ф) *-*¦ (/', ф') «2п-м е р н о г о
кольца». Производящая функция
S (/', Ф) = So (/') + е^ (/', ф), Г е= G CZ Rn, Ф е Тп.
Условие невырожденности
гарантирует сохранение большинства инвариантных торов невоз-
невозмущенного отображения ((/, ф) >->-(/, Ф + dSJdl)) при малом
возмущении (е <^ 1).
Если п = 1, то получается сохраняющее площади отображе-
отображение обычного кругового кольца на себя. Невозмущенное отобра-
отображение представляет собой на каждой окружности / = const
поворот. Условие невырожденности означает в этом случае, что
угол поворота от одной окружности к другой меняется.
Инвариантные торы в случае п = 1 превращаются в обычные
окружности. В этом случае теорема гарантирует, что при повторе-
повторении отображения все образы точки будут оставаться вблизи той
окружности, на которой лежала исходная точка, если возмущение
достаточно мало.
4. Окрестность положения равновесия
(автономный случа й). Положение равновесия пред-
предполагается устойчивым в линейном приближении, так что опре-
определены п собственных частот щ, . . ., со„. Предполагается, что
между собственными частотами нет резонансных соотношений
кгЩ + . . . + &ncon = 0 с целыми кг, 0 <^ S I &» ! <С 4.
Тогда функцию Гамильтона можно привести к нормальной форме
Биркгофа (см. добавление 7)
Я = Яо (т) + . . .,
где Н0(т) = \ щхк -f -3j- \ «OfcjTfcTj, а точки означают члены

378 ДОБАВЛЕНИЕ 8
выше четвертой степени относительно расстояния от положения
равновесия.
Условие невырожденности
det | cow | Ф О
гарантирует существование множества инвариантных торов почти
полной меры в достаточно малой окрестности положения равно-
равновесия.
Условие изоэнергетической невырожденности
СО.,, СО
гарантирует существование такого множества инвариантных торов
на каждом множестве уровня энергии (достаточно близком к кри-
критическому).
В случае п = 2 условие изоэнергетической невырожденности
заключается в том, что квадратичная часть функции Но не должна
делиться на линейную. В этом случае изоэнергетическая невырож-
невырожденность гарантирует устойчивость положения равновесия по
Ляпунову.
5. Окрестность положения равновесия
(периодический случай). Здесь снова предполагается
устойчивость в линейном приближении, так что определены п
собственных частот Юц . . ., юп. Предполагается, что между соб-
собственными частотами и частотой изменения коэффициентов (кото-
(которую мы будем считать равной единице) нет резонансных соотно-
соотношений
п
. ¦ . + кпап + К = 0 с
Тогда функцию Гамильтона можно привести к нормальной
форме Биркгофа такого же вида, как в автономном случае, но
с 2я-периодическим по времени остаточным членом.
Условие невырожденности
det | и>ы | ф О
гарантирует существование п + 1-мерных инвариантных торов
в In -f- 1-мерном расширенном фазовом пространстве, близких
к окружности т = 0, изображающей положение равновесия.
В случае п = 1 условие невырожденности сводится к отличию
от нуля производной периода малых колебаний по квадрату ам-
амплитуды малых колебаний. В этом случае невырожденность гаран-
гарантирует устойчивость положения равновесия по Ляпунову.
6. Неподвижная точка отображения. Здесь
предполагается, что все In собственных чисел линеаризации ка-
канонического отображения в неподвижной точке имеют модуль \

ТЕОРИЯ ВОЗМУЩЕНИЙ УСЛОВНО-ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ 379
и не удовлетворяют резонансным соотношениям низкого порядка
(где 2и собственных чисел— это Я^, . . ., Яп, %х, . . ., Кп).
Тогда отображение, если пренебречь членами выше третьей
степени в ряду Тейлора в неподвижной точке, записывается в нор-
нормальной форме Биркгофа
(т, ф) >-*- (т, ф + а (т)), где а (т) = dS/dx,
S = \ ft)kTk -\- -у \ сокгтлтг (обычные координаты в окрестности
положения равновесия — это р^ = |/Т][СО8 ф^, д^ = [/^2% sin фк).
Условие невырожденности
det | юи | ф О
гарантирует существование n-мерных инвариантных торов (близ-
(близких к торам т = const), образующих множество почти полной меры
в достаточно малой окрестности положения равновесия.
Если п = 1, то мы имеем дело с отображением обычной плос-
плоскости на себя, а инвариантные торы превращаются в окружности.
Условие невырожденности означает, что для нормальной формы
производная угла поворота окружности по площади, ограничен-
ограниченной этой окружностью, отлична от нуля (в неподвижной точке и,
следовательно, в некоторой ее окрестности).
В случае п = 1 условие невырожденности гарантирует устой-
устойчивость неподвижной точки отображения по Ляпунову. Заметим,
что в этом случае условие отсутствия младших резонансов имеет
вид
Таким образом, неподвижная точка сохраняющего площадь
отображения плоскости на себя устойчива по Ляпунову, если ли-
линейная часть отображения является поворотом на угол, не кратный
90° и 120°, и если отличен от нуля коэффициент со^ в нормальной
форме Биркгофа (гарантирующий нетривиальную зависимость
угла поворота от радиуса).
Выше мы нигде не останавливались на условиях гладкости,
предполагаемых в этих теоремах. Минимальная необходимая глад-
гладкость неизвестна ни в одном случае. В качестве примера можно
указать, что последнее предложение об устойчивости неповижных
точек отображений плоскости на себя было вначале доказано
Ю. Мозером в предположении 333-кратной дифференцируемости,
я лишь впоследствии (усилиями Мозера и Рюссмана) число про-
производных было понижено до 6.

380 ДОБАВЛЕНИЕ 8
Д. Приложения теоремы об инвариантных торах и ее обобще-
обобщений. Существует много механических задач, к которым приме-
применимы сформулированные выше теоремы. В качестве одной из прос-
простейших задач такого рода можно указать движение маятника под
действием периодически меняющегося внешнего поля или под
действием вертикальных колебаний точки подвеса.
Известно, что в отсутствие параметрического резонанса нижнее
положение равновесия маятника устойчиво в линейном прибли-
приближении. Устойчивость этого положения равновесия с учетом нели-
нелинейных эффектов (при дополнительном предположении отсутствия
резонансов порядков три и четыре) может быть доказана лишь
с помощью теорем об инвариантных торах.
Аналогичным образом можно использовать теорему об инва-
инвариантных торах для исследования условно-периодических движе-
движений системы связанных нелинейных осцилляторов.
Другой пример доставляет геодезический поток на выпуклой
поверхности, близкой к эллипсоиду. В этой системе две степени
свободы, и мы убеждаемся, что большинство геодезических на
близкой к трехосному эллипсоиду поверхности колеблется между
двумя «каустиками», близкими к линиям кривизны поверхности,
всюду плотно заполняя кольцо между ними. В то же время мы
приходим к теоремам об устойчивости двух замкнутых геодези-
геодезических, получившихся при деформации поверхности из двух эл-
эллипсов, содержащих среднюю ось эллипсоида (в отсутствие резо-
резонансов порядков 3 и 4).
В качестве еще одного примера можно рассмотреть замкнутые
траектории на бильярдном столе любой выпуклой формы. Среди
замкнутых бильярдных траекторий имеются устойчивые в ли-
линейном приближении, и мы можем заключить, что в общем случае
они по-настоящему устойчивы. Примером такой устойчивой биль-
бильярдной траектории является малая ось эллипса и, следователь-
следовательно, близкая к малой оси эллипса замкнутая бильярдная траек-
траектория на бильярде, близком к эллипсу, устойчива.
Применение теорем об инвариантных торах к задаче о враще-
вращении несимметричного тяжелого твердого тела позволяет рассмот-
рассмотреть неинтегрируемый случай тела, приведенного в быстрое вра-
вращение. Задача о быстром вращении математически эквивалентна
задаче о движении с умеренной скоростью в слабом поле тяжести:
существенным параметром является отношение потенциальной
энергии к кинетической. Если он мал, то мы можем использовать в
первом приближении эйлерово движение твердого тела.
Применяя теоремы об инвариантных торах к задаче с двумя
степенями свободы, которая получается после исключения цикли-
циклической координаты (вращения вокруг вертикали), мы приходим
к следующему выводу о движении быстро вращающегося тела:
если кинетическая энергия вращения тела достаточно велика по
сравнению с потенциальной, то длина вектора кинетического

ТЕОРИЯ ВОЗМУЩЕНИЙ УСЛОВНО-ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ 381
момента и его наклон к горизонту вечно остаются вблизи своих
начальных значений.
Из этого вытекает, что движение тела будет вечно близким
к комбинации движения Эйлера — Пуансо с азимутальной пре-
прецессией, исключая, однако, случай, когда начальные значения
кинетической энергии и полного момента близки к таким, для
которых тело может вращаться вокруг средней оси симметрии.
В этом последнем случае, реализующемся лишь при специальных
начальных условиях, вследствие расщепления сепаратрис вблизи
средней осп возникает более сложное кувыркание около средней
оси, чем в движении Эйлера — Пуансо.
Одним из обобщений теоремы об инвариантных торах является
теорема о вечной адиабатической инвариантности переменной
действия в одномерной колебательной системе с периодически
меняющимися параметрами. Здесь следует предположить, что
закон изменения параметров задан фиксированной гладкой пери-
периодической функцией медленного времени, а малым параметром
задачи является отношение периода собственных колебаний и
периода изменения параметров.
Тогда, если период изменения параметров достаточно велик,
то изменение адиабатического инварианта фазовой точки остается
малым в течение бесконечного промежутка времени.
Аналогичным образом доказывается вечная адиабатическая
инвариантность переменной действия в задаче о движении заря-
заряженной частицы в аксиально-симметричном магнитном поле.
Нарушение аксиальной симметрии в этой задаче увеличивает
число степеней свободы с двух до трех, так что инвариантные
торы перестают делить многообразие уровня энергии и становится
существенным блуждание фазовой кривой по резонансным зонам.
Наконец, в применении к задаче трех (или многих) тел удается
найти условно-периодические движения «планетного типа». Чтобы
описать эти движения, нужно сказать несколько слов о следующем
после кеплеровского приближения в задаче о движении планет.
Для простоты мы ограничимся здесь плоской задачей.
Рассмотрим для каждого кеплерова эллипса вектор, соединяю-
соединяющий фокус эллипса (т. е. Солнце) с центром эллипса. Этот вектор,
называемый вектором Лапласа, характеризует как величину экс-
эксцентриситета орбиты, так и направление на перигелий.
Взаимодействие планет друг с другом приводит к тому, что
кеплеров эллипс (и, следовательно, вектор Лапласа) слегка меня-
меняется со временем. При этом существует большая разница между
изменением большой полуоси и изменением вектора Лапласа.
А именно, большая полуось не имеет вековых возмущений, т. е.
в первом приближении лишь слегка колеблется вокруг своего
среднего значения («теорема Лапласа»). Вектор же Лапласа со-
совершает как периодические колебания, так и вековое движение.
Вековое движение получится, если размазать каждую планету по

382 ДОБАВЛЕНИЕ 8
ее орбите пропорционально времени, затрачиваемому на прохож-
прохождение участка орбиты, и заменить притяжение планет притяже-
притяжением полученных колец, т. е. если усреднить возмущения по быст-
быстрым движениям. Истинное движение вектора Лапласа получается
из векового наложением малых колебаний; эти колебания весьма
существенны, если нас интересует малый интервал времени (годы),
но их эффект становится малым по сравнению с эффектом веково-
векового движения, если рассмотреть большой интервал времени (тыся-
(тысячелетия).
Вычисления (проведенные еще Лагранжем) показывают, что
вековое движение вектора Лапласа каждой из п планет, движу-
движущихся в одной плоскости, состоит в следующем (если пренебречь
квадратами эксцентриситетов орбит по сравнению с самими экс-
эксцентриситетами) .
На плоскости орбиты планеты нужно расположить п векторов
фиксированных длин, равномерно вращающихся каждый со своей
угловой скоростью. Вектор Лапласа — их сумма.
Такое описание движения вектора Лапласа получается потому,
что усредненная по быстрым движениям гамильтонова система,
описывающая вековое движение вектора Лапласа, имеет положе-
положение равновесия, соответствующее нулевым эксцентриситетам.
Описанное движение вектора Лапласа — это разложение малых
колебаний вблизи указанного положения равновесия на собствен-
собственные колебания. Угловые скорости равномерно вращающихся со-
составляющих вектора Лапласа — это собственные частоты, а длины
этих составляющих определяют амплитуды собственных коле-
колебаний.
Заметим, что движение вектора Лапласа Земли является, по-видимому,
одним из факторов, с которыми связаны ледниковые периоды. Дело в том,
что при увеличении эксцентриситета орбиты Земли время, которое она
проводит вблизи Солнца, уменьшается, а вдали от него — увеличивается
(по закону площадей); итак, климат становится более суровым при увеличе-
увеличении эксцентриситета. Величина этого эффекта такова, что, например, коли-
количество солнечной энергии, получаемое за год на широте Ленинграда может
достигать значений, которые сейчас соответствуют широтам Киева (при умень-
уменьшении эксцентриситета) и Таймыра (при его увеличении). Характерное время
изменения эксцентриситета (десятки тысяч лет) хорошо согласуется с перио-
периодом наступления ледников.
Теоремы об инвариантных торах приводят к выводу, что при
достаточно малой массе планет в фазовом пространстве задачи
имеется множество положительной меры, заполненное такими ус-
условно-периодическими фазовыми кривыми, что соответствующее
движение планет близко к движению по медленно меняющимся
эллипсам малых эксцентриситетов, причем движение векторов
Лапласа близко к тому, которое дается описанным выше прибли-
приближением. Более того, если массы планет достаточно малы, то дви-
движения описанного типа заполняют большую часть области фазо-
фазового пространства, соответствующей в кеплеровом приближении

ТЕОРИЯ ВОЗМУЩЕНИЙ УСЛОВНО-ПЕРИОДИЧЕСКИХ ДВИЖЕНИЙ 383
движениям планет в одну сторону по непересекающимся эллип-
эллипсам малых эксцентриситетов.
Число степеней свободы в плоской задаче п планет равно 2п,
если считать Солнце неподвижным. Интеграл кинетического мо-
момента позволяет исключить одну циклическую координату, одна-
однако остается еще слишком много переменных, чтобы инвариантные
торы делили многообразие уровня энергии (даже если планет
всего две, это многообразие пятимерное, а торы трехмерные).
Поэтому в рассматриваемой задаче не удается сделать выводы
о сохранении больших полуосей в течение бесконечного интервала
времени для всех начальных условий, но только для большинства.
Задача с двумя степенями свободы получается при дальнейшей
идеализации. Заменим одну из двух планет «астероидом», кото-
который движется в поле второй планеты («Юпитера»), не возмущая
движения последнего.
Задача о движении такого астероида называется ограниченной
задачей трех тел. Плоская ограниченная задача трех тел приво-
приводит к системе с двумя степенями свободы, периодически завися-
зависящей от времени, для движения астероида. Если же вдобавок орбита
Юпитера круговая, то во вращающейся вместе с ним системе ко-
координат для движения астероида получается автономная гамиль-
тонова система с двумя степенями свободы — так называемая
плоская ограниченная круговая задача трех тел.
В этой задаче имеется малый параметр — отношение масс
Юпитера и Солнца. Нулевому значению параметра отвечает не-
невозмущенное кеплерово движение астероида, изображающееся
в нашем четырехмерном фазовом пространстве условно-периоди-
условно-периодическим движением по двумерному тору (так как система коорди-
координат вращается). Одна из частот этого условно-периодического дви-
движения одинакова при всех начальных условиях: это угловая ско-
скорость вращения системы координат, т. е. частота обращения Юпи-
Юпитера вокруг Солнца. Вторая же частота зависит от начальных
условий (это частота обращения астероида вокруг Солнца) и ме-
меняется на фиксированном трехмерном многообразии уровня функ-
функции Гамильтона.
Следовательно, условие невырожденности в нашей задаче не
выполняется, но условие изоэнергетической невырожденности
выполняется. Итак, теорема Колмогорова применима, и мы за-
заключаем, что большинство инвариантных торов с иррациональным
отношением частот сохраняется в случае, когда масса возмущаю-
возмущающей планеты (Юпитера) отлична от нуля, но достаточно мала.
Далее, двумерные инвариантные торы делят трехмерное мно-
многообразие уровня функции Гамильтона. Следовательно, величина
большой полуоси и эксцентриситет кеплерова эллипса астероида
будут вечно оставаться вблизи своих начальных значений, если
в начальный момент кеплеров эллипс не пересекал орбиту возмуща-
возмущающей планеты и если масса этой планеты достаточно мала.

384 ДОБАВЛЕНИЕ 9
При этом в неподвижной системе координат кепплеров эллипс
астероида может медленно поворачиваться, так как наша система
лишь изоэнергетически невырождена, и поэтому при возмущении
инвариантного тора сохраняются не частоты, а только их отно-
отношение. В результате возмущения частота азимутального движения
перигелия астероида в подвижной системе координат может сде-
сделаться слегка отличной от частоты Юпитера, и тогда в неподвиж-
неподвижной системе перигелий будет медленно поворачиваться.
Добавление 9
ГЕОМЕТРИЧЕСКАЯ ТЕОРЕМА ПУАНКАРЕ, ЕЕ ОБОБЩЕНИЯ
И ПРИЛОЖЕНИЯ
В своем исследовании периодических решений задач небесной
механики А. Пуанкаре построил весьма простую модель, уже
содержащую основную трудность задачи. Такой моделью является
сохраняющее площади отображение плоского кругового кольца
на себя.
Отображения указанного вида возникают при исследовании
динамических систем с двумя степенями свободы. А именно,
отображение двумерной поверхности сечения на себя строится
так: каждая точка поверхности сечения переходит в следующую
точку пересечения выпущенной из этой точки фазовой кривой с по-
поверхностью сечения (см. добавление 7).
При этом замкнутым фазовым кривым соответствуют непод-
неподвижные точки отображения или его степеней. И обратно, каждая
неподвижная точка отображения или его степени определяет зам-
замкнутую фазовую кривую.
Таким образом, вопрос о существовании периодических ре-
решений задач динамики сводится к вопросу о неподвижных точках
сохраняющих площади отображений кольца на себя.
Занимаясь такими отображениями, Пуанкаре пришел к сле-
следующей теореме.
А. Неподвижные точки отображения кольца на себя.
Теорема. Пусть дано сохраняющее площади гомеоморфное
отображение плоского кругового кольца на себя. Предположим,
что граничные окружности кольца сдвигаются отображением
в разные стороны. Тогда это отображение имеет не менее двух
неподвижных точек.
Условие, что граничные окружности сдвигаются в разные сто-
стороны, означает, что если выбрать в кольце координаты (х, у
mod 2я), так что граничные окружности будут х = а и .г — Ъ,
то отображение задается формулами
(х, у) -* (/ (х, у), у + g (х, у))

ГЕОМЕТРИЧЕСКАЯ ТЕОРЕМА ПУАНКАРЕ 385
где функции / и g непрерывны и 2я-периодичны по у, причем
/ («, У) = a, f (b, У) = Ь и g (a, j/)< 0, g (b, у)>0 при всех у.
Доказательство этой теоремы, опубликованной Пуанкаре не-
незадолго до его смерти, было дано лишь позже Дж. Д. Биркгофом,
см. его книгу «Динамические системы» (М.: Гостехиздат, 1941).
При этом до сих пор остаются открытыми многие вопросы,
связанные с этой теоремой и особенно с попытками ее многомер-
многомерного обобщения, важными для исследования периодических ре-
решений задач с большим числом степеней свободы.
Дело в том, что рассуждение, с помощью которого Пуанкаре
пришел к своей теореме, применимо в целом ряде других случаев.
Однако хитроумное доказательство, данное Биркгофом, плохо
поддается обобщению. Поэтому неизвестно, правильны ли выводы,
которые подсказывает рассуждение Пуанкаре, за пределами тео-
теоремы о двумерном кольце. Рассуждение, о котором идет речь,
состоит в следующем.
Б. Связь между неподвижными точками отображения и крити-
критическими точками производящей функции. Будем задавать симп-
лектический диффеоморфизм кольца
(*, у) -> (X, Y)
с помощью производящей функции Ху + S (X, у), где функция S
2я-периодична по у. Для такой записи диффеоморфизма нужно,
чтобы дХ/дх Ф 0. Тогда
dS = (x- X) dy + (Y - у) dX,
и следовательно, неподвижные точки диффеоморфизма являются
критическими точками функции F (х, у) = S (X (х, у), у). Послед-
Последнюю функцию F всегда можно построить, определив ее как инте-
интеграл от формы (х — X) dy + (Y — у) dX. Градиент этой функции
направлен либо внутрь кольца, либо наружу на обеих граничных
окружностях одновременно (в силу условия о вращении в разные
стороны).
Но всякая гладкая функция в кольце, градиент который на
обеих граничных окружностях направлен внутрь кольца (или
вовне его) имеет внутри кольца критическую точку (максимум
или минимум). Более того, можно показать, что число критических
точек такой функции в кольце не меньше двух. Следовательно, мы
могли бы утверждать, что наш диффеоморфизм имеет не менее
двух неподвижных точек, если бы мы были уверены, что каждая
критическая точка функции F является неподвижной точкой ото-
отображения.
К сожалению, последнее верно лишь при дополнительном ус-
условии, что дХ/дх Ф 0, при котором можно выразить F через X
и у. Таким образом, наше рассуждение проходит для отображений,
не слишком сильно отличающихся от тождественного. Например,

386 ДОБАВЛЕНИЕ 9
достаточно, чтобы производные производящей функции S были
меньше 1.
Некоторое усовершенствование того же рассуждения (с дру-
другим выбором производящей функции *)) показывает, что до-
достаточно даже, чтобы собственные числа матрицы Якоби
D (X,Y)/D (х, у) ни в одной точке не были равны —1, т. е. чтобы
наше отображение не переворачивало бы касательное пространство
ни в одной точке. К сожалению, все такие условия нарушаются в
некоторых точках для отображений, далеких от тождественного.
Доказательство теоремы Пуанкаре в общем случае использует
совсем иные соображения.
Связь неподвижных точек отображения с критическими точ-
точками производящих функций кажется более глубоким фактом,
чем сама теорема об отображениях двумерного кольца.
Ниже приведено несколько примеров, в которых эта связь
приводит к содержательным выводам, правда, при некоторых
ограничениях, необходимость которых неясна.
В. Симплектические диффеоморфизмы тора. Рассмотрим симп
лектпческий диффеоморфизм тора, оставляющий на месте центу)
тяжести
(хш y)~(x + f (х, у), y + g (х, у)) = (X, У),
где х и у modd 2я — угловые координаты на торе, симплектич-
ность означает равенство 1 якобиана D (X, Y)ID (ж, у), а условие
сохранения центра тяжести состоит в том, то средние значения
функций / и g равны нулю.
Теорема. Такой диффеоморфизм имеет не менее четырех
неподвижных точек, считая кратности, и не менее трех геометри-
геометрически различных, по меньшей мере в предположении, что собствен-
собственные числа матрицы Якоби ни в одной точке не равны —1.
Доказательство основано на рассмотрении функции на торе,
заданной формулой
Ф (х, У) - 4" $ (Х ~ x)(dY + йУ) ~(Y- У)@Х + dx),
и на том, что гладкая функция на торе имеет не менее четырех
критических точек (считая кратности), в том числе не менее трех
геометрически различных.
Попытки доказательства этой теоремы без ограничения на соб-
собственные числа наталкиваются на трудности, очень похожие на те,
с которыми столкнулся Пуанкаре в теореме о кольце.
Заметим, что теорема о кольце вытекала бы из теоремы о торе, если бы
в последней можно было отбросить условие на собственные числа. В самим
деле, составим тор из двух экземпляров нашего кольца, вставив вблизи каж-
каждой из двух граничных окружностей еще по узкому соединительному кольцу.
*)do = ±\x-x Y~y I
' . 2\dX + dx dV+dy\-

ГЕОМЕТРИЧЕСКАЯ ТЕОРЕМА ПУАНКАРЕ 387
Тогда мы можем достроить наше отображение кольца до симплекти-
ческого диффеоморфизма тора так, что: 1) на каждом из двух больших колец
диффеоморфизм будет совпадать с исходным, 2) на каждом из соединительных
колец диффеоморфизм не будет иметь неподвижных точек, 3) центр тяжести
будет оставаться на месте.
Построение такого диффеоморфизма тора использует свойство вращения
граничных окружностей в разные стороны. На каждом соединительном
кольце все точки сдвигаются в ту же сторону, что и на обеих окружностях,
ограничивающих соединительное кольцо. Поскольку направления сдвига
на обоих соединительных кольцах противоположны, величину сдвш а можно
подобрать так, чтобы обеспечить сохранение центра тяжести.
Теперь из четырех неподвижных точек на торе две должны лежать в ис-
исходном кольце, и мы получаем из теоремы о торе теорему о кольце.
Сформулированная выше теорема о торе допускает обобщение
на другие симплектические многообразия, как двумерные так и
многомерные. Чтобы сформулировать эти обобщения, нужно преж-
прежде всего переформулировать условие сохранения центра тяжести.
Пусть g: М —> М — симплектический диффеоморфизм. Мы
скажем, что диффеоморфизм g гомологичен тождественному, если
его можно соединить с тождественным диффеоморфизмом (оставляю-
(оставляющим на месте все точки многообразия М) гладкой кривой gt,
состоящей из симплектических диффеоморфизмов, так, чао поле
скоростей gt в каждый момент времени t имеет однозначную функ-
функцию Гамильтона. Можно доказать, что симплектические диффео-
диффеоморфизмы, гомологичные тождественному, образуют коммутант
связной компоненты единицы в группе всех симплектических диф-
диффеоморфизмов многообразия.
В случае, когда наше многообразие — двумерный тор, гомоло-
гомологичные тождественному симплектические диффеоморфизмы — это
в точности те, которые мы назвали выше сохраняющими центр
тяжести.
Таким образом, мы приходим к следующему обобщению тео-
теоремы Пуанкаре.
Теорема. Всякий гомологичный тождественному симплек-
симплектический диффеоморфизм компактного симплектического много-
многообразия имеет по меньшей мере столько неподвижных точек, сколь-
сколько критических точек имеет гладкая функция на этом многообра-
зииг во всяком случае, если этот диффеоморфизм не слишком да-
далек от тождественного.
Заметим, что условие гомологичное™ тождественному отобра-
отображению существенно, как видно уже из примера свига на торе, не
имеющего ни одной неподвижной точки.
Что касается последнего ограничения (диффеоморфизм не
слишком далек от тождественного), то неясно, существенно ли
оно. В случае, когда наше многообразие — 2п-мерный тор, доста-
достаточно, чтобы ни одно из собственных чисел матрицы Якоби диф-
диффеоморфизма (в какой-либо глобальной симплектической системе
координат, заданной в R2*1) не равнялось минус единице.

388 ДОБАВЛЕНИЕ 9
Ограничение такого рода, быть может, и необходимо в многомерных
задачах. Ибо не исключено, что теорема Пуанкаре является существенно
двумерным эффектом*), подобно следующей теореме А. И. Шнирельмана и
Н. А. Никишина. Всякий сохраняющий площадь диффеоморфизм двумерной
сферы на себя имеет по меньшей мере две геометрически различные неподвиж-
неподвижные точки.
Доказательство этой теоремы основано на том, что индекс векторного
поля градиента гладкой функции двух переменных в изолированной крити-
критической точке не может быть больше единицы (хотя может быть равен 1, О,
—1, —2, —3, . ..), а сумма индексов всех неподвижных точек сохраняющего
ориентацию диффеоморфизма двумерной сферы на себя равна двум.
Индекс же градиента гладкой функции большого числа переменных в
критической точке может принимать любые целые значения.
Г. Пересечения лагранжевых многообразий. Рассуждению
Пуанкаре можно придать несколько иную форму, если рассмот-
рассмотреть на каждом радиусе кольца точки, сдвигающиеся чисто ра-
диально. Такие точки есть на каждом радиусе, так как ограничи-
ограничивающие кольцо окружности поворачиваются в разные стороны.
Предположим, что нам удалось составить из радиально сдвигаю-
сдвигающихся точек замкнутую кривую, разделяющую внешнюю и внут-
внутреннюю окружности кольца. Тогда образ этой кривой при нашем
отображении должен пересекаться с самой кривой (так как об-
области, на которые кривая делит кольцо, переходят в области рав-
равной площади).
Если указанная кривая и ее образ пересекают каждый радиус
по одному разу, то точки пересечения кривой с образом являются,
очевидно, неподвижными точками отображения.
Кое-что из приведенного рассуждения можно перенести на
многомерный случай, и это дает полезные результаты о периоди-
периодических решениях задач динамики. Роль кольца в многомерном
случае играет фазовое пространство: прямое произведение области
в евклидовом пространстве на тор того же числа измерений (коль-
(кольцо — это произведение интервала на окружность). Симплекти-
ческая структура в фазовом пространстве задается обычным
образом, т. е. имеет вид Q = 2 dx^ Д dj/k, где х* — переменные
действия, а ^ — угловые переменные.
Нетрудно выяснить, какие симплектические диффеоморфизмы
нашего фазового пространства гомологичны тождественному.
Именно, симплектический диффеоморфизм А гомологичен тож-
тождественному, если его можно получить из тождественного непре-
непрерывной деформацией и кроме того,
ф xdy = (j) xdy
У AJ
для всякого замкнутого контура (не обязательно гомологичного
нулю). Условие гомологичности тождественному преобразованию
•) Это опасение не подтвердилось.

ГЕОМЕТРИЧЕСКАЯ ТЕОРЕМА ПУАНКАРЕ 389
запрещает систематический сдвиг вдоль ж-направления («эволюцию
переменных действия»), разрешая сдвиги вдоль торов.
Рассмотрим какой-нибудь из ю-мерных торов х = с = const
и применим к нему наш гомологичный тождественному симплек-
тический диффеоморфизм. Получим снова /г-мерный тор. Оказы-
Оказывается, исходный тор пересекается со своим образом по меньшей
мере в 2й точках (считая с кратностями), в том числе не менее
п -\- 1 из них геометрически различны, во всяком случае в предпо-
предположении, что тор-образ имеет уравнение вида х = / (у) с гладкой /.
При п = 1 выделенное утверждение означает, что каждая из
концентрических окружностей, составляющих кольцо, пересе-
пересекается со своим образом не менее чем в двух точках. Это сразу
следует из сохранения площадей, причем предположение о том,
что образ имеет уравнение х = f (у), не нужно. Если его при-
принять, то доказательство проходит следующим образом (без него
доказательство при п^>1 трудное).
Заметим, что исходный тор является лагранжевым подмного-
подмногообразием фазового пространства. Наш диффеоморфизм симплек-
тический, поэтому тор-образ также лагранжев. Стало быть,
1-форма (х — с) dy на нем замкнута. Более того, эта форма на
торе является полным дифференциалом некоторой однозначной
гладкой функции F, так как наш диффеоморфизм гомологичен
единице, и следовательно, для любого замкнутого контура
(х — с) dy = ф xdy — (? cdy = (f xdy — (j) cdy =
A A A
Ay Ay V Ay
У А\
Заметим, что точки пересечения тора с его образом являются
критическими точками функции F (поскольку в них dF =
= (x — c)dy = 0).
Из условия однозначной проектируемости тора-образа (т. е.
из того, что тор-образ имеет уравнение х = f (у)) вытекает, что и
обратно, все критические точки функции F являются точками пе-
пересечения наших торов. В самом деле, при указанном условии у
можно принять за локальную координату на торе, и следователь-
следовательно, равенство dF нулю для всех касательных к тору-образу век-
векторов влечет х = с.
Гладкая функция на n-мерном торе имеет не менее 2й крити-
критических точек, считая кратности, в том числе не менее п + 1 гео-
геометрически различных (см., например, М и л н о р. Теория Мор-
Морса.—М.: Мир, 1965).
Следовательно, наши торы пересекаются не менее чем в 2"
точках (считая кратности), причем геометрически различных
точек пересечения не менее п + 1.
Точно такое же рассуждение показывает, что образ любого
лагранжева тора пересекается с этим тором по меньшей мере

390 ДОБАВЛЕНИЕ 9
в 2п точках (в том числе геометрически различных точек не менее
п + 1), в предположении, что как исходный тор, так и его образ,
однозначно проектируются на у-пространстео, т. е. задаются
уравнениями х = / (у), х = g (у) соответственно.
Впрочем, это предложение сводится к предыдущему канони-
каноническим преобразованием (х, у) >-*¦ (х — / (у), у).
Д. Применения к отысканию неподвижных точек и периоди-
периодических решений. Рассмотрим теперь гомологичное тождественному
симплектическое преобразование того специального вида, который
возникает в интегрируемых проблемах динамики, т. е. вида
А- о (х, у) = (ж, у + о (х)), где со = dSldx.
Здесь х е= Rn—переменная действия, у modd2it E Г" — угловая
координата.
Предположим, что на торе х = х0 все частоты соизмеримы:
h
щ(х0) =~-2л с целыми кь Л7;
ы (х0) Ф 0,
и что выполнено условие невырожденности
det | ды1дх |ж, ф 0.
Теорема. Всякий гомологичный тождественному симплек-
тический диффеоморфизм А, достаточно близкий к Ао, имеет
вблизи тора х = х0 не менее 2п периодических точек | периода N
(так что AN\ = |), считая кратности.
Доказательство можно было бы свести к иссследованию пересечения
двух лагранжевых подмногообразий 4п-мерного пространства (Rn X
X f X R" X Тп) с Q — dx /\ dy — dX Д dY, одно из которых диагональ
(X = х, Y = у), а другое — график отображения Лл.
Однако проще непосредственно построить подходящую функцию на торе.
Действительно, отображение А^ имеет вид
{х, у) нч- (х, у + а (х)), где а (х0) = 0, det | да/дх ^ ф 0.
По теореме о неявной функции отображение AN имеет близ тора х = х0
тор, смещающийся чисто радиально ((я, у) >-*¦ {X, у)) и задающийся уравнени-
уравнением вида х = / (у), причем его образ также задается уравнением такого же
вида, х ~ g (у). В этих обозначениях X (/ (у), у) = g (у), Y (f(y), у) = у.
Из гомологичности отображения А единице вытекает, что AN имеет
однозначную глобальную производящую функцию вида Ху -\- S (X, у)г
где S имеет по переменным у период 2я.
Функция F (у) = S (X (/ (у), у), у) имеет на торе минимум 2п критичес-
критических точек j/jf. Все точки ?к = (/ (у^), у^) являются неподвижными точками
для AN. Действительно,
dF=(x- X) dy+(Y- у) dX = (x- X) dy = (/ (у) - g (у)) dy.
Поэтому из dF | = 0 вытекает, что / (уц) = g (ук), т. е. AnIk = |ftt чт° в
требовалось доказать.

ГЕОМЕТРИЧЕСКАЯ ТЕОРЕМА ПУАНКАРЕ 391
Обратимся теперь к замкнутым траекториям консервативных
систем. Пользуясь терминологией добавления 8, мы можем сфор-
сформулировать результат так.
Следствие. При распаде п-мерного инвариантного mopat
сплошь заполненного замкнутыми траекториями изоэнергетически
невырожденной системы с п степенями свободы, образуются не
менее 2"-1 замкнутых траекторий возмущенной задачи {считая
с кратностями), в том числе не менее п геометрически различных^
по меньшей мере если возмущение достаточно мало.
Доказательство сводится к предыдущей теореме при помощи
2п—2-мерной поверхности сечения. При этом следует вначале
выбрать угловые координаты у так, чтобы замкнутые траектории
невозмущенной задачи на торе задавались уравнениями у2 = . . .
. . . = i/n = 0, а затем определить поверхность сечения урав-
уравнением yt = 0.
В случае двух степеней свободы можно применять теорему
Пуанкаре к кольцам, которые образуются при пересечении ин-
инвариантных торов с двумерной секущей поверхностью. Мы полу-
получаем следующий результат.
В щели между двумя двумерными инвариантными торами
системы с двумя степенями свободы всегда есть не менее двух за-
замкнутых фазовых траекторий, если отношения частот условно-
периодических движений на этих торах различны.
Тем самым получается много периодических решений во всех
задачах с двумя степенями свободы, где найдены инвариантные
торы (например, в ограниченной круговой задаче трех тел, в за-
задаче о замкнутых геодезических и т. п.). Существует даже гипо-
гипотеза, что в гамильтоновых системах «общего вида» с компактным
фазовым пространством замкнутые фазовые кривые образуют
всюду плотное множество. Впрочем, если это и верно, замкнутость
большинства из таких кривых не имеет существенного значения,
так как их периоды чрезвычайно велики.
Примером применения методики Пуанкаре к системе с боль-
большим чем 2 числом степеней свободы является теорема Биркгофа
о существовании бесконечного числа периодических решений,
близких к данному линейно-устойчивому периодическому решению
общего вида (или о существовании бесконечного числа периоди-
периодических точек в окрестности неподвижной точки линейно-устой-
линейно-устойчивого невырожденного симплектического отображения простран-
пространства на себя). Доказательства заключаются в том, что сначала
отображение аппроксимируется своей нормальной формой, а по-
потом используется связь между неподвижными точками отображе-
отображения и критическими точками производящей функции.
Знание периодических решений позволяет, между прочим,
доказывать несуществование первых интегралов (отличных от клас-
классических) во многих задачах динамики. Предположим, например,
что на каком-либо многообразии уровня известных интегралов

392 ДОБАВЛЕНИЕ 9
обнаружена периодическая траектория, которая неустойчива.
Ее сепаратрисы в общем случае образуют сложную сеть, которую
мы рассматривали в добавлении 7. Если это явление расщепле-
расщепления сепаратрис удается обнаружить и если мы сумеем доказать,
что сепаратрисы не укладываются ни в какое многообразие мень-
меньшего числа измерений, чем рассматриваемое многообразие уров-
уровня, то мы можем быть уверенными, что система не имеет новых
первых интегралов.
Впрочем, сложное поведение фазовых кривых, препятствую-
препятствующее существованию первых интегралов, часто удается обнару-
обнаружить и без помощи периодических решений, просто с одного
взгляда на найденную вычислительной машиной картину, обра-
образованную пересечением фазовой кривой с поверхностью сечения.
Е. Инвариантность производящей функции. Выше мы уже
отмечали удручающую неинвариантность производящих функций
относительно выбора канонической системы координат в симплек-
тическом многообразии.
С другой стороны, мы неоднократно использовали связь между
неподвижными точками отображения и критическими точками
производящей функции.
Оказывается, хотя вообще производящая функция и неинва-
неинвариантно связана с отображением, вблизи неподвижной точки
инвариантная связь имеется.
Точнее, пусть дан оставляющий на месте некоторую точку
симплектический диффеоморфизм. Определим в окрестности этой
| l 2 «ИГ* + dlk
с помощью некоторой симплектической системы координат (х, у) *).
Далее, построим с помощью другой симплектической системы
координат (х', у') аналогично определяемую производящую функ-
функцию Ф'.
Теорема. Если линеаризация симплектического диффео-
диффеоморфизма в неподвижной точке не имеет собственных чисел, рав-
равных —1, то функции ФкФ' эквивалентны в ее окрестности в том
смысле, что существует такой диффеоморфизм g (вообще несимп-
лектический), что
Ф (z) == Ф' (g (z)) + const.
Доказательство см. в статье: Weinstein A. The invariance
of Poincare's generating function for canonical transformations //
Inventions Mathematicae.— 1972.— V. 16, № 3.— P. 202—214.
ффрф р р
точки «производящую функцию» Ф = 4" S Ц | dll +2, *
й й
*) Приращение этой функции вдоль какой-либо дуги равно интегралу
формы, задающей симплектическую структуру по полоске, образованной
прямолинейными отрезками, соединяющими каждую точку с ее образом.
Поэтому такая функция Ф связана с отображением инвариантно относитель-
относительно линейных канонических замен координат.

КРАТНОСТИ СОБСТВЕННЫХ ЧАСТОТ 393
Следует заметить, что два диффеоморфизма с эквивалентными
в окрестности неподвижной точки производящими функциями
не обязательно эквивалентны в классе симплектических диффео-
диффеоморфизмов.
Предположения, высказанные в первом издании этой книги
в виде гипотез, для торов и двумерных многообразий теперь дока-
доказаны. См.: Conley C.C., ZehnderE. The Birkhoff —
Lewis fixed point theorem and a conjecture of V. I. Arnold // Invent.
Math.— 1983.— V. 73.— P. 33—49; LandenbachF., Sico-
r a v J. C. Persistence d'intersection avec la section nulle au
cours d'une isotopie hamiltonienne dans un fibre cotangent//Invent
Math.— 1985.— V. 82.— P. 349—358; см. также: А р н о л ь д В. И.
Первые шаги симплектической топологии//УМН.— 1985.— Т. 41,
JY° 6.— С. 3—18. Развивающие эту тему работы Хофера, Флоера,
Громова, Элиашберга, Витербо, Вейнстейна, Гивенталя и др. уже
могли бы составить целую книгу.
Добавление 10
КРАТНОСТИ СОБСТВЕННЫХ ЧАСТОТ П ЭЛЛИПСОИДЫ,
ЗАВИСЯЩИЕ ОТ ПАРАМЕТРОВ
Семейства эллипсоидов в евклидовом пространстве встреча-
встречались нам несколько раз в этом курсе. Например, при изучении
зависимости собственных частот малых колебаний от параметров
мы встречались с зависящим от жесткости системы эллипсоидом
уровня потенциальной энергии в евклидовом пространстве (мет-
(метрика пространства определяется кинетической энергией). Другой
пример — эллипсоид инерции твердого тела (параметры здесь —
форма твердого тела и распределение масс в нем).
Здесь мы рассмотрим общий вопрос о том, при каких значе-
значениях параметров спектр собственных чисел вырождается, т. е.
соответствующий эллипсоид становится эллипсоидом вращения.
Заметим, что собственные числа квадратичной формы в евклидо-
евклидовом пространстве (или длины осей эллипсоида) непрерывно ме-
меняются при непрерывном изменении параметров системы (коэф-
(коэффициентов формы). Кажется естественным ожидать, что в зави-
зависящей от одного параметра системе при изменении параметра
в отдельные моменты одно из собственных чисел будет сталкивать-
сталкиваться с другим, так что при отдельных значениях параметра система
будет иметь кратный спектр.
Представим себе, например, что мы хотим превратить эллип-
эллипсоид инерции твердого тела в эллипсоид вращения, перемещая
по жестко закрепленной в теле штанге одну юстировочную массу,
так что в нашем распоряжении имеется один параметр. Три глав-
главные оси инерции а, Ъ, с будут непрерывными функциями от этого
параметра, и на первый взгляд кажется, что при надлежащем

394 ДОБАВЛЕНИЕ 10
значении параметра (р) можно добиться равенства двух осей,-
скажем а (р) = Ъ (р).
Оказывается, однако, что дело обстоит в действительности
не так и что, вообще говоря, нужно перемещать не менее двух
котировочных масс, чтобы сделать эллипсоид инерции эллип-
эллипсоидом вращения.
Вообще, кратный спектр в типичных семействах квадратич-
квадратичных форм наблюдается лишь при двух или более параметрах,
а в однопараметрических семействах общего вида спектр при
всех значениях параметра простой. Практически это проявля-
проявляется в том, что при изменении параметра в типичном однопара-
метрическом семействе собственные числа могут тесно сближать-
сближаться, но, подойдя достаточно близко одно к другому, как бы на-
начинают отталкивать друг друга и снова расходятся, обма-
обманув надежду меняющего параметр лица добиться кратного
спектра.
В настоящем добавлении рассматриваются причины этого
странного на первый взгляд поведения собственных чисел, а также
коротко обсуждаются аналогичные вопросы для систем с различ-
различными группами симметрии.
А. Многообразие эллипсоидов вращения. Рассмотрим множест-
множество всевозможных квадратичных форм в евклидовом п-мерном
пространстве Rn. Это множество само имеет естественную струк-
структуру линейного пространства размерности п (п -{- 1I2. Например,
все квадратичные формы на плоскости образуют трехмерное
пространство (форма Ах* + 2Вху + Су2 имеет координатами три
числа А, В, С).
Положительно определенные формы образуют в этом про-
пространстве квадратичных форм открытую область (например, в слу-
случае плоскости это внутренность одной из пол конуса В2 = АС,
образованного вырожденными формами).
Каждый эллипсоид с центром в начале координат задает по-
положительно определенную квадратичную форму, для которой
он является множеством уровня 1; обратно, множество уровня 1
любой положительно определенной квадратичной формы явля-
является эллипсоидом. Мы можем, следовательно, отождествить мно-
множества положительно определенных квадратичных форм и эллип-
эллипсоидов с центром в начале координат.
Тем самым мы введем в множестве эллипсоидов с центром О
в R*1 структуру гладкого многообразия размерности п (п + 1)/2
(это многообразие покрыто одной картой: указанной выше областью
в пространстве квадратичных форм).
Рассмотрим теперь множество всевозможных эллипсоидов вра-
вращения. Я утверждаю, что это множество имеет в рассматривае-
рассматриваемом пространстве коразмерность 2, т. е. задается двумя неза-
независимыми уравнениями, а не одним, как это кажется на первый
взгляд. Точнее, справедлива

КРАТНОСТИ СОБСТВЕННЫХ ЧАСТОТ 395
Теорема 1. Множество эллипсоидов вращения представ-
представляет собой конечное объединение гладких подмногообразий кораз-
коразмерности 2 и выше в многообразии всех эллипсоидов.
Здесь коразмерностью подмногообразия называется разность
между размерностью объемлющего пространства и размерностью
подмногообразия.
Доказательство. Рассмотрим вначале эллипсоиды в
/г-мерном пространстве, у которых две равные оси, а остальные
оси различны. Такой эллипсоид определяется направлениями
различных осей, что дает
(п — 1) + (п — 2) + . . . + 2 = (п + 1)(п — 2)/2
параметров, и еще величинами осей, что дает п — 1 параметр.
Итак, общее число параметров равно (п2 — п — 2 + 2/г — 2)/2,
что на два меньше размерности пространства всех эллипсоидов
(равной п (п -\- 1)/2). Приведенный подсчет параметров показы-
показывает также, что множество эллипсоидов с ровно двумя равными
осями является многообразием.
Что касается эллипсоидов с большим числом равных осей,
то ясно, что все они образуют множество еще меньшей размернос-
размерности. Строгое доказательство вытекает из следующей леммы.
Лемма. Множество всех эллипсоидов, имеющих v2 двукрат-
двукратных, v3 трехкратных, v4 четырехкратных осей и т. д., является
гладким подмногообразием многообразия всех эллипсоидов, имею-
имеющим коразмерность
Доказательство этой леммы проводится таким же подсчетом
параметров, как в разобранном выше частном случае (который
соответствует v2 — 1» v3 = v4 = . . . = 0). Читатель легко сам
проведет этот подсчет, заметив сперва, что размерность много-
многообразия всех ^-мерных подпространств в n-мерном линейном про-
пространстве равна к (п — к) (так как йьмерную плоскость общего
положения в n-мерном пространстве можно рассматривать как
график отображения из ^-мерного пространства в п — ^-мерное,
а такое отображение задается прямоугольной матрицей размера
к X (п — к)).
Пример. Рассмотрим случай п = 2, т. е. эллипсы на плос-
плоскости. Эллипс определяется тремя параметрами (например, двумя
длинами осей и углом, задающим направление одной из них).
Таким образом, многообразие эллипсов на плоскости трехмерно,
как и должно быть по нашей формуле.
Окружность же определяется одним параметром (радиусом).
Таким образом, многообразие окружностей в пространстве эллип-
эллипсов — это линия в трехмерном пространстве, а не поверхность^
как кажется на первый взгляд.

396 ДОБАВЛЕНИЕ 10
Этот «парадокс» становится, быть может, более понятным из следующего
вычисления. Квадратичные формы Ахг + 2Вху -\- Су2 с равными собственны-
собственными числами образуют в трехмерном пространстве с кс/ординатамн А, В, С
многообразие, заданное одним уравнением X,x = к2, где Xli2 (А, В, С) — соб-
собственные числа. Однако левая часть этого уравнения является суммой двух
квадратов, что видно из формулы для дискриминанта характеристического
уравнения
д = (Л + СJ — 4 {АС — Bz) = {А —1СJ + 4В2.
Таким образом, одно уравнение Д = 0 определяет в трехмерном простран-
пространстве квадратичных форм прямую (А = С, В = 0), а не поверхность.
Простейший вывод из того, что многообразие эллипсоидов
вращения имеет коразмерность 2, состоит в том, что это много-
многообразие не делит пространство всех эллипсоидов (а многообразие
квадратичных форм с кратным спектром не делит пространство
квадратичных форм), подобно тому как прямая не делит трехмер-
трехмерное пространство.
Следовательно, мы можем утверждать не только, что у эллип-
эллипсоида «общего положения» все оси разной длины, но и что любые
два такие эллипсоида можно соединить гладкой кривой в простран-
пространстве эллипсоидов, сплошь состоящей из эллипсоидов с осями разной
длины. Более того, если два эллипсоида общего положения соеди-
соединены гладкой кривой в пространстве эллипсоидов, на которой
есть точки, являющиеся эллипсоидами вращения, то сколь угодно
малым шевелением кривой можно снять ее с множества эллипсои-
эллипсоидов вращения, так что на новой кривой все точки будут эллип-
эллипсоидами без кратных осей.
Из сказанного вытекает, в частности, простое доказательство
теоремы о возрастании собственных частот при возрастании жест-
жесткости системы. Действительно, производные некратного собствен-
собственного числа квадратичной формы по параметру определяются про-
производной квадратичной формы по соответствующему собственному
направлению. Если жесткость растет, то потенциальная энергия
растет по каждому направлению, в том числе и по собственному.
Значит, и собственная частота растет. Тем самым мы доказали
теорему о возрастании частот в случае, когда от исходной системы
к более жесткой можно перейти, минуя кратный спектр. Доказа-
Доказательство в присутствии кратного спектра получается теперь пре-
предельным переходом на основании того, что внутреннюю часть
пути перехода от исходной системы к более жесткой можно сдви-
сдвинуть с множества систем с кратным спектром сколь угодно малым
шевелением.
Резюмируя, мы можем сказать, что типичное однопараметри-
ческое семейство эллипсоидов (или квадратичных форм в евклидо-
евклидовом пространстве) не содержит эллипсоидов вращения (квадра-
(квадратичных форм с кратным спектром). Применительно к эллип-
эллипсоиду инерции получаем приведенный выше вывод о необходи-
необходимости двух юстировочных масс.

КРАТНОСТИ СОБСТВЕННЫХ ЧАСТОТ 397
Обратимся теперь к двупараметрическим семействам. Из на-
наших подсчетов следует, что в типичных двупараметрических се-
семействах эллипсоиды вращения встречаются лишь в отдельных
изолированных точках плоскости параметров.
Рассмотрим, например, выпуклую поверхность в трехмерном евклидовом
пространстве. Вторая квадратичная форма поверхности определяет эллипс
в касательном пространстве в каждой точке. Поэтому возникает двупара-
метрическое семейство эллипсов (которые можно перенести в одну плоскость,.
выбрав вблизи точки на поверхности локальную систему координат). Мы
приходим к выводу, что в каждой точке поверхности, кроме отдельных изо-
изолированных точек, эллипс имеет оси разной длины. Следовательно, на поверх-
поверхности общего вида возникает два ортогональных поля направлений (боль-
(больших и малых осей эллипсов) с изолированными особыми точками. В диф-
дифференциальной геометрии эти направления называются направлениями
главных кривизн, а эти особые точки — омблическими точками. Например,
на поверхности эллипсоида имеется четыре омблическпе точки; они лежат
на содержащем большую и малую оси эллипсе и две ив них хорошо емдиы
на рисунке геодезических на эллипсоиде (см. рис. 207).
Точно так же в типичном т рехпараметрическом семействе
эллипсоиды вращения встречаются лишь на отдельных линиях
в трехмерном пространстве параметров. Например, еслп в каж-
каждой точке трехмерного евклидова пространства задан эллипсоид
(т. е. задан симметричный двухиндексный тензор), то особенности
полей главных осей будут, вообще говоря, на отдельных линиях
(где два из трех полей направлений терпят разрыв).
Эти линии, как и омблические точки в предыдущем прпмерет
бывают нескольких различных типов. Их классификацию (для
типичных полей эллипсоидов) можно получить из классификации
особенностей лагранжевых проекций, приведенной в добавле-
добавлении 12.
В типичном четырехпараметрическом семействе эллипсоиды
вращения встречаются на двумерных поверхностях пространства
параметров. Эти поверхности не имеют особенностей, кроме транс-
версальных пересечений в отдельных точках пространства пара-
параметров; этим значениям параметров отвечают эллипсоиды с двумя
(разными) парами равных осей.
Трехкратная ось появляется впервые при пяти параметрах,
в отдельных изолированных точках пространства параметров.
Значения параметров, соответствующие эллипсоидам с двукрат-
двукратной осью, образуют в пятимерном пространстве параметров трех-
трехмерное многообразие с особенностями двух типов: трансверсаль-
ными пересечениями двух ветвей вдоль некоторой кривой и кони-
коническими особенностями в отдельных (не лежащих на этой кривой^
точках, а именно в точках пространства параметров, соответст-
соответствующих эллипсоидам с трехкратной осью.
Указанная коническая особенность устроена так, что при пересечении че-
четырехмерной сферой малого радиуса с центром в особой точке получаются
два экземпляра проективной плоскости. Возникающие вложения проективной
плоскости в четырехмерную сферу диффеоморфны вложению, которое-

398
ДОБАВЛЕНИЕ 10
задается пятью сферическими функциями второй степени на двумерной сфере
¦(пять ортонормированных в пространстве функций на сфере х\ + х\ + г| = 1
линейных комбинаций функций xiij, ортогональных единице, задают четное
отображение Sz —» S* и, следовательно, вложение RP2-» S4).
Полезно разобраться еще, как ведут себя собственные числа
квадратичной формы из типичного двупараметрического семей-
семейства при подходе к особой точке, где два собственных числа сов-
совпадают. Небольшое вычисление показывает, что график указан-
указанной пары собственных чисел имеет над плоскостью параметров
вблизи особой точки вид двуполого конуса, вершина которого
отвечает особой точке, а каждая из половин — одному из собст-
собственных чисел (рис. 243).
Типичное одномерное подсемейство нашего двумерного семей-
семейства имеет вид кривой в плоскости параметров, не проходящей
через особую точку. Всякое одномерное подсемейство, содержа-
содержащее особую точку, можно сдвинуть с нее малым шевелением,
причем получающееся одно-
одномерное семейство будет кри-
кривой в пространстве парамет-
параметров, проходящей близко от
особой точки. График собст-
У^. у ^-^^ венных чисел над кривой на
уг \ к!!——" ^""> плоскости параметров, про-
проходящей вблизи особой точ-
точки, состоит из тех точек ко-
конуса, которые проектируют-
проектируются на эту кривую. Следова-
Следовательно, указанный график
вблизи особой точки близок к гиперболе, похожей на пару пере-
пересекающихся прямых (пара прямых получилась бы, если бы наше
однопараметрическое семейство проходило через особую точку).
Приведенное рассуждение о собственных числах двупарамет-
рических семейств квадратичных форм объясняет странное пове-
поведение собственных частот при изменении одного параметра: вооб-
вообще говоря (исключая случаи совершенно особые) при изменении
одного параметра собственные частоты могут подходить близко
друг к другу, но не могут обгонять друг друга, а должны, сбли-
сблизившись, снова разойтись в разные стороны.
Б. Применение к исследованию колебаний сплошных сред.
Приведенные выше общие соображения имеют многочисленные
приложения при исследовании зависимости от параметров собст-
собственных частот разнообразных механических систем с конечным
числом степеней свободы; однако, вероятно, наиболее интересные
их приложения относятся к системам с бесконечным числом сте-
степеней свободы, описывающим колебания сплошных сред. Эти
приложения основаны на том, что коразмерности многообразий
эллипсоидов с теми или иными кратностями осей определяются
Рис. 243. Собственные частоты одно- и двух-
параметрических семейств колебательных сис-
систем общего вида

КРАТНОСТИ СОБСТВЕННЫХ ЧАСТОТ 399
этими кратностями и не зависят от числа измерений простран-
пространства.
Например, коразмерность множества эллипсоидов вращения
в многообразии всех эллипсоидов равна двум в пространстве
любого числа измерений; поэтому естественно считать, что и в бес-
бесконечном «многообразии» эллипсоидов в бесконечномерном гиль-
гильбертовом пространстве множество эллипсоидов вращения имеет
коразмерность 2 (и, в частности, пространство эллипсоидов без
кратных осей связно).
Конечно, рассуждения подобного рода нуждаются в строгом
обосновании. Мы однако не будем этим заниматься, а посмотрим,
к каким выводам приводят развитые выше общие соображения,
«ели не побояться применить их к задаче о колебаниях сплош-
сплошной среды.
Кинетическая энергия сплошной среды, заполняющей компакт-
компактную область D, выражается через отклонение и точки х от равно-
равновесия формулой
2 )иах-
D
Среду мы будем для определенности считать мембраной (в этом
случае область D двумерна, а отклонение и одномерно). Кинети-
Кинетическая энергия задает евклидову структуру в конфигурационном
пространстве задачи (т. е. в пространстве функций и). Потен-
Потенциальная энергия дается интегралом Дирихле
U = -|- { (VuJ dx
D
(с математической точки зрения эти данные входят в определение
мембраны).
Квадраты собственных частот мембраны — это собственные
числа квадратичной формы U в конфигурационном пространстве,
метрика которого задана с помощью кинетической энергии. Мы
примем, что типичной мембране отвечает типичная квадратичная
¦форма (предположение это означает трансверсальность много-
многообразия квадратичных форм, соответствующих разным мембра-
мембранам, многообразию форм с кратными собственными числами).
Если поверить в это свойство общего положения, то мы приходим
к следующим выводам.
1. Для мембраны общего положения все собственные частоты
различны. От одной мембраны общего положения к другой можно
перейти непрерывным путем, сплошь состоящим из мембран
с простым спектром. Более того, типичный путь, соединяющий
две любые мембраны, не содержит ни одной мембраны с кратным
спектром (исключая, возможно, концы пути).

400 ДОБАВЛЕНИЕ 10
2. Меняя два параметра мембраны, можно добиться совпаде-
совпадения двух собственных частот; чтобы получить трехкратную
частоту, нужно иметь в своем распоряжении пять независимых
параметров, четырехкратную — девять и т. д.
3. Если, отправляясь от мембраны с простым спектром и
непрерывно деформируя ее, перейти к другой мембране с простым
спектром по любому пути общего положения, то в результате
такого продолжения из k-й по величине собственной частоты ис-
исходной мембраны получится независимо от пути деформации
всегда к-я по величине собственная частота конечной мембра-
мембраны; продолжение же собственных функций, вообще говоря, за-
зависит от пути деформации (а именно, при изменении пути может
измениться знак получающейся собственной функции).
В частности, если, начав с мембраны с простым спектром
и деформируя ее, мы опишем замкнутый путь в пространстве
мембран и вернемся к исходной мембране, обойдя вокруг мно-
множества мембран с кратным спектром (которое ведь имеет кораз-
коразмерность 2), то k-я собственная частота вернется к исходному
значению, а к-я собственная функция может сменить знак.
В. Влияние симметрии на кратность спектра. Кратный спектр
является исключением в системах общего вида, но он появляется
неустранимым малым шевелением образом в случаях, когда дан-
данная система симметрична и деформации сохраняют симметрию.
Рассмотрим, например, систему из трех одинаковых масс
в вершинах равностороннего треугольника, соединенных одина-
одинаковыми пружинами друг с другом и с центром треугольника
и способных двигаться в плоскости треугольника. Система имеет
поворотную симметрию третьего порядка. Следовательно, в кон-
конфигурационном пространстве (размерность коего равна 6) дейст-
действует линейный оператор g, куб которого равен 1, и который остав-
оставляет неизменной как евклидову структуру конфигурационного
пространства (заданную кинетической энергией), так и эллипсоид
в конфигурационном пространстве, задающий потенциальную
энергию.
Из сказанного следует, что этот эллипсоид должен быть
эллипсоидом вращения. Действительно, если g — указанный опе-
оператор действия симметрии в конфигурационном пространстве,
а | — вектор на главной оси эллипсоида, то ось направления
g| также является главной осью (ибо вращение g переводит эл-
эллипсоид в себя).
Для вектора gg возможны два случая: либо g| = |, либо
векторы § и g% линейно независимы. Во втором случае плоскость»
натянутая на векторы § и g%, сплошь состоит из главных осей.
Поэтому соответствующее такой оси собственное число как мини-
минимум двукратное. Пространство, натянутое на три вектора, |,
#1» ?21» инвариантно относительно g. Оно либо двумерно (тогда
g действует в нем как поворот на 120°), либо трехмерно (тогда g

КРАТНОСТИ СОБСТВЕННЫХ ЧАСТОТ 401
действует как такой же поворот вокруг оси § + g\ + g2?). В по-
последнем случае мы можем выбрать эту сумму в качестве направле-
направления одной из главных осей эллипсоида, а две другие оси в указан-
указанном трехмерном пространстве взять ему перпендикулярными.
Поэтому оси эллипсоида, переходящего в себя при ортогональ-
ортогональном преобразовании третьего порядка (в пространстве любого
числа измерений) можно выбрать так, что всякая ось при преоб-
преобразовании либо остается на месте, либо поворачивается на 120°
в инвариантной плоскости, натянутой на нее и на другую (орто-
(ортогональную ей, как и все другие оси) ось той же длины. В дальней-
дальнейшем мы считаем, что оси эллипсоида и соответственно направле-
направления собственных колебаний выбраны именно таким образом.
Наши рассуждения показывают, что собственные колебания
системы с поворотной симметрией третьего порядка могут быть
двух типов: выдерживающие поворот на 120° (g$ = 1) и перехо-
переходящие при таком повороте в независимое собственное колебание
с той же частотой (g§ и § независимы). Во втором случае возни-
возникают даже три формы собственных колебаний с одинаковой час-
частотой (|, g| и g%), но независимых среди них только две:
S + gl + g% = 0,
так как сумма трех векторов равной длины, образующих углы
по 120° на плоскости, равна нулю.
Общее число собственных колебаний нашей системы равно 6.
Чтобы узнать, сколько из них первого (симметричного) и второго
(несимметричного) типа, можно воспользоваться следующим рас-
рассуждением. Рассмотрим предельный случай, когда каждая из
масс колеблется независимо от других.
В этом случае мы можем выбрать в конфигурационном про-
пространстве ортонормированный базис из шести собственных ко-
колебаний, по два на каждую точку, при которых одна точка дви-
движется, а две другие нет. Обозначим через |,- и x\t соответствующие
*-й точке собственные векторы с собственными частотами а и Ъ
соответственно, и пусть Xi, у, — координаты в ортонормирован-
ном базисе ?г, ijj. Тогда потенциальная энергия запишется в виде
U = -|- (аЧ\
Оператор симметрии g переставляет оси координат:
= Чз,
Мы можем теперь представить наше шестимерное пространство
в виде ортогональной прямой суммы двух прямых и двух дву-
двумерных плоскостей, инвариантных относительно оператора
симметрии g. А именно, инвариантные прямые определяются

402 ДОБАВЛЕНИЕ 10
направляющими векторами
li + ?2 + Ъз, Ч1 + 42 + Чз,
а инвариантные плоскости — это их ортогональные дополнения
в пространствах, натянутых на орты |г и г\, соответственно.
При этом первая прямая является направлением симметрич-
симметричного собственного колебания с частотой а, а вторая — с часто-
частотой Ъ. Точно так же любой вектор первой плоскости является
направлением собственного колебания с частотой а, которое при
повороте на 120° переходит в независимое с ним колебание той
же частоты; для всех векторов второй плоскости колебание также
несимметричное, с частотой Ъ.
Итак, в рассматриваемом вырожденном случае трех незави-
независимых точек имеются два независимые собственные колебания
симметричного типа и четыре несимметричного, причем послед-
последние разбиты на две пары. В каждой паре колебания имеют оди-
одинаковую собственную частоту и получаются друг из друга пово-
поворотом плоскости наших точек на 120°.
Я утверждаю теперь, что подчеркнутый выше вывод остается
справедливым для любого закона взаимодействия между нашими
точками, лишь бы взаимодействие было симметричным, т. е. по-
потенциальная энергия системы сохранялась при повороте плос-
плоскости на 120°.
Действительно, инвариантные относительно g векторы кон-
конфигурационного пространства образуют двумерную плоскость.
Каждый вектор четырехмерного ортогонального дополнения к этой
плоскости при применении оператора g поворачивается на 120°.
Потенциальная энергия разлагается в прямую сумму форм на
описанных двумерном и четырехмерном инвариантных простран-
пространствах оператора g. Шесть собственных направлений выбираются
теперь так. Ровно два из шести векторов соответствуют симмет-
симметричным колебаниям, а остальные четыре лежат в ортогональном
им четырехмерном пространстве векторов, поворачивающихся на
120°. Возьмем один из этих векторов, применим к нему оператор
g и объявим полученный вектор парным с исходным направле-
направлением собственного колебания. Затем в ортогональном дополне-
дополнении к получившейся плоскости в четырехмерном пространстве
выберем любой вектор и в пару ему возьмем его образ при дейст-
действии оператора g. Мы получили систему из шести собственных
колебаний, обладающую требуемыми свойствами.
Таким образом, в системе общего вида трех точек на плос-
плоскости с поворотной симметрией третьего порядка имеются четы-
четыре различные собственные частоты, в том числе две простые
и две двукратные. При этом каждой из простых собственных
частот отвечает симметричное собственное колебание, а каждой
из двукратных — три собственные колебания^ получающиеся друг

КРАТНОСТИ СОБСТВЕННЫХ ЧАСТОТ 403<
из друга поворотом на 120° и дающие в сумме нуль (так что не-
независимых среди них только два).
Задача. Расклассифицировать собственные колебания системы
с симметрией правильного треугольника (допускающей не только повороты
на 120°, но также отражения относительно высот треугольника).
Задача. Расклассифицировать собственные колебания системы,
группа симметрии которой есть группа из 24 вращений куба.
Ответ. Колебания бывают пяти «шов. При вращениях из каждого-
колебания может получиться система из 8, либо 6, либо 4, либо 2, либо 1
независимого колебания (в последнем случае колебания полностью симмет-
симметричны).
3 амечавие. Для классификации колебаний в системах с любыми
группами симметрии разработан специальный аппарат (так называемая тео-
теория представлений групп). См., например, Л ю б а р с к и й Г. Я. Теория
групп и ее применение в физике.— М.: Физматгие, 1958, где имеются необ-
необходимые таблицы.
Г. Поведение частот симметричной системы при изменении
параметров, сохраняющем симметрию. Предположим теперь, что
наша симметричная система зависит общим образом от некото-
некоторого числа параметров, причем симметрия не нарушается при
изменении параметров. Тогда собственные частоты различных
кратностей также будут зависеть от параметров, и возникает
вопрос о столкновениях собственных частот. Я ограничусь фор-
формулировкой результата для простейшего случая систем с пово-
поворотной симметрией третьего порядка (для поворотной симметрии
любого порядка п !> 3 ответ такой же). Подробности можно
найти в статьях: Арнольд В.И. Моды и квазимоды // Функ-
Функциональный анализ и его приложения.— 1972.— Т. 6, № 2.—
С. 12—20; КарпушкинВ. Н. Об асимптотике собственных
чисел симметричных многообразий и о «наиболее вероятных»
представлениях конечных групп // Вестник МГУ. Сер. матем.—
1974.— № 2.— С. 8—13.
Собственные колебания любой системы с поворотной симмет-
симметрией третьего порядка делятся на два типа: симметричные коле-
колебания и колебания, переходящие при повороте на 120° в независи-
независимые с исходным. Для общей системы с поворотной симметрией
третьего порядка (не имеющей, в частности, никакой дополнитель-
дополнительной симметрии) все собственные частоты первого типа просты,
а второго — двукратны.
Далее оказывается, что если система зависит общим образом
от одного параметра и симметрична при всех значениях пара-
параметра, то при изменении параметра собственные частоты сим-
симметричных колебаний не сталкиваются друг с другом, а двукрат-
двукратные собственные частоты несимметричных колебаний не распа-
распадаются. Кроме того, двукратные собственные частоты несим-
несимметричных колебаний не сталкиваются друг с другом при изме-
изменении параметров. Однако собственные частоты симметричных
и несимметричных колебаний движутся при изменении параметра

404 ДОБАВЛЕНИЕ 10
независимо друг от друга, так что при отдельных значениях
параметра могут сталкиваться (и проходить друг сквозь друга)
собственная частота симметричного колебания и (двукратная)
собственная частота несимметричного колебания.
Чтобы столкнулись две собственные частоты симметричных
-колебаний, нужно менять как минимум два параметра, а две
собственные частоты несимметричных колебаний — минимум три.
Вообще, чтобы в типичном семействе систем с поворотной
симметрией третьего порядка встречались системы, соответствую-
соответствующие столкновению i простых собственных частот (i симметрич-
симметричных колебаний) и / двукратных (/ несимметричных колебаний),
число параметров семейства должно быть не менее, чем
(/ - l)(i + 2)/2 + f.
Применим сказанное к колебаниям симметричных мембран.
Здесь мы будем считать, что мембране общего вида, выдержи-
выдерживающей поворот на 120°, соответствует эллипсоид общего вида
в пространстве эллипсоидов конфигурационного пространства,
выдерживающих индуцированное поворотом мембраны преобра-
преобразование конфигурационного пространства.
Точная формулировка этого предположения заключается в трансвер-
трансверсальности отображения пространства симметричных мембран в пространство
симметричных эллипсоидов к многообразиям эллипсоидов с различными
числами кратных осей для всех мембран, исключая множество коразмер-
коразмерности бесконечность.
Если согласиться с этим предположением, то мы приходим
к следующим выводам о колебании симметричных мембран.
1. Для мембран общего вида, выдерживающих поворот на 120°,
асимптотически треть собственных частот (считая их с крат-
ностями) простая и соответствующие собственные колебания
выдерживают поворот на 120°. Остальные собственные частоты
двукратные, каждой двукратной собственной частоте соответст-
соответствуют три собственные функции, в сумме равные нулю и перехо-
переходящие друг в друга при повороте на 120°.
2. В однопараметрических семействах общего вида таких сим-
симметричных мембран встречаются при изолированных значениях
параметров столкновения однократной частоты с двукратной,
но не встречаются ни столкновения однократных частот друг
с другом, ни столкновения друг с другом двукратных частот.
3. Минимальное число параметров семейства мембран, в ко-
котором реализуются (неустранимо посредством сохраняющего сим-
симметрию малого шевеления) более сложные столкновения собствен-
мых частот, дается формулой

КРАТНОСТИ СОБСТВЕННЫХ ЧАСТОТ 405
где vtj —число точек столкновения i однократных и ] двукратных
частот.
В частности, при типичной малой деформации круглой мем-
мембраны, сохраняющей вращательную симметрию третьего порядка,
сразу же распадается треть двукратных собственных чисел (соот-
(соответствующих собственным функциям с азимутальной частью
cos З&ф и sin 3/яр). При дальнейшей однопараметрической дефор-
деформации простые и двукратные собственные частоты могут прохо-
проходить друг сквозь друга, но ни две простые, ни две двукратные
собственные частоты друг с другом не сталкиваются.(
Д. Обсуждение. Значение соображений общего положения
и симметрии состоит, в частности, в том, что они позволяют полу-
получить некоторую информацию в тех случаях, когда найти точное
решение задачи не удается.
В частности, почти ни для каких мембран не известны формы
собственных колебаний. Тем не менее из общих соображений
можно кое-что сказать, например, о кратностях собственных
чисел.
Исследование высокочастотных колебаний сплошных сред име-
имеет весьма большое значение для ряда областей (оптика, акустика
и т. д.), и для приближенного отыскания формы собственных
колебаний разработаны специальные приемы. Один из этих при-
приемов (так называемая квазиклассическая асимптотика) состоит
в том, что колебание ищется в виде, локально близком к простой
гармонической волне малой длины, у которой, однако, от точки
к точке слегка меняются амплитуда и направление фронта.
Анализ (на котором мы не можем здесь останавливаться),
показывает, что в некоторых случаях можно построить прибли-
приближенные решения уравнения собственных функций с указанными
свойствами. При этом приближенными решениями они являются
в том смысле, что почти удовлетворяют уравнению для собствен-
собственных' функций (а не в том, что близки к настоящим собственным
функциям).
В частности, если мембрана имеет форму равностороннего
треугольника со сглаженными и сильно затупленными углами,
то удается построить приближенное решение описанного типа,
которое заметно отличается от нуля лишь в окрестности одной
из высот треугольника. (Физики называют это приближенное
решение волновым аналогом луча, движущегося по высоте тре-
треугольника; этот луч является устойчивой *) траекторией биль-
бильярда, имеющего форму нашей мембраны; ср. добавление о ко-
коротковолновых асимптотиках).
*) Условие линейной устойчивости бильнрдной траектории имеет вид
(ri + г3 - 1)(п - 1)(г, - I) > 0,
где 2 — длина отрезка траектории, rjBr, — радиусы кривизны стенки в его
концах.

406 ДОБАВЛЕНИЕ 11
Из соображений симметрии и общего положения вытекает,
что у типичных мембран с поворотной симметрией третьего по-
порядка настоящих собственных колебаний описанного типа нет.
Действительно, предположим, что одно из собственных колебаний
мембраны сосредоточено близ высоты (но не вблизи центра мем-
мембраны). Тогда, повернув его на 120° и на 240°, мы получим три
собственные колебания с одинаковыми собственными частотами.
Эти три колебания независимы (это следует из отличия от нуля
их суммы). Следовательно, собственная частота трехкратна, что
у типичных систем с поворотной симметрией третьего порядка
не встречается.
Из приведенного рассуждения видно, что пытаться строить
строгую высокочастотную асимптотику собственных функций —
довольно безнадежное дело: лучшее, на что можно надеяться,—
это получить приближенные формулы для почти собственных ко-
колебаний. Такое почти собственное колебание может весьма сильно
отличаться от настоящих собственных колебаний, однако если
задать соответствующее начальное условие, то движение в тече-
течение длительного времени будет напоминать стоячую волну (соб-
(собственное колебание).
Пример почти собственного колебания — движение одного из
двух одинаковых маятников, соединенных очень слабой пружи-
пружиной. Если в начальный момент приведем в движение первый
маятник, а второй неподвижен, то в течение длительного времени
колебаться будет практически один лишь первый маятник, и ко-
колебания будут почти собственными. При настоящих же собствен-
собственных колебаниях амплитуды обоих маятников одинаковы.
Вопрос о свя8и геометрии мембраны со свойствами ее собственных коле-
колебаний в последние годы интенсивно изучался многими авторами (в том числе
Г. Бейлем, С. Минакпшсундарамом и А. Плейелем, А. Сельбергом, Дж.
Милнором, М. Кацем, И. Зингером, Н. Маккином, М. Берже, И. Ко-
лин де Вердье, Ж. Чезареном, Ж. Дюистермаатом, В. Ф. Лазуткиным,
А. И. Шнирельманом, - С. А. Молчановым).
На простейший вопрос «можно ли услышать форму барабана?» ответ
оказался отрицательным: существуют не изометричные римановы многооб-
многообразия с одинаковым спектром. С другой стороны, некоторые свойства много-
многообразия восстанавливаются по спектру собственных чисел оператора Лапла-
Лапласа и по свойствам собственных функций (например, восстанавливается пол-
полный набор длин замкнутых геодезических).
Добавление 11
КОРОТКОВОЛНОВЫЕ АСИМПТОТИКИ
Описание распространения света в геометрической оптике при
помощи лучей (т. е. с помощью канонических уравнений Гамиль-
Гамильтона) или волновых фронтов (т. е. с помощью уравнений Гамиль-
Гамильтона — Якоби) с точки зрения физической оптики является лишь
приближением. Согласно представлениям физической оптики
свет — это электромагнитные волны, а геометрическая оптика —

КОРОТКОВОЛНОВЫЕ АСИМПТОТИКИ 407
это первое приближение, хорошо описывающее явления, лишь
когда длина волны мала по сравнению с размерами рассматри-
рассматриваемых тел.
Математическим вариантом этих физических представлений
являются асимптотические формулы для решений соответствую-
соответствующих дифференциальных уравнений, формулы, которые дают тем
яучшее приближение, чем выше частота колебаний (т. е. чем
короче волны). Эти асимптотические формулы записываются в тер-
терминах лучей (т. е. движений в некоторой гамильтоновой динами-
динамической системе) или фронтов (т. е. решений уравнения Гамиль-
Гамильтона — Якоби).
Подобная коротковолновая асимптотика существует для реше-
решений многих уравнений математической физики, описывающих
всевозможные волновые процессы. При этом в разных областях
физики и математики ее связывают с различными именами. На-
Например, в квантовой механике коротковолновая асимптотика на-
называется квазиклассическим приближением, а ее отыскание —
методом ВКБДж (Вентцеля, Крамерса, Бриллюэна, Джефриса),
хотя гораздо раньше этим приближением пользовались, напри-
например, Лиувилль, Грин, Стоке и Релей.
Построение коротковолновой асимптотики основано на пред-
представлении, что локально в каждом месте наблюдается ряд почти
строго синусоидальных волн, однако амплитуда этих волн и на-
направление их фронтов медленно меняются от точки к точке.
Формальная подстановка функции такого вида в уравнение с ча-
частными производными, описывающее волновой процесс, приводит
(в первом приближении при малой длине волны) к уравнению
Гамильтона — Якоби для волновых фронтов. Следующие прибли-
приближения позволяют определить также и зависимость амплитуды
колебаний от точки.
Конечно, вся процедура требует математического обоснования.
Точная формулировка и доказательство соответствующих теорем
совсем не просты. Особенно большие затруднения вносят так на-
называемые каустики (иначе — фокальные или сопряженные точки,
или точки поворота).
Каустики — это огибающие семейств лучей; их можно видеть
на стене, освещенной лучами, отраженными от какой-либо глад-
гладкой кривой поверхности. Если лучи, возникающие при описании
волн, пересекаются и образуют каустики, то вблизи каустик
формулы коротковолновой асимптотики должны быть несколько
изменены. А именно, фаза колебаний вдоль каждого луча испыты-
испытывает стандартный разрыв (на четверть волны) при каждом прохо-
прохождении луча у каустики.
Точное описание всех этих явлений удобно проводить в тер-
терминах геометрии лагранжевых подмногообразий соответствующего
фазового пространства и их проекций на конфигурационное про-
пространство.

408 ДОБАВЛЕНИЕ ii
Каустики интерпретируются при этом как особенности проек-
проекции лагранжева многообразия, задающего семейство лучей, из
фазового пространства в конфигурационное. Таким образом, нор-
нормальные формы особенностей лагранжевых проекций, приведен-
приведенные в добавлении 12, доставляют, в частности, классификацию
особенностей каустик, образованных системами лучей «общего
положения».
В настоящем добавлении приведены (без доказательств) про-
простейшие формулы коротковолновой асимптотики для квантово-
механического уравнения Шредингера. Более подробное изло-
изложение имеется в следующих местах:
Хединг Дж. Введение в метод фазовых интегралов.— М.: Мир,
1965 (см. особенно Дополнение II в книге Хединга);
М а с л о в В. П. Теория возмущений и асимптотическое методы.— М.:
Изд-во МГУ, 1965;
Арнольд В. И. О характеристическом классе, входящем в условия
квантования // Функциональный анализ и его приложения.— 1967.—
Т. 1, вып. 1.— С. 1—14;
Хермандер Л. Интегральные операторы Фурье // Математика.—
1972.— Т. 16, № 1.— С. 17—61; 1972.— Т. 2, № 2.— С. 67—136; Acta Ma-
thematica.— 1971.— V. 127, № 1—2.— С. 119.
А. Квазиклассическое 'приближение для решений уравнения
Шредингера. Уравнением Шредингера для частицы в поле с по-
потенциалом U в евклидовом пространстве называется уравнение
относительно комплексной функции ty (q, t)
Здесь h — некоторая вещественная постоянная, которая и явля-
является малым параметром рассматриваемой задачи. А — оператор
Лапласа.
Предположим, что начальное условие имеет коротковолновый
вид
где гладкая функция ф отлична от нуля лишь внутри некоторой
ограниченной области. Мы укажем ниже асимптотическую (при
h -*- 0) формулу для решения уравнения Шредингера с таким
начальным условием.
Прежде всего рассмотрим движение классической "частицы
в поле с потенциалом U, т. е. рассмотрим уравнения Гамильтона
дН . дН „ 1 „ . ,,, .
9 = -gj-, Р= вГ» где H=^-P*+U{q)
в 2и-мерном фазовом пространстве. Решения этих уравнений оп-
определяют фазовый поток (при некоторых условиях на потенциал,
которые мы предположим выполненными; эти условия запрещают
уход на бесконечность за конечное время).

КОРОТКОВОЛНОВЫЕ АСИМПТОТИКИ
409
Р;
\м
\
д*М
Нашим коротковолновым начальным условиям мы сопоставим
лагранжево подмногообразие в фазовом пространстве (т. е. много-
многообразие, размерность которого равна размерности конфигурацион-
конфигурационного пространства и на котором обращается тождественно в нуль
2-форма dp /\ dq, задающая симплектическую структуру в фазо-
фазовом пространстве). А именно, мы определим «импульс», соответ-
соответствующий нашему начальному условию, как градиент фазы, т. е.
положим
Р (я) — dsldq.
Лемма. Какова бы ни была гладкая функция s, график пост-
построенной по ней функции р (q) в фазовом пространстве R2™ =
— {(Р- Я)) является лагранжевым многообразием. Обратно, если
лагранжево многообразие однозначно проектируется на q-npocm-
ранство (является графиком), то
оно задается некоторой производя-
производящей функцией s по предыдущей
формуле.
Обозначим лагранжево многооб-
многообразие, построенное по начальному
условию (по функции s) через М.
Фазовый поток #' за время t пере-
переводит многообразие М в другое мно-
многообразие g*M. Это новое многооб-
многообразие также лагранжево, так как
фазовый поток сохраняет симплек-
симплектическую структуру.
При малых t новое лагранжево многообразие, как и старое,
однозначно проектируется на конфигурационное пространство.
Однако при больших t это уже не обязательно так (рис. 244).
Иными словами, в одну точку Q конфигурационного прост-
пространства может проектироваться несколько точек нового лагран-
лагранжева многообразия. Мы предположим, что этих точек конечное
число, и что все они невырождены (т. е. что невырождена про-
производная отображения проектирования нового лагранжева много-
многообразия на конфигурационное пространство в каждой из точек,;
проектирующихся в заданную точку Q).
Условие невырожденности выполнено для почти всех точек Q. Те особен-
особенные точки Q, для которых оно не выполнено, образуют в конфигурационном
пространстве множество меры нуль. В общем случае это множество — поверх-
поверхность, размерность которой на 1 меньше числа измерений конфигурационного
пространства. Эта поверхность, играющая роль каустикиХв нашей задаче,
сама может иметь довольно сложные особенности.
Проектирующиеся в заданную точку Q точки нового лагранже-
лагранжева многообразия произошли при преобразовании фазового пото-
потока из некоторых точек исходного лагранжева многообразия (по-
(построенного по начальному условию). Иными словами, в точку Q
за время t приводит несколько траекторий классической частицы.
Рис. 244. Преобразование лагран-
жевых многообразии фазовым по-
потоком

410 ДОБАВЛЕНИЕ 11
начальные условия которых принадлежат исходному лагранжеву
многообразию.
Обозначим через (pj, gj) эти начальные точки фазового прост-
пространства, а через Sj действие вдоль траектории фазового потока,
выходящей из точки (pj, qj). Точнее, мы положим
где
? = -у U(q) и
Тогда при h—>-0 решение уравнения Шредингера с заданным
функциями s и ф осциллирующим начальным условием имеет
асимптотику
DQ
-1/2 4-S(Q,«)--V-
h } *
О (А),
где (х) — целое число (индекс Морса), определение которо-
которого дано ниже.
Чтобы разобраться в этой формуле, рассмотрим сперва случай,
когда промежуток времени t мал. В этом случае сумма сводится
к одному-единственному слагаемому, так как лагранжево много-
многообразие, полученное из исходного лагранжева многообразия пре-
преобразованием фазового потока за малое время, проектируется
на конфигурационное пространство однозначно. Иными словами,
из семейства частиц, соответствующих начальному условию для
уравнения Шредингера, только одна приходит в Q через малое
время t.
Для малых t индекс Морса равен нулю (как мы увидим ниже
из его определения). Таким образом, функция ч]з (Q, s) имеет, так
же как и начальное условие, быстро осциллирующий вид.
При этом функция S, определяющая фронты волн в момент t,
есть не что иное, как значение в момент t решения уравнения
Гамильтона — Як оби, начальное условие для которого задается
функцией s, определяющей фронты волн в начальный момент.
Амплитуда же волн в момент t в точке Q получается из их ампли-
амплитуды в начальный момент в исходной точке приходящей в Q тра-
траектории умножением на некоторый множитель. Этот множитель
подобран так, чтобы при движении частиц, соответствующих на-
нашему начальному условию, интеграл квадрата модуля функции
•ф по заполненной частицами области конфигурационного про-
пространства не менялся с течением времени. (Здесь предполагается,
что в начальный момент выделена любая область в конфигураци-
конфигурационном пространстве, затем- рассматриваются фазовые точки на
исходном лагранжевом многообразии, чьи проекции на конфи-
конфигурационное пространство лежат в этой области, далее — их

КОРОТКОВОЛНОВЫЕ АСИМПТОТИКИ 411
образы под действием фазового потока через время t и, наконец,
проекции последних на конфигурационное пространство образу-
образуют область, «заполненную частицами в момент ?».)
Б. Индексы Морса и Маслова. Число Hj определяется как
число фокальных к многообразию М точек на отрезке [0, t] фазо-
фазовой кривой, выходящей из точки (р}-, qf).
Определение фокальной к М точки состоит в следующем. Мы
выбрали точку Q так, что при проекции получившегося из М
в момент t лагранжева многообразия условие невырожденности
в этой точке выполняется. Однако если мы рассмотрим всю фазо-
фазовую кривую, выходящую из точки (pj, qj), то в некоторые момен-
моменты времени 0 между Ои f условие невырожденности может не вы-
выполняться в точке (р @), q @)) лагранжева многообразия g®M.
Такие точки и называются фокальными точками к многообра-
многообразию М вдоль рассматриваемой фазовой кривой.
Заметим, что определения фокальной к М точки и индекса Морса не зави-
зависят от уравнения Шредингера, а относятся просто к геометрии фазового пото-
потока в кокасательном расслоении к конфигурационному пространству (или, что
то же, к вариационному исчислению). В частности, в качестве лагранжева
многообразия М можно взять слой кокасательного расслоения, проходящий
через точку (р0, д0) (заданный условием д = д0).
В этом случае фокальная к М точка на выходящей иэ (р0, д0) фазовой
кривой называется сопряженной к исходной точке (точнее, проекция этой
фокальной точки на конфигурационное пространство называется сопряжен-
сопряженной точкой к точке д0 вдоль экстремали в конфигурационном пространстве,
выходящей из точки дв с импульсом р0). В еще более частном случае движе-
движения по геодезическим на римановом многообразии фокальная точка к слою
кокасательного расслоения называется сопряженной с начальной точкой
геодезической вдоль этой геодезической. Например, Южный полюс сферы —
сопряженная точка Северного полюса вдоль любого меридиана.
Индекс Морса отрезка геодезической, равный числу сопряженных нача-
началу точек, играет важную роль в вариационном исчислении. А именно, рас-
рассмотрим второй дифференциал действия как квадратичную форму на
пространстве вариаций изучаемой геодезической (с закрепленными концами).
Тогда отрицательный индекс инерции этой квадратичной формы равен ин-
индексу Морса (см., например, Милнор Дж. Теория Морса.—М.: Мир,
1965).
Таким образом, до первой сопряженной точки геодезическая реализует
минимум действия, чем и оправдывается название «принцип наименьшего
действия» для различных вариационных принципов механики.
Заметим, что при вычислении индекса Морса фокальные точки
нужно учитывать с кратностями (кратность фокальной точки
общего положения равна 1).
Индекс Морса является частным случаем так называемого
индекса Маслова, который определяется независимо от какого бы
то ни было фазового потока для любых кривых на лагранжевом
многообразии кокасательного расслоения над конфигурационным
пространством.
Рассмотрим проекцию нашего «-мерного лагранжева многооб-
многообразия на и-мерное конфигурационное пространство. Это — глад-
гладкое отображение многообразий одинаковой размерности. Оно

412 ДОБАВЛЕНИЕ 11
может иметь особые точки, т.е.точки, в которых ранг производной
отображения падает и в окрестности которых проекция не явля-
является диффеоморфизмом.
Оказывается, вообще говоря, множество особых точек само име-
имеет размерность п — 1 м состоит из объединения гладкого много-
многообразия размерности п — 1 простейших особых точек, в которых
ранг падает на 1, и из конечного набора многообразий, размер-
размерность которых п — 3 и меньше.
Здесь «вообще говоря» означает, что указанных свойств можно
добиться сколь угодно малым шевелением лагранжева многооб-
многообразия, при котором оно остается лагранжевым.
Существенно отметить, что среди частей разных рангов, на которые раз-
разбивается множество особых точек, нет части размерности п — 2. За простей-
простейшими особыми точками, образующими многообразие размерности п — 1,
следуют точки, где ранг падает на две единицы, и они образуют многообра-
многообразие размерности п — 3. Проекция множества особых точек на конфигура-
конфигурационное пространство (каустика) состоит, вообще говоря, из частей всех
размерностей от 0 до п — 1 без пропусков.
Далее, оказывается, что п — 1-мерное многообразие простей-
простейших особых точек расположено на лагранжевом многообразии дву-
сторонне, а именно можно следующим образом согласовать ори-
ориентации нормалей во всех его точках.
Рассмотрим какую-либо простейшую особую точку на лагран-
лагранжевом многообразии.
Рассмотрим систему координат q±, . . ., qn в окрестности про-
проекции этой точки на конфигурационное пространство. Пусть
рг, . . ., рп — соответствующие координаты в слоях кокасатель-
ного расслоения. В окрестности нашей особой точки лагранжево
многообразие можно рассматривать как график вектор-функции
(<Zi> />2> • • •» рп) от переменных (рг, q2, . . ., qn) (или вектор-функ-
вектор-функции аналогичного вида, в которой роль выделенной координаты
исполняет не первая, а какая-либо из остальных).
Особые точки вблизи данной определяются тогда из условия
dqjdp^ = 0. Для лагранжевых многообразий общего положения
эта производная меняет знак при переходе с одной стороны мно-
многообразия особых точек на другую в рассматриваемой окрестно-
окрестности простейшей особой точки. Мы выбираем за положительную
сторону ту, где эта производная положительна.
Заметим, что согласованность определения положительного направления
вблизи разных точек нуждается в доказательстве. Более того, нужно дока-
доказать, что положительное направление вблизи одной точки определено кор-
корректно, т. е. не зависит от координатной системы. Все это можно сделать
прямыми вычислениями (см. цитированную выше статью в «Функциональном
Теперь индекс Маслова ориентированной кривой на лагран-
лагранжевом многообразии определяется как число переходов с отри-
отрицательной стороны многообразия особенностей на положительную

КОРОТКОВОЛНОВЫЕ АСИМПТОТИКИ 413
минус число обратных переходов. При этом предполагается, что
концы кривой неособы и что кривая пересекает лишь многообра-
многообразие простейших особых точек и лишь под ненулевыми углами.
Определив индекс для таких кривых, можно определить его для
произвольной кривой, соединяющей две неособые точки: для это-
этого достаточно аппроксимировать кривую такой, которая пере-
пересекает лишь многообразие простейших особых точек и притом
под ненулевыми углами. Можно показать, что от выбора аппрок-
аппроксимирующей кривой индекс не зависит.
Задача. Найти индекс ориентированной параметром t, 0<t^ 2п,
окружности р = cos t, q = sin t на лагранжевом многообразии р2 -\- д2 = 1
фазовой плоскости.
Ответ. + 2.
Наконец, индекс Морса фазовой кривой в R2n можно теперь
определить как индекс Маслова кривой на п + 1-мерном лагран-
лагранжевом многообразии в подходящем 2п + 2-мерном фазовом про-
пространстве. Координатами в этом пространстве служат (р0, р; go,q)
(где (р, q) ЕЕ R2n). Если положить здесь q0 = t, р0 = —Н (р, q),
а точку (р, q) заставить пробегать /г-мерное лагранжево много-
многообразие в R2n, полученное из исходного за время t под действием
фазового потока^ то при изменении t полученные точки в R2n+2
заметут п + 1-мерное лагранжево многообразие. График движе-
движения фазовой точки под действием фазового потока можно рас-
рассматривать как кривую на этом п + 1-мерном лагранжевом мно-
многообразии. Можно проверить, что индекс Маслова этого графика
совпадает с индексом Морса исходной фазовой кривой.
В. Индексы замкнутых кривых. Индексы замкнутых кривых
на лагранжевых подмногообразиях линейного фазового простран-
пространства можно вычислять также с помощью комплексной структуры.
Введем в линейном фазовом пространстве R2n = {(p, q)}, кроме
симплектической структуры, dp Д dq еще евклидову структуру
(со скалярным квадратом р2 + q2) и комплексную структуру,
заданную умножением на мнимую единицу
/: R2» -^ R2», I(p,q) = (~q, p); z = р + iq, О = {z}.
Все три структуры связаны соотношением
[х, у] = Aх, у),
где квадратными скобками обозначено кососкалярное произведе-
произведение.
Линейные преобразования фазового пространства, сохраняю-
сохраняющие какие-нпбудь две (и тогда все три) структуры, называются
унитарными. Такие преобразования переводят лагранжевы плос-
плоскости в лагранжевы.
Каждая лагранжева плоскость может быть получена из ка-
какой-нибудь одной (например, из вещественной плоскости Rn, за-

414 ДОБАВЛЕНИЕ 11
данной уравнением д — 0) унитарным преобразованием. При этом
любые два унитарные преобразования А, В, переводящие вещест-
вещественную плоскость в одну и ту же лагранжеву плоскость, отли-
отличаются на унитарное преобразование, являющееся вещественным
ортогональным преобразованием:
В = АС, где CRn = R".
Обратно, любое предварительное ортогональное преобразова-
преобразование не меняет образа вещественной плоскости под действием уни-
унитарного преобразования.
Заметим теперь, что определитель ортогонального преобразо-
преобразования равен +1. Поэтому квадрат определителя унитарного пре-
преобразования, переводящего вещественную плоскость в данную
лагранжеву плоскость, зависит лишь от самой лагранжевой пло-
плоскости и совершенно не зависит от специального выбора унитар-
унитарного преобразования.
После этих предварительных замечаний вернемся к нашему
лагранжеву многообразию и лежащей на нем замкнутой ориен-
ориентированной кривой. В каждой точке кривой имеется касательная
плоскость к лагранжеву многообразию в линейном симплектичес-
ком пространстве. Квадрат определителя унитарного преобразо-
преобразования, переводящего вещественную плоскость в касательную,
есть комплексное число, по модулю равное единице. При движе-
движении точки по нашей замкнутой кривой это комплексное число
меняется.|3а время полного обхода кривой квадрат определителя
совершит некоторое целое число оборотов вокруг начала коор-
координат на плоскости комплексного переменного, ориентированной
от 1 к i. Это целое число и есть индекс рассматриваемой замкну-
замкнутой кривой.
Индексы замкнутых кривых входят в асимптотические форму-
формулы для стационарных задач (собственных колебаний). Предполо-
Предположим, что фазовый поток, соответствующий потенциалу U, имеет
инвариантное лагранжево многообразие, лежащее на уровне энер-
энергии Н — Е. Тогда уравнение
-к- Ai]) = л2 (U (q) — Е) г|)
имеет серию собственных чисел KN -*- эо с асимптотикой KN =
= Hw + О (jxjv)» если для всех замкнутых контуров у на нашем
лагранжевом многообразии выполняется сравнение
5indv(mod 4)i
В одномерном случае лагранжево многообразие — окружность,
ее индекс равен 2, и предыдущая формула превращается в так

ЛАГРАНЖЕВЫ ОСОБЕННОСТИ
называемое «условие квантования»:
415
Собственные функции, соответствующие этим собственным числам,
также связаны с лагранжевым многообразием, но эта связь не так проста.
В действительности удается написать не асимптотические формулы для соб-
собственных функций, а лишь формулы для функций, приближенно удовлетво-
удовлетворяющих уравнению собственных функций. Эти функции оказываются малыми
вне проекции лагранжева многообразия на конфигурационное простран-
пространство. Асимптотические формулы имеют особенности вблизи каустик, образую-
образующихся при проектировании.
Настоящие собственные функции могут, однако, вести себя совершенно
по-другому, по меньшей мере, если собственное число кратное или если
имеются близкие к нему собственные числа (см. добавление 10).
Индекс Маслова можно рассматривать как многомерное обобщение тео-
теории колеблемости Штурма. См.: Арнольд В.И. Теоремы Штурма в
симплектическая геометрия // Функциональный анализ и его приложения.—
1985.— Т. 19, № 4.- С. 1-10.
Добавление 12
ЛАГРАНЖЕВЫ ОСОБЕННОСТИ
Лагранжевы особенности — это особенности проекций лагран-
жевых многообразий на конфигурационное пространство. Такие
особенности встречаются при исследовании решений уравнения
Гамильтона — Якоби в целом, при изучении каустик, фокальных
или сопряженных точек, при анализе распространения разрывов
и ударных волн в механике сплошной среды, а также в задачах,
приводящих к коротковолновой асимп-
асимптотике (см. добавление 11).
Чтобы описать лагранжевы особен-
особенности, нужно вначале сказать несколь-
несколько слов об особенностях гладких отобра-
отображений вообще. Начнем с простейших
примеров.
А. Особенности гладких отображе-
отображений поверхности на плоскость. Ото-
Отображение проектирования сферы на
плоскость имеет особенность на эква-
экваторе сферы (в точках экватора ранг
производной падает на единицу). В ре-
результате на плоскости проекции обра-
образуется кривая (так называемый види-
видимый контур), разграничивающая обла-
области с разным числом прообразов точки: у каждой точки плоско-
плоскости внутри видимого контура два прообраза, а вне — ни одного.
В более сложных случаях «видимый контур» может иметь
более сложные особенности. Рассмотрим, например, поверхность,
Рис. 245. Сборка Уитни

416 ДОБАВЛЕНИЕ 12
заданную в трехмерном пространстве с координатами (х, у, z)
уравнением (рис. 245)
х = yz — z3
и отображение проектирования параллельно оси z на плоскость
с координатами (х, у).
Особые точки проектирования образуют на поверхности глад-
гладкую кривую (с уравнением 3z2 = у). Однако образ этой кривой
на плоскости (х, у) уже не является гладкой кривой. Этот об-
образ — полукубическая парабола с острием в точке @, 0) с урав-
уравнением
Такая кривая разделяет плоскость на две части: меньшую
(внутри острия) и большую (вне). Над каждой точкой меньшей
части имеются три точки нашей поверхности, а большей —• всего
одна.
Рассмотрим теперь любую малую деформацию нашей поверх-
поверхности. Оказывается, при проектировании всякой поверхности,
близкой к нашей, видимый контур всегда будет иметь подоб-
подобную же особенность (полукубическое острие) в некоторой точке,
близкой к особенности видимого контура исходной поверхности.
Иными словами, рассматриваемая особенность неустранима ма-
малым шевелением поверхности.
Более того, вместо деформации поверхности можно как угод-
угодно деформировать само отображение поверхности на плоскость
(не заботясь более, чтобы оно было проектированием), лишь бы
оно оставалось гладким и деформация была мала. Оказывается,
и при таких деформациях острие не исчезает, а лишь слегка
деформируется.
Приведенные здесь примеры исчерпывают все типичные осо-
особенности отображений поверхности на плоскость. Можно пока-
показать, что все более сложные особенности устранимы малым шеве-
шевелением . Поэтому, слегка продеформировав любое гладкое отобра-
отображение . можно всегда добиться того, что в окрестности любой точ-
точки отображаемой поверхности оно будет либо неособым, либо
будет устроено как отображение проектирования сферы на плос-
плоскость близ экватора, либо как отображение проектирования рас-
рассмотренной выше поверхности с кубическим острием на видимом
контуре.
Слова «устроено как» означают, что на поверхности-прообразе
и плоскости-образе можно выбрать локальные координаты (в ок-
окрестности рассматриваемой точки и ее образа) так, что в этих
координатах отображение запишется некоторым специальным об-
образом. А именно, нормальные формы, к которым приводится ото-
отображение поверхности на плоскость в окрестности точек трех
указанных выше типов, суть
У\ — xi, У2 = Х2 (неособая точка),

ЛАГРАНЖЕВЫ ОСОБЕННОСТИ 417
уг — х\, у2 = х2 (складка, как на экваторе сферы),
уг = х1х2 — х\, ya — ха (сборка с острием видимого контура).
Здесь (хг, х2) — локальные координаты в прообразе, а (уи у2) —
в образе.
Доказательства приведенных теорем (они принадлежат X. Уитни) и их
многомерные обобщения можно найти в работах по теории особенностей глад-
гладких отображений, см., например:
Арнольд В. И., Варченко А. Н., Г у с е й н-3 а д е СМ.
Особенности дифференцируемых отображений. Т. 1.— М.: Наука, 1982;
Т. 2— М.: Наука, 1984.
Том Р.,Левин Г., Мазер Дж. и др. Особенности дифференцируе-
дифференцируемых отображений.— М.: Мир, 1968.
Б. Особенности проектирования лаграыжевых многообразий.
Рассмотрим теперь и-мерное конфигурационное многообразие*
соответствующее 27г-мерное фазовое пространство и в нем и-мерное
лагранжево подмногообразие (т. е. и-мерное подмногообразие, на
котором 2-форма, задающая симплектическую структуру фазово-
фазового пространства, равна тождественно нулю).
Проектируя лагранжево многообразие на конфигурационное
пространство, мы получаем отображение одного гладкого 7г-мер-
ного многообразия на другое той же размерности.
В общей точке это отображение является локальным диффео-
диффеоморфизмом, однако в некоторых точках лагранжева многообразия
ранг дифференциала падает. Такие точки называются особыми.
При проекции множества особых точек в конфигурационном про-
пространстве образуется «видимый контур», который в лагранжевом
случае называется каустикой.
Каустики могут иметь сложные особенности, однако, как и
в обычной теории особенностей гладких отображений, от слишком
сложных особенностей можно избавиться малым шевелением.
(Здесь под малым шевелением подразумевается такая малая де-
деформация лагранжева многообразия в фазовом пространстве, при
которой это многообразие остается лагранжевым).
После этого останутся лишь простейшие неустранимые особен-
особенности, для которых можно выписать нормальные формы и кото-
которые можно раз навсегда подробно изучить. При рассмотрении
задач общего положения, не обладающих какими-либо специаль-
специальными свойствами симметрии, естественно ожидать появления
лишь этих простейших неустранимых особенностей.
Рассмотрим, например, каустики, образованные при освеще-
освещении стены светом от точечного источника, отраженным от какой-
либо гладкой искривленной поверхности (здесь четырехмерное
фазовое пространство образовано прямыми, пересекающими по-
поверхность стены по всевозможным направлениям, а лагранжево
подмногообразие — лучами света, выходящими из источника, при
пересечении ими стены). Перемещая источник, можно заметить,
что, вообще говоря, каустики имеют лишь простейшие особенно-

418 ДОБАВЛЕНИЕ 12
сти (полукубические острия), а более сложные особенности появ-
появляются лишь при специальных, исключительных положениях ис-
источника.
Ниже приведены нормальные формы для особенностей проек-
проектирования 7г-мерного лагранжева подмногообразия из 27г-мерного
фазового пространства на и-мерное конфигурационное простран-
пространство для п <^ 5. Этих нормальных форм конечное число, и их
классификация связана (довольно загадочным образом) с класси-
классификациями простых групп Ли, простейших вырожденных крити-
критических точек функций, правильных многогранников и многих
других объектов. При п ^ 6 нормальные формы некоторых осо-
особенностей неизбежно должны содержать параметры.
За дальнейшими подробностями читатель отсылается к статье:
Арнольд В. И. Нормальные формы функций вблизи вырожденных
критических точек, группы Вейля А%, D%, Ек и лагранжевы особенности //
Функциональный анализ и его приложения.— 1972.— Т. 6, № 4.— С. 3—25.
В. Таблица нормальных форм типичных особенностей проек-
проекций лагранжевых многообразий размерности п <^ 5. Мы будем
пользоваться следующими обозначениями:
(дъ . . ., дп) — координаты в конфигурационном пространстве,
{ри . . ., рп) — соответствующие импульсы, так что вместе р
ж д образуют симплектическую систему координат в фазовом про-
пространстве.
Лагранжево многообразие мы будем задавать при помощи
производящей функции F формулами
gt = dF/dpt, pj = -dF/dgj,
где индекс г пробегает некоторую часть множества A, . . ., п),
а индекс / — остальную часть. А именно, i = 1, j! ~^> 1 для осо-
особенностей, обозначенных в списке через Ак, и ? = 1,2, }^>2
для особенностей, обозначенных через DH и Ек.
При таких обозначениях одно и то же выражение F (pt, gj)
может рассматриваться как задающее лагранжево многообразие
в пространствах разного числа измерений: мы можем дописать
сколько угодно аргументов gj, от которых F на самом деле не за-
зависит.
Список нормальных форм типичных особенностей имеет теперь
следующий вид:
при п = 1
Ах: F = pl; A2: F = ±p\;
при п = 2, кроме двух предыдущих, еще
лри п = 3, кроме трех предыдущих, еще
At: F = + р\ + д3р\ 2
Dt: F = Ъ l

ЛАГРАНЖЕВЫ ОСОБЕННОСТИ
419
при т» = 4j кроме пяти предыдущих, еще
Аь: F = ±р\ + OP
q3Pi
Db- F = ± PxPi ± Pt +
+ qspl;
при т» = 5, кроме семи предыдущих, еще
De '• F = ±
Г. Обсуждение нормальных форм. Точка типа Ах неособая.
Особенность типа А2 — это особенность типа складки. Дейст-
Действительно, если за координаты на лагранжевом многообразии
взять (ри д2, . . ., дп), то отображение проектирования запишет-
запишется как
(Pi, ?а» • • -1 Qn) •-*¦ (± Зр1, да, . . ., дп).
Особенность типа А3 — это сборка с лолукубическим острием
на видимом контуре. Чтобы в этом убедиться, достаточно выписать
Рис. 246. Типичные особенности каустик в трехмерном пространстве
явно соответствующее отображение двумерного лагранжева мно-
многообразия на плоскость:
(Pi,
(± ^Р%
Особенность типа At впервые появляется в трехмерном слу-
чаея и соответствующая каустика представляет собой поверх-
поверхность в трехмерном пространстве (рис. 246) с особенностью, назы-
называемой ласточкиным хвостом (мы уже встречались с ней в § 46).
Каустика особенности типа Dt в трехмерном пространстве
представляет собой поверхность с тремя ребрами возврата (ти-

420 ДОБАВЛЕНИЕ 12
па А3), касающимися в одной точке; при этом два из этих ребер
возврата могут быть мнимыми, так что имеется два варианта
каустики ZL.
Д. Лагранжевы эквивалентности. Теперь следует сказать,
в каком смысле приведенные примеры являются нормальными
формами типичных особенностей проектирования лагранжевых
многообразий. Прежде всего мы определим, какие особенности
мы будем считать «одинаково устроенными».
Отображение проектирования лагранжева многообразия на
конфигурационное пространство будем для краткости называть
лагранжееым отображением. Пусть даны два лагранжевых ото-
отображения многообразий одинаковой размерности п (соответствую-
(соответствующие и-мерные лагранжевы многообразия лежат, вообще говоря,
в разных фазовых пространствах, являющихся кокасательными
расслоениями двух разных конфигурационных пространств). Мы
скажем, что два таких лагранжевых отображения лагранжево
эквивалентны, если существует симплектический диффеоморфизм
первого фазового пространства на второе, переводящий слои пер-
первого кокасательного расслоения в слои второго и переводящий
первое лагранжево многообразие во второе. Сам симплектический
диффеоморфизм называется тогда лагранжевой эквивалентностью
отображений.
Заметим, что два лагранжево эквивалентных лагранжевых
отображения превращаются одно в другое при помощи диффео-
диффеоморфизмов в пространстве-прообразе и пространстве-образе (или,
как говорят в анализе, приводятся одно к другому заменой коор-
координат в прообразе и в образе). Действительно, наш симплектиче-
симплектический диффеоморфизм, суженный на лагранжево многообразие,
задает диффеоморфизм прообразов; диффеоморфизм же конфигу-
конфигурационных пространств-образов возникает потому, что слои пе-
переходят в слои.
В частности, каустики двух лагранжево эквивалентных ото-
отображений диффеоморфны, поэтому классификация с точностью
до лагранжевой эквивалентности влечет за собой классификацию
каустик. Однако классификация с точностью до лагранжевой
эквивалентности, вообще говоря, тоньше, чем классификация
каустик, так как из диффеоморфности каустик вообще не вытека-
вытекает лагранжева эквивалентность отображений. Более того, клас-
классификация с точностью до лагранжевой эквивалентности тоньше,
чем классификация с точностью до диффеоморфизмов прообраза
и образа, так как не всякая такая пара диффеоморфизмов реали-
реализуется симплектическим диффеоморфизмом фазового пространства.
Лагранжево отображение, рассматриваемое в окрестности не-
некоторой выделенной точки, называется лагранжево эквивалентным
в этой точке другому лагранжеву отображению (также имею-
имеющему выделенную точку), если существует лагранжева эквива-
эквивалентность первого отображения в некоторой окрестности первой

ЛАГРАНЖЕВЫ ОСОБЕННОСТИ 421
точки на второе в некоторой окрестности второй tohkHj переводя-
переводящая первую точку во вторую.
Теперь мы можем сформулировать классификационную тео-
теорему для особенностей лагранжевых отображений в размерно-
размерностях п <^ 5.
Всякое п-мерное лагранжево многообразие (п <^ 5) можно сколь
угодно малой деформацией в классе лагранжевых многообразий
превратить в такое, что отображение проектирования на конфи-
конфигурационное пространство будет в каждой точке лагранжево эк-
эквивалентным одному из лагранжевых отображений приведенного
выше списка.
В частности, двумерное лагранжево многообразие можно сколь
угодно малым шевелением в классе лагранжевых многообразий
привести в «общее положение», так что отображение проектирова-
проектирования на конфигурационное (двумерное) пространство не будет иметь
других особенностей, кроме складок (которые лагранжевой эк-
эквивалентностью приводятся к нормальной форме А2) и сборок
(которые лагранжевой эквивалентностью приводятся к нормаль-
нормальной форме ^)
Заметим, что уже приведенное утверждение о двумерных лагранжевых
отображениях не вытекает из классификационной теоремы для общих (нела-
гравжевых) отображений. Ибо, во-первых, лагранжевы отображения состав-
составляют среди всех гладких отображений весьма узкий класс, и поэтому могут
иметь (и действительно имеют при п > 2) в качестве типичных для лагран-
лагранжевых отображений такие особенности, которые для отображений общего
вида нетипичны. Во-вторых же, из возможности привести отображение к
нормальной форме диффеоморфизмами прообраза и образа еще не сле-
следует возможность такого приведения с помощью лагранжевой эквивалент-
эквивалентности.
Таким образом, каустики лагранжева двумерного многообра-
многообразия общего положения имеют в качестве особенностей лишь
полукубические острия (и точки трансверсального самопересече-
самопересечения). Все более сложные особенности распадаются при малом
шевелении лагранжева многообразия, тогда как точки возврата
и точки самопересечения каустики неустранимы малым шевеле-
шевелением и лишь немного деформируются.
Нормальные формы следующих особенностей А4, D4l • • • мож-
можно подобным же образом использовать для исследования каустик
лагранжевых многообразий большего числа измерений, а также
для исследования перестроек каустик лагранжевых многообра-
многообразий небольшого числа измерений при изменении параметров, от
которых зависит многообразие.
Другие применения формулы настоящего раздела находят в теории
лежандроеых особенностей, то есть особенностей волновых фронтов, преобра-
преобразований Лежандра, огибающих и выпуклых оболочек (см. добавление 4,
стр. 333). Теории лагранжевых и лежандровых особенностей имеют очевид-
очевидные приложения не только в геометрической оптике и теории асимптотик
осциллирующих интегралов, го и в вариационном исчислении, в теории раз-

422 ДОБАВЛЕНИЕ 13
рывиых решений нелинейных уравнений с частными производными, в задачах
оптимизации, погони и т. п. Р. Том предложил для теории особенностей,
теории бифуркаций и их приложений объединяющее название теория катас-
катастроф.
Добавление 13
ПУАССОНОВЫ СТРУКТУРЫ
Наряду с классической скобкой Пуассона функций, встреча-
встречаются более общие скобки (вырождающиеся). Типичный пример —
скобка Пуассона функций от компонент Mt вектора кинетическо-
кинетического момента, {F, G} = S (dFldMt) (dG/dM,) {Mit M,}. Такие вы-
вырожденные скобки можно рассматривать как семейства обычных
скобок Пуассона функций на семействах симплектических мно-
многообразий. Однако эти семейства, вообще говоря, имеют особен-
особенности (не являются расслоениями): они состоят из симплектиче-
симплектических многообразий (листов) разных размерностей, соединенных
между собой условием гладкости заданной вырожденными скобка-
скобками пуассоновой структуры на пространстве — объединении.
(В описанном выше примере листы — концентрические сферы
и их центр.)
В настоящем добавлении перечислены простейшие элементар-
элементарные свойства пуассоновых структур на конечномерных многооб-
многообразиях. Но нужно иметь в виду, что в приложениях (особенно
в математической физике сплошной среды) часто встречаются и
пуассоновы структуры на бесконечномерных многообразиях. При
этом, впрочем, размерности или коразмерности листов часто (хо-
(хотя и не всегда) конечны.
А. Пуассоновы многообразия. Пуассоновой структурой на
многообразии называется структура алгебры Ли в пространстве
гладких функций на нем (т. е. билинейная кососимметрическая
операция «скобки Пуассона» функций, удовлетворяющая тожде-
тождеству Якоби), такая, что оператор ado= {а, } (взятие скобки Пуас-
Пуассона с любой функцией с) является оператором дифферен-
дифференцирования по направлению некоторого векторного поля va.
Векторное поле va называется тогда гамилыпоновым полем
с функцией Гамильтона а. Отображение ои-i?,, задает гомомор-
гомоморфизм алгебры Ли функций в алгебру Ли векторных полей. Мно-
Многообразие, снабженное пуассоновой структурой, называется пуас-
соновым многообразием.
Две точки на пуассоновом многообразии называются эквива-
эквивалентными, если их можно соединить ломаной ив отрезков фазо-
фазовых кривых гамильтоновых полей. Классы эквивалентных друг
другу точек называются листами пуассонова многообразия.
Векторы всевозможных гамильтоновых полей в каждой точке
пуассонова многообразия заполняют линейное пространство»
а именно касательное пространство листа. Таким образом, листы —

ПУАССОНОВЫ СТРУКТУРЫ 423
гладкие многообразия, но они, вообще говоря, не замкнуты и име-
имеют различные размерности.
Классический (явно указанный С. Ли, 1890, но по существу
рассматривавшийся уже Якоби) пример пуассонова многообра-
многообразия — дуальное пространство (конечномерной) алгебры Ли. Эле-
Элементы самой алгебры можно рассматривать как линейные функ-
функции на этом пространстве. Пуассонова структура определяется
как продолжение структуры алгебры Ли с этого конечномерного
подпространства пространства гладких функций (на дуальном
исходной алгебре Ли пространстве) на все пространство гладких
функций. Такое продолжение существует и единственно: если
<*>!, . . ., а>п — базис исходной алгебры Ли, то
{a, fc}poisson = 2 (да/дщ) {дЫдЫ]) [щ,
В этом примере листы — орбиты коприсоединенного представле-
представления группы Ли в дуальном к ее алгебре пространстве.
Каждый лист пуассонова многообразия имеет естественную
симплектическую структуру (замкнутую невырожденную на лис-
листе 2-форму). Эта форма определяется так. Рассмотрим два вектора
гамильтоновых полей, приложенные в одной точке листа. Значе-
Значение 2-формы на этой паре векторов определяется как значение
скобки Пуассона их функций Гамильтона в указанной точке (это
значение не зависит от выбора функций Гамильтона, но лишь от
векторов). Замкнутость формы на листе следует из тождества
Якоби, невырожденность — из равенства нулю вектора, вдоль
которого производная любой функции равна нулю. Фазовые по-
потоки гамильтоновых полей сохраняют симплектические формы
листов.
Таким образом, листы пуассонова многообразия четномерны,
и его можно рассматривать как объединение симплектических
многообразий (вообще разных размерностей), симплектические
структуры которых согласованы условием гладкости объединяю-
объединяющей скобки Пуассона.
Например, на орбитах коприсоединенного представления груп-
группы SOC) (сферах с центром в нуле) можно выбрать согласованные
локальные координаты Дарбу: в окрестности ненулевой точки
структура Пуассона в подходящих локальных координатах при-
принимает вид {х, у) = 1, {х, z) = {у, z} = 0. Эта нормальная фор-
форма структуры Пуассона пространства моментов полезна для иск-
исключения узла в задаче многих тел (см. п. 5 § 5 гл. III в статье:
Арнольд В. И. Малые знаменатели и проблемы устойчиво-
устойчивости в классической небесной механике // УМН.— 1963.— Т. 18,
вып. 6).
Якоби заметил, что скобку Пуассона (классическую) первых
интегралов любой гамильтоновой системы можно рассматривать
как структуру Пуассона (эта структура обсуждается в п. 3 § 1
гл. VI той же статьи).

424 ДОБАВЛЕНИЕ 13
Конструкция пуассоновой структуры на пространстве, дуаль-
дуальном алгебре Ли, приводит опять к алгебре Ли. Поэтому эту конст-
конструкцию можно повторять, получая все новые (бесконечномерные)
пуассоновы структуры. Более общим образом, пусть дана какая-
нибудь пуассонова структура на многообразии. Тогда простран-
пространство функций на этом многообразии получает структуру алгебры
Ли. Значит, пространство, дуальное к пространству функций, на-
наделяется пуассоновой структурой (как дуальное пространство
этой алгебры Ли функций). Элементы пространства, дуального
к пространству функций, интерпретируются как распределения
на исходном многообразии. Таким образом, пространство распре-
распределений на пуассоновом многообразии (например, на симплекти-
ческом фазовом пространстве) имеет естественную пуассонову
структуру. Эта структура позволяет применять гамильтонов фор-
формализм к уравнениям типа Власова, описывающим эволюцию
распределения частиц в фазовом пространстве под действием по-
поля, созданного самими частицами.
Б. Пуассоновы отображения. Пусть даны два пуассоновых
многообразия. Отображение первого во второе называется пуас-
соноеым, если оно уважает пуассоновы структуры. А именно, для
любой пары функций на втором многообразии их скобка Пуассо-
Пуассона, после перенесения отображением на первое многообразие,
должна совпадать со скобкой Пуассона на первом многообразии
перенесений самих исходных функций.
Например, вложение симплектического листа в пуассоново
многообразие является пуассоновым отображением.
Прямое произведение пуассоновых многообразий имеет ес-
естественную пуассонову структуру, в которой проекции на оба
сомножителя пуассоновы (скобки Пуассона функций, перенесен-
перенесенных с разных сомножителей, нулевые).
С. Ли доказал, что всякое пуассоново многообразие локально
(в окрестности точки, где размерности симплектических листов
постоянны, например — в окрестности точки общего положения,
где размерности максимальны) разлагается в прямое произведе-
произведение симплектического листа и дополнительного пространства, на
котором все скобки Пуассона нулевые.
В такой окрестности можно ввести координаты pt, qt, с} так,
что р и q имеют обычные симплектические скобки Пуассона,
а скобки Пуассона каждой из функций cj со всеми функциями тож-
тождественно равны 0. В физике координатыpt, qt называются перемен-
переменными Клебша, а функции Cj — функциями Казимира (Клебш ввел
свои переменные для гамильтонова описания гидродинамики
идеальной жидкости, а Казимир рассматривал центр алгебры Ли
функций на дуальном пространстве исходной алгебры Ли).
Размерности симплектических листов пуассонова многообра-
многообразия в точках не общего положения меньше, чем в точках общего
положения. В окрестности такой точки пуассоново многообразие

пуассоновы структуры 425
все равно можно представить в виде прямой суммы окрестности
этой точки на ее симплектическом листе и окрестности отмеченной
точки на некотором пуассоновом многообразии дополнительной
размерности. Иными словами, на минимальном трансверсальном
к симплектическому листу сечении возникает (единственная с точ-
точностью до диффеоморфизма) локальная пуассонова структура —
так называемая трансверсалъная пуассонова структура (см.:
WeinsteinA. The local structure, of Poisson manifolds //
J. Diff. Geom.— 1983.— V. 18.— P. 523—557) *). В трансвер-
сальной структуре скобки Пуассона всех функций в отмеченной
точке (начале координат) равны нулю. Структура задается скоб-
скобками Пуассона координат. Ряды Тейлора этих скобок начинаются с
{хи xj) = 2сг, jXH + . . .j
где с*, j — структурные константы конечномерной алгебры Ли
(линеаризованной трансверсалъпой структуры).
Возникает естественный вопрос: можно ли уничтожить высшие
члены ряда Тейлора за счет подходящего выбора системы коорди-
координат?
Вопрос о строении трансверсальных структур обсуждался
уже давно (см., например, п. 3 § 1 гл. VI цитированной выше
статьи в УМН, 1963, т. 18, вып. 6).
Если линеаризованная алгебра полупроста, а структура Пуас-
Пуассона аналитична, то от высших членов ряда Тейлора можно из-
избавиться аналитической заменой координат; см.: ConnJ. Li-
Linearization of analytic Poisson structures // Annals of Math. —
1984.—V. 119,—P. 577—601. Аналогичный результат справед-
справедлив в гладком случае при условии компактности группы Ли.
A. Вейнстейн, ранее доказывавший аналогичный результат
для формальных рядов, высказал гипотезу, что полупростота
необходима для такой уничтожимости нелинейных членов ряда.
Исследование особенностей пуассоновых структур на плоскости
(а значит, и вообще структур коранга 2) приводит, однако, к дру-
другому выводу.
B. Пуассоновы структуры на плоскости. С точки зрения диф-
дифференциальной геометрии пуассонова структура задается глад-
гладким бивекторным полем на многообразии. Действительно, скобка
Пуассона в каждой точке сопоставляет число паре кокасательных
векторов. Поэтому она является сечением расслоения внешних
квадратов касательных пространств, т. е. бивекторным полем.
Тождество Якоби означает своего рода «замкнутость» этого
бивекторного поля. На двумерном многообразии это условие замк-
замкнутости всегда выполнено автоматически, так что любое гладкое
бивекторное поле на плоскости задает пуассонову структуру. Это
обстоятельство позволяет применять при классификации пуассо-
*) Предостережение: теорема 3.1 этой работы неверна (А. Б. Гивенталь).

426
ДОБАВЛЕНИЕ 13
>новых структур на плоскости обычные соображения общего поло-
жепия (трансверсальность и т. п.). Через координаты х, у бивек-
торное поле выражается формулой /• (дх /\ ду), где / — гладкая
функция. Соответствующая пуассонова структура определяется
условием
{х, у) = f {х, у). A)
Пуассонову структуру на плоскости можно задать и диффе-
дифференциальной 2-формой dx Д dylf. Эта форма, как и бивекторное
доле, инвариантно связана с пуассоновой структурой, но имеет,
в отличие от него, на кривой / = О полярную особенность. Листы
в этом случае — точки кривой / = 0 и компоненты дополнения
к этой кривой на плоскости. Точки кривой / = 0 называются осо-
особыми точками пуассоновой структуры. В окрестности неособой
точки пуассонова структура на плоскости приводится к нормаль-
нормальной форме {х, у) = 1.
Начало иерархии особенностей пуассоновых структур на плос-
жости в окрестности особой точки таково:
\ \ \ \
6^—Ba^—Ba't^-l "
\ A
-Здесь буквы означают пуассоновы структуры, которые в окрест-
окрестности изучаемой особой точки записываются в подходящей систе-
системе локальйых координат с началом в этой точке в виде {х, у} = /,
•где функция / дается следующей таблицей:
У
тла
ж22/+2/2й
\-\-ax
а?+у*
4r-i
1+flJ/ft-l
Е«..
з?+ху3
1-ЫУ2
тла,Ь
хау±уъ'с-1
l-\-ax-\-byk
Еь
х*+уь
Теорема. Пуассонова структура на двумерном многообра-
многообразии либо в окрестности каждой точки приводится к одной из нор-
нормальных форм предыдущей таблицы, либо принадлежит множе-
множеству коразмерности 8 в пространстве пуассоновых структур.1^

пуассоновы структуры 427
Таким образом, пуассоновы структуры общего положения
в окрестности каждой точки приводятся к нормальным формам
{х, у} = 1 (неособая точка) или {х, у} = у (точка Ао). В однопа-
раметрических семействах общего положения встречаются еще-
при отдельных значениях параметра структуры Аг: {х, у} =
= Ь' (х2 ± У2), Ь Ф 0; в двупараметрических семействах А2т
и т. д.
Замечание 1. В двумерном случае все пуассоновы струк-
структуры образуют линейное пространство, поэтому можно говорить
о структурах или семействах общего положения (имея в виду
структуры (семейства), принадлежащие некоторому открытому
всюду плотному множеству пространства структур (семейств)).
Задача классификации пуассоновых структур в пространстве трех
или большего числа измерений с точки зрения общего положения
не поставлена однозначно, так как все структуры не образуют
единого многообразия (могут встречаться компоненты «разных
размерностей», как при классификации алгебр Ли).
Замечание 2. Структура {х, у} — у типа Ао — это стан-
стандартная пуассонова структура дуального пространства алгебры
Ли группы аффинных преобразований прямой. Эта структура
рассматривалась в 1965 г. в связи с изучением уравнений Эйле-
Эйлера левоинвариантной метрики на группе (в данном случае — мет-
метрики Лобачевского на полуплоскости), причем сразу же выясни-
выяснилось, что она устойчива и локально эквивалентна любой структу-
структуре вида {х, у} = у + . . ., где точки обозначают нелинейные чле-
члены (с нулем выше первого порядка). Это (очевидное) наблюдение
противоречит гипотезе А. Вейнстейна, согласно которой подоб-
подобная линеаризуемость всех не содержащих линейных членов воз-
возмущений — признак линейных пуассоновых структур дуальных
пространств полупростых алгебр Ли.
Замечание 3. Параметры а, Ъ в приведенной выше таб-
таблице — модули (непрерывно зависящие от структуры инвариан-
инварианты). Точнее говоря, структуры, эквивалентные данной, встреча-
встречаются при изменении параметров лишь конечное число раз. Таким
образом, уже в однопараметрических семействах общего положе-
положения на плоскости встречается континуум локально неэквивалент-
неэквивалентных друг другу пуассоновых структур.
Дроби в таблице можно было бы заменить многочленами, но
удобнее этого не делать. Числа модулей в знаменателях на едини-
единицу меньше чисел неприводимых компонент кривых / = 0. Такое
совпадение не случайно. Инвариантами пуассоновых структур на
плоскости являются вычеты, построенные по форме dx Д dylf
(сначала строится форма-вычет на каждой компоненте, а потом
ее вычет в нуле). Сумма вычетов, отвечающих всем компонентам,
равна нулю. Поэтому число модулей на 1 меньше числа компонент.
Г. Степени форм объема. Классификацию пуассоновых струк-
структур на плоскости можно рассматривать как классификацию диф-

428 ДОБАВЛЕНИЕ 13
•ференциальных форм вида / (dx Д dy)'1, где / — гладкая (или
голоморфная, или вещественно-аналитическая и т. п.) функция.
Более общим образом естественно рассмотреть формы вида
/ (dx)a = / (*lf • ¦ -, хп) (dx, Л • • ¦ Л dxnr, B)
тде а — фиксированное, вообще говоря, комплексное, число.
Классификация таких форм и их деформаций в одномерном слу-
•чае недавно получена В. П. Костовым, выявившим роль резонанс-
резонансных значений а (некоторых отрицательных рациональных зна-
значений), Функц. анализ и его прил. — 1984. — Т. 18, вып. 4. — С.
81-82.
Например, резонансный случай п = 1, а = —1 соответствует
классификации особенностей и бифуркаций особых точек вектор-
векторных полей на прямой, т. е. особых точек дифференциальных урав-
уравнений х = v (х) и их бифуркаций в конечнопараметрических се-
семействах. Однопараметрическое семейство общего положения
приводится гладкой (голоморфной) заменой переменной х, гладко
(голоморфно) зависящей от параметра, и гладкой заменой пара-
параметра к виду х = х2 + 8 + с (е) а? (при к параметрах ответ та-
такой: х = a*+i + 8^-1 + . . . + Ек + с (е) а?***).
Нерезонансный случай изучен С. Ландо и при любых п и а:
он показал, что почти всякая версальная деформация функции /
определяет, после умножения на (dx)a, версальную деформацию
формы^ если а — не резонансное (Функц. анализ и его прил. —
1985. — Т. 19, вып. 2. — С. 78—79).
Интересующий нас в связи со структурами Пуассона случай
а = —1, вообще говоря, резонансный. Вместо степеней B) форм
объема будем классифицировать дифференциальные формы
fdxx p-1/a, C)
что, очевидно, эквивалентно классификации форм B).
Гиперповерхность / = 0 инвариантно связана с формой C).
Поэтому классификация начинается с приведения к нормальной
-форме многообразия особенностей, / = 0. Начало иерархии осо-
особых точек гиперповерхностей известно. В подходящей системе
локальных координат гиперповерхность дается одним из уравне-
уравнений
А^. ± *i+1 ± А ± • • • ± 4 = 0, ц > 0;
D»- 4*2 ± я* ± г» ± . • • ± 4 = 0, [х > 4;
Е6: xf+ 4±4±-..±4 = 0;
Е7: х1 + хгх1±4±- ¦ -±xl = 0;
Es: xl+ х1±х*3±. . . ±xl = 0.
Приведя гиперповерхность к нормальной форме, мы сводим клас-
классификацию форм C) или B) к классификации дифференциальных

пуассоновы структуры 429
форм вида
fh (хх, ...,xn)dx, h @) Ф 0, D)
где / = 0 — выбранное уравнение гиперповерхности особеннос-
особенностей, h — гладкая (голоморфная...) функция, которую и остается
привести к нормальной форме.
Д. Квазиоднородный случай. Мы] рассмотрим здесь случай,
когда гиперповерхность особенностей / = 0 квазиоднородна (в
¦случаях A, D, Е классификации гиперповерхностей это так).
Определение. Функция / называется квазиоднородной
seca р при весах Wi переменных xt, если она является собственным
вектором оператора дифференцирования вдоль квазиоднородного
эйлерова поля э с собственным числом р (или нулем):
э/ = pf, где э = ^WtXidldXi.
Квазиоднородный многочлен называется невырожденным, если
критическая точка 0 конечнократна (С-изолирована). Мы будем
далее считать веса wt положительными числами.
Теорема. Пусть / — невырожденный квазиоднородный, мно-
многочлен веса 1. Тогда дифференциальная форма fJh dx (где dx =
= dxt Д . . . Д dxn и h — голоморфная в окрестности нуля функ-
функция, в нуле не равная 0) приводится биголоморфной в окрестности
нуля заменой координат к виду /Р A + ф) dx, где ф — квазиодно-
квазиоднородный многочлен веса — р — а, а = wt + • • • + wn-
Вес'ф определяется так, чтобы вес формы /f<p dx был нулем.
Аналогичная теорема верна для гладких h (и гладких замен
координат), но в вещественном слпгчае вместо 1 + ф следует поста-
поставить ±1 + ф (УМН. — 1984. — Т. 39, вып. 5. — С. 256).
Пример 1. Если р положительно, то ф = 0, так что комп-
комплексная форма приводится к виду ftdx.
Более общим образом, ф = 0, если (вообще комплексное) чис-
число р не является отрицательным рациональным числом: в этом
случае ненулевых квазиоднородных многочленов веса — Р — а
не бывает. Таким образом, резонансными значениями р являют-
являются лишь рациональные отрицательные числа. Если многочлен /
(или хотя бы его тип квазиоднородности w) фиксирован, то резо-
резонансные значения р образуют конечное число отрицательных ра-
рациональных арифметических прогрессий (для остальных р форма
/P/i dx приводится к виду f&dx).
Пример 2. Если р" = —1, то одночлены, входящие в ф,
нумеруются внутренними целыми точками диаграммы Ньютона /.
Одночлену хт = ж . . . х™п отвечает на диаграмме точка (т1 +
+ 1, . . ., тп + 1) (показатель формы xmdx).
Пример 3. Пусть Р = —1, п = 3 и / — один из приведен,
ных выше многочленов A, D, Е, определяющих простые особен-
особенности. Вычисляя веса, находим — р — а < 0, поэтому ф = 0,
откуда вытекает

430 ДОБАВЛЕНИЕ 13
Следствие 1. Форма с полярной особенностью
где f — один из многочленов A, D, Е, приводится к виду dx /\ dy Д
Д idzlf голоморфной {гладкой...) заменой координат.
Точно так же при любом и > 3 множитель h {хг, . . ., хп)г
не обращающийся в 0 в начале координат, можно обратить в еди-
единицу.
Следствие 2. Простые {не имеющие модулей) формы ви-
вида dxt Д . . . Д dxjf {xt, . . ., хп), где f — голоморфная {глад-
{гладкая...) в 0 функция un)>2, приводятся в окрестности точки О
к нормальной форме, в которой f — либо 1, либо — один из много-
многочленов A, D, Е, подходящим выбором локальных координат.
Следствие 3. Простые {не имеющие модулей) п-вектор-
ные поля в п-мерном пространстве {п ^> 2) локально эквивалентны-
нормальным формам /•(#! Д . . . Д дп), где f — либо 1, либо —
один из многочленов A, D, Е; дк — д/дхк.
Следствие 4. При I ^ 6 в 1-параметрических семействах'
общего положения п-векторных полей в п-мерном пространстве
{п ^> 2) поле в окрестности каждой точки при каждом значении
параметра эквивалентно одному из простых полей предыдущего
следствия.
Следствие 5. При 1^6 в l-параметрических семейст-
семействах общего положения форм dx Д dy Д dz/f {x, у, z) встречаются
лишь формы, которые в окрестности каждой точки в подходящих
координатах записываются в одном из 24 видов:
dx /\dy Д dz dx /\dy Д dz dx Д dy Д dz dx Д dy Д dz
1 ' x ' z2 + 2/2±z2 ' a^ + j/S-t-ja »
dx /\dy Д dz dx /\ dy Д dz dx /\dy Д dz dx Д dy Д dz
х*±у2 + г* » а*+2/2_)_:г2 ' я2у±У3 + 22 ' гв±У2±za »
dx /\dy /\ dz dx /\dy Д dz da: Д'Ду Д dz dx /\dy /\ dz
При п = 2, p = —1 теорема принимает такой вид:
Следствие 6. Пусть f — невырожденный квазиоднород~
ный многочлен веса 1 при весах аргументов wlf w2. Тогда форма
где h — гладкая {голоморфная...) в окрестности точки 0 функция
приводится к виду, в котором h = ±1 + ф» где q> — квазиоднород-
квазиоднородный многочлен веса 1 — wt — w2, при помощи гладкой {голоморф-
{голоморфной...) в окрестности точки О замены координат.

ПУАССОНОВЫ СТРУКТУРЫ 431
Соответственно бивекторное поле и пуассонова структура ло-
локально приводятся к виду
f(*,vH'xA°v) л _ f(x,y)
1ХШ
Вычисляя веса для простых особенностей A, D, Е функций /
от двух переменных, получаем из этого следствия приведенную
на с. 426 таблицу. Например, для Ах имеем wx = w2 = 1/2, вес
<р равен 0 и, значит, q> — константа.
Размерность пространства классов эквивалентности форм
hdx Д dylf, где h @) ф 0 и f — фиксированный невырожденный
квазиоднородный многочлен, равна размерности пространства
квазиоднородных многочленов веса 1 — а.
Е. Теоремы Варчснко. А. Н. Варченко указал ряд обобщений
предыдущих теорем (Функц. анализ и его прил.— 1985.— Т. 19,
вып. 4. — С. 23—31).
1. Пусть / — квазиоднородный многочлен веса 1 переменных
хх, . . ., хп весов wx, . . ., wn. Пусть классы смежности одночле-
одночленов хт, га €= /, порождают фактор-алгебру алгебры степенных
рядов
С [[*!, .. ., xj\!(df!dxx, . . ., df/dxn)
как линейное пространство.
Теорема. Всякий росток f$h dx эквивалентен ростку вида
/Р A + S^m, i xmf) dx, где неотрицательные целые I и т Е= I та-
таковы, что вес формы f®xmf dx равен нулю.
2. Назовем степенью неквазиоднородности ростка / размер-
размерность фактор-пространства
(/, df/дъ, . . ., df!dxn)W!dxx, . . ., df/dxn).
Теорема. Для почти всех р число модулей форм ff'hdx^ /\
/\ . . . Д dxn (с фиксированными р" и f и разными h, h @) Ф 0)
одинаково и равно степени неквазиоднородности ростка /. Исклю-
Исключительные (резонансные) значения р" составляют конечное число
арифметических прогрессий, составленных из отрицательных
рациональных чисел, с разностью — 1. В частности, для любого
|J ^ 0 число модулей равно степени неквазиоднородности.
3. Пример. При р = 0 получаем:
Следствие. Число модулей форм hdx (h @) Ф 0) относи-
относительно действия группы сохраняющих росток f — 0 диффеомор-
диффеоморфизмов равно степени неквазиоднородности f (равно нулю, если
росток f эквивалентен квазиоднородному).
4. В резонансном случае ответ сложнее.
Пример. Пусть п = 2, р" = —1 (пуассоновы структуры
на плоскости).

432 ДОБАВЛЕНИЕ 13
Теорема. Число модулей ростков структур Пуассона на
плоскости с данной особой кривой / = О равно степени некеазиод-
нородности ростка /, увеличенной на число неприводимых компонент,
ростка кривой / = О без единицы.
В резонансном случае число модулей ведет себя достаточно-
регулярно вдоль каждой арифметической прогрессии с разностью.
—1. А именно, при вычитании единицы из Р число модулей (не
строго) возрастает, пока не достигнет (при некотором р ^> —тг)
максимального значения, которое превосходит исходное значе-
значение (т. е. степень неквазиоднородности) на число жордановых
клеток с собственным числом егя1& оператора монодромии функ-
функции /.
Ж. Пуассоновы структуры и отображение периодов. Интерес-
Интересный источник пуассоновых структур доставляют отображения
периодов критических точек голоморфных функций (В а р ч е н-
к о А. Е, ГивентальА. Б. Отображение периодов и фор-
форма пересечений // Функц. анализ и его приложения.— 1982.—
Т. 16, вып. 2.— С. 7—20).
Отображение периодов позволяет переносить на базу расслое-
расслоения структуры, имеющиеся в пространстве (ко)гомологай слоя.
Пуассонова структура на базе возникает этим способом из формы
пересечений в средних гомологпях слоя, когда эта форма косо-
симметрична.
Отображение периодов определяется следующей конструкцией.
Пусть дано локально тривиальное расслоение. С таким расслое-
расслоением связаны расслоения гомологии и когомологий слоев с комп-
комплексными коэффициентами (база та же). Эти расслоения не только
локально тривиальны, но и канонически локально тривиализованы
(целочисленный цикл в слое перетаскивается в ^соседний слой го-
гомологически однозначно). Отображением периодов называется
сечение расслоения когомологий.
Пусть теперь на пространстве гладкого расслоения дана диф-
дифференциальная форма, замкнутая на слоях. Отображение перио-
периодов этой формы сопоставляет точке базы класс когомологий фор-
формы в слое над этой точкой.
Если на базе расслоения дано векторное поле, то любое (глад-
(гладкое) отображение периодов можно дифференцировать вдоль это-
этого поля, и производная также есть отображение периодов. Дейст-
Действительно, близкие слои расслоения когомологий канонически
отождествляются друг с другом целочисленной локальной тривиа-
лизацией, после чего сечение становится (локально) отображением
в один слой и дифференцируется, как обычная функция.
Предположим, что база — комплексное многообразие и что
комплексные размерности базы и слоя расслоения когомологий
одинаковы. Отображение периодов называется невырожденным,
если его производные вдоль любых С-независимых векторов в каж-
каждой точке линейно независимы. Иными словами, отображение пе-

ПУАССОНОВЫ СТРУКТУРЫ 433
риодов невырождено, если соответствующее локальное отображе-
отображение базы в один слой — диффеоморфизм.
Таким образом, производная невырожденного отображения
периодов изоморфно отображает касательное расслоение базы на
расслоение когомологий. Двойственный изоморфизм отображает
расслоение гомологии на кокасательное расслоение базы. Этот
изоморфизм и переносит имеющиеся в группе гомологии дополни-
дополнительные структуры на базу.
Предположим, что слои исходного расслоения — вещественные
ориентированные четномерные многообразия, и рассмотрим гомо-
гомологии средней размерности. В этом случае на пространстве гомо-
гомологии определена билинейная форма: индекс пересечения. Эта
форма симметрична, если размерность слоя кратна 4, и кососим-
метрична в противном случае. Она невырождена, если слой замк-
замкнут (компактен и не имеет края), но может вырождаться в против-
противном случае. Предположим, что форма кососимметрична.
В этой ситуации невырожденное отображение периодов инду-
индуцирует на базе пуассонову структуру. Действительно, построен-
построенный выше изоморфизм кокасательного пространства базы с груп-
группой гомологии (снабженной кососимметрической формой пересе-
пересечений) определяет билинейную кососимметрическую форму па-
пары кокасательных векторов. Скобка Пуассона двух функций
в точке определяется как значение этой формы на дифференциа-
дифференциалах функций.
Эта скобка определяет на базе структуру Пуассона (постоян-
(постоянного ранга). Это видно из того, что заданное отображением перио-
периодов локальное отождествление базы с группой когомологий слоя
вводит на базе такие локальные координаты, скобки Пуассона ко-
которых постоянны *).
Варченко и Гивенталь заметили, что построенные таким спо-
способом по 1-формам общего положения пуассоновы структуры на
дополнениях к дискриминантным многообразиям в базах версаль-
ных деформаций критических точек функций двух переменных (ес-
(если угодно, на дополнениях к волновым фронтам с типичными осо-
особенностями) голоморфно продолжаются на дискриминантное мно-
многообразие (волновой фронт). Мы ограничимся простейшим приме-
примером возникающих на этом пути пуассоновых структур.
Рассмотрим трехмерное пространство многочленов
С3 = {х* + Ijx2 + к>х + 13}
с координатами A,R. Многочлены с кратными корнями образуют
в нем дискриминантную поверхность (ласточкин хвост, рис. 247).
Пуассонова структура, возникающая из отображения периодов,
приводится (сохраняющим ласточкин хвост диффеоморфизмом)
*) В случае, когда форма пересечений симметрична, аналогичная кон-
конструкция определяет на базе плоскую псевдориманову метрику, быть может,
вырожденную.

434
ДОБАВЛЕНИЕ 13
отображения
структура на
Рис. 247. Пуассонова структура
пространства многочленов
к такому виду: симплектические слои — это плоскости Я,2 =
= const, их симплектическая структура — форма dkt /\ dka.
Расслоение, о котором здесь идет речь, образовано комплекс-
комплексными кривыми
{х, у: у* = х* + К х* + V + Я3},
отображение периодов задается, на-
например, формой ydx (см. книгу
Арнольд В. И., В а р ч е н-
ко А. Н., Г у с е й н-3 а д е С. М.
Особенности дифференцируемых отоб-
отображений. Т. 2.— М.: Наука, 1984,
§ 15).
Возникающая из
периодов пуассонова
пространстве ласточкина хвоста мо-
может быть локально определена как
структура общего положения сре-
среди обладающих следующим свойст-
свойством: линия самопересечения хвоста
вся лежит в одном симплектическом
листе.
Нужное здесь условие общности положения состоит в том, что
касательная плоскость листа в нуле не совпадает с касательной
плоскостью ласточкина хвоста в нуле. Всякая гладкая функция,
постоянная на линии самопересечения хвоста, имеющая ненуле-
ненулевой дифференциал на касательной плоскости хвоста в нуле, при-
приводится вблизи нуля сохраняющим хвост диффеоморфизмом к
виду A,2+const, a семейство голоморфных симплектических струк-
структур на плоскостях Я,2 = const приводится к виду dht Д dka голо-
голоморфным локальным диффеоморфизмом трехмерного простран-
пространства, сохраняющим ласточкин хвост и расслоение на плоскости
Х2 = const (УМН. — 1985. — Т. 40, вып. 5. — С. 236).
Можно предполагать, что и другие пуассоновы (в частности,
симплектические) структуры на базах версальных деформаций осо-
особенностей, индуцированные из формы пересечений инфинитези-
мально устойчивыми отображениями периодов, определяются ес-
естественными условиями на ранги ограничения пуассоновой
структуры на страты дискриминанта (с точностью ло сохраняющих
бифуркационное множество диффеоморфизмов). «Естественное ус-
условие» в разобранном выше трехмерном примере состоит в том, что
линия самопересечения ласточкина хвоста лежит в симплектиче-
симплектическом слое. В четырехмерном пространстве аналогичную роль,
видимо, играет условие лагранжевости многообразия многочле-
многочленов с двумя критическими точками с критическим значением нуль
в симплектическом пространстве многочленов х6 + Я2а? + Л

ОБ ЭЛЛИПТИЧЕСКИХ КООРДИНАТАХ 435
Добавление 14
ОБ ЭЛЛИПТИЧЕСКИХ КООРДИНАТАХ
С каждым эллипсоидом в конечномерном евклидовом простран-
пространстве связаны эллиптические координаты Якоби, с помощью кото-
которых интегрируются уравнения геодезических на этом эллипсоиде,
а также некоторые другие уравнения, например уравнения дви-
движения точки на сфере под действием сил с квадратичным потен-
потенциалом или тяжелой точки на параболоиде.
Это наводит на мысль, что и в бесконечномерном, гильберто-
гильбертовом пространстве с каждым симметрическим оператором должен
быть связан свой класс интегрируемых систем. Для исследова-
исследования этих систем нужно перенести на бесконечномерный случай
теорию эллиптических координат. А для этого нужно прежде все-
всего изложить обычную конечномерную теорию конфокальных по-
поверхностей второго порядка в бескоординатной форме.
Для перехода к бесконечномерному случаю нужно всюду за-
заменить симметрические операторы в евклидовом конечномерном
пространстве самосопряженными в гильбертовом. При этом, по-
поскольку эллиптические координаты связаны не с самим операто-
оператором, а с его резольвентой, неограниченность исходного оператора
(который может, например, быть дифференциальным) не является
слишком серьезным препятствием.
В некоторых случаях получаемые таким образом эллиптиче-
эллиптические координаты в гильбертовом пространстве образуют счетный
набор. Однако возможен и случай непрерывного спектра, когда
набор координат получается континуальным. В этом случае пере-
переход от исходной точки гильбертова (скажем, функционального)
пространства к континуальному набору эллиптических коорди-
координат этой точки может рассматриваться как нелинейное преобра-
преобразование функционального пространства. Это преобразование, по
аналогии с преобразованием Фурье, можно назвать преобразова-
преобразованием Якоби: исходной функции сопоставляется функция, выра-
выражающая зависимость континуальной эллиптической координаты
от ее номера (т. е. номера на оси спектрального параметра). Ве-
Вероятно, исследование функционально-аналитических свойств пря-
прямого и обратного преобразований Якоби — дело не слишком да-
далекого будущего.
Наряду с общей теорией эллиптических координат ниже об-
обсуждаются некоторые их применения в теории потенциала.
Настоящее дополнение основано на статье автора «Несколько замеча-
замечаний об эллиптических координатах», в посвященной 50-летию Л. Д. Фаддеева
книге «Записки научных семинаров ЛОМИ» (Л.: Изд-во ЛОМИ.— 1984.—
Т. 133.— С. 38—50) и докладах автора «Интегрируемые гамильтоновы
системы, связанные с квадриками (по Ю. Мозеру)» (УМН.— 1979.— Т. 34,
вып. 5.— С. 214); «Some algebro-geometrical aspects of the Newton attrac-
attraction theory» (в книге: Progress in Mathematics.— Boston:J Birkhauser, 1983.—

436 ДОБАВЛЕНИЕ 14
V. 36 (I. R. Shafarevich volume, p. 1—4)); «Магнитные аналоги теорем Нью-
Ньютона и Айвори» (УМН.— 1983.— Т. 38, вып. 5. — С. 145—146).
Дальнейшие подробности по поводу упомянутых в дополнении резуль-
результатов можно найти в работах:
Melrose R. В. Equivalence of glancing hypersurfaces // Invent.
Math.—1976.—V. 37.—P. 165—191; Мозер Ю. Некоторые аспекты
интегрируемых гамильтоновых систем//УМН.— 1981,—Т. 36, вып. 5.—
С. 109—151; Арнольд В. И. Л агранжевы многообразия с особенностями,
асимптотические лучи и раскрытый ласточкин хвост // Функциональный ана-
анализ и его приложения.— 1981.— Т. 15, № 4.— С. 1—14; Арнольд В. И.
Особенности в вариационном исчислении // Итоги науки. Современные
проблемы математики.— М.: ВИНИТИ.— 1983.— Т. 22. — С. 3—55; Г и-
венталь А. Б. Полиномиальность электростатических потенциалов //
УМН.— 1984.— Т. 39, вып. 5.— С. 253, 254; Арнольд В. И. О ньютонов-
ньютоновском потенциале гиперболических слоев//Труды Тбилисского университета.—
1982.— Т. 232—233. С. 23—28; ВайнштейнА. Д., Шапиро Б. 3.
Многомерные аналоги теоремы Ньютона и Айвори // Функциональный ана -
лиз и его приложения.— 1984.— Т. 18, № 4.
А. Эллиптические координаты и конфокальные квадрики.
Эллиптические координаты в евклидовом пространстве опреде-
определяются при помощи конфокальных квадрик (поверхностей второй
степени). Геометрия же конфокальных квадрик получается из
геометрии пучка квадратичных форм в евклидовом пространстве
(т. е. из теории главных осей эллипсоидов или из теории малых
колебаний) переходом в сопряженное пространство.
Определение 1. Евклидовым пучком квадрик (соответ-
(соответственно квадратичных форм) в евклидовом векторном простран-
пространстве V называется однопараметрическое семейство поверхностей
второй степени
-j-(AKx, эс) = 1
(соответственно форм А}), где
А,, = А — КЕ
в А — симметрический оператор:
A-.V-+V*, А*=А.
Определение 2. Конфокальным семейством квадрик
в евклидовом пространстве называется семейство квадрик, двой-
двойственных квадрикам одного евклидова пучка (квадрик в про-
пространстве, двойственном рассматриваемому):
Таким образом, конфокальные друг другу квадрики образуют
однопараметрическое семейство, но от параметра квадратичная
форма семейства зависит уже не линейно.
Пример. Плоские кривые, конфокальные фиксированному
эллипсу,— это все эллипсы и гиперболы с теми же фокусами.

ОБ ЭЛЛИПТИЧЕСКИХ КООРДИНАТАХ
437
На рис. 248 слева изображены кривые одного конфокального-
семейства, а справа — кривые соответствующего евклидова пучка.
Эллиптическими координатами точки называются значения
параметра Я, которым соответствуют проходящие через эту точку
квадрики фиксированного семейства конфокальных квадрик.
Зафиксируем в евклидовом пространстве эллипсоид, все оси
которого имеют неравные длины.
Теорема 1 (Якоби). Через каждую точку п-мерного евкли-
евклидова пространства проходит п квадрик, конфокальных выбранному
эллипсоиду. Гладкие конфокальные квадрики пересекаются под'
прямыми углами.
Доказательство. Отличная от 0 точка пространства
соответствует в двойственном пространстве аффинной гиперплос-
гиперплоскости: последняя состоит из линейных форм, равных 1 в этой точке»
Рис. 248. Конфокальное семейство и евклидов пучок
В терминах двойственного пространства теорема 1 означает, что
всякая гиперплоскость, не проходящая через 0 в n-мерном евкли-
евклидовом пространстве, касается ровно п квадрик евклидова пучка,
причем векторы, ведущие из 0 в точки касания, попарно ортого-
ортогональны (рис. 248 справа).
Доказательство указанного свойства евклидова пучка осно-
основано на том, что эти векторы определяют главные оси подходящей
1 1
квадратичной формы, а именно формы В = -н- (Ах, х) 5"(?, эс)\
где (I, х) = 1 — уравнение рассматриваемой гиперплоскости.
В самом деле, на главной оси любой квадратичной формы В,
отвечающей собственному числу К, форма В — %Е обращается в О
вместе со своим градиентом. Обращение в 0 самой этой формы
в точке пересечения главной оси с гиперплоскостью означает, что
точка пересечения лежит на квадрике -^(А^х, х) = 1, а обраще-
обращение в 0 градиента означает, что квадрика в этой точке касается
гиперплоскости.
Теорема 2 (Шаля). Общая прямая в п-мерном евклидовом
пространстве касается п—1-й различной квадрики семейства кон-

438 ДОБАВЛЕНИЕ 14
фокальных квадрик, причем плоскости, касающиеся каждая своей
квадрики в точке ее касания с прямой, попарно ортогональны.
Доказательство. Спроектируем квадрики конфокаль-
конфокального семейства пучком параллельных прямых на перпендикуляр-
перпендикулярную пучку гиперплоскость. Каждая квадрика определяет видимый
жонтур (множество критических значений проектирования квад-
квадрики). Для направления проектирования общего положения ви-
видимые контуры квадрик — это поверхности второй степени в ги-
гиперплоскости — образе проектирования.
Лемма. Видимые контуры квадрик конфокального семейства
сами образуют конфокальное семейство квадрик.
Доказательство. Переход к двойственным объектам
¦превращает сечения в проекции, а проекции в сечения. Видимые
контуры проектирования конфокальных квадрик пучком парал-
параллельных прямых двойственны поэтому сечениям двойственных
•квадрик проходящей через нуль гиперплоскостью.
Но сечения квадрик евклидова пучка гиперплоскостью, про-
проходящей через 0, образуют евклидов пучок квадрик в этой гипер-
гиперплоскости. По двойственности отсюда следует лемма.
Применим доказанную лемму к проектированию вдоль прямой,
о которой идет речь в теореме 2. По лемме видимые контуры проек-
проектирования конфокальных квадрик теоремы 2 образуют конфокаль-
конфокальное семейство квадрик в гиперплоскости. По теореме 1 эти видимые
контуры пересекаются под прямыми углами. Это доказывает тео-
теорему 2.
Теорема 3 (Якоби и Шаля). Касательные прямые к гео-
геодезической линии квадрики в п-мерном пространстве, проведенные
во всех точках геодезической, касаются, кроме этой квадрики, еще
п—2-х конфокальных с ней квадрик, одних и тех же для всех точек
геодезической.
Начало доказательства. Рассмотрим многооб-
многообразие ориентированных прямых евклидова пространства. Это
многообразие имеет естественную симплектическую структуру,
как многообразие характеристик гиперповерхности ра = 1 в фа-
фазовом пространстве свободной частицы, движущейся по инерции
в нашем евклидовом пространстве.
[Характеристика на гиперповерхности в симплектическом
многообразии — это интегральная кривая поля характеристи-
характеристических направлений, т. е. поля косоортогональных дополнений
ж касательной плоскости гиперповерхности. Иными словами,
характеристика гиперповерхности — это лежащая на этой ги-
гиперповерхности фазовая кривая уравнений Гамильтона с функ-
тщей Гамильтона, имеющей на этой гиперповерхности нуль пер-
первого порядка.
Симплектическая структура многообразия характеристик ги-
гиперповерхности симплектического многообразия определяется
тем, что кососкалярное произведение любых двух векторов, ка-

ОБ ЭЛЛИПТИЧЕСКИХ КООРДИНАТАХ 439'
сающихся гиперповерхности в исходном симплектическом много-
многообразии, равно кососкалярному произведению их проекций на-
многообразие характеристик].
Лемма А. Каждая характеристика многообразия всех пря-
прямых, касающихся заданной гиперповерхности в евклидовом про-
пространстве, состоит из касательных прямых одной геодезической-
гиперповерхности (во всех тонких геодезической).
Доказательство леммы А. Здесь мы для крат-
краткости отождествим кокасательные векторы евклидова простран-
пространства с касательными при помощи евклидовой структуры, так что-
исходное фазовое пространство будем представлять себе как про-
пространство векторов, приложенных в точках евклидова простран-
пространства (импульсы отождествляем со скоростями). Орты, приложенные-
в точках рассматриваемой гиперповерхности и касающиеся ее,
образуют в фазовом пространстве подмногообразие нечетной ко-
коразмерности (равной 3). Характеристики этого подмногообразия
определяют геодезический поток на рассматриваемой гиперпо-
гиперповерхности.
Отображение, сопоставляющее вектору прямую, на которой
он лежит, переводит указанное подмногообразие коразмерности 3
в многообразие касательных прямых гиперповерхности. При
этом отображении характеристики переходят в характеристики^
(по определению симплектической структуры пространства пря-
прямых). Это доказывает лемму.
Замечание. Проведенное рассуждение легко обобщается
на следующую общую ситуацию, впервые рассмотренную Мель-
розом. Пусть Y, Z — пара гиперповерхностей в симплектическом
многообразии X, трансверсально пересекающихся по подмного-
подмногообразию W. Рассмотрим многообразия характеристик В и С
гиперповерхностей Y и Z вместе с каноническими расслоениями
на характеристики, Y -**¦ В и Z -» С; многообразия В ж С насле-
наследуют из X симплектические структуры.
В пересечении W выделяется еще гиперповерхность (кораз-
(коразмерности 3 в X), в точках которой ограничение симплектической
структуры X на W вырождается. Эту гиперповерхность 2 в W
можно также определить как множество критических точек сквоз-
сквозного отображения W Q.Y -» В (или, по желанию, W Q Z -» С).
Введенные объекты образуют коммутативную диаграмму:

440 ДОБАВЛЕНИЕ 14
Аналог леммы А в этой ситуации утверждает, что характери-
характеристики на образах отображений 2 —»- В и 2 —> С являются образами
одних и тех же кривых на 2 (а именно — характеристик подмного-
подмногообразия 2 симплектического многообразия X).
Сама лемма А получается из этого утверждения в частном
случае, когда X = R2" — фазовое пространство свободной час-
частицы в R", гиперповерхность Y образована ортами (задается ус-
условием р2 = 1, т. е. является поверхностью уровня гамильтониана
свободной частицы), гиперповерхность Z образована всеми век-
векторами, приложенными в точках изучаемой поверхности в R".
В этом случае В есть многообразие всех ориентированных прямых
евклидова пространства, а 2 — многообразие касательных ортов.
Отображение 2 -> В сопоставляет касательному орту содержащую
его касательную прямую. Многообразие С есть пространство
(ко)касательного расслоения изучаемой поверхности. 2 -*- С —
вложение в это пространство пространства расслоения единичных
сфер (в иных терминах вложение гиперповерхности уровня ки-
кинетической энергии, т. е. гамильтониана движения со связями).
Приведенную выше диаграмму всегда полезно иметь в виду
при исследовании связей в симплектической геометрии.
Продолжение доказательства теоремы 3.
Предположим, что в евклидовом (конфигурационном) простран-
пространстве задана гладкая функция и что ограничение этой функции
на некоторую прямую имеет невырожденную критическую точку.
В таком случае такая же критическая точка (точка касания прямой
с поверхностью уровня функции) будет и на любой близкой пря-
прямой. Значение функции в критической точке является, таким
образом, функцией от прямой. Назовем эту функцию прямой ин-
индуцированной (из исходной функции точки).
Лемма В. Если функции точек евклидова пространства
таковы, что плоскости, касающиеся их поверхностей уровня в точ-
точках касания некоторой прямой с этими поверхностями *), орто-
ортогональны, то скобка Пуассона индуцированных функций обращается
е нуль в точке, являющейся рассматриваемой прямой.
Доказательство леммы В. Вычислим производную
второй индуцированной функции вдоль фазового потока, заданного
первой, как функцией Гамильтона. Фазовые кривые, заданные
первой индуцированной функцией на ее поверхности уровня,
являются характеристиками этой поверхности. Поверхность уров-
уровня первой индуцированной функции состоит из всех прямых,
касающихся фиксированного многообразия уровня первой функ-
функции точки. Каждая характеристика этого многообразия прямых,
по лемме А, состоит из прямых, касающихся одной геодезической
многообразия уровня первой функции точки.
*) Точка касания, вообще говоря, своя для каждой функции.

ОБ ЭЛЛИПТИЧЕСКИХ КООРДИНАТАХ 441
При бесконечно малом сдвиге точки по геодезической поверх-
поверхности касательная к геодезической прямая (с точностью до малых
высшего порядка) поворачивается в плоскости исходной каса-
касательной и нормали к поверхности. По условию, касательная плос-
плоскость к поверхности уровня второй функции в точке касания этой
поверхности с нашей прямой перпендикулярна касательной плос-
плоскости поверхности уровня первой функции. Поэтому при указанном
выше бесконечно малом повороте прямая сохранит касание с той
же самой поверхностью уровня второй функции (с точностью до
малых высшего порядка). Следовательно, скорость изменения
второй индуцированной функции под действием фазового потока,
заданного первой, обращается в нуль в изучаемой точке простран-
пространства прямых, что и доказывает лемму В.
Окончание доказательства теоремы 3.
Зафиксируем прямую общего положения в R". По теореме 2 она
касается п — 1 квадрик конфокального семейства в п — 1-й точке.
Построим в окрестности каждой из этих точек гладкую функцию,
без критических точек, поверхности уровня которой — квадрики
нашего конфокального семейства.
Зафиксируем одну из этих квадрик («первую») и рассмотрим
уравнения Гамильтона в пространстве прямых, функцией Гамиль-
Гамильтона которых является первая индуцированная функция прямой.
Каждая фазовая кривая на фиксированной поверхности уровня
функции Гамильтона состоит из касательных прямых одной гео-
геодезической квадрики (лемма А). Остальные индуцированные функ-
функции имеют с этой функцией нулевую скобку Пуассона по лем-
лемме В (ибо плоскости, касающиеся конфокальных друг другу
поверхностей в точках одной прямой, ортогональны по тео-
теореме 2).
Итак, все индуцированные функции суть первые интегралы
системы, функцией Гамильтона которой является любая из них.
Поскольку фазовые кривые этой системы — касательные к одной
геодезической первой поверхности, все индуцированные функции
принимают на всех этих касательных постоянные (не зависящие
от точки геодезической) значения. Отсюда вытекает как теорема 3,
так и
Теорема 4. Геодезический поток на центральной поверх-
поверхности второй степени в евклидовом пространстве — вполне ин-
интегрируемая по Лиувиллю система {имеющая столько независимых
интегралов в инволюции, каково число степеней свободы).
Замечание. Строго говоря, мы доказали теорему 3 лишь
для прямых общего положения, но результат по непрерывности
легко распространяется на исключительные случаи (в частности,
на асимптотические прямые наших квадрик). Точно так же теоре-
теорема 4 доказана для поверхностей с неравными главными осями, но
предельным переходом распространяется на более симметричные
квадрики вращения (а также на нецентральные, «параболоиды»).

442 ДОБАВЛЕНИЕ 14
Б. Магнитные аналоги теорем Ньютона и Айвори. Эллипти-
Эллиптические координаты позволяют распространить известные теоремы
Ньютона о притяжении сфер на случай притяжения эллипсоидов.
Определение. Гомеоидной плотностью на поверхности
эллипсоида называется плотность слоя между данным и беско-
бесконечно близким к нему гомотетичным эллипсоидом с тем же центром.
Теорема Айвори. Конечная масса, распределенная по
поверхности эллипсоида с гомеоидной плотностью, не притягивает
внутренние точки, а внешние точки притягивает так же, как
такая же масса, распределенная с гомеоидной плотностью по по-
поверхности меньшего конфокального эллипсоида.
Здесь притяжение определяется законом Ньютона или Кулона:
в n-мерном пространстве сила пропорциональна г1"" (как предпи-
предписывает фундаментальное решение уравнения Лапласа).
Теорема Ньютона о притяжении внутренних точек переносится
на случай гиперболических гомеоидных слоев и на случай при-
притяжения массой, распределенной по гиперповерхности уровня
гиперболического многочлена любой степени.
[Многочлен степени т, f (xlt . . ., хп) называется гиперболи-
гиперболическим (относительно точки 0), если его ограничение на любую
прямую, проходящую через 0, имеет лишь действительные корни.
Гомеоидная плотность заряда на гиперповерхности / = 0 оп-
определяется как плотность однородного бесконечно тонкого слоя
между гиперповерхностями / = 0 и / = е-*-0 (знаки зарядов
выбираются так, чтобы последовательные овалоиды были заря-
заряжены противоположно).
Гомеоидный заряд не притягивает точку 0 (и все точки внутри
самого внутреннего овалоида), и это свойство заряда сохраняется,
если умножить его плотность на любой многочлен степени
т — 2.
Обобщение: если умножить гомеоидную плотность заряда
на любой многочлен степени т — 2 + г, то потенциал такого
заряда внутри самого внутреннего овалоида будет гармоническим
многочленом степени г (А. Б. Гивенталь, 1983). Производные по-
потенциала высокого порядка алгебраичны и в следующих обла-
областях (В.А.Васильев, 1989) при п = 2].
При попытке перенести на гиперболоиды теоремы Айвори о
притяжении конфокальными эллипсоидальными слоями выяс-
выяснилось, что существенную роль играет топология гиперболоида.
При переходе к гиперболоидам различных сигнатур вместо гомео-
гомеоидных плотностей следует рассматривать гармонические на ги-
гиперболоидах дифференциальные формы различных степеней, а вмес-
вместо ньютоновского или кулоновского потенциала — соответствую-
соответствующим образом обобщенные потенциалы закона Био — Савара.
В простейшем нетривиальном случае однополостного гипер-
гиперболоида в трехмерном евклидовом пространстве результаты со-
состоят в следующем.

ОБ ЭЛЛИПТИЧЕСКИХ КООРДИНАТАХ 443
Гиперболоид делит пространство на две части: «внутреннюю»
и «внешнюю» (неодносвязную). Рассмотрим линии эллиптических
координат, поверхности уровня которых — квадрики, конфокаль-
конфокальные данному гиперболоиду.
Линии эллиптических координат на нашем гиперболоиде,
получающиеся пересечением его с эллипсоидами (замкнутые линии
кривизны гиперболоида), назовем параллелями гиперболоида.
Перпендикулярные им линии пересечения с двуполостными гипер-
гиперболоидами назовем меридианами.
Хотя эллиптические координаты и имеют особенности (на всех
плоскостях симметрии квадрик семейства), гиперболоид гладко
расслоен на параллели (диффеоморфные окружностям) и мери-
меридианы (диффеоморфные прямым).
Область внутри трубы гиперболоида также гладко расслоена
на меридианы (ортогональные конфокальным эллипсоидам се-
семейства), а кольцевая область вне гиперболоида — на параллели
(ортогональные двуполостным гиперболоидам).
Теорема. Ток надлежащей плотности, текущий вдоль
меридианов гиперболоида, создает магнитное поле, которое внутри
трубы гиперболоида равно нулю, а во внешней кольцевой области
направлено вдоль параллелей. Ток надлежащей плотности,
текущий вдоль параллелей гиперболоида, создает магнитное поле,
равное нулю во внешней, кольцевой области и
направленное вдоль меридианов внутри трубы
гиперболоида.
Плотности токов, создающих такие магнит-
магнитные поля, обобщают гомеоидные плотности на
поверхностях эллипсоидов и могут быть опи-
описаны следующим образом.
С семейством конфокальных квадрик в трех- рис 249 фокальный
мерном евклидовом пространстве связаны две эллипс и фокальная
«фокальные кривые»: эллипс (рис. 249) и ги- гипербола
пербола. Фокальный! эллипс — это край предельного эллипсоида
семейства, у которого малая ось сжалась в 0 (фокальная гипер-
гипербола получается так же из двуполостного гиперболоида).
Определим на фокальном эллипсе гомеоидную плотность сле-
следующим образом. Сначала рассмотрим какую-либо неплоскую
параллель, определенную как неплоское пересечение конфокаль-
конфокальных эллипсоида и однополостного гиперболоида. Гомеоидная
плотность на этой параллели определяется как плотность беско-
бесконечного тонкого слоя, получающегося при пересечении слоя между
данным эллипсоидом и бесконечно близким к нему гомотетичным
эллипсоидом с тем же центром, с одной стороны, и слоя меж-
между данным однополостным гиперболоидом и бесконечно близким
к нему гомотетичным гиперболоидом с тем же центром. Мы нор-
нормируем эту гомеоидную плотность на параллели так, чтобы масса
всей параллели была равна 1.

444
ДОБАВЛЕНИЕ 14
Теперь рассмотрим фокальный эллипс как предел неплоских
параллелей. Оказывается, нормированные гомеоидные плотности
параллелей имеют при стремлении параллелей к фокальному
эллипсу определенный предел. Этот предел и называется гомеоид-
ной плотностью фокального эллипса.
Гомеоидная плотность фокальной гиперболы определяется
аналогичным образом.
Теперь мы можем описать плотности токов, создающие опи-
описанные в теореме магнитные поля. Поверхность однополостного
гиперболоида расслоена над фокальным эллипсом (слой над точ-
точкой — меридиан, лежащий на том
же двуполостном гиперболоиде,
что рассматриваемая точка).
Поток меридианного тока,
описанного в теореме, через любую
кривую на гиперболоиде равен ин-
интегралу формы гомеоидной плот-
плотности на фокальном эллипсе по про-
проекции этой кривой на фокальный
эллипс (вдоль двуполостных гипер-
гиперболоидов).
Плотность тока, текущего
вдоль параллелей, индуцируется
аналогичным образом из гомеоидной плотности на фокальной
гиперболе (рис. 250).
Замечание. Магнитное поле параллельного тока ука-
указанной плотности внутри трубы гиперболоида совпадает во внеш-
внешней области каждого конфокального эллипсоида (с точностью до
знака) с ньютоновским и кулоновским полем заряда, распреде-
распределенного по поверхности этого эллипсоида с гомеоидной плотно-
плотностью *).
Точно так же магнитное поле меридианного тока в кольцевой
области вне однополостного гиперболоида совдадает (с точностью
до знака) в пространстве между полами каждого двуполостного
конфокального гиперболоида с кулоновским полем двух равных
зарядов разных знаков, распределенных по двум полам этого
двухполостного гиперболоида с гомеоидной плотностью (О. П. Щер-
Щербак).
Сформулированные выше результаты недавно перенесены
Б. 3. Шапиро и А. Д. Вайнштейном на гиперболоиды в евклидо-
евклидовых пространствах любого числа измерений. Для гиперболоида
в R", диффеоморфного S* X К', строится гармоническая Л-форма
во внешней области (диффеоморфной произведению Sk на полу-
полупространство) и гармоническая Z-форма во внутренней.
Рис 250. Магнитные поля токов на
гиперболоиде
*) Это именно та плотность, с которой сам собой распределяется заряд
на поверхности проводящего эллипсоида.

ОСОБЕННОСТИ СИСТЕМ ЛУЧЕЙ 445
Соответствующие гомеоидные плотности определяются на фо-
фокальном эллипсоиде размерности к и фокальном двуполостном
гиперболоиде размерности I таким же предельным переходом от
пересечений слоев между бесконечно близкими гомотетичными
квадриками, который выше описан для к = 1 = I.
Безвыкладочвые доказательства этих геометрических теорем
даже в частном случае магнитного поля в трехмерном простран-
пространстве неизвестны.
Замечание. Наличие выделенных гармонических форм
на гиперболоидах и в дополнительных к ним областях подсказы-
подсказывает, что на некомпактных (а возможно, и особых) вещественных
алгебраических или полу алгебраических многообразиях в про-
пространствах дифференциальных форм можно пытаться искать
фильтрации, аналогичные возникающим в теории смешанных струк-
структур Ходжа.
Добавление 15
ОСОБЕННОСТИ СИСТЕМ ЛУЧЕЙ
Простейший пример системы лучей — это система нормалей
к поверхности в евклидовом пространстве.
В окрестности гладкой поверхности система ее нормалей об-
образует гладкое расслоение, но на некотором расстоянии от поверх-
поверхности разные нормали начинают пересекаться (рис. 251). Сложную
Рис. 251. Система нормалей к параболе Рис. 252. Особенность эволь-
эвольвенты гладкой кривой
картину, которая при этом образуется, изучал уже Архимед, но
проясняться она начала лишь после того, как в 1972 г. была об-
обнаружена связь особенностей систем лучей с теорией групп, по-
порожденных отражениями.
Эта связь, для которой не видно никаких априорных причин
(столь же удивительная, как, скажем, связь задач о касательных
и площадях), оказалась мощным инструментом исследования
критических точек функций. К 1978 г. выяснилось, что теория

446 ДОБАВЛЕНИЕ 15
групп, порожденных отражениями, управляет также особенно-
особенностями эвольвент Гюйгенса.
Гюйгенс A654) обнаружил, что эвольвента плоской кривой
имеет точку возврата в том месте, где она подходит к кривой
(рис. 252). Эвольвенты и их многомерные обобщения — это вол-
волновые фронты на многообразии с краем. Особенности волновых
фронтов, как и особенности систем лучей, классифицируются
группами, порожденными отражениями.
В то время как лучи или фронты на многообразии без края
связаны с группами Вейля серий A, D и Е, особенности эвольвент
описываются группами В, С, F (с двойными связями в диаграммах
Дынкина).
Остающиеся группы, порожденные отражениями (/2 (/>), Н3, Нл),
до недавнего времени не находили приложений в теории особен-
особенностей. Положение изменилось после того, как осенью 1982 г,
выяснилось, что группа симметрии икосаэдра Н3 управляет осо-
особенностями системы эвольвент вблизи точки перегиба плоской
кривой.
Спрятанный около точки перегиба кривой икосаэдр представ-
представляется почти столь же мистическим, как икосаэдр в законе пла-
планетных расстояний Кеплера. Но здесь икосаэдр появился не слу-
случайно: при исследовании более сложных особенностей систем
лучей и фронтов в 1984 г. обнаружена и единственная оставшаяся
группа Я4.
В этом добавлении коротко описаны основные факты теории
особенностей систем лучей. Более подробное изложение имеется
в статьях:
Арнольд В. И. Особенности систем лучей // УМН.— 1983.— Т. 38,
вып. 2.— С. 77—147;
Арнольд В. И. Особенности в вариационном исчислении//Совре-
исчислении//Современные проблемы математики.— М.: ВИНИТИ.— 1983.— Т. 22.— С. 3—55
(другие статьи этого тома и тома 33 A988; также посвящены теории особен-
особенностей);
Ляшко О. В. Классификация критических точек функций на мно-
многообразии с особым краем // Функц. анализ и его приложения.— 1983.—
Т. 17, № 3.— С. 28—36;
Щербак О. П. Особенности семейства эвольвент в окрестности точки
перегиба кривой и группа Н3, порожденная отражениями // Функц. анализ
и его приложения.— 1983.— Т. 17, № 4.— С. 70—72;
Щербак О. П. Волновые фронты и группы отражений // УМН.—
1988.— Т. 43, вып. 3.— С. 125—160.
ВарченкоА. Н., Ч м у т о в С. В. Конечные неприводимые группы,
порожденные отображениями, суть группы монодромии подходящих осо-
особенностей // Функц. анализ и его приложения.— 1984.— Т. 18, JN° 3.—
С. 1—13;
Арнольд В. И. Особенности решений вариационных задач // УМН.—
1984.— Т. 39, вып. 5.— С. 256.
Многие из результатов, о которых пойдет речь, относятся к на-
настолько простым геометрическим объектам, что кажется удиви-
удивительным, как их не заметили классики. Например, локальная

ОСОБЕННОСТИ СИСТЕМ ЛУЧЕЙ 447
классификация проектирований поверхностей общего положения
в трехмерном пространстве была найдена лишь в 1981 г. Неэкви-
Неэквивалентных ростков проектирований оказалось конечное число,
а именно 14: столькими различными способами может выглядеть
окрестность точки на поверхности общего положения, если рас-
рассматривать ее из различных точек пространства.
. А. Симплектические многообразия и системы лучей.
1. Пространство ориентированных прямых в евклидовом про-
пространстве можно отождествить с пространством (ко)касательного
расслоения сферы (рис. 253) и так снабдить
симплектической структурой.
2. Более общим образом рассмотрим лю-
любую гиперповерхность в симплектическом
многообразии. Косоортогональное дополне-
дополнение к ее касательному пространству назы-
называется характеристическим направлением.
Интегральные кривые поля характеристи-
характеристических направлений на гиперповерхности
называются ее характеристиками. Многооб-
Многообразие характеристик наследует из исходного
многообразия симплектическую структуру.
3. В частности, многообразие экстремалей
общей вариационной задачи получает симп-
лектическую структуру.
4. Рассмотрим пространство бинарных форм (однородных
многочленов от двух переменных) нечетной степени. На этом
четномерном линейном пространстве действует группа линейных
преобразований плоскости. С точностью до множителя существует
ровно одна невырожденная кососимметрическая билинейная форма
на этом пространстве, инвариантная относительно действия груп-
группы SLB) линейных преобразований с определителем единица.
Эта форма задает на многообразии бинарных форм нечетной сте-
степени естественную симплектическую структуру.
5. Бинарные формы от ж и у с единичным коэффициентом при
д.гк+1 образуют гиперплоскость в пространстве всех форм. Много-
Многообразие характеристик этой гиперплоскости естественно отож-
отождествляется с многообразием многочленов четной степени х24 + - • •
... от ж. Мы определили естественную симплектическую струк-
структуру этого пространства многочленов.
6. Однопараметрическая группа сдвигов вдоль оси х сохраняет
указанную симплектическую структуру. Функция Гамильтона
этой группы — многочлен второй степени (найденный еще Гиль-
Гильбертом A893)). Многообразие характеристик поверхности уровня
функции Гамильтона отождествляется с многообразием многочле-
многочленов степени Ik — 1 от х со старшим коэффициентом 1 и суммой
корней 0. Мы получаем естественную симплектическую структуру
в этом пространстве многочленов.

448 ДОБАВЛЕНИЕ 15
Б. Подмногообразия симплектического многообразия. Огра-
Ограничение симплектической структуры на подмногообразие — замк-
замкнутая 2-форма, но она уже не обязательно невырождена. В евкли-
евклидовом пространстве, кроме внутренней геометрии подмногообра-
подмногообразий, имеется обширная теория внешних кривизн. В симплекти-
симплектической геометрии положение проще:
Теорема (А. Б. Гивенталь, 1981). Росток подмногообра-
подмногообразия симплектического многообразия определяется ограничением
на него симплектической структуры с точностью до симплекти-
симплектического диффеоморфизма.
Промежуточная теорема, в которой использовались значения
симплектической структуры на не касающихся подмногообразия
векторах, была ранее доказана А. Вейнстейном A973). В отличив
от теоремы Вейнстейна, теорема Гивенталя позволяет классифи-
классифицировать ростки подмногообразий общего положения в симплекти-
ческом пространстве: нужно лишь воспользоваться полученной
Ж- Мартине A970) и его последователями классификацией вырож-
вырождений симплектических структур.
Примеры. 1. Двумерная поверхность общего положения
в симплектическом пространстве в окрестности каждой своей точки
симплектически диффеоморфна поверхности р2 ~ р\ , р3 = q3 = . . •
. . . = 0 (в координатах Дарбу). 2. На четырехмерном под-
подмногообразии устойчиво встречаются линии эллиптических и
гиперболических особых точек Мартине с нормальной формой
Рг = PiPs ± ЧхЧт. + чЖ р3 = 0, /?4 = & = . . . = 0.
Эллиптичность и гиперболичность относятся к характеру движения в
динамической системе, инвариантно связанной с подмногообразием. Возника-
Возникающее бездивергентное векторное поле в трехмерном пространстве имеет
целую линию особых точек. Классификация особых линий оказывается менее
патологической, чем классификация особых точек (приближающаяся по
трудности к задачам небесный механики).
Таковы первые шаги теории симплектических особенностей
гладких подмногообразий.
В. Лагранжевы многообразия теории систем лучей. Напомню,
что лагранжевим многообразием называется подмногообразие симп-
симплектического пространства, на котором симплектическая структура
обращается в нуль и которое имеет наибольшую возможную раз-
размерность (равную половине размерности объемлющего многообра-
многообразия).
Примеры. 1. Слои кокасателъного расслоения лагранжевы.
2. Многообразие всех ориентированных нормалей к гладкому под-
подмногообразию (любой размерности) в евклидовом пространстве —
лагранжево подмногообразие пространства прямых. 3. Многообра-
Многообразие всех многочленов з?п + . . ., делящихся на хп, лагранжево.
Лагранжевым расслоением называется расслоение, слои кото-
которого лагранжевы.

ОСОБЕННОСТИ СИСТЕМ ЛУЧЕЙ 449
Примеры. 1. Кокасателъное расслоение лагранжево.
2. Гауссово расслоение, сопоставляющее ориентированной прямой
евклидова пространства ее орт, лагранжево.
Все лаграюкевы расслоения фиксированной размерности ло-
локально (в окрестности точки пространства расслоения) симплек-
тически диффеоморфны.
Лагранжевым отображением называется проектирование лаг-
раюкева подмногообразия на базу лагранжева расслоения, т. е.
тройка V ->- Е -*- В, где первая стрелка — иммерсия лагранжева
подмногообразия, а вторая — лагранжево расслоение.
Примеры. 1. Градиентное отображение q >->- dSldq. 2.
Нормальное отображение: вектору нормали к подмногообразию
евклидова пространства сопоставляется его конец. 3. Гуассово
отображение: точке трансверсально ориентированной поверх-
поверхности евклидова пространства сопоставляется орт нормали (со-
(соответствующее лагранжево многообразие образовано самими нор-
нормалями).
Эквивалентностью лагранжевых отображений называется симп-
лектическое отображение пространств расслоений, переводящее
слои в слои и первое лагранжево многообразие во второе.
Множество критических значений лагранжева отображения
называется каустикой. Каустики эквивалентных отображений
диффеоморфны.
Пример. Каустика нормального отображения поверхности
есть огибающая семейства нормалей, т. е. фокальная поверхность
(поверхность центров кривизны).
Всякое лагранжево отображение локально эквивалентно гра-
градиентному (нормальному, гауссовому). Особенности градиентных
(нормальных, гауссовых) отображений общего положения — те
же, что у общих лагранжевых отображений. Простейшие из них
классифицируются по группам отражений Ак, Dk, Ее, 2?71 Е8
(см. добавление 12).
Пример. Рассмотрим среду из пылевых частиц, движущихся
по инерции с потенциальным полем скоростей. Через время t
частица из х переходит в х + tdSldx. Мы получили однопарамет-
рическое семейство гладких отображений R3 -> R3.
Эти отображения лагранжевы. Действительно, потенциальное
поле скоростей задает лагранжево сечение пространства кокаса-
тельного расслоения. Фазовый поток уравнения Ньютона сохра-
сохраняет лагранжевость. Но это лагранжево многообразие при боль-
больших t перестает быть сечением: его проекция на базу имеет особен-
особенности. Каустики этого отображения — места бесконечной плот-
плотности частиц *). Согласно Я. Б. Зельдовичу A970) аналогичная
*) Связь каустик с плотностью пылевидной среды отмечали первыми
Лифшиц, Судаков и Халатников; см. обзор: LifshitzE.M., Halat-
tnikovJ.M. Investigations in relativistic cosmology.//Adv. Phys.—
1963.— V. 12.— P. 185.

450 ДОБАВЛЕНИЕ 15
модель (с учетом тяготения и расширения Вселенной) описывает
образование крупномасштабных неоднородностей в распределении
вещества во Вселенной.
По теории лаграгокевых особенностей, новорожденная каустика
имеет вид эллиптического блюдца (рис. 254) (через время t после
своего рождения блюдце имеет оси порядка ?/г, глубину порядка t
и толщину порядка tf*). Рождение блюдца соответствует А3.
Метаморфозы каустик в общем однопара-
метрическом семействе лагранжевых отоб-
отображений трехмерного пространства изобра-
изображены на рис. 255 (А г п о 1 d V. I. Wave
рис 254. новорожден- Front Evolution and Equivariant Morse Lem-
ная каустика ща//СРАМ.-1976.- V. 6, № 2.-P.319-335).
Теорема A972). Ростки лагранжевых отображений обще-
общего положения многообразий размерности <^5 в каждой точке просты
(не имеют модулей) и устойчивы. Простые устойчивые ростки лаг-
лагранжевых отображений классифицируются группами отражений
A, D, Е, как это объяснено ниже.
Г. Контактная геометрия систем лучей и волновых фронтов.
Напомню, что контактной структурой на нечетномерном гладком
многообразии называется невырожденное поле гиперплоскостей
в касательных пространствах. В чем именно состоит условие не-
невырожденности, несущественно, так как вблизи точки общего по-
положения все поля гиперплоскостей общего положения на много-
многообразии фиксированной нечетной размерности диффеоморфны
(контактная теорема Дарбу, Добавление 4).
Примеры. 1. Многообразие контактных элементов глад-
гладкого многообразия состоит из всех касательных гиперплоскостей.
Скорость перемещения элемента принадлежит плоскости, задаю-
задающей контактную структуру, если скорость перемещения точки кон-
контакта принадлежит элементу.
2. Многообразие 1-струй функций у = / (х) имеет контактную
структуру dy = pdx (p = df/дхдля 1-струи функции /).
Внешняя геометрия подмногообразия контактного пространст-
пространства локально определяется внутренней (контактная теорема Гивен-
таля).
Интегральное подмногообразие контактной структуры назы-
называется лежандровым, если оно имеет наибольшую возможную
размерность.
Примеры. 1. Множество всех контактных элементов, ка-
касающихся фиксированного подмногообразия (любой размерно-
размерности) — лежандрово многообразие.
2. В частности, все контактные элементы, приложенные в одной
точке, образуют лежандрово подмногообразие (слой расслоения
контактных элементов).
3. Множество всех 1-струй одной функции — лежандрово под-
подмногообразие пространства 1-струй.

о
о
о
и
н
о
Н
Q
в
Рис. 255. Типичные перестройки йаустик

452 ДОБАВЛЕНИЕ 15
Расслоение называется лежандровым, если его слои лежандровы.
Примеры. 1. Проективное кокасателъное расслоение (сопо-
(сопоставляющее контактному элементу его точку приложения) лежанд-
рово. 2. Расслоение 1-струй функций над 0-струями (забывание про-
производной) лежандрово.
Все лежандровы расслоения фиксированной размерности ло-
локально контактно диффеоморфны (в окрестности точки простран-
пространства расслоения).
Проектирование лежандрова подмногообразия на базу лежанд-
рова расслоения называется лежандровым отображением. Образ
лежандрова отображения называется фронтом.
Примеры. 1. Преобразование Лежандра: гиперповерхность
в проективном пространстве поднимается в пространство его кон-
контактных элементов в виде лежандрова подмногообразия. Много-
Многообразие контактных элементов проективного пространства рас-
расслоено и над двойственным проективным пространством (контакт-
(контактному элементу сопоставляется содержащая его плоскость). Это
расслоение лежандрово. Проекция поднятого лежандрова мно-
многообразия отображает его на гиперповерхность, проективно двой-
двойственную исходной.
Итак, проективно двойственная гладкой гиперповерхность есть
фронт лежандрова отображения.
2. Фронтальное отображение: отложим на каждой нормали
к гиперповерхности в евклидовом пространстве отрезок длины
t. Мы получим лежандрово отображение, фронт которого — эк-
видистанта данной гиперповерхности.
Всякое лежандрово отображение локально эквивалентно и
преобразованию Лежандра, и фронтальному отображению. Тео-
Теория лежандровых особенностей есть в точности теория особен-
особенностей преобразования Лежандра и волновых фронтов. Эквива-
Эквивалентность, устойчивость и простота лежандрова отображения оп-
определяется, как в лагранжевом случае.
Теорема A973). Ростки лежандровых отображений общего
положения многообразий размерности <^5 в каждой точке просты
и устойчивы. Простые устойчивые ростки лежандровых отобра-
отображений классифицируются группами A, D, Е: их фронты локаль-
локально диффеоморфны {в комплексной области) многообразиям нерегу-
нерегулярных орбит соответствующих групп, порожденных отражениями.
Пример. Типичный волновой фронт в трехмерном прост-
пространстве имеет особенностями лишь (полукубические) ребра возврата
(А2) и «ласточкины хвосты» (А3, рис. 256; в окрестности такой точ-
точки фронт диффеоморфен поверхности в пространстве многочленов
а;4 + ах2 + Ъх -\- с, образованных многочленами с кратными кор-
корнями). Разумеется, возможны также трансверсальные пересече-
пересечения ветвей фронта с описанными особенностями.
Замечание. Вещественные формы простых особенностей
фронтов также допускают описание в терминах групп отражений.

ОСОБЕННОСТИ СИСТЕМ ЛУЧЕЙ
453
Е. Лойенга показал, что вещественные компоненты дополнения к
простому ростку фронта нумеруются классами инволюций (эле-
(элементов порядка 2) в нормализаторе группы отражений, сопря-
сопряженных по отношению к действию этой группы отражений
Рис. 256. Типичные особенности волновых фронтов
(см.: Looijenga E.The discriminant of a real simple singularity.—
Compositio Math.—1978.— V. 37, Fasc. 1.— P. 51—62).
Д. Приложения контактной геометрии к симплектической.
Все лагранжевы особенности можно получить из лежандровых,
если реализовать последние проектированием лежандровых под-
подмногообразий пространства 1-струй функций на пространство
0-струй: достаточно забыть значение функции, чтобы пространство
1-струй превратить в фазовое пространство: лежандрово многооб-
многообразие первого изоморфно проектируется в лагранжево второго.
В частности, каустика лагранжева отображения есть проекция
ребра возврата фронта лежандрова отображения при общем
проектировании с одномерными слоями.
Теорема (О. В. Ляшко, 1979). Все голоморфные векторные
поля, трансверсалъные фронту простой особенности, локально
переводятся друг в друга голоморфным диффеоморфизмом, сохраняю-
сохраняющим фронт.
Пример. Векторное поле общего положения в окрестности
особой точки ласточкина хвоста {ж* + яя2 + Ъх + с = (х + аJ. . .}
сохраняющим хвост голоморфным диф-
диффеоморфизмом приводится к нормаль-
нормальной форме д/дс (рис. 257).
Приведение к нормальным формам
различных объектов диффеоморфизма-
диффеоморфизмами, сохраняющими волновые фронты
или каустики,— основное техническое
средство исследования геометрии си-
систем лучей и фронтов. Например, ис-
исследование метаморфоз движущегося
волнового фронта основано на результате, «двойственном» пре-
предыдущему:
Теорема A976). Голоморфные функции общего положения,
равные 0 в «самой особой» точке фронта простой особенности, ло-
\-С
Рис. 257. Векторное поле вбли-
аи ласточкиного хвоста

454
ДОБАВЛЕНИЕ 15
калъно переводятся друг в друга голоморфным диффеоморфизмом,
сохраняющим фронт.
Пример. В окрестности особой точки ласточкина хвоста
функция общего положения сохраняющим хвост диффеоморфиз-
диффеоморфизмом приводится к нормальной форме а.
Эта теорема — частный случай эквивариантной леммы Морса.
Применяется она так. Мгновенные волновые фронты образуют в
пространстве-времени «большой фронт». Время — функция в про-
пространстве времени. Приводим ее к нормальной форме сохраняющим
большой фронт диффеоморфизмом. Мы получили нормальную фор-
форму метаморфозы мгновенного фронта. Метаморфозы фронтов в R8
изображены на рис. 258. Точно так же решается задача о метамор-
Рис. 258. Типичные перестройки волновых фронтов
фозах каустик в однопараметрических семействах общего поло-
положения (рис. 255). Это — задача о приведении к нормальной форме
функции (времени) на пространстве — времени при помощи пре-
преобразования, сохраняющего «большую каустику». Если размер-
размерность пространства-времени не превосходит четырех, большая ка-
каустика имеет лишь особенности типов А и D.
Каустики лагранжевых особенностей серии А отличаются от
волновых фронтов серии А лишь сдвигом номера на единицу.
Поэтому и метаморфозы каустик серии А — такие же, как у
фронтов.
Каустики серии D отличаются от фронтов. Нормальные формы
функции времени общего положения в окрестности особенности
каустики серии D найдены В. М. Закалюкиным A975). Топологи-
Топологические нормальные формы функции времени особенно просты:

ОСОБЕННОСТИ СИСТЕМ ЛУЧЕЙ
455
Каустика
DC
D4+
Ал, A>3
R-случай
ki±Xz, Я.1+Я.4
С-случай
h + ^2
Xl + Ъ
Xi+k2
Здесь большая каустика D^ задается условиями:
{К: F(',k) имеет вырожденную критическую точку}, где
F(х, К) = ±
Приведение ростка функции времени к нормальным фор-
формам осуществляется локальным гомеоморфизмом пространства
R^ (О1), сохраняющим большую каустику и гладким всюду,
кроме точки О (В. И. Бахтин, Вестник МГУ.— 1987.— Вып. 4.—
С. 58—61).
Дж. Най (J. Nye, 1984)заметил, что не все метаморфозы каустик
и фронтов реализуются при движении фронта, определяемом урав-
уравнением эйконала (или Гамильтона — Якоби). Например, каусти-
каустика системы лучей не может иметь вид «губ» с двумя точками возвра-
возврата (хотя каустика лагранжева отображения — может). Дело в том,
что включение лагранжева или лежандрова многообразия в гипер-
гиперповерхность, заданную уравнением Гамильтона — Якоби или эй-
эйконала, накладывает топологические ограничения на сосущество-
сосуществование, а значит, и на метаморфозы особенностей (особенно в слу-
случае невырожденного, например, строго выпуклого по импульсам
гамильтониана),— хотя сами по себе особенности реализуются и на
гиперповерхности.
Диффеоморфизмам, сохраняющим фронт, отвечают векторные
поля, касающиеся его.
Исследование этих полей приводит к своеобразной операции
«сворачивания инвариантов» группы, порожденной отражениями.
Паре инвариантов (функций на пространстве орбит) мы сопостав-
сопоставляем новый инвариант — скалярное произведение градиентов
этих функций (поднятых с пространства орбит в исходное евкли-
евклидово пространство).
Линеаризация этой операции определяет билинейное симметри-
симметрическое отображение кокасательного пространства к пространству
орбит в себя.
Теорема A979). Линеаризованное сворачивание инвариан-
инвариантов группы, порожденной отражениями, изоморфно, как билиней-
билинейная операция, операции на локальной алгебре соответствующей
особенности, заданной формулой (р, q) *-*¦ S (p-q), где S = D +
+ B/h) Е, дифференцирование D — эйлерово квазиоднородное, h —
число Кокстера.

456 ДОБАВЛЕНИЕ 15
В 1981 г. А. Н. Варченко и А. Б. Гивенталь (которому принад-
принадлежит также доказательство этой теоремы для исключительных
групп) указали далекие ее обобщения. Евклидову структуру они
заменили формой пересечений подходящего невырожденного отоб-
отображения периодов семейства голоморфных дифференциальных форм
на слоях расслоения Милнора версального семейства функций.
Невырожденная форма пересечений определяет (в зависимости от
четности числа переменных) либо локально плоскую псевдоевкли-
псевдоевклидову метрику со стандартной особенностью на лежандровом фронте,
либо симплектическую структуру, голоморфно продолжающуюся
на фронт.
Пример. Пространство многочленов нечетной степени со
старшим коэффициентом 1 и суммой корней 0 получает еще одну
симплектическую структуру. Относительно этой структуры мно-
многообразие многочленов с максимально возможным числом дву-
двукратных корней оказывается лагранжевым.
При вырождении формы пересечений симплектическая струк-
структура заменяется пуассоновой (см. добавление 13).
Е. Тангенциальные особенности. Первые приложения, ради
которых и была развита (около 1966 г.) теория лагранжевых и
лежандровых особенностей, относились к коротковолновым асим-
асимптотикам, в том числе — асимптотикам осциллирующих интегра-
интегралов. Обзор этих приложений (вплоть до нахождения равномерных
оценок интегралов при слиянии точек перевала, вычисления асим-
асимптотик через многогранники Ньютона, построения смешанных
структур Ходжа, применений в теории чисел и теории выпуклых
многогранников, оценок индекса особой точки векторного поля и
числа особых точек алгебраической поверхности) можно найти в
книге: Арнольд В. И., Варченко А. Н., Гусейн-
3 а д е С. М. Особенности дифференцируемых отображений.
Т. 2: Монодромия и асимптотики интегралов.— М.: Наука, 1984,
и в докладе: Арнольд В. И. Особенности систем лучей.
Международный конгресс математиков в Варшаве, 1983.
Здесь обсуждаются другие приложения теорий лагранжевых
и лежандровых особенностей — к исследованию взаимного рас-
расположения проективного многообразия и касающихся его плоско-
плоскостей различных размерностей. К этим вопросам приводят как ва-
вариационные задачи с односторонними ограничениями (например,
задача об обходе препятствия), так и исследование показателей
крутизны Нехорошева невозмущенной функции Гамильтона (см.
добавление 8).
Рассмотрим поверхность общего положения в трехмерном про-
проективном пространстве (рис. 259). Кривая параболических точек
(р) делит поверхность на область эллиптических точек (е) и об-
область гиперболических точек (h), где лежит еще кривая перегибов
асимптотических линий (/)> с точками биперегиба (Ъ), самопересе-
самопересечения (с) и касания с параболической кривой (t).

ОСОБЕННОСТИ СИСТЕМ ЛУЧЕЙ 457
Из этой классификации выводится и оценка показателей кри-
кривизны, и классификация проектирований:
Теорема (О. А. Платнова и О. П. Щербак, 1981). Проек-
Проектирование гладкой поверхности общего положения в RP3 при любом
выборе центра проектирования {не на
поверхности) локально эквивалентно в каж-
каждой точке одному из проектирований по-
поверхностей z = / (х, у) прямыми, парал-
параллельными оси х, где / — одна из 14 функ-
функций:
х, х*, з? + ху, х3 ± ху2, х9 + ху3,
х* + ху, х* + х2у + ху2, х*±х*у + ху, рис 259 Классификация
Xs ± ху*, Ж4 + 3?У + ХуЪ, ХЪ + Ху. точек на поверхности
Здесь проектирование понимается как диаграмма V -*¦ Е -*¦ Вг
состоящая из вложения и проекции, а эквивалентность проекти-
проектирований — как коммутативная 3 X 2-диаграмма, вертикали ко-
которой — диффеоморфизмы.
Проектирование из центра общего положения имеет особен-
особенностями лишь складки и сборки Уитни. Сборка появляется при
проектировании вдоль асимптотического направления. Осталь-
Остальные особенности наблюдаемы лишь из некоторых точек. Конеч-
Конечность числа особенностей проектирований (и следовательно, чис-
числа особенностей видимых контуров) заранее не очевидна, так как
множество неэквивалентных особенностей в общих трехпараметри-
ческих семействах отображений поверхностей на плоскость кон-
континуально.
Разбиение пространства точек зрения на области, из которых
поверхность общего положения выглядит по-разному, и соответ-
соответствующие виды ростка поверхности изображены на рис. 260 (для
наиболее сложных случаев).
Иерархия касательных становится понятнее, если переформу-
переформулировать ее в терминах симплектической и контактной геометрии.
Р. Мельроз A976) заметил, что касательные к поверхности лучи»
описываются парой гиперповерхностей в симплектическом фазо-
фазовом пространстве: одна, р2 — 1, определяет метрику, а другая —
поверхность (стр. 439).
Значительная часть геометрии асимптотических может быть-
переформулирована в терминах этой пары. Тем самым мы переносим,
понятия геометрии поверхностей на общий случай любой пары ги-
гиперповерхностей симплектического пространства и можем исполь-
использовать геометрическую интуицию, накопленную в теории поверх-
поверхностей, для исследования общих вариационных задач с односторон-
односторонними фазовыми ограничениями.
Пусть Y TS.Z — гиперповерхности в симплектическом простран-
пространстве X, трансверсально пересекающиеся по подмногообразию W.

oo
g
Рис. 260. Двадцать четыре вида двух поверхностей

ОСОБЕННОСТИ СИСТЕМ ЛУЧЕЙ 459
Проектируя Y и Z на их многообразия характеристик U, V, полу-
получаем шестиугольную диаграмму:
в которой 2 — общее многообразие особых точек проекций W
на U и на V.
Пример. X = {q, р) — фазовое пространство свободной
частицы в евклидовом пространстве (q — положение частицы,
р — импульс); Y — многообразие ортов (р2 = 1); Z — много-
многообразие краевых векторов (q принадлежит гиперповерхности Г).
Тогда U — многообразие лучей, V — многообразие касательных
векторов Г, W — многообразие краевых ортов, 2 — многообра-
многообразие касательных ортов.
Если касательный орт не асимптотический, то особенность
обоих проектирований W -*¦ U и W -*¦ F в его окрестности — склад-
складки. Каждая из них определяет на W ин-
инволюцию, неподвижную на 2.
Пример. На многообразии крае-
краевых ортов выпуклой плоской кривой W
возникают две инволюции, а и т (рис. 261).
Их произведение — бильярдное пре-
преобразование Биркгофа A927).
ИСПОЛЬЗУЯ Пары ИНВОЛЮЦИЙ, МельроЗ рис. 261. Бильярдное пре-
нашел локальную нормальную форму па- обр^^вх Кинволюцийеде~
ры гиперповерхностей симплектического
пространства в описанной ситуации (в С°°-постановке, так как
в аналитическом случае ряды расходятся, как в теориях
Экаля A975) и Воронина A981) резонансных динамических
систем).
Для более сложных особенностей (например, вблизи асимпто-
асимптотического орта) пара гиперповерхностей имеет модули. Для двух
следующих за складкой особенностей можно привести (по мень-
меньшей мере формально) к нормальной форме пару (первая гиперпо-
гиперповерхность; след второй на ней). Это позволяет изучить особенности
отображения, сопоставляющего краевому орту определяемый им
луч в окрестности асимптотического и биасимптотического ортов.
Критические значения этого отображения в симплектическое про-
пространство прямых описывает

460 ДОБАВЛЕНИЕ 15
Теорема A981). Все симплектические структуры общего
положения в окрестности точки прямого произведения ласточкина
.хвоста на линейное пространство формально диффеоморфны.
Ибо вблизи биасимптотического луча многообразие касатель-
лых лучей локально диффеоморфно произведению ласточкина
хвоста на прямую.
Ж. Задача об обходе препятствия. Рассмотрим в евклидовом
.пространстве препятствие, ограниченное гладкой поверхностью.
•Задача об обходе препятствия состоит в исследовании особеннос-
особенностей кратчайшего расстояния от переменной точки пространства до
¦фиксированного начального множества в обход препятствия. (См.
Гивенталь А. Б. Особые лагранжевы многообразия и их лаг-
ранжевы отображения // Современные проблемы математики. Но-
Новейшее достижения. — 1988.—Т. 33, ВИНИТИ. С. 55—112).
Кратчайший путь состоит из отрезков прямых и отрезков гео-
геодезических на поверхности препятствия (рис. 262). Рассмотрим
лоэтому систему геодезических на поверхности препятствия, орто-
ортогональных фиксированному фронту. Си-
Система всех лучей, касательных к этим
геодезическим,— лагранжево подмного-
подмногообразие в симплектическом многообра-
многообразии прямых (как и всякая система экст-
экстремалей решения вариационной задачи).
.рис. 262. кратчайший путь в Но если в обычных вариационных зада-
обход препятствия чах лагранжево многообразие гладко
(даже в присутствии каустик), то в за-
задаче об обходе препятствия само лагранжево многообразие имеет
-особенности.
Из последней теоремы вытекает
Следствие A981). Лагранжево многообразие в задаче об
¦обходе препятствия общего положения имеет ребро возврата полу-
.кубического типа вблизи асимптотического луча и особенность,
диффеоморфную раскрытому ласточкину хвосту; вблизи биасимпто-
биасимптотического.
Раскрытый ласточкин хвост — это поверхность в четырехмер-
четырехмерном пространстве многочленов хъ + Axs + Вх2 + Сх + D, об-
образованная многочленами с трехкратными корнями. Дифферен-
Дифференцирование многочленов отображает раскрытый ласточкин хвост
в обычный; при раскрывании ласточкина хвоста ребро возврата
¦сохраняется, а самопересечение исчезает (рис. 263).
Теорема A981). При движении волнового фронта общего
положения ребра возврата мгновенных фронтов заметают раскры-
раскрытый ласточкин хвост в четырехмерном пространстве-времени
(над обычным ласточкиным хвостом каустики).
Теорема (О. П. Щербак, 1982). Рассмотрим общее однопа-
раметрическое семейство пространственных кривых и предположим,
что при некотором значении параметра (времени) одна из кривых

ОСОБЕННОСТИ СИСТЕМ ЛУЧЕЙ 461
имеет точку биуплощения (типа t1, f2, t5). Тогда проективно двой-
двойственные кривые образуют в пространстве-времени поверхность,
локально диффеоморфную раскрытому ласточкину хвосту.
Раскрытый хвост — первый представитель большой серии осо-
особенностей. Рассмотрим в многообразии многочленов хп + %1хп~2' +
+ . . . + %n-t_ множество всех многочленов с корнем фиксирован-
фиксированной кократности к, (х — а)п~к (хк + . . .). Дифференцирование
многочленов сохраняет кократность корня.
Теорема (А. Б. Гивенталь, 1981). Последовательность
пространств многочленов с корнем фиксированной кократности
стабилизируется с ростом степени, начиная
с п = 2к + 1 (т. е. с момента расщепления
самопересечений).
Пример. Раскрытый ласточкин хвост
— первое стабильное многообразие над
обычным.
Появление раскрытого хвоста в задаче
об обходе препятствия аксиоматизировано в
теории триад Гивенталя A982).
Определение. Симплектическая риС. 263. Раскрытый лас-
триада (Н, L, I) состоит из гладкой гипер- точкин хвост
поверхности Н в симплектическом много-
многообразии и лагранжева многообразия L, касающегося с ней с пер-
первым порядком касания вдоль своей гиперповерхности I.
Лагранжевым многообразием (с особенностями), порожденным
триадой, называется образ I в многообразии характеристик ги-
гиперповерхности Н.
Пример 1. Рассмотрим в задаче об обходе препятствия с
границей Г с R" расстояние вдоль геодезической до начального
фронта как функцию s: Г-vR. Многообразие L всех продолже-
продолжений 1-форм ds с Г на R" вместе с гиперповерхностью Н: р2 = 1 оп-
определяет триаду.
Эта триада порождает в точности многообразие лучей, каса-
касательных к геодезическим нашей системы экстремалей на Г.
Пример 2. Рассмотрим симплектическое многообразие
многочленов F = х1 + Я1ж'1~1 + - • ¦ + kd четной степени d =
= 2т. Многочлены, делящиеся на хт, образуют в нем лагранжево
подмногообразие.
Рассмотрим гамильтониан сдвигов вдоль оси х. [Этот многочлен
от К равен h = S (-1)*/™Я«, i + j = d, F& = d^FldxW Ги-
Гиперповерхность h = 0 касается лагранжева многообразия L по
пространству I многочленов, делящихся на хт+1, и образует с ними
триаду.
Эта триада порождает лагранжев раскрытый ласточкин хвост
размерности т — 1 (многообразие многочленов з?'1 + агх*~3 +
+ . . . + па-2, имеющих корень кратности большей половины
степени).

462 ДОБАВЛЕНИЕ 15
Т е о р е м а (А. Б. Гивенталь, 1982). Триада примера 2 устой-
устойчива. Ростки триад общего положения во всех точках симплекти-
чески диффеоморфны росткам триад примера 2.
Следствие. Многообразие лучей, касающихся геодезичес-
геодезических системы экстремалей задачи об обходе препятствия общего по-
положения, локально симплектически диффеоморфно лагранжеву
раскрытому ласточкину хвосту.
В контактной геометрии с задачей об обходе препятствия свя-
связаны два лежандровых многообразия с особенностями: многообра-
многообразие контактных элементов фронта и многообразие 1-струй функции
времени. Первое из них диффеоморфно накрывает лагранжев от-
открытый ласточкин хвост, второе диффеоморфно цилиндру под
первым.
Пример. Рассмотрим задачу об обходе препятствия на плос-
плоскости, ограниченного кривой с точкой перегиба. Фронты — эволь-
эвольвенты кривой. Они имеют по две точки возврата: обычная точка
возврата (порядка 3/2) на самой кривой и особенность порядка 5/2
на касательной перегиба (рис. 264). В точке над кривой лежандрово
многообразие неособо, а над точ-
точкой касательной перегиба лежанд-
рово многообразие имеет точку
возврата порядка 3/2.
Касательная
перегиба
/
Кридая Г
Рис. 264. Эвольвенты кубичес- Рис. 265. Поверхность много-
кой параболы членов с кратными корнями
Теорема A978). Поверхность в пространстве контактных
элементов плоскости, расслоенном над плоскостью, образованная
всеми контактными элементами эвольвент кривой общего положе-
положения вблизи точки перегиба кривой, локально диффеоморфна поверх-
поверхности, образованной всеми многочленами с кратными корнями
в пространстве многочленов х3 + ах* + Ъх + с, расслоенном на пря-
прямые, параллельные оси Ъ.
Эта поверхность (рис. 265), вместе с поверхностью с = 0 при-
приложенных на кривой элементов, образуют многообразие нерегу-
нерегулярных орбит группы отражений В3. Это наблюдение привело к
теории краевых особенностей A978).
Пример (И. Г. Щербак, 1982). Рассмотрим кривую общего
положения на поверхности в трехмерном евклидовом пространстве.
В отдельных точках направление кривой совпадает с направлени-

ОСОБЕННОСТИ СИСТЕМ ЛУЧЕЙ
463
ем линии кривизны. Из теории лагранжевых краевых особенностей
следует, что с такой точкой связана группа Вейля Ft: фокальные
точки поверхности (Аг), фокальные точки кривой (А$) и нормали
к поверхности в точках кривой (В2) образуют вблизи центра кри-
кривизны каустику Ft (рис. 266).
Не останавливаясь подробно на теории краевых особенностей,
етмечу «двойственность Лагранжа», переставляющую функцию и
ее ограничение на край (с точностью до стабильной эквивалент-
эквивалентности): такова современная трактовка правила множителей Лаг-
Лагранжа (И. Г. Щербак, 1982).
Возращаясь к точке перегиба плоской кривой, рассмотрим еще
график многозначной функции времени в задаче об обходе препят-
препятствия. Линии уровня времени — эвольвенты. Поэтому график име-
имеет вид изображенной на рис. 267 по-
поверхности с двумя ребрами возврата
(порядков 3/2 и 5/2). В этой нарисо-
ванной мной поверхности А. Б. Ги-
венталь опознал нарисованное
Рис. 266. Фокальные точки по-
поверхности с краем
Рис. 267. График функции вре-
времени вблизи точки перегиба гра-
границы препятствия
О. В. Ляшко многообразие 2 нерегулярных орбит группы Н3
(группы симметрии икосаэдра). Гипотеза Гивенталя вскоре была
доказана:
Теорема (О. П. Щербак, 1982). График (многозначной)
функции времени в задаче об обходе препятствия, ограниченного
плоской кривой общего положения, в окрестности точки перегиба
кривой диффеоморфен многообразию 2.
В доказательстве использована
Теорема (О. В. Ляшко, 1981). Многообразие^ диффеоморф-
но многообразию многочленов хъ + ах4 + Ьх2 + с, имеющих крат-
кратный корень.
Теорема Ляшко описывает многообразие нерегулярных орбит
группы Hs как объединение касательных к пространственной кри-
кривой (t, f3, tb), а теорема Щербака — к кривой (t + о (t), Р + о (Р),
* (*))
()
Такую же особенность имеет фронт общего положения в точке
касания асимптотического луча с поверхностью препятствия в R3.

464 ДОБАВЛЕНИЕ 15
Опишем, наконец, вариационную задачу, приводящую к осо-
особенности Ht (по О. П. Щербаку).
Группа Ht состоит из симметрии правильного многогранника
в R4. Его 120 вершин лежат на S3 ^s SUB) и образуют бинарную
группу икосаэдра (бинарная группа двулистно накрывает группу
вращений икосаэдра при накрытии S3 ->- SOC)).
Рассмотрим в евклидовом R3 препятствие, ограниченное глад-
гладкой поверхностью. Экстремали, соединяющие точку вне препят-
препятствия со всеми точками в обход препятствия, образуют на поверх-
поверхности препятствия пучок (однопараметрическое семейство) гео-
геодезических. Функцией времени называется расстояние до фиксиро-
фиксированного начального многообразия (например, точки) вдоль ста-
стационарного (не обязательно минимального) пути из отрезков гео-
геодезических и их касательных, рассматриваемое как (многозначная)
функция конечной точки пространства (решение уравнения Га-
Гамильтона — Якоби).
Теорема (О. С. Щербак, 1984). Для препятствия общего
положения график функции времени локально диффеоморфен много-
многообразию 2 нерегулярных орбит
группы НЛ в фокальной для пучка
точке асимптотической касатель-
касательной к геодезической пучка в пара-
параболической точке поверхности.
Явная параметризация 2:
(а, Ь2/2 + ас, с*/2 + аЬ3,
Ь6/5 + с3/3 + аЬ3с).
Рис. 268. Каустика группы Н4
Соответствующая каустика
изображена на рис. 268. Группа
Ht связана с четырехмерным пространством базы версальной де-
деформации Еа (эта связь уже указывалась в замечании 7 § 9 статьи:
Арнольд В. И. Индексы особых точек 1-форм на многообразии
с краем, сворачивание инвариантов групп, порожденных отраже-
отражениями, и особые проекции гладких поверхностей//УМН.—1979.—
Т. 34, вып. 2.— С. 3—38).
Соответствующее этому четырехмерному подпространству вло-
вложение локальной алгебры Dt в локальную алгебру Еь индуцирует
на первой именно ту градуировку, которая задается сворачива-
сворачиванием инвариантов НЛ. О. П. Щербак доказал, что эта связь до-
доставляет еще одно описание многообразия нерегулярных ор-
орбит Ht:
Т е о рема. Рассмотрим те значения К, для которых кривая
хъ + У3 + К3?]/ + ^г3? + ^ау + Х4 = 0 особа. Одна из неприводи-
неприводимых компонент этой трехмерной гиперповерхности {К} диф-
феоморфна многообразию нерегулярных орбит группы НА.

УРАВНЕНИЕ КОРТЕВЕГА — ДЕ ФРИЗА
465
а<о
а=0
Рис. 269. Типичная перестройка фронта при обходе препятствия
Три типичных сечения многообразия нерегулярных орбит Ht
изображены на рис. 269.
Добавление 16
УРАВНЕНИЕ КОРТЕВЕГА — ДЕ ФРИЗА
Не все первые интегралы уравнений классической механики
объяснены явной симметрией задачи (примеры — специфические
интегралы задачи Кеплера, задачи о геодезических на эллипсоиде
и т. п.). В таких случаях говорят о «скрытой симметрии».
Интересные примеры такой скрытой симметрии доставляет
уравнение Кортевега — де Фриза
щ — (зиих — их
A)

466 ДОБАВЛЕНИЕ 16
Это нелинейное уравнение с частными производными возникло
первоначально в теории мелкой воды; впоследствии оказалось, что
это же уравнение встречается в целом ряде задач математической
физики *).
В результате серии численных экспериментов были обнаружены
удивительные свойства решений этого уравнения с нулевыми гра-
граничными условиями на бесконечности: эти решения при t —> + оо
и t—+ — оо распадаются на «солитоны» — волны определенной
формы, бегущие с разными скоростями.
Чтобы получить солитон, бегущий со скоростью с, достаточно подста-
подставить в уравнение A) функцию и = <р (х — ct). Для ф получится тогда урав-
уравнение ф" = Зф2 -f- сф + d (d — параметр). Это — уравнение Ньютона с
кубическим потенциалом. На фазовой плоскости (ф, ф') имеется седло. Сепа-
Сепаратриса, идущая из седла в седло, в котором ф = 0, определяет стремящееся
к 0 при х —» Н^оо решение ф; оно и есть солитон.
При столкновениях солитонов наблюдается довольно сложное
нелинейное взаимодействие. Однако численный эксперимент пока-
показал, что размеры и скорости солитонов не меняются в результате
столкновения. Это обстоятельство навело на мысль о законах со-
сохранения. И действительно, Крускалу, Забусскому, Лаксу, Гард-
Гарднеру, Грину и Миуре удалось найти целую серию первых интегра-
интегралов для уравнения Кортевега — де Фриза. Эти интегралы^имеют
вид /s = J Ps (и, . . ., u(s>) dx' где Ps — многочлен." Например,
легко проверить, что первыми интегралами уравнения A) явля-
являются
1_г = jj udx, /0 = |j u*dx, 1г = ^ (-у- + u3) dx,
/2 = J (*L _ A UV + 4 ) dx.
Появление бесконечной серии первых интегралов легко объяс-
объясняется следующей теоремой Лакса**). Будем обозначать оператор
умножения на функцию от х знаком этой функции, а оператор диф-
дифференцирования по х — символом д. Рассмотрим зависящий от
функции и (х) оператор Штурма — Лиувилля L = —д2 + и. Не-
Непосредственно проверяется
Теорема. Уравнение Кортевега — де Фриза A) эквивалент-
эквивалентно уравнению и — [L, А], где А = 453 — 3 (ид -J- ди).
*) Уравнение Кортевега — де Фриза является уравнением Эйлера для
геодезического потока (ср. добавление 2).
Соответствующая бесконечномерная группа называется группой Вирасо-
ро и является одномерным центральным расширением группы диффеомор-
диффеоморфизмов окружности. См. Овсиенко В. Ю., ХесинБ. А. Суперуравнение
Кортевега — де Фриза как уравнение Эйлера//Функц. анализ и его прилож.—
1987.— Т. 21. вып. 4.— С. 81-82.
**) Л а к с П. Д. Интегралы эволюционных уравнений и уединенные
волны // Математика.— 1969.— Т. 13, № 5.— С. 128—150.

УРАВНЕНИЕ КОРТЕВЕГА — ДЕ ФРИЗА 467
Из этой теоремы Лакса непосредственно вытекает
Следствие. Операторы L, построенные по решению урав-
уравнения A), при всех t унитарно эквивалентны; в частности, каждое
из собственных чисел % задачи Штурма — Лиувилля Lf = Xf с нуле-
нулевыми условиями на бесконечности является первым интегралом
уравнения Кортевега — де Фриза.
В. Е. Захаров и Л. Д. Фаддеев заметили, что уравнение A)
является вполне интегрируемой бесконечномерной гамильтоновой
системой, и указали соответствующие переменные действие —
угол *). Симплектическая структура в пространстве убывающих
на бесконечности функций и (х) задается кососкалярным произве-
1 С
дением ю2 (dw, dv) = -^- \ (и> dv — v dw) dx, а гамильтонианом урав-
уравнения A) является интеграл Ix. Иными словами, уравнение A)
записывается в виде уравнения Гамильтона в функциональном
пространстве функций от а:, й = —r -s^— .
Каждый интеграл /s задает таким же образом «высшее урав-
непие Кортевега — де Фриза» и — Qs [u\, meQs = -^--т-5—поли-
-^--т-5—полином от и, и', , . ., и^+1. Интегралы /s находятся в инволюции, и
соответствующие им потоки в функциональном пространстве ком-
коммутируют. Явный вид полиномов Ps и Qs, а также явный вид
переменных действие—угол (и, следовательно, решений уравнения
A)), описывается в терминах решения прямой и обратной задач
теории рассеяния на потенциале и.
Явный вид.полиномов Qs можно получить также из следующей теоремы
Гарднера, обобщающей теорему Лакса. Рассмотрим в пространстве функций
от х дифференциальный оператор вида А = 2pidm~l, где р0 = 1, а остальные
коэффициенты р± — многочлены от и и производных и по х. Оказывается,
для каждого s существует такой оператор As порядка 2s + 1, что его комму-
коммутатор с оператором Штурма — Лиувилля L есть оператор умножения на
функцию: [L, As] = Qs.
Оператор As определяется выписанными условиями однозначно с точ-
точностью до добавления линейной комбинации А Т с г <^s; тем самым и много-
многочлены Qs от и и от производных и определены с точностью до прибавления
линейной комбинации предыдущих Qr.
В. Е. Захаров, А. Б. Шабат, Л. Д. Фаддеев и другие исследо-
исследовали с помощью приема Лакса и техники обратной задачи теории
рассеяния целый ряд физических важных уравнений, в том числе
уравнения ии — ихх = sin u, i\pt + \jpxx + я]) | ф |2 = 0.
Исследование задачи с периодическими граничными условиями
для уравнения Кортевега — де Фриза привело С. П. Новикова**)
*) 3 а х а р о в В. Е., Ф а д д е е в Л. Д. Уравнение Кортевега — де
Фриза — вполне интегрируемая гамильтонова система // Функциональный
анализ и его приложения.— 1971.— Т. 5, № 4.— С. 18—27.
**) Новикове.П. Периодическая задача для уравнения Кортеве-
Кортевега — де Фриза, I // Функциональный анализ и его приложения.— 1974.—Т. 8,
№ 3.— С. 54—66.

468 ДОБАВЛЕНИЕ 16
к открытию интересного класса вполне интегрируемых систем с ко-
конечным числом степеней свободы. Эти системы строятся следующим
образом.
Рассмотрим какую-либо конечную линейную комбинацию пер-
первых интегралов / = SciAi-i> и пусть с0 = 1. Множество стацио-
стационарных точек потока с гамильтонианом / в функциональном про-
пространстве инвариантно относительно фазовых потоков с гамильто-
гамильтонианами /s, в частности относительно фазового потока уравне-
уравнения A).
С другой стороны, эти стационарные точки определяются из
а ы п б/ , г,
уравнения ^— -г—= и, или -г— = а. Последнее уравнение пред-
представляет собой уравнение Эйлера — Лаграшка для функционала
/ — d/_i, включающего п-е производные. Следовательно, оно имеет
порядок 2ге и может быть записано как система уравнений Гамиль-
Гамильтона в 2и-мерном евклидовом пространстве.
Оказывается, получающаяся гамильтонова система с ге степе-
степенями свободы имеет ге интегралов в инволюции и может быть пол-
полностью проинтегрирована с помощью подходящих координат дей-
действие — угол. Таким образом получается конечномерное семейство
частных решений уравнения Кортевега — де Фриза, зависящее от
Зге + 1 параметров Bге фазовых координат и еще ге + 1 параметр
cv . . ., сп; d).
Найденные решения обладают, как показал Новиков, замеча-
замечательными свойствами: например, в периодической задаче они за-
задают функции и (х), для которых линейное дифференциальное
уравнение с периодическими коэффициентами —X" + и (х) X =
= XX имеет конечное число зон параметрического резонанса
(см. § 25) на оси Я.
Обзоры современного состояния теории интегрируемых систем
опубликованы в серии «Современные проблемы математики. Фун-
Фундаментальные направления», т. 4 (М.: ВИНИТИ, 1985) и т. 16 (М:
ВИНИТИ, 1987) Б. А. Дубровиным, И. М. Кричевером, С. П. Но-
Новиковым, М. А. Олыпанецким, А. М. Переломовым, М. А. Семено-
вьтм-Тян-Шанским, В.В.Трофимовым и А.Т.Фоменко.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Алгебра Ли 181, 284, 285
векторных полей 184
— — группы Ли 186
первых интегралов 190
— — функций Гамильтона 187, 190
Апоцентр 36
Атлас 72
— симплектический 201
Атласы эквивалентные 72
Базис симплектический 192
— эрмитово-ортонормированный 309
Биения 97, 98
Вариация 53
Вектор касательный к многообразию 74, 75
— кокасательный к многообразию 176
— Лапласа 381
— Пуассона 345
— формы нулевой 206
— характеристический 335
Векторы косоортогональные 192
Вихрь двумерного поля скоростей 300
Волчок быстро запущенный 140
— быстрый 137
— Лагранжа 132
— симметричный 132
— спящий 136
Вращение 112
— переносное 113
— равномерное 113
— стационарное 129, 293
Время 13
Гамильтониан квадратичный 347
— —, собственные числа 348
Гиперплоскость контактная 320
Гомологии 174
Граница цепи 162
График отображения 15
Группа галилеева 13
— диффеоморфизмов однопараметрическая
25, 182
— Ли 186, 284
¦— ортогональная 197
— параллельных переносов 12
— симплектическая 193
— стационарная 241
— унитарная 197
Движение в RN 14
— в галилеевой системе координат 15
— в лагранжевой системе 77
— в подвижной системе координат 111
— в центральном поле 32, 58
— поступательное 112
— условно-периодическое 251, 381
Действие 57
Действие группы Ли пуассоновское 339
Дивергенция 165
Диффеоморфизм 25
—, гомологичный тождественному 387
— контактный 325
Дифференциал функционала 53
Длина пути оптическая 220
Дополнение косоортогональное 192
Жесткость системы 99
Задача двух тел 49
— Кеплера 39
— трех тел 20
— — — ограниченная 383
Закон Кеплера второй 33, 34, 40
— первый 40
третий 40
— сохранения импульса 45
кинетического момента 33, 34, 42,
46, 47
— — циркуляции 298
энергии 21, 26, 42, 47—49, 181
Изотропность пространства 17
Импульс 45
— обобщенный 57
Инвариант адиабатический 262, 263, 380,
381
— интегральный 179
относительный 180
— — — Пуанкаре 209
Пуанкаре—Картана 208
Инволютивность 60
Инволюция Лежандра 332
Индекс Маслова 411—413
— Морса 410, 411, 413
Индикатриса 218
Интеграл формы по цепи 163
Интегрирование дифференциальных форы
158
Карта 72
Карты совместные 72
Каустика 407, 4С8, 417, 449
Квадрики конфокальные 436
Класс когомологий алгебры Ли 339
Клетки жордановы 348
— — неустранимые 349
Когомологий 173, 339
Колебания малые 88
— собственные 95
— фазовые 364
Количество движения 45
Коммутатор 181, 184
— Ли 186
Контактизация симплектического много-
многообразия 335

470
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Координаты обобщенные 57
— циклические 58, 64
— эллиптические 437
Коразмерность многообразия 395
Коцикл алгебры Ли двумерный 339
Кривая 15
— фазовая 22
Кривизна риманова 266, 269
по двумерному направлению 272
Кривые эквивалентные 75
Лагранжиан 57
Лемма Пуанкаре 172
— Стокса 205
— — многомерная 207
Линеаризация 91, 92
Линии вихревые 205
— ротора 205, 207
Линия мировая 15
Луч 220
Масса 20
Маятник Фуко 118
Медлительность фронта нормальная 220,
223
Метрика келерова 313
— риманова 76
левоинвариантная 287
правоинвариантная 295
Мир 13
Многообразие вложенное 74
— дифференцируемое 72, 73
— келерово 313
— лагранжево 409, 448
, порожденное триадой 461
— лежандрово 331
— параллелизуемое 121
— пуасооново 422
— риманово 76
— связное 73
•— симплектическое 175, 427
Многочлен гиперболический 442
— Чебышева 29
Множество эллипсоидов вращения 394
Момент 340
— вектора относительно оси 45
точки 33
— инерции относительно оси 123
— кинетический 32, 46, 289
— количества движения 32
Направление сопряженное 221
Невесомость 116
Неравенство Юнга 60
Нутация 135, 139
Обмотка тора 251
Образ контактной формы 326
Однородность пространства 17
Одночлены внешние 146
Окрестность точки многообразия 73
Оператор дифференциальный 183
— инерции 122, 289
Орбита 27
Особенности лагранжевы 415
— лежандровы 333, 421
Ось инерции 123
Отображение дифференцируемое 76
— за период 103
— каноническое 180, 210
— лагранжево 420, 449
— лежандрово 452
— периодов 432
— пуассоново 424
— Хопфа 28
Перегрузка 116
Перекачка энергии 97
Переменные действие — угол 246—248
— действия 245
— Нлебша i2i
Перемещение винтовое 115
— виртуальное 85
Перенесение вектора параллельное 267.
270
Перицентр 36
Плоскость контактная 322
— Лобачевского 268
— симплектического пространства изо-
изотропная 194
лагранжева 194
¦ нулевая 194
— фазовая 22
Плотность гомеоидная 442—444
Подалгебра 190
Подгруппа дискретная 242
Подмногообразие лежандрово 331, 450
Поле векторное вариации геодезической
275
гамильтоново 177, 422
• контактное 326
— — локально гамильтоново 191
фазовой Скорости 22
— гиперплоскостей 315
— — невырожденное 319
неинтегрируемое 316
— осесимметричное 43
— правоинвариантное 187
— приведенное 345
— силовое потенциальное 31, 42
— центральное 32, 42
Полином возвратный 198
Полиэдр сингулярный fc-мерный 161
Положение равновесия 22, 87, 90
Поля изозавихренные 298
Поток геодезический 278
— — ориентированных контактных эле-
элементов 326
— поля через поверхность 164
— фаговый 25, 65
— — гамильтонов 178
— — локально гамильтонов 191
Представление группы коприсоединенное
286
— — присоединенное 285
Преобразование галилеево 14
— каноническое 210
бесконечно малое 236
свободное 227, 234
— Лежандра 59, 332, 452
— симплектическое линейное 193
— —¦ сильно устойчивое 199
устойчивое 199
— унитарное 413
— эллиптическое 354
Прецессия 131, 136, 139
Принцип Гюйгенса 219, 326
— Даламбера—Лагранжа 84, 87
—• детерминированности Ньютона 12
— наименьшего действия Гамильтона 52,
56, 57
— Мопертюи 216
— относительности Галилея 12, 16
— усреднения 253
— Ферма 218
Проекция естественная 75
Произведение внешнее 145, 148
— внутреннее 173
— кососкалярное 187, 188, 191, 342
— прямое 14
— скалярное 13
— — эрмитово 309
Производная ковариантная 273, 275
— Ли 173

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
471
Производная отображения 76
-\ по направлению 182
— рыбака 173
— формы внешняя 166
Промежуток времени 13
Пространство аффинное 12
— галилеево 13
— — координатное 14
— евклидово 13
— касательное 74, 75
— кокасательное 176, 285, 320
— комплексное проективное 309
— конфигурационное 15, 52
системы со связями 71
твердого тела 119
— одновременных событий 13
— симплектическое линейное 191
— сопряженное 143
— фазовое 27, 65
приведенное 337, 342
Прямая Максвелла 226
Путь характерный 277
Пучок квадрик евклидов 436
Работа поля 30
— силы 30
Равновесие 22, 87, 90
— относительное 346
Размерность многообразия 73
Расслоение касательное 75
— кокасательное 176, 320
— лагранжево 448
— лежандрово 333, 452
Расстояние между одновременными собы-
событиями 13
— — точками аффинного пространства 13
комплексного проективного про-
пространства 309
Расстройка частоты 357
Расщепление сепаратрис 360
Резонанс параметрический 107, 192
Ротор 169
— двумерного поля скоростей 300
Связь 70, 72
— голономная 71, 72, 85, 88
— идеальная 85
Сдвиг правый 186
Семейство квадрик конфокальное 436
Сила 20, 44
— внешняя 45
— внутренняя 44
— инерции 87, 115
— — вращения 116
— Кориолиса 116
— обобщенная 57
— реакции связи 84
— центробежная 116
Силы взаимодействия 44
Симплекс 168
Симплектизация контактного векторного
поля 327
— — многообразия 322
Система голономная 70—72, 85
— замкнутая 16, 44
— интегрируемая невырожденная 255
— — — изоэнергетически 370
— координат галилеева 14
инерциальная 12
— — неподвижная 112
— — подвижная 112
— ¦— симплектическая 193
— консервативная 47
— лагранжева 77
— — натуральная 78
— ¦— неавтономная 80
Система механическая 15, 16
— натуральная 78
— потенциальная 20, 26, 47
— о двумя степенями свободы 26
— с одной степенью свободы 21
Скобка Пуассона 184, 187
Скорость 14
— вторая космическая 19
— обобщенная 57
— первая космическая 41
— секториальная 34
— угловая 113
След цепи при гомотопии 178
Сложение скоростей 112—115
Слой расслоения над точкой 75
Событие 13
События одновременные 13
Солитон 466
Соотношения между частотами 254
Среднее временнбе 251
— пространственное 251
Структура галилеева 13
— евклидова 12, 287
— комплексная 197
— комплексного проективного простран-
пространства симплектическая 311
эрмитова 309
— контактная 314, 315, 319, 450
— проективного алгебраического многооб-
многообразия симплектическая 312
— пуассонова 422
— — трансверсальная 425
— симплектическая 175
линейная 191
— — стандартная 191
Тело твердое 119
Тензор инерции 122, 289
¦— кривизны 272
Теорема Айвори 442
— Вильямсона 349
— Галина 350
— Гарднера 467
— Гюйгенса 219
— Дарбу 201, 328
Для контактных структур 328
— Клеро 79
— Колмогорова 372
— Лакса 466
— Лапласа 258
— Лиувилля 65, 178
— — об интегрируемых системах 238, 239
— Нётер 81, 188, 190
— Ньютона 42
— об усреднении 251
— Пуанкаре геометрическая 384
— — о возвращении 67
— Пуансо 129
— Пуассона 189, 190
— Рэлея 302
— Штейнера 125
— Якоби 228
Теоремы Варченко 431
Теория эргодическая 67, 256, 281
Течения стационарные 297
Тождество Якоби 181, 184, 189
Тор инвариантный 369
— — нерезонансный 369
— — резонансный 369
Точка контакта 320, 322
— мировая 13
— омблическая 397 „„,
— пространства моментов регулярная ^»»
— фазовая 22
— фокальная к многообразию 411
Траектория 15 ,Qfi
Трансверсальность подпространств i»o

472
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Триада симплектическая 461
Трубка ротора 205
Углы Эйлера 132, 133
Умножение внешнее 145, 148
Уравнение Гамильтона—Якоби 224
— Кортевега—де Фриза 465
— Матье 106
— Ньютона 16
— Шредингера 408
— Эйлера 127, 128
— — для угловой скорости 293
— Эйлера — Лагранжа 55
— Хилла 103
— Якоби 275
Уравнения Гамильтона канонические 62,
207, 212
— Лагранжа 57
— Ньютона 44
— с частными производными первого по-
порядка нелинейные 335
— Эйлера 127
— — для обобщенного твердого тела 290,
291
Ускорение 15, 16
— силы тяжести 19
Условие интегрируемости поля плоскостей
318
— — Фробениуса 318
Устойчивость 91
— асимптотическая 104
— по Ляпунову 91, 104
— сильная 105
Факторизация конфигурационного прост-
пространства 345
— фазового потока 291
Фигуры Лиссажу 29
Форма базисная 146, 147
— Биркгофа нормальная для гамильто-
гамильтониана 353
для преобразования 354
— внешняя 143, 144
— дифференциальная 153, 154
— замкнутая 171
— контактная 322
— кривизны 268
— неособая 206
Формула гомотопии 173
— Лейбница 182
— Стокса 167, 249
Фронт волновой 219
, скорость движения 220
— лежандрова отображения 452
Функции, двойственные по Юнгу 60
— Казимира 424
— находящиеся в инволюции 238
Функция Гамильтона 62, 177, 237, 347
контактная 329
, собственные числа 348
— действия 222
— квазиоднородная 429
— Лагранжа 52, 57
— производящая 227, 234
, инвариантность 392
— тока 299
Функционал 53
— дифференцируемый 53
Характеристика 207, 225, 336, 447
Хвост ласточкин 226, 334, 419, 433, 460,
461
Центр инерции 45
Цепь 161
Цикл 172
Циркуляция 163
Частота собственная 95
— условно-периодического движения 251
Частоты независимые 251
Число Бетти 173
— степеней свободы 74
Члены резонансные 358
Эволюция 258
Эквивалентность отображений лагранже-
ва 420
лежандрова 333
Экстремаль 54
— условная 85
Элемент контактный 314, 320
ориентированный 325
, геодезический поток 325
Эллипсоид инерции 124, 394
Энергия кинетическая 21, 47, 78
— немеханическая 49
— полная 21, 26, 63
— потенциальная 18, 20, 21, 31, 78
— — эффективная 35